Economie experimentale et théorie des jeux.

UNIVERSITE CADI AYYAD DE MARRAKECH

FACULTE DES SCIENCES JURIDIQUES

ECONOMIQUES ET SOCIALES

ÉCONOMIE EXPÉRIMENTALE  ET THÉORIE DES JEUX

MEMOIRE POUR L'OBTENTION DU DIPLOME DES ETUDES SUPERIEURES APPROFONDIES EN SCIENCES ECONOMIQUES

Option : Théorie Economique et Techniques Quantitatives

Présenté et soutenu par :

ADIL FERTAH

JURY

PRESIDENT : Mr. BACHIR. S. I. LAKHDAR

PROFESSEUR A L'UNIVERSITE DE MARRAKECH

SUFFRAGANTS :

Mr. Mohamed ABDAÏMI

PROFESSEUR A L'UNIVERSITE DE MARRAKECH

Mr. Mohamed BOUGROUM

PROFESSEUR A L'UNIVERSITE DE MARRAKECH

SEPTEMBRE 2003

SOMMAIRE

INTRODUCTION
CHAPITRE I : L'ÉCONOMIE EN LABORATOIRE
SECTION I : APERÇU SUR L'ÉCONOMIE EXPÉRIMENTALE
1-1- DÉFINITION
1-2- LA MÉTHODE EXPÉRIMENTALE
1-3- LA BONNE EXPÉRIENCE
1-4- CHAMP D'APPLICATION
SECTION 2- LE RECOURS EN LABORATOIRE : RAISONS ET OBJECTIONS
2-1- LES RAISONS DU RECOURS A L'EXPERIMENTATION
2-2- LES CRITIQUES ADRESSÉES À L'EXPÉRIMENTATION
CONCLUSION
CHAPITRE II THÉORIE DES JEUX ET MODÉLISATION DES
INTERRACTIONS INTERINDIVIDUELLES
SECTION I. BREF APERÇU SUR LA THÉORIE DES JEUX : NOTIONS DE BASE
1-1- THÉORIE DES JEUX : OBJET
1-2 - DÉFINITION D'UN JEU
1-3- FORMALISATION GÉNÉRALE DES JEUX
1-4- TYPOLOGIES DES JEUX
SECTION-2- FORMALISATION ET ANALYSE DES JEUX NON COOPÉRATIFS ET
DES JEUX COOPÉRATIFS
2-1-LES JEUX NON COOPÉRATIFS
2-2-LES JEUX COOPÉRATIFS
2-3- CONCEPTS DE SOLUTION
CONCLUSION
CHAPITRE III : LA THÉORIE DES JEUX AU LABORATOIRE
SECTION I : RAPPROCHEMENT ENTRE LA THÉORIE DES JEUX ET
L'ÉCONOMIE EXPÉRIMENTALE
1-1 DE LA THÉORIE DES JEUX À L'EXPÉRIMENTATION :
APERÇUS HISTORIQUES ET MÉTHODOLOGIQUES
1-2- L'INTUITION DERRIÈRE LE RAPPROCHEMENT ENTRE LA
THÉORIE DES JEUX ET L'EXPÉRIMENTATION
SECTION II- LES JEUX EXPÉRIMENTAUX : UNE DISCUSSION DE CAS
2-1- JEUX À DEUX JOUEURS ET À SOMME NON NULLE : UNE ÉTUDE EXPÉRIMENTALE
2-2 : LE FINANCEMENT D'UN BIEN PUBLIC ENTRE L'OPTIMALITÉ
ET LA RECHERCHE D'EQUILIBRE : UNE ÉTUDE EXPÉRIMENTALE
CONCLUSION
CONCLUSION GENERALE TABLE DES MATIÈRES
BIBLIOGRAPHIE
ANNEXES

INTRODUCTION

Il y avait un temps où l'opinion communément admise était que, parce que l'économie est une science caractérisée par la complexité, naturellement des expériences en laboratoires avaient peu à offrir aux économistes. L'idée qui prévalait était que l'économie, comme discipline, est une science de pensée et de réflexion plus qu'une science d'observation, par conséquent, on croyait que les problèmes économiques peuvent être compris et résolus seulement en pensant à eux. Cependant, l'essor et le développement des techniques expérimentales ont contribué grandement au changement de cette façon de voire les choses. Ainsi, selon les termes de V SMITH^1(*), en élaborant des expériences en laboratoire, nous pouvons rapidement nous apercevoir qu'un nombre important de résultats expérimentaux peuvent être répliqués par nous même et par d'autres. la conséquence, donc, est que la théorie économique sera de ce fait construite d'un ensemble de concepts et de propositions capable d'être, à n'importe quel moment et par n'importe qui, testée prouvant ainsi leur validité ou leur rejet. Le propos des techniques expérimentales ne s'arrête pas à ce stade, elles deviennent aussi un outil bien établi pour la prédiction^2(*) de nouvelles observations.

Cette transformation peut être expliquée par plusieurs raisons : Premièrement, comme la plupart des autres sciences, l'économie est considérée comme une science d'observation, les théories économiques sont conçues pour expliquer les activités de marchés. Toutefois, si les économistes ont développé un ensemble sophistiqué de modèles, leur capacité prédictive reste, jusqu'à présent, souvent en retrait. C'est, donc, pour pallier à cette insuffisance que les économistes ont adressé plus d'attention aux expériences en laboratoires. La deuxième raison est celle due au besoin accru des méthodes expérimentales dans les études de comportement du choix individuel. Comme les économistes se sont concentrés sur les théories microéconomiques qui dépendent des préférences des individus et du fait que celles-ci sont difficilement observables dans des environnements naturels, les économistes sont, en quelque sorte, devenu obliger de compter sur le laboratoire pour voir si les suppositions faites sur les individus étaient en fait descriptives de leur comportement effectif^3(*). L'expérimentation permet par exemple de fournir des données relatives aux croyances, à l'aversion au risque, à l'apprentissage, alors que ces mêmes éléments ne sont pas en général accessibles sous leur forme naturelle^4(*) (ni peuvent être produits par d'autres techniques). En plus l'environnement et l'institution qui caractérisent un protocole expérimental, non seulement ils garantissent le fait que les données produites n'ont pu être affectées par des chocs externes non pertinents, mais surtout il est possible d'effectuer plusieurs traitements expérimentaux selon que certains paramètres sont susceptibles d'affecter la prise de décision et les interactions stratégiques entre les individus.

De plus, la publication en 1944, par VON NEUMANN et MORGENSTERN^5(*) de leur ouvrage célèbre « Théorie des Jeux et Comportement Economique » a accéléré l'intérêt dans l'expérimentation puisque la théorie utilitaire qu'il ont présenté a ouvert la voie aux expérimentations concernées par le choix individuel. En effet, une vague d'essais expérimentaux dans le domaine économique à été lancé, au moins depuis L.L. THURSTONE (1931)^6(*) considéré par A. E. ROTH^7(*) un des premiers expérimentateurs en économie. Il a employé des techniques expérimentales communes dans la psychologie pour examiner si la représentation de la courbe d'indifférence des préférences pouvait avec cohérence organiser les choix des individus.

En effet, le principal objectif des travaux expérimentaux est définir le domaine de validité, la pertinence et la robustesse des prédictions de modèles économiques formels tout en leur offrant une assise empirique.

Les dernieres oeuvres qui peuvent être cité dans ce domaine sont celles de D. DAVIS et C. HOLT (1993)^8(*), A ROTH et J.H. KAGEL (1995)^9(*), T.C. BERGSTROM et J H. MILLER (1997)^1(*)0 et enfin les travaux de V L. SMITH titulaire du dernier Prix Nobel (2002).

Dans le but de mettre en lumière l'importance de cette méthode, notre travail a pour objectif d'évaluer l'intérêt scientifique, méthodologique et empirique du recours aux méthodes de l'économie expérimentale surtout dans le domaine de la théorie des jeux.

Cette évaluation consiste précisément à réaliser une revue sélective de la littérature sur le thème « théorie des jeux et économie expérimentale ». Ceci permettra de discuter des caractéristiques propres de la méthode expérimentale en économie « Quel est son projet ? Quel est son champ d'utilisation ? ». Notamment, Nous montrerons - à travers des exemples de jeux expérimentaux- l'intérêt de l'économie expérimentale comme méthode de production de données comportementales comparativement aux méthodes habituellement utilisées en théorie des jeux. D'autre part, cette revue permet de montrer la richesse des développements théoriques permis par l'économie expérimentale.

Ce travail est organisé de la façon suivante : Dans le premier chapitre nous présenterons l'économie expérimentale comme domaine de recherche bien établi. Dans un deuxième chapitre nous rappellerons (sans être exhaustif) les concepts de base de la théorie des jeux. Nous terminerons enfin avec le chapitre consacré à la mise en valeur du rapprochement entre la théorie des jeux et le laboratoire économique. Nous illustrons ce fait à travers les résultats de deux jeux expérimentaux.

CHAPITRE I : L'économie en laboratoire

L'idée prévalant il y a pas mal de décennies est que l'économie n'est pas une science expérimentale, et la plupart des économistes étaient convaincus que les expériences en laboratoire avaient peu à offrir aux économistes. LEMIEUX^1(*) a exprimé cette idée en disant que c'est cette impossibilité de l'expérimentation empirique qui distinguait les sciences sociales des sciences exactes. On n'arrivait plus à concevoir la possibilité de contrôler des conditions expérimentales dans une société humaine complexe c'est à dire que le fait de répliquer toute la complexité du monde pour tester une politique macroéconomique en laboratoire était certes impossible^2(*).

Aujourd'hui l'économie expérimentale est devenue un outil bien établi pour la recherche économique. On ira même jusqu'à dire que c'était un chemin indispensable à suivre pour arriver, actuellement, au (début du) stade de l'ingeneering microéconomique^3(*).

ROTH (1991), en essayant de spéculer sur l'avenir de l'économie expérimentale, stipule qu' « il y a beaucoup de questions pour lesquelles l'expérimentation en laboratoire constituera la voie la plus directe pour tester la théorie et pour examiner les effets des variables qui sont difficiles à mesurer et à contrôler par n'importe quelle autre méthode »^4(*).

En d'autres termes, la voie expérimentale nous permettra de répondre à la question suivante :

Comment peut-on, à travers l'utilisation du laboratoire économique, valider ou non une théorie économique. Cependant, avant d'aborder cette étape du travail, une remise en lumière de cette méthode s'impose. Ceci constituera l'objectif de ce premier chapitre où on essayera, dans un premier temps (Section I), de définir ce que l'on veut dire par l'expérimentation de la théorie, le deuxième point ( section II) se focalisera sur les différentes raisons qui ont conduit les économistes à suivre cette voie de recherche ainsi que les objections adressées à l'encontre de l'expérimentation.

Section I : Aperçu sur l'économie

EXPÉRIMENTALE

1-1- Définition

Selon O. BOISSIN et B. RUFFIEUX^5(*),  « l'économie expérimentale peut ainsi se définir comme l'activité de création, dans un cadre contrôlé par le chercheur, de situations économiques réelles impliquant des participants ( dans la plupart du temps des étudiants motivés par des récompenses monétaires) de façon à pouvoir observer leurs comportements économiques ».

De cette manière, le fait que l'économie est mise en laboratoire permet de tester, de valider, ainsi que de faire apparaître des régularités empiriques dans des situations économiques encore mal théorisées.

Pour V. L. SMITH^6(*)-^7(*), il s'agit en fait de l'application des méthodes de laboratoire pour l'étude du comportement économique d'un certain nombre de sujets motivés par des règles explicites ou implicites. Les règles explicites peuvent être définies par une séquence de mouvements contrôlés par l'expérimentateur. Les règles implicites sont les normes, les traditions et les habitudes que les gens (sujets) apportent avec eux au laboratoire comme partie de leur héritage culturel et biologique : elles ne sont pas normalement contrôlées par l'expérimentateur.

A coté de ce rôle pratique et dans un but pédagogique, l'expérimentation permet, à tout le moins, de démontrer aux étudiants la vraisemblance des théorèmes économiques élémentaires^8(*). Elle constitue par ceci un outil performant d'enseignement, car en impliquant directement les étudiants dans des situations économiques réelles, cette méthode permet une initiation aux modèles d'interactions interindividuelles, à la décision individuelle dans un environnement incertain, aux mécanismes des marchés et de la concurrence.

1 - 2 - La méthode expérimentale 

L'expérience économique, dans le but de création de situations économiques réelles, doit satisfaire à un certain nombre de principes très strictes. Il s'agit de préciser, selon Vernon L. SMITH^9(*) (1982) que chaque expérience en tant que système microéconomique ( artificiel) est constituée par un environnement qui « désigne l'ensemble des caractéristiques de tous les agents : les goûts et la technologie qui sont représentés respectivement par les relations de préférences ou les fonctions d'utilité et par les dotations initiales [ en compétence et en ressources] et les fonctions de coût et de production. A partir de ces éléments peuvent être dégagées les fonctions de demande des consommateurs et les fonctions d'offre des producteurs [ en général peuvent être tirés les résultats associés qui motivent les échanges entre les sujets] »* ^1(*)0. Cet environnement est contrôlé en utilisant un système de récompense monétaire afin de révéler de véritables comportements économiques. Ce système microéconomique définit aussi une institution qui établit le langage de communication, en général sous forme de messages qui révèlent des offres, des seuils d'acceptation, des valeurs de réserves, et les conditions sous lesquelles ces messages se transforment en engagement irrévocable c'est à dire les règles du jeu définissant les conditions dans lesquelles les messages et actions deviennent des contrats et par conséquent des allocations. L'institution peut soit mentionner, explicitement ou implicitement, l'ordre dans lequel les offreurs et les demandeurs parlent et agissent, soit stipuler que ceux-ci sont libres de parler et d'agir à leur guise. Enfin, les comportements observés des participants dans l'expérimentation doivent se déterminer en fonction de l'environnement et de l'institution qui constituent les variables contrôlées.

Selon DELOCHE, cette définition en forme de triptyque nous permet de parler de la fécondité de l'expérimentation et de sa supériorité sur l'économétrie. L'économiste-économétre ne contrôle aucun des trois ingrédients qui entrent dans la composition d'un système microéconomique ou d'une théorie. L'économiste-expérimentateur du laboratoire peut créer et contrôler les institutions en définissant à la fois les messages (actions) à la disposition des agents et les règles du jeu. L'économiste-expérimentateur du laboratoire peut contrôler non seulement les institutions mais encore l'environnement. Il peut donc vérifier les hypothèses de la théorie en ce qui concerne le comportement des agents à la double condition de disposer d'une théorie prenant en compte les institutions et d'utiliser un système de rémunération des participants aux expériences permettant de faire correspondre à chaque résultat une valeur monétaire déterminée.

La première condition prouve selon SMITH^1(*)1 que les expérimentateurs et leurs recherches ont été fortement influencés par la théories des institutions qui a commencé à se développer au début des années 60, ceci explique, selon DELOCHE, la solidité de l'union de la théorie des jeux et de l'économie expérimentale par l'importance que toutes les deux accordent aux institutions.

DELOCHE trouve dans la deuxième condition une mise en oeuvre, par les expérimentateurs, de la théorie de la valeur induite qui est constituée par cinq principes : Insatiabilité ; proéminence ; dominance ; secret et parallélisme. Les deux premiers principes - insatiabilité et proéminence - sont suffisants pour qu'une économie expérimentale existe puisqu'ils assurent respectivement que l'utilité de chaque agent soit une fonction connue de ses actions et de celles des autres agents. Pour qu'une économie expérimentale contrôlée existe, les deux

principes suivants - dominance et secret - doivent en outre être respectés. La dominance assure que, pour chaque agent, la récompense qu'il est susceptible d'obtenir pour avoir participer à l'expérience est le seul mobile , la seule raison significative de ses actes : les coûts et avantages (de penser, de calculer, d'agir) non monétaires de ceux-ci ne peuvent jouer qu'un rôle négligeable. Le secret, c'est à dire le fait que, au cours d'une expérience, chaque participant n'est informé que de ses propres dotations et récompenses, garantit l'autonomie de chaque agent. Joints aux deux premiers principes d'insatiabilité et de proéminence, la dominance et le secret certifient donc l'aptitude des données expérimentales à permettre des inférences de laboratoire, le cinquième et dernier principe - le parallélisme - doit, de plus, être satisfait au mieux. Le degré de réalisation de cette exigence mesure en effet l'ampleur de la ressemblance entre l'environnement du laboratoire et celui du monde réel. Le parallélisme assure donc que des propositions concernant le comportement des agents et les performances des institutions qui ont été vérifiées en laboratoire sont de même valables dans une économie réelle à l'image de celle construite par l'expérimentateur.

Revenons à la définition avancée au dessus du système microéconomique en forme de triptyque, SMITH^1(*)2 affirme, en adoptant cette conception, que l'économie expérimentale a découvert que les institutions importent parce que les règles ou les normes importent et les règles importent parce que les motivations importent. Mais les motivations auxquelles les gens répondent ne sont pas, parfois, celle espérées par la théorie économique. Ces contradictions

fournissent des indices précieux sur l'importance du rôle joué par les règles implicites^1(*)3 suivies par les gens, ce qui ouvre la voie, à l'examen en laboratoire, de nouvelles hypothèses théoriques.

RULLIÈRE^1(*)4 ajoute que le respect de cette définition en forme de triptyque du système microéconomique implique que les décisions soient prises de manière anonyme( par le cloisonnement des postes informatiques), dans un temps réduit afin d'éviter la fatigue ou la lassitude. En outre, pour un même protocole expérimental, les sessions doivent être rapprochées de façon à éviter des fuites d'information entre les sujets potentiels.

Par ailleurs, RULLIÈRE avance que outre l'anonymat les expérimentations tendent à devenir le plus souvent décontextualisées. Il illustre cette idée en affirmant que la meilleure façon d'apprécier le rôle joué par la mémoire, l'histoire, le passé des acteurs, du poids et de la nature de leurs relations sociales et des institutions dans lesquelles la vie économiques et sociale se déroule, consiste précisément à organiser les interactions économiques en neutralisant ces effets de contexte.

D'un autre coté, et en essayant d'appliquer la démarche expérimentale à l'économie, les expérimentalistes ont rencontré un problème technique qui est apparu à première vue comme difficile à évacuer. Il s'agit en effet de la représentation théorique de la structure des préférences. Normalement, dans la modélisation microéconomique. Cette représentation correspond de manière standard à la définition d'une fonction d'utilité. Cependant, dans le contexte expérimental, cette correspondance ne peut être établie. En effet, l'appréciation psychologique des plaisirs et des peines revêt, par nature, un caractère personnel propre à chaque sujet ( idiosyncrasique ).

SMITH a contourné cet obstacle en proposant en 1976^1(*)5 la méthode dite de la valeur induite. Par exemple, supposant que l'on souhaite qu'un participant à une expérience révèle sa fonction de demande D pour un certain bien homogène. Ne connaissant pas directement sa fonction d'utilité U(.), pour tout prix unitaire donné, on va lui demander d'exprimer la quantité désirée, q= D( p) ; pour cela, il suffit de construire dans le protocole expérimental une fonction de rémunération du sujet R(.) qui lui permette de gagner une somme monétaire équivalente à R(.) - pq.

En supposant que le participant se comporte comme si sa fonction d'utilité était monotone, croissante et concave, et comme le participant doit choisir q tel que R'(q) = p,

on obtient alors : D (p) = q = (R')^-1 ( p ) et avec

U [ R(q) D P.q] . [ R'(q) - p ] = 0

Cette méthode est maintenant couramment utilisée pour réduire un modèle microéconomique à un protocole expérimental.

Ce problème ainsi évité, nous pouvons dire qu'aujourd'hui les données une fois recueillis peuvent faire l'objet de traitements statistiques sophistiqués ( par rapport aux premiers travaux expérimentaux) dans la mesure où l'expérimentateur dispose actuellement d'un arsenal de technologie informatique assez développé ainsi que des progrès réalisés en économétrie des données expérimentales ( en particulier l'économétrie des données de panels). La mise à la disposition de ces nouveaux instruments permet aussi de répondre à la nécessité de répliquer et de répéter des protocoles expérimentaux. En effet, souvent des anomalies par rapport aux prédictions théoriques sont dues à l'absence totale de phase d'apprentissage. Pour cela il est devenu exigeant de passer par une telle phase surtout lorsqu'il s'agit d'un problème théorique difficilement maîtrisable par les sujets.

1 - 3 - La bonne expérience

Qu'est ce qu'une bonne expérience ?

SMITH^1(*)6 répond à cette question en affirmant que ceci dépend de ce que nous voulons évaluer et explorer, ainsi que de la manière avec laquelle nous abordons le sujet^1(*)7. SMITH ajoute aussi qu'une bonne expérience est celle qui contrôle les hypothèses alternatives les plus plausibles capables d'expliquer ce qui est observé et permet ainsi de distinguer entre elles. Ceci est dit, nous ajoutons que les hypothèses alternatives dépendent des développements récents dans la théorie, dans le laboratoire, ou dans le domaine. Donc « une bonne expérience » est une créature de son temps ( faisant du contrôle des hypothèses attachées une affaire inutile dans des expériences future). C'est pourquoi les expérimentalistes refusent de donner n'importe quelles directives méthodologiques strictes, des axiomes, des préceptes ou des règles précises. Et la bonne méthodologie expérimentale dépend des questions pour lesquelles on cherche à trouver une réponse à travers l'expérimentation.

Abordant maintenant un autre point, à savoir celui du contrôle par l'expérimentateur des préférences des sujets en utilisant une récompense monétaire. Il y en a différents points de vue : ROTH^1(*)8 dans « Handbook of Experimental Economics » a privilégié la voie libérale. Il a été contre l'établissement d'une orthodoxie rigide concernant la méthodologie des expériences. Il a affirmé que si, par contre, l'expérience était conçue d'une façon lilbérale (sans être contraingnée par l'utilisation des récompenses monétaires)

telle qu'on peut adresser des questions d'un intérêt particulier, les résultats expérimentaux seront pleinement riches surtout s'ils ont été répliqués par d'autres expérimentateurs, l'exigence d'une récompense monétaire peut mener à l'abondance d'un nombre important d'expériences surtout lors du manque de ressources financières^1(*)9. Cette approche suit l'adage stipulant que le `` parfait'' peut devenir l'ennemi du ` ``bon'' . Elle contrarie celle de BINMORE^2(*)0 (1994) qui argumente qu'il n'y a plus de crédibilité pour les expériences dans lesquelles la performance des sujets n'est pas récompensée par rapport à leurs coûts d'opportunité. En outre, BINMORE affirme que l'expérimentateur ne doit pas se présenter durant l'expérience et que « toute personne interagissant directement avec les sujets ne doit pas avoir un intérêt personnel dans leurs résultats »^2(*)1.

1 - 4 - Champ d'application

Plusieurs raisons justifient le recours à la méthode expérimentale ( voir section II) que ce soit en économie ( notamment en microéconomie des risques et de la décision individuelle dans un environnement incertain, en théorie des jeux et en microéconomie de l'organisation industrielle ou la théorie des marchés) ou en sciences de gestion ( notamment en marketing, en finance, en assurance, en théorie de l'organisation et en commerce électronique). L'utilisation de l'expérimentation dans ces différents domaines est considérée comme un moyen de production de données naturelles et de connaissance, qui est complémentaire aux méthodes statistiques de tout ordre, aux enquêtes et aux simulations.

Dans le domaine économique qui nous intéresse ici, nous pouvons distinguer, comme l'a fait ROTH^2(*)2, entre trois branches essentielles dans lesquelles l'expérimentation a attiré plus d'attention. Il s'agit en premier lieu des théories du choix individuel, deuxièmement les théories des organisations industrielles et en troisième lieu les théories des interactions comportementales. Il faut noter ici que l'avènement des expériences dans ces différents domaines a été fortement influencé  par la publication en 1944 du célèbre ouvrage de Von Neuman et Morgenstern, « Theory of Game and Economic Behavior »^2(*)3.

1-4-1 Les théories du choix individuel

Jusqu'à présent, l'expérience^2(*)4 de THURSTONE^2(*)5 en 1931 (examen de la vraisemblance de la théorie de l'utilité ordinaire), celle de MOSTELLER et NOGEE en 1951 et celle de ALLAIS^2(*)6 en 1953 ( qui établit quelques violations dans la théorie classique du choix individuel^2(*)7) restent les références les plus importantes dans ce domaine. En outre DAY^2(*)8 affirme qu'il faut, tout d'abord, associer à ce champ, qui s'intéresse à la décision en incertitude, la conférence dont le thème était « la conception des expériences sur les processus de décision » déroulant en 1952 au « RAND Corporation » à Santa Monica aux Etats Unis mettant ainsi en contact des mathématiciens, des psychologues, des économistes et des sociologues.

En général, ce genre d'expérience a pour objectif : premièrement de faire des tests des prédictions de la théorie du comportement rationnel et deuxièmement essayer d'expliquer et de faire des investigations concernant les régularités non prédites.

Mais, il y a différentes formulations du comportement rationnel qui influencent à leur tour la conception des expériences. Parmi ces différentes

formulations de la rationalité on peut citer : le comportement maximisateur, la maximisation de l'utilité ordinaire, la maximisation de l'utilité espérée et la maximisation de l'utilité espérée subjective.

Il faut noter ici que dans ce domaine, les expériences sont dans la plupart des cas simples. Souvent, il s'agit, seulement de poser des questions sur certains choix hypothétiques^2(*)9. Mais l'interprétation de ces choix observés ont des implications économiques très importantes. Parfois, et surtout pour les théories du choix basées sur les préférences, on essaye d'étudier les effets de présentation des décisions, puisque le choix entre deux alternatives peut dépendre de la façon avec laquelle la décision est présentée ou formulée ( ce genre d'études sont faites actuellement d'une manière importante dans des domaines tels que la communication des décisions publiques, le marketing).

Pour bien montrer ce point prenons, l'exemple de deux expériences développées par KAHNEMAN et TVERSKY (1979). Les décisions à prendre dans les deux expériences sont les mêmes, mais la façon avec laquelle elles sont présentées sont différentes.

Expérience 1 : Imaginez que vous avez décidé de voir un spectacle pour lequel le prix d'entrée est de 10 Dh. En entrant au théâtre vous découvrez la perte du billet à 10 Dh. Etes-vous prêt à payer 10 Dh pour le ticket du spectacle.

Résultat : Oui : 88 % NON : 12 %

Expérience 2 : Imaginez que vous avez décidé de voir un spectacle pour lequel vous avez payé 10 Dh pour le ticket d'entrée. En entrant au théâtre vous avez découvert la perte de votre ticket en sachant que ce dernier ne peut être remboursé. Etes-vous encore prêt à payer 10 Dh pour un autre ticket.

Résultat : Oui : 46 % NON : 54 %

N.B : le nombre de sujets enquêtés est 62 étudiants de collège.^3(*)0

On remarque donc que malgré que la décision à prendre dans les deux expériences soit la même, la façon de sa présentation a un effet important sur les résultats des expériences.

1-4-2 La théorie de l'organisation industrielle des

marchés.

Dans ce domaine on a eu recours à l'expérimentation depuis les années cinquante du siècle dernier. Cependant, les travaux de CHAMBERLIN^3(*)1 (en 1948), de FOURAKER et SIEGEL^3(*)2 (en 1960) et précisément de Vernon L SMITH sont à la base de presque tous les travaux contemporains.

CHAMBERLIN est considéré comme le précurseur de l'économie expérimentale grâce à sa contribution de 1948, dans laquelle il cherche à tester un modèle de la concurrence parfaite^3(*)3 entre les agents rationnels. Les résultats de cette première tentative étaient peu concluants, ce qui à poussé SMITH^3(*)4 après, à reproduire ce travail mais en modifiant l'expérience originelle de CHAMBERLIN. Cette contribution donnera très vite à SMITH le statut de fondateur de l'économie expérimentale. Selon RULLIERE^3(*)5, cette expérimentation reste à ce jour exemplaire sur au mois deux plans : d'un coté SMITH parvient à un résultat d'une grande élégance et d'un autre coté, il ouvre la voie à de nombreuses recherches en précisant les premiers éléments fondamentaux de la méthode expérimentale en économie.

SMITH organise un marché^3(*)6 en répartissant de manière aléatoire des sujets entre des acheteurs et des offreurs d'un seul bien pour lequel chacun se voit attribuer un valeur de réserve. Alors que chacun des sujets ne disposent pas de l'information pour calculer l'équilibre du marché, il parvient par cette méthode à mettre en évidence une convergence réelle vers le prix d'équilibre théorique et donc prouver l'efficience du marché.

En portant jugement sur ces travaux pionniers ( CHAMBERLIN ( 1948) et SMITH (1962))^3(*)7, NOUSSAIR et RUFFIEUX^3(*)8 affirment que ceux-ci portaient sur la vérification empirique de l'hypothèse fondamentale des modèles de la microéconomie des marchés, hypothèses selon laquelle la concurrence est efficace, l'efficacité était définie ici comme la réalisation de tout le surplus potentiel dans l'échange, autrement dit la maximisation de la valeur créée dans les échanges. Ces travaux entendaient explorer les conditions concrètes dans lesquelles les prix de marchés étaient stables et les quantités échangées correspondaient aux niveaux attendus par la théorie concurrentielle. Si les travaux de CHAMBERLIN (1948), utilisant des procédures d'échange décentralisées, ne furent pas concluants, ceux de SMITH (1962), utilisant les règles de la double enchère orale continue, montraient qu'il était possible de faire converger les prix et les quantités échangées d'une économie à marché unique vers l'équilibre concurrentiel.

Ce résultat était capital : il montrait que les propriétés d'optimalité d'un équilibre concurrentiel théorique, obtenu avec les comportements hypothétiques de l'Homo economicus pouvaient être obtenues, avec un environnement et des institutions adéquates, avec des Homo Sapiens, en l'occurrence avec des étudiants. Néanmoins, cette efficacité n'était justifiée que pour des marchés de biens et services non financiers. En essayant de faire pareil pour les marchés d'actifs^3(*)9, les expérimentalistes se sont convaincus que ceux-ci étaient loin d'avoir les mêmes propriétés d'efficacité que les marchés non financiers.

NOUSSAIR et RUFFIEUX affirment que si on accepte que, pour un marché financier, l'efficacité est définie comme l'aptitude à révéler la valeur fondamentale des actifs échangés, il est en effet saisissant que les prix constatés sur un marché financier de laboratoire n'ont pas tendance à converger vers cette valeur fondamentale, même lorsque celui-ci est obtenu de tous les participants et que l'information est commune.

Tout au long de presque 60 ans, les expérimentalistes des marchés ont réussit à construire une nouvelle méthode d'investigation des phénomènes liés à la théorie des organisations et des marchés, cette méthode a permis de trouver des réponses, auparavant impossibles ou difficiles à trouver, a des questions telles que : comment considérer par exemple l'hypothèse selon laquelle, sur un marché particulier de l'emploi, des considérations de bienveillance ou d'équité sont déterminantes dans la formation du salaire ?^4(*)0

L'idée pour tous ces auteurs, consiste donc à inverser la démarche scientifique : on reproduit artificiellement un contexte économique (un marché oligopolique, monopolique, concurrentiel,...etc) dans un laboratoire avec de vraie participants (des acheteurs et des vendeurs) et des transactions monétaires réelles^4(*)1. Cette méthode a le mérite d'isoler certaines variables constituants l'objet d'étude et par conséquent d'en considérer la pertinence. Ceci a permis de mettre en évidence le rôle crucial des institutions qui définissent un marché. Cette conclusion, selon RULLIERE, a eu un impact important sur le choix par exemple des mécanismes marchands de privatisation des services collectifs^4(*)2 comme l'électricité et l'eau.

Enfin, et afin de résumer en quelques mots ce qu'a apporté le laboratoire à la recherche scientifique dans le domaine de l'organisation industrielle, on atteste la citation suivante : «  Nous avons fait nos observations dans des conditions contrôlées,... Dans l'utilisation du laboratoire plutôt que le recours direct au champ, nous avons été capables d'isoler les phénomènes d'intérêt à la recherche .... Nous avons utilisé la méthode expérimentale, c'est à dire que nous avons manipulé certaines variables et avons observé les effets de variations de celles-ci sur certaines autres variables. En recourant, donc, a cette méthode, nous manifestons que la quantité d'information disponible à un commerçant et son niveau d'assimilation sont des déterminants significatifs des contrats ( prix-quantité) qui seront atteints. Nous déclarons que seulement la méthode expérimentale pourrait avoir démontrer l'influence et l'importance de ces déterminants ». ( SIEGEL et FOURAKER (1960)).^4(*)3

1-4-3- La théorie des interactions comportementales

Il y a dans notre vie réelle beaucoup de contextes économiques où les interactions des agents revêtent un caractère stratégique. L'articulation des politiques de relance de deux pays interdépendants, la politique de prix d'un monopole qui fait face à une menace d'entrée, la proposition de prix pour un marché public sont tout aussi des situations d'interaction stratégique où les choix

des autres agents influencent explicitement les gains de chaque agent.

Ces situations sont relativement complexes à analyser et seul le développement de la théorie des Jeux nous a permis de comprendre leur

fonctionnement. Nous présenterions dans le deuxième chapitre (sans être exhaustif) les différents concepts développés par ce champ de l'analyse économique.

Section II- Le recours au laboratoire : Raisons et Objections.

2-1-Les raisons du recours à l'expérimentation

Plusieurs raisons ont été avancées par les économistes ( quelque soit leur domaine d'activité) pour justifier le recours à l'expérimentation. la plupart de ces raisons ont été citées auparavant, mais nous essayerons dans ce point de les rassembler. Nous empruntons pour ceci la classification avancée par V SMITH^4(*)4 qui a essayé d'énumérer les différentes raisons citées dans la littérature économique, et il a réussi a en trouver sept.

2-1-1 Tester la théorie ou discriminer entre les théories

Cette motivation vient précisément des théoriciens des jeux. On teste la théorie en comparant son message ou ses implications en terme des résultats avec les observations expérimentales. Plus les prédictions théoriques heurtent (ou sont proche de) ce qui est observé plus la théorie est bonne.

2-1-2 Déterminer les causes d'échec d'une théorie

Lorsque les observations issu de l'expérience n'arrivent pas à se conformer avec les implications théoriques, la première chose à faire est de réexaminer la manière avec laquelle l'expérience est conçue et s'assurer qu'il s'agit bien d'une incapacité de la théorie à prédire les comportements des expérimentés et non pas d'une erreur de conception ( environnement non adéquat, non respect des règles du jeu, etc). On essayera donc de répliquer l'expérience et de voire si l'échec est sûr. L'échec de la théorie à prédire les comportement pousse aussi bien les théoriciens que les expérimentalistes à consentir des efforts supplémentaires pour découvrir les causes, ainsi que chercher de nouvelles suggestions théoriques.

2-1-3 Etablir des régularités empiriques pour de nouvelles théories.

Nous pouvons concevoir de nouvelles théories soit (comme précédemment ) à cause de la mise en doute de la prédictibilité d'une certaine théorie, ce qui impose la recherche d'un substitut, soit à travers le contrôle (au sein du laboratoire) par le théoricien-expérimentateur, de certaines variables difficilement observables et traitables à travers le seul travail théorique. Dans ce dernier cas, de nouvelles théories, de plus en plus proches de la réalité humaine, peuvent être élaborées.

2-1-4 Comparer les environnements

La comparaison des expériences ayant des environnements différents mais en utilisant la même institution peut nous renseigner sur la robustesse de cette institution, ainsi que sur les conditions sous lesquelles cette institution ne tient pas (déterminant par ceci les limites de cette institution).

2-1-5 Comparer les institutions

Dans le cas contraire, si, en utilisant le même environnement, la comparaison des institutions différentes (par exemple en changeant les règles d'échange dans un marché quelconque) permet de tirer des conclusions en ce qui concerne les propriétés de chaque institution et les effets de ces dernières sur la détermination des issues des jeux expérimentaux.

2-1-6 Evaluer les politiques économiques

Alors que le décideur se trouve face à un grand nombre d'options, il serait souhaitable qu'il puisse les tester et procéder à des allers-retours entre la paramétrisation de son modèle de décision et l'expérimentation. Or le laboratoire offre la possibilité de tester l'efficacité relative de politiques privées ou publiques alternatives, ou d'évaluer ex-post les éléments d'une décision, en réunissant des éléments de preuve dans un débat.

2-1-7 Conception de nouveaux designs institutionnels

Cette raison se déduit de la précédente. En évaluant ex-post les éléments d'une décision, la laboratoire permet de pré-évaluer de nouvelles politiques et de nouveaux designs institutionnels sans avoir à subir les coûts sociaux ou privés associés à leur mise en oeuvre réelle.

2-2- Les critiques adressées à l'expérimentation

N'importe quelle méthode d'investigation a des limites et les économistes réussissent toujours à trouver des objections à l'encontre de ces différentes méthodes d'investigation et le laboratoire économique ne se présente pas à cet égard, comme exceptionnel. Les économistes ont réussi à relever certaines faiblesses de la méthode expérimentale dont les principales sont énumérées par Bertrand MUNIER^4(*)5 qui a essayé d'apporter à ces objections les réactions et les réponses des expérimentalistes.

2-2-1- Les situations réelles sont plus complexes que les situations du laboratoire.

Sachant ceci, il est impossible de produire à partir du laboratoire des connaissances applicables aux situations réelles. Ce qui nous amène à affirmer que, par exemple, les marchés expérimentaux ne sont pas pertinents parce que les économies construites au laboratoire ont des structures beaucoup plus simples que celles qu'on trouve dans la réalité du terrain et qui sont celles qui nous intéressent en dernier ressort.

Cette critique est formulée d'une autre manière par COLMAN^4(*)6. En effet depuis la naissance de l'économie expérimentale, un groupe de commentateurs a émergé exprimant ses doutes à l'égard de ce qu'ils appelaient « la validité écologique » des jeux (du laboratoire) expérimentaux (expérimental). « La validité écologique » est un sujet sur lequel s'est déroulé un débat chaleureux entre sociologues et psychologues (surtout durant les années 70) et il exprime l'idée que les résultats expérimentaux peuvent être généralisés au monde réel naturel. A cette égard, il est à distinguer entre « validité interne » (le champ pour lequel, les conclusions de l'expérience sont vraies sous certaines conditions d'environnement et d'institution particulières) et la « validité externe » (l'état où les conclusions sont généralisées aux situations réelles). Les expériences expérimentales, à cause de leur nature abstraite et fortement artificielle, restent particulièrement vulnérables aux critiques qui portent sur leur « validité écologique ». On atteste à ce sujet les paroles de HAMBERGER : «Lorsque les gens sont mis dans une situation artificielle simple, on peut affirmer qu'ils se comporteront conformément à cette situation, de ce fait, cela ne révèle aucune information sur la manière avec laquelle ils se comporteront dans des vraies situations complexes »^4(*)7.

COLMAN^4(*)8 pense que c'est cette difficulté de prouver la validité écologique des expériences économiques qui explique le manque d'intérêt et la pénurie des travaux dans ce domaine durant les décennies 50, 60, 70. C'est pour cela qu'on trouve aussi, qu'il y a de rares tentatives de comparaison entre les comportements dans un environnement expérimental et ceux observés en réalité. WRIGHTSMAN, O'CONNOR et BAKER en essayant d'établir une revue séléctive des travaux expérimentaux effectués jusqu'alors exprime leur surprise à l'égard de la rareté des travaux de ce genre en disant : « ce qui nous a supris le plus, tout au long de notre recherche, c'est qu'il n'y avait aucune étude dont l'objectif était la comparaison entre le comportement au sein du laboratoire et celui dans les différentes situations du monde réel. Malgré que les manipulations au laboratoire permettent une meilleure évaluation du monde artificiel, la comparaison entre le comportement dans ces différents états s'impose. ».^4(*)9

La réponse à cette critique, selon les termes de NOUSSAIR et RUFFIEUX^5(*)0, est que le propos de l'expérimentation n'est pas nécessairement de reproduire la réalité que l'on trouve en dehors du laboratoire. L'intention première des expérimentalistes est d'évaluer les conditions dans lesquelles une théorie économique est pertinente. En économie, les modèles théoriques guident la structuration de la plupart des expériences. En d'autres termes, la simplicité vient plutôt de la théorie que de l'expérience et si on veut demander plus de ressemblance par rapport à la réalité c'est aux théoriciens de le faire et non plus aux expérimentalistes. Le souci de l'expérimentation n'est donc plus de copier la réalité mais créer une économie dont l'institution et l'environnement copient ceux du modèle théorique, et c'est cette possibilité de confrontation, des modèles théoriques et des expériences ayant les mêmes environnements et les mêmes institutions, qui permet de faire une comparaison directe des résultats.

Dans le même sens TEDESCHI, SCHLENKER et BONOMA^5(*)1 ont estimé que le critère de « validité écologique » des expérimentations en économie est inexistant et qu'aucune généralisation n'est admise des résultats expérimentaux vers le monde réel sans enquêtes et travaux ( a priori ) théoriques approfondies. En 1978, SCHLENKER et BONOMA^5(*)2 ont essayé d'expliquer ce jugement pris auparavant en mentionnant qu'il y a une réalité à ne pas oublier, c'est que ce sont les considérations théoriques qui déterminent notre jugement sur la généralisation et la validité écologique des résultats expérimentaux.

2-2-2- Le manque de motivation au sein du laboratoire

Les sujets ne sont pas vraiment motivés dans le laboratoire, c'est ce qui explique leur déviation par rapport au modèles théoriques. La réponse à cette objection est qu'il existe dans les protocoles « bien faits » des techniques de motivation et d'incitation des sujets semblables à celles qu'on trouve dans les modèles théoriques que l'on cherche à tester. Les participants doivent avoir les mêmes incitations que celles que le modèle suppose. Ceci est réalisé en créant une économie entièrement monétaire, où les valeurs et les coûts sont directement exprimés en numéraires. Les participants sont rémunérés en monnaie réelle, en fonction du montant du numéraire détenu, qu'ils conservent à l'issu de l'expérience. Ces montants ( en ECU)^5(*)3 sont proportionnels à la valeur de la fonction objectif qui résulte des décisions des sujets.

MUNIER avance une autre réponse à cette objection. Il affirme que si les sujets expérimentés ne répondaient pas en fonction d'une quelconque motivation dans l'expérience et dans l'expérience seulement, leurs réponses seraient distribuées au hasard et pour ce genre de situations il existe des techniques permettant d'écarter de tels sujets de l'échantillon. la répétition de l'expérience à une distance de temps adéquate pour tester la stabilité des réponses et recueillir les explications subséquentes des sujets (le debriefing) est un exemple des techniques utilisées pour faire face à ce genre d'obstacles.

2-2-3- La mal compréhension de la part des sujets de la situation

étudiée.

Les sujets sont obligés de répondre à une situation différente de leur

situation habituelle. La situation étudiée est, dans la plupart des cas, ignorée ou mal comprise de la part des sujets. S'ils avaient compris, leur réponses seraient plus proches de celles des modèles théoriques.

NEMETH^5(*)4 a expliqué cette idée en disant que le comportement irrationnel apparent dans les jeux expérimentaux est dû en grande partie à l'incompréhensibilité même de la situation dans laquelle les sujets sont placés.

Pour répondre à cette objection, nous pouvons dire que (comme on a déjà reproché à l'expérimentation économique) l'économie du laboratoire est souvent simplifiée et très loin de la complexité de la réalité économique. Mais pour tenir compte de cette objection, il est essentiel de savoir que les expérimentalistes s'assurent toujours, par une pré-expérimentation brève, que les sujets ont bien compris les questions. Par exemple au début d'une expérience du marché, les sujets apprennent à utiliser les institutions ( les règles de communication et d'échange) et à se familiariser avec l'environnement de l'expérience. Cette première phase d'apprentissage n'a pas d'influence sur les résultats de l'expérience et elle n'est pas prise en compte dans les gains des sujets.

2-2-4-La manipulation des sujets

L'objection stipule qu'on manipule les sujets et on leur fait répondre ce que l'on veut. En répondant à cette objection, MUNIER affirme que celle-ci ignore que des expériences telle que le paradoxe d'ALLAIS ont été faite des centaines de fois par des centaines d'expérimentateurs différents, ayant des objectifs divers et des cultures différentes ( psychologues, ingénieurs, civils, économistes, etc.), dans des pays et à des époques différentes et en usant des variantes diverses du protocole, alors que le résultat est étonnamment robuste. Serait-il envisageable que tous ces expérimentateurs aient formé un complot ? et pourquoi ? L'objection souligne que le protocole n'est pas complètement neutre par rapport aux réponses obtenues. La réponse à l'objection consiste à faire ce que l'on vient d'évoquer : répliquer les expériences sous des protocoles différents, des sujets différents, des expérimentateurs différents.

A ces quatre critiques énumérées par MUNIER, nous pouvons citer une autre avancée par COLMAN^5(*)5. Celle-ci porte sur l'incertitude qui touche la structure des paiements dans les expériences économiques. Les expériences se présentent comme moyen de prévoir les comportements des sujets en utilisant certaines propriétés stratégiques spécifiques. A cet égard, l'hypothèse qu'on se pose toujours est que les préférences individuelles dépendent seulement des récompenses monétaires. Mais il est tout à fait raisonnable de croire que les préférences individuelles peuvent être influencées par des facteurs autres que ceux supposés dans les jeux expérimentaux d'où les expériences actuellement utilisées pour tester des phénomènes (humains) tel que la réciprocité, l'aversion à l'inéquité ou à l'inégalité et la confiance.

Conclusion :

Au cours de ce chapitre, nous avons essayé de donner une idée générale sur ce qu'on entend par recherche expérimentale, ainsi nous avons avancé plusieurs arguments prouvant que l'économie expérimentale est un domaine de recherche bien établi, surtout lorsqu'il s'agit de l'examen de l'effet des variables qui sont difficiles à mesurer et à contrôler par n'importe quelle autre méthode. En effet, nous avons montré que la recherche expérimentale est un outil performant de la production des données. Notre jugement s'est basé premièrement sur la qualité des résultats attendus et deuxièmement sur sa comparaison par rapport aux autres techniques de production des données. Ainsi, notre définition du système microéconomique, en tant qu'entité composée de trois éléments à savoir l'institution, l'environnement et le comportement des agents, nous a permis de porter jugement sur la supériorité de l'outil expérimental par rapport aux autres techniques. En effet, l'expérimentateur peut

contrôler aussi bien l'institution que l'environnement, une chose qui est impossible par n'importe qu'elle autre outil. Cependant, malgré cette supériorité, les éxperimentateurs sont hostiles quant à l'unicité de cet outil pour la production des données, ils admettent que chaque outil a ses avantages et qu'une collaboration entre ces différentes techniques améliorera certainement la qualité des résultats attendus. L'exemple que nous pouvons avancer à cet égard est la naissance et le développement de l' « économétrie des données expérimentales », qui est considérée comme le fruit d'une union entre la modélisation économétrique et les techniques expérimentales.

D'un autre côté, et s'agissant seulement de l'économie, nous avons pu dégagé trois domaines d'application pour lesquels la méthode expérimentale a été bien établie. Il s'agit de la théorie du choix individuel, la théorie de l'organisation industrielle des marchés et la théorie des jeux bien que actuellement on constate, que dans la plupart des études expérimentales, il y a une tendance vers l'utilisation conjointe de plusieurs théories pour le traitement d'un seul problème, l'exemple le plus fréquent est celui des jeux expérimentaux dans lesquels la théorie des jeux est utilisée comme langage pour la description de la structure des marchés.

Dans un dernier point, nous avons pu découvrir que, malgré tous les avantages que procure la méthode expérimentale, il y a des faiblesses qui subsistes surtout celle concernant le parallélisme des résultats expérimentaux c'est à dire de degré de ressemblance entre l'environnement expérimental et celui du monde réel.

Après avoir présenter l'économie expérimentale comme domaine de recherche proprement dit, nous allons nous intéresser au cours du chapitre suivant au développement des différents concepts avancés par la théorie des jeux considérée comme un des champs d'application les plus prospères en terme d'études expérimentales.

Chapitre II Théorie des jeux et modélisation

des interactions interindividuelles

«Von Neumann and Morgenstern's theory is based on an analysis of the interrelationships of the various coalitions which can be formed by the players of the game.   Our theory, in contradiction is based on the absence of coalitions in that it is assumed that each participant acts independently, without collaboration of communication with any of the others.»(*)

Dans le chapitre précédent nous avons présenté l'économie expérimentale comme nouvelle technique d'investigation, en mettant, ainsi, en lumière les différentes raisons du recours au laboratoire sans oublier ses limites et faiblesses. Nous avons été intéressé aussi par les différents champs d'application de cette (nouvelle) méthode à savoir la théorie des marchés, la théorie des choix individuels et la théorie des interactions stratégiques entre individus. Et c'est sur cette dernière que nous allons nous concentrer dans le présent chapitre en essayant dans un premier point de présenter un bref aperçu sur l'objectif de cette discipline censée avoir intéresser un grand nombre d'expérimentateurs et présenter un champ d'application fertile pour eux ainsi que la présentation de ses notions de base ( Section I). Dans un deuxième point, nous essayerons d'analyser les deux situations importantes en théorie des jeux à savoir les interactions interindividuelles dans un environnement non coopératif et celles dans un environnement coopératif, ainsi que l'analyse des différents concepts de solution présentés dans chaque cas ( Section II ).

Section I. Bref Apercu sur la théorie des

jeux : notions de base

1 -1- Théorie des jeux : Objet

La théorie des jeux est une théorie dont on peut voir l'acte de naissance dans l'oeuvre de VON NEUMANN et MORGENSTERN publié en 1944 et intitulé «  Theory of Game and Economic Behavior ». Cet ouvrage se situe à la fois dans le prolongement et en rupture avec les réflexions sur les jeux de hasard, qui ont donné naissance au calcul des probabilités. L'objet de la théorie des jeux tel qu'on l'entend depuis Von NEUMANN et MORGENSTERN est l'étude des interactions des comportements de plusieurs individus ( au moins deux) qui sont conscient de l'existence de ces interactions. Avant cette période la seule conception du processus compétitif était celle véhiculée à travers l'Equilibre Economique Général ( EEG) dans lequel, comme l'atteste LAKHDAR^1(*), Communication et interdépendance sont médiatisées par le système prix. Toute communication interindividuelle autre que celle qui passe par les prix est bannie. Dans ce contexte les phénomènes de pouvoir, de mimétisme et de confiance sont occultés. Ceux-ci portent sur des relations interindividuelles et non sur des relations entre sujets et objets. L'étude de ces relations nécessite une logique autre par rapport au modèle de l'EEG. Une logique où la décision d'un agent est fonction de son comportement mais aussi des comportements de ses partenaires.^2(*)

A sa naissance, la théorie des jeux promettait de placer toute la théorie économique en forme stratégique dans laquelle le concept du processus compétitif devrait être restructuré et reformulé en fonction des jeux

stratégiques^3(*). Avant cette naissance^4(*) c'est à dire avant que le mathématicien VON NEUMANN et l'économiste MORGENSTERN ne publient en 1944, leur livre fondateur « Theory of Games and Economic Behavior » les économistes n'avaient guère de moyens pour analyser correctement les interactions stratégiques entre les entreprises. Les recherches se limitaient aux situations dans lesquelles ou bien les concurrents étaient trop nombreux sur un marché pour qu'une entente ait quelque poids( c'est la « concurrence parfaite »), ou bien une entreprise n'avait aucun concurrent ( c'est le « monopole »)^5(*)

A cette égard, nous pouvons affirmer , selon les termes de VERGARA^6(*), que les décisions prises par les individus en interactions ( les joueurs ) et la résultante ou les conséquences de ces décisions, pour eux et pour la collectivité qu'ils forment, représentent l'objet de la théorie des jeux . cette théorie s'applique à des jeux au sens strict ( lorsque je déplace ma tour sur un échiquier je modifie le domaine de choix de mon adversaire), mais aussi à l'économie (mes achats offrent des débouchés aux vendeurs), à la sociologie, à la science politique, à la psychologie^7(*) ...etc. Elle se propose, donc, de fournir un cadre unifié, ou un langage, permettant de traiter de façon unitaire des thèmes relevant de disciplines très diverses.

Revenons un peu à l'objectif de cette discipline pour donner plus d'éclaircissement, Bernard GUERRIEN^8(*) voit qu'il y a « confusion à ce propos, certains auteurs prétendant qu'elle cherche à expliquer les phénomènes observés, ou à faire des prédictions, d'autres qu'elle est prescriptive (normative), d'autres qu'elle est l'une et l'autre, d'autres (bien moins nombreux) enfin ne se prononçant pas ». Quelques exemples :

1- Version descriptive :

- Eric RASMUSSEN : « C'est là exactement le paradigme de la théorie des jeux, celui qui construit le modèle attribue des fonctions de gain et des stratégies aux joueurs puis OBSERVE se qui se passe lorsqu'ils choisissent des stratégies pour obtenir le gain maximum. »^9(*)

- Ken BINMORE : « la théorie (des jeux), telle qu'elle est développée actuellement, est surtout la DESCRIPTION de ce qui se passe lorsque des personnes interagissent rationnellement. »^1(*)0

- David KREPS : «  l'objet de la théorie des jeux est d'aider les économistes à COMPRENDRE et à PREDIRE ce qui se produit dans différentes situations économiques.»^1(*)1 P. 7

2 - Version Normative :

- VAN DAMME : « La théorie des jeux est une théorie normative : elle prescrit ce que chaque joueur dans les jeux doit faire afin de rendre ses intérêts optimaux ».^1(*)2

- LUCE et RAIFA : « il est essentiel, pour nous, que le chercheur en sciences humaines sache que la théorie des jeux n'est pas DESCRIPTIVE, mais plutôt (conditionnellement) NORMATIVE. Elle n'établit ni comment les gens se comportent, ni comment ils devraient le faire pour atteindre certains buts. Elle prescrit, avec des hypothèses données, des types d'action qui conduisent à des issues ayant un certain nombre de propriétés qui relèvent de l'optimalité. »^1(*)3

3 - Ambiguïté :

- OSBORNE et RUBINSTEIN : «  La théorie des jeux est un bagages d'outils analytiques désigné à nous AIDER A COMPRENDRE le phénomène que nous OBSERVONS lorsque les décisions interagissent.»^1(*)4

4 - Vague :

- Andrew COLMAN : «  la théorie des jeux est concernée par la logique de prise de décisions dans des situations sociales dans lesquelles les résultats dépendent des décisions prise par deux ou plusieurs agents autonomes »^1(*)5

- Robert AUMANN : « cette discipline concerne le comportement des joueurs dont les décisions affectent les uns les autres. »^1(*)6

- Bachir S.I. LAKHDAR : « Cette théorie se donnait pour but la prise en compte de la formalisation des phénomènes d'interaction et d'interdépendance directe entre les sujets économiques. »^1(*)7

En effet, cette multitude d'approches pour la théorie des jeux est considérée par les uns^1(*)8 (plus nombreux) une preuve de malléabilité et de flexibilité de cet outil ce qui justifie son utilisation dans plusieurs domaines, pour les autres^1(*)9 cette cacophonie à propos de la nature de la théorie des jeux - sur ce qu'elle fait ou permettrait de faire - découle de ce qu'elle ne « résout » rien et ne « propose » rien aux joueurs, elle permet essentiellement d'attirer l'attention sur les problèmes que posent les choix d'individus rationnel en interaction, lorsque toutes les hypothèses des modèles sont spécifiées. Ces derniers justifient leur point de vue en avançant l'idée que tandis que la théorie des jeux a adopté dès sa naissance le postulat de rationalité des individus, il est devenu usuel chez les théoriciens des jeux les plus réputés ( par exemple, AUMANN, KREPS, ROTH, RUBINSTEIN) d'affirmer que la seule issue pour la théorie des jeux, si elle veut rendre compte de ce qu'on observe dans le monde économique, est de faire appel à la « rationalité limitée » notion d'abord proposée par Herbert SIMON^2(*)0 ( qui depuis longtemps, nie toute pertinence et intérêt de la théorie des jeux ).

Mais tous ces auteurs quelque soit leur points de vue sont d'accords sur le fait que cette nouvelle discipline a promis dès son apparition de placer toute la théorie économique dans une nouvelle position stratégique dans laquelle le concept du processus compétitif doit être restructuré et reexprimé en termes de jeux et de stratégies.^2(*)1

A cet égard, il faut noter que la théorie des jeux contient et utilise des modèles mathématiques formels de jeux, que l'on analyse de manière déductive. Comme pour la théorie économique plus traditionnelle, on peut citer selon David KREPS^2(*)2 au moins trois avantages qui sont censés découler de la modélisation mathématique :

a- elle propose un langage clair et précis pour exprimer nos réflexions et nos idées. En particulier, elle fournit des hypothèses suffisamment générales pour transformer des idées et des intuitions d'une situation à une autre, ou de les confronter dans divers contextes.

b- Elle permet de tester la cohérence logique des intuitions et des idées proposées ;

c- Elle aide à remonter des `observations'  aux hypothèses sous-jacentes , de façon à déterminer celles d'entre elles qui sont véritablement essentielles pour parvenir à certaines conclusions.

Nous allons dans ce qui suit présenter un exposé^2(*)3 de quelques notions de base sans être exhaustif, travail que nous somme loin d'avoir les qualités pour le faire.

1-2 - Définition d'un jeu

Un jeu est un ensemble de règles, pour une situation particulière, délimitant les actions des joueurs et leur attribuant des résultats ( gains ou pertes) sur la base des actions choisies. Un jeu est une suite de décisions des joueurs, dans des situations régies par des règles.^{2(*)4 2(*)5}

Un jeu est une interdépendance de n libertés ( le libre arbitre stratégique de chaque joueur et de n intérêts des joueurs).^2(*)6

En effet, dans un contexte d'interaction, les différents choix des agents

( les joueurs ) constituent leur stratégies^2(*)7, le gain de chaque joueur dépend des stratégies choisies par chacun des joueurs. Par conséquent, les agents, leur stratégies possibles et la connexion entre ces stratégies et les gains des joueurs définissent ensemble un jeu.^2(*)8

Comme LAKHDAR l'a précisé, il convient de ne pas confondre les règles du jeu et les stratégies. Chaque joueur choisit librement ses stratégies : son principe de comportement. Les règles sont des contraintes intrangressibles. Les règles délimitent des frontières, des espaces à l'intérieur desquels (desquelles) les plans complets d'action, que sont les stratégies, sont opérationnel(les). Les stratégies spécifient ces mouvements à faire. Pour chaque n.tuple de stratégies - une stratégie par joueur et en présence de n joueurs - les règles du jeu spécifient le résultat, le paiement que procure le jeu à chaque joueur.

Il existe, en effet, plusieurs manières de décrire un jeu dont la forme extensive et celle normale sont les principales.

1-3- Formalisation générale des jeux.

La formalisation des situations de conflit a commencé par la création de jeu de société : jeux de dames, jeux d'échecs,...etc. Les règles de ces jeux sont des conventions qui représentent abstraitement des possibilité offertes aux acteurs représentés ( déplacements des pièces au jeu d'échecs). comme on l'a mentionné auparavant, un jeu est défini par l'ensemble des joueurs, les choix qui leur sont possibles et les conséquences ( gains ou pertes, paiements positifs ou négatifs) de ces choix. Afin de développer cette analyse des situations de jeux, il était nécessaire de formaliser les manières avec lesquelles un choix individuel est fait. On utilise principalement deux types de descriptions pour représenter un jeu : la forme EXTENSIVE et la forme NORMALE.

1-3-1-Les jeux sous forme stratégique ou sous forme normale.

Ce type de jeu se caractérise par trois éléments :

a- Une liste de participants, les joueurs : Prenons J l'ensemble de ces joueurs

avec j = 1,2,...,i,...n s'il y a n joueurs.

b- Un ensemble de stratégies ( Si)_{i J} , une stratégie par joueur.

c- Une fonction de résultat pour chaque joueur ( Ri)_{i J} , cette fonction dépend de l'ensemble des stratégies choisies par tous les joueurs. Elle est conçue de façon à représenter les préférences des joueurs.

Ri (s) est l'utilité associée au résultat pour i quand le vecteur de stratégie pour l'ensemble de joueurs est S = ( s₁, ...,s_i,...s_n ).

Dans les jeux sous forme normale, les joueurs sont supposés choisir leurs stratégies s_i S_i simultanément, ce choix ne concerne pas le temps en terme physique mais cela veut dire que chacun ignore les décisions prise par les autres joueurs. Si ce jeu statique est répété à l'infini alors la résultante est appelée Super Jeu.^2(*)9

On représente généralement la forme réduite d'un jeu à l'aide des matrices. Il faut noter ici que la forme normale d'un jeu est particulièrement adaptée à l'étude des situations de conflit sans possibilité de coopération. Les jeux coopératifs et en particulier ceux dans lesquels des paiements latéraux sont possibles entre les joueurs ( partage des gains ) sont plus difficiles à analyser dans ce contexte puisque les utilités doivent être exprimées dans une même unité, ce que la seule représentation du comportement individuel ne permet pas d'affirmer.

Pour donner une idée sur ce que permet la forme normale de décrire prenons un exemple.^3(*)0

Nous allons considérer deux entreprises, que nous appellerons Lacto et Lacta, qui se proposent de lancer un nouveau type de Yaourt, dont elles savent qu'il est possible d'écouler 10 millions d'unités, à 3 Dh pièce. On suppose que les deux entreprises ont le même coût marginal égal à 1 Dh. Par conséquent, le bénéfice - ou recette nette - par unité produite est de 2 Dh. Toutefois, les coûts fixes de Lacto sont supérieurs à ceux de Lacta, 15 millions de Dh contre 12 millions ( lorsqu'il n'y a pas production ces coûts sont nuls).

Ainsi, si Lacta satisfait toute la demande ( 10 millions d'unités), elle fait un profit de :

2 Dh * 10 millions d'unités - 12 M Dh = 8 M Dh

( Recettes nettes) (coûts fixes) ( profit )

Dans le cas ou Lacto est seule à produire, son profit est de :

2 Dh * 10 millions d'unités - 15 M Dh = 5 M Dh

Reste le cas où toute les deux décident de produire ; cas délicat, qui peut conduire à des guerres de prix, à un partage de marché ou à toute autre forme de conflit ou collusion. Ici, nous supposerons que si les deux entreprises se lancent dans la production, elles peuvent chacune écouler 5 millions d'unités ( mais alors Lacta perd 2 M Dh et Lacto 5 M Dh).

Ces précisions étant données, on peut construire le tableau suivant, dont on dit qu'il représente le jeu sous forme stratégique ou normale.

Tableau 1

Lacta

Produit

Lacto

ne produit pas

Produit ne produit pas

(- 5 , -2 )	( 5, 0)
( 0, 8)	( 0, 0)

Le vecteur ( x, y) signifie que Lacto à un profit égal à x et que Lacta réalise un profit égal à y.

1-3-2-Les jeux sous forme extensive.

Au cours du déroulement d'un jeu, chaque joueur, alternativement ou conjointement selon les règles du jeu, choisit une action parmi un ensemble de possibilités. A certains stades du jeu, son déroulement peut dépendre d'aléas que les joueurs ne peuvent prévoir mais sur lesquels ils peuvent connaître une distribution de probabilité : il est d'usage, pour décrire un jeu d'ajouter à la liste des joueurs un joueur n° 0 appelé «  la nature » dont les choix seraient ces événements aléatoires. Ces aléas peuvent représenter un jet de dés ou un tirage de cartes dans un jeu de société, il peuvent être les conditions climatiques, les résultats d'une recherche technologique ou de forage dans des situations réelles. Dans la représentation des jeux, on supposera qu'on est capable de définir l'ensemble des événements pertinents à chaque étape où ils interviennent.

La structure du jeu peut être représentée par un arbre ou un graphe. Les branches de l'arbre ou les arêtes du graphe représentent les différents choix possibles de chacun des joueurs et de la nature. Ces choix sont limités par les règles du jeu. En plus, ces règles spécifient l'information disponible pour les joueurs en indiquant ce qu'un joueur sait sur les actions antérieures des autres^3(*)1. Les sommets du graphe ( embranchement de l'arbre) représentent les étapes où ces choix sont faits. Les sommets terminaux du graphe indiquent les gains du chacun des joueurs à l'étape finale du jeu. Concernant les choix de la nature, lorsque cela est possible, on indiquera les probabilités de chaque possibilité.

Si la représentation extensive d'un jeu sous forme d'un arbre est théoriquement possible, elle est pratiquement difficile à utiliser vu la multitude de décisions conditionnelles attachées à chaque stratégie.

Comme pour la forme précédente prenons un exemple pour bien clarifier. Le jeu présenté précédemment, pour clarifier la forme normale, peut être aussi représenté par un jeu sous forme extensive c'est à dire sous la forme d'un arbre de jeu, dit arbre de Kuhn, comme dans la figure 1 si dessous, où les points noirs sont appelés « noeuds », chaque flèche représente un coup du jeu.

Figure 1 : un arbre de Kuhn

produit ( -5, -2 )

Lacta

ne produit pas

produit ( 5, 0 )

Lacto produit ( 0, 8 )

lacta

ne produit pas

ne produit pas ( 0, 0 )

Cette présentation est peut être « parlante » que celle donné par un tableau de chiffres. Toutefois elle suggère qu'il y a un certain ordre dans les actions, donné par le sens des flèches : Lacto « joue » d'abord, Lacta ensuite. Or, comme rien n'a été dit jusqu'à présent à ce propos, on peut considérer que la forme normale est moins ambiguë.

Quoi qu'il en soit, il apparaît que, pour que le jeu soit bien spécifié, il faut préciser l'ordre des coups ( cet ordre fait donc partie des règles du jeu). Ici, trois cas sont possibles : Lacto joue d'abord ( c'est le cas décrit dans la figure 1), Lacta joue d'abord ( figure 2), Lacto et Lacta jouent simultanément^3(*)2 (figure 3). Dans ce dernier cas, on « relie » par un pointillé ou on englobe dans un « ballon », les noeuds de l'arbre représentant les choix du « deuxième » joueur, pour signifier que celui-ci ignore le choix du « premier » joueur.

Figure 2 : Lacta « joue » d'abord

produit ( -2, -5 )

Lacto

ne produit pas

produit ( 8, 0 )

Lacta produit ( 0, 5 )

lacto

ne produit pas

ne produit pas ( 0, 0 )

Figure 3 : Jeu à coups simultanés

produit ( -2, -5 )

Lacto

Ne produit pas

produit ( 8, 0 )

Lacta produit ( 0, 5 )

lacto

ne produit pas

ne produit pas ( 0, 0 )

L'ensemble des noeuds se trouvant à l'intérieur d'un même « ballon » est appelé ensemble d'information. Evidemment, l'existence d'ensemble d'information comportant au moins deux noeuds va poser des problèmes au moment du choix des stratégies par les joueurs concernés (mais aussi pour les autres, qui doivent tenir compte de leur comportement). C'est pourquoi on dit que les jeux comportant de tels ensembles d'information sont des jeux à information imparfaite ( cas de la figure 3), les jeux à information parfaite n'ayant que des ensembles d'information réduits à un seul noeud ( ce sont des singletons : cas des figures 1 et 2, où on suppose que le « deuxième » joueur connaît le choix du premier).

Dans cette représentation, deux règles ne sont jamais violées. Premièrement, il y a au moins une flèche qui part de chaque noeud ( le joueur concerné par ce noeud a au moins une action à sa disposition). Et au plus une flèche qui y aboutit. En fait, tous les noeuds, en dehors du noeud initial, ont une flèche - et une seule - dirigée vers eux. Il s'ensuit que si on se situe à n'importe quel noeud autre que le noeud initial et si on se déplace à contre courant - c'est à dire dans le sens opposé des flèches -, alors il y a toujours une et une seule façon de remonter jusqu'au noeud initial. Deuxièmement, si on se déplace ainsi, à contre-courant, et à partir d'un noeud quelconque, alors on n'y revient jamais ; en fait, en poursuivant de la sorte, on aboutit au noeud initial.^3(*)3

Malgré cette différence en terme de présentation, on ne peut pas nier qu'il y a une relation entre ces deux formes. Ainsi David KREPS a résumé l'essentiel de ce qui peut être dit sur ce rapport en déclarant qu' «  à chaque jeu sous forme extensive correspond un jeu sous forme stratégique, dans lequel les joueurs choisissent simultanément les stratégies^3(*)4 qu'ils mettront en oeuvre. En revanche, un jeu sous forme stratégique donnée peut, en général, correspondre à plusieurs jeux sous forme extensive différents. ».

1-4- Typologies des jeux 

1-4-1-Typologie 1 : Jeux en terme de gain

Dans ce cadre on trouve les jeux à somme nulle et les jeux à somme non nulle. Un jeu est dit « à somme nulle »^3(*)5, si le montant du gain d'un joueur est toujours égal au montant de la perte de l'autre^3(*)6, autrement dit, si :

R₁ (s) = - R₂ (s)^3(*)7

La plupart des jeux de cartes sont de ce type, de même que les échecs et les dames. Quelques situations militaires, telles que les duels à mort, peuvent être considérées comme des jeux à somme nulle. La propriété principale d'un jeu à somme nulle est d'être une situation d'opposition pure. C'est un jeu strictement compétitif où il n'y a pas de possibilités d'entente car aucune stratégie jouée d'un commun accord ne peut améliorer la position des deux joueurs à la fois. Nous appelons, donc, un jeu dans lequel les pertes d'un côté  ne sont pas nécessairement égales aux gains de l'autre, un jeu à somme non nulle. Dans ce cas tous les agents peuvent, simultanément, retirer des bénéfices en jouant une certaines stratégie.

Exemple :

les deux matrices 1 et 2 ci-dessous décrivent les deux situations décrites auparavant.

Jeu à somme nulle jeu à somme non nulle

1 2	1	2
1	1 , -1	-1 , 1
2	-1 , 1	1 , -1
1 2	1	2
1	5 , 2	-10 , -13
2	4 , 1	-20 , -23

Remarquons donc qu'il s'agit bien de deux jeux opposés, dans la première matrice ( à gauche) la somme des gains mutuels ( des deux joueurs) est nulle, on dit aussi que ce jeu est à somme constante, dans la deuxième matrice ( à droite) cette somme est non nulle, le jeu est dit dans ce cas à somme non constante.

1-4-2-Typologie 2 : Jeux et coopération

La théorie des jeux est principalement divisée en deux principales branches ou disant deux approches pour traiter les relations interindividuelles, il s'agit de la vision non coopérative et de celle coopérative. La première met l'accent sur les comportements égoïstes des individus ou en d'autre termes les situations de conflit dont le cas extrême est celui du jeu à somme nulle^3(*)8 considéré comme situation de pure conflit, car tout ce qui est gagné par l'un et perdu par l'autre, et vice-versa. L'exemple type ici en est le jeu d'échecs où les joueurs ont des intérêts strictement opposés. Les échecs sont plus précisément un jeu à somme nulle à information complète puisque chaque joueur connaît précisément les conditions dans lesquels se trouve l'adversaire.^3(*)9

Dans les jeux non coopératifs il n'y a pas de communication directe entre les individus^4(*)0. chaque jeu décrit un cadre institutionnel dans lequel chaque joueur arrête seul ses choix sans consulter les autres joueurs. Cela pour une série de raisons, entre autres, soit parce qu'un mur empêche la communication, soit qu'il existe un manque de confiance entre les joueurs^4(*)1, soit qu'il y a manque de sympathie^4(*)2 entre eux ou d'autres sentiments pouvant aider à créer un environnement dans lequel une communication directe est possible.

La seconde vision est celle qui voie les relations interindividuelles d'un point de vue coopératif. Cette branche fait « intervenir d'autres facteurs, relevant de l'altruisme » incitant les individus à coopérer. Ainsi, le conflit pur est une abstraction théorique qui se rencontre rarement dans la réalité de l'existence. la plupart des situations dominées par le conflit comportent généralement une certaine dépendance mutuelle. C'est le cas des grèves, des négociations commerciales, de la dissuasion des criminels, des conflits de classe, des préparatifs de cessez-le-feu, du chantage, de la coercition exercée par les parents sur les enfants. Ainsi, dans une situation aussi problématique qu'une prise d'otage, les preneurs d'otage et les proches de ce dernier souhaitent les uns comme les autres que la négociation aboutisse. On parle alors de jeu coopératif, le mot coopération ne signifiant pas un accord amical, mais simplement un comportement qui accorde aux deux parties, un résultat relativement satisfaisant^4(*)3 ou selon les termes de B. GUERRIEN, « coopération » s'entend donc ici au sens de participation intéressée à une coalition.

Alors que la théorie des jeux non coopératifs prend l'individu pour point de départ, la théorie des jeux coopératifs envisage des coalitions formées par ces individus, sans préciser comment elles se sont constituées et comment s'effectue le partage des gains en leur sein.

Dans la réalité, la plupart des sujets traités par les scientifiques révèlent qu'il y a dans la majorité des cas un mélange de lutte et de coopération. Ainsi, on a ressenti un besoin de faire un mariage entre les deux approches. En effet, NASH a été le premier qui a rendu compte de cette nécessité.

RULLIERE^4(*)4 a bien décrit l'apport du « programme de NASH » dans ce sujet. Selon les termes de RULLIERE, NASH^4(*)5 a immédiatement ressenti la nécessité de justifier le choix de ses axiomes à partir d'un scénario décrivant de manière non coopérative le déroulement effectif de la négociation. Dans cette perspective, l'idéal serait bien évidemment que l'on puisse caractériser un équilibre de Nash unique soutenant ainsi la solution^4(*)6 de NASH.

Ainsi NASH écrivait : « L'auteur a développé une approche dynamique pour l'étude des jeux coopératifs fondée sur une réduction à la forme non coopérative. On procède en construisant un modèle de négociation préalable tel que les étapes de la négociation deviennent des coups dans un jeu non coopératif étendu(...)décrivant la situation. Ce jeu étendu est alors traité du point de vue de la théorie dans cet article(...) et si des valeurs sont obtenues, elles sont considérées comme les valeurs des jeux coopératifs. Dès lors, analyser un jeu coopératif revient à rechercher un modèle de négociation non coopératif approprié et convaincant. »^4(*)7

Cette articulation entre les concepts coopératif- la solution- et non coopératif - l'équilibre - recouvre ce qu'il est convenu d'appeler le programme

de NASH. D'emblée, il convient de souligner que NASH ne conçoit pas la théorie des jeux comme devant se développer en deux sphères indépendantes ou

opposées : il s'agirait « des deux faces d'une même pièce » qui sont chacune nécessaires l'une à l'autre. NASH nous donne donc la clé du développement moderne de la théorie des jeux en contraignant le modélisateur à tester sa construction coopérative par une maquette non coopérative.

Comme l'avait remarqué GUTH^4(*)8, le programme de NASH est loin aujourd'hui d'avoir été entièrement exploré. D'une part, de nombreuses configurations institutionnelles de la négociation restent à être mises en évidence. D'autre part, de nombreux modèles coopératifs de négociation ont été développés dans la lignée des propositions théoriques contenues dans l'ouvrage de LUCE et RAIFFA^4(*)9 . la plupart des ces constructions axiomatiques synthétisées par ROTH^5(*)0 ont cependant la caractéristique de s'être affranchies du programme de NASH. Par conséquent, elles sont toutes soumises à l'objection de NASH, à savoir qu'elles n'ont pas été chacune testées par une maquette non coopérative montrant comment les joueurs parviennent à prendre leur engagement pour atteindre la solution spécifiée.

Récemment les réflexions sur ce sujet ont été profondément renouvelées par plusieurs auteurs en essayant de trouver une réponse à une question devenue centrale de la théorie économique à savoir : comment la coopération peut-elle surgir entre des individus égoïstes ? Parmi ces auteurs on trouve Robert AXELROD^5(*)1, professeur de sciences politiques à l'université du Michigan. Il a invité des spécialistes de la théories des jeux et des passionnés d'informatique à lui soumettre des programmes pour un tournoi sur ordinateur du dilemme du prisonnier, chaque partie comptant 200 coups. Il a reçu 76 programmes, dont certains très complexes. C'est en fait le plus simple, « Donnant-donnant » (Tit for tat) qui s'est également montré le plus performant, « Donnant-donnant » commence par coopérer, puis répète systématiquement ce qu'à fait l'autre joueur au coup précédent (coopération, s'il y a eu coopération, défection, s'il y a eu défection). En effet, face à « Donnant-donnant », le joueur qui choisit de coopérer, aboutit à un résultat bénéfique pour les deux, alors que s'il opte pour la défection, le résultat s'avère funeste pour les deux.

Selon AXELROD, «  ce qui rend possible l'apparition de la coopération, c'est le fait que les joueurs peuvent être amenés à se rencontrer à nouveau ». La conclusion globale qu'il tire de ce tournoi informatique est que la coopération peut émerger dans un monde d'égoïstes en l'absence de pouvoir central. Cet auteur rapproche ces résultats du comportement de certains soldats allemands et français dans les tranchées de la première Guerre mondiale. Ils s'abstenaient souvent de tirer pour tuer, dès lors que ceux de l'autre côté adoptaient la même attitude, à tel point que dans certains lieux, des soldats pouvaient marcher à portée de fusil derrière leurs propres lignes. Ce qui n'était évidemment pas du goût des états-majors. Ce système « vivre et laisser vivre » démontre que l'amitié n'est pas nécessaire à l'apparition de la coopération. « Dans des conditions appropriées, la coopération fondée sur la réciprocité peut se développer même entre adversaires », conclut AXELROD.

Comme le souligne CORDONNIER^5(*)2, ce genre de comportement relève plus d'une approche coopérative du conflit que d'une approche stratégique. L'essentiel pour les joueurs semble être parvenir à coordonner leur comportement avec celui de leur alter ego, et non développer une stratégie optimale face à leur adversaire. » Considérant que les relations sociales ne sont pas seulement dominées par l'intérêt personnel, mais aussi par le lien social, CORDONNIER propose une nouvelle interprétation de ce qu'est la rationalité : «  Être rationnel, dans ces conditions, c'est faire en sorte que nos actions soient comprises et admises par les auteurs ».

Dans le point qui suit nous allons essayer de présenter comment formellement les jeux non coopératifs et les jeux coopératifs se présentent.

Section-2- Formalisation et analyse des jeux

non coopératifs et des jeux

coopératifs

2-1- Les jeux non coopératifs

Un cas particulier de jeux non coopératifs est le « jeu à deux joueurs de somme nulle », comme les échecs et les dames. Dans de tels jeux, l'absence de coopération vient de la nature des gains et non des règles du jeu. Les jeux à deux joueurs de somme nulle sont utilisés pour illustrer ou présenter la théorie des jeux non coopératifs.

Lorsque les ensembles de stratégies sont finis, la forme normale des tels jeux se présente comme un tableau à deux entrées qui sont les stratégies possibles de chaque joueur. Les éléments du tableau ci-dessous sont les gains du joueur I, ceux du joueur II leur étant opposés :

1 2	S1^2	...	Sj^2	...	S1^2
S1^1	a1 1				A1 n
...
Si^1	ai 1		ai j		Ai n
...
Sm^1	am 1				Am n

a_{i j}= R_I (S_i¹, S_j² ) = - R_II (S_i¹, S_j² )

La forme normale d'un jeu non coopératif à n joueurs est représentée par un tableau à n entrées qui sont les stratégies de chaque joueur, les éléments du tableau étant les listes des gains de chacun des joueurs correspondant au choix d'une stratégie par chacun d'eux. lorsque les ensembles de stratégies ne sont pas finis, le tableau ne représente que quelques valeurs des fonctions de gains.

Le concept de solution proposé ultérieurement, adapté à de tels jeux, est celui d'équilibre de NASH. Une telle solution n'existe pas toujours lorsque les ensembles des stratégies sont finis. Elle existe, en revanche, si ces ensembles sont assez riches, c'est à dire qu'ils contiennent toutes les combinaisons convexes de stratégies.

La combinaison convexe de deux stratégies S₁ et S₂ est une stratégie tS₁ + ( 1 - t) S₂ où t [ 0 , 1].

Tous les jeux à ensemble fini de stratégies peuvent être étendu en un jeu à ensemble convexe de stratégies : en effet, il suffit pour cela d'autoriser les joueurs « à tirer au hasard » leur stratégie. Selon la manière de « tirer au hasard » qu'ils utilisent, les joueurs ont à leur disposition de nouvelles possibilités de gain (se sont en fait de nouvelles espérances de gains).

On appelle stratégie mixte une distribution de probabilité sur l'ensemble des stratégies pures d'un joueur. Pratiquement, une stratégie mixte peut être obtenue par un mécanisme utilisant une expérience aléatoire :

- une pièce de monnaie équilibrée peut attribuer la probabilité 1/ 2 à une stratégies ( si face apparaît ) et 1/ 2 à une autre (si pile apparaît ) ;

- un dé peut attribuer la probabilité 1/ 3 à une stratégie ( si 1 ou 2 apparaît ), et 2/ 3 à une autre ( si 3, 4, 5 ou 6 apparaît ).

Pour se faire une idée de ce qu'est une stratégie mixte avec une distribution de probabilité P₁, P₂ , ..., P_n ( P₁ + P₂ + ...+ P_n = 1) sur n stratégies s₁ ... s_n, on peut songer à une roue divisée en n quadrants dont les arcs ont pour longueur les proportions P₁, ..., P_n du périmètre. Si la roue s'arrête sur l'arc i, la stratégie s_i est choisie avec la probabilité P_i : ici s₃ est choisie, la probabilité que la flèche indique le 3 est P₃.

Figure 4

P₂

P₁

P₃

P₄

Ce dernier mécanisme a incité les théoriciens à appeler aussi « loterie » une stratégie mixte.

Les stratégies mixtes ont plusieurs interprétations qui justifient leur emploi et l'intérêt de leur utilisation pour l'amélioration des résultats de la théorie.

- Si on imagine que le jeu est répété identiquement, la stratégie mixte : ts₁ + (1-t)s₂ se traduira par l'emploi de la stratégie pure s₁ pendant une proportion t du nombre de répétitions du jeu et de la stratégie pure s₂ pendant le reste du temps. Une telle manière de jouer rend imprédictible pour les observateurs la décision du joueur.

Ainsi, si une compagnie fait passer deux spots publicitaires à la télévision, soit 1/ 3 du temps pour l'un et 2/ 3 du temps pour l'autre, on pourra considérer qu'elle fait passer un spot mixte. Un téléspectateur aura une chance sur trois de voir le premier, à un instant donné.

- Si l'on considère que les joueurs annoncent leurs stratégies, on peut interpréter l'annonce d'une stratégie mixte comme un moyen de ne pas

révéler complètement les décisions prises. Ainsi dans le jeu suivant :

I II	s1^2		s2^2	S1^1
1, 1	1, 3		S2^1
0, 2	2, 1

Si le joueur I annonce s₁¹ il est sûr de gagner 1, s'il annonce s₂¹ , il peut gagner 0 ou 2 selon ce que joue le joueur II. S'il annonce s₂¹ , il peut supposer que le joueur II annoncera s₁² qui offre un supérieur. En annonçant qu'il suivra la stratégie s₁¹ avec la probabilité 1/ 2 et s₂¹ avec la probabilité 1/ 2, le joueur I laisse le joueur II dans l'incertitude par rapport à son gain, Mais peut-être que la probabilité 2/ 3 sur s₁¹ et 1/ 3 sur s₂¹ inciterait le joueur II à jouer plutôt la stratégie s₁² .

Dans le cas de l'utilisation des stratégies mixtes, le choix des joueurs porte sur la distribution selon laquelle ils choisissent leur stratégie, « ils créent (donc) de l'incertitude sur leurs propre stratégies ».^5(*)3

2-2- Les jeux coopératifs

Dans certaines configurations de jeux sous forme normal, une attitude entièrement non coopérative de la part des joueurs peut conduire à une catastrophe collective, on en verra quelques exemples ci-après. Il y a donc incitation à la coopération. Celle-ci peut prendre la forme d'une autorité qui coordonne les décisions de chaque joueur et dispose d'un certain pouvoir de coercition. Elle peut aussi être le fait d'un simple consensus entre les joueurs. Cet accord peut concerner tous les joueurs ou seulement certains groupes de joueurs : on définira alors les coalitions entre joueurs.

Quelques exemples illustrent de telles situations :

Deux entreprises en concurrence peuvent adopter chacune, soit une stratégie agressive se traduisant par le déclenchement de manoeuvre de conquête du marché, soit une stratégie préservant le statu quo. Il est clair que si les deux firmes adoptent la stratégie agressive et se ruinent en cherchant à conquérir le marché sans y réussir, le résultat est moins bon que le statu quo.

Le choix du lieu d'implantation d'un point de vente par des entreprises concurrentes est un autre exemple où l'absence de coopération peut se traduire par des conséquences désastreuses pour tous les concurrents.

Le rachat de parts du capital d'une société, l'enjeu étant le contrôle de la société, est un exemple où l'absence de consensus entre les acheteurs peut les amener à acheter très cher des parts dont le nombre restera insuffisant.

Ces exemples peuvent être traduits sous une forme voisine de celle du classique « dilemme de prisonnier ».^5(*)4 Ce jeu montre à travers un exemple folklorique comment des choix rationnels d'un point de vue individuel peuvent conduire à des situations sous-optimales (donc non rationnelles « collectivement ») pour l'ensemble des individus qui ont fait ces choix.

L'essence de ce type de situation peut être décrite par le jeu suivant^5(*)5 : Deux malfaiteurs ont été arrêtés et soupçonnés d'avoir commis un crime d'homicide volontaire, il ont été accusés à juste titre mais sans preuve suffisante. Il sont alors confrontés à la situation suivante : mis dans une cellule individuelle et privé de communiquer avec l'autre coupable, chacun doit choisir entre une stratégie pacifique et une stratégie agressive ( ici ne pas dénoncer = pacifique et dénoncer = agressive ), le juge essaye de sa part de les faire avouer tous deux pour les condamner à cinq ans chacun, faute de quoi il les condamnera à un an chacun pour le crime. Mais, il leur propose de relaxer celui qui témoignerait contre l'autre, ce dernier sera juger de vingt ans.

En suivant la logique du dilemme du prisonnier, on remarque qu'il y a un conflit curieux entre la rationalité individuelle et la rationalité collective. En suivant leurs motivations personnelles, il est clair qu'il est rationnel pour les deux joueurs de choisir leur stratégie agressive (dénoncer), mais si les deux se comportent d'une manière coopérative et optent pour la stratégie pacifique, le résultat sera bénéfique pour les deux, en d'autres termes, la coalition des deux joueurs leur assure un gain meilleur que celui qu'ils peuvent s'assurer individuellement. Ce qui complique les choses dans ce dilemme c'est que l'attaque surprise ( utiliser la stratégie agressive pendant que l'autre joueur est toujours pacifique) est payante, dans ce cas la perte est plus grave si on se place du côté du pacificateur.

Cependant, dans cette histoire, il y a quatre issues qui, du point de vue de l'un ou l'autre prisonnier, peuvent être classées de la façon suivante : la situation la plus avantageuse pour un prisonnier est celle où il dénonce l'autre sans être dénoncé par lui ; une situation un peu moins avantageuse est celle où il ne dénonce pas tout en n'étant pas dénoncé par lui ; une situation nettement moins avantageuse est celle où il dénonce l'autre, qui fait de même ; enfin, la situation la plus pire pour un prisonnier est celle où il est dénoncé alors qu'il se tait. Le tableau ci-dessous donne l'exemple chiffré de notre histoire et du classement qui vient d'être écrit.

I II	ne dénonce pas		Dénoncer	Ne dénonce pas
1, 1	20, 0		Dénoncer
0, 20	5, 5

On vérifie facilement que la stratégie pacifique ( ne dénonce pas) d'un joueur est dominée^5(*)6 par sa stratégie agressive. Donc le jeu possède un unique équilibre en stratégies dominantes^5(*)7 ( Dénoncer, Dénoncer) qui correspond à la guerre ouverte. Bien entendu une telle issue n'est pas satisfaisante du point de vue collectif puisque l'issue pacifique ( ne dénonce pas, ne dénonce pas) lui est strictement préférée par les deux joueurs. Etre agressif ( tous les deux) n'est pas un optimum de pareto. C'est là précisément que réside le dilemme : pour un joueur qui n'est pas entièrement assuré des intentions pacifiques de son partenaire, l'usage de la stratégie agressive s'impose au nom des intérêts individuels, mais l'intérêt commun recommande bien sûr de tout faire pour aboutir à l'issue de paix. Selon CORDONNIER « le dilemme de prisonnier est l'archétype des situations dans lesquelles l'intérêt individuel fait échec à la coopération... et fait échec à l'intérêt individuel »^5(*)8, et c'est dans la multitude de ce genre de situations ( dans des contextes très divers) dans la vie économique qu'a trouvé ce dilemme sa popularité.

Revenons au concept de stratégies mixtes afin d'établir sa relation avec les jeux coopératifs ainsi qu'avec notre exemple de dilemme de prisonnier. Ce concept correspond, dans les jeux coopératifs, à celui de stratégies corrélées. Les n joueurs d'une coalition jouent des stratégies corrélées s'ils choisissent leurs stratégies en s'en remettant à une loterie sur l'ensemble des vecteurs (s₁, s₂,..., s_n) de leurs stratégies pures de départ.

Ainsi dans notre dilemme de prisonnier, les deux joueurs peuvent choisir de jouer ( dénoncer, dénoncer) avec une probabilité de 1/ 5, ( ne dénonce pas, ne dénonce pas) avec une probabilité de 4/ 5 et une probabilité de 0 pour le reste ( c'est à dire qu'ils décident de ne pas dénoncer seuls). Il peuvent même décider de jouer ( ne dénonce pas, ne dénonce pas) avec une probabilité de 1, ce qui formalise la possibilité qu'ils ont de se mettre d'accord. le concept de stratégies corrélées permet donc de formaliser certains jeux avec communication entre les joueurs.

Ceci est dit nous pouvons maintenant aborder le point traitant les différentes solutions qui ont été proposées pour résoudre les situations de conflits issues que ce soit des jeux coopératifs ou des jeux non coopératifs.

2-3- Concepts de solution des jeux

Pour résoudre les situations de conflit, différents concepts de solution ont été proposés. Chaque situation requiert une solution qui lui est propre et les concepts généraux dégagés par la théorie doivent être considérés comme des outils d'analyse plus que comme des conseils d'aide à la décision. La théorie s'est attachée à définir des concepts pour les situations les mieux définies, celle des jeux non coopératifs et celle des jeux totalement coopératifs.

Cependant, lorsque la question à poser est celle de la définition d'une solution pour un jeu approprié, nous devons avant tout spécifier le type et la forme descriptive du jeu sous question. Par exemple, si le jeu est coopératif à n personnes, notre travail sera la recherche d'un vecteur d'utilité ou de paiement garantissant une meilleur dispersion de l'utilité pour les joueurs et ayant la propriété de stabilité dans un sens significatif. Dans ce cas l'objectif de la théorie des jeux sera de fournir certaines notions de stabilité. Dans l'autre côté, si le jeu est non coopératif à n personnes et à somme non nulle ( en forme normale), l'objectif de la théorie des jeux sera la recherche d'un vecteur n-tuple de stratégies qui lorsqu'elles seront prises ensemble, formeront donc un équilibre pour le jeu. Encore une fois, la contribution de la théorie des jeux sera de définir de manière convenable les notions d'équilibre qui vont être utilisées.

Ainsi, pour les jeux non coopératifs, le concept d'équilibre de NASH, qui généralise celui de la solution de Mini-Max de VON NEUMANN, s'est imposé. Ce concept correspond mathématiquement à la notion de point-selle, ou de col de montagne : un col, lorsqu'il existe, est à la fois le point le plus haut des points les plus bas et le point le plus bas des point les plus hauts. Ainsi le col est le point le plus haut par lequel passe une route qui cherche à monter le moins possible, c'est aussi le point le plus bas par lequel passerait un chamois qui cherche à rester le plus haut possible sur la montagne.^5(*)9

Dans un jeu sous forme normale, le concept d'équilibre de NASH s'applique à une liste de gains pour chacun des joueurs qui sont tels que ce sont les meilleurs qu'un joueur puisse obtenir parmi les pires que peuvent lui imposer les autres joueurs, de sorte que chacun puisse avec raison se dire la chose suivante : « Avec ma stratégie de NASH, mon gain est au moins aussi grand que pour toute autre stratégie, tant que l'autre ne change pas sa stratégie de NASH ». Il s'agit de minimiser les pertes et de maximiser les gains - et il ne s'agit pas d'une simple intelligence de la situation, mais bel et bien d'une traduction économique d'une théorie psychologique de l'intentionnalité qui fait appel à une coalition d'intérêts de joueurs supposés également compétents.

Pour les jeux coopératifs, le concept d'équilibre de NASH n'est pas le concept d'équilibre le plus adapté, comme on le voit dans le dilemme du prisonnier où le point d'équilibre est ( dénoncer, dénoncer) ce qui correspond à un résultat qui est moins bon pour chacun des deux joueurs que la solution ( ne dénonce pas, ne dénonce pas).

Un autre exemple classique argumentant contre l'équilibre de NASH comme concept de solution pour les jeux où la coopération est possible, est celui de la bataille des sexes. Ce jeu est appelé ainsi parce qu'on peut le présenter en considérant deux époux qui doivent décider de l'endroit où ils vont passer la soirée. Le mari préférerait aller à un match de Basket-ball , alors que sa femme désirerait aller voir un ballet. Mais tous deux préfèrent par dessus tout sortir ensemble à l'un ou l'autre spectacle, plutôt que d'assister seul à son spectacle préféré. La forme normale du jeu, où les gains sont des utilités, peut être représentée de la manière suivante ^6(*)0:

Femme mari	Basket-ball		Ballet	Basket-ball
4,5	0,0		Ballet
1,1	5,4

Ce jeu est représentatif de beaucoup de situations où les deux ( ou plus) parties cherchent à coordonner leurs actions, bien qu'elles aient des préférences opposées en ce qui concerne l'issue sur laquelle la coordination doit avoir lieu. En économie industrielle, la segmentation du marché par des entreprises rivales peut aussi être examinée dans cette perspective ; tel est le cas également de deux fabricants de biens complémentaires qui doivent adopter des normes- tous deux préfères que leurs normes soient compatibles, mais chacun aimerait que la sienne prévale. En économie du travail, un syndicat et une entreprise peuvent gagner à accepter les conditions de l'autre partie plutôt que d'endurer les conséquences d'une grève, mais même ainsi, chaque partie préfère que l'autre accepte ses exigences.

Revenons à notre exemple, les deux couples de stratégies ( basket-ball, basket-ball) et (ballet, ballet) sont des équilibres, mais l'un d'eux est préférable pour lui, l'autre pour elle. Ces équilibres ne sont pas stables en ce sens que chacun des joueurs à intérêt à ne pas jouer la stratégie qui lui est défavorable afin d'amener l'autre à jouer l'autre stratégie d'équilibre.

Remarquons que, pour ce jeu, une solution consiste à aller au match une fois sur deux et au ballet une fois sur deux, ou encore si le jeu n'est pas répété, à tirer à pile ou face le spectacle où aller. Cette solution est un équilibre corrélé ; c'est un concept de solution faisant intervenir des stratégies corrélées qui est adapté à certains jeux coopératifs.

Le concept de solution le plus répandu pour les jeux coopératifs est défini dans le cas où des paiements latéraux sont possibles ( partage des gains pour former des coalitions). Le Noyau ou Coeur ( deux traductions discutables de l'anglais « Core ») caractérise un ensemble de coalitions qui est stable dans le sens où les joueurs n'ont pas intérêt à quitter ces coalitions pour en former d'autres. il n'y a malheureusement pas de théorème général de non vacuité du noyau.

Un autre concept de solution pour les jeux où la coopération est possible est caractérisé par la valeur de SHAPLEY. La valeur de SHAPLEY attribue à chaque joueur un nombre qui représente son pouvoir dans la formation des coalitions, ou encore une valeur qu'il attribue au jeu ( semblable au maximum des gains minimaux qu'il peut obtenir) et qui est fonction du pouvoir que lui donne la structure du jeu pour se coaliser avec d'autres joueurs.

Nous allons essayer, dans ce qui suit, d'éclairer chacun de ces concepts ainsi que d'autres qui ne sont pas évoqués.

2-3-1-Jeux non coopératifs

Comme l'avait bien définit Hervé MOULIN, un contexte  non coopératif  est celui dans lequel « les joueurs se comportent comme s'ils n'avaient pas conscience de leur interdépendance stratégique : ils envisagent de changer de stratégie sans pouvoir anticiper la réaction des autres joueurs à ce changement, donc en supposant qu'ils ne réagiront pas .... Tout se passe comme si les joueurs ne ressentaient pas les effets externes de leur comportement, ne tenaient pas compte de l'influence qu'ils pourraient ainsi acquérir sur les autres joueur. »^6(*)1

La forme normale d'un jeu se prête particulièrement bien à l'analyse des jeux dans un contexte non coopératif à information complète. Dans un tel contexte, les stratégies des joueurs correspondent en effet à une description satisfaisante de leurs comportements : le choix d'une stratégie correspond au choix d'une suite d'actions et le critère est sans ambiguïté la maximisation du gain associé à une suite d'actions.

Le concept de solution qui s'impose pour l'analyse de tels jeux est celui d'équilibre de NASH^6(*)2 : C'est une liste des gains des joueurs ( c'est à dire une case du tableau de la forme normale du jeu) qui correspond à une liste de stratégies pour chaque joueur telles que aucun changement unilatéral de stratégie par l'un des joueurs ne lui permettrait d'augmenter son gain. On peut dire aussi qu'un équilibre de NASH est une liste de stratégie de chacun des joueurs telle qu'aucun d'eux n'a d'incitation à en changer unilatéralement.

Nous allons présenter la définition formelle d'un équilibre de NASH à travers l'exemple de deux jeux, à savoir le jeu à deux joueurs et le jeu à n joueurs.

Définition 1 : Pour un jeu à deux joueurs dont les ensembles de stratégies sont X et Y et les fonction de gains : U₁ : X x Y et U₂ : X x Y

Un équilibre de NASH est un couple ( x* , y* ) de X x Y tel que :

x X U1 ( x* , y* ) U1 ( x , y* )

x X U2 ( x* , y* ) U2 ( x* , y )

Définition 2

Dans un jeu à n personne où à la fois la communication directe entre les joueurs et la formation de coalition sont impossibles, une issue ( x1, ..., xn ) du jeu ( X1, ..., Xn , U1, ..., Un ) est un équilibre non coopératif ( ou équilibre de NASH ) si elle vérifie :

i ( 1, ..., n ) yi Xi U1 ( yi , xî ) Ui ( x1, ..., xn )

( la notation (y_i , x_î ) désignant l'issue (x₁,..., x_i-1 , y_i , x_i+1, ..., x_n ) )^6(*)3

Selon les termes de LAKHDAR, l'issue ( x₁, ..., x_n ) est dite équilibre non coopératif ou point d'équilibre de NASH si, étant donné n-1 stratégies, le nième joueur ne peut augmenter ses résultats en changeant sa propre stratégie.

Il s'agit donc bien d'un concept de solution du jeu puisque cet n-tuple de stratégies ( ou ce couple pour les jeux à deux joueurs) correspond à ce qu'un analyste du jeu pourrait conseiller à chacun des joueurs. C'est aussi un concept d'équilibre dans la mesure où la description du jeu contient la description du comportement des joueurs et que cette solution est un équilibre de ces comportements : le comportement des joueurs ne les incitant pas à dévier des stratégies proposées par la solution, parce que du point de vue individuelle cette dernière est la meilleure pour chacun tant que le choix des autres est fixé.

En revenant aux deux définitions précedentes, on peut remarquer leur forte tonalité non coopérative. Prenons, pour bien éclaircir l'idée, l'exemple présenté dans le tableau ci-dessous^6(*)4.

Prisonnier B Prisonnier A	Colonne 1		Colonne 2	Ligne 1
5, 5	-1, 6		Ligne 2
6, -1	0, 0

Ce jeu présente le cas d'un dilemme de prisonnier, Nous remarquons comme l'a fait David KREPS, que dans ce jeu l'ensemble formé par la ligne 2 et la colonne 2 est un équilibre de NASH. Mais s'il y a une possibilité de communication entre les joueurs, ceux-ci choisiront sans doute l'autre stratégie, à savoir la ligne 1 et la colonne 1 parce qu'il auront un gain de plus par rapport à la situation d'équilibre. Rappelons-nous cependant que nous nous intéressons ici à la théorie des jeux non coopératifs et que dans ce contexte la possibilité de telles actions n'existe en fait pas, les joueurs devant choisir leurs actions de façon simultanée et indépendante ; chaque joueur choisira donc probablement « l'action non coopérative », puisqu'il n'y a aucune façon pour un joueur de contraindre l'autre à respecter un éventuel accord, ni pour ce dernier d'infliger une punition quelconque pour son non respect.

Le concept d'équilibre de NASH soulève beaucoup de questions d'un grand intérêt. La plus évidente parmi elles est celle concernant l'existence de cet équilibre, c'est à dire dans quelles conditions un jeu possède-t-il au moins un équilibre ? Le théorème de NASH prouve qu'un équilibre existe pour tous les jeux dont les ensembles de stratégies sont des compacts convexes ( en particulier les stratégies mixtes sur un ensemble fini de stratégies pures) et dont les fonctions d'utilité sont continues et quasi-concave par rapport aux stratégies.^6(*)5 Nous trouverons dans l'ANNEXE I l'exemple d'un jeu ou ces propriétés ne sont pas respectées (un jeu fini où les joueurs complètent leurs ensembles de stratégies par l'utilisation des stratégies mixtes^6(*)6 ceci pour leur donner les propriétés voulues par le théorème de NASH, le concept utilisé dans ce cas devient Equilibre de NASH en stratégies mixtes considéré actuellement par de nombreux auteurs comme un véritable concept représentatif de la rationalité individuelle des joueurs surtout pour les prise de décision dans l'incertain ) .

La deuxième question qu'on peut poser à cet égard est celle concernant la stabilité de cet équilibre. Ce dernier une fois atteint est stable. Les individus n'en bougeront pas si l'histoire du jeu ou les événements les y conduisent. Si x^* est un équilibre de NASH, les agents ont toutes les chances de respecter ce vecteur. Ainsi, nous pouvons expliquer ceci, comme l'a fait Hervé MOULIN, par le fait que l'existence même d'une mince probabilité que les autres jouent x_-i^* augmente la probabilité que le joueur i joue x_i^* puisque cette dernière est la

meilleure réponse à x^*_-i , ce qui en retour augmente la probabilité que les autres jouent x^*_-i et ainsi de suite. Ce processus a été appelé par Hervé MOULIN « un phénomène de convergence psychologique » vers l'équilibre. En effet, les faibles probabilités ont un effet subjectif accru : cela contribue à l'attrait par exemple des billets de loterie et des assurances automobiles - tout ceci concerne des événements relativement improbables, mais à l'impact psychologique fort. En outre l'équilibre de NASH « apparaît en fait comme équilibre « auto-réalisateur », à savoir que les anticipations des joueurs sur leurs stratégies ( de NASH ) provoquent leurs réalisations »^6(*)7 effective.

Le défaut essentiel du concept d'équilibre de NASH est que l'issue correspondante peut être mauvaise du point de vue collectif, c'est dire aller à l'encontre de l'intérêt général. En effet, un équilibre de NASH n'est pas toujours Pareto-optimal. Si on prend les choses à l'envers il est facile de prouver qu'un optimum de Pareto^6(*)8 est un équilibre de NASH car personne ne peut améliorer sa situation sans détériorer celle d'un autre ( donc, si cet autre  ne bouge pas, une telle amélioration n'est pas possible). Mais la réciproque n'est pas vraie et c'est d'ailleurs cette non optimalité au sens de Pareto de certain équilibres de NASH qui est à l'origine de la naissance et la célébrité de fameux « dilemme du prisonnier »^6(*)9. Nous avons constaté dans ce jeu que l'issue d'équilibre

( équilibre en stratégie dominante qui est aussi l'unique équilibre de NASH ), malgré qu'elle s'impose du point de vue individuelle, est rejetée du point de vue collectif et donc n'est plus un optimum de Pareto.

Comme l'a fait remarquer LAKHDAR^7(*)0 la relation équilibre de NASH - optimalité dépend des situations que l'on doit analyser et plus exactement de la nature de la matrice des résultats.

Concernant la question d'unicité de l'équilibre, il est fermement prouvé qu'elle n'est jamais eu une réponse affirmative, cependant il demeure le problème de la sélection d'un état d'équilibre dans le cas ( fréquent) de multiplicité des états associés^7(*)1. Il se peut qu'un jeu comporte plus d'un équilibre de NASH, prenons l'exemple du tableau ci-dessous :

Joueur B Joueur A	t1	t2		t3	s1
( 4, 3 )	( 2, 7 )	( 7, 4 )		s2
( 5, 2 )	( 5, 1)	( 6, 0 )

Remarquons que dans ce jeu les couples ( s₂, t₁ ) et (s₂, t₂ ) sont tous deux des équilibres de NASH. Il y a là un problème sérieux, parce qu'un modèle comportant plusieurs équilibres est en quelque sorte « indéterminé »^7(*)2, dans ce cas ne nous permettant pas de désigner (de manière claire) l'un d'entre eux en tant que solution du jeu ; à supposer que celle-ci existe, elle ne nous aide pas à la trouver^7(*)3. Malheureusement cette situation est fréquente en théorie des jeux, où l'existence d'un et d'un seul équilibre est l'exception plutôt que la règle^7(*)4.

Comme l'a fait mentionner RULLIERE, NASH était lui même conscient de cette difficulté qui peut atténuer le pouvoir productif de son concept d'équilibre. Alors que les principaux critères de raffinement^7(*)5 ont été développés au cours des années 80^7(*)6, on néglige souvent le fait que là encore, NASH a été un précurseur. En particulier, il propose le concept d'équilibre interchangeable. NASH avait aussi proposé une heuristique, donnant lieu par la suite au mécanisme de sélection de la main tremblante^7(*)7 de Selten^7(*)8. Ce qui distingue NASH de SELTEN, cependant, tient au support de la perturbation : tandis que NASH introduit des perturbations sur les paiements en utilité, SELTEN introduit des perturbations sur les ensembles de stratégies ( interprétés comme des erreurs de la part des agents). Il est intéressant de noter que si les travaux de SELTEN portent sur les moyens de raffiner l'équilibre, ils traitent aussi des équilibres peu plausibles (imparfaits) dans une structure de jeu séquentiel. Ainsi, SELTEN a offert une des principales extensions de l'équilibre de NASH avec le critère de perfection en sous-jeu - a ce jour, l'un des concepts les plus utilisés dans la théorie économique contemporaine.

L'autre extension majeure^7(*)9 de l'équilibre de NASH est due à la contribution de HARSANYI^8(*)0. En introduisant la notion de type de joueur, elle permet de représenter l'incertitude aussi bien sur les actions passées que sur les caractéristiques des joueurs. Cette équivalence, plus connue sous le nom de « doctrine d'HARSANYI », a donné un caractère suffisamment général au concept d'équilibre de NASH. Ce type d'extension de l'équilibre de NASH a permis, par la suite, d'apporter une meilleure justification à l'usage de la stratégie mixte. Il s'agit là d'interpréter une stratégie mixte d'un joueur comme des croyance ou des conjectures de la part de ses adversaires concernant son propre comportement. Cette approche a donné lieu, d'une part, au concept d'équilibre corrélé de AUMANN^8(*)1 et, d'autre part, à la caractérisation des fondements épistémiques de l'équilibre de NASH^8(*)2.

Pour d'autres^8(*)3, dans certains cas on a pas besoin de tous ces raffinements, car le fait de connaître ( sans préciser comment) les conjectures de l'autre définit là encore un état parmi d'autres, la sélection peut s'effectuer grâce à des conventions qui sont de connaissance commune entre les joueurs portant généralement sur des phénomènes culturels hors modèles^8(*)4. Se sont là des hypothèses fortes considérées par pas mal d'auteurs comme source de faiblesse de ce concept d'équilibre. Ainsi, Olivier DE WOLF^8(*)5 pense que cet équilibre est moins une conséquence nécessaire de la rationalité. Pour lui cette solution ne paraît avoir du sens que si l'on suppose que chacun des joueurs, au moment de choisir sa stratégie, prédise correctement celles sélectionnées par ses adversaires. En d'autres termes, l'utilisation de cet équilibre suggère une sorte de don divinatoire de la part des joueurs ainsi qu'une capacité inimaginable de stockage d'information ( mémoire) ou de calcul. Un autre problème est que le théorème fondamental de NASH est basé sur la limite suivante : certes on pense à la place de l'autre (selon les principes classiques de la théorie de l'esprit), mais on ne pense pas un seul instant que l'autre puisse ne pas penser comme on pense qu'il devrait penser. Ces hypothèses portant sur les caractéristiques des joueurs étant très contraignantes. Bernard WALLISER^8(*)6 parle d'une analogie avec le commissaire-priseur walrassien qui fournit les prix d'équilibre aux agents économiques, puisqu'on peut introduire une entité fictive, le « régulateur nashien » qui calcule un état d'équilibre de jeu et suggère aux acteurs de l'adopter. Encore faut-il que les acteurs l'adoptent effectivement, ce qui n'est le cas que s'ils ont de bonnes raisons de penser que leurs adversaires l'adopteront aussi.

Ceci est dit, l'équilibre de NASH reste toujours un des concepts de base préconisé pour la construction de modèles s'appliquant à des domaines très variés ( économie industrielle, économie internationale, économie du travail, macro-économie, etc.).

2-3-2- Jeux coopératifs

Comme on l'a montré sur l'exemple du dilemme du prisonnier et sur celui de la bataille des sexes, l'équilibre de NASH n'est pas un concept de solution satisfaisant pour les jeux où la coopération est possible. La coopération qui est traduite par la formation de coalitions nécessite des concepts de solutions qui caractérisent les coalitions que les agents ont intérêt à former. Pour l'étude de tels jeux, la considération des stratégies individuelles n'est pas nécessairement utile, on préfère décrire le jeu par une forme dite forme « caractéristique » qui consiste à attribuer une valeur à chaque membre de la coalition, cette valeur étant ensuite répartie entre les joueurs.

La fonction caractéristique associe à chaque coalition un nombre : sa valeur. A chaque coalition correspond un jeu à deux joueurs ( cette coalition et la coalition formée par tous les autres joueurs) et à somme constante. Ce jeu a une valeur qui est le maximum des gains minimaux que la coalition peut obtenir en jouant contre celle formée par tous les autres joueurs. C'est cette valeur qui est donnée à cette coalition par la fonction caractéristique.

De façon générale, on peut définir un jeu coopératif de la façon suivante :

Un jeu coopératif ( I, v ) est donné par


· Un ensemble fini de joueurs I


· Un nombre v ( S ) pour chaque coalition S I

appelé valeur de S.

Pour bien éclaircir, prenons les trois exemple ci-dessous :

Exemple 1 :

On a un groupe de pécheurs, et un groupe de pilotes de bateaux. Pour partir à la pêche, il faut être un pilote et un pécheur.

Les pêcheurs : I = A B , ou A est l'ensemble des pêcheurs et B celui des pilotes. Pour S I , v ( S ) = min( S A, S B ) .

L'assemblée : I = { 1 , 2 , 3 } .

v ( S ) = 1 si card ( S ) 2 ,

v ( S ) = 0 sinon.

Exemple 2 :

Jeux d'unanimité

C'est un jeu dans lequel v ( I ) = 1 , et v ( S ) = 0 si S I .

Exemple 3 :

Jeux de majorité

On a I joueurs. Chaque joueur i possède p_i voix. La majorité est à q voix.

v ( I ) = 1 si _i p_i q

v ( I ) = 0 sinon.

Dans le but de garder les choses un peu claires, nous allons présenter seulement les concepts de solution les plus importants pour les jeux ayant un vecteur de paiements et une fonction d'utilité transférable.

Le concept le plus important dans ce cadre est celui « d'imputation ». Une imputation est une liste de paiements (ou une redistribution des ressources) proposés à chaque joueurs. Elle est telle que :

- chaque joueur reçoit au moins autant que ce qu'il peut s'assurer en jouant seul contre tous les autres joueurs,

- la somme des paiements de tous les joueurs est égale à la somme des paiements qu'ils obtiendraient en jouant tous ensemble.

Formellement une imputation est un vecteur8(*)7

x = ( x_i ) i I tel que _I x_i v ( I ).

IL s'agit donc d'une redistribution de la valeur totale (au plus) à tous les joueurs.

2-3-2-1- La solution de VON NEUMANN et MORGENSTERN

C'est une solution basée sur le concept de dominance : une imputation I domine une imputation J s'il existe une coalition dont la valeur ( définie par la fonction caractéristique) est au moins égale aux paiements proposés par l'imputation J.

Une solution est alors un ensemble d'imputations qui ne sont pas dominées et qui sont telles que toute imputation qui n'est pas solution est dominée par l'une des imputations de la solution.

La faiblesse de ce concept réside dans ce que le nombre d'imputations dans une solution et le nombre de solutions sont très grands : il n'a donc pas de pouvoir prédictif.

2-3-2-2- Le noyau^8(*)8

Le principe de cette solution a été avancé pour la première fois par EDGEWORTH^8(*)9 en 1981, le premier qui a constaté ce fait est SHUBIK^9(*)0 cependant, c'est à DEBREU et SCARF^9(*)1 qu'on doit la démonstration de cette liaison. DEBREU et SCARF fondaient leur démonstration sur la méthodes des duplication successives pour justifier que l'analyse en terme de la solution du noyau permet l'apparition d'un système de prix. En se basant sur la même méthode ( duplications successives) les deux auteurs pouvaient, en plus, généraliser considérablement le résultats précédent, ils montraient que « s'il y a des duplications successives, dans un marché avec n'importe quel nombre d'échangistes différents, le coeur se ``rétrécit'' (...) jusqu'à ce que l'on obtienne une^9(*)2 allocation limite, à laquelle peuvent être associés des prix, qui peut être considérée comme la limite du coeur. »^9(*)3. En d'autres termes, on peut dire qu'ils ont pu démontrer que : à la limite^9(*)4 les allocations du coeur et les allocations concurrentielles coïncident^9(*)5.

Formellement le noyau est défini de la façon suivante :

Une imputation u₁ ... u_n est bloquée par une coalition S formée de s joueurs, s'il existe des valeurs u₁^s ... u_n^s dont la somme est la valeur de la coalition et pour chaque joueur i : u_i^s u_i. Autrement dit, l'imputation u₁ ... u_n est bloquée par la coalition S si celle-ci offre aux joueurs qui la forment des gains supérieurs à ceux qui leur sont proposés par l'imputation u₁ ... u_n. Le noyau (ou coeur) est caractérisé par une série d'inégalités larges. C'est donc un ensemble fermé, et convexe. I. e. si x et y sont dans le noyau et [0 , 1], alors x + (1 - ) y est dans le noyau.

Le noyau du jeu est alors un ensemble d'imputations qui ne sont bloquées par aucune coalition. Cela signifie que tout ensemble d'agents, la somme de gains proposés par l'imputation est supérieure à celle qu'ils obtiendraient en se coalisant. C'est une condition très contraignante et pour de nombreux jeux le noyau est vide, c'est dire qu'une telle solution n'existe pas.

De nombreux concepts de solutions ont été proposés moins restrictifs que le noyau et plus restrictifs que la solution de VON NEUMANN et MORGENSTERN.

Une approche intéressante caractérise la valeur que chaque agent attribue au jeu en fonction des coalitions auxquelles il peut appartenir, nous la présentons ci-dessous.

2-3-2-3- La valeur de SHAPLEY

La valeur de SHAPLEY pour un jeu est en fait un vecteur : c'est une liste des valeurs que chaque joueur peut attendre du jeu. Le système de coalitions qui résout le jeu doit être tel que chaque joueur obtienne cette valeur.

La valeur de SHAPLEY existe et peut être calculée pour tous les jeux pour lesquels trois axiomes sont vérifiés :

- la valeur d'une coalition est la somme des valeurs de SHAPLEY des joueurs qui la forment ;

- la valeur de SHAPLEY de chaque joueur ne change pas si les rôles des joueurs sont permutés ;

- si un jeu est décomposé en deux sous jeux, la valeur de SHAPLEY du jeu est, pour chaque joueur, la somme des valeurs des deux sous-jeux.

La valeur de SHAPLEY de chaque joueur est donnée par la formule suivante : N est la coalition de tous les n joueurs, T est une coalition de t joueurs quelconques, V est la fonction caractéristique et V_i est la valeur de SHAPLEY du joueur i :

[ V(T) - V(T- i ) ]

(T - 1) ! (n - t) !

n !

T N i T

V_i =

La valeur de SHAPLEY à l'avantage d'être basée sur un axiome de symétrie et un axiome d'efficacité. On peut résumer ces deux axiomes en disant qu'à des droits égaux correspondent des rémunérations égales et que le résultat est optimal selon le critère de Pareto^9(*)6. A cet égard, il faut noter que là aussi il a été démontré^9(*)7 que lorsque le nombre d'agents augmente, la valeur de SHAPLEY tend vers l'allocation associé au système prix concurrentiel.

CONCLUSION

Comme conclusion, on peut dire que les apports potentiels de la théorie des jeux pour l'analyse du décideur sont difficiles à évaluer. A partir de la discussion qui précède, on peut définir deux utilisations très différentes:


· Premièrement, la théorie des jeux nous permet de définir formellement quelques unes des situations de conflit et de coopération ainsi que les choix offerts au joueurs. En effet,, si l'on arrive à classer une situation-type, on peut mieux décrire (du moins analytiquement) ce qu'un acteur peut potentiellement faire, même si cette théorie n'arrive pas souvent à fournir des recettes optimales. L'utilité principale de la théorie des jeux réside donc dans la compréhension de la structure de l'interaction entre les joueur, non seulement pour connaître la meilleure façon de jouer, mais aussi pour comprendre les différentes décisions possibles et les effets d'un changement des règles du jeu^9(*)8.


· Deuxièmement et paradoxalement, la théorie des jeux nous amène vers une négation de la pensée de la maximisation individuelle du profit. En effet, la méthode de choix rationnelle et formelle n'est applicable qu'à une partie infime de l'action humaine. Nous tirons une deuxième leçon de la théorie des jeux: des situations de décision qui ont l'air très simples ne sont pas si simples que cela. On constate très rapidement qu'un choix ne peut pas se fonder uniquement sur des règles de choix individuelles (utilité du type "maximin"), mais également sur la base de comportement ayant trait au raisonnement à long terme ainsi qu'à l'interaction entre joueurs.

Une troisième utilisation que nous n'avons encore pas discuté est la suivante :


· Les jeux comme cadre expérimental pour décortiquer le raisonnement de sujets dans des situations type: la discussion des jeux expérimentaux a montré les potentialités de cet usage, ainsi que l'apport des croyances dans la détermination de l'issue d'équilibre. Grâce à un environnement contrôlé d'action, il nous est possible de formuler quelques règles de décision, comme la règle "la confiance induit la confiance, et la méfiance induit la méfiance" applicable dans des situations où (1) la coopération est profitable, (2) la coopération de l'un et la non-coopération de l'autre est désastreuse pour l'un, et (3) la non-coopération des deux est mauvaise pour les deux. Nous essayerons dans le troisième chapitre de traiter avec plus de soin le rapprochement entre le laboratoire et la théorie des jeux pour découvrir et montrer la solidité de cette union.

Chapitre III : La théorie des jeux en

laboratoire

« the construction of a theory to deal with an unlimited or very large number of negotiation possibilities is as yet so difficult that it seems desirable to restrict and severely formalise the negotiation procedure to that point where a meaningful theory can be constructed (...) because of the relatively undeveloped status of the theory. The authors feel that the use of an experimental approach is strongly indicated »^*(*)

Dans les deux chapitres précédents nous étions amenés à présenter l'intérêt scientifique de la méthode expérimentale, en montrant qu'il s'agit bien d'un outil d'investigation différent des autres techniques traditionnelles ( une différence que les expérimentateurs la voie tantôt, comme supériorité, tantôt comme complémentarité). En outre, nous avions pu découvrir que, au moins pour l'économie, la méthode expérimentale ne cesse pas de se développer, ceci se justifie par sa couverture de plusieurs domaines d'investigation parmi lesquels nous avons cité la théorie des jeux au quelle nous avons donné plus d'importance. Notre choix s'explique par le fait que cette théorie a le privilège d'être (pour l'expérimentateur) à la fois, un champ d'application et l'outil le plus adéquat pour la conception des jeux expérimentaux. Pour cela nous examinerons, dans ce troisième chapitre, de façon un peu plus claire le rapprochement entre l'économie expérimentale et la théorie des jeux (section I). Dans un deuxième point (section II) et toujours dans le même but de mettre en lumière ce rapprochement fructueux entre ces deux disciplines, nous présenterons l'exemple de deux expériences expérimentales (ou plutôt deux jeux expérimentaux).

Section I : Rapprochement entre la

théorie des jeux et

l'économie expérimentale

« ... I am cautiously optimistic that, a hundred years from now, game theory will have become the backbone of a kind of micro-economic engineering that will have roughly the relation to the economic theory and laboratory experimentation of the time that chemical engineering has to chemical theory and bench chemistry »1(*)

1-1- De la théorie des jeux à l'expérimentation :

aperçus historiques et méthodologiques

Le développement de la théorie des jeux et le recours croissant à l'expérimentation en laboratoire ont constitué deux des principales innovations des soixante dernières années en science économique. Ainsi la théorie des jeux s'est présentée comme un outil fournissant un éclairage différent sur les problèmes posés par la microéconomie traditionnelle, elle a surtout fait apparaître de nouveaux problèmes. Elle est considérée par ses défenseurs comme un intéressant outil de réflexion.

Quant à la pratique de l'expérimentation en laboratoire elle est légèrement moins familière aux économistes. Elle consiste en une observation du comportement d'individus dont on tente de contrôler les dotations en biens, les préférences et les coûts, dans une situation caractérisée par un certain nombre de modes d'échange de l'information et de conclusion des contrats dont on essaie également de contrôler la nature. Elle se déroule souvent dans un lieu clos et utilise un matériel parfois sophistiqué (ordinateurs ou autres dispositifs de communication entre les joueurs et d'enregistrement des conduites)- d'où l'utilisation de l'expression « en laboratoire ». Elle a pour buts principaux de tester des théories, d'étudier les raisons des échecs de ces dernières à expliquer les comportements des individus, ou de découvrir des régularités empiriques susceptibles de constituer le socle de nouvelles théories^2(*). C'est à la fin des années 40 qu'on peut situer la naissance de l'économie expérimentale, avec les « expériences de marché » d' E. H. CHAMBERLIN^3(*) (en 1948). Tout comme la théorie des jeux, l'économie expérimentale a éprouvé quelques difficultés à s'imposer dans le champ de la pratique des économistes, mais on peut affirmer sans hésitation que sa position, sans toutefois l'emporter sur celle des travaux statistiques et économétriques, est à présent assez solidement établie. De nombreux économistes cherchent aujourd'hui à formuler des théories nouvelles ou à reformuler d'anciennes théories de manière notamment à ce que puisse être testée dans des conditions contrôlées telle ou telle proposition de la théorie^4(*).

L'étendue et la portée de cette union - forcée par à la fois le développement et l'utilisation de la théorie des jeux et par le recours croissant à l'expérimentation en laboratoire- sont attestées par le nombre des publications, la variété des applications théoriques, l'apparition d'enseignements spécifiques et la multiplication des manuels.

Dès le début, ou presque, du développement parallèle de ces deux approches ( théories des jeux d'un côté, expérimentation de l'autre), des chercheurs ont été amenés à les utiliser conjointement. En effet, à la fin des années 1950, soit peu de temps après la publication de Theory of Games and Economic Behavior et de l'expérience de marché de CHAMBERLIN, M FLOOD (1958)^5(*) et H RAIFFA (1962) mettent en oeuvre ce que nous appellerons, dans la suite, « des jeux expérimentaux »^6(*). Il s'agit d'expérimentations en laboratoire dans lesquelles on observe le comportement d'individus participant à des jeux- dans le sens que les théoriciens des jeux donnent à ce terme. L'expérimentation la plus connue de FLOOD consiste ainsi à faire jouer à deux individus le jeu matriciel décrit par le tableau suivant :

Joueur 1

1 2

1

joueur 2

2

-1 ; 2	0,5 ; 1
0 ; 0,5	1 ; -1

Qui est un jeu à « somme non nulle », puis à comparer le comportement observé des individus qui le jouent avec des « prédictions » s'inspirant des résultats de la théorie des jeux. Ces prédictions reposent sur l'idée que si les agents se comportent « rationnellement », alors il est possible qu'ils se conforment aux choix stratégiques mis en avant par la théorie des jeux. Dans son compte rendu expérimental, FLOOD se demande ainsi si les joueurs jouent ou non une « stratégie d'équilibre » compte tenu de la stratégie choisie par son adversaire. Dans son jeu^7(*), FLOOD se demande ainsi si l'équilibre de NASH correspondant au choix de la stratégie 2 pour le joueur 1 et de la stratégie 1 pour le joueur 2, soit l'issue dont le vecteur de gain est ( 0 ; 0,5), est un bon « prédicteur » du comportement des joueurs, ce qui serait le cas si chacun d'entre eux décidait de jouer une stratégie d'équilibre.

Autour des interrogations de ce type, la théorie des jeux et la recherche expérimentale ont ainsi commencé à entretenir des relations qui se sont, avec les années, progressivement intensifiées. En plus des premiers jeux expérimentaux recensés conçus par FLOOD et RAIFFA, on compte également dans la période pionnière une expérience réalisée en 1952 et cosignée par NASH lui-même (KALISCH, MILNOR, NASH et NEERING, 1954). A ce volet-ci, mariant la théorie des jeux et l'expérimentation, on doit, en premier lieu, faire correspondre les travaux fondateurs de RAPOPORT et CHAMMAH^8(*) (en 1965) concernant le dilemme du prisonnier. Puis, après quelques années d'hésitation, les chercheurs en sciences sociales commencent peu à peu à mettre régulièrement en oeuvre des jeux expérimentaux (plus souvent d'ailleurs en psychologie sociale, sociologie ou théorie du comportement qu'en économie). En 1962, RAPOPORT et ORWANT répertorient plus de vingt articles dont l'objet est un compte rendu expérimental, des articles où sont décrites en tout une trentaine de jeux expérimentaux différents.

Dans le champ de la psychologie sociale ou de la théorie du comportement, le succès est fulgurant à partir des années 1960, comme le décrit A COLMAN^9(*) :

« Vers 1965, les jeux expérimentaux étaient devenus si populaires que le Journal of Conflict Resolution commença à leur consacrer une section distincte dans chacun de ses numéros, et, en 1972, plus de 1000 études empiriques avaient été publiées dans cette revue ou ailleurs^1(*)0 (...). Depuis les premiers travaux expérimentaux jusqu'au milieu des années 1990, ce sont quelques 2000 jeux expérimentaux [experimental gaming] qui ont été publiés. » p. 13.

Dans le champ de l'économie, les travaux expérimentaux se développent initialement autour des thèmes liés à la théorie du duopole et d'oligopole, et à la théorie du marchandage^1(*)1. Puis, dans les années 1980, le nombre de jeux expérimentaux étudiés augmente régulièrement. Les jeux en question sont issus de toutes les parties de la théorie des jeux depuis la théorie des jeux non-coopératifs, sous forme normale ou extensive, jusqu'à l'étude des conditions d'information des joueurs, en passant par la coordination ou la théorie du marchandage - séquentiel ou non. En 1992, l'International Journal of Game Theory s'enrichit d'ailleurs d'une section spéciale intitulée « Games and Experiment » pour laquelle SELTEN joue le rôle d'éditeur . Depuis plusieurs années, la revue Games and Economic Behavior publie également des comptes rendus de jeux expérimentaux.

En plus de constituer un corpus de travaux en expansion, ces jeux expérimentaux représentent une fraction importante de la littérature expérimentale économique. On peut en prendre la mesure en considérant la place qu'ils occupent dans les premiers manuels d'économie expérimentale. En 1991, J. D. HEY^1(*)2 publie le premier de ces manuels, qui consacre des développements importants à la théorie du comportement interactif - dont un sixième de l'ouvrage pour les thèmes du marchandage et des jeux en général. Le Handbook of Experimental Economics de J. H. KAGEL et A ROTH^1(*)3 contient plusieurs chapitres portant sur les jeux expérimentaux. Par ailleurs, en

juin 1998 débute la publication de la revue Experimental Economics, dont une grande partie des articles traitent de problèmes liés à la théorie des jeux.

1-2- l'intuition derrière le rapprochement

entre la théorie des jeux et

l'expérimentation

Ce rapprochement des idées de la théorie des jeux et des méthodes de l'expérimentation, à l'oeuvre dans les jeux expérimentaux, était-il fortuit ? Non, semble-t-il. Des travaux de la pensée économique nous apprennent en effet que nombre important de spécialistes de la théorie des jeux ont fait appel aux méthodes de la recherche expérimentale. L'explication la plus fréquente du développement de l'expérimentation dans le champ de l'économie qui est alors proposée est que certains théoriciens des jeux ont souhaité produire de nouveaux énoncés théoriques au moyen d'observations expérimentales. Ainsi, par exemple, A ROTH déclare :

« Nombre des premiers économistes expérimentateurs sont aujourd'hui connus avant tout comme des théoriciens des jeux réputés ; ils ont été poussés vers l'expérimentation par le fait que cette dernière leur donnait la possibilité de tester les prédictions de la théorie des jeux et d'observer des comportements non prédits dans un environnement contrôlé ( voir par exemple le travail expérimental des années 1950 et 1960 de Maschler, Nash, Schelling, Shubik et Selten) »^1(*)4

En quoi l'expérimentation leur donnait-elle « l'occasion » de tester les prédictions de la théorie des jeux et d'observer les comportements non prédits ? En ce que, répond par exemple DELOCHE^1(*)5, l'expérimentation en laboratoire en économie entretient avec la théorie des jeux une relation privilégiée. Pour caractériser cette relation, il faut d'abord revenir à notre définition de la théorie économique comme étant un ensemble constitué par trois éléments : l' «environnement », l' « institution » et les « comportements ». et c'est à partir de cette définition, sous forme de trio, de la théorie économique qu'on retrouve ce que les défendeurs de l'expérimentation en laboratoire appelle une supériorité par rapport à l'économétrie, ainsi « l'économiste-expérimentateur de laboratoire peut contrôler non seulement les institutions, mais aussi l'environnement. »^1(*)6

L'expérimentation en laboratoire permet un contrôle plus étendu des conditions initiales des propositions théoriques testées ou des régularités observés. Toutefois cet avantage n'est intéressant que si, dans les théories testées et les régularités que l'on veut découvrir, l'institution^1(*)7 est définie avec précision.

Or, comme on a pu le voir dans la définition de la notion de jeu, la théorie des jeux accorde une grande importance à la caractérisation de l'institution. De la sorte que, non seulement des théoriciens des jeux ont-ils été tentés de réaliser des expérimentations mais encore des expérimentateurs ont-ils trouvé dans la théorie des jeux et les théories qui utilisaient la théorie des jeux une occasion propice à la réalisation de tels travaux. Selon DELOCHE, la solidité de l'union de la théorie des jeux et de l'économie expérimentale » s'explique ainsi « par l'importance que toutes les deux accordent aux institutions »^1(*)8.

Ainsi, le rapprochement décrit par DELOCHE, après d'autres, semble d'autant plus naturel  qu'il peut être facilement mis en pratique. Des théoriciens des jeux auraient voulu tester la théorie des jeux et observer le comportement des individus en situation de jeu, et des chercheurs intéressés par la réalisation d'expérimentations en laboratoire dans le champ des sciences économiques ( et sociales) auraient trouvé, dans les jeux et la théorie des jeux des concepts et des propositions particulièrement adaptés à ce type d'études^1(*)9.

Cependant, selon P MAMAS^2(*)0 cette explication, (avancée par DELOCHE) considérant le rapprochement entre la théorie des jeux et le laboratoire comme processus naturel, est insuffisante puisque en remontant à l'origine de l'apparition de la théorie des jeux on trouve que la possibilité d'établir des relations entre la démarche du théoricien des jeux et la recherche expérimentale ne va pas de soi puisque on sait déjà que la théorie des jeux des tout premiers fondateurs - E ZERMELLO (1913), E BOREL (1921), J VON NEUMANN (1928)- apparaît d'abord comme une mathématique, créée par des mathématiciens, pour des mathématiciens pour lesquels la rigueur de la démonstration mathématique compte plus que l'existence d'une quelconque référence empirique. Dans cette mesure, le théoricien des jeux ne recherche pas directement dans l'observation des conduites humaines un contrôle de son travail ou une source essentielle d'inspiration.

MAMAS continuent son raisonnement ( afin de trouver une autre explication à ce rapprochement entre la théorie des jeux et l'expérimentation) en affirmant que d'un autre point de vue, la théorie des jeux de ZERMELO, de BOREL et de VON NEUMANN est aussi une mathématique appliquée. On peut s'en persuader en remarquant que, d'une part, les notions de jeu, de joueur, de stratégie, renvoient directement, par leur nom même, à des objets empiriques, observables, et que d'autre part, il est possible de s'inspirer de la théorie des jeux pour formuler des conseils à l'attention de joueurs qui seraient placés dans les mêmes conditions que les joueurs de la théorie.

Les premiers théoriciens des jeux ne se privent d'ailleurs pas de donner ce genre de conseils. Ainsi, J VON NEUMANN indique en 1928 que, dans un jeu à deux joueurs et à somme nulle, un joueur qui cherche à obtenir le gain le plus avantageux possible doit jouer la stratégie qui maximise ( sur l'ensemble de ses stratégies) le minimum ( sur l'ensemble des stratégies de l'adversaire) de l'espérance mathématique de son gain - autrement dit sa stratégie « maximin ». MAMAS interprète ce genre de conseil comme une proposition « instrumentale-normative », c'est à dire comme un conseil (instrument) en termes de choix stratégique donné à un joueur dont les objectifs sont arbitrairement prédéfinis (norme). En ce sens, MAMAS considère que, dans les premières années de son existence, en se rapprochant des objets d'observation, la théorie des jeux fait simplement l'objet d'une interprétation « instrumentale-normative ».

Cependant, même en adoptant cette interprétation « instrumentale-normative » de la théorie des jeux, la relation de cette dernière aux faits d'observation reste limitée. En effet, dans la mesure où la démarche de la théorie des jeux, dans sa dimension appliquée des années 1910-1920, vise à conseiller des joueurs sur la base d'objectifs arbitraires et de raisonnements démonstratifs mathématiques, l'observation des choix des individus lui est de peu d'utilité. cette situation s'accorde mal avec l'utilisation ultérieure de la théorie des jeux en lien avec la recherche expérimentale. Le comportement des individus dans les jeux y devient au contraire un objet d'étude privilégié, observé en relation avec les idées et concepts de la théorie des jeux, et il est souvent utilisé pour « tester » cette dernière. En effet, cette interprétation « instrumentale-normative » décrit mal la situation actuelle de la relation entre la théorie des jeux et l'économie expérimentale.

Il a nécessairement fallu que, dans l'intervalle, une autre interprétation de la théorie des jeux apparaisse et se développe. Selon MAMAS, cette nouvelle lecture de la théorie des jeux se présente comme une interprétation « descriptive-prédictive », autrement dit elle consiste à dire que la théorie des jeux peut aider à décrire, prédire ou expliquer le comportement d'individus réels participant à des jeux. Cette interprétation s'inspire des propositions mathématiques centrales de la théorie des jeux pour formuler des énoncés de type:  si un joueur participe à un certain type de jeu et est caractérisé par certains objectifs et préférences spécifiées, alors il joue (ou jouera) telle stratégie. Par exemple, l'interprétation « descriptive-prédictive » de la proposition « instrumentale-normative » de VON NEUMANN énoncée précédemment est : dans un jeu à deux joueurs et à somme nulle, un joueur qui cherche à obtenir le gain le plus avantageux possible joue (ou jouera) sa stratégie maximin.

On peut conclure donc que, contrairement à DELOCHE qui voit dans le rapprochement actuelle entre la théorie des jeux et l'expérimentation un processus naturel ( soit parce que l'expérimentation en laboratoire se dote d'une supériorité par rapport aux autres types de techniques empiriques, soit parce que la théorie des jeux et l'expérimentation ont un point commun qui les rapproche à savoir l'importance que les deux accordent à l'institution), MAMAS affirme que les relations privilégiées qui existent aujourd'hui entre la théorie des jeux et les jeux expérimentaux, présupposent qu'on soit passé d'une interprétation mathématique ou « instrumentale-normative » de la théorie des jeux à une interprétation « descriptive-prédictive » de celle-ci^2(*)1.

Pour matérialiser le rapprochement entre la théorie des jeux et l'expérimentation ainsi que l'avantage qu'a procuré cette union pour résoudre des problèmes propres à d'autres domaines, nous allons donner, dans la prochaine section, deux exemples typiques de jeux expérimentaux.

Section II- les jeux expérimentaux :

une discussion de cas

Historiquement nous pouvons affirmer que le rapprochement entre la théorie des jeux et l'expérimentation a connu deux étapes d'évolution^2(*)2 :

- la première étape commence du début des années 50 jusqu'à la fin des années 60. durant cette période le recours au laboratoire avait pour objectif exclusif la validation théorique des concepts de solutions avancés par la théorie des jeux^2(*)3. Les chercheurs ont essayé pendant cette étape de gagner une certaine confiance quant à la fiabilité de la théorie des jeux comme outil performant qui permet une modélisation correcte des interactions stratégiques entre individus. En d'autres termes on a essayé pendant cette période d'avoir une réponse à la question suivante : Est ce que, en créant un environnement (expérimental) aussi semblable que celui préconisé par la théorie, le concept de solution avancé par cette dernière (tel que l'équilibre de NASH dans un environnement non coopératif) tiendra ?

En effet, nous essayerons dans un premier point de donner l'exemple d'une expérience de ce type. Nous avons choisi une expérience qui reste jusqu'à présent parmi les plus célèbres dans le domaine de la théorie des jeux, il s'agit de l'expérience réalisée par SHUBIK en 1962^2(*)4 dont l'objectif était la validation expérimentale des différentes concepts de solutions, connu jusqu'à cette date, pour des jeux à deux joueurs, à somme non nulle avec information incomplète sur les règles du jeux.

-La deuxième étape commence du début des années 70 jusqu'à nos jours. Cette période se caractérise par une conviction de la part des théoriciens des jeux ou plus généralement des économistes quant à la pertinence de la théorie des jeux comme outil performant de la modélisation des interactions interindividuelles. Une fois cette confiance établie, les économistes commence à utiliser le langage de la théorie des jeux dans plusieurs domaines (là où il y a interaction stratégique entre individus). Là encore on trouve que c'est SHUBIK qui était le précurseur, sa conviction quant à la pertinence de la théorie des jeux était même très précoce^2(*)5 par rapport à la plupart des autres économistes. Mais en général ce n'est que pendant cette deuxième période qu'on a pu abordé, en utilisant aussi bien l'expérimentation que le langage de la théorie des jeux, des questions en relations avec des sujets réels tels que l'étude des structures des marchés ( l'émergence des Cartel et leur stabilité, l'apparition des attaques spéculatives dans les marchés financiers, la réaction des marchés aux modifications de la réglementation), les relations internationales (les négociations bilatérales ou multilatérales), l'étude et l'analyse des décisions publiques ( les opérations de privatisation, la communication des décisions publique tel que la communication des risques).

Pendant cette deuxième période, on peut remarquer qu'il y avait un changement dimensionnel et formel de la relation entre la théorie des jeux et l'économie expérimentale. Cette relation prend parfois une forme bi-dimensionnelle («théorie des jeux-économie expérimentale »), il s'agit là de la forme classique dans laquelle le laboratoire est considéré comme outil de validation théorique seulement ou plutôt un outil de raffinement des processus d'équilibration. Dans d'autres cas cette relation prend une forme tri-dimensionnelle (ou plus) (« théorie des jeux-économie expérimentale-domaine(s) de référence »), dans ce cas l'objectif du « théoricien-expérimentateur » n'est pas seulement la recherche de la pertinence d'un certain concept théorique, mais il y a un second objectif aussi important que le premier. Il s'agit de chercher, à travers cette jonction entre théorie des jeux et économie expérimentale, la résolution des problèmes propres à certains domaines. On peut citer à titre d'exemple : la détermination des mécanismes de privatisation, la détermination des raisons des attaques spéculatives dans les marchés financiers, la conception de nouveaux marchés (boursiers). En d'autres termes, on dira qu'on a vécu pendant cette période la naissance de ce que nous appelons les « jeux expérimentaux appliqués » menant par la suite à la constitution d'un domaine de recherche proprement dit, ROTH l'a nommé le « Design Economics ».

Nous essayerons, donc, dans un deuxième point de présenter une expérience matérialisant ce changement dimensionnel en prenant comme « domaine de référence » la communication des décisions publiques et plus précisément les décisions publiques pour un financement efficient d'un bien public.

2-1- jeux à deux joueurs et à somme non nulle :

une étude expérimentale

Comme nous l'avons évoqué auparavant cette expérience à été réalisée par l'économiste SHUBIK et elle remonte à 1962 malgré son ancienneté elle reste toujours une référence importante pour les théoriciens-expérimentalistes, sa célébrité est due à la fois à sa simplicité, à sa clarté et à l'importance^2(*)6 des résultats qu'on a pu tirer.

Avant de présenter son expérience, SHUBIK commence son article par une présentation des différentes formalisations d'un jeu quelconque, une présentation sur laquelle nous ne revenons pas puisqu'elle est déjà évoquée dans le deuxième chapitre^2(*)7. Dans un deuxième point, l'auteur présente les différents concepts de solutions, connus jusqu'à cette date, pour les jeux à deux joueurs et à somme non nulle.

Dans les points qui suivent l'auteur présente l'expérience proprement dite ( les différents jeux expérimentaux qu'il a essayé d'étudier, les hypothèses et les conditions sous-tendant l'expérience, la confrontation des solutions théoriques et les choix des joueurs et enfin les résultats de cette confrontation).

2-1-1- les concepts de solutions proposés pour les jeux à deux

joueurs et à somme non nulle

SHUBIK affirmait que la théorie des jeux telle qu'elle se présentait à cette date était une théorie normative, il considérait que les efforts fourni dans le sens de la conception des jeux expérimentaux sont très importants pour l'acheminement vers, premièrement la validation des théories qui se prétendaient être descriptives et deuxièmement vers la production ou l'apparition de nouvelles théories descriptives.

L'auteur se limitait dans cette étude aux jeux à deux personnes, à durée finie, et à somme non nulle. Soit P₁(s₁, s₂) le paiement du premier joueur s'il joue sa stratégie s₁ et si le second joueur joue sa stratégie s₂ ; de manière similaire on peut définir P₂(s₁, s₂).

Soit le jeu présenté dans la matrice ci-dessous (figure 1) :

1

2

1 2

5 ; 2	-10 ; -13
4 ; 1	-20 ; -23

Fig 1

Nous remarquons qu'il s'agit d'un jeu à somme non nulle ou d'une manière générale d'un jeu à somme non constante ( la somme des paiements des deux joueurs diffère d'un casier à un autre).

VON NEUMANN et MORGENSTERN ont suggéré que dans les jeux à somme non constante les joueurs doivent maximiser conjointement leur bien être. Cela suppose évidemment qu'ils communiquent entre eux et qu'il y a possibilité de paiements latéraux. Mais dans leur description de ce jeu ils n'ont pas inclus d'une manière explicite ce processus de négociation ainsi que la possibilité de paiement latéraux. Ces opérations existent mais elles prennent place hors du jeu. La description du comportement des joueurs dans ce jeu est donnée mathématiquement par la condition suivante :

s₁ s₂

Max. Max. (P₁(s₁, s₂) + P₂(s₁, s₂)) [1]

Ceci veut dire que chaque joueur doit choisir sa stratégie telle que la somme des paiements soit maximum (choisir le maximum joint)^2(*)8. Appliquée au jeu de la figure 1 cette condition suggère que chaque joueur doit jouer sa première stratégie .

NASH avait introduit une théorie des jeux non coopératifs^2(*)9 qui se prétend être une généralisation de la théorie de l'Équilibre Economique Général. La théorie de NASH est appliquée pour les situations qui se caractérisent par l'absence de communication entre les joueurs ainsi que l'absence des paiements latéraux. NASH montre que pour n'importe quel jeu fini, il existe au moins une paire de stratégies s₁^* et s₂^* tel que les deux conditions suivantes :

[2]

s₁

s₁^* = Max. P₁(s₁, s₂^*)

s₂

s₂^* = Max. P₁(s₁^*, s₂)

sont simultanément satisfaites par le choix de s₁^* et s₂^* par le premier et le deuxième joueur respectivement. En d'autres termes, si le premier joueur croit que le second joueur utilisera s₂^* contre lui, sa meilleure réaction sera le choix de s₁^* et vice versa.

A coté de ces deux solutions, SHUBIK avance deux autres solutions moins acceptables mais possible dans un environnement tel que celui des jeux à deux joueurs à somme non nulle.

La troisième solution est envisageable dans le cas où les deux joueurs sont très pessimistes, dans ce cas ils s'efforcent à minimiser les pertes qu'ils peuvent concéder. En d'autres termes, en supposant que l'adversaire est un ennemi chacun croit que l'autre essayera toujours de minimiser sa récompense, il s'efforce donc de maximiser son résultat dans ces conditions. Formellement Ceci peut être exprimé de la façon suivante :

[3]

s₁ s₂

Max. Min. P₁(s₁, s₂)

s₁ s₂

Max. Min. P₂(s₁, s₂)

La quatrième solution avancée par SHUBIK est celle qui stipule que les joueurs peuvent trouver avantageux de maximiser la différence en terme de gain entre eux. La conséquence sera donc la maximisation du gain individuel. C'est la manière de penser qui prévalent chez les spéculateurs. Formellement, on peut représenter ce cas de la manière suivante :

s₁ s₂

Max. Min. (P₁(s₁, s₂) - P₂(s₁, s₂)) [4]

Ce sont là les quatre solutions proposées par SHUBIK pour les jeux à deux joueurs et à somme non nulle. Dans ce qui suit nous allons présenter comment SHUBIK a pu, en faisant recours aux jeux expérimentaux, étudier la validation théorique de ces concepts de solution.

2-1-2- Quelques jeux expérimentaux et leurs solutions

théoriques

1 2

SHUBIK donne l'exemple de six jeux joués par cinq paires de joueurs^3(*)0. On donne ci-dessous les matrices des gains pour ces jeux.

1

2

Jeu 1 :

6 ; 3	6 ; 7
10 ; 3	10 ; 7

Fig 2

1

2

1 2

Jeu 2 :

1 ; 3	2 ; 3
1 ; 1	2 ; 1

Fig 3

1 2

1

2

Jeu 3 :

2 ; 1	-1 ; -1
-1 ; -1	1 ; 2

Fig 4

1 2

1

2

Jeu 4 :

3 ; 3	-1 ; -1
-1 ; -1	2 ; 2

Fig 5

1 2

1

2

Jeu 5 :

3 ; 3	-2 ; 7
7 ; -2	-1 ; -1

Fig 6

1

2

Jeu 6 :

1 2

5 ; 2

	-10 ; -13
4 ; 1	-20 ; -23

Fig 7

Fig 8

Dans la figure 8 ci-dessous, tous les concepts de solutions qui ont été avancés précédemment sont maintenant appliqués aux six jeux ci-dessus. Les paires de stratégies représentant les solutions sont notées. Par exemple l'expression (1 ; 1) représente la solution selon laquelle chaque joueur joue sa première stratégie ( s₁ = 1 et s₂ = 2).

	Solution [1]	Solution [2]	Solution [3]	Solution [4]
Jeu 1	(2 ; 2)	(2 ; 2)	(2 ; 2)	(2 ; 2)
Jeu 2	(1 ; 2)	(1 ; 1) (1 ;2) (2 ; 1) (2 ; 2)	(1 ; 1) (1 ;2) (2 ; 1) (2 ; 2)	(2 ; 1)
Jeu 3	(1 ; 1) ou (2 ; 2)	(1 ; 1) ou (2 ; 2)	* (2/5 ; 3/5) et (3/5 ; 2/5)	(1 ; 2)
Jeu 4	(1 ; 1)	(1 ; 1) ou (2 ; 2)	* (3/7 ; 4/7) et (3/7 ; 4/7)	(1 ; 1) (1 ;2) (2 ; 1) (2 ; 2)
Jeu 5	(1 ; 1)	(2 ; 2)	(2 ; 2)	(2 ; 2)
Jeu 6	(1 ; 1)	(1 ; 1)	(1 ; 1)	(1 ; 1) (1 ;2) (2 ; 1) (2 ; 2)

* Ces deux solutions impliquent des stratégies mixtes. les paires entre parenthèses indiquent les probabilités employées par chaque joueur.

Lorsqu'il sont appliqués pour le premier jeu, les quatre concepts de solutions donnent la même solution (2 ; 2). SHUBIK affirme que, à travers une étude attentive de ce jeu, on peut constater qu'il y a des raisons structurelles pour l'apparition de ce résultat. Les joueurs sont stratégiquement indépendants de telle manière que leur sorts (ou leur destin) ne sont pas reliés. Ce jeu représente le cas où il y a une isolation complète des deux adversaires dans un marché de concurrence pure. En effet, sans tenir compte de leur intentions, les joueurs se trouvent dans une situation où leur comportement ne changera plus quel que soit les circonstances. SHUBIK appelle se genre de jeu «  un jeu inessentiel » où rien ne peut être gagner à travers la discussion, la négociation ou la collusion, tous ces termes n'ont pas de sens dans ce cas.

Remarquons aussi que dans les jeux 3 ; 4 et 6, la solution non coopérative [2] et celle du maximum joint [1] se coïncident ceci s'explique par le fait que la structure de ces jeux génère une sorte de collusion implicite.

2-1-3- Description de l'expérience : Hypothèses, Conditions

du travail et Résultats

En se référant à d'autres travaux précédents, SHUBIK suggère que le concept de solution non coopérative est le meilleur prédicteur ( parmi les quatre présentés dans cette expérience) dans une situation des jeux à somme non nulle. Ceci est vrai, ajoute-t-il, avec une seule modification. Les jeux seront joués sous la conditions d'information incomplète sur les règles. Cette incomplétude informationnelle est de deux sortes :

1- les joueurs seront informés seulement sur ses propres fonctions de paiements. Ils n'auront plus d'information sur les fonctions de paiements des autres joueurs. Pour chaque joueur, ses adversaires ( ou ses partenaires) seront choisi de manière aléatoire, en plus, toute communication sera interdite sauf celle via le moniteur qui transmettra l'information concernant les choix de chaque joueur après chaque période du Super Jeu.

2-les joueurs ne seront pas initialement informés sur le nombre de périodes pour les Super Jeux. Ceci pour éviter ce qu'a appelé l'auteur « les effets de conclusion », en d'autres termes afin d'éviter les raisonnement reposant sur le principe de la récurrence à rebours `` backward induction''. Les étudiants (joueurs) auront approximativement une minute par période.

Il faut noter ici que pour tester l'hypothèse selon laquelle la solution non coopérative est la meilleure parmi les quatre avancées, l'auteur ne s'est basé que sur les données des cinq dernières périodes pour chaque jeu. Le terme « meilleure » doit être compris dans un sens général parce qu'aucune solution ne peut être retenue pour tous les jeux.

La figure 9 ci-dessous donne les résultats observés pour les cinq dernières périodes.

	Les paires de stratégies	Paire (joueurs) 1	Paire 2	Paire 3	Paire 4	Paire 5	Prédiction des solutions [1] [2] [3] [4]
Jeu 1	(1 ; 1) (1 ; 2) (2 ; 1) (2 ; 2)	- - - 5	- - - 5	- - - 5	- - - 5	- - - 5	X X X X
Jeu 2	(1 ; 1) (1 ; 2) (2 ; 1) (2 ; 2)	- - 2 3	- - - 5	- - 3 2	- 1 2 2	- 5 - -	X X X X X X X X X X
Jeu 3	(1 ; 1) (1 ; 2) (2 ; 1) (2 ; 2)	- - - 5	- - - 5	- - - 5	5 - - -	5 - - -	X X 6/25 4/25 X 9/25 X X 6/25
Jeu 4	(1 ; 1) (1 ; 2) (2 ; 1) (2 ; 2)	5 - - -	5 - - -	5 - - -	5 - - -	3 1 1 -	X X 9/49 X 12/49 X 12/49 X 16/49 X
Jeu 5	(1 ; 1) (1 ; 2) (2 ; 1) (2 ; 2)	- - 3 2	- - 1 4	- - 1 4	- - - 5	- - 1 4	X X X X
Jeu 6	(1 ; 1) (1 ; 2) (2 ; 1) (2 ; 2)	5 - - -	5 - - -	5 - - -	5 - - -	5 - - -	X X X X X X X

Fig 9

En examinant les deux figures 8 et 9, on observe que l'ensemble des théories ont la même force prédictive pour le premier jeu, en plus cette observation est en complet accord avec les résultats concernant le jeu expérimental n°1. ceci affirme que les joueurs se dotent d'une rationalité effective.

Pour le deuxième jeu, les solutions [1] et [4] doivent être rejetées, tandis que les solutions [2] et [3] n'ont pas une force de résolution suffisante pour les prendre comme référence sur laquelle nous pouvons reposer notre prédiction des comportements réels des joueurs d'où leurs inconsistance par rapport aux données expérimentales. Ce que nous constatons pour ce jeu c'est qu'il y a une certaine tendance des joueurs à choisir la paire (2 ; 2) avec une grande fréquence, mais aucune des solutions n'a pu capter ce constat. L'auteur propose de rejouer ce jeu une deuxième fois mais en permutant les lignes et les colonnes parce qu'il pense que ce dernier constat ( le choix des joueurs de la paire (2 ; 2) ) ne se base pas sur le principe de rationalité, il avance, sans fermeté, qu'il y a derrière ce genre de comportement d'autres considérations (de type géométrique par exemple).

Pour le troisième jeu, les solutions [1] et [2] tiennent pour toutes les données, tandis que les solutions [3] et [4] doivent être rejetées.

Pour le quatrième jeu, les solutions [1] et [2] sont consistantes avec les donnés de l'expérience ( malgré que les données issues de la 5^ème paire de joueurs reflètent une certaine variabilité. La solution [3] doit être rejetée et la solution [4] n'a pas une force de résolution satisfaisante.

Pour le cinquième jeu, ce qui est remarquable c'est que les joueurs font preuve d'une difficulté d'apprentissage, ils n'arrivent pas à coordonner leurs stratégies pour améliorer leur profit joint. Par conséquent, la solution [1] est rejetée tandis que toutes les autres solutions restent acceptables.

Pour le sixième jeu, les solutions [1], [2] et [3] sont en complèt accord avec les données expérimentales ; la solution [4] n'a pas une force de résolution satisfaisante.

Le tableau ci-dessous résume en quelque sorte les résultats de cette expérience :

	Solutions
Jeux		1	2	3	4
	1	Oui	Oui	Oui	Oui
	2	Non	?^*	?	Non
	3	Oui	Oui	?	Non
	4	Oui	Oui	?	?
	5	Non	Oui	Oui	Oui
	6	Oui	Oui	Oui	?

* le point d'interrogation ( ? ) indique que la solution n'a pas une force de résolution

A travers les résultats de son expérience, SHUBIK a pu tirer la conclusion suivante : pour l'ensemble des jeux - pris dans cette expérience - aucun concept de solution n'est prédominant. Parfois on trouve qu'ils sont consistant par rapport aux données de l'expérience, dans d'autres cas on trouve qu'ils sont rejetés ( faute de force de résolution ou mauvaise prédiction). Des modifications s'imposent donc. Ces dernières doivent être faite dans le sens de rendre compte de certains aspects tels que la réciprocité, la confiance, l'équité et plein d'autres facteurs que des expériences ultérieures ont essayé de mettre en valeur.

L'expérience de SHUBIK n'a pas pu juger d'une manière un peu plus claire sur la pertinence des concepts de solutions avancés (ou plus précisément sur la pertinence de l'équilibre de NASH comme l'a souhaité SHUBIK lui-même). Ces conclusions insatisfaisantes^3(*)1 ont poussé l'auteur à se douter à propos de la méthode expérimentale comme outil de validation théorique. Ainsi il déclare dans la conclusion de son article : « there are great difficulties to be faced in attempting to use experimental games in vitro to learn about human processes in vivo.(...). The environnement of the simple experimental game probably destroys many of the factors contributing to the acceptance of stable standards of behaviour in societies or even in industries and trade associations »^3(*)2. Il avance que la meilleure façon qui peut mettre en valeur l'apport de la méthode expérimentale - ce qui peut en dernier lieu mettre en lumière ces facteurs encore négligés par les conditions expérimentales - est la clarification de la relation entre environnement social et environnement expérimental.

Actuellement on est allé très loin dans le processus de clarification de cette relation parce que tous les théoriciens sont convaincus maintenant de la chose suivante : il y a deux logiques du cheminement vers l'équilibre qui sont envisagées. Soit, l'équilibre est atteint à l'aide du mécanisme d'équilibration supposé par la théorie. Soit, le processus menant à l'équilibre est complété par la présence d'éléments extra-rationnels, partagés entre les individus. Ces éléments peuvent être d'ordre psychologique (la sensibilité à l'équité ou l'aversion à l'inéquité, la réciprocité et l'absence d'envie) ou d'ordre sociologiques ( moeurs et habitudes). L'incorporation de ces éléments dans les modèles théoriques améliore certainement leur pouvoir prédictif mais, en faisant, une question importante s'impose : celle concernant le fondement et l'origine de ces éléments extra-rationnels^3(*)3.

Dans ce qui suit on rencontrera un cas d'expérience où les jeux expérimentaux sont utilisés pour expliquer les comportements des gens lorsqu'il doivent choisir entre un investissement privé et un investissement public.

2-2 : Le financement d'un bien public entre

l'Optimalité et la recherche d'Equilibre :

une étude expérimentale3(*)4

Dans les jeux de contribution volontaire à un bien public, les membres d'un groupe font face à un dilemme social. Chaque individu doit investir tout ou une partie de ses ressources ( sa dotation) soit dans un bien privé, soit dans un bien public. Le bien privé rapporte à l'individu un gain qui est uniquement fonction de son investissement personnel dans ce bien, tandis que le bien public rapporte à chaque individu du groupe un gain qui est fonction de l'investissement collectif des membres du groupe pour le bien public. Le dilemme réside dans le fait que le gain marginal du bien privé est supérieur au gain marginal du bien public. La fonction de gain totale, telle que la définissent ISAAC, WALKER et THOMAS (1984)^3(*)5, connaît deux issues opposées. L'équilibre de NASH du jeu est atteint lorsque aucun des membres du groupe ne contribue au financement du bien public (c'est la stratégie dominante de sous jeu ou stratégie de passage clandestin « Free Riding ». L'optimum de Pareto est obtenu lorsque tous les membres du groupe avancent l'intégralité de leur dotation pour le bien public.

Les résultats des expérimentations précédentes portant sur les contributions volontaires (LEDYARD^3(*)6) montrent que les individus ne souhaitent ni contribuer par l'intégralité de leur dotation, ni jouer la stratégie de passage clandestin mais choisissent un niveau de contribution intermédiaire. Ces contributions diminuent avec les répétitions du jeu et approchent la contribution d'équilibre. Parmi les différentes hypothèses formulées pour expliquer ce comportement complexe, NEVEU avance  : les erreurs de compréhension des règles de l'expérience et la définition du niveau de financement efficient du bien public.

La première hypothèse tient au fait que les individus peuvent ne pas avoir saisi les règles de l'expérience. ANDREONI^3(*)7 explique ceci par le fait que les individus cotisent avec une partie de leur dotation sans véritablement savoir pourquoi. Toujours selon ANDREONI, les individus, suite à un apprentissage au cours des répétitions du jeu, assimilent les règles de l'expérience et les conséquences de leurs choix. Ils versent ainsi des sommes qui tendent vers la stratégie de passage clandestin et qui convergent vers l'équilibre de NASH du jeu. Pour rendre compte des comportements volontaires de contribution et de les distinguer des éventuelles erreurs de compréhension, beaucoup d'expérimentalistes^3(*)8 ont eu recours à la définition d'un jeu dont l'équilibre de Nash est obtenu par une contribution partielle des joueurs. Dans un tel jeu, des contributions supérieures et inférieures à la contribution d'équilibre doivent apparaître si des erreurs de compréhension sont à la source du choix des individus. En revanche, si les joueurs assimilent les règles mais tentent de développer un comportement coopératif, alors seules des contributions au-dessus de l'équilibre émergeront. Ces études montrent que les joueurs, en toute connaissance de cause, contribuent au bien public par des montants supérieurs à la contribution d'équilibre. Le phénomène de « sur-contribution » par rapport à la stratégie d'équilibre n'est donc plus lié à des erreurs de choix. Reste la question des choix de contributions sous optimales. Si les individus choisissent volontairement des contributions supérieures à la contribution d'équilibre, pourquoi ne choisissent-ils pas la pleine coopération, qui serait collectivement plus profitable ? Cette question suppose que le problème du passage clandestin n'est plus l'unique facteur explicatif du comportement non coopératif des individus. Il semble donc qu'il soit intéressant de comprendre pourquoi le bien public n'est que partiellement financé dans les jeux de contribution volontaire.

L'auteur propose dans un premier point une explication dans laquelle il modifie la définition de l'optimum de Pareto. Si les individus choisissent de conserver leur richesse au détriment du financement du bien public, la sous optimalité des contributions s'explique par l'aversion des joueurs à contribuer par l'intégralité de leur dotation. Un individu peut avoir saisi l'intérêt de la coopération mais ne souhaite pas investir l'intégralité de sa dotation, de peur d'être le seul à agir ainsi. La diminution dans le temps du taux de contribution serait alors due à la généralisation de ce type de comportements en réponse aux différents niveaux de contributions réalisés sur les périodes précédentes. Partant de cette hypothèse, on suppose donc qu'un bien public peut être financé sans qu'une contribution égale à la totalité de la dotation individuelle soit demandée aux membres du groupe. NEUVEU qualifie cette structure de financement volontaire de bien public un « optimum intérieur ». L'équilibre de NASH est toujours défini par une contribution nulle (c'est la stratégie dominante de sous jeu) ; en revanche, l'optimum de Pareto ne sera atteint que si les individus choisissent de contribuer par une partie de leur dotation.

Intégrer un optimum intérieur ouvre un problème de coordination des décisions individuelles. Une règle logique de décision de contribution, permettant d'atteindre le financement efficient, est que chaque joueur contribue par une part équivalente du montant requis. Dans ce cas, l'optimum de Pareto dit « symétrique » est atteint. Toutefois, si un joueur cotise moins que cette somme et qu'un autre individu cotise proportionnellement plus que cette somme, le bien public est également efficacement financé, et le résultat constitue également un optimum de Pareto mais « non symétrique ». Là, réside le problème de coordination des décisions individuelles pour atteindre le point optimal symétrique. Comprendre pourquoi les individus rencontrent ce problème de coordination et quelles motivations les conduisent à contribuer plus que la part équivalente qui leur assure un paiement Pareto optimal symétrique est rendu possible.

NEUVEU a fait recours à une comparaison expérimentale de deux jeux qui diffèrent selon leur niveau d'optimum. Dans le premier cas, le financement efficient du bien public est obtenu lorsque 30% de la dotation agrégée du groupe est cotisée ; dans le deuxième cas, le financement efficient est atteint avec 70% de la dotation agrégée. L'analyse des résultats de l'expérience met en évidence les conclusions suivantes. Concernant le problème des choix sous optimaux des individus, l'auteur conclut qu'une éventuelle mauvaise compréhension des règles de l'expérience est exclue. Les joueurs contribuent volontairement avec des montants positifs inférieurs à la contribution optimale (des sur-contributions sous optimales). De plus, selon la définition des optima testés (30% ou 70%), les individus n'ont pas un comportement de contribution identique. Le taux de financement du bien public se trouve amélioré dès que le point optimal se rapproche de la contribution d'équilibre. Enfin, les résultats obtenus permettent de comprendre comment les joueurs établissent leur choix de contribution. Voyons maintenant comment l'expérience conçue par NEUVEU a pu générer ces résultats.

2-2-1- Comparaison entre deux optima intérieurs

Afin de savoir d'une part, si une modification de la définition de l'optimum de Pareto influence le comportement de contribution des joueurs et, d'autre part, si les erreurs de contributions sont intentionnelles ou résultent d'un choix individuel délibéré, deux traitements ont été réalisés au cours de cette expérimentation.

Le financement efficient du bien public a été défini à 30% et 70% de la dotation agrégée du groupe^3(*)9. Ainsi la distance du premier optimum par rapport à l'équilibre se trouve égale à 30% de la dotation et la distance par rapport à la pleine contribution assure le complément de la dotation de 70%. Le deuxième optimum se définit alors logiquement comme le symétrique par rapport à 50% ; c'est à dire à 70% de la dotation par rapport à la contribution d'équilibre et à une distance de 30% de la dotation par rapport à la pleine contribution.(voir figure 10 ci-dessous).

Equilibre (0 % ) 50 %

70 % 100 %

Dotation

Equilibre (0 %)

30 % 50 % 100 %

Dotation

Fig 10

3-2-2-2- Détermination des solutions de jeu

2-2-2 Détermination des solutions du jeu.

Quelles que soient les caractéristiques du modèle (OP30 ou OP70)^4(*)0, l'équilibre du jeu est toujours obtenu par la contribution nulle de l'ensemble des membres du groupe. Cette stratégie de passage clandestin est la stratégie dominante du jeu. En revanche, l'optimum de Pareto est obtenu lorsque les individus ne contribuent par qu'une partie et non plus par l'intégralité de leurs dotations comme c'est le cas dans les autres expériences de contribution volontaire.

Il faut alors pouvoir différencier l'optimum de Pareto dit « symétrique », qui assure un paiement équivalent entre les membres du groupe, et l'ensemble des combinaisons de contributions qui assurent un financement également efficient du bien public mais qui sont des optima de Pareto « non symétriques ». Considérons le cas OP30 (resp OP70), le bien public est financé dès que la contribution globale du groupe atteint 30% de la dotation agrégée. Ainsi, toutes combinaisons de contributions individuelles permettant d'atteindre 30% des ressources totales du groupe assure une production efficiente de bien public. Avec une dotation individuelle de 10 jetons par période (40 jetons pour la dotation agrégée dans un groupe de 4 individus), le financement efficient du bien public est atteint dès que 12 jetons sont versés par le groupe. Ainsi, toutes combinaisons des contributions des joueurs qui permettent de recueillir 12 jetons se trouvent être un point de l'ensemble qui assure le financement efficient du bien public (optimum non symétrique). En revanche, un seul de ces points (une seule combinaison des décisions de contribution individuelles) est l'optimum de Pareto symétrique. Il s'agit du point défini par une contribution individuelle équivalente entre les joueurs et égale à 30% de la dotation individuelle soit 3 jetons par joueur.

Si tous les joueurs versent une part équivalente au bien public, chaque joueur du groupe obtient le paiement optimal symétrique. Les joueurs n'ont aucun intérêt à dépasser ce niveau de financement car le paiement associé au bien public diminuerait. Dans une telle situation, les joueurs reçoivent un paiement plus faible, à la fois du bien public mais aussi du bien privé (car plus de jetons sont investis dans le bien public). En revanche, chaque individu va être individuellement incité à dévier de la contribution symétrique optimale vers la stratégie de passager clandestin puisque la non contribution constitue la stratégie dominante. Ainsi, toute déviation unilatérale vers la contribution nulle aura pour effet d'augmenter le paiement du joueur déviant mais de diminuer le paiement des autres membres du groupe (car moins de jetons sont investis dans le bien public). Si chaque joueur suit ce raisonnement, il y aura convergence vers l'équilibre.

Le paiement maximum d'un joueur survient si ce joueur ne paye rien pour le financement du bien public et si dans un même temps, les autres membres du groupe assurent à eux seuls le financement complet du bien public. Par exemple^4(*)1, dans la condition OP30, le joueur passager clandestin profite du paiement maximum du bien privé (950 jetons) et du paiement maximum du bien public (607 jetons), soit un gain total de 1557 jetons. Les 3 autres joueurs auront un gain (1177 jetons, dont 607 du bien public et 577 du bien privé) moins important que le paiement à l'optimum « symétrique » (gain total de 1272 jetons par individu). Les joueurs coopérateurs auront une incitation plus forte à dévier de cette position puisqu'elle ne leur assure pas le paiement collectif optimal.

Une telle situation est cependant peu envisageable. Si un joueur agit comme passager clandestin, les autres joueurs du groupe n'ont aucun intérêt individuel à tenter de compenser cette défection par une augmentation de leur propre contribution au bien public. En effet, le paiement associé à une situation de sous financement du bien public est préférable au paiement associé à une situation de financement optimal mais asymétrique.

Au cours de l'expérience les individus n'ont donc aucun intérêt à dépasser la contribution symétrique optimale (i.e. 30 ou 70% de leur propre dotation). Sous l'hypothèse que les joueurs versent des sommes positives afin de signaler aux autres leurs intentions de coopérer, une contribution plus importante que la contribution symétrique optimale n'aurait pour effet que d'inciter les autres membres du groupe à diminuer leur contribution. Si cette hypothèse du signalement des intentions de coopération est vraie, les joueurs doivent contribuer des montants compris entre 0 et la contribution symétrique optimale (3 ou 7 jetons selon le traitement). Toute contribution au-dessus de la contribution symétrique optimale doit donc théoriquement être interprétée comme une erreur de compréhension du jeu.

A l'équilibre, le paiement individuel par période est de 950 jetons pour le traitement OP30 et de 300 jetons pour le traitement OP70. A l'optimum symétrique, ce paiement augmente à 1272 jetons pour le traitement OP30 et à 639 jetons pour le traitement OP70. La comparaison de ces deux traitements permet de mettre en évidence la sensibilité du financement efficient du bien public au niveau prédéfini de l'optimum. Fixer un optimum à 30%, plutôt qu'à 70%, conduit-il les individus à contribuer plus efficacement au bien public ?

2-2-3-Protocole expérimental

NEUVEU a réalisé son expérience au cours du printemps 2000 et a réuni un total de 60 étudiants en DEUG Sciences Economiques, répartis aléatoirement en 15 groupes de 4 joueurs. Ces groupes conservent la même composition au cours des différentes périodes et des différents traitements (pas de brassage des joueurs). Sur ce total de 15 groupes, 8 participent à l'expérience OP30 et 7 groupes participent à l'expérience OP70.

A leur arrivée sur les lieux de l'expérimentation, chaque étudiant tire au sort un numéro qui lui désigne sa place. A aucun moment les étudiants ne peuvent avoir accès à une quelconque information concernant leur numéro de groupe. Ainsi les participants ne savaient pas avec qui ils étaient en interaction.

Les décisions sont prises sur PC et l'expérience est gérée grâce au logiciel REGATE^4(*)2 . Seules les instructions sont distribuées sur papier et lues à voix haute par l'expérimentaliste. Il est précisé aux sujets que la rémunération en monnaie liquide s'effectuera à la fin de l'expérience, sur la base de leur gain cumulé au cours du jeu. Le taux de conversion appliqué est de : une unité monétaire pour 700 jetons dans la condition OP-30 et une unité monétaire pour 300 jetons dans la condition OP70. Les gains sont payés aux sujets de manière privée.

Chaque traitement comporte 20 périodes de décision et les sujets disposent d'une dotation de 10 jetons au début de chaque période. Durant l'expérience, les joueurs ne sont pas autorisés à communiquer. A la fin de chaque période, les joueurs disposent des informations suivantes réunies dans un tableau récapitulatif continuellement disponible à l'écran : le numéro de la période en cours, le montant de la dotation individuelle, leur choix individuel de contribution au cours des périodes passées, la somme des contributions du groupe pour chaque période (sans connaître le détail des contributions individuelles), ainsi que leurs gains individuels issus de chacun des deux biens, leur gain total de la période et leur gain cumulé en jetons depuis le début de l'expérience.

Nous allons à présent mettre en lumière quelques analyses faites par l'expérimentateur dans le but de tester les hypothèses posées au début.

2-2-4-Le rôle du niveau de l'optimum sur le comportement

individuel

L'objectif est de pouvoir isoler le comportement de contribution associé à la définition de l'optimum de Pareto symétrique.

- Différenciation des comportements de groupe

Lorsque le jeu de contribution volontaire définit un optimum intérieur, l'analyse des comportements agrégés doit s'effectuer sur deux variables distinctes qui se confondent lorsque les solutions des jeux de contribution volontaire sont en coin. Il s'agit du taux de contribution et du taux de financement du bien public. Dans le premier cas, il s'agit de la contribution au bien public faite par les joueurs, dans le second, il s'agit de la part du financement efficient du bien public atteinte par ce niveau de contribution.

Les résultats présentés révèlent les différences de comportement associées à chaque traitement.

- La contribution au bien public

Afin d'analyser les conséquences du niveau de l'optimum sur le comportement de contribution, NEUVEU procède à la comparaison des niveaux de contribution moyens réalisés par les joueurs dans chacun des traitements. Le graphique 1 met en relation l'évolution des taux de contribution moyens pour les groupes de chaque traitement. Les moyennes sont calculées par période pour chaque traitement sur les 32 (ou 28) joueurs^4(*)3 constituant les différents groupes d'un même traitement.



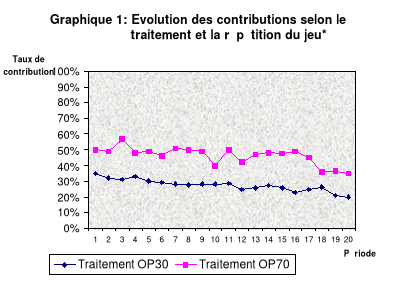
Observation 1 : Plus le niveau de financement efficient du bien public est haut,

plus la contribution moyenne des sujets est élevée.

On remarque que les joueurs contribuent significativement au bien public dans chacun des traitements étudiés. La moyenne des contributions, sur l'ensemble des périodes et des groupes, est de 2,68 jetons (écart type 1,84) pour le traitement OP30 et de 5,24 jetons (écart type 2,56) pour le traitement OP70. Un test unilatéral de Wilcoxon Mann Whitney a été effectué sur les contributions moyennes des joueurs de chaque groupe. L'hypothèse nulle d'équivalence des contributions moyennes des groupes entre les traitements est rejetée au seuil de 1%. La conclusion donc est que la contribution moyenne des sujets est plus forte sous OP70 que sous OP30.

Observation 2 : Le niveau de l'optimum n'a pas de conséquences sur la stabilité

du comportement de contribution entre les groupes.

Après cette dernière conclusion, l'auteur s'est attaché à vérifier les différences de contribution inter-groupes entre les traitements. Les écarts de contributions entre les groupes dans un même traitement sont-ils sensiblement différents des écarts de contributions entre les groupes pour un autre traitement ? Afin de vérifier cette hypothèse, on calcule l'écart absolu moyen des contributions des groupes du traitement OP30 par rapport à leur contribution moyenne (2,68) ainsi que l'écart absolu moyen des contributions des groupes du traitement OP 70 par rapport à leur contribution moyenne (5,24). Au seuil 1%, un test bilatéral de Wilcoxon Mann Whitney appliqué à ces mesures accepte significativement l'hypothèse nulle d'une équivalence des écarts de contribution entre les traitements. Il apparaît donc que les comportements de contribution inter-groupes sont équivalents entre les traitements.

Observation 3 : Les écarts des contributions entre les membres d'un même

groupe augmentent avec la définition du niveau optimal.

Toujours dans le cadre d'analyse des contributions, on s'intéresse à présent au problème des différences de contribution à l'intérieur d'un même groupe. NEUVEU a commencé par supposer que la différence des contributions dans un même groupe est fortement dépendante de la définition du niveau de financement optimal du bien public. Pour tester cette hypothèse, l'auteur envisage deux mesures. La première, est une analyse des écarts types des contributions sur l'expérience à l'intérieur d'un groupe de joueurs. La seconde, est la mesure de stabilité des décisions des groupes. Cette dernière se calcule comme la moyenne des changements absolus de contribution pour un individu d'une période à la suivante sur l'ensemble de l'expérience. La mesure de stabilité du groupe est la moyenne des stabilités individuelles pour chaque groupe.

Un test unilatéral de Wilcoxon Mann Whitney rejette, au taux d'erreur de 1%, à la fois l'hypothèse nulle supposant une équivalence des écarts types des contributions entre les traitements et l'hypothèse nulle d'équivalence entre les mesures de stabilité de décision entre les traitements. Avec un écart type global de 1,84 pour OP 30 et un écart type global de 2,56 pour OP 70, nous pouvons en conclure que les contributions des joueurs changent plus lorsque le niveau de financement optimal est haut. Ce constat est renforcé par le calcul de la stabilité des décisions individuelles puisque la stabilité moyenne des décisions est de 0,78 sous OP 30 alors qu'elle est de 1,41 sous OP 70.

Ces premiers résultats mettent en évidence une différence de contribution associée à chaque niveau Pareto optimal. Il reste à déterminer dans quelle mesure ces différences de comportement affectent le financement efficient du bien public.

2-2-5-Taux de financement et convergence vers un niveau

intermédiaire

Afin de savoir si l'un des deux traitements permet d'atteindre plus fréquemment le niveau de financement efficient, l'expérimentateur s'intéresse aux taux de financement du bien public pour chaque traitement. Le taux de financement se définit comme le ratio entre la somme versée par l(es)'individu(s) et la contribution optimale pour une période donnée. Ce taux de financement est analysé au niveau individuel et au niveau agrégé.

La première analyse porte sur l'évolution du taux de financement sur les 20 périodes de l'expérience pour chaque traitement. Cette analyse conclut que le taux de financement est plus important sous le traitement OP 30 que sous le traitement OP 70. D'autre part, avec la répétition du jeu, il semble que les écarts de financement entre les deux traitements se réduisent et que le taux de financement converge autour de 80% de l'optimum.

Observation 4 : Sur le premier tiers de l'expérience, le taux de financement est plus important lorsque le niveau optimal est bas.

Observation 5 : Sur les deux derniers tiers de l'expérience, il n'y a pas de différence de taux de financement entre les deux traitements.

Afin d'analyser la convergence des taux de financement entre les deux traitements, NEUVEU considère les écarts absolus des taux de financement entre OP 30 et OP 70. Pour repérer un éventuel changement de ces écarts, un test du changement de point est appliqué à ces mesures sur l'ensemble des 20 périodes. Au seuil 1% l'hypothèse nulle d'invariance des écarts de taux de financement est rejetée. Le calcul du test révèle que le changement s'effectue à la sixième période de jeu. Il existe donc une différence des écarts des taux de financement entre ces deux traitements. La sixième période constitue un point de rupture dans l'évolution de ces écarts. Il s'agit donc à présent de comparer les taux de financement moyens de chaque traitement avant et après cette période de rupture. Sur chacun de ces sous-ensembles (avant et après la 6ème période), l'objectif est de savoir si les taux de financement moyens des groupes sont propres à chaque traitement. En d'autres termes les écarts de financement entre les groupes d'un même traitement sont-ils sensiblement différents des écarts de financement entre les groupes pour un autre traitement ? Sur les périodes 1 à 6, un test bilatéral de Wilcoxon Mann Whitney appliqué à ces mesures rejette significativement à 1% d'erreur l'hypothèse nulle d'une équivalence des taux de financement entre les traitements. Avec un taux de financement moyen de 106% pour le traitement OP 30 contre 80% pour le traitement OP70 (l'analyse du graphique 1 donne aussi le même résultat). Il est donc évident de conclure que sur le premier tiers de l'expérience, le taux de financement est plus élevé lorsque le niveau optimal est faible.

Au contraire, sur les données de la fin de l'expérience (de la période 7 à la période 20), ce même test de Wilcoxon Mann Whitney accepte l'hypothèse nulle d'une équivalence des taux de financement entre les deux traitements. Avec une moyenne de financement à 82% pour le traitement OP 30 et une moyenne de 73% pour le traitement OP 70, il est acceptable de conclure qu'après le premier tiers de l'expérience, le taux de financement du bien public tend à converger vers 80%, quel que soit le traitement retenu.

2-2-6- Décisions individuelles et hypothèse d'erreur

Après avoir conclu que les différentes définitions du niveau optimal ne semblent pas influencer l'émergence de comportements extrêmes, NEUVEU a essayé de savoir si les décisions qui ne sont pas à l'optimum sont dues seulement aux erreurs associées à ces décisions.

Observation 6 : La décision de contribution sous optimale des joueurs ne sont ni la conséquence d'erreurs de compréhension, ni la conséquence d'une décision aléatoire.

Afin de différencier les contributions associées à des erreurs de compréhension de la part des individus, des contributions volontairement effectuées, l'auteur a comparé le nombre de contributions observées au-dessus de la contribution symétrique optimale au nombre de contributions en dessous de la contribution optimale symétrique. Si l'on retient l'hypothèse que les individus n'ont pas compris le but de l'expérience et que leurs contributions peuvent provenir d'erreurs, le nombre de contributions en dessous de l'optimum devrait être équivalent au nombre de contributions au-dessus de cet optimum. Pour chaque traitement un test bilatéral du ² est appliqué suivant l'hypothèse nulle que la distribution des contributions est symétrique autour de la contribution symétrique optimale. Cette hypothèse est rejetée au taux d'erreur de 1%. Ainsi, puisque les décisions en deçà de la contribution symétrique représentent respectivement 64,4% pour OP 30 et 82,08% pour OP 70, il est évident de conclure que les décisions des joueurs ne sont pas la conséquence d'erreurs de compréhension ou de décisions aléatoires.

Observation corollaire 7 : En jeu de contribution volontaire, les « sur

contributions » des individus par rapport à l'équilibre

sont des décisions intentionnellement sous optimales.

A partir des observations 1 et 6, nous pouvons déduire que les joueurs contribuent volontairement par des sommes positives au bien public mais que ces sommes sont plus souvent sous optimales que sur optimales.

Arrivant à ce stade^4(*)4, nous pouvons déjà conclure que l'expérimentateur à pu, en utilisant aussi bien le langage de la théorie des jeux que la technique expérimentale, trouver une explication convaincante au problème des contributions volontaires des individus dans le cas des financement des biens publics. Cette expérience en optimum intérieur a permis de révéler certain nombre de caractéristiques associées au comportement de contribution volontaire agrégé des individus. Le taux de contribution est fortement dépendant du niveau de financement efficient du bien public. Plus cet optimum est élevé, plus les contributions des joueurs sont importantes. Pourtant, ce fort taux de contribution doit être relativisé. Lorsqu'on s'intéresse au taux de financement du bien public, il apparaît que les conditions d'optimum faible assurent un financement plus efficient du bien public. D'autre part, quel que soit le niveau optimal, la répétition du jeu fait converger les taux de financement à environ 80% après un tiers des répétitions du jeu. Par ailleurs, compte tenu des distributions de choix des individus, l'hypothèse d'erreur de choix de contribution pour chacun des traitements effectués au cours de l'expérience est rejetée.

Conclusion :

Dans ce chapitre nous avons essayé de mettre en lumière le rapprochement qui s'est réalisé entre l'économie expérimentale et la théorie des jeux. En effet, nous avons montré qu'il y avait (depuis leur naissance) une sorte de consentement entre d'un côté l'expérimentateur, qui a vu dans la théorie des jeux un outil capable de fournir un éclairage différent et intéressant sur les problèmes posés par la microéconomie traditionnelle, la théorie des jeux a surtout fait apparaître de nouveaux problèmes, et de l'autre côté le théoricien des jeux qui s'est convaincu de la pertinence du laboratoire comme environnement acceptable pour la validation des théories existantes ainsi que pour le développement de nouvelles théories (rapprochées de plus en plus de la réalité humaine).

Dans la première section nous avons développé une approche historique et méthodologique. Cette dernière nous a permis de conclure que dès leur naissance, la théorie des jeux et l'économie expérimentale ont été amené à ce développer conjointement. Cependant, nous avons avancé deux explications différentes pour la justification de ce développement parallèle. La première prône pour un développement naturel tandis que la deuxième voie que c'est le passage d'une interprétation mathématique ou « instrumentale-normative » de la théorie des jeux à une interprétation « descriptive-prédictive » de celle-ci qui en est la cause.

Dans la deuxième section, nous avons présenté deux exemples concrets des expériences réalisées grâce à l'union entre le langage de la théorie des jeux et les techniques expérimentales.

CONCLUSION GÉNÉRALE

Nous avons voulu, à travers ce travail de recherche, répondre aux interrogations suivantes :

- Qu'est ce que l'économie expérimentale ?

- Quel est son projet ?

- Quel est son champ d'utilisation ?

- Sachant que la théorie des jeux est un des champs d'application les plus développés par les expérimentalistes, comment peut-on expliquer ce rapprochement fructueux ? ou alors est-il, seulement, fortuit ?

- Quel est l'intérêt de l'économie expérimentale comme méthode de production de données comportementales comparativement aux méthodes habituellement utilisées en théorie des jeux ? et comment pouvons-nous, à travers les jeux expérimentaux, prouver la validité ou non d'une théorie ?

Au terme de ce travail, nous pouvons conclure que :

L'économie expérimentale est devenue un outil bien établi pour la recherche économique. Le fait que l'économie est mise en laboratoire permet, aux théoriciens, de tester, de valider, ainsi que de faire apparaître des régularités empiriques dans des situations économiques encore mal théorisées. Ces facultés viennent du fait que l'expérimentation économique présente l'intérêt de mesurer ou de contrôler des éléments non observables et donc mal théorisés par d'autres méthodes. En outre, un des éléments les plus importants, rendant le travail au laboratoire si productif, est le fait que cette méthode n'est reliée à aucun espace de données quelconque, puisque l'expérimentateur génère ses propres données ce qui lui permet de tester des hypothèses précises. Un autre point positif en faveur de l'économie expérimentale est la replicabilité et le parallélisme des résultats expérimentaux ce qui permettra aux économistes-expérimentateurs d'avoir une conviction commune sur la validité ou non d'une quelconque théorie. En plus de cet apport théorique, l'économie expérimentale joue un rôle important en matière de politique économique, elle permet, en effet, de tester l'efficacité relative des politiques privées ou publiques alternatives.

Ceci dit, nous pouvons affirmer que, outre ces avantages d'ordre scientifique et pratique, l'économie expérimentale se présente comme outil pédagogique avec excellence. Elle facilite le contact (qui est toujours difficile) des étudiants avec la théorie microéconomique. On peut l'assimiler au même rôle que joue l'expérience dans l'enseignement de la physique. La difficulté, due à la plus ou moins grande conceptualisation des phénomènes étudiés, peut être-partiellement- levée grâce à la participation des étudiants à des expériences de laboratoire, mettant, par ceci, en évidence le rôle de la formalisation.

D'un autre côté, nous pouvons dire que si réussite il y a dans travaux expérimentaux c'est grâce à l'utilisation de la part des expérimentateurs d'un langage aussi simple et claire que celui de la théorie des jeux. Le développement de la théorie des jeux a rendu possible, pour les expérimentateurs, de rendre compte de certains phénomènes auparavant inobservables. Mais le développement même de cette discipline n'est et ne sera possible que grâce ou recours au laboratoire. ROHT explique cette idée en disant que :

« si nous ne progressons pas dans l'adjonction à la théorie des jeux de fondements empiriques solides, autrement dit si au contraire nous continuons à recourir à la théorie des jeux principalement en essayant d'obtenir des avancées conceptuelles (aussi profondes et satisfaisantes puissent-elles être), il est probable que, bien avant un siècle, la théorie des jeux connaîtra des rendements nettement décroissants. A cet égard, je pense que les cent prochaines années apportent vraisemblablement un changement dans la relation entre le travail théorique et le travail empirique en Economie en général, et que, dans le cas contraire, l'Economie tout entière pourrait bien ne pas porter tous ses fruits^1(*) ».

Ceci veut dire qu'il est préconisé d'avoir un développement parallèle de la théorie des jeux et des travaux expérimentaux.

En suivant le programme de recherche esquissé par ROTH, nous nous mettant devant une problématique. Il s'agit selon BULTER que « En choisissant d'étudier l'économie à travers la voie expérimentale, nous nous trouverons obligés de développer des modèles ayant un caractère de plus en plus comportemental^2(*)» et avec toute leur complexité. Et c'est cette complexité de la vie humaine qui pose problème, ainsi dans la plupart des expériences conçues jusqu'à présent il y a dominance d'une seule suggestion (dans le cas d'invalidité d'une théorie) à savoir que « la théorie standard a oublié une chose »^3(*) (on dit par exemple que le phénomène d'aversion d'inégalité est occulté dans tel ou tel cas), l'expérimentateur ne peut pas dire plus. Autrement dit on ressent une difficulté d'incorporation des facteurs exogènes dans les modèles standard^4(*).

La plupart des économistes-expérimentateurs pensent que la solution se trouve dans un compromis et une collaboration avec la psychologie cognitive et celle évolutionnaire. C'est à travers cette union, pensent-ils, qu'on pourra réconcilier les suppositions de la théorie économique à l'évidence empirique. il y a même ceux qui sont allés plus loin en incorporant les théories de l'imprécision et de l'erreur.

Cet appel à la collaboration entre économistes et psychologues est ressenti par l'attribution du Prix Nobel en Sciences Economiques 2002 à un économiste (Vernon SMITH) et un psychologue ( KAHNEMAN). Ceci veut dire que les mobiles du comportement économique ne se réduisent pas tous au simple argument de la défense de l'intérêt personnel ; bien d'autres ressorts psychologiques sont à l'oeuvre.

Alors que la main invisible d'Adam SMITH renvoie une image simple et dépouillé de la défense de l'intérêt personnel, l'économie expérimentale, en rendant (partiellement) visible les comportements économiques, ouvre la voie à la constitution d'une économie du comportement dans laquelle la défense de l'intérêt personnel peut se révéler sophistiquée.

Table des matières

INTRODUCTION..........................................................................................	4
CHAPITRE I : L'ÉCONOMIE EN LABORATOIRE..............................................	8

10

SECTION I : APERÇU SUR L'ÉCONOMIE EXPÉRIMENTALE............................

1-1- DÉFINITION.................................................................................	10
1-2- LA MÉTHODE EXPÉRIMENTALE.......................................................	11
1-3- LA BONNE EXPÉRIENCE..................................................................	16
1-4- CHAMP D'APPLICATION..................................................................	17
1-4-1-LES THÉORIES DU CHOIX INDIVIDUEL..........................................................	18
1-4-2- LA THEORIE DE L'ORGANISATION INDUSTRIELLE DES MARCHES..................	20
1-4-3- LA THEORIE DES INTERACTIONS INDIVIDUELLES.........................................	24
SECTION 2- LE RECOURS AU LABORATOIRE : RAISONS ET OBJECTIONS.........	24
2-1- LES RAISONS DU RECOURS A L'EXPERIMENTATION.........................	24
2-1-1 TESTER LA THÉORIE OU DISCRIMINER ENTRE LES THÉORIES........................	25
2-1-2 DÉTERMINER LES CAUSES D'ÉCHEC D'UNE THÉORIE.................................	25
2-1-3 ETABLIR DES RÉGULARITÉS EMPIRIQUES POUR DE NOUVELLES THÉORIES.......	25
2-1-4 COMPARER LES ENVIRONNEMENTS.....................................................	26
2-1-5 COMPARER LES INSTITUTIONS...........................................................	26
2-1-6 EVALUER LES POLITIQUES ÉCONOMIQUES.............................................	26
2-1-7 CONCEPTION DE NOUVEAUX DESIGNS INSTITUTIONNELS...........................	26
2-2- LES CRITIQUES ADRESSÉES À L'EXPÉRIMENTATION........................	26
2-2-1- LES SITUATIONS RÉELLES SONT PLUS COMPLEXES QUE LES SITUATIONS DU
LABORATORE..............................................................................	27
2-2-2- LE MANQUE DE MOTIVATION AU SEIN DU LABORATOIRE..........................	29
2-2-3- LA MAL COMPRÉHENSION DE LA PART DES SUJETS DE LA SITUATION
ÉTUDIÉE..................................................................................	30
2-2-4-LA MANIPULATION DES SUJETS..........................................................	31
CONCLUSION..........................................................................................	32
CHAPITRE II THÉORIE DES JEUX ET MODÉLISATION DES
INTERRACTIONS INTERINDIVIDUELLES..................................	34
SECTION I. BREF APERÇU SUR LA THÉORIE DES JEUX : NOTIONS DE BASE....	35
1-1- THÉORIE DES JEUX : OBJET............................................................	35
1-2 - DÉFINITION D'UN JEU...................................................................	40
1-3- FORMALISATION GÉNÉRALE DES JEUX...........................................	41
1-3-1-LES JEUX SOUS FORME STRATÉGIQUE...............................................	42
1-3-2-LES JEUX SOUS FORME EXTENSIVE...................................................	44
1-4- TYPOLOGIES DES JEUX .................................................................	48
1-4-2-TYPOLOGIE 1 : JEUX EN TERME DE GAIN.............................................	48
1-4-2-TYPOLOGIE 2 : JEUX ET COOPÉRATION .............................................	49
SECTION-2- FORMALISATION ET ANALYSE DES JEUX NON COOPÉRATIFS ET
DES JEUX COOPÉRATIFS.................................................	54
2-1-LES JEUX NON COOPÉRATIFS.........................................................	54
2-2-LES JEUX COOPÉRATIFS................................................................	57
2-3- CONCEPTS DE SOLUTION DES JEUX................................................	61
2-3-1-JEUX NON COOPÉRATIFS...............................................................	64
2-3-2- JEUX COOPÉRATIFS....................................................................	72
2-3-2-1- LA SOLUTION DE VON NEUMANN ET MORGENSTERN....................	74
2-3-2-2- LE NOYAU......................................................................	75

78

80

82

2-3-2-3- LA VALEUR DE SHAPLEY.....................................................

	76
CONCLUSION	74
CHAPITRE III : LA THÉORIE DES JEUX AU LABORATOIRE..............................
SECTION I : RAPPROCHEMENT ENTRE LA THÉORIE DES JEUX ET
L'ÉCONOMIE EXPÉRIMENTALE.................................................
1-1 DE LA THÉORIE DES JEUX À L'EXPÉRIMENTATION :
APERÇUS HISTORIQUES ET MÉTHODOLOGIQUES...........................	82
1-2- L'INTUITION DERRIÈRE LE RAPPROCHEMENT ENTRE LA
THÉORIE DES JEUX ET L'EXPÉRIMENTATION...............................	87

92

SECTION II- LES JEUX EXPÉRIMENTAUX : UNE DISCUSSION DE CAS.............

2-1- JEUX À DEUX JOUEURS ET À SOMME NON NULLE : UNE ÉTUDE
EXPÉRIMENTALE......................................................................	95
2-1-1 LES CONCEPTS DE SOLUTIONS PROPOSÉS POUR LES JEUX À
DEUX JOUEURS ET À SOMME NON NULLE.............................	96
2-1-2- QUELQUES JEUX EXPÉRIMENTAUX ET LEURS SOLUTIONS
THÉORIQUES.....................................................................	98
2-1-3- DESCRIPTION DE L'EXPÉRIENCE : HYPOTHÈSES, CONDITIONS
DU TRAVAIL ET RÉSULTATS..................................................	100
2-2 : LE FINANCEMENT D'UN BIEN PUBLIC ENTRE L'OPTIMALITÉ
ET LA RECHERCHE D'EQUILIBRE : UNE ÉTUDE EXPÉRIMENTALE...	106
2-2-1- COMPARAISON ENTRE DEUX OPTIMA INTÉRIEURS..................	110
2-2-2- DETERMINATION DES SOLUTIONS DU JEU.............................. 2-2-2-PROTOCOLE EXPÉRIMENTAL..................................................	111 113
2-2-3-LE RÔLE DU NIVEAU DE L'OPTIMUM SUR LE
COMPORTEMENT INDIVIDUEL.............................................	115
2-2-4-TAUX DE FINANCEMENT ET CONVERGENCE VERS UN
NIVEAU INTERMÉDIAIRE...................................................	118

122

123

127

129

139

2-2-5- DÉCISIONS INDIVIDUELLES ET HYPOTHÈSE D'ERREUR............

	120
CONCLUSION.........................................................................................
CONCLUSION GENERALE............................................................................
TABLE DES MATIERE.................................................................................. BIBLIOGRAPHIE..........................................................................................
ANNEXES....................................................................................................

BIBLIOGRAPHIE

ALLAIS M. (1953), « le coFmportement de l'homme rationnel devant le risque : critiques des postulats et axiomes de l'école américaine », économétrica, n°21, p. 503- 546.

ANDREONI J. (1995), « Coopération in Public Goods Experiments : Kindness or Confusion », American Economic Review, 85 (4), 891-904.

AUMANN R.J. (1974), « Subjectivity and Correlation in Randomized Strategies », Journal of Mathematical Economics, 1, p. 67-96.

AUMAN J. R. (1987), Game theory, the new Palgrave and dictionnary of economics, edited by Catwell, Migate, Neuman, Vol. 2.

AUMANN R.J., BRANDENBURGER A. (1991), « Epistemic Conditions for Nash Equilibrium », Working Paper, n°91-042, Harvard Business School.

AXELROD R. (1992), Donnant-donnant, théorie de comportement coopératif, Odile jacob.

^BERGSTROM T. C., ^MILLER J. (1997)^{, Experiments with Economic Principles, McGraw-Hill.}

BINMORE K. (1990), « Essays on the fondation of game theory », Oxford, Basil Blackwell.

BINMORE K. (1994), « Game theory and the social contract », Cambridge, MA, MIT Press.

BOISSIN O., RUFFIEUX B. (1996), « L'économie expérimentale », Revue Ingénieur INPG, N°96, 2 juin.

BOLTON G., OCKENFELS A. (2002), « ERC : a Theory of Equity, Reciprocity and Competition », American Economique Review, Novembre, Vol. 92, n°5, p 1125-1155.

BOUDON R. (2002), « Utilité ou rationalité ? rationalité restreinte ou générale ?, Revue d'Economie Politique, 112 (5), Septembte - Octobre.

BUTTER D. ( 1996), « The experimental economics' experiment », Journal of Economic Survey's, vol. 10, n° 3, p.347.

CACHON G.P., CAMERER C.F. (1996), « Loss-Avoidance and Forward Induction in Experimental Coordination Games », Quarterly Journal of Economics, February, 165-194.

CARLSSON H., VAN DAMME E. (1993), « Global Games and Equilibrium Selection », Econometrica , vol. 61, n° 5, Septembre, p. 989-1018.

CASTELLANOS S.G. (1998), « Analysis of Mexico's privatisation mechanisms and loan market regulation », UCLA.

CHAMBERLIN E.H. (1948), « An experimental imperfect market », Journal of Political Economy, 56, p. 95 - 108.

COLMAN A. (1982), Game theory and experimental Games : the study of strategic enteraction, Pergamon Press, USA.

COLMAN A. (1999), Game Theory and its Applications in the Social and Biological Sciences, Londres et New York: Routledge. (Seconde édition corrigée et augmentée- première impression en 1995 chez Butterworth-Heinemann - de Game theory and Experimental Games, 1982, Oxford, Pergamon Press.).

CORDONNIER L. (1997), Coopération et réciprocité, Puf.

DAVIS D., HOLT C.( 1993), Experimental Economics, Princeton NJ, Princeton University Press.

DAY R.H. (1993), « On the origins of experimentation in economics », dans DAY R.H., SMITH V.L, « Experiments in decision, organisation and exchange », Amsterdam, North-Holland,

DE WOLF O. (1998), « Fondements des concepts de solution en théorie des jeux », Annales d'économie et de statistique, N°51, p 2.

DEBREU G., SCARF H. (1966), « théorème de limite sur le coeur d'une économie », Techniques Economiques Modernes, N°5, Gauttier Villars, Paris, p 19-33.

DELOCHE R. (1995), « Expérimentation, science économique et théorie des jeux : Nunc est bibendum », Revue Economique, vol 46, n°3, mai, p. 951 - 960.

EDGEWORTH Y.F. (1881), Mathematical psychics : an assay on the application of mathematics to moral sciences, Kegan Paul, London.

FEHR E., SCHMIDT K. (1999), « A Theory of Fairness, Competition, and Cooperation », Quaterly Journal of Economics, August, 3, p. 769-816.

FLOOD, M.M. (1958), « Some experimental games », Management Science, Vol. 5, p. 5-26.

FOURAKER E.L et SIEGEL S. (1960), Bargaining and group decision making : Experiments in bilateral monopoly, New York, McGraw-Hill.

FREIDMAN W.J. (1979), « Non-cooperative Equilibria for Exit Super games » International Economic Review, Feb. Pp. 147-56.

FRIEDMAN D., SUNDER S. ( 1994), Experimenal methods : A primer for Economists, Cambridge, Cambridge University Press.

GAGEY F., REY P. (1986), « l'Economie expérimentale comme outil pédagogique : Elaboration d'un jeu d'incitation à la micro-économie », Revue Economique, N°1, Janvier.

GARICANO L. (2000), « comment mettre à profit la théorie des jeux », Problèmes Economiques, N° 2653, 23 janvier.

GUERRIEN B. (1999), dictionnaire d'analyse économique, Dunod.

GUTH W. (1998), « Negotiation Rules and Bargaining Behavior - what is known and what need to be further explored ? », Working Paper, Humboldt University of Berlin, Bepartement of Economics.

GUYER. M., PERKEL. B. (1972), Experimental games : a bibliography (1945-1971), Ann Arbor, Mich : Mental Health Research Institute, Communication 293.

HAMBERGER H. (1979), Games as Models of Social Phenomena, San Francisco : W. H. Freeman.

HARSANYI J.C. (1967-1968), « Games with Incomplete Information Played by Bayesian Players », Management Science, 14, p.159- 182, p. 320-334, p. 486-502.

HARSANYI J.C. (1982), « Morality and the theory of rational behavior », dans SEN A.K. et WILLIAMS B., Utilitarianism and Beyond, Maisons des Sciences de l'homme de Cambridge University Press.

HELLWIG C. (2001), « Public Information, Private Information and the Multiplicity of Equilibria in Coordination Games », London

School of Economics. http://econ.lse.ac.uk/phdc/papers/hellwig_jmp.pdf

HEY J.D. (1991), Experiments in Economics, Oxford, Royaume Uni.

ISAAC R.M., WALKER J., THOMAS S. (1984), « Divergent evidence on free riding:an experimental examination of some possible explanations », Public Choice, 43, 113-149.

ISAAC R.M., WALKER J. (1998), « Nash as an Organizing principle in the Voluntary Provision of Public Goods : Experimental Evidence», Experimental Economics, 1 (3), 191-206.

CLIFT J. (2003), « Le Chef du Labo », Finances et Développement, V. 40, N°1, mars.

^KAGEL ^J.^{H., R}OTH A.E^{. (1995), Handbook of Experimental economics, Princeton University Press.}

KAHNEMAN D., TVERSKI A. (1979), « Prospect theory : An analysis of décision under risk », Econometrica, n° 47, p. 263-291

KAJII A., MORRIS S. (1997), « The Robustness of Equilibria to Incomplete Information », Econometrica, p. 1283-1309.

KAJII A., MORRIS S. (1998), « Payoff Continuity in Incomplete Information Games », Journal of Economic Theory, vol. 82, p. 267- 276.

KAST R. (2002), La théorie de la décision, la Découverte, juin.

KESER C. (1996), « Voluntary Contribution to a Public Good When Partial Contribution is a Dominant Strategy », Economic Letters, 50, 359-366.

KREPS M.D. (1999), Théorie des jeux et modélisation économique, Dunod, Paris.

LAKHDAR S.I.B. (1985), Les processus de coordination : Prix, Normes et Ordre Social, Thèse d'Etat en sciences économiques, Aix Marseille III, p 327.

LECOMPTE J. (1999), « La théorie des jeux », Problèmes Economiques, N°2.599, 13 janvier.

LEDYARD J. (1995), « Public Goods : a survey of experimental research», 111-194, dans AE ROTH et J KAGEL (eds.), The Handbook of Experimental Economics, Princeton University Press.

LEMIEUX P. (1999), « L'économie comme science expérimentale », Le Figaro-Economie, 9 avril, P. XI.

LUCE R.D., RAIFFA H (1957), Games and Decisions : Introduction and Critical Survey, New York, wiley.

MAITRE P. ( 2000), « A l'origine de la coopération et de l'altruisme : l'hypothèse de sympathie », Problèmes Economique, N°2693, 20 décembre.

MAMAS P. (2001), Théorie des jeux et jeux expérimentaux : éléments d'histoire et d'épistémologie, Thèse de doctorat en sciences économiques, Décembre, Université Paris I.

MAUROY H. ( 2002), « Equilibre de NASH en stratégies mixtes, critères de classement des loteries et déformation des paiements », Revue Economie Appliquée, N°3, p.91-104.

MORRIS S. (2000), « Coordination, Communication and Common Knowledge: A Retrospective of the Electronic Mail Game », Août. http://www.econ.yale.edu/~smorris

MORRIS S., SHIN H. S. (2001), « Rethinking Multiple Equilibria in Macroeconomics », NBER Macroeconomics Annual, p. 139-161, M.I.T. Press. http://www.nuff.ox.ac.uk/users/Shin/working.htm

MORRIS S., SHIN H. S. (2001), « Global Games: Theory and Applications », Mars, Conference Volume of the Eighth World Congress of the Econometric Society.

MORRIS S., SHIN H.S. (1999), « A Theory of the Onset of Currency Attacks, in Asian Financial Crisis: Causes, Contagion, and Consequences », Septembre, édité par Agenor, Miller, Vines, and Weber, Cambridge University Press.

MOSTELLER F., NOGEE P. (1951), « An experimental measurement of utility », Journal of Political Economy, 59, p 371 - 404.

MOULIN H. (1981), Théorie des jeux pour l'économie et la politique, Hermann, Collection méthodes, Paris, P.245.

MUNIER B. (2001), « Expérimenter en économie ou en gestion», Revue d'Economie Politique, 111, N°1 janvier-fevrier, P.1- 6

NASH J.F. (1950a), « The Bargaining Problem », Econometrica, 18, p. 155-162.

NASH J.F. (1950b), « Equilibrium Points in n-person Games », Proceeding of the National Academy of Sciences fo the USA, 36, P. 48 - 49.

NASH J.F. (1951), « Non-cooperative Games », Annals of Mathematics, 54,p.286 - 295.

NASH J.F. (1999), « My Autobiography », dans Les prix Nobel, The Nobel Foundation, Stockholm.

NASH J.F., KALISH G.K., MILNOR J.W., NERING E.D. (1954), « Some Experimental n-person Games », dans THRALL R.M., COOMBS. Et DAVIS R.L. (eds), Decisions Processes, New York, p. 302

NEMETH C. (1970), Bargaining and reciprocity, Psychological Bulletin, 71, p. 297-308.

NEUMANN J.V., MORGENSTERN. O. (1944), Theory of game and economic behavior, Princeton University Press, Princeton.

NEUVEU M. (2002), « Optimum et financement efficient d'un bien public: une expérience », GATE, Document de travail 02-14, décembre.

NOUSSAIR A., RUFFIEUX B. (2002), « Un enseignement majeur de l'économie expérimentale des marchés : marchés non financiers et marchés financiers s'opposent en matière d'efficacité », Revus Economique, 53(5), p. 1051- 1074.

OSBORNE M., RUBINSTEIN A. (1998), « Games With Procedurally Rational Players », The American Economic Review, Vol. 88, N°4, Septembre, p. 834-847.

PLOTT C., GRAY P. (1990), « The multiple unit double auction », Journal of Economic Behavior and Organisation, 13 (2), p. 245 - 258.

RAPOPORT A., CHAMMAH. A.M, (1965), Prisoner's Dilemma: A Study in Conflict and Cooperation, Ann Arbor, University of Michigan Press.

RASMUSSEN E. (1994), Jeux et information, Basil Blackwell.

RASSENTI S.J., SMITH V.L., WILSON B.J. (2001), « Controling market power and price spikes in electricity networks demand-side bidding », Mimeo, George Masson Universituy.

ROTH A.E. (1979), Axiomatic Models of Bargaining, Berlin, Springer Verlag.

ROTH A.E. (1991), « Game Theory as a part of empirical economics », Economic Journal, January, vol.101, p. 107-114.

ROTH A.E. (1993), « On the early history of experimental economics », Journal of the History of Economic thought, 15, Fall, p. 184-209.

ROTH A.E. (1995), Handbook of Experimental economics, Princeton University Press.

ROTH A.E. (2002), «The Economist as Engineer: Game Theory, Experimental Economics and Computation as Tools of Design Economics », Econometrica, 70, 4, Juin, 1341-1378.

RUBINSTEIN A. (1989), « The Electronic Mail Game: Strategic Behavior Under "Almost Common Knowledge" », American Economic Review, vol. 79, n° 3, Juin, p. 385-391.

RULLIERE J.L. (2000), « L'indétermination et la méthode de Nash », Revue Economique, Vol. 51 N°. 5.

RULLIERE J.L. (2003), « D'Adam Smith à Vernon Smith : la main invisible observée à travers les comportements expérimentaux », Revue d'Economie Politique, N° 3, mai-juin, p. 309-322

SAUERMANN. H., SELTEN R. (1959), « Ein Oligopoleexperiment », Zeitschrift für die Gesamte Staatswissenschaft, vol. 115, p. 427-471.

SCHLENKER B.R., BONOMA T. V. (1978), « Fun and Games : The validity of games for the study of conflict », Jounal of Conflict Resolution, 22, p. 7-38.

SCHOTTER A., SCHWODIAUER G. (1980)., « Economics and the theory of games : A survey », Journal of Economic Literature, vol. XVIII, June, PP. 479-527.

SCHOTTER A., WEISS A., ZAPATER I. (1996), « Fairness and survival in ultimatum and dictatorship games », Journal of Economic Behavior and Economics, vol. 31, p. 745-779.

SEFTON M., STEINBERG R. (1996), « Reward Structures in Public Good Experiments », Journal of Public Economics, 61, 263-287.

SELTEN R. (1965), « spieletheoretische Behandlung eines Oligopolmodells mit Nash-frageragheit », Zeitschrift fur die Gesamte staatswissenschaft, 12, p. 301 -324.

SELTEN R. (1975), « Reexamination of the Perfectness Concepts for Equilibrium Points in Extensive Games », International Journal of Game Theory, 4, p. 25-55.

SHAPLEY L., SHUBIK M. (1967), « Concepts and theories of pure competition », dans « Essays in mathematical economics in honor of Oskar MORGENSTERN, édité par Martin SHUBIK, Princeton University Press, Princeton, p 63-79.

SHAPLEY L., SHUBIK M. (1969), « On market games », Journal of Economic Theory, Juin, p.9-25.

SHMIDT C. (2002), « Sur quelques difficultés d'appréhender les croyances dans l'analyse économique et la théorie des jeux », Revue d'Economie Politique, 112 (5), Sep - Oct.

SHUBIK M. ( 1959), Stratégie et structure de marché , New York: Wiley, Edition française (1964), Dunod, Paris.

SHUBIK M. (1961),« Comments Upon Games as a Teaching Device », in Proceedings of the Conference on Business Games ( avec DILL. W. T., JACKSON. J. R., SWEENEY J. W), New Orleans: Tulane University, 134-135.

SHUBIK M. (1962), « Some Experimental Non-Zero Sum Games With Lack of Information about the Rules » Management Science, Vol. 8, N° 2, January. dans SHUBIK M. (1999), Political economy, oligopoly and exp Games, Edward Elgar, Massachussetts.

SHUBIK M. (1963), Oligopoly Bargaining: The Quantity Adjuster Models, (avec FOURAKER L.E et SIEGEL S), Bargaining Behavior, Hightstown, NJ: McGraw-Hill.

SHUBIK M. (1964), «Experimental Gaming and Some Aspects of Competitive Behavior », New Perspectives in Organization Research, New York: Wiley, 449-463.

SHUBIK M. (1971), « The Dollar Auction Game: A Paradox in Noncooperative Behavior and Escalation », The Journal of Conflict Resolution, 15, 1, 109-111.

SHUBIK M. (1991), Théorie des jeux et sciences sociales, Economica, p 400.

SIEGEL S., FOURAKER L.E. (1960), Bargaining and Group Decision Making, New York : McGraw-Hill .

SMITH V.L. (1962), « An experimental study of market behavior », Journal of Political Economy, p. 111 - 137.

SMITH V.L. (1976), « Experimental Economics : Induced value theory », American Economic Review, Papers and Proceding, p. 275

SMITH V.L. (1982), « What is Experimental economics ? », American Economic Review, April, 72, p. 612-654.

SMITH V.L. (1982), « Microéconomic System as an experimental science », American Economic Review, Papers and Procedings, p. 274-9.

SMITH V.L., SUCHANEK G., WILLIAMS A. (1988), « Bubbles, Crashes ans Endogenous Expectations in Experimental Spot Asset Markets », Econometrica, p. 1119 - 1151.

SMITH V.L. (1989), « Theory, Experiment and Economics », Journal of Economic Perspectives, 3, p, 151 - 169.

SMITH V.L. (1994), « Economics in the laboratory », Journal of Economic Perspectives, 8, p. 113 - 131.

TEDESCHI J.T., SCHLENKER B.R., BONOMA T.V. (1973), Conflict, Power and Games, Chicago, Aldine.

THALER R. ( 1987), « The psychology of choice and the assumptions of Economics », dans ROTH A. E. « Laboratory Experimentation in Economics : six points of view », Cambridge University Press.

THURSTONE L.L. (1931), « The Indifference Function », Journal of Social Psychology Thurstone, 2, 139-167.

VAN DAMME E. (1987), Stability and perfection of Nash equilibria, Springer Verlag.

VERGARA F. (1992), « la concurrence imparfaite : Eléments de théorie des jeux », Cahiers Français, N°254, P. 42..

WALLISSER B. (2002), « les justifications des notions d'équilibre de Jeux », Revue d'Economie Politique, 112 (5), Sep-Oct.

WILLINGER M., ZIEGELMEYER A. (1999), « Non-Cooperative Behavior in Public Goods Experiment with Interior Solution », mimeo, Beta, Université de Strasbourg.

WRIGHTSMAN L.S., O'CONNOR J., BAKER N.J. (1972), Cooperation and Cometition Reading in Mixed-Motive Games, Belmont, Brookes-Cole.



Annexe 1

1- l'apport de SELTEN : l'équilibre parfait en sous-jeu

Il y a « équilibre parfait en sous-jeu » lorsque, dans la séquence de coups constituant le jeu, les joueurs, à chaque coup, donnent une « meilleure réponse » au regard du sous-jeu « pur » restant. On s'aperçoit toutefois immédiatement que lorsque les entreprises effectuent leur choix stratégiques de telle manière qu'aucune des deux ne connaît le choix de l'autre ( par exemple, lorsque leurs choix respectifs s'effectuent simultanément), le concept d'équilibre parfait en sous-jeu devient inopérant, car c'est alors l'ensemble du jeu qui constitue le seul sous-jeu restant et chacun des deux équilibres de Nash est aussi un équilibre parfait en sous-jeu. C'est pour résoudre cette difficulté que SELTEN a formulé en 1975, une analyse encore plus fine de l'équilibre de NASH, avec la théorie des équilibres séquentiellement rationnels dite encore « théorie de la main qui tremble ».

La main qui tremble repose sur l'idée que les joueurs commettent des erreurs au moment de choisir leurs stratégies d'équilibre et ont une probabilité faible, de choisir chacune des stratégies qui ne conduisent pas à la réalisation de l'équilibre. Plus simplement, un équilibre de NASH remplit les conditions de la main qui tremble lorsqu'il implique des meilleures réponses mutuelles même lorsque la main du joueur tremble et que tend vers zéro.

Prenons l'exemple d'une matrice de gain représentant la situation d'un monopoleur (entreprise 2) qui fait face à un nouveau venu (entreprise 1).

Entreprise 2 Entreprise 1	Se battre sur les prix	Ne pas se battre sur les prix
Ne pas entrer sur le marché	(0 ; 8)	(0 ;8)
Entrer sur le marché	(-2 ; -2)	(3 ; 3)

Appliquons la condition précédente au couple de stratégie « ne pas entrer sur le marché, se battre sur les prix ». nous constatons que « se battre sur les prix » ne constitue pas une meilleure réponse pour l'entreprise 2. S'il est possible, avec une probabilité 0, que l'entreprise 1 entre sur le marché, alors l'espérance mathématique de gain procuré par la stratégie « ne pas se battre sur les prix », soit [(1-).8 + 3. ], est supérieure à celle de « se battre sur les prix », soit [(1-).8 - 2.]. les deux stratégies ne promettent la même espérance de gain que lorsque = 0, autrement dit, que lorsque la probabilité que l'entreprise 1 entre sur le marché est nulle. Il s'ensuit que l'équilibre « ne pas entrer, se battre sur les prix » ne satisfait pas aux conditions de la « main qui tremble ». un raisonnement analogue montre qu'en revanche le couple de stratégie « entrer sur le marché, ne pas se battre » permet d'atteindre un équilibre séquentiellement rationnel.

2-l'apport de HARSANYI : le concept de formation des anticipations 

Dans le domaine de la théorie des jeux, l'apport essentiel d'HARSANYI réside dans la prise en compte des phénomènes d'information incomplète. Un joueur dispose d'une information complète lorsqu'il connaît toutes les composantes de la matrice de jeu qui décrit la situation de décision. Le nombre et l'identité des autres joueurs, les gains (ou évaluation des événements) qui leur sont associés. Ainsi, lorsque nous avons discuté le jeu de « monopole -nouveau entrant », ont est parti du principe que les joueurs connaissaient les composantes de la matrice. A partir du moment où un joueur ignore ne serait-ce qu'une de ces composantes, son information est incomplète.

Dans le jeu d'entrée sur un marché dans le tableau précédent (en supposant maintenant qu'il s'agit d'un monopoleur fort c'est que son gain en jouant sa stratégie « se battre sur les prix » est 5 au lieur de -2 lorsque son rival joue sa stratégie « entrer sur le marché » ), on ne peut aucune situation d'équilibre lorsque, par exemple, les gains associés à l'entrée sur le marché ne sont pas connus et le concept d'équilibre ne permet alors aucune prévision relative aux décisions des joueurs. Soit l'entreprise 2, monopoleur « fort », qui a opté, dans ce cas de figure, pour le couple stratégique « entrer sur le marché, se battre sur les prix », à laquelle est associé pour elle, un gain de 5 ; on s'aperçoit que si les gains des deux joueurs étaient égaux, « se battre sur les prix » serait une stratégie faiblement dominante et le couple « ne pas entrer sur le marché, se battre sur les prix » serait alors le seul équilibre de NASH ( qui remplirait aussi les conditions d'équilibre parfait en sous-jeu et celle de la « main qui tremble ») ; quelle stratégie l'entreprise 1 doit-elle adopter ?

Pour donner un commencement de réponse à cette question, HARSANYI a eu l'idée proprement géniale de transformer l'information incomplète en information imparfaite de manière que le jeu considéré puisse être discuté comme si les décisions étaient prises simultanément.

Pour cela, il introduit un joueur supplémentaire, la Nature (ou « joueur 0 »), qui décide si le monopoleur établi - l'entreprise 2- est un monopoleur « faible » (on se trouve alors dans le jeu décrit par la matrice précédente (sans modification) ou « fort » ( matrice modifiée). Bien entendu, l'entreprise 1 ne connaît pas l'arrêt de la Nature sur la force de l'entreprise 2 et elle ne sait pas d'avantage comment l'entreprise réagira à sa propre décision d' «entrée » ou de « ne pas entrer sur le marché ». Autrement dit, l'information de l'entreprise 1 est imparfaite. Dans la mesure où elle ne dispose d'aucune information supplémentaire, l'entreprise 1 part du principe qu'il existe une même probabilité (0,5) que l'entreprise 2 soit un monopoleur « faible » ou, au contraire, un monopoleur « fort », et , sur cette base, elle calcule les gains associés aux stratégie « entrer » et « ne pas entrer sur le marché » en combinant les deux matrice (avant modification et après modification ».

Si, par le passé, l'entreprise 1 a déjà eu l'occasion de constater que l'entreprise 2 avait barré un candidat à l'entrée en pratiquant une guerre des prix acharnée, suivant une logique bayésiènne, elle affectera d'une probabilité supérieure à 0.5 l'hypothèse que l'entreprise 2 est un monopoleur « fort ». d'où l'intérêt, pour un monopoleur « faible », de se forger une réputation de force, susceptible de dissuader, au moins jusqu'à un certain point, les candidats à l'entrée. Mais la fabrication d'une telle réputation à son prix : ici, c'est la différence entre le gain pour l'entreprise 2 aux conditions d'équilibre de la « main qui tremble » dans le jeu précédent, sans modification ( soit donc 3) et son gain, dans le même jeu, pour la stratégie « entrer sur le marché, se battre sur les prix » (-2). Le gain résultant de l'effort consenti pour se bâtir une réputation de force se mesure entre autres à la durée de la période pendant laquelle les candidats à l'entrée sont tenus à l'écart du marché.

Si à l'inverse, il apparaît à l'entreprise 1 que, dans le passé, l'entreprise 2 n'a pas fait obstacle à l'entrée d'un concurrent, elle est en droit de supposer que l'entreprise 2 est un monopoleur « faible » et, par conséquent, toujours selon la même logique bayésiènne, elle affecte d'une probabilité égale à 1 la matrice précédente (sans modification).

ANNEXE 2

L'option X correspond au bien privé et l'option Y au bien public.

Nombre de jetons alloué à l'option Y par l'ensemble du groupe	Gain issu de Y
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40	0 1 9 34 84 156 245 340 429 505 561 595 607 600 576 540 496 447 396 346 298 254 214 178 147 121 98 79 64 51 40 32 25 19 15 12 9 7 5 4 3

Grille des gains*(*) pour OP 30

Nombre de jetons alloué à l'option X	Gain issu de X
0 1 2 3 4 5 6 7 8 9 10	0 95 190 285 380 475 570 665 760 855 950

Grille des gains pour OP 70

Nombre de jeton alloué à l'option Y par l'ensemble du groupe		Gain issu de Y
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40		0 2 8 18 30 46 65 86 109 134 160 188 216 245 274 304 333 361 389 415 440 463 484 503 518 531 541 547 449 547 540 529 512 490 462 429 389 342 289 228 160
Nombre de jetons alloué à l'option X	Gain issu de X
0 1 2 3 4 5 6 7 8 9 10	0 30 60 90 120 150 180 210 240 270 300

* ¹ « experimentation changes the way you think about economics. If you do experiments you soon find that a number of important experimental results can be replicated by yourself and by others. As a consequence, economics begins to represent concepts and propositions capable of being or failing to be demonstrated ».p. 152 dans SMITH V. L. (1989), « Theory, Experiment and Economics », Journal of Economic Perspectives, Vol 3, N°1, p. 151-169.

* ² - A cet égart, le seul déterminant de la réussite des expérimentalistes est leur effort consenti dans ce sens. Comme l'a annoncé EINSTEIN : « [T]his theory is not speculative in origin ; it owes its envention entirely to the desire to make physical theory fit observed fact as well as possible... the justification for a physical concept lies exclusively in its clear and unambiguous relation to facts that can be experienced. » cité dans SMITH. (1989), op. cit. p. 152. Cette déclaration reste valable pour toute science qui se prétend être observationnelle.

* 3 - Voir Chapitre I (section 2) pour les autres raisons justifiant le recours aux techniques expérimentales.

* 4 - RULLIERE J L. (2003), «D'Adam Smith à Vernon Smith : la main invisible observée à travers les comportements expérimentaux, Revue

d'Economie Politique, N° 3, mai-juin, p. 309-322.

* 5 - VON NEUMANN J., MORGENSTERN O. (1944), Theory of Games and Economic Behavior, Princeton, Princeton University Press.

* 6 - THURSTONE L.L. (1931), «  The Indifference Function », Journal of Social Psychology, 2, p. 139-167.

* 7 - ROTH A E. (1993), « On the early history of experimental economics », Journal of the History of Economic thought, 15, Fall, p. 184- 209.

* 8 - DAVIS D. H. 1993), Experimental Economics, Princeton University Press.

* 9 - KAGEL J. H., ROTH A. E. (1995), Handbook of Experimental economics, Princeton University Press.

* 10-  BERGSTROM T. C., MILLER J. (1997), Experiments with Economic Principles, McGraw-Hill.

* 1 - LEMIEUX P. (1999), « L'économie comme science expérimentale », Le Figaro-Economie, 9 avril, P. XI.

* 2 - MUNIER B. (2001), « Introduction : expérimenter en économie ou en gestion », Revue d'Economie Politique, 111, N°1 janvier-fevrier, P.1- 6

* 3 - ROTH A. E. (1991), « Game Theory as a part of empirical economics », Economic Journal, January, vol.101, p. 107-114

* 4 - ROTH A. E. (1991), op. cit, p.107.

* 5 - BOISSIN O., RUFFIEUX B. (1996), « L'économie expérimentale », Revue Ingénieur INPG, N°96, 2 juin.

* 6 - SMITH L. V. (1982), « What is Experimental economics ? », American Economic Review, April, 72, p. 612-654.

* 7 - Vernon leon SMITH de l'université de George Masson en Virginie a été distingué en octobre 2002 par l'attribution du prix Nobel en Sciences Economiques pour avoir fait de l'expérimentation en laboratoire un instrument d'analyse économique empirique, en particulier dans l'étude des différentes structures du marché.

* 8 - LEMIEUX P, (1999), op. cit. P. 11.

* * ce qui est entre les crochets est hors citation.

9 - SMITH V. L. (1982), « Microéconomic System as an experimental science », American Economic Review, Papers and Procedings, p. 274 - 9.

* 10 - DELOCHE R. (1995), « Expérimentation, science économique et théorie des jeux : Nunc est bibendum », Revue Economique, vol 46, n°3, mai, p. 951 - 960.

* 11 - SMITH V.L. (1989), op. cit. Dans ce même article, et dans le but de faire différencier la méthode expérimentale par rapport à l'économétrie, SMITH avance : « In the testes based only on field data, the economist has no independent control over the environment and the institution ; as a result, the process is a composite test of the theory's assumptions about the environment, the institution and agent behavior. If the theory passes the test, it may be because all elements of the theory are `` correct'' or because `` incorrect'' elements of the theory had offsetting effects that could not be identified by the test. If the theory fails, the economist cannot know which of its elements accounted for the falsifying outcome ». p. 154.

* 12 - SMITH V. L. (1994), «  Economics in the laboratory », Journal of Economic Perspectives, 8, p. 113 - 131.

* 13 - SMITH écrit dans SMITH V.L. (1976), « Experimental Economics : Induced value theory », American Economic Review, Papers and Proceding, p. 275 : `` It's necessary to constantly remind ourselves that human activity is diffused and dominated by inconscious, autonomic, neuropsychological systems that enable people to function effectively without always calling upon the brain's scarcest resource : attentional circuity... if it were otherwise no one could get through the day under the burden of self-conscious monitoring and planning every trivial action in detail.'' `` il est nécessaire de se rappeler constamment que l'activité humaine est répandue et dominée par des systèmes inconscients, autonomes et neuropsychologiques qui permettent aux gens de fonctionner efficacement sans toujours faire appel à la ressource la plus rare du cerveau : circuit intentionnel ... si c'était autrement, personne ne pourrait passer le jour sous le fardeau du contrôle embarrassé et la planification de chaque action insignifiante en détail.''

Pour bien éclaircir cette idée, nous pouvons penser à la peine que peut souffrir un client si, au supermarché, il a été exigé pour explicitement évaluer l'utilité de chaque combinaison de dizaines de milliers des articles d'épicerie qui sont faisable pour un budget donné. ( l'exemple est cité dans SMITH. (1994), op. cit, p. 114.

* 14 - RULLIERE J. L. (2003), op. cit, p. 311.

* 15 - SMITH. ( 1976) op. cit, p. 275.

* 16 - SMITH. (1994). op. cit, p. 113-131.

* 17 - Parce que les économistes et les psychologues dirigent parfois des expériences plutôt différentes concernant des phénomènes grossièrement semblable. A titre d'exemple nous pouvons faire la comparaison entre les deux protocoles utilisés par les auteurs des deux articles suivant :

- ALLAIS M. (1953), « le comportement de l'homme rationnel devant le risque : critiques des postulats et axiomes de l'école américaine », économétrica, n°21, p. 503- 546 ( comme économiste).

- KAHNEMAN D., TVERSKY A. (1979), «  Prospect theory : ananalysis of décision under risk », économétrica, n° 47, p. 263-291 (comme psychologue). Il faut noter ici que D. KAHNEMANN a été illustré en l'an 2002 en s'attribuant le prix Nobel en sciences économiques partageant ainsi cette distinction avec V L. SMITH. L'académie Royale des sciences du suède a voulu à travers cette décision, confirmer l'idée selon laquelle les mobile du comportement économique ne se réduisent pas tous au simple argument de la défense de l'intérêt personnel, bien d'autres motifs psychologiques sont à l'oeuvre, comme la pression des groupes sociaux auxquels notre comportement fait référence, l'altruisme et la confiance.

* 18 - ROTH A.E. (1995),  Handbook of Experimental economics, Princeton University Press.

* 19 - BUTTER D. (1996), « The experimental economics' experiment », Journal of Economic Survey's, vol. 10, n° 3, p.347.

* 20 - BINMORE K. (1994), «  Game theory and the social contract », Cambridge, MA, MIT Press. Cité dans BUTTER David (1996), op. cit, p. 349.

* 21 - « Anyone who interacts directly with the subjects should have no personal interest in its outcome » in BINMORE ( 1994 ), op. cit.

* 22 - ROTH A E. (1993), op. cit, p. 184.

* 23 - NEUMANN J.V., MORGENSTERN O. (1944). op.cit.

* 24 - Dans son expérience, THURSTONE a été intéressé par le problème de la détermination ( de manière expérimentale ) de la courbe d'indifférence individuelle. Il a proposé une expérience dans laquelle chaque sujet a été demandé de faire plusieurs choix possibles entre des paquets de différents produits. Ces paquets peuvent contenir soit des chapeaux et des manteaux, soit des chapeaux et des chaussures soit des chaussures et des manteaux. En reportant des données détaillées sur un seul sujet, il a conclu que ces dernières peuvent adéquatement être représentées par des courbes d'indifférence ( hyperboliques).

* 25 - THURSTONE L.L. (1931), op. cit

* 26 - ALLAIS M. (1953). op. cit.

* 27 - ALLAIS s'est inspiré dans son expérience de l'article de MOSTELLER et NOGEE ( MOSTELLER F., NOGEE P. (1951), « An experimental measurement of utility », Journal of Political Economy, 59, p 371 - 404.) dans lequel ils ont conclu que malgré la possibilité de construction, de manière expérimentale, des fonctions d'utilité, les prédictions dérivées de celles-ci ne sont pas assez bonnes comme elles devraient. En effet, dans son expérience, ALLAIS a essayé de prouver expérimentalement que des violations systématiques da la théorie de l'utilité espérée peuvent être observées.

* 28 - DAY R.H. (1993), «  On the origins of experimentation in economics », dans DAY R.H., SMITH V.L, « Experiments in decision, organisation and exchange », Amsterdam, North-Holland, cité par DELOCHE Régis. (1995). op. cit, p. 952.

* 29 - Nous pouvons donner l'exemple suivant :

laquelle des options suivantes préférez-vous ?

gagner surement 30 Dh ; [ 78% ] Les résultats de l'expérience

avoir 80% de chance de gagner 45 Dh [ 22% ]

l'expérience est due à KAHNEMAN et TVERSKY. ( KAHNEMAN D., TVERSKY A. (1979), op. cit. Cité dans THALER R. ( 1987), « The psychology of choice and the assumptions of Economics », dans ROTH A. E. «  Laboratory Experimentation in Economics : six points of view », Cambridge University Press.

* 30- Experiment 1. Imagine that you have decided to see a play, admission to which is $10 per ticket. As you enter the theater you discover

that you have lost a $10 bill. Would you still pay $10 for the ticket to the play?

Yes: 88% No: 12%

Experiment 2. Imagine that you have decided to see a play and paid the admission price of $10 per ticket. As you enter the theater you

discover that you have lost your ticket. The seat was not marked and the ticket cannot be recovered. Would you pay $10 for another

ticket?

Yes: 46% No: 54%

Dans TVERSKY., KAHNEMAN. (1979), op.cit.

* 31 - CHAMBERLIN E.H. (1948), « An experimental imperfect market », Journal of Political Economy, 56, p. 95 - 108.

* 32 - ROURAKER E.L., SIEGEL S. (1960), « Bargaining and group decision making : Experiments in bilateral monopoly » , New York,

McGraw-Hill.

* 33 - Pour plus d'information sur l'Equilibre Economique Général voir LAKHDAR S.I.B. (1985), Les processus de coordination : Prix, Normes et Ordre Social, Thèse d'Etat en sciences économiques, Aix Marseille III, p 327.

* 34 - SMITH V.L, (1962), «  An experimental study of market behavior », Journal of Political Economy, p. 111 - 137.

* 35 - RULLIERE J L. (2003) op. cit, p. 311.

* 36 - Pour plus d'information sur les techniques et le matériel nécessaire à la conception d'un marché concurrentiel :

- PLOTT C., GRAY P. (1990), « The multiple unit double auction », Journal of Economic Behavior and Organisation, 13 (2), p. 245 -

258.

- DAVIS D., HOLT C. (1993), Experimental Economics, Princeton NJ, Princeton University Press.

- FRIEDMAN D., SUNDER S. (1994), Experimenal methods : A primer for Economists, Cambridge, Cambridge University Press.

* 37 - ces auteurs n'ont pas été les seuls à contribuer à l'essors de la l'économie expérimentale des marchés. On peut citer parmi ceux

récemment illustrés : WILLIAMS , HOLT , PLOTT et NOUSSAIR.

* 38 - NOUSSAIR A., RUFFIEUX B. (2002), « Un enseignement majeur de l'économie expérimentale des marchés : marchés non financiers et

marchés financiers s'opposent en matière d'efficacité », Revus Economique, 53(5), p. 1051- 1074.

* 39 - le premier travail établie dans ce sens était de SMITH, SUCHANEK et WILLIAMS ( SMITH V.L., SUCHANEK G., WILLIAMS A. (1988), «  Bubbles, Crashes ans Endogenous Expectations in Experimental Spot Asset Markets », Econometrica, p. 1119 - 1151.

* 40 - RULLIERE J L. (2003), op. cit, p. 317.

* 41 - Ce point, concernant la nature des transactions, constitue une des différences essentielles entre les contributions originelles de CHAMBERLIN (1948) et de SMITH (1962). A l'encontre de CHAMBERLIN, SMITH soutient que les sujets doivent être rémunérés en fonction de leurs décisions et des décisions des agents avec lesquels ils interfèrent : en d'autres termes, il est vain de croire que les comportements observés peuvent avoir du sens lorsqu'ils sont fondés uniquement sur des incitations monétaires fictives. Ceci constitue encore une différence notoire avec les travaux en psychologie expérimentale. Cette condition de rémunération substantielle est primordiale pour faire disparaître ou réduire certaines anomalies expérimentales.

* 42 - Pour de plus amples détails :

- CASTELLANOS S. G. (1998), «  Analysis of Mexico's privatisation mechanisms and loan market regulation », UCLA.

- RASSENTI S.J., SMITH V.L., WILSON B.J. (2001), « Controling market power and price spikes in electricity networks demand-

side bidding », Mimeo, George Masson University.

* 43 - SIEGEL., FOURAKER. (1960) op. cit. p. 72 - 73.

* 44 - SMITH V. L. (1994), op. cit, p. 115.

* 45 - MUNIER B. (2001), « expérimenter en économie ou en gestion », Revue d'Economie Politique, édition spéciale : Economie Expérimentale, Edition Dalloz, N°111, janvier-février.

* 46 - COLMAN M. A. (1982), Game Theory and Experimental Games, Pergamon Press, New York.

* 47 - « When people are put in a simple artificial situation, one might argue, they will behave in ways appropriate to a simple artificial

situation, thereby revealing nothing about How they will behave in a complex real situation », dans HAMBERGER H. (1979), Games as

Models of Social Phenomena, San Francisco : W. H. Freeman. Cité dans COLMAN (1982), op. cit. p. 231.

* 48 - COLMAN A. (1982), op.cit, p 232.

* 49 - « What surprises us most, in our review of research, is that apparently no studies have compaired (behavior) in a laboratory game with (behavior) in different real world tasks. While artificiality can also assessed throught laboratory manipulations, comparaison of behavior accross settings should be undertaken », dans WRIGHTSMAN. L. S., O'CONNOR. J., BAKER. N. J. (1972), Cooperation and Competition : Readings in Mixed-Motive Games, Belmont, Brookes-Cole, p. 227.

* 50 - NOUSSAIR C., RUFFIEUX B. (2002), « un enseignement majeur de l'économie expérimentale des marchés : marché non financiers et

marchés financiers s'opposent en matière d'efficacité », Revue Economique, Mai.

* 51 - TEDESCHI J. T., SCHLENKER B. R., BONOMA T. V. (1973), Conflict, Power and Games, Chicago, Aldine.

* 52 - SCHLENKER B. R., BONOMA T. V. (1978), « Fun and Games : The validity of games for the study of conflict », Jounal of Conflict

Resolution, 22, p. 7-38.

* 53 -- ECU : Experimental Currency Unit.

* 54 - NEMETH C. (1970), Bargaining and reciprocity, Psychological Bulletin, 71, p. 297-308.

* 55 - COLMAN A. (1982), op. cit, p 236.

* NASH J.F. (1999), « My Autobiography », dans Les prix Nobel, The Nobel Foundation, Stockholm, cité dans RULLIERE J.L. (2003), op.cit

* ¹ - LAKHDAR. (1985). op cit.

* ² - « Economist's interest in game theory was prompted by dissatisfaction with the assumption underlying the notion of competitive equilibrium that each economic agent ignores other agents' actions when making choices. Game theory analyses the interaction of agents who ``think strategically'', making their decisions rationally after forming beliefs about their opponents' moves, beliefs that are based on an analysis of the opponents' interests. » p. 834, dans OSBORNE M., RUBINSTEIN A. (1998), « Games With Procedurally Rational Players », The American Economic Review, Vol. 88, N°4, Septembre, p. 834-847

* ³ - SCHOTTER A., SCHWODIAUER G. (1980)., « Economics and the theory of games : A survey », Journal of Economic

Literature, vol. XVIII, June, PP. 479-527.

* ⁴ - Par mot naissance on veut dire l'apparition d'un nouveau outil d'analyse et on précisant de plus notre déclaration, il faut dire que le

travail de J. Von NEUMANN et O. MORGENSTERN a donné naissance à la théorie des jeux coopératifs quand à la théorie des jeux non coopératifs sa naissance est due à un autre nom à savoir J. Forbes NASH. Ainsi Jean Louis RULLIERE ( RULLIERE J L. (2000) « L'indétermination et la méthode de Nash » Revue Economique, Vol. 51 Num. 5 ) déclare : «  Tandis que le programme de la théorie des jeux a connu une rupture entre ses deux fondateurs et John NASH, on peut observer que les travaux postérieurs aux deux contributions de NASH de 1950 entrent dans le cadre des méthodes d'analyse développées par ce dernier et que de Nombreuses avancées apparaissent comme des extensions déjà formalisées, en particulier, dans sa thèse (...) c'est à ce titre que NASH apparaît finalement comme le fondateur de la théorie des jeux non coopératifs.

* ⁵ - GARICANO L. (2000), « comment mettre à profit la théorie des jeux », Problèmes Economiques, N° 2653, 23 janvier.

* ⁶ - VERGARA F. (1992), « la concurrence imparfaite : Eléments de théorie des jeux », Cahiers Français, N°254, P. 42.

* ⁷ - Il y a une autre typologie, il s'agit de celle qui distingue entre :

- Les jeux contre la nature où pour chaque joueur seule compte la réalisation éventuelle d'un événement aléatoire qui ne dépend ni de son propre choix ni de celui des autres ( choix au hasard, jeu de pile ou face).

- Les jeux de société où il y a au moins deux participants actifs dont les choix s'interagissent mutuellement, chacun en étant plus ou moins conscient.

Et c'est ce deuxième genre de jeux qui va intéresser l'économiste et précisément le théoricien des jeux où ce que vont faire les autres devient

un source fondamentale d'incertitude.

* ⁸ - GUERRIEN B. (2002), « Sur la théorie des jeux », http://www.lasavate.org/files/articles/thjeux.htm.

* ⁹ - RASMUSSEN E. (1994), « Jeux et information », Basil Blackwell.

* ¹⁰ - BINMORE K. (1990), « Essays on the fondation of game theory », Oxford, Basil Blackwell.

* ¹¹ - KREPS M. D. (1999), « Théorie des jeux et modélisation économique », Dunod, Paris.

* ¹² - VAN DAMME E. (1987), « Stability and perfection of Nash equilibria, Springer Verlag.

* ¹³ - LUCE R. D., RAIFFA H. (1957), Games and Decisions: Introduction and Critical Survey, New York, Wiley.

* ¹⁴ - OSBORNE M.J.,RUBINSTEIN A. (1995), A course in Game Theory, Cambridge, M.I.T. Press.

* ¹⁵ - COLMAN A. (1982), Game theory and experimental Games : the study of strategic enteraction, Pergamon Press, USA.

* ¹⁶ - AUMAN J.R. (1987), Game theory, the new Palgrave and dictionnary of economics, edited by Catwell, Migate, Neuman, Vol. 2.

* ¹⁷ - LAKHDAR B. (1985), op cit, p. 119.

* ¹⁸ - On peut citer par exemple : AUMANN, HARSANYI, KREPS, NASH, RUBINSTEIN et SELTEN.

* ¹⁹ - On peut citer à cet égard Herbert SIMON et Bernard GUERRIEN.

* ²⁰ - Rymond BOUDON (BOUDON R. (2002), « Utilité ou rationalité ? rationalité restreinte ou générale ?, Revue d'Economie

Politique, 112 (5), Septembte - Octobre ) avance : « Herbert SIMON a notamment assoupli la notion d'optimisation : le sujet social

prend selon lui des décisions plutôt satisfaisantes qu'optimales ; il a insisté sur le fait que l'information étant coûteuse, les décisions

doivent être analysées comme se fondant sur une rationalité limitée » P. 756.

Dans le même sens, Christian SHMIDT (SHMIDT C. (2002), « Sur quelques difficultés d'appréhender les croyances dans l'analyse économique et la théorie des jeux », Revue d'Economie Politique, 112 (5), Sep - Oct) avance que AUMANN a montré dans son article de 1992 intitulé « Irrationality in game theory » sur la base d'un exemple de jeu non coopératif à deux joueurs en forme normale, que chacun des joueurs pouvait effectuer un choix rationnel, sans être obligé de croire que le choix de l'autre joueur le fut également.

* ²¹ - SCHOTTER A., SCHWODIAUER G. (1980). op cit.

* ²² - KREPS D. (1999), op cit.

* ²³ - Nous nous inspirons pour la présentation de ces notions des travaux suivants :

- LAKHDAR B. (1985), op cit.

- SCHOTTER A., SCHWODIAUER G. (1980), op. cit.

- KREPS D. (1999), op cit.

- WALLISSER B. (2002), « Les justifications des notions d'équilibre de jeux », Revue d'Economie Politique, 112 (5), Sep-Oct.

- GUERRIEN B. (1999), Dictionnaire d'analyse économique, Dunod.

- MOULIN H. (1981), Théorie des jeux pour l'économie et la politique, Hermann, Collection méthodes, Paris, P.245.

* ²⁴ - LAKHDAR B. (1985), op. cit.

* ²⁵ - «  Nous pouvons associer au mot jeu, les mots règles, joueurs, mouvements, stratégies, paiements, certains concepts de concurrence et de

coopération, et quelques notions souvent mal définies sur la nature et l'importance de l'information... » SHUBIK M. (1964), Stratégie et

structure des marchés, Dunod, Paris.

* ²⁶ - MOULIN H. (1981), op. cit.

* ²⁷ - LAKHDAR ( dans LAKHDAR B. (1985) op. cit.) définit une stratégie comme un plan qui dit à chaque joueur ce qu'il doit faire dans

chaque circonstance du jeu.

* ²⁸ - Hervé MOULIN (dans MOULIN H. (1981) op. cit.) considère un jeu comme l'objet mathématique formalisant un conflit entre plusieurs

agents ( les joueurs) c'est à dire une situation qu'ils jugent selon des préférences contradictoires et dont ils peuvent influencer certains

paramètres.

* ²⁹ - Voir FREIDMAN W J. (1979), « Non-cooperative Equilibria for Exit Super games » International Economic Review, Feb. Pp. 147-56

cité dans SCHOTTER A., SCHWODIAUER G. (1981), op.cit.

* ³⁰ - l'exemple est de VERGARA F. (1992), op. cit.

* ³¹ - LAKHDAR. B. (1985), op.cit.

* ³² - La chronologie effective n'est importance ici que si elle intervient sur ce qu'un joueur sait à propos de l'action choisie par l'autre. Que

les joueurs choisissent simultanément ou l'un après l'autre, le point essentiel étant que chacun prend sa décision en ignorant ce que

l'autre va faire.

* ³³ - KREPS D. (1999), op. cit. Voir ce même ouvrage pour plus de détails.

* ³⁴ - Le caractère gras est propre à l'auteur.

* ³⁵ - Ce genre de jeux est appelé aussi les jeux strictement compétitifs dans lesquels l'augmentation du bien être d'un joueur implique la diminution du bien être de l'autre. pour plus de détails consulter l'article de SHUBIK M. (1962), « Some experimental non-zero sum games with ladk of information about the rules », Management Science, Vol. 8, N°. 2, January, dans SHUBIK M. (1999), Political economy, oligopoly and exp Games, Edward Elgar, Massachussetts.

* ³⁶ - SHUBIK M. (1964), op. cit.

* ³⁷ - Nous nous limitons ici au cas des jeux qui mettent en présence deux joueurs seulement.

* ³⁸ - cf . supra p. 45.

* ³⁹ - LECOMPTE J. (1999), « La théorie des jeux », Problèmes Economiques, N°2.599, 13 janvier.

* ⁴⁰ - Pourtant il y a communication entre eux. Hervé MOULIN ( MOULIN H. (1981) op. cit) à bien expliquer cette idée en disant que dans les situations non coopératives « les joueurs communiquent entre eux, ne serait-ce que par l'intermédiaire des coups qu'ils jouent et qu'ils s'observent jouer. Ils peuvent aussi échanger directement de l'information, se mettre d'accord sur telle ou telle issue, mais à condition qu'ils ne contractent pas d'accord contraignant : c'est à dire qu'ils vont peut-être convenir de jouer telle stratégie mais que jamais ceci ne constituera un réel engagement : ils n'abdiqueront jamais la moindre parcelle de souveraineté dans le choix de leur propre stratégie ».

* ⁴¹ - LAKHDAR B. (1985), op. cit.

* ⁴² - le concept de sympathie est très souvent évoqué en économie du bien-être comme en économie politique classique, pour expliquer les comportements coopératifs ou altruistes des agents. L'hypothèse de sympathie est définie par Philippe MAITRE ( MAITRE P. ( 2000), « A l'origine de la coopération et de l'altruisme : l'hypothèse de sympathie », Problèmes Economique, N°2693, 20 décembre) comme le fait « d'échanger momentanément son point de vue avec celui d'autrui, sans oublier que ce qui est bon pour les autres n'est pas nécessairement bon pour soi. ». Pour HARSANYI ( HARSANYI J.C. (1982), « Morality and the theory of rational behaviour », dans SEN A.K. et WILLIAMS B., Utilitarianism and Beyond, Maisons des Sciences de l'homme de Cambridge University Press. Cité dans MAITRE P (2000), op. cit ) il s'agit de se « mettre dans les chaussures des autres pur observer le monde de leur point de vue ».

* ⁴³ - LECOMTE Jacques (1999), op. cit.

* ⁴⁴ - Pour de plus amples détails voir RULLIERE J.L. (2000), « L'indétermination et la méthode de Nash », Revue Economique, Vol. 51 N° 5.

* ⁴⁵ - NASH J.F. (1950a), « The Bargaining Problem », Econometrica, 18, p. 155-162.

* ⁴⁶ - Comme le suggère la sémantique, l'équilibre étant redevable aux jeux non coopératifs et la solution aux jeux coopératifs.

* ⁴⁷ - NASH J.F. (1951), «  Non-cooperative Games », Annals of Mathematics, 54, p.286 - 295, cité dans RULLIERE (1999) op.cit, p. 1177.

* ⁴⁸ - GUTH W. (1998), «  Negotiation Rules and Bargaining Behavior - what is known and what need to be further explored ? », Working

Paper, Humboldt University of Berlin, Bepartement of Economics. Cité dans RULLIERE J. L. (1999), op.cit.

* ⁴⁹ - LUCE R. D., RAIFFA H. (1957), op. cit.

* ⁵⁰ - ROTH A.E. (1979), Axiomatic Models of Bargaining, Berlin, Springer Verlag.

* ⁵¹ - AXELROD R. (1992), Donnant-donnant, théorie de comportement coopératif, Odile jacob, 1992.

* ⁵² - CORDONNIER L. (1997), Coopération et réciprocité, Puf cité dans LECOMTE J. (1999), op.cit.

* ⁵³ - LAKHDAR B. (1985), op.cit, p. 129.

* ⁵⁴ - Un jeu inventé pour la première fois par Merrill FLOOD et Melvin DRESHER en 1951, il est formalisée peu après par TUCKER. L'appellation « dilemme de prisonnier » est originaire à ce dernier.

* ⁵⁵ - Nous nous somme inspirés pour la présentation de ce dilemme de : COLMAN A. (1982), op.cit. et MOULIN H. (1981), op cit.

* ⁵⁶ - Dans le jeu ( X₁, ..., X_n, u₁, ..., u_n ) on dit que la stratégie x_i X_i du joueur i domine sa y_i X_i stratégie si on a :

x _i X_î  :   u_i ( y_i , x_î ) u_i ( x_i , x_î )

x _i X_î  :   u_i ( y_i , x_î ) u_i ( x_i , x_î )

La notation ( y_i , x_î ) désignant l'issue ( x_i , ..., x_{î -1}, y_i , x_î+1, ..., x_n )

Dire que la stratégie y_i du joueur i est dominée par sa stratégie x_i revient à dire que quel que soit le choix stratégique des autres joueurs, employer x_i est au moins aussi profitable pour i qu'employer y_i , et que parfois ( pour au moins un (n-1) uple de stratégie des autres joueurs) la stratégie x_i est strictement meilleure que y_i. En d'autres termes, et selon les termes de bernard WALLISER (WALISER B. (2002) op.cit) une stratégie d'un acteur est dite dominée (fortement) lorsqu'il existe une autre stratégie de cet acteur qui lui donne une utilité (strictement) meilleure pour toute les stratégies de ses adversaires.

* ⁵⁷ - Pour de plus amples détails voir MOULIN H. (1981), op.cit.

* ⁵⁸ - CORDONNIER L. (1997), op. cit.

* ⁵⁹ - KAST R. (2002), La théorie de la décision, la Découverte, juin.

* ⁶⁰ - l'exemple est de KREPS D. (1999) op.cit.

* ⁶¹ - MOULIN H.(1981), op. cit p 58

* ⁶² - NASH J. F. (1950b), «  Equilibrium Points in n-person Games », Proceeding of the National Academy of Sciences fo the USA, 36,

P. 48 - 49.

* ⁶³ - MOULIN H. (1981), op.cit.

* ⁶⁴ - l'exemple est tiré de KREPS D. (1999), op.cit p27.

* ⁶⁵ - Hervé MOULIN (dans MOULIN H. (1981), op.cit) présente le Théorème de NASH comme suite : si pour tout i = 1, ..., n les ensembles X_i sont des sous-ensembles convexes et compacts d'un espace vectoriel et si les fonctions d'utilité vérifient :

Pour tout i, i = 1, ..., n, u_i est continue et x_i u_i (x_i , x_î) est quasi-convexe sur X_i

Alors le jeu possède au moins un équilibre non coopératif.

* ⁶⁶ - Pour de plus amples détails voir le travail de MAUROY H. ( 2002), « Equilibre de NASH en stratégies mixtes, critères de classement des loteries et déformation des paiements », Revue Economie Appliquée, N°3, p.91-104.

* ⁶⁷ - WALLISER bernard (2002), op. cit, p 699

* ⁶⁸ - Hervé MOULIN ((1981) op. cit) définit l'optimum de Pareto comme suit :

une issue ( x₁, ..., x_n ) du jeu ( X₁, ..., X_n , u₁, ..., u_n ) est dite dominée par l `issue ( y₁, ..., y_n ) si on a :

i 1, ...,n u_i ( x₁, ..., x_n ) u_i ( y₁, ..., y_n )

i 1, ...,n u_i ( x₁, ..., x_n ) u_i ( y₁, ..., y_n )

on appelle optimum de Pareto une issue qui n'est dominée par aucune autre issue.

* ⁶⁹ - cf. supra p. 55.

* ⁷⁰ - LAKHDAR B. (1985), op.cit, p 133

* ⁷¹ - Walliser B. (2002), op.cit

* ⁷² - VERGARA F. (1992), op. cit

* ⁷³ - KREPS D. (1999), op. cit p. 86

* ⁷⁴ - L'apport le l'économie expérimentale en ce qui concerne ce sujet est important, ainsi Gerard CACHON ET Colin CAMERER ont souligné que « In games with multiple equilibria ... players must somehow coordinate their choices to achieve Pareto efficiency...but generally leave unanswered a central question. Why is one equilibrium selected rather than another ? Experimental analysis is well suited to help answer this question because the specialized conditions of a coordination game can easily be created in the laboratory. Then a wide range of variables can be altered to help infer the principles that guide selection of equilibria » « dans les jeux à plusieurs équilibres... les joueurs doivent d'une manière ou d'une autre coordonner leurs choix afin d'atteindre l'efficience paretiènne. .. mais généralement reste encore une question centrale sans réponse : pourquoi un équilibre doit être choisi au lieu d'un autre ? l'analyse expérimentale est bien conçu pour répondre à de telle questions parce que les conditions spéciales des jeux de coordination sont faciles à créer dans le laboratoire. Donc, une large gamme de variables peuvent être modifiées dans le but de déduire les principes de sélection d'équilibre. » p. 165 dans CACHON G. .P., CAMERER C. F. (1996), « Loss-Avoidance and Forward Induction in Experimental Coordination Games », Quarterly Journal of Economics, February, 165-194.

* ⁷⁵ - les raffinements de l'équilibre sont des techniques consistant à invoquer une notion plus forte d'équilibre, ces raffinements de l'équilibre

sont en effet définis en imposant des conditions plus restrictives aux comportements qui constituent un équilibre de NASH ; en général, ils consistent à interdire aux joueurs d'effectuer des menaces ou des promesses qui ne sont pas crédibles ou de déduire des propositions non crédibles de leurs observations.

* ⁷⁶ - Pour de plus amples détails voir KREPS D. (1999), op. cit

* ⁷⁷ - Voir Annexe I

* ⁷⁸ - voir à cet égard:

- SELTEN R. (1965), « spieletheoretische Behandlung eines Oligopolmodells mit Nash-frageragheit », Zeitschrift fur die Gesamte

staatswissenschaft, 12, p. 301 -324.

- SELTEN R (1975), « Reexamination of the Perfectness Concepts for Equilibrium Points in Extensive Games », International Journal of Game Theory, 4, p. 25-55.

* ⁷⁹ - Cependant il existe d'autres techniques de raffinement, parmi les plus importantes d'entre elles on peut cité l'utilisation de la récurrence

à rebours et de la récurrence projective ( forward induction)

* ⁸⁰ - HARSANYI J.C. (1967-1968), « Games with Incomplete Information Played by Bayesian Players », Management Science, 14, p.159-

182, p. 320-334, p. 486-502 cité dans RULLIERE J. L. (2000), op. cit.

* ⁸¹ - AUMANN R.J. (1974), « Subjectivity and Correlation in Randomized Strategies », Journal of Mathematical Economics, 1, p. 67-96.

* ⁸² - AUMANN R.J., BRANDENBURGER A. (1991), « Epistemic Conditions for Nash Equilibrium », Working Paper, n°91-042, Harvard

Business School.

* ⁸³ - Comme bernard WALLISER

* ⁸⁴ - David KREPS ( KREPS D. (1999), op. cit ) avait exprimé différemment cette idée en disant : « ...dans certains jeux où il existe une multiplicité d'équilibres, les joueurs « savent » néanmoins comment se comporter. Ce savoir provient à la fois d'expériences passées directement utilisables et de connaissances sur la façon dont les individus agissent en général. » p 89.

* ⁸⁵ - DE WOLF O. (1998), « Fondements des concepts de solution en théorie des jeux », Annales d'économie et de statistique, N°51, p 2.

* ⁸⁶ - WALLISER B. (2002), op. cit, p 694.

* ⁸⁷ - SCHOTTER A., SCHWODIAUER G. (1981), op. cit, p 487.

* ⁸⁸ - Les termes Noyau et Coeur sont utilisés dorénavant comme synonymes.

* ⁸⁹ - EDGEWORTH Y. F. (1991), Mathematical psychics : an assay on the application of mathematics to moral sciences, Kegan Paul,

London.

* ⁹⁰ - SHUBIK M. ( 1959), Stratégie et structure de marché , New York: Wiley, 1959. Edition française (1964), Dunod, Paris.

* ⁹¹ - DEBREU G., SCARF H. (1966), « théorème de limite sur le coeur d'une économie », Techniques Economiques Modernes, N°5,

GAUTTIER - VILLARS, Paris, p 19-33.

* ⁹² - le caractère gras et le soulignement est le notre.

* ⁹³ - SHUBIK M. (1991), Théorie des jeux et sciences sociales, Economica, traduit par Bernard GUERRIEN, Nicolas PONTY et Raoul

SALOMON, p 399- 400.

* ⁹⁴ - Lorsque les trois hypothèses suivantes :

- Insatiabilité ;

- Convexité forte des préférences ;

- Continuité des préférences.

sont respectées par la fonction de préférence.

* ⁹⁵ - Voir LAKHDAR B. (1985), op. cit. p. 86 pour la démonstration.

* ⁹⁶ - SHUBIK M. (1991), op. cit p 401.

* ⁹⁷ - voir : - SHAPLEY L., SHUBIK M. (1967), « Concepts and theories of pure competition », dans « Essays in mathematical economics in honour of Oskar MORGENSTERN, édité par Martin SHUBIK, Princeton University Press, Princeton, p 63-79.

- SHAPLEY L., SHUBIK M. (1969), « On market games », Journal of Economic Theory, Juin, p.9-25.

* ⁹⁸ - GARICANO L. (2000), op. cit p 15.

* ^*- NASH J.F., KALISH G.K., MILNOR J.W., NERING E.D. (1954), « Some Experimental n-person Games », dans THRALL R.M., COOMBS. Et DAVIS R.L. (eds), Decisions Processes, New York, p. 302

* ¹ - ROTH. (1991), op. cit p 107.

«  je suis avec précaution optimiste que, cent ans dès maintenant, la théorie des jeux deviendra la colonne vertébrale de l'ingénierie microéconomique qui aura grossièrement avec la théorie économique et l'expérimentation en laboratoire de l'époque le même type de relation que l'ingénierie chimique entretient aujourd'hui avec la théorie chimique et la chimie de paillasse »

A cet égard Alvin ROTH parle déjà en 2002 de la naissance d'un nouveau domaine de recherche proprement dit qui est le « Design economics » qui est une sorte de cet « ingenieering » économique dont il avait parlé en 1991. Pour ROTH le « Design economics » est le fruit et le résultat de la jonction de trois autres domaines de recherche à savoir : l'économie expérimentale, la théorie économique traditionnelle et la théorie des jeux. Voir son article fondateur : «The Economist as Engineer: Game Theory, Experimental Economics and Computation as Tools of Design Economics », Econometrica, 70, 4, July 2002, 1341-1378, dans lequel il définit ce nouveau domaine comme étant « the part of economics intended to further the design and maintenance of markets and other economic institutions. » p 1342.

* ² - Voir SMITH V.L.(1994), p. 113-115.

* ³ - CHAMBERLIN E.H.(1948), op. cit.

* ⁴ - Pour un recensement des faits attestant le développement de la pratique de l'expérimentation en économie, voir par exemple DELOCHE R. (1995), notamment les pages 951-955, ou des manuels d'économie expérimentale tels que HEY (1991), DAVIS et HOLT (1992), FRIEDMAN et SUNDER (1994) ou KAGEL et ROTH (1995).

* ⁵ - FLOOD, M. M. (1958), « Some experimental games », Management Science, Vol. 5, p. 5-26.

* ⁶ - Une expression qu'utilise déjà FLOOD (1958), p. 6.

* ⁷ - Réaliser avec la collaboration de M DRESHER.

* ⁸ - RAPOPORT A., CHAMMAH. A.M, (1965), Prisoner's Dilemma: A Study in Conflict and Cooperation, Ann Arbor, University of Michigan Press. Voir aussi STRAFFIN P. (1980), The Prisoner's Dilemma, Umap Journal, N°1, p. 101-103 pour un historique de l'invention de ce jeu.

* ⁹ - COLMAN A. (1999), Game Theory and its Applications in the Social and Biological Sciences, Londres et New York: Routledge. ( Seconde édition corrigée et augmentée- première impression en 1995 chez Butterworth-Heinemann - de Game theory and Experimental Games, 1982, Oxford, Pergamon Press.) cité dans MAMAS P. (2001), op. cit p. 7.

* ¹⁰ - l'auteur renvoie aux publications suivantes :

- WRIGHTSMAN L.S., O'CONNOR. J., BAKER N. J. (1972), Cooperation and Competition : Readings in Mixed-Motive Games, Belmont : Brookes-Cole.

- GUYER. M., PERKEL. B. (1972), Experimental games : a b ibliography (1945-1971), Ann Arbor, Mich : Mental Health Research Institute, Communication 293.

* ¹¹ - Voir à ce sujet les travaux pionniers suivants :

- SAUERMANN. H., SELTEN R. (1959), « Ein Oligopoleexperiment », Zeitschrift für die Gesamte Staatswissenschaft, vol. 115, p. 427-471;

- SIEGEL S., FOURAKER L.E. (1960), Bargaining and Group Decision Making, New York : McGraw-Hill .

* ¹² - HEY J.D. (1991), Experiments in Economics, Oxford, Royaume Uni.

* ¹³ - ROTH A., KAGEL J, (1995), op. cit.

* ¹⁴ - ROTH A. (1991), op. cit p. 107.

* ¹⁵ - DELOCHE.(1995), op. cit, p 957

* ¹⁶ - DELOCHE.(1995), op. cit, p.957.

* ¹⁷ - Cf. supra, p . En plus de ce qui est dit dans cette dernière page il faut noter à cet égard que la distinction entre règle de comportement et institution ( règles d'échange et institution de marché par exemple) est utile en terme d'exposition. Pourtant, elle ne revêt pas un caractère économique fondamental car une institution sociale n'est autre qu'un ensemble de règles spécifiant le comportement de chaque joueur à chaque itération du jeu (organisant les échanges dans un marché). Le lecteur désirant plus d'information sur la relation règle de comportement - institution sociale et sur l'émergence, le rôle et le fonctionnement de cette dernière voir le travail de LAKHDAR (1985) op. cit.

* ¹⁸ - DELOCHE (1995), op. cit, p. 957.

* ¹⁹ - Parmi les domaines les plus familiarisés avec le langage de la théorie des jeux on peut citer les applications qui ont été faite dans les domaines monétaires et financières surtout les travaux considérant les attaques spéculatives comme des cas qui peuvent être modélisés comme un jeu global ( un jeu global sous-entend un jeu de coordination avec complémentarités stratégiques dans un environnement stochastique, où le vrai jeu est sélectionné aléatoirement parmi les jeux dont les fonctions de paiements des joueurs diffèrent. En d'autres termes on injecte dans l'environnement propre à ce jeu des signaux privés bruités concernant les paiements du jeu. ) le lecteurs désirant avoir plus d'information sur ce sujet peuvent consulter les travaux intéressants suivants :

- CARLSSON H., VAN DAMME E. (1993), « Global Games and Equilibrium Selection », Econometrica , vol. 61, n° 5, Septembre, p. 989-1018.

- HELLWIG C. (2001), « Public Information, Private Information and the Multiplicity of Equilibria in Coordination Games », London School of Economics. http://econ.lse.ac.uk/phdc/papers/hellwig_jmp.pdf

- KAJII A., MORRIS S. (1997), « The Robustness of Equilibria to Incomplete Information », Econometrica, p. 1283-1309.

KAJII A., MORRIS S. (1998), « Payoff Continuity in Incomplete Information Games », Journal of Economic Theory, vol. 82, p. 267- 276

- MORRIS S. (2000), « Coordination, Communication and Common Knowledge: A Retrospective of the Electronic Mail Game », Août. http://www.econ.yale.edu/~smorris

- MORRIS S., SHIN H.S. (1998), « A Theory of the Onset of Currency Attacks, in Asian Financial Crisis: Causes, Contagion, and Consequences », Septembre, édité par Agenor, Miller, Vines, and Weber, Cambridge University Press (1999). http://www.nuff.ox.ac.uk/users/Shin/working.htm

- MORRIS S., SHIN H. S. (2000), « Rethinking Multiple Equilibria in Macroeconomics », NBER Macroeconomics Annual 2000, p. 139- 161, M.I.T. Press, 2001. http://www.nuff.ox.ac.uk/users/Shin/working.htm

- MORRIS S., SHIN H. S. (2001), « Global Games: Theory and Applications », Mars, Conference Volume of the Eighth World Congress of the Econometric Society. http://www.nuff.ox.ac.uk/users/Shin/working.htm

- RUBINSTEIN A. (1989), « The Electronic Mail Game: Strategic Behavior Under "Almost Common Knowledge" », American Economic Review, vol. 79, n° 3, Juin, p. 385-391.

* ²⁰ - MAMAS P. (2001), Théorie des jeux et jeux expérimentaux : éléments d'histoire et d'épistémologie. Thèse de doctorat en Sciences Economiques de l'Université Paris I, p. 10.

* ²¹ - Pour plus de détails sur cette explication voir MAMAS P. (2001), op.cit, notamment le chapitre 4 (Multiplicité et complexité des relations possibles entre théorie des jeux et jeux expérimentaux).

* ²² - En ne parlant pas précisément de l'évolution conjointe de la théorie des jeux et les expériences en laboratoire, GAGEY et REY voient que en général l'expérimentation a parcouru trois étapes. Ainsi ils déclarent : « Les recherches menées en ce domaine se sont schématiquement déroulées en trois étapes. Tout d'abord, les expériences ont été mises au point pour tester, à l'aide de simulations, les conditions d'application à la réalité des modèles théoriques. Par la suite, de nombreuses études ont été consacrées à l'analyse de l'impact du contexte institutionnel (structure informationnelle, mode d'enchères,...) sur le déroulement et l'issue des expériences. Plus récemment, enfin, l'expérimentation a été utilisée comme instrument de prévision et effectivement appliquée à l'étude de situations réelles. » p. 6 dans GAGEY F., REY P. (1986), « l'Economie expérimentale comme outil pédagogique : Elaboration d'un jeu d'incitation à la micro-économie », Revue Economique, N°1, Janvier.

* ²³ - WRIGHTSMAN, O'CONNOR et BAKER (trois expérimentalistes éminents de cette époque) étaient conscient de l'absence de travaux rapprochants le laboratoire à la vie réelle. Ainsi ils déclaraient en 1972 que « apparently no studies have compared degreee of cooperative behavior in loratory mixed-motive game with cooperation in different real-world tasks » p207. dans WRIGHTSMAN L.S., O'CONNOR J., BAKER N.J. (1972), Cooperation and Cometition Reading in Mixed-Motive Games, Belmont, Brookes-Cole. Cité dans COLMAN. (1982). op. cit. p. 128-129.

* ²⁴ - SHUBIK M. (1962), « Some Experimental Non-Zero Sum Games With Lack of Information about the Rules » Management Science, Vol. 8, N° 2, January.

* ²⁵ - SHUBIK déjà en 1964 ( SHUBUK M. (1964). op.cit) utilisait le langage de la théorie des jeux pour la représentation des différentes structures de marché. Ainsi, il écrivait dans le premier chapitre de son ouvrage : « A l'origine de ce livre on trouve la conviction que les méthodes de la théorie des jeux nous aident à découvrir et à étudier cette structure ». Parallèlement il a conçu des expériences dont l'objectif était la validation de ses modèles théorique. Voir par exemple :

- « Comments Upon Games as a Teaching Device », in Proceedings of the Conference on Business Games ( avec DILL. W. T., JACKSON. J. R., SWEENEY J. W), New Orleans: Tulane University, 1961, 134-135.

- « Oligopoly Bargaining: The Quantity Adjuster Models » (avec FOURAKER L.E et SIEGEL S), Bargaining Behavior, Hightstown, NJ: McGraw-Hill, 1963.

- «Experimental Gaming and Some Aspects of Competitive Behavior », New Perspectives in Organization Research, New York: Wiley, 1964, 449-463.

- « The Dollar Auction Game: A Paradox in Noncooperative Behavior and Escalation », The Journal of Conflict Resolution, 15, 1, 1971, 109-111.

* ²⁶ - l'expression « résultats importants » ne doit pas être comprise dans un sens qualitatif. Comme on va le voir l'auteur a trouvé des difficultés pour conclure de manière ferme sur la validité théorique d'un des solutions théoriques proposées, mais son expérience a aidé beaucoup les expérimentalistes à changer leur manière de penser quant à la façon avec laquelle les expériences sont conçues, ceci afin de rendre compte de certains aspects humains dans leur modélisation (altruisme, réciprocité, confiance, sympathie, etc.).

* ²⁷ - Cf. supra chapitre II p.39.

* ²⁸ - LUCE et RAIFFA ( 1957) ont affirmé que la répétition des jeux à somme non nulle peut mener à l'adoption de la solution du maximum joint. Ainsi, ils déclaraient : « We feel that in most cases (  ils discutent ici le cas des jeux à somme non nulle) an unarticulated collusion between the players will develop....This arises from the knowledge that the situation will be repeated and that reprisals are possible » p. 101 dans LUCE R.D., RAIFFA H (1957), Games and Decisions : Introduction and Critical Survey, New York, wiley. Cité dans COLMAN A. (1981), op. cit, p. 115.

* ²⁹ - Cf. supra. p. 51.

* ³⁰ - les joueurs sont des étudiants en économie de l'université de Yale section Organisation Industrielle.

* ³¹ -il faut noter que ces résultats insatisfaisants sont dues en grande partie aussi à la nature même des jeux à joueurs et à somme non-nulle. Ainsi selon les termes de A. COLMAN : « The mathematical inconclusiveness of mixed-motive games (non-zero-sum games) can be explained by an abundance of psychologically interesting phenomena for which they provide precise models, such as cooperation and competition, risk taking and caution, trust and suspicion, altruism and spite, threats, retaliations, and commitments. ». Dans COLMAN. (1982). op.cit, p. 93.

* ³² - SHUBIK M. (1962), op. cit, p. 229. Outre le problème d'incompatibilité des environnements évoqué par SHUBIK dans cette citation , il y a celui de la capacité des joueurs à refléter des comportements conformes à la structure des paiements. COLMAN déclare à cet égard que : «  the finding of researches in this area therefore demonstrate beyond reasonable doubt that subjects in experimental games do not invariably play according to the explicit payoff structures presented to them. This problem strikes at the heart of experimental gaming and is badly in need of direct investigation » dans COLMAN (1982). op. cit, p. 118-119. Voir la réponse des éxpérimentalistes pour ce genre de critiques Supra. p. 25.

* ³³ - Voir pour ce sujet :

- BOLTON G., OCKENFELS A. (2002), « ERC : a Theory of Equity, Reciprocity and Competition », American Economique Review, novembre, Vol. 92, n°5, p 1125-1155.

- FEHR E., SCHMIDT K. (1999), «  A Theory of Fairness, Competition, and Cooperation », Quaterly Journal of Economics, August, 3, p. 769-816.

- SCHOTTER A., WEISS A., ZAPATER I. (1996), « Fairness and survival in ultimatum and dictatorship games », Journal of Economic Behavior and Economics, vol. 31, p. 745-779.

* ³⁴ - Cette expérience a été réalisé par NEVEU M. (membre groupe de recherche GATE :Groupe d'Analyse et de Théorie Économique à lyon 2). Il l'a publié dans son article : « Optimum et financement efficient d'un bien public : une expérience », GATE, Document de travail 02-14, décembre 2002.

* ³⁵ - ISAAC R.M., WALKER J., THOMAS S, (1984), « Divergent evidence on free riding : an experimental examination of some possible explanations », Public Choice, 43, 113-149.

* ³⁶ - LEDYARD J. (1995), « Public Goods : a survey of experimental research », 111-194, dans AE ROTH et J KAGEL (eds.), The Handbook of Experimental Economics, Princeton University Press.

* ³⁷ - Andréoni J. (1995), « Coopération in Public Goods Experiments : Kindness or Confusion », American Economic Review, 85 (4), 891-

904.

* ³⁸ - on peut citer à titre d'exemple :

- KESER C. (1996), « Voluntary Contribution to a Public Good When Partial Contribution is a Dominant Strategy », Economic Letters,

50, 359-366.

- SEFTON M., STEINBERG R. (1996), « Reward Structures in Public Good Experiments », Journal of Public Economics, 61, 263-287.

- ISAAC R.M., WALKER J. (1998), « Nash as an Organizing principle in the Voluntary Provision of Public Goods : Experimental

Evidence », Experimental Economics, 1 (3), 191-206.

- WILLINGER M., ZIEGELMEYER A. (1999), « Non-Cooperative Behavior in Public Goods Experiment with Interior Solution »,

mimeo, Beta, Université de Strasbourg.

* ³⁹ - Nous présentons ci-après les raisons, avancées par NEUVEU, du recours à ce choix :

- Les optima ne pouvaient être que des multiples de 10% de la dotation agrégée car la dotation individuelle par période était égale à 10 jetons et les contributions devaient être des nombres entiers.

- Les résultats expérimentaux précédents ont montré que les joueurs contribuent en première période entre 40 et 60% de leur dotation, les optima à 40, 50 et 60% de la dotation agrégée ont donc été éliminés.

- Les deux optima ont dû être caractérisés par une distance équivalente entre les solutions de coin (i.e. 0% ou 100%) pour pouvoir mesurer la distance entre le choix et la contribution optimale.

- L'optimum symétrique à 10% (1 jeton contribué par individu) n'a pas été retenu car l'espace des erreurs par rapport à l'équilibre (0 jeton contribué) aurait été quasi-inexistant. L'optimum à 20% (2 jetons contribués par individu) aurait également défini une zone d'erreur trop faible.

* ⁴⁰ - l'auteur note OP30 pour désigner le traitement expérimental se référant à l'optimum à 30% et OP70 celui de l'optimum à 70%.

* ⁴¹ - Pour les grilles des gains concernant les deux modes de financement (30% ou 70%) et pour les deux options ( bien privé ou bien public) voir l'annexe 2.

* ⁴² - Logiciel d'expérimentation du GATE, gratuitement téléchargeable sur http://www.gate.cnrs.fr

* *- Source : NEVEU M. (2002), op. cit, p. 17.

⁴³ - L'expérience a réuni 8 (respectivement 7) groupes de 4 joueurs dans le traitement OP30 (OP70)

* ⁴⁴ - Notons que le travail de NEUVEU ne s'arrête pas à ce niveau, d'autres analyses ont été effectué. Voir NEUVEU. ( 2002), op. cit pour les analyses et résultats complets de cette expérience. Nous donnant ci-dessous, en bref, les importants résultats non mentionnés dans cet exposé.

- La contribution la plus souvent réalisée est la contribution optimale symétrique définie par les règles de l'expérience. Néanmoins,

plus le niveau optimal est haut, plus la répartition des contributions s'étend sur l'ensemble des possibilités.

- Les individus choisissent plus fréquemment la contribution symétrique optimale lorsque l'optimum est faible.

- L'émergence d'un comportement du passager clandestin est indépendante de la définition du niveau optimal.

- L'émergence d'un comportement de coopérateur est indépendante de la définition du niveau optimal.

- Au niveau des choix individuels et du processus de décision, il apparaît que quelle que soit la définition du point optimal, les joueurs choisissent de contribuer principalement le montant optimal symétrique (3 ou 7 jetons selon l'optimum).

* ¹ - « However if we do not take steps in the direction of adding a solide empirical base to game theory, but instead continue to rely on game theory primarily for conceptual insights ( deep and satisfying as these may be), then it is likely that long before a hundred years game theory will have experienced sharply diminishing returns. In this respect, I think the next hundred years will likely bring about a change in the way theoretical and empirical work are related in economics generally, and that, if not, then the entire discipline of economics may alose fail to realize its potential. » dans ROTH A. E. (1991), op. cit. p 107.

* 2 -« by choosing to take economics down the experimental path, we are committing ourselves to developing models that are increasingly behavioural in character » dans BULTER D. (1996), « the `Experimental Economics' Experiment », Journal of Economic Surveys, Vol. 10, N°3, p. 347.

* 3 - BULTER exprime ceci en disant que « The suggestion that something is missing from the standard conception of rational economic man is the most consistent finding of the research (en économie expérimentale), but no general explanation is offered as to why this should be so. » dans BULTER. (1996). Op.cit.

* 4 - à l'exception des dernières tentatives d'incorporation de la réciprocité. Voir les travaux de ABDELLAOUI, de RUBINSTEIN et de HOLT.

* ^* - l'auteur s'inspire, pour le calcul des gains, des fonctions de paiement formulée dans Isaac R.M., Walker J., S. Thomas. (1984),

« Divergent evidence on free riding : an experimental examination of some possible explanations », Public Choice, 43, 113-149.