|

RAMUZ Loana Class 2020
Year 2019/2020
Engineering Degree
Télécom Physique Strasbourg
3rd YEAR INTERNSHIP REPORT
Machine learning for Big Data in Galactic
Archaeology

Astronomical Observatory of Strasbourg Supervisor: Rodrigo
Ibata
11 Rue de l'Université, Research director at the
CNRS
67000 Strasbourg
rodrigo.ibata@astro.unistra.fr
+33 (0) 3 68 85 24 10 From March 2nd, 2020
to August 14th, 2020

I
Machine Learning for Big Data in Galactic
Archaeology
Estimating heliocentric distances is a challenging task in
Astrophysics. There are different ways to do it including measuring geometric
parallaxes, and via spectroscopy, where absolute magnitudes are recovered
through comparison to stellar population models that are primarily dependent on
metallicity, i.e. the chemical composition. Spectroscopy is expensive and
time-consuming to obtain, but with multi-band photometry it is possible to
cover the whole spectrum for a huge number of stars in a small number of
exposures, and this amount of data naturally leads to machine learning. We
create a neural network using a simplified programming language called
fast.ai and Python module PyTorch, in order
to recover metallicity from multi-band photometry, and optimize it until it
reaches a precision of ó = 0.14dex. We then use this net to get
metallicity estimates for more than 18 million stars and generate maps of the
Milky Way to compare our results to other works. Once our results satisfactory,
we try to create an autoencoder based on the same data used for our previous
network, which would work with less complete photometry.

III
Machine learning pour le Big Data en archéologie
galactique
L'estimation des distances héliocentriques est d'une
importance primordiale en astrophysique pour définir la structure 3D de
notre univers, mais relève du défi. Il est possible de les
calculer de différentes façons, comme par exemple en se basant la
géométrie ou bien dans notre cas la spectroscopie, où les
magnitudes absolues sont calculées à partir de comparaison de
modèles de populations stellaires dépendant en premier lieu des
compositions chimiques des étoiles, aussi appelées
métallicités. Obtenir des données spectroscopiques est
long et compliqué, mais grâce à la photométrie
multi-bandes, il est possible de couvrir toute la plage d'émissions des
étoiles et d'obtenir des spectres à basse résolution en un
temps record pour de nombreuses étoiles à la fois. Ce volume de
données colossal permet d'entrer dans le monde du Big Data et du machine
learning. J'ai donc créé un réseau de neurones en
utilisant un langage de programmation dédié au machine learning
appelé
fast.ai et le module PyTorch de Python,
dans le but de retrouver les métallicités d'étoiles en se
basant sur la photométrie multi-bandes, réseau que j'ai
optimisé jusqu'à atteindre une précision de ó
= 0.14dex. Puis j'ai utilisé ce réseau sur 18 millions
d'étoiles, estimé leur métallicité et
créé une carte de la Voie Lactée pour comparer nos
résultats à d'autres travaux. Enfin, j'ai essayé de
créer un autoencoder se basant sur les mêmes données mais
fonctionnant avec moins de données photométriques.

V
Acknowledgements
I would like to pay my special regards to Rodrigo Ibata, my
amazing supervisor, for making this internship not only possible, but also
enlightening and rewarding, both scientifically and personnally. It allowed me
apply my knowledge in a domain that I love, to get a glimpse of the research
world and to better understand what I want for my future, and I am deeply
grateful for this chance.
I also wish to express my gratitude to Guillaume Thomas for
his highlights on the project and to Foivos Diakogiannis for his help and
everything he taught me about machine learning from Perth, a knowledge which
will be very useful going forward.
My fellow interns Elisabeth, Amandine, Théophile, Emilie,
Alexandre and Thomas are also to be thanked for their support and cheerfulness
in the Master Room, two things that I missed deeply during the lockdown.

VII
Contents
List of Figures IX
List of Tables XI
1 Introduction 1
1.1 The Astronomical Observatory of Strasbourg 1
1.2 The challenge of distances in Astrophysics 2
1.3 Machine learning for big data in Galactic archaeology
3
2 First test: a neural network for linear regression
5
2.1 Neural network vocabulary 5
2.2 Linear regression with
fast.ai 8
2.3 Training and getting predictions 9
3 Regression neural network for estimating metallicity
13
3.1 Input data: photometry 13
3.2 Output data: stellar parameter predictions 14
3.3 Data selection 15
3.4 First estimates of metallicity 15
3.5 Multi-tasking 17
4 Going further 19
4.1 Wrapping up data 19
4.2 Encoder/decoder, residuals and attention 19
4.3 Architecture of our net 20
4.4 Outputs and heads 21
4.5 Training 23
4.6 Getting predictions 24
5 Results 27
5.1 Comparison on metallicity and surface gravity predictions
27
5.2 Recovering distances 28
6 Auto-encoder 31
6.1 Architecture of the net 31
6.2 Training and precision 33
7 Conclusion 35
7.1 Conclusion & Discussion 35
7.2 Difficulties & Learnings 36
Bibliography 37

IX
List of Figures
1 The Astronomical Observatory of Strasbourg and its large
refracting tele-
scope at night 1
2 Explanatory scheme of a neural network for linear
regression (see Equation 2.2.1). The net feeds on a N x 8
dataset composed of 7 inputs (in our case photometric colours) in
the input layer and one output in the output layer. It has several hidden
layers (yellow and violet elements) whose number and type depends on the needs
of the situation, and obtains a prediction of the output. The activation
functions can be ReLu (maximum function), sigmoid or more complex if needed.
The loss function can be mean square error or otherwise, it helps compare the
predictions to the expected values and adjust
the weights and bias (values of parameters matrices) as needed.
6
3 Illustration of dropout from Srivastava et al. 2014 [1].
Up: a neural net with 2
hidden layers. Down: the same net but thinned using dropout
7
4 Hidden layers of the tabular model created for the
linear regression situation. The sigmoid layer, last layer which scales up the
predictions using the expected maximum and minimum value of the target, added
using the
y_range parameter, doesn't appear 9
5
fast.ai tools for choosing the learning
rate and training the net. 10
6 Visualisation of the expectations and the
predictions from the net with the normal fitting loop and the one cycle policy
fitting loop, for 10 epochs and a
given learning rate of 0.03. 11
7 Histogram of the difference between predictions and
expectations and fitted Gaussian, with values of amplitude, mean and standard
deviation at the top
respectively from left to right 11
8 Illustration of Gaia and SDSS photometric data
coverage in wavelength. . . 14
9 Results and accuracy for a three linear layer net with sizes
7x1024, 1024x512 and 512 x 1, trained for 20 epochs
and with a learning rate of 0.01 using the
one cycle policy 16
10 Results and precision for a five linear layers net with
sizes 7 x 64, 64 x 128, 128 x 128, 128 x 128 and 128 x 1,
trained for 20 epochs and with a learning
rate of 0.01 using the one cycle policy 16
11 Predictions of surface gravity and effective temperature
for a multi-tasking three linear layers net with sizes 7 x 1024, 1024 x 512
and 512 x 3, trained for
20 epochs and with a learning rate of 0.001 using the
one cycle policy 17
12 Results and precision for a multi-tasking three
linear layers net with sizes 7 x 1024, 1024 x 512 and 512 x
3, trained for 20 epochs and with a learning
rate of 0.001 using the one cycle policy. 17
13 An example of encoder/decoder architecture built using
ResDense blocks and AstroRegressor class working with depth. Are given
effective depth of 12 and minimum and maximum numbers of initial
features of 64 and 2048 respectively. The going up part
(left) is the encoder and the going down part
(right) is the decoder 21
X
14 Definition of head(s) whithin AstroRegressor class init
method. (a): one head for regression only, out_features
defines the number of outputs and each are computed independently. The outputs
are obtained by applying the regressor directly after the decoder.
(b): several heads for causality with regressor and
classifier, conv_dn is the table coming out of the encoder/de-coder backbone.
Teff is first computed from conv_dn , then [Fe/H] from
(conv_dn,Teff ), then log(g) from (conv_dn,
Teff , [Fe/H]), then classification from (conv_dn,
Teff , [Fe/H], log(g)). Outputs are Teff, FeH and logg
concate-
nated, and giant_pred 22
15 Visualisation of the predictions given by a regressor and
classifier multi-tasking net with attention, with the backbone shown in Fig. 13
(nfeatures_init=64, nfeatures_max=2048, depth=12). Top left: confusion
matrix for the 'pop' parameter. Top right, bottom left, bottom right:
scattering of predicted effective
temperature, surface gravity and metallicity respectively.
25
16 Training and results for a regressor only [Fe/H] and log(g)
guessing net with attention and with an encoder/decoder backbone of depth = 6
and nfea-tures_max = 4096. (a): History of the last epochs of
training, in red the best validation loss for which the model was saved.
(b): Histogram of the difference between predictions and
expectations and fitted Gaussian, with values of amplitude, mean and standard
deviation at the top respectively from left
to right. Precision of the net: ó 0.1446dex.
25
17 Comparison of metallicity as a function of (g -
r) color and surface gravity between Ivezié's Figure 1 (left)
and the same plot with our results (right). Color cuts are g<19.5 and
-0.1<g-r<0.9. On the left panel, the dashed lines correspond to main
sequence (MS) region selected for deriving photometric estimates for effective
temperature and metallicity. The giant stars (log(g)<3) can be found for
-0.1<g-r<0.2 (Bue Horizontal Branch stars) and for 0.4<g-r<0.65
(red giants). The features corresponding to red giants are easily identifiable
on our plot in the right panel, but not the BHB stars. However, a
strong low metallicity line appears for 0.4<log(g)<0.45
27
18 Iveziéet al. Figure 8: Dependence of the median
photometric metallicity for about 2.5 million stars from SDSS DR6 with
14,5<r<20, 0,2<g-r<0,4, and photometric distance in the 0.8-9 kpc
range, in cylindrical Galactic coordinates R and |Z|. There are about 40,000
pixels (50 pc ×50 pc) contained in this map, with a minimum of 5 stars per
pixel and a median of 33 stars. Note that the gradient of the median
metallicity is essentially parallel to the |Z|-axis, except
in the Monoceros stream region, as marked. 29
19 Dependence of raw predicted metallicity for about 1.18
million stars from Gaia, PS1, SDSS and CFIS joined together with are 14.5 <
r < 20, 0.2 < (g - r) < 0.4,
0.8kpc<dist<9kpc and -1.6<[Fe/H]<-0.5, using Galactic cylindrical
coordinates R and |Z|. Due to difference in metallicity, the disk appears
reddish on the bottom of the plot and the halo is mainly blue, visible for
|Z|>4kpc.
30
XI
20 Dependence of mean predicted metallicity for about 1.18
million stars from Gaia, PS1, SDSS and CFIS joined together with are 14.5 <
r < 20, 0.2 < (g - r) < 0.4,
0.8kpc<dist<9kpc and -1.6<[Fe/H]<-0.5, using Galactic cylindrical
coordinates R and |Z|. Binning is of size 0.015pc x 0.015pc in R and |Z|. The
disk and halo are still visible in the same colors but now the smooth
gradient
appears. 30
21 Scheme for an auto-encoder: left arrows represent the
encoder, right arrows are the decoder. The green square is a hypothetical
parameter to be added if
it doesn't work with Teff, logg and FeH only. 31
22 Structure and inside sizes of the auto-encoder.
(a): the encoder composed of a sandwich net of depth 6 and
predicting Teff, logg and FeH (width2=3 in the final layer).
(b): the decoder composed of a sandwich net of depth 6 and
predicting the missing colour (width2=1 in the final layer).
32
23 Evolution of the training (blue) and validation (orange)
losses as a function of the epochs. The red dot marks the lowest validation
loss, for which the parameters of the net are saved. Between 0 and 200 epochs,
the curves are
very bumpy but then they converge 33
24 Predictions of (g-r) colour in top left, effective
temperature in top right, surface gravity in bottom left and metallicity in
bottom right for a learning rate
of 10-3 and a hundred epochs. 34
25 Precisions, histograms and fitted gaussians for metallicity
(left) and (g-r) miss-
ing colour (right) 34
List of Tables
1 Description of the bands used as input data, the filters
mean wavelengths were taken from the SVO Filter Profile Service, and are given
for SDSS and
PS1 respectively. 13
2 Description of available outputs from the SEGUE survey 14

1
1 Introduction
1.1 The Astronomical Observatory of Strasbourg
The Astronomic Observatory of Strasbourg is at the same time
an Observatory for Universe Sciences, an intern school of the University of
Strasbourg and a Joint Research Unit between the University and the CNRS, the
French National Centre for Scientific Research. This Observatory funded in 1881
is presided by CNRS research director Pierre-Alain Duc since 2017. As a
research unit, it is organised in two teams: the Astronomical Data Centre of
Strasbourg (CDS) and the GALHECOS team.

Figure 1: The Astronomical Observatory of
Strasbourg and its large refracting telescope at night.
The "Galaxies, High Energy, Cosmology, Compact Objects &
Stars" team (GALHE-COS) studies the formation and evolution of galaxies
included our Milky Way in a cosmological context, considering their stellar
population and dark matter dynamics and the retroactive effects of their
central black hole. The objects it tackles can be Galactic and extra-Galactic
X-ray emitting sources, compact objects like neutron stars of white dwarves,
and Galactic active nuclei. Rodrigo Ibata, my supervisor, is part of this team
as a research director at the CNRS and specializes on the local group, the
Milky Way and dark matter. The will to acquire precise heliocentric distances,
and so to better understand the 3D construction of the Universe around us and
more particularly of the Milky Way, is what motivated my internship.
1.2 The challenge of distances in Astrophysics
Astrophysics is the discipline within science that focuses on
the understanding of our Universe. To get a glimpse of the fabric of its
gigantic structure, it is important to determine the place of the objects
within it. Various types of coordinates were developed to locate objects
depending on their place in our sky, but the crucial and most difficult
parameter to estimate is their heliocentric distance.
Spectroscopy provides useful data to estimate those distances.
In fact, spectral analysis of stars can provide information on their absolute
magnitude. The apparent magnitude of an object is a measure of its luminosity
when observed from Earth, on an inverse logarithmic scale. These apparent
magnitudes are biased by extinction from dust located in the interstellar
medium. The absolute magnitude of an object is its apparent magnitude if it
were observed from a distance of 10 parsecs, and corrected for extinction, so
it is distance-independent. Thus, using those two magnitudes, it is possible to
extract distances. This technique is called spectroscopic parallax, in contrast
to true parallax which is a geometric measurement. Recently, the European Space
Agency's Gaia mission has published over a billion (true) parallaxes of stars
in the sky, providing a huge leap in our understanding of the structure of the
Milky Way.
However, the accuracy of Gaia's parallax measurements decrease
rapidly with distance, and it is useful to consider alternative methods of
distance estimation. To estimate absolute magnitude, a metallicity-based
technique was developed by Iveziéet al. [2].
In Astrophysics, every element heavier than hydrogen or helium
is referred to as a metal. This comes from the fact that those metals are
really rare compared to hydrogen and helium which constitute 98% of the mass of
our baryonic Universe. That is why astrophysicists use the shorthand of
metallicity to refer to chemical composition. It is often quantified by the
[Fe/H] ratio defined as in Equation 1.2.1, where
Nx are the abundances in element x and the e
index refers to the values of the Sun. The spectrum of an object varies
substantially as a function of its metallicity, since the elements composing it
produce absorption rays. Hence Iveziéet al.'s approach of specifically
taking into account the metallicity of an object when computing its magnitude
is a reasonable data analysis strategy.
[Fe/H] = log10
(NFe/NH)e
NFe
-- log10 (1.2.1)
(NFe)e
NFe/NH
2
One issue with spectrometric data is that it is very costly in
instruments and time to acquire it. In fact, spectroscopy requires the
observatory to target a specific object to measure its parameters and the
exposure times can be huge for faint objects.
An alternative to real spectroscopy is to build up a very
low-resolution spectrum based on multi-band photometric data. Those are much
quicker to obtain since imaging cameras can record numerous objects (up to many
millions) at the same time. Indeed, photometric data are obtain by using
cameras with various filters (hence the "multi-band" qualification) which
allows one to cover all the wavelengths tackled in spectroscopy. Nowadays, with
various surveys like Gaia, Pan-STARRS or SDSS and others, a huge amount of
photometric data is available. This takes astrophysics into the world of big
data, which
3
is of no surprise since the number of objects in the Universe
itself is tremendous. And with big data it is natural to consider using
techniques like machine learning.
1.3 Machine learning for big data in Galactic
archaeology
Machine learning is a part of computer science that takes
advantage of big data to identify links between objects or entities. It usually
deals with image-type data but can work with all types of situations, from text
to sound waves, and including tabular data. It can be seen as an algorithm,
also called a neural network, which propagates knowledge coming from a dataset
to all data of the same form. For example, the work of Thomas et al. 2019 [3]
consisted of creating a neural network to distinguish dwarf and giant stars and
estimate their metallicities and distances. This network was trained on the
SEGUE spectrometric dataset and the Gaia DR2 and SDSS photometric dataset,
meaning it learned to recognize metallicities given by SEGUE from the
associated photometric data in Gaia and SDSS. Then it was used on Pan-STARRS,
CFIS and Gaia data to estimate metallici-ties for objects where this
information was unknown. This net obtained good estimations for metallicities,
with a precision of ó = 0.15dex. For comparison, a non-machine
learning way of getting metallicity estimation is using polynomial fitting,
tested by Ibata et al. 2017b [4]. This technique, obtained a precision of
ó = 0.20dex. This is a proof that machine learning is promising
for Galactic archaeology.
The aim of this internship was to create a neural network to
retrieve metallicity from photometric data. It builds on Thomas' work, but
instead of distinguishing giants and dwarfs to then determine their
metallicity, it directly tackles metallicity. For this, introductory lessons
from
fast.ai, a programming language based on
Python and its PyTorch module which simplifies machine learning, were taken to
first become acquainted with this technology, leading to a first neural network
on simulated data to test linear regression. Section 2 defines all the
vocabulary needed to understand our work and describes our first linear net as
an example. Then we dealt with real data, this first simple net was adapted to
the real situation and the first results came, as shown in Section 3. To get
better results, we set aside the
fast.ai modules and developed a more
complex net adapted from the work of Diakogionnis et al. 2020 [5] with the most
enlightening help of Foivos Di-akogiannis himself. Once the neural net reaches
convergence, distances were computed, and we compare our results to those
presented by Iveziéet al. 2008 [2] to map our Milky Way. We finally aim
to develop an auto-encoder, meaning an adaptation of the net to a less complete
photometric dataset which predicts spetrcometric parameters and gives an
estimation of the missing colour.

5
6
2 First test: a neural network for linear
regression
Machine learning consists of algorithms which automatically
learn to identify features in an entry set of data and associate it to one or
several output(s). It can be used for two aims: classification when it tackles
a categorical output, as done by Thomas et al. 2019 [3] for
distinguishing dwarf stars from giants, and estimating values for a continuous
output, like for example a value of metallicity for our objects. In our
situation, the net we created associates photometric values to a value of
metallicity, so it can be dealt with as a regression situation.
2.1 Neural network vocabulary
In this paragraph, we explain the basic vocabulary needed to
understand Machine Learning algorithms or neural networks. All of this
explanation will refer to Figure 2, which shows a visual example of a
neural net based on the data used for our first net, explained in Subsection
2.2.
As a first step, a neural network, also called a
net, can be considered as a black box algorithm, feeding on input data
in order to predict output data. Machine learning is almost always used for
images and computer vision but it also works on other data types like words,
time series or tabular data. The aim of a neural network is to train on a known
set of inputs and outputs to adjust itself, and finally to be used for
predicting unknown outputs based on known inputs. Physically, this technique
extrapolates the links between inputs and outputs within the black box and gets
to extend it to all inputs coming in a same way. For a net to work well, data
must be normalized between 0 and 1 (otherwise the huge number of matrix
multiplications can blow up values beyond the numerical precision range), and
well organized: there must be a training set, which contains inputs
and associated outputs and is used for adjusting the net predictions to those
outputs, and a test set, which is used to check the performance of the
adjusted net on a dataset it didn't train on. Furthermore, a net has to deal
with a huge amount of data but it cannot deal with everything at the same time:
it works on what is called a batch. The batch size is a hyperparameter
usually set to 64 (or another multiple of 2) but it is to be set by
taking into account other parameters. For this reason, it can be useful to
renormalize each batch before using it. This process is called
batch-normalization and is made by hidden layers called BatchNorm.
A net is structured in layers. The inputs are contained in the
input layer, the outputs in the output layer, both layers represented in blue
on Figure 2 and the black box is composed of layers referred to as
"hidden". Those hidden layers vary in number, size and complexity according to
the situation it is applied to. There are two types of hidden layers: the
parameters in yellow on Figure 2 and the activation
functions in purple on this same Figure. One can also speak about
activations (in red), the layers that don't require computing, which
help comprehension of what happens in the black box but is not used in the
process. The parameters can be considered as matrices that contain the
weights of the net, which are initially defined randomly or set to
arbitrary values and then adjusted in the training session. They can be for
example linear or convolutional layers. The activation functions are used to
help convergence during the training, and always keep the
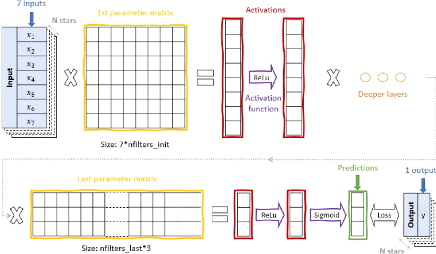
Figure 2: Explanatory scheme of a neural
network for linear regression (see Equation 2.2.1). The net feeds on a N
× 8 dataset composed of 7 inputs (in our case photometric colours) in
the input layer and one output in the output layer. It has several hidden
layers (yellow and violet elements) whose number and type depends on the needs
of the situation, and obtains a prediction of the output. The activation
functions can be ReLu (maximum function), sigmoid or more complex if needed.
The loss function can be mean square error or otherwise, it helps compare the
predictions to the expected values and adjust the weights and bias (values of
parameters matrices) as needed.
dimensions of the activations they apply to. For example, the
ReLu layer is basically a maximum function helping the predictions to
stay positive (since data inside the hidden layers are supposed to be between 0
and 1), the sigmoid layer is often used as the last activation
function as it allows to project the predictions between 0 and 1, ensuring the
respect of normalization, or between expected minimum and maximum if one wants
to denormal-ize within the algorithm.
The adjusting part we have been talking about is what is
called training. It is a step during which the net feeds on the
training set inputs, which is called the forward pass, computes a
prediction and compares it to the expected outputs. This comparison can be done
using different techniques called loss functions. The type of loss
function is to be chosen in line with the situation for which one wants to
develop a neural network. For classification there is for example the cross
entropy loss function which turns the predictions into probability of belonging
to different categorical classes. For regression, one of the simplest examples
is root mean square error, but one can use more complex functions that are less
prone to bias from outliers. After obtaining the loss, i.e. the difference
between expectation and prediction using the loss function, the weights in the
hidden layers are adjusted so as to decrease this loss. This is called the
backward pass and is done by a method called an optimizer.
For all our nets, we will use the default setting which is the Adam
optimizer, a gradient descent technique using adaptive learning rate from
moment estimates. The learning rate is the rate at which the
adjustment goes, a very important
and useful hyperparameter which also has to be adjusted during
training. It is highly dependent on the batch size, so those two have to be
taken into account together. Once the backward pass is done, the whole process
starts over. One fitting loop is called an epoch, and the number of
epochs is another hyperparameter to choose and adjust carefully.
During one epoch, there is not only training but also a
validation part. This part consists of doing just a forward pass on the test
set, i.e. a set which is not used for training and so is unknown by the net, to
test its efficiency on real conditions. Thus, at the end of each epoch, one
gets two important pieces of information: the training loss and the
validation loss. One way to check if a net is learning is to get the
predictions and compare them visually with the expected outputs, thus showing
the evolution of the efficiency of the net during training. The training
process is supposed to tend to decrease the training loss
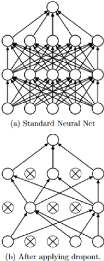
Figure 3: Illustration of dropout from
Srivastava et al. 2014 [1]. Up: a neural net with 2 hidden layers. Down: the
same net but thinned using dropout.
but sometimes it doesn't happen. This phenomenon is what is
called underfitting: the net doesn't catch the intrinsic links in the
training set and so can't improve itself. The validation loss doesn't take part
in the training process so it normally has no reason to decrease with the
number of epochs. If it does, everything is going well and the net is learning.
If it gets bigger, the net is overfitting: it becomes too specific to
its training dataset and is not able to extend to new data. One type of hidden
layer that can prevent the net from overfitting is Dropout. In fact,
overfitting can be seen as the net taking too much information from the
training dataset. So as to prevent from that, it is useful to skip some
parameters in the matrices as shown in Figure 3, an illustration of dropout by
Srivastava et al. 2014 [1], one of the first to develop this technique. The
upper net is fully connected, i.e. all of its parameters are active,
and in contrast, the second one has dropout. Dropout layers come with a dropout
probability, meaning a probability of dropping out a parameter in the following
layer. This quantity is another hyperparameter to optimize to improve the
performance of a net.
7
Therefore, creating a neural network requires one to organize
the data it will train on, decide of what type of net will be the most
efficient in this situation and adapt progressively all the hyperparameters to
get satisfying training and validation losses. Some of the hyperparameters will
of course depend on the situation, in particular as shown in Figure 2, the
sizes of the first and last parameter matrices depend respectively on the input
and output sizes. But basically, all other internal (number, types and other
sizes of hidden layers, loss function) and external (number of epochs, learning
rate) hyperparameters are to be adjusted by trial and error.
8
2.2 Linear regression with
fast.ai
To begin our machine learning project and create our first
neural network we decided to use
fast.ai, a package based on the Python
module PyTorch and created to simplify the creation and training of neural
networks and so to make it accessible for everyone no matter the domain of
application. It was founded by researcher Jeremy Howard and AI expert Rachel
Thomas. Together they published 14 video courses of about 2 hours each for
making
fast.ai clear and understandable to anyone
having basic notions of Python.
The first step of this internship consisted of taking those
courses to get comfortable with machine learning vocabulary and with
fast.ai. To test it on a close but
simplified situation, a linear regression solving net was created, based on
Equation 2.2.1:
y = a1 x1 + a2 ·
x2 + a3 · x3 + a4 · x4 +
a5 · x5 + a6 · x6 + a7
· x7 (2.2.1)
where {x1,...,x7} were the inputs, created
randomly to correspond approximately to our photometric data,
{a1,...,a7} were coefficients and y was the output,
corresponding to the value of metallicty expected for the object. The ai
coefficients were chosen arbitrarily to create artificially links between
the inputs and the output, as it is the case in our real data. Our dataset is
thus a huge table of size N x 8, N being the number of created objects
(N 100,000 since it is approximately the size of the catalogs we will
later work on), the seven first columns being the simulated photometric data
{xi } and the eighth column being the associated metallicity
y.
fast.ai has multiple tools for creating and
training a neural network, depending on the type of data one is dealing with.
In general machine learning is used for computer vision and image processing so
there are a lot of possibilities in
fast.ai for dealing with this kind of entry
data. In our case, our entry data is tabular, as described above, and the
networks developed with this type of data are basic and mostly linear.
Data used for training and testing are of upmost importance
since they are partially responsible for the precision of the net. In fact, the
amount and precision of data is crucial to get the best results possible.
That's why consolidating input and output data is the first and maybe most
important step in creating a neural network. A useful library for manipulating
data is the Pandas library, which is used to organize data within
fast.ai. It allows to gather all our data
in a table called DataFrame, determine which columns are to be considered as
categorical or continuous inputs and which one as output, apply some
pre-processes on it like normalizing, shuffling or filling if some data are
missing, etc. Once a training DataFrame and a test DataFrame are created, they
can be united into a DataBunch.
fast.ai has an integrated tool to create a
network, also called a learner, from a tabular DataBunch. This DataBunch, let's
call it data, having the inputs and outputs within it, the learner created from
it automatically knows part of the first layer and last layer sizes since it
has to match the input and output sizes as shown in Figure 2, but we still have
to give it information for the rest of the hidden layers. For a tabular
situation,
fast.ai creates automatically a linear
learner, i.e. the parameters matrices (yellow components in Figure 2) are
linear, and the activation functions are adapted to a linear situation. The
sizes of those matrices are to be given to the layers parameter. It is also
possible to add a
9
sigmoid layer at the end, by specifying the edges of the
sigmoid to the y_range parameter. This range is basically the minimal and
maximal values of the output of the DataBunch. Dropout is also available, by
adding a list of probabilities of dropout corresponding to each layer. Finally,
it is also possible to add metrics. Those don't change anything on the training
but compute and print values to help understand the evolution of the net. For
example, it can be accuracy, root mean square error or exponential root mean
square error. The following extremely simple line of code gives a working net
to begin with:
learn = get_tabular_learner(data, layers=[1024,512],
y_range=[min_y,max_y], dp=[0.001,0.01], metrics=exp_rmse)
This command creates a fully connected network with three
linear layers each coming with ReLU, dropout and BatchNorm layers, as can be
seen in Figure 4. The first linear layer is of size 7 x 1024, followed by ReLU
and BatchNorm layers of size 1024. Then a dropout layer of probability 0.001 of
dropping out a parameter applies to the next linear layer, of size 1024 x 512.
This layer is also followed by ReLU and BatchNorm layers of size 512. Then a
second dropout layer of probability 0.01 is applied to the last linear layer of
size 512 x 1 to coincide with the number of outputs. There is also a sigmoid
layer at the end of the net, created by adding the y_range parameter.
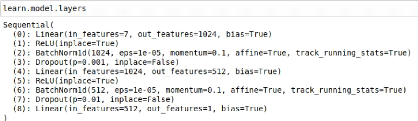
Figure 4: Hidden layers of the tabular model
created for the linear regression situation. The sigmoid layer, last layer
which scales up the predictions using the expected maximum and minimum value of
the target, added using the y_range parameter, doesn't appear.
2.3 Training and getting predictions
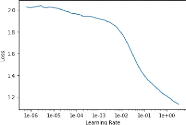
This net is ready to be trained, but first a learning rate has
to be chosen. This rate has to be adjusted during learning depending on the
smoothness and speed of convergence of the losses. For this,
fast.ai developed the lr_find() function,
which makes forward passes on the training dataset with different learning
rates and gets the associated losses. Then the curve can be plotted using the
recorder_plot() function, as shown on Figure 5a. It is recommended to choose at
first a learning rate which corresponds to the steepest slope. For example on
Figure 5a, the recommended learning rate would be 0.03.
To train the net we can use the fit() function which allows
one to train the net with a given learning rate for a given number of epochs.
This function shows the evolution of the training and test losses and a metric
to be chosen, like accuracy or root mean square
10
|
|
|
(a) Evolution of the loss as a function of the
learning rate.
|
(b) Display of the fit_one_cycle() function,
similar to the fit() function, with number of epoch, losses, metrics and
time.
|
Figure 5:
fast.ai tools for choosing the learning
rate and training the net.
error. There is also a special fitting loop called
fit_one_cycle(), which fits a given net following the one cycle policy defined
by Leslie Smith [6]. This sets a special schedule for the learning rate which
changes all along the training given a maximum value of the learning rate. It
helps the net to converge quicker, as shown later in Figure 6. Those two
functions allow one to follow up the training epoch by epoch, printing for each
epoch the value of the training loss, the validation loss, the metric(s)
requested when the net was created and the time the training and validation
sessions took. Figure 5b shows the display of those two fitting loop functions.
It is also possible to print the evolution of the losses at the end of the
fitting loop. Those losses are useful to evaluate the net tendency to overfit
or underfit. It is also an indicator as to when the learning rate must be
adapted: if the validation loss is unsteady, it may mean that the weights
changing step is too big and the net fails to get better precision so it could
be a good idea to lower the learning rate.
The evolution of the training and validation losses gives a
first idea of the precision of the net, but a visual check is more convincing.
After the training session, it is possible to get the predictions using the
test set, with the get_preds() function. Then they can be visualised using the
matlplotlib.pyplot module, as shown in Figure 6. There we can see clearly the
efficiency of the one cycle policy: for the same number of epochs, the
scheduled learning rate cycle (Fig 6b) gives a really convincing result whereas
the fixed learning rate of 0.03 barely begins to converge (Fig 6a).
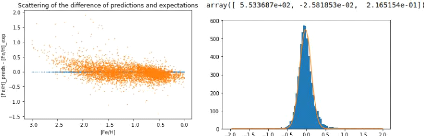
To quantify the precision of the net, we get the difference
between the predictions and the expectations, we create a histogram and fit a
Gaussian to it. This is shown in Figure 7 with a cut between -1 and 1 for
Figure 7a and a cut between -0.1 and 0.1 for Figure 7b. These plots also list
the values for the amplitude of the Gaussian, its mean and its standard
deviation. The standard deviation ó corresponds to the
precision of our net and depends on the cut we choose to apply, since bad
values on the edge of the histogram can easily be spotted and not taken into
account. Here for the [-1,1] cut, we get ó 0.012 and for the
[-0.1,0.1] cut, we get ó 0.007.
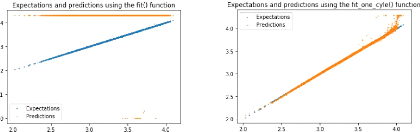
(a) Expectations and predictions using a net trained for 10
epochs and for a fixed learning rate of 0.03.
(b) Expectations and predictions using a net trained for 10
epochs and for a scheduled learning rate with maximum of 0.03.
11
Figure 6: Visualisation of the expectations
and the predictions from the net with the normal fitting loop and the one cycle
policy fitting loop, for 10 epochs and a given learning rate of 0.03.

(a) Histogram and fitted Gaussian with a [-1,1] cut. (b)
Histogram and fitted Gaussian with a [-0.1,0.1] cut.
Figure 7: Histogram of the difference between
predictions and expectations and fitted Gaussian, with values of amplitude,
mean and standard deviation at the top respectively from left to right.

13
3 Regression neural network for estimating
metallicity
The aim of this net is to estimate metallicities from training
on photometric data. So to get our network started, we need spectrometric
ground-truth data as well as photometric data. We have at disposition data from
various surveys:
· Spectroscopy: SEGUE (Sloan Extension for Galactic
Understanding and Exploration)
· Photometry: Gaia DR2, SDSS (Sloan Digital Sky Survey),
Pan-STARRS or PS1 (Panoramic Survey Telescop And Rapid Respond System), CFIS
(Canada-France Imaging Survey) and Pristine
3.1 Input data: photometry
Our input data is based on the photometric information we have
about our stars, meaning their magnitude in different bands and their
uncertainties. The bands we have at disposition are shown on Table1
hereafter.
|
Filter
|
Survey
|
Description
|
Mean wavelength
|
|
G
|
|
Visible band
|
6742.5Å
|
|
Bp
|
Gaia DR2
|
Blue photometer band
|
5279.9Å
|
|
Rp
|
|
Red photometer band
|
7883.7Å
|
|
u
|
CFIS
|
Ultra violet band
|
3549.1Å
|
|
CaHK
|
Pristine
|
Calcium »HK» doublet
|
3953.2Å
|
|
g
|
|
Green band
|
4718.9Å & 4900.1Å
|
|
r
|
SDSS &
|
Red band
|
6185.2Å & 6241.3Å
|
|
i
|
PS1
|
Optical infrared band
|
7499.7Å & 7563.8Å
|
|
z
|
|
Near infrared band
|
8961.5Å & 8690.1Å
|
Table 1: Description of the bands used as
input data, the filters mean wavelengths were taken from the SVO Filter Profile
Service, and are given for SDSS and PS1 respectively.
By their number and diversity, they manage to cover a large
part of the spectrum, as can be seen on Figure 8: Figure 8a shows Gaia DR2
photometric coverage and Figure 8b gives SDSS coverage and an idea of
Pan-STARRS and CFIS coverage. In fact, the values of the mean wavelength for
u,g,r,i,z filters can vary a little depending on the survey. The Ca H
& K filter by Pristine is a much narrower band between the u and
g bands, focused on the Balmer bumps in stars spectra, an area
displaying many metal absorption rays. It is thus useful to measure metallicity
with high accuracy.
The choice of the inputs to be kept for training is a
compromise between number of bands available and the number of objects we have
information about. In fact, Gaia covers the full sky, Pan-STARRS is three
fourths of the sky, SDSS is one fourth of the sky and CFIS is one eighth of the
sky. Pristine coverage is even smaller. It means that the more catalogs we
keep, the less objects we keep (as the area in common diminishes) but the more
information we have on those objects. Our raw photometric data is a combination
of all those surveys, in (at first) three catalogs. All three contain at least
Gaia DR2, PS1 and SDSS data, then one has the u band only, another one
has the CaH&K band only, and the last one has
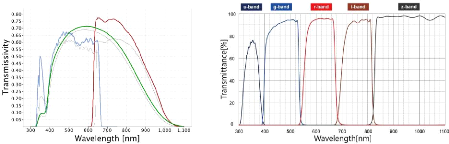
14
(a) Gaia DR2 passbands, in green the G
filter, blue the Bp (b) SDSS passbands, in dark
blue the u filer, blue the g filter, red the
filter and red the Rp filter, and in thin lines DR1
passbands. r filter, brown the i filter and black the z
filter.
Figure 8: Illustration of Gaia and SDSS
photometric data coverage in wavelength.
all bands. We proceed this way because of the differences in
survey coverage. Adding CFIS limits the training catalog to about 140,000
objects and Pristine narrows it down to 90,000. With all data, the number of
objects goes down to 49,000.
We train our algorithm on colors, i.e. differences between two
bands. The net precision highly depends on the input and output data, so the
amount of data we keep has to be optimized by trial and error. For example,
Thomas et al. 2019 [3] choose to keep (u -g), (g -
r), (r - i), (i - z) and (u
-G). Keeping all the colors would provide redundant information
to the network, so we choose to keep only n - 1 colours for n
available bands. At first, we keep only colours using the G-band as a
reference, since the G-band uncertainty is the lowest so the error propagation
should be optimized: the net is to train on (G - Bp), (G
- Rp), (G - g), (G - r),
(G - i), (G - z), (G - u)
and (G -CaHK), and once it gives satisfactory results, other
colors are to be tested.
3.2 Output data: stellar parameter
predictions
Spectroscopic studies have different physical parameters to
offer. Table 2 shows the three different spectrometric measurements coming from
the SEGUE survey. Those physical parameters are measured and presented in
different ways in SEGUE. We choose to work with the same data as Thomas et al.
2019 [3] which are the adopted metallicity fe-hadop, the adopted
surface gravity loggadop and the adopted effective temperature
tef-fadop.
|
Output
|
Name
|
Description
|
|
[Fe/H]
Log(g)
Teff
|
Metallicity
Surface gravity
Effective temperature
|
Chemical composition of an object
taken with a logarithmic
scale
Gravitational acceleration at the surface of an object
taken with a
logarithmic scale
Temperature (K) of a black body emitting
the same
amount of radiation as an object
|
Table 2: Description of available outputs from
the SEGUE survey
15
Of course metallicity is mandatory since the aim is to predict
it, but to add surface gravity and/or effective temperature can help the
network to converge. This is what is called multi-tasking. In fact, the more
links the network can find between inputs and outputs, the better and the
quicker the results converge. The dataset we use to train our model has within
it the inputs i.e. the colors we defined from the bands, and the outputs.
3.3 Data selection
It is obvious that the precision of the network depends on the
quality of input data, that's why an initial selection is done on the catalog
to obtain a clean input dataset. For this we use topcat, a software which comes
in handy when one has to manipulate this kind of catalog. We thus put a limit
on the signal to noise ration (SNR) and the uncertainties on all of the data
used. We can also put limits on the values of the bands and/or colors and on
the outputs. For example, limiting log(g) to values above 3 allows one
to delete most of the giant stars that are in the catalog and to focus on the
dwarf stars which are way more represented. It is also possible to make color
cuts to focus on the bluer stars, as done in the work of Iveziéet al.
2008 [2] and as we need to do to be able to use their photometric distance
formulae. The selection we make for our first attempt is as follows:
LOGG_ADOP> 3 & SNR>25 & g0-r0>0.2 &
g0-r0<0.6 & u0-g0>0.6 & u0-g0<1.35 & FEH_ADOP>-3 &
FEH_ADOP<0 & FEH_ADOP_UNC<0.1 & du<0.03 & dg<0.03 &
dr<0.03 & di<0.03 & dz<0.05 & eGmag<0.03 &
eBpmag<0.03 & eRpmag<0.03 & Gmag0<18 & g0<18.5 &
abs(g0-i0-0.45)<0.5 & abs(g0-z0-0.45)<0.5 &
abs(g0-Gmag0-0.35)<0.2
topcat also allows one to shuffle the data, a useful tool for
machine learning as it ensures that each row is independent from its neighbours
in the initial dataset. For example if stars in the initial dataset are sorted
according to their metallicity, then there is a risk for the network to train
only on low metallicities and then to test on higher metallicities which he
won't recognize as well as low ones.
With selection on the catalog containing Pristine data and not
CFIS, we can't do the color cuts on the u band. With all bands, the
number of available data goes from 49,000 down to 14,000, which may not be
enough, and with all bands but CaHK, a catalog initially containing more than
140,000 objects, only 41,000 are left. We choose to keep going with those are
the data to train our net.
3.4 First estimates of metallicity
The first net we created for linear regression is perfectly
usable here. The results given by this net when trained on our selected data as
presented above are shown in Figure 9. The predictions look quite smooth, no
big bias can be seen on Figure 9a, and after only 20 epochs with the one cycle
policy, which represents a handful for minutes, we get a precision of
ó 0.215dex, which is not far from the results of Ibata et al.
2017 [4]. The net thus has to be optimized to at least beat this limit of
ó = 0.2dex. Letting it train longer (up to 1000 epochs) doesn't
get ó much better, we win a few thousandth at most. In fact,
with the one cycle policy, nets converge very fast.
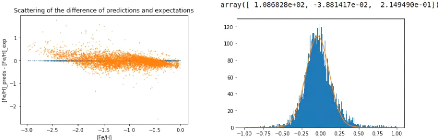
16
(a) Scattering of the error on the predictions with regard to (b)
Histogram and fitted gaussian for the difference between pre-
the expectations. dictions and expectations. Precision of the
net: u 0.215dex.
Figure 9: Results and accuracy for a three
linear layer net with sizes 7 x 1024, 1024 x 512 and 512 x 1, trained for 20
epochs and with a learning rate of 0.01 using the one cycle policy.
When the Pristine CaHK filter is added to the inputs, the
number of objects in the training and test sets is divided by three so the net
can't fit as well as before: the precision goes up to u 0.33dex. To
balance this problem, we try data augmentation using the uncertainties on each
bands to artificially inflate the size of the training and test sets, but the
precision only gets a little better, up to u 0.30dex. We thus decided
to work mainly with the catalog not containing the Pristine data.
Then, always with the same three linear layers inside the net,
different combinations of hyperparameters (number of epochs, learning rate,
dropout) are tested to optimize the efficiency of the net. After a long session
of trial and error, the net seemed to be stuck at an accuracy of u =
0.21dex. Since those three hyperparameters do not seem to be real
game-changers, the number and sizes of linear layers are to be tested as well.
Hereafter in Figure 10, we show the results obtained with a five layers net
with sizes 7x64, 64x128, 128x128, 128 x 128 and 128 x 1 with a dropout pf
probability 0.001 for each layer but the first. For 20 epochs, the precision
gets better than with the three linear layers net and comes to u
0.207dex. Trying different combinations of hyperparameters like for the
last net, the precision remains higher than u = 0.2dex, but it comes
closer.
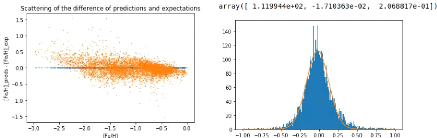
(a) Scattering of the error on the predictions with regard to (b)
Histogram and fitted Gaussian for the difference between pre-
the expectations. dictions and expectations. Precision of the
net: u 0.207dex.
Figure 10: Results and precision for a five
linear layers net with sizes 7x64, 64x128, 128x128, 128x128 and 128 x 1,
trained for 20 epochs and with a learning rate of 0.01 using the one cycle
policy.
3.5 Multi-tasking
Since we have at our disposition several stellar parameters
derived from spectrometric data, we can try what is called multi-tasking. In
fact, a neural network works by looking for links between the inputs and the
outputs, so by adding outputs, it can find more links. That's why we add the
surface gravity and the effective temperature to the outputs.
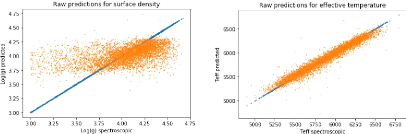
17
(a) Predictions for surface gravity: huge bias.
(b) Predictions for effective temperature: well fitted.
Figure 11: Predictions of surface gravity and
effective temperature for a multi-tasking three linear layers net with sizes 7
x 1024, 1024 x 512 and 512 x 3, trained for 20 epochs and with a learning rate
of 0.001 using the one cycle policy.
Figures 11 and 12 show the results we get for a three linear
layers net with sizes 7x1024, 1024x512 and 512x3. The effective temperature
predictions seem quite smooth (Fig. 11b) but for the surface gravity we can see
a huge bias on Figure 11a. This means that the net is working nicely on
Teff like it does for the metallicity but for surface gravity it may
be too simple. Multi-tasking is not really helping to guess better metallicity
for a net that simple. In fact on Figure 12a, the predictions don't seem to be
better than without multi-tasking, and we get a precision of ó
0.216dex.
(a) Scatter of the error on the predictions with
regard (b) Histogram and fitted Gaussian for the difference
between predictions
to the expectations. and expectations. Precision of the net:
ó 0.216dex.
Figure 12: Results and precision for a
multi-tasking three linear layers net with sizes 7x1024, 1024x512 and 512 x 3,
trained for 20 epochs and with a learning rate of 0.001 using the one cycle
policy.

19
4 Going further
fast.ai has only few options for tabular
data, so to get better results, we turned to a new algorithm that uses directly
the PyTorch module. This has been accomplished with the assistance of Foivos
Diakogiannis, an AI researcher at the University of Western Australia (Perth).
We also use new spectrometric data from LAMOST (Large Sky Area Multi-Object
Fibre Spectroscopic Telescope), which provides a wider number of stars. We also
play with all the colors in inputs, meaning the
g,r,i,z bands are doubled: one of each is
coming from Pan-STARRS and another from SDSS. This leads us to a total of 12
colors as inputs, which we can choose to use or not by turning Booleans to True
or False.
4.1 Wrapping up data
We first need to wrap up data properly to get it ready to be
trained on. To do so, we create a get_data_as_pandas() function which reads our
fits file and converts it to pandas, with possibility to shuffle data. Working
with joined surveys, we have a lot of unwanted fields so this function keeps
only the one we need as inputs or outputs, i.e. multi-band photometry,
spectrometric output as required (depending on if we want to do multi-tasking)
and associated uncertainties. In fact, uncertainties allow to do data
augmentation if needed and can be used in a customized loss function to prevent
the net from learning too much from not well measured stars.
Then we need a new data set class to wrap up, define training
and validation sets and normalize all of it. We call this new class
AstroDataset and implement its methods. The first one is the initialisation: we
use our get_data_as_pandas() function to get a raw data frame, which is then
normalised. The normalisation is done separately for the training and the test
sets, in order to not influence the training with values used on the test set
and getting a test set truly unseen during training, and all means and standard
deviations are stored for they will be needed for denormalisation afterwards.
This first method also allows to define in which mode to consider the
AstroDataset: train mode for training, test mode for validation or all to get
the whole data set, useful for example when we want to get predictions for a
whole data set once the net is trained enough. The two other methods are len
and getitem functions, which are basics in data sets. They respectively allow
to obtain the length of the data set in question and access to one or several
of its element(s). The getitem method separates the inputs from the outputs
when it is called. For our needs, it separates it in five categories: the
inputs (photometry), spectroscopy, measurement errors on spectroscopy, 'pop'
parameter (see in Section 4.4) and errors on 'pop' parameter.
4.2 Encoder/decoder, residuals and attention
The architecture of our new net is inspired from the ResUNet-a
framework developed by Diakogiannis et al. 2020 [5] in order to deal with scene
understanding of high resolution aerial images. It uses UNet encoder/decoder
backbone combined with residual connections, multi-tasking inference and other
complicated machine learning techniques.
20
The encoder/decoder architecture allows to go deeper and
deeper into inputs to find features at different scales. It is easy to
understand regarding translation. For example to translate the sentence THE
DARK SIDE OF THE FORCE from English to French, the net first feeds on it and
encodes each word into a number: the inputs become what is called a context
vector containing numerical codes for the words to be translated. Then this
vector is fed to a decoder and translates the numbers into French: LE
CÔTÉ OBSCUR DE LA FORCE. Literally, the translator would guess LE
OBSCUR CÔTÉ, since French and English people do not agree on the
order of words in sentences. In fact, a simple net feeds on the inputs and
forget them afterwards, soit would probably give this kind of error, even if an
encoder/de-coder architecture would naturally inspect the sentence at various
scales. To compensate, residuals are used at each step of the architecture so
that information contained on inputs can persist. Those techniques apply
perfectly on images: to go deeper in an image means to look for smaller and
smaller features, and the persistence of information allows to analyse those
features keeping on mind the context. Ronnenberg et al. 2015 [7]
created the U-Net architecture for biomedical image segmentation, net that
inspired Diakogiannis on his work and so on ours.
Another interesting technique is attention. Attention in
machine learning is used to rank input data in order of importance. It is a
computing translation of how we humans pay attention to important details
linked to one another in an image, a sentence or a table, and how the
background (i.e. less important pieces of information) seems blurred. For
example in computer vision, to recognize a dog's face it is essential to
identify its nose, eyes and ears and to compare their positions, sizes or
colors, but the details of the background are not important. Recurrent neural
networks already allow information persistence, but attention brings an order
to it. It can be seen as an importance weights vector, which quantifies the
correlation of a datum to other data.
4.3 Architecture of our net
This new architecture proposed by Diakogiannis et al. 2020
[5] can be adapted to work with 1D data such as ours. To implement it, we
create a residual building block class called ResDense_block, and from those
blocks we create a net class called AstroRegressor . They both have two
methods: init for initialisation where the layers to be used are declared and
forward for implementing the computational graph, i.e. the way the layers are
linked to one another.
Building blocks are handy when it comes to repetitive
networks. For example on
fast.ai, the get_tabular_learner function
uses linear building blocks, as can be seen on Figure 4 with the repetition of
Linear-ReLU-BatchNorm-Dropout layers. The ResDense block we implement is quite
similar to those. In fact, it is a simple net with only one activation funtion
(ReLU) and 4 declared layers: one BatchNorm layer BN1, one
linear layer dense1, another BatchNorm layer BN2 and another
linear layer dense2. The difference comes in the forward method, where
we implement the computational graph as shown in Equation 4.3.1: the output out
is computed by feeding the inputs in to the simple net and adding it back at
the end as residuals.
out = dense2(ReLU(BN2(dense1(ReLU(BN1(in)))))) + in
(4.3.1)
21
The AstroRegressor class is then created using the ResDense
blocks. Its init method is quite heavy since it has to define both the encoder,
the decoder and the last layers to define the outputs, which we call heads and
are detailed in the next subsection. The en-coder/decoder backbone must
absolutely symmetric. It can be defined using the minimum and maximum numbers
of features only, meaning the minimum and maximum sizes of the inner linear
layers, and then it is scaled with power of 2. For example for
(nfea-tures_init, nfeatures_max) = (64, 2048), the encoder and decoder sizes
would be as follows:
Encoder: 64 x 128 -+ 128 x 256 -+ 256 x 512 -+ 512 x 1024 -+
1024 x 2048 Decoder: 2048x1024-+1024x512-+512x256-+256x128-+128x64
This is often done because of the belief that computer science
works better with powers of 2. The problem is, to get a deep net using this
strategy brings to a huge amount of parameters. To keep it lighter, we define
our AstroRegressor by giving it still nfeatures_init and nfeatures_max but also
an effective depth, which quantifies the depth at which the middle layer is
reached. It requires an additional function to get the features scale, which we
define as another class called features_scale. Figure 13 shows an
encoder/decoder backbone obtained using this class with (nfeatures_init,
nfeatures_max) = (64, 2048) and depth = 12. This net is deeper and less heavy
than a net with features scaled by a power of 2 for a depth of 12, which would
go to 217 for nfeatures_max.
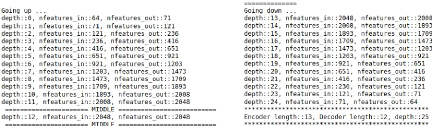
Figure 13: An example of encoder/decoder
architecture built using ResDense blocks and AstroRegressor class working with
depth. Are given effective depth of 12 and minimum and maximum numbers of
initial features of 64 and 2048 respectively. The going up part (left) is the
encoder and the going down part (right) is the decoder.
We also create a residual building block with attention class
called AResNet block net with attention class called AttAstroRegressor. The
AttAstroRegressor architecture is not really different from the AstroRegressor
one, the main changes are in the building blocks. The AResNet block is itself
based on the ResNet block with added an AttentionDense layer.
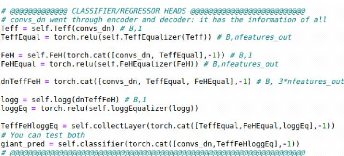
4.4 Outputs and heads
The last block is the one that defines the output(s), referred
to as head. It is also called classifier because it dispatches the outputs, but
as can be understood later, this name would be unsettling. It is this layer
that defines if we just guess metallicity, or try multi-tasking, or else. For a
simple guess of metallicity or for "simple" multi-tasking, we can use a simple
head, which is essentially a linear block. This is what our first
fast.ai
22
net did and what is shown in Figure 14a: out_features can be 1
if we want to guess only metallicity but also can be 2 or 3 if we want to add
effective temperature and/or surface gravity and do multi-tasking.
A new idea is to create a classification output to help the
net converge. In fact, we get predictions for the whole dataset using a
previous satisfying version of the net, one with precision of ó
0.15dex, and create a new field called pop in which we put 1 when
the prediction is bad ans 0 when it is good. With the same inner architecture
but a special head and a special loss function (see in next Subsection), we can
turn the regressor into a classifier. And by defining two different heads, one
for regression and one for classfication, it is possible to do both at the same
time. For consistency, an uncertainty field must be added in the AstroDataset
class so we create artificially an epop column which is all ones when
the dataset is deployed for training and all zeros when for validation.
Machine learning is the art of recognizing links between
inputs and outputs, so to improve the net we can add causality in it. Causality
means to add order in the predictions. For example and as illustrated on Figure
14b, we can have one head on the last layer of the backbone to first guess
effective temperature, then use this guess with the backbone to guess surface
gravity with a second head and finally use Teff , log(g)
and the backbone to guess metallicity. This can help creating links but this
can also transpose bias from one output to another. In fact, as we saw in the
previous Section, log(g) predictions are strongly biased so it may contaminate
metallicity predictions, thus the importance of the order.

(a)
(b)
Figure 14: Definition of head(s) whithin
AstroRegressor class init method. (a): one head for regression
only, out_features defines the number of outputs and each are computed
independently. The outputs are obtained by applying the regressor directly
after the decoder. (b): several heads for causality with
regressor and classifier, conv_dn is the table coming out of the
encoder/decoder backbone. Teff is first computed from
conv_dn , then [Fe/H] from (conv_dn,Teff ), then
log(g) from (conv_dn, Tef f , [Fe/H]), then classification from
(conv_dn, Teff , [Fe/H], log(g)). Outputs are Teff, FeH and
logg concatenated, and giant_pred.
23
4.5 Training
Many things occur during training, so we create various
functions to optimize the training loop. First, the loss function must be
adapted to the heads. For regression, we create a customized loss function
called custom_loss, working with predictions, expectations and uncertainties.
It gets the difference between expectations and predictions in absolute value
and divides it by normalised uncertainties: it is a weighted loss, which aims
to make the net learn more from stars with low uncertainties than with high
ones. Then it returns a mean of the loss over the dataset it is fed on. For
classification, we choose to use BCEWithLogitsLoss(), which is Binary Cross
Entropy with one Sigmoid layer. For both regression and classification, we use
respectively our custom_loss and BCEWithLogitsLoss() and use the sum as a total
loss. To make sure one doesn't take advantage on the other, we add a parameter
á to the sum and weight each sub-loss with respectively
á and 1-á. We adjust the á
parameter accordingly to the convergence speed during training. Be it for
regression, classification or both, the training loss is computed directly
inside the training loop.
For the validation loss, we create a function to evaluate it
to be used in the training loop, called eval_test_loss. This function uses the
same loss function than in the training loop but applies it to the validation
set and gets a mean of the loss over all the validation set. The aim is to
train the net and go for the lower validation loss, so using the result of this
function in the training loop, it is possible to save the parameters of the net
each time it improves and by doing so, always have the best fit model to check
out its precision, and not the last updated version as it was the case using
fast.ai. This is called checkpoint-ing.
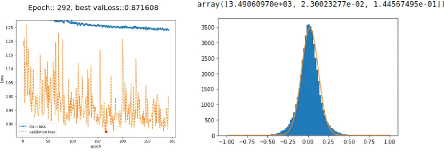
Also, having both training and validation losses stored in a 'history' list, it
is possible to plot the progress of the net at each epoch. To do so, we create
the generate_image function which plots the evolution of training and
validation losses as a function of the epoch, with adaptive edges, as shown in
Figure 16a. The red dot corresponds to the best validation loss for which
checkpointing saved the model.
Before entering the training loop, we must load the data we
want to work on using the AstroDataset class and the DataLoader from torch
module which allows to organize data onto batches and shuffle it if needed
(needed for the training session but not the test session). Then we must define
our net using one of the AstroRegressors (with or without attention) we created
and choose an optimizer. We keep the Adam optimizer which is the default set
for most nets and works well in many cases. We then must define our first
learning rate and number of epochs we want the training loop to run for, which
are both to be adapted accordingly to the net's response, i.e. the evolution of
the losses. The learning rate is passed as an argument to the optimizer so to
be able to change it inside the training loop, we create a function which puts
the optimizer's "lr" parameter to the new value. A last value to set is the
initial value for checkpointing: we fix acc=1.0e30 to be sure this threshold is
passed on the first epoch.
Now the training loop can begin. At each epoch, we first put
the net in train mode and set the initialise the training loss to 0. Then for
each batch on the training set, we reinitialise the optimizer gradients to 0,
we get the inputs, the expected outputs and their uncertainties and we send it
to the GPU. Once we have the inputs we can do the forward pass by feeding them
to the net and get the predictions, and from those and the expected
24
output we can compute the loss using our favourite loss
function. Now it is time for the backward pass: we compute the gradients using
the loss.backward() command and update our net's parameters using the
optimizer.grad() command. Then the value of the loss for this batch is added to
the training loss. At the end of the batch loop, the validation loss is
computed using the eval_test_loss function and and both training and validation
losses are added to the history list, in order to be plotted at the end of the
epoch using the generate_image function. The last action of the training loop
is to check if the net get better, i.e. if the validation loss get lower on
this epoch, and if it did, it saves the parameters of the net under a chosen
name.
This training loop is destined to trial and error. In fact,
there is no one cycle policy here so the learning rate has to be changed
manually when the net doesn't get more precise anymore or when it doesn't learn
enough. The aim is to train it again and again until the validation loss starts
to diverge to ensure that the best value is truly reached, and it can take a
few hours.
4.6 Getting predictions
To get our results, we create a get_preds function which
basically puts the net in test mode, feeds it the validation set and gets the
predictions. It returns the predictions and the expectations so we can compare
both. We can then plot the scattering of our results for regressions as did
with the
fast.ai net and as shown on Figure 15. To
visualise the results of the classification part, we create a function to plot
its confusion matrix. This matrix shows on the x-axis the predicted labels and
on the y-axis the true labels, then a color code shows the number of objects
well and wrongly predicted. That is what shows the top left panel on Figure
15.
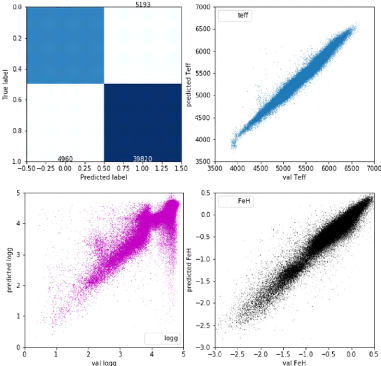
We can see on Figure 15 that biases for metallicity and
effective temperature are still quite low compared to our results with the
fast.ai net, but the surface gravity plot
evolved remarkably. The bias is way lower than with the old net (see Fig. 11a
for comparison), showing that our improvements were efficient. The top left and
bottom right cells in the confusion matrix correspond to the well identified
stars. They are way darker than the two other cells, meaning that our
classifier is working nicely. Those first visual results are satisfying.
Finally, Figure 16b shows the precision we obtain for an
encoder/decoder backbone net using attention and multi-tasking on metallicity
and surface gravity, with a depth of 6, a minimum number of features of 32 and
a maximum of 4096. With this net, we get a precision of ó
0.1446dex, which breaks the 0.2dex record of Ibata et al. [4] the 0.15dex
one of Thomas et al. [3].
25
Figure 15: Visualisation of the predictions
given by a regressor and classifier multi-tasking net with attention, with the
backbone shown in Fig. 13 (nfeatures_init=64, nfeatures_max=2048, depth=12).
Top left: confusion matrix for the 'pop' parameter. Top right,
bottom left, bottom right: scattering of predicted effective temperature,
surface gravity and metallicity respectively.
(a) (b)
Figure 16: Training and results for a
regressor only [Fe/H] and log(g) guessing net with attention and with an
encoder/decoder backbone of depth = 6 and nfeatures_max = 4096.
(a): History of the last epochs of training, in red the best
validation loss for which the model was saved. (b): Histogram
of the difference between predictions and expectations and fitted Gaussian,
with values of amplitude, mean and standard deviation at the top respectively
from left to right. Precision of the net: ó 0.1446dex.

27
5 Results
We use this last net with precision of ó
0.14dex on a huge photometric catalog containing data from Gaia, PS1, SDSS
and CFIS, to get photometric estimates of metallic-ity and surface gravity,
i.e. measures of those two spectrometric parameters, but based on photometry.
This gives us the photometric estimates of 18,183,767 stars. Let's then compare
it to the estimates of Iveziéet al. 2008 [2].
5.1 Comparison on metallicity and surface gravity
predictions
We propose to compare our metallicity and surface density
estimates to Iveziéet al. [2] work, using their Figure 1, which displays
mean metallicity color scale as a function of (g - r) color
and surface gravity. This figure is visible on Figure 17 left panel. In
particular, it allows us to identify giant stars in the log(g) < 3
region, which represents 4% of the objects in this plot. This region is
dominated by low metallicity stars with [Fe/H] < -1. Two types of giants are
visible on this figure: Blue Horizontal Branch (BHB) stars and red giants.
We do the same color cuts and plot raw metallicity. That is
what is plotted in the right panel of Figure17. The fraction of giants in this
plot is 2% so we found fewer giants than Ivezié. The rainbow feature
corresponding to the red giants is easily identifiable on our plot, but the
much rarer BHB stars are under-represented.
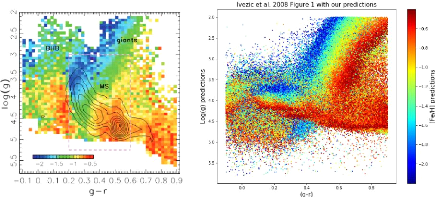
Figure 17: Comparison of metallicity as a
function of (g - r) color and surface gravity between
Ivezié's Figure 1 (left) and the same plot with our results (right).
Color cuts are g<19.5 and -0.1<g-r<0.9. On the left panel, the dashed
lines correspond to main sequence (MS) region selected for deriving photometric
estimates for effective temperature and metallicity. The giant stars
(log(g)<3) can be found for -0.1<g-r<0.2 (Bue Horizontal Branch stars)
and for 0.4<g-r<0.65 (red giants). The features corresponding to red
giants are easily identifiable on our plot in the right panel, but not the BHB
stars. However, a strong low metallicity line appears for
0.4<log(g)<0.45.
28
5.2 Recovering distances
Spectroscopic parallaxes are computed using magnitudes. In
fact, Equation 5.2.1 shows the way to get heliocentric distances dist
using absolute magnitudes Mr and apparent magnitudes
m. The m - Mr term is referred to as the
distance modulus and noted u.
|
m-Mr = 5log10
|
u di st
10pc
|
? dist= 101+u/5 (5.2.1)
|
The apparent magnitude of an object comes from photometry and
Ivezic et al. 2008 [2] developed a process to get its absolute magnitude from
its metallicity. As shown by Equation 5.2.2, absolute magnitude can be
decomposed on two factors: one depending on (g - i) color
called M0 r and one depending on metallicity called
AMr.
Mr (g -
i,[Fe/H]) = M0 r (g -
i) +AMr ([Fe/H]) (5.2.2)
Iveziélooked for a relationship between those values,
fitting it for five known globular clusters. Observations led to look for two
polynomial fits, one linking (g - i) color to M0
r and one linking metallicity to AMr. They came up
to Equations 5.2.3 and 5.2.4 below.
M0 r (g - i) = -2.85 +
6.29(g - i) - 2.30(g - i)2
(5.2.3)
AMr ([Fe/H]) = 4.50-
1.11[Fe/H] - 0.18[Fe/H]2
(5.2.4)
We apply this process to compute heliocentric distances, and then
transform to Galactic cylindrical coordinates. We have at our disposition right
ascension and declination from Gaia, so we use topcat to convert these to
Galactic longitudes and latitudes, later noted respectively l and
b. To convert those into cylindrical coordinates, we use the
trigonometrical relationships shown in Equations 5.2.5 and 5.2.6. The values of
cylindrical radius and distance to the galactic plane for the Sun come from two
different studies: R = 8.122#177;0.031kpc from Abuter et
al. 2018 [8] and Z = 0.017kpc from Karim et al. 2016
[9].
/
I X = di st ×
cos(l) × cos(b) - R = R
= X 2 + Y 2 (5.2.5)
Y = dist × sin(l) ×
cos(b)
Z = dist *sin(b)+
Z (5.2.6)
To compare our results with Ivezié's work, we reproduce
Figure 8 from his article, showing the dependence of the median photometric
metallicity as a function of the cylindrical radius R and the norm of the
distance to the Galactic plane |Z| for data from SDSS DR6. This figure is our
Figure 18 hereafter. The choice of coordinates puts the Galactic center at the
(0,0) point and the Sun at about (8,0.1). An interesting feature to notice is
the metallicity gradient which is quite linear with |Z|. The halo is made of
stars with low metallicities and the closer to the disk one gets, the higher
the metallicities. This change in metallicity allows us to identify the halo
(dark blue) and the thick and thin disks (green to red) of the Milky Way, but
also the Monoceros stream as pointed out on the figure.
We apply the same color, distance and metallicity cuts to zoom
on the same region, our sample being put down to 1,180,853 stars. We choose to
first reproduce Ivezié's map
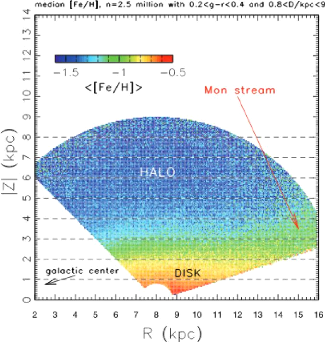
29
Figure 18: Iveziéet al. Figure 8:
Dependence of the median photometric metallicity for about 2.5 million stars
from SDSS DR6 with 14,5<r<20, 0,2<g-r<0,4, and photometric distance
in the 0.8-9 kpc range, in cylindrical Galactic coordinates R and |Z|. There
are about 40,000 pixels (50 pc ×50 pc) contained in this map, with a
minimum of 5 stars per pixel and a median of 33 stars. Note that the gradient
of the median metallicity is essentially parallel to the |Z|-axis, except in
the Monoceros stream region, as marked.
using raw metallicity. That is what is shown in Figure 19: |Z|
as a function of R with raw metallicity as color scale. We find back that the
stars of the disk have higher metallici-ties than the ones in the halo, but the
smooth metallicity gradient showing the difference between thin and thick disks
and the Monoceros stream disappeared. For the latter, the difference of
footprint is probably responsible, since our sample does not contain all the
SDSS data.
To uncover the smooth gradient, we compute and display mean
metallicities instead of raw ones. To do so, we bin the data on R and |Z| in
slices of 0.015 parsecs and get a mean for the other parameters. 0.015 parsecs
is a good compromise between clarity of results and number of data remaining.
In fact in Figure 20, the wings of the plots are a bit weak but information
remains: the smooth gradient appears.
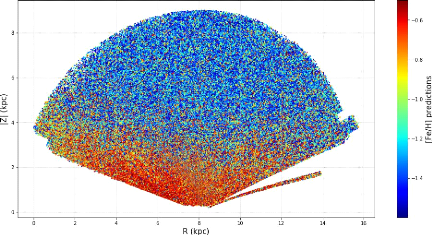
30
Figure 19: Dependence of raw predicted
metallicity for about 1.18 million stars from Gaia, PS1, SDSS and CFIS joined
together with are 14.5 < r < 20, 0.2 < (g
-r) < 0.4, 0.8kpc<dist<9kpc and -1.6<[Fe/H]<-0.5,
using Galactic cylindrical coordinates R and |Z|. Due to difference in
metallicity, the disk appears reddish on the bottom of the plot and the halo is
mainly blue, visible for |Z|>4kpc.
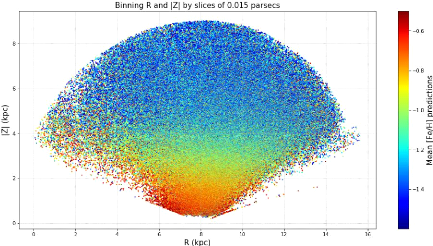
Figure 20: Dependence of mean predicted
metallicity for about 1.18 million stars from Gaia, PS1, SDSS and CFIS joined
together with are 14.5 < r < 20, 0.2 < (g
-r) < 0.4, 0.8kpc<dist<9kpc and -1.6<[Fe/H]<-0.5,
using Galactic cylindrical coordinates R and |Z|. Binning is of size 0.015pc x
0.015pc in R and |Z|. The disk and halo are still visible in the same colors
but now the smooth gradient appears.
31
6 Auto-encoder
One limit of the network we developed so far is that it
requires a certain amount of fields in the dataset, exactly seven colours,
which keeps stars with less photometric information getting a prediction of
their metallicities. We thus want to create a similar net which predicts the
same spectrometric parameters but with one colour missing. To that end, we
create an auto-encoder. Its aim is to extend the previously developed
net to datasets with one colour missing and also get a prediction for this
colour. This allows to increase the number of stars for which our net can
estimate the metallicity.
6.1 Architecture of the net
Figure 21 shows the principle of the auto-encoder, which has
two steps. The first step called encoder is a net identical to the
previous one but with one colour missing, soit predicts the spectrometric
parameters we want. The second step called decoder is mirror net which
takes the spectrometric parameters as inputs and predicts the missing colour.
To manipulate the missing colour, we create an index called missing_band. It is
to be used identify the missing colour field inside the dataset during
training. For easier understanding, the encoder/decoder architecture we
described in Section 5 is from now on referred to as a sandwich
net.
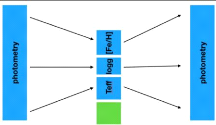
Figure 21: Scheme for an auto-encoder: left
arrows represent the encoder, right arrows are the decoder. The green square is
a hypothetical parameter to be added if it doesn't work with Teff, logg and FeH
only.
The architecture of the auto-encoder is thus composed by two
sandwich nets, as shown in Figure 22, each one's role being defined by their
first and last layers. The encoder aims to predict the effective temperature,
the surface gravity and the metallicity from the 11 colours we have as
photometric inputs minus the missing band, that's why the first layer is of
size 11 and the last one is of size 3. The decoder aims to predict the missing
band starting from all the photometric and spectrometric data we have, so its
first layer is of size 14 and its last is of size 1. The layers within the
sandwich nets are ResDense building blocks of a given size or linear layers to
increase or decrease linearly the size of the following ResDense layer.
In practice, we define subclasses to help implement the
auto-encoder. We first implement the sandwich net class, which is the previous
'encoder/decoder' structure we implemented in Section 4. It takes the input and
output sizes as explained in the previous paragraph, and create a sandwich
structure of ResDense and linear layers corresponding

(a) (b)
32
Figure 22: Structure and inside sizes of the
auto-encoder. (a): the encoder composed of a sandwich net of depth 6 and
predicting Teff, logg and FeH (width2=3 in the final layer). (b): the decoder
composed of a sandwich net of depth 6 and predicting the missing colour
(width2=1 in the final layer).
to each part of Figure 22. Then we create an Encoder class and
a Decoder class to implement separately the encoder and the decoder with the
right input and output sizes. Finally, we create an AutoEncoder class to
implement the final common structure, and organize the forward pass. We fix in
this method the part of the input data on which the net feeds.
The main difficulty we encounter doing those modifications is
the consistency between the sizes of the nets and the data going through it.
This consistency is to be reached to make sure the data on which the nets are
feeding are the good ones, so photometry minus one colours for the first and
spectrometry plus photometry minus one colour for the second. Basically, it all
depends on the definition of the getitem method inside the AstroDataset class
and how it is used in the eval_test_loss and get_preds functions and inside the
training loop. We decide that the getitem function has to separate the data
whithin five categories: the inputs (photometry minus one colour depending on
the index of the missing colour), ground truth spectrometry, errors on
spectromectry, ground truth of the missing colour and errors on the missing
colour. Those different categories are used in the forward pass to make sure
that the first sandwich net feeds on the photometry minus one colour (the
inputs) and the second feeds on the same inputs concatenated to the predictions
of the spectrometric parameters. The ground truths and errors are used inside
the custom loss function as before, in order to compute the training and
validation losses.
33
6.2 Training and precision
We then modify the eval_test_loss() function, the get_preds()
function and the training loop accordingly. To evaluate the loss between the
ground truth and the predictions of the encoder, we use our custom_loss()
function with special weights to give more or less importance to the parameters
we want to predict. The most important being metallicity, we give it an
artificial weight of 10, then 3 for surface gravity and 1 for effective
temperature. Then for the decoder we just compute the mean of the absolute
value of the difference between the ground truth and the predictions of the
missing colour. The total loss is thus the sum of each sandwich net's losses.
The rest of the eval_test_loss() function and the training loop are the same as
before: we get the predictions, compute the losses and adjust the net through a
backward pass. The training and validation losses are stored to plot the
learning history during training. We also kept checkpointing, which allows to
save the parameters of the net for the best value of validation validation
loss.
We first try and train an auto-encoder with the (G -
u) colour missing. As usual, we plot the evolution of the training and
validation losses during training to see its evolution, as can be seen on
Figure 23: the curves are quite bumpy but some converging parts appear, meaning
the auto-encoder still learns.
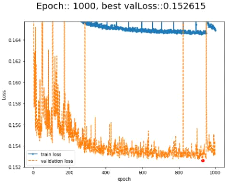
Figure 23: Evolution of the training (blue)
and validation (orange) losses as a function of the epochs. The red dot marks
the lowest validation loss, for which the parameters of the net are saved.
Between 0 and 200 epochs, the curves are very bumpy but then they converge.
To get a closer look to the results, we plot the predictions
of the net after a few hundreds epochs in Figure 24. The spectrometric
parameters don't seem too problematic but the missing colour is far away from
satisfactory. To get a more accurate measure of the precision of the net, we
can compute the differences between the expectations and the predictions for
both metallicity and missing colour, histogram them and get their standard
deviation ó, as shown in Figure 25. With more training and an
adaptive learning rate, we could probably a better precision for both parts. We
could also add an artificial weight in the loss for the missing colour like the
ones added in the loss for the spectroscopic parameters. Adding a weight of 10
for example would balance the loss and increase the impact of the missing band
on the adjustment of the net during the backward pass.
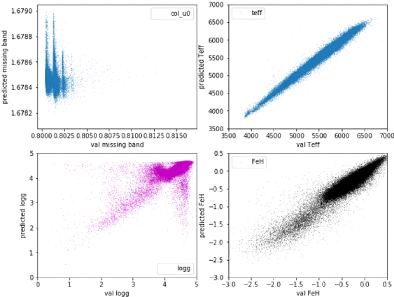
34
Figure 24: Predictions of (g-r)
colour in top left, effective temperature in top right, surface gravity in
bottom left and metallicity in bottom right for a learning rate of 10-3
and a hundred epochs.
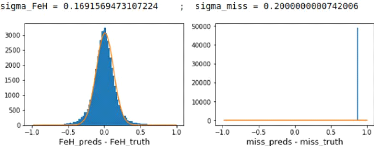
Figure 25: Precisions, histograms and fitted
gaussians for metallicity (left) and (g-r) missing colour (right).
35
7 Conclusion
7.1 Conclusion & Discussion
One challenge of Astrophysics is to estimate heliocentric
distances, and techniques to measure them are called parallaxes. Geometric
parallax is an efficient method but looses in precision with distance. However,
Iveziéet al. 2008 [2] developed a way to compute spectroscopic parallax
based on absolute magnitude recovered from metallic-ity. Moreover, with
multi-band photometry, it is possible to cover whole spectra of million of
stars at one go and get a huge amount of data quicker than with spectroscopy,
which easily leads to big data and machine learning.
The aim of this internship was to create a neural network to
propagate spectroscopic parallaxes to all stars with known multi-band
photometry. This net had to learn to associate photometric data (magnitudes in
u,g,r,i,z bands from Pan-STARRS,
SDSS and CFIS and G,Bp,Rp bands from Gaia) to
spectrometric data (metallicity, surface gravity and effective temperature from
SEGUE) in order to predict it for stars with no spectrometric data
available.
We ended up with two nets. The first one created with a
simplified programming language called
fast.ai, allowed to enter the world of
machine learning in a top down point of view and getting acquainted with the
main notions of this domain. The second one created using the Python module
PyTorch, and with the fabulous assistance of Foivos Diakogiannis, was brought
to work in a bottom up consideration, coding classes and functions used for our
first net and more from scratch. This second net was the most efficient,
reaching a precision of ó 0.1446dex.
This net was then used to estimate metallicities of about 18
million stars, which were used to compute their heliocentric distances as
proposed by Iveziéet al. 2008 [2]. Those distances were used to plot a
map of the distribution of metallicity inside the Milky Way, on which the halo,
thin and thick disks were clearly identifiable.
We finally developed an auto-encoder, which aim was to extend
our previous net to less complete entry datasets and to provide predictions for
this missing colour(s) in addition to the spectrometric predictions. For a
dataset missing the (G - u) colour, we get a precision of
ó 0.169dex for the metallicity and ó 0.2 for
the missing color.
With more time we could improve this auto-encoder to get a
really satisfying precision. To prove its efficiency, we could train it on the
(g - r) colour and get predictions for this colour, surface
gravity and metallicity and then use them to reproduce our Figure 17, for which
we would have the results of Iveziéet al. 2008 [2] and our first net as
a comparison. It would also be interesting to test other bands and see the
dependence of the precision as a function of it. Finally with significantly
more time, we could try to find the optimal amount of photometric information
to get satisfactory precision.
36
7.2 Difficulties & Learnings
This internship allowed me to acquire a solid knowledge basis
of Machine learning and its implementation using Python, which is a domain I
find highly interesting and promising for the years to come. Furthermore, the
discovery of
fast.ai and learning it by myself during
the first month made me work on my autonomy when handling a part of a project,
and then learning to use PyTorch with both Rodrigo and Foivos was a great
moment of team work. I am glad this project helped me develop both
competences.
The conditions of this internship were especially demanding
because of the Covid-19 pandemic. I am thankful that I was allowed to continue
it and not forced to stop after only one month like happened to some other TPS
interns in Strasbourg, but it was challenging. The lock-down was emotionally
rough, particularly in Alsace which was the main cluster in France, and
settling in teleworking outside the master room without having a dedicated room
for work was quite hard at the beginning. Nevertheless, after a few complicated
days, it allowed me to better organize myself in my work and to adapt to
extreme conditions. Regular and warm communication with Rodrigo (and Foivos)
via e-mails or Slack helped a lot.
This experience was an interesting leap into the research
world. They allowed me to get a further glimpse to it and to understand how it
works within Rodrigo's project. Using this insight, I could decide with more
confidence what I want for my professional career. Astrophysics are a part of
science that I love, and to be able to understand the discoveries that are to
come in this domain. It taught me to be curious about the Universe in which I
live while staying humble considering what I really understand of it. Even
though I am not carrying on with a thesis, I am going to apply this scientific
principle to my future job and life and stay in touch with Astrophysics.
In conclusion, those 6 months of internship were both a
challenge and a pleasure. They shaped my future career and the person I am
going to be in my professional life. I am deeply grateful to Rodrigo to have
made all of this possible, for his eternal cheerfulness and warm
encouragements. This experience prepared me to enter the labour force with more
serenity.
37
Bibliography
[1] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya
Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural
networks from overfitting. J. Mach. Learn. Res., 15(1):1929-1958,
January 2014.
[2] Zeljko Ivezic, Branimir Sesar, Mario Juric, Nicholas
Bond, Julianne Dalcanton, Constance Rockosi, Brian Yanny, Heidi Newberg,
Timothy Beers, Carlos Prieto, Ronald Wilhelm, Young Lee, Thirupathi Sivarani,
John Norris, Coryn Bailer-Jones, Paola Re Fiorentin, Alan Uomoto, Robert
Lupton, and Donald York. The milky way tomography with sdss. ii. stellar
metallicity. ApJ, 684, 05 2008.
[3] Guillaume F. Thomas, Nicholaas Annau, Alan McConnachie,
Sebastien Fabbro, Hossen Teimoorinia, Patrick Côté, Jean-Charles
Cuillandre, Stephen Gwyn, Rodrigo A. Ibata, Else Starkenburg, and et al. Dwarfs
or giants? stellar metallicities and distances from ugrizg multiband
photometry. The Astrophysical Journal, 886(1):10, Nov 2019.
[4] Rodrigo A. Ibata, Alan McConnachie, Jean-Charles
Cuillandre, Nicholas Fantin, Misha Haywood, Nicolas F. Martin, Pierre Bergeron,
Volker Beckmann, Edouard Bernard, Piercarlo Bonifacio, and et al. Chemical
mapping of the milky way with the canada-france imaging survey: A
non-parametric metallicity-distance decomposition of the galaxy. The
Astrophysical Journal, 848(2):129, Oct 2017.
[5] Foivos I. Diakogiannis, François Waldner, Peter
Caccetta, and Chen Wu. Resunet-a: A deep learning framework for semantic
segmentation of remotely sensed data. ISPRS Journal ofPhotogrammetry and
Remote Sensing, 162:94-114, Apr 2020.
[6] Leslie N. Smith. A disciplined approach to neural network
hyper-parameters: Part 1 - learning rate, batch size, momentum, and weight
decay, 2018.
[7] Olaf Ronneberger, Philipp Fischer, and Thomas Brox.
U-net: Convolutional networks for biomedical image segmentation, 2015.
[8] GRAVITY Collaboration, Abuter, R., Amorim, A., Anugu, N.,
Bauböck, M., Benisty, M., Berger, J. P., Blind, N., Bonnet, H., Brandner,
W., Buron, A., Collin, C., Chapron, F., Clénet, Y., dCoudé u
Foresto, V., de Zeeuw, P. T., Deen, C., Delplancke-Ströbele, F., Dem-bet,
R., Dexter, J., Duvert, G., Eckart, A., Eisenhauer, F., Finger, G.,
Förster Schreiber, N. M., Fédou, P., Garcia, P., Garcia Lopez, R.,
Gao, F., Gendron, E., Genzel, R., Gillessen, S., Gordo, P., Habibi, M.,
Haubois, X., Haug, M., Haußmann, F., Henning, Th., Hip-pler, S.,
Horrobin, M., Hubert, Z., Hubin, N., Jimenez Rosales, A., Jochum, L., Jocou,
L., Kaufer, A., Kellner, S., Kendrew, S., Kervella, P., Kok, Y., Kulas, M.,
Lacour, S., Lapeyrère, V., Lazareff, B., Le Bouquin, J.-B., Léna,
P., Lippa, M., Lenzen, R., Mérand, A., Müler, E., Neumann, U., Ott,
T., Palanca, L., Paumard, T., Pasquini, L., Perraut, K., Perrin, G., Pfuhl, O.,
Plewa, P. M., Rabien, S., Ramírez, A., Ramos, J., Rau, C.,
Rodríguez-Coira, G., Rohloff, R.-R., Rousset, G., Sanchez-Bermudez, J.,
Scheithauer, S., Schöller, M., Schuler, N., Spyromilio, J., Straub, O.,
Straubmeier, C., Sturm, E., Tacconi, L. J., Tristram, K. R. W., Vincent, F.,
von Fellenberg, S., Wank, I., Waisberg, I., Widmann, F., Wieprecht, E., Wiest,
M., Wiezorrek, E., Woillez, J., Yazici, S., Ziegler, D., and Zins, G. Detection
of the gravitational redshift in the orbit of the star s2 near the galactic
centre massive black hole. A&A, 615:L15, 2018.
38
[9] M. T. Karim and Eric E. Mamajek. Revised geometric
estimates of the north galactic pole and the sun's height above the galactic
mid-plane. Monthly Notices of the Royal Astronomical Society,
465(1):472-481, Oct 2016.
|
|



