Annexes
Annexe1 : Résultats de la synthèse passe-bande
obtenus avec l'ondulation maximale ou la moyenne des deux ondulations.
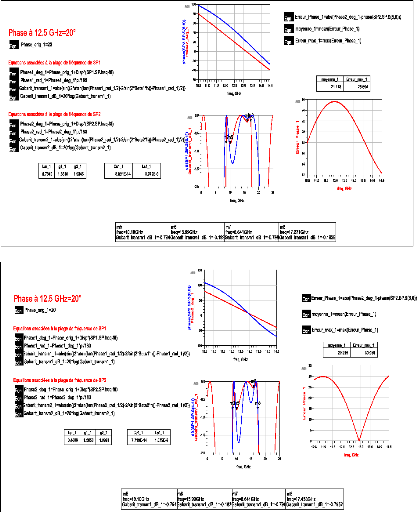
A1.1 Résultats obtenus avec la solution 1 pour une phase
à ??0, ?11(f0) = 20° et
(a)
(c)
??11(f0) = -30°/GHz
66
Annexes
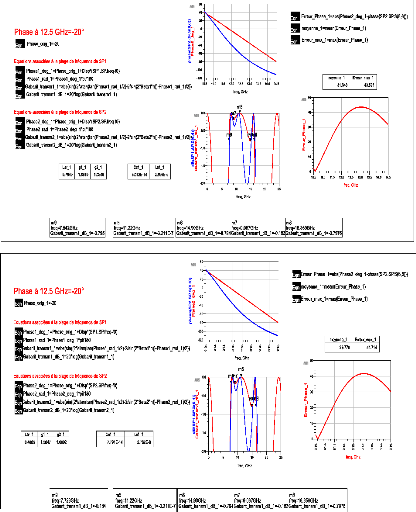
A1.2 Résultats obtenus avec la solution 2 pour une phase
à ??0, ?11(f0) = -20° et
??11(f0) = -30°/GHz
(b)
(a)
Figure A1. 2: Résultats de la synthèse
avec la solution 2 pour ??????(????) = -????° et
???????(????) = -????°/?????? (a)
ondulation
maximale. (b) ondulation moyenne
67
Annexes
Annexe 2 : Résultats de la synthèse passe-bande
solution 1 phases négatives et solution 2 phases positives
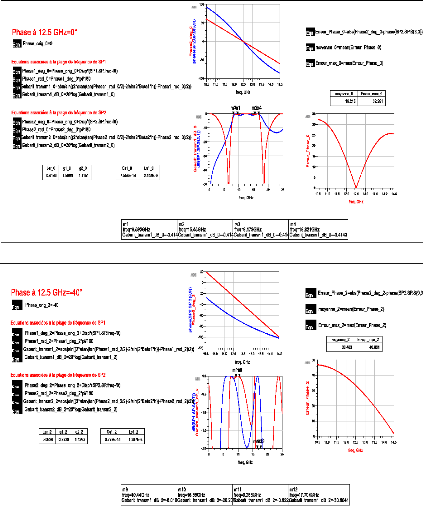
A2.1 Résultats obtenus avec la solution 1 pour une phase
à ??0, ?11(f0) = 0° ???? - 40° et
??11(f0) = -30°/GHz
(a)
(b)
Figure A2. 1: Résultats de la
synthèse solution 1 (a) ??????(????) =
??°. (b) ??????(????) = -????° ????????
???????(????) = -????°/??????
68
Annexes
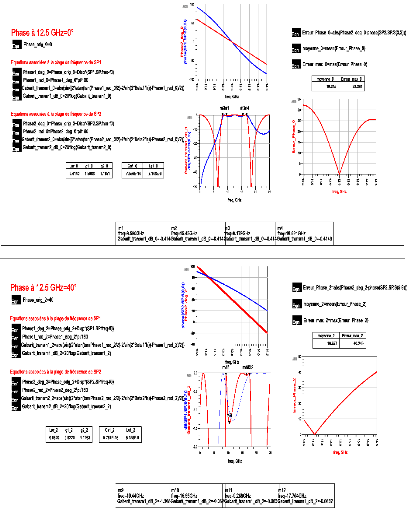
A2.2 Résultats obtenus avec la solution 2 pour une phase
à ??0, ?11(f0) = 0° ???? 40° et
??11(f0) = -30°/GHz
(a)
(c)
Figure A2. 2: Résultats de la
synthèse solution 2 (a) ??????(????) =
??°. (b) ??????(????) = ????° ????????
???????(????) = -????°/??????
69
Annexes
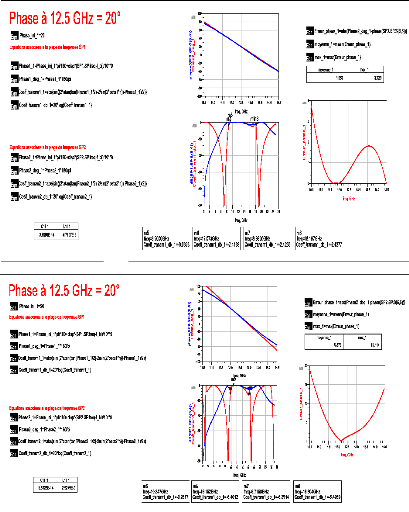
(b)
(a)
Annexe 3 : Résultats de la synthèse passe-bande h =
A/4 à ???????? = 15??????.
70
Annexes
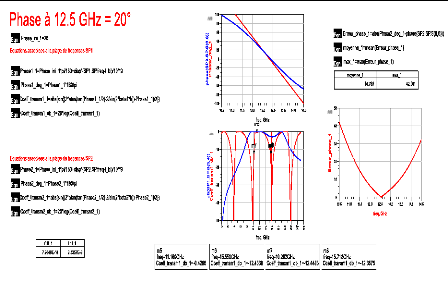
(c)
Figure A3. 1: Résultats de la
synthèse passe-bande ??????(????) =
????°. (a) ???????(????) =
-????°/??????. (b) ???????(????) =
-????°/??????. (c) ???????(????)
= -????°/??????.
|
???11(?? - ??0) (°/GHz)
|
??11(??0) (°)
|
???????? (°)
|
???????? (°)
|
|
-30
|
20
|
1,059
|
3,723
|
|
-45
|
20
|
5,876
|
19,114
|
|
-60
|
20
|
14,793
|
42,061
|
Tableau A3. 1: Erreurs moyenne et maximale h
à 15GHz avec ?????? (?? ??) = ????° pour
chaque dispersion
Liste des figures Corps du rapport
Figure 1. 1: : Schéma de principe d'une antenne
à réseau réflecteur avec une source primaire (a)
centrée. (b) décentrée 9
Figure 1. 2: Schéma du RA déployable avec une
grande ouverture rayonnante 10
Figure 1. 3 : Rayonnement dans l'axe du réseau (a) et
rayonnement avec dépointage (b) d'une
antenne à réseau réflecteur 11
Figure
1. 4: Vues satellitaires de deux diagrammes de rayonnements à lobes
formés pour assurer une
couverture donnée 11
Figure 1. 5: Réponse en phase (a) et réponse
fréquentiellle (b) d'une cellule déphaseuse 12
Figure 1. 6: Réponse fréquentielle et
dispersion associée 12
Figure 1. 7: Bande passante d'une cellule déphaseuse.
13
Figure 1. 8: Première antenne réseau
réflecteur à base de guides d'ondes métalliques 13
Figure 1. 9: Cellule patch microruban avec ligne à
retard 14
Figure 1. 10: Cellule patchs à dimensions variables
14
Figure 1. 11: Cellule à deux couches à base de
patchs de tailles différentes 15
Figure 1. 12: Cellule à une seule couche basée
sur l'association de deux résonateurs 15
Figure 1. 13: Augmentation de la taille de la fente annulaire
(a) entraine un décalage de la fréquence
de résonance vers les basses fréquences (b)
16
Figure 1. 14: Différentes configuration de cellules à une
ou deux fentes (a) et réponses en phase
associées (b) 17
Figure 1. 15: Evolution cyclique de la cellule Phoenix
17
Figure 1. 16: Six géométries différentes
réparties dans deux familles. 17
Figure 1. 17: Circuits équivalents associés aux
six géométries de la cellule Phoenix 18
Figure 1. 18: Méthodologie générale de
la synthèse d'un réseau réflecteur 18
Figure 1. 19: Utilisation d'un ANN pour la
génération de la base de données 20
Figure 1. 20 : Modélisation de la cellule Phoenix
d'ordre 2 par CE (a)Capacitive. (b) inductive 21
Figure 1. 21: Schéma électrique
équivalent des cellules Phoenix d'ordre 2. (a) capacitive.
(b)inductive. 21
Figure 2. 1: Dipôle équivalent d'une cellule
unitaire Phoenix monocouche de réseau réflecteur. 23
Figure 2. 2: Quadripôle équivalent
constitué de deux cellules unitaires montées
tête-bêche 23
Figure 2. 3: Quadripôle équivalent 23
Figure 2. 4: loi de phase 24
Figure 2. 5: Caractéristiques du gabarit en
transmission. (a) Zéros de transmission. (b) pôle à f0
25
Figure 2. 6: Evolution du gabarit pour une variation positive
de 0_11 (f_0) à dispersion constante 25
Figure 2. 7: Evolution du gabarit pour une variation
négative de 0_11 (f_0) à dispersion constante 26
Figure 2. 8: Evolution du gabarit pour une variation de la
dispersion pour 0_11 ((f_0) =0° 27
Figure 2. 9:Motif d'une cellule inductive de type Phoenix
d'ordre 2 : la fente annulaire 27
Figure 2. 10: Quadripôle équivalent du motif
inductif Phoenix d'ordre 2 28
Figure 2. 11: Prototype d'un filtre passe-bande d'ordre n=3
28
Figure 2. 12 : Exemples de lois de phase à
synthétiser dans la bande d'intérêt [10,5- 14, 5] GHz.
(a)
4)11(f0) = 20°. (b) 4)11(f0) = -20°. 29
Figure
2. 13: Gabarits en transmission associés aux lois sur la phase en
réflexion de la Figure 2. 12. .
(a) 4)11(f0) = 20°. (b) 4)11(f0) = -20°. 30
72
Liste des figures
Figure 2. 14: Prototype du filtre passe-bas
normalisé d'ordre n=3 31
Figure 2. 15: Filtre passe-bas
dénormalisé 32
Figure 2. 16: Filtre passe-bas avec inverseurs
d'admittances idéaux 32
Figure 2. 17: Opération de transformation d'un
filtre passe-bas en un filtre passe-bande 32
Figure 2. 18: Filtre passe-bande avec inverseurs
d'admittance idéaux 33
Figure 2. 19 : Circuit équivalent d'un inverseur
d'admittance constituée d'une structure en pi avec des
inductances 33
Figure 2. 20: Filtre
passe-bande d'ordre 3 constitué de résonateurs parallèles
et de deux structures en
pi avec des selfs 34
Figure 2. 21: Filtre
passe-bande constitué de 3 résonateurs parallèles
séparés par deux inductances34 Figure 2. 22: Circuit
équivalent d'un inverseur d'admittance constituée d'une structure
en pi avec des
capacités 34
Figure 2. 23: Filtre
passe-bande d'ordre 3 constitué de résonateurs parallèles
et de deux structures en
pi avec des capacités 35
Figure 2. 24: Filtre passe-bande constitué de 3
résonateurs parallèles séparés par deux
capacités 35
Figure 2. 25: Equivalence entre la structure en T centrale
et la ligne (2h, Zc) 35
Figure 2. 26: Résultats de la synthèse
passe-bande solution 1. (a) ???????? ?? = ??°. (b) ?????? ??
?? = ????° 39 Figure 2. 27: Résultats de la synthèse
passe-bande solution 1. (a) ???????? ?? = ??????°. (b)
???????? ?? =
??????° 40
Figure 2. 28: Erreur moyenne solution 1
lorsque ?????? ?? ?? ?????????? ???? ??° à ??????°
???????? ???????????=-
30°/GHz 41
Figure 2. 29: Résultats
de la synthèse passe-bande solution 1. (a) ??????? ??
??=-30°/GHz. (b)
??????? ?? ??=-45°/GHz. (c)
???????????=-60°/GHz 43
Figure 2. 30:
Résultats de la synthèse passe-bande solution 2. (a)
???????? ?? = ??°. (b) ?????? ?? ?? = -????°
45
Figure 2. 31: Résultats de la
synthèse passe-bande solution 1. (a) ???????? ?? =
-??????°. (b) ?????? ?? ?? =
-??????° 46
Figure 2. 32: Erreur moyenne solution
2 lorsque ?????? ?? ?? ?????????? ???? ??° à - ??????°
???????? ???????????=-
30°/GHz 47
Figure 2. 33: Résultats
de la synthèse passe-bande solution 2. (a) ???????????=
-30°/GHz. (b)
??????? ?? ??=-45°/GHz. (c)
???????????=-60°/GHz 49
Figure 2. 34: Bilan sur les performances de la
procédure de synthèse de type passe-bande 50
Figure 3. 1: Motif capacitif d'une cellule Phoenix d'ordre
2 51
Figure 3. 2: Quadripôle équivalent 51
Figure 3. 3: Prototype de filtre coupe-bande 52
Figure 3. 4: Lois de phase à synthétiser
dans la bande d'intérêt [10,5- 14, 5] GHz. (a) ?11(f0) =
160°.
(b) ?11(f0) = -160° 52
Figure 3. 5:
Gabarits en transmission associés aux lois sur la phase en
réflexion (a) ?11(f0) = 160°.
(b) ?11(f0) = -160°. 53
Figure 3. 6: Opération de transformation d'un
filtre passe-bas en un filtre coupe-bande. 54
Figure 3. 7: Filtre coupe-bande avec inverseurs
d'admittances 54
Figure 3. 8: Filtre coupe-bande d'ordre 3 constitué
de résonateurs séries et de deux structures en pi
avec des selfs 55
Figure 3. 9: Filtre
coupe-bande d'ordre 3 constitué de résonateurs séries et
de deux structures en pi
avec capas 55
Liste des figures
73
Figure 3. 10: Quadripôle équivalent obtenue
avec la solution 1 56
Figure 3. 11: Quadripôle équivalent obtenu
avec la solution 2 56
Figure 3. 12: Résultats de la synthèse
coupe-bande solution 2. (a) 0_11 (f0 )=100°. (b) 0_11 (f0
)=120° 59
Figure 3. 13: Erreur moyenne Solution 2 coupe-bande
011f 0 > 0° 60
Figure 3. 14: : Résultats de la synthèse
coupe-bande solution 2. (a) 0_11 (f0 )=-100°. (b) 0_11 (f0 )=-
120° 61
Figure 3. 15: Erreur moyenne Solution 2 coupe-bande 0_11
(f_0 )<0° 62
Figure 3. 16: Bilan sur les performances de la
procédure de synthèse de type coupe-bande
63
| 


