Chapitre 1- Généralités sur la
synthèse des réseaux réflecteurs
de fréquences dans laquelle les réponses en
phase sont parallèles (dispersion constante) diminue. Ceci a pour
conséquence de diminuer la bande passante de la cellule.
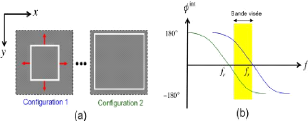
Figure 1. 13: Augmentation de la taille de la fente
annulaire (a) entraine un décalage de la fréquence de
résonance vers les basses fréquences (b)
Le concept de cellule Phoenix consiste à ajouter une
deuxième fente annulaire plus petite à l'intérieur de la
première. La Figure 1. 14 présente le principe de
fonctionnement de cette cellule. La cellule à une seule fente annulaire
(configuration1) résonne à une fréquence fr1 choisie ici
inférieure à la fréquence de travail
f0. Dès lors, la dispersion de la phase est quasi
nulle à f0. L'insertion d'une
seconde fente annulaire plus petite permet de créer une seconde
résonance fr2 située plus haut en fréquence, ici
au-delà de f0. Si les deux fréquences de
résonances sont trop éloignées entre elles, la phase
restera encore peu dispersive à f0 (configuration 2). Par contre le
rapprochement du périmètre des deux résonances
(configuration 3) permet de faire converger les deux fréquences de
résonances vers la fréquence de travail. Cette manoeuvre permet
alors de régler l'inclinaison du point d'inflexion et donc la
dispersion. La combinaison judicieuse de ces deux fentes permet de garantir une
gamme de phase de 360° sur une large gamme de fréquences.
1.3.3.2 Cycle de la cellule Phoenix
Dans [17] une évolution cyclique de la cellule Phoenix
a été présentée. Un exemple de cycle est
illustré sur la Figure 1. 15. Dans ce cas-ci, le cycle
débute par une cellule composée d'une seule fente annulaire. Il
continue en faisant croître un anneau métallique de longueur
Lr entre les deux fentes et se termine lorsque l'anneau
métallique disparaît à l'extérieur : il est revenu
à son état initial.
Il ressort que ce cycle permet d'obtenir une gamme de phase de
360° sur une large bande passante tout en garantissant une variation douce
de la géométrie du motif [2, p. 12]. C'est la
propriété dite de « renaissance » de la cellule
Phoenix.
1.3.3.3 Familles de la cellule Phoenix et circuits
équivalents
Dans un rapport interne à l'IETR, il a
été démontré que les caractéristiques sur la
phase et la dispersion, obtenues avec la cellule Phoenix, peuvent être
atteintes en utilisant deux familles de cellules : la famille capacitive et la
famille inductive (cf. Figure 1. 16). Chaque famille est
composée de trois géométries de cellules
différentes. Chaque géométrie permet ainsi de couvrir une
gamme de phase et de dispersion donnée.
Les six géométries de la cellule Phoenix peuvent
être représentées par un modèle comportemental. La
Figure 1. 17 présente les circuits équivalents
associés à chaque cellule. Les circuits équivalents ont
été développés et validés dans une
étude interne à l'IETR [Rapport interne, Simon Mener]. Cette
représentation en circuit équivalent est basée sur une
analyse théorique des composants de la cellule que nous verrons dans la
dernière partie de ce chapitre.
17
| 


