|

Université Gaston Berger de Saint-Louis
UFR des
Sciences Appliquées et de Technologie
Section Physique
Appliquée
RAPPORT DE STAGE DE FIN D'ETUDE
Pour obtenir le diplôme de Master
d'Ingénierie en
Electronique et Télécommunications (MIETEL)
|
|
|
Sujet :
|
|
Synthèse de cellules unitaires de réseaux
réflecteurs
basée sur des techniques de synthèse de
filtres
|
|
Stage effectué au sein du laboratoire IETR
Réalisé par : Fatou Gomis DIENG
Encadrant au laboratoire :
Erwan Fourn, Maître de
Conférence à l'INSA de RENNES
Raphaël Gillard, Professeur des
Universités à l'INSA de RENNES
Correspondant à l'université
:
Amadou Seidou Maiga, Professeur des
Universités à l'UGB de Saint-Louis
Année Universitaire 2017-2018
1
2
Dédicaces
Ames très chers Parents
Aucun hommage ne pourra être
à la hauteur de vos sacrifices, de l'amour et de l'affection dont vous
n'avez jamais cessé de m'entourer tout au long de
ces années d'études. J'espère que
vous trouverez dans ce travail, un vrai
témoignage de mon profond amour et
éternelle
reconnaissance.
Atoute ma famille.
Atous ceux qui m'aiment. Atous ceux que
j'aime.
3
Remerciements
Je tiens à remercier ici les personnes qui, de
près ou de loin, ont contribué à l'élaboration de
ce travail de mémoire de fin d'étude.
Je commence tout naturellement par mes encadrants : Erwan
Fourn et Raphaël Gillard envers qui je suis
extrêmement reconnaissante. Un grand merci à vous pour votre
disponibilité, votre gentillesse et votre sens de l'orientation qui
m'ont beaucoup apporté tant sur le plan technique que personnel, et qui
ont conduit à la concrétisation de ce travail.
J'adresse mes sincères remerciements à M.
Amadou Seydou Maiga, professeur à l'Université Gaston
Berger de Saint-Louis et M. Kidiyo Kpalma, professeur des
Universités à l'Institut National des Sciences Appliquées
(INSA) de Rennes sans qui, le partenariat entre les deux structures ne serait
né.
Je remercie vivement notre partenaire financier le programme
d'action européen pour la mobilité des étudiants,
ERASMUS pour m'avoir octroyé une bourse de mobilité
stage.
Je remercie également le CEA-MITIC (Centre
d'Excellence en Mathématiques, Informatique et Technologie de
l'Information et de la Communication), pour avoir pris en charge mes frais de
transports allée/retour.
Mes remerciements vont également à l'endroit de
tous les professeurs du MIETEL qui ont tout donné pour faire de nous des
ingénieurs capables de s'adapter à toute situation. Merci
énormément pour vos énormes sacrifices.
Je terminerai en adressant un chaleureux merci à toute
ma famille et à tous mes amis pour leur indéfectible soutien.
Merci !
4
Résumé
Combinant les atouts des réflecteurs classiques et ceux
des réseaux, les antennes réseaux réflecteurs ou RA
(Reflectarrays Antennas) pourraient remplacer, à terme, les
réflecteurs utilisés dans des domaines tels que le spatial et
l'aéronautique. Ce type d'antenne offre la possibilité de former
des diagrammes de rayonnement complexes avec une relative simplicité, un
faible coût de réalisation, de faibles pertes et un volume
réduit. Les antennes RA sont constituées d'une source primaire
placée au regard d'une surface réfléchissante
composée d'éléments rayonnants appelés cellules
unitaires. Si de nombreuses études portent déjà sur la
caractérisation des cellules, une des problématiques consiste
à les sélectionner judicieusement pour réaliser l'antenne
finale : c'est l'étape de synthèse.
Ce stage traite de la synthèse de cellules unitaires
des antennes réseaux réflecteurs. Aujourd'hui, les
méthodes utilisées pour les concevoir exploitent, pour la
majorité, des outils de simulations électromagnétiques
[1]. Elles ont pour inconvénient d'être coûteuse en temps et
en ressources de calcul. Récemment, une autre méthode
basée sur l'utilisation des circuits équivalents beaucoup moins
gourmands en temps et en ressources de calcul a été
proposée [2]. Elle s'appuie sur les techniques de synthèse de
filtres. Cependant, à l'issu de la synthèse, un certain nombre de
problèmes a été décelé dans la
procédure proposée.
Notre mission consiste alors à développer une
nouvelle méthode de synthèse plus fiable et plus précise
en éliminant notamment un certain nombre d'approximations et ceci dans
le but d'améliorer la première version. Cette méthode est
aussi basée sur l'utilisation des circuits équivalents et sur des
techniques de filtrage.
Un tour d'horizon sur les différentes cellules passives
utilisées pour la synthèse des réseaux réflecteurs
montre que la plupart est limitée en bande passante. La cellule Phoenix
est sélectionnée dans ce travail pour ses bonnes performances
puisqu'elle fournit toute la gamme de phase suivant un cycle continu de sa
géométrie.
Une nouvelle étape est franchie avec la méthode
de synthèse proposée. Elle permet de synthétiser les
éléments des circuits équivalents des cellules Phoenix
d'ordre 2 de type inductif et capacitif en utilisant respectivement un filtre
passe-bande et coupe-bande du troisième ordre de Tchebychev. Les
détails de cette procédure sont retracés au travers des
deux derniers chapitres. Finalement, les résultats obtenus avec cette
méthode révèlent que cette dernière est prometteuse
mais mérite d'être améliorer pour permettre une
synthèse complète du réseau réflecteur.
Table des matières
Remerciements 3
Résumé 4
Introduction générale 7
Chapitre 1 : Généralités sur la
synthèse des réseaux réflecteurs 8
1.1 Introduction 8
1.2 Présentation générale d'une antenne
à réseau réflecteur (RA) 8
1.2.1 Notion d'antenne à réseau réflecteur
(RA) 8
1.2.2 Architecture et principe de fonctionnement d'une antenne RA
8
1.2.3 Intérêts de la technologie RA imprimée
9
1.2.4 Concepts de base d'une antenne RA imprimée 10
1.2.5 Caractéristiques de la cellule unitaire d'un
réseau réflecteur 11
1.3 Choix de l'élément rayonnant 13
1.3.1 Historique sur les antennes réseaux
réflecteurs 13
1.3.2 Catégories de cellules déphaseuses 13
1.3.3 La cellule Phoenix 15
1.3.3.3 Familles de la cellule Phoenix et circuits
équivalents 16
1.4 Synthèse d'une antenne RA 18
1.4.1 Méthodologie générale de la
synthèse 18
1.4.2 Utilisation de modèles pour la synthèse 19
1.5 Conclusion 21
Chapitre 2 : Procédure de synthèse d'une cellule
inductive 22
2.1 Introduction 22
2.2 La loi de phase et le gabarit en transmission 22
2.2.1 Passage de la loi de phase au gabarit d'amplitude 22
2.2.2 Allure de la loi de phase et du gabarit en amplitude 23
2.3 Procédure de synthèse proposée pour une
cellule inductive (passe-bande) 27
2.3.1 Circuits équivalents du dipôle et du
quadripôle équivalent 27
2.3.2 Description de la procédure de synthèse 28
2.3.3 Spécifications 29
2.3.4 Etapes de la synthèse du quadripôle
équivalent 31
2.4 Résultats de la synthèse 37
2.4.1 Solution 1 : Structure en pi avec des inductances 38
2.4.2 Solution 2 : Structure en pi avec des capacités
44
6
Table des matières
2.4.3 Bilan sur la précision de la procédure de
synthèse passe-bande 49
2.5 Conclusion 50
Chapitre 3 : Procédure de synthèse d'une cellule
capacitive 51
3.1 Introduction 51
3.2 Procédure de synthèse proposée pour une
cellule capacitive 51
3.2.1 Circuits équivalents 51
3.2.2 Spécifications 52
3.2.3 Synthèse du quadripôle équivalent 53
3.3 Résultats de la synthèse 57
3.3.1 Première famille de spécification : ??11??0
> 0° 57
3.3.2 Deuxième famille de spécification : ??11??0
< 0° 60
3.3.3 Bilan sur la précision de la procédure de
synthèse passe-bande 62
3.4 Conclusion 63
Conclusion générale 64
Annexes 65
Annexe1 : Résultats de la synthèse passe-bande
obtenus avec l'ondulation maximale ou la
moyenne des deux ondulations. 65
A1.1 Résultats obtenus avec la solution 1 pour une phase
à ??0, ?11f0 = 20° et i?11f0 =
30°/GHz 65
A1.2 Résultats obtenus avec la solution 2 pour une phase
à ??0, ?11f0 = -20° et i?11f0 =
30°/GHz 66
Annexe 2 : Résultats de la synthèse passe-bande
solution 1 phases négatives et solution 2 phases
positives 67
A2.1 Résultats obtenus avec la solution 1 pour une phase
à ??0, ?11f0 = 0° et - 40° et
i?11f0 = 30°/GHz 67
A2.2 Résultats obtenus avec la solution 2 pour une phase
à ??0, ?11f0 = 0° et 40° et
i?11f0 = 30°/GHz 68
Annexe 3 : Résultats de la synthèse passe-bande h =
A/4 à ???????? = 15??????. 69
Liste des figures 71
Liste des tableaux 73
Bibliographie 74
7
Introduction générale
Les antennes jouent un rôle important, voire primordial
dans la chaine de communications. Les différentes applications civiles
et militaires, notamment dans le domaine du spatial et de
l'aéronautique, requièrent de plus en plus de performances pour
la réalisation de diagrammes directifs, multi-faisceaux ou formés
tout en restant exigeantes en termes de coût et de volume. A ce titre,
les antennes réseaux réflecteurs ou Reflectarrays Antennas (RA)
semblent être une alternative prometteuse aux antennes à
réflecteurs pour répondre à ces défis.
Constitués d'un grand nombre de cellules unitaires, dont il faut
optimiser la géométrie individuellement, ces antennes
réseaux réflecteurs demeurent toutefois difficiles à
concevoir.
L'Institut d'Electronique et de
Télécommunications de Rennes (IETR), à travers son
département ADH (Antennes & Dispositifs Hyperfréquences),
mène depuis le début des années 2000, des travaux de
recherche sur les antennes réseaux réflecteurs. Ces travaux sont
effectués par l'équipe dite BEAMS (BEam Antennas up to Mm and
Sub-mm waves) au sein de laquelle j'ai été accueillie du 22 Mai
2019 au 30 Septembre 2019 pour y effectuer mon stage de fin d'étude. Ce
dernier a été encadré par Erwan Fourn, maître des
conférences à l'Institut National des Sciences Appliquées
(INSA) de Rennes et Raphaël Gillard, professeur des universités
à l'INSA de Rennes.
Aujourd'hui, les méthodes utilisées pour
concevoir les cellules unitaires des réseaux réflecteurs
exploitent, pour l'essentiel, des simulations électromagnétiques
combinées à des méthodes d'optimisation [1]. Mais elles
sont très coûteuses en temps et en ressources de calcul.
Récemment, A. Grossetête a proposé une nouvelle
méthode [2] basée sur l'utilisation de circuits
équivalents, beaucoup moins gourmande en temps et en ressources de
calcul. Celle-ci s'appuie sur des techniques de synthèse de filtres.
Cependant, elle mérite d'être améliorée pour la
rendre plus fiable et plus précise en éliminant notamment un
certain nombre d'approximations. C'est dans ce contexte que s'inscrit ce projet
de fin d'étude. L'objectif est de développer une nouvelle
procédure de synthèse, basée aussi sur les techniques de
filtrage et sur l'utilisation des circuits équivalents, afin
d'améliorer la première version de la procédure
développée [2].
Ce rapport de stage s'articule autour de trois chapitres. Le
premier chapitre fait l'objet d'un état de l'art sur les antennes
réseaux réflecteurs. Il propose particulièrement un tour
d'horizon des différentes méthodes de synthèse
tirées de la littérature. La motivation du choix de la cellule
Phoenix y est aussi explicitée. Dans le deuxième chapitre, nous
déroulerons notre procédure de synthèse appliquée
à une cellule Phoenix d'ordre 2 de type inductif sur la base de trois
familles de spécifications. Enfin, dans le dernier chapitre, cette
méthode sera appliquée au motif capacitif de la cellule Phoenix
d'ordre 2 avant de donner le bilan sur les performances de la procédure
de synthèse.
Chapitre 1 : Généralités sur la
synthèse des réseaux réflecteurs
1.1 Introduction
L'objectif de ce chapitre est de présenter et de faire
l'état de l'art des antennes réseaux réflecteurs et les
méthodes de synthèse associées. Ce chapitre s'articule
autour de trois parties. La première partie est consacrée
à la présentation générale d'une antenne
réseau réflecteur. Pour ce faire, nous introduirons dans un
premier temps, la notion d'antenne RA imprimée, nous présenterons
également l'architecture de la structure, son principe
général de fonctionnement et les intérêts de la
technologie. Ensuite, nous balayerons les concepts de base d'une antenne RA
imprimée à savoir le champ incident, la phase introduite et les
rayonnements. Enfin, les caractéristiques de la cellule unitaire
(réponse en phase, bande passante) seront exposées.
Le plus important dans le processus de synthèse
étant le choix judicieux des propriétés EM des cellules en
fonctions de leurs géométries, substrats et incidence
d'excitation, la deuxième partie de ce chapitre propose un bref
état de l'art des catégories de cellules unitaires (passives,
actives) utilisées dans la littérature. Les avantages, le
principe de fonctionnement et les différentes familles de la cellule
passive, dite Phoenix, sélectionnée dans le cadre de cette
étude, seront détaillées. Afin d'introduire la principale
problématique de notre travail, à savoir le développement
de méthodes de synthèse de cellules unitaires de réseaux
réflecteurs basée sur des techniques de synthèse de
filtres, nous ferons, dans la troisième partie de ce chapitre, une revue
de la littérature sur la synthèse de ces structures. Tout
d'abord, nous présenterons le principe de la synthèse d'un
réseau réflecteur en présentant une méthodologie
générale. Ensuite, nous exposerons, les méthodes
basées sur des outils de simulations électromagnétiques et
des méthodes d'optimisations qui sont généralement
coûteuses en temps et en ressources de calcul. Enfin, nous
présenterons la méthode basée sur les circuits
équivalents.
1.2 Présentation générale d'une antenne
à réseau réflecteur (RA)
1.2.1 Notion d'antenne à réseau réflecteur
(RA)
Ces dernières décennies, les antennes
réseaux réflecteurs ont suscité beaucoup d'attention dans
le domaine des antennes à fort gain. Elles associent les concepts des
antennes réflecteurs et des réseaux d'antennes. Les antennes RA
sont très prometteuses dans le cadre des applications spatiales [3].
L'objectif consiste à bénéficier des atouts des antennes
réseaux pour la réalisation de diagrammes directifs et/ou
formés et ceux des réflecteurs qui n'utilisent qu'une seule
source primaire. Une antenne RA est donc constituée d'une source
primaire placée au-devant d'un réseau constitué
d'éléments rayonnants appelés cellules unitaires.
Pour une description plus exhaustive des
propriétés remarquables de cette structure, le lecteur pourra se
reporter à l'ouvrage de référence traitant exclusivement
des antennes à réseau réflecteur [4].
1.2.2 Architecture et principe de fonctionnement d'une antenne
RA
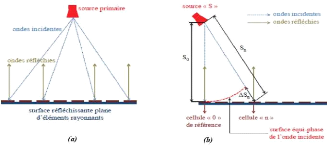
L'architecture d'un réseau réflecteur
imprimé est représentée sur la Figure 1. 1. Elle
est composée d'une antenne source, généralement de type
cornet et d'une surface plane réfléchissante constituée
d'un ensemble d'éléments rayonnants : le réseau. L'antenne
source peut être centrée ou décentrée (position
offset) par rapport au centre du réseau.
Le principe général de fonctionnement peut
être expliqué de la manière suivante : les ondes
incidentes, provenant d'une source primaire, atteignent la surface du panneau
déphasées les unes par rapport aux autres en raison de la
différence de trajet parcouru depuis la source primaire. Chaque
élément rayonnant doit alors introduire une certaine phase dite
« phase
Chapitre 1-Généralités sur la
synthèse des réseaux réflecteurs
introduite » afin de compenser ce déphasage et de
re-rayonner l'énergie dans une direction bien déterminée
pour former soit un lobe directif, soit une couverture particulière. Ces
éléments unitaires sont généralement appelés
cellules déphaseuses.
9
Figure 1. 1: : Schéma de principe d'une
antenne à réseau réflecteur avec une source primaire (a)
centrée. (b) décentrée
1.2.3 Intérêts de la technologie RA
imprimée
Il découle plusieurs avantages quant à
l'utilisation de cette technologie. Elle semble en effet prometteuse et
présente plusieurs avantages dans le contexte spatial, gourmand en
termes de performances et exigeant en coût.
Les réflecteurs formés nécessitent la
conception de moules très onéreux. Comparer à eux, les
antennes réseaux réflecteurs présentent un processus de
fabrication assez simple, des pertes faibles, un coût de production
relativement faible et un volume très réduit. Les RA classiques,
généralement plans sont fabriqués par superposition de
couches. Le panneau est constitué d'un plan de masse, d'une couche
intermédiaire de substrat, de plusieurs couches très fines de
colle et autres procédés chimiques et des motifs
métalliques permettant de réaliser le déphasage requis.
Dans le cadre de cette étude, l'utilisation d'éléments
rayonnants passifs est envisagée. Une des techniques de fabrication est
la photolithographie [5]. De plus, du fait de sa simplicité de
fabrication et de sa durée relativement courte, il est possible de
modifier ou d'améliorer le RA tardivement dans la gestion et la
planification de la conception.
Un autre avantage est la possibilité de réaliser
de grandes structures déployables. Ce modèle commence à
être utilisé dans les satellites. En effet, la masse et la
compacité constituent une contrainte très exigeante lors du
lancement des satellites et plus particulièrement pour les nouvelles et
futures générations (nano-satellites, Satcom, ...). Aussi, des RA
déployables comme présentés sur la Figure 1. 2
pourraient être une bonne alternative aux réflecteurs
formés de grandes dimensions et ainsi couvrir un grand nombre
d'applications par le biais de grandes couvertures rayonnantes (de l'ordre de 4
à 6 mètres). Les travaux illustrés dans [6]
présentent les développements d'un RA déployable
embarqué sur un nano-satellite. Le lancement du premier satellite, avec
un RA déployable, pour une mission spatiale, s'est fait en 2018. Le 23
Mars 2019, le satellite DARPA R3D2, constitué d'une antenne
réseau réflecteur déployable est monté en orbite
depuis la Nouvelle-Zélande [7]. Dans la même optique, des
structures déployables à base de RA gonflables ont aussi
été envisagées pour augmenter la compacité de
l'antenne embarquée [8, 9].
10
Chapitre 1- Généralités sur la
synthèse des réseaux réflecteurs

Figure 1. 2: Schéma du RA déployable
avec une grande ouverture rayonnante
1.2.4 Concepts de base d'une antenne RA imprimée
1.2.4.1 Champ incident provenant d'une source primaire
Comme mentionnée précédemment, les ondes
incidentes provenant de la source primaire atteignent la surface du panneau
déphasées les unes par rapport aux autres (cf. Figure 1.
1). L'expression du champ incident sur la cellule « n » est
donnée par l'équation (1. 1).
exp (-???2?? ?0????)
??? ?? ?????? = ??? 0??(????, ????) ???? (1.
1)
?
Où : ??0 représente l'amplitude et la
polarisation de champ électrique issu de la source « S », G
représente le gain de l'antenne source dans la direction (????, ????),
??0 est la longueur d'onde dans le vide à la fréquence ??0 et
???? représente la distance séparant le centre de phase de
l'antenne source et le centre de la cellule « n ».
Le champ incident arrive donc au centre de la cellule « n
» avec une phase ???????? ?? donnée par l'équation (1. 2) ;
le retard varie d'une cellule à une autre et dépend du chemin
???? parcouru.
?????????? = - ??????? ? ???? (1. 2)
En considérant la cellule « 0 » comme cellule
de référence (cf. Figure 1. 1(b)), la phase du champ
incident arrivant au centre de la cellule de référence est
donnée par l'équation (1. 3) :
????? ????? = - ???????? ???? (1. 3)
La phase du champ incident au centre de la cellule « n
» (?? ? 0) rend compte du retard de phase au centre de la cellule de
référence (?? = 0) augmenté du retard ?????, dû
à la différence entre le trajet associé à la
cellule « n » et le trajet associé à la cellule «
0 », soit :
?????? - ????
????? ????? = - ??????? ? ???? = - ??????? ? (???? +
?????) = ???? ???? ????? (1. 4)
1.2.4.2 Phase introduite et rayonnements
Une fois que l'onde d'excitation arrive sur la surface
réfléchissante, chaque cellule « n » du réseau
doit introduire une certaine phase dite « phase introduite » et
notée ?????????? afin de re-rayonner l'énergie dans une direction
bien déterminé. La phase de l'onde re-rayonnée par la
11
Chapitre 1-Généralités sur la
synthèse des réseaux réflecteurs
cellule « n », ???? ?????? correspond à la
somme de la phase incidente ???? ?????? relative à cette cellule et de
la phase ???? ?????? introduite par la cellule (cf. équation (1. 5)).
??????
???? ?????? = ???? ?????? + ???? (1. 5)
La distribution de la phase rayonnée par chaque cellule
du réseau réflecteur permet de générer
différents types de rayonnements. Trois types de rayonnement principaux
sont généralement recherchés, le premier est un
rayonnement dans l'axe du réseau dit rayonnement transversal (cf.
Figure 1. 3(a)), le second est un rayonnement avec dépointage
dans une direction bien définie (cf. Figure 1. 3(b)), le
dernier est un rayonnement à lobe formé fortement
recommandé dans les applications satellitaires [10] où le besoin
est de couvrir une zone bien précise de la terre (cf. Figure 1.
4). Par la suite, on entend par la loi de phase, la base de données
contenant la phase que doit introduire chacune des cellules unitaires du
réseau afin d'obtenir le rayonnement désiré.
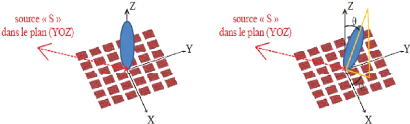
(a) (b)
Figure 1. 3 : Rayonnement dans l'axe du
réseau (a) et rayonnement avec dépointage (b) d'une antenne
à réseau
réflecteur
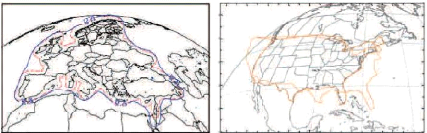
Figure 1. 4: Vues satellitaires de deux diagrammes de
rayonnements à lobes formés pour assurer une couverture
donnée
1.2.5 Caractéristiques de la cellule unitaire d'un
réseau réflecteur
1.2.5.1 Réponses d'une cellule déphaseuse
Une cellule déphaseuse doit pouvoir introduire
n'importe quelle phase dans l'intervalle [0°- 360°] afin de
générer n'importe quelle phase rayonnée à partir de
n'importe quelle phase incidente. Cette phase est contrôlée par un
ou plusieurs paramètre(s) lié(s) aux dimensions de la cellule
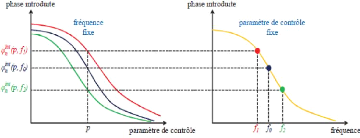
appelé(s) paramètre(s) de contrôle. La courbe qui
représente la variation de la phase introduite ???? ?????? par la
cellule « n » en fonction d'un paramètre de contrôle
à une fréquence donnée est appelée : réponse
en phase de la cellule (cf. Figure 1. 5(a)). D'autre part, pour un
paramètre de contrôle figé, la courbe représentant
la variation de la phase introduite par la cellule « n » en fonction
de la fréquence est appelée : réponse fréquentielle
de la cellule (cf. Figure 1. 5(b)).
Chapitre 1- Généralités sur la
synthèse des réseaux réflecteurs
(a) (b)
12
Figure 1. 5: Réponse en phase (a) et
réponse fréquentiellle (b) d'une cellule
déphaseuse
1.2.5.2 Dispersion fréquentielle et bande passante
d'une cellule déphaseuse
Le paramètre permettant d'évaluer les
performances d'une cellule déphaseuse dans une bande de fréquence
est la dispersion fréquentielle. Cette caractéristique donne des
renseignements sur la variation de la phase introduite en fonction de la
fréquence. La dispersion fréquentielle ??J?? (??)
obtenue sur une cellule « n » pour un paramètre
« p » fixé est donnée par l'équation (1. 6).
Elle correspond à la dérivée de la réponse
fréquentielle de la cellule concernée. La réponse
étant décroissante, la dispersion fréquentielle est
toujours négative (cf. Figure 1. 6).
??????(??,??-??)
??????(??) = ????m
????? (????
??????(??,??+??)-????
???? ) (1. 6)
La bande passante d'un réseau réflecteur est la
bande fréquentielle dans laquelle son diagramme de rayonnement reste
stable. Elle dépend de la bande passante de la cellule unitaire et de la
dispersion des trajets à compenser. La bande passante
[??1; ??2] d'une cellule
unitaire est la bande fréquentielle dans laquelle cette cellule admet
des réponses à variations linéaires et parallèles
lorsque le paramètre de contrôle « p » est
modifié (cf. Figure 1. 7). La variation linéaire de la
réponse fréquentielle (obtenue pour chaque valeur de p)
résulte en une dispersion fréquentielle constante dans cette
bande, et le parallélisme des différentes réponses
(obtenues en variant p) se traduit par des dispersions fréquentielles
identiques. De ce fait sachant que la loi pour un diagramme de rayonnement
donné varie linéairement en fonction de la fréquence, le
diagramme de rayonnement sera stable.
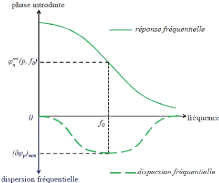
Figure 1. 6: Réponse fréquentielle et
dispersion associée
13
Chapitre 1-Généralités sur la
synthèse des réseaux réflecteurs
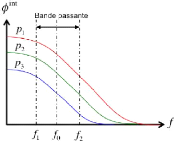
Figure 1. 7: Bande passante d'une cellule
déphaseuse.
1.3 Choix de l'élément rayonnant
1.3.1 Historique sur les antennes réseaux
réflecteurs
La première antenne réseau réflecteur
date de 1963 [11], elle était volumineuse (cf. Figure 1. 8). La
cellule unitaire qui la constituait était une guide d'onde
métallique terminée par un plan de court-circuit. Le
contrôle de la phase de l'onde réfléchie se fait par la
variation de la profondeur du guide. Ces structures ont ensuite
évolué en intégrant des déphaseurs de type
diaphragme (circuits intégrés hybrides) permettant un
contrôle dynamique de la phase de l'onde réfléchie [12].
Cependant, leurs inconvénients majeurs restent le poids et
l'encombrement, empêchant leur utilisation dans les applications
satellitaires.
Ce n'est que vers les années quatre-vingt que la
technologie imprimée [13] est appliquée aux antennes
réseaux réflecteurs ; le poids et l'encombrement se trouvent
alors réduits et leur utilisation dans le domaine spatial paraît
plus réaliste. Avec cette technologie, l'élément rayonnant
de la cellule déphaseuse est imprimé sur un substrat au-dessus
d'un plan de masse. Dans les antennes réseaux réflecteurs, la
source d'excitation est placée à une certaine distance de la
surface réfléchissante, supprimant ainsi la
caractéristique du volume.

Figure 1. 8: Première antenne réseau
réflecteur à base de guides d'ondes
métalliques
La suite de cette section traite les principales solutions de
cellules déphaseuses en technologie imprimée. La première
est consacrée aux réseaux réflecteurs reconfigurables, la
seconde aux réseaux réflecteurs passives elle dresse
particulièrement une liste des cellules déphaseuses passives qui
ont marqué l'avancement de l'étude des antennes réseaux
réflecteurs passives.
1.3.2 Catégories de cellules déphaseuses
Il existe deux grandes catégories de cellules
déphaseuses : les cellules passives pour les réseaux
réflecteurs passifs à diagramme de rayonnement figé, et
les cellules actives pour des réseaux réflecteurs reconfigurables
à rayonnement contrôlable.
14
Chapitre 1- Généralités sur la
synthèse des réseaux réflecteurs
Une antenne RA reconfigurable (ou active) offre la
possibilité de contrôler la loi de phase appliquée sur la
surface réfléchissante et dès lors, un même
réseau peut générer toute forme et direction de
rayonnement. Ce contrôle est assuré par des composants «
actifs » (sens reconfigurable) introduits dans l'élément
rayonnant d'où le nom attribué à la cellule
déphaseuse : « cellule déphaseuse active ». Parmi les
composants actifs les plus utilisés on peut citer :
· Les commutateurs à diodes PIN et les
commutateurs à MEMS1 qui assurent une variation
discrète de la phase ; un nombre de bits équivalent est alors
associé à la cellule.
· Les capacités variables dites
varactor2 pour lesquelles la variation de la phase est
continue.
Dans le cas d'une antenne réseau réflecteur
passive, chacune des cellules unitaires constitutives du réseau est
dimensionnée de manière à introduire une phase bien
définie dans le but de garantir un diagramme de rayonnement respectant
un certain gabarit. La loi de phase introduite et la loi de phase
rayonnée sont par conséquent figées et le diagramme de
rayonnement obtenu n'est pas modifiable. La phase introduite par la cellule est
contrôlée par l'intermédiaire d'un ou plusieurs de ses
paramètre(s) géométrique(s). Différents types de
géométries de cellule et plusieurs techniques permettant
d'élargir les performances de la cellule en termes de bande passante et
d'encombrement existent.
L'une des premières solutions proposées en
technologie imprimée consistait à utiliser un patch carré
de taille fixe. Le contrôle de la phase de l'onde réfléchie
se fait par l'intermédiaire d'une ligne à retard (stub) de
longueur variable rattaché au patch (cf. Figure 1. 9).
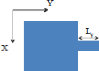
Figure 1. 9: Cellule patch microruban avec ligne
à retard
Afin de surmonter le problème de transfert
d'énergie lié au stub et la limitation de la bande passante de la
structure précédente, D. M. Pozar proposa dans [14] une cellule
à base de patch de taille variable. La modification de la taille du
patch (cf. Figure 1. 10) permet de modifier la fréquence de
résonnance de la cellule et donc la phase de l'onde
réfléchie. Ce type de structure atteint cependant difficilement
une gamme de phase de 360° et ceci au prix d'une résonnance souvent
abrupte3. Le même principe a été
développé en utilisant différentes
géométries telles que des dipôles, des anneaux et des
fentes.

Figure 1. 10: Cellule patchs à dimensions
variables
Dans le but d'améliorer la gamme de phases
assurée par la cellule déphaseuse et la bande passante, des
solutions à base de résonateurs multiples en technologie
multicouche ont été proposées par J. A. Encinar [15] (cf.
Figure 1. 11). Des patchs de tailles différentes sont
1 MEMS :
MicroElectromechanical Systems (microsystèmes
électromécaniques).
2 Varactor ou diode varicap
est une diode à capacité variable.
3 Dont la pente est presque
verticale.
15
Chapitre 1-Généralités sur la
synthèse des réseaux réflecteurs
superposés et résonnent les uns après les
autres. Cette solution permet d'obtenir une réponse en fréquence
plus douce et linéaire en fonction des dimensions des patchs et donc de
garantir une plus large bande-passante. La technologie multicouche n'est
cependant pas compatible avec les contraintes de fortes variations en
températures rencontrées dans le domaine spatial par exemple.
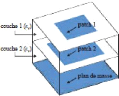
Figure 1. 11: Cellule à deux couches
à base de patchs de tailles différentes
M. R. Chaharmir proposa dans [16] une nouvelle technique
d'amélioration de la gamme de phases assurée et de la bande
passante tout en conservant une relative simplicité de
réalisation. Cette cellule se compose d'un assemblage de plusieurs
résonateurs concentriques imprimés au-dessus d'un plan de masse
(monocouche) (cf. Figure 1. 12). Une gamme de phases assurée
supérieure à 360° est atteinte en variant la taille des
résonateurs.
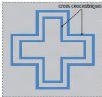
Figure 1. 12: Cellule à une seule couche
basée sur l'association de deux résonateurs
1.3.3 La cellule Phoenix
A l'IETR, un nouveau concept de cellule monocouche à
base de résonateur multiple a été développé
en 2011 : la cellule Phoenix [17, 18] . Ce concept de cellule permet de
répondre à deux problématiques bien connues dans le
domaine des réseaux réflecteurs. La première concerne la
faible bande passante des réseaux réflecteurs [19]. La seconde
concerne la difficulté pour prendre en compte les couplages
inter-élément lors de la conception d'un réseau
réflecteur. L'analyse classique suppose en effet que le couplage est
celui que l'on aurait dans un réseau infini d'éléments
périodiques. Or pour respecter cette hypothèse, il convient de
limiter les variations géométriques lorsque l'on passe d'une
cellule à une autre. Dans le cas contraire, le diagramme de rayonnement
se retrouverait fortement dégradé même si la loi de phase
est a priori respectée [20].
1.3.3.1 Principe de fonctionnement de la cellule Phoenix
Le concept de la cellule Phoenix a vu le jour d'une
problématique soulevée par la cellule à fente annulaire
[2, p. 10]. Le contrôle de la phase à une fréquence
donnée consiste à modifier la fréquence de
résonance de la fente. Le fait de diminuer le périmètre de
la fente entraine le déplacement de la fréquence de
résonance ???? vers les hautes fréquences et
vice-versa (cf. Figure 1. 13). Or ce type de motif dispose d'une
faible bande passante. En effet, le déplacement de la loi de phase a
pour conséquence un écrasement de la phase au voisinage de
#177;180°, la dispersion est par conséquent
modifiée. Il est donc difficile de maintenir une dispersion constante.
La plage
16
Chapitre 1- Généralités sur la
synthèse des réseaux réflecteurs
de fréquences dans laquelle les réponses en
phase sont parallèles (dispersion constante) diminue. Ceci a pour
conséquence de diminuer la bande passante de la cellule.
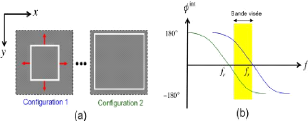
Figure 1. 13: Augmentation de la taille de la fente
annulaire (a) entraine un décalage de la fréquence de
résonance vers les basses fréquences (b)
Le concept de cellule Phoenix consiste à ajouter une
deuxième fente annulaire plus petite à l'intérieur de la
première. La Figure 1. 14 présente le principe de
fonctionnement de cette cellule. La cellule à une seule fente annulaire
(configuration1) résonne à une fréquence fr1 choisie ici
inférieure à la fréquence de travail
f0. Dès lors, la dispersion de la phase est quasi
nulle à f0. L'insertion d'une
seconde fente annulaire plus petite permet de créer une seconde
résonance fr2 située plus haut en fréquence, ici
au-delà de f0. Si les deux fréquences de
résonances sont trop éloignées entre elles, la phase
restera encore peu dispersive à f0 (configuration 2). Par contre le
rapprochement du périmètre des deux résonances
(configuration 3) permet de faire converger les deux fréquences de
résonances vers la fréquence de travail. Cette manoeuvre permet
alors de régler l'inclinaison du point d'inflexion et donc la
dispersion. La combinaison judicieuse de ces deux fentes permet de garantir une
gamme de phase de 360° sur une large gamme de fréquences.
1.3.3.2 Cycle de la cellule Phoenix
Dans [17] une évolution cyclique de la cellule Phoenix
a été présentée. Un exemple de cycle est
illustré sur la Figure 1. 15. Dans ce cas-ci, le cycle
débute par une cellule composée d'une seule fente annulaire. Il
continue en faisant croître un anneau métallique de longueur
Lr entre les deux fentes et se termine lorsque l'anneau
métallique disparaît à l'extérieur : il est revenu
à son état initial.
Il ressort que ce cycle permet d'obtenir une gamme de phase de
360° sur une large bande passante tout en garantissant une variation douce
de la géométrie du motif [2, p. 12]. C'est la
propriété dite de « renaissance » de la cellule
Phoenix.
1.3.3.3 Familles de la cellule Phoenix et circuits
équivalents
Dans un rapport interne à l'IETR, il a
été démontré que les caractéristiques sur la
phase et la dispersion, obtenues avec la cellule Phoenix, peuvent être
atteintes en utilisant deux familles de cellules : la famille capacitive et la
famille inductive (cf. Figure 1. 16). Chaque famille est
composée de trois géométries de cellules
différentes. Chaque géométrie permet ainsi de couvrir une
gamme de phase et de dispersion donnée.
Les six géométries de la cellule Phoenix peuvent
être représentées par un modèle comportemental. La
Figure 1. 17 présente les circuits équivalents
associés à chaque cellule. Les circuits équivalents ont
été développés et validés dans une
étude interne à l'IETR [Rapport interne, Simon Mener]. Cette
représentation en circuit équivalent est basée sur une
analyse théorique des composants de la cellule que nous verrons dans la
dernière partie de ce chapitre.
17
Chapitre 1-Généralités sur la
synthèse des réseaux réflecteurs
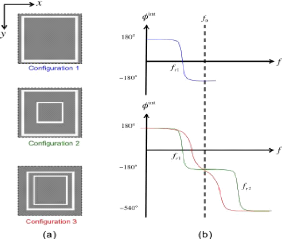
Figure 1. 14: Différentes configuration de
cellules à une ou deux fentes (a) et réponses en phase
associées (b)
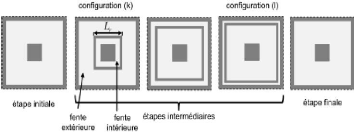
Figure 1. 15: Evolution cyclique de la cellule
Phoenix
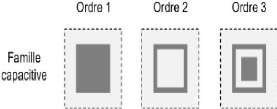

Figure 1. 16: Six géométries
différentes réparties dans deux familles.
18
Chapitre 1- Généralités sur la
synthèse des réseaux réflecteurs
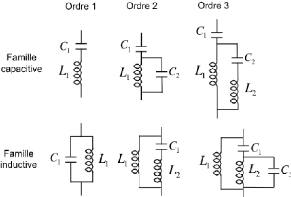
Figure 1. 17: Circuits équivalents
associés aux six géométries de la cellule
Phoenix
1.4 Synthèse d'une antenne RA
1.4.1 Méthodologie générale de la
synthèse
La synthèse d'un RA a pour but la conception et le
dimensionnement de l'antenne de manière à respecter les
spécifications sur le diagramme de rayonnement.
La première étape de la synthèse
consiste à fixer la distance focale (distance séparant l'antenne
source du réseau réflecteur) et les dimensions de l'ouverture
rayonnante.
L'étape suivante consiste à
synthétiser le diagramme de rayonnement. Sachant que l'amplitude sur
chaque cellule est fixée par l'antenne source, seule la phase
réfléchie peut être synthétisée, d'où
le nom donné à la méthode phase-only synthesis.
Synthétiser le diagramme de rayonnement consiste alors à
déterminer la loi de phase désirée à appliquer sur
l'ouverture rayonnante. Les méthodes de synthèses
diffèrent selon le rayonnement voulu. Pour des rayonnements canoniques
(transversal ou avec dépointage), la loi de phase à appliquer est
linéaire et peut être synthétisée grâce
à la théorie des réseaux linéaires. Pour des
rayonnements à lobes formés, la méthode d'optimisation
nommée intersection approach peut être utilisée [1].
L'objectif suivant consiste à dimensionner chacune des cellules
déphaseuses composant la surface rayonnante du réseau. La
géométrie de cellule qui permet de satisfaire la loi de phase
désirée est retenue pour chaque élément du
réseau, formant ainsi le layout du réseau réflecteur. Pour
être en mesure de réaliser cette dernière étape
(correspondance entre la phase introduite par la cellule et
géométrie de celle-ci), il faut un modèle de la cellule.
La méthodologie générale de la synthèse d'une
antenne réseau réflecteur est illustrée sur la Figure
1. 18.
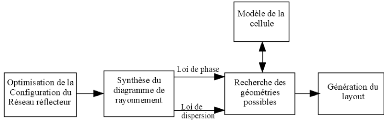
Figure 1. 18: Méthodologie
générale de la synthèse d'un réseau
réflecteur
19
Chapitre 1-Généralités sur la
synthèse des réseaux réflecteurs
1.4.2 Utilisation de modèles pour la synthèse
La modélisation de la cellule nécessite le
recours à des logiciels de simulation électromagnétiques
(par exemple HFSS ou CST). Toutefois, dans le cas où la cellule
présente de nombreux paramètres géométriques,
l'utilisation de ces outils peut s'avérer couteux en temps et en
ressources de calcul. La solution habituellement employée dans la
synthèse consiste à simuler la cellule pour quelques
géométries et à stocker la réponse obtenue dans une
base de données. Une alternative à la conception de bases de
données est l'utilisation de modèles comportementaux pour la
synthèse de RA. Ce paragraphe propose de classer quelques modèles
utilisés pour la caractérisation et pour la synthèse des
cellules unitaires.
1.4.2.1 Modèles basés sur les méthodes de
krigeage
Une méthode d'interpolation
généralisée consiste à utiliser le krigeage [21].
La méthode permet de modéliser de façon statistique un
ensemble de données connues. Plus précisément, comme les
algorithmes d'apprentissage par l'exemple, l'information est injectée
dans un processus d'entrainement où la relation Entrées (IN) /
Sorties (OUT) est connue afin de prédire la sortie de n'importe quel
autre jeu d'entrées. De plus le krigeage semble adapté au
processus déterministe. Un exemple en [22] propose de modéliser
la matrice de réflexion de la cellule de RA de type anneau
métallique rectangulaire. Les résultats sont encourageants
puisque l'erreur de prédiction sur le paramètre de phase du
coefficient de réflexion reste faible. Les avantages sont multiples : la
base de données, nécessaire à l'entrainement, n'a pas
besoin d'être aussi fournie que pour une synthèse classique, et
surtout le temps d'accès aux sorties du système non
linéaire est presque immédiat. Il en résulte que la
sélection des cellules pour la synthèse peut être
établie sans avoir recours à de nombreuses simulations
rigoureuses. La méthode de krigeage reste cependant difficile à
mettre en oeuvre et ne permet pas de modéliser précisément
l'amplitude des paramètres de la matrice de réflexion. Or les
pertes associées aux cellules sont importantes dans le processus de
synthèse.
1.4.2.2 Modèles basés sur les réseaux de
neurones artificiels (ANN)
Les réseaux de neurones artificiels (ANN pour
Artificial Neural Network en anglais) sont utilisés dans de
nombreux problèmes complexes non-linéaires. A partir d'un
ensemble d'échantillons issus de systèmes non-linéaires,
les réseaux de neurones artificiels sont capables d'approximer le
comportement de n'importe quel autre échantillon. Depuis peu, les
réseaux de neurones artificiels commencent à être
utilisés dans la synthèse des réseaux réflecteurs.
[23] présente les résultats obtenus sur la méthode de
caractérisation par ANN d'une cellule de type croix de malte (deux
paramètres géométriques). En effet, cet outil est
particulièrement adapté du fait que les cellules
déphaseuses ont un comportement non-linéaire en fonction de leurs
paramètres géométriques. Les réseaux de neurones
artificiels sont généralement utilisés de la
manière illustrée sur la Figure 1. 19.
Une base de données d'apprentissage est tout
d'abord générée à l'aide de logiciels de simulation
électromagnétique. Cette dernière comprend alors les
matrices de réflexion des cellules déphaseuses pour
différentes géométries, fréquences et angles
d'incidences. Après une phase d'apprentissage sur cette base de
données, le réseau de neurone artificiel sera capable
d'interpoler la réponse des autres cellules déphaseuses se
trouvant dans la gamme d'échantillon initiale formant ainsi une base de
données étendue.
Chapitre 1- Généralités sur la
synthèse des réseaux réflecteurs
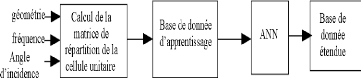
20
Figure 1. 19: Utilisation d'un ANN pour la
génération de la base de données
1.4.2.3 Modèles basés sur les circuits
équivalents (CE)
Une autre méthode plus rapide pour la synthèse
des panneaux réflecteurs consiste à modéliser chaque
cellule unitaire par son circuit équivalent (CE). La modélisation
consiste alors à dimensionner les éléments
localisés du circuit (capacité, inductance) de façon
à respecter la loi de phase spécifiée puis d'en
déduire analytiquement les valeurs des paramètres
géométriques. Cette méthode a été
utilisée pour synthétiser des surfaces sélectives en
fréquences (FSS) des réseaux transmetteurs et récemment
pour des réseaux réflecteurs. L'analyse des surfaces
périodiques par des circuits équivalents permet d'obtenir un
résultat immédiat de la réponse de la structure et
d'offrir une représentation intuitive des phénomènes
physiques qui ont lieu dans cette dernière. Différentes
méthodes permettant de calculer les valeurs des paramètres des
circuits en fonction des paramètres géométriques de la
cellule existent. Nous pouvons citer :
- La méthode de la moyenne "Averaged approach"
Cette méthode consiste à exprimer les
paramètres du circuit équivalent à partir d'une moyenne
sur le courant, dans le cas d'un motif de type patch, ou sur le champ
électrique, dans le cas d'un motif de type grille. Dans [24], O.
Luukkonen propose des géométries de FSS non résonantes de
types patch et grille métalliques.
- La méthode par interpolation
En 2015, une étude a été menée par
Nour Nachabe [25] sur la synthèse bi-fréquence de la
cellule Phoenix par les circuits équivalents. Ces travaux
ont permis de mettre en place des
équations permettant d'estimer les paramètres du
circuit équivalent en fonction des paramètres
géométriques pour trois ordres de la cellule Phoenix (cf.
Figure 1. 17). Cette étude s'appuie sur une analyse physique de
la géométrie de la cellule : une métallisation est
associée
à un effet inductif et une séparation entre
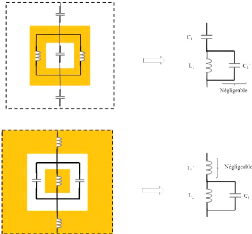
métallisation, à un effet capacitif. Les Figure 1. 20 Figure
1. 20 : Modélisation de la cellule Phoenix d'ordre 2 par CE
(a)Capacitive. (b) inductive(a) et (b) représentent respectivement
la modélisation de la cellule Phoenix d'ordre 2 capacitive et inductive.
En négligeant l'effet de la capacité ??1 ' dans schéma
global du motif « patch » et de la même manière, l'effet
de l'inductance ??1 ' devant l'impédance total du motif « grille
», on se retrouve finalement avec les CE de la Figure 1. 21(a) et
(b). Ils consistent simplement en une mise en série d'une
capacité et d'une inductance pour le cas capacitif et à la mise
en parallèle d'une capacité et d'une inductance pour le cas
inductif. Chacun des deux circuits étant fermé avec une ligne de
transmission pour modéliser le substrat et un court-circuit pour
modéliser le plan de masse [26].
La modélisation par circuit équivalent
présente de très bonnes performances c'est-à-dire qu'il
est possible de réaliser n'importe quel déphasage en jouant sur
les paramètres radioélectriques et ainsi déterminer la
géométrie de l'élément associé sans avoir
recours à la simulation rigoureuse. Cependant, cette modélisation
ne fonctionne qu'en incidence normale. Les erreurs
21
Chapitre 1-Généralités sur la
synthèse des réseaux réflecteurs
générées lorsque l'incidence devient
oblique [27] provoquent des différences de phase allant jusqu'à
5Ø°.
(b)
(a)
Figure 1. 20 : Modélisation de la cellule
Phoenix d'ordre 2 par CE (a)Capacitive. (b) inductive
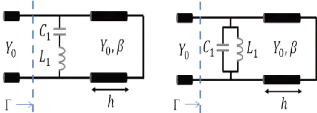
(a)
(b)
Figure 1. 21: Schéma électrique
équivalent des cellules Phoenix d'ordre 2. (a) capacitive.
(b)inductive.
1.5 Conclusion
A travers ce premier chapitre, nous avons pu présenter
la technologie des antennes RA qui combinent les technologies des
réflecteurs et des antennes réseaux en mettant l'accent sur ses
avantages notamment dans le domaine spatial. Nous avons également
explicité nos motivations sur le choix de la cellule unitaire dite
Phoenix par rapport aux autres géométries de cellules avant de
dresser quelques méthodes utilisées pour la modélisation
et la synthèse de la cellule unitaire. Ces méthodes sont, pour la
plupart, basées sur l'utilisation de base de données où
sont stockées les réponses de la cellule pour différentes
géométries, angles d'incidences et fréquences. Elles
s'appuient généralement sur des outils de simulations
électromagnétiques et des méthodes d'optimisations.
Cependant, ces méthodes ont l'inconvénient d'être
coûteuses en temps et en ressources de calcul. Une autre méthode
de synthèse d'un réseau réflecteur, plus rapide et moins
gourmande en ressource de calcul, consiste à modéliser chaque
cellule unitaire par son circuit équivalent. Une procédure de
synthèse de cellules de réseaux réflecteurs basée
sur cette approche et sur les techniques de synthèse de filtres sera
présentée dans la suite de ce rapport. Elle sera d'abord
appliquée à une cellule Phoenix d'ordre 2 de type inductif puis
de type capacitif.
Chapitre 2 : Procédure de synthèse d'une
cellule inductive
2.1 Introduction
A la suite des travaux d'Alexandre Grossetête [2], un
des problèmes majeurs identifié dans la procédure de
synthèse proposée a été la difficulté de
prendre en compte correctement la ligne centrale. Dans le modèle
proposé, la structure obtenue après transposition d'une
spécification en phase en une spécification en amplitude est
constituée de deux admittances parallèles identiques
séparées par une ligne de longueur 2h, h étant la longueur
de la cavité dans la cellule unitaire du réseau réflecteur
considéré (cf. Figure 2. 3). Si cette longueur h peut
être choisie initialement afin d'optimiser le fonctionnement du
réseau dans son ensemble, elle serait bien entendue la même d'une
cellule à une autre quel que soit la phase à
réfléchir. Or, deux phases réfléchies
différentes conduiront à deux comportements en amplitude
différents. Par conséquent, dans les modèles de filtres
passe-bande ou coupe-bande d'ordre 3 utilisés dans la procédure
développée, les caractéristiques du résonateur
central (L-C série dans le cas passe-bande et L-C parallèle dans
le cas coupe-bande), qu'on a naturellement associé à cette ligne
de longueur 2h, changent si on change la phase à réaliser. On se
trouve donc avec un paradoxe puisqu'on essaie d'associer des résonateurs
L-C différents à une même ligne de longueur 2h et
d'impédance caractéristique Z??.
Dans ce chapitre, nous proposons une nouvelle procédure
de synthèse de la cellule inductive Phoenix d'ordre 2 basée aussi
sur les techniques de synthèse de filtres passifs et qui permet de lever
ce paradoxe. L'idée est de ne plus considérer la ligne centrale
directement comme le résonateur série [2, pp. 120-124] mais de la
découper en plusieurs éléments en passant par
différentes étapes. Ainsi, à chaque configuration
différente correspondra une répartition différente des
valeurs des composants utilisés.
Dans la première partie de ce chapitre, nous
présenterons le concept de la méthode de synthèse.
Ensuite, dans la deuxième partie nous déroulerons notre
procédure de synthèse appliquée à la cellule
inductive en distinguant 2 solutions. Enfin dans la troisième partie,
les résultats de la procédure de synthèse, obtenus avec le
logiciel de simulation ADS (Advanced Design System), seront
présentés sur la base de trois familles de spécifications
faites sur la phase à synthétiser avant de dresser le bilan sur
la précision de la méthode de synthèse de ce type de
cellule.
2.2 La loi de phase et le gabarit en transmission
Dans la procédure de synthèse proposée,
nous serons amenés à faire des spécifications sur la phase
à réaliser et sur le gabarit en amplitude en vue de
déterminer les valeurs des composants du circuit équivalent. Pour
ce faire, nous allons dans cette première partie présenter le
concept développé pour la synthèse des
éléments du circuit équivalent.
2.2.1 Passage de la loi de phase au gabarit d'amplitude
Dans un rapport interne de l'IETR, R. Gillard montre le lien
entre la loi de phase d'une cellule unitaire Phoenix et le gabarit en
transmission du filtre équivalent. Plus précisément, il
établit la correspondance entre le module de S21 du filtre et la loi de
phase recherchée ??11 en utilisant la méthode paire/impaire.
Considérons une cellule unitaire représentable
par une admittance pure Y en parallèle sur un tronçon de ligne
court-circuité de longueur h et d'impédance
caractéristique Z?? égale à celle du
23
Chapitre 2- Procédure de synthèse d'une
cellule inductive
vide (cf. Figure 2. 1). On note ??11 =
??????11, le coefficient de réflexion à
l'entrée de la cellule, ??11 étant la phase à
synthétiser.
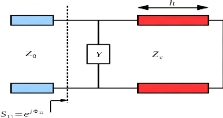
Figure 2. 1: Dipôle équivalent d'une
cellule unitaire Phoenix monocouche de réseau
réflecteur.
On cherche maintenant à relier la loi de phase à
l'amplitude du paramètre ??21 (et uniquement à celui-ci) d'un
circuit symétrique à 2 accès. On choisit le circuit
constitué par 2 cellules montées tête-bêche
créé par symétrie du premier (cf. Figure 2.
2).
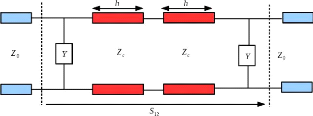
Figure 2. 2: Quadripôle équivalent
constitué de deux cellules unitaires montées
tête-bêche
En procédant par une analyse en mode pair/impaire, on
montre que le module de ??21 est directement lié à ??11 , la
phase à synthétiser par la relation suivante :
?????????????? [??????(?????? (??)
?? - ??
??????(??????))-?????? (??)]
|??????| = |?????? { ?? }| (2. 1)
La loi de phase initiale est donc transposée en un
gabarit en amplitude par la relation (2. 1). C'est le gabarit en amplitude que
nous allons utiliser pour déterminer l'inductance parallèle Y.
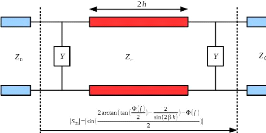
Figure 2. 3: Quadripôle
équivalent
2.2.2 Allure de la loi de phase et du gabarit en amplitude
2.2.2.1 Définition de la loi de phase
24
Chapitre 2-Procédure de synthèse d'une
cellule inductive
On considère une variation linéaire de la phase
??11 en fonction de la fréquence. Cette variation est décrite par
la relation suivante :
??11(??) = ????11(??- ??0) +
??11(??0) (2. 2)
????11(??0)
où ??11(??0) est la valeur de la phase à la
fréquence centrale ??0 et ???11 = ???? , la dispersion
de la phase en (°/GHz).
2.2.2.2 Illustration de la loi de phase et du gabarit en
transmission
Considérons la loi de phase illustrée sur la
Figure 2. 4 définie par le couple (phase à l'origine ;
dispersion) = (??11(??0); ???11) = (0°; -30°/??????) à la
fréquence centrale de la bande d'intérêt ??0=12,5GHz. La
loi équivalente sur l'amplitude du gabarit en transmission est
présentée sur la Figure 2. 5 avec une longueur de la
ligne fixée à h=??0/4 à ??0.
La réponse en amplitude présente 2 zéros
de transmissions situés de part et d'autre de la bande passante (cf.
Figure 2. 5(a)), et 3 pôles dont le pôle max est à
la fréquence centrale ??0. Cette courbe est
équivalente à la réponse d'un filtre passe-bande d'ordre 3
(3 pôles) et présente une ondulation en bande passante dont
l'amplitude est égale à 0,4137dB (cf. Figure 2.
5(b)).
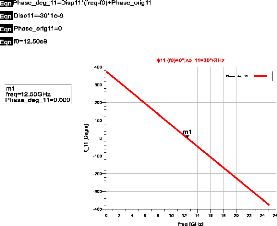
Figure 2. 4: loi de phase
2.2.2.3 Evolution du gabarit
Nous allons à présent étudier le
comportement des paramètres du gabarit (bande passante, les pôles,
les zéros de transmission, l'ondulation) en fonction d'une
évolution linéaire des paramètres de la loi de phase
(??11(??0); ???11). Nous analyserons ensuite
le comportement des paramètres du gabarit dans la bande
d'intérêt [10,5-14,5] GHz4.
La Figure 2. 6 montre l'évolution du gabarit
lorsque la phase à l'origine ??11(??0) varie de 0° à
180° par pas de 40° avec une dispersion fréquentielle
constante ???11 = -30°/??????.
4 Cette bande de fréquence
correspond à la bande Ku en liaison descendante (10,70-11,70 à
12,75 GHz) et montante (14 à 14,5). Ce spectre de fréquence est
utilisé dans les communications par satellite qui constitue
principalement le domaine d'utilisation des antennes RA.
25
Chapitre 2- Procédure de synthèse d'une
cellule inductive
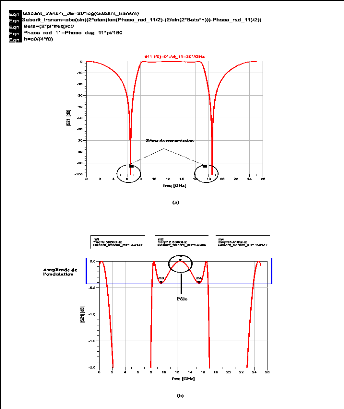
Figure 2. 5: Caractéristiques du gabarit en
transmission. (a) Zéros de transmission. (b) pôle à
f0
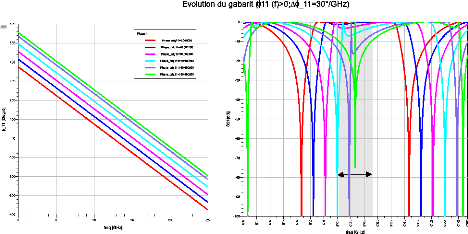
Bande
d'ntérêt
Figure 2. 6: Evolution du gabarit pour une
variation positive de ?_11 (f_0) à dispersion constante
26
Chapitre 2-Procédure de synthèse d'une
cellule inductive
Nous constatons un décalage du gabarit vers les
fréquences hautes. La bande passante se décale vers les hautes
fréquences et se déforme (l'ondulation n'est plus constante et le
pôle maximal n'est plus à ??0). Le zéro de
transmission qui précède la bande passante se rapproche
progressivement de la zone d'intérêt jusqu'à y entrer (cf.
Figure 2. 6).
La Figure 2. 7 présente une évolution
du gabarit d'amplitude pour une évolution négative de ??11(??0)
allant de 0° à -180° par pas de 40° avec une dispersion
???11 = 30°/??????.
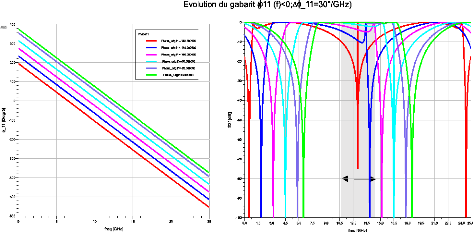
Bande
d'intérêt
Figure 2. 7: Evolution du gabarit pour une
variation négative de ?_11 (f_0) à dispersion
constante
Dans ce cas, l'effet inverse se produit. Le gabarit est
décalé cette fois ci vers les fréquences basses. La bande
passante s'éloigne de la bande d'intérêt, l'ondulation
n'est plus constante et le pôle maximal n'est plus centré à
??0. Et le second zéro de transmission se rapproche de la
zone d'intérêt jusqu'à y entrer (cf. Figure 2.
7).
A présent, on fait varier la dispersion ???11 avec une
phase à l'origine constante ??11(??0) = 0° et on obtient la
Figure 2. 8. Sur celle-ci, nous pouvons voir que la bande passante est
centrée à la même fréquence (la fréquence
centrale ??0) mais sa largeur diminue au fur et à mesure que
la dispersion augmente. Les zéros de transmission basse et haute
fréquence se rapprochent de la zone d'intérêt. L'ondulation
dans la bande passante reste constante mais sa valeur augmente avec la
dispersion (cf. Figure 2. 8).
2.2.2.4 Analyse et interprétation des résultats
En regardant la bande passante, la réponse en amplitude
du gabarit en transmission s'apparente à celle d'un filtre de type
passe-bande ou coupe bande selon la valeur de ??11(??0). Dans le cas
passe-bande, l'ondulation dans la bande passante et la présence des
zéros de transmission nous fait penser à un filtre elliptique (ou
au moins de Tchebychev si on ne prend pas compte la présence des
zéros de transmission). La présence des 3 pôles renseigne
sur l'ordre du filtre. Ainsi la synthèse des éléments du
circuit équivalent en l'occurrence l'admittance parallèle Y peut
dès lors s'opérer comme une synthèse de filtre classique.
Si le pôle de la bande passante se trouve dans la bande
d'intérêt défini, ce circuit sera synthétisé
par une synthèse de type passe-bande. Dans le cas où un des deux
zéros de transmission se trouve dans la bande d'intérêt, ce
dernier sera synthétiser par une synthèse de filtre
coupe-bande.
27
Chapitre 2- Procédure de synthèse d'une
cellule inductive
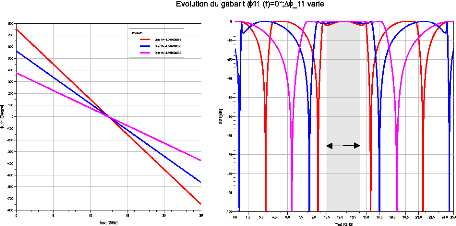
Bande d'intérêt
Figure 2. 8: Evolution du gabarit pour une
variation de la dispersion pour ?_11 ((f_0) =0°
2.3 Procédure de synthèse proposée pour une
cellule inductive (passe-bande)
2.3.1 Circuits équivalents du dipôle et du
quadripôle équivalent
On considère le motif d'une cellule inductive de type
Phoenix d'ordre 2 illustré sur la Figure 2. 9. Son admittance
équivalente est un résonateur parallèle composé par
une inductance L1 " et une capacité C1 ".
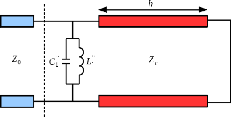
Figure 2. 9:Motif d'une cellule inductive de type
Phoenix d'ordre 2 : la fente annulaire
L'objectif consiste à synthétiser ce
résonateur à partir d'une spécification sur la loi de
phase en réflexion ??11(f) en passant par le gabarit en
amplitude équivalent présenté en section 2.2.1. Le
dipôle équivalent (Figure 2. 9) de la cellule est donc
transposé en un quadripôle équivalent
présenté sur la Figure 2. 10. On obtient deux
résonateurs parallèles identiques comprenant une inductance
L1 " et une capacité C1 " séparées par
une ligne de transmission de longueur 2h et d'impédance
caractéristique Z??. On note que ce résonateur est
identique à celui du dipôle équivalent (paragraphe 2.2).
Nous allons donc chercher à obtenir les valeurs de L1 " et
C1 " en synthétisant un filtre se rapprochant au mieux du
gabarit en transmission donné par l'équation (2. 1) afin de
remonter au dipôle.
28
Chapitre 2-Procédure de synthèse d'une
cellule inductive
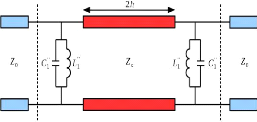
Figure 2. 10: Quadripôle équivalent du
motif inductif Phoenix d'ordre 2
2.3.2 Description de la procédure de synthèse
La cellule inductive de Phoenix d'ordre 2 se
caractérise par un comportement en amplitude de type passe-bande d'ordre
3 dans la bande d'intérêt [10,5-14,5] GHz. La structure de filtre
passe-bande d'ordre 3 se rapprochant au mieux est constituée de deux
résonateurs parallèles (??1 - ??1) séparés par un
résonateurs série (??2 - ??2), cf. Figure 2. 11.
L'objectif de cette procédure est de synthétiser le
quadripôle équivalent composé de deux résonateurs
parallèles d'entrée et de sortie (??1 " - ??1 ")
séparée par une ligne de transmission de longueur 2h et
d'impédance caractéristique ???? (cf. Figure 2. 10) en
utilisant le filtre passe-bande de la Figure 2. 11. L'idée est
de ne plus considérer la ligne centrale uniquement comme le
résonateur (??2 - ??2) mais de le découper
une plusieurs éléments (résonateurs parallèles et
inverseurs d'admittances) puis d'intégrer certains
éléments des inverseurs d'admittances dans les résonateurs
d'entrée et de sortie. A chaque étape différente de la
conception, correspondra une répartition différente des valeurs
des composants utilisés. Concrètement, au niveau de la cellule
unitaire cela revient à compenser au niveau du motif métallique
le fait que la longueur h de la cavité ait un comportement
différent en fonction de la fréquence considérer.
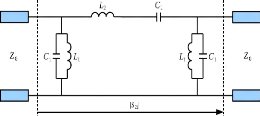
Figure 2. 11: Prototype d'un filtre passe-bande
d'ordre n=3
Les différents paramètres du module du gabarit en
transmission par la relation (2. 1) et les caractéristiques du
quadripôle équivalent (cf. Figure 2. 10) sont
définis comme suit :
- h : hauteur de la cavité (fixée, à
priori, par le cahier des charges et est égale à ??0/4 à
??0 = 12,5??????)
- ???? : impédance caractéristique de la ligne
associée à la cavité (prise égale à celle du
vide ??0)
- ??0 : impédance de référence
des ports 1 et 2 (égale à 120??)
2??
- ?? = ?? : constante de phase dans la cavité
- ?? : admittance associée à la cellule (au motif
en surface), a priori Y est un complexe.
- ???? : fréquence centrale de la réponse en
amplitude du filtre passe-bande.
- ??1, ??2 : fréquence de coupure basse et haute du filtre
passe-bande.
- ???? : pulsation correspondant à la fréquence
centrale du filtre passe-bande obtenu
(servira pour la transformation passe-bas/passe-bande)
29
Chapitre 2- Procédure de synthèse d'une
cellule inductive
- ??1, ??2 : les pulsations associées aux
fréquences de coupure basse et haute du filtre passe-bande
(définies à l'ondulation)
- ?????? : l'amplitude de l'ondulation dans la bande passante en
dB
- ?? = ??2-??1: la bande passante relative. ????
2.3.3 Spécifications
La prochaine étape consiste à relever un certain
nombre de paramètres (????, ??1, ??2 ???? ?????? ) sur le gabarit en
transmission obtenu à partir de l'équation (2. 1). Ces grandeurs
seront ensuite utilisées lors de la synthèse des cellules
unitaires du réseau réflecteur. Pour ce faire, des
spécifications doivent être faites sur la loi de phase en
réflexion ??11(??) en entrée du dipôle
équivalent.
A titre d'exemple, on considère les lois de phase
illustrées sur la Figure 2. 12 dans le cas d'une phase à
??0 positive ??11(??0) = 20° (Figure 2. 12 (a)) et
dans le cas où elle est négative ??11(??0) = -20°
(Figure 2. 12 (b)). Ces dernières sont obtenues avec la
même dispersion fréquentielle ???11(?? -
??0) = -30°/?????? et sont étudiées dans la bande
d'intérêt [10,5-14,5] GHz.
Ces lois sur la phase en réflexion peuvent
désormais se traduire en une loi sur l'amplitude en transmission sur les
deux axes du quadripôle équivalent (Figure 2. 13). Les
gabarits en transmission des Figure 2. 13(a) et Figure 2.
13(b) sont respectivement associés aux lois de phase des Figure
2. 12(a) et Figure 2. 12(b).
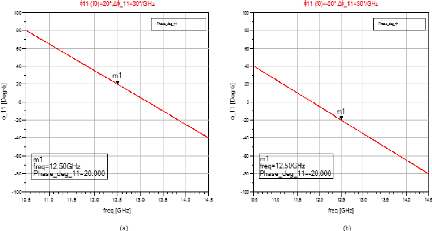
Figure 2. 12 : Exemples de lois de phase à
synthétiser dans la bande d'intérêt [10,5- 14, 5] GHz. (a)
??????(????) = 20°. (b)
?????? (?? ??) = -20°.
Le Tableau 2. 1 donne les valeurs des
paramètres relevées sur le gabarit en transmission (cf.
Figure 2. 13). La méthode suivie pour l'obtention de ces
valeurs est détaillée dans [2, pp. 117119]. L'ondulation choisit
est la plus faible. En effet, les résultats obtenus avec l'ondulation
maximale ou avec la moyenne des deux ondulations donnent globalement des
résultats moins satisfaisants. Ces résultats
révèlent des erreurs moyennes en phase non négligeables.
Quelques exemples vous seront présentés en Annexe 1.
30
Chapitre 2-Procédure de synthèse d'une
cellule inductive
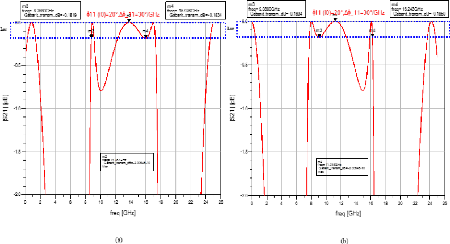
Figure 2. 13: Gabarits en transmission
associés aux lois sur la phase en réflexion de la Figure 2. 12. .
(a) ??????(????) = 20°.
(b) ??????(????) =
-20°.
|
???11,,11 11
|
0,, ~
11( 0)
|
spec Lar
|
r~ PeCs
|
spec
Îi
|
s??????
Î2
|
|
(°/??????)
|
(°)
|
(????)
|
(??????)
|
(??????)
|
(??????)
|
|
-30
|
20
|
0,1834
|
13,782
|
8,758
|
-
|
|
-30
|
-20
|
0,1834
|
11,218
|
-
|
16,24
|
Tableau 2. 1: Valeurs des paramètres du
gabarit à synthétiser
Comme mentionner plus haut, ces valeurs relevées serviront
ensuite à paramétrer la réponse du
prototype passe-bande à synthétiser. On note
????????6 : la fréquence du pôle ;
?????????? : l'ondulation dans la bande passante. Ces paramètres sont
définis comme suit :
??
???? ????????
?? = ????
????????
??????
???? = ??????
Les fréquences ??1 ???? et ??2 ???? sont les
fréquences de coupure définies à ??????????. Elles
délimitent la
bande passante du prototype de filtre passe-bande et sont
initialisées comme suit.
??1 ????????
???? ??11(??0) >0° ??2???????? ???? ??11(??0) <
0°
??1 ???? = { ????????2 ????????2
????
????
???????? ???? ??11(??0) < 0° et ??2 ????
= { ???????? ???? ??11(??0) > 0°
??2 ??1
Le Tableau 2. 2 donne les valeurs des paramètres
du filtre passe-bande à synthétiser (cf. Figure 2.
11)
5 L'exposant spec renvoie au terme
spécification
6 L'exposant PB fait référence aux
paramètres du filtre passe-bande
Chapitre 2- Procédure de synthèse d'une
cellule inductive
|
???11(°
/GHz)
|
??11(??0) (°)
|
P?? (d??) ??????
|
???? P?? (GHz)
|
??1P?? (GHz)
|
??2 P?? (GHz)
|
|
-30
|
20
|
0,1834
|
13,782
|
8,758
|
21,688
|
|
-30
|
-20
|
0,1834
|
11,218
|
7,749
|
16,24
|
Tableau 2. 2: Valeurs des paramètres de la
réponse du prototype passe-bande
2.3.4 Etapes de la synthèse du quadripôle
équivalent
Dans cette section, nous allons synthétiser le circuit
équivalent de la cellule inductive de Phoenix d'ordre 2 (cf. Figure
2. 10) à l'aide du prototype de filtre passe-bande d'ordre 3 (cf.
Figure 2. 11) et en utilisant les techniques classiques de filtrage
puis nous déterminerons les valeurs des éléments du
circuit à l'aide des équations établies lors de la
synthèse. Pour ce faire, nous procèderons par étape et
à chaque étape de la synthèse correspondra une
répartition différente des valeurs des éléments des
circuits que nous déterminerons en fin de synthèse.
2.3.4.1 Définition du filtre passe-bas normalisé
En filtrage, la synthèse du filtre passe-bande d'ordre
n (ou coupe-bande comme nous le verrons par la suite) commence par la
définition du prototype de filtre passe-bas d'ordre n. La Figure 2.
14 illustre la configuration du filtre passe-bas normalisé d'ordre
n=3.
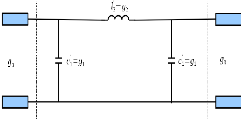
Figure 2. 14: Prototype du filtre passe-bas
normalisé d'ordre n=3
Les coefficients 90, 91 et 92 ,
associés aux éléments localisés définissent
la forme de la réponse du filtre passe-bande. Dans notre cas, nous
souhaitons avoir une ondulation dans la bande passante (cf. Figure 2.
13) donc nous allons synthétiser un filtre de type Tchebychev.
Les valeurs des éléments du filtre passe-bas de
Tchebychev peuvent dès lors être calculées [28, p. 99] en
calculant
31
D'abord :
??ar
?? = ??n(??????h (17,37)
y = sinh ??
(2n)
[(2??-1)??]
a?? = sin 2?? , ?? = 1, 2, ... , n
????
=y2+sin2(??????),
?? = 1,2, ... ,n
Ensuite,
2a1
y
9?? =
91 =
4????-1????
??= 1, 2,...,n
????-1????-1
9??+1 = 1 ????ur n im??air
= ??????h2 (??4) ????ur n
??air
Chapitre 2-Procédure de synthèse d'une
cellule inductive
2.3.4.2 Dénormalisation en impédance
En utilisant Z0 = 120ff impédance de l'air (milieu
d'arrivée de l'onde incidente) comme impédance de
référence, on obtient le circuit de la Figure 2. 15
suivante :
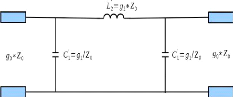
Figure 2. 15: Filtre passe-bas
dénormalisé
2.3.4.3 Introduction des inverseurs d'admittances
idéaux
Un inverseur d'admittance idéal, tel que défini
ici, est la représentation de l'admittance elle-même [28, pp.
144-145], c'est-à-dire qu'il fonctionne comme une ligne quart-d'onde
d'admittance caractéristique J à toutes les fréquences.
Ainsi, pour avoir les équations de conception de certains filtre
passe-bande ou coupe-bande, il est souhaitable de convertir le prototype
passe-bas d'ordre n=3 de la Figure 2. 15 en utilisant uniquement des
capacités parallèles (Ca1 et Ca2). Cela
peut être fait à l'aide des inverseurs d'admittances idéaux
(identiques dans notre cas J12) et on obtient le filtre passe-bas de la
Figure 2. 16.

32
Figure 2. 16: Filtre passe-bas avec inverseurs
d'admittances idéaux
L'équation (2. 3) donne la relation entre les
différents paramètres du circuit. La démarche à
suivre pour établir cette équation est donnée dans [28,
pp. 146-149].
CajCa2
I12 = 8i82 (2. 3)
2.3.4.4 Transformation passe-bas/passe-bande
L'étape suivante consiste à transformer le
filtre passe-bas avec des inverseurs d'admittances au filtre passe-bande avec
des inverseurs d'admittances correspondant [28, pp. 428-429]. En appliquant la
transformation illustrée sur la Figure 2. 17, on aboutit au
filtre passe-bande d'ordre n=3 avec inverseurs d'admittances de la Figure
2. 18.
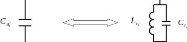
Figure 2. 17: Opération de transformation
d'un filtre passe-bas en un filtre passe-bande
Les éléments des résonateurs
parallèles (Lrj - Cri)sont calculés en utilisant
l'équation (2. 4).
Chapitre 2- Procédure de synthèse d'une
cellule inductive
?? ????' ??????
?? ???????? = = (2. 4)
?????????? ??
??1' : représente la
fréquence de coupure du prototype passe-bas normalisé ; cette
dernière est égale à 1.
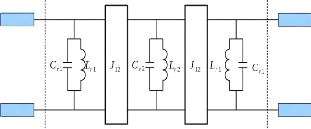
Figure 2. 18: Filtre passe-bande avec inverseurs
d'admittance idéaux
Finalement, Les valeurs des résonateurs (????1 - ????1)
et (????2 - ????2) sont données par les équations (2.
5) et (2. 6).
|
??????
??????
{
|
=
=
|
??????
|
(2.
|
5)
|
????
|
??????
??????
{
|
=
=
|
??????
|
(2. 6)
|
|
??.????
??
|
??.????
??
|
|
??????.????
|
??????.????
|
2.3.4.5 Implémentation des inverseurs d'admittances
idéaux
Dans cette étape, nous allons remplacer les inverseurs
d'admittances idéaux ??12 par leur circuit équivalent. Deux
solutions s'offrent à nous [28, p. 437], la structure en pi avec des
inductances et la structure en pi avec des capacités. Nous exploiterons
ces deux solutions.
a. Solution 1 : Structure en pi avec des inductances
Celle-ci est composée de deux inductances
négatives en parallèles séparées par une inductance
en série positive (cf. Figure 2. 19). La relation (2. 7) donne
la valeur de l'inverseur d'admittance en fonction de l'inductance et de la
pulsation ??0, associée à la fréquence de travail ??0 =
12,5??????. La Figure 2. 20 donne le circuit obtenu après
implémentation des inverseurs d'admittances idéaux.
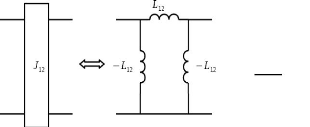
Avec :
??
?????? = (2. 7)
????·??????
33
Figure 2. 19 : Circuit équivalent d'un
inverseur d'admittance constituée d'une structure en pi avec des
inductances
Chapitre 2-Procédure de synthèse d'une
cellule inductive
En associant les admittances négatives
parallèles aux admittances des résonateurs parallèles, on
obtient le circuit de la Figure 2. 21. Les valeurs des
résonateurs parallèles (??1" -
??1") et (??2" -
??2") sont données par l'équation (2.8)
respectivement (2.9).
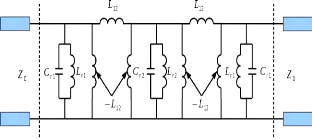
Figure 2. 20: Filtre passe-bande d'ordre 3
constitué de résonateurs parallèles et de deux structures
en pi avec des selfs
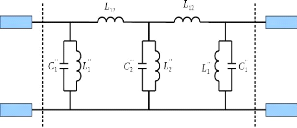
Figure 2. 21: Filtre passe-bande constitué
de 3 résonateurs parallèles séparés par deux
inductances
???? " = ?????? ???? " = ??????
{ ???? " = ??????\\(-??????) = ??????.?????? (2.
8) et { (2. 9)
???? " = (-??????)\\??????\\(-??????) = ??????.??????
??????-?????? ??????-????????
b. Solution 2 : Structure en pi avec des capacités
Cette structure est constituée de deux capacités
parallèles négatives séparées par une
capacité série positive (cf. Figure 2. 22). L'inverseur
d'admittance est exprimé ici en fonction de la capacité et de
??0 (équation (2. 10)). Le circuit équivalent obtenue
est illustré sur la Figure 2. 23.
|
Avec :
??????= ????· ?????? (2. 10)
|
34
Figure 2. 22: Circuit équivalent d'un
inverseur d'admittance constituée d'une structure en pi avec des
capacités
Comme pour la solution 1, on associe les capacités
négatives parallèles aux capacités positives des
résonateurs. On arrive au circuit de la Figure 2. 24, les
résonateurs parallèles (??1" -
??1") et (??2" -
??2") sont obtenue en appliquant les équations (2.
11) et (2. 12).
35
Chapitre 2- Procédure de synthèse d'une
cellule inductive
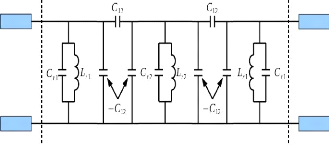
Figure 2. 23: Filtre passe-bande d'ordre 3
constitué de résonateurs parallèles et de deux structures
en pi avec des
capacités
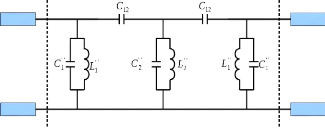
Figure 2. 24: Filtre passe-bande constitué
de 3 résonateurs parallèles séparés par deux
capacités
{
???? " = ?????? - ?????? (2. 11) et {???? " =
?????? - ???????? (2. 12)
???? " = ?????? ???? " =
??????
2.3.4.6 Equivalence de la structure en T centrale avec la ligne
(2h ; ????)
Dans cette étape, on cherche à remplacer la
structure centrale en T par une ligne de longueur 2h et d'impédance
caractéristique ???? (cf. Figure 2. 25) en utilisant les
matrices chaines des deux structures [28, p. 28].
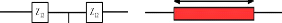
Figure 2. 25: Equivalence entre la structure en T
centrale et la ligne (2k, Zc)
On montre finalement que les deux structures de la Figure 2.
25 sont équivalente à la condition que :
|
??????
???? "
{
|
=
=
|
????????????(????)
????
|
(2. 13)
|
|
-?? ??????(??????)
|
36
Chapitre 2-Procédure de synthèse d'une
cellule inductive
On obtient ainsi le circuit équivalent final
constituée de deux résonateurs d'entrée et de sortie
(??1" - ??1") parallèles
séparés par une ligne de longueur 2h et d'impédance
caractéristique ???? (cf. Figure 2. 10).
2.3.4.7 Détermination des éléments des
circuits
Les expressions des impédances ??12 et
??2" seront définies dans les deux cas (solution 1
et solution 2) et avec le système d'équation (2.13)
établit précédemment, nous déterminerons les
valeurs des différents composants des circuits obtenues à chaque
étape de la synthèse pour obtenir enfin les valeurs des
composants (??1" - ??1") des
résonateurs d'entrée et de sortie du quadripôle
équivalent.
a. Solution 1 : Structure en pi avec des inductances
Sur la Figure 2. 21, on a : { ??12 = ????0??12 ")
??2 " = ????2 " ??0/(1 - ??02??2 " ??2
La première équation du système ci-dessus
et celle du système (2.13) impliquent que :
??
?????? =
??????????
|
??
??????????(????) (2. 14)
|
|
1
A partir de la seconde et sachant que ????2????2 = 2 , on trouve
les valeurs de ????2 ???? ????2
????
??
(2. 15)
?????? = ????(???? ??-??????)
?? ??????(????)(?? + ??????(????))
??????
??????????
{ ?????? = ??
???? ???????? =
????(??????-??????)??????(????)(??+??????(????))??
b. Solution 2 : Structure en pi avec des capacités
Avec la Figure 2. 24, on obtient : {??12 =
1/????0??12
??2 " = ????2 "?? 0/(1 -
??02??2" ??2")
De la même manière on trouve
??
?????? = ?????????? = - ??????????(????) (2.
16)
Et ensuite, on a de nouveau :
|
?????? = ????(????
??-????).??????(????).(??+??????(????))??
???????? ??
{ ????
?????? = ??
???? ???????? = ????(???? ??-????).??????(????).(??+??????(??
|
(2. 17)
??))??
|
D'après l'équation (2. 6), on a : ????2 =
????2?????? = ??
????????2
????2 ???? ????2 ayant les mêmes expressions dans les deux
solutions, on ne distinguera pas ici ces
deux solutions. On se retrouve dans les 2 cas avec :
????????????
?????? = ????(??????-??????)??????(????)(??+??????(????))??
(2. 18)
Or d'après l'équation (2. 3) , ????1 = ??1??2
??12
2
????2
??12 ayant la même expression dans les deux solutions mais
à un signe près de même que ????2, on ne distinguera pas
les deux solutions ici :
37
Chapitre 2- Procédure de synthèse d'une
cellule inductive
?????? = ???????? (???? ??-??????) ??????????
(2. 19)
?????????? (??????)
On peut ainsi en déduire l'admittance du résonateur
d'entrée/sortie. C'est-à-dire celle du motif métallique de
la cellule du RA qu'on synthétise :
1
??= ??????1+"
??????1

"
a. Solution 1 : Structure en pi avec des inductances
(???? ??-??????)
???? " = ?????? = ??????
?????? = ???????? ???????????? ??
?????????? (??????)
{ (2. 20)
??????????????????(??????)
???? " = ????????????
??????-?????? = ???????? (??????-??????)-????????????????????
(????)
b. Solution 2 : Structure en pi avec des capacités
{
?????????? (??????) ????????
???? = ?????? = ???????? (?????? -??????)
"= ?????? - ?????? = ????????(????
??-??????)+????????????????????(????)
???? ??????????????????
??????(??????)
(2. 21)
2.3.4.8 Cas particulier : ?? = 2?? à ???? =
??0
????
On rappelle que h =
??0à la fréquence ??0 = 12,5?????? et que
?? = ??2?? dépend de la fréquence. 4
Etant donné qu'il faut fixer ?? à une certaine
fréquence pour pouvoir calculer les composants des résonateurs
d'entrée/sortie (car il n'est pas encore envisageable d'utilisée
des composant à valeurs variable en fonction de la fréquence pour
la conception des cellules unitaires de RA imprimée) donc on la calcule,
a priori, à la fréquence centrale ???? du filtre passe-bande
à
2?? 2??
synthétiser (?? = ????). Il est à noter que, pour
ces deux solutions, si ?? = à ???? = ??0, on
????
obtient des valeurs des éléments qui sont sous une
forme indéterminée en 00. Le
problème peut
être contourner en faisant un développement
limité du premier ordre. On obtient ainsi dans les 2 solutions :
(2. 22)
?? { ??????????
???????????????????
?????? ? ??????????
??????????????
Nous pouvons dès lors passer à la conception et
à la simulation des circuits équivalents des cellules unitaires
en utilisant le logiciel ADS (Advanced Design System) et en faisant des
spécifications sur la loi de phase à réaliser comme
expliquer dans la section 2.3.3. Les résultats de ces simulations seront
présentés dans les paragraphes qui suivent.
2.4 Résultats de la synthèse
Dans cette partie, nous allons évaluer la
précision de la procédure de synthèse décrite
précédemment. Pour ce faire, nous considérons trois
familles de spécifications sur la loi de
38
Chapitre 2-Procédure de synthèse d'une
cellule inductive
phase en réflexion. Les lois de phases sont toutes
linéaires. On rappelle que la loi sur la phase en réflexion est
définie par sa valeur à la fréquence ??0 , ??11(??0), et
par sa dispersion ???11. Dans la première famille, nous allons faire
varier ??11(??0) de 0° à 180° avec une dispersion constante
fixée à ???11 = -30°/?????? . Dans la deuxième
famille, toujours avec la même dispersion, nous ferons varier ??11(??0)
de -0° à -180°. Enfin, dans la troisième famille, nous
ferons varier la dispersion ???11 avec une phase à ??0
fixée à 20°.
Pour chaque famille, nous appliquerons les résultats la
procédure décrite dans la section 2.3.4 aussi bien pour la
solution 1 que pour la solution 2.
A l'issue de la présentation des résultats de
chaque famille, nous présenterons les performances de la synthèse
passe-bande en termes de précision dans la bande d'intérêt
[10,5-14,5] GHz. Pour quantifier cette précision, nous calculerons, pour
chaque spécification, l'erreur moyenne entre la loi de phase
spécifiée ??11 (équation (2.23)) et la phase
réalisée par le dipôle équivalent
??11??????. Cette quantité est définie par
l'équation suivante :
|
???????? =
|
??1?|??11(????) - ??11
?? ??????(????)|
??=1 (2. 23)
|
?? : représente le nombre de points fréquentiels
définis dans la bande d'intérêt.
2.4.1 Solution 1 : Structure en pi avec des inductances
2.4.1.1 Première famille de spécification :
??11(??0) > 0°
Dans cette première famille, la phase à
??0, ??11(??0), varie de 0° à
180°avec un pas de 20°. La dispersion ???11(??0) est fixée
à -30°/GHz. Quelques résultats de la synthèse pour
cette famille sont présentés sur les Figure 2. 26 et
Figure 2. 27. Le Tableau 2. 3 donne les erreurs moyenne et
maximale des différentes cellules synthétisées pour des
phases à ??0 positives.
Dans toute la suite, les courbes en rouge
représentent les courbes de la phase et de l'amplitude
souhaitées obtenues avec les équations (2. 1) et (2. 2) et les
courbes en bleu, les courbes de la phase à l'entrée du
dipôle et de l'amplitude du gabarit en transmission obtenue avec la
synthèse.
|
??11(??0) (°)
|
0
|
20
|
40
|
60
|
80
|
90
|
|
????????7 (°)
|
7,545
|
16,453
|
17,557
|
15,480
|
15,924
|
17,536
|
|
????????8 (°)
|
13,551
|
18,782
|
29,053
|
32,051
|
34,532
|
40,421
|
(a)
|
??11(??0) (°)
|
100
|
120
|
140
|
160
|
180
|
|
???????? (°)
|
19,183
|
21,240
|
23,527
|
26,989
|
48,712
|
|
???????? (°)
|
48,730
|
54,178
|
59,411
|
67,396
|
96,087
|
(b)
Tableau 2. 3 : Erreurs moyenne et maximale solution
1. (a) ??????(????) ?????????? ???? ??° à ????°.
(b)
??????(?? ??) ?????????? ???? ????° à ??????°
???????? ???????(????)=-30°/GHz
7 Erreur moyenne en phase
8 Erreur maximale en phase
39
Chapitre 2- Procédure de synthèse d'une
cellule inductive
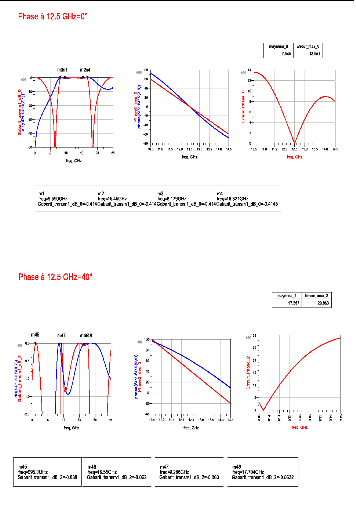
(a)
(c)
Figure 2. 26: Résultats de la
synthèse passe-bande solution 1. (a) ??????(????) =
??°. (b) ??????(????) = ????°
40
Chapitre 2-Procédure de synthèse d'une
cellule inductive
(a)
(b)
Figure 2. 27: Résultats de la
synthèse passe-bande solution 1. (a) 4)11(f 0) = 140°. (b) 4)11(f
0) = 180°
41
Chapitre 2- Procédure de synthèse d'une
cellule inductive
La Figure 2. 28 présente l'erreur moyenne en
fonction de la phase à f0, On(f0). Pour une spécification
fixée à On(f0) = 0° , l'erreur moyenne
entre la loi de phase souhaitée et la phase réalisée par
le dipôle est de 7,545°. Cette erreur augmente jusqu'à
17,557° pour On(f0) = 40°, puis diminue pour
des phases à f0 comprises entre 60° et 90°. Au-delà,
l'erreur augmente fortement.
En effet, lorsque O (f0) augmente, le pôle du gabarit se
déplace vers les hautes fréquences et s'éloigne ainsi de
la bande d'intérêt. De ce fait, l'approximation du gabarit dans la
bande d'intérêt perd en précision.
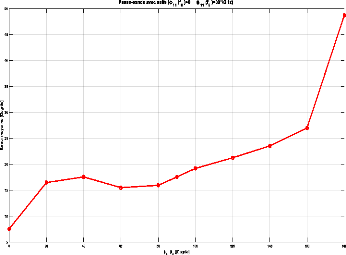
Figure 2. 28: Erreur moyenne solution 1 lorsque
4)11(f0) varie de 0° à 180° avec
?4)11(fo)=-30°/GHz
2.4.1.2 Deuxième famille de spécification : On(f0)
< 0°
Dans cette famille, la phase à f0,
On(f0) est négative et varie désormais de
0° à -180°. La dispersion ?Oii(f0) est fixée à
-30°/GHz. Les résultats pour des phases à f0 de
0° et -40° seront présentés en Annexe 2. Les erreurs
moyenne et maximale obtenues pour des phases comprises entre 0 et -90°
(Tableau 2. 4) révèlent que cette solution n'est pas
adaptée à la synthèse des phases négatives.
|
On(f0) (°)
|
0
|
-20
|
-40
|
-60
|
-80
|
-90
|
|
£moy (°)
|
31,037
|
11,782
|
30,402
|
24,996
|
126,222
|
164,832
|
|
£max (°)
|
45,335
|
27,608
|
46,891
|
51,760
|
146,116
|
193,124
|
Tableau 2. 4: Erreurs moyenne et maximale solution
1 lorsque 4)11(f??) varie de 0° à - 90° avec
?4)11 (f??)=-
30°/GHz
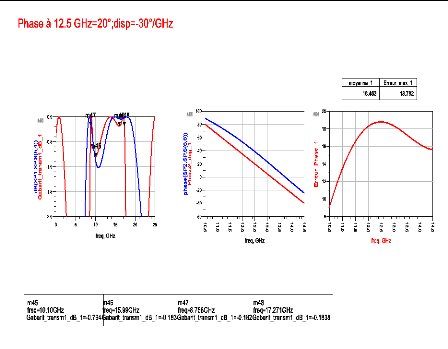
(a)
42
Chapitre 2-Procédure de synthèse d'une
cellule inductive
2.4.1.3 Troisième famille de spécification :
variation de ???11(??0)
Pour cette dernière famille, la phase à
??0, ??11(??0), est fixée à
20° et la dispersion ???11(??0) varie en prenant
trois valeurs : -30°/GHz, -45°/GHz et -60°/GHz. La Figure 2.
29 illustre les résultats de la synthèse. Nous notons que
cette spécification est un cas idéal puisque le pôle du
gabarit en transmission se trouve dans la bande d'intérêt et est
presque centré à la fréquence ??0. Le Tableau 2. 5
présente l'erreur moyenne et l'erreur maximale de la cellule pour
chaque dispersion. Nous remarquons que l'erreur moyenne ainsi que l'erreur
maximale augmentent avec la dispersion.
|
???11(?? - ??0) (°/GHz)
|
??11(??0) (°)
|
???????? (°)
|
???????? (°)
|
|
-30
|
20
|
16,463
|
18,782
|
|
-45
|
20
|
16,937
|
29,827
|
|
-60
|
20
|
25,980
|
44,126
|
Tableau 2. 5: Erreurs moyenne et maximale solution
1 avec ??????(????) = ????° pour chaque
dispersion
43
Chapitre 2- Procédure de synthèse d'une
cellule inductive
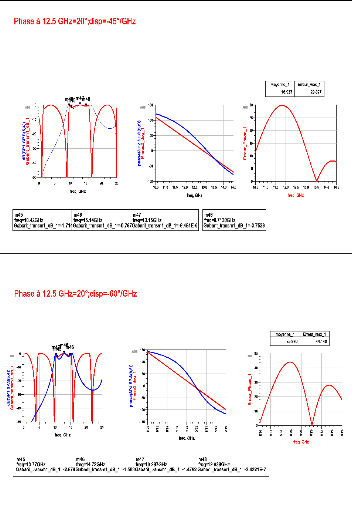
(b)
(c)
Figure 2. 29: Résultats de la
synthèse passe-bande solution 1. (a)
???????(????)=-30°/GHz. (b)
???????(????)=-45°/GHz. (c)
??????? (????)=-60°/GHz
44
Chapitre 2-Procédure de synthèse d'une
cellule inductive
2.4.2 Solution 2 : Structure en pi avec des capacités
2.4.2.1 Première famille de spécification :
??11(??0) > 0°
Dans cette famille, la phase à ??0, ??11(??0) est
positive et varie désormais de 0° à 180°. La dispersion
???11(??0) est fixée à -30°/??????.
Les résultats pour des phases à ??0 de 0°et
40° seront présentés en Annexe 2. Les erreurs moyenne et
maximale obtenues pour des phases comprises entre 0 et 90° (tableau 2.6)
montrent que cette solution n'est pas adaptée à la
synthèse des phases positives.
|
??11(??0) (°)
|
0
|
20
|
40
|
60
|
80
|
90
|
|
???????? (°)
|
30,812
|
16,460
|
19,637
|
31,753
|
124,292
|
145,815
|
|
???????? (°)
|
46,408
|
21,237
|
40,246
|
54,208
|
142,907
|
169,850
|
Tableau 2. 6: Erreurs moyenne et maximale solution
2 lorsque ?????? (????) ?????????? ???? ??° à ????
????????
???????(????)=-30°/GHz
2.4.2.2 Deuxième famille de spécification :
??11(??0) < 0°
Dans cette deuxième famille, la phase à ??0,
??11(??0), varie de 0° à -180°avec un pas de 20°. La
dispersion ???11(??0) est fixée à
-30°/GHz.
Quelques résultats de la synthèse pour cette
famille sont présentés sur les Figure 2. 30 et
Figure 2. 31. Les Tableau 2. 7(a) et Tableau 2. 7(b)
donnent les erreurs moyenne et maximale des différentes cellules
synthétisées pour des phases à ??0 négatives.
(a)
(b)
|
??11(??0) (°)
|
0
|
-20
|
-40
|
-60
|
-80
|
-90
|
|
???????? (°)
|
7,545
|
28,566
|
28,896
|
21,758
|
16,676
|
17,499
|
|
???????? (°)
|
13,552
|
35,706
|
37,681
|
41,613
|
33,978
|
42,785
|
|
??11(??0) (°)
|
-100
|
-120
|
-140
|
-160
|
-180
|
|
???????? (°)
|
19,102
|
21,322
|
24,174
|
27,845
|
39,521
|
|
???????? (°)
|
49,559
|
53,845
|
59,496
|
68,861
|
90,096
|
Tableau 2. 7 : Erreurs moyenne et maximale solution
2. (a) ??????(????) ?????????? ???? ??° à -
????°. (b)
??????(????) ?????????? ???? - ????° à -
??????° ???????? ???????(????)=-30°/GHz
45
Chapitre 2- Procédure de synthèse d'une
cellule inductive
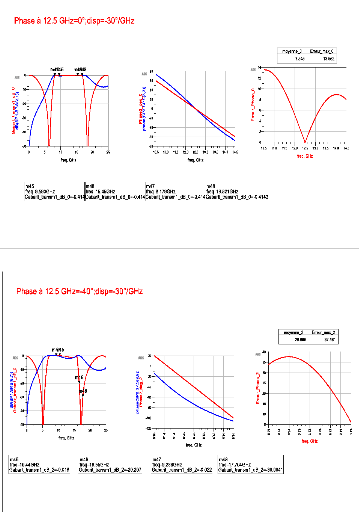
(a)
(b)
Figure 2. 30: Résultats de la
synthèse passe-bande solution 2. (a) 4 ii (Ï0) =
0°. (b) 4 ii (Ï0) = -40°
46
Chapitre 2-Procédure de synthèse d'une
cellule inductive
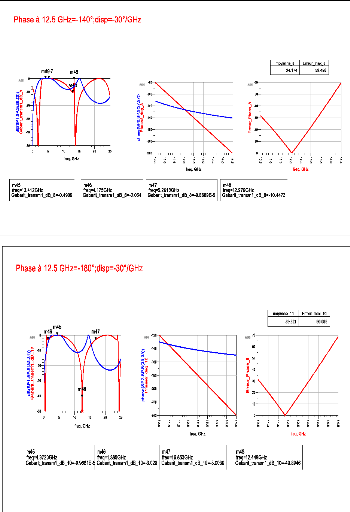
(a)
(b)
Figure 2. 31: Résultats de la
synthèse passe-bande solution 1. (a) ??????(????) =
-??????°. (b) ??????(????) = -??????°
47
Chapitre 2- Procédure de synthèse d'une
cellule inductive
La Figure 2. 32 présente l'erreur moyenne en
fonction de la phase à f0, ??11(f0).
Pour une spécification fixée à ??11(f0) = 0°
, l'erreur moyenne entre la loi de phase souhaitée et la phase
réalisée par le dipôle est de 7.545°. Cette erreur
augmente jusqu'à ??11(f0) = -40°, puis diminue
pour des phases à f0 comprises entre
-60° et -90°. Au-delà,
l'erreur augmente fortement.
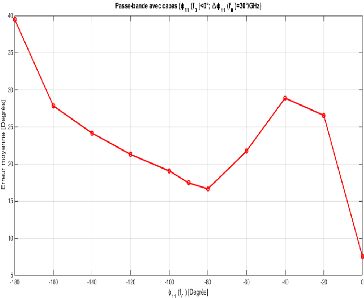
Figure 2. 32: Erreur moyenne solution 2 lorsque
??ll(????) v??r??e de ??° à - l????° ??vec
???ll (?? ??)=-30°/GHz
2.4.2.3 Troisième famille de spécification :
variation de ???11
Pour cette dernière famille, le phase à
f0, ??11(f0), est fixée à
-20° et la dispersion ???11(f0) varie en prenant trois
valeurs : -30°/GHz, -45°/GHz et -60°/GHz. La Figure 2. 33
illustre les résultats de la synthèse. Pour cette
spécification, le pôle du gabarit en transmission se trouve dans
la bande d'intérêt et est presque centré à la
fréquence f0. Le Tableau 2. 8 présente
l'erreur moyenne et l'erreur maximal de la cellule pour chaque dispersion. Nous
remarquons que l'erreur moyenne ainsi que l'erreur maximale augmentent lorsque
la dispersion augmente.
|
???11(°/GHz)
|
??11(f0) (°)
|
Em??y (°)
|
Em??x (°)
|
|
-30
|
-20
|
26,566
|
35,706
|
|
-45
|
-20
|
35,169
|
51,679
|
|
-60
|
-20
|
46,415
|
66,886
|
Tableau 2. 8: Erreurs moyenne et maximale solution
1 avec ??ll (?? ??) = -????° pour chaque
dispersion
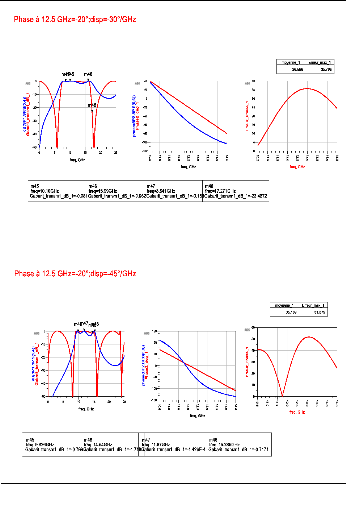
(a)
48
(b)
Chapitre 2-Procédure de synthèse d'une
cellule inductive
49
Chapitre 2- Procédure de synthèse d'une
cellule inductive
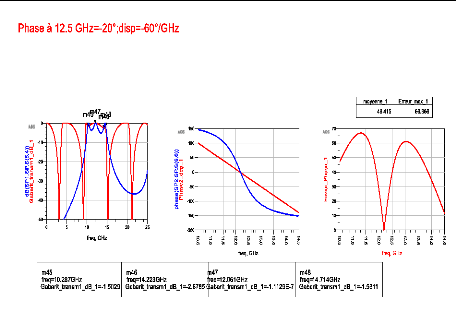
(c)
Figure 2. 33: Résultats de la
synthèse passe-bande solution 2. (a) ???????(??
??)= -30°/GHz. (b) ??????? (??
??)=-45°/GHz. (c)
???????(????)=-60°/GHz
2.4.3 Bilan sur la précision de la procédure de
synthèse passe-bande
La Figure 2. 34 présente l'évolution de
l'erreur moyenne en fonction de ??11(??0) pour trois dispersions ???11(??0) =
{-30°/??????; -45°/??????; -60°/??????}. Pour des valeurs de
?11(f0) comprises entre ]0° ; -40° ]et]0° ; 40°], l'erreur
augmente fortement en fonction de la dispersion. Bien que cette zone soit
idéale, dans le sens où le pôle du gabarit se trouve dans
la bande
40°; -60°/??????).
d'intérêt, l'erreur moyenne atteint une valeur
maximale de 32,914° pour (??11(??0); ???11) = (-
50
Chapitre 2-Procédure de synthèse d'une
cellule inductive
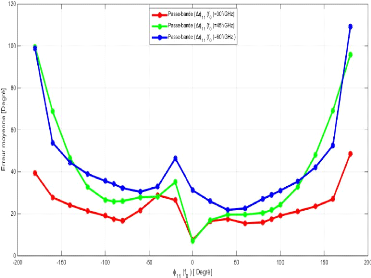
Figure 2. 34: Bilan sur les performances de la
procédure de synthèse de type passe-bande
Pour conclure, les résultats obtenus par l'utilisation
de la synthèse de type passe-bande ne sont pas globalement satisfaisants
et méritent d'être améliorés.
2.5 Conclusion
Dans ce chapitre, nous avons développé une
nouvelle méthode de synthèse d'une cellule Phoenix d'ordre 2 de
type inductif basée sur les techniques classiques de filtrage. Cette
méthode permet la conversion d'une loi à l'entrée d'un
dipôle équivalent en une loi sur le gabarit en transmission entre
les deux accès du quadripôle équivalent. Au cours de la
synthèse, deux solutions ont été retenues : la solution 1,
obtenue en remplaçant les inverseurs d'admittances par une structure en
pi avec des inductances et la solution 2, obtenue par utilisation d'une
structure en pi avec des capacités.
Pour tester les performances de la synthèse et
définir le domaine de validité de chaque solution, nous avons
considéré trois familles de spécifications sur la loi de
phase à synthétiser. Les résultats obtenus
révèlent que selon que ??11(J0) E [0°; 90°] ??u
[0°; -90°] , la solution 1 ou la solution 2 était la plus
appropriée. Ces résultats montrent aussi que dans ces deux
intervalles, la synthèse passe-bande offre de bonne précision qui
mérite néanmoins d'être améliorer et que les
performances se dégradent à mesure qu'on s'éloigne de ces
valeurs.
Nous allons maintenant montrer que pour les autres valeurs de
??11(J0), il est plus judicieux de s'appuyer sur une synthèse
coupe-bande.
Chapitre 3 : Procédure de synthèse d'une
cellule capacitive 3.1 Introduction
Dans ce dernier chapitre, nous proposons une nouvelle
procédure de synthèse appliquée à la cellule
Phoenix d'ordre 2 capacitive en utilisant les techniques classiques de
filtrage. Le motif capacitif de la cellule Phoenix d'ordre 2 se
caractérise par un comportement en amplitude de type coupe-bande d'ordre
3 dans la bande d'intérêt [10,5-14,5] GHz.
L'objectif de cette procédure est de synthétiser
le quadripôle équivalent composé de deux résonateurs
séries d'entrée et de sortie (L1 " - C1 ")
séparée par une ligne de transmission de longueur 2h et
d'impédance caractéristique Z?? (cf. Figure 3.
2) en utilisant le prototype de filtre coupe-bande se rapprochant au mieux
de l'amplitude du gabarit en transmission. Cette structure est
constituée de deux résonateurs séries (L1 - C1)
en parallèles dans le circuit séparés par un
résonateur parallèle (L2 - C2) en
série dans le circuit (cf. Figure 3. 3). L'idée est
comme précédemment de ne plus considérer la ligne centrale
directement comme le résonateur parallèle [2, pp. 149-151] mais
de la découper en plusieurs éléments en passant par
différentes étapes. Ainsi, à chaque configuration
différente correspondra une répartition différente des
valeurs des composants utilisés.
Le principe de la synthèse est le même que celui
du prototype passe-bande vue précédemment. Nous allons
découper le circuit en plusieurs éléments
(résonateurs séries en parallèles dans le circuit et
inverseurs d'admittances) puis intégrer certains éléments
des inverseurs d'admittances dans les résonateurs d'entrée et de
sortie. Les résultats obtenus sur la base de deux familles de
spécifications faites sur la loi de phase en réflexion seront
présentés avant de donner le bilan sur la précision de la
synthèse coupe-bande appliquée au motif capacitif.
3.2 Procédure de synthèse proposée pour une
cellule capacitive
3.2.1 Circuits équivalents
Le circuit équivalent du motif capacitif d'une cellule
Phoenix d'ordre 2 est un dipôle composé par un résonateur
série (L1 " - C1 ") à l'entrée du dipôle et
d'une ligne court-circuitée de longueur h et d'impédance
caractéristique Z?? (cf. Figure 3. 1). Le
quadripôle équivalent est présenté sur la Figure
3. 2. Il est composé de deux résonateurs séries
séparés par une ligne de transmission de longueur 2h et
d'impédance caractéristique Z??.
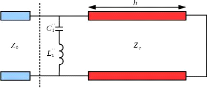
Figure 3. 1: Motif capacitif d'une cellule Phoenix
d'ordre 2
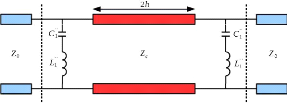
Figure 3. 2: Quadripôle
équivalent
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
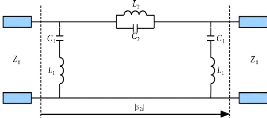
52
Figure 3. 3: Prototype de filtre
coupe-bande
3.2.2 Spécifications
Comme souligné à la section 2.2.2, lorsque les
zéros de transmissions basses et hautes de la réponse en
amplitude du gabarit entrent dans la zone d'intérêt [10,5-14,5]
GHz, la réponse du filtre s'apparente à celle d'un filtre
coupe-bande d'ordre n=3. La Figure 3. 4 présente les lois de
phase à synthétiser dans le cas d'une phase à
??0 positive ??11(??0) = 160° (Figure 3. 4 (a)) et
dans le cas où elle est négative ??11(??0) = -160°
(Figure 3. 4(b)). Ces dernières sont obtenues avec la
même dispersion fréquentielle ???11 = -30°/?????? et sont
étudiées dans la bande d'intérêt [10,5-14,5] GHz
avec ??0 = 12,5??????.
Ces lois sur la phase en réflexion peuvent dès
lors être traduites en une loi sur l'amplitude en transmission sur les
deux axes du quadripôle équivalent (Figure 3. 5). Les
gabarits en transmission des Figure 3. 5(a) et Figure 3. 5(b)
sont respectivement associés aux lois de phase des Figure 3.
4(a) et Figure 3. 4(b).
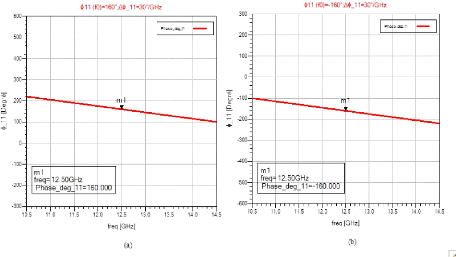
Figure 3. 4: Lois de phase à
synthétiser dans la bande d'intérêt [10,5- 14, 5] GHz. (a)
?11(f0) = 160°. (b) ?11(f0) = -160°
La zone remarquable que nous allons maintenant approximer est
celle contenant le zéro de transmission et non celle contenant le
pôle comme dans d'une cellule inductive.
A partir du gabarit en transmission, nous allons relever
différents paramètres décrivant le zéro de
transmission à savoir : la fréquence du zéro de
transmission ???? ????????, l'ondulation ??????
???????? prise
??11(??0) est négative ou après la bande
rejetée quand
avant la bande rejetée quand la phase à
??0,
53
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
??11(??0) est positive et ??1????????, ??2???????? les
fréquences de coupures basse et haute définies à
l'ondulation ??????
????????.
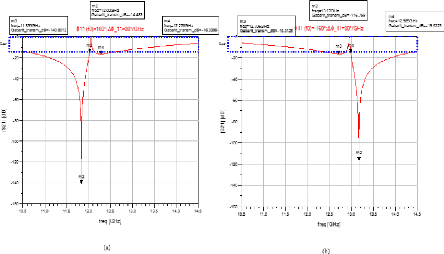
Figure 3. 5: Gabarits en transmission associés
aux lois sur la phase en réflexion (a) ?11(f0) = 160°. (b) ?11(f0)
= -160°.
Le Tableau 3. 1 donne les valeurs de ces
paramètres pour les spécifications précédentes. Ces
valeurs serviront ensuite à paramétrer la réponse du
prototype coupe-bande. En appliquant les formules de la section 2.3.3, on
obtient les valeurs des paramètres coupe-bande du Tableau 3.
2.
|
???11(°/??????)
|
??11(??0)(°)
|
???????? (????) ??????
|
?????? ?????? (??????)
|
??1?? ?????? (??????)
|
??2?? ?????? (??????)
|
|
-30
|
160
|
16,347
|
11,833
|
-
|
12,012
|
|
-30
|
-160
|
16,347
|
13,164
|
12,988
|
-
|
Tableau 3. 1: Valeurs des paramètres du
gabarit à synthétiser
|
???11(°/??????)
|
??11(??0) (°)
|
????9 (????) ??????
|
???? ???? (??????)
|
??1???? (??????)
|
??2 ???? (??????)
|
|
-30
|
160
|
16,347
|
11,833
|
11,657
|
12,012
|
|
-30
|
-160
|
16,347
|
13,164
|
12,988
|
13,342
|
Tableau 3. 2: Valeurs des paramètres de la
réponse du filtre coupe-bande
3.2.3 Synthèse du quadripôle équivalent
La procédure de la synthèse se fait par
étape comme nous l'avions défini dans le cas d'une cellule
inductive. Nous distinguerons aussi deux solutions que nous essayerons
d'exploiter. Les trois premières étapes de cette synthèse
sont équivalentes aux trois premières de celle
développée pour la cellule Phoenix d'ordre de type inductif.
9 L'exposant CB fait référence aux
paramètres du prototype coupe-bande
54
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
3.2.3.1 Transformation passe-bas/coupe-bande
Nous allons transformer le filtre passe-bas avec inverseurs
d'admittances idéaux de la Figure 2. 16 en un filtre
coupe-bande avec inverseurs d'admittances correspondant en s'appuyant sur les
transformations de la Figure 3. 6 [28, pp. 727-729].
On obtient le filtre coupe-bande d'ordre 3 constituée de
trois résonateurs séries séparés par deux
inverseurs d'admittance représenter sur la Figure 3. 7.
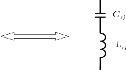
Figure 3. 6: Opération de transformation
d'un filtre passe-bas en un filtre coupe-bande.
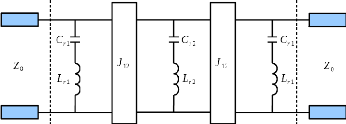
Figure 3. 7: Filtre coupe-bande avec inverseurs
d'admittances
Les éléments des résonateurs séries
(?????? - ??????) sont calculés en utilisant l'équation (3.
1).
?? ?? ?????????? = = ' ?????? (3. 1)
?????????? ??????
- ??1' : représente la
fréquence de coupure du prototype passe-bas normalisé ; cette
dernière est égale à 1.
- ???? : pulsation associée à la fréquence
du zéro.
Finalement, Les valeurs des résonateurs série
(????1 - ????1) et (????2 - ????2) sont données par les
équations (3. 2) et (3. 3).
|
??.??????
=
|
(3. 2)
??????.????.??
|
????
|
??.??????
=
|
(3. 3)
|
|
??????
??
??
{
=
|
??????
??
??
{
=
|
|
??????
|
??????
??????.????.??
|
3.2.3.2 Implémentation des inverseurs d'admittance
a. Solution 1 : Structure en pi avec des inductances
On utilise le circuit équivalent de l'inverseur
d'admittance de la Figure 2. 19 et on aboutit au circuit de la
Figure 3. 8.
55
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
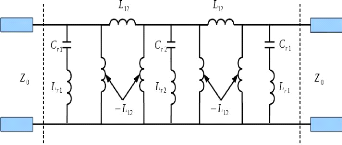
Figure 3. 8: Filtre coupe-bande d'ordre 3
constitué de résonateurs séries et de deux structures en
pi avec des selfs
b. Solution 2 : Structure en pi avec des capacités
On remplace les inverseurs d'admittance par la structure en pi
avec capacités de la Figure 2. 22. Et on obtient le circuit de
la
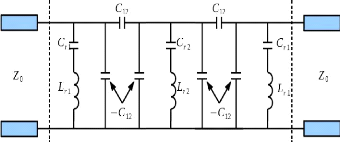
Figure 3. 9: Filtre coupe-bande d'ordre 3
constitué de résonateurs séries et de deux structures en
pi avec capas
A ce niveau, il nous est impossible d'intégrer les
inductances ou capacités négatives parallèles aux
résonateurs séries.
3.2.3.3 Equivalence de la structure en T centrale avec la ligne
(2h ; Zc)
On montre que la structure en T centrale des figures obtenue
après implémentation des inverseurs d'admittances est
équivalente à la ligne de longueurs 2h et d'impédance
caractéristique Zc à la condition que la relation (2.
13) soit vérifiée.
a. Solution 1 : Structure en pi avec des inductances
On aboutit au circuit illustré sur la Figure 3.
10. Ce dernier est composé de deux résonateurs
d'entrée/sortie identiques séparés par une ligne de
longueur 2h et d'impédance caractéristique Zc. Les
résonateurs d'entrée/sortie sont constitués de la mise en
parallèle d'un résonateur série (Lr1 - Cr1) avec une
inductance négative -L12.
b. Solution 2 : Structure en pi avec des capacités
Dans ce cas, le quadripôle équivalent
synthétisé est le même à la différence que
les résonateurs d'entrée/sortie sont ici composés par la
mise en parallèle d'un résonateur série (Lr1 - Cr1) avec
une capacité négative -C12 (cf. Figure 3. 11).
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
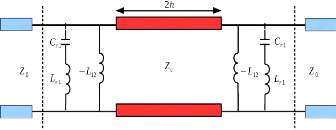
Figure 3. 10: Quadripôle équivalent
obtenue avec la solution 1
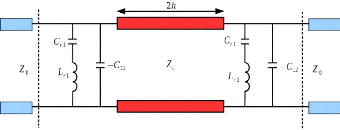
Figure 3. 11: Quadripôle équivalent
obtenu avec la solution 2
A l'issue de cette synthèse, les quadripôles
équivalents obtenus avec les deux solutions sont différents du
quadripôle souhaité de la Figure 3. 2.
Dans la prochaine étape, nous essayerons de simplifier ces
circuits et ainsi déterminer les composants (??1"
- ??1") du quadripôle équivalent final.
3.2.3.4 Détermination des éléments des
circuits
a. Solution 1 : Structure en pi avec des inductances
??12 = ????0??12
D'après la Figure 3. 8,
{2????2????2)
??2 " = ?? ??12??0(??0
2+??0 2????2(??12-2????2)
Avec la première équation du système
ci-dessus et celle du système (2. 13) on trouve que :
?????? = ??????????
????
= ?????? (?? ??) (3. 4)
????
??
56
1
A partir de la seconde et sachant que ????2????2 = 2 , on trouve
les valeurs de ????2 ???? ????2
????
|
?????? = (?? - ???? ??) [??????(??????)
?? ???????? - ??
???? ????????]
????
{
?????? = ??
???? ????????
|
(3. 5)
|
En remontant les équations, on trouve ????2 à
partir de la relation (3. 3), puis ????1 avec l'équation (2. 3) et enfin
????1 ???? ????1 peuvent être obtenus en appliquant la relation (3.
2).
Mais un problème important se pose dans la
réalisation de ces cellules, car nous ne savons pas encore faire des
inductances négatives.
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
Pour des phases à ??0, ??11(??0) ?
[90°;180°], ??12 est de l'ordre de 10-8. Cette
valeur est obtenue avec l'équation (3. 6). De ce fait, nous ne pouvons
pas négliger son impact dans le circuit ni l'associer aux autres
éléments puisqu'elle est montée en parallèle. Donc
nous utiliserons la solution 2 pour synthétiser des phases à ??0,
??11(??0) ? [90°;180°] même si, a priori les résultats
obtenus avec la solution 1 seraient meilleurs comme dans le cas passe-bande.
b. Solution 2 : Structure en pi avec des capacités
??12 = 1/????0??12
D'après la Figure 3. 9, {1-??0
2????2????2
??2 " = ????0[????2-2??12+2????2????2??12??0 2]
|
De la même manière on trouve :
?????? = ?????? ????
Ensuite :
|
-??
=
??????????????(????) (3. 6)
|
(3. 7)
????1 ???? ????1 peuvent ainsi être déterminer avec
la relation (3. 2).
?????? = (?? - ???? ??) [??????(??????)
??
???????? - ????????]
????
{ ??
??????= ???? ????????
57
Pour des phases ??11(f0) ? [-180°; -90°]
??12 est de l'ordre de 10-15 (3.8), son impédance
??12 sera de l'ordre de 104 qui est très grand. Donc ??12
sera vue comme un circuit ouvert dans le circuit. Le quadripôle de la
Figure 3. 11 peut dès lors être simplifier pour obtenir
le quadripôle équivalent de la Figure 3. 2.
Avec : {???? " = ?????? (3. 8)
???? " = ??????
3.3 Résultats de la synthèse
Dans cette partie nous allons déterminer la
précision de la méthode de synthèse
développée précédemment. Nous allons
considérer deux familles de spécifications sur la loi de phase.
Dans la première famille, la phase à ??0, ??11(??0) est positive
et varie de 0° à 180° avec une dispersion
???11(??0) = 30°/?????? alors que dans la
deuxième famille, elle est négative et varie de 0° à
- 180° avec la même dispersion. Nous ne présenterons ici que
les résultats obtenus avec la solution 2.
3.3.1 Première famille de spécification : ??11(??0)
> 0°
Les résultats de la synthèse pour ??11(??0) =
100° et ??11(??0) = 120° avec une dispersion constante égale
à ???11 = 30°/?????? sont présentés à travers
la Figure 3. 12. Le Tableau 3. 3 donne les erreurs moyennes
et maximales des différentes cellules synthétisées pour
des phases à ??0, ??11(??0) > 0°.
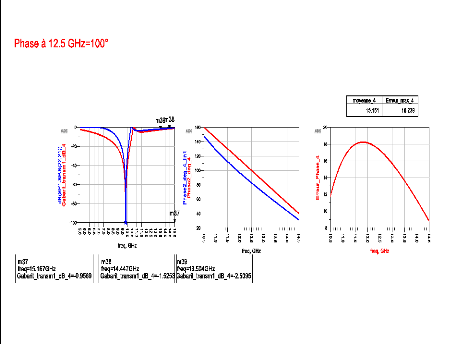
(a)
58
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
(a)
(b)
|
??11(??0) (°)
|
0
|
20
|
40
|
60
|
80
|
90
|
|
????????(°)
|
173,318
|
17,067
|
26,621
|
35,877
|
34,272
|
27,026
|
|
???????? (°)
|
202,603
|
40,765
|
51,186
|
54,872
|
42,287
|
31,716
|
|
??11(??0) (°)
|
100
|
120
|
140
|
160
|
180
|
|
???????? (°)
|
15,151
|
14,305
|
29,797
|
31,117
|
30,007
|
|
???????? (°)
|
18,239
|
30,036
|
69,102
|
74,903
|
60,000
|
Tableau 3. 3: Erreurs moyenne et maximale solution
2. (a) ??????(????) ?????????? ???? ??° à????°.
(b)
??????(????) ?????????? ???? ????° à ??????°
???????? ???????(????)=-30°/GHz
59
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
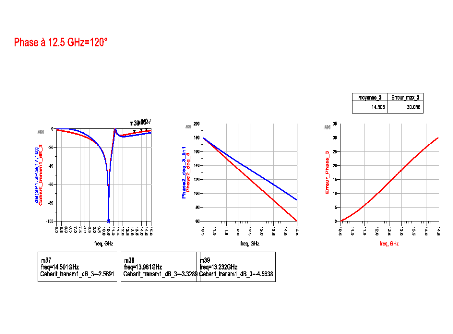
(b)
Figure 3. 12: Résultats de la
synthèse coupe-bande solution 2. (a) ?_11 (f0 )=100°. (b) ?_11 (f0
)=120°
La Figure 3. 13 présente l'erreur moyenne
réalisée par la synthèse coupe-bande pour la
première famille de spécification. Nous pouvons voir sur celle-ci
que la synthèse est plus adaptée à des phases
supérieures à 90° ce qui s'explique par la
complémentarité des deux structures (cellule Phoenix inductive et
capacitive).
Mais le résultat obtenu pour des phases à
f0, 411(f0) supérieures à 120° devraient
être meilleurs. En effet, c'est à partir de cette valeur que le
zéro de transmission rentre dans la bande d'intérêt
[10,5-14,5] GHz (section 2.2.2.3).
60
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
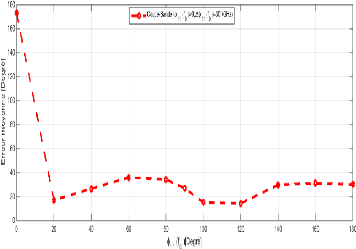
Figure 3. 13: Erreur moyenne Solution 2 coupe-bande
?????? (????) > ??°
3.3.2 Deuxième famille de spécification :
??11(f0) < 0°
Cette fois-ci, la phase à f0,
??11(f0) varie de 0° à -180°
par pas de 20° avec la même dispersion ???11 =
-30°/GHz. Sur la Figure 3. 14 sont
représentés les résultats de la synthèse pour une
??11(f0) = -100° (Figure 3. 14(a)) et
??11(f0) = -120° (Figure 3. 14(b)).
Les erreurs maximale et moyenne obtenues pour cette famille de
spécification sont répertoriées dans le Tableau 3.
4.
|
??11(f) (°)
|
0
|
-20
|
-40
|
-60
|
-80
|
-90
|
|
Env??y(°)
|
169,548
|
66,497
|
20,855
|
28,252
|
23,439
|
16,193
|
|
Env???? (°)
|
196,051
|
85,332
|
40,851
|
46,540
|
26,440
|
17,716
|
(a)
??11(f) (°)
|
-100
|
-120
|
-140
|
-160
|
-180
|
Env??y (°)
|
5,599
|
17,960
|
30,251
|
31,145
|
30,007
|
Env???? (°)
|
6,650
|
28,892
|
67,037
|
74,347
|
60,000
|
|
(b)
Tableau 3. 4: Erreurs moyenne et maximale solution 2.
(a) ??????(????) v??rie de ??° à - 9??°. (b)
??????(????) v??rie de - 9??° à - ??????° ??vec
???????(????)=-30°/GHz
61
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
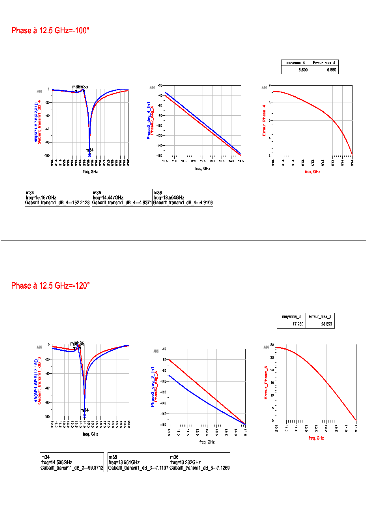
(a)
(c)
Figure 3. 14: : Résultats de la
synthèse coupe-bande solution 2. (a) q5_11 (f0 )=-100°. (b) q5_11
(f0 )=-120°
62
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
La courbe des erreurs moyennes en fonction de la phase à
??0, ??11(??0) est représentée sur la Figure 3. 15.
Cette courbe a le même comportement que celle obtenue pour des phases
à ??0 positives (cf. Figure 3. 13).
3.3.3 Bilan sur la précision de la procédure de
synthèse passe-bande
(180°; -30°/??????).
La Figure 3. 16 présente l'évolution de
l'erreur moyenne en fonction de la phase à ??0, ??11(??0)
pour une dispersion fréquentielle constante ???11 = -30°/??????.
Nous remarquons que pour des valeurs ?11(f0) comprises entre
]-100° ; -180° ]et]100° ; 180°], l'erreur augmente. Bien
que ces zones soient idéales, dans le sens où les zéros de
transmissions haute et basse rentrent dans la zone d'intérêt,
l'erreur moyenne atteint une valeur maximale de 30,007° pour (??11(??0);
???11) =
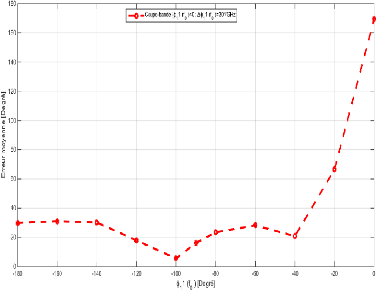
Figure 3. 15: Erreur moyenne Solution 2 coupe-bande
?_11 (f_0 )<0°
63
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
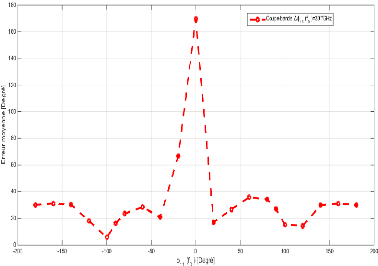
Figure 3. 16: Bilan sur les performances de la
procédure de synthèse de type coupe-bande
3.4 Conclusion
Dans ce dernier chapitre, nous avons présenté
une méthode de synthèse de la cellule Phoenix capacitive d'ordre
2 en utilisant les techniques de filtrage. Lors de cette synthèse, nous
avons distingué deux solutions : la solution 1, obtenue en
remplaçant les inverseurs d'admittances par une structure en pi avec des
inductances et la solution 2, obtenue par utilisation d'une structure en pi
avec des capacités. Mais, seule la solution 2 a été
exploitée à cause de la difficulté rencontrée avec
la solution 1 à introduire les inductances parallèles
négatives dans les résonateurs série.
Dans le but de tester la précision de la
synthèse, nous avons considéré deux familles de
spécifications sur la loi de phase à synthétiser. Les
résultats obtenus montrent que la synthèse coupe-bande est
adaptée à des phases à f0,
??11(f0) E [_90°; _180°] et
[90°; 180°] mais méritent d'être
améliorés.
Conclusion générale
L'objectif de ce stage était de tester une nouvelle
méthode de synthèse des cellules unitaires des réseaux
réflecteurs basée sur les techniques de synthèse de
filtres et permettant de résoudre un certain nombre de problèmes
décelés dans la première méthode proposée
par A. Grossetête [2]. Ces problèmes concernaient principalement
la difficulté à prendre en compte correctement la ligne centrale.
En effet, dans sa procédure, le résonateur central (L-C
parallèle ou série) était directement remplacé par
la même ligne de longueur 2h et d'impédance caractéristique
Zc. Ce qui faisait qu'on se retrouvait face à un
paradoxe.
La philosophie et le cheminement des différentes
étapes de la synthèse sont retracés au travers des
différents chapitres. Le premier chapitre fait l'état de l'art
sur le fonctionnement global des antennes réseaux réflecteurs qui
bénéficient des atouts des réflecteurs classiques et ceux
des antennes réseaux. L'utilisation de RA dans le spatial permet de
réduire le coût de fabrication. Ces antennes offrent
également un fort panel de possibilité pour améliorer les
performances globales des systèmes antennaires. La conception de RA
passe par la caractérisation de cellules à l'aide de base de
données ou de modèles comportementaux. Le point clé est
régi par la synthèse, c'est-à-dire la sélection
judicieuse des cellules unitaires constituant le réseau
réflecteur. A ce titre, des méthodes de synthèse des RA
tirées de la littérature sont listées en analysant les
avantages et les inconvénients de chacune d'entre elles. Une autre
contrainte majeure de la synthèse est de maintenir une variation
géométrique continue et régulière sur l'ensemble du
panneau pour garantir l'hypothèse de quasi-périodicité des
cellules. Pour ce faire, nous avons porté notre choix sur la cellule
Phoenix qui permet d'obtenir une gamme de phase de 360° sur une large
bande passante tout en garantissant une variation douce de la
géométrie du motif. Dans les deux derniers chapitres, nous avons
développé une méthodologie de synthèse des
composants du circuit équivalent de la cellule unitaire Phoenix d'ordre
2 inductive et capacitive basée sur les techniques de synthèse de
filtres. Pour ce faire, nous avons utilisé respectivement un filtre
passe-bande et coupe-bande du troisième ordre de Tchebychev. En
procédant par étape, nous avons réussi à prendre en
compte correctement la ligne centrale et à synthétiser les
résonateurs d'entrées et de sorties dans le cas d'une
synthèse passe-bande et celle coupe-bande. Cependant, les
résultats obtenus à l'issu de cette procédure ne sont pas
aussi satisfaisants et méritent d'être améliorés
pour pouvoir synthétiser la totalité du réseau
réflecteur. A l'issu de ces travaux, nous proposons les perspectives
à court et long terme suivantes. A court terme, nous proposons
d'optimiser la méthode de synthèse pour la rendre plus
performante. A cet effet, nous avons détecté certaines pistes qui
n'ont pas été exploité par contrainte de temps.
L'idée serait de modifier les paramètres relevés sur le
gabarit en transmission. L'ondulation est prise cette fois-ci comme
étant la moyenne des deux ondulations (maximale et minimale) avec
éventuellement une pondération, la hauteur de la cavité
est calculée à une fréquence hors de la bande
d'intérêt (fca = 15GHz par exemple) et les
fréquences de coupures (f1 ou f2) sont
déterminées à l'ondulation maximale. Les résultats
de quelques testes dans le cas d'une synthèse passe-bande vous sont
présentés en Annexe 3. Comme perspective à long terme,
nous proposons d'introduire les zéros de transmissions qui pourraient
améliorer les performances de la synthèse. A plus long terme,
nous proposons d'utiliser les fonctions de Zolotarev qui permettrait, a priori,
de mieux gérer l'ondulation variable dans la bande passante. Ceci reste
cependant à vérifier en mettant en oeuvre cette approximation.
Pour finir, ce stage a été d'un grand apport
tant sur le plan éducatif, professionnel que sur le plan social. Il m'a
permis de développer mes connaissances et compétences dans le
domaine des antennes réseaux réflecteurs et du filtrage. Ce stage
m'a également permis de découvrir le domaine de la recherche et
de me familiariser avec l'outil de conception et de simulation ADS (Advanced
Design System).
Figure A1. 1: Résultats de la synthèse
avec la solution 1 pour ?????? (????) = ????° et
???????(????) = -????°/?????? (a) ondulation
maximale. (b) ondulation moyenne
Annexes
Annexe1 : Résultats de la synthèse passe-bande
obtenus avec l'ondulation maximale ou la moyenne des deux ondulations.
A1.1 Résultats obtenus avec la solution 1 pour une phase
à ??0, ?11(f0) = 20° et
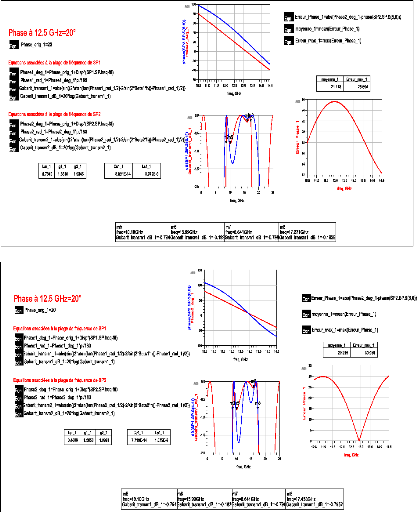
(a)
(c)
??11(f0) = -30°/GHz
66
Annexes
A1.2 Résultats obtenus avec la solution 2 pour une phase
à ??0, ?11(f0) = -20° et
??11(f0) = -30°/GHz
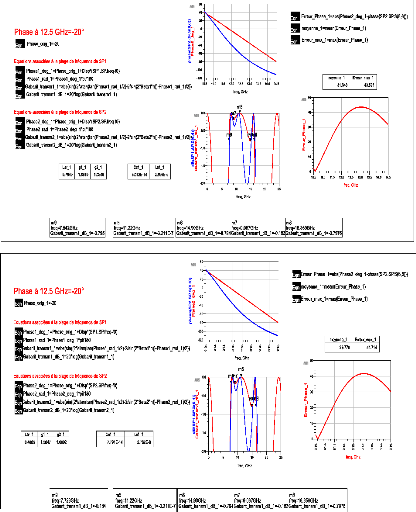
(b)
(a)
Figure A1. 2: Résultats de la synthèse
avec la solution 2 pour ??????(????) = -????° et
???????(????) = -????°/?????? (a)
ondulation
maximale. (b) ondulation moyenne
67
Annexes
Annexe 2 : Résultats de la synthèse passe-bande
solution 1 phases négatives et solution 2 phases positives
A2.1 Résultats obtenus avec la solution 1 pour une phase
à ??0, ?11(f0) = 0° ???? - 40° et
??11(f0) = -30°/GHz
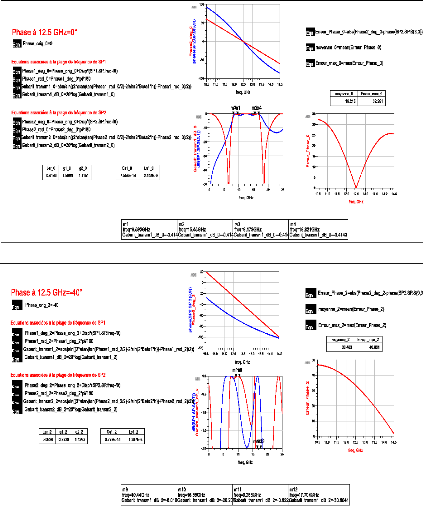
(a)
(b)
Figure A2. 1: Résultats de la
synthèse solution 1 (a) ??????(????) =
??°. (b) ??????(????) = -????° ????????
???????(????) = -????°/??????
68
Annexes
A2.2 Résultats obtenus avec la solution 2 pour une phase
à ??0, ?11(f0) = 0° ???? 40° et
??11(f0) = -30°/GHz
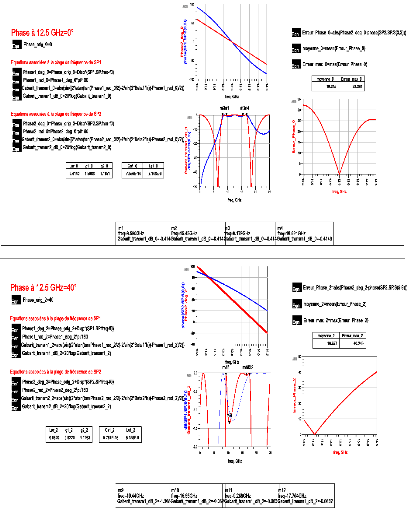
(a)
(c)
Figure A2. 2: Résultats de la
synthèse solution 2 (a) ??????(????) =
??°. (b) ??????(????) = ????° ????????
???????(????) = -????°/??????
69
Annexes
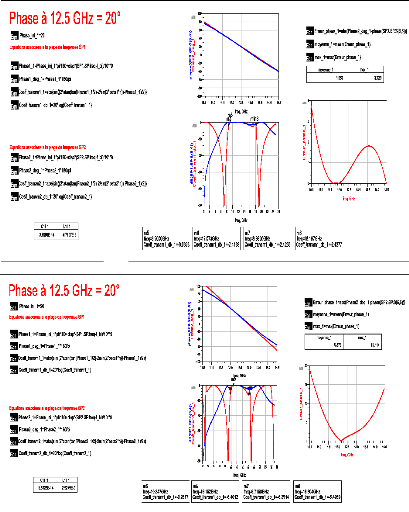
(b)
(a)
Annexe 3 : Résultats de la synthèse passe-bande h =
A/4 à ???????? = 15??????.
70
Annexes
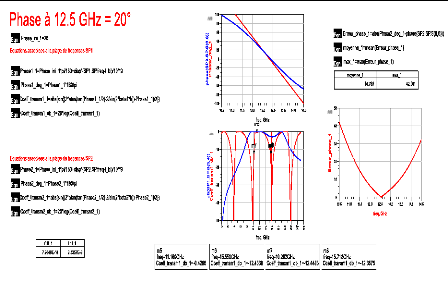
(c)
Figure A3. 1: Résultats de la
synthèse passe-bande ??????(????) =
????°. (a) ???????(????) =
-????°/??????. (b) ???????(????) =
-????°/??????. (c) ???????(????)
= -????°/??????.
|
???11(?? - ??0) (°/GHz)
|
??11(??0) (°)
|
???????? (°)
|
???????? (°)
|
|
-30
|
20
|
1,059
|
3,723
|
|
-45
|
20
|
5,876
|
19,114
|
|
-60
|
20
|
14,793
|
42,061
|
Tableau A3. 1: Erreurs moyenne et maximale h
à 15GHz avec ?????? (?? ??) = ????° pour
chaque dispersion
Liste des figures Corps du rapport
Figure 1. 1: : Schéma de principe d'une antenne
à réseau réflecteur avec une source primaire (a)
centrée. (b) décentrée 9
Figure 1. 2: Schéma du RA déployable avec une
grande ouverture rayonnante 10
Figure 1. 3 : Rayonnement dans l'axe du réseau (a) et
rayonnement avec dépointage (b) d'une
antenne à réseau réflecteur 11
Figure
1. 4: Vues satellitaires de deux diagrammes de rayonnements à lobes
formés pour assurer une
couverture donnée 11
Figure 1. 5: Réponse en phase (a) et réponse
fréquentiellle (b) d'une cellule déphaseuse 12
Figure 1. 6: Réponse fréquentielle et
dispersion associée 12
Figure 1. 7: Bande passante d'une cellule déphaseuse.
13
Figure 1. 8: Première antenne réseau
réflecteur à base de guides d'ondes métalliques 13
Figure 1. 9: Cellule patch microruban avec ligne à
retard 14
Figure 1. 10: Cellule patchs à dimensions variables
14
Figure 1. 11: Cellule à deux couches à base de
patchs de tailles différentes 15
Figure 1. 12: Cellule à une seule couche basée
sur l'association de deux résonateurs 15
Figure 1. 13: Augmentation de la taille de la fente annulaire
(a) entraine un décalage de la fréquence
de résonance vers les basses fréquences (b)
16
Figure 1. 14: Différentes configuration de cellules à une
ou deux fentes (a) et réponses en phase
associées (b) 17
Figure 1. 15: Evolution cyclique de la cellule Phoenix
17
Figure 1. 16: Six géométries différentes
réparties dans deux familles. 17
Figure 1. 17: Circuits équivalents associés aux
six géométries de la cellule Phoenix 18
Figure 1. 18: Méthodologie générale de
la synthèse d'un réseau réflecteur 18
Figure 1. 19: Utilisation d'un ANN pour la
génération de la base de données 20
Figure 1. 20 : Modélisation de la cellule Phoenix
d'ordre 2 par CE (a)Capacitive. (b) inductive 21
Figure 1. 21: Schéma électrique
équivalent des cellules Phoenix d'ordre 2. (a) capacitive.
(b)inductive. 21
Figure 2. 1: Dipôle équivalent d'une cellule
unitaire Phoenix monocouche de réseau réflecteur. 23
Figure 2. 2: Quadripôle équivalent
constitué de deux cellules unitaires montées
tête-bêche 23
Figure 2. 3: Quadripôle équivalent 23
Figure 2. 4: loi de phase 24
Figure 2. 5: Caractéristiques du gabarit en
transmission. (a) Zéros de transmission. (b) pôle à f0
25
Figure 2. 6: Evolution du gabarit pour une variation positive
de 0_11 (f_0) à dispersion constante 25
Figure 2. 7: Evolution du gabarit pour une variation
négative de 0_11 (f_0) à dispersion constante 26
Figure 2. 8: Evolution du gabarit pour une variation de la
dispersion pour 0_11 ((f_0) =0° 27
Figure 2. 9:Motif d'une cellule inductive de type Phoenix
d'ordre 2 : la fente annulaire 27
Figure 2. 10: Quadripôle équivalent du motif
inductif Phoenix d'ordre 2 28
Figure 2. 11: Prototype d'un filtre passe-bande d'ordre n=3
28
Figure 2. 12 : Exemples de lois de phase à
synthétiser dans la bande d'intérêt [10,5- 14, 5] GHz.
(a)
4)11(f0) = 20°. (b) 4)11(f0) = -20°. 29
Figure
2. 13: Gabarits en transmission associés aux lois sur la phase en
réflexion de la Figure 2. 12. .
(a) 4)11(f0) = 20°. (b) 4)11(f0) = -20°. 30
72
Liste des figures
Figure 2. 14: Prototype du filtre passe-bas
normalisé d'ordre n=3 31
Figure 2. 15: Filtre passe-bas
dénormalisé 32
Figure 2. 16: Filtre passe-bas avec inverseurs
d'admittances idéaux 32
Figure 2. 17: Opération de transformation d'un
filtre passe-bas en un filtre passe-bande 32
Figure 2. 18: Filtre passe-bande avec inverseurs
d'admittance idéaux 33
Figure 2. 19 : Circuit équivalent d'un inverseur
d'admittance constituée d'une structure en pi avec des
inductances 33
Figure 2. 20: Filtre
passe-bande d'ordre 3 constitué de résonateurs parallèles
et de deux structures en
pi avec des selfs 34
Figure 2. 21: Filtre
passe-bande constitué de 3 résonateurs parallèles
séparés par deux inductances34 Figure 2. 22: Circuit
équivalent d'un inverseur d'admittance constituée d'une structure
en pi avec des
capacités 34
Figure 2. 23: Filtre
passe-bande d'ordre 3 constitué de résonateurs parallèles
et de deux structures en
pi avec des capacités 35
Figure 2. 24: Filtre passe-bande constitué de 3
résonateurs parallèles séparés par deux
capacités 35
Figure 2. 25: Equivalence entre la structure en T centrale
et la ligne (2h, Zc) 35
Figure 2. 26: Résultats de la synthèse
passe-bande solution 1. (a) ???????? ?? = ??°. (b) ?????? ??
?? = ????° 39 Figure 2. 27: Résultats de la synthèse
passe-bande solution 1. (a) ???????? ?? = ??????°. (b)
???????? ?? =
??????° 40
Figure 2. 28: Erreur moyenne solution 1
lorsque ?????? ?? ?? ?????????? ???? ??° à ??????°
???????? ???????????=-
30°/GHz 41
Figure 2. 29: Résultats
de la synthèse passe-bande solution 1. (a) ??????? ??
??=-30°/GHz. (b)
??????? ?? ??=-45°/GHz. (c)
???????????=-60°/GHz 43
Figure 2. 30:
Résultats de la synthèse passe-bande solution 2. (a)
???????? ?? = ??°. (b) ?????? ?? ?? = -????°
45
Figure 2. 31: Résultats de la
synthèse passe-bande solution 1. (a) ???????? ?? =
-??????°. (b) ?????? ?? ?? =
-??????° 46
Figure 2. 32: Erreur moyenne solution
2 lorsque ?????? ?? ?? ?????????? ???? ??° à - ??????°
???????? ???????????=-
30°/GHz 47
Figure 2. 33: Résultats
de la synthèse passe-bande solution 2. (a) ???????????=
-30°/GHz. (b)
??????? ?? ??=-45°/GHz. (c)
???????????=-60°/GHz 49
Figure 2. 34: Bilan sur les performances de la
procédure de synthèse de type passe-bande 50
Figure 3. 1: Motif capacitif d'une cellule Phoenix d'ordre
2 51
Figure 3. 2: Quadripôle équivalent 51
Figure 3. 3: Prototype de filtre coupe-bande 52
Figure 3. 4: Lois de phase à synthétiser
dans la bande d'intérêt [10,5- 14, 5] GHz. (a) ?11(f0) =
160°.
(b) ?11(f0) = -160° 52
Figure 3. 5:
Gabarits en transmission associés aux lois sur la phase en
réflexion (a) ?11(f0) = 160°.
(b) ?11(f0) = -160°. 53
Figure 3. 6: Opération de transformation d'un
filtre passe-bas en un filtre coupe-bande. 54
Figure 3. 7: Filtre coupe-bande avec inverseurs
d'admittances 54
Figure 3. 8: Filtre coupe-bande d'ordre 3 constitué
de résonateurs séries et de deux structures en pi
avec des selfs 55
Figure 3. 9: Filtre
coupe-bande d'ordre 3 constitué de résonateurs séries et
de deux structures en pi
avec capas 55
Liste des figures
73
Figure 3. 10: Quadripôle équivalent obtenue
avec la solution 1 56
Figure 3. 11: Quadripôle équivalent obtenu
avec la solution 2 56
Figure 3. 12: Résultats de la synthèse
coupe-bande solution 2. (a) 0_11 (f0 )=100°. (b) 0_11 (f0
)=120° 59
Figure 3. 13: Erreur moyenne Solution 2 coupe-bande
011f 0 > 0° 60
Figure 3. 14: : Résultats de la synthèse
coupe-bande solution 2. (a) 0_11 (f0 )=-100°. (b) 0_11 (f0 )=-
120° 61
Figure 3. 15: Erreur moyenne Solution 2 coupe-bande 0_11
(f_0 )<0° 62
Figure 3. 16: Bilan sur les performances de la
procédure de synthèse de type coupe-bande
63
Annexes
Figure A1. 1: Résultats de la synthèse avec
la solution 1 pour 011f 0 = 20° et .6,011 f 0
=
- 30°/GHz (a) ondulation
maximale. (b) ondulation moyenne 65
Figure A1. 2:
Résultats de la synthèse avec la solution 2 pour 011f 0 =
-20° et .6,011 f 0 =
- 30°/GHz (a) ondulation
maximale. (b) ondulation moyenne 66
Figure A2. 1: Résultats de la synthèse
solution 1 (a) 011f 0 = 0°. (b) 011 f 0 =
-40°
avec .6,011f0 = -30°/GHz
67
Figure A2. 2: Résultats de la synthèse
solution 2 (a) 011f 0 = 0°. (b) 011 f 0 =
40°
avec .6,011f0 = -30°/GHz 68
Figure A3. 1: Résultats de la synthèse
passe-bande 011f0 = 20°. (a) .6,011f0 =
-30°/GHz. (b)
.6,011f0 = -45°/GHz. (c)
.6,011 f 0 = -60°/GHz . 70
Liste des tableaux
Tableau 2. 1: Valeurs des paramètres du gabarit
à synthétiser 30
Tableau 2. 2: Valeurs des paramètres de la
réponse du prototype passe-bande 31
Tableau 2. 3 : Erreurs moyenne et maximale solution 1. (a)
011 f 0 varie de 0° à 90°. (b)
011f 0 varie de 90° à 180° avec
.6,011f0=-30°/GHz
38
Tableau 2. 4: Erreurs moyenne et maximale
solution 1 lorsque 011 f 0 varie de 0° à -
90°
avec
.6,011f0=-30°/GHz
41
Tableau 2. 5: Erreurs moyenne et maximale solution 1 avec
011f0 = 20° pour chaque dispersion 42
Tableau 2. 6: Erreurs moyenne et maximale solution 2 lorsque
011 f0 varie de 0° à 90
avec
.6,011f0=-30°/GHz
44
Tableau 2. 7 : Erreurs moyenne et maximale solution 2. (a)
011f0 varie de 0° à - 90°. (b)
011f 0 varie de - 90° à - 180°
avec .6,011f0=-30°/GHz
44
Tableau 2. 8: Erreurs moyenne et maximale
solution 1 avec 011f0 = -20° pour chaque
dispersion
47
Tableau 3. 1: Valeurs des paramètres du gabarit
à synthétiser 53
Tableau 3. 2: Valeurs des paramètres de la
réponse du filtre coupe-bande 53
Tableau 3. 3: Erreurs moyenne et maximale solution 2. (a)
011 f 0 varie de 0° à90°. (b)
011f 0 varie de 90° à 180° avec
.6,011f0=-30°/GHz
58
Tableau 3. 4: Erreurs moyenne et maximale
solution 2. (a) 011 f 0 varie de 0° à - 90°.
(b)
011f 0 varie de - 90° à - 180°
avec .6,011f0=-30°/GHz 60
74
Bibliographie
[1] V. Richard, «Outils de synthèse pour les
réseaux réflecteurs exploitant la cellule Phoenix et les
réseaux de neurones,» 2018.
[2] A. Grossetête, «« Synthèse analytique
de panneaux réflecteurs imprimés - Utilisation de circuits
équivalents et de techniques de synthèse de filtres,» 19
Juin 2018.
[3] A. Z. Elsherbeni, P. Nayerie et F. Yang, «Reflectarray
antennas for space applications,» chez 2012 IEEE International
Conference on Ultra-Wideband, Sept 2012.
[4] J. Huang et J. A. Encinar, Reflectarray antennas, Wiley,
2007.
[5] M. D. Levenson, N. S. Viswanathan et R. A. Simpson,
«Improving resolution in photolithographie whith a phase-shifting
mask,» IEEE Transaction on Electron Devices, vol. 29, n°
%112, pp. 1828-1836, December 1982.
[6] R. E. Hodges, N. Chahat, D. J. Hoppe et J. D. Vacchione,
«A deployable high-gain antenna bound for mars : Developing a new
foldedpanel reflectarray for the first cubesat mission to mars,» IEEE
Antennas Propagation Magazine, vol. 59, n° %12, pp. 39-49, April
2017.
[7] S. Clack, «SPACEFLIGHT NOW,» 29 March 2019. [En
ligne]. Available:
https://spaceflightnow.com/2019/03/29/rocket-lab-launches-darpa-research-satellite/.
[Accès le 13 September 2019].
[8] J. Huang, «The development of inflatable array
antennas,» IEEE Antennas and Propagation Magazine, vol. 43,
n° %14, pp. 44-50, August 2001.
[9] H. Fang, M. Lou, J. Huang, L. M. Hsia, U. Quijano, G. Paleaz
et V. Svolopoulos, «Development of a 7-meter inflatable reflectarray
antenna.,» Pasadena, CA : Jet Propulsion Laboratory, National Aeronautics
and Space Administration, 2004.
[10] D. M. Pozar, S. D. Targonski et R. Pokuls, «A
Shaped-Beam Microstrip Patch Reflectarray,» IEEE Transactions on
Antennas and Propagation, vol. 47, pp. 1167-1173, July 1999.
[11] D. C. Berry, R. G. Malech et W. A. Kennedy, «The
Reflectarray Antenna,» IEEE Transactions on Antennas and
Propagation, Vols. %1 sur %2AP-11, pp. 645-651, November 1963.
[12] A. V. Chenakin, A. E. Martynyuk et V. I. Skachko, «A
new hybrid technology for millimeterwave integrated circuits,» chez
IEEE MTT-S International Microwave Symposium Digest, June 1997.
[13] R. Munson, «Conformal Microstrip Antennas and
Microstrip Phased Arrays,» IEEE Transactions on Antennas and
Propagation, vol. 22, n° %11, pp. 74-78, January 1974.
[14] D. M. Pozar et T. A. Metzler, «"Analysis of a
reflectarray using microstrip patches of variable size",» Electronics
Letters, vol. 29, n° %18, pp. 657-658, April 1993.
[15] J. A. Encinar, «Design of two-layor printed
reflectarrays using patches of a variable size,» IEEE Transactions on
Antennnas and Propagation, vol. 49, n° %110, pp. 1403-1410, October
2001.
[16] M. R. Chaharmir , J. Shaker, M. Cuhaci et A. Ittipiboon,
«Broadband reflectarray antenna with double cross loops,»
Electronics Letters, pp. 65-66, January 2006.
[17] L. Moustapha, R. Gillard, F. Peris, R. Loison, H. Legay et
E. Girard, «The Phoenix Cell: A New Reflectarray Cell with Large Bandwidth
and Rebirth Capabilities,» IEEE Antenna and Wireless Propagation
Letters, vol. 10, pp. 71-74, 2011.
[18] M. Kharbech, «Cellules à fentes pour
réseaux réflecteurs imprimés-Amélioration de la
stabilité du diagramme unitaire et extension à la
reconfigurabilité,» Octobre 2011.
75
Bibliographie
[19] D. M. Pozar, «Bandwidth of reflectarrays,»
Electronics Letters, vol. 39, n° %121, pp. 14901491, October
2003.
[20] M.-A. Milon, R. Gillard et H. Legay, «Rigorious
analysis of the reflectarray radiating elements: Charasterization of the
specular reflection effect and the mutual coupling effect,» chez 29th
ESA workshop on Multiple Beam and Reconfigurable Antennas, Netherlands,
April 18-20, 2007.
[21] M. L. Stein, «Interpolation of spatial data : some
theory for kriging,» Springer Science & Business Media,
2012.
[22] L. Tenuti, G. Oliveri, D. Bresciani et A. Massa,
«Avanced learning based approaches for reflectarrays design,»
chez 2017 11th European Conference on Antennas and Propagation
(EUCAP), March 2017.
[23] A. Freni, M. Musetta et P. Pirinoli, «Neural network
characterization of reflectarray antennas,» International Journal of
Antennas and Propagation, vol. 2012, 2012.
[24] O. Luukkonen, C. Simovski, G. Granet, D. Lioubtchenko, A.
Räisänen et S. Tretyakov, «Simple and accurate analytical model
of planar grids and hight impedance surfaces comprising metal strips or
patches,» IEEE Transaction on Antennas and Propagation, 2008.
[25] N. Nachabe, «Antenne reflectarray pour applications
spatiales,» 2015.
[26] A. Grossetete, E. Fourn et R. Gillard, «Single-layer
reflectarray cell synthesis based on filter synthesis techniques,»
chez 2016 Loughborough Antennas Propagation Conference (LAPC),
2016.
[27] R. J. Langley et E. A. Parker, «Equivalent circuit
model for arrays of square loops,» Electronics Letters, vol. 18,
n° %17, pp. 294-296, April 1982.
[28] G. Matthaei , L. Young et E. M. T. Jones, Microwave
filters, impedance-matching networks, and coupling structures, Norwood, MA:
Artech House, 1980.
| 


