III.2.CALCUL DU COEFFICIENT
DE CORRELATION SIMPLE
Avant de faire le calcul du coefficient de corrélation
simple, nous avons déterminé les variables dépendante ou
exogène et indépendante ou endogène. Nous avons
constaté que les offres d'emploi expliquent les demandes d'emploi. Pour
nos calculs, les offres d'emploi représentant la variable X (variable
explicative ou indépendante) tandis que les demandes d'emploi
représentent la variable Y (variable expliquée ou
dépendante).
Tableau N°3 : Procédure de calcul du
coefficient de corrélation
|
N°
|
X
|
Y
|
|
|
|
|
|
|
1
|
17
|
318
|
-31.3
|
-10.8
|
979.69
|
116.64
|
338.04
|
|
2
|
18
|
548
|
-30.3
|
219.19
|
918.09
|
48044.2561
|
-6641.457
|
|
3
|
16
|
334
|
-32.3
|
5.19
|
1043.29
|
26.9361
|
-167.637
|
|
4
|
8
|
203
|
-40.3
|
-125.8
|
1624.09
|
15825.64
|
5069.74
|
|
5
|
21
|
221
|
-27.3
|
-107.8
|
745.29
|
11620.84
|
2942.94
|
|
6
|
11
|
156
|
-37.3
|
-172.8
|
1391.29
|
29859.84
|
6445.44
|
|
7
|
16
|
113
|
-32.3
|
-215.8
|
1043.29
|
46569.64
|
6970.34
|
|
8
|
33
|
197
|
-15.3
|
-131.8
|
234.09
|
17371.24
|
2016.54
|
|
9
|
56
|
314
|
7.69
|
-14.8
|
59.1361
|
219.04
|
-113.812
|
|
10
|
22
|
417
|
-26.3
|
88.19
|
691.69
|
7777.4761
|
-2319.397
|
|
11
|
63
|
217
|
14.69
|
-111.8
|
215.7961
|
12499.24
|
-1642.342
|
|
12
|
31
|
897
|
-17.3
|
568.19
|
299.29
|
322839.876
|
-9829.687
|
|
13
|
85
|
270
|
36.69
|
-58.8
|
1346.1561
|
3457.44
|
-2157.372
|
|
14
|
34
|
219
|
-14.3
|
-109.8
|
204.49
|
12056.04
|
1570.14
|
|
15
|
55
|
393
|
6.69
|
64.19
|
44.7561
|
4120.3561
|
429.4311
|
|
16
|
47
|
397
|
-1.3
|
68.19
|
1.69
|
4649.8761
|
-88.647
|
|
17
|
33
|
226
|
-15.3
|
-102.8
|
234.09
|
10567.84
|
1572.84
|
|
18
|
50
|
205
|
1.69
|
-123.8
|
2.8561
|
15326.44
|
-209.222
|
|
19
|
79
|
337
|
30.69
|
8.19
|
941.8761
|
67.0761
|
251.3511
|
|
20
|
43
|
160
|
-5.3
|
-168.8
|
28.09
|
28493.44
|
894.64
|
|
21
|
56
|
238
|
7.69
|
-90.8
|
59.1361
|
8244.64
|
-698.252
|
|
22
|
39
|
259
|
-9.3
|
-69.8
|
86.49
|
4872.04
|
649.14
|
|
23
|
69
|
371
|
20.69
|
42.19
|
428.0761
|
1779.9961
|
872.9111
|
|
24
|
64
|
482
|
15.69
|
153.19
|
246.1761
|
23467.1761
|
2403.5511
|
|
25
|
65
|
700
|
16.69
|
371.19
|
278.5561
|
137782.016
|
6195.1611
|
|
26
|
61
|
267
|
12.69
|
-61.8
|
161.0361
|
3819.24
|
-784.242
|
|
27
|
95
|
325
|
46.69
|
-3.81
|
2179.9561
|
14.5161
|
-177.8889
|
|
28
|
35
|
285
|
-13.3
|
-43.8
|
176.89
|
1918.44
|
582.54
|
|
29
|
72
|
244
|
23.69
|
-84.81
|
561.2161
|
7192.7361
|
-2009.1489
|
|
30
|
49
|
432
|
0.69
|
103.19
|
0.4761
|
10648.1761
|
71.2011
|
|
31
|
79
|
374
|
30.69
|
45.19
|
941.8761
|
2042.1361
|
1386.8811
|
|
32
|
62
|
328
|
13.69
|
-0.81
|
187.4161
|
0.6561
|
-11.0889
|
|
33
|
82
|
299
|
33.69
|
-29.81
|
1135.0161
|
888.6361
|
-1004.2989
|
|
34
|
64
|
445
|
15.69
|
116.19
|
246.1761
|
13500.1161
|
1823.0211
|
|
35
|
61
|
325
|
12.69
|
-3.81
|
161.0361
|
14.5161
|
-48.3489
|
|
36
|
48
|
321
|
-0.3
|
-7.81
|
0.09
|
60.9961
|
2.343
|
|
Total
|
1739
|
11837
|
-
|
-
|
18898.6559
|
807755.206
|
14585.3503
|



Comme r est compris entre 0 et 0.5, c'est-à-dire il y a
une faible corrélation positive.
Le coefficient de détermination r2
est :
 =1,44% =1,44%
Comme r2=1,44%, cela signifie qu'il y a une
corrélation entre les offres d'emploi (X) et les demandes d'emploi (Y)
à 1,44%. Le 98,56% est expliqué par d'autres facteurs.
Le coefficient d'amélioration A est :

Interprétation
Comme A<50%, il n'y a pas présomption favorable
(0,7%) pour un lien corrélatif entre les demandes et les offres
d'emploi.
a)Calcul de l'Intervalle de Confiance de r (Cas d'un
échantillon d'effectif n<50)
Nous déterminons l'IC  à 95% à 95%
n=36
r=0,12
Avant d'y arriver, nous calculons d'abord le
paramètre
 = = =0.12 =0.12
Z=0.12
On calcule l'écart-type de Z
 
Les limites de confiance de Z sont :
 =-0.21 =-0.21
 =0.45 =0.45
En reconvertissant  en en  et et  en en  , on obtient : , on obtient :
 =-0,20 =-0,20
 =0,42 =0,42
L'intervalle de confiance (IC) du coefficient de
corrélation est :
 ou -0,20<R<0,42 ou -0,20<R<0,42
a)Test de signification du coefficient de
corrélation linéaire
Comme n<50, nous faisons appel au test T de Student
à n-2 degrés de liberté. Nous testons :
H0 : , il n'y a pas de corrélation entre X offres et Y demandes , il n'y a pas de corrélation entre X offres et Y demandes
Contre
H1 : , il y a une corrélation entre X offres et Y
demandes. , il y a une corrélation entre X offres et Y
demandes.
Notre test est unilatéral, c'est-à-dire à
1 issue.
Nous prenons le seuil de signification ?=5%
 = =

Comme cette valeur de t tabulée ne se trouve pas
exactement dans la table de T de Student, alors nous passons à
l'extrapolation :
 se trouve entre la valeur de se trouve entre la valeur de 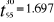 et la valeur de et la valeur de  . .
 




 =1.6918 =1.6918
Conclusion :
Comme au seuil de signification ?=0.05,  , on adopte H0 selon laquelle il y a absence de
corrélation entre les offres et les demandes d'emploi. , on adopte H0 selon laquelle il y a absence de
corrélation entre les offres et les demandes d'emploi.
III.2.1. L'AUTOCORRELATION DES
ERREURS31(*)
Il y a autocorrélation lorsque l'hypothèse
E(åå')=0 est violée. Dans ce cas, l'estimateur de Moindre
carré ordinaire (MCO) â reste sans biais, mais cet estimateur
n'est pas la variance minimale. Dans le cas de l'autocorrélation, le
modèle s'écrit :

avec  (autocorrélation d'ordre p) (autocorrélation d'ordre p)
Test de Durbin-Watson
Le test de Durbin-Watson (Dw) permet de détecter
l'autocorrélation des erreurs d'ordre 1 selon la forme :
 (2) (2)
Le test d'hypothèse est le suivant :
H0 : ñ=0, absence
d'autocorrélation
H1 : ñ 0, il y a doute et on ne peut pas conclure 0, il y a doute et on ne peut pas conclure
ou H1 : ñ>0 ou ñ<0, il
y a présence d'autocorrection positive ou négative.
Tableau N°4 : Procédure de calcul
d'autocorrélation de Durbin-Watson
|
N°
|
Y
|
|
|
 - -
|
|
|
|
|
1
|
318
|
304.62
|
13.384
|
0
|
0
|
13.384
|
179.13
|
|
2
|
548
|
305.39
|
242.614
|
13.384
|
179.13
|
229.23
|
58861.55
|
|
3
|
334
|
303.85
|
30.154
|
242.614
|
58861.55
|
-212.46
|
909.26
|
|
4
|
203
|
297.69
|
-94.686
|
30.154
|
909.26
|
-124.84
|
8965.44
|
|
5
|
221
|
307.7
|
-86.696
|
-94.686
|
8965.44
|
7.99
|
7516.2
|
|
6
|
156
|
300
|
-143.996
|
-86.696
|
7516.20
|
-57.3
|
20734.85
|
|
7
|
113
|
303.85
|
-190.846
|
-143.996
|
20734.85
|
-46.85
|
36422.2
|
|
8
|
197
|
316.94
|
-119.936
|
-190.846
|
36422.20
|
70.91
|
14384.64
|
|
9
|
314
|
334.65
|
-20.646
|
-119.936
|
14384.64
|
99.29
|
426.26
|
|
10
|
417
|
308.47
|
108.534
|
-20.646
|
426.26
|
129.18
|
11779.63
|
|
11
|
217
|
340.04
|
-123.036
|
108.534
|
11779.63
|
-231.57
|
15137.86
|
|
12
|
897
|
315.4
|
581.604
|
-123.036
|
15137.86
|
704.64
|
338263.21
|
|
13
|
270
|
356.98
|
-86.976
|
581.604
|
338263.21
|
-668.58
|
7564.82
|
|
14
|
219
|
317.71
|
-98.706
|
-86.976
|
7564.82
|
-11.73
|
9742.87
|
|
15
|
393
|
333.88
|
59.124
|
-98.706
|
9742.87
|
157.83
|
3495.65
|
|
16
|
397
|
327.72
|
69.284
|
59.124
|
3495.65
|
10.16
|
4800.27
|
|
17
|
226
|
316.94
|
-90.936
|
69.284
|
4800.27
|
-160.22
|
8269.36
|
|
18
|
205
|
330.03
|
-125.026
|
-90.936
|
8269.36
|
-34.09
|
15631.5
|
|
19
|
337
|
352.36
|
-15.356
|
-125.026
|
15631.50
|
109.67
|
235.81
|
|
20
|
160
|
324.64
|
-164.636
|
-15.356
|
235.81
|
-149.28
|
27105.01
|
|
21
|
238
|
334.65
|
-96.646
|
-164.636
|
27105.01
|
67.99
|
9340.45
|
|
22
|
259
|
321.56
|
-62.556
|
-96.646
|
9340.45
|
34.09
|
3913.25
|
|
23
|
371
|
344.66
|
26.344
|
-62.556
|
3913.25
|
88.9
|
694.01
|
|
24
|
482
|
340.81
|
141.194
|
26.344
|
694.01
|
114.85
|
19935.75
|
|
25
|
700
|
341.58
|
358.424
|
141.194
|
19935.75
|
217.23
|
128467.76
|
|
26
|
267
|
338.5
|
-71.496
|
358.424
|
128467.76
|
-429.92
|
5111.68
|
|
27
|
325
|
364.68
|
-39.676
|
-71.496
|
5111.68
|
31.82
|
1574.18
|
|
28
|
285
|
318.48
|
-33.476
|
-39.676
|
1574.18
|
6.2
|
1120.64
|
|
29
|
244
|
346.97
|
-102.966
|
-33.476
|
1120.64
|
-69.49
|
10602
|
|
30
|
432
|
329.26
|
102.744
|
-102.966
|
10602.00
|
205.71
|
10556.33
|
|
31
|
374
|
352.36
|
21.644
|
102.744
|
10556.33
|
-81.1
|
468.46
|
|
32
|
328
|
339.27
|
-11.266
|
21.644
|
468.46
|
-32.91
|
126.92
|
|
33
|
299
|
354.67
|
-55.666
|
-11.266
|
126.92
|
-44.4
|
3098.7
|
|
34
|
445
|
340.81
|
104.194
|
-55.666
|
3098.70
|
159.86
|
10856.39
|
|
35
|
325
|
338.5
|
-13.496
|
104.194
|
10856.39
|
-117.69
|
182.14
|
|
36
|
321
|
328.49
|
-7.486
|
-13.496
|
182.14
|
6.01
|
56.04
|
|
Total
|
11837
|
|
|
|
796474
|
|
796530.23
|
Pour tester ces hypothèses, on calcule la statistique
de Durbin-Watson comme suit :
 =1 =1
NB : Le Dw varie toujours entre 0 et 4
Où  est le résidu au temps t de l'estimation de l'équation
(1). est le résidu au temps t de l'estimation de l'équation
(1).
Cette statistique sera comparée aux valeurs
tabulées dans la table de Durbin et Watson au seuil de 5% en fonction de
la taille de l'échantillon n et du nombre de variations explicatives
(k).
La lecture de la table permet de déterminer deux
valeurs d1 et d2 comprise entre 0 et 2 qui
délimitent l'espace entre 0 et 4 selon le schéma
ci-après :
|
Autocorrélation
|
Doute
|
Pas de doute
|
Indépendance
|
Doute
|
Autocorrélation
|
|
?
|
|
|
?
|
|
|
0 d1 d2
2 4-d2 4-d1
4
|
Application
Si n=36 et k=2, alors d1=1.41 et d2=1.52. D'où on tire
4-d2=2.48 et
4-d1=2.59
Selon la position du Dw empirique dans l'espace ci-dessus, les
conclusions ci-après en découlent :
- Si  , il y a absence d'autocorrélation ; , il y a absence d'autocorrélation ;
- Si  , il y a autocorrélation positive ; , il y a autocorrélation positive ;
- Si  , il y a autocorrélation négative ; , il y a autocorrélation négative ;
Si  , il y a doute sur la présence d'autocorrélation. Ces deux
zones s'appellent zones d'indétermination. , il y a doute sur la présence d'autocorrélation. Ces deux
zones s'appellent zones d'indétermination.
Interprétation du test de
Dw
Comme Dw=1 tombe dans la condition 0<Dw,
c'est-à-dire il y a une autocorrélation positive. Le
modèle n'est pas bon.
* 31 BOFOYA KOMBA B., Principes
d'économétrie : cours et exercices résolus,
Inédit, L1 Economie rurale, Unigom, 2007-2008.
| 


