4.6 - Aspects théoriques : les
dépôts simples `monocouches'
Soit une couche mince et transparente d'indice n0,
déposée sur du verre d'indice n2. Un calcul simplifié avec
2 ondes donne facilement les conditions pour avoir un coefficient de
réflexion fort ou faible, selon que les ondes réfléchies 1
et 2 figure (45) sont en phase ou en opposition de phase.
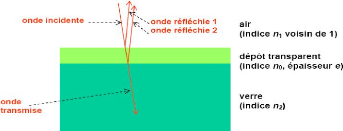
Figure 44. Ondes incidente, réfléchie et
transmise (verre à une seule couche).
La lumière réfléchie est composée
de deux ondes: une onde provenant de la réflexion sur la surface
air/dépôt et une onde réfléchie sur la surface
dépôt/verre. Les ondes étant cohérentes, il faut
additionner non pas les intensités mais les `vibrations' ou champs
électriques (interférences).
Le calcul plus rigoureux demande de prendre en
considération les réflexions multiples dans la couche dont les
coefficients de réflexion sont R1 et R2 figure (46). Après avoir
effectué la sommation des ondes multiples (il y en a une
infinité, et dont l'amplitude est décroissante), on peut calculer
les conditions et performances de traitements réfléchissants et
anti-réfléchissantes.
Deux cas sont à étudier : le revêtement
antireflet et le revêtement réfléchissant. Les
différents milieux sont supposés parfaits (donc non
absorbants).
Soit ë0 la longueur d'onde de la
lumière incidente.
4.6.1 - Traitement antireflet
Soit ë0 la longueur d'onde du rayonnement
incident. On peut montrer que le traitement antireflet est obtenu si les deux
conditions suivantes sont remplies :
a) l'indice de la couche n0 doit être inférieur
à celui du verre n2.n1<n0<n2
b) l'épaisseur e de la couche est donnée
par : n0 e = ë0/4 + k
ë0/2
Où k est un nombre entier.
Ce dépôt est donc une couche appelée lame
appelée `quart d'onde'. Le coefficient de réflexion minimum est
:
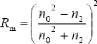
Le coefficient de réflexion est nul si :
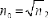
Pour qu'une surface de verre d'indice n2=1,5 présente
un coefficient de réflexion nul, il faudrait un dépôt
d'indice 1,23. C'est une valeur très faible. Il faut en outre que le
dépôt soit réalisé avec un matériau de bonne
durabilité chimique et mécanique, adhérant au verre et
pouvant être déposé par un moyen commode industriel (PVD
par exemple). Les matériaux qui conviendraient le mieux seraient:
- le fluorure de magnésium MgF2 (indice 1,38)
- la cryolite Na3AlF6 (indice 1,35)
Si :
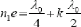
Alors le coefficient de réflexion sera minimum pour
ë = ë0.
Un traitement anti-réfléchissant par
dépôt de MgF2 abaisse le coefficient de réflexion de la
valeur initiale (verre sans dépôt) 4% à 1,2% (figure
47).
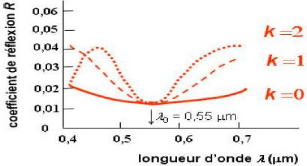
Figure 46. Réponse spectrale d'un dépôt
monocouche anti-réfléchissantes
Le dépôt est ajusté pour que le coefficient
de réflexion R soit minimum pour la longueur l'onde
ë 0=0,55 _m (centre du spectre visible).
A noter :
Si le dépôt est épais (k
élevé), alors l'intensité sera nulle pour plusieurs
valeurs de la longueur d'onde dans le domaine visible du spectre. Dans la
figure, on a représenté les cas k=0, k=1 et k=2.
La valeur de R en fonction de la longueur d'onde explique l'effet
décoratif obtenu par des couches minces d'oxyde de titane sur du
verre.
Mais il y a deux problèmes car :
1) le minimum n'est pas nul
2) le calcul suppose une lumière monochromatique de
longueur d'onde ë0
, alors qu'on souhaite en général une
réponse sur un spectre étendu (le spectre de lumière
visible, par exemple). Pour pallier ces inconvénients, il faut utiliser
des dépôts multicouches.
| 


