Impacts de la préssion du cout de ma vie sur les principaux indicateurs de la production nationale : Cas d'Haiti 1975@2005

IV.3.4) Test de détection de multicollinéarité

IV.3.4.1) Test de Klein

Ce test est fondé sur la comparaison du coefficient de détermination R²y calculé sur le modèle à k variables:

Y= A₀ +A₁X₁ +A₂X₂ +............+A_nX_n + å_t

Et les coefficients de corrélation simple r² x_iy_j entre les variables explicatives pour i?j.

Si R²_y < r² x_iy_j, il y a présomption de multicollinéarité.

Tableau XII

Vue des corrélations partielles

	TPIB	CG	IG	BC	DBE
TPIB	1.000000	-0.242039	0.267043	0.238947	0.468560
CG	-0.242039	1.000000	0.144508	-0.952151	-0.725593
IG	0.267043	0.144508	1.000000	0.018345	-0.006534
BC	0.238947	-0.952151	0.018345	1.000000	0.690852
DBE	0.468560	-0.725593	-0.006534	0.690852	1.000000

Source : Calculs effectués sur les données à partir du logiciel E-Views 5.

La lecture des données de la fig.5 permet de faire une comparaison entre les coefficients partiels et R²_y de la fig.1. La valeur de R²_y étant supérieur dans chaque cas, cela implique qu'il n'y a pas de présomption de multicollinéarité.

IV.3.4.2) Test de Farrar et Glauber

Ce test comporte deux étapes :

· La première étape consiste à calculer le déterminant (D) de la matrice des coefficients de corrélation entre les variables explicatives.

· La deuxième étape consiste à effectuer un test du ÷2, en posant les hypothèses suivantes:

H₀: D = 1 (les séries sont orthogonales)

H₁: D < 1 (les séries sont dépendantes)

Se servant de l'annexe IV, on trouve D = 0.070211721 <1, l'hypothèse H1 est acceptée, dans ce cas, il n'y a pas de problème de multicollinéarité. La valeur empirique du *Õ² calculée à partir de l'échantillon est égale à :

*Õ² = -[n-1-1/6(2K+5)]*lnD

Où n est la taille de l'échantillon, K le nombre de variables explicatives (terme constant inclus, K=k+1) et Ln le logarithme népérien.

· Si * Õ ² = Õ ² lu dans la table à ½ K(K-1) degrés de liberté et au seuil á choisi, alors l'hypothèse H₀ est rejetée. Il y a donc présomption de multicollinéarité.

· Si* Õ ² < Õ ², alors nous acceptons l'hypothèse d'orthogonalité.

En remplaçant les lettres par leur valeur on obtient :

*Õ² = -[30-1-1/6(2(5+1) +5)]*ln0.070211721

*Õ² = 88.21

Après calcul, le *Õ ² est égal à 88.21 et lorsque v > 30,on peut admettre que la quantitév2x² -v2v -1 suit la normale centrée réduite(annexe v).

IV.3.5) Test de Normalité des erreurs

Pour calculer les intervalles de confiance prévisionnels et aussi pour calculer les tests de Student sur les paramètres, il convient de vérifier la normalité des erreurs. Le test de Jarque et Bera (1984), fondé sur la notion de Skewness (asymétrie) et de Kurtosis (aplatissement), permet de vérifier la normalité d'une distribution statistique.

IV.3.5.1) Tests de Skewness et du Kurtosis

Soit u_k =1/n Ó(x_i -m)^k le moment centré d'ordre k,le coefficient de Skewness (â₁^½) est égal à : â₁^½ = u₃ / u₂^3/2 et le coefficient de Kurtosis : â₂ = u₃ / u_4. Si la distribution est normale et le nombre d'observations grand (n> 30) :

â₁^½ >N(0 ;?6/n) et â₂ ? (3, v24/n)

On construit alors les statistiques :

v₁=/â₁^½ - 0 / /v6/n et v₂ =/â₂ -3 //v24/n que l'on compare à 1.96 (valeur de la loi normale au seuil de 5%).

Si les hypothèses H₀ : v₁ = 0 (symétrie) et v₂ = 0 (aplatissement normal) sont vérifiées, alors v₁ = 1.96 et v₂ = 1.96 ; dans le cas contraire l'hypothèse de normalité est rejetée.

IV.3.5.2) Test de Jarque et Bera

Il s'agit d'un test qui synthétise les résultats précédents ; si â₁^½ et â₂ obéissent à des lois normales alors la quantité s : s =n/6 * â₁ + n/24*( â₂ -3) suit un x ² à deux degrés de liberté.

Donc, si s > Õ²_1-á (2) on rejette l'hypothèse H₀ de normalité des résidus au seuil á.

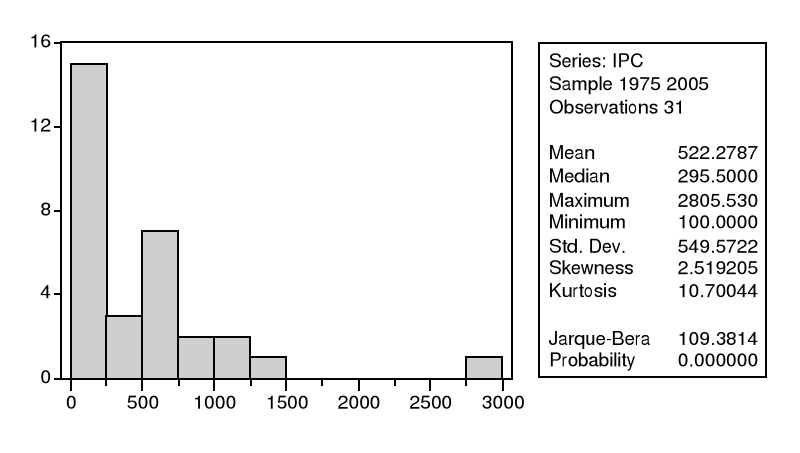
Donc, les tests effectués dans ce cas confirme l'hypothèse de normalité à partir des valeurs trouvées de v₁ = 2.51 et v₂ =10.7 que l'on compare à 1.96 et constaté également par la statistique de Jarque-Bera. Voir le schéma I, ci-dessous :

fig I : Test de Normalité des erreurs