Enrichissement du milieu et persistance des espèces dans les cha??nes trophiques : apport de la théorie DEB

Ismaël BERNARD Mémoire de stage de master 2 Biologie et Ecologie Marines

Enrichissement du milieu et persistance

des espèces dans les chaînes trophiques :

apport de la théorie DEB

UNIvERsITé DE LA MéDITERRANéE (AIX-MARsEILLE II)
CENTRE D'ocEANoLoGIE DE MARsEILLE
LABoRAToIRE DE MIcRoBIoLoGIE, GéocHIMIE ET EcoLoGIE MARINEs

Table des matières

Introduction 1

Modèles et méthodes 4

1 Le modèle de Rosenzweig - Mac Arthur 4

2 Le modèle de chalne trophique DEBf 6

3 Analyse des modèles 11

Résultats et discussion 13

4 Modèle de Rosenzweig MacArthur (R-M) 13

4.1 Dynamique en absence du superprédateur 13

4.2 Dynamique en présence du superprédateur 14

5 Modèle de chalne trophique DEBf 17

5.1 Dynamique en absence du superprédateur 17

5.2 Dynamique en présence du superprédateur 17

6 Étude comparée des deux modèles 19

6.1 Lien direct 19

6.2 Paradoxe de l'enrichissement 20

6.3 Persistance des chalnes trophiques a deux échelons 20

6.4 Temps de persistance des chalnes trophiques a trois échelons 22

Conclusion 26

Bibliographie 27

A Glossaire des termes de modélisation 32

B Dynamiques temporelles 34

C La méthode semi-numérique 36

Un grand merci a l'équipe du LMGEM pour son acceuil et plus particuliêrement a Jean-Cristophe Poggiale pour les discussions écologiques lumineuses.

Thank you to all the "DEB coursers' and more particularly, Bas Kooijman for his disponibility and his always clear explanations on DEB theory.

Merci a Marie et Laura, pour les conseils DEB éclairés et pour les footings endiablés.

Merci a Audrey pour les débats passionnés de politicomodélisation.

Merci a Annette pour le bleu du rêve et de l'aventure...

Merci a Andrea mi compañera de piso columbiana preferida.

Merci a Philippe pour les visions écologiques partagées.

Merci a mes parents dont le bon sens vaut tous les raisonnements scientifiques du monde.

Merci enfin a tous ceux qui ont participés a ces pénibles repas en terrasse ensoleillée de luminy...

Introduction

Un écosystème est un ensemble d'espèces ayant développé des relations entre elles en interaction avec un environnement physique particulier, on parle d'une biocénose en interaction avec son biotope. Parmi les relations interspécifiques, la prédation mérite particulièrement d'être considérée puisqu'elle est le principal mécanisme de transfert de l'énergie le long des échelons trophiques de l'écosystème. D'autre part, le biotope influe fortement sur la viabilité de la biocénose. Il convient donc d'étudier a la fois l'aspect interspécifique et l'interdépendance vis a vis du biotope. En ce sens, une chalne trophique constitue un écosystème simplifié dans lequel la biocénose comporte deux a trois espèces reliées par de la prédation et soumises a un biotope représenté par la richesse du milieu. C'est pour mieux comprendre les dynamiques engendrées dans cet écosystème simplifié que des modèles de chalnes trophiques a deux échelons ont été très tot développés (Volterra, 1931). Ces modèles autorisent, grace a leur dépouillement, une analyse théorique approfondie. L'idée est ensuite de comprendre le comportement du réseau trophique dans sa globalité en extrapolant les résultats obtenus sur ces briques de base de l'écosystème (Englund & Moen, 2003). Aujourd»hui, grace aux progrès de l'informatique, la complexité des modèles a augmenté pour prendre en compte un grand nombre de composantes des écosystèmes mais ne semble toujours pas suffisante pour effectuer des prédictions (Boero et al. , 2004). Entre ces deux extrémités se sont développés des modèles de chalnes trophiques a trois échelons qui rendent compte de la réalité d'un plus grand nombre de situations tout en conservant la simplicité nécessaire aux études analytiques (e.g. Cann & Yodzis, 1995). Le but est alors de dégager et de comprendre les schémas généraux que suivent les dynamiques.

Les modèles traditionnels, comme le modèle de Rosenzweig - Mac Arthur, expliquent la dynamique des populations en s'appuyant sur des hypothèses faites au niveau même de cette population et sont construits par des formules mathématiques d'origine empirique. Il est alors difficile de trouver une signification aux ajustements de ces modèles a des données expérimentales. Depuis les années 80, la modélisation des systèmes biologiques a considérablement gagné en réalisme au

niveau de l'individu grace a la théorie de modélisation DEB¹ (Kooijman, 2000a). Par extrapolation au niveau de la population, cette théorie est capable d'apporter une approche différente de la modélisation écologique oü la dynamique de plusieurs populations peut être décrite sur la base d'hypothèses faites au niveau de l'individu. L'individu est en effet un niveau d'organisation oü les bilans de masses et d'énergie sont plus aisés a effectuer. Cette plus grande facilité a paramètrer les modèles issus de la théorie DEB a conduit a de multiples applications de cette théorie en physiologie (Kooijman, 2000b), en écotoxicologie (DEBtox), pour les espèces a valeur commerciales (Pouvreau et al. , 2006) ou en dynamique des populations.

La comparaison entre le modèle de Rosenzweig & MacArthur (1963), noté R-M, et un modèle de chalne trophique issu de la théorie DEB, nommé DEBf (Kooi & Kooijman, 1994a), s'effectuera en suivant le fil du paradoxe de l'enrichissement. Ce phénomène popularisé par Rosenzweig (1971) postule que l'enrichissement peut avoir un impact négatif sur la stabilité de l'écosystème. Mathématiquement, il a été montré dans de nombreux modèles (e.g. Abrams & Roth, 1994) mais aussi dans quelques expérimentations (Fussmann et al. , 2000) que l'enrichissement du milieu transforme dans certains cas un équilibre stable en des fluctuations périodiques. Toutefois des mécanismes susceptibles de gommer ce phénomène dans les milieux naturels, tels des changements physiologiques ou la compétition d'algues non comestibles (McCauley et al. , 1999) ont aussi été mis en évidence. La présence du paradoxe de l'enrichissement sera vérifiée au sein des deux modèles, dans leurs versions a deux et trois espèces. Pour montrer l'effet dans les modèles de l'apparition de ces fluctuations, il est nécessaire de définir une méthode pour rendre compte du plus grand risque d'extinction encouru lorsque les populations fluctuent. La notion de persistance, c'est a dire de survie dans le temps d'une espèce par rapport a un seuil limite, sera utilisée a cette fin. La comparaison entre les deux modèles sur ces points permettra d'évaluer le gain apporté par le modèle issu de la théorie DEB.

A peu près a la même période que le paradoxe de l'enrichissement, les travaux précurseurs de May (1974) en écologie ont mis en évidence de nouvelles formes de régimes asymptotiques² pour ces modèles déterministes : c'est l'émergence du chaos en écologie. Ces systèmes ont la propriété, pour certaines gammes de valeur de paramètres, d'accentuer de manière exponentielle les incertitudes sur les mesures : on parle de sensibilité aux conditions initiales, ce qui constitue la définition la plus commune de la dynamique chaotique. L'évolution d'une variable au cours du temps a l'équilibre devient alors difficile a caractériser car elle n'est ni constante, ni périodique, ni quasipériodique. Depuis le chaos a été identifié aussi lorsque la

¹Dynamic Energy and Mass Budget

²Les mots en écriture penchée sont définis dans l'annexe A

structuration en taille, dans l'espace (e.g. Petrovskii et al. , 2004) ou génétique (e.g. Ferriére & Gatto, 1993) est prise en compte. La dynamique chaotique ne passe plus pour une curiosité en écologie mais bien pour un état envisageable de certains écosystèmes réel (Hastings et al. , 1993). L'importance du chaos en écologie est appuyée par plusieurs voies de recherche. Tout d'abord, des démonstrations expérimentales récentes assurent qu'il ne s'agit pas uniquement d'un phénomène propre aux modèles (Becks et al. , 2005). Ensuite, l'analyse de séries temporelles de terrain cherche a prouver l'existence de dynamiques chaotiques au sein même des écosystèmes (Turchin & Ellner, 2000). Enfin, l'analyse d'un nombre toujours plus grand de modèles renforce l'aspect ubiquiste du phénomène (Hastings et al. , 1993).

L'étude du chaos présente deux intérêts. Tout d'abord, s'il est évident qu'il constitue un défi a la prévision du devenir des écosystèmes, le chaos est aussi une barrière a l'explication de leurs dynamiques. C'est réellement en tant que nouveau type de dynamique de régime asymptotique, que son effet sur les populations doit être étudié et compris. En ce sens, l'introduction d'un troisième échelon trophique complexifie le schéma général d'évolution des types de dynamiques en fonction de l'enrichissement. La question sera alors de savoir quelle est la place de la dynamique chaotique, selon le critère de persistance, dans ce schéma général.

Trois questions seront donc mêlées dans les développements qui suivent: "Quel est l'apport de la théorie DEB pour la modélisation des chalne trophiques ?", "Quel est la robustesse du paradoxe de l'enrichissement?" et "Comment la dynamique chaotique influe-t-elle sur la persist ance des espèces ?".

Modèles et méthodes

1 Le modèle de Rosenzweig - Mac Arthur

Le modèle de Rosenzweig - Mac Arthur (R-M) est un modèle initialement a deux équations décrivant les interactions non spatialisées entre une proie et un prédateur (Rosenzweig & MacArthur, 1963). Historiquement, ce modèle fût utilisé pour mieux comprendre la dynamique induite par les relations de prédations dans l'écosystème. Il a ensuite été modiflé pour décrire les chalnes trophiques a trois échelons observées dans le milieu. Ce type de modèle très simple s'appuie sur de nombreuses hypothèses, dont entre autres :

- milieu de richesse constante

- prédateur monospécifique

- pas d'interactions avec d'autres espèces

- mortalité des proies négligeable par rapport au taux de prédation

- pas d'interaction des prédateurs entre eux (poursuite de la même proie)

- facteur de conversion de biomasse de proie en biomasse de prédateur constant Cette simplicité en permet une étude mathématique poussée et le rend comparable aux milieux expérimentaux contrôlés de type chemostat.

Dans la formulation mathématique de ce modèle de chalne trophique (Fig. 1), X1 représente la biomasse des proies, X2 celle des prédateurs et X3 celle des superprédateurs. La croissance des proies s'effectue selon la fonction logistique r X1 (1 - X1 _K ) oü r et K sont respectivement le taux de croissance et la capacité limite du milieu pour la population de proies. La prédation du prédateur (i = 2) comme celle du super-prédateur (i = 3) suit une réponse fonctionnelle de Holling

type _IIaiXi-1

bi+Xi-1 oü a et b sont respectivement le taux maximum de prédation et la constante de demi-saturation en proies. L'efficacité de la conversion d'un échelon trophique en l'échelon supérieur est déterminée par le coefficient e , supposé constant. La mortalité est considérée comme un phénomène linéaire ou la biomasse d'individus qui meurent est proportionnelle a la biomasse totale selon un taux d (Tab. 1).

MOdèlES ET méThOdES

FIG. 1 - Correspondance entre les processus a l'oeuvre au sein de la chalne trophique et leur formulation dans le modèle de R-M a trois échelons.

TAB. 1 - Interprétation des variables d'e'tat et des paramètres du modèle de Rosenzweig - Mac Arthur avec comme dimension M pour les masses et T pour le temps et valeurs prises par ces paramètres.

Notation	Interprétation	Dimension		Valeur i=(2,3)		r
taux de croissance des proies	T-1	i = 2		i = 3	K
capacité limite pour les proies	M	variable		X
biomasse de proie (i=1), de prédateur	M	-		-
(i=2) ou de superprédateur (i=3)					a
taux de prédation maximum du ^iièmeéchelon	M.T^-1	5/3		0,05	b
constante de demi-saturation de la pré- dation de i sur i-1	M	1/3		0,5	e
efficacité de la conversion entre l'éche- lon i-1 et l'échelon i	-	1		1	d
taux de mortalité du ^iièmeéchelon	T-1	0,4		0,01

Les variations de chaque compartiment du système peuvent ensuite être traduites en termes d'e'quations diffe'rentielles³ en faisant précéder les apports d'un signe positif et les pertes d'un signe négatif. On doit en outre remarquer que le terme qui est prélevé par la prédation ne correspond pas a ce qui est intégré dans l'échelon trophique supérieur du fait de l'introduction de l'efficacité de conversion: il y a une possibilité de perte d'énergie le long de la chalne trophique. Il en résulte le système d'équations différentielles suivant :

dX1 dt

dX2 dt dX3 dt

X1 a2 X1

=rX1(1-- _K) -- X2 (1a)
^b2+^X1

^a2^X1 a3 X2

= e2

= e3

^X2--d2^X2-- X3 (1b)

b2+^X1 b3+^X2

^X3^--d3^X3 (1c)

3+^X2

^a3^X2

^b

L'étude du modèle a été réalisée en considérant les paramètres utilisés dans de nombreuses études antérieures (e.g. Gragnani et al. , 1998). Ces paramètres ont la particularité de faire l'hypothèse d'une chalne trophique sans perte d'énergie, c'est a dire avec e = 1, i ? {2, 3} (Tab. 1). Il a été démontré que cela n'affectait pas la dynamique générale du modèle (Abrams & Roth, 1994).

2 Le modèle de chaîne trophique DEBf

La théorie DEB (Dynamic Energy and Mass Budgets) de Kooijman (2000a), offre une nouvelle approche pour la modélisation de nombreux processus du vivant. Le but de cette théorie est de décrire les processus physiologiques indépendamment de l'espèce considérée { 1 }⁴. L 'échelle de référence utilisée pour cela est l'individu {10} et plus précisément le niveau physiologique, pour éviter des modèles trop complexes. Le niveau individuel est naturel car il est facile de mesurer les masses et les énergies a cette échelle d'organisation {19}. La théorie est aussi basée sur des phénomènes actifs de niveau inférieur comme les unités de synthèse {43} qui traitent de la cinétique enzymatique ou la thermodynamique {3,35} qui traite du devenir de l'énergie. Des phénomènes de niveau supérieur sont aussi inclus comme les relations de forme entre aire et volume {23} ou la température {53}. Cette approche prend en compte certaines considérations importantes de modélisation sur l'utilisation des dimensions {12} ou sur le lien entre la testabilité d'un modèle et l'évaluation de paramètres {14}. Une autre idée clef est que, dans le vivant, les

³Les mots en écriture penchée sont définis dans l'annexe A

⁴Les nombres entre accolades renvoient pour ces deux paragraphes au numéro de la page de l'ouvrage de référence sur la théorie DEB : Kooijman, 2000

processus de production sont liés aux volumes tandis que les processus d'échange sont liés aux surfaces.

Ces réflexions mènent a un petit nombre de choix et d'hypothèses utilisées pour construire la théorie DEB. Les variables d'état sont choisies pour leur capacité a bien décrire le système {20}. La variable d' age est rejetée parce qu'elle ne prend pas en compte l'impact de l'environnement. Le volume, comme descripteur de la taille, est préféré au poids a cause des multiples relations impliquant des aires dans les processus physiologiques {22}. Les modèles issus de la théorie DEB décrivent un individu grace a deux variables d'état : la structure ou biomasse irréversible et les réserves ou biomasse réversible. Une variable de réserve de l'individu {20} est nécessaire pour pouvoir lisser l'influence des fluctuations de nourriture sur la croissance et pour assurer une maintenance continue de l'organisme. Une règle d'allocation énergétique, la règle ê {65,86}, stipule qu'il il y a une part ê de l'énergie dédiée au développement pour les juvénile et a la reproduction pour les adultes tandis qu'une part 1 - ê est allouée a la croissance. Ceci est mis en oeuvre pour autoriser la continuité de la croissance entre le stade juvénile et le stade adulte et pour autoriser différentes dynamiques de croissance avec un même mécanisme. Cette architecture est complétée par de la maintenance {89} prélevée sur chacune de ces deux partie pour respectivement l'entretien de maturité et l'entretien somatique. Les hypothèses d'homéostasie {30} traduisent le fait que la composition de la structure et de la réserve ne change pas au cours du temps (homéostasie forte) et que la composition globale de l'organisme ne change pas a ressource constante, c'est a dire sans fluctuation de nourriture (homéostasie faible). Ces hypothèses permettent de déterminer et de simplifier les équations dans le cadre de la théorie.

Le modèle de chalne trophique en chemostat issu de la théorie DEB, nommé modèle DEBf, a été pour la première fois présenté par Kooi & Kooijman (1994a). Il s'agit de la transposition au niveau de la population des mécanismes d'allocation énergétique de la théorie DEB. Ce modèle se démarque donc des modèles précédents dits de Monod (1942), de Droop (1973) et de Pirt (1965) par une formulation basée sur des hypothèses sur la gestion de l'énergie au niveau de l'individu. Selon ces hypothèses, chaque espèce (i E {1, 2, 3}) y est composée de deux variables d'état, une structure (Xi) et une réserve (ei). Ces variables d'état sont accompagnées d'une variable décrivant le substrat (X0). La dynamique des variables est régie par un ensemble de processus : maintenance, croissance, ingestion, assimilation, mobilisation et dilution (Fig. 2). La principale innovation de ce modèle par rapport a ses prédécesseurs est l'instauration a la fois d'un compartiment de réserve et d'une maintenance. Il est alors possible de se ramener a chacun de ces modèles antérieurs en faisant des hypothèses sur les paramètres du modèle DEBf (Tolla, 2006).

En plus des hypothèses incluses dans la théorie DEB, les hypothèses spécifiques au modèle DEBf sont les suivantes:

- Organismes dont la surface est proportionnelle a leur volume

- Propagation des individus par mitose, division en deux parties égales a une taille fixée

- Mélange homogène du chemostat

- Les réserves des proies ne sont pas digérées

Dans ce modèle, l'interprétation de chacun des paramètres du modèle est très précise (Tab. 2). Le substrat, X0, arrive dans le chemostat selon un taux de h ÿ Xr et en ressort selon un taux de h ÿ X0. La proie prélève le substrat et subit une prédation du prédateur selon des réponses fonctionnelles f et un taux maximum de jXm , avec i le rang de l'espèce prédatrice dans la chalne trophique. La réponse fonctionnelle utilisée est là aussi de Holling, type II.

X _1

f = XK +X _1

Une fois la nourriture assimilée, celle-ci est stockée dans un compartiment de réserve, e , avec une efficacité v . Pour diminuer le nombre de paramètre du modèle, les réserves utilisées sont normées par leur taille maximale. Cette réserve est ensuite utilisée pour la croissance selon un taux u qui dépend a la fois de la maintenance (^ÿkM ) et de la conductance énergétique (^ÿkE ).

^ÿkE e - ^ÿkM g

u =

Les espèces subissent un taux de lessivage qui supprime un biovolume ^ÿhX du chemostat.

TAB. 2 ~ Interprétation des variables et des paramètres du modèle DEB en chemostat

Notation		Interprétation	X0
Concentration en glucose		X
Biovolume de la population i		Xr
Concentration en glucose dans le réservoir du chemostat		h ÿ
Taux de dilution du chemostat		jXm
Taux maximum d'ingestion de l'espèce X sur X _1		XK
Constante de demi-saturation de l'espèce X sur X _1		^ÿkE
Conductance énergétique de l'espèce i		g
Ratio d'investissement énergétique de l'espèce i		^ÿkM
Ratio colits de maintenance et colits de croissance

L'ensemble de ces développements donne le système (Eq. 2), dans le cas d'une chalne trophique a trois échelons.

dX0 dt de1 dt dX1 dt de2 dt dX2 dt de3 dt dX3 dt

^=h^ÿ(^Xr-^X0)-^jXm1I1^X1(2a) = ^ÿkE1 (I1 - e1) (2b) = (u1-^ÿh)^X1-jXm2I2^X2 (2c) = ^ÿkE2 (I2 - e2) (2d) = (u2 - ^ÿh)X2 - jXm3I3^X3 (2e) = ^ÿkE3 (I3 - e3) (2f) = (u3 - ^ÿh) X3 (2g)

La microbiologie fournit le pendant expérimental idéal des modèles construits ainsi grace a la rapidité de succession des générations, a la petite taille des individus et au contrôle possible de tous les paramètres environnementaux (Jessup et al. , 2005). Deux jeux de paramètres issus de telles expérimentations ont été utilisés pour le modèle DEB (Tab. 3). Les valeurs des paramètres correspondent au meilleur ajustement possible du modèle sur des données expérimentales. Le premier jeu de paramètres est issue de l'étude de Kooi & Kooijman (1994b) des données d'un couple prédateur-proie Bactérie-Fungi représenté respectivement par Escherichia coli et Dictyostelium discoideum (Dent et al. , 1976). Le volume du chemostat est de 200 mL. Le taux de dilution du chemostat, ^ÿh, y est de 0, 064 h^-1 et la concentration du substrat de 1 mg.mL^-1. Le second est un paramétrage sur les données d'une expérience sur un couple Bactérie-Cillié (Cunningham & Nisbet, 1983) étendu de manière théorique a un troisième échelon (Kooi et al. , 1997). Ce second jeu de paramètres contient donc des valeurs pour trois échelons trophiques.

A cause de problèmes numériques, le modèle DEBf a trois échelons trophiques a été simpliflé en posant e1 = I1. Ce qui supprime la réserve de la proie et fait passer le nombre d'équations différentielles de sept a six.

¹Valeur tirée de Kooi & Kooijman (1994b) ²Valeur tirée de Kooi et al. (1997)

TAB. 3 - Valeur des deux jeux de paramètres utilisés pour le modèle DEBf, le premier considère un couple Bactérie-Fungi et le second un triplet Bactérie-CiliéCarnivore.

Variable	Jeu de paramètre ^11				Jeu de paramètre ^22
i=1	i=2		Unité	i=1	i=2	i=3	Unité	jXm
0,65	0,26		mg.mm^-3.h^-1 ,h^-1	1,25	0,333	0,25	h-1	XK
0,0004	0,18		mg.mL^-1	8	9	10	mg.L^-1
			,mm^3 .mL^-1					^ÿkE
0,67	2,05		h-1	40,0	0,2	0,0756	h-1	g
0,86	4,43		-	80,0	1,0	0,504	-	^ÿkM
0,0083	0,16		h-1	0,025	0,01	0,0075	h-1

3 Analyse des modèles

L'étude des modèles a été effectuée en deux temps : tout d'abord une analyse classique des équilibres et de leur stabilité puis une analyse de la capacité des différents échelons trophiques a se maintenir dans le temps, la persistance (Tab. 4). Toutes les analyses sont réalisées en fonction des paramètres d'enrichissement du système, nommés paramètres de bifurcation.

L'analyse classique a été menée soit de manière analytique pour les cas les plus simples (modèle R-M a deux équations), c'est a dire en calculant a la main la valeur des différents équilibres et les valeurs des paramètres de bifurcation pour lesquels il y a stabilité, soit de manière semi-numérique, c'est a dire en testant, en fonction des paramètres de bifurcation, le signe de la valeur propre maximale de la matrice jacobienne (Annexe C). Dans les deux cas, les domaines d'existence et de stabilité des différents équilibres en fonction des paramètres de bifurcations sont obtenus. Lorsque le modèle s'est avéré trop complexe pour le calcul des valeurs d'équilibre, ces domaines ont été tirés de la littérature scientifique lorsqu'il existent. Il est donc possible de caractériser, en fonction des valeurs des paramètres d'enrichissement, le type de la dynamique : stationnaire, périodique ou chaotique. Des diagrammes de bifurcations montrent ensuite les différents régimes asymptotiques selon les valeurs des paramètres de bifurcation.

Deux calculs différents de persistance ont été utilisés en fonction de la diversité des dynamiques rencontrées : la survie et le temps de persistance. Ces deux approches sont a chaque fois calculées lorsque la chalne trophique est a l'équilibre. Un calcul de survie a été effectué en considérant la valeur de l'équilibre ou le minimum des valeurs sur l'attracteur lorsque la dynamique du régime asymptotique, n'est pas constante. Cette valeur a ensuite été comparée a un seuil. Ce seuil a été

TAB. 4 - Méthodes d'analyses employées sur les quatre versions des différents modèles étudiés

	R-M a 2 espèces	R-M a 3 es- pèces	DEBf a 2 espèces		DEBf a 3 espèces	analyse des équilibres
analytique	Semi- numérique et littéra- ture	Semi-numérique	Littérature		analyse de persistance
Survie	Survie et temps de persistance	Survie	Survie et temps de persistance

déterminé comme le seuil le plus représentatif du schéma général qui apparalt lorsqu'on le fait varier. Le seuil utilisé pour le modèle R-M est de 0,05 pour la proie, pour le prédateur comme pour le superprédateur. Le seuil utilisé pour le modèle DEBf est la biomasse qui correspond a 1 individu. Pour les proies, il est évalué a 2, 8.10_¹² mm³.mL_¹ et a 1, 1.10_⁹ mm³.mL_¹ pour les prédateurs, d'après les données de Dent et al. (1976).

Pour les modèles possédant plusieurs types d'attracteurs complexes, cycles limites et attracteurs étranges, un calcul du temps moyen de persistance d'une espèce est possible. Pour effectuer ce calcul, une condition initiale aléatoire suivant une loi uniforme est prise au sein des bornes de l'attracteur. Pour un grand nombre de simulations (100), on calcule le temps avant que l'abondance d'un échelon ne devienne inférieure au seuil. La moyenne sur l'ensemble des simulations est le temps moyen de persistance de chaque échelon lorsque la chalne trophique se trouve a l'état d'équilibre. Ce calcul est répété en fonction des valeurs des paramètres de bifurcations. Pour ce calcul, un seuil arbitraire correspondant a une biomasse de 0, 5mm³.mL_¹ a été employé pour le modèle DEBf en remplacement du seuil a un individu dans le chemostat. Par ailleurs, pour diminuer la complexité de l'algorithme, le temps de persistance est limité par la durée de la simulation. Celle-ci est attribuée a l'espèce lorsqu'elle n'a pas franchie le seuil a la fin de la simulation.

Résultats et discussion

4 Modèle de Rosenzweig MacArthur (R-M)

4.1 Dynamique en absence du superprédateur

Ce modèle comporte trois points d'équilibres différents dont l'existence et la stabilité sont régies par la valeur de K, qui peut s'interpréter comme la richesse du milieu. Il s'agit donc du paramètre de bifurcation⁵ naturel du système (Fig. 3). Tout d'abord l'équilibre sans proies ni prédateurs dans le système, E1 = (0, 0), existe quelque soit la valeur de K. Il s'agit d'un point selle, stable selon l'axe des prédateurs et instable selon l'axe des proies. Le second équilibre qui correspond a l'établissement d'une certaine quantité de proies mais sans maintien du prédateur,

E2 = (K, 0), existe toujours lui aussi. Il est stable si K < X ₁ et se comporte en point selle sinon. Enfin, le troisième point d'équilibre, E3 = (X ₁, X ₂) (Eq. 3) n'existe que si K > X ₁.

d2 b2 E3 = (X 1, X 2) = , e2 a2 - d2

) rX (1 - K )(b2 + X 1 1)(3) a2

E3 est stable si K < b2 + 2X ₁ ou occupe le centre instable d'un cycle limite sinon. On remarque donc que l'enrichissement du milieu, c'est a dire l'augmentation de K, provoque des fluctuations de la biomasse des proies et des prédateurs par l'intermédiaire de l'apparition d'un cycle limite. La dynamique du modèle se décompose donc en trois phases selon l'augmentation de K :

Si K < X 1 , seule la proie se maintient a la capacité limite du milieu (E2).

Si x 1 < K < b2 + 2X ₁ , un équilibre stable entre proies et prédateurs est atteint dont la position est donnée par l'équilibre E3 (Eq. 3).

Si K> b2 + 2X ₁ , un cycle limite correspondant a des fluctuations périodique apparait. Ces fluctuations sont amplifiées par l'augmentation de K.

⁵Les mots en écriture penchée sont définis dans l'annexe A

FIG. 3 - Valeurs de bifurcation du modèle R-M, existence, stabilité et survie des deux espèces.

L'apparition de ces fluctuations d'effectifs pour des valeurs de K élevées rend les biomasses parfois très faibles ce qui augmente le risque d'extinction de la population de proie ou de prédateur. La définition d'un seuil en dessous duquel l'espèce est considérée comme éteinte permet de rendre compte de la baisse de la richesse spécifique. Les domaines d'extinction ou de persistance de la proie et de son prédateur en fonction de K et de r peuvent ensuite être considérés (voir section 6.2).

4.2 Dynamique en présence du superprédateur

Le modèle R-M a trois équations (Eq. 1) possède les trois points d'équilibres précédents sans superprédateur et deux équilibres propres autorisant le maintien du superprédateur (Eq. 4).

Ei = (X _1,i, X _2,i, X 3,i)

()) (e 2 a2 X 1,i = X 1,i, d3 b3 ,^b3 + X 2,i - d2 e3 a3 - d3^a3 b2 + X 1,i ( ) r 1 - X 1,i oü X 1,i est la solution de (b2 +X 1,i)= 0 pour i E {4, 5} a2 K

(4)

L'ajout du superprédateur fait apparaitre de nouvelles dynamiques d'équilibre plus complexes pour la chalne trophique (Fig. 4). En effet, lorsque les conditions sont favorables a son maintien, pour une capacité limite du milieu suffisamment importante et pour un taux de croissance assez élevé, quatre type de dynamiques

peuvent être observées : constante (A), périodique basse fréquence (B), chaotique (C) et périodique haute fréquence (D).

FIG. 4 - Différents régimes rencontrés a l'état d'équilibre pour le modèle R-M en présence du superprédateur. Les lettres A a D et les points associés situent les valeurs des paramètres choisis pour réaliser les portraits de phase présentés sur la figure suivante, d'après Gragnani et al. (1998)

Une manière simple de visualiser ces dynamiques au cours du temps (Annexe B) est d'en construire une représentation graphique oü chaque axe représente la biomasse d'un échelon trophique, une variable d'état différente du système. Dans un tel graphique, chaque point correspond a un état différent de la chalne trophique. Une trajectoire dans ce graphique rend donc compte de l'évolution du système puisqu'elle parcourt la succession de ses états au cours du temps. Comme il s'agit de modèles pour lesquels chaque état différents n'admet qu'un unique avenir, modèles dits déterministes, les trajectoires ne pourront se croiser. Ces trajectoires dépendent en outre du point de départ choisi, c'est a dire des valeurs des variables d'état au départ de la simulation, appelées conditions initiales. L'ensemble des trajectoires obtenues pour toutes les conditions initiales forme le portrait de phase tandis que l'ensemble des axes portant les variables constitue l'espace des phases.

Les différents portraits de phases obtenus selon un gradient d'enrichissement sur K et pour r = 1, 5 montrent la succession de quatre types de dynamique (Fig. 5). Le premier (A) correspond a l'attraction de la trajectoire vers un équilibre ponctuel constitué par le point noir. La trajectoire du système avant d'atteindre cet équilibre correspond au régime transitoire. Ce régime transitoire a été supprimé des repré-

10

10

0.3

1

1

0.5

X₁

C

0.1 X₂

0.20.4 0.6

X₁

K = 1

1

0.6 0.40 _.2

X₂

0

0

X₂

8

X₃ 7

6 2

K = 0,5 A K = 0,8 B

X₃

5

X₃

8

X₂

0

0

X₁

K = 1,5

D

1

1

2

6

0.5

0

2

12

X₃10

8

6

0.5

X₁

FIG. 5 - Portraits de phase présentant différentes dynamiques en présence du superprédateur. Ces dynamiques sont rencontrées de (A) a (D) selon un gradient d'enrichissement sur K pour r = 1, 5. (A) équilibre ponctuel, (B) cycle limite basse fréquence, (C) attracteur étrange et (D) cycle limite haute fréquence.

sentation suivante pour mieux mettre en évidence la complexité des attracteurs qui rend compte du régime a l'équilibre du système, dit régime asymptotique. Le second (B) correspond a un cycle limite qui se traduit par des oscillations lentes périodiques des biomasses des différentes espèces. Le troisième portrait de phase (C) est la représentation dans l'espace des phases d'une dynamique chaotique. L'attracteur est alors nommé attracteur étrange. Le dernier portrait de phase (D) est un cycle limite qui se traduit par des oscillations périodiques rapides des biomasses des différentes espèces. Cette séquence pour ce même modèle peut être plus compliquée ou plus simple selon la valeur des différents paramètres. Des états transitoires entre ces différentes dynamiques peuvent apparaltre comme la coexistence de deux attracteurs entre le chaos et le cycle limite a haute fréquence. La disparition de la dynamique chaotique est aussi possible avec un superprédateur qui ressemble au prédateur pour les paramètres de prédation et de croissance (Abrams & Roth,

1994).

RéSULTATS ET DISCUSSION

5 Modèle de chaîne trophique DEBf

5.1 Dynamique en absence du superprédateur

Ce modèle, dans sa version a deux échelons, possède lui aussi trois équilibres. E0 ₁ (Eq. 5) correspond au cas oü ni la proie nile prédateur ne peuvent se maintenir dans le chemostat tandis que E ₂ (Eq. 6) est l'équilibre oü seules les proies subsistent. E0 ₃ (Eq. 7) est l'équilibre qui permet la coexistence de la proie et du prédateur.

()

Xr,^Xr

E0 ₁ = ,0,0,0(5)

^Xk1 + Xr

E⁰₂ =(X* 0,2,^e* 1,2,^X* 1,2,^e* 2,2,^X*2,2)

=

^Xk1e*1 ,2 , 1 - e* 1,2

g1 (^ÿkM1 + ^ÿh) ÿkE1-hÿ ,

h ^ÿ(Xr - X* 0,2) (^Xk1 + X* 0,2) , J Xm1 ^X*0,2

) (6) X* 1,2, 0 ^Xk2+ ^X*1,2

E0 3 =(X* 0,3,^e* 1,3,^X* 1,3,^e* 2,3,^X*2,3)

= X* 0,3,	X*0,3 , ^Xk1+^X*0,3	^e*2,3^Xk2	g2(^ÿh+ ^ÿkM2) ÿkE2-hÿ ,	^Xk2 + X* 1,3 JXm1	ÿkE1 e* 1,3 - ^ÿkM1^g1		))^h^ÿ

(7)

Le diagramme de bifurcation synthétise les types de régime asymptotique atteints par le système (Fig. 6) pour des gammes de valeur des paramètres d'enrichissement, les paramètres de bifurcation. Il présente trois zones différentes selon Xr et ^ÿh. Tout d'abord une zone en arc de cercle pour des taux de dilution supérieurs a 0, 3 h^-1 ou des concentrations en glucose faibles (< 0, 2 mg.mL^-1) oü seule la proie peut se maintenir. Dans un autre arc de cercle atteint lorsqu'on augmente Xr et que l'on diminue ^ÿh, il y a coexistence de la proie et du prédateur autour d'un équilibre ponctuel. La dernière zone est obtenue pour Xr > 1, 2 mg.mL^-1 et pour des valeurs raisonnables de ^ÿh, la proie et le prédateur y subissent des fluctuations d'effectifpériodiques (Fig. 8).

Ces observations rejoignent des travaux antérieurs (Kooi & Kooijman, 1994a) et peuvent être complétées par une très petite zone de chaos située près du bord supérieur de la zone de fluctuation des abondances de la proie et du prédateur (Kooi & Hanegraaf, 2001).

5.2 Dynamique en présence du superprédateur

Le modèle DEB a trois échelons possédant six variables d'état, les véritables attracteurs du système se déploient dans un espace des phases a six dimensions. Les portraits de phase présentés ici (Fig. 7) correspondent donc a une projection dans

0.5 1 1.5 2

0.2

0.15

0.1

0.05

Proie
uniquement

Coexistence

stable de
la proie et du
prédateur

Fluctuations
périodiques
de la proie
et du prédateur

Concentration en glucose, X_r, en mg.mL^-1

FIG. 6 ~ Diagramme de stabilité des différents équilibres en fonction des deux paramètres de bifurcation du modèle DEBf, l'étoile signale les valeurs utilisées pour l'expérimentation de calibrage de Dent et al. (1976)

un espace des phases réduit composé uniquement des trois dimensions données par les biomasses des différents échelons trophiques. Selon un gradient d'enrichissement et avec un taux de dilution fixé a une valeur suffisamment basse, ici h ÿ = 0,02, on retrouve un équilibre ponctuel (A), des fluctuations pe'riodique de basse fréquence (B), une dynamique chaotique (C) et des fluctuations pe'riodiques de haute fréquence (D). Cette séquence de types d'équilibre est rigoureusement la même que pour le modèle R-M (Fig. 5). Elle a aussi été observée dans des modèles différents comme le modèle de Canale ou un modèle de métapopulation (Rinaldi & De Feo, 1999).

La dynamique en présence du superprédateur avec deux réserves (e2 et e3) est différente de ce qui se passe lorsque toutes les réserves sont supprimées du modèle en posant e, = f, pour i ? {1, 2, 3} (Kooi et al. , 1997). Le modèle présente alors une dynamique chaotique pour des zones différentes de l'espace des paramètres même si les mêmes dynamiques sont retrouvées. Les réserves semblent donc avoir une importance pour la description fine d'un système.

12 ₁

0

20

0

X₂

0

X₁

Xr = 170

Xr = 100 A B

4

2

0

4

X₃

2

510 1520 ²⁵

2

10

8

5

10

X₁

X₃

6₄

X₂

50

X₁

0

0

Xr = 350

Xr = 240 CD

4

5

4

3

2

X₃

20 40⁶⁰

1

0 40

15

100

5

X₁

X₃

2

10

X₂

20

X₂

FIG. 7 - Portraits de phase présentant différentes dynamiques en présence du superprédateur. Ces dynamiques sont rencontrées de (A) a (D) selon un gradient d'enrichissement sur Xr pour h ÿ = 0, 02. (A) équilibre ponctuel, (B) cycle limite basse fréquence, (C) attracteur étrange et (D) cycle limite haute fréquence.

6 Etude comparée des deux modèles

6.1 Lien direct

Il est tentant d'établir une relation directe entre les paramètres de bifurcation du modèles R-M, r et K, et ceux du modèle DEBf Xr et ^ÿh. Toutefois, l'exercice s'avère difficile et il n'est possible d'obtenir une équivalence entre les paramètres que dans quelques cas très restreints pour lesquels la réponse fonctionnelle est linéaire, de la forme ^X°

Xk1 , et l'espèce est soumise a un taux de mortalité de ^ÿh. Sous ces conditions, il apparait que les deux paramètres du modèle R-M sont liés entre eux et ne dépendent que de Xr (Kooi et al. , 1998).

Ceci rejoint l'observation que la dynamique du modèle R-M a deux échelons ne dépend que d'un seul paramètre de bifurcation tandis que celle du modèle DEBf dépend a la fois de Xr et de ^ÿh. L'équation logistique rassemble donc deux paramètres, la capacité limite du milieu K et le taux de croissance r, que semble capable de remplacer un seul paramètre mesurant directement la richesse nutritive du milieu (Kooi et al. , 1998). Rappelons en outre que l'équation logistique a été imaginée précisément dans l'hypothèse d'une limitation par le milieu de la population totale

par une force assimilée a un frottement, mais qu'elle n'explique pas le phénomène (Verhulst, 1838). L'implémentation dans le modèle DEBf d'une équation pour la concentration en nutriment abouti au même phénomène d'autolimitation de la population de proie mais sans en faire l'hypothèse. D'autre part le concept de capacité limite du milieu est une quantité qui varie dans le temps, ce qui empêche un bon paramétrage du modèle R-M et justifie son remplacement par une variable d'e'tat.

6.2 Paradoxe de l'enrichissement

En prenant un seul paramètre d'enrichissement, il est possible d'établir des diagrammes de bifurcations similaires pour chacun des deux modèles dans leur version a deux échelons (Fig. 8). La courbe tracée correspond a la biomasse de proie a l'équilibre. Cette courbe se sépare en deux lorsque le cycle limite apparalt, a la seconde valeur de bifurcation. Les deux valeurs de biomasse données correspondent alors au minimum et au maximum atteint lors des oscillations pe'riodiques sur le cycle limite.

Le diagramme de bifurcation obtenu pour le modèle R-M est valable de manière qualitative quelque soit la valeur des autres paramètres tandis que le diagramme de bifurcation du modèle DEBf n'est valable que pour certaines valeurs de ^ÿh. Le résultat est que le schéma classique du paradoxe de l'enrichissement, de déstabilisation d'un équilibre stable lorsqu'il y a enrichissement du milieu, perd de sa généralité pour ce second modèle.

D'autre part, dans les versions a trois échelons des deux modèles, la déstabilisation de l'équilibre au fil de l'enrichissement se traduit par la même séquence équilibre ponctuel, dynamique pe'riodique basse fréquence, dynamique chaotique et dynamique pe'riodique haute fréquence (Fig. 4). La complexité de la dynamique est donc croissante jusqu'à l'apparition du chaos puis décrolt vers un cycle limite (Fig. 5)(Fig. 7). L'ajout d'un superprédateur modifie donc la simple séquence de complexification de l'équilibre stable en cycle limite du modèle a deux niveaux trophiques. Ce schéma de complexification de l'attracteur d'une chalne trophique a trois échelons semble vrai pour une large variété de modèles (Rinaldi & De Feo, 1999) et correspond a la croissance de la biomasse moyenne du dernier échelon trophique.

6.3 Persistance des chaInes trophiques a deux echelons

Pour le modèle R-M, le paramètre de croissance r est intéressant en tant que facteur supplémentaire d'enrichissement du milieu. Malgré l'indépendance des bi-

RéSUlTaTS ET DISCUSSION

1

a

0.5

0 0.4

b

0.2

0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Capacité limite du milieu (K)

4

c

2

0

2

d

1

0

0 0.5 1 1.5 2 2.5

Xr en mg.mL^-1

FIG. 8 ~ Comparaison des diagrammes de bifurcation du modèle de R-M : (a) et (b), avec r = 1, et du modèle DEBf: (c) et (d) avec h ÿ = 0, 1

furcations de r, l'action de ce paramètre se situe sur la quantité de biomasses a l'équilibre et sur la vitesse d'ouverture du cycle limite lorsque K augmente. En effet, dans le domaine d'apparition du cycle limite, plus r sera petit plus le minimum de biomasse de prédateurs sera faible pour une même valeur de K. Cette démarche abouti a un découpage de l'espace des paramètres en quatre zones suivant si : les deux espèces sont sous le seuil, seule la proie est sous le seuil, seul le prédateur est sous le seuil ou aucune des deux espèces n'est sous le seuil (Fig. 9).

Pour le modèle DEBf, il a été possible d'utiliser des seuils naturels (Fig. 10). Le seuil correspond alors a la biomasse représentée par un seul individu dans le chemostat. Toutefois, pour observer l'effet d'éventuelles perturbations sur le milieu, un seuil beaucoup plus important a été choisi arbitrairement. Avec l'utilisation des seuils naturels, le modèle a deux échelons trophiques présente une large zone de coexistence pour une concentration en glucose supérieure a 0, 2 mg.mL^-1 et pour un taux de dilution inférieur a 0, 22 h^-1. Dans la version a trois échelons, on observe la même répartition imbriquée :

- pour une concentration en glucose faible ou un fort taux de dilution, seule la proie survie

- pour une concentration en glucose plus importante ou un taux de dilution moyen il y aura coexistence de la proie et du prédateur

0.2 0.4 0.6 0.8 1

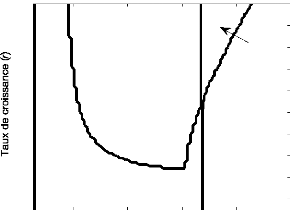
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1

Survie de la proie
uniquement

Survie de la
proie et
du prédateur

Survie ni de
la proie,
ni du
prédateur

Disparition
de la proie
entraine celle
du prédateur

Capacité limite du milieu (K)

FIG. 9 - Diagramme de survie des espèces du modèle R-M en fonction de K et de r pour un seuil de 0,05.

- pour une concentration en glucose suffisante ou un faible taux de dilution la coexistence des trois espèces sera possible

Dans un premier temps, l'enrichissement permet bien d'accroItre le nombre d'espèces de la chalne trophique mais cette possibilité est fortement contrainte par le taux de dilution. Avec ce seuil très bas, les oscillations ne provoquent pas de changement dans les zones de survie.

6.4 Temps de persistance des chaînes trophiques à trois échelons

Le temps de persistance (Fig. 11) pour chacun des échelons pour le modèle R-M apporte des informations supplémentaire car il permet de prendre en compte les différences de dynamique des attracteurs complexes, ce qui est impossible avec de simples portraits de phases. En ce sens, en les comparant a la figure qui présente la répartition des différents type de régimes asymptotiques (Fig. 4), il devient possible de classer les différentes dynamiques complexes précédemment rencontrées, a savoir fluctuations périodiques basse et haute fréquence et chaos en terme de persistance des espèces. Sans surprise, pour les trois échelons, les zones d'équilibre stationnaires offrent un temps de persistance soit infini soit nul.

Pour les proies, il apparalt peu de différences de temps de persistance entre

Concentration du substrat Xr Concentration en glucose Xr

Proie uniquement

Coexistence proie
et prédateur

Coexistence de la proie,
du prédateur et du
superprédateur

0.05

0.04

0.03

0.02

0.01

0

0.2

Survie de la
proie

0.15

0.1

Survie de la
proie
et du prédateur

0.05

0.5 1 1.5 2

0 100 200 300 400

FIG. 10 - Zones de survie des espèces du modèle DEBf en fonction de Xr et de h^ÿ avec un seuil d'un individu dans le chemostat pour des chalnes trophiques a 2 (a gauche) ou 3 (a droite) échelons.

les fluctuations périodiques basse fréquence et le chaos. La plus forte perte de persistance lorsqu'on enrichi le système selon K se trouve a la transition entre chaos et fluctuations périodiques haute fréquence. Le temps de parcours de l'attracteur est en effet plus faible et amène le système plus rapidement dans les zones d'extinction. Il est aussi remarquable que le chaos puisse localement augmenter le temps de persistance en fonction de l'enrichissement.

Pour les prédateurs, la perte de persistance lorsqu'on enrichi le système selon K apparait lors de deux changements de dynamique : entre la coexistence a biomasses constantes et les fluctuations périodiques basse fréquence et entre le chaos et les fluctuations périodiques haute fréquence. Il n'y a là aussi pas de différence importante de temps de persistance entre les fluctuations périodiques basse fréquence et la dynamique chaotique.

Pour le super-prédateur, la biomasse très supérieure de ce dernier échelon le place au-dessus du seuil d'extinction dans toute sa zone d'existence en régime asymptotique. Ceci provient probablement de l'absence de calibrage des paramètres du modèles sur des populations réelles. Une manière de le corriger serait de donner un seuil d'extinction différent au superprédateur, mais une telle démarche est difficile a justifier écologiquement.

L'analyse du temps moyen de persistance pour le modèle R-M renforce donc l'idée d'une persistance inversement proportionnelle a l'enrichissement avec des baisses importantes lors de l'apparition de fluctuations périodiques. Le chaos a une place a part dans ce schéma car son apparition ne provoque pas de baisse importante de la persistance avec l'enrichissement du milieu. La persistance est même plus importante sur le bord de la zone délimitant la dynamique chaotique,

FIG. 11 - Temps moyen de persistance pour les trois échelons du modèle R-M au sein de l'espace des paramètres de bifurcation.

ce qui rejoint des observations sur le maximum de biomasse du superprédateur (Rinaldi & De Feo, 1999). Pour ce qui est du taux de croissance de la proie, r, il doit être suffisant pour permettre la survie des échelons supérieurs, mais ne crée pas de variations continues de leur persistance.

FIG. 12 - Temps moyen de persistance pour les trois échelons du modèle DEBf au sein de l'espace des paramètres de bifurcation.

La même analyse sur le temps de persistance a été effectuée sur le modèle DEBf a trois espèces (Fig. 12). L'ajustement du modèle DEBf a des données expérimentales permet de donner une signification aux temps de persistance. Il s'agit ici du nombre d'heure moyen avant que les populations de proies, de prédateurs ou de superprédateurs qui forment la chalne trophique expérimentale ne passent sous un seuil de respectivement environ 10¹¹, 10⁹ et 10⁷ individus. Ces seuils correspondent a une même biomasse de 0, 5mm³.mL^-1. Même avec des seuils aussi élevé et peu réaliste, les temps moyens de persistance restent élevées : environ 1 jour dans la

zone la plus claire pour les proies, 1 a 2 jours pour les prédateurs. Le superprédateur fait preuve d'une très grande persistance sur toute sa zone de survie. Cette grande persistance du dernier échelon, déjà remarquée pour le modèle R-M, est associée pour le modèle DEB a des biomasses inférieures a celle des échelons de niveaux inférieurs. Cette robustesse peut être due a la linéarité de la mortalité du superprédateur qui est le terme de fermeture de la chalne trophique. ce terme semble avoir en effet une importance particulière pour les modèles de chalne trophique (Caswell & Neubert, 1998).

De tels temps de persistance dans des conditions d'équilibres, permettent de fournir une hypothèse pour expliquer la répartition très cosmopolite de nombreux micro-organismes. Les environnements naturels sont en effet, au contraire des hypothèses faites ici, fortement hétérogènes spatialement et subissent des conditions d'enrichissement qui ne sont pas constantes. Ces deux facteurs rendent d'autant plus difficile une extinction au niveau global. Ainsi même si, lorsque le milieu est enrichi, une plus grande instabilité est remarquée, cette instabilité paralt insuffisante pour causer la disparition des espèces de la chalne trophique étudiée ici.

Ces premiers résultats appellent plusieurs développements logiques. Des améliorations sont a apportées a la méthode de calcul de la persistance. Le choix d'une distribution uniforme n'est pas satisfaisant pour décrire la distribution des probabilités de biomasse sur l'attracteur. L'invariabilité de cette distribution au cours du temps peut en outre être utilisée pour identifier de manière numérique le passage du régime transitoire au régime asymptotique. Une optimisation de ce calcul permettrait aussi d'augmenter le temps maximum de persistance du système et donc la sensibilité de cette analyse. Ceci pourrait aussi se faire par le développement d'une méthode de calcul analytique de la persistance sur la base du travail de Mangel & Tier (1993).

Conclusion

L'apport de la théorie DEB réside dans la synthèse de plusieurs échelles et disciplines autour de l'individu. Comprendre l'individu permet ensuite de comprendre la population comme somme d'individus (Kooi & Kooijman, 1994a). La signification des paramètres des modèles issus d'une telle théorie est alors plus précise. La formulation des équations est contraintes de manière mécanique (thermodynamique, physiologie), ce qui semble important au vu de la grande sensibilité des modèles aux fonctions mathématiques employées (Fussmann & Blasius, 2005). Les modèles issus de la théorie DEB gagnent en réalisme et permettent de placer les modélisations dans un contexte expérimental précis. Le modèle présenté ici est donc pleinement opérationnel et possède un ancrage dans une réalité expérimentale en plus de l'objectif de généralité écologique auquel il prétend. Concrètement, cela se traduit par des résultats qui sont représentatifs : (i) quantitativement d'une réalité particulière, un temps moyen de persistance exprimé en heures pour les daphnies d'une chalne bactérie-cillié-carnivore et (ii) qualitativement de phénomènes écologiques, maintien de la persistance dans les modèles tritrophiques au fil de l'enrichissement pour des dynamiques complexes. La théorie DEB fait donc figure d'avancée vers une meilleur collaboration entre expérimentation et modélisation (Nisbet et al. , 2000).

Le paradoxe de l'enrichissement a été retrouvé dans les quatre cas de chalnes trophiques étudiés. Malgré les dissimilitudes d'approches des deux modèles, les résultats sont qualitativement similaires. Pour les chalnes trophiques a deux échelons, la même bifurcation d'un équilibre stable vers des fluctuations cycliques est retrouvée (bifurcation de Hopf). Pour les chalnes trophiques a trois échelons, la même séquence de types d'équilibre au fil de l'enrichissement a été mise en évidence au sein des deux modèles. Le premier équilibre permettant la coexistence est un équilibre ponctuel, puis viennent des fluctuations périodiques lentes, une dynamique chaotique et enfin des fluctuations périodiques rapides. Le paradoxe de l'enrichissement se maintien donc dans les chalnes tritrophiques mais il y suit un schéma plus complexe. Les analyses en temps de persistance montrent que c'est le changement d'une dynamique chaotique a une dynamique périodique rapide qui

CONCLUSION

est l'équivalent de la déstabilisation de l'équilibre ponctuel en un cycle limite des modèles a deux espèces. Toutefois, ces deux modèles utilisent la même réponse fonctionnelle de Holling type II et des termes de fermeture de la chalne trophique (mortalité du dernier échelon) linéaires. Au vu de l'influence de ces deux éléments sur la dynamique (Fussmann & Blasius, 2005; Caswell & Neubert, 1998), il conviendrait donc d'étudier la stabilité de ce schéma de complexification avec des réponses fonctionnelles et un terme de fermeture différents.

Le chaos apparait dans de nombreux modèles lorsque de nouveaux éléments sont pris en compte dans les modèles explicatifs. Il en est de même ici lors de l'inclusion d'un troisième échelon trophique. La complexification des modèles semble donc provoquer l'apparition du chaos. D'autre part, la dynamique chaotique demande bien une attention particulière puisqu'elle est un régime qui permet un temps de persistance important dans un milieu enrichi. L'hypothèse qui survient alors est que le chaos serait un régime optimum au-delà duquel l'écosystème perdrait en stabilité. Cette hypothèse est soutenue par la maximisation de la biomasse de superprédateurs dans de tels modèles pour des dynamiques chaotiques (Rinaldi & De Feo, 1999). Elle va a l'encontre de l'idée que le chaos est un phénomène qui n'existe pas dans les écosystèmes. Si le chaos tiens effectivement un role important dans les écosystèmes, cela doit remettre en cause la possibilité même de d'y réaliser des prédictions précises (Boero et al. , 2004). Le chaos nous apprend en effet que seules les tendances générales peuvent être prédites. Cela doit amener les écologistes a réfléchir a la formulation des questions posées pour que celles-ci restent solubles.

L'approche développée ici pour comprendre le role du chaos dans les écosystèmes n'apporte qu'un éclairage limité. Deux voies semblent particulièrement prometteuses pour mieux comprendre les dynamiques complexes de populations. En premier lieu, la spatialisation des modèles, même de manière simple, renforce l'idée d'un chaos qui favorise la survie des espèces (Allen et al. , 1993), ce qui peut même être décrit de manière analytique (Solé & Gamarra, 1998). En second lieu, la dynamique du régime transitoire, non considérée ici, semble elle aussi avoir un impact sur la persistance des espèces (Hastings, 2001).

Bibliographie

Abrams, P.A., & Roth, J.D. 1994. The Effects of Enrichment of Three-Species Food Chains with Nonlinear Functional Responses. Ecology, 75(4), 1118-1130.

Allen, J.C., Schaffer, W.M., & Rosko, D. 1993. Chaos reduces species extinction by amplifying local-population noise. Nature, 364, 229-232.

Becks, L., Hilker, F.M., Malchow, H., Jür^gens, K., & Arndt, H. 2005. Experimental demonstration of chaos in a microbial food web. Nature, 435, 1226-1229. .

Boero, F., Belmonte, G., Bussotti, S., Fanelli, G., Fraschetti, S., Gian^grande, A., Gravili, C., Guidetti, P., Pati, A., Piraino, S., Rubino, F., Saracino, O.D., Schmich, J., Terlizzi, A., & Geraci, S. 2004. From biodiversity and ecosystem functioning to the roots of ecological complexity. Ecological Complexity, 1(2), 101-109.

Cann, K. Mc, & Yodzis, P. 1995. Bifurcation structure of a three-species food chain model. Theoretical population biology, 48, 92-125.

Caswell, H., & Neubert, M.G. 1998. Chaos and closure terms in plankton food chain models. Journal of Plankton Research, 20(9), 1837-1845.

Cunnin^gham, A., & Nisbet, R.M. 1983. Transients and oscillations in continuous culture. Mathematical Methods in Microbiology, 77-103.

Dent, V.E., Bazin, M.J., & Saunders, P.T. 1976. Behaviour of dictyostelium discoideum amoebae and Escherichia coli grown together in chemostat culture. Archives of Microbiology, 109(1-2), 187-194.

Droo^p, M.R. 1973. Some thoughts in nutrient limitation Algae. Journal of Phycology, 9, 264-272.

En^glund, G., & Moen, J. 2003. Testing models of trophic dynamics : The
problem of translating from model to nature. Austral Ecology, 28(1), 61-69.

FErrIérE, R., & GattO, M. 1993. Chaotic population dynamics can result from natural selection. Proc. R. Soc. Lond. B, 251, 33-38.

FuSSmann, G.F., & BlaSIuS, B. 2005. Community response to enrichment is highly sensitive to model structure. Biology letters, 1, 9-12.

FuSSmann, G.F., EllnEr, S.P., ShErtZEr, K.W., & HaIrStOn, N.G. 2000. Crossing the Hopf Bifurcation in a Live Predator-Prey System. Science, 290, 1358-1360.

GraGnanI, A., FEO, O. DE, & RInaldI, S. 1998. Food Chains in the Chemostat : Relationships Between Mean Yield and Complex Dynamics. Bulletin of mathematical biology", 60, 703-719.

HaStInGS, A. 2001. Transient dynamics and persistence of ecological systems. Ecology Letters, 4, 215-20.

HaStInGS, A., HOm, C.L., EllnEr, S., TurChIn, P., & GOdfraY, H.C. J. 1993. Chaos in Ecology : Is Mother Nature a strange attractor? Annual Review of Ecology and Systematics, 24, 1-33.

JESSuP, C.M., FOrdE, S.B., & BOhannan, B.J.M. 2005. Microbial Experimental Systems in Ecology. Advances in ecological research, 37, 273-300.

KOOI, B.W., & HanEGraaf, P.P.F. 2001. Bi-trophic Food Chain Dynamics with Multiple Component Populations. Bulletin of mathematical biology, 63, 271-299.

KOOI, B.W., & KOOijman, S.A.L.M. 1994a. Existence and Stability of Microbial Prey-Predator Systems. Journal of theoretical biology, 170, 75-85.

KOOI, B.W., & KOOijman, S.A.L.M. 1994b. The transient behaviour of food chains in chemostats. Journal of theoretical biology, 170, 87-94.

KOOI, B.W., BOEr, M.P., & KOOijman, S.A.L.M. 1997. Complex dynamic behaviour of autonomous microbial food chains. Journal of mathematical biology, 36, 24-40.

KOOI, B.W., BOEr, M.P., & KOOijman, S.A.L.M. 1998. On the use of the logistic equation in models of food chains. Bulletin of mathematical biology, 60, 231-246.

KOOijman, S.A.L.M. 2000a. Dynamic Energy and Mass Budget in Biological Systems. Second edition edn. Cambridge University Press.

Kooijman, S.A.L.M. 2000b. Quantitative aspects of metabolic organization : a discussion of concepts. Philosophical Transactions of the Royal Society B : Biological Sciences, 356(1407), 331- 349.

Man^gel, M., & TIer, C. 1993. A Simple Direct Method for Finding Persistence Times of Populations and Application to Conservation Problems. PNAS, 90(3), 1083-1086.

MaY, R.M. 1974. Biological populations with nonoverlapping generations : stable points, stable cycles, and chaos. Science, 186, 645-647.

MCCaUleY, E., NIsbet, R.M., MUrdoCh, W.W., de Roos, A.M., & GUrneY, W.S.C. 1999. Large-amplitude cycles of Daphnia and its algal prey in enriched environments. Nature, 402, 653-656.

Monod, J. 1942. Recherches sur la croissance bactériennes. Paris : Hermann.

NIsbet, R.M., MUller, E.B., LIKa, K., & Kooijman, S A.L.M. 2000. From molecules to ecosystems through dynamic energy budget models. Journal of Animal Ecology, 69(6), 913-926.

PetroVsKII, S., LI, B.-L., & MalChoW, H. 2004. Transition to spatiotemporal chaos can resolve the paradox of enrichment. Ecological Complexity, 1(1), 37-47.

PIrt, S.J. 1965. The maintenance energy of bacteria in growing cultures. Proc. R. Soc. Lond. B, 163, 224-231.

PoUVreaU, S., BoUrles, Y., LefebVre, S., & AlUmno-BrUsCIa, M. 2006. Application of a dynamic energy budget model to the Pacific oyster, Crassostrea gigas, reared under various environmental conditions. Journal of Sea Research, 56(2), 156-167.

RInaldI, S., & De Feo, O. 1999. Top-predator abundance and chaos in tritrophic food chains. Ecology Letters, 2, 6-10.

RosenZWeI^g, M.L. 1971. Paradox of Enrichment : Destabilization of Exploitation Ecosystems in Ecological Time. Science, 171(Jan.), 385-387. .

RosenZWeI^g, M.L., & MaCArthUr, R.H. 1963. Graphical representation and stability conditions of predator-prey interactions. American Naturalist, 97, 209- 223.

Solé, R.V., & Gamarra, J.G.P. 1998. Chaos, Dispersal and Extinction in Coupled Ecosystems. Journal of Theoretical Biology, 193, 539-541.

TOlla, C. 2006. Modelling microbial populations in variable environments. Ph.D. thesis, Institute of the molecular and Cellular Biology, Vrije Universiteit.

TUrChIn, P., & Ellner, S.P. 2000. Living on the edge of chaos: Population dynamics of Fennoscandian voles. Ecology, 81, 3099-3116.

VerhUlSt, P.-F. 1838. Notice sur la loi que la population suit dans son accroissement. Correspondance mathe'matique et physique, Tome X, 113-121.

VOlterra, V. 1931. Leçon sur la the'orie mathe'matique de la lutte pour la vie. Paris : Gauthier-Villars.

Annexe A

Glossaire des termes de

modélisation

Attracteur : objet de l'espace des phases qui attire les trajectoires du système.

Attracteur étrange : objet complexe de l'espace des phases qui attire les trajectoires. Il correspond a une dynamique chaotique et est caractérisé par une dimension non entière, signe d'une grande complexité.

Bifurcation : changement de type de régime asymptotique du modèle selon la valeur de certains paramètres, nommés paramètres de bifurcation.

Chaotique : caractérisation d'une dynamique oü les différences entre les conditions initiales sont amplifiées de manière exponentielle tout en restant bornées. Cette dynamique correspond a un attracteur étrange dans l'espace des phases.

Cycle limite : attracteur de l'espace des phases ayant une forme de courbe fermée qui traduit une dynamique périodique.

Conditions initiales : valeurs des variables d'états au début de la simulation.

Diagramme de bifurcation : diagramme qui présente l'évolution des valeurs prises par les équilibres en fonctions de certains paramètres du modèle, les paramètres de bifurcation.

Equations différentielles : Equations régissant la variation des variables d'état,
ici les variables qui décrivent la chalne trophique, au cours du temps.

Espace des phases : espace dont les dimensions correspondent aux différentes variables d'états qui permettent la description de la chalne trophique (voir page 15 pour plus de détails). Chaque point de l'espace des phases représente un état possible du système, c'est a dire des variables d'état qui composent la chalne trophique.

ANNEXE A. GLOSSAIRE DES TERMES DE MODÉLISATION

Matrice jacobienne : matrice qui représente l'approximation linéaire du système. Elle permet de calculer comment évoluent les variations du système au voisinage d'un point de l'espace des phase, c'est a dire de savoir si un point d'équilibre est stable pour certaines valeurs de paramètres.

Paramètre : grandeur constante au cours du temps qui caractérise un processus ou une partie d'un processus a l'oeuvre au sein du système étudié, ici la chalne trophique.

Paramètre de bifurcation : paramètre pour lequel le système change d'e régime assymptotique.

Périodique : caractérisation d'une dynamique qui se répète aubout d'un certain temps. Cette dynamique correspond a un cycle limite dans l'espace des phases.

Point selle : équilibre stable dans certaines directions de l'espace des phases et instables dans d'autres.

Portrait de phase : représentation de la dynamique du système dans l'espace des phases.

Q uasipériodique : caractérisation d'une dynamique périodique couplant plusieurs périodes différentes.

Régime transitoire : dynamique observée avant d'atteindre l'attracteur du système.

Régime asymptotique : dynamique observée au bout d'un temps suffisament long, lorsque l'attracteur du système est atteint.

Trajectoire : représentation dans l'espace des phases de l'ensemble des états pris par le système au cours du temps lors d'une simulation.

Variable d'état : grandeur variant au cours du temps qui caractérise l'évolution du système, dans cette étude il s'agit des biomasses des différentes espèces, du nutriment ou des réserves. Sa variation est ici définie par une équation différentielle.

Annexe B

Dynamiques temporelles

6

4

2

0

8

A

X₁
X₂ X₃

12

B

10

8

6

4

2

0

0 200 400 600 800 1000
Temps

15

10

5

0

C

1700 1800 1900 2000
Temps

1700 1800 1900 2000
Temps

8

D

6

4

2

0

2700 2800 2900 3000

Temps

FIG. B.1 - Dynamiques temporelles rencontrées dans le modèle R-M au fil de l'enrichissement du système de A a D. Ces évolutions correspondent aux dynamiques dans l'espace des phases présentées sur la figure (Fig. 5).

Ces graphiques permettent de mieux visualiser les temps de parcours des attracteurs, c'est a dire les schémas répétitifs de la dynamique, tant pour le modèle R-M que pour le modèle DEB. Le régime transitoire est inclue pour le premier cas (A) mais absent des autres.

ANNEXE B. DYNAMIQUES TEMPORELLES

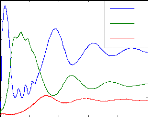
A

X₁

X₂

X₃

30

B

25

20

15

10

5

0

9000 9200 9400 9600 9800 10000

Temps

12 10 8 6 4 2 0

0 200 400 600 800 1000

Temps

80

C

60

40

20

0

7000 7200 7400 7600 7800 8000

100

D

80

60

40

20

0

9000 9200 9400 9600 9800 10000

Temps Temps

FIG. B.2 - Dynamiques temporelles rencontrées dans le modèle R-M au fil de l'enrichissement du système de A a D. Ces évolutions correspondent aux dynamiques dans l'espace des phases présentées sur la figure (Fig. 7).

Annexe C

La méthode semi-numérique

Voici le détail de la méthode employée pour calculer les valeurs des équilibres et tester leur stabilité dans le cas du modèle DEB a 2 échelons. Cette méthode présente la particularité d'allier des calculs analytiques traditionnels a des algorithmes informatiques.

L'existence des équilibres est tout d'abord testée numériquement pour les différentes valeurs des paramètres de bifurcation en regardant si les valeurs des variables d'état atteintes au point d'équilibre sont conformes aux hypothèses biologiques:> 0 et pour les réserves < 1. Le calcul de la matrice jacobienne permet de déterminer numériquement la stabilité de ces points d'équilibre suivant les paramètres de bifurcation. Cette matrice est obtenue en dérivant sur chaque ligne une équation du modèle en fonction de chacune des cinq variables en colonne.

?

? ? ? ? ? ? ? ? ? ?

J=

)

_(^ÿlb+^JXm1^X1^Xk1 0 _^JXm1^X0

(Xk1+X0)² Xk1+X0

^ÿkE1 0

^ÿkE1 ^Xk1

(Xk1+X0)²

0 g1( ^ÿkE1+ ^ÿkM1) ^ÿkE1e1^{-- ÿ}kM1^g1

(e1+g1)2 x1 e1+g1 _ lb ÿ _ ^JXm2^X2^Xk2

(Xk2+X1)² . . .

0 0

^ÿkE2 ^Xk2

(Xk2+X1 ⁾²

0 0 0

?

? ? ? ? ? ? ? ? ? ?

lb^ÿ

0 0

0 0

. . .

0 _^JXm2^X1

Xk2+X1

^ÿkE2 0

^ÿkE2 ^{e2-- ÿk}M2 ^g2
e2+^g2

g2 (^ÿkE2+^ÿkM2)

(e2+g2)2 x2

Le calcul numérique des valeurs propres de cette matrice pour les valeurs des points d'équilibre permet ensuite de tester leur stabilité : si la plus grande partie réelle des valeurs propres est négative, alors l'équilibre sera stable, sinon il sera

ANNEXE C. LA MÉTHODE SEMI-NUMÉRIQUE

instable. La confrontation ensuite des zones d'existence, de stabilité et d'instabilité pour différentes valeurs des paramètres de bifurcation permet de produire des figures comme la figure 6.

Résumé

Deux modèles de chaînes trophiques, dans leur version à deux et à trois échelons, sont comparés dans cette étude. Le premier modèle est un modèle traditionnel basé sur des hypothèses au niveau de la population. Le second modèle repose quant à lui sur des hypothèses d'allocation énergétique au niveau individuel, suivant la théorie des budgets dynamiques d'énergie et de masses (DEB). Ces deux modèles sont étudiés selon les paramètres qui décrivent la richesse du milieu. Dans les chaînes trophiques à deux échelons, il y a déstabilisation d'un équilibre constant en fluctuations périodiques selon le paradoxe de l'enrichissement. En revanche, dans les chaînes trophiques à trois échelons, une succession de dynamiques complexes est observée au fil de l'enrichissement : équilibre constant, fluctuations périodiques basse fréquence, dynamique chaotique et fluctuation périodique haute fréquence. Une analyse du temps de persistance des espèces dans ces systèmes montre que la réponse de ces différentes dynamiques à l'enrichissement varie. Le chaos ne produit pas de perte importante de persistance, contrairement à l'apparition de fluctuation périodiques. L'apport quantitatif de la théorie DEB est finalement souligné pour les chaînes trophiques de micro-organismes.

Mots clefs : Ecologie théorique, modélisation, chaîne trophique, théorie DEB, paradoxe de l'enrichissement, dynamique chaotique, persistance

Two kind of models are studied in their two or three trophic level version. The first one is a traditionnal approach with hypothesis made on the population. Le second one is based on energetic allocation at the individual level, following the Dynamic Energy and Mass Budgets theory (DEB). These two models are studied on the basis of enrichment parameters. In two trophic levels food chain, there is a destabilisation of constant coexistence state by periodic fluctuations acording to the paradox of enrichment. But, in three trophic level food chains, a sequence of complex dynamics is observed with enrichment: coexistence at constant value, low frequencies periodic oscillations, chaotic dynamic and hight frequencies periodic oscillations. A study ot the time of persistence, shows that persistence change with these different kind of dynamics. Chaotic dynamic does not produce a loss of persistence, contrary to periodic oscillations. The quantitave improvement of DEB theory for microorganims food chain is fynaly underlined.

Keywords: theoretical ecology, modelisation, food chains, DeB theory, enrichment paradox, chaotic dynamic, persistence