Equations differentials stochastics involving fractional brownian motion two parameter

University of Saïda
Faculty of Sciences and Technology
Department of Mathematics & Computer machine
Probability & Applications

Memory of Master

Equations Differentials Stochastics

Involving Fractional Brownian Motion

Two-parameter

HAMADA.I

Si tu veux courir, cours un kilomètre, si tu veux
changer ta vie, cours un marathon
Emil Zatopek1.

Contents

1 Element of Fractional Brownian Motion 5

1.1 Fractional Brownian Motion 5

1.1.1 Self-similarity 5

1.1.2 Hölder Continuity 6

1.1.3 Path Differentiability 7

1.1.4 The Fractional Brownian Motion is not a SemimartingaleforH=61 ₂ 7
1.1.5 Fractional Integrals and Fractional Derivatives of Func-

tions 8

1.2 Two-parameter Fractional Brownian Motion 9

1.2.1 The Main Definition 9

1.2.2 Fractional Integrals and Fractional Derivatives of Two-

parameter Functions 10

1.2.3 Hölder Properties of Two-parameter fbm 12

2 Stochastic Integration with Respect to Two-parameter Fractional Brownian Motion 15

2.1 Pathwise Integration in Two-parameter Besov Spaces 15

2.2 Some Additional Properties 23

3 Existence and Uniqueness of the Solutions of SDE with Two-Parameter Fractional Brownian Motion 25

4 CONTENTS

Chapter 1

Element of Fractional Brownian

Motion

1.1 Fractional Brownian Motion

Definition 1.1.0.1. The (two-sided, normalized) fractional Brownian motion (fBm) with Hurst index H E (0, 1) is a Gaussian process B^H = {BH _t , t E R} on (Ù, F, P), having the properties:

1. BH 0 = 0,

2. EBH t = 0; t E R,

1 (|t|^2H + |s|^2H - |t - s|^2H) ; t, s E R,

3. EBH t BH s = 2

1.1.1 Self-similarity

Definition 1.1.1.1. We say that an R^d-valued random process X = (Xt)t=0 is self-similar or satisfies the property of self-similarity if for every a > 0 there exist b > 0 such that:

law (Xat, t = 0) = law (bXt, t = 0) (1.1)

Note that (1.1) means that two process _Xat and bXt have the same finite-dimensional distribution functions, i.e., for every choice t1, ..., t_n E R,

P (Xat0 = x0, ..., Xat_n = x_n) = P(bXt₀ = x0, ..., bXt_n = x_n) For every x0, ..., x_n E R.

Definition 1.1.1. A stochastic process X = {Xt, t E R} is called b-selfsimilar if

{X_at,t E R} ^d ={a^bXt,t E R} in the sense of finite-dimensional distributions.

1.1.2 Hölder Continuity

We recall that according to the Kolmogorov criterion [3], a process X = (Xt)t?R admits a continuous modification if there exist constants á = 1, â > 0 and k > 0 such that

E [|X(t) - X(s)|^á] = k|t - s|^1+â

for all s,t E R.

Theorem 1.1.2.1. Let H E (0, 1). The fractional brownian motion B^H admits a version whose sample paths are almost surely Hölder continuous of order strictly less than H.

Proof. We recall that a function f : R -? R is Hölder continuous of order á, 0 < á = 1 and write f E C^á(R), if there exists M > 0 such that

|f(t) - f(s)| = M|t - s|^á,

For every s, t E R. For any á > 0 we have

E ~|BH t - BH _t |á] = E [|BH 1 |á] |t - s|^áH;

Hence, by the Kolmogorov criterion we get that the sample paths of B^H are almost everywhere Hölder continuous of order strictly less than H. Moreover, by [4] we have

lim t-+0+	sup	~~BH ~ (t)	= CH
		t^Hs/log log t-1

with probability one, where CH is a suitable constant. Hence B^H can not have sample paths with Hölder continuity's order greater than H.

1.1.3 Path Differentiability

By[5] we also obtain that the process B^H is not mean square differentiable and it does not have differentiable sample paths.

Proposition 1.1.3.1. Let H E (0, 1). The fractional brownian motion sample path B^H(.) is not differentiable. In fact, for every t0 E [0, 8)

~~~~

sup

lim

t--+t0

~~~~ = 8

B^H(t) - B^H(t0)

t - t0

With probability one.

1.1.4 The Fractional Brownian Motion is not a Semi-martingale for H =6 1 2

The fact that the fractional brownian motion is not a semimartingale for
H =61 ₂ has been proved by several authors. In order to verity B^H is not a
semimartingale for H =6 ¹ ₂, it is sufficient to compute the p-variation of B^H.

Definition 1.1.4.1. Let (X(t))tE[0,T ] be a stochastic process and consider a partition ð = {0 = t0 < t1 < ... < t_n = T}. Put

8_p(X,ð) := _Xn |X(ti) - X(ti_1)|^p

i=1

(i - 1

_~~B^H - BH

Ti Ti

Yn,p = TipH_1 _Xn

i=1

.

The p-variation of X over the interval [0, T] is defined as

Vp(X, [0, T]) := sup ð

8p(X, ð),

where ð is a partition of [0, T]. The index of p-variation of a process is defined as

I(X, [0, T]) := inf {p > 0; V_p(X, [0, T]) < 8}.

We claim that

I(B^H, [0, T ]) = 1H .

In fact, consider for p > 0,

81.1.5 Fractional Integrals and Fractional Derivatives of Functions

Since B^H has the self-similarity properity, the sequenceY_n,p, m ? N has the same distribution as

^eYn,p = m-1 _Xn ~_~B^H(i) - B^H(i - 1) ~~p

i=1

And by the Ergodic theorem [6] the sequence _eYn,p converges almost surely and in L¹ to E [~~BH(1) ^~~p] as n tends to infinity. It follows that

Vn,p =

Xn i=1

~( i "1 ~'\~~~~ ^p (i - 1 ~~B^H - BH m m

converges in probability respectly to 0 if pH > 1 and to infinity if pH < 1 as

1

n tends to infinity. Thus we can conclure that I(B^H, [0, T]) = H . Since for

every semimartingale X, the index I(X, [0, T]) must belong to [0, 1]?{2}, the

1

fractional brownian motion B^H can not be a semimartingale unless H = ₂.

1.1.5 Fractional Integrals and Fractional Derivatives of Functions

Let á > 0 (and in most cases below á < 1 though this is not obligatory). Define the Riemann-Liouville left- and right-sided fractional integrals on (a, b) of order á by

Z x

1

(I^á _a+f)(x) := f(t)(x - t)^á-1dt,

['(á) a

and

Z b

1

(I^á _b-f)(x) := f(t)(t - x)^á-1dt,

['(á) x

respectively.

We say that the function f ? D(Iá _a+(b-)) (the symbol D(.) denotes the domain of the corresponding operator), if the respective integrals converge for almost all (a.a.) x ? (a, b) (with respect to (w.r.t.) Lebesgue measure).

The Riemann-Liouville fractional integrals on R are defined as

(I^á +f)(x) :=

Z x 1 f(t)(x - t)^á-1dt, ['(á) -8

and

J 8

1

(I^á _-f)(x) := f(t)(t - x)^á-1dt,

['(á) x

respectively.

Z x

1 d

f(t)(x - t)^-ádt,

F(1 - á) dx -8

The Riemann-Liouville fractional derivatives of f of order á on R are defined by

(I+ - f)(x) = (D^á₊f)(x) :=

and

(I^?á -f)(x) = (D^á -f)(x) :=	-1	d 8 dx f (t)(t - x)^?á dt, x
	F(1 - á)

respectively.

For f ? I^á#177;(L_p(R)) with p > 1 the Riemann-Liouville derivatives coincide with the Marchaud fractional derivatives

_Z

( 15-7f)(x) := F(1 1 á) (f(x) - f(x - y)) R+

and

_Z

( ii^áf)(x) := F(1 1 á) (f(x) - f(x+ y)) R+

respectively.

1.2 Two-parameter Fractional Brownian Motion

1.2.1 The Main Definition

For technical simplicity we consider two-parameter fbm (fbm field) {B^H_t , t ? R²₊}, where t = (t1, t2). We suppose that s = t if s = (s1, s2), t = (t1, t2) and si = ti, i = 1, 2.

Definition 1.2.1. The two-parameter process {B^H_t ,t ? R²₊} is called a (normalized) two-parameter fBm with Hurst index H = (H1, H2) ? (0, 1)², if it satisfies the assumptions:

(a) B^H is a Gaussian field, Bt = 0 for t ? ?R²₊;

(b) EBt^i = 0, EBti B^H = 1 11 ^s 4 i=1,2

(ti ^2Hi + s2Hi i - |ti -si |2Hi)

Evidently, such a process has the modification with continuous trajectoires, and we will always consider such a modification. Moreover, consider "two-parameter" increments:Ä_sB^H_t := B^H_t - BHs1t2 - BHt1s2 + B^H_s for s = t. Then they are stationary. Note, that for any fixed ti > 0 the process B^H

(ti,.)

will be the fbm with Hurst index Hj, i = 1, 2, j = 3 - i, evidently, nonnormalized.

1.2.2 Fractional Integrals and Fractional Derivatives of 10 Two-parameter Functions

1.2.2 Fractional Integrals and Fractional Derivatives of Two-parameter Functions

For á = (á1, á2) denote (á) =

(á1)¹(á2)

Definition 1.2.2. [2] Let f ? T := [a, b] := 11 [ai, bi], a = (a1, a2), b =

i=1,2

(b1, b2). Forward and backward Reimann-Liouville fractional integrals of orders 0 < ái < 1 are defined as

(I _a^á_r¹² f)(x) := (á) 1,, f (u) ,x] ?(x, u, 1 - á) du,

and

_Z (Ir² f)(x) := (á)

f

u () ?(x, u ^du, 1 -- a) du,

+ E i=1,2,j=3--i	ái	áj	xi f (x) - f (ui, x j) % du i i), ai (xi -- Ui)^l#177;a
	xj - aj

correspondingly, where [a, x] = 11 [ai, xi], [x, b] = 11 [xi, bi], du = du1du2,

i=1,2 i=1,2

?(u,x, á) =| u1 - x1 |^á1| u2 - x2 |^á2 ,u, x ? [a, b].

Definition 1.2.3. Forward and backward fractional Liouville derivatives of orders 0 < ái < 1 are defined as

2

(Da

á1+ a
^a2 f)(x) := 1^-1(1 a) \
du 8x1?x2 I [a ,] ?(x f (u) u, á₎

and

(Dbá1á2

l f

x

\

A )

:= (1 - á)

?x1?x2 f[x ,b] ? (x u, á) x ? [a, b]

f(u)

Definition 1.2.4. Forward fractional Marchaud derivatives of orders 0 < ái < 1 are defined as

15r

( ² f)(x) :=(1 - á) f (x) +

á1á2 Ä_u f (x)du

?(x, u,á)i[a,x] 40(x, u, 1 + á)

1.2.2 Fractional Integrals and Fractional Derivatives of Two-parameter Functions 11

Let 1 = p = 8, the classes I₊ ^á1á2(L_p(T)) := ~f|f = I_a^á_rⁱ²?, ? ? L_p(T)}, I_- ^á1á2(L_p(T)) := {f|f = I_bJ^á2?, ? ? L_p(T)}

Further we denote Dá1á2

_a+ :=I-(á1á2)

_a+ . Of course, we can introduce the notion

of fractional integrals and fractional derivatives on R²₊. For exemple, the Riemann-Liouville fractional integrals and derivatives on R²₊ are defined by the formulas

(Iá1á2 f)(x) := (á) L8,x] ?(x^f(u^t) á) dt,

Z

(I1^1á2 f)(x) := (á) f(ut) á) dt,
?(x [x,8) 2

(I_V^á1á2) f)(x) = (DT^á2 f)(x) := (1 - á) O x1Oxe (t) dt,

x2 _(-8,x] ?(x,t, á)

and

O2 f f(t)

(I^-(á1á2)f)(x) (D^á1á2f)(x)

:= (1 - á) Ox1Ox2 _i[x,8)?(x,t, á)dt,

0 < ái < 1. Evidently, all these operators can be expanded into the product of the form Iá1á2 += Iá1

+ ? Iá2

+ , and so on. In what follows we shall consider only the case Hi ? (1/2, 1). Define the operator

YM#177; 1 H2 f := i=1,2

4) Iá1á2 #177; f.

Definition 1.2.5. A random field {Xt,t ? R²₊} is a field with independent
increments if its increments {ÄsiXti, i = 1, n} for any family of disjoint

rectangles {(si, ti], i = 1, n} are independent.

Definition 1.2.6. The random field {Wt,t ? R²₊} is called the Wiener field if W = 0 on OR²₊. W is the field with the independent increments and

E(Ä_sWt)² = area((s,t]) = II (ti - si).

i=1,2

Let we have a probability space (Ù,F, P) with two-parameter filtration {Ft, t ? R²₊} on it. It means that F_s ? Ft ? F for s < t. Denote F^* _s:= ó{F_u, s = u}.

Definition 1.2.7. An adapted random field {Xt,Ft,t ? R²₊} is a strong martingale if X vanishes on ?R²₊, E|Xt| < 8 for all t ? R²₊ and for any s < t E(Ä_sXt|F^* _s) = 0.

Evidently, any random field with constant expectation and independent increments is a strong martingale, in particular, the Wiener field is a strong martingale.

Definition 1.2.8. Let

~ f ? L21H2 := f : R² -->R : J ((M5^1H2f)(t))²dt < 8}

R

2

Then we denote I f (t)dBr1 ^H2 as .1 (M- ^H1H2 f)(t)dWt for the underlying R2 R2

Wiener process W.

1.2.3 Hölder Properties of Two-parameter fbm

We fix á = (á1, á2), ái ? (0,1] and let T = [a1, b1] × [a2, b2]. Let f the Riemann-Liouville fractional integral of order á i.e

1

,

(I^á_a+f)(x1, x2) = f(t1 ^t2)dt1dt2, x1x2) ? T

(á1)(á2) a1 a2 (x1 t1)^1-á1 (x2 - t2)^1-á2

x1

I

x2

The space Ëá,p = (I^á_a+)(L_p(T)) is called the Liouville space (or Besov space) and it becomes separable Banach space with respect to the norm IIáa+fIá,p = If1_p

Proposition 1.2.3.1. [7] For every á, â

Iá _a+I^â a+= Iá+â

_a+ ,

If f ? C²_b (T) and f = 0 on ?1T = ([a1,b1] × {b1}) ? ({a1} × [a2,b2])then the function

1 1x1 r2 _a²f (t1, t2) dt1dt2

+f (x1, x2) =

(1 - á1)(1 - á2) L₁ J_a2 ?t1?t2 (x1 - t1)^á1(x2 - t2)^á2

(1.2)

is the unique function from L₈(T) such that

I^á_a+D^á_a+f = f.

For a rectangle D = [s1, t1] × [s2, t2] ? T we define the increment on D of the function f : T ? IR by

f(D) = f(t1, t2) - f(t1, s2) - f(s1, t2) + ^f(s1, s2).

We denote by _C[ai,bi],ái the space of all ái-Hölder functions on [ai, bi] and

kfk[ai,bi],ái = sup u6=v,ai<u,v<bi

|f(u) - f(v)| (u - v)ái .

Also, we denote by _CT,á1,á2 the space of all (á1, á2)-Hölder functions on T, i.e., f ? CT,á1,á2 if f is continuous,

kf(a1, .)1[a2,b2],á2 < 8, 1f(., a2)I[a1,b1],á1 < 8

and

|f([u1, v1] × [u2, v2])|

< 8.

|u1 - v1|^á1|u2 - v2|^á2

1fkT,á1,á2 = sup

ui6=vi

Proposition 1.2.3.2. [8] Let 0 < â1 < á1,0 < â2 < á2 and p = 1. Then we have the continuous inclusions Ëá,p ? Ëâ,p,

Ëá,p ? Cá1_p^-1,á2_p^-1, Câ1,â2 ? Ëã,p if áip > 1, âi > ãi > 0

ici il faut tout d'abord définir la fonction généralisé

Proposition 1.2.3.3. [8] Assume that f, g are C¹([a, b])-function with f(a) = 0. Let á, â ? (0,1] be such that á+â > 1 and let ä := {a = t0 < ... < t_n = b} be a partition of [a, b] with the norm 1ä1 = max (tj+1 - tj). Then for every

j

0 < å < á + â - 1 the following estimates hold:

~~~~	fb f(t)dg(t)~~~~ = C(á, â)1fk[a,b],álgk[a,b],â(b - a)^1+å, (1.3) a

I^f b

~

f (t)dg(t) - E f(ti)[g(ti+1) - g(ti)]~= C(á, â)1f1[a,b],á1g1[a,b],â(b-a)^å.

~

i

(1.4)

14 1.2.3 Hölder Properties of Two-parameter fbm

Chapter 2

Stochastic Integration with

Respect to Two-parameter

Fractional Brownian Motion

2.1 Pathwise Integration in Two-parameter Besov Spaces

The next result gives an estimate of the Stieltjes integral for smooth functions in terms of Hölder norms and represents the essential step for extending the Stieltjes integral to Hölder functions of two variables.

Proposition 2.1.1. Let ái + âi > 1, ái, âi ? (0, 1], f, g ? C²(T) and let 0 < åi < ái + âi - 1. Then

i

~~~~

b1lb2 f (t1,t2)dg(t1,t2) a1 L

(2.1)

= C(ái, âi)kgkT,â1,â2 {1f1T,á1,á2(b1 - a1)^á1+â1(b2 -a2)^á2+â2 +1f(., a2) [a1,b1],á1(b1 - a1)^1+å1(b2 - a2)^â2

+1f(a1, .) [a2,b2],á2(b1 - a1)^â1(b2 - a2)^1+å2 + |f(a1, a2)| (b1 - a1)^â1(b2 - a2)^â2}

Moreover, for every partition Ä = (si, _tj)i,j, a1 = s1 < ... < sn1 = b1, a2 = t1 < ... < t_n2 = b2, 1Ä1 = max(si+1 - si) + max(tj+1 - tj) , we have

i j

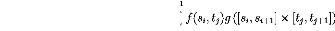
b1

f

b2 n1-1n2-

1

f(

74

,u2)dg(u1,u2) -

E E f(si, tj)g ([sisi+1] × [tj, tj+1])

fa1 a2 i=1

j

=1

(2.2)

+ ~kgkT,â1,â2 + kg(a1, .)k[a2,b2],â2kÄk^á1~ = C(ái, _{âi)kfkT,á1,á2} ~kgkT_,â_1,â₂kÄk^{á1+â1+á2+â2?2}

+ (1g1T,â1,â2 + kg(., _{a2)1[a1,b1],â11Älá2)]} .

Proof. Assume first that f = 0 on ?1T and define

h(t1, t2) = g(b1 - t1, b2 - t2) - g(b1 - a1, b2 - t2)

-g(b1 - t1, b2 - a2) + g(b1 - a1, b2 - a2). (2.3)

Then

Z _b1 Z b2 f(t1, _t2)?²g(t1, t2) dt1dt2 = ?²(f * h)(b1, b2) . ?t1?t2 ?t1, ?t2

a1 a2

Choose åi > 0, 0 < á⁰_i < ái, 0 < â0 i < âi with á⁰_i + â0 i = 1 + åi. By proposition the function f1 = D_a^á+^' f, h1 = D_a^â+^' h are in L₈ and satisfy

Iá0 = f , I_a^â+^" h1 = h. (2.4)

Then by proposition, 2.3 and 2.4 we have

Z _b1 Z b2 Z _b1 Z b2 f(t1, _t2)?²g(t1, t2)

f(t1, t2)dg(t1, t2) = dt1dt2

?t1?t2

a1 a2 a1 a2

?²(f * h)(b1, b2)

=

?2

_{h i}

_Iá⁰

a+f1 * Iâ0

a+h1 (b1, b2)

?t1?t2

=

?t1?t2

?2 _hi

_Iá⁰+â⁰

= _a+ (f1 * h1) (b1, b2)

?t1?t2

?2 ~I1

= _a+I^å_a+(f1 * h1)] (b1, b2)

?t1?t2
?2

= I^å _a+(f1 * h1)(b1, b2),

?t1?t2

= Ia(+ 1,1)_, å₌

such that Ia1+ Iå1,å2

_a+

and then

~Z

kf1 * h1k8

(b1 - a1)^1+å1(b2 - a2)^1+å2

= å1å2(å1)(å2) kf1k8kh1k8.

~Z ^{b2 b1} ~~~~ = (b1 - a1)^å1(b2 - a2)^å2
~~ f(t1, t2)dg(t1, t2) å1å2(å1)(å2)
a1 a2

Next, the integration by parts for functions of two variables (see[9]) yields

f1(x1, x2) = (1 - á^'o(1 - á^'2) fa x

, " (1 - t1 )á 4 (x2 - t2)^á4

1

r

2df ([t1,x1]× [t2,x2])

1 f ([t1,x1] × [t2, x2]) lim (1 ? áo(1 ? t%?x% (x1 - t1)^á4 (x2 - t2)^á4

lirn

x1 f ([t1, x1] [t2, x2])_,

- dt1
t2?x2 fa1 (x1 t1)^á1 (x2 - t2)^á2

x2 f ([t1, x1] × [t2, x2]) dt

lim

-

t1?x1 L2 (x1 _t1)á4 (x2 - t2)á2 2

f2 f ([t1,x1] × [t2, x2])

a1 a2 (xi - t1)^á4+1(x2 - t2)^á2+1

, dt1dt2}

+ác_.á⁰2

,0

á1u2 ix2 f ([t1,x1] × [t2, x2])

t, d dt
(1 - áo(1 - j_a2x1-t1)^á4+1(x2 t2)^á2+1

i 2,

so that

kf1k8 =

,0 á1u2 (1 ? ác)(1 ? T,á1,á2

(2.6)

x1 _fx2

× (x1 - t1 -á4-1 (x2 - t2)^á2-á4-1dt1dt2

a2

= - a1)^á1-á4(b2 - a2)^á2-á4.

Similary

- a1)^â1-âc(b2 - a2)^â2-â. (2.7)

By using (2.6) and (2.7) in (2.5) we obtain (2.1) if f = 0 on ?1T. If f is not necessarily null on ?1T then we define

f(t1,t2) = f ([a1,× [a2, t2])

Then f = 0 on ?1T and f, f have the same increments. Then we have

J b1 1b2

a2 f (t1,t2)?2 g(t1 t2)

?t1?t 2 dt1dt2

Z _b1 Z b2 Z _b1 Z b2

f(t1, _t2)?²g(t1, t2) f(a1, _t2)?²g(t1, t2)

= dt1dt2 + dt1dt2

?t1?t2 ?t1?t2

a1 a2 a1 a2

+ fa1 a2

b1

f

b

2

f(t1, a2)?2g(t1,

?t1?t2

t2) dt1dt2 + f (a1, a2)g(([a1,b1]× [a2, b2]))

,,

= I2 b2 f (t1,t2)?2 g(t1, t2)

dt1dt2 + ^b2 f(a1, t2) r?g(b1 t2) ?g(a1 ?t2 ?t2

t2) 1 dt2

a1 ?t1?t2

a2

a

?g(t1,b2) ? g(t1, a2)1 dt1 + f (a1, a2₎g(([a1,b1]×[a2, b2])

f21 ^b1 f(t1a2) [ ?t1

4

Jk.

k=1

(2.8)

From the previous reasoning we have

ja1 ^b1 l_a:² f (t1, t2) ?²g(t1 , t2)

dt1dt2

?t1?t2

= C(ái,âi)kfkT,á1,á2kgkT,â1,â2(b1 - a1)^á1+â1(b2 - a2)^á2+â2. (2.9)

Next by using (1.3) we have

~~Z b2 ~?g(b1, t2) ~

|J2| =

- ?g(a1, t2) ~~~~

~~ [f(a1, t2) - f(a1, a2)] dt2

?t2 ?t2

a2

+ |f(a1, _a2)g ([a1, b1] × [a2, b2])|

= C(ái, âi) kf(a1, .)1[a2,b2],á2kg(b1,.) - g(a1, .)k[a2,b2],â2 (b2 - a2)^1+å2

+ |f(a1, a2)| 1g1T,â1,â2(b1 - a1)^â1(b2 - a2)^â2,

so that

11 J2 11= C(ái, âi)11g1IT,â1,â2 { If(a1, .)1[a2,b2],á2 (b1 - a1)^â1(b2 - a2)^1+å2 + | f (a1, a2)| (b1 - a1)^â1(b2 - a2)^â2 1.

(2.10)

Similarly

n11J311 = C(ái, _{âi)1g1T,â1,â2} If(., a²)1[a1,b1],á1 (b1 - a1)^1+å1(b2 - a2)^â2 +|f(a1, a2)| (b1 - a1)^â1 (b2 - a2)^â2}.

(2.11)

Replacing (2.10) and (2.11) in (2.8) we obtain (2.2). Next we have

a¹ (12

IÄ f (u1,u2)dg(u1, u2) - E f (si,tj)g ([sisi+1] ×

= Ib1 b2

f

=E

[f(u1, u2) - f(si,tj)] dg(u1, u2)

i,j

=E

i,j

isi+1 itj+1

+E

+E

jsi+1 itj+1

jsi+1 itj+1

[f(u1,u2) - f(u1, tj) - f(si,u2) + f(si,tj)] dg(u1, u2) [f(u1, tj) - f(si,tj)] dg(u1, u2)

i,j t
·

isi+1 itj+1

8i 3 [f(si, u2) - f(si,tj)] dg(u1, u2)

= Ä + I_,²_6,

(2.12)

From (2.1) it follows that

|I^1Ä| = C1f11T,á1,á2110T,â1,â2E i,j

(si+1 - si)^á1+â1(tj+1 - tj)^á2+â2

(2.13)

I²Ä =E

i

Z b1

^,j Xtj)1 (u1, tj) [? g(u1, tj+1) ?g(u1,du1

?u1 ?u1

a1 j

₁si+1 ftj+1

Jsi[f (u1,tj) f (si, tj)]

3

?u1?u2

?²g(u1, u2) du1 du2

t
·

^i,j [f(u1, tj) - f (si,tj)]

[?g(u_?1_u,t₁ j+1) ?g(u1,tj)1 du1

?u1

₁s i +1

C11fkT,á1,á2kgkT,â1,â2MÄ1^{á1+â1+á2+â2-2}.

Next define

f1(u1, u2) = f(u1, u2) - f(si, u2) ifu1 ? [si, si+1).

Then (1.3),(1.4) imply

b1

I1 = C 11g(ui ) 11

fl (U1, -) 11 [a2,b2],á2 [a2 ,b2],â2 du1. (2.14)

a1

Since u1 ? [si, si+1) we have

If1(u1,.)1[a2,b2],á2 = 1f1T,á1,á2 (u1 - si)^á1 = 1f1T,á1,á2 IÄIá1

and

Mg(u1,.)1[a2,b2],â2 = (b1 - a1)â1 kg1T,â1,â2 + 1g(a1, .)1[a2,b2],â2 (2.15)

It follows by replacing in (2.14) that

11I²Ä11 = C111f11T,á1,á211Äll^á1 (11g11T,â1,â2 + 11g(a1,.)11[a2,b2],â2) . (2.16)

Similarly

11I³Ä11 (11g4,â1,â2 + 11g(.,a2)11[a1,b1],â1) . (2.17)

Finally using (2.13),(2.16) and (2.17) in (2.12) we (2.2).

Next we define CT,á1,á2,8 the space _CT,á1,á2 endowed with the norm

1x1T,á1,á2,8 = 1x1T,á1,á2+ sup a1=t1=b1

1x(t1, .)I[a2,b2],á2+ sup a2=t2=b2

kx(.,t2) [a1,b1],á1+1x T,á1,á2.

f (u, v)dg(u, v) f - a1)^â1(b2 - a2)^â2.

~

_.fb1 b2

a

2

The space _{(CT,á1,á2,8,1.1T,á1,á2,8)} is a Banach space.

The convergence of Riemann-Stieltjes sums to the integral for Hölder functions of one variable in shown in [[8],[10],[11]]. The corresponding result for functions of two variables is given in the next theorem.

Theorem 2.1.1. Let T0 = [a1 - å0, b1 + å0] × [a2 - å0, b2 + å0], å0 > 0, and let á1, á2, â1, â2 ? (0, 1] be such that ái + âi > 1. If f ? CT0,á1,á2, g ? CT0,â1,â2, then there exists a unique real number fb2

a

1

a

²

every sequence of partitions Äⁿ = (sⁿ_i ,tⁿ_j ), a1 = s0 < ... < sk(n) = b1, a2 = t0 < ... < tk(_n) = b2, with 1Äⁿ1 ? 0, the Riemann-Stieltjes sums

f(u,v)dg(u,v) such that for

Sog= E i

X(Es^Ti i,s7+1 ] × Et^rj ^i,t7+1]) j

b2

converge to f

f(u,v)dg(u,v). Moreover, the following estimate holds:

a

1

a

2

Proof. It is enough to prove that for every ä > 0 there exist ç > 0 such that for every two partitions (Äi)i=1,2, ai = uⁱ₀ < ... < uim(i) = bi with kÄik < ç we have

~_~~Sf,g

Ä1- _Sf,g ~~~ = ä. (2.19)

Ä-2

Let J ? C⁸(R²) be such that J = 0, J(x) = 0 if 114 = 1 and Iand define

R2

J_å(x) = å^-2J (^x). Consideer the regularizations of f_å, g_å of f,g. Recall that å

f_å(x) =R ₂ J_å(x - y)f (y)dy = f(x - åy)J(y)dy,
and for g_å similarly (as usual f,g are extended as 0 on R² \ T0). It is well
known that f_å ?f, g_å ? g uniformly on T . Also it is easily seen that

(2.20)

få ? CT,á1,á2, g_å ? CT,â1,â2.

Next we show that if 0 < á⁰_i < ái, 0 < â0 i < âi, then

f_å ? f in CT,á⁰ g_å ? g in CT,â⁰

1,á0 2, 1,â0 2,

f_å(a1, .) ? f(a1, .) in C[a2,b2],á⁰₂,

g_å(a1, .) ? g(a1,.) in C[a2,b2],â⁰₂, (2.21)

f_å(., a2) ? f(., a2) in C[a1,b1],á^'₁,

g_å(., a2) ? g(., a2) in C[a1,b1],â⁰₁. (2.22)

We have

(f_å - f) ([s1, t1] × [s², t²])

_Z

= J(u, v) {f ([s1 - åu, t1 - åu] × [s2 - åv, t2 - åv])}

B(0,1)

-f ([s1, t1] × [s2, t2]) dudv,

and then for every å,ä > 0,

sup

si6=ti

|(f_å - f) ([s1,t1] × [s2, t2])|

2

|s1 - t1|^{á0 1}|s2 - t2|^á0

= sup

~ ~|(få - f) ([s1, t1] × [s2, t2])| 2 , |si - ti| > ä, i = 1, 2 |s1 - t1|^á0 1|s2 - t2|^á0

~|(f_å - f) ([s1, t1] × [s2, t2])|

+ sup

₂ , |s1 - t1| > ä or |s2 - t2| > ä

|s1 - t1|^{á0 1}|s2 - t2|^á0

1

= sup {|f(u1, v1) - f(u2, v2)| , |ui - vi| < å, ui, vi ? T0, i = 1, 2}

äá⁰ 1+á0 2

+CkfkT,á1,á2 max(äá1-á0 1, äá2-á0 2) ? 0 as å ? 0, ä ? 0.

Similarly one prove(2.21),(2.22).

Next we choose 0 < á⁰_i < ái, 0 < â0 i < âi with á^'_i + â0 i > 1. Then from (2.20),(2.22) and (2.12) we obtain

~~~~~ + ~~~Sf,g

_~S^f,g

Ä1 - _Sf,g ~~~ = ~~~Sf,g

Ä1 - Sfå,gå Ä2 - _Sfå,gå ~~~

Ä2 Ä1 Ä2

ib1 fa2 b2 b1 _fb2

Qfå_l,gå

"Ä fådgå +Sk2 gå -

faa

1 1

a

2

+

~~

fådgå ~~

lim

å?

H

0

b1 _fb2 b1 _fb2

fådgå =

f dg,

1

1

12

²

1

1

I

~~~~~ + ~~~Sf,g = _~S^f,g

Ä1 - Sfå,gå Ä2 - _Sfå,gå ~~~

Ä1 Ä2

~ n ₁+á⁰ ₂+â⁰ ₂-2

+C ~kfåkT,á⁰ 1,á0 2 + kgåkT,â⁰ (kÄ1k + kÄ2k)á0 1+â0

1,â0 2

_2o

+ (kÄ1k + kÄ2k)á0 ¹ + (kÄ1k + kÄ2k)^á0

~~~~~ + ~~~Sf,g = _~S^f,g

Ä1 - Sfå,gå Ä2 - _Sfå,gå ~~~

Ä1 Ä2

_n

1

+ C1 (kÄ1k + kÄ2k)á0 ₁+â⁰ ₁+á⁰ ₂+â⁰ 2-2 + (kÄ1k + kÄ2k)^á0

+ (MÄ1M + 1Ä21)^á02/ ? 0, as å ? 0 and then IÄiI ? 0. The previous computation also shows that

2.2 Some Additional Properties 23

2.2 Some Additional Properties

24 2.2 Some Additional Properties

Chapter 3

Existence and Uniqueness of the

Solutions of SDE with

Two-Parameter Fractional

Brownian Motion

Next for K > 0 we define the closed sets

C[_a,b],H(K) = {? ? C[a,b],H : I?1[a,b],H = K},

and for ?i ? C[ai,bi],ái,

{CT,á1,á2,00(K, ?1, ?2) = x ? CT,á1,á2,00 : x(a1, .) = ?1, x(., a2) = ?2, 1x1T,á1,á2 = K,

sup

a1<t1<b1

< }

|x(., t2 ) | [a1 ,b1], K

_al - .

|x(t1, .)|[a2,b2],á2 = K, sup

a2<t2<b2

By using the Hölder spaces of functions we obtain the following local contraction property of an integral operator between such spaces, which is useful in the next existence and uniqueness result.

Proposition 3.1. Let â1, â2 ? (1/2, 1] and á1, á2 be such that âi > ái > 1 - âi.Let g ? CR²,â1,â2 and b, ó : R ? R be such that b is bounded and Lipschitz and ó ? C²_b(R) with ó^" Lipschitz. Then for every K > 0 and ai, bi ? R,ai < bi, i = 1, 2, there exists å0 > 0 independent of ai, bi, such that

,ái(K) the operator

for every ?i ? C[ai,ai+å0]

F : C[a1,a1+å0]x[a2,a2+å0],á1,á2,00(2K, ?1, ?2) ? C[a1,a1+å0]x[a2,a2+å0],á1,á2,00(2K,?1,?2)

defined by

Z s_J t s_f t

(F x)st = ?1(s) + ?2(t) + b(x_u,v)dudv + ó(x _u,v)dg(u, v),

a2 a1a2

Existence and Uniqueness of the Solutions of SDE with 26 Two-Parameter Fractional Brownian Motion

is a contraction.

Proof. Clearly we have

~ ~ Z .ja2b(xu,v)dudv T,á1,á2,8 = kb1₈(b1 - a1)^1-á1(b2 - a2)^1-á2 (3.1)

× [(b1 - a1)^á1(b2 - a2)^á2 + 1] .

By using (2.18) it follows

~ Z . ~Z. ~~ a1 a2

~ ~ ó(xu,v)dg(u, v) = Iló(x)11T,á1,á2,811g1IT,â1,â2 T,á1,á2

×(b1 - a1)^â1?á1(b2 - a2)^â2?á2 [(b1 - a1)^á1(b2 - a2)^á2 + 1] . (3.2)

Next

ó(x) ([s1, t1] × [s2, t2]) = (xt1,t2 - xt1,s2)

_- -(xs1 ,t2 xs1,s2)

(ëxt1,t2 + (1 - ë)xt1,s2) dë + (1 - ë)xs1,s2) dë

1

J0

1

Z0

Then

1

1

ó (x) ([s1,t1] × [s2, t2]) = (xt1,t2 - xt1,s2 - x _s1,t2 + xs1,s2) I ó' (ëxt1,t2 + (1 - ë)xt1,s2dë)

^+(x:(¹ëx

,t2 _s2 s1,s2) [ó^f _(ëxt1,t2 + (1 - ë)xt1,s2)

-ó

+ (1 - ë)xs1,s2)] dë.

(3.3)

Then (3.3) implies

{

|ó(x)([s1,t1] × [s2,t2])| 1,

110110011x1IT,aá2 + Iló^'IlL11x(s1, .)1[a2,b2],á2

1

×

o

[ë t2) II [a1,b1],á1 + (1 - ë) Mx(., s2)1[a1,b1],á1 ] dë} (t1 -s1)^á1(t2 -

and hence, if x ? CT,á1,á2,8(K, ?1, ?2), then

Ió(x)1T,á1,á2 = K (Mól8 + 1ó¹1_L) . (3.4)

Existence and Uniqueness of the Solutions of SDE with Two-Parameter Fractional Brownian Motion 27

From (3.2),(3.2) and (3.4) it follows that

Fx E C[a1,b1]x[a1,b1],á1,á2,00

if x E _{C[a1,b1]x[a1,b1],á1,á2,00} and also for å1 > 0 enough small,

Fx E C[a1,a1+å1]x[a2,a2+å1],á1,á2,00(2K, p1, p2)
if x E C[a1,a1+å1]x[a2,a2+å1],á1,á2,00(2K, p1, p2).

Next we have

[ó(x) - ó(y)] ([s1, t1] x [s2, t2])

Existence and Uniqueness of the Solutions of SDE with 28 Two-Parameter Fractional Brownian Motion

1

0₁

,

-(xt1,s2 - yt1,s2) I ó^' (ëxt1 s2 + (1 - ë)yt1,s2) dë

I 1

- (xs1,t2 - ys1,t2) a

I (ë - ë)ys1,t2) dë

o 1 _ol _(Ax_x,_: t_{2 82} + (¹

+(xs1,s2 - ys1,s2) j + (1 - ë)ys1,s2) dë

1

= (x - y) ([s1,t1] × [s2, t2]) I ó^f (ëxt1,t2 + (1 - ë)yt1,t2) dë

o

= (xt1 ,t2 - yt1 ,t2 ) ₁ ó^f (ëxt1,t2 + (1 - ë)yt1,t2) dë

1

+(xt1,s2

[ó^' (ëxt1 ,t2

- yt1,s2) I

- ó^' (ëx t1,s2 + (1 - ë)yt1 ,t2)

+ (1 - ë[ó) y, t(1ë, sx2d

t⁾1^] , t2 ë

1

(1 - ë)yt1,t2)

+(xs1,t2 - ys1,t2) I

+ (1 - ë_[ )_uy_,s₍1 _A, t _x2 )], , dë

t 2+

- ó^' (ëxs1,t2 0

1

- (xs1,s2 - ys1,s2) i + (1 - ë)yt1,t2)

0

- ó' (ëxs1,s2 + (1 - ë)ys1,s2)] dë

1

= (x - y) ([s1, t1] × [s2, t2]) j ^óf (ëxt1,t2 + (1 - ë)yt1,t2) dë

+ [(xs1,t2 - ys1,t2) - (xs1,s2 - ys1,s2)]

1

0

× 10 [a'(ëxt1,t2 + (1 .-, (ë) Y :2₂ ) - a' (ëxs1,t2 + (1 - ë)ys1,t2)] dë

+ +(óx:(1ë,sx2 s1,sy2 s1,s2) 11

[0 ëx _ti, + (1 - ë)ys1,s2) - ó^' (ëxt1,s2 + (1 - ë)yt1,s2)] dë

+ (1 - ë)yt1,t2) - ^ó' (ëxs1,t2 + (1 - ë)ys1,t2)

1

= (x - y) ([s1,t1] × [s2, t2]) I a' (ëxt1,t2 + (1 - ë)yt1,t2) dë

0

+ [(xs1,t2 - ys1,t2) - (xs1,s2 - ys1,s2)] 1

× jo [ó^f _(ëxt1,t2 + (1 - ë)yt1,t2) - ó^f (ëxs1,t2 + (1 - ë)ys1,t2)] dë

1

+(xs1,s2 - ys1,s2) [A(xt1,t2 - X81,t2 ) I + (1 - ë)(yt1,t2 - ys1,t2)]

1

0

× /

0 ó00 (u (ëxt1 ,t2 + (1 - ë)yt1,t2 ) + (1 - u) (ëxs1,t2 + (1 - ë)ys1,t2))dudë

1

- (xs1,s2 [A(xt1,82 - x81,82) Y81,82) I + (1 - A)(yt1,s2 - ys1,s2)]

1

o

×

+ (1 - ë)ys1,s2)) dudë

1

o ó00 (u _(ëxt1,s2 + (1 - ë)yt1,s2) + (1 - u) (ëxs1,s2

Existence and Uniqueness of the Solutions of SDE with Two-Parameter Fractional Brownian Motion 29

Therefore

[ó(x) - ó(y)] ([s1,t1] × [s2, t2])

1

= (x - y) ([s1, t1] × [s2, t2]) f ó^f (ëxt1,t2 (1 - ë)yt1,t2) dë

+ [(xs1,t2 - ys1,t2) - (xs1,s2 - ys1,s2)]

Z 1

×

[ó^f (ëxt1,t2 + (1 - ë)yt1,t2) - ó0 (ëxs1,t2 + (1 - ë)ys1,t2)] dë

0 1

+(xs1,s2 - ys1,s2) [ëx ([s1,t1]× [s2, t2]) + (1 - ë)y ([s1, t1] × [s2, t2])]

₁ 0

× ó⁰⁰ (u (ëxt1,t2 + (1 - ë)yt1,t2) + (¹ - u)(ëxs1,t2 + (1 - ë)ys1,t2))dudë

0 1

+ (xs1 ,s2 ys1,s2 ) f ,s2 xs1,s2) ( 1 - (yt1,s2 ys1,s2)]

0

1

× 0 [ó^" (u _(ëxt1,t2 + (1 - ë)yt1 ,t2 ) + (1 - u) (ëxs1,t2 + (1 - ë)ys1,t2))

-ó^" (u (ëxt1,s2 + (1 - ë)yt1,s2) + (1 - u) (ëxs1,s2 + (1 - ë)ys1,s2))]dudë.

(3.5)

If x, y ? C[a1,a1+å1]×[a2,a2+å1],á1,á2,8(K, ?1, ?2), then (3.5) yields

|ó(x) - ó(y)|T,á1,á2 = C (K, 1ó¹1₈, mó^tkL, ,ó^ffIL) Ilx - yIT,á1,á2. (3.6)

From (3.1), (3.2) and (3.6) it follows that there exists å2 > 0 enough small, independent of ai, bi, such that

1Fx - Fyk[a1,a1+å2]×[a2,a2+å2],á1,á2,8 = 11x - y1[a1,a1+å2]×[a2,a2+å2],á1,á2,8, (3.7)

for some 0 < d < 1, and hence, denoting å0 = min(å1, å2), we obtain that

F : C[a1,a1+å0]×[a2,a2+å0],á1,á2,8(2K, ?1, ?2) ? C[a1,a1+å0]×[a2,a2+å0],á1,á2,8(2K, ?1, ?2)

is a contraction.

An existence and uniqueness result for ordinary differential equations with Hölder continuous forcing is obtained in [12]. The global solution is constructed, first in small time interval, when the contraction principle can be applied, by using estimates in terms of Hölder norms. For the two-parameter case we have the following result.

Theorem 3.1. Let â1, â2 ? (1/2, 1] and á1, á2 be such that âi > ái > 1- âi. Let g ? CR²,â1,â2 and b, ó : R ? R be such that b is bounded and Lipschitz and ó ? C2 b (R) with ó⁰⁰ Lipschitz. Then for every a1 < b1, a2 < b2 and

Existence and Uniqueness of the Solutions of SDE with 30 Two-Parameter Fractional Brownian Motion

? ? C[ai,bi],ái with ?1(a1) = ?2(a2), the equation

Z ^sxs,t = ?1(s) + ?2(t) - ?1 (a1) + it

b(x_u,v)dudv

a2

(3.8)

s _ft

+ ó(x_u,v)dg(u, v), (s, t) ? T,

a1 a1

has a unique solution in CT,á1,á2,00.

Proof. Let K > 0 be such that ?i ? C[ai,bi],ái(K). Then from Proposition 3.1 we obtain the existence of the solution x of (3.8) on the rectangle [a1, a1 + å0]×[a2, a2+å0], å0 independent of ai, bi (but dependent on K). If a1+å0 < b1, let n0 be the biggest integer such that n0å < b1. Then x ? CT,á1,á2,00(2K) and inductively we obtain the existence of the solution on

[a1 + å0, a1 + 2å0] × [a2, a2 + å0], ..., [a1 + n0å0, b1] × [a2, a2 + å0], and then on

[a1, a1 + å0] × [a2 + å0, a2 + 2å0], ..., [a1 + n0å0, b1] × [a2 + å0, a2 + 2å0],

and continuing again by induction we obtain the existence on T . Let now x1, x2 be two solutions of (3.8). In particular, there is K > 0 such that x1, x2 ? CT,á1,á2,00(K). From (3.7) we deduce the existence of å0 > 0 (which does not depend on ai, bi) and 0 < d < 1 such that

1x1 -x21[a1,a1+å0]x[a2,a2+å0] = dlx1 - x21[a1,a1+å0]x[a2,a2+å0],

and therefore x1 = x2 on [a1, a1 + å0] × [a2, a2 + å0].Inductively (see the existence part) we obtain that x1 = x2 on T.

Bibliography

[1] Bass R.F., LEvin D.A., Harnack inequalities for jump processes, PoTEnTial Anal., 17 (4) (2002), 375-388.

[2] Bass R.F., Stochastic differential equations driven by symmetric stable processes, In SéminairE dE ProbabiliTés, XXXVI, 302-313, LEcTurE NoTEs in MaTH., 1801, SprinGEr, BErlin, 2003.

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]