3.3.3 Analyse des températures adimensionnelles
à l'interface MCP liquide / Paroi chaude.
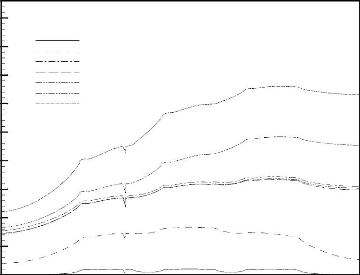
La Figure 3.3a illustre la distribution de la
température adimensionnelle le long de la paroi chaude,
constituée par les portions de la plaque conductrice (substrat) et les
faces des sources de chaleur en contact avec le MCP, pour différents
instants. L'analyse de cette figure montre que les courbes présentent
des minimums aux points B, D, E, F, I, J et M et des maximums aux points C, G,
H, K et L pour ô = 0,085. La présence des minimums est dû
à la minceur des couches limites formées aux faces horizontales
des sources de chaleur. Quant aux maximums, ils sont dus à
l'épaississement des couches limites, formées sur les faces des
sources de chaleur, aux points considérés. Un autre constat qui
peut se dégager de l'analyse de cette figure est l'uniformité de
la température à la surface des sources de chaleur et qui est
attribuée à la valeur relativement élevée de la
conductivité thermique du matériau constituant les sources de
chaleur (Kc=1130).
0.045
0.035
0.025
0.015
0.005
0.04
0.03
0.02
0.01
0
0.00011 0.007 0.029 0.051 0.085 0.096 0.105
ô=
è
i

A B C D E F G H I J K L M N
(a)
ô
èi
0.035
0.025
0.015
0.005
0.03
0.02
0.01
0
È X
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
X È
È X
X
È
È
È
X È X È È
X
X È
X X
s=
0.25 0.525 0.675 0.825 0.933 1.03 1.181 1.33 1.439 1.55 1.697
1.85 2.00
È
X
È
X
È
X
È
X
(b)
Figure 3.3: Distribution spatiale de la
température adimensionnelle à l'interface paroi
chaude/MCP liquide (a) et variation temporelle des
températures adimensionnelles à différentes positions de
cette même interface (b)
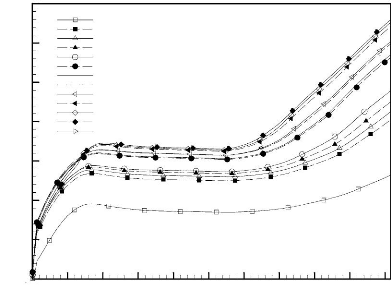
La Figure 3.3b présente la variation temporelle de la
température adimensionnelle pour différentes positions à
l'interface paroi chaude /MCP. A cause du stockage d'énergie sous forme
sensible, la température adimensionnelle s'accroît pendant les
périodes correspondant au début et la fin du processus de fusion.
On peut aussi constater que la température adimensionnelle est
stabilisée durant le régime quasi stationnaire correspondant
à l'établissement de la convection naturelle. L'accroissement et
la stabilité de la température peuvent être aussi
constatés à la Figure 3.3 a.
3.3.5 Analyse des nombres de Nusselt moyen des sources de
chaleur.
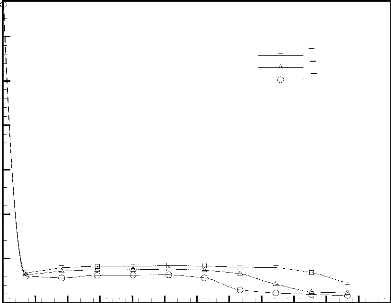
L'évolution du nombre de Nusselt moyen d'une source de
chaleur, Nu , est illustré à la Figure 3.4. Une des observations
qui se dégagent de l'analyse de ces courbes est que le
nombre de Nusselt Nu n'est pas proportionnel au rapport
. En effet, l'analyse de
~ max
1
1
Omax
l'équation (2.58) montre que le nombre de Nusselt moyen
Nu est le produit de
|
î ? î
o
et J ?ç
K d
0
|
. Ce dernier terme représente le flux thermique
adimensionnel évacué par les trois
|
faces de la source de chaleur au MCP. Au début, la
température maximale adimensionnelle et
le flux de chaleur
adimensionnel évacué par la source de chaleur s'accroissent.
Toutefois, le
|
rapport
|
1
Omax
|
l'emporte sur le flux de chaleur adimensionnel, si bien que le
produit
|
1
î ? ~ î ? ~
, max J ?ç
?ç 0
0 ~ 0
max
et diminuent avec le temps, respectivement. Le même
comportement est observé durant la
dernière phase. C'est la
raison pour laquelle le nombre de Nusselt diminue. Durant le régime
quasi stationnaire, °max et 0
î ? î
°
J ?ç demeurent constants, entraînant, ainsi, la
constance du
K d
nombre de Nusselt. L'évolution temporelle du nombre de
Nuselt moyen des sources de chaleur reflète fidèlement les
étapes du processus de fusion observées et analysées dans
les sections précédentes (conduction pure - convection-
conduction/convection).
300
Nu1
Nu2
Nu3
100
50
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12
250
0
200

Nu
150
ô
Figure 3.4: Evolution temporelle des nombres de
Nusselt moyen, (1): source située en bas de l'enceinte, (2): source
centrale, (3): source située en haut de la cavité.
| 


