|
N° d'ordre
Mustapha
Faraji
Etude Numerique des Transferts de Chaleur dans une Enceinte
Confinant un Materiau a Changement
de Phase et Chauffee par des Sources de
Chaleur Protuberantes sur une Paroi Conductrice Verticale
2010
P
UNIVERSITÉ CADI AYYAD N° d'ordre
:
FACULTÉ DES SCIENCES
SEMLALIA -
MARRAKECH
************************
THÈSE
présentée à la Faculté pour obtenir
le grade de :
Docteur
UFR : Thermique et Mécanique des Fluides
Spécialité : Mécanique des
Fluides et Energétique
Etude Numérique des Transferts de Chaleur dans
une Enceinte
Confinant un Matériau à Changement de Phase et
Chauffée
par des Sources de Chaleur Protubérantes sur une
ParoiConductrice Verticale
par :
Mustapha Faraji(Ingénieur
d'Etat - DESA : Mécanique des Fluides et Énergétique)
soutenue le : 08 mai 2010 devant la commission d'examen :
Président : E.K. LAKHAL
P.E.S. Faculté des Sciences Semlalia, Marrakech
Examinateurs : H. EL QARNIA
P.E.S. Faculté des Sciences Semlalia, Marrakech
A. AMAHMID P.E.S. Faculté des Sciences
Semlalia, Marrakech
S. ABBOUDI M.C. Université de Techn. de
Belfort- Montbéliard- France
A. AZIM P.E.S. Faculté des Sciences, El
Jadida
A. DRAOUI P.E.S. Faculté des Sciences et
Techniques, Tanger
H. CHEHOUANI P.E.S. Faculté des Sciences
et Techniques, Marrakech
Feat a/me etOitogete ytwie
iett46 Aarte ce heatiati
t9 la inejnobee A ma/n/lhee
t9imaja4 i t e A t91-meolwee/nto,
yetilho1126 ma, Got tab yinnook d oae/xtfiee et de
dehoffeilnew
DÉDICACES
AVANT PROPOS
- Nom et prénom de l'auteur: Faraji
Mustapha
- Intitulé du travail: Etude des Transferts de Chaleur
dans une Enceinte Confinant un Matériau à Changement de Phase et
Chauffée par des Sources de Chaleur Protubérantes sur une Paroi
Conductrice Verticale
- Nom et prénom du directeur de recherche: El
Qarnia Hamid
- Nom et prénom du co-encadrant:
- Laboratoire où ce travail a été
réalisé: Laboratoire de Mécanique des Fluides et
d'énergétique (LMFE) de la Faculté des Sciences et
Semlalia.
- Rapporteurs autres que l'encadrant et le co-encadrant:
- Cadre de coopération-soutien financier:
- Principales publications et communications auxquelles ce
travail a donné lieu:
Publications:
[1] M. Faraji and H. EL Qarnia, Passive
Cooling of Protruding Electronic Components by Latent Heat Fusion Storage,
Journal of Electronic Packaging (ASME), 2009 JEP. Volume 31, N°2, 021011
(10 pages).
[2] M. Faraji, H. EL Qarnia and J.C. Ramos,
Thermal control of protruding electronic components with PCM: A parametric
study, Numerical Heat Transfer, Part A, Volume 56, pp. 579-603, 2009.
[3] M. Faraji and H. EL Qarnia, Numerical study
of melting in an enclosure with discrete protruding heat sources, Applied
Mathematical Modelling, Volume 34, pp. 1258-1275, 2010.
[4] M. Faraji and H. EL Qarnia, Numerical
Study of Free Convection Melting within an Isolated Cavity Heated by Three
Protruding Electronic Components, IEEE Transactions on Components and Packaging
Technologies, Volume 33 (1), pp 167-177, 2010.
[5] M. Faraji, H. EL Qarnia and E. Lakhal,
Thermal Analysis of Phase Change Material Based Heat Sink for Cooling
Protruding Electronic Chips, Journal of Thermal Science, Volume 18, N°3,
pp. 268-275, 2009.
[6] M. Faraji and H. EL Qarnia, Numerical
Optimization of a Thermal Performance of a Phase Change Material based Heat
Sink, International Journal of Heat and Technology, Volume 26, N°2, pp.
17-24, 2008.
[7] M. Faraji, H. EL Qarnia, Etude
numérique des transferts de chaleur lors de la fusion d'un
matériau à changement de phase: Application Au refroidissement de
composants électroniques protubérants, International Journal of
Physical and Chemical News, Volume 47, pp. 58-67, 2009.
Communications:
[1] M. Faraji, H. El Qarnia, «Cooling
management of protruding electronic components by using a phase change material
heat sink», Proceeding of the 14th IEEE International Conference
Electronics, Circuits and Systems (ICECS), Special Issue: IEEE Library of
Congress, pp.174- 177, (2007).
[2] M. Faraji, H. El Qarnia, « Effet de
l'Epaisseur des Sources de Chaleur Protubérantes sur le Processus de
Fusion d'un Matériau à Changement de Phase?
9ème Congrès de Mécanique - (CDM 2009), Maroc
Marrakech, 21-24 avril, Tome 2 pp. 466-468 (2009).
[3] M. Faraji, H. El Qarnia, « PCM
Based-Heat Sink for Transient Thermal Management of Protruding Heat Sources ?
Proceedings of the Fourth International Exergy, Energy and Environment
Symposium, (IEEES4) April, AUS, Sharjah, UAE, 19-23, 2009.
[4] M. Faraji, H. El Qarnia, «Working
time of discreet protruding electronic components cooled by phase change
material» Proceedings of the 6th International Conference on
Computational Heat and Mass Transfer (ICCHMT) May 18-21, Guangzhou, China
(2009).
[5] M. Faraji, H. El Qarnia,
«Simulation numérique des transferts de chaleur lors de la fusion
d'un MCP chauffé par des sources de chaleur protubérantes?,
Colloque International sur les Méthodes Mathématiques et
Numériques en Mécanique des Fluides (CIMMNF'09), Maroc
Errachidia, 28-29 avril, pp. 40-41 (2009).
[6] M. Faraji, H. El Qarnia and El K.
Lakhal, «Stockage d'énergie dans un matériau fusible place
dans une enceinte rectangulaire a paroi verticale conductrice chauffée
par des sources discrètes protubérantes»,
7ème Colloque Interuniversitaire
Franco-Québécois sur la Thermique des Systèmes (CIFQ 09),
Lille France, mai 18-20 (2009).
[7] M. Faraji and H. El Qarnia, Application of
phase change material for cooling a protruding mounted power electronic
components, International conference on renewable energy and
power quality (ICREPQ'08), Santander, Spain, 11- 14 Mars (papers
contents published in CDR and on line:
http://www.icrepq.com/icrepq-08/programme-ICREPQ08.pdf).
[8] M. Faraji, H. El Qarnia and El K.
Lakhal, «Melting Natural Convection In an Enclosure Heated with Three
Discrete Protruding Heat Source «, 16th International
Conference on Thermal, Engineering and Thermo-grammetry (THERMO 09), Budapest,
Hungary, 1/3 -06 (2009). papers contents published in proceeding and CDR.
[9] M. Faraji, H. El Qarnia, «Numerical
Analysis of an Hybrid Heat Sink with using a Phase Change Material: Application
to a Cooling of an Electronic Component», Proceeding of the ASME 2008 Heat
Transfer Conference (HT2008), Jacksonville Florida USA August 10-14 (2008),
Paper No HT2008-56012 pp 771-777.
REMERCIEMENTS
Le travail présenté dans cette thèse a
été effectué au sein du Laboratoire de Mécanique de
Fluide et d'Energétique (LMFE) dans le cadre de l'UFR de Thermique et
Mécanique des Fluides à la Faculté des Sciences Semlalia,
Marrakech, sous la direction du Professeur Hamid EL Qarnia.
Je remercie sincèrement mon Directeur de thèse,
Mr. le Professeur Hamid EL Qarnia, pour sa contribution
majeure à l'orientation des travaux de recherche, pour son soutien non
seulement académique, mais aussi pour ses idées originales qui
ont servi à enrichir cette thèse, ses sages conseils et ses
directives magistrales et ses divers conseils et encouragements au cours de mes
études au DESA et durant la préparation de la Thèse. J'ai
particulièrement apprécié ses conseils et pour m'avoir
sensibilisé à l'importance de la communication scientifique. Sa
disponibilité, sa rigueur scientifique, ses remarques constructives, son
aide et ses qualités humaines, sont des atouts qui m'ont permis de
travailler avec joie et persévérance. Qu'il trouve ici
l'expression de mon sincère et profond respect.
Le Professeur El Khadir Lakhal de la
Faculté des Sciences Semlalia, m'a fait un honneur en acceptant la
présidence du jury de cette thèse. Je tiens à l'en
remercier profondément sans oublier de lui témoigner de
l'humanisme et du soutien dont il a fait preuve tout au long de ma
thèse.
Messieurs Abdelkhalek Amahmid, Professeur
à la Faculté des Sciences Semlalia, Said
Abboudi, Professeur à l'Université de Technologie de
Belfort- Montbéliard- France et Azzedine Azim,
Professeur à la Faculté des Sciences d'El Jadida ont
rapporté sur ce travail et siégé parmi les membres du
jury, malgré leurs préoccupations, qu'ils daignent trouver
l'expression de ma considération et mes remerciements les plus
sincères.
Que le Professeur Hassan Chehouani de la
Faculté des Sciences et Technique de Marrakech
et le Professeur Abdesslam Draoui de la
Faculté des Sciences et Technique de Tanger trouvent ici l'expression de
mes chaleureux remerciements pour l'intérêt qu'ils ont
manifesté envers mon travail en s'associant aux membres du jury.
Il est de mon devoir de formuler mes sincères
remerciements à l'ensemble du personnel enseignant du département
de physique.
Mes vifs et sincères remerciements vont aussi à
tous mes collègues du Laboratoire de Mécanique des Fluides et
d'Énergétique de Marrakech, pour leur encouragement et pour
l'ambiance de travail qu'ils ont su créer.
Enfin je dis: Louange à Dieu qui m'a donné le
courage et la foi nécessaires à la réalisation de ce
travail.
RÉSUMÉ
Le travail présenté dans ce mémoire
concerne l'étude numérique du transfert de chaleur dans une
enceinte confinant un matériau à changement de phase (MCP).
L'enceinte est chauffée par des sources de chaleur discrètes
protubérantes sur une paroi conductrice verticale. Cette enceinte joue
le rôle d'un puits de chaleur servant au refroidissement de composants
électroniques (les sources de chaleur) montés sur un substrat
vertical (la plaque conductrice). L'avantage d'utiliser cette stratégie
de refroidissement est que les MCP, caractérisés par une
densité de stockage d'énergie élevée et une plage
de température de transition étroite, sont capables de stocker
une importante quantité de chaleur générée par les
sources de chaleur ; ce qui permet d'assurer à ces dernières un
refroidissement passif. La stratégie proposée est aussi
convenable et efficace pour les situations où le refroidissement par
convection forcée à l'air ambiant n'est pas possible
(contrôle thermique des appareils électroniques utilisés en
métallurgie et dans les applications spatiales, par exemple). Pour
étudier les comportements thermique et hydrodynamique de l'enceinte, un
modèle mathématique (2D), basé sur les équations de
conservation de la masse, de l'énergie et de la quantité de
mouvement a été développé. Les paramètres de
contrôle sont ensuite identifiés, et les équations du
modèle sont discrétisées en adoptant la méthode des
volumes finis. L'équation d'énergie relative au MCP est
résolue en utilisant la méthode enthalpique. Le modèle
mathématique est confronté avec les résultats
expérimentaux disponibles dans la littérature. Plusieurs
investigations numériques ont été effectuées en vue
d'analyser l'effet des divers paramètres de contrôle sur les
comportements thermique et hydrodynamique et l'efficacité de
refroidissement du puits de chaleur. Des corrélations exprimant la
durée adimensionnelle de fonctionnement sécurisé des
sources de chaleur et la fraction liquide en fonction des paramètres de
contrôle ont été développées, moyennant la
technique d'expansion dynamique asymptotique appliquée à la
mécanique des fluides (Asymptotic Computational Fluid Dynamic expansion
technique) ACFD. Des abaques d'un intérêt pratique sont aussi
produits.
Mots clés: Matériau à
changement de phase ; fusion ; solidification ; méthode enthalpique ;
stockage de chaleur latente ; refroidissement de composants
électroniques.
ABSTRACT
The work presented in this dissertation is devoted to the
numerical study of the heat transfer during melting of a phase change material
(PCM) within a rectangular enclosure heated by protruding heat sources. This
enclosure plays the role of the heat sink for the cooling management of
electronic components simulated by protruding substrate-mounted heat sources.
The advantage of this cooling strategy is that PCMs, which characterized by
high energy storage density and small transition temperature interval, are able
to store a high amount of generated heat; which provides a passive cooling of
electronic components. The proposed strategy is suitable and efficient for
situations where the cooling by air convection is not possible (thermal control
of electronic devices for spatial and metallurgy applications, for example). In
order to numerically study the thermal and flow fields and explore the thermal
behaviour and the cooling efficiency of the proposed PCM based heat sink during
the melting process, a 2D mathematical model based on the mass, momentum and
energy conservation equations was developed. The control parameters are next
identified, and the equations are discretized using the volume control
approach. The energy equation for the PCM is solved using the enthalpy method.
The model has been checked and then validated comparing the numerical results
with available experimental results. Numerical investigations have been
conducted in order to examine the impact of various control parameters on the
thermal behaviour and efficiency of the proposed PCM-based heat sink.
Correlations encompassing a wide range of parameters were developed for the
non-dimensional secured operating time (non-dimensional time required by the
heat sink before reaching the critical temperature, Tcr) and the
corresponding liquid fraction using the asymptotic computational fluid dynamics
(ACFD) technique. Abacuses were also provided for practical use.
Keywords: Phase change material; melting;
solidification; enthalpy method; latent heat storage latent; cooling of
electronic components.
LiAti31A
44k) 1-1? el " 4.01° 14-.''SJA
Si.)14 a+.4.~~?) J U° 4)4?
44.A.) LAJJ `191-155
14-%9)41 bit
S ..Aila SA-41/41 P4,14 41}% &1,? S.1011
JS. i1, asjA.A?1 blit, 2 kpars 4jija j# j5
0$1 aik9AG ..49 ~~?)
|
2
|
If
|
a.13-1)
|
?
|
6
|
If
|
;Lii &A a?1-?1
|
J 1.%?1 j?l. 0.? .?1 tlia?$ Cj.i.j15
4.0.10 jAz:i. Lai& .1.44
j9.1 a?~&?1 to .J.ILA. t.1 ?1
yati
4?1 P.:~?1 CIO
4.:11?B1 . 1-2?$ .4.)11. J a- LA
C)A C.J". 4-441 S
·:4?1
.4-1+51i141 bit
24...1?B1
2 41:1 D1 4,$JA?$ jAa?l
jAa?l j L+ ~~?11 j.1.9:4. LIO: J.4?1 i111?1
IlA jAG i? ~' 4~?I 4.417u?1 cUs~?1 e.:a j lb5 "L?
4.0.1c j .a?l lak9
2 41?~.?1 ;?~-?I 4?1 a41.?1 ;?~-?I &A SA-?1 a?1- ...).0.1
jlitc,' VI air' l?'l t..4 4&si....$,a?l
2 1
J-y7il-q/1 j L19..A?1
f1÷&'11 .4412% .11..45014 .~31?1 cV.10-?1 &A
,LAW LL3?I 11T? Ll? y .1A?1 eAu, fq..3.4.2l. 1149 6WO J
·A.?1
IAj4+?1 4VA.~?1 4
·4311:1I ja?~
|
s_<9i4?1 '.~9,.:?1 41.1,"?$ t.A '~,11A?1. 4e.14,~?1
litt, 4.0.10 ;1.1. ?$ 1,4 j
|
.11
|
dii.)Ji"
|
Li &A
|
&A ..).a?l fitiii jAG, ...4.40.i. . Szli
eliala S?lli 4.010 111.4.46% j 441.?$
.1.4.4i A...,AA 1,x1; a4,1J. 4?1
402~?$ f.ti 4S?1.!?i as a.gas j LAIJ
·
1,11,1
sisi.~?$ &A :+1.4.11..1.; uAi 4t?$.A?1.
24S-1-:"?$ 4..&?1. 41)&?1
Y61÷?/

CAJI 4°..)4, 4% CJAJ
kA
·1?1 JA° S" 4% CJA liA:?1 a~?tai 4.01° JA1.2?$
CJA JAto J.1.).0i ala 4a.."-4
2 ~?ta?l i_~3~A i.1.?1
2 1 t?19-?$
.4-11+41-10 alhil-4-%'t
.4-4.... 4,1°
.11-41V1-: 44)1141? 44%4) & t-4:a.9 el 6Lj?i aT?
C.JA
&A IbUzil a~11A?1 S.A.?l 44!. A Ill j . sA?1
JAG LIA? ..~4,4?1 4,-?1 VA 44110?1 &w?l at 61.45
j
2 . sA?l jAl,G
2 4./~-?/ (6-?$ 6L$ A C.P..315 '1?~-?1 SJ744
SL4 6S:OU14 alj.)1?) . 1:° : ri_JtA cL.i. WS
TABLE DES MATIÈRES
Dédicace i
Avant Propos ii
Remerciements vi
Résumé viii
Abstract ix
~~~~~~ x
Table Des Matières xi
Nomenclature xiii
Introduction 1
CHAPITRE I: Revue Bibliographique
I.1 Stockage d'énergie par chaleur latente de fusion des
MCP 5
I.2 Refroidissement par convection naturelle et forcée
9
I.3 Refroidissement par les MCP 19
I.4 Position du problème 24
CHAPITRE II: Modélisation
2.1 Description du système de refroidissement
étudie 28
2.2 Modélisation mathématique 29
2.3 Validation du modèle numérique 52
2.4 Organigramme de calcul 58
CHAPITRE III: Résultats
3.1. Introduction 59
3.2. Choix des paramètres de simulation pour la
configuration de référence 59
3.3. Etude des comportements thermique et hydrodynamique de la
configuration de 62
référence
3.4. Etude paramétrique 76
3.4.1. Analyse de l'effet du nombre de Rayleigh, Ra 76
3.4.2. Effet de la distance adimensionnelle, Ä 85
3.4.3. Effet du rapport des diffusivités thermiques,
á s / á s,ref 91
3.4.4. Effet de la protubérance des sources de chaleur,
Ec 97
3.4.5. Effet de l'épaisseur adimensionnelle du substrat,
Es 107
3.4.6. Effet de la distance adimensionnelle, , séparant
les sources de chaleur 114
3.4.7. Effet du rapport de forme, A 120
3.4.8. Effet de la diffusivité thermique adimensionnelle
des sources de chaleur, 126
á c /á c,ref
CHAPITRE IV: Développement des
corrélations et abaques
4.1. Développement des corrélations 132
4.2. Elaboration des abaques 136
4.3. Exemple d'application 140
- Conclusion générale 142
- Références bibliographiques 146
Nomenclature
A rapport de forme, l/w
b constante paraissant dans l' Eq.(2.6)
C constante paraissant dans l' Eq.(2.6), kg m-3
s-1
C constante paraissant dans l' Eq.(2.21)
c chaleur spécifique, J kg-1 K-1
e épaisseur, m
E épaisseur adimensionnelle =e/lo
f fraction liquide
h enthalpie spécifique, J kg-1, ou coefficient
de convection, W m-2 K-1
k conductivité thermique, W m-1
K-1
K conductivité thermique adimensionnelle, k/km,l
l hauteur de la cavité, m
L hauteur adimensionnelle de la cavité =
l/lo
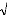
lo longueur caractéristique représentant
la masse du MCP = lw - 3e c l c , m
Lc hauteur adimensionnelle de la source de chaleur =
lc /lo
lc hauteur de la source de chaleur, m

lCE longueur caractéristique représentant le volume
de la source de chaleur = e c l c , m
Nu nombre de Nusselt moyen d'une source de chaleur c o
h l
=
km,l
p pression, Pa
Pr nombre de Prandtl = í m,l / á m ,l
qi'' densité de flux de chaleur adimensionnelle
à l'interface MCP/ source- plaque
conductrice, Eq(2.57)
Q puissance générée par une source de
chaleur, W
Q' puissance générée par unité de
longueur, W m-1
Rs résistance thermique, Eq(3.5), W K-1
|
Ra nombre de Rayleigh
|
g3l AT
3
o
~ ~
m,l m,l
|
s distance périphérique le long de la paroi
chaude
S terme source, surface, m2
Ste nombre de Stefan = (c p )
m,l AT
AH
t temps, s
T température, K
|
U,V vitesses adimensionnelles,
|
U=
|
u
|
|
V=
|
v
|
|
á m,l o
/l
|
,
|
á m,l o
/l
|
u, v vitesses dans les directions x et y, m s-1
w largeur de la cavité du MCP, m
W largeur adimensionnelle de la cavité = w
/lo
Symboles Grecques
ñ densité, kg m-3
á diffusivité thermique, m2 s -1
â facteur d'expansion thermique, K-1
è température adimensionnelle = (T-Tm)/
AT
è Ä Ä
X Y
ÄXÄY
~
èi température adimensionnelle moyenne d'une source
de chaleur source,i
=
~
source,i
ì viscosité
dynamique. kg m-1
s-1
õ viscosité cinématique,
m2 s-1
ä distance paroi inférieure- source de chaleur (S1),
m, Figure 2.1
position adimensionnelle de la source inférieure, ou
distance adimensionnelle
Ä séparant l'interface au noeud voisin = (ä
/lo)
AHf chaleur latente de fusion, J
kg-1
ÄT différence de température
caractéristique = '
3Q / k m,l , K
Äô pas de temps adimensionnel
ã distance entre deux sources de chaleur, m
î distance adimensionnelle périphérique des
sources de chaleur
ç distance adimensionnelle normale à la surface
d'une source de chaleur
distance adimensionnelle entre deux sources de chaleur =
ã /lo
|
á
ô temps adimensionnel, (nombre de Fourier) m,l
=
l 2
o
|
t
|
ã distance entre deux sources de chaleur, m
ù coefficient de sous relaxation pour la fraction
liquide
ø fonction de courant
Indices/Exposants
c convection, source de chaleur
cr valeur critique
e,n,s,w faces du volume de contrôle, Est, Nord, Sud et
Ouest
E,N,S,W volumes de contrôle, Est, Nord, Sud et Ouest
f fusion
fonc fonctionnement
i interface MCP/plaque conductrice- source de chaleur,
itération
l liquide
m liquide, MCP, fusion
max maximal
nv noeud voisin
o initiale
old pas de temps précèdent
p pression constante
ref valeur de référence
s plaque conductrice, périmètre de la paroi
chaude
S 1,2,3 source de chaleur inférieure, centrale et
supérieure
Introduction
Quand un matériau pur entre en fusion, en passant de
l'état solide à l'état liquide, quelque soit la
température de la source de chaleur qui provoque ce changement de phase,
la température du front de fusion demeure constante le long du processus
de fusion. Cette caractéristique peut être exploitée pour
le contrôle thermique des composants électroniques
générateur de chaleur, et ce en stockant la puissance
générée, en leur sein, dans un réservoir rempli
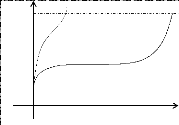
d'un matériau à changement de phase (MCP). La Figure 1
schématise une comparaison de l'évolution possible de la
température d'une source de chaleur refroidie par convection naturelle
à l'air ambiant et avec stockage dans un MCP.
Tcr
Tf
Ta
Sans MCP (a)
Avec MCP (b)
temps
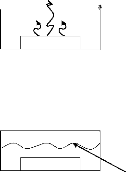
Air ambiant, T
Source, Q
(a)
MCP solide MCP liquide
Source, Q
(b) Front de fusion, T= Tf
Figure 1: Comparaison schématique entre
refroidissement d'une source de chaleur par convection naturelle à l'air
ambiant, (a) et par stockage dans un MCP, (b).
La source de chaleur, générant une puissance, Q,
s'échauffe avec le temps. Les faces de la source sont exposées
à l'air ambiant, et des mouvements de convection naturelle seront
induits par la différence des températures entre la source et
l'air ambiant. Dans le cas où la
source est enfermée dans une cavité remplie de
MCP, la puissance générée est absorbée par le MCP
solide. Quand la température de ce dernier atteint la température
de fusion, Tf, le MCP commence à fondre et la puissance
générée est absorbée sous forme de chaleur latente
par le front de fusion, ce qui permet de stabiliser la température de la
source de chaleur pendant une durée relativement longue car le
changement de phase se fait à une température constante, T=Tf,
pour la matière pure. Dans le cas du refroidissement par convection
naturelle à l'air, la température de la source augmente
incessamment et atteint rapidement la valeur critique, Tcr, fixée par le
manufacturier.
Le présent travail présente une étude
relative aux transferts thermiques se manifestant lors de la fusion d'un
matériau à changement de phase (MCP) et la dynamique de la fusion
de celui-ci. Le MCP est contenu dans une enceinte dont l'une des parois
verticales comporte trois sources de chaleur protubérantes. Le puits de
chaleur ainsi constitué peut jouer le rôle d'un refroidisseur de
composants électroniques (sources de chaleur) en stockant, dans le MCP,
sous formes sensible et latente, la chaleur dissipée par les composants
électroniques. Le système de refroidissement ainsi proposé
permet de dissiper la puissance générée par les sources de
chaleur en l'emmagasinant dans le MCP. Cette chaleur stockée est
transmise au MCP, soit directement (à travers les faces des sources de
chaleur), soit, indirectement (à travers la plaque conductrice).
L'avantage d'utiliser une telle stratégie de
refroidissement est que les MCP, caractérisés par une
densité énergétique élevée, sont capables
d'absorber une importante quantité de chaleur
générée par les composants électroniques sans avoir
recours aux ventilateurs. Cette méthode proposée est convenable
pour les situations où le refroidissement par convection naturelle et
forcée à l'air ambiant n'est pas pratique, comme c'est le cas des
appareils électroniques miniaturisés à usage intermittent.
Les consommateurs ont tendance à chercher des appareils
électroniques compacts et performants (téléphones
portables,
ordinateurs portables puissants, appareils photo
numériques haute résolution, etc ...), ce qui impose une
condensation croissante des circuits électroniques dans un espace
limité. Donc il faut prévoir des dissipateurs de chaleur de plus
en plus efficaces capables de maintenir la température de tels
équipements à un niveau acceptable. Il s'agit en fait de l'un des
principaux obstacles à surmonter afin d'augmenter la puissance des
appareils électroniques. La méthode de refroidissement par les
MCP peut aussi être une bonne solution pour des situations où le
refroidissement par convection forcée à l'air ambiant est
impossible, comme c'est le cas des appareils électroniques
utilisés dans les hauts fourneaux métallurgiques ou dans les
applications aérospatiales. Du point de vue économique et de
confort sonore, le mode de refroidissement par convection (naturelle ou
forcée) de l'air ambiant, le plus couramment utilisé, exige une
consommation énergétique pour le fonctionnement du ventilateur et
crée des problèmes liés aux bruits acoustiques lorsque
celui ci fonctionne. Afin de surmonter de telles difficultés, la
stratégie de refroidissement, basée sur les MCP peut être
envisagée. C'est une alternative très intéressante pour
dissiper l'énergie émanant des composants électroniques.
Aussi, il est possible de contrôler la température des composants
ultra sensibles au choc thermique étant donné que la fusion du
MCP se produit à l'intérieur d'une plage de température
étroite, et le MCP joue le rôle d'un amortisseur protecteur des
pics thermiques.
Le présent manuscrit comporte quatre chapitres. Le
premier chapitre est consacré à une étude bibliographique,
le second chapitre présente le modèle mathématique et la
méthode de résolution numérique et le troisième
chapitre présente l'analyse et les commentaires des résultats
obtenus. Le dernier chapitre expose la méthode de développement
des corrélations et des abaques pour la durée de fonctionnement
sécurisé et la fraction liquide.
Un modèle mathématique (2D) basé sur les
équations de conservation de la masse, de l'énergie et de la
quantité de mouvement est développé pour le puits de
chaleur proposé. Les paramètres de contrôle
régissant le fonctionnement du système sont identifiés. Le
modèle
mathématique est confronté aux résultats
expérimentaux disponibles en littérature. Plusieurs
investigations numériques ont été effectuées pour
analyser les comportements thermique et hydrodynamique du système de
refroidissement proposé.
Chapitre I
Revue Bibliographique
Quatre parties constituent le contenu du présent
chapitre. La première partie décrit le stockage d'énergie
par chaleur latente de fusion des MCP. La deuxième partie est
consacrée aux différentes réalisations relatives au
refroidissement des composants électroniques par convection
naturelle/forcée. La troisième partie analyse les travaux
théorique et pratique relatifs au refroidissement des composants
électroniques par stockage de l'énergie dans les MCP. Quant
à la quatrième partie, elle décrit la position du
problème.
1.1 Stockage d'énergie par chaleur latente de
fusion des MCP
Le stockage d'énergie thermique dans un MCP s'effectue
sous formes sensible et
latente.
1.1.1 Stockage d'énergie par chaleur sensible
Ce mode de stockage utilise les propriétés
calorifiques d'un corps. La quantité de chaleur (variation d'enthalpie
à pression fixe) stockée dépend alors de la
capacité calorifique du corps, et de l'écart entre sa
température initiale et la température de stockage.
Si on réchauffe (ou on refroidit) un corps de masse, m,
d'une température initiale, T1, à une température finale,
T2, l'énergie stockée est donnée par sa variation
d'enthalpie:
T2
AH = H -H = ~ mc dT (1.1)
2 1 (T)
p
T1
où cp (T) est la chaleur spécifique à
pression constante du corps.
Si la chaleur spécifique peut être
considérée comme constante dans l'intervalle de
températures [T1,T2] alors (cp (T) = c):
AH = m c p (T -T ) (1.2)
2 1
La quantité de chaleur stockée est
proportionnelle à l'écart de température: ce type de
stockage serait intéressant uniquement pour des grands écarts de
température et une chaleur spécifique élevée.
L'expression permet de distinguer deux cas:
si T2 > T1, le corps stocke la chaleur ;
si T2 < T1, le corps stocke le froid.
On utilise des corps ayant des chaleurs spécifiques
importantes comme le cas de l'eau pour les liquides et des lits de pierres pour
les solides.
1.1.2 Stockage d'énergie par chaleur latente de
fusion
A pression constante, la variation d'enthalpie d'un corps est
égale à la quantité de chaleur échangée lors
de la transformation. La chaleur latente de changement de phase d'un corps pur
à la température T est la variation d'enthalpie de celui-ci
passant d'un état (solide, liquide ou gazeux) à un autre. Ainsi,
la variation d'enthalpie du corps pour passer de l'état (1) à
l'état (2) est égale à la quantité de chaleur
échangée sur l'isobare, Figure 1.1.
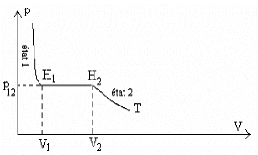
Figure 1.1: Variation d'enthalpie du corps
Le stockage d'énergie par chaleur latente met en jeu
l'énergie due au changement de phase. Soit Tf la température de
changement de phase d'un corps solide pur qui passe de la température
initiale T1 à la température finale T2, avec T1 < Tf < T2.
L'énergie stockée lors de cette transformation est:
T T
f 2
AH= ~ mc (T) dT + m AH + ~ mc
(T) dT (1.3)
p,s f p,l
T T
1 f
où cp,s (T): chaleur spécifique à
pression constante du corps à l'état solide. cp,l (T): chaleur
spécifique à pression constante du corps à l'état
liquide.
A H f : chaleur latente de changement de
phase.
Cette relation comporte deux termes représentant la
chaleur sensible et un terme représentant la chaleur latente, m
A Hf.
Le stockage d'énergie par chaleur latente de fusion est
plus bénéfique comparé à celui par chaleur
sensible. Une quantité importante d'énergie est stockée
lors de la fusion: Par exemple, dans un kilogramme de brique
réfractaire, il est possible de stocker environ 1 kJ pour chaque
degré d'élévation de la température, alors qu'en
faisant fondre un kilogramme de paraffine, environ 250 kJ sont
absorbés.
1.1.3 Utilité du stockage d'énergie par les
MCP
Dans le but d'économiser et de gérer
rationnellement la consommation énergétique, les recherches se
focalisent actuellement sur l'optimisation des systèmes
énergétiques.
L'une des stratégies d'économie de
l'énergie est le stockage. Les systèmes de stockage de
l'énergie par chaleur latente, utilisant des matériaux à
changement de phase (MCP), ont reçu, ces dernières années,
une attention particulière. La raison majeure de l'utilisation de tels
systèmes est leur densité énergétique
élevée, comparativement aux systèmes de stockage par
chaleur sensible, comme il a été illustré
ci-dessus. Ainsi le rapport "énergie stockée" au "poids et/ou
volume de stockage" est plus important en comparaison avec d'autre type de
stockage (sensible par exemple).
Le mode de stockage d'énergie thermique par chaleur
latente de fusion présente plusieurs avantages et trouve des
applications techniques variées dans divers domaines, parmi lesquels on
peut citer:
- Le stockage d'énergie solaire thermique pour
éviter les pics thermiques et réduire la charge de climatisation
dans l'habitat, pour réduire la charge de chauffage (en utilisant un
système de stockage d'énergie hybride emmagasinant
l'énergie électrique pendant les heures creuses, et
l'énergie solaire thermique pendant la phase diurne, pour la production
d'eau chaude, etc ;
- Le refroidissement des appareils fonctionnant dans des
conditions extrémales, comme le cas des caméras
électroniques utilisées lors des incendies [1], appareillage des
volcanologues, microprocesseur informatique, etc;
- Le stockage du froid qui permet une alimentation continue en
froid, en cas de panne des installations frigorifiques, surtout pour des
secteurs sensibles (pharmaceutique par exemple) ; - Les systèmes de
stockage de froid par chaleur latente peuvent être utilisés afin
de mieux gérer la consommation d'électricité
nécessaire à la climatisation des édifices.
1.1.4 Critères de choix d'un matériau
à changement de phase
Les conditions suivantes doivent être remplies par le MCP
pour un meilleur stockage d'énergie par chaleur latente de fusion:
- le MCP doit avoir une chaleur latente plus
élevée;
- la température de fusion du MCP doit correspondre
à la température d'utilisation ; - la conductivité
thermique doit être élevée pour accélérer le
changement de phase ;
- faible différence de masse volumique entre les phases
liquide et solide pour pouvoir les stocker dans le même volume
généralement fermé ;
- masse volumique élevée pour que le volume de
stockage soit faible ;
- stabilité chimique sur de longues périodes.
Certains MCP perdent leurs propriétés
thermo physiques après de nombreux cycles (charge /
décharge). La dégradation des
propriétés qui en résulte peut se traduire
par une variation du point de fusion ; - compatibilité avec les
matériaux en contact ;
- le MCP doit être non toxique et non nocif;
- abondance sur le marché et faible coût.
1.2 Refroidissement par convection naturelle et
forcée
1.2.1 Introduction
Dans le marché de l'électronique, les
consommateurs ont tendance à chercher des appareils de plus en plus
miniaturisés, ce qui oblige les fabricants à condenser les puces
électroniques et à augmenter leur fréquence interne.
Actuellement (2009) on arrive au nano technologie avec des transistors de
dimensions de l'ordre de 10-9 m [2]. La miniaturisation des puces
électroniques et l'augmentation de leur fréquence interne
incitent les fabricants à produire des circuits électroniques
réduits et à réduire la taille du système de
refroidissement. A cet effet, des problèmes liés à la
surchauffe des appareils électroniques sont survenus. Ce nouveau
paramètre, s'il est mal contrôlé, peut réduire
considérablement la durée de vie des composants
électroniques et réduire leur commercialisation. La
température maximale admissible par la majorité des composants
électroniques doit être inférieure à 75 °C - 80
°C [3]. Le défi consiste à bien dimensionner les puits de
chaleur afin d'éviter la surchauffe des composants électroniques.
La concurrence, de plus en plus croissante, entre les divers constructeurs du
matériel électronique, doit être accompagnée par des
stratégies de dissipation
de chaleur plus efficaces. Il s'agit en fait d'un des
principaux obstacles à surmonter afin d'augmenter la puissance des
ordinateurs et de l'électronique en général. Pour sa
simplicité, le mode de refroidissement couramment utilisé est la
convection (naturelle ou forcée) à l'air ambiant. Dans ce sens,
plusieurs initiatives de recherche ont été entreprises afin de
mettre en place des techniques de refroidissement plus efficaces permettant de
mieux dissiper la chaleur provenant des circuits électroniques. L'air
est le fluide préféré pour refroidir les circuits
électroniques suite à la facilité de sa mise en oeuvre et
à son faible coût. Toutefois, ses propriétés thermo
physiques font de lui un mauvais refroidisseur convectif. En effet, sa
conductivité thermique relativement faible (kair = 0,026W/m K) et son
nombre de Prandtl, (Pr = 0,7), entraînent un faible coefficient
d'échange par convection. La haute résistance thermique de l'air
et le besoin d'évacuer d'énormes quantités de chaleur ont
incité les chercheurs à repenser les techniques de
refroidissement afin d'intensifier le transfert de chaleur. Le flux de chaleur
évacué par la source de chaleur est donné par la loi de
refroidissement de Newton:
q = hc S (Tdissipateur - Tair) (1.4)
Ainsi, dans les puits de chaleur à base d'air,
l'amélioration d'échange de chaleur est assurée par
l'augmentation du coefficient de transfert de chaleur par convection,
hc, et de la surface d'échange de chaleur, S.
L'augmentation de la surface d'échange, S, est assurée par
l'introduction d'ailettes à la surface des composants
électroniques. Le coefficient d'échange par convection,
hc, est intensifié par l'augmentation du débit d'air
et la réduction de l'espace inter- ailettes. L'utilisation des jets
à grande vitesse sur les bouts d'ailette en direction de la base du
puits de chaleur, peut, aussi, augmenter notablement le coefficient de
transfert de chaleur mais il doit être testé in situ [3,4].
Toutefois, il faut noter que la réduction de l'espace
d'écoulement, résultant de l'ajout des ailettes, implique une
augmentation du poids de l'équipement et engendre des bruits acoustiques
[4,5].
Beaucoup de chercheurs ont contribué par leurs efforts
pour étudier les caractéristiques des écoulements à
flux convectif naturel ou forcé sur les blocs chauffants (sources de
chaleur). Les principaux axes de ces travaux portent sur l'estimation du
transfert thermique en convection naturelle et forcée, cette
dernière s'est avérée plus intéressante du fait
qu'elle offre une vaste marge de paramètres à varier, parmi ces
paramètres il y a le régime d'écoulement et la
configuration géométrique. L'analyse des travaux de recherche
relatifs au refroidissement des composants électroniques par convection
naturelle ou forcée permet de constater que les composants
électroniques sont généralement simulés par des
rectangles solides incrustés (surfacique) ou protubérants
(volumiques) montés sur l'une des parois de la cavité confinant
le fluide caloporteur. Aussi, dans ces études, il a été
démontré que la conductivité thermique du substrat, sur
lequel sont greffées les sources de chaleur, joue un rôle
important sur l'efficacité de refroidissement par convection naturelle
ou forcée à l'air ambiant. Dans les deux sections suivantes on va
exposer quelques travaux relatifs au refroidissement des sources de chaleur par
convection naturelle et forcée.
1.2.2 Refroidissement par convection forcée
Une étude numérique de la convection
forcée au sein d'un canal horizontal muni de trois blocs rectangulaires
disposés sur sa paroi inférieure a été conduite par
Davalath et Byazitoglu [6]. Les blocs chauffants sont identiques et
génèrent la chaleur de manière uniforme. Les auteurs ont
examiné les cas où les parois du canal sont adiabatiques ou
thermiquement conductrices. Cette étude a porté sur l'effet des
nombres de Reynolds et de Prandtl, des paramètres
géométriques (dimensions et espacement des blocs) et des
conductivités thermiques des parois du canal et des blocs. Ils ont
montré que la présence des blocs favorise la création des
zones de recirculation (entre les blocs) engendrant aussi une modification
considérable du profil de la vitesse imposée à
l'entrée. Ces tourbillons et
d'autres apparaissant en aval du dernier bloc, augmentent en
taille respectivement avec la distance entre les blocs et le nombre de
Reynolds. Aussi, l'augmentation du nombre de Reynolds et la diminution du
nombre de Prandtl agissent-ils en réduisant la température
maximale obtenue au voisinage du dernier bloc. Le nombre de Nusselt moyen
relatif à chaque bloc a été corrélé en
fonction des nombres de Reynolds et de Prandtl. De plus, il a été
établi que le nombre de Nusselt est quasiment indépendant de la
conductivité thermique des parois du canal, alors que la chaleur totale
transférée au fluide au dessus de la paroi active croît
avec ce paramètre.
Webb et Ramadhyani [7] ont étudié la convection
forcée dans un canal contenant des obstacles périodiquement
répartis sur ses deux parois et soumis à des flux de chaleur
constants. L'effet des nombres de Reynolds et de Prandtl et des
paramètres géométriques sur le transfert de chaleur a
été examiné. En profitant de la périodicité
des conditions aux limites de ce problème, ces auteurs ont
effectué les calculs numériques sur un domaine réduit et
ils ont montré qu'il est possible d'optimiser le transfert de chaleur et
la perte de charge en faisant un choix approprié des paramètres
géométrique du système.
Une étude numérique sur la convection
forcée en régime permanent dans un canal a été
menée par Wu et Perng [8]. Dans cette étude les auteurs ont
présenté une analyse des caractéristiques de
l'écoulement dans un canal vertical muni de blocs chauffants.
Young et Vafai [9] ont mené une étude
numérique paramétrique détaillée de la convection
forcée laminaire dans un canal horizontal muni d'un ensemble d'obstacles
chauffés. Dans le même sens, Tsay et Cheng [10] ont
présenté une étude numérique sur les
caractéristiques thermiques de l'écoulement de la convection
forcée laminaire dans un canal contenant plusieurs panneaux courts
montés avec des blocs générateurs de chaleur.
Najam et al. [11] ont traité le problème de la
convection mixte, en régime transitoire, dans un canal horizontal
chauffé périodiquement par des blocs chauffants isothermes.
Les
parois du canal sont adiabatiques. L'effet de
l'écoulement forcé sur les cellules issues de la convection
naturelle est étudié. Les conditions de déplacement de ces
cellules et l'instabilité de l'écoulement sont
analysées.
L'utilisation des logiciels commerciaux de calcul devient
très répandue. Lee et AbdelMoneim [12] ont utilisé un
modèle CFD pour étudier le transfert de chaleur et le
comportement de l'écoulement sur une surface horizontale à deux
nervures. Luo et al.[13] ont étudié le comportement thermique
d'un canal triangulaire équilatéral, à surface interne
nervurée. En adoptant un certain nombre d'hypothèses
simplificatrices, le problème 3D a été résolu par
deux approches 2D. Mathews et Balaji [14] ont utilisé un logiciel CFD
pour simuler la convection mixte conjuguée dans un canal vertical et ont
trouvé que la température maximale des composants
électroniques peut être réduite d'une façon
significative par l'augmentation de la conductivité thermique effective
des composants électroniques.
Perret et al.[15] ont proposé une méthodologie
de dimensionnement d'un refroidisseur à micro- canaux en cuivre, par
convection forcée d'eau en mode monophasique. Après une
étude par éléments finis de la structure proposée,
un modèle analytique est présenté. Celui-ci est
validé grâce à des mesures faites sur deux prototypes. Le
dimensionnement optimal de la structure est obtenu par le logiciel PASCOSMA,
basé sur l'utilisation extensive du calcul symbolique et la
programmation automatique et qui réalise la conception de dispositifs,
à partir de modèles analytiques, par une optimisation sous
contraintes.
Harnane et al.[16] ont abordé numériquement le
refroidissement par convection mixte turbulente de l'air des blocs
chauffés dans un canal vertical Les parois du canal sont adiabatiques.
L'approche numérique est basée sur la technique des volumes
finis. Le code FLUENT est appliqué pour intégrer ces
équations sur chaque volume de contrôle. Une description
détaillée de l'écoulement autour des blocs a
été présentée et la distribution du nombre de
Nusselt local est analysée.
1.2.3 Refroidissement par convection naturelle
L'étude des écoulements de convection naturelle
dans un canal vertical avec chauffage différentiel, trouve de nombreuses
applications pour le refroidissement des composants électroniques.
Vareilles et al.[17] ont étudié le refroidissement des cellules
photovoltaïques (PV) dont la perte de rendement est liée à
l'augmentation de la température. L'écoulement est
déstabilisé par l'alternance des sources de chaleur et des zones
froides (transparentes) sur les parois du canal. L'approche proposée est
numérique et s'appuie sur le code FLUENT.
Le problème de la convection naturelle dans un canal
horizontal muni de blocs rectangulaires sur sa paroi inférieure
adiabatique est examiné numériquement par El Alami et al. [18].
Les blocs sont maintenus à température constante. Des ouvertures
d'admission et d'évacuation d'air sont aménagées sur les
parois du canal. En raison de la périodicité du problème,
le domaine étudié a été réduit à une
cavité en forme de " "
T . Les résultats obtenus montrent que l'augmentation
du nombre de Rayleigh entraîne une augmentation du nombre de Nusselt
global et du débit d'air aspiré. La hauteur des blocs a un effet
important sur le débit massique ainsi que le nombre de Nusselt. Des
corrélations proches à celles rencontrées dans le cas du
canal vertical ou de la plaque verticale ont été
proposées.
Corvaro et Massimo [19] ont abordé une étude
expérimentale de la convection naturelle induite par une source de
chaleur protubérante enfermée dans une cavité
carrée pour deux différentes positions de la source de chaleur.
La comparaison est donnée en terme du nombre de Nusselt moyen pour
différentes valeurs du nombre de Rayleigh. Le champ des
températures est analysé par interférométrie
holographie et les résultats sont comparés avec les
résultats numériques obtenus en utilisant un logiciel
commercial.
Sivasankaran [20] a abordé l'étude de la
convection naturelle induite par des sources de chaleur montées sur une
paroi verticale isotherme d'une cavité chauffée d'une
manière
différentielle. Les parois horizontales sont
adiabatiques. Dans cette étude numérique, les champs thermique et
hydrodynamique sont analysés. L'auteur a conclut que le transfert de
chaleur au sein de la cavité est réduit à cause de la
présence des sources de chaleur et que le déplacement de
celles-ci vers le bas de la cavité permet de mieux transférer la
chaleur.
Desrayuad et al.[21] ont traité numériquement,
en régime permanent, le problème de la convection naturelle
à l'air ambiant pour le refroidissement d'une série de plaques
verticales chauffées par des sources de chaleur protubérantes. La
densité de flux de chaleur, imposée à la base de chaque
source de chaleur, est évacuée par conduction dans le substrat et
par convection naturelle. Le transfert de chaleur et l'écoulement sont
analysés et une étude paramétrique est menée. Les
auteurs ont conclu que la conductivité thermique du substrat a un effet
notable sur la température des sources de chaleur bien que la structure
de l'écoulement reste pratiquent intacte.
Le transfert de chaleur par convection naturelle laminaire
dans un canal vertical contenant deux obstacles rectangulaires disposés
symétriquement à la même hauteur sur les deux parois a
été examiné par Desrayaud et Fishera [22]. Les parois sont
isothermes et chauffées à la même température. Par
contre, les blocs sont soit adiabatiques, soit maintenus à la même
température que les parois du canal. Les résultats montrent que
le nombre de Nusselt moyen dans le cas des blocs isothermes est toujours
supérieur à celui généré dans le cas
où les blocs sont adiabatiques. Enfin, il a été
trouvé que l'augmentation de la longueur des blocs n'a qu'une influence
limitée sur le transfert de chaleur tandis que l'augmentation de sa
largeur conduit à une diminution considérable du débit
massique et du transfert de chaleur, particulièrement si la
moitié de l'ouverture est obstruée.
Kelkar et Choudhury [23] ont étudié
numériquement le problème de la convection naturelle dans un
canal vertical contenant des blocs rectangulaires chauffants sur l'une de ses
parois adiabatiques en utilisant les conditions d'un écoulement
périodique, pour les faibles
valeurs du nombre de Rayleigh. Les résultats de cette
investigation numérique, utilisant l'air comme fluide caloporteur,
montrent que le débit d'air aspiré par le canal augmente avec un
taux inférieur à la racine carrée de la longueur du
canal.
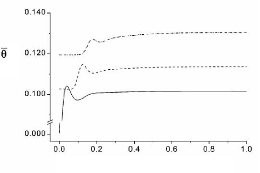
Temps adimensionnel, ô
S2
S1
S3
Figure 1.2: Evolution temporelle typique de
la température adimensionnelle moyenne de trois sources de chaleur
incrustées confinées dans une cavité rectangulaire et
refroidies par convection naturelle à l'air ambiant [24].
Il y a lieu à signaler qu'un nombre important de
travaux relatifs au refroidissement des composants électroniques par
convection naturelle se limite au régime permanent, mais il y a lieu de
noter que la connaissance du comportement du système lors des
marches/arrêts du système, ou lors de la variation d'un des
paramètres de contrôle, est essentielle pour un dimensionnement
correct des refroidisseurs, surtout quand il s'agit des équipements
électroniques très sensibles au choc thermique [24]. En effet, il
a été démontré que la température des
composants électroniques peut atteindre, en régime transitoire,
une valeur nettement supérieure à celle enregistrée en
régime permanent, comme il est illustré à la Figure
1.2.
1.2.4 Techniques avancées appliquées au
refroidissement de l'électronique
Dans les situations où l'air ambiant est absent ou sa
température dépasse la limite admissible par les composants
électroniques, comme c'est le cas de l'appareillage des volcanologues,
utilisé pour naviguer dans des zones enflammées où l'air
ambiant peut être chauffé à plus de 85 °C, ou dans les
zones ou l'air est absent, comme dans les applications spatiales, le
refroidissement des équipements électroniques par convection
naturelle ou forcée est délicat, et même impossible. Une
revue de la littérature spécialisée dans ce domaine montre
l'existence d'une limite de l'aptitude des fluides à évacuer
toute la puissance dissipée par les sources de chaleur. Dans ces
situations il faut prévoir d'autres stratégies de
refroidissement.
Les résultats expérimentaux obtenus par Kelleher
et al. [25] et Turner et al. [26] relatifs au transfert de chaleur par
convection naturelle au sein d'une cavité rectangulaire munie de sources
de chaleur démontrent aussi la limite de la capacité de l'air
à extraire naturellement toute la puissance dissipée par les
composants électroniques. D'autres investigations relatives au
refroidissement par convection naturelle par l'éthylène glycol
utilisé pour dissiper la puissance générée par des
sources de chaleur protubérantes sur un substrat vertical sont aussi
menées par Keyhani et al. [27] et Ju et Chen [28]. Dans ces
études, les auteurs montrent la limite de l'éthylène
glycol à refroidir les sources de chaleur.
Parmi les alternatives possibles, on peut citer la technique
de refroidissement par réfrigération qu'est utilisée pour
refroidir des super calculateurs, utilisés pour des missions
scientifiques [29]. La convection naturelle et forcée ne peut assurer le
refroidissement de l'appareil électronique qui doit être refroidi
par des méthodes non conventionnelles. La Figure 1.3 illustre une
unité centrale d'un serveur informatique utilisé dans un sous
marin avec un micro processeur de haute fréquence. Ce système est
refroidi par réfrigération à l'aide d'un
mini compresseur similaire à celui utilisé dans les
réfrigérateurs. Cette solution présente des défauts
tels que: encombrement, bruit sonneur et coût élevé.
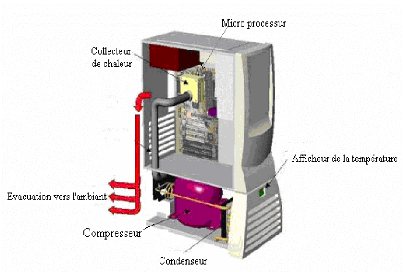
Figure 1.3: Prototype, `Kryotech IBM S/390
G4', pour le refroidissement du CPU utilisant un mini compresseur [29]
Dans le même sens, Joshi [30] a mis en oeuvre la
technique `Thermosiphon Biphasée' pour le refroidissement des composants
électroniques de haute puissance (Figure 1.4). Cette technique est
démontrée en 2001 avec succès pour des microprocesseurs de
type Pentium 4, dissipant une puissance de chaleur allant jusqu'à 85 W.
Cette méthode de refroidissement est actuellement utilisée dans
la majorité des unités centrales des ordinateurs de bureau.

Echangeur de chaleur croisé à ailettes plates
Caloduc
Absorbeur/collecteur
Microprocesseur
Ventilateur d'air
Figure 1.4: Refroidissement du microprocesseur
par 'Thermosiphon Biphasée', [30].
1.3 Refroidissement par les MCP
Parmi les solutions possibles dans les cas où le
refroidissement par convection naturelle et forcée à l'air
ambiant est impossible, on peut prévoir un réservoir rempli d'un
matériau à changement de phase (MCP) pour stocker la chaleur
générée par les composants électroniques. Cette
stratégie de refroidissement permet de réduire la taille du
système de refroidissement et doter les équipements d'une
capacité de refroidissement étendue. Pendant la période de
fonctionnement, les composants électroniques dissipent la chaleur
à travers leurs faces, entraînant ainsi la fusion du MCP solide.
L'unité de refroidissement doit fonctionner d'une manière
cyclique. La chaleur dissipée par les sources et stockée par le
MCP doit être rejetée à l'ambiance pendant les
périodes d'arrêt de l'équipement électronique.
Ainsi, le MCP ré- solidifié peut être
réutilisé lors des cycles suivants.
Le contrôle thermique des composants
électroniques par les MCP a reçu, récemment, une grande
attention due, fondamentalement, à leur haute capacité d'extraire
et de stocker la chaleur comparée aux liquides et à l'air [31].
Plusieurs stratégies ont été explorées pour
améliorer le refroidissement par stockage d'énergie sous forme de
chaleur latente de fusion. Ces stratégies envisagent l'ajout d'une
cavité remplie de MCP au puits de chaleur classiques ou le placement
d'une mince couche de MCP directement à la surface du composant
électronique pour absorber sa chaleur [32]. Ces études tentent
à effectuer un refroidissement sécurisé des composants
électroniques et à réduire le temps de fonctionnement des
ventilateurs. Faraji et El Qarnia [33] ont analysé un puits de chaleur
hybride constitué d'une cavité rectangulaire remplie d'un MCP
(SunTech P111) attachée à des ailettes rectangulaires. Plusieurs
simulations ont été menées pour optimiser le puits de
chaleur sans atteindre la surchauffe du microprocesseur. La configuration
optimale obtenue est, ensuite, soumise au fonctionnement cyclique
(charge/décharge), le régime périodique est établi
après trois cycles de fonctionnement.
Pal et al. [32] ont réalisé une étude de
refroidissement d'un composant électronique, d'une part, à
travers une cavité d'air de rapport de forme élevé
(>10) et, d'autre part, à travers une mince couche de MCP
(n-triacontane). Le composant électronique est installé sur un
substrat qui sépare la couche de MCP de l'enceinte d'air. Il s'agit
d'une étude numérique tridimensionnelle réalisée
avec et sans MCP. Les résultats montrent que la présence de la
couche de MCP diminue la température moyenne du composant
électronique pendant une durée relativement longue. Leur
modèle trouve des applications dans le secteur aéronautique.
Des études expérimentales, relatives à la
fusion du MCP (n-octadécane) à l'intérieur d'une
cavité chauffée par des sources de chaleur surfaciques
griffées sur une paroi verticale en Plexiglas, ont été
menées par Zhang et al. [34-36]. Les tests expérimentaux
effectués montrent que le refroidissement des composants
électroniques par le MCP permet de réduire leur
température jusqu'à 50 % en comparaison avec
leur refroidissement par convection naturelle avec l'éthylène
glycol. Les résultats montrent aussi que l'augmentation de la
conductivité thermique de la paroi chauffante permet d'uniformiser la
température des sources [36]. Les transferts de chaleur semblent
être meilleurs pour des sources de chaleur que pour une paroi
chauffée uniformément [35].
Binet et al. [37] ont développé un modèle
mathématique permettant de simuler le comportement thermique des sources
de chaleur dans une cavité similaire à celle
étudiée expérimentalement par Zhang et al. [34]. Une
série de simulations numériques a été menée
afin de déterminer les effets de la configuration des sources, du
rapport de forme de l'enceinte et des propriétés thermiques de la
paroi. Les résultats montrent que, pour des cavités de grand
rapport de forme (>4), le front de fusion se situe au dessus des sources et
se déplace horizontalement. La variation temporelle de la
température moyenne des sources, pour ce cas de front de fusion
horizontal, montre qu'il y a une montée suivie d'un état
quasi-stationnaire qui persiste jusqu'à la fin de la fusion. Cette
structure d'évolution des températures "à plateaux"
où la température présente une stabilité
couplée à une durée de fusion relativement longue, fait de
cette configuration un choix intéressant pour les applications
reliées au refroidissement des composants électroniques. Le MCP
solide et même le MCP fondu agissent comme un tampon thermique qui offre
l'avantage d'être situé au-dessus des sources de chaleur. Deux
zones optimales ont été obtenues. Pour dissiper la chaleur
émanant de composants électroniques, il serait ainsi
préférable de placer ces composants dans la partie
inférieure d'une enceinte de grand rapport de forme, ce qui garantit une
longue stabilité de leur température. Les résultats
montrent, aussi, que les cavités avec des rapports de forme > 4
contrôlent mieux la température des composants
électroniques et offrent une durée allongée de la
fusion.
Le refroidissement des appareils électroniques mobiles
(téléphones GSM, ordinateurs portatifs et les blocs notes
électroniques) utilisant une unité de stockage de chaleur remplie
par un MCP (n-eicosane) comme puits de chaleur, a été
exploré par Tan et Tso [38]. L'analyse des résultats montre que
la température des sources de chaleur a été
stabilisée à un niveau inférieur à 50 °C
pendant une durée de 2 heures sans avoir recours au ventilateur. Une
telle stabilité est due à la densité
énergétique relativement élevée du MCP. Cette
étude a permis, aussi, de conclure que la distribution de la
température est affectée par l'orientation de l'appareil dans le
champ de la pesanteur. La montée en puissance accélère la
fusion et améliore l'efficacité de refroidissement jusqu'à
la fusion complète du MCP, mais réduit la durée de
fonctionnent sécurisé de l'appareil. Les résultats des
investigations numériques indiquent la possibilité d'utiliser ce
type de puits de chaleur dans les appareils à usage intermittent.
L'effet de l'orientation du puits de chaleur sur la distribution et
l'évolution de la température a été
numériquement exploré par Wang et al. [39] et Zheng et al. [40].
Dans cette contribution, les auteurs rapportent que les transferts de chaleur
par convection naturelle dans la phase liquide ont un rôle majeur dans le
processus de fusion et que l'orientation du puits de chaleur dans le champ de
gravité influence son efficacité de refroidissement.
Le contrôle thermique des composants
électroniques par des matériaux à changement de phase est
aussi traité, expérimentalement et numériquement, par
Kandasamy et al. [41]. Les effets de la puissance imposée, l'orientation
de l'appareil, et la durée des périodes de fusion/solidification,
sur la performance thermique du refroidisseur ont été
examinés. L'étude numérique, basée sur un
modèle (CFD-2D), se compare bien avec les résultats
expérimentaux qui montrent que la montée en puissance
accélère la fusion. Cependant, l'orientation de l'appareil, dans
ce cas, a un faible effet sur la performance thermique du refroidisseur
à base de MCP.
Le processus de fusion d'un MCP (n-octadécane) dans une
cavité rectangulaire chauffée par trois sources de chaleur
protubérantes sur la paroi inférieure de la cavité est
étudié expérimentalement par Jianhua et al. [42]. Dans
cette étude les effets du nombre de Stefan, du sous refroidissement et
du rapport de forme sur la fusion du MCP ont été
analysés.
Ju et al. [43] analysent une configuration similaire à
celle traitée par Zhang et al. [34], mais avec des sources de chaleur
protubérantes sujettes à une densité de flux constante
à la base de chacune. Les résultats sont comparés avec
ceux rapportés dans l'article [34]. L'effet de la protubérance
sur l'allure du front de fusion et sur la température maximale des
sources est rapporté. Il s'est avéré que la
température des sources protubérantes est trouvée
inférieure à celle enregistrée par des sources
surfaciques. Une corrélation donnant le nombre de Nusselt moyen de
chaque source de chaleur, en régime quasi stationnaire, en fonction du
nombre de Rayleigh a été établie.
Hodes et al. [44] ont analysé expérimentalement
le refroidissement des casques (baladeur électronique) par des
matériaux à changement de phase. Les effets de la puissance
dissipée par le casque, le type du MCP ainsi que les pertes de chaleur
du casque par convection naturelle et par rayonnement vers l'ambiance, sur la
durée mise pour atteindre la température critique sont
numériquement analysés. Les auteurs ont conclut que l'usage des
MCP pour le refroidissement de l'électronique est une solution
prometteuse.
Akhilesh et al. [45] proposent une méthode pour
déterminer la configuration géométrique d'un puits de
chaleur à base de MCP pour une plage du flux de chaleur imposé et
pour une hauteur du puits de chaleur fixe en utilisant une analyse
d'échelle de l'équation d'énergie en régime
transitoire. Une relation entre la configuration optimale et la quantité
de MCP utilisée est déterminée. Ces résultats sont
validés par un modèle numérique. Des corrélations
sont proposées pour prédire, pour un MCP donné, les
dimensions optimales avec un écart de l'ordre de 10 %.
Les MCP sont caractérisés par leur faible
conductivité thermique. Pour améliorer les transferts de chaleur
à l'intérieur des cavités remplies de MCP il est possible
d'incorporer des ailettes métalliques dans le puits de chaleur à
base de MCP. Dans ce sens, Abhat [46] a effectué une étude
expérimentale et numérique pour examiner l'effet de
l'introduction des MCP sur l'évolution thermique d'une surface
chauffante, simulant un composant électronique. De leur
côté, Alawadhi et Amon [47], O'Connor et Weber [48] ont
vérifié la performance thermique d'un puits de chaleur à
base de MCP pour le refroidissement des équipements
électroniques. L'amélioration des transferts de chaleur au sein
des MCP a fait aussi l'objet des travaux de Yin et al. [49] qui ont
préparé un MCP composite avec une excellente performance
thermique. Les résultats montrent que l'introduction des MCP dans les
puits de chaleur protège les composants électroniques des chocs
thermiques suite aux éventuelles variations dans le flux de chaleur et
permet d'assurer des conditions opératoires sécurisées,
constantes et durables.
Dans la même optique, Nayak et al. [50] ont
étudié numériquement les possibilités
d'améliorer la performance du puits de chaleur hybride (ailettes
introduites dans le MCP) en examinant l'effet de la forme et du nombre
d'ailettes incorporées dans une cavité à MCP sur la
température maximal du microprocesseur et sur la fraction liquide. Les
résultats montrent que l'amélioration de la conductivité
thermique globale du puits de chaleur a un impact important sur sa performance
thermique et permet de mieux contrôler la température du composant
électronique de type CPU.
1.4 Position du problème
Dans les travaux antérieurs utilisant des
cavités remplies de MCP, les sources de chaleur sont soit volumiques et
incrustées dans une paroi adiabatique de la cavité soit
surfaciques. De plus, une condition de température ou de densité
de flux constantes sont
imposées à la base des sources de chaleur. En
ingénierie électronique, lorsque les sources de chaleur sont
mises sous tension, la puissance de chaleur y est générée
volumiquement. Ainsi, les conditions thermiques imposées:
température ou densité de flux constantes à la base des
composants électroniques ne reflètent pas les conditions
opératoires thermiques auxquelles sont réellement sujettes les
composants électroniques. A la limite de la connaissance de l'auteur,
aucune étude numérique relative au refroidissement des sources de
chaleur protubérantes, avec génération interne de chaleur
couplée à la conduction thermique dans le substrat et au
changement de phase solide\liquide, n'a été reportée dans
la littérature.
Le présent travail surmonte cette limitation, en
étudiant numériquement la performance thermique d'un dissipateur
de chaleur à base de MCP. Ce dissipateur est conçu pour
contrôler la température de trois sources de chaleur
protubérantes simulant des composants électroniques réels.
Les sources de chaleur sont griffées sur une plaque verticale
conductrice (substrat) d'une cavité remplie d'un MCP. Les parois de la
cavité sont adiabatiques. Les phénomènes de transferts
thermiques transitoires intervenant dans le système proposé,
combinent à la fois, les transferts de chaleur par conduction thermique
dans les sources de chaleur, dans le substrat et dans le MCP, conjugués
à la convection naturelle dans la cavité liquide du MCP, de
volume variable, formée suite à la fusion du MCP solide. Le MCP,
placé dans la cavité rectangulaire, est utilisé pour
dissiper la puissance générée par les sources de chaleur
(composants électroniques). L'avantage d'utiliser une telle
stratégie de refroidissement réside dans le fait que les MCP sont
capables d'absorber une importante quantité de chaleur
générée par les circuits intégrés, sans
recours à des ventilateurs. Cette méthode proposée est
convenable pour les situations où le refroidissement par convection
naturelle ou forcée à l'air ambiant n'est pas pratique, comme
c'est le cas pour les appareils électroniques utilisés dans les
applications aérospatiales, métallurgiques, extinction
d'incendies, etc...
Les objectifs visés dans cette étude peuvent se
résumer comme suit:
(1) modéliser et analyser les phénomènes
de transferts conjugués au changement de phase solide-liquide se
manifestant dans un MCP chauffé par des sources de chaleur
protubérantes sur une paroi conductrice verticale;
(2) développer un modèle mathématique
basé sur les équations de conservation de la masse, de
l'énergie et de la quantité de mouvement, et le valider par les
résultats expérimentaux disponibles en littérature;
(3) identifier les paramètres du modèle
contrôlant les comportements thermique et hydrodynamique du dissipateur
envisagé;
(4) examiner les comportements thermique et hydrodynamique du
dissipateur proposé par l'étude de la structure de
l'écoulement dans la phase liquide et l'analyse du champ de
température et des transferts de chaleur durant le processus de
fusion;
(5) mener une étude paramétrique du refroidisseur
pour étudier l'impact des différents paramètres sur la
performance thermique du refroidisseur;
(6) développer des corrélations pour la
durée adimensionnelle de fonctionnement sécurisé et la
fraction liquide obtenue à la fin du processus de fusion en fonction des
paramètres de contrôle;
(7) traduire les corrélations des résultats des
simulations numériques sous forme
d'abaques d'usage pratique relative au refroidissement des
composants électroniques par un MCP. De tels résultats sont d'une
grande importance pour la conception et le développement des
dissipateurs à base de MCP.
Chapitre II
Modélisation
Le présent chapitre est divisé en trois parties.
La première partie expose le modèle mathématique
basé sur les équations de conservation de la masse, de la
quantité de mouvement et d'énergie régissant les
comportements thermique et hydrodynamique des éléments
constituant le système de refroidissement (sources de chaleur, MCP,
plaque conductrice). La deuxième partie présente la
méthode de résolution numérique des équations
algébriques obtenues par la discrétisation des équations
constituant le modèle mathématique. La troisième partie
traite de la validation du code numérique, développé en
langage FORTRAN, en comparant les résultats prédits avec les
résultats expérimentaux disponibles dans la littérature.
Enfin, l'organigramme de calcul, décrivant les étapes de calcul,
est présenté à la fin de ce chapitre.
2.1 Description du système de refroidissement
étudié
La Figure 2.1 schématise le système de
refroidissement des composants électroniques
étudié. Il est formé d'une enceinte
rectangulaire contenant un MCP (n-eicosane, Tf = 36 °C). L'enceinte est de
hauteur, l, et de largeur, w. Ses frontières sont thermiquement
isolées. La base du refroidisseur est constituée d'une couche de
substrat solide (carte électronique imprimée) d'épaisseur,
es, qui supporte trois sources de chaleur rectangulaires et
identiques, notées (S1), (S2) et (S3). Elles sont
caractérisées par leur protubérance, ec, la
longueur de la face verticale, lc, l'espacement entre deux sources
successives, ã , et la position de la première
source (S1) par rapport à l'axe des abscisses, ä .
Chaque source de chaleur génère une puissance, par unité
de volume, constante et uniforme, Q'.
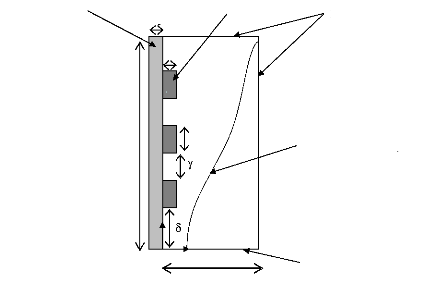
Plaque conductrice (Substrat)
es
Source de chaleur
Parois adiabatiques
e c
3
Cavité Liquide
l
Front de fusion, T=Tf
2
l c
1
MCP
Solide
y
Paroi adiabatique
0
x
w
Figure 2.1: Schéma du modèle
physique
La puissance générée par les trois
sources de chaleur est stockée, sous forme d'énergie sensible,
dans la plaque conductrice (substrat) et les sources de chaleur, alors qu'elle
est emmagasinée dans le MCP sous formes d'énergies sensible et
latente de fusion. Dès la mise sous tension de l'appareil
électronique, les composants électroniques et le substrat
s'échauffent et drainent la chaleur dans le MCP. Le front de fusion
prend naissance à proximité des sources de chaleur et se
développe en progressant vers la paroi droite de la cavité.
Après une certaine durée, l'une des trois sources de chaleur
atteindra la température critique fixée par le manufacturier
(Tcr). L'appareil doit alors s'arrêter pour éviter la
destruction des composants électroniques suite à leur
surchauffe.
2.2 Modélisation mathématique
2. 2. 1 Hypothèses simplificatrices
Pour modéliser les phénomènes
conjugués mis en jeu au sein du système proposé,
à
savoir les transferts de chaleur convectif et conductif et le
changement de phase, les hypothèses suivantes ont été
adoptées:
· le MCP est pure et le changement de phase est
isotherme;
· le MCP est homogène et isotrope;
· le MCP est initialement solide à sa
température de fusion (To = Tf);
· les propriétés thermophysiques sont
supposées constantes dans la plage de température
envisagée. La température de référence est
apportée au point de fusion: Tref = Tf. La densité de
référence: ñ ref = ñ (T = Tf));
· le contact entre le MCP et les frontières
solides est parfait et permanent;
· le MCP solide est immobilisé, même s'il
est entouré de liquide;
· l'écoulement est Newtonien, laminaire et
incompressible;
· les principaux modes de transfert de chaleur dans le MCP
sont la conduction et la convection naturelle;
· le transfert de chaleur et l'écoulement sont
transitoires et bidimensionnels;
· la dissipation visqueuse est négligée;
· l'approximation de Boussinesq qui consiste à
négliger les variations de la masse volumique avec la température
partout sauf dans le terme de poussée est valide. Ainsi, la masse
volumique figurant dans le terme qui génère le mouvement, varie
linéairement en fonction de la température selon la relation:
p(T) = p ref ~ 1 - !3
( T - T ref ) ~
~ ~
où, â est le coefficient de la dilatation
thermique donné par la relation:
1 ~ ?ñ ~
â = ? ~ ~
p(T) T
~ ? ) P
2. 2. 2 Présentation de la méthode
enthalpique
De multiples méthodes numériques sont
proposées dans la littérature pour résoudre les
problèmes de transfert de chaleur avec changement de phase (fusion ou
solidification). En général, ces méthodes cherchent
à calculer la position du front de fusion ou de solidification au cours
du temps, et se divisent en deux principales classes:
· méthodes à grille spatiale fixe ;
· méthodes à grille mobile ou
déformable.
Les méthodes à grille (maillage) fixe sont
basées sur une formulation enthalpique de l'équation de
conservation de l'énergie, et utilisent la fraction liquide locale pour
suivre le déplacement du front de fusion à travers le maillage
statique. En revanche, les méthodes à maillage déformable
se basent sur la formulation classique de Stefan où le bilan thermique
au front de fusion détermine la position de celui-ci; le maillage est
regénéré à chaque instant afin qu'une de ses lignes
se superpose à ce front. Ces deux méthodes,
considérées comme deux approches bien distinctes, ont fait
l'objet de plusieurs études comparatives [51-55]. La méthode
à maillage déformable est plus précise pour calculer la
position de l'interface solide/liquide. Toutefois, elle est plus lourde
à mettre en oeuvre, et demande plus de temps de calcul. La
méthode à maillage fixe demande moins de calculs. Ces
méthodes sont utilisées dans le domaine de la métallurgie,
dans le but de prévoir le comportement des métaux liquides au
cours de leur solidification dans les moules, ou dans les fours au cours de la
fusion. Un autre domaine dans lequel ces méthodes sont utilisées
est le stockage d'énergie par chaleur latente; des travaux ont
porté sur le comportement des MCP en solidification et en fusion, dans
différentes installations et configurations de stockage. Dans la
présente étude la méthode enthalpique à maillage
fixe sera adoptée.
2. 2. 3 Equations gouvernantes
Sur la base des hypothèses susmentionnées et en
utilisant la méthode d'enthalpie- porosité [52], les
équations gouvernant les transferts de masse, de la quantité de
mouvement et de chaleur au sein de la plaque conductrice, du MCP et des sources
de chaleur sont données comme suit:
- Equation de la conservation de la masse:
? ( ñ u) + ? ( ñv) = 0 (2.1)
? x ? y
- Equations de la quantité de mouvement:
? ? ?? ? ~ ? ~ ? ~ ? ~
p u u
( u) ( uu) ( vu)
ñ + ñ + ñ = - + ~ ì ~ + ~ ì ~
+ S (2.2)
u
? t ? x ? y ? ? ~ ? ~ ? ~ ? ~
x x x y y
? ? ?? ? ~ ? ~ ? ~ ? ~
p v v
( v) ( uv) ( vv)
ñ + ñ + ñ = - + ~ ì ~ + ~ ì ~
+ S (2.3)
v
? t ? x ? y ? ? ~ ? ~ ? ~ ? ~
y x x y y
- Equation de l'énergie
? ? ? ? ~ ? ~ ? ~ ? ~
k h k h
( h) ( uh) ( vh)
ñ + ñ + ñ = S (2.4)
h
? t ? x ? y ? ~ ? ? ?
~ + ~ ~ +
x c x
~ ~ ~ ~
y c y
p p
T
avec, h = f c p dT+h(T f) , (
h(Tf ) =0 ) (2.5)
Tf
(1-f)2
S u = -C
3
(f
+b) u (2.6)
|
(1 3 + b) - f)2
S v = - C (f v +ñ g â(T -T f)
|
(2.7)
|
~ ? f Q ' ~
S = ä ~ - - ä ñÄÇ
( )
1 + ä ~ (2.8)
h 1 2 f 2
~ ? t e c lc ~
L'équation de la quantité de mouvement est
similaire à celle d'un milieu poreux avec une porosité nulle dans
les zones solides et une porosité égale à 1 dans la zone
liquide, Eqs.(2.6 et 2.7). Les mêmes équations gouvernent les
transferts de chaleur et de la quantité de mouvement dans les
régions solides (MCP non fondu, sources de chaleur, plaque
conductrice)
et dans le MCP liquide avec la prise en compte d'une grande
valeur de la viscosité dynamique
dans les zones solides. Les
paramètres ä 1 et ä2 et la
conductivité thermique, k, figurant dans
l'équation de l'énergie, sont donnés comme
suit:
,
k MCP
m
~
~
k k plaque conductrice
= s
~L k sources de chaleur c
~
ä = ~~1
~
ä = ~~2
1 sourcesde chaleur et MCP 0 plaque conductrice
(2.9)
1 sources de chaleur 0 MCP
Conditions aux limites et initiales:
Les équations précitées sont assujetties aux
conditions aux limites et initiale suivantes: - Interface plaque conductrice
(s)- source de chaleur (c)
|
T =T et k
c s c
|
? T ? T
= k s
? x ? x
c
|
s
|
(2. 10)
|
|
|
- Interface plaque conductrice - MCP
T =T et k
s m m
k s
? x ? x
m
(2. 11)
? T
? T
s
- Interface MCP - source de chaleur
? T ? T
=km
? ?
c
T =T et k
c m c
m
ç
ç
(2. 12)
avec, ç ? interface.
- Sur les quatre parois adiabatiques de la cavité
|
? =
T
?ç
|
0 où, ç ? à la paroi (2. 13)
|
- Non glissement et imperméabilité sur toutes les
parois solides
u = v = 0 (2. 14)
- Condition initiale:
u = v = 0 , f = 0 , T =Tf (2. 15)
Les propriétés thermo- physiques du MCP sont
évaluées comme suit:
k m = f k m , l + ( 1 - f) k
m , s , á m = f á m,l + (1 - f
) ám,s (2. 16)
A l'interface `i' entre deux matériaux
différents (MCP, plaque conductrice ou sources de chaleur), la
conductivité thermique est estimée par la méthode des
moyennes harmoniques [56].
k i
k k ( ä + ä )
+ - + -
(2. 17)
ä + ä
k k
+ - - +
avec, ä + , est la distance séparant l'interface et
le point voisin appartenant au matériau `+' et, ä - , est la
distance séparant l'interface et le point voisin appartenant au
matériau `-'.
Dans les équations ci-dessus, Su et
Sv sont deux termes sources utilisés pour annuler la vitesse
dans les régions solides (MCP solide, plaque conductrice, sources de
chaleur). Une des techniques utilisée pour annuler la vitesse est
l'introduction d'un terme de Darcy [52], en choisissant C = 10 25 kg
m-3 s-1 et b = 0,005. La valeur de la constante C dépend, en
principe, de la morphologie du milieu poreux. La quantité b est
introduite ici simplement pour éviter une division par zéro dans
le cas d'une fraction liquide nulle. Numériquement, le rapport C/b doit
simplement être suffisamment élevé afin d'annuler les
vitesses dans la région solide. La comparaison des différentes
techniques d'immobilisation de la phase solide (y compris la variation de la
viscosité et le modèle du milieu poreux) est l'objet principal de
l'article de Voller et al. [52], et par la suite a fait l'objet d'un
`benchmark' prouvant son efficacité [55]. En résumé, cette
méthode offre l'avantage d'être souvent plus stable,
bénéficie d'une plus grande signification physique et peut servir
à modéliser des phénomènes de changement de phase
avec une zone pâteuse.
La méthode enthalpique consiste à formuler
l'équation d'énergie en terme d'enthalpie sensible. Le terme
source de cette équation reflète le changement de phase. Dans le
cas des corps purs, où le changement de phase se fait à
température constante, T = Tf, la fraction liquide, f, est
donnée par la relation suivante:
~L 0 < < 1 si T = T
f f
f= 1 si T > Tf
f= 0 si T < Tf
(2. 18)
Le système d'équations (2.1-2.3) est
intégré numériquement sur un maillage décalé
moyennant la méthode de volume de contrôle de Patankar [56].
L'algorithme SIMPLE (Semi Implicit Method for Pressure Linked Equation) est
utilisé pour traiter le couplage pression/vitesse. Ces techniques sont
explicitées dans les sections qui suivent.
2. 2. 4 Formulation adimensionnelle
Dans la présente étude les résultats
seront donnés sous une forme adimensionnelle. A cet effet, l'ensemble du
problème a été formulé à l'aide des
quantités représentatives sans dimension. Les équations et
les conditions aux limites et initiale seront adimensionnées en
utilisant les variables dépendantes et indépendantes et les
paramètres suivants:
Ä = , T T f
3Q ' -
T è = ,
k Ä T
m
,l
v
á m,l o
/l
,
,
l o
x
l o
X
Y
y
, ô = ,
l 2
o
á u
m,l t U =
á m,l o
/ l
,
V=
=
g l T
â Ä
3
o
Ste
,
õ
m ,l
Pr
,
á
m ,l
f
Ä H
P
, ( / l ) 2
ñ á m,l o
p
m,l
, á =
á
Ra =
õ á
m,l m,l
c T
ml,p Ä
á
(2. 19)
La quantité l o = lw - 3l c e c ,
représente la masse du MCP utilisée. Elle est retenue comme
longueur caractéristique.
Moyennant les quantités adimensionnées
susmentionnées, les équations gouvernantes
|
peuvent s'écrire sous la forme générale
adimensionnelle suivante:
2 2
? Ö ? Ö ? Ö
( ) U V ? Ö ? Ö
+ + = S
+
2 2
X Y X ? Y Ö
+
?ô ? ? ?
|
(2. 20)
|
Où est un coefficient de diffusion et SÖ
est un terme source associé à la variable
générale
Ö ( U, V ou è ). L'équation
générale se ramène donc à un terme d'accumulation
(terme d'inertie), un terme de convection, un terme de diffusion et un terme
source. Ces quantités sont explicitées au Tableau 2.1.
Tableau 2.1: Termes de l'équation
générale.
Ö SÖ
1 0 0
?
U Pr U
- +
P S
? X
?
V Pr V
- +
P S
? Y
è á Sè
|
avec,
|
( 1 f ) 2
-
S = - C U
U b f 3
+
|
(2. 21)
|
|
(1 f ) 2
-
S = - C V Ra Pr
+
V b f 3
+
|
è (2. 22)
|
~ 1 f
? ä "
2
S = ä ~ ä -
( )
1 + ~ (2. 23)
è 1 2
~ Ste ? ô 3E L
c c ~
L'équation (2.20) est soumise aux conditions aux limites
et initiale adimensionnelles suivantes:
- Conditions aux limites
- Frontières
adiabatiques
|
?è
? ç
|
paroi
|
= 0 où, frontière
ç ?
|
(2. 24)
|
|
|
|
- Interface plaque conductrice -( i ème) source
de chaleur
|
è = è
c
|
et K
s c
|
?è
|
|
|
K s
|
?è
|
|
|
(2. 25)
|
|
|
|
|
|
|
|
? X c
|
? X s
|
(X=0, i=1,2,3): Ä + (i - 1)( + L ) = Y = Ä + (i - 1) +
iL c
c
- Interface plaque conductrice - MCP
è = è
s
?è
?
s m
et K
m s
?è
? X
K m
X
(2. 26)
- Interface MCP- Source de chaleur
|
è = è
c
|
et K
m c
|
?è
? ç
|
c
|
Km
|
?è
? ç
|
m
|
(2. 27)
|
|
|
|
|
|
|
ç est la normale aux faces des sources de chaleur en
contact avec le MCP.
- Imperméabilité et non glissement sur les parois
solides
U=V=0 (2. 28)
Les propriétés thermo- physiques du MCP sont
évaluées comme suit:
K m = f + (1 - f) Km,s, á m = f + (1 - f) á m,s (2.
29)
Aux interfaces `i', entre deux matériaux
différents (MCP, plaque conductrice ou sources de chaleur), la
conductivité thermique adimensionnelle est estimée par la
méthode des moyennes harmoniques [56].
K K ( Ä + Ä)
+ - + -
K i
(2. 30)
K Ä + K
+
Ä
- - +
où, Ä + = ä + / l o est Ä - =
ä - / lo .
- Conditions initiales
è = U = V = f = 0 (2.31)
D'une manière générale, le système
peut être décrit, à partir de 5 groupements de
paramètres sans dimensions:
(1) Géométrie de l'enceinte:
Le rapport de forme de l'enceinte: A
~ 2 ~
~ + ~ ~ ~
~ ~
l CE
1 3
l o ~ ~ ~
Il est à noter que les dimensions adimensionnelles de la
cavité peuvent se déduire à partir des relations
suivantes:
L
~ ~ + ~ ~ ~ ~ ~ ~ = ~ ~ t\
2
l CE
A 1 3 , W
~ ~ ~ ~
l A
o
~ ~
où, lCE représente le volume de la
source de chaleur.
(2) Dynamique de la fusion et de l'écoulement:
Ste, Ra
(3) Propriétés thermophysiques du MCP:
|
k a
m,s m,s
K = , ~ =
m,s m,s
k ~
m,l m,l
|
, Pr
|
(4) Caractéristiques des sources de chaleur:
k ~
c c
, K = , a =
c c
k ~
m,l m,l
e ä ã
E = , = , =

c Ä
c l l l
o o o
(5) Caractéristiques de la plaque conductrice:
e s
E = ,
s l
k a
s s
K = , a =
s s
k ~
m,l m,l
o
2. 2. 5 Méthode de résolution
numérique
Le domaine de calcul est découpé en un ensemble
de volumes de contrôle [56] entourant le point de maillage sur lequel
l'équation générale (Eq. 2.20) est intégrée.
Le volume de contrôle est centré sur le noeud (P) et
délimité par les plans nord (n), sud (s), est (e) et ouest (w),
comme illustré sur la Figure 2.2. Ces volumes sont égaux à
ÄXÄY, ÄX et ÄY étant les pas d'espace selon les
directions (x) et (y). Cette méthode préserve les
propriétés de conservation des flux locaux et globaux, ce qui
joue un rôle important dans la stabilité des calculs lors de la
résolution numérique des équations.

ÄX
Figure 2.2: Volume de contrôle
En définissant les flux totaux (convectif et diffusif)
comme suit:
Jx U
= Ö -
?Ö (2.32)
? X
?Ö
Jy V
= Ö ?
? (2.33)
Y
l'équation (2.20) devient alors:
?Ö ? J xJ y S
?
+ + = (2.34)
?ô ? X ?Y
L'intégration de l'équation générale
Eq.(2.34) sur le volume de contrôle de la Figure 2.2 donne:
.f
? ? J ?Ö
x y
? ~~ ? ~~ ?ô
J dXdY + dXdY (S - )dXdY
= Ö
X Y
v v v
(2.35)
(I) (II) (III)

les termes (I), (II) et (III) sont développés comme
suit:
x e y
n? J x
(I) = dXdY J J Y J
= - Ä = Ä
( )
x w ys x e yn
xe xw x
~ ~ ? x
(II)
y
(2.36)
= Li y dXdY = ( J yn - J ys ) Ä X =
ÄJ
x w ys
??Jy
x y
e n 0
?Ö ~ Ö - Ö ~
P P
(III) (S- )dXdY S Ö
= ~ ~ = ~ - ~ Ä Ä
X Y
w s
y
?ô ~ Äô ~
x
|
avec
|
~ Ä = -
X x x
e w
~ ~Ä = -
Y y y
n s
|
et Äô désigne le pas de temps
adimensionnel
|
Ö p et o
Ö P sont les valeurs de la variable 0 au point P
respectivement aux instants actuel ô et
précédent ô-Äô. Le terme SÖ
est la valeur moyenne du terme source sur le volume de
contrôle. Il
dépend de Ö et il faut l'exprimer d'une manière
linéaire afin de l'utiliser dans le
système d'équations linéaires ( S Ö =
S c + SP Ö P ). Le terme SP
doit être négatif afin d'assurer la
stabilité de la solution et une convergence rapide
[56].
Pour établir les expressions des différents
coefficients, les différents flux aux faces du volume de contrôle,
peuvent être approximés par un schéma centré:
~ Ö+ Ö ~ ~ Ö - Ö ~
E P E P
J U ~ - ~
xe ~
e e ~
~ 2 ~ ~ X -X
E P ~
~ Ö + Ö ~ ~ Ö - Ö ~
W P P W
xw ~ ~ - ~ ~
w w
~ 2 ~ ~ X -X
P W ~
J U
(2.37)
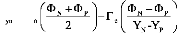
yn ~ ~
n n
J V
~ Ö + Ö ~ ~ Ö - Ö ~
S P P S
J V
ys ~ ~ ? ~ ~
s s
~ 2 ~ ~Y P -YS
En remplaçant les flux par leurs expressions dans
l'équation (2.35) et après réarrangement sous la forme
algébrique, on obtient:
a P Ö P = a E Ö E + a
W Ö W + a NÖ N + a SÖ
S + b (2.38)
on pose
Fe = U e ÄY, Fw = U
w ÄY , Fn = Vn ÄX, Fs =
VsÄX (2.39)
|
e w n s
D Ä
e = Y, D Ä
= Y, D = Ä X, D Ä
= X
w n s
Ä X Ä X Ä Y Ä Y
e w n s
|
(2.40)
|
avec, ÄX e = X E - XP, ÄX w = X P
- XW , ÄYn = YN - YP ,
ÄYs = YP - YS
Alors, les coefficients affectant la variable Ö de
l'équation (2.38) sont donnés comme suit:
F F F F
e w n s
a D
= - , a D
= + , a D
= - , a D
= + (2.41)
E e W w N n S s 2 2 2
2
Ä X Ä Y
a U Y U Y V X V X a a a a +
= Ä - Ä + Ä - Ä + + + + - Ä Ä
S X Y (2.42)
P e w n s E W N S P
Äô
En faisant appel à l'équation de continuité,
Eq (2.1), on obtient:
U e ÄY -- - U w ÄY +
Vn ÄX -- - VsÄX = 0 (2.43)
~ Ö + Ö ~ ~ Ö ? Ö ~
N P N P
~ ? ~
~ 2 ~ ~ Y -Y
N P ~
alors:
ÄXÄY
a a a a a
= + + + + - Ä Ä
S X Y (2.44)
P E W N S P
Äô
|
0
b S X Y ~ Ä Ä ~
X Y
= Ä Ä + ~ Ö
c P
~ Äô ~
|
(2.45)
|
La discrétisation des termes diffusif et convectif permet
d'exprimer les coefficients, a P ,a E ,a W ,a
N et aS par les relations suivantes [56]:

Ps
) Sup(0,F )
+ s
) Sup(0, F ) , a D A(
+ - =
n S s
a D A( P ) Sup(0, F ) , a D A( P
= + - =
E e e e W w w
a D A( P
=
N n n
) Sup(0,F )
+ w
(2.46)
Tableau 2.2: La fonction A( P ) pour
différents schémas.
Schéma Expression de A( P )
Différences Centrées 1 - 0,5 P
Upwind 1

Hybrid Sup(0,1 - 0,5 P )
5
P )

Sup(0,1 - 0,5
Loi de Puissance
|
F
Le rapport i
P =
i D i
|
est le nombre de Peclet sur la face `i' du volume de
contrôle,
|
exprimant le rapport du transfert de chaleur par convection
à celui par diffusion. A( P ) est
une fonction qui dépend du schéma adopté
pour la discrétisation des termes convectifs. Le
Tableau 2.2 donne
les expressions de la fonction A( P ) pour les schémas
fréquemment
utilisés. Patankar [56] a démontré que la
réalité physique du problème exige que
les
coefficients, a P ,a E ,a W ,a
N et aS soient positifs ou nuls. Cette condition n'est pas
toujours
vérifiée par le schéma centré quand
le nombre de Peclet, Pe > 2 , c'est-à-dire, lorsque la
convection naturelle est intense et prédomine la
diffusion. D'autres schémas sont proposés à savoir le
schéma hybride et le schéma en loi de puissance. Ce dernier
schéma est le plus recommandé dans la littérature [57].
Dans le présent travail, on a opté pour un schéma en loi
de puissance. Les coefficients a P ,a E ,a W
,a N et aS de l'équation Eq. (3.45) sont ajustés en
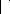
remplaçant la fonction A( P ) par l'expression:
|
A( P
|
) = sup 0, 1 - 0,1 P
( ( )5)
|
(2. 47)
|
2. 2.6 Couplage Vitesse /Pression
Si les vitesses intervenant dans le calcul des coefficients
convectifs sont estimées par la moyenne pondérée des
valeurs de la vitesse aux points de part et d'autre de la surface, des
oscillations de pression et de vitesse seront entraînées. Pour
remédier à ce problème, un maillage décalé
est utilisé. Le maillage principal est réservé pour la
pression, la température et la fraction liquide. Comme il est
indiqué sur les figures 2.3 et 2.4, le décalage est fait vers la
droite pour la composante de vitesse U et vers le haut pour la composante V.
Ainsi, les variables U et V seront calculées aux noeuds situés
respectivement sur les faces verticales et horizontales des volumes de
contrôle du maillage principal. Dans ce cas, le gradient de pression en
un noeud du maillage décalé est intégré en
considérant, tout simplement, la différence de pression entre les
deux points voisins du maillage principal. Les équations
discrétisées correspondant aux variables U et V s'obtiennent de
la même façon que l'équation générale (2.38)
en remplaçant Ö par chacune de ces variables et en
considérant les maillages décalés correspondants pour le
calcul des coefficients, ai. Les équations discrétisées
pour les composantes U (au noeud e) et V (au noeud n) sont respectivement
données par:
Ä Ä
X Y 0
a U = a U + U (P P ) Y
+ - Ä (2. 48)
e e nv nv e p E
Äô
Ä X Ä Y 0
a V = a V + V (P P ) X Pr Ra X. Y
+ ? Ä + è Ä Ä (2. 49)
n n nv nv n p N n
Äô
P E
Y
Figure 2.3. Maillage décalé pour
U.

X
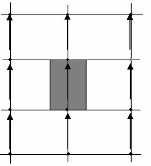
n
N
P
Figure 2.4. Maillage décalé pour
V.
L'algorithme SIMPLE (Semi Implicit Method for Pressure Linked
Equation), développé par Patankar [56], est utilisé dans
le présent code de calcul pour traiter le couplage pression/vitesse. Cet
algorithme consiste à estimer un champ de pression P*, dont le champ de
vitesse associé (V* et U*) doit vérifier l'équation de
continuité, ce qui nécessite un calcul itératif
jusqu'à la satisfaction de la conservation de la masse.
Une correction P' du champ de pression entraîne une
modification des composantes de la vitesse de telle sorte que:
P=P*+P', U=U*+U' , V=V*+V'
U' et V' étant les corrections de U et V,
respectivement. Ainsi, aux noeuds «e» et »n» , les
|
ÄY ÄX
corrections sont données comme suite: e
U ' = (P' P' ) , V '
- = (P' P' )
-
p E n p N
a a
e n
|
.
|
L'équation discrétisée associée
à la correction de pression P' a la même forme que
l'équation générale (2.38) [56]:
|
Avec,
|
ÄXÄY ÄXÄY ÄXÄY
ÄXÄY
a = , a = , a = , a = ,
E W N S
a a a a
e w n s
|
(2. 50)
|
b U* U* Y V* V* X
= ( - ) (
Ä + - ) Ä
w e s n
2. 2. 7 Mise à jour de la fraction liquide
Comme il a été mentionné auparavant,
l'équation d'énergie est résolue par la méthode
enthalpique [52]. Le terme source, 1 f
~ ? "
~ = -
S i , de cette équation est l'élément
moteur
è
~ Ste ? ô )
traduisant le processus de changement de phase, et la fraction
liquide, f, traduit son évolution. Du point de vue
numérique, la valeur de la fraction liquide est calculée
itérativement avec la solution de l'équation de l'énergie.
Dans l'équation de transport sous sa forme générale
discrète, Eq. (2.38), le terme source est:
1 old i X Y
Ä Ä
S = (f f )
- (2. 51)
Ste Äô
La fraction liquide, f, prend la valeur 1 dans les
volumes de contrôle situés dans la région liquide et 0 dans
la région solide, et elle est comprise entre 0 et 1 dans les volumes de
contrôle manifestant le changement de phase. Donc après la
(i+1)ème solution numérique, l'équation de
l'énergie peut être écrite sous la forme suivante:
|
1 (f f ) Ä Ä Ä Ä
X Y X Y
old i o
a è = è + è + è + è +
a a a a ? + è
P P E E S S W W N N P
Ste Äô Äô
|
(2. 52)
|
Si le MCP contenu dans le volume de contrôle (P) est
entrain de fondre, c. à. d, 0 < f <1, alors l'ancienne
valeur à la (i)ème estimation doit être mise
à jour: la partie gauche de
l'équation (2.52) est nulle ( è P =0). A cet effet,
on peut écrire:
|
1 + Ä Ä Ä Ä
X Y X Y
old i 1 o
0 a
= è + è + è + è +
a a a (f f )
? è
+
E E S S W W N N P
Ste Äô Äô
|
(2. 53)
|
En soustrayant l'équation (2.53) de l'équation
(2.52), la mise à jour de la fraction liquide f pour les noeuds
qui sont entrain de changer de phase est:
Äô
f f
i 1
+ = + ù
i Ste
a P P
è (2. 54)
Ä X Ä Y
où ù est un facteur de relaxation. La
mise à jour de la fraction liquide est appliquée à tous
les noeuds. Pour éviter des valeurs non physiques de la fraction
liquide, la correction (Eq. (2.55)) suivante, doit être prévue
immédiatement après l'équation Eq. (2.54).
|
f i 1
+
si = 0 : 0
f =
si 1 : 1
f i 1
+ = f =
|
(2. 55)
|
2. 2. 8 Nombre de Nusselt
Pour évaluer le taux de transfert de chaleur par
convection naturelle évacué par chaque source de chaleur, on
calcule le nombre de Nusselt moyen en procédant comme suit:
La densité de flux de chaleur locale à l'interface
MCP/source de chaleur est:
q k ? T
" = -
i i ?
( ç ? interface ) (2. 56)
i
ç
En utilisant la loi de refroidissement de Newton, cette
densité de flux chaleur peut s'exprimer à l'aide de la relation
suivante:
q i = h i (T max - Tf) (2. 57)
où hi est le coefficient local de transfert de chaleur par
convection à l'interface `i` basé sur la température
maximale Tmax.
En utilisant les deux expressions précédentes, le
nombre de Nusselt moyen, de chaque source de chaleur, basé sur la
température maximale, est:
|
h l 1 î ? °
c o
Nu = = -
j=1,2,3 i
k (L 2E ) O
+ ~ ?
K
0 ~
m,l c c max
|
i
|
dî
|
(2. 58)
|
|
|
où, dî désigne l'élément de
longueur adimensionnelle sur la source de chaleur.
2. 2. 9 Convergence
La nature des équations gouvernantes (couplage et non
linéarité des équations) nécessite un calcul
itératif. La convergence d'un tel calcul est déclarée
lorsque les trois critères suivants sont satisfaits:
- Critère mathématique:
|
~
|
k 1
+(i, j) (i, j)
- Ö k
Ö
|
|
i,j
|
|
|
|
|
< å
|
(2. 59)
|
|
~
i,j
|
Ö
|
k
|
(i, j)
|
où (i, j)
Ö k est la valeur de la variable
dépendante Ö ( è, U ou V) au noeud (i, j) à
l'itération
k. Le paramètre å doit être suffisamment petit
(= 10 -9).
- Critère physique traduisant la conservation de la masse
et de l'énergie:
Max ? in (i,j) -? out (i,j) < ~ m (2. 60)
1- (Q sen,s + Q sen,c + Q sen,l
+ Q lat ) < å T (2. 61)
où -8
å m =10 et å T= 10
-2
?in et ?out sont les
débits massiques adimensionnels entrant et sortant:
|
? (i,j) (U (i,j) AY V (i,j)
AX)
= + ~
in
~ ~
(i,j) (U (i 1,j) AY V (i,j 1)
AX)
+ + ~ ~
? = +
out
|
1 i M+1 ; 1 j N+1
= = = =
|
(2. 62)
|
La chaleur sensible stockée par la plaque conductrice, les
sources de chaleur et le MCP liquide sont exprimées par:
k 1
+ k
Q = ~ Ä Ä è - è ô (2. 63)
R X Y( ) / d
sen, s s
plaque conductrice
= ~ Ä Ä è - è ô (2. 64)
k 1
+ k
Q X Y( ) / d
sen, l
MCP liquide
k 1
+ k
Q = ~ Ä Ä è - è ô (2. 65)
R X Y( ) / d
sen, c c
source de chaleur 1,2,3
MCP
1 f
?
Q = ~ Ä Ä
X Y
lat Ste ?ô
(2. 66)
avec s p,s
ñ c ñ c
c p,c
R = ; R =
s c
ñ c ñ c
l p,l l p,l
2. 2. 10 Optimisation du maillage et du pas de temps
Afin de réaliser un compromis entre le temps de calcul
et la précision des résultats des simulations numériques,
une étude d'optimisation du maillage et du pas de temps a
été faite. Aussi, l'effet du nombre maximal d'itérations
internes sur les résultats obtenus a été analysé.
En se basant sur les données de la configuration de
référence données au Tableau 3.3 du chapitre III, les
résultas des effets des pas de temps et d'espace sont donnés au
Tableau 2.3 et à la Figure 2.5.
Le Tableau 2.3 donne l'effet de trois maillages
différents: 40x60, 60x80 et 80x100, sur la fraction liquide et la
température adimensionnelle maximale, à l'instant ô
= 0,0343. Le pas de temps choisi étant -4
~~ = 4,42x 10(20 s). L'effet du maillage sur
la durée adimensionnelle de fonctionnement sécurisé,
ôfonc (è max = è cr) et la fraction
liquide correspondante, f, est aussi
donné dans ce tableau. Comme on peut l'observer, le
passage du maillage de 60x80 à 80x100, entraîne des variations
relatives de la fraction liquide et de la température maximale
adimensionnelle de l'ordre de 0,82 % et 0,76 %, respectivement. Quant à
la durée maximale de fonctionnement sécurisé,
ôfonc , et la fraction liquide correspondante, f, les
variations
maximales sont estimées à 0,04 % et 0,11 %,
respectivement. Pour confirmer ces résultats, on a analysé
l'effet du maillage sur la position du front de fusion. Visuellement, la Figure
2.5.a montre que les fronts de fusion sont pratiquement confondus pour ces deux
maillages.
Tableau 2.3: Effet du maillage (a) et du pas
de temps (b) sur les résultats

èmax
ôfonc
M x N
Variation
relative
(%)
Variation
relative
(%)
Variation
relative
(%)
Variation
relative
(%)
f
(ô = 0,0343)
(ô = 0,0343)
(è max = è cr)
f
(è max = è cr)
Variation
relative
Variation
relative
Variation
relative
Variation
relative
èmax
f
ôfonc
f
Äô
40x60 0,3290 - 0, 01956 - 0,0964 - 0,801
60x80 0,3502 6,44 0, 01705 12,83 0,1013 4,83 0,868 7,72
80x100 0,3569 0,82 0, 01694 0,76 0,10134 0,04 0,869 0,11
(a, Äô = 4,42 x 10-4)
|
(ô = 0,0343)
|
(%)
|
(ô = 0,0343)
|
(%)
|
(è max = è cr )
|
(%)
|
(è max = è cr)
|
(%)
|
|
1,32x10-3 (60 s)
|
0, 3931
|
-
|
0, 01948
|
-
|
0,07250
|
-
|
0,758
|
-
|
|
7,73x10-4 (35 s)
|
0,3622
|
7,86
|
0,01772
|
9,03
|
0,08992
|
19,37
|
0,825
|
8,12
|
|
4,42x 10-4 (20 s)
|
0,3502
|
3,31
|
0,01705
|
3,78
|
0,10130
|
11,24
|
0,868
|
4,95
|
|
2,21x10-4 (10 s)
|
0, 3490
|
0,34
|
0,016970
|
0,46
|
0,10191
|
0,59
|
0,869
|
0,16
|
(c, M x N= 60x80)
Le Tableau 2.3.b montre que les pas de temps 4
~~ 4,42x10-
= et
At = 2,21x 10conduisent à des
variations relatives de la fraction liquide, de la température
-4
adimensionnelle maximale, de la durée adimensionnelle de
fonctionnement sécurisé, ôfonc ,
(è max = è cr) et de la fraction
liquide correspondante, f, de l'ordre de 0,34 %, 0,46 %, 0,59 % et
0,16 %, respectivement. La Figure 2.5.b montre que les fronts de fusion sont
pratiquement confondus pour des pas de temps inférieurs ( At
4,42x10- 4
= ).
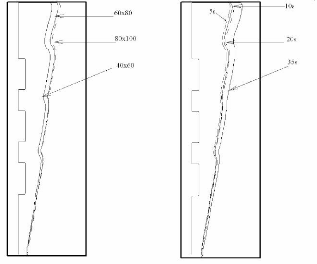
(a, Äô =4,42 x 10-4) (b: 60x80)
Figure 2.5: Effet du maillage, (a) et du pas de
temps, (b) sur la position du front de fusion, à l'instant ô =
0,0343
En conclusion, l'analyse des Tableaux 2.3 a et 2.3 b et des
Figures 2.5 a et 2.5 b
permet de conclure qu'un maillage de 60x80 et un pas
de temps 4
~~ 4,42x10-
= (20 s) sont
suffisants pour avoir des résultas insensibles aux pas
de temps et d'espace. D'autres pas de temps et d'espace ont été
testés, ces pas nécessitent une durée d'exécution
de calcul relativement longue sans, toutefois, apporter des variations
appréciables aux résultas.
Itérations internes:
Pour chaque variable Ö et pour chaque pas de temps, il
faut itérer jusqu'à résoudre le couplage spatial. A cet
effet, il faut que les itérations internes soient poursuivies
jusqu'à ce que la somme des résidus absolus soit réduite
à un niveau fixé, ou que le nombre maximal d'itérations
soit atteint. Le Tableau 2.4 donne l'effet du nombre maximum
d'itérations sur les résultats des simulations numériques,
en se basant sur les données de la configuration de
référence indiquées au Tableau 3.3 du Chapitre III.
Tableau 2.4: Effet du nombre maximal
d'itérations internes sur la fraction liquide, f, et la
durée adimensionnelle de fonctionnement sécurisé,
ôfonc
|
Nombre
d'itérations
|
f
( è max = è cr)
|
Variation relative
(%)
|
ôfonc
(è max = è cr)
|
Variation relative
(%)
|
|
5
|
0,7203
|
-
|
0,1140
|
-
|
|
7
|
0,7910
|
8,94
|
0,1075
|
6,05
|
|
10
|
0,853
|
7,27
|
0,1025
|
4,88
|
|
15
|
0,8685
|
1,78
|
0,1013
|
1,18
|
|
20
|
0,8700
|
0,17
|
0,1018
|
0,49
|
L'analyse des résultats obtenus montre qu'un nombre
maximal d'itération internes égale à 15 est suffisant pour
avoir des résultats précis. En effet, si on augmente le nombre
maximal d'itérations à 20, les variations relatives respectives
de la fraction liquide, f, et la durée adimensionnelle de
fonctionnement sécurisé, ôfonc sont égales
à 0,17 % et 0,5 %.
Les équations algébriques résultantes
sont résolues en utilisant l'algorithme de Thomas (TDMA), pour chaque
pas de temps. La durée d'exécution d'une simulation
numérique dépend directement du maillage et du pas de temps
utilisés. Le contrôle du nombre maximal d'itérations
internes permet de réaliser un compromis entre le temps de calcul et la
précision des résultats. La durée d'une simulation typique
(jusqu'à ce que è max = è cr (Tmax = Tcr)) est de
l'ordre de 9 heures de calcul itératif sur un ordinateur
de bureau équipé d'un microprocesseur 2.6 GHz avec 1 Gb de
RAM.
2.3 Validation du modèle numérique
2.3.1 Validation par l'expérience de Gau et al.
[58]
Dans un premier temps, les résultats du présent
code numérique, élaboré en Fortran, sont comparés
avec ceux obtenus par Gau et al. [58] relatifs au problème
bidimensionnel de changement de phase en présence de la convection
naturelle dans une enceinte rectangulaire. L'enceinte utilisée dans
cette expérience est de hauteur 6,35 cm et de largeur 8,89 cm. Les
parois horizontales sont adiabatiques tandis que les deux parois verticales
sont portées à des températures constantes; la paroi
chaude est portée à 311,15 K et la paroi froide est maintenue
à 302,93 K. Initialement, la cavité est remplie de Gallium pur
à l'état solide, à la même température que la
paroi froide. Les propriétés thermo physiques du Galium sont
données dans le Tableau 2.5. La durée de l'expérience de
la fusion du Galium est égale à 20 minutes. Le code de calcul est
adapté aux conditions de cette expérience. La comparaison entre
les prédictions numériques de la position du front de fusion avec
les résultats expérimentaux est présentée à
la Figure 2.6.
Tableau 2.5: Propriétés
thermophysiques du Galium [59]
Tf (K) k ( W/m K) cp (J/kg K) ñ m
(kg/m3) ì (kg/m s) â ( K-1)
AHf (J/kg)
302,93 32 381,5 6093 1,81x10-3 1,2 x10-4
80,16x103
L'analyse de la Figure 2.6 montre que l'accord entre les
prédictions numériques et l'expérience est satisfaisant;
le faible écart observé peut être expliqué par
l'instabilité de la température des parois du montage
expérimental. En effet, Gau et al. [58] signalent que la
température des parois n'a pas pu être réellement maintenue
constante pendant l'expérience.
6 min 10 min 19 min

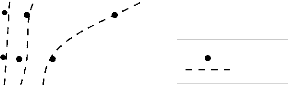
Expérience
Numérique
0 0.2 0.4 0.6 0.8 1 1.2 1.4
x/l
Figure 2.6: Comparaison entre les
prédictions numériques de la position du front de fusion et les
résultats expérimentaux de Gau et al. [58].
2.3.2 Validation par l'expérience de Ju et al.
[43]
Le problème de fusion d'un MCP dans une enceinte
chauffée par trois sources de chaleur protubérantes sur une paroi
verticale (Figure 2.7) a été étudié
expérimentalement par Ju et al. [43]. Le transfert de chaleur se fait
par conduction dans les sources de chaleur et par conduction et convection
naturelle dans la phase liquide du MCP.
Tableau 2.6: Propriétés thermo
physiques du n-octadecane [61-63]
|
Tf (K)
|
km,s
(W/m K)
|
km,l
(W/m K)
|
(c p ) m,s
(J/kg K)
|
(c p ) m,l
(J/kg K)
|
ñm
(kg/m3)
|
ì
(kg/m s)
|
AHf
â (K-1)
(J/ kg)
|
301,16 0,38 0,15 1891 2251 771, 2 3,6x10-3
9,1x10-4 2,434x105
w

|
|
air
|
|
ec
|
|
|
|
|
l c
ã
|
n-octadecane
|
|
|
ä
|
|

l


es
Figure 2.7: Configuration expérimentale
de Ju et al. [43]
L'enceinte utilisée dans cette expérience est
similaire à celle étudiée dans le présent travail.
Elle a une hauteur, l = 0,09 m, une largeur, w = 0,06 m, et une profondeur de
0,06 m. L'enceinte est chauffée par trois sources de chaleur,
d'épaisseur, ec=0,009 m, et de hauteur,
lc=0,015 m, avec une densité de flux de 900 W/m2,
imposée à la face gauche de chaque source de chaleur. Les sources
sont protubérantes sur une paroi verticale, en Plexiglas, non
conductrice de chaleur, d'épaisseur, es=0,02 m. La
source inférieure est placée à une distance, ä =
0,0075 m, de la paroi horizontale inférieure de la cavité.
La distance entre deux sources consécutives est ã =
0,015 m. Initialement la cavité est remplie de MCP solide
(noctadecane, Tf = 28 °C) et dont les propriétés
thermophysiques sont présentées dans le Tableau 2.6. Une couche
d'air ayant une épaisseur de 1 cm, est prévue pour l'expansion
thermique du MCP liquide. Le rapport de forme de cette cavité vaut 1,5.
Le code numérique est adapté aux conditions de cette
expérience et après le raffinement du maillage (MxN = 40x60) et
du pas de
temps ( Äô = 3,5 x 10 ), une comparaison entre les
prédictions numériques du front de fusion
-4
et les résultats expérimentaux, pour
différents instants est présentée à la Figure
2.8.
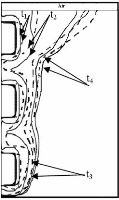
Figure 2.8: Comparaison entre les
prédictions numériques (lignes continues) et les résultats
expérimentaux [43] (lignes discontinues), t1 = 25 min, t2 = 50 min, t3 =
95 min et t4 = 110 min.
Compte tenu de la complexité des
phénomènes mises en jeu lors de la fusion, l'accord entre les
résultats numériques et l'expérience est satisfaisant. La
concordance est bonne pour les instants t1 = 25 min et t2 = 50 min,
excepté pour les zones supérieure et inférieure des
sources inférieure et supérieure, respectivement. Ces sources
semblent fournir moins de chaleur au MCP que prédit la simulation. Ceci
peut être attribué aux pertes thermiques par les parois de
l'enceinte, tout au long de l'expérience, à maintenir une
densité de flux constante et uniforme pour les trois sources de chaleur
ou lors de l'enlèvement de l'isolation au cours des prises des photos
pour déterminer la position de l'interface. L'accord est satisfaisant
pour les instants t3 = 95 min et t4 = 110 min, avec une déviation
à droite du front expérimental dans la partie supérieure.
Ceci est dû à l'expansion volumique du MCP au cours de la fusion,
un effet dont le modèle ne tient pas compte. En effet, l'expansion du
MCP provoque un débordement du liquide chaud à la surface libre
du MCP solide, accélérant ainsi la fusion dans la partie
supérieure. Aussi, une partie du liquide quitte le domaine de calcul en
modifiant notablement
la condition à la limite nord (adiabatique dans le
modèle). Il est donc normal d'observer un front de fusion
`expérimental' plus avancé vers la droite.
Aussi, l'évolution temporelle de la température
moyenne de chacune des trois sources de chaleur a été
déterminée par la même expérience [43] et est
comparée avec celle prédite par le code numérique. La
comparaison est illustrée à la Figure 2.9. L'analyse d'une telle
figure montre que l'accord est satisfaisant, en particulier pour t = 50 min.
Cette période est caractérisée par la prédominance
de la conduction thermique, les sources de chaleur ont pratiquement la
même température moyenne. En effet, la puissance fournie à
chaque source ne diffuse pratiquement pas au travers le Plexiglas à
cause de sa faible conductivité thermique. En conséquence, la
puissance fournie est stockée sous forme de chaleur sensible et cause
l'accroissement des températures des sources de chaleur. Avec la
progression de la fusion, les poches liquides entourant les sources de chaleur
fusionnent et les mouvements convectifs se manifestent dans toute la
région liquide. Ainsi, la puissance fournie aux sources de chaleur est
évacuée par convection naturelle au MCP liquide; le
système atteint, ainsi, un régime quasi stationnaire
marqué par une stabilité des températures moyennes des
sources de chaleur. Il est à noter que la différence des
températures moyennes des sources de chaleur est expliquée par le
fait qu'au début de la fusion les flux de chaleur évacués
par les sources diminuent dans le sens ascendant. Ceci est dû à
l'échauffement des particules liquides dans leur mouvement ascendant
(T1= 34 °C, T2 = 35 °C et T3 = 38 °C). La Figure 2.9 montre que
le présent code numérique reproduit fidèlement ce
comportement physique. L'écart maximal enregistré entre les
prédictions numériques et les résultats
expérimentaux a été estimé à 2 %.
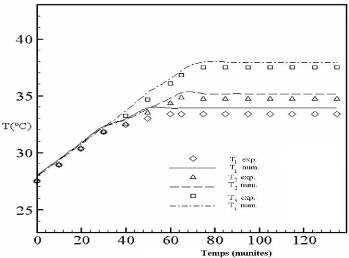
Figure 2.9: Evolutions temporelles des
températures moyennes expérimentales et numériques des
sources de chaleur.
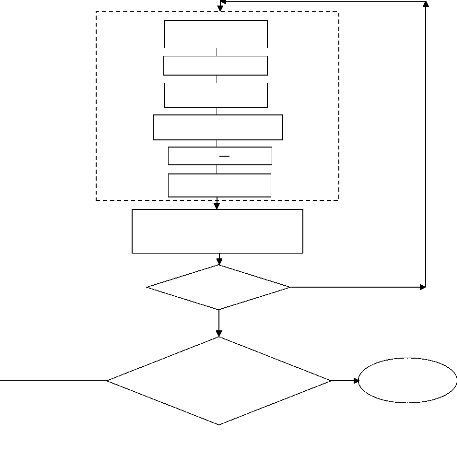
Correction P' et calcul de P
Calcul de è
Calcul de U
Calcul de V
Correction U'
Correction V'
Calcul de la nouvelle fraction liquide
f
et sa
mise à jour
Convergence
Oui
cr
Oui Non
et
è < è
max
Fin
f
< 1
58
Non
2. 4 Organigramme de calcul
Le déroulement du calcul de simulation s'effectue selon
l'organigramme ci-dessous:
Début
ô = 0
Initialisation

|
è 0 = è , U0 = U
V0 = V , P0=P
f0 = f , ô = ô + Äô
|
Chapitre III
Résultats
3.1 Introduction
Ce chapitre comporte trois parties. La première partie
définit les paramètres caractérisant la configuration de
référence. La deuxième partie présente l'analyse
des résultats obtenus par la simulation numérique des
comportements thermique et hydrodynamique de cette configuration. L'analyse
concerne l'évolution temporelle des températures moyennes
adimensionnelles des sources de chaleur et leur température maximale
adimensionnelle, les champs thermique et hydrodynamique et le profil de
température au sein de la plaque conductrice et à l'interface
paroi chaude /MCP liquide. Le nombre de Nusselt moyen des sources de chaleur,
la distribution de la densité de flux de chaleur adimensionnelle le long
de la paroi chaude et le flux thermique adimensionnel transmis par celles-ci
vers le MCP sont aussi présentés et analysés. Quant
à la troisième partie, elle expose les résultats de
simulations relatifs à l'étude paramétrique. Cette
étude a pour objectif la mise en évidence de l'impact des
paramètres de contrôle sur les comportements thermique et
hydrodynamique de l'enceinte du MCP.
3.2 Choix des paramètres de simulation pour la
configuration de référence
Le MCP utilisé dans cette étude est le
n-eicosane. Les sources de chaleur (composants électroniques) sont en
céramique. Elles sont attachées à une plaque conductrice
(substrat d'alumine). Les propriétés thermophysiques du MCP, les
sources de chaleur et la plaque conductrice sont indiquées au Tableau
3.1.
Tableau 3.1: Propriétés
thermophysiques [3, 5, 29, 59-64]
Source de chaleur
(alumine-céramique)
p c = 3260 kg/m3 cp ,c = 740 J/kg K
kc = 170 W/m K Tcr = 75 °C
Plaque
(substrat d'alumine)
p s = 3900 kg/m3 cp ,s = 900 J/kg K ks =
19,7 W/m K
13 =8,5x10 K -1
-4
Al-If = 2,47x105 J/kg
Tf = 36 °C
cp ,m =2460 J/kg K
km = 0,1505 W/m K p m = 769 kg/m3
Um = 4,15x10-3 kg/m s
MCP
(n-eicosane)
Les dimensions des sources de chaleur et de la plaque
conductrice sont indiquées au Tableau 3.2. Ces dimensions correspondent
à celles fréquemment utilisées en électronique. Les
dimensions de l'enceinte sont aussi indiquées dans le même
tableau.
Tableau 3.2: Dimensions (en m) des
différents composants de la configuration de référence
[3,5,29]
ec lc I ä l es w
0,003 0,015 0,01 0,03 0,121 0,005 0,035
Initialement le MCP est solide et la température du
système est To= Tf = 36 °C. Les composants
électroniques étudiés sont de type microprocesseur de
troisième génération à noyau double (CPU Core Duo),
«Chipset« ou contrôleurs graphiques de type (AGP 4). Dans la
présente étude, la puissance générée par
chaque source de chaleur, par unité de longueur, varie entre 7,5 W/m et
60 W/m. La température critique à ne pas dépasser pour
assurer un fonctionnement sécurisé des composants
électroniques est de l'ordre de 75 °C (Tcr =75 °C
[3]).
Les investigations numériques sont initialement conduites
en utilisant les données de la configuration de référence
des Tableaux 3.1 et 3.2. Le volume du MCP ( lw - 3e c l c
)
représenté par la longueur
caractéristique, lo , et le volume du composant
électronique ( e c l c ) représenté
par la longueur, lCE , sont maintenus constants pour toutes les
simulations numériques. La longueur lCE est calculée
en se basant sur les dimensions des composants électroniques les plus
fréquemment utilisées en électronique, 3
l CE = e c l c 6,7x10 m.
-
=
La longueur lo est choisie de telle sorte que la
durée minimale de fonctionnement du
puits de chaleur pour la puissance maximale par unité
de longueur (Q'= 60 W/m) soit de l'ordre d'une heure. Cette durée est
calculée en supposant que toute la puissance
générée par unité de longueur par les sources de
chaleur sert uniquement à la fusion du MCP (le stockage d'énergie
sensible est négligé). Cette durée est donnée par
l'expression:
2
m f o
ñ ÄÇ
l
3Q'
t =
min
Ainsi, en utilisant l'expression précédente, la
longueur l o = lw - 3e c l c = 0,06 m. Il
faut aussi noter que le calcul des nombres de Rayleigh et de
Stefan relatifs à la configuration de référence est
basé sur une puissance générée par unité de
profondeurde 60 W/m. Le Tableau 3.3 présente les valeurs des
paramètres de contrôle relatifs à la configuration de
référence.
Tableau 3.3: Paramètres de
contrôle de la configuration de référence
Es Ec Lc A I' A
Pr -
0,083 0,05 0,25 0,5 0,167 4,0 67,83 -
Km,s Ks Kc a m, s
as ac Ra Ste
1,0 130,9 1130 1,0 70,55 885,77 5,01x109 11,91
La température critique adimensionnelle pour la
configuration de référence est è cr = 0,033. Il est
à noter que cette quantité dépend de la puissance
générée par unité de
profondeur, Q'. La hauteur adimensionnelle, L, et la
largeur adimensionnelle, W, de l'enceinte sont égales à 2,016 et
0,583, respectivement.
3.3 Etude des comportements thermique et hydrodynamique
de la configuration de référence
3.3.1 Analyse de l'évolution des températures
moyennes adimensionnelles des sources de
chaleur, de la température maximale adimensionnelle
et de la fraction liquide.
La Figure 3.1 présente les variations temporelles des
températures moyennes adimensionnelles des sources de chaleur relatives
à la configuration de référence. L'analyse de cette figure
montre que l'évolution de la température moyenne adimensionnelle
de chaque source est caractérisée par quatre phases principales.
Durant la première phase, au début de l'échauffement, le
transfert de chaleur dans la couche du MCP liquide formée proche des
parois chaudes se fait essentiellement par conduction. Au début de la
fusion, une partie de la puissance générée par les sources
de chaleur est évacuée à travers les faces de celles-ci et
la plaque conductrice, alors que l'autre partie est emmagasinée sous
forme de chaleur sensible dans la plaque conductrice et les sources elles
mêmes. Le régime est purement conductif et l'épaisseur de
la couche liquide s'accroît avec le temps. La résistance thermique
de la cavité liquide augmente, réduisant ainsi le flux de chaleur
évacué et entraînant une augmentation de la
température moyenne adimensionnelle. Au début, cette
température augmente linéairement. Après une certaine
durée, son taux de variation commence à décroître
avec le temps. Ceci se traduit par une réduction de l'énergie
sensible stockée par les sources de chaleur et un accroissement du taux
de transfert de chaleur vers la plaque conductrice et la mince couche de MCP
fondue, au voisinage des parois chaudes. La température adimensionnelle
des sources de chaleur atteint un maximum local, alors que la fraction liquide
augmente linéairement durant cette première phase, indiquant que
le flux de chaleur transmis au front de fusion est constant.
Avec la progression de la fusion ( f
? 0,1) les poches liquides entourant les sources de chaleur commencent
à fusionner et à s'élargir (voir Figure 3.2a, ô
=0,007) favorisant, ainsi, le déclenchement de la
convection naturelle. C'est la deuxième phase au cours de laquelle, les
températures moyennes adimensionnelles des sources diminuent
légèrement à cause de leur brassage par les courants
froids provenant du front de fusion. Des constatations similaires ont
été rapportées par Zhang et al. [34].
è
è
è
è3
è
f
Plateau
x
x
x
x x x
x
x
x
0 0.02 0.04 0.06 0.08 0.1
ô
0.03
0.025
0.02
è
0.015
0.01
0.005
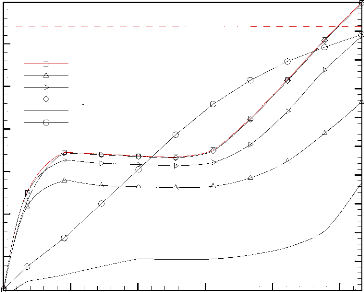
Temperature limite adimensionnelle , cr
è
|
1
0.9 0.8 0.7 0.6 0.5 f 0.4 0.3 0.2 0.1 0
|
max
1
2
x
mcp
x
Figure 3.1: Evolution temporelle de la
fraction liquide, de la température maximale adimensionnelle et des
températures moyennes adimensionnelles des sources de chaleur et du
MCP.
Les températures moyennes adimensionnelles des sources
de chaleur continuent leur légère chute et atteignent un plateau,
c'est la troisième phase. Durant cette période, la convection
naturelle se développe, et pratiquement toute la chaleur extraite des
sources de chaleur est absorbée au niveau du front de fusion par le MCP
solide qui se transforme en liquide. En
conséquence, les températures moyennes
adimensionnelles des sources de chaleur demeurent constantes, le régime
est quasi- permanent. Cette étape est la plus importante du cycle de
refroidissement. En effet, l'utilisation du MCP, comme moyen de refroidissement
passif des sources de chaleur, a permis d'obtenir un régime de
fonctionnement quasi-stationnaire, d'une durée relativement
élevée, durant laquelle les températures moyennes
adimensionnelles des sources de chaleur sont maintenues constantes. La
quatrième et dernière phase a lieu quand le processus de fusion
s'approche de sa fin (f 2 0,7). La température
moyenne adimensionnelle du MCP liquide augmente et le gradient de
température à l'interface (source - substrat) /MCP liquide
diminue, entraînant une baisse du taux de transfert de chaleur entre les
sources de chaleur et le MCP liquide. En conséquence, les
températures moyennes adimensionnelles des sources de chaleur augmentent
et atteignent la température critique adimensionnelle à l'instant
adimensionnel ô =0,1013.
L'analyse de la Figure 3.1 montre, aussi, que la source de
chaleur inférieure enregistre la température moyenne
adimensionnelle la plus basse. En effet, lors de sa descente, le MCP liquide
rejette sa chaleur le long du front de fusion causant ainsi la fusion du bloc
de MCP solide et se refroidit en passant par les zones centrales. Ainsi, le MCP
liquide se trouve déchargé au maximum de sa chaleur dans la
partie inférieure de la cavité. Ceci assure un transfert de
chaleur entre la source inférieure et le MCP liquide à un taux
relativement élevé. A l'inverse, dans la direction du courant
ascendant, le taux de transfert de chaleur devient de moins en moins intense en
passant d'une source de chaleur à l'autre. En effet, la structure de
l'écoulement, prés des sources de chaleur, et l'accroissement de
la température du MCP liquide, dans son mouvement ascendant, font que le
taux de transfert de chaleur le plus élevé est observé au
niveau de la source inférieure. Ce résultat est confirmé
par la Figure 3.5 (p. 74) où l'aire, de la surface
délimitée par l'axe des abscisses et la courbe de la
densité de flux de chaleur adimensionnelle, est plus
élevée pour la source de chaleur inférieure. Il est
important
de signaler que la température maximale adimensionnelle
est enregistrée par les sources de chaleur centrale et supérieure
durant la troisième et dernière phase, respectivement.
3.3.2 Analyse des champs de température et de
vitesse.
Les lignes de courant, ø , et les isothermes, è
, décrivant les champs d'écoulement et thermique, sont
illustrées aux Figures 3.2a et 3.2b, respectivement, pour
différents instants,
ô . Au début, 4
ô ? 1,1 x 10- (3 s), le transfert de chaleur
est purement conductif et pratiquement aucun mouvement de convection naturelle
ne se manifeste dans l'enceinte. Les isothermes sont parallèles aux
parois solides en contact avec le MCP (sources de chaleur et plaque
conductrice). Le front de fusion progresse parallèlement aux parois
chaudes. Au fur et à mesure que la fusion progresse, des poches de MCP
liquide prennent naissance au voisinage des sources de chaleur, comme
illustrées sur la Figure 3. 2a, à l'instant ô = 0,007 (317
s). On peut remarquer la formation de sept cellules horaires convectives (3
cellules en face des sources de chaleur, 2 cellules dans les
microcavités situées entre les sources et 2 autres cellules, une
en bas de la cavité et une autre en haut). Ce caractère
multicellulaire a été aussi rapporté par Pons [66], dans
le cas des cavités élancées (verticales) ayant des
rapports de forme élevés. Il est à noter que la
présence de ces cellules est à l'origine de la
légère distorsion des isothermes au voisinage des sources de
chaleur. La structure du front de fusion reflète la protubérance
des sources de chaleur. Les lignes de courant sont altérées par
la protubérance des sources de chaleur et une partie des cellules est
attirée par les microcavités. Ce comportement complexe n'est
observable que pour le cas des sources de chaleur protubérantes et il
est absent pour le cas simple des sources de chaleur surfaciques [34]. Avec la
progression de la fusion, ô = 0 ,029 (1312 s), les
zones liquides s'élargissent et fusionnent et l'écoulement
s'intensifie. Les cellules formées prématurément dans les
microcavités, tournent toujours dans le sens horaire,
s'élargissent d'avantage et ne peuvent y séjourner
longtemps. En effet, les forces de poussée,
crées par les parois chaudes, s'amplifient avec le temps et poussent les
petites cellules à l'extérieur des microcavités. Les
petites cellules entraînées par l'écoulement principal sont
englouties par les grandes cellules. L'écoulement ascendant brasse les
sources de chaleur. Le liquide se charge alors, continuellement, en chaleur et
la source de chaleur supérieure s'échauffe rapidement. En
conséquence, la fusion s'intensifie dans cette zone et donne lieu
à une progression plus rapide du front de fusion dans la partie
supérieure de la cavité. Dans cette dernière, le courant
liquide vire à droite et descend le long du front de fusion et contribue
à la fusion du reste du MCP solide, ce qui explique la courbure, de plus
en plus prononcée, caractérisant la structure du front de fusion.
Avec sa descente au fond de la cavité, le liquide se décharge de
sa chaleur et sa température atteint une valeur minimale au fond de la
cavité, entraînant un déplacement lent du front de fusion
dans la partie inférieure de la cavité. Ensuite, le courant
refroidi vire à gauche et se redirige vers le haut et contribue
directement au refroidissement de la source de chaleur inférieure. Comme
l'échauffement par les sources de chaleur est continu, le liquide
continue sa remontée, une nouvelle fois, vers la partie
supérieure de la zone liquide. Cette dernière s'élargit
d'avantage en favorisant l'établissement de la convection naturelle dans
la totalité de la région fondue. Il est important de noter
qu'avant que la paroi droite ne soit touchée par le front de fusion
(paroi froide), celui-ci offre une surface d'échange relativement
élevée. A cause de la descente du point d'intersection du front
de fusion le long de la paroi droite, la partie supérieure de la
cavité ne contient plus de MCP solide ( ô = 0
,062 ). L'intensité de l'écoulement s'affaiblit avec le
temps et les deux cellules, situées enter les sources de chaleur
inférieure et supérieure, se détachent et migrent vers le
sommet et le fond de la cavité pour ô = 0 ,08 5
. Ainsi, l'écoulement est divisé en deux cellules tournant
toujours dans le sens horaire et séparées par une région
où le MCP liquide est pseudo- stagnant. Alors que la cellule
supérieure s'intensifie avec le temps, celle
inférieure s'éclipse. Ce processus dynamique de
génération et de disparition des cellules est observé le
long du processus de fusion.
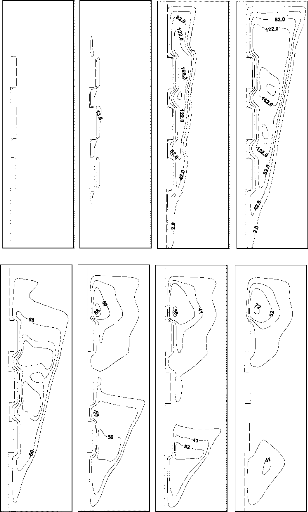
162.0
204.7
ø =204.7
max
ô=0.051
42.0
42.0
ø =160.3
max
ô=0.029
100
120
120
ô=0.062
ø =120
max
100
52
ø =90
max
ô=0.096
ø =72
max
41
ô=0.106
41
41
ø =86
max
ô=0.085
ô=1.1 10 ?4
x
ø =13.6
max
ô=0.007
Figure 3.2.a: Evolution temporelle des lignes de
courants
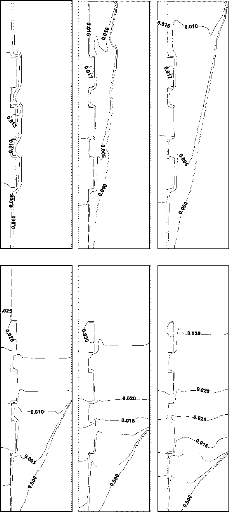
ô=0.007
è =0.013
max
è = 0.017
ô=0.029
max
è = 0.017
max
ô=0.051
ô=0.085
è =0.026
max
0.020
0.015
0.035
0.005
0.010
è =0.035
ô=0.106
max
0.025
0.010
0.005
è =0.030
max
ô=0.096

è ~ 0.001
max
ô=1.1 10 ?4
x
è =0.018
max
ô=0.062
Figure 3.2. b: Evolution temporelle des
isothermes et du front de fusion (isotherme è = 0)
La Figure 3.2b donne l'évolution des isothermes
à différents instants adimensionnels. L'analyse de cette figure
montre qu'au début du processus de fusion, la conduction
prédomine. En effet, les isothermes sont parallèles aux parois
chaudes ( r ~ 0 ,007 ). Le caractère bidimensionnel du
champ de température devient plus évident au cours du temps. La
distribution des isothermes au sein des sources de chaleur, sous forme de
contours concentriques fermés est caractéristique des sources de
chaleur avec génération interne de puissance. L'uniformité
de la température adimensionnelle des sources de chaleur est
attribuée à leur conductivité thermique relativement
élevée (Kc=1130). Au départ, la
température maximale adimensionnelle est enregistrée par la
source de chaleur centrale. Lorsque la convection naturelle se développe
et s'intensifie (t ? 0,007), la source de chaleur
supérieure devient la plus chaude. Ces résultats sont en parfait
accord avec les courbes de la Figure 3.1. Le resserrement des isothermes au
voisinage des parois verticales et du front de fusion est dû au
développement et à l'intensification de la convection naturelle.
L'écoulement se développe en régime de couche limite
durant la période quasi stationnaire, 0 , 02 ~ r ~ 0
,06, où la température maximale adimensionnelle des
sources de chaleur demeure constante, O max 0,017 ( Tmax ~ 57
°C, Figure 3.1). Durant cette période, la convection
naturelle est bien développée et prédomine. Les cellules
tournant dans le sens horaire forcent le fluide à extraire plus de
chaleur et la transférer ensuite au front de fusion. Avec la progression
du processus de fusion, le MCP solide est totalement fondu dans la partie
supérieure de la cavité. Le liquide s'y échauffe suite
à l'absence du puits de chaleur (MCP solide) dans cette zone ( r
~ 0 ,062 ). La température adimensionnelle s'uniformise au
centre de la cavité et des gradients thermiques importants
règnent au niveau des parois verticales de la cavité. Il est
à noter que l'écoulement est induit par une différence de
température, ( AO ), entre la paroi chaude et le MCP. Sa valeur maximale
est enregistrée pour le régime quasi permanent, AO = 0,017 (~21
°C). Il y a, aussi, lieu de noter que le modèle prend en
considération l'effet
de la conduction dans la plaque conductrice, et que la
différence maximale de température
dans la plaque conductrice,
( Äè s ), en régime quasi permanent,
dépasse, 0,015 ( ~18 °C). Ceci
montre que la plaque conductrice n'est pas isotherme et la raison
est due à sa conductivité thermique adimensionnelle finie
(Ks=131).
Lorsque le front de fusion intercepte la paroi droite et que
le point d'intersection se déplace vers le bas (t >
0,051), la surface d'échange offerte par le front de fusion diminue avec
le temps. En conséquence, le taux de transfert de chaleur au front de
fusion s'affaiblit, entraînant, ainsi, une réduction du taux de
fusion (traduite par une décroissance de la pente de la courbe donnant
l'évolution temporelle de la fraction liquide, telle que montrée
à la Figure 3.1). Le champ de température commence à se
stratifier à partir de la partie supérieure de la cavité,
et la source de chaleur supérieure se surchauffe ( è è
cr). A la fin du processus de fusion, un bloc de MCP solide non fondu persiste
autour du coin inférieur droit de la cavité.
3.3.3 Analyse des températures adimensionnelles
à l'interface MCP liquide / Paroi chaude.
La Figure 3.3a illustre la distribution de la
température adimensionnelle le long de la paroi chaude,
constituée par les portions de la plaque conductrice (substrat) et les
faces des sources de chaleur en contact avec le MCP, pour différents
instants. L'analyse de cette figure montre que les courbes présentent
des minimums aux points B, D, E, F, I, J et M et des maximums aux points C, G,
H, K et L pour ô = 0,085. La présence des minimums est dû
à la minceur des couches limites formées aux faces horizontales
des sources de chaleur. Quant aux maximums, ils sont dus à
l'épaississement des couches limites, formées sur les faces des
sources de chaleur, aux points considérés. Un autre constat qui
peut se dégager de l'analyse de cette figure est l'uniformité de
la température à la surface des sources de chaleur et qui est
attribuée à la valeur relativement élevée de la
conductivité thermique du matériau constituant les sources de
chaleur (Kc=1130).
0.045
0.035
0.025
0.015
0.005
0.04
0.03
0.02
0.01
0
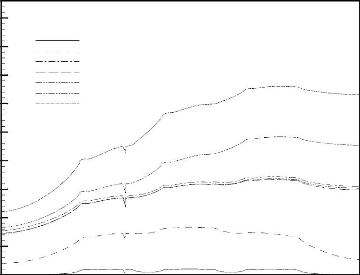
0.00011 0.007 0.029 0.051 0.085 0.096 0.105
ô=
è
i

A B C D E F G H I J K L M N
(a)
ô
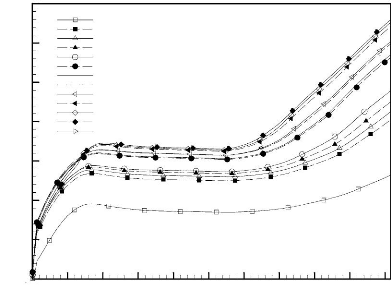
èi
0.035
0.025
0.015
0.005
0.03
0.02
0.01
0
È X
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
X È
È X
X
È
È
È
X È X È È
X
X È
X X
s=
0.25 0.525 0.675 0.825 0.933 1.03 1.181 1.33 1.439 1.55 1.697
1.85 2.00
È
X
È
X
È
X
È
X
(b)
Figure 3.3: Distribution spatiale de la
température adimensionnelle à l'interface paroi
chaude/MCP liquide (a) et variation temporelle des
températures adimensionnelles à différentes positions de
cette même interface (b)
La Figure 3.3b présente la variation temporelle de la
température adimensionnelle pour différentes positions à
l'interface paroi chaude /MCP. A cause du stockage d'énergie sous forme
sensible, la température adimensionnelle s'accroît pendant les
périodes correspondant au début et la fin du processus de fusion.
On peut aussi constater que la température adimensionnelle est
stabilisée durant le régime quasi stationnaire correspondant
à l'établissement de la convection naturelle. L'accroissement et
la stabilité de la température peuvent être aussi
constatés à la Figure 3.3 a.
3.3.5 Analyse des nombres de Nusselt moyen des sources de
chaleur.
L'évolution du nombre de Nusselt moyen d'une source de
chaleur, Nu , est illustré à la Figure 3.4. Une des observations
qui se dégagent de l'analyse de ces courbes est que le
nombre de Nusselt Nu n'est pas proportionnel au rapport
. En effet, l'analyse de
~ max
1
1
Omax
l'équation (2.58) montre que le nombre de Nusselt moyen
Nu est le produit de
|
î ? î
o
et J ?ç
K d
0
|
. Ce dernier terme représente le flux thermique
adimensionnel évacué par les trois
|
faces de la source de chaleur au MCP. Au début, la
température maximale adimensionnelle et
le flux de chaleur
adimensionnel évacué par la source de chaleur s'accroissent.
Toutefois, le
|
rapport
|
1
Omax
|
l'emporte sur le flux de chaleur adimensionnel, si bien que le
produit
|
1
î ? ~ î ? ~
, max J ?ç
?ç 0
0 ~ 0
max
et diminuent avec le temps, respectivement. Le même
comportement est observé durant la
dernière phase. C'est la
raison pour laquelle le nombre de Nusselt diminue. Durant le régime
quasi stationnaire, °max et 0
î ? î
°
J ?ç demeurent constants, entraînant, ainsi, la
constance du
K d
nombre de Nusselt. L'évolution temporelle du nombre de
Nuselt moyen des sources de chaleur reflète fidèlement les
étapes du processus de fusion observées et analysées dans
les sections précédentes (conduction pure - convection-
conduction/convection).
300
Nu1
Nu2
Nu3
100
50
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12
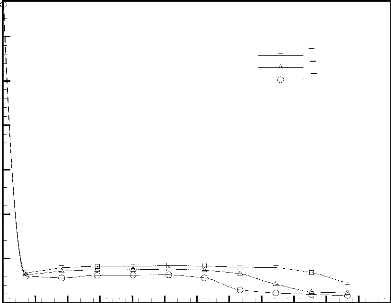
250
0
200

Nu
150
ô
Figure 3.4: Evolution temporelle des nombres de
Nusselt moyen, (1): source située en bas de l'enceinte, (2): source
centrale, (3): source située en haut de la cavité.
3.3.6 Analyse du flux de chaleur adimensionnel à
l'interface de la paroi chaude/ MCP liquide.
La distribution de la densité de flux de chaleur
adimensionnelle le long de l'interface paroi chaude /MCP liquide est
illustrée à la Figure 3.5, pour différents instants.
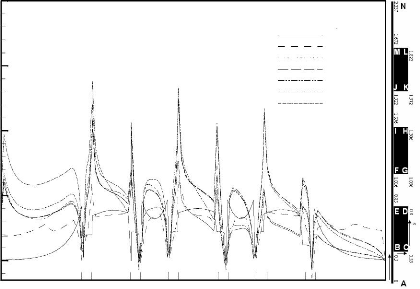
0.00011 0.007 0.029 0.051 0.085 0.096 0.105
ô=
2
1.5
0.5
0
q" i 1
A B C D E F G H I J K L M N
Figure 3. 5: Distribution de la densité
de flux de chaleur adimensionnelle le long de l'interface paroi chaude (plaque
conductrice- sources de chaleur)/MCP liquide
L'analyse de cette figure montre que cette distribution est
fortement non uniforme et
4
les courbes présentent des minimums et maximums locaux.
Au début ( ô = 1,1x10- ), la chaleur est
transférée par conduction pure, et comme il a été
prévu, la distribution de la densité de flux de chaleur
adimensionnelle le long de l'interface est symétrique. Le flux de
chaleur est faible au niveau des portions (AB) et (MN) de la plaque
conductrice. La raison est qu'au départ, la chaleur transmise par la
plaque conductrice est insuffisante pour déclencher la fusion du MCP.
Une grande partie de la puissance générée par les sources
de chaleur est stockée, sous forme d'énergie sensible, dans
celles-ci et la plaque conductrice. Quand la couche liquide s'élargit,
la convection naturelle s'y établit et des mouvements du liquide se
développent le long de l'interface plaque conductrice-sources/MCP. La
structure de
l'écoulement à proximité de la paroi
chaude, et la protubérance des sources de chaleur ont un effet sur la
distribution de la densité de flux de chaleur adimensionnelle à
l'interface plaque conductrice-sources/MCP. Des minimums et maximums locaux,
situés au niveau des coins (C,D,G,H,K,L), sont associés au
rétrécissement des couches limites. La formation de la couche
limite provoque une chute de la densité de flux de chaleur
adimensionnelle le long de la face verticale droite de chaque source de
chaleur. Ce comportement physique est rapporté dans d'autres travaux
relatifs au refroidissement des composants électroniques par convection
naturelle [70-72]. Au niveau des micro cavités, la densité de
flux de chaleur adimensionnelle est réduite à une valeur minimale
à coté des coins (B,E,F,I,J,M) où le liquide est pseudo
stagnant.
Tableau 3.4: Contribution des différentes
portions de l'interface paroi chaude-MCP au transfert de chaleur vers le MCP,
durant le régime quasi-permanent (%).
QAB QBCDE QEF QFGHI QIJ QJKLM QMN
(source 1) (source 2) (source 3)
18,74 18,63 7,24 19,85 6,78 17,3 8,5
Le Tableau 3.4 donne le pourcentage de contribution des
différentes parties de l'interface paroi chaude-MCP au transfert de
chaleur vers le MCP, durant le régime quasi-stationnaire. Il est
à noter que ces différentes valeurs restent constantes durant le
régime quasi-permanent ( 0 , 02 = ô = 0
,06). L'analyse du Tableau 3.4 montre que la contribution des quatre
portions de la plaque conductrice représente 41,26 % de la puissance
générée par les sources de chaleur, alors que les sources
de chaleur évacuent vers le MCP, environ 55,78 %. Ainsi, le MCP
emmagasine, environ, 97 % de la puissance générée par les
sources de chaleur. Ceci témoigne de l'intérêt pratique
d'utiliser le MCP dans les applications de refroidissement de composants
électroniques par stockage de chaleur latente de fusion.
3.4 Etude paramétrique
Dans le but d'étudier la sensibilité du
comportement thermique et hydrodynamique ainsi que la performance thermique de
l'enceinte de MCP aux paramètres de contrôle, une étude
paramétrique a été menée. La présente
section expose et analyse les résultats des investigations
numériques mettant en évidence l'impact des paramètres de
contrôle suivants:
Ra, A, F , Ec, Es, A, ct s et ct
c .
Il faut noter que les valeurs de ces paramètres ont
été normalisées par rapport à celles de
références données aux Tableaux 3.1 et 3.2. La
normalisation de ces paramètres de contrôle a été
effectuée dans un souci de simplification des corrélations
numériques qui seront développées au chapitre suivant.
3.4.1 Analyse de l'effet du nombre de Rayleigh, Ra.
Le nombre de Rayleigh représente l'intensité de
la convection naturelle se manifestant dans la cavité du MCP liquide.
Dans la présente étude, ce nombre varie entre 6,27x108
et 5,01x109. Sa variation résulte de celle de la puissance
générée, par unité de longueur, Q' par chaque
source de chaleur (Q'E [7,5 W/m - 60 W/m]).
La Figure 3.6-a illustre la variation temporelle de la
température adimensionnelle maximale, O max , pour
différentes valeurs du nombre de Rayleigh. Comme il peut être
constaté, l'évolution temporelle de O max passe
par les mêmes phases que celles décrites à
la section précédente. La phase
intermédiaire représente le régime quasi- stationnaire
de
l'enceinte, durant laquelle la température maximale
adimensionnelle demeure pratiquement
constante. Sa durée est d'autant
plus courte que le nombre de Rayleigh est élevé. Il faut
T T m
--
noter que dans la définition de la température
adimensionnelle, O = A , le
T
terme ÄT comporte la puissance
générée, par unité de longueur, Q'. Celle-ci figure
aussi dans la définition du nombre de Rayleigh. En conséquence,
et afin d'élucider l'effet du nombre de Rayleigh sur le comportement
thermique de l'enceinte, il s'est avéré méthodique
d'utiliser la température avec dimension, telle qu'illustrée
à la Figure 3.6.b.
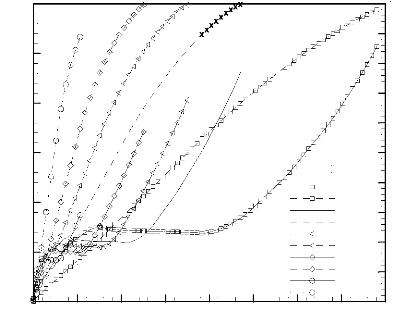
èmax
0.12
0.08
0.06
0.04
0.02
0.1
0 X 0.80
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
X
X
X
X
X
X
X
X
X
X
XXXXXXXXXXXXXXXXX X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
Ra /Ra
0.125
0.233
0.333
0.5
1
ref
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
1
f

Figure 3.6 a: Effet du nombre de Rayleigh sur la
variation temporelle de la température maximale adimensionnelle (lignes
continues) et de la fraction liquide (lignes discontinues).
L'analyse de cette figure montre que la température
maximale enregistrée, lors du régime quasi- stationnaire, est
d'autant plus élevée que le nombre de Rayleigh est
élevé. Quant à l'effet de Ra sur la fraction liquide, la
figure montre clairement que la durée de fusion est d'autant plus courte
que Ra est élevé. De ce qui précède, il est clair
que l'accroissement du nombre de Rayleigh entraîne une surchauffe rapide
de la source de chaleur. En pratique, il y a des situations où la
puissance générée par le composant électronique est
telle que le nombre
de Rayleigh correspondant est relativement élevé
et la source de chaleur risque de surchauffer rapidement. Pour surmonter cette
difficulté la géométrie de l'enceinte ainsi que les
propriétés thermo- physiques de la plaque conductrice doivent
être optimisées de telle sorte à maximiser la durée
de fonctionnement sécurisé des sources de chaleur.
75.0
70.0
65.0
60.0
T °(C)
max
55.0
50.0
45.0
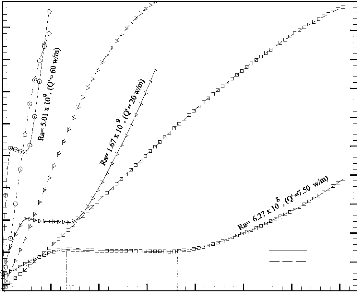
1
0.9 0.8 0.7 0.6 0.5 f 0.4 0.3 0.2 0.1
T f
ts1
ts2
40.0
35.0
0 5000 10000 15000 20000 25000 30000 35000
t(s)
Figure 3.6 b: Effet du nombre de Rayleigh sur la
variation temporelle de la température maximale Tmax (lignes
continues) et de la fraction liquide f (lignes discontinues)
La Figure 3.7 illustre les lignes de courants et les
isothermes décrivant les champs hydrodynamique et thermique,
respectivement, pour deux valeurs du nombre de Rayleigh: Ra/Raref = 0,33 et
Ra/Raref = 1, à l'instant t = 2900 s.
Ra/ Ra ref= 0.33 Ra/ Ra ref= 1 Ra/ Ra ref= 0.33 Ra/ Ra ref= 1
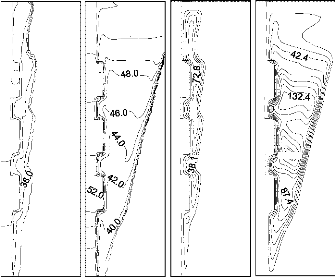
36.0
T = 45.3 °C max
45.3
44.0
44.0
57.0
56.0
36.0
T = 57.6 °C
max
50.0
52.0
72.8
ø = 72.8
max
72.4
150.4
ø = 150.4
max
Figure 3.7: Isothermes et lignes de courants
pour Ra /Raref =0,33 et Ra/Raref = 1 (t = 2900 s)
L'analyse des lignes de courant montre que l'écoulement
induit par la convection naturelle se fait dans le sens horaire; ascendant au
niveau de la paroi chaude gauche et descendant le long du front de fusion
(paroi froide). Le volume de la cavité liquide est plus grand pour le
cas des nombres de Rayleigh élevés. Dans les deux cas du nombre
de Rayleigh, l'écoulement est multi cellulaire et la valeur maximale de
la fonction de courant, ø max ,
s'accroît avec l'augmentation du nombre de Rayleigh
à cause de l'augmentation de la différence de température
induisant l'écoulement. Par exemple, à l'instant t = 2900 s la
différence maximale de température est Tmax
-Tm = 9,3 °C et 21 °C, et la fraction liquide
correspondante f est 0,23 et 0,66 pour Ra/Raref =0,33 et
Ra/Raref =1, respectivement. La Figure 3.7 montre que, pour les
grandes valeurs de Ra (Ra/Raref =1), le champ thermique se stratifie
rapidement dans la partie supérieure de la cavité alors que pour
le cas des sources de chaleur à faible puissance, les isothermes sont
nettement inclinés. Pour les deux valeurs de
Ra, la température maximale est enregistrée par
la source de chaleur placée au sommet de la cavité. Cette
température est d'autant plus élevée que le nombre de
Rayleigh est élevé (Tmax = 45,3 °C pour Ra /Raref = 0,33 et
Tmax = 57 °C pour Ra /Raref = 1). Le nombre de cellules convectives
décroît avec le nombre de Rayleigh. Elles sont
déformées par les coins des blocs protubérants. En effet,
de point de vue hydrodynamique, la protubérance des sources de chaleur
est considérée comme un obstacle à l'écoulement; la
rugosité de la paroi chaude est importante avec l'existence des blocs
protubérants, comme il a été observé
expérimentalement par Ju et al.[43]. Dans la présente situation,
les trois faces des sources de chaleur, exposées à
l'écoulement du MCP liquide, transfèrent directement la chaleur
au MCP. Ce comportement est absent dans le cas où les sources sont
incrustées dans la paroi de la cavité (paroi chaude lisse)
[34].
La Figure 3.8 met en évidence l'impact du nombre de
Rayleigh sur le profil de
température au sein de la plaque conductrice (milieu de la
plaque conductrice: E s
X= - ) à
2
l'instant t = 2900 s. Il ressort de l'analyse de cette figure
que la température s'accroît lorsque Ra augmente. Ceci est
dû au fait que la quantité de chaleur générée
par les sources de chaleur augmente avec Ra. Ainsi, pour une même
durée de stockage (t = 2900 s), le substrat stocke plus de chaleur
sensible pour les valeurs élevées de Ra. Un autre résultat
qui se dégage de l'analyse de la Figure 3.8 est que pour des valeurs
relativement faibles de Ra (Ra/Raref = 0,125), le gradient de
température vertical est faible en raison du transfert de chaleur
conductif qui prévaut dans la couche du MCP liquide avoisinant la paroi
chaude. Au fur et à mesure que Ra augmente, la convection naturelle
s'intensifie et le profil de température devient tributaire de la
structure de l'écoulement dans la phase liquide du MCP. On peut
constater, en particulier, le refroidissement relatif de la partie
inférieure du substrat et de la source de chaleur inférieure.
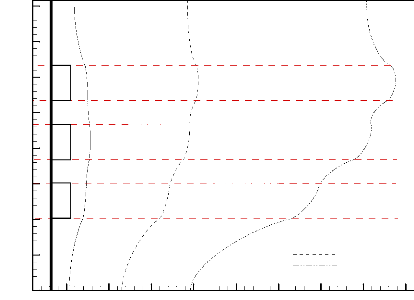
Y
0.75
0.25
1.75
1.25
0.5
1.5
2
0
1
S
S
S1
37.5 40 42.5 45 47.5 50 52.5 55 57.5
2
3
0,125 (7,5 W/m) 0,33 (20 W/m) 1,00 (60 W/m)
Ra /Raref
T(°C)
Figure 3.8: Profil de température au sein
du substrat (t = 2900 s, Es
X= - )
2
En effet, lorsque Ra augmente, les courants convectifs
impactant les faces des sources de chaleur et du substrat chaudes forcent le
liquide à extraire plus de chaleur au niveau de la partie
inférieure de la cavité et de la véhiculer, ensuite, vers
les zones supérieures de la cavité. Il en résulte une
remarquable montée en température dans la partie
supérieure de la plaque conductrice, en particulier au niveau de la
source de chaleur supérieure. Pour ce cas, la plaque conductrice n'est
plus isotherme, et la différence de température
enregistrée au sein de la plaque conductrice dépasse 12
°C.
Le Tableau 3.5 donne, en termes de pourcentages, les flux de
chaleur dissipés par les différentes surfaces de la plaque
conductrice et par les faces des sources de chaleur (Figure 3.9), durant le
régime quasi permanent, pour trois valeurs du nombre de Rayleigh.
Plaque conductrice (substrat)
Source de chaleur (composant électronique)
Figure 3.9: Définition des
différentes surfaces de la paroi gauche (interface séparant le
MCP liquide et la paroi gauche)
Tableau 3.5: Contribution, en régime
quasi- permanent, des différentes surfaces de la paroi gauche au
transfert de chaleur (exprimée en % de la puissance
générée par les sources de chaleur).
Ra/ Raref 0,125 0,33 1
AB
BCDE (S1)
EF
FGHI (S2)
IJ
JKLM (S3)
MN
Flux de chaleur évacué par les trois sources de
chaleur vers le MCP
Flux de chaleur évacué par la plaque vers le MCP
Chaleur sensible stockée dans la plaque conductrice
Chaleur sensible stockée dans les sources de chaleur
Chaleur stockée par le MCP
22,04
|
%
|
20,34
|
%
|
18,74
|
%
|
|
19,10
|
%
|
18,95
|
%
|
18,63
|
%
|
|
7,00
|
%
|
7,26
|
%
|
7,24
|
%
|
|
19,56
|
%
|
19,60
|
%
|
19,85
|
%
|
|
6,10
|
%
|
6,42
|
%
|
6,78
|
%
|
|
16,76
|
%
|
17,02
|
%
|
17,30
|
%
|
|
7,70
|
%
|
8,05
|
%
|
8,50
|
%
|
|
55,42
|
%
|
55,57
|
%
|
55,78
|
%
|
|
42,84
|
%
|
42,07
|
%
|
41,26
|
%
|
|
0,62
|
%
|
0,93
|
%
|
1,13
|
%
|
|
0,47
|
%
|
0,61
|
%
|
0,70
|
%
|
|
98,26
|
%
|
97,64
|
%
|
97,04
|
%
|
L'analyse des données du Tableau 3.5 montre que la
contribution au transfert de chaleur des surfaces des sources (BCDE), (FGHI) et
(JKLM) vers le MCP liquide varie légèrement avec le nombre de
Rayleigh. Les portions de la plaque conductrice situées entre les
sources de chaleur, (EF), (IJ) et la portion supérieure (MN)
transfèrent moins de chaleur au MCP en comparaison avec la portion
inférieure de la plaque (AB). Il ressort aussi de l'analyse du Tableau
3.5 que, pour la plage considérée du nombre de Rayleigh, plus de
41 % de la puissance générée par les sources de chaleur
est transférée à la plaque conductrice et
convectée, ensuite, au MCP liquide au travers les faces (AB), (EF), (IJ)
et (MN), alors qu'environ 55 % de la puissance générée par
les sources de chaleur est transférée au MCP à travers
leurs surfaces exposées à l'écoulement. En
conséquence, durant le régime quasi permanent, la fusion du MCP
absorbe plus de 97 % de la puissance générée par les
sources de chaleur. La température de ces dernières reste
constante pendant ce régime. Ceci est justifié par les valeurs
relativement faibles des énergies stockées sous forme sensible
par les sources de chaleur, la plaque conductrice et le MCP.
La Figure 3.10 donne la durée de fonctionnement
sécurisé, ô fonc , et la fraction liquide,
f, en fonction du nombre de Rayleigh. L'analyse de cette figure montre
que la durée ô fonc
diminue avec l'accroissement du nombre de Rayleigh. Pour les
faibles valeurs de Ra (Ra /Raref < 0,4) le MCP solide est totalement fondu
(f ~ 1) avant que la température maximale n'atteigne la
température critique, è cr .
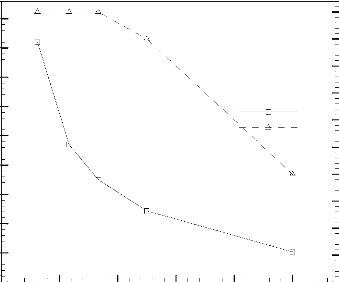
ô
fonc
f
0.9 0.8 0.7 0.6
ô
fonc
0.5 0.4 0.3 0.2 0.1 0
0.98
0.96
0.94
0.92
f
0.9
0.88 0.86 0.84 0.82 0.8
0 0.2 0.4 0.6 0.8 1
Ra/ Raref
Figure 3.10: Durée de fonctionnement
sécurisé, ô fonc , et la fraction liquide
correspondante, f, en fonction du nombre de Rayleigh.
La Figure 3.10 permet de développer les
corrélations donnant la durée de fonctionnement
sécurisé, ôfonc , et la fraction liquide
correspondante, f, en fonction du rapport Ra /Raref:
0,6
,
~ ~
Ra
~ ~
Raref
ô fonc= - 0,186594 + 0,287894 ~ ~
2,7
~ l
Ra
f = 1,00273 - 0,134833 ~~ ~ (3.1)
~
Ra ref
avec 0,12 < Ra /Raref <
1,0
Le Tableau 3.6 montre un bon accord entre les résultats
numériques et ceux obtenus par les corrélations Eq. (3.1). Les
variations maximales pour ôfonc et f sont égales
à 6,45 % et
2,22 %, respectivement.
Tableau 3.6: Comparaison des résultats
numériques avec ceux obtenus par la corrélation Eq. (3.1).
|
Ra /Raref
|
ôfonc
numérique
|
ôfonc
corrélation
|
Variation
(%)
|
f
numérique
|
f
corrélation
|
Variation
(%)
|
|
0,125 0,23 0,333 0,50 1,00
|
0,819 0,470 0,351 0,244 0,101
|
0,81391 0,50064 0,36789 0,24777 0,09929
|
0,67 6,45 4,90 1,54 1,97
|
1,000 1,000 0,992 0,980 0,868
|
0,99789 0,98959 0,97947 0,95825 0,86790
|
0,21 1,04 1,26 2,22 0,01
|
3.4.2 Effet de la distance adimensionnelle, Ä
La Figure 3.11 illustre l'effet de la distance adimensionnelle,
Ä, sur l'évolution temporelle de la température maximale
adimensionnelle des sources de chaleur, Omax , et
la fraction
liquide. Cette figure montre que le positionnement des sources
de chaleur en bas de la cavité
favorise un meilleur refroidissement
de celles-ci. Plus la distance adimensionnelle, Ä,
diminue, plus la
température maximale adimensionnelle, Omax ,
diminue et plus les durées du
régime quasi-stationnaire et de fonctionnement
sécurisé sont élevées. En effet, le
déplacement des sources de chaleur à la partie inférieure
de la cavité leur permet d'être en contact avec du MCP liquide
relativement froid, et par conséquent un échange de chaleur
important. Les températures maximales adimensionnelles atteintes par les
sources de chaleur en régime quasi stationnaire (à ô =
0,04), pour Ä /Ä ref = 1,667 et 0,667, sont respectivement
Omax = 0,0196
(Tmax= 59,44 °C) et Omax =
0,0157 (Tmax= 54,78 °C), soit une chute de température
de 5 °C.
Quant aux durées des régimes quasi-permanent, elle
sont respectivement 0,022 et 0,064, soit un accroissement de 0,042 ( ~1900 s =
31,67 minutes).
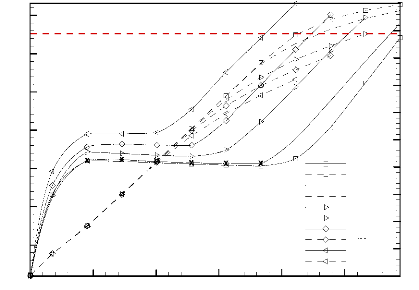
0.035
0.015
0.005
0.03
0.01
X
0
0 0.02 0.04 0.06 0.08 0.1
ô
Température limite adimensionnelle,
X
X
X
X
X
ècr
X
X
X
X
X
X
X
X
X
Ä /Ä
1.667
0.167
0.5
1
1.334
X
X
ref
X
X
0.9
0.8
0.7
0.2
0.1
1
0.025
è
max
0.02
0.6
f
0.5
0.4
0.3
Figure 3.11: Effet de la distance
adimensionnelle, Ä, sur la température adimensionnelle maximale
(traits continus) et la fraction liquide (traits discontinus)
L'effet de la distance adimensionnelle, Ä, sur le profil
de température au sein de la plaque conductrice est
présenté à la Figure 3.12, pour deux instants
adimensionnels différents (ô = 0,04 et ô = 0,084). En
analysant les Figures 3.12a et 3.12b, il ressort que pour une distance
adimensionnelle donnée, Ä, la température adimensionnelle
augmente à cause du stockage d'énergie sensible dans la plaque
conductrice. L'accroissement de la température adimensionnelle est
d'autant plus élevé que la distance adimensionnelle, Ä, est
grande. Pour les faibles valeurs de Ä ( Ä /Ä ref 0,167) la
température adimensionnelle subit une légère
augmentation à cause du positionnement des sources de
chaleur en bas de la cavité. Ceci est dû à
l'intensification du transfert de chaleur entre le MCP liquide et les sources
de chaleur lorsque celles-ci sont positionnées en bas de la
cavité. Les profils de température présentés aux
Figures 3.12 a et 3.12 b présentent des maximums locaux localisés
prés des sources de
chaleur. Ces maximums se déplacent du coté droit
lorsque la distance adimensionnelle, Ä, s'accroît (sources se
déplaçant vers le haut de la cavité). L'intersection des
courbes de température résulte du rapprochement de la source de
chaleur supérieure de la paroi horizontale supérieure et de
l'éloignement de la source de chaleur inférieure de la paroi
horizontale inférieure, lorsque la distance adimensionnelle, Ä,
augmente. Le déplacement ascendant des sources de chaleur entraîne
un échauffement et un refroidissement de la plaque conductrice au niveau
des parties supérieure et inférieure, respectivement.
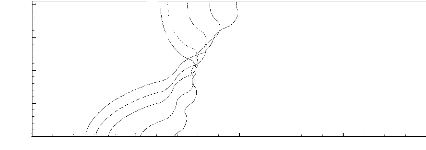
0,5
1
1,334
1
Y
1,667
(a)
0.5
0 0 0.01
0.02 0.03
è
2
1.5
ô =0.04 (1800 s )
A/A =0,167 ref

1
1,334
ô =0.084 (3800 s)
A/A =0,167 ref
0,5
(b)
1,667
0 0.01 0.02 0.03
è
Figure 3.12: Effet de la distance
adimensionnelle Ä / Ä ref sur le profil de
température au sein de la plaque conductrice ( E s
X= - ) aux instants adimensionnels, t = 0.04 et
0.084
2
La Figure 3.13 donne l'évolution temporelle du champ
thermique au sein de la cavité pour deux valeurs de la distance
adimensionnelle: Ä / Ä ref = 0,167 et Ä / Ä ref
=1,667.
ô= 1.105 x 10 -4 0,029 0,051 0,0733 0,0844
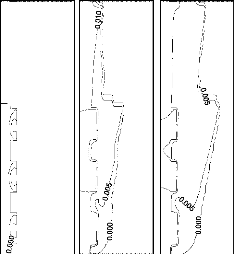
0.001
0.001
0.001
MCP solide
0.016
0.015
0.016
MCP solide
0.015
0.015
0.015
MCP solide
MCP solide

MCP solide
0.010
0.015
0.015
MCP solide
0.015
0.016
0.005
0.015
MCP solide

MCP solide
(a)
ô= 1.105 x 10 -4 0,029 0,051 0,0733 0,0844
0.001
0.001
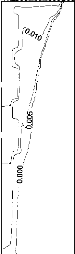
0.020
0.015
0.015

0.020
0.015
0.020
0.015
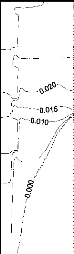
0.020
0.025
0.030
0.025
0.005

0.030
0.020
0.005
0.030
(b)
Figure 3.13: Isothermes et position du
front de fusion (isotherme 0 =0): (a): Ä /Ä
ref =0,167,
(b): Ä /Ä ref =1,667.
L'analyse de cette figure montre que la position et la forme
du front de fusion et la structure des isothermes dépendent
étroitement de la position des sources de chaleur. En suivant le front
de fusion (isotherme 0 = 0) et en analysant sa forme les
remarques suivantes ont été dégagées:
· Pour le cas des sources de chaleur situées dans
la partie supérieure de la cavité ( Ä /Ä ref
=1,667), un bloc de MCP solide reste dans la partie inférieure de la
cavité.
Ce puits de chaleur refroidi inutilement la portion de la plaque
située en dessous de la source de chaleur inférieure (0 Y
Ä) ;
· Lorsque les sources de chaleur sont placées en bas
de la cavité ( Ä /Ä ref =0,167), un
bloc de MCP solide se détache et se localise devant la
source de chaleur située en haut de la cavité, à l'instant
ô = 0,0733. Ce bloc de MCP joue le rôle d'un puits de chaleur pour
la source de chaleur supérieure. C'est la raison pour laquelle les
sources de chaleur supérieure et centrale restent à l'abri de la
surchauffe ( è 1 et è 2 < è cr = 0,032),
pendant une durée relativement élevée;
· Les trois sources de chaleur sont bien refroidies
quand elles sont positionnées en bas de la cavité. Lorsque elles
sont déplacées vers le haut de la cavité, la source de
chaleur supérieure est rapidement surchauffée et sa
température adimensionnelle atteint la valeur critique. En effet,
après une durée adimensionnelle de fonctionnement ô
= 0,0844 (~ 3820 s) la température adimensionnelle de la source
de chaleur supérieure dépasse la valeur critique (
è 3 > è cr = 0,032), alors que les sources de chaleur centrale
et inférieure restent à l'abri d'une telle surchauffe.
La Figure 3.14 donne la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et la fraction
liquide correspondante, f, en fonction de la distance adimensionnelle,
Ä / Ä ref . L'analyse de cette figure montre que la
durée ôfonc et la fraction liquide, f, diminuent
avec l'augmentation du rapport Ä / Ä ref . Pour les
faibles valeurs du rapport Ä /Ä ref ( Ä /Ä ref
< 0,5),
tout le MCP solide est pratiquement fondu (f ~1)
à la fin du processus de fusion, tandis que
pour le cas où les
sources de chaleur sont placées dans la partie supérieure de la
cavité, plus
de 20 % du MCP reste à l'état solide (pour
Ä /Ä ref > 1,25), et le système atteint la
température
critique d'arrêt ( è max è cr ).
Ce cas n'est pas pratique pour le design des systèmes de refroidissement
de l'électronique (poids inutile).
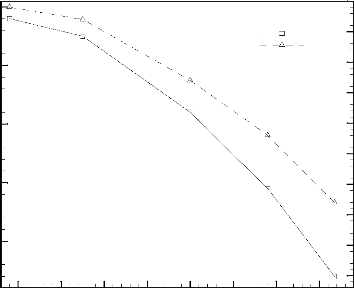
ôfonc
f
0.12 0.11 0.1
ôfonc
0.09
0.08
1
0.95
0.9
0.85
0.8
f
0.75
0.7
0.65
0.6
0.55
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
Ä/Äref
Figure 3.14: Effet de la distance
adimensionnelle, Ä /Ä ref , sur la durée
adimensionnelle de fonctionnement sécurisé, ôfonc
, et la fraction liquide, f.
Les résultats de la Figure 3.14 peuvent être
traduits par des corrélations exprimant la durée adimensionnelle
de fonctionnement sécurisé, ôfonc , et la fraction
liquide, f, en fonction de la
distance adimensionnelle, Ä /Ä ref . Ces
corrélations sont données comme suit:
)1,6 1,8
Ä [ Ä )
ô fonc = 0,12134 - 0,02004 , f= 0,99937
- 0,13137 (3.2)
Ä ref Ä ref
avec 0,667 < Ä /Ä ref
< 1,667.
Le Tableau 3.6 montre un bon accord entre les résultats
numériques et ceux obtenus par les corrélations, Eq.(3.2). Les
variations maximales pourôfonc et f sont de
3,68 % et 0,87 %,
respectivement.
Tableau 3.6: Comparaison des résultats
numériques (Figure 3.14) avec ceux calculés par la
corrélation (Eq. 3.2).
|
Ä /Ä ref
|
ôfonc
numérique
|
ôfonc
corrélation
|
Variation
relative
(%)
|
f
numérique
|
f
corrélation
|
Variation
relative
( %)
|
|
0,167
|
0,115
|
0,11962
|
3,68
|
0,990
|
0,99743
|
0,75
|
|
0,50
|
0,115
|
0,11416
|
1,03
|
0,968
|
0,96500
|
0,31
|
|
1,00
|
0,101
|
0,10073
|
0,56
|
0,868
|
0,87136
|
0,39
|
|
1,334
|
0,089
|
0,08823
|
1,30
|
0,780
|
0,77605
|
0,51
|
|
1,667
|
0,074
|
0,07533
|
1,63
|
0,667
|
0,67278
|
0,87
|

3.4.3 Effet du rapport des diffusivités thermiques,
á s / á s,ref
Dans cette section, l'effet de la diffusivité thermique
adimensionnelle de la plaque conductrice sur le comportement thermique des
sources de chaleur sera analysé. Les simulations numériques ont
été effectuées en considérant la plage de variation
du rapport des diffusivités thermiques á s / á s,ref :
0,02-2,38 avec á s,ref = 70,55, correspondant aux
valeurs fréquemment utilisées en
électronique. La Figure 3.15 illustre l'effet du rapport
á s /
á s,ref sur l'évolution temporelle de la
température maximale adimensionnelle des sources
de chaleur. Comme illustré sur cette figure, plus le
rapport á s / á s,ref augmente, plus la
montée de la température maximale adimensionnelle
des sources de chaleur est lente
(pour á s / á
s,ref >1). En effet, l'accroissement de á s / á
s,ref augmente l'habilité de la plaque
conductrice à diffuser la chaleur en son sein, au lieu
de la stocker sous forme sensible, et d'uniformiser sa température. La
résistance thermique de la plaque conductrice diminue, favorisant,
ainsi, la diffusion de la chaleur vers les parties inférieure et
supérieure de la plaque conductrice. En conséquence, les
températures moyennes adimensionnelles des sources de chaleur subissent
une nette diminution.
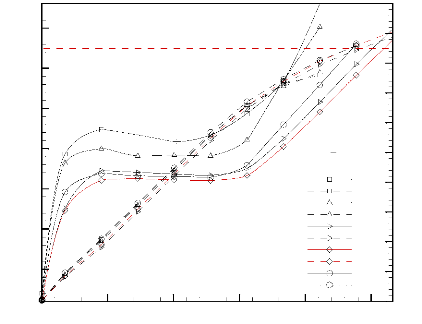
0.035
0.015
0.005
0.03
0.01
0.1 0
0 0.02 0.04 0.06 0.08
Température limite adimensionnelle, cr
è
á s / __ á s,ref
0.02
0.21
2.38
1
1.75
0.9
0.8
0.7
0.6
0.2
0.1
1
ô
f
.
0.025
èmax
0.02
0.5
0.4
0.3
Figure 3.15: Effet de la diffusivité
thermique adimensionnelle de la plaque conductrice, á s / á
s,ref, sur l'évolution temporelle de la température
maximale adimensionnelle des sources
de chaleur (traits continus) et la fraction liquide (traits
discontinus).
Il a été, aussi, constaté que la valeur
optimale du rapport á s / á s,ref correspondant
à un meilleur
refroidissement des sources de chaleur, durant le régime
quasi-stationnaire, est estimée à 1,75.
La température
maximale adimensionnelle correspondant à ce régime est de l'ordre
de 0,0160
(Tmax ~ 55,02°C). Pour des valeurs de á s / á
s,ref > 1,75, la température adimensionnelle de la
plaque conductrice s'uniformise davantage (Figure 3.16),
entraînant, ainsi, une diminution du gradient de température et du
transfert de chaleur des sources de chaleur vers la plaque conductrice. Ceci se
traduit par une légère augmentation de la température
maximale adimensionnelle et du flux de chaleur adimensionnel à
l'interface sources de chaleur- MCP liquide.
Ces résultats sont confirmés par l'analyse des
Figures 3.16 et 3.17, illustrant le profil de température
adimensionnelle de la plaque conductrice et la forme et la position du front de
fusion pour différentes valeurs du rapport des diffusivités
thermiques, á s / á s,ref. L'analyse de
la Figure 3.16 montre que l'accroissement du rapport á s
/ á s,ref réduit la température
maximale adimensionnelle et favorise l'isothermie de la plaque
conductrice. Aussi, il est
important de signaler l'apparition de gradients
thermiques élevés au sein de la plaque
conductrice, au niveau
des jonctions des sources de chaleur, pour les faibles valeurs du
rapport á s / á s,ref ( á s /
á s,ref = 0,21). Ces gradients thermiques élevés risquent
d'engendrer une déformation de la plaque conductrice (fissuration de la
carte mère de l'ordinateur).
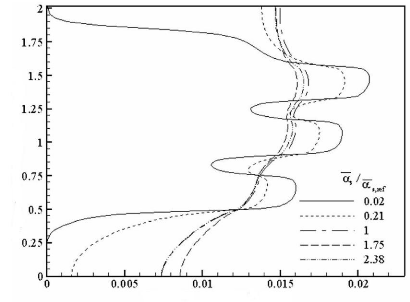
Y
Figure 3.16: Effet de la diffusivité
thermique adimensionnelle de la plaque conductrice
è
á s / á s,ref sur le profil de
température adimensionnelle au sein du substrat en Es
X= - 2
L'analyse de la Figure 3.17 montre que pour les faibles
valeurs de á s / á s,ref (~ 0,02), la plaque est
similaire à une paroi non conductrice et transmet moins de chaleur. La
chaleur est essentiellement évacuée par les faces des sources de
chaleur. Au début de la fusion, des poches de MCP liquides prennent
naissance autour de chaque source de chaleur. Les mouvements convectifs se
manifestant dans cette zone sont insuffisants pour dissiper toute la puissance
générée par les sources de chaleur. Ceci explique
l'échauffement relativement rapide de ces dernières. Plus le
rapport á s / á s,ref s'accroît, plus la plaque
conductrice contribue au transfert de la chaleur, en véhiculant celle-ci
à partir des sources de chaleur vers le MCP. Le MCP liquide
s'étale sur toute la surface chaude. Pour des valeurs de á s /
á s,ref = 1 la courbure du front de fusion devient moins
prononcée et indépendante du rapport á s / á
s,ref .
Il est à noter que la diffusion de la chaleur vers les
parties inférieure et supérieure de la plaque conductrice
entraîne un allongement de la cavité liquide et une diminution du
volume des poches liquides entourant les sources de chaleur. Dans ce cas, la
forme du front de fusion ressemble à celle obtenue pour le cas de la
fusion par une paroi isotherme.
|
_
á /
s
|
ás,ref
|
= 0,02 0,21 1 1,75 2,38
|
|
è max = 0,0209 (61°C)
|
0,0192 (59 °C)
|
0,0167(56 °C)
|
0,0151(54 °C)
|
0,0159(55 °C)
|
|
f = 0,207
|
0,203
|
0,180
|
0,190
|
0,210
|
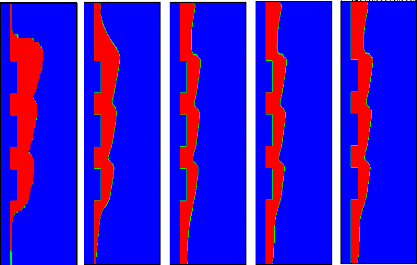
Figure 3.17: Effet du rapport des
diffusivités thermiques, á s / á s,ref , sur la
forme et la position du front de fusion à ô = 0,018
La Figure 3.18 présente la variation de la durée
adimensionnelle de fonctionnement sécurisé mise par les sources
de chaleur pour atteindre la température adimensionnelle critique (
è max è cr), pour différentes valeurs du
rapport á s / á s,ref. Il ressort de l'analyse de
cette figure que l'augmentation du rapport á s /
á s,ref a un effet appréciable sur la durée
adimensionnelle de fonctionnement sécurisé,
ôfonc . En effet, lorsque le rapport á s / á
s,ref varie
de 0,02 à 1, la durée adimensionnelle
de fonctionnement sécurisé s'accroît en passant de
ôfonc = 0 ,08 à ô
fonc = 0 ,102. Mais à partir de á s / á
s,ref ~1, le taux de variation de ôfonc diminue
lorsque á s / á s,ref augmente. Pour des rapports plus
élevés ( á s / á s,ref> 1,75), la
durée adimensionnelle de fonctionnement sécurisé,
ôfonc , décroît. A cet effet, l'utilisation d'une
plaque conductrice ayant un rapport á s / á s,ref
~1,75 (substrat d'alumine, á s ~123,28)
0.11
0.105
0.1
ô
fonc
0.095
0.09 0.085 0.08
0.9
0.85
f
0.8
0.75
constitue un choix pratique correspondant à la valeur
maximale de la durée adimensionnelle de fonctionnement
sécurisé, ôfonc = 0 ,105
(tmax= 4752 s).
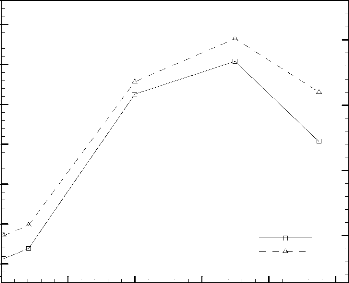
ô
f
fonc
0 0.5 1 1.5 2 2.5
á /á
s s,ref
Figure 3.18: Durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et
fraction liquide, f, en fonction du rapport á s / á
s,ref.
L'analyse de la Figure 3.18 montre, aussi, une augmentation du
volume de MCP fondu avec la diffusivité thermique adimensionnelle de la
plaque conductrice pour á s / á s,ref <
1,75.
Pour des rapports á s / á s,ref > 1,75, le
volume du MCP fondu diminue.
2,8
La durée adimensionnelle de fonctionnement
sécurisé et la fraction liquide ont été
corrélées à partir des résultats numériques
de la Figure 3.18. Elle sont données comme suit:
ôfonc =
,
(3.3)
~ 1 ~
á á
s s
0,078847 + 0,0264467 ~ ~ - 0,004074 ~
~
á
~ )
á s ref
, ~ ~
s ref ,
2,7
\
~ ~
á f á
s s
f = 0,7393 + 0,15176 - 0,02298
~ ~ ~
á á
s ref
, ) s ref
,
avec 0,02 < á s / á s,ref
< 2, 38
Le Tableau 3.7 montre un bon accord entre les résultats
numériques et ceux obtenus par les corrélations (Eq.3.3). Les
variations maximales pour ôfonc et f sont
estimées à 2,42 % et
1,44 %, respectivement.
Tableau 3.7: Comparaison des résultats
numériques (Figure 3.18) avec ceux obtenus par l'équation
Eq.(3.3).
|
ás
|
ôfonc
numérique
|
ôfonc Variation
corrélation ( %)
|
f
numérique
|
f
corrélation
|
Variation
(%)
|
|
ás,ref
|
|
|
|
|
|
|
|
0,02 0,081 0,07908 1,96 0,750 0,74108 1,19
0,21 0,082 0,08393 2,42 0,758 0,76889 1,44
1,00 0,101 0,10092 0,37 0,868 0,86679 0,14
1,75 0,105 0,10532 0,08 0,901 0,89946 0,17
2,38 0,095 0,09543 0,07 0,860 0,86077 0,09
3.4.4. Effet de la protubérance des sources de
chaleur, Ec

Il est important de rappeler que les simulations
numériques ont été conduites en utilisant les
données des Tableaux 3.1 et 3.2. Les volumes du MCP et des sources de
chaleur représentés
par leurs longueurs caractéristiques respectives, l o =
lw - 3l c e c et l CE = l c e c ,
sont
maintenus constants pour toutes les simulations numériques, (
lo = 0,06 m, lCE = 0,0067 m).
Dans cette section, l'effet de l'épaisseur
adimensionnelle des sources de chaleur, Ec, sur leur refroidissement
sera étudié. Puisque les dimensions de la cavité et la
quantité du MCP sont maintenues constantes, la hauteur adimensionnelle
de la source, Lc, doit être ajustée en utilisant la
relation: Lc = LCE / Ec où LCE = lCE/
lo, à chaque fois que l'épaisseur adimensionnelle,
Ec, varie. Plusieurs simulations numériques ont
été effectuées en considérant la plage de variation
de Ec/Ec,ref: 0,667 - 4.
Un exemple illustrant le champ de température, la
structure de l'écoulement, la forme et la position du front de fusion
est donné à la Figure 3.19, pour deux instants adimensionnels,
ô1 =
0,0181 (soit 820 s) et ô2 =0,0733 (soit
3320 s). Comme on peut le constater, la forme et la
position du front de fusion, les isothermes et le champ des
vitesses sont fortement altérés par la protubérance des
sources de chaleur. Le profil des vitesses est parabolique dans la couche
limite qui se développe prés des parois solides. Pour les faibles
rapports Ec/Ec,ref, et dans son mouvement ascendant de convection
naturelle, le MCP liquide récupère la chaleur
évacuée par les trois sources de chaleur et la plaque
conductrice. Lorsque le MCP liquide atteint la paroi supérieure, il
subit une déflexion et descend le long du front de fusion en lui
transférant la chaleur avec une densité de flux de chaleur
décroissante dans la direction descendante. La nature
décroissante, dans le sens descendant, de la densité de flux de
chaleur, à l'interface solide- liquide, entraîne des taux de
fusion décroissant dans le même sens. Ceci explique la
déformation prononcée du front de fusion dans la partie
supérieure de la cavité. La présence

0.019
0.016
0.013
0.027
0.021
0.014
Ec/Ec,ref =0,667 1 2 4
(b)
(a)

0.02
0.018


0.021
0.022
0.020
0.017
.018
0.016

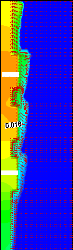
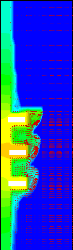
0.015
0.014
0.016
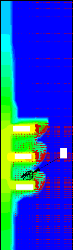
0.014
0.015
0.014
-
0.017
0.014

0.030 0.028 0.026 0.024 0.022 0.020 0.018 0.016 0.014 0.012
0.010 0.008 0.006 0.004 0.002 0.000

0.019 0.018 0.017 0.016 0.015 0.014 0.013 0.012 0.011 0.010
0.009 0.008 0.007 0.006 0.005 0.004 0.003 0.002 0.001 0.000

Figure 3.19: Effet de l'épaisseur
adimensionnelle des sources de chaleur, Ec/Ec,ref, sur les champs de
température, de vitesse, la position et la forme du front de fusion
(isotherme, è =0) aux instants adimensionnels (a):
ô1 = 0,0181 soit 820 s et (b):
ô2 = 0,0733 soit 3320 s
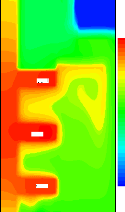
0.022
0.020
0.021
Figure 3.19.c: Structure en
plume au dessus de la
source
supérieure (ô =0,0733)
0.021 0.020 0.018 0.017 0.016 0.015 0.015 0.014 0.013 0.012
0.010 0.009 0.007 0.007 0.005 0.005 0.004 0.003 0.000
d'une cellule de convection prés de la source de
chaleur supérieure améliore le transfert de chaleur entre
celle-ci et le MCP liquide. Ce qui explique la température relativement
basse de la source supérieure et la déformation locale
marquée de l'interface solide-liquide. La chaleur
récupérée par le MCP liquide, lors de son mouvement
ascendant, est transférée au front de fusion qui avance plus
lentement dans la partie supérieure de la cavité en comparaison
avec sa progression dans la partie inférieure. Pour des rapports
Ec/Ec,ref élevés, la situation est localement
similaire à une cavité chauffée par le bas,
caractérisée par l'apparition de ` jets ` et une
structure en plume `panaches `. Cette structure altère
l'écoulement et donne naissance à un vortex anti-horaire au
dessus de la troisième source de chaleur (voir détail figure
ci-contre, Ec/Ec,ref = 4, ô = 0,0733). Ce vortex sépare
deux zones d'écoulement principales: zone inférieure et
supérieure. Dans la zone inférieure, le MCP liquide extrait la
chaleur des faces des sources de chaleur et de la plaque conductrice, pour
l'évacuer, en grande partie, au front de fusion, expliquant le
rapprochement rapide de celui-ci de la paroi droite. Dans la zone
supérieure, et dans son mouvement de convection naturelle, le MCP
liquide extrait la chaleur de la partie supérieure de la plaque
conductrice et de la face supérieure de la source de chaleur
supérieure et la transfère à l'interface solide- liquide.
Dans la partie inférieure de l'enceinte, la fusion est plus rapide en
comparaison à celle dans la partie supérieure. En effet, le
positionnement des sources de chaleur en bas de l'enceinte, où le MCP
liquide est relativement froid, contribue à l'amélioration du
transfert de chaleur et par conséquent à la fusion rapide du
MCP.
Une autre remarque qui se dégage de l'analyse de cette
figure est que la zone la plus chaude comporte les trois sources de chaleur et
une partie de la paroi conductrice. Il faut noter
que cette zone se déplace vers le bas de la
cavité lorsque l'épaisseur adimensionnelle, Ec,
augmente. Quant à la zone la plus froide, dépendamment de
l'épaisseur, Ec, elle peut être située soit en
bas soit en haut de la cavité. Cette zone renferme le MCP liquide ayant
déjà évacué sa chaleur au front de fusion lors de
son mouvement descendant. Il y a lieu de signaler que la Figure 3.19b
correspondant à l'instant ô2 = 0,0733 montre
l'état thermique et
hydrodynamique avancé du système (proche de la
fin du processus de fusion). On peut bien remarquer, que pour une
épaisseur adimensionnelle faible (Ec /Ec,ref
1), la fin du processus de fusion est marquée par la
présence d'un seul bloc de MCP solide dans la zone inférieure
droite de la cavité, alors que pour une épaisseur adimensionnelle
élevé (Ec /Ec,ref > 1) un bloc de MCP solide se
détache et se localise dans la zone supérieure du coté
droit de la cavité.
La Figure 3.20, donne le profil de température
adimensionnelle dans la plaque conductrice
en Es
X= - 2 , pour différentes valeurs de
l'épaisseur adimensionnelle, Ec/Ec,ref, à des
instants
adimensionnels représentant trois régimes du
processus de fusion. Cette figure montre que les faces latérales des
sources de chaleur, caractérisées par leur protubérance,
Ec, influencent fortement le transfert de chaleur. Les courbes de
cette figure sont ondulées au niveau des sources de chaleur. Les
maximums se situent directement près des sources de chaleur. Cette
figure montre aussi que, pour les faibles épaisseurs adimensionnelles
(Ec/Ec,ref = 0,667), le maximum est situé à
proximité de la source de chaleur supérieure, alors que pour les
épaisseurs adimensionnelles relativement élevées
(Ec/Ec,ref = 4), ce maximum est localisée près de la source
centrale. Il est à signaler que pour les faibles valeurs de
l'épaisseur adimensionnelle, Ec, la plaque est mal refroidie.
Ceci est dû à la structure de l'écoulement qui change avec
la variation de Ec, comme il a été décrit
précédemment. Il y a lieu de noter qu'à l'instant
ô = 0,095 la différence de température
adimensionnelle enregistrée dans la plaque, Äè s
, est de l'ordre de 0,026 (soit 31 °C) pour les faibles épaisseurs
adimensionnelles
(Ec/Ec,ref = 0,667); une valeur à comparer à 10,5
°C pour Ec/Ec,ref = 4.

E /E
c
ô= 0,018
4
0,667
1
c,ref
ô= 0,051
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
0

0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
ô= 0,095
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
è
Figure 3.20: Effet de l'épaisseur
adimensionnelle, Ec/Ec,ref, sur le profil de température
adimensionnelle au sein du substrat en Es
X= - 2 , à différents instants.
Les constatations précédentes sont
confirmées par l'analyse de la Figure 3.21 qui donne la variation du
nombre de Nuselt moyen, Nu, de chaque source de chaleur et la variation de la
température maximale adimensionnelle en fonction de Ec/Ec,ref
durant le régime quasi stationnaire. Lorsque l'épaisseur
adimensionnelle des sources augmente, le nombre de Nusselt moyen augmente et
atteint sa valeur maximale au voisinage de Ec/Ec,ref =1,2,
puis diminue avec l'accroissement de Ec. Pour Ec/Ec,ref
< 3, le nombre de Nusselt le plus faible correspond
à la source de chaleur supérieure, alors que pour
Ec/Ec,ref >3, c'est la source de chaleur centrale qui
présente le nombre de Nusselt moyen le plus faible. Ces
résultats reflètent fidèlement les
constatations observées précédemment
(Figure 3.19) concernant la localisation de la température maximale
adimensionnelle. Celle-ci est localisée sur la source de chaleur
supérieure pour Ec/Ec,ref < 1, alors que pour
Ec/Ec,ref > 1, cette température est enregistrée par la source
de chaleur centrale. La valeur de cette température augmente avec
l'accroissement du rapport Ec/Ec,ref. Ceci explique la
décroissance aiguée du nombre de Nusselt (qui est inversement
proportionnel à Omax , voir équation
(2.58) ). Lorsque Ec/Ec,ref = 3, la source
centrale présente le nombre de Nusselt le plus petit.
Nu 1
Nu 2
Nu 3
è max
1 2 3 4
E / E
c c,ref
Nu
30
40
20
60
50
10
0
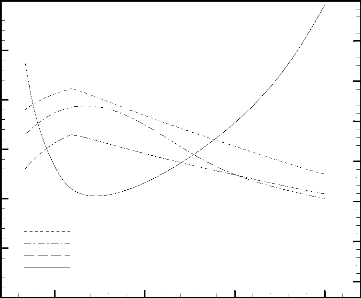
0.021
0.02
0.019 0.018
è
max
0.017
0.016
0.015
0.014
Figure 3.21: Effet de l'épaisseur
adimensionnelle, Ec/Ec,ref, sur la température maximale
adimensionnelle, èmax , et le nombre de Nusselt moyen des
sources de chaleur, Nu, en régime quasi stationnaire, ô =
0,051.
Tableau 3.8: Effet de l'épaisseur
adimensionnelle des sources de chaleur sur le taux de transfert de chaleur
échangé entre le MCP et les des différentes surfaces de la
plaque conductrice et des sources de chaleur en régime quasi- permanent
(ô = 0,051).
|
Ec /Ec,ref
|
Valeurs exprimées en % de la puissance
générée dans les sources de chaleur
|
|
|
0,667
|
17,00
|
20,30
|
7,23
|
22,30
|
7,32
|
17,00
|
4,07
|
|
1
|
18,74
|
18,63
|
7,24
|
19,85
|
6,78
|
17,30
|
8,50
|
|
1,2
|
19,13
|
17,80
|
7,28
|
20,01
|
6,68
|
16,20
|
11,25
|
|
2,6
|
21,07
|
18,20
|
6,01
|
17,12
|
4,01
|
15,40
|
16,80
|
|
4
|
23,40
|
18,64
|
5,97
|
15,03
|
3,23
|
15,04
|
17,85
|
S1 S2 S3
Plaque conductrice
Le Tableau 3.8 donne la contribution au transfert de chaleur
des différentes faces de la paroi chaude, exposées à
l'écoulement, pour différentes épaisseurs adimensionnelles
Ec. L'analyse des données du Tableau 3.8 permet de confirmer
les constatations susmentionnées. Avec l'augmentation de Ec,
les surfaces de la plaque conductrice, situées dans les
microcavités, évacuent de moins en moins la chaleur en
comparaison avec les autres portions. Ceci est dû au faible mouvement du
MCP liquide capturé par les microcavités. La conduction thermique
prédomine au sein des microcavités, conduisant, ainsi, à
la surchauffe locale du liquide. La Figure 3.22 donne plus de détails
sur l'écoulement à l'intérieur des microcavités et
dévoile l'existence d'un faible mouvement comparativement à celui
trouvé dans la zone d'écoulement principale. Ce faible mouvement
est aussi à l'origine de la décroissance des taux de transfert de
chaleur transmis par les faces des sources de chaleur avec l'accroissement de
l'épaisseur Ec. L'accroissement de l'épaisseur
adimensionnelle, Ec, des sources de chaleur se traduit par le
déplacement descendant des centres des sources de chaleur et par
conséquent une augmentation de la surface d'échange de la partie
de la plaque conductrice située au dessus de la source
supérieure. Cet effet contribue à l'intensification du taux de
transfert de chaleur tel qu'illustré au Tableau 3.8.
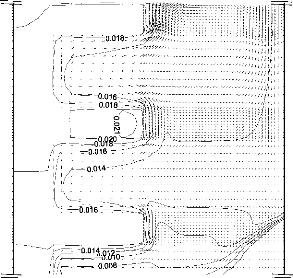
S3
0.020
Plaque conductrice
S2
0.020
0.014
S1
0.018
0.016
Figure 3.22: Champ de vitesses au niveau des
microcavités pour Ec/Ec,ref =4, à l'instantô
= 0,051.
L'analyse du Tableau 3.8 montre que, pour la plage de
variation de Ec considérée, quelque soit
l'épaisseur adimensionnelle, Ec, pas moins de 35 % de la
puissance générée par les sources de chaleur est
transférée par les faces verticales arrières des sources
au MCP liquide. La contribution de la plaque conductrice, assurant la diffusion
de la chaleur, s'intensifie avec l'augmentation de l'épaisseur
adimensionnelle, Ec. Le Tableau 3.8 montre que lorsque le rapport
Ec/Ec,ref varie de 0,667 à 4, le taux de transfert de chaleur
évacué au MCP liquide correspond à 35,62 % et 50,45 % de
la puissance générée, respectivement. Quant aux faces des
sources de chaleur en contact avec le MCP liquide, leur contribution au
transfert de chaleur subit une décroissance en passant de 59,60 %
à 48,71 %, lorsque le rapport Ec/Ec,ref s'accroît de 0,667
à 4. De ce qui précède, il en résulte que le taux
de transfert de chaleur vers le MCP s'intensifie sous l'effet de l'augmentation
de l'épaisseur adimensionnelle en passant
d'une valeur de 95,22 % à 99,16 % de la puissance
générée par les sources.
La Figure 3.23 présente l'effet du rapport
Ec/Ec,ref sur la durée adimensionnelle de fonctionnement
sécurisé, ôfonc , et la fraction liquide, f.
L'analyse de cette figure permet de
constater une nette amélioration de la durée
ôfonc avec l'augmentation du rapport Ec/Ec,ref.
Les
valeurs respectives de ôfonc , pour Ec/Ec,ref = 0,67 et 4
sont 0,0887 (~ 4013 s) et 0,117 (~
5294 s). En effet, comme il a été
susmentionné, l'accroissement de l'épaisseur Ec se
répercute sur le taux de transfert de chaleur en intensifiant celui-ci.
En conséquence, les sources de chaleur se refroidissent davantage et la
durée adimensionnelle de fonctionnement sécurisé
s'allonge. La fraction liquide, f, augmente, aussi, suite à
l'augmentation du taux de transfert de chaleur et de la durée de
fonctionnement sécurisé, ôfonc .
0 0.5 1 1.5 2 2.5 3 3.5 4
E c /E c,ref
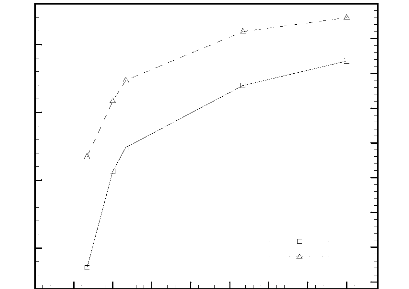
0.85
f
0.8
1
ô
fonc
f
0.95
0.9
0.75
0.7
0.65
0.6
0.12
0.11
ô
fonc
0.1
0.09
Figure 3.23: Effet de l'épaisseur
adimensionnelle, Ec/Ec,ref, sur la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et la fraction
liquide, f.
En s'inspirant de la Figure 3.23, les corrélations
exprimant la durée adimensionnelle de fonctionnement
sécurisé, ôfonc , et la fraction liquide,
f, en fonction du rapport Ec/Ec,ref sont
-1,17 - 1 4
,
données par l'équation Eq.(3.4). La variation
maximale entre les résultats numériques et ceux donnés par
l'expression Eq.(3.4) est estimée à 2 %.
(3.4)
~
E ~ ~
E
c c
ô = 0 12243 0,02113
, - ~ ~ , 0 99107 0 12307
f ,
= - , ~ ~
fonc
~ )
E E
c ref
, ~ ~
c ref
,
avec 0,667 < Ec/Ec,ref <
4,0
3.4.5 Effet de l'épaisseur adimensionnelle du
substrat, Es
Dans cette section, on étudie l'effet de
l'épaisseur adimensionnelle de la plaque conductrice (substrat),
Es, sur le refroidissement des sources de chaleur. Les simulations
numériques ont été effectuées en variant le
paramètre Es /Es,ref dans la plage: 0,4 - 2.
L'effet de ce paramètre sur Omax et
f est illustré à la Figure 3.24. L'analyse de cette
figure montre que la température maximale adimensionnelle la plus
élevée et la durée adimensionnelle de fonctionnement
sécurisé la plus courte sont obtenues pour le cas d'une plaque
conductrice (substrat) de faible épaisseur, à cause de son
inertie thermique relativement faible. Par exemple, la température
è max atteinte durant le régime quasi
permanent est de l'ordre de 0,017 (soit 57 °C) et 0,016
(soit 55 °C) pour Es/Es,ref = 0,4 et 2, respectivement. Aussi, il ressort
de l'analyse de cette figure que l'accroissement de l'épaisseur
adimensionnelle de la plaque conductrice Es, donc de son inertie
thermique, provoque un allongement de la durée de ce régime
quasi- stationnaire. Les valeurs respectives de cette durée pour
Es/Es,ref = 0,4 et 2, sont 0,022 (soit 996 s) et 0,032 (soit 1448 s). Ce
régime quasi- stationnaire s'achève lorsque la fraction liquide,
f, atteint des valeurs excédant 0,6. Lorsque la
température è max atteint la valeur critique, è
cr , la fraction liquide, f, atteint une
valeur d'autant plus proche de l'unité que
l'épaisseur adimensionnelle de la plaque est élevée.

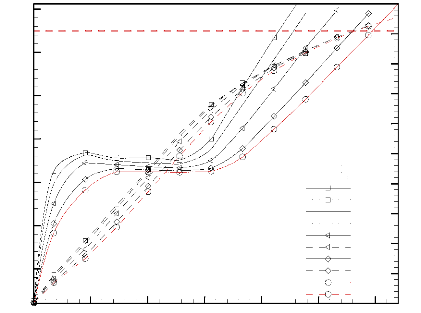
0.035
1
0.9
0.03
0.12 0
0 0.02 0.04 0.06 0.08 0.1
X
Température limite adimensionnelle, cr
è
X
X
X
X
X
X
X
X
X
X
X X X
X
E /E
s
s,ref
0.4
X
X
X
0.6
1
X
1.6
X
2
X
0.025
èmax
0.02
0.015
0.01
0.005
0.8
0.7
0.6
f
0.5
0.4
0.3
0.2
0.1
Figure 3.24: Effet de l'épaisseur
adimensionnelle de la plaque conductrice sur les variations temporelles de la
température maximale adimensionnelle des sources de chaleur (traits
continus) et la fraction liquide (traits discontinus).
L'effet de l'épaisseur, Es, sur la
distribution de la température adimensionnelle dans la plaque
conductrice en X = - Es/2 est donné à la Figure 3.25,
à trois instants différents représentant les trois
régimes du processus de fusion. Comme il peut être observé,
au début du processus de fusion, les courbes relatives aux
différentes épaisseurs adimensionnelles présentent des
maximums situés à proximité de la source de chaleur
centrale. Ces maximums se déplacent près de la source de chaleur
supérieure pour les instants ultérieurs. A noter qu'au
début de la fusion du MCP, cette distribution de température est
pratiquement symétrique, à cause du transfert de chaleur
conductif qui prévaut durant cette période. Au cours du temps,
les mouvements convectifs s'établissent dans la cavité liquide
ainsi formée, et perturbent cette
symétrie. Lors du processus de fusion, la cavité
liquide s'élargit et la partie inférieure de la plaque
conductrice (0 < Y < 0,5) se refroidit
mieux comparativement à la partie restante de la plaque. Ce
refroidissement devient plus important avec la réduction de
l'épaisseur adimensionnelle, Es (voir Figure 3.25). Quant
à la partie restante de la plaque conductrice, l'impact de
l'accroissement de l'épaisseur adimensionnel, Es, se
répercute par une élévation de la température.
Aussi, on peut constater que l'augmentation de l'épaisseur
adimensionnelle, Es /Es,ref, entraîne une réduction de
la différence de température adimensionnelle au sein de la plaque
conductrice. Par exemple, à l'instant, ô = 0,051, cette
différence est égale à 0,0117 (14 °C) pour une
épaisseur adimensionnelle, Es/Es,ref = 0,4, tandis que pour une
épaisseur adimensionnelle, Es/Es,ref = 2, cette différence est
inférieure à 0,0066 (8 °C).
2
E s /Es,ref
0,4
1
2
ô=0,007
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035

ô=0,051
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
2
1.5
1
0.5
Y

ô=0,0844

0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
è
Figure 3.25: Profil de température
adimensionnelle au sein de la plaque conductrice pour
différentes épaisseurs adimensionnelles,
Es/Es,ref ( Es
X= - 2 ).
Le Tableau 3.9 donne la contribution au transfert de chaleur
des différentes surfaces de la paroi conductrice, exposées
à l'écoulement, pour différentes valeurs de
l'épaisseur adimensionnelle de la plaque conductrice, Es/Es,ref.
Tableau 3.9: Effet de l'épaisseur
adimensionnelle de la plaque conductrice sur le transfert de chaleur
échangé entre le MCP et les des différentes surfaces de la
plaque conductrice et des sources de chaleur à ô =
0,051.
Es /Es,ref Valeurs exprimées en % de la
puissance générée dans les sources de chaleur
0,4 14,00 19,00 7,70 21,00 7,20 18,50 7,00
0,6 16,05 18,60 7,60 19,87 7,00 17,80 7,70
1 18,74 18,63 7,24 19,85 6,78 17,30 8,50
1,6 20,60 18,10 7,10 18,30 6,40 15,90 8,70
2 22,40 18,10 6,90 17,70 6,00 15,40 8,73

S1 S2 S3
Plaque conductrice
L'analyse des données du Tableau 3.9 permet de
constater que l'accroissement de l'épaisseur adimensionnelle de la
plaque conductrice entraîne une augmentation des taux de transfert de
chaleur échangée par les parties inférieure et
supérieure de la plaque conductrice (de 14 % à 22,4 % pour la
partie inférieure et de 7 % à 8,73 % pour la partie
supérieure). Pour expliquer ce comportement, on peut faire appel, pour
le régime quasi permanent, à l'expression usuellement
utilisée pour l'approximation de la résistance de l'ailette
[21]:
1
R (3.5)
s (k h e l) 0.5
s c s
L'expression (3.5) montre que la résistance thermique
du substrat décroît avec l'accroissement de l'épaisseur du
substrat, es. Par conséquent, le transfert de
chaleur entre le MCP liquide et la paroi chaude s'intensifie. Le taux de
transfert de chaleur évacué par la
paroi chaude au MCP représente 94,2 % et 95,25 % de la
puissance générée par les sources de chaleur pour
Es/Es,ref = 0,4 et 2, respectivement. Ceci explique la chute de la
température maximale adimensionnelle durant le régime quasi
permanent (Figures 3.24 et 3.26).
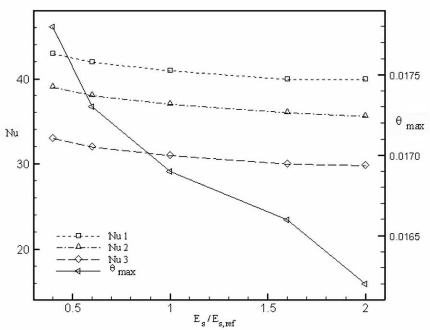
Figure 3.26: Effet de l'épaisseur
adimensionnelle, Es/Es,ref , sur la température
maximale
adimensionnelle, èmax , et le nombre de Nusselt
moyen des sources de chaleur, Nu, à ô =0,051
(régime quasi stationnaire).
La Figure 3.26 illustre l'effet de l'épaisseur
adimensionnelle, Es/Es,ref, sur le nombre de Nusselt moyen et la
température maximale adimensionnelle des sources de chaleur, durant la
régime quasi- permanent. L'effet de l'accroissement de
l'épaisseur adimensionnelle, Es est traduit par une
décroissance de la température maximale adimensionnelle (Figure
3.26) et des flux de chaleur adimensionnels évacués par les faces
des sources de chaleur (Tableau 3.9). L'expression (2.58) montre que le nombre
de Nusselt moyen de chaque source de chaleur est
Es augmente). Ainsi, la décroissance de J
?ç est légèrement compensée par
î ? î
O
K d
0
|
l'augmentation de
|
1
O , si bien que le nombre de Nusselt moyen de
chaque source de chaleur
max
|
subit une légère chute lorsque Es
s'accroît.
La Figure 3.27 donne l'effet de l'épaisseur
adimensionnelle, Es/Es,ref, sur la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et la fraction
liquide, f.
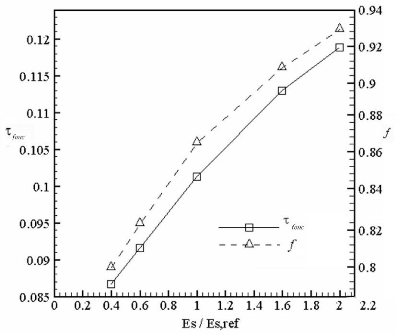
Figure 3.27: Effet de l'épaisseur
adimensionnelle, Es/Es,ref, sur la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et la fraction
liquide, f.
L'analyse des courbes de cette figure montre que la durée
ôfonc et la fraction liquide, f,
|
varient, approximativement, linéairement en fonction du
rapport
|
0.5
/ '
E s
~ ~
~ ~
Es,ref
|
dans la plage: 0,2 -
|
0,5
~~ ,
4. Les corrélations suivantes ont été
déduites:
~ E s
ô fonc = 0,059375 + 0,041925 ~ ~ E
s,ref
0,5
( ~
E s
f ,
= 0 70036 + 0,167647 (3.6)
~ ~
~ , )
E s ref
avec 0,4 < Es /Es,ref
< 2.
La comparaison des résultats numériques avec
ceux obtenus à partir des corrélations (3.6) est donnée
à la Figure 3.28, représentant la courbe de parité. Un
accord satisfaisant est obtenu. En effet, les variations maximales pour la
durée ôfonc et la fraction liquide, f, sont de
l'ordre
de 3 % et 1,5 %, respectivement.
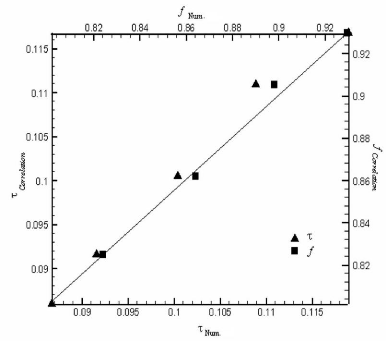
Figure 3.28: Courbe de parité
3.4.6 Effet de la distance adimensionnelle séparant
les sources de chaleur
Cette section présente les résultats relatifs
à l'effet de l'espacement sur le comportement thermique de l'enceinte
du MCP. Plusieurs simulations numériques ont été conduites
en considérant la marge de variation du rapport / ref : 0,5 - 2,2.
ô
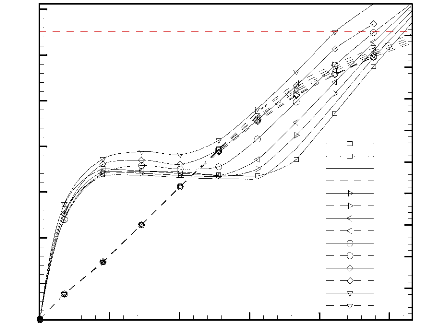
0.6
f
0.5
0.035
0.015
0.005
0.03
0.01
X
0
0 0.02 0.04 0.06 0.08 0.1
Température limite adimensionnelle, cr
è
X
X
X X X X X
X
X
X
X
X
X
X
X
X
X
X
/
ref
X
X
2
2.2
0.5 0.8 1
1.3
1.7
0.9
0.8
0.7
0.4
0.3
0.2
0.1
1
0.025
è
max
0.02
Figure 3.29: Effet de la distance
adimensionnelle / ref sur l'évolution temporelle de la
température maximale adimensionnelle (lignes continues) et
la fraction liquide (lignes discontinues).
La Figure 3.29 illustre l'évolution temporelle de la
température maximale adimensionnelle des sources de chaleur et de la
fraction liquide pour différentes valeurs du
rapport / ref . L'analyse de cette figure montre que
durant la première phase du processus
de fusion (dominée par la conduction thermique) la
montée en température est d'autant plus rapide que la distance
adimensionnelle est élevée. En effet, l'accroissement de la
distance adimensionnelle se traduit par l'éloignement des sources entre
elles. La fusion du MCP se manifeste essentiellement autour de chaque source de
chaleur. Ainsi, les zones liquides n'interfèrent pas rapidement et les
mouvements de convection naturelle deviennent moins intenses. Par
conséquent, le taux de transfert de chaleur évacué par les
sources de chaleur est réduit avec l'accroissement de . C'est la raison
pour laquelle la température adimensionnelle des sources de chaleur
augmente lorsque augmente. Quant à la durée du régime
quasi- stationnaire, elle est d'autant plus élevée que est
faible. En effet, pour les valeurs relativement élevées de , la
source de chaleur supérieure s'approche davantage de la paroi
supérieure adiabatique. La quantité du MCP emprisonnée
entre la paroi supérieure adiabatique et la source de chaleur
supérieure diminue. Ainsi, et après fusion de cette
quantité du MCP, la source de chaleur supérieure se trouve
rapidement entourée d'une zone liquide relativement chaude, à
cause des mouvements convectifs naturels se manifestant dans la cavité
liquide. Tous ces effets entraînent la réduction du gradient
thermique entre le MCP liquide et la source de chaleur supérieure. Cette
dernière stocke la chaleur sous forme sensible, ce qui se traduit par sa
rentrée précoce et rapide dans la troisième phase du
processus de fusion. Par ailleurs, le système évolue plus
rapidement vers l'état critique ( è max = è cr
),
pour les valeurs élevées du rapport /
ref . Il ressort aussi de la Figure 3.29 que la fraction
liquide
évolue linéairement et indépendamment du rapport /
ref , jusqu'à ce que le système
quitte le plateau et atteint la troisième phase du
processus de fusion. A partir de ce moment, la vitesse de fusion devient
tributaire du rapport / ref , sa valeur est d'autant petite que /
ref
est elevé.
La Figure 3.30 illustre le profil de température
adimensionnelle au sein de la plaque
conductrice ( Es
X= - ) pour différentes valeurs du rapport /
ref et pour trois différents
2
instants adimensionnels. Ces instants correspondent aux trois
principaux régimes du processus de fusion. Comme il peut être
constaté de l'analyse de cette figure, le maximum est situé
près de la source de chaleur supérieure quelque soit le rapport
/ ref , à l'exception de la première phase
(régime de conduction) où il est situé prés de la
source centrale pour / ref < 1.
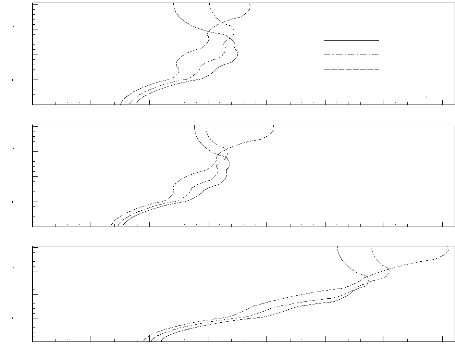
1.5
Y
1
0.5
0
2
1.5
Y
1
0.5
2
1.5
Y 1
0.5
0
2
/
ref
0,5
1
2,2
ô=0,018
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
ô=0,051
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
0
ô=0,095
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
è
Figure 3.30: Profil de température
adimensionnelle au sein de la plaque pour différentes valeurs de la
distance adimensionnelle / ref ( Es
X= - ).
2
Il ressort, aussi, de l'analyse de ces figures qu'il faut
distinguer entre deux parties de la plaque conductrice: partie
inférieure (0 = Y = 1,7) et supérieure (Y > 1, 7 ). Dans la
partie
inférieure, la température adimensionnelle est
d'autant plus élevée que / ref est petit, alors que
c'est l'effet inverse qui se manifeste dans la partie supérieure.
Pour confirmer les constatations susmentionnées,
à la Figure 3.29, on analyse le Tableau 3.10 donnant la contribution, au
transfert de chaleur, des différentes surfaces de la paroi chaude,
exposées à l'écoulement, pour différentes valeurs
du rapport / ref à
l'instantô = 0,051. Ce tableau montre que la
plaque conductrice évacue plus de 35 % de la
puissance
générée par les sources de chaleur. L'accroissement du
rapport / ref cause une
réduction de la surface d'échange de la partie
supérieure de la plaque conductrice et par
conséquent une
réduction de sa contribution au transfert de chaleur (de 11,2 % à
0,08 % pour
/ ref = 0,5 et 2,2, respectivement). Ceci se traduit par une
surchauffe très rapide de la source
supérieure et, par la suite, une réduction de la
durée adimensionnelle de fonctionnement sécurisé.
Tableau 3.10: Effet du rapport /
ref sur la contribution des différentes surfaces
exposées
de la plaque conductrice et des sources de chaleur au transfert
de chaleur vers le MCP, ô = 0,051 (régime quasi stationnaire).
|
/ ref
|
Valeurs exprimées en % de la puissance
générée dans les sources de chaleur
|
|
0,5
|
20,64
|
20,50
|
3,08
|
18,80
|
2,55
|
17,80
|
11,20
|
|
0,8
|
19,31
|
18,8
|
5,90
|
18,10
|
5,40
|
17,90
|
9,55
|
|
1,0
|
18,74
|
18,63
|
7,24
|
19,85
|
6,78
|
17,30
|
8,50
|
|
1,7
|
16,63
|
16,20
|
12,80
|
19,50
|
13,40
|
17,00
|
0,12
|
|
2,2
|
16,35
|
15,80
|
13,62
|
19,40
|
15,40
|
16,50
|
0,08
|
S1 S2 S3
Plaque conductrice
La Figure 3.31 illustre la forme et la position du front de
fusion pour trois valeurs du rapport / ref à
l'instantô = 0,051. L'analyse de cette figure permet de
constater que pour
un rapport / ref faible, le front de fusion
progresse rapidement prés de la source de chaleur
supérieure. Ceci cause une déflexion de la forme
du front de fusion. Cette déflexion devient
moins prononcée
avec l'augmentation du rapport / ref ( / ref >1).
Il faut noter que pour
des valeurs élevées du rapport / ref
, le front de fusion intercepte la paroi adiabatique
verticale droite. Ainsi, le bloc du MCP solide, en face de la
source de chaleur supérieure, fond rapidement en causant la surchauffe
de celle-ci.

Figure 3.31: Forme et position du front de
fusion pour différents rapports / ref (ô =
0,051).
La Figure 3.32 relate l'effet du rapport / ref sur la
durée adimensionnelle de
fonctionnement sécurisé du
puits de chaleur, ôfonc , et la fraction liquide, f.
L'analyse de cette
figure montre que la durée adimensionnelle,
ôfonc , et la fraction liquide, f, sont d'autant
plus
élevées que les sources de chaleur sont plus
rapprochées. La durée ôfonc et la fraction
liquide, f, varient, approximativement,
linéairement avec le rapport / ref . Les
corrélations suivantes ont été établies:
~
~
ô = 0,1093 - 0,008 , = 0,9208 - 0,05277
~ ~ f ~ ~ (3.7)
fonc
~ ~
ref ~ ~
ref
avec 0,5 < / ref < 2,
2
La comparaison des résultats numériques avec
ceux obtenus à partir des corrélations Eq.(3.7), donnée
à la Figure 3.33, montre un bon accord. Les variations maximales sont
estimées à 3,5 %.
ô
fonc
f
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 2.2
/ ref
0.108
0.106 0.104
0.102
ô
fonc
0.1
0.098
0.096 0.094
0.092
0.09
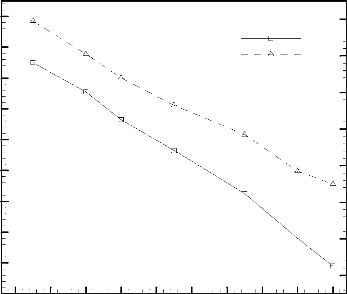
0.9
0.88
0.86 0.84
f
0.82
0.8
0.78
0.76
Figure 3.32: Durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et fraction
liquide, f, en fonction du rapport / ref
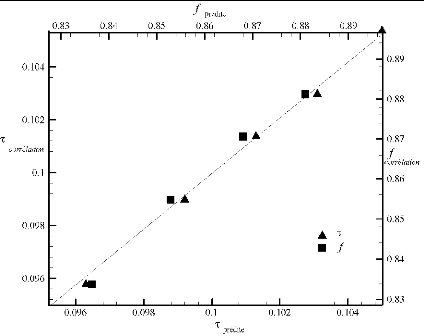
Figure 3.33: Courbe de parité.
3.4.7 Effet du rapport de forme, A.
Cette section présente les principaux résultats
relatifs à l'effet du rapport de forme, A, sur le comportement et la
performance thermiques de l'enceinte. Plusieurs investigations
numériques ont été effectuées en considérant
la marge de variation du rapport de forme A/Aref: 0,75 - 2,5. Il faut
signaler que le volume du MCP, contenu dans l'enceinte, est constant. Par
ailleurs, la forme de l'enceinte varie avec le rapport de forme, A. Une valeur
élevée du rapport de forme, A, correspond à une
cavité élancée verticale, alors que pour une valeur
relativement faible de A, correspond une cavité allongée
horizontalement.
La Figure 3.34-a donne les isothermes et la structure des
lignes de courant pour deux valeurs du rapport de forme de l'enceinte du MCP,
à l'instant ô = 0,0734. L'analyse de cette figure montre
que pour les valeurs élevées du rapport de forme
(A/Aref =2,5 (A = 10)), le système est en régime
quasi- stationnaire et l'écoulement induit par la convection naturelle
est mono cellulaire et se fait dans le sens horaire; ascendant au niveau de la
paroi chaude à gauche, et descendant le long du front de fusion (paroi
froide). La valeur maximale de la fonction de courant, ø max
, s'accroît avec l'augmentation du rapport A/Aref suite
à
l'élancement de la cavité liquide favorisant
l'écoulement du MCP liquide. La Figure 3.34-a montre, aussi, que pour
les faibles valeurs du rapport A/Aref, le champ thermique se
stratifie rapidement dans la partie supérieure de la cavité alors
que pour le cas des cavités élancées, de grand rapport de
forme, les isothermes sont nettement inclinés. Pour le cas des
cavités ayant un rapport de forme élevé, les sources de
chaleur sont mieux refroidies et la température maximale
adimensionnelle, enregistrée par les sources de chaleur, est d'autant
plus élevée que le rapport A/Aref est faible. (
è max = 0,026 (Tmax = 61 °C ) pour A/Aref = 0,75 alors que
è max =0,014 (Tmax = 53 °C) pour
A /Aref = 2,5).
Ces résultats sont, aussi, vérifiés en
analysant l'évolution temporelle de la forme et la position du front de
fusion, pour les rapports 0,75 et 2,5 (Figure 3.34 b). L'examen de cette figure
permet de remarquer le détachement d'un bloc de MCP solide dans la
partie supérieure de la cavité pour les rapports de forme
élevés (A/Aref = 2,5 (A = 10)). Le positionnement de ce bloc de
MCP, dans la partie supérieure de la cavité, fait de lui un puits
de chaleur pour la source de chaleur supérieure. Cette situation est
absente pour le cas des cavités de faibles rapports de forme (A/Aref =
0,75 (A = 3)) pour lesquelles le MCP est totalement fondu dans la partie
supérieure de la cavité, ce qui cause une surchauffe rapide de la
source de chaleur supérieure.
è
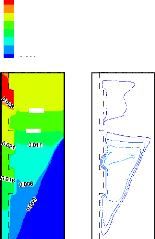
A/A ref= 0,75
80.0
0.026 0.026 0.021 0.016 0.011 0.006 0.000
0.016
0.021
A/A ref= 2,5
ø
367.9 360.0 340.0 320.0 300.0 280.0 260.0 240.0 220.0 200.0
180.0 160.0 140.0 120.0 100.0 80.0 60.0 40.0 20.0
0.0


367.9
(a)

0.016
0.016
0.011
A/A ref= 0,75

ô1
ô2
ô3
A/A ref= 2,5
ô1
ô
3
(b)

ô
3
ô2
Figure 3.34: Effet du rapport de forme sur les
isothermes et les lignes de courant à l'instant,
ô =
0,0734 (a). Evolution temporelle de la forme et la position du front de fusion
pour les
rapports de forme 0,75 et 2,5, aux instants adimensionnels:
ô1 =0,0197, ô2 = 0,051 et
ô3 = 0,0844 (b).
En effet, à l'instant ô =0,0844, la
température maximale adimensionnelle est très proche de la valeur
critique, alors qu'il reste environ 20 % du MCP solide. Avec un rapport de
forme élevé, et bien que seulement 8 % du MCP reste à
l'état solide, la température maximale adimensionnelle est de
loin inférieure à la température critique
adimensionnelle.
ô
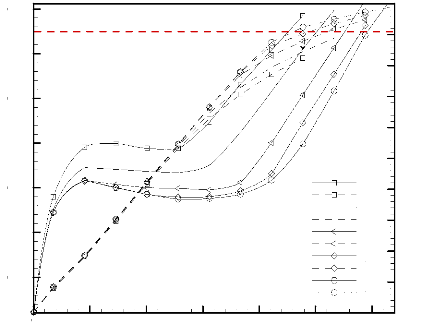
0.035
0.015
0.005
0.03
0.01
X
0.12 0
0 0.02 0.04 0.06 0.08 0.1
Température limite adimensionnelle, cr
è
X
X
X X
X X X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
A /A
0,75
2
2,5
1
1,5
ref
0.9
0.8
0.7
1
0.025
èmax
0.02
0.6
f
0.5
0.4
0.3
0.2
0.1
Figure 3.35: Effet du rapport A/Aref
sur l'évolution temporelle de la température maximale
adimensionnelle, è max , (lignes continues) et la fraction
liquide, f, (lignes discontinues).
L'effet du rapport de forme, A, de l'enceinte sur la variation
temporelle de è max et f est donné à
la Figure 3.35. L'analyse d'une telle figure montre que les durées du
régime quasi stationnaire et du fonctionnement sécurisé
diminuent lorsque le rapport de forme décroît. En effet, la
réduction du rapport de forme, A, conduit à une réduction
de la surface d'échange de la paroi gauche et par conséquent une
baisse du transfert de chaleur transmis au MCP. Ceci se traduit par une hausse
de l'énergie accumulée sous forme sensible par les sources de
chaleur
et donc une hausse de leurs températures moyennes et
une rentrée rapide dans la phase de surchauffe. A cet effet, il faut,
aussi, ajouter que pour les faibles valeurs du rapport de forme, A, le MCP
contenu dans la partie supérieure fond complètement et la source
de chaleur supérieure surchauffe rapidement, comme il a
été mentionné précédemment. L'effet du
rapport de forme, A, sur la fraction liquide, f, ne se fait ressentir
qu'après le régime de fonctionnement quasi- stationnaire
où la fraction liquide subit une variation d'autant plus lente que le
rapport de forme, A, est réduit. Ceci est dû à la
réduction du flux de chaleur transmis au MCP lorsque A
décroît.
Ainsi, on conclut que les cavités ayant des rapports de
forme élevés constituent une bonne solution pour le
refroidissement des composants électroniques.
La Figure 3.36 présente la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et la
fraction liquide, f, pour différents rapports
de forme, A/Aref. Il ressort de l'analyse de
cette
figure que les cavités ayant un rapport de forme
élevé n'assurent pas seulement l'allongement
de la durée de fonctionnement sécurisé,
ôfonc , mais aussi une fusion pratiquement totale du
MCP.
En adoptant la même procédure de
développement des corrélations que dans le cas des autres
paramètres de contrôle, il ressort de la Figure 3.36 que les
corrélations pour la durée
adimensionnelle, ôfonc , et la fraction liquide,
f, sont:
|
- 0 95
, - 1 05
,
~ ~
A ~ ~
A
ô = 0,1324 - 0,03109 , =1,0467 - 0,1787
~ ~ f ~ ~
fonc
~ ~
A A
ref ~ ~
ref
|
(3.8)
|
avec 0,75 < A/Aref < 2,
5
La variation maximale, obtenue lors de la comparaison des
résultats numériques et ceux de l'expression (3.8), est de
l'ordre de 1 %.
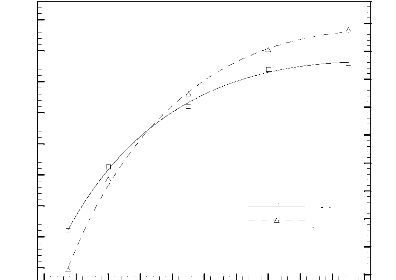
0.125 0.12 0.115 0.11
ô fonc
0.105
0.1 0.095 0.09 0.085
0.98 0.96 0.94 0.92 0.9 f 0.88 0.86 0.84 0.82 0.8
ô
fonc
f
0.6 0.8 1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6
A /A ref
Figure 3.36: Durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et fraction
liquide, f, pour différents rapports de forme, A/Aref.
3.4.8 Effet de la diffusivité thermique
adimensionnelle des sources de chaleur, á c /á c,ref
L'effet du rapport des diffusivités thermiques
adimensionnelles des sources de chaleur, á c /á
c,ref, sur la variation temporelle de la température maximale
adimensionnelle des sources
de chaleur, Omax , et la fraction
liquide, f, est illustré à la Figure 3.37. Les
simulations
numériques ont été effectuées en
considérant la marge de variation du rapport á c
/á c,ref: 0,1 -
20. Comme il est montré sur cette figure, durant la
première phase du processus de fusion,
caractérisée par
la prédominance de la conduction thermique, plus le rapport á
c /á c,ref est
élevé, plus l'augmentation de la
température maximale adimensionnelle des sources de
chaleur est
lente. Ceci est dû au fait que l'accroissement de la diffusivité
thermique
adimensionnelle des sources de chaleur augmente leur
habilité à uniformiser leur température et à
diffuser plus facilement la chaleur générée en leur sein
au lieu de la stocker sous forme sensible; favorisant ainsi le transfert de
chaleur vers la plaque conductrice et la couche du MCP liquide entourant les
faces des sources de chaleur. Ces constatations sont en accord avec les
résultats obtenus par Jaluria et al. [67], lors de l'étude du
refroidissement d'un composant électronique enfermé dans une
enceinte rectangulaire confinant l'air comme fluide de refroidissement. Le
système atteint rapidement le régime quasi- stationnaire
(plateau, Figure 3.37) pour les faibles valeurs du rapport á
c /á c,ref, à l'encontre du cas avec des
sources de
chaleur de diffusivité thermique adimensionnelle
élevée, pour lequel la première phase du processus de
fusion, dominée par la conduction thermique, persiste plus longtemps.
ô
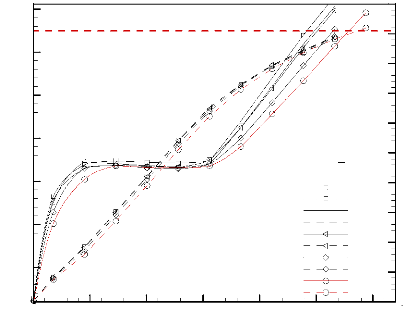
èmax
0.035
0.025
0.015
0.005
0.03
0.02
0.01
X
0 0.02 0.04 0.06 0.08 0.1 0.12
Température limite adimensionnelle, cr
è
X
X
X X
X X X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
á /á
__
c
0.1
0.5
20
1
10
c,ref
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1
f
Figure 3.37: Effet du rapport des
diffusivités thermiques adimensionnelles, á c
/á c,ref, sur
l'évolution temporelle de la température maximale
adimensionnelle des sources de chaleur et la fraction liquide.
Une autre constatation qui peut être
dégagée de l'analyse de la Figure 3.37 est qu'en régime
quasi- stationnaire, la température maximale adimensionnelle des sources
de chaleur la plus basse est enregistrée pour le cas des sources de
chaleur ayant une diffusivité thermique adimensionnelle
élevée. La température maximale adimensionnelle,
°max , atteinte par les
sources de chaleur, en régime quasi- stationnaire, est
égale à 0,017 (Tmax= 56.33 °C) pour
á
c /á c,ref = 0,1 et 0,016 (Tmax= 55,13 °C)
pour á c /á c,ref= 20. Quant aux fractions
liquides,
obtenues à la fin du processus de fusion ( O
max = O cr ), elles sont, respectivement,
0,84 et 0,9.

L'effet du rapport á c /á c,ref sur le
profil de température adimensionnelle de la plaque
conductrice ( Es
X= - ) est donné à la Figure 3.38. A l'exception du
régime quasi stationnaire
2
( ô = 0 ,051), pour lequel le profil de
température est quasi indépendant du rapport á
c /á c,ref ,
les deux autres régimes ( ô = 0,007 et ô
=0,0844) sont tels que l'accroissement du rapport
á c
/á c,ref entraîne une baisse de température non
pas seulement des sources de chaleur mais
aussi celle de la plaque conductrice. En effet, comme il a
été expliqué précédemment,
l'augmentation
de ác/ác,ref rend les sources de chaleur plus habiles
à diffuser la chaleur au
lieu d'en stocker, ce qui cause une intensification du
transfert de chaleur et par conséquent une baisse de la
température adimensionnelle des sources de chaleur et de la plaque
conductrice. Ce résultat est aussi confirmé à la Figure
3.39, illustrant le champ de température, la position et la forme du
front de fusion aux instants ô = 0,007, ô = 0
,051 et ô =0.0844, représentant les trois phases
du processus de fusion. On remarque bien les températures
élevées dans le cas où á c /á
c,ref =0,1.

__ __
á /á
c
ô=0,007
0,1 1
20
c,ref
|
2
1.5
Y 1
0.5
0
2
1.5
Y
1
0.5
0
2
1.5
Y 1
0.5
|
0.01 0.015 0.02 0.025 0.03
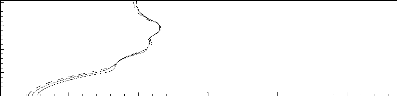
ô=0,051
0.01 0.015 0.02 0.025 0.03

ô=0,0844
0.01 0.015 0.02 0.025 0.03
è
Figure 3.38: Effet du rapport
ác/ác,ref sur le profil de température
adimensionnelle au sein de la plaque conductrice en Es
X= - .
2
è
0.012 0.011 0.010 0.009 0.008 0.007 0.006 0.005 0.004 0.003
0.002 0.001 0.000
ô = 0,007
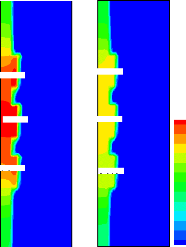
0.0120
0.0120
0.0111
0.0101
0.0091
0.0091
á c /á c,ref = 0,1 f = 0,085
á c /á c,ref = 20 f = 0,075
ô = 0,051 ô = 0,0844
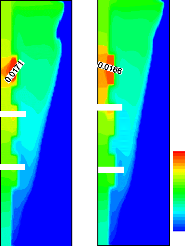
0.0133
0.0162
0.0157
0.0133
è
0.017 0.017 0.016 0.015 0.012 0.010 0.007 0.004 0.001
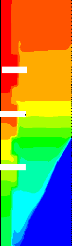
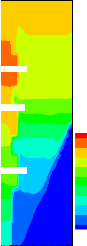
0.0196
0.0221
0.0147
è
0.025 0.022 0.020 0.017 0.015 0.012 0.010 0.007 0.005 0.000
0.0245
0.0245
0.0172
á c /á c,ref = 0, 1 f = 0,53
á c /á c,ref = 20 f = 0,51 á
c /á c,ref= 0,1 f = 0,79 á c /
á c,ref= 20 f = 0,78
Figure 3.39: Effet du rapport á c /
á c,ref sur le champ thermique.
La durée adimensionnelle de fonctionnement
sécurisée, ôfonc , et la fraction liquide,
f, sont données à la Figure 3.40 pour différents
rapports á c /á c,ref. Il ressort de
l'analyse de cette
figure que la durée ôfonc et la fraction
liquide, f, augmentent lorsque á c /á
c,ref s'accroît.
Toutefois, pour ác/ác,ref > 10, la durée,
ôfonc , et la fraction liquide, f, subissent une
légère augmentation.
0.12
0.115
0.11
ô
fonc
0.105
0.1
0.095
1
0.98
0.96
0.94
f
0.92
0.9
0.88
0.86
0.84
0 5 10 15 20
_
á /á
c c,ref
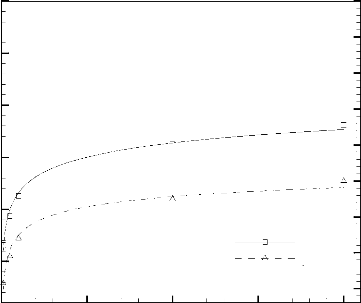
f
ô
fonc
Figure 3.40: Durée de fonctionnement
sécurisé, ôfonc , et fraction liquide, f,
en fonction du
rapport á c / á c,ref.
En adoptant la même procédure de
développement des corrélations que dans le cas des autres
paramètres de contrôle, il ressort de la Figure 3.40 que les
corrélations donnant la
durée adimensionnelle, ôfonc , et la
fraction liquide, f, sont:
|
- 0 07
, - 0 15
,
( '
á ~ '
á
c c
ô = 0,13363 - 0 0320248
, , = 0,9430688 - 0 0731999
f ,
fonc ~ á ~ ~ á
~
~ )
c ref
, ~
c ref
,
|
(3.9)
|
avec 0,1 < á c /á
c,ref < 20
Un accord satisfaisant est obtenu entre les résultats
numériques et ceux de la corrélation (3.9). La variation maximale
est de l'ordre de 1 %.
Chapitre IV
Développement des corrélations et
abaques
4.1 Corrélations
L'un des objectifs visés lors de la conception des
systèmes de refroidissement de composants électroniques, à
base de MCP, est la prévention de ces derniers de la surchauffe. Pour le
cas des systèmes de refroidissement actif, un tel objectif est atteint
en ayant recours à un mode de refroidissement par convection naturelle
et/ ou forcée à l'air ou à un liquide (eau ou liquide
diélectrique, tel que le FC 72, par exemple). Dans le cas d'un
système de refroidissement utilisant un MCP fonctionnant selon un mode
passif, la surchauffe peut se manifester après une certaine durée
de fonctionnement. L'efficacité de refroidissement est d'autant
élevée que cette durée est maximale et la fusion du MCP
est totale (f ~ 1). Ainsi, il serait pratique de développer des
corrélations et/ou des abaques permettant le calcul de la durée
de fonctionnement sécurisé et la fraction liquide au lieu du
Nombre de Nusselt moyen pour chaque source de chaleur. De tels abaques et
corrélations sont très utiles pour les concepteurs oeuvrant dans
le domaine du contrôle thermique des équipements
électroniques. Ils permettent de déterminer les paramètres
de contrôle correspondant à une durée de fonctionnement
sécurisé donnée.
La présente section expose la méthode
adoptée pour élaborer les corrélations exprimant la
durée adimensionnelle, ôfonc, et la fraction liquide,
f, en fonction des différents paramètres de
contrôle. Cette méthode est basée sur l'approche de
développement asymptotique qui consiste à développer la
solution d'un problème au voisinage d'une solution particulière,
appelée solution de référence. La procédure
détaillée d'une telle méthode est
rapportée par Balaji et Herwig [68]. Il est à
rappeler que les valeurs de référence des variables
indépendantes qui correspondent à la solution de
référence (ôfonc,réf = 0,1013 et
fréf = 0,868) sont données au Tableau 3.3. Les Figures
4.1.a et 4.1.b illustrent les variations respectives de ôfonc
et f en fonction des variables indépendantes
normalisées, ë i = 1,...8 ,
suivantes:
-
~~
Pour la durée, ôfonc:
0.6 i X1.6
(4.1)
0.07
, aR 1 LAÄ
A1 , ',2 A
Ra ref ref
2.8
[
[-1.17
ë3 = á s 0.154
ás , X,4 = Ec '
f
á s,ref Ec,ref
~ ~ ~
0.5 -0.95
E s ) A ) ác
LE s,ref ref A ref á c,ref
-
-
~
~
~
~
L
2.7 1.8
· = Ra Ä
Ra ref 2 Äref
· = [[ á s )-0.151[ ás = Ec
á s,ref á s,ref Ec,ref
2.7 -1.4
Pour la fraction liquide, f:
(4.2)
-
~á ~
c
, ë =
8
~ ~
~á ~
c,ref
0.15
0.5 11.05
= E s
A
ë5 E = [ ref =[Aref
s,ref
Il est clair, de ce qui précède, que les valeurs de
référence des variables susmentionnées sont:
- Pour la durée adimensionnelle, ôfonc
réf = 1, ë2, réf = 1, ë3, réf =
0,846, ë4, réf = 1, (4.3)
ë5, réf = 1, ë6, réf = 1, ë7,
réf = 1, ë8, réf = 1
- Pour la fraction liquide, f
ë1, réf = 1, ë2, réf = 1, ë3,
réf = 0,849, ë4, réf = 1, (4.4)
ë5, réf = 1, ë6, réf = 1, ë7,
réf = 1, ë8, réf = 1
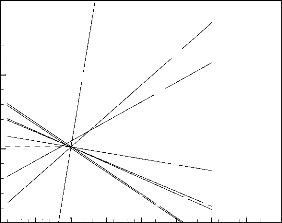
ë1
ë7 ë8 ë4 ë2
ë3
ë5
ë6
0 0.5 1 1.5 2 2.5 3 3.5 4
ë
(a)
ë3
0.8
ë5
ë6
ë4
ë1
ë2
0 0.5 1 1.5 2 2.5 3
ë
0.2
ô fonc
1
f
0.15
ô fonc,ref
0.1
0.05
0.9
fref
0.7
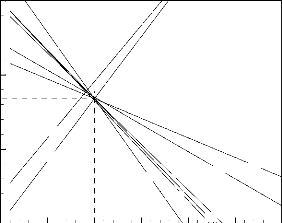
ë7
ë8
(b)
Figure 4.1: Variations de la
durée de fonctionnement sécurisé, ôfonc,
(a) et la fraction liquide,
f, (b) en fonction des variables indépendantes,
ë1, ....., ë8
Il ressort d'une simple analyse des figures
précédentes que la variation de ces deux solutions autour des
solutions de référence est linéaire. Ainsi, le
développement en série de Taylor, autour des solutions de
référence, permet d'écrire ôfonc et
f, comme suit:
ôfonc= ôfonc, réf + ~ (ë i -
ë i, réf) [? ôfonc/ ? ë i] ëi=ëi, réf
(4.5)
i = 1 , 8
f = f réf + ~ (ë
i - ë i, réf) [? f fonc/ ? ë i]
ëi=ëi, réf (4.6)
i = 1 ,8
Les dérivées partielles figurant dans les
expressions (4.5) et (4.6) sont les pentes des courbes linéaires des
Figures 4.1.a et 4.1.b. Par exemple, pour ôfonc, la
dérivée partielle ?ôfonc / ? ëi| ëi=ëi,
réf, est la pente de la courbe représentant la variation de
ôfonc en fonction de ëi, les autres variables
indépendantes, ë j(j ? i), étant constantes et égales
à leurs valeurs de référence. Cette pente est
déduite directement de la corrélation (3.1),
développée au chapitre précédent. Le même
raisonnement s'applique pour le calcul des autres dérivées
partielles. Ainsi, après substitutions des valeurs des
différentes dérivées partielles, les corrélations
suivantes on été déduites:
ôfonc = 0,1013 + 0,288 (ë1 - 1) - 0,02 (ë2 - 1) +
0,02645 (ë3 - 0,846) - 0,02113 (ë4 - 1)
+ 0,042 (ë5 - 1) - 0,008 (ë6 - 1) - 0,0311 (ë7 -
1) + 0,03202 (ë8 - 1) (4.7)
f = 0,868 - 0,135 (ë1 - 1) - 0,1314 (ë2 - 1) +
0,152 (ë3 - 0,849) - 0,1231 (ë4 - 1)
+ 0,168 (ë5 - 1) - 0,0528 (ë6 - 1) - 0,1787 (ë7 -
1) + 0,0732 (ë8 - 1) (4.8)
Les courbes de parité (Figure 4.2) relatives à
ôfonc et f montrent que les résultats de
simulation se comparent de manière satisfaisante à ceux obtenus
par les corrélations (4.7) et (4.8). L'écart maximal est de
l'ordre de 8 %.
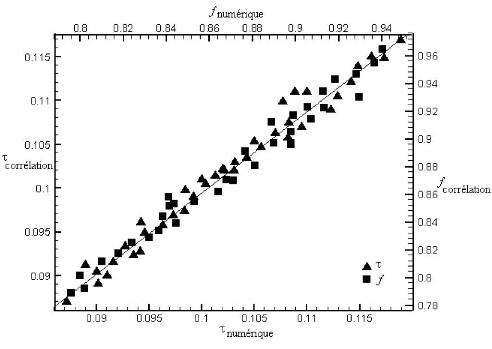
Figure 4.2: Courbes de parité pour
ôfonc et f.
4.2 Elaboration des abaques
Pour faciliter l'exploitation des corrélations (4.7) et
(4.8), deux abaques, Abaque I et Abaque II, ont été
élaborés. Pour une valeur de la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , on choisi le
contour correspondant: c'est l'iso- durée sur l'Abaque I. Les
valeurs des huit paramètres de contrôle du puits
de chaleur (A, Es, Ec, A , ,
as , Ra, ~c ) sont
aussi déterminées, en faisant une projection orthogonale sur
chaque coté de l'octogone. Connaissant les valeurs des huit
paramètres de contrôle, la fraction liquide, f , est
ainsi déduite de l'Abaque II.
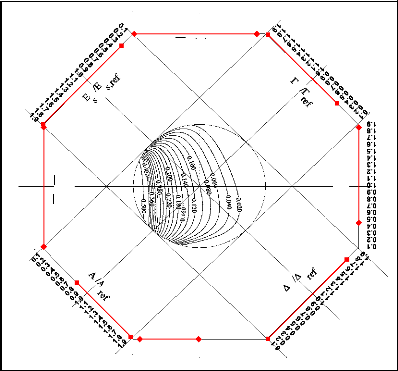
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3
1.4 1.5 1.6 1.7 1.8 1.9
ac /ac,ref
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3
1.4 1.5 1.6 1.7 1.8 1.9
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3
1.4 1.5 1.6 1.7 1.8 1.9
Ra /Ra
á /á
s s,ref
ref
c c, ref
E /E
Abaque I: Durée adimensionnelle de
fonctionnement sécurisé, ôfonc
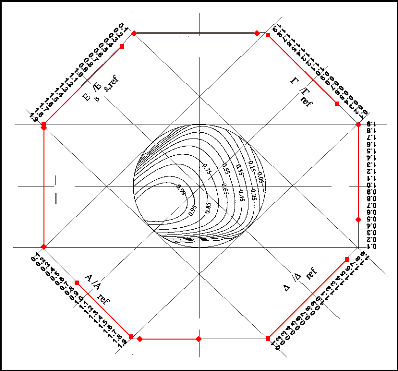
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3
1.4 1.5 1.6 1.7 1.8 1.9
ac /ac,ref
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3
1.4 1.5 1.6 1.7 1.8 1.9
Ra /Ra
ref
E c /E c, ref
Abaque II: Fraction liquide, f
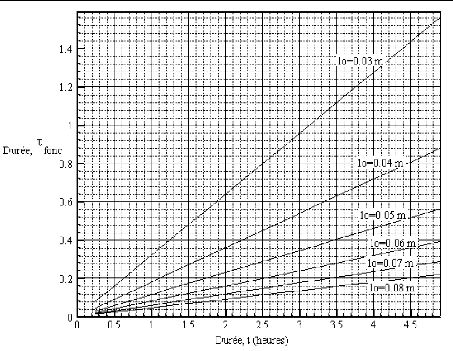
Abaque III: Durée adimensionnelle de
fonctionnement sécurisé en fonction de la durée
dimensionnelle de fonctionnement sécurisé pour différentes
valeurs de lo.
4.3 Exemple d'application
L'objectif est de faire fonctionner un puits de chaleur durant
une période, t =90 minutes, durant laquelle la température
maximale des trois composants électroniques doit être
inférieure à la valeur critique, Tcr, La puissance
générée par unité de longueur par chacune des
sources de chaleur est, Q'= 58,5 W/m. Quelles sont les valeurs des
paramètres de contrôle permettant de réaliser un tel
objectif ?
Un abaque supplémentaire a été
élaboré pour éviter les calcules intermédiaires, il
s'agit
de l'Abaque III donnant la durée adimensionnelle,
ôfonc , correspondant à la durée
réelle pour
différentes valeurs du paramètre, lo
(représentant la masse du MCP).
Pour lo=0,062 m, cette durée est
ôfonc = 0,105. Ainsi, l' iso- durée sur l'Abaque I, est
celui
correspondant à ôfonc =0,105.
|
En remarquant que
|
Ra Q'
=
|
et que Q' =58,5 W/m, Q 'ref =60 W/m, le rapport
|
|
Ra Q'
ref ref
|
Ra Q'
= = 0,975. Sur l'Abaque I on obtient un point d'intersection
entre la normale sur
Ra Q'
ref ref
le coté de l'octogone
= 0,975, et le contour ôfonc =0,105. A partir de
ce point, les valeurs
Ra
Ra ref
des autres paramètres de contrôle sont
déduites par des projections normales sur les côtés
correspondantes de l'octogone. Ainsi, on obtient les valeurs suivantes, pour
les différents paramètres de contrôle:
0.0161 et Ä f
Äô fonc
ô fonc
0,0023
Ra/ Ra réf = 0,975 Es Es réf
= 1,1
Ä/ Ä réf = 0,62 / réf = 1,4
á s / á s, réf = 0,48 A/ A
réf =1,5
Ec/ Ec, réf =0,65 á c / á c,
réf =1,35
La fraction liquide, f, est déduite
directement de l'Abaque II, de même échelle que l'abaque I. Les
huit valeurs des paramètres de contrôle, déterminées
sur l'Abaque I, doivent être positionnées sur les cotés
correspondants de l'Abaque II. Le point d'intersection des droites verticales
issues des cotés de l'octogone de l'Abaque II et passant par les valeurs
des paramètres de contrôle, donne, f = 0,85.
La vérification par les expressions (4.7) et (4.8) a
donné:
ôfonc = 0,106723 et f = 0,852
Abaques: ô fonc = 0,105 et f = 0,85
CONCLUSION GENERALE
Au terme de ce travail, la présente section
récapitule les principaux résultats obtenus dans cette
étude. Les perspectives immédiates qu'ouvre la présente
étude sont aussi évoquées.
Dans ce mémoire, une étude numérique
relative aux transferts thermiques, se manifestant lors de la fusion d'un
matériau à changement de phase dans une enceinte chauffée
par des sources de chaleur protubérantes, est présentée.
Un modèle mathématique, basé sur les équations de
conservation de la masse, de l'énergie et de la quantité de
mouvement, a été développé pour le puits de chaleur
proposé. Ensuite, ce modèle, traduit en un code numérique
basé sur la méthode des volumes de contrôle, a
été développé puis confronté aux
résultats expérimentaux disponibles dans la littérature.
Plusieurs investigations numériques ont été
effectuées pour analyser les comportements thermique et hydrodynamique
du système de refroidissement proposé. Les principaux
résultats dégagés, de cette étude, peuvent
être récapitulés comme suit:
- L'analyse des variations temporelles des températures
moyennes des sources de chaleur, relatives à la configuration de base,
montre que l'évolution de la température moyenne de chaque source
passe par trois phases principales. Durant la première phase, le
transfert de chaleur dans la couche du MCP liquide, formée proche des
parois chaudes, est dominé par la conduction. Durant la deuxième
phase, le transfert de chaleur par convection prévaut, et la
température moyenne des sources de chaleur demeure constante : il s'agit
du régime quasistationnaire. Quant à la dernière phase
(lorsque le processus de fusion s'approche à sa fin), elle est
marquée par une augmentation brusque des températures moyennes
des sources de chaleur.
- La durée de fusion est d'autant plus courte que le
nombre de Rayleigh est élevé ;
- L'accroissement du nombre de Rayleigh entraîne une
surchauffe rapide des sources de chaleur ;
- Aux valeurs élevées du nombre de Ra,
correspond une stratification rapide du champ thermique dans la partie
supérieure de la cavité, tandis que pour le cas des sources de
chaleur à faible puissance, les isothermes sont nettement
inclinés ;
- Pour la plage considérée du nombre de Rayleigh,
plus de 41 % de la puissance générée par
les sources de chaleur est transférée à la
plaque conductrice et convectée, ensuite, au MCP liquide ;
- Environ, 55 % de la puissance générée par
les sources de chaleur est transférée au MCP à travers
leurs surfaces, exposées à l'écoulement ;
-Durant le régime quasi permanent, la fusion du MCP
absorbe plus de 97 % de la puissance générée par les
sources de chaleur ;
- Les trois sources de chaleur sont bien refroidies quand
elles sont positionnées en bas de la cavité. Lorsque elles sont
déplacées vers le haut de la cavité, la source de chaleur
supérieure est rapidement surchauffée et sa température
adimensionnelle atteint la valeur critique.
- Les profils de température verticaux
présentent des maximums locaux localisés prés des sources
de chaleur ;
- La position et la forme du front de fusion et la structure
des isothermes dépendent étroitement de la position des sources
de chaleur ;
- Pour le cas des sources de chaleur situées dans la
partie supérieure de la cavité, un bloc de MCP solide reste dans
la partie inférieure de la cavité. Ce puits de chaleur refroidi
inutilement la portion de la plaque située en dessous de la source de
chaleur inférieure ;
- Lorsque les sources de chaleur sont placées en bas de
la cavité, un bloc de MCP solide se détache et se localise devant
la source de chaleur située en haut de la cavité. Ce bloc de MCP
joue le rôle d'un puits de chaleur pour la source de chaleur
supérieure ;
- Plus la diffusivité thermique du substrat est
élevée, plus la montée de la température moyenne
adimensionnelle des sources de chaleur est lente ;
- Existence d'une valeur optimale de la diffusivité
thermique du substrat correspondant à un meilleur refroidissement des
sources de chaleur, durant le régime quasi-stationnaire ;
- L'accroissement de la diffusivité thermique du
substrat réduit la température maximale adimensionnelle et
favorise l'isothermie de la plaque conductrice ;
- Apparition de gradients thermiques élevés au
sein de la plaque conductrice, au niveau des jonctions des sources de chaleur,
pour les faibles valeurs de la diffusivité thermique du substrat. Ces
gradients thermiques élevés risquent d'engendrer une
déformation de la plaque conductrice (fissuration de la carte
mère de l'ordinateur) ;
- Pour les faibles épaisseurs des sources de chaleur,
la fin du processus de fusion est marquée par la présence d'un
seul bloc de MCP solide dans la zone inférieure droite de la
cavité, alors que pour les épaisseurs élevées, un
bloc de MCP solide se détache et se localise dans la zone
supérieure du coté droit de la cavité.
- La température maximale adimensionnelle est
localisée sur la source de chaleur supérieure
pour les épaisseurs des sources de chaleur faibles ;
alors que pour les épaisseurs élevées elle est
enregistrée par la source de chaleur centrale. Sa valeur est d'autant
élevée que l'épaisseur des sources de chaleur est
élevée ;
- La température maximale adimensionnelle la plus
élevée et la durée adimensionnelle de fonctionnement
sécurisé la plus courte sont obtenues pour le cas d'une plaque
conductrice de faible épaisseur ;
- L'accroissement de l'épaisseur adimensionnelle de la
plaque conductrice provoque un allongement de la durée de fonctionnement
sécurisé ;
- L'augmentation de l'épaisseur adimensionnelle de la
plaque conductrice entraîne une réduction de la différence
de température adimensionnelle au sein de la plaque ;
- L'accroissement de l'épaisseur adimensionnelle de la
plaque conductrice entraîne une diminution de la température
maximale adimensionnelle et les flux de chaleur évacués par les
faces des sources de chaleur ;
- Durant la première phase, dominée par la
conduction thermique, la montée en température est d'autant plus
rapide que l'espacement des sources de chaleur est élevé ;
- La durée du régime quasi- stationnaire est
d'autant plus élevée que l'espacement des sources de chaleur est
faible ;
- L'accroissement de l'espacement des sources de chaleur
provoque une augmentation de la température adimensionnelle des sources
;
- Pour les faibles valeurs du rapport de forme le champ
thermique se stratifie rapidement dans la partie supérieure de la
cavité alors que pour le cas des cavités élancées,
de grand rapport de forme, les isothermes sont nettement inclinés. Pour
le cas des cavités ayant un rapport de forme élevé, les
sources de chaleur sont mieux refroidies et la température maximale
adimensionnelle, enregistrée par les sources de chaleur, est d'autant
plus élevée que le rapport de forme est faible ;
- Pour les rapports de forme élevés, un bloc de
MCP solide se détache et se positionne dans la partie supérieure
de la cavité. Cette position fait de lui un puits de chaleur pour la
source de chaleur supérieure.
-Pour les faibles valeurs du rapport de forme, le MCP contenu
dans la partie supérieure fond complètement, et la source de
chaleur supérieure surchauffe rapidement ;
- Les durées du régime quasi stationnaire et du
fonctionnement sécurisé s'allongent lorsque le rapport de forme
augmente ;
- L'effet du rapport de forme sur la fraction liquide ne se
fait ressentir qu'après le régime de
fonctionnement
quasi-stationnaire. La fraction liquide subit une variation d'autant plus
rapide
que le rapport de forme est élevé.
- Les cavités ayant un rapport de forme
élevé n'assurent pas seulement une durée de fonctionnement
sécurisé allongée mais aussi une fusion pratiquement
complète du MCP. En conséquence, ces cavités constituent
une bonne solution pour le refroidissement des composants
électroniques.
- En régime quasi-stationnaire, la température
maximale adimensionnelle des sources de chaleur la plus basse est
enregistrée pour le cas des sources de chaleur ayant une
diffusivité thermique élevée ;
- Durant la première phase et la dernière phase
du processus de fusion, l'accroissement de la diffusivité thermique des
sources de chaleur entraîne une baisse de la température des
sources de chaleur et de la plaque conductrice.
Également, des corrélations exprimant la
durée adimensionnelle de fonctionnement sécurisé et la
fraction liquide en fonction des différents paramètres de
contrôle, ont été élaborées moyennant la
technique d'expansion dynamique asymptotique appliquée à la
mécanique des fluides ACFD. Ces corrélations
sont transformées en abaques d'un intérêt pratique pour les
ingénieurs impliqués dans le domaine de contrôle thermique
des composants électroniques.
En perspectives, on compte étendre cette étude
à d'autres configurations géométriques de puits de chaleur
récemment utilisées dans les équipements
électroniques et soumises à des conditions thermiques variables
dans le temps. Cette stratégie de refroidissement à base de MCP
peut, aussi, trouver des applications dans les équipements
aérospatiaux où le champ de gravité est
réglé par d'autres lois (g variable). Les transferts de chaleur
et de la quantité de mouvement dans l'enceinte du MCP seront, dans ce
cas, régis par d'autre lois, plus compliquées.
RÉFÉRENCES BIBLIOGRAPHIQUES
[1] Jason McKenzie Leland. Numerical optimization of a phase
change heat sink. MSME Thesis, Portland State University, (2002).
[2] M. Dreyer, New Thermal Cooling Addresses the Shrinking
Electronics Issue, Equipments Protection Magazine, (4), 12-15, (2006).
[3] R. R. Tummala, Fundamentals of Micro Systems Packaging,
McGraw Hill, (2001).
[4] S. C. Lin and C. L. Huang, The study of a small centrifugal
fan for notebook computer. Journal of the Chinese Society of Mechanical
Engineers, 22 (5), 421-431, (2001).
[5] F. P. Incropera, Liquid cooling of electronics devices by
single phase convection, Wiley series in Thermal Management of Microelectronics
and Electronics Systems, Wiley Inter Science Publications, (1999).
[6] J. Davalath,Y. Bayazitoglu, Forced convection cooling across
rectangular blocks, ASME J. Heat transfer (109), 321-328, (1987)
[7] B. W. Webb,S. Ramadhyani, Conjugate heat transfer in a
channel with staggered ribs, Int. J. Heat and Mass Transfer, (28),1679-1687,
(1985).
[8] H.W. Wu, S.W. Perng, Turbulent Flow and Heat Transfer
Enhancement of Mixed Convection over Heated Blocks in a Channel, International
Journal for Numerical Methods in Heat and Fluid Flow, 15 (2), 205 - 225,
(2005).
[9] T.J. Young, K. Vafai, Convective cooling of heated obstacle
in a channel, International Journal of Heat and Mass Transfer, 3131 - 3148,
(1998).
[10] Y.L. Tsay, J.C. Cheng, Analysis of Convective Heat
Transfer Characteristics for a Channel Containing Short Multi-Boards Mounted
with Heat Generating Blocks, International Journal of Heat and Mass Transfer,
2511- 2524, (2007).
[11] M. Najam, A. Amahmid, M. Hasnaoui et M. El Alami,
Unsteady mixed convection in a horizontal channel with rectangular blocks
periodically distributed on its lower wall, International Journal of Heat and
fluid Flow, (24), 726-735, (2003).
[12] C.K. Lee and S.A. Abdel-Moneim, Computational Analysis
of Heat Transfer in Turbulent Flow Past a Horizontal Surface with
Two-Dimensional Ribs, International Comm. Heat and Mass Transfer, 28(2),
161-170, (2001).
[13] D.D. Luo, C.W. Leung, T.L. Chan and W.O. Wong,
Simulation of Turbulent Flow And Forced Convection in a Triangular Duct with
Internal Ribbed Surfaces, Numerical Heat Transfer, Part A, (48), 447 - 459,
(2005).
[14] R.N. Mathews, C. Balaji, Numerical Simulation of
Conjugate, Turbulent Mixed Convection Heat Transfer in Vertical Channel with
Discrete Heat Sources, International Comm. Heat and Mass Transfer, (33), 908 -
916, (2006).
[15] C. Perret, I. Fandino, C.Schaeffer, J.Boussey,
S.Räe, Conception et optimisation d'un micro refroidisseur en cuivre pour
composants électroniques, European Journal of Electrical Engineering,
4(34), 255-272, (2001).
[16] Y. Harnane et R. Bessaih, Etude numérique de
l'écoulement de la convection mixte turbulente dans un canal vertical
muni de blocs chauffés - Revue des Energies Renouvelables CISM'08 Oum El
Bouaghi, 165 - 174, (2008).
[17] J. Vareilles, C. Muresan, S. G-Julien, C. Menezo, Etude
numérique des transferts de chaleur et de masse en convection naturelle
dans un canal vertical soumis a des perturbations thermiques
périodiquement reparties sur ses parois, 12ème
Journées Internationales de Thermique,Albi, France (2007).
[18] M. El Alami, M.Najam, E. Semma, A. Oubarra, F. Penot,
Electronic components cooling by natural convection in horizontal channel with
slots, Energy Conversion and Management, (4), 2762-2772, (2005).
[19] F. Corvaro et M. Paroncini, The Natural Convective Heat
Transfer in a Partially Divided Enclosure: A Study on the Influence of the
Source Position, Journal of Thermodynamics, Article ID: 792370,10 pages,
doi:10.1155/2009/792370, (2009).
[20] S. Sivasankaran, Buoyant convection in a cavity with
discrete heat sources and internal heat generating, International Journal of
Applied Mathematics and Mechanics, 2(2), 63-74, (2006).
[21] G. Desrayaud, A. Fichera, G. Lauriat, Natural convection
air cooling of a substrate mounted protruding heat sources in a stack of
parallel boards, International Journal of Heat and Fluid Flow,(28) 469-482,
(2007).
[22] G. Desrayaud and A. Fichera, Laminar natural convection
in a vertical isothermal channel with symmetric surface-mounted rectangular
ribs, Int. J. Heat and Fluid Flow, (23), 519-529, (2002).
[23] K. M. Kelkar and D. Choudhury, Numerical prediction of
periodically fully developed natural convection in a vertical channel with
surface mounted heat generating blocks, Int. J. Heat and Mass Transfer, (36),
1133-1145, (1993).
[24] J. H. Bae, J. M. Hyun, Time-dependent buoyant convection in
an enclosure with discrete heat sources, International Journal of Thermal
Sciences, (43), 3-11, (2004).
[25] M. D. Kelleher, R. H. Hnock, K. T. Yang, Laminar natural
convection in a rectangular enclosure due to a heated protrusion on one
vertical wall, Part 1: Experimental investigation. Proceeding of the ASME/JSME
Thermal Engineering Joint Conf, (2), 169-177, (1987).
[26] B. L. Turner, R. D. Flack, The experimental measurement
of Natural Convection heat transfer in a rectangular enclosure with
concentrated energy sources, ASME J. Heat transfer, (102), 236-241, (1980).
[27] M. Keyhani, L. Chen and D. R. Pitts, The aspect ratio
effect on natural convection in an
enclosure with discrete heat sources, ASME J. Heat Transfer,
(113),883-891, (1991).
[28] Y. L. Ju and Z. Q. Chen, Numerical simulation of natural
convection in an enclosure with discrete protruding heaters, Numerical Heat
Transfer, 30(2), 207-218, (1996).
[29] A. Bar-Cohen, Thermal Management of Electronics- Energy
Conversion Issues Refrigeration Technologies for Microelectronics, Rohsenow
Symposium - MIT, Cambridge, Mass, May 16th -(2003).
[30] Y. Joshi, Heat Out of Small Packages, Journal of Mechanical
Engineering, (123), 56-58, (2001).
[31] V. Shanmugasundaram, J. R. Brown, K. L. Yerkes, Thermal
management of high heat flux sources using phase change material, a design
optimization, AIAA -2451-2460, (1997).
[32] D. Pal, Y. K. Joshi, Melting in a side heated tall
enclosure by a uniformly dissipating heat sources, International Journal of
Heat and Mass Transfer (44), 375-387, (2001).
[33] M. Faraji, H. El Qarnia, Numerical Optimization of a
Thermal Performance of a Phase Change Material based Heat Sink, International
Journal of Heat and Technology, 26 (2), 17- 24, (2008).
[34] Y. Zhang, Z. Chen, Q. Wang, Q. Wu, Analysis of melting in
an enclosure with discrete heating at a constant rate, Int. J. heat Fluid Flow,
(15),79-82, (1994).
[35] Y. Zhang, A. Bejan, The problem of time-dependent natural
convection melting with conduction in the solid, Int. J. Heat Mass Transfer,
32(12), 2447-2457, (1989).
[36] Y.Zhang, Z. Q. Chen, Analysis of melting in an enclosure
with discrete heating at constant temperature, Proceedings of the Tenth
International Heat Transfer Conference, Brighton, UK, (1994).
[37] B. Binet, M. Lacroix, Melting from heat sources flush
mounted on a conducting vertical wall, Int. J. Num. Methods for Heat and Fluid
Flow, 10(3), 286 -307, (2000).
[38] F. L. Tan, C. P.Tso, Cooling of mobile electronic devices
using phase change materials,
Applied Thermal Engineering, (24), 159-169, (2004).
[39] X. Q. Wang, Ch. Yap, A. S. Mujumdar A parametric study of
phase change material (PCM)-based heat sinks, International Journal of Thermal
Sciences (47), 1055-1068, (2008).
[40] N. Zheng, R. Wirtz, Methodology for designing hybrid
thermal energy storage, Part I: Design methodology, ASME Journal of Electronic
Packaging, (126), 1-7, (2004).
[41] R. Kandasamy, X. -Q. Wang, A. S. Mujumdar, Application of
phase change materials in thermal management of electronics, Applied Thermal
Engineering 34 (7) 801-808, (2007).
[42] Z. Jianhua, C; Zhongqi, L. Dengying, L. Ji, Experimental
study on melting in a rectangular enclosure heated below with discrete heat
sources, Int. J. Thermal Science, (10), 254-259, (2001).
[43] Y. Ju, Z.Chen, Y. Zhou, Experimental Study of melting
heat transfer in an enclosure with three discrete protruding heat sources,
Experimental Heat Transfer (11), 171-186, (1998).
[44] M. Hodes, R. D. Weinstein, S. J. Pence, J. M. Piccini,
L. Manzione, and C. Chen, Transient thermal management of a handset using phase
change material (PCM). ASME Journal of Electronic Packaging, (124), 419-426,
(2002).
[45] R. Akhilesh, A.Narasimhan, C.Balaji, Method to improve
geometry for heat transfer enhancement in PCM composite heat sinks,
International Journal of Heat and Mass Transfer, 48 (13), 2759-2770, (2005).
[46] A. Abhat, Experimental investigation and analysis of a
honeycomb packed phase change material device, AIAA. 426-437, (1976).
[47] E. M Alawadhi, C. H. Amon, PCM thermal control unit for
portable electronic devices: experimental and numerical studies. IEEE
Transactions on Components and Packaging Technology, (26) 116-25, (2003).
[48] J. O'Conner, R. Weber, Thermal management of electronic
packages using solid-toliquid phase change techniques, International Journal of
Microcircuits and Electronic Packaging (20) 593-601, (1997).
[49] H. Yin, X. Gao, J. Ding, Z. Zhang, Experimental research
on heat transfer mechanism of heat sink with composite phase change materials,
Energy Conversion and Management (49) 1740-1746, (2008).
[50] K. C. Nayak, S. K. Saha, K. Srinivasan, P. Dutta, A
numerical model for heat sinks with phase change materials and thermal
conductivity enhancers, International Journal of Heat and Mass Transfer (49)
1833-1844, (2006).
[51] R. Viswanath, et J Y. Jaluria, A comparison of different
solution methodologies for melting and solidification problems in enclosures,
Numerical Heat Transfer Part B, (24), 77- 105, (1993).
[52] V. R, Voller, M. Cross, N. C. Markatos, An enthalpy method
for convection/diffusion phase change, Int. J. for Num. Meth. Engng, (24),
271-284, (1987).
[53] V. R. Voller, C. Prakash, A fixed grid numerical
modeling methodology for convection diffusion mushy region phase-change
problems, Int. J. Heat Mass Transfer, 30(8), 1709-1719, (1987).
[54] V. R. Voller, An overview of numerical methods for
solving phase change problems, Advances in Numerical Heat Transfer, vol. 1, W.
J. Minkowycz et E. M. Sparrow, Taylor & Francis, (1997).
[55] O. Bertrand, B. Binet, H. Combeau, S. Couturier, Y.
Delannoy, D. Gobin, M. Lacroix, P. Le Quéré, M. Médale, J.
Mencinger, H. Sadat, G. Vieira, Melting driven by natural convection. A
comparison exercise: First results, Int. J. Thermal Sciences, (38), 5-26,
(1999).
[56] S. V.Patankar, «Numerical Heat Transfer and Fluid
Flow», Hemisphere, washington, D. C., (1980).
[57] A Amahmid, Contribution à l'étude
numérique de convection mixte dans deux cavités contigués
semi ouvertes: Application au cellule -patio. Thèse de DES, Physique,
Faculté des Sciences Semlalia, Marrakech, Maroc, (1993).
[58] C. Gau, R. Viskanta, Melting and solidification of a metal
system in a rectangular cavity, Int. J. Heat Mass Transfer,(27), 113-123,
(1984).
[59] T. E. Daubert, R. P. Danner, Physical and thermodynamic
properties of pure chemicals, data compilation, Hemisphere, (1989).
[60] E. Dorre, H.Hubner, Alumina- Processing, properties and
applications, Berlin, Springer- Velarj, (1984).
[61] W.R. Humphries, E.I.Griggs, A Design Handbook for Phase
Change Thermal Control and Energy Storage Devices, NASA Technical Paper 1074,
NASA Scientific and Technical Information Office, (1977).
[62] D. Gobin, Changement d'état solide- liquide:
Évolution temporelle du couplage entre la convection naturelle dans la
phase liquide et la conduction dans la phase solide. Étude
numérique et expérimentale, Thèse de Doctorat
d'état, Université Paris VI, (1984).
[63] S. Hirman, A.Suwono, G. A. Mansoori, Characterization of
alkenes and paraffin waxes for application as phase change energy storage
medium, Energy Sources, (16), 17-128, (1994).
[64] Alloy Digest, Engineering Alloy Digest Inc., Upper
Montclair, NJ, (2004).
[65] S. Krishnan, S. V.Garimella, S. S.Kang, A novel hybrid
heat sink using phase change materials for transient thermal management of
electronics, IEEE Transactions on Components Packaging and Manufacturing
Technology, 28 (2), 281-289, (2005).
[66] Michel Pons, Transition from Single-to Multi-Cell
Natural Convection of Air in Cavities with an Aspect Ratio of 20: A
Thermodynamic Approach, International Journal of Thermodynamics, 11 (2), 71-79,
(2008).
[67 ] Y. Jaluria, E. Papanolaou, «Mixed convection from a
localized heat source in a cavity with conducting walls: A numerical
study» Numerical Heat transfer Part A, vol. 23, pp. 463- 484, (1993)
[68] C. Balaji, H, Herwig, The use of ACFD approach in
problems involving surface radiation and free convection. International
Communication Heat Mass Transfer, (30), 251- 259, (2003).
|
|



