CHAPITRE
IV
RESULTAS ET
VALIDATIONS
SOMMAIRE PAGE
IV.1. Introduction 59
IV.2. Les Conditions aux limites 59
IV.3. Première simulation 59
IV.4. Deuxième simulation 64
IV.5. Contours de coefficient de pression 72
IV.6. Troisième simulation 75
IV.7. Forces de chaque angle d'incidence 82
IV.8.Calcule des coefficients pour chaque á
82
IV.9. Conclusion 84
IV.1.Introduction
Dans cette section, nous allons présenter les
résultats obtenus avec le code Fluent utilisé dans le cadre de ce
travail, ainsi une vue d'ensemble du procédé de la
vérification et de la validation des simulations. Le traitement consiste
donc à visualiser les résultats. On utilise pour cela les
logiciels de visualisation TECPLOT, ORIGIN et GRAFWIN. L'utilisation de ces
logiciels est a raison plus simple qu'ils permettent de visualiser/tracer des
résultats directement à partir d'un fichier.
La visualisation peut être sous forme des
contours (Mach, Pression) ou sous forme des graphes (Cl, Cd, Cm, Cp...) afin de
les tracer avec des données expérimentales dans le même
plan pour facilité l'interprétation et voir clairement la
différence.
IV.2.Les Conditions aux limites
Cette phase est la plus importante, par ce qu'on doit
savoir le type de condition qui convient à chaque zone. Il existe
plusieurs types de conditions aux limites dans fluent, dans notre travail on
fait la simulation pour un écoulement compressible on utilise dans ce
cas les conditions suivantes : voir tableau (IV.1)
Tableau (IV.1) : Définition des conditions aux
limites
|
Nom
|
Type
|
|
ff/s_entre
|
Pressure-far-field
|
|
ff/s_far
|
Pressure-far-field
|
|
ff/s_sort
|
Pressure-far-field
|
|
avion/s_body
|
Wall
|
|
avion/s_extra
|
Wall
|
|
avion/s_intra
|
Wall
|
|
avion/s_tip
|
Wall
|
|
int_fluid
|
Interior
|
|
symetry/s_sym
|
Symmetry
|
IV.3.Première simulation
IV.3.1. Calcule non visqueux
IV.3.1.1. Configuration d'écoulement
Lors de cette première simulation nous
considérons : Angle d'attaque : 2.873 degrés.
Nombre de mach : 0.8027.
Nombre de Reynolds : 13.1 E+06.
IV.3.1.2. L'histoire de convergence des
résidus
La figure ci-dessous montre l'histoire de convergence
exprimée en termes de résidus.
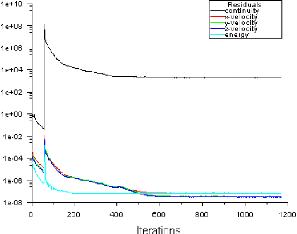
Figure (IV.1) : Historique des résidus
IV.3.1.3. L'histoire de convergence des coefficients
Cd, Cl et Cm
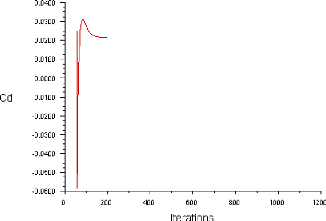
Figure (IV.2) : Historique des Coefficient de
trainée (ORIGIN)
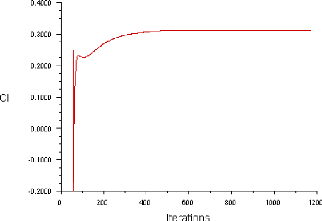
Figure (IV.3) : Historique des Coefficient de Portance
(ORIGIN)
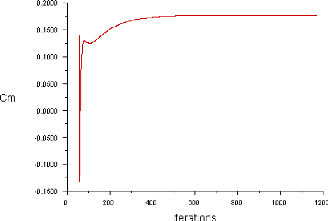
Figure (IV.4) : Historique des Coefficient de Moment
(ORIGIN)
D'après les figures ci-dessus, on peut dire que
la solution a été convergée ; d'une part, parce que le
résidu des variables conservatives a une allure presque constante en
dépassant 600 itérations Figure (IV.1) et d'autre part pour
confirmer la convergence, les Figures (IV.2), (IV.3) et (IV.4) montre l'allure
des coefficients des forces en fonction d'itération dont ces
coefficients prennent des valeurs constantes au dessus de 500
itérations.
| 


