Calcul des performances aérodynamiques de la configuration aile-fuselage Ara M100 par maillage hybride

MÉMOIRE

Présenté à

L'UNIVERSITÉ SAAD DAHLEB

DÉPARTEMENT D'AÉRONAUTIQUE

DE BLIDA

par MOURAD BOUDJERIS

Pour obtenir le grade

d'INGÉNIEUR d'ÉTAT

en AÉRONAUTIQUE

Spécialité : PROPULSION

THÈME

CALCUL DES PERFORMANCES

AÉRODYNAMIQUES DE LA

CONFIGURATION AILE-FUSELAGE ARA

M100 PAR MAILLAGE HYBRIDE

Rapporteur :

M. ALI.T AHI

Soutenu en Septembre 2011

RÉSUMÉ

Le succès des méthodes de résolution numériques, les progrès dans la Conception Assistée par Ordinateur (C.A.O), et le développement des outils de visualisation font que les méthodes de génération de maillage ont connu de nombreux progrès au cours des dernières années pour devenir aujourd'hui un sujet d'étude à part entière. Notre projet porte sur la génération de maillages hybride par ANSYS 13 sur la configuration AileFuselage d'ARA M100 et les solutions correspondantes, ainsi la validation avec l'expérimentale.

ABSTRACT

The success of the numerical methods of resolution, progress in the Computer-aided design (D.A.O), and the development of the tools for visualization make that the methods of generation of mesh knew many progress during the last years to become today a subject of study to whole share. Our project thus carries on the hybrid mesh generation by ANSYS 13 on the configuration ARA M100 Wing-Body and the solutions corresponding, thus the validation with the experimental.

REMERCIEMENTS

Avant tout je remercie ALLAH qui m'a donné la volonté, la foi et le courage pour mener à bien ce travail.

Un remerciement particulier et spécial à mes chers parents qui m'ont aidé et conseillé, sans eux je ne serais jamais arrivée à ce stade.

Le travail présenté dans ce mémoire a été effectué au sein de l'institut d'Aéronautique de Blida sous la direction de monsieur A. TAHI, à qui je présente mes sincères remerciements pour avoir accepté de diriger ce travail.

J'exprime mes remerciements aux membres du jury de nous avoir honoré en acceptant de juger notre travail,

Enfin à tout mes camarades qui m'ont aidé beaucoup durant la réalisation de cette mémoire surtout Mr : Mohammed Taifour Abdelouahab, Belbaki Abderrahman, et à tous ceux qui ont contribués de prés ou de loin.

NOMENCLATURE

a Vitesse du son [m/s]

A Surface [m²]

Cd Coefficient de trainée

Cl Coefficient de portance

Cm Coefficient du moment
Cp Coefficient de pression

ñ Masse volumique de en [kg/m3]

F Forces extérieures [N/kg]

R Constante du gaz [J/kg K]

í La viscosité cinématique en [m2/s]

L La corde en [m]

T La température [°K]

t Temps [s]

g Gravité [m/s²]

U Vitesse du fluide [m/s]

L Longueur caractéristique [m]

P Pression [Pa]

Pt Pression totale [Pa]

Ps Pression de statique [Pa]

ã Forces d'inertie

Re Nombre de Reynolds

á Angle d'incidence [°]

ë Allongement

ä Dièdre d'une voilure

M Nombre de mach

ä* Epaisseur de déplacement de la couche limite [mm]

è Epaisseur de quantité de mouvement [mm]

H Facteur de forme

ã Rapport des chaleurs spécifiques (Cp/Cv)

Y+ Distance adimensionnée de la première maille à la paroi M8 Nombre de Mach à l'infini Nombre de Mach à l'infini

u Composante horizontale de la vitesse [m/s]

v Composante verticale de la vitesse [m/s]

ô ù Cisaillement pariétal

h Hauteur initiale (initial height) [mm]

r Facteur de progression (height ratio)

n Nombre des couches (layer number)

ABRÉVIATIONS

AGARD Advisory Group for Aerospace Research and Development

DNS Direct Numerical Simulation

LES Large Eddy Simulation

SST Shear Stress Tensor

RSM Reynolds Stress Model

CFD Computational Fluid Dynamics

B-REP Boundary Représentation

CAO Conception Assisté par Ordinateur

CSG Constructive Solid Geometry

RNG Reynolds Normalisation Group

LISTE DES FIGURES

Figure (I.1) : Plaque plane mise à l'écoulement. [3] 7

Figure (I.2) : Fumée d'une cigarette. 9

Figure (I.3) : Forme de la couche limite sur une plaque plane 9

Figure (I.4) : Epaisseur de la Couche Limite 9

Figure (I.5) : Décollement de la Couche Limite 11
Figure (I.6) : Ecoulement avec gradient longitudinal de pression positif (D est le point de

décollement de la couche limite). 11

Figure (I.7) : Conceptions simples du décollement. 12

Figure (I.8) : Division de la région proche paroi 18

Figure (I.9) : Modélisation de la couche limite. 19

Figure (II.1) : Méthodologie de résolution d'un problème numérique 23

Figure (II.2) : Exemples de mailles utilisées en Volumes Finis. 24

Figure (II.3) : Composant d'un maillage. 25

Figure (II.4). Exemple de maillage structuré et non structuré autours d'un profil. [14] 26

Figure (II.5) : La distorsion. 27

Figure (II.6) : Déviation angulaire. 28

Figure (II.7) : Maillage couche limite. 29

Figure (II.8) : Indépendance de la solution du maillage. 30

Figure (II.9) : Interface d'ICEM CFD 32

Figure (II.10) : Interface FLUENT 13. 33

Figure (II.11): Exemple de Marcum (1995) faisant passer le nombre de triangle de 11544 au niveau de la couche limite (maillage non-structuré pur, figure à gauche) à

5772 quadrilatères (maillage hybride, figure à droite). 34

Figure (II.12) : Croissances des prismes. 36

Figure (II.13) : Hauteur des prismes. 36

Figure (III.1) : Dimensions d'ARA M100 39

Figure (III.2) : Importation de la géométrie et nettoyage de la CAO 40

Figure (III.3) : Création des familles 41

Figure (III.4) : Création d'un point matériel 42

Figure (III.5) : Affichage de maillage (Tecplot) 43

Figure (III.6) : Paramètres de la hauteur des prismes 44

Figure (III.7) : Génération de maillage prismatique (Tecplot) 46

Figure (III.8) : Importation du maillage 48

Figure (III.9) : Vérification du maillage sou Fluent 48

Figure (III.10) : Lissage du maillage 49

Figure (III.11) : Vérification des unités 49

Figure (III.12) : Choix du modèle de turbulence 50

Figure (III.13) : Définition des caractéristiques du fluide 52

Figure (III.14) : Choix de la pression de référence 52

Figure (III.15) : Pressure-far-field pour tout le domaine 53

Figure (III.16) : Wall 54

Figure (III.17) : Symétrie 54

Figure (III.18) : Choix et affichage pendant les calculs des critères de convergence (residuals) 55
Figure (III.19) : Choix et affichage pendant les calculs des critères de convergence

(Drag & Lift) 55

Figure (III.20) : Initialisation des calculs 56

Figure (III.22) : Lancement de la simulation 57

Figure (III.21) : Création d'animation 58

Figure (IV.1) : Historique des résidus 60

Figure (IV.2) : Historique des Coefficient de trainée (ORIGIN) 60

Figure (IV.3) : Historique des Coefficient de Portance (ORIGIN 61

Figure (IV.4) : Historique des Coefficient de Moment (ORIGIN) 61

Figure (IV.5) : Répartition de la pression statique sur ARA M100 extrados (Tecplot) 62

Figure (IV.6) : Répartition de la pression statique sur M100 intrados (Tecplot) 62

Figure (IV.7) : Répartition du nombre de mach sur ARA M100 extrados (Tecplot) 63

Figure (IV.8) : Répartition du nombre de mach sur ARA M100 intrados (Tecplot) 63

Figure (IV.9) : Historique des résidus 64

Figure (IV.10) : Historique des Coefficient de trainée (ORIGIN) 64

Figure (IV.11) : Historique des Coefficient de Portance (ORIGIN) 65

Figure (IV.12) : Historique des Coefficient de Moment (ORIGIN) 65

Figure (IV.13) : Maillage de l'avion ARA M100 (Tecplot) 66

Figure (IV.14) : Variation d'Y⁺ plus sur chaque station de l'aile (GRFWIN) 66

Figure (IV.15) : Répartition de la pression statique sur ARA M100 extrados (Tecplot) 67

Figure (IV.16) : Répartition de la pression statique sur ARA M100 intrados(Tecplot) 67

Figure (IV.17) : Contours de pression sur le profil d'aile 68

Figure (IV.18) : Contours de Mach sur l'avion 68

Figure (IV.19) : Contours de Mach sur le profil d'aile 69

Figure (IV.20) : Vecteurs vitesse sur l'avion au plan de symétrie 70

Figure (IV.21) : Vecteurs vitesse sur le profil d'aile 71

Figure (IV.22) : Stations de mesure de Cp sur l'aile d'ARA M100 (Tecplot) 73

Figure (IV.23) : Distribution du coefficient de pression calculé et expérimental sur l'intrados et l'extrados pour la station 0.019 (GRAFWIN) 73
Figure (IV.24) : Distribution du coefficient de pression calculé et expérimental sur

l'intrados et l'extrados pour la station 0.325 (GRAFWIN) 74
Figure (IV.25) : Distribution du coefficient de pression calculé et expérimental sur

l'intrados et l'extrados pour la station 0.635 (GRAFWIN) 74
Figure (IV.26) : Distribution du coefficient de pression calculé et expérimental sur

l'intrados et l'extrados pour la station 0.936 (GRAFWIN) 75

Figure (IV.27) : Contours de pression pour á=-3.017⁰ (Tecplot) 76

Figure (IV.28) : Contours de pression pour á=-2.873⁰ (Tecplot) 76

Figure (IV.29) : Contours de pression pour á=0⁰ (Tecplot) 76

Figure (IV.30) : Contours de pression pour á=3.017⁰ (Tecplot) 77

Figure (IV.31) : Contours de pression sur le profil à á=3.017⁰, -2.8730, 0⁰ et 3.017⁰

(Tecplot) 77

Figure (IV.32) : Contours de Mach pour á=-3.017⁰ (Tecplot) 78

Figure (IV.33) : Contours de Mach pour á = -2.873⁰ (Tecplot) 78

Figure (IV.34) : Contours de Mach pour á=0⁰ (Tecplot) 78

Figure (IV.35) : Contours de Mach pour á=3.017⁰ (Tecplot) 79

Figure (IV.36) : Contours de Mach sur le profil à á=3.017⁰, -2.8730, 0⁰ et 3.017⁰ (Tecplot)

79

Figure (IV.37) : distribution de Cp dans la station 0.019 (GRAFWIN) 80

Figure (IV.38) : distribution de Cp dans la station 0.325 (GRAFWIN) 80

Figure (IV.39) : distribution de Cp dans la station 0.635 (GRAFWIN) 81

Figure (IV.40) : distribution de Cp dans la station 0.936 (GRAFWIN) 81

Figure (IV.41) : Variation de Cl en fonction de Alpha (ORIGIN) 83

Figure (IV.42) : Variation de Cd en fonction de Alpha (ORIGIN) 83

Figure (IV.43) : Variation de Cl en fonction de Cd (ORIGIN) 84

LISTE DES TABLEAUX

Tableau (II.1) : La variation de la qualité de maillage 28

Tableau (III.1) : Paramètres de maillage tétraédrique 42

Tableau (III.2) : Valeurs des hauteurs 44

Tableau (III.3) : Paramètres de maillage prismatique 45

Tableau (III.4) : Modèles de turbulence [20] 51

Tableau (IV.1) : Définition des conditions aux limites 59

Tableau (IV.2) : Forces de pression 82

Tableau (IV.3) : Forces de viscosité 82

Tableau (IV.4) : Valeurs de Cl et Cd pour chaque á 82

TABLE DES MATIÈRES

INTRODUCTION 1

CHAPITRE I : PAPPEL DE LA DYNAMIQUE DES FLUIDES

I.1. Introduction 3

I.2. Les équations fondamentales de la dynamique des fluides 3

I.2.1. Principe de conservation de la masse 3

I.2.2. Principe de conservation de la quantité de mouvement 4

I.2.3. Les équations de Navier-Stokes 5

I.3. Les différents types d'écoulements 6

I.3.1. Ecoulements incompressibles et compressibles 6

I.3.2. Ecoulement laminaire et écoulements turbulent 7

I.3.3. Ecoulement stationnaire et instationnaire 7

I.3.4. Ecoulement irrotationnel 8

I.4. Couche Limite 8

I.4.1. Epaisseur de la Couche Limite 9

I.4.1.1. Epaisseur de déplacement ä* 9

I.4.1.2. Epaisseur de quantité de mouvement è 10

I.4.1.3. Facteur de forme H 10

I.4.2. Décollement de la Couche Limite 10

I.4.3. Couche limite turbulente 12

I.5. Turbulence 13

I.5.1. Modélisation de la turbulence 14

I.5.2. Nombre de Reynolds 14

I.5.3. Nombre de Mach" M " 15

I.5.4. Les modèles de turbulence 15

I.5.4.1. Le modèle Spalart-Allmaras 15

I.5.4.2. Le modèle k-å 16

I.5.4.3. Le modèle k-ù standard et le modèle k- ù -SST 16

I.5.4.4. Modèle à contrainte de Reynolds RSM (Reynolds Stress Model) 16

I.5.4.5. Large Eddy Simulation (LES) 17

I.5.4.6. Simulation directe (DNS) ou Direct Numerical Simulation 17

I.5.5. Calcul en proche paroi 17

I.5.5.1. Modélisation de l'écoulement en proche paroi 18

I.6. Les conditions aux limites 19

I.6.1. Condition de pression à l'entrée 19

I.6.2. Condition de vitesse à l'entrée 20

I.6.3. Condition de débit massique à l'entrée 20

I.6.4. Condition de pression à la sortie 20

I.6.5. Condition de parois 20

I.7. Conclusion 21

CHAPITRE II : SIMULATION NUMERIQUE & MAILLAGE HYBRIDE

II.1. Introduction 22

II.2. Processus de simulation numérique 22

II.2.1. Modélisation Géométrique 23

II.2.2. Maillage 23

II.2.2.1. Génération de maillage 24

II.2.2.2. Composants du maillage 24

II.2.2.3. Choix du type de maillage 25

II.2.2.4. Techniques générales de génération du maillage 27

II.2.2.5. Qualité d'un maillage 27

II.2.2.6. Génération de maillage couche limite 29

II.2.2.7. Indépendance de la solution du maillage 29

II.2.3. Resolution 30

II.2.4. Analyse et Visualisation 30

II.3. Les Logiciels de Simulation Numérique 31

II.3.1. ICEM CFD 31

II.3.2. Le Solveur Fluent 32

II.4. Maillage hybride 33

II.4.1. Position du problème 33

II.4.2. Historique des maillages hybrides 33

II.4.3. Processus de génération de maillage hybride (prisme) 35

II.4.3.1. Lois de croissance (Growth Law) 35

II.5. Conclusions 37

CHAPITRE III : GENERATION DE MAILLAGE HYBRIDE & SOLUTION SUR ARA M100

III.1. Introduction 38

III.2. Définition de la géométrie ARA M100 Aile-Fuselage 38

III.2.1. Plan de symétrie 38

III.2.2. Aile 38

III.2.3. Extrémité d'aile (Tip) 38

III.2.4. Dimensions de la géométrie ARA M100 39

III.3. Génération du maillage (ICEM CFD 13) 40

III.3.1. Génération de maillage tétraédrique 40

III.3.1.1. Importation de la géométrie et nettoyage de la CAO 40

III.3.1.2. Création des familles 41

III.3.1.3. Définition du domaine « FLUID » 41

III.3.1.4. Paramètres de maillage 42

III.3.1.5. Choix et génération de type de maillage 43

III.3.1.6. Vérification de maillage 43

III.3.2. Génération des couches de prisme sur ARA M100 44

III.3.2.1. Paramètres général des prismes 44

III.3.2.2. Paramètres de prismes sur chaque partie de la géométrie 45

III.3.2.3. Lancement de maillage prismatique 45

III.3.3. Exportation vers Fluent 13 47

III.4. Solution par Fluent 47

III.4.1. Principales étapes de simulation sous Fluent 47

III.4.1.1. Importation du fichier (*.msh) 47

III.4.1.2. Vérification du maillage importé 48

III.4.1.3. Lissage du maillage (Smooth and Swap the Grid) 49

III.4.1.4. Vérification de l'échelle 49

III.4.1.5. Choix du modèle de turbulence 50

III.4.1.6. Définition des caractéristiques du fluide 51

III.4.1.7. Conditions opérationnel 52

III.4.1.8. Conditions aux limites 53

III.4.1.9. Choix des critères de convergence 54

III.4.1.10. Initialisation des calculs 56

III.4.1.11. Animation 56

III.4.1.12. Sauvegarde du fichier *.cas 57

III.4.1.13. Lancement de la simulation 57

III.5. Conclusion 58

CHAPITRE IV : RESULTATS ET VALIDATION

IV.1. Introduction 59

IV.2. Les Conditions aux limites 59

IV.3. Première simulation 59

IV.3.1. Calcule non visqueux 59

IV.3.1.1. Configuration d'écoulement 59

IV.3.1.2. L'histoire de convergence des résidus 60

IV.3.1.3. L'histoire de convergence des coefficients Cd, Cl et Cm 60

IV.1.3. Les contours de pression et vitesse autour d'ARA M100 62

IV.1.3.1. Contours de pression statique sur 62

IV.1.3.2. Contours de Mach sur ARA M100 63

IV.4. Deuxième simulation 64

IV.4.1. Calcule visqueux pour le model de turbulence K epsilon 64

IV.4.1.1. L'histoire de convergence des résidus 64

IV.4.1.2. L'histoire de convergence des coefficients Cd, Cl et Cm 64

IV.4.1.3. Vérification de maillage 66

IV.4.1.4. Contours de pression statique sur ARA M100 67

IV.4.1.5. Contours de pression statique sur le profil d'aile 68

IV.4.1.6. Contours de mach sur l'avion 68

IV.4.1.7. Contours de Mach sur le profil d'aile 69

IV.4.1.8. Vecteurs vitesse sur l'avion au plan de symétrie 70

IV.4.1.9. Vecteurs vitesse sur le profil d'aile 71

IV.5. Contours de coefficient de pression 72

IV.5.1. Distribution du coefficient de pression sur l'intrados et l'extrados 73

IV.6. Troisième simulation 75

IV.6.1. Calcule visqueux pour le model de turbulence K epsilon 75

IV.6.1.1. Configuration d'écoulement 75

IV.6.1.2. Contours de pression statique sur ARA M100 pour chaque á 76

IV.6.1.3. Contours de pression statique sur le profil d'aile pour chaque á 77

IV.6.1.4. Contours de Mach sur ARA M100 pour chaque á 78

IV.6.1.5. Contours de Mach sur le profil d'aile pour chaque á 79

IV.6.1.6. Coefficient de pression pour chaque á 80

IV.7. Forces de chaque angle d'incidence 82

IV.8.Calcule des coefficients pour chaque á 82

IV.8.1. Courbe du coefficient de portance Cl 83

IV.8.2. Courbe du coefficient de trainée Cd 83

IV.8.3. La polaire 84

IV.9. Conclusion 84

CONCLUSION GENERALE 85

ANNEXE A
ANNEXE B

INTRODUCTION

La simulation numérique est une activité du processus de conception de produits manufacturiers. Sa mise en oeuvre dans les systèmes de production industrielle se base essentiellement sur des méthodes aux éléments finis. Cette méthode requiert basiquement un maillage comme représentation du système étudié. De nombreux travaux de recherche, depuis plusieurs décennies [1, 2], ont porté sur la mise en place de mailleurs. Toutefois l'activité de maillage demeure fastidieuse et couteuse en temps ingénieur. Plusieurs jours, semaines ou mois sont consacrés au maillage de structures, maillage parfois exploité dans une unique simulation.

Ce mémoire présent une approche pour la gestion de processus de maillages hybrides. Les maillages hybrides concernent des maillages pour lesquels les spécifications de construction ne sont pas uniformes sur l'ensemble du système. Cette classe de maillage évoque des maillages associant différents types d'éléments, différentes variétés pour leurs sous-domaines, différents modes de constructions, différentes sources de définition, etc. Ainsi la production de maillages hybrides passe souvent par l'association de plusieurs techniques de maillages.

La conception de grands systèmes, correspond souvent à l'assemblage de la conception de systèmes plus petits, qui sont modélisés dans des environnements logiciels hétérogènes. Ainsi l'activité de production de maillages ne s'appuie pas sur un mais plutôt plusieurs supports géométriques issus de logiciels ou de pratiques différents (plans papier, outils CAO divers, ingénierie inverse, etc.). Avant toute procédure de maillage, l'intégration des différents supports sources doit être envisagée. Cette intégration s'appuie en général sur des techniques d'échanges de données qui imposent des conversions et des duplications explicites des supports initiaux, taches induisant des erreurs de modélisation dans les objets finalement utilisés.

L'intégration dans un même modèle est aussi une source de difficultés (positionnement, fusion des sous domaines, etc.). Enfin une idéalisation des supports intervient à tout moment dans ces procédures. Le ou les supports géométriques sont alors maillés avec les outils à disposition. Si plusieurs supports géométriques sont maillés indépendamment, une fusion des maillages est finalement nécessaire. Beaucoup d'outils de maillages sont disponibles et le choix des outils est alors affaire de spécialiste.

Architecture du mémoire

Ce travail a été développé à partir du plan suivant :

Afin d'exposer les différents types d'écoulements, le premier chapitre débute par quelques notions de base en mécanique des Fluides, et un rappel sur les principes généraux de la couche limite, la dynamique des différentes structures de la couche limite laminaire et turbulente et la physique de décollement de la couche limite. En fin une modélisation de la turbulence et quelques définitions de ces model les plus utilisés dans la simulation numérique.

Au cours du deuxième chapitre, une étude générale des processus de simulation numérique appliqué à la mécanique des fluides a été définie, pour cela nous avons décrit le choix du type de maillage et les techniques générales de génération de maillage et Une définition des logiciels utilisés dans notre simulation (ICEM et FLUENT). En fin une historique des maillages hybrides et les lois correspondantes pour générer un maillage prismatique.

Dans le troisième chapitre, nous avons présenté une définition de la géométrie ARA M100, ainsi que les processus de génération de maillage tétraédrique et prismatique dans ICEM CFD 13 sur la configuration Ail-Fuselage du model ARA M100. Et en fin les étapes de la solution dans Fluent 13.

Le quatrième chapitre présente les différents résultats obtenus par Fluent, ainsi que leur validation avec l'expérimental et leur interprétation en vue de les exploités.

Le présent mémoire se termine par une conclusion générale résumant les contributions de la thèse et présentant les difficultés et perspectives à court terme qui en découlent.



CHAPITRE

I RAPPEL DE LA

DYNAMIQUE DES

FLUIDES

SOMMAIRE PAGE

I.1. Introduction 3

I.2. Les équations fondamentales de la dynamique des fluides 3

I.3. Les différents types d'écoulements 6

I.4. Couche Limite 8

I.5. Turbulence 13

I.6. Les conditions aux limites 19

I.7. Conclusion 21

=

OZ CI (I. 1)

, div pU

=0=

Ou Ox +

Ov Oy +

Ow

I.1.Introduction

L'utilité pratique de la mécanique des fluides est évidente à partir de ces applications technologiques qui couvrent tout un ensemble de domaines ceci est appuyé par l'avancement spectaculaire des secteurs technologiques dans les quels la qualité et l'originalité des solutions des problèmes d'écoulement ont joué un rôle primordial dans le développement des secteurs de transport (avion, bateaux, voitures) et le secteur de production d'énergie (turbines, compresseurs, réacteurs).

L'étude théorique dans ces domaines nécessite l'utilisation des équations non linéaire de base comme les équations de Navier Stokes. Cette dernière résout les problèmes de la dynamique des fluides qui sont généralement difficiles à résoudre. C'est pour cela que la résolution de ces équations nécessite les méthodes de calculs numériques.

I.2.Les équations fondamentales de la dynamique des fluides

On peut définir le comportement d'un fluide à partir de la résolution des équations mathématiques fondamentales, mais il faut tenir compte des principes de conservation, tirés de la physique de ce fluide, ces principes sont :

· Principe de la conservation de la masse.

· Principe de la conservation de la quantité de mouvement.

I.2.1. Principe de conservation de la masse

C'est un principe de physique, qui permet d'établir une relation entre certaines caractéristiques du fluide et ses mouvements, indépendamment des causes qui le provoquent. {Quelque soit le volume D du fluide que l'on suit dans son mouvement, sa masse m reste constante (Fluide Conservatif)}.

Il se traduit par l'équation de continuité, sous sa forme générale.

Dans le cas d'un fluide permanent (stationnaire), et incompressible, ou la masse volumique est invariable, l'équation de continuité se réduit à :

I.2.2. Principe de conservation de la quantité de mouvement

C'est un principe de mécanique qui permet d'établir des relations entre les caractéristiques du fluide, celles de ces mouvements et les causes qui les produisent (Forces).

Ce principe se traduit par les équations de Navier- Stokes, qui ont été établies en 1822 par ces derniers. On les obtient en écrivant l'équilibre du système de forces s'exerçant sur un parallélépipède élémentaires dx, dy, dz :

Forces extérieures : F ~~~~		(force de volume)		Forces de Pression : - grad ~~~~~~~~~~~ P Forces d'inertie i Forces de Viscosité fi?v
P (forces de surface)

Pour un fluide incompressible, on a :

1 grad ~~~~~~~~~~~~~ P

~ P = F

- i + fi?v (I. 2)

Et sous forme cartésiennes, par projections sur les trois axes :

1 P

OP = ~~ ~~

au a + v?u (I. 3)

av

a + v?v (I. 4)

OP

= F_Y

~~

1
P



OP

=

~$

~~

Ow

a + v?w (I. 5)

1
P



Avec :

0^2 ?= axe +

a^2 aye +

a^2 az2 (I. 6)

a

+ u

a

a

+ v

ax

a

+ w

ay

a²

az2 (I.7)

a

?

a

=



D'une manière générale, lorsque le fluide en écoulement est newtonien (c'est-a-dire lorsque la relation contrainte-taux de déformation est linéaire et isotrope), les équations de conservation de la quantité de mouvement prennent la forme particulièrement simple des équations de Navier Stokes.

I.2.3. Les équations de Navier-Stokes

Nous allons maintenant établir ces équations en supposant, pour simplifier, que la viscosité dynamique ì reste constante dans tout l'écoulement. Si cette viscosité n'est pas constante, des termes supplémentaires apparaissent dans les équations du mouvement. Nous parlons ici de l'équation de conservation de la quantité de mouvement projetée suivant l'axe i.

= - + ~~) +

dill

_dxi(I..8))

^P

dvi OP

Cette équation exprime l'égalité entre la quantité d'accélération par unité de volume et les forces extérieures qui s'appliquent l'unité de volume (pression, forces volumiques, contraintes visqueuses). Dans le cas d'un fluide newtonien, les contraintes visqueuses ont pour forme :

*)+ = - .~~) + ~~+ / - 2 3 -0?. 3⁴)+ (I. 9)

~~+ ~~)

Nous devons maintenant calculer^6789' commeìp est constant, on a :6:8i

dill dx1

= - ;~&~) + ~ <~~) => - 2 3 - ~ 0?. 3^4)+ ~~+~~+ ~~) ~~) ~~+ )

(I. 10)

Ou encore :

[

dill

dXj

0². 022 0= = 1.1 v
^is+ + ?V.. v)- 1¹ ?.. v)
OxiäXj 0.7Ci33 0.7Ci(I. .11)
On obtient finalement :

dill dXj

= -?&~) + - 0?. . v) (I. 12) 3 Oxi

Etl'équationn (I.10) devient :

dvi OP

+ ~~) + -?&~) + -

~ = - 0?. 3 (I. 13)

~ ~~) 3 ~~) i

Sous forme explicite, on peut écrire :

dVi ~ d

OP ~

+ ~~~ + -?&~~ + -

= - 0?. 3 (I. 14)

~~~

3 oxi

dv2 OP ~

+ ~~& + -?&~& + -

~ = - 0?. 3 (I. 15)

~ ~~& 3 ~~&

dv3 OP~

+ ~~? + -?&~? + -

~ = - 0?. 3 (I. 16)

~ ~~? 3 ~~?

On peut aussi représenter ces troiéquationsns sous forme vectorielle compacte. Les expressions précédentes sont appeléeéquationsns de Navier-Stokes.

Lorsque le fluide est incompressibleÄ.õti = 0 et le dernier termdisparaîtit on a alors

^:

~ dv -?PVP + pg p?²v²v (I. 17)

Leéquationsns de Navier-Stokes sontrèses complexes, des solutions Analytiques lie peuvenêtrere obtenues que par certaines configurations simples. On peut dire que si on sait leintégrer,r, on pourrairésoudrere analytiquement leproblèmeses d'hydrodynamique. I.3.3. Ledifférentsts typed'écoulementsts

Nous allons maintenant donner une description qualitative rapide de quelques

^{typed'écoulements.s}

I.3.1.1. Ecoulements incompressibles et compressibles

On dit qu'un fluide est incompressible si sa massspécifiqueue varie faiblement avec la pression ou ltempérature.e. Ainsi la variation relative de massspécifiqueue pour l'eau esÄñ/ñ/p = 5x10⁴ pour une variation dtempératurerÄTAT = 1⁰K eÄñ/ñ/p = 2x10^-4 pour une variation de pressioÄñOp = 1bar. On peut donc souvent traiter l'eau comme un fluide incompressible et utiliser dans leéquationsns du mouvement undensité tñ=ño=constante.e. Dans le cas des gaz trèses généralement, les gaz sont traités comme des fluides compressibles. Cependant nous verrons qu'aux faibles vitesses d'écoulement (aux nombre de mach petits devant uM<<M« 1, les variations de densité sont faibles grandeur du carre du nombre de mach

?p ₌Ap

/4M « 1<<1 (I. 18 ~

)

Dans ces conditions, on peut traitel'écoulementnà a l'aide deéquationsns qurégissentnt ^leécoulementsts incompressibles.

I.3.2. Ecoulement laminaire et écoulements turbulent

Un écoulement turbulent peut être caractérise par une orientation aléatoire (ou fluctuation) des vecteurs vitesses en chaque point ; autrement dit chaque composante u(M, t), v(M, t), w(M, t), de V(M, t) Obéissent à des lois de distributions (au sens probabiliste) en fonction de l'espace et du temps. On dit que le régime de l'écoulement est turbulent. Un écoulement turbulent peut posséder une composante moyenne a (le mouvement global se fait d'ouest en est par exemple) pouvant dépendre du temps mais de manière plus « régulière »; les fluctuations ont alors lieu autour de cette composante moyenne, de sorte que la vitesse s'écrit :

B0@, 3 = ~~~ + D (I.19)

C'est alors Sur v' que l'on fait apparaitre des lois statistiques.

Dans un écoulement laminaire, le mouvement du fluide s'effectue en « couches » parallèle entre elles, chaque couche possédant sa propre vitesse ; le profit de vitesses dans le fluide en mouvement est biens ordonne. Les vecteurs vitesses conservent une orientation stable au cours du temps. On dit que le régime de l'écoulement est laminaire. Lorsque le mouvement laminaire du fluide dégénère en un écoulement turbulent, il perd son caractère ordonne et stable ; on dit qu'il y a transition du régime laminaire vers le régime turbulent, ou plus simplement transition laminaire turbulent.

La différence entre le régime turbulent et le régime laminaire peut être représenté par les courbes donnant la vitesse en fonction du temps en un point M fixe.



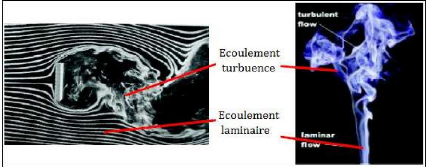
Figure (I.1) : Plaque plane mise à l'écoulement. [3] Figure (I.2) : Fumée d'une cigarette.

I.3.3. Ecoulement stationnaire et instationnaire

On dit qu'un écoulement est stationnaire si en tout point M de Ù, toutes les variables décrivant le mouvement sont indépendants du temps. Ainsi la pression P, la vitesse õ, la densité ñ, l'énergie e d'un écoulement stationnaire sont des quantités indépendantes du temps.

I7(m, 3 = I⁷(m) ?M ? c/ (I. 20)

Tous les phénomènes de propagation d'onde dans les fluides appartiennent à cette catégorie (onde à surface d'un liquide, rayonnement d'ondes sonores à partir d'un jet libre turbulent...), les écoulements atmosphériques sont aussi essentiellement instationnaires. Les écoulements turbulents sont aussi par nature instationnaire, cependant on dit qu'un écoulement turbulent est instationnaire si les variables moyennes sont indépendantes du temps et si les corrélations d'ordre deux constituées a partir de ces variables sont invariantes par transition.

I.3.4. Ecoulement irrotationnel

On dit qu'à un instant t donne, l'écoulement est irrotationnel dans le domaine D si le rotationnel de la vitesse V(M, 3 est nul en chacun des points M de D.

ro f, = 0 (I. 21)

Le rotationnel est un vecteur (défini en cinématique des fluides) qui caractérise en un point M, la rotation dans l'espace de la particule fluide.

Il s'écrit symboliquement :

.o V(M, 3 = ?^~~^V(M, 3 (I. 22)

Il s'écrit par exemple en coordonnées cartésiennes :

law(M, 3av(M,Trau(M, 3 aw(M,1-- rav(M, 3 au(M, 3].

r;'^, I7(M, 3 ay az X + az ax Y + ax ay Z (I. 233


I.4. Couche Limite

Si le fluide était parfait, la seule force crée par le positionnement d'un profil dans un écoulement est une force de portance perpendiculaire à la vitesse.

Mais l'air n'est pas un fluide parfait. Il est visqueux, ce qui engendre un frottement le long du profil de l'aile.

La partie du fluide qui est infiniment proche de la paroi d'un profil possède donc une vitesse nulle. Il en résulte un accroissement progressif de la vitesse au fur et à mesure que l'on s'éloigne de la paroi. La zone dans laquelle l'écoulement est freiné de par sa proximité avec la paroi est appelée couche limite. Il s'agit de la zone dans laquelle la vitesse de l'écoulement est comprise entre 0 et 99% de la vitesse à l'infini sur la normale à la paroi.

Cette couche limite est également dépendante de l'état de surface du profil, donc on peut dire que :

La couche limite est la mince pellicule entourant un corps en mouvement dans un fluide (air). Dans cette mince pellicule les forces de viscosité sont importantes.

La couche limite conditionne directement la résistance de frottement du corps en mouvement dans le fluide.



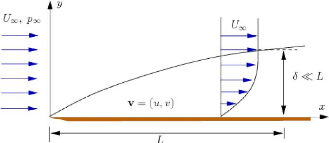
Figure (I.3) : Forme de la couche limite sur une plaque

I.4.1. Epaisseur de la Couche Limite

L'épaisseur de la couche limite croit de l'amont (quelque mm) vers l'aval (quelque Cm). Conventionnellement l'épaisseur de la couche limite est la distance à la paroi à partir de laquelle U = 0,99 U0

I.4.1.1. Epaisseur de déplacement ä*

Les lignes de courants en écoulement visqueux sont déplacées par rapport à leurs positions en fluide non-visqueux.



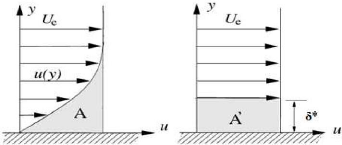
Figure (I.4) : Epaisseur de la Couche Limite

Ce déplacement est exploites pour définir une épaisseur tel que les aires A et A' soient égales :

S 4* = O <1 - ~ P= 0

dy (I.24)

I.4.1.2. Epaisseur de quantité de mouvement è

Correspond à la perte de quantité de mouvement dans la CL par rapport à un écoulement de fluide parfait (à débit masse équivalent)

8 = OR

SU (1 - U Ue) d)1 (I. 25)

Ue

I.4.1.3. Facteur de forme H

Rapport des deux épaisseurs précédemment définies :

8*

H = 8 (I. 26)

I.4.2. Décollement de la Couche Limite

La théorie de la couche limite laminaire montre que le profil des vitesses se modifie sous l'effet d'un gradient longitudinal de pression positif.

La pente à l'origine peut devenir nulle, caractérisant le point de décollement. Il est en est de même pour une couche limite turbulente.

· De A à T les vecteurs vitesses restent parallèles entre eux sur une normale à la paroi : la couche limite est laminaire.

· A partir de T, les vecteurs vitesses ne sont plus parallèles entre eux, mais les vecteurs vitesse moyenne restent parallèles entre eux. La couche limite est turbulente. T est le point de transition, sa position dépend essentiellement du nombre de Reynolds, de l'état de surface et du nombre de Mach. La couche limite turbulente est d'autant plus importante que Re est grand.

· A partir de D, la couche limite se décolle, les particules près de la paroi voient leur mouvement s'inverser et entraînent la formation de tourbillons (d'où forte augmentation de la traînée). D est le point de décollement.



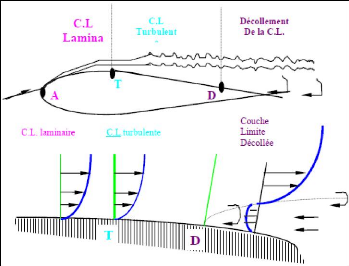
Figure (I.5) : Décollement de la Couche Limite

La figure (I.5) montre l'évolution progressive du profil des vitesses d'amont en avale: lorsque la vitesse s'annule dans les couches inférieures, le fluide sous l'effet de la pression plus grande en aval qu'en amont prend une vitesse de sens opposé à celui de la vitesse de l'écoulement extérieur, créant un courant de retour. [4]

L'expérience met en évidence le phénomène très important dit « décollement libre » dont la position peut être prévue lorsqu'on étudie le développement d'une couche limite et en particulier l'évolution du coefficient local de frottement puisque celui-ci s'annule au point de décollement.



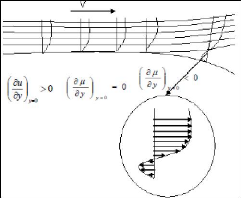
Figure (I.6) : Ecoulement avec gradient longitudinal de pression positif (D est le point de décollement de la couche limite).

Pour les applications, il est très important de noter qu'une couche limite turbulente décolle moins facilement qu'une couche limite laminaire, étant donné l'échange intense d'énergie à l'échelle macroscopique qui existe entre les couches inférieures dans une couche limite turbulente.

Les écoulements décollés tridimensionnels sont caractérisés par la présence de structures tourbillonnaires définies comme des concentrations spatiales de vorticité résultant du décollement de la couche limite figure (I.6).

Une fois que le décollement a eu lieu, la vorticité tend à se concentrer au voisinage de surfaces dont l'enroulement forme les tourbillons. Dans la réalité, de telles surfaces définies comme support de discontinuités (ou singularités) n'existent pas. Ces concepts appartiennent aux modèles de fluide parfait. Dans le monde réel, la vorticité est répartie dans l'espace et occupe un certain volume dans le voisinage de ce que l'on appelle une surface de décollement.



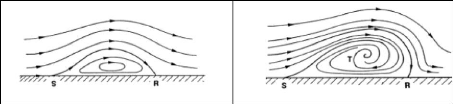
(a) écoulement bidimensionnel (b) écoulement tridimensionnel

Figure (I.7) : Conceptions simples du décollement.

I.4.3. Couche limite turbulente

Profil de vitesse dans la couche limite turbulente :

· Équation de quantité de mouvement :

äu U + v äx

äu = äy

äy <v äu ä äy= + ä äy U-~^'v^'WWWWWX (I. 27)

· Proximité immédiate de la paroi : terme de frottement laminaire dominant (vitesses moyennes et fluctuations de vitesses ?0 quand y ?0

Y" Zv Ou

O Y"\ 0 Quand y ? 0 ~ = dy = ef g y (I. 28)

Zone de très proche paroi = sous-couche visqueuse (viscous sub-layer)

· Echelle caractéristique de la vitesse = vitesse de frottement

T(() =

T(() (I. 29) p

· Variables sans dimension pertinentes dans la zone proche paroi :

U U_t)'

U+ = , y⁺ = (I.30)

U_e

· Relation de très proche paroi valable jusqu'à y⁺ ? [10, 5]

u = i (I.31)

· Lorsque l'on quitte la sous-couche visqueuse, le frottement turbulent devient peu à peu prépondérant par rapport au frottement laminaire (faibles vitesses termes d'inertie négligeables) -dans cette zone, le frottement total reste à peu près constant et égal à -la vitesse moyenne reste de l'ordre de la vitesse de frottement -l'échelle caractéristique de longueur reste

Ui = f(yⁱ) (I.32)

· Lorsque l'on continue à s'éloigner de la paroi, frottement turbulent et inertie deviennent dominants devant le frottement laminaire -déficit de vitesse de l'ordre de la vitesse de frottement -échelle de longueur de l'ordre de l'épaisseur de CL

Ue - U = g (^y ₄) = 0k3 (I. 33)

UT

· Lorsque l'on est à l'extérieur de la CL seul le terme d'inertie est dominant, les frottements laminaire et turbulent devenant négligeables

I.5. Turbulence

Le phénomène de turbulence se manifeste par un champ de vitesse fluctuant. Ces fluctuations des variables de l'écoulement peuvent être d'un petit ordre de grandeur et atteindre des hautes fréquences. La résolution directe des équations régissant les écoulements turbulents est extrêmement onéreuse, compte tenu des temps de calcul et des moyens informatiques requis.

Cependant, la solution instantanée (exacte) des équations gouvernantes peut être
moyennée en temps, tout en éliminant les grandeurs de faible échelle de turbulence, ce
qui rend la résolution des équations résultantes moins coûteuse. Néanmoins, cette

modélisation fait apparaître des variables inconnues supplémentaires qui doivent être déterminées en utilisant des modèles dits de turbulence.

I.5.1. Modélisation de la turbulence

Il n'y a pas de modèle de turbulence universel valable pour modéliser tous les cas d'écoulements. Le choix d'un modèle de turbulence dépend de certaines considérations telles que la physique du problème traité, le niveau de précision exigé, les ressources informatiques disponibles et le temps disponible pour effectuer la simulation.

Afin de choisir le modèle le plus approprié à chaque application donnée, il est nécessaire de comprendre les principes et les limites de chaque modèle de turbulence.

I.5.2. Nombre de Reynolds

Le nombre de Reynolds (Re) est un nombre sans dimension utilisé en mécanique des fluides. Il a été mis en évidence en 1883 par Osborne Reynolds. Il caractérise un écoulement, en particulier la nature de son régime laminaire, transitoire, et turbulent. Le nombre de Reynolds représente le rapport entre les forces d'inertie et les forces visqueuses. On le définit par:

L.0

R_e = V (I. 34)

Avec :

U : vitesse du fluide [m/s]

L : longueur caractéristique [m]

í : viscosité cinématique du fluide : [m²/s]

Le nombre de Reynolds s'interprète alors comme le rapport entre forces d'inertie et forces visqueuses. Donc on distingue trois principaux régimes :

· Aux faibles valeurs du Reynolds (inférieures à 2000) : les forces de viscosité sont prépondérantes, l'accélération convective étant négligée ; L'écoulement est laminaire. De plus, comme l'inertie est négligeable, l'écoulement du fluide est réversible. C'est-àdire si les forces extérieures sont soudainement stoppées, le fluide s'arrête immédiatement, et si les forces extérieures sont inversées, le fluide repart en sens inverse.

· Aux valeurs intermédiaires du Reynolds (entre 2000 et 3000 environ) : les forces d'inertie sont prépondérantes, mais l'écoulement reste laminaire. Cependant, il n'est plus réversible: si l'on stoppe les forces extérieures, le fluide continu partiellement sur sa lancée.

· Aux fortes valeurs du Reynolds (au-delà d'environ 3000) : les forces d'inertie sont si importantes que l'écoulement devient turbulent. Entre les régimes laminaire et turbulent, on parle de régime transitoire.

I.5.3. Nombre de Mach" M "

Pour comparer la vitesse « U» d'un écoulement et la vitesse « a » du son, il est intéressant d'introduire le rapport sans dimension « U/a » appelé Nombre de Mach.

U

M =

a (I.35)

* Si U < a ? M < 1 : l'écoulement est subsonique.

* Si U > a ? M > 1 : l'écoulement est supersonique. * Si U = a ? M = 1 : l'écoulement est sonique.

En mécanique de vol on définie plusieurs nombres de Mach:

· Le nombre de Mach général : C'est le nombre de Mach correspondant à la vitesse de l'avion « U » et la vitesse du son « a » à l'altitude de Vol.

· Les nombres de Mach locaux: Qui correspondent par exemple à des survitesses locales sur l'extrados.

I.5.4. Les modèles de turbulence

Les écoulements turbulents sont caractérisés par les champs de fluctuation de Vitesse.

Ces fluctuations mélangent des quantités transportées telle que l'énergie, la concentration D'espèce,... Ces fluctuations peuvent être de petite échelle et de haute fréquence, elles sont d'un point de vue informatique trop ardu pour être simuler directement dans des calculs pratiques en technologie.

En alternative les équations régissantes (exactes) instantanées peuvent être remplace
par des équations a variables moyennes temporelles ramenée a des structures a petites
échelles, afin d'obtenir un ensemble d'équations modifie qui sont plus simple à résoudre.

I.5.4.1. Le modèle Spalart-Allmaras

Le modèle Spalart-Allmaras est une formulation simple à une équation. Ce modèle est surtout destiné à des applications aérospatiales, et il a donné des résultats satisfaisants concernant les calculs des couches limites soumises à de très forts gradients de pressions. Il devient de plus en plus populaire dans d'autres applications telles que les turbomachines.

Sous sa formulation originale, le modèle Spalart-Allmaras est un modèle de turbulence à bas nombre de Reynolds nécessitant la résolution complète des équations de la couche limite.

Cependant, certains codes de CFD couplent ce modèle avec des fonctions de parois lorsque la résolution du maillage n'est pas suffisamment fine. En outre, ce modèle est moins sensible aux erreurs numériques que les modèles k-å et k-ù.

Cependant, les équations modifiées contiennent des variables inconnues additionnelles, et des modèles de turbulence sont nécessaires pour déterminer ces variables en termes de quantités connues.

I.5.4.2. Le modèle k-å

Les modèles de turbulence les plus populaires sont les modèles dits à deux équations dont le modèle k-å. Il est fréquemment utilisé dans de nombreux calculs d'ingénierie. Il est basé sur la formulation proposée par Launder et Spalding. [5]

La robustesse, l'économie, et la précision dans la prédiction d'une large gamme de problèmes d'écoulements turbulents, expliquent sa popularité dans la simulation des écoulements industriels et les problèmes de transfert de chaleur. Le modèle k-å est un modèle semi empirique et les équations utilisées découlent des considérations phénoménologiques et empiriques.

Par rapport à sa formulation d'origine, le modèle a subi des améliorations pour l'adapter au mieux à certains cas d'écoulement. On retrouve ainsi la variante k-å - RNG (Re Normalisation Group) [6] et k-å modifié. [7]

I.5.4.3. Le modèle k-ù standard et le modèle k- ù -SST

Le modèle k-ù est basé sur la formulation de Wilcox [8], dans laquelle il a introduit des modifications qui tiennent compte des effets liés aux bas Reynolds et à la compressibilité. Les deux variantes du modèle k- ù, Standard et SST, sont des modèles semi empiriques et ils ont la même forme mathématique que les équations de transport de k et de ù. Le modèle k- ù -SST est basé sur la formulation proposée par Menter. [9]

I.5.4.4. Modèle à contrainte de Reynolds RSM (Reynolds Stress Model)

Ce modèle est encore plus sophistiqué. Il évite de faire l'hypothèse d'isotropie de la viscosité turbulente, car il résout les équations pour les six composantes des contraintes de Reynolds et pour å. Ce modèle est donc très lourd numériquement et la convergence est souvent difficile. Il existe de nombreuses variantes de ce modèle, qui concernent en particulier la façon de modéliser la corrélation de la fluctuation de la pression et la déformation. Ce modèle est préconisé dans le cas des écoulements fortement tourbillonnaires, comme par exemple dans le cas d'un cyclone ou d'un injecteur dans une chaudière à combustion. [10.11.12]

I.5.4.5. Large Eddy Simulation (LES)

Dans l'approche LES, toutes les échelles de la turbulence sont résolues sauf celle relative à la dissipation, qui est modélisée. Il faut donc utiliser un maillage très fin et opter pour une solution instationnaire dans la résolution des équations. Après un temps de calcul assez long, la solution peut reproduire toutes les échelles de la turbulence. Ce modèle est très puissant dans le cas où les écoulements ne sont pas dominés par la présence des parois parce qu'il faut alors un maillage très fin ou l'utilisation d'une fonction de parois dans cette région. Ce modèle permet d'accéder à un tel niveau de détails qu'il peut être utilisé pour la prédiction du bruit.

Avec l'augmentation de la puissance des ordinateurs, ce modèle est devenu plus intéressant. Mais il faut éviter de l'utiliser avec un maillage trop lâche, ou pour des simulations en deux dimensions parce que le modèle s'appuie sur des phénomènes tridimensionnels.

I.5.4.6. Simulation directe (DNS) ou Direct Numerical Simulation

DNS est théoriquement l'approche la plus puissante car elle fait appel à un maillage très fin et à un pas de temps très petit pour résoudre les équations de Navier-Stokes sans aucun modèle. Mais avec les plus puissants ordinateurs, on ne peut aujourd'hui étudier que les écoulements simples. Donc, cette approche n'a encore aucune utilité industrielle. Elle reste réservée à la recherche et à la construction de modèles.

I.5.5. Calcul en proche paroi

Les écoulements turbulents sont sensiblement influencés par la présence des parois. Dans les zones très proches des parois, les effets de viscosité réduisent les fluctuations des vitesses tangentielles. En dehors de la zone de proche paroi, la turbulence apparaît plus rapidement par la production d'énergie cinétique turbulente due au gradient de vitesse moyenne.

La modélisation des zones de proche paroi a un impact significatif sur les résultats de la simulation numérique car la présence des parois constitue la principale source de vorticité et de turbulence et les variables de l'écoulement turbulent y présentent un fort gradient. Les modèles de turbulence définis précédemment (k-å, RSM, LES), demeurent valables pour le calcul des écoulements turbulents loin des parois, cependant ces modèles doivent être développés initialement pour être appliqués dans toute l'étendue de la couche limite à condition que la résolution du maillage soit satisfaisante.

Beaucoup d'expériences ont montré que la région proche paroi peut être divisée en trois couches. Dans la première couche appelée sous-couche visqueuse, l'écoulement est presque laminaire, la viscosité joue un rôle dominant sur l'écoulement et les phénomènes physiques associés (transferts de chaleur, etc.). Dans la zone externe



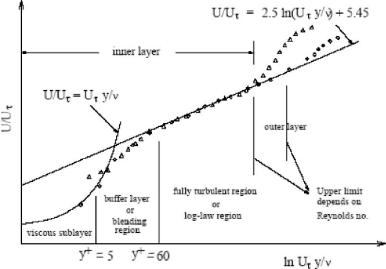
appelé zone logarithmique, c'est plutôt la turbulence qui joue un rôle prépondérant. Finalement une zone intermédiaire entre la sous couche visqueuse et la zone logarithmique associe les effets de la turbulence et les effets de la viscosité est définie. Figure (I.8) illustre la subdivision de la zone de proche paroi.

Figure (I.8) : Division de la région proche paroi

I.5.5.1. Modélisation de l'écoulement en proche paroi

Il existe deux approches pour modéliser l'écoulement en proche paroi. La première approche consiste à ne pas résoudre l'écoulement dans la région de la sous couche visqueuse et d'appliquer des fonctions empiriques dites fonctions de paroi. Cependant, l'utilisation de ces fonctions exige la modification et l'adaptation des modèles de turbulence pour tenir compte de la présence des parois dans l'écoulement.

Dans la deuxième approche, les modèles de turbulence sont adaptés afin de résoudre toutes les sous-couches y compris la sous couche-visqueuse, cette approche appelée approche proche paroi nécessite un maillage très raffiné près des parois. Figure (I.9) résume la différence entre ces deux approches :



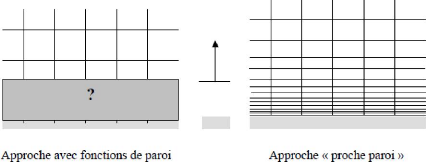
Figure (I.9) : Modélisation de la couche limite.

Dans la plupart des écoulements turbulents à haut Reynolds, l'approche basée sur fonctions de paroi réduit considérablement les besoins en ressources informatiques. Cette approche demeure très populaire pour sa robustesse, son économie et sa précision, et elle est largement utilisée dans beaucoup d'applications industrielles.

Cependant, cette approche est inadéquate pour la modélisation des écoulements où les effets liés aux bas Reynolds sont prépondérants et les hypothèses concernant les fonctions de paroi ne sont plus valables.

I.6. Les conditions aux limites

En fonction du problème physique traité, les conditions aux limites sont différentes et leur compatibilité avec les modèles numériques associés à un impact direct sur la convergence et le réalisme des résultats des simulations numériques. Plusieurs types de conditions aux limites sont proposés en CFD.

I.6.1. Condition de pression à l'entrée

Ce type de condition aux limites est employé lorsqu'on veut imposer une pression à l'entrée du volume de contrôle à étudier. Cette condition est valable aussi bien en écoulement compressible qu'en écoulement incompressible, elle est utilisable lorsqu'on connaît la pression à l'entrée et qu'on recherche la vitesse de l'écoulement correspondante. La pression totale imposée s'exprime, en écoulement incompressible, par la relation suivante:

1

Pt = P_p + ₂pv² (I.36)

En écoulement compressible cette expression devient :

Po = Pp + (1 + ' - 1 2 M2)

y y-1

(I.37)

Avec :

Pt : Pression totale Ps : Pression statique

ã : Rapport des chaleurs spécifiques (Cp/Cv)

M : Nombre de Mach

I.6.2. Condition de vitesse à l'entrée

Cette condition aux limites sert à imposer une vitesse d'entrée au volume de contrôle. Une fois la vitesse fixée, on remonte aux autres grandeurs de l'écoulement. Cette condition aux limites est utilisable en général dans les écoulements supposés incompressibles. Pour des raisons d'instabilités numériques il est déconseillé d'appliquer la condition de vitesse à l'entrée dans le cas des écoulements compressibles.

I.6.3. Condition de débit massique à l'entrée

A l'inverse de la condition de pression à l'entrée, cette condition aux limites consiste à fixer le débit de l'écoulement à l'entrée pendant que la pression totale de l'écoulement varie. Dans plusieurs applications, la condition de pression à l'entrée rend la convergence des calculs plus lente, il est conseillé dans ces cas d'appliquer la condition de débit massique à l'entrée. Pour les calculs des écoulements incompressibles, il n'est pas nécessaire d'imposer le débit massique à l'entrée. La vitesse de l'écoulement impose la valeur du débit massique du fait que la masse volumique du fluide est constante.

I.6.4. Condition de pression à la sortie

Permet d'imposer une valeur de la pression statique à la sortie du volume de contrôle. La valeur de la pression statique ne peut être imposée que lorsque l'écoulement est subsonique.

Le processus de convergence devient plus rapide lorsque la valeur de la pression à la sortie imposée est proche de la réalité.

I.6.5. Condition de parois

Cette condition aux frontières permet de spécifier les parois du volume de contrôle.

Les parois peuvent être déclarées fixes ou en mouvement relatif à l'exemple des rotors de machines rotodynamiques.

Pour des écoulements visqueux, la condition de non glissement est associée à cette condition aux limites. La contrainte de cisaillement associée à la présence des parois dans le domaine de calcul en régime d'écoulement laminaire est donnée par la relation suivante :

Tw = J1

av (I. 38) an

I.7. Conclusion

Dans ce chapitre, nous avons présenté quelques notions de base en mécanique des Fluides, et un rappel sur les principes généraux de la couche limite, la dynamique des différentes structures de la couche limite laminaire et turbulente et la physique de décollement de la couche limite. En fin une modélisation de la turbulence et quelques définitions de ces model les plus utilisés dans la simulation numérique.



CHAPITRE

II

SIMULATION NUMERIQUE

&

MAILLAGE HYBRIDE

SOMMAIRE PAGE

II.1. Introduction 22

II.2. Processus de simulation numérique 22

II.3. Les Logiciels de Simulation Numérique 31

II.4. Maillage hybride 33

II.5. Conclusions 37

II.1.Introduction

La CFD (Computational Fluid Dynamics) est simplement le calcul numérique appliqué à la mécanique des fluides. Cela consiste à résoudre dans une géométrie donnée les équations fondamentales de la mécanique des fluides, que l'on peut éventuellement coupler aux équations de transfert thermique ou de réaction chimique. Historiquement, la CFD a commencé à se développer en génie mécanique, pour étudier les écoulements autour d'un objet afin de mieux le profiler (ailes d'avions, automobiles). Dans le domaine du génie chimique, les problèmes sont, en général, beaucoup plus complexes de par, en particulier, le caractère multiphasique des écoulements, les réactions chimiques et le comportement rhéologique des fluides.

Le résultat d'une opération unitaire est souvent sous-tendu par la qualité des écoulements qui sont produits dans l'appareil, car l'intensité des transferts en dépend fortement (mise en contact d'espèces, de fluides, de phases, d'internes, de parois). La connaissance des écoulements dans une installation, et des grandeurs locales ou globales que l'on peut en déduire (champs de concentration, de dissipation énergétique, de température, puissance dissipée, perte de charge, distribution de temps de séjour, etc.), aide alors l'ingénieur de procédé à mieux définir la géométrie de son équipement et à régler avec pertinence ses paramètres opératoires.

II.2.Processus de simulation numérique

Les développements et les progrès réalisés au cours des deux dernières décennies ont conduit à l'apparition d'une méthodologie qui est devenue standard. Comme pour tout système complexe, la clef de la maîtrise réside dans l'identification et la modularisation des tâches. Actuellement, la méthodologie standard découpe le processus de simulation en quatre tâches distinctes, qui sont :

· Modélisation Géométrique

· Maillage

· Résolution

· Analyse et Visualisation

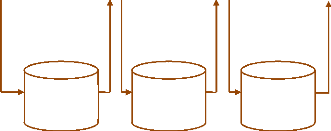
La Figure (II.1) montre comment ces quatre modules s'intègrent dans le processus de simulation numérique, et comment ils communiquent entre eux. La transmission d'information, c'est-à-dire la façon dont les objets sont échangés entre modules, se fait sous la forme de fichiers informatiques. [13]



MODELEUR
GEOMETRIQUE

GENERATEUR
DE MAILLE

RESOLUTEUR
D'EQUATIONS

ANALYSE ET
VISUALISATION



Géométrie

Maillage

Solution

Figure (II.1) : Méthodologie de résolution d'un problème numérique

II.2.1. Modélisation Géométrique

Le rôle du modeleur géométrique est de traduire la géométrie des objets, en deux ou trois dimensions sous la forme d'une représentation informatique. Les entités constituant la description complète de la géométrie sont des formes élémentaires assemblées pour former la géométrie. La modélisation solide appelée CSG (Constructive Solid Geometry) est basée sur des volumes élémentaires tels que cubes, sphères, cônes, et autres volumes géométriques de base. Le modèle final est obtenu en appliquant des opérations booléennes sur ces volumes élémentaires. Les opérations sont l'union, l'intersection, la soustraction, etc. La modélisation B-rep (Boundary Représentation) utilise, comme son nom l'indique, les frontières pour construire le modèle. Cette modélisation définit un volume à partir des surfaces qui le bornent. Les techniques de représentation de ces surfaces sont issues des développements mathématiques sur les fonctions splinaires, de Bézier et plus récement les NURBS. Ces surfaces sont ellesmêmes délimitées par des courbes qui sont définies par des points.

Un modeleur géométrique produit un fichier qui contient une représentation informatique de la géométrie. Le format est souvent propre au modeleur géométrique, même si des efforts sont faits pour arriver à une norme (telles que les normes IGES ou STEP). Souvent, le format utilise la représentation la plus simple soit une facettisation plane obtenue par des triangles

II.2.2. Maillage

Un maillage est une partition de l'espace ou d'un domaine en cellules appelées éléments. Le mailleur prend en entrée la géométrie, c'est-à-dire le fichier produit par le modeleur géométrique, et fournit en sortie un maillage. Ceci comprend une information

géométrique sur les sous-volumes et une information topologique sur la connectivité entre les éléments. Les maillages non structurés sont sous la forme d'une liste d'éléments interconnectés. Les formes sont souvent des triangles ou des quadrilatères en deux dimensions, et des tétraèdres, des cubes ou des hexaèdres en trois dimensions. La connectivité d'un élément est la liste de ses voisins. Un élément possède un voisin par arête ou par face, selon que le maillage est bi- ou tridimensionnel. Dans le cas des maillages structurés, la connectivité est par définition implicite, et donc le maillage se résume à une simple liste de noeuds.

II.2.2.1. Génération de maillage

La génération du maillage (2D ou 3D) est une phase très importante dans une analyse CFD, vu l'influence de ses paramètres sur la solution calculée.

La technique de génération de maillage peut être résumée sous la forme suivante :

La géométrie doit être préparée au préalable, avec la définition de tous les composants de la géométrie fuselage, aile, extrados, intrados...etc., sous forme de données numériques, fichier CAD pré-établi ou plutôt sous forme de fichier maillage qu'on peut importer sous ICEM CFD.

La géométrie qui représente les différents domaines fluides est décomposée en sous domaines « maillables ».

Maillages des sous domaines fluides.

La réduction du temps nécessaire à la génération du maillage est un critère de bonne maîtrise de l'utilisation des outils CFD.



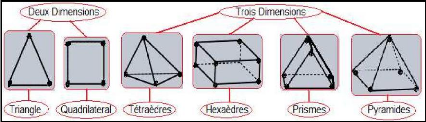
Figure (II.2) : Exemples de mailles utilisées en Volumes Finis.

II.2.2.2. Composants du maillage

Les composants sont définis dans un processeur : Cell = volume de contrôle divisant la géométrie

Le domaine de calcul est défini par un maillage qui représente le fluide et les faces solides qui interviennent.

Face = frontière d'une cell

Edge = frontière d'une face

Node = point de maillage

Zone = groupe de noeuds, face et/ou cell

Les conditions limites sont assignées aux faces zones.

Les d onnées des matériaux et les termes sources sont assignés aux cell zones.



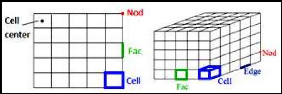
Figure (II.3) : Composant d'un maillage.

II.2.2.3. Choix du type de maillage

> Maillage structuré (quadra/hexa)

Il est beaucoup plus facile de le générer en utilisant une géométrie multi bloc. Cette technique consiste à diviser les domaines de calcul en plusieurs compartiments de

mailler séparément.

formes géométriques simplifiées et de les

Les avantages

· Economiq

ue en nombre d'éléments, présente un nombre inférieur de mailles par rapport à un maillage non structuré équivalent.


·

Réduit les risques d'erreurs numériques dues à la diffusion numérique si l'écoulement est aligné avec le maillage.

Ses inconvénients

· Difficile à générer dans le cas d'une géométrie complexe.


·

Difficile d'obtenir une bonne qualité de maillage pour certaines géométries complexes.


·

Dans la majorité des cas, la division du domaine de calcul est nécessaire pour faciliter sa génération.

> Maillage non structuré (tri/tétra.)

Les éléments de ce type de maillage sont générés arbitrairement sans aucune contrainte quant à leur disposition.

Ses avantages

· Peut être généré sur une géométrie complexe tout en gardant une bonne qualité des éléments.

· Les algorithmes de génération de ce type de maillage (tri/tétra) sont très automatisés d'où un gain de calcul énorme.

Ses inconvénients

· Très gourmand en nombre de mailles comparativement au maillage structuré.

· Engendre des erreurs numériques (diffusion numérique) qui peuvent être plus importantes si l'on compare avec le maillage structuré.



Figure (II.4). Exemple de maillage structuré et non structuré autours d'un profil. [14]

> Maillage hybride

Maillage généré par un mélange d'éléments de différents types, triangulaires ou quadrilatéraux en 2D, tétraédriques, prismatiques, ou pyramidaux en 3D.

Ses avantages

Combine les avantages du maillage structuré et ceux du maillage non structuré en réduisant les erreurs dues à la diffusion numérique.

Ses inconvénients

Ce type de maillage demeure encore difficile à générer notamment dans les endroits de liaison entre le maillage structuré et le maillage non structuré

II.2.2.4. Techniques générales de génération du maillage

Pratiquement, il n'existe pas de règle précise pour la création d'un maillage valable, cependant il existe différentes approches qui permettent d'obtenir une grille acceptable. Nous pouvons résumer ces règles ainsi :

· Maintenir une bonne qualité des éléments.

· Assurer une bonne résolution dans les régions à fort gradient.

· Assurer un bon Lissage dans les zones de transition entre les parties à maillage fin et les parties à maillage grossier.

· Minimiser le nombre Total des éléments (temps de calcul raisonnable).

II.2.2.5. Qualité d'un maillage

La génération d'une très bonne qualité de maillage est essentielle pour l'obtention d'un résultat de calcul précis, robuste et signifiant.

Une bonne qualité de maillage repose sur les éléments suivants:

· Minimisation des éléments présentant des distorsions (skewness).

· Une bonne résolution dans les régions présentant un fort gradient (couches limites, ondes de choc ...etc).

Enfin, la qualité de maillage à un sérieux impact sur la convergence, la précision de la solution et surtout sur le temps de calcul.

> Distorsion

Une bonne qualité de maillage est synonyme d'absence de grandes distorsions d'éléments (Bon skewness).

Le facteur de distorsion Fd (skewness) se calcule de deux façons différentes :

1. Calcul basé sur le volume équilatéral :



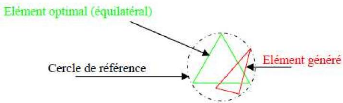
Figure (II.5) : La distorsion.

Fd =

Tai//ee'te'mentoptimal - Tailiee'le'mentge'ne're'

Taillee'we'mentoptimal (II. 1)

= 1.2 (II. 3)

?K)



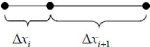
?xi+1

Applicable uniquement pour les éléments triangulaires ou tétraédriques 2. Calcul basé sur la déviation angulaire :

t = ~~ €Gmax - 90 90 , 90 - ^8min 90 (II. 2)

Figure (II.6) : Déviation angulaire. Applicable pour tout type d'élément.

· Notons que les grandes valeurs du facteur de distorsion induisent des erreurs de calcul et ralentissent considérablement le processus de convergence.

· Quelques distorsions peuvent être tolérées si elles sont situées dans des régions à faible gradient.

Ce tableau illustre la variation de la qualité des éléments de maillage en fonction de la valeur du coefficient de distorsion Fd :

Tableau (II.1) : La variation de la qualité de maillage

Fd	0-0.25	0.25-0.50	0.50-0.80	0.80-0.95	0.95-0.99		0.99-1.00	Qualité
excellent	Bon	Acceptable	Pauvre	Très Pauvre	Mauvais

· La valeur maximale du "skewness" tolérée pour un maillage volumique doit être inférieure à 0.90.

· La valeur maximale du "skewness" tolérée pour un maillage surfacique structuré ou non, hexaédrique ou tétraédrique doit être inférieure à 0.75.

> Lissage

Le changement dans la taille des éléments de maillage d'une zone maillée à une autre doit être graduel, la variation de la taille des éléments de deux zones adjacentes ne doit pas dépasser 20%.

> Nombre total d'éléments

Un nombre important d'éléments de maillage permet sans doute d'améliorer la précision des calculs, mais pénalise les ressources informatiques en terme de mémoire et alourdit le système. Par voix de conséquence, un compromis entre précision et temps de calcul s'impose. Des techniques existent pour économiser un certain nombre d'éléments :

· Utilisation des maillages non uniformes, en concentrant la bonne qualité du maillage uniquement dans les zones où c'est nécessaire.

· Utilisation de la fonction adaptation de maillage pour raffiner uniquement sur des zones bien précises.

· Utilisation des éléments de maillage hexaédriques dans les zones adéquates.

II.2.2.6. Génération de maillage couche limite

La notion de résolution concerne plus particulièrement les zones qui présentent un fort gradient, ainsi une bonne résolution permet de mieux décrire les phénomènes physiques qui existent dans ces zones telles que les ondes de choc, ou les phénomènes lies a la couche limite.



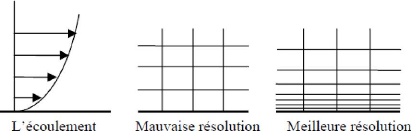
Figure (II.7) : Maillage couche limite.

II.2.2.7. Indépendance de la solution du maillage

Dans une modélisation CFD, la solution doit être indépendante de la densité du maillage pour être sûr du réalisme de la solution que donne le solveur après convergence.



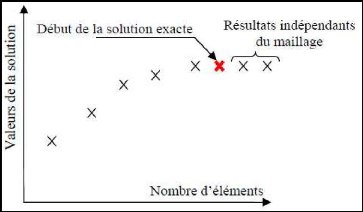
Figure (II.8) : Indépendance de la solution du maillage.

II.2.3. Resolution

Au cours de cette étape, les équations différentielles décrivant le phénomène physique sont discrétisées et transformées en un système d'équations algébriques. Les techniques utilisées sont les différences finies, les volumes finis ou bien les éléments finis, et permettent d'exprimer les variables des problèmes sur le support géométrique que constitue le maillage. Des conditions aux frontières et ou des conditions initiales viennent compléter ces équations, rendant la solution du système unique. Le résoluteur prend donc en entrée un maillage et avec le schéma de discrétisation retenu, construit le système d'équation. La solution de système algébrique, c'est-à-dire la liste des valeurs, Pour chaque point du maillage, de la ou les variables est obtenue par différents schémas itératifs.

II.2.4. Analyse et Visualisation

Les résultats fournis par la résolution des équations constituent une ^quantitéphénoménale de données qui dans leur forme brute défient toute analyse par un

humain. Les outils d'analyse permettent d'extraire les informations utiles pour fins d'analyse et de compréhension. Utilisant des procédures de post-traitement, les caractéristiques globales qui sont l'objectif final de la simulation numérique, sont calculées à partir des données ponctuelles de la solution. Par exemple, lors de l'étude d'une aile d'avion, la traînée et la portance font partie de ces caractéristiques obtenues par l'intégration numérique des valeurs surfaciques.

La visualisation regroupent l'ensemble des techniques qui permettent de représenter les quantités physiques (telles les vitesses, les températures etc...) sous une forme graphique pour faciliter la compréhension des résultats.

II.3. Les Logiciels de Simulation Numérique

Le développement du calcul scientifique a entraîné le développement de nouveaux algorithmes, de nouvelles méthodes de calcul, d'interfaces plus conviviales et plus puissantes. Combinés aux progrès très rapide du matériel informatique, ces développements assurent la progression des performances des logiciels et par conséquent la réduction du temps de simulation numérique.

Dans notre travail on utilise le logiciel de simulation ANSYS 13; (ICEM CFD) pour généré le maillage tétra/prisme et (FLUENT) pour la simulation d'écoulement fluide.

II.3.1. ICEM CFD

ICEM est un mailleur commercial ouvert (par opposition à limité à seul code de calcul. Il peut lire des géométries venant des logiciels de CAO classiques : SOLIDWORKS, CATIA, etc., ou générer lui-même ses géométries. ICEM sauvegarde les maillages soit aux formats des codes classiques de mécanique des fluides (Fluent, CFX, ...) et de mécanique du solide (Nastran, Patran, ...), soit dans des formats définis par l'utilisateur lui-même par le biais de routines en Fortran ou C.

Par rapport à la concurrence, ICEM est un mailleur très puissant en termes de génération des géométries complexes et d'optimisation de maillage. La contre partie de cette puissance vient de la complexité de l'outil (il existe de multiples options) et d'une convivialité perfectible.

ICEM génère des maillages 2D ou 3D structurés, non structurés et hybride à base d'hexaédriques, prismatiques, tétraédriques. Permet de mailler des domaines de géométrie d'un problème de CFD (Computational Fluid Dynamics). Il génère des fichiers *.msh pour Fluent. Ce dernier est un logiciel qui est basé sur l'utilisation de la méthode des volumes finis des problèmes de mécanique des fluides et de transferts thermiques.

En résumé, ICEM est pour la mécanique des fluides un des mailleurs les plus performants mais il nécessite un investissement en temps conséquent.

ICEM-CFD regroupe trois fonctions : définition de la géométrie du problème (construction si la géométrie est simple ou bien import de la géométrie CAO), le maillage et sa vérification, la définition des frontières (Types de conditions aux limites) et définitions des domaines de calculs.



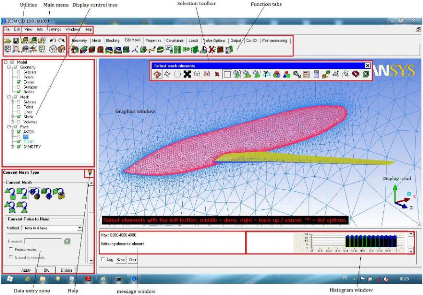
Figure (II.9) : Interface d'ICEM CFD

II.3.2. Le Solveur Fluent

Fluent est un solveur qui utilise des maillages non-structurés 2D ou 3D (avec la méthode des volumes finis). Ces maillages sont : soit des maillages triangulaires (tétraédriques en 3D), soit des maillages structurés interprétés en format nonstructurés comme des rectangles (hexaèdres), pour une simulation de tous les écoulements fluides, compressibles ou incompressibles, impliquant des phénomènes physiques complexes tels que la turbulence, le transfert thermique, les réactions chimiques, les écoulements multiphasiques... et ce sur les géométries complexes industrielles. Ce produit inclut également un véritable environnement CAO et un mailleur paramétrique de dernière génération, permettant de mettre en place

rapidement les modèles numériques ou de s'intégrer aux outils de conception ^déjàexistants (SOLIDWORKS, CATIA, I-DEAS, Pro/E...)

Le maillage est lu dans fluent comme un nouveau cas et il est possible de l'améliorer : lissage (grid smoothing) ou permutation des arêtes (grid swapping). Pour débuter une simulation, il faut passer dans chaque menu déroulant de Fluent (en commençant par la gauche) pour initialiser les différents paramètres de la simulation (modèle de turbulence, condition aux limites, etc.).



Figure (II.10) : Interface FLUENT 13.

II.4. Maillage hybride

II.4.1. Position du problème

Généralement on dit que, aucune des techniques de génération automatique, telles qu'elles existent aujourd'hui, ne peut seule respecter l'ensemble des critères imposés à un maillage. Ainsi un bon maillage pour un programme qui résout les équations de type Euler peut être de mauvaise qualité pour un programme traitant les équations de type Navier- Stokes. Dans le premier cas (Euler), il est fondamental d'avoir des éléments qui ne soient pas aplatis alors que dans le second cas, on demande un élancement important des éléments dans La direction de L'écoulement.

La technique des maillages hybrides trouve sa justification et sa motivation dans La tentative de résoudre cette contrainte. Dans cette partie nous faisons d'abord un historique des maillages hybrides, ensuite le processus de génération de maillage hybride prismatique proche parois et ses déférentes lois correspondantes.

II.4.2. Historique des maillages hybrides

Depuis la fin des années 80 les maillages hybrides ont commencé à attirer l'attention des chercheurs comme alternative à l'utilisation de maillages non structurés dans tout le domaine. Dans l'approche non-structurée pure et pour avoir une certaine

précision numérique, il faut utiliser beaucoup de tétraèdres dans la région de la couche limite, augmentant ainsi la probabilité d'avoir des éléments de pauvre qualité connus sous le nom de Slivers à l'origine de certaines imprécisions et singularités numériques. On a don un impact direct négatif sur la précision, le temps de calcul, et sur la robustesse des programmes informatiques dont le maillage est le support. Les premiers résultats concrets dans cette nouvelle approche de maillages hybrides datent de 1993 avec Nakahashi (1993) [15], Kallinderis et Ward (1993) [16]. Marcum (1995) [17], par l'exemple que nous illustrons ci-dessous montre que l'utilisation de quadrilatères à la place de triangles au niveau de la couche limite, a pour effet à précision numérique égale de réduire le nombre d'éléments, donc le temps de calcul. Kallinderis (1995), montre l'avantage de l'utilisation de maillage structurés par rapport aux non structurés pour mieux capter la physique du problème dans la couche limite, et réduire par la même occasion les temps de calculs.



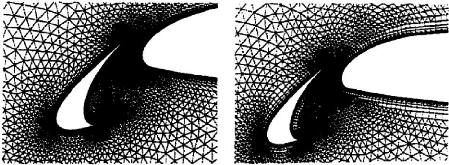
Figure (II.11): Exemple de Marcum (1995) faisant passer le nombre de triangle de
11544 au niveau de la couche limite (maillage non-structuré pur, figure à gauche) à
5772 quadrilatères (maillage hybride, figure à droite).

Pour des raisons d'espace mémoire, de vitesse d'exécution, et le désir d'avoir des éléments étirés à grand coefficient de forme, ils ont proposé l'utilisation d'éléments prismatiques structurés au niveau de la couche limite pour former le maillage, zone ou les effets visqueux sont dominants, et d'éléments tétraédriques à l'extérieur de la couche limite ou l'écoulement est non visqueux.

II.4.3. Processus de génération de maillage hybride (tétra/prisme)

II.4.3.1. Lois de croissance (Growth Law)

Détermine la hauteur totale des couches données, la hauteur de la première couche et le facteur de progression pour les trois types suivants : [18]

> Linéaire

La hauteur de la couche particulière d'un prisme est définie par :

H = h[1 + (n - 13(r - 13] (II. 4)

Avec:

h=hauteur initiale (initial height) r=facteur de progression (height ratio) n=nombre des couches (layer number)

La hauteur totale à la couche n est :

[(n - 13(r - 13 + 2]

ho = nh (II. 5)

2

> Exponentiel

La hauteur de la couche particulière d'un prisme est définie par :

H = h * r(y-1) (II. 6)

La hauteur totale à la couche n est :

(1 - rⁱ')

ho = h (1 - r) (II. 7)

> WB-Exponential

C'est la loi de croissance exponentielle est définie dans l'ANSYS Workbench. La hauteur de la couche particulière d'un prisme est définie par :

H = h * exp[(~_13(1_~3] (II. 83



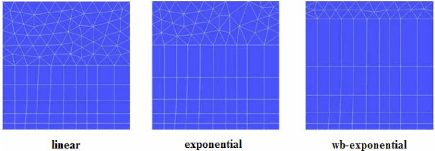
Figure (II.12) : Croissances des prismes. > La hauteur initiale (Initial height)

Est la hauteur d'élément de la première couche.

Si la hauteur initiale est placée à 0, la maille d'entrée elle sera calculée automatiquement

> Facteur de progression (Height ratio)

Est le facteur de progression de la première couche. Ce rapport sera multiplié par la taille d'élément de la couche précédente pour définir la taille de la prochaine couche.

> Nombres des couches de prisme (Number of layers) Est le nombre de couches à développer.

> La hauteur totale (Total height)

Est la hauteur totale de toutes les couches de prisme.



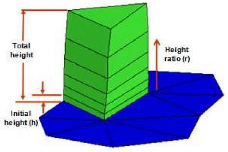
Figure (II.13) : Hauteur des prismes.

II.5. Conclusions

Ce chapitre nous a permis de nous familiariser avec les techniques générales de la simulation numérique et comprendre l'outil de génération de maillage et solution le très utilisées en aérodynamique. La méthode qui nous intéresse dans notre travail est celle de type hybride.

Dans l'utilisation d'un maillage hybride, un bon compromis entre les critères robustesse offerte, résolution et précision souhaité et coûts de calculs induits doit être trouvé. D'une manière générale, approximativement 50% des noeuds de maillage se trouveront dans les couches limites, essentiellement composées d'hexaèdres et/ou des prismes, et 50% dans le restant du domaine de calcul, essentiellement composé de tétraèdres. Le choix final de discrétisation devra refléter cette situation.



CHAPITRE

III GENERATION DE

MAILLAGE HYBRIDE &

SOLUTION SUR

ARA M100

SOMMAIRE PAGE

III.1. Introduction 38

III.2. Définition de la géométrie ARA M100 Aile-Fuselage 38

III.3. Génération du maillage (ICEM CFD 13) 40

III.4. Solution par Fluent 47

III.5. Conclusion 58

III.1. Introduction

Dans cette section, on présente les étapes de génération de maillage hybride (tétra/prisme) sur la configuration Ail-Fuselage ARA M100, ensuite les étapes dans fluent par le logiciel ANSYS 13.

III.2. Définition de la géométrie ARA M100 Aile-Fuselage

La configuration aile-fuselage du model ARA M100 c'est une géométrie d'un modèle de soufflerie examiné dans United Kingdom's Aircraft Research Association. L'aile est montée approximativement centralement sur l'axe de fuselage. [19]

La géométrie contienne des ensembles des points (x, y, z) définissent cette
configuration.

Avec :

· X : axe orienté dans la direction d'écoulement, positif en aval.

· Y : axe orienté verticalement, positif vers le haut.

· Z : axe orienté dans la direction de l'envergure, positif à l'extérieur.

L'origine des axes est située au nez du fuselage.

III.2.1. Plan de symétrie

C'est un plan 2D définissent le fuselage est donnée par un ensemble de 38 points dans le plan xy de l'avion.

III.2.2. Aile

La surface de l'extrados et l'intrados représenté par des 22 courbes suivant la direction de l'envergure apartir de l'emplanture jusqu'à l'extrémité de l'aile (tip), Chacune de ces courbes est définie par un ensemble de 52 points.

III.2.3. Extrémité d'aile (Tip)

L'extrémité de l'aile (Tip) est représentée par 9 courbes, chacune d'elles est définie par un ensemble de 51 points.

III.2.4. Dimensions de la géométrie ARA M100





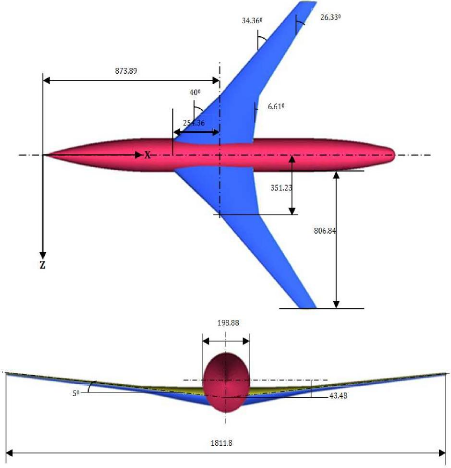
Figure (III.1) : Dimensions d'ARA M100

III.3. Génération du maillage (ICEM CFD 13)

La génération du maillage est une phase très importante dans le cadre d'une modélisation CFD, compte tenu de son influence sur la solution calculée. La technique de génération de maillage peut être résumée par les étapes suivantes :

· La géométrie doit être préparée au préalable, avec la définition de tous les composants sous forme, fichier TIN ou sous forme de fichier maillage qu'on peut importer sous ICEMCFD.

· La géométrie qui représente les différents domaines fluides est décomposée en sous

domaines «maillables».

· Maillage des sous domaines fluides.

Le maillage qui peut être utilisé sur ARA M100 est de type hybride (tetra/prisme). La forme géométrique des cellules de discrétisation sont triangulaires et prismatiques. Cette variété d'éléments assure une certaine flexibilité lors de la génération du maillage et permet ainsi de choisir l'élément adéquat pour épouser au mieux la forme géométrique du problème.

III.3.1. Génération de maillage tétraédrique

III.3.1.1. Importation de la géométrie et nettoyage de la CAO

Dans ce cas, on a recours à l'importation de la géométrie. Il est conseiller d'importer des fichiers sous format TETIN (*.tin). Souvent il est indispensable de nettoyer la géométrie.



File

Geometry

Open Geometry

Figure (III.2) : Importation de la géométrie et nettoyage de la CAO

III.3.1.2. Création des familles

Dans cette étape on va subdiviser l'élément importé (la géométrie et le Domaine) en plusieurs sous éléments de point de vue surfaces et courbes pour chacun, avec une association des noms de familles pour éviter le désordonnément.



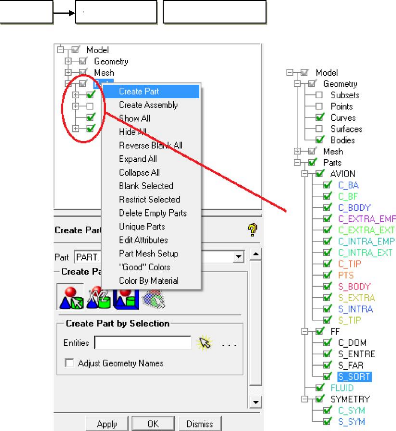
Parts

Create Parts

Create Assembly

Figure (III.3) : Création des familles

III.3.1.3. Définition du domaine « FLUID »

Lors de la création des parties, il est obligatoire de créer un point qui n'appartient pas à la géométrie elle-même, mais qui est contenu dans le domaine de calcul. Ce point va permettre de déterminer le domaine à maillé (far-field).

			Create Body	Geometry





Figure (III.4) : Création d'un point matériel

III.3.1.4. Paramètres de maillage

Les paramètres de maillage sont choisis de telle manière à avoir un maillage voulu (raffiné ou gros). La précision de la solution dépend de la qualité du maillage obtenu.

			Part Mesh Setup	Mesh

Tableau (III.1) : Paramètres de maillage tétraédrique



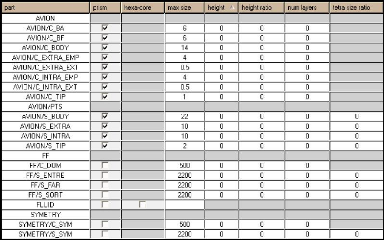
III.3.1.5. Choix et génération de type de maillage

Mesh

Compute Mesh

Tetra/mixed

Compute

Cette étape consiste à choisir le type de maillage à générer (Tétraédrique).





Figure (III.5) : Affichage de maillage (Tecplot)

III.3.1.6. Vérification de maillage

Pour dire que notre maillage est faisable, il faut vérifier les conditions suivantes :

· Si le domaine n'est pas ouvert dans quelque part de la géométrie.

· S'il n'y a pas d'écrasement des éléments.

· Si le maillage est raffiné ou non dans chaque partie de la géométrie selon les besoins.

III.3.2. Génération des couches de prisme sur ARA M100

Après avoir le maillage tétra, on peut générer les couches de prisme sur la géométrie pour simulé mieux l'écoulement dans la couche limite sur toute la géométrie, pour cela on a suivi les étapes suivantes :

III.3.2.1. Paramètres général des prismes



Mesh

Global Mesh

Prism Meshing Parameters



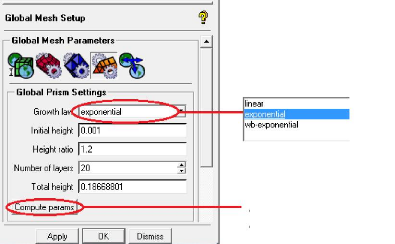
Compute parameters pour calculer la hauteur totale des couches de prisme

Figure (III.6) : Paramètres de la hauteur des prismes Tableau (III.2) : Valeurs des hauteurs

Parameters	Paramètres	Description		Valeurs	Initial height
Hauteur initiale	Hauteur initiale de la première couche des prismes.	0.001 mm		Height ratio
Facteur de progression	Ce rapport sera multiplié par la taille d'élément de la couche précédente pour définir la taille de la prochaine couche.	1.2 mm		Numbre of layers
Nombre de couches	Est le nombre de couches à développer.	20 couches		Total height
Hauteur totale	Est la hauteur totale de toutes les couches.	0.1866mm

III.3.2.2. Paramètres de prismes sur chaque partie de la géométrie

Mesh
			Part Mesh Setup

· sélectionner seulement les parties qui contiennent les couches de prisme.

· Remplir les valeurs des hauteurs (Height), facteur de progression (Height Ratio) et nombre de couches (Num Layers) de toutes les parties contiennent les couches de prisme.

· Mettant zéro dans les autres parties.

Tableau (III.3) : Paramètres de maillage prismatique



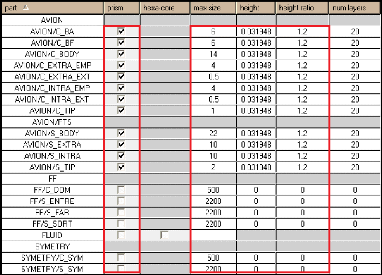
III.3.2.3. Lancement de maillage prismatique

Séléctionner create prism layers pour générer les couches de prisme sur le maillage tetra.

Mesh
			Compute Mesh				Volume Mesh



Enfin, Pour avoir les couches de prisme, on clic sur Compute pour commencer à générer le maillage.

Mesh

Compute

Compute Mesh

Prism Mesh







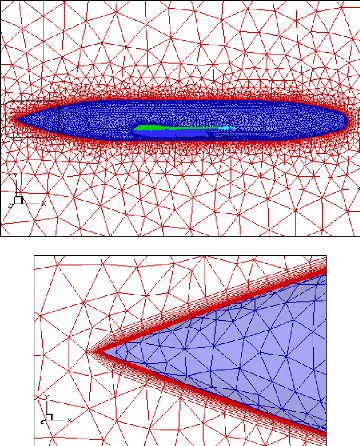
Figure (III.7) : Génération de maillage prismatique (Tecplot)

Paramètres de maillage obtenu Total elements 908699 Total nodes 354044 Min -4000 -4000 0 Max 8000 4000 4000

III.3.3. Exportation vers Fluent 13

Pour enregistrer le maillage sous format (*.msh), il faut spécifier le solveur. Dans notre cas, nous choisissons : Fluent_V6.

Output
			Select Solver

Tout est ainsi défini (géométrie, maillage). Il ne reste plus qu'à sauver l'ensemble au format Fluent.

Output
			Write Input

Le fichier d'enregistrement se retrouve dans le répertoire choisi.

III.4. Solution par Fluent

Fluent est un solveur qui utilise des maillages non-structurés 2D ou 3D (avec la méthode des volumes finis). Ces maillages sont : soit des maillages triangulaires (tétraédriques en 3D), soit des maillages structurés interprétés en format nonstructurés comme des rectangles (hexaèdres), pour une simulation de tous les écoulements fluides, compressibles ou incompressibles, impliquant des phénomènes physiques complexes tels que la turbulence, le transfert thermique, les réactions chimiques, les écoulements multiphasiques... et ce sur les géométries complexes industrielles. Ce produit inclut également un véritable environnement CAO et un mailleur paramétrique de dernière génération, permettant de mettre en place rapidement les modèles numériques ou de s'intégrer aux outils de conception déjà existants.

III.4.1. Principales étapes de simulation sous Fluent

Cette partie fournie une introduction à FLUENT, une explication de ses aptitudes, et des instructions afin de citer les paramètres du solveur. Il explicite les étapes nécessaires pour réussir une simulation d'un problème en mécanique des fluides.



File

Read

Mesh...

III.4.1.1. Importation du fichier (*.msh)

Pour commencer la simulation il faut importer le fichier (*.msh) généré sous ICEM CFD.



Figure (III.8) : Importation du maillage

III.4.1.2. Vérification du maillage importé

Mesh
	Check

Ceci permet de vérifier si le maillage importé ne contient pas d'erreurs ou de volumes négatifs.



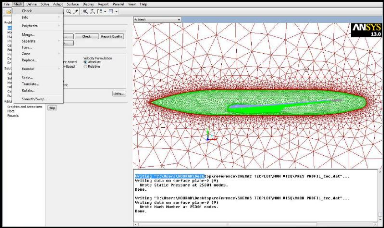
Figure (III.9) : Vérification du maillage sou Fluent

III.4.1.3. Lissage du maillage (Smooth and Swap the Grid)

Mesh

Smooth/Swap..



Pour s'assurer de la qualité du maillage, il est pratique de lisser le maillage, cliquez sur le bouton Smooth puis sur le bouton Swap. Répétez jusqu'à ce que FLUENT affiche que zéro faces sont swapped.



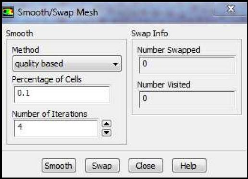
Figure (III.10) : Lissage du maillage

III.4.1.4. Vérification de l'échelle





Mesh

Scale

Il faut toujours vérifier que les dimensions affichées correspondent aux dimensions physiques du problème.



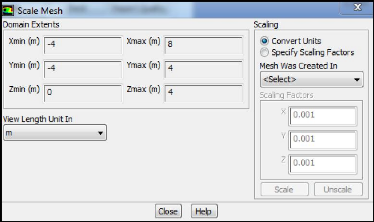
Figure (III.11) : Vérification des unités

III.4.1.5. Choix du modèle de turbulence

Define

Models

Viscous

Fluent propose différentes modélisations de l'écoulement turbulent. Soit des écoulements non visqueux, laminaires, turbulents ... etc.



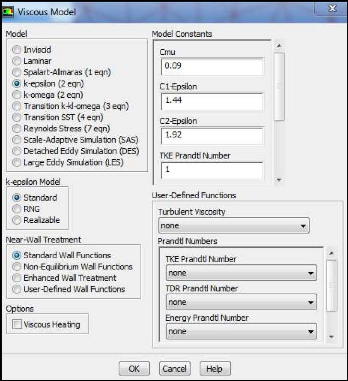
Figure (III.12) : Choix du modèle de turbulence

Tableau (III.4) : Modèles de turbulence [20]

Modèles	Avantages		Inconvénients	Spalart-Allmaras
Economique (1 equ). Bon pour les écoulements moyennement complexes.	N'est pas largement testé.		STD k-?
Robuste, économique et relativement précis.	Résultats médiocre pour des écoulements complexes (fort gradient de pression, rotation et swirl).		RNG k-?
Bon pour des écoulements moyennement complexes (impact de jet, séparation d'écoulements, écoulements secondaires...)	Limité par l'hypothèse de viscosité turbulente isotrope.		Realizable k-?
Offre les mêmes avantages que le RNG. Recommandé dans le cas des turbomachines.	Limité par l'hypothèse de viscosité turbulente isotrope.		Reynolds Stress Model (RSM)
Le modèle le plus complet Physiquement (transport et l'anisotropie de la turbulence sont tenus en compte)	Requiert plus de temps CPU. Les équations de quantité de mouvement et turbulence sont étroitement liées.		SST et standard k-ù
Modèle le plus recommandé pour les problèmes liés aux turbomachines, meilleur que le Realizable k-?.	Nécessite une plus grande résolution du maillage aux frontières (pas de aux murs).

III.4.1.6. Définition des caractéristiques du fluide

			Materials	Define

Les caractéristiques du fluide sont chargées à partir de la bibliothèque de données de Fluent.



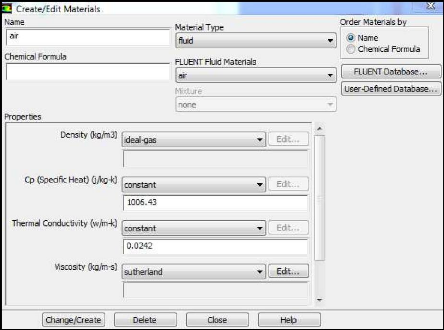
Figure (III.13) : Définition des caractéristiques du fluide III.4.1.7. Conditions opérationnel



Define Operating conditions

Avant de choisir les conditions aux limites, il faut choisir d'abord la valeur de la pression de référence « operating conditions ».



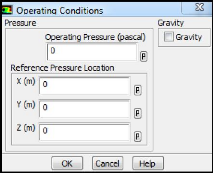
Figure (III.14) : Choix de la pression de référence

En effet, Fluent effectue tous les calculs, avec une pression appelée gauge pressure et ce afin d'éviter les erreurs d'ordre numérique lors du calcul pour des écoulements à faible nombre de mach. La relation liant la pression absolue à la « gauge pressure » est donnée par :

Pabs = P0p + Pgauge

Fluent prend par défaut la valeur de la pression atmosphérique comme operating pressure.

Ensuite, il faut choisir les conditions aux limites :

III.4.1.8. Conditions aux limites

			Boundary Conditions	Define

Ensuite, il faut fixer les valeurs des conditions aux limites : Pour le domaine :

Pressure-far-field : Utilisée pour des écoulements compressibles, quand le nombre de mach et l'angle d'incidence sont connus.

· ff/s_entre : Ps = 101325 pa, M =0.8027, á = 2.873°.

· ff/s_sort : Ps = 101325 pa, M =0.8027, á = 2.873°.

· ff/s_far : Ps = 101325 pa, M =0.8027, á = 2.873°.

· volume du domaine "fluide" : "fluid" (garder par défaut).



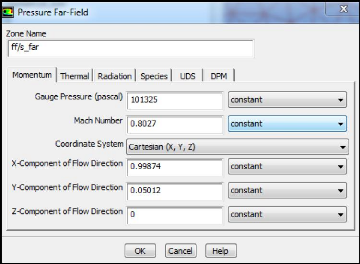
Figure (III.15) : Pressure-far-field pour tout le domaine

Wall : est utilisé pour délimiter les régions solides des régions fluides. En général on utilise les propriétés d'une paroi lisse i-e Roughness Height = 0 et Roughness Constant = 0.5 (sur toute la géométrie ARA M100).



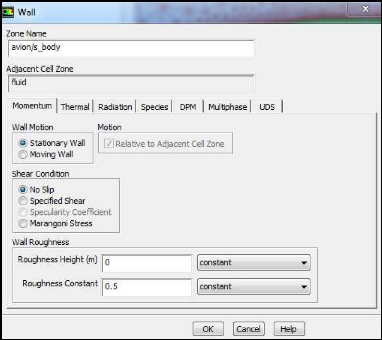
Figure (III.16) : Wall

Symétrie : Les gradients normaux et la vitesse normale au plan de symétrie sont nuls.



Figure (III.17) : Symétrie

III.4.1.9. Choix des critères de convergence

Solve		Monitors		Residual...



Il s'agit ici de choisir les critères qui doivent être vérifiés pour que les calculs de la simulation s'arrêtent.



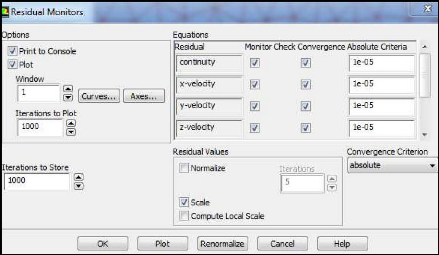
Figure (III.18) : Choix et affichage pendant les calculs des critères de convergence
(residuals)



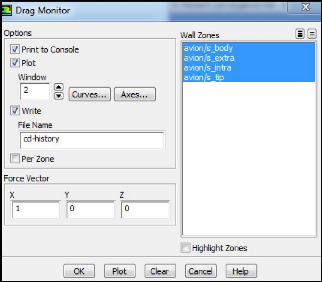
Figure (III.19) : Choix et affichage pendant les calculs des critères de convergence
(Drag & Lift)

Pour afficher la convergence à l'écran pendant les calculs sous forme d'un graphe, il faut activer l'option Plot. Il est possible de désactiver certains critères d'arrêt de la simulation en décochant la case de convergence.

Remarque importante

Les résidus sont calculés à partir des corrections dans les variables ; pression, vitesse, température... du problème entre la présente itération et l'itération précédente. Dans la plupart des cas, le critère de convergence par défaut dans FLUENT (residual) est suffisant. La solution converge quand les résidus atteignent 10^-3. Toutefois, dans certains cas il faut pousser les calculs à 10^-4 voir 10^-6. Il n'y a pas de règle universelle ! Dans le cas des écoulements diphasiques, il faut impérativement pousser la convergence à 10^-4. [18]

III.4.1.10. Initialisation des calculs

Solve

Inisialization



Il est conseillé dans nombreux cas d'initialiser les calculs aux conditions de l'entrée. Toutefois s'il y a un calcul qui a déjà convergé et que vous désirez changer juste un paramètre (exp. Vitesse d'entrée), il est préférable d'initialiser au calcul précédent déjà convergé.



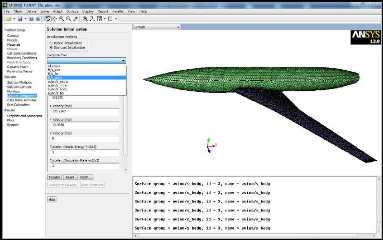
Figure (III.20) : Initialisation des calculs

III.4.1.11. Animation

Solve
		Calculation activities



Pour créer une vidéo qui affiche la solution il faut activer l'option "Animate"



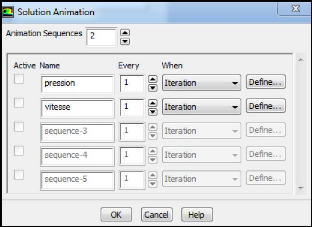
Figure (III.21) : Création d'animation

Il faut spécifier le type de contour que l'on veut visualiser : champs de pression, champs de vitesses, etc.

III.4.1.12. Sauvegarde du fichier *.cas

File
			Write			Case & Data

Il est conseillé qu'une fois le paramétrage est effectué, de sauvegarder le fichier en format *.cas. S'il y a un bug durant les calculs, il suffit de charger le fichier *.msh, on n'aura pas à refaire le paramétrage.

III.4.1.13. Lancement de la simulation

Solve

Run calculation



Le paramétrage étant effectué, il ne reste plus qu'à choisir le nombre d'itérations que Fluent devra réaliser.



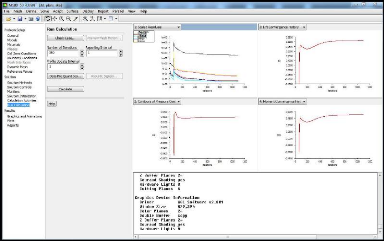
Figure (III.22) : Lancement de la simulation

III.5. Conclusion

Dans ce chapitre nous avons décrire les étapes générales de génération de maillage hybride dans ICEM CFD et solution dans Fluent.

Dans l'étape de l'affichage des résultats, tous les résultats de la simulation peuvent être affichés, tels que la vitesse, la pression et d'autres paramètres obtenus lors des calculs. Il est possible de visualiser les contours de pression, le champ des vecteurs de vitesse, etc.



CHAPITRE

IV

RESULTAS ET

VALIDATIONS

SOMMAIRE PAGE

IV.1. Introduction 59

IV.2. Les Conditions aux limites 59

IV.3. Première simulation 59

IV.4. Deuxième simulation 64

IV.5. Contours de coefficient de pression 72

IV.6. Troisième simulation 75

IV.7. Forces de chaque angle d'incidence 82

IV.8.Calcule des coefficients pour chaque á 82

IV.9. Conclusion 84

IV.1.Introduction

Dans cette section, nous allons présenter les résultats obtenus avec le code Fluent utilisé dans le cadre de ce travail, ainsi une vue d'ensemble du procédé de la vérification et de la validation des simulations. Le traitement consiste donc à visualiser les résultats. On utilise pour cela les logiciels de visualisation TECPLOT, ORIGIN et GRAFWIN. L'utilisation de ces logiciels est a raison plus simple qu'ils permettent de visualiser/tracer des résultats directement à partir d'un fichier.

La visualisation peut être sous forme des contours (Mach, Pression) ou sous forme des graphes (Cl, Cd, Cm, Cp...) afin de les tracer avec des données expérimentales dans le même plan pour facilité l'interprétation et voir clairement la différence.

IV.2.Les Conditions aux limites

Cette phase est la plus importante, par ce qu'on doit savoir le type de condition qui convient à chaque zone. Il existe plusieurs types de conditions aux limites dans fluent, dans notre travail on fait la simulation pour un écoulement compressible on utilise dans ce cas les conditions suivantes : voir tableau (IV.1)

Tableau (IV.1) : Définition des conditions aux limites

Nom	Type
ff/s_entre	Pressure-far-field
ff/s_far	Pressure-far-field
ff/s_sort	Pressure-far-field
avion/s_body	Wall
avion/s_extra	Wall
avion/s_intra	Wall
avion/s_tip	Wall
int_fluid	Interior
symetry/s_sym	Symmetry

IV.3.Première simulation

IV.3.1. Calcule non visqueux

IV.3.1.1. Configuration d'écoulement

Lors de cette première simulation nous considérons : Angle d'attaque : 2.873 degrés.

Nombre de mach : 0.8027.

Nombre de Reynolds : 13.1 E+06.

IV.3.1.2. L'histoire de convergence des résidus

La figure ci-dessous montre l'histoire de convergence exprimée en termes de résidus.



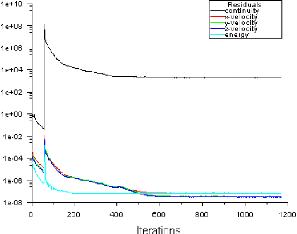
Figure (IV.1) : Historique des résidus

IV.3.1.3. L'histoire de convergence des coefficients Cd, Cl et Cm



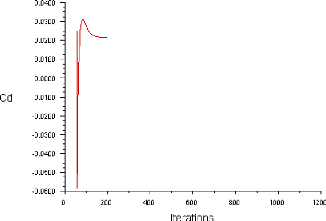
Figure (IV.2) : Historique des Coefficient de trainée (ORIGIN)



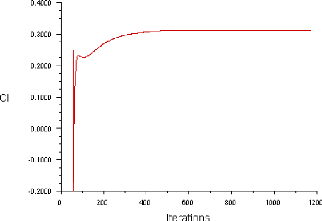
Figure (IV.3) : Historique des Coefficient de Portance (ORIGIN)



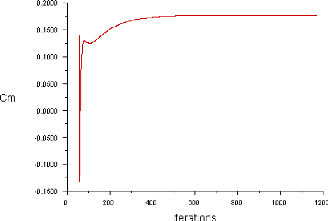
Figure (IV.4) : Historique des Coefficient de Moment (ORIGIN)

D'après les figures ci-dessus, on peut dire que la solution a été convergée ; d'une part, parce que le résidu des variables conservatives a une allure presque constante en dépassant 600 itérations Figure (IV.1) et d'autre part pour confirmer la convergence, les Figures (IV.2), (IV.3) et (IV.4) montre l'allure des coefficients des forces en fonction d'itération dont ces coefficients prennent des valeurs constantes au dessus de 500 itérations.

IV.1.3. Les contours de pression et vitesse autour d'ARA M100

Dans l'étape de l'exploitation des résultats, tous les résultats de la simulation peuvent être exploités, tels que la vitesse, la pression et autres paramètres obtenus lors des calculs. Il est possible de visualiser les contours de pression, le champ des vecteurs de vitesse, etc. Voici ci-dessous quelques résultats obtenus :

IV.1.3.1. Contours de pression statique sur ARA M100



Figure (IV.5) : Répartition de la pression statique sur ARA M100 extrados (Tecplot)



Figure (IV.6) : Répartition de la pression statique sur ARA M100 intrados (Tecplot)



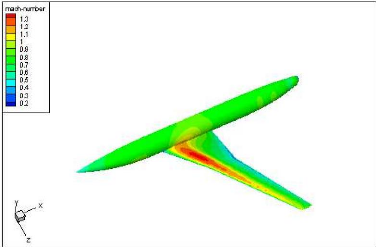
IV.1.3.2. Contours de Mach sur ARA M100



Figure (IV.7) : Répartition du nombre de mach sur ARA M100 extrados (Tecplot)
Figure (IV.8) : Répartition du nombre de mach sur ARA M100 intrados (Tecplot)

D'après les contours que l'on a obtenus nous permet de faire les remarques suivantes :

· Apparition d'une zone de suppression sur l'intrados et une dépression sur l'extrados due à la direction de l'écoulement sur le long de l'aile.

· Apparition de deux zones : l'une ou la pression est maximale (en rouge) qui correspond aux points de vitesse nulle c'est-à-dire la pression statique est la pression totale .la deuxième zone ou la pression atteint sa valeur minimale (en bleu).

IV.4. Deuxième simulation

IV.4.1. Calcule visqueux pour le model de turbulence K epsilon

IV.4.1.1. L'histoire de convergence des résidus



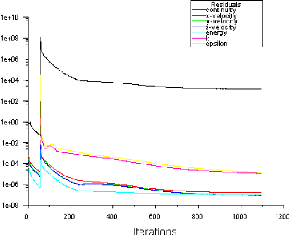
Figure (IV.9) : Historique des résidus

IV.4.1.2. L'histoire de convergence des coefficients Cd, Cl et Cm



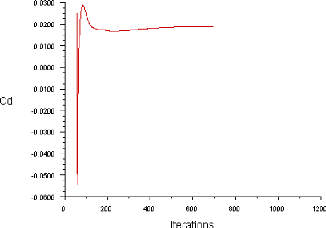
Figure (IV.10) : Historique des Coefficient de trainée (ORIGIN)



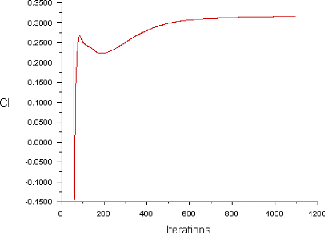
Figure (IV.11) : Historique des Coefficient de Portance (ORIGIN)



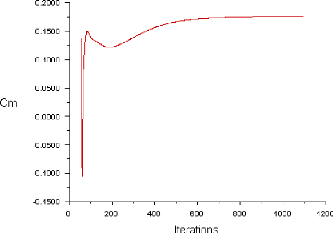
Figure (IV.12) : Historique des Coefficient de Moment (ORIGIN)

D'après les figures de convergence, on peut dire que la solution a été convergée, parce que le résidu des variables conservatives a une allure presque constante en dépassant 1000 itérations Figure (IV.9), et d'autre part pour confirmer la convergence, les figures (IV.10), (IV.11) et (IV.12) montre l'allure des coefficients des forces en fonction d'itération dont ces coefficients prennent des valeurs constantes au dessus de 1000 itérations.

IV.4.1.3. Vérification de maillage

La figure (IV.13) nous donne un aperçu général sur le maillage obtenu. La distribution de y+ à la paroi solide autour d'ARA M100 pour le maillage utilisée est de valeur y+ = 28.



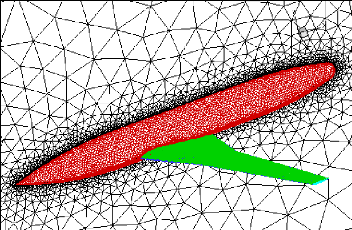
Figure (IV.13) : Maillage de l'avion ARA M100 (Tecplot)

La figure (IV.14) montre la variation d'Y⁺ plus a la paroi solide de l'aile sur les stations 0.019, 0.325, 0.635 et 0.936



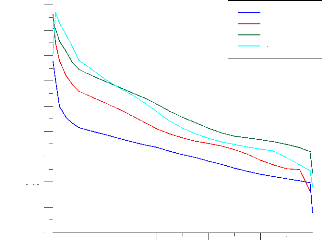
Y Plus

17.00

16.00

15.00

14.00

13.00

12.00

11.00

10.00

9.00

8.00

STATION 0.019 STATION 0.325 STATION 0.635 STATION 0.936

0.00 0.20 0.40 0.60 0.80 1.00

X/C

Figure (IV.14) : Variation d'Y⁺ plus sur chaque station de l'aile (GRFWIN)

IV.4.1.4. Contours de pression statique sur ARA M100

Les figures (IV.13), (V.14) et (IV.15) montrent respectivement la distribution de pression sur toute la surface de l'avion ainsi que la distribution sur le profil d'aile.



Figure (IV.15) : Répartition de la pression statique sur ARA M100 extrados (Tecplot)



Figure (IV.16) : Répartition de la pression statique sur ARA M100 intrados(Tecplot)

IV.4.1.5. Contours de pression statique sur le profil d'aile



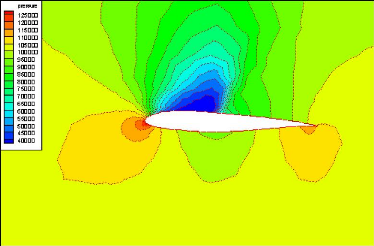
Figure (IV.17) : Contours de pression sur le profil d'aile IV.4.1.6. Contours de mach sur l'avion



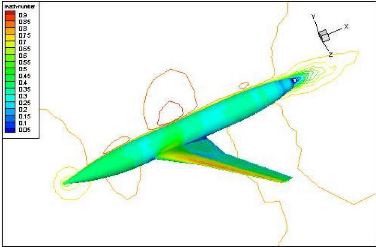
Figure (IV.18) : Contours de Mach sur l'avion

IV.4.1.7. Contours de Mach sur le profil d'aile



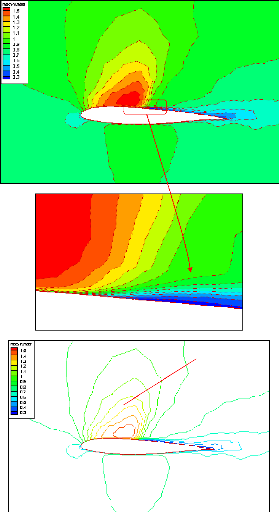
Ligne sonique

Figure (IV.19) : Contours de Mach sur le profil d'aile

IV.4.1.8. Vecteurs vitesse sur l'avion au plan de symétrie



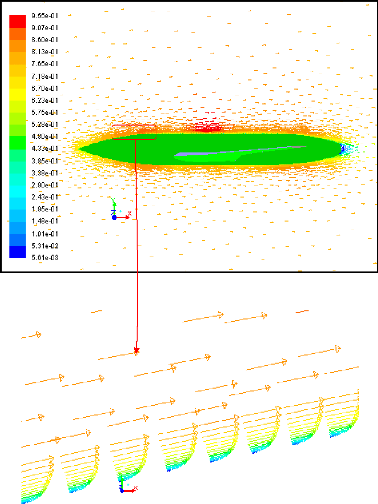
Figure (IV.20) : Vecteurs vitesse sur l'avion au plan de symétrie

IV.4.1.9. Vecteurs vitesse sur le profil d'aile



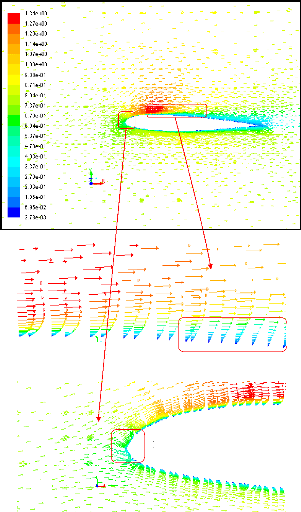
Décollement de la
couche limite

Point d'arrêt

Figure (IV.21) : Vecteurs vitesse sur le profil d'aile

Interprétation des résultats

L'écoulement amont arrive avec un angle d'incidence de 2.873⁰ degrés et il est entièrement subsonique. Au bord d'attaque se situe le point d'arrêt de l'écoulement, autour duquel se présente une zone de ralentissement (basses vitesses), due aux forts gradients de pression. Ensuite le fluide subit une accélération dans son mouvement sur l'extrados du profil qui conduit a la présence d'une zone localement supersonique (1 < M < 1.34). Cette zone est séparée de l'écoulement extérieur par la ligne sonique (figure IV.17). On observe alors la formation d'une onde de choc droite forte (avec une petite courbure), a l'extrados en aval du bord d'attaque. En aval du choc l'écoulement devient subsonique et décélère en dehors de la couche limite jusqu'a atteindre le nombre du Mach infini M₈.

Jusqu'à l'apparition de l'onde de choc, la couche limite est complètement attachée sur la

paroi. Lorsque l'onde incidente rencontre la couche limite, elle provoque une forte augmentation de la pression statique, qui se propage en aval du choc et entraine l'épaississement de la couche limite.

Sur l'intrados du profil, l'écoulement est complètement attaché à la paroi solide. Dans la
partie concave on observe une accélération. Le nombre de Mach atteind des valeurs de

l'ordre de 0.8 et la pression statique diminue. Ensuite le fluide décélère sur la partie convexe, ce qui provoque une élévation de la pression statique.

IV.5. Contours de coefficient de pression

Le coefficient de pression est un facteur très important dans l'aérodynamique, c'est

le rapport de la pression totale par rapport à la pression de référence. Le coefficient de pression est défini comme suit:

P-P₈

d_† = ₂ (IV.1)

1 2ñ8Vref

Les résultats de la simulation sont comparés avec celles expérimentaux en terme de la distribution du coefficient de pression sur l'intrados et l'extrados dans les stations radiales suivantes : ç = 0.019, 0.325, 0.635 et 0.936. De la demi-envergure comme montré dans la figure (IV.22).



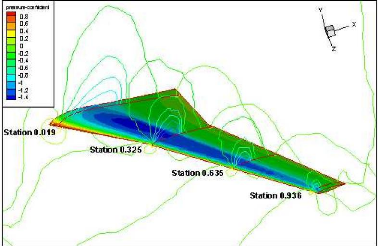
Figure (IV.22) : Stations de mesure de Cp sur l'aile d'ARA M100 (Tecplot) IV.5.1. Distribution du coefficient de pression sur l'intrados et l'extrados

Les résultats obtenus pour les deux cas de simulation précédente (non visqueux et K epsilon) sont présentés dans même figure avec les résultats expérimentaux trouvés par AGARD pour chaque station.

Station 0.019 :

0.80





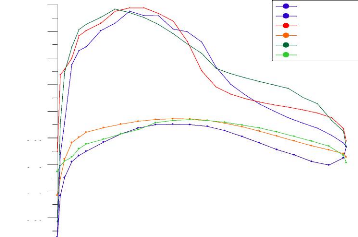
CP

-1.00

-0.80

-0.60

-0.40

-0.20

0.00

0.60

0.20

0.40

STATION 0.019

Cp EXT-EXPR

Cp INT-EXPR

Cp EXT-K epsilon

Cp INT-K epsilon

Cp EXT-NON visqueux
Cp INT-NON visqueux

0.00 0.20 0.40 0.60 0.80 1.00

X/C

Figure (IV.23) : Distribution du coefficient de pression calculé et expérimental sur l'intrados et l'extrados pour la station 0.019 (GRAFWIN)



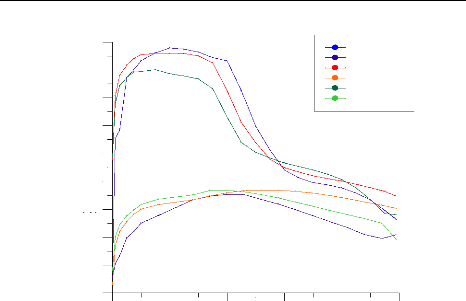
Cp

Station 0.325 :

STATION 0.325

-0.75

-0.50

-0.25

0.00

0.25

0.50

0.75

-1.50

-1.25

-1.00

Cp EXT-EXPR

Cp INT-EXPR

Cp EXT-K epsilon

Cp INT-K epsilon

Cp EXT-NON visqueux
Cp INT-NON visqueux

0.00 0.20 0.40 0.60 0.80 1.00

x/C

Figure (IV.24) : Distribution du coefficient de pression calculé et expérimental sur l'intrados et l'extrados pour la station 0.325 (GRAFWIN)



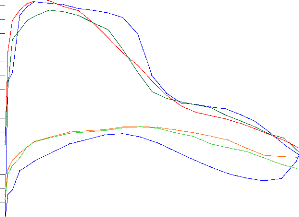
Cp

Station 0.635 :

-1.50

-1.25
-1.00

-0.75

STATION 0.635

Cp EXT-EXPR

Cp INT-EXPR

Cp EXT-K epsilon

Cp INT-K epsilon

Cp EXT-NON visqueux Cp INT-NON visqueux



-0.50

-0.25

0.00

0.25

0.50

0.75



0.00 0.20 0.40 0.60 0.80 1.00

x/C

Figure (IV.25) : Distribution du coefficient de pression calculé et expérimental sur l'intrados et l'extrados pour la station 0.635 (GRAFWIN)



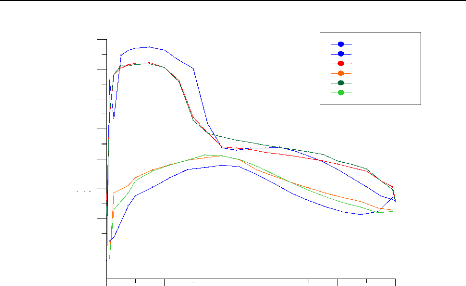
Station 0.936 :

STATION 0.936

-0.50

-0.25

0.00

0.25

0.50

0.75

CP

-1.25

-1.00

-0.75

Cp EXT-EXPR

Cp INT-EXPR

Cp EXT-K epsilon

Cp INT-K epsilon

Cp EXT-NON visqueux
Cp INT-NON visqueux

0.00 0.20 0.40 0.60 0.80 1.00

X/C

Figure (IV.26) : Distribution du coefficient de pression calculé et expérimental sur l'intrados et l'extrados pour la station 0.936 (GRAFWIN)

On s'intéresse à l'évolution du coefficient de pression Cp intrados et extrados du profil en fonction de la corde adimensionnel x/c. Cette évolution est représentée sur les figures (IV.20), (IV.21), (IV.22) et (IV.23). La courbe supérieure se réfère à l'extrados et la courbe inférieure se réfère à l'intrados. À l'extrados, on met clairement en évidence la forte dépression près du bord d'attaque du profil. Sur la fin du profil, la pression augmente. Pour ce qu'est de l'intrados, on observe aussi une dépression près du bord d'attaque, mais bien moins intense que celle de l'extrados. En comparant avec les valeurs expérimentales, on remarque que le Cp a presque la même allure à mois qu'il y a une faible différence.

IV.6. Troisième simulation

IV.6.1. Calcule visqueux pour le model de turbulence K epsilon IV.6.1.1. Configuration d'écoulement

Lors de cette troisième simulation nous considérons :

· Angle d'attaque variable : -3.017⁰, -2,8730, 0⁰ et 3.017⁰ degrés.

· Nombre de mach : 0,8027.

· Nombre de Reynolds : 13,1 E+06.



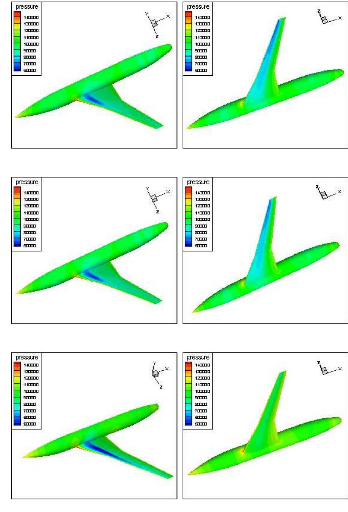
Figure (IV.27) : Contours de pression pour á=-3.017⁰ (Tecplot)

á = -2.873⁰

Figure (IV.28) : Contours de pression pour á=-2.873⁰ (Tecplot)

á = 00

Figure (IV.29) : Contours de pression pour á=0⁰ (Tecplot)

IV.6.1.2. Contours de pression statique sur ARA M100 pour chaque á á = -3.017⁰

á = 3.017⁰



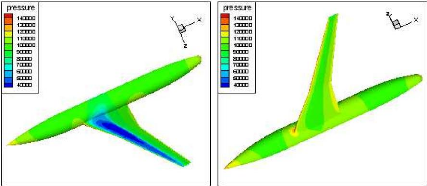
Figure (IV.30) : Contours de pression pour á=3.017⁰ (Tecplot) IV.6.1.3. Contours de pression statique sur le profil d'aile pour chaque á á = -3.017⁰ á = -2.873⁰



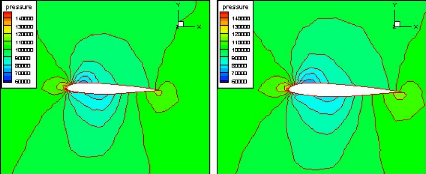
á = 00 á = 3.017⁰



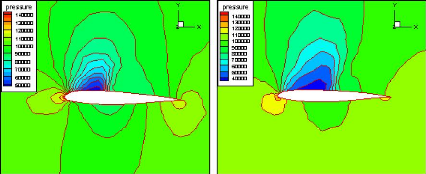
Figure (IV.31) : Contours de pression sur le profil à á=3.017⁰, -2.8730, 0⁰ et 3.017⁰
(Tecplot)



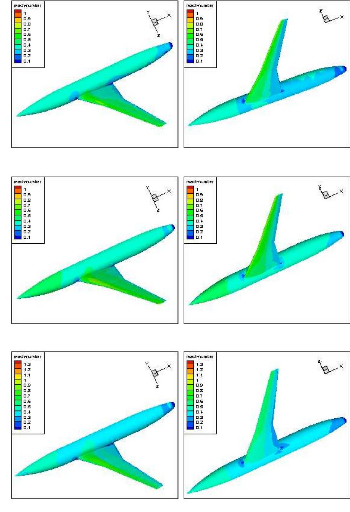
Figure (IV.32) : Contours de Mach pour á=-3.017⁰ (Tecplot)

á = -2.873⁰

Figure (IV.33) : Contours de Mach pour á = -2.873⁰ (Tecplot)

á = 00

Figure (IV.34) : Contours de Mach pour á=0⁰ (Tecplot)

IV.6.1.4. Contours de Mach sur ARA M100 pour chaque á á = -3.017⁰

á = 3.017⁰



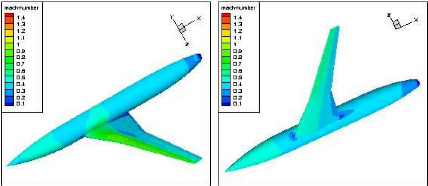
Figure (IV.35) : Contours de Mach pour á=3.017⁰ (Tecplot) IV.6.1.5. Contours de Mach sur le profil d'aile pour chaque á

á = -3.017⁰ á = -2.873⁰



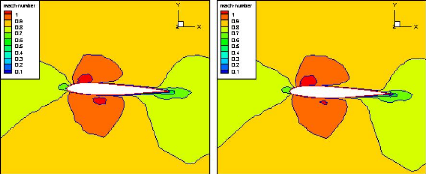
á = 00 á = 3.017⁰



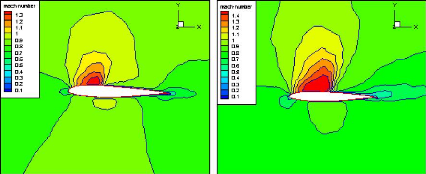
Figure (IV.36) : Contours de Mach sur le profil à á=3.017⁰, -2.8730, 0⁰ et 3.017⁰
(Tecplot)

IV.6.1.6. Coefficient de pression pour chaque á

Les résultats des coefficients de pression obtenus pour l'écoulement visqueux K epsilon dans les différents angles d'incidence á = -3.017⁰, á = -2.873⁰, á = 0⁰ et á = 3.017⁰ sont présentés dans même figure pour les stations 0.019, 0.325, 0.635 et 0.936. De la demi-envergure.



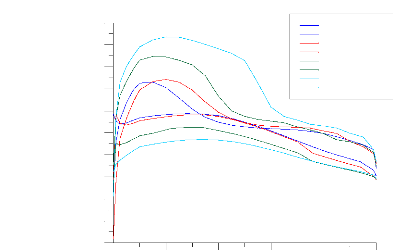
- 0.20

0.00

0.20

0.40

0.60

0.80

CP

STATION 0.019

Cp EXT- ALPHA=-3.017 Cp INT- ALPHA=-3.017 Cp EXT- ALPHA=-2.873 Cp INT- ALPHA=-2.873

Cp EXT- ALPHA=0 Cp INT- ALPHA=0

Cp EXT- ALPHA=3.017
Cp INT- ALPHA=3.017

Station 0.019 :

- 1.20

- 1.00

- 0.80

- 0.60

- 0.40

0.00 0.20 0.40 0.60 0.80 1.00

X/C

Figure (IV.37) : distribution de Cp dans la station 0.019 (GRAFWIN)



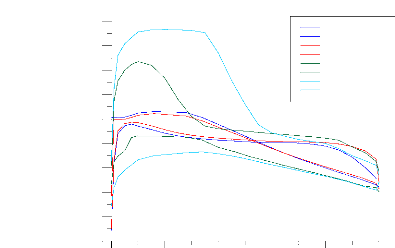
eP

Station 0.325 :

- 1.50

- 1.25

- 1.00

- 0.75

- 0.50

STATION 0.325

- 0.25

0.00

0.25

0.50

0.75

Cp EXT- ALPHA=-3.017 Cp INT- ALPHA=-3.017 Cp EXT- ALPHA=-2.873 Cp INT- ALPHA=-2.873 Cp EXT- ALPHA=0

Cp INT- ALPHA=0

Cp EXT- ALPHA=3.017 Cp INT- ALPHA=3.017

0.00 0.20 0.40 0.60 0.80 1.00

X/C

Figure (IV.38) : distribution de Cp dans la station 0.325 (GRAFWIN)



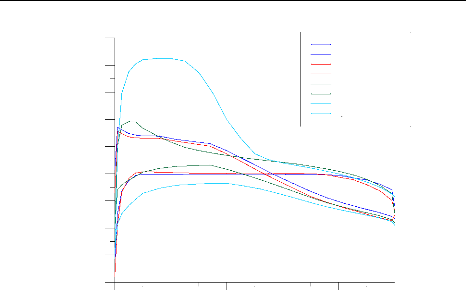
CP

Station 0.635 :

-1.50

STATION 0.635

-0.50

-0.25

0.00

0.25

0.50

0.75

-1.25

-1.00

-0.75

Cp EXT- ALPHA=-3.017 Cp INT- ALPHA=-3.017 Cp EXT- ALPHA=-2.873 Cp INT- ALPHA=-2.873 Cp EXT- ALPHA=0

Cp INT- ALPHA=0

Cp EXT- ALPHA=3.017 Cp INT- ALPHA=3.017

0.00 0.20 0.40 0.60 0.80 1.00

X/C

Figure (IV.39) : distribution de Cp dans la station 0.635 (GRAFWIN)



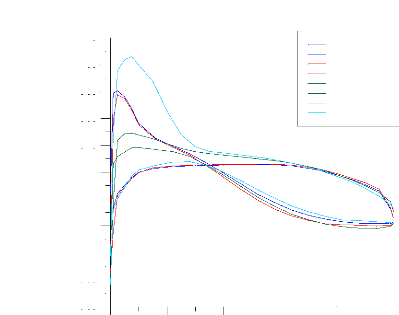
-1.20

-1.00

-0.80

-0.60

-0.40

C p

-0.20

0.00

0.20

0.40

0.60

0.80

Station 0.936 :

STATION 0.936

Cp EXT- ALPHA=-3.017 Cp INT- ALPHA=-3.017 Cp EXT- ALPHA=-2.873 Cp INT- ALPHA=-2.873 Cp EXT- ALPHA=0

Cp INT- ALPHA=0

Cp EXT- ALPHA=3.017 Cp INT- ALPHA=3.017

0.00 0.20 0.40 0.60 0.80 1.00

X/C

Figure (IV.40) : distribution de Cp dans la station 0.936 (GRAFWIN)

IV.7. Forces de chaque angle d'incidence

Tableau (IV.2) : Forces de pression

Vecteur force : (0 Y 0)
NOM DE ZONE	Force (N) á=-3.017^0	Force (N) á=-2.873^0	Force (N) á=0^0	Force (N) á=2.873^0	Force (N) á=3.017^0
s-body	115.465	142.445	452.058	773.929	789.647
s-extrados	1508.474	1595.735	2781.304	4219.39	4289.822
s-intrados	-1764.418	-1674.777	-625.895	157.91	189.432
s-tip	-0.324	-0.285	0.939	2.528	2.608
force totale (avion)	-140.803	63.118	2608.406	5153.759	6071.511

Tableau (IV.3) : Forces de viscosité

Vecteur force : (X 0 0)
NOM DE ZONE	Force (N) á=-3.017^0	Force (N) á=-2.873^0	Force (N) á=0^0	Force (N) á=2.873^0	Force (N) á=3.017^0
s-body	51.526	42.894	42.677	42.697	42.701
s-extrados	26.752	22.615	22.741	21.747	21.621
s-intrados	25.375	21.311	21.804	22.055	22.071
s-tip	0.178	0.15	0.142	0.151	0.152
force totale (avion)	103.833	86.971	87.365	86.651	86.747

IV.8.Calcule des coefficients pour chaque á

ct =

F"

2 pV2S

1

F_~

Cd =

2 PV&S 1

(IV. 2)

(IV. 3)

Tableau (IV.4) : Valeurs de Cl et Cd pour chaque á

Angles Coefficients	á=-3.017^0	á=-2.873^0	á=0^0	á=2.873^0	á=3.017^0
Coefficient de portance(Cl)	-0.006	0.004	0.184	0.365	0.433
Coefficient de trainée(Cd)	0.00308	0.00258	0.00259	0.00258	0.00258

IV.8.1. Courbe du coefficient de portance Cl

Les calculs ont été effectuées pour un nombre de Mach à l'infini M=0.8027 et un nombre de Reynolds de 13.1*10⁶. Les mesures des coefficients aérodynamiques Cd (coefficient de trainée) et Cl (coefficient de la portance) pour ce cas sont présentés dans les figures (IV.41), (IV.42). Les graphes de Cl et Cd en fonction de l'angle á est tracé par logiciel ORIGIN.



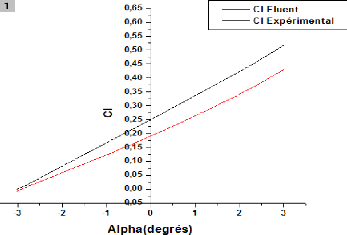
Figure (IV.41) : Variation de Cl en fonction de Alpha (ORIGIN)

IV.8.2. Courbe du coefficient de trainée Cd



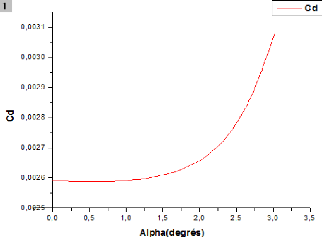
Figure (IV.42) : Variation de Cd en fonction de Alpha (ORIGIN)

IV.8.3. La polaire

La variation des coefficients de portance et de traînée en fonction de l'angle d'incidence est souvent représentée sur un seul diagramme (IV.43). Un tel diagramme s'appelle la polaire, c'est une courbe de Cd en fonction de Cl pour différents angles d'incidence.



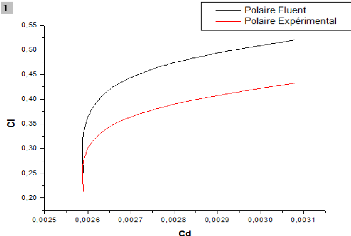
Figure (IV.43) : Variation de Cl en fonction de Cd (ORIGIN)

Les résultats obtenus par fluent sont comparés avec l'expérimental et [22, 23].

On voit que le coefficient de portance est proportionnel à l'angle d'incidence tant que l'écoulement est laminaire, puis augmente ensuite moins rapidement en écoulement turbulent. L'avion à une portance négative ceci signifie qu'il y a une surpression à l'extrados et une dépression à l'intrados.

On voit également que le coefficient de trainée varie relativement peu dans la zone des petits angles d'incidence, ensuite il augmente rapidement dans la zone des grands angles.

Donc l'évolution des ces courbes obtenus ont presque une même allure que l'expérimental et [22, 23].

IV.9. Conclusion

Dans ce chapitre nous avons présenté les résultats des calculs visqueux et non visqueux obtenus par FLUENT pour la configuration 3D aile/fuselage du model ARA M100, ainsi la validation avec l'expérimentale.

CONCLUSION GENERALE

CONCLUSION

L `industrie aéronautique est longtemps considérée comme un secteur très particulier, et le domaine par excellence où les technologies de pointe se développent. Les constructeurs disposent actuellement de plusieurs méthodes de simulation numérique sous forme de codes de calcul. Néanmoins, il est indispensable de savoir comment ces méthodes sont élaborées de façon à ne pas appliquer aveuglément les codes de calcul sous peine de commettre de lourdes erreurs d'interprétation. C'est notamment dans l'interprétation que se situe l'art de l'ingénieur.

Notre objectif est d'obtenir les performances aérodynamique de la configuration Ail-Fuselage du model ARA M100 par maillage hybride.

Cette étude est une simulation numérique visant à présenter les capacités du code de calcul FLUENT sur le traitement de ce genre de problème. Mais aussi de connaitre l'influence des couches de prisme générées sur l'épaisseur de la couche limite et le temps de simulation. L'emploi du code de calcul FLUENT 13 avec un maillage hybride réalisé par le logiciel ICEM CFD13, a permis d'obtenir des résultats approchant ceux obtenus expérimentalement.

Grâce à cette étude, on a su connaître les différentes étapes d'une simulation CFD. Elle nous a aussi permis de se familiariser avec les logiciels utilisés (ICEM-CFD et FLUENT) pour la simulation, (TECPLOT, ORIGIN et GRFWIN) pour la présentation des résultats. Ainsi qu'une connaissance plus approfondie des problèmes d'écoulement autour de la configuration Aile-Fuselage du modèle ARA M100, ce qui est un plus dans notre formation en aéronautique.

Dans la réalisation de ce travail on a réussi à surmonter les difficultés qui sont :

> L'adaptation du maillage hybride c-à-dire, la création des couches de prisme sur notre géométrie, ainsi le raffinage de maillage.

> Manque de documentations dans ce domaine (maillage 3D hybride).

> Les moyens de calcul ne sont pas très puissants pour ce genre de calcul qui nécessite des supers calculateurs.

Le but de ce travail n'est pas de trouver de bons résultats mais de montrer la possibilité de l'utilisation de la CFD pour la résolution des problèmes liés aux écoulements complexes.

REFERENCES

[1]: W.C. Thacker. A brief review of techniques for generating irregular computational grids.

International Journal For Numerical Methods In Engineering, 15 :1335.1341, 1980.

[2]: S. J. Owen. A survey of unstructured mesh generation technology, pages 239.267, 1998.

[3]: H. OUALLI. « Influence de la vibration radiale et de la rotation d'un cylindre circulaire sur l'évolution du sillage proche ». Thèse de doctorat (2006), U.S.T.H.B Alger.

[4]: M. Gad-El-Hak. (2003), « Flow control: passive, active and reactive flow management »Cambridge University Press, United Kingdom.

[5]: B. E. Launder and D. B. Spalding Lectures in Mathematical Models of Turbulence Academic Press, London, England, 1972

[6]: V. Yakhot, S. A. Orszag. Renormalization Group Analysis of Turbulence: I. Basic Theory.Journal of Scientific Computing, 1(1):1-51, 1986.

[7]: T.-H. Shih, W. W. Liou, A. Shabbir, Z. Yang, and J. Zhu, A New k-å Eddy Viscosity Model for High Reynolds Number Turbulent Flows - Model Development and Validation. Computers Fluids, 24(3):227-238, 1995.

[8]: D. C.Wilcox. Turbulence Modeling for CFD, DCW Industries, Inc., La Canada, California, 1998

[9]: F. R. Menter, M. Kuntz, and R. Langtry, Ten Years of Experience with the SST Turbulence Model, In K. Hanjalic, Y. Nagano, and M. Tummers, editors, Turbulence, Heat and Mass Transfer 4, pages 625-632. Begell House Inc., 2003.

[10]: M. M. Gibson and B. E. Launder, Ground Effects on Pressure Fluctuations in the Atmospheric Boundary Layer J. Fluid Mech., 86:491-511, 1978.

[11]: B. E. Launder. Second-Moment Closure: Present... and Future? Inter. J. Heat Fluid Flow, 10(4):282-300, 1989.

[12]: B. E. Launder, G. J. Reece, and W. Rodi, Progress in the Development

[13]: Génération de maillage département de génie mécanique Ecole Polytechnique de Montréal janvier 2008

[14]: Ecole doctorale n° 432 : Sciences des Métiers de l'Ingénieur Thèse doctorat Mohand YOUNSI le 16 novembre 2007

[15]: NAKAHASHI.K (1993). External viscous flow computations using prismatic grids.

S. Verlag, éditeur, Lecture Notes in Physics 414, Thirteenth Int. Conf. on Num. Meth. In Fluid. Dynam. 280-284.

[16]: KALLINDERIS.J et WARD.S,(1993). Prismatic grid generation for three dimensional complex geometries. AIAA Journal, Volume 31.

[17]: MARCUM.D (1995). Generation of unstructured grids for viscous flow applications, 129-151.

[18]: Tutorials ANSYS 13 (IECM CFD).

[19]: Carr, M.P. and Pallister,K.C., Pressure distributions measured on Research Wing M100 Mounted on an Axysymmetric Body. AGARD AR-138 Addendum, 1984.

[20]: l'laboratoire d'énergétique et de mécanique des fluides interne ANSAM, CER de paris

Simulation numérique des écoulements interne dans les turbomachines PFE octobre

2007.

[21]: Academic College of Tel-Aviv-Yaffo, Computer Science Department 4 Antokolsky St, Tel Aviv 64044, Israel. Israel Aircraft Industries, Aerodynamic Dept. CFD Group BenGurion International Airport, Lod, Israel (ICAS 2002 CONGRESS).

[22]: Marconi, F., Siclary, N., Carpenter, G. and Chow, R., Comparison of TLNS3D Computations with Test Data for a Transport Wing/Simple Body Configuration. AIAA paper 94-2237.

[23]: website ht pp : _hpccp_www_larc_nasa_gov



ANNEXES

ANNEXE A

ANNEXE B

ANNEXE A

1. L'histoire de convergence des résidus

Les figures ci-dessous montrent l'histoire de convergence exprimée en termes de résidus pour chaque angle d'incidence á=-3.017⁰, -2.873⁰, 0⁰, 3.017⁰.

On peut dire que les solutions a été convergées ; d'une part, parce que le résidu des variables conservatives a une allure presque constante en dépassant 600 itérations.

Pour á=-3.017⁰



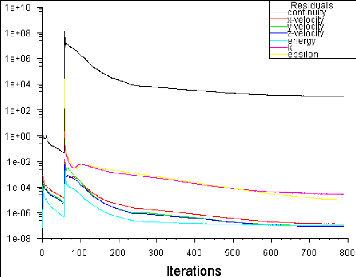
Pour á=-2.873⁰



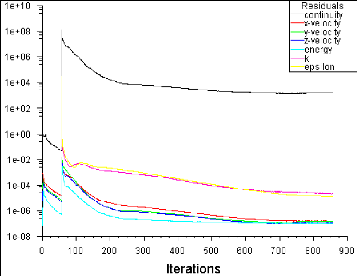
Figure (2) : Historique des résidus Pour á=-2.873⁰

Pour á=0⁰





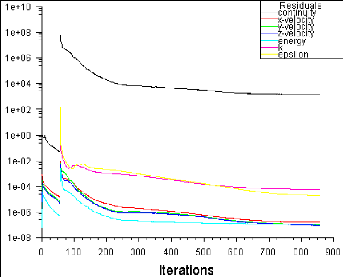
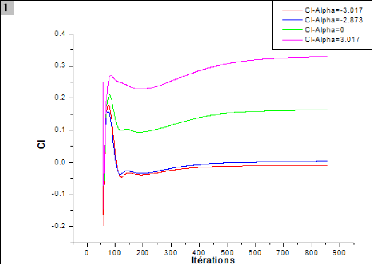
Pour á=3.017⁰



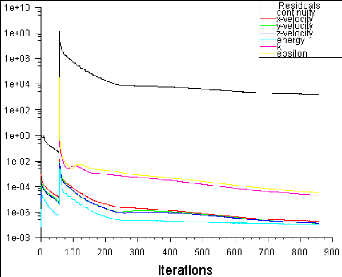
Figure (4) : Historique des résidus Pour á=3.017⁰ 2. L'histoire de convergence des coefficients Cd, Cl et Cm

Les figures ci-dessous montrent l'histoire de convergence des coefficients de portance, de trainée et de moment en fonction d'itérations pour chaque angle d'incidence.

2.1. Historique de convergence des Coefficient de Portance Cl





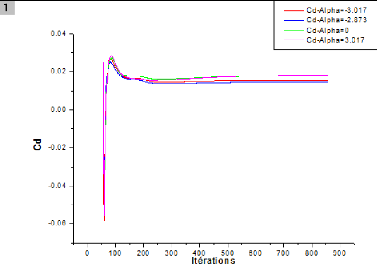
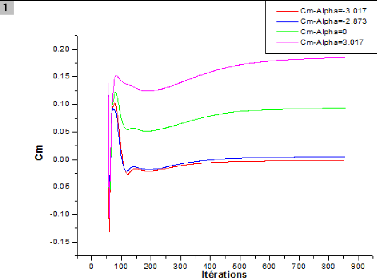
2.2. Historique des Coefficient de trainée

Figure (6) : Historique des Coefficient de trainée (ORIGIN) 2.2. Historique des Coefficient de moment

ANNEXE B

Données Expérimentales

Dans cette annexe, se regroupent tous les données expérimentales du coefficient de pression qui ont été utilisées pour la validation.

Coefficient de pression CP expérimentale pour: ETA=0.019

X/C	Cp
0.0000000000E+00	0.7454000115
0.9999999776E-02	0.1265999973
0.2500000037E-01	-0.1181999967
0.5000000075E-01	-0.5508000255
0.7500000298E-01	-0.6563000083
0.1000000015	-0.6841999888
0.1500000060	-0.8065999746
0.2000000030	-0.8626000285
0.2500000000	-0.9520999789
0.3000000119	-0.9183999896
0.3499999940	-0.9179000258
0.4000000060	-0.8177999854
0.4499999881	-0.7979999781
0.5000000000	-0.7206000090
0.5500000119	-0.5311999917
0.6000000238	-0.4031000137
0.6499999762	-0.3244999945
0.6999999881	-0.2547000051
0.7500000000	-0.2011999935
0.8000000119	-0.1508000046
0.8500000238	-0.1105000004
0.8999999762	-0.7360000163E-01
0.9499999881	-0.1869999990E-01
0.9900000095	0.3810000047E-01
1.000000000	0.6530000269E-01
0.9999999776E-02	0.4345000088
0.2500000037E-01	0.2973000109
0.5000000075E-01	0.1785999984
0.7500000298E-01	0.1322000027
0.1000000015	0.1005999967
0.1599999964	0.3159999847E-01
0.2199999988	-0.2999999933E-01
0.2800000012	-0.7440000027E-01
0.3400000036	-0.9929999709E-01
0.4000000060	-0.1032000035
0.4600000083	-0.9920000285E-01
0.5199999809	-0.8649999648E-01
0.5799999833	-0.5480000004E-01
0.6399999857	-0.1040000003E-01
0.6999999881	0.3720000014E-01
0.7599999905	0.8810000122E-01
0.8199999928	0.1278000027
0.8799999952	0.1773999929
0.9399999976	0.2043000013
0.9900000095	0.1500999928

Coefficient de pression CP expérimentale pour: ETA=0.325

X/C	Cp
0.0000000000E+00	0.6146000028
0.9999999776E-02	0.6384000182
0.2500000037E-01	0.7091000080
0.5000000075E-01	-1.183599949
0.7500000298E-01	-1.254600048
0.1000000015	-1.334900022
0.1500000060	-1.404199958
0.2000000030	-1.448199987
0.2500000000	-1.437500000
0.3000000119	-1.411499977
0.3499999940	-1.362900019
0.4000000060	-1.333799958
0.4499999881	-1.064299941
0.5000000000	-0.7462999821
0.5500000119	-0.5303999782
0.6000000238	-0.3533000052
0.6499999762	-0.2824000120
0.6999999881	-0.2409999967
0.7500000000	-0.2198999971
0.8000000119	-0.1908999979
0.8500000238	-0.1469999999
0.8999999762	-0.8309999853E-01
0.9499999881	0.1030000020E-01
0.9900000095	0.9009999782E-01
0.9999999776E-02	0.4859000146
0.2500000037E-01	0.4178000093
0.5000000075E-01	0.2558000088
0.7500000298E-01	0.1969999969
0.1000000015	0.1228000000
0.1599999964	0.5499999970E-01
0.2800000012	-0.8420000225E-01
0.3400000036	-0.1185000017
0.4000000060	-0.1344999969
0.4600000083	-0.1316999942
0.5199999809	-0.8820000291E-01
0.5799999833	-0.4569999874E-01
0.6399999857	0.5100000184E-02
0.6999999881	0.5730000138E-01
0.7599999905	0.1111999974
0.8199999928	0.1636999995
0.8799999952	0.2257999927
0.9399999976	0.2617000043
0.9900000095	0.2287999988

Coefficient de pression CP expérimentale pour: ETA=0.635

X/C	Cp
0.0000000000E+00	0.6557999849
0.9999999776E-02	-0.5781999826
0.2500000037E-01	-0.6524000168
0.5000000075E-01	-1.165300012
0.7500000298E-01	-1.241299987
0.1000000015	-1.284999967
0.1500000060	-1.271700025
0.2000000030	-1.259099960
0.2500000000	-1.224099994
0.3000000119	-1.209900022
0.3499999940	-1.184900045
0.4000000060	-1.145200014
0.4499999881	-0.9991000295
0.5000000000	-0.6259999871
0.5500000119	-0.4677999914
0.6000000238	-0.3826999962
0.6499999762	-0.3716999888
0.6999999881	-0.3467000127
0.7500000000	-0.3321000040
0.8000000119	-0.2806000113
0.8500000238	-0.2196000069
0.8999999762	-0.1206000000
0.9499999881	-0.1219999976E-01
0.9900000095	0.6069999933E-01
1.000000000	0.7680000365E-01
0.9999999776E-02	0.4309999943
0.2500000037E-01	0.3892999887
0.5000000075E-01	0.2185000032
0.7500000298E-01	0.1770000011
0.1000000015	0.1327999979
0.1599999964	0.5420000106E-01
0.2199999988	-0.2050000057E-01
0.3400000036	-0.1001000032
0.4000000060	-0.1106999964
0.4600000083	-0.8160000294E-01
0.5199999809	-0.2740000002E-01
0.5799999833	0.4690000042E-01
0.6399999857	0.1199000031
0.6999999881	0.1871999949
0.7599999905	0.2467000037
0.8199999928	0.2845999897
0.8799999952	0.3093000054
0.9399999976	0.2881999910
0.9900000095	0.1333999932

Coefficient de pression CP expérimentale pour: ETA=0.936

X/C	Cp
0.0000000000E+00	0.5993999839
0.9999999776E-02	-0.9096999764
0.2500000037E-01	-0.5863000154
0.5000000075E-01	-1.156200051
0.7500000298E-01	-1.208600044
0.1000000015	-1.206599951
0.1500000060	-1.184000015
0.2000000030	-1.159899950
0.2500000000	-1.086300015
0.3000000119	-1.036399961
0.3499999940	-0.5430999994
0.4000000060	-0.3443000019
0.4499999881	-0.3231999874
0.5000000000	-0.3438999951
0.5500000119	-0.3429000080
0.6000000238	-0.3490999937
0.6499999762	-0.3188999891
0.6999999881	-0.2741999924
0.7500000000	-0.2263000011
0.8000000119	-0.1633999944
0.8500000238	-0.9099999815E-01
0.8999999762	-0.1840000041E-01
0.9499999881	0.5959999934E-01
0.9900000095	0.8760000020E-01
1.000000000	0.9950000048E-01
0.9999999776E-02	0.4347000122
0.2500000037E-01	0.4052999914
0.7500000298E-01	0.1415999979
0.1000000015	0.5640000105E-01
0.1599999964	-0.1549999975E-01
0.2199999988	-0.9420000017E-01
0.2800000012	-0.1631000042
0.3400000036	-0.1787000000
0.4000000060	-0.1993000060
0.4600000083	-0.1852999926
0.5199999809	-0.1202000007
0.5799999833	-0.4610000178E-01
0.6399999857	0.3500000015E-01
0.6999999881	0.9730000049E-01
0.7599999905	0.1512999982
0.8199999928	0.1934999973
0.8799999952	0.2138999999
0.9399999976	0.1895000041
0.9900000095	0.6949999928E-01