Bond graphs couplés pour la surveillance

UNIVERSITE D'ORAN

FACULTE DES SCIENCES

Departement d'Informatique

2005

THESE DE VIAGISTER

Discipline : Informatique
Option : Informatique et Automatique

presentee et soutenue publiquement par
Fatima Zohra LEBBAH

juin 2005

an Departement d'Informatique, Es-senia

Bond graphs couples pour la surveillance

President Examinateur Examinateur Examinateur Rapporteur

Mustapha Kamel Rahmouni Djilali Benhamamouch Mohamed Faycal Khelfi Larbi Sekhri

Hafid Haffaf

Professeur, universite d'oran, es-senia

Maitre de conferences, universite d'oran, es-senia Maitre de conferences, universite d'oran, es-senia Chargé de corers, universite d'oran, es-senia Maitre de conferences, universite d'oran, es-senia

Remerciements

Je remercie Monsieur le Professeur Mustapha Kamel Rahmouni d'avoir accepte d'examiner ce travail et de presider le jury de cette these de magister.

Mes remerciements s'adressent egalement a Messieurs les Maitres de conferences Djilali Benhamamouch et Mohamed Faycal Khelfi ainsi que Monsieur le chargé de cours Larbi Sekhri qui ont accepte d'examiner et de juger ce travail.

Je remercie Monsieur le Maitre de conferences Hafid Haffaf, directeur de cette these de m'avoir initiee a la theorie des bond graphs ainsi que la surveillance industrielle. Je le remercie pour m'avoir cider a bien mener cette these.

Mes remerciements vont egalement a tout enseignant avant honorer sa noble mission.

Plus largement, je remercie tous les gens qui ont contribue de pres ou de loin a mon aboutissement de mon parcours d'etudiante. Qu'ils trouvent ici mes sinceres vceux.

J'adresse un remerciement particulier a mon frere Yahia pour sa precieuse aide le long de ma post-graduation. Je le remercie pour ses encouragements et ses precieux commentaires pour la realisation de ce travail.

Mes parents et mes sceurs m'ont toujours soutenue avec une grande determination. Ma mere et mon pere m'ont apportee plus que je ne saurais decrire en quelques mots. Je leur souhaite ce qu'il y a de meilleur dans la vie ici-bas et dans Pau-dela.

Enfin, je remercie profondement L.Abdenour pour son soutien le long de ce travail. Je le remercie sincerement pour ses encouragements .

Résumé

L'outil de modelisation bond graph permet la representation des informations structurelles et comportementales d'un systeme physique. En consequence, les Relations de Redondance Analytique (RRAs) peuvent etre generees. Ces dernieres permettent la detection et la localisation des defaillances dans une installation industrielle. En d'autres termes, la determination des RRAs constitue une phase essentielle dans la procedure de detection et de localisation de defaillances (FDI : Fault Detection and Isolation procedure) dans la surveillance des systemes physiques.

Les methodes appliquees sur les bond graphs, jusqu'a, present, sont classees en deux types : methodes directes et methodes indirectes. Ce memoire presente l'application de l'approche des cycles de l'analyse structurelle pour la determination des RRAs directement du modele bond graph simple ou couple.

Nous proposons un nouvel algorithme qui exploite la notion des chemins causaux en modelisation bond graph. Le but de notre travail est de tirer profit des avantages des methodes directes et ceux de l'approche des cycles, pour la generation d'un ensemble de RRAs permettant une forte localisation de defaillances. Initialement, nous avons concu cet algorithme sur le graphe structurel correspondant au systeme a surveiller. Une adaptation a ete faite par la suite, pour les bond graphs couples.

Mots Iles : Bond Graph, Surveillance, Redondance Analytique, Detection de

defaillances, Theorie des graphes, Analyse structurelle.

Abstract

The bond graph model is a unified tool for modelling dynamics systems. It represents the structural and the behaviour information of a physical system. It enables to generate the Analytical Redundancy Relationships (ARRs). The ARRs allow the faults detection and isolation. In other words, the generation of the ARRs constitutes an essential step in the Fault Detection and Isolation procedure (FDI) in the physical systems monitoring.

Two main types of methods are used in the literature. The first one works directly on the bond graph model, whereas the second exploits an intermediate model. This master thesis introduces the application of cycles approach of the structural analysis to generate ARRs, directly from the bond graph model.

We propose a new algorithm, which exploits the advantages of the direct methods and the cycle approach. This algorithm works directly on the bond graph model and uses a search procedure of causal paths. Initially, this algorithm was designed to be applied on the system structural graph. An extension of this algorithm is given on bond graph model with multiports elements.

Key words : Bond Graph, Monitoring, Analytical Redundancy, Fault Detection, Graphs theory, Structural Analysis.

Table des matieres

1	La surveillance des systemes physiques			7
	1.1		Introduction	7
	1.2		Notions fondamentales de la surveillance	8
	1.3		Supervision et surveillance	11
	1.4		Detection et localisation de defaillances	12
	1.5		Methodes de surveillance	13
			1.5.1 Methodes avec modele	13
			1.5.2 Methodes sans modele	17
	1.6		Conclusion	18
2	Generation des relations de redondance analytique			21
	2.1		Introduction	21
	2.2		Notion de la redondance	22
	2.3		La redondance analytique	24
	2.4		Les relations de redondance	25
			2.4.1 Relations de redondance directes	25
			2.4.2 Relations de redondance indirectes	26
	2.5		L'approche espace de parite	27
			2.5.1 Espace de parite statique	27
			2.5.2 Espace de parite dynamique	29
			2.5.3 Theorie d'elimination	32
	2.6		Conception et evaluation des residus	33
			2.6.1 Generation des residus	34
			2.6.2 Evaluation des residus	36
			2.6.3 Table de signatures	37
	2.7		Conclusion	39
3		Analyse structurelle		41
		3.1	Introduction	41
		3.2	Systeme physique	41
			3.2.1 Le modele structurel	42
			3.2.2 Caracterisation des sous-systemes	44
		3.3	L'approche des couplages	46
			3.3.1 Couplages et generation des RRAs	46
			3.3.2 Decomposition canonique	51
		3.4	L'approche des cycles	54
		3.5	Conclusion	56
4		Modelisation bond graph		57
		4.1	Introduction	57
		4.2	Bond graphs simples	57
			4.2.1 Les elements bond graph	57
			4.2.2 Les ports	59
			4.2.3 Notion de causalite	64
			4.2.4 Les chemins causaux	69
			4.2.5 Representation matricielle	71
		4.3	Bond graphs couples	75
			4.3.1 Les elements multiports	75
			4.3.2 Les chemins causaux	78
		4.4	Conclusion	84

5 Contribution : Les bond graphs couples et la surveillance 87

5.1 Introduction 87
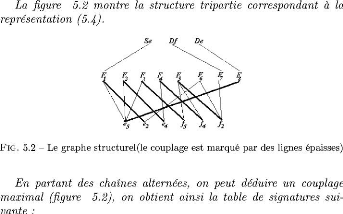
5.2 Generation des RRAs a partir d'un modele bond graph 88

	5.2.1 5.2.2	Generation indirecte des RRAs Generation directe des RRAs	88 89
5.3	Nouvel algorithms de generation des RRAs		93
	5.3.1	Principe de l'algorithme	93
	5.3.2	Le graphe structurel	94
	5.3.3	Complexite de l'algorithme	99
	5.3.4	Extension aux bond graphs simples	100
	5.3.5	Extension aux bond graphs couples	103
5.4	Conclusion		107

Introduction generale

L'automatisation des systemes de fabrication contribue enormement dans le developpement de l'industrie. La taille et la complexite de ces systemes posent des difficultes dans la conception et la mise en ceuvre des differentes methodes de surveillance. Pour garantir le bon fonctionnement de ces systemes, it y a besoin de faire appel aux techniques de controle et de verification, dices techniques de surveillance.

La detection et la localisation des defaillances au niveau d'une installation industrielle, constitue une Cache essentielle dans le pro-cede de surveillance.

Pour assurer la surveillance des systemes physiques, d'une maniere generale, une procedure de detection et de localisation des erreurs (FDI : Fault Detection and Isolation procedure), permet de suivre un processus de comparaison entre le comportement voulu (ideal) et le comportement reel (calcule) du systeme. La structure d'un FDI est composee de deux etapes de detection et de localisation de defaillances. La redondance analytique represente une des possibilites de la realisation de la FDI. Elle est bask sur l'utilisation des signaux d'informations disponibles et le modele mathematique du systeme physique. Les relations de redondance analytique (RRAs) decrivent les relations existant entre les elements pris en consideration par le cahier des charges (les variables a surveiller). Le bon fonctionnement du systeme physique est deduit de la satisfiabilite des RRAs qui verifie la conformite du comportement du systeme avec le modele de reference. Le choix du modele pour la conception d'un systeme de surveillance, est une etape importante et difficile, puisque la qualite des RRAs et la performance du systeme en dependent. Il existe differents modeles de surveillance dans la litterature : requation d'etat, la matrice de transfert, le modele structurel et le schema bloc.

Le bond graph est un outil unifie de modelisation des systemes dynamiques et it permet la conception, la simulation et l'analyse des systemes complexes. C'est une representation graphique qui genere les informations structurelles et comportementales du systeme physique.

L'approche structurelle est une notion qui est bask sur la theorie des graphes. Deux methodes a specifier : celle des couplages et celle des cycles. Elle est appliquee sur le graphe biparti decrivant la structure du systeme physique.

L'approche analytique, est celle appliquee sur le modele math& matique du systeme a surveiller. Deux methodes analytiques sont decrites dans le deuxieme chapitre, celles d'espace de parite statique et dynamique et celle de la theorie d'elimination.

Notre travail consiste a trouver un algorithme de generation des RRAs directement a partir du modele bond graph, en utilisant l'approche structurelle. Ceci, en combinant les deux approches suivantes :

1. l'approche des cycles, appliquee sur le modele structurel du systeme. Elle est bask sur des notions de la theorie des graphes.

2. l'approche des chemins causaux generalises, appliquee sur le modele bond graph du systeme. Elle est bask sur la structure de jonction et les chemins causaux.

Le but de ce travail, consiste a generer une table de signature permettant une forte localisation de defaillances.

Dans le premier chapitre, nous presentons une introduction generale a la supervision et a la surveillance. Nous donnons, par la suite, les stapes de la procedure de detection et de localisation des defaillances (FDI).

Dans le deuxieme chapitre, nous nous interessons aux notions fondamentales des redondances physique et analytique. Une vue intentionnee sera port& sur la redondance analytique qui represente un concept fondamental de noire travail. Nous introduisons par la suite les differents types de relations de redondance. Une definition detainee des methodes de generation des RRAs est dorm& dans la section 2.4. Nous introduisons dans la section 2.6 d'autres notions cies dans le processus de diagnostic : la generation des residus et de la table des signatures avec ses types.

Le troisieme chapitre est consacre a l'analyse structurelle qui en-globe les deux approche de couplages et celle des cycles. Des notions de la theorie des graphes sont introduites, pour permettre une bonne explication des resultats de la recherche des couplages maximaux et ceux des cycles. Nous presentons par la suite une comparaison entre les deux approches, pour mettre en evidence les avantages et les inconvenients de chacune des deux approches. Notre algorithme est fonds sur l'approche de cycles et it permet la recherche de l'ensemble des cycles permettant la determination d'une table de signature a defaillances fortement localisables.

Le quatrieme chapitre est destine aux details de la modelisation bond graph. Nous decrivons au depart les elements et notions de base d'un bond graph simple, ainsi les differents types de chemins causaux. Nous continuons, avec les bond graphs couples en definissant les elements multiports et les differents types de chemins causaux.

Le cinquieme chapitre comporte deux parties. Dans la premiere, nous exposons les differentes methodes directes et indirectes, de generation des RRAs a partir d'un modele bond graph. La deuxieme est consacree aux details de noire algorithme de generation des RRAs. Nous commencons par exposer l'idee de base et le but de la methode. Initialement, nous avons concu l'algorithme pour etre appliqué sur la representation structurelle du systeme physique. Par la suite, nous l'avons adapts pour les bonds graphes simples puis les bonds graphs couples.

Chapitre 1

La surveillance des systemes

physiques

1.1 Introduction

Avec l'automatisation des systemes industrials, une demande croissante est apparue en matiere de surveillance. Celle-ci a permis le passage de la maintenance curative a une maintenance preventive, permettant ainsi la mutation d'une situation ou on subit les pannes a une situation ou on maitrise les pannes. En se basant sur les donnees quantitatives et/ou qualitatives fournies par le systeme physique, la fonction "surveillance" permet de prevenir les dysfonctionnements et d'ecarter les fausses alarmes qui peuvent ralentir la production. L'importance du domaine de la surveillance dans l'industrie peut etre interpretee par la variete et la diversite des ouvrages abordant le sujet des differents cotes [12] [1611411134111511171143114511141130].

L'objectif de ce chapitre est d'initier le lecteur a la notion de surveillance en donnant les definitions necessaires pour aborder le domaine. Nous presentons, par la suite un kat de l'art sur les methodes de surveillance, afin de pouvoir se situer correctement dans le probleme etudie. Afin d'eviter toute ambiguIte entre la modelisation bond graph et la surveillance, nous avons prefers ne pas introduire ici leurs liens.

t1 > 0 y [0,t1]

x(0)

Definition 3 (Surveillance) La surveillance a pour objectif d'elaborer et de fournir des informations structurees sur la situation du systeme observe. Elle met en oeuvre des mecanismes d'observation, de detection et de filtrage pour generer des indicateurs pertinents.

Definition 4 (Defaillance) Une defaillance est l'alteration ou la cessation de l'aptitude d'un ensemble a accomplir ses fonctions requises avec les performances definies dans les specifications techniques. Les defaillances peuvent etre classifiees selon leers degres de severite, comme suit :

-- defaillance critique : necessite une intervention d'urgence,

-- defaillance significative : necessite un processus de traitements, -- defaillance absorbable : pouvant etre ignoree dans un premier

temps au moins.

·
·
·

Definition 5 (Panne) C'est l'inaptitude d'un dispositif a accomplir sa fonction requise.

Definition 6 (defaut) Tout ecart entre la caracteristique observee sur le dispositif et la caracteristique de reference, lorsque celui-ci est en dehors des specifications

Definition 7 (Detection) La detection des defaillances d'un systeme physique, ne peut etre faite sans la classification des situations observables comme etant normales ou anormales. Cette classification n'est pas triviale etant le manque d'informations caracterisant generalement les situations anormales. Une situation communement adoptee consiste a considerer toute situation qui n'est pas normale comme etant une situation anormale.

Definition 8 (Diagnostic) C'est une determination du type, de la taille, de l'endroit et de l'instant d'apparition d'un &Put. Elle Suit la detection de defaut, inclut la localisation et l'identification d'un defaut

Definition 9 (Mode de fonctionnement) Trois types de fonctionnement peuvent etre cites a ce niveau :

Mode de fonctionnement nominal : c'est le mode ou le systeme industriel remplit sa mission dans les conditions de fonctionnement requises par le constructeur et avec les exigences de l'exploitant.

Mode de fonctionnement degrade : correspond soit a l'accomplissement partici de la mission, soit a l'accomplissement de celle-ci avec des performances moindres. Autrement dit, it y a eu une degradation an niveau du systeme mais pas de defaillance.

Mode de defaillance : correspond an mauvais fonctionnement du systeme, dic a une defaillance apparue apres une degradation ou une defaillance brusque. Un mode de defaillance est caracterise par les effets (mesurables ou qualifiable& causes par cette defaillance. On associe par la suite une analyse de cause a effet. Ce qui correspond a associer un mode de defaillance du systeme industriel. A noter qu'un systeme ne possede qu'un seul mode nominal (cas de fonctionnement normal; par contre it possede plusieurs mode de defaillance.

Definition 10 (Cahier des charges) Il est difficile de localiser l'origine de la defaillance dans un processus industriel. Ceci est chi a

la diversite des composants pouvant etre responsables de cette defaillance. Autrement dit, une defaillance pent etre reperee an niveau d'un capteur, un parametre physique (ex : changement de la valeur de la resistance a cause d'une variation de la temperature), un actionneur ou un autre.

Le cahier des charges doit repondre aux questions suivantes :

1. Definition des objectifs : que vent-on surveiller ?

2. Definition des criteres : comment evaluer la qualite du systeme concu ?

3. Definition des contraintes : quelles sont les limites que doit respecter le systeme concu ? (delai de detection maximum, coilt... etc.

Par consequent le cahier des charges pent etre defini en trois etapes :

-- Etape 1 : Specifier les causes de defaillance (les composants

pouvant etre responsables de la defaillance) et definir celles qui

devraient etre prises en compte.

-- Etape 2 : Fixer les criteres de qualite concernant la detection (fausse alarme, non detection, et delai de detection) et localisation.

-- Etape 3 : Definir une architecture d'instrumentation optimale (du systeme de surveillance), vis-a-vis des contraintes de coilt, de disponibilite de base de donnees brute, incomplete, ... etc. en respectant le cahier des charges. Cette etape doit etre effectuee par le concepteur du systeme de surveillance.

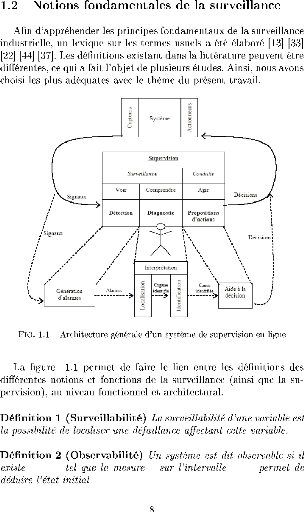
1.3 Supervision et surveillance

Pour pouvoir separer la surveillance de la supervision (figure 1.1), it est indispensable de passer par la definition de chacune d'elles. La surveillance [44] consiste a &teeter et classer les defaillances du systeme en observant son evolution, puis a les diagnostiquer en localisant les elements defaillants et en identifiant les causes premieres. Autrement dit, la surveillance comporte deux fonctions principales, la detection et le diagnostic.

Les principales raisons qui conduisent a concevoir un systeme de surveillance sont :

la conduite : son but est d'optimiser les Caches en lignes (la production maximale, securite et non degradation des equipements). Ceci passe par la surveillance du procede afin de &- teeter toute anomalie de fonctionnement et de l'identifier aussi bien que possible. Ce type d'action est aussi appele supervision : surveillance + conduite.

la maintenance : Il s'agit toujours de l'optimisation, mais uniquement au niveau des equipements, Celle que le remplacement ou la reparation des equipements uses ou defectueux. On peut citer trois types de maintenance :

La maintenance corrective, elle intervient apres la detection et la localisation d'un defaut.

La maintenance preventive, elle est effectuee dans le but de reduire la probabilite d'apparition de defaillance. C'est une maintenance prevue, preparee et programmee avant la date probable d'apparition d'une defaillance.

La maintenance conditionnelle, elle represente une alternative a la maintenance systematique, fait l'objet d'une demande croissants dans les grandes industries. Elle est bask sur la surveillance en continu de revolution du systeme, afin de prevoir un dysfonctionnement avant qu'il ne surgisse. La decision d'intervention preventive est prise lorsqu'il y a evidence experimentale de defaut imminent ou approche d'un seuil de degradation predeterminee.

Le role de la supervision [13] est de controler et surveiller rex& cution d'une operation dans un systeme de production sans rentrer dans les details de cette execution. Autrement dit elle recouvre l'aspect fonctionnel du processus industrial :

FDI

H0 H1

H0 H1

n

n

H1i,i = 1..n i

Surveillance sans
modèle

Surveillance avec
modèle

Outils statistiques

Reconnaissance de
formes

Approche statistique

Approchefloue Réseaux de neurones

Redondances physique et analytique

Méthodes d'estimation Paramétrique

Test de franchissement de

seuil

Test de moyenne
Test de variance

Existence d'un
modèle?

Surveillance industrielle

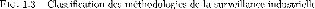
x(k + 1) = A.x(k) + B.u(k)
y(k) = C.x(k)

x(k) u(k)

A B C

F_p(k) b_p(k)

x(k + 1) = Ax(k) + Bu(k) + PF_p(k) + Qb_p(k)

y(k)

F_u(k) F_y(k)

eu(k) = u(k) + F_u(k) + b_u(k)
ey(k) = y(k) + F_y(k) + b_y(k)

A B C

Ae = A + AA(k) B^e = B + AB(k) C^e = C + Ac(k)

eu(k) u(k)

ey(k) y(k)

e e e

u(t) y(t)

y(t) = f(u(t), è)

àp(t) = g-1(è(t))

p

è p

è = g(p)

èà è

u(t) y(t)

èà = h(y(1)...y(t); u(1)...u(t))

èà p

è

è

èà p

pà

Ti

ã

maintenance preventive ; et seuil d'alarme qui impose l'arret de la production et l'engagement d'une action de maintenance corrective. C'est une technique dont la mise en ceuvre est tres facile et ne per-met pas d'etablir un diagnostic des defaillances. Elle est aussi tres sensible aux fausses alarmes.

Surveillance par reconnaissance des formes

Elle permet d'associer un ensemble de mesures (continues ou discretes) effectuks sur le systeme a des etats de fonctionnement connus. Ceci permet d'avoir une relation d'un espace caracteristique vers un espace de decision, en minimisant les risques de mauvaise classification. On peut citer comme techniques de surveillance par reconnaissance des formes, technique classique bask sur les outils de la probabilite, et les techniques bask sur l'intelligence artificielle (logique floue, reseaux de neurones, ...). La premiere technique n'est pas tres utilisee puisqu'elle suppose une reconnaissance a priori de tous les etats du systeme, et ne prend pas en consideration revolution du systeme. Le deuxieme type de techniques permet d'eviter rinconvenient de l'approche probabiliste puisqu'elle est bask sur une phase d'apprentissage.

1.6 Conclusion

L'objectif de ce chapitre etait de donner un apercu sur les techniques habituelles utilisees pour resoudre les problematiques de la surveillance.

Nous avons commence par une presentation des definitions des mots cies de la surveillance industrielle. Cette derniere se base sur la detection et le diagnostic. La detection permet de signaler toute situation autre qu'une situation normale, dice anormale, suivie par la fonction diagnostic qui va localiser le composant defaillant du systeme et identifier la ou les causes avant provoque cette defaillance.

Pour resoudre le probleme d'ambiguIte pose entre surveillance et supervision, nous avons essaye de decrire la position fonctionnelle et architecturale de chacun des deux dispositifs, permettant ainsi de specifier le role de chacun dans la siirete d'un procede industrial.

Le classement des techniques de surveillance s'effectue en fonction de l'existence ou non d'un modele formel (correspondant au systeme

physique). Nous avons presente comme methodes avec modele, la redondance physique, la redondance analytique et l'estimation parametrique. Et pour les methodes sans modele , nous avons deux categories : la surveillance avec outils statistiques et la surveillance avec reconnaissance des formes, dont chacune comprend plus d'une technique.

La procedure de detection et de localisation des defaillances (FDI), est une procedure qui est citee generalement dans les cas de surveillance avec modele. Les etapes fondamentales de cette derniere ont ete donnees, avec integration des differentes hypotheses connues en matiere de surveillance.

FDI

m1f m2f

m1 m2 m1f - m2f

m1 m2

r1 = m1f - m2f

r2 = m1f - m3f

r3 = m2f - m3f

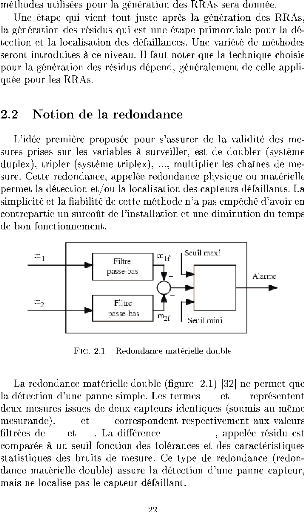
soient ou non de meme nature. Cette methode (voir chapitre precedent) ne peut etre appliquk qu'en se basant sur un modele formel statique ou dynamique, lineaire ou non lineaire, deterministe ou stochastique du systeme industrial.

2.3 La redondance analytique

La redondance analytique permet une exploitation optimale des informations structurelles du systeme physique. C'est une technique bask sur une redondance implicite au niveau des mesures des grandeurs. La disponibilite d'un modele formel est une condition necessaire pour l'utilisation de cette technique. Il faut prkiser que l'approche analytique ne va pas remplacer l'approche physique, mais elle constitue un complement de cette derniere [32](voir figure 2.3). Par consequent, la redondance analytique permet de :

augmenter l'ordre de redondance,

augmenter la fiabilite et la siirete du systeme de surveillance, remplacer un capteur materiel par un capteur mathematique ou informationnel,

implanter un voteur pour un systeme duplex (redondance physique double), comme illustre sur la figure 2.3.

FIG. 2.3 -- Redondance materielle et analytique

La redondance analytique est une technique qui repose sur les actions de cause a effet statiques ou dynamiques entre les entrées et les sorties du systeme physique. Cela permet de surpasser la detection des defaillances capteurs et le passage vers la detection des defaillances produites des actionneurs ou du procede lui meme. Ceci

F Fk

F' F

Vf E F',Vx E X,S(f,x) = 0 Fk

f1(x1,y1) = 0 f2(x2, y2) = 0 f3(y1, y2, y3) = 0

		x1		x2		y1		y2	y3
f1
f2
f3

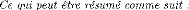
f3 y1y2 y3

F_x

Fk F F_x = F -- Fk

	y1	y2	x	X -- {x}
f1
f2

x

x

f1 f2

f1(y1,x) = 0
f2(y2,x) = 0

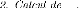
x

x = f-1

1 (y1)

x = f-1

2 (y2)

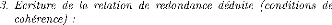
_f-1

1 (y1) -- f-1

2 (y2) = 0

k

yk xk fk ek

C
F

yk = Cxk + ek + Ffk

x ? IRⁿ y ? IR^m f ? IR^p e ? IR^m C ? IR^m.n F ? IR^m.p

pk

yk

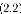
pk = Wyk

W q.m

WC = 0

pk = Wek + WFfk

pk

yk

fk = 0 pk

Wyk = 0

~yk = Cxk + ek + F fk Axk = 0

( ₁ ~ ( _C ~ ( ₁ ~ ( _F ~

yk = xk + ek + fk

0 A 0 0

( C xk ~

W W = 0

A

p

( ₁ )

pk = W yk

0

( ₁ ) ( _F )

pk = W ek + W fk

0 0

( _I )

xk = xk2

_A^-1

1 A2

xk

( _I ~

yk = C xk2 + ek + F fk

_A^-1

1

( _yk )

(I _ C) = ek + F fk
xk

A A1 A

((A1A2)

~

xk1

xk2

A1

Mzk = bk

xk+1 = Axk + Buk + F1fk yk = Cxk + Duk + F2fk

C
CA

?
????

?
????

?
????

?
????

?
????

?
????

?
????

?
????

+ H2

=

CA^s

fk -- s

fk-s+1

fk

uk-s
uk-s+1

uk

xk-s

yk -- s + 1

yk

xk-s + H1

?
????????

H1 =

D 0

CB D

CAB CB

CA^8-1B CA^8-2

H1 H2

F2 ? CF1 CAR1 H1 = ???????? CA^8^-1F1

0 F2 CF1 CA^8^-2F1

0 0 F2 CA^8^-3F1

· · · · · · · · · · · · · · · · · ·

0 0 0 0 0 CF1

0 0 ? 0 ???????? 0 0 F2

x E IR^Th

u E IR^r B

y E IR^m

f E IR F1 F2

s

C
CA

?
????

xk-s + H2

?fk-s

fk-s+1 ? ? ? ?

fk

=

- H1

?
????

CA^s

?
????

?
????

?
????

? ?

yk-s
? ? yk-s+1 ? ?

? ?

? ?

yk

uk-s
uk-s+1

uk

0	· ·	·	0		0 ?	0
· ·	·	0	0		D
· · · ·	· ·	0 0	0 0 ????????
· ·	·	0	0		CA^8^-3
· ·	·	CB	D

pk = (W1(z)F1 + W2(z)F2)fk

pk = --(W1(z)B + W2(z)D)uk + W2(z)yk

?
????

? ?

? ?

? ?

? ?

? ?

?
????

T

- H1

rk = w

uk-s
uk-s+1

uk

= _wT _H2

_?fk-s

_fkfk -s+1

? ? ?

yk-s

? _?yk-s+1 ?

? ? ?

? ? ?

? ? ?

yk

W^T

?

?

_wT ? ?

CA^s

A
CA

?
? ? ?

= 0

xk

rk

s

( A -- zI

C ) xk +

F2 ) ^{k =}--D I ) yk )

W(z) = W1(z) + W2(z)

W(z) (A -- zI

C ) = 0

pk

fk

W(z)

( A - zI F _ )

1

W (z) = = 0

C F _ 2

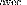
? ? Y ( -I H1 O ) ? U ? = H2f xk_s

? ?

yk-s
? yk - s + 1 ?

? ?

? ?

? ?

yk

et O =

uk-s
uk-s+1

uk

C
CA

CA^s

y =

?
????

?
????

U=

_?fk-s

fk-s+1 ? ? ? ?

fk

? ???? ? ????

f =

? ????

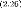
fi = E

j

c_j ...x^aj,p

aj,1 _pkbj,1

1 ...kbj,q

p

cj E IR aj,k, bj,k E IN

F = f1, ..., f_m
X = x1, ..., x_p
K = k1, ..., k_q

F

fi

K

R[x1
·
·
· x_p, k1
·
·
· kq] fi

f f = á1f1 + á2f2 +
·
·
· +

ámfm ái E IR

?(u, y) = 0 u y

(f1,
·
·
· , fm)

X

fi(x1, ...,x_p, k1, ..., k_q) = 0

x1
·
·
· x_p k1
·
·
· k_q

IR R[x1
·
·
· x_p, k1
·
·
· k_q]

f1
·
·
· f_m E

ri = yui - yui

i ? K K

K = {1, 2, · · · }

ri ime

yui ime

cyui ime

ri 0

|ri| > ki > 0 ki ? IR

yu è cyu

yu

ryu = yu-

yu

u(t) f(t)

y(s) = G_u(s)u(s) + Gf(s)f(s)

?(u,y) = r

(yui) ( cyui)

H_u(s) H_y(s)

r(s) = H_u(s)u(s) + H_y(s)y(s)

y(s)

r(s) = (H_u(s) + H_y(s)G_u(s))u(s) + H_y(s)Gf(s)f(s)

y

è

è y

H_u(s) H_y(s)

H_u(s) + H_y(s)G_u(s) = 0

y ènom

r_y = y -- y y rè = ènom

r_y

rè

è

r(t) = (r1(t)r2(t) · · · r_p(t))^T r(t) E IR^p

p

{ 1 si |ri(t)| = ki ei(t) = 0 si |ri(t)| < ki

e(t) = (e1(t)e2(t) · · · ep(t))T

e(t)

i ? p ki

t ri(t)

ki

Ö

í(t) = (í1(t)í1(t) · · · ík(t))^T

r ? - - Öí

ime Ö

Öi = _eíi eíi e ime

Ö p × k

0 1 ? --

r ? - - 0

r

ri(t)

íi(t) k

p p = k = 3

_ime

_ime

?

^r = ?

? ? ? ? ? r1 í1 1 0 0 r2 ? ? - - ? í2 ? = ?0 1 0 ? r3 í3 0 0 1

? ?

í1 í2 í3

? ?

Se. _{z } |._soo. }

Ö í

0

1

p1	p2	p3	p4	Re1
1	1	0	0	Re2
1	1	1	0	Re3
1	1	0	1	Re4
0	0	1	1

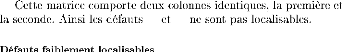
p1 p2

p1	p2	p3	p4	Re1
1	1	0	0	Re2
1	0	1	0	Re3
1	1	0	0	Re4
0	0	1	1

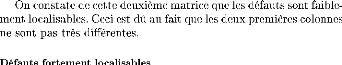
	p1	p2	p3		p4	Re1
1	1	0	0		Re2
1	0	1	0		Re3
0	1	0	1		Re4
0	0	1	1

p1	p2	p3	p4	Re1
0	1	1	1	Re2
1	0	1	1	Re3
1	1	0	1	Re4
1	1	1	0

40

Umi=1 Ci fi

zj,j = {1,...,n}

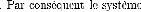
fi(z1, ...,zp) = 0 1 = p = n

Z = {z1, ..., z_n}

F = {f1, ..., f_m}

Z

				u(t)
			d(t)
			ä(t)
			x(t)
			y(t)
			å(t)
			è

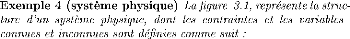
F = {f1, f2, f3, f4, f5, f6,f7,f8,f9, f10, f11} K = {c1,c2, c3, c4, c5}

Z Z = X ? K X

K

F

K

K = U ? P ? Y U P Y

X = {x1, x2, x3, x4, x5, x6, x7, x8, x9, x10}

F

Z

G(F, Z, A) A c (F x Z)

? ?

?

A :FxX-->10,11

A* :XxF-->10,11
KF :FxK-->10,11

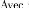
~ 0 si fi s'applique sur xj

(fi, xj) = aij E A, aij =

1 sinon

~ 0 si xi est calculable en utilisant xj

(xi, fj) = a* ij E A, a^*ij =

1 sinon

~ 0 si fi s'applique sur kj

=

(fi,kj) = kifj E A,kifj

1 sinon

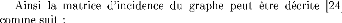
Z

K	F	X	K
0	KF	0	F
KF^T	0	A	X
0	A^*	0

c1

c2

c3

c4

c5

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

f1

f2

f3

f4

f5

f6

f7

f8

f9

f10

f11

(F, Q(F))
F F_x Q(F) = Qk(F) U

Q_x(f) Qk(f) Q_x(f)

F(Qk(F),Q_x(F))

Q_x(F)

Qk(F)

Card_sol(F, Q(F))

(F, Q(F))

(F, Q(F))

Qk(F)

(F, Q(F))

?ö c F Ö = F Q_x(Ö) = Q_x(F)

Qk(F) Qx(Ö)

ö Q_x(F)

Card_sol(F, Q(F)) = 1

(F, Q(F))

Q_x(Ö) = Q_x(F)

(F, Qx(F),Qk(F)) Q_x(F)

(F, Q(F))

(F, Q(F)) Qk(F)

Q_x(F) F
Card_sol(F, Q(F)) > 1

Q_x(F) F

Card_sol(F, Q(F)) =6 ⁰

F

G+

G(X,U) K ? U

K

i ? X

K ? U K i

Qk(F) F

(F, Q_x(F), Qk(F))

Q_x(F)

Qk(F) F

(F, Q_x(F), Qk(F))

Q_x(F)

Qk(F)

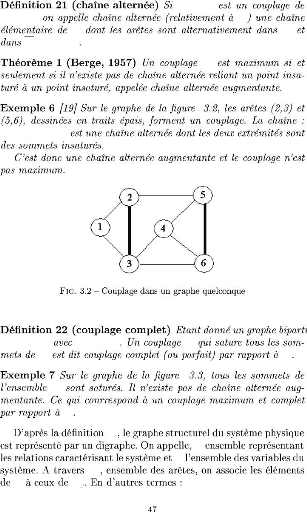
F A_z

K ? U

G(X,U) K

G K

L = {1,2,3,4}

G(X,Y, U) |X| = |Y | K

X X

K = U - K

X

X

A_z

10

Z

F

K

(f, z) E A_z ? S(f, z) = 1 G(FX, X, AX)

a = (FX(a),X(a))

FX(a) X(a)

AXC c AX

Va1, a2 E _AXC a1 =6 a2 ? FXC(a1) ⁼⁶ FXC(a2) A XC(a1) =6 XC(a2)

G+ = (F ⁺,X⁺,A⁺) Q(F +) = X+

X+ F +

G(FX_C, XC, AXC)

G(FX,X,AX) _FXC c FX XC c X

G(FX, X, AX)

G= = (F ⁼,X⁼,A⁼) Q(F ⁼)X⁼ nX⁺

_X= _F=

G- = (F ^-,X^-,A^-)

_F- X-

_G+

|F +| > |X⁺|

_X+

G+

x

_X+

F +

x _G= _G-

x1 x2

x1 x2

Knew = K U {x1, x2}

f1 f2

K

x3 x4

f3 f4

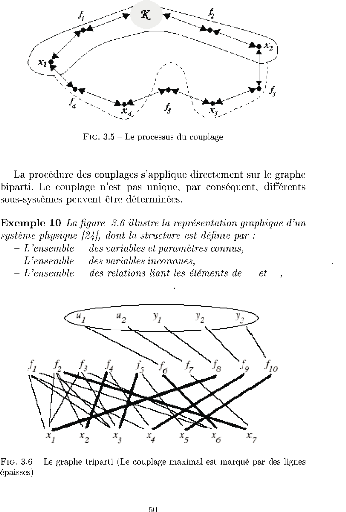
K K = {u1,u2,y1,y2,y3}

X X = {x1,x2,x3,x4,x5,x6,x7}

R K XR =

{f1, f2, f3,f4,f5,f6,f7,f8,f9, f10}

y2 - f9 = x4 - f4 = x2 - f2 = x7 - f7 = u2 y1 - f8 = x1 - f2 = x7 - f7 - u2

y3 - f10 - = x5 - f5 - = x3 - f2 - = x7 - f7 - u2

	u1	u2	y1	y2		y3	Re1
0	1	0	1	0		Re2
0	1	1	0	0		Re3
0	1	0	0	1

u1

u1

u2

u2

u1

u2

G(Fx, X, Ax)

a

(a, 3)

a ? Fx ? 3 ? X Ax n (a, 3) = ö a 3

Fx 3 X

x

G(Fx, X, Ax)

G(Fx, X, Ax)

dim(G(Fx, X, Ax)) = min(a,$)?X (|a| + |3|)

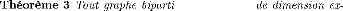
G(FX, X, AX)

(á_*, â^*)

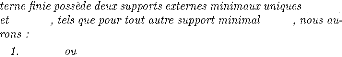
(á^*, â_*) (á, â)

á_* ? á á_* = ö

á ? á*

â_* ? â â_* = ö â ? â*

G(FX, X, AX)

B+ = G(á^*, â_*, A⁺_X) B- = G(á_*, â^*, A⁺_X) B0 = G(á^* \ á*, â^* \ â_*, A⁰_X)

á* = {f1, ..., fk} â_* = {x1, ..., xl} ? k > l

â*

_á*

(á^*, â_*)

G(FX, X, AX)

(á^*, â_*)

A⁺_X = AX n (á^*.â_*)

A^-_X = AX n (á_*.â^*)

A⁰_X = AX n (á^* \ á_*,â^* \ â_*)

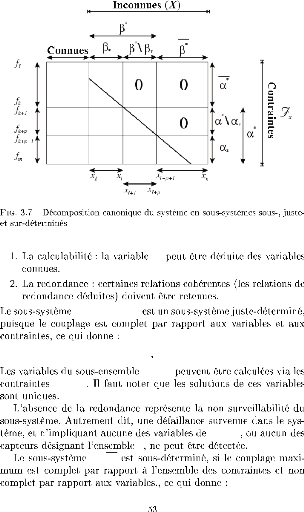
(á^*\á_*, â^*\â_*)

â_*

á* \ á_* = {fk+1, ..., fk+p} â* \ â_* = {xl+1,...,xl+p}

â* \ â*

á* \ á_*

á* \ á_*

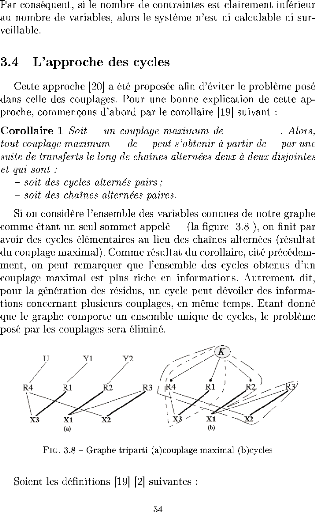
C G = [X,U]

C' G C

K

á_* = {fk+p+1, ..., fm} â^* = {xl+p+1, ..., x_n} ? m - k < n - l

K = {U,Y1,Y2}

C1 : u1 -- f6^--f3^--x3^--f5^--x5^--f10^--y3

C2 : u1 -- f6 -- x6 -- f1 -- x1 -- f8 -- y1

C3 : u2--f7--x7--f2--x2--f4--x4--f9--y2

C4 : y2--f9--x4--f1--x1--f8--y1

C5 : y2--f9--x4--f1--x3--f5--x5--f10--y3

{i0,i1,...,i_q}

C6 : y2 - f9 - x4 - f1 - x6 - f6 - u1

C7 : y3 - f9 - x4 - f4 - x2 - f2 - x3 - f5 - x5 - f10 - u2

C8 : y1 - f8 - x1 - f2 - x3 - f7 - u2

C9 : y3 - f10 - x5 - f5 - x3 - f2 - x7 - f7 - u2

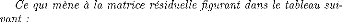
	u1	u2	y1	y2		y3	Re1
0	1	0	1	0		Re2
1	0	0	0	1		Re3
1	0	1	0	0		Re4
0	0	1	1	0		Re5
0	0	0	1	1		Re6
1	0	0	1	1		Re7
0	0	0	1	1		Re8
0	1	1	0	0		Re9
0	0	0	1	1

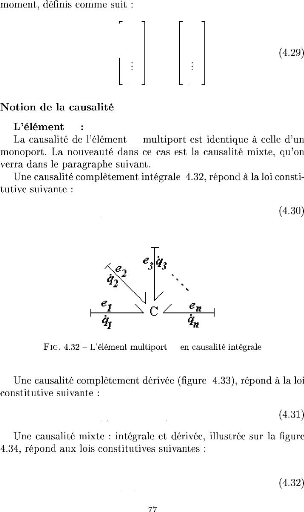
Chapitre 4

odelisation bond graph

4.1 Introduction

Le modele bond graph a ete invente par H.Paynter en 1961 et developpe ensuite par Karnopp et Rosenberg en 1983, Thoma en 1975 et 1991 et Breedveld en 1984 [26]. C'est un outil unifie de modelisation des systemes dynamiques et it permet la conception, la simulation et l'analyse des systemes complexes. Il est totalement in-dependant du domaine auquel appartient le systeme physique. C'est une reproduction graphique du systeme, en utilisant les sommets et les liens pour representer respectivement les composants et les relations definissant le systeme.

Dans ce chapitre, nous introduisons les fondements de base de la modelisation bond graph comportant une classification des elements mono et multiports ainsi la notion de la causalite. Le concept, chemin causal sera, par la suite decrit en detail pour les bond graphs simples et les bond graphs multiports.

4.2 Bond graphs simples

4.2.1 Les elements bond graph Le bond

Les elements bond graphs s'echangent l'energie a travers les bonds. La puissance est le ratio de la derivee de l'energie par rapport au temps ; la puissance est le produit de l'effort et du flux. Les directions des deux variables flux et effort sont opposees. A partir de ces

0 1

i V

e f

P = ef

P

u F

p(t) = R 0 t e(ô)d(ô) q(t) = f0 t f(ô)d(ô)

Z t

E(t) = p(ô)d(ô)

0

e	i	F	q
F	v	p	x
t	w	H	q
P	Q	Pp	V

(R, C, I, Se, Sf)

(TF,GY ) (0,1)

p(0) q(0)

p(t) q(t)

Se,Sf 0,1,TF,GY

R

ÖR(e,f) = 0

R

C

ÖC(e,q) = 0

R,C,I

C

I

Sf

Se

I

ÖI(p,f) = 0

R,C,I

0,1,TF,GY

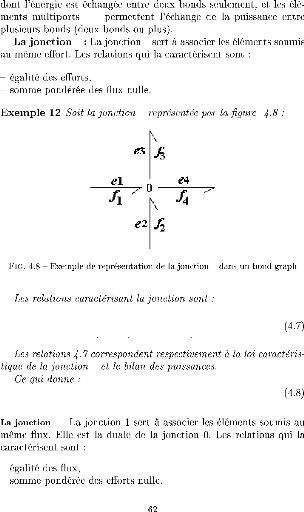
e1 = e2 = e3 = e4
e1f1 + e2f2 - _e3f3 - e4f4 = 0

0

f1 + f2 - f3 - f4 = 0

1

0, 1

0

0

0 0

e1 = me2
f2 = mf1

0

1

f1 = f2 = f3 = f4
e1f1 + e2f2 - _e3f3 - e4f4 = 0

1

e1 + e2 - e3 - e4 = 0

TF

m

TF

e1 = rf2

e2 = rf1

0 1

A B A

B p = ef

A B

e A

f

A B f

e

GY

GY

r

FIG. 4.12 -- Position du trait causal au niveau d'un bond

Ces deux cas conduisent a deux schemas blocs differents, illustres sur la figure 4.13.

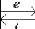
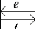
FIG. 4.13 -- Les deux differentes situations de la causalite

Comme la position du trait causal est tout a fait independante du sens de la demi-fleche, on obtient les deux cas illustres sur la figure 4.14.

FIG. 4.14 -- Independance de la position du trait causal par rapport au sens du bond

Les differents types de la causalite :

Ports avec causalites fixes : Ce sont les elements de sources d'effort et de flux qui possedent une causalite fixe (voir figure 4.15). Cependant, si l'objectif de noire analyse est la derivation du modele mathematique (Equations d'etat), alors les elements non-lineaires seront consideres comme des ports avec causalite fixe. C'est le cas ou la relation constitutive de l'element non-lineaire ne peut pas etre exprimee par une forme arbitraire de causalite.

Ports avec causalites preferees : Pour des considerations d'ordre
numerique et souvent physique, it est plus aise d'integrer que de de-
river, par consequent on essaiera d'affecter aux elements de stockage

I C

f CI e

eC = 1 f fcdt

C
eI = I dfI

dt

C I

e C I

f

fC = C deC

f eIdt

dt

fI = I 1

C I

e = Rf f R

f = e e R

R

R

TF GY 0 1

0

e2

e1 = e2, e3 = e2, e4 = e2

f2 = --f1 + f3 + f4

1 n

n -- 1

0

1

1

f1 = f2 = f3 = f4

e3 = e1 + e2 - e4

e1 - e2 - e3 - e4 = 0

0

f1 = f3, f2 = f3, f4 = f3

1

0 1 TF GY

1 -

2 - 3 - 4 I R

I R

E = {C, I, Se, Sf, De, Df}

{R,C,I}

I R 1 - 2 - 3 - 4 -

4 - 3 - 2 - 1

X p

I q C

1 - 5 - 5 - 1 4 - 3 - 6 - 6 - 3 - 4

xi xd

Xÿ X

ÿxi xi

ÿxd xd

Z f

I C

Zi Zd

Y

Din R

Dout R

S

ÿxi		S11	S12	S13	S14		Zi	Zd
=	S21	S22	S23	S24	ÿxd		Din
	S31	S32	S33	S34	Dout		Y
	S41	S42	S43	S44	U

U

S (n_c +n_s) (n_c +ne)

n_c (R,C,I)

n_s
n_e

Dout = L.Din

s 1/s

Zi = H(s) ÿxi

Zd = H^'(1/s) ÿxd

L H(s) H'(1/s)

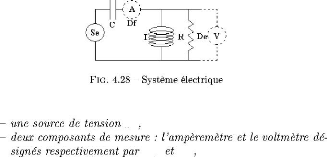
Se

Df De

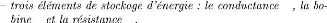
C

I R

(a) (b)

ÿxd = [f2, e5]^tÿxi = []^t Zd = [e2, f5]^t Zi = []^tt Dout[f4]^tDin = [e4]^t
U = [Se]^t Yout = [De, Df]^t
V = [Se, e2, e5, e4, f5, f4, f2, De, Df]t

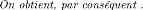
e2
f5
e4

Df
De

f2
e5
f4

Se

?
?

?

? =

Zd
Din

Y

?

0 --1 0 1

? 1 0 --1 0

?

= ? 0 1 0 0

? ?1 0 0 0

0 1 0 0

R CISe Sf De Df TF GY

0 1

R C I

C I

C C

n C

ime ÿqi

C

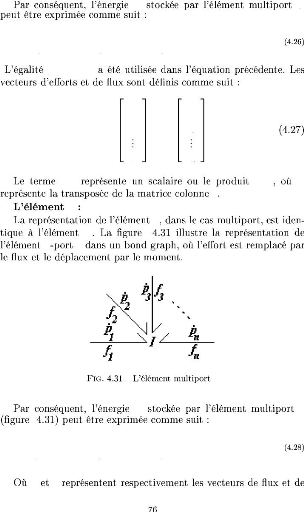
Z t _>n Z t _>n Z t _>n Z q

E = (eifi)dt = (ei ÿqi)dt = (eiq()dqi = e(q)dq = E(q)

t0 i=1 t0 i=1 t0 i=1 q0

q1

q2

q3

e1

e2

e3

q =

, e =

q_n

e_n

Z t _>n Z t _>n Z t >:n Z p

E = (fiei)dt = (fi ÿpi)dt = (fip()dpi = f(p)dp = E(p)

t0 t0 t0 p0

i=1 i=1 i=1

E C

fidt = dqi

edq etdq et

e

I

I

C

n I

I

E I

f p

ei = ÖCi(q1, q2, · · · , qj, ej+1,· · · , e_n), i = 1,2,· · · ,j

f1

f2

f3

,f =

f_n

C

ei = Ö-1

Ci (q1,q2,···,q_n),i = 1,2,···,n

? p1

? p2 ?

p = ? p3

p_n

C

C

qi = ÖCi(e1,e2,·· · ,e_n),i = 1,2, · ··,n

qk = Ö-1

Ci (q1, q2, · · ·, qj, _ej+1,···, e_n),k = j, 2,··· ,m

C

C

I

I

C

fi = Ö-1

Ci (p1,p2, · · · ,p_n), i = 1,2, · · · ,m

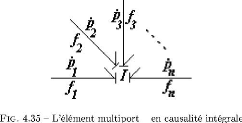
I

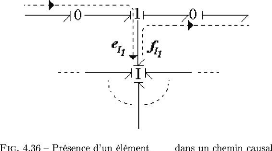
MP

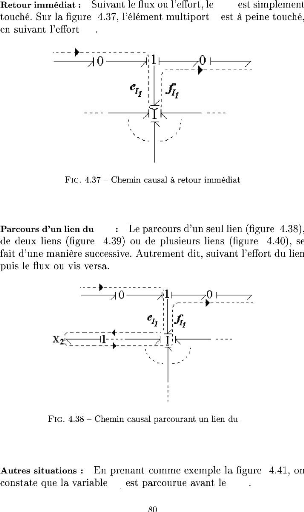
MP

MP

eI% MP

eI1

MP I

MP

MP

MP

0 C0

MP

1 C1

MP

2 C2

MP

1 - 2 C1 - 2

MP

MP

MP

MP

0 C0

MP

{R,C,I}

t Tt 1 < t < dim(M) dim(M)

MP t

1 C1

MP

2 C2

MP

1-2 C1-2

MP

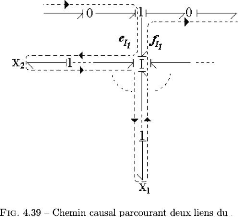
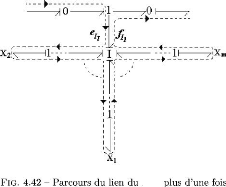
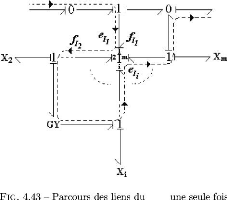
le cas des multiports, le probleme combinatoire de parcours des chemins causaux est accentue. La notion de chemins causaux et leur classification ont ete fournies par la suite afin de mieux aborder le chapitre suivant.

Chapitre 5

Contribution : Les bond

graphs couples et la

surveillance

5.1 Introduction

Il existe differentes methodes de generation de RRAs a partir d'un modele bond graph. Deux possibilites peuvent etre proposees pour la classification de ces methodes :

classification [29] en methodes directes et indirectes, classification [37] en methodes analytiques et structurelles.

Dans ce chapitre, nous allons presenter les differentes methodes appliquees dans la surveillance des systemes physiques. Nous presentons les methodes directes qui permettent une generation des RRAs directement du bond graph, et celles qui determinent les RRAs a partir d'un modele intermediaire. Nous exposons, par la suite, noire algorithme avec sa complexite. Nous decrivons la conception de l'algorithme [29] pour le graphe structure) et son extension vers les bond graphs simples et les bond graphs couples.

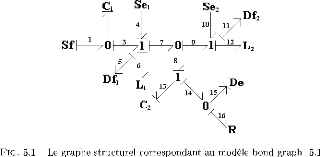
p

I

C

I C R

I q C

ABC D

R TF GY

?
????

1

?
?

D(s)

?

? =

De1

Df1

Df2

b1 M1

_s2

? ? ? ? ? ? ?

V1 F1 F2

? ?

(1+M2 s2

k1 )

--b1s b1M1 s3

k1 k2

k1 (1+b1 k1 s )

1 + b1 s (1 + M2 k1 s ) k1 s + (1 + b1 k1 s ) s s

k1 k1 k2

(1+b1 s (1+b1 k1 s +M1 s2

k1 )

1 + b1 k1 s + M1 s2 k1 )

s s

k1 k2 k2

F2

F1 F2

V1F1 F2

V1F1

D(s) = 1 + M2s2

k2 + M1s2

k2 + M1s2

k1 + b1s

k1 + b1s

k1 (M2s2

k2 + M1s2

k2 ) + M1M2s4

k1k2

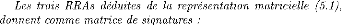
	De1	Df1	Df2	V1	F1		F2	Re1
1	0	0	1	1	1		Re2
0	1	0	1	1	1		Re3
0	0	1	1	1	1

~

-I -M'

~ S

M = I

Y

MT(s)

S

M

U

S11 ? ? S31 M =? ? S41 ? ? I1 ?0 0

S12 S22 S32 S42 0 I2 0

? ? S21 S13 S23 S33 S43 0 0 I3

S14 S24 S34 S44 0 0 0

-I1 0 0 0 -H(1/s) 0 0

0 -I2 0 0 0 -H^'(1/s) 0

0 0 -I3 0 0 0 -L

0 0 0 -I4 0 0 0

_M'

?

M'.V = 0

M

Mij

i j

(2m_c + m_s) 2m_c

m_s

I1I2I3 I4

M.V = 0

M

V

M

M 1

_M*

M*

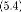
F1 F5 F2 M* = F7 F8 F6 F3 F4

? ? ? ? ? ?

0 1 0 1 0 1 0 0

1 0 1 0 1 0 1 0

0 1 0 0 0 0 0 1

1 0 0 0 0 0 0 0

1 0 0 0 0 1 0 0

0 1 0 0 0 0 1 0

0 0 1 0 0 0 0 1

0 0 0 1 0 0 0 0

0 0 0 0 1 0 0 0

	Se	De		Df	Re1
1	1	0		Re2
0	1	1

0 1

0

1

0

1

0 1

0 1

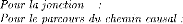
0 e2 = e1 - e3

e3 = De e1 = Se Df = (Cs)e2

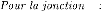
1 f5 = f3 - f4

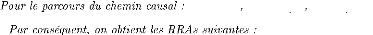
f3 = Df f4 = De/R De = (Is)f5

Df = Cs(Se - De) De = Is(Df - De/R)

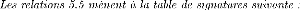
	Se	De		Df	Re1
1	1	1		Re2
0	1	1

1

	y1	y2	y3	· · ·		yn	Re1
1	1	0	· · ·	0		Re2
0	1	1	· · ·	0
				1		Ren
1	0	0	· · ·	1

CHEM

d d

q

q - 1

1 C

q

C[i,j] = 1 1

i j

C[i,j] = 0

1

_C,

sommet C'

sommet E K0

K0 = K0 - {sommet} K1 = K1 U {sommet}

NR = |K|

K0 = K1 = ö

sommet E K1

K1 = K1 - {sommet} K+ 2 = K+ 2 U {sommet}

C,	10	11	C, 1^+2
	d	f
			df

2

NR |K|

3 4

K0 0

K1 1

1

K+ = 2

2

l 1

i Kd

j Kf

? l i j

C

l 1

i Kdf

? l i i

C

l

d f

5

RRAs

K0 = K K1 = ö K+ 2 = ö

C

	Se	De	Df
C1	1	1	0
C2	1	0	1
C3	0	1	1

	Se	De	Df
Re1	1	1	0
Re2	1	0	1
Re2	0	1	1

C' N

sommet

1 N sommet E K0

sommet E K0 sommet E K0

sommet E K1

N * 3

O(N)

2

1 1 1

1 1

3

O(1)

l i j

1 N

l i

j O(N)

RRA

N

O(N) N *N *

N * (3N) O(N⁴)

O(N4)

{,,,,}

l i

i O(N)

l i

1 N

O(N)

N *N *

RRA

N

(3N) O(N³)

3

O(1)

C

O(N²) 5

O(N⁴) O(N³)

O(1)

_Ci _ime

Ca

_Ei _ime

Ce

C1 Ca= {Se, e2, f2, Df} C²Ca = {Se, e5, De}

C³Ca = {Df, f2, f5, e5, De}

E1 Ce= {Se, e2, f2, Df} E²Ce = {Se, e2, f2, f3, f5, e5, De}

0	f(ei, ej) f(fi, fj)
1	f(ei, ej) f(fi, fj)
C	f(ei, fj)
I	f(fi, ej)
R	f(ei, fj)

Se De Df

MP

C

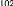
	Se	De	Df
C1	1	1	0
C2	1	0	1

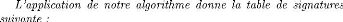
	Se	De	Df
Re1	1	1	0
Re2	1	0	1
Re2	1	1	1

eh
et

e_c

?

E = ?

? ? ?

fh

? , F = ? ft ?

fc

fhft f_c

ehet e_c

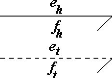
FIG. 5.7 -- Representation du couplage des energies par deux liens en pointilles et en trait plein

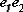
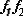
FIG. 5.8 -- Representation du couplage des energies par deux liens separes

Les bond graphs couples ne sont pas directement utilises comme support a la surveillance. Afin de generer les RRAs, des transformations doivent etre effectuees au niveau du bond grah couple. L'utilisation de la causalite integrals permet d'eviter les difficultes de calculs numeriques de la derivee du residu lors de la simulation.

Les methodes de redondance analytique et de l'analyse structurelle ont fait l'objet d'application a des processus thermofluides, tels que :

-- un generateur de vapeur,

un condensateur d'une installation pilote complexe representant le fonctionnement d'une centrale a echelle reduite.

Les deux approches initialement proposees [11], pour la surveillance

avec les bond graphs couples sont :

1. &coupler les liens couples en liens simples puis appliquer les outils déjà developpes pour les bond graphs monoenergie,

2. proposer une methode de linearisation des muliports permettant ensuite une analyse du bond graph par un parcours de chemins causaux generalises.

Notre but dans ce travail est de permettre la surveillance par les bond graphs couples sans transformations. Ceci en adaptant le nouvel algorithms (1' algorithme 5) directement sur le modele bond graph.

_Xn
i=1

Ö_s : mÿ +

ai ÿmi = 0

^ÿH)

_Xn
i=1

ai ÿmi = 0

_ö-1

h (P, ^ÿH) +

Pn i=1 ai ÿmi

R C I RRA

0h

ai #177;1

mÿ
Hÿ

C

Öb : P = öh( ÿm,

ÿmi (i = 1 · m)

mÿ

Sfh

fh = Pn i=1 ai ÿmi

I

	E1	E2	E3	u1	u2	u3	Df1	Df2	Df3
C1	1	0	0	1	0	0	1	0	0
C2	1	0	0	1	0	0	0	1	0
C3	1	0	0	1	0	0	0	0	1
C4	0	1	0	0	1	0	1	0	0
C5	0	1	0	0	1	0	0	1	0
C6	0	1	0	0	1	0	0	0	1
C7	0	0	1	0	0	1	1	0	0
C8	0	0	1	0	0	1	0	1	0
C9	0	0	1	0	0	1	0	0	1

(E1,u1) (E2,u2) (E3,u3)

	E1	E2	E3	u1	u2	u3	Df1	Df2	Df3
Re1	1	0	0	1	0	0	1	0	0
Re2	1	0	0	1	0	0	0	1	0
Re3	1	0	0	1	0	0	0	0	1
Re4	0	1	0	0	1	0	1	0	0
Re5	0	1	0	0	1	0	0	1	0
Re6	0	1	0	0	1	0	0	0	1
Re7	0	0	1	0	0	1	1	0	0
Re8	0	0	1	0	0	1	0	1	0
Re9	0	0	1	0	0	1	0	0	1

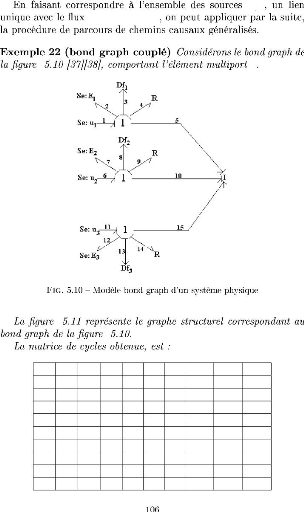
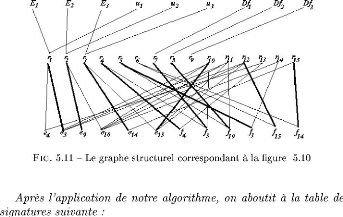
Nous avons commence par la presentation du principe (l'idee de base) de l'algorithme et son application sur le graphe structurel correspondant au systeme physique. A ce niveau, un exemple illustratif de l'algorithme a ete donne.

L'interet du present travail etait de permettre une generation de la table de signatures, directement du modele bond graph, autrement dit sans utilisation d'un modele intermediaire (graphique ou mathematique). Ceci a ete realise via l'adaptation de l'algorithme aux bond graphs couples (systemes complexes). Par consequent, notre contribution est celle de permettre la surveillance des systemes complexes avec les bond graphs couples ( 5.12).

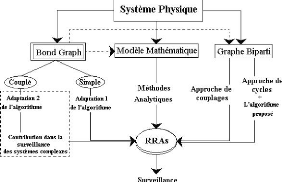
FIG. 5.12 -- Schema qui situe notre contribution en surveillance par les bond graphs

M

M

M*

Symbol's 2000

6.0

C

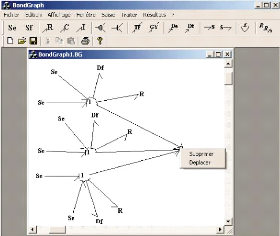
FIG. 5.13 -- Interface de saisie du modele bond graph

0 1 TF GY

R

I C

I C

R

C

C

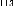
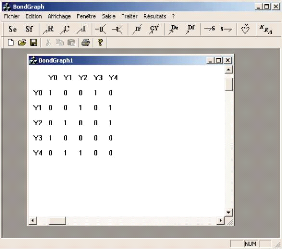
FIG. 5.14 -- Interface d'affichage de la matrice des cycles

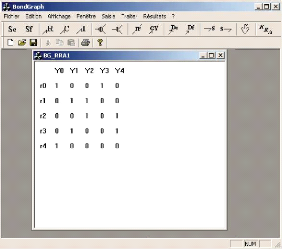
FIG. 5.15 -- Interface d'affichage de la table de signatures

Bibliographie

[1] M. BelaIguid. Generation des relations de redondance analytique (rra), 2005. Universite d'oran, Es-Senia. Institut d'Informatique.

[2] C. Berge. Graphes. 3eme edition, Paris, Editions gauthiervillars, 1983.

[3] P. Borne, G. Dauphin-Tanguy, J.P. Richard, F. Rotella, and I. Zambettakis. Modelisation et identification des processus, Tome 2. Editions technip, Paris, 1992.

[4] B. Ould Bouamama. Model builder for thermo-fluid systems using a bond graph and functional modelling. 13th European Simulation Symposium, ESS01, pages 822-826,2001. Marseille, France.

[5] B. Ould Bouamama. Modelisation et supervision des systemes en genie des procedes - approche bond graphs, 2002.

[6] B. Ould Bouamama. Design of supervision platforms based on bond graph theory. ON-LINE DIAGNOSIS SCHEDULING OPERATION SUPPORT FOR INDUSTRIAL PROCESSES, line FRANCE, 2004.

[7] B. Ould Bouamama, G. Dauphin-Tanguy, and M. Staroswiecki. Integration des modeles externes et bond graphs pour la supervision des processus en genie des procedes. Journee d'etudes de diffusion technologique. Instrumentation et traitement du signal et des images, Dans les procedes agroalimentaires et biotechnologiques, 2002. Ecole centrale de Nantes.

[8] B. Ould Bouamama, G. Dauphin-Tanguy, M. Staroswiecki, and D. Del Amo Bravo. Bond graph analysis of structural fdi properties in mechatronics system. 1st IFAC Conference on mechatronic systems. Vol. 3. IFAC. Darmsdadt, Germany, 2000.

[9] P. C. Breedveld. Multibond elements in physical systems theory. Special issue of journal of Franklin Institute, pages 1-36, 1985.

[10] Brow and F. T. Direct application of the loop rule to bond graphs. Journal of Dynamics Systems, Measurement and Control, pages 253-261, 1972.

[11] F. Busson and B. Ould Bouamama. Monitoring of steam generator using a bond graph approach. Symposium On Power Plant and Power Systems Control, 2000. Brussels, Belgium.

[12] M. Combacau. Commande et surveillance des systemes a evenements discrets complexes : application aux ateliers flexibles. PhD thesis, Universite P.Sabatier de TOULOUSE, 1991.

[13] M. Combacau, P. Berruet, P. Charbonnaud, and A. Khatab. Reflexions sur la terminologie surveillance - supervision. http ://www.laas.fr/ combacau/SPSF/sursup. html, 2000.

[14] C. Combastel. Methodes d'aide a la decision pour la detection et la localisation de defauts dans les entrainements electriques. PhD thesis, INPG, 2000.

[15] C. Cussenot. Surveillance et diagnostic de la chaine de depollution d'une automobile. PhD thesis, Universite de Rennes 1, 1996.

[16] G. Devauchelle. Diagnostic mecanique des fatigues sur les structures soumises a des vibrations en ambiance de travail. PhD thesis, Universite de Paris IX Dauphine, 1991.

[17] A. Evsukoff. Raisonnement approche pour la surveillance des procedes. PhD thesis, INPGrenoble, 1998.

[18] A. Golynski and J.D. Horton. A polynomial time algorithm to find the minimal cycle basis of a regular matroid. ?, 2001.

[19] M. Gondron and M. Minoux. Graphes et Algorithmes. 3eme edition, Paris, Editions Eyrolles, 1995.

[20] H. Haffaf, B. Ould Bouamama, and M. Staroswiecki. Structural analysis and fdi : A cycle approach. soumis a Automatica, 2004.

[21] R. Isermann. Process fault diagnosis based on modelling and estimation methods-a survey. Automayica, pages 387-404, 1984.

[22] R. Isermann and P. Bane. Terminology in the field of supervision, fault detection and diagnosis. http ://w3.rte-technik.tudarmstadt.de/institut/terminology.en.html, 2003.

[23] R. Izadi-Zamanabadi. Fault detection and isolation using analytical redundancy relations for the ship propulsion benchmark. Technical report, LAIL URA 1440D, University of sciences and technologies of Lille, France, 1998.

[24] R. Izadi-Zamanabadi and M. Blanke. Structural analysis for diagnosis - the matching problem revisited. Proceedings of 15th IFAC World Conferences, Barcelona Spain, 2002.

[25] R.C. Karnopp and S. Azerbaijani. Pseudo bond graphs for generalised comportemental models in engineering and physiologie. Journal of the Franklin Institute, pages 95-108, 1981.

[26] R.C. Karnopp, D. Margolis, and R. C. Rosenberg. System Dynamics : A unified Approach. 2nd edition, J.Willey editions, 1990.

[27] P. Kubiak. Analyse symbolique des systemes physiques par bond graph et comportant des elements multiports. PhD thesis, Universite des Science et Technologies de Lille, 1996.

[28] F. Z. Lebbah. Affectation de la causalite aux bond graphs acausaux avec mrcap et pses. Universite d'Oran. Es-Senia. Departement d'informatique, 1999. Memoire de fin d'etudes en vue de l'obtention du diplOme : Ingenieur d'Etat en Informatique.

[29] FZ. Lebbah and H. Haffaf. Surveillance et bond graphs-nouvel algorithms de generation de relations de redondance analytique. Colloque International MOAD'2004, Saida, Algerie, 2004.

[30] D. Lefebvre. Contribution a la modelisation des systemes dynamiques a evenements discrets pour la commande et la surveillance, 2000.

[31] L.TROMP. Surveillance et diagnostic de systemes industriels complexes : une approche hybride numerique/symbolyque. PhD

thesis, Universite de Rennes, Ecole Doctorale : Science Pour l'Ingenieur, 2000.

[32] Didier MAQUIN. Diagnostic a base de modeles des systemes technologiques, 1997. Institut National de Lorraine,Ecole doctorale IAE#177;M, DFD Automatique.

[33] S. Ploix and S. Giuliani. Glossaire des termer

usuels du diagnostic de defauts. http ://www-

lag.ensieg.inpg.fr/ploix/glossaire/DiagnosticGlossaire.htm.

[34] H. Poulard. Statistiques et reseaux de neurones pour un systeme de diagnostic. Application au diagnostic de pannes automobiles.

PhD thesis, LAAS/France, 1996.

[35] Hector E. Rubio Scola. Information criteria for residual generation and fault detection and isolation. Technical report, Publication interne n 1008, Institut fr Recheche en Informatique et Systemes Aleatoires, 1996.

[36] Hector E. Rubio Scola. Detection signal for failure detection and isolation for linear dynamic systems. Technical report, Rapport de recherche n 3935L URA 1440D, Universidad Nacional de Rosario, Argentina, 1998.

[37] M. Tagina. Application de la modelisation bond graph a la surveillance des systemes complexes. PhD thesis, University des Science et Technologies de Lille, 1995.

[38] M. Tagina, JP. Cassar, G. Dauphin-Tanguy, and M. Staroswiecki. Monitoring of systems modelled by bond-graphs.

ICBGMS95. International Conference on Bond Graph Modelling. Las Vegas, 1995.

[39] Tako and F.Lootsma. Observer-based Fault Detection and Isolation for nonlinear systems. PhD thesis, Department of control engineering. Alborg University, 2001.

[40] J. U. Thoma and B. Ould Bouamama. Modelling and Simulation in Thermal and Chemical Engineering . bond Graph Approach. Springer Verlag, 2000.

[41] A.K.A. Toguyeni. Surveillance et diagnostic en ligne dans les ateliers flexibles de l'industrie manufacturiere. PhD thesis, Universite de Lille, 1991.

[42] P. Vismara. Union of all minimum cycle bases of graph. The electronic journal of combinatorics, 1997.

[43] P. Weber. Diagnostic de procedes par l'analyse des estimations parametriques de modeles de representation a temps discret.

PhD thesis, INPG, 1999.

[44] Mohamed Ryad ZEMOURI. Contribution a la surveillance des systemes de production a l'aide des reseaux de neurones dynamiques : Application a la e-maintenance. PhD thesis, L'UFR des sciences et techniques de l'Universite de Franche Comte, 2003.

[451 Q. Zhang. Identification et Surveillance de systemes Dynamiques, Habilitation a diriger les recherches. PhD thesis, Universite de Rennesl, Institut de Formation Superieure en Informatique et en Communication, 1999.

Table des figures

1.1	Architecture generale d'un systeme de supervision en
	ligne	8
1.2	Classification des methodologies de la surveillance in-
	dustrielle	13
1.3	Classification des methodologies de la surveillance in-
	dustrielle	14
2.1	Redondance materielle double	22
2.2	Redondance materielle double	23
2.3	Redondance materielle et analytique	24
2.4	Structure generale de generateurs de residus	35
3.1	Exemple d'un systeme physique	43
3.2	Couplage dans un graphe quelconque	47
3.3	Couplage maximum d'un un graphe biparti	48
3.4	Couplage maximum sur le graphe structurel d'un sys-
	teme physique	49
3.5	Le processus du couplage	50
3.6	Le graphe triparti (Le couplage maximal est marque
	par des lignes epaisses) 50
3.7	Decomposition canonique du systeme en sous-systemes
	sous-, juste- et sur-determines	53
3.8	Graphe triparti (a)couplage maximal (b)cycles . . . .	54
4.1	Les differentes formes d'un bond	58
4.2	Representation des bonds avec le flux et l'effort . . .	58
4.3	Representation du flux et de l'effort dans les domaines
	electrique et mecanique	59
4.4	Representation de l'element R dans le bond graph . .	60
4.5	Representation de l'element C dans le bond graph . .	60

0

1

TF
GY

C I

C I

R

0

1

I R

1-5-5-1 4-3-6-6-3-4

C I C C C I

MP

MP

MP

MP

MP

MP MP