III. MODELISATION DU SYSTEME
1. INTRODUCTION
Le but de ce chapitre est de présenter les
modèles classiques de générateurs hydroélectriques
et de leurs régulateurs. Ces modèles servent à comprendre
le comportement des générateurs et le réglage de leurs
régulateurs à l'aide de la théorie du contrôle.
Les différentes configurations de réseau
possibles aux bornes du générateur sont d'abord
illustrées. Le rôle du générateur pour chaque
configuration est défini ainsi que les actions qu'il effectue pour
réguler la fréquence. Les hypothèses de
linéarité utilisées pour la modélisation sont par
la suite présentées. La modélisation du régulateur
de vitesse mécanique du type accélerotachymétrique est par
la suite effectuée. Les paramètres typiques du
générateur sont donnés ainsi que les paramètres du
procédé étudié. En fin en fonction des
données provenant de la centrale de Mwadingusha, nous déduirons
les paramètres du régulateur dans son fonctionnement normal ou
fonctionnement sans défaut.
Pour une bonne supervision de la boucle de réglage,
nous présenterons la plage de bon fonctionnement du système sans
défauts et au delà de la quelle, on qualifie le système
comme défaillant.
2. MODELISATION DU GENERATEUR
Dans cette section, nous présentons le
générateur comme situé dans l'ensemble du réseau
électrique c'est-à-dire dans son fonctionnement à vide, en
îlotage et en réseau. Les relations entre les
entrées-sorties du générateur et du régulateur
ainsi que les directions des actions sont aussi présentées.
La turbine de la centrale de Mwadingusha étant du type
Francis, les hypothèses faites pour la modélisation
sont :
F La résistance hydraulique est négligeable dans
la conduite forcée,
F L'eau dans la conduite forcée est
inélastique
F La puissance active de sortie de la machine est
proportionnelle à la position des directrices
F La dynamique de la charge est négligée, sa
relation entrée-sortie est statique ;
F Le couple et la puissance sont équivalents dans le
système par unité ;
F L'utilisation du modèle linéaire est
limitée à la région autour du point de l'opération
en puissance où il a été identifié.
2.1. Fonctionnement à vide
Les éléments du modèle de
générateur à vide sont la conduite forcée, la
turbine et l'alternateur. La conduite forcée crée la pression
nécessaire à la production d'énergie, elle est
constituée d'un tuyau ou une conduite fermée qui comporte une
dénivellation. L'eau y transite entre la chambre de mise en charge en
amont et le générateur en aval. Son comportement est
caractérisé par l'inertie de translation de l'eau et par la
pression sur les aubes de la turbine. L'inertie contraint les variations de
vitesse brusque afin d'éviter la surpression importante en aval (coup de
bélier). Elle dépend de la longueur et de la section de la
conduite ainsi que de la vitesse de l'eau. La pression dépend de la
différence des hauteurs entre l'entrée de la conduite et sa
sortie en régime permanent et des variations des vitesses de l'eau en
régime transitoire.
Les directrices sont réparties tout autour de la
turbine et contrôle le débit et la direction de propagations de
l'eau sur les aubes de la turbine et forment ce qu'on appelle cercle de
vannage.
La turbine sert à transformer l'énergie
cinétique de translation de l'eau en énergie cinétique de
rotation du rotor. Le modèle de la turbine comprend la dynamique de
l'ouverture des vannes d'eau et l'interaction entre l'eau et les aubes.
Effectivement la puissance de la machine est proportionnelle au produit du
débit par la pression. Lors d'une augmentation rapide de l'ouverture des
directrices, l'eau ne peut accélérer immédiatement dans la
conduite forcée, le débit est donc constant. Cependant,
l'ouverture plus grande entraîne une baisse de pression sur les aubes de
la turbine et produit une diminution de la puissance.
L'alternateur fait la transformation entre l'énergie
mécanique et électrique. Du côté mécanique,
il s'agit de l'arbre sur lequel sont situés des pièces
tournantes, son comportement est donc celui d'une inertie de rotation. Du
coté électrique, l'alternateur est un ensemble de bobinages, il
se comporte comme un circuit inductif.
Les pertes par fiction surviennent entre les parties mobiles
et les parties fixes. La friction est considérée linéaire
par rapport à la vitesse de rotation, ce qui est valide pour une plage
restreinte d'opération.
a) Modèle
mathématique du système
Au cours de ce paragraphe, nous désignons par ?p
l'écart relatif instantané entre la puissance de la turbine, sous
hauteur de chute constante H0 et sous ouverture variable du
vannage, et la puissance initiale de l'alternateur.
En tenant compte aussi des hypothèses
énoncées, nous admettons que cette valeur de ?p est
proportionnelle à la variation relative de l'ouverture du vannage
qu'elle peut ainsi servir à représenter à une certaine
échelle.
y = k (1 - ?p)
Où y est l'ouverture relative du vannage
k est un coefficient de proportionnalité
Signalons en plus que pour la modélisation du
système, nous avons utilisé les variables en grandeur relative.
Le débit de la turbine est la somme du débit
correspondant à l'ouverture du vannage et par suite proportionnel
à  et du débit supplémentaire provenant de la surpression
dans la conduite forcée, proportionnellement à la racine
carrée de la hauteur de chute, soit en valeur absolue à 0,5?h.
L'expression du débit est ainsi donnée
par :
 (1)
La surpression ?h dans la conduite forcée est
proportionnelle à la variation instantanée du débit ?q
selon l'expression :
 (2)
Où Te est la constante d'inertie hydraulique
de l'eau dans la conduite forcée. Cette constante est donnée par
l'expression :
 (3)
Où L est la longueur de la conduite forcée en
mètre ;
V : la vitesse initiale de l'eau engagée
dans la conduite forcée en m/s
g : est l'accélération de pesanteur
en m/s2
H0 est la hauteur nette de chute en
mètre.
En substituant les expressions (1) et (3) dans l'expression
(2), on trouve :
 (4)
L'expression (4) est celle de la surpression. Elle donne
l'écart de pression ?h du coup de bélier de masse entendue que
cette expression n'est valable que pour des chutes basses et moyennes dans
lesquelles on peut négliger les effets de la dilatation des conduites et
de la compressibilité de l'eau (le coup de bélier d'onde). Donc
cette expression convient le mieux pour la modélisation du coup de
bélier de la centrale de Mwadingusha qui a une chute moyenne.
Du côté de la turbine, le mouvement s'obtient,
toujours en grandeur relative, en écrivant que le couple
accélérateur fait équilibre à la somme
algébrique des puissances ?p, de l'excès de puissance introduit
par le coup de bélier de masse qui, étant proportionnel à
l'exposant 3/2 de l'écart de hauteur ?H donne en valeur relative 1,5?h
et enfin de la variation de puissance apportée par l'autoréglage
ou perte par friction, soit -ã?f.
D'où l'équation de la masse tournante :
 (5)
La deuxième équation tient compte de la
variation de la puissance apportée par l'autoréglage ou perte par
friction.
Où Tm est la constante
d'accélération appelée aussi temps de lancer du groupe ou
encore la constante de temps mécanique.
Il est donné par l'expression :
 (6)
Où ù est la vitesse angulaire en rad/sec.
P est la puissance active nominale en kW
J est le moment d'inertie du groupe.
Les praticiens ont pris l'habitude, que rien ne justifie
d'ailleurs, de substituer au moment d'inertie MR2 par le moment de
giration PD2, produit du poids en kg par le carré du
diamètre de giration. Le PD2 est une grandeur qui n'a pas les
mêmes dimensions que le moment d'inertie MR2 ; mais sa
valeur numérique est le quadriple du moment d'Inertie.
 (7)
Jù2 est le double de l'inertie
cinétique emmagasinée ; Tm qui est le temps de
lancer en seconde représente le temps fictif nécessaire pour
qu'un groupe au repos atteigne la vitesse ù sous l'action du couple
constant correspondant à la puissance nominale P.
Ainsi les relations importantes retenues pour la
modélisation du système fonctionnant à vide sont
formées par le système d'équations (4) et (5).
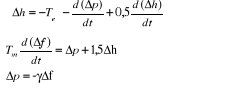
En appliquant la transformation de Laplace, on a :
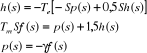
De la première équation, nous tirons :
 et nous l'insérons dans la deuxième équation, on
avons alors :
La fonction de transfert du générateur à
vide est alors donnée par le système d'équation
(8):
 (8)
| 
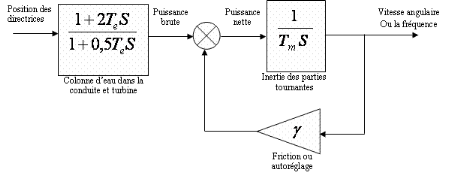
