DEDICACE
A mon père NKULU NTAMBO André, qui
malgré la conjoncture, se donne toujours corps et âme pour notre
instruction et par sa tolérance et son optimisme nous a permis à
monter lentement mais sûrement les gradins du savoir ;
A ma mère NGOY KABILA Béatrice, par son
affection et ses conseils moraux et spirituels qui nous réconfortent
dans des durs moments, voici le fruit de ton travail, première soupire
de soulagement pour tout ce que tu consentis pour nous.
A toi Bijou MADIKA MWENZE Placide, par ton amour si grand et
inégalable, tu as ouvert tout coeur pour braver les dures
épreuves et Dieu Tout-Puissant t'a sortie gagnante, trouve dans ce
travail l'expression de mon enthousiasme d'être ensemble et mes
sincères gratitudes.
A toi NKULU NTAMBO Yves Prémices mon cher fils, voici
ce que ton père te donne comme le précepte : « Si
tes rêves ne te font pas peur, tu rêves petit ». Cela
veut dire que tu es fais pour des grandes choses, tu es né pour
être Seigneur dans ta cour féodale et non pas vassal au service
d'un maître. Pour y arriver, ceci est le droit chemin que ton père
te montre pour atteindre tes objectifs bien que dure et escarpé, tu dois
être résolu de le suivre par un travail bien fait !
A mes frères et soeurs : Patrick NKULU NTAMBO,
Gerry NKULU KABILA, Nadine NKULU KILUMBA, Laurence NGOY KABILA, Thierry
KABILA et Josky BANZE, vous qui subissez les retombées de notre
comportement, voici le fruit de nos efforts conjugués en commun.
A ma regrettée grand-mère Gaudence NKULU
KILUMBA, par son assistance à la prière dans les jours de sa vie,
ceci est l'oeuvre de ta progéniture qui t'immortalise,
Je dédie ce travail
AVANT-PROPOS
Il nous incombe l'agréable devoir de témoigner
en ce moment un signe de reconnaissance envers ceux qui nous ont assisté
tant moralement que matériellement à l'élaboration de ce
travail.
Nos remerciements s'adressent premièrement au corps
professoral de la faculté polytechnique en général et
celui du département d'électromécanique en particulier
pour leur contribution intellectuelle combien de fois louable faisant de nous
une pépinière du savoir durant tout notre parcours universitaire
et particulièrement au chef des travaux ILUNGA MWANZA, secrétaire
académique de la Faculté polytechnique pour cette phrase qui nous
interpelle toujours à nous mettre au travail : « Je veux
savoir ».
Nous témoignons notre gratitude et remercions Le Pr.
Dr. Ir Pierre KAMULETE M, qui, en dépit de ses multiples occupations, a
accepté de diriger ce travail et l'Assistant Ingénieur Civil
Moïse MUKEPE qui, a accepté de coordonner ce travail et d'en
suivre son évolution malgré ses lourdes charges.
Nous ne pouvons pas fermer cette page sans citer
l'Ingénieur civil Boniface MABONZO MUAKA, chef d'entretien
mécanique à la centrale hydroélectrique de Mwadingusha,
pour toutes ses remarques et suggestions portées à ce travail, et
pour sa disponibilité de nous fournir une documentation
nécessaire pour amener à bien la rédaction de travail.
Nos sentiments de gratitude s'adressent aux familles des
oncles : Papa François MULONGO et Maman Concilia KASONGO, Papa
Adonis BANZE et Maman Aimérance, Papa René KABILA, Gérard
KABILA pour leurs soutiens tant moral que matériel.
Nous serons très ingrat si nous passons sous silence la
grande famille KABALE MULOPWE : Maman Modestine NKULU, Roseline KIBALE,
KIBALE Muley, Anna-Maria KIBALE, Gaudemus KIBALE l'aigle fort, Christiane
KIBALE, Prince KIBALE le sage ministre de porte-feuille, Vincent KIBALE, Alice
KIBALE et Sabine Magera KIBALE, pour leur hospitalité à notre
égard ainsi que leur preuve de bonne fois par leur assistance dans nos
multiples difficultés.
A nos cousins : Gaëtan MULONGO, Vevette MULONGO et
François KABWANGA, Patient MULONGO, Gerry KITOBELO, Donatien
KIBALAMATA, Hortance NGOY, Ricky BULEMBU, Nesy KITWA, Léonard NSUNGU
pour le soutien moral que vous nous exprimez dans nos relâchements et
durs moments.
A vous Ir Nelly MUKABE, Ir Patrick, Dr Franck OTETE, le temps
passé à vos côtés n'est pas un grain semé
dans le vent ou sur un sol infertile, c'est un plaisir aussi grand qu'immense
de vous avoir rencontré dans ma vie et pour cela je m'en réjouis,
car ensemble on se sait trouver la définition de la vie sans se le dire,
trouvez dans ce travail l'expression vos encadrements tant moraux et que dire
en plus.
A nos compagnons de lutte Didier KIKONKO Seigneur Râ,
Mathias MASES le master, Serge SIMBI Octave, Séraphin KABAMBA, Patrick
KALENDA CIPOYA et NKULU YMBA Eddy pour votre apport moral très
stratégique dans les moments de désespoir dans notre struggle for
life.
A tous mes collègues de la promotion en
général et à Vanexel MUKUPA, Alain NZUMBA, Williams BETU,
Nicolas AKILIMALI, Katou KABAMBA, Séliana NAVEMBA de manière
particulière pour s'être assisté mutuellement en tout
occasion.
A mes amis et connaissances : Eulalie KASONGO, Blaise
NSENGA, Michel-Ange ASANI, Eric MPOYO, Dady LENGE, Jean MAYEBA, Serge NGANDU,
Ladislas KANGAJI, Patrick TSHIKALA, Patrick KISIMBA, Gabriel KISHENKE, ,
Patient KASHOBA, Sadiel KALONJI, Hugue NSENGA, Francl NAMEGABE, Félix
OMARI, Justin YUMALUHOLE, Fanfan KALEND, Serge MUSOYA pour votre sympathie
à notre égard.
Par ce qu'il nous est difficile de reprendre toutes nos
connaissances ici, que ceux qui de loin ou de près ont participé
à l'élaboration de ce travail, y trouvent l'expression de notre
profonde gratitude.
Alain Nazaire NGOY MWANABUTE
INTRODUCTION GENERALE
Les générateurs hydroélectriques sont la
source primaire d'énergie sur le réseau électrique de la
République Démocratique du Congo de par sa situation
géographique et ses conditions climatiques qui lui donnent une
hydrographie favorable à cette production.
Ces générateurs doivent fournir
l'électricité de qualité en maintenant l'amplitude et la
fréquence de l'onde de tension à des valeurs acceptables par
rapport aux normes de l'industrie. C'est ainsi qu'il est prévu deux
régulateurs sur chaque générateur ; le
régulateur de vitesse maintient la fréquence et le
régulateur de tension maintient l'amplitude de l'onde de tension.
Des défauts peuvent apparaître sur le groupe de
production hydroélectrique, soit sur le régulateur ou dans le
générateur lui-même. L'opération optimale doit
permettre de rejeter le plus rapidement possible les variations des charges
raccordées au réseau. Lorsque la qualité de
l'asservissement est dégradée par la présence d'un
défaut sur le groupe de production, les variations de charges engendrent
des oscillations des fréquences et de tensions indésirables.
En plus, étant donné que les
générateurs sont des équipements coûteux, ils
doivent être en état de production le plus longtemps possible pour
pouvoir amortir les frais d'investissement. C'est ainsi qu'il est important
d'augmenter leur disponibilité et leur fiabilité.
En outre, les pertes de synchronisme posant des interruptions
d'alimentation chez les clients peuvent être réprimandées
par des pénalités financières qui sont donc des manques
à gagner de l'entreprise productrice.
S'assurer que la machine est dans un état optimal, une
diminution du nombre d'arrêts non planifiés et de l'usure des
actionneurs peut être anticipée. Une évaluation du besoin
de maintenance est obtenue grâce aux techniques de diagnostic qui
permettent de maintenir le fonctionnement de l'outil de production pendant une
période prolongée. Les générateurs bien
régulés fournissent une énergie électrique tout en
diminuant l'impact des perturbations et en assurant sa stabilité.
Les diagnostics des défauts sont difficiles lorsque les
centrales sont raccordées à un grand réseau du fait que
les variations des charges sont généralement beaucoup plus
faibles que la capacité du réseau ; ce qui masquerait les
mauvais réglages des centrales. De plus, la présence d'un couple
synchronisateur permet de maintenir raccordée une machine mal
régulée.
Le réglage d'une centrale hydroélectrique
étant en effet un terrain très complexe, la demande du
réseau électrique varie sans cesse et les turbomachines au sein
des centrales de production électriques doivent adapter en permanence
leur point de fonctionnement surtout pour les centrales qui travaillent sur le
réseau presque isolé ou moins interconnecté.
I. CONSIDERATIONS GENERALES SUR LES CENTRALES
HYDROELECTRIQUES
1. CENTRALES HYDROELECTRIQUES
1.1.
Ecoulement transitoire
Le but d'une installation hydraulique étant de
fonctionner au régime nominal de manière stationnaire afin
d'exploiter les machines dans leur plage de rendement maximum, il se fait que
la réalité diffère nettement de cette situation
idéale. En effet, un réseau étant constamment soumis
à des perturbations de l'ensemble des consommateurs, les machines
doivent en permanence s'adapter à la demande variable. A travers le
système de contrôle - commande, qui agit sur les directrices des
turbomachines, le mouvement de l'eau engagée dans le réseau de
conduites hydrauliques est influencé, ce qui mène à des
phénomènes transitoires tels que le coup de Bélier dans
les conduites ou des oscillations de masse entre la cheminée et le
bassin amont ou aval, ainsi que la cavitation sur les aubages des
turbomachines. Ces phénomènes peuvent soumettre l'installation
à des fortes sollicitations mécaniques, qui nécessitent
d'être prises en compte dans le dimensionnement de la centrale ou
être contrôlé ou supervisé lors du fonctionnement de
la centrale.
C'est ainsi que partant de ces considérations, nous
parlerons dans cette partie du phénomène de coup de bélier
dans les conduites forcées et la cavitation.
Pour chacun de ces deux phénomènes, nous
essayerons de donner une description et les différentes sortes qu'on
peut rencontrer.
1.1.1. Phénomène de coup de Bélier
1.1.1.1. Description du
phénomène
Le coup de bélier est une onde de choc qui se propage
dans un tronçon de conduite lors d'un changement brusque de ses
conditions aux limites.
Etant donné que le phénomène du coup de
bélier entraine une augmentation de la hauteur apparente de chute sur la
turbine du fait de l'inertie de l'eau dans la conduite, cela exerce une action
de sens contraire à l'autoréglage.
On distingue deux sortes de coup de bélier : le
coup de bélier d'onde et le coup de bélier de masse.
1.1.1.2. Sortes des coups de
bélier
a) Le coup de bélier
d'onde.
Il est important surtout dans les longues conduites
forcées des hautes chutes qui tiennent compte de la
compressibilité de l'eau et de la déformation élastique
des parois des conduites forcées.
Ce phénomène est répétitif et se
produit avec une période de 
où le rapport 
est définit comme étant le temps caractéristique
du tronçon de conduite.
Avec :
L : longueur de la conduite forcée.
a : vitesse de propagation de l'onde.
Ainsi pour éviter le phénomène de coup de
bélier dans ce type d'installation, on prévoit une chambre
d'équilibre ou cheminée d'équilibre en amont, celle-ci est
placée sur une dérivation en pression de la turbine d'un groupe
générateur. Signalons que cette chambre d'équilibre de
l'installation s'ouvre et se ferme lorsque les oscillations du plan d'eau
résultant des manoeuvres d'ouverture ou de fermeture de
générateur tendent à s'amplifier.
b) Coup de bélier de
masse
Il se produit surtout dans les conduites forcées de
moyenne chute supposée incompressible et les parois
indéformables.
La centrale de Mwadingusha ayant une chute moyenne chute, se
trouve exposer à ce type de coup de Bélier.
Pour protéger les installations hydrauliques des
conséquences néfastes du coup de bélier, un orifice
compensateur est aménagé en dérivation de la bâche
spirale et commandé par le régulateur lui-même.
Cet orifice compensateur joue le rôle d'une soupape de
sécurité comme dans tout circuit hydraulique.
1.1.2. La cavitation
1.1.2.1. Description du
phénomène
La cavitation est le phénomène par lequel il y a
formation de la vapeur au sein d'un liquide, lorsque la pression locale chute
en dessous de la pression de vapeur saturante du liquide
considéré.
C'est un problème crucial auquel s'affrontent
concepteurs et utilisateurs des machines hydrauliques.
En effet le développement du phénomène de
cavitation à l'entrée de l'aubage d'une machine hydraulique est
souvent à l'origine d'une érosion sévère qui peut
conduire à l'arrêt prématuré de la machine avec des
conséquences économiques considérables (arrêt de
production, frais de maintenance, etc.). La cavitation s'accompagne
également d'une chute de performance de la machine (hauteur
absorbée et rendement), d'une génération de vibrations de
la structure mécanique et d'une émission d'un bruit intense qui
peut gêner l'utilisateur et l'environnement.
1.1.2.2. Sortes de
cavitations
Nous distinguons principalement trois types de
cavitation :
a) Cavitation de Vortex
Ce type de cavitation est couramment rencontré dans les
hélices marines. Il est dû à la grande dépression
créée dans le coeur d'un tourbillon, c'est ce qui provoque la
vaporisation de l'eau dans cette zone.
b) Cavitation à
bulles séparées
Cette cavitation se manifeste sur un profil bidimensionnel
lorsque l'incidence de l'écoulement aux bords d'attaques est voisine de
l'incidence nulle. Les bulles de vapeurs subissent des expansions explosives
déclenchées dans les zones de dépressions puis elles
implosent dans les zones de compression. Les pulsations de ce type de
cavités sont à l'origine du bruit de cavitation dans les machines
hydrauliques.
La cavitation à bulle se produit principalement
à la sortie des aubes des turbines Francis sur les côtés
extrados ainsi que dans les pompes au voisinage du point de fonctionnement
optimum.
c) Cavitation par poche
attachée
La cavitation à poche, appelée aussi cavitation
du bord d'attaque ou cavitation d'entrée, se développe sur un
profil en incidence. Elle se caractérise par une poche de vapeur
attachée au bord d'attaque qui génère des cavités
transitoires. Ces cavités de vapeur sont entraînées par
l'écoulement et implosent dans la zone de compression, du
décollement de la couche limite laminaire sur une paroi.
2. THEORIE DE REGLAGE DES PROCESSUS DYNAMIQUES
I.2.1. Processus dynamique
Le processus dynamique est caractérisé par des
phénomènes possédant une variation continue en fonction du
temps. Il se déroule en principe dans le système analogique.
Les variables en jeu sont des grandeurs physiques
analogiques ; et comme modèle mathématique pour la
description de ces processus, on fait appel soit à des équations
différentielles soit à des équations d'état ou soit
encore à des fonctions de transfert.
2.2. Conduite de processus
La notion des conduites de processus est importante dans le
domaine d'automatisation. La conduite de processus se compose en
général de plusieurs fonctions à savoir :
ü La surveillance
ü Le traitement des données
ü Commandes logiques et analogiques
ü Les organes de réglage
a) La surveillance
Consiste à vérifier continuellement ou
périodiquement, l'état des certaines grandeurs qui sont
déterminant pour le bon fonctionnement d'une installation.
Lors de la détection d'un état
indésirable, la surveillance doit déclencher un avertissement
(alarme) ou provoquer une intervention sur la commande et réglage, cette
surveillance est assurée grâce à un traitement des
données qui consiste à visualiser les grandeurs
intéressantes.
b) Le réglage
Le schéma de réglage est de la forme
suivante :
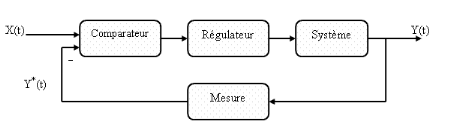
Figure I.1 : Diagramme fonctionnel de la
chaîne de réglage.
Légende :
X(t) : variable d'entrée
Y(t) : variable de sortie
Y*(t) : grandeur mesurée
La chaîne de réglage est constituée
de :
Ø La partie commande ou régulateur qui se
compose d'un régulateur déterminant l'écart entre la
consigne et la mesure d'un correcteur qui élabore à partir d'un
signal d'erreur l'ordre de commande.
Ø D'un actionneur, l'organe d'action qui apporte
l'énergie au système pour produire l'effet souhaité.
Ø Le capteur qui prélève sur le
système la grandeur réglée, l'information physique et le
transforme en un signal compréhensible par le régulateur.
Les informations que donnent l'organe de réglage se
présentent sous forme de :
· La consigne qui est la grandeur réglante du
système ;
· La sortie réglée, présente le
phénomène physique que doit régler le système.
C'est la raison d'être du système ;
· Les perturbations sont l'ensemble de tout
phénomène physique qui intervient sur le système et
modifie l'état de sortie
· L'écart est la différence entre la sortie
et la consigne.
2.3. Modèle d'état d'un système
2.3.1. Variables
d'état
Qualitativement, l'état d'un système se
réfère au comportement initial, courant et futur d'un
système.
Quantitativement, il est défini par un ensemble minimum
des variables notées X1(t0),
X2(t1), ..., Xn(tn) qui sont
spécifiées à l'instant t = ti et qui, ensemble
avec les entrées données U1(t1),
U2(t2), ...,Un(tn) pour t=0
déterminent l'état pour n'importe quel instant futur t >
t0.
Les variables appelées variables d'état,
Xi(t) définit un ensemble minimum des variables qui
déterminent l'état d'un système ; ils sont des
informations minimales pour pouvoir décrire les comportements futurs.
L'ensemble de ces variables constituent les composantes d'un vecteur
appelé vecteur d'état du système.
Ainsi le vecteur d'état est un vecteur qui
décrit le comportement dynamique du système en termes de n
variables.
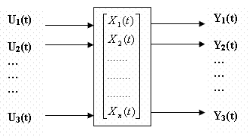
Figure I.2. Vecteur
d'état d'un système dynamique
2.3.2. Modèle d'état d'un
système
Etant donné que la dynamique d'un système est
complètement définit pour vecteur d'état. Ce
système peut être alors modélisé par le
modèle d'état dont les équations sont données
par :
Où :
U(t) : Vecteur d'entrée ou vecteur de commande
Y(t) : la sortie réglée du
système
A : matrice dynamique du système
B : matrice de commande du système
C : matrice d'observation
D : matrice de liaison directe
Généralement, il n'y a pas liaison directe entre
la variable de commande et la sortie réglée et le modèle
se réduit à :
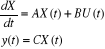
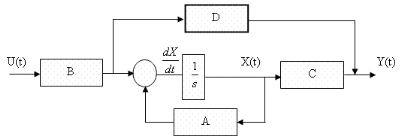
Figure I.3. Diagramme en bloc de la modélisation
d'Etat d'un système ).
2.3.3.
Contrôlabilité et Observabilité
2.3.3.1.
Contrôlabilité
Les problématiques générales de
l'automatisme consistent à commander et à contrôler un
système de manière à ce qu'il évolue depuis un
état initial vers un état final déterminé.
En représentation d'état, il s'agira de
déterminer le signal de commande U(t) entre deux états
donnés t1 et t2 pour ramener le système de
l'état X(t1) vers un état X(t2).
Critère de Kalman
Un système est complètement accessible,
commandable ou contrôlable si et seulement si les vecteurs 
sont linéairement indépendants ou si la matrice de
commande Q définit par 
est de rang n.
2.3.3.2.
Observabilité.
Des nombreuses méthodes de commande de processus
utilisent le principe de retour d'état. Comme dans la plus part des cas,
les seules grandeurs accessibles du système sont les variables
d'entrée et de sortie.
Il est nécessaire, à partir des ces informations
de construire l'état du modèle choisi pour élaborer la
commande. Un reconstructeur d'état ou estimateur est un système
ayant comme entrées, les entrées et sorties du système
réel et dont la sortie est une estimation de l'état de ce
système.
En plus, certaines variables d'état sont très
faciles à mesurer et les autres sont non mesurables. Les variables non
mesurables peuvent, comme celles mesurables influencer la sortie y(t) du
système. Il est donc possible à partir de la mesure de la sortie
de déduire les grandeurs considérées.
Un système est donc observable à un instant
t1 si la connaissance du signal d'entrée et du signal de
sortie sur un intervalle de temps [t1, t2] permet de
calculer l'état du système à l'instant t1.
a) Critère
d'observabilité
Un système est complètement observable si et
seulement si les vecteurs lignes 
où n est l'ordre de la matrice A, sont linéairement
indépendants, ou si la matrice colonne d'observabilité N est de
rang n.
b) Reconstructeur d'état
Sous l'hypothèse de linéarité du
modèle du processus, la structure de base de l'estimateur est toujours
la même, mais sa réalisation dépendra du contexte
choisit : continu ou discret, déterministe ou stochastique.
Dans le cas où ce modèle est
déterministe, le reconstructeur d'état est appelé
observateur.
Dans le cas des systèmes bruité, où
intervient de phénomène aléatoire, on parle de filtres.
1°) Principe des
observateurs
Soit un système continu décrit par
l'équation d'état (déterministe non
bruité) :
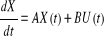
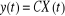
Comme l'état n'est pas généralement
accessible, l'objectif d'un observateur consiste en vue de réaliser une
commande par retour d'état, d'estimer cet état par une variable
notée
. Cette estimation est réalisée par un système
dynamique dont la sortie est précisément 
et l'entrée sera constituée de U(t) et y(t). La structure
de l'observateur est de la forme :
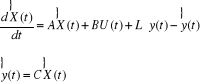
Où L est le gain de l'observateur.
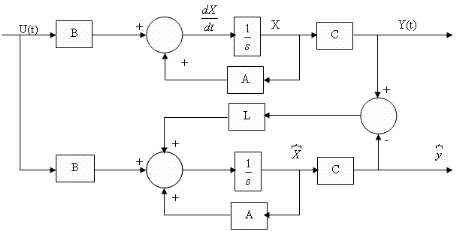
Figure I.4. Diagramme en bloc d'un estimateur
d'état d'un système
2°) Observateur
prédicteur ou correcteur.
Considérons le système discret stationnaire
défini par :
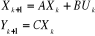
Où k appartient à N, 
est l'état du modèle, Uk est l'entrée
du processus et yk est la sortie du processus.
A, B, C sont les matrices définies par le modèle
d'état.
Soit un observateur pour ce système dont le principe
est le même que dans le cas des systèmes continu.
Où Gk est le terme de correction.
a) PREDICTEUR
Pour un prédicteur, on envisage 
où Lp est le gain du prédicteur, ce qui conduit
au constructeur d'état définit par :
Ce qui peut s'écrire également :
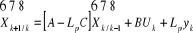
Cette structure est identique à celle définie
dans le cas des systèmes continus. En notant 
l'erreur de reconstruction, il convient :
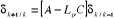
Le reconstructeur est asymptotique si le gain Lp
est choisit de sorte que les valeurs propres de la matrice A- LpC
sont, en module, inférieurs à l'unité.
b) LE CORRECTEUR
Dans le cas où yk+1 est connue, on peut
envisager que 
où Lc est un gain et 
représente l'estimation de la sortie à l'instant k+1 qui
peut être réalisée de deux façons
différentes : par anticipation ou par prédiction.
L'estimation de Xk+1 est fournie par le
reconstructeur :
Anticipation : si on suppose connue
, on se pose dans le cas : 
ce qui conduit à écrire l'observateur sous la
forme :
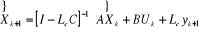
L'erreur de reconstruction 
est définit par l'équation récurrente :
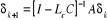
Le reconstructeur est asymptotique si le gain Lc
est choisit de telle sorte que la matrice 
ait les valeurs propres dont le module est inférieur à
l'unité.
Prédiction : dans ce cas, yk+1 est la
meilleure estimation que l'on puisse faire de la sortie à partir de
l'information disponible avant le calcul de
, on pose donc :
Ce qui conduit à la deuxième forme du reconstructeur -
correcteur.
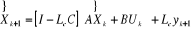
Dans ce cas, l'erreur du reconstructeur devient :
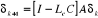
Signalons cependant que dans le cas des systèmes
discrets, il existe un choix particulièrement intéressant qui
consiste à déterminer L tel que la matrice 
soit nilpotente, c'est-à-dire que toutes les valeurs propres
soient nulles.
3°) OBSERVATEUR
DETECTEUR DES DEFAUTS
Outre la reconstruction de l'état pour élaborer
une commande par retour d'état, une autre application importante des
observateurs est celle utilisée en diagnostic et détection.
Dans cette optique on utilise l'observateur pour
générer des résidus permettant d'élaborer une
décision dans un étage de surveillance (supervision) et
diagnostic du système lorsque les perturbations ou des défauts
apparaissent sur un processus. On a en effet des variables qui agissent sur le
système mais qui ne peuvent être mesurée et l'objectif
consiste ici à construire des résidus qui doivent être
sensibles aux défauts du système et en plus doivent permettre de
les retrouver et dans ce cas on parle de l'isolation des défauts.
Considérons le modèle :
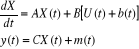
Où b(t) représente une défaillance des
actionneurs,
m(t) : défaillance des capteurs
L'utilisation d'un observateur donné par :
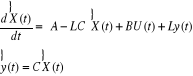
Conduit au résidu :
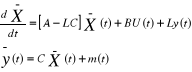
Si L est telle 
soit une matrice de Hurwitz, le résidu 
tend bien vers O en l'absence de défauts. Le transfert entre
défauts et le résidu s'écrit :
Ce qui, en tenant compte du lemme d'inversion, se met sous la
forme :
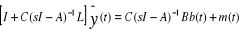
A partir de cette relation, on peut construire :
Ø En l'absence de défauts actionneurs, le
système permettant d'isoler les défauts capteurs à partir
des résidus :
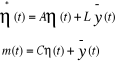
Ø En l'absence de défauts capteurs, le
système permettant d'isoler les défauts actionneurs à
partir des résidus et construit à partir de la variable
î(t) définit par :
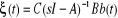
Cette variable est estimée à partir du
système :
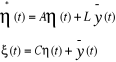
Et l'estimation d'une défaillance capteur est
donnée par l'inversion du système initial à
savoir :
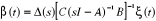
Où 
est la matrice du filtre tel que 
soit bicausale.
Â(t) n'est pas une estimation des défauts mais
plutôt un filtre de défauts, cependant le caractère
diagonal de 
permet l'isolation de défauts.
Dans le cadre de notre travail, un observateur
détecteur de défauts est d'une grande importance pour la
supervision des boucles de régulations dont les défauts peuvent
affecter soit l'actionneur, soit le capteur ou l'organe de mesure ou soit
encore le processus lui-même.
II. METHODES DE REGLAGE DES CENTRALES HYDROELECTRIQUES
1. INTRODUCTION
On désigne par régulateur, l'ensemble des
organes de mesure et réglage, non compris le servomoteur commandant
l'organe d'adduction d'eau de la turbine et par régleur les organes de
mesure et de réglage qui sont souvent standardisés, commandant le
tiroir de distribution, non compris ce dernier.
La figure suivante représente les organes de
réglage d'un groupe hydroélectrique complet avec deux consignes
de vitesse et de puissance, les chaînes de réaction
fréquence et puissance et enfin un régulateur de
réseau.
Cette figure met en évidence le fait que ce
régulateur peut faire partie d'un ensemble de trois boucles de
régulation, à savoir : celle de la vitesse (ou
fréquence), celle de puissance du groupe et celle par exemple, d'un
réseau électrique. Dans ce trois cas, la grandeur réglante
est la même, c'est-à-dire la position du vannage de la turbine. Ce
sont donc des régulateurs convergents.
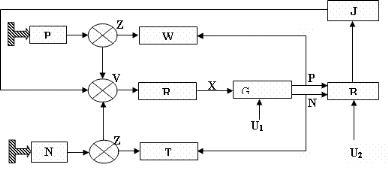
Figure II.1. Structure de la chaîne de
réglage à consigne de vitesse et de puissance avec
régulateur de réseau intégré d'un groupe
hydroélectrique .
La solution traditionnelle actuelle consiste à utiliser
la position du vannage de la turbine comme mesure ou comme moyen
d'asservissement de sa puissance. Ce procédé présente
cependant quelques inconvénients qui sont : premièrement,
à une ouverture donnée du vannage correspondent des puissances
différentes suivant la valeur de la chute nette de la turbine ;
deuxièmement, la loi liant la puissance à l'ouverture du vannage
n'est pas linéaire. Au lieu de chercher à corriger des
défauts par l'introduction d'une ou plusieurs cames dans l'organe de
mesure ou d'asservissement de la position du vannage, il est plus logique, au
point de vue réglage, de mesurer directement la puissance de
l'alternateur, opération que la régulation électronique
permet de faire sans difficulté.
Rappelons maintenant quelques exemples, tout à fait
classiques, destinés à illustrer principalement les fonctions des
boucles de régulation de vitesse et de puissance :
1. Le groupe n'est pas couplé sur un
réseau : la puissance électrique est alors nulle, seule la
boucle de régulation de la vitesse est en action. Son rôle est
d'amener ou de ramener au plus vite la vitesse de la turbine à sa valeur
de consigne dans le but de pouvoir coupler rapidement le groupe au
réseau lors d'un démarrage ou après déclenchement.
Pendant cette opération, la consigne de vitesse est en principe
pilotée par le coupleur automatique de la centrale.
2. le groupe est chargé de régler seul la
fréquence d'un réseau : dans ce cas extrêmement rare
mais intéressant à décrire, le réglage de vitesse
est en fait seul en action, il cherche à maintenir la puissance du
groupe égale à celle du réseau. Malgré les
variations de cette dernière, afin que la fréquence garde une
valeur la plus proche possible de sa valeur de consigne.
3. le groupe débite sur un réseau dont la
puissance est beaucoup plus grande que la sienne : la puissance est alors
imposée par le réseau et la boucle de régulation de la
puissance permet précisément de régler la puissance
fournie par la machine.
Par l'intermédiaire du sommateur du régleur, les
deux boucles de réglage de vitesse et de puissance lient la
fréquence à la puissance.
En effet, pour que le vannage reste immobile (régime
permanent), il faut que le sommateur du régleur ne délivre aucun
signal, ce qui implique que ses signaux d'entrée, provenant des
chaînes de vitesse et de puissance, doivent être en valeur absolue,
et de signes contraires ou nuls.
Cette liaison entre la fréquence et la puissance est
donnée par la caractéristique du statisme. Qui est une droite,
si les organes de mesure de la vitesse et de la puissance sont
linéaires. Cette caractéristique permet de définir le
statisme permanent fréquence -puissance et montre bien que le groupe
participe au réglage de la fréquence du réseau (cette
participation est d'autant plus forte que le statisme est faible). Une
variation de la valeur de consigne de la puissance provoque une translation de
la caractéristique de la fig.3 donc une variation de la puissance de la
machine pour une même fréquence. Le même effet peut
être par un ordre régulateur de réseau.
4. Un cas, moins rare que celui décrit plus haut sous
2, est réalisé lorsqu'une centrale ou groupe de centrales est
chargé de régler la fréquence d'un réseau dans
lequel les variations normales de puissance sont importantes par rapport
à sa puissance totale. la répartition de la puissance exige,
comme en 3, la présence des boucles de régulation de la puissance
de chaque machine, en d'autres termes un statisme individuel. La
fréquence est liée à la puissance totale par un statisme
global. Elle peut différer de la fréquence nominale, par exemple,
si la somme des puissances de consigne n'est pas égale à la
puissance du réseau. On peut éviter cet écart en
supprimant l'effet de la chaîne de puissance d'un groupe. C'est alors ce
dernier qui subira toutes les variations de puissance du réseau afin de
maintenir la fréquence constante pour autant que sa capacité de
réglage ne soit dépassée ; c'est le réglage en
« chef d'orchestre ».
Ainsi s'agissant de la boucle de régulation de la
vitesse dans notre travail, considérons que seule la boucle de
régulation de vitesse est en service. A cet égard, les turbines
hydrauliques sont, d'une façon générale, à classer
dans des systèmes difficiles à régler à cause du
phénomène du coup de bélier. Pour obtenir un
réglage de qualité dans tous les cas qui peuvent se
présenter, mêmes les plus défavorables, au double point de
vue de la stabilité en régime transitoire et de la
précision en régime permanent la construction d'un
régulateur PID est nécessaire.
Les spécialistes de réglage automatique, aussi
bien dans les domaines électriques, pneumatiques ou hydrauliques, ont
introduit une classification des régulateurs à action continue
basée sur le mode de régulation qui comprend principalement les
trois modes d'action : proportionnel P, par intégration I, par
dérivation D ainsi que les modes d'actions composées
résultant de leurs combinaisons.
Après avoir rapidement rappelé le sens et
l'utilité des régulations P, I et D et de leurs combinaisons,
nous allons établir une parallèle entre cette classification et
celle que l'on rencontre habituellement pour les régulateurs de vitesse
des turbines hydrauliques, soit : le régulateur
tachymétrique, accélérotachymétrique ou
régulateur à asservissement transitoire, et les
régulateurs accélérotachymétrique à
asservissement transitoire à avanceur des phases (régulateurs
accélérotachymétriques à dashpot) ; mais la
description complète des derniers sera faite dans le paragraphe
suivant.
Principalement la classification selon les modes d'action P,
I, et D est basée sur la forme mathématique de la relation liant
la grandeur réglante à l'écart de régulation,
c'est-à-dire, pour le réglage de la vitesse des turbines
hydrauliques, celle de la position du servomoteur du vannage à la
différence entre la valeur de consigne et la vitesse réelle du
groupe. Dans ce qui suit la valeur de consigne de la vitesse est
supposée maintenue constante.
Les régulateurs réalisant une
proportionnalité entre la grandeur réglante et l'écart de
régulation sont désignés par Régulateur P. En
ce qui nous concerne, aussi bien pour le réglage de la vitesse que pour
celui de la puissance, cette régulation présente
l'inconvénient de lier de manière gênante et permanente la
position du servomoteur à la valeur de la grandeur réglée.
Il s'ensuit donc des valeurs de la grandeur réglée
dépendant non pas seulement de sa valeur de consigne mais aussi de la
valeur de la grandeur réglante.
Afin d'éviter cet inconvénient, on superpose au
mode d'action proportionnelle le mode par intégration I. Le
régulateur devient PI. La grandeur réglante est alors la somme
d'un terme proportionnel à l'écart de régulation et d'un
terme proportionnel à l'intégral dans le temps de cet
écart. Comme en régime permanent la grandeur réglante est
constante, l'intégral cité ci-dessus l'est aussi, ce qui n'est
réalisé que si l'écart de régulation est nul. Le
mode d'action I introduit, par contre, un retard c'est-à-dire un
déphasage qui joue un rôle défavorable en ce qui concerne
la stabilité en régime transitoire.
Lorsque des difficultés de stabilisation apparaissent,
il est avantageux d'introduire un effet d'anticipation en ajoutant à la
grandeur réglante une composante proportionnelle à la
dérivée par rapport au temps de la grandeur réglée.
C'est le mode d'action par dérivation D.
Pour le réglage de vitesse envisagée
ici :
· L'action D est proportionnelle à
l'accélération du groupe, donc à l'écart entre les
couples moteur et résistant.
· L'action P est proportionnelle à l'écart
de vitesse.
· On peut représenter l'action I de plusieurs
manières. Elle est proportionnelle, par exemple, à la
différence entre la phase c'est-à-dire la position angulaire de
la machine et celle d'une référence tournant à vitesse
constante, en d'autres termes, l'écart entre les heures affichées
par une horloge synchrone et une horloge astronomique.
Ainsi en bref, nous pouvons dire que l'introduction d'une
action I dans un régulateur P améliore la
« Précision » en régime permanent
(indépendance entre les grandeurs réglante et
réglée) mais nuit à la stabilité ; celle d'une
action D améliore la stabilité, par conséquent les
performances en régime transitoire, sans affecter le fonctionnement en
régime permanent. Le meilleur régulateur est dans le cas qui nous
occupe certainement celui qui cumule les trois modes d'actions, P, I et D, donc
le régulateur PID.
2. PRINCIPALES METHODES DE REGLAGE ET REGULATEURS ASSOCIES
Les régulateurs de vitesse utilisés sur les
turbines hydrauliques sont toujours à action indirecte, à cause
de l'effort énorme nécessité par la commande du vannage.
Ils sont de deux types principaux : les régulateurs purement
tachymétriques qui agissent uniquement par la vitesse du groupe à
régler et les régulateurs
accélérotachymétrique, qui font intervenir à la
fois la vitesse et l'accélération.
Dans les domaines des turbines hydrauliques, le
régulateur comprend :
a) un régleur ou tachymètre, constitué
par l'organe de mesure de la vitesse et les dispositifs d'ajustage
b) le servomoteur de commande du vannage et son tiroir de
distribution.
L'entraînement du régleur peut s'effectuer soit
à partir de l'arbre du groupe générateur, soit à
partir des bornes de l'alternateur principal de ce groupe.
Ces deux cas vont être examinés :
Premier cas : - Le régleur est
entraîné soit par l'arbre du groupe au moyen d'un dispositif
mécanique, soit par un moteur qu'alimente un alternateur pilote, donc
l'inducteur est formé d'aimants permanents ou d'enroulements
alimentés spécialement au démarrage. Ainsi,
l'entraînement du régleur est indépendant de la puissance
fournie par l'alternateur.
Deuxième cas : - Le moteur du
régleur est alimenté par le circuit de l'alternateur principal
grâce à un transformateur spécial branché sur ce
circuit.
Toute fois, comme un alternateur ne peut être
excité que pour une valeur de la vitesse égale à environ
70% de la vitesse nominale, le réglage automatique ne peut être
assuré que pour une vitesse supérieure. De plus, il y a lieu de
prévoir un dispositif de sécurité pour le cas où la
tension au démarrage demeurerait insuffisante (par exemple en cas de
court-circuit), d'où résulterait un danger d'emballement du
groupe.
Nous allons étudier maintenant le rôle de
l'asservissement dans la stabilité du fonctionnement d'un
régulateur.
2.1. Réglage tachymétries et régulateur
associé
Considérons un équipement de réglage dans
lequel un régulateur centrifuge à boules ou tachymètre A
(figure II.2) commandé par l'intermédiaire d'une tige AC,
supposée d'abord mobile autour d'un point fixe B, un système de
tiroirs D, réglant l'admission d'un fluide moteur dans les deux
extrémités d'un cylindre Q qui renferme un piston P dont la tige
T actionne le vannage de la turbine.
Figure II.2. Régulateur tachymétrique avec
asservissement
Si le groupe ralenti par suite d'une surcharge, le manchon du
tachymètre A s'abaisse, le tiroir
p1p2 s'élève, le fluide
moteur est admis en e1 et évacué en e2 et
le piston P se meut de droite à gauche ouvrant le vannage ; quand
la vitesse revient à sa valeur normale, le tachymètre
arrête à nouveau l'admission.
La théorie montre qu'un pareil régulateur ne
peut assurer la marche d'une turbine : il pompe d'une façon
permanente.
Cela tient au fait suivant : supposons que la vitesse du
groupe varie suivant une loi sinusoïdale de période
T1 ; le déplacement du tiroir sens où il tend
à ouvrir du tiroir, pris positivement dans le sens où il tend
à ouvrir le vannage, exécutera une oscillation en opposition avec
celle le l'écart de vitesse ; mais l'ouverture du vannage sera en
retard de T1/4 sur la courbe du tiroir et par la suite en avance de
T1/4 sur la courbe de la vitesse. L'ouverture de vannage et le
couple seront donc maxima au moment où la vitesse ayant la valeur
moyenne augmente vers son maximum et par suite l'oscillation sera
entretenue.
Pour stabiliser le fonctionnement, il faut asservir le
régulateur, c'est-à-dire faire en sorte que, comme dans un
régulateur direct de machine à vapeur, à chaque position
du tachymètre corresponde une vitesse bien définie : le
régulateur asservi n'est pas isodrome, mais il a une certaine courbe
caractéristique et un certain écart de réglage. On obtient
ce résultat en rendant mobile le point B, autour duquel oscille la tige
de commande AC ; l'articulation B est maintenant portée par une
tige, coulissant dans des guides g1 et g2 et s'appuyant
en permanence, par son poids ou par des ressorts non indiqués au moyen
d'un galet G sur une came E, dite came d'asservissement, portée
par la tige de commande du vannage. Grâce à la tige à la
came d'asservissement, la position du point B varie avec l'ouverture du vannage
et le couple développé, et à chaque degré de cette
ouverture correspond une position d'équilibre différente du
tachymètre et une valeur de la vitesse du groupe, comme dans un
régulateur direct de machine à vapeur. En faisant varier la
longueur de la tige d'asservissement, on fera varier la caractéristique
du Régulateur et sa vitesse de régime pour une charge
donnée.
L'écart de réglage, ou différence
relative entre les vitesses à vide et en charge,
nécessaire pour une stabilité convenable du
système, est assez grand et il en résulte une trop forte
variation de fréquence, inadmissible dans un groupe
générateur à courant alternatif. Pour éliminer cet
écart et le ramener à une valeur très faible, on utilise
des compensateurs
Il existe des compensateurs des différents
systèmes mécaniques, hydrauliques... mais le principe de leur
action est le même, avec des modes de fonctionnement
différents.
La compensation d'un régulateur asservi consiste
à ramener lentement l'articulation B de la tige à une même
place fixe, après que le réglage de vannage aura
été effectué par le servomoteur avec déplacement
convenable de ce point d'articulation.
Un schéma de compensation mécanique est
donné à la figure précédente (figure II.2). La tige
d'asservissement est composée d'une tige filetée H portant le
galet G coulissant dans le guide g1, et venant se visser dans le
manchon L qui porte l'articulation B et glisse dans le guide g2, et
venant se visser dans le manchon L qui porte l'articulation B et glisse dans le
guide g1. En faisant tourner le manchon L à la main, ou
mécaniquement, on ferait varier la caractéristique du
régulateur et la vitesse correspondant à une charge
donnée, comme il est dit plus haut.
Dans la compensation, on le fait tourner automatiquement au
moyen d'un plateau de friction N, entraîné par un arbre R à
mouvement lent et commandant le manchon par l'intermédiaire du plateau
M.
Dès que par le jeu du réglage et de
l'asservissement, le manchon L se déplace verticalement, le plateau N
fait tourner le manchon jusqu'à ce qu'il revienne, par rotation autour
de la vis H, présenter le plateau M dans l'axe du plateau N, seule
position d'équilibre pour ce plateau M. Après tout
réglage, la vitesse revient donc à la même valeur fixe,
suffisamment d'une manière lente pour ne pas compromettre la
stabilité du réglage.
Un régulateur asservit n'a donc plus d'écart de
réglage en régime : sa caractéristique est une
horizontale. Cette disposition convient fort bien pour la marche isolée
d'un groupe générateur à courant alternatif, dont la
fréquence est maintenue rigoureusement constante ; mais elle ne
permet pas la marche en parallèle de groupes générateurs
alternatifs, puisque la réparation de la charge entre groupes
dépend uniquement des caractéristiques de régulateur et
est définie, pour deux groupes, par l'intersection de ces
caractéristiques après renversement des abscisses de l'une
d'elles. Le groupe dont le régulateur fournirait la plus grande vitesse
prendrait toute la charge, et entre deux groupes de vitesses rigoureusement
égales, la répartition de charge serait
indéterminée.
Un certain écart de réglage (au moins 3%) est
nécessaire pour permettre la marche en parallèle de groupes
alternatifs. Pour obtenir cet écart, il faut décompenser
partiellement les régulateurs, en provoquant un léger
déplacement de l'articulation B entre les marches à vide et
à pleine charge. On y arrive par différents artifices, variables
avec le mode de compensation employé ; dans le cas de la figure
ci-dessus, on pourrait provoquer un léger déplacement vertical de
l'arbre R et du manchon M (commandé par flexible à cet effet).
Cet écart de réglage est le statisme, dont il serrait
question un peu plus loin ; il détruit en quelque sorte l'effet de
la compensation.
2.1. Réglage accélérotachymétrique
et régulateur associé
2.1.1 Description d'un accéléromètre
L'accéléromètre est constitué par
une masse pesante destinée à détecter
l'accélération angulaire.
L'accélération donne naissance à un
couple qui commande l'organe de réglage. Ce couple a pour
expression :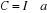
Avec: - I : moment d'inertie de la masse
tournante
-a : accélération
angulaire (
)
Pour que l'effort soit sensible, il faut que la masse soit
considérablement plus lourde que celle du tachymètre (100 fois
environs)
L'accéléromètre peut être
constitué par un anneau relié à l'organe d'entrainement
par l'intermédiaire des lames élastiques.
Si l'accélération est positive, a
supérieur à zéro, il est décalé en avance.
C'est le décalage ainsi obtenu qui contrôle le réglage.
2.1.2 Régulateur
accélérotachymétrique
On peut réaliser un régulateur stable, sans
recourir à l'asservissement, en faisant agir à la fois
l'écart de vitesse et l'accélération ; d'où le
nom du régulateur accélérotachymétrique. Cet
appareil est constitué par un relais différentiel à huile
dans le quel la pression variable est réglé par
l'échappement des deux tuyères dont le débit dépend
respectivement de la vitesse et de l'accélération du groupe.
Cette pression variable s'exerce sur un piston tournant terminé par un
pointeau, qui commande, par l'intermédiaire des relais, le mouvement du
tiroir de commande d'huile au servomoteur du régulateur. Un dispositif
mécanique assez complexe réalise cette condition que la course du
tiroir de distribution, proportionnelle à celle du piston, est
comptée à partir d'une position moyenne d'équilibre ne
commandant aucun mouvement, est une fonction bien déterminée de
l'accélération et de l'écart de vitesse du groupe, ou des
différentes paires des valeurs de ces deux grandeurs ; le dosage
accélérometrique du réglage est défini par le
nombre m de seconde nécessaire à
l'accélération mise en jeu pour produire un écart de
vitesse fournissant le même effort dans le régleur que
l'accélération considérée.
L'accélération étant en avance sur
l'écart de vitesse d'un quart de période, l'effet sur le tiroir,
de sens opposé à l'accélération, est en retard de
T1/4 sur l'écart de vitesse et l'ouverture du tiroir ainsi
que l'écart de couple se trouve en opposition avec l'écart de
vitesse, ce qui tend à amortir l'oscillation et stabiliser le
fonctionnement.
Un régulateur
tachyaccélérométrique bien entendu, fonctionne d'une
manière stable, sans asservissement et par suite sans écart de
réglage, c'est-à-dire d'une façon isodrome :il peut
servir à commander , à vitesse parfaitement constante, un groupe
générateur à courant alternatif indépendant ou
encore un groupe à courant alternatif chef d'orchestre,
c'est-à-dire chargé à maintenir la fréquence
constante dans un ensemble des groupes fonctionnant en parallèle avec
d'autre groupes, pour pouvoir repartir la puissance entre ces groupes, il faut
qu'il possède un certain écart ou statisme, résultant d'un
degré convenable d'asservissement, au moyen d'un dispositif prévu
à cet effet. Cette commande peut se produire automatiquement par exemple
lorsqu'on veut réaliser le mode réglage dit
fréquence-puissance, dont il sera question plus loin.
Pour obtenir, avec le régulateur tachymétriques
les résultats comparables à ceux que fournit le régulateur
accélérotachymétrique, du point de vue grande
rapidité de réglage combiné avec une bonne
stabilité de marche on emploie maintenant, dans ce but, sur les groupes
électrogènes hydrauliques de grande puissance de centrales
modernes, des régulateurs tachymétriques qui comportent deux
asservissements, l'un permanent correspondant à un statisme dont la
faible valeur, de l'ordre de 0,030, suffit à assurer une bonne
répartition de charge entre groupe en parallèle et l'autre
temporaire, avec un statisme d'une valeur beaucoup plus grande de l'ordre de
0,20 à 0,30.
Cet asservissement temporaire est réalisé au
moyen d'un Dashpot ou une cataracte (Voir figure II.3). La came
d'asservissement temporaire C', au profil beaucoup plus élevé que
celui de la came d'asservissement permanent C est relié au levier de
commande de tachymètre par une tige dans laquelle est
inséré un Dashpot D et aboutit à un fort ressort D'.
Lorsque le galet C' s'élève sur sa came, le
Dashpot D, constitué par l'ensemble d'un cylindre remplit d'huile et
d'un piston munis d'un petit trou, se déplace d'abord comme un seul bloc
et soulève le point B en forçant le ressort, ce qui a pour
conséquence de limiter le mouvement du tiroir et du distributeur par un
asservissement rapide ; mais sous l'action du ressort, le point B'
redescend d'autant plus rapidement que le ressort est plus rigide et le
mouvement du piston est plus facile dans son cylindre ; la position du
distributeur est finalement assuré par la came C.
Figure II.3. Régulateur tachymétrique à
dashpot avec asservissements temporaire et permanent
Le fonctionnement du système est
caractérisé par le statisme provisoire 
et le temps 
de relaxation du Dashpot, ce temps 
étant défini comme nécessaire pour que le
déplacement du dashpot ait atteint 63% de sa course totale
supposée effectuée suivant une loi exponentielle.
3. NOTION DU STATISME
D'une manière générale, le statisme d'un
équipement de réglage automatique est le rapport entre variation
de la grandeur réglée et la variation correspondante de la
grandeur de réglage. On distingue ainsi dans le réglage des
centrales hydroélectriques, deux sortes de statismes : le statisme
local et le statisme total.
3.1
LE STATISME LOCAL
Le statisme local pour une puissance déterminée
d'un groupe générateur est défini par la pente, au point
correspondant à cette puissance, de la courbe de statisme obtenu
emportant en abscisse la puissance exprimée en pourcentage de la
puissance Pop correspondant à la pleine ouverture du vannage
de la turbine et en ordonnée la vitesse exprimée en pourcentage
de la vitesse nominale. Le statisme local pour la puissance P1 sera
ainsi donné par :
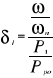
Si la courbe de statisme était une droite, on aurait
P1 = P et le statisme local 
serait en tout point égal au statisme total.
Toujours en assimilant la courbe du statisme à sa
tangente, l'énergie réglante K du groupe
générateur, évaluée en kilowatts, à la
puissance considérée, est :
: fn étant la fréquence nominale.
L'énergie réglante K est la variation de puissance par Hertz,
produite par le groupe lorsque la fréquence du réseau, sur lequel
il débite, varie légèrement autour d'une fréquence
voisine de la fréquence nominale.
3.2. LE STATISME
Soit ùo la vitesse en marche à vide
d'un alternateur excité, ùpo la vitesse à
pleine ouverture du vannage, ùn la vitesse nominale, le
statisme total est :
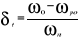
Selon la recommandation du comité de l'association
suisse des Electriciens, la valeur du statisme total devra pouvoir être
ajustée entre ämin = 0% et ämax = 6%.
III. MODELISATION DU SYSTEME
1. INTRODUCTION
Le but de ce chapitre est de présenter les
modèles classiques de générateurs hydroélectriques
et de leurs régulateurs. Ces modèles servent à comprendre
le comportement des générateurs et le réglage de leurs
régulateurs à l'aide de la théorie du contrôle.
Les différentes configurations de réseau
possibles aux bornes du générateur sont d'abord
illustrées. Le rôle du générateur pour chaque
configuration est défini ainsi que les actions qu'il effectue pour
réguler la fréquence. Les hypothèses de
linéarité utilisées pour la modélisation sont par
la suite présentées. La modélisation du régulateur
de vitesse mécanique du type accélerotachymétrique est par
la suite effectuée. Les paramètres typiques du
générateur sont donnés ainsi que les paramètres du
procédé étudié. En fin en fonction des
données provenant de la centrale de Mwadingusha, nous déduirons
les paramètres du régulateur dans son fonctionnement normal ou
fonctionnement sans défaut.
Pour une bonne supervision de la boucle de réglage,
nous présenterons la plage de bon fonctionnement du système sans
défauts et au delà de la quelle, on qualifie le système
comme défaillant.
2. MODELISATION DU GENERATEUR
Dans cette section, nous présentons le
générateur comme situé dans l'ensemble du réseau
électrique c'est-à-dire dans son fonctionnement à vide, en
îlotage et en réseau. Les relations entre les
entrées-sorties du générateur et du régulateur
ainsi que les directions des actions sont aussi présentées.
La turbine de la centrale de Mwadingusha étant du type
Francis, les hypothèses faites pour la modélisation
sont :
F La résistance hydraulique est négligeable dans
la conduite forcée,
F L'eau dans la conduite forcée est
inélastique
F La puissance active de sortie de la machine est
proportionnelle à la position des directrices
F La dynamique de la charge est négligée, sa
relation entrée-sortie est statique ;
F Le couple et la puissance sont équivalents dans le
système par unité ;
F L'utilisation du modèle linéaire est
limitée à la région autour du point de l'opération
en puissance où il a été identifié.
2.1. Fonctionnement à vide
Les éléments du modèle de
générateur à vide sont la conduite forcée, la
turbine et l'alternateur. La conduite forcée crée la pression
nécessaire à la production d'énergie, elle est
constituée d'un tuyau ou une conduite fermée qui comporte une
dénivellation. L'eau y transite entre la chambre de mise en charge en
amont et le générateur en aval. Son comportement est
caractérisé par l'inertie de translation de l'eau et par la
pression sur les aubes de la turbine. L'inertie contraint les variations de
vitesse brusque afin d'éviter la surpression importante en aval (coup de
bélier). Elle dépend de la longueur et de la section de la
conduite ainsi que de la vitesse de l'eau. La pression dépend de la
différence des hauteurs entre l'entrée de la conduite et sa
sortie en régime permanent et des variations des vitesses de l'eau en
régime transitoire.
Les directrices sont réparties tout autour de la
turbine et contrôle le débit et la direction de propagations de
l'eau sur les aubes de la turbine et forment ce qu'on appelle cercle de
vannage.
La turbine sert à transformer l'énergie
cinétique de translation de l'eau en énergie cinétique de
rotation du rotor. Le modèle de la turbine comprend la dynamique de
l'ouverture des vannes d'eau et l'interaction entre l'eau et les aubes.
Effectivement la puissance de la machine est proportionnelle au produit du
débit par la pression. Lors d'une augmentation rapide de l'ouverture des
directrices, l'eau ne peut accélérer immédiatement dans la
conduite forcée, le débit est donc constant. Cependant,
l'ouverture plus grande entraîne une baisse de pression sur les aubes de
la turbine et produit une diminution de la puissance.
L'alternateur fait la transformation entre l'énergie
mécanique et électrique. Du côté mécanique,
il s'agit de l'arbre sur lequel sont situés des pièces
tournantes, son comportement est donc celui d'une inertie de rotation. Du
coté électrique, l'alternateur est un ensemble de bobinages, il
se comporte comme un circuit inductif.
Les pertes par fiction surviennent entre les parties mobiles
et les parties fixes. La friction est considérée linéaire
par rapport à la vitesse de rotation, ce qui est valide pour une plage
restreinte d'opération.
a) Modèle
mathématique du système
Au cours de ce paragraphe, nous désignons par ?p
l'écart relatif instantané entre la puissance de la turbine, sous
hauteur de chute constante H0 et sous ouverture variable du
vannage, et la puissance initiale de l'alternateur.
En tenant compte aussi des hypothèses
énoncées, nous admettons que cette valeur de ?p est
proportionnelle à la variation relative de l'ouverture du vannage
qu'elle peut ainsi servir à représenter à une certaine
échelle.
y = k (1 - ?p)
Où y est l'ouverture relative du vannage
k est un coefficient de proportionnalité
Signalons en plus que pour la modélisation du
système, nous avons utilisé les variables en grandeur relative.
Le débit de la turbine est la somme du débit
correspondant à l'ouverture du vannage et par suite proportionnel
à 
et du débit supplémentaire provenant de la surpression
dans la conduite forcée, proportionnellement à la racine
carrée de la hauteur de chute, soit en valeur absolue à 0,5?h.
L'expression du débit est ainsi donnée
par :
(1)
La surpression ?h dans la conduite forcée est
proportionnelle à la variation instantanée du débit ?q
selon l'expression :
(2)
Où Te est la constante d'inertie hydraulique
de l'eau dans la conduite forcée. Cette constante est donnée par
l'expression :
(3)
Où L est la longueur de la conduite forcée en
mètre ;
V : la vitesse initiale de l'eau engagée
dans la conduite forcée en m/s
g : est l'accélération de pesanteur
en m/s2
H0 est la hauteur nette de chute en
mètre.
En substituant les expressions (1) et (3) dans l'expression
(2), on trouve :
(4)
L'expression (4) est celle de la surpression. Elle donne
l'écart de pression ?h du coup de bélier de masse entendue que
cette expression n'est valable que pour des chutes basses et moyennes dans
lesquelles on peut négliger les effets de la dilatation des conduites et
de la compressibilité de l'eau (le coup de bélier d'onde). Donc
cette expression convient le mieux pour la modélisation du coup de
bélier de la centrale de Mwadingusha qui a une chute moyenne.
Du côté de la turbine, le mouvement s'obtient,
toujours en grandeur relative, en écrivant que le couple
accélérateur fait équilibre à la somme
algébrique des puissances ?p, de l'excès de puissance introduit
par le coup de bélier de masse qui, étant proportionnel à
l'exposant 3/2 de l'écart de hauteur ?H donne en valeur relative 1,5?h
et enfin de la variation de puissance apportée par l'autoréglage
ou perte par friction, soit -ã?f.
D'où l'équation de la masse tournante :
(5)
La deuxième équation tient compte de la
variation de la puissance apportée par l'autoréglage ou perte par
friction.
Où Tm est la constante
d'accélération appelée aussi temps de lancer du groupe ou
encore la constante de temps mécanique.
Il est donné par l'expression :
(6)
Où ù est la vitesse angulaire en rad/sec.
P est la puissance active nominale en kW
J est le moment d'inertie du groupe.
Les praticiens ont pris l'habitude, que rien ne justifie
d'ailleurs, de substituer au moment d'inertie MR2 par le moment de
giration PD2, produit du poids en kg par le carré du
diamètre de giration. Le PD2 est une grandeur qui n'a pas les
mêmes dimensions que le moment d'inertie MR2 ; mais sa
valeur numérique est le quadriple du moment d'Inertie.
(7)
Jù2 est le double de l'inertie
cinétique emmagasinée ; Tm qui est le temps de
lancer en seconde représente le temps fictif nécessaire pour
qu'un groupe au repos atteigne la vitesse ù sous l'action du couple
constant correspondant à la puissance nominale P.
Ainsi les relations importantes retenues pour la
modélisation du système fonctionnant à vide sont
formées par le système d'équations (4) et (5).
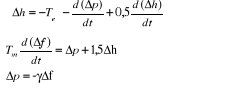
En appliquant la transformation de Laplace, on a :
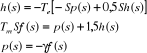
De la première équation, nous tirons :
et nous l'insérons dans la deuxième équation, on
avons alors :
La fonction de transfert du générateur à
vide est alors donnée par le système d'équation
(8):
(8)
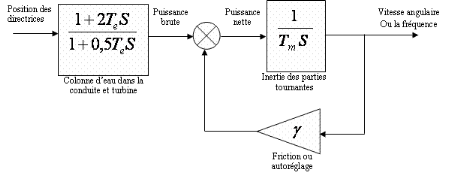
Figure III.1. Diagramme
fonctionnel du groupe à vide
La fonction de transfert du générateur à
vide avec la boucle d'autoréglage fermé est donnée par
l'expression :
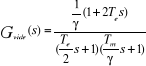
b) Calcul des paramètres caractéristiques
du système
1. Présentation des
données
Ø Longueur des conduites forcées : 312 m
Ø Vitesse de l'eau dans la conduite
forcée : 4m/s
Ø Hauteur de chute nette : 110 m
Ø Vitesse nominale de la roue: 375 tr/min
Ø Survitesse du groupe : 450 tr/min
Ø Vitesse d'emballement : 700 tr/min
Ø Débit : 13050 dm3/s
Ø Puissance hydraulique : 17000 CV sous 116,5 m de
chute nette.
Ø Puissance active électrique du groupe :
12 MW sous cosö=0,9
Ø Fréquence industrielle : 50Hz
Ø Moment de giration PD2 : 180
Tm2 soit 180 000 kgfm2
Ø Pour les alternateurs de construction normale, le
coefficient d'autoréglage ã est compris entre 1 et 1,5. Dans le
cas de notre travail, nous prendrons la valeur maximale de 1,5.
2. Calcul des
paramètres
La constance d'inertie hydraulique
(9)
La constante de temps d'accélération ou
constante de temps mécanique
(10)
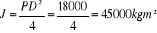
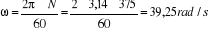
(11)
3) Expression numérique de la fonction de transfert
En remplaçant chaque paramètre par sa valeur
numérique dans l'expression de la fonction de transfert, nous obtenons
l'expression numérique de la fonction de transfert du système
étudié.
(12)
Et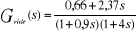 
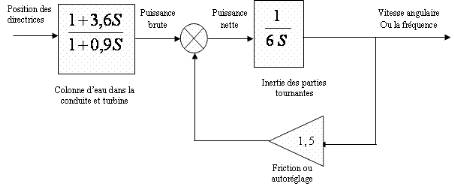
Figure III.2. Diagramme fonctionnel du
générateur à vide avec des valeurs
numériques.
III.1.2 Fonctionnement en autonome
La configuration du générateur autonome est
celle dans laquelle le générateur alimente seul la charge dont la
puissance apparente est inférieure à celle du
générateur lui-même. C'est le cas par exemple, quand un
groupe perd le synchronisme avec le réseau et n'alimente que la
consommation locale de la cité et du centre urbain de Mwadingusha.
La modélisation de cette configuration se
diffère de celle du générateur en fonctionnement à
vide par l'apparition d'un courant qui circule au stator de l'alternateur pour
alimenter la charge locale. Bref ce là caractérise l'influence de
l'amortissement de la charge qui implique une proportionnalité entre la
puissance nette et la variation de la vitesse angulaire.
D'une manière générale, la puissance
absorbée par la charge augmente avec la fréquence ce qui a un
effet stabilisateur puisque la puissance livrée par un
générateur non régulé augmente avec la vitesse de
rotation proportionnellement. La constance de proportionnalité est
nommée coefficient d'amortissement de la charge qui est le rapport en
per unit de la puissance active sur la fréquence. Ayant un effet
stabilisateur, elle vient s'ajouter à l'effet de l'autoréglage et
renforce celui-ci.
Concordia et Ihara dans leur travail intitulé
« Load representation in power stability studies » ont
montré que pour un générateur de construction normale, les
valeurs typiques d'amortissement de la charge varient entre 0 et 3. Ainsi, pour
ce qui concerne notre travail, nous avons considéré un
coefficient d'amortissement de la charge de 3.
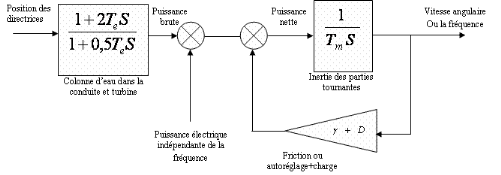
Figure III.3. Diagramme fonctionnel du
générateur en autonome
La fonction de transfert du générateur autonome
ou en fonctionnement autonome est donc :
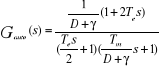
Le diagramme bloc du système avec ses paramètres
numérique.
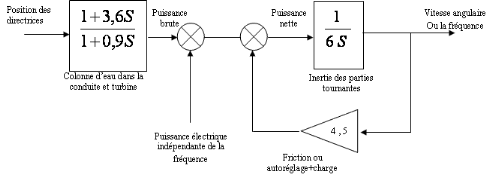
Figure III.4. Diagramme fonctionnel du
générateur en autonome avec des valeurs
numériques.
La fonction de transfert de notre site en autonome est
donc :
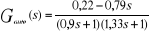
III.1.3. Fonctionnement en
réseau
Le modèle du générateur en réseau
est dérivé du modèle de générateur à
vide et de l'équivalent du réseau vu à ses bornes. La
majorité des générateurs possèdent des amortisseurs
qui servent à amortir les oscillations de vitesse du rotor lors du
fonctionnement en régime transitoire en réseau. En fonctionnement
normal, le rotor tourne à la vitesse synchrone et aucune induction n'a
lieu dans les amortisseurs. Cependant, lorsque la vitesse de rotation du
générateur est différente de celle du réseau, des
courants sont induits dans le rotor du générateur. Ces
amortisseurs, étant des enroulements en court-circuit au rotor, ils
permettent la dissipation de l'énergie des oscillations. Le couple
tiré de la machine par ces enroulements en court-circuit est
proportionnel à la différence de vitesse entre le rotor et le
champ tournant au stator. L'énergie cinétique emmagasinée
dans les parties tournantes cause le dépassement angulaire suite
à un changement de consigne ou une perturbation. L'oscillation qui en
résulte vise à éliminer l'énergie cinétique
excédentaire emmagasinée dans le rotor pendant la période
transitoire. La dissipation de l'énergie est effectuée par les
courants induits dans les enroulements amortisseurs au rotor de la machine qui
voient une oscillation sous synchronisme du rotor par rapport au stator.
Le modèle du générateur à vide est
augmenté du calcul du décalage interne ou angle interne par
rapport à la référence tournante qui est l'intégral
de la différence de vitesse de rotation. Le gain constant appelé
couple synchronisant multiplie le décalage interne pour donner la
puissance électrique échangée entre la machine et le
réseau.
Le diagramme fonctionnel du générateur en
réseau est présenté à la figure suivante.
Figure III.5.Diagramme fonctionnel du générateur en
réseau
La fonction de transfert de la vitesse du
générateur en fonction de la position des directrices
est :
(13)
Où ks est couple synchronisant du
réseau.
ks est le coefficient d'amortissement de
l'alternateur du groupe.
Pour le réseau de la SNEL et pour les alternateurs de
Mwadingusha, on a les caractéristiques suivantes :
N = 375 trs/min et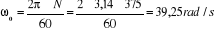 
kp = 0,44
ks = 0,66
L'expression numérique de la fonction de transfert est
donnée par :
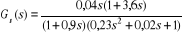
III.2. MODELISATION DU
REGULATEUR DE VITESSE
Dans la modélisation des régulateurs de
centrales hydroélectriques, l'entrée du régulateur de
vitesse est l'erreur de vitesse et la sortie de celui-ci est la position des
directrices dans le cas de la turbine Francis bien entendu.
III.2.1. Régulateur
accélérotachymétrique mécanique.
Lorsqu'un groupe fonctionne couplé à un
réseau important, il n'y a pas de question grave de stabilité
hydraulique, puisque sa vitesse est maintenue par le couple synchronisant
exercé par les autres groupes ; mais il faut que son
régulateur soit assez rapide pour que le groupe obéisse
suffisamment vite à une demande d'augmentation ou de diminution de la
charge.
Par contre, lorsque le même groupe sera appelé
à fonctionner seul sur le réseau, il faudra que son
régulateur ajuste sa vitesse à la valeur normale, à la
suite d'une accélération produite par une variation de charge,
assez rapidement pour éviter de trop grandes variation de
fréquences.
L'autoréglage facilite cette opération, mais
l'inertie hydraulique de l'eau s'y oppose et empêche de réaliser
un réglage à la fois stable et infiniment rapide sur le
réseau autonome.
Une caractéristique d'un régulateur est donc sa
promptitude de réglage, qui peut être définie
comme l'inverse de la constante de temps ô du mouvement de vannage,
supposé d'allure exponentielle ; M. Stein a proposé de
donner à cette constante ô le nom de « lenteur de
réglage ».
Le régulateur
accélérotachymétrique est soumis à la fois à
une action proportionnelle à l'écart de fréquence Äf
et à une action proportionnelle à l'accélération
soit 
, où le coefficient de proportion m représentant le temps
en secondes nécessaire à l'accélération mis en jeu
de produire un écart de vitesse fournissant le même effort dans le
régleur que l'accélération considérée. Cette
constante est appelé dosage
accélérotachymétrique.
Bien que le régulateur puisse fonctionner sans
asservissement, on lui confère toujours un certain statisme permanent
ó, généralement assez petit de l'ordre de 3 à 4
%.
Ainsi, l'équation du mouvement du régulateur
accélérotachymétrique est donnée par les
expressions suivantes :
(17)
Dont la première équation de ce système
donne le modèle de la chaîne directe et le second le modèle
de chaîne de contre-réaction négative.
L'application de la transformation de Laplace au
système d'équation donne :
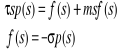
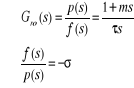
Ainsi, le diagramme fonctionnel du régulateur
accélérotachymétrique est donné par le
schéma de la figure ci-dessous.
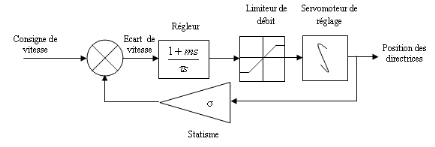
Figure III.6. Diagramme fonctionnel du régulateur
accélérométrique.
Ainsi la fonction de transfert du régulateur en
bouclé fermée ou du régulateur avec asservissement est
donc donnée par l'équation suivante :
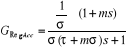
Calcul des paramètres du régulateur
Considérons le système d'équations
différentielles du modèle de la surpression dans les conduites
forcées, de la masse tournante et du régulateur
ci-dessous :
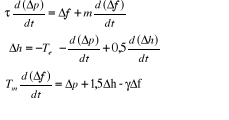
En appliquant la transformation de Laplace à ce
système d'équations, on a :
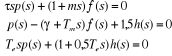
En annulant le déterminant des coefficients des
variables p(s), f(s) et h(s), on a :
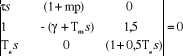
Ou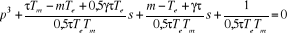 
En appliquant le critère de stabilité de ROUTH
à l'équation caractéristique ci-haut trouvée et en
identifiant que :
, 
et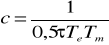 
On a :
s3
s²
s1
s0
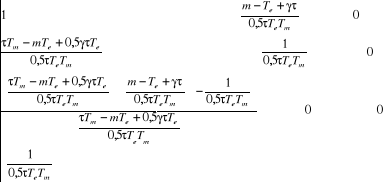
Pour que le système soit stable, il faut que les
éléments de la première ligne soient tous
supérieurs à zéro.
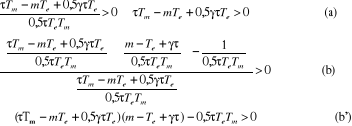
Pour trouver les paramètres du régulateur, il
sied de faire une discussion sur les conditions de stabilité
ci-dessus.
Discussion du fonctionnement :
Sans autoréglage
Si on considère ã = 0, les conditions de
stabilité du critère de ROUTH deviennent :
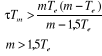
Ce qui veut dire que :
1°) le dosage accélérométrique m
doit être au moins égal à 1,5Te.
2°) le produit des constantes de temps du groupe et du
générateur doit avoir une certaine valeur minimum.
3°) cette valeur minimum est elle-même susceptible
de passer par un minimum pour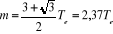 
4°) si on donne à m cette valeur optimum, on
trouve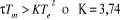 
Les conditions de stabilité de ROUTH
énoncées dans ce cas précis sont appelées
critère fondamental établi par D. Garden.
Influence de l'autoréglage.
Les relations (a) et (b') peuvent se mettre sous la
forme :
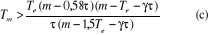
Cela entraîne comme condition préalable 
La valeur qui donne le minimum du second membre de la relation
( c) et celle qui annule sa dérivée première,
soit :
(e)
A condition que sa dérivée seconde soit
positive, ce qui exige :
(f)
En nous basant sur les relations (c), (d), (e) et (f), on peut
déduire les paramètres du régulateur :
Et en remplaçant cette expression dans la relation (e), on
trouve l'expression du dosage accélérométrique en fonction
de la constante d'inertie hydraulique :
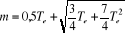
Les valeurs numériques de m et ô
respectivement dosage accélérométrique et lenteur
de réglage sont données par :
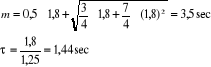
La fonction de transfert du régulateur est donc
donnée par sa forme numérique :
