|
Conception d'Antenne Radiofréquence Dédiée
à
l'Imagerie par Résonance Magnétique

Dédicace :
Je dédie ce mémoire
à
mes Parents .
ii
Remerciements
Je voudrais exprimer ma profonde gratitude à tous ceux
qui de près ou de loin ont contribué à la
réalisation de ce travail. Mes sincères remerciements :
I Au Seigneur DIEU Tout Puissant qui m'a
accordé la grâce de réaliser ce travail; I A mon Directeur
de mémoire, Dr. Olivier VIDEME BOSSOU pour avoir accepté de
diriger ce travail : votre rigueur scientifique, votre disponibilité,
votre esprit de travail et vos nombreux conseils ont contribué à
l'amélioration de ce travail.
I Au corps enseignants du Département de physique de la
Faculté des Sciences, particulièrement au Pr NDJAKA Jean Marie,
Chef de Département de Physique à l'Université de
Yaoundé1; au Pr. ESSIMBI ZOBO Bernard responsable du laboratoire des
systèmes électriques et électroniques et aux autres
enseignants du laboratoire : le Pr. EYEBE FOUDA Jean-sire, le Pr. BODO
Bertrand, le Pr. Frederic BIYA MOTTO et le Dr MBINACK Clement, pour leurs
disponibilités, leurs conseils et encouragements tout au long des
années d'enseignements;
I Au Pr Giulio Giovannetti, du conseil national de la
recherche italien (CNR) pour ses conseils, sa collaboration, son orientation et
ses encouragements
I A mon papa NKENGNE Jacques et ma mère chérie
KENGNI Paulette Vos encouragements et vos prières m'ont
été d'un grand soutien et réconfort;
I A mes frères et soeurs : Entcheu Armel, Cheudong
Florian, Djouffo Oivier, Fokoua Serge, Mikam Merlin, Cheudong Cedric, Guede
gaelle, Huitmo Kelly, Mangang Imelda pour tout l'amour dont vous me comblez
I A Mr Gatcho Modeste, du Minsanté, pour son soutien
morale, ses conseils et ses encouragements dans les moments difficiles.
I A mes camarades de laboratoire, Cesar Djoumessi, Malla
sophie, Mirene jules, Tchinda leibniz, Dejo Arlette, Tohou Gandha, pour le
climat chaleureux qu'ils ont entretenu durant tout notre travail;
I A mes amis pour leurs conseils et encouragements
I Enfin, à tous ceux ou celles que nous avons
involontairement omis de citer. Qu'ils trouvent ici l'expression de ma profonde
reconnaissance.

Table des matières
Dédicace i
Remerciements ii
Table des matières iv
Table des figures v
iv
Table des figures

Liste des tableaux
vi
TABLE 1 - Listes des Abréviations
|
RF
|
RadioFréquence
|
|
IRM
|
Imagerie par Résonance Magnétique
|
|
RMN
|
Résonance Magnétique nucléaire
|
|
FID
|
free induction decay
|
|
(SNR/RSB)
|
signal to noise ratio(rapport signal sur bruit)
|
|
FEM
|
Finite Element Method(Méthode des élément
finies)
|
|
MOM
|
Moment Method( Méthode des Moments)
|
|
FDTD
|
Finite Difference in Time Domain(différence finie dans
le domaine temporel)
|
|
ROI
|
Region of interest (région d'intéret)
|
|
SAR
|
specific absorption rate (taux d'absorption
spécifique)
|
|
IDL
|
Interactive Data Language
|
|
BEM
|
Boundary Element method
|
|
FOV
|
Field Of View
|
|
EM
|
ElectroMagnétique
|
|
VPC
|
Vector Potentiel Calcul
|
|
MATLAB
|
Matrix laboratory
|
|
CST
|
computer simulation technology
|
|
ICE
|
induced current compensation or elimination
|
|
MWS
|
MicroWave
|
|
MHz
|
Mega Herzt
|
|
EFIE
|
Electric Field Integral Equation
|
|
MFIE
|
Magnetic Field Integral Equation
|
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
vii
Résumé
Les travaux de recherches de ce mémoire s'inscrivent
dans le cadre de la conception d'une antenne radiofréquence
appliquée en imagerie par résonance magnétique (IRM). La
qualité des examens dus à la sensibilité de l'antenne ou
l'inhomogénéité du champ magnétique et parfois
même l'échauffement de l'élément rayonnant pouvant
causer des brûlures cutanées est un problème.
L'originalité de notre travail consiste à faire une étude
mathématique du champ magnétique radiofréquence d'une
boucle circulaire de 20 cm de diamètre, à la fréquence de
64 MHz relative à une antenne de surface. Nous nous sommes basés
sur les techniques de la magnétostatique combinées à la
méthode de Gauss-Legendre pour intégrer le champ
magnétique B de l'équation de Biot-Savart. Ce champ
magnétique, simulé dans un espace tridimensionnel (3D)
présente une bonne homogénéité; le champ par
unité de courant, également simulé sur l'axe (oz)
renseigne sur la forte sensibilité de l'antenne donnant ainsi un
meilleur Rapport Signal sur Bruit. Les résultats obtenus ont
été jugés satisfaisant, et obéissent à ceux
de certains travaux de la littérature.
Mots clés : antenne
radio-fréquence, IRM.
Abstract
The research works on this thesis are based on design of radio
frequency antenna applied in magnetic resonance imaging (MRI). The quality of
examinations due to the sensitivity of antenna or the inhomogeneity of magnetic
field and sometimes the heating of radiating element which can cause skin
burns, is a problem. The originality of our work is to make a mathematical
study of radiofrequency magnetic field of a circular loop of 20 cm of diameter,
at the frequency of 64 MHz relative to a surface antenna. We used magnetostatic
techniques combined with the Gauss-Legendre method to integrate the magnetic
field B of the Biot-Savart equation. This magnetic field simulated in a 3D
space has a good homogeneity; the field per unit of current also simulated on
the axis (oz) informs about the sensitivity of the antenna which gives a better
signal to noise ratio. The results obtained are satisfact and in agreement with
those of certain works of the literature.
viii
Keywords : radiofrequency antenna,
magnetic resonance imaging
1
Introduction générale
Dans le domaine de l'exploration et de l'imagerie
médicale, l'Imagerie par Résonance Magnétique « IRM
» est devenue un outil quasiment incontournable dans de nombreux domaines
cliniques et a connu une avancée considérable tant sur le plan
technologique que sur le plan de ses applications; c'est une technique
d'imagerie qui utilise des champs électromagnétiques induisant un
effet de résonance dans les atomes d'hydrogènes pour visualiser
les organes et structures internes du corps. Un système informatique
dédié enregistre et traite l'énergie
électromagnétique émise en retour par les atomes
d'hydrogène, et produit ainsi des images des structures internes du
corps. Les médecins utilisent ces images pour diagnostiquer diverses
pathologies. A la différence des scanners et des appareils de
radiographie conventionnelle, les appareils IRM n'exposent pas le patient
à des rayonnements ionisants. Mais lors de leur application dans
certains laboratoires cliniques, les problèmes qui subsistent sont
parfois : la qualité des examens qui n'est pas de bonne qualité
soit à cause du faible rapport signal sur bruit (RSB/SNR) et le
phénomène d'échauffement des tissus dû au port
d'implant métallique par le patient causant des brûlures
cutanées. Cet ainsi qu'intervient l'antenne RF qui est un
élément majeur à développer pour palier à
ces problèmes. L'IRM continue de connaitre un développement
important avec l'utilisation de champs magnétiques de plus en plus
intense; deux champs perpendiculaires sont alors à considérer :
le champ fondamental Bo crée par l'aimant principal et le champ
magnétique radiofréquence ou onde radiofréquence B1
crée par l'antenne. Nous y portons souvent peu d'attention sur l'antenne
en IRM, pourtant son rôle est primordial dans la chaîne de
réception. C'est un outil fondamental du système IRM; il a pour
rôle de détecter le signal émis lors du retour à
l'équilibre des noyaux d'atomes d'hydrogènes préalablement
excités par le champ RF. Le signal mesuré étant
très faible, Il est donc important de comprendre le fonctionnement des
antennes et de savoir ce que ce signal y devient. Aussi simples qu'elles
paraissent, les antennes sont de plus en plus complexes, avec une technologie
optimisée afin «d'écouter» le mieux possible les
protons. Dans ce travail, nous nous sommes concentrés sur la
problématique liée aux antennes en particulier l'étude du
champ magnétique radiofréquence en accord avec les
différentes études qui ont été menées.
L'objectif de ce mémoire est de concevoir une antenne RF simple boucle
circulaire capable de produire des images homogènes de qualité et
qui sera en conformité avec les normes sanitaires définies pour
l'IRM. Ce mémoire s'articule autour de trois chapitres, des
exposés précis et concis y sont
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2
présentés :
Le chapitre 1 résume l'état actuel des
connaissances sur les antennes RF et donne des éclaircissements sur les
problématiques spécifiques à l'IRM.
Le travail de ce mémoire et la démarche
scientifique suivie sont quant à eux détaillés dans le
chapitre 2 divisé en 3 parties, La première partie
s'intéressera à une brève description du fonctionnement de
l'appareil IRM et des outils et environnements logiciels utilisés dans
cette étude; La seconde partie portera sur les antennes
radiofréquence en IRM où nous les aborderons en
énumérant les différents types d'antennes et en
présentant leurs paramètres caractéristiques. La
troisième partie portera sur la conception d'une antenne à boucle
circulaire, où nous présenterons une méthode analytique
exprimant le champ magnétique par unité de courant
(sensibilité de l'antenne) sur l'axe (oz); nous présenterons
également une méthode d'intégration numérique celle
de Gauss-Legendre pour discrétiser le champ magnétique B1 de
l'équation de Biot-savart dans le plan (xoy) généralement
utiliser pour les antennes de formes plus simple. Nous présenterons
enfin quelques méthodes numériques de calculs du champ
électromagnétique (FEM, FDTD et MOM) basée sur des
équations de maxwell pour la conception d'antenne plus complexe.
Le chapitre 3 présente les différents
résultats de simulations réalisés ainsi que les
discussions relatives à ces résultats. Ce chapitre est suivi
d'une conclusion générale dans laquelle, quelques perspectives
pour des travaux ultérieurs y sont proposées.
CHAPITRE I
ETAT DE L'ART SUR LES ANTENNES RF
POUR IRM
3
Les antennes RF encore appelées bobines RF sont de nos
jours un outil très important dans un système IRM; dans la
littérature de nombreux travaux sur des antennes en IRM ont
été effectué allant des chronologies anciennes aux
nouvelles techniques. Les premières publications qui en font état
sur les antennes IRM datent de la fin des années 80; depuis l'abondante
littérature médicale, les conférences, le nombre important
de revues générales, certains auteurs démontrent la
maturité d'une discipline dont les avancées significatives au
cour de la dernière décennie ont concerné un grand nombre
de domaines d'applications. L'utilisation des systèmes plus simples
permettant de modéliser et concevoir des antennes RF. L'objectif de ce
chapitre est de présenter exhaustivement les travaux actuels
menés par les chercheurs et les industriels dans la problématique
liée aux antennes.
En 1985, Hayes et al.[1] ont décrit
pour la première fois l'utilisation des bobines de cage d'oiseaux
(bobine volumique) comme étant des bobines émettrices et
réceptrices dans les systèmes IRM à champ faible et
élevé. Ces bobines sont populaires en raison de leur
capacité à générer un champ magnétique RF
très homogène avec un RSB élevé. Leur
méthode de conception est basée sur une ligne de retard à
élément localisé; cette méthode présente
beaucoup d'avantage et l'utilisation de ces bobines montre que les
résultats attendus ont été obtenus : l'augmentation quasi
linéaire du RSB en fonction de la fréquence à 64 MHz
correspondant au champ magnétique statique Bo de 1.5 T, c'est A cette
même fréquence qu'ils dimensionnent et construisent leurs bobines.
Les bobines cage d'oiseaux sont des résonateurs
caractérisés par plus d'un mode de résonance; en fait, une
bobine de N jambes fournit 1+N/2 modes de résonance distincte même
si le mode de travail utilisé en IRM est généralement
celui qui garantit la meilleure homogénéité du champ
magnétique. La méthode utilisée est une méthode
itérative utilisant le complexe d'onde et est basée non pas sur
les champs électriques et magnétiques comme d'autres
méthodes numériques telles que MoM, EFIE ou MFIE. Leur domaine
d'étude est totalement différent du nôtre; Nous nous sommes
attardés sur l'étude du champ magnétique RF crée
par l'antenne RF.
En 1988, H. Tsuboi et al. [2]
déterminent la taille et la structure géométrique d'une
antenne radiofréquence qui est utilisée à la fois comme
émetteur et récepteur et exige qu'il
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
4
y ait un facteur de qualité (Q) élevé, un
grand gain et un champ magnétique uniforme élevé pour une
bonne résolution de l'image. Ils ont utilisé la méthode
des moments pour calculer le champ magnétique propre à l'antenne
et la distribution du courant sur l'an-tenne; ils ont ensuite utilisé
des méthodes analytiques [3] pour optimiser la géométrie
de l'antenne. Ils comparent les résultats de calcul (par méthode
des moments) et les résultats expérimentaux (utilisant le model
d'antenne dipolaire). Les résultats de calculs utilisant presque 63
segments sont en accord avec les résultats expérimentaux; la
fréquence de résonance par calcul est de 22 MHz, ce qui est
largement inférieure à la fréquence de résonance
théorique de 50 MHz. Ceci est dû à l'influence des facteurs
externes. Les résultats attendus ont été obtenus et il est
vérifié que la méthode des moments est praticable pour la
conception d'antenne RF en IRM. Par rapport à leur fréquence de
travail (expérimental et théorique), nous nous sommes
basés sur l'étude du champ magnétique par Biot-Savart
à la fréquence de 64 MHz qui est la plus adapté aux IRM
actuels à des champs faibles. Et contrairement à eux qui
appliquent la MoM sur les équations de Maxwell pour le calcul du champ
électromagnétique, MoM est plus adapté aux antennes de
formes plus complexes.
En 1990, M. Fujita et al. [4] emploient
également la méthode des moments pour analyser le champ
électromagnétique de l'antenne, également pour calculer la
distribution du courant; ils développent un programme efficace pour
analyser la distribution d'une antenne de forme compliquée, ils
examinent les dimensions adaptatives d'une antenne RF multi-tour pour obtenir
un champ EM uniforme; ils développent aussi un algorithme pour concevoir
l'antenne adaptative pour IRM. Il est plus commode de déterminer les
dimensions de l'antenne et les configurations adaptatives de celle-ci, que
d'évaluer sa qualité avec la valeur macroscopique Q (facteur de
qualité); les dimensions adaptatives de cette antenne RF multi-tour sont
calculées pour émettre un champ électromagnétique
sur l'uniformité de l'espace d'imagerie en supposant en supposant qu'un
courant continu circule sur l'antenne. Les résultats de calculs des
admittances d'entrées par la méthode des moments sont en accord
avec les résultats expérimentaux lors des comparaisons; les
angles adaptatifs ont été recalculés et par rapport aux
anciens, il y a une différence de 0,3 degré et il est donc
possible de déterminer la configuration adaptative d'une antenne RF.
Cette technique bien que meilleure, a été réalisée
avec des logiciels de simulations très ancien et aujourd'hui on assiste
à des logiciels plus évolués dites modernes. La MoM est
détaillée à la fin du chapitre suivant.
En 1994, Li et al. [5] ont utilisé la
méthode des éléments finis (FEM) bidimensionnel pour
calculer des solutions pour le champ B1 de certaines bobines
représentatives (cage à oiseaux, bobine de selle, bobine à
éléments multiples, bobine à plaque radiale). Les
résultats de leurs travaux décrivent le domaine B1 plus
réaliste que les solutions analytiques ordinaires, en tenant compte des
courants de Foucault. L'une des premières oeuvres exploitant une FEM 3D
a été développée par Guclu et ses
collègues (1997) [6], le champ magnétique est
déterminé par le courant total; les courants de foucaults
étant proportionnels
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
5
à la dérivée temporelle du champ
magnétique, il est très difficile de calculer
simultanément la distribution du champ et du courant dans les
conducteurs au moyen des approches analytiques. D'où l'idée
d'utiliser la méthode numérique FEM qui a beaucoup d'avantage
dans leur utilité. Ils ont caractérisé le champ
généré par une bobine de cage à oiseaux dans
l'échantillon de tissu dans une bobine à 64 et 223 MHz (cette
fréquence correspond à un champ non conventionnel de 5,25 T). Ils
comparent les résultats de la simulation avec les solutions analytiques
sous-tendant les avantages de la modélisation. Ils montrent comment la
modélisation 3D FEM peut être utilisée pour étudier
les problèmes techniques qui affectent la qualité de l'image; par
exemple, une cartographie précise des champs peut être utile dans
le développement de nouvelles séquences d'impulsions pour
minimiser les perturbations du terrain. Ils utilisent donc la FEM pour des
conceptions plus complexes. Avec ces méthodes, on connait beaucoup de
cas d'inhomogénéité de champ magnétique; nous
choisissons travailler avec l'équation de Biot-savart parce que en terme
de conception d'antenne elle est très simple et la mieux adapté
pour générer un champ uniforme. La FEM est également
explicité plus bas.
En 2001, Ibrahim et al. [7] décrivent
l'analyse de la performance d'une bobine de cage à oiseaux à
basse et haute fréquence. Ils ont utilisé la méthode FDTD
pour modéliser une bobine de cage à oiseaux avec tous les
composants, y compris les fils, les condensateurs localisés et la
source. La bobine cage d'oiseaux a été chargé avec un
modèle de tête humaine et l'homogénéité du
champ magnétique, ainsi que le taux d'absorption spécifique, ont
été calculés à deux fréquences
différentes (1,5 et 4,7 T). Les résultats pour la distribution du
taux d'absorption spécifique SAR sont présentés. Le
modèle des épaules donne des résultats plus précis
dans le réglage des bobines et le calcul du SAR. Les résultats
numériques sont présentés pour montrer
l'homogénéité du champ magnétique et du SAR dans le
modèle de tête humaine à l'intérieur de la bobine
cage d'oiseaux sous excitation en quadrature à 64 MHz et 200 MHz. Un
code informatique pour générer ces résultats a
été validé (Ibrahim et al, 2000 b) contre
des mesures prises avec un système IRM GE Signa 1,5T. Nous utilisons
Gauss-Legendre pour intégrer numériquement le champ de
l'équation de Biot-Savart. Ces méthodes numériques seront
détaillées dans le chapitre suivant.
En 2002, G. Giovannetti et al. [8]
décrivent un programme capable d'évaluer toutes les
fréquences de résonances des bobines et de tracer les diagrammes
de distribution du champ magnétique sous forme de contour, de
représentation 3D et de coupe axiale. Ils utilisent la méthode
des circuits équivalents pour faire une analyse magnétostatique
de la bobine. Et ils développent un logiciel pour simuler des bobines
cage d'oiseaux à l'aide de l'environnement IDL (Interactive Data
Language). Ce logiciel prend en compte les inductances mutuelles entre tous les
conducteurs. Ils ont également testé le simulateur à
l'aide des données décrites dans la littérature [9] pour
une bobine de cage d'oiseaux passe-haut, accordé à une
fréquence beaucoup plus grande que le prototype passe-bas
développé; les comparaisons faites, indiquent un écart
inférieur à 4,500 (alors que l'autre simulateur donne
une erreur
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
6
de 8,800 ) Il a été
démontré que le simulateur proposé était capable
d'obtenir un spectre de fréquence de résonance complet et les
modèles de champ magnétique avec une grande précision et
un temps très bref. Pour la même bobine, la fréquence de
résonance du mode dominant obtenu à l'aide des deux simulateurs
disponibles dans la littérature est 9.291 MHz et 7.730 MHz, avec une
précision de 15 et 4,300 respectivement; une mesure de
l'uniformité du champ a été effectuée pour le mode
d'onde sinusoïdale dans le centre plan transversal perpendiculaire
à l'axe de la bobine cage d'oiseaux, obtenant une valeur satisfaisante
de 7200 . Le logiciel développé permet a priori la
connaissance de la configuration du champ magnétique à
l'intérieur de la bobine, vérifiant ainsi le degré
d'homogénéité. Dans cet article la modélisation
avec cette méthode nécessite la présence de sources
virtuelles d'admittance ou l'opérateur d'impédance et de sources
d'excitation.
En 2004, G. Giovannetti et Al. [10]
conçoivent et construisent 4 prototypes de bobine basse fréquence
pour montrer comment le choix de la géométrie croisée du
conducteur et de la qualité du condensateur affectent la performance de
la bobine. Il est a noté qu'un fil conducteur est difficile à
gérer lors de la construction de bobine et cela nécessite une
bonne compétence des mécanismes. Lors de l'utilisation d'un
conducteur à bande pour une conception de bobine RF, l'épaisseur
de la bande doit être au moins 6 fois celle de la profondeur de peau
à la fréquence utilisée afin de maximiser la surface
où le courant circule et de minimiser les résistances du
conducteur. Les résultats de la littérature soulignent le mieux
les performances d'une bobine constituée d'un fil conducteur, ce qui est
imputable à une meilleure répartition des courants à
l'intérieur, par rapport à un conducteur à ruban, comme
prédit théoriquement. Les résultats ont montré
l'importance d'utiliser des condensateurs de haute qualité et des
conducteurs de tige cylindriques au lieu des bandes ceux pour réaliser
des bobines de cage d'oiseaux efficaces. Les résultats obtenus semblent
être très prometteur, compte tenu du fait que les performances des
bobines cage d'oiseaux peuvent être améliorées avec une
meilleure optimisation électronique.
En 2004, Rogovich et al. [11] ont
utilisé une technique de MoM pour concevoir une bobine de cage d'oiseaux
à 8 pattes, passe-bas et une bobine en cage d'oiseaux à 16
pattes, passe-haut. Dans ce travaille le simulateur a été
utilisé pour déterminer les caractéristiques principales
des bobines, telles que le mode de résonance, le facteur Q et
l'homogénéité du champ magnétique. Les
résultats pertinents pour une bobine de cage à oiseaux à 8
jambes, passe bas sont montrés et proposés dans [12]. Les
résultats des simulations ont été comparés par
rapport aux mesures établies pour démontrer l'utilité des
méthodes numériques dans la conception de la bobine. En
considérant le cas d'une bobine de cage à oiseaux à 16
pattes proposée dans [13], les résultats confirment la
précision de la technique et le mode de résonance de Helmholtz
est correctement prédit, alors que les modèles de circuits
localisés proposés n'ont pas été en mesure de le
prédire. Les techniques de MoM sont également utilisées
dans la littérature afin d'analyser et d'optimiser les bobines
superficielles telles que les bobines à 2 canaux, une bobine en forme de
8 et une bobine à papillon; Lemdiasov (2005)
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
7
et al. [14] ont utilisé une
formulation en MoM pour calculer la matrice de paramètres S pour une
Bobine superficielle à 2 canaux sans composants localisés
(réglage et adaptation des condensateurs). Puis ils calculent la matrice
S élargie, en tenant également compte des éléments
localisés, et extrait de certains paramètres de performance de la
bobine, par exemple, le facteur de qualité, facteur de remplissage et le
SNR. Kumar et Bottomley (2008) [15] ont également
utilisé MoM pour calculer l'amplitude des composants polarisés
circulairement de la gauche du champ magnétique RF transverse produit
par 2 bobines superficielles, une bobine en forme de 8, et une bobine à
papillon. Cette information a ensuite été utilisée pour
optimiser le SNR des bobines. Pour alléger les calculs fastidieux dans
les problèmes de bobines RF chargées, certains travaux
récents proposés utilisant des techniques hybrides connues sous
le nom de MoM / FDTD ou MoM / FEM. Dans ces approches, MoM est utilisé
avec FEM ou FDTD pour exploiter sa force pour modéliser une bobine RF et
FDTD ou FEM pour calculer le champ à l'intérieur d'un objet
diélectrique compliqué. Par exemple, Li et al.(2006)
[16] ont fourni un bref aperçu des méthodes
numériques pour la conception de bobines RF et ont discuté de
l'hybridation de ces méthodes. Une méthode hybride MoM / FEM a
été utilisée pour des exemples de modélisation de
bobines RF (2 bobines superficielles et une bobine de tête à 4
éléments). Les résultats simulés et
expérimentaux ont été comparés pour
démontrer la précision de la méthode hybride. FEKO, est un
logiciel commercial basé sur MoM, qui implémente également
un algorithme hybride MoM / FEM. Ces articles présentent l'hybridation
des méthodes numériques de calcul du champ
électromagnétique; et sont simulées avec différents
logiciels.
En 2007, D. Doty et al. [17]
présentent une approche d'optimisation et d'utilisation des bobines
radiofréquences RF pour l'IRM de petits animaux en faisant une analyse
du rapport signal sur bruit (S/N) et les discussions sur les différentes
bobines communément utilisé en IRM de petits animaux telles que :
bobine de surface, bobine à volume linéaire et à cage
d'oiseaux; ils se limitent sur des bobines milieu de gamme où le produit
(f*d) de la fréquence f et du diamètre de la bobine d est dans la
plage 2-30 MHz.m; gamme à laquelle toutes les sources de pertes (bobine,
condensateur, échantillon, blindage, ligne de transmission) sont
importantes. L'optimisation des bobines RF se fait en deux étapes
principales : - le logiciel pleine onde avec des algorithmes efficaces pour
gérer les pertes de surfaces des conducteurs est utilisé pour la
minimisation de l'intégral de E/B1 pour la bobine de
l'échantillon; - les simulateurs de circuits linéaires connus
tels que : Spice, Ansoft designer ou Genesys sont utilisés pour
maximiser l'efficacité de la puissance fournie à la bobine RF du
point de vue de la transmission même si la bobine sert uniquement
à concevoir. La plupart des logiciels de validations 3D sur des bobines
IRM n'ont pas confirmé l'exactitude du logiciel pour bobines complexes
de milieu de gamme où tous les types de pertes sont importants. Certains
travaux assez détaillés des évaluations de trois
progiciels de pointe « électromagnétisme 3D à onde
pleine» ont été effectués dans les années 2002
et ont conclu pour la plupart que, des problèmes de bobine de RMN et IRM
de milieu de gamme, Micro-ondes (MWS) par des technologies de simulations
informatique (CST) était
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
8
mieux adapté et plus précis que les autres
logiciels qui ont été évalués (HFSS par Ansoft et
XFDTD par REMCOM). D'autres ont plus récemment montré qu'Ansoft
HFSS donne également des résultats précis pour certains
aspects des problèmes de petites bobines. Les fréquences de mode
sont généralement calculées à moins de
200 des valeurs expérimentales (même pour les bobines
à double résonance) et la magnitude B1 calculé est souvent
inférieure à 500 avec l'expérience de l'IRM.
avec l'expérience de l'IRM. Alors que la magnitude B1 peut parfois aller
jusqu'à 2500 , l'intégrale E/B1 est probablement
précis de quelque pourcent. Les résultats montrent qu'il y a
souvent plus à gagner de l'espacement accru par rapport à
l'échantillon segmentation capacitive accrue. Les Simulations de champ
en pleine onde et circuit linéaire sont susceptibles de jouer un
rôle de plus en plus important dans les avancées futures dans la
technologie des bobines RF.
En 2008, Solis et al.[18] ont
récemment décrit la conception d'une bobine de cage à
oiseaux pour l'IRM du genou humain à haut champ. Des simulations de
champ magnétiques B1 utilisant la méthode des
éléments finis (FEM) ont été effectuées
à différentes fréquences de résonance et en faisant
varier le nombre de pattes. Un design optimal à 4 T a
résulté en une bobine cage à oiseaux à quatre
pattes pour l'émetteur-récepteur. Les résultats
numériques ont ensuite été comparés aux
résultats expérimentaux, montrant une bonne correspondance. La
FEM peut également être utilisé pour concevoir et optimiser
les bobines de réceptions multiéléments. Vojtisek
et al.(2009) [19] ont traité les données extraites des
simulations et calculé des paramètres importants, tels que la
géométrie, le facteur de qualité, la sensibilité.
Les codes informatiques les plus utilisés sur la FEM sont HFSS de
ANSYS62 et Multi physics. Naturellement, l'accord et le découplage
corrects des bobines sont inévitables pour obtenir les meilleurs
résultats.
En 2009, Mikhail Kozlov et al. [20]
présentent une approche de l'utilisation du lien bidirectionnel
indépendamment du fournisseur et permettant l'utilisation d'un seul
outil RF avec plusieurs différents outils EM 3-D, réalisant une
flexibilité souhaitable du flux d'ana-lyse de bobines tout en
réduisant le coût des licences de l'outil de simulation. Ils
ajustent les paramètres de l'alimentation réseaux utilisant des
outils de circuit RF, suivis d'un nouveau calcul (basé sur les
données de simulation de circuit RF) du champ lointain à l'aide
d'outils EM 3D. La conception de la bobine RF 3D en IRM implique une simulation
en champ proche, et les réseaux de bobines d'alimentations et des
réglages sont souvent des circuits indépendants. Un diagramme de
flux de travail de cette approche est proposé. La procédure de
combinaison des résultats consiste en une superposition linéaire
de E et B pondéré par les ports P et
u fourni pour chacun des Ports. Cette procédure peut être
exécutée en dehors de l'environnement d'outils EM à l'aide
d'un logiciel externe tel que Matlab. Le calcul EM 3D nécessite beaucoup
de temps, en particulier quand une résolution spatiale
élevée est requise, alors que le circuit simulation est assez
rapide, car l'analyse de circuit RF nécessite beaucoup moins de
ressources informatiques que n'importe quelle approche de simulation EM 3-D qui
doit traiter avec un corps humain réaliste précisément un
modèle spécifié. Le
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
9
temps de calcul pour la procédure de résultat
combiné dépend linéairement du nombre
d'éléments de maillage et de ports, et ne prend pas beaucoup de
temps. Dans les études numériques, ADS a été
utilisé comme circuit RF; CST Microwave Studio et HFSS ont
été utilisés en tant qu'outils d'EM tridimensionnels et
Matlab a été utilisé en post-traitement. Cette approche a
été validée en effectuant un certain nombre de simulations
pour la bobine analysée où les réseaux d'alimentations et
de réglages n'ont pas été remplacés par des ports.
Les résultats de ces simulations pour les valeurs optimisées
d'alimentations et de réglages du condensateur étaient exactement
les mêmes que pour les simulations de substitution de port
correspondante. La différence maximale entre les données B1 et le
SAR 3D entre ces deux les simulations étaient inférieures
à 0,500 .
En 2010, G.Shou et al. [21] proposent une
approche permettant l'étude numérique des bobines RF
conventionnelle à gradient en utilisant un schéma de conception
avec une régularisation pratique des contraintes. Les méthodes
basées sur les algorithmes numériques avancés tels que la
méthode des éléments limites (BEM) et la méthode
des éléments finis (FEM) sont décrites dans ce travail.
Cependant, la conception de bobines de gradient à base de BEM se heurte
à un problème mathématique mal posé, traité
de manière classique au moyen d'une méthode de multiplication de
Lagrange. Ce travail tente d'améliorer la méthode BEM pour la
conception de bobines IRM en appliquant la méthode de Tikhonov. Les
exemples démontrent que la méthode proposée est efficace
et flexible pour la conception de bobines IRM avec des géométries
et des contraintes d'ingénieries arbitraires. Cette méthode
évite un calcul itératif de sorte que le coût de calcul
soit beaucoup moins que les techniques d'optimisation stochastique. En raison
de la relation directe des valeurs actuelles sur les noeuds limites et les
contraintes physiques spatiales des bobines peuvent être directement
introduites dans la formulation BEM, simplifiant ainsi la procédure de
conception. L'algo-rithme BEM a été codé en langage C et
la fonction d'interface a été utilisée pour interfacer
l'optimisation / régularisation de Tikhonov effectuée à
Matlab. Le maillage BE dans cette étude était
généré pour les noeuds couche par couche et codé
dans Matlab, et le les chemins de câbles discrets sont exportés
à l'aide de Tecplot.
En 2011, Ye. LI et al. [22] présentent
une approche de développement d'une nouvelle méthode basée
sur la compensation ou l'élimination du courant induit (ICE) pour le
découplage amélioré des éléments de la
bobine et l'étude de ses performances dans les images IRM
fantômes. Une méthode de découplage
électromagnétique basée sur la compensation ou
l'élimination du courant induit pour les réseaux de bobines RF
sans chevauchement a été développée avec les
critères de conception de haute efficacité, mise en oeuvre facile
et pas de connexion physique aux éléments du tableau RF. Une
méthode d'analyse des valeurs propres / vecteurs propres est
appliquée pour analyser le mécanisme de découplage et
calculer les conditions de découplage. Un réseau de micro-rubans
à deux canaux et un réseau de bobines à huit canaux ont
été construits pour tester les performances de la méthode.
Après les essais sur banc d'essai, des expériences d'imagerie IRM
ont été réalisées sur un scanner IRM 7T. Les essais
au banc ont montré que les deux matrices obtenaient un
découplage
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
10
suffisant avec un S21 inférieur
à 25 dB parmi les éléments de bobine à 298 MHz. Les
images fantômes IRM ont montré des distributions de
sensibilité bien définies pour chaque élément de la
bobine et la capacité de découplage unique du modèle ICE
proposé des techniques de découplages. Les distributions de champ
B1 des différents éléments ont également
été mesurées et calculées. L'analyse
théorique et les expériences ont démontré la
faisabilité de la méthode de découplage pour des
conceptions de réseaux de bobines RF à champ élevé
sans chevauchement ni connexions physiques directes entre les
éléments de bobines, ce qui offre davantage la flexibilité
pour la conception et l'optimisation de réseaux de bobines. La
méthode offre une nouvelle approche pour résoudre le
problème du découplage des réseaux de bobines RF, qui
constitue un défi majeur pour la mise en oeuvre de l'imagerie
parallèle. En 2011, Lingzhi et al, [23] proposent et
testent une stratégie universelle pour la construction de bobine RF
bi-fréquence 19F/ 1H permettant la
géométrie de bobines multiples. Ils étudient la
faisabilité de concevoir une bobine RF bi-fréquence 19F/
1H basée sur un modèle de résonateur
couplé; Un réseau d'appariement capacitif en série permet
une adaptation d'impédance robuste pour les deux harmoniques modes
oscillants du résonateur couplé; où deux conceptions
typiques de bobines de volume 19F/ 1H (cage à
oiseaux et selle) à 4,7T ont été mises en oeuvre et
évaluées avec un test électrique au banc et une imagerie
in vivo à double noyau 19F/ 1H.
Pour différentes combinaisons de résistances internes de la
bobine d'échantillonnage et du résonateur secondaire, des
solutions numériques pour les condensateurs accordables afin d'optimiser
l'adaptation d'impédance ont été obtenues à l'aide
d'un programme de recherche de racine. Distribution du champ B1 identique et
homogène aux fréquences 19F/et 1H ont
été observées au banc d'essai et image fantôme.
Enfin, l'imagerie in vivo chez la souris a confirmé la
sensibilité et l'homogénéité de la conception de la
bobine bi-fréquence 19F/ 1H. Une
distribution de champ B1 identique et homogène aux fréquences
19F/ 1H a été observée dans le test au
banc et en image fantôme. L'imagerie in vivo sur la souris a
confirmé la sensibilité et l'homogénéité de
la conception de la bobine à double fréquence
19F/ 1H. Et une caractéristique
unique de cette conception est qu'elle préserve
l'homogénéité du champ B1 de la bobine RF aux deux
fréquences de résonance. Cela minimise ainsi l'effet de
susceptibilité sur le Co-enregistrement d'image.
En 2014, S-M. Sohn et al.
[24] proposent dans cette étude, un élément de
ligne de transmission à micro-ruban de forme trapézoïdale
double pour obtenir une distribution uniforme du champ B1 par variation
d'impédance. Deux bobines de tête RF à huit canaux ont
été construites avec la forme du conducteur : un
élément micro-ruban uniforme, et un élément
micro-ruban à double trapèze, où chaque
élément comprend un substrat en téflon à faibles
pertes avec une hauteur et une longueur de 1,9 et 16 cm, respectivement. Une
méthode utilisant des impédances échelonnées ou
alternées avec des sections conductrices épaisses et minces
répétitives, afin de réduire le champ magnétique
inhomogène RF; Celles-ci, cependant, créent des bosses dans le
champ proche magnétique RF. Les données de simulation
électromagnétiques (modales pilotées du type solution dans
HFSS) ont été utilisées pour évaluer et analyser la
forme trapézoïdale proposée en comparant les
résultats avec autres
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
11
structures. Les résultats sont cohérents avec
ceux de simulations. Par rapport au résultat du conducteur de forme
uniforme, la forme du double trapézoïde a une distribution de champ
plus uniforme avec un signal plus élevé de profondeur de
pénétration. Les résultats de simulations et
expériences, la bobine de tête RF proposée compense la
détérioration du champ aux extrémités et
démontre amélioration de l'uniformité du champ proche
magnétique RF ainsi intensité. Par rapport au résultat de
la forme uniforme du conducteur, la forme du double trapézoïde a
une distribution de champ plus uniforme avec un signal plus élevé
de profondeur de pénétration. Les améliorations
calculées ont la fourchette de 70,'0 à
610,'0 et la moyenne de 29, 30,'0 .
En 2014, G. Giovannetti et al. [25], lors du
développement moderne des bobines de résonance magnétique,
stipulent que ces bobines lorsqu'elles sont émettrices doivent produire
un champ magnétique homogène dans un large champ de vision (FOV),
et lorsqu'elles sont réceptrices elles doivent maximiser la
détection du signal et minimiser le bruit. L'utilisation des
méthodes numériques pour ce développement permettent de
simuler le comportement de la bobine en présence de charges
réalistes et d'étudier le rendement de la bobine à des
champs magnétiques élevés. Et après toutes
constructions, pour des tests les bobines doivent être
caractérisées en laboratoire pour optimiser leur positionnement
et leurs performances en extrayant plusieurs indices de qualité. Et
ensuite les performances de ces bobines doivent être
évaluées dans un scanner utilisant des paramètres de
qualité d'image standardisés avec des expériences
fantômes et humaines. Dans cet article, hormis le principe des bobines
radiofréquences présenté, un bref aperçu des
développements futurs de la technologie de ces bobines RF a
été inclus. La valeur élevée de l'intensité
du champ magnétique statique utilisé dans les scanners modernes
IRM a entraîné l'utilisation de méthodes numériques.
En réalité, à B0 superieur 3 T, la haute valeur de la
fréquence de Larmor ne permet pas l'utilisation d'hypothèses
magnétostatiques parce que la longueur d'onde du champ est comparable
aux dimensions de la bobine. De plus, à ces fréquences,
l'échantillon interagit fortement avec le champ
généré et affecte les performances de la bobine.
L'utilisation de bobines RF supraconductrices pour réduire les pertes
résistives ont également été brièvement
examinés, et les solutions actuelles proposées pour
résoudre les problèmes de sécurité et techniques
ont été discutées. Ces auteurs utilisent une bobine
à boucle circulaire de 16.7mm de rayon, et 2 mm de rayon de fil
conducteur, ce qui correspond à la taille de l'étude d'un
fantôme en spectroscopie par résonance magnétique; Le rayon
de la boucle utilisé est extrêmement petit pour des études
cliniques. Nous nous sommes contentés de retrouver les résultats
de cet article tout en augmentant la taille de la boucle (20 cm
diamètre) et à 1.5 T qui est réglementée aux
études cliniques chez certains patients en IRM; nous avons donc
étudié le champ magnétique radiofréquence par
l'équation de Biot et savart; car elle est la méthode
appropriée pour des hypothèses de magnétostatiques
à des champs Bo inférieur à 3 T.
En 2016, G. Giovannetti et al. [26] examine
une méthode de développement du modèle SNR de bobine
utilisant un circuit électrique équivalent et l'applique à
la conception
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
12
de boucles carrées et circulaires. Inductance de bobine
et la résistance ont été calculées de
manière analytique en tenant compte des conducteurs la
géométrie croisée et la configuration du champ
magnétique ont été estimées à l'aide de la
loi de Biot-Savart, tandis que la résistance induite par
l'échantillon a été calculée avec une
méthode utilisant une approche quasi statique. La prévision de
performance de bobine a permis de comparer les boucles circulaires et boucles
carrées et a démontré que lorsqu'une simple relation entre
la taille des boucles est satisfaite, la performance des deux bobines s'est
avérée très similaire en termes de SNR. La formulation de
l'approche théorique étant largement détaillée, cet
article pourrait être intéressant pour les étudiants
diplômés et les chercheurs travaillant dans le domaine de la
conception de bobine et développement.
Rtotal est la somme de toutes les
résistances pouvant être associé à un
mécanisme de perte dans les conducteurs et au sein de
l'échantillon. En particulier : Rbobine prend
en compte les pertes dans les conducteurs de bobine et dépend de la
géométrie du conducteur.
Rchantillon sont les pertes
d'échantillon causées par les courants RF, induites par le champ
magnétique alternatif, et par les champs électriques dans
l'échantillon, principalement générés par les
condensateurs à bobine. Les Rextra
comprennent les pertes radiatives, condensateurs d'accord et pertes de
soudure, bien que les pertes radiatives peuvent être
négligées dans de nombreuses applications bobines
accordées basse fréquence. La définition du facteur de
qualité de la bobine fournit une mesure quantitative de la
qualité du circuit, Un paramètre commun d'évaluation de la
performance de la bobine est le rapport r entre le facteur de qualité du
résonateur vide (Qvide) et le
résonateur avec l'échantillon
(Qchantillon), qui peut être
défini comme la sensibilité à la charge où r doit
être maximisé pour fournir un SNR d'IRM maximal. De ces travaux,
nous nous sommes servis pour des différents calculs des dimensions de
bobine boucle (résistance de la bobine, résistance de
l'échantillon, facteur de qualité et le rapport r entre les Q)
En 2017, Nan Li et al. [27] décrivent
une méthode permettant d'améliorer l'effica-cité de la
simulation dans la conception de bobines radiofréquences; tout en
optimisant la performance des bobines afin d'améliorer la
sensibilité de détection du signal et d'obte-nir des IRM de haute
qualité. À travers la simulation, on peut étudier la
distribution du champ électromagnétique (EM) et le taux
d'absorption spécifique (SAR) pour assurer la qualité de
l'imagerie et la sécurité des patients. Ils présentent une
méthode de Co-simulation qui combine la simulation de champ EM et la
simulation de circuit; elle fournit un choix plus efficace pour les circuits RF
complexes. Ils effectuent donc une comparaison entre les paramètres de
diffusion et les résultats de distribution de champ avec la
méthode de simulation conventionnelle (principalement basée sur
la méthode des éléments finis et la méthode des
différences finies) et observe que la méthode de Co-simulation
est très précise. Sans structure de résonance dans la
Co-simulation, la convergence de la simulation de champ
électromagnétique est plus rapide que la méthode
conventionnelle. Et à travers le double accord à trois canaux de
simulation de bobine radiofréquence, la Co-simulation proposée
réduit de 4000 la durée de simulation dans une
simulation de champ électromagnétique. En
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
13
ce qui concerne l'optimisation des valeurs des
éléments localisés, la Co-simulation permet
d'économiser plus de 9000 du temps total. L'écart du
champ électromagnétique et le taux d'absorption spécifique
(SAR) entre la Co-simulation proposée et la simulation conventionnelle
sont tous inférieurs à 400 ; ce qui valide donc la
précision de la méthode proposée.
En 2017, Giulio Giovannetti et al. [28] se
concentre sur une tâche fondamentale pour optimiser le rapport signal sur
bruit dans les applications de résonance magnétique : La
simulation et la conception des bobines. Les techniques de conception de ces
bobines tirent parti des simulations sur ordinateur en fonction de la longueur
d'onde du champ magnétique et les tailles de bobines. Certaines
caractéristiques de la bobine, telles que
l'ho-mogénéité du champ magnétique, peuvent
être estimées par la théorie
électromagnétique sous le nom de Biot-Savart aussi longtemps que
l'hypothèse de champ presque statique est vérifiée, mais
avec l'augmentation de l'intensité du champ statique dans les scanners
modernes, cette condition est rarement satisfaite. Une question sur l'analyse
précise des antennes de communication s'est développée au
cours des dernières années; De plus, lorsque la bobine est
chargée avec un échantillon, les propriétés
électromagnétiques de l'échantillon ont une incidence
importante sur la répartition du rapport signal / bruit (SNR). C'est
pour cela que le développement moderne de bobines de résonance
magnetique exploite des méthodes numériques qui permettent de
simuler le comportement de la bobine en présence de charges
réalistes et d'étudier l'efficacité de la bobine à
haute fréquence, et à ces fréquences-là, les
bobines commencent à se comporter comme des antennes; ainsi, Ce
développement exploite les méthodes numériques
généralement utilisées pour la simulation d'antennes. Ils
présentent aussi les paramètres de performance des bobines et des
antennes et se concentrent sur les différentes approches de simulation.
En fonction des zones de champ proche ou lointain et de la fréquence de
fonctionnement.
En 2018, C. stumpf et al. [29] proposent une
description mathématique pour le calcul du rapport signal sur bruit
(SNR) maximal combiné de Réseaux de bobines de réception
IRM utilisant des valeurs numériques de champs B1 et des
paramètres S, et comprenant un nouveau modèle complet de la
contribution du bruit dans le préamplificateur, qui permet une
prédiction précise de la valeur absolue. Ils utilisent la
méthode du facteur Y décrite dans [30] pour mesurer les
paramètres de bruit des préamplificateurs dans un environnement
blindé; ils présentent également une méthode qui
maximise le RSB dans chaque voxel [31]; et le résolveur de la
méthode des éléments finis du logiciel CST microwave
studio est également utilisée. Les valeurs SNR du modèle
sont en bon accord avec les valeurs mesurées, présentant un
écart maximal de 1,1 dB à une distance de bobine de l = 290 mm.
Cet écart peut être dû à des imprécisions de
mesure. De plus, les conditions aux limites de la simulation de champ
électromagnétique ne couvrent pas tous les détails du
système de numérisation complet. Cependant, la précision
résultante du modèle SNR montre que le couplage du bruit des
préamplificateurs et la dégradation du SNR sont bien
reproduit.
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
14
Pour l = 20 mm, représentant les bobines fortement
couplées, le rapport SNR estimé entre les
préamplificateurs physiques et sans bruit est d'environ 16 dB. Cela
montre que réduire le facteur de bruit des préamplificateurs et
optimiser le découplage des éléments de bobines peuvent
avoir un impact majeur sur le RSB résultant pour les réseaux de
bobines faiblement chargés. Comme la charge de la bobine augmente,
l'effet sera affaibli car le bruit de l'échantillon deviendra le facteur
dominant en ce qui concerne le SNR. Les résultats de mesure du RSB et le
modèle du réseau à quatre éléments peuvent
également être considéré comme étant en bon
accord. L'écart maximum entre les valeurs mesurées et
modélisées est observé dans les régions où
le signal IRM est de faible amplitude. Cela peut s'expliquer par une onde
stationnaire qui s'est accumulée dans le fantôme
enquêté. Les résultats des réseaux de bobines
à deux et à quatre canaux montrent que l'approche proposée
pour la modélisation du SNR peut être utilisé pour
prédire les valeurs de SNR absolues avec une bonne précision,
même pour éléments légèrement chargés.
Le modèle de préamplificateur passif permet la
modélisation de l'ensemble du réseau en Paramètres S, en
tenant compte de tous les effets de couplage.
Tout au long de ce chapitre, nous avons pu nous rendre compte
des difficultés liées à la conception d'antennes RF en
IRM. Malgré ces difficultés des méthodes numériques
pour les solutionner existent et la communauté de chercheur en IRM ne
cesse de travailler à l'élaboration des techniques nouvelles de
conceptions capables d'apporter des améliorations (la
sensibilité, l'homogénéité du champ, le rapport
signal sur bruit). Ainsi dans la suite de ce travail, nous nous sommes
intéressés aux travaux de Giulio Giovannetti et al.
[25] qui par une étude magnétostatique exploitent le
champ magnétique de l'équation de Biot et savart pour concevoir
une antenne de surface simple boucle circulaire de 16.7 mm de rayon et 2 mm de
rayon du fil; nous cherchons ici à reproduire les résultats de
leurs travaux en modifiant la taille de la boucle (20 cm diamètre)
à 1.5 T qui est réglementée pour des études
cliniques chez certains sujets en IRM; ceci dans le but de mieux comprendre les
techniques de conceptions d'antennes RF employées par ces auteurs qui
utilisent le logiciel IDL pour simuler le champ de l'équation de
Biot-savart. Nous utiliserons également cette équation que nous
allons l'intégrer numériquement par Gauss-Legendre et la
simulé dans le logiciel Matlab. Le chapitre suivant présente les
différents outils et méthodes utilisés pour la conception
de cette antenne.
CHAPITRE II
IMAGERIE PAR RéSONANCE
MAGNéTIQUE, ANTENNES
RADIOFRéQUENCES ET SIMULATION
D'ANTENNE RF
15
2.1 Introduction
Ce chapitre est consacré à une brève
présentation des généralités sur l'IRM, où
nous présenterons ses différents constituants; ensuite les
généralités sur les antennes radiofréquences,
où nous présenterons les différents types d'antennes et
les paramètres de caractérisations de ces antennes; enfin une
modélisation d'une antenne boucle circulaire, où nous ferons
l'étude du champ magnétique crée par une antenne à
boucle circulaire; ce champ est généralement appelé champ
radiofréquence dans la littérature car sa pulsation se situe dans
la gamme des ondes radio; où nous présenterons enfin quelques
méthodes de conceptions des antennes RF.
2.2 L'imagerie par résonance magnétique (IRM)
2.2.1 Historique
L'IRM est fondée sur une découverte faite dans
les années 1930 dans le domaine de la physique, appelée
résonance magnétique nucléaire (RMN). Felix Bloch, de
l'Université Stanford, et Edward Purcell, de l'Uuniversité
Harvard, ont découvert que l'interaction entre les champs
magnétiques et les ondes radioélectriques fait que les atomes
émettent un petit signal radio; ces signaux radio peuvent ensuite
être détectés pour former une image. Cette
découverte a aidé de nombreux scientifiques à mieux
comprendre les structures internes des objets sans avoir à les
disséquer et à les détruire, c'est ce qu'on appelle essai
non destructif. La première image unidimensionnelle par IRM a
été obtenue en 1952; Puis en 1974, Paul Lauterbur a
réalisé la première image en coupe d'une souris et en
1972, Peter Mansfield a mis au point des méthodes mathématiques
qui ont permis d'obtenir des images claires et
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.2. L'IMAGERIE PAR RÉSONANCE MAGNÉTIQUE (IRM)
16
rapides, faisant passer la durée d'analyse de quelques
heures à quelques secondes.
2.2.2 Fonctionnement
L'IRM fournit des images en tranche de l'organisme grâce
à des champs magnétiques et des ondes radio de forte
intensité. Les images obtenues par résonance magnétique
sont le résultat de l'interaction entre un champ magnétique
créé par la machine et les atomes d'hy-drogènes contenus
dans l'organisme du patient. L'appareil est en effet équipé d'un
aimant très puissant et envoyant des ondes qui vont faire vibrer les
noyaux d'hydrogènes contenus dans les tissus organiques. Le retour de
ces noyaux d'hydrogènes à leur état d'équilibre va
engendrer la formation d'un signal dans une antenne réceptrice et
analysé par des ordinateurs qui vont ensuite convertir ce signal en une
image.
2.2.3 Déroulement de l'examen
L'examen dure en général de 15 à 30
minutes, mais pour un examen plus complet la durée peut aller
jusqu'à une heure. Le patient après avoir enlevé ses
vêtements, est allongé sur un lit, l'appareil (antenne) est alors
disposé sur la zone à examiner, puis le lit coulisse doucement
dans le mini-tunnel; c'est à l'intérieur de ce mini-tunnel qu'est
produit le champ magnétique (voir figure 2.3). Durant l'examen, le
patient doit rester parfaitement immobile mais dispose, si quelque chose ne va
pas, d'une sonnette pour prévenir le manipulateur. L'examen est
totalement indolore et ne présente aucun risque pour le patient, il doit
cependant avoir retiré absolument tous les objets métalliques
(montres, ceinture, bijoux, etc...). Il doit aussi signaler à son
médecin le port d'une pile cardiaque, valve ou prothèse qui
pourraient perturber le déroulement de l'examen et présenter des
risques chez le patient. Le seul inconvénient est le bruit de la machine
et la sensation d'enfermement qui peuvent perturber certains patients. Une fois
les images prises, celles-ci vont être interprétées par un
radiologue.
2.2.4 Principe de la RMN
Le principe de fonctionnement de l'IRM consiste d'abord
à aimanter le corps humain par le biais d'un champ magnétique
statique uniforme très intense (de l'ordre du Tesla), auquel vient
s'ajouter une onde radiofréquence (20-400 MHz) accordée sur la
fréquence de résonance des atomes d'hydrogène
(fréquence de Larmor). Le noyau généralement
utilisé lors des applications en IRM est celui d'hydrogène en
raison de sa grande abondance dans le corps humain (celui-ci contient environ
7500 d'eau). En l'absence de champ magnétique
extérieur, le spin d'un noyau d'hydrogène est orienté de
façon aléatoire. Sous l'influence d'un champ magnétique
statique et uniforme ~E0, le spin du noyau
d'hydrogène effectue un mouvement de rotation autour de la direction du
vecteur ~E0 ; on dit que le spin effectue un mouvement de
précession. La fréquence de rotation, appelée
fréquence de Larmor, est
2.2. L'IMAGERIE PAR RÉSONANCE MAGNÉTIQUE (IRM)
17
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
|
caractéristique du noyau étudié et
proportionnelle à l'intensité du champ
|
~B0 :
|
f0 = ã 2ð B0 (2.1)
Où ã est le rapport gyromagnétique de
l'espèce considérée (le rapport gyromagnétique de
l'hydrogène vaut 42,58 MHz/T). Les atomes d'hydrogènes entrent en
résonance et lorsque le champ alternatif est brutalement interrompu il
est possible de mesurer la perturbation du champ magnétique due aux
vibrations de ces atomes. Pour obtenir des images localisées, on joue
sur le fait que cette fréquence de résonance dépend de
l'intensité du champ magnétique. On superpose alors un gradient
statique de champ pour moduler cette fréquence, selon l'endroit
où l'on souhaite mettre en résonance les atomes. Une antenne dite
émettrice génère un champ radio-fréquence
noté ~B1 perpendiculaire au champ ~B0
et effectuant un mouvement de rotation à la fréquence de
Larmor des noyaux d'hydrogènes. Une fois l'émission du champ
radio-fréquence finie, les protons retournent à
l'équilibre en émettant à leur tour un signal
radio-fréquence à la fréquence de Larmor. Celui-ci est
capté par des antennes dites réceptrices. C'est ce signal qui,
une fois numérisé, traité puis analysé permet
d'obtenir les propriétés physiques et chimiques de
l'échantillon étudié. La qualité des
résultats obtenus lors de la RMN est donc en partie liée à
la qualité d'émission et de réception des antennes. Pour
avoir une bonne qualité, le champ émis doit être aussi
homogène que possible dans la région étudiée et
effectuer un mouvement de rotation à une fréquence la plus proche
possible de la fréquence de Larmor afin d'exciter uniformément
les noyaux voulus. De plus, les antennes réceptrices doivent avoir un
rapport signal sur bruit élevé. Pour cela, il faut rendre la
résistance de ces antennes la plus faible possible. C'est pourquoi les
antennes sont composées de matériaux ayant une bonne
conductivité tel que le cuivre ou l'or.
|
2.2.5 Le signal RMN
2.2.5.1 Détection du signal RMN
Lors du retour à l'équilibre, si une bobine de
réception d'axe perpendiculaire à
|
~B0 est
|
placée à proximité du système de
spin, la composante transversale du signal RF émis peut induire dans la
bobine une tension sinusoïdale amortie de pulsation ù0.
L'amplitude de ce signal, appelé signal de précession libre
(FID), décroît exponentiellement avec le temps (Figure
2.1).
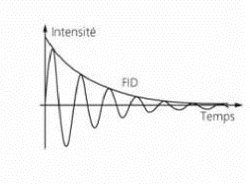
2.2. L'IMAGERIE PAR RÉSONANCE MAGNÉTIQUE (IRM)
18
B1 -? (2.2)
-?
S = ùo sin(á).8íMo
I
FIGURE 2.1 - signal de précession libre
En ce qui concerne l'instrumentation, le champ statique est
créé à l'aide d'un aimant dont l'intensité varie
selon les applications (de 0,5 à 17 T). Une antenne RF d'émission
génère
|
le pulse du champ
|
~B1 et une antenne RF de
réception détecte le signal émis lors du retour
|
à l'équilibre thermique de l'aimantation
macroscopique. Notons qu'une seule et unique antenne peut jouer les deux
rôles à la fois. Pour une bonne efficacité, ces antennes
doivent être finement accordées à la fréquence de
résonance fo des spins des noyaux analysés. Afin de reconstruire
une image à partir du signal capté, il est nécessaire de
localiser le plus précisément possible son origine spatiale. La
méthode mise en oeuvre est basée sur une discrimination des
éléments de volumes (voxels) par leur fréquence de
résonance. Pour cela, un système de gradient de champ est
utilisé. Le signal acquis est ensuite traité par un
système informatique afin de reconstruire les images en 2 ou 3
dimensions.
2.2.5.2 Expression analytique du signal
détecté
L'application du principe de réciprocité qui
stipule: <qu'une antenne, en régime stationnaire, dans un milieu
linéaire et isotrope, présente les mêmes
caractéristiques magnétiques (sensibilité, champ
généré) lorsq'elle est utilisée en émission
ou en réception > permet alors de calculer la valeur du signal RMN
perçu par une antenne en mode réception à partir du champ
magnétique ~B1 créé par cette
antenne en mode émission par unité de courant I. Alors, le signal
S émis par les spins contenus dans un élément de volume
8v et capté par l'antenne de réception est une force
électromotrice d'expression :
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.2. L'IMAGERIE PAR RÉSONANCE MAGNÉTIQUE (IRM)
19
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
Le rapport B' I est appelé coefficient d'induction
de l'antenne. C'est un critère d'efficacité de l'antenne IRM
puisqu'il traduit l'aptitude de l'antenne à générer un
champ par unité de courant circulant dans celle-ci.
2.2.6 Composantes d'un équipement IRM
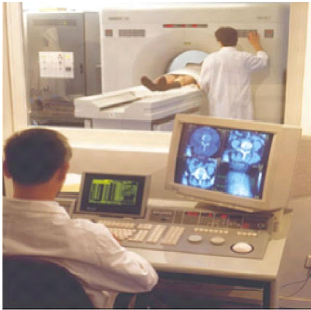
Un système IRM se compose de trois parties : la salle
d'examen, la salle de commande et la salle technique (Fig.2.2).

FIGURE 2.2 - les différentes parties du système
IRM. [41]
2.2.6.1 La salle d'examen :
C'est la partie principale du système, on y retrouve le
tunnel de l'aimant où le patient est allongé sur la table, puis
sera introduit automatiquement tout en préservant son confort par une
ventilation et un éclairage adapté ainsi qu'un système de
communication personnel médical/patient. Le diamètre du tunnel
est d'environ 60 cm selon les fabricants. (Fig.2.3). IL'aimant
permanent : C'est le composant essentiel de l'appareil IRM, il est
dans la grande majorité supraconducteur car c'est le type d'aimant qui
possède les meilleures caractéristiques
d'homogénéité et de puissance. Pour obtenir cette
supraconductivité l'aimant
2.2. L'IMAGERIE PAR RÉSONANCE MAGNÉTIQUE (IRM)
20
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
doit être refroidit par de l'hélium liquide et
doit donc être constitué d'un système complexe de
refroidissement. Son rôle est de produire un champ magnétique
équivalent à 30000 fois le champ magnétique terrestre. On
distingue trois types d'aimants : les aimants permanents, les aimants
résistifs et les aimants supraconducteurs.
'Les bobines de gradient : Elles introduisent
une inhomogénéité dans le champ magnétique, de
façon à ce que l'on puisse savoir différencier deux points
avec précision en fonction des valeurs des champs magnétiques en
ces points. En pratique, on trouve la plupart du temps 3 bobines qui jouent ce
rôle dans les imageurs IRM. Chaque bobine sert à
caractériser une direction de l'espace, ce qui permet d'accéder
à des informations en 3 dimensions. 'Les antennes
radio-fréquences : Elles jouent un rôle multiple et
essentiel dans l'appa-reil IRM. Elles permettent d'émettre le signal
d'excitation (quand elles servent d'émetteur) et de recueillir le signal
émis au moment de la relaxation (quand elles servent de
récepteur); elles assurent l'interface entre le patient et l'aimant; des
antennes dédiées, positionnées sur le patient, permettent
d'améliorer le rapport signal-bruit (S/B) pour un organe
donné.

FIGURE 2.3 - salle d'examen. [41]
2.2.6.2 La salle de commande :
Elle doit être positionnée de façon
à donner aux opérateurs le meilleur angle de vue du patient,
à travers un châssis de vision (Fig.2.4). C'est l'endroit
où le manipulateur enregistre, par l'intermédiaire du pupitre de
commande les différents paramètres de l'IRM et réceptionne
les données sous forme d'image à la fin de l'examen.
2.2. L'IMAGERIE PAR RÉSONANCE MAGNÉTIQUE (IRM)
21
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
FIGURE 2.4 - salle de commande. [41]
2.2.6.3 La salle technique :
La salle technique regroupe les multiples armoires techniques
telles que le groupe de puissance (alimentation de l'aimant, des bobines de
gradient, émetteur...) (Fig.2.5), elle doit être
positionnée à proximité de la salle d'examen pour limiter
les longueurs de câbles mettant en jeux des puissances importantes. Le
groupe informatique assurant l'interface entre la salle examen/salle de
contrôle est également situé dans ce local pour
protéger ses organes (ordinateurs et périphériques) du
champ magnétique produit par l'IRM tout comme le groupe de puissance.
Cette salle doit être climatisée pour protéger ces
installations sensibles à la température.

2.3. LES ANTENNES RADIOFRÉQUENCES 22
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
FIGURE 2.5 - salle technique. [41]
.
2.3 Les Antennes Radiofréquences
Contrairement à la majorité des applications
où les antennes sont utilisées pour transférer de
l'information sur de grandes distances, les antennes utilisées en
imagerie par résonance magnétique sont situées très
près du récepteur et de l'émetteur du signal,
c'est-à-dire du corps du patient. Le rôle de l'antenne est de
faire le lien entre le circuit électrique et l'es-pace environnant.
L'antenne peut être vue comme une impédance complexe d'un circuit
électrique dont la partie réelle possède une composante
radiative, c'est-à-dire une résistance qui transforme
l'énergie électrique en ondes électromagnétiques.
Pour des valeurs du champ magnétique statique délivré par
les aimants utilisés en pratique la fréquence de résonance
( 42,6 MHz/T) appartient au domaine des radiofréquences (RF).
2.3.1 Éléments constitutifs d'une
antenne.
Celle-ci est constituée d'une boucle conductrice qui
forme un circuit fermé autour ou à proximité d'un
échantillon ainsi que d'un circuit électronique relié
à la boucle et composé de capacités de diodes et parfois
d'inductances.
2.3. LES ANTENNES RADIOFRÉQUENCES 23
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
I Boucle de l'antenne.
La boucle métallique est plus souvent constituée
d'un fil ou ruban de cuivre qui forme un contour fermé. Cette boucle a
pour fonction de convertir par induction le faible signal
électromagnétique de la relaxation de l'aimantation transverse de
fréquence en une tension électrique de même
fréquence à ses bornes. D'un point de vue électrique, la
boucle de l'antenne chargée par l'échantillon est
équivalente à une inductance L en série avec une faible
résistance Req. L'inductance est définie
comme le flux à travers la section S de la boucle du champ B1
(en T) divisé par le courant I (en A) dans la boucle :
fZ
1 B1 (q) · ?-
---?
L = ds (2.3)
I q?s
En calculant B'
I (sensibilité de l'antenne) en
tout point de la surface S, il est théoriquement possible d'estimer
l'inductance propre L d'une antenne. En pratique, L est donnée par des
modèles de la littérature pour les antennes aux
géométries simples ou par simulation numérique pour les
plus complexes.
I circuit de l'antenne
L'antenne peut être vue comme une impédance
complexe d'un circuit électrique dont la partie réelle
possède une composante radiative, c'est-à-dire une
résistance qui transforme l'énergie électrique en ondes
électromagnétiques. L'impédance Za
peut donc être écrite comme:
|
Vin
Za =
Iin
|
= Ra + jXa (2.4)
|
où Vin et Iin
sont respectivement la tension et le courant aux bornes de
l'entrée de l'antenne. Ra est la partie
réelle (active) de l'antenne, c'est-à-dire la partie
associée au rayonnement et aux pertes joules, alors que Xa
est la partie imaginaire (réactive) de l'antenne,
c'est-à-dire la partie due aux champs d'induction au voisinage de
celle-ci. Ra peut être réécrit comme :
Ra = Rri + Rpertes où Rpertes
comprend les pertes ohmiques et les pertes diélectriques.
Rri est la résistance de rayonnement vue à
l'entrée, qui relie la puissance totale rayonnée <P> au
courant efficace i :
< p >= Rrii2 (2.5)
La puissance rayonnée par une antenne n'est
généralement pas isotrope. C'est la géométrie de
l'antenne et son impédance vue du côté circuit qui
déterminent comment le courant est distribué dans la structure de
l'antenne et donc comment la puissance sera rayonnée. Pour que le
transfert de puissance soit maximal, le circuit récepteur ou
émetteur doit être adapté de façon à ce que
son impédance soit égale au conjugué de Za
à la fréquence centrale d'opération
ùL vue aux bornes de l'antenne, formant ainsi un circuit
résonant.
2.3. LES ANTENNES RADIOFRÉQUENCES 24
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.3.2 Principaux paramètres de
Caractérisation d'antennes RF
2.3.2.1 Fréquence de résonance
Le signal RMN provenant de l'échantillon étant
extrêmement faible, il est alors nécessaire d'utiliser des
antennes de détection résonante, dont la fréquence de
résonance est ajustée à la fréquence du signal RMN
(fréquence de Larmor). La résonance de l'antenne se traduit par
une sélectivité fréquentielle et permet donc de filtrer
une partie du bruit associé à la détection du signal. Une
antenne IRM peut-être représentée classiquement par un
circuit RLC. (Fig.2.6). R est la somme de toutes les résistances pouvant
être associé au mécanisme de perte au sein des conducteurs
et au sein de l'échantillon. En particulier,
R = Rbobine +
Rchantillon (2.6)
Rbobine Prend en compte les pertes
au sein du conducteurs de la bobine du récepteur et dépend de la
géométrie du conducteur; Rchantillon
correspond aux pertes causés par les courants RF
induits par la fluctuation du champ magnétique et du champ
électrique dans l'échantillon, principalement
générée par les condensateurs. L est l'inductance du
système tenant compte de l'énergie qui peut être
stockée dans le champ magnétique, et est liée à la
géométrie et la taille du conducteur; C la capacité du
système résultant principalement de la contribution de
condensateur discret; I est le courant qui circule dans la bobine. En
appliquant la loi de Kirchhoff, la fréquence de résonance du
circuit correspondant à la fréquence pour laquelle le courant est
maximal, peut être calculée comme suit :
1
fo = v (2.7)
2ð LC
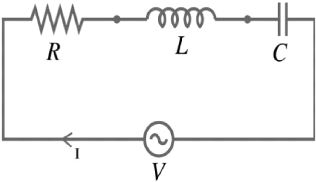
FIGURE 2.6 - circuit RLC équivalent d'une antenne
radio-fréquence [25]
2.3. LES ANTENNES RADIOFRÉQUENCES 25
2.3.2.2 Facteur de qualité de l'antenne
Le facteur de qualité Q d'une antenne RF en
réception peut être traduit par son aptitude à transmettre
le signal à la fréquence de résonance tout en
atténuant le bruit aux autres fréquences. Il peut être
défini comme le rapport de la fréquence de résonance
fo à la largeur de la bande
passante Äf autour de la résonance :
fo fo
Q = = (2.8)
f1 - f2
Äf
où f1 et f2
sont les deux fréquences de coupure à -3dB.
Äf correspond ainsi à la bande passante à -3dB de
l'antenne. Pour une antenne ayant un facteur de qualité
élevé, sa bande passante est étroite et il est donc
important d'accorder le plus précisément possible la
fréquence de résonance de l'antenne à la fréquence
de Larmor des spin. Le facteur de qualité peut également
être abordé d'un point de vue énergétique au travers
de l'expression ci-dessous :
Energie.totale.stockee.par.l'antenne
Q = 2ð
(2.9)
Energie.dissipee.par.cycle
- L'énergie stockée par l'antenne correspond
à l'énergie magnétique emmagasinée dans
l'in-ductance de l'antenne (12
Li2, avec i le courant
parcourant l'antenne).
- L'énergie dissipée par cycle correspond
à l'énergie dissipée dans la résistance
équivalente de l'antenne
(12
Ri2, normalisée par
la fréquence de résonance)
Le facteur de qualité Q est alors relié aux
paramètres électriques équivalents du circuit par :
/
Lwo
2ðf0L 1 L
Q = R = R = (2.10)
R C
Avec wo, la pulsation de
résonance de l'antenne. Une mesure de la performance de l'antenne est le
rapport r entre le facteur Q d'une bobine non chargée et le Q d'une
bobine chargée :
|
r =
|
Qnon charg Qcharg
|
Rbobine +
Rchantillon
= (2.11)
Rbobine
|
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.3. LES ANTENNES RADIOFRÉQUENCES 26
Où Rbobine est la
résistance de la bobine et Rchantillon
est la résistance induite par l'échan-tillon.
L'indice r devrait être maximisé pour fournir un RSB/SNR maximal
en IRM, puisque
/
1 - 1
SNRá r
2.3.2.3 Homogénéité du champ
magnétique
Lorsqu'un courant parcourt l'enroulement d'une antenne, il
crée un champ magnétique ~B1
au voisinage de l'antenne. L'homogénéité de
ce champ peut donc être un paramètre critique car elle conditionne
un basculement homogène de l'aimantation de chaque voxel dans le volume
observé et donc l'uniformité de l'intensité du signal RMN
détectable. Une
antenne doit donc produire un champ le plus homogène
possible pour exciter en même temps tout le volume observé.
2.3.2.4 Facteur de sensibilité d'une antenne
La sensibilité de la bobine est un autre
paramètre important qui caractérise les performances des bobines
RF. elle est défini comme le rapport entre le champ magnétique
B1 induit par la bobine RF en un point donné
et la puissance totale délivrée par la bobine P, elle
s'écrit comme suit :
17 '
17
B1
v (2.12)
P
B1 (2.13)
d'où
i Le théorème de réciprocité
permet d'utiliser l'équation (2.13) pour caractériser les deux
performances d'émissions et de réceptions d'une bobine. Il est
important de noter que maximiser la sensibilité de la bobine maximisera
aussi le RSB.
2.3.2.5 Rapport signal sur bruit (RSB)
C'est certainement le plus important parmi les
paramètres qui caractérisent une bobine et c'est aussi le plus
problématique à mesurer en laboratoire. Le signal capté
par l'antenne est composé à la fois du signal RMN utile et des
signaux parasites dus aux pertes. La qualité d'une analyse IRM peut
être représentée par l'intensité relative du signal
utile par rapport à l'intensité du bruit : c'est le rapport
signal sur bruit (RSB). A la sortie de l'antenne, ce rapport est défini
comme:
S B=
amplitude du signal RMN (2.14)
amplitude moyenne de bruit
Considérons uniquement les deux principales sources de
bruit, c'est-à-dire les pertes propres de l'antenne et celles induites
par l'échantillon. Il est possible d'exprimer leur influence sur la
puissance dissipée à l'aide de leurs résistances
équivalentes (Rb et Ri
respectivement). La tension moyenne de bruit est définie
comme la somme quadratique des tensions de bruit exprimées à
partir de ces résistances équivalentes. Alors, l'expression du
RSB devient :
S ùo
sin(á).8íM0
B=
B1 (2.15)
I
J
4KBB(TbRb
+ TiRi)
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
á : l'angle de basculement.
M0 : l'aimantation macroscopique de
l'échantillon.
8v : élément de volume de
l'échantillon analysé (voxel). Tb :
température de l'antenne.
2.3. LES ANTENNES RADIOFRÉQUENCES 27
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
Ti : température du sujet d'étude.
B : bande passante de fréquence en hertz.
Si le signal sur bruit est mauvais, la plupart du temps le
technicien est contraint de remplacer l'antenne, (chaque antenne a son
signal/bruit). Le RSB dépend aussi des : Facteurs non modifiables tels
que l'intensité du champ, séquence d'ondes RF,
caractéristiques tissulaires et des facteurs modifiables :
antenne utilisée.
2.3.3 Les différents types d'antennes RF
~B1
Pour la conception des antennes RF en IRM, un des
critères importants est que l'antenne doit présenter une
sensibilité optimale dans la région d'intérêt.
L'homogénéité du champ
créé par l'antenne doit également
être considérée pour certaines applications. De nombreuses
bobines RF ont été conçues [32] et ils peuvent être
classés en 2 grand groupes selon leurs formes : les antennes de volumes
et les antennes de surfaces.
2.3.3.1 Les antennes de surfaces
Lorsque l'on souhaite observer des zones de dimensions
réduites, situées en périphérie d'un
échantillon de grande taille, l'utilisation d'antenne de volume n'est
pas adaptée car la taille de l'antenne (imposée par la taille de
l'échantillon devant être inséré dans l'antenne) est
beaucoup plus grande que celle de la zone d'intérêt. D'où
la nécessité d'utiliser des antennes de surfaces qui feront
également l'objet de ce présent mémoire car elles sont
plus simple à concevoir, elles sont généralement
constituées d'un enroulement (souvent circulaire ou rectangulaire) qui
fixe l'inductance et de condensateurs soudés sur l'enroulement pour
créer la résonance (voir Fig.2.7). Ce sont des antennes de petite
taille, ayant une sensibilité de détection locale et
placées au contact de la zone à observer, leur utilisation permet
d'améliorer le rapport signal sur bruit en IRM. Cependant, l'antenne de
surface présente une carte de champs moins homogène que l'antenne
de volume, ce qui crée des problèmes si celle-ci est
utilisée à la foi en réception et en émission,
entrainant un basculement inhomogène des spins nucléaires,
d'où la nécessité d'utiliser une antenne de volume pour
l'excitation et une antenne de surface pour la réception. Tout en tirant
profit de la grande sensibilité des antennes de surface, ces
dernières sont utilisées en réseau [33]. Néanmoins,
le champ B1 généré par une antenne de surface
décroît rapidement avec la distance à l'antenne et n'est
pas homogène dans le volume imagé. Pour cette raison, les
antennes de surface ne sont efficaces que pour imager des zones peu profondes
et de dimension latérale réduite; de nombreuses applications
cliniques ont été réalisées en profitant de la
haute sensibilité des antennes de surface.

2.3. LES ANTENNES RADIOFRÉQUENCES 28
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
FIGURE 2.7 - bobines planes circulaires (à gauche),
carrées (au milieu) et papillons (à droite) [25J.
2.3.3.2 Les antennes de volumes
Elles comprennent principalement des spirales de Helmholtz et
de cage d'oiseaux souvent utilisées à la fois en transmission et
en réception. Ces bobines peuvent générer un champ
uniforme dans une grande région lorsqu'elles entourent
l'échantillon et elles sont caractérisées par une
induction magnétique induite homogène. Une bobine de Helmholtz
est faite en haut par 2 boucles circulaires identiques séparées
par une distance égale au rayon de la boucle; elle a la forme d'un
solénoïde (fig.2.8, à gauche), et elle est capable de
générer un champ uniforme à proximité de leur
milieu [34].
Une bobine cage d'oiseau (birdcage) est composée de N
jambes reliées à chaque extrémité par 2 boucles
circulaires, appelées bagues d'extrémité (fig.2.8,
à droite); la présence de condensateurs rend la structure
résonante. Les antennes de volumes sont utilisées à la
fois comme bobines émettrices et réceptrices dans les
systèmes IRM à champ faible et élevé; en raison de
leur capacité à générer un champ magnétique
RF hautement homogène avec un RSB élevé, elles sont
très populaires.
Le principe de base de ce type d'antennes est de faire
circuler un courant le long des conducteurs, dont l'amplitude varie
sinusoïdalement avec la position azimutale dans l'antenne cylindrique afin
de générer un champ le plus homogène possible. Le
principal inconvénient de ce type d'antennes est dû au fait que le
bruit collecté provenant de tout le volume de l'échantillon
limite ainsi leur sensibilité de détection.
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 29
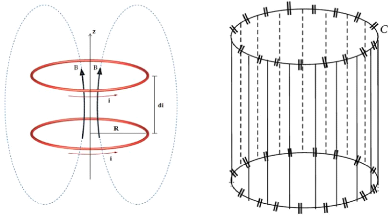
FIGURE 2.8 - Représentation schématique
d'une bobine de Helmholtz (à gauche) et d'une bobine de cage à
oiseaux (à droite) [25J.
2.4 Simulation d'une antenne de surface : cas d'une antenne
simple boucle circulaire
Il existe différentes catégories de bobines de
surfaces telles que : les bobine à boucle circulaire ayant plusieurs
formes (bobine simple boucle, bobine en forme de 8, bobine en forme de double
cône) et les bobines à boucle carrées ou rectangulaires.
Des simulations ont été effectuées pour tracer le profil
du champ magnétique B1 généré par une
bobine de surface accordée à la fréquence de
précession de Larmor à 64 MHz correspondant à un champ
magnétique statique de 1.5 T. Cette bobine a ensuite été
fabriquée et utilisée pour certaines études.
2.4.1 Géométrie et matériaux
L'antenne de surface a une forme circulaire avec un
diamètre de 20 cm. Le conducteur est un fil cylindrique de rayon a=2mm.
La définition de la géométrie est planifiée, ce qui
a été réalisé en utilisant une structure circulaire
à laquelle deux petites parties ont été enlevées
pour permettre d'insérer le condensateur d'accord et la source (fig
2.9).
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 30

FIGURE 2.9 - géométrie de l'antenne de
surface
2.4.2 Eléments de circuit et réglage de la
bobine
* Calcul de la résistance de la bobine pour une
boucle circulaire
La résistance de la bobine peut être estimée
en utilisant la formule classique
Rbobine = ñl (2.16)
S
Qui prend en compte la géométrie du fil
conducteur, où l et S sont respectivement la longueur totale du
conducteur et l'aire de la section transversale. Pour une boucle circulaire de
rayon b constituée d'un fil conducteur (forme cylindrique) de rayon a
(fig 2.10), la longueur du conducteur vaut l = 2ð.b; S la section totale
dans laquelle le courant circule effectivement vaut S = 2ða.ä, ce qui
caractérise l'effet de peau lié à la circulation du
courant RF dans «l'épaisseur de peau» ä du conducteur.
ä dépend de la fréquence de travail f et est
donné par:
r ñ
ä = (2.17)
ðfu0
Où ñ est la résistivité du
conducteur ( ñ=1.68*10-8m.Ù pour le cuivre) f est la
fréquence d'accord de la bobine et u0 est la perméabilité
magnétique dans le vide.
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 31
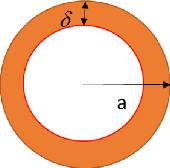
FIGURE 2.10 - conducteur cylindrique de rayon a et de
section S caractérisé par l'épaisseur de peau ä
[25J
La résistance de la bobine peut être calculée
comme suit :
Rbobine(f) = ñ2ðb ðfu0ñ (2.18)
2ðaä ? Rbobine(f) = b \/
a
* Calcul de résistance induit par
l'échantillon
Pour estimer les pertes dues à la résistance
induite par l'échantillon, nous avons utilisé une méthode
utilisant le calcul de potentiel vectoriel (VPC) pour l'estimation des pertes
d'échantillons. Il est basé sur l'approche
magnétostatique, mis en oeuvre mathématiquement pour le calcul de
résistance induite par l'échantillon des bobines simples et des
géométries d'échantillon. En fonction de la
géométrie et de la forme de la bobine, une estimation de la
résistance induite par échantillon peut être donnée
par :
|
fRchantillon = óù2
vol
|
A * AdV (2.19)
|
Où ó est la conductivité de
l'échantillon, A est le potentiel de vecteur magnétique produit
par le courant I circulant dans la bobine; il s'exprime comme suite :
|
Z
A(r) = u0I dl
4ð w
c
|
(2.20)
|
En moyennant certaines approximations (conductivité
constante sur le volume semi-infini de l'échantillon, courant unitaire
uniforme dans la boucle), on peut dans le cas d'une boucle circulaire de rayon
b réécrire :
Rchantillon = 3u2
1 0ù0 2ób3 (2.21)
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 32
* Calcul de l'inductance pour une boucle
circulaire
L'inductance des boucles a été calculée en
utilisant les valeurs suivantes :
|
L 4ðI2 ZZZ
V
|
ZZZ
V
|
J(r).J(r') dvdv' (2.22)
W
|
Où J est la densité de courant dans le
conducteur, u0 est la perméabilité de l'espace libre, I
représente le courant total dans le conducteur, V est le volume du
conducteur, et W=|r-r'|. Pour les géométries simples, de
nombreuses tables et formulations existent pour le calcul de l'inductance de la
boucle de l'antenne L. par exemple, pour une boucle circulaire de rayon b
constitué d'un fil de rayon a, l'inductance L (en H) s'écrit
simplement :
L = u0bl ln l âb l - 1.75 I (2.23)
2.4.3 Modélisation analytique d'une antenne à
boucle circulaire
2.4.3.1 Calcul du champ magnétique B~ par
Biot-savart
Les expériences montrent que le champ magnétique
est créé par des particules chargées
?-
en mouvement (courants électriques). Le champ
magnétostatique B obéit à deux lois :
~ Le champ magnétique
?- Bcréé par un courant I est donné par le
théorème d'Ampère :
Ic
B.-?
-? dl = u0I (2.24)
?- j ,
où C est une courbe fermée quelconque
traversée par le courant électrique I et u0 =
4ð.10-7H.m-1 est la perméabilité
magnétique du vide. Si le courant I correspond à une distribution
de charges électriques mobiles définissant un vecteur
densité de courant
?-
alors le courant I encerclé par la boucle fermée C
est le flux de j à travers une surface
quelconque délimitée par C :
I = 1111>is (2.25)
Le théorème d'ampère s'écrit alors
:
Ic dl = u0 Z f?-j.dS (2.26)
En tenant compte du théorème de Stokes :
ic B = ZP ??-B . dS (2.27)
On obtient :
ZZ ? B c = u0 Zf .7
·'`
db (2.28)
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 33
Cette égalité étant vraie quelle que soit
la surface S, on obtient la forme locale du théorème
d'Ampère qui s'écrit :
?- ?? ?- B = u0-? j (2.29)
-Le flux du champ magnétique à travers une
surface fermée S quelconque est nul. On dit que le champ
magnétostatique est à flux conservatif. Cette
propriété est traduite par l'intégrale suivante :
ZZ
~
?-B.-?dS = 0 (2.30)
En tenant compte du théorème de
Gauss-Ostrogradski, on obtient l'équation du flux magnétique :
?- ?.-? B= 0 (2.31)
?-
Sachant que ?.-?B = 0 et que la divergence du
rotationnel d'un champ vectoriel est nulle, on
?-
vectoriel ?- A' tel que : A' =
?- A+ ?- ?ö; calculons le champ magnétostatique ?- B
' associé à
en déduit qu'il existe un champ vectoriel ?- A
appelé potentiel vecteur tel que : ?- B = ?- ? ? ?- A Ce potentiel
vecteur n'est pas défini de manière unique. En effet
considérons un autre champ
?- -?A'
? ?+ ?-? ?ö
?-
= ?? ?-A
?- A' :
-?
B' =
(2.32)
Car le rotationnel du gradient d'un champ vectoriel est
égal à zéro. Nous voyons donc que
- ?A' et -?A'=
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
= ?- B
les deux potentiels vecteurs
?- A+ ?- ?ö qui ne diffèrent que par ?- ?ö
conduisent
?-
au même champ magnétostatique B . On dit que le
potentiel vecteur est défini à un gradient
?-
près. Pour définir A de manière unique, il
faut imposer une condition supplémentaire à ?-A. Cette
condition est appelée condition de jauge. La plus utilisée en
magnétostatique est la
?- ?.-? A = 0 ; En remplaçant ?- B par ?- B = ?- ? ?
?-
condition de jauge de Coulomb qui s'écrit : A
?- Adans le théorème d'Ampère :
?- ?? ?- B = u0-?j (2.33)
Et en tenant compte de la jauge de Coulomb
?-?.-?A = 0 on obtient :
?- -? ? ? ?- = u0-?
? ? A j
?- -? ?.-? - ?2-? A = u0-?
? A j .
-?2-? A = u0-? j
Ce résultat constitue l'équation de Poisson pour le
potentiel vecteur :
?2-?A = -u0-? j (2.34)
|
?-
En absence de courants, on obtient l'équation de Laplace
pour A : ?2
|
-? A= -u0
|
-? j Pour
|
?-
trouver une solution à l'équation de Poisson pour
A, nous procéderons par analogie avec la
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 34
solution obtenue dans le cas de l'électrostatique pour
le potentiel électrostatique. L'équation de Poisson pour le
potentiel électrostatique U :
|
?2-?U = - ñ
å0
|
admet comme solution :
|
|
|
ZZZU(M) =
|
ñ(p) dv (2.35)
4ðå0 k --?
P M k
|
?-
De même, l'équation vectorielle pour A, peut
s'écrire comme un ensemble de trois équations
?-
aux dérivées partielles pour chacune des
composantes Ax, Ay et Az de A :
|
?
??
??
|
?2Ax = -ujx
?2Ay = -ujy ?2Az =
-ujz
|
(2.36)
|
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
Chacune de ces équations scalaires admet, par analogie
avec la solution pour le potentiel scalaire, une solution sous la forme :
|
?
????
????
|
Ax(M) = fff u0jx(p)
4ðk--? P Mkdv
Ay(M) = fff u0jy(p)
4ðk--? P Mkdv
Az(M) = fff u0jz(p)
4ðk--? P Mkdv
|
(2.37)
|
_ u0 ( )
?-A(M) -fff4 PM
7r
~
-? jp
Ce qui peut s'écrit sous une forme vectorielle qui
constitue la loi de Biot-Savart pour le potentiel vecteur :
dv (2.38)
Dans un système de coordonnées cartésiennes,
la loi de Biot-Savart s'écrit :
1(x z) = u0j (xp, yp, zp) dv
(2.39)
y' ,fff /
4ðy (x -
xp)2 + (y - yp)2 + (z -
zp)2
?-
Cette expression permet de calculer le potentiel vecteur A au
point M (x, y, z) créé par une distribution de courants
électriques dans un volume (v) qui est découpé en
éléments de volumes dv localisés aux points où les
courants sont définis localement par le vecteur
|
?-
densité de courant j (xp, yp,
zp). Le champ magnétique
?- B = ?- ? ? ?-
potentiel vecteur par : A
|
?- Bpeut être obtenu à partir du
|
=? ?.111 // u0 j (xp, yp,
zp) dv (2.40)
4ð 1/(x - xp)2 + (y -
yp)2 + (z - zp)2
Le rotationnel étant calculé autour du point M,
les opérations de dérivation se font par rapport aux
coordonnées x, y et z. Comme l'intégration se fait par rapport
aux coordonnées
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 35
xp, yp et zp nous pouvons
écrire :
=
fff?u0j (xp, yp, zp)
dv (2.41)
47r\/(x -- xp)2 + (y _
yp)2 + (z _
zp)2
7r1//(x--x7,)2+(y-yy)2+(z-zz)2
?- u + f-?
Rappelons que : ? ? (f-? u ) = ?- ?f ? ?- ? ? ?- u
d'où
|
(?- ? ?
|
?-
v(x-xp)2+(y-yp)2+(z-zp)2 j
(xp,yp,zp)
|
1 ((x--xp)2#177;(y--yp)2#177;(z_zp)2) ?
?-(p)
?- j (p)
= ?- ?
(2.42)
1
+ v(x-xp)2+(y-yp)2+(z-zp)2
?- ? ?
or
-? ?
(x-xp)2+(y-yp)2+(z-zp)2)
1 P M
k--?
=-PMk3
et comme on calcule le rotationnel en dérivant par rapport
à x, y et z et que ne dépend que
de ?- j (P) :
?- ? ? ?-j (P) = ?-0 (2.43)
?-
On obtient la loi de Biot-Savart pour le champ magnétique
B :
4ð fff
~ ~ --? ~ ~ PM
?- j (p) ?--?
P M
3 dv (2.44)
Dans le cas particulier d'un circuit filiforme parcouru par un
courant I, le volume élémentaire s'écrit : d3v
= d2S.dl où d2S est un élément de
surface situé en un point M et dl un élément de longueur
du fil ; en considérant que le point M est situé à une
distance du fil supposé très mince, ainsi on écrit :
|
u0I
Bz(0,0,z) = 4ð
|
2ð
f
0
|
b2dè
|
|
[(bcosè)2 + (bsinè)2
+ z213/2
|
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
u0I =
|
4ð
|
b22ð
|
(2.45)
|
|
(b2 + z2)3/2
|
u0I b2
Bz(0 0 z) = 2 (b2 + z2)3/2
?-
Cette expression constitue la loi de Biot-Savart pour le champ
magnétique B
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 36
2.4.3.2 Champ magnétique B~ pour une antenne boucle
circulaire
?-
Une forme analytique de B (en fonction des paramètres
géométriques de l'antenne)
est relativement simple à obtenir si on se limite
à des profils simples, comme sur l'axe de symétrie par exemple.
Pour l'intégration de Biot-savart, l'épaisseur du conducteur
électrique n'a pas été considérée et un
modèle linéique a été utilisé, bien qu'une
approche volumique soit possible. Le dipôle magnétique est
constitué d'une boucle circulaire de courant dont le nom plus usuelle
est antenne boucle. C'est une antenne de surface; dont on s'intéresse
à exprimer son champ magnétique. Considérons une boucle de
rayon b parcouru par un courant I (fig. 2.11).

FIGURE 2.11 - géométrie de la boucle
circulaire [25]
La loi de Biot-savart pour cette antenne s'écrit :
|
I
?- B (r) = uoI
4ð C
|
?- dl ? ?- R (2.46)
R3
|
Les composantes du segment infinitésimal le long du
conducteur sont données par :
?- dl = (dx, dy, dz) = b(-sinè, cosè, 0) (2.47)
?-
Et les coordonnées du vecteur R sont :
?- R = (x - bcosè,y - bsinè,z) (2.48)
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 37
Où e est l'angle est l'angle de balayage de
l'anneau circulaire. En utilisant l'équation (Biot-savart), les trois
composantes du champ magnétique peuvent être calculées
comme suite :
|
u0I
Bx(x,y,z) = 47r
|
27r
0
|
bz cos ede
3 (2.49)
[(x - bcose)2 + (y -
bsine)2 + z2] 2
|
|
u0I
By(x,y,z) = 47r
|
27r
0
|
bz sin ede
3 (2.50)
[(x - bcose)2 + (y -
bsine)2 + z2] 2
|
(b2 - by sin e - bx cos
e)de
[(x - bcose)2 + (y -
bsine)2 + z2]3
2
(2.51)
Bz(x,y,z) = 47r
u0I
27r
0
2.4.3.2.1 Méthode analytique de calcul du champ pour
une antenne le long de l'axe oz
Pour une boucle circulaire de rayon b parcouru par un courant
permanent I, le champ magnétique le long de l'axe z ne contient que les
composantes z et peut être calculé comme suit :
|
u0I
Bz(0,0,z) = 47r
|
27r
0
|
b2de
|
u0I =
47r
|
b227r
|
|
|
[(bcose)2 + (bsine)2 + z2]3/2
|
(b2 + z2)3/2
|
(2.52)
|
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
b2
Bz(0,0,z) = u0I 2 (b2 + z2)3/2
Ce champ par unité de courant n'est autre que
l'expression analytique de la sensibilité d'une simple boucle circulaire
de rayon b, le long de l'axe (oz) de l'antenne :
Bz = u0
I 2
b2
(2.53)
(b2 + z2)3/2
2.4.3.2.2 Méthode d'intégration
numériquement du champ : Gauss-Legendre
Quand il est impossible de déterminer analytiquement la
primitive d'une équation, ou qu'il n'est pas possible de ramener le
calcul d'une intégrale à une autre dont on connaît une
solution, la façon d'obtenir un résultat est de procéder
à une intégration numérique. La méthode de Gauss
est celle qui permet d'avoir une formule exacte pour les polynômes de
plus haut degré en choisissant au mieux à la fois les points
d'évaluation de la fonction et les coefficients correspondants. On peut
ainsi obtenir des valeurs approchées acceptables avec un nombre de
points assez réduit, pourvu que la fonction à intégrer ne
présente pas de trop grandes variations. L'intégration des
équations (2.49), (2.50), (2.51) de Biot et savart par la méthode
de Gauss-Legendre, En ce qui concerne la méthode de Gauss, on
développe B(e) dans une base de polynômes orthogonaux
dont les ei sont les racines de ces polynômes, qui sont alors
irrégulièrement espacés. Ces polynômes sont
définis sur l'intervalle [-1,1]. Dans
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 38
ce cas, il faut faire un changement de variable sur 0
qui permet de transformer 0 E [01, 02]
en î E [-1, 1] ; c'est à dire :
|
On obtient donc :
|
02 + 01
0 = +
2
|
02 - 01? (2.54)
2
|
B(0) d0 = (02 -01) Xn
2
wk.B(0k) (2.55)
Zè2
è1
k=1
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
Où wk et ?k sont tabulés.
Ainsi, l'intégrale de B(0), peut être
évaluée en suivant la procédure :
on choisit la valeur n qui donne le nombre de points où
la fonction doit être évaluée,
on lit dans la table donnant wk et ?k les n valeurs
de ?k qui sont deux à deux symétriques par rapport
à zéro (qui sont les racines du polynôme de Legendre
d'ordre n) qui correspondent à la valeur de n choisie,
on calcule 0k par l'équation (2.54), ensuite
on évalue l'intégrale de B(0) (expression (2.55)).
Le principe de cette méthode est simple :
· On subdivise l'intervalle [01, 02]
en n sous-intervalles de longueur égale
02 - 01
h = n
délimités par les points de subdivisions 0i =
01 + ih, i = 0, ...n.!
· La méthode de Gauss-Legendre de rang k consiste,
sur chaque sous-intervalle
|
(2.56)
|
[0i, 0i+1] , i = 0, ...n - 1,
à remplacer B par son polynôme d'interpolation de
degré k passant par les points d'abscisses rkj, j = 0,...k, les
rkj étant les racines du polynôme de Legendre
de degré k + 1, noté Pk+1(0) :
P0(0) = 1, P1(0) = 0 Puis
kPk(0) = (2k - 1)0Pk-1(0) - (k
- 1)Pk-2(0) avec k = 2, 3, ... (2.57)
2.4.4 Quelques méthodes numériques de
conceptions d'antennes
Pour estimer le champ magnétique de la bobine RF (non
chargé ou chargé) avec le modèle du corps exposé et
de fournir une solution numérique aux équations de Maxwell avec
conditions aux limites spécifiques, des méthodes
numériques sont utilisées. Le développement moderne de
bobine de résonance magnétique exploite des méthodes
numériques telles que : la méthode des moments (MoM),
méthode des éléments finis (FEM), et la méthode des
différences finies dans le domaine temporel (FDTD). Ces méthodes
sont adéquates pour des bobines de forme plus complexe. Vue la
complexité et la difficulté de leur implémentation,
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE
ANTENNE
SIMPLE BOUCLE CIRCULAIRE 39
il a été choisi de mettre en place une
méthode de conception simple basée principalement sur la loi de
Biot-Savart [35]. Où nous avons utilisé la Méthode de
Gauss-Legendre pour discrétiser son équation.
2.4.4.1 Méthode des éléments finis
(FEM)
La méthode des éléments finis [36] est
une approche par équation différentielle basée sur la
discrétisation des éléments de maillage. La FEM est
largement utilisé en ingénierie et applications scientifiques en
raison de son excellente capacité de modélisation
géométrique. Cependant, la matrice dimension de l'équation
peut être très grande, en particulier lors-qu'elle est
utilisée pour une bobine RF chargée avec un modèle humain
précis; donc le FEM n'est pas la méthode la plus utilisée
pour les applications IRM. Cependant, la FEM a été
utilisée dans la littérature pour modéliser les bobines RF
et les interactions entre les champs RF et le corps humain en IRM [37].
Premièrement, le modèle géométrique du
problème réel doit être planifié dans une conception
assistée par ordinateur, alors l'équation différentielle
des systèmes partielles et les conditions aux limites doivent être
déterminées. Enfin, les propriétés des
matériaux et le signal d'excitation doit être
spécifié. La géométrie doit être
discrétisée par un maillage FEM en utilisant triangles ou
quadrangles dans un dessin à 2 dimensions et des
tétraèdres ou des hexaèdres dans une conception 3D. Dans
les simulations FEM, il est possible d'incorporer des éléments de
circuit, tels que des résistances, des inductances et condensateurs,
dans le modèle de bobine RF.
2.4.4.2 Méthode des moments (MoM)
MoM est une méthode basée sur la
résolution des équations intégrales dans le domaine
fréquentiel. Pour calculer la solution sur une bande de
fréquence, les calculs doivent être répétés
à chaque fréquence. Le problème
électromagnétique est réduit à la solution d'un
système d'équations linéaires. MOM est très
efficace pour traiter des problèmes avec des sources parfaitement
conductrices (par exemple les bobines RF) et des milieux homogènes. Le
principal avantage du MoM est que la bobine et l'échantillon doivent
être discrétisé. Néanmoins, les besoins en
mémoire échelle proportionnellement à la taille du
problème et à la fréquence requise, donc pour des
problèmes d'IRM réalistes la charge de calcul peut être
considérablement élevée. En conséquence, une bobine
non chargée peut être analysée avec haute précision
et efficacité [38]. Un autre avantage dans la MOM, est que la
discrétisation des fils est divisée en segments et les surfaces
sont divisées en petites pièces triangulaires. La dimension
maximale de ces éléments est choisie pour être une petite
fraction, typiquement 1/10, d'une longueur d'onde à la plus haute
fréquence à simuler. Les courants sur ces les
éléments sont ensuite décomposés en une combinaison
linéaire de fonctions de base. Après avoir effectué des
tests pour chaque fonction de base, les équations intégrales sont
finalement
2.5. CONCLUSION 40
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
transformées en une matrice d'équations :
[Z][I] = [V ] (2.58)
où [Z] est la matrice d'impédance pouvant
incorporer des termes représentant des éléments
localisés tels que le condensateurs dans la bobine de cage à
oiseaux, [I] est le vecteur de courant à déterminer et [V] est le
vecteur de tension, y compris la source d'excitation. Pour alléger les
calculs fastidieux dans les problèmes de bobines RF chargées,
certains travaux récents proposés utilisant des techniques
hybrides connues sous le nom de MoM / Méthodes FDTD ou MoM / FEM. Dans
ces approches, MoM est utilisé avec FEM ou FDTD pour exploiter sa force
pour modéliser une bobine RF et FDTD ou FEM pour calculer le champ
à l'intérieur d'un objet diélectrique compliqué
[39].
2.4.4.3 Méthodes des différences finies dans
le Domaine temporel (FDTD)
La méthode des différences finies dans le
domaine temporel (FDTD) résout les équations de Maxwell en
utilisant une discrétisation aux différences finies centrales des
dérivés temporel et spatial (les détails seront
expliqués plus loin dans le paragraphe). Cette méthode est
très simple en termes conceptuels et est également simple
à mettre en oeuvre. L'algorithme, introduit pour la première fois
en 1966 par Kane Yee [40], exprime les équations de Maxwell dans le
domaine temporel avec une discrétisation spatiale et temporelle, qui est
suivie par des réarrangements appropriés, il permet d'exprimer la
valeur des champs à l'étape d'échantillonnage n + 1 en
fonction de la valeur du champ à l'étape d'échantillonnage
n. itérer cette procédure jusqu'au temps d'observation
souhaité, nous obtenons la tendance temporelle de champs au point en
question. La résolution du problème dans le domaine temporel
plutôt que dans le domaine fréquentiel, il permet de
résoudre en une seule exécution du programme également des
problèmes caractérisés par une large bande de
fréquence. En outre, la discrétisation d'un volume entier
d'intérêt permet, comme dans le cas de la méthode FEM,
l'introduction au problème des charges biologiques. Donc La
méthode FDTD est considérée comme la meilleure
méthode pour les simulations électromagnétiques et la plus
efficace.
2.5 Conclusion
Dans ce chapitre nous avons reconsidéré
l'équation électromagnétique de Biot et Savart. En
transformant cette équation, nous avons montré que le
paramètre le plus important de cette équation était la
forme du circuit de la bobine. Nous avons passé en revue les
différents types de bobines et donc les différents types de
champs magnétiques générés. Il existe encore
d'autres types de bobines, mais elles restent peu décrites et nous ne
les avons pas étudiées. Nous avons par la suite
considéré plusieurs méthodes numériques de calcul
de champ électromagnétique (FEM, MoM et FDTD) et retenu une
technique à base d'ap-
2.5. CONCLUSION 41
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
proximation polynomiale (utilisant des polynômes de
Gauss-Legendre). Enfin nous avons donc cherché à simuler : le
comportement du champ sur l'axe (oz) et un exemple d'an-tenne simple boucle
circulaire sous le logiciel Matlab. Le chapitre suivant va présenter la
conception d'une antenne intégrant tous ces aspects.
CHAPITRE III
RÉSULTATS DE SIMULATIONS ET
DISCUSSIONS
42
3.1 Introduction
L'analyse théorique impliquée dans la conception
de quelques types d'antennes, est devenue très complexe, et dans
beaucoup de cas une solution exacte est impossible. Des logiciels de
simulations ont donc facilité l'analyse des problèmes et la
conception des structures de plus en plus complexes. Dans ce chapitre, nous
décrivons l'environnement de simulation que nous avons utilisé,
nous présentons également les résultats de simulation de
notre antenne qui sont évalués par la simulation du champ
magnétique B dans le plan (sensibilité) et dans l'espace. Ces
simulations sont réalisées avec le logiciel MATLAB version R2018b
(9.5.0.944444) installé dans un ordinateur personnel de
caractéristiques 64 bits, 3 GB de RAM, 2.16 GHz.
3.2 Présentation de l'outil de simulation :
logiciel Mat-lab
MATLAB signifie Matrix laboratory. C'est un logiciel
distribué par la société Math-Works qui fournit
principalement des moteurs de calcul numériques, et une interface de
programmation simple. Il est distribué avec un grand nombre d'options,
appelées Toolbox. Sans option, MATLAB n'est pas capable de proposer des
résultats de calcul formel, et permet principalement de résoudre
des problèmes matriciels, c'est à dire linéaires (fig
3.1).
3.3. RÉSULTATS DE SIMULATIONS 43
FIGURE 3.1 - interface MATLAB
3.3 Résultats de simulations 3.3.1 Approche analytique
Pour la bobine de surface boucle circulaire, le champ
magnétique par unité de courant B/I (sensibilité) a
été calculé analytiquement (eq 2.55) à la
fréquence de 64 MHz le long de l'axe (oz), de part et d'autre du maximum
en z=0 qui correspond au centre de la bobine. La figure 3.2 montre le
tracé (le long de l'axe des z) du profil champ magnétique par
unité de courant (sensibilité) en fonction de la profondeur
variant de 0 à 50 mm pour une Boucle circulaire de 20 cm de
diamètre. En règle générale, pour avoir un bon SNR
dans la ROI, le rayon de l'antenne doit correspondre à peu près
à la profondeur d'un échantillon à l'étude.
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
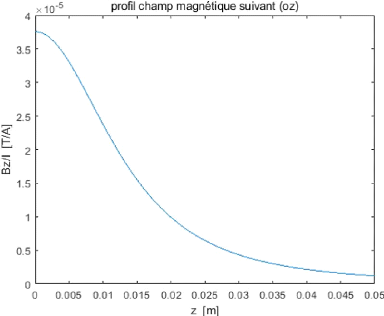
3.3. RÉSULTATS DE SIMULATIONS 44
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
FIGURE 3.2 - Profil champ magnétique par unité
de courant en fonction de la profondeur z pour la boucle circulaire
La rapide décroissance en z est caractéristique
de cette antenne qui présente une forte sensibilité mais à
une distance réduite, à l'inverse des antennes volumiques comme
ceux à base de solénoïde. L'allure des sensibilités
des géométries circulaire et carrée sont relativement
similaires.
3.3.2 Approche numérique
Pour obtenir la variation spatiale du champ magnétique
sur des profils moins élémentaires tels que des plans ou
même un volume, une formulation analytique simple n'est plus possible.
Une intégration numérique de Biot-savart est donc
nécessaire. Le résultat du calcul numérique sur MATLAB
concernant le champ magnétique dans le plan (xoy) pour l'an-tenne de
surface à boucle circulaire est illustré à la figure 3.3;
Le champ magnétique B généré pendant la phase de
transmission pour la même antenne a également été
calculé à la fréquence de 64 MHz dans un plan orthogonal
au plan de la bobine traversant son centre. Le profil de champ
magnétique extrapolé à partir de l'antenne et sa
représentation dans le plan (2D) sont représentés sur les
figures suivantes :
3.3. RÉSULTATS DE SIMULATIONS 45
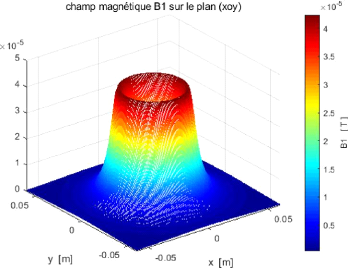
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
FIGURE 3.3 - Profil du champ magnétique B pour une
antenne de surface simple boucle circulaire

FIGURE 3.4 - représentation dans le plan (2D) du champ
magnétique
3.4. DISCUSSION 46
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
Comme on pouvait s'y attendre, le champ est très
homogène près du plan de stock de la bobine et son amplitude
décroît rapidement au fur et à mesure qu'il
s'éloigne de ce plan. Cela est très évident si on observe
la ligne de profil suivant l'axe oz passant par le centre de la bobine comme
vue à la figure 3.2.
La figure 3.3 est le tracée du champ magnétique
en tout point de l'espace; plus on s'éloigne du centre de la bobine,
plus le champ magnétique devient intense en surface; cela est visible
par des couleurs allant de la bleu (au centre) jusqu'à la rouge (en
surface). La bobine transporte des courants électriques dans la
même direction pour améliorer la sensibilité du champ au
centre de l'antenne; le champ magnétique auquel on associe une pulsation
très homogène et non nul au centre l'antenne.
L'amélioration de la sensibilité permet alors d'obtenir un RSB
beaucoup plus élevé à la surface de l'échantillon
grâce à un meilleur couplage magnétique local et un
filtrage spatial du bruit provenant de l'échantillon.
La figure 3.4 est la représentation dans le plan (2D)
du champ magnétique le long d'un cylindre avec un courant I
distribué à la surface du cylindre.
Le tableau 3.1 indique les paramètres de boucle
évalués à une fréquence de 64 MHz pour une boucle
circulaire dont les dimensions satisfont au rayon de la boucle 20 cm. Cette
fréquence correspond à la fréquence du proton dans un
scanner IRM de 1,5 T. La résistance de la bobine a été
calculée avec équation (2.18) pour la boucle circulaire en
considérant un rayon de fil de 2 mm pour cette boucle, tandis que la
résistance induite dans l'échantillon a été
estimée en utilisant l'équation (2.21). Les dimensions de cette
antenne ont été calculées pour avoir un champ
électromagnétique uniforme.
TABLE 3.1 - Estimation des paramètres
à 64 MHz
|
bobine
|
Rbobine(mÙ)
|
Rchantillon(mÙ)
|
L(mH)
|
r
|
|
diamètre de la boucle circulaire 20 cm
|
53.9
|
51.01
|
52.5
|
1.95
|
3.4 Discussion
Le calcul du champ magnétique décrit dans cet
article est basé sur l'équation de Biot-Savart. Cette
théorie peut être employée pour l'analyse et la conception
de bobines dont la taille est une petite fraction de longueur d'onde. Par
exemple à 64 MHz, la longueur d'onde associée est de 4,7 m et
l'hypothèse quasi statique est valable pour toutes les dimensions de la
bobine. En augmentant l'intensité du champ magnétique,
l'approximation est la même que lorsque la dimension de l'antenne
diminue. La géométrie circulaire est la conception la plus simple
pour une bobine à surface unique. Cependant, une bobine
constituée par une boucle de géométrie différente
pourrait être nécessaire lorsque des champs de vision (FOV) sont
souhaités. En particulier, les formes rectangulaires et elliptiques
pourraient être préférées lorsqu'une zone doit
être imagée, mais à condition de faire intervenir la
profondeur
3.4. DISCUSSION 47
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
de pénétration. Dans les cas où la bobine
et l'échantillon ont des formes géométriques
différentes, les antennes de surfaces sont incurvées autour des
anatomies, la littérature propose l'application des méthodes
numériques pour la conception et la simulation des antennes, qui
tiennent compte du rendement de l'antenne, même à fort champs
magnétiques.
48
Conclusion Générale et Perspectives
L'objectif de notre travail était de concevoir une
antenne radiofréquence pour l'IRM. Les antennes RF sont des composants
clés dans les systèmes à résonance
magnétique qui devraient être capable de supporter un champ de
vision avec une forte homogénéité du champ
magnétique pendant la transmission et atteindre un Rapport signal sur
bruit élevé lors de la réception Afin d'obtenir des images
de haute qualité. Nous avons choisi d'étudier une antenne de
surface à boucle circulaire de 20 cm de diamètre pour un
système IRM de 1.5 T. Partant des principes théoriques des
antennes RF, nous avons décrit les paramètres de performance des
antennes, leurs techniques d'estimations dans la phase de développement.
Nous nous sommes basés sur les techniques magnétostatiques
où nous utilisons la méthode de Gauss-Legendre pour
intégrer le champ magnétique B de l'équation de
Biot-Savart. Ce champ est ensuite simulé dans un espace tridimensionnel
(3D) nous renseignant sur son homogénéité; le champ par
unité de courant est également simulé sur l'axe (oz) et
nous renseigne sur la sensibilité de l'antenne. Cette approche
utilisée reste valable pour les champs magnétiques statiques de
faible intensité (inférieur à 3 T) ou avec de très
petites bobines telles que celles utilisées dans les études
animales. Nous avons également introduit les méthodes
numériques (MoM, FEM et FDTD) et montré comment elles peuvent
être utilisées pour simuler les performances de l'antenne à
un niveau de champ supérieur. Ces méthodes offrent la
possibilité d'évaluer et optimiser les conceptions des antennes
RF complexes. Compte tenu des difficultés techniques liées
à l'utilisation de très hauts champs (3 Teslas et plus), la
qualité des antennes reste toujours un élément majeur
à développer afin d'améliorer la qualité des
examens en IRM. Ce mémoire nous a permis d'acquérir des bases
solides sur la conception d'antenne RF en imagerie médical permettant
une bonne résolution de l'image, à la lumière des
technologies et des outils de conception actuels. En ce qui concerne les
développements futurs, les résultats étant prometteurs,
Bien que le champ généré à partir d'une antenne
simple boucle soit très homogène. Il serait donc
intéressant d'envisager des conceptions différentes, en utilisant
par exemple des méthodes numériques pour la conception des
antennes multi-éléments (réseaux d'antennes) introduit
dans des systèmes avec plusieurs canaux de réceptions pour tirer
parti de l'amélioration de la sensibilité.
49
Bibliographie
[1] CE.Hayes et al, An efficient, highly homogeneous
radiofrequency coil for whole-body NMR imaging at 1.5 T, Magn Reson.,
1985,
[2] H.Tsuboi, T.Misaki, H.Tanaka and M.Fujita,
Electromagnetic field analysis of RF antenna for MRI, IEEE transaction
on magnetics, 1988.
[3] D.M.Ginsberg and M.J.Melchner, optimum geometry of
saddle shaped coil for generating a uniform magnetic field, The Review of
Scientific Instruments, pp 122-123, 1970.
[4] M.fujita et al, design of the RF antenna for MRI,
IEEE transaction on magnetics, 1990.
[5] S.Li, MB.Smith, QX.Yang, RF coil optimization
evaluation of B1 field homogeneity using field histograms and finite element
calculations, Magn Reson Imaging, 1994.
[6] C.Guclu, Hacinliyan.a, Nalcioglu.O, Kashmar.G, An FEM
approach for the characterization of the RF field homogeneity at high field,
Magn Reson Med, pp 76-83, 1997.
[7] Ibrahim TS, Baertlein, BA Robitaille, Lee R, B1 field
homogeneity and SAR calculations for the birdcage coil, Phys Med Biol,
2001.
[8] G. Giovannetti et al, A fast and accurate simulator
for the design of birdcage coils in MRI, Magnetic Resonance Materials in
Physics, Biology and Medicine, pp 36-44, 2002.
[9] PML Ibrahim, BA.Baertlein, Y.Robitaille R.Lee,
Computational analysis of the high pass birdcage resonator finite
difference time domain simulations for high-field MRI, Magn. Reson.
Imaging, 2000.
[10] Giovannetti G, Landini, Santarelli, Positano, Benassi A,
Francesconi R, Conductor geometry and capacitor quality for performance
optimization of low-frequency birdcage coils, Concepts Magn Reson Part B
Magn Reson Eng., 2004.
[11] Rogovich A, Nepa P Manara G Giovannetti G Landini L,
Monorchio A. Design of magnetic resonance imaging (MRI) RF coils by using
the method of moments, IEEE Antennas and Propagation Society Symposium,
2004.
[12] G. Giovannetti, M.F. Santarelli V. Positano, L. Landini,
A fast and accurate simulator for the design of birdcage coils in MRI,
Magnetic Resonance Materials in Physics, Biology and Medicine, 2002.
[13]
BIBLIOGRAPHIE 50
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
Leifer et al, Resonance modes of the birdcage coil,
J. Magn. Reson., 1997.
[14] lemdiasov et al, A stream function method for
gradient coil design, Concept. Magn. Reson. B, 2005.
[15] Kumar et Bottomley, optimized quadrature surface
coil designs, resonance materials in physics, biology and medicine,
2008.
[16] Li BK, Crozier S, Liu F. High-field magnetic
resonance imaging with reduced field/tissue RF artefacts-A modeling study using
hybrid MoM/FEM and FDTD technique, IEEE Trans Electromagn Compat, pp
28-33, 2006.
[17] D. Doty et al, Radio frequency coil technology for
small-animal MRI, NMR Biomed, pp 304-325, 2007.
[18] Solis S, Wang R Tomasi D Rodriguez A , Cuellar G,
Transceiver 4-leg birdcage for high field MRI : knee imaging, Rev Mex
Física., pp 15-20, 2008.
[19] Vojtisek L, Valkovic L , Frollo I. Phased array
receiving coils for low field lungs MRI : design and optimization, Meas
Sci Rev, 2011.
[20] Mikhail Kozlov et al, Fast MRI coil analysis based
on 3-D electromagnetic and RF circuit co-simulation, Journal of Magnetic
Resonance, pp 147-152, 2009.
[21] G.Shou et al, MRI Coil Design Using Boundary-Element
Method With Regularization Technique : A Numerical Calculation Study, IEEE
transaction, 2010.
[22] Ye LI et al, ICE decoupling technique for RF coil
array designs, Med. Phys, 2011.
[23] Lingzhi et al, A Generalized Strategy for Designing
19F/1H Dual-Frequency MRI Coil for Small Animal Imaging at 4.7 Tesla,
JOURNAL OF MAGNETIC RESONANCE IMAGING, pp 245-252, 2011.
[24] M. Sohn et al, RF Head Coil Design With Improved RF
Magnetic Near-Fields Uniformity for Magnetic Resonance Imaging (MRI) Systems,
Med. Phys, 2011.
[25] Giulio Giovannetti et al, Radiofrequency Coils for
Magnetic Resonance Applications : Theory, Design, and Evaluation, Critical
Reviews in Biomedical Engineering, pp 109-135, 2014.
[26] Giulio Giovannetti et al, Comparison between
circular and square loops for
low-frequency magnetic resonance applications
: theoretical performance estimation, Concepts Magn Reson Part B, 2016.
[27] Nan Li et al, Electromagnetic Field and Radio
Frequency Circuit Co-Simulation for Magnetic Resonance Imaging Dual-Tuned Radio
Frequency Coils, IEEE transaction on Magnetics, 2017.
[28] G Giovannetti G tiberi, Radiofrequency magnetic
resonance coils and communication antennas : Simulation and design strategies,
Magnetic Resonance Imaging, pp 1-7, 2017.
[29]
BIBLIOGRAPHIE 51
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
C.stumpf et al, Radio Frequency Modeling of Receive Coil
Arrays for Magnetic Resonance Imaging, Magnetic Resonance Imaging, pp 67,
2018.
[30] D Pozar, Microwave Engineering, Wiley, 2004.
[31] C.E.Roemer, Souza, P. Mueller, Hayes, Edelstein, The
NMR phased array, Magn. Reson. Med., pp 192-225, 1990.
[32] Vaughan JT, Griffiths JR, RF coils for MRI,
Wiley, 2012.
[33] S.Lambert, Modélisation et
caractérisation d'antennes supraconductrices pour la micro IRM du
cerveau de souris à 4.7 T, PhD thesis, 2011.
[34] Haacke EM, Thompson MR Venkatesan R , Brown RW.
Magnetic resonance imaging: physical principles and sequence design,
Wiley-Liss, 1999.
[35] Nadeem.M, Gandhi.O Thorlin.T, and Persson,
Computation of electric and magnetic stimulation in human head using the
3-d impedance method, IEEE Transactions on Biomedical Engineering, pp
900-907, 2003.
[36] Jin JM, The finite element method in
electromagnetics, John Wiley and Sons, 1993.
[37] Li.S, Smith.MB, Yang QX, RF coil optimization:
evaluation of B1 field homogeneity using field histograms and finite element
calculations, Magn Reson Imaging, pp 79-87, 1994.
[38] Rogovich.A, Giovannetti.G, Landini L, Manara.G,
Monorchio.A, Design of magnetic resonance imaging (MRI) RF coils by using
the method of moments, IEEE Antennas and Propagation Society Symposium,
2004.
[39] Liu.F, Fitzsimmons.JR, Blackband.SJ, Crozier.S, Xu.B,
Beck.BL, Numerical modeling of 11.1 T MRI of a human head using a MoM/FDTD
method, Magn Reson Eng, pp 28-38, 2005.
[40] K.Yee, Numerical solution of initial boundary value
problems involving Maxwell's equations in isotropic media, IEEE
Transactions on antennas and propagation, pp 900-907, 1966.
[41] http ://
www.utc.fr/abih.
| 


