|
REPUBLIQUE DU BENIN
N
|
|
********
|
|
MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE LA
RECHERCHE SCIENTIFIQUE
(M.E.S.R.S.)
|
|
********
|
|
UNIVERSITE D'ABOMEY-CALAVI
(U.A.C.)
|
|
********
|
|
ECOLE NATIONALE D'ECONOMIE APPLIQUEE ET DE
MANAGEMENT
(E.N.E.A.M.)

****
|
|
|
Filière :Statistique
AppliquéeDiplôme :Master
INVESTISSEMENTS ET CROISSANCE ECONOMIQUE: Cas des
secteurs de l'énergie et de l'eau au Bénin
THEME

0
|
Réalisé et présenté
par :Mahougnon Raymonde M. C. HOUANGNI
|
|
Sous la supervision de :
|
|
Maître de stage :
|
Maître de Mémoire
|
|
Mr Aristide MEDENOU, en service à la
Direction Générale de l'Analyse Economique
|
Dr Barthélemy SENOU, enseignant à
l'Ecole Nationale d'Economie Appliquée et de Management
|
SOMMAIRE
SOMMAIRE
2
DEDICACE
3
REMERCIEMENTS
4
LISTE DES TABLEAUX
5
LISTE DES GRAPHIQUES
6
SIGLES ET ABREVIATIONS
7
RESUME
9
INTRODUCTION
10
CHAPITRE 1: CADRE THEORIQUE ET ANALYTIQUE DE
L'ETUDE
14
1. PROBLEMATIQUE, OBJECTIFS, HYPOTHESES ET REVUE DE
LITTERATURE
14
1.1. Problématique de
l'étude
14
1.2. Objectifs et hypothèses de
recherche
15
2. REVUE DE LITTERATURE ET METHODOLOGIE
16
2.1. Revue de
littérature
16
2.2. Méthodologie de l'étude
et Présentations des données
41
_Toc448995411
CHAPITRE 2: ANALYSE DESCRIPTIVE ET ECONOMETRIQUE
DES INVESTISSEMENTS PUBLICS DANS LES SECTEURS DE L'ENERGIE ET DE L'EAU, ET LA
CROISSANCE ECONOMIQUE AU BENIN
3
1. ANALYSE DESCRIPTIVE DES INVESTISSEMENTS DANS LES
SECTEURS DE L'ENERGIE ET DE L'EAU, ET LA CROISSANCE ECONOMIQUE AU BENIN
52
1.1. Analyse de l'évolution des
dépenses d'investissements publics dans les secteurs de l'énergie
et de l'eau par rapport au Secteur Productif
52
1.2. Analyse de l'évolution des
dépenses d'investissements publics dans les secteurs de l'énergie
et de l'eau par rapport aux dépenses d'investissements
nationales
53
2. ANALYSE ECONOMETRIQUE DES INVESTISSEMENTS DANS
LES SECTEURS DE L'ENERGIE ET DE L'EAU, ET LA CROISSANCE ECONOMIQUE AU BENIN
54
2.1. Analyse de causalité entre
investissement et croissance
54
2.2. Analyse économétrique
des investissements dans les secteurs de l'Energie et de l'eau, et croissance
économique
57
CONCLUSION
71
REFERENCES BIBLIOGRAPHIQUES
72
ANNEXES
76
TABLE DES MATIERES
103
DEDICACE
A celui qui est, qui était et qui vit
éternellement !
REMERCIEMENTS
J'adresse mes sincères remerciements :
- A mon Mari Albérick N. BOCOVO, qui m'a
encouragée à faire cette formation ;
- A Monsieur Aristide MEDENOU en service à la
Direction Générale de l'Analyse Economique ;
- Au Docteur Barthélemy SENOU, enseignant à
l'Ecole Nationale d'Economie Appliquée et de Management;
- A Monsieur François ANAGO, en service à
la Caisse Autonome d'Amortissement ;
- A tous ceux qui ont contribué à
l'avènement de ce jour.
LISTE
DES TABLEAUX
Tableau n°1 : Présentation des
variables
3
Tableau n°2 : Stationnarité des
variables
55
Tableau n°3 : Estimation du modèle
avec les dépenses d'investissements publics gouvernementales globales
(INVG)
58
Tableau n°4 : Estimation du modèle
avec les dépenses d'investissements publics dans le secteur de l'eau
(INVG_EAU)
61
Tableau n°5 : Estimation du modèle
avec les dépenses d'investissements publics dans le secteur de
l'énergie (INVG_ENERGIE)
63
LISTE
DES GRAPHIQUES
Graphique n°1 : Evolution des
dépenses d'investissements publics dans les secteurs de
l'énergie et de l'eau par rapport au Secteur Productif
3
Graphique n°2 : Evolution des
dépenses d'investissements publics dans les secteurs de
l'énergie et de l'eau par rapport aux dépenses d'investissements
nationales
53
SIGLES
ET ABREVIATIONS
|
ABERME
|
:
|
Agence Béninoise de l'Electrification Rurale et de la
Maîtrise d'Energie
|
|
ADF
|
:
|
Dickey-Fuller Augmenté
|
|
AIE
|
:
|
Agence Internationale de l'Energie
|
|
AR
|
:
|
AutoRegressive
|
|
BiPEN
|
:
|
Bilan et Perspectives à court et moyen termes de
l'EconomieNationale
|
|
BPO
|
:
|
Budget Programme par Objectifs
|
|
CEB
|
:
|
Communauté Electrique du Bénin
|
|
CEREG
|
:
|
Centre d'Etudes et de Recherche en Economie et Gestion
|
|
DG Eau
|
:
|
Direction Générale de l'Eau
|
|
DGAE
|
:
|
Direction générale de l'Analyse Economique
|
|
DPC
|
:
|
Direction de la Prévision et de la Conjoncture
|
|
DS
|
:
|
Differency Stationnary
|
|
FBCF
|
:
|
Formation Brute de Capital Fixe
|
|
HD
|
:
|
Harrod et Domar
|
|
INSAE
|
:
|
Institut National de la Statistique et de l'Analyse Economique
|
|
MCO
|
:
|
Moindres Carrés Ordinaires
|
|
MDAEP
|
:
|
Ministère du Développement de l'Analyse Economique
et de la Prospective
|
|
MDMCS
|
:
|
Méthode des Doubles Moindres Carrés en
Système
|
|
MEFPD
|
:
|
Ministère de l'Economie, des Finances et des Programmes de
Dénationalisation
|
|
MERPMEDER
|
:
|
Ministère de l'Energie, des Recherches
Pétrolières et Minières de l'Eau et du
Développement des Energies Renouvelables
|
|
MMG
|
:
|
Méthode des Moments Généralisés
|
|
MMG
|
:
|
Méthode des Moments Généralisés
|
|
OMD
|
:
|
Objectifs du Millénaire pour le Développement
|
|
OSD
|
:
|
Orientations Stratégiques de Développement
|
|
PIB
|
:
|
Produit Intérieur Brut
|
|
PNB
|
:
|
Produit National Brut
|
|
PTF
|
:
|
Partenaires Techniques et Financiers
|
|
RDC
|
:
|
République Démocratique du Congo
|
|
RNBD
|
:
|
Revenu National Brut Disponible
|
|
SBEE
|
:
|
Société Béninoise d'Energie Electrique
|
|
SCRP
|
:
|
Stratégie de Croissance pour la Réduction de la
Pauvreté
|
|
SONEB
|
:
|
Société Nationale des Eaux du Bénin
|
|
SS
|
:
|
Services Statistiques
|
|
SUR
|
:
|
Seemingly Unrelated Regression
|
|
TS
|
:
|
Trend Stationnary
|
|
UEMOA
|
:
|
Union Economique et Monétaire Ouest Afraicain
|
|
USA
|
:
|
United States of America
|
|
USD
|
:
|
United States Dollar
|
|
VAR
|
:
|
Vector AutoRegressive
|
RESUME
Les secteurs de l'énergie et de l'eau sont deux
secteurs très importants pour la prospérité d'une nation.
Le secteur de l'énergie, parce qu'il propulse la production des
institutions, entreprises et ménages. Quant au secteur de l'eau, il
contribue à la bonne santé du capital humain pour
développement économique, participe au développement des
entreprises agricoles, pastorales et alimentaires. C'est dans ce contexte que
nous avons étudié le thème :
« Investissements et la croissance économique :
cas des secteurs de l'énergie et de l'eau au Bénin ».
Cette étude analyse l'effet de l'investissement en
énergie et en eau sur la croissance économique au Bénin,
à l'aide d'un modèle économétrique par la
méthode des moments généralisés. Il en ressort
que : les investissements dans les secteurs Energie et Eau favorisent la
croissance économique.
A cet effet, il est important que le gouvernement mette en
place des dispositifs nécessaires afin attirer les investissements dans
les secteurs de l'Energie et de l'Eau.
INTRODUCTION
L'investissement est l'emploi de capitaux visant à
accroître la production d'une institution ou à améliorer sa
rentabilité. Selon François Perroux, la croissance
économique correspond à « l'augmentation soutenue
pendant une ou plusieurs périodes longues du produit global net en
termes réels » (F. Perroux, La pensée
économique de Joseph Schumpeter)1(*). De même, Pierre Maillet ; identifie
plusieurs types de déterminants à la croissance : les
richesses naturelles, l'environnement extérieur, la population,
l'innovation, l'investissement, la connaissance, la cohérence du
développement(Pierre Maillet, La croissance
économique)2(*).
Les théories de la croissance endogène ont
revalorisé le rôle de l'Etat dans les secteurs de la santé,
de l'éducation et des infrastructures. Etant donné qu'elles
produisent des externalités positives , et qu'elles remplissent au moins
partiellement les caractéristiques de non exclusion et de non
rivalité, les infrastructures publiques (routes, chemins de fer, ports,
aéroports, barrages hydroélectriques, centrales thermiques,
télécommunications etc.) sont considérées comme des
biens publics dont le financement ne peut être assuré de
manière optimale par des agents privés individuels. Elles
constituent donc le secteur par excellence de l'intervention de l'Etat dans
l'économie, et les dépenses publiques qui y sont engagées
sont généralement classées au rang des dépenses
productives (Barro, 1991)3(*).
A la suite de la Conférence nationale des forces vives
de février 1990, le Bénin a renoué avec la
démocratie et le libéralisme économique. Depuis lors, les
indicateurs macroéconomiques demeurent instables. En effet, le taux de
croissance économique s'est établi en moyenne à 4,7% sur
la période 1991-2002 puis à 3,4% en moyenne sur la période
2003-2005. Il est remonté à 3,8% en 2006 et à 5% en 2008,
et se situe au-delà de 5% depuis 2012, 5,6% en 2013, 5,4% en
2014 et 5,6% en 2015 (DGAE 2016).
En raison de la dynamique démographique importante, ce
rythme de la croissance économique est encore insuffisant pour
améliorer le bien-être des populations béninoises et faire
reculer les frontières de la pauvreté. En conséquence,
l'accélération de la croissance économique
nécessite une impulsion significative du taux d'investissement aussi
bien privé que public.
Le secteur de l'énergie est un des secteurs clé
du développement. Au Bénin, il est constitué à
59,4% de la biomasse énergie (bois de feu et charbon de bois), à
38,4% des produits pétroliers et à 2,2% de l'énergie
électrique (en 2006). 80% de l'énergie électrique et 100%
des hydrocarbures utilisés au Bénin proviennent de
l'extérieur (en 2006). Cette forte dépendance extérieure
est à la base des différentes crises énergétiques
de 1984, 1994, 1998, 2006- 2007(BiPEN, 2007).
Actuellement, l'énergie électrique
consommée est importée et transportée par la
Communauté Electrique du Bénin (CEB), pendant que sa distribution
est assurée par la Société Béninoise d'Energie
Electrique (SBEE). Par ailleurs, l'Agence Béninoise de l'Electrification
Rurale et de la Maîtrise d'Energie (ABERME) s'occupe du raccordement des
zones rurales au réseau conventionnel de la SBEE et de la maitrise de
l'énergie.
Par ailleurs, d'après le rapport d'avancement 2012 de
la Stratégie de Croissance pour la Réduction de la
Pauvreté (SCRP), le Gouvernement béninois s'est engagé
à garantir la disponibilité permanente et suffisante des
ressources en eau en tant que facteur de production, et l'accès à
l'eau potable aux populations. En effet, l'eau est une denrée
nécessaire au renforcement et au développement du capital humain.
Sans l'eau potable, le capital humain est vulnérable et exposé
aux maladies hydriques. Par contre avec l'eau potable, des économies
sont faites en termes de dépenses sanitaires et revenus
épargnés peuvent servir pour le financement des secteurs
productifs.
Il semble donc important, que le Bénin accroisse ses
investissements publics dans les infrastructures afin d'améliorer son
niveau de développement. C'est dans cette logique que nous nous
proposons de travailler sur le thème :
« Investissements et la croissance économique :
cas des secteurs de l'énergie et de l'eau au
Bénin ».
La présente étude s'articule autour de deux
chapitres. Le premier chapitre présente le cadre théorique et
analytique de l'étude. Le deuxième chapitre fait : une
analyse descriptive et économétrique des investissements dans les
secteursde l'énergie et de l'eau, et la croissance économique au
Bénin. Cette dernière partie est soutenue par la formulation de
limites et suggestions.
CHAPITRE 1: CADRE THEORIQUE ET ANALYTIQUE DE L'ETUDE
CHAPITRE 1: CADRE THEORIQUE ET
ANALYTIQUE DE L'ETUDE
1. PROBLEMATIQUE, OBJECTIFS,
HYPOTHESES ET REVUE DE LITTERATURE
1.1. Problématique de
l'étude
L'énergie électrique est utilisée par les
agents économiques pour leurs activités de production ainsi que
pour leurs besoins quotidiens. Ainsi elle occupe une place importante dans le
processus de développement de toute nation. Le rôle que joue
l'énergie électrique dans la croissance économique n'est
plus à démontrer. En effet, elle a été d'une
grande utilité dans le processus de développement des pays
industrialisés. Selon les statistiques de l'Agence Internationale de
l'Energie (AIE) publiées en 2009, il existe une forte corrélation
entre la consommation d'électricité et la richesse d'un pays. Des
études empiriques établissent aussi que le service de
l'électricité semble être l'un des services les plus
importants pour améliorer le bien-être de l'individu pauvre
(AIE 2002). De même, la production de l'eau potable
nécessite l'utilisation de l'énergie électrique ;
donc de consommation d'électricité. Or cette dernière ne
serait possible sans la production de l'énergie électrique. Par
ailleurs, d'après A.Direr, l'investissement dépend du coût
du capital et des variations de la demande souvent matérialisée
par la consommation(A. Direr, Note de macroéconomie, 2009).
Des études empiriques établissent aussi que le
service de l'électricité semble être l'un des services les
plus importants pour améliorer le bien-être de l'individu pauvre
(AIE 2002). De même, la production de l'eau potable
nécessite l'utilisation de l'énergie électrique ;
donc de consommation d'électricité. Or cette dernière ne
serait possible sans la production de l'énergie électrique. Par
ailleurs, d'après A.Direr, l'investissement dépend du coût
du capital et des variations de la demande souvent matérialisée
par la consommation (A. Direr, Note de macroéconomie, 2009).
Il s'agit pour le Bénin de porter la proportion de la
population ayant accès à l'eau potable de 35% en 2002 à
67,3% en 2015. Ce taux s'est établi à 65,6% en 2013 (Rapport
d'exécution BPO gestion 2013 du MERPMEDER). De même, l'une
des Orientations Stratégiques de Développement (OSD) est le
renforcement du capital humain. Ceci, en facilitant la satisfaction des
besoins essentiels de la population et en réduisant la pauvreté
de façon durable. L'exécution de cette orientation
stratégique se fait en partie par le Ministère en charge de
l'énergie et de l'eau. D'après le rapport BPO de la Direction
Générale de l'Eau (DG Eau) de ce département
ministériel, les activités du secteur de l'eau sont
financées à plus de 86% par les Partenaires Techniques et
Financiers (PTF). Or pendant la décennie écoulée, ces
derniers ont diminué,voire annulé leur intervention dans le
secteur. Pour atteindre les objectifs fixés dans le secteur de l'eau, le
Gouvernement béninois se doit de combler le vide financier laissé
par les PTF.
Par ailleurs, le Bénin connaît des
problèmes structurels en matière d'énergie
électrique. Il s'agit : d'une forte dépendance de
l'extérieur pour son approvisionnement, d'une production nationale peu
compétitive, des délestages électriques récurrents
et d'un service aux consommateurs peu performant.
Ces derniers ont des conséquences sur l'économie
nationale et la croissance économique (BIPEN 2007 ; Impact de
la crise de l'énergie électrique sur l'économie
béninoise). Ce niveau de croissance est loin des objectifs de
développement. Depuis 20134(*), le taux de croissance économique du
Bénin tourne autour de 5% (DGAE 2014). Afin d'améliorer
le bien-être des populations béninoises et faire reculer les
frontières de la pauvreté, il est nécessaire d'investir
dans les secteurs de l'Energie et de l'Eau.
Au regard de tout ce qui précède, il est
opportun de réaliser une étude afin d'analyser les
Investissements et la croissance économique : cas des secteurs de
l'énergie et de l'eau au Bénin.
1.2.
Objectifs et hypothèses de recherche
1.2.1. Objectif
général
Cette étude vise à analyser la relation qui
existe entre les investissements dans les secteurs de l'énergie et de
l'eau, et la croissance économique.
1.2.2. Objectifs
spécifiques
De façon spécifique, il s'agira :
§ d'analyser l'évolution des investissements dans
les secteurs de l'énergie électrique et de l'eau et la croissance
économique au Bénin ;
§ d'analyserla relation de causalité entre les
investissements dans les secteurs de l'énergie électrique et de
l'eau et la croissance économique au Bénin ;
§ d'évaluer l'impact sur la croissance
économique des investissements dans les secteurs de l'énergie
électrique et de l'eau.
1.2.3.
Hypothèses
Pour cette étude nous posons les hypothèses
ci-après :
§ Hypothèse 1 : les investissements dans les
secteurs de l'énergie électrique et de l'eau et la croissance
économique au Bénin ont une tendance croissante ;
§ Hypothèse 2 : il existe une causalité
positive réciproque entre les investissements dans les secteurs de
l'énergie électrique et de l'eau et la croissance
économique.
§ Hypothèse 3 : les investissements dans les
secteurs de l'énergie et de l'eau affectent positivement la croissance
économique.
2. REVUE DE LITTERATURE ET
METHODOLOGIE
2.1. Revue de
littérature
L'analyse des relations entre les investissements dans les
secteurs de l'énergie et de l'eau et la croissance économique
exige une revue de littérature sur les différents théories
et travaux empiriques sur le sujet. Cette dernière nous permettra de
prendre connaissance des travaux déjà effectués dans le
domaine afin de déterminer la méthodologie adéquate pour
l'atteinte des objectifs de la présente étude.
Les relations de causalité entre l'investissement dans
les secteurs de l'énergie et de l'eau et la croissance économique
n'ont pas fait l'objet d'étude statistique à notre connaissance.
Le sujet le plus abordé s'appariant à cette étude est
l'analyse de la relation de causalité entre la consommation de
l'énergie électrique et la croissance économique.
Toutefois, les résultats de nos recherches sont présentés
selon une approche théorique et une approche empirique.
2.1.1. Approche
théorique
2.1.1.1. Approche théorique
de l'investissement public
2.1.1.1.1. Fondement de l'Action Publique
Dans la Théorie générale, Keynes (1936)
met l'accent sur le rôle des dépenses publiques dans la relance
économique par un processus multiplicateur. A la fin des années
1960 et au début des années 1970, alors que se dissipe l'euphorie
liée à la croissance économique, le monde assiste à
un retour en force de thèses libérales qui s'attaquent à
la macro-économie keynésienne. Ainsi, l'apparition de la
stagflation - développement simultané de l'inflation et du
chômage- remet en cause la loi de Phillips5(*) (1958). On a alors expliqué les
difficultés croissantes des années 1970 par les effets
secondaires des politiques keynésiennes. Avec Friedman6(*) (1968), le monétarisme
est devenu le premier grand courant anti-keynésien. En allant
au-delà de ses premières critiques du keynésianisme
concernant la réalité du mécanisme du multiplicateur
budgétaire, Friedman a déstabilisé la
macro-économie standard en réinterprétant la loi de
Phillips. Son raisonnement a permis de mettre en cause toute la logique du
keynésianisme. Cependant, les études économétriques
ne permettent pas de trancher nettement ce débat entre
keynésiens et monétaristes. Selon que les auteurs des
modèles sont ou non partisans de l'«effet d'éviction»,
leurs résultats confirment (Spencer et Yoke, 7(*)1970) ou infirment
(Blinder et Solow,8(*)
1973) cette thèse. Force est de conclure que le débat sur
l'efficacité à court terme de la politique budgétaire n'a
pas été tranché par les tests
économétriques (Aftalion et Ponvet, 9(*)1981). Cette conclusion se
trouve renforcée par l'école des anticipations rationnelles
(Muth10(*), 1961;
Lucas11(*), 1972)
qui, en cherchant à donner un fondement micro-économique aux
recommandations macro- économiques des monétaristes, conduit
à une position «radicale»: l'inefficacité totale des
politiques de régulation conjoncturelle, qu'elles soient
budgétaires ou monétaires (Sargent et Wallace,12(*) 1975). Ainsi, les
dépenses publiques ont fait l'objet de différentes
interprétations selon les courants de la pensée
économique, principalement à travers les modèles de
croissance qui ont révélé des répercussions
très différenciées des différentes composantes des
dépenses sur les variables macro-économiques et sur le
bien-être. Dès lors, une kyrielle de travaux aussi bien
théoriques qu'empiriques se sont penchés sur la question pour
justifier le bien fondé des dépenses publiques en capital
humain.
2.1.1.1.2. Infrastructures publiques
Les infrastructures sont le plus souvent définies comme
des biens collectifs mixtes à la base de l'activité productive.
Deux notions sous-tendent cette définition : celle de bien collectif ou
de bien public, et celle de facteur productif. La notion de bien collectif,
définie par Samuelson13(*)(1954) et Musgrave 14(*)(1959), repose sur les
critères de non rivalité et de non exclusion. Un bien est
qualifié de non rival si son utilisation par un agent ne réduit
pas la quantité disponible pour les autres agents. La « non
rivalité » s'accompagne, en fait, de l'indivisibilité
d'usage, c'est-à-dire d'une consommation en totalité de ce bien
qui ne pourra être partagé entre divers utilisateurs. Les exemples
traditionnels sont ceux de la justice, de la sécurité ou de
l'éclairage public. La non-exclusion par les mécanismes de
marché caractérise, de son côté, des biens dont
aucun agent ne peut être exclu des bénéfices. Celle-ci
découle également de l'impossibilité de fractionner le
service entre divers consommateurs, c'est à dire de
l'indivisibilité. Ainsi, les caractéristiques intrinsèques
de ces biens, en entraînant une impossibilité de reposer sur les
mécanismes de marché, justifient l'intervention de l'Etat dans
leur production ou leur réglementation. Dans la réalité,
les biens publics purs sont l'exception et l'on a plutôt à faire
à des biens publics mixtes, c'est à dire partiellement rivaux. Le
relâchement partiel de l'hypothèse de « non
rivalité » recoupe, notamment, les problèmes de
congestion des services publics qui peuvent apparaître au-delà
d'un certain seuil d'utilisation (voir l'exemple des transports
modélisé par Aschaue15(*)r, 1990c), et celui de l'hypothèse de
« non exclusion » la possibilité de relever les
droits d'utilisation. Un classement des infrastructures selon ces
critères établi par Eden et Mc Millan16(*) (1991) comme la boite de
Musgrave-Samuelson est repris plus récemment par la Banque mondiale en
(1994). Le caractère productif des infrastructures relève de son
côté de plusieurs logiques. La production de services publics
constitue, en tant que telle, une activité économique à
part entière. Mais une caractéristique propre de ces biens
réside surtout dans le facteur de potentialité qu'ils
constituent. A la suite de Hirschman17(*) (1958), on peut définir les infrastructures
comme les biens et les services qui rendent possible l'activité
économique. Cette définition, particulièrement large, est
reprise par Hansen18(*)
(1965) qui est le premier à proposer une classification précise.
Il distingue : les infrastructures sociales, dont la fonction est d'entretenir
et de développer le capital humain (comme l'éducation, les
services sociaux et de santé) et les infrastructures
économiques, dont la caractéristique est de participer au
processus productif.
Selon Meade19(*) (1952), ce facteur de potentialité est tout
d'abord direct, le rôle productif des infrastructures passant par la
fourniture de biens et de services intermédiaires qui participent au
processus de production. Mais surtout, la particularité des
infrastructures réside dans la faculté d'améliorer
l'utilisation des autres facteurs de production. Il s'agit ici d'un effet
indirect d'augmentation de la productivité des autres facteurs de
production. Cet effet indirect consiste, tout d'abord, en une diminution des
coûts de production et un accroissement de la rentabilité des
activités. Certains travaux soulignent que la pénurie chronique
d'infrastructures d'un grand nombre de pays en développement explique
des coûts de production élevés et une
compétitivité dégradée voire l'impossibilité
de développement de certaines activités ou régions
(Wheeler et Mody20(*),
1993). Mais cette rentabilité passe également par la
réduction des coûts de transport permise par le
développement des infrastructures (Banque mondiale21(*), 1994). Ces
améliorations sont également liées à
l'accroissement de la taille du marché permis par le
développement des infrastructures, et par l'intensification des
échanges qui lui est consécutif. Ces caractéristiques
conduisent à la possibilité d'économies d'échelle
et de diffusion du progrès technique, de même qu'à une
division du travail accrue. Celle-ci, en rendant possible l'apparition de
synergies et de complémentarités entre entreprises,
régions ou activités, contribue encore d'une autre façon
au caractère productif des infrastructures. En stimulant de la sorte
l'apparition d'externalités de type marshallien, les infrastructures
trouvent ici une autre justification économique à l'intervention
de l'Etat dans la fourniture ou la réglementation de certaines d'entre-
elles.
2.1.1.2. Théorie de la
croissance
Depuis Adam Smith et sa « richesse des
nations », la croissance occupe l'esprit de nombreux
économistes. De nos jours, deux (02) analyses tendent à
être privilégiées :
§ la première et la plus ancienne repose sur le
modèle néo-classique développé par Ramsey22(*) (1928), Solow23(*) (1956), Swan24(*) (1956), Cass25(*) (1965) et Koopmans26(*) (1965) ; avec Solow (Prix
Nobel 1987), la figure pensante. Cette théorie des années 60, a
été enrichie durant les années 80 afin de tenir compte
d'un certain nombre de critiques ;
§ la seconde, la croissance endogène, semblerait
ouvrir de nouvelles perspectives.
2.1.1.2.1. Analyse néoclassique de la croissance :
modèle de Solow
A la suite d'une réflexion critique sur le
modèle keynésien de croissance développé par Harrod
et Domar (HD)27(*), Robert
Solow a construit un modèle qui s'inscrit ainsi dans une perspective
néo-classique et est à la base des théories de la
croissance endogène apparues dans les années 1980.
Le modèle HD distingue trois (03) taux de croissance
différents : (i) le taux de croissance naturel (taux de
croissance de la population active, exogène), (ii) le taux de
croissance effective (taux de croissance observé) et (iii) le taux de
croissance garanti (celui qui assure l'équilibre sur le
marché des biens). La stabilité de la croissance est
garantie par l'égalité entre le taux de croissance effective et
le taux de croissance garanti; ce qui est rarement le cas, même sur le
long terme. Le modèle HD décrit donc une croissance
fondamentalement instable qualifiée d'être sur le « fil
du rasoir », (ou encore en anglais « on a knife-edge of
equilibrium growth »). C'est sur ce résultat que Solow va
formuler sa principale critique à l'encontre du modèle HD.
Pour remédier à l'opposition entre taux de
croissance naturel et taux de croissance garanti, Solow se débarrasse du
postulat des proportions fixes, c'est-à-dire de la
non-substituabilité des facteurs de production capital et travail. Le
modèle de Solow se fonde sur l'hypothèse que les facteurs de
production connaissent séparément des rendements
décroissants : une même augmentation du volume d'un des facteurs
de production répétée plusieurs fois entraîne une
augmentation de moins en moins grande de la production. Par contre, les
rendements d'échelle sont supposés constants. Il pose
également comme hypothèse que les facteurs de production sont
utilisés de manière efficace par tous les pays. En posant que la
population connaît un taux de croissance qu'il qualifie de « naturel
» (non influencé par l'économie), le modèle
déduit trois (03) prédictions :
§ augmenter la quantité de capital
(c'est-à-dire investir) aura pour effet d'augmenter la croissance : en
effet, avec un capital plus important, la main d'oeuvre augmente sa
productivité apparente ;
§ les pays pauvres auront un taux de croissance plus
élevé que les pays riches. Ils ont en effet accumulé moins
de capital, et connaissent donc des rendements plus faiblement
décroissants, c'est-à-dire que toute augmentation de capital y
engendre une augmentation de la production proportionnellement plus forte que
dans les pays riches ;
§ en raison des rendements décroissants des
facteurs de production, les économies vont atteindre un point où
toute augmentation des facteurs de production n'engendrera plus d'augmentation
de la production par tête. Ce point correspond à l'état
stationnaire. Solow note toutefois que cette troisième prédiction
est irréaliste : en fait, les économies n'atteignent jamais ce
stade, en raison du progrès technique qui accroît la
productivité des facteurs. Autrement dit, pour Solow, sur le long terme,
la croissance provient du progrès technique. Toutefois, ce
progrès technique est exogène au modèle,
c'est-à-dire qu'il ne l'explique pas mais le considère comme
donné (telle une « manne tombée du
ciel »).
Ce modèle, développé dans un
environnement de concurrence pure et parfaite, utilise une fonction de
production néo-classique à rendements factoriels
décroissants et à rendements d'échelle constants avec
substituabilité des facteurs de production28(*) On se situe en économie
fermée dans laquelle l'entreprise produit un bien unique à partir
de la combinaison de trois (03) facteurs : le travail (L), le capital (K) et
les connaissances (A), c'est-à-dire l'efficacité du facteur
travail ou encore le progrès technique. Le modèle postule en
outre que les niveaux initiaux du capital, du travail et du progrès
technique sont fixés, et que L et A croissent à un taux
exogène constant.
Partant de ces hypothèses, le modèle de
croissance néo-classique implique l'épuisement à terme de
la croissance du capital par tête et par conséquent celle de la
croissance du revenu par tête. Un épuisement qui s'explique par
les rendements marginaux décroissants du facteur accumulable, le
capital. Comme les facteurs sont rémunérés à leurs
productivités marginales, la décroissance des rendements a pour
effet une diminution de l'incitation à investir.
Du fait de l'épuisement du revenu par tête, la
croissance de long terme n'est expliquée que de manière
exogène par la croissance de la population et la nécessité
de couvrir la dépréciation du capital. Seule(s) la croissance de
la population et/ou l'introduction d'un progrès technique exogène
permettraient d'augmenter la productivité des facteurs. La mise en
évidence de l'existence d'un facteur résiduel représentant
le niveau de la technologie ne permet pas de pallier les faiblesses du
modèle de croissance néoclassique dans la mesure où le
progrès technique reste exogène.
Aussi, l'une des implications du modèle de Solow est
qu'en considérant que le progrès technique est universellement
partagé, deux (02) pays l'un développé et l'autre moins
développé, mais ayant le même taux d'épargne vont
tendre vers un même PIB par tête. Ce principe connu sous le nom de
« Principe de convergence » n'est en réalité
vérifié que pour peu de pays, ce qui constitue l'une des
critiques majeures à l'encontre du modèle de Solow.
Dès lors, le modèle de Solow qui ajoute un
investissement en capital humain à l'investissement en capital
technique, permet à la fois d'expliquer la convergence de certains pays
et l'accentuation des inégalités mondiales entre pays pauvres et
pays riches. La convergence provient des efforts d'investissement en capital
humain et en capital technique de pays qui comblent ainsi leur retard (ils
peuvent transférer chez eux les techniques de production des pays les
plus en avance, grâce à une main d'oeuvre mieux
formée).Le modèle de Solow s'est cependant
écarté de la réalité en considérant que la
croissance économique par tête devait peu à peu diminuer et
finir par cesser de progresser : ainsi en l'absence d'innovations
technologiques continues, la croissance du produit/habitant cesse
(application de l'hypothèse des rendements décroissants et
d'une croissance limitée : Ricardo et Malthus). Les observations
ont montré que la croissance économique progressait même
à un rythme ralenti et demeurait un fait majeur de toutes les
économies développées.
En outre, dans le modèle de Solow, l'Etat ne peut jouer
aucun rôle particulier dans le processus de croissance, puisque ce
dernier relève des facteurs exogènes. Les tenants de la
croissance endogène vont montrer au contraire qu'une intervention de
l'Etat peut stimuler la croissance en incitant les agents à investir
davantage dans le progrès technique. Pour inciter à investir en
capital humain, l'Etat peut aussi favoriser l'accès à
l'éducation. On assiste ainsi à une réhabilitation des
dépenses publiques, non pas dans une perspective de régulation
conjoncturelle, mais dans une perspective structurelle de croissance à
long terme (effets d'apprentissage de Romer (1986)29(*), l'accumulation du capital
humain par Becker ( 1962 )30(*), gains de productivité de Barro(1997
)31(*)).
2.1.1.2.2. Croissance endogène
L'arrivée des théories sur la
Recherche-Développement (des objectifs volontaires en matière
de recherche développement), la diffusion progressive des
innovations technologiques, et plus précisément les travaux de
Romer (1986, 1987, 1990) sont à l'origine des théories de la
croissance endogène. Cette dernière est assimilée à
un phénomène auto-entretenu par accumulation de quatre (04)
facteurs principaux : le capital physique, la technologie, le capital humain et
le capital public. Le rythme d'accumulation de ces variables dépend de
choix économiques, c'est pourquoi on parle de théories de la
croissance endogène
2.1.1.2.2.1. Capital physique
C'est l'équipement dans lequel investit une entreprise
pour la production de biens et de services. Romer (1986) a cependant
renouvelé l'analyse en proposant un modèle qui repose sur les
phénomènes d'externalités entre les firmes : en
investissant dans de nouveaux équipements, une firme se donne les moyens
d'accroître sa propre production mais également celles des autres
firmes concurrentes ou non.
2.1.1.2.2.2. Technologie
Cette théorie repose sur l'analyse des conditions
économiques qui favorisent le changement technique. Chaque changement
technique provient d'une idée mise en forme et testée. Cependant,
entre l'émergence d'une idée nouvelle et sa mise en oeuvre
concrète, il peut y avoir un très long chemin (test,
essais-erreurs...) qui nécessite le concours de plusieurs personnes.
D'un point de vue économique, cette théorie
porte atteinte au cadre concurrentiel et permet l'incorporation
d'éléments de concurrence imparfaite qui rendent possibles
l'apparition de produits nouveaux et de nouvelles idées. Si au travail
et au capital utilisé, on ajoute des idées nouvelles
génératrices de changement technique, tout sera modifié.
Car contrairement au capital dont les rendements sont décroissants et au
travail dont les rendements sont constants (si on effectue sans cesse un
investissement humain supplémentaire), les idées ont un rendement
croissant : plus on s'appuie sur un stock d'idées importantes, plus on
aura de nouvelles idées. Chaque idée ouvre le champ à
d'autres idées potentielles. Par conséquent, en l'absence de
progrès technique, le modèle de Solow s'applique à long
terme, la croissance ne dépend pas du taux d'investissement. Le
progrès existe, et est d'autant plus intense que le nombre de chercheurs
est élevé et le stock de connaissances important. Le nombre de
chercheurs dépend de la capacité du système
économique à leur offrir des rentes de monopole en cas de
réussite.
2.1.1.2.2.3. Capital humain
Il a été mis en évidence par deux (02)
économistes de l'Ecole de Chicago, TheodorSchultz et Gary Becker, et est
au centre des études menées par R.E Lucas (Prix Nobel en 1995).
Le capital humain désigne l'ensemble des capacités apprises par
les individus et qui accroissent leur efficacité productive. Chaque
individu est en effet, propriétaire d'un certain nombre de
compétences, qu'il valorise en les vendant sur le marché du
travail.
Cette vision n'épuise pas l'analyse des processus de
détermination du salaire individuel sur le marché du travail,
mais elle est très puissante lorsqu'il s'agit d'analyser des processus
plus globaux et de long terme. Dans ce schéma, l'éducation, est
un investissement dont l'individu attend un certain retour. Il est alors
naturel de souligner que la tendance plus que séculaire dans les pays
occidentaux à un allongement de la durée moyenne de la
scolarité est une cause non négligeable de la croissance.
2.1.1.2.2.4. Capital public
En théorie, le capital public n'est qu'une forme de
capital physique. Il résulte des investissements opérés
par l'Etat et les collectivités locales. En mettant en avant le capital
public, cette nouvelle théorie de la croissance souligne les
imperfections du marché. Outre l'existence de situations de monopole,
ces imperfections tiennent aux problèmes de l'appropriation de
l'innovation. Du fait de l'existence d'externalités entre les firmes,
une innovation, comme il a été dit précédemment, se
diffuse d'une façon ou d'une autre dans la société. La
moindre rentabilité de l'innovation qui en résulte, dissuade
l'agent économique d'investir dans la recherche-développement.
Dans ce contexte, il pourra incomber à l'Etat de créer des
structures institutionnelles qui soutiennent la rentabilité des
investissements privés et de subventionner les activités
insuffisamment rentables pour les agents économiques et pourtant
indispensables à la société.
Par ailleurs, les auteurs ont mis en évidence plusieurs
facteurs dont la prise en compte dans les fonctions de production favorise la
croissance endogène. Ainsi, Riadh Ben Jelili (2000) a isolé
quatre (04) facteurs de la croissance endogène présentés
comme suit : (i) rendements croissants des facteurs, (ii)
investissements en recherches et développement, (iii) accumulation du
capital humain, (iv) capital public à travers l'implantation des
infrastructures.
Le modèle de Solow n'expliquait pas tous les facteurs
qui concourent à la croissance, il signalait simplement que grâce
au progrès technique, la croissance peut perdurer. Pour les tenants de
la théorie de la croissance endogène, le progrès technique
ne tombe pas du ciel. La croissance est ainsi assimilée à un
phénomène auto-entretenu par accumulation de quatre facteurs
principaux: (i) la technologie, (ii) le capital physique, (iii) le capital
humain et (iv) le capital public. Le rythme d'accumulation de ces variables
dépend de choix économiques, c'est pourquoi on parle de
théories de la croissance endogène. L'opinion considère
Paul Romer (1986) comme le chef de file d'une nouvelle vague d'auteurs qui ont
profondément renouvelé la théorie de la croissance. Dans
la file nous retrouvons des noms aussi prestigieux que Frankel, Lucas, Barro,
Howitt, Aghion, Mankiw, etc. C'est Frankel qui, avec le modèle AK, a
esquissé en 1962 l'épure de la croissance endogène mais
c'est Lucas qui l'a popularisée en 1988.
Pour sortir de l'impasse de l'exogénéité
des déterminants de la croissance, ces auteurs ont introduit de
nouvelles hypothèses et apporté de nouveaux
éléments dans l'analyse.
Ils poussent l'audace jusqu'à quitter le cadre
d'analyse néo-classique en remettant en cause de façon radicale
deux (02) de ses postulats de base : les rendements décroissants et le
marché de concurrence pure et parfaite pour leursubstituer les postulats
de rendements croissants et de concurrence monopolistique.
Les théoriciens de la croissance endogène vont
reprendre cette idée et l'élargir. Si l'on peut parler de
croissance endogène c'est parce que les facteurs qui expliquent la
croissance trouvent leurs origines dans les décisions endogènes
des agents économiques.
Ces modèles ont porté un nouvel éclairage
sur les raisons du progrès technique, mettant en avant le rôle
primordial joué par les innovations dans la croissance
économique. Ils ont également réhabilité les
politiques économiques comme facteurs influents de la croissance
économique. Les théories de la croissance endogène tentent
ainsi d'apporter une solution aux problèmes suivants : peut-on expliquer
la croissance par des éléments propres au système ?
Par conséquent, il résulte du fonctionnement
même de l'économie. C'est cette idée que Paul Romer a
développé dans les années 80-90.
Aussi, d'après Dominique Guellec, le coeur de la
croissance endogène réside dans l'hypothèse que la
productivité marginale du capital ne s'annule pas lorsque le stock de
capital devient grand.
Les modèles récents de croissance (pour
l'essentiel, les modèles dits de croissance endogène) estiment
pour la plupart qu'en dehors de la prise en compte des effets externes, l'Etat
exerce une influence directe sur l'efficacité du secteur privé:
les investissements publics concourent à la productivité
privée. Ainsi, sans routes, quelle serait la productivité d'une
entreprise de transport ? C'est dans cette optique que Barro (1990, 1991)
présente un modèle de croissance où les dépenses
publiques jouent un rôle moteur (Agenor, 2000).
2.1.1.3. Théories
économiques sur le rôle de l'énergie dans la croissance
économique
La relation entre la croissance économique et
l'énergie électrique est très ancienne. En effet,
l'utilité de l'énergie dans le processus de développement
s'estfait ressentir depuis 1780 avec la révolution industrielle. Durant
cette période, le souci d'apporter un nouveau souffle à une
économie anglaise basée sur l'utilisation de techniques
rudimentaires a permis à certains pionniers de l'époque
(James Watt, 1763)32(*) de découvrir de nouvelles sources
d'énergie et des machines utilisant de façon abondante
l'énergie. Ces découvertes ont ainsi permis une véritable
mutation de l'activité économique.
C'est en effet à partir de la fin du XVIIIème
siècle que de nombreuses découvertes eurent lieu, tant en chimie
qu'en innovations techniques et mécaniques. Ce processus
d'industrialisation a provoqué un changement des habitudes, de la nature
de la production et une redynamisation de l'économie provoquant un exode
rural vers les villes qui se développèrent autour des nouveaux
sites de production. L'agriculture fut ainsi mécanisée ; les
paysans passèrent ainsi d'une agriculture manuelle traditionnelle
à une révolution agricole basée sur des machines et des
produits chimiques. Ces innovations techniques n'auraient pas été
possible sans le fruit des nouvelles inventions qui nécessitaient une
utilisation massive de l'énergie pour fabriquer des machines à
vapeur, tout d'abord, puis électriques par la suite.
Le rôle de l'énergie dans le processus de
croissance d'une nation a connu une évolution particulière dans
la théorie économique. En dépit de l'importance du
rôle qu'elle a joué pendant la révolution industrielle, les
auteurs classiques et néo-classiques n'intègrent pas directement
l'énergie comme facteur de production dans la détermination du
produit global. Adam Smith, avec sa théorie de la valeur33(*) montre que la valeur d'un bien
dépend uniquement de la quantité de travail nécessaire
à sa production. La valeur d'un bien est donc déterminée
par le seul facteur travail utilisé dans le processus de production.
Tenir compte de cette conception de la valeur revient implicitement à
occulter le rôle joué par l'énergie dans une période
marquée par l'utilisation à grande échelle de machines
durant la révolution industrielle. Pour pallier à cette
insuffisance, Adam Smith va donc considérer que les plus-values
tirées de l'utilisation des machines se diluent sous formes de profits
et salaires. A l'instar d'Adam Smith, les théories de Jean Baptiste Say
et de Ricardo n'intègrent pas l'énergie comme facteur de
production. Cependant, c'est avec les travaux de Stanley Jevons en 1865 sur
l'impact de la limitation de la production du charbon sur le
développement industriel en Royaume Uni que l'introduction de
l'énergie comme facteur de production va connaitre un essor.
Malgré l'avertissement de Jevons sur l'utilité de
l'énergie dans la croissance économique anglaise, les
économistes classiques ne vont pas faire de l'énergie un facteur
essentiel dans la détermination de la production nationale. Avec
l'avènement des nouvelles théories de la croissance
économique, le rôle que joue l'énergie dans la production
sera également occulté. Ces auteurs (Solow, Barro, Becker,
Romer) à l'instar de leurs prédécesseurs expliquent
les performances des nations à partir d'autres facteurs (le
progrès technique, l'innovation, les dépenses publiques, le
capital humain et l'apprentissage par la pratique) autres que
l'énergie. Les théoriciens de la croissance endogène ont
retenu quatre (04) sources principales : l'accumulation de la connaissance,
l'accumulation du capital humain, l'accumulation du capital technologique et
les dépenses d'infrastructures publiques. Cette situation va perdurer
jusqu'à l'avènement de la crise pétrolière en
1973.
C'est à la suite des crises pétrolières
et de ses impacts sur les économies que l'intérêt pour
l'énergie comme facteur de production s'est fait ressentir dans les
recherches économiques.
Dans les années 1970, la nécessité de
comprendre les liens entre les évolutions des ressources naturelles, en
l'occurrence énergétique et l'économie a conduit à
la reconnaissance de l'énergie, puis des matières
premières, en tant que facteur de production. Cette prise de conscience
a permis l'apparition des fonctions de production intégrant
l'énergie et les matières premières comme facteur de
production. Il s'agit des fonctions de production KLE (capital, travail,
énergie)ou Klem (capital, travail, énergie,
matière)34(*).
Ces nouvelles fonctions de production se proposent d'étudier la
croissance économique en intégrant un nouveau facteur de
production qui est l'énergie. Cependant, la question relative aux
hypothèses concernant la substituabilité se pose dans la
formulation des fonctions de production (Percebois, 1989)35(*).
La plupart des modèles macro-énergétiques
ont longtemps utilisé des fonctions de production de type Cobb Douglas
admettant une substituabilité parfaite entre ces facteurs de production.
Elle suppose que quel que soit le niveau de production et la proportion des
facteurs, l'élasticité de substitution est toujours égale
à l'unité et la part relative en valeur des facteurs toujours
constante (Gregory, Griffin 1976)36(*).
Berndt et Wood (1979) soutiennent par contre
l'existence d'une complémentarité entre le capital et
l'énergie. Cette controverse pose le problème de
«substituabilité technique brute» et de
«complémentarité économique nette» entre
l'énergie et le capital dans les processus de production.
Par ailleurs, la compréhension de la dynamique de la
relation entre l'énergie et la croissance économique doit tenir
compte des autres facteurs de production.
A l'instar des théories économiques sur le
rôle de l'énergie dans la croissance économique, plusieurs
études empiriques ont été menées dans le but de
comprendre cette relation.
2.1.2. Approche
empirique
A notre connaissance, il n'y a pas de
travaux empiriques ayant étudié la causalité entre
l'investissement dans les secteurs de l'énergie et de l'eau, et la
croissance économique.
Néanmoins, plusieurs études ont traité
de « L'analyse de la causalité entre la consommation
d'énergie électrique et la croissance
économique ». Cependant, les conclusions de ces études
conduisent à des résultats antagonistes.
2.1.2.1. Absence de
relation de causalité entre la croissance et la consommation
d'énergie
Pour Akarca et Long (1980), les résultats auxquels sont
parvenues Kraft and Kraft sont biaisés dans la mesure où la
période choisie pour les études est jugée instable car
elle incluait le premier choc pétrolier. Ainsi, en écourtant la
période d'étude de 1950 à 1968, ces auteurs montrent une
absence de relation de causalité entre le PIB et la consommation
d'énergie.
Au même moment, Yu et Choi (1985) étudient
l'existence de relation entre la consommation d'énergie et le PNB sur un
panel de pays composé du Brésil, des USA, du Royaume Uni, de la
Pologne, des Philippines et de la Corée du Sud. Ils parviennent à
la conclusion qu'il n'existe aucune relation de causalité entre la
consommation totale d'énergie et le PNB pour les USA, le Royaume Uni et
la Pologne.
Wolde Rufael (2004) à la question de savoir les
relations entre la consommation d'électricité et la croissance a
utilisé les nouvelles techniques de Pesaran, Shin et Smith (2001) sur
quinze (15) pays africains. Wolde Rufael montre en utilisant le PIB comme
variable explicative qu'il existe une relation de long terme pour quatre (04)
pays (Gabon, Côte d'Ivoire, Nigéria, et le Soudan). Par
contre, lorsque la consommation d'électricité est utilisée
comme variable endogène, il obtient une relation de cointégration
pour quatre (04) pays (Algérie, RDC, Ghana). Pour les onze (11) autres
pays de l'étude, les tests de cointégration indiquent une absence
de cointégration quelque soit la variable utilisée comme
endogène.
2.1.2.2. Présence de
relation unidirectionnelle allant de la croissance vers la consommation
d'énergie
En effet, c'est à Kraft and Kraft 37(*)(1978) que l'on doit les
premières études sur les relations de causalité entre la
consommation d'énergie et le produit national brut. Dans le but de
mettre en évidence l'existence d'un lien entre le PNB et la demande
d'énergie aux USA, Kraft and Kraft partent d'une analyse sur la
consommation d'énergie et le PNB des Etats Unis sur la période
1947-1974 pour parvenir à la conclusion qu'il existe une relation
unidirectionnelle allant du Produit National Brut vers la consommation
d'énergie. Ainsi, les conclusions des travaux impliquent alors que toute
action visant à promouvoir et redynamiser le secteur de l'énergie
n'aurait aucune influence sur l'évolution du Produit National Brut.
Yu et Choi (1985) étudient l'existence de relation
entre la consommation d'énergie et le PNB sur un panel de pays
composé du Brésil, des USA, du Royaume Uni, de la Pologne, des
Philippines et de la Corée du Sud. Ils parviennent à la
conclusion qu'il n'existe aucune relation de causalité entre la
consommation totale d'énergie et le PNB pour les USA, le Royaume Uni et
la Pologne.
2.1.2.3. Présence de
relation unidirectionnelle allant de la consommation d'énergie vers la
croissance
Yu et Choi (1985) étudient l'existence de relation
entre la consommation d'énergie et le PNB sur un panel de pays
composé du Brésil, des USA, du Royaume Uni, de la Pologne, des
Philippines et de la Corée du Sud. Ils détectent un lien causal
allant de la consommation d'énergie au PNB pour les Philippines.
En Chine, Shiu et Lam (2004) ont eu recours au test de
causalité de Granger pour mettre en évidence le lien causal entre
la consommation d'électricité et le PIB réel sur la
période 1971- 2000. Ils aboutissent au fait que la consommation
d'électricité cause le PIB au sens de Granger. De tout ce qui
précède, on pourrait penser que les initiatives et innovations
dans le domaine de l'électricité contribuent à
l'amélioration de l'activité économique.
Par ailleurs, en Turquie, Galip Altinay et al (2005) ont eu
recours à deux (02) tests à savoir le test de
Dolado-lukepohl38(*) dans
un VAR à niveau et celui de Granger selon la procédure de
Toda-Yamamoto39(*) (1995)
pour mettre en évidence les relations entre la consommation
d'électricité et le PIB réel sur la période
1950-2000. Après estimation, les deux (02) tests utilisés pour
leur modélisation ont donné une preuve solide de la
présence d'une causalité unidirectionnelle allant de la
consommation d'électricité au revenu. Au vu de ces
résultats, Galip Altinay et al encouragent des politiques visant
à améliorer les services de fourniture
d'électricité car elles sont d'une importance vitale pour une
augmentation de la consommation d'électricité qui permettrait de
soutenir la croissance économique.
Sur les îles Fidji, pays dépendant de
l'énergie pour son développement, P. Narayan et Singh (2006) ont
réalisé une étude sur les liens entre la consommation
d'électricité et le Produit Intérieur Brut. Ces auteurs
utilisent dans leurs analyses les nouvelles techniques de
cointégrationdéveloppée par Pesaran, Shin et al
(2001)40(*) et la
causalité de Granger. Les tests économétriques
appliqués pour ce pays révèlent qu'il existe une relation
de causalité de long terme allant de la consommation
d'électricité vers le PIB. Narayan et Singh proposent d'engager
des politiques visant à faciliter l'accès à
l'électricité dans la mesure où les actions ayant pour but
de conserver l'énergie auront un impact négatif sur la croissance
économique.
Toujours dans cette même optique, Yoo et Kwak (2010)
étudient la consommation d'électricité et le PIB
réel sur un panel de sept (07) pays de l'Amérique du Sud à
savoir : l'Argentine, le Brésil, le Chili, la Colombie, l'Equateur,
le Pérou et le Venezuela sur la période 1975-2006. Yoo et Kwak
parviennent à la conclusion qu'il existe une relation de
causalité unidirectionnelle de la consommation
d'électricité vers le PIB pour l'Argentine, le Brésil, le
Chili, la Colombie et l'Equateur. Cela veut dire que toute action ou politique
visant à améliorer les performances du secteur de
l'énergie électrique affecte directement la croissance
économique de ces pays. Pour le Venezuela par contre, les
résultats montrent qu'il y a une causalité bidirectionnelle entre
la consommation d'électricité et la croissance économique.
Cela implique qu'une augmentation de la consommation
d'électricité affecte directement la croissance économique
et cette croissance économique stimule aussi la consommation
d'électricité dans ce pays. Concernant le Pérou, les
conclusions de l'étude de Yoo et Kwak indiquent une absence de lien de
causalité entre la consommation d'électricité et la
croissance économique.
2.1.2.4. Présence de
relation bidirectionnelle entre la consommation d'énergie vers la
croissance
En Afrique, peu d'études se sont consacrées au
lien entre le niveau de richesse d'un pays et sa consommation
d'électricité (Jumbe, 2004). Cependant, il existe
certains auteurs qui ont essayé de mettre en évidence ces
relations soit sur des pays pris individuellement ou sur des groupes de pays.
Tout comme dans le cas des pays industrialisés, les études sur
les relations entre la consommation d'électricité et la
croissance en Afrique indiquent une absence de consensus sur le sens de
causalité.
Jumbe (2004) a abordé la question dans ces travaux sur
le Malawi. Il a montré qu'il existe une relation de causalité
unidirectionnelle du PIB vers la consommation d'électricité sur
la période de 1970 à 1999 dans ce pays.
2.1.2.5. Autres
résultats
Idrissa Ouedraogo (2010) utilise les techniques de
cointégration aux bornes de Pesaran et al pour mettre en évidence
la relation entre la consommation d'électricité et la croissance
économique au Burkina Faso sur la période 1968-2003. Il
intègre dans sa modélisation certaines variables à savoir
; la Formation Brute de Capital Fixe (FBCF), le PIB et la consommation
d'énergie électrique. Après application de la
méthode de Pesaran, l'auteur aboutit au fait qu'il existe une relation
de long terme bidirectionnelle entre la consommation d'énergie et
l'investissement. Les travaux de Ouédraogo révèlent
également l'existence d'une relation rétroactive positive entre
les investissements et le Produit Intérieur Brut.
En ce qui concerne les études empiriques sur l'analyse
des relations existantes entre les investissements dans les secteurs
l'énergie et de l'eau, et la croissance économique, les
résultats sont similaires.
Ainsi, Global Water Partnerships Central Africa a
travaillé sur le « Développement d'une stratégie
de financement du secteur de l'eau en Afrique centrale : Etude nationale
sur le financement du secteur de l'eau» ; en Juin 2010. L'approche
méthodologique utilisée est composée : de recherche
documentaire ; des enquêtes enrichies des observations ; des
échanges et des estimations et extrapolations statistiques. Au cours de
cette étude les investissements dans l'hydraulique urbaine de 2004
à 2007 ; les ressources exploitables pour
l'hydroélectricité et les enjeux majeurs dans le secteur de
l'eau ont été présentés. Par ailleurs, les auteurs
ont fait le diagnostic du financement du secteur de l'eau en
s'intéressant aux financements et aux besoins en investissements des
sous-secteurs de l'eau ; par une analyse descriptive. Comme
résultats, cette étude a permis de : dresser l'état
des lieux général du secteur de l'eau et de faire un diagnostic
de son financement ; et présenter une analyse prospective dudit
financement.
Par ailleurs, Ongono Patrice du Centre d'Etudes et de
Recherche en Economie et Gestion (CEREG) Université de Yaoundé II
Cameroun a étudié les « Investissements en
Infrastructures Publiques et Performances Economiques au Cameroun »
pour évaluer l'impact de l'investissement public routier, de
l'investissement public en énergie, et de l'investissement public en
télécommunications sur la croissance du PIB par tête et
l'investissement privé. Pour cette étude, il a été
défini : une équation de croissance qui s'inspire du
modèle de Solow augmenté (Mankiw, Romer et Weil41(*) 1992) ; et une
équation d'investissement. L'étude a porté sur la
période 1970 à 2008. Les méthodes utilisées sont
les suivantes : la Méthode des Moindres Carrés ordinaires,
la Méthode des Variables Instrumentales proposée par Arellano
& Bond (1991) et la Méthode des Moments
Généralisés (MMG). L'estimation de l'équation de
la croissance a révélé que : seuls l'investissement
routier a des effets sur la croissance économique ; les
investissements en énergie sont actuellement insuffisants pour que les
effets bénéfiques soient ressentis sur la croissance du PIB par
tête ; et les investissements en télécommunications ne
sont pas alloués dans les secteurs productifs. De même,
l'estimation de l'équation d'investissement montre que :
l'investissement public routier et l'investissement public en énergie
sont respectivement complémentaires de l'investissement
privé ; et l'investissement public dans le secteur des
télécommunications évince l'investissement privé.
De même, « l'Unité de Coordination de
la Formulation du 2ième programme et suivi des
réformes du MCA-Bénin » et « le Millenium
Challenge Corporation » ont commandité en juillet 2012 une
étude sur le thème : « Analyse des contraintes
à l'investissement privé et à la croissance
économique au Bénin », afin d'identifier les obstacles
à l'investissement privé en vue de les lever pour
favoriser : le développement du secteur privé,
l'éclosion d'une masse critique d'entrepreneurs, la création
d'emplois durables et la réalisation d'une croissance forte et soutenue
dans le temps. La méthode utilisée est celle de l'arbre de
diagnostic de la croissance proposé par Hausman, Rodrik et Velasco
(2005). Pour établir le caractère actif (ou majeur) des
contraintes, chaque contrainte a été soumise à la
série des quatre (04) tests proposés par Hausmann, Klinger et
Wagner dans leur manuel de diagnostic de la croissance. L'analyse approfondie
des contraintes potentielles a permis de faire ressortir celles qui ont un
impact déterminant sur le niveau de l'investissement privé et de
la croissance économique. Il s'agit : de la défaillance de
la coordination dans la formation ; du déficit en infrastructures
d'énergie électrique ; du déficit en infrastructures
routières dans les zones rurales ; de la corruption le long des
principaux corridors commerciaux ; du déficit en infrastructures de
transport ferroviaire ; de l'inadéquation de l'environnement des
affaires.
Aussi, les Nations Unies dans leur 3è Rapport mondial
des sur la mise en valeur des ressources en eau ont-elles rédigé
un article sur « l'eau dans un monde qui change ». Dans ce
document, il a été rappelé que : les investissements
dans l'eau potable et l'assainissement contribuent à la croissance
économique et la pauvreté reste élevée en Afrique
subsaharienne. Ainsi, près de 50 % de la population vit en dessous du
seuil de pauvreté absolue d'1,25 USD. De même, Il existe une
relation forte entre les investissements dans l'eau et la croissance. Par
ailleurs, il est financièrement difficile pour les ménages
d'investir dans l'amélioration de leur accès à
l'assainissement. Selon le type d'opération, chaque dollar investi dans
l'amélioration de l'approvisionnement en eau et de l'assainissement a
en moyenne un gain de rendement de 4 USD à 12 USD. Près d'un
dixième de la morbidité mondiale pourrait être
évité par une amélioration de l'approvisionnement en eau,
de l'assainissement, de l'hygiène et de la gestion des ressources en
eau. L'hydroélectricité fournit environ 20% de
l'électricité mondiale, une part qui est restée stable
depuis les années 90.
Parmi ces rares études, on peut aussi
énumérer celui de Kane (2009). Cet auteur analyse
l'intensité énergétique du PIB dans la zone UEMOA en
utilisant les données de panels hétérogènes non
stationnaires et les tests de cointégration basés sur les
données de panel. Il met en évidence un modèle
économétrique en prenant en compte quatre (04) variables :
l'investissement, la structure productive, le PIB par tête, et le taux
d'urbanisation. Les résultats de sa modélisation
révèlent que l'intensité
énergétique42(*) du PIB au sein de l'UEMOA dépend largement du
niveau d'investissement, de la structure des économies et du taux
d'urbanisation. Il montre également que la consommation d'énergie
est dominée par le secteur industriel.
Au Nigéria, ce sont les travaux d'Akinlo (2009) qui ont
été les premiers à s'intéresser à cette
problématique. En effet, pour faire ressortir le lien entre la
consommation d'électricité et la croissance du PIB, l'auteur
décompose les séries sur la consommation
d'électricité et le taux de croissance réelle en utilisant
le filtre de Hodrick-PrescottEn appliquant ce filtre, il parvient à
décomposer chaque série en sa composante saisonnière,
cyclique et sa tendance. Les résultats des estimations montrent qu'il y
a cointégration entre la tendance et les composantes cycliques des deux
(02) séries, ce qui semble suggérer que la causalité de
Granger est probablement liée au cycle économique. L'auteur
suggère donc d'investir davantage dans le secteur de
l'électricité afin de réduire l'inefficacité dans
la fourniture et dans l'utilisation de l'électricité pour
stimuler la croissance économique au Nigéria.
2.2.Méthodologie de l'étude et
Présentations des données
2.2.1.
Méthodologie
L'analyse des investissements dans les secteurs de
l'énergie et de l'eau débutera par une analyse descriptive de
l'évolution des investissements dans les secteurs l'énergie et de
l'eau, et la croissance économique au Bénin. Ensuite, nous
ferons une analyse de causalité au sens de Granger et l'étude de
la stationnarité des variables. Pour finir, nous procéderons
à l'élaboration d'un modèle économétrique
pour appréhender l'impact de l'investissement dans les secteurs de
l'énergie et de l'eau sur la croissance économique..
2.2.1.1. Analyse
descriptive
Avec le logiciel Excel nous analyseronsl'évolution des
séries :
· des investissements dans les secteurs de l'Energie et
de l'Eau par rapport au secteur productifs ;
· des investissements dans les secteurs de l'Energie et
de l'Eau par rapport aux investissements publics en général.
2.2.1.2. Analyse de
causalité au sens de Granger
En économétrie, la causalité entre deux
(02) chroniques est généralement étudiée en termes
d'amélioration de la prévision selon la caractérisation de
Granger, ou en termes d'analyse impulsionnelle, selon les principes de Sims. Au
sens de Granger, une série « cause » une autre série si
la connaissance du passé de la première améliore la
prévision de la seconde. Selon Sims, une série peut être
reconnue comme causale pour une autre série, si les innovations de la
première contribuent à la variance d'erreur de prévision
de la seconde. Entre ces deux (02) principaux modes de caractérisation
statistique de la causalité, l'approche de Granger est certainement
celle qui a eu le plus d'échos chez les économètres ; elle
sera donc retenue dans le cadre de notre recherche.
Le fondement de la définition de Granger est la
relation dynamique entre les variables. Comme indiqué ci-dessus, elle
est énoncée en termes d'amélioration de la
prédictibilité d'une variable. Chez Granger, la succession
temporelle est centrale et on ne peut discuter de la causalité sans
prendre en considération le temps. On peut formaliser la
causalité au sens de Granger comme suit : si l'on note par 
 et
et 
 deux (02) séries stationnaires ; en effectuant la
régression linéaire de
deux (02) séries stationnaires ; en effectuant la
régression linéaire de 
 sur les valeurs passées
sur les valeurs passées
 , s < t, et sur les valeurs passées
, s < t, et sur les valeurs passées
 , s < t ; si l'on obtient des coefficients significatifs, alors la
connaissance de leurs valeurs peut améliorer la révision de
, s < t ; si l'on obtient des coefficients significatifs, alors la
connaissance de leurs valeurs peut améliorer la révision de 
 : on dit que
: on dit que 
 cause
cause 
 unidirectionnellement. Il y a causalité instantanée
lorsque la valeur courante
unidirectionnellement. Il y a causalité instantanée
lorsque la valeur courante 
 apparaît comme une variable explicative supplémentaire
dans la régression précédente.
apparaît comme une variable explicative supplémentaire
dans la régression précédente.
Une version du test de Granger issue directement de la
représentation autorégressive précédente, propose
d'estimer par la méthode des moindres carrés les deux
équations suivantes :

 (1)
(1)

 (2)
(2)
Où 
 représente le produit intérieur brut au temps t et
représente le produit intérieur brut au temps t et 
 les dépenses d'investissements publics dans le secteur de
l'énergie au temps t.
les dépenses d'investissements publics dans le secteur de
l'énergie au temps t.
En utilisant cette représentation autorégressive
(équations (1) et (2)), 
 ne cause pas
ne cause pas 
 au sens de Granger si i =0 ;
au sens de Granger si i =0 ; 
 ne cause pas
ne cause pas 
 si
si 
 =0
=0
2.2.1.3. Analyse de
stationnarité des variables
Les caractéristiques stochastiques d'une série
chronologique ne peuvent être observées que si elle stationnaire
c'est-à-dire lorsque son espérance mathématique, sa
variance sont des constantes finies et que sa covariance est une fonction finie
indépendante du facteur temporel.
Pour ce faire, il est nécessaire d'étudier la
stationnarité des différentes séries à travers
l'étude des fonctions d'autocorrélation et des tests de racine
unitaire. Les fonctions d'autocorrélation permettront de
détecter une éventuelle tendance ou une saisonnalité dans
le processus stochastique. En ce qui concerne les tests de racine unitaire, ils
renseigneront sur le type de non stationnarité de la série qui
peut être de type déterministe TS ( Trend Stationnary )
ou de type aléatoire DS (Differency Stationnary ). Quelque soit
leurs natures, les séries sont stationnarisées par écart
à la tendance et par le filtre aux différences dont le nombre
permet de déterminer l'ordre d'intégration de la variable
(Bourbonnais, 2005).
Pour étudier la stationnarité des variables nous
avons utilisé le test de Dickey-Fuller Augmenté (ADF).
2.2.1.4. Le modèle
économétrique
Nous allons nous inspirer du modèle de Solow tel que
spécifié par Mankiw, Romer &Weil (1992). Dans ce
modèle, le capital humain est traité comme facteur de production
additionnel au capital physique, à la population, et à la
technologie comme dans l'équation ci-dessous :
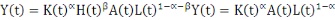
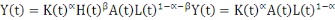 (1)
(1)
Y, K, H, A et L représentant respectivement le niveau
de la production, le capital physique, le capital humain, la technologie et la
force de travail.
En dissociant le capital privé du capital public, nous
obtenons la fonction de production définie par l'équation (2)
ci-après :
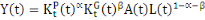
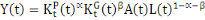 (2)
(2)
Dans cette équation nous avons fait une distinction
entre le capital privé 
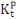 et le capital public
et le capital public
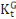 . Les fonctions d'accumulation du capital privé et du capital
public sont données par les équations 3 et 4
respectivement :
. Les fonctions d'accumulation du capital privé et du capital
public sont données par les équations 3 et 4
respectivement :
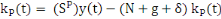
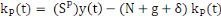 (3)
(3)
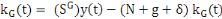
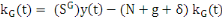 (4)
(4)
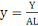
 ,
, 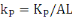
 ,
, 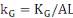
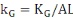 représentant respectivement la production, le capital physique
et le capital humain par unité de travail effectif.
représentant respectivement la production, le capital physique
et le capital humain par unité de travail effectif. 
 et
et 
 sont les taux de croissance de la population et de la technologie. Nous
avons supposé que le capital privé et le capital public se
déprécient au même taux.
sont les taux de croissance de la population et de la technologie. Nous
avons supposé que le capital privé et le capital public se
déprécient au même taux. 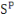
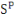 et
et 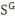
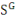 sont les parts de la production investies dans le capital privé
et dans le capital public. En combinant la fonction de production et les
équations d'accumulation, on a :
sont les parts de la production investies dans le capital privé
et dans le capital public. En combinant la fonction de production et les
équations d'accumulation, on a :
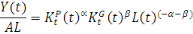

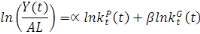
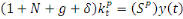
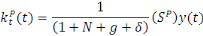
De même
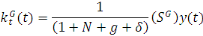
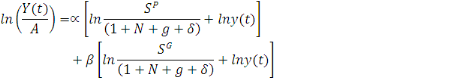
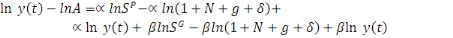


Posons 
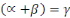 , on a :
, on a :
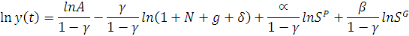
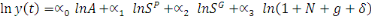
Or 
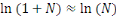
Ainsi 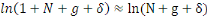

Alors
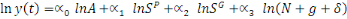
Comme nous sommes dans un modèle de Solow, A(t)
étant exogène, le capital ne se déprécie pas 
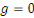 (
( 
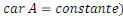 .
.
De plus, on considère le fait que dans la
réalité, la population ne croît pas à un taux
constant et on obtient l'équation 5 ci-après :
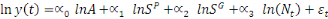
 (5)
(5)
L'équation 5 montre que le PIB par tête
dépend à chaque période de la technologie, de
l'investissement privé, de l'investissement public et de la croissance
démographique. L'équation à estimer peut alors se
présenter de la manière suivante:
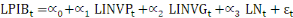
 (6)
(6)
Avec « L » désignant le logarithme
de la variable concerné ; PIB le Produit Intérieur Brut par
tête,
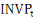 la formation brut de capital fixe du secteur privé en
pourcentage du PIB,
la formation brut de capital fixe du secteur privé en
pourcentage du PIB, 
 la formation brut de capital fixe du secteur public en pourcentage du
PIB, et
la formation brut de capital fixe du secteur public en pourcentage du
PIB, et 
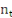 le taux de croissance de la population.
le taux de croissance de la population.
En considérant que l'investissement privé et
l'investissement public dans l'équation 6 sont des variables
endogènes, on peut également définir deux équations
d'investissement.
En 2001, Kamgnia & Touna Mama ont défini une
fonction d'investissement pour le Cameroun où la variable
dépendante, l'investissement privé, dépend du PIB
réel, du crédit au secteur privé, de l'investissement
public, du taux de change, du déficit budgétaire, et de la dette
extérieure. Cette analyse ne fait cependant pas de distinction entre les
secteurs (transport, énergie, télécommunication),
et ne prend pas en compte l'impact de la maintenance. En s'inspirant de ce
travail, nous définissons deux fonctions d'investissement telle que
spécifiées dans les équations 7 et 8 ci-après :

 (7)
(7)

 (8)
(8)
En effet, l'investissement Privé est influencé
par la production de l'année antérieure, le crédit
à l'économie, l'investissement public, la dette extérieure
et les recettes fiscales.
De même, l'action gouvernementale en investissement est
soumise à des pressions sociales liées à la demande en
énergie et en eau ; ici respectivement matérialisée
par la consommation en énergie de la SBEE et la vente d'eau de la SONEB.
CRED représente le crédit au secteur
privé en pourcentage du PIB, TAXE représente le pourcentage des
recettes fiscales dans le PIB. DET représente la dette extérieure
en pourcentage du revenu national, CONS désigne la consommation en
énergie ou en eau. Sur la base des équations 6, 7 et 8, nous
définissons un système :
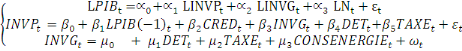
(9)
2.2.2. Présentation
des données
2.2.2.1. Description des
variables
§ Le Produit Intérieur Brut
Le Produit Intérieur Brut est l'indicateur
économique principal qui mesure la production économique
réalisée à l'intérieur d'un pays en une
année donnée. Il reflète l'activité
économique interne d'un pays. Le Produit Intérieur Brut
divisé par la population est appelé le PIB par habitant. Il
mesure le niveau de vie et, de façon approximative, celui du pouvoir
d'achat. Dans le cadre cette étude, le Produit Intérieur Brut
par habitant est désigné par la variable PIB_TETE
ou par sa valeur loguée libellée
LPIB.
§ La Formation Brute de Capital Fixe
La Formation Brute de Capital Fixe est
l'agrégat qui mesure en comptabilité nationale l'investissement
en capital fixe des différents agents économiques
résidents. Elle est mise en pourcentage du PIB et représente la
variable INVG
§ Le Crédit à l'économie
Le Crédit à l'économie est
l'ensemble des ressources financières mise à disposition du
secteur privé, sous forme de prêt. Il est mis en pourcentage du
PIB et représente la variable CRED.
§ Le Revenu National Brut Disponible
Le Revenu National Brut Disponible (RNBD) est
l'ensemble des revenus perçus par les différents secteurs
institutionnels, utilisés pour la consommation et l'épargne.
§ Encours
L'encours est le solde comptable d'un compte d'épargne,
de prêt, de stock, après comptabilisation des entrées et
sorties. C'est la situation de la dette extérieure. Il est mis en
pourcentage du RNBD et représente la variable DET.
§ Les Recettes Fiscales
Les Recettes Fiscales constituent l'ensemble des
impôts et taxes perçus par l'Etat. Elle est mise en pourcentage du
PIB et représente la variable TAXE
§ La Consommation totale
d'électricité
La Consommation totale d'électricité
est la quantité totale d'énergie électrique en
kwh vendue par la SBEE. Elle représente la variable
CONSENERGIE.
§ Les Ventes d'eau de la SONEB
Les ventes d'eau de la SONEB sont la quantité
totale d'eau potable en 
 vendue par la SONEB à la population. Elle représente la
variable VENTE_EAU.
vendue par la SONEB à la population. Elle représente la
variable VENTE_EAU.
§ L'Investissement Public
Le Programme d'Investissement Public est l'ensemble des
dépenses d'investissements de l'Etat pour un secteur au cours d'une
année. Il représente la variable INVG.
§ L'Investissement Privé
L'Investissement Privé est l'ensemble des
dépenses d'investissements effectuées par le secteur privé
sur une période donnée. Il est mis en pourcentage du PIB et
représente la variable INVP.
§ Le Taux de croissance démographique
Le taux de croissance démographique est
l'évolution de la population d'un pays d'une année sur l'autre.
Il permet de voir la progression annuelle de la population en prenant en compte
les mouvements migratoires et la croissance naturelle. Il représente le
capital humain par la variable N.
§ Le Secteur Productif
Le Secteur Productif est l'ensemble des
dépenses d'investissements de l'Etat dans les secteurs
générateurs de revenu à savoir :le Rural,
l'Industrie, l'Artisanat, l'Eau, l'Electricité, les Infrastructures, le
Commerce, le Service et le Tourisme. Il est mis en pourcentage du PIB et
représente la variable SECTEUR PRODUCTIF.
Tableau n°1 :
Présentation des variables
|
N°
|
Variable
|
Unité de valeur
|
Effet attendu sur la croissance économique
|
|
1
|
Produit Intérieur Brut (PIB ou PIB_TETE)
|
ratio
|
Positif
|
|
2
|
Formation Brute de Capital Fixe (INVG)
|
Milliers de FCFA
|
Positif
|
|
3
|
Crédit à l'économie (CRED)
|
Milliers de FCFA
|
Positif
|
|
4
|
Revenu National Brut Disponible (RNBD)
|
Milliers de FCFA
|
Positif
|
|
5
|
Encours (DET)
|
Milliers de FCFA
|
Positif
|
|
6
|
Recettes Fiscales (TAXE)
|
Milliers de FCFA
|
Négatif
|
|
7
|
Consommation totale d'électricité (CONSENERGIE)
|
1000 kwh
|
Positif
|
|
8
|
Ventes d'eau de la SONEB (VENTE_EAU)
|
|
Positif
|
|
9
|
Investissement Public (INVP)
|
Milliers de FCFA
|
Positif
|
|
10
|
Taux de croissance de l'économie (N)
|
%
|
Positif
|
|
11
|
Secteur Productif
|
Milliers de FCFA
|
Positif
|
2.2.2.2. Source des
données
Les données utilisées ont été pour
la plupart collectées à la Direction de la Prévision et de
la Conjoncture de la Direction Générale de l'Analyse Economique
(DPC/DGAE) du Ministère de l'Economie, des Finances et des Programmes de
Dénationalisation (MEFPD) et à l'Institut National de la
Statistique et de l'Analyse Economique (INSAE) du Ministère du
Développement de l'Analyse Economique et de la Prospective (MDAEP). Ceci
à l'exception de la Consommation d'électricité, de la
Vente d'eau potable, des Dépenses d'Investissements Publics dans le
domaine de l'eau et de l'énergie, qui ont été
collectées auprès des Services Statistiques (SS) de la
Société Béninoise de l'Energie Electrique (SBEE), de la
Société Nationale des Eaux du Bénin. Les données
recueillies couvrent la période de 1982 à 2013. Toutefois, il
convient de notifier que nous avons eu recourt à des techniques
d'extrapolation, afin de compléter la série de certaines
variables.
CHAPITRE 2:
ANALYSE DESCRIPTIVE ET ECONOMETRIQUE DES
INVESTISSEMENTS PUBLICS DANS LES SECTEURS DE L'ENERGIE ET DE L'EAU, ET LA
CROISSANCE ECONOMIQUE AU BENIN
CHAPITRE 2: ANALYSE DESCRIPTIVE ET
ECONOMETRIQUE DES INVESTISSEMENTS PUBLICS DANS LES SECTEURS DE L'ENERGIE ET DE
L'EAU, ET LA CROISSANCE ECONOMIQUEAU BENIN
1. ANALYSE DESCRIPTIVE DES
INVESTISSEMENTS DANS LES SECTEURS DE L'ENERGIE ET DE L'EAU, ET LA CROISSANCE
ECONOMIQUE AU BENIN
L'analyse descriptive se fera respectivement par le
biais : d'un graphique en aires empilées pour observer la relation
entre les investissements publics dans le secteur énergie, le secteur
eau et le secteur productif ; et d'un histogramme empilé pour
comparer les investissements publics dans les secteurs énergie et eau
et l'ensemble des dépenses d'investissements de l'Etat.
1.1. Analyse de l'évolution
des dépenses d'investissements publics dans les secteurs de
l'énergie et de l'eau par rapport au Secteur Productif
De 1982 à 2000, la part des investissements publics
dans les secteurs énergie et eau, dans les investissements du secteur
productif a une tendance globalement haussière ; avec sa plus
grande valeurs atteinte de 89.707.230FCFAen l'an 2000.De 2002 à 2004,
cette performance a régressé jusqu'à 81.928.169 FCFA en
2004. De 2006 à 2008, la part des investissements publics dans les
secteurs énergie et eau, dans les investissements du secteur productif
s'est accrue jusqu'à atteindre la valeur maximale de 118.409.677 FCFA.De
2009 à 2013, cette proportion a repris une tendance baissière.
Toutefois, il convient de remarquer que, à partir de
2001, les investissements dans le secteur de l'énergie, sont plus
importants que ceux du secteur de l'eau. En particulier, les investissements
publics dans le domaine de l'énergie semblent représenter le
double des investissements publics dans le domaine de l'eau.
Graphique n°1 : Evolution des dépenses
d'investissements publics dans les secteurs de l'énergie et de l'eau
par rapport au Secteur Productif

Source : DPP/MERPMEDER et
DPP/MEFPD
1.2. Analyse de l'évolution
des dépenses d'investissements publics dans les secteurs de
l'énergie et de l'eau par rapport aux dépenses d'investissements
nationales
De 1982 à 1994, les dépenses d'investissement
publiques nationales ont augmenté progressivement, pendant que les
investissements publics dans les secteurs eau et énergie sont quasi
inexistantes. Mais en 1995 et 1996, les dépenses d'investissement
publiques nationales ont chuté, tandis que les investissements publics
dans les secteurs eau et énergie sont demeurés stables. A partir
de 1997, les dépenses d'investissement publiques nationales et les
investissements publics dans les secteurs eau et énergie se sont accrus
jusqu'à atteindre leur valeur maximale respective en 2009 pour commencer
par décroître de 2010 à 2011, avant de reprendre leur
ascension en 2012.
Graphique n°2 : Evolution des dépenses
d'investissements publics dans les secteurs de l'énergie et de l'eau
par rapport aux dépenses d'investissements nationales
Source : DPP/MERPMEDER et 
DGAE/MEFPD
2. ANALYSE ECONOMETRIQUE DES
INVESTISSEMENTS DANS LES SECTEURS DE L'ENERGIE ET DE L'EAU, ET LA CROISSANCE
ECONOMIQUE AU BENIN
2.1. Analyse de causalité
entre investissement et croissance
2.1.1. Analyse de causalité
entre les investissements publics, dans les secteurs de l'énergie et de
l'eau, et la croissance économique
L'analyse de causalité au sens de Granger,
révèle que :
· Les investissements dans le secteur de l'énergie
(INVG_ ENERGIE) causent le niveau de la croissance économique
(PIB_TETE) ; « P= 0.0028». De même, la
croissance économique (PIB_TETE) cause le niveau des
investissements dans le secteur de l'énergie (INVG_ ENERGIE),
« P= 0.0000» ;
· Les investissements dans le secteur de l'eau
(INVG_EAU) causent le niveau de la croissance économique
(PIB_TETE), « P= 0.0020». De même, la
croissance économique (PIB_TETE) cause le niveau des
investissements dans le secteur de l'eau (INVG_ EAU),
« P= 0.0000» ;
· Les investissements dans le secteur de
l'énergie (INVG_ ENERGIE) causent l'accélération de
la croissance économique (LPIB), « P= 0.0057».
Réciproquement, la croissance économique (LPIB) cause les
investissements dans le secteur de l'énergie (INVG_ ENERGIE),
« P= 0.0000».
Les résultats ci-dessus se justifient par les
théories sur l'utilité des infrastructures publiques pour le
développement en particulier : les travaux de Meade (1952), Wheeler
et Mody (1993), de Romer (1986) et de Barro (1997).
De même, les résultats implicites obtenus sont
les suivants :
· L'accroissement des investissements dans le
secteur de l'énergie (LINVG_ ENERGIE) et l'accroissement des
investissements dans le secteur de l'eau (LINVG_ EAU) causent l'accroissement
de la croissance économique (LPIB), respectivement de
probabilité « P= 0.0000» pour l'énergie et de
« P= 0.0000» pour l'eau. Réciproquement,
l'accroissement de la croissance économique (LPIB) cause
l'accroissement des investissements dans le secteur de l'énergie (LINVG_
ENERGIE) et l'accroissement des investissements dans le secteur de l'eau
(LINVG_ EAU) respectivement de probabilité
« P= 0.0000» pour l'énergie et de
« P= 0.0000» pour l'eau ;
· L'accroissement des investissements dans le secteur de
l'énergie (LINVG_ ENERGIE) et l'accroissement des investissements dans
le secteur de l'eau (LINVG_ EAU) causent le niveau de la croissance
économique (PIB_TETE), respectivement de probabilité
« P= 0.0000» pour l'énergie et de
« P= 0.0000» pour l'eau. Réciproquement, la
croissance économique (PIB_TETE) cause l'accroissement des
investissements dans le secteur de l'énergie (LINVG_ ENERGIE) et
l'accroissement des investissements dans le secteur de l'eau (LINVG_ EAU)
respectivement de probabilité « P= 0.0000» pour
l'énergie et de « P= 0.0000» pour l'eau.
2.1.2. Analyse de causalité
de Granger entre les investissements publics dans le secteur de
l'énergie électrique et dans le secteur de l'eau
Le test de causalité de Granger a permis d'observer
que :
· Les investissements publics dans le secteur de
l'énergie (INVG_ENERGIE) causent le niveau des investissements publics
dans le secteur de l'eau (INVG_EAU), « P=
0,0000 » ;
· Les investissements publics dans le secteur de l'eau
(INVG_ EAU) causent le niveau des investissements publics dans le secteur de
l'énergie (INVG_ ENERGIE), « P= 0,0000 » ;
Ces résultats s'expliquent par le fait que la
construction des barrages hydroélectriques nécessite des cours
d'eau à fort débit d'eau afin de les faire tourner. Il faut donc
aménager ces cours d'eau en investissant. De plus, les pompes qui
assurent le refoulement dans les châteaux d'eau sont alimentées
par l'électricité.
De même, les résultats implicites obtenus sont
les suivants :
· Les investissements publics dans le secteur de
l'énergie (INVG_ENERGIE) causent l'accroissement des investissements
publics dans le secteur de l'eau (LINVG_EAU), « P=
0,0000 » ;
· Les investissements publics dans le secteur de l'eau
(INVG_ EAU) causent l'accroissement des investissements publics dans le secteur
de l'énergie (LINVG_ ENERGIE), « P=
0,0000 » ;
· L'accroissement des investissements dans le secteur de
l'énergie (LINVG_ ENERGIE) cause le niveau des investissements publics
dans le secteur de l'eau (INVG_EAU), « P=
0,0000 » ;
· L'accroissement des investissements dans le secteur de
l'énergie (LINVG_ ENERGIE) cause l'accroissement des investissements
publics dans le secteur de l'eau (LINVG_ EAU), « P=
0,0000 » ;
· L'accroissement des investissements dans le secteur de
l'eau(LINVG_ EAU) cause l'accroissement des investissements publics dans le
secteur de l'énergie (LINVG_ ENERGIE), « P= 0,0000 .
2.2. Analyse
économétrique des investissements dans les secteurs de l'Energie
et de l'eau, et croissance économique
2.2.1. Analyse de la stationnarité
des variables
Pour étudier la stationnarité des variables nous
avons utilisé le test de Dickey-Fuller Augmenté (ADF). Les
résultats obtenus sont les suivantes :
Tableau n°2 : Stationnarité des variables
|
N°
|
VARIABLE
|
ADF
|
NIVEAU
D'INTEGRATION
|
|
Prob critique
|
Lag
|
Max lag
|
|
1
|
VENTE_EAU
|
0,0165
|
6
|
7
|
I(0)
|
|
2
|
LINVG
|
0,0357
|
1
|
7
|
I(0)
|
|
3
|
LINVG_EAU
|
0,0001
|
2
|
7
|
I(0)
|
|
4
|
TAXE
|
0,0201
|
0
|
7
|
I(0)
|
|
5
|
LINVG_ENERGIE
|
0,0001
|
4
|
7
|
I(0)
|
|
|
6
|
LINVP
|
0,0002
|
0
|
6
|
I(1)
|
|
7
|
LN
|
0,0001
|
0
|
6
|
I(1)
|
|
8
|
CONSENERGIE
|
0,0003
|
0
|
6
|
I(1)
|
|
9
|
CRED
|
0,0135
|
0
|
6
|
I(1)
|
|
10
|
DET
|
0,0228
|
0
|
6
|
I(1)
|
|
11
|
INVG
|
-
|
0
|
6
|
I(1)
|
|
12
|
INVP
|
0,0003
|
0
|
6
|
I(1)
|
|
13
|
LPIB
|
0,0002
|
0
|
6
|
I(1)
|
|
14
|
INVG_EAU
|
0,0004
|
3
|
4
|
I(1)
|
|
15
|
INVG_ENERGIE
|
0,0001
|
1
|
4
|
I(1)
|
Source : Nous même
Le tableau ci-dessus indique que les variables VENTE_EAU,
LINVG, LINV LN G_EAU, TAXE et LINVG_ENERGIE sont stationnaires à niveau.
Tandis que les variables : LINVP, LN, CONSENERGIE, CRED, DET, INVG, INVP,
LPIB, INVG_EAU et INVG_ENERGIE sont stationnaires en première
différence. Dans la suite du travail, toutes les variables ont
été rendues stationnaires au regard de la méthodologie
retenue.
2.2.2. Estimation du
modèle
L'estimation du système 9 par les Moindres
Carrés Ordinaires (MCO) pose un problème
d'endogéneité des variables. En effet, une des conditions pour
l'estimation par les MCO est que toutes les variables explicatives soient
exogènes, c'est-à-dire qu'elles ne soient pas
corrélées avec le terme d'erreur. Si cette condition est
violée, les estimateurs des MCO sont biaisés et ne sont plus
convergents. Pour notre étude (système 9), la variable
LINVP qui est une variable explicative pour l'équation du LPIB
(1ière équation), se retrouve comme variable
expliquée par d'autres variables au niveau de la seconde
équation ; sous la forme INVP. De même, la variable INVG qui
est une variable explicative dans la première et la deuxième
équation, constitue une variable expliquée par d'autres variables
au niveau de la troisième équation. De plus, la variable LPIB qui
est expliquée dans la première équation, explique à
son tour la variable INVP dans l'équation suivante. Pour
remédier à ce problème, il est conseillé d'utiliser
la méthode des variables instrumentales qui consiste à trouver
des variables qui sont fortement corrélée avec les variables
explicatives endogènes (INVP, INVG et LPIB) mais qui ne sont pas
corrélée au terme d'erreur.
Dans notre système, seules les variables : LN,
CRED, DET, TAXE, CONS et VENTE_EAU sont purement exogènes. Par contre,
les variables INVP, LINVP, INVG et LPIB sont source
d'endogénéité. Quant aux autres variables, les valeurs
retardées ont été utilisées comme des instruments
conformément à la méthode proposée par Arellano
& Bond (1991).
Par ailleurs, une des conditions pour utiliser la
méthode des variables instrumentales est que le nombre d'instruments
soit au moins égal au nombre de variables endogènes dans chaque
équation (Johnston & Dinardo, 1997). Les variables
exogènes au sens strict peuvent être utilisées comme des
instruments pour elles-mêmes.
Dans le cadre des systèmes d'équations, trois
(03) principales méthodes permettent l'usage des instruments. La
première est la Méthode des Doubles Moindres Carrés en
Système (MDMCS) qui est la version système des doubles moindres
carrés appliqués à une seule équation. Cette
méthode est appropriée lorsque certaines variables explicatives
sont corrélées au terme d'erreur et qu'il
n'existe pas de problème
d'hétéroscédasticité ou de corrélation
contemporaine entre les résidus. La deuxième est la
méthode des triples moindres carrés est la version doubles des
moindres carrées des modèles SUR (Seemingly Unrelated
Regression). Les modèles SUR sont des régressions
multivariées qui prennent en compte
l'hétéroscédasticité et la corrélation
contemporaine des erreurs entre les équations. Cette technique est donc
appropriée lorsque les variables explicatives sont
corrélées au terme d'erreur et qu'il y a à la fois
hétéroscédasticité et autocorrélation entre
les erreurs contemporaines des équations. La troisième est la
Méthode des Moments Généralisés (MMG). Elle permet
d'obtenir des estimateurs robustes puisqu'elle ne requiert pas d'information
sur la distribution exacte des erreurs. Cette méthode est donc robuste
même lorsque l'hétéroscédasticité et
l'autocorrélation sont de forme inconnue. Cette méthode apparait
donc être la plus appropriée pour l'utilisation des variables
instrumentales, et c'est elle qui a été retenue pour les
estimations de la présente étude.
De façon empirique, nous ferons trois (03) estimations
avec le système d'équation 9 :
§ la première serait avec la variable INVG, afin
d'apprécier l'effet des investissements publics gouvernementales de
façon globale ;
§ la deuxième serait avec la variable INVG_EAU,
afin d'apprécier l'effet des investissements publics dans le secteur de
l'eau ;
§ la troisième serait avec la variable
INVG_ENERGIE, afin d'apprécier l'effet des investissements publics dans
le secteur de l'énergie.
2.2.3. Résultats,
limites et suggestions
2.2.2.1. Estimation du modèle avec les dépenses
d'investissements publics gouvernementales globales (INVG)
2.2.2.1.1. Résultats
de l'estimation du modèle avec les dépenses d'investissements
publics gouvernementales globales
Le système d'équations estimé est
présenté dans le tableau suivant :
Tableau n°3 : Estimation du modèle avec les
dépenses d'investissements publics gouvernementales globales (INVG)
|
System: SYST1 (dépenses d'investissements publics
gouvernementales globales)
|
|
Estimation Method: Generalized Method of Moments
|
|
Included observations: 31
|
|
Var endogène
|
Var exogène
|
Coefficient
|
Std. Error
|
|
LPIB
|
C(1)
|
12.53050
|
0.132221
|
|
LINVP
|
0.058838
|
0.015027
|
|
LINVG
|
0.280288
|
0.016902
|
|
LN
|
0.096343
|
0.054199
|
|
Adjusted R-squared
|
0.904002
|
|
Durbin-Watson stat
|
1.055643
|
|
INVP
|
C(5)
|
4.385246
|
0.897401
|
|
LPIB(-1)
|
-0.366396
|
0.078247
|
|
CRED
|
0.121815
|
0.011153
|
|
INVG
|
0.390505
|
0.373874
|
|
DET
|
0.040047
|
0.004077
|
|
TAXE
|
-5.243205
|
0.420268
|
|
Adjusted R-squared
|
0.722956
|
|
Durbin-Watson stat
|
1.291036
|
|
INVG
|
C(11)
|
-0.055147
|
0.007176
|
|
TAXE
|
0.456286
|
0.054111
|
|
DET
|
0.000815
|
0.000504
|
|
CONSENERGIE(-1)
|
0.471431
|
0.017973
|
|
VENTE_EAU(-1)
|
0.024623
|
0.002707
|
|
Adjusted R-squared
|
0.882518
|
|
Durbin-Watson stat
|
1.172121
|
|
|
Determinant residual covariance
|
1.32E-12
|
|
|
J-statistic
|
0.259817
|
Source : Nous même
2.2.2.1.2. Test de
normalité des résidus de Cholesky (Lutkepohl) de l'estimation du
modèle avec les dépenses d'investissements publics
gouvernementales globales
Afin de nous assurer que les termes d'erreur sont normaux,
nous allons procéder au test de normalité des résidus. Il
en ressort que :
la probabilité « joint Skewness »
est égale à 0,1119 >0,05 ; le coefficient
d'asymétrie des résidus n'est pas celui d'une loi
normale ;
la probabilité « joint Kurtosis »
est égale à 0,8158 >0,05 ; le coefficient d'aplatissement
n'est pas celui de la loi centrée réduite ;
la probabilité « joint
Jarque-Berra » est égale à 0,3271 >0,05 ; les
résidus sont donc normaux.
2.2.2.1.3. Commentaires de
l'estimation du modèle avec les dépenses d'investissements
publics gouvernementales globales
L'équation du LPIB est globalement significative avec
le 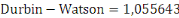
 et le
et le 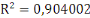
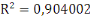 .Cette valeur du
.Cette valeur du 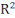
 stipule que les variables dans leur ensemble contribue à
expliquer plus de 90% des variations du Produit Intérieur Brut par
tête. De façon individuelle, les variables impactent
différemment sur le PIB par tête.
stipule que les variables dans leur ensemble contribue à
expliquer plus de 90% des variations du Produit Intérieur Brut par
tête. De façon individuelle, les variables impactent
différemment sur le PIB par tête.
Ainsi, un accroissement de 1% de l'Investissement Privé
(INVP) entraine un accroissement de 0,06% de la croissance économique.
Une augmentation de 1% de l'Investissement Public Global (INVG) entraine une
augmentation de 0,28% de la croissance économique. Par contre, le taux
de croissance de la population a un impact positif non significatif sur la
croissance économique au seuil de 5%.
En ce qui concerne l'équation de l'Investissement
Privé (INVP), elle est globalement significative avec le 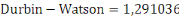
 et le
et le 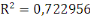
 .Cette valeur du
.Cette valeur du 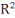
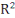 stipule que les variables dans leur ensemble contribue à
expliquer plus de 72% des variations de l'Investissement Privé (INVP).
Ainsi, une augmentation de 1 point du Produit Intérieur Brut par
tête (LPIB) de l'année t-1 et des recettes fiscales
(TAXE) cause la diminution de l'Investissement Privé (INVP)
respectivement de 0,37 point et de 5,24 %. Une augmentation de 1% du
Crédit à l'Economie et de la Dette Extérieure favorise
l'augmentation de l'Investissement Privé (INVP) respectivement de 0,12
point et de 0,04 point. Cependant, l'Investissement Public Global (INVG) a un
impact positif non significatif sur l'Investissement Privé (INVP).
stipule que les variables dans leur ensemble contribue à
expliquer plus de 72% des variations de l'Investissement Privé (INVP).
Ainsi, une augmentation de 1 point du Produit Intérieur Brut par
tête (LPIB) de l'année t-1 et des recettes fiscales
(TAXE) cause la diminution de l'Investissement Privé (INVP)
respectivement de 0,37 point et de 5,24 %. Une augmentation de 1% du
Crédit à l'Economie et de la Dette Extérieure favorise
l'augmentation de l'Investissement Privé (INVP) respectivement de 0,12
point et de 0,04 point. Cependant, l'Investissement Public Global (INVG) a un
impact positif non significatif sur l'Investissement Privé (INVP).
Quant à l'équation de l'Investissement Public
Global (INVG) elle est globalement significative avec le 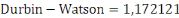
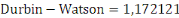 et le
et le 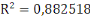
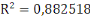 .Cette valeur du
.Cette valeur du 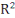
 stipule que les variables dans leur ensemble contribue à
expliquer plus de 88% des variations d de l'Investissement Privé
(INVP).
stipule que les variables dans leur ensemble contribue à
expliquer plus de 88% des variations d de l'Investissement Privé
(INVP).
De façon particulière, les variables Recettes
fiscales (TAXE), Consommation de l'énergie électrique
(CONSENERGIE) et Consommation de l'Eau (VENTE_EAU(-1) ) ont un effet
positif sur l'Investissement Public Global (INVG) dans des proportions
différentes. Ainsi, un accroissement de 1% de chacune de ces variables
entraine respectivement l'accroissement de l'Investissement Public Global
(INVG) de 0,46 point, de 0,47 point et de 0,02 point. La pression sociale
liée au besoin en énergie a un effet plus important sur
l'investissement public que celle de l'eau.
2.2.2.2. Estimation du modèle avec les dépenses
d'investissements publics dans le secteur de l'eau (INVG_EAU)
2.2.2.2.1. Résultats
de l'estimation du modèle avec les dépenses d'investissements
publics dans le secteur de l'eau
Le système d'équations estimé est
présenté dans le tableau le suivant :
Tableau n°4 : Estimation du modèle avec les
dépenses d'investissements publics dans le secteur de l'eau
(INVG_EAU)
|
System: SYST2 (dépenses d'investissements publics
secteur eau)
|
|
Estimation Method: Generalized Method of Moments
|
|
Included observations: 31
|
|
Var endogène
|
Var exogène
|
Coefficient
|
Std. Error
|
|
LPIB
|
C(1)
|
11.95342
|
0.111139
|
|
LINVP
|
0.042907
|
0.007184
|
|
LINVG_EAU
|
0.065111
|
0.005886
|
|
LN
|
0.160893
|
0.065109
|
|
Adjusted R-squared
|
0.936582
|
|
Durbin-Watson stat
|
0.468798
|
|
INVP
|
C(5)
|
1.889943
|
0.312125
|
|
LPIB(-1)
|
-0.151185
|
0.026651
|
|
CRED
|
0.138374
|
0.005155
|
|
LINVG_EAU
|
-1.619628
|
0.200913
|
|
DET
|
0.026751
|
0.003458
|
|
TAXE
|
-4.141386
|
0.282805
|
|
Adjusted R-squared
|
0.806297
|
|
Durbin-Watson stat
|
1.734317
|
|
INVG_EAU
|
C(11)
|
-0.098959
|
0.013780
|
|
TAXE
|
0.082155
|
0.178161
|
|
DET
|
-0.007364
|
0.000392
|
|
VENTE_EAU(-1)
|
0.036366
|
0.003599
|
|
Adjusted R-squared
|
0.504682
|
|
Durbin-Watson stat
|
0.837783
|
|
|
Determinant residual covariance
|
8.46E-13
|
|
|
J-statistic
|
0.241671
|
Source : Nous même
2.2.2.2.2. Test de
normalité des résidus de (Doornik-Hansen) de l'estimation du
modèle avec les dépenses d'investissements publics dans le
secteur de l'eau
Pour nous assurer de la qualité du modèle, nous
faire recourt au test de normalité des résidus. Il en
ressort que :
la probabilité « joint Skewness »
est égale à 0,0003< 0,05 ; le coefficient
d'asymétrie des résidus est celui d'une loi normale ;
la probabilité « joint Kurtosis »
est égale à 0,4473 >0,05 ; le coefficient d'aplatissement
n'est pas celui de la loi centrée réduite ;
la probabilité « joint
Jarque-Berra » est égale à 0,6666> 0,05 ; les
résidus sont donc normaux
2.2.2.2.3. Commentaires de
l'estimation du modèle avec les dépenses d'investissements
publics dans le secteur de l'eau
L'équation du Produit Intérieur Brut (LPIB) est
globalement significatif avec le 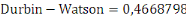
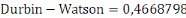 et le
et le 
 . Ainsi, les variables dans leur ensemble contribue à expliquer
environ 94% des variations du Produit Intérieur Brut béninois.
Les variables de cette équation contribuent toutes positivement et
significativement à l'évolution de la variable endogène.
En effet, une augmentation de 1% des variables Investissement Privé
(LINVP), Investissement public dans le secteur Eau (LINVG_EAU) et Taux de
croissance de la population (LN) entraine respectivement l'accroissement du
Produit Intérieur Brut (LPIB) de 0,04%, de 0,07% et de 0,16%.
. Ainsi, les variables dans leur ensemble contribue à expliquer
environ 94% des variations du Produit Intérieur Brut béninois.
Les variables de cette équation contribuent toutes positivement et
significativement à l'évolution de la variable endogène.
En effet, une augmentation de 1% des variables Investissement Privé
(LINVP), Investissement public dans le secteur Eau (LINVG_EAU) et Taux de
croissance de la population (LN) entraine respectivement l'accroissement du
Produit Intérieur Brut (LPIB) de 0,04%, de 0,07% et de 0,16%.
L'équation de l'Investissement Privé (INVP) est
aussi globalement significatif avec le 
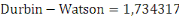 et le
et le 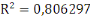
 . Les variables exogènes de cette équation, dans leur
ensemble, permettent d'expliquer environ 81% des variations du Produit
Intérieur Brut béninois. De plus, un accroissement de 1% du
Produit Intérieur Brut (LPIB) de l'année t-1, de l'Investissement
Public en Eau (LINVG_EAU) et des Recettes Fiscales (TAXE) cause la diminution
de l'Investissement Privé (INVP) respectivement de 0,15 point, de 1,62
point et de 4,14 point.
. Les variables exogènes de cette équation, dans leur
ensemble, permettent d'expliquer environ 81% des variations du Produit
Intérieur Brut béninois. De plus, un accroissement de 1% du
Produit Intérieur Brut (LPIB) de l'année t-1, de l'Investissement
Public en Eau (LINVG_EAU) et des Recettes Fiscales (TAXE) cause la diminution
de l'Investissement Privé (INVP) respectivement de 0,15 point, de 1,62
point et de 4,14 point.
De même, l'équation de l'Investissement Public en
Eau (INVG_EAU) est globalement peu significatif avec le 
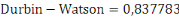 et le
et le 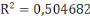
 . Une augmentation de 1% des Recettes fiscales (TAXE) et de la
Consommation en Eau (VENTE_EAU) induit respectivement une augmentation de 0,08
point et de 0,04 point de l'Investissement Public en Eau (INVG_EAU). Par
contre un accroissement de 1% de la Dette extérieure (DETTE) entraine
une diminution de 0,007 point de l'Investissement Public en Eau (INVG_EAU).
L'effet de l'eau sur l'eau est beaucoup plus important que l'effet de l'eau sur
le global.
. Une augmentation de 1% des Recettes fiscales (TAXE) et de la
Consommation en Eau (VENTE_EAU) induit respectivement une augmentation de 0,08
point et de 0,04 point de l'Investissement Public en Eau (INVG_EAU). Par
contre un accroissement de 1% de la Dette extérieure (DETTE) entraine
une diminution de 0,007 point de l'Investissement Public en Eau (INVG_EAU).
L'effet de l'eau sur l'eau est beaucoup plus important que l'effet de l'eau sur
le global.
2.2.2.3. Estimation du
modèle avec les dépenses d'investissements publics dans le
secteur de l'énergie (INVG_ENERGIE)
2.2.2.3.1. Résultats
de l'estimation du modèle avec les dépenses d'investissements
publics dans le secteur de l'énergie
Le
système d'équations estimé est présenté dans
le tableau le suivant :
Tableau n°5 : Estimation
du modèle avec les dépenses d'investissements publics dans le
secteur de l'énergie (INVG_ENERGIE)
|
System: SYST3 (dépenses d'investissements publics
secteur énergie)
|
|
Estimation Method: Generalized Method of Moments
|
|
Included observations: 31
|
|
Var endogène
|
Var exogène
|
Coefficient
|
Std. Error
|
|
LPIB
|
C(1)
|
11.88070
|
0.032370
|
|
LINVP
|
-0.016299
|
0.003327
|
|
LINVG_ENERGIE
|
0.024937
|
0.000603
|
|
LN
|
-0.012690
|
0.025063
|
|
Adjusted R-squared
|
0.960679
|
|
|
Durbin-Watson stat
|
0.714530
|
|
|
INVP
|
C(5)
|
2.585659
|
0.191796
|
|
LPIB(-1)
|
-0.211374
|
0.016068
|
|
CRED
|
0.204610
|
0.003405
|
|
LINVG_ENERGIE
|
-2.477182
|
0.166818
|
|
DET
|
0.027955
|
0.002022
|
|
TAXE
|
-4.914213
|
0.306585
|
|
Adjusted R-squared
|
0.656991
|
|
|
Durbin-Watson stat
|
1.152078
|
|
|
LINVG_ENERGIE
|
C(11)
|
-0.020320
|
0.001031
|
|
TAXE
|
0.285237
|
0.042793
|
|
DET
|
-0.008447
|
0.000346
|
|
CONSENERGIE(-1)
|
0.417217
|
0.013152
|
|
Adjusted R-squared
|
0.585209
|
|
|
Durbin-Watson stat
|
0.735471
|
|
|
|
Determinant residual covariance
|
3.72E-13
|
|
|
J-statistic
|
0.214709
|
Source : Nous même
Nous obtenons un effet négatif de l'investissement sur
la croissance économique.Ce qui n'est pas conforme à la
théorie économique. Pour tenir compte du fait que dans la
réalité économique les chocs que subissent certaines
variables n'ont pas d'effets instantanés sur la croissance
économique dont notamment l'investissement (Catherine B. et Olivier
B., 1998), nous introduisons dans le modèle en lieu et place de la
variable LINVP, sa valeur retardée de deux années ; à
savoir LINVP(-2).
Les résultats obtenus avec la variable LINVP(-2), se
présentent ci-contre :
|
System: SYST31 (dépenses d'investissements publics
secteur énergie)
|
|
Estimation Method: Generalized Method of Moments
|
|
Included observations: 31
|
|
Var endogène
|
Var exogène
|
Coefficient
|
Std. Error
|
|
LPIB
|
C(1)
|
11.96806
|
0.076172
|
|
LINVP (-2)
|
0.056300
|
0.023105
|
|
LINVG_ENERGIE
|
0.021425
|
0.00109
|
|
LN
|
0.033996
|
0.037252
|
|
Adjusted R-squared
|
0.960679
|
|
|
Durbin-Watson stat
|
0.622164
|
|
|
INVP
|
C(5)
|
2.461003
|
0.282366
|
|
LPIB(-1)
|
-0.200745
|
0.023731
|
|
CRED
|
0.203724
|
0.004610
|
|
LINVG_ENERGIE
|
-2.554160
|
0.177535
|
|
DET
|
0.027227
|
0.002511
|
|
TAXE
|
-4.803093
|
0.407870
|
|
Adjusted R-squared
|
0.633848
|
|
|
Durbin-Watson stat
|
1.113533
|
|
|
LINVG_ENERGIE
|
C(11)
|
-0.020996
|
0.001031
|
|
TAXE
|
0.318050
|
0.038263
|
|
DET
|
-0.008144
|
0.000985
|
|
CONSENERGIE(-1)
|
0.416044
|
0.027967
|
|
Adjusted R-squared
|
0.584657
|
|
|
Durbin-Watson stat
|
0.732457
|
|
|
|
Determinant residual covariance
|
3.86E-13
|
|
|
J-statistic
|
0.218840
|
Nous nous apercevons que le remplacement de la variable LINVP
par la variable LINVP(-2) améliore non seulement la
significativité des coefficients mais aussi l'effet de l'investissement
sur la croissance ; qui est désormais positif .
2.2.2.3.2. Test de
normalité des résidus de Cholesky (Lutkepohl ) de l'estimation du
modèle avec les dépenses d'investissements publics dans le
secteur de l'énergie
Avant d'interpréter les résultats du
modèle, il est important de vérifier la normalité des
résidus. Le test de normalité des résidus montre
que :
la probabilité « joint Skewness »
est égale à 0.1908>0,05 ; le coefficient
d'asymétrie des résidus n'est pas celui d'une loi
normale ;
la probabilité « joint Kurtosis »
est égale à 0.0919 >0,05 ; le coefficient
d'aplatissement n'est pas celui de la loi centrée
réduite ;
la probabilité « joint
Jarque-Berra » est égale à 0.0825 >0,05 ;
les résidus sont donc normaux.
2.2.2.3.3. Commentaires de
l'estimation du modèle avec les dépenses d'investissements
publics dans le secteur de l'énergie
L'équation décrivant le PIB (LPIB) par
tête est globalement significative avec le 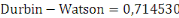
 et le
et le 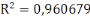
 .Cette valeur du
.Cette valeur du 
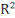 stipule que les variables dans leur ensemble contribue à
expliquer plus de 96% des variations du LPIB.
stipule que les variables dans leur ensemble contribue à
expliquer plus de 96% des variations du LPIB.
En effet, un accroissement de 1% de l'Investissement
Privé (INVP) et du taux de croissance de la population (LN) fait chuter
le PIB par tête, respectivement de 0,02% et de 0,01%. Toutefois, une
augmentation de 1% de l'Investissement Public en Energie (INVG_ENERGIE)
entraine une augmentation de 0,25% de la croissance économique.
Pour l'équation de l'Investissement Privé
(INVP), le 
 et le
et le 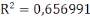
 ; le modèle est globalement significatif. La valeur du
; le modèle est globalement significatif. La valeur du 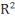
 renseigne que les variables dans leur ensemble contribue à des
variations de l'Investissement Privé (INVP) à près de 66%.
Une hausse de 1 % du Produit Intérieur Brut par tête (LPIB), de
l'Investissement Public en Energie (LINVG_ENERGIE) et des recettes fiscales
(TAXE) entraine la baisse de l'Investissement Privé (INVP)
respectivement de 0,21 point, de 2,48 point et de 4,91 point. Par contre une
hausse de 1% du Crédit à l'Economie et de la Dette
Extérieure entraine l'augmentation l'Investissement Privé (INVP)
respectivement de 0,20 point et de 0,02 point.
renseigne que les variables dans leur ensemble contribue à des
variations de l'Investissement Privé (INVP) à près de 66%.
Une hausse de 1 % du Produit Intérieur Brut par tête (LPIB), de
l'Investissement Public en Energie (LINVG_ENERGIE) et des recettes fiscales
(TAXE) entraine la baisse de l'Investissement Privé (INVP)
respectivement de 0,21 point, de 2,48 point et de 4,91 point. Par contre une
hausse de 1% du Crédit à l'Economie et de la Dette
Extérieure entraine l'augmentation l'Investissement Privé (INVP)
respectivement de 0,20 point et de 0,02 point.
En ce qui concerne l'équation de l'Investissement
Public en Energie (INVG_ENERGIE) elle est globalement significative avec le

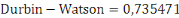 et le
et le 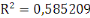
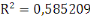 . Alors les variables dans leur ensemble contribue à expliquer
environ 59% des variations de l'Investissement Public en Energie
(INVG_ENERGIE). L'effet de l'énergie sur l'énergie est moins
important que l'effet de l'énergie sur le global car l'énergie
joue un rôle sur l'eau, l'énergie et l'économie.
. Alors les variables dans leur ensemble contribue à expliquer
environ 59% des variations de l'Investissement Public en Energie
(INVG_ENERGIE). L'effet de l'énergie sur l'énergie est moins
important que l'effet de l'énergie sur le global car l'énergie
joue un rôle sur l'eau, l'énergie et l'économie.
Individuellement, les variables Recettes fiscales (TAXE) et
Consommation de l'énergie électrique (CONSENERGIE) ont un effet
positif sur l'Investissement Public en Energie (INVG_ENERGIE). En effet, un
accroissement de 1% de chacune de ces variables entraine respectivement
l'accroissement de l'Investissement Public en Energie (INVG_ENERGIE) de 0,28
point et de 0,41 point. Cependant, une augmentation de 1% de la Dette
Extérieure (DETTE) cause la diminution de l'Investissement Public en
Energie (INVG_ENERGIE) de 0,008 point.
2.2.2.4. Limites et suggestions de l'étude
Dans le cadre de cette étude les limites que nous avons
observées sont les suivantes :
· la variable VENTE_EAU utilisée pour quantifier
la consommation d'eau potable de la population est réduite à la
quantité d'eau vendue par la SONEB et ne comporte pas l'eau fournie par
les forages cnstruites par la DG Eau ;
· la variable CONSENERGIE utilisée pour quantifier
la consommation d'énergie électrique n'est pas
représentative de la quantité réelle d'énergie
consommée par la population ;
· les problèmes internes à la gestion des
secteurs de l'énergie et de l'eau ne sont pas examinés.
Ces deux variables ne captent pas l'effet de la pression
sociale dans son entièreté.
Eu égard à tout ce qui précède
nous suggérons que:
o le Ministère en charge de l'énergie et de
l'eau en collaboration avec l'INSAE initie des études afin de quantifier
les consommations réelles de la population en énergie
électrique et en eau potable ;
o la gestion au sein des secteurs de l'énergie et de
l'eau soit assainie ;
o L'Etat investisse d'avantage dans les secteurs de
l'énergie et de l'eau pour réduire la dépendance
énergétique du Bénin vis-à-vis de
l'extérieur et , à long terme , le rendre autonome.
CONCLUSION
Leprésent travail de recherche a permis
d'étudier les Investissements dans les secteursde l'Energie et de l'Eau,
et la croissance économique au Bénin. Cette étude a
révélé que de 1960 à 2009, la croissance
économique et les investissements publics dans les secteurs de l'Energie
et de l'Eau ont une évolution tendanciellement ascendante. Elle a aussi
montré que : la croissance économique cause l'investissement
dans le secteur de l'Eau ; l'Investissement dans le secteur de l'Energie
électrique cause l'Investissement dans le secteur de l'Eau ; et
l'Investissement dans le secteur de l'Eau cause dans le secteur de l'Energie
électrique. L'analyse économétrique nous a permis de
spécifier trois (03) modèles dans les trois (03) situations
ci-après : le secteur public global ; le secteur Eau et le
secteur Energie électrique. Les résultats de ces estimations
témoignent que : les investissements dans les secteurs Energie et
Eau favorise légèrement la croissance économique.
Somme toute, cette étude a permis de confirmer la
première hypothèse « il existe une faible
corrélation entre les investissements et la croissance
économique ». Par contre, en ce qui concerne la
deuxième hypothèse « il existe une causalité
réciproque entre l'investissement et la croissance
économique », elle n'est pas confirmée. En effet
seul la croissance économique cause les investissements uniquement dans
le secteur de l'eau. La troisième hypothèse
« l'investissement a un effet positif sur la croissance
économique » est aussi confirmé dans le secteur de
l'eau, le secteur de l'énergie et dans le public en
général.
REFERENCES BIBLIOGRAPHIQUES
AARON, H. et MCGUIRE, M. (1970), « Public goods and
Income Distribution », Economica, vol. 38 No.6. pp. 907
AFLALION, Florin et PONCET, Fabrice (1981), Le
monétarisme
AGBODAN, Mavor Michel et AMOUSSOUGA, ýFulbert Gero
(1995), Les facteurs de performance de l'entreprise - Page 207
AGÉNOR, P. R. et MORENO-DODSON, B. (2006), Public
Infrastructure and Growth: New Channels and Policy Implications. The World Bank
Policy Research Working Paper 4064
AGENOR, P-R. (2000) «L'ECONOMIE DE L'AJUSTEMENT ET DE LA
CROISSANCE», MIMEO BANQUE MONDIALE, WASHINGTON, 2000, 848P
ANAGO, Gildas (2011), Consommation d'électricité
et croissance économique en Côte d'Ivoire, p37-49
ASCHAUER, David Alan (1990), Highway capacity and economic
growth
BARRO, R. (1990), « Government spending in a simple model
of endogeneous growth », the Journal of Political Economy, Vol.98,
N°5 pp. S103-S125
BARRO, R.J (1991), Economic Growth in a Cross Section of
Countries. Quartely Journa l of Economies Volume 2, N°106, May. PP
407-444
BARRO, R.J : Economic Growth in a Cross Section of Countries.
Quartely Journal 1 of Economies Volume 2, N°106, May. p 407-444.
BEN, S. et HASSAD, M., (2006), « Efficience du
financement des services publics et croissance économique dans les pays
en développement : Analyse en coupe transversale », Journées
scientifiques du réseau « analyse économique et
développement », 37p
CHAMAK, Alain et FROMAGE, ýCéline (2006), Le
capital humain - Page 21
DGAE, (2007), BIPEN : Impact de la crise de
l'énergie électrique sur l'économie béninoise,
p52-70
DICKEY, D.A. et FULLER, W.A. (1981). Likelihood Ratio
Statistics for Autoregressive Time Series With a Unit Root, Econometrica, 49,
1057-1072
DOMAR (1947), « Expansion et Emploi »
DOUCOURE, F. B. (2007), « Méthode
économétrique : cours et travaux pratiques »
DUKES, Paul (2011), Minutes to Midnight: History and the
Anthropocene Era from 1763 - Page 11
EASTERLY, W. et Rebelo, S. (1993), Fiscal Policy and Economie
Growth
ENGLE, R.F., et GRANGER, C.W.J. (1987), Co-integration
and Error Correction : Représentation, Estimation and Testing,
Econometrica, 55, 251-276
FRIEDMAN, Milton, the American Ecomic Review (1968), The role
of monetary policy
Global Water Partnership Central Africa (2010), Etude national
sur le financement du secteur de l'eau, rapport Cameroun, p33-87
HARROD (1948), « Théorèmes Dynamiques
Fondamentaux »
HAUSEN, Alvin (1965), The dollar and the international
monetary system
HIRSCHMAN, Albert (1958), The strategy of economic
development
JORLAND, Gérard (1995), Paradoxes du capital - Page
40
Journal of Monetary Economies, Empirical Investigation»,
n° 32, décembre, p. 417
KEPTER , Jan Horst et SCHULKE, Christian (2008), Investir dans
le secteur de l'énergie : une équation de gouvernance,
p122-160
KOOPMANS (1965), On the concept of optimal economic growth
KRAFT, J. et KRAFT, A. (1978), Note and comments: on the
relationship between Energy and GNP
KÜMMEL, Reiner (2011), The Second Law of Economics:
Energy, Entropy, and the Origins of Wealth, Page 180
LeCAILLON, Jean-Didier , Le PAGE, ýJean-Marie et
ý OTTAVJ, Christian (2008), Économie contemporaine: Analyse et
diagnostics - Page 242
LORRAINE, Eden et McMILLAN, L. (1991), Local public goods shup
revised
LUCAS, Robert (1972), journal of economy, Expectations and the
neutrality of money
MANKIW, ROMER et WEIL (1992), A contribution as the empirics
of economic growth
MARKANDYA, Anil et ý PEDROSO-GALINATO, Suzette (2005),
How Substitutable is Natural Capital? - Page 12
MUSGRAVE, Richard (1959), The theory of public finance
MUTH, John (1961), Rational Expectations and the Theory of
Price Movements
ONGONO, Patrice (2012), investissement en Infrastructures
publiques et performances économiques au Cameroun, p18-30
PERROUX, F. (1965), La pensée économique de
Joseph Schumpeter. Les dynamiques du capitalisme, Librairie Droz,
Genève, p 1935
PHILLIPS, A.W.H. (1958), Relationship between unemployment and
the rate of change of money wages in the UK 1891-1957
Pierre Maillet (1967), La croissance économique,
Quarterly Journal of Economics, (1956) « A contribution
to the thery of economic growth»
RAMSEY (1928), Mathematical theory of saving (economic
journal), Rapport sur le développement dans le monde 1994: une
infrastructure pour le développement 1984
REYNIER, Audrey (2008), Progrès technique et innovation
- Page 26
ROMER, Paul (1987), ``Crazy explanations for the productivity
slowdown'', NBER Macroéconomic Annual
SAMUELSON, Paul (1954), The pure theorh of public
expenditure
SARGENT, Thomas et WALLACE, Neil, Rational expectations and
the theory of economic policy.
SPENCER, R. and YOKE, W., The crowding out of private
expenditure by fiscal policy actions
SWAN (1956), Economic growth and capital accumulation
WHEELER, D et Mody, A. (1992), International investissement
location decisions: the case of US firms
ANNEXES
ANNEXE 1 : Séries des variables
|
Année
|
PIB
|
INVP
|
INVG
|
INVG_EAU
|
INVG_ENERGIE
|
|
1982
|
98277,7858
|
25417,6213
|
12246,2956
|
203,614002
|
0,023886959
|
|
1983
|
99638,1502
|
27431,3713
|
13179,091
|
241,155141
|
0,042344234
|
|
1984
|
101017,345
|
29604,6636
|
14182,9369
|
285,617891
|
0,075063308
|
|
1985
|
102415,63
|
31950,1384
|
15263,2455
|
338,278419
|
0,133064167
|
|
1986
|
103833,271
|
34481,437
|
16425,8406
|
400,648183
|
0,235881857
|
|
1987
|
105270,534
|
37213,2815
|
17676,9902
|
474,517312
|
0,418146013
|
|
1988
|
106727,693
|
40161,5607
|
19023,4393
|
562,005992
|
0,741244324
|
|
1989
|
108205,021
|
46612,3578
|
18399,6267
|
665,625315
|
1,313998295
|
|
1990
|
109702,798
|
50976,1022
|
18274,8203
|
788,349352
|
2,329314996
|
|
1991
|
110860,995
|
52073,0092
|
22927,0178
|
933,700517
|
4,129159353
|
|
1992
|
110550,351
|
45733,4235
|
27752,5678
|
1105,85067
|
7,319730047
|
|
1993
|
113369,21
|
53560,7938
|
31256,7734
|
1309,74083
|
12,97563096
|
|
1994
|
112071,698
|
53969,4395
|
32164,3006
|
1551,22306
|
23,00180441
|
|
1995
|
115166,326
|
65533,7988
|
27782,9367
|
1837,22834
|
40,77512745
|
|
1996
|
116394,503
|
70694,2059
|
26588,5894
|
2175,96558
|
72,28176489
|
|
1997
|
119203,038
|
74072,0417
|
30481,7141
|
2577,15717
|
128,1333465
|
|
1998
|
120008,069
|
72590,1763
|
40327,88
|
3052,31809
|
227,1410295
|
|
1999
|
122398,78
|
76362,3408
|
45024,5697
|
3615,08634
|
402,6512122
|
|
2000
|
124244,001
|
79731,1941
|
50759,7346
|
4281,61447
|
713,7768063
|
|
2001
|
127759,501
|
87372,9567
|
54862,1556
|
5071,03308
|
1265,306831
|
|
2002
|
129089,283
|
84173,3453
|
60337,5289
|
6006
|
2243
|
|
2003
|
129734,113
|
88126,1897
|
62165,1194
|
7465,153
|
1273
|
|
2004
|
129398,906
|
93136,2115
|
64669,663
|
6123,382
|
2317,727
|
|
2005
|
128719,858
|
99351,3033
|
67922,9237
|
10050,322
|
620,203
|
|
2006
|
129122,195
|
107597,462
|
73560,5264
|
13126,864
|
3599,649
|
|
2007
|
130590,631
|
96484,8774
|
89473,7971
|
30210,368
|
10658,15086
|
|
2008
|
132543,61
|
99030,1902
|
75956,9226
|
28278,9877
|
35575,524
|
|
2009
|
131475,103
|
101115,409
|
83370,931
|
36097,284
|
48895,495
|
|
2010
|
130254,369
|
107947,505
|
84958,2878
|
23603,367
|
37527,366
|
|
2011
|
130164,707
|
188697,312
|
90960,1834
|
19576,054
|
20727,5275
|
|
2012
|
132526,972
|
203647,146
|
97888,5834
|
16775,5289
|
19688,84843
|
|
2013
|
133379,218
|
219781,402
|
105344,717
|
19515,5361
|
21597,20439
|
ANNEXE 2 : Séries des variables (suite)
|
Année
|
CRED
|
TAXE
|
DET
|
CONSENERGIE
|
VENTE_EAU
|
SP
|
|
1982
|
77136,5463
|
10008,0989
|
-11920,348
|
109304,57
|
9898886,61
|
16436,7575
|
|
1983
|
84928,0337
|
10195,2383
|
-9394,9668
|
117527,672
|
10294554,1
|
18071,132
|
|
1984
|
93506,5316
|
10385,8769
|
-7404,5990
|
126369,407
|
10706036,7
|
19868,0191
|
|
1985
|
102951,535
|
10580,0803
|
-5835,9
|
135876,316
|
11133966,7
|
21843,578
|
|
1986
|
113350,569
|
10777,9151
|
-5531
|
146098,439
|
11579001,4
|
24015,5749
|
|
1987
|
124800
|
10979,4491
|
-15438
|
157089,584
|
12041824,6
|
26403,5425
|
|
1988
|
137840
|
10167,5229
|
7011
|
168907,605
|
12523147,2
|
29028,9554
|
|
1989
|
103428,7
|
7396,25887
|
-16782,8
|
181614,708
|
13023708,7
|
31915,424
|
|
1990
|
102070,9
|
7420,72473
|
11168,3
|
195277,781
|
13544278,2
|
30897,733
|
|
1991
|
85853,6
|
8424,29309
|
-559
|
209968,742
|
14085655,2
|
29156,068
|
|
1992
|
69394
|
9604,44812
|
13341
|
225764,919
|
14648671,6
|
28069,947
|
|
1993
|
67720,6
|
10169,8994
|
321350
|
242749,461
|
15234192,3
|
34530,897
|
|
1994
|
76021,5
|
10232,1388
|
628430
|
261011,767
|
15843116,7
|
68970,972
|
|
1995
|
81447,1
|
11359,4385
|
703070
|
280647,967
|
16476380,4
|
76842,126
|
|
1996
|
102395,9
|
11806,5905
|
757160
|
301761,42
|
17134956,3
|
66879,122
|
|
1997
|
71700
|
11994,8637
|
748220
|
324463,261
|
17819856
|
57188,011
|
|
1998
|
100130
|
12607,8851
|
771500
|
348872,987
|
18532131,8
|
58344,864
|
|
1999
|
154637
|
13105,3387
|
847700
|
375119,082
|
19272877,8
|
63020,778
|
|
2000
|
194030
|
13937,5095
|
910470
|
403339,7
|
20043232,2
|
89707,23
|
|
2001
|
192837
|
13496,2777
|
974366,787
|
460448,63
|
20844378,3
|
97219,422
|
|
2002
|
222228
|
14436,0678
|
941640
|
551544,91
|
21677547
|
71664,629
|
|
2003
|
293849
|
14858,7906
|
832600
|
572832,3
|
22544018,2
|
80029,659
|
|
2004
|
312052
|
14551,313
|
826250
|
606411,4
|
23445123
|
81928,169
|
|
2005
|
375102
|
14530,2944
|
919452,832
|
641025,8
|
25689675
|
44790,6918
|
|
2006
|
415821
|
15400,7688
|
519765
|
669801,2
|
24899032
|
66804,09
|
|
2007
|
527641
|
16928,1245
|
299733
|
726466,774
|
24256657
|
88692,626
|
|
2008
|
624476
|
17241,6023
|
415090
|
798232,612
|
27882157
|
122237,88
|
|
2009
|
698548
|
16095,2392
|
463310,434
|
843367,389
|
28070545
|
108592,25
|
|
2010
|
757818
|
16181,9874
|
582884,602
|
915930,445
|
28789460
|
63437,6546
|
|
2011
|
844960
|
15544,6384
|
613652,545
|
900744,585
|
31949723
|
97960
|
|
2012
|
924440
|
15531,9367
|
638883,878
|
955864,497
|
32580517
|
107700,566
|
|
2013
|
1022600
|
16278,8186
|
834777,966
|
1021628,68
|
32881269
|
118409,677
|
ANNEXE 3: Test ADF
|
Null Hypothesis: LINVG has a unit root
|
|
|
Exogenous: None
|
|
|
|
Lag Length: 3 (Automatic - based on t-statistic, lagpval=0.1,
maxlag=7)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-2.289360
|
0.0237
|
|
Test critical values:
|
1% level
|
|
-2.650145
|
|
|
5% level
|
|
-1.953381
|
|
|
10% level
|
|
-1.609798
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(LINVG)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/14/15 Time: 10:08
|
|
|
|
Sample (adjusted): 1986 2013
|
|
|
|
Included observations: 28 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
LINVG(-1)
|
-0.014860
|
0.006491
|
-2.289360
|
0.0312
|
|
D(LINVG(-1))
|
0.036379
|
0.182049
|
0.199832
|
0.8433
|
|
D(LINVG(-2))
|
-0.135615
|
0.180223
|
-0.752486
|
0.4591
|
|
D(LINVG(-3))
|
-0.430452
|
0.182206
|
-2.362442
|
0.0266
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.233960
|
Mean dependent var
|
0.027488
|
|
Adjusted R-squared
|
0.138205
|
S.D. dependent var
|
0.097681
|
|
S.E. of regression
|
0.090680
|
Akaike info criterion
|
-1.831401
|
|
Sum squared resid
|
0.197348
|
Schwarz criterion
|
-1.641086
|
|
Log likelihood
|
29.63962
|
Hannan-Quinn criter.
|
-1.773220
|
|
Durbin-Watson stat
|
2.240796
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Null Hypothesis: LINVG has a unit root
|
|
|
Exogenous: None
|
|
|
|
Lag Length: 3 (Automatic - based on t-statistic, lagpval=0.1,
maxlag=7)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-2.289360
|
0.0237
|
|
Test critical values:
|
1% level
|
|
-2.650145
|
|
|
5% level
|
|
-1.953381
|
|
|
10% level
|
|
-1.609798
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(LINVG)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/14/15 Time: 10:11
|
|
|
|
Sample (adjusted): 1986 2013
|
|
|
|
Included observations: 28 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
LINVG(-1)
|
-0.014860
|
0.006491
|
-2.289360
|
0.0312
|
|
D(LINVG(-1))
|
0.036379
|
0.182049
|
0.199832
|
0.8433
|
|
D(LINVG(-2))
|
-0.135615
|
0.180223
|
-0.752486
|
0.4591
|
|
D(LINVG(-3))
|
-0.430452
|
0.182206
|
-2.362442
|
0.0266
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.233960
|
Mean dependent var
|
0.027488
|
|
Adjusted R-squared
|
0.138205
|
S.D. dependent var
|
0.097681
|
|
S.E. of regression
|
0.090680
|
Akaike info criterion
|
-1.831401
|
|
Sum squared resid
|
0.197348
|
Schwarz criterion
|
-1.641086
|
|
Log likelihood
|
29.63962
|
Hannan-Quinn criter.
|
-1.773220
|
|
Durbin-Watson stat
|
2.240796
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Date: 03/14/15 Time: 10:37
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sample: 1982 2013
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Included observations: 32
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Autocorrelation
|
Partial Correlation
|
|
AC
|
PAC
|
Q-Stat
|
Prob
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |******|
|
. |******|
|
1
|
0.816
|
0.816
|
23.385
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |***** |
|
. | . |
|
2
|
0.686
|
0.058
|
40.430
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |***** |
|
. |* . |
|
3
|
0.641
|
0.199
|
55.826
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |**** |
|
. *| . |
|
4
|
0.520
|
-0.195
|
66.339
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |*** |
|
. | . |
|
5
|
0.437
|
0.056
|
74.032
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |*** |
|
. | . |
|
6
|
0.389
|
-0.005
|
80.377
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |*** |
|
. |* . |
|
7
|
0.353
|
0.096
|
85.792
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |**. |
|
. *| . |
|
8
|
0.277
|
-0.146
|
89.272
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |* . |
|
. *| . |
|
9
|
0.176
|
-0.135
|
90.737
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |* . |
|
. | . |
|
10
|
0.108
|
-0.055
|
91.315
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. | . |
|
. | . |
|
11
|
0.043
|
-0.018
|
91.410
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. | . |
|
. | . |
|
12
|
-0.019
|
-0.006
|
91.430
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. *| . |
|
. *| . |
|
13
|
-0.077
|
-0.087
|
91.771
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. *| . |
|
. *| . |
|
14
|
-0.131
|
-0.067
|
92.802
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. *| . |
|
. | . |
|
15
|
-0.180
|
-0.059
|
94.873
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.**| . |
|
. | . |
|
16
|
-0.225
|
-0.005
|
98.323
|
0.000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Null Hypothesis: VENTE_EAU has a unit root
|
|
|
Exogenous: Constant
|
|
|
|
Lag Length: 6 (Automatic - based on SIC, maxlag=7)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-3.503698
|
0.0165
|
|
Test critical values:
|
1% level
|
|
-3.724070
|
|
|
5% level
|
|
-2.986225
|
|
|
10% level
|
|
-2.632604
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(VENTE_EAU)
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/14/15 Time: 10:51
|
|
|
|
Sample (adjusted): 1989 2013
|
|
|
|
Included observations: 25 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
VENTE_EAU(-1)
|
-0.369450
|
0.105446
|
-3.503698
|
0.0027
|
|
D(VENTE_EAU(-1))
|
-0.429563
|
0.176851
|
-2.428958
|
0.0265
|
|
D(VENTE_EAU(-2))
|
-1.315453
|
0.221755
|
-5.932005
|
0.0000
|
|
D(VENTE_EAU(-3))
|
-0.610754
|
0.268575
|
-2.274056
|
0.0362
|
|
D(VENTE_EAU(-4))
|
-1.639922
|
0.363150
|
-4.515820
|
0.0003
|
|
D(VENTE_EAU(-5))
|
-0.850218
|
0.261002
|
-3.257510
|
0.0046
|
|
D(VENTE_EAU(-6))
|
-1.466231
|
0.380437
|
-3.854070
|
0.0013
|
|
C
|
1.286396
|
0.340052
|
3.782936
|
0.0015
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.820861
|
Mean dependent var
|
0.018269
|
|
Adjusted R-squared
|
0.747098
|
S.D. dependent var
|
0.110492
|
|
S.E. of regression
|
0.055566
|
Akaike info criterion
|
-2.688162
|
|
Sum squared resid
|
0.052488
|
Schwarz criterion
|
-2.298122
|
|
Log likelihood
|
41.60203
|
Hannan-Quinn criter.
|
-2.579981
|
|
F-statistic
|
11.12833
|
Durbin-Watson stat
|
1.916537
|
|
Prob(F-statistic)
|
0.000029
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Null Hypothesis: LINVG has a unit root
|
|
|
Exogenous: Constant, Linear Trend
|
|
|
Lag Length: 1 (Automatic - based on SIC, maxlag=7)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-3.728543
|
0.0357
|
|
Test critical values:
|
1% level
|
|
-4.296729
|
|
|
5% level
|
|
-3.568379
|
|
|
10% level
|
|
-3.218382
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(LINVG)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/14/15 Time: 10:57
|
|
|
|
Sample (adjusted): 1984 2013
|
|
|
|
Included observations: 30 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
LINVG(-1)
|
-0.643053
|
0.172468
|
-3.728543
|
0.0009
|
|
D(LINVG(-1))
|
0.427067
|
0.181022
|
2.359199
|
0.0261
|
|
C
|
-2.197424
|
0.598908
|
-3.669049
|
0.0011
|
|
@TREND(1982)
|
0.019574
|
0.005628
|
3.478105
|
0.0018
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.355692
|
Mean dependent var
|
0.027779
|
|
Adjusted R-squared
|
0.281349
|
S.D. dependent var
|
0.094259
|
|
S.E. of regression
|
0.079906
|
Akaike info criterion
|
-2.092361
|
|
Sum squared resid
|
0.166010
|
Schwarz criterion
|
-1.905535
|
|
Log likelihood
|
35.38542
|
Hannan-Quinn criter.
|
-2.032594
|
|
F-statistic
|
4.784460
|
Durbin-Watson stat
|
2.215236
|
|
Prob(F-statistic)
|
0.008735
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Null Hypothesis: LINVG_EAU has a unit root
|
|
|
Exogenous: Constant, Linear Trend
|
|
|
Lag Length: 2 (Automatic - based on SIC, maxlag=7)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-6.251435
|
0.0001
|
|
Test critical values:
|
1% level
|
|
-4.309824
|
|
|
5% level
|
|
-3.574244
|
|
|
10% level
|
|
-3.221728
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(LINVG_EAU)
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/14/15 Time: 10:57
|
|
|
|
Sample (adjusted): 1985 2013
|
|
|
|
Included observations: 29 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
LINVG_EAU(-1)
|
-0.920844
|
0.147301
|
-6.251435
|
0.0000
|
|
D(LINVG_EAU(-1))
|
0.648468
|
0.156140
|
4.153116
|
0.0004
|
|
D(LINVG_EAU(-2))
|
0.981641
|
0.147273
|
6.665442
|
0.0000
|
|
C
|
-7.140680
|
1.162948
|
-6.140152
|
0.0000
|
|
@TREND(1982)
|
0.120287
|
0.020054
|
5.998144
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.697438
|
Mean dependent var
|
0.104160
|
|
Adjusted R-squared
|
0.647011
|
S.D. dependent var
|
0.216535
|
|
S.E. of regression
|
0.128650
|
Akaike info criterion
|
-1.107861
|
|
Sum squared resid
|
0.397218
|
Schwarz criterion
|
-0.872120
|
|
Log likelihood
|
21.06398
|
Hannan-Quinn criter.
|
-1.034030
|
|
F-statistic
|
13.83064
|
Durbin-Watson stat
|
2.181326
|
|
Prob(F-statistic)
|
0.000006
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Null Hypothesis: TAXE has a unit root
|
|
|
Exogenous: None
|
|
|
|
Lag Length: 0 (Automatic - based on SIC, maxlag=7)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-2.355232
|
0.0201
|
|
Test critical values:
|
1% level
|
|
-2.641672
|
|
|
5% level
|
|
-1.952066
|
|
|
10% level
|
|
-1.610400
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(TAXE)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/14/15 Time: 11:02
|
|
|
|
Sample (adjusted): 1983 2013
|
|
|
|
Included observations: 31 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
TAXE(-1)
|
-0.031139
|
0.013221
|
-2.355232
|
0.0252
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.051074
|
Mean dependent var
|
-0.000479
|
|
Adjusted R-squared
|
0.051074
|
S.D. dependent var
|
0.001381
|
|
S.E. of regression
|
0.001345
|
Akaike info criterion
|
-10.35298
|
|
Sum squared resid
|
5.43E-05
|
Schwarz criterion
|
-10.30672
|
|
Log likelihood
|
161.4712
|
Hannan-Quinn criter.
|
-10.33790
|
|
Durbin-Watson stat
|
1.364688
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Null Hypothesis: LINVG_ENERGIE has a unit root
|
|
Exogenous: None
|
|
|
|
Lag Length: 4 (Automatic - based on SIC, maxlag=7)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-4.482267
|
0.0001
|
|
Test critical values:
|
1% level
|
|
-2.653401
|
|
|
5% level
|
|
-1.953858
|
|
|
10% level
|
|
-1.609571
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(LINVG_ENERGIE)
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/14/15 Time: 11:04
|
|
|
|
Sample (adjusted): 1987 2013
|
|
|
|
Included observations: 27 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
LINVG_ENERGIE(-1)
|
-0.085918
|
0.019168
|
-4.482267
|
0.0002
|
|
D(LINVG_ENERGIE(-1))
|
-0.120258
|
0.178441
|
-0.673937
|
0.5074
|
|
D(LINVG_ENERGIE(-2))
|
0.300489
|
0.160607
|
1.870951
|
0.0747
|
|
D(LINVG_ENERGIE(-3))
|
-0.458546
|
0.165237
|
-2.775084
|
0.0110
|
|
D(LINVG_ENERGIE(-4))
|
-0.466936
|
0.190369
|
-2.452799
|
0.0226
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.485638
|
Mean dependent var
|
0.381636
|
|
Adjusted R-squared
|
0.392117
|
S.D. dependent var
|
0.588063
|
|
S.E. of regression
|
0.458494
|
Akaike info criterion
|
1.443838
|
|
Sum squared resid
|
4.624775
|
Schwarz criterion
|
1.683808
|
|
Log likelihood
|
-14.49182
|
Hannan-Quinn criter.
|
1.515194
|
|
Durbin-Watson stat
|
2.064935
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Null Hypothesis: LINVG_EAU has a unit root
|
|
|
Exogenous: None
|
|
|
|
Lag Length: 4 (Automatic - based on SIC, maxlag=7)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-3.433706
|
0.0013
|
|
Test critical values:
|
1% level
|
|
-2.653401
|
|
|
5% level
|
|
-1.953858
|
|
|
10% level
|
|
-1.609571
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(LINVG_EAU)
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/14/15 Time: 11:05
|
|
|
|
Sample (adjusted): 1987 2013
|
|
|
|
Included observations: 27 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
LINVG_EAU(-1)
|
-0.033877
|
0.009866
|
-3.433706
|
0.0024
|
|
D(LINVG_EAU(-1))
|
0.057854
|
0.198032
|
0.292143
|
0.7729
|
|
D(LINVG_EAU(-2))
|
0.547584
|
0.166522
|
3.288365
|
0.0034
|
|
D(LINVG_EAU(-3))
|
-0.633283
|
0.167891
|
-3.771983
|
0.0011
|
|
D(LINVG_EAU(-4))
|
-0.455337
|
0.247754
|
-1.837860
|
0.0796
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.576997
|
Mean dependent var
|
0.102419
|
|
Adjusted R-squared
|
0.500088
|
S.D. dependent var
|
0.224608
|
|
S.E. of regression
|
0.158808
|
Akaike info criterion
|
-0.676671
|
|
Sum squared resid
|
0.554837
|
Schwarz criterion
|
-0.436701
|
|
Log likelihood
|
14.13506
|
Hannan-Quinn criter.
|
-0.605315
|
|
Durbin-Watson stat
|
1.964500
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ANNEXE 4 : Tests de causalité de Granger
|
VAR Granger Causality/Block Exogeneity Wald Tests
|
|
Date: 03/09/16 Time: 14:00
|
|
|
Sample: 1982 2013
|
|
|
|
Included observations: 25
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: LPIB
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_ENERGIE
|
19.95735
|
7
|
0.0057
|
|
INVG_EAU
|
20.90530
|
7
|
0.0039
|
|
|
|
|
|
|
|
|
|
All
|
34.00754
|
14
|
0.0021
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
LPIB
|
97.78135
|
7
|
0.0000
|
|
INVG_EAU
|
801.2399
|
7
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
1636.650
|
14
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_EAU
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
LPIB
|
1040.107
|
7
|
0.0000
|
|
INVG_ENERGIE
|
53599.41
|
7
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
405464.4
|
14
|
0.0000
|
|
VAR Granger Causality/Block Exogeneity Wald Tests
|
|
Date: 03/09/16 Time: 13:39
|
|
|
Sample: 1982 2013
|
|
|
|
Included observations: 25
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: PIB_TETE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_ENERGIE
|
21.74814
|
7
|
0.0028
|
|
INVG_EAU
|
22.63209
|
7
|
0.0020
|
|
|
|
|
|
|
|
|
|
All
|
37.84423
|
14
|
0.0005
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
PIB_TETE
|
97.48514
|
7
|
0.0000
|
|
INVG_EAU
|
747.4835
|
7
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
1631.831
|
14
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_EAU
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
PIB_TETE
|
1165.521
|
7
|
0.0000
|
|
INVG_ENERGIE
|
51038.34
|
7
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
454214.5
|
14
|
0.0000
|
|
|
|
|
|
|
|
|
|
VAR Granger Causality/Block Exogeneity Wald Tests
|
|
Date: 03/09/16 Time: 17:56
|
|
|
Sample: 1982 2013
|
|
|
|
Included observations: 28
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_EAU
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_ENERGIE
|
246946.0
|
4
|
0.0000
|
|
LINVG_EAU
|
53425.97
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
22172.12
|
4
|
0.0000
|
|
LPIB
|
13432.50
|
4
|
0.0000
|
|
PIB_TETE
|
14360.59
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
4.89E+08
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
49592.41
|
4
|
0.0000
|
|
LINVG_EAU
|
25355.92
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
24260.11
|
4
|
0.0000
|
|
LPIB
|
98075.49
|
4
|
0.0000
|
|
PIB_TETE
|
119192.9
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
1.33E+08
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: LINVG_EAU
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
55527.46
|
4
|
0.0000
|
|
INVG_ENERGIE
|
65417.59
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
60905.38
|
4
|
0.0000
|
|
LPIB
|
43828.44
|
4
|
0.0000
|
|
PIB_TETE
|
45705.22
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
1.26E+08
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: LINVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
30181.91
|
4
|
0.0000
|
|
INVG_ENERGIE
|
96028.79
|
4
|
0.0000
|
|
LINVG_EAU
|
21173.25
|
4
|
0.0000
|
|
LPIB
|
42850.84
|
4
|
0.0000
|
|
PIB_TETE
|
51729.93
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
6106794.
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: LPIB
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
429.6642
|
4
|
0.0000
|
|
INVG_ENERGIE
|
369.1419
|
4
|
0.0000
|
|
LINVG_EAU
|
638.2744
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
542.1127
|
4
|
0.0000
|
|
PIB_TETE
|
250.2691
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
4191.993
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: PIB_TETE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
439.5930
|
4
|
0.0000
|
|
INVG_ENERGIE
|
360.8051
|
4
|
0.0000
|
|
LINVG_EAU
|
651.9976
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
540.5400
|
4
|
0.0000
|
|
LPIB
|
370.9961
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
5082.092
|
20
|
0.0000
|
|
Vector Autoregression Estimates
|
|
|
|
|
|
Date: 03/09/16 Time: 17:45
|
|
|
|
|
|
Sample (adjusted): 1986 2013
|
|
|
|
|
|
Included observations: 28 after adjustments
|
|
|
|
|
Standard errors in ( ) & t-statistics in [ ]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
INVG_ENERGIE
|
LINVG_EAU
|
LINVG_ENERGIE
|
LPIB
|
PIB_TETE
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
INVG_EAU(-1)
|
1.119259
|
-7.548870
|
125.3474
|
-3380.591
|
-86.22501
|
-9730268.
|
|
(0.03471)
|
(0.08439)
|
(3.26998)
|
(45.0735)
|
(33.7313)
|
(3745570)
|
|
[ 32.2472]
|
[-89.4559]
|
[ 38.3328]
|
[-75.0018]
|
[-2.55623]
|
[-2.59781]
|
|
|
|
|
|
|
|
|
INVG_EAU(-2)
|
-8.556350
|
15.17003
|
-1272.455
|
5215.429
|
850.3604
|
96768970
|
|
(0.10856)
|
(0.26395)
|
(10.2279)
|
(140.982)
|
(105.506)
|
(1.2E+07)
|
|
[-78.8149]
|
[ 57.4740]
|
[-124.410]
|
[ 36.9936]
|
[ 8.05986]
|
[ 8.25992]
|
|
|
|
|
|
|
|
|
INVG_EAU(-3)
|
3.604295
|
7.754199
|
703.8456
|
4302.769
|
-659.6048
|
-73844302
|
|
(0.08496)
|
(0.20656)
|
(8.00431)
|
(110.332)
|
(82.5680)
|
(9168463)
|
|
[ 42.4232]
|
[ 37.5392]
|
[ 87.9333]
|
[ 38.9985]
|
[-7.98863]
|
[-8.05416]
|
|
|
|
|
|
|
|
|
INVG_EAU(-4)
|
7.706079
|
-15.26753
|
753.7551
|
-5581.114
|
-279.2164
|
-33108752
|
|
(0.09147)
|
(0.22238)
|
(8.61721)
|
(118.780)
|
(88.8903)
|
(9870498)
|
|
[ 84.2508]
|
[-68.6554]
|
[ 87.4709]
|
[-46.9871]
|
[-3.14114]
|
[-3.35431]
|
|
|
|
|
|
|
|
|
INVG_ENERGIE(-1)
|
4.008724
|
-5.010438
|
484.5387
|
-2502.051
|
-235.4617
|
-27050188
|
|
(0.03771)
|
(0.09169)
|
(3.55281)
|
(48.9720)
|
(36.6488)
|
(4069538)
|
|
[ 106.302]
|
[-54.6482]
|
[ 136.382]
|
[-51.0914]
|
[-6.42481]
|
[-6.64699]
|
|
|
|
|
|
|
|
|
INVG_ENERGIE(-2)
|
-7.416046
|
9.352842
|
-857.4442
|
3830.174
|
430.7465
|
49427814
|
|
(0.07164)
|
(0.17417)
|
(6.74916)
|
(93.0305)
|
(69.6206)
|
(7730764)
|
|
[-103.521]
|
[ 53.6990]
|
[-127.045]
|
[ 41.1711]
|
[ 6.18706]
|
[ 6.39365]
|
|
|
|
|
|
|
|
|
INVG_ENERGIE(-3)
|
5.201903
|
-10.47298
|
557.8797
|
-4766.420
|
-223.4408
|
-25984806
|
|
(0.04207)
|
(0.10227)
|
(3.96314)
|
(54.6280)
|
(40.8816)
|
(4539544)
|
|
[ 123.660]
|
[-102.401]
|
[ 140.767]
|
[-87.2523]
|
[-5.46557]
|
[-5.72410]
|
|
|
|
|
|
|
|
|
INVG_ENERGIE(-4)
|
-6.533936
|
10.44506
|
-795.2436
|
3917.134
|
411.0884
|
47136895
|
|
(0.06574)
|
(0.15984)
|
(6.19371)
|
(85.3742)
|
(63.8908)
|
(7094526)
|
|
[-99.3874]
|
[ 65.3481]
|
[-128.395]
|
[ 45.8820]
|
[ 6.43423]
|
[ 6.64412]
|
|
|
|
|
|
|
|
|
LINVG_EAU(-1)
|
-0.000831
|
0.035125
|
-3.544785
|
10.57981
|
4.478161
|
499058.9
|
|
(0.00035)
|
(0.00086)
|
(0.03316)
|
(0.45707)
|
(0.34205)
|
(37982.2)
|
|
[-2.35981]
|
[ 41.0473]
|
[-106.901]
|
[ 23.1470]
|
[ 13.0919]
|
[ 13.1393]
|
|
|
|
|
|
|
|
|
LINVG_EAU(-2)
|
0.046099
|
0.048515
|
10.79319
|
29.75469
|
-10.58201
|
-1190703.
|
|
(0.00121)
|
(0.00294)
|
(0.11403)
|
(1.57176)
|
(1.17625)
|
(130612.)
|
|
[ 38.0882]
|
[ 16.4868]
|
[ 94.6539]
|
[ 18.9308]
|
[-8.99640]
|
[-9.11631]
|
|
|
|
|
|
|
|
|
LINVG_EAU(-3)
|
-0.003052
|
-0.208431
|
-5.421741
|
-90.61683
|
8.321437
|
917850.1
|
|
(0.00090)
|
(0.00220)
|
(0.08508)
|
(1.17273)
|
(0.87763)
|
(97453.3)
|
|
[-3.37924]
|
[-94.9318]
|
[-63.7257]
|
[-77.2697]
|
[ 9.48171]
|
[ 9.41836]
|
|
|
|
|
|
|
|
|
LINVG_EAU(-4)
|
0.001744
|
0.080082
|
5.735815
|
44.21204
|
-7.260576
|
-799947.2
|
|
(0.00051)
|
(0.00124)
|
(0.04787)
|
(0.65986)
|
(0.49382)
|
(54834.1)
|
|
[ 3.43242]
|
[ 64.8229]
|
[ 119.817]
|
[ 67.0019]
|
[-14.7030]
|
[-14.5885]
|
|
|
|
|
|
|
|
|
LINVG_ENERGIE(-1)
|
-0.007126
|
0.008092
|
-0.985313
|
3.545118
|
0.802021
|
91394.74
|
|
(0.00011)
|
(0.00027)
|
(0.01033)
|
(0.14243)
|
(0.10659)
|
(11835.9)
|
|
[-64.9702]
|
[ 30.3452]
|
[-95.3553]
|
[ 24.8901]
|
[ 7.52435]
|
[ 7.72182]
|
|
|
|
|
|
|
|
|
LINVG_ENERGIE(-2)
|
0.006275
|
-0.002369
|
1.894722
|
1.053511
|
-1.951971
|
-218586.0
|
|
(0.00019)
|
(0.00046)
|
(0.01784)
|
(0.24591)
|
(0.18403)
|
(20435.1)
|
|
[ 33.1389]
|
[-5.14641]
|
[ 106.204]
|
[ 4.28410]
|
[-10.6067]
|
[-10.6966]
|
|
|
|
|
|
|
|
|
LINVG_ENERGIE(-3)
|
-0.004039
|
-0.044793
|
-2.362182
|
-20.07406
|
2.582373
|
287617.3
|
|
(0.00025)
|
(0.00060)
|
(0.02344)
|
(0.32314)
|
(0.24182)
|
(26852.5)
|
|
[-16.2326]
|
[-74.0412]
|
[-100.763]
|
[-62.1224]
|
[ 10.6787]
|
[ 10.7110]
|
|
|
|
|
|
|
|
|
LINVG_ENERGIE(-4)
|
-0.006461
|
0.049139
|
-0.273671
|
17.36785
|
-0.094346
|
-8454.654
|
|
(0.00014)
|
(0.00033)
|
(0.01281)
|
(0.17652)
|
(0.13210)
|
(14668.3)
|
|
[-47.5304]
|
[ 148.693]
|
[-21.3709]
|
[ 98.3930]
|
[-0.71422]
|
[-0.57639]
|
|
|
|
|
|
|
|
|
LPIB(-1)
|
0.066640
|
-0.623074
|
8.120464
|
-223.0022
|
4.338246
|
396554.2
|
|
(0.00107)
|
(0.00260)
|
(0.10081)
|
(1.38956)
|
(1.03989)
|
(115471.)
|
|
[ 62.2792]
|
[-239.503]
|
[ 80.5528]
|
[-160.484]
|
[ 4.17182]
|
[ 3.43423]
|
|
|
|
|
|
|
|
|
LPIB(-2)
|
0.100774
|
-0.137504
|
19.14090
|
-36.62380
|
-13.77810
|
-1438286.
|
|
(0.00339)
|
(0.00823)
|
(0.31895)
|
(4.39647)
|
(3.29015)
|
(365343.)
|
|
[ 29.7666]
|
[-16.7056]
|
[ 60.0115]
|
[-8.33028]
|
[-4.18768]
|
[-3.93681]
|
|
|
|
|
|
|
|
|
LPIB(-3)
|
-0.186221
|
0.395220
|
-38.23456
|
121.6921
|
30.82067
|
3562175.
|
|
(0.00207)
|
(0.00504)
|
(0.19546)
|
(2.69421)
|
(2.01625)
|
(223887.)
|
|
[-89.7597]
|
[ 78.3530]
|
[-195.614]
|
[ 45.1680]
|
[ 15.2862]
|
[ 15.9106]
|
|
|
|
|
|
|
|
|
LPIB(-4)
|
0.091630
|
0.506212
|
22.11596
|
220.6689
|
-25.61946
|
-3104818.
|
|
(0.00332)
|
(0.00808)
|
(0.31301)
|
(4.31451)
|
(3.22882)
|
(358532.)
|
|
[ 27.5796]
|
[ 62.6686]
|
[ 70.6562]
|
[ 51.1458]
|
[-7.93463]
|
[-8.65981]
|
|
|
|
|
|
|
|
|
PIB_TETE(-1)
|
-6.57E-07
|
5.65E-06
|
-0.000108
|
0.001994
|
4.10E-06
|
1.257448
|
|
(7.3E-09)
|
(1.8E-08)
|
(6.8E-07)
|
(9.4E-06)
|
(7.1E-06)
|
(0.78422)
|
|
[-90.3465]
|
[ 320.001]
|
[-157.049]
|
[ 211.335]
|
[ 0.58037]
|
[ 1.60344]
|
|
|
|
|
|
|
|
|
PIB_TETE(-2)
|
-6.65E-07
|
1.88E-06
|
-8.99E-05
|
0.000677
|
3.33E-05
|
2.823076
|
|
(2.6E-08)
|
(6.3E-08)
|
(2.5E-06)
|
(3.4E-05)
|
(2.5E-05)
|
(2.80866)
|
|
[-25.5352]
|
[ 29.7624]
|
[-36.6642]
|
[ 20.0251]
|
[ 1.31699]
|
[ 1.00513]
|
|
|
|
|
|
|
|
|
PIB_TETE(-3)
|
1.63E-06
|
-5.53E-06
|
0.000282
|
-0.001951
|
-0.000189
|
-22.30357
|
|
(1.6E-08)
|
(3.8E-08)
|
(1.5E-06)
|
(2.1E-05)
|
(1.5E-05)
|
(1.70714)
|
|
[ 103.010]
|
[-143.710]
|
[ 188.924]
|
[-94.9701]
|
[-12.3210]
|
[-13.0649]
|
|
|
|
|
|
|
|
|
PIB_TETE(-4)
|
-7.55E-07
|
-3.49E-06
|
-0.000141
|
-0.001469
|
0.000161
|
20.28348
|
|
(2.8E-08)
|
(6.9E-08)
|
(2.7E-06)
|
(3.7E-05)
|
(2.8E-05)
|
(3.05676)
|
|
[-26.6704]
|
[-50.6991]
|
[-52.7353]
|
[-39.9339]
|
[ 5.84950]
|
[ 6.63562]
|
|
|
|
|
|
|
|
|
C
|
-0.656353
|
-1.626504
|
-101.3093
|
-901.8811
|
42.98881
|
4752360.
|
|
(0.03602)
|
(0.08757)
|
(3.39339)
|
(46.7745)
|
(35.0043)
|
(3886927)
|
|
[-18.2226]
|
[-18.5735]
|
[-29.8549]
|
[-19.2815]
|
[ 1.22810]
|
[ 1.22265]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
1.000000
|
1.000000
|
1.000000
|
1.000000
|
0.999991
|
0.999992
|
|
Adj. R-squared
|
1.000000
|
1.000000
|
1.000000
|
1.000000
|
0.999921
|
0.999932
|
|
Sum sq. resids
|
1.72E-12
|
1.02E-11
|
1.52E-08
|
2.90E-06
|
1.62E-06
|
20006.27
|
|
S.E. equation
|
7.57E-07
|
1.84E-06
|
7.13E-05
|
0.000983
|
0.000735
|
81.66245
|
|
F-statistic
|
1.47E+08
|
44136716
|
2.49E+08
|
14183802
|
14302.76
|
16447.51
|
|
Log likelihood
|
386.1792
|
361.3035
|
258.9038
|
185.4455
|
193.5618
|
-131.7326
|
|
Akaike AIC
|
-25.79851
|
-24.02168
|
-16.70741
|
-11.46039
|
-12.04013
|
11.19519
|
|
Schwarz SC
|
-24.60904
|
-22.83221
|
-15.51794
|
-10.27093
|
-10.85066
|
12.38466
|
|
Mean dependent
|
0.008464
|
0.006365
|
-5.281414
|
-8.072018
|
11.70167
|
121170.2
|
|
S.D. dependent
|
0.008659
|
0.011524
|
1.060373
|
3.489358
|
0.082923
|
9874.109
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Determinant resid covariance (dof adj.)
|
2.70E-73
|
|
|
|
|
|
Determinant resid covariance
|
4.09E-79
|
|
|
|
|
|
Log likelihood
|
2288.566
|
|
|
|
|
|
Akaike information criterion
|
-152.7547
|
|
|
|
|
|
Schwarz criterion
|
-145.6179
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VAR Granger Causality/Block Exogeneity Wald Tests
|
|
Date: 03/09/16 Time: 17:56
|
|
|
Sample: 1982 2013
|
|
|
|
Included observations: 28
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_EAU
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_ENERGIE
|
246946.0
|
4
|
0.0000
|
|
LINVG_EAU
|
53425.97
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
22172.12
|
4
|
0.0000
|
|
LPIB
|
13432.50
|
4
|
0.0000
|
|
PIB_TETE
|
14360.59
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
4.89E+08
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
49592.41
|
4
|
0.0000
|
|
LINVG_EAU
|
25355.92
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
24260.11
|
4
|
0.0000
|
|
LPIB
|
98075.49
|
4
|
0.0000
|
|
PIB_TETE
|
119192.9
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
1.33E+08
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: LINVG_EAU
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
55527.46
|
4
|
0.0000
|
|
INVG_ENERGIE
|
65417.59
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
60905.38
|
4
|
0.0000
|
|
LPIB
|
43828.44
|
4
|
0.0000
|
|
PIB_TETE
|
45705.22
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
1.26E+08
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: LINVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
30181.91
|
4
|
0.0000
|
|
INVG_ENERGIE
|
96028.79
|
4
|
0.0000
|
|
LINVG_EAU
|
21173.25
|
4
|
0.0000
|
|
LPIB
|
42850.84
|
4
|
0.0000
|
|
PIB_TETE
|
51729.93
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
6106794.
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: LPIB
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
429.6642
|
4
|
0.0000
|
|
INVG_ENERGIE
|
369.1419
|
4
|
0.0000
|
|
LINVG_EAU
|
638.2744
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
542.1127
|
4
|
0.0000
|
|
PIB_TETE
|
250.2691
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
4191.993
|
20
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: PIB_TETE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
INVG_EAU
|
439.5930
|
4
|
0.0000
|
|
INVG_ENERGIE
|
360.8051
|
4
|
0.0000
|
|
LINVG_EAU
|
651.9976
|
4
|
0.0000
|
|
LINVG_ENERGIE
|
540.5400
|
4
|
0.0000
|
|
LPIB
|
370.9961
|
4
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
5082.092
|
20
|
0.0000
|
|
Vector Autoregression Estimates
|
|
|
|
Date: 03/09/16 Time: 18:05
|
|
|
|
Sample (adjusted): 1987 2013
|
|
|
|
Included observations: 27 after adjustments
|
|
|
Standard errors in ( ) & t-statistics in [ ]
|
|
|
|
|
|
|
|
|
|
|
|
|
LINVG_EAU
|
LINVG_ENERGIE
|
INVG_EAU
|
INVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
|
LINVG_EAU(-1)
|
0.249228
|
-15.91418
|
0.001907
|
-0.039946
|
|
(0.57441)
|
(5.25815)
|
(0.00217)
|
(0.01433)
|
|
[ 0.43388]
|
[-3.02658]
|
[ 0.87840]
|
[-2.78752]
|
|
|
|
|
|
|
LINVG_EAU(-2)
|
3.103490
|
-14.81887
|
0.020478
|
-0.041949
|
|
(1.10412)
|
(10.1071)
|
(0.00417)
|
(0.02755)
|
|
[ 2.81082]
|
[-1.46619]
|
[ 4.90642]
|
[-1.52291]
|
|
|
|
|
|
|
LINVG_EAU(-3)
|
-8.137393
|
68.50680
|
-0.036963
|
0.207891
|
|
(4.24502)
|
(38.8588)
|
(0.01605)
|
(0.10590)
|
|
[-1.91693]
|
[ 1.76297]
|
[-2.30351]
|
[ 1.96301]
|
|
|
|
|
|
|
LINVG_EAU(-4)
|
-3.178201
|
31.35771
|
-0.012361
|
0.079624
|
|
(1.75030)
|
(16.0222)
|
(0.00662)
|
(0.04367)
|
|
[-1.81580]
|
[ 1.95714]
|
[-1.86828]
|
[ 1.82347]
|
|
|
|
|
|
|
LINVG_EAU(-5)
|
6.894626
|
-77.09660
|
0.026558
|
-0.216709
|
|
(3.38414)
|
(30.9783)
|
(0.01279)
|
(0.08443)
|
|
[ 2.03733]
|
[-2.48873]
|
[ 2.07610]
|
[-2.56682]
|
|
|
|
|
|
|
LINVG_ENERGIE(-1)
|
-1.590760
|
20.87588
|
-0.008076
|
0.053884
|
|
(0.75041)
|
(6.86925)
|
(0.00284)
|
(0.01872)
|
|
[-2.11985]
|
[ 3.03904]
|
[-2.84708]
|
[ 2.87825]
|
|
|
|
|
|
|
LINVG_ENERGIE(-2)
|
1.246151
|
-20.78323
|
0.003367
|
-0.058182
|
|
(0.80385)
|
(7.35838)
|
(0.00304)
|
(0.02005)
|
|
[ 1.55023]
|
[-2.82443]
|
[ 1.10818]
|
[-2.90122]
|
|
|
|
|
|
|
LINVG_ENERGIE(-3)
|
3.020359
|
-23.39009
|
0.014982
|
-0.068276
|
|
(1.77977)
|
(16.2920)
|
(0.00673)
|
(0.04440)
|
|
[ 1.69705]
|
[-1.43568]
|
[ 2.22701]
|
[-1.53770]
|
|
|
|
|
|
|
LINVG_ENERGIE(-4)
|
-2.039492
|
1.952857
|
-0.013650
|
0.017622
|
|
(1.05242)
|
(9.63382)
|
(0.00398)
|
(0.02626)
|
|
[-1.93791]
|
[ 0.20271]
|
[-3.43111]
|
[ 0.67119]
|
|
|
|
|
|
|
LINVG_ENERGIE(-5)
|
-0.135873
|
24.32515
|
0.003469
|
0.057796
|
|
(0.44014)
|
(4.02902)
|
(0.00166)
|
(0.01098)
|
|
[-0.30870]
|
[ 6.03748]
|
[ 2.08484]
|
[ 5.26346]
|
|
|
|
|
|
|
INVG_EAU(-1)
|
813.0458
|
-5774.726
|
4.361761
|
-16.32337
|
|
(410.579)
|
(3758.43)
|
(1.55200)
|
(10.2430)
|
|
[ 1.98024]
|
[-1.53647]
|
[ 2.81041]
|
[-1.59360]
|
|
|
|
|
|
|
INVG_EAU(-2)
|
-1671.411
|
14820.35
|
-9.175640
|
41.66988
|
|
(684.904)
|
(6269.59)
|
(2.58896)
|
(17.0869)
|
|
[-2.44036]
|
[ 2.36385]
|
[-3.54414]
|
[ 2.43871]
|
|
|
|
|
|
|
INVG_EAU(-3)
|
1612.942
|
-15256.69
|
7.161701
|
-47.06755
|
|
(835.048)
|
(7644.00)
|
(3.15651)
|
(20.8326)
|
|
[ 1.93156]
|
[-1.99590]
|
[ 2.26887]
|
[-2.25932]
|
|
|
|
|
|
|
INVG_EAU(-4)
|
2148.676
|
-16029.00
|
11.96578
|
-45.23051
|
|
(984.380)
|
(9010.99)
|
(3.72099)
|
(24.5581)
|
|
[ 2.18277]
|
[-1.77883]
|
[ 3.21575]
|
[-1.84177]
|
|
|
|
|
|
|
INVG_EAU(-5)
|
-3433.233
|
25553.05
|
-14.77250
|
77.54015
|
|
(1719.86)
|
(15743.6)
|
(6.50114)
|
(42.9068)
|
|
[-1.99623]
|
[ 1.62308]
|
[-2.27230]
|
[ 1.80718]
|
|
|
|
|
|
|
INVG_ENERGIE(-1)
|
860.6510
|
-9337.757
|
4.767891
|
-23.46538
|
|
(338.495)
|
(3098.57)
|
(1.27952)
|
(8.44471)
|
|
[ 2.54258]
|
[-3.01357]
|
[ 3.72630]
|
[-2.77871]
|
|
|
|
|
|
|
INVG_ENERGIE(-2)
|
-2192.888
|
24261.53
|
-10.80427
|
66.40600
|
|
(1013.54)
|
(9277.95)
|
(3.83123)
|
(25.2857)
|
|
[-2.16358]
|
[ 2.61497]
|
[-2.82005]
|
[ 2.62623]
|
|
|
|
|
|
|
INVG_ENERGIE(-3)
|
1375.666
|
-20394.47
|
6.030291
|
-55.11402
|
|
(783.568)
|
(7172.75)
|
(2.96191)
|
(19.5483)
|
|
[ 1.75564]
|
[-2.84333]
|
[ 2.03594]
|
[-2.81938]
|
|
|
|
|
|
|
INVG_ENERGIE(-4)
|
758.4344
|
6562.156
|
3.446275
|
14.55468
|
|
(804.319)
|
(7362.71)
|
(3.04035)
|
(20.0660)
|
|
[ 0.94295]
|
[ 0.89127]
|
[ 1.13351]
|
[ 0.72534]
|
|
|
|
|
|
|
INVG_ENERGIE(-5)
|
-1526.395
|
2878.184
|
-8.478241
|
9.583156
|
|
(955.667)
|
(8748.14)
|
(3.61245)
|
(23.8418)
|
|
[-1.59721]
|
[ 0.32901]
|
[-2.34695]
|
[ 0.40195]
|
|
|
|
|
|
|
C
|
-6.166127
|
-19.36448
|
0.004008
|
-0.021232
|
|
(6.79835)
|
(62.2319)
|
(0.02570)
|
(0.16960)
|
|
[-0.90700]
|
[-0.31117]
|
[ 0.15598]
|
[-0.12518]
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.999989
|
0.999909
|
0.999998
|
0.999946
|
|
Adj. R-squared
|
0.999951
|
0.999607
|
0.999990
|
0.999764
|
|
Sum sq. resids
|
0.000310
|
0.026001
|
4.43E-09
|
1.93E-07
|
|
S.E. equation
|
0.007191
|
0.065829
|
2.72E-05
|
0.000179
|
|
F-statistic
|
26398.52
|
3308.307
|
132996.8
|
5504.469
|
|
Log likelihood
|
115.2356
|
55.45251
|
265.8422
|
214.8917
|
|
Akaike AIC
|
-6.980412
|
-2.552038
|
-18.13646
|
-14.36235
|
|
Schwarz SC
|
-5.972539
|
-1.544165
|
-17.12858
|
-13.35448
|
|
Mean dependent
|
-5.217852
|
-7.836348
|
0.008743
|
0.006601
|
|
S.D. dependent
|
1.024773
|
3.320989
|
0.008695
|
0.011674
|
|
|
|
|
|
|
|
|
|
|
|
Determinant resid covariance (dof adj.)
|
1.24E-30
|
|
|
|
Determinant resid covariance
|
3.03E-33
|
|
|
|
Log likelihood
|
857.6048
|
|
|
|
Akaike information criterion
|
-57.30406
|
|
|
|
Schwarz criterion
|
-53.27257
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vector Autoregression Estimates
|
|
|
|
Date: 03/09/16 Time: 18:05
|
|
|
|
Sample (adjusted): 1987 2013
|
|
|
|
Included observations: 27 after adjustments
|
|
|
Standard errors in ( ) & t-statistics in [ ]
|
|
|
|
|
|
|
|
|
|
|
|
|
LINVG_EAU
|
LINVG_ENERGIE
|
INVG_EAU
|
INVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
|
LINVG_EAU(-1)
|
0.249228
|
-15.91418
|
0.001907
|
-0.039946
|
|
(0.57441)
|
(5.25815)
|
(0.00217)
|
(0.01433)
|
|
[ 0.43388]
|
[-3.02658]
|
[ 0.87840]
|
[-2.78752]
|
|
|
|
|
|
|
LINVG_EAU(-2)
|
3.103490
|
-14.81887
|
0.020478
|
-0.041949
|
|
(1.10412)
|
(10.1071)
|
(0.00417)
|
(0.02755)
|
|
[ 2.81082]
|
[-1.46619]
|
[ 4.90642]
|
[-1.52291]
|
|
|
|
|
|
|
LINVG_EAU(-3)
|
-8.137393
|
68.50680
|
-0.036963
|
0.207891
|
|
(4.24502)
|
(38.8588)
|
(0.01605)
|
(0.10590)
|
|
[-1.91693]
|
[ 1.76297]
|
[-2.30351]
|
[ 1.96301]
|
|
|
|
|
|
|
LINVG_EAU(-4)
|
-3.178201
|
31.35771
|
-0.012361
|
0.079624
|
|
(1.75030)
|
(16.0222)
|
(0.00662)
|
(0.04367)
|
|
[-1.81580]
|
[ 1.95714]
|
[-1.86828]
|
[ 1.82347]
|
|
|
|
|
|
|
LINVG_EAU(-5)
|
6.894626
|
-77.09660
|
0.026558
|
-0.216709
|
|
(3.38414)
|
(30.9783)
|
(0.01279)
|
(0.08443)
|
|
[ 2.03733]
|
[-2.48873]
|
[ 2.07610]
|
[-2.56682]
|
|
|
|
|
|
|
LINVG_ENERGIE(-1)
|
-1.590760
|
20.87588
|
-0.008076
|
0.053884
|
|
(0.75041)
|
(6.86925)
|
(0.00284)
|
(0.01872)
|
|
[-2.11985]
|
[ 3.03904]
|
[-2.84708]
|
[ 2.87825]
|
|
|
|
|
|
|
LINVG_ENERGIE(-2)
|
1.246151
|
-20.78323
|
0.003367
|
-0.058182
|
|
(0.80385)
|
(7.35838)
|
(0.00304)
|
(0.02005)
|
|
[ 1.55023]
|
[-2.82443]
|
[ 1.10818]
|
[-2.90122]
|
|
|
|
|
|
|
LINVG_ENERGIE(-3)
|
3.020359
|
-23.39009
|
0.014982
|
-0.068276
|
|
(1.77977)
|
(16.2920)
|
(0.00673)
|
(0.04440)
|
|
[ 1.69705]
|
[-1.43568]
|
[ 2.22701]
|
[-1.53770]
|
|
|
|
|
|
|
LINVG_ENERGIE(-4)
|
-2.039492
|
1.952857
|
-0.013650
|
0.017622
|
|
(1.05242)
|
(9.63382)
|
(0.00398)
|
(0.02626)
|
|
[-1.93791]
|
[ 0.20271]
|
[-3.43111]
|
[ 0.67119]
|
|
|
|
|
|
|
LINVG_ENERGIE(-5)
|
-0.135873
|
24.32515
|
0.003469
|
0.057796
|
|
(0.44014)
|
(4.02902)
|
(0.00166)
|
(0.01098)
|
|
[-0.30870]
|
[ 6.03748]
|
[ 2.08484]
|
[ 5.26346]
|
|
|
|
|
|
|
INVG_EAU(-1)
|
813.0458
|
-5774.726
|
4.361761
|
-16.32337
|
|
(410.579)
|
(3758.43)
|
(1.55200)
|
(10.2430)
|
|
[ 1.98024]
|
[-1.53647]
|
[ 2.81041]
|
[-1.59360]
|
|
|
|
|
|
|
INVG_EAU(-2)
|
-1671.411
|
14820.35
|
-9.175640
|
41.66988
|
|
(684.904)
|
(6269.59)
|
(2.58896)
|
(17.0869)
|
|
[-2.44036]
|
[ 2.36385]
|
[-3.54414]
|
[ 2.43871]
|
|
|
|
|
|
|
INVG_EAU(-3)
|
1612.942
|
-15256.69
|
7.161701
|
-47.06755
|
|
(835.048)
|
(7644.00)
|
(3.15651)
|
(20.8326)
|
|
[ 1.93156]
|
[-1.99590]
|
[ 2.26887]
|
[-2.25932]
|
|
|
|
|
|
|
INVG_EAU(-4)
|
2148.676
|
-16029.00
|
11.96578
|
-45.23051
|
|
(984.380)
|
(9010.99)
|
(3.72099)
|
(24.5581)
|
|
[ 2.18277]
|
[-1.77883]
|
[ 3.21575]
|
[-1.84177]
|
|
|
|
|
|
|
INVG_EAU(-5)
|
-3433.233
|
25553.05
|
-14.77250
|
77.54015
|
|
(1719.86)
|
(15743.6)
|
(6.50114)
|
(42.9068)
|
|
[-1.99623]
|
[ 1.62308]
|
[-2.27230]
|
[ 1.80718]
|
|
|
|
|
|
|
INVG_ENERGIE(-1)
|
860.6510
|
-9337.757
|
4.767891
|
-23.46538
|
|
(338.495)
|
(3098.57)
|
(1.27952)
|
(8.44471)
|
|
[ 2.54258]
|
[-3.01357]
|
[ 3.72630]
|
[-2.77871]
|
|
|
|
|
|
|
INVG_ENERGIE(-2)
|
-2192.888
|
24261.53
|
-10.80427
|
66.40600
|
|
(1013.54)
|
(9277.95)
|
(3.83123)
|
(25.2857)
|
|
[-2.16358]
|
[ 2.61497]
|
[-2.82005]
|
[ 2.62623]
|
|
|
|
|
|
|
INVG_ENERGIE(-3)
|
1375.666
|
-20394.47
|
6.030291
|
-55.11402
|
|
(783.568)
|
(7172.75)
|
(2.96191)
|
(19.5483)
|
|
[ 1.75564]
|
[-2.84333]
|
[ 2.03594]
|
[-2.81938]
|
|
|
|
|
|
|
INVG_ENERGIE(-4)
|
758.4344
|
6562.156
|
3.446275
|
14.55468
|
|
(804.319)
|
(7362.71)
|
(3.04035)
|
(20.0660)
|
|
[ 0.94295]
|
[ 0.89127]
|
[ 1.13351]
|
[ 0.72534]
|
|
|
|
|
|
|
INVG_ENERGIE(-5)
|
-1526.395
|
2878.184
|
-8.478241
|
9.583156
|
|
(955.667)
|
(8748.14)
|
(3.61245)
|
(23.8418)
|
|
[-1.59721]
|
[ 0.32901]
|
[-2.34695]
|
[ 0.40195]
|
|
|
|
|
|
|
C
|
-6.166127
|
-19.36448
|
0.004008
|
-0.021232
|
|
(6.79835)
|
(62.2319)
|
(0.02570)
|
(0.16960)
|
|
[-0.90700]
|
[-0.31117]
|
[ 0.15598]
|
[-0.12518]
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.999989
|
0.999909
|
0.999998
|
0.999946
|
|
Adj. R-squared
|
0.999951
|
0.999607
|
0.999990
|
0.999764
|
|
Sum sq. resids
|
0.000310
|
0.026001
|
4.43E-09
|
1.93E-07
|
|
S.E. equation
|
0.007191
|
0.065829
|
2.72E-05
|
0.000179
|
|
F-statistic
|
26398.52
|
3308.307
|
132996.8
|
5504.469
|
|
Log likelihood
|
115.2356
|
55.45251
|
265.8422
|
214.8917
|
|
Akaike AIC
|
-6.980412
|
-2.552038
|
-18.13646
|
-14.36235
|
|
Schwarz SC
|
-5.972539
|
-1.544165
|
-17.12858
|
-13.35448
|
|
Mean dependent
|
-5.217852
|
-7.836348
|
0.008743
|
0.006601
|
|
S.D. dependent
|
1.024773
|
3.320989
|
0.008695
|
0.011674
|
|
|
|
|
|
|
|
|
|
|
|
Determinant resid covariance (dof adj.)
|
1.24E-30
|
|
|
|
Determinant resid covariance
|
3.03E-33
|
|
|
|
Log likelihood
|
857.6048
|
|
|
|
Akaike information criterion
|
-57.30406
|
|
|
|
Schwarz criterion
|
-53.27257
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VAR Granger Causality/Block Exogeneity Wald Tests
|
|
Date: 03/09/16 Time: 18:07
|
|
|
Sample: 1982 2013
|
|
|
|
Included observations: 27
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: LINVG_EAU
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
LINVG_ENERGIE
|
83.87515
|
5
|
0.0000
|
|
INVG_EAU
|
56.63411
|
5
|
0.0000
|
|
INVG_ENERGIE
|
48.09128
|
5
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
10599.98
|
15
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: LINVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
LINVG_EAU
|
27.73492
|
5
|
0.0000
|
|
INVG_EAU
|
64.03684
|
5
|
0.0000
|
|
INVG_ENERGIE
|
132.6841
|
5
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
959.2716
|
15
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_EAU
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
LINVG_EAU
|
196.3591
|
5
|
0.0000
|
|
LINVG_ENERGIE
|
664.8819
|
5
|
0.0000
|
|
INVG_ENERGIE
|
181.7997
|
5
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
256242.7
|
15
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dependent variable: INVG_ENERGIE
|
|
|
|
|
|
|
|
|
|
|
Excluded
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
LINVG_EAU
|
25.13038
|
5
|
0.0001
|
|
LINVG_ENERGIE
|
31.26578
|
5
|
0.0000
|
|
INVG_EAU
|
68.55523
|
5
|
0.0000
|
|
|
|
|
|
|
|
|
|
All
|
12679.48
|
15
|
0.0000
|
|
|
|
|
|
|
|
|
ANNEXE 5 : Estimations économétriques
|
System: SYST1
|
|
|
|
|
Estimation Method: Generalized Method of Moments
|
|
Date: 01/27/15 Time: 22:32
|
|
|
|
Sample: 1983 2013
|
|
|
|
Included observations: 31
|
|
|
|
Total system (balanced) observations 93
|
|
|
Kernel: Bartlett, Bandwidth: Fixed (4), No prewhitening
|
|
Linear estimation after one-step weighting matrix
|
|
|
|
|
|
|
|
|
|
|
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
C(1)
|
12.53050
|
0.132221
|
94.76924
|
0.0000
|
|
C(2)
|
0.058838
|
0.015027
|
3.915588
|
0.0002
|
|
C(3)
|
0.280288
|
0.016902
|
16.58329
|
0.0000
|
|
C(4)
|
0.096343
|
0.054199
|
1.777576
|
0.0794
|
|
C(5)
|
4.385246
|
0.897401
|
4.886610
|
0.0000
|
|
C(6)
|
-0.366396
|
0.078247
|
-4.682555
|
0.0000
|
|
C(7)
|
0.121815
|
0.011153
|
10.92166
|
0.0000
|
|
C(8)
|
0.390505
|
0.373874
|
1.044483
|
0.2995
|
|
C(9)
|
0.040047
|
0.004077
|
9.822384
|
0.0000
|
|
C(10)
|
-5.243205
|
0.420268
|
-12.47587
|
0.0000
|
|
C(11)
|
-0.055147
|
0.007176
|
-7.685347
|
0.0000
|
|
C(12)
|
0.456286
|
0.054111
|
8.432428
|
0.0000
|
|
C(13)
|
0.000815
|
0.000504
|
1.619002
|
0.1095
|
|
C(14)
|
0.471431
|
0.017973
|
26.22954
|
0.0000
|
|
C(15)
|
0.024623
|
0.002707
|
9.097295
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
Determinant residual covariance
|
1.32E-12
|
|
|
|
J-statistic
|
0.259817
|
|
|
|
|
|
|
|
|
Equation: LPIB= C(1) + C(2)*LINVP+C(3)*LINVG+ C(4)*LN
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
CONSENERGIE(-1)
VENTE_EAU(-1) C
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.913601
|
Mean dependent var
|
11.68439
|
|
Adjusted R-squared
|
0.904002
|
S.D. dependent var
|
0.095305
|
|
S.E. of regression
|
0.029529
|
Sum squared resid
|
0.023543
|
|
Durbin-Watson stat
|
1.055643
|
|
|
|
|
|
|
|
|
|
Equation: INVP=C(5)+ C(6)*LPIB(-1)+
C(7)*CRED+C(8)*INVG+C(9)*DET
|
|
+C(10)*TAXE
|
|
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
CONSENERGIE(-1)
VENTE_EAU(-1) C
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.769130
|
Mean dependent var
|
0.098647
|
|
Adjusted R-squared
|
0.722956
|
S.D. dependent var
|
0.022096
|
|
S.E. of regression
|
0.011630
|
Sum squared resid
|
0.003382
|
|
Durbin-Watson stat
|
1.291036
|
|
|
|
|
|
|
|
|
|
Equation:
INVG=C(11)+C(12)*TAXE+C(13)*DET+C(14)*CONSENERGIE(-1)
|
|
+C(15)*VENTE_EAU(-1)
|
|
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
CONSENERGIE(-1)
VENTE_EAU(-1) C
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.898182
|
Mean dependent var
|
0.055764
|
|
Adjusted R-squared
|
0.882518
|
S.D. dependent var
|
0.015677
|
|
S.E. of regression
|
0.005373
|
Sum squared resid
|
0.000751
|
|
Durbin-Watson stat
|
1.172121
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
System: SYST2
|
|
|
|
|
Estimation Method: Generalized Method of Moments
|
|
Date: 01/27/15 Time: 22:47
|
|
|
|
Sample: 1983 2013
|
|
|
|
Included observations: 31
|
|
|
|
Total system (balanced) observations 93
|
|
|
Kernel: Bartlett, Bandwidth: Fixed (4), No prewhitening
|
|
Linear estimation after one-step weighting matrix
|
|
|
|
|
|
|
|
|
|
|
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
C(1)
|
11.95342
|
0.111139
|
107.5542
|
0.0000
|
|
C(2)
|
0.042907
|
0.007184
|
5.972154
|
0.0000
|
|
C(3)
|
0.065111
|
0.005886
|
11.06121
|
0.0000
|
|
C(4)
|
0.160893
|
0.065109
|
2.471145
|
0.0156
|
|
C(5)
|
1.889943
|
0.312125
|
6.055085
|
0.0000
|
|
C(6)
|
-0.151185
|
0.026651
|
-5.672673
|
0.0000
|
|
C(7)
|
0.138374
|
0.005155
|
26.84472
|
0.0000
|
|
C(8)
|
-1.619628
|
0.200913
|
-8.061341
|
0.0000
|
|
C(9)
|
0.026751
|
0.003458
|
7.736023
|
0.0000
|
|
C(10)
|
-4.141386
|
0.282805
|
-14.64399
|
0.0000
|
|
C(11)
|
-0.098959
|
0.013780
|
-7.181547
|
0.0000
|
|
C(12)
|
0.082155
|
0.178161
|
0.461127
|
0.6460
|
|
C(13)
|
-0.007364
|
0.000392
|
-18.78086
|
0.0000
|
|
C(14)
|
0.036366
|
0.003599
|
10.10576
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
Determinant residual covariance
|
8.46E-13
|
|
|
|
J-statistic
|
0.241671
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Equation: LPIB= C(1) + C(2)*LINVP+C(3)*LINVG_EAU+
C(4)*LN
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
VENTE_EAU(-1)
C
|
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.942923
|
Mean dependent var
|
11.68439
|
|
Adjusted R-squared
|
0.936582
|
S.D. dependent var
|
0.095305
|
|
S.E. of regression
|
0.024001
|
Sum squared resid
|
0.015553
|
|
Durbin-Watson stat
|
0.468798
|
|
|
|
|
|
|
|
|
|
Equation: INVP=C(5)+ C(6)*LPIB(-1)+
C(7)*CRED+C(8)*INVG_EAU+C(9)
|
|
*DET+C(10)*TAXE
|
|
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
VENTE_EAU(-1)
C
|
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.838581
|
Mean dependent var
|
0.098647
|
|
Adjusted R-squared
|
0.806297
|
S.D. dependent var
|
0.022096
|
|
S.E. of regression
|
0.009725
|
Sum squared resid
|
0.002364
|
|
Durbin-Watson stat
|
1.734317
|
|
|
|
|
|
|
|
|
|
Equation: INVG_EAU=C(11)+C(12)*TAXE+C(13)*DET+C(14)*VENTE_EAU(
|
|
-1)
|
|
|
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
VENTE_EAU(-1)
C
|
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.554213
|
Mean dependent var
|
0.007714
|
|
Adjusted R-squared
|
0.504682
|
S.D. dependent var
|
0.008539
|
|
S.E. of regression
|
0.006010
|
Sum squared resid
|
0.000975
|
|
Durbin-Watson stat
|
0.837783
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
System: SYST3
|
|
|
|
|
Estimation Method: Generalized Method of Moments
|
|
Date: 01/29/15 Time: 19:46
|
|
|
|
Sample: 1983 2013
|
|
|
|
Included observations: 31
|
|
|
|
Total system (balanced) observations 93
|
|
|
Kernel: Bartlett, Bandwidth: Fixed (4), No prewhitening
|
|
Linear estimation after one-step weighting matrix
|
|
|
|
|
|
|
|
|
|
|
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
C(1)
|
11.88070
|
0.032370
|
367.0244
|
0.0000
|
|
C(2)
|
-0.016299
|
0.003327
|
-4.899542
|
0.0000
|
|
C(3)
|
0.024937
|
0.000603
|
41.38790
|
0.0000
|
|
C(4)
|
-0.012690
|
0.025063
|
-0.506334
|
0.6140
|
|
C(5)
|
2.585659
|
0.191796
|
13.48128
|
0.0000
|
|
C(6)
|
-0.211374
|
0.016068
|
-13.15467
|
0.0000
|
|
C(7)
|
0.204610
|
0.003405
|
60.09367
|
0.0000
|
|
C(8)
|
-2.477182
|
0.166818
|
-14.84965
|
0.0000
|
|
C(9)
|
0.027955
|
0.002022
|
13.82228
|
0.0000
|
|
C(10)
|
-4.914213
|
0.306585
|
-16.02885
|
0.0000
|
|
C(11)
|
-0.020320
|
0.001031
|
-19.70896
|
0.0000
|
|
C(12)
|
0.285237
|
0.042793
|
6.665424
|
0.0000
|
|
C(13)
|
-0.008447
|
0.000346
|
-24.44386
|
0.0000
|
|
C(14)
|
0.417217
|
0.013152
|
31.72267
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
Determinant residual covariance
|
3.72E-13
|
|
|
|
J-statistic
|
0.214709
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Equation: LPIB= C(1) + C(2)*LINVP+C(3)*LINVG_ENERGIE+
C(4)*LN
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
CONSENERGIE(-1)
C
|
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.964611
|
Mean dependent var
|
11.68439
|
|
Adjusted R-squared
|
0.960679
|
S.D. dependent var
|
0.095305
|
|
S.E. of regression
|
0.018899
|
Sum squared resid
|
0.009643
|
|
Durbin-Watson stat
|
0.714530
|
|
|
|
|
|
|
|
|
|
Equation: INVP=C(5)+ C(6)*LPIB(-1)+
C(7)*CRED+C(8)*INVG_ENERGIE
|
|
+C(9)*DET+C(10)*TAXE
|
|
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
CONSENERGIE(-1)
C
|
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.714159
|
Mean dependent var
|
0.098647
|
|
Adjusted R-squared
|
0.656991
|
S.D. dependent var
|
0.022096
|
|
S.E. of regression
|
0.012941
|
Sum squared resid
|
0.004187
|
|
Durbin-Watson stat
|
1.152078
|
|
|
|
|
|
|
|
|
|
Equation: INVG_ENERGIE=C(11)+C(12)*TAXE+C(13)*DET+C(14)
|
|
*CONSENERGIE(-1)
|
|
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
CONSENERGIE(-1)
C
|
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.626688
|
Mean dependent var
|
0.005749
|
|
Adjusted R-squared
|
0.585209
|
S.D. dependent var
|
0.011099
|
|
S.E. of regression
|
0.007148
|
Sum squared resid
|
0.001380
|
|
Durbin-Watson stat
|
0.735471
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
System: SYST31
|
|
|
|
|
Estimation Method: Generalized Method of Moments
|
|
Date: 03/07/16 Time: 13:48
|
|
|
|
Sample: 1983 2013
|
|
|
|
Included observations: 31
|
|
|
|
Total system (unbalanced) observations 92
|
|
|
Kernel: Bartlett, Bandwidth: Fixed (4), No prewhitening
|
|
Linear estimation after one-step weighting matrix
|
|
|
|
|
|
|
|
|
|
|
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
C(1)
|
11.96806
|
0.076172
|
157.1191
|
0.0000
|
|
C(2)
|
0.056300
|
0.023105
|
2.436732
|
0.0171
|
|
C(3)
|
0.021425
|
0.001090
|
19.65404
|
0.0000
|
|
C(4)
|
0.033996
|
0.037252
|
0.912606
|
0.3643
|
|
C(5)
|
2.461003
|
0.282366
|
8.715655
|
0.0000
|
|
C(6)
|
-0.200745
|
0.023731
|
-8.459047
|
0.0000
|
|
C(7)
|
0.203724
|
0.004610
|
44.19210
|
0.0000
|
|
C(8)
|
-2.554160
|
0.177535
|
-14.38681
|
0.0000
|
|
C(9)
|
0.027227
|
0.002511
|
10.84393
|
0.0000
|
|
C(10)
|
-4.803093
|
0.407870
|
-11.77604
|
0.0000
|
|
C(11)
|
-0.020996
|
0.001375
|
-15.27168
|
0.0000
|
|
C(12)
|
0.318050
|
0.038263
|
8.312165
|
0.0000
|
|
C(13)
|
-0.008144
|
0.000985
|
-8.269467
|
0.0000
|
|
C(14)
|
0.416044
|
0.027967
|
14.87646
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
Determinant residual covariance
|
3.86E-13
|
|
|
|
J-statistic
|
0.218840
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Equation: LPIB= C(1) + C(2)*LINVP(-2)+C(3)*LINVG_ENERGIE+
C(4)*LN
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
CONSENERGIE(-1)
C
|
|
|
|
Observations: 30
|
|
|
|
R-squared
|
0.968217
|
Mean dependent var
|
11.69022
|
|
Adjusted R-squared
|
0.964550
|
S.D. dependent var
|
0.091126
|
|
S.E. of regression
|
0.017157
|
Sum squared resid
|
0.007654
|
|
Durbin-Watson stat
|
0.622164
|
|
|
|
|
|
|
|
|
|
Equation: INVP=C(5)+ C(6)*LPIB(-1)+
C(7)*CRED+C(8)*INVG_ENERGIE
|
|
+C(9)*DET+C(10)*TAXE
|
|
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
CONSENERGIE(-1)
C
|
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.694873
|
Mean dependent var
|
0.098647
|
|
Adjusted R-squared
|
0.633848
|
S.D. dependent var
|
0.022096
|
|
S.E. of regression
|
0.013371
|
Sum squared resid
|
0.004469
|
|
Durbin-Watson stat
|
1.113533
|
|
|
|
|
|
|
|
|
|
Equation: INVG_ENERGIE=C(11)+C(12)*TAXE+C(13)*DET+C(14)
|
|
*CONSENERGIE(-1)
|
|
|
|
Instruments: LPIB(-1) LINVP(-1) DET LN INVP(-1) CRED TAXE
|
|
CONSENERGIE(-1)
C
|
|
|
|
Observations: 31
|
|
|
|
R-squared
|
0.626191
|
Mean dependent var
|
0.005749
|
|
Adjusted R-squared
|
0.584657
|
S.D. dependent var
|
0.011099
|
|
S.E. of regression
|
0.007153
|
Sum squared resid
|
0.001381
|
|
Durbin-Watson stat
|
0.732457
|
|
|
|
|
|
|
|
|
ANNEXE 6 : Test de normalité
Système1
|
System Residual Normality Tests
|
|
|
|
Orthogonalization: Cholesky (Lutkepohl)
|
|
|
Null Hypothesis: residuals are multivariate normal
|
|
|
Date: 03/15/15 Time: 16:06
|
|
|
|
Sample: 1983 2013
|
|
|
|
|
Included observations: 31
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Skewness
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0.221869
|
0.254335
|
1
|
0.6140
|
|
2
|
-0.838857
|
3.635686
|
1
|
0.0566
|
|
3
|
0.638083
|
2.103605
|
1
|
0.1470
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
|
5.993626
|
3
|
0.1119
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Kurtosis
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
1
|
2.567931
|
0.241133
|
1
|
0.6234
|
|
2
|
3.717638
|
0.665214
|
1
|
0.4147
|
|
3
|
2.839331
|
0.033344
|
1
|
0.8551
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
|
0.939691
|
3
|
0.8158
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Jarque-Bera
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0.495468
|
2
|
0.7806
|
|
|
2
|
4.300900
|
2
|
0.1164
|
|
|
3
|
2.136949
|
2
|
0.3435
|
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
6.933317
|
6
|
0.3271
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Système2
|
System Residual Normality Tests
|
|
|
|
Orthogonalization: Cholesky (Lutkepohl)
|
|
|
Null Hypothesis: residuals are multivariate normal
|
|
|
Date: 03/15/15 Time: 16:09
|
|
|
|
Sample: 1983 2013
|
|
|
|
|
Included observations: 31
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Skewness
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0.628812
|
2.042925
|
1
|
0.1529
|
|
2
|
-1.156694
|
6.912696
|
1
|
0.0086
|
|
3
|
1.194837
|
7.376117
|
1
|
0.0066
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
|
16.33174
|
3
|
0.0010
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Kurtosis
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
1
|
3.117686
|
0.017890
|
1
|
0.8936
|
|
2
|
5.843421
|
10.44318
|
1
|
0.0012
|
|
3
|
5.014845
|
5.243650
|
1
|
0.0220
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
|
15.70472
|
3
|
0.0013
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Jarque-Bera
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
2.060814
|
2
|
0.3569
|
|
|
2
|
17.35588
|
2
|
0.0002
|
|
|
3
|
12.61977
|
2
|
0.0018
|
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
32.03646
|
6
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Système3
|
System Residual Normality Tests
|
|
|
|
Orthogonalization: Cholesky (Lutkepohl)
|
|
|
Null Hypothesis: residuals are multivariate normal
|
|
|
Date: 03/15/15 Time: 16:10
|
|
|
|
Sample: 1983 2013
|
|
|
|
|
Included observations: 31
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Skewness
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
1
|
-0.026836
|
0.003721
|
1
|
0.9514
|
|
2
|
-0.127228
|
0.083632
|
1
|
0.7724
|
|
3
|
-0.501149
|
1.297609
|
1
|
0.2547
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
|
1.384962
|
3
|
0.7091
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Kurtosis
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
1
|
4.133088
|
1.658356
|
1
|
0.1978
|
|
2
|
3.121899
|
0.019193
|
1
|
0.8898
|
|
3
|
3.152818
|
0.030165
|
1
|
0.8621
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
|
1.707714
|
3
|
0.6352
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Jarque-Bera
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
1.662077
|
2
|
0.4356
|
|
|
2
|
0.102826
|
2
|
0.9499
|
|
|
3
|
1.327774
|
2
|
0.5148
|
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
3.092676
|
6
|
0.7971
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Système31
|
System Residual Normality Tests
|
System 31
|
|
|
Orthogonalization: Cholesky (Lutkepohl)
|
|
|
Null Hypothesis: residuals are multivariate normal
|
|
|
Date: 03/07/16 Time: 14:34
|
|
|
|
Sample: 1983 2013
|
|
|
|
|
Included observations: 31
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Skewness
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0.770997
|
3.071255
|
1
|
0.0797
|
|
2
|
-0.189188
|
0.184925
|
1
|
0.6672
|
|
3
|
0.538253
|
1.496869
|
1
|
0.2212
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
|
4.753049
|
3
|
0.1908
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Kurtosis
|
Chi-sq
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
1
|
3.404160
|
0.210988
|
1
|
0.6460
|
|
2
|
5.073502
|
5.553405
|
1
|
0.0184
|
|
3
|
3.725190
|
0.679288
|
1
|
0.4098
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
|
6.443681
|
3
|
0.0919
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Component
|
Jarque-Bera
|
df
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
3.282242
|
2
|
0.1938
|
|
|
2
|
5.738331
|
2
|
0.0567
|
|
|
3
|
2.176157
|
2
|
0.3369
|
|
|
|
|
|
|
|
|
|
|
|
|
Joint
|
11.19673
|
6
|
0.0825
|
|
|
|
|
|
|
|
|
|
|
|
TABLE
DES MATIERES
SOMMAIRE
2
DEDICACE
3
REMERCIEMENTS
4
LISTE DES TABLEAUX
5
LISTE DES GRAPHIQUES
6
SIGLES ET ABREVIATIONS
7
RESUME
9
INTRODUCTION
10
CHAPITRE 1: CADRE THEORIQUE ET ANALYTIQUE DE
L'ETUDE
14
1. PROBLEMATIQUE, OBJECTIFS ET HYPOTHESES ET REVUE
DE LITTERATURE
14
1.1. Problématique de
l'étude
14
1.2. Objectifs et hypothèses de
recherche
15
1.2.1. Objectif général
15
1.2.2. Objectifs spécifiques
16
1.2.3. Hypothèses
16
2. REVUE DE LITTERATURE ET METHODOLOGIE
16
2.1. Revue de
littérature
16
2.1.1. Approche théorique
17
2.1.1.1. Approche théorique de
l'investissement public
17
2.1.1.1.1. Fondement de l'Action Publique
17
2.1.1.1.2. Infrastructures publiques
18
2.1.1.2. Théorie de la croissance
21
2.1.1.2.1. Analyse néoclassique de la
croissance : modèle de Solow
21
2.1.1.2.2. Croissance endogène
25
2.1.1.3. Théories économiques sur le
rôle de l'énergie dans la croissance économique
29
2.1.2. Approche empirique
32
2.1.2.1. Absence de relation de causalité
entre la croissance et la consommation d'énergie
32
2.1.2.2. Présence de relation
unidirectionnelle allant de la croissance vers la consommation
d'énergie
33
2.1.2.3. Présence de relation
unidirectionnelle allant de la consommation d'énergie vers la
croissance
34
2.1.2.4. Présence de relation
bidirectionnelle entre la consommation d'énergie vers la croissance
36
2.1.2.5. Autres résultats
37
2.2. Méthodologie de l'étude
et Présentations des données
41
2.2.1. Méthodologie
41
2.2.1.1. Analyse descriptive
41
2.2.1.2. Analyse de causalité au sens de
Granger
41
2.2.1.3. Analyse de stationnarité des
variables
42
2.2.1.4. Le modèle
économétrique
43
2.2.2. Présentation des données
47
2.2.2.1. Description des variables
47
_Toc443306021
2.2.2.2. Source des données
3
CHAPITRE 2: LES INVESTISSEMENTS DANS LES SECTEURS
DE L'ENERGIE ET DE L'EAU, ET LA CROISSANCE ECONOMIQUE AU BENIN : UNE
ANALYSE DESCRIPTIVE ET ECONOMETRIQUE
52
1. ANALYSE DESCRIPTIVE DES INVESTISSEMENTS DANS LES
SECTEURS DE L'ENERGIE ET DE L'EAU, ET LA CROISSANCE ECONOMIQUE AU BENIN
52
1.1. Analyse de l'évolution des
dépenses d'investissements publics dans les secteurs de l'énergie
et de l'eau par rapport au Secteur Productif
52
1.2. Analyse de l'évolution des
dépenses d'investissements publics dans les secteurs de l'énergie
et de l'eau par rapport aux dépenses d'investissements
nationales
53
2. ANALYSE ECONOMETRIQUE DES INVESTISSEMENTS DANS
LES SECTEURS DE L'ENERGIE ET DE L'EAU, ET LA CROISSANCE ECONOMIQUE AU BENIN
54
2.1. Analyse de causalité entre
investissement et croissance
54
2.1.1. Analyse de causalité entre les
investissements publics dans les secteurs de l'énergie et de l'eau et la
croissance économique
54
2.1.2. Analyse de causalité de Granger entre
les investissements publics dans le secteur de l'énergie
électrique et dans le secteur de l'eau
56
2.2. Analyse économétrique
des investissements dans les secteurs de l'Energie et de l'eau, et croissance
économique
57
2.2.1. Analyse de la stationnarité des
variables
57
2.2.2. Estimation du modèle
58
2.2.3. Résultats, limites et suggestions
60
2.2.2.1. Estimation du modèle avec les
dépenses d'investissements publics gouvernementales globales (INVG)
60
2.2.2.1.1. Résultats de l'estimation du
modèle avec les dépenses d'investissements publics
gouvernementales globales
60
2.2.2.1.2. Test de normalité des
résidus de l'estimation du modèle avec les dépenses
d'investissements publics gouvernementales globales
61
2.2.2.1.3. Commentaires de l'estimation du
modèle avec les dépenses d'investissements publics
gouvernementales globales
61
2.2.2.2. Estimation du modèle avec les
dépenses d'investissements publics dans le secteur de l'eau
(INVG_EAU)
63
2.2.2.2.1. Résultats de l'estimation du
modèle avec les dépenses d'investissements publics dans le
secteur de l'eau
63
2.2.2.2.2. Test de normalité des
résidus de l'estimation du modèle avec les dépenses
d'investissements publics dans le secteur de l'eau
64
2.2.2.2.3. Commentaires de l'estimation du
modèle avec les dépenses d'investissements publics dans le
secteur de l'eau
64
2.2.2.3. Estimation du modèle avec les
dépenses d'investissements publics dans le secteur de l'énergie
(INVG_ENERGIE)
65
2.2.2.3.1. Résultats de l'estimation du
modèle avec les dépenses d'investissements publics dans le
secteur de l'énergie
65
2.2.2.3.2. Test de normalité des
résidus de l'estimation du modèle avec les dépenses
d'investissements publics dans le secteur de l'énergie
67
2.2.2.3.3. Commentaires de l'estimation du
modèle avec les dépenses d'investissements publics dans le
secteur de l'énergie
68
2.2.2.4. Limites et suggestions de
l'étude
69
CONCLUSION
71
REFERENCES BIBLIOGRAPHIQUES
72
ANNEXES
76
TABLE DES MATIERES
103
* 1F. Perroux, La pensée
économique de Joseph Schumpeter. Les dynamiques du capitalisme,
Librairie Droz, Genève 1965, p 1935
* 2Pierre Maillet, La croissance
économique, 1967
* 3 Barro R.J : Economic
Growth in a Cross Section of Countries. Quartely Journal 1 of Economies Volume
2, N°106, May. p 407-444.
* 4 Le taux de croissance est
5,6% en2013 et de 5,4% en 2014.
* 5 Relationship between
unemployment and the rate of change of money wages in the UK 1891-1957, A.W.H.
Phillips, Ecomica, 1958
* 6The role of monetary policy,
Milton Friedman, the American Ecomic Review, 1968
* 7The crowding out of private
expenditure by fiscal policy actions, Spencer R. and W. Yoke
* 8 Cité dans
Documentation économique volume 39, p51
* 9 Le monétarisme,
Florin Aflalion et Fabrice Poncet, 1981
* 10Rational Expectations and
the Theory of Price Movements, John Muth, Econometrica, 1961
* 11Expectations and the
neutrality of money, Robert Lucas, journal of economy, 1972
* 12Rational, expectations and
the theory of economic policy, Thomas Sargent and neil Wallace
* 13The pure theorh of public
expenditure, Paul Samuelson, 1954
* 14The theory of public
finance, Richard Musgrave, 1959
* 15Highway capacity and
economic growth, David Alan Aschauer, 1990
* 16Local public goods shup
revised, Eden Lorraine and L. McMillan, 1991
* 17The strategy of economic
development, Albert Hirschman, 1958
* 18The dollar and the
international monetary system, Alvin hausen 1965
* 19The theory of international
economic policy_the balance of payments, 1951
* 20International
investissement location decisions: the case of US firms, Wheeler D et A. Mody
1992
* 21 Rapport sur le
developpement dans le monde 1994: une infrastructure pour le
développement, 1984
* 22Mathematical theory of
saving (economic journal), Ramsey, 1928
* 23« A contribution
to the thery of economic growth», Quarterly Journal of Economics, 1956
* 24 Economic growth and
capital accumulation, Swan, 1956
* 25 Optinium growth in an
aggregative mode of capital accumulation
* 26 On the concept of optimal
economic growth, Koopmans, 1965
* 27« Expansion et
Emploi », (Domar, 1947) et « Théorèmes
Dynamiques Fondamentaux » (Harrod, 1948)
* 28Une fonction de
production Y = F(K,L) est dite néoclassique quand les
propriétés suivantes sont satisfaites :
· 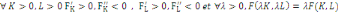

· les conditions d'Inada (1963) : 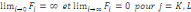
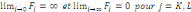
* 29 D'après P. Romer,
1986, Le progrès technique est issu de l'apprentissage par la
pratique.Audrey Reynier (2008), Progrès technique et innovation - Page
26
* 30Alain Chamak,
?Céline Fromage (2006), Le capital humain - Page 21
* 31Jean-Didier Lecaillon,
?Jean-Marie Le Page, ?Christian Ottavj (2008), Économie contemporaine:
Analyse et diagnostics - Page 242
* 32 Paul Dukes (2011), Minutes
to Midnight: History and the Anthropocene Era from 1763 - Page 11
* 33 Gérard Jorland
(1995), Paradoxes du capital - Page 40
* 34 Reiner Kümmel (2011),
The Second Law of Economics: Energy, Entropy, and the Origins of Wealth, Page
180
* 35Mavor Michel Agbodan,
?Fulbert Gero Amoussouga (1995), Les facteurs de performance de l'entreprise -
Page 207
* 36 Anil Markandya, ?Suzette
Pedroso-Galinato (2005), How Substitutable is Natural Capital? - Page 12
* 37Note and comments: on the
relationship between Energy and GNP, Kraft J. and kraft A. , (1978)
* 38Association pour le
développement de la recherche en économie et en statistique,
2001, Annales d'économie et de statistique, Numéros 61 à
64 (test de Dolado-lukepohl)
* 39 A recent procedure
proposed by Toda and Yamamoto (1995) bypasses the need for potentially biased
pre-tests for unit. The Toda and Yamamoto (1995) procedure for testing Granger
causality is performed directly on the least squares estimators of the
coefficients of the levels VAR
* 40 The Pesaran and Shin
(1999) test consists of adding, in the first differenced version of Equation
(7.5), lags of first . Pesaran et al. (2001), tabulate the relevant critical
bounds for I(0) and I(1).
* 41 A contribution as the
empirics of economic growth, Mankiw, Romer et Weil, 1992
* 42 L'intensité
énergétique (IE) est une mesure de l'efficacité
énergétique d'une économie. C'est la consommation
d'énergie par unité de PIB ; en 2000 elle de 301,1 tep/M$
au Bénin et 154 tep/M$ au Japon



