Application des générateurs de scénarios économiques en alm pour les compagnies d'assurance

Mémoire présenté devant l'Université de Paris-Dauphine

Tunis

pour l'obtention du diplôme du Master Actuariat

Par : Zribi Mohamed Mahdi

Titre : Application des générateurs de scénarios économiques en ALM pour les compagnies d'assurances

Confidentialité: Non Oui (Durée : 1 an 2 ans)

Les signataires s'engagent à respecter la confidentialité ci-dessus

Membres présents du jury du Master Entreprise :

Actuariat de Tunis-Dauphine : Nom: ERM Partners

Racem KETATA (président de jury) Signature:

Abdelwaheb MAHJOUB Directeur de Mémoire en entreprise:

Med Najed KSOURI Nom: M.Ksouri Mohamed Najed

Signature :

Tutrice académique:

Nom: Mme.Rihani Sinda Signature :

Autorisation de publication et de mise en ligne sur un site de diffusion de documents actuariels (après expiration de l'éventuel délai de confidentialité)

Signature du responsable entreprise

Signature du candidat

Secrétariat :

Bibliothèque :

Institut Tunis-Dauphine - 20 rue Baudelaire, 1005 El Omrane

2

Table des matières

Liste des tableaux 4

Table des figures 5

Résumé 7

Abstract 9

Remerciements 11

Note de Synthèse 12

Synthesis note 16

Introduction 20

1 Contexte et Cadre réglementaire 21

1.1 Présentation de ERM Partners 21

1.2 Normes réglementaires en assurance : Solvabilité I et Solvabilité II 22

1.2.1 Solvabilité I : Principes et Limites 22

1.2.2 De Solvabilité I vers Solvabilité II 24

1.2.3 Solvabilité II 25

1.3 Contexte historique de la gestion actif-passif 28

1.3.1 Introduction à la gestion actif-passif 28

1.3.2 Evolution des outils de la gestion actif-passif à travers les

générations 29

1.3.3 Limites d'un modèle de gestion actif-passif 31

2 Les générateurs de scénarios économiques 32

2.1 Introduction et motivation 32

2.2 Définition d'un GSE 32

2.3 Etapes de la construction d'un GSE 33

2.4 Principaux modèles d'un GSE 43

2.4.1 Modèle de WILKIE - 1986 43

2.4.2 Modèle de Brennan and Xia 46

2.4.3 Modèle d'Ahlgrim et AL 48

2.4.4 Avantages et limites des modèles de références 50

3 La gestion actif passif dans le cadre de l'assurance 52

3.1 Présentation d'un contrat d'assurance vie 53

3.2 Présentation de l'assurance non-vie 55

3.3 Modélisation Actif - Passif 57

3

TABLE DES MATIÈRES

3.4 Modélisation de l'actif 57

3.4.1 Modélisation de l'actif en assurance vie 58

3.4.2 Modélisation de l'actif en assurance non-vie 59

3.5 Modélisation du passif 59

3.5.1 Modélisation du passif en assurance vie 59

3.5.2 Modélisation du passif en assurance non-vie 60

3.6 Interaction actif-passif 60

3.7 Projection des éléments de comptabilité 62

3.7.1 Revalorisation de l'actif 63

4 Application pratique de la mise en place d'un GSE et projection au sein du

modèle ALM 66

4.1 Analyse des données 66

4.1.1 Taux d'inflation 67

4.1.2 Taux d'intérêt 69

4.1.3 Rendement des actions 71

4.1.4 Rendement de l'immobilier 72

4.2 Calibrage des données 74

4.3 Projection 78

4.3.1 Projection issues du calibrage du modèle d'Ahlgrim et Boostrap 80

4.4 Réalisation d'un cas pratique pour une compagnie d'assurance 88

4.4.1 Cas pratique en assurance non-vie 88

4.4.2 Résultats en assurance non-vie 92

4.4.3 Cas pratique en assurance vie 93

4.4.4 Résultats en assurance vie 96

Conclusion 99

4

Liste des tableaux

1.1 Comparaison entre Solvabilité 1 et Solvabilité 2 25

2.1 Tests statistiques et intérêts 41

2.2 Comparaison entre un monde réel et un monde risque neutre 43

2.3 Avantages et limites des modèles de référence 51

4.1 Statistiques du taux d'inflation entre 1990-2021 68

4.2 Statistique du Taux réel à court terme entre 1990-2020 70

4.3 Statistique du Taux réel à long terme entre 2007-2021 70

4.4 Statistique du rendement de l'action entre 1997-1990 72

4.5 Statistique du rendement de l'immobilier entre 2000-2020 74

4.6 Ahlgrim : Estimation des paramètres du modèle sur l'inflation 74

4.7 Ahlgrim : Test d'adéquation du modèle sur l'inflation 74

4.8 Ahlgrim : Estimation des paramètres du modèle sur l'immobilier . . 75

4.9 Ahlgrim : Test d'adéquation du modèle sur l'immobilier 75

4.10 Ahlgrim : Estimation des paramètres du modèle sur le taux d'intérêt

réel à long et court terme 76
4.11 Ahlgrim : Test d'adéquation du modèle sur le taux d'intérêt réel à

long terme 77
4.12 Ahlgrim : Test d'adéquation du modèle sur le taux d'intérêt réel à

court terme 77
4.13 Ahlgrim : Estimation des paramètres du modèle sur le rendement

d'actions 78

4.14 Ahlgrim and Al : Matrice de corrélation de l'historique des résidus . 79

4.15 Ahlgrim and Al : Matrice de corrélation - Décomposition de Cholesky 79

4.16 Ahlgrim and Al : Matrice de corrélation projeté 80

5

Table des figures

1 Résultats des projections Ahlgrim et Al. réalisés 13

2 Résultats des projections par Boostrap réalisés 14

3 Distribution des NAV selon les deux scénarios 15

1.1 Métiers du cabinet ERM partners 22

1.2 Bilan sous Solvabilité 1 23

1.3 Passage d'un bilan comptable a un bilan économique 24

1.4 Principes de la norme prudentielle Solvabilité 2 26

2.1 Les étapes de la construction d'un GSE 33

2.2 Structure do modèle de WILKIE [1] 45

2.3 Structure du modéle de Brennan-Xia [1] 48

2.4 Structure du modéle de Ahlgrim-Al [1] 50

3.1 Démarche de calcul du BE et NAV 61

3.2 Démarche de projection en assurance non-vie [8] 62

3.3 Démarche de projection des éléments de comptabilité 63

4.1 Evolution de l'inflation entre 1990-2020 (Source : INS ) [12] 68

4.2 Evolution du TMM entre 1990-2020 (Source : INS) [23] 69

4.3 Evolution de TUNINDEX entre 1997-2020 (Source : INS) [12] 71

4.4 Evolution du rendement de l'action entre 1997-2020 (Source : INS) [12] 72 4.5 Evolution du rendement de l'immobilier entre 2000-2020 (Source :

INS) [12] 73

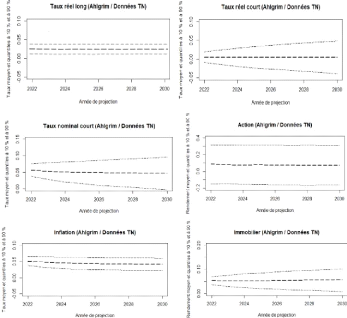
4.6 Ahlgrim et Al. : projection de l'inflation 80

4.7 Boostrap : projection de l'inflation 80

4.8 Ahlgrim et Al. : projection de l'éxcedent de rendement de l'action . 81

4.9 Boostrap : projection de l'éxcedent de rendement de l'action 81

4.10 Ahlgrim et Al. : projection de l'immobilier 82

4.11 Boostrap : projection de l'immobilier 82

4.12 Ahlgrim et Al. : projection de rendement de l'action 83

4.13 Ahlgrim et Al. : projection de Taux court 83

4.14 Ahlgrim et Al. : projection de Taux court 84

4.15 Boostrap : projection de Taux court 84

4.16 Ahlgrim et Al. : projection de Taux long 85

4.17 Boostrap : projection de Taux long 85

4.18 Ahlgrim et Al. : projection de taux réel court 86

4.19 Boostrap : projection de taux réel court 86

4.20 Ahlgrim et Al. : projection de Zero coupon nominal 87

4.21 Ahlgrim et Al. : projection de Zero coupon réel 87

4.22 Hypothéses de construction du bilan en assurance non-vie 88

4.23 Triangle PSAP 88

6

TABLE DES FIGURES

4.24 Règlements et charges des sinistres 89

4.25 Bilan économique 89

4.26 Compte de résultat technique 90

4.27 Etat de flux de trésorerie 91

4.28 Allocation stratégique des actifs 91

4.29 Rendements macro-économiques prospective issus des GSE 92

4.30 Hypothéses de projection en assurance-vie 94

4.31 Résultat de projection des facteurs financiers 95

4.32 Projection des cash-flows passif en assurance-vie 96

4.33 Résultats BE(0) et NAV(0) 96

4.34 Evolution du NAV selon le premier scénario 97

4.35 Evolution du NAV selon le deuxième scénario 97

7

Résumé

Les compagnies d'assurances sont exposées à plusieurs enjeux, parmi ceux on cite les engagements qui durent a long terme (les engagements liés aux produits d'épargne-retraite à titre d'exemple en assurance-vie et les rentes suite à des sinistres corporels en automobile pour l'assurance non-vie). De ce fait un risque de sous-investissement s'impose à l'activité, l'assureur doit donc disposer des outils nécessaires pour faire face à ses engagements envers ses assurés et ses actionnaires.

L'objectif de ce mémoire est de mettre en place des outils de l'analyse prospective de gestion actif-passif stochastique pour des compagnies d'assurances offrant des produits d'assurance vie et des produits d'assurance non-vie sous la probabilité historique et sur la base des données économiques et financières tunisiennes.

La mise en place de ces outils s'est déroulée en plusieurs étapes, en effet il est tout d'abord nécessaire de rappeler le cadre réglementaire (solvabilité 2 dans notre étude) qui constitue le principal enjeu pour les assureurs : des règles particulières pour la modélisation de l'actif et la modélisation du passif (soit en valeur de marché).

Ainsi, les compagnies d'assurances sont amenées à évaluer leur valeur économique et fournir une vision prospective sur leurs activités d'investissement pour faire face à toute fluctuation de sinistralité et l'apparition de nouveaux risques inhérents à l'activité.

Pour ce faire il est nécessaire d'implémenter un modèle ALM qui s'appuie sur des scénarios stochastiques fournis par le générateur de scénarios économiques (GSE)

Les outputs de ce GSE seront des outils utiles pour déterminer :

· Le bilan et le compte de résultat et l'état de flux de trésorerie.

· Le best estimates BE.

· La valeur de l'actif net « VAN ».

Dans le cadre de ce mémoire, nous construisons un générateur de scénarios économiques permettant de projeter les indices économiques suivant : le taux d'intérêt tel que l'inflation, le taux court et long et les rendements des actions et immobiliers en utilisant le modèle de Wilkie, Brennan and Xia et Ahlgrim et Al. Ce dernier est choisi car il s'adapte mieux à la nature des données du marché tunisien.

Au final, nous proposons une analyse des résultats obtenus, ces analyses seront exploitées par la suite pour l'élaboration d'un business plan pour une compagnie d'assurance tunisienne.

Notre étude traitera ce business plan sous les différents scénarios afin de fournir une allocation stratégique optimale des actifs.

8

TABLE DES FIGURES

Mots-clés: Générateur de scénarios économiques, Gestion actif-passif, Solvabilité 2, Best Estimate, Valeur de l'actif net, assurance vie, assurance non-vie, PM, PSAP, bilan, Compte de resultat.

Our study will treat this business plan under the different scenarios in order to provide an optimal strategic allocation of assets.

Abstract

Insurance companies are exposed to several issues, among those we cite long-term commitments (commitments related to retirement savings products for example in life insurance and annuities following bodily injury claims for non-life insurance). As a result, a risk of underin-vestment is imposed on the activity, the insurer must therefore have the necessary tools to meet its commitments to its policyholders and shareholders.

The objective of this thesis is to set up prospective analysis tools for stochastic asset-liability management for insurance companies offering life insurance products and non-life insurance products under the probability historical data and on the basis of Tunisian economic and financial data.

The implementation of these tools took place in several stages, indeed it is first of all necessary to recall the regulatory framework (solvency 2 in our study) which constitutes the main issue for insurers : specific rules for the modeling of the assets and the modeling of the liabilities (either in market values).

Thus, insurance companies are required to assess their economic value and provide a forward-looking view of their investment activities to deal with any fluctuation in claims and the emergence of new risks inherent in the activity.

To do this it is necessary to implement an ALM model which is based on stochastic scenarios provided by the economic scenario generator (GSE)

The outputs of this GSE will be useful tools to determine :

· The balance sheet and the income statement and the cash flow statement.

· The best estimates BE.

· The value of the "NAV" net assets.

As part of this thesis, we are building an economic scenario generator allowing the projection of the following economic indices : the interest rate such as inflation, short and long rate and returns on stocks and real estate using the model of Wilkie, Brennan and Xia and Ahlgrim and Al. The latter is chosen because it best fits the nature of the market data Tunisian.

In the end, we propose an analysis of the results obtained, these analyzes will be used in the following for the development of a business plan for a Tunisian insurance company.

TABLE DES FIGURES

Key words : Economic scenario generator, Asset liability Manegement, Solvency 2, Best Estimate, Net asset value, life insurance, non-life insurance, MP, IBNYR¹, balance, income statement.

10

1. Incurred But Not Yet Reported

11

Remerciements

La réalisation de ce mémoire était possible grâce au concours de plusieurs personnes à qui je voudrais témoigner toute ma gratitude.

Je voudrais tout d'abord adresser toute ma reconnaissance au directeur de ce mémoire, M.Ksouri Mohamed Najed, pour sa patience, sa disponibilité et surtout ses judicieux conseils, qui ont contribué à alimenter ma réflexion.

Je tiens à remercier également Mme.Rihani Sinda tutrice académique de ce mémoire pour avoir eu la patience de répondre à mes innombrables questions, ses nombreux conseils ainsi ses instructions pertinentes pour la rédaction de ce mémoire.

Je désire aussi remercier les professeurs de l'université de Tunis-Dauphine en particulier Rammeh Hichem, qui m'ont fourni les outils nécessaires à la réussite de mes études universitaires.

Je remercie également Mme.Dhuin Claudine (paix à son âme) chargée de la coordination entre Tunis-Paris dauphine pour son professionnalisme et sa disponibilité.

Je remercie également toute l'équipe ERM Partners, en particulier Chammem Irad et Dridi Imen pour leur accueil chaleureux et leur bienveillance.

Finalement, je tiens à remercier tous les membres de ma famille pour leurs supports, leurs encouragements et leur confiance.

12

Note de Synthèse

1. Introduction

La gestion actif-passif constitue un manuel d'organisation dans les compagnies assurances pour mesurer, analyser et gérer les risques inhérents à l'activité.

Une vision prospective de ce fait devient indispensable afin d'assurer une suffisance de capital afin de faire face aux engagements futurs. En assurance vie, les contrats d'épargne prévoient un certain nombre de garanties financières tel que le TMG, taux de revalorisation en contre partie d'une prime et des risques tel que la mortalité et le rachat pour ce faire l'assureur doit :

· Prévenir une stratégie d'investissement.

· Fixer une allocation optimale de ces générateurs d'intérêts.

· Traiter ses hypothèses sous diffèrent scénarios afin qu'ils soient capables pour n'importe quelle déviation du marché.

En assurance non-vie, la prime payée doit couvrir totalement le risque souscrit en particulier les risques qui durent à long terme tel que les rentes suite à des sinistres corporels en automobile ou bien les rentes suite à une erreur médical en assurance santé dans ce contexte l'assureur doit étudier :

· Les différents scénarios financiers, permettant de choisir l'une des différentes allocations gérées d'actifs en fonction du ratio S/P.

· L'impact de la variation du ratio S/P.

· L'impact d'un excès de sinistralité.

Les compagnies d'assurances dépendent alors fortement de la situation économique du marché, ce facteur constitue un élément inhérent de l'activité puisque l'assureur s'engage à :

· Fournir l'interaction actif-passif.

· Choisir une allocation optimale d'actif répondant au besoin des assurés et des actionnaires.

· Respecter un cadre réglementaire et comptable.

D'où la nécessité d'un modèle ALM (Asset Liability Management) afin de projeter les flux des actifs et passifs et prévoir l'évolution de l'activité de l'entreprise à long terme.

2. Une analyse des résultat obtenus

Nous travaillons sur les deux volets d'assurance : l'assurance vie et non-vie dans l'objectif

13

TABLE DES FIGURES

de fournir des outils d'aide à la décision.

Nous commençons à projeter nos variables macro-économiques : l'indice inflation, le rendement de l'action, le rendement de l'immobilier, le taux réel long, le taux réel court et les prix de zéro-coupon nominal et réel.

Cette projection constitue la force motrice de ce mémoire intitulé « Application des générateurs de scénarios économiques en ALM pour les compagnies d'assurances », elle est assuré comme l'indique son nom par les GSE en particulier le modèle de référence AHLGRIM et AL . : un modèle qui demande des données disponible au niveau du marché tunisien dont ces derniers répondent aux contraintes qu'il demande singularisé par rapport au autres modèle (WILKIE, BRENNAN AND XIA dans notre étude) par l'indice immobilier qui constitue un pilier d'investissement chez les assureurs tunisien ainsi la simplicité d'implémentation. Nous obtenons les résultats suivants :

FIGURE 1 - Résultats des projections Ahlgrim et Al. réalisés Ces outputs sont utilisés dans la suite pour :

· Projeter le bilan, le compte de résultat technique et l'état de flux de trésorerie.

· Calculer le Best Estimate et la NAV.

· Analyser les différentes allocations des actifs.

14

TABLE DES FIGURES

Pour la projection (en assurance non-vie) on s'appuie sur les techniques de boostrapping afin de rééchantillonner à chaque fois un nouveau scénario.

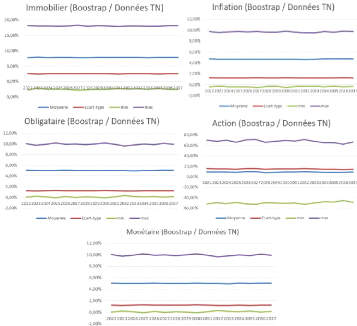
FIGURE 2 - Résultats des projections par Boostrap réalisés

En assurance non-vie nous avons analysé l'évolution des fonds propres selon deux scénarios économiques dont la répartition du premier définie par : 15% en monétaire, 15% en action, 10% en immobilier et 50% en obligataire.

L'allocation proposée pour le deuxième scénario est la suivante : 20% en monétaire, 30% en action, 20% en immobilière et 20% en obligataire.

Pour l'assurance vie on trouve les deux histogrammes de la distribution du NAV suivantes: Dont le premier scénario est défini par l'allocation suivante :

· 80% en action.

· 20% en obligataire

Pour le deuxième scénario on propose le cas contraire (80% en obligation et 20% en action (courbe au-dessous)).

3. Conclusion

Pour l'assurance non-vie nous choisissons d'investir selon l'allocation proposée dans le deuxième scénario, en effet un coefficient de variation de 14% contre celle des 30% pour le premier scénario.

15

TABLE DES FIGURES

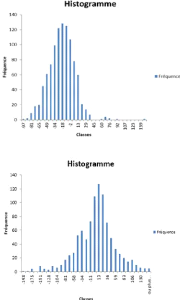
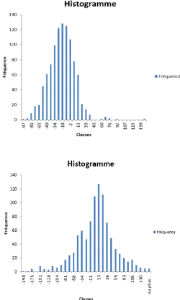
FIGURE 3 - Distribution des NAV selon les deux scénarios

Pour l'assurance vie on choisi également le deuxième scénario, ce choix est motivé par la valeur du NAV de 93,01 contre -12,08, ce choix est renforcé également par une interprétation graphique en effet la première distribution est plus aplati par rapport à la deuxième ce qui implique que notre investissement est plus risqué et plus étalé ainsi on peut expliquer aussi ce choix par la volatilité élevée du marché donc les assureurs recourent vers les obligations pour se couvrir.

Les résultats réalisés n'impliquent pas de se limiter aux décisions fournies par le code, en effet :

· Un modèle est l'outil d'approximation et d'aide à la décision, certes son utile mais reste est limité : on peut renforcer le choix par d'autres outils

· Un assureur est exposé aux différents risques, il n'est pas évident de corréler entre eux : on peut modéliser des corrélations au sein d'un GSE par les méthodes des vraies semblances et les copules

· Mesurer les différents degrés d'aversion de risque : utiliser les fonctions d'utilité (Von Neuman Morgenstein)

16

Synthesis note

1. Introduction

Asset-liability management constitutes an organizational manual in insurance companies for measuring, analyzing and managing the risks inherent in the activity.

A forward-looking view of this fact becomes essential in order to ensure sufficient capital to meet future commitments. In life insurance, savings contracts provide for a certain number of financial guarantees such as the TMG, revaluation rate in return for a premium and risks such as mortality and redemption for to do so, the insurer must:

· Prevent an investment strategy.

· Set an optimal allocation of these interest generators.

· Treat his assumptions under different scenarios so that he is capable for any deviation from the market.

In non-life insurance, the premium paid must fully cover the risk taken out, in particular risks that last in the long term such as annuities following bodily injury in the automobile or annuities following a medical error in health insurance in this context. the insurer must study:

· The different financial scenarios, allowing to choose one of the different managed asset allocations according to the S / P ratio.

· The impact of changing the S / P ratio.

· The impact of excess claims.

Insurance companies are therefore highly dependent on the economic situation of the market, this factor is an inherent element of the activity since the insurer is committed to:

· Provide active-passive interaction.

· Choose an optimal asset allocation that meets the needs of policyholders and shareholders.

· Respect a regulatory and accounting framework.

Hence the need for an ALM (Asset Liability Management) model in order to project the flows of assets and liabilities and forecast the evolution of the activity of the company in the long term.

2. Une analyse des résultat obtenus

We are working on both sides of insurance: life and non-life insurance with the aim of providing decision support tools.

17

TABLE DES FIGURES

We begin to project our macroeconomic variables: the inflation index, the stock yield, the real estate yield, the real long rate, the real short rate and the nominal and real zero-coupon prices.

This projection constitutes the driving force of this thesis entitled "Application of the generators of economic scenarios in ALM for the insurance companies", it is ensured as indicated by its name by the GSE in particular the reference model AHLGRIM et al . : a model which requires data available at the level of the Tunisian market of which the latter responds to the constraint that it requests singled out compared to the other model (WILKIE, BRENNAN AND XIA in our study) by the real estate index which constitutes a pillar of investment in Tunisian insurers and simplicity of implementation. We obtain the following results:

These outputs are used in the following for :

· Project the balance sheet, the technical income statement and cash flow statement.

· Calculate the Best Estimate and the NAV.

· Analyze the different asset allocations.

18

TABLE DES FIGURES

For the projection (in non-life insurance), we rely on boostrapping techniques in order to resample a new scenario each time.

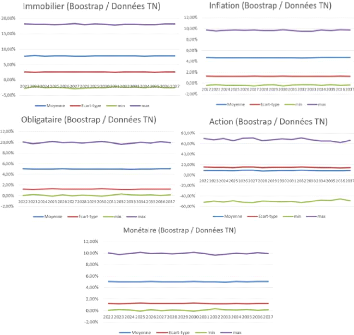
In non-life insurance, we have analyzed the evolution of own funds according to two economic scenarios, the distribution of the first of which is defined by: 15% in money market, 15% in equities, 10% in real estate and 50% in bond.

The allocation proposed for the second scenario is as follows: 20% in money market, 30% in equities, 20% in real estate and 20% in bonds.

For life insurance we find the following two histograms of the NAV distribution: The first scenario of which is defined by the following allocation:

· 80% in equity.

· 20% in bounds.

For the second scenario, we propose the opposite case (80 % in bonds and 20 % in shares (curve below)).

3. Conclusion

For the non-life insurance we choose to invest according to the allocation proposed in the second scenario, in fact a coefficient of variation of 14 % against that of the 30 % for the first scenario thus this choice is reinforced by a graphic interpretation: equity at the end of the period is higher than the first amount invested at the initial.

19

TABLE DES FIGURES

For the life insurance we also choose the second scenario, this choice is motivated by the value of the NAV of 93,01 against -12,08, this choice is also reinforced by a graphic interpretation in fact the first distribution is more flattened compared to the second which implies that our investment is more risky and more spread out so we can also explain this choice by the high volatility of the market therefore the insurers resorts green bonds to hedge.

The results achieved do not imply limiting oneself to the decisions provided by the code, in fact:

· A model is an approximation and decision-aid tool, certainly useful but these are limited: we can reinforce the choice by other tools.

· An insurer is exposed to different risks, it is not easy to correlate between them: we can model correlations within a GSE by the likelihood methods and them copulas.

· A person averse to risk and seek to hedge is not capable of generating more return: we resort to utility functions in microeconomics to reinforce the degree of risk aversion.

20

Introduction

Dans un contexte lié à la sensibilité du secteur financier à toute variation du taux l'assurance fait face à plusieurs enjeux parmi ceux on cite : le risque de sous-investissement, le risque de contre partie et le risque de change.

En outre, le passage vers les nouvelles normes réglementaires et comptables représente un enjeu pour l'assurance de point de vue implémentation, cout de passage et mise en vigueur.

Pour ces raisons fondamentales, l'assureur doit avoir une vision quotidienne et prospective sur l'activité de son entreprise pour faire face à n'importe quel scénario aberrant et satisfaire ses contraintes envers assurés.

D'ou la nécessité de la mise d'un générateur de scénario économique pour l'exécution simultanée des milliers de scénarios, projeter les facteurs de risque tel que l'inflation, le taux d'intérêt et les rendements action et immobilier tout en intégrant les contraintes économiques de long terme et la dépendance des actifs.

Nous proposons d'élaborer un GSE qui sera nécessaire pour la modélisation de la gestion actif passif dans le cadre d'assurance vie et non vie. afin d'analyser, mesurer et gérer les différents risques encourus.

Le premier chapitre est une brève introduction aux travaux de ce mémoire dans lequel nous présentons le cadre réglementaire , une introduction également de la gestion actif-passif.

Le deuxième chapitre souligne la force motrice de ce mémoire nommé les générateurs de scénarios économiques, ce dernier nous permettra de projeter les variables macro-économiques d'intérêt tel que l'inflation, le taux court et à long terme et les rendements des actions et immobiliers sous les modèles de références : Wilkie, Brennan and Xia et Ahlgrim et Al. Nous détaillerons également dans ce chapitre les étapes de constructions et les tests statistiques nécessaires pour la validation d'un modèle.

Dans le troisième chapitre de ce mémoire nous présentons la gestion actif-passif dans le cadre de l'assurance vie et non-vie, nous proposons également une modélisation de l'actif et une modélisation du passif et nous terminons avec une construction du compte de résultats et le bilan comptable.

Finalement avec le quatrième chapitre nommé modélisation d'un cas pratique : une application de ce qui était présenté en théorique pour les deux volets d'assurances : vie et non-vie. La dernière phase consiste à analyser les résultats obtenus et l'élaboration d'un business plan pour une compagnie d'assurance Tunisienne réelle.

21

Chapitre 1

Contexte et Cadre réglementaire

1.1 Présentation de ERM Partners

ERM² Partners est un cabinet de conseil et de formation professionnelle en Risk Management et en Actuariat dans les secteurs de l'assurance, de la finance et de l'industrie, basé principalement à Tunis, le cabinet possède une représentation commerciale à Dakar pour la zone CIMA³[15].

L'équipe d'actuaires et de consultants intervient sur l'ensemble des sujets liés aux problématiques actuarielles et financières et dispose d'une excellente connaissance des outils informatiques ainsi que des logiciels mathématiques et statistiques.

Le réseau international pluridisciplinaire de partenaires accompagne également dans les évolutions réglementaires, financières, économiques et technologiques du secteur pour les aider à en tirer la meilleur partie.

L'expertise opérationnelle du cabinet est mise en service de ses clients couvrant l'ensemble d'épargne, retraite, prévoyance, santé, responsabilité et dommages reposant sur une large spectre de sujets tant pour la mise en oeuvre que pour la revue :

· La conception et l'analyse de rentabilité des produits Vies et IARD

· Le provisionnement selon divers référentiels (Comptable et réglementaire)

· Les techniques de calcul (ALM ⁴, Embedded Value, Goodwill, ...)

· La gouvernance (Gestion des risques, Conformité, Actuariat, ...)

ERM partners fait partie du réseau international d'actuaires indépendants GLOBACS⁵, le plus grand et ancien regroupement d'actuaires dans le monde, comptant environ 40 cabinets membres et plus de 2000 actuaires.

2. Entreprise Risk Management

3. Chartered Institute of Management Accountants : Société qui aident les entreprises du monde entier à gérer leurs finances

4. Asset Liability Management

5. Global Actuarial and Consulting Services

22

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

FIGURE 1.1 - Métiers du cabinet ERM partners

1.2 Normes réglementaires en assurance : Solvabilité I et Solvabilité II

La solvabilité en assurance est définie comme la capacité de la société à faire face à ses engagements envers les assurés et les actionnaires. Elle doit générer suffisamment d'activité pour pouvoir rembourser ses dettes envers ses créanciers, ses actionnaires (dettes financières) et ses assurés à travers les provisions techniques.

Selon les conditions imposées par le marché, les autorités des normes comptables et règle-mentaires assurent le contrôle du secteur assurantiel en développant des normes qui répondent aux besoins des compagnies.

Pour exercer le métier, les autorités de contrôle de sa part obligent les assurances de fournir un capital règlementaire requis, ce capital réglementaire est limité par un minimum de capital de solvabilité requis permettant d'assurer la bonne pratique de l'activité.

1.2.1 Solvabilité I : Principes et Limites

La directive européenne sur la solvabilité a déclaré en deux moments différents la mise en vigueur des premierer réformes réglementaires pour améliorer l'activité du secteur assurantiel; la première en 1973 lors du conseil pour les assureurs non-vie et la deuxième en 1979 lors du conseil pour les assureurs vie.

Vers 1994, tenant compte du développement du marché ainsi que l'évolution remarquable de la population au cours du temps, la troisième directive s'engage à la mise des règles sur la solvabilité des assureurs fondes sur des principes rigoureux et stricts.

Février 2002, la norme solvabilité 1 est entrée en vigueur officiellement dans l'objectif d'harmoniser la réglementation européenne et de renforcer les contrôles du secteur assurantiel.

Le bilan sous Solvabilité 1 est en norme comptable dont l'actif est constitué essentiellement de placement enregistré en valeur comptable , le passif également englobe l'ensemble des provisions techniques et le fonds propres qui doivent être supérieurs au minimum du capital réglementaire imposé par l'autorité.

D'une manière générale, le bilan comptable sous solvabilité I a la forme suivante:

23

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

FIGURE 1.2 - Bilan sous Solvabilité 1

Les principes de solvabilité I

Cette norme réglementaire s'articule autour de trois points essentiels :

1. Fournir une marge de solvabilité qui doit être supérieure à un minimum réglementaire (exigence d'une marge de solvabilité).

2. Posséder suffisamment d'actifs réels que de dettes et engagements.

3. Le passif doit être adéquat avec l'actif (Construction des provisions techniques prudentes). Sous la directive solvabilité I, les fonds propres sont fondés sur 3 points principaux :

· Le surplus de capital

C'est la composante principale des fonds propres que considère cette première réglementation dans le bilan d'une entreprise, il tient compté des capitaux propres qu'on l'appelle aussi l'excédent de capital ou primes d'émission.

Ce surplus désigne la marge ajoutée sur la valeur nominale de la vente d'une action ordinaire.

· Exigence de la marge de solvabilité (EMS)

Dans un deuxième moment solvabilité I exige les compagnies d'assurances à disposer d'une marge de solvabilité pour renforcer leur capacité à faire face à des événements imprévus qui doivent être supérieurs à un minimum réglementaire mentionné par le régulateur. En cas du non-respect de cette note la compagnie d'assurance sera sanctionnée.

· Le fonds de garantie

Fond dédie spécialement pour financer et protéger les compagnies d'assurances en cas d'insolvabilité à travers le remboursement des assurés dans ce contexte.

24

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

Les limites de solvabilité I

Le régime prudentiel du secteur assurantiel dit Solvabilité 1 a été remis en question pour plusieurs avantages tel que la simplicité de le mettre en vigueur et la facilité du calcul de la marge de solvabilité, néanmoins ces dernières années le secteur a marqué une refonte très profonde en raison de :

· La vision rétrospective sur l'activité de l'entreprise : un bilan comptable qui limite la vision du marché.

· Les risques de marché qui ne sont pas pris en considération pour le calcul de l'SCR.

· Le manque d'un aspect qualitatif et d'un aspect de communication avec le régulateur et le public.

Nous détaillerons dans la section suivante les conditions d'imposition d'une nouvelle norme plus prudentielle ainsi que les conditions de la mise en vigueur.

1.2.2 De Solvabilité I vers Solvabilité II

Pour renforcer l'activité de l'assurance due à l'évolution imposée par le marché concurrentiel, les autorités de contrôle font face à plusieurs nouveaux enjeux tels que l'apparition de nouveaux risques techniques, juridiques, financiers qui impactent fortement la gestion des portefeuilles des compagnies d'assurances.

Une évolution au niveau du bilan devient indispensable pour le secteur, une valorisation plus économique non comptable, a cet effet le bilan devient :

FIGURE 1.3 - Passage d'un bilan comptable a un bilan économique

Le changement au niveau du bilan observé ci-dessus tient compte des challenges nécessaires, en effet :

Au niveau de l'actif

· Une évaluation des actifs en valeur de marché et non plus en valeur comptable.

25

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

· Tenir compte de la duration et la sensibilité de l'actif pour mettre en évidence une technique d'adossement du passif à travers le calcul des SCR permettant d'avoir une évolution cohérente entre l'actif et le passif.

Au niveau du passif

· Introduction d'une nouvelle modélisation des provisions techniques.

· Une réforme considérable et plus logique au niveau du calcul de SCR¹, MCR² ainsi que la marge pour risque.

· Les fonds propres (SCR, MCR et la marge pour risque) reflètent les risques de l'activité ainsi les engagements ce qui permet d'avoir une meilleure protection pour les assurés et les investisseurs.

· Une nouvelle notion de la marge de solvabilité assure une pratique plus simple.

Le tableau ci-dessous met en relief les principaux points de différence entre solvabilité I et solvabilité II :

	Solvabilité I	Solvabilité II
Pour les exigences	Pas d'exigences quantitatives Suivi classique du profil de risque Absence de communication avec les tiers : régulateur et investisseurs	Des exigences qualitatives et quantitatives Des exigences de reporting et de publication Basée sur des principes plutôt que des règles de calcul
Pour les régles	La norme n'était pas harmonisée au niveau de l'union Européenne	Une harmonisation entre les pays du continent Européen
Pour la gestion actif-passif	Actif est en valeur comptable Provision non prudente	Introduction des outils mathématiques garantissant une évolution économique adéquate du passif avec l'actif
Pour le calcul des risques	Niveau de prudence des provisions insuffisant Pas de formule unique	La formule standard Le modèle interne Le modèle interne partiel

TABLE 1.1 - Comparaison entre Solvabilité 1 et Solvabilité 2

L'objectif de la section suivante est de présenter la norme prudentielle Solvabilité 2, les piliers sur lesquels elle se base ainsi les notions de la formule standard, le modèle interne et le modèle interne partiel.

1.2.3 Solvabilité II

Le 1^er janvier 2016 la directive Solvabilité II rentre en vigueur : une réforme réglementaire équivalente à Bale II pour les banques marquées par une évolution énorme au niveau du bilan

1. Solvency Capital Requirement

2. Minimum Capital Requirement

26

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

et la communication.

Elle a pour ambition d'harmoniser le calcul de solvabilité des compagnies d'assurances en Europe et renforcer l'aspect qualitatif et la relation entre l'assureur et le régulateur et l'assureur et les assurés, les actionnaires. Elle sert à mieux protéger tous les tiers intervenants dans le secteur.

Depuis sont rentrés en vigueur, l'EIOPA¹ exige l'application de 3 piliers dans l'ordre d'harmonisation de la norme surtout l'échelle européenne :

FIGURE 1.4 - Principes de la norme prudentielle Solvabilité 2

Pilier I : Exigence quantitatives

Le premier pilier détermine les exigences quantitatives de solvabilité sur laquelle s'appuie la réforme. Il vise à calculer principalement :

· SCR : Le capitale de solvabilité requise dont l'assureur doit disposer pour faire face à ses engagements et honorer ses assurés en cas de réalisation d'un événement extrême où un choc provoque par un risque majeur.

Le calcul du SCR se fait par deux principaux moyens:

1. Soit par la formule standard publiée par l'autorité de contrôle européenne (l'EIOPA) dite approche standard dont la formule donnée par le régulateur s'adapte avec toutes les compagnies existantes sur le marché prenant en compte les risques significatifs et quantifiables.

L'objectif de cette formule est d'avoir un niveau de couverture égale à 99, 5% sur le

1. European Insurance and Occupational Pention Authority: C'est un organe consultatif indépendant auprès du Parlement européen, au Conseil de l'Union européenne et la Commission européenne ayant pour objectif le contrôle et la bonne surveillance du secteur financier.[28]

27

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

risque global de la compagnie à l'horizon d'un an c'est dire une seule ruine dans 200 ans.

2. Soit par un modèle interne établi par la compagnie elle-même sous l'accord du régulateur, ce phénomène est rare vue le cout de passage.

3. Soit par un modèle interne partiel en complément de la formule standard à condition qu'il soit validé par les autorités de contrôle.

· MCR : C'est le capital minimum requis au-dessous duquel l'entreprise n'aura pas le droit de poursuivre son activité, sinon le régulateur imposera des mesures de sanctions.

· Best Estimate of liabilities : Les provisions techniques sous solvabilité II sont valorisées en matière de best estimate (BE) qui reflète la moyenne des couts des engagements contractuels et futurs de l'organisme, compte tenu de la valeur temporelle de l'argent estimée sur la base de la courbe des taux sans risque pertinent.

On peut aussi le définir comme la moyenne de l'écart entre les flux futurs entrants et sortants pondérés par leur probabilité de réalisations actualisées par la valeur future de l'argent.

Avec :

BEL = EP N Q(X t>0

Ft * ät) (1.2.1)

- Ft = F entrant -_F sortant : différence entre les flux futurs entrants et les flux futurs

t t

sortants.

- ät : facteur d'actualisation tient compte du taux sans risque et le correcteur de volatilité.

- Q : probabilité risque neutre

- P : probabilité réelle qui valorise les actifs financiers

On rappel que la courbe des taux généralement donnée par l'EIOPA.

Pilier II : Exigence qualitatives

Le deuxième pilier du régime prudentiel dédié a contrôlé la bonne application de celle du premier, il est destiné à effectuer des contrôles internes et externes et instaurer une formule mathématique unique qui sert de référence à toutes les entreprises d'assurance et de réassurance, mais cette dernière ne quantifie pas parfaitement les risques propres à chaque compagnie.[9]

IL souligne également la bonne gouvernance et la maitrise du risque pour l'assureur, l'efficacité de la vision mise en hypothèse et assure une solvabilité prudente respectant les règles imposées par la directive.

La particularité de ce pilier réside au niveau de l'ORSA 1 : un outil avec lequel l'assureur aura plus de capacités pour identifier, clarifier et gérer ses risques, il assure un système de contrôle et d'évaluation interne des risques et impose un suivi continu.

1. Own Risk and Solvency Assessment

28

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

Ce processus se manifeste à partir d'une démarche ERM ¹ et exige les responsables à mieux réagir sur leur gestion des risques et leur stratégie commerciale adoptée : ils déterminent leurs BGS² en prenant en considération de leur profil de risque particulier, des limites approuvées de tolérance aux risques et de la stratégie commerciale de l'entreprise.

De ce fait, le processus ORSA tient compte des risques qui ne sont pas mentionnés dans le premier pilier en respectant des exigences de capital SCR et MCR également des exigences concernant les provisions techniques ou Best Estimate.

Pilier III : Exigence de l'information

Le troisième pilier souligne la discipline de la transparence des compagnies d'assurances envers le marché financier, de ce fait la directive prévoit la publication de deux rapports chaque année : un rapport SFCR³ pour les assurés et les investisseurs et un rapport RSR⁴ pour le régulateur.

Nous nous restreindrons seulement au premier pilier dans le cadre de ce mémoire en particulier le calcul du best estimate qui donne une vision prospective sur le portefeuille passif de la compagnie, en effet à l'aide des résultats de projection qu'on réalisera par la suite on peut limiter l'intervalle des valeurs possibles du BE.

Nous avons détaillé de ce qui précède les piliers de solvabilité 1 et ses limites ainsi les conditions de passage de solvabilité 1 vers solvabilité 2 et nous arrivons à expliquer les 3 piliers sur lesquels s'appuie la norme prudentielle Solvabilité 2 ainsi les différentes notions relatives.

Nous décrivons par la suite le contexte historique et l'évolution de la gestion actif-passif à travers les générations.

1.3 Contexte historique de la gestion actif-passif 1.3.1 Introduction à la gestion actif-passif

À partir de 1930 le secteur assurantiel a marqué un progrès exponentiel à l'échelle mondiale , une nouvelle culture envers l'assurance oblige les assureurs de la mise en place d'une nouvelle stratégie pour capter le maximum des souscriptions et garantir une qualité de service répondant aux besoins des assurés.

Une pensée de la part des états en particulier les pays du continent européen suite aux difficultés des grandes institutions financières dues au post premiere guerre mondial.

Les gouvernements ont mis en place une surveillance et une réglementation pour le secteur de l'épargne et des concepts financiers comme l'immunisation et la duration sont apparues.

La crise des années 80 a été la conséquence d'engagements à des taux élevés qui se sont révélés difficiles à honorer : baissent des taux d'intérêt et de moins-value constatées sur des

1. Entreprise Risk Management

2. Besoin Global de Solvabilité

3. Solvency and Financial Condition Report

4. Regular Supervisory Report

29

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

actifs supposés les plus rémunérateurs/risqués (tel que l'immobilier,...) la liquidité des actifs était parfois insuffisante pour faire face à la baisse de la collecte et à l'augmentation du taux de rachat anticipé obligeant les assureurs à céder les actifs dépréciés.

Pour ces raisons les autorités de contrôle des sociétés d'assurance ont intégré progressivement des outils de gestion actif-passif dans les éléments de reporting.

Les difficultés financières à partir de 2000 dues au terrorisme, les guerres successives,... ont mis en évidence la faible résistance de certaines réglementations en cas de baisse de la bourse : les règles comptables et prudentielles de l'assurance-vie et des fonds de pension ont des êtres revus.

Evolution de l'ALM : de la banque vers l'assurance

La gestion actif-passif¹ est apparue dans les banques pour une prise de conscience plus poussée des risques financiers.

Pour les compagnies d'assurances le besoin de l'ALM est dans le cadre de satisfaire leurs engagements envers les assurés (les rentes, prestations, capitales,...), ceci est dû à :

· L'explosion des totaux de bilan grâce au fort développement de l'assurance-vie, qui est passée de la prévoyance a l'épargne.

· L'emergence de la banque assurance (assurance emprunteur).

· Contexte porteur d'une baisse des taux continue depuis 15ans.

1.3.2 Evolution des outils de la gestion actif-passif à travers les générations

1. Les outils de la 1^ére génération : une approche statique

Ces outils se basent sur une projection statique des flux financiers générés par l'actif et le passif, ils sont généralement utilisés pour mesurer l'adéquation entre ces derniers, en effet :

· La projection des flux de l'actif basé sur un scénario économique moyennant un scénario pour la structure par terme de taux, un scénario du marché des actions et un scénario de l'immobilier.

· La projection des flux du passif se fait d'une manière indépendante de l'actif, en effet elle dépend des caractéristiques des contrats d'assurance telles que TMG², montant investit, durée du contrat et rachat, décès...

Le recours à ces outils permettent d'avoir une vision des trésoreries et mesurer les enjeux de l'adéquation actif-passif, leurs durations, sensibilité et convexités ainsi utilisation pour la gestion des risques de taux valable pour des déplacements parallèles de courbe des taux.

Les limites de la première génération

1. Asset Liability Management en Anglais

2. Taux Minimum Garanti

30

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

· Des approches statistiques fondées sur des données réelles donc pas de vision prospective.

· Seuls les risques de taux sont étudiés.

· Les flux du passif sont très volatils et se prêtent mal aux calculs de duration.

2. Pour la 2^éme génération : une approche dynamique

L'approche dynamique est un outil qui vise à actualiser la totalité des cash-flows issus de l'actif et passif donnés au moment où l'étude est réalisée, ou constituée à une date prochaine en fonction de la stratégie qui sera adoptée par la société d'assurance.

Cette approche est plus favorisée que l'approche statique parce qu'elle n'est pas limitée par la stratégie définie en amont.

Comme déjà noté dans les limites de la première génération il s'agit d'une vision rétrospective, une vision basée sur des données des cash-flows issus de l'actif et passif au moment où l'étude est réalisée ne permettant pas d'avoir et d'estimer les flux futurs : une simulation déterministe du bilan et identification des risques ALM.

Cette vision est la plus proche de la nouvelle norme réglementaire solvabilité 2, elle vise à :

· Approcher les résultats des flux financiers futur.

· Avoir une vision plus globale du bilan économique (Vision dynamique) en fonction des perturbations, stress-test d'un paramètre selon le choix de l'assureur.

· Varier des paramètres fixés par l'assureur.

Dans ce cas, un risque pour une compagnie d'assurance est caractérisé par des indicateurs qui vont mesurer la dégradation de richesse via des stress-test, ces outils de cette génération se résument en 4 étapes :

· Prise en compte des hypothèses déterministe en interne.

· Définir un scénario central et les scénarios extrêmes par simulation (Simulation déterministe).

· Analyse et interprétation des différents risques.

· Un scénario résultant de la corrélation des scénarios étudiés.

Les limites de la deuxième génération

· Le nombre réduit des simulations.

· Il est difficile de tirer des stress-testes fiables relatives à la situation économique.

· Pas d'allocation optimale en environnement multi-variable (corréler tous les stress-testes).

3. La 3^éme génération : Vers une approche plus stochastique

Les outils de la 3^ème génération constitue l'introduction a les mathématiques financières, ces outils introduitsent des approches stochastiques par le biais des modèles prédéfinis dans le but de fournir le maximum de scénarios.

31

CHAPITRE 1. CONTEXTE ET CADRE RÉGLEMENTAIRE

C'est l'approche la plus forte puisqu'elle tient compte des outils des deux dernières générations et génère des scénarios futurs selon le contexte économique dans l'ordre de fournir une mesure cohérente des risques actif-passif. Cette génération opte à construire des outils de simulation financière tels que le rendement monétaire, le taux obligataire, le rendement des actions, l'inflation, le rendement locatif : Un processus stochastique qui peut générer une densité de probabilité conditionnelle (dépend du temps et d'une valeur initiale) pour les variables étudiées.

Les méthodes de Monte-Carlo

Désigne une famille de méthodes algorithmiques visant à calculer une valeur numérique approchée en utilisant des procédés aléatoires, elle s'appuie sur la loi forte des grands nombres. constitue un outil d'exploration, c'est la méthode la plus utilisée.

Générateur de scénario économique :

C'est un scénario économique défini par une simulation chronique d'indices économiques et financiers sur un horizon T d'intérêt : taux d'intérêt, prix des actions, taux obligataires... Un GSE constitue une nouvelle théorie actuarielle dont leurs applications sont diverses et variées parmi ceux on cite : ALM, ORSA, ...

4. La 4^éme génération : une approche d'optimisation stochastique

· Programmation d'algorithmes d'optimisation stochastique.

· Recherche automatique d'allocation stratégique.

1.3.3 Limites d'un modèle de gestion actif-passif

Le modèle de la gestion actif/passif présente des contraintes pouvant être prises en compte, parmi ces contraintes on cite :

· Choix d'investissement : Immobilier, Obligations, Actions.

· Hypothèses inhérentes à l'actif: La pertinence des hypothèses du système d'information.

· Présentation du passif.

· Détermination de l'allocation optimale.

· Politique de la participation aux bénéfices.

· L'application du modèle théoriquement émise : un contexte politique et économique s'impose (confinement, instabilité, conflits sociaux ...)

Nous avons expliqué dans ce qui précède le cadre réglementaire en assurance ainsi les conditions et les limites qui ont été prises en compte pour réaliser une réforme plus prudentielle ensuite nous avons détaillé le contexte de la gestion actif-passif et ses évolutions à travers les générations et ses limites.

Dans le chapitre suivant nous décrivons la force motrice de ce mémoire : Les générateurs de scénarios économiques l'outil avec lequel on va projeter notre bilan en assurance vie et en assurance non-vie.

32

Chapitre 2

Les générateurs de scénarios

économiques

2.1 Introduction et motivation

Les institutions financières telles que les banques et les compagnies d'assurances sont exposées aux différents risques du marché, elles sont sensibles à toutes variations des taux ce qui impacte fortement l'évolution prévue du bilan, la valorisation des engagements et leurs revalorisations également.

Avec la mise en place de la directive Solvabilité 2 de nouveaux challenges font face aux assureurs en particulier le bilan économique qui doit être réalisé. De ce fait l'utilisation des générateurs de scénarios économiques est devenue une pratique courante et indispensable dans le monde de l'assurance.

Grâce à cette pratique l'assureur aura une vision plus prospective sur l'activité de l'entre-prise ainsi une modélisation plus cohérente entre l'actif et le passif.

En assurance vie les assureurs utilisent les GSE pour simuler des trajectoires simultanées de tous les facteurs de risques financiers présents au bilan : Taux, crédit, actions, immobilier, investissements alternatifs, changes, etc...

En assurance non-vie les assureurs utilisent les GSE pour projeter les variables macroéconomiques telleque; l'inflation, le taux court, le taux réel ... afin d'avoir une vision prospective sur l'évolution du bilan.

2.2 Définition d'un GSE

Le générateur de scénario économique (GSE) est un outil de simulation qui permet de projeter dans le temps des trajectoires de grandeurs économiques telles que les taux d'intérêts, les taux d'inflations, les rendements des actions, les rendements obligataires, les rendements immobiliers qui interviennent dans la valorisation des engagements d'un assureur quel que soit le référentiel considéré (règlementaire ou comptable).

L'objectif de ce mémoire est d'utiliser les générateurs de scénarios économiques pour projeter les flux d'actif (actions, obligation, l'immobilier, ...) afin de calculer le BE et NAV ²

2. Net Asset Value

33

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

dans le cadre de l'assurance vie et l'assurance non-vie.

Les enjeux d'un GSE

Un scénario économique correspond aux rendements de grandeurs économiques sur un horizon de temps, ce scénario doit respecter certains points fondamentaux, parmi ceux on cite :

1. Etre prudent dans l'estimation des rendements.

2. Intégrer toutes les fluctuations possibles à court terme et tenir compte des impacts à long terme.

3. Avoir une vision prospective sur les contraintes économiques à long terme.

4. Intégrer la dépendance entre les actifs et modéliser la matrice de corrélation selon le besoin.

5. Respecter les tests statistiques et martingales dans le cadre de la calibration des variables choisies.

Les compagnies d'assurances sont soumises aux plusieurs risques commerciaux, operationnels, juridiques, techniques et financières.

Notons que les GSE contribuent à la prise des décisions stratégiques qui seront adoptées par les compagnies, ils permettent ainsi d'évaluer la juste valeur de l'entreprise assurantielle.

Il est aussi à noter que la prise de la décision et l'évaluation de la juste valeur passe par une gestion actif-passif, cette dernière permet de capter les risques inhérents qui peuvent être face a l'assureur ainsi il assure une vision prospective motivée par les outputs des GSE.

Nous détaillerons dans la suite les étapes de la construction d'un générateur des scénarios économiques ainsi les tests statistiques nécessaires pour la validation et leurs intérêts.

2.3 Etapes de la construction d'un GSE

Dans cette partie, nous allons citer les étapes de la construction d'un Générateur de Scénario économique [10], le schéma suivant illustre la démarche adoptée :

FIGURE 2.1 - Les étapes de la construction d'un GSE

34

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

1. Choix des inputs

Le choix des variables macro-économiques a modélisé dans un univers probabilisé¹ dépend de la qualité du portefeuille d'investissement étudié.

Il s'agit de construire des modèles mathématiques sur des variables d'intérêts tels que le taux d'intérêt, le rendement des actions, le rendement des immobiliers, ...

Pour assurer une bonne projection répondant au besoin fallait bien choisir les inputs et les bien modéliser, ceci est garanti :

(a) Soit par l'expérience.

(b) Soit par un avis de l'expert.

(c) Soit par des approximations aux données réelles.

2. Choix du modèle

Une fois qu'on a choisi les variables inputs, le choix du modèle devient nécessaire, ce choix dépend du type des variables macro-économiques ainsi la structure demandée :

· Soit un modèle en cascade (intégré) : Une seule variable parmi toutes les variables sera choisie pour déduire les autres grandeurs macro-économiques à titre d'exemple on cite le modèle de Wilkie qui sera expliqué dans la section modèle de référence.

· Soit un modèle par corrélation (composite) : C'est le modèle le plus utilisé dans les compagnies d'assurances : il est simple à implémenter et considérer une structure de dépendance linéaire que l'on détaillera dans le paragraphe suivant puis chaque classe d'actif est modélisée par un processus stochastique indépendamment des autres variables à titre d'exemple on cite le modèle de Brennan and Xia ou bien le modèle d'Ahlgrim et Al. qui sera expliqué également dans la section modèle de référence.

3. Structure de dépendance

L'objectif de cette étape est d'avoir une projection à minima acceptable à travers une structure de dépendance entre les sources des risques afin d'obtenir des projections cohérentes, trois structures de dépendance sont proposées :

· Une matrice de corrélation linéaire permettant d'étudier la dépendance entre les variables du GSE : c'est la structure la plus simple au niveau de l'estimation et la mise en oeuvre pratique.

Néanmoins plusieurs travaux ont montré que la dépendance linéaire peut conduire à une sous-estimation des paramètres cherchés.

· Une structure non-linéaire (dynamique) où la modélisation de l'interdépendance est basée sur les copules (archimédienne, gaussienne, ...) : ils permettent l'augmentation de la dépendance en période de crise.

1. Probabilité historique ou probabilité risque neutre

35

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

· Une structure développée par A.Faleh-Planchet[18] dans ses travaux en 2011 "pour les modèles qui s'avèrent difficiles à calibrer et à implémenter on segmente la matrice de corrélation selon la nature de la volatilité forte ou bien faible."

Dans le cadre de ce mémoire, nous modéliserons la dépendance par une matrice de corrélation qui sera soumise à un backtesting pour la validation.

4. Calibration

L'objectif de cette étape se résume en ces points spécifiques :

· Déterminer les valeurs des paramètres manquantes.

· Discrétisatier des états continues en un équivalent discret. Dans notre mémoire nous utilisons la discrétisation des processus d'Orstein-Uhlenbeck, Hull and White à deux facteurs et black and scholes .

Rappelons que La discrétisation en mathématiques appliquées, c'est la transposition d'un état continue (fonction, modèle, variable, équation) en un équivalent discret.

· Respecter les modèles de calibration que demande le modèle choisit.

Ce procédé constitue en général une étape préliminaire à la résolution numérique d'un problème ou sa programmation sur machine.[25]

Méthode de projection

La méthode de projection des scénarios consiste à utiliser les processus précédemment calibrés en utilisant une matrice de corrélations. Nous présentons par la suite les processus utilisés ainsi que leurs discrétisation[20], soit :

(a) Processus de Black and Scholes

Appelé aussi mouvement brownien géomètrique : il s'agit d'un processus stochastique utilisé pour la modélisation de l'action et l'inflation adopté dans le cadre de ce mémoire.

Soit St le cours d'une action suit un mouvement brownien géomètrique :

dSt St

= udt + ódBt (2.3.1)

avec:

· u Rendement espéré.

· ó Volatilité.

La résolution de l'équation différentiel stochastique donne :

_ó2

St = S0 exp((u - 2 )t + ó(Bt - B0)) (2.3.2)

Après discrétisation exacte on obtient :

_ó2 v

St+o = St exp((u - 2 )ä + ó ä c) (2.3.3)

avec:

36

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

· ä : Pas de discrétisation

· E : Variable aléatoire de loi normale centrée réduite.

(b) Processus d'orstein-uhlenbeck

Ce processus est utilisé dans le cadre de l'estimation des paramètres du modèle AR ¹(k) basé sur la méthode classique des MCO ², on se restreint à k = 1 dans le cadre de ce mémoire.

Ce processus est déjà utilisé pour modéliser l'inflation, le taux d'intérêt réel, le rendement de l'immobilier.

On suppose que X suit un processus d'Orstein-Uhlenbeck :

dXt = ê(u - Xt)dt + ódBt (2.3.4)

avec :

· ê : le vitesse de retour à la moyenne.

· u : la moyenne à long terme de X.

· ó : le terme de volatilité.

Ce processus est caractérisé par une oscillation autour de sa valeur moyenne, en effet u - Xt aura tendance à converger vers ê

La résolution de l'EDS donne :

t

Xt = X0 exp(-êt) + u (1 - exp(-êt)) + ó exp(-êt) ^f exp(-ês) dBS (2.3.5)

Après discrètisation exact on obtient :

X X p(-- ) ,u ( p(-- )) \I1 - e2(-2êä) (2.3.6)

t+a = _t ex r~S + 1 -- exp(--k S + o- Ex.t 2.3.6

avec :

· ä : Pas de discrétisation.

· E : Variable aléatoire de loi normale centrée réduite.

On considére dans notre mémoire que ä = 1 : l'estimation des paramètres est effectuè par une régression linéaire simple :

Xt+1 = Xt â + á + à~x.t (2.3.7)

Après une estimation de á, â il vient que :

· ê = -ln(â)

á

· = u

1-âV 1-exp(-2ê

· ó est égal à l'écart type de l'erreur du modèle estimé divisé par

2ê

(c) Processus de Hull-White à deux facteurs

Le modèle Hull-White a deux facteurs consiste en une dynamique du taux court rt et une dynamique du taux long lt reprenant l'approche de retour à la moyenne de Vasicek. Les équations différentielles stochastiques associées sont :

drt = êr(lt - rt)dt + órdBr,t (2.3.8)

dlt = êl(ut - rt)dt + óldBl,t (2.3.9)

avec :

1. autorégressif

2. Moindre carré

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

· rt : Taux court.

· lt : Taux long.

· ê_r : Vitesse de retour à la moyenne des Taux court.

· êl : Vitesse de retour à la moyenne des taux long.

· ó_r : Volatilité des taux courts.

· ól : Volatilité des taux longs.

· Bl,t, Br,t : Mouvement brownien.

Après une discrétisation exact on obtient :

rt+1 = rt exp(-ê_r) + lt (1 - exp(-êt)) + ór 1 - exp(-2êr) ~r.t (2.3.10)

2ê_r

_s

1 - exp(-2êl)

lt+1 = lt exp(-êl) + ul (1 - exp(-êl)) + ól ~l.t (2.3.11)

2êl

Déterminer les paramètres lt et rt nécessite une double régression linéaire, cette méthode consiste à appliquer en deux étapes les MCO.

lt+1 = â1 + â24 + Eî,t (2.3.12)

rt+1 = á1à+ _â21t + EZt (2.3.13)

La première étape consiste à estimer â1 et â2 et on déduit que :

· r1-exp(-2êl)

2êl

êl = -ln(â2)

â1

· ul = 1-â2

· ól : l'écart-type de l'erreur du modèle estimé divisé par

Une fois les paramèetres du premier modèle sont estimés, il convient de modèliser les tauxd'intérêt réel à court terme en retenant les taux réels a long terme estimé comme variable explicatif, soit donc :

· á2 = exp(-ê_r)

· á1 = 1 - exp(-ê_r) = 1 - á2

et donc :

Art + 1 = rt+1 - rt = á1(rt - rt) + cr,t (2.3.14)

Parsuite :

· ê_r = -ln(1 - á1)

q1-exp(-2ê_r)

· ó_r : l'écart-type de l'erreur du modèle estimé divisé par

2ê_r

Généralement les modèles mathématiques de calibration classiques oscillent autour du mouvement brownien géométrique, Orstein Uhlenbeck et Hull White dans le cadre de ce mémoire.

Nous utilisons également le théorème de cholesky : dans la formule de discrétisation, le résidu suit une loi normale. La génération des trajectoires revient alors à générer des lois normales corrélées. Pour ce faire, nous allons nous baser sur le théorème de cholesky.[14]

Théorème de cholesky :

Soit[27] M une matrice symétrique définit positive, à déterminer une matrice triangulaire 37

38

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

inférieure L et sa transposée telle que M = L^T L = LL^T Avec :

· L : La matrice triangulaireinférieure liée à M issue de la formule de décomposition de Cholesky.

· L^T : La transposée de L.

De l'égalité M = L^TL on déduit : mij = (LL^T )ij = ~ⁿk=1 likljk = ~min(i,j)

k=1 likljk, 1 < i, j <

n

5. Analyse des résultats

Lors de la calibration des paramètres choisis on doit analyser les résultats obtenus en adoptant des testes statistiques particuliers, ceci revient à :

· Mesurer la qualité et la performance du modèle.

· Mesurer la qualité d'ajustement : coefficient de détermination.

· Réaliser des tests statistiques que nous allons expliciter par la suite.

La robustesse d'un GSE est garantie à travers des testes statistiques pour valider le caractère martingale et s'assurer de la bonne convergence des prix estimés vers les prix de marché.

(a) Test d'ajustement

Ce test mesure la qualité de calibrage des paramètres par rapport aux données historiques, on définit tout d'abord SST ( Total Sum of Square) :

SST = _Xn (yi - y)² (2.3.15)

i=1

Où :

· yi : représente les observations étudiées.

· y : représente la moyenne empirique des observations yi.

Le SST représente l'écart quadratique entre les observations et leur moyenne, il peut être décomposé en somme des variances du modèle noté SSR ( Regression Sum of

Square) et des variations résiduelles notée SSE (Error Sum of Squares) :

SST = SSR + SSE (2.3.16)

Avec,

SSR = _Xn ( ^byi- y)² (2.3.17)

i=1

Et,

SSE = _Xn (yi - yi)² = _Xn Ê_i (2.3.18)

i=1 i=1

Où g_i représente les observations estimées.

Le coefficient de détermination ajusté R² est défini par :

R2 = SSR SSt

SSE = 1 - (2.3.19) SST

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

À noter que ce dernier ne doit pas dépasser 1, on définie dans la suite le coefficient de détermination ajustée corrigé _R2corrigé corrigé pour que ce dernier soit adéquat lors de l'introduction de certaines variables ailleurs :

R2corrigé = 1 - (n - 1)SSE (2.3.20)

(n - p - 1)SST

avec n taille de l'échantillon et p le nombre des variables explicatives.

(b) Test de Fisher

Le test de Fisher permet de valider globalement le modèle, ce test repose sur les variances soit :

H0 : u_á = uâ contre H1 : u_á =6 uâ La statistique de Fisher est définie comme suit :

SSR/(p - 1)

F = (2.3.21)
SSE/(n - 1)

Sous l'hypothèse H0, la statistique F suit la loi de Fisher de paramètres (p-1,n1) au risque á, si une valeur théorique soit supérieure à F alors on rejet H0 au risque d'erreur á donc le modèle n'est pas significatif et inversement.

(c) Test de student

Le test de Student est un test de significativité sur chaque coefficient du modèle, en effet il est défini comme suit :

Hj 0 : u_x= u_y contre H^j₁ : u_x =6 u_y La statistique du test est :

.Vn + p - 2

T = V 1 +

n p 1

.VSSR² + SSE2 (2.3.22)

(Y - Y)

39

Où Y est la moyenne empirique de l'échantillon et Y est la moyenne empirique des variables estimées.

Sous H0, T suit une loi de Student à n+p-2 degrés de libertés au risque á. (d) Test de Breusch-Godfrey

Le test de Breusch-Godfrey d'ordre p se base sur l'autocorrélation pour mesurer l'indépendance des résidus, dans notre mémoire on prend p=1.

On suppose que les résidus suivent un processus autorégressif d'ordre p :

Et = p1Et-1 + + _ppEt-p + ut (2.3.23)

Avec :

40

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

· Et : les résidus issus du modèle de régression,

· ñi, i = 1..p : les coefficients d'autocorrélation des résidus,

· ut : Bruit blanc fort (moyenne nulle et variance constante).

Les ñi sont obtenus à travers de la méthode des moindres carrés grâce à une régression des résidus sur les variables explicatives et sur les résidus retardés.

Le test proposé est le suivant :

H0 : ñ1 = ... = ñ_p = 0 contre H1 : ? i0 / ñi0 =60

L'hypothèse H0 implique l'absence de l'autocorrélation des résidus, en revanche l'acceptation de H1 montre qu'il existe une corrélation entre eux.

(e) Test de Jarque-Bera

Ce test s'intéresse aux lois des résidus s'ils suivent une loi normale centrée réduite ou pas, ceci ce manifeste à partir du couple du coefficient d'asymétrie et du moment d'ordre 4 (Skewness, Kurtosis) que l'on note dans la suite (S, K).

Le test permet également de déterminer l'écart-type simultané entre (S_€, K) calculé à partir de l'échantillon des résidus et la valeur (S, k) calculé à partir d'une loi normale centrée réduite.

Le test statistique est donné par :

H0 : S = 0 et K = 3 contre H1 : S =60 et K =63 La statistique du test est donnée par :

n

JB = 6 (S² + (K - 3)²

4 ) (2.3.24)

Avec

· n : Taille de l'échantillons

· S : Skewness

· K : Kurtosis

(f) Test ARCH

Le test s'appuie sur les séries temporelles ARCH (AutoRegressive Conditionally Heteroscedastic) a été introduit en 1982, il permet de prendre en compte la dépendance entre les résidus d'un modèle de régression.

Dans le cas de la régression d'une variable à expliquer Yt à partir d'une variable explicative Xt le modèle linéaire a la forme suivante :

Yt = á + âXt + t (2.3.25)

Où :

\/

Et = ut á0 + á1E2 _{t_1} + .... + á_pE² (2.3.26)

t-p

Tel que á0, á1, ,á_p > 0 et ut suit une loi normale centré réduite

Le test est le suivant :

41

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

H0 : á0 = á1 = ... = á_p contre H1 : ? i0 / ái0 =60

Dans le cas ou l'hypothése H0 est acceptée, Et = Iit/á0 ce qui implique que les résidus sont identiquement distribués.

Pour conclure nous proposons le tableau suivant qui résume les testes statistiques nécessaire pour un GSE ainsi leurs intérêts :

Test statistique	Intérêt
Test d'ajustement	Mesurer de la qualité de calibrage
Test de Fisher	Valider globalement le modèle
Test de Student	Vérifier la significativité des coefficients du modèle
Test de Breusch-Godfrey	Mesurer l'indépendance des résidus
Test de Jarque-Bera	Vérifier la normalité des résidus
Test ARCH	Mesure la dépendance des résidus d'un modèle de régression

TABLE 2.1 - Tests statistiques et intérêts

Il est à noter que les résultats des tests statistiques présentés ci-après, lorsque la probabilité associée est inférieure à 5 % l'hypothèse H0 sera rejetés et on accepte l'hypothèse H1.

6. Projection

Après la modélisation de la structure de dépendance, la calibration des données et la validation des différents tests de marginalités et d'ajustement l'étape finale consiste a projeter les variables macro-économiques.

Les deux natures du modèle que nous allons détailler par la suite (Wilkie, Brennan Xia, Ahlgrim et Jarrow Yildrim) : soit par cascade, soit par corrélation possèdent deux structures schématiques différentes dont l'une structure linéaire et l'autre une structure par arbres, l'intérêt de choix se manifeste à travers la modélisation de l'évolution dans le temps des variables de GSE.

A un instant "t" de temps, une variable macro-économique choisie comme input est représentée par un noeud, l'ensemble des noeuds cumulés est relié par des droites forment un scénario économique futur possible.

Pour la structure linéaire, elle est généralement dédiée pour les modèles en cascade : une seule trajectoire est dérivée à partir de chaque noeud sauf pour le noeud de départ dont chaque noeud généré dispose d'une trajectoire.

En second lieu on trouve la structure par arbre à partir d'un seul noeud considéré comme la force motrice du modèle, on peut y avoir plusieurs noeuds qui peuvent eux-mêmes générer plusieurs scénarios.

En comparant les deux structures, la structure linéaire est préférable.

En effet, ceci est expliqué par le nombre élevé de scénarios économiques générés lors de la projection en utilisant une structure par arbre ce qui engendre une difficulté d'implémentation.

Dans le cadre de ce mémoire on adopte la structure linéaire pour la projection.

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

42

Schéma 2.2 Comparaison entre deux structures de projection des scénarios
(source : les GSE en assurance Faleh-Planchet)

L'objetif de ce mémoire est d'utiliser des modèles de GSE de référence : Wilkie, Brennan and Xia, Ahlgrim et Jaroow-yilrim afin de générer des flux d'actif pour projeter le bilan, le compte de résultats et l'état de flux de trésorerie dans le cadre de l'obtention d'une vision plus prospective en assurance vie et en assurance non vie.

Les classes d'un GSE

Il existe principalement deux familles :

1. La première s'agit d'un GSE composite,il sert à décrire indépendamment l'évolution de chacun des actifs à travers un processus stochastiques, il définit une structure de dépendance des actifs à partir de la matrice de corrélation pour proposer une description globale. Ce GSE est simple à implémenter et le plus utilisé par les praticiens.

2. La deuxième s'agit d'un GSE intégré, ce GSE considère une seule variable explicative à partir de laquelle les autres variables sont décrites appelées variables explicatives.

Monde réel ou monde risque neutre

On distingue entre deux approches de GSE : un générateur de scénarios économiques dans un univers "monde réel" ou historique et un générateur de scénarios économiques dans un univers "risque neutre".

Le tableau ci-dessous met en relief une comparaison entre le deux univers (réel et risque-neutre) :

43

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

	Monde réel	Monde risque-neutre
Objectif	Projeter les valeurs réelles et les données observées sur le marché. Pilotage financier de la compagnie et la stratégie d'allocation d'actifs.	Intégration de scénarios économiques pour fournir un modèle prospectif d'évaluation des engagements futurs.
Hypothéses	Tenir compte d'une prime de risque	L'agent économique est neutre au risque
Utilité	Modélisation actif-passif(ALM). Projection du bilan dans le cadre ORSA. Calcul du Capital économique.	Etude de pricing dans le cadre de l'ALM. Valorisation du Best estimate dans le cadre de l'ORSA.
Calibrage	Seule les modèles fondés sur des données historiques.	Tous les modèles qui respectent l'hypothèse risque neutre.
Limite	Modélisation d'une prime de risque. Actualisation des flux futurs dépend de la prime de risque.	Pas de réalité exacte et observable. Ne répond pas aux besoins de l'assureur.

TABLE 2.2 - Comparaison entre un monde réel et un monde risque neutre

Rappelons que la prime de risque est le supplément de rendement dont l'investisseur bénéficie en compensation de son investissement dans un actif risqué cette problématique nous mène à une nouvelle théorie des GSE suivant l'approche « Risque-neutre » qui suppose que tous les agents économiques sont neutres au risque et que les primes de risque sont nulles.

2.4 Principaux modèles d'un GSE

Nous adoptons dans la suite la liste des variables macro-économiques suivantes :

· St : Valeur de l'action à l'instant t.

· DIVt : Valeur du dividende à l'instant t.

· IMBt : Valeur de l'immobilier à l'instant t.

· Rt : Valeur du taux d'intérêt nominal à l'instant t.

· Dt : Valeur de l'indice déflateur à l'instant t.

· Rr,t : Valeur du taux d'intérêt réel à l'instant t.

· Init : Valeur du taux d'inflation à l'instant t.

· It : Indice des Prix à la Consommation à l'instant t.

2.4.1 Modèle de WILKIE - 1986

Historiquement, tenant compte des tailles des portefeuilles réduits dans les compagnies d'assurances chaque classe d'actif financier est traitée indépendamment des autres actifs sans prise en compte de la corrélation entre eux, ce qui implique que la projection des actifs ou la modélisation des engagements futurs ne répondent pas réellement aux besoins de l'assureur.

44

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

À partir de 1986, des nouvelles prospectives actuarielles de modélisation des Générateurs de scénarios économiques sont apparus : Ce sont les travaux des GSE de WILKIE.

C'est le premier modèle fondé, élaboré par David WILKIE actuaire associé, il s'agit d'un modèle de GSE en cascade considérant l'inflation comme force motrice, à partir duquel il considère que "Toutes les autres variables sont déduites".

L'inflation correspond à l'augmentation généralisée des prix au sein d'une économie. Ce phénomène est persistant et implique une diminution du pouvoir d'achat avec une somme constante dans le temps. L'augmentation des prix est différente pour chacun; en fonction des habitudes de consommation.

Une mesure de l'inflation souvent utilisée est la variation annuelle de l'Indice des Prix à la Consommation (IPC)[21].

Ce modèle fixe une variable centrale puis déduit les autres à partir des coefficients estimés à l'aide des études statistiques, c'est la philosophie adoptée par David Wilkie.

Le modèle de WILKIE repose sur cinq variables fondamentales:

· L'indice d'inflation It qui est la variable centrale

· L'indice de rendement de l'immobilier

· L'indice du rendement de l'action

· L'indice du rendement des dividendes

· Le taux d'intérêt à long terme

· Le taux d'intérêt à court terme

Depuis 1995 ce modèle est devenu le modèle de référence, c'est le premier modèle reconnu sur les générateurs de scénario économique, à partir duquel les autres souches se basent.

Les variables modélisées

· Processus d'inflation

Lors de ses premiers travaux, David WILKIE a modélisé l'inflation 'mit par un processus AR (1) (Auto-regressive d'ordre 1), rappelons que l'inflation est l'écart entre le rendement de l'IPC (Indice des prix à la consommation) et l'inflation à long terme, l'équation est la suivante:

'mit = ç1 * 'mit-1 + Et (2.4.1)

Avec :

- ç1 : Structure de corrélation - Et : Bruit Blanc

· Le rendement de l'immobilier

Ces variables sont déterminées par une relation de causalité modélisée par les séries temporelles avec l'inflation.

45

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

· Processus de rendement des actions

Ce rendement nécessite l'inflation et d'autres paramètres relatifs au dividende, soit la modélisation de Black and scholes proposé comme suit :

dSt = u St dt + St ó_a dWt (2.4.2)

Avec :

- St : Actif sous-jacent

- u : Drift

- ó_a : Volatilité constante

- Wt : Mouvement Brownien

· Taux d'intérêt à long terme

Il est déduit directement à partir de l'inflation .

· Processus des taux d'intérêts à court terme : mentionné dans le schéma ci-dessous le taux d'intérêt à court terme est déduit du taux d'intérêt long terme.

· Processus des dividendes

Ces variables sont déduites de l'inflation de du rendement des actions.

Le schéma explicite suivant illustre l'idée du modèle en cascade et le rôle central que joue l'inflation :

FIGURE 2.2 - Structure do modèle de WILKIE [1]

46

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

2.4.2 Modèle de Brennan and Xia

En 2000, un variant du modèle de WILKIE des générateurs de scénarios économiques est apparu, il s'agit d'un modèle singularisé par sa structure de corrélation, plus précisément à partir des données historiques disponibles, il est possible de tirer une structure de dépendance entre les variables pour assurer une projection cohérente.

Ce variant prend plus de paramètres par rapport à celle du modèle de WILKIE et prend l'inflation et l'indice action comme inputs et ne prend pas l'indice immobilier malgré son importance dans le secteur d'assurance.

L'objectif de ce modèle est de déterminer le prix d'une obligation zéro coupon sous la probabilité historique.

Il est aussi basé sur les données historiques et prend en considération deux hypothèses fondamentales :

· Constance des prix du marché de risque

· Le modèle d'équilibre décrit l'état stationnaire des facteurs observés

Les variables modélisées

1. Processus d'inflation

Modélisé par un processus de retour à la moyenne d'Orstein-Uhlenbeck sous la probabilité historique :

dInft = ê (u - Inft)dt + ó dBt (2.4.3)

Avec :

· ê : Vitesse de retour à la moyenne

· u : Moyenne long terme de Inft

· ó : Volatilité

· B : Mouvement brownien

Cette équation discrétisée soit l'approximation suivante :

_s

1 - e_2ê

Inft+1 = Inft e^-ê + u(1 - e^-ê) dt + Inft,t (2.4.4)

2ê

2. Processus d'action

Sous la probabilité historique, le prix des actions est représenté par la dynamique brownienne géométrique prend en considération l'hypothèse de constance de la prime de risque:

dSt St

= u_sdt + ó_sdB^P (2.4.5)

s

47

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

Avec :

· u_s = Rt + ëS ó_s

· Rt : Taux d'intérêt nominal.

· ëS ó_s : La prime de risque.

Où ó_s la volatilité des actions et ëS la prime de risque unitaire.

3. Taux réel

Sous la probabilité risque neutre, le taux réel _Rr,t est représenté par un modèle d'équilibre de retour à la moyenne d'Ornstein-Uhlenbeck à un facteur (modèle de taux court à un facteur), soit :

dRr,t = ê(u_r - Rr,t)dt + órdW r Q (t) (2.4.6)

Avec

· ê : Vitesse de retour à la moyenne

· u_r : Moyenne à court terme de Rr,t

· ó_r : Volatilité du taux réel

· W _r Q(t) : Mouvement Brownien

· Q : Probabilité risque neutre

4. L'indice de prix à la consommation (IPC)

Dans notre mémoire on considère que l'inflation est le dérivé de l'IPC, sous la probabilité historique ,le modèle de Black and Scholes, soit :

dIt It

= Inftdt + óIdW ^P (2.4.7)

I

Avec

· I : L'indice des Prix a la Consommations

· óI : Volatilité des Indices de Prix à la Consommations

· I : Mouvement brownien

· P : Probabilité Historique

5. Taux Réel

Dédier lorsqu'on utilise la monnaie étrangère, sous la probabilité risque neutre étrangère, la dynamique du taux réel suit un modèle de Hull and White à un facteur.

Le schéma suivant montre la structure du fonctionnement du modèle :

48

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

FIGURE 2.3 - Structure du modéle de Brennan-Xia [1]

2.4.3 Modèle d'Ahlgrim et AL

En 2005, une nouvelle souche des générateurs de scénarios économiques est apparue développée par Ahlgrim et AL : ils s'aperçoivent que les paramètres estimés pour le modèle de taux d'intérêt réel conduisent à une estimation des taux d'intérêt nominaux insatisfaisantes[1].

Aussi, Ahlgrim et al. fixent la valeur des paramètres sur la vitesse de retour à la moyenne et sur la volatilité des modèles de taux d'intérêt réel[1].

Ce modèle est plus adapté à la gestion de portefeuilles d'actifs que le modèle de WILKIE et BRENNAN XIA, il est soutenu par les associations professionnelles d'actuariat et que CAS ¹ et SOA², il est également dernier caractérisé par une structure de corrélation globale, ce qui enlève une partie de l'hypothèse de causalité.

Dans la littérature du modèle d'AHLGRIM et AL les actifs qui forment le portefeuille sont : le rendement action, les taux obligataires et le rendement immobilier comme le modèle de Brennan and XIA, ce modèle place le taux d'intérêt réel et le taux d'inflation au centre du modèle.

1. Causalité Actuariel society : une société professionnelle d'actuaires et l'organisme d'agrément pour les désignations Associate of the Casualty Actuarial Society (ACAS) et Fellow of the Casualty Actuarial Society (FCAS), elle se concentre sur les risques et les dangers liés à l'assurance de dommages (par exemple, l'assurance soins et habitation), et non l'assurance vie ou l'assurance maladie.[7]

2. Society Of ACTUARIES : est une organisation professionnelle mondiale pour les actuaires. Elle a été fondée en 1949 à la suite de la fusion de deux grandes organisations actuarielles aux États-Unis : l'Actuarial Society of America et l'American Institute of Actuaries. C'est une organisation membre à part entière de l'International Actuarial Association.[26]

49

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

Les variables à modéliser

1. L'inflation

Le modèle d'Ahlgrim et Al Modélise sous la probabilité historique, l'inflation par un processus d'ornstein-uhlenbeck de retour à la moyenne, soit :

dInft = êa(ua,t - Inft)dt + óadBa,t (2.4.8)

Avec

· ê_a : Vitesse de retour à la moyenne

· ua,t : Moyenne long terme de dInft

· ó_a : Volatilité

· Ba,t : Mouvement brownien

2. Taux d'intérêt réel

Concernant le taux d'intérêt réel, il est modélisé sous la probabilité risque neutre par un cas d'application du modèle Hull and White a deux facteurs.

A noter que le taux court réel r_r(t) oscille autour du taux long ll(t), soit :

dr_r(t) = u_r[ll(t) - r_r(t)]dt + ó_rdW_r(t) (2.4.9)

dl_r(t) = ur,l[êr(t) - ll(t)]dt + óldWl(t) (2.4.10)

3. Taux d'intérêt nominale

Sous la probabilité risque neutre, les taux d'intérêt nominaux sont déduits, des taux d'intérêt réels et des anticipations d'inflation en utilisant la relation classique de Fischer

P_n(t, T) = PT(t,T) * EQ t [ ^Inft ] (2.4.11)

InfT

4. Rendement des actions

C'est la somme du taux sans risque, spread aléatoire dépendant d'un modèle à changement de régime.

St = r_r(t) + Inft + xt (2.4.12)

avec :

· xt : Prime de risque

50

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

Dividendes des actions

Le logarithme des dividendes suit un processus d'Ornstein-Uhlenbeck de retour à la moyenne,soit :

dln(St) = ic_s(t_s - ln(St))dt + usdBs,t (2.4.13)

56. L'immobilier, chômage

Indexé sur les données du marché qui sont modélisées par un processus d'Ornstein-Uhlenbeck de retour à la moyenne.

Le schéma suivant met en relief le fonctionnement du modèle :

FIGURE 2.4 - Structure du modéle de Ahlgrim-Al [1]

En conclusion : Dans le cadre de ce mémoire nous adopterons deux modèles de base pour les Générateurs de scénarios économiques : le modèle de Brennan and Xia et le modèle d'Ahlgrim.

2.4.4 Avantages et limites des modèles de références

Nous proposons pour cette partie le tableau suivant qui résume les 3 modèles cités ci-dessus :

CHAPITRE 2. LES GÉNÉRATEURS DE SCÉNARIOS ÉCONOMIQUES

51

Modèle

Wilkie	Brennan Xia	Ahlgrim	Avantages
Ouvert à être varié. Dépend d'une seule variable. Modèle de références.	Déduire un IPC stochastique et un facteur d'actualisation réelle.	Une vision plus claire partant de l'inflation. Prise en compte d'une structure de corrélation.	Modèle Inflation - Taux d'interet
AR(1) - Déduit de l'inflation	Processus de retour à la moyenne - Orstein-Uhlenberck	Orstein-Uhlenberck - Hull and White	Modèle action
Déduit de l'inflation	Orstein-Uhlenberck.	Déduite du taux d'intérêt à court terme.	Limites
Modèle d'inflation est mal adapté aux données. Modèle purement théorique.	Absence de l'actif immobilier. Modèle compliqué pour la mise en place Il tient compte beaucoup de paramètres.	Modèle très long à l'exécution et pose souvent un problème de paramétrisation.

TABLE 2.3 - Avantages et limites des modèles de référence

52

Chapitre 3

La gestion actif passif dans le cadre de

l'assurance

La Gestion Actif-Passif (GAP) ou Asset-Liability Management (ALM) en anglais englobe l'ensemble des techniques visant d'analyser, mesurer et gérer les différents risques encourus dans les entreprises d'assurances et sert également à faire de l'optimisation au cours du temps à travers des calculs actuariels dans un cadre respectant les normes réglementaires (la norme prudentielle Solvabilités 2 à titre d'exemple) et comptables (IFRS² par exemple) afin de modéliser un scénario économique adéquat pour l'assureur à un niveau de risque défini.

Un modèle ALM permet de donner une vision prospective de l'actif et du passif en prenant en compte les interactions Actif/Passif. Il fait partie des outils mis à disposition de la gestion Actif-Passif contribuant à la maîtrise des risques financiers.

En assurance-vie, le modèle de gestion actif-passif constitue un pilier dans l'activité il permet de [16] :

· Identifier et évaluer les risques ALM présents ou prévisibles au binal compte tenu des hypothèses prospectives financières, techniques et commerciales en date d'évaluation.

· Identifier et mettre en oeuvre les actions de remédiation envisageables pour faire face à ces risques ALM, lorqu'ils vont au-delà de l'appétit au risque de l'assureur.

· Projeter les différents flux d'une compagnie d'assurance. En assurance non-vie, le modèle de gestion actif-passif consiste à

· Procurer de l'information sur l'interaction des décisions opérationnelles.

· Fournir un outil d'aide à la décision pour la mise en place d'une stratégie prospective.

· Garder un suivi simultané quantitative sur l'évolution du couple rendement, risque inhérent.

De ce fait, l'ALM s'engage à répondre aux questions relatives au pilotage de l'activité des compagnies par une stratégie commerciale permettant le bon déroulement du portefeuille des contrats d'assurance sous des contraintes prédéfinies, soit par une allocation optimale d'actif qui limite les risques financiers liés aux conditions du marché pour que l'assureur soit prêt pour faire face aux engagements futurs envers ses assurés.

Dans cette partie, nous présentons le cadre général du présent travail. Pour ce faire, nous

2. International financial reporting standards

53

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

allons nous intéresser, dans un premier temps, aux généralités sur l'assurance-vie également en assurance non-vie, les caractéristiques, les particularités et les produits garantis pour chaque type d'assurance. Puis, nous présenterons la modélisation d'un actif et un passif et l'interaction entre eux.

Au final nous détaillerons les outils de construction du bilan comptable et le compte de résultats technique.

3.1 Présentation d'un contrat d'assurance vie

1. Définition : L'assurance-vie est un contrat par lequel l'assureur s'engage à verser une rente ou un capital à une personne, le souscripteur, moyennant une prime. Ce versement se fait selon le type de contrat souscrit. En effet dans un contrat d'assurance-vie, il faut distinguer deux sortes de contrats : un contrat d'assurance en cas de décès et un contrat d'assurance vie[6].

Il existe trois types de contrats d'assurance-vie : l'assurance vie, l'assurance en cas de décès et un contrat mixte offrant une garantie à la fois vie et en cas de décès. L'épargne accumulée sera versée selon le type de garantie :

· La garantie en cas de vie : Versement d'un capital ou d'une rente si l'assuré est encore en vie a la fin du contrat.

· La garantie en cas de décès : un capital ou une rente sera versé au bénéficiaire désigné par le souscripteur.

2. Principaux risques en assurance-vie

· Risque de rachat : risque résultant d'une modification du comportement des assurés en matière de rachat de contrats.

Lors de cette opération l'assuré peut être soumis à des sanctions en fonction de l'ancienneté du contrat et ce que fixe les closes lors de la souscription ^1.

· Risque de longévité : est le risque de voir la durée de vie humaine se raccourcie de manière non déterministe, il s'articule autour de trois points :

- Les assurés survivent plus longtemps que prévu.

- Baisse de la mortalité de la population assurée.

- Tendance temporelle due aux progrès médicaux et l'avancée technologique.

· Risque de mortalité : Ce risque est expliqué par un excès/choc inattendu de la mortalité à cause d'un événement imprévu (catastrophe/épidémie) de ce fait l'assureur ne peut plus faire face à ses engagements.

3. Présentation d'un contrat d'épargne Dans la suite du rapport, nous nous intéresserons à l'élaboration d'un modèle de gestion actif passif pour un portefeuille de contrats d'épargne en dinars tunisiens simplifié.

On considère une unique police soumise au risque de mortalité et pouvant racheter à tout moment son contrat. Le terme du contrat est fixé à 10 ans.

En effet durant la vie du contrat l'assuré bénéficie d'une revalorisation annuelle correspondant au maximum entre :

1. Il peut être exonéré de tous types de sanctions

54

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

· Un taux minimum garanti fixé à 2%.

· Une quote-part (fixée à 90%) des produits financiers générés par les actifs en représentation des PM.

4. Quelques notions de comptabilité

(a) Les provisions mathématiques

Les provisions mathématiques désignent les réserves obligatoires, qu'elles sont tenues de constituer et qui doivent rester disponibles à tout moment. Ainsi, en cas de besoin, elles peuvent immédiatement débloquer des fonds en faveur de leurs souscripteurs. Elle représente la différence entre les valeurs actuelles des engagements respectivement pris par l'assureur et par les assurés

A un instant t donné, les provisions mathématiques sont définies comme suit :

PM(t) = V AP^assureur(t) - V AP^assuré(t) (3.1.1)

La provision mathématique se caractérise par le faite quelle est individuelle, calculée tête par tête, ne peut pas être négative, ne peut pas être inférieure à la valeur de rachat du contrat.

(b) Provision pour participation aux bénéfices

Provision destinée à prendre en charge le montant des participations aux bénéfices attribués aux bénéficiaires de contrats lorsque ces bénéfices ne sont pas payables immédiatement après la liquidation de l'exercice qui lui a produit.

L'une des spécificités de l'assurance-vie est la participation aux bénéfices qui doit être provisionnée pour que l'assureur soit prêt, la dotation à la participation aux bénéfices doit être au moins égale à :

90 % du benéfice technique + 85 % du bénéfice financiére (3.1.2)

ou

10 % de la perte technique + 15 % de la perte financière (3.1.3)

Le Minimum de participation des assurés aux bénéfices est donné par:

90 % du bénéfice technique + 85 % du bénéfice financier - Intérets techniques

(3.1.4)

ou

55

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

10 % du bénéfice technique + 15 % du bénéfice financier - Interets techniques

(3.1.5)

(c) Provision globale de gestion

Destinée à couvrir les charges de gestion futures des contrats non couverts par ailleurs.

Elle est calculée par groupes homogènes de contrats (il n'y a pas de compensation possible entre les contrats).

Les contrats dont les chargements de gestion sont insuffisants doivent faire l'objet d'une PGG.

(d) Provision pour risque d'exigibilité (PRE)

Destinée à faire face aux engagements dans le cas de moins-value de l'ensemble des actifs autre qu'amortissable, hors obligations indexées sur l'inflation (par exemple les placements en représentation des contrats en unités de compte).

La PRE est constituée lorsque les actifs décrivent ci-dessus se trouvent en situation de moins-value latente nette globale (constatée lorsque la valeur nette comptable de ces placements est supérieure à leur valeur de réalisation).

Principes comptables des provisions en assurance vie Les calculs des provisions techniques en assurance vie doivent :

· Respecter les règles actuarielles : loi de probabilité, taux d'actualisation.

· Etres traités contrat par contrat selon les particularités.

· Assurer un rendement d'actif adéquat compatible avec le passif.

· Disposer tout au long de la vie du contrat de revenus compatibles avec le taux technique.

3.2 Présentation de l'assurance non-vie

1. Définition : L'assurance non-vie est l'ensemble des opérations d'assurances dont le fait générateur ne dépend pas de la vie de l'assuré. Elle est donc principalement composée des assurances de choses ou de biens, des assurances de responsabilité ou de dettes, et des assurances de personnes.

L'engagement de l'assureur est la prestation en cas de réalisation de sinitralité subit par l'assuré pendant la période garantie au contrat.

Il est également manifestement clair qu'en assurance non-vie le coût d'un sinistre est inconnu a priori et reste aléatoire.

2. Principaux risques en assurance non-vie

En assurance non-vie le secteur est caractérisé par le cycle de production inversée en

56

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

effet l'assureur perçoit généralement les primes avant de verser les prestations. Les coûts réalisés de production ne sont connus qu'à posteriori.

Cette problématique cause des problèmes inhérents pour l'activité d'assurance en cas d'excès de sinistralité ainsi l'investissement réalisé doit couvrir le risque assuré (à court et à long terme) on parle alors d'un risque de sous-investissement.

3. Quelques éléments de comptabilité

(a) Provision pour prime non-acquise (PPNA)

Provision dédiée pour la part des primes non encore émises lors de la souscription du contrat d'assurance, on peut encore le définir comme étant les primes restantes à émettre se rapportant à un exercice futur.

Le calcul de la provision se fait contrat par contrat sinon le total des contrats d'échéances voisines.

L'objectif de cette provision est de réaliser une répartition du risque prorata temporise.

(b) Prime acquise non émise (PANE)

Provision destinée pour les primes qui ont été souscrites par l'assuré mais qui n'ont pas encore été émises, notamment à cause du retard administratif.

(c) Provision pour sinistre à payer (PSAP)

C'est le pilier principal des provisions en assurance non-vie elle désigne la valeur estimative des dépenses en principal et en frais, tant internes qu'externes, nécessaires au règlement de tous les sinistres survenus et non payés, y compris les capitaux constitutifs des rentes non encore mises à la charge de l'entreprise[2].

Principes comptables des provisions en assurance non-vie Les calculs des provisions techniques en assurance non-vie doivent :

· Constituer des provisions techniques suffisantes.

· Les sinistres non survenus font l'objet de la PPNA¹ et de la PREC ^2.

· Assurer un rendement d'actif adéquat compatible avec le passif.

Pour simplifier, nous intéressons seulement aux provisions pour sinistre à payer dans le cadre de ce mémoire, nous détaillerons dans le dernier chapitre les hypothèses nécessaires pour cette provision.

Nous avons présenté dans ce qui précède la gestion actif-passif dans le cadre de l'assurance. Nous avons également défini son activité et rappeler quelques éléments de comptabilité qui seront utiles pour le cas pratique dans le chapitre suivant.

L'objectif des sections suivantes est de modéliser ce qui décrit les moyens dont une compagnie d'assurances dispose pour s'acquitter de ses engagements envers ces assurés (ou bien l'actif) ainsi modéliser ce qui explique l'activité de la compagnie (l'engagement ou passif) tenant compte de l'interaction entre eux afin de construire un bilan et un compte de résultats.

1. Provision Pour Prime Non Acquise

2. Provision Pour Risque en Cours

57

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

3.3 Modélisation Actif - Passif

Les modèles actif-passif apportent de l'information sur l'interaction des décisions opérationnelles d'une compagnie d'assurances, une vision quantitative et qualitative sur les décisions stratégiques proposées et constituent également un outil d'aide à la décision et la mise en place d'un business plan.

La mise en place d'un processus de gestion actif-passif est avant tout conditionnée par la disponibilité de données permettant de projeter passif et/ou actif, et ensuite par la disponibilité d'outils ou de modèles pour traiter ces projections[3].

Dans le cadre de ce mémoire, nous avons proposé un processus simplifié de gestion actif-passif nommé "mini-ALM" pour une compagnie d'assurances offrant des produits d'assurances vie et des produits d'assurances non-vie.

Nous proposons un modèle stochastique permettant d'effectuer des simulations du bilan et du compte de résultats afin d'avoir un modèle simplifié d'aide à la décision contenant des règles de pilotage automatique permettant de réaliser des simulations en stochastiques à travers le logiciel VBA-Excel.

Un modèle de gestion actif-passif sera utile pour des différentes applications[3], parmi ceux on cite :

1. Structure de la réassurance.

2. Besoin en capital.

3. Allocation en capital.

4. Allocation stratégique.

5. Réalisation d'un buisness plan.

6. Gestion actif-passif.

7. Analyse d'une stratégie d'investissment.

3.4 Modélisation de l'actif

Nous proposons dans cette section de détailler les portefeuilles d'actifs considérés pour la construction d'un modèle ALM pour les deux volets d'assurances : l'assurance vie et l'assurance non-vie.

On rappelle les différentes classes d'actif développé dans notre modèle ALM proposé :

· Les obligations

Une obligation est un instrument financier représentant une part de la dette. Il existe plusieurs types d'obligations parmi eux on cite : l'obligation à taux fixe, l'obligation à taux variable et l'obligation zéro coupon.

· Les actions

Une action est un titre financier représentant la part au capital de l'entreprise, garantissant à son porteur un revenu appelé dividende.

58

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

· L'immobilier

Un actif immobilier est un ensemble de biens immobiliers et fonciers détenu par la compagnie d'assurance, c'est un actif qui est caractérisé par un manque de liquidité.

· L'actif monétaire

L'actif monétaire désigne les liquidités que dispose la compagnie d'assurance, il est placé au taux sans risque de maturité à un an chaque exercice.

3.4.1 Modélisation de l'actif en assurance vie

Dans cette sous-section, nous détaillerons les différents choix de modélisation effectués pour la projection du portefeuille d'actifs dans notre étude mini-ALM proposée.

Pour faire face à ses engagements envers ses assurés disposant des contrats d'épargne, les compagnies d'assurances vie investissent les primes acquises collectées dans des actifs de types différents, à titre d'exemple on cite les actions, les obligations, l'immobilier et la construction,... qui sont générateurs de revenus : dividendes, coupons, loyers et intérêts monétaires.

Nous supposons dans notre étude que l'assureur investit seulement en obligation (part majoritaire) et en action, ce qui est le cas en Tunisie.

Ce choix chez les assureurs tunisiens est expliqué par la volatilité élevée du marché. Ainsi, ils recourent majoritairement aux obligations pour garder plus de protection.

Nous allons décrire dans la suite la dynamique que nous avons choisie pour décrire chacun de ces actifs.

Portefeuille action : Mouvement Brownien géométrique

Le portefeuille action est modélisé par un processus de black-scholes :

dSt St

= .utdt + 8tdBt (3.4.1)

Où :

· B_s : Un mouvement brownien géométrique.

· S(0) = 1

Portefeuille immobilier : Modélisation CIR

On s'intéresse maintenant à la calibration de la dynamique des obligations de notre portefeuille d'étude proposé, nous utiliserons le modèle CIR (Cox-Ingersoll-Rox) pour la valorisation d'une obligation zéro coupon de maturité 10 ans.

La calibration du taux d'intérêt est réalisée à l'aide de la dynamique:

drt = ii(e - rt)dt + o,/rtdWt (3.4.2)
Le prix du zéro coupon à l'instant t et de maturité m est donné par:

p (t, in) = A(in) exp(-r(t)B(in)) (3.4.3)

59

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

Avec :

2 exp((k + )m ₂

A (m) = ( (3.4.4)
(k + ) * (exp ( .m) - 1) + 2 ₎2 ê O

_a2

Et :

2(exp( .m) - 1)

B (m) = (3.4.5)
(k + e) * (exp ( .m) - 1) + 2 )

_V"

= k² + 2ó² (3.4.6)

On rappelle la condition de Feller qu'on doit respecter afin de garantir des taux presque surement positifs :

2k e ~ 2 (3.4.7)

Notons p la corrélation des mouvements browniens des diffusions taux zéro-coupon et actions, soit :

dWt.dBt = p dt (3.4.8)

Le facteur d'actualisation flux par flux le déflateur est donné par:

Z t

D(t) = D(t - 1) exp (- ₀ r(u)du) avec D(0) = 1 (3.4.9)

3.4.2 Modélisation de l'actif en assurance non-vie

Le but de cette sous-section est de présenter les différentes classes d'actif proposé pour la modélisation de l'actif.

Nous souhaitons projeter le bilan, le compte de résultats techniques et l'état de flux de trésorerie à un horizon de 15 ans, nous s'appuyons donc sur des données historiques pour la première année et des données projetées résultatant du GSE pour les projections souhaitées.

On ne dispose pas donc d'une dynamique pour décrire les actifs nous avons juste proposé une structure de répartition des actifs (monétaires, action, obligataire et immobilière).

3.5 Modélisation du passif

Nous proposons également dans cette section de détailler les passif considérés pour la construction d'un modèle ALM pour les deux volets d'assurances : l'assurance vie et l'assurance non-vie.

3.5.1 Modélisation du passif en assurance vie

Le portefeuille d'un assureur vie est constitué de plusieurs contrats dont chacun fait l'objet d'une particularité selon les éléments qui lui sont propres (propriétaire du contrat, taux de revalorisation, sexe, prime versée, ...)

Dans un modèle ALM, parmi les données qu'un assureur doit disposer on cite :

· Age, sexe de l'assuré.

· La prime versée.

· Taux minimum garantie (TMG) associé au contrat.

60

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

· Les frais dédiés à la gestion du contrat et à la prestation en cas de rachat et décès.

Dans le cadre de notre étude et pour simplifié on dispose d'un horizon de projection de 10 ans d'un contrat d'épargne simplifier dont les hypothèses de projection sont les suivantes :

· Le taux de mortalité constant tout au long de la période.

· Le taux de rachat constant tout au long de la période.

· Pas de primes périodiques.

· Les provisions mathématiques à la date initiale "=" 100 dt.

· La date d'écheance du contrat est dans 10 ans.

· Un taux technique de 2%, constant tout au long de la période.

· Un taux de participation à la bénéfice de 90%.

3.5.2 Modélisation du passif en assurance non-vie

Dans cette sous-section nous présentons les choix effectués pour la modélisation du passif proposé en assurance non-vie au sein du modèle Mini-ALM. On suppose que le passif est découpé en deux principales parties : les capitaux propres et les provisions techniques.

· Les capitaux propres : Ce sont les capitaux versés par les propriétaires de la compagnie d'assurances ( les actionnaires à titre d'exemple). Généralement divisés en deux :

1. Montant versé par les actionnaires.

2. Produit financier généré non encore distribué en dividendes.

· Les provisions techniques : On se restreint seulement à la provision pour sinistre à payer (PSAP).

3.6 Interaction actif-passif

L'intérêt d'un modèle ALM en assurance est de projeter sur un horizon temporel défini en amont (durée de validité d'une stratégie) les flux de trésorerie des portefeuilles d'une compagnie d'assurance et modéliser l'interaction entre l'actif et le passif afin de :

· Projeter le bilan, le compte de résultat et l'état de flux de trésorerie.

· Calculer le BE et NAV avant de réaliser l'investissement.

· Modéliser les différents risques inhérents à l'activité de la compagnie d'assurance.

Dans le cadre de ce mémoire la projection des flux de trésorerie est assurée à l'aide d'un générateur de scénarios économiques dont les flux générés sont utilisés pour réaliser un bilan économique stochastique pour l'assurance non-vie et calculer les engagements futurs de l'assureur envers ses assurés le BE, mesurer l'efficacité de l'investissement NAV en assurance vie à l'instant initial avant de lancer l'investissement.

Ce qui fait la particularité en assurance vie, par rapport à l'assurance non-vie réside sur le fait qu'il existe des interactions entre le passif et l'actif plus dépendante. Cette dépendance

61

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

entre l'actif et le passif se traduit essentiellement par les comportements des assurés en termes de rachat et le niveau de revalorisation de leurs contrats via la participation aux bénéfices. Cette participation aux bénéfices quant à elle dépend du rendement issu des différents investissements sur l'actif[19].

Le modèle prend en input 1000 scénarios économiques générés fournis par le GSE et projette sur un horizon de 10 ans. Pour chaque simulation, le modèle ALM projette l'actif et le passif de la compagnie d'assurance en prenant compte les interactions actif-passif dans le calcul des flux de trésorerie utilisés pour valoriser le BE et le NAV[19].

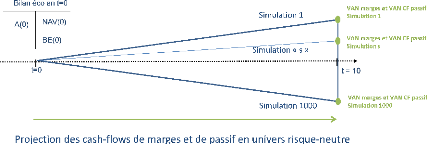
FIGURE 3.1 - Démarche de calcul du BE et NAV

En revanche, en assurance non-vie la situation est différente de celle en assurance vie, les différentes simulations stochastiques qui seront présentées dans le chapitre suivant ont pour objectif de définir une structure d'investissements répartie entre actions, immobilier, obligataire optimale au vu des contraintes supposées pour satisfaire les contraintes envers les assurés et capter un maximum de rendement.

Cette définition passe par la mise des hypothèses indicatrices telles que le ratio S/P, les différents taux : d'encaissement, acquisition et frais afin d'atteindre la variable cible.

Notre objectif dans le cadre de ce mémoire est mis d'une stratégie afin de réaliser une augmentation de capital au bout de 15 ans de projection provenant seulement des résultats techniques internes de la compagnie et non pas d'ailleurs (versement de la part des actionnaires) .

Cette observation s'est déroulée en plusieurs étapes pour les modélisations stochastiques, afin de mieux comprendre les différentes interactions actif-passif (simulations stochastiques des actifs et des passifs) mais également afin d'optimiser les temps de calcul.

Nous avons de plus testé différentes politiques d'investissements obligataires, actionnaires et immobilières (structure de répartition des réinvestissements) afin de choisir une allocation optimale.

Généralement, les modèles de projection ALM sont utilisés en assurance vie qu'en non-vie, peu d'acteurs ont mis en place ces outils pour plusieurs raisons parmi ceux on cite [8] :

· La duration courte du passif: un engagement ne dépasse pas un an pour l'assurance santé et l'assurance automobile.

62

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

· Les rentabilités gérées et les risques couverts sont relatifs essentiellement aux résultats techniques et le risque de souscription.

· La mise en place est plus couteuse qu'en assurance vie puisque les produits sont plus variés.

Ces éléments nécessitent cependant d'être critiqués [8] :

· Si en moyenne la duration des passifs est courte, il existe des branches à développement long, comme les rentes suite à des sinistres corporels en automobile par exemple. Une approche ALM visant à compenser la faiblesse du résultat technique par le résultat financier à tout son sens, à condition qu'elle ne vienne pas surajouter au risque technique un risque de marché mal maitrisé.

· Si l'essentiel des risques et de leur suivi provient du résultat technique, il n'en demeure pas moins que la plupart des sociétés Non Vie sont exposées au risque de marché.

· Si la mise en place d'un outil de projection est couteuse, il constitue un outil d'optimisation avec lequel on garantie plus de gain et un processus de contrôle.

FIGURE 3.2 - Démarche de projection en assurance non-vie [8]

Les apports d'un outil ALM stochastique

Selon le besoin, la mise en place d'un outil stochastique au sein d'une compagnie d'assurances vie ou non-vie devient indispensable, en particulier si on s'intéresse à :

· L'étude de différents scénarios financiers, permettant de choisir l'une des différentes allocations gérées d'actifs en fonction d'un couple (rendement,risque).

· L'étude de l'impact d'augmentation du ratio S/P.

· L'étude approfondie de l'appétit au risque inhérent.

3.7 Projection des éléments de comptabilité

Les étapes retenues dans ce mémoire lors de la projection du bilan comptable, compte de résultats et l'état de flux de trésorerie sont synthétisés dans la figure suivante :

63

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

FIGURE 3.3 - Démarche de projection des éléments de comptabilité

La projection des éléments comptables (bilan, compte de résultat et l'état de flux de trésorerie) s'articule autour de trois principales parties.

L'instant initiale, il convient d'alimenter ces outils avec les données historiques disponibles sur le marché ainsi que les produits financiers récoltés.

Ensuite, nous introduisans les taux d'inflation, monétaires, actions et les rendements immobilier et obligataires issus de la projection à l'aide des générateurs de scénarios économiques (modèle d'Ahlgrim et Al).

Ces taux et rendement permettent de projeter les rendements financiers, les primes acquises et les engagement futures (provision pour sinistre à payer) en assurance non-vie, le montant de la participation aux bénéfices, les provisions mathématiques, le Best Estimate, les intérêts générés et les rentes futures en assurance vie.

Au final, nous changeons l'allocation des actifs selon le scénario économique afin d'avoir un outil d'aide à la décision pour le choix d'investissement.

3.7.1 Revalorisation de l'actif

Dans notre modèle proposé, le portefeuille d'actifs en assurance non-vie est constitué d'actions, d'immobiliers, monétaires et d'obligations. En assurance vie nous proposons un portefeuille constitué d'obligations et actions seulement.

Notre objectif est de fournir une allocation optimale d'actif selon les indices d'aide à la décision sur lequel on s'appuie parmi ceux on cite :

· Valeur du NAV et BE.

· Valeur des capitaux propres à la fin de l'investissement.

Cette section est orientée pour l'assurance vie plus que l'assurance non-vie vu la sensibilité de l'activité ainsi le modèle proposé par l'entreprise chez qui j'ai fait mon stage.

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

Gestion du portefeuille obligataire

Les assureurs vie recourent généralement aux obligations pour se couvrir du risque de marché, néanmoins ce dernier reste difficile à modéliser ainsi sa gestion nécessite de recalculer les valeurs de marché, les valeurs comptables également à chaque arrêt comptable.

Mise à jour des valeurs comptables

Chaque exercice, la VNC ¹ est recalculée afin de prendre en compte la dépréciation de l'obligation [22]. La revalorisation dans le bilan comptable s'exprime par :

V Mt =

XT i=t+1

CFi * exp((-r(t, i - t) + s) * (i - t)) (3.7.1)

avec:

· T la maturité de l'obligation.

· CFi les flux de l'obligation.

· r le taux d'intérêt.

· Dt = exp((-r(t, i - t) + s) * (i - t)) : le déflateur.

Gestion des portefeuilles action

Le portefeuille action est modélisé de la même façon que le portefeuille obligataire dont la valeur du marché est évaluée selon le déflateur, le rendement sur lequel nous avons déterminé ce déflateur est fourni par le GSE :

V Mt = V Mt_1 * exprt (3.7.2)

Modélisation des produits financiers

Nous avons décidé, pour simplifier de négliger cette partie dans le cadre de ce mémoire est de restreindre seulement au résultat que donne le code (une simple application numérique) notre objectif est de fournir un outil d'aide à la décision pour une stratégie d'investissement, déterminer l'allocation optimale des actifs et projeter les engagements futurs.

Néanmoins nous mettons un focus sur cette partie issue d'une littérature des travaux de Damien Tichit dans son mémoire "Construction d'un modèle ALM pour une analyse de l'impact d'une remontée des taux sur la solvabilité d'un assureur vie"[22].

Récolte des coupons

Le générateur d'intérêt pour les obligations est appelé coupon, on distingue les obligations à taux fixe et les obligations à taux variable. Les coupons sont calculés sur la base du nominal dont le montant total collecté est calculé par [22] :

Coupon =

XM k=1

Taux Couponk * Nominalk (3.7.3)

64

avec: M le nombre d'obligation dans le portefeuille.

1. Valeur Nette Comptable

65

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

Récolte des dividendes

Les dividendes sont les revenus des actions et elles sont calculés sur la base de la valeur de marché de l'actif.

Dividendest = V Mt * Txdiv (3.7.4)

Stratégie de réinvestissement

Au final, la rentabilité des investissements réalisé se mesure par l'allocation cible fixée au début. Néanmoins dans un contexte d'excès de rachat ou de mortalité l'assureur sera obligé de liquide les titres financiers afin de bien gérer ses risques et d'assurer des projections plus réalistes.

De ce fait on retient le même travail, on re projette de nouveau le panier d'actif à l'aide des générateurs de scénarios économiques et on fixe de nouveau une allocation optimale d'actifs.

On introduit ces outputs de nouveau dans le moteur ALM afin de mieux clarifier les nouveaux risques issus de ce nouveau mécanisme.

66

Chapitre 4

Application pratique de la mise en

place d'un GSE et projection au sein

du modèle ALM

Introduction

Ce chapitre propose l'élaboration d'un Générateur de Scénarios Economiques pour une compagnie d'assurance qui permet de projeter des facteurs de risques économiques et financiers. Ces derniers seront utilisés pour la projection du bilan, du compte de résultat technique (en cas d'assurance non-vie) et l'état de flux de trésorerie (en cas assurance non-vie) .

Pour rappel, ce mémoire est élaborée dans un cadre tunisien² nous avons rencontré certaines difficultés au niveau des études pratiques :

· Insuffisance des données.

· L'instabilité du climat économique et politique.

· Incomplétude de marché financier tunisien due à une économie stationnaire avec de faibles performances.

Néanmoins, nous arrivons à collecter des données historiques à des horizons variables pour calibrer et projeter chaque variable selon le modèle retenu (modèle de référence).

Nous rappelons que dans ce mémoire, le modèle de référence utilisé pour projeter les variables macro-économiques est Ahlgrim et Al. présenté au niveau du chapitre 2.

Dans la section suivante nous allons présenter une analyse des données utilisées dans notre étude.

4.1 Analyse des données

Les facteurs des risques considérés dans notre analyse sont : le taux d'inflation, le taux d'intérêt, le rendement des actions et le rendement immobilier.

Ce choix des variables est efféctué car elles représentent les inputs du modèle de référence

2. Source des données

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

choisi. Ces dernières sont calculées à un pas annuel.

Les différents tests et modélisation statistiques dans la suite ont été réalisés à l'aide du logiciel libre statistique R.

Nous avons utilisé pour ce fait les librairies : Moments, tseries (pour les séries temporelles) et GLM.

Les codes R relatifs à la calibration et la projection du modèle d'Ahlgrim et Al. sont disponibles sur le site Ressources actuarielles [18] .

4.1.1 Taux d'inflation

L'inflation est définie par : "la perte du pouvoir d'achat de la monnaie qui se traduit par une augmentation générale et durable des prix. ... La perte de valeur de la monnaie est un phénomène qui frappe l'économie nationale dans son ensemble (ménages, entreprises, etc."[5] Pour la Tunisie, comme pour d'autres pays, l'inflation se calcule sur la base de l'indice des prix à la consommation (IPC) ¹ base 100 en 2015. Le calcul de l'IPC est donné par:

Prix d^'un panier de biens et de services d^'une année t

IPCt = * 100 (4.1.1)
P rix d'un panier de biens et de services de l'année de base

Ensuite, nous proposons dans le cadre de l'élaboration de ce mémoire une construction de taux d'inflation par la formule suivante :

Inft = ( IP Ct ) - 1 (4.1.2)

IP Ct-1

Pour la modélisation de cette variable nous choisissons un historique de l'IPC de 30 ans entre 1990 et 2021, les données utilisées sont disponibles sur le site de l'institu national de la statistique.

La figure ci-dessous, publié par la banque illustre l'évolution de l'inflation en Tunisie depuis 1990 jusqu'au 2020 en citant les principaux facteurs de déviation de l'inflation :

67

1. L'indice des prix à la consommation est l'instrument de mesure de l'inflation. Il permet d'estimer, entre deux périodes données, la variation moyenne des prix des produits consommés par les ménages. C'est une mesure synthétique de l'évolution de prix des produits, à qualité constante.[13]

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

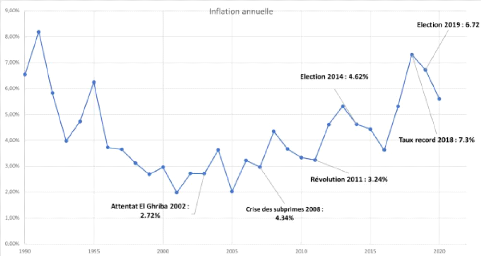
FIGURE 4.1 - Evolution de l'inflation entre 1990-2020 (Source : INS ) [12]

En Tunisie l'inflation garde une évolution en exponentielle depuis l'année 2011 ¹ et atteint un pique de 7.3% en 2018 et se stabilise à 6.2% fin 2020. Ceci est conséquence de l'instabilité économique et politique qui se traduit par l'augmentation du taux de déficit commercial : une vision stratégique doit être prise en compte pour lutter ce phénomène qui menace l'économie. Le tableau (4.1) ci-dessus représente les caractéristiques statistiques de la série des données utilisées :

		Taux d'inflation entre 1990-2020	Moyenne
0.042		Ecart type
0.015		Médiane
0.037		Maximum
0.082		Minimum
0.010		Skewness
0.725		Kurtosis
2.802		Jarque-Bera
0.0610

TABLE 4.1 - Statistiques du taux d'inflation entre 1990-2021

Les résultats obtenus permettent de conclure que :

· L'hypothèse de normalité est à rejeter (Test de Jarque-Bera).

· Une asymétrie de la distribution empirique de l'échantillon à droite (Skewness et Kurtosis).

Ces données sont utilisées pour le calibrage et la projection du modèle retenu pour le taux d'inflation qu'on détaillera dans la section suivante, nous étudions par la suite les données relatives au Taux d'intérêt.

1. Année de la révolution

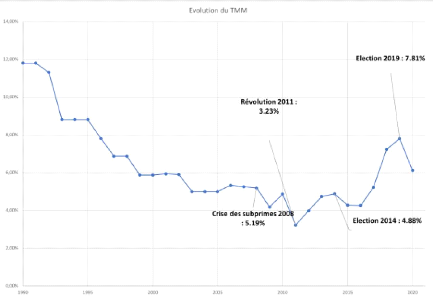
CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

4.1.2 Taux d'intérêt

Le Taux moyen du marché monétaire ¹ correspond au taux auquel les banques s'empruntent et se prêtent de l'argent entre elles. Il joue un rôle essentiel dans l'activité financière et fluctue en fonction de l'inflation, du chômage, mais aussi de la conjoncture internationale.[4]

Dans le cadre tunisien, le TMM est fixé par la BCT² et varie soit à la hausse soit à la baisse selon le contexte économique. En effet, une baisse de TMM conduit à une hausse des demandes de crédits par les investisseurs avec des coûts non élevés mais un retour sur investissement qui peut être rentable. Cependant, une augmentation de TMM est effectuée afin de limiter et régulariser la demande de crédit et créer une marge d'intérêt plus importante.[11].

La courbe suivante souligne l'évolution du taux d'intérêt réel durant les 30 dernières années en Tunisie :

FIGURE 4.2 - Evolution du TMM entre 1990-2020 (Source : INS) [23]

Le TMM a passé de 4,11% à 7,24% entre 2011 et 2019, la banque centrale de Tunisie considère que cette augmentation de 3,13% grave sur les budgets et la trésorerie des ménages dans un pays qui connait une hausse des prix en exponentielle.³

Le taux de marché monétaire est un taux nominal déterminé à partir de l'inflation par une intégration. En revanche, pour avoir une vision plus réaliste de ce que rapportera le placement du préteur, ou bien qu'il coutera à l'emprunteur, il est nécessaire de tenir compte de l'inflation et de raisonner en terme de taux réel plutôt qu'en terme de taux nominal. Ainsi la relation qui relie ces taux se traduit par :

1. Abrégé TMM

2. Banque Centrale de la Tunisie

3. Inspiré de la note banque centrale 2019

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Taux réel = Taux nominal - Taux inflation[30]

On distingue entre un taux d'intérêt à court terme et un taux d'intérêt à long terme, en effet :

· Taux d'intérêt à court terme est déterminé à partir du TMM que publie la BCT et en utilisant la relation précédente 29.

· Taux d'intérêt à long terme est celui des obligations d'État à échéance de 10 ans. Les taux dépendent essentiellement du prix facturé par le prêteur, du risque propre à l'emprunteur et de la réduction de la valeur du capital. ... Les taux d'intérêts à long terme sont un déterminant de l'investissement des entreprises.[17]

Nous présenterons dans la suite les statistiques des données collectées sur le taux d'intérêt à long terme et le taux d'intérêt à court terme.

Concernant la modélisation du taux d'intérêt à long terme, nous utilisons un historique de 30 ans entre 1990 et 2020 partagé par la banque centrale.

Les tableaux (4.2) et (4.3) ci-dessus présentent les mêmes caractéristiques statistiques des séries des données utilisées :

		Taux réel à court terme entre 1990-2020	Moyenne
0.194		Ecart type
1.811		Médiane
2.287		Maximum
5.548		Minimum
-0.932		Skewness
0.142		Kurtosis
1.856		Jarque-Bera
1.792

TABLE 4.2 - Statistique du Taux réel à court terme entre 1990-2020

		Taux réel à long terme entre 2007-2020	Moyenne
0.245		Ecart type
0.016		Médiane
0.0663		Maximum
0.103		Minimum
0.051		Skewness
0.672		Kurtosis
2.107		Jarque-Bera
1.629

TABLE 4.3 - Statistique du Taux réel à long terme entre 2007-2021

Les résultats permetent de conclure que :

· L'hypothèse de normalité est à rejeter (Test de Jarque-Bera).

· Une asymétrie de la distribution empirique de l'èchantillon à droite (Skewness et Kurtosis).

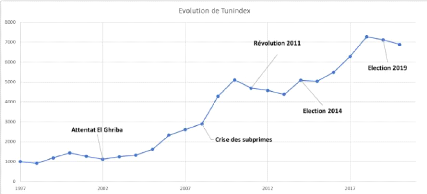
CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

4.1.3 Rendement des actions

Pour la collecte des historiques des rendements des actions tunisiennes nous nous se focalise sur l'indice boursier Tunindex¹.

Les données sont récupérées à partir de l'institut nationale de la statistique (INS) entre 1997 et 2020[12], le graphique ci-dessous illustre l'évolution de TUNINDEX en tenant compte les principaux facteurs de volatilités au cours de la période d'étude.

FIGURE 4.3 - Evolution de TUNINDEX entre 1997-2020 (Source : INS) [12]

Dans le cadre de ce mémoire la construction de l'historique des rendements de l'action à partir de l'indice boursier Tunindex est donnée par la formule suivante :

Rendaction n = ( ^indn ) - 1 (4.1.3)
indn-1 Où Rendaction

n représente le rendement de l'action et ind_n représente l'indice Tunindex avec
dividendes réinvestis à l'année n.

Le rendement de l'action associé à l'historique du rendement annuel construit entre 1997 et 2020 est présenté dans la figure ci-dessous :

1. L'indice TUNINDEX est un indice boursier tunisien pondéré par les capitalisations boursières flottantes avec une base 1000, C'est un indice statistique, de type rendement (les dividendes sont réinvestis), qui mesureent la tendance générale des marchés des titres de capital de la Cote de la Bourse, composés des cinquantes principales capitalisations boursières du pays.[24]

L'indice des prix immobilier IPM est utilisé pour la projection du rendement de l'immobilier. c'est un indice trimestriel établi dans le cadre d'un projet de suivi des prix de l'immobilier à

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

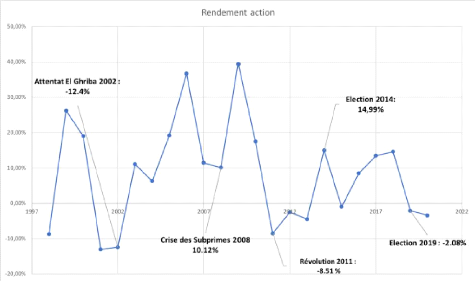
FIGURE 4.4 - Evolution du rendement de l'action entre 1997-2020 (Source : INS) [12]

Le tableau ci-dessous représente les caractéristiques statistiques de la série des données utilisées :

		Rendement de l'action entre 1997-2020	Moyenne
0.093		Ecart type
0.162		Médiane
0.097		Maximum
0.483		Minimum
-0.121		Skewness
0.771		Kurtosis
3.098		Jarque-Bera
2.389

TABLE 4.4 - Statistique du rendement de l'action entre 1997-1990

Les résultats permet de conclure que :

· L'hypothèse de normalité est rejetée (Test de Jarque-Bera).

· Une légère asymétrie de la distribution empirique de l'echantillon à gauche (Skewness).

Ces données sont utilisées pour le calibrage et la projection du modèle retenu pour le rendement de l'action que nous détaillerons dans la section suivante, nous étudions dans la suite les données relatives au rendement de l'immobilier.

4.1.4 Rendement de l'immobilier

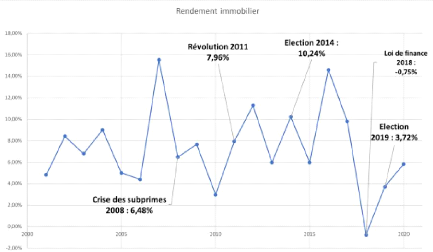
CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

usage d'habitation au sein de l'institut national de la statistique (INS).

Dans le cadre de ce mémoire et pour simplifier nous considérons que les indices du quatrième trimestre représentent les indices immobiliers annuels.

L'historique du rendement immobilier pour chaque année est construit à partir de la relation suivante:

Im_n = ( IP Mn ) - 1 (4.1.4)

IP Mn-1

Où IPM_n représente l'indice des prix immobiliers à l'année n. La figure ci-dessous illustre l'évolution du rendement de l'immobilier entre 2000 et 2020 :

FIGURE 4.5 - Evolution du rendement de l'immobilier entre 2000-2020 (Source : INS) [12]

Le tableau ci-dessous représente les caractéristiques statistiques de la série des données utilisées, les résultats réalisés permetent de conclure que :

· L'hypothèse de normalité des données est accepter (Test de Jarque-Bera).

· Une légère asymétrie de la distribution empirique de l'èchantillon à gauche (Skewness).

· Aplatissement proche de celui d'une loi normale centrée réduite (Kurtosis).

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

		Rendement de l'immobilier entre 2000-2020	Moyenne
0.075		Ecart type
0.038		Médiane
0.077		Maximum
0.154		Minimum
-0.012		Skewness
0.044		Kurtosis
3.117		Jarque-Bera
0.730

TABLE 4.5 - Statistique du rendement de l'immobilier entre 2000-2020

4.2 Calibrage des données

Nous proposons dans la suite une calibration des variables macro-économique selon le modèle d'Ahlgrim et Al. ^1.

Le modèle d'Ahlgrim et Al présenté dans le deuxieme chapitre sert à déterminer le rendement des actions en prenant comme inputs le taux d'inflation et le taux d'intérêt réel.

Modèle sur l'inflation

Ahlgrim et Al. modélise le taux d'inflation par un processus d'Orstein-Uhlenbeck.

Dans le cadre de ce mémoire nous adoptons ce modèle pour modéliser le taux d'inflation tunisien.

En se basant sur les données tunisiennes sur l'inflation présentées dans la section précédente, les paramétres obtenues sont résumés dans le tableau suivant :

Paramètre		Valeur	Taux d'inflation moyen :
0.041		Ecart-type de l'erreur :u
0.013		Vitesse de retour à la moyenne : k
0.381

TABLE 4.6 - Ahlgrim : Estimation des paramètres du modèle sur l'inflation

Test		Résultat	R2 corrigé
0.481		Fisher
P = 3,559 e5		Moyenne des résidus
6.089 e^-17		Student(constante)
P = 0.048		Student(variable)
P = 3.57 e-5		Breusch-Godfrey
P = 0.549		ARCH(1)
P = 0.633		Jarque-Bera
P = 0.049

TABLE 4.7 - Ahlgrim : Test d'adéquation du modèle sur l'inflation

Le tableau ci-dessus résume les résultats des différents tests d'adéquation sur le modèle, nous pouvons conclure que :

1. Vois chapitre 2 section modèle d'Ahlgrim et Al pour plus de détails.

1. entre 2000 et 2021

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· Le test d'ajustement permet de conclure que le pouvoir explicatif est de 48.1%.

· Le test de Fisher permet de dire que le modèle est globalement significatif.

· La moyenne des résidus est presque nulle.

· Le couple du test de student (constante,variable) affirme que les paramétres utilisés sont significatifs.

· Le test de Breusch-Godfrey montre l'abscence de l'autocorrélation d'ordre P = 1.

· Le test ARCH(1) montre l'abscence de l'hétéroscédasticité d'ordre q = 1.

· Le test de Jarque-Bera permet de validé la normalité des résidus.

L'ensemble des tests réalisés permettent de valider globalement l'adéquation du modèle d'Orstein-Uhlenbeck pour le taux d'inflation.

Modèle sur l'immobilier

Dans le cas tunisien, l'immobilier joue un rôle central dans les portefeuilles des assureurs tunisiens il permet de freindre les conséquences de l'inflation, vu la rentabilité qu'il procure. Ahlgrim et Al dans ses traveaux modélisent cette varibale par un processus d'orstein-uhlenbeck, nous adoptons cette modélisation dans le cadre de ce mémoire. En se basant sur les données tunisiennes sur l'immobilier ¹ présentées dans la section précédente, les paramétres obtenus sont résumés dans le tableau suivant :

Paramètres		Résultat	Vitesse de retour à la moyenne
0.570		Espérance du taux de rendement de l'immobilier
0.073		Ecart type de l'erreur
0.066

TABLE 4.8 - Ahlgrim : Estimation des paramètres du modèle sur l'immobilier

Paramètres	Résultat			R2 corrigé
0.365			Fisher
P = 0.01			Student (Constante)
P = 0.00001			Student (Variable)
P = 1.41 e -	7		Moyenne des résidus
1.301 e - 18			Breusch-Godfrey
P = 0.520			ARCH (1)
P = 0.289			Jarque-Bera
P = 0.049

TABLE 4.9 - Ahlgrim : Test d'adéquation du modèle sur l'immobilier

Le tableau ci-dessus résume les résultats des différents tests d'adéquation sur le modèle, ceci permet de conclure que :

· Le test d'ajustement permet de conclure que le pouvoir explicatif est de 36%.

· Le test de Fisher permet de dire que le modèle est globalement significatif.

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· La moyenne des résidus, on peut le considére nulles.

· Le couple du test de student (constante,variable) affirme que les paramétres sont significatifs.

· Le test de Breusch-Godfrey montre l'abscence de l'autocorrélation d'ordre P = 1.

· Le test ARCH(1) montre l'abscence de l'hétéroscédasticité d'ordre q = 1.

· Le test de Jarque-Bera permet de validé la normalité des résidus.

L'ensemble de ces tests valident les conditions posées pour la validation du modèle et du calibrage. Nous concluons que la modélisation par le processus d'Orstein uhlenbeck est bien adapté au rendement de l'immobilier.

Modèle sur les taux d'intérêt réel

Concernant le taux d'intérêt réel, il est modélisé sous la probabilité risque historique par le processus de Hull and White à deux facteurs.

A noter que le taux court réel r_r(t) oscille autour du taux long ll(t), soit :

dr_r(t) = u_r[ll(t) - r_r(t)]dt + ó_rdW_r(t) (4.2.1)

dl_r(t) = ur,l[êr(t) - ll(t)]dt + óldWl(t) (4.2.2)

En se basant sur les données tunisiennes sur le taux d'intérêt réel ¹ à long et à court terme présentés dans la section précédente, on obtient les paramètres de besoin qui sont résumés dans le tableau ci-dessous.

Paramètres		Résultat	Vitesse de retour à la moyenne (CT)
0.194		Ecart type de l'erreur (CT)
0.018		Vitesse de retour à la moyenne (LT)
2.454		Taux d'intérêt réel moyen (LT)
0.027		Ecart type de l'erreur (LT)
0.020

TABLE 4.10 - Ahlgrim : Estimation des paramètres du modèle sur le taux d'intérêt réel à long et court terme

1. entre 2007 et 2020

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Le tableau suivant représente les tests statistiques nécessaires pour l'adéquation du modèle de taux d'intérêt réel à long terme :

Test	Résultat			R2 corrigé
-0.0834			Fisher
P = 0.716			Student (Constante)
P = 0.006			Student(Variable)
P = 0.716			Moyenne des résidus
2.271 e^-19			Breusch-Godfrey
P = 0.635			ARCH(1)
P = 0.733			Jarque-Bera
P = 9.295	e^-13

TABLE 4.11 - Ahlgrim : Test d'adéquation du modèle sur le taux d'intérêt réel à long terme

Ceci permet de conclure que :

· Le test d'ajustement permet de conclure que le pouvoir explicatif est de -8%.

· Le test de Fisher permet de dire que le modèle est globalement significatif.

· La moyenne des résidus est presque nulle.

· Le couple du test de student (constante,variable) affirme que les paramétres sont significatifs.

· Le test de Breusch-Godfrey montre l'abscence de l'autocorrélation d'ordre P = 1.

· Le test ARCH(1) montre l'abscence de l'hétéroscédasticité d'ordre q = 1.

· Le test de Jarque-Bera permet de valider la normalité des résidus.

Le tableau suivant représente les tests statistiques nécessaire, pour l'adéquation du modèle de taux d'intérêt réel à court terme :

Test		Résultat	R2 corrigé
0.0078		Fisher
P = 0.321		Student(Variable)
P = 0.322		Moyenne des résidus
-0.0004		Breusch-Godfrey
P = 0.238		ARCH(1)
P = 0.763		Jarque-Bera
P = 0.502

TABLE 4.12 - Ahlgrim : Test d'adéquation du modèle sur le taux d'intérêt réel à court terme

Ceci permet de conclure que :

· Le test d'ajustement permet de conclure que le pouvoir explicatif est de 0.8%.

· Le test de Fisher permet de dire que le modèle est globalement significatif.

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· La moyenne des résidus est presque nulle.

· Le test de student (variable) affirme que les paramétres sont significatifs.

· Le test de Breusch-Godfrey montre l'abscence de l'autocorrélation d'ordre P = 1.

· Le test ARCH(1) montre l'abscence de l'hétéroscédasticité d'ordre q = 1.

· Le test de Jarque-Bera permet de valider la normalité des résidus.

L'ensemble de ces tests montre que le modèle de Hull-White n'est pas parfaitement adapté aux données tunisiennes pour les taux d'intérêt réel à long et à court terme, car les testes de fisher et le test d'ajustement ne sont pas tout à fait validés. Cependant nous retenons ces données vu que les résultats issus de ces deux tests sont proches de zéro.

Modèle sur les actions

La modèlisation de l'excès du rendement actions dans le cadre du modèle d'ahlgrim se base sur le processus de Black et Scholes. En se basant sur les données annuelles tunisienne entre la période de 1997 et 2020 des rendements des actions, on obtien l'excès du rendement de l'action par la formule suivante :

Excès du rendement actions = Rendement actions - TMM

On peut donc déduire les paramètres nécessaires pour alimenter le processus de black and Scholes, soit alors :

Paramètre		Résultat	Excès de rendement moyen
0.037		Ecart type de l'excès des actions
0.148

TABLE 4.13 - Ahlgrim : Estimation des paramètres du modèle sur le rendement d'actions

4.3 Projection

Dans cette section nous présentons les résultats de la projection issue des variables validées dans la section précédente pour le modèle d'Ahlgrim.

La projection est réalisée par la génération de trajectoires en utilisant la formule de discrétisation, nous définissons une structure de dépendance pour effectuer des projections cohérentes. Pour le choix de cette structure nous allons adopter la structure de corrélation linéaire ^1.

Hypothèses de projection

Nous présentons dans cette sous-section les hypothèses de projection pour le modèle Ahlgrim and Al ainsi les paramétres et les valeurs initiales nécessaires pour la projection.

· NS = 10000 : Le nombre de simulations.

· T = 10 ans : La maturité de projection.

· Les quantiles sont présentées à 10 % et à 90 %. On suppose que l'année d'origine de projection est t = 2020.

1. Voir la 3^éme étape de construction d'un GSE 2^éme chapitre pour plus de détail.

1. Matrice ci-dessus

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Matrice de corrélation entre les variables du GSE

Pour la modélisation de la dépendance on se focalise sur la matrice de corrélation. Les résidus suivent une loi normale, la génération des trajectoires revient alors à générer des lois normales corrélées, d'où le recours vers la décomposition de Chlesky.

Nous nous intéressons à une projection annuelle, les matrices de corrélations présentées ci-dessous sont estimées à partir des données à fréquences annuelles dont l'historique des variables du GSE est récupéré entre 2007-2020 pour des raisons d'absence de suffisamment des données sur le taux réel long. La matrice de corrélation est intégrée alors comme un paramètre dans le GSE.

Nous présentons dans la suite les matrices de corrélations pour le modèle de référence Ahlgrim and Al ainsi qu'un backtesting sur les résultats obtenus afin d'effectuer des projections cohérentes dans la suite.

Données	Res_Tx_In	Res_Rdt_Im	Res_Tx_rl	Res_Tx_rc		Res_Rdt_ex	Res_Tx_In
1	-0.025	0.693	-0.132	-0.0026		Res_Rdt_Im
-0.025	1	-0.493	-0.005	0.016		Res_Tx_rl
0.693	-0.493	1	0.051	0.020		Res_Tx_rc
-0.132	-0.005	0.051	1	0.228		Res_Rdt_ex
-0.0026	0.016	0.020	0.228	1

TABLE 4.14 - Ahlgrim and Al : Matrice de corrélation de l'historique des résidus Backtesting sur la matrice de corrélation

Comme la matrice de corrélation de l'historique des résidus est symetrique, définie et positive, d'aprés le théoréme de Cholesky, on peut la décomposer comme le produit d'une matrice triangulaire et de sa transposée, soit :

Données	Res_Tx_In	Res_Rdt_Im	Res_Tx_rl	Res_Tx_rc		Res_Rdt_ex	Res_Tx_In
1	0	0	0	0		Res_Rdt_Im
-0.0258	0.999	0	0	0		Res_Tx_rl
0.693	-0.475	0.541	0	0		Res_Tx_rc
-0.132	-0.008	0.257	0.957	0		Res_Rdt_ex
-0.0026	0.015	0.054	0.22	0.973

TABLE 4.15 - Ahlgrim and Al : Matrice de corrélation - Décomposition de Cholesky

Nous proposons une mesure de qualité pour notre GSE de référence Ahlgrim et Al. sur la matrice de corrélations : nous comparons la matrice de corrélations issue des données historiques ¹ avec celle projetée pour vérifier si la structure de dépendance est conservée ou pas. La matrice projetée est présentée ci-dessous.

FIGURE 4.7 - Boostrap : projection de l'inflation

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Données	Inflation	Immobilier	Tx long	Tx court		Excès_action	Inflation
1	-0.023	0.670	-0.127	0.008		Immobilier
-0.023	1	-0.471	-0.004	0.019		Tx long
0.670	-0.471	1	0.043	0.0208		Tx court
-0.127	-0.004	0.043	1	0.221		Excès_action
0.008	0.019	0.0208	0.221	1

TABLE 4.16 - Ahlgrim and Al : Matrice de corrélation projeté

Les valeurs des deux matrices sont très proches donc la structure de dépendance est conservée.

4.3.1 Projection issues du calibrage du modèle d'Ahlgrim et Boos-trap

Nous restreindrons dans cette partie seulement pour présenter les schémas issus du code R

lors de la projection. Voici ci-dessous la chronique des rendements de l'inflation issus du modèle Ahlgrim et Al :

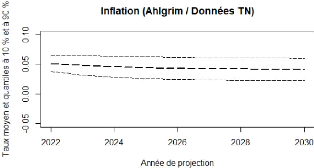
FIGURE 4.6 - Ahlgrim et Al. : projection de l'inflation

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Vous trouvez ci-dessous l'évolution de l'action à long terme des rendements de l'action issus du modèle Ahlgrim et Al et boostrap :

FIGURE 4.8 - Ahlgrim et Al. : projection de l'éxcedent de rendement de l'action

FIGURE 4.9 - Boostrap : projection de l'éxcedent de rendement de l'action

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Ci-dessous la chronique de l'immobilier issus du modèle Ahlgrim et Al et boostrap :

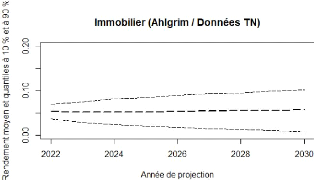
FIGURE 4.10 - Ahlgrim et Al. : projection de l'immobilier

FIGURE 4.11 - Boostrap : projection de l'immobilier

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

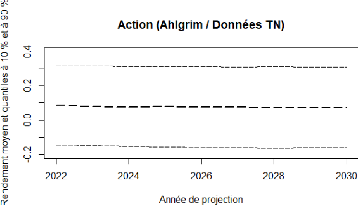
FIGURE 4.12 - Ahlgrim et Al. : projection de rendement de l'action

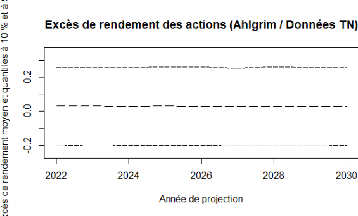
FIGURE 4.13 - Ahlgrim et Al. : projection de Taux court

Vous trouvez ci-dessous la chronique des taux à court et à long terme ainsi la projection des zéro coupon issus du modèle d'Ahlgrim et Al :

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

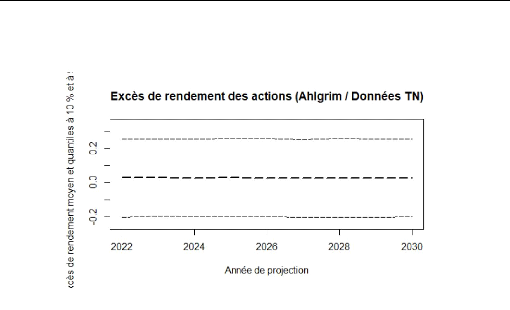
FIGURE 4.14 - Ahlgrim et Al. : projection de Taux court

FIGURE 4.15 - Boostrap : projection de Taux court

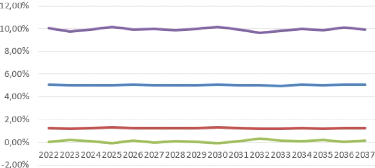
CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

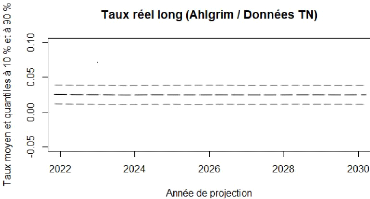
FIGURE 4.16 - Ahlgrim et Al. : projection de Taux long

FIGURE 4.17 - Boostrap : projection de Taux long

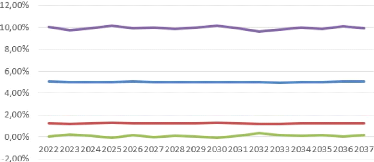
CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

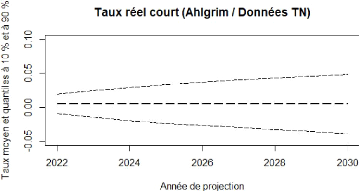
FIGURE 4.18 - Ahlgrim et Al. : projection de taux réel court

FIGURE 4.19 - Boostrap : projection de taux réel court

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

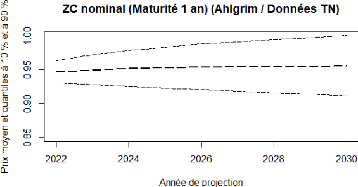
FIGURE 4.20 - Ahlgrim et Al. : projection de Zero coupon nominal

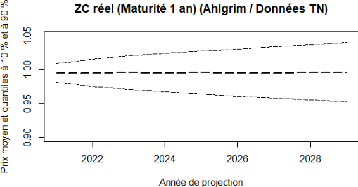
FIGURE 4.21 - Ahlgrim et Al. : projection de Zero coupon réel

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

4.4 Réalisation d'un cas pratique pour une compagnie d'assurance

4.4.1 Cas pratique en assurance non-vie

L'objectif de cette section est de construire un modèle ALM simplifié pour une compagnie d'assurance non-vie offrant des produits d'assurances automobiles et des produits d'assurances santé. La projection des variables macro-économiques du modèle d'Ahlgrim et Al. du bilan, du compte de résultats et de l'état de flux de trésorerie sera alimentée par les résultats issus des projections.

1. Contruction du Bilan comptable

Le tableau ci-dessous représente les hypothèses retenues pour le portefeuille étudié :

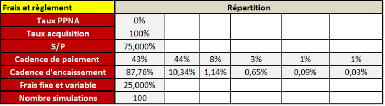
FIGURE 4.22 - Hypothéses de construction du bilan en assurance non-vie

Dans le cadre de ce mémoire et pour simplifier nous supposons que le passif est constitué seulement des capitaux propres et provisions pour sinistre à Payer (PSAP).

Pour le calcul de la psap¹ nous réalisons un triangle en fonction de la cadence de paiement on multiplie la prime acquise par le ratio s/p pour obtenir la charge sinistre qui sera répartie sur 6 ans.

A ce stade nous pouvons projeter le triangle de développement.

FIGURE 4.23 - Triangle PSAP

La variation PSAP est donnée par :

1. Provision pour sinistre à payé

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

VAR PSAP = PSAP(t) - PSAP(t - 1) Pour valider le résultat nous adaptons un back-testing:

Reglement - VAR PSAP = charge de sinistre

FIGURE 4.24 - Règlements et charges des sinistres

L'actif est constitué des placements, créance et l'avoir en banque.

Pour les créances nous réalisons un triangle d'encaissement dont la somme de chaque colonne du triangle donne le montant du règlement et la somme restante de la ligne en dehors de cette colonne donne le montant de la créance restante.

Les avoirs en banque représentent la différence entre la clôture de l'exercice présenté au niveau l'état de flux de trésorerie et l'investissement en action, obligation, monétaire et immobilier à l'année n.

Pour que le bilan soit cohérent nous vérifions que :

Total actif (t) - total passif (t) = 0

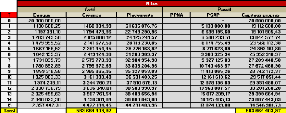
FIGURE 4.25 - Bilan économique

2. Construction du compte de résultat technique

Le compte du résultat technique nommé aussi état des résultats ou compte du résultat est un état financier synthétisant l'ensemble des charges et des produits d'une entreprise ayant une activité marchande.

Le compte de résultat technique étudié est constitué de .

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· Primes acquises

Prime acquise(t) = prime émise(t) * taux d^'acquisition avec:

(a) Prime émise(t) = prime émise (t - 1) * (1 + taux d^'inflation(t) + 2%)

(b) Taux d'acquisiton = 100% défini en hypothèse.

· Charge de sinistre

La charge de sinistre est constitué de la varisation PSAP et des sinistres réglés obtenus du triangle de développement élaboré précédemment.

· Frais d'exploitation

Frais d^'acquisiton(t) = prime émise(t) * taux de frais

· Produit financier

Ainsi le résultat tehnique est obtenu comme :

Résultat technique (t) = prime acquise (t) + sinistre réglé (t) + variation PSAP (t) + frais(t) + produit financier (t)

FIGURE 4.26 - Compte de résultat technique

3. Construction d'un état de flux de trésorerie

L'état de flux de trésorerie appelé aussi l'évolution de la situation financière indique comment l'encaisse a évolué au cours de l'exercice.

L'état des flux de trésorerie est subdivisé en trois types d'activité : l'activités d'exploitation, l'activité d'investissement et l'activité de financement.

· Activité d'exploitation elle est définie par deux éléments : l'ouverture et la clôture.

(a) L'ouverture est définie comme suit

Ouverture (0) = capitaux propres (0) pour t = 0 Ouverture (t) = clôture (t - 1) pour t > 0

(b) La clôture est définie comme la somme du solde avant placement et le produit financier de la même année.

· L'activité de financement est constituée de :

(a) Primes encaissées résultantes du triangle réalisé par la cadence d'encaissement.

(b) Sinistre (t) = sinistre réglé (t) provenant du compte de résultat technique.

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

(c) Frais (t) provenant du compte de résultat technique.

· L'activité d'investissement

Le montant à placer est défini comme suit :

(a) Montant à placer (0) = 0.

(b) Montant à placer (t) = Clôture (t-1).

(c) Excédent (t) = Prime encaissés (t) + sinistre (t) + frais (t)

(d) Solde avant placement (t) = excédent (t) + ouverture (t)

Le produit financier à l'année t est défini comme étant le total des rendements nets obtenus suite aux investissements.

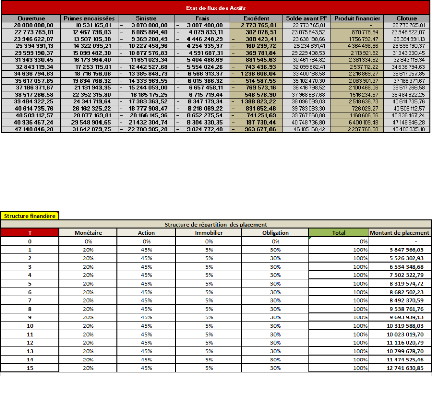
FIGURE 4.27 - Etat de flux de trésorerie

FIGURE 4.28 - Allocation stratégique des actifs

Dans ce paragraphe, nous proposons différentes allocations d'actifs afin d'étudier leur impact sur la variation du passif:

· Scénario 1 : 5 % en monétaire, 10 % en action, 10 % en immobilier et 65 % en obligation.

· Scénario 2 : 5 % en monétaire, 25 % en action, 50 % en immobilier et 10 % en obligation.

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· Scénario 3 : 5 % en monétaire, 45 % en action, 10 % en immobilier et 40 % en obligation.

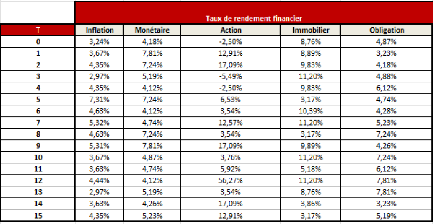
FIGURE 4.29 - Rendements macro-économiques prospective issus des GSE

4.4.2 Résultats en assurance non-vie

Nous avons développé un outil sur VBA-Excel pour projeter le bilan économique, le compte de résultat technique et l'état de flux de trésorerie au sein d'une entreprise d'assurance à l'aide des résultats issus des techniques de boostrapping sous l'allocation d'actif proposée. Les différents résultats statistiques s'affichent lors de l'exécution du code par le bouton "simuler".

Les statistiques relatives aux capitaux propres obtenus suite à l'exécution de ce scénario à l'aide de la commande VBA "Simuler" sont :

· Une moyenne de 47100.

· Un écart-type de 6465.

· Un Coefficient de variation de 14%.

Pour le deuxième scénario nous proposons l'allocation suivante: 10 % en monétaire, 10%

en action, 50 % en immobilière et 20% en obligataire, les statistiques relatives aux capitaux propres issus de ce scénario :

· Une moyenne de 55433.

· Un écart-type de 4844.

· Un Coefficient de variation de 9%.

Pour le dernier scénario proposé, l'allocation prise en compte est la suivante : 20 % en

monétaire, 30% en action, 20 % en immobilière et 20% en obligataire, les statistiques relatives à ce scénario donnée sont :

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· Moyenne: 58833.

· Ecart-type : 17900.

· Coefficient de variation: 30%.

Conclusion :

Pour le premier scénario, nous optons d'investir plus en obligataire qu'en action et immobilier nous trouvons une moyenne assez réduite par rapport aux autres scénarios, une volatilité plus élevée ainsi un coefficient de variation élevé en moyenne de 14%.

Pour le deuxième scénario, nous choisissons d'investir la moitié du montant dédié en immobilier, nous arrivons à avoir un coefficient de variation la plus réduite, une moyenne de 55433 acceptable par rapport aux autres scénarios, et un écart-type légèrement élevé en comparant les valeurs d'écart-type réalisé.

Le dernier scénario possède le coefficient de variation le plus élevé soit de 30% néanmoins on remarque qu'il possède la moyenne la plus élevée.

En effet plus que la moyenne est élevée plus que l'investissement est rentable et plus que l'écart-type est élevé plus que l'investissement est risqué, autrement dit l'investissement le plus rentable est celui qui possède le coefficient de variation le plus réduit, nous choisissons pour ce fait le deuxième scénario.

4.4.3 Cas pratique en assurance vie

Dans cette partie nous étudions le cas d'un contrat d'épargne en assurance vie afin de calculer la « Valeur Actuelle Net » et le « Best Estimate ».

Nous rappelons ces notions :

· Le VAN ¹ est défini comme étant la marge de l'assureur attendue lors d'un investissement proposé : c'est la somme actualisée de la marge de l'assureur sur les investissements.

· Pour le best estimate correspond à la moyenne pondérée par leur probabilité des flux de trésorerie futurs compte tenu de la valeur temporelle de l'argent (valeur actuelle attendue des flux de trésorerie futurs) estimée sur la base de la courbe des taux sans risque pertinent.

· Hypothèses Les hypothéses qu'ona retenus sont : - Hypothèses relatives à l'actif

Pour simplifier l'étude nous nous restreindrons à un actif constitué des actions et des obligations.

On suppose que les produits financiers à chaque période correspondent à 1 - á du rendement zéro-coupon 10 ans et á du rendement action, on note TPF (t) le taux de produits financiers et on le définit par :

T P Ft = á( P (t, M) (4.4.1)

P (t - 1, M + 1) - 1) + (1 - á)( 8(t)

8(t - 1) - 1)

Avec :

1. Valeur Actuelle Net

1. Cox-Ingersoll-Ross

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

* á : Part de l'investissment à partir du montant dédié.

* P(t,M) : Prix du zéro-coupon à un instant t de maturité M. * S(t) : Prix de l'action.

- Hypothèses relatives au passif

A noter que ce contrat est soumis au risque de mortalité et pouvant être racheté a tous moment.

L'assuré de ça part, avec un PM initial égal à 100 bénéficie d'une revalorisation annuelle correspondant au maximum entre un TMG fixé à 2% et une quote-part (fixée à 90%) des produits financiers générés par les actifs en représentation des PM.

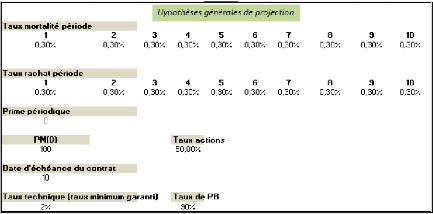
FIGURE 4.30 - Hypothéses de projection en assurance-vie

Pour la projection des facteurs financiers :

· Projections des actions

Les actions retenus pour la projection du portefeuille sont issues du GSE construit dans la premiére section de ce chapitre.

· Projection des prix zéro-coupon

Les prix zéro-coupon sont calculés à partir des taux zéro-coupon issus du GSE modèlisé. Pour passer au monde risque-neutre, nous avons utilisé le modèle CIR¹ (nous n'avons pas utilisé la méthode de risque neutralisation habituelle car nous ne disposons pas d'une courbe de taux sans risque).

Pour la projection des cash-flows:

· L'évolution du nombre de contrat (N(t)) est proportionnelle au taux de survie (S(t) = 1-q(t)) et le taux de non-rachat (r(t)).

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

FIGURE 4.31 - Résultat de projection des facteurs financiers

· L'évolution du nombre de décès (q(t)) est le produit du nombre de contrat pour l'année précédente (N(t-1)) et le taux de mortalité (q(t)).

· Le nombre de rachat (r(t)) est le produit du nombre de contrat pour l'année précédent et le taux de survie (1-q(t)) avec le taux de rachat.

· Sous l'hypothèse de l'absence des primes périodique la prime ici est nulle (nombre de contrats * prime).

· La prestation au décès est égale à la provision mathématique dédiée à l'année précédente (PM (t-1)) multiplié par le taux de mortalité (q (t)).

· La prestation au rachat est égale à la PM de l'année précédente (PM(t-1)) multiplié par le taux de rachat (r(t)) tant que l'assureur en vie (1-q(t)).

· Le montant total de bénéfice (IC Stock) dédié à être servie aux assurés est égal au montant des provisions mathématiques PM(t-1) tant que les assurés sont en vie (1-q(t)) et n'ont pas racheté leur contrat (1-r(t)) : c'est ce que la compagnie doit fournir comme stock pour faire face à ses engagements de revalorisation envers ses assurés.

· Ce que doit l'assureur avoir en stock pour servir les prestations en cas de rachat ou de mortalité (PB stock) est le maximum entre TMG et le taux de participation au bénéfice projeté pour l'année précédente (PB(t-1) projeté) pour les assurés en vie (1-q(t)) et non-racheté (1-r(t)).

· L'IC (ce que l'assureur doit l'avoir) pour les prestations est la multiplication de la PM(t) et le TMG pour les rachetés et non décès (r(t) (1-q(t)) où pour les décès (q(t)).

· La provision (PB Prest) est donné donc par le maximum entre la différence Tx PB projetée, TMG multiplié par PM(t-1) pour les rachetés et non décès ou bien décès.

· A un instant t, la PM est la somme de la PM(t-1) pour les non-décès et non rachetés, le montant de PB que doit l'assureur fournir (IC stock) et la provision dédiée pour les prestations (PB stock).

· La marge de l'assureur est PM(t-1) multiplié par la différence entre le taux du produit financier et le max (tx pb projeté; TMG) (qui sera servie à l'assuré)

· Le cash-flow du passif de l'assureur est la somme des engagements de l'assureur en éliminant la prime (elle est nulle dans notre cas).

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

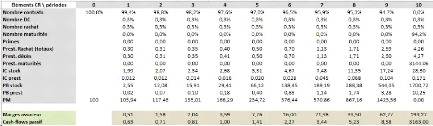
FIGURE 4.32 - Projection des cash-flows passif en assurance-vie

Pour le calcul du BE(0) et NAV(0) on recoure aux techniques des simulations à l'aide du logiciel VBA-Excel.

Une fois qu'on a déterminé la marge assureur et le cash-flow passif on s'arrange au calcul du VAN grâce au déflateur.

On effectue 1000 simulations pour la VAN marges-assureur et pour la VAN cash-flows passi et on aura:

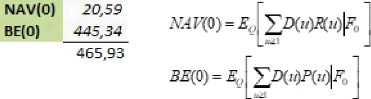
FIGURE 4.33 - Résultats BE(0) et NAV(0)

4.4.4 Résultats en assurance vie

On refait le même travail élaboré en assurance non-vie, nous utilisons VBA-Excel pour développer un bouton "Simulation VAN" afin de simuler la VAN marge assureur et la VAN cash-flow passif pour plusieurs scénarios selon le choix de á nous disposons pour ce fait deux scénarios possibles.

Le premier scénario prend une valeur de á = 20% soit une allocation de : 20% en actions et 80% en obligataires. Les valeurs issues de ce scénario sont :

· NAV(0) = -12,08.

· BE(0) = 161,95.

Pour le deuxième scénario nous changeons la valeur de á afin d'interpréter l'investissement le plus rentable, nous prenons á = 80% et nous obtenons :

FIGURE 4.35 - Evolution du NAV selon le deuxième scénario

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

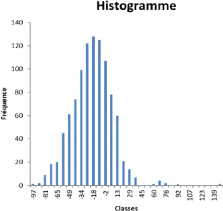
FIGURE 4.34 - Evolution du NAV selon le premier scénario

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· NAV(0) = 93,01.

· BE(0) = 1187,81. Conclusion

Pour le premier scénario nous proposons d'investir majoritairement en action soit de 80% et le reste en obligations, nous trouvons un NAV négatif et un BE trés réduit en le comparant par rapport au deuxiéme scénario.

En revanche pour le deuxiéme scénario nous prennons le cas contraire; investir à 80% en obligations et le reste en actions, nous arrivons à trouver un NAV positif et un BE beaucoup plus élevé que celle du premier scénario.

Comme indiqué dans la partie théorique le NAV constitue un outil d'aide à la décision du coup plus que ma valeur NAV est élevée plus que mon investissement est rentable de ce fait nous s'arrangeons pour le deuxième scénario et on recommande d'investir majoritairement en obligataire.

Ce choix peut être renforcé par une interprétation graphique, en effet on remarque que notre premier histogramme la distribution est plus aplati par rapport à celle du deuxième scénario, elle donne l'intuition que notre investissement est plus risqué et plus étalé.

Critiques des modèles proposés

Les résultats réalisés en amont n'impliquent pas de se limiter aux décisions fournies par le code, en effet :

· Un modèle est outil d'aide à la décision, certes son utile mais certes limitée.

· Un assureur est exposé aux différents risques, il n'est pas certain de corréler entre eux.

· Une personne averse au risque et cherche à se couvrir n'est pas capable de générer un plus de rendement.

Conclusion

A l'occasion de ce mémoire, nous avons construit un outil d'aide à la décision pour les compagnies d'assurances a travers des techniques acturielles tel que la NAV et le BE.

Dans un premier temps, nous avons pris les générateurs de scénarios économiques comme étant un outil de projection, le modèle d'Ahlgrim a été choisi parmi tous les modèles pour assurer cette projection. Ce choix est dû aux disponibilités des données tunisiennes pour les inputs, simplicité d'exécutions et répond à nos besoins pour les out-put.

Pour respecter les contraintes qu'impose ce modèle nous avons réalisé des tests statistiques pour vérifier certains critères parmi ceux on cite : la qualité de calibrage, l'indépendance et la normalité des résidus afin d'avoir une projection cohérente.

Nous avons choisi dans la suite de développer un modèle de gestion actif-passif stochastique permettant d'avoir une vision très cohérente avec les pratiques actuarielles et de l'ensemble des outils comptables intervenant dans la modélisation des engagements d'une compagnie d'assurances combinant les deux volets : l'assurance vie et l'assurance non-vie.

Pour ce fait nous avons développé un outil de simulation sur VBA-Excel permettant à chaque fois de simuler un nouveau scénario économique en se basant sur les techniques de bootstrapping qui ont été alimentées par les résultats de projection issus du modèle d'Ahlgrim et Al par le logiciel statistique libre R.

Pour l'assurance non-vie nous avons projeté le bilan, le compte de résutats techniques et l'état de flux de trésorerie à l'aide des rendements projeté issus du générateur de scénario économique et nous cherchons si notre investissement est rentable ou pas, Notre variable cible est la valeur des capitaux propres apres 15ans. Pour ce fait nous avons changé à chaque fois l'allocation des actifs afin d'avoir l'allocation optimale selon le scénario économique proposé.

Pour l'assurance vie nous avons projeté le taux d'intérêt et le prix du zéro-coupon à maturité 10 ans a l'aide des résultats issus du générateur de scénario économique et à chaque fois nous avons cherché une allocation optimale répartie entre l'action et l'obligation. Le choix de l'allocation dépend de la valeur du NAV, en effet plus ma NAV est élevée plus mon investissement est rentable.

Pour renforcer nos choix, nous avons tracer les courbes d'evolution et réaliser des tests statistiques.

Enfin, nous avons cité les limites des modèles développés : d'autres études et variantes pourraient être réalisées à ce titre, d'autres modélisations de comportement des assureurs et des assurés pouvant être changées et d'autres normes comptables et réglementaires pouvant améliorer ce travail.

Annexes

Lemme d'Itô

Un processus stochastique (Xt) est appelé processus d'Itô s'il est de la forme :

Z t Z t

Xt = X0 + ₀ á_udu + 0 HudBu (4.4.2)

Où X0 est F0 mesurable, át et Ht sont deux processus F-adapté, át est intégrable et Ht est de carré intégrable et Bt un mouvement brownien stochastique.

On note également sous la forme intégrale :

dXt = átdt + HtdBt (4.4.3)

Pour une fonction f de classe C^1,2 (Ou bien dérivable et que son dérivé est continue) et (Xt) un processus d'Itô alors Yt = f(t, Xt) est un processus d'Itô et ona :

?f

2

f(t, Xt) = f(0, X0)+ ~t ?t (u, Xu)du+Jot _?x(u, ^Xu)dXu+ 2 Jot ?x2f(u, X_u)d < X >_u (4.4.4)

fot ?f ?f 21?2f ft ?f

= f(0, X0) + ( _?t + áu _?x + Hu 2 ?x2)(u, X_u)du + o Hu (u, X_u)dB_u (4.4.5)

Où encore, en formation différentielle

?²f

df(t, Xt) = (?f ?t + át ?f 1

?x + H2 ?x2 )(t, Xt)dt + Ht ?f

?x(t, Xt)dBt (4.4.6)

^t 2

Rappel des expressions statistiques

Le coefficient d'asymétrie (Skewness en anglais) pour n réalisation (x1, ..., x_n) d'une variable aléatoire X de moyenne u et écart-type ó est défini par :

1 SK = ó3	E(xi - u)^3		(4.4.7)

Le coefficient d'aplatissement (Kurtosis en anglais) pour n réalisation (x1, ..., x_n) d'une variable aléatoire X de moyenne u et écart-type ó est défini par :

1 K = ó4	E(xi - u)^4		3 (4.4.8)

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Soit X, Y deux variables aléatoires réelles de variance finis noté respectivement óX, óY alors le le coefficient de corrélation noté COR(X,Y) ou _ñXY est défini par:

ñXY =

COV (X, Y ) (4.4.9) óXóY

Où COV(X,Y) est la covariance de X et Y définie par:

COV (X, Y ) = E(XY ) - E(X)E(Y) (4.4.10)

Série temporelle ARCH

Le modèles ARCH (Auto Regressive Conditional Heteroskedacity) utilisés en économétrie pour la modélisation des séries chronologiques et les séries temporelles financières à volatilité variable.

Un modéle ARCH de paramétre q noté ARCH(q) est définie par:

Et = ótZt (4.4.11)

Avec :

· Et : Les innovations de le série.

· Zt : Variable aléatoire qui suit une loi normale centrée réduite.

· ót = á0 + Pq i=1 áiE2 t_i

Modéle Linéaire Généralisé (GLM)

En statistiques, en économétrie et en apprentissage automatique, un modèle de régression linéaire est un modèle de régression qui cherche à établir une relation linéaire entre une variable dite expliquée et une ou plusieurs variables dites explicatives.

Le modèle s'écrit de la maniére suivante :

Y = Xâ + E (4.4.12)

Avec :

· Y : Variable endogéne.

· X : Variable explicative.

· â : Paramétre à expliquer.

· E : Erreur.

On définit la valeur prédite où ajustée par la relation suivante Yà = X â^à et le résidu comme la différence entre la valeur observée et la valeur prédite, soit ~à = Y - Yà .

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

L'estimateur des Moindre Carré Ordinaire (MCO) s'écrit:

â à= (X^'X)^-1y (4.4.13)

Où y est la réalisation de Y[29].

Coefficient de variation = Ecart-type

Moyenne

Martingale : On dit que la variable aléatoire Xt est martingale pour la filtration Ft sous la probabilité P si et seulement si :

EP (Xt+1/Ft) = Xt (4.4.14)

Pour la réalisation du projet, nous avons utilisé :

Marque, modèle PC	Acer, PC du cabinet ERM Partners
Système d'exploitation	Windows 10 Education
Processeur	Intel(R) core(TM) i5-7200U CPU @ 2.50Hz 2.70 GHz
R studio	R i386 2.15.1 64bits
Excel - VBA Excel	Microsoft office 2010
Document interne de ERM Partners	Scénarios économique en assurance : Simulation et projection (A.Faleh-Frederic Planchet) Gestion Actif-Passif en assurance-vie (Véronique Mattei) GSE en assurance : Cas d'application ALM (Faleh-Planchet) Mémoire développé en interne du cabinet ERM : GSE Tunisien: Calibration et projection élaborée par Zeineb Ghardallou

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Variable macro économique	Equation	Modélisation
Inflation + Immobilier	Processus d'Orstein - Uhlenbeck	dut = ka(iLa,t - ut)dt + UadBa,t
Taux d'intérêt nominale	Déduit des taux d'intérêts réels ^etPn(t,T) des anticipations d'inflation	PT(t,T) EQ Inft
		= * t [ InfT ]
Taux d'intérêt réel	Modèle de Hull and White	drr(t) = iir[ll(t) - rr(t)]dt + rdWr(t)
Rendement des actions	Somme du taux sans risque taux d'inflation et une prime de risque	St = rr(t) + mnit + xt

Bibliographie

[1] Frédéric planchet - AYMRIC KAMEGA. Générateurs de scénarios économiques (GSE) en assurance [Consulté le 22/5/2021]. 2021. URL : http : / / www . ressources - actuarielles.net/EXT/ISFA/fp- isfa.nsf/34a14c286dfb0903c1256ffd00502d73/ fe8ad6d32b953971c125773300703808/$FILE/GSE_AK_v1.3.pdf.

[2] Institut des ACTUAIRES. Cahier des régles professionelles. 2004. URL : https://www. institutdesactuaires . com / global / gene / link . php ? doc _ id = 100 & fg = 1 % 20 % 5Ctextbf%7B[Consult%C3%A9%20le%2020%20et%2023/8/2021]%7D.

[3] Institut des ACTUAIRES. Etude sur la situation actif-passif d'une compagnie d'assurance Non Vie. 2019. URL : http://www.ressources-actuarielles.net/EXT/ISFA/1226-02.nsf/0/a102cebaea592f35c1257562006654b0/%20%5Ctextbf%7B[Consult%C3%A9% 20le%2016/8/2021]%7D.

[4] Expert crédit et ASSURANCE. Taux du marché monétaire(TMM) [Consulté le 21/9/2021]. URL : . https://www.empruntis.com/credits-consommation/lexique/taux-du-marche-monetaire.php.

[5] Institu national de la statistique et des études ÉCONOMIQUES. Inflation/Taux d'inflation [Consulté le 15/9/2021]. URL : https://www.insee.fr/fr/metadonnees/ definition/c1473.

[6] Article EMPUNTIS. Définiton de l'assurance vie [Consulté le 20/12/2021]. URL : https://www.empruntis.com/epargne/assurances- vie/guide/qu- est- ce- que-assurance-vie.php.

[7] The press FREE. «Qu'est-ce que la Casualty Actuarial Society (CAS) ?» In : (). URL : https://thepressfree.com/casualty- actuarial- society- cas/%20%5Ctextbf% 7B[Consult%C3%A9%20le%2012/7/2021]%7D.

[8] Cabinet d'étude GALEA. DES PROJECTIONS ACTIF/PASSIF EN NON VIE, POUR QUOI FAIRE ? [Consulté le 18/11/2021]. 2016. URL : https://www.galea-associes. eu/2016/09/des-projections-actifpassif-en-non-vie-pour-quoi-faire/.

[9] Estelle GERONDEAU. Ratio de couverture Solvabilité 2 d'un contrat d'épargne en euros, quels leviers de pilotage pour l'assureur ? [Consulté le 28/5/2021]. URL : https://www. institutdesactuaires.com/docs/mem/3bba19a8cd26f7c5fc133d41bad3a095.pdf.

[10] Zeineb GHARDALLOU. Générateur de scénarios économiques Tunisien : Calibration et Projection [Mémoire de Référence tout au long du stage] Mémoire développé au sein d'ERM Partners. 2020.

[11] Ezzeddine ben HAMIDA. Tunisie - L'augmentation du TMM : Une orthodoxie monétaire inefficace et nuisible [Consulté le 22/9/2021]. URL : https://www.leaders.com. tn/article/26557-tunisie-l-augmentation-du-tmm-une-orthodoxie-monetaire-inefficace-et-nuisible.

[12] INS. Historique des rendements [Consulté le 5/10/2021]. URL : http://dataportal. ins.tn/fr.

BIBLIOGRAPHIE

[13] INSEE. def/l'IPC [Consulté le 15/9/2021]. URL : https : / / www . insee . fr / fr / metadonnees/definition/c1557.

[14] Sarra ISMAIL. Construction d'un générateur de Scénarios economique pour une compagnie d'assurance [Consulté le 22/10/2021] Document EY. 2021. URL : https://www.ey. com/en_tn.

[15] MOHAMED NAJED KSOURI. Site officiel de ERM Partners [Consulté le 12/4/2021]. URL: http://www.erm-partners.com/.

[16] Jean-Baptiste MONNIER. Pilotage ALM et référentiels market consistent en assurance vie [Consulté le 20/11/2021]. 2019. URL : https://www.institutdesactuaires. com/docs/mem/de9eb88ab5971a73adc99f61d8a8d1a8.pdf.

[17] OCDE. Taux d'intérêt à long terme [Consulté le 27/9/2021]. URL : https://data. oecd.org/fr/interest/taux- d- interet- a- long- terme.htm#:~:text=%C3%A0% 20long%20terme-,Les%20taux%20d'int%C3%A9r%C3%AAt%20%C3%A0%20long%20terme% 20sont%20ceux%20des,de%20la%20valeur%20du%20capital.&text=par%20l'%C3% 89tat.-,Les%20taux%20d'int%C3%A9r%C3%AAt%20%C3%A0%20long%20terme%20sont% 20un,de%20l'investissement%20des%20entreprises.

[18] Frederic PLANCHET. Scénarios économiques en assurance : Modélisation et Simulations [Consulté le 30/4/2021]. 2015. URL : http://www.ressources-actuarielles.net/.

[19] HOUNKONNOU PRUDENCE. Modélisation ALM et Estimation efficace du SCR d'un assureur vie en modèle interne avec le Krigeage stochastique [Consulté le 26/10/2021]. 2020. URL : https://www.institutdesactuaires.com/docs/mem/cf2fb92cc76e4a70207bafecc882437f pdf.

[20] Guibert QUANTIN. Simulation en assurance [Consulté le 7/7/2021]. 2018.

[21] Bastien ROSSPOPOFF. Modèles historique et risque neutre de taux et l'inflation pour l'assurance [Consulté le 3/5/2021]. 2013. URL : https://www.institutdesactuaires. com/docs/mem/8dbba0a293fb0592a65e49c51cd7aa9d.pdf.

[22] Damien TICHIT. Construction d'un modèle ALM pour une analyse d'impact d'une remontée des taux sur la solvabilité d'un assureur vie [Consulté le 22/12/2021]. 2020. URL : https://www.institutdesactuaires.com/docs/mem/cf2fb92cc76e4a70207bafecc882437f. pdf.

[23] Banque Centrale de TUNISIE. Evolution du TMM [Consulté le 27/9/2021]. URL : https://www.bct.gov.tn/bct/siteprod/stat_index.jsp.

[24] Guide des indices boursiers TUNISIEN. Bourse des Valeurs Mobilières de Tunis [Consulté le 1/10/2021]. URL : http://www.bvmt.com.tn/sites/default/files/documentation/ indices/Guide-Indices-Boursiers.pdf.

[25] WIKIPEDIA. «Discrétisation [Consulté le 13/7/2021]». In : (). URL : https://fr. wikipedia.org/wiki/Discr%C3%A9tisation.

[26] WIKIPEDIA. Society of Actuaries [Consulté le 12/7/2021]. URL : https://en. wikipedia.org/wiki/Society_of_Actuaries.

[27] WIKIPEDIA. Matrice de Cholesky [Consulté le 13/10/2021]. URL : https://fr. wikipedia.org/wiki/Factorisation_de_Cholesky.

[28] WIKIPEDIA. «Autorité européenne des assurances et des pensions professionnelles [Consulté le 8/6/2021]». In : (). URL : https://fr.wikipedia.org/wiki/Autorit% C3%A9_europ%C3%A9enne_des_assurances_et_des_pensions_professionnelles.

BIBLIOGRAPHIE

[29] WIKIPEDIE. Regression lineaire [Consulté le 12/10/2021]. URL : https : / / fr . wikipedia.org/wiki/R%C3%A9gression_lin%C3%A9aire.

[30] Jihane ben YAACOUB. Modélisation de la courbe des taux et valorisation des produits dérivés de taux [Consulté le 19/6/2021]. URL : https://www.actuarialab.net/ storage/BOUYACOUB-Jihane.pdf.