à‰tude de l'initiation et de la propagation de la détonation dans les aérosols de kérosène liquide.

HAUTE ECOLE LOUVAIN EN HAINAUT
Catégorie technique
Type long
Master en sciences de l'ingénieur industriel finalité Electromécanique

Etude de l'initiation et de la

propagation de la détonation dans

les aérosols de kérosène liquide

Directeur de stage : Bernard VEYSSIERE

Travail de fin d'étude présenté par Ghiles BERREFAS en vue de l'obtention du grade de Master en sciences de l'ingénieur industriel finalité Electromécanique

Avant-propos

Les travaux de recherche présentés dans ce travail de fin d'étude ont été effectués à l'institut P' dans le département D2 « Fluides, Thermique, Combustion » au sein de l'axe de détonique situé sur le site du Futuroscope.

Je tiens à remercier Monsieur Bernard VEYSSIERE, directeur au sein de l'axe détonique en sa qualité de tuteur et je le remercie pour m'avoir proposé cette thématique de recherche et de m'avoir encadré durant ces 5 mois de stage. Je suis particulièrement reconnaissant par sa disponibilité et l'ensemble des précieux conseils apportés au cours du stage.

Je voudrais remercier particulièrement Monsieur Vincent MONTASSIER, qui a énormément investi, de son temps et de sa personne, plus qu'indispensable à la réalisation des dispositifs expérimentaux. Je lui exprime également ma gratitude pour son partage de connaissances et ses compétences techniques mais aussi pour son sens de l'humour et le travail dans la bonne humeur.

Je remercie également Alain CLAVERIE pour ses explications du système de fonctionnement par PDI. Mes remerciements vont aussi à Florent VIROT et Pierre VIDAL pour leurs aides dans l'analyse de la structure cellulaire et les notions de différents régimes de détonation. J'ai réellement apprécié les échanges avec mon collègue thésard Stéphane BOULAL avec qui j'ai passé de très bons moments durant ce stage.

Je remercie l'ensemble du corps professoral de l'ISICHt pour m'avoir transmis les connaissances de base qui m'ont permis d'effectuer ce stage. Plus particulièrement, je voudrais exprimer ma gratitude envers Monsieur Adrien POURBAIX et Monsieur Christophe SPENS, professeurs à la Haute Ecole Louvain en Hainaut, ISICht pour leur suivi, je les remercie d'avoir été mes coordinateurs de stage en institut.

Le travail au cours de ce stage était laborieux mais très agréable car il s'est déroulé dans de très bonnes conditions. Chacune des personnes que j'ai rencontrées durant ce stage, ont contribué à leur manière, à ce que la tâche soit agréable. Je suis ainsi reconnaissant envers tout le personnel du laboratoire qui a consacré, en plus de l'attribution normale de ses tâches, du temps et de l'énergie pour effectuer un dépannage. Merci pour la contribution de chacun.

Enfin, je remercie toutes les personnes, familles et amis, pour votre soutien tout au long de ces années d'études et votre collaboration afin de m'aider au mieux dans la rédaction de ce mémoire.

Table des matières

Introduction 1

Chapitre 1 5

1 Détonations en phase gazeuse et détonations hétérogènes gouttelettes liquide/gaz 5

1.1. Généralités sur les détonations en phase gazeuse 5

1.1.1. Introduction 5

1.1.2. Modélisation de la détonation [Chapman, 1899 ; Jouguet 1905] 5

1.1.3. Modèle de Zeldovich - Von Neumann - Döring (ZND) 9

1.2. Détonation en milieu hétérogènes gaz/gouttelettes liquides 10

1.2.1. Les détonations hétérogènes 10

1.2.2. Synthèse des principaux travaux antérieurs 10

1.3. La structure cellulaire 12

1.3.1. Structure cellulaire tridimensionnelle 12

1.3.2. Structure cellulaire des détonations hétérogènes 13

Chapitre 2 15

2. Influence des mécanismes de désintégration et de vaporisation des gouttelettes sur la détonation

des aérosols de carburants liquides 15

2.1 Propagation d'une détonation en présence d'aérosols de gouttelettes liquides 15

2.2 Mode et régime de désintégration de gouttelettes liquides 16

2.2.1 Désintégration d'un jet liquide 16

2.2.2 Modes et régimes de désintégration de gouttelettes liquides 18

2.2.2.1 Modèle d'atomisation secondaire 18

2.2.2.2 Modèle de Reitz Diwakar [Reitz, 1986] 18

2.2.3 Caractéristiques des gouttelettes et leur mesure 19

2.2.3.1 Grandeurs caractéristiques des gouttelettes issus d'un aérosol 19

2.2.3.2 Techniques de mesures granulométrique de l'aérosol 21

2.3 Mécanisme de vaporisation des gouttelettes liquides 21

2.4 Diamètre de gouttelette et déficit de célérité de détonation hétérogène 23

Chapitre 3 25

3. Montage expérimental 25

3.1 Introduction 25

3.2 Le tube à détonation 25

3.3 Le tube à choc 28

3.4 Génération des aérosols de gouttelettes liquides 28

3.4.1. Les atomiseurs ultrasoniques 29

3.4.2. Le générateur 30

3.4.3. Alimentation de l'atomiseur 30

3.5 Dispositifs de mesure 31

3.5.1 Granulométrie de l'aérosol 31

3.5.2 Mesure de la célérité et de la pression de détonation 31

3.5.3 Enregistrement de la structure cellulaire 32

3.6 Système de commande et protocole 32

3.6.1 Système de commande 32

3.6.2 Protocole d'essai 33

Chapitre 4 35

4 Caractérisation de la distribution granulométrique des gouttelettes d'un aérosol 35

4.1 Introduction 35

4.2 Méthode de mesure granulométrique par PDI (Phase Doppler Interferometry) 35

4.2.1 Principe de mesure par PDI 35

4.2.2 Montage expérimental et protocole d'essai 39

4.3 Etude de la distribution granulométrique des gouttelettes produites par les atomiseurs 41

4.3.1 Atomiseur ultrasonique 41

4.3.2 Variation du D10 et D32 en fonction du débit d'oxydant 44

4.3.3 Conclusions 46

Chapitre 5 47

5 Les mélanges réactifs 47

5.1 Introduction 47

5.2 Produits étudiés 47

5.3 Caractéristiques de détonation CJ 50

5.4 Détermination de la richesse du mélange 51

6. Etude expérimentale de l'influence de la taille des gouttelettes sur la détonation d'aérosols de

carburants liquides 53

6.1 Introduction 53

6.2 Initiation de la détonation par un tube à choc (booster) 53

6.3 Détonation dans le mélange d'aérosol de gouttelettes de kérosène/air 55

6.3.1 Formation de la détonation 55

6.3.2 Célérité de détonation 56

6.3.3 Pression de détonation 61

6.3.4 Structure cellulaire de détonation 62

6.3.5 Influence de la pression initiale du booster 63

6.3.5.1 Célérité de détonation 64

6.3.5.2 Pression de détonation 65

6.3.6 Synthèse des résultats obtenus pour le mélange kérosène/air 66

6.3.7 Bilan pour le mélange kérosène/air 68

6.4 Détonation dans le mélange d'aérosol de gouttelettes de kérosène/air suroxygéné 69

6.4.1 Richesse r = 1 69

a. Formation de la détonation 69

b. Célérité de la détonation 70

c. Pression de détonation 71

6.4.2 Richesse r = 1,3 72

a. Célérité de détonation 72

b. Pression de la détonation 73

6.4.3 Synthèse des résultats obtenus pour les mélanges kérosène/air suroxygéné 74

Synthèse et conclusion 75

Bibliographie 77

Annexes 79

Annexe AI : Etude à l'état Chapman-Jouguet (CJ) 79

Annexe AII : Calibrage du système d'atomisation de gouttelettes et détermination de la richesse 83

a. Introduction 83

b. Calibrage massique 83

c. Détermination de la richesse 85

i. Introduction 85

ii. Méthodologie de calcul de la richesse 85

d. Vitesse et temps de balayage dans le tube 92

Annexe AIII: Specification Jet-A1 de l'American Society for Testing and Materials (ASTM) 96

Annexe AIV : Calcul des caractéristiques de la bouteille de mélange O2 + 2 N2 par la méthode des

pressions partielles via EES. 97

Table des figures

FIGURE 1.1 - L'ONDE DE DETONATION DANS DIFFERENTS SYSTEMES DE COORDONNEES (A) PAR RAPPORT AU

LABORATOIRE ET (B) PAR RAPPORT A L'ONDE 6

FIGURE 1.2 - DROITE DE RAYLEIGH-MICHELSON ET ADIABATIQUE DE CRUSSARD DANS LE PLAN (p, y) 8

FIGURE 1.3 - PRINCIPE DU MODELE DE ZEDOVICH VON NEUMAN DORING 9

FIGURE 1.4 - DROITE DE RAYLEIGH-MICHELSON, ADIABATIQUE D'HUGUONIOT ET ADIABATIQUE DE CRUSSARD

DANS LE PLAN (p, y) 10
FIGURE 1.5 - SCHEMA D'UNE CELLULE DE DETONATION ET DE LA VARIATION DE LA CELERITE DE L'ONDE DE

DETONATION LE LONG DE L'AXE DE LA CELLULE 12

FIGURE 2.1 - DESCRIPTION SCHEMATIQUE D'UNE DETONATION DANS UN AEROSOL DE GOUTTELETTES 15

FIGURE 2.2 - MODE DE FRAGMENTATION MECANIQUE D'UN JET LIQUIDE DANS UN MILIEU GAZEUX SELON REITZ

[1987] 17

FIGURE 2.3 - SCHEMA DESCRIPTION DU BAG BREAKUP 18

FIGURE 2.4 - SCHEMA DESCRIPTION DU STRIPPING BREAKUP 19

FIGURE 3.1 - SCHEMA DU MONTAGE EXPERIMENTAL 26

FIGURE 3.2 - MONTAGE EXPERIMENTAL 27

FIGURE 3.3 - GAMME DE FREQUENCE ULTRASONIQUE ET DESINTEGRATION D'UN FILM LIQUIDE PAR ATOMISATION

ULTRASONIQUE 29

FIGURE 3.4 - GENERATEUR DE GOUTTELETTES LIQUIDES (ATOMISEUR ULTRASONIQUE) 30

FIGURE 3.5 - TABLEAU DE COMMANDE DU DISPOSITIF D'ALIMENTATION DE DEBIT EN OXYDANT (ROTAMETRE

D'OXYDANT A DROITE) 31

FIGURE 3.6 - TABLEAU DE COMMANDE ET DE CONTROLE DE SECURITE 33

FIGURE 4.1 - PRINCIPE DE MESURE GRANULOMETRIQUE PAR PDI (PHASE DOPPLER INTERFEROMETER) 36

FIGURE 4.2 - INTERACTION DES FAISCEAUX LASERS AVEC UNE GOUTTELETTE LIQUIDE 37

FIGURE 4.3 - PRINCIPE DE DETECTION DES RAYONS LUMINEUX REFRACTES 37

FIGURE 4.4 - VARIATION DU DEPHASAGE EN FONCTION DE LA TAILLE DES GOUTTELETTES 38

FIGURE 4.5 - PRINCIPE DE MESURE DE VELOCIMETRIE DES GOUTTELETTES 39

FIGURE 4.6 - DISPOSITIF DE MESURE GRANULOMETRIQUE PAR PDI 40

FIGURE 4.7 - SPECTRE GRANULOMETRIQUE D'UN AEROSOL D'EAU A UNE COTE D'OBSERVATION Z = 160 MM,

????AIR = 1,42 M³/H 42
FIGURE 4.8 - SPECTRE GRANULOMETRIQUE D'UN AEROSOL DE (A) KEROSENE JET-A1, (B) DODECANE A UNE COTE

D'OBSERVATION Z = 160 MM, ????AIR = 1,42 M³/H 42
FIGURE 4.9 - EVOLUTION DE LA GRANULOMETRIE D'AEROSOLS D'EAU GENERES PAR L'ATOMISEUR EN FONCTION DU

DEBIT D'AIR POUR DIFFERENTES COTES D'OBSERVATION Z 44

FIGURE 4.10 - VARIATION DE LA GRANULOMETRIE D'AEROSOLS DE KEROSENE ET DODECANE GENERES PAR

L'ATOMISEUR EN FONCTION DE LA RICHESSE A UNE COTE D'OBSERVATION Z = 16 CM 45

FIGURE 5.1 - EVOLUTION DE LA CELERITE IDEALE CJ DE DETONATION DU MELANGE KEROSENE ~ AIR EN

FONCTION DE LA RICHESSE 50

FIGURE 6.1- EVOLUTION DE LA CELERITE DE LA DETONATION EN FONCTION DE LA DISTANCE DE PROPAGATION

DANS LE TUBE PRINCIPALE INITIE PAR UN BOOSTER SEUL DE PREMELANGE C2H4/O2 54
FIGURE 6.2 - SIGNAUX DE PRESSION LE LONG DU TUBE PRINCIPAL AVEC BOOSTER SEUL DE PREMELANGE C2H4/O2

SOUS 2 BARS DE PRESSION INITIALE 54
FIGURE 6.3 - PROFILS DE PRESSION ET DIAGRAMME DE MARCHE, ENREGISTRES EN K1, K2, K3, K4, K5, K6 ET K7

DE LA DETONATION DU MELANGE KEROSENE/AIR, C11H22 + 16,5 (O2 + 3.76); R=1,1 ET D0 = 5uM 55
FIGURE 6.4 - CELERITE MOYENNE DU FRONT EN FONCTION DE LA DISTANCE DE PROPAGATION ET ENREGISTREMENT

DE LA STRUCTURE CELLULAIRE POUR LE MELANGE KEROSENE/AIR AVEC UNE RICHESSE = 1,1 56

FIGURE 6.5 - ENREGISTREMENT DE LA STRUCTURE CELLULAIRE DU MELANGE KEROSENE/AIR - R=1,1 - TEST 1 57

FIGURE 6.6 - PROFILS DE PRESSION ET DIAGRAMME DE MARCHE, ENREGISTRES EN K1, K2, K3, K4, K5, K6 ET K7

DE LA DETONATION DU MELANGE KEROSENE/AIR, C11H22 + 16,5 (O2 + 3.76); R=1,3 ET D0 = 5uM 58
FIGURE 6.7 - CELERITE MOYENNE DU FRONT EN FONCTION DE LA DISTANCE DE PROPAGATION ET ENREGISTREMENT

DE LA STRUCTURE CELLULAIRE POUR LE MELANGE KEROSENE/AIR AVEC UNE RICHESSE = 1,3 59

FIGURE 6.8 - ENREGISTREMENT DE LA STRUCTURE CELLULAIRE DU MELANGE KEROSENE/AIR - R=1,3 - TEST 4 60

FIGURE 6.9 - ENREGISTREMENT DE LA STRUCTURE CELLULAIRE DU MELANGE KEROSENE/AIR - R=1,3 - TEST 5 60

FIGURE 6.10 - ENREGISTREMENT DE LA STRUCTURE CELLULAIRE DU MELANGE KEROSENE/AIR - R=1,3 - TEST 6 60

FIGURE 6.11 - PROFILS DE PRESSIONS DES CAPTEURS K4, K5, K6 ET K7 EN FIN DE PROPAGATION DANS LE TUBE A

DETONATION POUR LE MELANGE KEROSENE/AIR AVEC UNE RICHESSE = 1,3 61
FIGURE 6.12 - PRINCIPE DE DETERMINATION DE LA VALEUR EXPERIMENTALE DE LA PRESSION DE DETONATION PEXP

62
FIGURE 6.13 - CELERITE DU FRONT DE DETONATION EN FONCTION DE LA DISTANCE DE PROPAGATION DANS LE TUBE A DETONATION POUR LE MELANGE KEROSENE/AIR AVEC UNE RICHESSE = 1,5 ET PRESSION BOOSTER 2

BARS. 63
FIGURE 6.14 - CELERITE DU FRONT DE DETONATION EN FONCTION DE LA DISTANCE DE PROPAGATION DANS LE

TUBE A DETONATION POUR LE MELANGE KEROSENE/AIR AVEC UNE RICHESSE = 1,5 ET BOOSTER DE 3 BARS. 64 FIGURE 6.15 - PROFILS DE PRESSIONS DES CAPTEURS K4, K5, K6 ET K7 EN FIN DE PROPAGATION DANS LE TUBE A

DETONATION POUR LE MELANGE KEROSENE/AIR AVEC UNE RICHESSE = 1,5 ET BOOSTER DE 3 BARS 65
FIGURE 6.16 - EVOLUTION DE LA CELERITE MOYENNE DE DETONATION EXPERIMENTALE DEXP EN FONCTION DE LA

RICHESSE DU MELANGE REACTIF KEROSENE/AIR 66
FIGURE 6.17 - EVOLUTION DE LA PRESSION MOYENNE DE DETONATION EXPERIMENTALE PEXP EN FONCTION DE LA

RICHESSE DU MELANGE DU MELANGE REACTIF KEROSENE/AIR 67
FIGURE 6.18 - EVOLUTION DE LA TAILLE DE LA CELLULE DE DETONATION EN FONCTION DE LA RICHESSE DU

MELANGE DU MELANGE REACTIF KEROSENE/AIR 67

FIGURE 6.19 - PROFILS DE PRESSION ET DIAGRAMME DE MARCHE, ENREGISTRES EN K1, K2, K3, K4, K5, K6 ET K7

DE LA DETONATION DU MELANGE KEROSENE + (O2+2N2); R=1 ET D0 = 5uM 69
FIGURE 6.20 - CELERITE DU FRONT DE DETONATION EN FONCTION DE LA DISTANCE DE PROPAGATION DANS LE

TUBE A DETONATION DU MELANGE KEROSENE + (O2+2N2); R=1 ET D0 = 5uM 70
FIGURE 6.21 - PROFILS DE PRESSIONS DES CAPTEURS K4, K5, K6 ET K7 EN FIN DE PROPAGATION DANS LE TUBE A

DETONATION DU MELANGE KEROSENE + (O2+2N2); R=1 ET D0 = 5uM 71
FIGURE 6.22 - CELERITE DU FRONT DE DETONATION EN FONCTION DE LA DISTANCE DE PROPAGATION DANS LE

TUBE A DETONATION DU MELANGE KEROSENE + (O2+2N2); R=1,3 ET D0 = 5uM 72
FIGURE 6.23 - PROFILS DE PRESSIONS DES CAPTEURS K4, K5, K6 ET K7 EN FIN DE PROPAGATION DANS LE TUBE A

DETONATION DU MELANGE KEROSENE + (O2+2N2); R=1,3 ET D0 = 5uM 73
FIGURE 6.24 - ENREGISTREMENT DE LA STRUCTURE CELLULAIRE DU MELANGE KEROSENE + (O2 + 2 N2), R=1 -

TEST 10 74
FIGURE 6.25 - ENREGISTREMENT DE LA STRUCTURE CELLULAIRE DU MELANGE KEROSENE + (O2 + 2 N2), R=1,3 -

TEST 11 74

FIGURE AII.1 - CALIBRAGE EN MASSE DE L'ATOMISEUR AVEC DE L'EAU A DIFFERENTS DEBITS D'AIR DE REFERENCE

83

FIGURE AII.2 - EVOLUTION DE LA RICHESSE DU KEROSENE JET-A1 AVEC LE DEBIT D'AIR POUR L'ATOMISEUR DE

GOUTTELETTES DE 5 uM ET COURBE DE TENDANCE DE TYPE PUISSANCE 88
FIGURE AII.3 - EVOLUTION DE LA RICHESSE DU DODECANE AVEC LE DEBIT D'AIR POUR L'ATOMISEUR DE

GOUTTELETTES DE 5 uM ET COURBE DE TENDANCE DE TYPE PUISSANCE 90
FIGURE AII.4 - COMPARAISON DES PLAGES DE RICHESSE ENTRE LES ATOMISEURS GENERANT DES TAILLES DE

GOUTTELETTES DE 5 uM ET 8uM (COURBE DE TENDANCE DE TYPE PUISSANCE) 91

Table des tableaux

TABLEAU 3.1 - DISTANCES ENTRE CAPTEURS 31

TABLEAU 4.1 - GAMMES DE MESURE DE TAILLE ET DE VITESSE DES GOUTTELETTES 36

TABLEAU 4.2 - RESULTATS DE MESURE AVEC L'ATOMISEUR 43

TABLEAU 5.1 - FORMULE CHIMIQUE DU KEROSENE CONVENTIONNEL 48

TABLEAU 5.2 - COMPARATIF DE QUELQUES CARACTERISTIQUES CHIMIQUES ET PHYSIQUES ENTRE LE JET-A1 ET LE

C11H22 49

TABLEAU 5.3 - CARACTERISTIQUES PHYSIQUES ET CHIMIQUES DU DODECANE 49

TABLEAU 5.4 - CELERITE ET PRESSION DE DETONATION CJ POUR DIFFERENTS RATIO O2/N2 51

TABLEAU 6.1 - CONDITIONS EXPERIMENTALES DES DIFFERENTS TESTS REALISES 53

TABLEAU A.1 - CARACTERISTIQUES DE DETONATION CJ POUR UN GAZ POLYTROPIQUE A F CONSTANT SOUS

L'HYPOTHESE D'UN CHOC FORT 82

TABLEAU AII.1 - RESULTATS DE L'ETALONNAGE EN MASSE DE L'ATOMISEUR AVEC DU DODECANE C12H26 84

TABLEAU AII.2 - RESULTATS DE L'ETALONNAGE EN MASSE DE L'ATOMISEUR AVEC DU KEROSENE JET-A1 84

TABLEAU AII.3 - VALEURS DE RICHESSE DU KEROSENE JET-A1 OBTENUES POUR DIFFERENTS COUPLES DE

TRAVAIL (MJET-A1;MAIR) 87

TABLEAU AII.4 - RECAPITULATIF DES VALEURS DE RICHESSE DU DODECANE C12H26 OBTENUES 90

TABLEAU AII.5 - VALEURS DE RICHESSE DU DODECANE OBTENUES DANS LES TRAVAUX ANTERIEURS REALISES PAR

MODOU MAR (2012) 91

TABLEAU AII.6 - TEMPS DE MONTEE DES GOUTTELETTES AU SEIN DU TUBE A DETONATION 93

TABLEAU AII.7 - NOMBRE DE REYNOLDS RE EN FONCTION DU DEBIT D'AIR DE TRAVAIL 94

TABLEAU AIII.1 - SPECIFICATIONS ASTM DU KEROSENE JET-A1 96

Page | 1

Introduction

L'étude de la détonation dans les aérosols de carburants liquides, dispersés sous forme d'aérosols de fines gouttelettes, est un domaine d'étude relativement récent qui intéresse la sécurité industrielle, le domaine militaire et de défense ou encore le domaine aéronautique notamment en propulsion.

En effet, pour optimiser la sécurité dans le domaine de la propulsion aéronautique et spatiale, il est nécessaire de mieux connaître le risque de détonation dans le cas d'éclatement des réservoirs et de dispersion sous forme pulvérisée. Il s'agit également d'éviter toutes explosions accidentelles de suspensions d'aérosols de gouttelettes combustibles. En 1975, l'explosion de l'usine chimique de Flixborough a entrainé la vaporisation de 45 tonnes de cyclohexane chaud et sous pression à la suite de la rupture d'une conduite engendrant des dégâts dans un rayon d'un peu plus de 2km.

Concernant le domaine militaire, les premières générations d'armes à effet de souffle furent conçues à la fin des années 1960, mais c'est vers le milieu des années 1970 qu'apparaissent les premières versions d'armes plus efficaces, désignées sous l'appellation de FAE (Fuel-Air Explosives). Récemment, des conceptions proches ont été créées sous la désignation d'explosifs thermobariques ou explosifs à effet de souffle augmenté. Dans ces systèmes explosifs, un matériau combustible est dispersé dans l'air, au moment de l'explosion initiale de la munition, afin de créer un brouillard (poussière ou aérosols liquides). Ce brouillard de combustible est mis en détonation et engendre une onde de souffle qui génère de grandes surpressions, ainsi qu'une boule de feu. Dans ce type d'armes, les niveaux de surpression peuvent atteindre 2 fois la surpression créée par des armes conventionnelles.

Toutefois, l'application la plus intéressante concerne le domaine de la propulsion et consiste à utiliser ce type de système réactif hétérogène pour la propulsion par onde de détonation. De nombreuses recherches en ce domaine ont déjà été effectuées depuis les années 40 mais c'est vers la fin des années 90 que les premiers moteurs utilisant ce principe de fonctionnement fait l'objet de développements dans le secteur aéronautique et spatial. Ces moteurs seront connus sous le nom de moteur à détonation pulsée (Pulsed Detonation Engine, PDE) ou moteur à détonation rotative (RDE). Parmi les solutions envisagées pour faire

Page | 2

fonctionner le PDE, l'utilisation d'aérosols de gouttelettes liquides injectés dans la chambre de combustion est une voie prometteuse.

Comparativement aux connaissances sur les détonations gazeuses homogènes, les connaissances sur celles des mélanges hétérogènes gaz-aérosols de gouttelettes liquides sont limitées. Cela s'explique notamment en raison des difficultés de réalisation d'expériences dans des aérosols de caractéristiques bien contrôlées et reproductibles et la complexité de la détonation dans ce type de milieu. Modou MAR [2012] et Mohamed El-Amine BENHAMMED [2012], durant leur thèse, ont tous deux contribué à la compréhension des processus physiques et chimiques qui entrent en jeu dans les détonations hétérogènes d'aérosols de gouttelettes liquides d'hydrocarbures en atmosphère oxydante. L'étude de la structure cellulaire de détonation s'est faite avec une intention toute particulière car en ce domaine, les résultats sont quasiment inexistants. MAR s'est concentré sur l'influence de la granulométrie sur la détonation et BENHAMMED a étudié l'influence de la cinétique chimique sur le phénomène de détonation.

L'objectif de ce mémoire sera d'alimenter la base de données existantes sur le sujet, et dont la nouveauté sera de travailler avec un nouvel atomiseur permettant de produire des aérosols de granulométrie théoriquement inférieur à 5 um. Une autre nouveauté sera de travailler avec un carburant utilisé en propulsion qui est le JET-A1 et, éventuellement, des monergols.

Ce travail de fin d'étude est organisé autour de 7 chapitres et scindé en deux parties. La première est consacrée à l'état de l'art sur les détonations organisée en deux chapitres :

Le chapitre 1 rappelle les notions générales des détonations à travers une étude bibliographique. Les différentes notions employées tout au long de ce mémoire sont progressivement introduites.

Le chapitre 2 est consacré aux modes de désintégration des gouttelettes par interaction avec une onde de choc.

La deuxième partie est dédiée à l'étude expérimentale des détonations de mélanges hétérogènes et s'organisera autour de quatre chapitres :

Le chapitre 3 décrit le dispositif expérimental et les techniques d'analyse qui lui sont associées.

Page | 3

Le chapitre 4 présente la caractérisation granulométrique des aérosols.

Le chapitre 5 détaille les mélanges réactifs utilisés pour cette étude, la phase d'étalonnage de l'atomiseur générant les gouttelettes ainsi que le calcul des paramètres de travail (couple de débits, richesse, vitesse, temps de balayage,...).

Le chapitre 6 présente les résultats expérimentaux obtenus dans des aérosols de carburant liquides.

Enfin, ce travail de fin d'étude s'achèvera par un chapitre de synthèse des résultats expérimentaux ainsi qu'une conclusion.

Page | 4

Page | 5

Chapitre 1

1 Détonations en phase gazeuse et détonations hétérogènes gouttelettes liquide/gaz

1.1. Généralités sur les détonations en phase gazeuse

1.1.1. Introduction

Dans les années 1870-1883, les premières observations des détonations en phase gazeuse ont vu le jour. Ce n'est qu'en 1881, que Berthelot et Vieille ainsi que Mallard et Le Chatelier mettent en évidence un phénomène de propagation stationnaire d'ondes supersoniques de combustion. Ce phénomène sera nommé onde explosive et actuellement connu sous l'appellation de détonation.

Le premier modèle de détonation voit le jour avec Chapman [1889] et Jouguet [1905]. Ce modèle assimile la détonation à une discontinuité monodimensionnelle plane se propageant avec une célérité supersonique dans un fluide réactif supposé parfait et qui transforme instantanément le fluide réactif (milieu des gaz frais) en produits de détonation c'est-à-dire en gaz brûlés à l'équilibre thermodynamique dit état final « Chapman-Jouguet » CJ.

Zeldovitch, Von Neumann et Döring ont proposé dans les années 40, un modèle plus réaliste décrivant l'onde de détonation plane et stationnaire comme étant une onde de choc dont la propagation supersonique est entretenue par les réactions chimiques qu'elle initie avec un certain délai.

1.1.2. Modélisation de la détonation [Chapman, 1899 ; Jouguet 1905]

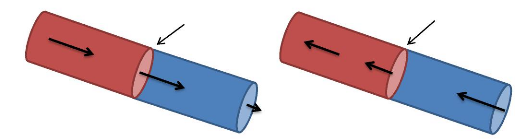
Le modèle Chapman-Jouget (CJ) assimile la détonation à une surface de discontinuité plane, d'épaisseur infiniment mince, perpendiculaire à l'écoulement et totalement réactive qui se propage à la célérité D. L'onde de détonation ? se déplace à une célérité de propagation D dans le référentiel lié au laboratoire. (figure 1.1)

Gaz frais

????, ????, ????, ????

Gaz brûlés E

W1

D

????, ????, ????, ????

W0

Gaz brûlés

Gaz frais

????, ????, ????, ????

E

??1

????, ????, ????, ????

D

??0

référentiel lié au laboratoire (a) référentiel lié à l'onde (b)

Figure 1.1 - L'onde de détonation dans différents systèmes de coordonnées (a) par rapport au laboratoire et (b) par rapport à l'onde

W0 = -(D - ??0) ???? W1 = -(D - ??1) (1.1)

avec : W₀ et W₁ qui sont respectivement la vitesse du gaz frais et des gaz brûlés par rapport à l'onde de détonation.

Ce modèle a pour hypothèses que :

· l'onde de détonation est supposée plane, monodimensionnelle et stationnaire.

· le mélange réactif est parfait et uniforme

· l'écoulement est adiabatique, sans pertes d'énergie aux parois et les phénomènes de dissipation sont négligés.

Les équations de conservation de masse, de quantité de mouvement et d'énergie par rapport au référentiel lié à l'onde découlent de ces hypothèses :

??1W1 = ??0W0 (1.2)

??1W1² = ??0W0² (1.3)

h1 +

W2 1 2

= h0 +

W2 0 (1.4) 2

Page | 6

Page | 7

Où ??, ?? ???? h représentent respectivement la masse volumique, la pression et l'enthalpie absolue. Par combinaison de l'équation de conservation de masse (1.2) et celle de

la quantité de mouvement (1.3) dans un plan (??, ??) (figure 1.2) avec ?? = ¹/?? qui est le volume spécifique, l'expression du débit massique est la suivante :

??^2 -??^2 = -??0 = 0 ??0 2

??1 - ??0 = (1.5) ??1 - ??0

De cette équation (1.5) et par combinaison de (1.2) et (1.3), on trouve les vitesses relatives à l'onde :

??1 - ??0

??0 = ??0v (1.6)
??0 - ??1

??1 - ??0

??1 = ??1v (1.7)
??0 - ??1

En substituant ??₀ ???? ??₁ à l'équation de conservation d'énergie (1.4) à l'aide des expressions (1.6) et (1.7), l'équation de l'adiabatique dynamique ou adiabatique de Crussard dans le plan (??, ??) est obtenu :

1

h1 - h0 = 2 (??1 - ??0)(??0 + ??1) (1.8)

En ajoutant la chaleur de réaction ?????? = -??? h* = h₀^* - h₁^* ( h* est l'enthalpie de

^ ^

référence à la température ??*), et l'enthalpie sensible h

telle que : h

= h - h*.

Il vient :

1

^ - h0

h1 ^ - ??P?? = 2 (??1 - ??0)(??0 + ??1) (1.9)

P

zone de détonations

fortes

zone de détonations

faibles

Pcj

Po

F

CJ

f

v

vcj

vo

Page | 8

Figure 1.2 - Droite de Rayleigh-Michelson et adiabatique de Crussard dans le plan (p, y)

L'étude de l'existence de solutions physiques au système peut être illustrée par la représentation dans le plan (P, y). Les droites de Rayleigh-Michelson (RM) et l'adiabatique de Crussard (C) issues des conditions initiales du mélange réactif, sont représentées à la figure 1.2. Trois cas existent :

· la droite de Rayleigh-Michelson n'a pas d'intersection avec l'adiabatique de Crussard, il n'y a donc pas de solution pour la propagation de la détonation.

· la droite de Rayleigh-Michelson coupe la droite de Crussard en deux points « F » et « f » se situant respectivement dans une zone de détonations « fortes » et une zone de détonations « faibles ». Il est à noter que les détonations faibles n'ont jamais été observées expérimentalement, seul le point F est observé pour des célérités D supérieures à Dcj.

· la droite de Rayleigh-Michelson est tangente à l'adiabatique de Crussard au point CJ dit Chapman-Jouguet : cette solution unique correspond à une propagation d'onde de détonation sonique par rapport aux gaz brûlés, cela permet à l'onde de ne pas être rattrapée par une onde de détente, et donc de se propager de façon stable et autonome. En ce point, la célérité de détonation est minimale.

Graphiquement, lorsque la pression atteint une valeur au-delà de Pcj , la zone de détonations fortes est atteinte, en deçà de celle-ci la zone de détonations faibles est atteinte. (cf. Annexe AI : étude détaillée de l'état Chapman-Jouguet)

1.1.3. Modèle de Zeldovich - Von Neumann - Döring (ZND)

Le modèle de Chapman Jouguet possède l'inconvénient de ne pas prendre en compte l'évolution du milieu réactif entre l'état initial et l'état final. Zeldovich, Von Neumann et Döring ont pris en compte l'extension de la zone de réaction qui s'appuie sur la description physique d'une onde de détonation afin d'établir un modèle. Ce modèle ZND permet ainsi d'associer la cinétique chimique au processus thermodynamique du modèle CJ.

Dans ce modèle, la détonation est définie comme la propagation d'une onde d'épaisseur finie monodimensionnelle, plane et stationnaire dans un milieu réactif. La zone de réaction est alors scindée en deux parties : un choc frontal considéré comme inerte provoque une augmentation brutale de la pression et de la température des gaz frais (état ZND, compression du mélange de façon adiabatique), générant après une période d'induction l'initiation de réactions chimiques (zone de combustion amorcée par auto-allumage). L'énergie libérée par la combustion entretient l'onde de choc. Le temps d'induction est compté entre le passage du choc et l'instant où le maximum d'énergie est libéré. Il est associé à la longueur d'induction Äi (figure 1.3). A la sortie de la zone de réaction, lorsque l'ensemble de l'énergie chimique a été libérée, l'écoulement est sonique par rapport aux gaz brûlés : on retrouve alors l'état CJ du modèle précédent.

Gaz brûlés (état final)

TCJ

PCJ

T,P

TZND

P0 x

T0

PZND

Gaz choqués

DCJ

Gaz frais (état initial)

Pic ZND

Page | 9

Recombinaison

Zone d'induction Äi

Figure 1.3 - Principe du modèle de Zedovich Von Neuman Doring

VZND

vcJ

v0

P

PZND

ZND

CJ

PcJ

P0

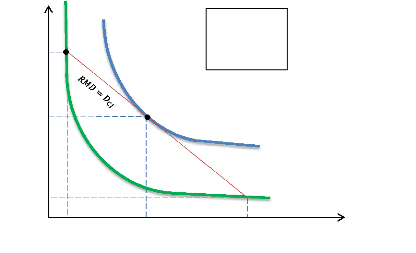
Figure 1.4 - Droite de Rayleigh-Michelson, adiabatique d'Huguoniot et adiabatique de Crussard dans le plan (p, y)

v

Crussard

Rayleigh-Michelson Huguoniot

Page | 10

L'intersection de la droite de Rayleigh-Michelson, tangente à l'adiabatique de Crussard, avec l'adiabatique d'Huguoniot correspond aux caractéristiques du point ZND (figure 1.4), obtenue à partir de l'équation (1.9) en considérant QPT = 0. L'adiabatique d'Huguoniot représente la compression adiabatique du milieu réactif par l'onde de choc. La réaction chimique fait passer le mélange de l'état ZND à l'état CJ avec augmentation du volume spécifique.

1.2. Détonation en milieu hétérogènes gaz/gouttelettes liquides

1.2.1. Les détonations hétérogènes

Les premières études de détonations de gouttelettes liquides ont débutées dans les années cinquante. Burgoyne et Cohen ont observé une détonation ou quasi-détonation d'aérosols liquides en atmosphère oxydante en 1954. Ce n'est que dans les années 80 et jusqu'au milieu des années 90 que des études sur la détonation d'aérosols de carburants liquides ont été menées pour déterminer la détonabilité de ces mélanges. Toutefois, les résultats expérimentaux restent en nombre limité.

1.2.2. Synthèse des principaux travaux antérieurs

Dans les années 50, les premières études de détonations de gouttelettes liquides ont vu le jour. C'est en 1954 que Burgoyne et Cohen ont observé une détonation d'aérosols liquides en atmosphère oxydante. Entre les années 80 et 90, des études pour déterminer des limites de détonabilité ont été réalisées sur des aérosols de carburants liquides.

Page | 11

Les applications en lien avec ces recherches, concernent le domaine de l'aéronautique, des applications en matière de propulsion, les réacteurs aéronautiques, les moteurs diesels mais aussi la sécurité industrielle ainsi que des applications de défense. Récemment, le moteur à détonation pulsée (PDE, Pulse Detonation Engine) suscite un intérêt croissant. L'utilisation de carburants liquides dans le PDE présente l'avantage de réduire le volume et le poids du moteur.

Dans les années 60, les travaux de Williams concernent l'analyse théorique monodimensionnelle des détonations de brouillard de gouttelettes liquides très peu volatiles en atmosphère gazeuse. Par la suite, Webber [1962] et Cramer [1963] ont conduit des expériences systématiques sur la détonation d'aérosols liquides. Cramer relève que la désintégration mécanique des gouttelettes est nécessaire pour produire un aérosol de gouttelettes de taille inférieure à 10 um afin d'apporter une quantité suffisante de vapeur pour entretenir la détonation. De plus, il remarque qu'une richesse élevée est une condition favorable à l'entretien de la détonation. D'autres études ont été menées dans la seconde moitié des années 60. De ces études est ressorti que la structure de l'onde de détonation d'un mélange hétérogène constitué d'aérosols de gouttelettes liquides est plus complexe que celle d'une détonation gazeuse. Durant les années 90, des études concernant l'initiation et la détonabilité de mélanges biphasiques ont vu le jour : citons les travaux de Benedick et al. [1989], Boiko et al. [1991]; Dabora et al. [1991], Papavassilou et al. [1993] ... Plus particulièrement, les travaux de Brophy et al. [2000] et Zhang et al. [2001] ont établis une série de résultats concernant la détonabilité de différents carburants suivant leur taille de gouttelettes et différentes méthodes d'initiation.

Globalement, l'ensemble des travaux expérimentaux effectué sur les détonations hétérogènes gaz/gouttelettes, beaucoup moins avancé que l'étude des détonations en phase gazeuse, montre que si les gouttelettes sont de tailles assez petites, ces détonations peuvent se propager à des célérités suffisamment proches de celles observées en phase gazeuse. Par contre, pour les tailles de gouttelettes d'aérosol plus importantes, de l'ordre du millimètre, la détonation pour les mélanges biphasiques est difficilement observable. De plus, la célérité observée est souvent inférieure à la célérité du mélange gazeux équivalent. Toutefois, les pertes pariétales, la divergence de l'écoulement, la combustion incomplète des gouttelettes avant le plan CJ et la déperdition d'énergie libérée due à son transport vers l'arrière de l'onde de choc sont considérés comme étant la cause du déficit en célérité.

Page | 12

1.3. La structure cellulaire

1.3.1. Structure cellulaire tridimensionnelle

L'onde de détonation possède une structure réelle beaucoup plus complexe que celle présentée dans les modèles de CJ et ZND. C'est en 1927 que Campbell et Woodhead ont montré le caractère non plan de la détonation. La structure tridimensionnelle de détonation a été mise en évidence grâce à des procédés optiques [Voitsekhovskii et al.,1958], [White, 1961] et par la technique des traces sur les feuilles de suie [Denisov et Troshin, 1960], [Shchelkin et Troshin, 1965], [Strehhlow et al., 1967]. La propagation d'une onde de détonation se réalise avec la formation de points triples, résultant de la collision de :

? l'onde incidente, qui se propage dans la direction de la propagation dans le tube

? l'onde de Mach, qui est une onde transverse forte

? l'onde réfléchie, qui est également une onde transverse

Les points triples évoluent de manière périodique sur le front dans la direction perpendiculaire à la direction de propagation. La trajectoire de ces points triples prend alors la forme de cellules (figure 1.5) dites « cellules de détonation » [Denisov et Troshin, 1962].

L'ensemble des chocs de tête se déplace dans le sens longitudinal avec une célérité proche en moyenne de la valeur DCJ. En effet, sur l'axe longitudinal d'une cellule élémentaire, la célérité du choc varie de 1,6 ~ 1,8 DCJ à 0,8 ~ 0,6 DCJ. (figure 1.5)

Figure 1.5 - Schéma d'une cellule de détonation et de la variation de la célérité de l'onde de détonation le long de l'axe de la

cellule

Page | 13

1.3.2. Structure cellulaire des détonations hétérogènes

Les preuves expérimentales de l'existence de la structure cellulaire de détonation dans les milieux hétérogènes biphasiques gaz/gouttelettes liquides sont en nombre très restreint notamment pour les expériences réalisées dans les conditions standards de température et de pression (T = 293 K et 1 bar).

Quelques études expérimentales ont été réalisées soit dans des aérosols très volatils, soit après préchauffage du mélange, ou encore à des pressions initiales très basses. Dans toutes ces situations, le carburant était vaporisé dans des proportions très importantes avant l'initiation de la détonation.

Papavassilou et al. [1993] ont étudié la détonation dans un tube vertical des aérosols de décane de 5 um dans de l'oxygène pur à température et pression ambiante. Ils ont observé l'amorçage de la détonation dans des mélanges décane/oxygène et une propagation stationnaire et autonome de la détonation même pour les mélanges hétérogènes à la température ambiante. Ils ont trouvé que les célérités mesurées sont inférieures de 10 % aux célérités théoriques CJ des mélanges gazeux équivalents. Pour les mélanges très pauvres (r < 0,6), le déficit en célérité est très important. Ils ont observé une structure cellulaire similaire à celle observée en phase gazeuse. Dans un certain nombre d'expériences, les gouttelettes de carburant ont été vaporisées par chauffage préalable du tube.

La comparaison de la taille de la structure cellulaire de détonation pour les mêmes mélanges, d'une part, en phase condensée hétérogène et, d'autre part, en phase vapeur homogène indique que les processus physiques intervenant dans la détonation des aérosols sont responsables de l'augmentation de la taille de la cellule de détonation.

Les études antérieures, expérimentales ou numériques, montrent que la détonation n'a été obtenue que dans le cas de gouttelettes suffisamment fines et une pré-vaporisation importante. Toutefois, des travaux récents [Modou MAR, 2012] ont montré que l'on pouvait observer des détonations d'aérosols dans l'air dans les conditions standards de température et de pression à condition que les gouttelettes initiales soient suffisamment fines.

Page | 14

Page | 15

Chapitre 2

2. Influence des mécanismes de désintégration et de vaporisation des gouttelettes sur la détonation des aérosols de carburants liquides

Ce chapitre a pour but d'exposer les phénomènes présents lors de l'interaction d'un aérosol de gouttelettes liquides avec une onde de choc incidente, incluant le processus de déformation et désintégration des gouttelettes ainsi que le processus de vaporisation de celles-ci.

2.1 Propagation d'une détonation en présence d'aérosols de gouttelettes liquides

Le schéma reprend la description de la structure d'une détonation hétérogène dans des

aérosols de gouttelettes : Onde de choc

Sens de propagation

Gaz brûlés

Zone de gouttelettes en suspension

Zone d'induction

Zone de réaction

Figure 2.1 - Description schématique d'une détonation dans un aérosol de gouttelettes

? Au sein du mélange frais (gouttelettes en suspension), se déplace un front de choc incident en comprimant et chauffant la phase gazeuse du milieu hétérogène de la même manière que lors d'une détonation en phase gazeuse. Considérant la vitesse des gouttelettes au niveau du front comme nulle, une grande différence entre les vitesses matérielles des gaz et des gouttelettes dans l'écoulement apparait derrière le front.

? Une déformation et une désintégration rapide des gouttelettes constituant la phase dispersée [Nicholls, 1969] s'explique par le fait que l'écoulement convectif derrière l'onde de choc est caractérisé par des valeurs élevées des nombres de Weber et de Reynolds. Les nombres de Weber et de Reynolds sont des nombres sans dimension, le

Page | 16

premier correspond au rapport des forces d'inertie et la tension superficielle du liquide, et le second, permet de caractériser un écoulement, en particulier sa nature et son régime laminaire, transitoire ou encore turbulent.

? les fines gouttelettes obtenues par la désintégration se mélangent avec la phase gazeuse comprimée, s'échauffent et se vaporisent rapidement sous l'effet de l'écoulement convectif, pour finalement s'enflammer. La propagation de la détonation est assurée par la combustion du mélange dans la zone de réaction.

? des explosions secondaires locales peuvent apparaître dans le cas de grosses gouttelettes et engendrer des ondes de chocs secondaires. Ces ondes peuvent rattraper l'onde de choc de tête et renforcer la propagation de l'onde de détonation.

Dabora et al. [1979] soulignent que la mise en vitesse de la phase dispersée se produit avec un délai derrière le front de détonation, de par l'inertie et la densité des gouttelettes liquides. Ce phénomène de relaxation a pour conséquence directe d'allonger les temps d'induction et de réaction, ce qui peut se traduire par un déficit de la célérité de détonation et par un découplage du front de combustion et du front de choc. Un déficit trop important de célérité peut conduire une extinction de la détonation, en raison d'une désintégration initiale des gouttelettes insuffisante (gouttelettes très grosses, faible pression de vapeur saturante).

2.2 Mode et régime de désintégration de gouttelettes liquides

2.2.1 Désintégration d'un jet liquide

Quand un jet liquide débouche à l'atmosphère sous forme de cylindre, la compétition entre forces cohésives et forces « destructrices » à la surface du jet donne lieu à des oscillations et des perturbations. Rayleigh a montré que le jet est par nature instable et que les oscillations s'amplifient jusqu'à désintégration en gouttes. Les gouttes ainsi formées peuvent être elles-mêmes instables, d'où possibilité d'atomisation secondaire. Ce n'est que si la longueur disponible pour le jet est inférieure à la distance à laquelle la désintégration se produit qu'il peut paraître stable.

Plusieurs mécanismes de fragmentation se succèdent lorsque l'on augmente progressivement la vitesse du jet. Le premier (pour des écoulements très lents c'est à dire à bas nombre de Reynolds) est le mécanisme de Rayleigh, instabilité dynamique intrinsèque au jet, qui conduit à des gouttes dont le diamètre est supérieur à celle de la buse.

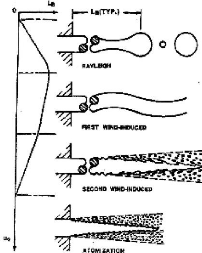
Lorsque la vitesse du jet augmente, les forces aérodynamiques renforcent le mécanisme de Rayleigh, produisant des gouttes dont la distribution granulométrique est plus dispersée. Reitz parle de « first wind induced breakup » (première zone d'instabilité aérodynamique), pour lequel la fragmentation se produit au bout d'un nombre important de diamètres en aval de l'orifice, et pour lequel le diamètre des gouttes reste de l'ordre du diamètre du jet. Arrive ensuite le « second wind induced breakup » (deuxième zone d'instabilité aérodynamique), lié à des petites vagues à la surface du jet. La fragmentation a lieu après quelques diamètres de l'orifice seulement et le diamètre des gouttes est très inférieur au diamètre de l'orifice car le jet est déstabilisé par la force aérodynamique de cisaillement. Si la vitesse d'injection augmente encore, la force de cisaillement devient telle que le jet se désintègre dès la sortie de l'orifice et les tailles de gouttelettes sont très fines.

Page | 17

Figure 2.2 - Mode de fragmentation mécanique d'un jet liquide dans un milieu gazeux selon Reitz [1987]

2.2.2 Modes et régimes de désintégration de gouttelettes liquides

2.2.2.1 Modèle d'atomisation secondaire

L'atomisation secondaire concerne la fragmentation des gouttelettes issues de l'atomisation primaire du jet sous l'effet de l'accélération imposée par un écoulement externe. Le passage à la désintégration secondaire est favorisée lorsque les nombres de Weber We et de Reynolds Re sont grands et que la différence de vitesse entre les phases gazeuses et liquides est grande.

De nombreux modèles d'atomisation secondaire existent et le but de cette partie n'est pas de dresser une liste exhaustive. Beaucoup de modèles sont disponibles dans la littérature, citons Hsiang [1992], Shraiber [1996], Patterson [1998]. Seront décrits, ici, simplement des modèles représentatifs. Un modèle d'atomisation secondaire sera présenté au point 2.2.2.2.

2.2.2.2 Modèle de Reitz Diwakar [Reitz, 1986]

Ce modèle de fractionnement secondaire a été développé à partir des corrélations obtenues par Nicholls [Nicholls, 1972]. À partir de ces travaux, Reitz et Diwakar [Reitz, 1986] ont proposé de retenir trois types de fractionnement secondaire qui dépendent directement du nombre de Weber gazeux de la goutte.

? Le bag breakup - « Cassure en parachute » (We>12)

Ce premier régime d'atomisation a lieu pour des nombres de Weber gazeux supérieurs à 12. La gouttelette est déformée par l'écoulement d'air. Elle forme alors un sac dont la membrane se rompt en petites gouttelettes, ne laissant intact qu'un anneau qui, lui-même, se fractionne en plus petites gouttelettes.

Ecoulement

Page | 18

Figure 2.3 - Schéma Description du bag breakup

Page | 19

? Le stripping breakup - « atomisation par arrachement » (We>100)

Dans cette configuration, l'écoulement gazeux est plus rapide et le nombre de Weber est supérieur à 100. Il y a alors arrachage de ligaments liquides sur les bords des gouttelettes sous la contrainte de cisaillement aérodynamique imposé par l'écoulement. Ces ligaments sont ensuite rapidement fractionnés.

Figure 2.4 - Schéma Description du stripping breakup

Pour les nombres de Weber compris entre 12 et 100, d'autres modes de désintégration existent, il est possible de trouver dans la littérature une explication pour chacun de ces modes présentés en détail par Shraiber et al. [1996].

2.2.3 Caractéristiques des gouttelettes et leur mesure

2.2.3.1 Grandeurs caractéristiques des gouttelettes issus d'un aérosol

Un aérosol se définit comme un brouillard de gouttelettes issues de l'atomisation d'un jet primaire évoluant dans un milieu gazeux. Les gouttelettes constituant l'aérosol ont des tailles et des vitesses différentes. Toutefois, il est nécessaire de chiffrer ces grandeurs.

Les gouttelettes liquides sont supposées sphériques, leurs tailles sont donc représentées par leur diamètre. La distribution des tailles est représentée en nombre ou en volume sous forme d'histogramme. Cet histogramme contient plusieurs plages de diamètres caractéristiques. Dès lors, pour chaque distribution de gouttelettes, deux familles de diamètres caractéristiques sont associées à savoir les diamètres moyens et les diamètres représentatifs de la distribution.

? Les diamètres moyens :

D10 : diamètre correspondant à la moyenne numérique des diamètres des gouttelettes de l'aérosol appelé « Arithmetic Mean Diameter (AMD) et il se définit :

Page | 20

? ?? ????(??)????

??10 = (2.1)
? ?? ????(??)

avec ????(??) et ???? étant respectivement le nombre de gouttelettes et le diamètre géométrique de chaque gouttelette.

D20 : diamètre de la gouttelette dont la surface est la surface moyenne des gouttelettes de l'aérosol considéré, il est défini comme :

??20v??????(??)????2 (2.2)
= ??? ????(??)

D30 : correspond à la gouttelette dont le volume est le volume moyen des gouttelettes de l'aérosol considéré.

??30 = v? ????(??)???? 3

3 ?? (2.3)

??? ????(??)

D32 : correspond au diamètre de la gouttelette qui a le même rapport volume sur surface que celui de la totalité de l'aérosol. Ce diamètre est intéressant pour les aérosols pour lesquels la vaporisation joue un rôle important. Ce diamètre est appelé « Sauter Mean Diameter (SMD) » et se définit comme :

? ????(??)????³

?? (2.4)

??? ????(??) ????²

? Les diamètres représentatifs :

La distribution volumique de gouttelettes est une autre manière de caractériser une distribution de gouttelettes. Ces diamètres sont déterminés à partir de la fraction volumique de l'aérosol noté fV et du volume total noté tV.

???

6????(??)????³

??

???? = ???? ???????? ???? = ?????(??)????

?? (2.5)

3

Page | 21

2.2.3.2 Techniques de mesures granulométrique de l'aérosol

De nombreuses techniques de mesures granulométriques existent, le choix de la technique dépend des paramètres à étudier et de l'environnement du milieu étudié. Les principales techniques de mesure utilisées de nos jours sont des systèmes optiques qui offrent l'avantage d'être rapides et non intrusifs. Deux grandes techniques de mesure d'aérosols sont utilisées :

? La granulométrie à diffraction : la mesure est effectuée à l'aide d'un faisceau laser se basant sur la théorie de Mie de diffusion de la lumière [J. Swithenbank et al., 1976]. Le principe est basé sur l'interaction du faisceau avec la gouttelette, le faisceau de diffraction sur la gouttelette présente un angle de déviation dépendant de la taille de la gouttelette rencontrée. Cette méthode permet d'obtenir la distribution volumique des tailles de gouttelettes présentes dans le volume de mesure.

? Le PDI (Phase Doppler Interferometer), le PDPA (Phase Doppler Particule Analyser) dont le principe s'appuie sur la théorie de la diffusion de Mie de la lumière. Le volume de mesure est délimité par la cohérence des faisceaux lasers par paires de deux, formant ainsi un réseau de franges. Lorsque la gouttelette traverse le volume délimité par les faisceaux, le mouvement crée une lumière diffusée qui sera récupérée au voisinage de l'ange de diffusion. Le déphasage entre signaux est ainsi récupéré, ce dernier est proportionnel à la vitesse et au diamètre de la gouttelette. Une distribution granulométrique numérique de tailles et de vitesses caractérisant l'aérosol est ainsi obtenue.

2.3 Mécanisme de vaporisation des gouttelettes liquides

De nombreux modèles d'évaporation sont disponibles dans la littérature. Les principales différences entre ces modèles sont liées à la modélisation de la phase liquide qui contrôle le débit d'évaporation de la gouttelette dans une atmosphère gazeuse à haute température. Citons quelques un de ces modèles :

1. Modèle à température constante de gouttelette (loi en d²),

2. Modèle à conductivité du liquide infinie (température de la gouttelette uniforme mais variant avec le temps),

3. Modèle de chauffage de la gouttelette transitoire,

4.

Page | 22

Modèle à conductivité effective,

5. Modèle basé sur la solution des équations de Navier-Stockes.

Le modèle classique d'évaporation a été élaboré par Godsave [1953], Spalding [1953], Goldsmith & Penner [1954] et Wise et al. [1955].

Les hypothèses du modèle standard menant à la loi en d² sont applicables pour l'évaporation de gouttelettes mono-constituantes et sont les suivantes :

· La symétrie sphérique car les effets de la convection naturelle et forcée sont négligés en supposant que la goutte est immobile par rapport au milieu ambiant.

· La goutte est isolée et plongée dans un environnement au repos.

· Les processus sont considérés comme isobares et la pression est égale à celle du milieu ambiant.

· Les propriétés de la phase gazeuse (capacité calorifique, conductivité thermique et coefficient de diffusion) sont constantes. Le nombre de Lewis est supposé égal à l'unité. Soit l'égalité entre le nombre de Schmidt et le nombre de Prandtl.

· Les phénomènes sont quasi-stationnaires dans la phase liquide. La température de la goutte est uniforme et constante.

· La phase gazeuse est quasi-stationnaire, ce qui signifie que l'écoulement s'adapte instantanément aux conditions, aux limites et aux dimensions de la goutte. Tenant compte de cette hypothèse et de la précédente, on peut constater que le débit de vapeur est constant.

· Le changement de phase entre le liquide et sa vapeur est beaucoup plus rapide que le phénomène de transport dans la phase gazeuse, ce qui entraîne un équilibre liquide-vapeur à tout instant à la surface de la goutte, qui est à la pression de vapeur saturante correspondant à la température de surface de la goutte.

· Les phénomènes de décomposition de la phase gazeuse, le rayonnement, les effets de Soret (la diffusion massique provenant d'un gradient thermique), et de Dufour (flux de chaleur produit par un gradient de concentration) sont négligés.

De par ces hypothèses, la loi en d² est établie et décrit l'évolution du diamètre initial d'une gouttelette d en fonction du temps t :

??² = ??0 2 - ??.?? (2.6)

Page | 23

avec d étant le diamètre instantané de la goutte, d0 est son diamètre initial, t est le temps et K représente le taux de vaporisation définit par :

Pyaz

K = 8 Dyaz ln(1 + B) (2.7)
Pliquide

Où Dgaz représente la diffusivité, _Pyaz et Pliquide sont les densités respectives de la vapeur et du combustible en présence à la température de gouttelette et B est la constante de transfert de Spalding.

Brophy et al. [1998 ,2000] ont montré que la vitesse à laquelle des mélanges combustible/air atteignent l'équilibre dépend du taux de transfert de chaleur entre l'air et les gouttelettes, de la pression de vapeur saturante du combustible. D'où l'importance de connaitre le taux de vaporisation.

2.4 Diamètre de gouttelette et déficit de célérité de détonation hétérogène

Pour des gouttelettes de petites tailles devant l'épaisseur de la zone d'induction, le comportement de la détonation est identique à celui d'une détonation gazeuse. Par contre, dans le cas d'une gouttelette de taille importante, la zone d'induction doit inclure la phase de désintégration et d'évaporation partielle des gouttelettes. La propagation de la détonation dépend donc de la désintégration des gouttelettes et de leur temps de combustion dans la zone de réaction [Dabora et al., 1969, Bar-Or et al., 1981, Lin et al., 1984].

Les expériences menées sur les espèces chimiques de faible volatilité, telles que le kérosène, ont montré qu'existait un déficit en célérité de 23,5% par rapport à la célérité de détonation idéal CJ. Par contre, dans le cas d'espèces à volatilité plus importante, cas de l'heptane par exemple, le déficit n'est que de 3.3 %. De ces observations, on en conclut que pour des combustibles de volatilité importante, il y a peu de différence au point de vue de la célérité entre le cas où l'on vaporise partiellement ou complétement les gouttelettes liquides. Lin [1984] a montré que pour la détonation de combustibles peu volatils, la longueur d'induction augmente ce qui veut dire qu'une énergie élevée est requise pour l'initiation de la détonation.

Dabora et al. [1969] ont montré l'influence de la taille des gouttelettes sur la détonabilité des mélanges. Il s'avère que plus la taille de gouttelettes est petite, plus on atteint le régime stable de détonation. Pour les gouttelettes de taille allant de 290 à 940 um, le déficit

Page | 24

de célérité va de 2 à 10% tandis que pour les tailles de l'ordre de 2600 um, le déficit peut atteindre 30%. Les pertes aux parois sont considérées comme le facteur dominant expliquant ce déficit en célérité, à cause de l'augmentation de la longueur d'induction.

Page | 25

Chapitre 3

3. Montage expérimental

3.1 Introduction

Dans ce chapitre, l'ensemble des éléments constituant le dispositif expérimental, ainsi que les différentes techniques de mesure et procédures expérimentales mises en oeuvre lors des expériences seront décrits. Le montage expérimental a été conçu pour permette de produire des aérosols de carburants, de caractéristiques contrôlées sur toute la longueur du tube, et d'enregistrer les caractéristiques de la structure cellulaire de détonation (taille et régularité). Cela a pour objectif de pouvoir acquérir de nouvelles connaissances sur les détonations hétérogènes gouttelettes liquides/gaz et sur leurs caractéristiques.

3.2 Le tube à détonation

Le tube à détonation vertical (figure 3.1 et 3.2) est constitué dans sa partie principale de tronçons de section carré de 53*53 mm. Il est composé de bas en haut :

· d'un dispositif de génération de l'aérosol,

· d'une électrovanne à boule, à commande électropneumatique, permettant la fermeture du tube à détonation,

· d'un tube à choc auxiliaire pour l'initiation de la détonation du mélange,

· de six tronçons de section carrée 53*53 mm instrumentés, le tronçon terminal permettant l'enregistre ment de la structure cellulaire de détonation,

· d'une électrovanne à boule similaire à celle du bas du tube permettant la fermeture du tube à sa partie supérieure (la distance entre ces deux électrovannes est de 4,036m),

· d'un tube d'évacuation vers l'extérieur de la pièce.

· Le tube à détonation est instrumenté sur toute la longueur et l'ensemble des opérations expérimentales est piloté par un dispositif de commande et de sécurité géré par logiciel informatique.

Evacuation des gaz brûlés

Prémélanges C2H4 + 3O2

Figure 3.1 - Schéma du montage expérimental

Page | 26

Pompe à vide

Membrane en mylar

Jauge de contrainte (MKS 4000)

Booster (tube à choc)

Système
d'amorçage

Bouteille des prémélanges

Tube à détonation

Electrovanne

Système de
production
d'aérosols de
carburants liquides

Plaque de suie
(Chambre
d'enregistrement)

Mélange biphasique

K7

K6

K5

K4

K3

K2

K1

Electrovanne

Acquisition de données

Capteurs
piézoélectriques

Partie supérieure tube Chambre d'enregistrement

Partie inférieure tube

Tube à choc « booster »

Figure 3.2 - Montage expérimental

Page | 27

Page | 28

3.3 Le tube à choc

Dans les détonations gazeuses, un dispositif à spirale de Schelkin est souvent utilisé pour amorcer la détonation. Ce dispositif permet d'obtenir une longueur de pré-détonation la plus courte possible. Mais ce dispositif engendre des perturbations importantes lors de l'écoulement de l'aérosol de gouttelettes dans la première partie du tube à détonation ce qui engendrerait des dépôts non négligeables de gouttelettes sur les parois du tube.

Le tube à choc remplit le rôle de dispositif d'amorçage, l'amorçage de mélange hétérogène est réalisé par une onde de choc. Celle-ci est générée par la détonation d'un mélange contenu dans un tube à choc auxiliaire, dit booster, débouchant dans le tube principal, au-dessus de la vanne inférieure de fermeture du tube (la distance entre le point de raccordement et la vanne supérieure de fermeture du tube est de 3,9 m). Ce tube à choc (figure 3.1) est de section circulaire de diamètre 69 mm et de longueur 1,7 m avec une capacité de volume de 6 litres. Il est muni à ses deux extrémités de deux brides permettant d'une part de le connecter au tube à détonation principal par l'intermédiaire d'une membrane en mylar intercalée entre deux joints toriques, et, d'autre part, de fermer l'extrémité opposée par un couvercle muni du système d'allumage par inflammateur électrique. Ce tube à choc est connecté à une croix de distribution comportant 4 vannes pour la connexion à une pompe à vide, à une jauge de pression (MKS PR 4000) et à un réservoir de mélange, ce qui permet de faire le vide dans le tube , puis de le remplir avec un prémélange réactif d'éthylène ~ oxygène stoechiométrique, préparé au préalable par la méthode des pressions partielles et stocké dans un réservoir sous pression. La pression initiale du prémélange est de 2 bars ou 3 bars.

3.4 Génération des aérosols de gouttelettes liquides

Le remplissage du tube à détonation, de manière uniforme, sur toute sa longueur avec un aérosol de caractéristiques contrôlées et reproductibles était l'une des principales difficultés. Les méthodes traditionnelles de génération d'un aérosol par injecteur mécanique, ne permettent pas de satisfaire cette condition. En effet, par injection mécanique l'aérosol se désintègre de façon non contrôlée en une série aléatoire de ligaments et de gouttelettes de diverses tailles. De plus, l'atomisation du liquide nécessite des vitesses très élevées entre les différents fluides. L'écoulement qu'engendre cette technique est très turbulent lors du remplissage du tube, avec comme inconvénient de favoriser les dépôts de gouttelettes aux parois. Les aérosols sont donc produits en utilisant la technique des atomiseurs ultrasoniques.

Page | 29

3.4.1. Les atomiseurs ultrasoniques

Le principe de fonctionnement des atomiseurs ultrasoniques utilisés, est celui décrit par Lacas et al. [1994]. La technique des atomiseurs ultrasoniques consiste à créer des instabilités hydrodynamiques à la surface d'un film liquide en le soumettant à des fréquences d'excitation ultrasoniques. Avec cette gamme de fréquence d'excitation appliquée, la désintégration du film est obtenue (figure 3.3).

Le liquide va alors développer en surface des ondes capillaires transverses. La longueur d'onde des vibrations créées est fonction de la fréquence, de la tension superficielle du liquide, ainsi que de sa masse volumique. Dans le cas où l'amplitude des ondes générées est suffisante, le film liquide est déstabilisé en une série de petites gouttelettes.

Figure 3.3 - Gamme de fréquence ultrasonique et désintégration d'un film liquide par atomisation ultrasonique

Les gouttelettes ainsi formées ont leur diamètre d0 relié à la fréquence d'excitation f par la formule de Kelvin :

1 3

d0 = 2 v o???? (3.1)

P????²

Où : k est une constante empirique (typiquement 0,25 - 0,33), o?? représente la tension surfacique de la gouttelette et P?? sa densité.

L'ensemble des gouttelettes forme un aérosol au-dessus du film liquide dans une atmosphère gazeuse à vitesse nulle.

Page | 30

3.4.2. Le générateur

Pour l'expérience, un nouveau type de générateur de gouttelettes (figure 3.4) venant du commerce est utilisé, son fonctionnement est basé sur le principe des atomiseurs ultrasoniques.

Le fonctionnement est basé sur la mise en vibration d'une lame métallique situé sous une couche d'eau ou de carburants. Celui-ci devrait couvrir une plage de granulométrie permettant de passer en dessous de 5 um. (Etude plus approfondie de la granulométrie au chapitre 4)

Figure 3.4 - Générateur de gouttelettes liquides (atomiseur ultrasonique)

3.4.3. Alimentation de l'atomiseur

? Le débit d'oxydant est contrôlé par un rotamètre "Brooks" (GT/1000, flotteur : 8 - RS14), dont la sortie est reliée à la base d'un boitier mélangeur où l'admission se fait en trois points différents

? L'ensemble des rotamètres et des vannes de contrôle des circuits d'alimentation est regroupé sur un tableau de commande que l'on peut voir sur la figure 3.5.

Page | 31

Figure 3.5 - Tableau de commande du dispositif d'alimentation de débit en oxydant (rotamètre d'oxydant à droite)

3.5 Dispositifs de mesure

3.5.1 Granulométrie de l'aérosol

Ce point est abordé en détail au chapitre 4.

3.5.2 Mesure de la célérité et de la pression de détonation

Le tube est instrumenté, sur toute sa longueur, de capteur de pression piézoélectriques Kistler 603B dont le temps de réponse est de 1 us. Ces capteurs sont positionnés en sept points, répartis le long du tube à 1350 mm, 1850 mm, 2091 mm, 2591 mm, 2821 mm, 2956 mm et 3126 mm à partir du point d'initiation. Ces différents capteurs sont reliés à des amplificateurs de charges Kistler Type 5011. Le tableau 3.1 reprend les distances entre capteurs.

Capteurs	0-K1	K1-K2	K2-K3	K3-K4	K4-K5	K5-K6		K6-K7	Distances (mm)
1350	500	241	500	230	135	170

Tableau 3.1 - Distances entre capteurs

Page | 32

Afin de filtrer les vibrations acoustiques se propageant dans les parois du tube, chaque capteur est inséré dans un support en téflon. Ils sont maintenus par une entretoise et une vis de serrage. Le support est ensuite monté sur la paroi du tube principal. Afin d'éviter des problèmes de dérive de signaux pouvant être provoqués par des sollicitations thermiques, une couche de graisse protectrice en silicone couvre la partie sensible métallique du capteur.

Les signaux délivrés par les amplificateurs de charge sont envoyés sur une unité centrale « Graphtec Hard Disk Logger GL1100 ». Cette unité centrale possède 8 voies ainsi qu'une vitesse d'échantillonnage pouvant aller jusqu'à 25 ns, celle-ci étant pilotée par un ordinateur. L'enregistrement des sept signaux de pression provenant des capteurs se fait ainsi de manière synchronisé dès l'allumage. La célérité moyenne de détonation se déduit par la connaissance du temps de passage du front de discontinuité incident et le signal de pression permet de déterminer sa valeur et son évolution.

3.5.3 Enregistrement de la structure cellulaire

L'existence d'un régime de détonation se fait par l'analyse des structures cellulaires tridimensionnelles obtenu par l'intermédiaire de plaque rectangulaires (420 mm * 53 mm). L'une des faces, polie « miroir », est enduite d'un dépôt de suie afin de mettre en évidence une éventuelle structure par la méthode des traces de Mach. En effet, les points triples caractéristiques de la structure inscrivent la trace de leur trajectoire en arrachant les particules de suie en raison des niveaux élevés de température et pression existant à ces points. Un enregistrement bidimensionnel de la structure tridimensionnelle est ainsi obtenu et la taille, la forme et la régularité sont ainsi étudiés.

3.6 Système de commande et protocole

3.6.1 Système de commande

Un système automatisé régi par un logiciel géré par ordinateur permet de commander et contrôler l'ensemble des opérations de remplissage du tube à détonation, d'isolement du tube par fermeture des électrovannes, d'arrêt des débits des fluides et de mise à feu. 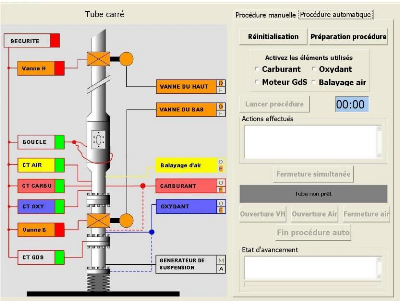Ce logiciel intègre également la gestion de tous les dispositifs de sécurité permettant ainsi d'éviter tous risques d'incidents, de manipulations ou encore toutes pannes et dysfonctionnements. La figure 3.6 reproduit le tableau de commande et de contrôle du logiciel.

Page | 33

Figure 3.6 - Tableau de commande et de contrôle de sécurité

3.6.2 Protocole d'essai

Pour des raisons de sécurité, l'ensemble du tube est tout d'abord mis sous vide afin de localiser des éventuelles fuites. Un protocole bien défini est à suivre et ce pour n'importe quel type de tirs :

Phase préparatoire

· Mise sous tension de l'ensemble des appareils de contrôle,

· Enfumage des plaques de suie et fixation de ces plaques sur leur support,

· Mise en route du logiciel de commande de la procédure, des systèmes d'acquisition de données, des électrovannes, du boîtier d'alimentation électrique de l'injecteur,

· Test de fonctionnement de l'enregistreur "Graphtec",

· Mise en place de la membrane en mylar entre tube principal et tube à choc,

· Mise en place du système d'initiation par inflammateur,

· Verrouillage de la boucle de sécurité.

Page | 34

Phase de remplissage du tube

· Faire le vide dans le tube de pré-détonation,

· Remplissage du prémélange C2H4/O2, dans le tube à choc sous 2 bars ou 3 bars,

· Lancement de la procédure automatique : vannes haute et basse ouvertes, ouverture des circuits d'alimentation en oxydant et du générateur d'aérosols,

· Branchement des conducteurs électriques du dispositif de mise à feu,

· Réglage des débitmètres carburant et oxydant selon la richesse désirée,

· Mise en marche de l'atomiseur, et accouplement à la partie inférieure du tube principal,

· Remplissage du tube principal par balayage des différents composants : aérosol de carburants et air.

Phase de tir

· Mise sous tension électrique de commande de mise à feu,

· Activation des amplificateurs de charge,

· Fermeture simultanée des vannes d'alimentation en carburant et en air et des électrovannes de fermeture du tube; retrait de l'atomiseur,

· Initiation du tir (activation de la touche départ du "Graphtec"),

· Mise à feu.

Acquisition de données

· Sauvegarde des données à partir du "Graphtec",

· Mise en position "stand-by" des amplificateurs de charge,

· Ouverture de la vanne haute (vanne basse fermée), et mise en route du balayage d'air et sa connexion au tube de pré-détonation (évacuation des gaz brûlés),

· Arrêt du balayage d'air,

· Dégager le support de l'atomiseur du tube principal,

· Ouverture de la vanne basse

· Nettoyage et remise en état du tube,

· Exploitation des données.

Page | 35

Chapitre 4

4 Caractérisation de la distribution granulométrique des gouttelettes d'un aérosol

4.1 Introduction

Ce chapitre a pour but de déterminer la granulométrie des aérosols générés par l'atomiseur utilisé pour nos expériences. Pour comprendre le dispositif expérimental utilisé, deux points seront développés.

Le premier consistera à expliquer le principe de mesure de la granulométrie par PDI (Phase Doppler Interferometry), celui-ci permet d'obtenir la caractéristique de la distribution en terme de diamètre moyen (D10) et diamètre de sauter SMD (D32). Deuxièmement, l'analyse des histogrammes de distributions de gouttelettes, et l'évolution des diamètres D10 et D32 en fonction du débit d'air de travail seront abordées.

4.2 Méthode de mesure granulométrique par PDI (Phase Doppler Interferometry)

La détermination de la granulométrie des aérosols se fait par la technique de mesure par interférométrie Phase Doppler PDI dont l'avantage est d'être non intrusive.

4.2.1 Principe de mesure par PDI

Le principe de mesure repose sur l'utilisation de la cohérence de deux faisceaux laser produit par un émetteur, qui crée un réseau de franges d'interférence dans un volume, et l'analyse des signaux résultant du passage des gouttelettes au sein de ce réseau de franges, appelées « bouffées Doppler ». La figure 4.1 représente la disposition des composants (émetteur et récepteur) du système de mesure. Il est important de focaliser précisément le point d'intersection des faisceaux lasers et le point définissant la zone de mesure, et de positionner le récepteur dans l'axe des rayons réfléchis par les gouttelettes, de manière à positionner le système optique du récepteur sur le volume de mesure. Les angles de collection de l'axe du récepteur sont typiquement de 30 ou 40° par rapport aux rayons lasers issus de l'émetteur. Durant l'expérience, l'angle a été fixé à 40° pour optimiser la réfraction du 1er ordre.

Page | 36

Figure 4.1 - Principe de mesure granulométrique par PDI (Phase Doppler Interferometer)

Les lasers vert et bleu, respectivement de longueur d'onde de 532 et 473 nm, sont issus de l'émetteur. Une gamme de focales de 350 à 2000 mm est disponible. Pour la partie expérimentale, deux focales de longueur de 500 mm sont utilisés, l'une pour l'émetteur, et l'autre pour le récepteur. Ces focales permettent d'effectuer des mesures dans les gammes de tailles de gouttelettes allant de 1,5 à 160 um. Les caractéristiques des focales sont reprises dans le tableau 4.1.

Focale émetteur (mm)	Focale récepteur (mm)	Gamme de tailles mesurables (um)	Vitesse min (m/s)		Vitesse max (m/s)	500
500	1.5~160	-100	400

Tableau 4.1 - Gammes de mesure de taille et de vitesse des gouttelettes

L'indice de réfraction est un paramètre important qui caractérise la vitesse de la lumière à travers les gouttelettes de l'aérosol. Il est de l'ordre de 1,33 pour les gouttelettes d'eau. Pour nos autres liquides de travail l'indice change : soit 1,42 pour le dodécane et 1,45 pour le kérosène.

Page | 37

La granulométrie

L'interaction entre le faisceau laser incident et la gouttelette liquide sphérique est représenté à la figure 4.2. Le point intéressant est la réfraction du 1^er ordre et les variations de phases qui s'ensuivent. Les méthodes de mesures reposent sur la variation de trajet optique des faisceaux lors du passage à travers la gouttelette vue par des détecteurs placés à des angles azimutaux différents (figure 4.3). Cette variation est à l'origine du déphasage entre le rayon incident et le rayon réfracté.

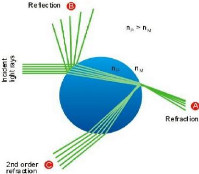
Figure 4.2 - Interaction des faisceaux lasers avec une gouttelette liquide

Connaissant la distance séparant les détecteurs, la longueur d'onde du laser et le déphasage entre les deux signaux à chaque « bouffée Doppler », la taille de la gouttelette peut être calculée. Dans ce cas-ci, trois photomultiplicateurs (PM, 1, 2, 3) sont utilisés pour effectuer des mesures de déphasage. Ces mesures servent à vérifier la sphéricité des gouttelettes mais également à éliminer les gouttelettes ayant un déphasage de plus de 360° qui sortent de la gamme d'échantillon mesurable.

Figure 4.3 - Principe de détection des rayons lumineux réfractés

La détermination du diamètre de gouttelettes repose sur le fait que le déphasage spatial Ö est proportionnel à la taille des gouttelettes présentes dans le volume de mesure. Le déphasage ??1-2 entre deux photomultiplicateurs est calculé comme suit : ??1-2 = (??1-2/?? ) * 360, où P est la période du signal sinusoïdal issu de la bouffé e Doppler.

La mesure du déphasage ??1-2 permet donc de remonter au déphasage spatial et ainsi au diamètre de la gouttelette. Cependant, trois photomultiplicateurs (PM, 1, 2, 3) sont nécessaires pour une mesure correcte du diamètre de la gouttelette, car, l'analyse de la déviation des faisceaux laser dans la gouttelette repose sur les lois de l'optique géométrique qui ne sont applicables qu'à des gouttelettes sphériques. La comparaison entre les mesures des PM (1-2) et des PM (1-3) (figure 4.4) permet ainsi de vérifier cette sphéricité, et de valider les gouttelettes pour lesquelles les mesures sont exactes. De plus, l'utilisation d'un troisième photomultiplicateur permet l'élimination directe des gouttelettes dépassant la borne supérieure de la gamme de diamètre mesurable (avec un déphasage de plus de 360°).

Page | 38

Figure 4.4 - Variation du déphasage en fonction de la taille des gouttelettes

La vélocimétrie

Cette technique s'appuie sur l'utilisation de la cohérence de deux faisceaux lasers pour créer un réseau de franges d'interférence dans un volume de mesure (typiquement quelque mm³, cf. figure 4.5) et d'utiliser ce réseau de franges pour analyser le signal lumineux obtenu par le passage d'une gouttelette liquide.

Page | 39

Figure 4.5 - Principe de mesure de vélocimétrie des gouttelettes

L'intersection de deux faisceaux lasers cohérents permet d'obtenir un réseau d'interfranges connu, et la gouttelette animée d'une vitesse non nulle, diffuse la lumière modulée au passage du réseau. Il s'ensuit un signal sinusoïdal de période correspondant au passage de la gouttelette d'une raie à la suivante (pourvu que la taille de la gouttelette soit inférieure à l'interfrange). La connaissance de l'interfrange et de la période de passage de la gouttelette permet de calculer la vitesse de la gouttelette dans le plan des franges et perpendiculairement au réseau de franges.

4.2.2 Montage expérimental et protocole d'essai

Le montage expérimental utilisé pour les mesures de granulométrie est photographié sur la figure 4.6. Il comporte :

- le générateur d'aérosols,

- un tube transparent cylindrique en plexiglas, de diamètre 53 mm, fixé à la sortie de

l'atomiseur,

- un bâti d'assemblage,

- l'émetteur de faisceaux lasers (bleu et vert),

- le récepteur fixé sur un bâti

- le système d'alimentation en oxydant et en carburant (cf. chapitre 3),

- le système d'acquisition et d'exploitation de données

Le protocole d'essai suivi est le suivant :

- mise en route des appareils et initialisation de la granulométrie en faisant une acquisition en l'absence d'émission de rayon laser,

- calibrage du laser ; réglage des distances focales; réglage de l'amplitude et de la fréquence du signal Doppler, indication de l'indice de réfraction, réglage du gain (une valeur de 350 V est typiquement employée),

- réglage de la bonne convergence des faisceaux laser dans la zone de mesure,

- réglage du critère de sphéricité des gouttelettes,

- choix du nombre d'échantillons mesurés, les valeurs typiques sont de 5.000 à 10.000 gouttelettes. La bonne représentation statistique des plus grosses gouttelettes dans la distribution exige un grand nombre d'échantillons,

- mise en marche du générateur d'aérosols, réglage des débits de liquide et d'oxydant, - démarrage de l'acquisition de données ; le système réalise l'acquisition jusqu'à ce que le nombre d'échantillons soit atteint,

- enregistrement et sauvegarde des données.

Emetteur

Injecteur ultrasonique

Tube

Récepteur

Figure 4.6 - Dispositif de mesure granulométrique par PDI

Page | 40

Page | 41

4.3 Etude de la distribution granulométrique des gouttelettes produites par les atomiseurs

La distribution granulométrique des aérosols générés par l'atomiseur sera étudiée dans ce paragraphe. Tout d'abord, les expériences sont effectuées sur des aérosols d'eau ensuite sur différents carburants. Les caractéristiques intéressantes sont le diamètre moyen D10, le diamètre de sauter D32, les histogrammes du nombre de gouttelettes et le LWC (Liquid Water Content), défini comme étant la masse des gouttelettes liquides dans un volume de l'espace donné. Il est exprimé en g/m³ et se calcule via la formule suivante :

??

??????= 6 ?? D30

3 ND (4.1)

Où ND ( 1

????3) représente le nombre de gouttelettes par unité de volume dans l'espace de

mesure et D30, correspond à la gouttelette dont le volume est le volume moyen des gouttelettes de l'aérosol considéré.

Différentes séries de mesures ont été effectuées en faisait varier certains paramètres :

? le débit d'air d'entrainement de l'aérosol

? la hauteur du point de mesure dans le tube au-dessus de l'atomiseur.

Les essais ont été effectués sur des échantillons de 10000 gouttelettes.

4.3.1 Atomiseur ultrasonique

Les histogrammes ont été obtenu pour un aérosol d'eau à une hauteur z = 50 mm et 160 mm au-dessus de l'atomiseur pour différentes valeurs de débits d'air d'entrainement. Ces mesures de granulométrie sont effectuées au centre de l'écoulement. Sur ces histogrammes, la répartition du nombre de gouttelettes en fonction de leur diamètre peut être observée. L'allure de l'histogramme est gaussienne, le diamètre pris comme valeur représentative pour les expériences de détonation est le diamètre moyen D10 qui prend en compte les autres diamètres de gouttelettes par pondération de leur nombre dans le volume de mesure.

Nombre de gouttelettes

2500 2000 1500 1000 500 0

1 3 5 7 9 11 13 15 17 19 21 Diamètre des goutellettes [um]

Figure 4.7 - Spectre granulométrique d'un aérosol d'eau à une cote d'observation z = 160 mm, ??_??air = 1,42 m³/h

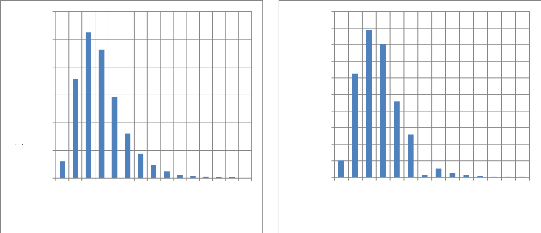
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29

Diamètre des goutellettes [um]

(a)

Nombre de goutellettes

3000

2500

2000

1500

1000

500

0

1 3 5 7 9 11 13 15 17 19 21 23 25 27

Diamètre des goutellettes [um]

(b)

Nombre de goutellettes

4500

4000

5000

3500

3000

2500

2000

1500

1000

500

0

Figure 4.8 - Spectre granulométrique d'un aérosol de (a) kérosène Jet-A1, (b) dodécane à une cote d'observation z = 160 mm, ??_??air = 1,42 m³/h

Avec le même atomiseur et dans la même configuration, des mesures granulométriques avec le kérosène Jet-A1 et le dodécane ont été prises. Les Figures 4.8 (a) et (b), donnent la distribution des gouttelettes à une cote d'observation z = 16 cm. On constate qu'avec le dodécane (figure 4.8 (b)) la majorité des gouttelettes a une taille comprise entre 3 et 11 ìm avec un maxima centré autour de 6 ìm. Le calcul de la moyenne arithmétique du D10 par le système PDI renvoie une valeur D10 = 4,3 ìm (tableau 4.2). Concernant le kérosène, le maximum est centré à environ 6 ìm. La majorité des gouttelettes de kérosène ont une taille variant de 3 à 13 ìm et le diamètre moyen D10 est de 4,7 ìm. La présence de plus grosses gouttelettes dans l'aérosol de kérosène se traduit par des diamètres SMD (D32) plus importants que dans le cas du dodécane.

Page | 42

Page | 43

Z [cm]	D10 [um]	D32 [um]	D30 [um]	LWC [g/m^3]	Kérosène Jet-A1
16	4,7	73,6	15,9	16,47	Dodécane
16	4,3	69,1	14	10,78

Tableau 4.2 - Résultats de mesure avec l'atomiseur

Le tableau reprend les informations principales permettant de caractériser l'aérosol. Par comparaison des LWC avec le kérosène et le dodécane dans les mêmes conditions opératoires, on voit que ce paramètre est plus élevé pour le kérosène. Cela est dû au fait que la masse volumique est plus élevée et que ce carburant est peu volatil d'où une proportion de phase liquide plus importante.

Pour l'ensemble des mesures effectuées, les diamètres D10 mesurés varient entre 4 et 6 um en fonction de la dispersion expérimentale et de la nature du liquide testé. Pour la suite, afin de faciliter l'analyse expérimentale au chapitre 6, un diamètre moyen unique des gouttelettes pour tous les aérosols produits avec cet atomiseur est fixé. L'atomiseur générant majoritairement des gouttelettes de taille de 5 um le diamètre sera alors fixé à D10 = 5 um.

Page | 44

4.3.2 Variation du D10 et D32 en fonction du débit d'oxydant

Les figures montrent la variation des diamètres D10 et D32 dans des aérosols de gouttelettes d'eau en fonction du débit d'air et ceux pour deux cotes d'observations z différentes par rapport à la sortie du jet liquide. Pour le débit d'air d'entrainement, celui-ci à peu d'influence sur la valeur de D10 et D32. Cependant, ces deux paramètres dépendent fortement de la cote d'observation.

0,00 0,50 1,00 1,50 2,00 2,50 3,00 3,50 4,00 4,50 5,00

Débit d'air [m³/h]

Cote z=5cm Cote z=16cm

14

12

10

D10 [um)

8

6

4

2

0

0,00 0,50 1,00 1,50 2,00 2,50 3,00 3,50 4,00 4,50 5,00

Débit d'air [m³/h]

Cote z=5cm Cote z=16cm

120

100

80

D32 [um]

60

40

20

0

Figure 4.9 - Evolution de la granulométrie d'aérosols d'eau générés par l'atomiseur en fonction du débit d'air pour différentes

cotes d'observation z

Page | 45

Le travail réalisé par Modou MAR [2012], montre qu'à partir d'une hauteur donnée, la valeur de débit d'air a peu d'influence sur la valeur de D10 et D32. Cela serait probablement dû à la vitesse d'écoulement faible, excepté à une cote z = 50 mm où une dispersion de la taille des gouttelettes est observée.

Ces comportements sont également observés dans le cas d'un aérosol de dodécane et de kérosène. Dès lors, quelle que soit la valeur de la richesse du mélange, la taille des gouttelettes est la même. Cependant, une différence notable est constaté pour les variations du diamètre de sauter D32. Cela pourrait être dû à l'instabilité du nombre des très grosses gouttelettes qui ont un poids important dans le calcul de SMD.

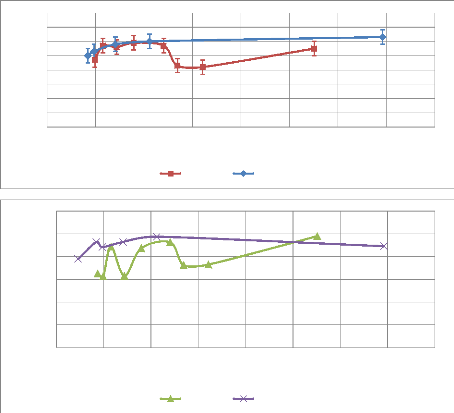
0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60

Richesse

Kérosène Dodécane

8,0

7,0

6,0

5,0

D10 [um]

4,0

3,0

2,0

1,0

0,0

0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60

Richesse

Kérosène Dodécane

120,0

100,0

80,0

D32 [um]

60,0

40,0

20,0

0,0

Figure 4.10 - Variation de la granulométrie d'aérosols de kérosène et dodécane générés par l'atomiseur en fonction de la
richesse à une cote d'observation z = 16 cm

Page | 46

Idéalement, il aurait fallu effectuer nos mesures granulométriques à une hauteur de 3 ou 4 m. Malheureusement, il n'est pas possible dans les conditions de cette étude de procéder à des mesures de granulométries à ces hauteurs d'observation.

4.3.3 Conclusions

Les mesures granulométriques par la méthode PDI effectuées sur des aérosols générés par l'atomiseur, ont conduit aux résultats suivant :

? la distribution granulométrique des aérosols produits est de type gaussien, avec un écart type maxima de 11 um

? le débit d'air a peu d'influence sur les valeurs du diamètre moyen D10 et sur le diamètre de sauter D32. Toutefois, une dispersion en D32 est constatée à cause du poids relatif des grosses gouttelettes dans le calcul du D32.

? Le générateur d'aérosols fournit des gouttelettes de taille comprise entre 4 et 6 um. Pour la suite des travaux, une taille de diamètre moyen unique sera prise en compte à savoir d0 = 5um.

Page | 47

Chapitre 5

5 Les mélanges réactifs

5.1 Introduction

Ce chapitre abordera la présentation des mélanges réactifs étudiés à savoir comme produit principal, le kérosène Jet-A1, et comme produit secondaire le dodécane.

5.2 Produits étudiés

? Kérosène Jet-A1

Le kérosène est essentiellement utilisé dans la fabrication de carburant pour l'aviation (turboréacteur et turbopropulseur) notamment le Jet A-1, le principal d'entre eux. Le Jet A-1 est le carburéacteur le plus utilisé, il est destiné à l'alimentation des avions à réaction civils et militaires (avions équipés de turboréacteurs). Ce dernier est obtenu à partir de pétrole brut selon une coupe de distillation comprise entre 150 et 250°C. Il est constitué de centaines de composés (environ 300 produits "majoritaires") dont la chaîne carbonée est principalement comprise entre 9 et 15 atomes de carbones (C9 à C15).

Les contraintes propres aux applications aéronautiques (volume disponible, conditions rencontrées en altitude, sécurité d'utilisation) font du kérosène un produit aux spécifications sévères et soigneusement contrôlées à tous les stades de son élaboration, depuis la fabrication jusqu'au stockage avant distribution. Le Jet A-1, comme tous les carburants, ne possède pas une composition figée mais est défini selon un ensemble de normes ou spécifications, les normes les plus courantes proviennent de l'American Society for Testing and Materials ou ASTM. (cf. Annexes AIII)

Les kérosènes Jet A et Jet A-1 sont composés de milliers d'hydrocarbures. On y retrouve principalement une composition volumique de 80 % d'hydrocarbures saturés, tels que les paraffines linéaires, ramifiées ou cycliques, 15 à 20 % d'espèces mono voire bi-aromatiques et moins de 5 % d'oléfines.

Le kérosène Jet-A1 répond à des caractéristiques bien définies et strictes, liées aux conditions d'utilisation en sol ou en vol. Ce carburéacteur doit pouvoir répondre aux contraintes liées au moteur et à son fonctionnement comme :

·

Page | 48

la viscosité, la densité et le point de congélation (-47°C pour le Jet-A1) ;

· la chaleur de combustion ;

· le pouvoir corrosif et lubrifiant ;

· la stabilité thermique.

D'autres contraintes dépendent des conditions de sécurités (stockage et manutention), de vol ou environnementales comme :

· le point éclair (« flash point ») définissant la température la plus basse à laquelle le liquide fournit suffisamment de vapeur pour former en contact avec l'air, un mélange gazeux qui peut s'enflammer au contact d'une source d'énergie calorifique mais insuffisante pour entretenir la déflagration (combustion) ;

· la conductivité électrique. Le kérosène possède une faible conductivité électrique, il peut potentiellement se produire une décharge électrique brusque, par accumulation des charges électrostatiques, qui enflammera le mélange air ~ carburant. La conductivité électrique du Jet-A1 est comprise entre 0,5 et 4,5 pS/cm ;

· le point de congélation (« freezing point ») doit se situer à la température la plus basse (-47°C pour le Jet-A1) afin d'éviter que le carburéacteur gèle en altitude et entraine de sérieux dysfonctionnements du moteur.

La composition chimique du kérosène n'étant pas connue avec exactitude pour des raisons de secret professionnel, il nous a fallu trouver une molécule s'approchant au mieux des caractéristiques du Jet-A1.

Il s'avère que dans la littérature le kérosène est souvent assimilé, selon la source, à une formule chimique variant de ??10,9??20,9 ^à ??12??23 (tableau 5.1). Quelques caractéristiques chimiques et physiques de comparaison avec le Jet-A1 sont reprises dans le tableau 5.2.

Sources Formule chimique approchée

Gracia-Salcedo et al. ??12??23

Edwards et Maurice ??11??21

Martel ??11.6??22

Guéret ??11??22

Nguyen et Ying ??11??23

Tableau 5.1 - Formule chimique du kérosène conventionnel

Page | 49

	JET-A1	C11H22
Density [g/cm3]	0,7825	0,79
Boiling Point [°C]	130 ~ 290	218,4
Flash Point [°C]	>38	73,7
Indice réfraction	1,45 ~ 1,46	1,433

Tableau 5.2 - Comparatif de quelques caractéristiques chimiques et physiques entre le JET-A1 et le C11H22

Au regard des grandeurs ci-dessus, les valeurs étant relativement proches, l'hypothèse consistera à approximer le kérosène par une molécule de C11H22 pour pouvoir évaluer la richesse. Tout au long de ce travail, la formule chimique approchée du kérosène adoptée est celle de Guéret.

? Dodécane

Le dodécane est un alcane linéaire de formule brute C12H26. C'est un liquide huileux de la série des paraffines. Il possède 355 isomères structuraux. Ces dernières années, le dodécane a retenu l'attention comme possible substitut aux carburants à base de kérosène tels que le Jet-A, le S-8, et d'autres carburants d'aviation conventionnels. Il est considéré comme un substitut de carburant de deuxième génération, conçu pour émuler la vitesse de flamme laminaire, supplantant largement le n-décane, principalement en raison de sa masse moléculaire plus élevée et de son ratio hydrogène/carbone qui correspond mieux à ceux des n-alcanes de carburéacteurs. Ses caractéristiques sont résumées dans le tableau 5.3.

Propriétés chimiques et physiques Formule brute C12H26
MC12H26 [g/mole]	170,3348 #177; 0,0114 C 84,62 %, H 15,39 %
Diamètre moléculaire	0,761 nm
T° fusion	-9,65 °C
T° ébullition	216,32 °C
Masse volumique	0,7455 g/cm^3à 24,95 °C
T° d'auto-inflammation	200 °C
Point d'éclair	74 °C
Viscosité dynamique	1,324 mPa.s à 24,95 °C 0,891 mPa.s à 49,95 °C
Point critique	1 820 kPa, 385,1 °C

Tableau 5.3 - Caractéristiques physiques et chimiques du dodécane

5.3 Caractéristiques de détonation CJ

Les caractéristiques idéales de détonation en célérité et pression sont calculées à partir d'un logiciel de thermochimie GASEQ pour les conditions initiales T0=298K et P0=1bar. Ces caractéristiques serviront de base de comparaison avec les résultats expérimentaux exposés au chapitre 6. Il est à noter que ce logiciel ne fournit des résultats que pour les molécules gazeuses alors que notre molécule de travail est un liquide. Néanmoins, la valeur de célérité de détonation obtenue par ce logiciel donne un bon ordre de grandeur des célérités, assez proche d'un cas où la molécule serait liquide. L'évolution de la célérité de détonation CJ en fonction de la richesse est indiquée sur la figure 5.1, ainsi que sur le tableau 5.4.

0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60 1,80 2,00

Richesse

D [m/s]

2100

1900

1700

1500

1300

1100

900

700

500

Figure 5.1 - Evolution de la célérité idéale CJ de détonation du mélange kérosène ~ air en fonction de la richesse

Page | 50

Page | 51

Richesse	DCJ [m/s]	PCJ [bar]	Nb mole O2	Nb mole N2
0,38	872,46	4,303	43,61	163,99
0,51	1232,61	8,388	32,47	122,09
0,61	1417,74	11,09	27,13	102,00
0,57	1348,77	10,034	29,06	109,28
0,68	1521,44	12,791	24,34	91,51
0,63	1447,74	11,568	26,30	98,88
0,64	1470,21	11,933	25,69	96,61
0,67	1508,31	12,568	24,68	92,81
0,94	1784,41	17,772	17,57	66,08
1,00	1808,48	18,301	16,50	62,04
1,16	1838,03	19,026	14,18	53,31
1,21	1840,96	19,121	13,63	51,24
1,40	1837,84	19,192	11,79	44,31
1,50	1829,34	19,084	11,00	41,36
1,60	1818,3	18,923	10,31	38,78
1,80	1791,54	18,504	9,17	34,47

Tableau 5.4 - Célérité et pression de détonation CJ pour différents ratio O2/N2

5.4 Détermination de la richesse du mélange

La méthodologie et les résultats des essais effectués pour étalonner les débits de liquide fournis par l'atomiseur, ainsi que la détermination de la richesse du mélange réactif qui en découle sont exposés dans l'annexe AII.

Page | 52

Page | 53

Chapitre 6

6. Etude expérimentale de l'influence de la taille des gouttelettes sur la détonation d'aérosols de carburants liquides

6.1 Introduction

Ce chapitre a pour but d'exposer les résultats expérimentaux sur la formation de la détonation dans les aérosols des carburants étudiés. Afin de caractériser la détonation, des mesures de célérité et de pression sont effectuées et les caractéristiques de la structure cellulaire sont également étudiées. Ces résultats permettront de mettre en évidence l'influence éventuelle de la granulométrie sur la détonation des carburants étudiés.

Pour l'ensemble des expériences effectuées, les conditions expérimentales correspondantes sont reprises dans le tableau 6.1.

Dispositif d'atomisation	Dispositif d'amorçage	Conditions initiales de tir				Dimensions de la plaque de suie (mm)
Taille de l'aérosol (um)	Prémélange gazeux	Pression d'initiation (bars)	Inflammateur	Température (K)	Pression (bars)	420 * 53
5	C2H4/O2 richesse 1	2 ou 3	Electrique	293	1

Tableau 6.1 - Conditions expérimentales des différents tests réalisés

6.2 Initiation de la détonation par un tube à choc (booster)

Le dispositif d'amorçage de la détonation se fait par tube à choc dont le fonctionnement est décrit au chapitre 3. Ce dispositif permet d'obtenir la propagation d'un choc sur toute la longueur du tube. Dans un premier temps, les caractéristiques de l'onde de choc produite par le booster seul dans le tube principal sont étudiées pour les conditions initiales suivantes :

? prémélange C2H4/O2 stoechiométrique sous 2 bars de pression initiale, ? prémélange C2H4/O2 stoechiométrique sous 3 bars de pression initiale

Les célérités moyennes du choc en fonction de la distance de propagation le long du tube principal sont indiquées à la figure 6.1. Les courbes montrent que quelle que soit la pression initiale, l'onde de choc ralentit lors de sa propagation. On notera que sous une pression initiale de 3 bars, la célérité du choc est supérieure à celle initiée sous 2 bars, ce qui serait à priori une situation plus favorable à la transition choc/détonation pour amorcer la détonation.

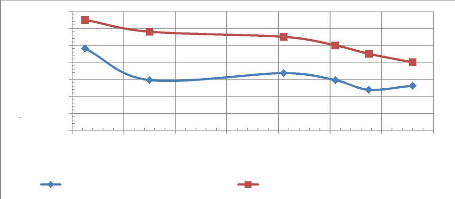
Célérité de choc (m/s)

1500,00

1400,00

1300,00

1200,00

1100,00

1000,00

900,00

800,00

1800 2000 2200 2400 2600 2800 3000 3200

distance de propagation (mm)

Booster seul - Pression initiale 2 bars Booster seul - Pression initiale 3 bars

Figure 6.1- Evolution de la célérité de la détonation en fonction de la distance de propagation dans le tube principale initié
par un booster seul de prémélange C2H4/O2

Les signaux de pression enregistrés lors de la propagation du choc sont reproduits sur la figure 6.2.

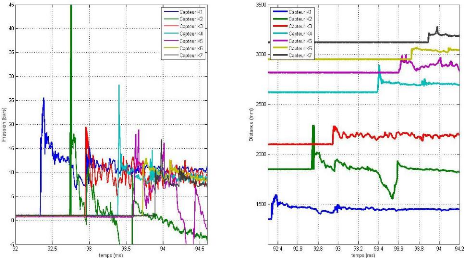
Figure 6.2 - Signaux de pression le long du tube principal avec booster seul de prémélange C2H4/O2 sous 2 bars de pression

initiale

Page | 54

Page | 55

Cette expérience sera utilisée par la suite comme base de comparaison avec les valeurs de célérité et de pression enregistrées dans le cas du booster + mélange réactif.

6.3 Détonation dans le mélange d'aérosol de gouttelettes de kérosène/air

Nous présentons ici, les résultats des expériences effectuées sur la détonation hétérogène du mélange kérosène Jet-A1 ~ Air. Les gouttelettes sont de taille moyenne 5 à 6 um et le domaine de richesse est compris entre 1,1 et 1,5. Le but est de se placer dans conditions optimales pour faciliter l'établissement d'une détonation stable et autonome en vue d'obtenir des structures cellulaires.

La détonation s'effectue avec un booster contenant un prémélange ??2??4/??2 sous 2 bars de pression initiale.

6.3.1 Formation de la détonation

Après la détonation du prémélange introduit dans le booster, la membrane de mylar est rompue et un choc est généré dans le tube principal et se propage jusqu'à la partie supérieure du tube. Sur la figure 6.3, l'évolution de la pression dans le tube à détonation enregistrée entre les capteurs K1 et K7 est représentée pour une richesse r = 1,1.

Figure 6.3 - Profils de pression et diagramme de marche, enregistrés en K1, K2, K3, K4, K5, K6 et K7 de la détonation du
mélange Kérosène/Air, C11H22 + 16,5 (O2 + 3.76); r=1,1 et d0 = 5um

6.3.2 Célérité de détonation

K7

K6

K5

Célérité de détonation (m/s)

1600,00

1500,00

1400,00

1300,00

1200,00

1100,00

1000,00

900,00

800,00

1800 2000 2200 2400 2600 2800 3000 3200

distance de propagation (mm)

Test 2,3 ~ Kérosène/Air ~ r=1,1 ~ Booster seul _H4/O2 à 2 bars

Booster seul Test 2 Test 3

Aucune structure cellulaire relevée sur la plaque de suie

Page | 56

Capteur K4 Capteur K5 Capteur K6 Capteur K7

Figure 6.4 - Célérité moyenne du front en fonction de la distance de propagation et enregistrement de la structure cellulaire pour le mélange kérosène/air avec une richesse = 1,1

La figure 6.4 montre que la célérité décroit à partir de 1400 m/s jusqu'à passer à une valeur de célérité inférieure à celle du booster seul, il n'y a donc pas détonation mais bien extinction puisque dans ce cas-ci, la célérité ne se stabilise pas à une valeur constante. Le système tend à revenir vers l'état caractérisé au point 6.2 lors du tir booster seul.

Trois tests ont été réalisés pour cette valeur de richesse afin de tester la reproductibilité des résultats, deux d'entre eux ont fourni les mêmes constations repris à la figure 6.4. Toutefois, l'un des tests a fourni une structure cellulaire bien particulière (figure 6.5) cependant le système d'acquisition de pression ne s'est pas mis en marche suite à un problème d'ordre électrique sur le système. Les valeurs de pressions et de célérité sont donc

inconnues pour ce test.

Sens de propagation

Figure 6.5 - Enregistrement de la structure cellulaire du mélange kérosène/air - r=1,1 - Test 1

L'enregistrement révèle sur la plaque de suie une structure de type hélicoïdale. Cette structure est bien connue et s'obtient souvent lorsque l'on est proche des limites de détonation. N'ayant pas obtenu de structure avec les autres tests, la richesse 1,1 correspond surement à la limite inférieure de détonabilité de l'aérosol de kérosène. Afin d'essayer d'initier de nouveau une détonation, l'amorçage de nouveaux essais ont été effectuée à une pression initiale du booster de 3 bars et une richesse de 1,3. Les enregistrements de pression sont reproduits sur la figure 6.6 et ceux de célérité et de la structure cellulaire sur les figures 6.7 à 6.10.

Page | 57

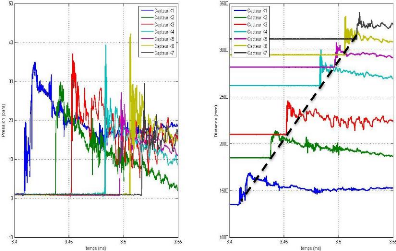
Page | 58

Figure 6.6 - Profils de pression et diagramme de marche, enregistrés en K1, K2, K3, K4, K5, K6 et K7 de la détonation du mélange Kérosène/Air, C11H22 + 16,5 (O2 + 3.76); r=1,3 et d0 = 5um

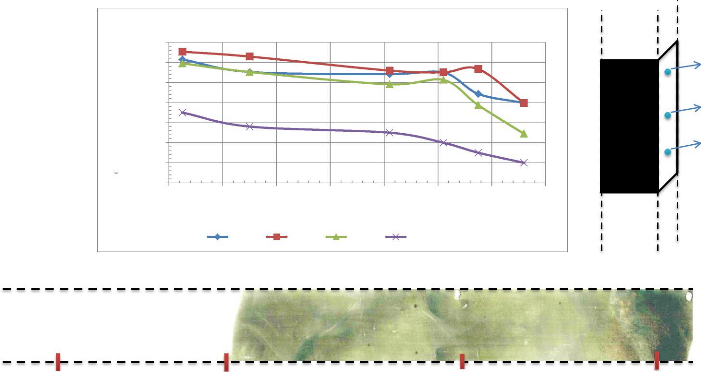
Célérité de détonation (m/s)

1800,00

1700,00

1600,00

1500,00

1400,00

1300,00

1200,00

1100,00

1800 2000 2200 2400 2600 2800 3000 3200

distance de propagation (mm)

Test 4,5,6 ~ Kérosène/Air ~ r=1,3 ~ Booster _H4/O2 à 3 bars

Test 4 Test 5 Test 6 Booster seul

K7

K6

K5

Page | 59

Capteur K4 Capteur K6

Capteur K5 Capteur K7

Figure 6.7 - Célérité moyenne du front en fonction de la distance de propagation et enregistrement de la structure cellulaire pour le mélange kérosène/air avec une richesse = 1,3

? Structures cellulaires enregistrées pour ce mélange

Sens de propagation

Figure 6.8 - Enregistrement de la structure cellulaire du mélange kérosène/air - r=1,3 - Test 4

Figure 6.9 - Enregistrement de la structure cellulaire du mélange kérosène/air - r=1,3 - Test 5

Figure 6.10 - Enregistrement de la structure cellulaire du mélange kérosène/air - r=1,3 - Test 6

La figure 6.7 montre que la célérité décroit jusqu'à une valeur de #177; 1500 m/s. Les figures 6.8 à 6.10 montrent différentes structures, en effet à la figure 6.9 on observe une demi-cellule de cellule plus large que le tube >> 53 mm.

Page | 60

6.3.3 Pression de détonation

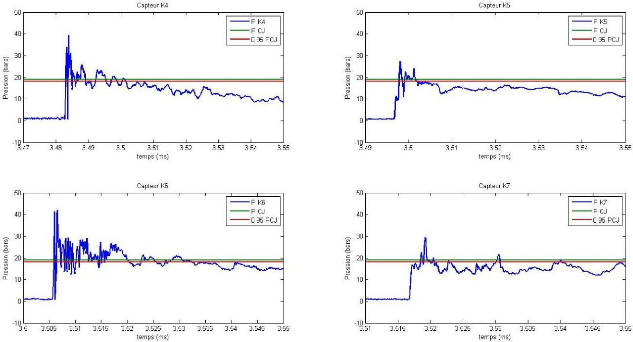
Page | 61

Figure 6.11 - Profils de pressions des capteurs K4, K5, K6 et K7 en fin de propagation dans le tube à détonation pour le mélange kérosène/air avec une richesse = 1,3

Page | 62

La détermination de la pression de détonation n'est pas simple car le signal de pression comporte une plage importante de fluctuations. La lecture de pression qui correspond à la pression de détonation au point CJ est donc difficile. De plus, l'identification des points ZND et CJ est entachée d'incertitude. En effet, si la taille des cellules est grande, la position relative du capteur de pression par rapport à la trajectoire du point triple joue un rôle important sur l'amplitude des pressions enregistrées au point de mesure.

En général, la détermination graphique de la pression de détonation est obtenue par l'intersection du front de choc avec la droite reproduisant l'évolution moyenne du signal après le pic de pression (figure 6.12).

Figure 6.12 - Principe de détermination de la valeur expérimentale de la pression de détonation Pexp

Les pressions idéales PCJ sont obtenues en utilisant le logiciel de thermochimie GASEQ (cf. Chapitre 5) et servent de base de comparaison avec la pression expérimentale mesuré Pexp. La détonation pourra être considérée stable et autonome si la célérité du front reste constante au niveau des capteurs K5 ... K7 et que la pression expérimentale Pexp reste comprise entre 0,95 PCJ et PCJ. Dans les expériences présentes, il n'est pas sûr que le régime de propagation observé soit complétement autonome.

6.3.4 Structure cellulaire de détonation

Les enregistrements effectués sur les plaques de suie (figure 6.8, 6.9 et 6.10) fournissent pour les mêmes conditions expérimentales des résultats différents. A la figure 6.8, il semblerait que l'on voit des cellules entières, tandis qu'à la figure 6.9 il semblerait que cela

Page | 63

correspond à de la demi-cellule ou à une structure hélicoïdale. Concernant la figure 6.10, on voit une trace en début de plaque uniquement. Ces différentes observations indiquent que le régime de propagation dans ces conditions est proche de la limite de détonabilité. Après l'examen qualitatif des structures cellulaires, une taille de la cellule peut être estimée comme supérieure à 53 mm.

6.3.5 Influence de la pression initiale du booster

Afin de compléter l'étude du kérosène, d'autres tests expérimentaux ont été réalisés cette fois-ci à une richesse plus élevé, à savoir 1,5 et avec une pression initiale de booster de 2 bars et 3 bars. Les résultats précédents ont montré que le kérosène est difficile à détoner et qu'une chute de célérité assez importante apparait entre les capteurs K6 et K7. Ce dernier phénomène est constaté de nouveau dans le cas d'un allumage du mélange r=1,5 avec un booster de 2 bars (figure 6.13).

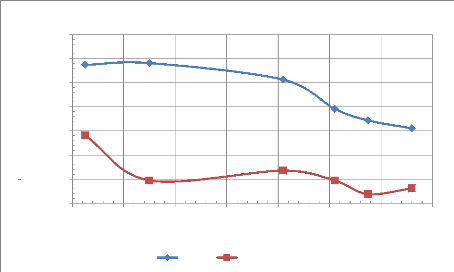
Célérité de détonation (m/s)

1700,00

1600,00

1500,00

1400,00

1300,00

1200,00

1100,00

1000,00

1800 2000 2200 2400 2600 2800 3000 3200

distance de propagation (mm)

Test 8 ~ Kérosène/Air ~ r=1,5 ~ Booster _H4/O2 à 2 bars

Test 8 Booster 2 bars

Figure 6.13 - Célérité du front de détonation en fonction de la distance de propagation dans le tube à détonation pour le
mélange kérosène/air avec une richesse = 1,5 et pression booster 2 bars.

Aucune structure cellulaire n'a été observée dans ce test. L'évolution de célérité montre que celle-ci ne se stabilise pas et diminue progressivement jusqu'à une valeur de 1300 m/s. Ce test confirme que pour initier une détonation avec le kérosène une pression au booster importante est nécessaire.

Page | 64

Dans le cas d'un allumage avec un booster de 3 bars, les observations sont les suivantes : 6.3.5.1 Célérité de détonation

Célérité de détonation (m/s)

1900,00

1800,00

1700,00

1600,00

1500,00

1400,00

1300,00

1200,00

1100,00

1000,00

1800 2000 2200 2400 2600 2800 3000 3200

distance de propagation (mm)

Test 9 ~ Kérosène/Air ~ r=1,5 ~ Booster H4/O2 3 bars

Booster 3 bars Test 9 DCJ

K7

K6

K5

Capteur K4 Capteur K6 Capteur K7

Capteur K5

Figure 6.14 - Célérité du front de détonation en fonction de la distance de propagation dans le tube à détonation pour le mélange kérosène/air avec une richesse = 1,5 et booster de 3 bars.

6.3.5.2 Pression de détonation

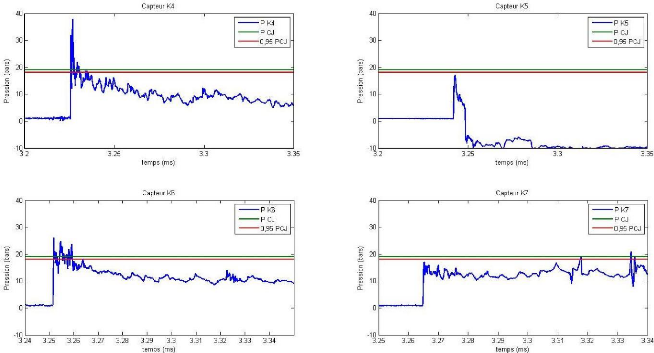
Page | 65

Figure 6.15 - Profils de pressions des capteurs K4, K5, K6 et K7 en fin de propagation dans le tube à détonation pour le mélange kérosène/air avec une richesse = 1,5 et booster de 3 bars

Page | 66

6.3.6 Synthèse des résultats obtenus pour le mélange kérosène/air ? Célérité moyenne de détonation

L'évolution de la célérité moyenne de détonation déterminée expérimentalement Dexp en fonction de la richesse est indiquée à la figure 6.16. Il en ressort qu'à richesse faible, le déficit de célérité est de l'ordre de 15%, cet écart a tendance à diminuer puisque à une richesse de 1,3 le déficit est de 12% et à la richesse 1,5 il n'est plus que de 10%.

Cependant, les valeurs de célérité expérimentales restent inférieures aux valeurs de célérités idéales DCJ (calculées avec le logiciel de thermochimie GASEQ, le mélange en phase gazeuse, alors que dans cette étude expérimentale, le kérosène utilisé est à l'état liquide). En prenant en compte cette remarque, le déficit de célérité est probablement plus faible.

1 1,1 1,2 1,3 1,4 1,5 1,6

richesse

Dexp DCJ 0,85 DCJ 0,9 DCJ

Célérité de détonation (m/s)

1900

1800

1700

1600

1500

1400

1300

1200

1100

1000

Figure 6.16 - Evolution de la célérité moyenne de détonation expérimentale Dexp en fonction de la richesse du mélange

réactif kérosène/air

? Pression de détonation

Les pressions mesurées juste à l'arrière du front de détonation sont rassemblées sur la figure 6.17 et comparées aux valeurs de pressions idéales PCJ.

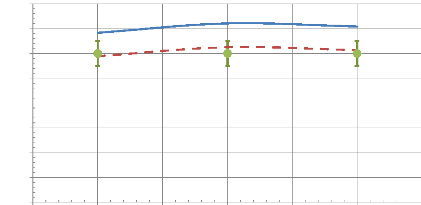
Pression de détonation (bars)

20

19

18

17

16

15

14

13

12

1 1,1 1,2 1,3 1,4 1,5 1,6

richesse

Pexp PCJ 0,95 PCJ

Page | 67

Figure 6.17 - Evolution de la pression moyenne de détonation expérimentale Pexp en fonction de la richesse du mélange du mélange réactif kérosène/air

La figure 6.17 montre une évolution de la pression expérimentale très similaire à celle de la pression moyenne de détonation de Chapman-Jouguet.

? Structure cellulaire

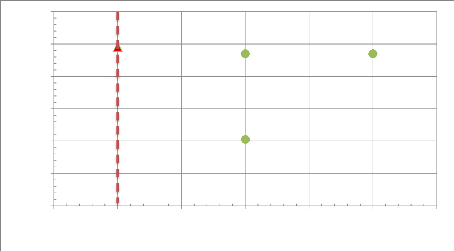
ë (mm) Pas P(mm)

132

112

92

72

32

52

12

1 1,1 1,2 1,3 1,4 1,5 1,6

richesse

Figure 6.18 - Evolution de la taille de la cellule de détonation en fonction de la richesse du mélange du mélange réactif

kérosène/air

Page | 68

La figure 6.18 montre différentes structures cellulaires obtenues en fonction de la richesse. Pour une richesse r = 1,1, ce régime particulier correspond à de l'hélicoïdale et se caractérise par un pas de détonation de l'ordre de 110 mm. A richesse plus élevée r = 1,3 et r = 1,5, on observe une demi-cellule de cellule plus large que le tube >> 53 mm (#177; 106 mm).

6.3.7 Bilan pour le mélange kérosène/air

Les expériences dans les aérosols de kérosène dans l'air montrent qu'il est possible d'initier la détonation sans vaporisation préalable, bien que l'amorçage soit difficile. En effet, pour l'initiation une énergie importante est nécessaire, et le régime de détonation n'a pas toujours été atteint pour les tirs réalisés à une pression de booster de 2 bars. Une pression de 3 bars était plus favorable. La détonation s'initie mais on ne peut affirmer avoir atteint un régime stable et autonome, la distance d'observation étant insuffisante pour trancher.

La structure tridimensionnelle de détonation est mise en évidence pour ces mélanges biphasiques. Différents régimes de propagation ont été observés et dans certains cas pour les mêmes conditions expérimentales. Plusieurs structures cellulaires ont été relevées pour des conditions identiques : hélicoïdale, demi-cellule, cellule entière. La dimension de ces structures est importante. Tout cela montre que le comportement est proche des limites de propagation. De manière générale, ce mélange biphasique est difficile à faire détoner.

Remarque : La plupart des évolutions de célérité moyenne sont qualitativement identiques. Entre le capteur K4 et K5, une baisse de célérité est à chaque fois constatée et ce, même pour le cas du booster seul. Cela peut s'expliquer par la géométrie du tube, en effet, entre K4 et K5 se trouve un léger changement de section. Au départ, le tube carré a une forme arrondie au niveau des angles et une fois arrivé au niveau de la chambre d'enregistrement de la cellule les coins sont de forme aigue. Ce changement de section qui se produit à 2,75 m du bas du tube peut expliquer la décélération locale du front.

6.4 Détonation dans le mélange d'aérosol de gouttelettes de kérosène/air suroxygéné

Quelques expériences ont été effectuées sur la détonation hétérogène du mélange kérosène Jet-A1 ~ Air suroxygéné (O2 + 2N2). Un mélange avec de l'air suroxygéné est utilisé afin de diminuer la taille de cellule. (Mélange air suroxygéné cf Annexes AIV)

6.4.1 Richesse r = 1

a. Formation de la détonation

La figure 6.19 reprend l'évolution de la pression de détonation du mélange kérosène air suroxygéné à richesse 1, entre les capteurs K1 et K7.

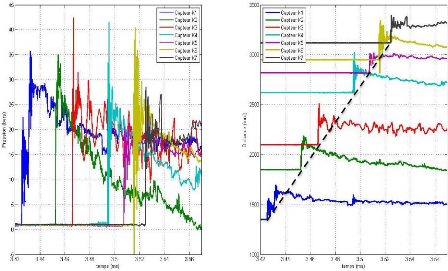
Page | 69

Figure 6.19 - Profils de pression et diagramme de marche, enregistrés en K1, K2, K3, K4, K5, K6 et K7 de la détonation du mélange Kérosène + (O2+2N2); r=1 et d0 = 5um

b. Célérité de la détonation

Célérité de détonation (m/s)

1900,00

1800,00

1700,00

1600,00

1500,00

1400,00

1300,00

1200,00

1100,00

1000,00

1800 2000 2200 2400 2600 2800 3000 3200

distance de propagation (mm)

Test 10 ~ Kérosène + (O₂+2N₂) ~ r=1 ~ Booster _H4/O2 à 3 bars

Booster 3 bars DCJ Test 10

K7

K6

K5

Page | 70

Capteur K4 Capteur K6 Capteur K7

Capteur K5

Figure 6.20 - Célérité du front de détonation en fonction de la distance de propagation dans le tube à détonation du mélange Kérosène + (O2+2N2); r=1 et d0 = 5um

c. Pression de détonation

Page | 71

Figure 6.21 - Profils de pressions des capteurs K4, K5, K6 et K7 en fin de propagation dans le tube à détonation du mélange Kérosène + (O2+2N2); r=1 et d0 = 5um

Page | 72

6.4.2 Richesse r = 1,3

a. Célérité de détonation

Célérité de détonation (m/s)

2000,00

1900,00

1800,00

1700,00

1600,00

1500,00

1400,00

1300,00

1200,00

1100,00

1000,00

Test 11 ~ Kérosène + (O₂+2N₂) ~ r=1,3 ~ Booster _H4/O2 à 3 bars

1800 2000 2200 2400 2600 2800 3000 3200

distance de propagation (mm)

Booster 3 bars DCJ Test 11

K7

K6

K5

Capteur K4 Capteur K6 Capteur K7

Capteur K5

Figure 6.22 - Célérité du front de détonation en fonction de la distance de propagation dans le tube à détonation du mélange Kérosène + (O2+2N2); r=1,3 et d0 = 5um

b. Pression de la détonation

Page | 73

Figure 6.23 - Profils de pressions des capteurs K4, K5, K6 et K7 en fin de propagation dans le tube à détonation du mélange Kérosène + (O2+2N2); r=1,3 et d0 = 5um

6.4.3 Synthèse des résultats obtenus pour les mélanges kérosène/air suroxygéné

L'analyse des évolutions de célérité et des profils de pression ainsi que de la structure cellulaire, permet d'affirmer qu'une détonation stable et autonome est atteinte et cela pour les deux richesses étudiées. En effet, la figure 6.19 montre que la détonation est formée dès le capteur K1, les pics de pression sont relativement élevés et la célérité de détonation est quasi-constante. L'évolution de la célérité moyenne de détonation comme le montre la figure 6.20, est très proche de la valeur théorique de Chapman Jouguet. Le déficit de célérité mesuré est de 3%. La pression expérimentale mesurée à partir des profils de pressions de la figure 6.21 est de l'ordre de 18,1 bars soit très proche de la pression idéale de Chapman Jouguet qui est de 18,3 bars. Les mêmes constatations sont faites pour l'expérience à richesse plus élevée r =1,3. En effet, l'analyse de l'évolution de célérité et du profil de pression ainsi que de la structure cellulaire obtenue (figure 6.22 et 6.23) permettent d'affirmer l'établissement d'un régime de détonation autonome.

Le kérosène détone difficilement avec de l'air, par contre avec de l'air suroxygéné, sa réactivité est plus importante. En effet, un régime de détonation multicellulaires est obtenu (figure 6.24 et 6.25). La taille caractéristique des cellules de détonation X est de l'ordre de 30 mm à richesse 1 et de 22 mm à une richesse de 1,3. Dans la configuration expérimentale considérée, le kérosène peut détonner avec de l'air suroxygéné, sans vaporisation préalable des gouttelettes.

ë

Figure 6.24 - Enregistrement de la structure cellulaire du mélange kérosène + (O2 + 2 N2), r=1 - Test 10

L

L

ë

Figure 6.25 - Enregistrement de la structure cellulaire du mélange kérosène + (O2 + 2 N2), r=1,3 - Test 11

Page | 74

Page | 75

Synthèse et conclusion

L'objectif de ce TFE était d'apporter une meilleure connaissance des caractéristiques et des mécanismes de propagation des détonations dans des milieux hétérogènes composés d'aérosols de gouttelettes liquides de kérosène dans une atmosphère gazeuse oxydante. Le travail a consisté à mettre en évidence l'existence de la structure cellulaire de détonation, avec un aérosol de gouttelettes de kérosène de taille 5 um. Ainsi, une étude purement expérimentale a été menée.

Le montage expérimental mis au point pour cette étude est composé principalement d'un tube à détonation vertical, d'environ 4 m de longueur et de section carrée 53*53 mm. Le tube est instrumenté sur toute sa longueur de capteurs de pressions pour suivre l'évolution de la pression et de la célérité au cours de la propagation de l'onde incidente, ainsi que de plaques disposées en paroi permettant le relevé de la structure cellulaire par la méthode des traces de suie, sur une distance de 400 mm. Cette installation possède une caractéristique importante qui est la génération de l'aérosol par atomiseur ultrasonique. La méthodologie utilisée permet de remplir le tube à détonation sur toute sa longueur tout en ayant des aérosols de caractéristiques contrôlées et une distribution granulométrique quasi monodispersée.

Les expériences ont été réalisées avec du kérosène Jet-A1 dispersé dans de l'air pour une granulométrie d'aérosols de 5 um, dans des conditions de température et de pression ambiante.

Les résultats ont mis en évidence qu'il était possible d'observer les traces de la structure cellulaire de détonation dans les mélanges d'aérosols de gouttelettes liquides combustibles étudiés. Ce résultat est important, puisque les résultats expérimentaux obtenus sont novateurs.

Il a été possible durant la phase expérimentale, de dégager des conditions opératoires permettant d'initier des détonations dans des aérosols dispersés dans l'air. Par contre, il est très difficile d'affirmer si la détonation obtenue est stable et autonome, ce qui nécessiterait l'observation de la propagation du front sur une distance plus longue. Néanmoins, dans le cas du mélange avec l'air suroxygéné, il semble qu'un régime de propagation de détonation stable et autonome ait été atteint.

Page | 76

En conséquence, il apparait que les aérosols de gouttelettes liquides de kérosène dans l'air, de granulométrie suffisamment petite, peuvent détoner. La plupart des travaux antérieurs s'accordaient à dire qu'il était très difficile, voire même impossible, de faire détoner cet aérosol dans de l'air. Les détonations n'étaient obtenues que dans de l'oxygène pur ou dans le cas d'air mais avec un préchauffage permettant la vaporisation des gouttelettes afin de générer la propagation en phase gazeuse.

Ce travail complète les travaux antérieurs réalisés sur l'influence de la granulométrie sur la détonation des mélanges diphasiques et montre que la granulométrie des gouttelettes est un paramètre physique influençant la détonation.

L'ensemble des résultats obtenus montre que le kérosène Jet-A1 est un carburant difficile à faire détoner avec l'air. L'influence de la granulométrie des gouttelettes sur les mécanismes de propagation des détonations en milieu biphasique doivent être poursuivis. En effet, les résultats ont été obtenus avec une granulométrie très fine. La taille des cellules de détonation obtenues avec le kérosène est assez importante. Il est donc nécessaire d'étudier plus en détail l'influence de la richesse, de la granulométrie et de la dilution du mélange sur la détonation du kérosène.

Des perspectives peuvent être envisagées afin d'améliorer les résultats obtenus avec le kérosène. La taille de la cellule obtenue étant de l'ordre de grandeur de la section du tube, une manière de la diminuer serait d'agir sur la réactivité du mélange par exemple en travaillant à des conditions de pression supérieure à 1 atm dans le tube à détonation, tout en veillant à conserver des caractéristiques d'aérosols reproductibles. Une autre voie explorable est l'utilisation de mélange hybrides deux combustibles (l'un gazeux, l'autre liquide) + un oxydant.

Page | 77

Bibliographie

[1] Benmahammed M. A., « Détonations dans les aérosols de gouttelettes liquides réactives. Etude de l'influence des propriétés physicochimiques de la phase liquide et de l'oxydant gazeux » Thèse de doctorat ENSMA, Poitiers, janvier 2013.

[2] Castanet G.; « Etude aérothermique d'un jet de gouttes monodispersé en évaporation et en combustion à l'aide de méthodes optiques », Thèse de doctorat, Vandoeuvre-lès-Nancy, 1er Octobre 2004.

[3] Chang C.T., Farrell P.V., 1998, Spray characteristics and near injector tip effects of injection pressure and ambient density, Comodia, p. 1973.

[4] Lassauce A. ; « Visualisation, granulométrie et évaporation de gouttes et de sprays - Etude dans une atmosphère close et pressurisée » Thèse de doctorat, Alès, 22 février 2011.

[5] Lebas R. ; « Modélisation Eulérienne de l'Atomisation Haute Pression Influences sur la Vaporisation et la Combustion Induite » Thèse de doctorat, Rouen, 26 octobre 2007.

[6] Mar M., « Détonations dans les aérosols de gouttelettes liquides réactives. Etude de l'influence de la granulométrie des gouttelettes » Thèse de doctorat ENSMA, Poitiers, 26 janvier 2012

[7] Reitz, R.D. and Diwakar, R., «Structure of High-Pressure Fuel Spray, » SAE Technical Paper Series 870598.

[8] Reitz R.D. Modeling atomization processes in high-pressure vaporizing sprays. Atom. SprayTech, 3: 309-337, 1987.

[9] Reitz R.D. and Diwakar R. Effect of drop break-up on fuel sprays. Technical Report 860469, SAE paper, 1986.

[10]

Page | 78

Reitz R.D. Atomization and other break-up regimes of a liquid jet. PhD thesis, Princeton University USA, 1978.

[11] Reitz R.D. et Bracco F.V. - Mechanisms of breakup of round liquid jets. In: Encyclopedia of Fluid Mechanics. pp. 233-249. - NJ, 1986. 34, 36, 43.

[12] Abdellah TOUIL. ; « Modélisation des jets diphasiques liquide vapeur et du « rain out » » Thèse de doctorat, Saint Etienne, 2 janvier 2004.

[13] Virot F. « Contribution à l'étude expérimentale et numérique du régime hélicoïdal de détonation dans les systèmes H2, CH4, C2H6 - O2 dilués ou non par N2 ou Ar. » Thèse de Docteur Ingénieur, ENSMA, Université de Poitiers (France), 2009.

[14] Woldon Fickett and William C. Davis; « Detonation Theory and Experiment ». Dover Publication, INC. Mineola, New York, 1997

[15] Fan Zhang; « Shock Wave Science and Technology Reference Library Volume 6 », Detonation Dynamics, Publisher Springer, 2012.

[16] Edwards T., «Kerosene Fuels for Aerospace Propulsion-Composition and Properties, 38^th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, 7-10 July 2002, Paper 2002-3874, Indianapolis, Indiana

[17] P. Dagaut and M. Cathonnet, « The ignition, oxidation and combustion of kerosene: A review of experimental and kinetic modelling », Energy and Combustion, 2006, vol. 32.

Annexes

Annexe AI : Etude à l'état Chapman-Jouguet (CJ)

En différenciant l'équation (1.8) et en sachant que h0, ??0, ??0 sont des constantes, on obtient :

1

??h1 = ??1????1 + ??1????1 = 2 [????1(??0 + ??1) + ????1(??1 - ??0)] (1.10)

Où ?? représente l'entropie.

Le point Chapman-Jouguet (CJ) correspond à l'état de mélange réactif où la condition de tangence entre la droite de Rayleigh-Michelson et l'adiabatique de Crussard est satisfaite, dans ce cas ????1 = 0.

???? = ??1 - ??0 = ??1 (1.11)

( ????)?? ??0 + ??1

Où ??1 représente la célérité du son. Avec l'équation (1.10), on en déduit :

2 = ????₁

2 +

????₁

??²??1

2 > 0 (1.12)

^????1

??²??1 ??0 - ??1 ??²??1

2??1

1

2??1

L'équation (1.12) montre dans le plan (??, ??) que le point CJ correspond à un minimum d'entropie sur la branche des détonations. Dès lors, la condition de sonicité au point de tangence CJ est établie comme suit :

2??1	??^2??1	??^2 1	??1 - ??0	??1^2 + ????1 ??1^2 = 0 = ??1 - ??1 (1.13)
		= ??0 - ??1
	????1		??0 - ??1

Page | 79

On a alors ??₁ = ??₁.

Cas des gaz polytropiques :

Le gaz polytropique est un gaz qui obéit à la loi des gaz parfaits ???? = ???? et qui vérifie

??

la relation ?????? = ???????? (avec ?? = ???? le rapport des chaleurs massiques et ?? = où

???? ????

????: masse molaire). De ces expressions, de nombreuses simplifications apparaissent pour les équations (1.2), (1.3) et (1.4) en supposant que l'enthalpie vaut h = ?????? = ?????? ??-1 et en tenant

compte de la chaleur libérée par les réactions chimiques Q reliant h0 et h1. Dès lors, le système devient :

??1 - ??0

|??0| = ?? - ??0 = ??0v (1.14)
??0 - ??1

|??0| - |??1| = ??1 - ??0 = v(??1 - ??0)(í0 + ??1) (1.15)

??1??1 ??1 ??0 ??1 - 1	??0??0	1 ?? = 2 (??1 - ??0)(??0 + ??1) (1.16)
	??0 - 1

(- ???? = ??1 ??1 = ??1 - ??0

????)(1.17) ??₁ ??1 ??0 - ??1

Si la détonation est dite forte c'est-à-dire que ??^2 » ??0^2 = ??0 ??0 ??0

, ??0 étant la célérité du

son, les valeurs de ??₀, ??₁ peuvent différer fortement lorsqu'il y a une forte libération d'énergie.

Le rapport ^??1 peut s'exprimer à l'aide de l'équation (1.16) :

??0

??0 + 1

= ??0

??0 + 1

??0

1

??1

??0 - 1

??0+ 2????0

??1 ??0 - 1 ??1 ??1

(1.18)

(1.19)

??0[ 2

??1 - 1 ??1 - ??0 2 - 1 ??0 - 2??0??

??0² = (??- ??0)² =

(??1 - ??0) (??0 + 1

??0 - 1 ??1 + ??0)

Page | 80

Des équations (1.14) et (1.15) en substituant ??₁ il vient :

La condition de tangence (1.17) s'écrit comme ceci :

??1	??12	=	0	(1.20) (1.21) (1.22) (1.23)
??1 ??0 ??1 ??0 =
??0 ??1 1) ??1 1
(??1 + ??0 - Ou encore : (??1 - ??0)
??0 ??1 = - ??0 ??1 (??1 + 1) - ??0 Dès lors d'après (1.14) on peut écrire : ??0(?? - ??0)^2 = ??1 (??1 + 1) - ??0 On injecte ainsi ??1 dans l'expression (1.19) 4 2 ??0 (??1^2 - 1)?? 2(??- ^??0 [ ??1^2 - ??0 ] (??- ) )
- + 2 ??0 ??0 (??0 - 1)??0 ??0	+ 2 ??0

La solution de cette équation, dans le cas de détonation, est fournie par Stanyukovich :

?? - ??0 = ??0 v(??1	-	1 )	??	??0 +	+ ??1
	2		2 ??0	(??0

- 1)??0

+ v(??1 + 1

2 ) ?? 2 + ??0 - ??1 (1.24)

??₀ (??0 - 1)??0

Avec la chaleur de réaction Q qui peut s'exprimer comme ceci :

4

(?? - ??0 + ??12

??0² ??0 2

??0 )

(?? - ??0) ??0

??1² - ??0

(1.25)

(??0 - 1)??0

)

??=

??₁² - 1

2

2

Le tableau A.1 reprend les grandeurs caractéristiques à l'état CJ dans un gaz polytropique avec ?? constant (?? = ??0 = ??1) , et dans le cas d'un choc forts ??² » ??₀² .

Page | 81

Page | 82

			Gaz idéal Cp constant			Gaz idéal Cp constant et choc fort ??^2 » ??0^2
??	-	??0 =
			?? 1 v(??2 - v(??2 - 1	1	??
						??= v2(??^2 - 1)?? ??0??2
	??0	??1 ??0	2 ) 2 + + ??0 2 1 ??0 = + 1) ((?? - ??0)2	)	??0 2
			?? + 1 ??0 ??1 ??0 ?? + 1 ??0 = = +			??1 = ?? + 1 ??1 ?? + 1 =
			??0 ??1 ?? ????1 ??1 ??1??1 =			??0 ?? T1 ?? ??^2 =
			??0 ??0??0 ??1 = ??1 = v??????1 ??1 + ??1 = ?? - ??0			2 ??0 ?? + 1 ??0 ????
						??1 = ?? + 1 ??
						??1 = ??+ 1

Tableau A.1 - Caractéristiques de détonation CJ pour un gaz polytropique à ã constant sous l'hypothèse d'un choc fort

Page | 83

Annexe AII : Calibrage du système d'atomisation de gouttelettes

et détermination de la richesse

a. Introduction

Un étalonnage en masse de l'atomiseur de 5 um doit être réalisé afin de connaître le débit liquide injecté dans le tube en fonction du débit d'air d'entrainement. La technique utilisée consiste simplement à mettre l'atomiseur sur une balance précise au centième de gramme près, le mettre en fonctionnement durant un temps de trois minutes et de relever à chaque intervalle de quinze secondes, la perte de masse. Dans un premier temps, le calibrage massique est réalisé avec de l'eau afin de voir le comportement de l'atomiseur et par après avec le kérosène et dodécane. Ultérieurement, la courbe de richesse sera établie et le calcul des caractéristiques de vitesse et temps de balayage seront effectués.

b. Calibrage massique

Dans un premier temps afin de voir le comportement de l'atomiseur, celui-ci est étalonné avec de l'eau. Les résultats sont repris à la figure AII.1

dm (g)

14

12

10

8

4

6

2

0

0 20 40 60 80 100 120 140 160 180

t (s)

m_AIR ref = 50 m_AIR ref = 80

m_AIR ref = 120 m_AIR ref = 30

m_AIR ref = 90 m_AIR ref = 110

Linéaire (m_AIR ref = 50) Linéaire (m_AIR ref = 80)

Linéaire (m_AIR ref = 120) Linéaire (m_AIR ref = 30)

Linéaire (m_AIR ref = 90) Linéaire (m_AIR ref = 110)

y = 0,0448x R² = 0,9993

y = 0,0467x R² = 0,9976

y = 0,0672x R² = 0,9985

y = 0,0435x R² = 0,9905

Perte de masse en fonction du temps

y = 0,0478x R² = 0,9957

y = 0,0743x R² = 0,9993

Figure AII.1 - Calibrage en masse de l'atomiseur avec de l'eau à différents débits d'air de référence

Après calibrage, la figure AII.1 montre que la perte de masse reste linéaire et ce, peu importe le débit d'air d'entrainement de référence. Cet étalonnage permet ainsi d'établir les différents couples (mAir,mCarburant) nécessaires au calcul de la richesse (exposé au point c). Une

Page | 84

différence est à noter avec cet atomiseur. En effet, l'atomiseur utilisé en 2012 par Modou MAR produisait une perte de masse en liquide constante quel que soit le débit d'air de référence, ce qui n'est pas le cas de ce dernier. L'étalonnage est également réalisé avec le kérosène et le dodécane. Les résultats sont reportés dans les tableaux AII.1 et AII.2

Indication mAIR 120	mAIR [m^3/h] 5,68	mC12H26 [g/h] 30,24	mAIR [kg/h] 7,34	m C12H26 [kg/h] 0,030
100	4,71	9,36	6,09	0,009
90	4,32	11,53	5,59	0,012
80	3,81	14,4	4,92	0,014
65	3,23	16,34	4,17	0,016
50	2,45	20,52	3,17	0,021
40	1,87	28,8	2,42	0,029
30	1,42	25,2	1,84	0,025
25	1,23	31,68	1,59	0,032
20	0,94	36,36	1,22	0,036
10	0,45	56,88	0,58	0,057

Tableau AII.1 - Résultats de l'étalonnage en masse de l'atomiseur avec du dodécane C12H26

Indication mAIR 120	mAIR [m^3/h] 5,68	mJET-A1 [g/h] 68,43	mAIR [kg/h] 7,34	mJET-A1 [kg/h] 0,068
110	5,26	68,14	6,80	0,068
100	4,71	68,04	6,09	0,068
90	4,32	65,62	5,59	0,066
80	3,81	62,28	4,92	0,062
65	3,23	61,63	4,18	0,062
50	2,45	58,32	3,17	0,058
40	1,87	55,44	2,42	0,055
30	1,42	56,52	1,84	0,057
25	1,23	54,72	1,59	0,055
20	0,94	49,94	1,22	0,050
10	0,45	41,04	0,58	0,041

Tableau AII.2 - Résultats de l'étalonnage en masse de l'atomiseur avec du kérosène JET-A1

c. Détermination de la richesse

i. Introduction

La richesse se définit comme un rapport de masses. Celle-ci (notée Ö), s'écrit :

'P = Dosage massique stoe??hiomét??ique

D????

= (5.1)

D????

Dosage massique ??éel

Dans nos expériences, les valeurs de débit d'air de travail sont connues. A ces débits correspond une valeur de débit de liquide bien définie, déduite de l'étalonnage massique du paragraphe b. Enfin, à partir de la composition chimique du mélange, la richesse sera calculée.

ii. Méthodologie de calcul de la richesse

? Kérosène

1. Méthode 1

Equation chimique à la stoechiométrie c'est-à-dire quand la richesse vaut 1 :

'P?? ??11H22 +

17.5 0.21 (0.21 ??2 + 0.79N2) ? ????2 + H2?? + N2 (5.2)

Il est à noter que l'équation n'est pas pondérée mais nous ne nous intéressons qu'à la partie des réactifs pour chiffrer la richesse.

Connaissant les débits et les masses molaires des composants, l'expression du nombre de moles/h de liquide X?????? correspondant au nombre de moles/h d'air X?????? peut être établi. Par conséquent, la richesse 'P?? peut se calculer par simple règle de trois par rapport à la stoechiométrie. La relation suivante est ainsi établie :

X = Masse molai??e du fluide

m

= M Fmole

h ] (5.2)

Débit du fluide

Page | 85

X?????? 'P?? = X??????

17.5 * (5.3) 0.21

2. Méthode 2

Pour confirmer les résultats obtenus, le calcul de la richesse se fera suivant une autre méthode.

Le calcul consistera à procéder par un rapport de dosage massique. Cela consistera à procéder au rapport du dosage massique réel ?????? par rapport au dosage massique dans les conditions stoechiométrique.

L'équation d'équilibre chimique à la stoechiométrie est la suivante :

1 2 H2O + 3,76?? (x + C??H ?? + ?? (x + ^y4) (O2 + 3,76N2) ? xCO2 + y C11H22 + ??????(O2 + 3,76N2) ? 12CO2 + 13H2O + ?????? N2 1 y 22 le (x 11	y 4) N2 = 16,5	(5.4) (5.5) (5.6)
avec + 4) = + c??efficien?? s????echi??mé????ique ?????? = ?? 4

Détermination de la valeur du dosage massique à la stoechiométrie :

Dans le dosage stoechiométrique, il y a une mole de carburant de masse égale à 154.29 g. De plus, il y a de l'air dont la masse vaut 16.5 * 4.76 * 28.96 = 2274.52 g.

Par définition, le dosage massique :

?? = Masse d^'ai??????

= = 0.068 (5.7)

²²⁷⁵

Masse essence????

154.29

.52

Page | 86

Ce dosage massique calculé est celui correspondant à la stoechiométrie et sera noté ??????. Connaissant maintenant ?????? procédons au calcul du dosage réel ?????? avec les valeurs obtenues par étalonnage pour ainsi chiffrer la richesse selon le rapport de dosage massique :

ö JET-A1= ?????? (5.8)

??????

Page | 87

Comparatif des résultats obtenus par les 2 méthodes :

(mJET-A1;mAIR) [kg/h] (0,068 ; 7,34)		ö JET-A1 Méthode 1 0,15	ö JET-A1 Méthode 2 0,14
(0,068 ;	6,80)	0,16	0,15
(0,068 ;	6,09)	0,17	0,16
(0,066 ;	5,59)	0,18	0,17
(0,062 ;	4,92)	0,20	0,19
(0,062 ;	4,18)	0,23	0,22
(0,058 ;	3,17)	0,29	0,27
(0,055 ;	2,42)	0,36	0,34
(0,057 ;	1,84)	0,48	0,45
(0,068 ;	1,84)	0,58	0,54
(0,055 ;	1,59)	0,54	0,51
(0,050 ;	1,22)	0,64	0,61
(0,041 ;	0,58)	1,10	1,04

Tableau AII.3 - Valeurs de richesse du kérosène JET-A1 obtenues pour différents couples de travail (mJET-A1;mAIR)

Les valeurs de richesse obtenues suivant les 2 méthodes sont relativement proches. Les débits de liquide obtenus avec la technologie du brumisateur de gouttelettes de 5 um sont relativement petits.

La plus grande valeur de richesse obtenue est de l'ordre de 1,1 et celle-ci s'obtient avec un débit d'air de l'ordre de 0.58 kg/h. Lorsque le débit d'air est très important, nous sommes en excès d'air d'où les valeurs plus petites de richesse et donc moins de chance d'obtenir une détonation. L'évolution de la richesse est reportée graphiquement à la figure AII.2.

Débit d'air [m3/h]

4,00

6,00

3,00

2,00

0,00

5,00

1,00

0,00 0,20 0,40 0,60 0,80 1,00 1,20

Richesse

Evolution de la richesse en fonction du débit d'air

y = 0,576x-1,192

Figure AII.2 - Evolution de la richesse du kérosène JET-A1 avec le débit d'air pour l'atomiseur de gouttelettes de 5 um et
courbe de tendance de type puissance

La plage de richesse étant définie, afin de tenter d'initier une détonation, les richesses de travail seront fixées entre 1 et 1,2 et les résultats exposés au chapitre 6.

? Dodécane

La même démarche est tenue ici avec le dodécane. Un comparatif sera ensuite réalisé avec les résultats antérieurs obtenus par Modou MAR (2012) qui a travaillé avec atomiseur générant des tailles de gouttelettes de l'ordre de 8 um.

Calcul de la richesse

1. Méthode 1

Equation chimique à la stoechiométrie c'est-à-dire quand la richesse vaut 1 :

???? C12H26 +

17.5 0.21 (0.21 ??2 + 0.79N2) ? C??2 + H2?? + N2 (5.9)

X = Masse molaire du fluide

m _M Fmole

h ] (5.10)

Débit du fluide

Page | 88

???????? ???? = ????????

17.5 * (5.11) 0.21

2. Méthode 2

L'équation d'équilibre chimique à la stoechiométrie est la suivante :

C??H ?? + ??(x + ^y ₄)(??2 + 3,76N2) ? xC??2 + y 2 H2?? + 3,76??(x + ^y ₄) N2 (5.12)

C12H26 + _??????(??2 + 3,76N2) ? 12C??2 + 13H2?? + ?????? N2 (5.13)

avec le c??efficien?? s????echi??mé????ique ?????? = ?? (x + ^y ₄) = 12 + 26 4 = 18,5 (5.14)

Détermination de la valeur du dosage massique à la stoechiométrie :

Dans le dosage stoechiométrique, il y a une mole de carburant de masse égale à 170.33 g. De plus, il y a de l'air dont la masse vaut 18.5 * 4.76 * 28.96 = 2550.52 g.

Par définition, le dosage massique :

?? = Masse d^'ai??????

= = 0.067 (5.15)

²⁵⁵⁰

Masse essence????

170.33

.52

Page | 89

Ce dosage massique calculé est celui correspondant à la stoechiométrie et sera noté ??????. Connaissant maintenant ?????? procédons au calcul du dosage réel ?????? avec les valeurs obtenues par étalonnage pour ainsi chiffrer la richesse selon le rapport de dosage massique :

??C12H26 = ?????? (5.16)

??????

Page | 90

Comparatif des résultats obtenus par les 2 méthodes :

(mC12H26;mAIR) [kg/h] (0,068 ; 7,34)		ö C12H26 Méthode 1 0,06	ö C12H26 Méthode 2 0,06
(0,068 ;	6,80)	0,02	0,02
(0,068 ;	6,09)	0,03	0,03
(0,066 ;	5,59)	0,04	0,04
(0,062 ;	4,92)	0,06	0,06
(0,062 ;	4,18)	0,09	0,10
(0,058 ;	3,17)	0,17	0,18
(0,055 ;	2,42)	0,19	0,21
(0,057 ;	1,84)	0,24	0,25
(0,068 ;	1,84)	0,28	0,30
(0,055 ;	1,59)	0,42	0,45
(0,050 ;	1,22)	1,39	1,46

Tableau AII.4 - Récapitulatif des valeurs de richesse du dodécane C12H26 obtenues

Les deux méthodes de calcul donnent quasiment les mêmes valeurs de richesse. La valeur de richesse ö la plus élevée, avoisine les 1,4 ~ 1,5 et s'obtient pour une valeur de débit d'air de l'ordre de 1,22 kg/h. Sous forme graphique, l'évolution de la richesse est indiquée sur la figure AII.3.

Débit d'air [m3/h]

4,00

6,00

3,00

2,00

0,00

5,00

1,00

0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60

Richesse

Evolution de la richesse en fonction du débit d'air

y = 0,5853x-0,603

Figure AII.3 - Evolution de la richesse du dodécane avec le débit d'air pour l'atomiseur de gouttelettes de 5 um et courbe de
tendance de type puissance

? Comparaison avec les résultats antérieurs

Les conditions des expérimentés de Modou MAR avec le dodécane sont identiques aux nôtres mais l'atomiseur utilisé est différent. En effet, celui-ci permet de générer des tailles de gouttelettes de l'ordre de 8 um. Modou MAR [2012] a travaillé dans une plage de débits d'air comprise entre 2 et 5 m³/h. Dans son cas, le débit de liquide est constant quel que soit la valeur de débit d'air, sa valeur est de 0,21 l/h.

La richesse correspondante est calculée sur le tableau AII.5 et la comparaison avec nos résultats sur la figure AII.4:

m C12H26 [kg/h]	m AIR [kg/h]	X C12H26 [mole/h]	X AIR [mole/h]	ö C12H26
0,158	5,69	0,925	196,450	0,39
0,158	4,53	0,925	156,267	0,49
0,158	3,36	0,925	116,084	0,66
0,158	2,72	0,925	93,760	0,82

Tableau AII.5 - Valeurs de richesse du dodécane obtenues dans les travaux antérieurs réalisés par Modou MAR (2012)

Débit d'air [m3/h]

4,00

6,00

3,00

2,00

0,00

5,00

1,00

0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60

Richesse

Evolution de la richesse en fonction du débit d'air

Atomiseur 5um Atomiseur 8um

Puissance (Atomiseur 5um) Puissance (Atomiseur 8um)

y = 1,7258x^-1

y = 0,5853x-0,603

Figure AII.4 - Comparaison des plages de richesse entre les atomiseurs générant des tailles de gouttelettes de 5 um et 8um (courbe de tendance de type puissance)

Page | 91

Le fait d'avoir changé de brumisateur modifie considérablement les résultats. La plage de richesse est complétement différente et cela peut se justifier par une différence de fonctionnement technologique du brumisateur.

La plage de richesse avec l'atomiseur de 5 um est beaucoup plus petite que celle obtenue avec l'atomiseur de gouttelettes de 8 um pour une même plage de débit d'air de travail. Cela peut s'expliquer par le fait que pour un même débit d'air, le brumisateur générant des plus petites tailles de gouttelettes travaille avec un débit de liquide très petit par rapport à l'autre. Pour un même débit d'air, la proportion de liquide est différente d'un facteur 10, d'où des plages de richesses différentes. Vu les proportions de liquides mise en jeu, il sera nécessaire de travailler à bas débit d'air pour le brumisateur de 5 um afin d'avoir une valeur importante de richesse et optimiser ainsi la probabilité de détonation.

d. Vitesse et temps de balayage dans le tube

Il est important de pouvoir chiffrer le temps nécessaire au balayage des gouttelettes dans le tube, ainsi que la vitesse d'entrainement de celles-ci afin de savoir si elle sera suffisante pour vaincre la force due à la pesanteur, et ainsi atteindre le haut du tube. Le tube à détonation est un tube de section carrée de 53*53 mm et de longueur de 4,036 m. Chiffrons le temps de balayage au sein du tube.

L = 4,036 m

Q AIR

La relation reliant le débit à la section est la suivante :

M

3600

= V * S (5.17)

avec

_m3

* m : débit volumique du fluide

h

*

m

V : vitesse d^'entrainement des gouttelettes s

* S : section d'étude m2

La vitesse est considérée comme constante. Dès lors, son expression peut s'écrire :

L dt

?x

V = ?t

m

-, 3600

at * S -, dt = L * S * 3600 (5.18)

m

Page | 92

Temps de balayage 2 ou 3 * dt (5.19)

Page | 93

Les valeurs de temps de balayage en fonction du débit d'air sont reprises dans le tableau AII.6.

???? AIR [m^3/h]	Ventrainement [m/s]	?t [s]	tbalayage [s]
1,42	0,14	28,74	57,48
1,23	0,12	33,18	66,36
0,94	0,09	43,42	86,84
0,45	0,04	90,70	181,4

Tableau AII.6 - Temps de montée des gouttelettes au sein du tube à détonation

Fixer un temps de balayage entre 3 et 4 min sera donc suffisant pour assurer le balayage au sein du tube. Il reste maintenant à vérifier si nos vitesses d'entrainements sont suffisantes pour que les gouttelettes montent jusqu'en haut du tube.

Pour cela, il faut calculer la vitesse de chute d'une particule dans l'air. Pour les gouttelettes de petites tailles, le modèle de Stokes est envisageable.

La vitesse de chute diminue, le nombre de Reynolds devient faible devant l'unité et le mécanisme de frottement dominant n'est pas l'inertie. La force de friction est alors donnée par la formule suivante :

??

??= ??0 2 ?? (5.20)

Où ??0 désigne la viscosité dynamique de l'air, ?? le diamètre de la gouttelette et ?? la vitesse de chute de la goutte.

Le poids d'une goutte sphérique de diamètre ?? s'écrit :

3

4

?? = 3 ?? (?? ₂) ???? (5.21)

Où ?? est la masse volumique du liquide considéré et ?? est l'accélération de la pesanteur. L'équilibre de ces forces permet d'obtenir l'expression de la vitesse de chute :

2

4 3 ?? (?? ₂) ????

?? = (5.22)

??0

Les tests granulométriques par méthode PDI ont fait ressortir des tailles de gouttelettes de l'ordre de 4 à 6 um. En moyenne, le diamètre avoisine les 5 um, dès lors la vitesse de chute dans l'air sera égale à :

Page | 94

Vchute kérosène =

	2 4 3 T1 * (5 * 10^-6 2 ) * 782,5 * 9,81			cm = 1,17 s
	1,71 * 10-^5
Vchute dodécane =		2 4 3 T1 * (5 * 10^-6 2 ) * 750 * 9,81	cm = 1,13 s
		1,71 * 10-^5

Le modèle de Stokes n'est applicable que pour les tailles de gouttelettes très petites et si le nombre de Reynolds est inférieur à l'unité. Vérifions cette dernière condition (tableau 5.9)

V * d

R_e = ?0 (5.23)

???? AIR [m^3/h] 5,68	VENTRAINEMENT [m/s] 0,56	Re 0,16
4,71	0,47	0,14
4,32	0,43	0,12
3,81	0,38	0,11
3,23	0,32	0,09
2,45	0,24	0,07
1,87	0,18	0,05
1,42	0,14	0,04
1,42	0,14	0,04
1,23	0,12	0,04
0,94	0,09	0,03
0,45	0,04	0,01

Tableau AII.7 - Nombre de Reynolds Re en fonction du débit d'air de travail

Ce modèle considère également que les gouttelettes sont parfaitement sphériques, c'est-à-dire la situation où les forces capillaires dominent la friction de l'air, qui serait susceptible de déformer les gouttes. La force capillaire typique est proportionnelle à la taille de la gouttelette R et à la tension superficielle y qui est une force par unité de longueur. On peut se la représenter comme la force de tension de surface appliquée par une moitié de la goutte sur l'autre moitié. Pour qu'une goutte soit considéré comme sphérique, il faut donc que la condition suivante soit vérifiée :

Ffriction air < Fcapillaire (5.24)

ñ_aV²R² < yR (5.25)

Page | 95

En remplaçant Vpar l'expression obtenue en (5.21), le critère devient :

2

5 ã?0

R < v = ? (5.26)

16 9 ð2ñañ2g2

En résumé, la gouttelette sera sphérique si son rayon ne dépasse pas la longueur capillaire ? du liquide utilisée. Vérifions cette dernière condition sachant que :

- la tension superficielle du kérosène ã est comprise entre 0.023 et 0.032 N/m

- la viscosité de l'air ?0 vaut 1,71 * 10^-5 Pa.s

- la densité de l'air ñ?? vaut 1,292 kg/m³

- la densité du kérosène ñ vaut 782,5 kg/m³

- la force de pesanteur g vaut 9,81 m/s²

En remplaçant les données dans l'équation (5.26), la longueur capillaire ? = 8,717*10^-5 m. Soit 87,17 um, le rayon de nos gouttelettes R valant 2,5 um, la condition de sphéricité est vérifiée.

Notons également que le modèle de Stokes reste en adéquation avec le test de mesure de granulométrie par PDI (cf. Chapitre 4). En effet, durant cette phase expérimentale, des mesures de vitesse de gouttelettes sont relevés et la montée des gouttelettes au sein du tube a été observée durant la phase de calibrage du système avec le tube en plexiglas.

e. Conclusion

Pour conclure ce chapitre, concernant l'atomiseur utilisé, changer le débitmètre utilisé afin de minimiser l'erreur sur la richesse. En effet, un constructeur garantit en général sur l'instrumentation, une imprécision minime entre 5 et 95% de l'échelle de mesure, alors que notre plage de travail se situe entre 0 et 5% de l'échelle où la précision qui règne sur cette gamme est inconnue.

Annexe AIII: Specification Jet-A1 de l'American Society for Testing and Materials

(ASTM)

Tableau AIII.1 - Specifications ASTM du kérosène Jet-A1

Page | 96

Page | 97

Annexe AIV : Calcul des caractéristiques de la bouteille de mélange O2 + 2 N2 par

la méthode des pressions partielles via EES.

// Equation à la stoechiométrie avec l'air + caractéristiques -> C11H22 + z (O2 + 3,76 N2) // // Caractéristiques connus par calibrage cf. Chapitre 5 //

r = 1,5 /* Richesse */

z_st = 16,5 /* Dosage massique stoechiométrique */

z= z_st/r /* Dosage massique réel */

nb_moles_O_2 = z /* Nombre de moles O2*/

nb_moles_N_2 = z/r * 3,76 /* Nombre de moles N2*/

Q_air = 0,3 /* Débit massique d'air [kg/h] */

Q_c = 0,031 /* Débit massique de carburant [kg/h] */

// Conversion en indication débitmètre de travail // ind_Q_air = (20,919*Q_air / 1,293) + 0,134

// Pour ces mêmes caractéristiques de travail, si proportion du mélange change, et qu'on utilise de l'air suroxygéné -> C11H22 + â (O2 + 2 N2) //

// Calcul rapport de débit et de la nouvelle richesse et pression partielle //

beta = Q_air/ Q_c /* Dosage massique réel */

r_newmélange = z_st/beta*(3/4,76) /* Calcul de la nouvelle richesse */

nb_moles_O_2_new = beta /* Nombre de mole de O2 */

nb_moles_N_2_new = beta/r_newmélange*2 /* Nombre de moles de N2*/

// Calcul de la fraction massique de O2 et de N2 //

x_O_2 = nb_moles_O_2_new/( nb_moles_O_2_new+nb_moles_N_2_new) x_N_2=1-x_O_2

// Temps de balayage en secondes et volume en litres // // Dimension tube //

L = 4,036 /* Longueur tube en mètre */

S = 0,053 * 0,053 /* Section tube en mètre carré */

t_balayage =( (L/Q_air/1,293)*S*3600*2) /* Calcul du temps de balayage en

secondes */

Volume_3manip = t_balayage * 3 * (Q_air/1,293)/3600*1000 /* Calcul du volume nécessaire pour un

total de 3 manipulations */

Volume_manip = Volume_3manip / 3 /* Volume pour une manipulation */

p_bouteille = 12 /* On fixe une pression de 12 bars dans

la bouteille */

V_bouteille = 43 /* Capacité de la bouteille 43 litres*/

p_O_2 = x_O_2 * p_bouteille /* Pression partielle en O2 */

P_N_2 = x_N_2 * p_bouteille /* Pression partielle en N2 */