à‰tude de l'initiation et de la propagation de la détonation dans les aérosols de kérosène liquide.

Chapitre 1

1 Détonations en phase gazeuse et détonations hétérogènes gouttelettes liquide/gaz

1.1. Généralités sur les détonations en phase gazeuse

1.1.1. Introduction

Dans les années 1870-1883, les premières observations des détonations en phase gazeuse ont vu le jour. Ce n'est qu'en 1881, que Berthelot et Vieille ainsi que Mallard et Le Chatelier mettent en évidence un phénomène de propagation stationnaire d'ondes supersoniques de combustion. Ce phénomène sera nommé onde explosive et actuellement connu sous l'appellation de détonation.

Le premier modèle de détonation voit le jour avec Chapman [1889] et Jouguet [1905]. Ce modèle assimile la détonation à une discontinuité monodimensionnelle plane se propageant avec une célérité supersonique dans un fluide réactif supposé parfait et qui transforme instantanément le fluide réactif (milieu des gaz frais) en produits de détonation c'est-à-dire en gaz brûlés à l'équilibre thermodynamique dit état final « Chapman-Jouguet » CJ.

Zeldovitch, Von Neumann et Döring ont proposé dans les années 40, un modèle plus réaliste décrivant l'onde de détonation plane et stationnaire comme étant une onde de choc dont la propagation supersonique est entretenue par les réactions chimiques qu'elle initie avec un certain délai.

1.1.2. Modélisation de la détonation [Chapman, 1899 ; Jouguet 1905]

Le modèle Chapman-Jouget (CJ) assimile la détonation à une surface de discontinuité plane, d'épaisseur infiniment mince, perpendiculaire à l'écoulement et totalement réactive qui se propage à la célérité D. L'onde de détonation ? se déplace à une célérité de propagation D dans le référentiel lié au laboratoire. (figure 1.1)

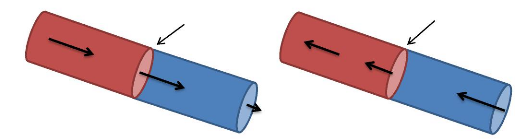
Gaz frais

????, ????, ????, ????

Gaz brûlés E

W1

D

????, ????, ????, ????

W0

Gaz brûlés

Gaz frais

????, ????, ????, ????

E

??1

????, ????, ????, ????

D

??0

référentiel lié au laboratoire (a) référentiel lié à l'onde (b)

Figure 1.1 - L'onde de détonation dans différents systèmes de coordonnées (a) par rapport au laboratoire et (b) par rapport à l'onde

W0 = -(D - ??0) ???? W1 = -(D - ??1) (1.1)

avec : W₀ et W₁ qui sont respectivement la vitesse du gaz frais et des gaz brûlés par rapport à l'onde de détonation.

Ce modèle a pour hypothèses que :

· l'onde de détonation est supposée plane, monodimensionnelle et stationnaire.

· le mélange réactif est parfait et uniforme

· l'écoulement est adiabatique, sans pertes d'énergie aux parois et les phénomènes de dissipation sont négligés.

Les équations de conservation de masse, de quantité de mouvement et d'énergie par rapport au référentiel lié à l'onde découlent de ces hypothèses :

??1W1 = ??0W0 (1.2)

??1W1² = ??0W0² (1.3)

h1 +

W2 1 2

= h0 +

W2 0 (1.4) 2

Page | 6

Page | 7

Où ??, ?? ???? h représentent respectivement la masse volumique, la pression et l'enthalpie absolue. Par combinaison de l'équation de conservation de masse (1.2) et celle de

la quantité de mouvement (1.3) dans un plan (??, ??) (figure 1.2) avec ?? = ¹/?? qui est le volume spécifique, l'expression du débit massique est la suivante :

??^2 -??^2 = -??0 = 0 ??0 2

??1 - ??0 = (1.5) ??1 - ??0

De cette équation (1.5) et par combinaison de (1.2) et (1.3), on trouve les vitesses relatives à l'onde :

??1 - ??0

??0 = ??0v (1.6)
??0 - ??1

??1 - ??0

??1 = ??1v (1.7)
??0 - ??1

En substituant ??₀ ???? ??₁ à l'équation de conservation d'énergie (1.4) à l'aide des expressions (1.6) et (1.7), l'équation de l'adiabatique dynamique ou adiabatique de Crussard dans le plan (??, ??) est obtenu :

1

h1 - h0 = 2 (??1 - ??0)(??0 + ??1) (1.8)

En ajoutant la chaleur de réaction ?????? = -??? h* = h₀^* - h₁^* ( h* est l'enthalpie de

^ ^

référence à la température ??*), et l'enthalpie sensible h

telle que : h

= h - h*.

Il vient :

1

^ - h0

h1 ^ - ??P?? = 2 (??1 - ??0)(??0 + ??1) (1.9)

P

zone de détonations

fortes

zone de détonations

faibles

Pcj

Po

F

CJ

f

v

vcj

vo

Page | 8

Figure 1.2 - Droite de Rayleigh-Michelson et adiabatique de Crussard dans le plan (p, y)

L'étude de l'existence de solutions physiques au système peut être illustrée par la représentation dans le plan (P, y). Les droites de Rayleigh-Michelson (RM) et l'adiabatique de Crussard (C) issues des conditions initiales du mélange réactif, sont représentées à la figure 1.2. Trois cas existent :

· la droite de Rayleigh-Michelson n'a pas d'intersection avec l'adiabatique de Crussard, il n'y a donc pas de solution pour la propagation de la détonation.

· la droite de Rayleigh-Michelson coupe la droite de Crussard en deux points « F » et « f » se situant respectivement dans une zone de détonations « fortes » et une zone de détonations « faibles ». Il est à noter que les détonations faibles n'ont jamais été observées expérimentalement, seul le point F est observé pour des célérités D supérieures à Dcj.

· la droite de Rayleigh-Michelson est tangente à l'adiabatique de Crussard au point CJ dit Chapman-Jouguet : cette solution unique correspond à une propagation d'onde de détonation sonique par rapport aux gaz brûlés, cela permet à l'onde de ne pas être rattrapée par une onde de détente, et donc de se propager de façon stable et autonome. En ce point, la célérité de détonation est minimale.

Graphiquement, lorsque la pression atteint une valeur au-delà de Pcj , la zone de détonations fortes est atteinte, en deçà de celle-ci la zone de détonations faibles est atteinte. (cf. Annexe AI : étude détaillée de l'état Chapman-Jouguet)