íãáÚáÇ
ËÍÈá Çæ
íáÇÚáÇ
âþàÌà'
ÉÑÇÒ?
ÉÜÈÇäÚ

BADJI MOKHTAR- ANNABA UNIVERSITY UNIVERSITE BADJI MOKHTAR
ANNABA
-ÑÇÊÎã ????
?????
Année : 2015
Faculté: Sciences de l'Ingéniorat
Département: Electronique
MEMOIRE
Présenté en vue de l'obtention du
diplôme de :MASTER
Intitulé
Modélisation et diagnostic des
systèmes non linéaires par ACP
à
noyaux
Domaine : Sciences et Technologies Filière :
Génie électrique
Spécialité:
Robotique et informatique industrielle
Par :DJOUDI Chemse-Eddine
DEVANT Le JURY
Président: BENSAOULA.Salah M.C.A
U.ANNABA
Directeur de mémoire: HARKAT.Mohamed-Faouzi Pr
U.ANNABA
Examinateur: BOULEBTATECHE.Brahim M.C.A
U.ANNABA
i
.emerciementf
Les travaux présentés dans ce mémoire ont
étéréaliséau sein du laboratoire des
Systèmes et Matèriaux Avancés (LASMA) - Universit Badji
Mokhtar Annaba
Je remercie tout d'abord Dieu tout puissant de m'avoir
donnéle courage, la force et la patience d'achever ce modeste
travail.
Je remercie tous les enseignants que j'ai eu tout au long de
cette formation, qui m'ont appris énormément.
Je tiens à exprimer mon respect et gratitude à mon
tuteur et encadreur Professeur Mohamed-Faouzi HARKAT pour le suivi de mon
mémoire, son aide ainsi que disponibilité.
Mes remerciements vont également à Monsieur Tarek
AIT IZEM pour ces judicieux conseils et soutien.
Je remercier également les membres de jury d'avoir
acceptéd'examiner et de juger ce travail.
Ainsi que je ne saurais trop remercier mes parents pour leur
soutien tout au long du parcours.
ii
A` ma mère
A` mes proches et amis
A`
tout ceux qui m'ont soutenu
A` ceux que j'aime et
qui m'aiment et
comptent pour moi
Chemse-?ddine.
iii
?'esum'e
Dans ce travail, nous avons présentéune approche
statistique multi-variables pour la modèlisation et le diagnostic des
sysèmes non linéaires. Cette approche, appelée analyse en
composantes principales à noyau, qui est une extension de l'ACP
classique au cas non linéaire, est basée sur une transformation
des données en utilisant une fonction Noyau(Kernel) pour la
linéairasation des des variables non linéaires initiales.
Ce travail est partagéen quatre chapitres,
organiés de la façon suivante :
Le premier chapitre présente un aperçu sur le
principe de diagnostic. Nous exposant les différentes étapes pour
la mise en place d'un système de surveillance, la structure
générale et la classification des méthodes
utilisées dans un système de diagnostic.
Dans le deuxième chapitre on à
présentéla description de la méthode ACP classique, ainsi
que ses différentes étapes pour la modèlisation,
détection et localisation de défauts.
Le troisième chapitre est consacréà l'ACP
à noyau. Oùla transformation noyau effectuant un changement de
base qui permet de projeter les données dans un nouvel espace est mise
en oeuvre, La modélisation est ainsi facilitée, par l'application
de l'ACP linéaire, puisque on passe d'un système initialement non
linéaire, à un autre linéaire. Par contre l'espace de
représentation sera de dimension plus importante que l'espace de
départ.
Le dernier chapitre compte à lui a
étéconsacréà l'application de la méthode du
diagnostic, oùle principe de l'ACP à noyau et de
modélisation et la génération de résidus sont
présentés à l'aide d'un simulateur du processus chimique
Tennessee Estman Challange Process (TECP).
Mots-clés : Diagnostic, Détection et localisation
de défauts capteurs, Analyse en Composantes Principales a' noyau,
Tennessee Estman
iv
?bstract
In this work, we presented a statistical multivariable
approach used for modeling and diagnosis of nonlinear systems, namely, Kernel
Principal Component Analysis (KPCA). This approach, which is an extension of
the classical PCA for nonlinear data, is based on a transformation of the
nonlinear input data using a kernel function, thus resulting in a new
representation with linear relations among the variables, where conventional
PCA can be used for modeling and diagnosis. This work is composed of four
chapters and is organized as follows:
The first chapter presents a global preview of diagnosis,
different steps for the establishment of a monitoring system are explained,
along with the different methods and approaches used in diagnosis, organized in
different classes.
In the second chapter we presented the classical principal
component analysis method, and its different steps, applied for modeling, and
fault detection and isolation.
The third chapteris devoted to the Kernel PCA, where a kernel
transformation is used for the projection of nonlinear data into a new linear
presentation space. The use of conventional PCA for modeling of the data is
then possible because of the new linear nature of the obtained data. However,
the new representation space is of higher dimension compared to the initial
space.
Finally, the last chapter contains the application of the
kernel PCA method for the modeling phase as well as fault diagnosis by
generating residuals on a chemical process, namely, the Tennessee Eastman
challenge process TECP.
Keywords : Diagnosis, Sensor fault detection and isolation,
Kernel Principal Components Analysis, Tennessee Estman
v
Table des matières
Table des Figures vii
Introduction générale 1
Chapitre 1
Introduction au diagnostic
1.1 Introduction 2
1.2 Principe du diagnostic et définitions 3
1.2.1 Principe du diagnostic 3
1.2.2 Définitions 4
1.3 Les différentes étapes du diagnostic d'un
système 4
1.4 Classification des approches de diagnostic 5
1.4.1 Les approches relationnelles 6
1.4.2 Les méthodes de traitement de données
6
1.4.3 Les méthodes à base de modèles
7
Chapitre 2
Analyse des composantes principale
2.1 Introduction à l'ACP 8
2.2 Identification du modèle ACP 9
2.3 Estimation des paramètres du modèle ACP
10
2.4 Détermination de la structure du modèle
14
2.4.1 Pourcentage cumuléde la variance totale (PCV)
14
2.4.2 Variance non reconstruite (VNR) 15
2.4.3 Validation croisée 16
2.4.4 Moyenne des valeurs propres 17
2.5 Détection et localisation de défauts 18
2.5.1 Génération de résidus par
estimation d'état 18
2.5.2 Statistique SPE 21
2.5.3 Statistique T2 de Hotelling 22
2.5.4 Localisation de défauts par ACP partielle 22
vi
Table des matières
Chapitre 3
L'ACP à Noyau (Kernel PCA)
3.1 Introduction 25
3.2 Méthodes à noyaux et Kernel PCA 26
3.2.1 Méthodes à noyaux 26
3.2.2 Kernel PCA 28
3.3 Détection et localisation en Kernel PCA 30
3.3.1 Détection en Kernel PCA 30
3.3.1.1 Statistique SPE . 31
3.3.1.2 Statistique T2 32
3.3.2 Localisation de défauts par KPCA partielle 32
3.4 Algorithme de base du Kernel PCA 33
4.1 Introduction 35
4.2 Description du processus 36
4.3 Identification du modèle Kernel PCA . 38
4.4 Détection et localisation de défauts 38
4.4.1 Détection de défauts 38
4.4.2 Localisation de défauts 39
Annexes
Conclusion générale 42
Bibliographie 43
vii
Table des figures

1.1 Structure générale d'un système de
diagnostic 3
1.2 Les différentes étapes d'un système
4
1.3 Les différentes méthodes de diagnostic 6
2.1 Déroulement D'une analyse en composantes
principales.(a) Distribution
d'entrée.(b) Centrage et réduction de cette
distribution 10
2.2 Mesures simulées de x1...x7 du premier exemple
d'illustration 12
2.3 Évolution de toutes les composantes du premier exemple
d'illustration . 13
2.4 Évolution du PCV en fonction du nombre de composantes
15
2.5 Évolution du VNR en fonction du nombre de composantes
16
2.6 Évolution du PRESS en fonction du nombre de
composantes 17
2.7 Évolution des Valeurs propres en fonction du nombre de
composantes . . 18
2.8 Évolution de La projection de X sur les premiers
(l) et dernièrs (in - l)
vecteurs propre de 20
2.9 Comparaison entre X et l'estimationXà à
partir des composantes principale . 20 2.10 Indice SPE dans le cas sain et le
cas défaillant avec un seuil de 95% . . . . 21
2.11 Indice T2 dans le cas sain et le cas
défaillant avec un seuil de 95% 22
2.12 Procèdure de structuration de résidus par ACP
partielles 23
2.13 Procèdure de localisation par ACP partielles
structurée 23
2.14 L'évolution des SPE des modèles réduits
24
2.15 Table des signatures théoriques 24
3.1 Représentation des données non linéaire
par ACP classique 25
3.2 Représentation des données non linéaire
par KPCA . 26
3.3 Représentation en utilisant des fonctions de bases
Ö 26
3.4 Concept global du KPCA . 31
3.5 Procédure de structuration de résidus par KPCA
partielles 33
3.6 Procédure de localisation par KPCA partielles
structurée 33
3.7 Représentation de l'algorithme de KPCA . 34
4.1 La description du procéssus 36
4.2 La description des variables mesurées 36
4.3 Les variables mesurées pour la simulation 37
4.4 Simulateur Tennessee Estman Process 37
4.5 Évolution de l'indice SPE cas sain et
défaillant 38
4.6 Table des signatures théoriques 39
4.7 L'évolution des SPE des modèles réduits
40
1
ntroduction générale
Certes, l'automatisation des procédés
industriels, de plus en plus complexes, a permis des gains importants en termes
de productivitéet de qualité. Cependant, les systèmes
automatisés de production sont devenus vulnérables
aux défaillances. Une
vulnérabilitéàl'origine de coûts
importants en termes de sécuritépour faire face aux risques
d'accidents,
de pollutions, ... et en termes de disponibilitépour
améliorer la productivité, ... En fait, une défaillance
d'une partie du processus peut endommager tout le système de production
pouvant engendrer des pertes en vies humaines et des dommages sur le plan
économique et écologique. Ainsi, les défaillances plus ou
moins critiques représentent une limite aux bénéfices
résultant de l'automatisation.
Cette situation a justifiéla mise en oeuvre d'une
recherche scientifique ayant pour objectif le développement des
approches fiables de surveillance de systèmes afin de détecter de
façon précise et précoce l'apparition des défauts
et de trouver des solutions adaptées à chaque
procédéindustriel.
Dans la littérature, il existe une multitude de
méthodes pour aborder ce type de
problème, parmi ces méthodes, l'Analyse en
Composantes Principales (ACP), qui a étélargement
utilisée pour la détection et la localisation des défauts
de capteurs. Cette technique est classée parmi les méthodes sans
modèle à priori, le modèle se révèle
àposteriori par la collecte de données recueillies sur
le systéme en fonctionnement normal
sans effectuer une distinction entre ses entrées et ses
sorties.
Son principe consiste à transformer les variables d'un
système en un nombre restreint de nouvelles variables, appelées
composantes principales, via une projection orthogonale exploitant les
combinaisons linéaires ou quasi-linéaires entre les variables
d'origine. Le nouvel espace de repr'sentation réduit est
partitionnéen deux parties, à savoir, l'espace principal et
résiduel, à partir desquels les techniques de détection et
de localisation des défauts sont utilisées pour la surveillance
du processus.
Seulement, la plupart des systémes sont dynamiques et
non linéaires. Ainsi l'application de l'ACP classique n'est pas
trés adaptée à ce type de données, afin de
contourner cette difficulté, plusieurs approches ont
étédéveloppées, l'ACP non linéaire
basée sur les réseaux de neurones (Tan and Mavrovouniotis, 1995),
l'ACP non linéaires avec l'utilisation de la programmation
génétique (Hiden et al. 1999), l'ACP à noyau (Kernel PCA)
(Schokopf et al. 1998). d'autre auteurs y ont contribué, on peut en
citer Jie Yu(2012), Qin et al(2001), Lee et al(2004).
Dans ce travail, nous avons choisi d'exploiter l'ACP à
noyau (kernel PCA), pour aborder la modèlisation et le diagnostic des
défauts dans les applications industrielles qui possèdent un
grand nombre de variables (capteurs/actionneurs) non linéaires. L'ACP
à noyau, a attirél'attention des chercheurs, par sa
capacitéd'extraire la corrélation non linéaire entre les
variables et du fait qu'elle ne fait appel à aucune procédure
d'optimisation pour l'estimation du modèle ACP non linéaire,
comme c'est le cas de l'ACP utilisant les réseaux de neurones. C'est ce
qui conforte notre choix.

2
ntroduction au diagnostic
Sommaire
1.1 Introduction 2
1.2 Principe du diagnostic et définitions
3
1.3 Les différentes étapes du diagnostic
d'un système 4
1.4 Classification des approches de diagnostic
5
1.1 Introduction
En raison d'une modernisation incessante des outils de
production, les systèmes industriels deviennent de plus en plus
complexes et sophistiqus. En parallèle, la fiabilité, la
sûretéde fonctionnement sans oublier la protection de
l'environnement sont devenues de véritables enjeux pour les entreprises
actuelles. Le diagnostic des systèmes est apparu dans le but
d'améliorer les points précédents. Discipline de
l'automatique à part entière, ce module de surveillance qu'est le
diagnostic fait l'objet d'un engouement prononcédepuis des
décennies. En effet, la recherche dans ce domaine n'a fait que prendre
de l'importance dans le monde entier, aussi bien de manière
théorique que pratique.
Dans ce contexte, de nombreuses approches sont
développées, en vue de la détection de défaillances
et du diagnostic, par les différentes communautés de recherche en
automatique, intelligence artificielle... etc. Les méthodes se
différencient par rapport au type de connaissance a priori sur le
processus qu'elles nécessitent. Ainsi, elles peuvent être
classées, de faon générale, comme des méthodes
à base de modèles, à base de connaissances et des
méthodes à base de données historiques. Les
méthodes à base de modèles considèrent un
modèle structurel du comportement du processus basésur des
principes physiques fondamentaux. Ces modèles peuvent être de type
quantitatif, exprimés sous forme d'équations mathmatiques ou bien
de type qualitatif, exprimés par exemple sous forme de relations
logiques. Les méthodes à base de connaissance exploitent les
compétences, le raisonnement et les connaissances des experts sur le
processus pour les transformer en règles, de manière à
résoudre des problèmes spécifiques. Enfin, les
méthodes à base de données cherchent à
découvrir des informations, sous forme d'exemples type ou tendances, au
sein des mesures venant des capteurs et des actionneurs, pouvant identifier le
comportement du procédé. Ces méthodes comprennent, parmi
d'autres, les méthodes d'apprentissage et de classification (ou
reconnaissance de formes).
Principe du diagnostic et définitions Introduction au
diagnostic
Sachant que nous ne disposons pas souvent d'un modèle
de comportement réel, un travail de simulation s'impose. Au cours de ces
vingt dernières années, les outils informatiques pour la
modélisation et la simulation des procédés se sont
développés conjointement avec les outils et techniques
informatiques. La technologie des ordinateurs a considérablement
évoluéet les langages ont progressé, passant d'une
approche procédurale à une approche orientée objet. En
cette dernière décennie, les simulateurs dynamiques se sont
améliorés en termes de structure et de fonctionnalité.
L'informatique est aujourd'hui le carrefour de plusieurs voir toutes
sciences.
1.2 Principe du diagnostic et définitions
1.2.1 Principe du diagnostic
De manière générale, un système
industriel est composéde trois parties : - Les actionneurs
- Le procédé- Les capteurs
Les défauts peuvent survenir sur chacune de ces trois
parties.
Le diagnostic de défaut consiste donc en la
détermination du type, de l'amplitude,
de la localisation et de l'instant d'occurrence td d'un
défaut, il comprend trois étapes
successives :
- La détection du défaut
- l'isolation du défaut
- L'identification du défaut
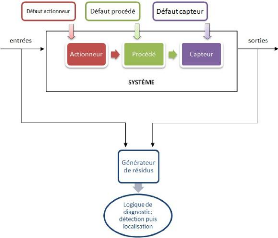
3
Figure 1.1 - Structure générale d'un système
de diagnostic
Principe du diagnostic et définitions
Introduction au diagnostic
1.2.2 Définitions
La surveillance et la supervision
constituent un complément du diagnostic. La
surveillance d'un système est une tâche continue
et en temps réel pour déterminer l'état d'un
système. Elle se fait à travers l'enregistrement des informations
pouvant indiquer la survenue d'éventuelles anomalies dans le
comportement du système. Quant à la supervision, elle consiste en
la prise de décisions appropriées, lors de l'étape de
surveillance du système, afin de maintenir le
fonctionnement nominal du système malgrél'apparition
de défauts.
L'ensemble de ces tâches vise à assurer les
performances optimales du système, en termes de disponibilité,
fiabilitéet maintenabilité. Cela équivaut à
prévenir la survenue de pannes. Une panne est un dysfonctionnement voire
une défaillance autrement dit un arrêt de fonctionnement
momentanéet accidentel, d'une partie ou de tous les composants d'un
système matériel.
Il est opportun, lors du diagnostic d'un système, de
différencier défaut et perturbation. Une perturbation
est une entrée inconnue et non commandée qui agit sur un
système. Contrairement au défaut, qui est
interne au système, une perturbation est une entrée
exogène au système.
1.3 Les différentes étapes du diagnostic
d'un système
Le diagnostic d'un système industriel nécessite un
certain nombre d'étapes (Fig 1.2)
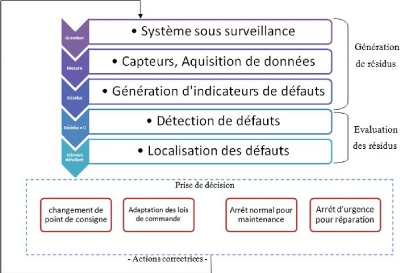
Figure 1.2 - Les différentes étapes d'un
système
4
Les différentes étapes du diagnostic d'un
système Introduction au diagnostic
5
Acquisition de données : La
procédure de diagnostic nécessite de disposer de l'information
sur le fonctionnement du système à surveiller, les fonctions
suivantes doivent être réalisées:
- conditionnement et pré-traitement du signal.
- validation du signal de mesure.
Étape d'élaboration d'indicateurs de
défauts: À partir des mesures réalisées et
des observations issues des opérateurs en charge de l'installation, il
s'agit de construire des indicateurs permettant de mettre en évidence
les éventuels défauts pouvant apparaître au sein du
système. Dans le domaine de diagnostic, les indicateurs de
défauts sont couramment dénommés les résidus aux
symptômes. Un résidu représente un écart entre une
grandeur estimées et mesurées. Cet écart de comportement
doit donc être idéalement nul en l'absence de défaut et
différent de zéro dans le cas contraire.
Étape de détection : C'est
l'opération qui permet de décider si le système est en
fonctionne- ment normal ou non. On pourrait penser qu'il suffit de tester la
non nullitédes résidus pour décider de l'apparition d'un
défaut.
Étape de localisation: la localisation
suit l'étape de détection, elle attribue le défaut
à un sous-système particulier (capteur, actionner, organe de
commande, processus...).
Étape de prise de décisions :
le fonctionnement incorrect du système étant constaté, il
s'agit de décider de la marche à suivre afin de conserver les
performances souhaitédu système sous surveillance. Cette prise de
décision doit permettre de générer, eventuelle-
ment sous le contrôle d'un opérateur humain, les
actions correctrices nécessaires à un retour à la normale
du fonctionnement de l'installation.
1.4 Classification des approches de diagnostic
La classification des approches est
déterminéselon le type de méthode ou de modèle
utilisés. Dans la plupart des cas, les méthodes du diagnostic
sont liées à la connaissance disponible sur le
procédéou à sa représeutation et sont
classées de différentes façons.
A partir de ces considérations, nous proposons une
classification non exhaustive des méthodes de diagnostic selon trois
axes : les approches relationnelles, les méthodes de traitement de
données (méthodes qualitatives et méthodes quantitatives)
et les approches à base de modèles. Pour ce dernier, nous avons
fait apparaître deux branches concernant les méthodes
quantitatives et les méthodes qualitatives liées au domaine du
continu et une branche spécifique concernant les méthodes
discrètes. Cette organisation est présentée sur la (Fig
1.3)
6
Classification des approches de diagnostic Introduction au
diagnostic
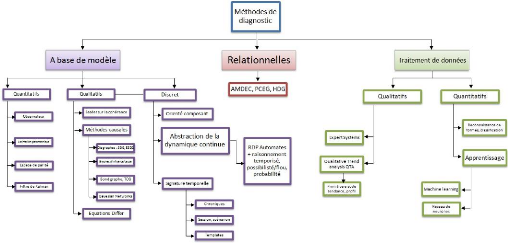
Figure 1.3 - Les différentes méthodes de
diagnostic
1.4.1 Les approches relationnelles
Les approches relationnelles sont des méthodes issues
du contexte de la sûretéde fonctionnement qui associe des causes
à des symptômes. Elles sont basées, en
général, sur des systèmes à base de règles,
de dictionnaires de défauts ou de graphes avec un raisonnement de
parcours ou adductif, sur la méthode AMDEC (Analyse des Modes de
D'efaillance, de leurs Effets et de lours Criticités), sur les
graphes PCEG (Possible Cause and effect graph), HDG
(Hazap-digraph) ou sur les réseaux Boyesians. Ce sont des
approches de diagnostic fondées sur une connaissance associative
dépendante du système et sur une connaissance a priori des
défauts et de leurs effets. Elles manquent d'un pouvoir de
réutilisabilitéet nécessitent une
énumération de tous les défauts possibles. Dans le cas des
prorédés complexes qui nous préoccupe, le nombre
élevéde variables, de composants et de modes opératoires,
rend leur utilisation peu adaptée.
1.4.2 Les méthodes de traitement de
données
Les méthodes de traitement de données exploitent
des observations quantitatives et/ou qualitatives disponibles sous la forme de
données historiques ou de résultats de traitement en ligne de
signaux issus des capteurs. Ce sont des approches envisageables quand
l'obtention d'un modèle analytique du
procédés'avère difficile, et lorsqu'un raisonnement sur
les comportements dynamiques (variables et relations) du
procédén'est pas utile. Le comportement de
référence d'un signal, en général statistique,
peut être représentatif de l'état normal de
l'installation ou d'un défaut particulier. Les approches de
classification
Classification des approches de diagnostic Introduction au
diagnostic
7
de données (reconnaissance de formes) sont
fondées sur l'analyse des données issues des signaux
corrélés entre eux pour la discrimination des différentes
modes de fonctionnement et certains modes de défaut. Toutes ces
approches sont fortement dépendantes d'un grand volume des
données, ce qui les limitent en général à la
détection. Le diagnostic dépend donc de la représentation
et de la discrimination de tous les modes de défaut. Dans le cadre du
suivi de régions transitoires, les méthodes d'AQT sont les plus
utilisées. Le diagnostic cependant est fondésur un
mécanisme d'inférence qui dépend d'une connaissance assez
large des modes de défaut et de la prise en compte des techniques
d'alignement temporel.
1.4.3 Les méthodes à base de
modèles
Les approches à base de modèles
s'appuient sur des modèles comportementaux explicites du
système soumis au diagnostic. Un grand avantage de ces approches par
rapport aux approches relationnelles et de traitement de données,
réside sur le fait que seule l'information du comportement normal du
procédéest prise en compte par l'intermédiaire d'un
modèle de référence. La précision du modèle,
liée aux besoins de la surveillance et aux critères de
performance du diagnostic, définit le choix de l'utilisation de
modèles quantitatifs, qualitatifs ou semi-qualitatifs. Selon, les
méthodes de diagnostic à base de modèles présentent
les avantages suivants :
- La connaissance sur le système est
découplée de la connaissance de diagnostic
- Il s'agit de connaissance de conception plutôt que
d'exploitation
- Les fautes et les symptômes ne doivent pas être
anticipés
- Le coût de développement et de maintenance est
moindre
- Les modèles fournissent un rapport adéquat pour
l'explication (structure du système explicitement
repnésentée).

8
?nalyse en composantes principales
Sommaire
2.1 Introduction à l'ACP 8
2.2 Identification du modèle ACP
9
2.3 Estimation des paramètres du modèle
ACP 10
2.4 Détermination de la structure du
modèle 14
2.5 Détection et localisation de défauts
18
2.1 Introduction à l'ACP
L'analyse en composantes principales (ACP) est une
méthode mathématique d'analyse graphique de données qui
consiste à rechercher et mettre en évidence les relations qui
existent entre les variables, sans tenir compte, à priori d'une
quelconque structure, et élabore un modèle du système
à partir de données prélevées sur ce dernier L'ACP
élabore un modèle du système à partir de
données prélevées sur ce dernier.
L'identification du modèle repose sur deux
étapes : la première consiste à estimer ses
paramètres alors que la seconde consiste à déterminer sa
structure.
Une fois le modèle ACP identifié, des
résidus peuvent être générés en comparant le
comportement observéà celui donnépar le modèle ACP
de référence, Ces résidus permettent de détecter
puis de localiser l'ensemble des variable en défaut.
Le but de l'ACP est donc de trouver un ensemble de facteurs
(composantes) qui ait une dimension inférieure à celle de
l'ensemble original de données et qui puisse décrire correctement
les tendances principales.
Ce chapitre concernera la présentation et le
développement des différentes procédures de diagnostics
à base d'ACP en termes de traitement de données recueillies, et
détection et de localisation de défauts capteurs.
Identification du modèle ACP Analyse en composantes
principales
9
2.2 Identification du modèle ACP
L'identification du modèle ACP débute par la
construction d'une matrice contenant l'ensemble des données disponibles
sans distinction entre les entrés et les sorties du système.
Ces données sont supposées être recueillies
sur un système statique en fonctionnement normal (données
saines).
Au départ on aura des données recueillies sur
différents capteurs x1 xm :
Notre matrice de données Xd ?
[N×m]
formée par la concaténation des vecteurs xi(K)
obtenus à différents instants est :
Xd (k) = [x1(K)T x2(K)T ... ...
xm(K)T
Où: i [1 : m]
N étant le nombre de mesure ou itération (k) m est
le nombre de capteurs ( variables ) Ce qui donnera la Matrice de données
suivante :
|
x1 (1) ? x1 (2)
Xd = ???????
.
x1 (N)
|
x2 (1) .
x2 (2) .
.
x2 (N) .
|
. . xm (1)
. . xm (2) ?
???????
.
. . xm (N)
|
Généralement les données sont
exprimées par des unités et des échelles
différentes. Pour cela on centre les données en premier lieu.
Puis afin de rendre les résultats indépendants des unités
utilisées pour les différentes variables, on réduit ces
dernières par rapport a leur variance respective. Les données
ainsi obtenues sont centrées et réduites, elles sont de moyenne
nulle et de variance unité.
Chaque colonne Xj de la nouvelle matrice de donnée
centré-réduite est donnée par :
Où: Mj = La moyenne de tout les prélèvements
[1 : N] de la colonne j ój = écart type ( qui est égale
à la racine carrée de la variance)
Xd j - Mj pour le centrage de nos données,
qu'on divise par la suite sur ój pour la réduction.
La moyenne est donnée par :
Identification du modèle ACP Analyse en composantes
principales
La variance est donnée par :
|
XN
ó2 j = 1
N
k=1
|
(xj (k) -
Mj)2
|
10
La nouvelle matrice des données normalisées est
donnée par :
X = ( X1 ...
Xm)
La matrice de corrélation est donnée par :
l'effet du centrage et de réduction d'une distribution
de données est illustrépar la Figure ci-dessous :
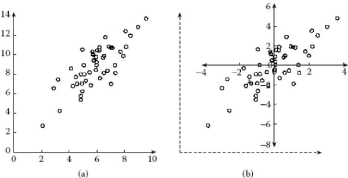
Figure 2.1 - Déroulement D'une analyse en composantes
principales.(a) Distribution
d'entrée.(b) Centrage et
réduction de cette distribution
2.3 Estimation des paramètres du modèle
ACP
L'estimation des paramétres du modèle ACP se
résume en une estimation des valeurs et vecteurs propres de la matrice
de corrélation Ó . Une décomposition spectrale de cette
dernière nous donne :
Estimation des paramètres du modèle ACP Analyse
en composantes principales
|
> >m
= P ? PT =
i=1
|
ëipipTi
|
Où: pi est le ieme vecteur propre de Ó
et ëi est la valeur propre correspondante.
S'il existe q relations linéaires entre les colonnes de
X, on aura q valeurs propres nulles. La matrice X peut être
représentée par les première (m-q) = l composantes
principales.
l correspond au nombre de valeurs propres non nulles.
Toutefois les valeurs propres égales à zéro sont rarement
rencontrées en pratique (relation quasi-linéaire, bruits, ...
etc). Donc, il est nécessaire de déterminer le nombre l
représentant le nombre de vecteurs propres correspondant aux valeurs
propres dominantes.
Pour illustrer ce qui a étédit jusqu'a
présent sur l'ACP linéaire, on va présentéun
exemple de simulation, qui sera ensuite utilisépour illustrer les
différentes méthodes
présentéprécédemment, et qui va nous suivre tout au
long de ce chapitre.
Nous disposons de 7 variables qui représentent notre
système et qui sont décrites par les équations suivantes
:
x1 = u1 + î1
x2 = u2 + î2
x3 = x1 + î3
x4 = x1 + î4
x5 = x2 + î5
x6 = x2 + î6
x7 = x2 + î7
Où: les bruits de mesureîi,j sont des
bruits aléatoires qui prennent des valeurs réparties entre -0.05
et + 0.05, u1 et u2 sont des signaux en forme créneaux dont les
amplitudes sont comme suite :
1
u1 = sin t - 3 sin 3t +
1
5 sin 5t
11
1 1
u2 = cos t- 3 cos 3t + 5 cos 5t
Les mesures simulées des variables sont
représentéci-dessous :
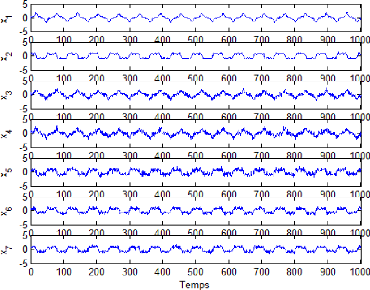
Estimation des paramètres du modèle ACP Analyse
en composantes principales
Figure 2.2 - Mesures simulées de x1...x7 du premier
exemple d'illustration
La matrice de corrélation des variables est
donnée par :
|
1.0000
|
0.0056
|
0.9269
|
0.8714
|
-0.0013
|
0.0170
|
-0.0070
|
?
|
|
0.0056
|
1.0000
|
-0.0043
|
0.0131
|
0.8807
|
0.9509
|
0.9488
|
?
|
|
0.9269
|
-0.0043
|
1.0000
|
0.8098
|
-0.0097
|
0.0029
|
-0.0151
|
? ?
|
|
0.8714
|
0.0131
|
0.8098
|
1.0000
|
0.0016
|
0.0268
|
0.0010
|
? ?
|
|
-0.0013
0.0170
|
0.8807
0.9509
|
-0.0097
0.0029
|
0.0016
0.0268
|
1.0000
0.8431
|
0.8431
1.0000
|
0.8422
0.9013
|
? ? ?
|
|
-0.0070
|
0.9488
|
-0.0151
|
0.0010
|
0.8422
|
0.9013
|
1.0000
|
?
|
X= [
12
Les matrices des valeurs et vecteurs propres sont données
par :
ë = [
|
3.6883
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
2.7443
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0.1967
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0.1845
|
0
|
0
|
0
1
|
|
0
|
0
|
0
|
0
|
0.0913
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0.0657
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0.0291
|
Estimation des paramètres du modèle ACP Analyse
en composantes principales
|
?
p=
?????????
|
0.0061 0.5133 0.0003 0.0100 0.4831 0.5018 0.5013
|
-0.5902 0.0034 -0.5772 -0.5642 0.0083 -0.0038 0.0110
|
0.1817 -0.0490 0.5537 -0.7533 0.2658 -0.1217 -0.0716
|
-0.0534 -0.1848 -0.1744 0.2411 0.8284 -0.2938 -0.3191
|
0.0393 0.0164 -0.0113 -0.0481 -0.0074 0.7006 -0.7106
|
0.7837 -0.0129 -0.5742 -0.2315 -0.0011 -0.0292 0.0390
|
0.0089 0.8364 -0.0126 0.0027 -0.0978 -0.3942 -0.3678
|
?
? ? ? ? ? ? ? ? ?
|
t1 =
t2 =
t3 =
t4 =
t5 =
t6 =
t7 =
|
+0.0061x1
|
+ 0.5133x2
|
+ 0.0003x3
|
+ 0.0100x4
|
+ 0.4831x5
|
+ 0.5018x6
|
+ 0.5013x7
|
|
-0.5902x2
|
+ 0.0034x2
|
- 0.5772x3
|
- 0.5642x4
|
+ 0.0083x5
|
-
|
0.0038x6
|
+ 0.0110x7
|
|
+0.1817x1
|
- 0.0490x2
|
+ 0.5537x3
|
- 0.7533x4
|
+ 0.2658x5
|
-
|
0.1217x6
|
- 0.0716x7
|
|
-0.0534x1
|
- 0.1848x2
|
- 0.1744x3
|
+ 0.2411x4
|
+ 0.8284x5
|
-
|
0.2938x6
|
- 0.3191x7
|
|
+0.0393x1
|
+ 0.0164x2
|
- 0.0113x3
|
- 0.0481x4
|
- 0.0074x5
|
+ 0.7006x6
|
- 0.7106x7
|
|
+0.7837x1
|
- 0.0129x2
|
- 0.5742x3
|
- 0.2315x4
|
- 0.0011x5
|
-
|
0.0292x6
|
+ 0.0390x7
|
|
+0.0089x1
|
+ 0.8364x2
|
- 0.0126x3
|
+ 0.0027x4
|
- 0.0978x5
|
-
|
0.3942x6
|
- 0.3678x7
|
Ainsi, on peut tracer l'évolution des composantes t1, ...,
t7 de cet exemple.
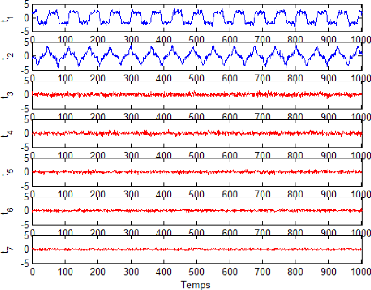
13
Figure 2.3 - Evolution de toutes les composantes du premier
exemple d'illustration
Détermination de la structure du modèle Analyse
en composantes principales
14
A partir de (Fig 2.3), on remarque que les composantes t1,
..., t7 ne représentes que du bruit alors que les deux premières
composantes sont porteuse d'information et sont corrélées avec
les variables originelles (car elle sont obtenues par combinaison linaire de
ces dernires).
Cependant, pour l'estimation des variables originelles on ne
doit conserver que les composantes porteuses d'information significative
permettant d'expliquer les différentes variables. La prochaine partie de
ce chapitre sera consacréla détermination de la structure du
modèle ACP, c'est a dire la détermination du nombre de
composantes à conserver ou à retenir dans le modèle.
2.4 Détermination de la structure du
modèle
L'analyse en composantes principales a pour but
d'établir une approximation de la matrice initiale des données X,
par une matrice de rang inférieur. La question qui se pose alors et qui
a étélargement débattue dans la littérature,
concerne le choix du nombre de composantes à retenir, de nombreuses
règles sont proposées dans la littérature pour
déterminer ce nombre.
Dans le carde de l'application de l'ACP au diagnostic, le
nombre de composantes a un impact significatif sur chaque étape de la
procédure de détection et de localisation, si peu de composantes
sont utilisées, on risque de perdre des informations et voir
établir un faux diagnostic ce qui provoquera des fausses alarmes, si par
contre beaucoup de composantes sont utilisées, on risque de prendre des
composantes ayant les valeurs propres les plus faibles, qui sont porteuses de
bruit ce qui est indésirable. On peut voir ce type de composantes dans
la (Fig 2.3).
En plus il y a risque de non détection des
défauts, si certaines variables sont projetées dans le
sous-espace des composantes principale alors qu'elles doivent être
projetées dans le sous-espace résiduel.
On va citéquelques critères qui vont nous
permettre de bien choisir ce nombre.
2.4.1 Pourcentage cumuléde la variance totale
(PCV)
Il mesure le pourcentage de la variance capturée par les l
composantes retenues. Sachant que chaque composantes principale est
représentative d'une portion de la variance des mesures du processus
étudié. Les valeurs propres de la matrice de corrélation
sont les mesures de cette variance et peuvent donc être utilisées
dans la sélection du nombre de composantes principale.
Le nombre de composantes est alors le plus petit nombre pris
de telle sorte que ce pourcentage soit atteint ou dépassépar
exemple 90% ou 95% ou voir 99%.
Pl j=1 Àj
P CV (l) = 100(Im )%
j=1 Àj
Détermination de la structure du modèle Analyse
en composantes principales
15
Sa capacitéa fournir le nombre correct de composantes
principale dépend fortement du rapport signal sur bruit, car la variance
du bruit est inconnue à priori, donc ce critère reste un peut
subjectif.
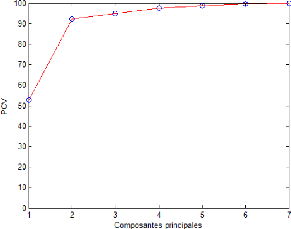
Figure 2.4 - Évolution du PCV en fonction du nombre de
composantes 2.4.2 Variance non reconstruite (VNR)
Lorsque le modèle ACP est utilisépour
reconstruire des valeurs manquantes ou des variable défectueuses,
l'erreur de reconstruction est une fonction du nombre de composantes
principale. Le minimum trouvédirectement dans le calcul du V NR
(variance non reconstruite) détermine le nombre de composantes
à retenir, le V NR de la jemme variable est
une fonction de l.
|
ój (l) = var {îT j
(x - xj)} =
|
îT P îj j
|
|
( )2
îT j îj
|
Où: îj =
Cîj et îj
correspond au jemme colonne de la matrice
identité.
Détermination de la structure du modèle Analyse
en composantes principales
Pour trouver le nombre optimal des composantes, il faut
minimiser la variance ój (l). En considérant tous les
défauts possibles, le critère VNR à minimiser est le
suivant :
|
V NR (l) =minl
|
Xm j=1
|
ój (l)
var {îT j
x}
|
=minl
|
Xm j=1
|
ój (l)
îT P îj j
|
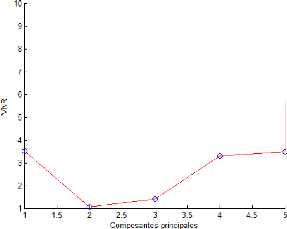
16
Figure 2.5 - Évolution du VNR en fonction du nombre de
composantes 2.4.3 Validation croisée
La validation croisée est un critère statistique
très populaire pour le choix du nombre de composantes utile pour un
modèle ACP. Cette procédure de validation croisée est
basée sur la minimisation de la somme des carrées des erreurs de
prédiction (PRESS) entre les données observées et celles
estimées par le modèle obtenu à partir d'un jeu
d'identification différent :
|
XN
1
PRESS (l) = Nm
k=1
N étant la taille du jeu de validation.
|
Xm i=1
|
( )2
àx(l)
i (k) - xi (k)
|
Détermination de la structure du modèle Analyse
en composantes principales
17
Une version simplifiée de l'algorithme permettant le
calcul du nombre de composantes principales par la validation croisée
est la suivante :
1 - Diviser les données en un jeu d'identification et un
jeu de validation.
2 - Réaliser une ACP avec l composantes (l
= 1,...., in) sur le jeu d'identification et calculer les
critère correspondant sur le jeu de validation PRESS(1), ...,
PRESS(in).
3 - La leme composante
pour laquelle le minimum de PRESS apparait sera la dernière
composante à retenir et l sera le nombre de composantes
retenu.
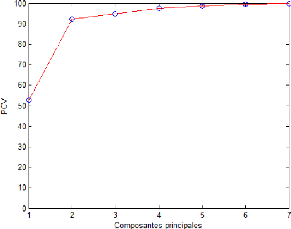
Figure 2.6 - Évolution du PRESS en fonction du nombre de
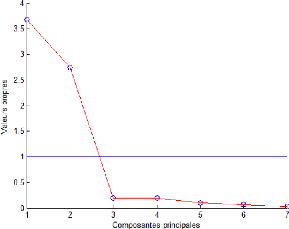
composantes 2.4.4 Moyenne des valeurs propres
Il consiste à prendre en considération que les
composantes pour lesquelles la valeur propre est supérieure à la
moyenne arithmétique de toutes les valeurs propres.
En ACP on travaille sur des données centrées
réduites, cela revient à négliger les composantes ayant
une variance inférieur a l'unité
1
in
strace( ) = 1
Détection de défauts Analyse en composantes
principales
18
Figure 2.7 - Évolution des Valeurs propres en fonction du
nombre de composantes 2.5 Détection de
défauts
En diagnostic à base de modèle analytique, la
phase de détection de défaut est liée à
l'étape de génération de résidus qui a pour but de
générer, à partir d'un modèle de bon fonctionnement
du processus et des mesures disponibles, des signaux révélateurs
de la présence de défauts, appelés résidus. A
partir de l'analyse de ces résidus, l'étape de prise de
décision doit alors indiquer si un défaut est présent ou
non. Il existe deux approches pour la génération des
résidus : l'approche par estimation d'état et l'approche par
estimation des paramètres. Dans ce memoire on va utiliséla
première approche.
2.5.1 Génération de résidus par
estimation d'état
La présence d'un défaut affectant l'une des
variable provoque un changement dans les corrélations entre les
variables indiquant une situation inhabituelle, les relations entre les
variables ne seront plus vérifiées.
La projection du vecteur de mesures dans le sous-espace des
résidus va croitre par rapport à sa valeur dans les conditions
normales, et le défaut nous sera alors visible, pour détecter un
tel changement dans les corrélation entre les différentes
variables, l'ACP utilise plusieurs indices,notamment La statistique SPE, ou
T2de Hotelling.
Détection de défauts Analyse en composantes
principales
19
Une fois le nombre de composantes à retenir est
déterminé, la matrice X peut être approximée
à partir des l premières composantes principale qui correspondent
au l plus
grandes valeurs propres de la matrice :
|
Xà =
|
Xl i=1
|
TipT i =
|
Xl i=1
|
XpipT i
|
La matrice des vecteurs propres et la matrice des composantes
principales peuvent
|
être décomposées en deux sous-matrices : P
= [ Pà P] et T = [
|
Tà T ]
|
Où:
P à et
T àreprésentent les matrices des l
premiers vecteurs propres qui correspondent aux l premières composantes
principale, et l'inverse pour P et T représentent les matrices des (m
- l) vecteurs propres qui correspondent aux dernières composantes
principales. Sachant que TN×m est
donnée par:
T = X P = X [ Pà P]
On peut dire ainsi que:
Tà = X Pà
Et :
Xà = Tà Pà T
T àreprésente la projection de X sur l
les premiers vecteurs propre de .
T = X P
Et :
X = T P T
Où:
T représente la projection de X sur les (m - l) derniers
vecteurs propres. X représente la matrice des résidus qu'on
notera E.
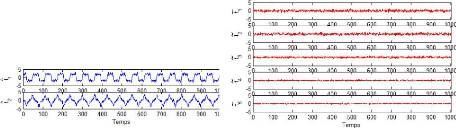
Détection de défauts Analyse en composantes
principales
20
Figure 2.8 - Évolution de La projection de X sur les
premiers (l) et dernièrs (m - l)
vecteurs propre de E
La décomposition de la matrice X donnera :
X = Xà + X = Xà + E
On note :
E = X C et Xà = X Cà
Oû:
Cà= PàPàT
et C = (I - Cà)
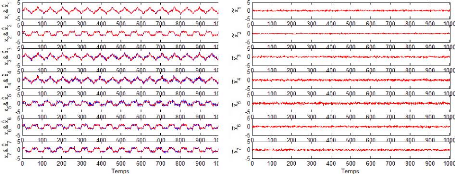
Figure 2.9 - Comparaison entre X et son estimation
Xà à partir des l premières
composantes
principale
Détection de défauts Analyse en
composantes principales
2.5.2 Statistique SPE
L'indicateur de détection SPE (Squared Prediction
Error) réalise la détection de défauts dans l'espace
résiduel. A l'instant k, il est donnépar :
SPE (k) = k1 (k)k 2 = xTx = Êm
~x2j(k)
j=1
Le processus est considéréen fonctionnement
anormal (présence d'un défaut) à l'instant ksi:
SPE (k) > ä2á
Oùä2 est le seuil de détection du
SPE(k) qui est approximépar : :
|
" 2
cá V2è2h6 è2h0(h0 - 1)
äá = è1 è1 + 1 +
è2
1
|
1 h0
|
Soit :
Pour i=1,2,3 et ëi est la jemme valeur
propre de la matrice E .
|
Où: h0 = 1 - 2è1è3
3è2 2 et Cá =
|
[(11e112)h0-1-è2h0(hè20-1
1
|
|
v2è2h2
0
|
|
Cá est la limite au seuil de confiance (1 -
á).
21
Figure 2.10 - Indice SPE dans le cas sain et le cas
défaillant avec un seuil de 95%
Détection de défauts Analyse en composantes
principales
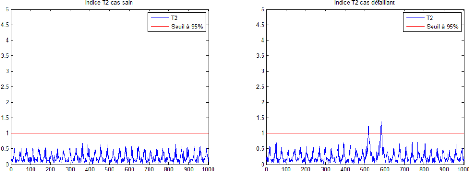
2.5.3 Statistique T2 de Hotelling
L'indice T2 de Hotelling mesure les
variations des projections des observations dans l'espace principal. Il est
calculéà partir des l premières composantes
principales :
|
T2(k) =
|
Xl i=1
|
àt2 i (k) Ài
|
Le seuil de détection peut être approximé,
pour un seuil de confiance á donné, par une distribution
du x2.
Le processus est considéréen fonctionnement
anormal (présence d'un défaut) à l'instant k si
:
T2 (k) > x2
l,á
Où:
x2 l,á = l(N - 1)(N
+ 1)
N(N - l)
Fl,(N-l),á
Fl,(N-l),á est la
distribution de Fisher avec : l, N - l degrés
de liberté, et N nombre d'observations.
22
Figure 2.11 - Indice T2 dans le cas sain
et le cas défaillant avec un seuil de 95% 2.5.4 Localisation de
défauts par ACP partielle
L'ACP partielle consiste à utiliser des bancs de
modèles avec des ensembles de variables réduits et
différents d'un modèle à l'autre. L'application d'une ACP
sur un vecteur de données réduit oùquelques variables sont
écartées par rapport au vecteur originel. Donc les résidus
deviennent sensibles uniquement aux défauts associeés aux
variables qui forment le vecteur réduit, et insensibles aux
défauts associés aux variables éliminées.
Détection de défauts Analyse en composantes
principales
La procédures consiste à structurer les indices
de détection en calculant les ACP partielles ainsi que les seuils de
détection des indices correspondants (Fig 2.13).
Procédure de structuration des
résidus
1. Appliquer l'ACP sur la matrice des données.
2. Construire une matrice d'incidence fortement localisable
(Matrice des signatures théoriques).
3. Construire un ensemble de modèles d'ACP partielles,
chacune correspondant à une ligne de matrice d'incidence (prendre les
variable ayant un 1 sur cette ligne).
4. Déterminer les seuils pour la détection des
défauts (seuil pour T i 2 ou
SPEi).
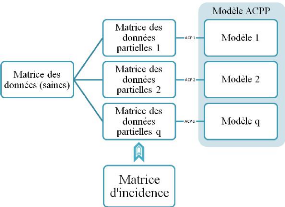
Figure 2.12 - Procèdure de structuration de
résidus par ACP partielles
23
Figure 2.13 - Procèdure de localisation par ACP
partielles structurée
Localisation de défauts Analyse en composantes
principales
Cette approche sera utilisée pour localiser le
défaut simulésur la première variable de notre exemple et
qui a étédétectéprécédemment. Dans ce
cas simple d'un seul défaut, on aura besoin de déterminer
plusieurs modèle dont chacun est insensible à une seule variable.
Par la suite, le calcul des indices de détection pour les
différents modèles réduits nous permettra de localiser le
défaut détecté.
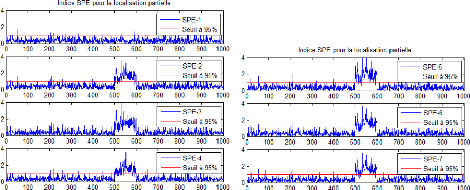
Figure 2.14 - L'évolution des SPE des modèles
réduits
On remarque que le modèle ACP1 n'est pas affectépar
le défaut ce qui implique que l'ACP1 est insensible à la variable
en défaut X1.
24
Figure 2.15 - Table des signatures théoriques

?'ACP à Noyau (Kernel PCA)
Sommaire
3.1 Introduction 25
3.2 Méthodes à noyaux et Kernel PCA
26
3.3 Détection et localisation en Kernel PCA
30
3.4 Algorithme de base du Kernel PCA 33
3.1 Introduction
L'Analyse en composantes principale à montréson
efficacitédans le traitement des données linéaire comme on
la vu dans le chapitre précédent, par contre quand il s'agit de
données non linéaires on aura des difficultés à
exploiter la corrélation potentielle entre les variables pour
réduire la dimension. Car l'ACP consiste à trouver des relations
linéaires entre les variables, or dans la projection de données
non linéaires il nous est impossible de faire une séparation
linéaire. Celle-ci sera erronée et pas représentative de
nos variables et données. Comme le montre la figure ci-dessous :
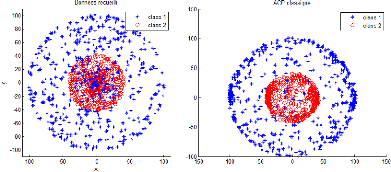
Figure 3.1 - Représentation des données non
linéaire par ACP classique
25
Méthodes à noyaux et Kernel PCA L'ACP à
Noyau (Kernel PCA)
26
Afin de corriger ce problème, la Kernel PCA entre en
jeu, en exploitant des relations potentiellement non linéaires entre les
variables. Qui aboutira par une représentation plus correct de nos
données, comme le montre la figure ci-dessous :
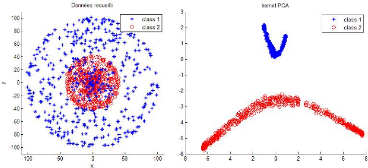
Figure 3.2 - Représentation des données non
linéaires par KPCA 3.2 Méthodes à noyaux et Kernel
PCA
L'ACP à noyau est une extension de l'ACP classique, qui
permet d'exploiter les relations potentielles non linéaires entre les
variables. Le principe de cette extension est d'envoyer nos données par
une application I : RN -? F , X -? ?(x) appelée Feature map
dans un nouvel espace de grande dimension H muni d'un produit scalaire.
La kernel PCA agit sur les ?(x) de la même façon
que l'ACP agit sur les Xj. Les données dans le nouvel espace fonctionnel
deviennent linéairement séparables.
3.2.1 Méthodes à noyaux
Pour se familiariser avec l'astuce de noyau on va
donnéquelques notions :
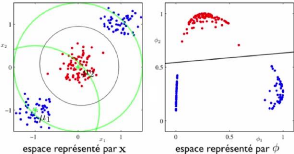
Figure 3.3 - Reprsentation en utilisant des fonctions de bases
I
Méthodes à noyaux et Kernel PCA L'ACP à
Noyau (Kernel PCA)
Dans la Figure (3.3) : on a deux classe différentes
(bleu et rouge), il nous est impossible de trouver tout d'un seul coup une
séparation linéaire entre ces deux dernières. Par contre
si on utilise seulement deux fonctions de bases gaussiennes à noter :
Ij = e(-
kX-ujk2
2ó2 )
OùX est le vecteur de données, et
uj est un vecteur de moyenne qu'on a placéjudicieuse-ment comme
le montre la Figure (3.3)
On obtient un système de représentation I1 , I2.
Ainsi avec des fonctions de base on a finalement pu convertir notre
problème qui était pas résolvable avec une méthode
ou modèle linéaire en un problème facilement
résolvable avec un modèle linéaire.
Par contre lorsque X est de grande dimension, notre
représentation dans le Feature space sera d'une dimension
gigantesque.
Exemple d'un mapping polynômial de X E
Rd, de degréK(tous les produits entre k
éléments de X), on doit calculer un (x)
dans un espace de dimension et d'ordre dk . Ex: d
= 100, k = 5 donne 10000000000, ou même infinie si on
prends le cas de l'exemple d'illustration gaussien-(Figure 3.3) avec X
de grande dimension.
Dans la kernel PCA on utilise l'astuce du noyau qui nous
laisse supposer qu'on peut calculer le produit scalaire ( (xi),
(xj)) directement sans jamais avoir à calculer
explicitement un (x).
Notre but est de calculer la matrice K : k(Xi,
Xj) = ( (xi), (xj))
Dans la kernel PCA on utilisera le noyau gaussien pour le
calcul de la matrice, ce choix est fais après le test de plusieurs
noyaux connus.
K(X, Y ) = e(- 'IX-Y
"2
2ó2 )
On rappelle que le noyau gaussien est bien un noyau valide, et
cela peut être démontréfacilement.
Règles pour construire de nouveaux noyaux valides :
k(X, Y ) = ck1(X, Y )
k(X, Y ) =
f(X)k1(X, Y )f(Y )
k(X,Y ) = q(k1(X,Y ))
k(X, Y ) =
e(k1(X,Y ))
k(X, Y ) = k1(X, Y )) +
k2(X, Y ))
k(X,Y ) = k1(X,Y
)k2(X,Y ) k(X, Y ) = k3(
(X), (Y )) k(X, Y ) =
XTAY
k(X, Y ) =
ka(Xa, Ya) +
kb(Xb, Yb) k(X, Y ) =
ka(Xa,
Ya)kb(Xb, Yb)
27
Oùc > 0, f(x)est une
fonction, q(a)est un polynôme avec coefficients
positifs, A est une matrice définie positive et X =
(Xa, Xb). Les noyaux k1, k2,
k3, ka, et kb doivent être valides.
Méthodes a` noyaux et Kernel PCA L'ACP a` Noyau
(Kernel PCA)
'Ix-Y"2
K(X, Y ) = e(- PU H2)
On a` :
11X - Y 112 = (X - Y )T(X - Y ) =
XTX - 2XTY + YTY
K(X,Y ) = e( XT X
2ó2 )e( XT2ó2Y)e( Y T Y
2ó2 )
Ainsi on a démontréque ce noyau est bien valide
et les règles utilisées pour arriver au noyau gaussien sont les
suivantes :
1 - k(X, Y ) = ck1(X, Y )
2 - k(X, Y ) = e(k1(X,Y ))
3 - k(X,Y ) = f(X)k1(X,Y )f(Y )
3.2.2 Kernel PCA
Aprés avoir transforménos données, on doit
construire notre modèle. On suppose
ö(Xn) = 0 )
N
pour l'instant que les données (transformées) sont
centrées (
n=1
La matrice de covariance est alors :
|
1
C = N
|
XN n=1
|
ö (Xn)ö (Xn)T
|
28
Et on cherche ses vecteurs propres vi :
Cvi = ëivi
(le défi est de trouver les vi sans vraiment calculer
explicitement la matrice C) Équivaut a` ce que vi satisfasse :
1
N
XN n=1
ö (Xn){ö (Xn)T vi} =
ëivi
On divise sur ëi et on note le scalaire : ain =
ö(Xn)T vi
ëiN
On peut donc écrire vi sous la forme :
vi = XN ainö (Xn) n=1
Méthodes à noyaux et Kernel PCA L'ACP à
Noyau (Kernel PCA)
On replace vi par cette forme et on aboutit à :
|
1 N
|
XN n=1
|
ö (Xn)ö (Xn)T
|
N m=1
|
aimö (Xm) = ëi
|
XN n=1
|
ainö (Xn)
|
Le but étant d'éliminer les ö(Xn),
et de n'avoir que des évaluations de noyau. On multiplie par
ö(Xl)T les deux côtés (Xl tiréde mon
exemple d'entrainement)
|
1 N
|
XN n=1
|
k(Xl, Xn)
|
N m=1
|
aimk(Xn, Xm) = ëi
|
XN n=1
|
aink(Xl, Xn)
|
Avec : k(Xl, Xn) = ö (Xl)T ö (Xn)
Et : k(Xn, Xm) = ö (Xn)T ö
(Xm)
OùK est la matrice de Gram : Kn,m = k(Xn,
Xm)
Sachant qu'une somme de deux éléments peut
être notéde la sorte :
N
E aink(Xl, Xn) = Kl,:ai
n=1
Où: ai est le vecteur contenant toutes les valeurs
ain comme suit :
ai = [ai1 ai2 . . . ain]T Et : Kl,: est le vecteur
contenant la lemme rangée de la matrice de Gram. On
répète la même opération pour ces sommes ce qui nous
donnera :
1
N Kl,:Kai =
ëiKl,:ai
On a ainsi obtenu une équation, on doit maintenant
généraliser ca, et générer N équations en
considérant n'importe quel Xl de l'ensemble de l'entrainement :
K2ai = ëiNKai
En multipliant par K-1, on obtient :
Kai = ëiNai
Pour obtenir les ai, on trouve les M vecteurs propres (ai) de
K ayant les plus grandes valeurs propres (ëiN)
Au final, on doit s'assurer que les vi soient de norme 1 :
|
1 = vT i vi =
|
XN n=1
|
N m=1
|
ainaimö (Xn)T ö (Xn)
= aTi Kai = ëiNaTi ai
|
29
On divise les ai par la racine carrée des valeurs propres
ëiN
Méthodes à noyaux et Kernel PCA L'ACP à
Noyau (Kernel PCA)
On peut finalement calculer chaque élément
ti(X) de la projection t(X) comme suit :
ti(X) =
0(X)Tvi = XN ain0
(Xn)T 0 (Xn) =
XN aink(X, Xn)
n=1 n=1
Centrage du noyau
On a supposéque les 0(Xn)
sont centrés, mais ce n'est probablement pas le cas. Pour avoir des
données centrés, Il nous faudrait donc soustraire la moyenne,
dans l'espace des 0(Xn) tel que :
|
1 N
(Xn) = 0(Xn)
- N E
l=1
|
0(Xl)
|
Par contre, on ne peut pas travailler avec les
0(Xn) directement, puisqu'ils peuvent être
de taille infinie. On va travailler avec la matrice (K) de
Gram tel que :
Kn,m =
0(Xn)T
0(Xm)
|
N
=
0(Xn)T0(Xm)
- N E
l=1
|
0(Xn)T
0(Xl) - 1N
|
N 1 N
0(Xl)T
0(Xm) + N2 E
l=1 j=1
|
l=1
|
0(Xj)T0(Xl)
|
30
Qui va nous donner :
|
1 ~N`
Kn,m =
k(Xn,Xm)
-NL~
l=1
|
XN
1
k(Xl, Xm) - N
l=1
|
k(Xn, Xl) +
N1 2
|
H
XN
j=1 l=1
|
k(Xj, Xl)
|
D'oùl'expression finale :
K = K - 1NK - K1N +
1NK1N Avec : 1N est une matrice N x N oùtous les
éléments sont 1N
La première chose à faire donc est de calculer
notre noyau K grâce auquel on va pouvoir trouver le nouveau
noyau K, dont on va extraire les valeurs et vecteurs
propres.
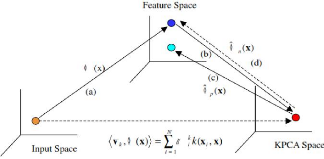
Détection et localisation en Kernel PCA L'ACP à
Noyau (Kernel PCA)
31
Figure 3.4 - Concept global du KPCA
3.3 Détection et localisation en Kernel PCA
3.3.1 Détection en Kernel PCA
Une approche pour la surveillance des processus par ACP
à noyau implique l'utilisation des indices de détection tel que
les deux statistiques T2(Hotlling) et Q (SPE).
3.3.1.1 Statistique Q (SPE)
La technique de surveillance de la KPCA est similaire à
la procédure utilisée dans l'ACP classique mais calculée
dans l'espace caractéristique (Feature space). La statistique SPE pour
la détection de défauts est donnée par :
SPE = kÖ(X) -
bÖp(X)k2 =
k4;N(X) -
bÖp(X)k2_
= ÖN(X)TbÖN(X)
- 2bÖN(X)T
Öp(X) + Öp(X)T
Öp(X)
|
=
|
XN j=1
|
tjVjT
|
XN k=1
|
tkVk - 2
|
XN j=1
|
tjVjT
|
X p
k=1
|
tkVk +
|
X p
j=1
|
tjVjT
|
X p
k=1
|
tkVk
|
|
=
|
XN j=1
|
t2j - 2
|
X p
j=1
|
t2j +
|
X p
j=1
|
t2 = j
|
XN j=1
|
t2j -
|
X p
j=1
|
t2 j
|
On donne :
N N
tk = hVk,
Ö(Xt)i = aki
hÖ(Xi), Ö(Xt)i =
akikt(Xi,
Xt)
i=1 i=1
Détection et localisation en Kernel PCA L'ACP à
Noyau (Kernel PCA)
32
tk représente les dernières
composantes. Le processus est considéréen fonctionnement anormal
(présence d'un défaut) à l'instant k si :
SPE(k) > ä2 á
Oùä2 est le seuil, le même
que pour l'ACP classique (voir chapitre 2).
3.3.1.2 Statistique T2
T2 =
tË-1tT
Oùt sont les composantes principales et Ë les
premières valeurs propres de la matrice de Gram.
Le seuil de détection peut être approximé,
pour un seuil de confiance á donné, par une distribution du
÷2.
Le processus est considéréen fonctionnement
anormal (présence d'un défaut) à l'instant k si :
T2 (k) > ÷2 l,á
Où:
÷2 l,á = l(N - 1)(N + 1)
N(N - l) Fl,(N-l),á
3.3.2 Localisation de défauts par KPCA partielle
Le principe est le même que l'ACP classique, la
procédures consiste à structurer les indices de détection
en calculant les KPCA partielles ainsi que les seuils de détection des
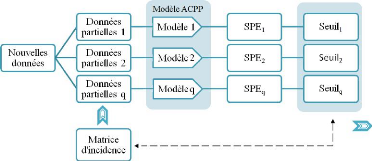
indices correspondants (Fig 3.6).
Procédure de structuration des
résidus
1. Appliquer l'ACP à noyaux sur la matrice des
données.
2. Construire une matrice d'incidence fortement localisable
(Matrice des signatures théoriques).
3. Construire un ensemble de modèles de KCPA
partielles, chacune correspondant àune ligne de matrice
d'incidence (prendre les variable ayant un 1 sur cette ligne).
4. Déterminer les seuils pour la détection des
défauts (seuil pour T i 2 ou SPEi).
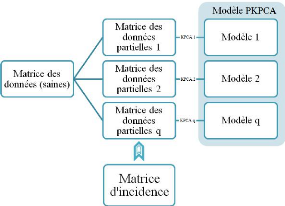
Algorithme de base du Kernel PCA L'ACP à Noyau (Kernel
PCA)
33
Figure 3.5 - Procèdure de structuration de résidus
par KPCA partielles
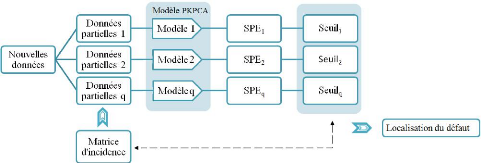
Figure 3.6 - Procèdure de localisation par KPCA partielles
structurée 3.4 Algorithme de base du Kernel PCA
A la fin de ce chapitre on peut dire que l'algorithme de base
de modèlisation et diagnostic à base du Kernel PCA se
décompose en deux parties:
Partie 1 : Transformation de la fonction Kernel.
1. La matrice X qui contient les échantillons des
différentes variables du système en bon fonctionnement.
2. Calcul de la matrice K :
k(Xn,
Xm) =
(ö(xn),
ö(xm)).
3. Calcul de la matrice K centrée (matrice de
Gram) : G = K - 1nK
- K1n +
1nK1n.
Algorithme de base du Kernel PCA L'ACP à Noyau (Kernel
PCA)
Partie 2 : Application de l'ACP.
1. Diagonalisation de la matrice G (trouver les
valeurs/vecteurs propres).
2. Calcul des projections sur les composantes principales.
3. Calcul des indices de détection SPE et
T2.
4. Développement de la procédure de localisation
et isolation.
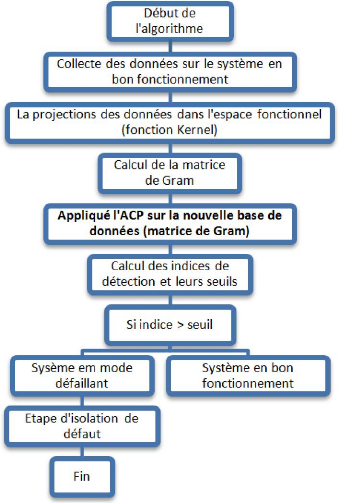
34
Figure 3.7 - Reprsentation de l'algorithme de KPCA

35
?pplication
Sommaire
4.1 Introduction 35
4.2 Description du processus 36
4.3 Identification du modèle Kernel PCA
38
4.4 Détection et localisation de défauts
38
4.1 Introduction
Tennesse Estman Challenge Process a
étépubliépar le Tennessee Estman Compagnie (Downs et
Vogel, 1993) comme une simulation du processus pour la recherche acadmique. Le
simulateur du processus chimique (TECP), considérécomme une
installation pilote de l'industrie chimique, il est largement utilisépar
la communautéscientifique pour évaluer les performances des
algorithmes de commande et de diagnostic. Le TECP est un réacteur
chimique multi-variable non linéaire, de grande dimension. Ce processus
fournit les produits chimiques finis G et H à partir de quatre
réactifs A, C, D et E. L'installation possède 7 modes de
fonctionnement opératoire, 41 variables mesurées et 12 variables
manipulées, il existe en plus 20 perturbations IDV1 à IDV20 qui
peuvent être simulées pour perturber le fonctionnement. Le TECP
offre une opportunitépour les études qui concernent la commande,
la détection et le diagnostic des défauts. Un diagramme
simplifiédu processus est montrédans la (Fig 4.1). Les 41
variables mesurésont un mélange de continu et discret et de
dynamiques rapides et lentes incluent le niveau, pression, température,
courant et indicateurs de la composition (des variables qui sont mesurés
d'une façon continue (chaque seconde) et d'autres avec une
pèriode d'échantillonnage T ), tel que 22 variables sont
continues et le reste 19 variables sont les mesures des concentration de
l'alimentation du réacteur, gaze purgéavec différentes
fréquences d'échantillonnage 6 ou 15 minutes. Chaque mesure est
corrompue par un bruit additif, les propriétés statistiques du
bruit sont inconnues. Dans notre cas on a choisis 20 variables parmi 41, qui
sont mesurées d'une façon continue (chaque seconde). La liste de
ces variables est montrédans (Fig 4.2)
Description du processus Application
36
4.2 Description du processus
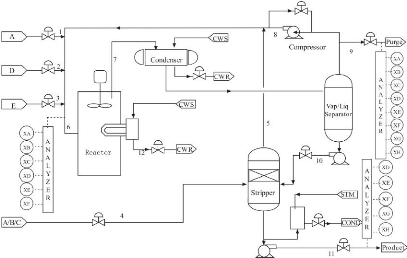
Figure 4.1 - la description du processus
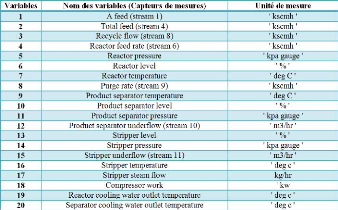
Figure 4.2 - La description des variables mesurées
Description du processus Application
Pour bien illustrer ces variables on va présenter
quelques unes sur la (Fig 4.4). Ces figures représentent
l'évolution des mesures des capteurs de température, pression et
niveau du réacteur et séparateur de produits pendant 10 heurs de
mesures avec une pèriode d'échantillonnage T = 1 seconde.
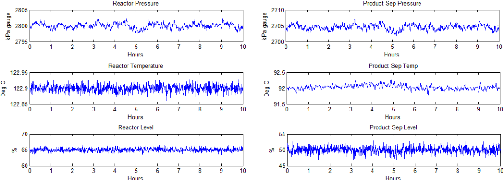
Figure 4.3 - Les variables mesurées pour la
simulation
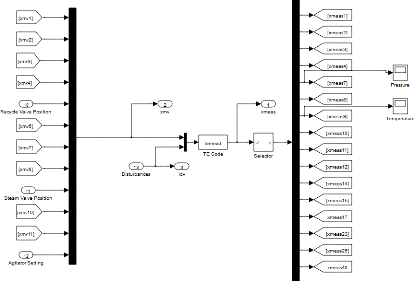
37
Figure 4.4 - Simulateur Tennessee Estman Challange Process
Identification du modèle Kernel PCA Application
4.3 Identification du modèle Kernel PCA
Dans cette partie on va appliquer l'ACP à noyau sur ces
20 variables qui sont mesurées de façon continue. Les sets de
données (entrainement et test) sont généréà
partir du simulateur (TECP). Le choix du nombre de composantes principales est
important, on utilisera le critère PCV à 95% tel que : on prend
les composantes dont la somme de leurs valeurs propres dépasse 95% de la
somme de toutes les valeurs propres. Ainsi qu'un u approprié, on abouti
à un nombre de composantes principales l = 7
Remarque : Dans
l'intègralitédes figures de localisation ainsi que
détection, les SPE, T2 ont
étédivisépar leurs seuils respectives, ainsi que pour les
seuils (prennent la valeur 1).
4.4 Détection et localisation de
défauts
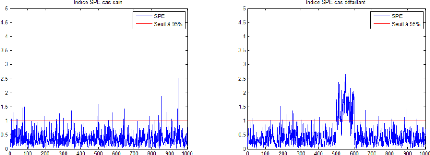
4.4.1 Détection de défauts
Une fois que le modèle KPCA a bien
étéidentifié, on peut passer à l'étape de
détection et localisation de défauts. Deux défauts ont
étésimulées sur les variables X3, X18 du nouveau set de
données, entre les instants [450, 550] et [650, 750] respectivement,
avec une amplitude qui s'élève à environ 25% de la plage
de variation de ces variables.
KPCA Indice SPE cas sain
4
2
8
6
0
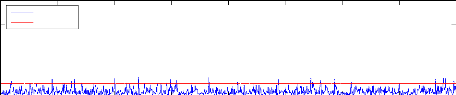
SPE
Seuil à 95%
100 200 300 400 500 600 700 800

KPCA - Indice SPE cas défaillant
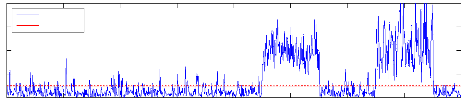
4
2
8
6
0
SPE
Seuil à 95%
100 200 300 400 500 600 700 800
38
Figure 4.5 - Évolution de l'ndice SPE cas sain et
défaillant
Détection et localisation de défauts
Application
39
4.4.2 Localisation de défauts
Une fois le défaut est bien détectépar
l'indice de détection, une étape d'isolation de ce défaut
intervient pour savoir la provenance de cette défaillance. On utilisera
la méthode du Kernel PCA partielle pour l'isolation des défauts.
Elle permet une structuration des résidus par construction d'un ensemble
de modèles, de tel sorte que chaque modèle est sensible à
certaines variables et insensible à d'autres. Les modèles sont
construits d'après la matrice d'incidence suivante (Table des signatures
théoriques).
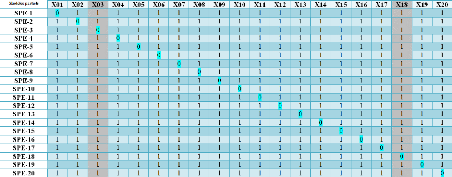
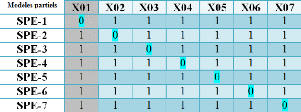
Figure 4.6 - Table des signatures théoriques
Dans cette approche on a construit 20 modèles du KPCA.
Chaque modèle est insensible à une (01) variable comme il est
bien illustrésur la table des signatures théoriques qui montre la
structuration des modèles choisis. La (Fig 4.7) montre
l'évolution de la signature expérimentale lorsqu'un défaut
intervient sur les variables (capteur/actionneur)
du système. La signature expérimentale est
obtenue après codification des résidus. Oùun
dépassement est codépar 1 et un non dépassement est
codépar 0. Ce qui permet d'obtenir les deux signatures théoriques
:
La premiére : ( 1 1 0 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 ). Cette signature est identique à la
3emme colonne de la table des signatures
théoriques. Cela veut dire que la variable (capteur/Actionneur)
affectépar le premier défaut est X3.
La deuxième : ( 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 0 1 1 ). Cette signature est identique à la
18emme colonne de la table des signatures
théoriques. Cela veut dire que la variable (capteur/Actionneur)
affectée par le deuxième défaut est X18.
Détection et localisation de défauts
Application
40
KPCA Indice SPE pour les dix premiers modèles
réduits
5
0

SPE 1
100 200 300 400 500 600 700 800
5
0

SPE 2
0 100 200 300 400 500 600 700 800
5
0

SPE 3
0 100 200 300 400 500 600 700 800
5
0

SPE 4
100 200 300 400 500 600 700 800
5
0

SPE 5
100 200 300 400 500 600 700 800
5
0

SPE 6
100 200 300 400 500 600 700 800
5
0

SPE 7
0 100 200 300 400 500 600 700 800
5
0

SPE 8
0 100 200 300 400 500 600 700 800
5
0

SPE 9
100 200 300 400 500 600 700 800
5
0

SPE 10
100 200 300 400 500 600 700 800
Détection et localisation de défauts
Application
KPCA - Indice SPE pour les dix derniers modèles
réduits

5
0
SPE-11
0 100 200 300 400 500 600 700 800

5
0
SPE-12
0 100 200 300 400 500 600 700 800

5
0
SPE-13
0 100 200 300 400 500 600 700 800

5
0
SPE-14
0 100 200 300 400 500 600 700 800
5
0

SPE-15
0 100 200 300 400 500 600 700 800

5
0
SPE-16
0 100 200 300 400 500 600 700 800

5
0
SPE-17
0 100 200 300 400 500 600 700 800
5
0

SPE-18
0 100 200 300 400 500 600 700 800

5
0
SPE-19
0 100 200 300 400 500 600 700 800
5
0

SPE-20
0 100 200 300 400 500 600 700 800
41
Figure 4.7 - L'évolution des SPE des modèles
réduits
42
Conclusion générale
Dans ce mémoire, nous avons présentéun
outil flexible et puissant pour l'analyse et la modèlisation des
systèmes non linéaires en vue du diagnostic, à savoir,
l'Analyse en composantes principales à noyaux. Deux approches ont
étéprésentées : d'une part, l'analyse en
composantes principales conventionnelle pour les données
linéaires, ainsi que son application pour le diagnostic, et d'autre part
sa variante non linéaire à base de noyau et son adaptation pour
la détection et la localisation des défauts.
Nous avons expliquéen détails, dans un premier
temps,la mise en oeuvre d'un modèle ACP linéaire et son
exploitation pour la détection et la localisation des défauts.
Nous avons mis l'accent particulièrement sur les différentes
méthodes existantes pour la détermination de la structure
optimale du modèle ACP, ainsi que les différentes approches et
techniques de détection en utilisant des indices statistiques,
notamment, la statistique Q aussi dénommée SPE et la statistique
T2 de Hotteling. Plusieurs techniques de localisation à base d'ACP
existent dans la littérature. Toutefois, nous n'avons
présentéque l'approche dite ACP partielle qui se base sur des
modèles réduits pour la localisation de défauts, pour sa
forte adaptabilitédans le cas non linéaire à noyau. Pour
illustrer la procédure de surveillance en utilisant l'ACP classique,
nous avons démontréles performances des approches citées
par un exemple de simulation.
Par la suite, nous avons entaméla variante non
linéaire de l'ACP qui repose sur la notion de noyau pour la
linéarisation des données, et son application pour le diagnostic.
D'abord, un aperu général des différents noyaux
utilisés, et la logique suivie pour définir un noyau valide a
étéprésenté, puis nous avons
expliquél'utilisation de cette notion pour l'exploitation des
données à tendance non linéaire. A l'aide d'une
transformation vers un nouvel espace appeléespace des
caractéristiques, les méthodes à noyaux nous permettent de
linéariser les données non linéaires, qui passe notamment
par la construction de la matrice dite 'de Gram', oùl'utilisation de
l'ACP classique devient possible pour la modèlisation en vue d'une
application au diagnostic et à la surveillance à l'aide des
différents indices de détections et des approches de
localisation. Enfin, une application sur un processus réel a
étéabordée pour illustrer le principe de l'ACP à
noyau. Le système proposé, appeléEastman Tennessee, est un
processus chimique à plusieurs variables non linéaires et
fortement corrélées, qui offre un environnement parfait pour la
validation de la méthode présentée. L'ACP à noyau a
démontréson efficacitéà parfaitement
détecter et localiser les défauts capteurs.
L'ACP à noyau présente toutefois des
désavantages quant au temps de calcul due à l'immense taille de
la matrice de Gram, ce qui engendre bien évidemment quelques
complications dans le cadre d'une supervision en ligne des processus. Autour du
thème de l'optimalitéde l'espace de représentation, il
serait intéressant d'étudier les différentes
possibilités pour la réduction du temps de calcul, une approche
particulière et bien prometteuse est appelél'ACP à noyau
locale qui permet de diminuer la taille de la matrice de Gram (m × m) au
lieux de (N × N) mais qui comporte bien des inconvénients reste
àétudier.
?ibliographie
[1] Nello Cristianini. John Shawe-Taylor.
Book Kernel Methods for Pattern
Analysis,.
Cambridge university press, 2004.
[2] M. Jelali A. BAthelt, N. Lawrence-Ricker. Revision of the
tennessee east-man process model. International Symposium on Advanced
Control of Chemical Processes, 2015.
[3] Smola-K. R Muller B. Scholkpof, A.j. Nonlinear component
analysis as a kernel eigenvealue problem. Neural Computation Vol 10, pp
1299-1319, Jully 1998.
[4] Mohamed-Faouzi HARKAT. Détection et
localisation de d'efauts par analyse en composantes principales.
Automatic. PhD thesis, Institut National Polytechnique de Lorraine - INPL,
2003.
[5] Chakour.C Harkat.M-F, Djeghaba.M. New adaptive kernel
principal component analysis for nonlinear dynamic process monitoring.
Applied Mathematics & Information Science Vol 9, pp 1833-1845,
2015.
[6] J. j. Downs and E. F. Vogel. A plant-wide industrial
process control problem. Computers & Chemical Engineering, Vol 17, pp
245-255, Marche 1993.
[7] J. M Lee S.W Choi D. K Lee I. B Lee J. H, Cho. Fault
identification for process monitoring using kernel principal component
analysis. Chemical Engineering Science Vol 60, pp 279-288, Jan
2005.
[8] Choi S W et al Lee J M, Yoo C K. Nonlinear process
monitoring using kernel
43
principal component analysis. Chemical Engeneering
Science. Vol 59, pp. 223-234, 2004.
[9] Guizeng Wang Peiling Cui, Jun-hong Li. Improved kernel
principal component analysis for fault detection. Expert Systems with
Applications Vol 34, pp. 1210-1219, 2008.
[10] Yvon Tharrault. Diagnostic de
fonctionnement par
analyse en com-
posantes principales application a'
une station de
traitement des eaux usées. Automatic. PhD thesis, Institut National
Polytechnique de Lorraine - INPL, 2008.
[11] Sheng Chen Xiaogang Deng,
Xuemin Tian. Modified kernel
principal component analysis
based on local structure analysis and its application to nonlinear process
fault diagnosis. Chemometrics and Intelligent Laboratory Systems Vol 127,
pp. 195-209, 2013.
[12] H. Zhou S. J Qin Y. W, Zhang. Decentralized fault
diagnosis of large scale processes using multiblock kernel principal component
analysis. Act Auto-matica Sinica Vol 36, pp 593-597, April 2010.
[13] Jie Yu. A nonlinear kernel gaussian mixture model based
in ferential monitoring approach for fault detection and diagnosis of chemical
processes nature. 2012.
[14] Q. X Zhu Z. Q, Geng. Multiscale non linear principal
component analysis (nlpca) and its application for chemical process monitoring.
Industrial and Engineering Chemistry Research Vol 44, pp 3585-3593,
2005.
?'esum'e ?bstract
Dans ce travail, nous avons présentéune approche
statistique multi-variables pour la modèlisation et le diagnostic des
sysèmes non linéaires. Cette approche, appelée analyse en
composantes principales à noyau, qui est une extension de l'ACP
classique au cas non linéaire, est basée sur une transformation
des données en utilisant une fonction Noyau(Kernel) pour la
linéairasation des des variables non linéaires initiales.
Ce travail est partagéen quatre chapitres,
organiés de la façon suivante:
Le premier chapitre présente un aperçu sur le
principe de diagnostic. Nous exposant les différentes étapes pour
la mise en place d'un système de surveillance, la structure
générale et la classification des méthodes
utilisées dans un système de diagnostic.
Dans le deuxième chapitre on à
présentéla description de la méthode ACP clas-
sique, ainsi que ses différentes étapes pour la
modèlisation, détection et localisation de défauts.
Le troisième chapitre est consacréàl'ACP
à noyau. Oùla transformation noyau
effectuant un changement de base qui permet de projeter les
données dans un nouvel espace est mise en oeuvre, La modélisation
est ainsi facilitée, par l'application de l'ACP linéaire, puisque
on passe d'un système initialement non linéaire, à un
autre linéaire. Par contre l'espace de représentation sera de
dimension plus importante que l'espace de départ.
Le dernier chapitre compte à lui a
étéconsacréà l'application de la
méthode du di-
agnostic, oùle principe de l'ACP à noyau et de
modélisation et la génération de résidus sont
présentés à l'aide d'un simulateur du processus chimique
Tennessee Estman Chal-lange Process (TECP).
Mots-clés : Diagnostic, Détection
et localisation de défauts capteurs, Analyse en Composantes Principales
a' noyau, Tennessee Estman
44
In this work, we presented a statistical multivariable
approach used for modeling and diagnosis of nonlinear systems, namely, Kernel
Principal Component Analysis (KPCA). This approach, which is an extension of
the classical PCA for nonlinear data, is based on a transformation of the
nonlinear input data using a kernel function, thus resulting in a new
representation with linear relations among the variables, where conventional
PCA can be used for modeling and diagnosis. This work is composed of four
chapters and is organized as follows:
The first chapter presents a global preview of diagnosis,
different steps for the establishment of a monitoring system are explained,
along with the different methods and approaches used in diagnosis, organized in
different classes.
In the second chapter we presented the classical principal
component analysis method, and its different steps, applied for modeling, and
fault detection and isolation.
The third chapteris devoted to the Kernel PCA, where a kernel
transformation is used for the projection of nonlinear data into a new linear
presentation space. The use of conventional PCA for modeling of the data is
then possible because of the new linear nature of the obtained data. However,
the new representation space is of higher dimension compared to the initial
space.
Finally, the last chapter contains the application of the
kernel PCA method for the modeling phase as well as fault diagnosis by
generating residuals on a chemical process, namely, the Tennessee Eastman
challenge process TECP.
Keywords : Diagnosis, Sensor fault detection and
isolation, Kernel Principal Components Analysis, Tennessee Estman



