|

REPUBLIC OF CAMEROON
REPUBLIQUE DU CAMEROUN Paix - Travail -
Patrie
Peace - Work - Fatherland
*********
**********
MINISTERE DE L'ENSEIGNEMENT SUPERIEUR
**********
MINISTRY OF HIGHER EDUCATION
***********
UNIVERSITE DE NGAOUNDERE
THE UNIVERSITY OF NGAOUNDERE
ECOLE NATIONALE SUPERIEURE DES SCIENCES
AGRO-
INDUSTRIELLES
NATIONAL ADVANCED SCHOOL OF
AGRO-INDUSTRIAL
SCIENCES
B.P:455
Ngaoundéré-CAMEROUN Tel / Fax: (+237) 22 15 81 89
DEPARTEMENT DE GENIE ELECTRIQUE, ENERGETIQUE ET
AUTOMATISME DEPARTMENT OF ELECTRIC, ENERGETIC AND AUTOMATISM
ENGINEERING
Mémoire de Master en Sciences et Technologie Parcours :
Ingénierie des Equipements Agro - Industriels (IEAI)
Spécialité : Energétique et Procédé (EP)
*****************************
Présenté par
:
TIENTCHEU NSIEWE Maxwell
Matricule : 010S203EN
********************************
ETUDE DE LA CONVECTION NATURELLE
TURBULENTE DANS UNE
ENCEINTE A PAROI
CHAUFFÉE
********************************
Sous la Direction de :
KUITCHE Alexis et
TCHEUKAM-TOKO
*********************************
Soutenue le 05 Décembre 2013
*************************************
- Jury -
TIEUDJO Daniel Maitre de conférences ENSAI -
Ngaoundéré Président
EDOUN Marcel Chargé de Cours ENSAI -
Ngaoundéré Examinateur
TCHEUKAM-TOKO Maitre de Conférences IUT -
Ngaoundéré Rapporteur
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page i
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
DEDICACE
Je dédie ce travail à la grande
famille NSIEWE, et demande à Dieu tout puissant de l'agrandir
d'avantage dans la joie et l'amour
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page ii
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
REMERCIEMENTS
Je tiens avant tout à reconnaitre la grâce qui
m'a été accordée de mener à terme cette formation,
pour cela je remercie Dieu tout puissant pour la merveille que je suis. Ma
reconnaissance va également à l'endroit de tous ceux qui d'une
manière ou d'une autre ont su m'apporter leur soutien. Je souhaite
qu'ils trouvent dans ce rapport le témoignage de ma gratitude à
leur endroit. Je pense particulièrement au :
? Le Recteur de l'Université de
Ngaoundéré, le Pr. AMVAM ZOLO Paul Henry, pour nous avoir
autorisés à poursuivre nos études en Master au sein de son
Institution ;
? Directeur de l'Ecole Nationale des Sciences
Agro-industrielles, le Pr NSO Emmanuel Jong, pour ses encouragements et sa
qualité de père des enfants de l'ENSAI ;
? Pr. KUITCHE Alexis, Chef de Division des Affaires
Académiques, de la Coopération, de la Recherche et de la
Scolarité, par ailleurs Chef de Département de Génie
Electrique, Energétique et Automatisme (GEEA) et Responsable de
l'Unité de Formation Doctorale Physique Applique et Ingénieur
(UFD-PAI) de l'ENSAI, pour son encadrement, ses efforts fournis pour mon
encadrement paternel et académique depuis le master 1, et pour toute la
patience. Qu'il trouve dans ce travail mes sincères remerciements ;
? Pr. TCHEUKAM TOKO Denis, pour son encadrement
académique et paternel durant tout mon cursus académique de l'IUT
à l'ENSAI de Ngaoundéré, les mots ne suffiront pour le
remercier ;
? Dr. MOUANGUE Ruben, Chef de Département de
Génie Energétique de l'IUT de Ngaoundéré, pour son
encadrement et son soutien permanent dans ma vie d'étudiant et d'homme,
et aussi pour sa disponibilité, pour l'initiation au calcul
numérique, ses documents et ses multiples conseils. Merci
l'engagé ;
? Dr. DJEUMAKO Bonaventure, Chef de Département de
Génie Mécanique a l'ENSAI, pour son amour de la famille, sa
disponibilité, ses sacrifices pour la résolution de mes
problèmes, ses encouragements et son soutien parental et
académique incontournable dans ma vie à Ngaoundéré
;
? Dr. DJANNA KOFFI Francis Lénine, pour nous avoir
fourni des documents traitants du transfert thermique ;
? Mes parents M. NSIEWE Augustin et Mme NSIEWE née
NGUITCHOU Anne, aujourd'hui s'achève la deuxième partie de mon
cursus scolaire grâces aux efforts et aux sacrifices que vous fournissez
chaque jour. Merci de toujours croire en moi ;
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page iii
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
? Le Groupement Camerounais de Combustion (GCC) en particulier
le Dr. OBOUNOU Marcel, BOGNING Saccarose, Chelem, Clovis... pour les multiples
conseil et aides logistique et scientifique qu'ils m'ont fourni ;
? Tous les enseignants de l'IUT-ENSAI, pour leurs conseils et
la formation qu'ils m'ont offerte, en particulier le Dr. EDOUN, le Pr. NJIOKAP,
le Pr. KAMTA, le Pr. TIEUDJO, le Dr. KAMGANG, le Dr. NZIE, le Pr. EKOBENA...
;
? Toute l'équipe des chercheurs du département
de G.E.E.A. je pense particulièrement à mon Responsable
Pédagogique TETANG, ainsi qu'à KOUENI, NDJIYA, BOUKAR, TCHAMI,
BOSCO à qui je souhaite du courage pour la thèse ;
? Mes frères et soeurs FEUGANG Fabrice, NGANDJEU
Beauté, DJEUMO Cyrus, DJINE Vinyl, TEKENG Eddie, ma nièce
Freshnelle et mon neveu Landry ;
? La grande famille SOH ZINGA, pour les encouragements et le
soutien constant sans faille ;
? La grande famille FEUGANG, pour tout le soutient sans frein
qu'elle m'accorde depuis ma naissance ;
? La famille KIENANG, qui ma chaleureusement accueilli a
Ngaoundéré depuis mon premier cycle universitaire ;
? La mère de mon petit gar EYANGA Maguy Florice, pour
son amour et sa maternité en mon endroit, ainsi que sa soeur MENDOUGA
Marie laure ;
? Mes frères jumeaux TCHUITCHOU, DONGMO, DJEUFACK et
NGANDJUI, ainsi que mes collaborateur du GIC Univers Sans Frontière,
TCHIO et NONO ;
? Mes amis de toujours : HEUSSEIN, MBOUOPDA, NGATTAT, TAMKAM,
TATSINKOU, KAMNENG, JOGO, KEUBOU, KOUAMOU ;
? La grande famille de la JESHN de Ngaoundéré,
ma première famille à Ngaoundéré ;
? La grande famille du NSIE'SI, du HAUT-NKAM, de l'ACE, du
2@GTE,
? Mes camarades de promotion d'IEAI ;
Ainsi qu'a tous ceux qui, de près ou de loin ont
contribué à la réussite de ce travail.
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page iv
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
SOMMAIRE
DEDICACE i
REMERCIEMENTS ii
SOMMAIRE iv
LISTE DES FIGURES vi
LISTE DES TABLEAUX ix
NOMENCLATURE x
SYMBOLES GRECS : xii
RESUME xiii
ABSTRACT xiv
INTRODUCTION 1
chapitre I. ETUDE BIBLIOGRAPHIQUE 3
I.1 Quelques définitions 4
I.1.1 Notion de convection 4
I.1.2 Convection turbulente 6
I.1.3 Couche limite dynamique et thermique 8
I.1.4 Convection en enceinte différentiellement
chauffée 11
I.2 La convection naturelle en cavité
differentiellement chauffée. 13
I.2.1 Les bases de la convection naturelle en cavité 13
I.2.1.1 La cellule de Rayleigh-Bénard 13
I.2.1.2 Problème posé par la convection naturelle
14
I.2.2 Paramètres influençant l?écoulement de
convection naturel en cavité 15
I.2.2.1 Influence du nombre de Rayleigh 15
I.2.2.2 Influence du rapport de forme 22
I.2.2.3 Influence du nombre de Prandtl 25
I.2.2.4 Influence du rayonnement sur la stratification thermique
et le nombre de
Rayleigh 26
chapitre II. DESCRIPTION DU PROBLEME
ET FORMULATION
MATHEMATIQUE 34
II.1 Description du problème physique
35
II.2 Mise en équation 36
II.2.1 Formulation mathématique 36
II.2.1.1 Hypothèses simplificatrices 36
II.2.1.2 Equation générale de la convection
naturelle 37
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page v
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
II.2.1.3 Equations adimensionnées 38
II.2.1.3.1 Grandeurs adimensionnelles caractéristiques du
problème 38
II.2.1.3.2 Système d'équations
adimensionnées 39
II.2.2 Conditions aux limites 40
chapitre III. OUTILS NUMERIQUES ET METHODES DE
RESOLUTION 41
III.1 Architecture du logiciel Fluent 42
III.2 Déroulement du calcul dans Fluent
42
III.2.1 Intégration des équations de transport
43
III.2.2 Discrétisation spatiale 45
III.2.3 Problème de Couplage pression-vitesse 48
III.2.3.1 Équation algébrique de pression 49
III.2.3.2 Méthode « Semi-Implicit Method for
Pressure-Linked » 50
III.2.4 Sous relaxation et Convergence 51
III.2.4.1 Sous relaxation 51
III.2.4.2 Convergence 51
III.2.5 Etapes de la simulation numérique 51
chapitre IV. RESULTATS ET DISCUSSION
55
IV.1 Etude de sensibilité 56
IV.1.1 Sensibilité par rapport au maillage 56
IV.1.2 Maillage de la géométrie 57
IV.2 Validation du model 57
IV.2.1 Champs thermiques de l'écoulement de convection
naturelle 58
IV.2.2 Champs dynamiques de l'écoulement de convection
naturelle 61
IV.3 Etude de la convection naturelle turbulence à
Rayleigh de 107 62
IV.3.1 Etude de la stratification thermique 63
IV.3.2 Etude du champ dynamique pour quatre nombres de Rayleigh
66
IV.4 Influence du rayonnement de surface sur
l'écoulement de convection naturelle
turbulente 68
IV.4.1 Etude du champ thermique 68
IV.4.2 Etude du champ dynamique 73
CONCLUSION GENERALE 76
Bibliographie 77
Annexes 81
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page vi
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
LISTE DES FIGURES
Figure 1 : couche limite
dynamique Graf et Altinakar [1995] 9
Figure 2 : couche limite
thermique Graf et Altinakar [1995] 10
Figure 3 : Profils des vitesses
pour les couches limites laminaire et turbulente dans un
écoulement sur une plaque plane Tcheukam T. et al
[2012] 11
Figure 4 : schéma représentant la
configuration de la convection de Rayleigh-Bénard cité
par Mabrouk G. [2010] 11
Figure 5 :
schéma représentant le déplacement d'une goutte de fluide
Bejan A. et Kraus A.
[2003 ] 12
Figure 6 : schéma de
la convection dans une enceinte avec gradient horizontal de
température Wang H. et al [2006 ]
12
Figure 7 : enceinte rectangulaire comportant plusieurs
sources de chaleur surfaciques Binet
B. [1998 ] 13
Figure 8 :
Représentation schématique de l'écoulement pour
un nombre de Rayleigh égal à
1,5×109 Salat J. [2004]
15
Figure 9 : Comparaison des courbes correspondant
à la transition à l'instationnarité pour des parois
addiabatiques (---) ou conductrices (-) en cavité remplie d'air A= (H/l)
Le Quéré
[1987] 17
Figure 10 :
représentation des lignes de courant. Aklouche S. et al, [2005 ]
18
Figure 11 :
représentation des isothermes. Aklouche S. et al
[2005] 18
Figure 12 : a) lignes de
courants, b) Isothermes, c) Iso lignes de l'énergie
cinétique
turbulente. Lasfer K. et al [2007] 20
Figure 13
: Profil des composantes verticale et horizontale de vitesse dans les
couches limites montante et descendante, à la position z = 2,69 m pour
un écoulement de convection
naturelle. (Ra = 1,2.1011 ; å = 0,1 ;
ÄT = 20 K). Saury D. et al [2008] 20
Figure 14 :
Effets du nombre de Rayleigh en régime stationnaire sur: (a) les
isothermes; (b) le nombre de Nusselt local relevé sur la paroi chaude;
(c) le profil de température relevée sur
le plan médian horizontale. (Pr = 7; Bn = 5 et
Ä = 5.104). Boutra A. et al [2011] 21
Figure 15
: Comparaison de l'allure des fonctions de courant. (a) et (b) : AH=
2, Ra = 2×106
Le Quéré [1987] ; (c) et (d) AH= 1, RaH =
1,7×108 (c) ; Ra = 1×106 (d) Henkes [1990]
23
Figure 16 : écart de température critique
d'apparition des différents modes d'instationnarité
Benkhelifa A. et Penot F. [ 2005] 25
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page vii
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Figure 17 . Effets du nombre de
Prandtl en régime stationnaire sur. (a) les isothermes; (b) le nombre de
Nusselt local relevé sur la paroi chaude; (c) le profil de
température relevée sur le
plan médian horizontale. (Ra = 105; Bn =
5 et Ä = 5 104). Boutra A. et al [2011] 26
Figure 18
: influence de l'émissivité sur l'écoulement
à Ra = 106 avec (a) e = 0, (b) e = 0.1, (c) e = 0.4, (d) e =
0.8 et (e) e = 0 avec parois horizontales conductrices. Wang H. et al
[2006] 27
Figure 19 .
température (à gauche) et densité de flux net radiatif
(à droite) en parois haute et
basse à Ra = 10 6. Wang H. et al[ 2006]
28
Figure 20 : Stratification thermique avec des parois
d'émissivité importante pour différents
ÄT Djanna F. [2010] 29
Figure 21 :
Stratification thermique obtenue avec des parois de faible
émissivité pour
différents ÄT Djanna F. et al [2008].
30
Figure 22 : Stratification thermique pour ?T=10, 15,
17,4 et 20 K. Djanna F. et al [2008] . 31 Figure 23 .
représentation de la cavité différentiellement
chauffée avec conditions aux limites
thermiquesde 0,335 x 0,335 m Wang H. et al [2006]
35
Figure 24 . volumes finis
bidimensionels patankar [1980] 44
Figure 25 . démarche de
simulation avec Gambit-Fluent 54
Figure 26 . temperature axiale
du fluide en fonction de la densité du maillage 56
Figure 27 . domaine
maillé avec un reserrage plus poussée au niveau des parois
57
Figure 28 . Comparaison des
isothermes . (à droite) Wang H. et al [2006] (à gauche)
Présente étude, dans le cas de la convection
pure 58
Figure 29 . comparaisons des
profils de température en x = 0,5 à Rah = 106.
59
Figure 30 . comparaisons des
profils de température en paroi basse à Ra = 106
60
Figure 31 . comparaisons des
profils de température en paroi haute à Ra = 106.
60
Figure 32 . Comparaison des
champs de vitesse . (à droite) Wang H. et al [2006] (à
gauche)
Présente étude, dans le cas de la convection
pure 61
Figure 33 . comparaison du
profil de vitesse a mi largeur de la cavite a Ra = 106 61
Figure 34 : influence du nombre
de Rayleigh sur le contour de température 63
Figure 35 . profil de
temperature en paroi basse et haute pour 4 nombres de Rayleigh 64
Figure 36 . stratification
thermique au coeur de la cavite a mi-hauteur (a gauche) et a mi-
largeur (a droite) 65
Figure 37 . champs dynamiques de
vitesse pour les 4 valeurs du Rayleigh 66
Figure 38 . profils des
composantes verticales a mi-largeur (a gauche) et a mi-hauteur (a
droite) de la vitesse 67
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page viii
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Figure 39 : contour de
temperature dans la cavité avec emissivité des parois passives
69
Figure 40 : comparaison des
profils de température en paroi basse et haute avec
émissivité
de paroi et sans émissivité 69
Figure 41 : profils de
temperature a mi profondeur et a mi largeur de la cavitee. 71
Figure 42 : densité de
flux net radiatif en paroi basse et haute pour les deux valeurs de dt
(3
et 8) 72
Figure 43 : contours du champ
dynamique a Ra= 1,04 x 107 (a gauche) et Ra= 2,79 x107
(a
droite) 73
Figure 44 : profils de la
composante verticale et horizontale de la vitesse au coeur de la
cavité
a Ra=107 74
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page ix
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
LISTE DES TABLEAUX
Tableau 1 : Paramètre de
stratification mesuré avec rayonnement important des parois
passives. Djanna F. et al [2008] 30
Tableau 2
: Paramètre de stratification avec rayonnement faible des
parois passives. Djanna
F. et al [2008] 31
Tableau 3 : récapitulatif
de quelques configurations étudiées Djanna F. et al [2008]
32
Tableau 4: differents termes de
l'equation de transport globale 44
Tableau 5: fonction A(|Pe|) des
schemas de discretisation, 48
Tableau 6 : effet du maillage sur la température du
fluide 56

Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page x
H Hauteur de la cavité, longueur de
référence
[m]
I Intensité de turbulence []
k Energie cinétique turbulente
n Coordonnée normale à la paroi
[]
Nu Nombre de Nusselt []
Nuc Nombre de Nusselt convectif []
Nur Nombre de Nusselt radiatif []
Nut Nombre de Nusselt total : Nuc + Nur []
p Pression [Pa]
Pm Pression motrice : P + [Pa]
Pl Nombre de Planck : []
Pr Nombre de Prandtl :
[g.s-1m-1]
Q Débit massique linéique
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
NOMENCLATURE
AH Rapport de forme horizontal =
AT Rapport de forme transversal =
[]
Cp Capacité calorifique massique du fluide
[J.kg-1K-1]
D Profondeur de la cavité [m]
f Fréquence [Hz]
g Accélération de la pesanteur
l Largeur de la cavité
Densité de flux radiatif [W.m-2]
Flux radiatif adimensionné []
RaH Nombre de Rayleigh basé sur la hauteur : []
Ral Nombre de Rayleigh basé sur la largeur :
Re Nombre de Reynolds
S Paramètre de stratification de la cavité []
Sr* Terme source radiatif [W.m-3]
Sr Terme source radiatif adimensionné []
| | Norme du taux de déformation des échelles
résolues []
AV Rapport de forme vertical =
[m.s-2]
[]
[]
[]
[m2.s-2]
[m]
[]
[]
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page xi
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
t* Temps adimensionné []
t Temps [s]
T Température locale de l?air [°C]
Tc Température de la paroi chaude [°C]
Tf Température de la paroi froide [°C]
T0 Température moyenne des parois actives :
Tc
ZT f [°C]
0T Ecart de température : Tc-Tf [°C]
[m]
X,Y,Z Coordonnées cartésiennes
adimensionnées []
Vref Vitesse de référence : Vref = a
11Rah
x,y,z Coordonnées cartésiennes
dimensionnelles
[m.s-1]
[m.s-1] [m.s-1]
VMAX Vitesse maximale atteinte dans toute la cavité
u,v,w Composantes transversal, horizontale et verticale de la
vitesse
, ; ., ) []
U,V,W Composantes de la vitesse adimensionnée : (=
Tiv TiTi Tiw

Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page xii
[K-1]
[m2s-1]
á Diffusivité thermique
â Coefficient de dilatation thermique
ì, ç, î Cosinus directeurs de la direction
suivant x, y, et z []
å Emissivité des parois []
X Conductivité thermique
[W.m-1.K-1]
y Viscosité cinématique
[m2s-1]
ì Viscosité dynamique [Pa.s]
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
SYMBOLES GRECS :
Température adimensionnée : []
Taille du filtre []
Coefficient d?absorption [m-1]
ç Epaisseur optique []
æ Constante de Stephan Boltzmann (5,67 x
10-8) [W.m-2.K-4]
è Densité de flux [W.m-2]
Ù Angle solide [sr]
ñ Masse volumique du fluide [kg. m-3]
Symbole de Kronecker []
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page xiii
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
RESUME
Nous avons mené des investigations numériques
sur l'étude de la convection naturelle turbulente dans une cavité
carrée à paroi différentiellement chauffée, dans
laquelle nous soumettons une différence de température de 10 K
entre les parois verticales actives correspondant à une valeur
caractéristique du nombre de Rayleight de 107. Le model de
turbulence K-å standard est utilisé pour la résolution des
équations mathématique de Navier-Stokes a deux dimensions avec la
moyenne de Reynolds (RANS), discrétisé au « second ordre
Upwind scheme ».L'algorithme SIMPLE développé, utilise la
méthode des volumes finis pour la résolution numérique.
Nous effectuons donc des calculs pour plusieurs valeurs du nombre de Rayleigh
correspondant à différents écoulements et
température de parois. Les résultats montrent que, en augmentant
le nombre de Rayleigh, la distribution de température et de vitesse ont
des valeurs très élevé à l'entrée de la
cavité. Nos résultats numériques comparés avec ceux
de la littérature sont satisfaisante.
Mots clefs : convection naturelle turbulence,
enceinte différentiellement chauffée, champ dynamique, champ
thermique, couche limite.
Mémoire de MASTER rédigé et soutenu par
TIENTCHEU NSIEWE Maxwell Page xiv
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
ABSTRACT
We investigate numerically the turbulent natural convection
flow that develops in a differentially heated in square cavity, submitted to a
temperature difference between the active vertical walls equal to 10 K
resulting in a characteristic Rayleigh number equal to 107. The
turbulent model has been applied a standard K-E two equations model and the
two-dimensional Reynolds Averaged Navier-Stokes (RANS), equations are
discredited with the second order upwind scheme. The SIMPLE algorithm, which is
developed using control volumes, is adopted as the numerical procedure.
Calculations were performed for a wide variation of the Rayleigh number
corresponding respectively to different flow and wall temperature. The results
reveal that with increasing Rayleigh number, distributions of temperature and
velocity show higher values at the entrance region of the cavity. Comparison of
numerical results with the experimental data available in the literature is
satisfactory.
Key words : turbulent natural convection,
differentially heated cavity, thermal field, dynamic field, boundary layer.
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
INTRODUCTION
L'équilibre statique d'un fluide dans le champ de
pesanteur est une situation bien moins anodine qu'il n'y paraît. Pour que
cet état soit possible, les forces volumiques telles que le poids,
doivent être compensées exactement par les gradients de pression,
lesquels sont eux-mêmes contraints par la condition de conservation de la
masse. Il suffit de modifier localement la densité du fluide, par
exemple par dissolution d'un sel ou encore en provoquant sa dilatation
thermique, pour briser ce fragile équilibre. Le mouvement qui
résulte de cette variation de densité est appelé
«convection naturelle» ou «convection libre» ou tout
simplement «la convection» par opposition aux convections
forcées mécaniquement (Roche, 2001). Ces phénomènes
de rupture d'équilibre sont tellement présents dans la nature que
trouver un fluide en équilibre statique est en fait une véritable
gageure. Il faut pourtant attendre le début du XXème
siècle pour que la convection soit conceptualisée et
étudiée par Bénard en 1901 et Rayleigh plus tard en 1916.
Le contrôle du gradient de température dans une enceinte
chauffée est un processus complexe, mal maîtrisé, il peut
entrainer une grande perte pour l'industrie (Tcheukam-Toko D. et al.,
2012) (explosion d'unité de chauffage, consommation intense
d'énergie fossile et électrique, mauvais traitement des produits,
brulure de personne voir incendie) et être un danger pour l'environnement
(le rejet de monoxyde de carbone (CO), de l'oxydes d'azote (NO), de soufre
(SOx)... dans l'atmosphère contribue au réchauffement
de la planète). Caractériser l'ambiance thermique d'une enceinte
contribuerait à réduire la dépense
énergétique et ouvrir une voie vers un développement
durable dans l'industrie comme dans le bâtiment.
Dans ce secteur, la principale utilisation de l'énergie
concerne le confort, à savoir le chauffage en hivers et la climatisation
en été (Rouger N., 2009). Elles entraînent des
écoulements de convection naturelle et mixte très importants dans
la pièce d'habitation. Par conséquent, afin d'optimiser ces
systèmes, il devient important de connaître les écoulements
de convection (naturelle ou mixte) induits par le chauffage ou la
climatisation. En effet, pour maitriser les échanges de chaleur dans
l'enceinte et la qualité des ambiances intérieures, la
conduction, le rayonnement puis la convection doivent être pris en compte
de façon précise (Djanna F., 2011). Notons que, les transferts de
chaleur au sein d'une enceinte sont principalement dus aux effets
couplés de convection naturelle et de rayonnement. S'il faut
contrôler ce gradient de température, il est nécessaire
d'étudier la convection naturelle qui s'y déroule. Le cas
étudié est une cavité différentiellement
chauffée. Celle-ci consiste en une enceinte carrée fermée
possédant une paroi chaude et une paroi froide en vis-à-vis. Les
quatre autres parois sont, le plus souvent, considérées comme
adiabatiques pour les simulations numériques. La littérature fait
état de plusieurs travaux
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 1
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
dans le domaine : (Batchelor, 1954), (Le Quéré,
1987), (Boutra A. et al., 2011) (Aklouche S. et al., 2005), (Saury D. et al.,
2008), ont examinés en détail les régimes
d'écoulement pour de faibles nombres de Rayleigh (Ra <
105) et la transition à la turbulence en cavité
différentiellement chauffée. (Salat J., 2004), (Mergui S., 1993),
(Benkhelifa A. et al., 2007), (Djanna F., 2011), ont fait une analyse
qualitative et quantitative pour des valeurs plus élevées du
nombre de Rayleigh (109 à 1012). Par la suite,
(Wang H. et al., 2006), (Adel I., 2010), (Djanna F., 2011) ont montrer
l'influence qu'a le rayonnement de surface sur la stratification thermique au
centre ainsi que dans la couche limite. Pour compléter la base de
données sur ces écoulements, notre intérêt portera
donc sur le thème « étude de la convection naturelle
turbulente dans une enceinte à paroi chauffée ».
Dans ce mémoire, la première partie est
consacrée à un rappel bibliographique sur les études
réalisées dans le domaine de la convection libre d'une part et la
convection radiative d'autre part, afin de poser le problème de la
convection naturelle en cavité différentiellement
chauffée. Passant par la définition des mots clés. Dans le
deuxième chapitre, le problème physique la mise en
équations de la convection naturelle est présentée. En
troisième partie les outils numériques de résolution sont
décrient. En quatrième partie les résultats obtenus dans
une cavité différentiellement chauffée de 0.335 m de
hauteur avec comme paramètre caractéristique Ra = 107
avec de l'air.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 2
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
CHAPITRE I. ETUDE BIBLIOGRAPHIQUE
Les premières études de convection naturelle
concernent les écoulements de couche limite sur plaque plane (à
température ou à flux imposé). Ensuite, les chercheurs
vont se pencher sur les écoulements de convection naturelle en espace
confiné avec comme principale illustration, une cavité
parallélépipédique remplie d'air possédant deux
parois opposées soumises à un écart de température
constant (une paroi chauffée et la paroi opposée refroidie). Une
telle cavité est le siège d'écoulements de convection
naturelle et fait l'objet de nombreuses études tant
expérimentales que numériques.
La littérature montre que plusieurs paramètres
influencent la stratification des écoulements dans ces types de
cavité, dont le nombre de Rayleigh principalement, le nombre de Prandtl,
le rapport de forme verticale ainsi que le rayonnement de surface,
éléments clés des conditions imposées aux parois.
Nous allons donc partir de la définition des mots clés de notre
travail, afin de mieux situer le lecteur dans l'étude, ensuite montrer
comment les paramètres cités ci-haut, influencent sur la
stratification de l'écoulement. Notre objectif sera donc de :
? Préciser le cheminement de l'écoulement dans
la cavité afin de mieux explorer le parcours du fluide au sein de la
cavité ;
? sortir les fluctuations de température et la
stratification thermique de la température dans l'enceinte;
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 3
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
I.1 Quelques définitions
I.1.1 Notion de convection
Ce mode de transfert est basé sur le fait qu'il y'a
déplacement de matière : il ne concerne donc que les fluides
(liquides et gaz). Contrairement à la conduction où le transfert
de chaleur se fait « par contact », dans le fluide, la
possibilité de déformation sous l'effet de la température
permet de mettre en oeuvre des mouvements de ce fluide plus ou moins important.
Ces mouvements sont dus à des différences de température
et/ou des différences de pression. Ce couplage fort entre la thermique
et la dynamique fait de ce type d'écoulement un sujet d'étude
particulièrement attractif (Djanna F., 2011).
On peut exprimer la quantité de chaleur transmise par
convection entre une paroi solide et un fluide au moyen de l'équation
suivante :
Sous cette forme, l'équation de la convection semble
être tout à fait simple. En réalité, il n'en est
rien, car cette équation est une définition de l'unité de
conductance thermique moyenne par convection plutôt qu'une loi de
transmission de la chaleur par convection. Le coefficient d'échange de
chaleur par convection est, en effet, une fonction de l'écoulement du
fluide, des propriétés thermiques du milieu fluide et de la
géométrie du système. Sa valeur numérique n'est
généralement pas uniforme sur une surface et elle dépend
également du lieu où on mesure la température. Elle est
naturelle si le nombre de Richardson (Zermane S. et al., 2005),
Gr/Re2, est supérieur à 16 ou forcé si ce
dernier est inférieur à 0,1.
? Convection naturelle : ou "convection
libre" (Natural Convection), est le régime
d'écoulement obtenu
lorsque l'on chauffe un fluide sans qu'il n'y ait d'écoulement
"extérieur" imposé. Cet écoulement est inexplicable dans
le cadre précédent car aucun mouvement ne serait possible de par
le découplage entre les équations de la dynamique et de la
thermique. Pour lever ce paradoxe, on tient compte d'un phénomène
que l'on avait négligé : la légère
dilatabilité du fluide. C'est donc la force d'Archimède
provoquée par les variations de densité induites par le chauffage
qui fait se déplacer le fluide. La "thermique" et la "dynamique" sont
alors très fortement couplés. La convection naturelle est en fait
un mouvement de fluide induit par des forces pesantes ou forces de
poussée d'Archimède. Ces dernières sont dues à des
différences de masse volumiques (Rouger N., 2009).
?
? I-1
A priori ñ la densité est fonction de la
température et de la pression par la loi d'état (pour un
gaz mais aussi pour un liquide). Il est donc naturel de penser
que si l'on chauffe une paroi, la
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 4
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
température du fluide environnant augmente par
diffusion. La stratification de pression s'en trouve changée, le
gradient de pression crée le mouvement.
En général, c'est un gradient thermique qui est
la cause de cet écoulement de convection naturelle. En effet, du fait de
l'agitation thermique, la masse volumique des fluides diminue quand la
température augmente (Rouger N., 2009). La différence de
densité qui est la plupart du temps provoquée par la
différence de la température, avec la force de gravité,
créée une force de flottabilité qui créée
par conséquent une différence de quantité de mouvement.
Cependant, on devra mentionner que, ce n'est pas n'importe quel gradient de la
température qui causera le mouvement dans le fluide. En
réalité, la différence de température devrait
être d'une manière qui provoque l'instabilité du fluide. Il
est conventionnel d'employer la différence de la température
instable pour assurer le mouvement du fluide ;
? L'approximation de Boussinesq : Grâce
à elle, on transforme un fluide faiblement dilatable en un fluide
incompressible mais avec un terme de force d'Archimède. Le nombre sans
dimension pertinent est le nombre de Grashof (ou son faux jumeau le nombre de
Rayleigh). Les équations sans dimension (en négligeant la
dissipation visqueuse) à résoudre sont couplées (au sens
où la dynamique et la thermique sont liés et qu'il faut
connaître les conditions aux limites en vitesse et en température
pour résoudre) aux conditions aux limites associées... Cette
approximation n'est pas mauvaise pour les liquides mais est à manier
avec précautions pour les gaz. Dans tous les cas on ne chauffera pas
trop! Des phénomènes très variés peuvent se
produire : écoulements pariétaux ou rouleaux ou hexagones.
Cette approximation permet d'écrire une équation
d'état du fluide qui relie les variables d'état : densité,
pressions et température. La simulations (air) utilise la loi des gaz
parfaits. Dans l'approximation de Boussinesq, on suppose que les
propriétés du fluide sont constantes, à l'exception de la
masse volumique dans le terme des forces volumique. Cependant si les
variations
de température sont peu importantes on peut écrire
que : °P = f3(T -- To) = (T-T0) «
1. L'équation
P To
de la masse volumique peut être présentée par
une fonction linéaire de T :
;
? Convection forcée : contrairement
à la convection naturelle qui est causée par une
différence de masse ou d'énergie, elle est
provoquée par une circulation artificielle (pompe, turbine) d'un fluide.
Le transfert y est plus rapide. Dans un environnement comme dans l'espace, la
convection naturelle n'est pas possible puisque la poussée
d'Archimède ne s'exerce pas. Ainsi la circulation de la chaleur doit
être forcée dans une capsule spatiale. Une flamme aurait
également de
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 5
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
la difficulté à exister car les gaz de
combustion resteraient près de la flamme, la coupant de l'apport
d'oxygène. Il faut pour l'entretenir une circulation forcée pour
éloigner ces gaz et amener l'oxygène ;
? Convection mixte : Il existe un grand
nombre de situations intermédiaires où les
mécanismes
de convection forcée et de convection libre coexistent avec des ordres
de grandeur comparables. Parmi les exemples de cette mixité, on peut
citer : les écoulements lents en canalisations (comme dans les
radiateurs à eau), les écoulements atmosphériques et les
courants marins. Dans nombre de situations pratiques on se trouve en
régime de convection mixte. Tandis que, les situations de convection
naturelle dominante et de convection forcée dominante doivent être
caractérisées par des critères de discrimination clairs et
physiquement fondés, définies plus souvent par des nombres
adimensionnels.
La première approche physique de la convection a
été mise en place par Henri Bénard, avec l'étude de
la convection dans une couche de fluide soumise à un gradient de
température vertical. Ces expériences sont connues sous le nom de
cellules de Bénard. Les équations de conservation mise en jeu
constaté par celui-ci sont entre autre :
? La conservation de la masse :
? La conservation de la quantité de mouvement ;
? La conservation de l'énergie.
Le Nombre de Rayleigh (Ra) est le paramètre de
contrôle de la convection (elle donne la transition entre le laminaire et
le turbulent à travers le Rayleigh critique et varie en fonction des
configurations). Il représente le terme moteur de poussée
d'Archimède rapporté au produit des deux termes diffusifs.
Expérimentalement, on observe qu'au bout d'un certain temps, le fluide
se met en mouvement spontanément :
I-2
I.1.2 Convection turbulente
Comme le transfert d'énergie par convection est
très intimement lié au mouvement du fluide, il est
nécessaire de connaître le mécanisme de l'écoulement
du fluide avant d'examiner celui de l'écoulement de la chaleur. Un des
plus importants aspects de l'étude hydrodynamique est d'établir
si le mouvement du fluide est laminaire ou turbulent.
La turbulence se décrit généralement
comme étant un écoulement désordonné, en temps et
en espace, opposé à l'écoulement laminaire qui est
parfaitement ordonné. Elle est imprévisible au sens qu'une petite
perturbation initiale à un instant donné s'amplifie rapidement et
rend impossible une prédiction déterministe de son
évolution. Chacun est capable de citer des éffets bien visibles
de celle-ci : Les flots tumultueux, les rafales de vent frais, la fumée
d'une cigarette ou le développement d'un filet d'eau coulant d'un
robinet, sont des phénomènes de turbulence. Et dans
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 6
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
chacun de ces cas, on constate des structures tourbillonnaires
plus ou moins organisées, rendant l'écoulement complexe et
difficile d'appréhender les détails, d'en prédire
précisément l'évolution instantanée et locale.
La turbulence se manifeste sur toutes les quantités qui
interviennent dans la définition des écoulements et dans leurs
propriétés fondamentales et appliquées. Son investigation
expérimentale nécessite donc la mesure instantanée de
nombreuses grandeurs physiques : vitesse, température, pression, masse
volumique, indice de réfraction, champ électrique...
Les situations à aborder dans les mesures sont
variées. Il y a d'abord celles que l'on crée au laboratoire et
qui sont relativement bien définies : couches limites, jets,
sillages, modèles de turbulence isotrope ou anisotrope. Il y a
ensuite les situations plus complexes que l'on rencontre dans les
réalisations techniques actuelles (réacteurs, turbomachines,...)
ou celles qui apparaissent dans la nature (couche limite atmosphérique,
turbulence de ciel clair, nébuleuses, courants marins...) (Comte-Bellot
G., 1976). L'intermittence qui apparaît à la frontière
libre d'un écoulement turbulent exige en effet la séparation des
caractéristiques propres au champ turbulent considéré et
à l'écoulement extérieur. A l'intérieur même
d'un champ turbulent existent de grandes structures organisées en
liaison avec les instabilités et déformations imposées par
le champ de vitesse. En outre, les zones où l'énergie
cinétique est dissipée en chaleur sont concentrées en
certaines régions effilochées à travers le champ. Toutes
ces structures particulières retiennent actuellement l'attention des
chercheurs. Pour les atteindre, il faut, d'une part, disposer de capteurs
fournissant des signaux continus et, d'autres parts, réaliser les
circuits électroniques aptes à fournir les traitements
appropriés (moyennes conditionnelles, échantillonnages...).
Un écoulement turbulent présente un grand nombre
de degrés de liberté spatiale proportionnel à
Re9/4 pour une turbulence tridimensionnelle
(respectivement temporelle en Re 11/4) (Tamman H., 2004). Par
conséquent, il est difficile de prédire théoriquement son
évolution à partir des conditions initiales notamment dans la
plupart des applications industrielles. Les tourbillons présentent des
dimensions comparables à la longueur caractéristique du domaine
de l'écoulement (diamètre du canal, épaisseur de la couche
de mélange,...), les plus petites sont des structures dissipatrices
dites structures de Kolmogorov dont les dimensions sont proportionnelles
à Re -3/4 (Tamman H., 2004).
La mise en mouvement du fluide commence à
apparaître pour un nombre de Rayleigh critique d'environ Rac = 3,5 ×
104. Pour Ra < Rac le transfert thermique est purement diffusif.
Le seuil de l'instabilité est indépendant de la nature du fluide.
Ensuite avec l'augmentation du Rayleigh apparaît un régime de
convection stationnaire suivie par une zone dite de « transition vers le
chaos » caractérisée par l'apparition d'oscillations
périodiques puis instationnaire du champ de température
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 7
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
et de vitesse autour de Ra = 106. Nous distinguons
ensuite le régime de turbulence douce et le régime de turbulence
dure qui apparaît autour de Ra = 2 X 108 Pour une cellule de
rapport d'aspect 0,5. Elle est établie également à partir
d'un nombre de Reynold de l'ordre de 3200.
I.1.3 Couche limite dynamique et thermique
Lorsqu'un fluide s'écoule le long d'une surface,
indépendamment de la nature de l'écoulement (laminaire ou
turbulent), les molécules à proximité de la surface sont
ralenties à cause des forces visqueuses. Les molécules du fluide
adjacentes à la surface y adhèrent et ont une vitesse nulle par
rapport à la paroi. Les autres molécules du fluide
s'efforçant de glisser sur les premières sont ralenties,
phénomène qui donne naissance aux forces de cisaillement
(Tcheukam Toko T., 1997). Dans un écoulement laminaire, l'interaction
appelée cisaillement visqueux, s'effectue entre les molécules
à une échelle microscopique. Dans l'écoulement turbulent
une interaction entre les masses du fluide à une échelle
macroscopique, appelée cisaillement turbulent, se superpose au
cisaillement visqueux. Les effets des forces visqueuses qui prennent naissance
à la paroi s'étendent dans la masse du fluide, mais à une
faible distance de la paroi, la vitesse des particules fluides atteint celle de
l'écoulement libre non perturbé. La région dans laquelle
sont localisées les variations notables de la vitesse est appelée
couche limite hydrodynamique. L'épaisseur de cette couche est
définie comme étant la distance comptée à partir de
la paroi où la vitesse locale atteint 99 % de la vitesse uoe
du fluide loin de la paroi. Le profil des vitesses à l'intérieur
de la couche limite dépend de la nature de l'écoulement. Comme le
fluide poursuit son écoulement le long de la plaque, les forces de
cisaillement ralentissent de plus en plus son mouvement et l'épaisseur
de la couche limite augmente. Elle est un élément important en
mécanique des fluides, (aérodynamique, hydrodynamique), en
météorologie, en océanographie, etc.
Lorsqu'un fluide réel s'écoule le long d'une
paroi supposée fixe, les vitesses sur la paroi sont nulles alors
qu'à l'infini (c'est-à-dire loin de l'obstacle) elles sont
égales à la vitesse de l'écoulement non perturbé.
La loi de variation dépend de la viscosité du fluide qui induit
un frottement entre les couches voisines : la couche la plus lente tend
à freiner la couche la plus rapide qui, en retour, tend à
l'accélérer. Dans ces conditions, une forte viscosité
égalise au maximum les vitesses. Au contraire, si le fluide est peu
visqueux, les différentes couches sont beaucoup plus
indépendantes : la vitesse à l'infini se maintient jusqu'à
une courte distance de l'obstacle et il y a une variation plus forte des
vitesses dans la petite épaisseur de la couche limite.
Considérons l'écoulement turbulent d'un fluide
à l'intérieur d'un tube de section circulaire,
présenté à la figure 1. On remarque que l'adhérence
du fluide à la paroi provoque l'apparition d'une couche limite
dynamique, qui tend à se développer au fur et à mesure que
l'on s'éloigne de l'entrée
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 8
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
du tube. Une autre zone centrale de pleine turbulence
où le gradient de vitesse est très faible avec un profil aplati
en son centre est présente.
Par définition, la couche limite est la région
dans laquelle la variation normale de la vitesse est suffisamment rapide pour
que la force de cisaillement à laquelle elle donne lieu soit de l'ordre
de grandeur de la force d'inertie. Par convention, l'épaisseur de la
couche limite ô correspond à une composante u égale
à 0,99U ; où U est la composante de la vitesse du fluide libre.
Elle est aussi la couche dans laquelle l'écoulement est
significativement influencé par les propriétés du fluide
(Tcheukam Toko T., 1997).

Figure 1 : couche limite
dynamique (Graf W. et Altinakar M., 1995)
Lorsque le fluide, entre avec une température
différente de celle de la paroi, des échanges thermiques
s'établissent. Les particules du fluide s'échauffent ou se
refroidissent par conduction au contact de la paroi et par convection en
s'échangeant entre elles la chaleur de proche en proche. La
température varie depuis celle de la surface jusqu'à la
température du fluide libre au centre de l'écoulement et on
assiste alors à la formation d'une couche limite thermique.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 9
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »

Figure 2 : couche limite
thermique (Graf W. et Altinakar M., 1995)
Pour un tuyau très long et de faible rayon, la couche
limite dynamique finit par envahir tout le tube, sauf près de sa section
d'entrée. Son épaisseur dépend de plusieurs facteurs tels
que la viscosité du fluide, la masse volumique et le niveau de
turbulence. Une étude numérique récente menée par
(Tcheukam-Toko D. et al., 2012) sur un fond hydrauliquement lisse,
révèle que lorsque le nombre de Reynolds augmente,
l'épaisseur de la couche limite dynamique diminue
L'épaisseur de la couche limite thermique quant
à elle n'est pas celle de la couche limite dynamique : elle peut
être plus grande (pour les métaux liquides par exemple) ou plus
petite (liquides en général) et à peu près
égale pour les gaz à pression ordinaire. On évoque
l'aspect thermique pour bien montrer que la physionomie de l'écoulement
général est conditionnée par ce qui se passe au voisinage
immédiat de l'obstacle. Le traitement mathématique de la couche
limite dynamique ne peut être isolé de celui de la couche limite
thermique que par l'hypothèse d'une viscosité indépendante
de la température
Nous remarquons sur les deux figures ci-dessus, une longueur
d'entrée qui est la distance requise dans le sens d'écoulement
pour que les couches limite thermiques de part et d'autre de la canalisation
fusionnent au centre de l'écoulement (confère figure 2
ci-dessus). Cette distance ne peut pas être prédite avec
exactitude, mais de nombreuses expériences ont été
menées pour sa détermination dans des conditions
d'écoulements différents.
La figure 3 montre l'accroissement de la couche limite et les
profils des vitesses en différents points de la plaque.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 10
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »

Figure 3 : Profils des vitesses
pour les couches limites laminaire et turbulente dans un
écoulement sur une plaque plane (Tcheukam-Toko D.
et al., 2012)
Les profils des vitesses près du bord d'attaque sont
représentatifs des couches limites laminaires. Cependant
l'écoulement à l'intérieur de la couche limite reste
laminaire seulement sur une certaine distance à partir du bord d'attaque
et devient ensuite turbulent. A l'intérieur de la couche limite
turbulente, il subsiste, tout contre la paroi, une très mince couche en
écoulement presque laminaire appelée sous couche limite laminaire
ou film laminaire. La distance entre le bord d'attaque et le point de
transition où la couche limite devient turbulente est appelée
longueur critique.
I.1.4 Convection en enceinte différentiellement
chauffée
On distingue principalement deux configurations, la
première est celle d'une enceinte contenant un fluide et soumise
à un gradient vertical de température (convection de
Rayleigh-Bénard), la seconde étant celle d'une cavité avec
un gradient horizontal de température.
L'enceinte qui est chauffée par le bas et refroidie par
le haut correspond à la configuration de la convection de Rayleigh
Bénard qui traite de la stabilité et le mouvement d'un fluide
confiné entre deux plaques horizontales qui sont maintenues à des
températures uniformes et distinctes. La convection de
Rayleigh-Bénard a une longue et riche histoire, elle a été
étudiée durant des décennies aussi bien pour ses
différentes applications industrielles que du point de vue recherche
fondamentale (Mabrouk G., 2010).
Paroi froide Tf

Adiabatique
Adiabatique
Paroi chaude TC
Figure 4 : schéma
représentant la configuration de la convection de Rayleigh-Bénard
cité par
(Mabrouk G., 2010)
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 11
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Pour illustrer le mécanisme de base de la convection de
Rayleigh-Bénard et les forces en présence qui sont en
compétition, on considère le mouvement d'une goutte de fluide
selon ce qui suit.
Tout d'abord, considérons une goutte située dans
le fond d'une couche de fluide, où la densité est plus faible que
la densité moyenne. Tant que la goutte reste immobile, elle est
entourée de fluides de même densité et la poussée
d'Archimède est nulle. Supposons maintenant une perturbation
aléatoire provoquant un léger déplacement de la goutte
vers le haut. Cette dernière est alors entourée de fluides de
densité plus grande et de température plus petite. Ainsi la
poussée d'Archimède, proportionnelle à la
différence de densité et au volume de la goutte, va s'exercer
vers le haut et va amplifier le mouvement ascendant initial de la goutte. On
peut raisonner de la même façon pour une goutte de fluide
située au sommet de la couche. La goutte subissant un léger
déplacement aléatoire vers le bas est alors entourée d'un
fluide moins dense et tend à s'enfoncer vers le bas de la couche.
Ces écoulements ascendants et descendants
définissent la convection naturelle. La convection s'amorce lorsque le
nombre de Rayleigh dépasse une valeur de 1700 (Bejan A. et Kraus A.,
2003).
Paroi froide Tf
Adiabatique
Paroi chaude TC
Figure 5 : schéma
représentant le déplacement d'une goutte de fluide (Bejan A.
et Kraus A., 2003)
Dans la 2éme configuration, l'une des parois
verticales est chauffée tandis que l'autre est refroidie, les parois
horizontales étant considérées comme adiabatiques (Figure
6). Dans ce cas, il n'y a pas de gradient critique de température et le
fluide est alors ascendant le long de la paroi chaude et descendante le long de
la paroi froide.

Adiabatique
Paroi chaude TC
Adiabatique
Paroi froide Tf
Figure 6 : schéma de la
convection dans une enceinte avec gradient horizontal de température
(Wang H. et al., 2006)
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 12
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Il existe des configurations donc la source de chaleur n'est pas
répartir sur toute la paroi
horizontale ou verticale. Mais il y'a plutôt des sources
de chaleur qui sont introduites dans l'enceinte (Binet B., 1998).

Figure 7 : enceinte rectangulaire
comportant plusieurs sources de chaleur surfaciques (Binet B.,
1998)
On peut retrouver les éléments suivants dans la
définition d'une cavité différentiellement chauffée
:
? Les parois actives, dont l'une est
chauffée à flux uniforme, et l'autre est refroidie (avec
un
écart de température constant) ;
? parois passives, qui sont
supposées adiabatiques ou libre selon le phénomène
étudié ;
? Un rapport de forme verticale qui est
le rapport de la longueur sur la largeur.
I.2 La convection naturelle en cavité
differentiellement chauffée.
I.2.1 Les bases de la convection naturelle en
cavité
L'étude de la convection naturelle dans les enceintes a
fait l'objet d'un très grand nombre de travaux tant théoriques
qu'expérimentaux. L'intérêt de telles études
réside dans son implication dans de nombreuses applications
industrielles telles que le refroidissement des composants
électroniques, la thermique des bâtiments, l'industrie
métallurgique, la croissance des cristaux pour l'industrie des semi
conducteurs, et le cas d'une génération de chaleur accidentelle
due à un incendie dans un bâtiment pour réacteur
nucléaire, etc.... L'enceinte rectangulaire continue à être
la géométrie qui présente le plus
d'intérêt.
I.2.1.1 La cellule de
Rayleigh-Bénard
C'est Henri Bénard à la fin du XIXe
siècle fut l'un des premiers à mener une étude en
laboratoire sur les courants de convection. Dans son article intitulé
Les tourbillons cellulaires dans une nappe de liquide, (Bénard H.,
1901), étudie des couches minces de fluides (environ 1 mm)
chauffées en-dessous, la surface supérieure du liquide
étant libre. La cellule de Rayleigh-Bénard est plus proche de
celle définie théoriquement par Lord Rayleigh en 1916.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 13
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
En effet, contrairement au dispositif expérimental de
H. Bénard, il fait l'hypothèse dans son article que le fluide est
contenu entre deux plaques planes infiniment grandes. Lors du calcul du seuil
d'instabilité du fluide, c'est-à-dire la différence de
température pour laquelle le fluide se met en mouvement, l'auteur
introduit également une quantité qui deviendra par la suite le
nombre de Rayleigh (Rayleigh L., 1916). Rayleigh place lui même son
travail dans la continuité de celui de H. Bénard qu'il cite
dès la première phrase de son article. En réalité,
nous savons maintenant que la théorie développée par
Rayleigh ne s'applique pas à l'expérience de H. Bénard.
En 1900, H. Bénard commente son travail en ces termes :
« Je n'est pas la prétention d'avoir épuisé un sujet
aussi nouveau : bien des points restent à éclaircir, même
sans sortir du point de vue expérimental ; mais je serais heureux si mon
travail, tout incomplet qu'il est, contribuait à attirer l'attention des
expérimentateurs sur les domaines inexplorés de la Physique
moléculaire et de la Mécanique des fluides. ». Il semble que
son souhait ait été réalisé : la cellule de
Rayleigh-Bénard reste encore aujourd'hui un dispositif d'étude de
la convection thermique très utilisé. Il s'agit en effet d'une
géométrie simple avec peu de paramètres de contrôles
qui peuvent être ajustés indépendamment les uns des autres.
Cependant, malgré le grand nombre d'études sur ce sujet, des
zones d'ombre persistent, en particulier la compréhension du
mécanisme de transport de la chaleur par l'écoulement turbulent
à haut nombre de Rayleigh.
I.2.1.2 Problème posé par la convection
naturelle
Le problème de la convection naturelle dans les
cavités différentiellement chauffées a été
posé par Batchelor en 1954 (Djanna F., 2011), il fut le premier à
définir les régimes de conduction
et de couches limites. Il a examiné en détail
les cas de faibles nombres de Rayleigh (Ra < ) et a
fait une analyse
qualitative pour des valeurs plus élevées du nombre de Rayleigh.
Il ressort de son étude que, lorsque l'on soumet les parois verticales
d'une cavité remplie d'air à un écart de
température constant, les paramètres principaux donc
dépend l'écoulement engendré sont :
? Le nombre de Rayleigh :
? le nombre de Prandtl:
? le rapport de forme vertical :
Les nombreuses publications de (Busse F., 1967)
témoignent de l'intérêt qu'il a porté à
l'étude des instabilités de Rayleigh-Bénard. Il a en effet
établi un diagramme qui donne les différentes instabilités
en fonction de trois paramètres, à savoir: le nombre d'onde, le
nombre de Prandtl et le nombre de Rayleigh.
Le cheminement principal du fluide dans une cavité
différentiellement chauffée avec parois en vis-à-vis est
donné ci-dessous : une fois l'écart de température
imposé, le fluide monte au niveau
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 14
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
de la paroi chaude, rejoint la paroi froide en longeant le
plafond (jet pariétal), puis, redescend au niveau de la paroi froide,
enfin, rejoint la paroi chaude par le plancher. De plus, suivant les conditions
limites imposées, il se peut que des zones de recirculation
apparaissent. On peut également observer suivant les cas de figure, le
développement des couches limites le long des parois chaude et froide,
ainsi que la transition vers la turbulence ou même la turbulence
pleinement développée (Ra grand).

Figure 8 : Représentation
schématique de l'écoulement pour un nombre de Rayleigh
égal à
1,5×109 (Salat J., 2004)
Une question centrale est notamment de savoir comment
évolue l'efficacité du transfert thermique avec l'augmentation du
nombre de Rayleigh. Le nombre de Rayleigh (Ra) est un paramètre de
contrôle du système. Il peut être vu comme la
différence de température sans dimension, c'est-à-dire que
plus il est élevé, plus l'échange de chaleur est important
(Gautier F., 2008). Nous verrons que peu importe le régime, le Rayleigh
est le moteur de la modification de la stratification thermique de
l'écoulement, et qu'a une valeur dite Rayleigh critique (transition
entre le régime laminaire et le régime turbulent), il change
complètement l'allure de l'écoulement.
I.2.2 Paramètres influençant
l'écoulement de convection naturel en cavité
I.2.2.1 Influence du nombre de Rayleigh
Le nombre de Rayleigh (Ra) est le paramètre de
contrôle de la convection thermique. Plus le nombre de Rayleigh est
grand, plus la convection est intense. Il s'écrit sous la forme :
Où g est l'accélération
de la pesanteur, f.? le coefficient de dilatation thermique isobare,
h la hauteur de la cellule de convection, ?T la
différence de température entre le haut et le bas de la cellule,
á la diffusivité thermique et y
la viscosité cinématique du fluide. Le nombre de
Rayleigh
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 15
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
peut s'interpréter comme une mesure de l'importance du
mécanisme responsable de l'instabilité du fluide (la
poussée d'Archimède) par rapport aux mécanismes de
freinage (la diffusivité thermique et la viscosité). Il est
également possible de voir le nombre de Rayleigh comme la
différence de température ?T adimensionnée (Djanna F.,
2011).
En général, les écoulements de convection
se présente sous forme de rouleaux contra-rotatifs bidimensionnels
d'axes parallèles qui apparaissent au seuil d'instabilité
correspondant à une valeur du nombre de Rayleigh critique (Rac) de
l'ordre de 1708. Au-dessous de cette valeur critique, on a un régime
conductif. En augmentant la valeur du nombre de Rayleigh au-delà de la
criticalité, des modifications dans la structure de l'écoulement
apparaissent. Dans ce sens, (Krisnamurti R., 1970) a effectué des
études sur le Rayleigh, et a constaté différentes
transitions vers le régime turbulent en fonction du nombre de Prandtl.
Il a montré que pour un fluide donné, en augmentant le nombre de
Rayleigh, l'écoulement, depuis l'état stationnaire, passe par
différents régimes; à savoir le régime
périodique, quasi-périodique et turbulent. Néanmoins, pour
les faibles valeurs du nombre de Prandtl (cas de l'air), la transition d'un
état stationnaire à la turbulence s'opère directement et
elle se fait pour une faible valeur du nombre de Rayleigh (Ra = 4,8 x
103). Dans le même ordre, (Revnic C. et al., 2009), fait des
expériences pour deux valeurs du nombre de Rayleigh (102 et
103) et fait le constat qu'effectivement, plus il augmente le nombre
de Rayleigh, plus les lignes des isothermes se déforment et tendent
à être parallèle au plafond, en tendant vers la turbulence.
Il en va de même pour le champ dynamique, qui tourne autour du centre de
la cavité et s'en rapproche en fonction de l'augmentation du nombre de
Rayleigh.
Lorsque le nombre de Rayleigh augmente, l'écoulement
horizontal à proximité du plafond (resp. planché) est
refroidi (resp. réchauffé) le long de son parcours, et lorsque le
gradient local excède celui que le fluide peut supporter, ce dernier
éjecte une perturbation thermique qui peut alors être
absorbée par la couche limite. Cette perturbation va ensuite être
amortie ou amplifiée par la couche limite verticale suivant un processus
de filtrage tel que décrit par (Gebhart B., 1973). Cette perturbation
est généralement amortie sur la première moitié de
la couche limite avant d'être amplifiée sur la deuxième
moitié. Ces perturbations thermiques ont un effet plus
déstabilisant sur l'écoulement que les perturbations d'origine
hydrodynamique rencontrées pour des cavités à parois
adiabatiques. En effet, pour une cavité carrée remplie d'air par
exemple, le nombre de Rayleigh critique pour lequel apparaissent les
premières instationnarités est de l'ordre de 2×108
(Le Quéré P., 1987), (Mergui S., 1993) dans le cas
adiabatique alors qu'il passe à 2×106 dans le cas
conducteur (Le Quéré P., 1987). On peut le voir sur la figure
ci-dessous qui présente la valeur du nombre de Rayleigh critique pour
des cavités de rapport de forme compris entre 1 et 10. Les valeurs du
nombre
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 16
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
de Rayleigh critique ont été confirmées
numériquement par (Winters K., 1987), (Jones D. et Briggs D., 1989).

Figure 9 : Comparaison des courbes
correspondant à la transition à l'instationnarité pour
des
parois addiabatiques (---) ou conductrices (-) en cavité remplie
d'air A= (H/l) (Le Quéré P., 1987)
(Ampofo F. et Karayiannis T., 2003) Ressortent les profils de
température au coeur de la cavité pour un nombre de Rayleigh de
1,5 x 109, et a les mêmes profils.
L'étude de la convection naturelle en régime
instationnaire obéit aux Hypothèses simplificatrices suivantes
(Aklouche S. et al., 2005) :
? le fluide doit être newtonien ;
? L'écoulement doit être laminaire et
bidimensionnelle ;
? les propriétés physiques du fluide doivent
être constantes hormis la masse volumique qui obéit à
l'approximation de Boussinesq ;
? Les échanges radiatifs entre les parois, la
dissipation visqueuse et le terme de pression dans l'équation de la
chaleur doivent également être négligeables.
Les calculs d'Aklouche S. et al. (2005) ont
été effectués pour trois valeurs du nombre de Rayleigh
thermique (103, 104, 105) et un nombre de
Prandtl de l'air pris égal à 0,71. Les résultats sont
présentés sous la forme de lignes de courant, d'isothermes et de
portrait de phase. Pour les nombres de Rayleigh égaux à 103
et 105, l'écoulement est caractérisé
respectivement par quatre et trois cellules. Les quatre cellules sont
assimilables à des tourbillons symétriques 2 à 2 par
rapport au plan médian aux parois horizontales figure 10a.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 17
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »

Figure 10 : représentation
des lignes de courant. (Aklouche S. et al., 2005)
Les deux cellules localisées dans la partie
inférieure gauche de l'enceinte et celles situées dans la partie
supérieure droite tournent dans le sens trigonométrique tandis
que les deux autres cellules tournent dans le sens horaire. La
répartition des isothermes présente, comme les lignes de courant,
une symétrie par rapport au plan médian aux parois horizontales.
L'écoulement caractérisé par trois cellules résulte
de la fusion des deux cellules situées à gauche de la diagonale
de l'enceinte et la cellule du milieu tourne dans le sens
trigonométrique (fig.10b et 10c).

Figure 11 : représentation
des isothermes. (Aklouche S. et al., 2005)
Par contre, au milieu de l'enceinte, la forme des isothermes
varie au cours du temps. Il y a un resserrement d'autant plus prononcé
que le nombre de Rayleigh est élevé, des isothermes,
caractérisant la prédominance du transfert de chaleur par
conduction (fig.11b et 11.c).
On remarque que l'écoulement en régime chaotique
apparaît pour un nombre de Rayleigh égal à 7,5
105 et se manifeste jusqu'à un nombre de Rayleigh égal
à 3,10 6. Les différents portraits de phase
caractérisant l'état stationnaire (point limite), l'état
périodique (cycle limite), l'état quasi périodique
(dédoublement de période), (tore) et l'état chaotique
(chaos) montrent la mise en évidence de la multiplicité des
solutions lorsque le nombre de Rayleigh augmente. Des fenêtres laminaires
apparaissent pour un nombre de Rayleigh égal à 3,7 106
dont le portrait de phase est caractérisé par un tore. Le
dimensionnement des portraits de phase a révélé
l'existence d'attracteurs étranges.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 18
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Ces résultats sont confirmés à une couche
de différence lors des campagnes de mesure de vitesse, par PIV-2D
effectué par (Benkhelifa A. et al., 2007), dans le plan vertical
médian à mi-profondeur d'une cavité, L'examen de son champ
moyen, montre que l'écoulement est caractérisé par un
arrangement sous forme de trois rouleaux contrarotatifs. Qui persiste
même à des écarts de température de l'ordre de
40°C pour un même nombre de Rayleigh. On observe également
deux petits tourbillons de coin respectivement au niveau du coin en haut
à gauche et en bas à droite. Il est intéressant de
constater que cette structure organisée fait apparaître trois
rouleaux, alors que l'on aurait pu s'attendre à trouver une structure
à quatre rouleaux comme présenté
précédemment.
Reprenons toujours un cas d'instationnarités en
ajoutant dans la cavité un linteau mais pour une valeur du nombre de
Rayleigh de 1,5.109 (Rouger N. et al., 2007). On observe
immédiatement que la circulation d'air se caractérise
essentiellement par des écoulements qui suivent les parois, sans aucun
décollement appréciable. En descendant le long de la paroi
froide, il fait apparaître un développement de couche limite qui
s'épaissit dans la partie basse. La partie inférieure de la
cavité devient le siège de l'épanouissement d'un jet
pariétal horizontal accompagné au-dessus, d'une recirculation
bien visible à travers les vecteurs. Le long de la paroi verticale
chaude, la couche limite montante se développe même au-delà
de Y = 0,7 (coté inférieure du linteau), sans que l'on puisse
distinguer un échappement horizontal important à cette même
cote, comme cela est observé dans les cas tests de simulations
numériques à plus haut nombre de Rayleigh.
Il n'y a donc apparemment pas de zone morte dans la partie
supérieure gauche de la cavité, l'écoulement principal
longe les parois et contourne sans décollement le linteau qui,
normalement, n'est qu'un obstacle passif (adiabatique). Le linteau introduit
des différences de température entre l'amont et l'aval car
l'alimentation de l'espace semi-confiné en aval du linteau se fait
principalement par de l'air à une température
adimensionnée de l'ordre de 0,15 et qu'il n'y a plus aucun apport de
chaleur en aval du linteau. Nous remarquons que le Linteau en fait ne modifie
vraiment pas l'allure de la stratification thermique de l'écoulement.
Elle est juste un obstacle passif pour l'écoulement qui reste
influencé par le nombre de Rayleigh.
On augmente cette fois ci d'une puissance (Rayleigh de
5,85x1010 (Lasfer K. et al., 2007) en introduisant une inclinaison
ô de la cavité sur l'intervalle comprises entre 70 et 110°.
La figure 12 illustre la distribution des lignes de courant, des isothermes et
des iso-lignes de l'énergie cinétique turbulente imposée
par le nombre de Rayleigh obtenu. Nous remarquons que l'écoulement
présente un aspect parallèle et une stratification thermique
prononcée au coeur de la cavité et que la majeure partie de
l'écoulement se déplace au niveau des parois latérales.
Ceci se traduit par la formation d'une couche limite aux proximités de
ces parois. On peut distinguer aussi que les lignes de courant
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 19
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
deviennent de plus en plus distordues dans la partie
supérieure ou la partie inferieure de la cavité, respectivement
si on augmente ou on diminue l'inclinaison à partir de 90°. Cette
structure est accompagnée par des zones de recirculation dans le coin
inférieur droit et le coin supérieur gauche de la
cavité.

Figure 12 : a) lignes de
courants, b) Isothermes, c) Iso lignes de l'énergie cinétique
turbulente.
(Lasfer K. et al., 2007)
Le modèle de turbulence utilisé est le k-w de
Peng-Davidson-Holmberg. Cette investigation
a permis de mettre en évidence les effets de
l'inclinaison sur l'intensité de l'écoulement dans la
cavité et sur le transfert de chaleur à travers les parois
latérales. Le profil reste le même que dans une cavité
rectangulaire avec le même nombre de Rayleigh sans inclinaison.
De Saury D. et al. (2008) on avance encore d'un cran
avec le nombre de Rayleigh (1,2.1011) sans inclinaisons et sans
obstacle dans la cavité, et on obtient les mêmes résultats.
Intéressons nous plutôt aux profils de vitesse dans la direction
normale et à proximité des parois chaude, Z = 0,7 (z = 2,69 m) et
froide, Z = 0,3 (AT = 20 °C) qu'ils présentent. On peut noter une
faible intensité du mouvement (le maximum de vitesse ne dépasse
pas 25 cm/s). Par contre, la couche limite montante est particulièrement
épaisse car elle atteint 145 mm à la cote Z = 0,7.
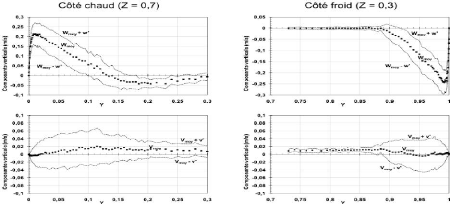
Figure 13 : Profil des composantes
verticale et horizontale de vitesse dans les couches limites
montante et
descendante, à la position z = 2,69 m pour un écoulement de
convection naturelle. (Ra
= 1,2.1011 ; å = 0,1 ; AT = 20
K). (Saury D. et al., 2008)
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 20
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Pour montrer que le paramètre principal qui gouverne la
convection thermique naturelle est le nombre de Rayleigh, qui représente
le rapport des forces de flottabilité (Poussée
d'Archimède) aux forces visqueuses, et est proportionnel au gradient de
température appliqué, Boutra A. et al (2011) sortent
l'évolution de la cartographie des isothermes pour différentes
valeurs du nombre de Rayleigh. Pour les faibles valeurs du nombre de Rayleigh,
il montre que la structure des isothermes reste parallèle à la
paroi verticale de la cavité ce qui signifie que le transfert thermique
est purement conductif dans cette zone. Remarquons que pour Ra =
106, les isothermes sont plus incurvées, indiquant ainsi des
gradients de température plus importants.
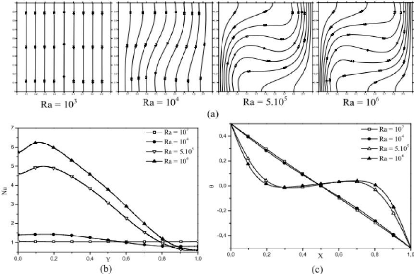
Figure 14 : Effets du nombre de Rayleigh en
régime stationnaire sur: (a) les isothermes, (b) le nombre de Nusselt
local relevé sur la paroi chaude, (c) le profil de température
relevée sur le plan médian horizontale. (Pr = 7, Bn = 5 et Ä
= 5.104). (Boutra A. et al., 2011)
La figure 14 (b) représente l'évolution du
nombre de Nusselt local le long de la paroi chaude (paroi verticale de gauche)
pour différents nombres de Rayleigh. Nous remarquons que l'augmentation
du nombre de Rayleigh augmente le nombre de Nusselt local. Les profils des
températures relevées sur le plan médian horizontal (Y =
0,5) pour les différents nombres de Rayleigh sont donnés sur la
figure 14(c). Pour Ra = 103, le profil de température est
linéaire étant donné que le transfert thermique est
purement conductif. Pour des valeurs élevées du nombre de
Rayleigh, les profils de températures se caractérisent par une
épaisseur de couche limite thermique (sur les deux faces verticales) qui
diminue avec l'augmentation de ce dernier.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 21
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
On peut donc conclure en disant que, le nombre de Rayleigh
permet de voir la stratification thermique de l'écoulement de convection
naturelle (Pour les faibles valeurs du nombre de Rayleigh, la structure des
isothermes reste parallèle à la paroi verticale de la
cavité et pour des Rayleigh élevé, elle est oblique et
forme des tourbillons dans l'enceinte). Et aussi que la présence d'un
élément dans la cavité, ou l'inclinaison de celle-ci
n'influe vraiment pas sur la stratification à un nombre de Rayleigh
donnée. Nous allons maintenant voir si la variation du rapport de forme
(rapport entre les dimensions de la cavité) influence sur cette
stratification.
I.2.2.2 Influence du rapport de forme
Dans le cas de parois horizontales adiabatiques, Le
Quéré (1987) identifie deux classes d'écoulement selon le
rapport de forme vertical de la cavité :
? Pour Av = 4, l'instationnarité résulte de
l'instabilité intrinsèque des couches limites verticales sous
forme d'ondes progressives se propageant dans le sens de l'écoulement.
La période associée à ces instabilités
évolue au voisinage de Rac comme Ra-1/2 ;
? Pour Av < 4, l'instationnarité est due à la
déstabilisation d'une zone à forte divergence dans les coins en
sortie de couche limite d'après Paolucci et Chenoweth en 1989. La
période relative à ces instabilités évolue au
voisinage de Rac comme Ra-1/2.
Si les conditions aux limites influent notablement sur
l'apparition des instabilités, elles agissent également sur la
structure de l'écoulement. La figure 15 (a)-(d), représentent les
lignes de courant correspondant au cas d'écoulement d'air dans une
cavité de rapport de forme égal à 2 ((a) et (b)) pour Ra =
2×106. On peut constater la présence de mouvements de
recirculation dans la partie haute et basse de la cavité dans le cas
conducteur (b), inexistants dans le cas adiabatique (a). En revanche, on
observe nettement la présence d'un ressaut hydraulique en aval des
couches limites verticales dans le cas adiabatique (c) à Ra =
1,7×108 tandis que pour le cas conducteur (d) à Ra =
1×106, l'écoulement est formé par deux zones de
couches limites prolongées par des écoulements horizontaux le
long du plafond et du plancher. On ne note plus ici la présence de la
zone décollée observée pour le cas adiabatique (c). Enfin
on constate que pour cette gamme de Rayleigh, la centro-symétrie de
l'écoulement est conservée aussi bien pour le cas de parois
horizontales adiabatiques que pour le cas de parois conductrices.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 22
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »

Figure 15 : Comparaison de l'allure des
fonctions de courant. (a) et (b) : AH= 2, Ra = 2×106 (Le
Quéré P., 1987) ; (c) et (d) AH= 1, RaH = 1,7×108
(c) ; Ra = 1×106 (d) (Henkes W., 1990)
Prenons les travaux de (Benkhélifa A. et Pénot
F., 2005) effectués avec un rapport de forme vertical Av (Av = H/L) de
4. Afin de repérer les premières instationnarités pour une
inclinaison è donnée (è est l'angle formé par
l'horizontale et la paroi chaude de la cavité pouvant varier entre 0 et
180°), ils font varier graduellement l'écart de température
entre les parois. Les mesures de température locale, associées
aux visualisations par tomographie laser, lui ont permis de distinguer les
différentes situations suivantes :
? Pour les faibles inclinaisons, è = 40°, le
régime turbulent est atteint très tôt (dès un
écart de température ?T = 1,6°C pour è = 40° et
à partir de ?T = 1°C pour è = 15 et 0°). Pour è
= 40°, ils ont observé un écoulement de couche limite, le
long des parois actives, caractérisé par de grosses structures
tourbillonnaires qui affectent le reste de la cavité. Toutefois, pour
les faibles inclinaisons, l'examen attentif des visualisations fait ressortir
une tendance très nette avec l'existence d'une structure
cohérente organisée en trois rouleaux contrarotatifs de taille et
de formes irrégulières. Pour toutes ces inclinaisons, il y a par
moment, apparition de bouffées provenant de la 3ème
direction montré également par (Benkhelifa A. et al.,
2007). Ces cas correspondent à des situations du type convection de
Rayleigh-Bénard. On voit bien que le rapport de forme change l'instant
de la stratification et non la stratification ;
? Pour è = 60°, l'écoulement passe de
l'état stationnaire à deux états successifs, à
savoir l'état monopériodique à un écart de
température de 2°C et l'état chaotique à partir d'un
écart de
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 23
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
température de 3,6°C. En effet, les visualisations
effectuées à ?T = 1°C montrent principalement un
écoulement de couche limite laminaire le long des parois
différentiellement chauffées. Cependant, pour un écart de
température de 6°C, de grosses structures tourbillonnaires
circulent le long de ces parois, provoquant des mouvements secondaires
très instables au coeur de la cavité ;
? Pour 60° < O = 100°, ont retrouve trois
régimes d'écoulement qui se succèdent depuis l'état
stationnaire ; à savoir, le régime monopériodique, le
régime quasi-périodique et le régime chaotique. La
différence réside uniquement dans les valeurs de l'écart
de température d'apparition de ces différents modes. Par
ailleurs, les visualisations effectuées pour chacun des régimes
font apparaître d'abord le régime de couche limite laminaire le
long des parois actives avec un coeur pratiquement au repos (mode
stationnaire), puis un régime oscillatoire en haut de la couche limite
chaude et en bas de la couche limite froide (mode monopériodique). En
augmentant l'écart de température, ces oscillations s'amplifient
avec l'apparition de temps en temps de structures tourbillonnaires ; c'est le
régime quasi-périodique qui s'installe. Si l'on se situe à
des écarts plus élevés, nous franchissons le seuil de
l'écoulement turbulent caractérisé par des structures
tourbillonnaires qui prennent naissance cette fois-ci en bas de la couche
limite chaude et en haut de la couche limite froide et se développent
tout le long vers l'aval. Pour ces différents régimes, ont
constate des écoulements secondaires caractérisés par deux
tourbillons co-rotatif et contrarotatif proches de chacun des planchers haut et
bas provoqués par les décharges des couches limites sur ces
parois ;
? Pour O = 120°, les analyses spectrales des fluctuations
de température en haut de la couche limite chaude révèlent
l'apparition successive, à des écarts de température ?T =
21,6, 26 et 31°C, de trois fréquences distinctes. Puis, deux
nouvelles fréquences accompagnées d'une multiplication de pics
secondaires sont perceptibles sur le spectre de puissance à partir de ?T
= 33°C. En effet, si le long des parois actives un écoulement de
couche limite laminaire perdure jusqu'à un écart de
température égal à 33°C (où l'on observe des
oscillations en haut de la couche limite chaude, et inversement en bas de la
couche limite froide), le reste de la cavité semble en revanche
être affecté par des bouffées 3D. Ces dernières
seraient dues à la présence d'ondes de gravité et seraient
à l'origine des trois premières fréquences
évoquées ci-dessus, les autres fréquences sont
causées par les instabilités de couche limite avec des ondes
progressives de Tolmien-Schlichting.
? Pour O = 140°, un seul mode monopériodique
dû aux instabilités d'ondes de gravité est observé
dès un écart de température égal à 29°C
et jusqu'à un écart de l'ordre de 40°C.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 24
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
? Au-delà de 140°, aucune fréquence n'est
perceptible sur les spectres, le régime conductif reste bien stable
même pour les grands écarts de température (?T =
42°C).

Figure 16 : écart de
température critique d'apparition des différents modes
d'instationnarité
(Benkhélifa A. et Pénot F.,
2005)
Pour chacun de ces résultats, On voit bien que le
rapport de forme change et influence le temps d'initiation de la
stratification, mais en aucun cas ne change la stratification thermique
imposé par le nombre de Rayleigh. Un autre nombre adimensionnel modifie
cette stratification.
I.2.2.3 Influence du nombre de Prandtl
(Boutra A. et al., 2011), montre l'influence du nombre de
Prandtl sur l'évolution des isothermes dans une cavité
chauffée, en sortant la cartographie des isothermes pour
différentes valeurs du nombre de Prandtl. Pour les faible nombre de
Prandtl (Pr » 7), ces courbes mettent en évidence un transfert
convectif traduit par une forte distorsion des isothermes. En revanche, Pour
les grandes valeurs du nombre de Prandtl (Pr = 10 et 20), on assiste à
un comportement totalement différent du précédent,
caractérisant un transfert conductif représentatif des milieux
solides ou des milieux liquides pour lesquels une structure en forme de bouchon
apparaitrait et occuperait la région centrale de la cavité et
dont l'étendue augmenterait avec l'augmentation du nombre du Prandtl.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 25

|
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
|
|
Figure 17 : Effets du nombre de Prandtl en
régime stationnaire sur: (a) les isothermes; (b) le nombre de Nusselt
local relevé sur la paroi chaude; (c) le profil de température
relevée sur le plan médian horizontale. (Ra = 105; Bn
= 5 et Ä = 5 104). (Boutra A. et al., 2011)
(Aounallah M. et al., 2006), La résolution
numérique est basée sur la méthode de Boltzmann sur
réseau. Les présents résultats montrent que les
caractéristiques du transfert thermique sont fortement affectées
par la variation des nombres de Rayleigh et de Prandtl.
En fait, le Prandtl en soit ne modifie pas la stratification,
mais crée une forte distorsion des isothermes. Lesquels peuvent avoir
une structure en forme de bouchon, et occuperait la région centrale de
la cavité et dont l'étendue augmenterait avec l'augmentation du
nombre du Prandtl. Le dernier paramètre et non le moindre est le
couplage convection-rayonnement.
I.2.2.4 Influence du rayonnement sur la stratification
thermique et le nombre de Rayleigh
La convection naturelle en cavité carrée a fait
l'objet de nombreuses études numériques en tant que configuration
générique représentative des applications potentielles.
Mais rares sont des études qui tiennent compte du couplage de la
convection naturelle avec le rayonnement même si ce couplage est
inhérent en convection naturelle.
Afin d'enrichir la base de données en couplage
convection naturel et rayonnement de surfaces et comprendre l'effet du
rayonnement de surfaces sur la convection naturelle, un code numérique
2D a été mis en oeuvre par (Wang H. et al., 2006). Ils
réalisent des études en cavité carrée remplie d'air
dont les quatre parois ont la même émissivité å. En
faisant intervenir
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 26
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
est la
conductivité de l'air, T est la température et
qr est la densité de flux net radiatif. qr est déterminée
par les systèmes d'équations.
Sur l'écoulement stationnaire, ils montrent que le
rayonnement fait varier jusqu'à 10 % le nombre de Nusselt convectif. Et
illustre à Ra = 106 l'influence du rayonnement de surfaces
sur la structure d'écoulement : les effets visibles se trouvent le long
des parois horizontales et dans le coeur de la cavité.
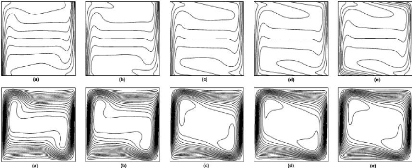
Figure 18 : influence de
l'émissivité sur l'écoulement à Ra = 106
avec (a) e = 0, (b) e = 0.1, (c) e = 0.4, (d) e = 0.8 et (e) e = 0 avec parois
horizontales conductrices. (Wang H. et al., 2006)
Par rapport au cas sans rayonnement (E = 0), les isothermes ne
sont plus normales aux parois horizontales du fait de l'échange net
radiatif, la stratification diminue au centre de la cavité, les couches
limites horizontales sont renforcées et enfin la paroi haute est
refroidie et la paroi basse est réchauffée. Ce comportement de la
température sur les paroi horizontales s'explique par le fait que la
paroi haute perd de la chaleur (flux net radiatif essentiellement positif) et
que la paroi basse reçoit de la chaleur (flux net radiatif
essentiellement négatif). De façon qualitative, le rayonnement de
surfaces a pour effet d'induire une structure d'écoulement qui ressemble
plus à celle dans une cavité avec parois horizontales
parfaitement conductrices (Fig. 18).
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 27
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
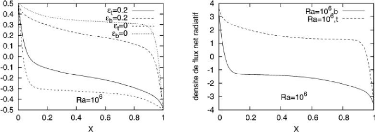
Figure 19 : température
(à gauche) et densité de flux net radiatif (à droite) en
parois haute
et basse à Ra = 10 6. (Wang H. et al.,
2006)
Pour å = 0,2, le rayonnement de surfaces modifie le
transfert thermique global au moins à la hauteur de 20 % pour la gamme
du nombre de Rayleigh considéré. Il est à noter que pour
å fixe le nombre de Nusselt radiatif augmente non seulement avec le
nombre de Rayleigh mais aussi en proportion par rapport au nombre de Nusselt
convectif correspondant. Du fait que
( ) , ce qui est le cas dans ce travail à petit nombre de
Rayleigh,
et que la densité de flux conductif , est
utilisée pour définir Nur, le nombre de Nusselt radiatif
n'est
plus qu'une fonction linéaire de H. Bien que le nombre de Nusselt
convectif soit proportionnel à , il reste constant à un nombre de
Rayleigh fixe. Comme Nur ~ H, pour un
nombre de Rayleigh et les
émissivités fixes l'influence du rayonnement de surfaces est
d'autant plus importante que H est grand sur l'écoulement
instationnaire, à Ra = 1,82 X 108 pour les parois
horizontales adiabatiques et à Ra = 2,08 X 106 pour celles
parfaitement conductrices. Comme en présence du rayonnement de surfaces
la structure d'écoulement ressemble plutôt à celle dans une
cavité avec parois horizontales conductrices, on s'attend à un
nombre de Rayleigh critique intermédiaire. Ils ont procédé
de façon classique en augmentant progressivement le nombre de Rayleigh
en examinant pour chaque nombre de Rayleigh étudié le
comportement en temps des solutions numériques. Les premiers calculs ont
été faits pour H variant de 0,265 m à 0,420 m et å =
0,2. Comme un des premiers écoulements instationnaire a
été observé à Ra = 2,0 X 107 avec
T = 5 K et H = 0,333 m, H. Wang et al choisissent alors de
travailler avec H = 0,335 m et å = 0,2 et toute variation du nombre de
Rayleigh correspond à celle de T.
Par la suite ils ont diminué progressivement le nombre
de Rayleigh : 1,9 X 107, 1,8 X 107, 1,2 X 107
et ont obtenu des solutions périodiques
caractérisées par une période sans dimension de T = 5.
Lorsqu'ils partent avec la solution obtenue à Ra = 1,2 X 107
comme conditions initiales pour étudier Ra = 1,1 X107,
ils ont observé, après un long temps transitoire, une solution
périodique en temps caractérisée par une période
sans dimension de T = 6,5. Il s'agit d'une autre branche de solutions
périodiques. En continuant de diminuer le nombre de Rayleigh, des
solutions périodiques jusqu'à
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 28
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Ra = 9,4 × 106 sont obtenus. Repartant de Ra =
1,1 × 107 pour des nombres de Rayleigh plus
élevés des solutions périodiques avec T = 6,5
jusqu'à Ra = 1,3 × 107 sont obtenu. En faisant le
passage Ra = 1,3 × 107 ? 1,5 × 107, la solution
périodique finale a une période de T = 5 est découverte.
La Figure suivante résume les procédures suivies et les
résultats obtenus, notamment les deux branches de solutions
périodiques.
Par rapport aux études antérieures
réalisées en convection naturelle pure dans une cavité
carrée différentiellement chauffée avec parois
horizontales adiabatiques, on conclut en premier que la présence du
rayonnement de surfaces avec une émissivité des quatre parois
égale à å = 0,2, fait baisser le nombre de Rayleigh
critique. Comme vu ci-dessus, le rayonnement de surfaces fait tendre la
structure de l'écoulement vers celle d'une cavité avec parois
horizontales conductrices, il semble normal que le rayonnement de surfaces fait
baisser le nombre de Rayleigh critique. Il est vraisemblable que le nombre de
Rayleigh critique baissera d'avantage pour å plus grande.
(Djanna F., 2011) donne un meilleur éclaircissement en
sortant la stratification thermique de l'écoulement de convection
naturelle turbulente dans une cavité chauffée avec rayonnement de
parois passives important. Il analyse plusieurs cas de figure :
? Stratification dans la cavité avec
rayonnement de parois passives important : les parois
latérales, le plancher et le plafond sont laissés bruts. Des
profils verticaux de température au centre de la cavité ont
été obtenus pour plusieurs écarts de température,
et donc pour différents nombre de Rayleigh.

Figure 20 : Stratification
thermique avec des parois d'émissivité importante pour
différents AT
(Djanna F., 2011)
Cette figure donne l'évolution de la température
adimensionnée O (= (T - Tm)/AT) en fonction de la hauteur
adimensionnée Y (= y/H). On constate, sur cette figure que,
l'écart de température ne modifie pas de façon
significative l'évolution de la température au centre de la
cavité. Cette évolution est d'ailleurs relativement
linéaire au coeur de la cavité, et on retrouve la
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 29
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
tendance centro-symétrique de ce type
d'écoulement. Cette linéarité disparaît lorsque l'on
s'approche du plafond ou du plancher et l'on observe une dispersion des
températures. Ceci s'explique en partie par un rayonnement de paroi non
négligeable.
Afin de mieux comparer, les phénomènes qui se
produisent au centre de la cavité, le paramètre de stratification
thermique S a été calculé pour chaque essai. Ce
paramètre traduit l'évolution du gradient vertical sans dimension
de température. Il est définit par
H0T 09
s= = I-3
L'évolution de ce paramètre, en fonction de la
différence de température entre les deux parois actives ou en
fonction du nombre de Rayleigh, est reportée dans le tableau 1.
Toutefois ce nombre reste quasiment constant égal à une valeur de
0,45 quelque soit la différence de température. L'étude de
l'incertitude sur S montre que la dispersion sur ce paramètre ne
dépasse pas 8 % avec peut être une tendance vers la diminution
avec l'augmentation (tendance régressive due à l'augmentation) du
nombre de Rayleigh.
Tableau 1 : Paramètre de
stratification mesuré avec rayonnement important des parois
passives.
(Djanna F., 2011)
|
LT(K)
|
10,0
|
15,0
|
17,4
|
20,0
|
|
Ra
|
5,8 x 1010
|
8,6 x 1010
|
1 x 1011
|
1,2 x 1011
|
|
S
|
0,47
|
0,44
|
0,44
|
0,41
|
? Stratification dans la cavité avec
émissivité faible des parois passives : Les parois avant
et arrière, le plancher et le plafond sont maintenant recouverts des
feuilles d'aluminium de très faible émissivité (å =
0,10#177; 0,05) et d'épaisseur 40 um. Comme précédemment,
des profils verticaux de température ont été obtenus pour
plusieurs différences de température, et donc pour
différents nombre de Rayleigh.

Figure 21 : Stratification
thermique obtenue avec des parois de faible émissivité pour
différents AT
(Djanna F. et al., 2008).
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 30
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
On constate, sur cette figure, que comme dans la configuration
précédente et quel que soit l'écart de température
entre les parois actives, l'évolution de la température reste
linéaire au coeur de la cavité. On note également la
centro-symétrie des profils de température caractéristique
de ce type de configuration. Les résultats obtenus sont reportés
dans le tableau ci-dessous. L'étude d'incertitude montre que l'erreur
commise sur ce paramètre ne dépasse pas 8 %. On peut donc
conclure que le paramètre de stratification thermique est
indépendant de l'écart de température.
Tableau 2 : Paramètre de
stratification avec rayonnement faible des parois passives. (Djanna F.
et
al., 2008)
|
LT(K)
|
10,0
|
15,0
|
17,4
|
20,0
|
|
Ra
|
5,8.1010
|
8,6.1010
|
1,0.1011
|
1,2.1011
|
|
S
|
0,59
|
0,57
|
0,56
|
0,54
|
En comparant les résultats, il ressort l'influence du
rayonnement des parois « passives » sur la stratification
thermique.

Figure 22 : Stratification
thermique pour ?T=10, 15, 17,4 et 20 K. (Djanna F. et al., 2008)
On peut remarquer que, dans tous les cas, l'augmentation de
l'émissivité fait baisser le paramètre de stratification.
Ceci peut s'expliquer par l'influence du rayonnement des parois actives qui
n'est pas négligeable et intensifie les écoulements secondaires.
Ainsi, l'augmentation du rayonnement à l'intérieur de la
cavité se traduit par des écoulements secondaires non
négligeables
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 31
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
entraînant ainsi une homogénéisation de la
température dans toute la cavité (y compris au coeur) et
réduisant ainsi le gradient vertical de température. Ceci est
observé sur tous les essais réalisés par (Djanna F. et
al., 2008), puisque le paramètre de stratification passe de 0,57 dans le
cas où le rayonnement des parois passives est faible (E = 0,10 #177;
0,05) à 0,45 lorsque ce rayonnement devient plus important (E = 0,60
#177; 0,02) soit une diminution d'environs 22%. Ces résultats sont
à rapprocher de ceux obtenus par Salat J. [2008], qui
présente une diminution de l'ordre de 30 % lorsque
l'émissivité passe de 0,10 à 0,95 (0,72 Ô 0,54) avec
un rapport de forme horizontal proche du cas étudié ici.
Le tableau suivant rassemble les résultats
expérimentaux obtenus pour différentes configurations. Ce tableau
confirme les observations précédentes, à savoir que pour
une configuration géométrique donnée, la stratification
diminue lorsque l'émissivité des parois passives augmente.
L'étude des écoulements devrait permettre de confirmer les
résultats thermiques, c'est-à-dire la présence
d'écoulements secondaires non négligeables lorsque
l'émissivité des parois passives augmente. On note
également l'influence des rapports de forme. En effet, il apparait dans
ces travaux que si le rapport de forme vertical Av n'influence pas de
manière significative le paramètre de stratification thermique,
le rapport de forme horizontal Ah a quant à lui une influence notable
sur la stratification en température. Ceci peut s'expliquer par un effet
de confinement et des écoulements secondaires tridimensionnels qui ne
sont plus du second ordre lorsque la géométrie de la
cavité varie. Ces conclusions sont à modérer étant
donné que les cavités étudiées ne sont pas de
géométrie « atypique » (cavité aplatie par
exemple).
Tableau 3 : récapitulatif de
quelques configurations étudiées (Djanna F. et al., 2008)

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 32
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Le rayonnement de paroi induit une modification des
écoulements secondaires qui conduit à une modification de la
stratification thermique de la cavité. La centrosymétrie qui
traduit, en grande partie, la validité des hypothèses de
Boussinesq est cependant bien conservée.
En somme, que ce soit le nombre de Rayleigh, le nombre de
Prandtl, le rapport de forme ou le couplage convection-rayonnement,
l?écoulement se trouve soit transformer soit modifier. Sans oublier une
interdépendance entre les différents paramètres.
Maintenant que nous avons montré cette influence nous pouvons aborder
plus en profondeur les configurations les plus utilisé dans la
littérature.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 33
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
CHAPiTRE II. DESCRIPTION DU PROBLEME ET
FORMULATION MATHEMATIQUE
Dans ce chapitre nous allons faire une description succincte
et précise du problème que nous nous proposons de
résoudre, dans le cadre de ce mémoire de master. En
présentant le model expérimental sur lequel nous allons nous
basé pour validé notre étude numérique (sachant
pertinemment que le numérique ne peut se faire sans
l?expérimentale). Ensuite nous allons poser les équations
mathématiques (adimensionnelles et non adimensionnelles) qui
régissent le système. Et enfin présenter la méthode
de résolution numérique utilisée par le logiciel FLUENT
pour déterminer cette évolution de température.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 34
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
II.1 Description du problème physique
Le modèle physique considéré est
présenté sur la figure 23. Il s'agit d'une cavité
carrée
différentiellement chauffée dont les quatre
parois internes sont supposées grises, diffuses, opaques et les surfaces
sont supposées adiabatiques et ont la même valeur
d'émissivité, å. Les parois
verticales sont isothermes et maintenues à un
écart de température constante (Tc pour la
paroi
chaude, et Tf pour la paroi froide). Les parois hautes, basse avant et
arrière sont isolées. La cavité 2D est remplie d'un fluide
transparent de l'air (Pr = 0,71), et le mouvement d'air est gouverné par
les équations de Navier Stokes sous l'hypothèse de Boussinesq.
De manière classique, sans rayonnement de surfaces, la
condition adiabatique implique que le gradient de température normal
à ces parois est nul. En présence du rayonnement elle est
traduite par l'équilibre entre les flux convectif et radiatif. Il s'est
avéré que le rayonnement de surfaces ne modifie pas les
équations gouvernant le mouvement du fluide mais altère seulement
les conditions aux limites thermiques. Le couplage de la convection naturelle
avec le rayonnement de surfaces se fait uniquement à travers les
conditions aux limites thermiques.

Figure 23 : représentation
de la cavité différentiellement chauffée avec conditions
aux limites
thermiquesde 0,335 x 0,335 m (Wang H. et al., 2006)
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 35
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
II.2 Mise en équation
II.2.1 Formulation mathématique II.2.1.1
Hypothèses simplificatrices
Les équations présentées dans cette partie
sont basées sur des hypothèses qu'il convient de rappeler :
> l'écoulement est stationnaire ;
> le fluide est supposé newtonien ;
> la variation de la masse volumique n'est
considérée que dans le terme de la poussée thermique
d'Archimède et elle est supposée constante (égale à
ñ0) pour les autres termes des équations : c'est
l'hypothèse de Boussinesq ;
> le volume reste constant sous l'action d'une pression
externe (fluide isovolume), alors que sa masse volumique varie
linéairement telle que p = po[ 1 -- fJ(T -- To)] où
fJ est le coefficient d'expansion thermique et po la masse
volumique à la température de référence To
définie par :
;
> la seule source interne d'énergie est celle issue
du bilan local entre l'absorption et l'émission volumique du rayonnement
au sein du fluide.
Nous avons --A +qr= et A +qr= en z = H,
où ë = 0.025 W/ (K m) est la
conductivité de l'air, T est la température et
qr est la densité de flux net radiatif. qr est
déterminée par les systèmes d'équations : qr
=E1 E (6T 4 -- J) et AJ = b où æ est la constante
de Stefan- Boltzmann, J représente le vecteur radiosité, A la
matrice dont ALS = 8 , -- (1 -- e)F11 avec Fij le
facteur de forme et b (b1 = ea Th le vecteur
émission propre.
En convection naturelle les équations sont
classiquement rendues sans dimension. Pour cela nous utilisons l'écart
de température entre les parois actives OT et la
température moyenne T0 pour définir une température
réduite 0 = (T -- To)/OTT et, comme longueur et
vitesse de référence, respectivement la hauteur H et
áRa1/2/H avec á la diffusivité thermique de
l'air et Rah =
3
(gfJ T H )/(v ) le nombre de Rayleigh. Nous
poursuivons cette logique pour rendre sans dimension les équations du
problème avec rayonnement, à savoir que qr et J sont
rendues sans dimension par AOT /H, comme la définition du
nombre de Nusselt en convection naturelle pure. Notons que le problème
avec rayonnement fait apparaître conventionnellement deux
paramètres sans dimension additionnels, outre Ra et Pr, le rapport de
température, Bo = To/OT , et le nombre de
rayonnement, Nr = ea Tô H/(AOT ) (ou son inverse le nombre de
Planck). Comme il est difficile de faire varier un nombre sans dimension en
maintenant constants les trois autres en
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 36
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
couplage convection naturelle-rayonnement, nous n'avons pas
jugé nécessaire de faire apparaître è0 et Nr dans
cette étude outre la mention de T0, T et H.
II.2.1.2 Equation générale de la convection
naturelle
La détermination de l'écoulement de convection
pour un fluide newtonien se fait grâce aux équations de
Navier-Stokes qui regroupent trois équations (continuité,
conservation de quantité de mouvement et conservation d'énergie).
Voici l'expression de ce système d'équations dans le cas de la
convection naturelle :
? Equation de continuité :
? ? ? ?
II-1
? Equation de conservation de quantité de mouvement :
? ? ? ? ? ?
II-2
? Equation de conservation d'énergie, sous forme
d'enthalpie :
? ? ?
II-3
Où est la pression motrice qui correspond à
l'état de référence telle que
. Et á est la diffusivité thermique du fluide : /
.
est le terme source qui caractérise la participation
radiative du fluide (absorption,
émission) telle que ? . Ce terme se
calcule une fois le champ spatial et directionnel de la
luminance connu dans
tout le domaine de calcul. Il est à noter que les luminances sont
solutions de l'équation de transfert radiatif qui exprime en chaque
point d'un chemin optique et suivant une direction donnée, le bilan
entre la perte (absorption et diffusion) et le gain (émission et
renforcement par diffusion) de photons. soit :
? ? ( ) ? ? II-4
Dans le cadre des hypothèses de Boussinesq, les
caractéristiques physiques sont considérées comme
constantes. L'évolution de la masse volumique étant la cause des
mouvements, seules les variations de la masse volumique en fonction de la
température sont considérées dans le terme de
l'équation de conservation de la quantité de mouvement. Les
équations de Navier-Stokes deviennent donc :
? Equation de continuité :
?
II-5
? Equation de conservation de la quantité de mouvement
:
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 37
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
?
? ? ? II-6
> Equation de conservation de l''énergie :
?
II-7
II.2.1.3 Equations adimensionnées
II.2.1.3.1 Grandeurs adimensionnelles
caractéristiques du problème
>

Rapport de forme vertical :
> Rapport de forme transverse :
> Rapport de forme Horizontale :
> Coordonnées adimensionnées
:
> Température adimensionnée
:
> Vitesses adimensionnées :
·rre
V' W V v
H
> Temps adimensionné : t avec tref =
Lref = a~
V F
> Rapport de température :
> Nombre de Planck : 6T (son inverse le nombre
de rayonnement Nr)
> Terme source adimensionné :
v
> Flux radiatif adimensionné :
> Nombre de Rayleigh : le nombre de Rayleigh est le
rapport entre le phénomène moteur du mouvement (la poussée
d'Archimède) et les phénomènes résistants
(diffusion de chaleur et frottements visqueux). Dans le cas où
l'élément moteur du mouvement est un écart de
température, ce qui est tout le temps le cas dans des cavités
différentiellement chauffées, ce nombre s'exprime de
la façon suivante
> Nombre de Prandtl : afin de caractériser le
fluide, le nombre de Prandtl est introduit. Il s'agit du rapport entre la
diffusivité de quantité de mouvement (viscosité
cinématique) et la
diffusivité thermique
> -Nombre de Nusselt : C'est le flux de chaleur
échangé de manière conduction, convection et radiation,
adimensionnée par un flux de conduction de référence. Il
peut se
décomposer en deux parties : d'une part le nombre de
Nusselt conducto-convectif noté et le
nombre de Nusselt radiatif noté . On écrit :
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 38
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Le flux de conduction de référence est
basé sur l'écart de température entre les parois
différentiellement chauffées et sur la hauteur
de la cavité (en général, on le base sur la largeur de
la
cavité), soit :
Le flux conducto-convectif s'exprime à partir du
gradient normal à la paroi considérée, soit
? ?
|
Le flux radiatif quant à lui, est défini tel que
:
|
??
|
? [ ]
|
? Paramètre de stratification thermique est donné
par :
II.2.1.3.2 Système d'équations
adimensionnées
En adimensionnant le système formé par les
équations de bilan au paragraphe 2.2.1.3.1 avec les grandeurs de
référence, le système s'exprime sous la forme :
II-8
[ (
)] II-9
[ ( )]
II-10
v
Ou encore ramenées dans un repère cartésien,
ces équations s'écrivent :


II-11
II-12
II-13
(
) II-14
(
) II-15
Nous obtenons ainsi le système d'équations dont
l'ensemble des variables est sans dimension.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 39
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
II.2.2 Conditions aux limites
Les conditions aux limites associées au système
d'équations précédent sont les suivantes :
? Condition d'adhérence aux parois : U = V = W =0
8(y=A1V)
? Conditions aux limites thermiques :
· Paroi chaude
· Paroi froide
· Au plancher :
· Au plafond :
· Paroi arrière :
· Paroi avant :
Ce chapitre a permis de présenter les équations
régissant la convection naturelle ainsi que les conditions limite
à apporter aux différentes parois. De plus, les différents
nombres adimensionnels apparaissant pour caractériser la cavité
et les résultats ont été présentés
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 40
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
CHAPITRE III. OUTILS NUMERIQUES ET METHODE DE
RESOLUTION
A partir du chapitre précédent nous remarquons
que l'écoulement d'un fluide dans un conduit chauffé, quelque
soit le régime, est décrit par un ensemble d'équations aux
dérivées partielles dont les équations de Navier-Stockes
et l'équation de conservation d'énergie. Ces équations,
qui expriment des lois physiques de conservation, relient la vitesse, la
pression et la température en chaque point de l'écoulement.
Ainsi, leur résolution permettra de connaître par exemple, les
caractéristiques des champs thermique et dynamique. Cependant, les
équations de Navier-Stokes sont des équations non
linéaires, pour lesquelles une solution analytique n'est pas
jusqu'à présent connue. A cela s'ajoute la forte
interdépendance entre les champs thermique et dynamique,
modélisée par l'équation de conservation
d'énergie.
Pour établir un schéma numérique de
résolution de ces équations, de nombreux aspects autres que
physiques doivent être pris en compte : il s'agit notamment de la
discrétisation des équations. Parmi les méthodes de
discrétisation les plus fréquemment utilisées, on peut
citer les méthodes des différences finies,
d'éléments finis et de volumes finis. Ces méthodes
permettent de transformer les équations différentielles du
modèle mathématique en systèmes d'équations
algébriques linéaires avant de procéder à la
résolution.
Dans le cadre de ce travail, un code de calcul
numérique utilisant la méthode des volumes finis pour la
discrétisation puis, la simulation numérique du problème
d'écoulement est utilisée : il s'agit du code de calcul
industriel FLUENT. Dans ce chapitre nous allons présenter l'architecture
du code en question, puis les différentes étapes requises pour la
simulation numérique que nous allons effectuer.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 41
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
III.1 Architecture du logiciel Fluent
FLUENT est l'un des logiciels de simulation numérique
en mécanique des fluides intégrés dans la suite ANSYS
(Swanson Analysis Systems, Inc.). Il dispose d'un grand nombre de
modèles de turbulence permettant de faire face à de nombreux
problèmes physiques dont les écoulements monophasiques,
diphasiques (miscibles ou non), les écoulements en milieux poreux, la
combustion (pré mélangé et non pré
mélangé), le transport de particules Etc. La résolution
d'un problème physique par ce logiciel passe par les trois étapes
suivantes : la définition des caractéristiques
géométriques du domaine physique, le choix numérique des
conditions opératoires et enfin la résolution itérative
des équations puis la visualisation des résultats.
La définition de la géométrie du
problème à résoudre s'effectue à l'aide d'un
préprocesseur (GeoMesh, preBFC, Gambit, Tgrid,...). Il permet de
représenter la géométrie du problème à
étudier, de le mailler, de définir les types de conditions aux
frontières du domaine physique et aussi de spécifier le type de
matériau utilisé (fluide ou solide). Numériquement, les
conditions opératoires (gravité, pression) dans lesquelles est
effectuée la simulation, ainsi que la spécification des
conditions aux limites se font via un solveur. Il permet aussi de choisir le
processus itératif à utiliser en proposant des schémas
numériques de discrétisation et des algorithmes pour
résoudre le problème de couplage vitesse-pression. Une interface
permettant de contrôler à tout moment l'état d'avancement
des calculs y est aussi intégré.
Le postprocesseur est l'élément qui permet de
visualiser la géométrie et le maillage du domaine, mais surtout
d'afficher les résultats. Il est ainsi possible de visualiser les champs
de vitesse, de température, de pression, de turbulence ainsi que de
toutes les autres grandeurs calculées sur un segment, une section ou sur
tout le volume du domaine.
III.2 Déroulement du calcul dans
Fluent
La résolution numérique des équations par
FLUENT peut se faire en régime instationnaire
ou permanent. Les étapes que nous présentons ci
après sont propres aux régimes permanents.
Généralement, on distingue (Versteeg H. et
Malalasekera W., 1995) :
? Intégration des équations de transport ;
? Discrétisation spatiale ;
? Couplage vitesse-pression ;
? Sous relaxation et Convergence.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 42
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
III.2.1 Intégration des équations de
transport
La méthode des volumes finis consiste à
subdiviser le domaine en petit volumes, puis d'intégrer les
équations de conservation sur chacun de ces volumes finis (volume de
control). Les valeurs des variables de l'écoulement pour chaque volume
de control sont définies au centre du volume tandis qu'au niveau des
surfaces de ces volumes, on utilise des schémas d'interpolation pour les
évaluer. Cette méthode permet de prendre en compte la
présence d'obstacles dans l'écoulement des fluides et garantit la
conservation de masse et de quantité de mouvement dans tout le domaine
de calcul. Un autre avantage de cette méthode sur les différences
finies est qu'elle s'adapte facilement à des géométries
complexes qui interviennent dans de nombreux problèmes industriels. La
difficulté essentielle réside dans l'estimation des flux aux
frontières de chaque volume de contrôle (Patankar V., 1980). Le
maillage contenant le volume de contrôle est représenté
à la figure ci-dessous. Il s'agit d'une subdivision du domaine
d'étude en grilles longitudinales et transversales dont l'intersection
représente un noeud, où on trouve les variables (pression,
énergie cinétique, taux de dissipation...) tandis qu'au milieu
des segments reliant deux noeuds adjacents on trouve les composantes du vecteur
vitesse (u et v). Si nous appelons P le noeud considéré, les
points qui lui sont adjacents tout comme les faces du volume de contrôle
seront dénommés : East (E), West(W), North (N), et South(S) pour
des écoulements bidimensionnels.
Les équations « moyennées » et de
fermetures présentées dans le chapitre ci dessus permettent, en
distinguant les termes convectif et diffusif, d'aboutir à une
équation de transport globale suivante :
III-1
Ou
W est la grandeur transportée c'est-à-dire la
variable indépendante ; ø est le coefficient de
diffusion de la variable indépendante ; Sø
représente le terme source de la grandeur
considérée.
Le premier terme à gauche de l'égalité
représente le terme entrée (ou sortie) de ø dans le
volume de contrôle V dû à la convection, le
deuxième terme à gauche de l'égalité est la
variation de ø par diffusion et le terme à droite de
l'égalité est le terme source (ou puits).
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 43
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »

Figure 24 : volumes finis bidimensionels
(Patankar V., 1980)
Seule cette équation (III.1) sera
discrétisée et le système d'équations aux
dérivées partielles est résolu pour chaque valeur de yr.
Elle s'écrit encore :
( ) III-2a
Le théorème d'Ostrogradski permet de
l'écrire sous la forme intégrale suivante :
? ? ( ) ? III-3b
Le tableau ci-dessous résume tous les différents
termes de l'équation de transport globale (III.1) en se
référant aux modèles mathématiques
présentés plus haut. On constate sur ce tableau cinq (5)
variables indépendantes associées à 6 équations, le
système est donc fermé grâce au modèle de turbulence
qui lui est associé et sa résolution est possible.
Tableau 4: differents termes de
l'equation de transport globale

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 44
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
III.2.2 Discrétisation spatiale
Sous forme bidimensionnelle stationnaire l'équation de
transport est :
( ) III-4
Désignons par Jx et Jr, les flux totaux (de convection
et de diffusion) par unité de surface dans les directions x et r
respectivement par :
( ) III-4a
( ) III-4b
Nous pouvons écrire sous forme condense :
III-5
L'equation 3-5 est integree sur le volume de controle comme
suit:
? ? ? ? III-6
En supposant que la variable généralisée
yr varie linéairement entre les noeuds principaux dans les deux
directions, que les termes convectifs et diffusifs sont uniformes à
travers les faces correspondantes et un terme source uniforme sur le volume de
contrôle; nous pouvons intégrer séparément les
termes de l'équation de transport comme suit :
> Intégration du flux total :
? ? [ ] [ ] III-7a
Si nous posons :
[ III-7b
III-8
> Intégration du terme source :
? ? III-9
Où Syr est la valeur moyenne du terme source
sur ce volume et est le volume du volume
de contrôle. Quand la valeur moyenne du terme source
dépend de la variable dépendante, cette dépendance doit
être linéariser comme suit (Patankar V., 1980) :
Où Sc est la partie constante qui ne
dépend pas explicitement de yrp et Sp est la pente de
yrp. Il est nécessaire que le coefficient Sp soit
inférieur à zéro pour que la solution soit
numériquement stable et que la convergence soit plus rapide.
La forme linéarisée de l'équation de
transport globale (III.5) est :
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 45
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
III-11
Ou sont les flux a travers les faces Est, Ouest, Nord et Sud du
volume de
contrôle donnees par :
III-12a
( )
III- 12b
( )
( ) III-12c
III-12d
( )
Considérons par exemple l?équation de
continuité moyenne où yr =1, Syr =0 et Fyr = 0, la
forme linéarisée est :
III-13
Posons Qi (i= E, W, N, S), le débit volumique à
travers les faces du volume Nous obtenons le système suivant :
Multiplions (2) par yrP et soustrayons cette équation de
l'équation (1), nous obtenons :
( ) ( ) ( ) III-14
Les termes entre parenthèse de gauche de
l'équation (III.14) peuvent se mettre sous la forme suivante [Patankar
1980] :
III-15
Où les ai (i= E, W, N, S) sont les coefficients voisins
du point P du volume de contrôle (la notation ||A, B || désigne la
valeur maximale de A et de B ).
| | ? ?
| | ? ?
| | ? ?
| | ? ?
Les Di et Pi (i = E, W, S, N) sont les coefficients de diffusion
et les nombres de Peclet donnés par :
III-15a III-15b
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 46
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
L'équation de continuité moyenne
discrétisée s'écrit donc finalement sous la forme
suivante:
III-16c
Où III-17d
Toutes les équations de transport, après avoir
été discrétisées, peuvent être mises sous la
forme générale linéarisée suivante :
? III-186
Où nb représente le nombre d'indices des
cellules voisines. Ce nombre dépend de la topologie du maillage (il y a
6 cellules voisines pour un maillage hexaédrique par exemple).
Cette équation est à écrire pour chaque
cellule de centre P du domaine. Le système d'EDP est transformé
en système d'équation algébrique avec des coefficients
matriciels. FLUENT résous ce système en utilisant la
méthode de résolution numérique de Gauss-Seidel.
> Schémas de discrétisation
L'approximation de la variable
généralisée øp aux interfaces du volume
de contrôle se fait avec un schéma de discrétisation
approprié. Le rôle du schéma intervient pour expliquer
comment évaluer les flux de diffusion et de convection sur les faces du
volume de contrôle après intégration. Nous ressortons ici
quelques schémas discrétisation disponibles dans le code de
calcul FLUENT. Parmi ces schémas, nous avons :
V' Le schéma aux différences centrées
(Central Difference Scheme) ;
V' Le schéma aux différences
décentrées (Upwind Scheme) ;
V' Le schéma hybride mis au point par Spalding (1972) qui
est la combinaison des deux schémas précédents
(Centré et Upwind) ;
V' Le schéma à loi de puissance (Power law Scheme)
développé par Patankar (1980) ; V' Le schéma
Exponentiel.
Ces schémas sont choisis, en fonction du
problème traité, suivant la concordance des résultats
qu'ils donnent avec les résultats physiques et la stabilité
numérique. Le schéma exponentiel par exemple requiert un temps de
calcul important, la procédure aux différences
décentrées est moins précis que celui aux
différences centrées et n'est pas adaptée aux
écoulements qui ne sont pas à convection dominée (Baliga
B. et Patankar S., 1980). Le schéma de la loi de puissance est le plus
recommandé dans la littérature car, moins coûteux en temps
de calcul. Les schémas hybrides et "loi de puissance" n'ont
été utilisés que dans le cadre de méthodes de
volumes finis classiques sur maillages structurés.
Le tableau ci après proposé par (Patankar V.,
1980) donne les expressions de la fonction A(|Pe|) relatif aux
différents schémas de discrétisation.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 47
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Tableau 5: fonction A(|Pe|) des
schemas de discretisation,

Il ressort de ce tableau que les schémas
numériques peuvent être vus comme des choix particuliers de la
fonction A(|Pe|) de l'équation de discrétisation
générale.
III.2.3 Problème de Couplage pression-vitesse
La résolution numérique de l'équation
(III.17) n'est pas facile et directe surtout si la variable est l'une des
composantes de vitesse, parce que les coefficients ai (i= E, N, W, S)
apparaissant dans l'équation de discrétisation dépendent
de ces variables et les termes de sources des équations de
quantités de mouvement, impliquent les gradients de pression or nous ne
disposons pas d'équation pour cette variable jusqu'à
présent. Pourtant, la résolution numérique consiste en une
résolution séquentielle des équations de conservation de
la quantité de mouvement et de continuité. Ce couplage
pression-vitesse qui fait la particularité des écoulements
incompressibles, rend la résolution difficile et plusieurs algorithmes
ont été développés pour pouvoir faire intervenir la
pression dans l'équation de continuité.
Parmi ces algorithmes, nous avons entre autres :
> MAC (Marker-And-Cell) de Harlow & Wesh (1965) ;
> Projection Method de Chorin (1968) ;
> SMAC (Simplified MAC )de Amsden & Harlow (1970) ;
> FS (Fractional Step) de Yanenko (1971) ;
> HSMAC (High Simplified MAC) de Hirt & Cook (1972) ;
> SIMPLER (SIMPLE Revised) de Patankar (1980) ;
> SIMPLE (Semi-Implicit Method for Pressure-Linked Equations)
de Patankar (1980); > SIMPLEC (SIMPLE Consistent) ;
> PISO (Pressure-Implicit with Splitting of Operators).
Les trois derniers algorithmes à savoir le SIMPLEC,
SIMPLE et PISO sont intégrés dans le code de calcul FLUENT. Nous
portons notre choix sur l'algorithme de SIMPLE, qui est recommandé pour
les écoulements en régime permanent. Avant de présenter
cet algorithme, nous commençons par décrire la procédure
pour établir l'équation algébrique de la pression.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 48
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
III.2.3.1 Équation algébrique de
pression
Lorsque le champ de pression est connu, le champ de vitesse est
obtenu directement par la
résolution des équations de quantité de
mouvement. Dans le cas où ce champ est inconnu, l'établissement
d'une équation de pression est nécessaire par
établissement d'une correction. L'intégration de
l'équation générale de transport pour l'équation de
quantité de mouvement sur le volume de contrôle donne les
équations suivantes+ :
? III-19a
? III-20b
Avec bu et bv contenant tous les termes
sources de l'équation sauf ceux de la pression, les deux autres termes
(Pp Pi) Ai et (Pp Pi) Ai représentent
les forces de pression à travers les surfaces Ai (i=E, N, S, W).
Supposons, pour démarrer que la pression est connue (estimation P*) et
calculons le champ des vitesses correspondant à vi* et ui*.
? III-21 a
? III-22 b
Les vitesses calculées avec une estimation de la pression
ne satisfont pas, en général
l'equation de continuité, nous les corrigeons en
utilisant, comme précédemment, une correction en posant :
(Exposant :(*) pour l'estimation, (^) pour sa correction.
III-23a
III-24b III-25c
Si l'on retranche les équations estimées de celles
corrigées on trouve :
? III-26a
? III-27a
Pour des raisons numériques on néglige les termes ?
et ?
par rapport aux termes de pression, les équations
deviennent respectivement (Patankar V., 1980) :
III-28a
|
Les champs des vitesses seront corrigés à partir
de (3.22) par les équations suivantes :
|
III-29b
III-30a III-31b
|
Définissons les pseudo-vitesses Ui» et Vi» selon
les expressions suivantes :
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 49
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
? III-32a
? III-33b
Les équations (3.23) peuvent être écrites
sous la forme :
III-34a
III-35b
Pour trouver l'équation discrétisée de p'
(équation de correction de pression), il suffit
d'écrire l'équation de continuité comme
une équation de correction de pression. L'équation de
continuité discrétisée pour un volume de contrôle
limité par les faces E, N et S s'écrit :
III-36
L'introduction des expressions (III.24) dans (III.25) nous
donne l'équation algébrique de la pression suivante :
III-37
Où ( )
(
)
III.2.3.2 Méthode « Semi-Implicit Method for
Pressure-Linked »
Il s'agit d'un algorithme avec lequel il est possible de tirer un
champ de pression et de
vitesse vérifiant à la fois les équations
de quantité de mouvement et celle de continuité (Patankar V.,
1980). Les séquences peuvent être résumées comme
suit:
1) Estimer un champ de vitesse ;
2) Calculer les coefficients des équations du mouvement
et déterminer u^ et v^ ;
3) Calculer les coefficients pour l'équation de pression
et obtenir le champ de pression ;
4) Considérer le champ de pression P comme champ
estimé P* et résoudre les équations de mouvement pour
obtenir les vitesses u* et v* ;
5) Calcul du terme « b » de l'équation de
correction de pression et puis la résoudre pour obtenir les corrections
de pression P* ;
6) Correction des valeurs des vitesses pour obtenir les
vitesses u et v ;
7) Résoudre les équations de transport
discrétisées pour t, E et k et réitérer le calcul
jusqu'à convergence.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 50
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
III.2.4 Sous relaxation et Convergence
III.2.4.1 Sous relaxation
A cause de la nature non-linéaire des équations, il
est important de contrôler (amplifier ou
atténuer) les changements des valeurs de la variable WP
calculés lors des itérations successives. Pour ce faire on
introduit un facteur de sous relaxation 0= á =1 tel que De
l'équation (III.17) nous avons :
III-38
: est la valeur obtenue de l'itération
précédente ;
: est la valeur obtenue de la résolution en
A chaque équation correspond un facteur de sous
relaxation á qui peut varier d'une équation à une autre.
Plus á est faible, plus la sous relaxation est forte et plus la
convergence est lente, plus il est fort, plus la sous relaxation est faible et
plus des instabilités dans le processus itératif peuvent
apparaître. Il n'existe pas de règle générale pour
choisir les coefficients de sous relaxation. Cela peut dépendre de la
nature du problème, du nombre et de la taille des cellules du maillage,
de la procédure itérative choisie.
III.2.4.2 Convergence
Une résolution est convergente si toute erreur tend
à décroître au cours des itérations et les
itérations ne produisent plus de changements significatifs sur les
variables selon un critère bien défini. En d'autres termes, pour
avoir une solution convergente, il faut que la différence entre le
débit entrant et le débit sortant d'un volume de contrôle
soit négligeable. Afin de contrôler la convergence du calcul, des
critères de convergences basés sur les résidus absolus des
équations à résoudre sont intégrés dans le
code FLUENT. Le résidu correspond au déséquilibre,
à l'erreur de l'équation (3.17) sommé sur toutes les
cellules du domaine, soit :
? | ? III-39
|
Cette formulation ne permet pas de bien appréhender la
convergence du calcul, un résidu relatif est adopté par
défaut dans le code FLUENT. Il est défini par :
? | ? |
III-40
?
Dans l'équation de quantité de mouvement, le
terme du dénominateur ap Wp est remplacé
par ap Vp où Vp est la vitesse maximale
au niveau de la cellule P.
III.2.5 Etapes de la simulation numérique
En guise de rappel, soulignons que dans ce travail, la situation
physique correspond à un
écoulement naturel bidimensionnel, turbulent
incompressible dans une cavité ou nous avons impose
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 51
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
un écart de température entre les parois
verticales, et les parois horizontales sont supposé adiabatique. La
cavité a les dimensions HxlxD = 3,84m x 1m x 0,86m. Les
différentes étapes pour réaliser cette simulation
numérique (c'est-à-dire le passage du domaine physique au domaine
numérique) sont énumérées ci-après :
1ère étape : Maillage du domaine
physique
Le premier travail à accomplir dans la
réalisation d'une simulation numérique est la définition
d'un maillage adapté au problème physique après l'avoir
esquissé. De sa qualité dépend la précision des
calculs.
Un nombre de mailles insuffisant fera par exemple diverger le
calcul ou sera responsable d'une diffusion numérique trop importante
tandis qu'un maillage trop fin alourdira le calcul ou peut causer des
variations trop grandes dans les grosseurs de maille à travers le reste
du domaine. Il faut donc trouver un compromis entre les deux situations.
Le logiciel Gambit, est le préprocesseur dont nous
disposons. Nous avons utilisé un maillage régulier avec des
cellules de forme quadrilatérale. Un raffinement des zones au voisinage
de la paroi a été pris en compte pour ressortir les
différents phénomènes qui peuvent intervenir dans ces
zones, notamment les gradients de température et de vitesse.
Le résultat de la discrétisation des
équations différentielles de transport est un ensemble
d'équations algébriques. Nous avons donc divisé le domaine
de calcul en N mailles suivant x et en M mailles suivant r, nous aurons donc un
système de M x N d'équations algébriques non
linéaires pour chaque variable considérée. Après
avoir achevé cette étape, il faut exporter le domaine
maillé vers le solveur FLUENT.
2ème étape : Exportation du domaine et
spécifications des conditions initiales
Une fois importé le domaine maillé dans FLUENT,
on peut vérifier le maillage pour détecter d'éventuelles
erreurs qui pourrait fausser le calcul, le lisser s'il le faut et ensuite
préciser l'échelle du domaine physique étudié.
Ensuite il faudra choisir avec délicatesse et en fonction du
problème étudié, les modèles à utiliser
à savoir :
Le type de solveur pour la résolution des
équations (solveur découplé pour une résolution
séquentielle individuelle des équations ou solveur
couplé), la dimension du domaine (2D, axisymétrique, 3D...) ainsi
que le régime d'écoulement (permanent ou non);
Les modèles de fermeture du système
d'équations. Le code FLUENT dispose des modèles à
viscosité turbulente à une équation (modèle de
Spalart-allmaras) et à deux équations (les variantes du
modèle k?) de fermeture, des modèles aux tensions de Reynolds et
la simulation des grosses structures (LES).
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 52
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Les fonctions de parois pour traiter la turbulence près
des parois dont FLUENT propose sont: les fonctions standard de parois
(«Standard Wall-Functions''), les fonctions de parois non
équilibrées (Non-equilibrium wall-function'') et un
traitement amélioré des lois de parois («Enhanced wall
treatment'').
Enfin, il faut fixer les conditions initiales qui sont
l'état de base du modèle à l'instant où la
simulation commence. Ici on évalue les propriétés
thermophysiques du fluide en écoulement ainsi que celles de la paroi en
contact avec le fluide à l'instant initiale (c'est-à-dire
à la température de référence pour le cadre de ce
travail et le flux de chaleur sur les parois). On pourra aussi définir
la valeur de la pression si l'on travaille à pression imposée et
l'accélération si la poussée d'Archimède ou
l'hypothèse de Boussinesq est considérée.
3ème étape : Spécification des
conditions aux limites
Le choix des conditions aux limites est une étape
déterminante dans un tel travail. Plusieurs types de conditions aux
limites existent. Nous utiliserons essentiellement la condition au limites
« wall » est une condition de flux de chaleur constant sur les parois
verticales de la conduite. Notre écoulement est délimité
par des parois imperméables et le fluide d'essai est de l'air, donc un
fluide supposé compressible.
4ème étape : Résolution proprement
dite des équations
Pour la résolution proprement dite des équations
qui gouvernent le problème, on procède comme suit dans FLUENT
:
y' Choix du facteur de relaxation pour chaque équation
;
y' Choix des schémas de discrétisation spatiale des
termes convectifs présent dans ces équations
y' Choix de l'algorithme de résolution pour le
problème de couplage pression-vitesse ; y' Choix des critères de
convergence ;
y' Exécution du calcul itératif.
Une fois la résolution effectuée nous pouvons
visualiser les champs de vitesse, de
température, de pression, de turbulence sur tout le
volume du domaine et aussi tracer différentes courbes
souhaitées.
En définitif, rappelons que dans la simulation
numérique de l'écoulement d'un fluide, on résout au moyen
d'un ordinateur, les équations préalablement
discrétisées suivant un schéma numérique. La
difficulté est liée à la physique du problème
traité, c'est-à-dire à la turbulence et le choix de
l'utilisation d'une méthode numérique va dépendre
essentiellement du type et de la
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 53
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
complexité du problème à résoudre
: la nature du fluide, le comportement thermodynamique, la modélisation
du milieu et l'aspect stationnaire ou instationnaire problème.
La figure ci après, résume, les étapes
à franchir pour simuler l'écoulement du fluide avec le code de
calcul industriel FLUENT.
1ère étape : Définition et
maillage du domaine physique
2ème étape : importation du domaine
physique maillé et définition des conditions
initiales
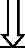
3ème étape : spécification des
conditions opératoires et des conditions aux limites
4ème étape : résolution proprement
dite des équations
5ème étape : visualisation et traitement
des résultats
Figure 25 : démarche de
simulation avec Gambit-Fluent
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 54
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
CHAPiTRE IV. RESULTATS ET DISCUSSION
L'objectif de ce paragraphe est de présenter dans un
premier temps l'influence du nombre de Rayleigh et de
l'émissivité des parois sur le paramètre de stratification
thermique. Ensuite, une comparaison de la stratification thermique dans des
cavités différentiellement chauffées expérimentales
est effectuée. Nous présentons les résultats obtenus lors
de notre simulation numérique réalisée avec le code de
calcul industriel FLUENT, sur un ordinateur de 2,30 x 2,29 GHz de
fréquence et de 2Go de capacité de mémoire.
L'approche « segregated solution method » (solveur
découplé) a été choisie pour la résolution
des différentes équations. Les termes de diffusion correspondant
aux équations de quantité de mouvement et de turbulence sont
discrétisés en utilisant le schéma de
discrétisation « Upwind » du second ordre et un critère
de convergence de 10-8 est adoptée Pour toutes les
équations. A cause du couplage et de la non linéarité des
équations, la stabilité du processus itératif est
assurée par l'utilisation de coefficients de sous relaxation. Pour
traiter la turbulence près des parois, l'approche «Standard
Wall-Functions'' est utilisée. La convergence du calcul numérique
est contrôlée par l'examen de l'évolution des
résidus relatifs à chacune des équations.
L'écoulement du fluide à l'intérieur de la cavité
dont la paroi est chauffée uniformément par un flux de chaleur
est contrôlé par les nombres adimensionnels suivants :
? Le nombre de Rayleigh (Rah), correspondant au rapport entre
les forces de pesanteur et les forces de diffusion de chaleur et frottements
visqueux ;
? Le nombre de Prandlt (Pr), (exprimant le rapport entre la
diffusivité de quantité de mouvement et la diffusivité
thermique);
? Le nombre de Nusselt (Nu), relatif aux taux d'échange
de chaleur paroi- fluide, est le rapport de la résistance thermique de
conduction par la résistance thermique de convection. Il est d'autant
plus élevé que la convection est prédominante sur la
conduction. Il caractérise le type de transfert de chaleur.
Apres avoir valide le model, nous présentons les
différents résultats obtenus. Les champs thermiques et dynamiques
et les profils de température et vitesse adimensionné tout au
long des parois sont mises en forme grâce au logiciel Tecplot 8.0.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 55
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
IV.1 Etude de sensibilité
Un maillage de qualité est primordial pour obtenir une
bonne convergence du calcul numérique et de bons résultats lors
de la simulation. Diverses configurations de maillage composée de
cellules quadrilatères ont été testées dans
l'optique de déterminer le meilleur compromis entre la précision
des résultats et la durée nécessaire pour que le calcul
converge. Après avoir choisi une densité de maillage, un test de
sensibilité par rapport aux modèles de turbulence à deux
équations de fermeture (test pour le modèle K-E standard et le
modèle Réalisable K-E) a été effectué. Tout
comme le maillage, le choix du modèle de turbulence lors de la
simulation est aussi déterminant pour la qualité des
résultats.
IV.1.1 Sensibilité de la température
à l'évolution du maillage
Le test de sensibilité par rapport au maillage a
été effectué pour trois densités différentes
de maillage (70×200, 75×100 et 100x100) en comparant les profils
axiales de température d'écoulement dans les mêmes
conditions aux limites (Ra = 107). Le tableau ci-après
compare les différentes valeurs maximales de la température du
fluide pour les trois différentes densités de mailles.
Tableau 6 : effet du maillage sur la température du
fluide
|
Densité de maillage
|
75 X 100
|
100 X 100
|
70 X 200
|
|
Température max
|
0.480
|
0.482
|
0.485
|
Nous remarquons sur le tableau ci-dessus, que, pour le
maillage moins dense (75 x 100) la valeur maximale de la température de
l'écoulement est faible par rapport aux deux maillages plus denses (100
x 100 et 70 x 200) avec une erreur relative de 0,05% entre les valeurs
maximales évaluées.

Figure 26 : temperature axiale du
fluide en fonction de la densité du maillage
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 56
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Nous pouvons donc porter notre choix sur un maillage 100 x
100, quadrille. Il en va de même pour le champ dynamique de
l'écoulement. Mais nous présentons celui-ci car ce sont les
phénomènes thermiques qui nous intéressent le plus. Bien
qu'avec l'hypothèse de Boussinesq, il y'a une coexistence entre la
dynamique et la thermique.
IV.1.2 Maillage de la géométrie
La création de la géométrie et son
maillage sont réalisés grâce au logiciel Gambit. Plusieurs
méthodes permettent la création de cette géométrie
; soit on se base sur des géométries prédéfinies,
soit il suffit d'entrer les coordonnées des différents points (x,
r) en 2D, de créer les limites et enfin de créer la surface. Deux
choix principaux du maillage sont proposés à savoir : un maillage
à base de cellules quadrilatères, soit à base de cellules
triangulaires. L'utilisation d'un maillage triangulaire induirait un surplus du
nombre de cellules par rapport au maillage quadrilatère et
nécessiteras plus de ressources et de temps de calcul.

Figure 27 : domaine maillé
avec un reserrage plus poussée au niveau des parois
La figure ci-dessus représente le domaine physique
après maillage. Il est composé de 112 225 cellules. Comme nous
pouvons le voir, le maillage utilisé est un ensemble de cellules
quadrilatères (maillage uniforme et structuré). Il est
très densifié proche des parois afin de bien y prendre en compte
les effets de forts gradients de température, de vitesse ou de
frottement.
IV.2 Validation du model
Nous avons comparé nos résultats avec ceux issus
des travaux de (Wang H. et al., 2006), concernant l'écoulement de
convection naturelle en présence des parois grises, dans une
cavité différentiellement chauffée remplie d'air
(Pr=0,71). L'écart de température imposé entre les parois
actives est de 10 K et la température de référence T0 est
égale à 293,5 K. L'émissivité de parois est nulle.
Pour ce qui est de la méthode numérique de (Wang H. et al.,
2006), les équations de Navier- Stokes sont discrétisées
classiquement par une approche Volumes Finis avec un schéma d'ordre 2
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 57
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
en temps et en espace sur un maillage décalé non
uniforme (progression géométrique) et le flux radiatif
dérive du flux de radiosité, elle- même
évaluée à partir des facteurs de forme. Au final, c'est
une méthode directe et exacte qui est utilisée pour les
échanges radiatifs. Notons par ailleurs que ces auteurs ont travaille
avec des parois émissive et non émissive.
Notre code de calcul est de type Volume Fini pour les
équations de transport et la résolution du problème
radiatif est basée sur la méthode des ordonnées
discrètes utilisant la quadrature S8, qui est de fait une méthode
approchée. Nos résultats sont donc, de facto moins précis
que ceux de Wang et al. Même si qualitativement, ils sont en bon accord.
Par ailleurs, le champ de température et la fonction de courant que nous
obtenons montre une bonne concordance avec ceux de (Wang H. et al., 2006). On
retrouve également pour ces deux études une parfaite
centro-symétrie de l'écoulement en présence ou non du
rayonnement surfacique et indépendamment de la valeur des
émissivités de parois.
IV.2.1 Champs thermiques de l'écoulement de
convection naturelle sans rayonnement
La première caractéristique de
l'écoulement de convection naturelle turbulente ou laminaire
réside sur la forme des contours. Comme décrit
précédemment dans la littérature la température
suit le mur chaud jusqu'au plafond, le longe et redescend par le mur froid
avant de rejoindre le mur chaud par le plancher. Et il peut y avoir des zones
de recirculation, du moment où le gradient de température va du
haut vers le bas.

a b
Figure 28 : Comparaison des isothermes :
(à droite) (Wang H. et al., 2006) (à gauche)
Présente
étude, dans le cas de la convection pure
D'une façon générale, nous retrouvons
qualitativement la même tendance, en ce qui
concerne le champ de température que celle obtenue par
Wang H. et al., en 2006, ainsi que (Djanna F., 2011). La
Centro-symétrie de l'écoulement est également bien
préservée.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 58
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
De même en ce qui concerne les profils de
température à mi largeur de la cavité, les courbes
obtenues concordent parfaitement avec ceux de (Wang H. et al., 2006).
Même si on note cependant une différence significative autour de
la cote Y=0,25 et 0,75. En effet, dans notre cas, les zones de recirculation
sont observées à des cotes plus proches du coeur de la
cavité que dans le cas de (Wang H. et al., 2006), ceci peut être
dû à la différence au niveau du nombre de Rayleigh (15%),
ou alors aux effets pariétaux.
Dans la couche limite chaude, on note une décroissance
monotone de la température quand on s'éloigne de la paroi chaude,
la température atteint un minimum puis augmente pour atteindre la valeur
de la température de coeur. Ceci est dû à l'entrainement
par la couche limite chaude de l'air plus frais depuis les couches
inférieures (environnement stratifié). Cet air plus frais,
entraîné par effet visqueux, redescend ensuite pour rejoindre son
isotherme (présence d'un écoulement descendant).

Figure 29 : comparaisons des profils de
température en x = 0,5 à Rah = 106.
Cette inversion des profils de température est
caractéristique d'un écoulement en milieu stratifié, et
est également observée expérimentalement par (Rouger N.,
2009). En effet, cette situation typique des écoulements de convection
naturelle en milieu stratifié se produit lorsque la quantité de
chaleur reçue par le fluide à la frontière de la couche
limite est insuffisante pour réchauffer rapidement le fluide à la
température du coeur. Ce comportement, est également
observé par (Djanna F., 2011) sur les profils en bordure de la couche
limite froide où pour 0,65 = Z <0,95, la température
croît de façon monotone quand on s'éloigne de la paroi
froide tandis que pour 0,30 = Z <0,60, la température atteint un
maximum avant de diminuer pour retrouver la valeur de température de
coeur à cette altitude. Ceci n'est pas surprenant, la
centro-symétrie semble respectée. La valeur de la
température adimensionnée au centre de la cavité est
très proche de la valeur 0 attendue pour les écoulements
respectant la propriété de centro-symétrie. Il faut noter
que la
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 59
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
température des parois (O (Y=0) = 0,5 et O (Y=0,26) =
-0,5) n'est jamais exactement retrouvée malgré toutes les
précautions prises.
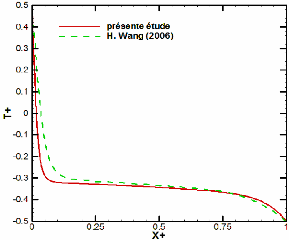
Figure 30 : comparaisons des profils de
température en paroi basse à Ra = 106

Figure 31 : comparaisons des profils de
température en paroi haute à Ra = 106.
Ce comportement de la température sur les parois
horizontales (basse et haute), s'explique par le fait que la paroi haute perd
de la chaleur (flux net radiatif essentiellement positif) et que la paroi basse
reçoit de la chaleur (flux net radiatif essentiellement négatif)
(Djanna F., 2011).
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 60
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
IV.2.2 Champs dynamiques de l'écoulement de
convection naturelle sans rayonnement
Au niveau des champs de vitesse, nous obtenons qualitativement
les mêmes contours que ceux de la littérature et de (Wang H. et
al., 2006).

a b
Figure 32 : Comparaison des
champs de vitesse : (à droite) (Wang H. et al., 2006) (à
gauche)
Présente étude, dans le cas de la convection
pure
De même en ce qui concerne les profils de vitesse
à mi largeur de la cavité, les courbes obtenues concordent
parfaitement avec ceux de (Wang H. et al., 2006). Et on observe
également comme dans le cas du profil de température, une
différence significative autour de la cote Y=0,25 et 0,75. Les raisons
semblent être les mêmes.

Figure 33 : comparaison du profil
de vitesse a mi largeur de la cavite a Ra = 106
Ces différences observe quantitativement sur les profils
de température et de vitesse
permettent de conclure a la Centro-symétrie de
l'écoulement. En effet les effets pariétaux entrainent un
déplacement de la couche limite vers le bas de la cavité, ce qui
affecte tout l'écoulement de
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 61
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
convection. En plus l'inversion observe sur les deux courbe a
la cote y = 0,5, prouve cette Centro-symétrie.
IV.3 Etude de la convection naturelle turbulence
à un Rayleigh de 107 sans rayonnement
Nous allons à présent, pousser nos recherches
vers plus de ressources pour enrichir la base de données sur les calculs
numériques en convection naturelle turbulente. Nous avons vu
précédemment que le nombre de Rayleigh était le moteur de
la convection naturelle, ceci parce qu'elle est le rapport de forces de
pesanteurs sur les forces de dissipation. Nous allons voir comment celui-ci
influe sur les paramètres thermiques et dynamiques de l'enceinte.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 62
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
IV.3.1 Etude de la stratification thermique
Les figures suivantes présentent les champs de
température adimenssionnée pour les quatres valeurs de Rayleigh
calculé :

Ra = 1,04 107 Ra = 2,79 107

Ra = 3,14 107 Ra = 3,94 107
Figure 34 : influence du nombre de
Rayleigh sur le contour de température
Dans toutes ces cavités différentiellement
chauffées, on distingue un écoulement principal formé de
couches limites le long des parois actives (une montante le long de la paroi
chaude et une descendante le long de la paroi froide), ainsi que des jets
pariétaux le long du plancher et du plafond reliant ces deux couches
limites. De plus, la présence de zones de recirculation secondaires est
également à noter au-dessus du jet pariétal au plancher et
en-dessous de celui au plafond. De manière qualitative, le champ de
température ne varie pas, tout simplement parce que le régime
d'écoulement (turbulent) n'a pas changé (Salat J. et al., 2004).
Par contre si nous regardons de manière quantitative la stratification
thermique au centre de la cavité, elle n'est pas la même. Il faut
les comparer avec les résultats de (Wang H. et al., 2006) pour observer
que des différences existent entre les différents nombres de
Rayleigh. Les profils de la composante verticale de la température
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 63
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
adimensionné dans les couches limites chaude et froide
sont tracés respectivement sur la Figure 33 et 34. De plus, le profil de
la composante horizontale de la température moyenne à mi-largeur
et a mi hauteur tracé et concordent avec celles obtenues par (Rouger N.
et al., 2007).

a b
Figure 35 : profil de temperature
en paroi basse et haute pour 4 nombres de Rayleigh
Les profils sont identiques qualitativement et approchent
quantitativement celles obtenues par (Wang H. et al., 2006).
On constate qu'en paroi haute, la couche limite thermique se
rapproche de plus en plus de la paroi au fur et mesure que le nombre Rayleigh
s'affaibli et inversement au niveau de la paroi basse. Par contre, en regardant
les profils au centre de la cavité (à mi-largeur et à
mi-hauteur), on retrouve un écoulement relativement linéaire au
coeur la cavité, et on retrouve une tendance centro-symétrique de
ce type d'écoulement. Cette linéarité disparaît
lorsque l'on s'approche du plafond ou du plancher. Ceci s'explique
principalement par le jet pariétal et probablement en partie par un
rayonnement de paroi non négligeable. Le même cas a
été identifie par (Rouger N., 2009), (Djanna F., 2011).
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 64
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »

Figure 36 : stratification
thermique au coeur de la cavite a mi-hauteur (a gauche) et a mi-largeur
(a
droite)
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 65
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
IV.3.2 Etude du champ dynamique pour quatre nombres de
Rayleigh
En ce qui concerne le champ dynamique de l'écoulement,
le Rayleigh modifie de manière qualitative et quantitativement celui-ci.
Si l'on maintient entre les parois actives des différences de
température, on peut voir la présence du jet pariétal au
plafond et la formation d'un écoulement secondaire dans la partie haute,
d'un écoulement « retour » en bordure de la couche limite
chaude, des couches limites dynamiques en développement le long des
parois actives.

Ra = 2,79 x 107
Ra = 1,04 x 107

Ra = 3,14 x 107 Ra = 3,94 x 107
Figure 37 : champs dynamiques de
vitesse pour les 4 valeurs du Rayleigh
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 66
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
La remarque est la même que sur le champ thermique de
température observe plus, plus le Rayleigh est élevé, plus
la couche limite dynamique tarde à décoller de la paroi. Les
profils au coeur de la cavité le démontrent aisément.
Cette cartographie du module de la vitesse moyenne nous donne
de constater que les vitesses les plus importantes sont localisées dans
les couches limites verticales, toutefois il convient de souligner que
l'intensité du mouvement est particulièrement faible : le maximum
de vitesse ne dépasse pas 14% de la vitesse de référence
de convection.
Les profils de la composante verticale de la vitesse moyenne
dans les couches limites chaude et froide sont tracés respectivement sur
la Figure 38 a et b.
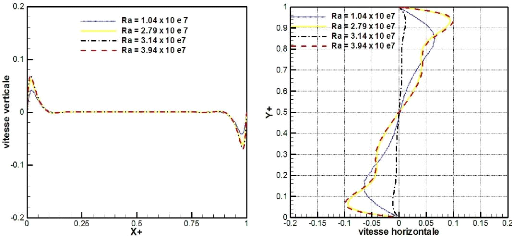
a b
Figure 38 : profils des
composantes verticales a mi-largeur (a gauche) et a mi-hauteur (a
droite)
de la vitesse
L'examen de la figure 38 montre que la vitesse maximale du jet
pariétal au voisinage du plafond à mi largeur est pratiquement la
même quelles que soient les quatre configurations (l'écart relatif
est inférieur à 6%).
On peut dire que le niveau de turbulence a tendance à
décroitre lorsqu'on remonte le long du mur chaud (inversement au niveau
du mur froid). Toutefois l'intensité de turbulence dans la couche limite
chaude et froide reste élevée ; on trouve à la cote Z=0,70
une intensité de turbulence maximale de l'ordre de 27%. En suivant la
direction horizontale de l'écoulement le long du plafond, on enregistre
également un niveau de turbulence assez élevé allant
jusqu'à 24% à Y=y/H=0,06 du mur chaud. En effet, l'interaction
entre l'écoulement principal et l'écoulement secondaire
génère une zone de cisaillement, qui, associée à
l'impact de l'écoulement principal sur le plafond
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 67
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
pourraient expliquer ce niveau de turbulence. Les fluctuations
de vitesse sont faibles à mi largeur au plafond, d'où une
intensité de turbulence relativement faible. Ensuite l'impact du jet
pariétal sur la paroi froide va accroître les fluctuations,
augmentant ainsi l'intensité de turbulence en aval du jet.
D'une manière générale le cheminement du
fluide dans la cavité pour les trois configurations
étudiées est similaire. Cet écoulement est
caractérisé globalement par : la présence d'une couche
limite ascendante le long de la paroi chaude et d'une couche limite descendante
le long de la paroi froide reliée entre elles par un jet pariétal
au plafond et au plancher ; la présence au plafond, d'une recirculation
dans une zone de circulation secondaire, à contre courant de la zone de
circulation principale qui la jouxte et qui s'étend sur toute la largeur
de l'enceinte. La présence d'un écoulement secondaire descendant
à la frontière de la couche limite chaude, alimentant la couche
limite froide en partie haute de la cavité et la couche limite chaude en
dessous.
IV.4 Influence du rayonnement de surface sur
l'écoulement de convection naturelle turbulente
Depuis quelques décennies le paramètre de
stratification thermique constitue un point de divergence entre les
expérimentateurs et les numériciens qui étudient la
convection naturelle en espace confiné. Si expérimentalement, la
valeur obtenue se situe autour de 0,5, les calculs qui traitent des
configurations idéales (parois passives adiabatiques) prédisent
une valeur proche de l'unité. La prise en compte du rayonnement de
parois par certains auteurs (Salat J. et al., 2004), (Wang H. et al., 2006) a
modifié de façon notable la stratification thermique. Une
étude expérimentale dont le but est de déterminer
l'influence du rayonnement de parois sur la stratification thermique dans une
cavité à haut nombre de Rayleigh a été menée
dans un premier temps
Des mesures de température sont ainsi faites à
mi largeur, dans le plan médian et sur toute la hauteur de la
cavité. Un profil vertical est établi pour deux écarts de
températures de 3 et 8 10 K, soient respectivement des valeurs du nombre
de Rayleigh de 1,04 x 107 et 2,79 x 107.
IV.4.1 Etude du champ thermique
Afin d'étudier l'influence des parois « passives
» sur le champ thermique, les profils verticaux de température dans
les couches limites chaude et froide établis dans le cas où les
parois passives sont non émissive (å= 0) et dans le cas où
elles ont une émissivité faible (å= 0,20) sont
comparés un à un sur la figure 39.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 68
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Ra = 2,79 x 107
Ra = 1,04 x 107
Figure 39 : contour de
temperature dans la cavité avec emissivité des parois
passives
Le rayonnement volumique seul fait apparaître deux
nouvelles zones de recirculation dans les coins (en haut à gauche et en
bas à droite), au détriment des ressauts hydrauliques
observés en convection pure. Le même cas a été
observé par (Djanna F., 2011).
La figure 39 montre que le rayonnement de parois accentue
encore l'affaiblissement des zones de recirculation à proximité
des parois actives et modifie considérablement la structure de
l'écoulement, avec l'apparition de nouvelles zones de recirculation en
parties amont des couches limites chaude et froide. On peut aussi observer une
distorsion de la zone de recirculation au voisinage des parois actives avec une
tendance plus forte à alimenter la couche limite opposée.

Figure 40 : comparaison des profils
de température en paroi basse et haute avec émissivité de
paroi et sans émissivité
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 69
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
On peut remarquer que, dans tous les cas, l'augmentation de
l'émissivité fait baisser le paramètre de stratification.
Ceci peut en partie s'expliquer par les échanges radiatifs entre les
parois haute et basse qui tendent à uniformiser les écarts de
température entre ces deux parois, réduisant ainsi la
stratification. Ceci est observé sur tous les essais
réalisés.
En prenant le cas Ra = 1,04 x107, le
paramètre de stratification passe de 0,33 dans le cas sans rayonnement
des parois passives à 0,40 avec rayonnement (E= 0,20) soit une
diminution d'environ 32%. Ce résultat est à rapprocher de celui
obtenu par (Djanna F., 2011) qui présente une diminution de l'ordre de
34 % lorsque l'émissivité des parois avant et arrière
passe de 0,10 à 0,95, mais à une valeur de Rayleigh plus
élevé.
Des mesures de température ont été
effectuées dans les couches limites ascendante et descendante à
différentes altitudes (de Z=0,30 à Z=0,95). Les profils sont
représentés sur la figure 41 pour ces différentes
élévations.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 70
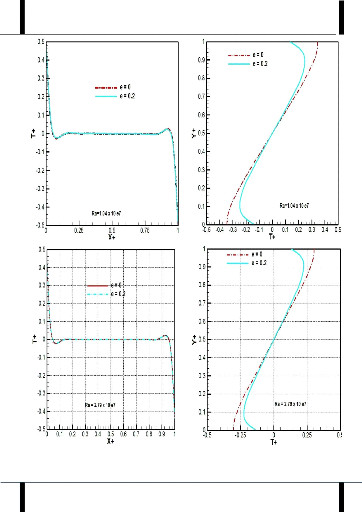
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Figure 41 : profils de temperature
a mi profondeur et a mi largeur de la cavitee.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 71
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Il ressort que la centro-symétrie est conservée
en convection pure et en rayonnement de surface. En revanche, le rayonnement
surfacique semble déplacer légèrement l'écoulement
dans toute la cavité, même si les différences
observées restent faibles. La figure 42 montre que le rayonnement
volumique diminue également la stratification thermique au coeur de la
cavité, mais dans une mesure moindre par rapport à ce qui est
observé avec le rayonnement de surface.

Figure 42 : densité de
flux net radiatif en paroi basse et haute pour les deux valeurs de dt (3 et
8)
D'emblée on peut relever que le flux de chaleur
pariétal augmente avec l'écart de température et donc,
avec le nombre de Rayleigh. Cette représentation nous permet de mieux
caractériser les différents régimes d'écoulement au
sein de la cavité en fonction du nombre de Rayleigh local.
Il ressort de notre étude que la partie centrale de
cette cavité est stratifiée en température. De plus, Une
investigation portant sur la contribution du rayonnement de parois à
parois à la stratification thermique a été soigneusement
menée et montre que la prise en compte du rayonnement est incontournable
pour l'évaluation correcte des champs de température dans la
cavité. On remarque qu'en baissant l'émissivité des parois
de 0,6 à 0,1, le paramètre de stratification augmente de 0,41
à 0,54 soit de 25% environ pour un Ra = 1,2×10 11. En effet le
rayonnement intensifie les écoulements secondaires dans la
cavité, ce qui génère un mélange plus important de
fluide, par conséquent la température est beaucoup plus
homogène dans le coeur réduisant ainsi la stratification
thermique. Toutefois, bien que le rayonnement de paroi induise une modification
de la stratification thermique, la centro-symétrie reste
conservée.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 72
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
IV.4.2 Etude du champ dynamique
La figure 43 montre que le rayonnement de parois accentue
encore l'affaiblissement des zones de recirculation à proximité
des parois actives et modifie considérablement la structure de
l'écoulement, avec l'apparition de nouvelles zones de recirculation en
parties amont des couches limites chaude et froide. On peut aussi observer une
distorsion de la zone de recirculation au voisinage des parois actives avec une
tendance plus forte à alimenter la couche limite opposée.

a b
Figure 43 : contours du champ
dynamique a Ra= 1,04 x 107 (a gauche) et Ra= 2,79 x107 (a
droite)
On voit bien l'apparition de nouvelles zones de recirculation
autour de la couche limite chaude et froide. L'émissivité des
parois a des effets notables aussi sur le contour de champ dynamique.
L'écoulement est également perturbé dans toutes la
cavité, on peut mieux observe cette différence en regardant les
profils au coeur de la cavité.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 73
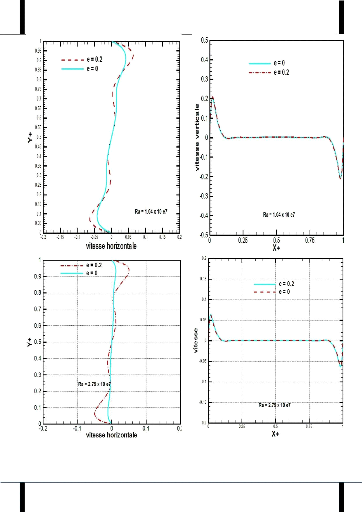
Figure 44 : profils de la
composante verticale et horizontale de la vitesse au coeur de la cavité
a
Ra=107
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 74
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
La différence est immédiatement visible à
mi largeur de la cavité. Le rayonnement inverse carrément la
symétrie de l'écoulement. Par contre à mi-hauteur, on ne
note aucun changement dans l'allure de la courbe de vitesse.
Le rayonnement de parois introduit des modifications
relativement importantes sur la structure de l'écoulement en favorisant
la formation d'écoulements secondaires à proximité des
parois horizontales. Il provoque une distorsion des zones de recirculation
tourbillonnaire observées en bordure de couches limites verticales. On a
noté que pour les nombres de Rayleigh considéré, le
rayonnement de parois diminue considérablement la stratification
thermique dans le coeur de la cavité et influe sensiblement sur le
transfert thermique au voisinage des parois actives. De même, il
génère un flux de chaleur turbulent important dans les couches
limites verticales et dans les coins (en haut à gauche et en bas
à droite). Lorsqu'il est seul, le rayonnement de parois induit une
croissance de l'énergie cinétique turbulente près des
parois adiabatiques. En effet, en convection pure les effets de turbulence se
manifestent uniquement dans les couches limites verticales tandis que quand on
prend en compte le rayonnement surfacique, la turbulence est présente
également au voisinage des parois horizontales.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 75
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
CONCLUSION ET PERSPECTIVES
Nous avons présenté dans ce mémoire les
données issues d'investigations numériques de convection
naturelle turbulente en cavité différentiellement chauffée
de type habitat et les résultats numériques du couplage de la
convection naturelle turbulente avec le rayonnement, ont également
été étudié. Nous avons comparé nos calculs
grâce à des données issues de la littérature
particulièrement celles de (Wang H. et al., 2006).
Ainsi nous avons pu montrer que l'écoulement de
convection naturelle en cavité différentiellement
chauffées est gouverné par le nombre de Rayleigh, donc le
paramètre variant est la différence de température entre
le mur froid et le mur chaud (dans le cas actuel 10 K). Nous avons ainsi
représenté les champs de température et de vitesses dans
l'enceinte pour plusieurs valeurs du nombre de Rayleigh (1,04 x 107,
2,71 x 107, 3,14 x 107 et 3,94 x 107), et
ainsi caractériser l'ambiance thermique d'une enceinte soumise à
des différences de température. Ensuite, nous avons
démontré que le fait de rendre les murs d'une cavité
émissive, modifie la thermique et la dynamique de l'écoulement de
convection naturelle au centre, au plancher et au plafond de la
cavité.
Au regard de l'intérêt croissant porté par
la communauté « convectionniste » sur une meilleure
connaissance des écoulements turbulents et une maitrise des transferts
de chaleur, cette contribution pourra servir pour de nouvelles perspectives. Le
rayonnement volumique affecte la stratification thermique d'après les
simulations, alors des expériences avec peu de vapeur d'eau et en
remontant les températures pourraient s'envisager. En
réalité, dans une pièce d'habitation, l'air qui s'y trouve
est un mélange de gaz (air sec, vapeur d'eau, CO2...) et donc, dans
notre code de calcul, la modélisation du fluide comme un gaz réel
et non pas un gaz gris, semble indispensable pour une meilleure analyse de
l'effet de rayonnement de gaz sur les écoulements de convection
naturelle turbulents. Il pourrait également être envisagé
dans un avenir proche une étude des instabilités
thermo-convectives au sein de cette grande cavité. Les
écoulements dans l'habitat sont généralement
tridimensionnels. Cette dernière constatation reste une
préoccupation et c'est en cela qu'une extension du code de simulation
(LES-2D en présence du rayonnement) à des configurations 3D
semble nécessaire
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 76
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
BIBLIOGRAPHIE
Adel I. couplage de la convection naturelle
et du rayonnement dans des mélanges gazeux absorbants-emettants
[Rapport] : thése de doctorat. - poitier, France : [s.n.], 2010.
Aklouche S., Zeghmati B., Bouhadef K., Daguenet
M. etude numèrique de lq convection nqturelle instqtionnaire
bidimensionnelle dans une enciente fermée. identification des routes
vers le chaos [Conférence] = S. Aklouche et al, 2005 // journée
international de thermique. - maroc : [s.n.], 2005. - pp. 65-68.
Ampofo F. et Karayiannis T. Experimental
benchmark data for turbulent natural convection in an air filled square cavity
[Revue] // International Journal of Heat and Mass Transfer 46. - 2003. - pp.
3551-3572.
Aounallah M. et al. Aounallah M., Addad Y.,
Benhamadouche S., Imine O., Adjlout L., Laurence D. Numerical
investigation of turbulent natural convection in an inclined square cavity with
a hot wavy wall [Revue] // International Journal of Heat and Mass Transfer. -
2006.
Baliga B. et Patankar S. A new finite element
formulation for convection-diffusion problem. ,, 3. [Revue] // Numerical Heat
Transfer. - 1980. - Part B : Vol. 3.
Batchelor G. K. Heat transfer by free
convection across a closed cavity between vertical boundaries at different
temperatures. [Revue] // Quaterly of Applied Mathematics. - 1954. - Vol. 12. -
pp. 209-233.
Bejan A. et Kraus A. "Heat transfer" [Rapport].
- Canada : John Wiley & Sons , Inc, 2003.
Bénard H. Les Tourbillons cellulaires
dans une nappe liquide transportant de la chaleur par convection en
régime permanent. [Revue]. - [s.l.] : Ann. Chim. Phys., 1901. - 7(Ser.
23): 62..
Benkhelifa A., Fuentes C., Tuhault J. L., penot F.,
convection naturelle à grand nombre de Rayleigh dans une couche
horizontale de fluide, approche expérimentale [Conférence] //
journées Internationales de Thermiques. - Albi-France : [s.n.], 2007. -
pp. 1-5.
Benkhélifa A. et Pénot F.
étude espérimentale des mouvements de convection
naturelle dans une cavité différentiellement chauffée
inclinée, influence de l'inclinaison [Conférence] //
12èmes Journées Internationales de Thermique. - Tanger, Maroc :
[s.n.], 2005. - pp. 117-120.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 77
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Binet B. "Etude de la fusion dans des enceintes
munies de sources de chaleurdiscrètes". , [Rapport] : Thèse de
Doctorat en génie mécanique. - Canada : Université de
Sherbrooke (Québec), 1998.
Bougoul S., Zeroual S., Boulard T., Azil F.,
Simulation numérique du mouvement d'air et de la variation de
température dans des serres chauffées [Revue] // Revue des
Energies Renouvelables. - 2007. - pp. 209-212.
Boutra A., Benkahla Y. K., Ameziani D. E., et Labs
N., Etude numérique du transfert de chaleur pour un fluide de
Bingham dans une cavité carrée en mode de convection naturelle
instationnaire [Conférence] // 20iéme Congrés
Français de Mécanique. - Besançon : [s.n.], 2011. - pp.
1-6.
Busse F. The Stability of Finite
Amplitude Cellular Convection and its Relation to an Extremum Principle'
[Revue] // J. Fluid Mech.. - 1967. - 4 : Vol. 30. - pp. 625 - 649.
Comte-Bellot G. les méthodes de mesure
physique de la turbulence [Revue] // journal de Physique. - Janvier 1976. - 1 :
Vol. tome 37. - pp. supplément au n° 1, Tome 37, Cl-67.
De Laroche Lambert étude
expérimentale et numérique des transferts de chaleur en
convection naturelle le long des parois verticales épaisses rayonnantes
fortement chauffées [Revue] // congés français de
thermique. - 2009.
Djanna F. convection naturelle turbulente en
cavité différentiellement chauffée a grands nombres de
Rayleigh : caratérisation expérimentale des écoulements et
des transferts thermiques, étude numérique du couplage
convection-rayonnement [Rapport] : thése de doctorat / Ecole Nationale
Superieure De Mecanique Et D'aerotechnique Poitier. - poitier : [s.n.],
2011.
Francis Djanna, Nicolas Rouger, Didier Saury,
François Penot Stratification thermique de l'air dans une
cavité en convection naturelle à grand nombre de Rayleigh
[Conférence]. - 2008.
Draoui A. Contribution à la
modélisation des transferts de chaleur couples par convection naturelle
laminaire et rayonnement dans une cavité carrée à haut
nombre de Rayleigh [Rapport] : thése de doctorat. - Tétouan :
[s.n.], 1991.
Draoui B., Benyamine M., Taïbi R. et Hami O.
Simulation Numérique de la Convection Naturelle en
Régime Laminaire et Transitoire d'une Serre Monochapelle Chauffée
par le bas (Flux) [Revue] // Rev. Energ. Ren. / éd. Chemss. - 2000. -
pp. 67-73.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 78
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Gautier F. Convection turbulente dans une
cellule de Rayleigh-Bénard cryogénique : de nouveaux
éléments en faveur du Régime Ultime de Kraichnan [Rapport]
: Thèse de doctorat préparée à l'Institut
Néel, CNRS. - 2008.
Gebhart B. Instability transition and turbulence
buoyancy induced flows, [Revue] // Annual review of Fluid Mechanics, 5. - 1973.
- p. 213.
Graf W. et Altinakar M. Hydrodynamique : une
introduction [Rapport] : Traité de Génie Civil. - universitaire
romanes : Presse polytechnique et Ecole polytechnique fédérale de
Lausanne, 1995.
Hadji T. "Phénomènes
couplés thermo-acoustiques dans la convection de Rayleigh-Bénard"
[Rapport] : Mémoire de magistère en mécanique. -
Université de Batna, Algérie : [s.n.], 2003.
Henkes W. Turbulent natural boundary layers
[Rapport]. - [s.l.] : PHD Thesis University of Delft, 1990.
Jackson T. W., Spurlock J. M., Purdy K. R.,
Combined Free and Forced Convection in a Constant Temperature
Horizontal Tube. [Revue] // A.I.Ch.E. Journal,. - 1961. - 1 : Vol. 7. - pp.
3841.
Jeanot Y. transfert et échangeur de
chaleur [Livre]. - 2003.
Jones D. et Briggs D. Periodic two-dimensional
cavity flow: effect of linear horizontal thermal boundary condition, [Revue]. -
[s.l.] : Journal of Heat Transfer, 1989. - Vol. Vol. 111. - pp. pp 8691, .
Krisnamurti R. 'On the Transition to Turbulent
Convection; Part 2: The Transition Time Dependant flow' [Revue] // J. Fluid
Mech.. - 1970. - 2 : Vol. 42. - pp. 309 - 320.
Krisnamurti R. 'Some Further Studies on the
Transition to Turbulent Convection' [Revue] // J. Fluid Mech. - 1973.. - Vol.
60. - pp. 285 - 303.
Lasfer K., Bouzaiane M., Lili T.,
étude numérique de la convection naturelle turbulente
dans une cavité trapézoïdale [Conférence] //
Journées International de Thermique. - Albi, France : [s.n.], 2007. -
pp. 1-5.
Le Quéré P. Etude de la
transition à l'instationnarité des écoulements de
convection naturelle en cavité verticale différentiellement
chauffée par méthodes spectrales Chebyshev [Rapport] :
Thèse de doctorat ès Sciences. - Université de Poitiers :
[s.n.], 1987.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 79
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Mabrouk G. Modélisation de la Convection
Naturelle Laminaire dans Une Enceinte Avec Une Paroi Chauffée
Partiellement [Rapport] : mémoire de Magister. - Université de
Mentouri Constantine : [s.n.], 2010.
Mergui S. Caractérisation
expérimentale des écoulements d'air de convection naturelle et
mixte dans une cavité fermée. , 1993 [Rapport] : Thèse de
doctorat. - Université de Poitiers : [s.n.], 1993.
Moudil L. Couplage Fluide-Structure pour la
simulation num'erique des 'ecoulements fluides dans une conduite `a parois
rigides ou 'elastiques, en pr'esence d'obstacles ou non [Rapport] :
thése de doctorat. - Universit'e d'Artois : [s.n.], 2008.
Padet J. Fluides en écoulement -
méthodes et modèles [Livre]. - [s.l.] : Masson, 1991.
Patankar V. Numerical heat transfer and fluid flow [Revue] //
Mc Graw Hill. - 1980.
Phllippe-Emmanuel R. "Convection thermique
turbulente en cellule de Rayleigh-Bénard cryogénique". [Rapport]
: Thèse de Doctorat,. - Université de Grenoble, France, : [s.n.],
2001.
Rayleigh L. On convection currents in a
horizontal layer of fluid, when he higher temperature is on the underside..
[Revue]. - [s.l.] : Phil. Mag. 32: 529, 1916.
Revnic C., Grosan T., Pop I., Ingham D. B., Free
convection in a square cavity filled with a bidisperse porous medium [Revue] //
International Journal of Thermal Sciences. - 2009. - Vol. 48. - pp.
1876-1883.
Rouger N., Joubert P., Penot F.,
Caractérisation dynamique et thermique de la convection
naturelle turbulente dans une cavité différentiellement
chauffée comportant un linteau [Conférence] // Congrés
Français de Thermique. - Iles des Embiez : [s.n.], 2007.
Rouger N. Sensibilité de la convection
naturelle en cavité différentiellement chauffée à
des variations de paramètres géométriques, thermiques et
massiques [Rapport] : thése / École Doctorale : Sciences pour
l'Ingénieur et Aérotechnique Secteur de recherche :
Énergétique, Thermique, Combustion. - Poitier : [s.n.], 2009.
Saeidi S. et Khodadadi J. Forced convection
in a square cavity with inlet and outlet ports [Revue] // International Journal
of Heat and Mass Transfer / éd. ELSEVIER. - 2006. - Vol. 49. - pp.
1896-1906.
Salat J. Contribution à l'étude de
la convection naturelle tridimensionnelle en cavité
différentiellement chauffée [Rapport] : Thèse de Doctorat.
- Université de Poitiers : [s.n.], 2004.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 80
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Salat J., Xin S., Joubert P., Sergent A., Penot F., Le
Queret P. Experimental and numerical investigation of turbulent
natural convection in a large air-filled cavity [Revue] // International
Journal of Heat and Fluid Flow / éd. ELSEVIER. - 2004. - Vol. 25. - pp.
824-832.
Sartipi A., Laouadi A., Naylor D., Dhib R.
Convective heat transfer in domed skylight cavities [Revue] // Journal
of Building Performance Simulation / éd. Francis Taylor &. - 2010. -
4 : Vol. 3. - pp. 269-287.
Saury D., Rouger N., Djanna F., Penot F.
caracterisation des écoulements de convection naturelle
turbulente à grand nombre de Rayleigh [Conférence] //
Congrés Francophone de Techniques Laser. - 2008.
Tamman H. contribution à la
modélisation de la turbulence en convection naturelle [Rapport] :
thése de doctorat. - 2004.
Tcheukam Toko T. Etude de la couche limite
générée par l'action de la houle/courant sur fond
hydrauliquement lisse : Application aux transports des sédiments
[Rapport] : thése de doctorat / université du Havre. - 1997.
Tcheukam-Toko D., Kongue L., Koueni-Toko C. A.,
Mouangue R., Bélorgey M. Numerical Simulation and Experimental
Validation of Boundary Layer Generated by a Turbulent Flow on a hydraulically
Smooth Bed [Revue] // Res. J. of Applied Sci.,. - 2012. - (2) : Vol. Vol. 7. -
pp. pp.108-112.
Versteeg H. et Malalasekera W. An
introduction to Computational Fluid Dynamics, the finite volume method [Livre].
- england : Addison Wesley Longman Limited, 1995.
Wang H., Xin S., Le Quéré P.
Étude numérique du couplage de la convection naturelle
avec le rayonnement de surfaces en cavité carrée remplie d'air
[Revue] // Elsevier, Comptes Rendus de Mécanique. - 2006. - pp.
48-57.
Winters K. hopf bifurcation in the
double-glazing problem with conducting boundaries [Revue]. - [s.l.] : Journal
of Heat Transfer, 1987. - Vol. Vol. 109. - pp. pp 894-898,.
Zermane S., Boudebous S., Boulkroune N., Etude
numérique de la convection mixte laminaire dans des cavités
ventilés [Revue] // Sciences & Technologie B - N°23. - 2005. -
pp. PP. 34-44.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 81
MEMOIRE DE MASTER EP« étude de la
convection naturelle turbulente dans une enceinte à paroi chauffé
»
ANNEXES A : interface de fluent
The user interface to FLUENT consists of a graphical interface
with pull-down menus,
panels, and dialog boxes, as well as a textual command line
interface (described in the User's Guide).
1) GUI Components
FLUENT's graphical user interface (GUI) is made up of four
main components: a console window, control panels, dialog boxes, and graphics
windows. When you use the GUT, you will be interacting with one of these
components at all times. Figure 5.1.1 is a sample screen shot showing all of
the GUT components. The four GUT components are described below.
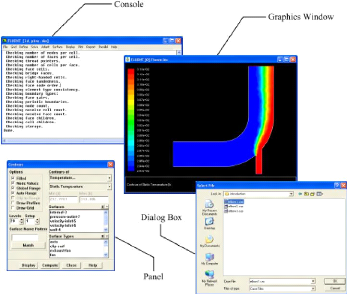
Figure 45 : FLUENT GUT Components
2) Console
The FLUENT Console is the main window that controls the
execution of the program. When using the Console to interact with FLUENT, you
have a choice between a text user interface (TUT) and a graphical user
interface (GUT). The Console contains a terminal emulator for the TUT and a
menu bar for the GUT. An overview of the GUT is described in this chapter,
while a more detailed description of the GUI is located in the User's Guide.
For more information about using the TUI, see the User's Guide as well.
Rédigé et soutenu par TTENTCHEU NSTEWE Maxwell
Phidelo Page a
MEMOIRE DE MASTER EP« étude de la convection
naturelle turbulente dans une enceinte à paroi chauffé »
Figure 46 : the Comsole
2.1) Terminal Emulator
The terminal emulator is similar in behavior to
«xterm» or other Linux/UNIX command shell tools, or to the Command
Prompt window on Windows systems. It allows you to interact with the text
command interface (TUI). All textual output from the program (e.g., error
messages) is printed in the terminal emulator, and all typing is displayed on
the bottom line. As the number of text lines.
Grows, the lines will be scrolled off the top of the window.
The scroll bar on the right allows you to go back and look at the preceding
text. The terminal emulator accepts <Control-C> to let you interrupt the
program while it is working. It also lets you perform text copy and paste
operations between the Console and other X Window (or Windows) applications
that support copy and paste.
2.2) Menu Bar
The menu bar organizes the GUI menu hierarchy using a set of
pull-down menus. A pull-down menu contains items that perform commonly executed
actions. Figure 47 shows the FLUENT menu bar. Menu items are arranged to
correspond to the typical sequence of actions that you perform in FLUENT (i.e.,
from left to right and from top to bottom).
Figure 47 : The FLUENT Menu Bar
In addition to using the mouse, you can also select a pull-down
menu item using the
keyboard. Each pull-down menu label or menu item contains one
underlined character, known as
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page b
MEMOIRE DE MASTER EP« étude de la convection
naturelle turbulente dans une enceinte à paroi chauffé »
the mnemonic. Pressing the <Alt> key plus the mnemonic
character of a pull-down menu will display the menu. Once the pull-down menu is
selected and displayed, you can type a mnemonic character associated with an
item to select that item. If at any time you wish to cancel a menu selection
while a pull-down menu is posted, you can press the <Esc> key. For
example, to display the Help menu and select the Using Help...option, press
<Alt> h, then h.
A pull-down menu item may also have an accelerator key
associated with it. An accelerator key can be used to select a menu item
without displaying the pull-down menu. If a menu item has an associated
accelerator key, the key will be shown to the right of the item. For example,
if a pull-down menu contains the item Iterate... Ctrl+I, you can select this
item by holding down the <Ctrl> key and pressing the «I»
key.
3) Dialog Boxes
Dialog boxes are used to perform simple input/output tasks, such
as issuing warning and
error messages, or asking a question requiring a yes or no
answer. The following describes each type of dialog box:
> The Information dialog box is used to report some
information that FLUENT thinks you
should know. Once you have read the information, you can click
the OK button to close the dialog box ;
> The Warning dialog box is used to warn you of a potential
problem and ask you whether
or not you want to proceed with the current operation. If you
click the OK button, the operation will proceed. If you click the Cancel
button, the operation will be canceled;
> The Error dialog box is used to alert you of an error
that has occurred. Once you have read the error information, you can click the
OK button to close the dialog box.
> The Working dialog box is displayed when FLUENT is busy
performing a task. This is a special dialog box, because it requires no action
by you. It is there to let you know that you must wait. When the program is
finished, it will close the dialog box automatically. You can, however, abort
the task that is being performed by clicking the Cancel button.
> The Question dialog box is used to ask you a question
that requires a yes or no answer. You can click the appropriate button to
answer the question.
> The Select File dialog box enables you to choose a file
for reading or writing. You can
use it to look at your system directories and select a file.
This is a special type of dialog box that is described in more detail in the
following section.
Select File Dialog Box
Selecting Files in Windows
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page c
MEMOIRE DE MASTER EP« étude de la convection
naturelle turbulente dans une enceinte à paroi chauffé »
File selection in Windows systems is accomplished using the
standard Windows Select File dialog box (see Figure 48).
Figure 48 :The select file dialog box for Windows
See documentation regarding your Windows system for further
instructions on file selection. Selecting Files in UNIX or
Linux
For UNIX or Linux systems, note that the appearance of the
Select File dialog box will not always be the same.
Figure 49 : the select file dialog box for UNIX or Linux
Platform
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page d
MEMOIRE DE MASTER EP« étude de la convection
naturelle turbulente dans une enceinte à paroi chauffé »
The version shown in Figure 5.3.2 will appear in almost all
cases, but it will be different if
you are loading external data files for use in an XY plot (see
the User?s Guide for more information). In such cases, the dialog box will look
like Figure 50.
The steps for file selection are as follows:
1. Go to the appropriate directory. You can do this in two
different ways:
? Enter the path to the desired directory in the Filter text
entry box and then press the <Enter> key or click the Filter button. Be
sure to include the final / character in the pathname, before the optional
search pattern (described below);
? Double-click a directory, and then a subdirectory, etc. in
the Directories list until you reach the directory you want. You can also click
once on a directory and then click the Filter button, instead of
double-clicking. Note that the «.»item represents the current
directory and the «..» item represents the parent directory.
Figure 50 : another version select file dailog box for Unix or
Linux platforms
2. Specify the file name by selecting it in the Files list or
entering it in the File text entry box (if available) at the bottom of the
dialog box. The name of this text entry box will change depending on the type
of file you are selecting (Case File, Journal File, etc.).
That if you are searching for an existing file with a
nonstandard extension, you may need to modify the «search pattern» at
the end of the path in the Filter text entry box. For example, if you are
reading a data file, the default extension in the search path will be *.dat*,
and only those files that have a .dat extension will appear in the Files list.
If you want files with a .DAT extension
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page e
MEMOIRE DE MASTER EP« étude de la convection
naturelle turbulente dans une enceinte à paroi chauffé »
to appear in the Files list, you can change the search pattern
to *.DAT*. If you want all files in the directory to be listed in the Files
list, enter just * as the search pattern.
3. If you are reading multiple XY-plot data files, the
selected file will be added to the list of XY File(s). You can choose another
file, following the instructions above, and it will also be added to this list.
(If you accidentally select the wrong file, you can choose it in the XY File(s)
list and click the Remove button to remove it from the list of files to be
read.) Repeat until all of the desired files are in the XY File(s) list.
4. If you are writing a case, data, or radiation file, use
the Write Binary Files check box to specify whether the file should be written
as a text or binary file. You can read and edit a text file, but it will
require more storage space than the same file in binary format. Binary files
take up less space and can be read and written by FLUENT more quickly.
5. Click the OK button to read or write the specified file.
Shortcuts for this step are as follows:
? If your file appears in the Files list and you are not
reading an XY file, double-click it instead of just selecting it. This will
automatically activate the OK button. (If you are reading an XY file, you will
always have to click OK yourself. Clicking or double-clicking will just add the
selected file to the XY File(s) list.);
? If you entered the name of the file in the File text entry
box, you can press the <Enter> key instead of clicking the OK button.
4) Panels
Panels are used to perform more complicated input tasks.
Similar to a dialog box, a panel is displayed in a separate window, but working
with a panel is more akin to filling out a form. Each panel is unique and
employs various types of input controls that make up the form (see Figure 51).
The types of controls you will see are described in more detail in the User?s
Guide.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page f
MEMOIRE DE MASTER EP« étude de la convection
naturelle turbulente dans une enceinte à paroi chauffé »
Figure 51 : the components of a typical FLUENT Panel
When you have finished entering data in a panel?s controls, you
will need to apply the
changes you have made, or cancel the changes, if desired. For
this task, each panel falls into one of two behavioral categories, depending on
how it was designed:
? The first category of panels is used in situations where it
is desirable to apply the changes and immediately close the panel. This type of
panel includes two button controls as described below.
OK applies any changes you have made to the panel, then closes
the panel.
Cancel closes the panel, ignoring any changes you have
made.
? The other category of panels is used in situations where it
is desirable to keep the panel displayed on the screen after changes have been
applied. This makes it easy to quickly go back to that panel and make more
changes. Panels used for postprocessing and grid adaption often fall into this
category. This type of panel includes two button controls as described
below.
Apply applies any changes you have made to
the panel, but does not close the panel. The name of this button is often
changed to something more descriptive. For example, many of the postprocessing
panels use the name Display for this button, and the adaption panels use the
name Adapt.
Close closes the panel.
All panels include the following button used to access on-line
help:
Help displays information about the controls
in the panel. The help information will appear in your web browser.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page g
MEMOIRE DE MASTER EP« étude de la convection
naturelle turbulente dans une enceinte à paroi chauffé »
Each type of input control utilized by the panels is described in
greater detail in the User's
Guide.
5) Graphics Display Windows
Graphics display windows (e.g., Figure 52) are separate
windows that display the program's graphical output.
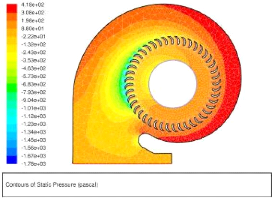
Figure 52 : sample graphics display Window
The Display Options panel can be used to change the attributes of
the graphics display or to
open another display window. The Mouse Buttons panel can be
used to set the action taken when a mouse button is pressed in the display
window.
To cancel a display operation, press <Control-C> while
data are being processed in preparation for graphical display. You cannot
cancel the operation after the program begins to draw in the graphics
window.
For Windows systems, there are special features for printing
the contents of the graphics window directly. These features are not available
on UNIX systems. See the User's Guide for further details.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page h
MEMOIRE DE MASTER EP« étude de la convection
naturelle turbulente dans une enceinte à paroi chauffé »
ANNEXE B : article de comparaison
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page i
| 


