Une nouvelle approche de la determination de taux d'envasement des barrages

CHAPITRE II

Où :

Pf : périmètre mouillé correspondant au fond ;

P_p : périmètre mouillé correspondant aux parois.

P= Pf + P_p ;

K : KF, Kp : coefficient de strickler (global, fond et parois).

0.8

10

0.1

1

6

2

'U_c

2

W?

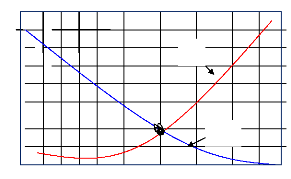
Fig. II.6. Variation de la contrainte critique ô et le paramètre W
De la formule de Boys (.Sidi Adda M, 2004)

b. formule de Mayer Peter et Muller 1948

Est une formule expérimentale ajustée pour des sédiments dont le 0.4< _d50< 30 mm et 1.02 10³ < q <4 . 310³ Kg/m³

{

J

.R_F.

ÇO_g

ÇO - ÇO K

s f

0 . 047 ( ) 0 . 25 ( ) 1 / 3 ( ) 2 / 3 2 / 3 ( ) 3 / 2

' - ÇO gd + ? q =

s

ÇO

s ^s KF

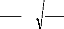
K_F

F

V

2

=

8 2

K

'

f

R J

F

													(	II	.	6	)

46

Où : XF est le coefficient de Darcy Weisbach relatif au fond et à la rugosité, on obtient à l'aide des abaques de Nikuradse dans lesquelles on remplace d, diamètre de la conduite, par 4Rf et K_s, rugosité équivalente, par dg_o pour des valeurs telle que :

> 100 (II.7)

2_F Vdg o

8 V

CHAPITRE II

On admet formule (régime hydraulique rugueux) :

26

K ' = (II.8)

o

1 / 6

^f dg

Kf est le coefficient strickler du fond, RF étant obtenu selon la méthode indiquée précédemment pour la formule de Du Boys.

c. Formule de Shields

Elle s'exprime sous la forme suivante :

c

g_s= 10q .J (

2

-

(II.9)

ô - ô

Où : ô_c est la contrainte critique de début d'entraînement, donnée par la courbe de Shields.

d. Formule de Van Rijn

Elle est exprimée sous la forme suivante:

? U - U cr g = 0 . 005 ?? s ? g ( s - 1 ) d

2. 4 ? ? d ? ?? ?? ?? R ?

1/ 2

UhB (II.10)

Où, U : vitesse moyenne d'écoulement, Ucr : vitesse moyenne critique d'écoulement. h : profondeur d'eau, B : largeur de canal.

d: diamètre des sédiments ; S= P_s/P : densité des particules solides.

e. Formule d'Einstein-Brown

La formule d'Einstein-Brown s'exprime sous forme suivante

ö	3 ? 1 ? 1 40 ? ? pour = 0.09 ? ? ø ø		(II.11)

??

?

? ö =

? ?

g F g ( ? / ? - 1 ) d

s 1 s

?

(II.12)

g s

3

s

47

1 ô

=

ø

( p - ? ) s

g d

s

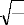
2

2

CHAPITRE II

2 36 V 36 V

1 3 )

F : + - ...( II .

1 3 3

3 gd (? / ? - 1 ) gd (? /? -1 )

s s s s

d_s est soit pris égal à _d50 soit à la moyenne géométrique d_g. La formule d'Einstein-Brown dérive des données de Gilbert et Meyer-Peter-Muller (pour 0.3 mm<dm<7mm).

II.5.2. Débit solide en suspension

De nombreuses formules ont été établies pour le calcule du débit solide par suspension et la formule d'Einstein représente l'approche la plus complète du phénomène.

Il s'agit en fait d'une méthode d'évaluation du transport solide total qui prend en compte les différentes classes granulométriques on pose : g_s= Óigssi

G_s : débit solide total en suspension, gssi : débit solide en suspension en poids par unité de largeur pour la calasse granulométrique de diamètre moyen d_s i :

g = g [p I₁(ç ,Z ) + I₂(ç ,Z )] ( II. 14 )

ss sbi r oi i oi i

gsbi: débit solide charrié en poids par unité de largeur.

Z i - 1 1

ç 1 - ç

o J Z i

I = 0. 216 ( ) d (II.15)

I o i Z i ç .

?

(1 - ç

oi

çç

)

Z - 1 1

i

I₂ = 0 . 0 6 ç?1-ç

o i ?

Z i ?

(1 - ç ) ? ç

o i ç

? ? log ç dç (II.16)

?

Z i

On peut évaluer I, I2 à l'aide des abaques de la Fig. II.8.

P_r= 2.31 log1030.2 á Rf / d65 (II.17)

2 d si --(II.18)

ço i R_f^, Rf i 0 .4U

w_i

'...................

48

á est un nombre sans dimension caractérisant le profil de la vitesse logarithmique. On l'obtiendra à partir de la Fig. II.7.en fonction de K_s/ä c'est-à-dire : U d65/11.6 V Wi est la vitesse de chute dans une eau calme.

U' = gR_F' J (II .19)