Modélisation du coefficient apparent d'utilisation de l'azote issu d'un engrais minéral apporté sur blé tendre d'hiver

"Les analyses et les conclusions de ce travail d'étudiant n'engagent
que la responsabilité de son auteur et non celle d'AGROCAMPUS OUEST".

AGROCAMPUS OUEST Arvalis - Institut du Végétal

CFR Rennes Station Expérimentale de la Jaillère

65 rue de Saint-Brieuc 44370 LA CHAPELLE SAINT SAUVEUR

35042 RENNES

Mémoire de Fin d'Études

Diplôme d'Ingénieur de l'Institut Supérieur des Sciences
Agronomiques, Agroalimentaires, Horticoles et du Paysage

Année universitaire : 2011-2012

Spécialisation ou option : Statistiques appliquées

Modélisation du coefficient apparent d'utilisation de l'azote
issu d'un engrais minéral apporté sur blé tendre d'hiver

Par : François COLLIN

Date : 20/09/2012 Autorisation de diffusion : Oui

Devant le jury : Soutenu à Rennes le : 10 septembre 2012

Sous la présidence de : Jérôme PAGES Maître de stage : Jean-Pierre COHAN Enseignant référent : Julie JOSSE

Mémoire de fin d'études

Modélisation du coefficient apparent d'utilisation de l'azote issu d'un engrais minéral apportésur blétendre d'hiver

François Collin Maître de stage :

Etudiant ingénieur agronome Jean-Pierre Cohan

Master de statistiques appliquées Agronome spécialiséthématique fertilisation

Soutenance

10 septembre 2012

Remerciements

Jean-Pierre Cohan, agronome spécialisésur les thématiques de fertilisation et maître de stage, m'a accordésa confiance pour mener à bien ce projet. Malgréses nombreuses missions, il s'est ^montrédisponible dans la mesure du possible et a veilléàla bonne marche du stage. Pour l'attention et la sympathie dont-il a fait preuve àmon égard je le remercie sincèrement.

Je remercie également Jean-Charles Deswarte, écophysiologiste àArvalis - Institut du Végétal. Il a participéau suivi des travaux en répondant présent aux comités de pilotages au cours desquels il a pu apportéson expérience et son regard critique.

De même, je dois remercier François Piraux, statisticien àArvalis - Institut du Végétal qui a fait preuve de patience pour répondre àmes doutes et interrogations.

Je remercie mes collègues de bureau : Gérald, Pauline et Olivier. Nous avons partagéde bons moments et j'espère que nos routes se croiserons de nouveaux, d'ici làje leur dit merci et leur souhaite une bonne continuation.

Enfin, je remercie l'ensemble du personnel d'Arvalis - Institut du Végétal de la station de La Jaillière qui m'a réservéun accueil des plus agréables, permettant à ce stage de se dérouler dans des conditions très appréciables. Outre l'expérience professionnelle que m'a apportéce stage, je garderai un souvenir plus personnel du partage d'expérience et de points de vue autour de l'agriculture.

Riche de cette expérience tant professionnelle que personnelle, je ne peux qu'être enthousiaste ^àl'idée de renouveler ma collaboration avec Arvalis - Institut du Végétal lors ma prochaine affectation. Merci et àbientôt.

Table des matières

Liste des figures Liste des tableaux

1	Introduction : la modélisation du CAU, une réponse aux enjeux de la fertilisation
	azotée		1
	1.1	Le CAU : indicateur de l'efficacitédes apports d'engrais azotés	1
		1.1.1 Un Coefficient Apparent différent du Coefficient Réel d'Utilisation	2
		1.1.2 Complément à 100 du CAU : les pertes d'azote issue de l'engrais	2
	1.2	Utilisation du CAU dans la détermination des doses d'engrais à apporter aux cultures	3
	1.3	Travaux de modélisation	3
		1.3.1 La vitesse de croissance pour expliquer le CAU	3
		1.3.2 Introduction de variables climatiques et de l'état de nutrition azotée	4
	1.4	Problématique de l'étude	5
2	Matériel et méthodes		7
	2.1	Préparation et présentation des données	7
		2.1.1 Les essais : acquisition de données brutes	7
		2.1.2 Calculs des variables d'intérêt	8
		2.1.2.1 Détermination du CAU	8
		2.1.2.2 Estimation de la vitesse de croissance	10
		2.1.2.3 Comment estimer l'état de nutrition azotéde la culture?	11
		2.1.2.4 Relevédes variables pluviométriques	11
		2.1.3 ~Elaboration du jeu de données pour l'étude du CAU	12
	2.2	Exploration et compréhension du jeu de données	13
		2.2.1 Modèles généraux d'analyses statistiques	13
	2.3	~Elaboration d'un modèle explicatif du CAU	14
		2.3.1 Analyse factorielle	14
		2.3.2 Approche linéaire de la sélection de modèles	15
		2.3.3 Introduction de relations non linéaires	16
		2.3.4 Validation du modèle	16
	2.4	Moyens informatiques	16
3	Résultats		17
	3.1	Préparation des données	17
		3.1.1 Examen des données	17
		3.1.2 La variable à expliquer, le CAU calculéàla récolte	18
		3.1.3 Les variables explicatives	21
		3.1.3.1 La vitesse de croissance	21
		3.1.3.2 ~Etat de nutrition azotée	24
		3.1.3.3 Variables pluviométriques	24
	3.2	~Elaboration d'un modèle explicatif du CAU	27

3.2.1 Analyse multidimensionnelle 27

3.2.2 Modèles linéaires 30

3.2.2.1 Un point de départ : le modèle nul et le modèle VC 30

3.2.2.2 L'INN apporte-t-il une amélioration au modèle? 33

3.2.2.3 Qu'en est-il de la pluviométrie? 33

3.2.2.4 Synthèse des ajustements linéaires 38

3.2.3 Modélisation non linéaire 39

4 Discussion - conclusion 43

Bibliographie 46

Glossaire, liste des abréviations et formulaire 48

Annexes i

I Répartition des sites de l'étude i

II 'Echelle Zadoks ii

III Extrait du jeu de données iii

IV Fonctions de Weibull : variations des paramètres de formes et d'échelle iv

V Algorithme de Backfitting v

VI Algorithme de Newton, annexe du cours de P.A. Cornillon vi

VII Déterminer la structure de variance-covariance d'un effet aléatoire : réponse de Dou-

glas Bates à Michael Kubovy sur le R-SIG vii

VIII Fonctions d'estimation des RMSEP pour des modèles de classe R nls ou mer . . . ix

IX Résultats détaillés de l'ACP sur variables pluviométriques x

X Catégorisation des groupes issues d'une classification ascendante hiérarchique . . . xi

Liste des figures

1.1 Les formes d'azote dans le sol 2

1.2 Le modèle VC 4

2.1 Courbe de dilution critique 12

2.2 Construction des jeux de données 13

3.1 Examen de cinétiques de croissances, de l'évolution des teneurs en azote et des quan-

tités d'azote absorbées 17
3.2 Relation entre les quantités d'azote apportées par l'engrais et les quantités d'azote

absorbées 18

3.3 'Evolution du CAU moyen en cours de culture de 6 essais 19

3.4 Distribution du CAU selon les stades de fertilisation et comparaison des CAU obtenus

pour chaque modalité 20

3.5 Qualitédes ajustements des modèles de croissance 21

3.6 Estimations des paramètres des cinétiques de croissance obtenus par régression non

linéaire 22

3.7 Ajustement de cinétiques de croissance 23

3.8 'Evolution de la VC 23

3.9 Teneurs en azote mesurées et INN calculés 24

3.10 Distribution des variables pluviométriques 25

3.11 Distribution des variables pluviométriques selon les stades d'apport 26

3.12 Exploration du jeu de données par AFM 28

3.13 Premier plan de l'espace décrit par la pluviométrie 29

3.14 Représentations du CAU en fonction des variables explicatives 30

3.15 Confrontation des données de l'étude au modèle VC 31

3.16 Effets marginaux du modèle 4 36

3.17 'Evolution du résidu du modèle 1 au modèle 4 et confrontation des estimations aux

données réelles 37

3.18 'Evolution du REQMP entre le modèle nul et le modèle 4 38

3.19 CAH sur les écarts au modèle général du modèle 4 selon les essais 39

3.20 Ajustement du modèle non linéaire 1 40

3.21 Ajustement du modèle non linéaire 2 41

Liste des tableaux

2.1 Variables étudiées du jeu de données 8

2.2 Description de l'échelle Zadoks 9

2.3 Modalités de fertilisation 9

2.4 Mesures réalisées 9

3.1 Estimation des coefficients liés aux modalités 20

3.2 Analyse des composantes de la variance de l'INN 25

3.3 Estimation des effets aléatoires du modèle 0 31

3.4 Test des effets du modèle 1 31

3.5 Estimation des effets aléatoires du modèle 1 32

3.6 Test des effets du modèle 2 32

3.7 Estimations des effets fixes du modèle 2 32

3.8 Estimation des effets aléatoires du modèle 2 32

3.9 Test des effets du modèle 3 33

3.10 Comparaison des modèles 2 et 3 33

3.11 Estimations des effets fixes du modèle 3 33

3.12 Estimation des effets aléatoires du modèle 3 34

3.13 Test des effets du modèle 4 34

3.14 Comparaison du modèle 4 au modèle 3 35

3.15 Estimations des effets fixes du modèle 4 35

3.16 Estimation des effets aléatoires du modèle 4 35

3.17 Estimation des paramètres du modèle non linéaire (VC) 41

3.18 Estimation des paramètres du modèle non linéaire (VC + pl) 41

3.19 Comparaison des modèles obtenus par régression non linéaire après ajout de la variable

pluviométrique 42

1

1 Introduction : la modélisation du CAU, une

réponse aux enjeux de la fertilisation azotée

La disponibilitéen azote minéral constitue un des principaux facteurs limitants de la production quantitative et qualitative des céréales à pailles. Pour des raisons économiques (tendance à la hausse du prix des engrais, notamment liée à l'évolution du prix des énergies fossiles) et réglementaires (durcissement des contraintes environnementales liéau transfert d'azote réactif hors de la parcelle agricole), il deviendra nécessaire à l'avenir de recourir à de moindres quantités d'engrais minéraux azotés de synthèse. Sous cette contrainte, le maintien des niveaux de productions actuels, voire leur augmentation, nécessitera de maintenir un état de nutrition azotée optimal des cultures. Cela pourra passer par le recours àd'autres sources d'azote (fixation symbiotique par l'emploi de légumineuses dans les systèmes de culture, recyclage de l'azote des produits résiduaires organiques, ...), et par l'amélioration significative de l'efficacitédes apports d'engrais azotés de synthèse (Cohan et al., 2011). C'est dans le contexte de cette seconde option que se situe le travail de ce stage.

1.1 Le CAU : indicateur de l'efficacitédes apports d'engrais azotés

L'azote contenu dans un engrais apportéàune culture n'est pas intégralement utilisépar cette dernière. Les micro-organismes du sol sont responsables de l'immobilisation d'une fraction de l'azote minéral par organisation. Des phénomènes physico-chimiques, liés aux caractéristiques du sol ou à l'activitédénitrifiante de certains processus, provoquent des pertes par voie gazeuse. Enfin, la lixiviation de l'azote nitrique entraîne des pertes en profondeur. Pour rendre compte de la part de l'azote de l'engrais valorisée par la culture, on quantifie l'accroissement de l'absorption d'azote permis

par l'apport, en comparaison àune situation non fertilisée. On traduit ainsi l'efficacitéde l'apport, ^àn'importe quel moment survenant après la date de fertilisation. Indépendamment de la dose d'azote

apportée, cette conception de l'efficacitéreprésente la coefficient directeur d'une relation linéaire de l'azote absorbéen fonction de l'azote apporté(équation 1.1). Cette relation est vraie tant que les quantités apportées demeurent inférieures àl'optimum technique de nutrition azotée de la culture. Au delà, la fraction d'azote absorbée diminue, l'efficacitémarginale de l'engrais décroît.

CAU = QND - QN0 D

ÄQN (1.1) ÄD

- CAU : Coefficient Apparent d'Utilisation

- QND : azote absorbépour une fertilisation de D kg N ha^-1 - QN0 : azote absorbéen l'absence de fertilisation

Le CAU se présente comme un indicateur de l'efficacitédes apports d'engrais azotés minéraux. En outre, le CAU est un coefficient apparent car il simplifie les processus complexes en jeu àl'échelle de la plante. A ~ ce titre, il est nécessaire de comprendre ce à quoi correspond un coefficient réel pour justifier l'emploi du terme simplificateur. Enfin, si le CAU quantifie l'azote absorbé, qu'advient-il de l'azote non-absorbé?

2

1.1.1 Un Coecient Apparent différent du Coecient Réel d'Utilisation

Le CAU représente l'utilisation apparente de l'engrais, supposant que les fournitures du sol soient indépendantes des apports. Le recours au marquage isotopique ¹⁵N permet de déterminer le coefficient réel d'utilisation (CRU) : l'azote de l'engrais réellement absorbépar le peuplement végétal. Pour une situation agronomique donnée, le CAU est supérieur ou égal au CRU, car en situation fertilisée

l'azote fourni par le sol peut être supérieur à QN0. Il existe donc une interaction entre l'azote apportéet l'azote du sol s'expliquant par des phénomènes de resubstitution de pools. En effet, une partie

des besoins en azote de la microflore du sol est assurée par l'azote de l'engrais alors que la biomasse microbienne restitue de l'azote minéral utilisépar la culture (Limaux, 1999; Recous et al., 1997). Finalement, en ne relevant pas les phénomènes de resubstitution, l'interprétation du CAU comporte moins de biais que celle du CRU (Recous et al., 1997). Le CAU est globalement proportionnel au CRU en étant plus facile à acquérir dans des dispositifs expérimentaux au champ.

1.1.2 Complément à 100 du CAU : les pertes d'azote issue de l'engrais

L'azote est au coeur d'une compétition entre la demande en azote du peuplement végétal, l'or-ganisation (Ix), les pertes par voie gazeuse (Gx) et par lixiviation (Lx) (fig. 1.1). Le complément ^à100 du CAU intègre ces pertes (équation 1.2).

(1-CAU)·D=ÄRf+Gx+Lx+Ix (1.2)

- ÄRf : la différence de stock d'azote minéral du sol après récolte par rapport àune culture non fertilisée.

Minéralisation

Ammonium

Dénitrification

N gazeux

Volatilisation

Absorption

N minéral

Nitrate

N plante

Nitrification

Lixiviation

Organisation

N organique

Figure 1.1 - Les formes d'azote dans le sol. L'azote minéral de la solution du sol se trouve sous deux formes : ammoniacale et nitrique. La ressource est partagée par différents processus entre le peuplement végétal (absorption), les micro-organismes du sol (organisation), les pertes par voies gazeuses (volatilisation et dénitrification) et la lixiviation (Recous et al., 1997).

Pour des doses d'azote inférieures ou égales à l'optimum technique de nutrition azotée de la culture, ÄRf et la lixiviation sont négligeables (Meynard et al., 1997). La somme des pertes gazeuses et d'organisation est proportionnelle àla dose d'engrais pour des apports sous-optimaux (équation 1.3).

(1-CAU)·D=Gx+Ix (1.3)

3

Les pertes I_x sont des pertes temporaires à l'échelle du système de culture (mais définitives ^àl'échelle de la phase d'absorption de la culture) puisque l'azote immobilisésous forme organique par

les microorganismes est minéraliséà la morts de ceux-ci (Recous et al., 1997) ou incorporéàl'humus (Nicolardot et al., 1997). Au contraire, les pertes G_x sont des pertes sèches : l'azote gazeux est définitivement perdu pour le système sol-plante. Les pertes par voie gazeuse concernent en premier lieu la volatilisation de l'ammoniac (COMIFER, 2012). Ainsi, toutes les formes d'engrais ne sont pas exposées au même risque : les engrais nitriques ne sont pas concernés, l'ammonitrate est associéàun risque faible tandis que les formes ammoniacales sont impactées par ces pertes (COMIFER, 2012).

1.2 Utilisation du CAU dans la détermination des doses d'engrais àapporter aux cultures

Aujourd'hui, le raisonnement de la fertilisation consiste àestimer les fournitures en éléments minéraux du sol afin de déterminer la dose d'engrais nécessaire et suffisante pour assurer une production visée. Cette dose, notée X, représente une estimation de l'optimum technique (COMIFER, 2012) 1. Sur cette base, des méthodes d'estimations de l'optimum technique de fertilisation par l'approche du bilan de masse de l'azote minéral du sol ont vu le jour. Hébert propose dès 1969 la méthode du bilan prévisionnel de l'azote minéral du sol, complétée par Rémy-Hébert en 1977. A ` l'échelle de la parcelle, cette méthode, la plus largement utilisée aujourd'hui, détermine les besoins du peuplement et propose l'inventaire des ressources disponibles et envisageables pendant la durée de prélèvement d'azote de la culture, expliquant le passage d'une situation initiale représentée par la quantitéd'azote minéral R (àl'ouverture du bilan) àune situation finale Rf (quantitéd'azote minéral du sol à la fermeture du bilan)(COMIFER, 2012). Le COMIFER (2012) propose en plus la prise en compte des pertes aux dépens de l'engrais, par voie gazeuse Gx et par organisation Ix, gràace au CAU, intégrateur des processus de compétition, améliorant ainsi la précision de la méthode. L'expression du bilan de masse devient l'équation 1.4, adaptée des écritures du COMIFER. Selon les contraintes locales, certains postes du modèle peuvent être difficiles à estimer, ils sont substitués par un terme général représentant les fournitures du sol P0, intégrédans l'équation d'efficience de l'azote (équation 1.5).

Pf = P + Ri + Mn + A + Nirr + X - CAU -- L -- Rf (1.4)

Pf = P0 + X - CAU (1.5)

- Pf - P : azote prélevépar le peuplement végétal entre l'ouverture et la fermeture du bilan;

- Rf - R : quantitéd'azote minérale entre l'ouverture et la fermeture du bilan;

- Mn : minéralisation de la matière organique (humus, résidus de cultures, produits résiduaires

organiques);

- A : apports atmosphériques;

- Nirr : azote apportépar l'eau d'irrigation;

- X : dose d'azote (optimum technique de fertilisation);

- L : lixiviation de l'azote.

1.3 Travaux de modélisation

1.3.1 La vitesse de croissance pour expliquer le CAU

Dans sa thèse François Limaux (1999) étudie les termes de l'équation d'efficience (équation 1.5). Il met en évidence un lien fort entre le CAU et la vitesse de croissance (VC) du blétendre d'hiver au moment de l'apport, pour des apports précoces. Cette relation se base sur des essais réalisés en

1. L'optimum technique n'est pas nécessairement un optimum économique. L'optimum économique dépend du rapport du prix de l'engrais au prix de vente de la culture. La dose optimale technique est la base de toute approche économique ultérieure (COMIFER, 2012).

Lorraine fournissant des valeurs de CAU et des suivis de croissance permettant d'estimer les VC. Il établit une relation linéaire entre le CAU et la VC, éprouvée sur un jeu de données de validation externe dont les résultats sont encourageants mais suggèrent des relations plus complexes (fig. 1.2, VC exprimée en g MS m^-2dj^-1 ; dj : degrés jours base 0°C).

Construction du modèle VC

CAU (%)

0 20 40 60 80 100 120

COUR94 JOV94

LIFF94 MAN93

MON90

l ROS93

0,0 0,2 0,4 0,6 0,8 1,0

VC en gr de MS m^-2dj^-1 Validation externe du modèle VC

0,0 0,2 0,4 0,6 0,8 1,0

CAU (%)

0 20 40 60 80 100 120

l BOU96
DIE96
LIX95

LIXN295

l MEL96 MIR95

MIRD196 MIRD296 SEI96

l SIE96 STA196 STA296

VC en gr de MS m^-2dj^-1

4

Figure 1.2 - Le modèle VC (Limaux, 1999). CAU = 38,24 + 73,924 · V C ; R² = 0,86; RMSEP = 13,6 pour la validation externe

L'utilisation de l'isotope ¹⁵N met en évidence la concurrence forte pour la ressource azotée entre les besoins de la culture, les pertes par voie gazeuse et l'organisation (Limaux et al., 1999; Recous,

1988). Il démontre que les quantités d'azote de l'engrais absorbées par la plante et retrouvées ^àla récolte sont déterminées très précocement (quelques jours àquelques semaines après l'apport)

(Limaux et al., 1999; Recous et al., 1997). Ceci suggère de s'intéresser aux conditions qui caractérisent le moment de l'apport pour comprendre l'absorption de l'azote. La VC traduirait justement la demande en azote de la culture au moment de l'apport et représente un facteur explicatif de la compétitivitéde la culture pour l'azote vis àvis des processus concurrents (Limaux et al., 1999).

1.3.2 Introduction de variables climatiques et de l'état de nutrition azotée

À plus large échelle, le modèle de Limaux (1999) (notémodèle VC par la suite) a étéconfrontéaux résultats acquis par 38 essais répartis en France conduits par Arvalis - Institut du Végétal couvrant une importante diversitéde conditions pédoclimatiques (Le Souder et al., 2007). Après avoir vérifiéla relation entre VC et CAU, de nouveaux facteurs ont étéintroduits. En effet, le modèle ne convient

pas pour des valeurs de CAU qui deviennent de plus en plus variables pour des apports de plus en plus tardifs. On suppose que les cultures sont exposées àdes conditions de pluviométrie plus variables qu'àla sortie de l'hiver et, étant donnée l'implication de l'eau dans les processus physiques de mise àdisposition de l'azote, on peut penser qu'une variable de régime hydrique influence le CAU (Bouthier, 1997). L'état de nutrition azotée de la culture a également étéintroduit dans un modèle, il est supposétraduire en partie la dynamique d'absorption de l'azote par la culture. Ces premiers résultats suggèrent l'existence d'un lien entre variables climatiques, VC, état de nutrition azotée et CAU. Cependant le travail dissocie les facteurs selon les stades, bien que les stades et VC soient liés, et les relations mises en évidence sont fragiles (variabilitérésiduelle forte).

5

1.4 Problématique de l'étude

La connaissance du raisonnement de la fertilisation amène àconsidérer le CAU comme un indicateur de l'efficacitédes apports d'engrais azotés. Il présente l'avantage d'être mesurable par des dispositifs expérimentaux au champ sans recourir à l'emploi de techniques lourdes de marquage de l'azote. ^{^}Etre capable de prévoir le CAU représenterait une avancée importante en matière de fertilisation puisqu'il s'agit d'une variable déterminante pour le calcul d'une dose prévisionnelle. Ainsi, la détermination des doses techniques optimales pourraient intégrer ce CAU pour rendre compte de manière plus fidèle des pertes d'azote de l'engrais. D'un point de vue pratique, ceci constitue une avancée pour le conseil en fertilisation puisqu'il serait possible de proposer des recommandations qui soient fonction d'un contexte agroclimatique variable pour que l'agriculteur retire la plus grande efficacitédes apports qu'il réalise (et diminuer les pertes qui sont tant une atteinte pour l'environ-nement qu'une pénalisation économique pour l'exploitation). Enfin, cette information, àpartir des facteurs explicatifs du CAU au moment de l'apport, pourrait être intégrée aux modèles dynamiques d'estimation de croissance du couvert auxquels ont recours un nombre croissant d'outils d'aide àla décision, proposés par Arvalis - Institut du Végétal, destinés à l'utilisateur final qu'est l'agriculteur.

Des travaux ont déjàétémenés à ce sujet. Ils supposent l'effet de trois principaux facteurs caractérisant le moment de l'apport : la vitesse de croissance, le régime hydrique et l'état de nutrition azotée de la culture. Fort de ces hypothèses il est important d'affiner les connaissances que l'on a du CAU.

Les objectifs sont donc :

i) d'élaborer un modèle explicatif du CAU d'un point de vue global sur l'ensemble du cycle de croissance du blétendre d'hiver;

ii) d'étudier le domaine de validitéde ce modèle.

6

7

2 Matériel et méthodes

Dans un premier temps il s'agit de construire le jeu de données qui permet d'obtenir les variables d'intérêt pouvant expliquer le CAU. Dans un second temps, il convient d'apprécier la qualitédes données àla fois à travers la détection des individus aberrants mais aussi en assurant que les données sont en adéquation avec les connaissances actuelles. Ensuite, l'exploration des données doit permettre

i) de dissocier l'information utile du bruit liéau hasard, ii) de juger des conséquences de la structure des données sur l'information qu'elle contient. Enfin, ayant construit le jeu de données, et compris sa structure on pourra valoriser l'information par la construction d'un modèle statistique explicatif du CAU.

2.1 Préparation et présentation des données

L'étude amène àconsidérer un certain nombre de variables. Tout d'abord certaines sont relatives ^àl'organisation du réseau d'essais. D'autres ont étéacquises lors des phases de terrain, elles constituent

l'ensemble des mesures. Enfin des variables s'obtiennent par le calcul pour répondre aux objectifs de modélisation (table 2.1).

2.1.1 Les essais : acquisition de données brutes

Les données disponibles sont pour partie les données utilisées par François Laurent et Christine Le Souder, Arvalis - Institut du Végétal, pour la validation du modèle VC (Le Souder et al., 2007). Elles se composent de 38 essais répartis sur l'ensemble du territoire français, menés en 2004, 2005 et 2006 (localisation : annexe I).

Principe : des micro-parcelles sont semées en blétendre d'hiver (Triticum aestivum L. supsp. aestivum) puis exposées àdes modalités de fertilisations variables. A ` partir d'un suivi de la croissance des cultures et de l'accumulation d'azote dans la biomasse aérienne, on obtient des valeurs de CAU et de VC (la désignation des stades auxquels interviennent ces mesures correspond à l'échelle Zadoks détaillée tableau 2.2, illustrée en annexe II et utilisée par la suite (Zadoks et al., 1974)). Les modalités se différencient par le stade d'apport et les quantités apportées exprimées en kg N ha^-1 (tab. 2.3). Les CAU ne peuvent être calculés qu'en référence àun témoin. Les modalités 2 à6 permettent de déterminer des CAU pour des apports précoces : au début du tallage (stade Z21), ou au stade épi à 1 cm (stade Z30), par rapport à une modaliténon fertilisée (modalité1). Les modalités 7 à10 correspondent àun fractionnement de la fertilisation ¹. Le premier apport équivaut à la modalité4, et le second àun apport aux stades Z32 ou Z39. Ce dispositif permet de déterminer le CAU d'un

apport de second rang spécifiquement en utilisant la modalité4 comme témoin des modalités 7 ^à10. Les modalités d'implantation caractérisent l'essai (densité, précocité, variété, ...), tout comme la nature de la matière fertilisante employée (ammonitrate ou solution azotée à39% en volume²).

1. Le dispositif ayant étéreconduit sur 3 ans, suite à un ajustement du protocole de 2004, la modalité10 n'a ^étéappliquée qu'àpartir de 2005

2. ammonitrate : 50% NH+ ₄ - 50%NO- 3 ; solution azotée à 39% : 50% urée - 25% NO- ₃ - 25% NH+ 4

Table 2.1 - Variables étudiées du jeu de données

Groupe Variable Notation Description

Année a A_a année de l'essai

Essai e Ee|a identifiant de l'essai, chaque essai est

propre à une année

Réseau d'essais

Bloc b Bb|e|a bloc, chaque bloc est propre àun essai

Modalitém m_m modalitéde fertilisation

Stade S_s stade de fertilisation auquel a lieu la fer-

ff matière fertilisante appliquée (ammoni-

trate ou solution à 39%)

tilisation, dépend de la modalitéFertilisant f

Densitéd densitéde semis

Mesures terrain

Matière sèche MS Matière Sèche mesurée ou calculée ^àpartir d'une hauteur de couvert, en t ·

ha^-1

Teneur en azote %N teneur en azote mesurée en laboratoire,

en % MS

Azote absorbéQN quantitéd'azote absorbée obtenue par

le produit de la teneur en azote par la matière sèche, en kg N ha^-1.

Var. à expliquer

CAU y CAU à Z92, en référence à un témoin

VC vc vitesse de croissance instantanée dé-

Var. explicatives

terminée au moment de l'apport en g MS m^-2dj^-1 (dj : degrés jours base 0°C)

INN inn Indice de Nutrition Azotée déterminéau

moment de l'apport

Cumul de pluies pxj cumul de pluies pendant x jours après

apport en mm

Cumul de pluies efficaces pexj cumul de pluies efficaces pendant x

jours après apport en mm

8

2 à 6 mesures sont réalisées par microparcelle du début du tallage (stade Z21) à la maturité(stade Z92) selon les modalités (tab. 2.4) puisque les mesures des témoins sont extrapolées aux modalités testées tant que celles-ci n'ont pas étéfertilisées. Notons que certaines mesures sont estimées par la hauteur du couvert, àpartir de l'étalonnage d'une relation linéaire par essai entre la hauteur du couvert et la biomasse produite pour des stades antérieurs à la mi-floraison (stade Z65). L'ensemble du dispositif est répétésur 3 ou 4 blocs selon les essais.

2.1.2 Calculs des variables d'intérêt

Les hypothèses de travail introduisent de nouvelles variables calculées au moment de l'apport pour tenter d'expliquer le CAU : vitesse de croissance, état de nutrition azotée et variables pluviométriques.

2.1.2.1 Détermination du CAU

Le CAU peut être calculéàtout moment après l'apport d'engrais, dès que des mesures de biomasse et de teneur en azote sont disponibles. Le CAU déterminéàla récolte rend compte de l'efficacitéfinale de l'apport, c'est donc le CAU à Z92 qui est modélisédans cette étude. Les mesures de biomasse et de teneur en azote àla récolte déterminent les quantités d'azote absorbées (QN). Le CAU est

Table 2.2 - Description de l'échelle Zadoks, stades rencontrés dans l'étude (Zadoks et al., 1974)

Stade Zadoks Description du stade

Z21 début du tallage

Z30 épi à1 cm

Z32 deuxième noeud visible

Z39 apparition de la ligule de la dernière feuille

Z65 demi-floraison

Z92 maturitédu grain

Table 2.3 - Modalités de fertilisation, X est l'optimum technique calculépar la méthode du bilan, fertilisation exprimée en kg N ha^-1

ModalitéFertilisation par stade Témoin

	Z21	Z30	Z32	Z39
1
2	40				1
3	80				1
4		X-120			1
5		X-80			1
6		X-40			1
7		X-120	40		4
8		X-120	80		4
9		X-120		40	4
10		X-120		80	4

Table 2.4 - Mesures réalisées : B (mesure de biomasse), N(mesure de teneur en azote), H(mesure de hauteur du couvert)

		Stades de mesures
Traitement	Z21	Z30	Z32	Z39	Z65	Z92
1	BN	BNH	NH	BNH	BN	BN
2		HN	HN	HN		BN
3		BNH	HN	HN		BN
4			BNH	BNH	BN	BN
5						BN
6			BNH	HN	BN	BN
7						BN
8				BNH	BN	BN
9						BN
10					BN	BN

9

10

calculépour chaque bloc, de chaque modalitéde chaque essai. En référence àla définition du CAU, et en intégrant le cas du calcul de CAU des apports de rang 2 (T7 à T10), les CAU sont calculés selon l'expression 2.1.

CAU = QN_m - QNt (2.1)

D_m - Dt

Où:

- QN_m - QNt : azote absorbéen plus par une modalitém par rapport au témoin ;

- D_m - Dt : différence de fertilisation entre la modalitém et son témoin. Pour les modalités

composées d'un unique apport, le CAU est calculéen référence au témoin non fertilisé(modalité1), donc Dt=1 = 0 <=> D_m - Dt=1 = D_m. En revanche, pour les modalités composées de deux apports successifs, le calcul du CAU spécifique au deuxième apport est réaliséen référence à la modalitéayant reçu un premier apport identique. Dans l'étude, ce témoin est la modalité4,

donc Dt=4 = D - 120.

On dispose d'autant de résultats de CAU que de mesures MS et %N, soit une mesure par bloc et par modalité.

2.1.2.2 Estimation de la vitesse de croissance

La vitesse de croissance (VC) correspond au gain de biomasse par unitéde temps, soit la dérivée de la cinétique de croissance (dMS/dt, le temps t expriméen degrés jours dj de base 0°C). Pour obtenir les VC, les cinétiques de croissance correspondantes àchaque modalitéde chaque essai sont ajustées.

Dans son travail, François Limaux considère la cinétique de croissance de la biomasse comme une fonction exponentielle, et approxime la VC par l'équation 2.2 (Limaux, 1999).

V C1 = ln(MS2) - ln(MS1) T2 - T1

· MS1 · 10^-2 (2.2)

- V C1 : VC à l'instant 1 en g MS · 10^-2 · m^-2dj^-1 ;

- MS2/MS1 : la biomasse en matière sèche au prélèvement 2 / 1 en g MS · m^-2 ;

- T2 - T1 : la somme de degrés jours en base 0 cumulée entre le prélèvement 1 et 2.

François Laurent adopte une approche logistique, avec des ajustements de cinétiques de MS de la forme de l'équation 2.3 permettant l'expression paramétrique de la VC (équation 2.4) (Le Souder et al., 2007).

K

MS(t) = (2.3)

-

S

K

M

0 ~

-at

MS0 exp

1 +

K - MS0 1

V C(t) = K · · a exp^-at ·

(1 + K

2 (2.4)

MS0 - MS0 exp-at

MS0· )

Cependant, d'un point de vue agronomique, cette approche est discutable car MS0 est nécessairement nulle puisque la biomasse aérienne au semis est nulle. L'utilisation des fonctions de Weibull permet de pallier ce point. Elles peuvent être présentées comme une généralisation du modèle exponentiel proposédans certains ajustements de modèles de croissances biologiques (Jolivet et al., 1982). La cinétique est obtenue par l'équation 2.5, dont la dérivée fournit l'expression de la VC (équation 2.6).

1 - e-(t/ë)â~

MS(t) = K (2.5)

VC(t) = MS(t)^' = K · _ëâ^â·tâ^-1 · exp^-x/^ëâ (2.6)

11

K correspond àla limite du milieu, À est relatif à l'échelle de temps nécessaire pour atteindre K (paramètre d'échelle) et fi traduit le taux de croissance (paramètre de forme) (annexe IV).

Déterminer les paramètres des cinétiques impose un ajustement non linéaire de la fonction 2.7. Les estimations sont obtenues par la méthode de minimisation des moindres carrés (MMC), l'algorithme Gauss-Newton converge vers les estimations de K, fi et À (annexe VI). Toutefois, il est nécessaire de fournir des valeurs initiales des paramètres obtenus par régression linéaire de l'expression 2.8.

( 1 - e-(t/ë)â)

MSt = K + st (2.7)

s ~ N (0, ó) s ~ N (0, ó)

( ( ln - ln 1

~~ MS = fi ln t - fi ln À + st (2.8) K t

Concrètement l'obtention des paramètres des fonctions de Weibull suit 4 étapes :

1. rassemblement des données brutes de cinétiques;

2. correction ou suppression des données aberrantes;

3. extrapolation des données des témoins aux modalités avant apport;

4. ajustement des cinétiques et vérifications.

Par la suite, disposant des paramètres des modèles de croissance et des cumuls de degrés jours, il est possible d'estimer la VC pour tout t positif. La VC calculée dépend de la date d'apport, elle est constante pour les modalités d'un essai qui partagent le même stade de fertilisation.

2.1.2.3 Comment estimer l'état de nutrition azotéde la culture?

La teneur en azote de la biomasse évolue au cours de la culture, elle peut être perçue comme une dilution de l'azote dans la biomasse et représentée par une courbe qui relie la teneur en azote à la matière sèche. Il en existe une infinitéqui varient avec la fertilisation appliquée. L'une d'entre elles est dite »critique» et marque le passage entre deux situations :

- au dessous de la courbe, le peuplement est en situation oùl'azote est limitant (carence);

- au dessus, l'azote n'est plus limitant (consommation de luxe).

La frontière entre ces deux situations est objectivement repérable par des chiffres techniquement satisfaisants qui peuvent servir de référence. D'oùla construction en 1989 par Lemaire et son équipe d'un indicateur de diagnostic de situation d'une culture vis à vis de l'azote : l'indice de nutrition azotée (INN, équation 2.9).

N%

INN = (2.9)
N%_c

La détermination des valeurs de teneurs en azote critiques dépend de la matière sèche : N_c = á · MSâ, á et fi étant des valeurs fixées par type de culture (fig. 2.1) (Lemaire et al., 1989). L'INN est utilisépour quantifier l'état de nutrition azoté. Toutefois, les mesures de teneurs en azote des modalités n'intervenant qu'après la différenciation de fertilisation azotée par rapport aux témoins (au stade suivant, cf. tab.2.4 et 2.3), le calcul de l'INN est basésur les mesures de matière sèche des témoins à la date de l'apport. En conséquence pour un même stade d'apport, l'INN pour un bloc est constant pour les modalités partageant le même témoin.

2.1.2.4 Relevédes variables pluviométriques

Le choix des variables climatiques repose sur les résultats de travaux antérieurs réalisés sur la station Arvalis - Institut du Végétal du Magneraud (Bouthier, 1997). Ils suggèrent un effet déterminant de la pluviométrie dans les 10 à15 jours après l'apport, àtravers une mise en solution puis mise

12

Teneur en azote critique du blé tendre

Teneur en azote

0 1 2 3 4 5

1,56 t/ha

4,4%

%N = 5,35MS(-0,442) Carence en azote

0 5 10 15

MS (t/ha)

Figure 2.1 - Courbe de dilution critique %N_c = 5.35 · MS-0.442 avec %N_c maximum à 4,4% pour une MS de 1,56 t · ha^-1, pour des biomasses mesurées entre Z10 et Z65 (Justes et al., 1994). Au dessus de la courbe le peuplement est en situation de consommation de luxe, en dessous en situation de carence pour la production de biomasse

à disposition racinaire de l'azote de l'engrais. Pour tenir compte du bilan hydrique, le champ des variables étudiées est élargi àla pluviométrie efficace : la différence entre la pluviométrie journalière et l'évapotranspiration (équation 2.10). Huit variables sont calculées : les cumuls de pluies sur 5, 10, 15 ou 20 jours après l'apport et les pluies efficaces exprimées en mm sur les mêmes périodes de calcul. Le réseau de stations et les bases de données de Arvalis - Institut du Végétal permettent de disposer d'informations météorologiques complètes de manière localisée. Les données sont relatives à un site, en référence à une date, donc les données pluviométriques sont constantes pour un site et une date d'apport.

Pe = P - ETP (2.10)

- Pe : pluviométrie efficace (mm);

- P : pluviométrie (mm);

- ETP : évapotranspiration potentielle

2.1.3 Élaboration du jeu de données pour l'étude du CAU

Les données initiales sont contenues dans une base de données Arvalis - Institut du Végétal. On édite une table par essai qui croise des parcelles en lignes et des colonnes de mesures aux stades auxquels elles ont étéréalisées. Ce premier format de données est rendu nécessaire pour l'exploitation des données pour d'autres travaux au sein d'Arvalis - Institut du Végétal. A ` partir des 38 tables on en construit une commune aux essais oùune ligne correspond àl'ensemble des mesures d'une parcelle d'un essai à une date donnée à laquelle on intègre l'ensemble des variables calculées. Ce jeu de données est le jeu de données brutes, à partir duquel on peut suivre l'évolution des variables (cinétiques). Enfin, on souhaite expliquer le CAU à la récolte, on transforme donc le jeu de données pour qu'àun CAU correspond l'ensemble des valeurs des variables explicatives déterminées au moment de l'apport (fig. 2.2, extrait du jeu de données en annexe III).

Base de données
Arvalis

Institut du végétal

Essai 38

Essai 37

Parcelle x mesure par stade

Parcelle x mesure par stade

Parcelle x mesure par stade

Essai

Parcelle x mesure par stade

Essai 1

Parcelle x mesure par stade

Essai 2

Mesure
(Essai bloc
date organe)

X

Variables
(MS - %N -
récolte)

CAU

(Essai - parcelle - rang apport)

X

Variables
(caractéristiques
essai f modalité,

VCi, INN,

pluviométrie)

Base de données

Format destiné à Données

Données de l'étude

I Arvalis - Institut II brutes III

du végétal (cinétiques)

13

Figure 2.2 - Construction des jeux de données

2.2 Exploration et compréhension du jeu de données

Les données disponibles vérifient-elles les connaissances acquises au sujet du CAU? Quelles méthodes statistiques déployer pour extraire l'information puis construire un modèle explicatif du CAU? La VC, les variables pluviométriques, l'INN sont des effets fixes qu'on souhaite quantifier. De la même manière on peut être amenéàconsidérer des variables liées àl'implantation de la culture, ou d'autres variables relatives àla fertilisation qui pourraient expliquer le CAU (par exemple la forme du

fertilisant employé). En revanche, l'année, le site et le bloc sont des effets aléatoires et les données ^àl'intérieur d'un groupe sont corrélées, ce qui ne sera pas sans impact dans la construction de modèles.

Notons que ces effets sont hiérarchisés : chaque année a ses essais et chaque essai a ses blocs (tab. 2.1, page 8).

2.2.1 Modèles généraux d'analyses statistiques

Outre les vérifications des hypothèses biologiques de départ, on tente d'expliquer les relations entre variables. La compréhension du jeu de données s'acquiert progressivement par des analyses bivariées qui permettent de mettre en lumière les relations 2 à 2 des variables (notamment entre CAU et variables explicatives), puis par des analyses multivariées pour estimer les effets et interactions. Les facteurs explicatifs sont pour une première approche supposés linéairement reliés au CAU comme

proposépar François Limaux. On s'oriente donc vers des modèles d'analyse linéaire, orientation ^àconfirmer par des représentations graphiques et des analyses des distributions des résidus. Ceci inclut des modèles d'analyses de variances ou de régressions linéaires (équation 2.11) .

Y = Xâ + E (2.11)

- Y : vecteur réponse;

- X : matrice des prédicteurs;

- â : vecteur des p + 1 paramètres;

- E : vecteur des résidus;

- E(E) = 0 et V(E) = ó².

Les mesures faites sur un même essai partagent le même effet aléatoire, elles sont donc corrélées. Cette corrélation peut être induite par exemple par la nature complexe du sol fortement variable

14

d'un essai àl'autre. Pour les prendre en compte, on a recours àl'utilisation de modèles mixtes. De fait, chaque analyse inclut les effets aléatoires année, essai et bloc. L'estimation est réalisée par maximisation de la vraisemblance (ML) ou de la vraisemblance restreinte (REML). ML est utilisée lorsqu'on souhaite comparer des modèles emboîtés avec des structures d'effets fixes différentes. REML propose une correction de la distribution de la fonction de vraisemblance pour obtenir de meilleures estimations, moins sensibles aux valeurs extrêmes (Crawley, 2007). L'écriture matricielle des modèles d'analyses étudiés devient l'équation 2.12.

y = Xfi + Zb + E (2.12)

- E Jf(0, a²I)

- b ~ Jf(0,W)

- E I b

y est le vecteur réponse de n dimensions, X la matrice du modèle de dimensions nxp pour le vecteur

des effets fixes fi de p dimensions. Z est la matrice n x q pour le vecteur des effets aléatoires b de

dimension q (Bates and DebRoy, 2004). Considérer des effets aléatoires implique 5 hypothèses :

- les erreurs intra-groupes sont indépendantes, d'espérance nulle et de variance a² ;

- les erreurs intra-groupes sont indépendantes des effets aléatoires;

- les effets aléatoires sont distribués selon une loi normale de moyenne nulle et de matrice de

covariance W;

- les effets aléatoires sont indépendants dans les différents groupes;

- la matrice de covariance ne dépend pas du groupe.

Pour vérifier ces hypothèses, différentes méthodes peuvent être déployées, basées sur l'observation

du résidu, des valeurs ajustées et des estimations des effets aléatoires. Sur la base des estimations

des effets aléatoires, on quantifie la part de variabilitéimputable àun facteur à travers une analyse

des composantes de la variance (Crawley, 2007).

2.3 Élaboration d'un modèle explicatif du CAU

Les objectifs de modélisation sont de deux ordres. Le premier est cognitif, on souhaite comprendre la nature des relations : quelles sont les variables explicatives du CAU? Les hypothèses de travail posées par François Limaux et François Laurent se vérifient-elles? Le second est prédictif. Avec la connaissance que l'on a de la nature des relations, et si les hypothèses de travail sont vérifiées, peut-on prédire le niveau de CAU d'un apport? Un objectif poséen introduction est de produire un modèle pour l'ensemble du cycle de la culture. A ` travers l'étude des trois variables calculées (VC puis INN puis une variable issue des groupes de mesures pluviométriques) on tente d'expliquer le CAU sur l'ensemble du cycle.

2.3.1 Analyse factorielle

Dans un premier temps il convient d'obtenir une représentation synthétique des données. Disposant de plusieurs variables quantitatives on opte pour un outil d'analyse factorielle. Néanmoins, on souhaite équilibrer le poids des variables dans le jeu de données, notamment celui des huit variables pluviométriques probablement fortement corrélées entre elles. L'Analyse Factorielle Multiple (AFM) permet de représenter l'espace des variables prenant en compte les groupes de variables pluviométriques, la VC et l'INN formant chacun un groupe. Le CAU, variable à expliquer, est projetédans cet espace en illustratif ainsi que le stade de fertilisation pour observer la liaison linéaire des variables au

temps. L'individu projetécorrespond àune microparcelle d'un essai appliquéune année, exposée ^àune modalitéde fertilisation, pour laquelle il a étépossible de calculer l'efficacitéde la fertilisation.

15

2.3.2 Approche linéaire de la sélection de modèles

Si rien ne contredit les hypothèses de linéarité(sur représentation graphique) une approche linéaire des effets est adoptée, en tenant compte des interactions possibles (ce qui peut introduire des réponses non linéaires). L'élaboration d'un modèle linéaire est le choix qu'a réaliséFrançois Limaux, et présente une simplification intéressante pour appréhender les relations existantes.

La sélection du modèle est ascendante. A ` partir du modèle nul on apporte de nouvelles variables pour expliquer le CAU, justifiées a priori par des représentations graphiques des données. L'ordre dans lequel les variables sont ajoutées est dictépar les connaissances que l'on a des relations entre variables et CAU. On commence par étudier la relation qui lie le CAU à la VC, en comparant nos résultats obtenus à ceux de François Limaux puis on ajoute ensuite l'effet du fertilisant, l'INN et enfin la pluviométrie. Cette démarche se justifie par la volontéd'apprécier le progrès qu'apporte chacune des hypothèses de travail.

On sait que les effets aléatoires induisent une structure particulière des données, on veut donc les prendre en compte pour améliorer les estimations des différents modèles (cf paragraphe précédent). Une couche de complexitésupplémentaire est donc introduite par la prise en compte des effets aléatoires. En effet, les méthodes d'ajustement des modèles mixtes demandent d'avoir des hypothèses sur la structure de covariance mais nous ne disposons pas d'information spécifique permettant de nous orienter. On simplifie le problème en ne considérant que deux types de structures de covariances :

- les effets aléatoires sont indépendants (structure de covariance diagonale);

- les effets aléatoires ne sont pas indépendants, il faut estimer les corrélations entre effets aléatoires.

(Annexe VII : choix d'une structure de variance-covariance, D.Bates)

A ` chaque niveau du modèle, àchaque ajout de variable, on détermine dans un premier temps la structure des effets aléatoires, puis la structure des effets fixes (quels effets, quelles interactions?). Les effets aléatoires sont sélectionnés sur la base de la probabilitécritique associée à un test de x2 pour des modèles ajustés par maximisation de la vraisemblance restreinte (REML). La combinaison des effets fixes de chaque modèle testéest sélectionnée sur la base de la probabilitécritique d'un test F (approximation des degrés de libertéde Sattertwhaite) (Kuznetsova and Brockhoff, 2012). La qualitéd'ajustement de chacun des modèles est appréciée par le BIC (équation 2.13), le BIC permettant de pénaliser la variabilitéexpliquée par le nombre de paramètres ajoutés dans le modèle. On compare également les modèles et sous modèles, de structure aléatoire identique, par un test de rapport de vraisemblance. On construit la statistique de test qui suit une loi de x² sous H0 (H0 : la vraisemblance du modèle est égale àla vraisemblance du sous modèle V1 = V2), elle permet de juger de l'amélioration apportée par le modèle en comparaison àun sous modèle (équation 2.14). Cependant, pour comparer des modèles emboîtés avec des structures d'effets fixes différents, il est recommandéd'utiliser un ajustement de modèle maximisant la vraisemblance (ML) et non plus la vraisemblance restreinte (REML) (Crawley, 2007). Tests F et tests du x² fournissent des probabilités critiques considérées significatives au seuil á = 5%.

BIC= -2-lnV+K-lnn (2.13)

- V : vraisemblance;

- K : nombre de paramètres indépendants; - n : nombre d'individus.

-2 [ln V2 - ln V1] H9 x2 (2.14)

ddl

- V1,V2 : vraisemblance respective des modèles 1 et 2;

- ddl : degrés de liberté.

La normalitéet l'homogénéitédes variances de chaque modèle sont vérifiées par une représentation graphique du résidu contre les valeurs ajustées, de la distribution du résidu, et de la confrontation des valeurs observées contre les valeurs estimées.

16

2.3.3 Introduction de relations non linéaires

Une approche fonctionnelle envisageant des effets non linéaires peut apporter des améliorations aux modèles. Le choix des formes des fonctions se base sur des représentations graphiques et, autant que possible, sur des hypothèses biologiques. Comme pour les ajustements de cinétiques, les paramètres des fonctions non linéaires sont ajustées par MMC. L'algorithme de Gauss-Newton converge vers les estimations des différents paramètres et demande des paramètres initiaux. Lorsque plusieurs fonctions sont »additionnées» pour fournir un modèle, les estimations initiales sont fournies par une procédure de back fitting (annexe V). BIC et rapports de vraisemblance permettent d'orienter la construction du modèle pour expliquer au mieux le CAU.

2.3.4 Validation du modèle

Les résultats de modélisation sont appréciés par une procédure de validation pour mesurer la précision de la prédiction. On opère par validation croisée, de type leave-one-out (nombre de données faibles), pour déterminer une Racine de l''Ecart Quadratique Moyen de Prédiction (REQMP, équation 2.15). Le modèle est ajustésur n - 1 (équation 2.15 : -j) observations puis confrontéà la n-ième observation, l'opération est répétée n fois. Pour fixer les idées, une REQMP de 20 constitue a minima le niveau que l'on souhaite atteindre pour l'estimation du CAU.

1 n

àó2 0 =

_Xn i=1

tu u v

[ _]2

Yi - ^àY-i (2.15)

2.4 Moyens informatiques

Afin de prévoir les retours possibles aux données initiales, le travail de formatage des jeux de données est automatisé. L'agrégation des données brutes issues des 38 tables individuelles est assez aisée bien que la nature des lignes et colonnes change. En revanche l'automatisation des calculs de variables caractérisant l'apport est plus compliqué. Il faut prendre en compte des témoins variables des stades variables, et des nombres de mesures variables d'un essai à l'autre. Toutes les données ont étéanalysées en utilisant R (R Core Team, 2012) et plus spécifiquement les paquets :

- doBy (Højsgaard et al., 2012)

- FactoMineR (Husson et al., 2012)

- lme4 (Bates et al., 2011)

- MixMod (Kuznetsova and Brockhoff, 2012)

- MuMIn (Barto'n, 2012)

Les calculs de REQMP (leave-one-out) ont donnélieu àla programmation de deux fonctions adaptées aux modèles mixtes, ou aux modèles non linéaires (annexe VIII). Les ajustements non linéaires faisant intervenir plusieurs fonctions sont initialisés par back-fitting (annexe V) pour déterminer un jeu de paramètres qui atteigne un minimum total de la grandeur estimée par l'algorithme de Gauss-Newton.

3 Résultats

3.1 Préparation des données

3.1.1 Examen des données

Les tables des données brutes et des données étudiées sont éditées. Les données brutes rassemblent l'ensemble de toutes les mesures réalisées sur les parcelles. Chacune des 9643 lignes de ce jeu de données correspond à l'ensemble des mesures réalisées sur un organe (PA, grain, pailles) à un stade donné. Les représentations graphiques permettent d'apprécier la qualitédes données et détecter les anomalies. Par exemple, l'essai qui a étémenéà Labergement (département 21) en 2005 (figure 3.1) montre des mesures de MS élevées pour le bloc 1, ce qui se ressent en cours de culture sur l'azote absorbé. A contrario, la dernière mesure de teneur en azote du graphique (teneur des parties aériennes àZ65, les données de Z92 dissociant l'azote des pailles de l'azote du grain ne figurent pas), inférieure à1 est une mesure particulièrement faible. En conséquence, les CAU obtenus durant la culture à Labergement en 2005 risquent d'être très variables d'un bloc à l'autre. L'expertise démontre que ces valeurs restent tout de même dans un domaine de validitéagronomique : ces données sont conservées. Cet exemple est représentatif du point de vue de la composition des données : les MS sont disponibles pour chaque bloc alors que bien souvent la mesure de %N est unique pour un stade et extrapolée à chaque bloc. À partir des %N et MS, on détermine les quantités d'azote absorbées QN par bloc.

MS (t/ha)

0 2 4 6 8

l

l bloc 1 bloc 2 bloc 3 bloc 4 moyenne +/ - s

500 1500 2500

Degrés jours

labergement 2005

600 1000 1400

Teneur en azote (%MS)

1 2 3 4

Azote absorbé (KgN/ha)

20 40 60

Degrés jours

500 1500 2500

l

Degrés jours

17

Figure 3.1 - Examen de cinétiques de croissances, de l'évolution des teneurs en azote et des quantités d'azote absorbées. Exemple de la modalité1, de l'essai de Labergement (21), conduit en 2005

Globalement, parmi les erreurs relevées notons :

- 13 données de matières sèches sur tous les cycles (valeurs hors normes); - 141 données relatives àl'azote (teneurs et azote absorbé), dont :

- 27 données aberrantes sans explication (erreurs de saisie par exemple);

18

- 22 mesures de QN antérieures à la date de l'apport;

- 92 mesures sur des modalités présentant un écart important au protocole.

En prenant en compte les données aberrantes déterminées graphiquement et confirmées par un retour aux données brutes, nous éliminons 149 lignes soit 1,5% des données brutes. Globalement, les données sont de bonne qualitéet correspondent à ce qui peut normalement être obtenu en pareilles conditions.

3.1.2 La variable à expliquer, le CAU calculéà la récolte

Dans un premier temps on observe la relation entre azote apportéet azote absorbéà partir de l'ensemble des mesures d'absorption d'azote réalisées dans les essais. Le coefficient de corrélation linéaire entre les deux grandeurs atteint 0,79, ce qui montre l'intensitéforte de la liaison. Une représentation graphique permet de confirmer les hypothèses de linéaritéposées en introduction (fig. 3.2), le CAU correspondant àla pente de la relation pour les données d'un essai et les modalités d'un stade d'apport.

Azote absorbé à la récolte en fonction de l'azote apporté

0 50 100 150 200 250 300 350

Azote absorbé (kg N /ha)

250

200

150

100

50

0

l

l

l

r = (0,79)

l

l

l

l

l

l

modalités

1 0

2 40Z21

3 80Z21

4 (X-120)Z30

5 (X-80)Z30

6 (X-40)Z30

7 (X-120)Z30+40Z32

8 (X-120)Z30+80Z32

9 (X-120)Z30+40Z39

10 (X-120)Z30+80Z39

azote apporté (kg N /ha)

Figure 3.2 - Relation entre les quantités d'azote apportées par l'engrais et les quantités d'azote absorbées

Le CAU est calculépour chaque bloc, de chaque modalité, de chaque essai, suite àà un apport d'engrais. Sur l'ensemble des valeurs de CAU obtenues durant le cycle de culture, certaines sont beaucoup trop fortes ou trop faibles pour être réalistes, on borne les CAU entre 0% et 150%, éliminant ainsi 71 données, laissant 2050 calculs de CAU. L'évolution du CAU en fonction du temps depuis le moment de l'apport peut être représenté. La figure 3.3 permet d'apprécier cette évolution en se basant sur quelques essais représentatifs. On remarque que le CAU évolue rapidement, ce qui appuie l'intérêt d'utiliser des variables relatives au moment de l'apport. Le CAU a étésystématiquement mesuréà la récolte, on se base donc dorénavant sur le CAU Z92 : on veut prévoir l'efficacitéde

Évolution du CAU de 6 essais

0 500 1000 1500 2000

21							22				34
C C
									C
											C		C
				6					8				18
											C
													C
CAU	1,2 1,0 0,8 0,6 0,4 0,2 0,0

1,2

1,0

0,8

Modalités

C 2

3

4

5

6

7

8

9

10

0,6

0,4

0,2

0,0

19

0 500 1000 1500 2000 0 500 1000 1500 2000

Cumul de températures après apport (dj)

Figure 3.3 - Évolution du CAU moyen en cours de culture de 6 essais

l'engrais au terme de la période d'absorption de la culture.

La distribution des 765 valeurs de CAU déterminés à la récolte évolue selon les stades d'apport (figure 3.4) : plus l'apport est tardif, plus la distribution des valeurs semble variable. En considérant les connaissances actuelles du CAU on veut i) rendre compte des variations entre CAU obtenus pour des stades d'apports différents, ii) vérifier que le CAU est constant pour les apports d'un même stade. Une analyse de variances est réalisée sur l'ensemble des CAU mesurés àZ92. Elle tend à expliquer le CAU par les modalités de fertilisation. Les étapes de l'analyse amènent à considérer l'effet aléatoire de l'essai et son interaction avec la modalité(équation 3.1). Le test de l'effet du fertilisant fournit une probabilitécritique 0,008, au seuil de risque : á = 5% on rejette l'hypothèse H0 ?m m_m = 0. Les tests des coefficients (avec pour contrainte >m2 = 0) mettent en évidence une différence

significative des apports àZ30 ou àZ39, par rapport aux apports à Z21 (représentés par la modalité2) : des apports à des stades différents entraînent des variations du CAU (tab 3.1). Ensuite, au regard

de la représentation graphique, les différences entre modalités 7 et 8 (apport Z32) d'une part, 9 et 10 (apport Z39) d'autre part, même si elles ne sont pas significatives, ne semblent pas négligeables, les CAU entre modalités fertilisées au même stade semblent variables. Or, l'apport d'azote étant au maximum inférieur de 40 kg N ha^-1 àla dose optimale X, on peut aisément supposer que les doses apportées aient toujours étésous optimales : en conséquence les CAU étaient attendus constants. Il faudra donc chercher d'autres explications, notamment du côtéde la pluviométrie ou de l'INN. Mais attention, bien que l'on perçoive des différences entre modalités d'un même stade d'apport on ne pourra pas les expliquer. En effet, les variables dont nous disposons ne permettent pas de différencier les modalités d'un même stade, puisque à un stade donnénous disposons :

- de VC relatives àun cumul de degrés jours (équivalentes pour des apports réalisés le même jour);

- d'INN relatifs àune mesure du témoin commun aux modalités d'un même stade (deux modalités partageant le même témoin sont décrites par les mêmes valeurs d'INN);

- de pluviométries calculées pour une date d'apport (équivalentes pour un apport le même jour).

Un modèle explicatif du CAU ne discriminera pas les modalités d'un même stade avec le jeu de données dont nous disposons. Autrement dit, la variabilitépour un même stade d'apport ne pourra être expliquée. D'ailleurs, cette variabilitéest importante en ordre de grandeur puisque pour un essai,

20

les CAU mesurés à la récolte, et pour les modalités qui partagent le même stade d'apport, l'écart type moyen est de 14,9%.

yiem = u + m_m + E_e + MEme + åiem (3.1)

- E_e iid, : E_e ~ .V(0,óE);

- å iid, : å .V(0, ó);

- MEme iid, : MEme .V(0, óME);

- E_e, MEme ^et åmei indépendants deux à deux.

Distribution du CAU selon le stade d'application

Moyennes aujustées de CAU en fonction de la modalité de fertilisation

Densité

0,0 0,5 1,0 1,5 2,0

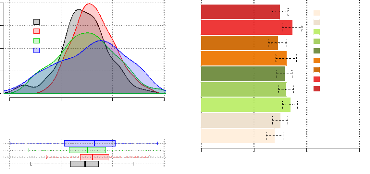
0,0 0,5 1,0 1,5

Stade d'application

Z21 Z30 Z32 Z39

l

CAU

10

4

2

9

8

7

6

5

3

0,0 0,5 1,0 1,5

CAU

40Z21

80Z21 (X-120)Z30 (X-80)Z30 (X-40)Z30 (X-120)Z30+ (X-120)Z30+ (X-120)Z30+ (X-120)Z30+

Figure 3.4 - Distribution du CAU selon les stades de fertilisation et comparaison des CAU obtenus pour chaque modalité(moyennes ajustées des CAU par modalitéde fertilisation et leur intervalle de confiance)

Table 3.1 - Estimation des coefficients liés aux modalités

	Estimation	ó	test t
u	0,70	0,04	17,04
Modalité3	0,05	0,04	1,22
Modalité4	0,15	0,04	3,42
Modalité5	0,11	0,04	2,55
Modalité6	0,09	0,04	2,18
Modalité7	0,11	0,05	2,06
Modalité8	0,03	0,05	0,56
Modalité9	0,16	0,05	3,17
Modalité10	0,05	0,05	1,03

fréquence

0 10 30 50

3.1.3 Les variables explicatives 3.1.3.1 La vitesse de croissance

Les calculs de cinétiques ont étéautomatisés. Pour chaque modalitéde chaque essai on dispose d'une expression de la cinétique de croissance à trois paramètres (K, fi et À, équation 2.5, p. 10). De manière générale, les ajustements obtenus sont de bonne qualité(fig. 3.5). En effet, le biais est environ nul et la Racine de l''Ecart Quadratique Moyen (REQM) est en moyenne de 0,40 t/ha (en sachant que àla récolte, la biomasse maximale mesurée était de : 14 t/ha). Cependant, les valeurs des paramètres ajustés sont parfois très variables, notamment K, qui correspond àla limite de production permise, qui atteint des valeurs supérieures à30 t/ha : ces ajustements ne peuvent être admis car hors du domaine de validitéagronomique. De même, des valeurs de À très fortes sont détectées; celles-ci sont corrélées àK (r = 0,40) puisque pour atteindre un K hors norme il faut une échelle de temps supérieure que peut représenter À. Le retour sur les données montre que ces valeurs sont associées à des ajustements de cinétiques fragilisés par le manque de données acquises pendant la culture, notamment entre Z39 et Z92. Au total, ce sont 17 ajustements qui sont problématiques sur les 340 possibles.

fréquence

0 10 20 30 40 50 60

Distribution des REQM

0,0 0,2 0,4 0,6 0,8 1,0 REQM

Distribution du biais

-0,05 0,00 0,05 0,10 0,15

Biais

21

Figure 3.5 - Qualitédes ajustements des modèles de croissance. Distribution de la Racine de l'Erreur Quadratique d'Estimation et du biais (différence moyenne) entre estimations et valeurs observées

Il est possible d'ajuster un modèle de croissance pour chaque essai et chaque modalité(Le Souder et al., 2007). On s'attend à ce que la différenciation en terme de VC n'apparaisse qu'après l'apport. Autrement exprimé, avant la fertilisation, rien ne distingue la modalitéde son témoin : leur régimes de croissance sont analogues. Cependant, le niveau de fertilisation conditionne la production de biomasse

à la récolte. De fait, le paramètre K, qui représente la capacitélimite du milieu, varie d'une modalitéà l'autre. Ces variations se ressentent sensiblement sur les autres paramètres de l'expression de la

cinétique, il en résulte que les VC aux dates d'apport différent en moyenne de 0,2 g MS m^-2dj^-1 entre la modalitéet son témoin, la différence maximale étant de 0,45 g MS m^-2dj^-1. La figure 3.7 fournit un exemple d'ajustement de cinétiques illustrant ces écarts d'estimations de VC entre modalitéet témoin. On est donc contraint d'utiliser les VC calculées sur les témoins, en considérant un régime de croissance de la modalitéanalogue àcelui de son témoin évitant ainsi d'introduire une variabilité»artificielle».

En comparaison aux VC des expérimentations de Limaux (1999), la gamme obtenue est plus grande : elle varie de 0,004 à1,81 g MS m^-2dj^-1 (moyenne = 0,60, écart-type = 0,47) contre un intervalle de VC de 0,15 à0,91 g MS m^-2dj^-1 pour Limaux (1999) (moyenne = 0,42, écart type = 0,21), ceci s'expliquant par l'ajout dans le protocole de CAU pour des apports tardifs pour lesquelles

Estimation des paramètres

K

50

40

30

20

10

7 6 5 4 3 2

4000

3500

3000

2500

2000

1500

l

ë

â

22

Figure 3.6 - Estimations des paramètres des cinétiques de croissance obtenus par régression non

( 1 - e-(t/ë)â)

linéaire, MS(t) = K

les VC sont encore plus fortes (Z32 et Z39) (figure 3.8). Le graphique 3.8 illustre le lien fort qui existe entre VC et stade de fertilisation, la VC est d'autant plus forte que le stade physiologique du bléest avancé. Ceci est vrai parce que la fertilisation intervient avant le point d'inflexion de la cinétique de croissance. La VC, par sa construction dépendante des sommes de températures, est donc porteuse pour partie de l'information liée au stade physiologique du bléau moment de l'apport.

Cinétique labergement 2005

Vitesse de croissance (agrandissement)

800 900 1100 1300

VC (gr de MS m^-2dj^-1)

0,0 0,5 1,0 1,5 2,0

Z21

0

40Z21

80Z21

(X-120)Z30 (X-80)Z30 (X-40)Z30 (X-120)Z30+40Z32 (X-120)Z30+80Z32 (X-120)Z30+40Z39 (X-120)Z30+80Z39

Z30

Z32

Z39

0 500 1500 2500

0 5 10 15 20

MS (t/ha)

Z92

Z21

Z30 Z32 Z39

Z65

Vitesse de croissance

0 500 1500 2500

Z21 Z30

Z32 Z39

Z65

Z92

0,0 0,5 1,0 1,5 2,0

VC (gr de MS m^-2dj^-1)

23

Degrés jour Degrés jour

Figure 3.7 - Ajustement de cinétiques de croissance. Exemple des modèles de croissance ajustés pour les modalités de l'essai de Labergement (21), conduit en 2005

Évolution de la VC au cours du temps, selon les stades

VC à l'apport (gr de MS m^-2dj^-1)

0,0 0,5 1,0 1,5

l

l

Z21 Z30 Z32 Z39

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

0 500 1000 1500 2000

Somme de températures depuis le semis (dj)

Figure 3.8 - Évolution de la VC

24

3.1.3.2 État de nutrition azotée

Mesures de teneurs en azote

Stade de fertilisation

Année

0 1 2 3 4 5

l

l

l

l

l

l

l

l

l

l

l

l

Teneur en azote %

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

données brutes
données brutes

à l'apport

teneur en azote critique carence en azote

0 5 10 15

Matière sèche t/ha

2004 2005 2006

N Ncrit

INN =

0,6 0,9 1,2

0,6 0,9 1,2

N Ncrit

INN =

Z21 Z30 Z32 Z39

Figure 3.9 - Teneurs en azotes mesurée et INN calculés selon l'année ou le stade de fertilisation

La figure 3.9 représente les teneurs en azote mesurées au cours de la culture en fonction des mesures de biomasses correspondantes. Globalement, la majoritédes teneurs mesurées révèlent une teneur en azote inférieure à la teneur en azote critique. Toutefois le nombre de cas oùl'azote est en excès augmente pour des valeurs de matières sèches plus faibles, concernant donc les mesures les plus précoces. L'INN traduit l'éloignement àla teneur en azote critique. Au moment de l'apport, on calcule 440 valeurs d'INN. L'INN varie de 0,54 à1,26 (écart type : 0,17). Pour connaître l'implication des effets aléatoires on réalise l'analyse des composantes de la variance du modèle 3.2 (tab. 3.2). Le stade est ce qui induit le plus de variabilitédans les mesures, devant l'essai. À eux deux ils expliquent 62% de la variabilitéde l'INN.

INNiaes = u + A_a + S_s + Ee|a + ASas + åiaes (3.2)

3.1.3.3 Variables pluviométriques

Ayant au plus 4 dates d'acquisition des données de pluviométrie par essai (une donnée par stade d'apport), et certains essais dépendant de la même station météorologique, on dispose de 99 données pour chaque variable pluviométrique dont les distributions sont représentées figure 3.10. Étant »imbriquées», les 8 variables de pluviométrie sont corrélées : plus elles sont proches dans le temps plus le coefficient de corrélation entre deux variables est fort. En moyenne, la pluviométrie journalière est de 2,07 mm, alors que la pluviométrie efficace journalière est de -0,53 mm. Notons la

25

Table 3.2 - Analyse des composantes de la variance de l'INN

Groupes	Variance	ó
Essai :Année	0,0086	0,093
Année :Stade	0,0029	0,054
Stade	0,0125	0,112
Année	0,0005	0,023
Résidu	0,0092	0,096

pluviométrie exceptionnelle ayant suivi les apports àZ30 pour l'essai de Satolas en 2005 qui cumule déjàplus de 80 mm en 5 jours et 140 mm en 20 jours. Pour chaque variable pluviométrique, cet essai apparaît comme exceptionnel, ce qui lui vaut d'être exclu du jeu de données lors des analyses faisant appel àla pluviométrie. Comme le suggère la figure 3.11 la pluviométrie efficace semble davantage limitante à mesure que l'on avance dans l'année (stade d'apport plus tardif). On cherche àsavoir si la pluviométrie est équivalente d'un stade d'apport à l'autre (facteur stade s_s) et si cela dépend de l'année (SA_as). Dans cette approche qui se veut descriptive des variables de pluviométrie, le stade d'apport devient un effet fixe, on souhaite quantifier les différences de pluviométrie selon les stades pour mieux appréhender ces variables. On étudie donc un modèle mixte avec l'ensemble de ces effets pour comprendre les variations des variables climatiques (équation 3.3).

Cumul de pluies (mm)

5 jours 10 jours 15 jours 20 jours

0 50 100 150

pluie (mm)

l

l

Cumul de pluies efficaces (mm)

-100 -50 0 50 100

pluie efficace (mm)

l

l

densité	0,06 0,05 0,04 0,03 0,02 0,01 0,00
densité	0,04 0,03 0,02 0,01 0,00

Figure 3.10 - Distribution des variables pluviométriques

- Aa iid : Aa .'V(0,óA); - SAas iid : SAas .'V(0, óas); - åia iid : åia .'V(0, ó); - Aa et åia indépendants deux à deux.

Vi, a plx (ou plex) = it + ss + Aa + SAsa + åiaz (3.3)

L'analyse de variance permet de révéler l'effet significatif de l'année pour des cumuls de pluies et cumuls de pluies efficaces de 10 jours et plus, en interaction avec le stade d'apport : selon l'année, les mesures de pluviométrie pour un stade sont variables. Ajoutons que plus le nombre de jours de cumul est important, plus les particularités liées àl'année sont importantes. Concrètement, l'interaction est responsable de 20% de la variabilitédes données, ce qui représente 12 mm autour de l'estimation.

26

Quel que soit le stade d'apport, la pluviométrie quotidienne est équivalente, il tombe en moyenne 2 mm de pluies par jour, que ce soit pour un apport précoce Z21 ou plus tardif à Z39 : il n'y a pas d'effet du stade d'apport sur les cumuls de pluie ou cumul de pluies efficaces après l'apport. Les variations importantes observées sont le résultat d'un effet aléatoire de l'interaction stade / année : l'effet du stade àpartir duquel est mesuréle cumul de pluie dépend de l'année ou les variations peuvent être très fortes d'une année à l'autre pour un stade donné.

Cumul de pluies (mm)

0 20 40 60 80

Cumul de pluies efficaces (mm)

-60 -40 -20 0 20

Pluviométrie selon les stades d'apport

Z21 Z30 Z32 Z39 + - s

Z21 Z30 Z32 Z39 + - s

5 jours 10 jours 15 jours 20 jours

Figure 3.11 - Distribution des variables pluviométriques selon les stades d'apport

27

3.2 Élaboration d'un modèle explicatif du CAU

Pour répondre à l'objectif de base, on tente d'expliquer le CAU par les variables construites pour l'ensemble du cycle.

3.2.1 Analyse multidimensionnelle

L'AFM rend compte des liaisons entre variables (fig. 3.12). Les individus forment un nuage homogène autour de l'origine du repère. Du point de vue des variables, étant donnéleur faible nombre dans l'analyse, chaque groupe décrit un axe. Le premier axe est très majoritairement expliquépar les deux groupes de variables pluviométriques. Plus un individu se trouve àdroite du repère, plus les valeurs de pluviométrie ou pluviométrie efficace sont fortes. Dans le carrédes liaisons, le premier axe est un facteur commun entre les deux groupes de variables pluviométriques. Le second axe est expliquépar la vitesse de croissance. Notons en parallèle, conformément à ce qui a étépréciséplus tôt, que le stade d'apport est très bien projetéle long de cette variable : VC et stade d'apport sont très liés. La forme de fertilisant employée est discriminée par la troisième dimension de variabilité. Enfin, l'INN est liéau quatrième axe. Le groupe illustratif CAU n'est jamais bien projeté, la nature de la liaison du CAU aux autre variables n'est probablement pas uniquement linéaire, elle est plus complexe.

Nuage des individus

Nuage des individus

-1.0 -0.5 0.0 0.5 1.0

Dim 1 (32.89 %)

Carré des liaisons

-1.0 -0.5 0.0 0.5 1.0

Dim 3 (18.45 %)

Carré des liaisons

-0.2 0.0 0.2 0.4 0.6 0.8 1.0 1.2

Dim 1 (32.89 %)

-0.2 0.0 0.2 0.4 0.6 0.8 1.0 1.2

Dim 3 (18.45 %)

-1.0 -0.5 0.0 0.5 1.0

-1.0 -0.5 0.0 0.5 1.0

vc

inn

pluvio.J15

pluvio.J10

Dim 2 (24.23 %)

vc

CAU

CAU pluvio.J5

pluvio.J20

pluieEff.J15 pluieEff.J20

pluvio.J10 pluvio.J15

inn

Dim 4 (14.29%)

pluvio.J20 pluvio.J5

pluieEff.J5 pluieEff.J10

pluieEff.J20pluieEff.J5

pluieEff.J10 pluieEff.J15

0.0 0.2 0.4 0.6 0.8 1.0

0.0 0.2 0.4 0.6 0.8 1.0

fertiStadeTh

VC

Dim 2 (24.23 %)

Di m 4 (14.29 %)

INN

fertiStadeTh

VC

pluieEff

pluieEff

fertilisant

CAU

pluie

fertilisant

CAU

INN pluie

-2 0 2 4

Dim 1 (32.89 %)

Cercle des corrélations

-2 -1 0 1 2

Dim 3 (18.45 %)

Cercle des corrélations

-3 -2 -1 0 1 2 3

-1 0 1 2

Z39

Dim 4 (14.29 %)

Dim 2 (24.23 %)

Z32

Z32

Z39

solution39

Z30

Z21

ammonitrate

solution39

ammonitrate

Z30

Z21

28

Figure 3.12 - Exploration du jeu de données par AFM

29

Les variables pluviométriques sont fortement corrélées, toutes les introduire induirait de la redondance dans l'information apportée. On cherche donc la meilleure variable pluviométrique. Les résultats de l'AFM justifient d'utiliser une variable synthétique : une dimension commune aux 8 variables. Une ACP entre les variables pluviométriques permet de produire cette dimension commune, indépendamment de la variable àexpliquer comme l'aurait permis une régression PLS (fig. 3.13). La première composante capte 68,7% de la variabilitédes données et le premier plan 83%. Les pluviométries efficaces à 15 ou 20 jours avec des coordonnées sur le premier axe de 0,83 et 0,75 respectivement sont les moins bien projetées. Le second axe semble décrire une part de la pluviométrie efficace, la partie supérieure du graphique correspondant à des situations négatives en terme de bilan hydrique. Par la suite, les coordonnées des individus sur l'axe 1 sont utilisées pour synthétiser l'information des variables de pluviométrie, au travers d'une nouvelle variable notée pl.

Dim 2

-3 0 2

Cercle des corrélations

-4 0 2 4 6

pluieEff.J20

pluieEff.J15

pluieEff.J10
pluvio.J20
pluvio.J15

pluieEff.J5

pluvio.J10

pluvio.J5

-2 -1 0 1 2

Dim 1 (68.9%)

Dim 1

Di m 2 ( 13. 98 % )

-1.0 -0.5 0.0 0.5 1 . 0

Figure 3.13 - Premier plan de l'espace décrit par la pluviométrie. Premier plan d'une ACP, espace des variables et représentation du nuage des individus dans le coin supérieur droit.

3.2.2 Modèles linéaires

La représentation graphique du CAU en fonction des variables explicatives ne contredit pas les hypothèses de linéarités entre variables même si elles n'apparaissent pas non plus évidentes (fig. 3.14). Adopter une modélisation linéaire permet de confronter les résultats à ceux de Limaux (1999), et tenter de proposer sur cette base des améliorations du modèle.

CAL

150

100

50

0

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

CAL

l

l

l

l

l

l

l

150

100

50

0

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

CAL

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

100

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

^CAU

150

50

0

l

l Ammonitrate Solution39

l

l

l

0,0 0,5 1,0 1,5

VC (gr de MS m^-2dj^-1)

-4 0 2 4 6

Pluviométrie

(coord ACP dim. 1) 0,6 0,8 1,0 1,2

INN

yie = u + E_e + åie (3.4)

30

Figure 3.14 - Représentations du CAU en fonction des variables explicatives

3.2.2.1 Un point de départ : le modèle nul et le modèle VC

La figure 3.15 représente l'ensemble des valeurs de CAU calculées à la récolte en fonction des VC au moment de l'apport. En vert, on retrouve l'intervalle de valeurs de CAU et de VC rencontrés dans les travaux de Limaux (1999). Bien que l'ensemble de nos données soient obtenues par le calcul et donc susceptibles de cumuler plusieurs erreurs lors de leur obtention (teneur en azote, matière sèche, méthode d'estimation de la VC), 50% des données sont comprises dans le même intervalle. Les points les plus àdroite du graphique, pour lesquelles les valeurs de VC sont plus importantes, correspondent à des valeurs acquises pour des apports plus tardifs (Z32 et Z39) sur lesquels n'a pas travailléLimaux (1999). Le modèle VC passe au travers du nuage de points. Il suit la même allure que le début de la courbe de lissage obtenue par régression Loess. Globalement, le modèle semble sous-estimer les valeurs de CAU pour des valeurs de VC inférieures à0,6g MS m^-2dj^-1, et surestimer par la suite, puisque le modèle dépasse rapidement 100%. De ce point de vue, le modèle comporte une anomalie. En effet, les VC du jeu de données peuvent atteindre 1,8g MS m^-2dj^-1alors que pour un CAU de 100%, la VC du modèle VC est de 0,84g MS m^-2dj^-1 : la relation doit être réajustée.

Pour fournir une seconde référence, un modèle nul est ajusté(notémodèle 0) : un modèle expliquant le CAU (y) par la moyenne (équation 3.4, un modèle n'expliquant pas mieux le CAU que la moyenne est àrejeter). La meilleure combinaison d'effets aléatoires pour le modèle nul est sélectionnée : seul l'effet de l'essai est conservé(expression 3.4). Une analyse des composantes de la variance du modèle montre qu'il est responsable de plus de 36% de la variabilitédes données. L'analyse du résidu confirme les hypothèses de normalitéde sa distribution. Par ailleurs, l'écart type résiduel est fort : 19.

CAU en fonction de la vitesse de croissance

0 50 100 150

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

CAU (%)

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

Données de l'étude

l

Données et zone de définition du modèle VC

Modèle VC : CAU = 38,24 + 73,92VC

l

Reg. Loess á = 0,75

l

0,0 0,5 1,0 1,5 2,0

VC à l'apport (gr de MS m^-2dj^-1)

Figure 3.15 - Confrontation des données de l'étude au modèle VC Table 3.3 - Estimation des effets aléatoires du modèle 0

Groupe Variance ó

Essai (Intercept) 230.43 15.180

Residual 375.67 19.382

Introduisons la variable VC comme explicative du CAU : le modèle 1. La sélection des effets aléatoires aboutit aux mêmes résultats que pour le modèle nul : l'effet de l'essai induit une grande variabilité. L'expression du modèle ajustéest de la forme de l'équation 3.5. Toutefois, le test de l'effet VC aboutit àune probabilitécritique de 0,5 (tab. 3.4), si l'effet a étésélectionnédans le modèle c'est davantage pour sa prise en compte dans les effets aléatoires (tab. 3.5). Ce modèle n'est donc pas explicatif des CAU obtenus, on le rejette.

yie = u + âvci + E_e + åie (3.5)

Table 3.4 - Test des effets du modèle 1

ddl numérateur ddl dénominateur test F Pc

vc 1,00 25,05 0,39 0,54

Cependant, un modèle qui ne tienne pas compte du fertilisant employén'est pas réaliste étant donnéce que l'on sait du poids de la forme d'engrais sur les phénomènes de pertes. Le modèle 2 permet l'introduction de l'effet du fertilisant (ammonitrate ou solution 39). Le test des effets fixes exclut l'effet de la VC sur le CAU ; en revanche, la forme de fertilisant employée est hautement significative. Les coefficients obtenus révèlent la différence prépondérante entre matières fertilisantes, l'utilisation d'ammonitrate augmente en moyenne le CAU de 16,18 par rapport àune modalitéfertilisée par une solution à39% (tab.3.7). L'effet aléatoire liéà l'essai est très important, il explique une grande part de la variabilitéobservée àtravers son effet sur la moyenne et la pente de la relation (tab. 3.8). L'écriture du modèle 2 devient l'équation 3.6.

yife = u + ff + E_e + åife (3.6)

31

32

Table 3.5 - Estimation des effets aléatoires du modèle 1

Groupe Variance ó

Essai (Intercept) 280.94 16.761

vc 646.37 25.424

Residual 288.84 16.995

Table 3.6 - Test des effets du modèle 2

ddl numérateur ddl dénominateur test F Pc

fertilisant 1,00 33,18 11,77 0,00

Table 3.7 - Estimations des effets fixes du modèle 2

Estimation ó test t

(Intercept) 68,34 3,56 19,21

fertilisantammonitrate 16,18 4,72 3,43

Table 3.8 - Estimation des effets aléatoires du modèle 2

Groupe Variance ó

Essai (Intercept) 170.73 13.066

Residual 375.60 19.380

33

3.2.2.2 L'INN apporte-t-il une amélioration au modèle?

Les modèles basés sur la variable VC ne sont pas concluants. On introduit l'INN puisqu'on sait que selon les stades il varie de manière substancielle. La sélection des effets aléatoires retient l'effet de l'essai sur la pente et la moyenne de la relation. La sélection des effets fixes écarte les interactions entre variables (équation 3.7) et on ne peut conserver l'effet de VC dans le modèle, le test F le rejetant. Le modèle 3 est un sous modèle du modèle 2. La comparaison du modèle nul au modèle 3 par le rapport de vraisemblance démontre l'intérêt de l'INN (tab. 3.10). Notons la forte diminution du BIC marquant l'amélioration du modèle par la prise en compte de l'INN.

yife = u + ff + âinni + E_e (3.7)

Table 3.9 - Test des effets du modèle 3

	ddl numérateur	ddl dénominateur	test F	Pc
fertilisant	1,00	33,07	13,09	0,00
inn	1,00	697,47	4,05	0,04

Table 3.10 - Comparaison des modèles 2 et 3

ddl BIC ln(V ) ÷² Pc

mod2 4,00 6645,19 -3309,37

mod3 5,00 6249,78 -3108,51 401,72 0,00

Table 3.11 - Estimations des effets fixes du modèle 3

Estimation ó test t

(Intercept) 76,04 5,25 14,49

fertilisantammonitrate 16,88 4,67 3,62

inn -9,46 4,70 -2,01

3.2.2.3 Qu'en est-il de la pluviométrie?

Les valeurs de pluviométrie correspondant à l'essai de Satolas (2005) sont exclues. La sélection des effets aléatoires retient une structure de covariance partiellement indépendante entre l'effet de l'essai sur la pente liéàla pluviométrie d'une part et l'effet sur la moyenne de la relation d'autre part. Les tests des effets retiennent l'INN en interaction avec la pluviométrie et la VC en interaction avec la pluviométrie, auxquels s'ajoute l'effet du fertilisant (expression 3.8). Pour comparer le modèle 4 au modèle 3, ce dernier doit être réajustésur le jeu de données réduit (retrait de Satolas). La comparaison au modèle précédant montre une amélioration de la qualitéde l'ajustement (tab. 3.14). L'écart type du modèle est de 17, on reste dans les ordres de grandeur attendus, variabilitéà laquelle s'ajoute celle liée au facteur essai de niveau équivalent.

yife = u + ff + â1pli + â2vci + â3inni + ff + â4vc pl + â5inn pl + Ee|â1 (3.8)

L'observation des effets marginaux tempère l'amplitude des coefficients estimés. Si l'effet de la pluviométrie est compris entre -70 et 80, et l'INN entre -5 et -10, l'interaction montre que l'effet de l'INN est très fortement conditionnépar la pluviométrie. La représentation de la surface de réponse

34

Table 3.12 - Estimation des effets aléatoires du modèle 3

Groupe Variance ó

Essai (Intercept) 165.76 12.875

Residual 373.71 19.332

Table 3.13 - Test des effets du modèle 4

	ddl numérateur	ddl dénominateur	test F	Pc
pl	1,00	268,39	10,26	0,00
vc	1,00	404,63	0,46	0,50
inn	1,00	445,61	1,87	0,17
fertilisant	1,00	31,89	9,68	0,00
pl :vc	1,00	328,34	11,86	0,00
pl :inn	1,00	347,52	20,36	0,00

estimée en »selle de cheval», met en évidence l'interaction (fig. 3.16). L'effet de la vitesse de croissance instantanée apparaît plus limité, et fortement dépendant de la pluviométrie. On traduit donc bien le terme d'interaction entre pluviométrie et VC.

Table 3.14 - Comparaison du modèle 4 au modèle 3

ddl BIC ln(V ) x² Pc

mod3 5,00 5926,12 -2946,81

mod4 10,00 5875,88 -2905,44 82,73 0,00

Table 3.15 - Estimations des effets fixes du modèle 4

	Estimation	a	test t
(Intercept)	78,35	6,47	12,12
pl	8,96	2,80	3,20
vc	-1,52	2,25	-0,68
inn	-7,97	5,82	-1,37
fertilisantammonitrate	14,87	4,78	3,11
pl :vc	3,47	1,01	3,44
pl :inn	-12,84	2,85	-4,51

35

Table 3.16 - Estimation des effets aléatoires du modèle 4

Groupe Variance a

Essai (Intercept) 159.321 12.6222

Essai pl 17.605 4.1958

Residual 304.225 17.4421

Pluviométrie

-4 -2 0 2 4 6

CAU

-20

-40

40

20

60

0

l

l

l

l

l

l

l

l

l

Effets marginaux
de la pluviométrie
de l'INN
et de la VC

pluviométrie

20

0

-20

-40

4

2

0,6

0,8

-2

0

1,0 -4

50

0

-50

₂4

0,5

1,0

-4

0

-2

1,5

INN

CAU

-5

-6 -7 -8 -9 -10

l l l l l l

0,6 0,7 0,8 0,9 1,0 1,1 1,2

INN

VC

0,0 0,5 1,0 1,5

CAU

-0,5

-1,0

-1,5

-2,0

-2,5

0,0

VC

36

Figure 3.16 - Effets marginaux du modèle 4

Modèle 1 Modèle 1

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

100

40

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

80

20

l

l

observé

résidu

60

0

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

40

l

- 20

20

l

- 40

0

0 50 100 150 0 40 80 120

valeurs ajustées estimé (effets fixes)

Modèle 2

Modèle 2

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

100

40

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

80

20

observé

l

résidu

l

l

60

l

l

0

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

40

- 20

20

- 40

0

0 50 100 150 0 40 80 120

valeurs ajustées estimé (effets fixes)

Modèle 3

Modèle 3

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

100

40

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

80

20

observé

l

résidu

60

0

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

40

- 20

l

20

- 40

0

0 50 100 150 0 40 80 120

valeurs ajustées estimé (effets fixes)

Modèle 4

Modèle 4

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

100

40

l

l

l

l

l

l

80

20

l

l

l

l

l

l

l

l

l

l

l

observé

résidu

60

0

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

40

- 20

20

- 40

0

0 50 100 150 0 40 80 120

valeurs ajustées

valeurs ajustées estimé (effets fixes)

estimé (effets fixes)

Figure 3.17 - Évolution du résidu du modèle 1 au modèle 4 et confrontation des estimations aux données réelles

37

38

3.2.2.4 Synthèse des ajustements linéaires

Chaque facteur est porteur d'une information qui permet de mieux comprendre les évolutions

du CAU.

À chaque étape, le modèle sélectionnéest globalement inclus dans le modèle sélectionné

à l'étape suivante. L'effet aléatoire de l'essai apparaît continuellement comme très significatif, il est responsable d'une grand part de variabilitéque les variables introduites ne permettent pas d'expliquer. Une connaissance plus fine àl'échelle de l'essai peut donc se révéler déterminante dans la prédiction d'un CAU. Du côtédes effets fixes, le modèle 4 semble être le plus explicatif du CAU, notamment

à travers les variables pluviométriques et l'INN. En revanche, la VC ne semble pas significative ^àl'exception de l'interaction avec la variable pluviométrique.

L'examen du résidu, obtenu pour chacun des modèles proposés montre une amélioration, en augmentant la complexitédu modèle on disperse les estimations qui se rapprochent un peu plus des valeurs observées et le résidu se concentre de plus en plus autour de 0 (fig. 3.17). Enfin, d'un point de vue des prédictions permises par ce modèle si la qualitédes ajustements s'est améliorée, il est possible que l'augmentation du nombre de paramètres dans le modèle soit responsable d'un sur-ajustement. On étudie donc l'évolution de la REQMP du modèle nul jusqu'au modèle 4. La figure 3.18 montre l'évolution du REQMP. Globalement le REQMP est mauvais, les ajustements ne sont pas de bonne qualité, l'incertitude autour des prédictions est grande, ces modèles ne sont donc pas d'une grande qualitéprédictive, même s'ils apportent une amélioration par rapport au modèle nul. On passe ainsi d'une REQMP de 22,2 à 21,1.

Évolution du REQMP (unité de CAU)

RMSEP (leave-one-out)

20 21 22 23 24 25

l

l

0 1 2 3 4

Modèles

Figure 3.18 - Évolution du REQMP entre le modèle nul et le modèle 4

Le dernier modèle produit montre un effet aléatoire de l'essai sur la moyenne de la relation et sur la pente liée àla pluviométrie : d'un essai àl'autre, on observe des écarts à la relation plus ou moins grands. Sur la base de la différence de chaque essai àla relation générale, on tente de rendre compte de l'existence de groupes d'essais qui seraient proches du point de vue de ces écarts au modèle global. On propose donc une classification ascendante hiérarchique (CAH, agrégation méthode Ward) qui aboutit àla construction de trois groupes que les variables caractéristiques des essais décrivent (fig. 3.19). Les effets de ces variables sont testés par un test V et mettent en avant le rôle de la variété, de la longitude, du pH et de la CEC du sol dans la caractérisation des groupes (annexe X). On retrouve làdeux aspects : un aspect purement biologique et un aspect pédologique, dépendant de l'essai. Ce sont autant de pistes suggérées àexplorer dans un prochain travail de modélisation, qui n'entre pas dans le cadre de l'étude de la relation du CAU àla VC, l'INN et la pluviométrie.

Factor map Cluster Dendrogram

Dim 2 (43,85%)

-3 -2 -1 0 1 2 3

Height

0,0 0,2 0,4 0,6 0,8

11

28

20

13 1 6

27

30

26 5 3 8

25

29 9

21 7

15

16

32

34

17

31

23

12

33

24

18

19

22

14 4 2

10

cluster 1
cluster 2
cluster 3

39

-3 -2 -1 0 1 2

Dim 1 (56,15%)

Figure 3.19 - CAH sur les écarts au modèle général du modèle 4 selon les essais 3.2.3 Modélisation non linéaire

La construction d'un modèle linéaire ne donne pas de résultats satisfaisants. D'après les travaux de François Limaux la VC permet d'expliquer l'évolution du CAU mais cette relation ne se vérifie pas au regard de nos résultats sur l'ensemble du cycle de culture. Mais comme préciséplus tôt la relation de François Limaux est limitéà des stades pour lesquels la VC est inférieure à 0,80 (fig. 3.15, 31). Cette observation démontre un plafonnement de la relation, qu'il est possible de traduire par une régression asymptotique, c'est à dire une expression exponentielle.

Le choix de la relation se porte vers une équation àtrois paramètres (équation 3.9). Sur cette base, on inclut l'effet du fertilisant qui peut avoir un impact sur un ou plusieurs paramètres du modèle. On sélectionne les paramètres du modèle sur la base de la minimisation du BIC. Le modèle qui minimise le plus le BIC est un modèle dont l'asymptote varie avec le fertilisant employé. Ceci semble cohérent au regard des résultats précédents pour lesquels la forme du fertilisant est le facteur le plus important pour déterminer un CAU. Les résultats sont encourageants, en incluant le seul effet de la VC et du fertilisant employé(tab. 3.17). Les paramètres obtenus apportent de l'information comme le montre la représentation graphique (fig. 3.21). La fonction représente bien deux phases, une phase ou la relation entre VC et CAU semble linéaire et évolue très rapidement, puis tend vers une asymptote pour des valeurs de VC supérieures à 0,3g MS m^-2dj^-1. Par la suite on tente d'ajouter les effets linéaires de l'INN, la pluviométrie et leur interaction. Les représentations graphiques, et les différentes transformations des données ne permettent pas de révéler une structure particulière des données, on s'appuie donc sur les résultats des modèles mixtes pour supposer la relation linéaire (fig. 3.14 page 30). Les effets sont supposés additifs àl'expression du CAU en fonction de la VC, on estime des paramètres initiaux à partir des premiers tours d'un algorithme de back fitting. Parmi l'ensemble des modèles possibles, seul un modèle incluant l'effet de la pluviométrie apporte de l'information

(équation 3.10, tab. 3.18). Ce paramètre permet de nuancer l'effet de la VC : en s'intéressant ^àl'effet marginal de cet effet on voit qu'il peut faire varier de -5 à + 10 unités de CAU (fig. ??). Cette

information est significative au regard d'une comparaison des sommes de carrés des écarts résiduels entre modèle 1 et modèle 2 (tab. 3.19).

CAU = Asym + (RU - Asym) · exp- exp(^lrc) V C (3.9)

CAU = Asym + (R0 - Asym) · exp- exp(^lrc) V C +â · pl (3.10)

CAU estimé

CAU observé

20 60 100 140

l

l

l

l

l

l

l

l

20 60 100 140

CAU estimé

Résidu centré réduit

-3 -1 1 2 3 4

65 75 85

l

l

l

l

l

l

l

l B

l

l

l

l

l

l

·

0,0 0,5 1,0 1,5

CAU

20 40 60 80 100 120 140

l

l

l

l

l

l

l

Kf + (R0 - Kf)e(-exp(lrc)VC)

vc

40

Figure 3.20 - Ajustement du modèle non linéaire 1. Représentation de l'effet de la VC, du résidu du modèle et de la confrontation entre données estimées et données observée

On détermine alors des REQMP des deux modèles pour les comparer entre eux et s'assurer que l'ajout de la variable pluviométrique n'est pas une surparamétrisation du modèle. De cette manière, la REQMP descend respectivement à 20,93 et 20,60. En comparaison au dernier modèle linéaire ajusté, avec un paramètre de moins on obtient une REQMP bien inférieure, proche de 20.

Table 3.17 - Estimation des paramètres du modèle non linéaire (VC)

Estimate Std. Error t value Pr(>Itl)

Asym1 87,45 1,54 56,62 0,00

Asym2 70,07 1,46 47,91 0,00

R0 60,38 5,01 12,06 0,00

lrc 2,31 0,40 5,82 0,00

Table 3.18 - Estimation des paramètres du modèle non linéaire (VC + pl)

Estimate Std. Error t value Pr(>Itl)

Asym1 87,54 1,46 60,06 0,00

Asym2 70,26 1,43 49,11 0,00

R0 55,97 5,65 9,90 0,00

lrc 2,46 0,36 6,80 0,00

b 1,51 0,38 3,97 0,00

Effet marginal VC

0 50 100 150

CAU

- 5 0 5 10

CAU

l

l

l

l

l

l

Kf + (R0 - Kf)e(-exp(lrc)VC) + b × pl

l

l

l

l

l

l

l

l

l

l

l

l

l

l

- 3 -2 -1 0 1 2 3

Résidu centré réduit

0,0 0,5 1,0 1,5

VC

Effet marginal pl

-4 -2 0 2 4 6

CAU observé

l

l

l

l

pl (ACP)

20 60 100

60 70 80 90

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

CAU estimé

20 60 100

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

l

CAU estimé

41

Figure 3.21 - Ajustement du modèle non linéaire 2. Représentation des effets marginaux de la VC et de la pluviométrie pl, du résidu du modèle et de la confrontation entre données estimées et données observée

42

Table 3.19 - Comparaison des modèles obtenus par régression non linéaire après ajout de la variable pluviométrique

Res.Df Res.Sum Sq Df Sum Sq F value Pr(>F)

1 661 340216,55

2 660 332258,15 1 7958,41 15,81 0,0001

43

4 Discussion - conclusion

L'élaboration d'un modèle explicatif du CAU permet de mettre en évidence les effets des variables:

- le fertilisant est le facteur le plus déterminant. Il quantifie la différence de réponse en terme de valorisation de l'engrais entre un apport d'ammonitrate et un apport de solution azotée à 39%. La nature de la relation du CAU aux autres variables n'est pas modifiée quelque soit le fertilisant employé, puisque l'effet du fertilisant n'est en interaction ni avec l'INN, ni la pluviométrie, ni la VC. Les CAU à la récolte sont améliorés ou pénalisés selon la matière fertilisante apportée. Cette idée se retrouve en modélisation non linéaire du CAU en fonction de la VC oùle seul paramètre qui dépende du fertilisant est l'asymptote de la relation ;

- la pluviométrie : cet effet est important. Globalement, un contexte de régime hydrique humide permet une meilleure valorisation de l'engrais, probablement à travers une mise en solution de l'azote améliorée;

- la VC : d'un point de vue non linéaire la relation qui lie le CAU à la VC est de type exponentielle. La réponse évolue rapidement pour atteindre une asymptote. L'effet de la VC semble donc déterminant pour des VC plus faibles (entre 0 et 0,5g MS m^-2dj^-1);

- l'INN : l'état de nutrition azotée de la culture influe sur la réponse au CAU;

- la pluviométrie en interaction avec la VC et l'INN : les effets de l'INN et de la VC dépendent de la pluviométrie.

Les modèles obtenus ne sont pas d'une grande précision mais confirment les hypothèses agronomiques posées. Ainsi, l'hypothèse de Limaux (1999) est vérifiée : il existe un lien entre VC et CAU. Compte tenu de la variabilitéentre essais nos résultats corroborent pour partie les conclusions de Limaux (1999). Les hypothèses proposées par Le Souder et al. (2007) sont soutenues par les travaux, appuyant l'importance de la pluviométrie et l'influence de l'INN dans la réponse observée à l'azote apporté. Enfin, la forme du fertilisant conditionne effectivement le CAU comme le présente Recous et al. (1997).

Bien que les qualités explicatives du modèle soient avérées, le pouvoir prédictif est beaucoup plus limité. L'incertitude du modèle se décompose principalement dans l'erreur résiduelle (qui s'explique par la variabilitéforte intrinsèque àl'estimation du CAU) et la variabilitéentre essais. D'un point de vue méthodologique, la variabilitéforte de l'estimation du CAU pose une question : comment affiner l'estimation de cette valeur? En effet, travailler sur une valeur mieux définie permettrait de clarifier les relations entre CAU et variables explicatives.

Par ailleurs, une stratégie de type leave-one-out a étéadoptée pour le calcul des REQMP. Toutefois, étant donnéles structures de corrélations induites par l'effet aléatoire de l'essai, les données d'un même essai apporte une information redondante. Retirer un individu ne retranche pas toute l'information qu'il véhicule puisque les autres individus sont encore présents. De ce constat on peut affirmer que la procédure de validation REQMP adoptée présente un biais puisqu'en toute rigueur ce sont l'ensemble des données d'un essai qui devraient être retirées dans les phases d'apprentis-sage/prédiction. Faute de temps, la mise en oeuvre d'une nouvelle fonction pour calculer un REQMP pour lequel le nombre de données exclues correspondrait aux individus d'un essai n'a pas étéréalisé.

Le développement du modèle VC (Limaux, 1999) a étéréalisésur des sols de Lorraine, et uniquement pour des apports à épi 1 cm : par conséquent ses résultats sont plus précis et traduisent

44

la relation pour des valeurs de VC faibles en étant soumis àun effet aléatoire liéà l'essai limité. Dans notre étude, les modèles établis sont très variables selon les essais. Le territoire français est une échelle d'étude qui induit une diversitéde réponses trop large pour mettre un place un modèle global. Par conséquent le résidu du modèle reste très fort. L'effet de l'essai est déterminant dans la variabilitédes résultats, comment expliquer ces différences entre essais? Dans le devenir de l'azote, les pertes par organisation sont supposées constantes d'un type de sol à l'autre et la lixiviation de l'azote est nulle pour de bonnes conditions de fertilisation (apport inférieur à l'optimum technique, fragmentation de l'apport), restent les pertes par voie gazeuse. Ces pertes sont principalement liées à de la volatilisation de l'ammoniac (NH3), conditionnée par des caractéristiques physico chimiques du sol : CEC et pH. Ces caractéristiques ressortent par classification ascendante hiérarchique et justifient par la suite de proposer des facteurs explicatifs àl'échelle de l'essai (hors cadre de l'étude qui visait à expliquer le CAU par la VC, l'INN et la pluviométrie). De plus, une nouvelle question peut être posée : la valorisation de l'azote est-elle variable d'un cultivar à l'autre? Il est communément admis que la valorisation de l'azote par les différentes variétés cultivées en France est équivalente, rentre-t-on dans un niveau de détail qui n'admette plus ce postulat?

En somme, le CAU apparaît comme une grandeur complexe. VC, INN, pluviométrie et fertilisant l'influencent, mais il faut désormais s'intéresser à l'échelle de l'essai, pour comprendre les déterminants locaux influant les relations établies.

45

Bibliographie

Barto'n, K. (2012). MuMIn : Multi-model inference. R package version 1.7.7.

Bates, D., Maechler, M., and Bolker, B. (2011). lme4 : Linear mixed-effects models using S4 classes. R package version 0.999375-42.

Bates, D. M. and DebRoy, S. (2004). Linear mixed models and penalized least squares. J. Multivar. Anal., 91(1) :1-17.

Bouthier, A. (1997). Efficacitéd'un apport d'azote sur blétendre - la pluie est rarement limitante courant montaison. Perspectives Agricoles, 220 :56-59.

Cohan, J.-P., Laurent, F., and Lellahi, A. (2011). Fertiliser les cultures : Concilier efficacitétechnique et défis environnementaux. DEMETER, 2011 :269-327.

COMIFER (2012). Calcul de la fertilisation azotée - Guide méthodologique pour l'étalissement des prescriptions locales - Cultures annuelles et prairies. COMIFER.

Crawley, M. J. (2007). The R Book, chapter Mixed-Effects Models, pages 627-660. John Wiley & Sons.

Hébert, J. (1969). La fumure azotée du blétendre d'hiver. Bulletin technique d'information, 254 :755- 766.

Højsgaard, S., with contributions from Jim Robison-Cox, U. H., Wright, K., and Leidi., A. A. (2012). doBy : doBy - Groupwise summary statistics, general linear contrasts, population means (least-squares-means), and other utilities. R package version 4.5-3.

Husson, F., Josse, J., Le, S., and Mazet, J. (2012). FactoMineR : Multivariate Exploratory Data Analysis and Data Mining with R. R package version 1.19.

Jolivet, E., Lebreton, J.-D., and Millier, C. (1982). Modèles dynamiques déterministes en biologie, chapter Courbes de réponse, pages 151-170. Masson.

Justes, E., Mary, B., Meynard, J.-M., Machet, J.-M., and Thelier-Huche, L. (1994). Determination of a critical nitrogen dilution curve for winter wheat crops. Annals of Botany, 74(4) :397-407.

Kuznetsova, A. and Brockhoff, P. B. (2012). MixMod : Analysis of Mixed Models. R package version 1.0.

Le Souder, C., Cohan, J.-P., and Laurent, F. (2007). Eléments de prévision du cau de l'azote de l'engrais sur blétendre d'hivers. In Congrès COMIFER-GEMAS, Blois, France.

Lemaire, G., Gastal, F., and Salette, J. (1989). Analysis of the effect of N nutrition on dry matter yield of a sward by reference to potential yield and optimum N content. In XVI International Grassland Congress, Nice, page 179-180.

46

Limaux, F. (1999). Modélisation des besoins du bléen azote, de la fourniture du sol et de l'utilisation de l'engrais. Application au raisonnement de la fertilisation en Lorraine. PhD thesis, Institut national polytechnique de Lorraine.

Limaux, F., Recous, S., Meynard, J., and Guckert, A. (1999). Relationship between rate of crop growth at date of fertiliser N application and fate of fertiliser N applied to winter wheat. Plant and Soil, 214(1) :49-59. 10.1023/A :1004629511235.

Meynard, J. M., Justes, E., Machet, J., and Recous, S. (1997). Fertilisation azotée des cultures annuelles de plein champ. Les colloques de l'INRA, 83 :183-199.

Nicolardot, B., Mary, B., Houot, S., and Recous, S. (1997). La dynamique de l'azote dans les sols cultivés. Les colloques de l'INRA, 83 :87-103.

R Core Team (2012). R : A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0.

Recous, S. (1988). The fate of labelled ¹⁵N urea and ammonium nitrate applied to a winter wheat crop. II. Plant uptake and N efficiency. Plant and Soil, 112 :215-224.

Recous, S., Loiseau, P., Machet, J., and Mary, B. (1997). Transformations et devenir de l'azote de l'engrais sous cultures annuelles et sous prairies. Les colloques de l'INRA, 83 :105-120.

Rémy, J. and Hébert, J. (1977). Le devenir des engrais azotés dans le sol. Comptes rendus des séances de l'Académie d'agriculture de France, 11 :700-714.

Zadoks, J. C., Chang, T. T., and Konzak, C. F. (1974). A decimal code for the growth stages of cereals. Weed Research, 14(6) :415-421.

Glossaire, liste des abréviations et formulaire

AFM

Analyse Factorielle Multiple.

BIC

Critère d'information Bayésienne, permet de traduire la qualitéde l'ajustement d'un modèle, il est une pénalisation de la log-vraisemblance (ln V ) par le nombre de paramètres du indépendants K du modèle et du nombre d'individus n sur lesquels a étéajustéle modèle. K - lnn représente le terme de pénalité:

BIC = -2 - lnV + K - lnn

.

CAU

Coefficient Apparent d'Utilisation.

CRU

Coefficient Réel d'Utilisation.

EQM

_Xn i=1

[ _]2

Yi - ^àYi

Écart Quadratique Moyen (anglais : MSE) :

EQMP = 1

n

.

47

EQMP

Écart Quadratique Moyen de Prédiction (anglais : MSEP), déterminée ci-dessous par leave-one-out:

1 EQMP = n

Xn i=1

[ ]2 Yi - ^àY-i

.

ETP

Évapotranspiration potentielle.

INN

Indice de Nutrition Azotée.

lixiviation

transfert d'un élément dissous dans la solution du sol par transfert vertical de l'eau en profondeur (drainage) (COMIFER, 2012).

48

ML, log-likelihood

Maximisation de la log-vraisemblance :

_Xn _~2

n

log L = -₂ ln (2ðó²) - 1 (Yi - u

2 ó

i=1

.

MMC

méthode de Minimisation des Moindres Carrés.

MS

Matière Sèche.

Nc

teneur en azote critique.

organisation

processus biologique d'assimilation de l'azote minéral par les micro-organismes d'un substrat qui conduit à la formation d'azote organique dans la biomasse microbienne.

REML, log-likelihood

Maximisation de la log-vraisemblance restreinte :

? _)2? [ )2]

log L = ?-1 (2ðó2 ) ( _-n - 1

- 1 y - u 2 ln (2ðó²) - 2 1 ln(n) - 1 X (Yi - y

?+

2 n 2 vn 2 ó

.

REQMP

Racine [carrée] de l'Écart Quadratique Moyen de Prédiction (anglais : RMSEP).

VC

Vitesse de Croissance.

bignan

l

saint-pierre-damilly

ouzouer-le-marche

barran

vraignes-en-vermandois

l

cesseville matougues

l berni

enville vrau

saint-pierre

l labergement-foigney

thizay

colombier-saugnieu

satolas-et-bonce

l .,

2004

2005

2006

i

Annexes

Annexe I : Répartition des sites de l'étude

Répartition des essais

ii

Annexe II : Échelle Zadoks

Stade Zadoks Description du stade

Z21 début du tallage

Z30 épi à1 cm

Z32 deuxième noeud visible

Z39 apparition de la ligule de la dernière feuille

Z65 demi-floraison

Z92 maturitédu grain

Annexe III : Extrait du jeu de données

annee

numeroApport

numeroModaliteTh

lieu

Essai

inn

CAU

bloc

vc

fertiStadeTh

fertiCumul

fertilisant

558

		24	saintPierreAmilly				2005		1	ammonitrate			92,65		2		Z21	I	0,00	3,94	1,08
559		24	saintPierreAmilly				2005		1	ammonitrate			92,65		2		Z21	II	0,00	33,02	1,08
560		24	saintPierreAmilly				2005		1	ammonitrate			92,65		2		Z21	III	0,00	73,13	1,08
561		24	saintPierreAmilly				2005		1	ammonitrate			92,65		3		Z21	I	0,00	57,63	1,08
562		24	saintPierreAmilly				2005		1	ammonitrate			92,65		3		Z21	II	0,00	52,59	1,08
563		24	saintPierreAmilly				2005		1	ammonitrate			92,65		3		Z21	III	0,00	79,81	1,08
451		20	saintPierre				2004		1	solution39			443,75		3		Z21	I	0,01	100,32	0,97
452		20	saintPierre				2004		1	solution39			443,75		3		Z21	II	0,01	74,20	0,97
453		20	saintPierre				2004		1	solution39			443,75		3		Z21	III	0,01	69,13	0,97
712		30	villejouet				2004		1	ammonitrate			530,30		3		Z21	II	0,02	85,22	1,05
713		30	villejouet				2004		1	ammonitrate			530,30		3		Z21	III	0,02	72,05	1,05
714		30	villejouet				2004		1	ammonitrate			530,30		3		Z21	IV	0,02	95,51	1,05
55		3	bignan				2005		1	ammonitrate			476,20		2		Z21	II	0,03	73,01	0,96
56		3	bignan				2005		1	ammonitrate			476,20		2		Z21	III	0,03	60,75	0,96
57		3	bignan				2005		1	ammonitrate			476,20		2		Z21	IV	0,03	69,18
58		3	bignan				2005		1	ammonitrate			476,20		3		Z21	II	0,03	76,87	0,96
59		3	bignan				2005		1	ammonitrate			476,20		3		Z21	III	0,03	86,19	0,96
60		3	bignan				2005		1	ammonitrate			476,20		3		Z21	IV	0,03	58,88
586		25	thizay				2004		1	solution39			506,75		2		Z21	I	0,04	74,53	0,99
587		25	thizay				2004		1	solution39			506,75		2		Z21	II	0,04	10,13	0,99
588		25	thizay				2004		1	solution39			506,75		2		Z21	III	0,04	35,48	0,99
589		25	thizay				2004		1	solution39			506,75		2		Z21	IV	0,04	58,37	0,99

pluvio.J5

pluieEff.J20

pluieEff.J15

pluieEff.J10

pluieEff.J5

pluvio.J20

pluvio.J15

pluvio.J10

558

	0,40	14,80	36,00	47,40	0,23	14,39	35,26	46,53
559	0,40	14,80	36,00	47,40	0,23	14,39	35,26	46,53
560	0,40	14,80	36,00	47,40	0,23	14,39	35,26	46,53
561	0,40	14,80	36,00	47,40	0,23	14,39	35,26	46,53
562	0,40	14,80	36,00	47,40	0,23	14,39	35,26	46,53
563	0,40	14,80	36,00	47,40	0,23	14,39	35,26	46,53
451	4,90	13,20	14,00	25,80	1,03	4,10	-3,47	0,12
452	4,90	13,20	14,00	25,80	1,03	4,10	-3,47	0,12
453	4,90	13,20	14,00	25,80	1,03	4,10	-3,47	0,12
712	16,20	37,60	44,80	44,80	15,20	35,93	42,14	40,20
713	16,20	37,60	44,80	44,80	15,20	35,93	42,14	40,20
714	16,20	37,60	44,80	44,80	15,20	35,93	42,14	40,20
55	16,20	18,80	22,60	34,80	12,30	10,70	12,10	20,40
56	16,20	18,80	22,60	34,80	12,30	10,70	12,10	20,40
57	16,20	18,80	22,60	34,80	12,30	10,70	12,10	20,40
58	16,20	18,80	22,60	34,80	12,30	10,70	12,10	20,40
59	16,20	18,80	22,60	34,80	12,30	10,70	12,10	20,40
60	16,20	18,80	22,60	34,80	12,30	10,70	12,10	20,40
586	19,60	23,60	35,00	35,40	16,00	16,00	24,90	22,30
587	19,60	23,60	35,00	35,40	16,00	16,00	24,90	22,30
588	19,60	23,60	35,00	35,40	16,00	16,00	24,90	22,30
589	19,60	23,60	35,00	35,40	16,00	16,00	24,90	22,30

iv

Annexe IV : Fonctions de Weibull : variations des paramètres de formes et d'échelle

Influence du paramètre de forme sur la cinétique de croissance

0 1 2 3 4 5

y

0,0 0,4 0,8

F(ë = 2, â = 3)
F(ë = 2, â = 2)
F(ë = 2, â = 1)

Influence du paramètre d'échelle sur la cinétique de croissance

x

y

0,0 0,4 0,8

F(ë = 1, â = 2)
F(ë = 2, â = 2)
F(ë = 3, â = 2)

0 1 2 3 4 5

v

Annexe V : Algorithme de Backfitting

1. Initialisation :

^àâ0 =

Y,

^àfj =

àf(^0) j

2. Itération : estimer tout àtour fk par le modèle

??Y - ^àâ0 -

Xp j=1,j6=k

? ( àfj (xj) x(k)) ? = fk + å

3. Arrêt : l'itération laisse inchangée l'estimation.

vi

Annexe VI : Algorithme de Newton, annexe du cours de P.A. Cornillon

Pierre AndréCornillon écrit :

»Nous rappelons brièvement le principe de cet algorithme. L'étude de sa convergence

et des vitesses associées peuvent être trouver dans un livre d'optimisation. Soit g une fonction àminimiser, par exemple l'opposéde la log-vraisemblance.

g : R^s -> R

0 i-> g(0).

On cherche la valeur de qui réalise le minimum de g, valeur que nous noterons ^à0. Pour cela on utilise une procédure itérative qui va procéder par approximations successives. D'abord, on prend un point de départ 00 puis on chercher autour de celui ci une valeur 01 qui fasse diminuer la fonction g (ie g (01) < g (00)).

Plaçons nous à l'étape k + 1. Nous avons donc 0k qui est connu et nous souhaitons trouver 0k+1 au voisinage de. Comme nous ne savons pas minimiser g, on va l'approxi-mer par une fonction au voisinage de 0k. Cette approximation est choisie de telle sorte qu'un minimum est directement calculable. On va donc approximer la fonction g par une fonction quadratique, grâce àune développement de Taylor :

g (0) ^ g (0k) + (0 - 0k)^' Vg + ₂ (0 - 0k)' V² (0 - 0k)

1

oùles vecteur des dérivées sont évalués au point 0k.

Remplaçons maintenant g(0) par h(0) = g (0k)+(0 - 0k)^' Vg+¹₂ (0 - 0k)' V² (0 - 0k) et cherchons en donc le minimum. Comme il s'agit d'une fonction quadratique, l'unique minimum est le point 0k+1 qui annule la dérivée de h par rapport à 0. La dérivée est donc :

h^'(0) = Vg + V² (0 - 0k)

et elle s'annule au point 0k+1 :

Vg + V² (0 - 0k) = 0

0k+1 = 0k - (V2)-1 Vg

oùchaque dérivée est évaluée au point 0k.»

web.supagro.inra.fr/partage/cornillo/COURS/MODELES-MIXTES/mixtes.pdf

consultéle 23 août 2012.

vii

Annexe VII : Déterminer la structure de variance-covariance d'un effet aléatoire : réponse de Douglas Bates à Michael Ku-bovy sur le R-SIG

Réponse de Douglas Bates, le 7 avril 2008,

https://stat.ethz.ch/pipermail/r-sig-mixed-models/2008q2/000789.html

On Mon, Apr 7, 2008 at 12 :34 PM, Michael Kubovy <kubovy at virginia.edu> wrote :

> Dear lme4 folk

> The lmer help page gives two examples :

> (fm1 <- lmer(Reaction Days + (Days|Subject), sleepstudy))

> (fm2 <- lmer(Reaction Days + (1|Subject) + (0+Days|Subject), sleepstudy))

> How is the following different, in principle, from the above? Is it that the

> above treats (Intercept) and Days as orthogonal, whereas the latter checks

> to see if they are? What would be appropriate if the correlation between

> Days and Intercept (here 0.067, apparently) were large?

> (fm3 <- lmer(Reaction Days + (1 + Days | Subject), sleepstudy))

Model fm3 is equivalent to model fm1. In the linear model formula language used in the S language, the intercept term is implicit so the random-effects term (Days|Subject) is equivalent to (1+Days|Subject). Some authors, notably Gelman and Hill in their 2007 book, prefer to use the second form so that the presence of the intercept is explicit. I can see the point of that.

Every random effect is associated with one and only one random-effects term in the model formula and with one and only one level of the grouping factor for that random-effects term. The general rules for determining the variance-covariance of the random effects (as fit in lmer) are :

- random effects associated with different terms are independent

- random effects associated with the same term but with different levels of the grouping factor are independent

- within a term the random effects may be partitioned according to the levels of the

grouping factor. The variance-covariance matrix of the vector of random effects associated with each of these levels of the grouping factor is a constant, symmetric, positive semidefinite matrix. It has no additional constraints other than being symmetric and positive semidefinite. (In SAS-speak this is called an »unstructu-red»variance-covariance matrix but the mathematician in me refuses to accept the concept of an unstructured, symmetic, positive semidefinite matrix.)

(Note that when I refer to »levels» in the above description I am referring to the S-

language concept of the levels of a factor, not levels of random effects in the sense of

multilevel models.)

In practice the difference between the two models is that fm2 is a restricted form of

fm1/fm3 in which the correlation of the random effects has been set to zero.

> Random effects :

> Groups Name Variance Std.Dev. Corr

> Subject (Intercept) 610.8 24.72

> Days 35.1 5.92 0.067

> Residual 655.1 25.59

> Professor Michael Kubovy > University of Virginia

viii

> Department of Psychology

> USPS : P.O.Box 400400 Charlottesville, VA 22904-4400

> Parcels : Room 102 Gilmer Hall

> McCormick Road Charlottesville, VA 22903

> Office : B011 [phone]

> Lab : B019 [phone]

> Fax: [phone]

> WWW : http ://www.people.virginia.edu/ mk9y/

ix

Annexe VIII : Fonctions d'estimation des RMSEP pour des modèles de classe R nls ou mer

function (lmer)

{

system.time({

RMSEP <- data.frame(iIndex = 1, iDonnees = 1, realiseDeI = 1,

predictionMoinsI = 1, ecartPrediction = 1)

RMSEP <- cbind(RMSEP, t(data.frame(lmer@fixef)))

jdd <- lmer@frame

X0 <- lmer@X

nlignes <- nrow(jdd)

for (i in 1:nlignes) {

updateLmer <- update(lmer, data = jdd[-i, ], REML = T)

predit <- as.numeric(X0[i, ] %*% updateLmer@fixef)

realise <- lmer@y[i]

RMSEP[i, ] <- c(i, rownames(jdd[i, ]), realise, predit,

(realise - predit)^2, updateLmer@fixef)

cat(round(i/nlignes * 100))

}

res.EQMP = sum(as.numeric(RMSEP$ecartPrediction))/nlignes

res.REQMP = sqrt(res.EQMP)

cat("----")

res = list(simulations = RMSEP, estimation = c(EQMP = res.EQMP,

REQMP = res.REQMP))

print(res$estimation)

})

return(res)

}

function (nls, reponse, data)

{

resultat = cbind(data.frame(ind = 1, predit = 1, realise = 1,

ecartSq = 1), t(data.frame(coefficients(nls))))

for (i in 1:nrow(data)) {

modeleMoinsUn <- update(nls, data = data[-i, ])

predit = predict(modeleMoinsUn, newdata = data[i, ])

realise = data[i, reponse]

ecartSq = (predit - realise)^2

resultat[i, ] = c(rownames(data[i, ]), predit, realise,

ecartSq, coefficients(modeleMoinsUn))

cat(round(i/nrow(data) * 100), "")

}

cat("%\n")

EQMP = sum(as.numeric(resultat$ecartSq))/nrow(data)

REQMP = sqrt(EQMP)

res = list(estimations = resultat, validation = c(BIC = BIC(nls),

AIC = AIC(nls), EQMP = EQMP, REQMP = REQMP))

return(res)

}

Annexe IX : Résultats détaillés de l'ACP sur variables pluviométriques

Valeurs propres :

comp 1 comp 2 comp 3 comp 4 comp 5 comp 6 comp 7 comp 8

eigenvalue

	percentage of variance	cumulative percentage of variance
5,51	68,90	68,90
1,12	13,98	82,89
0,87	10,91	93,80
0,30	3,78	97,58
0,18	2,22	99,80
0,01	0,12	99,92
0,01	0,06	99,98
0,00	0,02	100,00

x

Coordonnées des variables :

Dim.1 Dim.2

pluvio.J5	0,80	-0,56
pluvio.J10	0,88	-0,32
pluvio.J15	0,85	-0,04
pluvio.J20	0,80	0,08
pluieEff.J5	0,84	-0,28
pluieEff.J10	0,88	0,08
pluieEff.J15	0,83	0,47
pluieEff.J20	0,75	0,62

Contribution des variables :

Dim.1 Dim.2

pluvio.J5	11,63	27,54
pluvio.J10	13,94	9,38
pluvio.J15	13,19	0,11
pluvio.J20	11,53	0,58
pluieEff.J5	12,78	7,17
pluieEff.J10	14,15	0,58
pluieEff.J15	12,57	19,98
pluieEff.J20	10,21	34,65

Loadings :

	comp 1	comp 2
pluvio.J5	0,34	-0,52
pluvio.J10	0,37	-0,31
pluvio.J15	0,36	-0,03
pluvio.J20	0,34	0,08
pluieEff.J5	0,36	-0,27
pluieEff.J10	0,38	0,08
pluieEff.J15	0,35	0,45
pluieEff.J20	0,32	0,59

xi

Annexe X : Catégorisation des groupes issues d'une classification ascendante hiérarchique

> load("../../../RoutputsV2/tables/analysesModeleVC/lsHCPC.Rda") > lsHCPC$HCPC$desc.var

$test.chi2

p.value df

precocite 0,03649405 2

annee 0,09044460 4

$category

$category$`1` NULL

$category$`2`

Cla/Mod Mod/Cla Global p.value v.test
precocite=tardif 52,94118 81,81818 50,00000 0,02550983 2,233594

annee=2006 71,42857 45,45455 20,58824 0,04752830 1,981562
precocite=precoce 11,76471 18,18182 50,00000 0,02550983 -2,233594

$category$`3` NULL

$quanti.var

Eta2 P-value

(Intercept) 0,7046974 6,153793e-09

pl 0,5053773 1,824934e-05

CEC 0,1992899 3,190564e-02

$quanti $quanti$`1`

v.test Mean in category Overall mean sd in category Overall sd

longitude -1,97590 1,130244 2,648291e+00 2,962962 2,448134

pl -4,03478 -4,298241 6,452763e-15 2,340266 3,394581
p.value

longitude 4,816607e-02

pl 5,465349e-05

$quanti$`2`

v.test Mean in category Overall mean sd in category Overall sd

pl 2,130394 1,820358 6,452763e-15 2,6454204 3,3945814

pH 1,831482 7,609091 7,270588e+00 0,7597303 0,7342581

latitude 1,743900 48,690307 4,818540e+01 1,0359882 1,1502074

CEC -2,340972 9,563636 1,271059e+01 2,0920945 5,3405160

(Intercept) -3,673128 -10,342040 -9,748985e-14 6,0222612 11,1856060
p.value

pl 0,033139066

pH 0,067028569

latitude 0,081176544

CEC 0,019233595
(Intercept) 0,000239599

$quanti$`3`

v.test Mean in category Overall mean sd in category Overall sd

(Intercept) 4,722153 10,34841 -9,748985e-14 5,394961 11,185606

CEC 2,264556 15,08000 1,271059e+01 5,656996 5,340516
p.value

(Intercept) 2,333612e-06

CEC 2,353992e-02

attr(,"class")

[1] "catdes" "list "

Résumé

Le contexte économique et les risques de transfert dans l'environnement amènent à limiter le recours aux engrais azotés de synthèse. Pour maintenir les niveaux de productions actuelles, l'amélioration de l'efficacitédes apports d'engrais azotés apparaît comme une solution tangible. Le Coefficient Apparent d`Utilisation de l'engrais (CAU) est la grandeur adéquate pour quantifier l'efficacitéde l'apport. Des travaux antérieurs suggèrent que le CAU estiméàla récolte est déterminédès le moment de l'apport par : la vitesse de croissance de la culture (VC), la pluviométrie, l'Indice de Nutrition Azotée (INN) et la forme du fertilisant ((Limaux, 1999; Recous et al., 1997; Le Souder et al., 2007)). A partir de ces hypothèses, on souhaite établir un modèle explicatif du CAU. 38 essais ont étéconduits par Arvalis - Institut du Végétal de 2004 à2006, répartis en France, semés en blétendre d'hiver (Triticum aestivum) et exposés àdes modalités de fertilisation variables. Par le suivi de l'évolution de la biomasse et de la teneur en azote des tissus végétaux il est possible de déterminer : les CAU, la VC à partir d'ajustement des cinétiques de croissance, l'INN, et des variables pluviométriques. La construction d'un modèle explicatif met en évidence le rôle prépondérant de la forme du fertilisant. La pluviométrie, par la modulation de la mise en solution de l'azote de l'engrais, explique le CAU en interaction avec la VC et l'INN. La variabilitédes résultats entre essais àgrande échelle diminue le pouvoir prédictif de la relation obtenue et souligne la nécessitécaractériser davantage le milieu dans de prochaines expérimentations.

The economic context and environmental transfer hazard lead to limit using of synthetic N fertilizer. To maintain current production levels, improving the fertilizer efficiency appears as a tangible solution. Nitrogen Use Efficiency (NUE) is the right indicator to quantify the fertilization effectiveness. Previous works suggest the harvest stage NUE is determined at fertilization application date by : the growth rate of the culture (GR), rainfall, Nitrogen Nutrition Index (NNI) and the fertilizer form (Limaux 1999, Recous 1997, Souder et al., 2007). From these assumptions, we need to establish an explanatory model of NUE. 38 trials were conducted by Arvalis - Institut du végétal from 2004 to 2006, located in France, sown with winter wheat (Triticum aestivum) and exposed to variable fertilization application. Following the biomass evolution and plant nitrogen content it is possible to determine : NUE, the GR from growth kinetics adjustments, NNI, and rainfall. The explanatory model adjustment highlights the fertilizer form role. Rainfall, by modulating the dissolution of nitrogen fertilizer in interaction with the GR and NNI explain NUE. The results variability within large-scale trials reduces the predictive power of the relationship and underline the requirement to characterize the environment in future experimentations.

	Diplôme : Ingénieur Agronome Spécialité : Statistiques appliquées Enseignant référent : Julie JOSSE
Auteur : François COLLIN Date de naissance : 2 avril 1989		Organisme d'accueil : Arvalis - Institut du végétal Adresse : Station Expérimentale de la Jaillière 44 370 LA CHAPELLE SAINT SAUVEUR Maître de stage : Jean-Pierre COHAN
Nb pages : 48 Annexes : 10
Année de soutenance : 2012
Titre français : Modélisation du coefficient apparent d'utilisation de l'azote issu d'un engrais minéral apporté sur blé tendre d'hiver Titre anglais : Modelling the Nitrogen Use Efficiency of a inorganic nitrogen fertilizer application on winter wheat
Résumé Le contexte économique et les risques de transfert dans l'environnement amènent à limiter le recours aux engrais azotés de synthèse. Pour maintenir les niveaux de productions actuelles, l'amélioration de l'efficacité des apports d'engrais azotés apparaît comme une solution tangible. Le Coefficient Apparent d`Utilisation de l'engrais (CAU) est la grandeur adéquate pour quantifier l'efficacité de l'apport. Des travaux antérieurs suggèrent que le CAU estimé à la récolte est déterminé dès le moment de l'apport par : la vitesse de croissance de la culture (VC), la pluviométrie, l'Indice de Nutrition Azotée (INN) et la forme du fertilisant (Limaux 1999, Recous 1997, Le Souder et al., 2007). A partir de ces hypothèses, on souhaite établir un modèle explicatif du CAU. 38 essais ont été conduits par Arvalis - Institut du végétal de 2004 à 2006, répartis en France, semés en blé tendre d'hiver (Triticum aestivum) et exposés à des modalités de fertilisation variables. Par le suivi de l'évolution de la biomasse et de la teneur en azote des tissus végétaux il est possible de déterminer : les CAU, la VC à partir d'ajustement des cinétiques de croissance, l'INN, et des variables pluviométriques. La construction d'un modèle explicatif met en évidence le rôle prépondérant de la forme du fertilisant. La pluviométrie, par la modulation de la mise en solution de l'azote de l'engrais, explique le CAU en interaction avec la VC et l'INN. La variabilité des résultats entre essais à grande échelle diminue le pouvoir prédictif de la relation obtenue et souligne la nécessité caractériser davantage le milieu dans de prochaines expérimentations.
Abstract The economic context and environmental transfer hazard lead to limit using of synthetic N fertilizer. To maintain current production levels, improving the fertilizer efficiency appears as a tangible solution. Nitrogen Use Efficiency (NUE) is the right indicator to quantify the fertilization effectiveness. Previous works suggest the harvest stage NUE is determined at fertilization application date by: the growth rate of the culture (GR), rainfall, Nitrogen Nutrition Index (NNI) and the fertilizer form (Limaux 1999, Recous 1997, Souder et al., 2007). From these assumptions, we need to establish an explanatory model of NUE. 38 trials were conducted by Arvalis - Institut du végétal from 2004 to 2006, located in France, sown with winter wheat (Triticum aestivum) and exposed to variable fertilization application. Following the biomass evolution and plant nitrogen content it is possible to determine: NUE, the GR from growth kinetics adjustments, NNI, and rainfall. The explanatory model adjustment highlights the fertilizer form role. Rainfall, by modulating the dissolution of nitrogen fertilizer in interaction with the GR and NNI explain NUE. The results variability within large-scale trials reduces the predictive power of the relationship and underline the requirement to characterize the environment in future experimentations.
Mots-clés : Fertilisation, CAU, blé tendre d'hiver, cinétique, vitesse de croissance, INN