Etude de la demande de monnaie selon ses différentes formes. Cas du Maroc

Année universitaire : 2012/2013

Université Hassan II Mohammedia

Faculté des Sciences Juridiques Economiques et Sociales

Master : Techniques de Modélisation Economiques et Econométrie

Mémoire de Master d'université sous le thème

Etude de la demande de monnaie selon ses

différentes formes : Cas du Maroc

Préparé par : Mr Amine TEFFAL

Sous la direction de : Mr. Ahmed HEFNAOUI

Mr. Ahmed HEFNAOUI , professeur d'enseignement supérieur à la faculté des sciences juridiques, économiques et sociales de Mohammedia

Membres de jury :
Président : Ahmed HEFNAOUI
Suffragants :
Mr . Aziz OUIA : Professeur à la FSJES Mohammedia
Mr . Mohammed MOUTMIHI : Professeur à la FSJES Mohammedia
Mr . Mbarek AOUFIR : Professeur à la FSJES Mohammedia

2

Résumé

La littérature est abondante en ce qui concerne les études économétriques réalisées sur la demande de monnaie. La plupart de ces études utilisent l'agrégat large M3 et dans une moindre mesure l'agrégat étroit M1, mais rares sont celles qui traitent d'un agrégat plus étroit. Dans cette étude, nous avons donc tenté de modéliser la demande de monnaie fiduciaire, scripturale et enfin celle contenue dans le sous-agrégat M3-M1. Les variables explicatives que nous avons utilisés sont le PIB et le taux sur compte de carnet publié par Bank Al-Maghrib.

Dans un premier temps nous avons fait recours à la modélisation univariée, puis dans un second temps à une modélisation multivariée. Dans la première, nous avons adopté une spécification en niveau puis une autre en termes de logarithme. Dans la deuxième, nous n'avons adopté que la spécification logarithmique qui a donné de meilleurs résultats dans le cas univarié. Les coefficients obtenus dans la spécification logarithmique ont été interprétés comme des élasticités-revenu et comme des semi-élasticité-taux. L'hypothèse d'une élasticité-revenu unitaire qui permet d'interpréter la relation de long terme comme une équation de vitesse de circulation a été donc testée.

3

Abstract

The literature is abundant with respect to econometric studies on the demand for money. Most of these studies use the broad aggregate M3 and to a lesser extent the narrow aggregate M1, but rare are those that deal with a more narrow aggregate. In this study, we have therefore tried to model the demand of currency, bank money and that contained in the M3 - M1 sub-aggregate. The explanatory variables we used are GDP and the rate on account of book published by Bank Al-Maghrib. Initially we have use univariate modeling, then in a second step a multivariate modeling. In the first one, we adopted a level specification and then another one in terms of the logarithm. In the second, we did adopt the logarithmic specification which gave better results in the univariate case. The coefficients obtained in the logarithmic specification have been interpreted as income's elasticity and as the interest's semi-elasticity. The hypothesis of a unitary income's elasticity that allows interpreting the long-term relationship as a velocity equation has been so tested.

4

Dédicace

je dédi,e ce modeste travai,L

A mes chers parewts

A mow épouse bi,ew ai,mée

A mes deux chers ewfawts ALi, et Mohammed

A ma saur K.haouLa bi,ew ai,mée

A mes deux frères Abdou et gi,LaL bi,ew .ai,més

A toute La fami,LLe

5

Remerciements

Au terme de ce travail, j'aimerai exprimer mes profonds remerciements à mon Directeur de mémoire monsieur Ahmed Hefnaoui pour l'intérêt et l'effort particulier qu'il a déployé, pour sa disponibilité, ses conseils et ses encouragements permanents, et ce, durant toutes les deux années de ce Master ainsi que durant l'élaboration de ce travail.

Je remercie également monsieur Aziz Ouia, qui n'a aménagé aucun effort pour m'apporter l'aide et le soutien nécessaire tout au long de la réalisation du mémoire.

Mes sincères reconnaissances vont à tous ceux qui, de près ou de loin, ont contribué à l'aboutissement de ce projet.

6

SOMMAIRE

Résumé

Abstract

Dédicace

Remerciements

Introduction Générale

Chapitre I : La demande de monnaie

Section 1 : La monnaie

Section 2 : La fonction de demande de monnaie

Section 3 : La demande de monnaie au Maroc

Chapitre II : Etude des séries utilisées pour l'estimation de la demande de monnaie

Section 1 : Rappel sur les stratégies de tests de Dickey-Fuller

Section 2 : Etude des séries utilisées

Chapitre III : Estimation de la demande de monnaie dans le cas du Maroc

Section 1 : ESTIMATION D'UNE FONCTION DE DEMANDE DE MONNAIE POUR LA ZONE EURO PAR LA

BANQUE DE FRANCE

Section 2 : Estimation univariée de la demande de monnaie Section 3 : Estimation multivariée de la demande de monnaie Conclusion

Bibliographie

ANNEXE : Données utilisées

7

Introduction Générale

Durant les deux siècles qui ont précédé, plusieurs théories économiques se sont succédées pour essayer d'expliquer le rôle de la monnaie dans l'économie d'un pays. Certaines de ces théories ont vu le jour lorsque que la monnaie n'était que sous forme de pièces de monnaie et billets de banque, alors que d'autres sont apparues avec le processus de dématérialisation de la monnaie qui a donné naissance à la « monnaie scripturale ». Cette nouvelle forme de monnaie a la particularité unique de pouvoir être créée selon certains "ex nihilo" (à partir de rien, mais en réalité en contrepartie d'engagements économiques).

Ces différentes théories s'opposent sur le rôle de la monnaie dans l'économie. Les classiques et néo-classiques considèrent que la monnaie est neutre, les keynésiens affirment que la monnaie est active et qu'elle peut être utilisée pour améliorer les performances économiques, et les monétaristes pensent que la monnaie est active, mais que son utilisation est surtout nocive à l'économie. Pour ces derniers, la monnaie n'aurait aucun effet sur le niveau de production d'une économie. Cependant, si on exclut l'équation de FISHER sous sa forme séparant d'une part la monnaie sous forme de pièces et de billets, et d'autre part les dépôts bancaires, aucune de ces théories ne focalise sur le rôle de chacune des formes de monnaie séparément : monnaie fiduciaire et monnaie scriptural. De même, les différentes études empiriques réalisées sur la demande de monnaie utilisent très souvent l'agrégat large M3 ou dans une moindre mesure l'agrégat étroit M1.

C'est à partir de ce dernier constat, qu'il nous est venu l'idée de mener cette étude qui a pour objectif de modéliser la demande de monnaie fiduciaire (M1_FID), la demande de monnaie scripturale (M1_SCR), qui contient essentiellement les dépôts à vue, et enfin la demande de monnaie qui ne contient que les comptes d'épargne auprès des banques et les comptes sur livrets auprès de la caisse d'épargne nationale ainsi que les comptes à terme et bons de caisse auprès des banques (M3_M1).

La modélisation de ces trois formes de monnaie, nous permettra de répondre aux deux questions suivantes :

- Est-ce que le motif se spéculation, tel que défini par Keynes, peut être mis en évidence pour chacune de ces trois formes ou bien ne concerne t-il qu'une seule forme ?

- Est-ce que les vitesses de circulation, les élasticité-revenu et les semi-élasticité-taux sont les mêmes pour ces trois forme ?

Pour répondre à la première question, nous adopterons une spécification additive de la demande en niveau en se basant sur la formule de Keynes : M = L1(R) +L2(i). Keynes n'émettant aucune hypothèse sur les formes analytiques de L1 et L2, nous adopterons la plus simple à savoir la forme linéaire bien que celle-ci ne prend pas en compte la présence de « la trappe à la liquidité ».

En ce qui concerne la deuxième question, il se trouve que la spécification en termes de logarithme est la plus adaptée puisque les coefficients sont interprétés directement comme des élasticités ou semi-élasticités.

Ainsi, notre travaille sera structuré comme suit : dans le premier chapitre nous présenterons dans la première section une définition de la monnaie selon la pensée classique et néoclassique, la pensée Keynésienne et enfin selon la pensée des monétaristes notamment celle de Friedman. Nous y aborderons également les formes de la monnaie ainsi que les différents agrégats monétaires. Dans la deuxième section, nous allons aborder la fonction de demande de monnaie, toujours selon les trois pensées précitées mais cette fois-ci en détaillant plus celle de Keynes étant donné qu'elle servira de base pour notre étude empirique dans le troisième chapitre. La troisième section sera consacrée à l'étude de la demande de monnaie au Maroc.

8

Dans le deuxième chapitre nous allons commencer par faire un rappel sur les stratégies de tests de Dickey-Fuller (Section 1) puis nous finirons par l'étude de la stationnarité des différentes séries que nous avons utilisées pour estimer la demande de monnaie (Section 2).

Enfin, le troisième chapitre sera consacré à l'estimation de la demande de monnaie dans le cas du Maroc. Il nous a apparu essentiel de disposer d'une base de comparaison pour nos résultats. Par conséquent, nous avons consacré la première section de ce chapitre à la présentation des résultats d'une étude économétrique de la demande de monnaie réalisée sur des données de la zone euro, et ce n'est que dans la deuxième et la troisième section que nous avons abordé l'estimation univariée et celle multivariée de la demande de monnaie au Maroc.

Nous finirons notre travaille par une synthèse des résultats obtenus et une conclusion.

9

Chapitre I : La demande de monnaie

Ce chapitre sera consacré à la présentation du cadre théorique sur lequel portera notre analyse empirique. Nous présenterons dans la section 1 une définition de la monnaie selon la pensée classique et néo-classique, la pensée Keynésienne et enfin selon la pensée des monétaristes notamment celle de Friedman. Nous y aborderons également les formes de la monnaie ainsi que les différents agrégats monétaires. Dans la section 2, nous allons aborder la fonction de demande de monnaie, toujours selon les trois pensées précitées mais cette fois-ci en détaillant plus celle de Keynes étant donné qu'elle fera l'objet de notre étude empirique dans la partie empirique. La section 3 sera consacrée à l'étude de la demande de monnaie au Maroc.

Section 1 : La monnaie

La monnaie est mieux définie par les fonctions qu'elle remplie :

Fonction d'échange : La monnaie sert de moyen de paiement, reconnu par tous, dans toutes les transactions.

Fonction de compte : La monnaie sert d'unité de compte c'est-à-dire d'instrument de mesure de la valeur des biens. Elle le fait par leur prix : il s'agit donc de la valeur d'échange des biens, qui n'est pas nécessairement la même que leur valeur intrinsèque. Dans la mesure où tous les biens ont un prix dans une économie de marchés, la monnaie offre un moyen de comparer tous les biens entre eux.

Fonction de réserve de valeur : Celle-ci résulte de ce que la monnaie permet de séparer dans le temps les actes de vente et d'achat. L'encaisse monétaire obtenue lors d'une vente est un pouvoir d'achat mis en réserve, qui pourra être réutilisé lors d'un achat ultérieur. À ce titre, elle est une forme possible d'épargne, un « actif », et joue donc un rôle d'intermédiaire entre les ressources présentes et les biens futurs.

I- La monnaie chez les classiques et les néo-classiques

Pour les classiques et les néo-classiques, la monnaie n'est qu'un bien comme les autres, choisi comme étalon de référence pour fixer le prix des autres biens. Elle n'est donc qu'un moyen d'échange et le seul motif de sa détention est le motif de transaction.

Pour J.B Say, l'échange à l'aide de la monnaie n'est qu'une illusion d'optique : dans tout échange monétaire (biens contre monnaie, ou services contre monnaie) se cachent en fait des échanges réels : biens contre services, biens contre biens, services contre services

10

Dans son ouvrage « Traité d'économie politique - Livre I - chapitre XXI », il affirme même que l'idée selon laquelle les échanges sont le fondement essentiel de la production des richesses est fausse et qu'elle n'est que accessoire étant donnée que si chaque famille dans une société peut produire tous ce dont elle a besoin, il n'y aurait pas d'échanges.

Mais ensuite, il a souligné l'indispensabilité des échanges dans les sociétés modernes en montrant combien il serait difficile si les échanges se faisaient en nature. Ainsi, il admet la nécessité d' « une marchandise qui soit recherchée non à cause des services qu'on en peut tirer par elle-même, mais à cause de la facilité qu'on trouve à l'échanger contre tous les produits nécessaires à la consommation, une marchandise dont on puisse exactement proportionner la quantité qu'on en donne avec la valeur de ce qu'on veut avoir ». C'est cette marchandise qu'il dénomme monnaie.

Ensuite, il définit deux qualités essentielles que la monnaie possède et qui la rend préférable à un bien de valeur:

- Etre un moyen d'échange acceptable par tout le monde - Etre parfaitement divisible

Pour Ricardo, La valeur d'une marchandise, ou la quantité de toute autre marchandise contre laquelle elle s'échange, dépend de la quantité relative de travail nécessaire pour la produire et non de la rémunération plus ou moins forte accordée à l'ouvrier. Ainsi, pour lui ni l'or, ni aucun autre objet ne peuvent servir à mesurer exactement la valeur des marchandises.

II- La monnaie chez Maynard Keynes

Contrairement aux classiques et aux néo-classiques, Keynes accorde une grande importance à la monnaie. Il l'introduit dans sa théorie générale à travers la théorie de la préférence pour la liquidité (liquidity-preference) et celle du taux d'intérêt, moyennant la formule ci-dessous :

M = L(r)

Où : M est la quantité de monnaie, L la fonction de préférence pour la liquidité et r le taux d'intérêt qu'il définit comme étant le « prix » qui équilibre le désire de détenir la richesse sous forme de « cash » avec la quantité de « cash » disponible.

Pour lui, la monnaie possède des caractéristiques spéciales qui la différencient par rapport aux autres biens. Il résume ses caractéristiques comme suit :

· La monnaie a un rendement nul que ce soit dans le court ou dans le long terme,

· son élasticité-production est égale à zéro ou au moins très petite,

· elle a une élasticité de substitution presque égale à zéro, c'est-à-dire qu'il n'y a aucun autre bien qui peut lui être substitué.

11

III. La monnaie chez Friedman

Pour Friedman, la monnaie n'est qu'un actif comme les autres et il ne lui reconnaît aucune propriété particulière à part le fait qu'elle est la plus liquide et celle qui a le rendement le plus bas par rapport à tous les actifs. D'ailleurs, il l'analyse avec la théorie générale de la demande d'actifs.

Selon lui, la monnaie est un patrimoine parmi les autres, qu'il classe en quatre catégories :

- Le stock de monnaie

- Les actifs financiers (Actions, obligations,...)

- Les actifs réels (Maisons, immeubles, terrains,...)

- Les actifs humains : Le capital humain des individus (Formation, instruction, compétences,...)

IV. Les formes de la monnaie

La monnaie a connu au cours de son histoire plusieurs formes. Ainsi, les premières formes de la monnaie ont été la monnaie marchandise et la monnaie métallique (pièce) qui présente l'intérêt d'être homogène, divisible et de faible volume.

Les formes actuelles de la monnaie sont :

· La monnaie divisionnaire : c'est l'ensemble des pièces ou monnaie métallique. Elle est utilisée dans les transactions de faibles montants (pièces de 5, 10, 20 et 50 centimes, pièces de 1, 2, 5 et 10 Dirhams)

· La monnaie fiduciaire : c'est une monnaie dont la valeur repose uniquement sur la confiance que lui accordent les agents économiques. Ainsi, la valeur d'une pièce n'a aucun lien avec la valeur du métal qui la constitue. De même, la valeur d'un billet ne correspond pas à une contrepartie en métal physique qu'une banque garantirait. Cette définition ne se réfère pas à la forme physique de la monnaie (métal ou papier). Par conséquent on comprend que la monnaie fiduciaire inclut aussi bien les pièces métalliques que les billets de banque (Billets de 20, 25, 50, 100 et 200 Dirhams)

· La monnaie scripturale¹ : comme son nom l'indique, cette monnaie n'existe que sous forme d'écritures comptables. Le support monétaire de la monnaie scripturale est, aujourd'hui, une information contenue dans des fichiers informatiques. Elle est constituée de l'ensemble des dépôts dans les organismes financiers. Elle circule par jeux d'écritures (électroniques le plus souvent) entre comptes par l'intermédiaire d'instruments tels que les chèques ou les virements. La monnaie scripturale doit normalement être considérée comme monnaie fiduciaire puisqu'il est évident que les agents économiques lui accordent la même confiance accordée aux pièces et billets de banque. Cependant, on réserve exclusivement le terme de "fiduciaire" à la monnaie qui se présente sous la forme de billets et de pièces.

¹ Définition LAROUSSE : Relatif à l'écriture.

V- Les agrégats monétaires

Les agrégats monétaires comme définis par Bank Al-Maghrib (BAM) sont comme suit :

V-1- L'agrégat M1

Cet agrégat comprend, d'une part, la monnaie fiduciaire qui inclut les billets et monnaies mis en circulation par BAM et les encaisses des banques², et d'autre part, la monnaie scripturale qui inclut :

· les dépôts à vue auprès de la banque centrale,

· les dépôts à vue auprès des banques,

· les dépôts à vue auprès du CCP³ et

· les dépôts à vue auprès du Trésor.

V-2- L'agrégat M2

Cet agrégat comprend, en plus de M1, les comptes d'épargne auprès des banques et les comptes sur livrets auprès de la CEN⁴.

V-3- L'agrégat M3

Cet agrégat contient, en plus de M2, les comptes à terme et bons de caisse auprès des banques.

12

²Liquidités leurs permettant de faire face aux retraits des clients.

³ Compte Chèque Postal

⁴ Compte d'Epargne Nationale

13

Section 2 : La fonction de demande de monnaie

I- La demande de monnaie chez les classiques et les néo-classiques

Pour les classiques, le seul motif de détention de la monnaie est le motif de transaction. En plus, ils considèrent qu'il y a absence d'interaction entre ce qui est monétaire et ce qui est réel (activité économique de production et de consommation des biens) et supposent même, que les agents économiques font une évaluation précise de la monnaie à court terme comme à long terme c'est-à-dire qu'ils anticipent le niveau général des prix, ce qui est bien sûr irréaliste. On comprend donc de l'analyse classique que la monnaie n'est pas détenue comme réserve de valeur.

Cette approche par les transactions a été formalisée à l'aide de deux équations bien connues : l'équation de FISHER et celle de MARSHALL.

I-1- L'équation de FISHER

L'équation de FISHER s'écrit comme suit :

M.V + M'.V' = PT

Où :

M : représente les pièces de monnaie et les billets de banques

M' : représente les dépôts bancaires

V : représente la vitesse de circulation des pièces de monnaie et des billets de banque

V' : représente la vitesse de circulation des dépôts bancaire

P : représente le niveau général des prix

T : représente le volume des transactions dans l'unité de temps.

Une formulation plus simple confondant les deux formes de monnaie s'écrit : M.V = P.T

La vitesse de circulation est en fait le nombre de fois où une unité de monnaie est échangée dans les transactions. Il s'agit donc d'une vitesse moyenne puisque toutes les unités monétaires ne s'échangent pas le même nombre de fois.

Cette équation est basée sur le principe évident suivant :

Toute transaction met en relation un acheteur et un vendeur et par conséquent, chaque vente correspond un achat et le montant des ventes est nécessairement égal au montant des ventes et ce, pour l'ensemble de l'économie.

Cette équation nous dit tout simplement que les dépenses totales mesurées par la quantité de monnaie multipliée par le nombre moyen des échanges qu'une unité monétaire a été échangée durant une période donnée, sont nécessairement égales aux nombre total de transactions effectuées durant cette même période, multipliés par le prix moyen des biens échangés.

Pour illustrer ce principe, considérons une économie où il y a trois agents et un seul bien. En début de période :

· Le premier agent possède 100 unités d'un bien dont le prix est 1 DH mais ne possède pas de monnaie

· Le deuxième agent ne possède aucun bien mais par contre possède 100 DH

· Le troisième agent lui aussi ne possède aucun bien mais possède 200DH.

Agent 2 :

· 0 bien

· 100 DH

Agent 3 :

· 0 bien

· 200 DH

Début de période :

Agent 1 :

· 100 biens (prix unitaire 1 DH)

· 0 DH

14

Au cours de la période, les deux échanges ont eu lieu :

Echange 1 : l'agent 1 vend les 100 biens à l'agent 2 au prix unitaire de 1 DH Echange 2 : l'agent 2 revend les 100 biens à l'agent 3 au prix unitaire de 1 DH A la fin de la période on a la situation ci-dessous :

Fin de période :

				Agent 1 :
Agent 2 :	Agent 3 :		· 0 bien · 100 DH
· 0 bien · 100 DH	· 100 biens · 100 DH

Vérifions si l'équation de FISHER est vraie pour cet exemple et calculons donc chacun des termes de cette équation :

- Calcul de M :

La masse monétaire en circulation est évidemment égale à 300 DH

15

- Calcul de V :

Il y a eu deux échanges : le premier échange concerne les 100 DH qui étaient chez l'agent 2. Chaque unité de ces cents dirhams a donc une vitesse de 1 (échangée une seule fois dans la période).

Le deuxième échange concerne les 100 DH qui étaient chez l'agent 3 (parmi les 200 DH qu'il avait en début de période). Chaque unité de ces cents dirhams a donc une vitesse de 1 (échangée une seule fois dans la période).

Par contre, les 100 unités monétaires non utilisées par l'agent 3 durant la période, ont une vitesse égale à zéro (non échangées dans la période). La vitesse moyenne est donc :

(? 1 ? 0 200 ~~~ i=1 300		200 ~ 300

- Calcul de P :

Nous n'avons qu'un seul bien, donc le prix moyen est évidement égal au prix de ce bien c'est-à-dire 1 DH.

- Calcul de T :

Pour le premier et le deuxième échange nous avons 100 transactions pour chaque échange (100 biens échangés pour un prix unitaire de 1 DH). Donc, T = 200.

On peut maintenant vérifier l'équation :

Le membre droit de l'équation vaut : M. V = 300 X ~~~

~~~ = 200

Le membre gauche vaut : P.T = 1 x 200 = 200

L'équation est donc bien vérifiée.

D'une manière générale, on peut démontrer cette équation de la façon suivante :

Soit une économie avec M unités monétaires. Supposons qu'au cours d'une période il ya eu T Transactions et que lors de chaque transaction un bien Bi a été vendu au prix Pi (les T biens peuvent être identiques ou non). Supposons de plus que chaque unité monétaire a été échangée ni fois (ni peut être nul). Alors, étant donné que tous les échanges de monnaie correspondent à toutes les transactions effectuées durant la période, on a nécessairement :

M T

>n1 = >pi

i=1 j=1

Si on définit la vitesse moyenne comme suit :

? ni

M

i=l

~ ~ M

Alors on a : M.V = ? ~~

~ ~~~

De même, si on définit le prix moyen comme suit :

? ~~ ~

~~~

~ ~ ~

Alors on a : P.T = ? ~~

~~~

~

Et par conséquent ; on a : M.V = P.T

Cette équation n'est pas une véritable fonction de demande de monnaie. Elle ne traduit pas une encaisse monétaire désirée, mais une encaisse nécessaire pour effectuer les transactions. En effet, dans une économie, la monnaie qui circule est nécessairement égale à la monnaie que réclament les agents économiques en contrepartie de la valeur de leurs transactions économiques.

I-2- L'équation de MARSHALL

L'équation de Marshall se présente sous la forme suivante :

1

P .M = K.R

Où :

M : représente la masse monétaire

P : représente le niveau général des prix et 1/P le pouvoir d'achat de la monnaie K : représente la vitesse de transformation de la monnaie en revenu

R : représente le montant des revenus dans l'unité de temps.

Même si cette équation paraît différente de celle de FISHER, elle peut être mise sous une forme équivalente. En effet,

1 ~ .M = K.R M.

1 K

= P.R

16

Et on voit donc que (1/K) et R correspondent respectivement à V et T dans l'équation de FISHER.

II- La demande de monnaie chez Maynard Keynes

Dans son ouvrage « Théorie générale de l'emploi, de l'intérêt et de la monnaie » John Maynard Keynes renonce à l'hypothèse fondamentale des classiques selon laquelle la vitesse de circulation de la monnaie est constante. Sa nouvelle théorie dite théorie de la préférence pour la liquidité se base plutôt sur les motifs de détention de la liquidité par les agents économiques. Selon Keynes, il y a trois motifs de détention de liquidité :

17

- Le motif de transaction - Le motif de précaution

- Le motif de spéculation.

II-1- Le motif de transaction

Chez les classiques, les individus détiennent la monnaie pour sa fonction d'échange pour effectuer des transactions quotidiennes. Keynes suppose en plus que cette demande est proportionnelle au revenu.

II-2- Le motif de précaution

Pour Keynes, non seulement les agents détiennent la monnaie pour effectuer des transactions quotidiennes, mais également pour se prémunir de dépenses imprévisibles et inattendues comme par exemple les réparations automobiles de voiture, les frais d'hospitalisation, les amendes de circulation,...etc. Là encore, Keynes suppose que la monnaie détenue pour ce motif est proportionnelle au revenu.

II-3- Le motif de spéculation

La grande différence entre la théorie de Keynes et celle des classiques et des néoclassiques, c'est qu'il suppose qu'en plus du motif de transaction et de précaution, les agents détiennent la monnaie également pour un motif de spéculation. Selon lui, la monnaie est une réserve de richesse (ou de valeur) et pas seulement un moyen d'échange. Il suppose toujours que la quantité de monnaie détenue pour motif de spéculation est proportionnelle au revenu mais aussi et surtout du taux d'intérêt. Keynes distingue deux types d'actifs seulement utilisables comme réserve de valeur : La monnaie et les titres.

Pour lui, la monnaie a un rendement nul, mais les agents n'y renonceront pour les titres que si la somme des intérêts perçus de la détention de ces titres et la variation du prix de ceux-ci est supérieure à leur valeur d'achat. Keynes va plus loin et suppose que les agents pensent que le taux d'intérêt fluctue autour d'une valeur normale de telle sorte que lorsque celui-ci est très inférieur à cette valeur, alors les agents anticipent une hausse des taux et par conséquent une baisse de la valeur de leurs titres et préfèrent donc détenir la monnaie. Dans cette situation la demande de monnaie est forte. Au contraire, lorsque les taux sont très supérieurs à cette valeur, alors les agents anticipent une baisse des taux et par conséquent une hausse de la valeur de leurs titres et préfèrent donc les garder. Dans cette situation la demande de monnaie est faible. Ainsi, la principale conclusion de son raisonnement, est que la demande de monnaie pour motif de spéculation est une fonction décroissante du taux d'intérêt.

II-4- Fonction de préférence pour la liquidité

Même si Keynes distingue trois motifs de demande de monnaie, il ne propose en fait qu'une seule fonction unique de demande de monnaie qu'il appelle « fonction de préférence pour la liquidité ». Mais il précise que cette demande doit être évaluée à son pouvoir d'achat étant donné que lorsque les prix sont multiplié par un coefficient k (2 par exemple), alors la quantité de biens qu'on peut avoir avec la même monnaie se trouve divisée par ce même coefficient k. Ainsi, la fonction de demande de monnaie que propose Keynes relie la demande d'encaisses réelles, M/P (avec P le niveau général des prix), au taux d'intérêt i et au revenu Y. La formulation mathématique de la fonction qu'il propose s'écrit alors comme suit :

18

M

~ = f(i,!)

Où :

M : est la quantité de monnaie demandée

P : est l'indice général des prix

i : est le taux d'intérêt

Y : est le revenu

D'après les raisonnements qui ont précédé, f est une fonction décroissante en i et croissante

en Y.

La principale différence entre la théorie de Keynes et celle de FISHER est que la demande

de monnaie chez Keynes dépend du taux d'intérêt alors que chez FISHER celui-ci ne joue

aucun rôle.

De cette équation on peut déduire l'expression de la vitesse de circulation de la monnaie

définie par : V = "# ~ :

P.! P.! !

V =		P.f(i,!) =

Deux conclusions peuvent être tirées de cette équation :

· La vitesse de circulation n'est pas constante

· La vitesse de circulation varie dans le même sens que le taux i : A revenu constant, lorsque i augmente f (i,Y) diminue et donc V augmente et vice-versa.

III- La demande de monnaie chez Friedman

La principale critique de Friedman concernant la théorie de demande de monnaie de Keynes porte sur les variables expliquant cette demande, à savoir le revenu et le taux d'intérêt. Pour lui, la demande de monnaie ne dépend pas du revenu quotidien, mais de l'ensemble des revenus présents, passés et futurs. En plus, elle ne dépend pas uniquement du taux d'intérêt, mais de tous les actifs financiers disponibles. En effet, l'agent économique détermine sa demande de monnaie en tenant compte de toutes les autres formes possibles qu'il peut donner à ses actifs : sa préférence dépendra de leurs rendements et de leurs gains respectifs.

Friedman n'explique pas la demande de monnaie en analysant ses motifs de détention comme a fait Keynes, mais il la considère plutôt analogue à la demande de n'importe quel actif. Par conséquent, il l'analyse avec la théorie générale de la demande d'actifs.

Selon cette théorie, la demande de monnaie est une fonction de la richesse des individus et des différentiels des rendements anticipés des différents titres disponibles par rapport au rendement anticipé de la monnaie, ce qui la traduit par l'équation ci-dessous :

Mp = f(!",$% & $',$( & $', )( & $')

19

Où :

M/P : est la demande d'encaisses réelles

YP : est la richesse au sens de Friedman, appelée « revenu permanent ». Elle est égale à la valeur actualisée de tous les revenus futurs anticipés qui correspond à un revenu moyen anticipé de long terme.

r_m : est le rendement anticipé de la monnaie

rb : est le rendement anticipé des titres autres que les actions r_e : est le rendement anticipé des actions.

ðe : est le taux d'inflation qui est ici considéré comme étant une approximation du rendement des actifs réels (maisons, immeubles,...)

La fonction f est croissante par rapport à Y_p et décroissante par rapport aux autres variables.

Comme on peut le constater d'après cette fonction, Friedman répartit les actifs en trois catégories : les titres autres que les actions, les actions et la monnaie. Les rendements anticipés des deux premières catégories de ces actifs ne sont pas introduites dans son modèle directement mais indirectement via leurs différences par rapport à celui de la monnaie à savoir r_m. Pour lui, ce rendement dépend de deux éléments :

· Les services fournis par les banques sur les dépôts : Quand la qualité ou la quantité de ces services augmentent sans hausse de leurs coûts, le rendement anticipé de la monnaie augmente

· Les intérêts payés sur les encaisses monétaires : Dans les pays, où les banques rémunèrent les comptes courants alors le rendement anticipé de la monnaie croit avec l'augmentation de cette rémunération.

Le terme ð^e-r_m dans la formule ci-dessus représente le rendement relatif anticipé des actifs réels (Maisons, immeubles,...) par rapport à la monnaie. Pour ces actifs, l'inflation anticipée ðe peut être considérée comme une approximation grossière du taux de rendement attendu. En effet, si on considère par exemple un appartement loué, alors ð^e est certainement une sous estimation du rendement anticipé qui inclut les entrées de loyers.

20

Section 3 : La demande de monnaie au Maroc

Avant d'aborder la demande de monnaie au Maroc, il est important de cerner d'abord les principes d'élaboration des statistiques monétaires servant de mesure pour cette demande.

I- Principes d'élaboration des statistiques monétaires au Maroc

Pour élaborer ces statistiques monétaires, les agents économiques sont classés en trois secteurs :

1. Le secteur émetteur de la monnaie

2. Le secteur détenteur de la monnaie

3. Le secteur neutre

I-1- Le secteur émetteur de la monnaie

Ce secteur comprend l'ensemble des sociétés financières résidentes qui ont pour principale fonction d'assurer l'intermédiation financière et qui comptent dans leur passif des éléments entrant dans la définition nationale de la monnaie au sens large. Au Maroc, ce secteur est composé de :

· Bank Al-Maghrib ;

· les banques commerciales

· les OPCVM monétaires.

Les sociétés financières émettrices de la monnaie sont dites Institutions de Dépôts (ID). On distingue entre la banque centrale d'un côté et les Autres Institutions de Dépôts (AID) d'un autre côté. Ces dernières comprennent les banques commerciales et les OPCVM monétaires.

Les OPCVM monétaires créent de la monnaie, d'une manière différente des établissements de crédit, en émettant des titres convertibles à tout moment et sans risque important de perte en capital.

En plus des actifs monétaires auprès des ID, les dépôts ouverts auprès du Trésor sont inclus dans M3 dans la mesure où ils répondent aux critères d'inclusion dans les agrégats de monnaie.

De même, les dépôts ouverts auprès de la Caisse d'Epargne Nationale (CEN) et du Centre des Chèques Postaux (CCP) étaient, avant juin 2010 inclus dans la masse monétaire. A partir de juin 2010, les services financiers de la Poste se sont transformés en banque postale (Al Barid-Bank) qui fait partie désormais des autres institutions de dépôts.

21

I-2- Le secteur détenteur de la monnaie

Ce secteur inclut tous les secteurs résidents, à l'exception des Institutions de Dépôts et de l'Administration Centrale. Il comprend :

· Les sociétés non financières publiques et privées (SNFPu et SNFPr) ;

· Les collectivités locales ;

· Les administrations de sécurité sociale ;

· Les ménages composés des particuliers, des entrepreneurs individuels et des MRE,

· Les institutions sans but lucratif au service des ménages (ISBLSM) et ;

· Les autres sociétés financières⁵ (ASF).

I-3- Le secteur neutre

L'Administration Centrale est considérée comme un secteur neutre dans la mesure où l'évolution de ses actifs financiers n'est pas déterminée par l'activité économique. En effet, les dépôts de l'AC ne réagissent pas aux phénomènes macroéconomiques de la même manière que les dépôts des secteurs détenteurs de la monnaie, compte tenu de ses spécificités, de ses contraintes de financement et de la nature de ses dépenses ainsi que des techniques de gestion de sa trésorerie.

I-4- Sources de données pour l'élaboration des statistiques monétaires

Les statistiques monétaires regroupent la situation monétaire et les situations analytiques des autres sociétés financières.

I-4-1 La situation monétaire :

L'élaboration de la situation monétaire repose sur :

1- La situation comptable de Bank Al-Maghrib qui est élaborée à partir de la situation consolidée de la Banque, conformément au plan comptable de BAM adopté en janvier 2005.

2- La situation comptable des banques commerciales et ses états annexes. Ces états fournissent des informations, en fonction de la résidence, de la monnaie et par catégorie de contrepartie sur :

· Les opérations des banques avec les établissements de crédit et assimilés

· Les opérations des banques avec la clientèle financière

· Les opérations des banques avec la clientèle non financière

· Les créances sur la clientèle par secteur d'activité

· Les titres en portefeuille par catégorie d'émetteur

⁵ Les sociétés financières autres que les Institutions de Dépôts

·

22

Les emplois et les ressources des banques en fonction de la durée initiale

· Les créances en souffrance, provisions et agios réservés

3- Les déclarations des sociétés gestionnaires d'OPCVM monétaires, transmises par le Conseil Déontologique des Valeurs Mobilières (CDVM) et établies conformément aux prescriptions du plan comptable des OPCVM, approuvé en 1995, il s'agit de :

· La répartition mensuelle de l'actif net des OPCVM monétaires par agent économique

· L'actif net hebdomadaire des OPCVM monétaires arrêté à la dernière valeur liquidative du mois

· La ventilation des titres détenus par nature, par émetteur et par unité de monnaie, arrêtée à la dernière valeur liquidative du mois.

· La ventilation des composantes des autres éléments d'actifs et des dettes, par émetteur et par unité de monnaie (dernière valeur liquidative du mois).

4- L'encours des dépôts auprès du Trésor communiqué, mensuellement, par la TGR relevant du Ministère de l'Economie et des Finances

5- La ventilation des bons du Trésor par catégorie de détenteurs

6- La ventilation des titres de créances négociables (Certificats de dépôt, Bons de sociétés de financement et billets de trésorerie) par catégorie de souscripteur à l'émission et par durée initiale et résiduelle.

I-4-2 La situation analytique des Autres Sociétés de Financement

La situation analytique des ASF, repose sur :

1- La situation comptable agrégée des sociétés de financement et par catégorie, à savoir:

· crédit à la consommation

· crédit-bail

· affacturage

· cautionnement

· crédit immobilier

· gestion des moyens de paiement.

2- La situation comptable agrégée des banques off-shores

3-La situation comptable agrégée des associations de microcrédit et les annexes relatives à la ventilation des dettes par catégorie de prêteurs. Les états comptables des associations de microcrédit sont établis conformément aux prescriptions de leur plan comptable, entré en vigueur en 2008.

4- Les déclarations des sociétés gestionnaires d'OPCVM autres que monétaires, transmises par le Conseil Déontologique des Valeurs Mobilières (CDVM) et établies conformément aux prescriptions du plan comptable des OPCVM, approuvé en 1995, il s'agit de :

· La répartition mensuelle de l'actif net des OPCVM autres que monétaires par agent économique

·

23

La ventilation hebdomadaire de l'actif net par catégorie d'OPCVM arrêtée à la dernière valeur liquidative du mois

· La ventilation des titres détenus par les OPCVM autres que monétaires par nature, par émetteur et par unité de monnaie, arrêtée à la dernière valeur liquidative du mois.

· La ventilation des composantes des autres éléments d'actifs et des dettes des OPCVM autres que monétaires par instrument, par émetteur et par unité de monnaie (dernière valeur liquidative du mois).

II- La demande de monnaie au Maroc

Nous aborderons la demande de monnaie au Maroc à travers l'analyse de l'évolution des agrégats monétaires M1, M2 et M3, d'une part, et d'autre part en analysant la vitesse de circulation de la monnaie.

II-1- Evolution des agrégats monétaires

Evolution agrégats monétaires au Maroc

01/12/01 01/05/02 01/10/02 01/03/03 01/08/03 01/01/04 01/06/04 01/11/04 01/04/05 01/09/05 01/02/06 01/07/06 01/12/06 01/05/07 01/10/07 01/03/08 01/08/08 01/01/09 01/06/09 01/11/09 01/04/10 01/09/10 01/02/11 01/07/11 01/12/11 01/05/12 01/10/12

M1 M2 M3



1 200 000

1 000 000

800 000

600 000

400 000

200 000

0

Le graphique ci-dessous montre l'évolution des agrégats monétaires M1, M2 et M3 pour le Maroc, et ce, depuis le début de l'année 2001 jusqu'à octobre 2012. On constate d'après ce graphique que les trois agrégats évoluaient pratiquement au même rythme.

24

Le graphique ci-dessous nous amène presque au même constat quant à l'évolution de la monnaie scripturale (M1_SCR) et de M3-M1. Par contre, la monnaie fiduciaire (M1_FID) est restée pratiquement stable:



1 200 000

1 000 000

400 000

800 000

600 000

200 000

0

01/12/01 01/05/02 01/10/02 01/03/03 01/08/03 01/01/04 01/06/04 01/11/04 01/04/05 01/09/05 01/02/06 01/07/06 01/12/06 01/05/07 01/10/07 01/03/08 01/08/08 01/01/09 01/06/09 01/11/09 01/04/10 01/09/10 01/02/11 01/07/11 01/12/11 01/05/12 01/10/12

Evolution de la monnaie fiduciaire, la monnaie scripturale et M3 - M1 au Maroc

M1_FID M1_SCR M3 - M1

Poids des sous-agrégats monétaires au Maroc

17%

37%

46%

M1_FID M1_SCR M3-M1



Ce graphique montre également que sur toute la durée de l'observation, c'est la monnaie scripturale qui a le poids le plus élevée. En effet, comme le montre le graphique ci-dessous qui représente la moyenne historique de ces sous-agrégats monétaires, la monnaie scripturale vient en premier lieu avec un poids de 46%, suivi par M3-M1 avec un poids de 37%, et enfin on trouve la monnaie fiduciaire avec un poids de 17%.

25

Pour ce qui est de l'évolution de ces poids, le graphique ci-dessous montre que le poids de M1_FID est resté pratiquement stable autour de sa moyenne historique.



45%

40%

50%

35%

30%

25%

20%

15%

Evolution des poids de M1_FID, de M1_SCR et de M3 - M1 au

Maroc

%M1_FID %_M1_SCR %_M3-M1

Ce graphique montre que le poids de la monnaie fiduciaire dans M3 a connu une légère tendance baissière en passant de 19% en décembre 2001 à 17% en décembre 2007. A partir de mars 2008 il va se stabiliser à 16 % jusqu'à septembre 2011 où il va monter à 17%, niveau qu'il va garder jusqu'à septembre 2012. En ce qui concerne la monnaie scripturale, ce graphique montre que son poids a connu une croissance continue sur la période janvier 2002 - juin 2006 en passant de 43% seulement, à 47%. Durant les deux derniers trimestres de 2006 et le premier trimestre de 2007, il est s'est stabilisé autour de 46%, puis il a bondi à 48% lors du deuxième trimestre de 2007, niveau qu'il va garder jusqu'au premier trimestre de 2008. A partir de là, il va continuer à diminuer progressivement pour atteindre un niveau moyen de 45% qu'il va garder jusqu'à la fin de la période. Enfin, pour M3-M1, le graphique fait apparaître une évolution symétriquement opposée à celle de M1_SCR. En effet, le poids de M3-M1 a connu une tendance baissière sur la période janvier 2002 - juin 2006 en passant de 38% à 35%, puis une quasi-stagnation autour de 36% durant la période septembre 2006 - mars 2008. A partir de cette date, il va commencer une tendance haussière pour atteindre 40% à fin juin 2010. Au troisième trimestre de 2010 il va redescendre à 39%, niveau qu'il va garder jusqu'à la fin de la période.

26

II-2- Evolution de la vitesse de circulation

Selon la théorie quantitative, cette vitesse est définie comme suit :

V = PIB*IPC/M3

Evolution de la vitesse de circulation de M3 au Maroc

01/12/2001 01/05/2002 01/10/2002 01/03/2003 01/08/2003 01/01/2004 01/06/2004 01/11/2004 01/04/2005 01/09/2005 01/02/2006 01/07/2006 01/12/2006 01/05/2007 01/10/2007 01/03/2008 01/08/2008 01/01/2009 01/06/2009 01/11/2009 01/04/2010 01/09/2010 01/02/2011 01/07/2011 01/12/2011 01/05/2012 01/10/2012



31

30

29

28

27

26

25

24

23

22

Le graphique ci-dessous montre que l'hypothèse prônée par les quantitativiste et les monétaristes, selon laquelle la vitesse de circulation est constante n'est pas vérifiée pour le Maroc sur toute la durée d'observation. En effet, la vitesse de circulation ne peut être considérée comme presque stable que sur la période 2007-2012, par contre, pour la période 2001-2007 on voit clairement que celle-ci a une tendance nettement décroissante avec une variation annuelle moyenne de -1%. Entre 2007 et 2001, la vitesse de circulation a baissé de 20% alors qu'elle n'a baissé que de 0.58% entre 2008 et 2012.

27

Chapitre II : Etude des séries utilisées pour

l'estimation de la demande de monnaie

Ce chapitre sera consacré à l'étude de la stationnarité des différentes séries que nous allons utiliser pour estimer la demande de monnaie. Mais avant, nous allons commencer dans la section 1 par présenter la stratégie de tests de Dickey-Fuller que nous avons adoptée.

Section 1 : Rappel sur les stratégies de tests de Dickey-Fuller

Avant d'exposer la stratégie des tests ADF que nous allons adopter, il est nécessaire de faire d'abord un bref rappel sur les processus stationnaires.

I- Définition d'un processus stochastique stationnaire (au deuxième ordre)

Un processus stochastique Xt est dit stationnaire au deuxième ordre s'il vérifie les conditions suivantes :

i. Vt >_ 0,E[Xt] < +00

ii. Vt >_ 0, E[X_t] = it

iii. Vt, h >_ 0, cov(Xt,Xt+n) = E[(X_t -- it). (Xt+n -- it)] = Y(h), indépendant de t

La condition (i) veut dire que le moment d'ordre 2 doit être fini.

La condition (ii) veut dire que la moyenne de la variable aléatoire Xt est finie et indépendante du temps t.

Enfin, la condition (iii) veut dire que la covariance de Xt et _Xt' ne dépend que de la différence entre t et t' mais pas de t ou t'. Ainsi, (iii) est équivalente à :

Vt,t' >_ 0, cov(X_t,X_t,) = E[(X_t -- it). (X_ti -- it)] = Y(t -- t') = Y(t' -- t)

La fonction y s'appelle fonction d'autocovariance et elle est nécessairement pair (y(h) = y(-h) ? h=0).

D'après cette définition, on conclut qu'un processus est non stationnaire lorsque l'une seulement de ces trois conditions n'est pas vérifiée, ou lorsque deux de ces conditions ne sont pas vérifiées, ou lorsqu'aucune des trois conditions n'est vérifiée. Par conséquent, on aura C3 + C3 + C3 = 3 + 3 + 1 = 7 causes possibles qui font qu'un processus n'est pas stationnaire. Cependant, nous n'allons aborder que deux classes de processus stochastiques : les processus TS (Time Stationary) et les processus DS (Diferency Stationary) et qui concerne d'ailleurs la majorité des séries économiques.

28

II- Les processus non stationnaires TS

Un processus _{(Xt)t>_0} est dit TS s'il peut s'écrire sous la forme suivante :

xt = f(t) + zt

où :

f : est une fonction déterministe du temps (ex : t, t², sin(t),...) zt : est un processus stationnaire.

L'exemple le plus simple d'un processus TS est celui d'une tendance linéaire perturbée par un bruit blanc. C'est-à-dire que f (t) = a0 + a1.t et zt = Et avec Et - iid N(0,6²) par exemple et donc :

xt = a0 + a1.t + Et

Calculons l'espérance et la variance pour ce processus :

· E[xt] = E[a0 + a1.t + Et] = a0 + a1.t + E[Et] = a0 + a1.t , par conséquent l'espérance dépend de t.

· V[xt] = V[a0 + a1.t + Et] = V[Et] = 6² <+oc


· D78(F0,F09:) = -.(F₀ & -.F₀1). (F09: & -.F09:1)1 = -.G₀. G09:1 = H0 I 5 J 0

K I 5 ~ 0,

donc

cov(xt,xt+h) est indépendant du temps.

Ce processus ne vérifie pas la deuxième condition de staionnarité et est donc non stationnaire.

L'une des propriétés importantes des processus TS est que l'influence d'un choc sur Et à la date T est amortie dans le temps de telle sorte que le processus converge toujours vers sa moyenne à savoir f(t).

III- Les processus non stationnaires DS

Un processus _{(xt)t>_0} est dit DS intégré d'ordre 1, si le processus Axt = (xt-xt-1) est stationnaire. L'opérateur A s'appelle « opérateur différence première ».

D'une manière générale si on définit A^dxt (d>_1) par la relation de récurrence suivante : A¹xt=Axt=xt-xt-1 et A^dxt=A^d-1(Axt) pour d>_2, alors :

Un processus _{(xt)t>_0} est dit DS intégré d'ordre d (d>_1), si le processus A^dxt est stationnaire. L'opérateur A^d s'appelle « opérateur différence d'ordre d », c'est-à-dire que l'appliquer à une série donnée, revient à appliquer l'opérateur différence première A à cette série, puis à appliquer d-1 fois ce même opérateur à chaque nouvelle série.

Les tests de Dickey-Fuller (DF) et les tests de Dickey-Fuller Augmenté (ADF) permettent de tester si une série est stationnaire ou non et plus particulièrement tester la présence ou non d'une racine unitaire. Le résultat de ces tests indique que :

·

29

Soit la série est stationnaire

· Soit qu'elle contient un trend déterministe (processus TS)

· Soit qu'elle est un DS sans drift

· Soit qu'elle est un DS avec drift

IV- Stratégie de tests ADF adoptée

La stratégie de tests ADF que nous allons adopter est schématisée par la figure ci-dessous :

Estimation du modèle 3

bx_t = (P.xt_i + c + f3. t + E_t

Estimation du modèle 2
bx_t = (P. xt_i + c + E_t



Test H0 : Ö=0

â?0

H0,3 acceptée

â=0

H0,3 rejetée

x_t est I(0) + c + â.t

Test â=0
Test de Student :
seuils loi normal

H₀ rejetée H₀ acceptée

Test H0,3 :
(c,â,Ö)=(c,0,0)
Statistique F3

x_t est I(1) + c+ â.t



x_t est I(0) +c

c?0

Test c=0

Test de Student : seuils loi normal

H₀ rejetée

c=0

Estimation du modèle 1 bx_t = (P. xt_i + E_t

Test H0 : Ö=0

H0,2 acceptée

H₀ acceptée

Test H0,2 : (c,Ö)=(0,0) Statistique F2

(seuil Dickey-Fuller)

x_t est I(1) + c

H0,2 rejetée

30



x_t est I(0)

H₀ rejetée

Test H0 : Ö=0

H₀ acceptée

x_t est I(1)

31

Les tests des hypothèses _H0,3 ^et _H0,2 sont effectués à l'aide de Eviews en estimant un modèle (Quick-*Estimate Equation...) avec la même variable dépendante et les mêmes variables explicatives telles que affichées dans les résultats du test ADF (y compris les différences des retards de la variable d'intérêt), puis en conduisant un test de Wald de restriction sur les coefficients (View-*Coefficient Diagnostics-*Wald Test-Coefficient Restrictions...). L'hypothèse nulle sera rejetée si la p-value relative à la statistique F calculée par ce test est inférieure au seuil retenu (généralement 5%)

Section 2 : Etude des séries utilisées

L'objectif de cette étape est d'étudier les propriétés des différentes séries de notre étude du point de vu de stationnarité et d'ordre d'intégration.

Etude de la série M1FID :

M1_FID

160,000 140,000 120,000 100,000 80,000 60,000

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

Le graphe de cette série se présente comme suit :

Ce graphe laisse apparaître une tendance évidente, mais pour déterminer est ce qu'il s'agit d'une tendance déterministe ou stochastique nous allons procéder aux tests ADF selon la stratégie présentée ci-dessus :

32

Estimation du modèle [3] pour M1FID :

L'estimation du modèle [3] donne les résultats suivants :

Null Hypothesis: M1_FID has a unit root Exogenous: Constant, Linear Trend Lag Length: 5 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -3.242139	0.0934
Test critical values: 1% level -4.252879
5% level -3.548490
10% level -3.207094
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(M1_FID)
Method: Least Squares
Date: 05/24/13 Time: 10:39
Sample (adjusted): 2003Q3 2011Q4
Included observations: 34 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M1_FID(-1) -0.335364 0.103439 -3.242139	0.0032
D(M1_FID(-1)) -0.014894 0.164667 -0.090447	0.9286
D(M1_FID(-2)) -0.098877 0.134004 -0.737867	0.4672
D(M1_FID(-3)) 0.103223 0.130458 0.791232	0.4360
D(M1_FID(-4)) 0.673247 0.126661 5.315339	0.0000
D(M1_FID(-5)) 0.170749 0.174354 0.979325	0.3364
C 18003.83 5251.900 3.428060	0.0020
@TREND("2002Q1") 874.8233 265.4699 3.295377	0.0028
R-squared 0.736755 Mean dependent var	2545.475
Adjusted R-squared 0.665881 S.D. dependent var	2592.404
S.E. of regression 1498.488 Akaike info criterion	17.66462
Sum squared resid 58382109 Schwarz criterion	18.02377
Log likelihood -292.2986 Hannan-Quinn criter.	17.78710
F-statistic 10.39532 Durbin-Watson stat	1.999826
Prob(F-statistic) 0.000004

La statistique t relative à Ö1 est de -3.24 qui est supérieur à sa valeur critique de -3.54, on accepte donc H0 : Existence d'une racine unitaire. On passe donc au test de l'hypothèse H0,3 :

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 5.474813 Chi-square 10.94963	(2, 26) 2	0.0104 0.0042
Null Hypothesis: C(1)=0,C(8)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(8)	-0.335364 874.8233	0.103439 265.4699
Restrictions are linear in coefficients.

La p-value relative à la statistique F est inférieure à 5%, on rejette donc H0,3.

Donc M1_FID est un DS avec trend. Il convient donc de la stationnariser en la différenciant puis en retirant la tendance. Ceci peut se faire en prenant le résidu de la régression suivante : M1_FID_t - M¹_FIDt_1 = C + a. t + E_t

Les résultats de cette régression sont comme suit :

33

Dependent Variable: D(M1_FID) Method: Least Squares Date: 05/24/13 Time: 15:53 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	1412.492	814.8924 1.733348	0.0914
TEMPS	47.32875	35.50850 1.332885	0.1907
R-squared	0.045816	Mean dependent var	2359.067
Adjusted R-squared	0.020027	S.D. dependent var	2521.092
S.E. of regression	2495.720	Akaike info criterion	18.53246
Sum squared resid	2.30E+08	Schwarz criterion	18.61777
Log likelihood	-359.3830	Hannan-Quinn criter.	18.56307
F-statistic	1.776582	Durbin-Watson stat	2.115850
Prob(F-statistic)	0.190719

L'allure du résidu de cette régression est comme suit :



-2000

-4000

-6000

4000

2000

8000

6000

0

02 03 04 05 06 07 08 09 10 11

M1_FIDRES

Il faut vérifier si cette nouvelle série est stationnaire. Pour ce faire nous allons effectuer les tests ADF sur cette série.

Estimation du modèle [3] pour M1_FIDRES :

34

Null Hypothesis: M1_FIDRES has a unit root Exogenous: Constant, Linear Trend Lag Length: 3 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -1.531751	0.7990
Test critical values: 1% level -4.243644
5% level -3.544284
10% level -3.204699
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(M1_FIDRES)
Method: Least Squares
Date: 05/27/13 Time: 16:31
Sample (adjusted): 2003Q2 2011Q4
Included observations: 35 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M1_FIDRES(-1) -0.554647 0.362100 -1.531751	0.1364
D(M1_FIDRES(-1)) -0.499938 0.296196 -1.687865	0.1022
D(M1_FIDRES(-2)) -0.713168 0.204692 -3.484095	0.0016
D(M1_FIDRES(-3)) -0.650302 0.139206 -4.671509	0.0001
C 110.7541 687.1455 0.161180	0.8731
@TREND("2002Q1") -3.392676 28.43693 -0.119305	0.9059
R-squared 0.818554 Mean dependent var	4.097143
Adjusted R-squared 0.787270 S.D. dependent var	3666.745
S.E. of regression 1691.200 Akaike info criterion	17.85907
Sum squared resid 82944533 Schwarz criterion	18.12570
Log likelihood -306.5337 Hannan-Quinn criter.	17.95111
F-statistic 26.16543 Durbin-Watson stat	1.951792
Prob(F-statistic) 0.000000

La statistique t relative à Ö1 est supérieure à sa valeur critique qui est de -3.54, on accepte donc H0 : Existence d'une racine unité. On passe à l'hypothèse H0,3 :

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 1.173217 Chi-square 2.346434	(2, 29) 2	0.3236 0.3094
Null Hypothesis: C(1)=0,C(6)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(6)	-0.554647 -3.392676	0.362100 28.43693
Restrictions are linear in coefficients.

La p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,3 et on passe à l'estimation du modèle [2].

35

Estimation du modèle [2] pour M1_FIDRES :

Null Hypothesis: M1_FIDRES has a unit root Exogenous: Constant Lag Length: 3 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -1.552880	0.4955
Test critical values: 1% level -3.632900
5% level -2.948404
10% level -2.612874
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(M1_FIDRES)
Method: Least Squares
Date: 06/07/13 Time: 11:42
Sample (adjusted): 2003Q2 2011Q4
Included observations: 35 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M1_FIDRES(-1) -0.550914 0.354769 -1.552880	0.1309
D(M1_FIDRES(-1)) -0.502986 0.290203 -1.733223	0.0933
D(M1_FIDRES(-2)) -0.715364 0.200486 -3.568158	0.0012
D(M1_FIDRES(-3)) -0.651102 0.136741 -4.761571	0.0000
C 36.23362 281.6450 0.128650	0.8985
R-squared 0.818465 Mean dependent var	4.097143
Adjusted R-squared 0.794260 S.D. dependent var	3666.745
S.E. of regression 1663.182 Akaike info criterion	17.80242
Sum squared resid 82985243 Schwarz criterion	18.02461
Log likelihood -306.5423 Hannan-Quinn criter.	17.87912
F-statistic 33.81432 Durbin-Watson stat	1.952070
Prob(F-statistic) 0.000000

La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,2 :

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 1.223492 Chi-square 2.446984	(2, 30) 2	0.3085 0.2942
Null Hypothesis: C(1)=0,C(5)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(5)	-0.550914 36.23362	0.354769 281.6450
Restrictions are linear in coefficients.

La p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,2 et passe à l'estimation du modèle [1].

Estimation du modèle [1] pour M1_FIDRES :

Null Hypothesis: M1_FIDRES has a unit root Exogenous: None Lag Length: 3 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -1.584318	0.1052
Test critical values: 1% level -2.632688
5% level -1.950687
10% level -1.611059
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(M1_FIDRES)
Method: Least Squares
Date: 06/07/13 Time: 11:49
Sample (adjusted): 2003Q2 2011Q4
Included observations: 35 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M1_FIDRES(-1) -0.552670 0.348838 -1.584318	0.1233
D(M1_FIDRES(-1)) -0.501083 0.285192 -1.757007	0.0888
D(M1_FIDRES(-2)) -0.714493 0.197167 -3.623791	0.0010
D(M1_FIDRES(-3)) -0.650365 0.134437 -4.837712	0.0000
R-squared 0.818365 Mean dependent var	4.097143
Adjusted R-squared 0.800787 S.D. dependent var	3666.745
S.E. of regression 1636.588 Akaike info criterion	17.74583
Sum squared resid 83031026 Schwarz criterion	17.92358
Log likelihood -306.5519 Hannan-Quinn criter.	17.80719
Durbin-Watson stat 1.951237

La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et conclut que M1_FIDRES est DS. La meilleure façon de la stationnariser est de la différentier.

La figure ci-dessous présente l'allure de cette nouvelle série :

M1_FIDRESD1

6,000 4,000 2,000 0 -2,000 -4,000 -6,000 -8,000 -10,000 -12,000
	2002 2003 2004 2005 2006 2007 2008 2009 2010 2011
Les tests ADF			réalisés sur cette série montrent qu'elle est stationnaire.

36

Conclusion :

M1 FID est _

I(2)

37

Etude de la série LNM1FID

LNM1_FID

12.0 11.8 11.6 11.4 11.2 11.0
	2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

L'allure de cette série est comme suit :

Estimation du modèle [3] pour LNM1_FID :

Null Hypothesis: LNM1_FID has a unit root Exogenous: Constant, Linear Trend Lag Length: 4 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -3.105322	0.1208
Test critical values: 1% level -4.243644
5% level -3.544284
10% level -3.204699
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNM1_FID)
Method: Least Squares
Date: 06/07/13 Time: 16:03
Sample (adjusted): 2003Q2 2011Q4
Included observations: 35 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
LNM1_FID(-1) -0.255569 0.082300 -3.105322	0.0043
D(LNM1_FID(-1)) 0.149941 0.130256 1.151131	0.2594
D(LNM1_FID(-2)) 0.011778 0.125990 0.093486	0.9262
D(LNM1_FID(-3)) 0.152784 0.118425 1.290133	0.2076
D(LNM1_FID(-4)) 0.746140 0.112628 6.624839	0.0000
C 2.822126 0.904551 3.119919	0.0042
@TREND("2002Q1") 0.006113 0.002012 3.037807	0.0051
R-squared 0.707246 Mean dependent var	0.022879
Adjusted R-squared 0.644513 S.D. dependent var	0.023358
S.E. of regression 0.013927 Akaike info criterion	-5.533148
Sum squared resid 0.005431 Schwarz criterion	-5.222079
Log likelihood 103.8301 Hannan-Quinn criter.	-5.425767
F-statistic 11.27390 Durbin-Watson stat	2.417134
Prob(F-statistic) 0.000002

La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,3 :

38

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 4.901437 Chi-square 9.802875	(2, 28) 2	0.0150 0.0074
Null Hypothesis: C(1)=0,C(7)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(7)	-0.255569 0.006113	0.082300 0.002012
Restrictions are linear in coefficients.

La p-value relative à la statistique F étant inférieure à sa valeur critique, on rejette _H0,3 et on conclut que LNM1_FID est I(1) + C + â.t. Pour la stationnariser, il suffit de prendre le résidu de la régression suivante :

LNM1_FID_t-LNM1_FID_t-₁ = C + â.t + å_t



-.02

-.04

-.06

.06

.04

.02

.00

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

LNM1_FIDRES

On va procéder aux tests ADF sur cette série pour voir est ce qu'elle est stationnaire ou non.

39

Estimation du modèle [3] pour LNM1_FIDRES :



La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,3 :



La p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,3 et on passe à l'estimation du modèle [2].

40

Estimation du modèle [2] pour LNM1_FIDRES :



La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,2 :



La p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,2 et on passe à l'estimation du modèle [1].

41

Estimation du modèle [1] pour LNM1_FIDRES :



La statistique t relative à Ö étant supérieure à sa valeur critique on accepte H0 et on conclut que LNM1_FIDRES est DS. Pour la stationnariser nous allons la différencier.

Le graphe de la nouvelle série obtenue par différenciation de LNM1_FIDRES se présente comme suit :



-.04

-.08

-.12

.08

.04

.00

02 03 04 05 06 07 08 09 10 11

LNM1_FIDRESD1

Les tests ADF conduits sur cette série montrent qu'elle est stationnaire. Conclusion : LNM1_FID est I(2)

42

Etude de la série M1_SCR

L'allure de cette série se présente comme suit :

M1_SCR

450,000 400,000 350,000 300,000 250,000 200,000 150,000 100,000

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

L'allure de cette courbe montre une tendance évidente, mais pour savoir est ce qu'il s'agit d'un TS ou d'un DS, nous allons procéder aux tests ADF :

Estimation du modèle [3] pour M1SCR:

Null Hypothesis: M1_SCR has a unit root Exogenous: Constant, Linear Trend Lag Length: 4 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -2.907396	0.1725
Test critical values: 1% level -4.243644
5% level -3.544284
10% level -3.204699
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(M1_SCR)
Method: Least Squares
Date: 05/28/13 Time: 10:23
Sample (adjusted): 2003Q2 2011Q4
Included observations: 35 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M1_SCR(-1) -0.300336 0.103301 -2.907396	0.0071
D(M1_SCR(-1)) 0.184157 0.165543 1.112447	0.2754
D(M1_SCR(-2)) 0.361189 0.155440 2.323655	0.0276
D(M1_SCR(-3)) -0.090752 0.169185 -0.536410	0.5959
D(M1_SCR(-4)) 0.505137 0.166857 3.027369	0.0052
C 37884.91 11829.86 3.202480	0.0034
@TREND("2002Q1") 2346.179 813.0235 2.885746	0.0074
R-squared 0.570931 Mean dependent var	7255.411
Adjusted R-squared 0.478987 S.D. dependent var	7735.274
S.E. of regression 5583.415 Akaike info criterion	20.26985
Sum squared resid 8.73E+08 Schwarz criterion	20.58091
Log likelihood -347.7223 Hannan-Quinn criter.	20.37723
F-statistic 6.209585 Durbin-Watson stat	1.841756
Prob(F-statistic) 0.000310

La statistique t relative à Ö1 est égale à -2.91 qui est largement supérieure à sa valeur critique de -3.54. On accepte donc H0 et on passe donc au test de l'hypothèse H0,3 :

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 4.226668 Chi-square 8.453336	(2, 28) 2	0.0249 0.0146
Null Hypothesis: C(1)=0,C(7)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(7)	-0.300336 2346.179	0.103301 813.0235
Restrictions are linear in coefficients.

La p-value relative à la statistique F étant inférieure à 5%, on rejette H0,3.

Donc M1_SCR est un DS avec trend. Il convient donc de la stationnariser en la différenciant puis en retirant la tendance. Ceci peut se faire en prenant le résidu de la régression suivante :

M1_SCR_t -- M¹_SCRt_1 = C + a. t + E_t

Les résultats de cette régression sont comme suit :

Dependent Variable: D(M1_SCR) Method: Least Squares Date: 05/28/13 Time: 10:25 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	6915.111	2474.213 2.794873	0.0082
TEMPS	14.21291	107.8125 0.131830	0.8958
R-squared	0.000469	Mean dependent var	7199.369
Adjusted R-squared	-0.026545	S.D. dependent var	7479.002
S.E. of regression	7577.616	Akaike info criterion	20.75371
Sum squared resid	2.12E+09	Schwarz criterion	20.83902
Log likelihood	-402.6973	Hannan-Quinn criter.	20.78431
F-statistic	0.017379	Durbin-Watson stat	2.644121
Prob(F-statistic)	0.895833

L'allure de la série des résidus issus de cette régression, M1_SCRRES, se présente comme suit :



-10,000

-15,000

-20,000

20,000

15,000

10,000

-5,000

5,000

0

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

M1_SCRRES

43

44

Nous allons vérifier si cette nouvelle série est stationnaire ou non, en procédant aux tests ADF :

L'allure de la courbe montre l'absence d'une tendance déterministe, on passe donc directement à l'estimation du modèle [2].

Estimation du modèle [2] pour M1_SCRRES :

Null Hypothesis: M1_SCRRES has a unit root Exogenous: Constant Lag Length: 2 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -3.568796	0.0116
Test critical values: 1% level -3.626784
5% level -2.945842
10% level -2.611531
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(M1_SCRRES)
Method: Least Squares
Date: 05/28/13 Time: 10:28
Sample (adjusted): 2003Q1 2011Q4
Included observations: 36 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M1_SCRRES(-1) -1.012331 0.283662 -3.568796	0.0012
D(M1_SCRRES(-1)) -0.069432 0.259108 -0.267964	0.7904
D(M1_SCRRES(-2)) 0.319140 0.174602 1.827818	0.0769
C -151.4609 1071.078 -0.141410	0.8884
R-squared 0.760596 Mean dependent var	130.9706
Adjusted R-squared 0.738152 S.D. dependent var	12545.93
S.E. of regression 6419.891 Akaike info criterion	20.47663
Sum squared resid 1.32E+09 Schwarz criterion	20.65258
Log likelihood -364.5793 Hannan-Quinn criter.	20.53804
F-statistic 33.88843 Durbin-Watson stat	1.696606
Prob(F-statistic) 0.000000

La statistique t relative à Ö1 est égale à -3.57 qui est inférieure à sa valeur critique (-2.94), on rejette donc H0. Cependant, la constante n'est pas significativement différente de zéro (p-value=0.8884 > 5%) , on passe donc à l'estimation du modèle [1].

45

Estimation du modèle [1] pour M1_SCRRES :

Null Hypothesis: M1_SCRRES has a unit root Exogenous: None Lag Length: 2 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -3.620154	0.0006
Test critical values: 1% level -2.630762 5% level -1.950394 10% level -1.611202
*MacKinnon (1996) one-sided p-values. Augmented Dickey-Fuller Test Equation Dependent Variable: D(M1_SCRRES) Method: Least Squares Date: 05/28/13 Time: 10:33 Sample (adjusted): 2003Q1 2011Q4 Included observations: 36 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M1_SCRRES(-1) -1.010782 0.279210 -3.620154 D(M1_SCRRES(-1)) -0.070055 0.255194 -0.274518 D(M1_SCRRES(-2)) 0.319123 0.171989 1.855479	0.0010 0.7854 0.0725
R-squared 0.760446 Mean dependent var Adjusted R-squared 0.745928 S.D. dependent var S.E. of regression 6323.846 Akaike info criterion Sum squared resid 1.32E+09 Schwarz criterion Log likelihood -364.5906 Hannan-Quinn criter. Durbin-Watson stat 1.697218	130.9706 12545.93 20.42170 20.55366 20.46776

La statistique t relative à Ö1 est égale à -3.62 qui est inférieure à sa valeur critique (-1.95), on rejette donc H0 et conclut que M1_SCRRES est stationnaire.

Conclusion : M1_SCR est I(1)

Etude de la série LNM1SCR



13.0

12.8

12.6

12.4

12.2

12.0

11.8

02 03 04 05 06 07 08 09 10 11

LNM1_SCR

Ce graphe fait apparaître une tendance évidente. Nous allons donc procéder aux tests ADF pour déterminer sa nature.

46

Estimation du modèle [3] pour LNM1_SCR :



La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,3 :



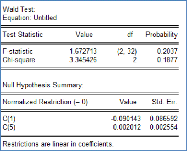
La p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,3 et on passe à l'estimation du modèle [2].

47

Estimation du modèle [2] pour LNM1_SCR :



La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,2 :



La p-value relative à la statistique F étant inférieure à 5%, on rejette _H0,2, on conclut que LNM1_SCR est I(1) + C. La meilleure façon de la stationnariser est de la différencier.

Le graphe de cette nouvelle série se présente comme suit :



-.02

-.04

.10

.08

.06

.04

.02

.00

02 03 04 05 06 07 08 09 10 11

LNM1_SCRD1

48

Estimation du modèle [3] pour LNM1_SCRD1 :



La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,3 :



La p-value relative à la statistique F étant inférieure à 5%, on rejette _H0,3 et on conclut que LNM1_SCRD1 est I(1) + C + â.t. Pour la stationnariser il faut la différencier puis retirer la tendance. Cela revient à prendre le résidu de la régression suivante :

LNM1_SCRD1t - LNM1_SCRD1t-1 = C + â.t + åt

Le résultat de cette régression est comme suit :



Le graphe du résidu issu de cette régression se présente comme suit :



-.04

-.08

-.12

.08

.04

.00

02 03 04 05 06 07 08 09 10 11

LNM1_SCRD1RES

49

50

Les tests ADF réalisés sur cette série montent qu'elle est stationnaire. Conclusion : LNM1_SCR est I(2)

Etude de la série M3- M1 :

Pour rappel ce sous-agrégat contient les comptes d'épargne auprès des banques et les comptes sur livrets auprès de la caisse d'épargne nationale ainsi que les comptes à terme et bons de caisse auprès des banques.

Le graphe de la série M3_M1 se présente comme suit :

M3_M1

400,000 350,000 300,000 250,000 200,000 150,000 100,000

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

Nous allons procéder aux tests ADF pour déterminer la nature de cette série. Estimation du modèle [3] pour M3_M1 :

51

Null Hypothesis: M3_M1 has a unit root Exogenous: Constant, Linear Trend Lag Length: 1 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -2.027535	0.5680
Test critical values: 1% level -4.219126
5% level -3.533083
10% level -3.198312
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(M3_M1)
Method: Least Squares
Date: 06/11/13 Time: 12:41
Sample (adjusted): 2002Q3 2011Q4
Included observations: 38 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M3_M1(-1) -0.119044 0.058714 -2.027535	0.0505
D(M3_M1(-1)) 0.279879 0.157088 1.781668	0.0837
C 13065.24 5402.700 2.418279	0.0211
@TREND("2002Q1") 951.8607 441.6675 2.155152	0.0383
R-squared 0.194343 Mean dependent var	6298.051
Adjusted R-squared 0.123256 S.D. dependent var	6843.559
S.E. of regression 6407.940 Akaike info criterion	20.46776
Sum squared resid 1.40E+09 Schwarz criterion	20.64014
Log likelihood -384.8875 Hannan-Quinn criter.	20.52909
F-statistic 2.733869 Durbin-Watson stat	2.004488
Prob(F-statistic) 0.058801

La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de H0,3

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 2.383466 Chi-square 4.766931	(2, 34) 2	0.1075 0.0922
Null Hypothesis: C(1)=0,C(4)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(4)	-0.119044 951.8607	0.058714 441.6675
Restrictions are linear in coefficients.

La p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,3 et on passe donc à l'estimation du modèle [2].

Estimation du modèle [2] pour M3_M1 :

52

Null Hypothesis: M3_M1 has a unit root Exogenous: Constant Lag Length: 0 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic 0.811014	0.9930
Test critical values: 1% level -3.610453 5% level -2.938987 10% level -2.607932
*MacKinnon (1996) one-sided p-values. Augmented Dickey-Fuller Test Equation Dependent Variable: D(M3_M1) Method: Least Squares Date: 06/11/13 Time: 13:10 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M3_M1(-1) 0.010779 0.013291 0.811014 C 3599.584 3274.426 1.099302	0.4225 0.2787
R-squared 0.017466 Mean dependent var Adjusted R-squared -0.009089 S.D. dependent var S.E. of regression 6896.838 Akaike info criterion Sum squared resid 1.76E+09 Schwarz criterion Log likelihood -399.0260 Hannan-Quinn criter. F-statistic 0.657743 Durbin-Watson stat Prob(F-statistic) 0.422544	6099.587 6865.709 20.56543 20.65074 20.59604 1.416664

La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de H0,2 :

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 15.58117 Chi-square 31.16235	(2, 37) 2	0.0000 0.0000
Null Hypothesis: C(1)=0,C(2)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(2)	0.010779 3599.584	0.013291 3274.426
Restrictions are linear in coefficients.

La p-value relative à la statistique F étant inférieure à 5%, on rejette _H0,2 et on conclut donc que M3_M1 est DS avec Drift. La meilleure façon de la stationnariser est de la différencier. Le graphe de cette nouvelle série se présente comme suit :

M3_M1D1

25,000 20,000 15,000 10,000 5,000 0 -5,000

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

53

Nous allons procéder aux tests ADF pour voir est ce qu'elle est stationnaire. Estimation du modèle [3] pour M3_M1D1 :

Null Hypothesis: M3_M1D1 has a unit root Exogenous: Constant, Linear Trend Lag Length: 0 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -4.478063	0.0052
Test critical values: 1% level -4.219126
5% level -3.533083
10% level -3.198312
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(M3_M1D1)
Method: Least Squares
Date: 06/11/13 Time: 13:16
Sample (adjusted): 2002Q3 2011Q4
Included observations: 38 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M3_M1D1(-1) -0.733409 0.163778 -4.478063	0.0001
C 3139.038 2384.404 1.316487	0.1966
@TREND("2002Q1") 77.79646 100.2276 0.776198	0.4428
R-squared 0.364285 Mean dependent var	430.6905
Adjusted R-squared 0.327958 S.D. dependent var	8156.632
S.E. of regression 6686.656 Akaike info criterion	20.52927
Sum squared resid 1.56E+09 Schwarz criterion	20.65856
Log likelihood -387.0562 Hannan-Quinn criter.	20.57527
F-statistic 10.02805 Durbin-Watson stat	1.974543
Prob(F-statistic) 0.000361

La statistique t relative à Ö étant inférieure à sa valeur critique, on rejette H0. Cependant, la tendance n'est pas significative au seuil de 5%, on doit tester le modèle [2].

54

Estimation du modèle [2] pour M3_M1D1 :

Null Hypothesis: M3_M1D1 has a unit root Exogenous: Constant Lag Length: 0 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -4.435181	0.0011
Test critical values: 1% level -3.615588 5% level -2.941145 10% level -2.609066
*MacKinnon (1996) one-sided p-values. Augmented Dickey-Fuller Test Equation Dependent Variable: D(M3_M1D1) Method: Least Squares Date: 06/11/13 Time: 13:18 Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
M3_M1D1(-1) -0.712925 0.160743 -4.435181 C 4613.677 1432.875 3.219874	0.0001 0.0027
R-squared 0.353342 Mean dependent var Adjusted R-squared 0.335379 S.D. dependent var S.E. of regression 6649.636 Akaike info criterion Sum squared resid 1.59E+09 Schwarz criterion Log likelihood -387.3804 Hannan-Quinn criter. F-statistic 19.67083 Durbin-Watson stat Prob(F-statistic) 0.000083	430.6905 8156.632 20.49371 20.57990 20.52437 1.982157

La statistique t relative à Ö étant inférieure à sa valeur critique, on rejette H0. La constante est significativement différente de zéro, donc M3_M1D1 est stationnaire autour d'une moyenne.

Conclusion : M3_M1 est I(1)

Etude de la série LNM3M1 :

LNM3_M1

13.0 12.8 12.6 12.4 12.2 12.0 11.8 11.6

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

Le graphe de cette série se présente comme suit :

55

Estimation du modèle [3] pour LNM3_M1 :

Null Hypothesis: LNM3_M1 has a unit root Exogenous: Constant, Linear Trend Lag Length: 0 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -1.474968	0.8212
Test critical values: 1% level -4.211868
5% level -3.529758
10% level -3.196411
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNM3_M1)
Method: Least Squares
Date: 06/12/13 Time: 09:31
Sample (adjusted): 2002Q2 2011Q4
Included observations: 39 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
LNM3_M1(-1) -0.108287 0.073416 -1.474968	0.1489
C 1.287443 0.855440 1.505007	0.1410
@TREND("2002Q1") 0.003483 0.002377 1.465434	0.1515
R-squared 0.057134 Mean dependent var	0.026420
Adjusted R-squared 0.004752 S.D. dependent var	0.029508
S.E. of regression 0.029438 Akaike info criterion	-4.139289
Sum squared resid 0.031196 Schwarz criterion	-4.011323
Log likelihood 83.71613 Hannan-Quinn criter.	-4.093376
F-statistic 1.090721 Durbin-Watson stat	1.505514
Prob(F-statistic) 0.346819

La statistique relative à Ö1 (-1.47) est supérieure à sa valeur critique (-3.53). On accepte donc H0, et on passe au test de l'hypothèse H0,3 :

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 1.090721 Chi-square 2.181442	(2, 36) 2	0.3468 0.3360
Null Hypothesis: C(1)=0,C(3)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(3)	-0.108287 0.003483	0.073416 0.002377
Restrictions are linear in coefficients.

La p-value relative à F étant supérieure à 5%, on accepte _H0,3 et on passe à l'estimation du modèle [2].

56

Estimation du modèle [2] pour LNM3_M1 :

Null Hypothesis: LNM3_M1 has a unit root Exogenous: Constant Lag Length: 0 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -0.181452	0.9325
Test critical values: 1% level -3.610453 5% level -2.938987 10% level -2.607932
*MacKinnon (1996) one-sided p-values. Augmented Dickey-Fuller Test Equation Dependent Variable: D(LNM3_M1) Method: Least Squares Date: 06/12/13 Time: 09:36 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
LNM3_M1(-1) -0.002384 0.013137 -0.181452 C 0.055712 0.161502 0.344962	0.8570 0.7321
R-squared 0.000889 Mean dependent var Adjusted R-squared -0.026114 S.D. dependent var S.E. of regression 0.029891 Akaike info criterion Sum squared resid 0.033057 Schwarz criterion Log likelihood 82.58628 Hannan-Quinn criter. F-statistic 0.032925 Durbin-Watson stat Prob(F-statistic) 0.857003	0.026420 0.029508 -4.132630 -4.047319 -4.102021 1.582537

La statistique relative à Ö1 (-0.18) est supérieure à sa valeur critique (-2.94). On accepte donc H0, et on passe au test de l'hypothèse H0,2 :

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 15.25127 Chi-square 30.50254	(2, 37) 2	0.0000 0.0000
Null Hypothesis: C(1)=0,C(2)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(2)	-0.002384 0.055712	0.013137 0.161502
Restrictions are linear in coefficients.

La p-value relative à F étant inférieure à 5%, on rejette _H0,2 et on conclut que LNM3_M1 est DS avec Drift. La meilleure façon de la stationnariser est de la différencier. Le graphe de cette nouvelle série se présente comme suit :

LNM3_M1D1

.10 .08 .06 .04 .02 .00 -.02 -.04

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

57

Les tests ADF conduits sur cette série montrent qu'elle est stationnaire autour d'une moyenne.

Conclusion : LNM3_M1 est I(1)

Etude de la série PIB :

PIB

220,000 200,000 180,000 160,000 140,000 120,000 100,000

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

Le graphe de la série PIB se présente comme suit :

L'allure de cette courbe montre une tendance croissante évidente. Mais pour savoir est ce qu'elle est de type DS ou TS nous allons procéder aux tests ADF :

Estimation du modèle [3] pour PIB:

L'estimation du modèle [3] donne les résultats suivants :

58

Null Hypothesis: PIB has a unit root Exogenous: Constant, Linear Trend Lag Length: 1 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -2.016811	0.5737
Test critical values: 1% level -4.219126
5% level -3.533083
10% level -3.198312
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(PIB)
Method: Least Squares
Date: 05/27/13 Time: 16:48
Sample (adjusted): 2002Q3 2011Q4
Included observations: 38 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
PIB(-1) -0.212330 0.105280 -2.016811	0.0517
D(PIB(-1)) -0.388025 0.148629 -2.610691	0.0133
C 23633.98 10408.13 2.270724	0.0296
@TREND("2002Q1") 601.0285 278.0961 2.161226	0.0378
R-squared 0.316615 Mean dependent var	2483.421
Adjusted R-squared 0.256316 S.D. dependent var	2755.606
S.E. of regression 2376.355 Akaike info criterion	18.48382
Sum squared resid 1.92E+08 Schwarz criterion	18.65620
Log likelihood -347.1926 Hannan-Quinn criter.	18.54515
F-statistic 5.250782 Durbin-Watson stat	1.921014
Prob(F-statistic) 0.004372

La statistique relative à Ö1 (-2.017) est supérieure à sa valeur critique (-3.53). On accepte donc H0, et on passe au test de l'hypothèse H0,3.

· Estimation du modèle : D(PIB) = PIB_t - PIBt_1 = C + e_t Les résultats de cette estimation sont comme suit :

Dependent Variable: D(PIB) Method: Least Squares Date: 05/27/13 Time: 16:49 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments					Variable
Coefficient		Std. Error t-Statistic	Prob.	C
2445.359		437.0660 5.594942	0.0000	R-squared
0.000000		Mean dependent var	2445.359	Adjusted R-squared
0.000000		S.D. dependent var	2729.476	S.E. of regression
2729.476		Akaike info criterion	18.68691	Sum squared resid
2.83E+08		Schwarz criterion	18.72957	Log likelihood
-363.3948		Hannan-Quinn criter.	18.70222	Durbin-Watson stat
2.887832

· Calcul de F3 : F3 = (

2,83.10^8-1,92.10^8 192108 ) = 8.53 > 6.73 4 on rejette H0,3 . Par conséquent ^,39-3^)

la série D(PIB) est un TS. La meilleure façon de la dessaisonaliser est de prendre les résidus de la régression suivante :

D(PIB) = PIB_t - PIBt_1 = C + a. t + e_t

Les résultats de cette régression sont comme suit :

59

Dependent Variable: D(PIB) Method: Least Squares Date: 05/27/13 Time: 16:51 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	1788.695	894.6456 1.999334	0.0530
TEMPS	32.83320	38.98371 0.842229	0.4051
R-squared	0.018811	Mean dependent var	2445.359
Adjusted R-squared	-0.007708	S.D. dependent var	2729.476
S.E. of regression	2739.975	Akaike info criterion	18.71921
Sum squared resid	2.78E+08	Schwarz criterion	18.80452
Log likelihood	-363.0245	Hannan-Quinn criter.	18.74981
F-statistic	0.709349	Durbin-Watson stat	2.942842
Prob(F-statistic)	0.405071

Le graphe de la série des résidus, PIBRES, issus de cette régression se présente comme suit :



-2,000

-4,000

-6,000

-8,000

4,000

2,000

8,000

6,000

0

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

PIBRES

De la même façon, nous allons vérifier est ce que la nouvelle série, PIBRES est stationnaire ou non. Pour ce faire, nous allons procéder aux tests ADF. L'allure de la courbe montre qu'il n'y a pas présence d'une tendance déterministe, on passe donc directement au modèle [2] :

Estimation du modèle [2] pour PIBRES :

Les résultats de l'estimation de ce modèle sont comme suit :

60

Null Hypothesis: PIBRES has a unit root Exogenous: Constant Lag Length: 0 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -10.04259	0.0000
Test critical values: 1% level -3.615588 5% level -2.941145 10% level -2.609066
*MacKinnon (1996) one-sided p-values. Augmented Dickey-Fuller Test Equation Dependent Variable: D(PIBRES) Method: Least Squares Date: 05/27/13 Time: 16:56 Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
PIBRES(-1) -1.472644 0.146640 -10.04259 C 21.01350 396.4659 0.053002	0.0000 0.9580
R-squared 0.736945 Mean dependent var Adjusted R-squared 0.729638 S.D. dependent var S.E. of regression 2443.979 Akaike info criterion Sum squared resid 2.15E+08 Schwarz criterion Log likelihood -349.3449 Hannan-Quinn criter. F-statistic 100.8536 Durbin-Watson stat Prob(F-statistic) 0.000000	22.98259 4700.291 18.49184 18.57803 18.52250 1.947267

La statistique t relative à Ö1 est égale à -10.04 qui est largement inférieure à sa valeur critique (-2.94), on rejette donc H0. Cependant, la constante n'est pas significativement différente de zéro (p-value = 0.958 >5%), on passe donc à l'estimation du modèle [1].

Estimation du modèle [1] pour PIBRES :

Les résultats de l'estimation de ce modèle sont comme suit :

61

Null Hypothesis: PIBRES has a unit root Exogenous: None Lag Length: 0 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -10.18074	0.0000
Test critical values: 1% level -2.627238 5% level -1.949856 10% level -1.611469
*MacKinnon (1996) one-sided p-values. Augmented Dickey-Fuller Test Equation Dependent Variable: D(PIBRES) Method: Least Squares Date: 05/27/13 Time: 16:59 Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
PIBRES(-1) -1.472648 0.144650 -10.18074	0.0000
R-squared 0.736925 Mean dependent var Adjusted R-squared 0.736925 S.D. dependent var S.E. of regression 2410.821 Akaike info criterion Sum squared resid 2.15E+08 Schwarz criterion Log likelihood -349.3464 Hannan-Quinn criter. Durbin-Watson stat 1.947107	22.98259 4700.291 18.43929 18.48238 18.45462

La statistique t relative à Ö1 est égale à -10.18 qui est largement inférieur à sa valeur critique (-1.95) on rejette donc H0 et on conclut que la série PIBRES est stationnaire.

Conclusion : PIB est I(1)

Etude de la série LNPIB (ln(PIB)) :

LNPIB

12.3

12.2 12.1 12.0 11.9 11.8 11.7 11.6
	2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

Le graphe de cette série se présente comme suit :

62

Estimation du modèle [3] pour LNPIB :

Null Hypothesis: LNPIB has a unit root Exogenous: Constant, Linear Trend Lag Length: 0 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -2.572014	0.2944
Test critical values: 1% level -4.211868
5% level -3.529758
10% level -3.196411
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNPIB)
Method: Least Squares
Date: 06/07/13 Time: 14:45
Sample (adjusted): 2002Q2 2011Q4
Included observations: 39 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
LNPIB(-1) -0.317133 0.123302 -2.572014	0.0144
C 3.685184 1.426432 2.583498	0.0140
@TREND("2002Q1") 0.005447 0.002137 2.549222	0.0152
R-squared 0.155371 Mean dependent var	0.016032
Adjusted R-squared 0.108447 S.D. dependent var	0.016604
S.E. of regression 0.015678 Akaike info criterion	-5.399362
Sum squared resid 0.008848 Schwarz criterion	-5.271396
Log likelihood 108.2876 Hannan-Quinn criter.	-5.353449
F-statistic 3.311132 Durbin-Watson stat	2.364630
Prob(F-statistic) 0.047862

La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,3 :

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 3.311132 Chi-square 6.622265	(2, 36) 2	0.0479 0.0365
Null Hypothesis: C(1)=0,C(3)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(3)	-0.317133 0.005447	0.123302 0.002137
Restrictions are linear in coefficients.

La p-value de la statistique F étant inférieure à 5% on rejette _H0,3. Donc, LNPIB est I(1) + C + â.t. La meilleure façon de la stationnariser est de la différentier puis de retirer la tendance. Ceci est équivalent à prendre le résidu de la régression suivante :

LNPIBt-LNPIBt-1 = C+ â.t + åt

Les résultats de cette régression sont comme suit :

Dependent Variable: D(LNPIB) Method: Least Squares Date: 06/07/13 Time: 14:57 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	0.016405	0.005494 2.986136	0.0050
@TREND("2002Q1")	-1.87E-05	0.000239 -0.078008	0.9382
R-squared	0.000164	Mean dependent var	0.016032
Adjusted R-squared	-0.026858	S.D. dependent var	0.016604
S.E. of regression	0.016825	Akaike info criterion	-5.281951
Sum squared resid	0.010474	Schwarz criterion	-5.196640
Log likelihood	104.9980	Hannan-Quinn criter.	-5.251342
F-statistic	0.006085	Durbin-Watson stat	2.780079
Prob(F-statistic)	0.938242

L'allure du résidu issu de cette régression se présente comme suit :



-.01

-.02

-.03

-.04

-.05

.04

.03

.02

.01

.00

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

LNPIBRES

Les tests ADF conduits sur cette série montrent qu'elle est stationnaire. Conclusion : LNPIB est I(1) + C + â.t

Etude de la série PIBDEF (PIB/IPC) :

63

Le graphe de cette série se présente comme suit :



1900

1800

1700

1600

1500

1400

1300

1200

1100

02 03 04 05 06 07 08 09 10 11

PIB_DEF

64

Estimation du modèle [3] pour PIB_DEF :



La statistique t relative à Ö étant supérieure à sa valeur critique de 5%, on accepte H0 et on passe au test de l'hypothèse H0,3 :



65

La p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,3 et on passe à l'estimation du modèle [2].

Estimation du modèle [2] pour PIB_DEF :



La statistique t relative à Ö étant supérieure à sa valeur critique au seuil de 5%, on accepte H0 et on passe au test de l'hypothèse H0,2 :



66

La p-value relative à la statistique F étant inférieure à 5%, on rejette H0 _;2 et on conclut que PIB_DEF est un DS avec Drift. La meilleure façon de la stationnariser est de la différencier. Le graphe de cette nouvelle série se présente comme suit :



-100

150

100

-50

50

0

02 03 04 05 06 07 08 09 10 11

PIB_DEFD1

Les tests ADF effectués sur cette série montrent qu'elle est stationnaire autour d'une moyenne.

Conclusion : PIB_DEF est I(1)

67

Etude de la série LNPIBDEF (ln(PIB/IPC))

L'allure de cette série se présente comme suit :

LNPIB_DEF

7.6 7.5 7.4
7.3 7.2 7.1 7.0

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

Estimation du modèle [3] pour LNPIB_DEF :

Null Hypothesis: LNPIB_DEF has a unit root Exogenous: Constant, Linear Trend Lag Length: 1 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -2.749248	0.2240
Test critical values: 1% level -4.219126
5% level -3.533083
10% level -3.198312
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNPIB_DEF)
Method: Least Squares
Date: 06/07/13 Time: 15:15
Sample (adjusted): 2002Q3 2011Q4
Included observations: 38 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
LNPIB_DEF(-1) -0.641837 0.233459 -2.749248	0.0095
D(LNPIB_DEF(-1)) -0.384677 0.161500 -2.381896	0.0230
C 4.540629 1.643448 2.762868	0.0092
@TREND("2002Q1") 0.007878 0.002906 2.711539	0.0104
R-squared 0.591977 Mean dependent var	0.012196
Adjusted R-squared 0.555975 S.D. dependent var	0.024161
S.E. of regression 0.016100 Akaike info criterion	-5.320756
Sum squared resid 0.008813 Schwarz criterion	-5.148379
Log likelihood 105.0944 Hannan-Quinn criter.	-5.259426
F-statistic 16.44287 Durbin-Watson stat	2.056803
Prob(F-statistic) 0.000001

La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de H0,3 :

68

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 3.839309 Chi-square 7.678618	(2, 34) 2	0.0314 0.0215
Null Hypothesis: C(1)=0,C(4)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(4)	-0.641837 0.007878	0.233459 0.002906
Restrictions are linear in coefficients.

La p-value relative à la statistique F étant inférieure à 5%, on rejette _H0,3 et on conclut que LNPIB_DEF est I(1) + C + â.t. La meilleure façon de la stationnariser est de la différencier et de retirer la tendance. Ceci est équivalent à prendre le résidu de la régression ci-dessous :

LNPIB_DEFt-LNPIB_DEFt-1 = C + â.t

Les résultats de cette régression sont comme suit :

Dependent Variable: D(LNPIB_DEF) Method: Least Squares Date: 06/07/13 Time: 15:22 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	0.012961	0.007889 1.642885	0.1089
@TREND("2002Q1")	-3.45E-05	0.000344 -0.100251	0.9207
R-squared	0.000272	Mean dependent var	0.012272
Adjusted R-squared	-0.026748	S.D. dependent var	0.023845
S.E. of regression	0.024162	Akaike info criterion	-4.558136
Sum squared resid	0.021601	Schwarz criterion	-4.472825
Log likelihood	90.88365	Hannan-Quinn criter.	-4.527527
F-statistic	0.010050	Durbin-Watson stat	3.405660
Prob(F-statistic)	0.920687

L'allure des résidus issus de cette régression se présente comme suit :



LNPIB_DEFRES

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

.08

.06

.04

.02

.00

-.02

-.04

-.06

-.08

Les tests ADF réalisés sur cette série montrent qu'elle est stationnaire. Conclusion : LNPIB_DEF est I(1) + C + â.t

69

Etude de la série TauxCC :

TAUXCC

.040 .036 .032
.028 .024 .020

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

L'allure de cette série est comme suit :

Vu l'allure de la courbe ci-dessus, il est évident qu'il ne s'agit pas d'un bruit blanc. Ceci est confirmé par la lecture du corrélogramme de la série :

Date: 05/20/13 Time: 15:00 Sample: 2002Q1 2011Q4 Included observations: 40
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	0.702	0.702	21.233	0.000
	2	0.404	-0.17...	28.455	0.000
	3	0.277	0.135	31.934	0.000
	4	0.149	-0.13...	32.975	0.000
	5	0.180	0.282	34.526	0.000
	6	0.210	-0.07...	36.707	0.000
	7	0.112	-0.08...	37.347	0.000
	8	0.014	-0.08...	37.358	0.000
	9	-0.03...	0.035	37.426	0.000
	1...	-0.08...	-0.08...	37.830	0.000
	1...	-0.17...	-0.20...	39.637	0.000
	1...	-0.26...	-0.12...	43.954	0.000
	1...	-0.28...	0.047	48.910	0.000
	1...	-0.29...	-0.11...	54.579	0.000
	1...	-0.29...	-0.05...	60.338	0.000
	1...	-0.28...	-0.12...	66.195	0.000
	1...	-0.25...	0.156	71.103	0.000
	1...	-0.22...	-0.09...	75.114	0.000
	1...	-0.27...	-0.20...	81.342	0.000
2...	-0.32...	-0.14...	90.428	0.000

On va procéder aux tests ADF pour déterminer la nature de la non stationnarité.

70

Estimation du modèle [3] pour TAUXCC :

Null Hypothesis: TAUXCC has a unit root Exogenous: Constant, Linear Trend Lag Length: 0 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -3.302619	0.0808
Test critical values: 1% level -4.211868
5% level -3.529758
10% level -3.196411
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(TAUXCC)
Method: Least Squares
Date: 05/15/13 Time: 09:39
Sample (adjusted): 2002Q2 2011Q4
Included observations: 39 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
TAUXCC(-1) -0.313552 0.094940 -3.302619	0.0022
C 0.007270 0.002736 2.657565	0.0117
@TREND("2002Q1") 6.50E-05 3.85E-05 1.687440	0.1002
R-squared 0.261083 Mean dependent var	-0.000254
Adjusted R-squared 0.220032 S.D. dependent var	0.003049
S.E. of regression 0.002693 Akaike info criterion	-8.922779
Sum squared resid 0.000261 Schwarz criterion	-8.794813
Log likelihood 176.9942 Hannan-Quinn criter.	-8.876866
F-statistic 6.359969 Durbin-Watson stat	2.007363
Prob(F-statistic) 0.004312

La statistique t relative à Ö1 est égale à -3.30 qui est supérieure à sa valeur critique au seuil de 5%, mais inférieure à celle au seuil de 1%. Pour cette série, nous allons retenir un seuil de 1%, et donc nous rejetons H0. D'autre part, le coefficient relatif à la tendance n'étant pas significativement différent de zéro, on doit passer à l'estimation du modèle [2].

71

Estimation du modèle [2] pour TAUXCC :



La statistique t relative à Ö étant supérieure à sa valeur critique (au seuil de 1%), on accepte H0 et on passe au test de l'hypothèse H0,2 :



La p-value relative à la statistique F est supérieure à 1%, on accepte donc _H0,2 et on passe à l'estimation du modèle [1].

72

Estimation du modèle [1] pour TAUXCC :



La statistique t relative à Ö étant supérieure à sa valeur critique au seuil de 1%, on accepte H0 et on conclut que TAUXCC est un DS. La meilleure façon de la stationnariser est de la différencier. Le graphe de cette nouvelle série se présente comme suit :

.012 .008 .004 .000 -.004 -.008 -.012 -.016

02 03 04 05 06 07 08 09 10 11

TAUXCCD1

Les tests ADF conduits sur cette série montrent qu'elle est stationnaire. Conclusion : TAUXCC est I(1).

73

Etude de la série IPC :

IPC

112 108 104 100 96 92

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

Le graphe de cette série se présente comme suit :

Estimation du modèle [3] pour IPC :

Null Hypothesis: IPC has a unit root Exogenous: Constant, Linear Trend Lag Length: 1 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -2.042331	0.5601
Test critical values: 1% level -4.219126
5% level -3.533083
10% level -3.198312
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(IPC)
Method: Least Squares
Date: 06/07/13 Time: 11:12
Sample (adjusted): 2002Q3 2011Q4
Included observations: 38 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
IPC(-1) -0.325196 0.159228 -2.042331	0.0489
D(IPC(-1)) -0.537607 0.139479 -3.854387	0.0005
C 30.31981 14.55012 2.083819	0.0448
@TREND("2002Q1") 0.166680 0.081162 2.053664	0.0478
R-squared 0.526030 Mean dependent var	0.408513
Adjusted R-squared 0.484209 S.D. dependent var	1.447662
S.E. of regression 1.039691 Akaike info criterion	3.015024
Sum squared resid 36.75253 Schwarz criterion	3.187402
Log likelihood -53.28546 Hannan-Quinn criter.	3.076355
F-statistic 12.57814 Durbin-Watson stat	1.714527
Prob(F-statistic) 0.000011

La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,3 :

74

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 2.118157 Chi-square 4.236313	(2, 34) 2	0.1358 0.1203
Null Hypothesis: C(1)=0,C(4)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(4)	-0.325196 0.166680	0.159228 0.081162
Restrictions are linear in coefficients.

La p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,3 et on passe à l'estimation du modèle [2].

Estimation du modèle [2] pour IPC :

Null Hypothesis: IPC has a unit root Exogenous: Constant Lag Length: 1 (Automatic - based on SIC, maxlag=9)
t-Statistic	Prob.*
Augmented Dickey-Fuller test statistic -0.131131	0.9386
Test critical values: 1% level -3.615588
5% level -2.941145
10% level -2.609066
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(IPC)
Method: Least Squares
Date: 06/07/13 Time: 11:21
Sample (adjusted): 2002Q3 2011Q4
Included observations: 38 after adjustments
Variable Coefficient Std. Error t-Statistic	Prob.
IPC(-1) -0.004142 0.031587 -0.131131	0.8964
D(IPC(-1)) -0.682672 0.125677 -5.431960	0.0000
C 1.113076 3.211811 0.346557	0.7310
R-squared 0.467236 Mean dependent var	0.408513
Adjusted R-squared 0.436792 S.D. dependent var	1.447662
S.E. of regression 1.086429 Akaike info criterion	3.079327
Sum squared resid 41.31150 Schwarz criterion	3.208610
Log likelihood -55.50720 Hannan-Quinn criter.	3.125324
F-statistic 15.34755 Durbin-Watson stat	1.829766
Prob(F-statistic) 0.000016

La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,2 :

Wald Test: Equation: Untitled
Test Statistic Value	df	Probability
F-statistic 7.127342 Chi-square 14.25468	(2, 35) 2	0.0025 0.0008
Null Hypothesis: C(1)=0,C(3)=0 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
C(1) C(3)	-0.004142 1.113076	0.031587 3.211811
Restrictions are linear in coefficients.



4.72

4.68

4.64

4.60

4.56

4.52

02 03 04 05 06 07 08 09 10 11

LNIPC

75

La p-value relative à la statistique F étant inférieure à sa valeur critique, on rejette _H0,2. Par conséquent, IPC est I(1) + C et la meilleure façon de la stationnariser est de la différencier.

IPCD1

5 4 3 2 1 0 -1 -2 -3 -4
	2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

Le graphe ci-dessous représente la série IPCD1, différence première de IPC :

Les tests ADF réalisés sur cette série montrent qu'elle est stationnaire. Conclusion : IPC est I(1)

Etude de la série LNIPC :

Le graphe de cette série se présente comme suit :

76

Estimation du modèle [3] pour LNIPC :



La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,3 :



La p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,3 et on passe à l'estimation du modèle [2].

77

Estimation du modèle [2] pour LNIPC :



La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on passe au test de l'hypothèse H0,2 :



Encore une fois, la p-value relative à la statistique F étant supérieure à 5%, on accepte _H0,2 et on passe à l'estimation du modèle [1].

78

Estimation du modèle [1] pour LNIPC :



La statistique t relative à Ö étant supérieure à sa valeur critique, on accepte H0 et on conclut que LNIPC est un DS. La meilleure façon de la stationnariser est de la différencier. Le graphe de cette nouvelle série se présente comme suit :



-.01

-.02

-.03

-.04

.04

.03

.02

.01

.00

02 03 04 05 06 07 08 09 10 11

LNIPCD1

Les tests ADF conduits sur cette série montrent qu'elle est stationnaire. Conclusion : LNIPC est I(1)

79

Le tableau ci-dessous récapitule la nature des différentes séries étudiées en termes de stationnarité et ordre d'intégration :

Série	Définition	Stationnaire	Ordre d'intégration
M1_FID	Monnaie fiduciaire	Non	I(2)
LNM1_FID	Logarithme de M1_FID	Non	I(2)
M1_SCR	Monnaie scripturale	Non	I(1)		LNM1_SCR
Logarithme de M1_SCR	Non	I(2)
M3_M1	Agrégat monétaire M3 - M1	Non	I(1)
LNM3_M1	Logarithme de M3 M1	Non	I(1)
PIB	Produit Intérieur Brut	Non	I(1)
LNPIB	Logarithme de PIB	Non	I(1)
PIB_DEF	PIB déflaté par l'indice des Prix à la Consommation(IPC)	Non	I(1)
LNPIB_DEF	Logarithme de PIB DEF	Non	I(1)
TAUXCC	Taux sur compte carnet	Non	I(1)
IPC	Indice des Prix à la Consommation	Non	I(1)
LNIPC	Logarithme de IPC	Non	I(1)

Toutes les séries sont intégrées d'ordre 1, à l'exception de M1_FID, LNM1_FID et LNM1_SCR qui sont intégrées d'ordre 2.

80

Chapitre III : Estimation de la demande de

monnaie dans le cas du Maroc

Avant d'aborder l'estimation de la demande de monnaie dans le cas du Maroc, on se propose d'abord de présenter les résultats d'une étude économétrique de la demande de monnaie réalisée pour la zone euro. Ces résultats nous servirons comme une base de comparaison avec nos résultats. Ce choix a été dicté principalement par l'intensité et l'importance des échanges économiques du Maroc avec cette zone ce qui, à notre avis, fait d'elle, le meilleur repère pour situer nos résultats et conclusions.

Section 1 : ESTIMATION D'UNE FONCTION DE DEMANDE DE MONNAIE POUR LA ZONE EURO PAR LA BANQUE DE FRANCE

Cette étude économétrique a été réalisée en 2003 par un groupe de travail, interne à la Banque de France, rassemblant des experts rattachés à différentes unités administratives. Le BULLETIN DE LA BANQUE DE FRANCE - N°111 - MARS 200 3 propose une synthèse des résultats des estimations de la fonction de demande de monnaie de la zone euro dans le cadre d'un système multivarié.

Le modèle qu'ils ont estimé s'écrit en univarié sous la forme suivante :

m_t -- P_t = Y_o + Y_i. Y_t + Y₂. rown_t + Y₃. ra_t + Y₄. rlt_t + Y5. 7T_t + £_t

Où

mt : est le logarithme du stock de monnaie à la période t,

pt : est le logarithme du déflateur d'une composante de la demande ou du PIB,

~t : est le taux d'inflation,

yt est le logarithme du PIB réel,

rownt : est le taux d'intérêt intrinsèque,

rctt : est le taux d'intérêt nominal de court terme

rltt : est les taux d'intérêt nominal de long terme

Et : est un terme d'erreur.

Les yi sont les paramètres à estimer et vérifient les inégalités suivante : y1 > 0, y2 < 0, y3 < 0, y4 < 0, y5 < 0.

81

Il ressort de leur étude que l'approche univariée donne une élasticité de la demande de monnaie au revenu très supérieure à 1 ce qui n'est pas conforme à la théorie économique.

En revanche, l'approche multivariée (VECM), leur a permis d'obtenir des résultats nettement plus intéressants, tant du point de vue statistique qu'économique. En effet, les différents tests statistiques conduits leur ont permis, d'une part, de valider les spécifications retenues et d'autre part, d'identifier deux relations de cointégration, interprétées respectivement comme une équation de vitesse de circulation de la monnaie et comme une relation de Fisher (relation liant l'inflation et le taux d'intérêt de long terme). En outre, l'hypothèse d'une élasticité unitaire des encaisses réelles au revenu, rejetée dans le cas univarié, a été acceptée dans cette approche, ce qui a permis de réconcilier les données et la théorie économique.

Les deux tableaux ci-dessous présentent les résultats qu'ils ont obtenus pour la demande de monnaie et ceux pour la relation de FISHER :

Variables Coefficients

cst 1.297

yt 1.000

rownt 0.063

rctt -0.039

rltt -0.020

Equation de demande de monnaie

Variables Coefficients

cst -0.363

rltt 0.502

Relation de FISHER (ðt = â0+â1.rltt)

Dans ce bulletin, ils présentent également un tableau comparant leurs résultats avec ceux obtenus par d'autres auteurs (Brand et et Cassola, 2000 ; Calza et alii, 2001 ; Coenen et Vega, 2001 ; Gerlach et Sevensson, 2001) :

82

Auteurs	Périodes	yt	rownt	rctt	rltt	rctt-rownt	rltt-rctt	ðt
BC	1980Q1-	1.331			-0.0040
	1999Q3
CGL	1980Q1-	1.336				-0.0086
	1999Q4
CV(a)	1980Q4-	1.125					-0.0087	-0.0151
	1998Q4
GS(a)	1981Q1-	1.510					0.0156
	1998Q4
BdF	1987Q1-	1.000	-0.063	-0.039	-0.020
	2002Q1

BC : Brand et Cassola CGL : Calza et alii

CV : Coenen et Verga GS : Gerlach et Svensson (a) : Analyse univariée BdF : Banque de France

L'objectif principal recherché dans la section suivante est d'estimer la fonction de demande de monnaie pour le cas du Maroc selon la théorie Keynésienne mais en se basant sur les trois forme de monnaie suivantes : monnaie fiduciaire (M1_FID), monnaie scripturale(M1_SCR) et enfin M3-M1 . Pour rappel, Keynes distingue trois motifs de détention de la monnaie : motif de transaction, motif de précaution et motif de spéculation, mais en ce qui concerne sa formulation mathématique, il regroupe ces trois motifs de détention de la monnaie en une seule équation de demande de monnaie qu'il appel fonction de préférence pour la liquidité. La formulation qu'il propose est comme suit :

_M'

~ = L₁(Y)+L₂(i)

Où :

Md : est la demande de monnaie P : est le niveau général des prix i : est le taux d'intérêt

Y : est le revenu réel

L1 : est la fonction de demande pour les motifs transaction et précaution

L2 : est la demande de monnaie pour le motif spéculation.

Pour le motif de transaction, nous allons nous baser sur le sous-agrégat de M1 ne contenant que les billets de banque et les pièces de monnaie (monnaie fiduciaire), que nous allons noter M1_FID.

Pour le motif de précaution, nous allons étudier le sous-agrégat de M1 qui ne contient que la monnaie scripturale, nous noterons ce sous-agrégat M1_SCR.

83

Notre choix de ces sous-agrégats est motivé par le fait suivant, et que nous considérons comme une hypothèse à tester :

Hypothèse (H) : pour leurs transactions de tous les jours les agents gardent, pour des raisons pratiques, une grande partie de leurs revenus sous forme liquides (billets et pièces) et non sous forme de dépôt à vue, bien que les paiements par cartes connaissent une évolution croissante ces dernières années. Par contre, pour le motif de précaution, il devrait être sous forme de dépôt à vue ou dans les comptes à court terme (et donc inclut dans M1_SCR et M3_M1).

Enfin, le motif de spéculation sera appréhendé en étudiant l'agrégat M3 duquel on retranchera l'agrégat M1, ce sous agrégat sera noté M3_M1.

L'objectif est de vérifier est ce que les hypothèses émises par Keynes selon lesquelles le motif de transaction et le motif de précaution dépendent du revenu et seulement de celui-ci, et que le motif de spéculation dépend du taux d'intérêt uniquement.

Ainsi, le taux sur compte de carnet (TAUXCC) sera toujours inclut dans les estimations, et à chaque fois la significativité de son coefficient sera testée. Si notre hypothèse est vraie, ce coefficient ne devrait être significativement différent de zéro que pour M1_SCR et M3_M1.

La démarche que nous allons adopter pour les différents modèle se présente comme suit :

· Spécification du modèle (formulation mathématiques et hypothèses économiques sur ses coefficients)

· Estimation du modèle (sous Eviews)

· Validation du modèle par les tests statistiques

· Interprétation des résultats du modèle retenu

Mais avant de passer à l'estimation des modèles il nous a apparu important de faire un rappel de la stratégie de tests de Dickey-Fuller que nous allons adopter vu leurs importance dans la stationnarisation des séries étudiées et dans la détermination de leurs ordres d'intégration le cas échéant.

84

Section 2 : Estimation univariée de la demande de monnaie

Dans cette partie, nous allons utiliser un modèle univarié dans lequel la demande de monnaie M1_FID puis M1_SCR et enfin M3_M1 seront expliquées par le PIB et par TAUXCC. Le but étant d'essayer de capturer la demande incombant au motif de transaction et de précaution et celle incombant au motif de spéculation selon la théorie Keynésienne. A chaque fois, nous allons estimer un modèle en niveau puis en logarithme.

I- Etude de la demande de monnaie fiduciaire (M1_FID)

I-1- Spécification en niveau :

Le modèle à estimer s'écrit comme suit :

M1_FID_t = C + a. PIB_t + b. TAUXCC_t + å_t

Dans cette spécification nous utilisons le PIB nominal et par conséquent, M1_FID ne sera pas divisée par l'IPC.

Selon la théorie de Keynes le coefficient a doit être positif et le coefficient b négatif, alors que la constante C ne devrait pas être significativement différente de zéro.

Les résultats de régression de ce modèle sont comme suit :

Dependent Variable: M1_FID Method: Least Squares Date: 06/10/13 Time: 10:14 Sample: 2002Q1 2011Q4 Included observations: 40
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	-36052.02	3774.096 -9.552492	0.0000
PIB	0.938953	0.017182 54.64664	0.0000
TAUXCC	-55292.24	115442.9 -0.478957	0.6348
R-squared	0.988238	Mean dependent var	106440.8
Adjusted R-squared	0.987602	S.D. dependent var	28967.35
S.E. of regression	3225.388	Akaike info criterion	19.06753
Sum squared resid	3.85E+08	Schwarz criterion	19.19420
Log likelihood	-378.3507	Hannan-Quinn criter.	19.11333
F-statistic	1554.353	Durbin-Watson stat	0.921204
Prob(F-statistic)	0.000000

Modèle 1 : M1_FID C,PIB,TAUXCC

Le coefficient relatif à la constante C est significativement différent de zéro ce qui contredit notre hypothèse.

85

Le coefficient relatif à PIB est positif et significativement différent de zéro, en plus il est inférieur à 1 ce qui est logique puisque la demande de monnaie ne peut pas être supérieure au revenu.

Par contre, le coefficient relatif à TAUXCC n'est pas significatif au seuil de 5% et même au seuil de 10%, ce qui contredit une deuxième fois notre hypothèse.

Ces conclusions sont conditionnées par la validité du modèle. C'est ce qu'on se propose de faire par la suite.

Le R² est très satisfaisant (0.987), de même que le R² ajusté. Cependant, la statistique de Durbin-Watson est proche de zéro ce qui laisse présager d'une autocorrélation des erreurs.

En effet, l'analyse des résidus de cette régression montre qu'on est en présence d'une autocorrélation des erreurs :

Date: 06/10/13 Time: 10:17 Sample: 2002Q1 2011Q4 Included observations: 40
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	0.522	0.522	11.746	0.001
	2	0.271	-0.00...	14.992	0.001
	3	0.209	0.095	16.983	0.001
	4	0.236	0.127	19.589	0.001
	5	-0.06...	-0.35...	19.784	0.001
	6	-0.41...	-0.43...	28.125	0.000
	7	-0.18...	0.353	29.864	0.000
	8	-0.14...	-0.12...	30.973	0.000
	9	-0.34...	-0.37...	37.443	0.000
	1...	-0.51...	-0.06...	52.118	0.000
	1...	-0.35...	-0.14...	59.247	0.000
	1...	-0.22...	-0.31...	62.259	0.000
	1...	-0.39...	-0.07...	72.142	0.000
	1...	-0.33...	0.056	79.390	0.000
	1...	0.001	0.012	79.390	0.000
	1...	0.234	0.069	83.225	0.000
	1...	0.185	0.062	85.717	0.000
	1...	0.158	-0.21...	87.627	0.000
	1...	0.327	-0.21...	96.206	0.000
2...	0.335	0.025	105.64	0.000

En effet, les coefficients d'ordre 1, 6, 9 et 10 sont significativement différents de zéro.

On s'attendait à ce résultat étant donné qu'aucune des séries présentes dans ce modèle n'est stationnaire. En effet, M1_FID est I(2), PIB et TAUXCC sont I(1).

Les conclusions ci-dessus ne sont donc pas à prendre en compte étant donné que le modèle ne peut pas être validé.

Nous allons donc estimer le modèle ci-dessus avec les séries stationnarisées :

M1_FIDRESD1_t = C + a. PIBRES_t + b.TAUXCCD1 + E_t

Avec les hypothèses suivantes : C non significativement différent de zéro, 1> a >0 et b <0 Les résultats de l'estimation de ce modèle sont comme suit :



86

Modèle 2 : M1_FIDRESD1 C,PIBRES,TAUXCC

Les résultats de cette estimation montrent qu'aucun des coefficients n'est significatif, même si leurs signes sont conforme à la théorie (1> a >0 et b <0). En plus, le R² et le R² ajusté se sont beaucoup détériorés (0.068700 pour R² et 0.01548 pour R² ajusté).

L'analyse du corrélogramme des résidus issus de cette régression montre en fait qu'il y a présence d'une forte autocorrélation des erreurs. En effet, comme le montre la figure ci-dessous, les coefficients d'ordre 2, 4 et 6 sont significativement différents de zéro.



Cette autocorrélation est sûrement dû à l'omission de quelque variables étant donnée le R2 très bas.

Nous allons donc voir à l'aide du test de causalité de Granger si des retards de PIBRES et de TAUXCCD1 peuvent améliorer le modèle :

En prenant un retard de 4, on obtient les résultats suivants :



87

Comme on peut le voir sur ce tableau, l'hypothèse « PIBRES ne cause pas M1_FIDRESD1 » est rejetée au seuil de 5% (p-value = 0.04556). Par contre, l'hypothèse « TAUXCC ne cause pas M1_FIDRESD1 » est acceptée au seuil de 5%.

On se propose donc d'introduire dans le modèle précédent les retards jusqu'à l'ordre 4 de la variable PIBRES. Les résultats de ce modèle sont comme suit :



Modèle 3 : M1_FIDRESD1 C, PIBRES, PIBRES(-1 à -4) TAUXCCD1

D'après ces résultats on voit que le R² s'est amélioré mais les coefficients sont toujours non

significatifs. En plus, les erreurs sont toujours autocorrélées comme le montre le
corrélogramme ci-dessous :



88

Pour remédier à ce problème, nous avons testé plusieurs modèles incluant différents retards pour les erreurs (termes MA : Moyenne mobile). Le meilleur modèle est celui avec 4 retards des erreurs :



Modèle 4 : M1_FIDRESD1 C, PIBRES, PIBRES(-1 à -4) TAUXCCD1 MA(1 à 4)

En effet, comme on peut le constater, le R² s'est nettement amélioré en passant à 0,76 et le R2 ajusté à 0.66. Cependant, on constate que les coefficients relatifs à PIBRES d'ordre 1, 3 et 4 sont négatifs ce qui soulève des questions quant à leur signification et justification économique.

Le corrélogramme des résidus ci-dessous, montre qu'aucun des coefficients d'autocorrélation n'est significativement différent de zéro :



89

Cependant, le test de Breusch-Godfrey ne permet pas d'accepter l'hypothèse H0 selon laquelle il y a absence de corrélation :



En effet, les p-value relatives aux statistiques F et n*R² sont toutes les deux inférieures à 5% et même 1%.

Donc même si le R² du dernier modèle est assez satisfaisant, on ne peut pas le valider si on se fie au test de Breusch-Godfrey.

Si on retire les retards de PIBRES, on obtient les résultats suivants :

90

Dependent Variable: M1_FIDRESD1 Method: Least Squares Date: 06/11/13 Time: 12:21 Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after adjustments Convergence achieved after 25 iterations MA Backcast: 2001Q3 2002Q2
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	29.25949	346.0383 0.084556	0.9332
PIBRES	0.237446	0.112671 2.107434	0.0433
TAUXCCD1	58860.98	162633.2 0.361925	0.7199
MA(1)	-0.181954	0.068648 -2.650542	0.0125		MA(2)
-0.594425	0.087771 -6.772448	0.0000	MA(3)
-0.153580	0.063892 -2.403742	0.0224	MA(4)
0.919146	0.042208 21.77641	0.0000
R-squared	0.709423	Mean dependent var	11.29564
Adjusted R-squared	0.653183	S.D. dependent var	3630.246
S.E. of regression	2137.896	Akaike info criterion	18.33785
Sum squared resid	1.42E+08	Schwarz criterion	18.63951
Log likelihood	-341.4192	Hannan-Quinn criter.	18.44518
F-statistic	12.61406	Durbin-Watson stat	2.534566
Prob(F-statistic)	0.000000
Inverted MA Roots	.84-.51i	.84+.51i -.75-.63i	-.75+.63i

Modèle 5 : M1_FIDRESD1 PIBRES, MA(1 à 4)

Comme on peut le voir, tous les coefficients relatifs aux retards MA ainsi que celui relatif à PIBRES sont significativement différents de zéro au seuil de 5% et le R²s'est détérioré par rapport au modèle 4. En plus, le corrélogramme ci-dessous, montre que les résidus sont autocorrélés :

Date: 06/11/13 Time: 12:26 Sample: 2002Q3 2011Q4 Included observations: 38 Q-statistic probabilities adjusted for 4 ARMA term(s)
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	-0.29...	-0.29...	3.5042
	2	-0.17...	-0.27...	4.7278
	3	0.049	-0.11...	4.8305
	4	0.358	0.348	10.569
	5	-0.10...	0.192	11.095	0.001
	6	-0.28...	-0.18...	15.026	0.001
	7	-0.03...	-0.35...	15.069	0.002
	8	0.286	-0.07...	19.210	0.001
	9	-0.05...	0.162	19.352	0.002
	1...	-0.48...	-0.27...	31.946	0.000
	1...	0.248	0.004	35.411	0.000
	1...	-0.00...	-0.29...	35.412	0.000
	1...	0.008	-0.08...	35.417	0.000
	1...	-0.25...	0.023	39.602	0.000
	1...	0.034	-0.13...	39.680	0.000
	1...	0.152	-0.12...	41.274	0.000

On conclut donc que la spécification en niveau de la demande de monnaie M1_FID ne permet pas de mettre en évidence la présence d'un motif de spéculation comme c'est postulé par la théorie Keynésienne. Ceci conforte tout de même notre hypothèse (H).

I-2- Spécification logarithmique :

Selon cette spécification, le modèle à estimer est comme suit :

LNM1_FID - LNIPC = C + a. LNPIB_DEF + b. TAUXCC + å

91

Cette fois-ci, nous allons utiliser le PIB réel et par conséquent l'agrégat M1_FID sera divisé par l'IPC. L'avantage de ce modèle est que les coefficients a et b ont une signification économique. En effet, a sera interprété comme étant l'élasticité de M1_FID par rapport au PIB et b sera interprété comme étant la semi-élasticité de M1_FID par rapport à TAUXCC.

Nous allons directement passer au modèle avec les variables stationnarisées, soit le modèle ci-dessous :

LNM1_FIDRESD1 - LNIPCD1 = C + a. LNPIB_DEFRES + b. TAUXCCD1 + å avec åt ~ N (0, ó²)

Les résultats de l'estimation de ce modèle sont comme suit :

Dependent Variable: LNM1_FIDRESD1-LNIPCD1 Method: Least Squares Date: 06/11/13 Time: 09:08 Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	-0.004432	0.005463 -0.811244	0.4227
LNPIB_DEFRES	0.429837	0.228411 1.881859	0.0682
TAUXCCD1	-2.906281	1.786115 -1.627152	0.1127
R-squared	0.146873	Mean dependent var	-0.003700
Adjusted R-squared	0.098123	S.D. dependent var	0.035332
S.E. of regression	0.033554	Akaike info criterion	-3.875692
Sum squared resid	0.039404	Schwarz criterion	-3.746409
Log likelihood	76.63816	Hannan-Quinn criter.	-3.829694
F-statistic	3.012772	Durbin-Watson stat	2.452892
Prob(F-statistic)	0.062050

Modèle 6 : (LNM1_FIDRESD1-LNIPC) C,LNPIB_DEFRES,TAUXCCD1

Ces résultats montrent qu'aucun des coefficients n'est significativement différent de zéro au seuil de 5%. Par contre, celui relatif à LNPIB_DEFRES peut être accepté au seuil de 10%. Le R2 et le R² ajusté sont très bas (0.15 et 0.098 respectivement).

L'analyse du corrélogramme des résidus ci-dessous, montre une forte corrélation d'ordre 4 :

Date: 06/11/13 Time: 09:12 Sample: 2002Q3 2011Q4 Included observations: 38
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	-0.26...	-0.26...	2.8870	0.089
	2	-0.41...	-0.51...	10.039	0.007
	3	-0.12...	-0.63...	10.732	0.013
	4	0.708	0.318	33.121	0.000
	5	-0.20...	0.057	35.088	0.000
	6	-0.38...	-0.07...	42.062	0.000
	7	0.006	0.018	42.064	0.000
	8	0.482	-0.06...	53.815	0.000
	9	-0.15...	-0.02...	55.024	0.000
	1...	-0.38...	-0.19...	63.201	0.000
	1...	0.066	-0.23...	63.450	0.000
	1...	0.388	-0.13...	72.231	0.000
	1...	-0.05...	0.059	72.422	0.000
	1...	-0.45...	-0.21...	85.280	0.000
	1...	0.166	0.004	87.107	0.000
	1...	0.249	-0.24...	91.379	0.000

92

Le coefficient d'autocorrélation d'ordre 2 est également significativement différent de zéro. On se propose donc d'introduire un terme MA d'ordre 2 et un autre d'ordre 4 dans le modèle et de retirer la constante étant donné sa p-value très élevée. Les résultats obtenus à partir de l'estimation de ce modèle sont comme suit :

Dependent Variable: LNM1_FIDRESD1-LNIPCD1 Method: Least Squares Date: 06/11/13 Time: 09:14 Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after adjustments Convergence achieved after 14 iterations MA Backcast: 2001Q3 2002Q2
Variable	Coefficient	Std. Error t-Statistic	Prob.
LNPIB_DEFRES	0.611350	0.081798 7.473899	0.0000
TAUXCCD1	-0.938386	0.993148 -0.944861	0.3514
MA(2)	-0.426607	0.071263 -5.986364	0.0000
MA(4)	0.948616	0.028556 33.21933	0.0000
R-squared	0.725462	Mean dependent var	-0.003700
Adjusted R-squared	0.701238	S.D. dependent var	0.035332
S.E. of regression	0.019312	Akaike info criterion	-4.956878
Sum squared resid	0.012680	Schwarz criterion	-4.784501
Log likelihood	98.18069	Hannan-Quinn criter.	-4.895548
Durbin-Watson stat	2.466296
Inverted MA Roots	.77+.62i	.77-.62i -.77+.62i	-.77-.62i

Modèle 7 : Modèle 6 : (LNM1_FIDRESD1-LNIPC) LNPIB_DEFRES,TAUXCCD1 MA(2) MA(4)

Comme on peut le voir, à l'exception du coefficient relatif à TAUXCCD1, tous les autres coefficients sont significativement différents de zéro, et le R² et le R² ajusté se sont nettement améliorés (0.72 et 0.70 respectivement).

L'analyse du corrélogramme des résidus ci-dessous, montre qu'à part le coefficient d'ordre 8, tous les autres coefficients d'autocorrélation sont non significatifs :

Date: 06/11/13 Time: 09:19 Sample: 2002Q3 2011Q4 Included observations: 38 Q-statistic probabilities adjusted for 2 ARMA term(s)
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	-0.26...	-0.26...	2.8881
	2	-0.09...	-0.17...	3.2481
	3	-0.14...	-0.24...	4.1981	0.040
	4	0.301	0.188	8.2432	0.016
	5	-0.17...	-0.10...	9.6949	0.021
	6	-0.19...	-0.26...	11.429	0.022
	7	0.034	-0.07...	11.486	0.043
	8	0.409	0.324	19.973	0.003
	9	-0.01...	0.262	19.991	0.006
	1...	-0.35...	-0.23...	26.692	0.001
	1...	0.140	0.014	27.797	0.001
	1...	-0.05...	-0.26...	27.959	0.002
	1...	0.021	-0.05...	27.987	0.003
	1...	-0.33...	-0.11...	34.955	0.000
	1...	0.144	-0.19...	36.321	0.001
	1...	0.175	-0.06...	38.434	0.000

Par contre, le test de Breusch-Godfrey conduit avec 20 retards permet d'accepter l'hypothèse d'abscence d'autocorrélation des erreurs au seuil de 5%, comme le montre les deux p-values des deux statistique de test :

Breusch-Godfrey Serial Correlation LM Test:

F-statistic 1.608733 Prob. F(20,14) 0.1829

Obs*R-squared 26.35360 Prob. Chi-Square(20) 0.1544

93

Ces différents tests nous permettent d'accepter le modèle.

Ce modèle nous donne une élasticité-revenu (élasticité de M1_FID par rapport au PIB_DEF) égale à 0.61 et une semi-élasticité-taux égale à -0.94. On peut donc dire qu'une augmentation de 1% du PIB entraîne une augmentation de seulement 0.61% de M1_FID et vice-versa. Une augmentation de 1 point du taux sur compte de carnet entraîne une diminution de -0.94% de M1_FID et vice-versa.

D'autre part, les résultats de test d'une élasticité unitaire ne permettant pas d'accepter cette hypothèse, la constante, qui est ici égale à zéro, ne peut pas être interprétée comme une vitesse de circulation :

Wald Test: Equation: EQ07
Test Statistic Value	df	Probability
t-statistic -4.751348 F-statistic 22.57531 Chi-square 22.57531	34 (1, 34) 1	0.0000 0.0000 0.0000
Null Hypothesis: C(1)=1 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
-1 + C(1)	-0.388650	0.081798
Restrictions are linear in coefficients.

Ces deux modèles nous permettent de conclure que le motif de spéculation est absent pour M1_FID, c'est-à-dire que le seul motif de détention de M1_FID est le motif de transaction et celui de précaution ce qui est conforme à notre hypothèse (H).

II- Etude de la demande de monnaie scripturale (M1_SCR)

II-1- Spécification en niveau :

Le modèle à estimer s'écrit comme suit :

M1_SCR_t = C + a. PIB_t + b. TAUXCC_t + å_t Avec C non significativement différent de zéro, 0 <a < 1 et b<0

Nous allons suivre la démarche que nous avons adoptée pour M1_FID.

Dans cette spécification nous utilisons le PIB nominal et par conséquent, M1_SCR ne sera pas divisée par l'IPC.

94

Les résultats de régression de ce modèle sont comme suit :

Dependent Variable: M1_SCR Method: Least Squares Date: 06/10/13 Time: 10:19 Sample: 2002Q1 2011Q4 Included observations: 40
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	-138975.7	13143.42 -10.57379	0.0000
PIB	2.910663	0.059838 48.64253	0.0000
TAUXCC	-753078.9	402034.1 -1.873172	0.0690
R-squared	0.985039	Mean dependent var	286346.5
Adjusted R-squared	0.984231	S.D. dependent var	89448.33
S.E. of regression	11232.53	Akaike info criterion	21.56305
Sum squared resid	4.67E+09	Schwarz criterion	21.68972
Log likelihood	-428.2611	Hannan-Quinn criter.	21.60885
F-statistic	1218.085	Durbin-Watson stat	0.773446
Prob(F-statistic)	0.000000

Modèle 8 : M1_SCR C, PIB, TAUXCC

Les résultats de cette estimation montrent que les coefficients relatifs à la constante et à PIB sont significatifs au seuil de 5%, mais pas celui relatif à TAUXCC. Toutefois, la significativité de ce dernier coefficient peut être acceptée au seuil de 10% contrairement à ce qu'on a obtenu pour M1_FID. Cependant, le coefficient relatif à PIB est égal à 2.9 et est donc supérieur à 1 ce qui contredit notre hypothèse.

Le R² est très élevé (0.98) au même titre que le R² ajusté. Cependant, la statistique DW est proche de 0 ce qui laisse présager d'une autocorrélation des erreurs.

En effet, l'analyse du corrélogramme des résidus issus de cette régression montre qu'il y a présence d'une forte autocorrélation des erreurs. En effet, comme le montre la figure ci-dessous, les coefficients d'ordre 1, 2, 15 et 16 sont significativement différents de zéro.

Date: 06/10/13 Time: 10:26 Sample: 2002Q1 2011Q4 Included observations: 40
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	0.606	0.606	15.840	0.000
	2	0.508	0.223	27.269	0.000
	3	0.331	-0.07...	32.233	0.000
	4	0.200	-0.07...	34.106	0.000
	5	0.075	-0.08...	34.377	0.000
	6	-0.11...	-0.21...	34.976	0.000
	7	-0.04...	0.174	35.097	0.000
	8	-0.06...	0.069	35.321	0.000
	9	-0.06...	-0.04...	35.535	0.000
	1...	-0.04...	0.001	35.651	0.000
	1...	-0.21...	-0.34...	38.221	0.000
	1...	-0.21...	-0.11...	40.899	0.000
	1...	-0.35...	-0.14...	48.622	0.000
	1...	-0.36...	-0.04...	57.425	0.000
	1...	-0.44...	-0.09...	70.427	0.000
	1...	-0.40...	0.030	81.716	0.000
	1...	-0.32...	-0.08...	89.193	0.000
	1...	-0.21...	0.054	92.840	0.000
	1...	-0.09...	0.033	93.498	0.000
2...	-0.00...	0.019	93.498	0.000

95

On s'attendait à ce résultat étant donné qu'aucune des séries présentes dans ce modèle n'est stationnaire. En effet, M1_SCR, PIB et TAUXCC sont toutes I(1). Nous allons donc estimer le modèle avec les séries stationnarisées :

M1_SCRRES_t = C + a. PIBRES_t + b. TAUXCCD1_t + E_t

Avec C non significativement différent de zéro, 0 <a < 1 et b<0 Les résultats de l'estimation de ce modèle sont comme suit :

Dependent Variable: M1_SCRRES Method: Least Squares Date: 06/10/13 Time: 12:21 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	52.04004	1201.138 0.043326	0.9657
PIBRES	0.554593	0.456707 1.214329	0.2325
TAUXCCD1	205006.2	404997.2 0.506192	0.6158
R-squared	0.053561	Mean dependent var	1.87E-13
Adjusted R-squared	0.000981	S.D. dependent var	7477.246
S.E. of regression	7473.578	Akaike info criterion	20.74994
Sum squared resid	2.01E+09	Schwarz criterion	20.87791
Log likelihood	-401.6238	Hannan-Quinn criter.	20.79585
F-statistic	1.018654	Durbin-Watson stat	2.637168
Prob(F-statistic)	0.371252

Modèle 9 : M1_SCRRES C,PIBRES,TAUXCCD1

Les résultats de cette estimation montrent qu'aucun des coefficients n'est significatif, en plus, celui relatif à TAUXCC n'est pas négatif comme on s'y attendait et R² est très bas (0.05356).

L'analyse du corrélogramme des résidus issus de cette régression montre en fait qu'il y a présence d'une forte autocorrélation des erreurs. En effet, comme le montre la figure ci-dessous, les coefficients d'ordre 1 jusqu'à 5 sont significativement différents de zéro.

Date: 06/10/13 Time: 12:24 Sample: 2002Q2 2011Q4 Included observations: 39
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	-0.35...	-0.35...	5.2131	0.022
	2	0.437	0.358	13.478	0.001
	3	-0.42...	-0.26...	21.655	0.000
	4	0.439	0.225	30.477	0.000
	5	-0.46...	-0.22...	40.617	0.000
	6	0.182	-0.24...	42.224	0.000
	7	-0.38...	-0.07...	49.717	0.000
	8	0.344	0.100	55.838	0.000
	9	-0.23...	0.078	58.887	0.000
	1...	0.252	-0.00...	62.377	0.000
	1...	-0.25...	-0.10...	66.139	0.000
	1...	0.167	-0.21...	67.797	0.000
	1...	-0.21...	-0.07...	70.727	0.000
	1...	0.015	-0.19...	70.741	0.000
	1...	-0.20...	-0.05...	73.440	0.000
	1...	0.082	-0.00...	73.911	0.000

Cette autocorrélation est sûrement dû à l'omission de quelque variables étant donnée le R2 très bas.

96

Nous allons donc voir à l'aide du test de causalité de Granger si des retards de PIBRES et de TAUXCCD1 peuvent améliorer notre modèle :

En prenant un retard de 4, on obtient les résultats suivants :

Pairwise Granger Causality Tests Date: 06/10/13 Time: 12:27 Sample: 2002Q1 2011Q4 Lags: 4
Null Hypothesis:	Obs	F-Statistic	Prob.
PIBRES does not Granger Cause M1_SCRRES	35	0.69468	0.6024
M1_SCRRES does not Granger Cause PIBRES		1.74064	0.1714
TAUXCCD1 does not Granger Cause M1_SCRRES	35	1.85745	0.1482
M1_SCRRES does not Granger Cause TAUXCCD1		2.42500	0.0735
TAUXCCD1 does not Granger Cause PIBRES	35	0.61497	0.6557
PIBRES does not Granger Cause TAUXCCD1		0.95067	0.4508

Comme on peut le voir sur ce tableau, l'hypothèse « PIBRES ne cause pas M1_SCRRES » est acceptée au seuil de 5% (p-value = 0.60) de même que l'hypothèse « TAUXCC ne cause pas M1_SCRRES » (p-value = 0.15). Donc, l'introduction de retards de PIBRES et de TAUXCC ne permettra pas d'améliorer notre modèle. On passe donc directement à l'introduction de retards MA. Le corrélogramme précédent nous suggère les retards suivants : 1 jusqu'à 5 et 7. Les résultats de ce modèle sont comme suit :

Dependent Variable: M1_SCRRES Method: Least Squares Date: 06/10/13 Time: 12:35 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments Convergence achieved after 75 iterations MA Backcast: 2000Q3 2002Q1
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	468.7053	504.7014 0.928679	0.3605
PIBRES	0.051861	0.326631 0.158774	0.8749
TAUXCCD1	515578.6	364890.6 1.412967	0.1680
MA(1)	-0.189860	0.106689 -1.779560	0.0853		MA(2)
0.351219	0.143100 2.454355	0.0201	MA(3)
-0.295310	0.104069 -2.837629	0.0081	MA(4)
0.513939	0.087905 5.846532	0.0000	MA(5)
-0.624400	0.110982 -5.626117	0.0000
MA(7)	-0.646027	0.141060 -4.579810	0.0001
R-squared	0.608232	Mean dependent var	1.87E-13
Adjusted R-squared	0.503760	S.D. dependent var	7477.246
S.E. of regression	5267.292	Akaike info criterion	20.17559
Sum squared resid	8.32E+08	Schwarz criterion	20.55949
Log likelihood	-384.4241	Hannan-Quinn criter.	20.31333
F-statistic	5.821986	Durbin-Watson stat	1.821757
Prob(F-statistic)	0.000163
Inverted MA Roots	.98	.55+.83i .55-.83i	-.20-.81i
	-.20+.81i	-.75-.63i -.75+.63i

Modèle 10 : M1_SCRRES C, PIBRES, TAUXCCD1, MA (1 à 7)

L'examen de ces résultat montre que le R² et le R² ajusté se sont nettement améliorés bien qu'ils ne soient pas très satisfaisants (0.61 pour R² et seulement 0.50 pour R² ajusté). Cependant, aucun des coefficients relatifs à C, PIBRES et TAUXCCD1 n'est significatif. En plus, celui relatif à TAUXCCD1 est positif contrairement à nos attentes.

97

D'autre part, le corrélogramme des résidus ci-dessous, montre qu'aucun des coefficients d'autocorrélation n'est significativement différent de zéro :

Date: 06/10/13 Time: 12:50 Sample: 2002Q2 2011Q4 Included observations: 39 Q-statistic probabilities adjusted for 6 ARMA term(s)
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	0.076	0.076	0.2441
	2	-0.07...	-0.07...	0.4627
	3	-0.15...	-0.14...	1.5139
	4	0.153	0.175	2.5780
	5	-0.09...	-0.15...	3.0410
	6	-0.09...	-0.07...	3.4299
	7	-0.01...	0.043	3.4404	0.064
	8	0.148	0.073	4.5766	0.101
	9	-0.11...	-0.13...	5.2184	0.156
	1...	0.076	0.149	5.5371	0.236
	1...	-0.14...	-0.19...	6.7736	0.238
	1...	-0.02...	-0.05...	6.7992	0.340
	1...	-0.15...	-0.06...	8.1996	0.315
	1...	-0.10...	-0.20...	8.8373	0.356
	1...	-0.10...	-0.06...	9.5809	0.385
	1...	0.057	0.025	9.8085	0.457

Le test de Breusch-Godfrey , conduit avec 20 retards, permet également d'accepter l'hypothèse H0 selon laquelle il y a absence de corrélation :

Breusch-Godfrey Serial Correlation LM Test:
F-statistic 0.508332 Prob. F(20,10) Obs*R-squared 19.63172 Prob. Chi-Square(20)	0.9051 0.4812
Test Equation: Dependent Variable: RESID Method: Least Squares Date: 06/10/13 Time: 12:51 Sample: 2002Q2 2011Q4 Included observations: 39 Presample missing value lagged residuals set to zero.

En effet, les p-value relatives aux statistiques F et à n*R² sont toutes les deux inférieures à 5%.

Même si ces résultats nous permettent de valider le modèle, on ne peut pas l'accepter puisque aucun des coefficients relatifs à PIBRES et TAUXCCD1 n'est significativement différent de zéro.

II-2- Spécification logarithmique :

Selon cette spécification, le modèle à estimer s'écrit comme suit :

LNM1_SCR - LNIPC = C + a. LNPIB_DEF₀ + b. TAUXCC + å 0

Comme on l'a fait pour M1_FID, nous allons directement passer au modèle avec les variables stationnarisées, soit le modèle ci-dessous :

LNM1_SCRD1RES - LNIPCD1 = C + a.LNPIB_DEFRES + b. TAUXCCD1 + å 0

98

Les résultats de l'estimation de ce modèle sont comme suit :

Dependent Variable: LNM1_SCRD1RES-LNIPCD1 Method: Least Squares Date: 06/10/13 Time: 14:28 Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	-0.003134	0.006469 -0.484442	0.6311
LNPIB_DEFRES	0.954624	0.270494 3.529188	0.0012
TAUXCCD1	3.181393	2.115194 1.504067	0.1415
R-squared	0.300279	Mean dependent var	-0.004019
Adjusted R-squared	0.260295	S.D. dependent var	0.046201
S.E. of regression	0.039736	Akaike info criterion	-3.537485
Sum squared resid	0.055262	Schwarz criterion	-3.408202
Log likelihood	70.21221	Hannan-Quinn criter.	-3.491487
F-statistic	7.509967	Durbin-Watson stat	3.105043
Prob(F-statistic)	0.001933

Modèle 11 : (LNM1_SCRD1RES-LNIPCD1) C,LNPIBDEFRES,TAUXCCD1

Ces résultats montrent que les coefficients relatifs à la constante et à TAUXCCD1 ne sont pas significativement différents de zéro. Le coefficient relatif à LNPIB_DEFRES est par contre significativement différent de zéro. Le R² et le R² ajusté sont bas (0.30 et 0.26 respectivement) mais nettement supérieurs à ceux obtenu pour l'estimation de M1_SCR. L'analyse du corrélogramme des résidus ci-dessous, montre que les résidus sont fortement autocorrélés :

Date: 06/10/13 Time: 14:59 Sample: 2002Q3 2011Q4 Included observations: 38
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	-0.57...	-0.57...	13.432	0.000
	2	0.440	0.168	21.596	0.000
	3	-0.40...	-0.15...	28.795	0.000
	4	0.440	0.198	37.447	0.000
	5	-0.42...	-0.11...	45.912	0.000
	6	0.213	-0.23...	48.073	0.000
	7	-0.24...	-0.09...	51.027	0.000
	8	0.350	0.202	57.227	0.000
	9	-0.21...	0.207	59.543	0.000
	1...	0.226	0.129	62.326	0.000
	1...	-0.20...	-0.09...	64.753	0.000
	1...	0.204	-0.13...	67.196	0.000
	1...	-0.24...	-0.12...	70.951	0.000
	1...	0.076	-0.11...	71.315	0.000
	1...	-0.19...	-0.10...	73.941	0.000
	1...	0.162	-0.04...	75.752	0.000

Nous procéderons de la même manière que précédemment et nous allons donc voir à l'aide du test de causalité de Granger si des retards de LNPIB_DEFRES et de TAUXCCD1 peuvent améliorer le modèle. Le test conduit avec un retard de 4 donne les résultats suivants :

99

Pairwise Granger Causality Tests Date: 06/10/13 Time: 15:11 Sample: 2002Q1 2011Q4 Lags: 4
Null Hypothesis:	Obs	F-Statistic	Prob.
LNPIB_DEFRES does not Granger Cause LNM1_SCRD1RES-LNIPCD1	34	0.82453	0.5220
LNM1_SCRD1RES-LNIPCD1 does not Granger Cause LNPIB_DEFRES		3.27102	0.0275
TAUXCCD1 does not Granger Cause LNM1_SCRD1RES-LNIPCD1	34	2.04005	0.1193
LNM1_SCRD1RES-LNIPCD1 does not Granger Cause TAUXCCD1		2.74934	0.0506
TAUXCCD1 does not Granger Cause LNPIB_DEFRES	35	0.78277	0.5467
LNPIB_DEFRES does not Granger Cause TAUXCCD1		0.32898	0.8559

Ces résultats montrent que les deux hypothèses « LNPIB_DEFRES ne cause pas LNM1_SCRD1RES » et « TAUXCCD1 ne cause pas LNM1_SCRD1RES » ne peuvent pas être rejetées au seuil de 5% et par conséquent des retards de LNPIB_DEFRES ou de TAUXCCD1 ne permettrait pas d'améliorer le modèle. Nous allons donc plutôt introduire des retards MA. Le corrélogramme précédent suggère les retards suivants : 1 à 5.

Les résultats obtenus avec ce nouveau modèle sont comme suit :

Dependent Variable: LNM1_SCRD1RES-LNIPCD1 Method: Least Squares Date: 06/10/13 Time: 15:20 Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after adjustments Convergence achieved after 14 iterations MA Backcast: 2001Q2 2002Q2
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	-0.006028	0.001066 -5.656917	0.0000
LNPIB_DEFRES	0.589797	0.152884 3.857808	0.0006
TAUXCCD1	-0.564812	1.756201 -0.321610	0.7500
MA(1)	-0.584466	0.043000 -13.59219	0.0000		MA(2)
0.548561	0.053112 10.32839	0.0000	MA(3)
-0.544149	0.053952 -10.08578	0.0000	MA(4)
0.577043	0.043373 13.30420	0.0000	MA(5)
-0.917183	0.021424 -42.81103	0.0000
R-squared	0.863995	Mean dependent var	-0.004019
Adjusted R-squared	0.832261	S.D. dependent var	0.046201
S.E. of regression	0.018922	Akaike info criterion	-4.912318
Sum squared resid	0.010741	Schwarz criterion	-4.567563
Log likelihood	101.3341	Hannan-Quinn criter.	-4.789657
F-statistic	27.22578	Durbin-Watson stat	2.281620
Prob(F-statistic)	0.000000
Inverted MA Roots	.98	.41+.89i .41-.89i	-.61-.78i
	-.61+.78i

Modèle 12 : (LNM1_SCRD1RES-LNIPCD1) C,LNPIBDEFRES,TAUXCCD1,MA51 à 5)

Le modèle est beaucoup plus meilleur puisque le R² est passé à 0.86 et le R² ajusté à 0.83. Tous les coefficients, à l'exception du coefficient relatif à TAUXCCD1, sont significativement différents de zéro.

Le corrélogramme des résidus montre que ceux-ci ne sont pas autocorrélés :

100

Date: 06/10/13 Time: 15:25 Sample: 2002Q3 2011Q4 Included observations: 38 Q-statistic probabilities adjusted for 5 ARMA term(s)
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	-0.15...	-0.15...	0.9948
	2	0.058	0.035	1.1391
	3	-0.16...	-0.15...	2.3497
	4	0.161	0.117	3.5063
	5	-0.28...	-0.25...	7.3617
	6	0.073	-0.02...	7.6136	0.006
	7	-0.11...	-0.07...	8.2928	0.016
	8	0.083	-0.03...	8.6412	0.034
	9	-0.01...	0.071	8.6478	0.071
	1...	0.256	0.184	12.194	0.032
	1...	-0.35...	-0.31...	19.153	0.004
	1...	-0.06...	-0.20...	19.392	0.007
	1...	-0.13...	-0.13...	20.412	0.009
	1...	-0.07...	-0.29...	20.727	0.014
	1...	-0.09...	-0.01...	21.327	0.019
	1...	0.238	0.113	25.248	0.008

Le test de Breusch-Godfrey confirme cette conclusion au vu des p-values des statistiques F et n*R²

Breusch-Godfrey Serial Correlation LM Test:
F-statistic 1.055596 Prob. F(20,10) Obs*R-squared 25.76967 Prob. Chi-Square(20)	0.4859 0.1736
Test Equation: Dependent Variable: RESID Method: Least Squares Date: 06/10/13 Time: 15:25 Sample: 2002Q3 2011Q4 Included observations: 38 Presample missing value lagged residuals set to zero.

Le modèle peut donc être accepté.

Ce modèle nous donne une élasticité-revenu (élasticité de M1_SCR par rapport au PIB_DEF) égale à 0.59 et une semi-élasticité-taux égale à -0.56. On peut donc dire qu'une augmentation de 1% du PIB entraîne une augmentation de seulement 0.59% de M1_SCR et vice-versa. Une augmentation de 1 point du taux sur compte de carnet entraîne une diminution de -0.56% de M1_SCR et vice-versa.

Etant donné la non significativité du coefficient relatif à TAUXCCD1, on peut émettre la même conclusion que celle relative à M1_FID, à savoir qu'il n'y pas présence de motif de transaction dans la demande de M1_SCR, c'est-à-dire que le seule motif de sa détention est celui relatif au motif de transaction et celui de précaution, ce qui confirme une deuxième fois notre hypothèse (H).

D'autre part, les résultats de test d'une élasticité unitaire ne permettant pas d'accepter cette hypothèse, la constante, qui est ici égale à -0.0060, ne peut pas être interprétée comme une vitesse de circulation :

101

Wald Test: Equation: EQ12
Test Statistic Value	df	Probability
t-statistic -2.683099 F-statistic 7.199020 Chi-square 7.199020	30 (1, 30) 1	0.0118 0.0118 0.0073
Null Hypothesis: C(2)=1 Null Hypothesis Summary:
Normalized Restriction (= 0)	Value	Std. Err.
-1 + C(2)	-0.410203	0.152884
Restrictions are linear in coefficients.

Ces deux modèles nous permettent de conclure que le motif de spéculation est absent pour M1_FID, c'est-à-dire que le seul motif de détention de M1_FID est le motif de transaction et celui de précaution ce qui est conforme à notre hypothèse (H).

III- Estimation de la demande de monnaie M3_M1 :

III-1- Spécification en niveau :

Le modèle à estimer s'écrit comme suit :

M3_M1_t = C + a. PIB_t + b. TAUXCC_t + å_t

Cette fois ci, le coefficient b devrait être positif étant donné que M3_M1 inclut les comptes d'épargne auprès des banques et les comptes sur livrets auprès de la caisse d'épargne nationale ainsi que les comptes à terme et bons de caisse auprès des banques. Par conséquent, plus le taux est élevé et plus les agents vont faire des dépôts.

Les contraintes sur C et a restent inchangées : C non significativement différent de zéro et 0 < a <1.

Les résultats de l'estimation de ce modèle sont comme suit :

Dependent Variable: M3_M1 Method: Least Squares Date: 06/11/13 Time: 15:40 Sample: 2002Q1 2011Q4 Included observations: 40
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	-221137.2	11793.69 -18.75047	0.0000
PIB	2.729762	0.053693 50.84028	0.0000
TAUXCC	1338605.	360748.2 3.710635	0.0007
R-squared	0.986941	Mean dependent var	235375.5
Adjusted R-squared	0.986235	S.D. dependent var	85906.82
S.E. of regression	10079.03	Akaike info criterion	21.34634
Sum squared resid	3.76E+09	Schwarz criterion	21.47301
Log likelihood	-423.9268	Hannan-Quinn criter.	21.39214
F-statistic	1398.117	Durbin-Watson stat	1.353598
Prob(F-statistic)	0.000000

Modèle 13 : M3_M1 C,PIB,TAUXCC

102

Ces résultats montrent que le coefficient relatif à la constante est significativement différent de zéro ce qui contredit notre hypothèse.

Le coefficient relatif à PIB est également significatif mais il est largement supérieur à 1 (2.73) ce qui contredit également notre hypothèse.

Le coefficient relatif à TAUXCC est cette fois ci très significatif et son signe est bien positif comme on s'y attendait.

Le R² et le R² ajusté sont très satisfaisant (0.99 pour les deux)

L'analyse du corrélogramme montre qu'à part le premier coefficient qui est dans la limite du rejet, tous les autres coefficients d'autocorrélation sont non significativement différents de zéro:

Date: 06/11/13 Time: 15:44 Sample: 2002Q1 2011Q4 Included observations: 40
Autocorrelation Partial Correlation		AC	PAC	Q-Stat	Prob
	1	0.313	0.313	4.2271	0.040
	2	0.206	0.120	6.1084	0.047
	3	-0.10...	-0.22...	6.5927	0.086
	4	-0.22...	-0.18...	8.9125	0.063
	5	-0.09...	0.097	9.3405	0.096
	6	-0.25...	-0.22...	12.507	0.052
	7	0.151	0.280	13.675	0.057
	8	0.007	-0.09...	13.677	0.091
	9	-0.08...	-0.28...	14.049	0.121
	1...	-0.03...	0.097	14.120	0.168
	1...	-0.26...	-0.19...	18.104	0.079
	1...	-0.11...	-0.14...	18.860	0.092
	1...	-0.20...	0.046	21.573	0.062
	1...	0.037	0.007	21.662	0.086
	1...	0.006	-0.25...	21.665	0.117
	1...	-0.01...	0.094	21.682	0.154
	1...	0.034	-0.12...	21.769	0.194
	1...	0.035	0.053	21.863	0.238
	1...	-0.01...	-0.09...	21.871	0.291
2...	-0.05...	-0.10...	22.081	0.336

D'ailleurs, le test de Breusch-Godfrey conduit avec 20 retards permet d'accepter l'hypothèse d'absence d'autocorrélation des erreurs :

Breusch-Godfrey Serial Correlation LM Test:

F-statistic 1.187337 Prob. F(20,17) 0.3634

Obs*R-squared 23.31155 Prob. Chi-Square(20) 0.2738

Etant donné que toutes les séries du modèle sont I(1), nous allons étudier la série des résidus (RESID18) pour voir si elle est stationnaire, auquel cas il y a risque de cointégration.

Le graphe de la série des résidus se présente comme suit :



-10,000

-20,000

20,000

30,000

10,000

0

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

RESID18

103

L'allure de cette série montre qu'elle pourrait bien être stationnaire. Pour s'en convaincre, nous avons mené les tests ADF sur cette série et il s'est avéré qu'il s'agit bien d'un processus stationnaire sans Drift.

Nous allons donc voir est ce qu'une spécification ECM est possible.

D'abord, on commence par tester la cointégration entre d'une part M3_M1 et PIB, et d'autre part entre M3_M1 et TAUXCC.

Test de cointégration entre M3M1 et PIB :

Les résultats de test de Johansen pour M3_M1 et PIB sont comme suit :

Date: 06/12/13 Time: 13:54 Sample (adjusted): 2003Q2 2011Q4 Included observations: 35 after adjustments Trend assumption: Linear deterministic trend Series: M3_M1 PIB Lags interval (in first differences): 1 to 4 Unrestricted Cointegration Rank Test (Trace)
Hypothesized Trace No. of CE(s) Eigenvalue Statistic	0.05 Critical Value	Prob.**
None 0.305202 13.54182 At most 1 0.022518 0.797143	15.49471 3.841466	0.0964 0.3719

L'hypothèse d'absence de cointégration est acceptée au seuil de 5% (p-value = 0.0964 >5%) Test de cointégration entre M3M1 et TAUXCC :

Les résultats de test de Johansen pour M3_M1 et TAUXCC sont comme suit :

104

Date: 06/12/13 Time: 13:57 Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after adjustments Trend assumption: Linear deterministic trend Series: M3_M1 TAUXCC Lags interval (in first differences): 1 to 1 Unrestricted Cointegration Rank Test (Trace)
Hypothesized Trace No. of CE(s) Eigenvalue Statistic	0.05 Critical Value	Prob.**
None * 0.386148 18.54429 At most 1 5.61E-06 0.000213	15.49471 3.841466	0.0168 0.9902

Contrairement au résultat précédent, l'hypothèse d'absence de cointégration est rejetée au seuil de 5%.

Il n'y a donc qu'une seule relation de cointégration, et par conséquent on peut appliquer la méthode de Engle and Granger en deux étapes.

La première étape consistant à estimer la relation de long terme a déjà été effectuée (cf. ci-dessus).

La deuxième étape consiste à estimer la relation du modèle dynamique avec les séries stationnaires :

M3_M1D1 = a.PIBRES + b.TAUXCCD1 + c.RESID18 _{_1} + 8 Avec c qui doit être négatif.

Les résultats de l'estimation de ce modèle sont comme suit :

Dependent Variable: M3_M1D1 Method: Least Squares Date: 06/12/13 Time: 14:52 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
PIBRES	0.370941	0.584151 0.635008	0.5294
TAUXCCD1	-41666.61	477798.9 -0.087205	0.9310
RESID18(-1)	-0.365316	0.158302 -2.307721	0.0269
R-squared	-0.572578	Mean dependent var	6099.587
Adjusted R-squared	-0.659943	S.D. dependent var	6865.709
S.E. of regression	8845.696	Akaike info criterion	21.08705
Sum squared resid	2.82E+09	Schwarz criterion	21.21502
Log likelihood	-408.1975	Hannan-Quinn criter.	21.13297
Durbin-Watson stat	0.563174

Modèle 19

Ces résultats montrent que le coefficient de rappel (relatif à RESID18) est significativement négatif. Cependant, les coefficients relatifs à PIBRES et à TAUXCCD1 ne sont pas significativement différents de zéro. Par conséquent, le modèle ECM n'est pas validé.

105

III-2- Spécification logarithmique :

Selon cette spécification le modèle à estimer s'écrit :

LNM3_M1_t -- LNIPC_t = C + a.LNPIB_DEF_t + b.TAUXCC_t + E_t

Les résultats de l'estimation de ce modèle sont comme suit :

Dependent Variable: LNM3_M1-LNIPC Method: Least Squares Date: 06/12/13 Time: 15:12 Sample: 2002Q1 2011Q4 Included observations: 40
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	-8.017620	0.395961 -20.24853	0.0000
LNPIB_DEF	2.129795	0.054761 38.89246	0.0000
TAUXCC	5.361269	1.739840 3.081472	0.0039
R-squared	0.977209	Mean dependent var	7.680200
Adjusted R-squared	0.975977	S.D. dependent var	0.317424
S.E. of regression	0.049199	Akaike info criterion	-3.113861
Sum squared resid	0.089559	Schwarz criterion	-2.987195
Log likelihood	65.27722	Hannan-Quinn criter.	-3.068063
F-statistic	793.2223	Durbin-Watson stat	1.394813
Prob(F-statistic)	0.000000

Modèle 20

Ces résultats montrent que tous les coefficients sont significatifs au seuil de 5% et même au seuil de 1%.

Le signes des coefficients relatifs à LNPIB_DEF et TAUXCC sont conformes aux hypothèses (a, b >0). Cependant, on constate que, contrairement à M1_FID et M1_SCR, l'élasticité-revenu de M3_M1 est largement supérieure à 1 (2.13) et que la semi-élasticité-taux est très élevée en valeur absolue (5.36 contre -0.94 pour M1_FID et -0.56 pour M1_SCR).

Comme on l'a fait pour la spécification précédente nous devons tester le risque d'une cointégration étant donné que toutes les séries du modèle sont I(1).

Nous commencerons d'abord par voir est ce que les résidus issus de la régression précédente (RESID20) sont stationnaires.

Le graphe de la série de ces résidus se présente comme suit :



-.025

-.050

-.075

-.100

.100

.075

.050

.025

.000

2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

RESID20

106

Les résultats des tests ADF conduits sur cette série montrent qu'elle est en fait stationnaire. Nous allons donc voir est ce qu'une spécification ECM est possible.

D'abord, on commence par tester la cointégration entre d'une part LNM3_M1-LNIPC et LNPIB_DEF, et d'autre part entre LNM3_M1-LNIPC et TAUXCC.

Test de cointégration entre LNM3M1 -LNIPC et LNPIBDEF :

Les résultats de test de Johansen pour LNM3_M1 -LNIPC et LNPIB_DEF sont comme suit :

Date: 06/12/13 Time: 15:56 Sample (adjusted): 2003Q2 2011Q4 Included observations: 35 after adjustments Trend assumption: Linear deterministic trend Series: LNM3_M1-LNIPC LNPIB_DEF Lags interval (in first differences): 1 to 4 Unrestricted Cointegration Rank Test (Trace)
Hypothesized Trace 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None 0.335383 14.54138 15.49471 At most 1 0.006899 0.242305 3.841466	0.0692 0.6225
Trace test indicates no cointegration at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values Unrestricted Cointegration Rank Test (Maximum Eigenvalue)
Hypothesized Max-Eigen 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None * 0.335383 14.29907 14.26460 At most 1 0.006899 0.242305 3.841466	0.0494 0.6225
Max-eigenvalue test indicates 1 cointegrating eqn(s) at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values

Si on se fit à la statistique « Trace », l'hypothèse selon laquelle il n'y a pas de relation d'intégration est acceptée au seuil de 5% (p-value = 0.0692 > 5%) mais rejetée au seuil de 10%. Cependant, si on se fit à la statistique « Max Eigen », l'hypothèse est rejetée au seuil de 5% (p-value = 0.0494).

On accepte donc l'hypothèse de l'existence d'une relation de cointégration entre LNM3_M1 - LNIPC et LNPIB_DEF.

107

Test de cointégration entre LNM3M1 -LNIPC et TAUXCC :

Les résultats de test de Johansen pour LNM3_M1 -LNIPC et TAUXCC sont comme suit :

Date: 06/12/13 Time: 16:01 Sample (adjusted): 2003Q2 2011Q4 Included observations: 35 after adjustments Trend assumption: Linear deterministic trend Series: LNM3_M1-LNIPC TAUXCC Lags interval (in first differences): 1 to 4 Unrestricted Cointegration Rank Test (Trace)
Hypothesized Trace 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None 0.105052 7.046903 15.49471 At most 1 0.086389 3.162265 3.841466	0.5722 0.0754
Trace test indicates no cointegration at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values Unrestricted Cointegration Rank Test (Maximum Eigenvalue)
Hypothesized Max-Eigen 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None 0.105052 3.884638 14.26460 At most 1 0.086389 3.162265 3.841466	0.8713 0.0754
Max-eigenvalue test indicates no cointegration at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values

Ces résultats montrent que les deux statistiques de tests, Trace et Max Eigen, nous permettent d'accepter l'hypothèse d'absence de relation de cointégration au seuil de 5% (p-values égales à 0.57 et 0.87).

Il n'y a donc qu'une seule relation de cointégration, et par conséquent on peut appliquer la méthode de Engle and Granger en deux étapes.

La première étape consistant à estimer la relation de long terme a déjà été effectuée (cf. ci-dessus).

La deuxième étape consiste à estimer la relation du modèle dynamique avec les séries stationnaires :

LNM3_M1D1 - LNIPCD1 = a.LNPIB_DEFRES + b. TAUXCCD1 + c.RESID20 _{_i} + 8 Avec c < 0

Les résultats de l'estimation de ce modèle sont comme suit :

108

Dependent Variable: LNM3_M1D1-LNIPCD1 Method: Least Squares Date: 06/12/13 Time: 16:11 Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after adjustments
Variable	Coefficient	Std. Error t-Statistic	Prob.
LNPIB_DEFRES	0.461306	0.310757 1.484459	0.1464
TAUXCCD1	-1.537898	2.012952 -0.764001	0.4498
RESID20(-1)	-0.168200	0.157200 -1.069976	0.2918
R-squared	-0.443656	Mean dependent var	0.022661
Adjusted R-squared	-0.523859	S.D. dependent var	0.030533
S.E. of regression	0.037692	Akaike info criterion	-3.644946
Sum squared resid	0.051144	Schwarz criterion	-3.516980
Log likelihood	74.07645	Hannan-Quinn criter.	-3.599033
Durbin-Watson stat	0.907814

Le coefficient de rappel est bien négatif, mais il n'est pas significatif, au même titre que ceux relatifs à LNPIB_DEFRES et TAUXCCD1.

La spécification ECM ne peut donc pas être validée. Et seule la relation de long terme est validée (modèle 20). Encore une fois, les résultats de test d'une élasticité-revenu unitaire ne permettant pas d'accepter cette hypothèse, la constante de ce modèle ne peut pas être interprétée comme une vitesse de circulation.

On constate donc après l'estimation de ces différents modèles, que c'est la spécification logarithmique qui donne de meilleurs résultats du point de vue statistique. Ainsi, le tableau ci-dessous récapitule les résultats de ces modèles retenus :

Forme de	Modèle retenu	Elasticité-	Semi-élasticité-	Constante
monnaie		revenu	taux
M1_FID	Logarithme sur les séries stationnarisées	0.61	-0.94	0
M1_SCR	Logarithme sur les séries stationnarisées	0.59	-0.56	-0.006028
M3_M1	Logarithmique sur les séries non stationnarisées	2.13	5.36	-8.0176
M3 (BdF)	VECM	1.00	0.004	1.297

109

Section 3 : Estimation multivariée de la demande de monnaie

Dans ce paragraphe nous allons essayer d'estimer la demande de monnaie pour les différentes formes de la monnaie : M1_FID, M1_SCR et M3-M1 en adoptant une modélisation VECM. Nous nous contenterons de la spécification logarithmique étant donné que les résultats du paragraphe précédent ont montré qu'elle est plus adaptée.

I- Etude de la demande de monnaie fiduciaire (M1_FID)

Le modèle à estimer s'écrit comme suit :

pN1

LNM1_FID_t - LNIPC_t LNM1_FID_t_ - LNIPC_t_ LNM1_FID_t__i - LNIPCt_i

? m hl~RU_S-Q₀ n ~ ~ . ? m hl~RU_S-Q_0N n ~ a. O^A. m hl~RU_S-Q_0N~ n ~ G₀

~jk/DD₀ ~~ ~jk/DD_0N ~jk/DD0N~

Avec : p le nombre de retards, des matrices (3×3), á une matrice (3×r) et â une matrice (r×3) où r est le nombre de relations de cointégration.

Dans un premier temps, il faut déterminer le nombre de retards p en se basant sur le critère AIC et SC.

Le retard 3 est celui qui minimise le critère SC (AIC reste décroissant même après 6 retards).

Dans un second temps on va déterminer le nombre de relations de cointégration r à l'aide du test de Johansen. Ce test conduit avec un retard de 3 donne les résultats ci-dessous :

Date: 06/14/13 Time: 09:08 Sample (adjusted): 2003Q1 2011Q4 Included observations: 36 after adjustments Trend assumption: Linear deterministic trend Series: LNM1_FID-LNIPC LNPIB_DEF TAUXCC Lags interval (in first differences): 1 to 3 Unrestricted Cointegration Rank Test (Trace)
Hypothesized Trace 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None * 0.692129 52.06600 29.79707 At most 1 0.206012 9.655373 15.49471 At most 2 0.036822 1.350627 3.841466	0.0000 0.3082 0.2452
Trace test indicates 1 cointegrating eqn(s) at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values Unrestricted Cointegration Rank Test (Maximum Eigenvalue)
Hypothesized Max-Eigen 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None * 0.692129 42.41063 21.13162 At most 1 0.206012 8.304746 14.26460 At most 2 0.036822 1.350627 3.841466	0.0000 0.3486 0.2452
Max-eigenvalue test indicates 1 cointegrating eqn(s) at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values

Comme on peut le voir, l'hypothèse « Aucune relation de cointégration » est rejetée au seuil de 5% (p-value =0.0000 pour Trace et pour Max-Eigen), alors que l'hypothèse « Au plus 1 relation de cointégration » est acceptée au seuil de 5% (p-value=0.3082 pour Trace et 0.3486

110

pour Max-Eigen). Par conséquent, le nombre de relations de cointégration est égale à 1 (rang=1).

Les résultats de l'estimation du VECM avec un retard = 3 et un rang =1 sont comme suit :

Vector Error Correction Estimates Date: 06/14/13 Time: 09:23 Sample (adjusted): 2003Q1 2011Q4 Included observations: 36 after adjustments Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq:	CointEq1
LNM1_FID(-1)-LNIPC(-1)	1.000000
LNPIB_DEF(-1)	-3.525606
	(0.34423)
	[-10.2419]
TAUXCC(-1)	100.4708
	(13.5230)
	[ 7.42962]
C	16.09792
Error Correction:	D(LNM1_FID-...D(LNPIB_DE...		D(TAUXCC)
CointEq1	-0.002451	0.005150	-0.008168
	(0.01360)	(0.01256)	(0.00162)
	[-0.18016]	[ 0.41005]	[-5.04386]

Les trois premiers coefficients (en colonne) sont ceux de la relation de long terme, alors que les trois autres (en ligne) sont ceux de la correction d'erreur (EC).

VAR Model - Substituted Coefficients:

D(LNM1_FID-LNIPC) = - 0.00245093897749*( (LNM1_FID(-1)-LNIPC(-1)) - 3.52560621374*LNPIB_DEF(-1) + 100.470770368*TAUXCC(-1) + 16.0979194181 ) - 0.0386240926276*D(LNM1_FID(-1)-LNIPC(-1)) - 0.434461085892*D(LNM1_FID(-2)-LNIPC(-2)) + 0.117077961329*D(LNM1_FID(-3)-LNIPC(-3)) - 0.691484831794*D(LNPIB_DEF(-1)) + 0.084820268205*D(LNPIB_DEF(-2)) - 0.0463174749808*D(LNPIB_DEF(-3)) + 1.76474683212*D(TAUXCC(-1)) - 1.31084514852*D(TAUXCC(-2)) + 2.9512637919*D(TAUXCC(-3)) + 0.033316038374

D(LNPIB_DEF) = 0.0051499698875*( (LNM1_FID(-1)-LNIPC(-1)) - 3.52560621374*LNPIB_DEF(-1) + 100.470770368*TAUXCC(-1) + 16.0979194181 ) - 0.106340101178*D(LNM1_FID(-1)-LNIPC(-1)) + 0.154569919217*D(LNM1_FID(-2)-LNIPC(-2)) + 0.097502761406*D(LNM1_FID(-3)-LNIPC(-3)) - 0.878161955204*D(LNPIB_DEF(-1)) - 0.39235582078*D(LNPIB_DEF(-2)) - 0.116758818226*D(LNPIB_DEF(-3)) - 1.0738686604*D(TAUXCC(-1)) + 0.668725120837*D(TAUXCC(-2)) + 0.968668497263*D(TAUXCC(-3)) + 0.0263109155596

D(TAUXCC) = - 0.00816825543014*( (LNM1_FID(-1)-LNIPC(-1)) - 3.52560621374*LNPIB_DEF(-1) + 100.470770368*TAUXCC(-1) + 16.0979194181 ) - 0.0128730931781*D(LNM1_FID(-1)-LNIPC(-1)) - 0.0135595348404*D(LNM1_FID(-2)-LNIPC(-2)) - 0.0236696311332*D(LNM1_FID(-3)-LNIPC(-3)) + 0.0126601581239*D(LNPIB_DEF(-1)) + 0.0336734094083*D(LNPIB_DEF(-2)) + 0.0313589799341*D(LNPIB_DEF(-3)) + 0.20336751738*D(TAUXCC(-1)) - 0.0626619825146*D(TAUXCC(-2)) - 0.0494287780443*D(TAUXCC(-3)) - 0.000176630596422

Ces résultats montrent que l'élasticité-revenu est de 3.52, ce qui semble très élevé, de même, la semi-élasticité-taux est égale à 100 ce qui n'est pas normal. Nous avons donc refait l'estimation avec un retard = 4. Les résultats obtenus sont comme suit :

111

Vector Error Correction Estimates Date: 06/14/13 Time: 09:27 Sample (adjusted): 2003Q2 2011Q4 Included observations: 35 after adjustments Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq:	CointEq1
LNM1_FID(-1)-LNIPC(-1)	1.000000
LNPIB_DEF(-1)	-1.377910
	(0.06888)
	[-20.0039]
TAUXCC(-1)	-5.983027
	(3.05480)
	[-1.95857]
C	3.302775
Error Correction:	D(LNM1_FID-...D(LNPIB_DE...		D(TAUXCC)
CointEq1	-0.179125	0.253918	0.045247
	(0.09416)	(0.12243)	(0.00978)
	[-1.90234]	[ 2.07402]	[ 4.62765]

VAR Model - Substituted Coefficients:

D(LNM1_FID-LNIPC) = - 0.179125190791*( (LNM1_FID(-1)-LNIPC(-1)) - 1.37791029902*LNPIB_DEF(-1) - 5.98302714503*TAUXCC(-1) + 3.30277458086 ) + 0.212716148846*D(LNM1_FID(-1)-LNIPC(-1)) + 0.0507815970433*D(LNM1_FID(-2)-LNIPC(-2)) + 0.265528020739*D(LNM1_FID(-3)-LNIPC(-3)) + 0.780115757551*D(LNM1_FID(-4)-LNIPC(-4)) - 0.941335655784*D(LNPIB_DEF(-1)) - 0.446245681687*D(LNPIB_DEF(-2)) - 0.33799716824*D(LNPIB_DEF(-3)) - 0.53497011045*D(LNPIB_DEF(-4)) + 1.35719772703*D(TAUXCC(-1)) + 0.219217900337*D(TAUXCC(-2)) + 1.7084792386*D(TAUXCC(-3)) + 0.98714473878*D(TAUXCC(-4)) + 0.0227779641747

D(LNPIB_DEF) = 0.253918118396*( (LNM1_FID(-1)-LNIPC(-1)) - 1.37791029902*LNPIB_DEF(-1) - 5.98302714503*TAUXCC(-1) + 3.30277458086 ) - 0.451272453638*D(LNM1_FID(-1)-LNIPC(-1)) - 0.154204219809*D(LNM1_FID(-2)-LNIPC(-2)) - 0.19833562006*D(LNM1_FID(-3)-LNIPC(-3)) - 0.213663079595*D(LNM1_FID(-4)-LNIPC(-4)) - 0.58766506885*D(LNPIB_DEF(-1)) - 0.281599733338*D(LNPIB_DEF(-2)) - 0.182027422701*D(LNPIB_DEF(-3)) - 0.102139784617*D(LNPIB_DEF(-4)) - 0.945013946652*D(TAUXCC(-1)) + 0.985275355366*D(TAUXCC(-2)) + 0.647217307699*D(TAUXCC(-3)) - 0.364855991582*D(TAUXCC(-4)) + 0.0442724593759

D(TAUXCC) = 0.0452469030339*( (LNM1_FID(-1)-LNIPC(-1)) - 1.37791029902*LNPIB_DEF(-1) - 5.98302714503*TAUXCC(-1) + 3.30277458086 ) - 0.0300464056903*D(LNM1_FID(-1)-LNIPC(-1)) - 0.0636867654248*D(LNM1_FID(-2)-LNIPC(-2)) - 0.026542598053*D(LNM1_FID(-3)-LNIPC(-3)) - 0.0632688417305*D(LNM1_FID(-4)-LNIPC(-4)) + 0.0447369399994*D(LNPIB_DEF(-1)) + 0.073693374048*D(LNPIB_DEF(-2)) + 0.0156158387238*D(LNPIB_DEF(-3)) + 0.0157848549298*D(LNPIB_DEF(-4)) + 0.0697169751847*D(TAUXCC(-1)) - 0.579145237923*D(TAUXCC(-2)) + 0.0989906924098*D(TAUXCC(-3)) - 0.28106640147*D(TAUXCC(-4)) + 0.00160067046242

Cette fois-ci on a une élasticité-revenu qui semble plus réaliste (1.37), de même que la semi-élasticité-taux qui est égale à 5.98, mais qui n'est pas significative au seuil de 5% (t-statistic < 1.96). D'autre part, le coefficient EC relatif à D(LNM1_DEF-LNIPC) n'est pas significativement différent de zéro, alors que ceux relatifs à D(LNPIB_DEF) et D(TAUXCC) le sont. D'après la littérature, on peut tolérer que certains coefficients soient non significatifs. Il nous reste donc, pour valider le modèle, que le test de Ljung-Box sur les résidus. Ce test conduit avec un retard de 12 nous donne les résultats suivants :

112

VEC Residual Portmanteau Tests for Autocorrelations Null Hypothesis: no residual autocorrelations up to lag h Date: 06/14/13 Time: 09:51 Sample: 2002Q1 2011Q4 Included observations: 35
Lags	Q-Stat	Prob.	Adj Q-Stat	Prob.	df
1	12.17393	NA*	12.53199	NA*	NA*
2	14.38999	NA*	14.88235	NA*	NA*
3	20.20585	NA*	21.24345	NA*	NA*
4	38.02597	NA*	41.36294	NA*	NA*
5	44.51416	0.0001	48.93249	0.0000	15
6	52.00817	0.0008	57.97699	0.0001	24
7	62.79026	0.0013	71.45461	0.0001	33
8	65.99616	0.0105	75.61040	0.0011	42
9	73.74180	0.0203	86.03722	0.0016	51
10	86.46436	0.0143	103.8488	0.0004	60
11	94.22581	0.0235	115.1676	0.0004	69
12	102.7954	0.0315	128.2083	0.0003	78
*The test is valid only for lags larger than the VAR lag order.
df is degrees of freedom for (approximate) chi-square distribution

Comme on peut le voir, l'hypothèse nulle d'absence d'autocorrélation est rejetée au seuil de 5% à partir du retard 5 jusqu'à 12. Le modèle ne peut donc être validé.

II- Etude de la demande de monnaie scripturale (M1_SCR)

Le modèle à estimer s'écrit comme suit :

LNM1_SCR - LNIPCt pN1 LNM1_SCR - LNIPCt_~ LNM1_SCR₀_₁ - LNIPCt_i

? m hl~RU_S-Q₀ n ~ ~ ~. ? m hl~RU_S-Q_0N~ n ~ p. O^A. f hl~RU_S-Q_0N~ n ~ e₀

~jk/DD₀ ~~~ ~jk/DD0N~ ~jk/DD0N~

Avec : p le nombre de retards, ~ des matrices (3×3), á une matrice (3×r) et â une matrice (r×3) où r est le nombre de relations de cointégration.

Nous allons suivre la même démarche précédente : Détermination du nombre de retards p :

Après avoir testé différents retards, nous avons retenu un retard =2 puisque c'est lui qui minimise SC.

Détermination du nombre de relations de cointégration r :

Le test de Johansen conduit avec 2 retards donne les résultats ci-dessous :

113

Date: 06/14/13 Time: 10:01 Sample (adjusted): 2002Q4 2011Q4 Included observations: 37 after adjustments Trend assumption: Linear deterministic trend Series: LNM1_SCR-LNIPC LNPIB_DEF TAUXCC Lags interval (in first differences): 1 to 2 Unrestricted Cointegration Rank Test (Trace)
Hypothesized Trace 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None * 0.444852 32.15363 29.79707 At most 1 0.198187 10.37837 15.49471 At most 2 0.057874 2.205811 3.841466	0.0263 0.2527 0.1375
Trace test indicates 1 cointegrating eqn(s) at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values Unrestricted Cointegration Rank Test (Maximum Eigenvalue)
Hypothesized Max-Eigen 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None * 0.444852 21.77525 21.13162 At most 1 0.198187 8.172564 14.26460 At most 2 0.057874 2.205811 3.841466	0.0406 0.3614 0.1375
Max-eigenvalue test indicates 1 cointegrating eqn(s) at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values

Ces résultats montrent qu'il n'y a encore qu'une seule relation de cointégration ( p-value pour « None » inférieure à 5% mais supérieure à cette valeur pour « At most 1).

Estimation du VECM :

Les résultats de l'estimation du VECM avec un retard = 2 et un rang =1 sont comme suit :

Vector Error Correction Estimates Date: 06/14/13 Time: 10:05 Sample (adjusted): 2002Q4 2011Q4 Included observations: 37 after adjustments Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq:	CointEq1
LNM1_SCR(-1)-LNIPC(-...	1.000000
LNPIB_DEF(-1)	-1.660235
	(0.15561)
	[-10.6690]
TAUXCC(-1)	-15.54804
	(4.94513)
	[-3.14411]
C	4.648512
Error Correction:	D(LNM1_SC... D(LNPIB_DE...		D(TAUXCC)
CointEq1	-0.049755	0.020376	0.021616
	(0.05036)	(0.03358)	(0.00488)
	[-0.98806]	[ 0.60680]	[ 4.42762]

VAR Model - Substituted Coefficients:

D(LNM1_SCR-LNIPC) = - 0.0497549843899*( (LNM1_SCR(-1)-LNIPC(-1)) - 1.66023510698*LNPIB_DEF(-1) - 15.548042806*TAUXCC(-1) + 4.64851233776 ) - 0.149927610723*D(LNM1_SCR(-1)-LNIPC(-1)) + 0.648770623836*D(LNM1_SCR(-2)-LNIPC(-2)) - 0.491819392128*D(LNPIB_DEF(-1)) - 0.360089737157*D(LNPIB_DEF(-2)) + 2.887946213*D(TAUXCC(-1)) - 1.31302506145*D(TAUXCC(-2)) + 0.0206868985366

D(LNPIB_DEF) = 0.0203759746284*( (LNM1_SCR(-1)-LNIPC(-1)) - 1.66023510698*LNPIB_DEF(-1) - 15.548042806*TAUXCC(-1) + 4.64851233776 ) - 0.10855843069*D(LNM1_SCR(-1)-LNIPC(-1)) + 0.267114957297*D(LNM1_SCR(-2)-LNIPC(-2)) - 0.73485012642*D(LNPIB_DEF(-1)) - 0.404500877963*D(LNPIB_DEF(-2)) - 0.0455678533531*D(TAUXCC(-1)) + 0.753589441159*D(TAUXCC(-2)) + 0.0219914276927

D(TAUXCC) = 0.0216159395815*( (LNM1_SCR(-1)-LNIPC(-1)) - 1.66023510698*LNPIB_DEF(-1) - 15.548042806*TAUXCC(-1) + 4.64851233776 ) - 0.0620197753036*D(LNM1_SCR(-1)-LNIPC(-1)) - 0.0464342421669*D(LNM1_SCR(-2)-LNIPC(-2)) + 0.0357181232932*D(LNPIB_DEF(-1)) + 0.0191766157533*D(LNPIB_DEF(-2)) - 0.141198885971*D(TAUXCC(-1)) - 0.178225684303*D(TAUXCC(-2)) + 0.00160049305981

114

Ces résultats nous donnent une élasticité-revenu de 1.66, significativement différente de zéro, et une semi-élasticité-taux de 15.55, également significative mais qui est d'une part très élevée et d'autre part a un signe contraire à nos attentes (elle devrait être négative !). Ceci est dû à la présence de la constante qui est égale à -4.648.

Les coefficients CE sont non significatifs à l'exception de celui relatif à D(TAUXCC). Test de Ljung-Box sur les résidus

Ce test conduit avec un retard de 12 donne les résultats suivants :

VEC Residual Portmanteau Tests for Autocorrelations Null Hypothesis: no residual autocorrelations up to lag h Date: 06/14/13 Time: 10:13 Sample: 2002Q1 2011Q4 Included observations: 37
Lags	Q-Stat	Prob.	Adj Q-Stat	Prob.	df
1	3.302544	NA*	3.394281	NA*	NA*
2	8.524384	NA*	8.914512	NA*	NA*
3	9.746380	0.8354	10.24433	0.8041	15
4	12.01020	0.9798	12.78255	0.9696	24
5	21.38729	0.9404	23.62482	0.8853	33
6	26.19743	0.9732	29.36595	0.9296	42
7	34.05835	0.9673	39.06108	0.8891	51
8	39.58851	0.9806	46.11680	0.9064	60
9	53.03386	0.9226	63.88388	0.6516	69
10	59.28237	0.9434	72.44665	0.6561	78
11	65.24880	0.9607	80.93734	0.6627	87
12	69.74079	0.9800	87.58547	0.7182	96
*The test is valid only for lags larger than the VAR lag order.
df is degrees of freedom for (approximate) chi-square distribution

Ces résultats montrent que l'hypothèse d'absence d'autocorrélation des erreurs est acceptée au seuil de 5% à partir du retard 3 jusqu'à 12.

Le modèle est donc validé.

115

III- Etude de la demande de monnaie M3_M1 :

Le modèle à estimer s'écrit comme suit :

(LlM3_M1₀ & hlRPD0\ oN1 (LlM3_M1₀ & hlRPD0Ni1 hlM3_M1_0N1 & hlRPD0N11

? \ hTjk/DDQ0 / - 1 ~.? \ hTAUXC_CF0N1 J + p. O^A. ~ LTAUXCCQ0N1 J + G₀

0 -1 t t i.

Avec : p le nombre de retards, ~ des matrices (3×3), á une matrice (3×r) et â une matrice (r×3) où r est le nombre de relations de cointégration.

Nous allons suivre la même démarche précédente : Détermination du nombre de retards p :

Le retard =2 est lui qui minimise SC, mais nous avons préféré retenir un retard de 3 car celui permet d'accepter l'hypothèse d'une seule relation de cointégration.

Détermination du nombre de relations de cointégration r :

Le test de Johansen conduit avec 3 retards donne les résultats ci-dessous :

Date: 06/14/13 Time: 11:06 Sample (adjusted): 2003Q1 2011Q4 Included observations: 36 after adjustments Trend assumption: Linear deterministic trend Series: LNM3_M1-LNIPC LNPIB_DEF TAUXCC Lags interval (in first differences): 1 to 3 Unrestricted Cointegration Rank Test (Trace)
Hypothesized Trace 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None * 0.606085 47.10605 29.79707 At most 1 0.268165 13.56769 15.49471 At most 2 0.062633 2.328484 3.841466	0.0002 0.0956 0.1270
Trace test indicates 1 cointegrating eqn(s) at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values Unrestricted Cointegration Rank Test (Maximum Eigenvalue)
Hypothesized Max-Eigen 0.05 No. of CE(s) Eigenvalue Statistic Critical Value	Prob.**
None * 0.606085 33.53836 21.13162 At most 1 0.268165 11.23921 14.26460 At most 2 0.062633 2.328484 3.841466	0.0006 0.1426 0.1270
Max-eigenvalue test indicates 1 cointegrating eqn(s) at the 0.05 level * denotes rejection of the hypothesis at the 0.05 level **MacKinnon-Haug-Michelis (1999) p-values

Ces résultats montrent qu'il n'y a qu'une seule relation de cointégration ( p-value pour « None » inférieure à 5% mais supérieure pour « At most 1).

Estimation du VECM :

Les résultats de l'estimation du VECM avec un retard = 3 et un rang =1 sont comme suit :

116

Vector Error Correction Estimates Date: 06/14/13 Time: 11:11 Sample (adjusted): 2003Q1 2011Q4 Included observations: 36 after adjustments Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq:	CointEq1
LNM3_M1(-1)-LNIPC(-1)	1.000000
LNPIB_DEF(-1)	-0.990113
	(0.25159)
	[-3.93544]
TAUXCC(-1)	-60.02277
	(9.09428)
	[-6.60005]
C	1.177629
Error Correction:	D(LNM3_M1-... D(LNPIB_DE...		D(TAUXCC)
CointEq1	0.001494	-0.001082	0.014835
	(0.03282)	(0.02003)	(0.00246)
	[ 0.04552]	[-0.05399]	[ 6.03922]
VAR Model - Substituted Coefficients: D(LNM3_M1-LNIPC) = 0.00149388799484*( (LNM3_M1(-1)-LNIPC(-1)) - 0.990113181775*LNPIB_DEF(-1) - 60.0227668734*TAUXCC(-1) + 1.17762921534 ) + 0.0958873073059*D(LNM3_M1(-1)-LNIPC(-1)) + 0.00634757208945*D(LNM3_M1(-2)-LNIPC(-2)) - 0.170385593728*D(LNM3_M1(-3)-LNIPC(-3)) - 0.526357934018*D(LNPIB_DEF(-1)) - 0.164175584669*D(LNPIB_DEF(-2)) + 0.145004649661*D(LNPIB_DEF(-3)) + 4.38127871713*D(TAUXCC(-1)) + 1.78617522569*D(TAUXCC(-2)) + 1.20143242085*D(TAUXCC(-3)) + 0.0327283068862 D(LNPIB_DEF) = - 0.00108151021694*( (LNM3_M1(-1)-LNIPC(-1)) - 0.990113181775*LNPIB_DEF(-1) - 60.0227668734*TAUXCC(-1) + 1.17762921534 ) + 0.169314144719*D(LNM3_M1(-1)-LNIPC(-1)) + 0.038610796323*D(LNM3_M1(-2)-LNIPC(-2)) - 0.0685767679637*D(LNM3_M1(-3)-LNIPC(-3)) - 0.940985751794*D(LNPIB_DEF(-1)) - 0.251748628444*D(LNPIB_DEF(-2)) - 0.0348357550129*D(LNPIB_DEF(-3)) - 0.821599570807*D(TAUXCC(-1)) - 0.0696168110819*D(TAUXCC(-2)) + 0.514731521183*D(TAUXCC(-3)) + 0.0237746862837 D(TAUXCC) = 0.0148348116881*( (LNM3_M1(-1)-LNIPC(-1)) - 0.990113181775*LNPIB_DEF(-1) - 60.0227668734*TAUXCC(-1) + 1.17762921534 ) + 0.000976188968862*D(LNM3_M1(-1)-LNIPC(-1)) - 0.0122295280252*D(LNM3_M1(-2)-LNIPC(-2)) - 0.0172217763177*D(LNM3_M1(-3)-LNIPC(-3)) + 0.0349025865627*D(LNPIB_DEF(-1)) + 0.0664440030856*D(LNPIB_DEF(-2)) + 0.0440123674837*D(LNPIB_DEF(-3)) + 0.276094254917*D(TAUXCC(-1)) - 0.127990502783*D(TAUXCC(-2)) - 0.0199823898347*D(TAUXCC(-3)) - 0.0012239646529

Ces résultats nous donnent une élasticité-revenu de 0.99, significativement différente de zéro, et une semi-élasticité-taux de 60.02, également significative mais qui nous semble très élevée.

Les coefficients CE sont non significatifs à l'exception de celui relatif à D(TAUXCC).

Test de Ljung-Box sur les résidus

Ce test conduit avec un retard de 12 donne les résultats suivants :

117

VEC Residual Portmanteau Tests for Autocorrelations Null Hypothesis: no residual autocorrelations up to lag h Date: 06/14/13 Time: 11:17 Sample: 2002Q1 2011Q4 Included observations: 36
Lags	Q-Stat	Prob.	Adj Q-Stat	Prob.	df
1	4.706038	NA*	4.840497	NA*	NA*
2	7.470616	NA*	7.767696	NA*	NA*
3	14.66009	NA*	15.61076	NA*	NA*
4	25.05978	0.0491	27.31042	0.0263	15
5	29.91455	0.1876	32.94820	0.1052	24
6	35.79826	0.3384	40.00866	0.1870	33
7	44.55120	0.3649	50.87438	0.1638	42
8	53.99917	0.3605	63.02177	0.1205	51
9	57.94700	0.5511	68.28554	0.2164	60
10	64.44783	0.6328	77.28669	0.2311	69
11	75.15634	0.5702	92.70694	0.1224	78
12	79.38465	0.7068	99.04940	0.1776	87
*The test is valid only for lags larger than the VAR lag order.
df is degrees of freedom for (approximate) chi-square distribution

Ces résultats montrent que l'hypothèse d'absence d'autocorrélation des erreurs est acceptée au seuil de 5% à partir du retard 5 jusqu'à 12. Par contre, pour le retard 4, on est dans la limite du rejet (0.0491) mais on peut accepter.

Le modèle est donc validé.

Etant donné que l'élasticité-revenu de ce modèle (0.99) est très proche de 1, on se propose de tester l'hypothèse d'une élasticité-revenu unitaire. Pour ce faire, nous allons imposer à chacun des deux coefficients relatifs à LNM3_M1-LNIPC et à LNPIB_DEF d'être égal à 1, puis nous allons mener un test de Portmantau sur les résultats, si l'hypothèse nulle de ce test est acceptée, alors on conclut que l'hypothèse d'une élasticité-revenu unitaire peut être acceptée. Les résultats du modèle avec les restrictions précitées sont comme suit :

Vector Error Correction Estimates Date: 06/14/13 Time: 15:45 Sample (adjusted): 2003Q1 2011Q4 Included observations: 36 after adjustments Standard errors in ( ) & t-statistics in [ ]
Cointegration Restrictions:
B(1,1)=1,B(1,2)=1
Convergence achieved after 6 iterations.
Restrictions identify all cointegrating vectors
LR test for binding restrictions (rank = 1):
Chi-square(1) 0.349049
Probability 0.554652
Cointegrating Eq: CointEq1
LNM3_M1(-1)-LNIPC(-1) 1.000000
LNPIB_DEF(-1) 1.000000
TAUXCC(-1) -146.4650
(19.8656)
[-7.37278]
C -11.01070
Error Correction: D(LNM3_M1-... D(LNPIB_DE...		D(TAUXCC)
CointEq1 0.000902	-0.002525	0.005601
(0.01259)	(0.00767)	(0.00096)
[ 0.07162]	[-0.32916]	[ 5.80826]

Les résultats du test de Portmantau, ci-dessous, montrent que l'hypothèse d'une élasticité-revenu unitaire ne peut pas être acceptée :

118

VEC Residual Portmanteau Tests for Autocorrelations Null Hypothesis: no residual autocorrelations up to lag h Date: 06/14/13 Time: 15:50 Sample: 2002Q1 2011Q4 Included observations: 36
Lags	Q-Stat	Prob.	Adj Q-Stat	Prob.	df
1	4.736215	NA*	4.871536	NA*	NA*
2	7.514210	NA*	7.812942	NA*	NA*
3	14.91199	NA*	15.88324	NA*	NA*
4	25.85395	0.0270	28.19295	0.0134	14
5	30.27453	0.1417	33.32652	0.0755	23
6	36.55232	0.2655	40.85988	0.1355	32
7	45.29907	0.2973	51.71791	0.1218	41
8	56.03565	0.2588	65.52209	0.0693	50
9	60.22406	0.4312	71.10663	0.1342	59
10	67.11728	0.5075	80.65109	0.1400	68
11	78.21121	0.4401	96.62635	0.0646	77
12	82.43786	0.5888	102.9663	0.1025	86
*The test is valid only for lags larger than the VAR lag order.
df is degrees of freedom for (approximate) chi-square distribution

En effet, la p-values relative au retard 4 est supérieure à 5%.

Le tableau ci-dessous récapitule les résultats des différents modèles estimés :

Forme de monnaie	Elasticité-revenu	Semi-élasticité-taux	Constante	Paramètres du Modèle VECM(retard,rang)
M1_FID	1.37	5.98	-3.303	p=4,r=1
M1_SCR	1.66	15.55	-4.648	p=2,r=1
M3_M1	0.99	60.023	-1.178	p=3,r=1
M3 (BdF)	1.00	0.004	1.297	p=2,r=2

119

Conclusion

Les différentes études économétriques réalisées sur la demande de monnaie utilisent généralement l'agrégat large M3 ou dans une moindre mesure l'agrégat étroit M1, à notre connaissance, rares sont les études économétriques réalisées sur des agrégats encore plus étroits comme la monnaie fiduciaire ou scripturale. Aussi, à travers cette modeste étude nous avons tenté de combler ce vide en modélisant la demande de monnaie fiduciaire(M1_FID), scripturale (M1_SCR) et celle ne contenant que les comptes d'épargne auprès des banques et les comptes sur livrets auprès de la caisse d'épargne nationale ainsi que les comptes à terme et bons de caisse auprès des banques (M3_M1), et ce, en se basant sur des données marocaines couvrant la période 2002Q1-2011Q4. Nous avons utilisé comme valeurs explicatives de cette demande, le PIB et le taux sur compte de carnet publié par Bank Al-Maghrib. Nous avons essayé deux types de modélisations, une modélisation univariée, dans laquelle nous avons estimé, pour chacune de ces trois formes de monnaie, un modèle linéaire en niveau puis un modèle en termes de logarithme, puis une modélisation multivariée de type VECM dans laquelle nous avons adopté une spécification logarithmique.

Il ressort de notre étude que pour le cas univarié, la spécification en termes de logarithme donne de meilleurs résultats. En effet, en ce qui concerne M1_FID, seul le modèle de la spécification logarithmique sur les séries stationnarisées a pu être validé. Celui-ci nous a donné une élasticité-revenu de 0.61 ce qui est bien inférieure à celle obtenu par la Banque de France (BdF) pour l'agrégat M3. Quant à la semi-élasticité-taux, le modèle nous a donné - 0.94 ce qui est très supérieure en valeur absolue à la somme des semi-élasticités de la BdF (0.004).

Pour M1_SCR, même si le modèle en spécification non logarithmique sur les séries stationnarisées avec l'introduction de retards MA a été validé par les tests statistiques, il n'a pas été retenu à cause de la non significativité de tous ses coefficients. C'est encore une fois le modèle de la spécification logarithmique sur les séries stationnarisées qui a pu être retenu. Ce modèle nous a donné une élasticité-revenu de 0.59, inférieure mais proche de celle de M1_FID, et une semi-élasticité de -0.56, largement inférieure à celle obtenu pour M1_FID, ce qui veut dire que M1_FID est plus sensible au taux sur compte de carnet que M1_SCR. La comparaison avec BdF nous amène au même constat que pour M1_FID.

Et enfin, pour M3_M1, le modèle avec spécification logarithmique sans correction d'erreurs (ECM) sur les séries non stationnarisées a été retenu. Celui-ci nous a donné une élasticité-revenu égale à 2.13, largement supérieure à 1, et une semi-élasticité revenu égale à 5.36. Ces deux chiffres sont largement supérieurs à ceux obtenus par la banque de France (respectivement 1 et 0.004)

Pour chacun de ces modèles nous avons testé l'hypothèse d'une élasticité-revenu unitaire, cependant elle n'a pas été acceptée dans aucun d'eux, ce qui veut dire que la constante obtenue dans chacun d'eux ne peut être interprétée comme une vitesse de circulation.

120

En ce qui concerne la modélisation VECM, les résultats obtenus sont différents. En effet, les élasticités-revenu de M1_FID et M1_SCR sont supérieures à 1 (respectivement 1.37 et 1.66) alors que celle de M3_M1 est inférieure mais très proche de 1 (0.99). Les semi-élasticités sont également très supérieures à celle obtenues dans le cas univarié : 5.98 pour M1_FID,

15.55 pour M1_SCR et 60.023 pour M3_M1.

Pour M3_M1, nous avons testé l'hypothèse d'une élasticité-revenu unitaire, mais elle n'a pas été acceptée, par conséquent l'équation de long terme ne peut être interprétée comme une équation de vitesse de circulation de M3_M1.

Enfin, notons que notre choix du taux sur compte de carnet (TAUXCC) pour représenter le coût d'opportunité de la détention de la monnaie, a été essentiellement dicté par la disponibilité des données. Aussi, cette étude pourrait-elle être améliorée en se basant, sur des taux d'intérêt plus représentatifs de ce coût. On pense également à l'introduction de taux différents pour le court et le long terme pour mieux capter le motif de spéculation qui, de notre point de vue, dépend beaucoup de l'horizon de placement. Du côté de la modélisation, le VECM peut être estimé pour l'ensemble des variables de notre étude pour tenter de détecter les interactions qui pourraient exister entre les trois formes de la monnaie, le PIB et les taux d'intérêt utilisés.

121

Bibliographie

Mishkin, F (2010), « Monnaie, banque et marchés financiers », Pearson Education, 9ème édition.

Alphandery, E (1976), « Cours d'analyse macroéconomique », Economica.

Contensou, F et Vranceanu, R (1996), « Introduction à la théorie macroéconomique », Editions ESKA.

Védie, H (2008), « Macroéconomie », Dunod, 2^ème édition.

Bourbonnais, R (2009), « Econométrie. Manuel et exercices corrigés », Dunod, 7ème édition.

Maynard Keynes, J , « Théorie générale de l'emploi, de l'intérêt et de la monnaie » : http://classiques.uqac.ca/classiques/keynesjohnmaynard/keynesjm.html

SAY, JB, Traité d'économie politique :

http://classiques.uqac.ca/classiques/say jean baptiste/say jb.html

Estimation d'une fonction de demande de monnaie pour la zone euro : une synthèse des résultats :

http://www.banque-

france.fr/fileadmin/userupload/banquedefrance/archipel/publications/bdfbm/etudesb dfbm/bdfbm111etu2.pdf

Fiche N°5: La Demande de Monnaie

http://theo-monetaire.e-monsite.com/medias/files/fiche-n-5-la-demande-de-monnaie.pdf

Cours « Systèmes monétaires et financiers », chap II, Le marché de la monnaie, Arnaud Diemer, MCF Université d'Auvergne, Faculté de Sciences économiques et de Gestion, 2ème année DEUG :

http://www.oeconomia.net/private/cours/monnaie/chapitre23.pdf

La théorie quantitative de la monnaie Extraits wikipédia :

http://postjorion.wordpress.com/2010/10/26/132-la-theorie-quantitative-de-la-monnaie/

Théorie générale de l'emploi, de l'intérêt et de la monnaie - Traduit de l'Anglais par Jean- de Largentaye (1942) :

Histoire de la monnaie :

http://fr.wikipedia.org/wiki/Histoiredelamonnaie

122

ANNEXE : Données utilisées

Date	M1_FID	M1_SCR	M3 - M1	PIB	TauxCC	IPC
31/12/2001	66 829	149 262	129 732	109472	4,72%	92,81
31/03/2002	66 284	147 714	132 001	109787	3,95%	94,65
30/06/2002	66 564	155 481	130 558	110786	3,95%	94,08
30/09/2002	70 493	159 592	135 191	111209	3,42%	93,10
31/12/2002	70 361	173 437	137 699	113644	3,42%	94,13
31/03/2003	71 069	174 550	140 123	115380	2,15%	93,56
30/06/2003	71 742	174 545	135 648	119480	2,15%	94,19
30/09/2003	75 392	182 110	138 783	120561	2,95%	96,27
31/12/2003	75 694	192 452	143 361	121601	2,95%	95,81
31/03/2004	76 234	194 350	152 125	124364	2,49%	95,92
30/06/2004	76 634	201 418	150 306	127706	2,49%	95,86
30/09/2004	80 225	204 159	149 341	127301	2,35%	97,07
31/12/2004	80 243	212 052	153 588	125644	2,35%	96,32
31/03/2005	81 319	217 100	166 415	128578	2,27%	97,13
30/06/2005	82 464	220 095	172 461	130787	2,27%	96,32
30/09/2005	87 200	232 577	174 182	133457	2,28%	97,42
31/12/2005	89 906	239 000	179 664	134856	2,28%	98,34
31/03/2006	91 934	245 349	184 281	139952	2,57%	99,15
30/06/2006	94 940	253 375	185 510	143142	2,57%	99,96
30/09/2006	100 820	261 293	202 271	143645	2,49%	101,45
31/12/2006	109 177	276 044	215 342	150605	2,49%	101,57
31/03/2007	107 038	287 237	230 183	149312	2,49%	101,60
30/06/2007	108 802	307 701	225 831	151846	2,49%	101,70
30/09/2007	115 144	318 066	239 928	154724	2,41%	104,00
31/12/2007	120 045	337 138	248 760	160368	2,41%	103,80
31/03/2008	117 462	342 777	257 655	167053	3,11%	105,10
30/06/2008	119 662	353 080	280 136	169582	3,11%	106,20
30/09/2008	125 869	346 747	297 211	176935	3,10%	107,70
31/12/2008	128 091	360 796	311 494	175273	3,10%	108,00
31/03/2009	126 734	350 151	329 561	178307	3,29%	108,00
30/06/2009	129 397	359 934	332 434	182066	3,29%	105,60
30/09/2009	134 697	363 827	333 314	181561	3,11%	109,80
31/12/2009	136 664	388 726	331 629	190515	3,11%	106,30
31/03/2010	134 747	383 982	343 986	185813	2,87%	109,00
01/06/2010	137 505	391 149	346 978	191138	2,87%	107,60
04/09/2010	142 263	389 952	346 075	191898	3,11%	109,50
08/12/2010	144 660	404 828	348 851	195181	3,11%	108,60
01/03/2011	146 612	402 401	353 235	197807	2,99%	109,60
09/06/2011	149 473	410 765	354 069	197608	2,99%	108,30
13/09/2011	155 780	409 418	354 960	202036	2,96%	110,40
16/12/2011	158 288	428 489	369 884	205156	2,96%	109,60

123

Tables des matières

Résumé 2

Abstract 3

Dédicace 4

Remerciements 5

Introduction Générale 7

Chapitre I : La demande de monnaie 9

Section 1 : La monnaie 9

I- La monnaie chez les classiques et les néo-classiques 9

II- La monnaie chez Maynard Keynes 10

III- La monnaie chez Friedman 11

IV- Les formes de la monnaie 11

V- Les agrégats monétaires 12

V-1- L'agrégat M1 12

V-2- L'agrégat M2 12

V-3- L'agrégat M3 12

Section 2 : La fonction de demande de monnaie 13

I- La demande de monnaie chez les classiques et les néo-classiques 13

I-1- L'équation de FISHER 13

I-2- L'équation de MARSHALL 16

II- La demande de monnaie chez Maynard Keynes 16

II-1- Le motif de transaction 17

II-2- Le motif de précaution 17

II-3- Le motif de spéculation 17

II-4- Fonction de préférence pour la liquidité 17

III- La demande de monnaie chez Friedman 18

Section 3 : La demande de monnaie au Maroc 20

I- Principes d'élaboration des statistiques monétaires au Maroc 20

I-1- Le secteur émetteur de la monnaie 20

I-2- Le secteur détenteur de la monnaie 21

I-3- Le secteur neutre 21

I-4- Sources de données pour l'élaboration des statistiques monétaires 21

I-4-1 La situation monétaire : 21

I-4-2 La situation analytique des Autres Sociétés de Financement 22

II- La demande de monnaie au Maroc 23

II-1- Evolution des agrégats monétaires 23

II-2- Evolution de la vitesse de circulation 26

124

Chapitre II : Etude des séries utilisées pour l'estimation de la demande de monnaie 27

Section 1 : Rappel sur les stratégies de tests de Dickey-Fuller 27

I- Définition d'un processus stochastique stationnaire (au deuxième ordre) 27

II- Les processus non stationnaires TS 28

III- Les processus non stationnaires DS 28

IV- Stratégie de tests ADF adoptée 29

Section 2 : Etude des séries utilisées 31

Chapitre III : Estimation de la demande de monnaie dans le cas du Maroc 80

Section 1 : ESTIMATION D'UNE FONCTION DE DEMANDE DE MONNAIE POUR LA ZONE EURO PAR LA BANQUE

DE FRANCE 80

Section 2 : Estimation univariée de la demande de monnaie 84

I- Etude de la demande de monnaie fiduciaire (M1_FID) 84

I-1- Spécification en niveau : 84

I-2- Spécification logarithmique : 90

II- Etude de la demande de monnaie scripturale (M1_SCR) 93

II-1- Spécification en niveau : 93

II-2- Spécification logarithmique : 97

III- Estimation de la demande de monnaie M3_M1 : 101

III-1- Spécification en niveau : 101

III-2- Spécification logarithmique : 105

Section 3 : Estimation multivariée de la demande de monnaie 109

I- Etude de la demande de monnaie fiduciaire (M1_FID) 109

II- Etude de la demande de monnaie scripturale (M1_SCR) 112

III- Etude de la demande de monnaie M3_M1 : 115

Conclusion 119

Bibliographie 121

ANNEXE : Données utilisées 122