Memoire Online - La mécanique statistique des membranes biologiques confinées

We re-examine here the phase separation between phospholipids and adsorbed polymer chains on a fluid membrane with a change in some suitable parameter (temperature). Our purpose is to quantify the significant effects of the solvent quality and of the polydispersity of adsorbed loops formed by grafted polymer chains on the segregation phenomenon. To this end, we elaborate on a theoretical model that allows us to derive the expression for the mixing free energy. From this, we extract the phase diagram shape in the composition-temperature plane. Our main conclusion is that the polymer chain condensation is very sensitive to the solvent quality and to the polydispersity of loops of adsorbed chains.

Biological membranes are of great importance to life, because they separate the cell from the outside environment and separate the compartments inside the cell in order to protect important processes and specific events.

Nowadays, it is largely recognized that biological membranes are present as a lipid bilayer composed of two adjacent leaflets [1, 2], which are formed by amphiphile molecules possessing hydrophilic polar-heads pointing outward and hydrophobic fatty acyl chains that form the core. The majority of lipid molecules are phospholipids. These have a polar-head group and two non-polar hydrocarbon tails, whose length is of the order of 5 nm.

Also, the cell membranes incorporate another type of lipid, cholesterol [1, 2]. The cholesterol molecules have several functions in the membrane. For example, they give rigidity or stability to the cell membrane and prevent crystallization of hydrocarbons. The biomembranes also contain glycolipids (sugars), which are lipid molecules that microaggregate in the membrane, and may be protective and act as insulators. Certain kinds of molecules are bounded by sphingolipids such as cholera and tetanus toxins. Sphingolipids and cholesterol favor the aggregation of proteins in microdomains called rafts. In fact, these play the role of a platform for the attachment of proteins while the membranes are moved around the cell and also during signal transduction.

Proteins (long macromolecules) are another principal component of cell membranes. Transmembrane proteins are amphipathic and are formed by hydrophobic and hydrophilic regions having the same orientation as other lipid molecules. These proteins are also called integral proteins. Their function is to transport substances, such as ions and macromolecules, across the membrane. There exist other types of proteins that may be attached to the cytoplasm surface by fatty acyl chains or to the external cell surface by oligosaccharides. These are termed peripheral membrane proteins. They have many functions; in particular, they protect the membrane surface, regulate cell signaling and participate in many other important cellular events. In addition, some peripheral membrane proteins (those having basic residues) tend to bind electrostatically to negatively charged membranes, such as the inner leaflet of the plasma membrane.

We note that the majority of macromolecules forming the bilayer are simply anchored on the membrane and form a soft branched polymer brush [3, 4].

The study of grafted polymers on soft interfaces was motivated by the fact that they have potential applications in biological materials, such as liposomes [5-8]. These soft materials were discovered by A Bangham. Currently, they are major tools in biology, biochemistry and medicine (as drugs transport agents). Liposomes are artificial vesicles of spherical shape that can be produced from natural nontoxic phospholipids and cholesterol. But the lipid bilayers have a short lifetime, because of the weak stability of the vesicles and their extermination by white blood cells. To have stable vesicles in time, one useful method consists of protecting them with a coat of flexible polymer chains (coat size of the order of 50 nm [1]), which prevents the adhesion of marker proteins [6, 7]. In fact, these polymer chains stabilize the liposomes, due to the excluded volume forces between monomers [8]. Liposomes can also be synthesized from A-B diblock-copolymers immersed in a selective solvent that prefers to be contacted by the polymer A. The hydrophobic B-polymer chains then aggregate and form a thin bilayer, while the hydrophilic polymer chains A float in the solvent. These copolymer-based liposomes have properties that are slightly different from those of the lipid ones [9] (high resistance, high rigidity and weak permeability to water). Depending on the choice of copolymers, these liposomes are resistant to detergents [10].

The grafting of polymers onto lipid membranes was considered in a very recent paper [11]. More precisely, the purpose was to investigate of the phase separation between phospholipids and anchored polymers. As assumptions, the aqueous medium was assumed to be a good solvent, and in addition, the polymer chains were anchored to the interface only by one extremity, a big amphiphile molecule. The latter is chemically different from the phospholipid molecules. In this paper, however, we assume that the polymer chains may be adsorbed on the membrane by many monomers that are directly attached to some polar-heads of the host lipid molecules (mobile anchors), and then organize in polydisperse loops. The surrounding liquid may be a good solvent or a theta solvent. As we shall see below, the loops' polydispersity and solvent quality drastically affect the phase behavior of the system. Under a change in a suitable parameter, such as temperature, the phospholipids and adsorbed polymer chains phase separate into macroscopic domains alternately rich in the two components. For the determination of the phase diagram shape, we elaborate on a theoretical model that takes into account both the loops' polydispersity and the solvent quality.

This paper is organized as follows. In section 2, we derive the expression for the mixing free energy of the phospholipid-anchor mixture. To investigate the phase diagram shape is the aim of section 3. Finally, some concluding remarks are given in section 4.

Polymers can adhere to biomembranes in several ways: (i) by lipid anchors; that is, the polymer is covalently

bound to the polar-head of a lipid molecule (for many proteins, the lipid anchors are glycosylphosphatidylinositol units) [12, 13]; (ii) by hydrophobic side-groups of the polymers which are integrated into the bilayer [14, 15]; (iii) by membrane spanning hydrophobic domains of the polymer (membrane-bound proteins, for example); and (iv) by a strong adsorption that drives the polymer from a desorbed state to an adsorbed one [16]. For a single polymer chain, the adsorption (on solid substrates) can be theoretically studied using a scaling argument [17], for instance. In addition to the polymerization degree of the polymer chain, N, and the excluded volume parameter, v, the study was based on an additional parameter, 8, which is the energy (per kBT unit) required to adsorb one monomer on the surface. For a strong adsorption, 8-¹defines the adsorbed-layer thickness. An adsorption transition takes place at some typical value 8* of 8 scaling as [17]: 8^*~ R-1 F ~ aN^-VF(VF = 3/5), where RF is the Flory radius of the polymer chain. For dilute and semi-dilute polymer solutions, the adsorption phenomenon depends, in addition to the parameter 8, on the polymer concentration.

In this paper, we consider situation (iv), where each monomer has the same probability of being adsorbed on the membrane surface [18]¹. More precisely, a given monomer is susceptible to becoming linked to a polar-head of a phospholipid molecule (anchor). As a result, the polymer chains form polydisperse loops (with eventually one or two tails floating in the aqueous medium). In fact, this assumption conforms to what was considered in [19]. The case where no loops are present (adsorption only by one extremity) was considered in [11]. Contrary to the adsorption on the solid surface, the anchored polymer chains are mobile on the host membrane and may undergo the aggregation transition that we are interested in. To be more general, the fluid membrane is assumed to be in contact with a good solvent or a theta solvent.

The purpose is to write a general expression for the mixing free energy. The latter will allow the determination of the phase diagram related to the aggregation of anchored polymer chains.

First, we start with the free energy (per unit area) of the polymer layer (for solid substrates), which is given by [20]

F0 ' kBT

Z _N(

1 [b²S (n)]^â+ [-b²S⁰(n)] ln

b2 1

~ _l\

- S0 (n) dn.

(1)

For the configuration study, Guiselin [21] considered that each loop can be viewed as two linear strands (two half-loop). Here, S(n) is the number of strands having more than n monomers per unit area, and b represents the monomer size. The number N denotes the length of the longest strand. Hereafter, we shall use the notation S1 = /a, which denotes the total number of grafted chains per unit area, with 8 being the volume fraction of anchors and a their area. If the mixture is assumed to be incompressible, then 1 - 8 is the volume fraction of the phospholipid molecules.

Let us come back to the free energy expression (1); note that the first term of the right-hand side represents the

1 The adsorption of an adequate polymer on a fluid membrane made of two phospholipids of different chemical nature may be a mechanism of phase separation between these two unlike components as was pointed out.

contribution of the (two- or three-body) repulsive interactions between monomers belonging to the polymer layer. The second term is simply the entropy contribution describing all possible rearrangements of the grafted chains in the polymer layer. There, the exponent â depends on the solvent quality [20]. When the grafting is accomplished in a dilute solution with a good solvent or a theta solvent, the values of â are â = 11/6 (blob model) or â = 2, respectively.

For polydisperse polymer layers, the distribution S(n) is known in the literature [20]. This can be obtained by minimizing the above free energy with respect to this distribution.

S(n) ~

an⁶/⁵

with f (n) ~ 1/n¹/⁽â-¹⁾, for polydisperse polymer layers, and f (n) = 1 (for all n), for polymer brushes. Therefore, F0 can be approximated by

where the linear term in 8 describes the contribution of entropy to the free energy, where the coefficient ç(N) is as follows (see the appendix):

Note that æ(N) < 1, since, in all cases, â > 1. Therefore, the polydispersity of loops decreases the repulsive interaction energy.

Now, we have all the ingredients for the determination of the expression for the mixing free energy. To this end, we imagine that the interface is present as a two-dimensional (2D) Flory-Huggins lattice [17, 22], where each site is occupied by an anchor or by a phospholipid molecule. Hence, we can regard the volume fraction of anchors 8 as the probability that a given site is occupied by an anchor. Therefore, 1 - 8 is the occupation probability of phospholipids.

Before the determination of the desired mixing free energy (per site), we note that the latter is the sum of three contributions, which are the mixing entropy (per site), the volume free energy (per site) and the interaction energy (per site) coming from the membrane undulations. Actually, the induced attractive forces due to the membrane undulations are responsible for the condensation of anchors. These forces balance the repulsive ones between monomers along the connected polymer chains. We then write

We note that, for polymer chains anchored by one extremity, a big amphiphile molecule (the polymer brush case), the first contribution of entropy, 8 ln 8, should be divided by some factor q, which represents the ratio of the anchor area to the area of polar-heads of the host phospholipids. In the present case, we have q = 1. In equality (11), ÷ accounts for the Flory interaction parameter

+ N1/(1-â) ln N }. (7)

â -1 JJJ

÷ = ÷0

(14)

1 D
A2 C -_kBT ,

ç(N) ? a^-1 [â +ln(â - 1)], (8)
provided that â > 1 (note that â = 11/6, for good solvents, and â = 2, for theta ones). This asymptotic limit is always positive definite and inversely proportional to the polar-head area a. In fact, the positive sign of the coefficient ç(N) agrees with the entropy loss due to the polymer chains grafting. As we shall see below, this linear contribution does not change the phase diagram in the composition-critical parameter plane. Here, the coupling constant u is as follows:

Here, U(r) is the pair potential induced by the membrane undulations ([11]; [24] and references therein)

where ó is the hard disc diameter, which is proportional to the square root of the anchor area a. There, the potential amplitude AH plays the role of the Hamaker constant. It was found that the latter decays with the bending rigidity constant according to ([11]; [24] and reference therein)

But this amplitude is also sensitive to temperature. We remark that the above mixing free energy is not symmetric under the change 8 ? 1-8.

Some straightforward algebra gives the following expression for the attraction parameter D:

Therefore, those membranes with a small bending modulus induce significant attraction between anchors.

In formula (12), ÷0 > 0 is the Flory interaction parameter describing the chemical segregation between amphiphile molecules that are phospholipids and anchors. This segregation parameter is usually written as

where the coefficients á0 and ã0 depend on the chemical nature of the various species. Also, the total interaction parameter ÷ can be written as

These coefficients then depend on the chemical nature of the unlike components and on the membrane's characteristics through its bending modulus ê.

If we admit that the coupling constant u has a slight dependence on temperature, we will draw the phase diagram in the plane of variables (8, ÷). Indeed, all of the temperature dependence is contained in the Flory interaction parameter ÷. interactions widen the compatibility domain, and then, the separation transition appears at low temperature.

Now, to see the influence of the solvent quality, we rewrite the interaction parameter u as u = u0æ(N) ~ u0Nâ/(1-â) < u0, where u0 is the interaction parameter relative to a monodisperse system. Thus, the polydispersity of loops has a tendency to reduce the compatibility domain in comparison with the monodisperse case.

The critical volume fraction, 8_c, can be obtained by minimizing the critical parameter ÷(8) with respect to the 8-variable. We then obtain

Therefore, the critical volume fraction is the abscissa of the intersection point of the curve of the equation (2x - 1)/ x⁵/⁶(1 - x)²and the horizontal straight line of the equation y = (55/216)u. Note that this critical volume fraction is unique, and in addition, it must be greater than the value 1/2 (for mathematical compatibility). The coordinates of the critical point are (8_c, ÷_c), where 8_csolves the above equation and ÷_c= ÷(8_c). The latter can be determined by combining equations (19) and (21). For theta solvents (â = 2), the coordinates of the critical point are exact,

With the help of the above mixing free energy, we can determine the shape of the phase diagram in the (8, ÷)-plane that is associated with the aggregation process that drives the anchors from a dispersed phase (gas) to a dense one (liquid). We focus only on the spinodal curve along which the thermal compressibility diverges. The spinodal curve equation can be obtained by equating to zero the second derivative of the mixing free energy with respect to the anchor volume fraction 8; that is, ?²F/?8²= 0. Then, we obtain the following expression for the critical Flory interaction parameter:

Above this critical interaction parameter appear two phases: one is homogeneous and the other is separated. Of course, the linear term in 8 appearing in equality (11) does not contribute to the critical parameter expression.

We remark that, in usual solvents, this critical interaction parameter is increased due to the presence of (two-or three-body) repulsive interactions between monomers belonging to the polymer layer. This means that these

The above relation clearly shows that the polymer chains' condensation rapidly takes place only when the characteristic mass N is high enough. The same tendency is also seen in the case of good solvents.

It is straightforward to show that the critical fraction and the critical parameter are shifted to lower values in the case of polydisperse systems, whatever be the quality of the surrounding solvent.

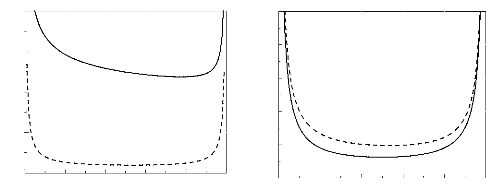
In figure 1, we present the spinodal curve for monodisperse (with no loops) and polydisperse (with loops) systems, with a fixed parameter N. We have chosen the good solvents situation. For theta solvents, the same tendency is seen.

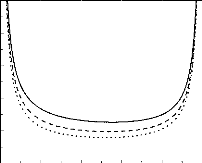
We present in figure 2 the spinodal curve for a polydisperse system (with loops), at various values of the parameter N. As expected the critical parameter is shifted to higher values when we augmented the typical polymerization degree.

Finally, we compare, in figure 3, the spinodal curves for a polydisperse system (with loops) for the case of theta solvents and those for the case of good solvents, at fixed parameters b and N. All the curves in the figure reflect our discussions above.

Figure 1. Spinodal curves (in a good solvent) for monodisperse (dashed line) and polydisperse (solid line) systems, when N = 100, with the parameter b²= 0.5a.

Figure 2. Spinodal curves for a polydisperse system, when N = 50 (solid line), 100 (dashed line) and 150 (dotted line), with the parameter b²= 0.5a . We assumed that the surrounding liquid is a good solvent. For theta solvents, the tendency is the same.

This paper is devoted to the thermodynamic study of the aggregation of the polymer chains adsorbed on a soft surface. Such an aggregation is caused by competition between the chemical segregation between phospholipids and grafted polymer chains, their volumic interactions and the membrane undulations. More precisely, we addressed the question of how these polymer chains can be driven from a dispersed phase (gas) to a dense one (liquid), under a change in a suitable parameter, e.g. the absolute temperature.

To be more general, we achieved the study in a unified way; that is, we have considered more realistic physical situations: the solvent quality (good or theta solvents) and the polydispersity of the adsorbed loops formed by the grafted

Figure 3. Superposition of spinodal curves for a polydisperse system for the case of theta solvents (solid line) on those for the case of good solvents (dashed line). For these curves, we chose N = 100 and b²= 0.5a.

polymer chains. The latter were taken into account through the well-known form of the chains' length distribution.

In doing so, we first computed the expression for the mixing free energy by adopting the Flory-Huggins lattice image usually encountered in polymer physics [17, 22]. Such an expression shows that there is competition between four contributions: entropy, chemical mismatch between unlike species, interaction energy induced by the membrane undulations and the interaction energy between monomers belonging to the grafted layer. Such a competition governs the phases succession.

We emphasize that the present work and a previous work [11] differ from another previous work that was concerned with the same problem, but in which the substrate was assumed to be a rigid surface [3]. Therefore, the membrane undulations were neglected. As we have seen, these undulations increase the segregation parameter ÷ by an additive term, ÷_m, scaling as ê-². This means that the phase separation is accentuated due to the presence of thermal fluctuations. Compared with the previous work [11], which was concerned with soft brushes with monodisperse end-grafted polymers, the present work is more general, since it takes into account both the polydispersity of loops forming the adsorbed polymer chains and the solvent quality. Thus, the present study was achieved in a unified way. As we have seen, these details drastically affect the phase diagram architecture.

Now, let us discuss further the influence of solvent quality on the critical phase behavior. We recall that the solvent quality appears in the free energy (11) through the repulsion parameter u, defined in equation (7). We find, in the N ? 8 limit, that u_g~ N¹/⁵uè, where the subscripts g and è stand for good and theta solvents, respectively. This implies that the good solvent plays the role of a stabilizer regarding the phase separation.

Finally, this work must be considered as a natural extension of a study reported previously [11], which was concerned with monodisperse end-grafted polymer chains

trapped in a good solvent. Therefore, the present work presents a wide perspective on the phenomenon of segregation between the host phospholipids and grafted polymer chains on bilayer membranes.

We are indebted to Professors T Bickel, J-F Joanny and C Marques for helpful discussions during the First International Workshop on Soft-Condensed Matter Physics and Biological Systems (14-17 November 2006, Marrakech, Morocco). MB thanks Professor C Misbah for fruitful correspondence and the Laboratoire de Spectroscopie Physique (Joseph Fourier University of Grenoble) for their kind hospitality during his visit. We are grateful to the referee for critical remarks and useful suggestions that helped us to improve the scientific content of this paper.

The aim is to determine the coefficient ç(N) appearing in formula (6). We start with the entropy contribution to the free energy

Fentropic
kBT

Z N

1 (~-b²S⁰(n)~ ln
' b2 1

~ ~~

- S0(n)

dn, (A.1)

where the loop-size distribution is defined in equation (2). Then, the above expression can be rewritten as

La mécanique statistique des membranes biologiques confinées

Abstract