III. STATIC CASIMIR FORCE
When viewed under the microscope, the membranes of vesicles
present thermally excited shape fluctuations. Generally, objects such as
interfaces, membranes or polymers undergo such fluctuations, in order to
increase their configurational entropy. For bilayer biomembranes and
surfactants, the consequence of these undulations is that, they give rise to an
induced force called Casimir force.
To compute the desired force, we start from the partition
function constructed with the Hamiltonian defined in Eq. (13). This partition
function is the following functional integral
f { }
-H0 [h]
Z = Dh exp , (3.0)
kBT
where integration is performed over all height-field
configurations. The associated free energy is such that : F = -kBT
lnZ, which is, of course, a function of the separation D. If we
denote by Ó = L2 the common area of plates, the
Casimir force (per unit area) is minus the first derivative of the
free energy (per unit area) with respect to the film-thickness D, that
is
This force per unit area is called disjoining pressure. In
fact, II is the required pressure to maintain the two plates at some distance
D apart. In term of the partition function, the disjoining pressure
rewrites
|
II
kBT =
|
1 Ó
|
? lnZ 1 ?u ? lnZ
?D = ?u . (3.0)
Ó ?D
|
Using definition (19) together with Eqs. (23) and (24) yields
1 ?u
II = -(3.0)
2 ?D L2 ? .
Explicitly, we obtain the desired formula
êD3 . (3.0)
3
II = 8
(kBT)2
106
From this relation, we extract the expression of the disjoining
potential (per unit area) [25]
f D II (D') dD'
= 3 (kBT )2
Vd (D) = - êD2 . (3.0)
16
8
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
107
The above expression of the Casimir force (per unit area)
calls the following remarks.
Firstly, this force decays with distance more slowly in
comparison to the Coulombian one that decreases rather as
D-2.
Secondly, this same force depends on the nature of lipids
forming the bilayer (through ê). In this sense, contrarily to
the Casimir effect in Quantum Field Theory [16] and in Critical Phenomena [20],
the present force is not universal. Incidentally, if this force is
multiplied by ê, then, it will become a universal quantity.
Thirdly, at fixed temperature and distance, the force amplitude has significant
values only for those bilayer membrane of small bending rigidity constant.
Fourthly, as it should be, such a force increases with
increasing temperature. Indeed, at high temperature, the membrane undulations
are strong enough.
Finally, the numerical prefactor 3/8 (Helfrich's
cH-amplitude [9]) is close to the value obtained using Monte Carlo
simulation [26].
In Fig. 1, we superpose the variations of the reduced static
Casimir force Ð/kBT upon separation D, for two
lipid systems, namely SOPC and DAPC [27], at temperature T =
18?C. The respective membrane bending rigidity constants are :
ê = 0.96 x 10-19 J and ê =
0.49 x 10-19 J. These values correspond to the renormalized
bending rigidity constants : ?ê = 23.9 and ?ê
= 12.2. The used methods for the measurement of these rigidity
constants were entropic tension and micropipet [27]. These
curves reflect the discussion made above.
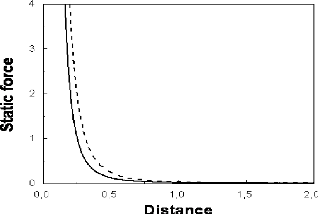
FIG. 1. Reduced static Casimir force,
ll/kBT, versus separation D, for two lipid
systems that are SOPC (solid line) and DAPC (dashed line), of respective
membrane bending rigidity constants : k = 0.96 ×
10-19 J and k = 0.49 ×
10-19 J, at temperature T =
18?C. The reduced force and separation are expressed in
arbitrary units.
| 


