|

Centre d'Etudes Doctorales Sciences et
Applications
Faculté des Sciences Ben M'Sik
Casablanca
THESE
Présentée pour l'obtention du
DOCTORAT

Par : Khalid EL HASNAOUI
Titre de la thèse : La Mécanique
Statistique des Membranes Biologiques Confinées
Formation Doctorale : Physique & Applications
(PA)
Laboratoire Physique des Polymères et
Phénomènes Critiques (LPPPC) Membres du Jury :

Pr. H. Ridouane Faculté des Sciences Ben M'Sik
Président
Pr. N. Benayad Faculté des Sciences Ain Chock
Rapporteur
Pr. A; Derouiche Faculté des Sciences Ben M'Sik
Rapporteur
Pr. M. Rahmoune EST, Meknès, Maroc
Rapporteur

Pr. A. Rahmani Faculté des Sciences, Meknès
Examinateur
Pr. M. Benhamou Faculté des Sciences Ben M'Sik
Encadrant
Pr. M. Chahid Faculté des Sciences Ben M'Sik
Co-Encadrant
Date de soutenance : Samedi 15 octobre 2011 à 10
heures Lieu : Salle 18
Centre d'Etudes Doctorales Sciences et Applications
Université Hassan II-Mohammedia-Casablanca,
Faculté des Sciences Ben M'sik, BP 7955 Casablanca.
Tél. 05 22 70 46 71-75 Fax. 05 22 70 46 75, E-mail
:
secretariat.cedfsb@yahoo.fr,
secretariat.cedfsb@univh2m.ac.ma
Remerciements
Le travail de recherche présenté dans cette
thèse a été effectué au sein du
Laboratoire de Physique des Polymères et
Phénomènes Critiques (LPPPC), de la faculté
des Sciences Ben M'sik de Casablanca, Sous la direction de Monsieur le
Professeur Mabrouk BENHAMOU.
J'exprime ma profonde gratitude et ma reconnaissance au
Professeur M. Benhamou, le Directeur de (LPPPC) pour m'avoir accueilli au sein
de son laboratoire et pour l'aide précieuse qu'il m'a apportée.
Je le remercie également pour m'avoir encadré, pour ses conseils,
son soutien, sa disponibilité et surtout pour ses qualités
humaines.
Le Professeur M. Chahid a contribué à
l'encadrement de ce travail et participé à son
élaboration, je le remercie chaleureusement pour l'intérêt
qu'il a apporté à mon travail et pour sa disponibilité et
son conseil.
Mes vifs remerciements et mes amitiés les plus
sincères s'adressent à Mesdames et Messieurs les Professeurs, H.
Ridouane, F. Ben2ouine, A. Derouiche, et A. Bettachy pour avoir
participé à ma formation en Master de Physique
Matière et Rayonnement.
J'exprime mes sincères remerciements à Messieurs
N. Benayad, de la Faculté des Sciences A4n Chok de Casablanca, M.
Rahmoune, Professeur à la Faculté des Sciences et Technique de
Méknes,A. Derouiche, Professeur à la Faculté des Sciences
Ben M'sik de Casablanca, pour l'intérêt qu'ils ont porté
à ce travail, en acceptant de le juger et, de surcroît, en
être rapporteurs.
Je remercie aussi chaleureusement Mr H. Ridouane pour avoir
accepté de présider mon jury de thèse.
Une thèse, c'est aussi un laboratoire où l'on
passe de nombreuses heures et où il est bon de se sentir bien. Alors un
grand merci à tous les membres du LPPPC, passés et
présent, en particulier,T. El khalefi, H.Kaidi, E. Elkennassi ,Y.
Madmoune, F. El Hajjaji, H. Qamar, R. Elmiles, A. Charekaoui, A. Nidam,... pour
l'ambiance scientifique et amicale qui règne au sein du laboratoire.
Je remercie infiniment tous les membres de ma famille pour
leur soutien et leurs encouragements tout au long de mon cursus. A la fin,
j'aurais l'immense plaisir de dédier ce manuscrit à ma
mère, ma soeur khadija et ma femme qui m'ont particulièrement
soutenu au temps des difficultés, sans ce soutien, je n'aurais sans
doute pas eu la persévérance de mener ce travail à
terme.
Toutes mes excuses à celles et à
ceux que j'ai oublié(e)s, et encore merci à toutes et à
tous.
Résumé de la thèse :
Cette thèse visait des études
étendues des propriétés statistiques des
biomembranes.
Plus exactement, nous avons à chercher à
quantifier les effets de confinement sur ces mêmes
propriétés.
Le premier objectif était
l'étude de la dynamique Brownienne de particules
entourant une membrane biologique, confinée entre deux parois
réfléchissantes parallèles.
En effet, les biomembranes se sont jamais
à l'état pure, car elles sont souvent en
présence d'entités (particules,
macromolécules et autres). Pour simplifier
l'étude, ces entités étaient
considérées comme des colloïdes ponctuels. Nous avons
étudié cette dynamique, à travers la densité locale
des particules, qui est fonction non seulement de la distance, mais aussi du
temps. Les résultats obtenus généralisent ainsi ceux
relatifs aux biomembranes non confinées.
Le second objectif avait trait à
l'étude de l'effet Casimir des biomembranes
confinées entre deux parois réfléchissantes
parallèles. En fait, les fluctuations thermiques de la
membrane induisent une force répulsive entre les deux
plaques. Cette force, d'origine entropique, a
été calculée, du point de vue statique et
dynamique.
Le troisième objectif retracé était
une étude statistique des biomembranes, immergées dans un liquide
trouble, c'est-à-dire contenant des impuretés.
Nous avons étudié les effets de ces impuretés sur le
spectre de fluctuations des membranes presque planes, sur la forme
d'équilibre des vésicules (membranes lipidiques fermées),
et sur la transition de délocalisation des phases
lamellaires.
Le quatrième objectif était
l'étude de la conformation des polymères, à
connectivité arbitraire, confinés dans une phase lamellaire ou
à l'intérieur d'une vésicule
tubulaire. Une telle étude a été
motivée par des intérêts d'ordre biologique.
Le dernier objectif était la séparation
de phase entre les phospholipides et des polymères greffés sur
une membrane fluide. L'étude a été menée, pour
diverses situations, à savoir la qualité du solvant et la
polydispersité des chaînes de polymère.
Nous avons montré que ces deux facteurs
induisent des changements drastiques du comportement de phase.
L'ensemble des résultats obtenus ont fait
matière de plusieurs publications dans des revues scientifiques
spécialisées et d'un nombre important de communications
(orales ou par affiche), présentées lors de congrès
nationaux ou internationaux.
Mots clés : Membranes biologiques - Dynamique
Brownienne - Particules - Effet Casimir - Confinement - Milieux troubles -
Polymères greffés.
N°d'ordre:

www.univh2m.ac.ma
Avenue Hassan II B.P. 150, Mohammedia, Maroc Tél :
+212 5 23 31 46 35/36 Fax : +212 5 31 46 34 E-mail :
presidence@univh2m.ac.ma
8
Table des matières
|
Résumé.
|
12
|
|
1
|
Introduction générale.
|
14
|
|
2
|
Composition et fonction des membranes
biologiques.
|
21
|
|
2.1
|
Représentation des biomembranes. . . . . . .
. . . . . . . . . . . . .
|
21
|
|
2.2
|
Membranes lipidiques. . . . . . . . . . . . . . . .
. . . . . . . . . . .
|
25
|
|
|
2.2.1 Organisation. . . . . . . . . . . . . . . . .
. . . . . . . . . . .
|
25
|
|
|
2.2.2 Lipides membranaires. . . . . . . . . . . . .
. . . . . . . . . .
|
27
|
|
|
2.2.3 Protéines. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
|
30
|
|
|
2.2.4 Cholestérol. . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
|
31
|
|
|
2.2.5 Mouvements à l'intérieur de la
membrane. . . . . . . . . . . .
|
32
|
|
|
2.2.6 Perméabilité membranaire.. . . .
. . . . . . . . . . . . . . . .
|
33
|
|
2.3
|
Membranes artificielles.. . . . . . . . . . . . . .
. . . . . . . . . . . .
|
36
|
|
|
2.3.1 Définition. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
|
36
|
|
|
2.3.2 Liposomes. . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
36
|
|
|
2.3.3 Applications des liposomes. . . . . . . . . .
. . . . . . . . . .
|
38
|
|
2.4
|
Conclusions. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . .
|
40
|
|
Table de matière
3 Mécanique Statistique des
biomembranes.
|
9
45
|
|
3.1
|
Introduction. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
45
|
|
3.2
|
Compositions et fonctions des biomembranes. . . . . . .
. . . . . . .
|
48
|
|
|
3.2.1 Les vésicules. . . . . . . . . . . . . . .
. . . . . . . . . . . . .
|
48
|
|
|
3.2.2 Les lipides. . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
49
|
|
|
3.2.3 Les liposomes.. . . . . . . . . . . . . . . . . .
. . . . . . . . .
|
51
|
|
3.3
|
Propriétés statistiques des biomembranes.
. . . . . . . . . . . . . . .
|
52
|
|
|
3.3.1 Description thermodynamique. . . . . . . . . . .
. . . . . . .
|
52
|
|
|
3.3.2 Théorie de Canham-Helfrich.. . . . . . . .
. . . . . . . . . . .
|
53
|
|
|
3.3.3 Spectre de fluctuations thermiques. . . . . . . .
. . . . . . . .
|
56
|
|
|
3.3.4 Interaction d'Helfrich. . . . . . . . . . . . . .
. . . . . . . . .
|
58
|
|
|
3.3.5 Longueur de persistance. . . . . . . . . . . . .
. . . . . . . . .
|
60
|
|
3.4
|
Conclusions. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . .
|
62
|
|
4
|
Effet de Casimir dans les biomembranes
confinées.
|
66
|
|
4.1
|
Introduction. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
66
|
|
4.2
|
Formulation théorique. . . . . . . . . . . . . .
. . . . . . . . . . . . .
|
70
|
|
4.3
|
Force de Casimir statique. . . . . . . . . . . . . . .
. . . . . . . . . .
|
78
|
|
4.4
|
Force de Casimir dynamique. . . . . . . . . . . . . . .
. . . . . . . .
|
81
|
|
4.5
|
Conclusions. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . .
|
90
|
|
Dynamique Brownienne de colloïdes au contact d'une
biomem-
|
|
|
brane confinée.
|
95
|
|
5.1
|
Introduction. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
96
|
|
5.2
|
Formulation théorique. . . . . . . . . . . . . .
. . . . . . . . . . . . .
|
100
|
Table de matière 10
5.3 Evolution temporelle de la densité de
particules. . . . . . . . . . . . . 106
5.3.1 Equations de base. . . . . . . . . . . . . . . .
. . . . . . . . . 106
5.4 Conclusions. . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . 112
6 Mécanique Statistique des membranes
confinées dans un liquide
trouble. 118
6.1 Introduction . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . 119
6.2 Hamiltonien effectif. . . . . . . . . . . . . . .
. . . . . . . . . . . . . 121
6.3 Membranes presque-plates
isolées. . . . . . . . . . . . . . . . . . . . . 124
6.4 Vésicules isolées. . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . 135
6.5 Phases lamellaires. . . . . . . . . . . . . . . .
. . . . . . . . . . . . . 140
6.6 Conclusions. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . 146
7 Conformation d'un polymère confiné dans
des domaines délimités
par des biomembranes. 1 50
7.1 Introduction. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . 151
7.2 D-manifolds non confinés . . . . . . . . . . .
. . . . . . . . . . . . . . 153
7.3 D-manifolds confinés en
Géométrie I. . . . . . . . . . . . . . . . . . .
156
7.3.1 Relations utiles.. . . . . . . . . . . . . . . . .
. . . . . . . . . 156
7.3.2 Extension parallèle à l'axe du
cylindre. . . . . . . . . . . . . . 158
7.4 D-manifolds confinés en
Géométrie II. . . . . . . . . . . . . . . . . .
160
7.4.1 Séparation moyenne. . . . . . . . . . . . .
. . . . . . . . . . . 160
7.4.2 Extension parallèle du polymère. . .
. . . . . . . . . . . . . . 161
7.5 Conclusions. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . 163
Table de matière 11
8 Condensation des polymères greffés sur
une biomembrane. 169
8.1 Introduction. . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . 170
8.2 Energie libre du mélange.. . . . . . . . .
. . . . . . . . . . . . . . . . 173
8.3 Diagramme de phase.. . . . . . . . . . . . . . . .
. . . . . . . . . . . 180
8.4 Conclusions. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . 184
9 Conclusions générales. 190
10 Appendice A. 194
11 Appendice B. 196
Résumé.
Cette thèse visait des études
étendues des propriétés statistiques des biomem-branes.
Plus exactement, nous avons à chercher à quantifier les effets de
confinement sur ces mêmes propriétés.
Le premier objectif était l'étude de la
dynamique Brownienne de particules entourant une membrane biologique,
confinée entre deux parois réfléchissantes
parallèles. En effet, les biomembranes se sont jamais à
l'état pure, car elles sont souvent en présence d'entités
(particules, macromolécules et autres). Pour simplifier l'étude,
ces entités étaient considérées comme des
colloïdes ponctuels. Nous avons étudié cette dynamique,
à travers la densité locale des particules, qui est fonction non
seulement de la distance, mais aussi du temps. Les résultats obtenus
généralisent ainsi ceux relatifs aux biomembranes non
confinées.
Le second objectif avait trait à l'étude
de l'effet Casimir des biomembranes confinées entre deux parois
réfléchissantes parallèles. En fait, les fluctuations
thermiques de la membrane induisent une force répulsive entre les deux
plaques. Cette force, d'origine entropique, a été
calculée, du point de vue statique et dynamique.
Le troisième objectif retracé
était une étude statistique des biomembranes, immergées
dans un liquide trouble, c'est-à-dire contenant des impuretés.
Nous avons
Table de matière 13
étudié les effets de ces
impuretés sur le spectre de fluctuations des membranes presque planes,
sur la forme d'équilibre des vésicules (membranes lipidiques
fermées), et sur la transition de délocalisation des phases
lamellaires.
Le quatrième objectif était
l'étude de la conformation des polymères, à
connec-tivité arbitraire, confinés dans une phase lamellaire ou
à l'intérieur d'une vésicule tubulaire. Une telle
étude a été motivée par des intérêts
d'ordre biologique.
Le dernier objectif était la séparation
de phase entre les phospholipides et des polymères greffés sur
une membrane fluide. L'étude a été menée, pour
diverses situations, à savoir la qualité du solvant et la
polydispersité des chaînes de polymère. Nous avons
montré que ces deux facteurs induisent des changements drastiques du
comportement de phase.
L'ensemble des résultats obtenus ont fait
matière de plusieurs publications dans des revues scientifiques
spécialisées et d'un nombre important de communications
(orales ou par affiche), présentées lors de congrès
nationaux ou internationaux.
Mots clés : Membranes biologiques - Dynamique
Brownienne - Particules - Effet Casimir - Confinement - Milieux troubles -
Polymères greffés.
14
Chapitre 1
Introduction générale.
Les méthodes utilisées pour
l'étude des propriétés mecoscopiques de la matière
molle (cristaux liquides, films amphiphiles, membranes biologiques,
polymères, colloïdes, milieux granulaires....), dont les bases ont
été jetées par le Professeur Pierre-Gilles de Gennes (Prix
Nobel de Physique, 1991), ont contribué, d'une
manière déterminante, au nouvel essor de la biologie cellulaire
et au développement de nouvelles méthodes thérapeutiques.
Dans l'espace de quelques dizaines d'années, grâce à ces
techniques empruntées à la matière, l'on a plus saisir les
structures, la manipulation de molécules individuelles, les moteurs
biologiques, et la motilité et l'adhésion cellulaires.
Actuellement, l'intérêt accordé à ce domaine prend
plus d'ampleur.
Ces dernières années, les
matériaux biologiques (biomembranes, ADN, ARN, etc.) ont attiré
l'attention des Physiciens, mais aussi des Chimistes et Biologistes. En
particulier, les physiciens ont mis à la disposition des ces
matériaux tout un arsenal d'outils théoriques adaptés aux
phénomènes faisant intervenir un grand nombre de
molécules, à savoir la Mécanique Statistique, la
Théorie de Champ et la Simu-
Résumé. 15
lation (essentiellement, les méthodes Monte
Carlo et Dynamique Moléculaire). En parallèle, la visualisation
en temps réel, facilitée par les énormes progrès
des moyens optiques, s'est révélée un outil puissant
[1]. Ces techniques de visualisation a permis le
contrôle de la présence ou l'absence d'effets indésirables,
et aussi de présenter le système sous différents aspects
(zoom, angles d'observation, éclairement, marquages fluorescents,...).
Les techniques de diffusion (rayons-X, lumière et neutrons) ont
été déterminantes pour explorer les matériaux
biologiques, à toutes les échelles.
Des expériences ont montré que les
membranes biologiques peuvent incorporer de grosses molécules
(inclusions), telles que des protéines, des particules
colloïdales ou d'autres macromolécules [2]. En
plus des interactions directes entre ces diverses inclusions, les fluctuations
thermiques des membranes engendrent des interactions effectives entre elles
[3 - 9]. Notons que ces fluctuations
thermiques ont pour origine les chocs incessants de la part des
molécules et ions formant le liquide hôte. Donc, une
membrane biologique est un système capable de passer par une
infinité de configurations. L'apparition des ondulations thermiques ont
reçu leur confirmation expérimentale, même sous des
conditions physiologiques.
Les matériaux biologiques présentent un
grand intérêt, en raison de leurs nombreuses applications dans
divers secteurs [10, 11]. Sur le plan
conceptuel, leurs principales caractéristiques découlent de leur
structure bidimensionnelle et de la richesse de leur comportement
thermodynamique.
Aujourd'hui, la structure en bicouche diffuse des
membranes biologiques est largement admise par la communauté
scientifique. Le dénominateur commun de ces bicouches est qu'elles sont
formées de molécules amphiphiles. La majorité des
molécules de lipide sont les phospholipides. Une molécule
amphiphile est composée d'une
Résumé. 16
tête polaire hydrophile (qui aime l'eau) et
d'une queue hydrophobe [12]. Cette queue qui n'aime pas, est
naturellement repoussée par le milieu aqueux. Cette double
affinité fait que les molécules s'assemblent de façon
à exposer leur tête et protéger leur
extrémité lipidique. En plus de ces molécules lipidiques,
une membrane cellulaire comporte des protéines transmembranaires et
périphériques, des glycoprotéines, des glycolipides, et
dans certains cas, du cholestérol et des lipoprotéines
[13]. Signalons qu'il existe des membranes biologiques, qui
sont dépourvues de cholestérol. C'est le cas des
bactéries, par exemple.
Les phospholipides sont loin d'être immobiles,
car ils peuvent diffuser librement sur la surface de la membrane. Aussi, ils
subissent de rotations autour de leur axe principal [13]. De
plus, l'épaisseur de la couche lipidique est de l'ordre de 100
Angströms, qui est naturellement plus faible que son extension
latérale. De ce fait, une membrane biologique peut être
considérée comme un liquide bidimensionnel. En langage de
Géométrie Différentielle, une membrane est une surface
fluctuante plongée dans l'espace euclidien à trois dimensions
[14 - 16].
Le grand nombre de molécules impliquées
et la géométrie locale souvent complexe [14 -
16] rendent difficile le traitement des membranes biologiques,
à partir d'interactions microscopiques réalistes. C'est la raison
pour laquelle l'on a vu se développer, progressivement, des
théories phénoménologiques ignorant les détails
microscopiques, mais permettant de prédire la majorité des
comportements généraux. Les membranes sont
considérées comme des surfaces fluctuantes continues,
décrites par une énergie effective qui dépend de la forme
locale de la membrane, de son élasticité, de sa topologie, et
éventuellement des degrés de liberté
supplémentaires en relation les spécificités des diverses
espèces chimiques présentes [17,
18].
Résumé. 17
Mais, très souvent, une biomembrane est en
présence de petites entités baignant dans le milieu aqueux
(macromolécules ou autres). Bien évidemment, celles-ci influent
sur le comportement de cette membrane (spectre de fluctuations,
séparation de phase, etc.). Pour mener des études quantitatives
des effets de ces corps étrangers, l'on peut les assimiler à des
particules colloïdales de forme sphérique (nanoparti-cules). Cette
hypothèse n'est valable que si la taille des particules est bien
inférieure à la taille caractéristique de la membrane, qui
est sa rugosité moyenne.
Cette thèse s'inscrit précisément
dans le cadre de la Physique Statistique des biomembranes confinées,
pour diverses situations.
La première contribution est le calcul
de la force de Casimir entre deux plaques interactives parallèles
délimitant un liquide comptant une biomembrane immergée
[19]. Cette force répulsive provient des ondulations
thermiques de la membrane. Nous avons traité aussi bien l'aspect
statique que l'aspect dynamique.
La deuxième contribution se rapporte
à une solution colloïdale au contact d'une biomembrane, qui est
confinée dans une fente [20]. L'épaisseur de
cette fente est supposée beaucoup plus petite que la rugosité en
volume, afin d'assurer le confinement de la membrane. Le but étant
l'étude de la dynamique Brownienne de ces particules, sous la variation
d'un paramètre adéquat, tel que la température, par
exemple. L'objet de base est la densité locale des particules. Nous
avons déterminé exactement cette densité, qui est fonction
de la distance et du temps. L'outil pour cela est l'équation de
Smoluckowski.
La troisième contribution est une
étude détaillée des effets d'impuretés sur les
propriétés statistiques des membranes fluides
[21]. Celles peuvent être attractives ou
répulsives. En premier lieu, nous avons déterminé la
rugosité moyenne de la
Résumé. 18
membrane, en combinant la technique des
répliques avec la méthode variationnelle. Le résultat
s'exprime en fonction de la concentration des impuretés et l'amplitude
de leur interaction avec la membrane. En second lieu, nous avons
évalué la taille d'une vésicule isolée, en fonction
de ces mêmes paramètres. Enfin, l'étude est étendue
à l'adhésion membranaire.
La quatrième contribution est une
étude conformationnelle d'un polymère isolé, qui est
confiné entre deux membranes lipidiques parallèles ou dans une
vésicule tubulaire [22]. Pour rester plus
général, nous avons supposé que le polymère est de
topologie arbitraire, qu'on appelle D-manifold, où
D est la dimension spectrale (par exemple, D =
1, pour les polymères linéaires, et D =
4/3, pour les polymères
branchés). En fait, D est le nombre de coordonnées
locales permettant de caractériser géométriquement le
polymère.
La dernière contribution est une
investigation de la séparation de phase entre les phospholipides et des
polymères greffés sur une membrane fluide [23].
L'étude a été menée, pour diverses situations,
à savoir la qualité du solvant et la polydispersité des
chaînes de polymère. Nous avons montré que ces deux
facteurs induisent des changements drastiques du comportement de
phase.
Le mémoire suit l'organisation
suivante.
Les deux premiers chapitres sont à
caractère bibliographique, où nous rappelons les
éléments nécessaires à la présente
étude.
Les résultats trouvés sont
décrits aux chapitres 3 à
7.
Enfin, nous retraçons nos conclusions et
présentons certains détails techniques (Appendices A et
B) à la fin de ce mémoire.
19
Bibliographie
[1] D.R. Nelson, T. Piran, S. Weinberg,
éditeurs, Statistical Mechanics of Membranes and Surface, World
Scientific, Singapore, 1989.
[2] C. Fradin, A. Abu-Arish, R. Grank, M. Elbaum,
Biophys. J. 84, 2005 (2003).
[3] P.G. Dommersnes, J.-B. Fournier, Europhys. Lett. 46,
256 (1999).
[4] S. Safran, Statistical Thermodynamics of
Surfaces, Interface and Membranes, Addision-Wesly, Reading,
1994.
[5] D. Bartol, J.-B. Fournier, Eur. Phys. J. E 11, 141
(2003).
[6] H. Kaïdi, T. Bickel, M. Benhamou, Eur. Phys.
69, 15 (2005).
[7] T. Bickel, M. Benhamou, H. Kaïdi, Phy. Rev. E
70, 051404 (2004).
[8] A. Bendouch, H. Kaïdi, T. Bickel, et M.
Benhamou, J. Stat. Phys. : Theory and Experiment P01016, 1 (2006).
[9] A. Bendouch, M. Benhamou, et H. Kaidi, E. J.
Theoretical Physics 5, 17, 215230. (2008).
[10] H. Lodish, A. Berk, S.L. Zipursky, P. Matsudaira,
D. Baltimore, J. Darnell, Molecular Cell Biology, Freeman &
Company, New York, 2002.
[11]
Résumé. 20
S. Safran, Statistical Thermodynamics of Surface,
Interfaces and Membranes, Addison-Wesley, Reading, MA, 1994.
[12] E. Evans, D. Needham, J. Phys. Chem. 91, 4219
(1987).
[13] R. Lipowsky, S. Sasckmann, éditeurs,
Structure and Dynamics of Membranes : From Cells to Vesicles, Volume 1A,
Elsevier Science B.V., 1995.
[14] P.B. Canham, Theoret. Biol. J. 26, 61
(1970).
[15] W. Helfrich, Z. Naturforsch. 28, 693
(1973).
[16] S. Safran, Statistical Thermodynamics of
Surfaces, Interface and Membranes, Addision-Wesly, Reading,
1994.
[17] F. Brochard, J.-F. Lennon, J. Physique
(Paris) 36, 1035 (1975).
[18] V.I. Marchenko, C. Misbah, Eur. Phys. J. E 8,
477 (2002).
[19] K. Elhasnaoui, Y. Madmoune, H. Kaidi, M. Chahid,
M. Benhamou, African Journal of Mathematical Physics 8, 101 (2010).
[20] Y. Madmoune, K. El Hasnaoui, A. Bendouch, H.
Kaidi, M. Chahid, M. Benha-mou, African Journal of Mathematical Physics 8, 91
(2010).
[21] M. Benhamou, K. Elhasnaoui, H. Kaidi, M. Chahid,
Physica A 389, 3465 (2010).
[22] M. Benhamou, K. El Hasnaoui, H. Kaidi, M.
Chahid, à paraître dans African Journal of Mathematical
Physics, 2011.
[23] M. Benhamou, I. Joudar, H. Kaidi, K. Elhasnaoui,
H. Ridouane, H. Qamar, Phys. Scr. 83, 065801 (2011).
Chapitre 2
Composition et fonction des
membranes biologiques.
Dans ce premier chapitre, à caractère
bibliographique, nous rappelons, dans un premier temps, la
représentation des membranes biologiques, ensuite, les
découvertes et les premières observations de la cellule, enfin,
la structure et les propriétés des membranes biologiques,
principalement pour leurs capacités de séparer deux milieux
aqueux l'un de l'autre. Plus exactement, nous explorons la composition des
cellules biologiques. En particulier, nous mettons l'accent sur le rôle
de chacune de ses composantes. Nous terminons en précisant quelques
intérêts et applications des vésicules.
2.1 Représentation des biomembranes.
saires pour le maintien de la vie. La cellule est donc
l'unité structurale et fonction-
21
La cellule est la plus petite unité vivante,
capable d'accomplir les fonctions néces-
hapitre 1 : Composition et fonction des membranes
biologiques. 22
nelle fondamentale des organismes vivants. Sa taille
est de l'ordre du micromètre. C'est d'ailleurs l'une des raisons qui
laisse cette brique élémentaire de tous les êtres vivants
un objet d'une extrême complexité. La découverte des
cellules était intervenue avec la mise au point du
microscope.
Ainsi, en 1665, Robert Hooke
[1] observa, pour la première fois, des cellules
à l'aide d'un microscope à deux lentilles. En
1838, M. Schleiden et Theodor Schwann [2]
s'étaient mis d'accord sur la même conclusion. C'est que
tous les organismes se composent de cellules, qui y sont décrites comme
des petite chambres limitées par une paroi ou encore membrane
cellulaire. Cette dernière est alors considérée comme
une simple enveloppe renfermant différents constituants de la cellule.
En 1847, Théodore Nicolas Gobley [45]
isola la lécithine du jaune d'oeuf et découvrit les
phospholipides. Singer et Nicolson [11] partirent du
modèle de bicouche lipidique de Gorter et Grendel et utilisèrent
les découvertes de Frye et Edidin [10], en
matière de fluidité de la membrane et de mobilité des
protéines. Ce modèle de fluide mosaïque
[11] reste le modèle de référence,
même s'il a subi quelques aménagements. Dans ce modèle, la
membrane plasmique est décrite comme une bicouche lipidique fluide, dans
laquelle flottent des protéines, et où les molécules de
lipide et protéines sont distribuées plus ou moins
aléatoirement. Les protéines sont insérées
profondément dans la bicouche lipidique, sous forme compacte. Les
protéines peuvent être intégrales (protéines
transmembranaires) ou adsorbées à la surface de la bicouche. Les
chaînes polypeptidiques, le plus souvent organisées sous forme
d'hélices á [12] et contenant de nombreux
résidus d'acides aminés hydrophobes, prennent la place des
lipides et assurent ainsi la continuité de la partie hydrophobe de la
membrane. Alors que es parties les plus hydrophiles des protéines
émergent sur au moins une
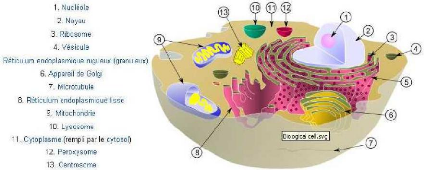
hapitre 1 : Composition et fonction des membranes
biologiques. 23
FIG. 2-1 -- Schéma d'une cellule
eucaryote.
des deux faces de la bicouche. La face externe de la
membrane est rendue encore plus hydrophile, par la présence de
résidus osidiques (Fig.
1.1).
L'agitation thermique est responsable de la diffusion
et de la rotation de toutes les molécules dans le plan de la
membrane.
Des études récentes
[13, 14] révélèrent que
les lipides et les protéines ne diffusent pas aussi librement. Ce qui
contredit alors les prédictions du modèle original de Singer et
Nicolson. En effet, les structures membranaires observées à
l'aide de techniques nouvelles, comme les pièges optiques, le SPT
(Simple Particle Tracking) et le SMT (Simple Molecule
Tracking). Cette technique relativement récente a permis le suivi
du déplacement de molécules individuelles par
vidéomicroscopie couplée à l'analyse d'images. Les sondes
utilisées sont soit des particules submicrométriques (particules
de latex, nanocristaux ou colloïdes d'or, couplés à la
molécule d'intérêt
hapitre 1 : Composition et fonction des membranes
biologiques. 24
par un anticorps), et l'on parle alors de suivi de
particule unique ou SPT [15, 16], soit des
molécules fluorescentes (suivi de molécule unique ou SMT
[17]). En fait, la résolution spatiale est de l'ordre
du manomètre et la résolution temporelle,
généralement imposée par la cadence vidéo, peut
atteindre la centaine de Hertz. A partir des trajectoires des molécules,
le calcul du déplacement quadratique moyen de la position en fonction du
temps permet de déterminer les modes de diffusion.
La méthode de FRAP (Fluorescence Recovery
After Photobleaching ) réalise une mesure moyenne sur un grand
nombre de molécules. La FCS (Fluorescence Correlation
Spectroscopy) effectue une mesure moyenne sur un petit nombre de
molécules et nécessite de ce fait un certain nombre de
répétitions pour obtenir une valeur finale significative.
L'avantage de cette technique de FCS réside dans l'utilisation d'un
faible marquage : une faible suppression des molécules
d'intérêt est suffisante et même nécessaire pour
réaliser des mesures. En effet, la FCS est sensible à l'amplitude
des variations de fluctuation d'intensité et donc aux fluctuations du
nombre de molécules présentes dans le volume confocal qui a une
taille de l'ordre du femtolitre
(10-i5L) , ceci correspond
à une concentration volumique de l'ordre de quelques dixièmes de
nanomolaires (10-9M) à un
micromolaire (10-6M).
Les SPT et SMT permettent alors une
caractérisation plus fine des sous-populations. Au contraire, ces trois
dernières techniques autorisent la mise en évidence de
phénomènes qui auraient pu être masqués par l'effet
de moyenne de la FRAP. Dans certaines situations ce sont donc des techniques
complémentaires.
Malgré la diversité des êtres
vivants, les cellules ont des caractères anatomiques, biochimiques et
fonctionnels communs.
hapitre 1 : Composition et fonction des membranes
biologiques. 25
2.2 Membranes lipidiques.
2.2.1 Organisation.
Les membranes cellulaires sont formés de
molécules amphiphiles, qui présentent une partie hydrophobe
et un groupement hydrophile [18]. La
majorité des molécules lipidiques d'une membrane sont des
phospholipides. Ceux-ci contiennent une tête hydrophile attachée
à deux chaînes carbonées, contrairement aux surfactants qui
ne possèdent qu'une seule chaîne aliphatique.
La solubilité des molécules amphiphiles
dépend de la longueur et le nombre des chaînes carbonées..
Les lipides sont très peu solubles. Leur concentration micellaire est de
l'ordre de 10-10M, et au
delà de cette concentration, ils s'assemblent en structures qui
dépendent de la géométrie de la
molécule.
La formation d'une bicouche nécessite que
l'aire de la tête hydrophile soit légèrement plus grande ou
de la même taille que la section de la chaîne carbonée.
Certaines molécules de ce genre s'auto-assemblent, non pas en feuillet,
mais en vésicule, c'est-à-dire en structure fermée. En
effet, d'un point de vue énergitique, un ensemble de vésicules
est plus stable qu'une bicouche infinie, en raison de l'entropie de translation
des vésicules [19]. Le rayon minimum de la
vésicule est alors fixé par la géométrie de la
molécule. Les têtes des lipides sont séparées d'une
distance optimale qui résulte de la balance entre l'attraction des
parties hydrophobes, qui se protègent de l'eau, et la répulsion
(d'origine stérique, électrostatique, etc.) des chaînes.
Lorsque les molécules s'auto-assemblent en vésicule, les
têtes doivent conserver leur espacement optimal. Cela impose un rayon
minimal à la vésicule. Sa taille réelle dépend des
conditions de fabrication, et peut aller jusqu'à 100pm
pour des vésicules géantes.
hapitre 1 : Composition et fonction des membranes
biologiques. 26
Les lipides composant la membrane peuvent former un
liquide bidimensionnel ou un gel. La température de transition de l'un
à l'autre dépend de la longueur des chaînes aliphatiques.
Plus les chaînes sont longues, plus cette température est
élévée [19]. Au-dessus de cette
température critique (typiquement de l'ordre de
25?C), la bicouche est fluide, et
les lipides diffusent dans le plan de la membrane. Ainsi, pour une composition
homogène, le coefficient de diffusion est de l'ordre
10-12m2/s,
c'est-à-dire qu'un lipide parcourt environ 1um en
1s [19]. La conséquence de la
fluidité de la bicouche est qu'elle ne présente aucune
résistance au cisaillement.. Ce n'est pas entendu le cas en phase
gel.
La fonction spécifique des systèmes
biologiques vivants (cellules, organites cellulaires et autres
organismes) est essentiellement reliée à la structure des
membranes plasmiques. Ces dernières protègent la cellule de son
environnement. La majorité des cellules procaryotes contiennent un grand
nombre de compartiments formant les organites cellulaires, qui sont
bordés par une ou deux membranes. Enfin, certains organites responsables
de la conversion d'énergie (mitochondries, chloroplastes)
contiennent un nombre important de membranes internes, ou bien
présentent des repliements très complexes de l'une des membranes
qui les protègent.
Nous soulignons que les membranes ne se limitent pas
à celui d'un sac mou et inert, mais elles interviennent aussi dans les
différentes processus biologiques indispensables à la vie, comme
les phénomènes de transport, les processus de conversion
d'énergie, la reconnaissance cellulaire, etc. De plus, la membrane
plasmique repose sur une charpente dynamique ou cytosquelette. Ce dernier est
formé d'un réseau de filaments de protéines, qui favorise
la mobilité cellulaire, et contribue à maintenir la forme de la
cellule et la cohésivité des tissus. Aussi, il sert comme guide
pour le

hapitre 1 : Composition et fonction des membranes
biologiques. 27
FIG. 2-2 -- Structure de la bicouche
membranaire.
transport des molécules indispensables à
l'activité cellulaire.
Enfin, chez tous les êtres vivants, les
membranes sont formées, essentiellement, de lipides, disposés en
double feuillet (Fig. 1.2), de faible
épaisseur, c'est-à-dire de l'ordre de 5 à
10nm. Ces membranes constituent alors une barrière
infranchissable pour les ions ou les grosses molécules. En plus des
lipides, la membrane cellulaire comporte des protéines, des sucres, etc.
C'est donc un milieu complexe, chimiquement actif et en renouvellement
constant.
2.2.2 Lipides membranaires.
Les lipides de la membrane cellulaire sont tous des
amphiphiles possédant des groupements aliphatiques ou aromatiques (comme
le cholestérol) et des groupements polaires variés. La
géométrie de chaque chaîne aliphatique dépend de
l'existence ou non d'insaturations.. Les chaînes d'acides gras non
saturées sont très flexibles et possèdent un très
grand nombre de conformations possibles. Chaque liaison possède
3
hapitre 1 : Composition et fonction des membranes
biologiques. 28

FIG. 2-3 -- Composition lipidique de
différentes types de membranes cellulaires (pourcentage en
poids).
degrés de liberté de rotation. La
conformation la plus probable est celle de l'extension maximale de la
chaîne (configuration trans), conduisant à une
énergie minimale. Une chaîne insaturée possède au
moins une double liaison. La configuration cis, largement plus
probable que la configuration trans, conduit à un coude dans la
chaîne carbonée de l'ordre de
30?.
La tête polaire est attachée à
deux chaînes carbonées, par l'intermédiaire d'une
molécule servant de lien entre les trois groupements. Ce lien jouant le
rôle de squelette pour l'ensemble de la molécule, est
généralement réalisé par un alcool, comme le
glycérol, ou une sphingosine. Les groupements polaires sont, le plus
souvent, basés sur un groupe phospho ou glyco,
d'autres molécules venant s'y greffer.
La composition lipidique des membranes cellulaires
eucaryotes est très variée (Fig.
1.3). La majorité des molécules de
lipide constituant une membrane biologique,

hapitre 1 : Composition et fonction des membranes
biologiques. 29
FIG. 2-4 -- Structure d'un phosphoglycérol , le
phosphatidyléthanolamine (PE) : (a) formule chimique, (b) modèle
compact et (c) représentation symbolique
sont des phospholipides (Fig.
1.4a).
Selon le type d'organites, les lipides membranaires,
représentant 30% à 50% de la
masse de la membrane, sont, le plus souvent, des lipides amphipolaires
(Fig. 1.4b), qui comportent une tête
polarisable hydrophile (le phosphoglycérol substitué,
par exemple) et une ou deux queues hydrophobes, formées de
longs résidus d'acides gras, qui sont des chaînes
hydrocarbonées (Fig. 1.4c). Un exemple
de ces lipides est le phosphatidyléthanolamine (Fig.
1.4a).
Pour assurer l'équilibre thermodynamique, un
mélange de lipides baignant dans un milieux aqueux, s'organise
spontanément en structure lytrope séquestrant les
parties hydrophobes des molécules au centre des agrégats. Le
contact avec les molécules d'eau étant assuré par les
parties polaires (dans l'eau, la concentration micellaire critique est de
l'ordre de 10-12), avec une couche
d'hydratation d'épaisseur de l'ordre
hapitre 1 : Composition et fonction des membranes
biologiques. 30
de 10 Angströms
[20].
Nous signalons que les constituants d'une membrane
tiennent ensemble, grâce à l'existence des attractions
hydrophobes, qui sont plus faibles que les liaisons covalentes.
2.2.3 Protéines.
Une membrane cellulaire renferment, également,
des protéines, qui sont intégrées dans la bicouche
lipidique. Ce sont des grosses molécules ou encore
macromolécules, dont la fonction est d'assurer les échanges de
matière et d'énergie entre l'intérieur et
l'extérieur de la membrane. Les lipides servent de solvant pour les
protéines membranaires.
L'on distingue des protéines
intégrales et protéines
périphériques. Les premières
pénètrent assez profondément dans la bicouche lipidique,
et forment des canaux assurant le passage des ions et autres entités
d'un côté à l'autre de la membrane. Les parties hydrophobes
de ces protéines se trouvent naturellement entourées par les
queux hydrocarbonées des lipides, alors que les régions polaires
sont au contact avec le solvant environnant (milieu aqueux). En revanche, les
protéines périphériques ne pénètrent pas du
tout dans la membrane, et se trouvent plutôt greffées sur la
surface membranaire (Fig. 1.2).
Sur la surface interne de la membrane plasmique, des
filaments du cytosque-lette aident à maintenir en place certaines
protéines périphériques et les protéines
intramembranaires associées. Nous signalons que les surfaces interne et
externe des membranes sont bien distinctes. En effet, ils ne présentent
pas la même compo-

hapitre 1 : Composition et fonction des membranes
biologiques. 31
FIG. 2-5 -- Protéines de transport dans une
membrane : (a) Protéines porteuses (trans-porteurs),(a) Protéines
tunnels (canaux)
sition lipidique et l'orientation des protéines
y diffère. Seule la surface externe de la membrane plasmique contient
des glycoprotéines [21]. Ces dernières sont
d'une importante capitale, car elles participent à un grand nombre de
fonctions biologiques, telles que la signalisation, la
bioénergétique, l'adhésion, la reconnaissance, et le
transport de soluté (Fig.
1.5).
Enfin, nous notons que sur les 20000
structures de protéines solubles connues, seules 48
protéines membranaires sont actuellement identifiées
[22].
2.2.4 Cholestérol.
Le cholestérol est un autre constituant des
membranes plasmiques, qui possède une structure très
différente. C'est une molécule très hydrophobe, rigide, et
dotée d'une petite tête hydrophile. Il est plus petit que les
autres lipides formant la membrane. Le cholestérol peut interagir avec
les lipides environnants, soit par des liaisons hydrogénes, soit en
favorisant la condensation des chaînes. La proportion du
cholestérol est de l'ordre de 15% à
50%, selon les cellules et les tissus. Son rôle
est
hapitre 1 : Composition et fonction des membranes
biologiques. 32
de permettre à la membrane de conserver sa
fluidité, quelque soit la température. Toutefois, il faut
souligner que la structure du cholestérol varie fortement, suivant
l'organisme considéré.
Le cholestérol est l'unique stérol des
membranes plasmiques de mammifères, mais, également,
présent chez nombre d'eucaryotes. Ainsi, chez les levures et les
plantes, ce dernier est, respectivement, remplacé par
l'ergostérol et des phytostérols, comme le sitostérol ou
le stigmastérol. Le cholestérol ne présente pas une
distribution homogène au sein des cellules des mammifères, et se
retrouve extrêmement concentré au sein de la membrane plasmique,
alors qu'il est très peu présent dans les membranes enveloppant
les organites à l'intérieur des cellules
[23].
2.2. 5 Mouvements à l'intérieur de la
membrane.
Des études montrèrent que, suivant la
nature de leurs symétrie et environnement, les molécules de
lipides sont en mouvement de rotation, autour de deux directions
perpendiculaires. Les axes de rotation subissent aussi des oscillations. Les
deux mouvements de rotation sont caractérisés par un temps moyen,
nécessaire pour qu'une molécule puissent tourner de 1
radian. Les temps de corrélation rotationnels ôilot et T
ôt sont de l'ordre de
10-9s à
10-lis. Pour les lipides, ces
ordres de grandeur dépendent, naturellement, du mécanisme et du
modèle utilisé, pour la description du mouvement des
molécules sondées [24,
25].
D'un autre côté, les molécules
lipidiques peuvent aussi passer d'une bicouche à l'autre (mouvement
en flip-flop). Néanmoins, c'est un phénomène qui
reste lent, car il est très défavorable de faire passer la
tête polaire des lipides à l'intérieur de la
zone
hapitre 1 : Composition et fonction des membranes
biologiques. 33
hydrophobe constituée par les queues des
lipides. On a un coefficient de diffusion de l'ordre de Df =
10-8s-1
[18]. Il faut noter que ce passage d'un feuillet à l'autre a
bien lieu dans les membranes biologiques, avec un temps de corrélation,
de l'ordre de l'heure ou du jour, selon la nature du phospholipide
[26].
Les molécules lipidiques sont sujet,
également, de mouvements intramoléculaires, tels que les
mouvements d'isomérisation trans/gauche des chaînes
hydrocarbonées et des rotations des liaisons carbone-carbone, avec des
temps de corrélation, respectivement, de l'ordre de
10-10s et
10-11s.
2.2.6 Perméabilité membranaire.
Notons que la cellule est capable d'accepter de
nombreuses variétés de petites molécules, et de refuser
d'autres. Evidemment, toutes les substances ne traversent pas la membrane
à la même vitesse. D'un autre côté, la cellule,
entant que système thermodynamique ouvert fonctionnant dans des
conditions hors d'équilibre, effectue, en permanence, des
échanges de la matière et du combustible avec le milieu
environnant. En fait, ces échanges permettent à la cellule de
maintenir les concentrations des solutés dans le cytoplasme,
différentes de celles du milieu extracellulaire. Pour préserver
l'équilibre à l'intérieur de la cellule, la membrane
cellulaire joue le rôle de barrière hautement sélective, en
imposant à chacune des substances qui la traversent un bilan positif ou
négatif (Fig. 1.7).
Contrairement aux membranes artificielles, les
membranes biologiques peuvent être traversées par des ions et
molécules. Ces substances hydrophiles évitent le contact avec la
bicouche lipidique, et passent au travers des protéines. Deux types
de

hapitre 1 : Composition et fonction des membranes
biologiques. 34
FIG. 2-6 -- (a) simple et (b) Diffusion
facilitée à l'aide d'une protéine porteuse. La
barriére de potentiel G(b) que doit passer le soluté par
diffusion facilitée à travers la membrane est abaissée par
rapport à la diffusion simple G(a).
protéines transmembranaires spécifiques
sont utilisées par la cellule : protéines porteuses et
canaux protéiques. Les premières subissent un changement
de conformation pour faire passer les solutés spécifiques d'un
côté à l'autre de la membrane. Les canaux protéiques
qui se présentent comme des pores étroits traversant la membrane,
sont remplis d'eau. Chaque protéine assure le transport d'une classe
particulière de molécules ou d'ions. La
perméabilité sélective de la membrane dépend donc
des propriétés chimiques de la bicouche et des protéines.
A côté de la perméabilité sélective, propre
à la membrane, deux facteurs physico-chimiques essentiels
déterminent l'am-
hapitre 1 : Composition et fonction des membranes
biologiques. 35
plitude de transport, qui est due à un gradient
de concentration, ou à une différence de potentiels
électriques des deux côtés de la membrane.
Les transports biologiques peuvent être
classés en deux catégories, distincts, selon que le flux de
matière est dirigé dans le sens du gradient de potentiel
électrochimque de l'espèce déplacée ou dans le sens
opposé. Le premier cas correspond à un transport passif,
et le second à un transport actif au travers des
protéines porteuses. L'on distingue deux types de transports actifs :
primaire ou secondaire. Ce dernier est une diffusion d'un
soluté (généralement H+ ou
Na+) dans le sens de son gradient de concentration. Aussi, il
peut entraîner le mouvement d'un autre soluté dans le sens
opposé à son gradient. Dans ce cas, l'énergie
nécessaire au mouvement contre-gradient a pour origine un gradient de
concentration du soluté co-transporté. A titre d'exemple, les
cellules épithéliales contiennent des transporteurs d'oses ou
d'acides aminés, qui sont commandés par le gradient de
Na+. Le transport contre-gradient est dfl à une
réaction métabolique, lumino-chimique ou autres
[27].
Un autre type de transport est le transport de
macromolécules. C'est l'endocytose. D'abord, la
macromolécule contacte la membrane, en formant une pochette
(invagination), puis un pincement, suivi d'un détachement d'une
vésicule. Ensuite, cette vésicule relâche la
macromolécule à l'intérieur. L'on parle, aussi, de
l'exodocytose, qui consiste à un transport de macromolécules de
l'intérieur vers l'extérieur.
hapitre 1 : Composition et fonction des membranes
biologiques. 36
2.3 Membranes artificielles.
2.3.1 Définition.
Les membranes fluides artificielles sont des
enveloppes inertes, à structures fixes, douées de fonctions
dynamiques, et en interaction directe avec le milieu ambiant. Toutefois, ces
objets restent encore d'une grande complexité, en raison de leur
cytos-quelette qui leur confère des propriétés
viscoélastiques et du nombre important de leur constituants. Ils
choisirent alors d'enlever tout ce qui dépasse la membrane
(gly-cocalix), puis, tout ce qui n'en constitue pas l'élément
dominant (enzymes, protéines membranaires...).
2.3.2 Liposomes.
Les liposomes sont des vésicules
sphériques, dont le diamètre est de quelques milliers de
manomètres. Elles ont été synthétisées,
volontairement, par Bangham, en 1968. Ces vésicules
sont composées d'une ou plusieurs bicouches lipidiques permettant de
séparer un milieu intravésiculaire d'un milieu extérieur.
Au sein de ces bicouches, tout comme pour les membranes biologiques, les
mouvements des phospholipides sont observés. Les liposomes sont faciles
à pré parer. L'hydratation d'un film phospholipidique permet
d'obtenir des liposomes multilamellaires. Pour obtenir ces liposomes, des
étapes supplémentaires sont nécessaires.
Les liposomes sont utilisés dans l'industrie,
comme vecteurs de substances en cosmétologie (crèmes hydratantes,
antioxydants...), ou en pharmacologie, en tant que vecteurs de transport de
médicaments vers l'organisme cible [28]. Aussi, ils
sont
hapitre 1 : Composition et fonction des membranes
biologiques. 37
parfois employés comme vecteurs de
thérapie génique, ou encore comme supports de
vaccins.
Tous les liposomes submicroniques SUV (Liposome
Unilamellaire de petite taille : 30 -
50nm, de diamètre) et LUV (Liposome Unilamellaire
de grande taille : 50 - 500nm, de
diamètre) ont été intensivement étudiés.
Mais de par leurs dimensions, ils possèdent une courbure plus
élevée que les membranes plasmiques, et de ce fait, ils
constituent des modèles assez éloignés de la cellule. Ils
s'apparentent d'avantage à certains organites comme les vésicules
de sécrétion, les liposomes ou les endosomes. La
préparation de populations unimodales de vésicules unilamellaires
nécessite, pour être reproductible, l'utilisation des
méthodes hautement invasives telles que la so-nication
[29], l'ulrafiltration [30] ou
l'évaporation de solvants organiques [31]. De plus, le
résultat de ces préparations est souvent instable dans le sens
où les objets obtenus changent aisément de forme et de taille.
Toutefois, il n'est pas encore clair que l'état vésiculaire soit
un état d'équilibre ou seulement un état
intermédiaire par lequel passe le mélange lipide-eau avant
d'atteindre sa configuration d'équilibre final [32,
33].
Les vésicules unilamellaires de taille proche
de la cellule GUV (Giant Unilamellar Vesicles -Liposome unilamellaire
géant : 1-200pm, de diamètre)
ont, ensuite, attiré l'attention, car elles constituent un
système idéal pour l'observation directe, par les techniques de
microscope optique (contraste de phase, fluorescence, RICM (Fig.
1.9), des propriétés physiques et
chimiques des membranes, et pour leurs applications techniques
[34]. Plusieurs travaux ont été consacrés
à l'inventaire, par exemple, des formes d'équilibre et aux
propriétés mécaniques des GUVs
[35].
L'étude des formes d'équilibre d'une
vésicule sans contrainte extérieure,
nécessité

hapitre 1 : Composition et fonction des membranes
biologiques. 38
largement utilisées dans d'autres applications,
principalement pour leur capacité à
FIG. 2-7 -- (a) Vésicule géante (b) Une
membrane constitué d'un double feuillet
des efforts considérables théoriques,
numériques et expérimentaux [36]. L'observation
expérimentale a permis de confirmer la validité de certains
travaux théoriques. En retour, ces modèles théoriques
servent à interpréter les manipulations menées sur des
vésicules, afin de mesurer des paramètres physiques de la
membrane elle-même, à savoir la constante de courbure, la tension,
ou le couplage avec un réseau réticulé ou avec des
protéines adsorbées.
2.3.3 Applications des liposomes.
En plus d'être un système mimétique
de la membrane cellulaire, les vésicules sont
Chapitre 1 : Composition et fonction des membranes
biologiques. 39
séparer deux milieux aqueux l'un de
l'autre.
Intérêt thérapeutique.
Les vésicules utilisées à des
fins thérapeutiques sont appelées liposomes. Elles peuvent
être utilisées pour transporter dans l'organisme des
médicaments hydro-p hiles ou non : un médicament soluble dans
l'eau sera dissout dans le milieu aqueux à l'intérieur de la
vésicule alors qu'un médicament hydrophobe sera dissout dans la
bicouche [37]. Par contre, la capacité à exposer
des protéines à la surface permet d'utiliser les liposomes comme
vaccins, ayant l'avantage de ne pas contenir de matériel
génétique tout en présentant la molécule
antigénique [38].
Intérêt cosmétologique.
Les vésicules utilisées dans la
cosmétique sont aussi appelées liposomes. Tout comme celles
utilisées en pharmacie, elles servent à appliquer localement une
substance, sur la peau dans le cas présent.
Intérêt biochimiques et
biophysiques.
Les vésicules, utilisées comme
systèmes modèles de la membrane cellulaire, ont largement
contribué à en comprendre les propriétés
mécaniques. Mais leur intérêt biomimétique ne
s'arrête pas là : elles permettent aussi de mimer des processus
cellulaires impliquant la membrane [39].
De même, il est possible de reconstituer dans
une vésicule un aster de microtu-bules, c'est à dire une
structure de microtubules en étoile [40]. Les
microtubules sont des filaments de tubulines polymérisées et sont
utilisés par la cellule comme compo-
hapitre 1 : Composition et fonction des membranes
biologiques. 40
sants de son cytosquelette ; lors de la
réplication de la cellule, il apparaît un aster de microtubules
qui va permettre de tirer de part et d'autre le matériel
génétique. Comprendre comment ces structures grandissent et
interagissent avec la membrane est une étape dans la
compréhension du processus de division.
Intérêt en micro-manipulation.
Les vésicules forment des réservoirs de
petits volumes, isolés du milieu environnant. Aussi, il est possible de
les utiliser comme des petits réacteurs chimiques, en induisant des
réactions à l'intérieur de l'espace confiné d'une
vésicule [41 - 43]. La
possibilité de connecter les vésicules par des tubes de membrane
permet aussi de former des circuits micro-fluidiques [44]. Les
contenus peuvent être transférés d'une vésicule
à une autre simplement en appuyant sur la vésicule à
remplir : la présence d'un obstacle augmente la tension de surface, qui
provoque un flux de lipides et un écoulement depuis la vésicule
voisine.
2.4 Conclusions.
Ce chapitre a été destiné
à une revue de la description des membranes biologiques. Plus
exactement, nous avons explicité leurs compositions, ainsi que le
rôle de chacune des composantes de la membrane. Aussi, nous nous
étions tardés sur tous les modes de transport au travers une
membrane cellulaire. Egalement, l'accent a porté sur les
vésicules et leur grande importance surtout en biologie, en
pharmacologie ,en cosmétologie ,en biochimie, et en biophysique
.
Enfin, cette description est d'une grande
utilité d'un côté pour avoir une idée
hapitre 1 : Composition et fonction des membranes
biologiques. 41
général sur les membranes biologiques et
leurs rôle dans la régulation de différence de potentiel
entre le milieux intérieur et le milieux extérieur de la cellule
et d'un autre côté pour comprendre la physique des membranes
esquissée dans les chapitres qui suivront.
42
Bibliographie
[1] R. Hooke, Royal Society of London 8, 167177
(1665).
[2] T. Schwann, Encyclop3dia Britannica,
11ème édition, Cambridge University
Press, 1835.
[3] E. Overton, Vierteljahrschrift der
Naturforschende Gesellschaft 44, 88 (1899).
[4] I. Langmuir, Journal of the American Chemical
Society 39, 18481906 (1917).
[5] E. Gorter, F. Grendel, J. Experimental Medicine
41, 439 (1925).
[6] J.H. Danielli, H. Davson, J. of Cell and
Comparative Physiology 5, 495 (1935).
[7] J.D. Robertson, Biochim 16, 3 (1959).
J.D. Sleigh et al., An International Journal of Obstetrics
& Gynaecology 71,
7481 (1964).
[8] L. Silva, A. Coutinho, A. Fedorov, M. Prieto, J.
Biophys. 90, 3625 (2006).
[9] L.D. Frye, M. Edidin, Science 7, 319
(1970).
[10] S.J. Singer, G.L. Nicholson, Science 17 5, 731
(1972).
[11] N. Unwin, R. Henderson, Scientific American 2
50, 78 (1984).
[12] M. Forstner, D. Martin, M. Naver, J. Kas,
Langmuir 19, 4876 (2003).
[13] G. Vereb et al., Proc. Natl. Acad. Sci.
USA 100, 8053 (2003).
[15]
hapitre 1 : Composition et fonction des membranes
biologiques. 43
A. Kusumi, Y. Sako, M. Yamamoto, J. Biophys. 6 5, 2021
(1993).
[16] K. Ritchie et al., J. Biophys. 88, 2266
(2005).
[17] V. Kiessling, J.M. Crane, L.K. Tamm, J. Biophys.
91, 3313 (2006).
[18] B. Alberts et al., Molecular
Biology of the Cell, 4ème edition, Inc. Garland
Publishing, New York, 2002.
[19] Voir, par exemple, T. Bickel, Thèse
de Doctorat, Université Louis Pasteur, Stras-
bourg I, 2001.
J. Israelachvili, Intermolecular and Surface Force,
Academic Press, San Diego,
4ème édition, 1994.
[20] D. Jones, FEBS Lett. 423, 281(1998).
[21] A. Bendouch, Thèse de Doctorat,
Université Hassan II Mohamadia, Faculté des
Sciences Ben M'Sik Casablanca, 2008.
G. Staneva, Thèse de Doctorat, Université de
Paris VI,Pierre et Marie Curie,
2004.
[22] A. Jutila, P. Kinnunen, J. Phys. B 101, 7635
(1997).
[23] P. Devaux, Biochemistry 30, 1163
(1991).
[24] T. Kirchhausen, Nat. Rev. Mol. Cell. Biol. 1,
187 (2000).
[25] L. Pelkamans, A. Helenius, Il Nuovo Cimento D 3,
174 (2002).
[26] B. Kloesgen,W. Helfrich, J. Eur. Biophys. 22,
329 (1993).
[27] R. MacDonald et al., Biochim. Biophys.
Acta 1061, 297 (1991).
[28] S. Kim, G. Martin, Biochim. Biophys. Acta 646, 1
(1981).
[29] W. Harbich, W. Helfrich, Chem. Phys. Lipids 55,
191 (1990).
[32]
hapitre 1 : Composition et fonction des membranes
biologiques. 44
P. Luisi, P. Walde, éditeurs, Giant
Vesicles, dans : Perspectives in Supramole-
cular Chemistry, Volume 6, John Wiley &
Sons, Chichister, 2000.
[33] W. Helfrich, B. Kltisgen, J. Thimmel, Pramana,
J. Phys. (Paris) 53, 13 (1999).
D. Baeriswyl, M. Droz, A. Malaspinas, P. Martinoli,
éditeurs, Tenth Gwatt
Worshop : Physics in Matter, Volume
284, Switzerland. Springer-Verlay, 1986.
[34] U. Seifert, Eur. Phys. J. B 8, 405
(1997).
[35] B. Martin et al., Curr. Pharm. Design
11, 375 (2005).
[36] A. Lorin, et al., Biotechnol. Agron.
Soc. Environ. 8, 163176 (2004).
[37] A. Roux et al., PNAS 99, 5399
(2002).
[38] D. Chiu, et al., Science 283, 1892
(1999).
[39] M.R. Helfrichet al., J. Am. Chem. Soc.
124, 13374 (2002).
[40] S.Kulin, el al., Langmuir 19, 8206
(2003).
[41] M. Karlsson et al., PNAS 99, 11573
(2002).
[42] R. Karlsson, A. Karlsson, O. Orwar, J. Phys.
Chem. B 107, 11201 (2003).
[43] M.B. Forstner, D.S. Martin, A.M. Navar, J.A.
Kas, Langmuir 19, 4876 (2003).
[44] T. N. Gobley, J. Pharm. Chim. 11, 409412
(1847).
Chapitre 3
Mécanique Statistique des
biomembranes.
Dans ce chapitre, à caractère
bibliographique, nous donnons un aperçu sur les
propriétés statistiques des membranes lipidiques, à
l'équilibre thermodynamique. Le sujet est très riche, mais nous
nous contentons de présenter ici une revue succinte des
propriétés thermiques de ces interfaces molles.
Nous rappelons, également, les outils de la
Physique Statistique permettant la description des membranes fluides, entant
que systèmes incorporant un nombre considérable de
molécules et macromolécules.
3.1 Introduction.
Les membranes cellualires jouent un rôle crucial
pour la vie, car elles protègent la cellule de son environnement, et les
organites à l'intérieur de cette cellule [1]. En
fait, ces membranes constituent une barrière étanche protegeant
les cellules, et à

hapitre 2 :Mécanique Statistique des
biomembranes. 46
FIG. 3-1 -- Molécule amphiphile de
phospholipide
travers lesquelles s'effectuent les échanges
d'ions et du matériel.
Les chercheurs s'accordent à ce que les
membranes biologiques se présentent essentiellement comme une bicouche,
formée de molécules amphiphiles. La majorité de ces
molécules sont des phospholipides, qui possèdent une tête
polaire hydrophile (qui aime l'eau), liée chimiquement à deux
chaînes d'acides gras hydrophobes (qui n'aiment l'eau), une
saturée et l'autre insaturée (Fig.
2.1).Aussi, les membranes biologiques contiennent du
cholestérol, des protéienes et des glucides. Chacune de ces
composantes a un rôle spécifique à jouer. Par exemple, le
cholestérol permet la rigidification et la fluidité de la
membrane. Les protéines assurent le transport d'ions, de
molécules et de macromolécules. L'on distingue des transports
passifs et actifs, l'endocytose et l'exoendocytose. Les glucides ressembles aux
phospholipides, mais ne contiennent pas de goupements phosphates, plutôt
des résidus sucrés.
En milieux aqueux, les lipides s'organisent, le plus
souvent, en bicouche. Celle-ci contient une partie apolaire au centre
où l'eau n'a pas accès, et une partie
polaire

hapitre 2 :Mécanique Statistique des
biomembranes. 47
FIG. 3-2 -- Représentation schématique
de la membrane cellulaire montrant les différentes molécules
constituant la membrane. La membrane est constituée d'un double feuillet
phos-pholipidique associé à des protéines .
en contatct avec le milieu aqueux de part et d'autre
de la bicouche. La structure se referme sur elle-même, et l'on obtient,
ainsi, une vésicule fermée, qui sépare un compartiment
interne aqueux du milieu aqueux externe (Fig.
2.2). C'est le modèle de fluide
mosaïque, largement reconnu par la communauté
scientifique.
Ce chapitre s'organise comme suit. En Sec. I,
nous esquissons les compositions et fonctions des membranes biologiques. Nous
décrivons, en Sec. II, leurs propriétés
statistiques. Certaines remarques concluantes sont retracées dans la
dernière section.
hapitre 2 :Mécanique Statistique des
biomembranes. 48
3.2 Compositions et fonctions des biomembranes.
La vie dans toute sa diversité n'est devenue
possible qu'après l'apparition des membranes. Ces entités
séparent et protègent les systèmes vivants primitifs de
leur environnement, tout en autorisant des échanges
régulés de matière avec ce même environnement
[2] (Fig. 2.2).
Pour comprendre les propriétés des
membranes biologiques, il est possible d'utiliser un système
modèle formé uniquement de lipides. Ces derniers ont la
capacité de s'assembler spontanément en une double couche de
molécules, comme dans la membrane cellulaire. Plongée dans l'eau,
la bicouche se referme sur elle-même pour former une vésicule. En
fait, cette organisation spontanée est due au caractère
am-phiphile et à la forme cylindrique des lipides. Aussi, les
vésicules présentent des similitudes avec les bulles de savon et
avec les cristaux liquides smectiques.
3.2.1 Les vésicules.
Les vésicules ont été
découvertes volontairement par Bangham, en 1968 [3].
Elles se présentent dans la nature comme des capsules biologiques
nécessaires au transport de molécules entre les différents
milieux membranaires (cellules, mitochondries, appareil de Golgi, ....).
Actuellement, les vésicules sont utilisées dans diverses
applications, comme éléments actifs en industries
pharmaceutique et en cosmétiques [4], ou
comme modèle très simplifié des cellules vivantes au
laboratoire. Généralement, les vésicules sont des
coquilles fluctuantes en suspension dans l'eau ; leur taille peut varier de
quelques dizaines de nanomètres à quelques centaines de
micromètres. Dans la nature, les vésicules sont
constituées de molécules biologiques
hapitre 2 :Mécanique Statistique des
biomembranes. 49

FIG. 3-3 -- Schéma de représentation des
trois modes élastiques de déformation des membranes
(phospholipides, protéines, cholestérol,
...), mais pour les physiciens, elles peuvent aussi être formées
à partir de tensio-actifs ou de molécules polymérisables
[5] ; ce qui modifie considérablement leurs
propriétés mécaniques (Fig.
2.3). Objets bidimensionnels sans tension de surface,
les propriétés physiques des vésicules sont fixées
par la connaissance de trois grandeurs : le module de cisaillement,
d'élasticité et de courbure.
Si la formation de bicouches de lipides et de
tensio-actifs est relativement bien comprise [6,
7], la formation des vésicules et les conditions de
leur stabilité restent encore mystérieuses. Dans la
majorité des cas, en particulier celui des vésicules de lipides,
l'état thermodynamique des bicouches est la structure smectique des
lamelles empilées.
3.2.2 Les lipides.
Les lipides jouent un rôle important dans la
cellule, et constituent les composantes majeures des membranes. Ils renferment
également une importante quantité
hapitre 2 :Mécanique Statistique des
biomembranes. 50
d'énergie stockée, et ils sont
directement impliqués dans la signalisation cellulaire
[2], à la fois comme hormones stéroïdes
(oestrogènes et testostérone) et comme messagers potentiels
transportant les signaux des récepteurs membranaires aux cibles
situées à l'intérieur de la cellule.
Les acides gras.
Les acides gras sont des acides carboxyliques
possédant une chaîne aliphatique hydrophobe saturée ou
insaturée. Il s'agit d'une longue chaîne hydrocarbonée
comportant le plus souvent 16 à 18
atomes de carbones, avec un groupe carboxyle (COO-) à une
extrémité.
Il faut noter que la nature hydrophobe de ces
chaînes d'acides gras est responsable de la plupart des comportements des
lipides complexes, et particulièrement de la formation des membranes
biologiques.
Les phospholipides.
Les phospholipides sont les principaux constituants
des membranes cellulaires. Ces lipides possédant un groupe phosphate,
sont des molécules amphiphiles. Leur tête polaire
hydrophile détermine le type de phospholipide. En fait, plusieurs
variétés peuvent coexister, et se distinguent uniquement par la
longueur de leur queue, c'est-à-dire les acides gras les
constituant.
Les phospholipides se différencient les uns des
autres par la nature de leur tête polaire, c'est-à-dire l'alcool
qui estérifie une seconde fois l'acide phosphorique, et également
par leurs acides gras qui déterminent la longueur de l'encombrement
stérique des molécules. Par ailleurs, d'autres molécules,
comme le cholestérol, sont
hapitre 2 :Mécanique Statistique des
biomembranes. 51
susceptibles de s'ajouter aux phospholipides, pour
modifier sensiblement certaines propriétés des membranes comme
par exemple la fluidité, ou la manière dont les phospholipides de
même type s'associent préférentiellement pour former des
micro-domaines ou rafts.
La portion glycérole et phosphate de la
molécule est dite hydrophile, alors que les acides gras sont
hydrophobes. Dons, la partie hydrophile est soluble dans l'eau, alors que la
partie hydrophobe ne l'est pas (elle est soluble dans les lipides) (Fig.
2.1).
3.2.3 Les liposomes.
Nous avons noté, auparavant, que les liposomes
sont des vésicules sphériques, dont le diamètre varie de
quelques dizaines à quelques milliers de nanomètres. Ces
vésicules sont composées d'une ou de plusieurs bicouches
lipidiques permettant de séparer un milieu intravésiculaire d'un
milieu extérieur. Au sein de ces bicouches, tout comme dans les
membranes biologiques, les mouvements des phospholipides sont observés.
Les liposomes sont faciles à préparer [8]. En
effet, l'hydratation de film phospholipidique permet d'obtenir des liposomes
multilamellaires. Les liposomes possèdent un grand potentiel
d'applications, en particulier, ils sont utilisés dans l'industrie,
comme vecteurs de substances cosmétologiques ou de thérapie
génique, pour délivrer des médicaments, ou encore comme
supports de vaccins. Les liposomes constituent surtout un bon modèle
membranaire, et sont largement employés, pour mieux comprendre les
mécanismes intervenant au niveau de la membrane, comme la
perméabilité, la fluidité, l'ancrage de protéines
ou encore la fusion de deux mem-

hapitre 2 :Mécanique Statistique des
biomembranes. 52
FIG. 3-4 -- Evolution d'une vésicule de SOPC
lorsque la température augmente
branes.
Notons que les phospholipides se réorganisent
dans une configuration la plus thermodynamiquement stable (énergie
minimale) (Fig. 2.5).
3.3 Propriétés statistiques des
biomembranes.
Dans ce paragraphe, nous rappelons l'essentiel de
l'étude des propriétés mécaniques de la bicouche
lipidique ainsi que le formalisme associé. L'outil pour cela est une
approche élaborée par Helfrich, basée sur l'énergie
de courbure.
3.3.1 Description thermodynamique.
Parmi les paramètres pertinents dans la
description d'une membrane fluide, nous pouvons citer son aire totale,AT, et
son aire projetée, AP. Ces aires sont deux variables thermodynamiques
indépendantes [6, 7]. En effet, l'aire
totale ne peut être modifiée que par échange de
molécules avec un réservoir ou par effet de dilatation (due aux
fluctuations thermiques de la membrane). Des expériences d'aspiration
par
hapitre 2 :Mécanique Statistique des
biomembranes. 53
micropipette ont montré que les
vésicules sont très résistantes aux déformations de
compression et de dilatation [9] : les membranes sont peu
extensibles et peuvent donc être considérée comme
incompressibles. La variable conjuguée à l'aire totale AT
est alors directement proportionnelle au potentiel chimique des
tensio-actifs.. En revanche, l'aire projetée AP dépend
des contraintes appliquées : cisaillement, adhésion, ..., le
paramètre conjugué étant une tension de surface. Une
propriété spéciale de ces systèmes
auto-assemblés est que, en l'absence de contraintes, l'aire
projetée d'une membrane fluctuante s'adapte, de manière à
minimiser l'énergie, et donc s'ajuste pour annuler la tension de
surface. Notons que ce point n'est pas forcément vrai pour une surface
fermée, comme par exemple une vésicule, où les
fluctuations thermiques sont responsables de la tension
[10,11].
3.3.2 Théorie de Canham-Helfrich.
La description théorique des membranes a
réellement débuté avec les travaux de Canham puis ceux de
Helfrich [12, 13]. En s'inspirant des
propriétés des films minces, les auteurs proposèrent une
approche phénoménologique basée sur l'énergie
élastique de courbure suivante
H = 2 f (C1 +
C2 - Co)2 dS
+ êG J
C1C2dS +
ã f dS , (2.1)
où C1 = R-1
1 et C2 = R-1
2 sont les deux courbures principales,
(C1 + C2) /2
la courbure moyenne (Fig.
2.6),
et C1C2 la courbure
totale (de Gauss) (Fig. 2.7).
L'énergie (2.1) peut être vue
comme un développement en puissance des invariants du tenseur de
courbure. Le der-
hapitre 2 :Mécanique Statistique des
biomembranes. 54
fCiC2dS
= 4ð (1 - g) ,
(2.2)
FIG. 3-5 -- Une forme de selle de cheval »dans le
cas ci=-1/ Ri<0, c2
=1/R2>0.
nier terme de cette équation est un terme de
tension de surface, et Co est la courbure spontanée
de la membrane, qui peut être associée à une
asymétrie de composition de la bicouche. Le paramètre K est la
constante de rigidité de courbure. Cette dernière a
été mesurée expérimentalement par des
méthodes d'aspiration par micropipette, ou par l'étude de
l'amplitude des fluctuations thermiques de la membrane
[14,15]. Les valeurs obtenues sont de
10 à 50kBT, pour les
membranes phospholipidiques. Quant au paramètre KG, il
représente la constante élastique de courbure
gaussienne, et est associé à la topologie de la membrane. Le
théorème de Gauss-Bonnet [16] permet
d'évaluer l'intégrale de la courbure gaussienne pour une surface
fermée sans bords. Ce théorème stipule que cette
intégrale dépend uniquement de la topologie de la surface, et
s'exprime sous la forme suivante

hapitre 2 :Mécanique Statistique des
biomembranes. 55
hapitre 2 :Mécanique Statistique des
biomembranes. 56
FIG. 3-6 -- Une forme ellipsoïydale d'une surface
dans le cas : c1 =1/R1>0 ,c2
=1/R2< 0
.
où la constante g est le genre
topologique, et correspond au nombre de poignées de la
surface (g = 0, pour la sphère, g
= 1, pour le tore). Pour un système
constitué de plusieurs surfaces fermées, on peut écrire la
contribution de la courbure gaussienne à l'énergie de courbure
comme
JêG
C1C2dS =
4ðêG (N -
Nh) . (2.3)
Ici, N est le nombre de composants
déconnectées et Nh est le nombre total de
poignées.
En fait, cette contribution à l'énergie
de courbure agit comme un potentiel chimique qui gouverne la topologie du
système. En particulier, il est important de connaître le signe de
R. C'est lui qui contrôle l'apparition de
poignées sur la surface, c'est-à-dire la formation de point
selle de courbure moyenne quasi-nulle et de
courbure gaussienne négative.
Revenons à l'énergie de courbure de
Cahnam-Helfrich et notons qu'il est possible, à partir de cette
énergie, d'étudier la stabilité d'une phase lamellaire..
Nous avons vu que le terme de courbure gaussienne est celui qui contrôle
la topologie du système, alors que les fluctuations de forme de la
surface sont gouvernées par la courbure moyenne. On peut imaginer deux
mécanismes de déstabilisation de la membrane : (i) par la
création d'un passage qui coûte une énergie
-47ri (en première approximation, le
passage est une surface minimale de courbure moyenne nulle), et l'on gagne donc
de l'énergie à créer des passages, si k
> 0, (ii) ou par formation d'une vésicule
(l'énergie de courbure d'une vésicule sphérique
étant 47r (2k + R),
et l'on gagne donc de l'énergie à créer des
vésicules, si k < -2k .
3.3.3 Spectre de fluctuations thermiques.
Sous l'effet de l'agitation thermique, les
molécules du milieu aqueux diffusent sur la membrane, et donc celle-ci
fluctue autour de sa position d'équilibre. De nombreuses études
[17] ont été consacrées à la
quantification de l'effet de ces fluctuations sur la forme des
vésicules. Nous nous limiterons ici au cas de membranes presque-planes.
Dans ces conditions, on peut décrire la forme de la surface dans la
représentation de Monge, où la position d'un point de la membrane
est repérée par sa hauteur h (r) =
h (x, y), par rapport à un
plan de référence parallèle à la position moyenne
de la membrane (Fig. 2.7).
L'énergie de la membrane peut alors être
linéarisée et s'exprime comme suit
hapitre 2 :Mécanique Statistique des
biomembranes. 57
kBT
\|uq|2%
U?+
ãq2 +
êq4 . (2.7)
FIG. 3-7 -- Représentation de Monge.
f [ê
]
H [h] =
d2~r 2
(?h)2 + ã
2 (?h)2 + U
(h) , (2.5)
avec le potentiel extérieur U
(h), qui décrit les
interactions entre la membrane et un substrat solide ou une autre membrane.
Ici, ã est le coefficient de tension interfaciale.
Si, maintenant, on linéarise le potentiel U
autour de l'équilibre, l'énergie devient quadratique dans la
déformation h (r).
On peut donc décomposer la déformation de la membrane en mode de
Fourier d'amplitude
ti
hq = f
(27)2 h
(-r) eig.T .
(2.6)
Par ailleurs, le théorème
d'équipartition de l'énergie permet d'écrire l'amplitude
carrée moyenne de chaque mode, et l'on a
hapitre 2 :Mécanique Statistique des
biomembranes. 58
3.3.4 Interaction d'Helfrich.
Les fluctuations de forme d'une membrane lorsqu'elle
se trouve au voisinage d'un substrat solide ou d'une autre membrane, conduisent
à une interaction d'origine entropique dépendant de la
rigidité des membranes et de la température. Cette interaction a
été décrite, pour la première fois, par Helfichen
1978. Elle permet, en particulier, de comprendre la
remarquable stabilité des phases lamellaires des tensio-actifs
neutres.
Considérons une membrane de module de courbure
ê, et négligeons, dans un premier temps, la tension de surface.
Les fluctuations de cette membrane sont confinées entre deux murs
distants d'une distance finie î? (Fig.
2.9a). L'on suppose qu'il n'existe que des
interactions stériques à très courte portée entre
les murs et la membrane. L'amplitude des fluctuations de la membrane est donc
limitée par la présence des murs. On peut raisonnablement
supposer qu'un choc de la membrane sur un mur décorrélé
complètement les fluctuations. On voit alors la membrane comme une
mosaïque de patch indépendants de taille
î2II et d'amplitude de fluctuation
moyenne
î2?.
Ici, îII représente la longueur de
corrélation dans le plan. On peut maintenant relier ces deux grandeurs
en utilisant l'expression du spectre de fluctuations, définie par la
relation (2.8), avec U?=
0 et ã = 0. Alors, l'on a
kBT
0uq|2)
(2.8)
êq, ,
f d2~q
~|uq|2) ~
kBT
î2 ? ~ ê
î2 II . (2.9)

hapitre 2 :Mécanique Statistique des
biomembranes. 59
FIG. 3-8 - Une membrane liquide fluctuante , qui est
confinée entre deux plaques parallèles
.
Il reste à calculer la variation
d'énergie libre, ?FS, par unité de surface due
au confinement de la membrane. La courbure de la membrane liée à
la présence des murs est simplement donnée par
R-1 ~
îL/î2II. On en déduit la
contribution enthalpique
2
kBT
?Ec ~ ê .
(2.10)
î
2 II
Les bouts de la membrane, de taille
î2II, étant indépendants, le confinement
réduit leur entropie de kB et l'on obtient
kBT
?Sc ~ .
(2.11)
î
2 II
A l'aide de ces considérations, l'on
déduit que la variation de l'énergie libre due au confinement
est
hapitre 2 :Mécanique Statistique des
biomembranes. 60
kBT
?THelfrich ~
?Ec - T?S
~
ê
1
(2.12)
.
î~ ?
Il s'agit d'une interaction répulsive,
qui est proportionnelle à l'énergie d'agitation thermique
kBT, et inversement proportionnelle au module de courbure de la
membrane. Traditionnellement, l'on introduit une constante, cH, et
l'on écrit l'énergie de répulsion de Helfrich comme
suit
|
kBT
VHelrich `v cH
ê
|
1 .
(2.13)
î~ ?
|
Nous rappelons que de nombreuses études
théoriques et numériques ont suivis les travaux pionniers de
Helrich. Ainsi, Seifert [19] a proposé une
généralisation de l'interaction de Helfrich au cas des membranes
sous tension (ã =
0).
Dans le cas asymétrique d'une membrane neutre
qui fluctue près d'un seul substrat (ou d'une seule autre membrane),
l'interaction entropique (répulsion de Helfrich) repousse la membrane
qui peut décoller.
Noter également que les fluctuations thermiques
influent également sur les propriétés élastiques de
la membrane.
3.3. 5 Longueur de persistance.
Nous finissons cette section par un rappel de la
notion importante de longueur de persistance,
îp, qui est liée au phénomène de
froissement de la membrane. Cette longueur a été introduite, pour
la première fois, par de Gennes et Taupin [20,
21]. Cette idée a donné lieu, par la suite,
à une quantité impressionnante de travaux sur les surfaces
fluctuantes. Cette longueur de persistance peut être comprise en
notant
hapitre 2 :Mécanique Statistique des
biomembranes. 61
qu'une surface, si elle n'est soumise à aucune
tension latérale (u = 0), reste rigide
jusqu'à une certaine longueur îp. C'est la
longueur au-delà de laquelle la membrane perd sont ordre
orientationnel, et plus froissée à des échelles
supérieures à cette même longueur. Afin de
déterminer une telle longueur, il suffit de calculer la fonction de
corrélation du vecteur normal n
(-?n (0)
.-?n (-?r
)) ~ exp
{-r/îp} , (2.14)
avec la longueur de persistance
îp =
ao exp
{2ðk/kBT} , (2.15)
où ao
représente la taille typique des lipides. La relation
précédente montre que la longueur de persistance est d'autant
plus importante que la rigidité de courbure est forte. Aussi, cette
même échelle de longueur est sensible à la
température, et qu'elle se déplace vers ces faibles valeurs
à mesure que la température augmente. La formule
(2.14) suggère que pour des
échelles inférieures à îp, la
membrane est plane, et ses orientations sont alors
corrélées. En revanche, au-dessus de
îp, la membrane est plutôt
froissée, et ses orientations sont
décorrélées [21]. Nous
soulignons, de passage, qu'au-dessus de îp, la
description d'une membrane quasi-plane, gouvernée par le Hamiltonien de
Canham-Helfrich, n'a plus de sens.
Revenons à la définition
(2.15) et notons le point important
suivant. C'est que la longueur de persistance îp
dépend du rapport k/kBT, et ceci d'une
manière exponentielle. Une petite variation de k entraîne
donc une grande variation de îp.
hapitre 2 :Mécanique Statistique des
biomembranes. 62
Ainsi, si ê N
10kBT, cette longueur est astronomique, et la
membrane est lisse, à toutes les échelles. Si
ê N kBT, îp N 0,
5 pm, pour la valeur ao
N 10 Angströms, les fluctuations
de courbure sont assez fortes, pour des vésicules géantes ou des
globules rouges. Si ê N 0,
1kBT, îp N
230 Angströms.
Enfin, soulignons que, pour les
micro-émulsions, la longueur îp fixe
l'échelle de taille de la dispersion de l'huile dans l'eau ou
l'inverse.
3.4 Conclusions.
Dans ce chapitre, nous avons passé en revue les
différentes composantes des biomembranes. Les lipides ont la
caractéristique de s'auto-organiser spontanément en une bicouche.
Cette structure, à la base de la membrane cellulaire, a des
propriétés très anisotropes. Les vésicules, des
bicouches refermées sur elles-mêmes, quant à elles, sont
largement utilisées à la fois en biologie, comme systèmes
modèle de la membrane cellulaire, et en physico-chimie, en particulier
pour leur capacité à séparer physiquement un petit volume
d'eau du milieu aqueux environnant.
Les propriétés de la bicouche
homogène sont aujourd'hui bien comprises. Pour progresser dans la
modélisation de la membrane, des vésicules composées de
plusieurs types de lipides ont été développées. De
tels mélanges présentent des séparations de phases,
conduisant à la formation des domaines de compositions
différentes, flottant dans une membrane classique
[1].
Aussi, nous avons présenté les
propriétés élastiques des bicouches lipidiques, en se
basant sur une description phénoménologique de Canham-Helfrich.
Nous avons rappelé, également, comment on en déduit le
spectre de fluctuations, ainsi que la
hapitre 2 :Mécanique Statistique des
biomembranes. 63
répulsion entropique due au confinement de la
membrane. L'accent a été, également, mis sur la notion
importante de longueur de persistance.
64
Bibliographie
[1] J.-M. Allain, Thèse de Doctorat,
Université Paris VII, 2005.
[2] C. Lales, Thèse de Doctorat,
Université Bordeaux I, 2007.
[3] A.D. Bangham, M.M. Standish, J.C. Watkins, J.
Mol. Biol. 13, 238 (1965).
[4] D.D. Lasic, Liposomes : From Physics
to Applications, Elsevier Sciences, 1993.
[5] B.M. Disher et al., Science 284, 1143
(1999).
[6] T. Bickel : Thèse de Doctorat,
Université Strasbourg I, 2001.
[7] J. Israelachvili, dans : Intermoleculat And
Surfaces Forces, pp. 366-394, Academic
Press, San Diego, 1991.
[8] A. Lorin et al., Biotchnol. Agron. Soc.
8, 163 (2004).
[9] E. Evans, D. Needham, J. Phys. Chem. 91, 4219
(1987).
[10] U. Seifert, Z. Phys. B 97, 299
(1997).
[11] J.-B. Fournier, A. Ajdari, L. Peliti, Phys. Rev.
Lett. 86, 4970 (2001).
[12] P. Canham, J. Theor. Bio. 26, 61
(1970).
[13] W. Helfrich, Zeitschrift far Naturfoschung 28,
693 (1970).
[14] F. Brochard, J.-F. Lennon, Journal de Physique
(Paris) 36, 1035 (1975).
[15]
hapitre 2 :Mécanique Statistique des
biomembranes. 65
E. Evans, W. Rawicz, Phys. Rev. Lett. 64, 2094
(1990).
[16] R. Willmore, Total Curvature In Riemannian
Geometry, NY-Brisbane-Chichester-Toronto, 1982.
[17] U. Seifert, Advances In Physics 46, 13
(1997).
[18] W. Helfrich, Zeitschrift für Narurforshung 33,
305 (1978).
[19] U. Seifert, Phys. Rev. Lett. 74, 5060
(1995).
[20] L. Peliti, S. Leibler, Phys. Rev. Lett. 54, 1690
(1985).
[21] P.-G. de Gennes, C. Taupin, J. Phys. Chem. 86, 2294
(1982).
[22] D. Nelson, T. Piran, S. Weinberg, Statistical
Mechanics of Membranes And Surfaces, World Scientific, 1988.
Chapitre 4
Effet de Casimir dans les
biomembranes confinées.
Dans ce chapitre, qui consiste notre
première contribution originale, nous réexaminons le
calcul de la force de Casimir entre deux plaques interactives parallèles
délimitant un liquide comptant une biomembrane immergée. Nous
désignerons par D, la distance qui sépare les deux
plaques, et l'on suppose que cette dernière est beaucoup plus petite que
la rugosité en volume, afin d'assurer le confinement de cette membrane.
Cette force répulsive provient des ondulations thermiques de la
membrane. Nous avons traité aussi bien l'aspect statique que l'aspect
dynamique.
Pour plus de détails, le lecteur peut
être renvoyé à la Réf.
[1].
4.1 Introduction.
parent la cellule de son environnement, et agissent
alors comme une barrière sélective
66
Les membranes cellulaires ont une importance cruciale
dans la vie, car elles sé-
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 67
de la matière. Les détails descriptifs
de l'organisation structurale et des fonctions de base des biomembranes peuvent
être trouvés dans Réfs. [2 -
8].
Les membranes cellulaires sont formées par une
bicouche de phospholipide combinée avec une variété de
protéines et de cholestérol. Particulièrement, ces
derniers assure la fluidité des bicouches. Un phospholipide est une
molécule amphiphile qui possède une tête polaire hydrophile
(qui aime le milieu aqueux) attachée à deux chaînes
carboniques hydrophobes (qui n'aiment pas le milieu aqueux).
Les phospholipides se déplacent librement dans
la bicouche membranaire, dont l'épaisseur est de l'ordre de 50
Angströms. En fait, ces deux propriétés permettent
de considérer la membrane comme une membrane fluide à deux
dimensions.
La membrane fluide, auto-s'assemblée de
solutions du surfactant, peut avoir une variété de formes et de
topologies [9], qui ont été expliquées en
terme de l'énergie de courbure [10,
11].
Dans de vraies situations, les biomembranes ne sont
pas confinées dans les liquides à extension infinie, mais elles
sont plutôt confinées par des frontières
géométriques, telles que les globules blancs et rouges ou des
liposomes, comme vecteurs de transport de médicaments dans les vaisseaux
sanguins [11 - 14]. Pour la
simplicité, nous considérons la situation où la
biomembrane est confinée dans un domaine liquide, qui est fini dans une
direction spatiale donnée. Nous désignons par D, la
taille géométrique de ce domaine. Pour un tube, D
étant le diamètre, et pour un domaine liquide
délimité par deux plaques parallèles, cette taille est
simplement la séparation entre les murs. Naturellement, la longueur
D doit être comparée à la rugosité en
volume, Li, qui est la taille typique des bosses
provoquées par les fluctuations thermiques de la membrane. Ces
fluctuations dépendent naturellement de la nature
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 68
des molécules de lipide formant la bicouche. La
biomembrane est confinée seulement quand D est beaucoup plus
petite que la rugosité en volume
L~?. Cette
condition est semblable à celle habituellement rencontrée dans le
contexte des polymères confinés
[15].
Les ondulations de la membrane provoquent des
interactions effectives répulsives entre les frontières
géométriques confinantes.. La force induite ou encore force
du Casimir, qui est manifestement fonction de la taille D, doit
s'atténuer avec la distance. Dans ce chapitre, nous sommes
intéressés par la façon dont cette force diminue avec la
distance. Pour simplifier les calculs, nous supposons que la membrane est
confinée entre deux plaques parallèles, qui sont à une
distance finie l'une de l'autre, c'est-à-dire D <
Li.
Le mot "Casimir" est inspiré de l'effet Casimir
traditionnel. Un tel effet, prédit pour la première fois par
Hendrick Casimir, en 1948 [16], peut être
considéré comme l'une des découvertes fondamentales du
siècle dernier. Selon Casimir, les fluctuations quantiques du vide d'un
champ électromagnétique confiné produisent une force
attractive entre les deux plaques parallèles non chargées et
parfaitement conductrices. L'effet Casimir a été confirmé
dans des expériences plus récentes par Lamoreaux [17]
et par Mohideen et Roy [18]. Par la suite, Fisher et
de Gennes [19] remarquèrent que l'effet Casimir
apparaît aussi pour les systèmes critiques, tels que les fluides,
les mélanges de liquides simples ou de polymères, l'hélium
liquide 4He ou les liquide-cristaux, dans des
géométries restreintes ou en présence de particules
colloïdales immergées. Pour ces systèmes, les fluctuations
critiques du paramètre d'ordre jouent le rôle des fluctuations
quantiques du vide, et conduisent à des forces de longue portée
entre les plaques confinantes ou entre les colloïdes immergés
[20, 21].
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 69
Pour calculer la force de Casimir entre les plaques
parallèles, nous élaborons d'abord une théorie des champ
générale, qui prend en considération les interactions
primitives senties par la membrane confinée. Comme nous verrons
ci-dessous, en régime de confinement, ce modèle de champ
dépend seulement de deux paramètres, qui sont la constante de
rigidité de courbure de la membrane et d'une constante de couplage
contenant toute les informations sur le potentiel d'interaction exercé
par les plaques. En outre, le dernier paramètre est une fonction connue
de la séparation D. A l'aide de l'énergie libre
construite, nous avons calculé, pour la première fois, la force
de Casimir statique (par unité d'aire), fJ. Les calculs
exacts montrent que cette dernière diminue avec la
séparation D, selon une loi de puissance, c'est-à-dire
f ~ ê-1
(kBT)2
D-3, avec une
amplitude connue. Ici, kBT désigne l'énergie thermique,
et ê est la constante de rigidité de courbure de la
membrane. Naturellement, cette force augmente avec la température, et a
des valeurs significatives seulement pour des biomembranes à faible
ê. Le deuxième problème que nous avons
examiné est le calcul de la force de Casimir dynamique,
n(t). Plus
précisément, nous avons considéré une biomembrane
à une température T, qui est au début dans un
état d'équilibre où elle est presque plate, et nous
étions intéressés par la façon dont la force
induite se développe dans le temps, avant que l'état final soit
atteint. En utilisant un argument d'échelle, nous avons montré
que la rugosité de membrane, L?
(t), augmente avec le temps, comme
L? (t) ~
t1/4
(t < ô), avec ô
~ D4, est le temps
final, durant lequel la membrane atteint son état d'équilibre
final. En plus, nous constatons que la force augmente avec le temps selon
n (t) ~
t1/2
(t < ô). La discussion est
étendue à la vraie situation où la biomembrane est en
présence d'interactions hydrodynamiques, provoquées par le
liquide ambiant. Dans ce cas,
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 70
nous montrons que L?
(t) ~
t1/3
(t < Th) et FI
(t) ~
t2/3
(t < Th), avec le nouveau temps
final Th ~
D3.
En conséquence, les interactions
hydrodynamiques provoquent des changements drastiques des
propriétés dynamiques de la membrane confinée, puisque la
rugosité et la force induite se développent plus
rapidement.
Ce chapitre est organisé comme suit. En Sec.
II, nous présentons le modèle de champ permettant la
détermination de la force Casimir, du point de vue statique et
dynamique. Les Secs. III et IV sont consacréss au
calcul des forces induites statiques et dynamiques. Nous retraçons nos
conclusions dans la dernière section. Quelques détails techniques
sont présentés dans l'Appendice A.
4.2 Formulation théorique.
Nous considérons une membrane liquide
fluctuante, qui est confinée entre deux plaques parallèles
interactives 1 et 2,
séparées par une distance finie D. Naturellement, la
séparation D doit être comparée à la
rugosité en volume de la membrane,
L°?,
quand le système est illimité (la membrane est libre). La
membrane est confinée seulement quand la condition L <<
L°? est
satisfaite. Pour la situation opposée, c'est-à-dire L
>> L°?,
nous nous attendons à des corrections de taille finie,
expo-nentiellement petites. Ici, z =
-D/2 et z
= D/2 sont les positions des
deux plaques, dans la direction perpendiculaire. Pour la simplicité,
nous supposons que les deux surfaces sont physiquement identiques. Nous
désignons par V (z),
le potentiel d'interaction exercé par une plaque sur la membrane fluide,
en l'absence de l'autre. Habituellement, V
(z) est la somme de deux
potentiels, l'un est répulsif et l'autre
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 71
est attractif. Un exemple typique est fourni par le
potentiel suivant [2]
V (z) =
Vh (z) +
Vvdw (z)
, (3.1)
où
Vh (z) =
Ahe-z/ëh (3.1a)
représente le potentiel d'hydratation
répulsif, qui est dû aux molécules d'eau
insérées entre les têtes hydrophiles des molécules
de lipide [22]. L'amplitude Ah et la
portée du potentiel, ëh, sont de l'ordre de Ah '
0.2J/m2
et ëh ' 0.2
- 0.3nm. En fait,
l'amplitude Ah est Ah = Ph X
lh, avec la pression d'hydratation Ph '
108 -
109Pa. Ici,
VvdW(z) est le
potentiel de van der Waals entre une plaque et la biomembrane, qui sont
séparées par une distance z. Sa forme est comme suit
_
COH 1 2 1
Vvdw l --
12ð Lz2
(z +
ä)2 + (z +
2ä)2 (3.1b)
Ici, H désigne la constante d'Hamaker,
qui est homogène à une énergie. Pour des surfaces de
basses énergies (solides organiques), H est de d'ordre de
10-21J, soit du
même ordre de grandeur que l'énergie thermique kBT. En
revanche, elle ne dépasse pas
10-18J, pour des surfaces
de hautes énergies (métaux, céramiques, ...). Dans les
phases vapeurs, H est totalement négligeable. Dans la formule
précédente, ä est l'épaisseur de membrane, qui est de
quelques nanomètres. Pour des grandes valeurs de la distance z, l'on
a
U
(h)
W(h) =
L2 , (3.4)
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 72
Vvdw(z) ~
Wä2. (3.1c)
z4
Généralement, en plus de la distance z,
le potentiel d'interaction, V
(z), dépend de
certaines échelles de longueur,
(î~, ...,
în), qui sont les portées des
interactions. La membrane fluide sent alors le potentiel total
suivant
lD
) lD
) D D
U(z) =
V 2 - z +
V 2 + z ,- <
z < . (3.2)
2 2
Comme la membrane peut être regardée
comme une plaque élastique à deux dimensions, alors, dans la
représentation de Monge, un point de surface peut être
décrit par un vecteur-position tridimensionnel r =
(ñ, z) E
R3, où ñ =
(x, y) E R2 est le
vecteur transverse, et z = h
(x, y) E
[-D/2,
D/2] est la distance perpendiculaire à la
plaque localisée à z = 0. Ici, la
fonction de hauteur h (x, y)
peut prendre des valeurs positives ou négatives.
L'Hamiltonien total, H, du système est donné par
[9, 23]
f [ê
]
H [h] =
d2ñ 2
(?h)2 +
W (h) .
(3.3)
Ici, ê est la constante de rigidité de
courbure. Cette dernière est comparable à l'énergie
thermique kBT, où T est la température absolue et kB est la
constante de Boltzmann. W(h)
est le potentiel d'interaction par unité d'aire, qui se
présente comme suit
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 73
où le potentiel U(h)
est celui défini par la relation
(3.2), et L est la taille linéaire
latérale de la biomembrane.
Maintenant, discutons les propriétés
analytiques du potentiel d'interaction, W
(h). Premièrement, la relation
(3.2) suggère que ce potentiel total
est une fonction paire de la distance perpendiculaire h,
c'est-à-dire
W (-h) = W
(h) . (3.5)
En particulier, nous avons W
(-D/2) = W (D/2)
.
Deuxièmement, quand ils existent, les
zéros, ho, de la fonction potentielle W
(h) sont tels que
lD ) lD
)
V 2 - ho = -V
2 + ho . (3.6)
Cette égalité indique que, si
ho est un zéro de la fonction potentielle W
(h), alors -ho l'est aussi.
Le nombre de zéros est alors un nombre pair. En outre, dans tous les
cas, les ho sont différents de 0. En
effet, la quantité V (D/2) est non non
nulle, puisqu'elle représente le potentiel créé par une
plaque au milieu du film. Nous soulignons que, lorsque le potentiel
considéré est différent de zéro, il est
répulsif ou attractif. Quand ce même potentiel s'annulent en
quelques points, alors il est soit répulsif ou attractif entre deux
zéros consécutifs.
Troisièmement, nous notons d'abord que, de la
relation (3.2), nous déduisons que la
dérivée première de la fonction potentielle est une
fonction impaire, auquel cas W' (-h) =
-W'(h). En appliquant
cette relation à la médiane h = 0, nous obtenons
que W' (0) = 0. Par conséquent, le potentiel
W présent un extremum à h = 0,
quelle
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 74
que soit la forme de la fonction V
(h). Nous trouvons aussi que
l'extremum h = 0 est un maximum, si V
?(D/2) <
0, et est un minimum, si V
?(D/2) >
0. Le potentiel W présente une tangente
horizontale à h = 0, si seulement si V
?(D/2) = 0. D'une
part, la condition générale donnant les extrema
{hm} est
|
dV
|
|
dV =
dh
|
|
|
(3.7)
|
|
dh
|
h=
D -hm
|
h=D+hm
|
.
|
Puisque la dérivée première
W'(h) est une
fonction impaire de la distance h, elle doit avoir un nombre impair de
points extremum. Le point h = hm
est un maximum, si
|
et est un minimum, si
|
d2V
dh2
|
h=
D -hm
|
<
|
dV 2
dh2
|
h=D+hm
|
,
|
(3.8)
|
|
d2V
|
|
>
|
dV 2
|
|
|
(3.9)
|
|
dh2
|
h=
D -hm
|
dh2
|
h=D+hm
|
.
|
Au point h =
hm, nous avons une tangente horizontale,
si
|
d2V
dh2
|
~~~~h=D
-hm
|
= -
|
dV 2
dh2
|
h=
D
+hm
|
.
|
(3.10)
|
Notons que les déductions ci-dessus
dépendent, naturellement, de la forme du potentiel d'interaction V
(h).
Enfin, une analyse dimensionnelle simple montre que le
potentiel d'interaction total peut être réécrit sous la
forme d'échelle suivante
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 75
|
W (h)
kBT
|
1 (h
æ1
æn)
3. l11)
= D2
D, D, ...,
D)
|
où
(î1, ...,
în) sont les diverses échelles de
longueurs, et Ö (x1, ...,
xn+1) est une fonction d'échelle à n
+ 1 facteurs. En conclusion, nous notons que le potentiel de
paire, W (h), ne peut pas être
singulier à h = 0. C'est plutôt une fonction
analytique dans la variable h. Par conséquent, aux rapports fixés
æi/D, un développement limité, au second ordre,
de la fonction d'échelle Ö, autour de la valeur h
= 0, donne
ã h2+ O
(h4) . (3.12)
W (h)
kBT
2 D4
Nous nous limitons à la classe des potentiels
qui présentent un minimum autour du plan d'équilibre,
situé à h = 0. Dans ce cas, le coefficient
ã est défini positif, c'est-à-dire ã >
0. Bien-sûr, un tel coefficient dépend des
rapports æi/D. Dans le régime de confinement, où la
distance h est assez petite, nous pouvons assimiler le potentiel d'interaction
total par la partie quadratique. Dans ces conditions, le Hamiltonien Can
ham-Helfrich devient
Ho [h] = 2
J d2ñ [ê
(?h)2 +
ph2] , (3.13)
avec la constante élastique
Le préfacteur ã sera calculé plus
loin. L'expression ci-dessus de la constante élastique u donne une
idée sur sa dépendance de l'épaisseur du film D. En outre,
nous soulignons que ce coefficient peut être considéré
comme un multiplicateur de Lagrange
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 76
que l'égalité précédente
indique que la rugosité de la membrane est
indépendante
fixant la valeur de la rugosité de la
membrane.
Nous aurons besoin de la fonction de
corrélation (ou fonction de Green) hauteur-hauteur
G(ñ -
ñ') =
(h(ñ)h(ñ'))
- (h
(ñ))
(h
(ñ'))
. (3.14)
Cette fonction est solution de l'équation
différentielle
(~ê?2ñ
+~p)
G(ñ -
ñ') =
ä2 (ñ -
ñ') .
(3.15)
Ici, ä2
(x) est la fonction de Dirac
bidimensionnelle, et ?ñ =
?2/?x2
+
?2/?y2
représente l'opérateur Laplacien en dimension
2. Nous avons employé les notations
~ê = ê/kBT
et u = p/kBT, pour désigner
les constantes d'élasticité de la membrane
réduites.
A partir de ce propagateur, nous déduisons
l'expression de la rugosité de la membrane, ou encore le carré
moyen de déplacement,
L2?
=
(h2) -
(h)2 = G
(0, 0) . (3.16)
Une telle quantité mesure l'amplitude des
fluctuations thermiques de la membrane, autour du plan d'équilibre,
situé à h = 0. Nous montrons, dans
l'Appendice B, que la rugosité de la membrane est exactement
donnée par
D2
L2?
= , (3.17)
12
à condition qu'on soit dans le régime de
confinement, c'est-à-dire D << Li.
Notons
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 77
des propriétés
géométriques de la membrane (à travers ê). Nous
soulignons que cette même relation peut être retrouvée en
utilisant l'argument que chaque point de la membrane a la même
probabilité de se retrouver en n'importe quel point entre les deux
plaques [24].
La constant élastique u peut être
calculée, en utilisant la relation connue
(3.18)
8
uê .
L1 =
2 1 kBT
v
Ce qui donne
u = 9 (kBT)24
êD4 . (3.19)
Cette formule indique clairement que cette constante
élastique décroît avec la séparation D, comme
D-4. Le terme
uh2/2 décrit alors un
potentiel de confinement, qui assure la localisation de la membrane autour du
plan d'équilibre. L'intégrale spatiale de ce terme
représente la perte d'entropie causée par le confinement de la
membrane. La valeur (3.19) de la constante
élastique est compatible avec la contrainte
(3.17). Par conséquent, le
modèle élaboré est basé sur le Hamiltonien
(3.13), avec un potentiel de confinement
quadratique.
Nous considérons une membrane confinée
entre deux parois impénétrables, séparées par une
distance D. Dans ce cas, la décroissance exponentielle des
corrélations d'orientation est gouvernée par la longueur L11. Les
fluctuations de la hauteur de la membrane sont caractérisées par
l'échelle L1, qui doit rester en dessous de la séparation D. De
la relation standard
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 78
libre associée est tel que : F
= -kBT ln Z, qui est,
naturellement, une fonction de la
kBT
L1 =L2 11
, (3.20)
16ê
nous déduisons
(k:T)
1/2
L11 =N/3T
D D. (3.21)
Contrairement à L1, l'extension latérale
L11 dépend des caractéristiques de la membrane (à travers
ê).
Les étapes suivantes consisteront au calcul de
la force de Casimir en équilibre et hors équilibre.
4.3 Force de Casimir statique.
Les membranes des vésicules présentent
des fluctuations thermiquement excitées. Généralement, les
objets tels que des interfaces, les membranes ou les polymères subissent
de telles fluctuations, afin d'augmenter leur entropie de configuration. Pour
des biomembranes et des agents tensio-actifs de la bicouche lipidique, la
conséquence de ces ondulations provoquent une force induite,
appelée force de Casimir. Pour calculer la force
désirée, nous partons de la fonction de partition, construite
avec le Hamiltonien (3.13). Cette fonction de
partition est l'intégrale fonctionnelle suivante
Z =
IDh exp --
kBT] } . (3.22)
L'intégrale fonctionnelle s'étend sur
toutes les configurations du champ h. L'énergie
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 79
séparation D. Si nous désignons par E
= L2 l'aire de la surface
commune des deux plaques, la force de Casimir (par unité d'aire), fJ,
est moins la dérivée première de l'énergie
libre (par unité d'aire) par rapport à la séparation D,
c'est-à-dire
L'expression ci-dessus de la force de Casimir (par
unité d'aire) appelle les re-
Cette force par unité d'aire est
homogène à une pression. En fait, fJ est la pression suffisante
pour maintenir les deux plaques à une certaine distance D l'une de
l'autre. En terme de la fonction de partition, nous avons
Il
kBT
1 ?p ? lnZ
E
. (3.24)
?D ?~
En utilisant la définition
(3.19) et les relations
(3.23) et
(3.24), nous trouvons que
11 = - 2 ?D
1 ?p L2?
·
(3.25)
Explicitement, nous obtenons la formule
désirée, à savoir
T7 3 (kBT
)2. (3.26)
11 8
êD3
De cette relation, nous extrayons l'expression du
potentiel de séparation (par unité d'aire) [25]
Vd (D) = -
fD Ð
(D') dD = 3
(kBT )2 . (3.27)
16 êD2
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 80
marques suivantes.
Premièrement, cette force décroît
plus vite que la force de Colomb, qui se comporte plutôt comme
D-2.
Deuxièmement, cette même force
dépend de la nature des lipides formant la bicouche lipidique (à
travers la constante de rigidité de courbure de la membrane ê).
Notons que la présente force n'est pas universelle, contrairement
à l'effet Casimir rencontré habituellement en Théorie
Quantique des Champs [16] et en Phénomènes
Critiques [20]. Cela tient au fait que l'amplitude de cette
même force dépend de la nature des molécules de lipide
formant la bicouche.
Troisièmement, à température et
à distance fixées, l'amplitude de force n'a de valeurs
significatives que pour les petites constantes de rigidité de courbure
de la membrane.
Enfin, comme elle se doit, cette force augmente avec
la température. En effet, à température
élevée, les ondulations de la membrane sont très
fortes.
En conclusion, le préfacteur numérique
3/8 (ou amplitude d'Helfrich cH
[9]) est proche de la valeur obtenue en utilisant la
simulation Monte Carlo [26].
Dans la Fig. 3.1,
nous superposons les variations de la force statique réduite,
fJ /kBT, en fonction de la séparation D, pour deux
systèmes lipidiques, à savoir les SOPC et DAPC
[27], à la température T =
18C?. Les constantes de rigidité de courbure
respectives sont : ê = 0.96×
10-19J et ê =
0.49 ×
10-19J. Ces valeurs
dimensionnées correspondent aux constantes : /Z =
23.9 et ~ê =
12.2. La méthode courante pour la mesure de ces
constantes de rigidité est la méthode de micro-pipette
[27]. Les courbes tracées reflètent la
discussion faite ci-dessus.

hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 81
FIG. 4-1 -- Les variations de la force statique
réduite, fJ /kBT, en fonction de la
séparation D, pour deux systèmes lipidiques, à
savoir SOPC ( ligne continue) et DAPC (ligne pointillés ), à la
température T = 18C?
4.4 Force de Casimir dynamique.
Pour étudier les phénomènes
dynamiques, la quantité d'intérêt est la fonction hauteur,
h (r, t), qui dépend
du vecteur-position r = (x, y)
E R2 et du temps, t. Cette
dernière représente l'observation dans le temps du
système, avant qu'il atteigne son état d'équilibre final.
Nous rappelons que la fonction h (r,
t) est solution de l'équation non-dissipative de
Langevin (avec bruit) [28]
|
ah(r, t)
at
|
= -Fan°
[h] +
í(r, t)
. (3.28)
ah(r, t)
|
Ici, n° est le Hamiltonien
statique (divisé par kBT) et F >
0 est le coefficient cinétique. Ce dernier a les
dimensions : [F] = L
°T -1
° , où L° est
une certaine échelle
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 82
de longueur et T°
est l'unité de temps. Ici, v
(r, t) est une force
aléatoire Gaussienne,
(v(r,
t)) = 0 , (3.29a)
(v(r,
t)v(r',
t')) =
28e (r - r')
8 (t - t')
. (3.29b)
La fonction de corrélation temporelle, dont la
transformée de Fourier est le facteur de structure dynamique, est
définie par la valeur moyenne suivante (par rapport au
bruit),
G (r - r', t -
t') =
(h(r,t)h(r',t'))í
-
(h(r,t))í
(h(r',t'))
í , t > t' .
(3.30)
L'équation dynamique
(3.28) montre que la fonction
hauteur h est une fonctionnelle du bruit v, et nous
écrivons : h = h
[v]. Au lieu de résoudre
l'équation de Langevin pour h
[v], puis moyenner, ensuite,
sur la distribution du bruit, P
[v], les fonctions de
corrélation et de réponse peuvent être directement
calculées à l'aide de la théorie du champ usuelle,
d'action [28 - 31]
Ah,~h = dt
derr~h?th +
~h h°
-~h~h} , (3.31)
de sorte que, pour une observable arbitraire, O
[î], l'on a
|
(O)í =
[dv] O [?
[v]] P
[v] =
|
DhD~hOe-A[h,h]
(3.32)
DhD~he-A[h,h]
,
|
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 83
où h (r, t)
est un champ auxiliaire, couplé au champ externe h
(r, t).
Les fonctions de corrélation et de
réponse peuvent être calculées en remplaçant le
Hamiltonien statique, H0, défini par la
relation (3.13), par un nouveau, qui
est : H0 [h, J] =
H0 [h] - f
derJh. En conséquence,
pour une observable quelconque O, nous avons
|
ä (O)J
äJ (r,t)
|
J=0
|
~ ~
= h (r,t)O
. (3.33)
|
~ ~
La notation ~O~J est la moyenne
calculée avec l'action A h, h, J , associée à
l'Ha-
miltonien H0 [h,
J]. En raison de la structure de l'égalité
(3.33), le champ conjugé
h est appelé champ de réponse. Maintenant, si O
= h, nous obtenons la réponse
du champ de hauteur à la perturbation externe J,
R(r -
r',t - t') =
ä äJ (r,t'))J
= Ch(r,t)
h(r',t')> _
.(3.34)
J=0 J=0
La causalité implique que la fonction de
réponse est nulle pour t < t'. En fait, cette
fonction peut être reliée à la fonction de
corrélation temporelle, en utilisant le théorème de
dissipation-fluctuation, selon lequel
~ ~
h (r,t)
h(r',t') =
-è (t -
t')?t
~h(r,t)h(r',t')~c
. (3.35)
La formule ci-dessus montre que la fonction de
corrélation temporelle, C (r
- r', t -
t') = (cp
(r, t) cp
(r',
t'))c, peut être
déterminée par la connaissance de la fonction réponse. En
particulier, nous trouvons que
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 84
?F ~ kBT/L2~ax ~
kBT
(B/L1)2/æ
, (3.37)
t
L21(t)
= (h2 (r,
t))c = -2
f (h, (r, t) h
(r',
t')) . (3.35a)
La limite t -* -oo donne la valeur normale
L21
(-oo) = 0, car l'état initial correspond
à une interface complètement plate.
Considérons, maintenant, une membrane à
la température T, qui est initialement dans un état
d'équilibre thermique où elle est plate. A un temps
postérieur, t, la membrane possède une certaine
rugosité, L1(t).
Naturellement, cette dernière est une fonction du temps. Nous sommes
intéressés par la façon dont il augmente au cours du
temps. Nous précisons que les fluctuations thermiques provoquent une
rugosité de la membrane, qui est caractérisée par
l'apparition des bosses anisotropes. Par conséquent, un segment de
taille linéaire L effectue des excursions de taille
[32]
L1 = BLæ .
(3.36)
Une telle relation définit l'exposant de
rugosité, (. Notons que L est de l'ordre de la
longueur de corrélation parallèle , L11. De la relation
(3.20), nous déduisons
l'exposant ( et la valeur de l'amplitude B. Alors, nous avons
( = 1 et B ~
(kBT/ê)1/2.
Afin de déterminer la croissance de la
rugosité dans le temps, L1
(t), la clé est de
considérer l'excès d'énergie libre (par unité
d'aire) ?F, due au confinement (perte
d'entropie). La formule (3.27)
nous indique que ?F doit diminuer avec la
séparation. Le résultat s'écrit [32]

hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 85
~ =-??F
~ L? (1+2/0 (3.37a)
?L? .
En outre, une analyse attentive de l'équation de
Langevin (3.28) montre que
|
?L? ??F
~ -
?t ?L?
|
= .Ð ~
.L-(1+2/æ~ . (3.38)
?
|
Nous soulignons que cette loi d'échelle est
conforme aux prédictions de Monte Carlo [32,
33]. La solution de cette équation, de premier ordre,
est [34]
e? e?æ
1
L?(t) t , è?
= =
4 . (3.39)
2 + 2æ
Ceci implique la forme d'échelle suivante de la
taille linéaire
LII(t) ~
eute° B --
, 1
æ
"" 2 + 2
4 . (3.40)
où Lmax représente une certaine longueur d'onde,
au-dessus de toutes les fluctuations
de forme, qui ne sont pas accessibles par la membrane
confinée. L'interaction de
fluctuations induite (répulsive) conduit à la
pression de séparation
Commentons le résultat obtenu
(3.39).
Premièrement, la rugosité augmente avec
le temps (l'exposant è? étant défini positif). En plus,
l'exposant è? est universel, indépendamment de la
constante de rigidité de courbure ê.
Deuxièmement, notons que, dans
l'égalité (3.39), nous avons
ignoré une certaine amplitude, qui n'est pas universelle et se
comportant comme ê-1/4. Cela signifie
que la rugosité temporelle est significative, seulement pour ces
biomembranes de petite
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 86
constante de rigidité de courbure.
Quatrièmement, cette rugosité peut
être interprétée comme la taille perpendiculaire des trous
et vallées, au temps t.
Enfin, la rugosité augmente jusqu'à un
temps final, ô. Ce dernier peut être interprété comme
le temps au bout duquel le système atteint son état
d'équilibre final. Le temps caractéristique se comporte
comme
ô ~
-1L1/è?
L , (3.41)
où nous avons ignoré une certaine
amplitude dépendant de ê. Ici, LL ~ D
est la rugosité finale. Explicitement, nous avons
ô ~
-1D4 .
(3.42)
Comme qu'il devrait être, le temps final
augmente avec l'épaisseur du film D. d'une part, nous pouvons
réécrire le comportement (3.39)
comme suit
|
LL(t)
LL(ô)
|
( t)è?
= .
ô
|
(3.43)
|
Cette égalité signifie que le rapport de
rugosité, en fonction du temps réduit, t/ô, est
universel.
Maintenant, pour calculer la force de Casimir
dynamique, nous partons d'une formule analogue à
(3.24), c'est-à-dire
1 ?p ? ln Z~
(3.44)

?D ?p ,
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 87
avec la nouvelle fonction de partition
fZ =
DhD~he-A[h,~h]
. (3.45)
Un calcul simple, en considérant la relation de
base (3.35a),
donne
1 ?~
L
2
?D1(t) ,
(3.46)
Ce qui est très semblable à la relation
statique (3.25), mais avec une
rugosité de membrane dépendant du temps , L1
(t). La combinaison des formules
(3.43) et (3.46)
mène à l'expression désirée de la force de
Casimir (par unité d'aire), en fonction du temps,
t e
) f
= ô
ri(t)
ri(ô)
, (3.47)
où ri(ô)
est la force de Casimir statique finale, définie par la relation
(3.25). L'exposant de force,
èf, est tel que
æ 1
èf = 2è1
= 1 + æ = 2 . (3.48)
Alors, la force induite se développe dans le
temps comme t1/2,
jusqu'à ce qu'elle atteigne sa valeur finale, ri
(ô). Au temps ô, l'amplitude de
la force diminue comme ê-3/2.
En outre, notons que l'égalité ci-dessus signifie que le rapport
de force, en fonction du temps réduit, est universel.
Dans la Fig. 3.2,
nous reportons la force de Casimir dynamique réduite, ri
(t) / ri
(ô), en fonction du temps
renormalisé t/ô.

hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 88
où (ôh)
est la force de Casimir statique, relation
(3.25). Le nouvel exposant de
FIG. 4-2 -- La force de Casimir dynamique
réduite, (t) /
(ô), en fonction du temps
renormalisé t/ô.
Considérons cette fois-ci une membrane, qui en
présence d'interactions hydrodynamiques. Dans ce cas, la rugosité
se développe dans le temps comme [35]
|
~L?(t) ~
t~e? ,
|
~è? =î
1 + 2î
|
1
=(3.49) 3 .
|
Donc, l'augmentation de la rugosité avec le
temps est relativement plus rapide que celle où la membrane est en
absence d'interactions hydrodynamiques. Dans cette situation, la force de
Casimir dynamique est telle que
|
h (t)
(ôh)
|
~ t ~
= ô
|
êf
|
,
|
(3.50)
|

hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 89
FIG. 4-3 -- La force dynamique réduite (avec
des interactions hydrodynamiques), Hh
(t) /H
(Th), en fonction du temps renormalisé
t/Th.
force est alors
|
2æ
èf =
2~è? = 1 +
2æ
|
2
= 3
· (3.51)
|
Ici, Th ~
D3 est la nouvelle échelle de
temps, au bout duquel la membrane confinée atteint son état
d'équilibre final. Par conséquent, la force de Casimir dynamique
croit avec du temps comme
t2/3, donc
plus rapidement que celle en l'absence d'interactions hydrodynamiques, qui
croit plutôt comme
t1/2.
Nous illustrons, dans la Fig.
3.3, la variation de la force
dynamique réduite (avec des interactions hydrodynamiques),
Hh (t)
/H (Th), en
fonction du temps renormali-sée t/Th.
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 90
Après, nous avons abordé le calcul de la
force de Casimir statique, fJ. A l'équi-
4. 5 Conclusions.
Dans ce chapitre, nous avons réexaminé
le calcul de la force de Casimir entre deux parois parallèles
délimitant une membrane lipidique fluctuante, qui est immergée
dans un certain liquide. Cette force est provoquée par les fluctuations
thermiques de la membrane. Nous avons étudié le problème,
du point de vue statique et dynamique. Nous nous étions
intéressés, pour la première fois, à la variation
temporelle de la rugosité, Li, en partant d'une membrane qui
est initialement dans un état plat, et à une certaine
température.
Naturellement, cette rugosité se
développe avec le temps, et nous avons trouvé que
Li(t) ,,,
te? (èi
= 1/4), à condition que les
interactions hydrodynamiques soient ignorées. Pour de vrais
systèmes, toutefois, ces interactions sont importantes, et
|
nous avons montré que la rugosité
augmente plus rapidement, comme
|
.Li(t)
, t~e?
|
( )
.èi = 1/3
. Le processus dynamique est alors arrêté à un
ô (ou ôh) final, qui re-
présente le temps nécessaire pour que la
biomembrane atteigne son état d'équilibre final. Ce temps final
se comporte comme : ô ~,
D4 (ôh
~, D3),
avec D l'épaisseur du film.
Maintenant, supposons que le système est
exploré à des échelles de l'ordre de la longueur d'onde,
q-1, où q
= (4ð/ë) sin
(è/2) est le module du vecteur d'onde,
ë est la longueur d'onde du rayonnement incident, et è est l'angle
de diffusion. Dans ces conditions, le taux de relaxation,
ô(q), comme fonction de q, se comporte
comme ô-1
(q) N
q1/3? =
q4
(.ô-1(q)
t,, q1/ê? =
q3) . Physiquement parlant, le
taux de relaxation caractérise la croissance locale des fluctuations de
taille
q-1.
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 91
libre, en utilisant une Théorie de Champ
appropriée, nous avons montré que cette force
décroît avec la séparation D comme : f ~
D-3, avec une
amplitude se comportant comme
ê-1, où ê
est la constante de rigidité de courbure de la membrane. Une telle force
est alors très petite, en comparaison à la force de Coulomb. En
outre, cette force a tendance à disparaître, quand la
température du milieu est suffisamment abaissée.
La force de Casimir dynamique,
fJ(t), a été
calculée, en utilisant une équation de Langevin non-dissipative
(avec un bruit), satisfaite par la fonction hauteur. Nous avons montré
que II (t) ~
tèf
(èf =
2è? =
1/2). Quand les effets
hydrodynamiques
d'interactions sont importants, nous avons trouvé
que la force dynamique augmente
~ ~
plus rapidement comme : ~ h
(t) ~
tè~ ~èf
= 2~è?
= 2/3 .
Enfin, notons que nous avons ignoré certains
détails, tels que le rôle des inclusions (protéines,
cholestérol, glycolipides, et autres macromolécules) et la
différence chimique entre espèces sur l'expression de la force.
Il est bien établi que ces détails conduisent simplement à
une renormalisation additive de la constante de rigidité de courbure de
la membrane. En effet, nous écrivons êeffective =
ê + äê , avec ê
la constante de rigidité de courbure de la membranes dépourvue
d'inclusions, et äê est la contribution des entités
incorporé. Généralement, le décalage äê
est une fonction de la concentration des inclusions et de la composition des
espèces de la nature chimique différente (divers phospholipides
formant la bicouche). Par conséquent, pour prendre en
considération la présence des inclusions et de la
différence chimique, il serait suffisant de remplacer la constante
ê par une effective ê+äê, dans
les relations établies ci-dessus.
·
92
Bibliographie
[1] K. Elhasnaoui, Y. Madmoune, H. Kaidi, M. Chahid, M.
Benhamou, African Journal of Mathematical Physics 8, 101 (2010).
[2] M.S. Bretscher, S. Munro, Science 261, 12801281
(1993).
[3] J. Dai, M.P. Sheetz, Meth. Cell Biol. 55, 157171
(1998).
[4] M. Edidin, Curr. Opin. Struc. Biol. 7, 528532
(1997).
[5] C.R. Hackenbrock, Trends Biochem. Sci. 6, 151154
(1981).
[6] C. Tanford, The Hydrophobic Effect,
2ème édition, Wiley, 1980.
[7] D.E. Vance, J. Vance, éditeurs,
Biochemistry of Lipids, Lipoproteins, and Membranes, Elsevier,
1996.
[8] F. Zhang, G.M. Lee, K. Jacobson, BioEssays 1 5,
579588 (1993).
[9] S. Safran, Statistical Thermodynamics of
Surfaces, Interfaces and Membranes, Addison-Wesley, Reading, MA,
1994.
[10] W. Helfrich, Z. Naturforsch. 28c, 693
(1973).
[11] Pour une revue récente, voir U. Seifert,
Advances in Physics 46, 13 (1997).
[12] H. Ringsdorf, B. Schmidt, How to Bridge the Gap
Between Membrane, Biology and Polymers Science, P.M. Bungay et
al., éditeurs, Synthetic Membranes :
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 93
Science, Engineering and Applications, p.
701, D. Reiidel Pulishing Compagny, 1986.
[13] D.D. Lasic, American Scientist 80, 250
(1992).
[14] V.P. Torchilin, Effect of Polymers Attached
to the Lipid Head Groups on Properties of Liposomes, D.D. Lasic, Y.
Barenholz, éditeurs, Handbook of Nonmedical Applications of
Liposomes,Volume 1, p. 263, RCC Press, Boca Raton, 1996.
[15] R. Joannic, L. Auvray, D.D. Lasic, Phys. Rev.
Lett. 78, 3402 (1997).
[16] P.-G. de Gennes, Scaling Concept in Polymer
Physics, Cornell University Press, 1979.
[17] H.B.G. Casimir, Proc. Kon. Ned. Akad. Wetenschap
B 51, 793 (1948).
[18] S.K. Lamoreaux, Phys. Rev. Lett. 78, 5
(1997).
[19] U. Mohideen, A. Roy, Phys. Rev. Lett. 81, 4549
(1998).
[20] M.E. Fisher, P.-G. de Gennes, C. R. Acad. Sci.
(Paris) Série B 287, 207 (1978) ; P.-G. de Gennes, C. R. Acad.
Sci. (Paris) II 292, 701 (1981).
[21] M. Krech, The Casimir Effect in Critical
Systems, World Scientific, Singapore, 1994.
[22] Des références plus
récentes peuvent être trouvées dans : F. Schlesener, A.
Hanke, S. Dietrich, J. Stat.Phys. 110, 981, 2003 ; M. Benhamou, M. El Yaznasni,
H. Ridouane, E.-K. Hachem, Braz. J. Phys. 36, 1 (2006).
[23] R. Lipowsky, Handbook of Biological
Physics, R. Lipowsky, E. Sackmann, éditeurs, Volume 1, p. 521,
Elsevier, 1995.
[24] P.B. Canham, J. Theoret. Biol. 26, 61
(1970).
[25]
hapitre 3 : Effet de Casimir dans les biomembranes
confinées. 94
O. Farago, Phys. Rev. E 78, 051919 (2008).
[26] Nous retrouvons la loi de puissance f ~
D-3, qui est
connue dans la littérature (voir, par exemple, la Réf.
[8], mais l'amplitude correspondante dépend du
modèle utilisé).
[27] G. Gompper, D.M. Kroll, Europhys. Lett. 9, 59
(1989).
[28] U. Seifert, R . Lipowsky, dans : Structure and
Dynamics of Membranes, Handbook of Biological Physics, R. Lipowsky, E.
Sackmann, éditeurs, Elsevier, North-Holland, 1995.
[29] J. Zinn-Justin, Quantum Field Theory and
Critical Phenomena, Clarendon Press,Oxford,1989.
[30] H.K. Jansen, Z. Phys. B 23, 377 (1976).
[31] R. Bausch, H.K. Jansen, H. Wagner, Z. Phys. B 24,
113 (1976).
[32] F. Langouche, D. Roekaerts, E. Tirapegui, Physica A
9 5, 252 (1979).
[33] R. Lipowsky, dans : Random Fluctuations and
Growth, H.E. Stanley, N. Os-trowsky, éditeurs, p. 227-245, Kluwer
Academic Publishers, Dordrecht, 1988.
[34] R. Lipowsky, J. Phys. A 18, L-585
(1985).
[35] R. Lipowsky, Physica Scripta T 29, 259
(1989).
[36] F. Brochard, J.-F. Lennon, J. Phys.
(Paris) 36, 1035 (1975).
95
Chapitre
Dynamique Brownienne de
colloïdes au contact d'une
biomembrane confinée.
Dans ce chapitre, qui consiste notre
deuxième contribution originale, nous considérons une
solution colloïdale au contact d'une biomembrane, qui est confinée
dans une fente. L'on suppose que l'épaisseur de cette fente est beaucoup
plus petite que la rugosité en volume, afin d'assurer le confinement de
la membrane. Le but étant l'étude de la dynamique Brownienne de
ces particules, sous la variation d'un paramètre adéquat, tel que
la température, par exemple. L'objet de base est la densité
locale des particules. Nous déterminons exactement cette densité,
qui est fonction de la distance et du temps. L'outil pour cela est
l'équation de Smolokowski.
Pour plus de détails, le lecteur peut
être renvoyé à la Réf.
[1].
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 96
.1 Introduction.
Les membranes biologiques constituent un
élément fondamental dans l'organisation cellulaire, car elles
séparent la cellule de son environnement, et agissent comme une
barrière sélective vis-à-vis de la matière. Les
détails descriptifs de l'organisation structurale et les fonctions de
base des biomembranes peuvent être trouvés dans les Réfs.
[2 - 8].
Les membranes cellulaires sont formées par une
bicouche de phospholipides combinée avec une variété de
protéines et de cholestérol. Particulièrement, ces
derniers assure la fluidité de la bicouche. Un phospholipide est une
molécule amphiphilique possédant une tête polaire
hydrophile attachée à deux chaînes carboniques hydro-p
hobes.
Les phospholipides se déplacent librement sur
la surface de la membrane, et l'épaisseur de la bicouche membranaire est
de l'ordre de 50 Angströms. En fait, ces deux
propriétés permettent de considérer la membrane comme une
membrane fluide à deux dimensions.
Les membranes fluides, auto-s'assemblées de
solutions du surfactant, peuvent avoir une variété de formes et
de topologies [9], qui ont été expliqués
en terme de l'énergie de courbure [10,
11].
Généralement, les biomembranes ne sont
pas immergées dans les liquides d'extension infinie, mais elles sont
confinées dans des domaines à frontières
géométriques. Des exemples typiques sont fournis par les globules
blancs et rouges ou liposomes (agents de transport de médicaments
[12 - 15]), dans les vaisseaux sanguin. Pour
obtenir des résultats quantitatifs, nous considérons la situation
où la biomembrane
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 97
est piégée dans un liquide
délimité par deux parois parallèles, qui sont
séparées par une distance finie, L. Cela veut dire que
la séparation L est plus petite que la rugosité moyenne
de la membrane, eL (géométrie en
film). Cette dernière peut être considérée
comme la dimension typique des bosses, causée par les fluctuations
thermiques de la membrane. Bien sûr, l'échelle
et dépend de la nature des molécules de
lipide formant la bicouche. Alors, la condition L < eL
assure le confinement de la biomembrane. Une telle condition est
semblable à cela rencontrée habituellement dans le contexte des
polymères confinés [16].
Généralement, les membranes fluides ne
sont pas pures. En effet, elles sont en présence d'entités, comme
les protéines, les petits et les macro-ions, ou des structures complexes
[17]. Par exemple, les suspensions des membranes
utilisées dans les détergents et les produits de beauté
sont habituellement en contact avec de nombreux additifs (macromolécules
ou colloïdes), dans le but d'améliorer leur efficacité et de
contrôler leurs propriétés de
visco-élasticité [18]. Pour modéliser
l'organisation de ces entités externes ainsi que leur influence sur les
propriétés mécaniques et topologiques de la membrane
fluide, la manière la plus simple consiste à considérer
ceux-ci comme de petites colloïdes sphériques. Nous croyons que
cette considération a une bonne signification physique, lorsque les
tailles de certaines phénomènes sont plus grandes que les
dimensions caractéristiques des entités voisines (diamètre
des particules, rayon de giration des macromolécules, etc.).
L'organisation des nanoparticles autour d'une membrane
fluide fluctuante, dans un domaine liquide infini, est le sujet de nombreux
travaux théoriques très récents [19 -
21]. La question a été adressée aux
propriétés statistiques des particules médiatisées
par les ondulations de la membrane. En particulier, il a été
trouvé que
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 98
ces ondulations induisent une agrégation des
perles, au voisinage de la membrane fluide. Une telle agrégation est
causée par l'apparition des forces attractives due à leur contact
avec la membrane. Aussi, l'attention a été prêtée
sur la transition de phase [19] conduisant les colloïdes
d'une phase dispersée (gaz) à une phase dense
(liquide).
Dans un travail très récent
[22], on a étudié la dynamique Brownienne des
nano-particules, de faible densité, qui sont au contact d'une membrane
fluide pénétrable. Les colloïdes et la membrane ont
été supposées qu'elles baignent dans un domaine liquide
infinie. Plus précisément, le problème posé
était comme ces particules sont poussées par le potentiel externe
vers l'interface. Cette dynamique Brownienne sera étudiée,
à travers l'évolution dans le temps de la densité de
particules, sous l'effet de certains paramètres convenables
(température, pression, environnement, etc.), lorsqu'elle est
passée d'une valeur initiale à une autre finale.
Nous rappelons que le mouvement Brownien gouverne
plusieurs phénomènes dépendant du temps, en allant des
suspensions [23 - 28] aux solutions de
polymère [29]. Ce mouvement peut être
traité, en utilisant deux approches, à savoir l'équation
de Smoluckowski ou l'équation de Langevin. Bien que ces deux
formulations théoriques soient différentes, elles sont
physiquement équivalentes. L'équation de Smoluckowski qui est une
généralisation de l'équation de diffusion habituelle, a
une pertinence claire des processus thermodynamiques irréversibles. En
revanche, l'équation de Langevin n'a aucun rapport direct avec la
thermodynamique, mais elle fournit un outil prospère pour la description
de larges classes de processus stochastiques.
Dans ce chapitre, le but est d'étendre
l'étude de la dynamique Brownienne au cas où les particules
colloïdales sont au contact d'une membrane fluide fluctuante,
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 99
qui est trompée dans un liquide
délimité par deux parois impénétrables. Plus
précisément, la question est de savoir comment cette dynamique
peut être affectée par le confinement de la membrane. Comme nous
verrons ci-dessous, ce confinement induit des changements drastiques des
propriétés statistiques des perles.
Pour étudier la dynamique Brownienne d'une
suspension colloïdale, près d'une membrane fluide fluctuante
confinée, nous utilisons une approche basée sur l'équation
de Smoluckowski. Cette dernière décrit l'évolution dans le
temps de la densité de particules. Pour cela, nous rappelons d'abord la
détermination du potentiel externe de la force moyenne induit par les
fortes fluctuations thermiques de la membrane [20]. Pour
simplifier l'étude, nous supposons que les particules sont ponctuelles
et de très faible densité. La première hypothèse
reste valable tant que nous nous sommes intéressés par de fortes
ondulations de la membrane, alors que la deuxième signifie que les
interactions mutuelles entre particules peuvent être ignorées.
Donc, l'interaction restante provenant d'un potentiel externe, tire son origine
des fluctuations thermiques de l'interface. Dans le domaine de distance
d'intérêt, qui est la région autour de la membrane fluide,
nous déterminons la forme exacte de la densité locale de
particules. Cette forme dépend de la distance perpendiculaire z,
comptée à partir d'une paroi prise comme origine, le temps t, et
d'un certain temps caractéristique, T ~
L3/w, où L est la
séparation entre les murs confinants et w est une constante de couplage
mesurant l'amplitude de la force d'interaction colloïde-membrane. Cette
échelle de temps peut être interprétée comme le
temps nécessaire pour que les particules occupent les nouveaux trous et
vallées de la membrane.
Notons que l'étude présentée dans
ce chapitre, est une extension naturelle de l'étude statique de
l'organisation de particules colloïdales, au contact d'une
seule
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 100
7-lo [h] = 21 J
d2p [ê
(?h)2 +
uh2] ,
(4.1)
membrane fluide fluctuante
(géométrie semi-infinie).
Ce chapitre s'organise comme suit. Dans Sec.
II, nous présentons l'essentiel de la Théorie de Champ
permettant le calcul d'une quantité de base, qui est le potentiel de la
force moyenne, dû aux ondulations de la membrane. L'étude de la
dynamique Brownienne est le but de la Sec. III. Quelques remarques
finales sont retracées dans la dernière section.
.2 Formulation théorique.
Nous considérons une membrane liquide
fluctuante, qui est confinée entre deux murs parallèles
interactifs 1 et 2. Nous
désignons par L leur distance de séparation finie.
Naturellement, la séparation L doit être comparée
à la rugosité en volume de la membrane,
eo?, quand le système est
illimité (membrane libre). La membrane est confinée
seulement lorsque la condition L <<
eo? est satisfaite.
Dans la représentation de Monge, un point de la
surface peut être décrite par un vecteur-position
tridimensionnels, r = (p, z)
E R3, où p
= (x, y) E R2
est le vecteur transverse et z = h
(x, y) E
[-L/2,
L/2]. La distance perpendiculaire est comptée du
plan localisé à z = 0. Ici, la
fonction de hauteur h (x, y)
peut prendre des valeurs positives ou
négatives.
Le Hamiltonien, 7-lo, est celui de
Canham-Helfrich [10, 30], avec une
tension de surface nulle (u =
0),
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 101
avec la constante élastique [31]
_ 9kBT
u L4 .
(4.2)
4
Ici, ê est la constante de
rigidité de courbure. Cette dernière est comparable à
l'énergie thermique kBT, où T est la
température absolue et kB est la constante de Boltzmann. En
fait, le terme
uh2/2
décrit le potentiel de confinement assurant la localisation de
la membrane autour d'un plan d'équilibre. L'intégrale ci-dessus
représente la perte d'entropie due au confinement de la membrane. La
valeur (4.2) de la constante
élastique est compatible avec la contrainte que
1 kBT L2
2? =
(h2) - (h)2 =8
vuê 12 , (4.3)
à condition qu'on soit dans le régime de
confinement où L << e1. La
quantité mesurant les fluctuations, est une fonctionnelle de la hauteur
(amplitude de fuctuations) autour d'un plan d'équilibre,
localisé à z = 0. Nous rappelons que le
résultat (4.3) a
été obtenu récemment dans la Réf. [31]
.
Maintenant, nous considérons un assemblage de
N particules colloïdales qui sont mobiles autour d'une membrane
fluide fluctuante. Pour simplifier les calculs, les particules sont
supposées ponctuelles. En fait, cette supposition a un sens, seulement
si la dimension des particules est plus petite que la rugosité de la
membrane, e? =
L/2v3. Typiquement,
les particules considérées ont un diamètre de quelques
nanomètres, en comparaison avec la rugosité qui est de l'ordre de
1 micromètre. De plus, nous supposons qu'il n'y a
aucune interaction directe colloide-colloide. Cette hypothèse reste
valable tant que la dispersion colloïdale est de faible densité.
Nous rappelons que, dans ce chapitre, nous nous intéressons à
l'influence des ondulations
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 102
de la membrane sur le mouvement des particules. Bien
sflr, les interactions mutuelles primitives entre nanoparticles devraient
être prises en considération, quand on s'intéresse à
leur transition de la phase (agrgation collodale), près d'une
interface fluide attractive [20].
Le Hamiltonien total décrivant la physique des
colloids et membrane, s'écrit [19].
H [h] =
Ho [h] + Hcm
[h] , (4.4)
avec le Hamiltonien Ho
[h], relation
(4.1). Dans la définition
précidente, Hcm représente l'interaction colloïde-interface.
Généralement, cette dernière est une fonction
compliquée des positions des particules et des configurations de la
surface. Il est alors naturel de comparer la distance caractéristique
î? (de l'ordre du micromètre) à la taille des particules
(de l'ordre de quelques nanomètres). Si nous nous intéressons au
régime où l'interface subit de fortes fluctuations, la taille des
particules est plus petite queî?. En fait, cette hypothèse permet
de négliger les effets de taille finie. Même avec cette
simplification, Hcm reste encore être compliqué. Pour simplifier,
nous supposerons que le potentiel d'interaction colloïde-surface est de
contact, c'est-à-dire
|
w
Hcm = -
2
|
N i=1
|
S [zi - h
(pi)] . (4.5)
|
Ici, S (z) est la
fonction de Dirac. Dans cette définition, la somme discrète porte
sur toutes les positions des particules, ri = (pi,
zi), avec 1 = i = N. Ici, w > 0
est la constante de couplage de surface. En fait, w joue le rôle
de la longueur d'extrapolation, rencontré habituellement dans
le contexte des Phénomènes Critiques
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 103
de Surface [32 -
34]. Dans ce modèle, l'interface est supposée
pénétrable, et les colloïdes peuvent se trouver des deux
côtés de l'interface. Comme il est montré dans Réf.
[20], les ondulations de la membrane induisent des
interactions à un et deux corps, et même plus, entre les
colloïdes. Le calcul exact de ces interactions effectives a
été accompli en utilisant la méthode du cumulant
standard, qu'on rencontre en Théorie de Champ Statistique
[35, 36].
Le système physique que nous
considérons, par la suite, est une suspension très diluée
de colloïdes identiques, qui sont au contact d'une membrane fluide
fluctuante. Donc, les interactions mutuelles entre particules peuvent
être ignorées, et la seule interaction restante est un potentiel
à un seul corps (attractif), U
(z), entre colloïdes et interface. Son
expression est [20]
~ --
2
U (z) =
Uo exp L2, (4.6)
avec l'amplitude négative
Uo = - \/3 2ð L
kBT . (4.7)
La quantité |Uo| est la
profondeur du potentiel. Notons que, dans l'expression du potentiel
d'interaction obtenue dans un travail antérieur [20],
la rugosité î? est remplacée par son expression : î?
= L/2s/3.
Faisons des commentaires à propos de
l'expression du potentiel extérieur ci-dessus, ressenti par les
nanoparticules.
Premièrement, en plus de la distance
perpendiculaire z, le potentiel d'interaction dépend naturellement de la
séparation L entre les parois réfléchissantes et de la
constante couplage de surface w.
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 104
Deuxièmement, le potentiel à un corps
passe par un seul minimum situé à z =
0. De plus, il est symétrique autour du point
minimum.
Troisièmement, la remarque est que la
profondeur de potentiel, |U0|, dépend de trois
types de paramètres, qui sont la température absolue T,
la constante de couplage de surface et l'épaisseur du film L.
Par exemple, si T et w sont fixées, la profondeur du
potentiel est inversement proportionnelle à la séparation
L. Cela signifie que le potentiel externe ressenti par les perles n'a
de valeurs appréciables, que pour des membranes se trouvant dans des
fentes très étroites. Si T et L sont maintenant
fixées à certaines valeurs, la profondeur du potentiel augmente
linéairement avec la constante de couplage surface
w.
Quatrièmement, nous soulignons que
|U0| doit être petite, en comparaison avec
l'énergie thermique kBT. Cela implique que la constante de
couplage de surface w !doit bornée supérieurement,
c'est-à_dire w < w* = L
x 2ð/3.
Enfin, comme il se doit, en l'absence d'interactions
entre colloïdes et membrane (w =
0), le potentiel à un corps disparaît. Le potentiel
(réduit) ressentis par les nanoparticules,
U(z)/kBT, en
fonction de la distance perpendiculaire renormalisée, z/L, est
celui représenté sur la Fig.
4.1, pour deux valeurs de la constante de
couplage de surface : w1 = 0, 5
x L et w2 = 0, 9
x L. La courbe dessinée avec le paramètre
w2 est naturellement en dessous de celle avec une
constante de couplage de surface w1 <
w2.
L'expression ci-dessus du potentiel à un corps
est l'ingrédient principal pour l'étude de la dynamique Browienne
des particules de très faible densité, qui sont situées
à proximité d'une membrane souple. Mais, afin de faciliter les
calculs et obtenir des résultats exacts, l'expression ci-dessus pour le
potentiel extérieur doit
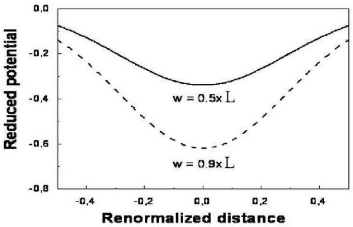
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 105
est la constante élastique. La relation
précédente montre que la constante élasique
FIG. 5-1 -- Le potentiel (réduit) ressentis par
les nanoparticules, en fonction de la distance perpendiculaire
renormalisée, z/L , pour deux valeurs de la constante de couplage de
surface : w1 = 0, 5 x L et w2 =
0, 9 x L
être simplifiée. Puisque l'essentiel du
phénomène se produit dans l'intervalle |z| < î?
= L/2V3, un tel potentiel
peut être approximé par [22]
U (z) ' Uo +
W (z) , z < î? ,
(4.8)
avec le potentiel harmonique
1
W(z) =
2kz2 , (4.9)
où
k = - U° =
121J2ð
L3kBT > 0 (4.10)
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 106
k se comporte, en fonction de la
séparation L, comme k ~
L-3.
.3 Evolution temporelle de la densité de
particules.
Considérons est une suspension colloïdale,
de très faible densité, qui est au contact d'une membrane fluide
fluctuante. Sous un changement d'un certain paramètre physique
convenable (la température, par exemple), le système est hors
équilibre. Maintenant, nous nous intéressons à
l'évolution dans le temps de la densité de particules, avant que
la suspension colloïdale atteigne son état d'équilibre
final. Hors équilibre, cette densité dépend de la distance
perpendiculaire z, à partir du plan horizontal localisé
à z = 0, et du temps t. La
densité de particules, n (z, t)
représente le nombre de colloïdes par unité de
volume, à la distance z et au temps t. Pour simplifier
l'étude, nous considérons que la suspension est de très
faible densité, c'est-à-dire qu'l n'y a pas d'interactions
mutuelles entre particules. Donc, la seule interaction induite entre les
petites particules est un potentiel externe causé par les ondulations de
la membrane.
.3.1 Equations de base.
neq
(z) =
Aexp{-kBT
1 , (4.11)
Nous rappelons l'expression de la densité de
particules à l'équilibre
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 107
où A est une constante de normalisation, et U
(z) est un potentiel à un corps
(attractif ), développé par la membrane fluctuante. La
densité de particules à l'équilibre peut s'écrire
comme
|
neq
(z) ' no exp
|
1
_W
(z) , (4.12)
kBT
|
où le potentiel harmonique W
(z) est celui défini par la relation
(4.9). Dans la relation
(4.12), no n'est
rien d'autre que la valeur maximale de la densité de particules à
l'origine z = 0. Par conséquent, la formule
(4.12) peut être supposée
valable, pour toutes les valeurs de z, et en particulier, n
(oo) -* 0.
Quand la dispersion colloïdale est hors
équilibre, en plus de distance, la densité dépend du
temps. Cela veut dire que les nanoparticles sont sujet d'une dynamique
Brownienne, en présence du potentiel harmonique W
(z). Pour calculer cette densité
locale, nous rappelons que le phénomène de diffusion peut
être correctement décrit par la loi de Fick. Cette dernière
suggère que, si la densité est non uniforme, le flux, j
(z, t), est directement proportionnel au
gradient spatial de la densité, c'est-à-dire
j = _D?n_ 1?W
(4.13)
?z æ ?z .
C'est la loi de Fick modifiée. Ici, le coefficient
de diffusion D est donné par
kBT
D = æ . (4.14)
C'est la relation d'Einstein
(théorème de fuctuation-dissipation
[28, 29]), qui affirme que la
quantité D caractérisant le mouvement thermique est reliée
au coefficient de friction æ, qui spécifie la réponse
à une force extérieure. Le coefficient de diffusion
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 108
ou diffusivité des particules, D, contient
alors toutes les informations concernant les propriétés
statistiques des particules. Notons que, plus ce coefficient de diffusion est
important, plus importante sera la vitesse à laquelle se
déplacent les particules. Pour une température plus
élevée, les particules diffusent beaucoup, par contre, pour des
solutions plus visqueuses, les particules diffusent moins. Le signe moins
indique que le courant des particules se déplace des zones
où la concentration en particules est élevée vers les
zones où elle est faible. Revenons au coefficient de friction æ
(æ-1 étant la
mobilité), et rappelons que si les particules sont assimilées
à des billes de rayon a, ce coefficient a pour expression [37]
: æ = 6ðçsa,
où çs est la viscosité du
solvant.
En plus, nous avons l'équation de
continuité, ou la loi de conservation des espèces (la variation
de la quantité d'espèces dans un volume est égale au bilan
de flux entrant et sortant),
|
?n
+
?t
|
?j ?z
|
= 0 . (4.15)
|
Une combinaison des relations
(4.13) et (4.15)
donne l'équation de Smoluckowski (à une
dimension)
1n
?z
Ç kBT ?z +
n
?n
?t =
?z) , (4.16)
satisfaite par la densité de particules locale
n (z, t). A l'équilibre, nous avons
?n/?t = 0, et alors, le vecteur densité de courant de
particule j ne dépend ni du temps, ni de la position. Dans ces
conditions, l'équation différentielle
(4.16) devient :
kBT?n/?z+n? W/?z = 0, dont la
solutution est neq (z) =
no exp {-W (z)
/kBT}.
Si nous remplaçons le potentiel harmonique W
(z) par sa forme explicite
(4.9),
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 109
nous obtiendrons
|
?n D?2n
?t=?z2 +
|
kæ z
|
?n
+ ?z
|
kæ n . (4.17)
|
1 (L)3, ôf = =
V
32ð
(L)3<ôi , (4.22)
w% f
æ 2ð
ôi = ki 3
Cette nouvelle équation de Smoluckowski doit
satisfaire les deux conditions aux limites
n (z,t = 0) = ni
(z) , n (z,t =
oo) = nf (z) .
(4.18)
Si la température T et la séparation L
sont fixées, les densités de particules initiale et finale
à l'équilibre, ni (z) et nf
(z), sont complitement
déterminées par les constantes de couplage de surface initiale et
finale w% et wf. Par conséquent, la dynamique
Browienne peut être causée par un changement de l'environnement
membranaire.
Un calcul algébrique simple donne la solution
suivante [22]
[ni (y) - nf
(y)
(4.19)
où les deux densités de particules à
l'équilibre initiale et finale sont données par
" #
T 2
n (z, t) = nf
(z)+et/ôf
[2ðDô (e2t/ôf -
1)]-1/2 +8 dy exp
- (zet/ f - y)
2Dôf (e2t/ôf -
1)
-8
|
kiz2 _
ni (z) =
ñô exp { - 2kBT }
= ñio exp
|
{ }
-z2
, (4.20)
2Dôi
|
z2-z2
nf (z) =
ñô _ eXp { -- 2kBT }
-- ñfO exp {
2Dôf } . (4.21)
avec les échelles de temps ôi et ôf.
Explicitement, nous avons
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 110
où w. et wf > wi sont les
constantes de couplage de surface initiale et finale. Cela veut dire que
l'interaction colloïde-membrane est soudainement augmentée de w.
à wf. Comme il devrait être, le temps ô
dépend des caractéristiques de la membrane fluide, et de ses
interactions avec les petites particules, à travers la rugosité
moyenne î?, et la constante de couplage de surface w. En particulier,
ôf peut être interprété comme un temps
au-delà duquel le système colloïdal atteint son état
d'équilibre final. Les fortes ondulations de la membrane (ou les fortes
intéractions colloïdes-membrane) nécessitent un petit temps
avant que le système colloïdal atteigne son état
d'équilibre final. En fait, l'échelle de temps ôf
peut avoir une autre signification physique, et peut être
regardée comme un temps pour que les particules occupent les nouveaux
trous et vallées de la membrane.
Une intégration sur la variable y dans la
relation (4.19) donne la forme de la
densité de particules temporelle
" 2
n (z, t) = no
[1 + ç
(e-2t/ôf
- 1)]-1/2 exp
-1 + ç (e2t/ôf _
1) (
2Dôi) ,
(4.23)
avec le temps réduit
|
ç=
|
ôi - ôf
ôi
|
=
|
w. wf
|
> 0 . (4.24)
|
r r+8
Jni (z) dz
= J dznf (z) -
.
+00
(4.25)
La notation est l'adsorbance
moyenne. Cette dernière est définie comme le
nombre
En utilisant la loi de consevation de la matière,
nous trouvons que
Chapitre 4 : Dynamique Brownienne de colloïdes
au contact d'une biomembrane confinée. 111
total de colloïdes (par unité d'aire)
localisés près de l'interface
! !
2ðDôfnf ~ =
2ðDôini ~ = F .
(4.26)
Le résultat (4.23)
appelle les remarques suivantes.
Premièrement, il est facile de vérifier
que la solution (4.23) satisfait les deux
conditions aux limites (4.18), où les
états à l'équilibre initial et final sont définis
par les relations (4.20) et
(4.21).
Deuxièmement, quant la densité de
particules est réduite par ni, elle devient une
fonction d'échelle universelle, indépendamment de tous
les détails particuliers de la membrane, et de ses interactions avec les
colloïdes. Cette fonction dépend de trois facteurs sans dimensions,
qui sont la distance renormalisée
z/v2Dôi, le rapport de temps t/ôf
et l'écart réduit ç = (ôi
- ôf) /ôi. Notons que tous
les détails microscopiques (interactions membrane-colloïde) sont
entièrement contenus dans ôi et
ôf.
Finalement, nous notons que la courbe
représentant la densité de particules temporelle, à temps
fixé, atteint un maximum unique à z = 0, et
présente une symétrie autour de ce même point, pour toutes
les valeurs de t/ôf et ç.
Dans la Fig. 4.2,
nous reportons la densité de particules temporelle réduite, n
(z, t) /ni, en fonction
de la distance renormalisée z/v2Dôi, en
choisissant trois valeurs du rapport de temps t/ôf :
0, 0.5, et oo. La
première et la troisième valeur correspondent, respectivement,
aux états initial et final. Ces courbes sont tracées avec le
paramètre ç = 0.5.

hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 112
FIG. 5-2 -- la densité de particules
temporelle réduite, n (z, t)
/ni, en fonction de la distance renormalisée
z/v2Dôi, en choisissant trois valeurs du
rapport de temps t/ôf : 0 ( ligne
pointillée ) , 0.5 (
ligne continue), et 8 (ligne en pointillée). La première et la
troisième valeurs correspondent, respectivement, aux états
initial et final. Ces courbes sont tracées avec le paramètre
ç = 0.5 (wf
= 2wi)
.4 Conclusions.
Ce travail est consacré à l'étude
de la dynamique Brownienne de petites particules colloïdales, qui sont au
contact avec une membrane fluide pénétrable attractive. Le
liquide hôte est délimité par deux parois parallèles
séparées par une distance finie. La membrane entourée par
des colloides est confinée si seulement si l'épaisseur de la
bicouche est plus petite que la rugosité moyenne en volume de la
membrane.
La physique a été discutée, en
fonction de trois paramètres pertinents, qui sont la
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 113
Enfin, notons que, quand la séparation L est
beaucoup plus grande que la rugosité
température absolue, T, la séparation
entre les parois, L, et l'amplitude d'interaction colloïde-membrane, w.
Dans notre étude, nous avons fixé la température et
l'épaisseur du film à quelques valeurs, et varié la
constante de couplage de surface. Cela peut être réalisé
expérimentalement en changeant l'environnement de la membrane (force
ionique).
Pour la présente étude, nous avons fait
trois hypothèses : (i) les particules sont ponctuelles, (ii) de
très faible densité (pour ignorer leurs interactions mutuelles),
et (iii) interagissent fortement avec la membrane. Pour accomplir
l'étude de la dynamique Brownienne, nous avons été
utilisé un formalisme théorique basé sur l'équation
de Smoluchowski. Cette dernière est satisfaite par la densité de
particules temporelle, à laquelle nous nous étions
intéressés. Nous avons calculé cette quantité
physique exactement, autour du plan d'équilibre où l'essentiel du
phénomène se produit. Dans ce domaine, le potentiel externe de la
force moyenne a été approximé par un potentiel harmonique.
Cela signifie que nous étions en présence de particules
Browniennes se mouvant dans un potentiel harmonique. En plus de la diffusion
habituelle, ces particules effectuent de petites oscillations, avec une
fréquence se comportant comme /ù ~
w/L3. Comme nous avons montré, la
densité de particules dépend du temps et de la distance
perpendiculaire, et fait intervenir un temps caractéristique se
comportant comme ô ~ L3/w.
Nous avons interprété cette échelle de temps comme la
durée au bout de laquelle les nanoparticles atteignent leur état
d'équilibre final . Aussi, elle peut être considéré
comme le temps où les particules sont piégées dans les
nouveaux trous et vallées, de taille légèrement plus
petite que l'épaisseur du film L.
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 114
en volume, î1, en plus des
paramètres évoqués ci-dessus, le phénomène
physique dépend des caractéristiques de la membrane (à
travers les constantes élastiques de la membrane). Dans ce cas, la
dynamique Brownienne peut être aussi causée par un changement de
ces paramètres.
Comme dernier mot, nous soulignons que les
résultats obtenus dans ce chapitre, peuvent être étendus
à des bicouches de tensio-actifs, bien que les deux systèmes ne
soient pas des mêmes structure et composition.
·
115
Bibliographie
[1] Y. Madmoune, K. El Hasnaoui, A. Bendouch, H. Kaidi,
M. C hahid, M. Benha-mou, African Journal of Mathematical Physics 8, 91
(2010).
[2] M.S. Bretscher, S. Munro, Science 261, 12801281
(1993).
[3] J. Dai, M.P. Sheetz, Meth. Cell Biol. 55, 157171
(1998).
[4] M. Edidin, Curr. Opin. Struc. Biol. 7, 528532
(1997).
[5] C.R. Hackenbrock, Trends Biochem. Sci. 6, 151154
(1981).
[6] C. Tanford, The Hydrophobic Effect,
2ème édition, Wiley, 1980.
[7] D.E. Vance, J. Vance, éditeurs,
Biochemistry of Lipids, Lipoproteins, and Membranes, Elsevier,
1996.
[8] F. Zhang, G.M. Lee, K. Jacobson, BioEssays 1 5,
579588 (1993).
[9] S. Safran, Statistical Thermodynamics of
Surfaces, Interfaces and Membranes, Addison-Wesley, Reading, MA,
1994.
[10] W. Helfrich, Z. Naturforsch. 28c, 693
(1973).
[11] U. Seifert, Advances in Physics 46, 13
(1997).
[12]
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 116
H. Ringsdorf, B. Schmidt, How to Bridge the Gap
Between Membrane, Biology and Polymers Science, P.M.Bungay et al., eds,
Synthetic Membranes : Science, Engineering and Applications, p. 701, D.
Reiidel Pulishing Compagny, 1986.
[13] D.D. Lasic, American Scientist 80, 250
(1992).
[14] V.P. Torchilin, Effect of Polymers Attached
to the Lipid Head Groups on Properties of Liposomes, D.D. Lasic and Y.
Barenholz, eds, Handbook of Nonmedical Applications of Liposomes, Volume
1, p. 263, RCC Press, Boca Raton, 1996.
[15] R. Joannic, L. Auvray, D.D. Lasic, Phys. Rev.
Lett. 78, 3402 (1997).
[16] P.-G. de Gennes, Scaling Concept in Polymer
Physics, Cornell University Press, 1979.
[17] C. Fradin, A. Abu-Arish, R. Granek, M. Elbaum,
Biophys. J. 84, 2005 (2003).
[18] D.F. Evans, H. Wennerstrom, The Colloidal
Domain, Wiley, New-York, 1999.
[19] T. Bickel, M. Benhamou, H. Kaïdi, Phy. Rev.
E 70, 051404 (2004).
[20] H. Kaidi, T. Bickel, M. Benhamou, Europhys.
Lett. 69, 15 (2005).
[21] A. Bendouch, H. Kaidi, T. Bickel, M. Benhamou,
J. Stat. Phys. : Theory and Experiment P01016, 1 (2006).
[22] A. Bendouch, M. Benhamou, H. Kaidi, Elec. J.
Theor. Phys. 5, 215 (2008).
[23] A. Einstein, Ann. Physik. 17, 549 (1905) ; 19,
371 (1906) ; voir, aussi, Investigation on the Theory of the Brownian
Movement, E.P. Dutton and Copy Inc, New York, 1926.
[24] N. Wax, Noise and Stochastic Processes,
Dover Publishing Co., New York, 1954.
[25] M. Lax, Rev. Mod. Phys. 32, 25 (1960) ; 38, 541
(1966).
[26]
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 117
R. Kubo, Rep. Prog. Phys. 29, 255 (1966).
[27] C.W. Gardiner, Handbook of Stochastic
Methods, 3ème édition, Springer, 2004.
[28] H. Risken, T. Frank, The Focker-Planck
Equation : Methods of Solutions and Applications, 2ème
édition, Springer, 1989.
[29] M. Doi, S.F. Edwards, The Theory of Polymer
Dynamics, Clarendon Press Oxford, 1986.
[30] P.B. Canham, J. Theoret. Biol. 26, 61
(1970).
[31] K. El Hasnaoui, Y. Madmoune, H. Kaidi, M.
Chahid, M. Benhamou, African Journal of Mathematical Physics
8, 101 (2010).
[32] K. Binder, dans : Phase Transitions and
Critical Phenomena, Volume 8, édité par C. Domb et J.L.
Lebowitz, Academic Press, London, 1983.
[33] H.W. Diehl, dans : Phase Transitions and
Critical Phenomena, édité par C. Domb et J.L. Lebowitz,
Volume 10, Academic Press, London, 1986.
[34] S. Dietrich, dans : Phase Transitions and
Critical Phenomena, édité par C. Domb et J.L. Lebowitz,
Volume 12, Academic Press, London, 1988.
[35] C. Itzykson, J.-M. Drouffe, Statistical
Field Theory : 1 and 2, Cambridge University Press,
1989.
[36] J. Zinn-Justin, Quantum Field Theory and
Critical Phenomena, Clarendon Press, Oxford, 1989.
[37] G.K. Batchelor, An Introduction to Fluid
Dynamics, Chap. 4, Cambridge University Press, 1970.
Chapitre 6
Mécanique Statistique des
membranes confinées dans un
liquide trouble.
Dans ce chapitre, qui consiste notre
troisième contribution originale, nous étudions les
effets d'impuretés sur les propriétés statistiques des
membranes fluides. Celles peuvent être attractives ou
répulsives.
En premier lieu, nous déterminons la
rugosité moyenne de la membrane, en combinant la technique des
répliques avec la méthode variationnelle. Le résultat
s'exprime en fonction de la concentration des impuretés et l'amplitude
de leur interaction avec la membrane. En second lieu, nous déterminons
la taille d'une vésicule isolée, en fonction de ces mêmes
paramètres. Enfin, l'étude est étendue à
l'adhésion membranaire.
Pour plus de détails, nous renvoyons le lecteur
à la Réf. [1].
hapitre 5 : Mécanique Statistique des
membranes confinées .. 119
6.1 Introduction
En général, un milieu aqueux qui
supporte des membranes biologiques est supposé homogène. En fait,
tout système réel contient obligatoirement des impuretés.
Dans la plupart des circonstances, on essaie de les éliminer, sous des
conditions bien contrôlées. Mais, si ces entités sont
présentes, il est aussi intéressant d'étudier leurs effets
sur les propriétés statistiques des biomembranes, tel que le
spectre de fluctuations et le comportement dynamique. Dans le cas
général, les inhomogénéités
aléatoires ont tendance à provoquer le désordre du
système. Il est important de faire une distinction entre deux
états de désordre : recuit et trempé. Le
premier est utilisé, lorsque les impuretés et les constituants
hôte (phospholipides) sont en équilibre [2]. Cela
signifie que leurs mobilités respectives sont comparables. Si ce n'est
pas le cas, ces constituants hôte et les impuretés sont hors
équilibre, et le désordre est plutôt trempé
[2]. Lorsque la Mécanique Statistique est
utilisée, celle-ci consiste à faire la trace sur toutes les
ondulations membranaires, avant d'effectuer la sommation sur le désordre
des impuretés. Bien que le désordre trempé soit plus
difficile à analyser, il reste plus réaliste que son homologue
recuit. En effet, la thermique et l'étalement du bruit ont des
rôles très différents.
Dans ce chapitre, le système physique que nous
considérons est une membrane fluide (presque-plane ou fermée),
trompée dans un milieu aqueux trouble. Ce dernier est
imprégné par une faible quantité d'impuretés, qui
peuvent être attractives ou répulsives vis-à-vis de la
membrane. L'objectif est de montrer comment ces entités peuvent modifier
les propriétés statistiques de la membrane fluide. Ces
propriétés seront étudiées à travers
l'amplitude de fluctuations. Afin de modéliser le
système,
hapitre 5 : Mécanique Statistique des
membranes confinées .. 120
nous supposons que les impuretés agissent comme
un potentiel aléatoire externe, avec une distribution Gaussienne
(désordre non corrélé). En outre, nous supposons
que le désordre est trempé. Pour faire les calculs, nous
utilisons la théorie mathématique des répliques
[3, 4], basée sur une
méthode analytique, combinée avec la méthode
variationnelle, généralement rencontrée en
Mécanique Quantique [5] et en Phénomènes
Critiques [6, 7].
Dans ce chapitre, nous calculons, dans un premier
temps, la rugosité moyenne d'une membrane quasi-plane, en fonction des
paramètres primitifs de la membrane pure (sans
impuretés) et un certain paramètre dépendant de la
fraction volumique d'impuretés et l'amplitude de leur force
d'interaction avec la membrane. La conclusion essentielle est que les
impuretés attractives augmentent les fluctuations de la forme dues aux
ondulations thermiques, alors que les impuretés répulsives ont
tendance à supprimer ces fluctuations, et conduisent alors au
confinement de la membrane. En second lieu, nous analysons les effets
d'impuretés sur la forme d'équilibre des vésicules
(fermées), à travers la résolution de l'équation de
courbure (pour les vésicules sphériques). Nous montrons que la
vésicule est plus stable en présence d'impuretés
répulsives, en comparaison avec celles attractives. En troisième
lieu, nous étendons l'étude à des phases lamellaires, qui
sont formées par deux membranes fluides parallèles. Nous montrons
que la présence des impuretés aléatoires affectent
drastiquement les propriétés physiques de l'adhésion
membranaire.
Ce chapitre est organisé comme suit. Dans la
Sec. II, nous décrivons les fondements du modèle
utilisé. La Sec. III traite du calcul de l'amplitude des
fluctuations d'une membrane fluide isolée presque-plane et du
diamètre à l'équilibre d'une vésicule
fermée, entourées par des impuretés attractives ou
répulsives. L'extension de
hapitre 5 : Mécanique Statistique des
membranes confinées .. 121
l'étude aux phases lamellaires est l'objectif
de la Sec. IV . Quelques remarques finales sont retracées dans
la dernière section.
6.2 Hamiltonien effectif.
Nous considérons une membrane fluide
fluctuante, immergée dans un liquide à trois dimensions, qui
contient de très petites impuretés. Pour simplifier
l'étude, nous supposons que les impuretés sont
ponctuelles.
Dans la représentation de Monge, un point de
l'interface peut être repéré par les coordonnées
(x, y, h (x,
y)). Ici, (x, y)
représentent les coordonnées sur le plan de projection,
et h (x, y) la fonction
hauteur pouvant prendre des valeurs positives ou négatives.
Dans ce qui suit, nous adopterons la notation (r, z
= h
(r)), où r
= (x, y) ? R2
est le vecteur transverse et z la distance
perpendiculaire au plan de projection.
La Mécanique Statistique des membranes fluides,
sans impuretés, est basée sur l'énergie libre de courbure
de Canham-Helfrich [8]
~ ~ê 2
h2
Ho [h] =
d2r 2
(?h)2 + ~ ,
(5.1)
avec ê la constante de rigidité
de courbure, et u > 0 est le paramètre de
confinement. La membrane est supposée sans tension. En fait, cette
supposition ne change pas les conclusions faites ci-dessous. Le terme de
confinement est responsable de la localisation de la membrane dans quelque
région de l'espace Euclidien, où elle fluctue autour d'un plan
d'équilibre. Pour modéliser les effets d'impuretés sur les
propriétés statistiques du système, nous supposons que
celles-ci ont tendance à renforcer le
hapitre 5 : Mécanique Statistique des
membranes confinées .. 122
confinement de la membrane, si elles sont
répulsives, et elles rendent cette membrane plus libre, si les
particules sont plutôt attractives. Ces tendances peuvent être
expliquées par le fait que le paramètre température est
supposé local dans l'espace, et en faisant la substitution
u (r) = u +
V (r) . (5.2)
Le déviation V (r)
peut être regardé comme un potentiel externe
aléatoire. Pour simplifier, la distribution de probabilité
correspondante est supposée être Gaussienne (désordre
non carrelées), et l'on a alors
V (r) = 0 , V
(r) V
(r') = -vä2
(r - r') . (5.3)
Ici, -v est une constante positive, qui est
proportionnelle à la concentration des impuretés et à
l'amplitude de leur force d'interaction avec la membrane. La notation
ä2 (r) signifie la fonction de Dirac
à deux dimensions.
Par conséquent, le Hamiltonien de
Canham-Helfrich revêt la nouvelle forme suivante
~ ~ê
~
H [h] =
d2r 2
(?h)2 + 2 1 (~ + V
(r)) h2 .
(5.4)
Pour des impuretés répulsives, il suffit
de remplacer V (r) par iV
(r), avec i2 =
-1. Puisque la distribution de désordre est
Gaussienne, tous ses moments impairs sont nuls. Cela implique que toutes les
grandeurs physiques calculées avec le potentiel imaginaire pur iV sont
des nombres réels.
hapitre 5 : Mécanique Statistique des
membranes confinées .. 123
Les impuretés et la membrane ne sont pas en
équilibre, donc le désordre est plutôt
trempé. Dans ce cas, nous n'avons pas à moyenner la
fonction de partition, Z, mais plutôt son logarithme, ln
Z. Ce dernier, définit l'énergie libre. La fonction de
partition, à une configuration d'impuretés donnée,
s'écrit
Z =
Dhe-A[h]
, (5.5)
avec l'action
A [h] =
l~B[T =
d2r
(?h)2 +
2 +
V~(r)h2
. (5.6)
Nous avons utilisé les notations
|
~ê =
|
ê
|
|
u=
|
u
|
|
V~= V
kBT . (5.7)
|
|
|
|
|
|
kBT ,
|
kBT ,
|
En terme du potentiel aléatoire réduit, V,
la deuxième loi du désordre apparaissant
dans la relation
(5.3), devient : V
(r) V~
(r') = -vä
(r - r'), avec la constante de
couplage renormalisée : v = v/
(kBT)2. Une simple
analyse dimensionnelle montre que :
[îZ] = L0,
[u] =
L-4 et
[v] =
L-s, avec L une certaine
longueur pouvant être l'épaisseur de la membrane.
Pour calculer la moyenne ln Z, la
procédure standard consiste à utiliser la méthode des
répliques [3], basée sur la limite
|
ln Z = lim
n?0
|
Zn - 1
|
|
(5.8)
|
|
n
|
.
|
hapitre 5 : Mécanique Statistique des
membranes confinées .. 124
En moyennant sur le désordre, l'on
obtient
~Zn =
Dh1...Dhne-A[h~,...,h~]
,(5.9)
avec l'action effective, obtenue après n
répliques,
A [h1, ...,
hn] = f d2r $2
~
(?há)2 +
2 h2á +
v8 ~ ha (2_,
h2â ,

á=1
á=1
á=1â=1
(5.10) où les indices grecs désignent
les répliques. Le dernier terme est responsable de l'interaction
effective entre les répliques, dues à la présence
d'impuretés (i < 0). L'action
ci-dessus décrit des impuretés attractives. Pour des
impuretés répulsives, le couplage i doit être
remplacé par -v. L'apparition de ce terme signifie que la
présence des impuretés augmente l'entropie, si elles sont
attractives, et la diminue lorsqu'elles sont répulsives.
Au paragraphe qui suit, l'objectif est une
détermination quantitative du spectre de fluctuations d'une membrane
presque-plate, en présence d'impuretés.
6.3 Membranes presque-plates isolées.
Nous commençons en considérant des
impuretés attractives. Bien sûr, l'intégrale fonctionnelle
(5.9) ne peut être calculée
exactement. Pour faire les calculs, nous ferons usage de la méthode
variationnelle. Pour cela, nous introduisons l'action d'essai
suivante
hapitre 5 : Mécanique Statistique des
membranes confinées .. 125
[h1, ..., hn] =
f d2r
n n
Aç
[jz
E
(?há)2 + 2
E h2á ,
(5.11)
á=1 á=1
avec le nouveau paramètre de confinement
ri. Avec cette action, la fonction de partition, Zç,
est exacte, et nous avons
Zç =
(Zo)n , (5.12)
où
f { f
1~ê ]~
Z = Dhexp -
d~r 2 (?h)~ +
~ç
2h
(5.13)
est la fonction de partition habituelle d'une membrane
libre.
Introduisons alors la valeur moyenne d'une
fonctionnelle X [h1, ...,
hn], calculée avec l'action Aç
[h1, ...,
hn],
(X)0 = Zç f
Dh1...DhnX
[hl, ..., hn] exp
{-Aç [h1, ...,
hn]1 . (5.14)
En terme de cette valeur moyenne, la fonction de
partition moyenne s'écrit
Zn = Zç (exp
{- (A -
Aç)1)0 .
(5.15)
En utilisant l'inégalité
standard
(eX)0
> e<X>o ,
(5.16)
hapitre 5 : Mécanique Statistique des
membranes confinées .. 126
nous obtenons
Zn = Zç exp {- (A -
Aç~0} . (5.17)
Cela implique
|
|
|
1 - Zn
|
|
1 - Zç exp{-(A -
Aç)0}
n
|
|
|
-ln Z = lim
n?0
|
= lim
n?0
|
. (5.18)
|
|
n
|
D'autre part, nous avons
$ %
(A - A00 = f d2r u
2 E
(h2á)o
+ 8 E E
(h2áh2â)0 .
(5.19)
á=1 á=1
â=1
Il est facile de voir que
|
En á=1
|
(h2)0
= nue , á
|
En
á=1
|
En â=1
|
(h2áh2â)0
= n (n + 2)
(u2)2 , (5.19a)
|
Avec le carré de la rugosité de la
membrane
u2(ç)
=8~ ê ç . (5.20)
A l'aide de ces considérations, nous trouvons
que
-ln Z = - ln
Zo + E I u 2 u2 +
4 (u2)2] , (5.21)
avec E l'aire d'un plan de
référence. Notons le second membre de cette
inégalité
hapitre 5 : Mécanique Statistique des
membranes confinées .. 127
dépend du paramètre variationnel ri. Une
assez bonne approximation de - ln Z est
- [ln Z] CM = min r-
ln Zo + Ó (ît 2
ç~2 + 4
(ó2)2)1 (5.22)
(L'indice CM est pour thorie de champ moyen). Le
paramètre variationnel ri est tel
que
ar- ln Zo + ÓI
~u 2ç ó2 + 4
(ó2)2)1 0 .
(5.23)
La combinaison de la relation
ó2 = - 2
Ó
~ln Zo
(5.24)
En introduisant le carré de la rugosité de
la membrane habituelle (sans impuretés),
et des formules (5.19)
et (5.19a) donne la
valeur minimale de ri, qui satisfait la relation suivante
~ç =
u + . (5.25)
Le carré de la rugosité de la membrane,
ó2, est donné par les
équations paramétriques
|
{ ó2 = 1 1
8 V ç /
~ç =
~~ +
~vó2
.
|
(5.26)
|
L'élimination de ri entre ces équations
aboutit à la relation implicite
|
ó2 = 1
8
|
1
(5.27)
Vê(~u+
vó2) .
|
hapitre 5 : Mécanique Statistique des
membranes confinées .. 128
Vó~ ~ = 1/8
~ê~~, nous obtenons la
relation importante
1
ó~ =
ó~ (5.28)
V1 + vó2/~~
,
ou encore
ó2
ó2
0
1
=(impurities attractives) ,
(5.29)
V1 -
wó2/óo ,
avec la nouvelle constante de couplage sans dimensions
w = -64I
(óg)3 >
0. Notons que la constante de couplage w > 0
est directement proportionnelle à la fraction volumique des
impuretés et à l'amplitude de leur force d'interaction avec la
membrane.
Le résultat obtenu
(5.29) appelle les remarques
suivantes.
Premièrement, il n'a de sens que si
ó2/ó < 1/w. Cette
condition est remplie pour de très faibles désordres (w est assez
petite).
Deuxièmement, puisque w est défini
positive, nous avons : ó2 >
óô. Une comparaison entre cette
inégalité et celle juste évoquée au-dessus implique
que 0 < w < 1. Troisièmement, si
nous choisissons comme variable x =
ó2/óô,
nous aurons
Par conséquent, w est en fonction de x
(Fig. 5.1). Cette formule peut être
expérimentalement utilisée pour estimer le couplage
d'impuretés w, à travers la mesure du rapport de rugosité
ó2/óô. Si w
est fixée à une certaine valeur, la variable x est
Chapitre 5 : Mécanique Statistique des
membranes confinées .. 129
alors solution de l'équation algébrique de
troisième degré
wx3 - x2
+ 1 = 0 . (5.31)
L'existence de ses racines dépend de la valeur
de la constante de couplage renorma-lisée w. Nous montrons qu'il existe
une valeur typique w* =
2/3V3 du couplage w séparant
différents régimes :
(i) w > w*
(désordre fort) : Dans ce régime, nous avons
une seule racine qui est négative ;
(ii) w = w*
(désordre moyen) : Dans ce cas, nous avons une
racine négative et une racine unique positive qui est x =
o2/o =
V3. Alors, la valeur maximale de la rugosité de
la membrane est o* =
31/4o0. Cette
contrainte signifie que la bicouche lipidique ne peut pas supporter les
ondulations de taille perpendiculaire supérieure à
o*. Ceci est réalisé si la fraction volumique
d'impuretés 0 est inférieure à une certaine valeur
0*, directement proportionnelle au seuil w*
;
(iii) w < w*
(désordre faible ) : Dans ce régime, nous
avons une racine négative et deux autres positives. Une seule racine
positive est acceptable (la plus petite). A cette racine particulière,
l'énergie libre -kBT [ln Z]
MF est minimale. Nous montrons que le
minimum absolu vérifie l'inégalité
Dans ce cas, le rapport
o2/o peut être obtenu en résolvant
numériquement l'équation algébrique
(5.31).
-4wx6 +
3x4 - 1 > 0
. (5.32)
hapitre 5 : Mécanique Statistique des
membranes confinées .. 130
Table 1
Certaines valeurs du couplage d'impuretés w et
les valeurs correspondantes du rapport de rugosité
u2/u2. Pour les impurities
attractives.
|
w
|
u2/uô
|
|
0.1
|
1.0575
|
|
0.15
|
1.0937
|
|
0.2
|
1.1378
|
|
0.25
|
1.1378
|
|
0.3
|
1.2715
|
|
w*
|
v3
|
Nous reportons, au Tab. I, certaines valeurs du
couplage d'impuretés w et les valeurs correspondantes du rapport de
rugosité
u2/u~~.
Il est facile de voir que ce rapport
u2/u augmente avec le couplage w, pourvu que w soit
dans l'intervalle w < w*.
Maintenant, pour des impuretés
répulsives, le rapport (5.28) doit
être remplacé
par
|
u2
u2
0
|
1
= (impuretés répulsives) ,
(5.33)
V1 +
wu2/u~o
|
ou d'une manière équivalente,
-wx3 - x2
+ 1 = 0 , (5.34)
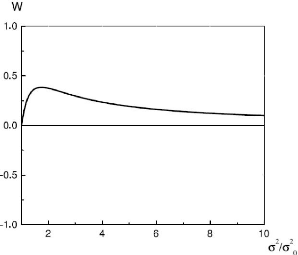
hapitre 5 : Mécanique Statistique des
membranes confinées .. 131
Comme il devrait être, la rugosité de la
membrane est réduite par la présence
FIG. 6-1 -- Le couplage d'impuretés w en
fonction du rapport de rugosité
o2/o2 , pour les
impuretés attractives .
avec la condition de stabilité
4wx6 +
3x4 - 1 > 0
. (5.35)
L'égalité (5.34)
peut être transformée en la forme suivante (Fig.
5.2)
1 - x2
w =
s (5.36)
x
avec x < 1 et w <
0.
hapitre 5 : Mécanique Statistique des
membranes confinées .. 132

FIG. 6-2 -- Le couplage d'impuretés w
en fonction du rapport de rugosité
u2/u2
, pour le cas impuretés répulsives .
d'impuretés répulsives,
c'est-à-dire u2 <
uô. En fait, l'effet de ces particules est de
renforcer le confinement de la membrane fluide considérée. Par
conséquent, la présence d'impuretés répulsives peut
être un mécanisme de confinement d'une membrane en bicouche. Dans
ce cas, il est facile de voir que l'équation algébrique a une
seule racine positive. Au Tab. II, nous donnons quelques valeurs du
couplage w et celles du rapport
u2/uô
correspondant.
Table 2
Certaines valeurs du couplage d'impuretés w
et les valeurs correspondantes du rapport de rugosité
u2/uô.
Pour les impurities répulsives.
hapitre 5 : Mécanique Statistique des
membranes confinées .. 133
Cette définition indique que l'objet principal
à calculer est la fonctionnelle généra-
|
w
|
ó2/ó~~
|
|
-0.1
|
0.9554
|
|
-0.15
|
0.9364
|
|
-0.2
|
0.9190
|
|
-0.25
|
0.9032
|
|
-0.3
|
0.8885
|
|
-0.4
|
0.8622
|
|
~~
ä~ln Z
[J]
~
G (r -
r') = ~
äJ (r)
äJ (r')
~
|
J=0
|
.
|
(5.38)
|
Une autre quantité physique
d'intérêt est la fonction de corrélation hauteur-hauteur :
G (r - r') =
(h (r) h
(r')) - (h
(r)) (h
(r')).
Cette dernière mesure les fluctuations de la fonction hauteur h
autour d'une certaine valeur moyenne (h). Ici, (.)
désigne la moyenne thermique, qui ne doit pas être confondue
avec la moyenne sur le désordre. Pour calculer les fonctions de
corrélation, nous partons de la fonctionnelle
génératrice
Z [J] =
Dh exp -A~
[h] +
d~rJ
(r) h
(r) ,
(5.37)
avec l'action Ao
[h] = xo
[h] /kBT, où
xo [h] est le Hamiltonien
standard de Canham-Helfrich, défini par la relation
(5.1). Ici, J
(r) est une source
couplée au champ h. Les dérivées fonctionnelles
de Z [J] par rapport
à la source J définissent toutes les fonctions de
corrélation hauteur-hauteur. En particulier, le propagateur est
donné
par
hapitre 5 : Mécanique Statistique des
membranes confinées .. 134
trice connexe ln Z
[J].
Pour déterminer ln Z
[J], nous utilisons la
méthode des répliques, qui consiste à calculer la
limite
|
|
Zn
[J] - 1
n
|
|
|
|
ln Z [J] =
lim
n?0
|
,
|
(5.39)
|
avec
contribuent pas au propagateur. Après avoir
effectué la limite n = 0, nous
trouvons
" #
r
Zn [J] =
f
Dh1...Dhn
exp -A [hi,
..., hn] + J
d2rJ
(r) hi
(r) , (5.40)
i=1
où A
[h1, ...,
hn] est l'action, relation
(5.10).
Notons que l'intégrale ci-dessus ne peut
être calculée exactement. Pour avoir une valeur approximative de
cette intégrale, nous utilisons la méthode standard du cumulant
[6, 7], basée sur la
formule
(exp {X})0
= exp {(X)0 +
(1/2!)
((X2)0 -
(X) ~ + ...} .
(5.41)
~
Nous montrons que
Zn [J]
^~ Zç (exp {n
fder
fd2r'J
(r) Go
(r - r') J
(r')
/2» , (5.42)
l o
avec la fonction de corrélation
habituelle
= f
d2qGo(r
- r')
eiq.(r-r')
(5.43)
(2ð)~~êq~
+ ~ç .
Dans la relation
(5.42), nous avons
négligé les termes d'ordres supérieurs en J, qui
ne
hapitre 5 : Mécanique Statistique des
membranes confinées .. 135
que la moyenne ln Z
[J] est telle que
ln Z [J]
- ln Zo+Ó
(;ó2 +
(ó2)2)
+ 2 fd2r
f
d2r'J
(r) Go
(r - r') J
(r') .
(5.44)
Par une simple dérivation fonctionnelle, nous
obtenons l'expression du propagateur
G(r -
r') = Go
(r - r') =f
q2~ (5.45)
(2ð) rie
+~ç .
Ainsi, le propagateur attendu s'identifie avec
l'usuel. Ici, le paramètre variationnel ~ç
satisfait la relation explicite
(5.24). De cette expression, nous
déduisons la rugosité ó
(~ç)
= G (0), qui est exactement définie
par la relation (5.20).
Le but du paragraphe suivant est une extension de
l'étude à des vésicules fermées. Plus exactement,
nous chercherons à quantifier les effets de la présence
d'impuretés sur leur forme d'équilibre.
6.4 Vésicules isolées.
D'entrée de jeu, nous rappelons que la forme
d'équilibre des vésicules peut être
déterminée en utilisant les techniques de la
Géométrie Différentielles.
Une vésicule est formée par deux
monocouches adjacentes (interne et externe). A leur tour, ces feuillets sont
formés de molécules amphiphiles. Naturellement, celles-ci
diffusent en permanence avec les molécules du milieu aqueux entourant la
membrane. Une telle diffusion provoque des variations thermiques (ondulations)
de la membrane. Cela veut dire que le dernière subit des variations
autour d'une configuration
hapitre 5 : Mécanique Statistique des
membranes confinées .. 136
F = 2 f
(2C)2 dA +
êG f KdA
+ fãdA + p
f dV . (5.48)
d'équilibre.
Considérons une biomembrane à topologie
arbitraire. Un point de cette membrane (surface) peut être décrit
par deux coordonnées locaux
(u1, u2).
A chaque point de la surface, il existe deux courbures particulières
(minimale et maximale), appelé courbures principales à la
surface [9], notées C1 =
1/R1 et C2 =
1/R2. Les quantités
R1 et R2 sont les rayons de
courbure principaux. Avec ces courbures principales, l'on construit deux
invariants, qui sont la courbure moyenne
1
C = 2 (C1 +
C2) , (5.46)
et la courbure Gaussienne
K =
C1C2 .
(5.47)
L'on a besoin d'un bon modèle, qui permet de
comprendre les propriétés géométriques et physiques
des biomembranes. Le modèle largement accepté est ce lui du
fluide mosaïque, proposé par Singer et Nicholson, en
1972 [10]. Ce modèle consiste à
considérer la membrane de la cellule comme une bicouche lipidique,
où les molécules de lipide peuvent diffuser librement sur la
surface de la membrane fluide, alors que les protéines et autres
molécules amphiphiles sont enfoncées dans les deux feuillets de
la bicouche lipidique. Nous rappelons que les propriétés
élastiques des biomem-branes en bicouche ont été
étudiées, pour la première fois, par Helfrich, en
1973 [8]. L'auteur proposa l'énergie libre de courbure
(sans impuretés) suivante
hapitre 5 : Mécanique Statistique des
membranes confinées .. 137
Ici, dA désigne
l'élément de surface sur la membrane, et V est le volume
délimité par la bicouche lipidique. Dans la définition
précédente, ê est la constante de rigidité
de courbure, qui contrôle l'amplitude des fluctuations thermiques de la
membrane, du fait qu'elle contient tous les détails microscopiques de la
bicouche, à savoir la rigidité et la longueur des chaînes
carbonées hydrophobes, la nature des interactions entre têtes
polaires, etc. D'ailleurs, les valeurs typiques de ce module varient de
quelques kBT, pour les membranes les plus souples, à
quelques dizaines de kBT, pour les membranes les plus
rigides. La valeur de ê dépend naturellement de la nature
des molécules de lipide formant la bicouche. Dans la définition
(5.48), êG est le
module élastique de Gauss, -y est la tension de surface, et
p est la différence de pressions entre les faces
extérieure et intérieure de la vésicule. Un calcul
variationnel, de premier ordre, donne l'équation de forme
d'équilibre des vésicules [11]
p - 2-yC +
4êC (C2
- K) + êV2
(2C) = 0 ,
(5.49)
avec l'opérateur de Laplace-Bertlami (de
surface)
|
V2 = 1
N/g
|
a ~N/ggij a ~ ,
(5.49a)
aui auj
|
où gij est le tenseur
métrique sur la surface, et g = det
(gij) est son déterminant.
Pour des vésicules ouvertes ou fermées avec une ligne de tension,
l'équation différentielle locale
(5.49) doit être
complétée par des conditions aux limites additionnelles que nous
n'écrivons pas [12]. L'équation
précédente a trois solutions analytiques, qui correspondent
à une sphère [11], au tore-N/2
[13 - 16], et au disque biconcave
[17].
hapitre 5 : Mécanique Statistique des
membranes confinées .. 138
~F ? F #177; kBT öCdA .
(5.52)
Pour le cas cylindrique (vésicules tubulaires),
l'une des deux courbures principales est nulle, et l'on a
1
C = - K = 0 ,
(5.50)
R
où R est le rayon du cylindre. Si nous ignorons
la condition aux frontières (supposition valable pour les très
longs tubes), la solution constante de l'équation
(5.49) est
4ê\
1/3
H = 2( I
p
(5.51)
où H est le diamètre à
l'équilibre. Nous avons négligé la tension de surface et
la contribution provenant de la courbure spontanée, pour avoir une
expression simplifiée du diamètre à
l'équilibre.
La relation précédente a de sens tant
que la différence de pressions est plus petite qu'une valeur critique
pc, donnée par [54] : pc
~
ê/R3. Cette
dernière est de 1 à 2Pa. La
signification de la pression critique est qu'au-delà de
pc, la vésicule est instable. Cela implique que le
diamètre à l'équilibre doit être plus grand qu'une
valeur critique Hc = 2
(4ê/pc)1/3.
Maintenant, nous supposons que la vésicule
fermée est immergée dans un milieu aqueux trouble,
c'est-à-dire renfermant des impuretés attractives ou
répulsives. Habituellement, on prend en considération la
présence des impuretés, par l'ajout d'un terme en couplant leur
fraction volumique, ö, et la courbure moyenne C de la membrane, à
l'énergie libre précédente F,
c'est-à-dire
hapitre 5 : Mécanique Statistique des
membranes confinées .. 139
Le signe positif est pour des impuretés
attractives, et le signe négatif pour les répulsives. La nouvelle
énergie libre est alors
F = 2 f (2C +
2Co)2 dA
+ êG fKdA +
f "-ãdA +
p f dV , (5.53)
avec la notation
Co = kBT ö
(5.54)
4ê , "-ã =
ã - 2êC2
o .
Alors, les impuretés produisent une courbure
spontanée.. Cela veut dire que celles-ci donnent lieu à une
asymétrie de la vésicule, quand sa membrane est traversée.
De plus, ces impuretés renormalisent additivement le coefficient de
tension interfaciale. La minimisation de la nouvelle énergie libre
donne
p - 2"-ãC +
ê (2C + Co)
(2C2 #177;
CoC - 2K) +
êv2 (2C) = 0
. (5.55)
Pour une vésicule sphérique, nous trouvons
que la solution est
2
ö2
R = 2
(2ã2 +
(kBT)2
16r~1 +
2kBTöp + 2ã +
(kBT)2
16ê . (5.56)
p /
Pour une fraction volumique très faible,
c'est-à-dire ö << 1, nous trouvons, au
premier ordre, que
R Ro
= 1 +
pgB2 ö +
C) (ö2) (5.57)
ã
hapitre 5 : Mécanique Statistique des
membranes confinées .. 140
ou encore
|
~~~~
|
R - Ro
|
~~~~
|
? pkB2 0 . (5.58)
8'y
|
|
Ro
|
membrane immergée dans un milieu aqueux, qui est
imprégné par de petites impu-
Les signes + et - sont pour
impuretés attractives et répulsives, respectivement. Ici
Ro = 2'y/p désigne le rayon à
l'équilibre d'une vésicule en l'absence d'impuretés. Les
résultats ci-dessus appellent les remarques suivantes.
En premier lieu, comme il se doit, le rayon
d'équilibre de la vésicule augmente avec la fraction volumique
d'impuretés, lorsqu'elles sont attractives. Cela signifie que la
vésicule est gonflée, mais son rayon reste proche du rayon non
perturbé Ro, tant que la fraction volumique
d'impuretés est très faible. Pour les impuretés
répulsives, toutefois, l'on assiste à l'effondrement de la
vésicule.
En second lieu, la formule
(5.57) n'a de sens que lorsque la
fraction volumique 0 est inférieure à un certain seuil
0* =
8'y2/kBTp. Celle-ci doit
être naturellement faible devant l'unité. Cela implique que la
tension de surface ne doit pas dépasser !une certaine valeur
typique 'y* =
kBTp/8.
Enfin, à une fraction de volume fixée
0 < 0*, la formule
(5.58) peut être
utilisée pour estimer la valeur expérimentale du rapport
p/'y2, par une simple mesure des rayons
d'équilibre R (avec impuretés) et Ro
(sans impuretés).
Le paragraphe suivant sera consacré à
l'étude des phases lamellaires, constituées de deux bicouches
lipidiques parallèles.
6. 5 Phases lamellaires.
La question naturelle est l'extension de l'étude
au cas où nous avons plus d'une
hapitre 5 : Mécanique Statistique des
membranes confinées .. 141
retés aléatoires.
Dans notre analyse, nous partons d'une phase
lamellaire composé de deux membranes fluides parallèles (neutres)
sans impuretés. Les effets de ces entités sur la physique seront
discutées ci-dessous. La cohésion entre ces membranes en bicouche
est assurée par des interactions attractives de van der Waals
[18], qui sont équilibrées, à courte
distance de séparation, par une répulsion forte provenant des
forces d'hydratation [19] et des fluctuations de forme
stériques résultant des ondulations membranaires
[8].
Pour deux bicouches lipidiques parallèles
séparées par une distance finie l, l'énergie
totale d'interaction (par unité d'aire) est donnée
par
V (l) =
VH (l) + VW
(l) + VS
(l) .
(5.59)
Le premier terme représente l'énergie
d'hydratation, qui agit à petite distance de séparation (de
l'ordre de 1nm). Ces forces d'hydratation ont
été découvertes pour les multi-bicouches sous contrainte
externe [18]. La forme proposée pour cette
énergie est
VH (l) =
AHe-l/ëH . (5.60)
Les valeurs typiques de l'amplitude AH et de
la portée ëH sont de l'ordre de AH ?
0.2J/m2
et ëH ?
0.3nm.
Le deuxième terme désigne
l'énergie d'interaction de van der Waals, qui résulte de la
polarisabilité des molécules lipidiques et aussi de celle des
molécules d'eau. Cette énergie d'interaction a la forme
standard
hapitre 5 : Mécanique Statistique des
membranes confinées .. 142
VW (l) =
-12ð
I_l2-2
(l + ä)2 + (l
+ 2ä)2] . (5.61)
La constante d'Hamaker est dans l'intervalle W '
10-22 -
10-2iJ. Dans l'expression
ci-dessus, l'épaisseur de la bicouche lipidique ä est de l'ordre de
ä ' 4nm.
Le troisième terme représente
l'énergie d'interaction stérique, qui est due aux ondulations de
la membrane. D'après Helfrich [8], cette énergie
(par unité d'aire) est donnée par
2
Vs (l) =
cH.
(kBT)2
Ici, kB est la constante de Boltzmann, T est
la température absolue, et ê est le module de courbure usuel des
deux membranes. Pour deux bicouches ayant des constantes de rigidité de
courbure êi et ê2, nous avons
ê = êiê2/
(êi + ê2). La
valeur précise du coefficient cH est encore sujet de
controverses. En effet, d'après Helfrich cH '
0.23 [8], mais les simulations
numériques prédisent des valeurs bien inférieures,
à savoir cH ' 0.16 [24],
cH ' 0.1 [25], cH '
0.07 [26], et cH '
0.08 [27]. Par conséquent,
l'énergie d'interaction stérique est considérable,
uniquement pour des membranes ayant de petits modules de courbure.
Généralement, cette énergie s'annule, pour des interfaces
rigides (ê -* oo).
Notons, tout d'abord, que la phase lamellaire reste
stable, pour une énergie potentiel minimale, à condition que la
profondeur du potentiel soit comparable à l'énergie thermique
kBT. Elle dépend, en particulier, de la valeur de l'amplitude
W. Pour des membranes non chargées, la constante d'Hamaker peut varier
en changeant la polarisabilité du milieu aqueux.
D'un point de vue théorique, Lipowsky et
Leibler [20] ont prédit une transition
hapitre 5 : Mécanique Statistique des
membranes confinées .. 143
avec l'exposant critique 0
[20], qui est de l'ordre de 0 '
1.00#177;0.03.
Un tel exposant a
de phase, qui fait passer le système d'un
état où les deux membranes sont en contact, à un
état où ils sont totalement séparées. Une telle
transition est de premier-ordre, si l'énergie stérique
est prise en compte. Par contre, si cette énergie est ignorée
(pour les membranes relativement rigides), la transition est plutôt de
second-ordre. Nous nous limitons au cas où la transition est de
seconde ordre. Il a été montré qu'il existe un certain
seuil W,, au-delà duquel l'interaction de van der Waals est suffisante,
pour que les deux membranes soient en contact. Au-dessus de cette amplitude
caractéristique, les ondulations des membranes deviennent plus
dominantes que les forces attractives, ce qui conduit alors à une
séparation totale des deux membranes . En fait, la valeur critique W,
dépend des paramètres du problème, tels que la
température T, l'amplitude AH, la portée ëH,
l'épaisseur S de la bicouche, et le module de courbure i. A
température ambiante, et pour AH ' 0.2
J/m2, ëH '
0.3 nm et S ' 4 nm, W, a
été trouvé de l'ordre de W, '
(6.3 - 0.61)
x 10-21J, quand la
constante de rigidité est de l'ordre de i ' (1 -
20) x 10-19J. Par
exemple, pour la lécithine d'oeuf, la constante de rigidité de
courbure est de l'ordre de i ' (1 -
2)x10-19J
[25], et la valeur critique correspondante W, se trouve dans
l'intervalle W, ' (6.3 -
4.1)x10-21J.
Notons que la valeur typique W, correspond à une certaine
température, appelée température de
délocalisation T, [20,
21].
En particulier, il a été trouvé
[20] que, lorsque la valeur de l'amplitude critique est
approchée par dessus, la séparation moyenne entre les deux
membranes diverge comme
(l)0 =
î0? ~ (T, -
T)-o , T T,- ,
(5.63)
hapitre 5 : Mécanique Statistique des
membranes confinées .. 144
tô "' 1 + 4
+ O (w2~
S1
, (impuretés attractives) ,
(5.65)
été calculé, en utilisant la
théorie de champ moyen et le Groupe de Renormalisation.
Maintenant, nous supposons que la phase lamellaire est
piégée dans un milieu aqueux trouble. Comme première
implication, les impuretés modifient subtantielle-ment le
phénomène de transition de délocalisation, en particulier,
la température critique. Pour la simplicité, nous admettons que
les deux membranes fluides adjacentes sont physiquement identiques. Alors, nous
devons considérer deux situations physiques distinctes, selon que les
impuretés attirent ou repoussent les deux membranes. Comme nous avons
montré au-dessus, pour les impuretés attractives, la
rugosité de la membrane, î1, est importante. Dans ce cas,
l'énergie stérique domine. Par conséquent, nous nous
attendons à ce que la transition de délocalisation se produise
à une température critique, T7 , plus faible que celle sans
impuretés, Te. Toutefois, pour des impuretés
répulsives, nous avons une tendance opposée, à savoir que
la transition de phase se passe à une température critique
supérieure à Te (sans impuretés). Cela peut
être expliqué par le fait que la rugosité de la membrane
est moins importante, et que l'énergie de van der Waals domine.
Dans tous les cas, la séparation moyenne (l) se
comporte comme
(l) = î1
~ (T: - T)-O
, T ? T*-
e . (5.64)
La nouvelle température critique
Te* peut être estimée comme suit. En
utilisant les relations (5.28) et
(5.31), nous montrons, au premier ordre dans
le couplage d'impuretés w, que
x*e -
xe ti -w + O
(w2) , (impurets
rpulsives) . (5.71)
hapitre 5 : Mécanique Statistique des
membranes confinées .. 145
|
î? w
LN 1
-4
|
+ O
(w2) , (impurets
rpulsives) .
|
(5.67)
|
En combinant les relations
(5.63) à
(5.66), nous trouvons que la
différence entre les deux températures critiques
Te et Te* (sans et avec
impuretés) est comme suit
Te -
Te* ti w +
O (w2) ,
(impuretés attractives) , (5.67)
Te -
T*e ti -w +
O (w2) ,
(impurets rpulsives) . (5.68)
Les préfacteurs dans les comportements
précités restent inconnu. Le changement de température est
alors proportionnel à la fraction volumique d'impuretés et leur
force d'interaction avec les membranes formant la phase lamellaire. Alors, nous
sommes dans une situation semblable aux effets de taille finie. Pour les
membranes chargées, qui forment une phase lamellaire, il a
été trouvé [20] que la séparation
moyenne entre deux bicouches adjacentes se comporte comme
(l)0 =
î0? ti
(x -
xe)-ø ,
x ? xe , (5.69)
avec x la concentration ionique moyenne du
milieu aqueux, et xe sa valeur critique. Par exemple, pour
le DPPC dans la solution de CaCl2,
xe est dans l'intervalle [22] :
xe N 84 -
10mM. En présence d'impuretés, la
séparation moyenne se comporte comme : (l)
=î? ti (x -
x*e)-ø,
avec le même exposant ø. Dans ce cas, nous
avons
x*e -
xe ti w + O
(w2) , (impurets
attractives) , (5.70)
hapitre 5 : Mécanique Statistique des
membranes confinées .. 146
Notons, enfin, que nous aurons les mêmes
commentaires qu'avant.
6.6 Conclusions.
Dans ce chapitre, nous avons présenté
une étude détaillée des effets d'impuretés sur les
propriétés statistiques des membranes fluides. En fait, celles-ci
affectent substantiellement le comportement des systèmes vivants. Comme
exemple, nous pouvons citer une étude expérimentale très
récente [23], où les auteurs ont entrepris une
série d'expériences comparatives, pour explorer les effets
d'impuretés sur la cristallisation des protéines
membranaires.
Pour l'étude de l'influence des
impuretés, attractives ou répulsives, nous avons combiné
la technique des répliques avec la méthode variationnelle, pour
calculer la rugosité moyenne, en fonction des paramètres de la
membrane pure et certains paramètres, qui sont proportionnels à
la fraction volumique des impuretés et leur force d'interaction. La
principale conclusion est que, pour les impuretés attractives, les
ondulations de la membrane augmentent la forme des fluctuations de la membrane.
Mais, les impuretés répulsives ont tendance à supprimer
ces fluctuations.
En suite, nous avons étendu l'analyse aux
vésicules, qui sont immergées dans un milieu aqueux trouble. La
conclusion essentielle est que les impuretés attractives ont tendance
à gonfler la membrane, alors qu'en présence d'impuretés
répulsives, la vésicule s'effondre sur
elle-même.
La discussion a été
généralisée à des phases lamellaires,
formées par deux membranes fluides parallèles, qui sont
séparées par une distance finie. Ces phases lamellaires peuvent
subir à une transition de délocalisation. En particulier, nous
avons
hapitre 5 : Mécanique Statistique des
membranes confinées .. 147
montré que les impuretés attractives
augmentent la température critique, alors que les répulsives ont
tendance à diminuer cette température.
Notons que l'incorporation d'une petite quantité
d'impuretés dans un milieux aqueux peut être un nouveau
mécanisme permettant la suppression ou la production d'une transition de
phase.
Enfin, l'étude présentée ici
pourrait être étendue à des systèmes à
plusieurs phases lamellaires parallèles.
148
Bibliographie
[1] M. Benhamou, K. Elhasnaoui, H. Kaidi, M. Chahid,
Physica A 389, 3465 (2010).
[2] J. Cardy, Scaling and Renormalization in
Statistical Physics, Cambridge, University Press, 1996.
[3] V.J. Emery, Phys. Rev. B 11, 239 (1975).
[4] S.F. Edvards, P.W. Anderson, J. Phys.
(Paris) 5, 965 (1975).
[5] L.D. Landau , E.M. Lifshitz, Quantum
Mechanics, 3ème édition, Pergamin Press, 1991.
[6] J. Zinn-Justin, Quantum Field Theory and
Critical Phenomena, Clarendon Press, Oxford, 1989.
[7] C. Itzykson, J.-M. Drouffe, Statistical Field
Theory : 1 and 2, Cambridge University Press, 1989.
[8] W. Helfrich, Z. Natureforsch 28c, 693
(1973).
[9] K. Wolfgang, Differential Geometry :
Curves - Surfaces - Manifolds, American Mathematical Society,
2005.
[10] S.J. Singer, G.L. Nicolson, Science 17 5, 720
(1972).
[11] 0.-Y. Zhong-Can, W. Helfrich, Phys. Rev. Lett. 59,
2486 (1987).
[12]
hapitre 5 : Mécanique Statistique des
membranes confinées .. 149
Z.C. Tu, Z.C. Ou-Yang, Phys. Rev. E 68, 061915
(2003).
[13] O.-Y. Zhong-Can, Phys. Rev. A 41, 4517
(1990).
[14] Z. Lin, R.M. Hill, H.T. Davis, L.E. Scriven, Y.
Talmon, Langmuir 10, 1008 (1994).
[15] M. Mutz, D. Bensimon, Phys. Rev. A 43, 4525
(1991).
[16] A.S. Rudolph, B.R. Ratna, B. Kahn, Nature 3 52, 52
(1991).
[17] H. Naito, M. Okuda, O.Y. Z hong-Can, Phys. Rev. E
48, 2304 (1993).
[18] J.N. Israelachvili, Intermolecular and Surface
Forces, 2ème édition, Academic Press, London,
1991.
[19] R.P. Rand, V.A. Parsegian, Biochim. Biophys. Acta
988, 351 (1989).
[20] R. Lipowsky, S. Leibler, Phys. Rev. Lett. 56, 2541
(1986).
[21] R. Lipowsky, E. Sackmann, éditeurs,
Structure and Dynamics of Membranes : Generic and Specific Interactions,
Volume 1B, Elsevier, 1995.
[22] L.J. Lis, W.T. Lis, V.A. Parsegian, R.P. Rand,
Biochemistry 20, 1771 (1981).
[23] A. Christopher et al., Acta Cryst. D 6 5,
10621073 (2009).
[24] R. Lipowsky, B. Zielinska, Phys. Rev. Lett. 62,
1572 (1989).
[25] N. Gouliaev, K.J.F. Nagle, Phys. Rev. Lett. 81,
2610 (1998).
[26] W. Janke, H. Kleinert, Phys. Rev. Lett. 58, 144
(1987) ; Phys. Lett. A 117, 353 (1986).
[27] G. Gompper, D.M. Kroll, Europhys. Lett. 9, 59
(1989).
Chapitre 7
Conformation d'un polymère
confiné dans des domaines
délimités par des biomembranes.
Dans ce chapitre, qui consiste notre
quatrième contribution originale, nous étudions la
conformation d'un polymère isolé, qui est confiné entre
deux membranes lipidiques parallèles ou dans une vésicule
tubulaire.
Pour rester plus général, nous supposons
que le polymère est de topologie arbitraire, qu'on appelle
D-manifold, où D est la dimension spectrale
(par exemple, D = 1, pour les
polymères linéaires, et D =
4/3, pour les polymères branchés).
En fait, D est le nombre de coordonnées locales permettant de
caractériser géométriquement le
polymère.
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..151
7.1 Introduction.
Le confinement d'un polymère a des nombreuses
applications dans divers domaines, tels que les fonctions biologiques, la
filtration, la chromatographie à gel, et la récupération
assistée du pétrole.
La physique des polymères confinés est
un problème très riche et passionnant. Récemment, une
grande attention a été portée sur la structure et la
dynamique des chaînes de polymère, confinées à
l'intérieur de pores cylindriques [1 -
7]. Par la suite, l'étude a été
étendue à des polymères plus complexes ou D-manifolds
[8], qui sont restreints aux même
géométries. Ici, D est la dimension spectrale, qui mesure le
degré de connectivité des monomères à
l'intérieur du polymère [9]. Par exemple, cette
dimension intrinsèque est de 1, pour les
polymères linéaires, et 4/3
pour les polymères branchés. Les D-manifolds peuvent
être polymérisés et organisés en vésicules
[10].
Le confinement des polymères entre deux
surfaces planes ou avec des ondulations sinusoïdales a également
été étudiée [11,
12].
Les géométries de confinement peut
être solides ou molles (biomembranes en bicouche ou tensio-actifs,
vésicules sphériques ou des tubulaires). Une question
particulière a été adressée au confinement d'un
polymère dans des bicouches de tensioactives formant une phase
lamellaire lyotrope [13], où les auteurs ont
réalisé des mesures en utilisant la diffusion de rayons-X aux
petites-angles, et étudié le phénomène de fracture
libre, par microscopie électronique, d'un surfactant non ionique /
système eau / polyélectrolyte, dans la région de la phase
lamellaire. La remarque fondamentale est que les molécules de
polymère provoquent à la fois déformation
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..152
locale et le ramollissement de la
bicouche.
Dans le même contexte, il a été
démontré expérimentalement [14] que le
confinement des polymères peut induire une transition nématique
de gouttelettes de microémulsion. Plus précisément, les
auteurs ont montré que, lors de confinement, les gouttelettes
sphériques se déforment en gouttelettes ellipsoïdales.
L'origine d'une telle transition structurelle peut être attribuée
à une perte d'entropie de conformation des chaînes de
polymère, en raison de confinement.
Dans d'autres expériences [15
- 17], une nouvelle phase a été
observée, en ajoutant un polymère hydrosoluble neutre (PVP) dans
la phase lamellaire lyotrope (CPCI -hexanol - eau). En outre, on a
étudié l'effet de l'eau sur un polymère neutre et soluble
dans la phase lamellaire d'un système de tensioactifs zwitterioniques
[18].
Le confinement des polymères est
également pertinente pour les systèmes vivants et régit de
nombreux processus biologiques. Comme exemple, nous peut citer les nanotubes de
membranes qui jouent un rôle majeur dans le trafic intracellulaire. En
particulier, nous pouvons citer des lipides et protéines, qui assurent
l'échange entre les différents compartiments dans les cellules
eucaryotes [19 - 22]. Le trafic des
macromolécules et des vésicules dans nanotubes est assurés
par des moteurs moléculaires [23]. En outre, ils sont
responsables de l'extraction des nanotubes [24]. La formation
d'attaches membranaires tubulaires ou spicules [25 -
33] résulte de l'action des forces localisées,
qui sont perpendiculaires à la membrane. Ces forces peuvent provenir de
la polymérisation des fibres [34], d'actine
[35], de la tubuline [36], ou
d'hémoglobine faucille [37].
Inspiré par des processus biologiques, comme
des macromolécules et des vésicules de transport, nous visons
l'étude de la conformation des polymères, confinés
dans
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..153
des milieux aqueux délimité par des
biomembranes. Plus précisément, le but est de voir comment ces
biomembranes peuvent modifier les propriétés de conformation du
polymère contraint. Dans ce but, nous choisissons deux
géométries : une vésicule tubulaire
(Géométrie I), et deux biomembranes parallèles
(Géométrie II). Pour être plus
général, nous considérons un polymère à
connectivité arbitraire ou encore D-manifold
[38]. Les polymères linéaires et
branchés, et les vésicules polymérisées en
constituent des exemples typiques. Notons que cette étude de
conformation est nécessaire pour la description des
propriétés dynamiques des polymères limités par des
parois géométriques. Comme nous le verrons plus loin, le
confinement d'un polymère est entièrement contrôlé
par l'état des biomembranes. En effet, pour la Géométrie
I, le polymère ne peut être confiné que si la
vésicule tubulaire est à l'équilibre. Pour la
Géométrie II, le confinement n'est possible que si les deux
membranes parallèles sont à l'état lié.
Ce chapitre suit l'organisation suivante. En Sec.
II, nous rappelons brièvement l'étude conformationnelle
d'un D-manifold non confiné, trompé dans un bon solvant.
La Sec. III est destinée à l'étude de la
conformation des polymères confinés à l'intérieur
d'une vésicule tubulaire. En Sec. IV , nous étendons
l'étude à des D-manifolds, confinés, cette
fois-ci, entre deux biomembranes parallèles. Nous retraçons
quelques remarques finales dans la dernière section.
7.2 D-manifolds non confinés
par
Considérons un D-manifold isolé,
immergé dans un bon solvant. Nous désignons
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..154
RF ~
aM1/dF (6.1)
son rayon de giration (ou de Flory), où dF
est la dimension fractale (ou d'Hausdorff), M est le poids
moléculaire (masse totale) du polymère considéré,
et a désigne la taille du monomère. La masse M
est liée à la dimension linéaire N par :
M = ND, où D est
la dimension spectrale [9]. Cette dernière est
définie comme la dimension de Hausdorff correspondant à
l'extension maximale de la fractale.
Naturellement, la dimension d'Hausdorff dépend
de la dimensionalité euclidienne d, la dimension spectrale
D et la qualité du solvant. Quand le polymère est
idéal (absence du volume exclu ), la dimension fractale correspondante,
d°F,
est simplement fonction de la dimension spectrale D
[9], et est donnée par
d°F
= 2D (6.2)
2 - D .
Pour les polymères linéaires
(D = 1),
d°F = 2
[2], pour les polymères branchés (D
= 4/3),
d°F = 4
[9], et pour les membranes (D =
2),
d°F =
8.
En raison de la positivité de la dimension
d'Hausdorff, l'expression ci-dessus n'a de sens que si D <
2. En effet, cette condition est remplie, pour tous les
polymères complexes, de dimension spectrale dans l'intervalle 1
= D < 2 [9].
Un D-manifold, en bon solvant, est
gonflée, en raison de la présence des forces de volume exclu. La
taille du polymère augmente avec la masse totale M,
conformément à la loi de puissances
(6.1).
La première implication du gonflement du
polymère est que sa dimension fractale réelle, dF, est
tout à fait différente de la dimension fractale Gaussienne,
relation
Par exemple, pour les polymères linéaires,
dF (3) = 5/3,et dF (3) = 2,
pour les
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..155
(6.2).Toutefois, il existe une valeur
spéciale de la dimension euclidienne appelé dimension
critique supérieure duc [39], au-delà de
laquelle la fractale polymérique devient idéale. Cette dimension
supérieure est naturellement une fonction de D, et qui peut être
déterminée, en utilisant un critère de type
Ginzburg, habituellement rencontré en Phénomènes
Critiques [41, 42]. D'après la
Réf. [39], duc est donnée par
4D duc =(6.3) 2 - D
.
Par exemple, la dimension critique supérieure
est 4 pour les polymères linéaires
[2], et 8 pour les polymères
branchés [39]. Par exemple, la dimension critique
supérieure est 4, pour les polymères
linéaires [2], et 8 pour les plus
branchés [39].
Nous notons que, dans le cas général, la
dimension fractale dF ne peut être calculée exactement. Plusieurs
techniques ont été utilisées, pour déterminer sa
valeur approximative, en particulier, la théorie de Flory-de Gennes
(TFD) [2]. Dans le cadre de cette approche
générale, il a été trouvé que la dimension
fractale a pour expression [39]
dF = Dd+2
D + 2 , (6.4)
qui est fonction des dimensions euclidienne d et
spectrale D. Notons que la relation précédente n'est valable que
si d est inférieure à la dimension critique supérieur duc.
En dimension 3, nous avons
dF (3) = D + 2 .
(6.5)
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..156
branchés (animaux).
Au paragraphe suivant, nous nous intéresserons
à l'étude de la conformation d'un D-manifold, confiné dans
une vésicule tubulaire.
7.3 D-manifolds confinés en
Géométrie I.
7.3.1 Relations utiles.
Avant d'étudier la conformation d'un D-manifold
isolé, confiné dans une vésicule tubulaire, nous allons
rappeler certaines relations de base, nécessaires pour la
présente étude, et qui se rapportent à la
Géométrie Différentielle.
La vésicule tubulaire est essentiellement
formée par deux feuillets adjacents (interne et externe),
composés de molécules amphiphiles. Celles-ci diffusent en
permanence avec les molécules du milieu aqueux support. Une telle
diffusion provoque des variations thermiques (ondulations) de la
membrane.
Nous considérons une biomembrane, qui peut
être comme une surface, dont la normale est n
(u1, u2), où
u1 et u2 sont les paramètres
curvilignes au point considéré. Bien-entendu, ce vecteur normal
dépend de la base choisie. Cependant, deux quantités issues des
dérivées premières de la normale sont indépendantes
de la base choisie. Il s'agit de la courbure moyenne
|
1
C = -
2
|
Tr
(?i?jR.n) = 2
(C1 + C2) , (6.6)
|
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..157
et la courbure Gaussienne
K = det (?i?
R.n) = C1C2 .
(6.7)
Ici, C1 = 1/R1 et
C2 = 1/R2 désignent les courbures
principales à la surface [43],
-?
c'est-à-dire les valeurs propres de la matrice des
dérivées secondes ?i?jR.-? n ,
ou
encore tenseur de courbure. L'énergie
étant une quantité intrinsèque, qui doit être
indépendante de la base choisie. Donc, elle ne doit faire intervenir que
les grandeurs intrinsèques C et K. C'est l'énergie de courbure de
Canham-Helfrich [43, 44], qui décrit
au Chapitre 5. Aussi, dans ce même chapitre, nous avons
écrit l'équation de la courbe à l'équilibre. En
particulier, pour un vésicule tubulaire, nous trouvons que son
diamètre à l'équilibre est donnée par
4k1/3
H = 2 ,
(6.8)
p
où k est la constante de rigidité de
courbure de la membrane (sans tension), et p est la différence de
pressions de part et d'autre de la surface. La formule précédente
n'est valable que si le diamètre H excède une valeur critique
Hc = 2
(4k/pc)1/3, ou
pc est la pression seuil.
Dans ce qui suit, nous utiliserons l'idée qui
consiste à considérer la vésicule tubulaire comme un
cylindre rigide, de diamètre effective H, qui dépend des
caractéristiques de la bicouche lipidique, à travers les
paramètres k et p.
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..158
7.3.2 Extension parallèle à l'axe du
cylindre.
Considérons un D-manifold quelconque,
confinée à l'intérieur d'une vésicule tubulaire, de
diamètre à l'équilibre H. Le solvant hôte
est supposé être un bon dissolvant. Le polymère n'est
confiné que si son rayon de Flory à trois dimensions,
RF3, est plus grand que le diamètre
H, c'est H << RF3. A paramètres
ê et p fixés, cette condition implique que la
masse du polymère, M, doit être plus grande qu'une
certaine valeur typique, M, se comportant comme M*
~
(ê/p)5D/3(D+2).
Maintenant, si M est fixée, le polymère n'est
confiné que si ê << ê*
~
pM3(D+2)/5D. Ce
comportement indique clairement que le confinement est plus favorable, quand la
vésicule tubulaire est de petite constante de rigidité de
courbure. Notons que la condition de confinement dépend de la nature de
la fractale polymérique, à travers sa dimension spectrale
D. Aussi, la qualité du solvant est un autre facteur influant
sur le confinement.
Le confinement des polymères, à
topologie arbitraire, à l'intérieur d'un tube rigide, est en
grande partie étudié dans la Réf. [8].
Dans ce travail publié, la méthode utilisée, pour
l'étude du confinement, est une TFD étendue, qui se base sur
l'énergie libre suivante [8]
|
R2
F
kBT = 2 +
v
RF,
|
M2
R~~H2
(6.9) ,
|
où R11
désigne l'extension parallèle du polymère,
v est le paramètre volume exclu, et
RiiH2 est le volume
occupé par le D-manifold. Ici, Ro ~
aMi/d~~
est le rayon de giration du polymère lorsqu'il est idéal (sans
volume exclu), où doF
est la dimension fractale correspondante, relation
(6.2).
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..159
La minimisation de cette énergie, par rapport
à R11, donne le comportement
suivant
-2/9
RH ~
aM(D+2)/3D
(a-3ê)
. (6.10)
p
Nous avons utilisé la relation
(6.8).
Le résultat (6.10)
appelle les commentaires suivantes.
Premièrement, nous faisons remarquer que le
rayon parallèle dépend naturellement des caractéristiques
du polymère confiné et des vésicules tubulaires, à
travers M et les paramètres (ê,
p), respectivement.
Deuxièmement, à une masse de
polymère fixée M, l'extension parallèle RH n'est
importante que pour les vésicules tubulaires, de faible module de
courbure.
Enfin, notons que le comportement ci-dessus n'est
valable que si l'extension parallèle RH reste en dessous de l'extension
maximale du polymère, Rmax ~
aM1/D,
c'est-à-dire RH < Rmax. Cela donne un
diamètre de tube minimal
Hmin ~
aM(D-1)/2D
. (6.11)
Par conséquent, le confinement de la fractale
polymérique implique que le diamètre du tube est dans
l'intervalle Hmin < H < RF3.
Par exemple, pour les polymères linéaires, Hmin ~
a, et Hmin ~
aM1/8,
pour les polymères branchés. La taille du pore minimale pour les
polymères linéaires est alors indépendante de son poids
moléculaire. Cela signifie que les polymères linéaires
trouvent toujours leur chemin à travers des pores, même de
très faible diamètre. Ce n'est pas le cas pour les
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..160
polymères ramifiés, pour lesquels la
taille minimale des pores augmente avec leur masse totale. Comme il a
été souligné dans la Réf. [8], il
serait possible de construire un milieu poreux, qui peut séparer un
mélange de molécules linéaires ou ramifiés, sur la
base de leur connectivité. En effet, on peut choisir une taille minimale
appropriée des pores, au travers lesquels peuvent passer des
polymères linéaires, alors que les polymères
ramifiés ne le peuvent pas. Maintenant, en combinant les
(6.8) et
(6.11), nous trouvons une valeur seuil de la
constante de rigidité de courbure,
kmin ~
a3pM3(D-1)/2D
.(6.12)
Donc, une membrane tubulaire confine une fractale
polymérique, que si le module
de courbure est dans l'intervalle kmin
< k < k*, avec la valeur typique
k* ~
pM3(D+2)/5D.
Le paragraphe suivant sera consacré au
confinement d'un polymère, de topologie arbitraire, entre deux membranes
parallèles fluides fluctuantes.
7.4 D-manifolds confinés en
Géométrie II.
7.4.1 Séparation moyenne.
Considérons une phase lamellaire, formée
par deux membranes parallèles. Les interactions spécifiques entre
ces membranes sont largement discutées au Chapitre 5.
Notons simplement que les membranes adjacentes peuvent subir une transition de
délocalisation, qui les conduit d'un état lié à un
état séparé. En fait, ce phénomène
dépend de la température ou de la polarité du milieu
ambiant.
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..161
Au chapitre précédent, nous avons
écrit le comportement de la séparation moyenne entre les
membranes (neutres) formant la phase lamellaire,
c'est-à-dire
H ~
(Tc -
T)-ø , T
--* T- c, (6.13)
où Tc est la
température critique. Ici, l'exposant critique 0 est
donné par [45]
0 N 1.00
#177; 0.03 .
(6.14)
Un tel exposant a été calculé, en
utilisant la Théorie de la Renormalisation.
D'un point de vue expérimentale, les
fluctuations critiques des membranes ont été
considérées dans plusieurs expériences
[46], et en particulier, l'on avait mesuré cette
séparation moyenne.
Nous avons maintenant tous les ingrédients
nécessaires, pour étudier la conformation d'une fractale
polymérique isolée, de topologie arbitraire, qui est
confinée entre deux membranes fluides parallèles formant une
phase lamellaire.
7.4.2 Extension parallèle du polymère.
En premier lieu, notons que le polymère est
confiné, seulement quand son rayon de giration à trois
dimensions, RF3 ~
aM(D+2)/5D,
est beaucoup plus grand que la séparation moyenne H
~ (Tc -
T)-ø, c'est
H << RF3. Cette condition implique que
le confinement du polymère n'est possible que si la température
T est en dessous d'une certaine valeur T*
= Tc -
aM-(D+2)/5Dø.
Cette température est alors plus petite que la température
critique Tc, et la distance Tc -
T* dépend essentiellement
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..162
de la masse du polymère M et de sa
dimension spectrale D.
La première implication du confinement du
polymère est que son comportement devient à deux dimensions. Cela
veut dire que le polymère peut être considéré comme
une fractale polymérique à deux dimensions, formée par
des pancakes de dimension H.
Pour la détermination de l'extension
parallèle du polymère, RII, nous utilisons, comme avant,
la TFD, basée sur l'énergie libre
kBR2
T = Ro2 +
v
R2H ,
(6.15)
II
M2
où v est le paramètre volume
exclu. Ici, Ro ~
aMi/d~~
est le rayon idéal, et R2IIH
représente le volume occupé par la
fractale. La minimisation de cette énergie libre, par rapport à
RII, donne
RII ~
aM(D+2)/4D
(Tc -
T)ø/4
, T << T* . (6.16)
Nous avons utilisé la relation
(6.8).
Le résultat central appelles les remarques
suivantes.
Premièrement, l'expression de l'extension
parallèle d'un polymère combine deux phénomènes
critiques, en rapport avec la limite de grand poids moléculaire de la
fractale, d'une part, et la criticalité de la transition de
délocalisation, d'autre part.
Deuxièmement, dans cette formule,
apparaît naturellement la dimension fractale (D
+ 2) /4D à deux
dimensions.
Troisièmement, le rayon parallèle
devient de plus en plus petit, à mesure qu'on
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..163
s'approche du point de transition. En d'autres termes,
ce rayon est important, seulement quand les deux membranes adjacentes sont
fortement liées.
Enfin, l'expression du rayon parallèle peut
être utilisée pour déterminer l'expression de l'exposant
critique ø.
7. 5 Conclusions.
Dans ce chapitres, nous avons deux objectifs, à
savoir l'étude conformationnelle d'une fractale polymérique,
confinée à l'intérieur d'une vésicule tubulaire ou
entre deux membranes parallèles formant une phase lamellaire à
l'équilibre. Pour la première géométrie,
l'échelle de longueur étant le diamètre à
l'équilibre, qui dépend des caractéristiques de la
membrane, à travers la constante de rigidité de courbure et la
différence de pressions. Pour la deuxième
géométrie, l'échelle de longueur est la séparation
moyenne entre les membranes adjacentes.
La quantité principale à
considérer était l'extension parallèle de la fractale
poly-mérique confinée. Une telle quantité a
été calculée, en étulisant une théorie
Flory-de Gennes étendue.
Notons que le même résultat pourrait
être retrouvé, en faisant usage du modèle de blobs
[8].
Une autre quantité physique
d'intérêt est l'énergie libre de confinement, notée
OF. C'est l'énergie libre nécessaire
pour confiner le polymère, à partir de l'état avec H
= 8. Ici, H est le diamètre de
tube ou la séparation moyenne. L'énergie libre de confinement
doit avoir la forme d'échelle : OF =
kBT f
(RF3/H),
où f (x) est une
fonction d'échelle universelle inconnue, et dont les comportements sont
: f (x) ~
0,
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..164
pour x << 1
(régime non confiné), et f
(x) ti
xm, pour x >> 1
(régime confiné). L'exposant m peut être
obtenu, en utilisant le fait que ?F doit être
proportionnelle à la masse totale M. Cela donne m
= dF (3) = 5D/
(D + 2). Par conséquent,
?F = kBTM
(H/a)-5D/(D+2),
avec H ti
(ê/p)1/3,
pour les vésicules tubulaires, et H ti
(Tc -
T)-ø, pour
les phases lamellaires. Remarquer que ?F peut
être mesurée, par comparaison des concentrations dans le pore
(tube) et dans la solution en volume. Nous avons Cpore/Cbulk
= á exp
(-?F/kBT), avec
á est certain coefficient dépendant du rapport
RF3/H.
Pour des membranes chargées, il a
été démontré [45] que la
séparation moyenne entre deux bicouches adjacentes se comporte comme :
H ti (x -
xc)-ø,
lorsque x -f
x+c
, avec x la concentration ionique, et xc sa valeur
critique. Bien sûr, cette dernière dépend de la nature du
lipide considéré. Par exemple, pour le DPPC en solution de
CaCl2, l'expérience a montré
[47] que xc est dans l'intervalle
xc ' 84 - 10mM.
Dans ce cas, le rayon parallèle du polymère se comporte :
R11 ti
aM(D+2)/4D
(x -
xc)ø/4.
Notons que la transition de délocalisation peut
se produire, même pour T > Tc. Pour cela, il
suffit d'exercer une pression externe P. Dans ces conditions, il a
été trouvé [48] que la séparation
moyenne H se comporte comme : H ti
îl ti
P-1/3(îl
étant la rugosité moyenne de la membrane). Un tel comportement
est en accord avec les données de la simulation Monte Carlo
[49]. Dans ce cas, l'extension parallèle du polymère
obéit à la loi d'échelle : R11
ti
aM(D+2)/4DP1/12.
Comme il devrait être, l'extension parallèle augmente avec la
pression externe.
Aussi, la transition de délocalisation peut se
produire en présence d'une tension latérale. Celle-ci tend
à supprimer les ondulations de la membrane. Ce qui permet de rapprocher
plus les deux membranes adjacentes. Il a été trouvé que
[48] que la sé-
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..165
paration moyenne se comporte comme : H ~
î? ~ E-1/2,
avec E la tension latérale. Dans ce cas, l'extension
parallèle du polymère obéit à la loi : R11
~
aM(D+2)/4DE1/8.
Comme il se doit, ce rayon parallèle augmente avec la tension
latérale.
Pour des vésicules tubulaires, nous avons
supposé qu'elles sont sans tension. Si ce n'est pas le cas, et si la
différence de pressions peut être négligée, nous
montrons que le diamètre d'équilibre est : H = 2
(2ê/'y)1/2. Ici, 'y
est le coefficient de tension interfaciale. Dans ce cas, l'extension
parallèle du polymère est : R11 ~
aM(D+2)/3D
(a2'y/ê)1/3.
Naturellement, cette extension augmente avec le coefficient de tension de
interfaciale. Le diamètre minimal correspond à une valeur
typique, 'ymin ~
a-2êM(1-D)/D,
de 'y (ê étant fixée). Par conséquent, le
polymère est confiné si 'y <
'ymin.
Enfin, certaines questions en relation avec le sujet
sont en cours d'étude.
166
Bibliographie
[1] E.F. Cassasa, J. Polym. Sci. B 5, 773
(1967).
[2] P.-G. de Gennes, Scaling Concepts in Polymer
Physics, Cornell University Press,
Ithaca, 1979.
[3] M. Daoud, P.-G. de Gennes, J. Phys.
(Paris) 38, 85 (1977).
[4] F. Brochard, P.-G. de Gennes, J. Phys.
(Paris) 40, L-399 (1979).
[5] E. Raphael, P. Pincus, J. Phys. II
(Paris) 2, 1341 (1992).
[6] J.T. Brooks, M.E. Cates, J. Chem. Phys. 99, 5467
(1993).
[7] J. Lal, S.K. Sinha, L. Auvray, J. Phys. II
(Paris) 7, 1597 (1997).
[8] T.A. Vilgis, P. Haronska, M. Benhamou, J. Phys.
II (Paris) 4, 2139 (1994).
[9] S. Alexander, R. Orbach, J. Phys. (France) 43,625
(1982).
[10] B. Duplantier, Phys. Rev. Lett. 62, 23372341
(1989).
[11] T. Dotera, Y.Y. Suzuki, Phys. Rev. E 62,
53185323 (2000).
[12] Y.Y. Suzuki, T. Dotera, M. Hirabayashi,
Simulation of Gaussian and Excluded-
Volume Chains in Curved Slits, 3rd
International Symposium on Slow Dynamics
in Complex Systems, AIP Conference
Proceedings, Volume 708, pp. 257-258, 2004.
[13] E.Z. Radlinska et al., Phys. Rev. Lett.
74, 42374240 (1994).
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..167
[14] K. Nakaya et al., Europhys. Lett. 71, 494
(2005).
[15] G. Bouglet, Thèse de Doctorat,
Université Montpellier II, France, 1997.
[16] C. Ligoure, G. Bouglet, G. Porte, Phys. Rev. Lett.
71, 3600 (1993).
[17] C. Ligoure, G. Bouglet, G. Porte, O. Diat, J. Phys.
II (Paris) 7, 473 (1997).
[18] A. Maldonado et al., Journal of Colloid
and Interface Science 296, 365 (2006).
[19] P.A. Halban, J.C. Irminger, Biochem. J. 299, 1
(1994).
[20] M.G. Farquhar, H.P. Hauri, Protein Sorting and
Vesicular Traffic in the Golgi Apparatus, dans The Golgi
Apparatus, E.G. Berger et J. Roth, éditeurs, pp. 63129,
1997.
[21] B. Alberts, Transport des Protéines dans
la Cellule : Essentiel de la Biologie Cellulaire, Garland ,
éditeurs, 1999.
[22] C. Leduc et al., PNAS 101, 17095
(2004).
[23] J.C. Howard, Mechanics of Motors Proteins and
the Cytoskeleton, Sinauer, Sunderland, MA, 2001.
[24] A. Roux et al., Proc. Nath. Acad. Sci. USA
99, 5394 (2002).
[25] I. Derenyi, F. Julicher, J. Prost, Phys. Rev. Lett.
88, 238101 (2002).
[26] B. Bozic, V. Heinrich, S. Svetina, B. Zeks, Eur.
Phys. J. E. 6, 91 (2001).
[27] D.J. Bukman, J.H. Yao, M. Wortis, Phys. Rev. E. 54,
5463 (1996).
[28] V. Heinrich, B. Bozic, S. Svetina, B. Zeks,
Biophys. J. 76, 2056 (1999).
[29] S. Zhang, J. Phys. Soc. Japan. 68, 3603
(1999).
[30] A. Smith, E. Sackmann, U. Seifert, Phys. Rev. Lett.
92, 208101 (2004).
hapitre 6 :Conformation d'un polymère
confiné dans des domaines délimités ..168
[31] T.R. Powers, G. Huber, R.E. Goldstein, Phys.
Rev. E. 6 5, 041901 (2002).
[32] D. Raucher, M.P. Sheetz, Biophys. J. 77, 1992
(1999).
[33] D.K. Fygenson et al., Phys. Rev. Lett.
79, 4497, 1997.
[34] Plus de détails peuvent être dans :
D.R. Daniels , M.S. Turner, Phys. Rev. Lett.
9 5, 238101 (2005).
[35] D. Boal, Mechanics of the Cell,
Cambridge University Press, 2001.
[36] B. Alberts et al., Molecular
Biology of the Cell, Garland, New York, 2002.
[37] R.W. Briehl et. al., J. Mol. Biol. 24
5, 710 (1995).
[38] Voir Réf.
[8].
[39] D. Lhuillier, J. Phys. (Paris) 49, 705
(1988).
[40] T.A. Vilgis, J. Phys. (Paris) 49, 1481
(1988).
[41] J. Zinn-Justin, Quantum Field Theory and
Critical Phenomena, Clarendon
Press, Oxford, 1989.
[42] C. Itzykson, J.-M. Drouffe, Statistical
Field Theory : 1 and 2, Cambridge Uni-
versity Press, 1989.
[43] K. Wolfgang, Differential Geometry :
Curves - Surfaces - Manifolds, American
Mathematical Society, 2005.
[44] S.J. Singer, G.L. Nicolson, Science 17 5, 720
(1972).
[45] R. Lipowsky, S. Leibler, Phys. Rev. Lett. 56,
2541 (1986).
[46] R. Zhang et al., Phys. Rev. Lett. 74,
2832 1995.
[47] L.J. Lis, W.T. Lis, V.A. Parsegian, R.P. R ,
Biochemistry 20, 1771 (1981).
[48] R. Lipowsky, B. Zielinska, Phys. Rev. Lett. 62,
1572 (1989).
Chapitre 8
Condensation des polymères
greffés sur une biomembrane.
Dans ce chapitre, qui constitue notre
cinquième contribution originale, nous présentons une
vue large sur le phénomène de ségrégation entre les
phospholipides et des chaînes de polymère greffées sur une
membrane en bicouche.
En particulier, nous discutons l'influence de la
qualité du solvant et la poly-dispersité des chaînes de
polymère greffées sur le comportement de phase critique du
mélange. Nous rappelons que la qualité du solvant apparaît
à travers l'expression générale de l'énergie libre
du mélange, qui nous permettra la détermination du diagramme de
phase relatif à l'agrégation des chaînes de polymère
ancrées.
Pour plus de détails, le lecteur pourra
consulter la Réf. [1].
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 170
8.1 Introduction.
Les membranes biologiques sont d'une importance
cruciale pour la vie, parce qu'elles séparent la cellule de son
environnement extérieur, et les compartiments à
l'intérieur de la cellule, afin de protéger les processus
importants et des événements spécifiques.
Aujourd'hui, il est largement reconnu que les
biomembranes se présentent sous forme d'une bicouche lipidique,
composée de deux feuillets adjacents [2,
3], qui sont formés de molécules amphiphiles
possédant des têtes polaires hydrophiles, attachées
chimiquement à des chaînes d'acides gras hydrophobes. La
majorité des molécules de lipide sont des phospholipides. Ceux-ci
ont un groupe polaire et deux queues hydrocarbonées non-polaires, dont
la longueur est de l'ordre de 5nm.
En plus, les membranes cellulaires incorporent un
autre type de lipides, qui est le cholestérol [2,
3]. Les molécules de cholestérol ont plusieurs
fonctions dans la membrane. Par exemple, ils donnent la rigidité ou la
stabilité de la membrane cellulaire, et évitent la
cristallisation des hydrocarbures.
Les biomembranes contiennent, également, des
glycolipides (résidus de sucre), qui sont des molécules
lipidiques s'agrégeant dans la membrane. Certains types de
molécules sont limités par des sphingolipides, des toxines du
choléra et du tétanos. Les sphingolipides et le
cholestérol favorisent l'agrégation des protéines dans des
microdomaines, appelés râteaux ou rafts. En
fait, ceux-ci jouent le rôle de plates-formes pour la fixation de
protéines sur les membranes, et jouent un rôle dans la
transduction du signal.
Les protéines (macromolécules
géantes) sont une autre composante principale des
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 171
membranes cellulaires. Les protéines
transmembranaires sont amphipathiques et formées par des régions
hydrophobes et hydrophiles ayant la même orientation que les autres
molécules lipidiques. Ces protéines sont aussi appelées
protéines intrinsèques. Elles ont la fonction de transporter des
substances à travers la membrane, comme les ions et les
macromolécules. Il existe d'autres types de protéines, qui
peuvent être attachées à la surface par des chaînes
d'acides gras ou à la surface cellulaire externe. Ce sont les
protéines membranaires périphériques, qui ont de
nombreuses fonctions. En fait, ils protègent la surface de la membrane,
régulent la signalisation cellulaire et participent à de nombreux
autres événements cellulaires importants. En outre, certaines
protéines membranaires périphériques ont tendance à
se lier aux membranes électrostatiquement chargées
négativement, sur le feuillet interne de la membrane
plasmique.
Notons que la majorité des
macromolécules formant la bicouche sont tout simplement ancrées
sur la membrane et forment une brosse de polymères ramifiés
[4, 5]
.
Nous nous intéressons aux polymères
greffés sur des interfaces molles, comme les liposomes [6
- 9]. Ces matériaux souples ont
été fabriqués volontairement par A. Bangham, en
1968. Actuellement, ils sont devenus des objets de grand
intérêt en biologie, biochimie et particulièrement en
médecine, pour leur rôle comme agents de transport de
médicaments. Les liposomes sont des vésicules artificielles de
forme sphérique, qui peuvent être produites à partir de
phospholipides naturels et de cholestérol, mais les bicouches lipidiques
qui constituent ces vésicules ont une durée de vie courte, en
raison de leur faible stabilité et aussi suite à leur
extermination dans le sang par les globules blancs. Pour avoir des
vésicules plus stables, un moyen utile
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 172
consiste à les protéger en les enrobant
d'une couche de polymères flexibles (la taille de pelage est de l'ordre
de 50nm [2]) qui empêche
l'adhérence de protéines [7,
8]. En fait, ces chaînes de polymère stabilisent
les liposomes, en raison des forces de volume exclu entre monomères
[9]. Les liposomes peuvent être, également,
synthétisés à partir des copolymères en dibloc,
dans un solvant sélectif qui préfère être
contacté par le polymère préféré. Les
chaînes de polymère hydrophobes s'agrègent pour
former une bicouche mince, tandis que les chaînes de polymères
hydrophiles flottent dans le solvant. Naturellement, ces liposomes de
copolymère ont des propriétés légèrement
différentes, en comparaison avec ceux à base de lipides
[10] (une grande résistance, forte rigidité et
faible perméabilité à l'eau). Selon le choix des
copolymères, ces liposomes résistent aux détergents
[11].
Le greffage des polymères sur des membranes
lipidiques a été considéré dans un travail
récent [12]. Le but était l'étude de la
séparation de phase entre les phospholipides et des polymères
ancrés. Comme hypothèse, le milieu aqueux est supposé
être un bon solvant, et en plus, les chaînes de polymère
sont ancrées à l'interface par une seule extrémité
(ancres). Les ancres sont des grandes molécules amphiphiles
chimiquement différentes des molécules de phospholipide. Dans ce
chapitre, nous supposons que les chaînes de polymère peuvent
être adsorbées à la membrane par plus d'une
extrémité (polydispersité), et le liquide support peut
être un bon solvant ou un solvant thêta. Comme nous le verrons
ci-dessous, la polydispersité et la qualité du solvant affectent
considérablement le comportement de phase du mélange. Par
changement d'un paramètre approprié, comme la température,
les phospholipides et les chaînes de polymère ancrées se
séparent en domaines macroscopiques, alternativement riches en ces deux
composantes. Pour la détermination de l'architecture
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 173
du diagramme de phase, nous élaborons un
modèle théorique, qui prend en compte à la fois de la
polydispersité et la qualité du solvant. Nous déterminons,
d'abord, l'expression de l'énergie libre du mélange de
phospholipides et d'ancres, ensuite, nous déterminons la forme du
diagramme de phase, et enfin, calculons le facteur de structure associé,
comme fonction du vecteur d'onde de transfert et des paramètres
pertinents du problème.
8.2 Energie libre du mélange.
Les polymères peuvent adhérer à
la biomembranes de plusieurs façons : (i) par de grosses
molécules amphiphiles (pour de nombreuses protéines, les ancres
lipidiques sont des unités de glycosylphosphatidylinositol)
[13, 14], (ii) par des groupements
latéraux hydrophobes de polymères, qui sont
intégrés dans la bicouche [15,
16], (iii) par une membrane couvrant des domaines hydrophobes
du polymère (protéines mem-branaires, par exemple), et (iv) par
une forte adsorption qui entraîne le polymère d'un état
désorbé à un état adsorbé
[17]. Pour une chaîne de polymère isolée,
l'adsorption (sur des substrats solides) peut être théoriquement
étudiée, en utilisant un argument d'échelle
[18], par exemple. Outre le degré de
polymérisation de la chaîne polymère, N, et le
paramètre de volume exclu, v, l'étude a été
basée sur un paramètre supplémentaire, 8, qui est
l'énergie nécessaire (par kBT ) d'absorber un
monomère sur la surface. Pour une forte adsorption,
8-1 définit l'épaisseur de
la couche adsorbée. Une transition d'adsorption a lieu, à une
certaine valeur typique 8* de 8 [17] : 8*
~ R-1
F ~
aN-íF (íF
= 3/5), avec RF le rayon de
Flory de la chaîne de polymère. Pour des solutions
semi-diluées de polymères, le phénomène
d'adsorption
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 174
Pour l'étude configurationnelle, Guiselin
[22] a considéré que chaque boucle
peut
dépend, en plus du paramètre
ä, de la concentration en polymère.
Dans ce chapitre, nous considérons la situation
(iv), où chaque monomère a la même probabilité
d'être adsorbé sur la surface de la membrane
[19]. Plus précisément, un monomère
donné est susceptible d'être lié à une tête
polaire d'une molécule de phospholipide (ancre). Comme
résultat, les chaînes de polymère forment des boucles
polydisperses (avec éventuellement un ou deux queues flottant dans le
milieu aqueux). En fait, cette hypothèse est conforme à ce qui a
été considéré dans la Réf.
[20]. Le cas où aucune boucle n'est présente
(adsorption par une seule extrémité) a été
examiné dans la Réf. [12]. Contrairement
à l'adsorption sur une surface solide, les chaînes de
polymère ancrées sont mobiles sur la membrane hôte, et
peuvent subir une transition d'agrégation qui nous intéresse ici.
Pour être plus général, la membrane fluide est
supposée être en contact avec un bon solvant ou un solvant
thêta.
Le but est d'écrire l'expression
générale de l'énergie libre du mélange, qui nous
permettra la détermination du diagramme de phase relatif à
l'agrégation des chaînes de polymère
adsorbées.
Notre point de départ est l'énergie
libre (par unité d'aire) de la couche poly-mérique (pour des
substrats solides). Par exemple, dans un contexte biologique, les
macromolécules peuvent être liées à la surface par
des monomères extrémités. Cette énergie est
donnée par [21]
|
F0
?
|
kBTi
bfN
([b2S
(n)]â
+
[-b2S'
(n)] ln
[-SSn)11
dn . (7.1)
|
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 175
être envisagée comme deux demi-boucles
(brins). Ici, S (n)
est le nombre de brins comportant plus de n monomères
par unité de surface, et b représente la taille de
monomère. Pour les couches de polymère monodisperses, N
dénote le degré de polymérisation commun des
chaînes greffées. Ici, N est plutôt le nombre de
monomères des brins les plus longs. Par la suite, nous utiliserons la
notation Si = Ö/a, qui est
le nombre total de brins adsorbés par unité de surface, avec
Ö la fraction volumique des monomères
adsorbés, et a est l'aire des têtes polaires. Si le
mélange est supposé être incompressible, 1
- Ö sera donc la fraction volumique des
molécules de phospholipide.
Revenons à l'expression de l'énergie
libre volumique (7.1) et notons que
le premier terme de l'égalité représente la contribution
des interactions répulsives (à deux ou à trois corps)
entre monomères appartenant à la couche polymérique, alors
que le second est tout simplement la contribution d'entropie décrivant
tous les réarrangements possibles des chaînes de polymère
greffées. Dans l'égalité
(7.1), l'exposant 0
dépend de la qualité de solvant [21].
Lorsque le greffage est réalisé en solution diluée, avec
un bon solvant ou un solvant thêta, ses valeurs sont, respectivement,
0 = 11/6 (modèle
de blob) ou 0 = 2.
Pour les couches de polymère polydisperses, la
distribution S (n) est bien
connue dans la littérature [21]. Celle-ci peut
être obtenu en minimisant l'énergie libre précédente
par rapport à cette distribution. Sans détails, nous nous
contentons du résultat général [21]
suivant
Ö
S (n) ~
an1/(â?1) .
(7.2)
Pour les solvants habituels, nous avons
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 176
do
S (n) ~
an6/5 , (bon
solvant) , (7.3)
|
do
S (n)
~
an
|
,
|
(solvant thta) . (7.4)
|
Nous réécrirons, ensuite, la distribution
S (n) sous la
forme
|
do
S (n) =
a
|
f (n)
, (7.5)
|
avec f (n)
~
n1/(1-â),
pour les couches de polymères polydisperses, et f
(n) = 1 (pour tous n),
pour les monodisperses.
Par conséquent, F0
peut être approchée par
|
F0
kBT =
a
|
-1udoâ
+ ç
(N) do .
(7.6)
|
Ici, le terme linéaire en do
décrit la contribution de l'entropie à l'énergie
libre volumique, où le coefficient ç
(N) est (voir l'annexe
B)
ç (N)
= a-1
{[0 + ln (0 -
1)] (1 -
N1/(1-â))
+ 0 -
1N1/(")~)
ln N} . (7.6a)
Dans la limite asymptotique N ? oo, ce
coefficient se réduit à
ç (N)
? a-1 [0
+ ln (0 - 1)] ,
(7.6b)
pourvu que 0 > 1 (noter que
0 = 11/6, pour les bons
solvants, et 0 = 2, pour
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 177
les solvants thêta). Cette limite asymptotique
est toujours définie positive, et inversement proportionnelle à
l'aire des têtes polaires a. En fait, le signe positif du
coefficient ç (N)
est en accord avec la perte d'entropie, due aux chaînes de
polymère greffées. Comme nous le verrons ci-dessous, cette
contribution linéaire n'affecte pas le diagramme de phase, dans le plan
composition-température. Ici, la constante de couplage u est la
suivante
(a)b2=
N( (N) ,
(7.7)
avec
N
( (N) = N
f [f
(n)]fi dn
. (7.8)
Explicitement, nous avons
( (N) = 1
, (pour les syst mes monodisperses) ,
(7.9)
( (N) ~
Nfi/(") , (pour les syst mes polydisperses)
. (7.10)
Notons que (
(N) < 1,
puisque, dans tous les cas, â > 1.
Par conséquent, la poly-dispersité diminue l'énergie
d'interaction répulsive.
Maintenant, nous avons tous les ingrédients
nécessaires pour la détermination de l'expression de
l'énergie libre du mélange. Pour ce faire, nous imaginons que
l'interface se présente comme un réseau de Flory-Huggins
bidimensionnel [18, 23], où
chaque site est occupé par un ancre ou par une molécule de
phospholipide. Par conséquent, nous pouvons regarder la fraction
volumique des ancres Ö comme la
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 178
8
D = -ð ~ rU
(r) dr , C =ð
ó2 (covolume) . (7.13)
probabilité pour qu'un site donné soit
occupé par un ancre, et 1 - Ö la
probabilité d'occupation de ce site par un phospholipide.
Avant de déterminer l'énergie libre (par
site) du mélange (ancre-phospholipide), nous constatons que celle-ci est
la somme de trois contributions : L'entropie de mélange (par site),
l'énergie libre volumique (par site), et l'énergie d'interaction
(par site) provenant des ondulations de la membrane. En réalité,
les forces attractives induites par les ondulations de la membrane sont
responsables de la condensation des ancres. Ces forces contrebalancent les
forces répulsives entre monomères le long des chaînes de
polymère connectées. Nous écrivons donc
|
F Ö kBT
=q
|
lnÖ + (1 - Ö) ln(1 -
Ö) + ÷Ö(1 - Ö) +
u(q) Öâ
. (7.11)
|
Notons que, pour les chaînes de polymère
ancrées par une extrémité, qui est une grosse
molécule amphiphile (cas des brosse de polymère), la
première contribution de l'entropie, Ö ln Ö,
devrait être divisée par certain facteur, q, qui représente
le rapport de l'aire des ancres à celle des têtes polaires des
phospholipides hôte. Dans le cas présent, nous avons q =
1. Dans l'égalité
(7.11), ÷ est le paramètre
d'interaction de Flory
÷ = ÷o
- A2 I C +
+~)
,)
(7.12)
où les coefficients positifs C et D (en dimension
2) sont tels que [24]
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 179
Ici, U (r) est le
potentiel de paire induit par les ondulations membranaires
[11, 24]
|
U (r) =
|
{
|
8 , r < ó ,
(ó )4
, r > ó ,
-AH r
|
(3.14)
|
où ó est le diamètre du disque-dur,
qui est proportionnel à la racine carrée de l'aire des ancres, a.
L'amplitude de potentiel, AH, joue le rôle de la constante de
Hamaker. Il a été montré que celle-ci
décroît avec la constante de rigidité comme
[12, 25]
AH ~
ê-2 . (3.15)
Mais cette amplitude est également sensible
à la température. De ce qui précède, nous pouvons
remarquer que l'énergie libre de mélange n'est pas
symétrique par le changement : Ö ? 1
- Ö.
Pour le paramètre d'attraction D, nous trouvons
l'expression suivante
|
ð
D = AH
2ó2
|
ê-2
~ ó2,
(3.16)
|
qui montre que les membranes de faible module de
courbure induisent une attraction importante entre les ancres.
Dans l'expression
(7.12), ÷o
> 0 est le paramètre d'interaction de Flory
décrivant la ségrégation chimique entre les phospholipides
(molécules amphiphiles) et les
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 180
ancres. Le paramètre de ségrégation
s'écrit, généralement, comme
ão
÷o = áo
+ T , (7.17)
où les coefficients áo
et ão dépendent de la nature
chimique des différentes espèces. En outre, le paramètre
d'interaction totale ÷ s'écrit comme
÷ = á +T ,
(7.18)
avec les nouveaux coefficients
C
á = áo -
A2 , ã = ão +
D
kBA2 . (7.18a)
Ces coefficients dépendent alors de la nature
chimique des différentes composantes et des caractéristiques de
la membrane, à travers le module de rigidité ê.
Si nous admettons que la constante de couplage u est
peu dépendante de la température, nous pourrons tracer le
diagramme de phase dans le plan des variables (Ö,
÷). En effet, toute la dépendance en
température est entièrement contenue dans le paramètre
d'interaction de Flory ÷.
8.3 Diagramme de phase.
Avec l'aide de l'énergie libre du
mélange (7.11), nous pouvons
déterminer l'architecture du diagramme de phase, dans le plan des
variables (Ö, ÷), en relation avec
le processus d'agrégation, qui mène les ancres d'une phase
dispersée (gaz) à une phase
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 181
|
1
|
1
Ö2
c
|
+ /3 (/3 - 1) (/3 -
2) uÖâ?3
c = 0 . (7.20)
|
|
(1 -
Öc)2
|
dense (liquide). Nous nous intéressons
ici seulement à la courbe spinodale, le long de laquelle la
compressibilité thermique diverge. L'équation de cette courbe
spinodale peut être obtenue en annulant la dérivée seconde
de l'énergie libre du mélange par rapport à la fraction
volumique des ancres Ö :
?2F/?Ö2 = 0.
Alors, nous obtenons l'expression suivante pour le paramètre
d'interaction de Flory critique
x(Ö) = 2
(Ö(11 Ö) + /3
(/3 - 1)
uÖâ-2) .
(7.19)
Au-dessus de ce paramètre d'interaction
critique, apparaissent deux phases, l'une est homogène et l'autre est
séparée. Bien sûr, le terme linéaire en
Ö figurant dans l'égalité
(7.11) ne contribue pas à l'expression
du paramètre d'interaction critique.
Remarquons que, dans les solvants habituels, ce
paramètre interaction critique est augmenté par la
présence d'interactions répulsives (deux ou trois corps) entre
monomères appartenant à la couche de polymère. Cela
signifie que ces interactions élargissent le domaine de
compatibilité, et donc la séparation de phase se produit à
basse température.
Maintenant, pour voir l'influence de la qualité
du solvant, nous réécrivons le paramètre d'interaction u
comme u = u0æ
(N) ~
u0Nâ/(1?â)
< u0, où u0 est celui
relatif à un système monodisperse. Ainsi, la
polydispersité a tendance à réduire le domaine de
compatibilité, par rapport au cas monodisperse.
La fraction volumique critique,
Öc, peut être obtenue
en minimisant le paramètre critique x (Ö) par
rapport à la variable Ö. Nous obtenons
alors
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 182
Pour de bons solvants (/3 =
11/6), nous avons
|
1 1
(1 -
Öe)2
-Ö2e
|
-
|
55
216uÖ-7/6
= 0 . (7.21)
|
Par conséquent, la fraction volumique critique
est l'abscisse du point d'intersection de la courbe d'équation
(2x - 1)
/x5/6 (1 -
x)2 et la droite horizontale d'équation y
= (55/216) u. Notons que cette fraction
volumique critique est unique, et en plus, elle doit être
supérieure à la valeur 1/2
(pour la compatibilité mathématique). Les
coordonnées du point critique sont
(Öe,
÷e), où
Öe est solution de
l'équation ci-dessus : ÷e = ÷
(Öe). Ce dernier peut
être déterminé en combinant
(7.19) et
(7.21). Pour les solvants thêta
(/3 = 2), les coordonnées du point
critique sont exactes,
1
Öe = 2 ,
÷e = 2 + u . (7.22)
Le paramètre d'interaction u se comporte
comme
b2
u = a
N-1 . (7.22a)
La relation ci-dessus montre clairement que la
condensation des chaînes de polymère se produit rapidement,
seulement lorsque le rapport des aires b2/a est
suffisamment élevée.
Cette tendance est également présente
pour les bons solvants.
Il est facile de montrer que la fraction critique et
le paramètre critique sont déplacés vers leur valeurs les
plus basses, pour les systèmes polydisperses, quelque soit la
qualité du solvant. Dans la Fig. 7.1,
nous traçons la courbe spinodale, pour des

hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 183
FIG. 8-1 -- La courbe spinodale (bon solvant), pour
des systèmes monodisperse (ligne pointillés) et polydisperse
(ligne continue), à paramètre N = 100 et b2 =
0.5a.
systèmes monodisperse (sans boucles)
et polydisperse (avec boucles), à paramètre N
fixé. Nous avons choisi le cas d'un bon solvant. Pour les solvants
thêta, la tendance est la même.
Nous reportons sur la Fig.
7.2, la courbe spinodale d'un système
polydisperse, pour déférentes valeurs du paramètre N.
Comme il se doit, le paramètre critique est déplacé vers
ses valeurs les plus élevées, à mesure que le degré
de polymérisation typique N est augmentée.
Enfin, nous comparons, dans la Fig.
7.3, les courbes spinodale d'un système
polydisperse, avec un bon solvant et un solvant thêta, aux
paramètres b et N fixés. Toutes les courbes tracées
reflètent les discussions faites ci-dessus.

hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 184
FIG. 8-2 -- la courbe spinodale d'un système
polydisperse, pour déférentes valeurs du paramètre N avec
b2 = 0.5a.
8.4 Conclusions.
Ce chapitre a été consacré
à l'étude thermodynamique de l'agrégation des
chaînes de polymère, qui sont adsorbées à une
surface molle, par plus d'un point d'ancrage. Cette agrégation est due
à une compétition entre la ségrégation chimique
entre les phospholipides et les chaînes de polymère
greffées, leurs interactions volumiques et les ondulations de la
membrane. Plus précisément, la question posée est comment
ces chaînes de polymère peuvent être menée d'une
phase dispersée à une phase dense (à l'instar de la
transition gaz-liquide pour les fluides), suite au changement d'un
paramètre approprié, qui peut être la
température.
Pour être plus général, nous avons
considéré des situations physiques les plus réalistes,
telles que la qualité du solvant (bon solvants ou solvants thêta)
et la po-

hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 185
FIG. 8-3 -- Les courbes spinodales d'un système
polydisperse, avec un bon solvant et un solvant thêta, aux
paramètres b et N fixés.
lydispersité des chaînes
connectées. Cette dernière a été prise en compte,
à travers la forme de la distribution des boucles. Nous avons, d'abord,
déterminé l'expression de l'énergie libre du
mélange, en adoptant le modèle de Flory-Huggins, habituellement
rencontrés en physique des polymères [18,
23]. Une telle expression montre qu'il existe une
compétition entre trois contributions : l'entropie, la
ségrégation chimique entre les espèces différentes
(phospholipides et polymères greffés), l'énergie
d'interaction induite par les ondulations de la membrane, et l'énergie
d'interaction entre les monomères appartenant à la couche
adsorbée. Une telle compétition règle la succession des
phases.
Nous soulignons que le présente étude et
une précédente déjà publiée [12]
diffèrent de celle relative à une surface rigide
[4]. Par conséquent, les ondulations
membra-
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 186
naires ont été ignorées. Comme
nous l'avons vu plus haut, ces ondulations augmentent le paramètre de
ségrégation, x, par un terme additif,
xm, se comportant comme comme
i-2. Cela signifie que
la séparation de phase est accentué, par la présence des
fluctuations thermiques. Si elle est comparée à une étude
faisant déjà matière de publication [12],
et qui portait sur des brosses monodisperses de polymères
greffés, la présenté est plus générale, car
elle tient compte à la fois de la polydispersité des
chaînes et la qualité du solvant. Ainsi, la présente
étude a été réalisée de façon
unifiée. Comme nous l'avons constaté, ces détails
affectent drasti-quement l'architecture du diagramme de phase.
Maintenant, discutons l'influence de la qualité
du solvant sur le comportement de phase critique. Nous rappelons que la
qualité du solvant apparaît dans l'énergie libre
(7.11), à travers le
paramètre de répulsion u, défini par la relation
(7.7). Nous trouvons, dans la limite
N ? 8, que
ug(q) ~
N1/5uè,
où les indices g et B sont pour bon solvant
et solvant thêta, respectivement. Cela implique que le bon
solvant joue un rôle stabilisateur, en ce qui concerne la
séparation de phase.
Enfin, soulignons que l'étude
présentée dans ce chapitre, est une suite naturelle d'une
précédente étude [12], qui
considérait des chaînes de polymère monodisperses,
ancrées sur une membrane fluide, en bon solvant. Par conséquent,
cette nouvelle présente une vue large sur le phénomène de
ségrégation entre les phospholipides et des chaînes de
polymère greffées sur une membrane en bicouche.
187
Bibliographie
[1] M. Benhamou, I. Joudar, H. Kaidi, K. Elhasnaoui,
H. Ridouane, H. Qamar, Phys. Scr. 83, 065801 (2011).
[2] R. Lipowsky, S. Sasckmann, éditeurs,
Structure and Dynamics of Membranes : From Cells to Vesicles, Volume 1A,
Elsevier Science B.V., 1995.
[3] M. Benhamou, Lipids Insights 1, 2
(2008).
[4] A. Nicolas, B. Fourcade, Eur. Phys. J. E 10, 363
(2003).
[5] M. Aubouy et al., Phys. Rev. Lett. 84,
4858 (2000) ; M. Aubouy et al., Macromolecules 29, 7261
(1996).
[6] H. Ringsdorf, B. Schmidt, How to Bridge the
Gap Between Membrane, Biology and Polymers Science, P.M. Bungay et
al., éditeurs, Synthetic Membranes : Science, Engineering and
Applications, p. 701, D. Reiidel Pulishing Compagny, 1986.
[7] D.D. Lasic, American Scientist 80, 250
(1992).
[8] V.P. Torchilin, Effect of Polymers Attached
to the Lipid Head Groups on Properties of Liposomes, D.D. Lasic , Y.
Barenholz, éditeurs, Handbook of Nonmedical Applications of
Liposomes, Volume 1, p. 263, RCC Press, Boca Raton, 1996.
[9]
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 188
R. Joannic, L. Auvray, D.D. Lasic, Phys. Rev. Lett.
78, 3402 (1997).
[10] B.M. Discher et al., Science 284, 1143
(1999).
[11] M.G.L. Elferink et al., Biochim.
Biophys. Acta 1106, 23 (1992).
[12] M. Benhamou, J. Joudar, H. Kaidi, Eur. Phys. J.
E 24, 343 (2007).
[13] G. Blume, G. Cev, Biochim. Biophys. Acta 1029,
91 (1990).
[14] D.D. Lasic, F.J. Martin, A. Gabizon, S.K. Huang,
D. Papahadjopoulos, Bio-chim. Biophys. Acta 1070, 187 (1991).
[15] G. Decher et al., Angew. Makromol.
Chem. 166-167, 71 (1989).
[16] J. Simon, M. Kuhner, H. Ringsdorf, E. Sackmann,
Chem. Phys. Lipids 76, 241 (1995).
[17] T. Garel1, M. Kardar, H. Orland, Europhys. Lett.
29, 303 (1995) ; X. Chatellier, D. Andelman, Europhys. Lett. 32, 567 (1995) ;
R. Lipowsky, Europhys. Lett. 30, 197 (1995) ; A.F. Xie, S. Granick, Nature
Materials 1, 129 (2002).
[18] P.-G. de Gennes, Scaling Concept in Polymer
Physics, Cornell University Press, 1979.
[19] L'adsorption d'un polymère adéquat
sur une membrane liquidique, constituée de deux phospholipides, de
nature chimique différente, peut être un mécanisme de la
séparation de phase entre ces deux composantes, comme il est
souligné dans : W.H. Binder, V. Barragan, F.M. Menger, Chem. Int. Ed.
42, 5802 (2003).
[20] M. Manghi, M. Aubouy, Adv. Coll. Interf. Sci.
94, 21 (2001).
[21] M. Manghi, M. Aubouy, Phys. Rev. E. 68, 041802
(2003).
[22] O. Guiselin, Euro. Phys. Lett. 17, 225 (1992) ;
Thèse de Doctorat, Université Paris VI,
1992.
[23]
hapitre 7 : Condensation des polymères
greffés sur une biomembrane. 189
P.J. Flory, Principles of Polymer Chemistry,
Cornell University Press, Ithaca, 1953.
[24] R. Balian, From Microphysics to Macrophysics
- Methods and Applications of Statistical Physics, Springer Verlag,
2006.
[25] V.I. Marchenko, C. Misbah, Eur. Phys. J. E
8, 477 (2002).
190
Chapitre 9
Conclusions générales.
Cette thèse avait comme objectif principal
l'étude de la Mécanique Statistique des biomembranes
confinées dans le milieu aqueux support. Il s'agit d'une série de
contributions qui étendaient le cas des biomembranes pures,
c'est-à-dire en l'absence de bords géométriques, de
particules ou dépourvues de chaînes de polymères
greffées.
La première contribution porte sur
l'effet Casimir entre deux plaques interactives parallèles
délimitant un liquide comptant une biomembrane immergée. Cette
force répulsive provient des ondulations thermiques de la membrane. Plus
exactement, nous avons réexaminé le calcul de la force de Casimir
entre deux parois parallèles délimitant une membrane lipidique
fluctuante, qui est immergée dans un certain liquide. Cette force est
provoquée par les fluctuations thermiques de la membrane. Nous avons
étudié le problème, du point de vue statique et dynamique.
Les quantités d'intérêt étaient la rugosité
de la membrane, qui est une échelle de distance caractéristique
mesurant l'étendue des fluctuations thermiques dans la direction
perpendiculaire à la biomembrane.
onclusions générales.
191
D'entrée de jeu, nous avons
déterminé la rugosité de la membrane, lorsque celle-ci est
à l'équilibre. Puis, nous avons montré que lorsque la
température du système est augmentée, la rugosité
croît avec le temps, selon une loi de puissance. Ensuite, l'accent a
été mis sur le calcul de la force induite entre deux parois
parallèles délimitant un liquide où baigne une membrane
lipidique. Le calcul a été achevé, du point de vue
statique et dynamique. Il a été mis en évidence que la
force induite croît avec l'importance des fluctuations thermiques de la
membrane.
La deuxième contribution avait trait
à une solution colloïdale au contact d'une biomembrane, qui est
confinée dans une fente. L'épaisseur de cette fente était
supposée beaucoup plus petite que la rugosité en volume, afin
d'assurer le confinement de la membrane. Le but étant l'étude de
la dynamique Brownienne de ces particules, sous la variation d'un
paramètre adéquat, tel que la température, par exemple.
L'objet de base était la densité locale des particules. Nous
avons déterminé exactement cette densité, qui est fonction
de la distance et du temps. L'outil pour cela est l'équation de
Smoluckowski, satisfaite par cette densité. Dans, un premier temps, nous
avons précisé le potentiel extérieur induit par les
ondulations de la membrane. De tel potentiel est symétrique, par rapport
à l'origine de la coordonnée perpendiculaire. En plus, il
dépend naturellement des caractériques de la membrane, à
travers sa rugosité, et de l'interaction colloïde-membrane. Pour
simplifier les calculs, nous avons approximé ce potentiel par un
potentiel harmonique. Cette hypothèse reste valable, car l'essentiel du
phénomène se passe autour de la membrane, sur des distances
inférieures à la rugosité en volume. La conclusion
essentielle est les particules sont poussées vers l'interface en
occupant les nouveaux trous et vallées..
La troisième contribution est une
étude détaillée des effets d'impuretés sur
les
onclusions générales.
192
propriétés statistiques des membranes
fluides. Celles peuvent être attractives ou répulsives. En premier
lieu, nous avons déterminé la rugosité moyenne de la
membrane, en combinant la technique des répliques avec la méthode
variationnelle. Le résultat s'exprime en fonction de la concentration
des impuretés et l'amplitude de leur interaction avec la membrane. En
second lieu, nous avons évalué la taille d'une vésicule
isolée, en fonction de ces mêmes paramètres. Enfin,
l'étude est étendue à l'adhésion membranaire. Le
résultat fondamental est que la présence des impuretés
induit un changement substantiel des propriétés
d'équilibre de la membrane se trouvant dans un liquide trouble. Une
discussion des effets de courbure a été faite, en
considérant une vésicule sphérique fermée. Pour ce
qui des phases lamellaires, l'étude peut être étendue pour
plus de deux membranes.
La quatrième contribution est une
étude conformationnelle d'un polymère isolé, qui est
confiné entre deux membranes lipidiques parallèles ou dans une
vésicule tubulaire. Pour rester plus général, nous avons
supposé que le polymère est de topologie arbitraire,
appelé D-manifold, où D est la
dimension spectrale. Cette dernière représente le nombre de
coordonnées locales permettant de caractériser
géométriquement le polymère. En particulier, nous avons
mis en évidence de cette dimension intrinsèque sur le confinement
du polymère. Ce sujet a été inspiré des
phénomènes biologiques.
La dernière contribution est une
étude de la séparation de phase entre les phospholipides et des
polymères greffés sur une membrane fluide. L'étude a
été menée, pour diverses situations, à savoir la
qualité du solvant et la polydispersité des chaînes de
polymère. Nous avons montré que ces deux facteurs induisent des
changements drastiques du comportement de phase.
onclusions générales.
193
Enfin, il serait intéressant d'étendre
la présente étude à des biomembranes chargées.
194
Chapitre 10
Appendice A.
Le but est de montrer comme on a obtenu la formule
(3.17). Pour cela, nous partons de la
fonction de partition que nous réécrivons comme
D/2
Z = f Dh exp
{
-
Ho } =
dzÖ (z) . (A.1)
kBT -D/2
D'un autre côté, il est facile de voir que
la rugosité de la membrane est donnée par
L2 f
DD/2 dzz2Ö
(z) A.2
? f DD/2
dz4 (z) (
)
avec la fonction de partition restreinte
Ö(z) = fDh
ä [z -
h(xo, yo)] exp
{HBo
[T] }
· (A.3)
k
Ici,H [h] est le
Hamiltonien original, relation (3.3).
Naturellement, cette définition est indépendante du point choisi
(xo, yo), en raison de la
symétrie de translation le long des directions parallèles aux
parois.
Appendice A. 195
Notons que la fonction Ö n'est
pas singulière, quelque soit la valeur de la distance perpendiculaire.
Puisque nous sommes intéressés par le régime de
confinement, où la séparation D est beaucoup plus petite que la
rugosité de la membrane, c'est-à-dire L? <<
Li, nous pouvons remplacer la fonction paire Ö
par sa valeur à z = 0, notée
Öo. Dans cette limite, l'on obtient le résultat
désiré.
Ceci termine la démonstration de la formule
attendue.
·
196
Chapitre 11
Appendice B.
L'objectif est la détermination du coefficient
ç (N) apparaissant dans la formule
(7.6), du Chapitre 7. Pour
cela, nous commençons par la contribution de l'entropie à
l'énergie libre
|
Fentropique kBT
|
b2 %N
([-b2S'(n)]
ln I -S'
(n)1) dn , (B.1)
1 L J/
|
où la distribution des tailles des boucles est
définie par la relation (7.2), du
même chapitre. L'expression ci-dessus peut être
réécrite comme
|
Fentropique kBT
|
= ç (N) Ö
, (B.2)
|
avec
ç (N) =
a-1 11 J N (nâ/(")
ln fâ - JJ 1 1
nâ/(1-âl)
dn . (B.3)
Appendice B. 197
Un calcul simple aboutit à la formule
désirée
ç (N) =
a-1 {[â
+ ln (â - 1)] (1 -
N1/(")) + â - 1
JJJ NI-â) ln
N } . (B.4)
Ceci termine la détermination du coefficient
ç (N).

Dans cette première contribution
originale, nous réexaminons le calcul de la force de
Casimir entre deux plaques interactives parallèles délimitant un
liquide comptant une biomembrane immergée. Nous désignerons par
D, la distance qui sépare les deux plaques, et l'on suppose que
cette dernière est beaucoup plus petite que la rugosité en
volume, afin d'assurer le confinement de cette membrane. Cette force
répulsive provient des ondulations thermiques de la membrane. Nous avons
traité aussi bien l'aspect statique que l'aspect dynamique
Article N°1
Effet de Casimir dans les biomembranes
confinées.
101

|
African Journal Of Mathematical Physics Volume
8(2010)101-114
|
Casimir force in confined biomembranes
K. El Hasnaoui, Y. Madmoune, H. Kaidi,
M. Chahid, and M.
Benhamou
Laboratoire de Physique des Polymères et
Phénomènes Critiques Facultédes Sciences Ben M'sik, P.O.
7955, Casablanca, Morocco
m.benhamou@univh2m.ac.ma
abstract
We reexamine the computation of the Casimir force between two
parallel interacting plates delimitating a liquid with an immersed biomembrane.
We denote by D their separation, which is assumed to be much smaller
than the bulk roughness, in order to ensure the membrane confinement. This
repulsive force originates from the thermal undulations of the membrane. To
this end, we first introduce a field theory, where the field is noting else but
the height-function. The field model depends on two parameters, namely the
membrane bending rigidity constant, k, and some elastic constant,
u - D-4. We first compute the static Casimir force
(per unit area), 11, and find that the latter decays with separation D
as : 11 - D-3, with a known amplitude scaling as
k-1. Therefore, the force has significant values only for
those biomembranes of small enough k. Second, we consider a
biomembrane (at temperature T) that is initially in a flat state away
from thermal equilibrium, and we are interested in how the dynamic force, 11
(t), grows in time. To do calculations, use is made of a
non-dissipative Langevin equation (with noise) that is solved by the time
height-field. We first show that the membrane roughness, L?
(t), increases with time as : L? (t) -
t1/4 (t < r), with the final time
r - D4 (required time over which the final
equilibrium state is reached). Also, we find that the force increases in time
according to : 11 (t) - t1/2 (t
< r). The discussion is extended to the real situation where the
biomembrane is subject to hydrodynamic interactions caused by the surrounding
liquid. In this case, we show that : L? (t) -
t1/3 (t < rh) and 11h
(t) - t2/3 (t < rh),
with the new final time rh - D3. Consequently, the
hydrodynamic interactions lead to substantial changes of the dynamic properties
of the confined membrane, because both roughness and induced force grow more
rapidly. Finally, the study may be extended, in a straightforward way, to
bilayer surfactants confined to the same geometry.
Key words: Biomembranes - Confinement - Casimir force -
Dynamics.
I. INTRODUCTION
The cell membranes are of great importance to life, because
they separate the cell from the surrounding environment and act as a selective
barrier for the import and export of materials. More details concerning the
structural organization and basic functions of biomembranes can be found in
Refs. [1 - 7]. It is well-recognized by the scientific community that the cell
membranes essentially present as a phospho-lipid bilayer combined with a
variety of proteins and cholesterol (mosaic fluid model). In
particular, the function of the cholesterol molecules is to ensure the bilayer
fluidity. A phospholipid is an amphiphile
0 ?c a GNPHE publication 2010,
ajmp@fsr.ac.ma
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
102
molecule possessing a hydrophilic polar head attached to two
hydrophobic (fatty acyl) chains. The phos-pholipids move freely on the membrane
surface. On the other hand, the thickness of a bilayer membrane is of the order
of 50 Angstroms. These two properties allow to consider it as a two-dimensional
fluid membrane. The fluid membranes, self-assembled from surfactant solutions,
may have a variety of shapes and topologies [8], which have been explained in
terms of bending energy [9, 10].
In real situations, the biomembranes are not trapped in
liquids of infinite extent, but they rather confined to geometrical boundaries,
such as white and red globules or liposomes (as drugs transport agents [11 -
14]) in blood vessels. For simplicity, we consider the situation where the
biomembrane is confined in a liquid domain that is finite in one spatial
direction. We denote by D its size in this direction. For a tube,
D being the diameter, and for a liquid domain delimitated by two
parallel plates, this size is simply the separation between walls. Naturally,
the length D must be compared to the bulk roughness, L0
1, which is the typical size of humps caused by the thermal
fluctuations of the membrane. The latter depends on the nature of lipid
molecules forming the bilayer. The biomembrane is confined only when D
is much smaller than the bulk roughness L0
1. This condition is similar to that usually
encountered in confined polymers context [15].
The membrane undulations give rise to repulsive effective
interactions between the confining geometrical boundaries. The induced force we
term Casimir force is naturally a function of the size D, and
must decays as this scale is increased. In this paper, we are interested in how
this force decays with distance. To simplify calculations, we assume that the
membrane is confined to two parallel plates that are a finite distance D
< L01 apart.
The word »Casimir» is inspired from the traditional
Casimir effect. Such an effect, predicted, for the first time, by Hendrick
Casimir in 1948 [16], is one of the fundamental discoveries in the last
century. According to Casimir, the vacuum quantum fluctuations of a confined
electromagnetic field generate an attractive force between two parallel
uncharged conducting plates. The Casimir effect has been confirmed in more
recent experiments by Lamoreaux [17] and by Mohideen and Roy [18]. Thereafter,
Fisher and de Gennes [19], in a short note, remarked that the Casimir effect
also appears in the context of critical systems, such as fluids, simple liquid
mixtures, polymer blends, liquid 4He, or liquid-crystals, confined
to restricted geometries or in the presence of immersed colloidal particles.
For these systems, the critical fluctuations of the order parameter play the
role of the vacuum quantum fluctuations, and then, they lead to long-ranged
forces between the confining walls or between immersed colloids [20,
21].
To compute the Casimir force between the confining walls, we
first elaborate a more general field theory that takes into account the
primitive interactions experienced by the confined membrane. As we shall see
below, in confinement regime, the field model depends only on two parameters
that are the membrane bending rigidity constant and a coupling constant
containing all infirmation concerning the interaction potential exerting by the
walls. In addition, the last parameter is a known function of the separation
D. With the help of the constructed free energy, we first computed the
static Casimir force (per unit area), II. The exact calculations show that the
latter decays with separation D according to a power law, that is II
#c-1 (kBT)2
D-3, with a known amplitude. Here, kBT
denotes the thermal energy, and #c the membrane bending rigidity
constant. Of course, this force increases with temperature, and has significant
values only for those biomembranes of small enough #c. The second
problem we examined is the computation of the dynamic Casimir force, II
(t). More precisely, we considered a biomembrane at temperature T
that is initially in a flat state away from the thermal equilibrium, and
we were interested in how the expected force grows in time, before the final
state is reached. Using a scaling argument, we first showed that the membrane
roughness, L1 (t), grows with time as : L1
(t) t1/4 (t < r), with
the final time r D4. The latter can be interpreted as the
required time over which the final equilibrium state is reached. Second, using
a non-dissipative Langevin equation, we found that the force increases in time
according to the power law : II (t) t1/2
(t < r). Third, the discussion is extended to the real
situation where the biomembrane is subject to hydrodynamic interactions caused
by the flow of the surrounding
liquid. In this case, we show that : L1 (t)
t1/3 (t < rh) and II (t)
t2/3 (t < rh), with the new
final
time rh D3. Consequently, the
hydrodynamic interactions give rise to drastic changes of the dynamic
properties of the confined membrane, since both roughness and induced force
grow more rapidly.
This paper is organized as follows. In Sec. II, we present the
field model allowing the determination of the Casimir force from a static and
dynamic point of view. The Sec. III and Sec. IV are devoted to the computation
of the static and dynamic induced forces, respectively. We draw our conclusions
in the last section. Some technical details are presented in Appendix.
K. El Hasnaoui et al. African Journal Of Mathematical
Physics Volume 8(2010)101-114
103
II. THEORETICAL FORMULATION
Consider a fluctuating fluid membrane that is confined to two
interacting parallel walls 1 and 2. We denote by D their finite
separation. Naturally, the separation D must be compared to the bulk
membrane roughness, L01, when the system is
unconfined (free membrane). The membrane is confined only when the condition
L << L01 is fulfilled. For the opposite
condition, that is L >> L01, we expect
finite size corrections.
We assume that these walls are located at z =
-D/2 and z = D/2, respectively. Here, z
means the perpendicular distance. For simplicity, we suppose that the two
surfaces are physically equivalent. We design by V (z) the
interaction potential exerted by one wall on the fluid membrane, in the absence
of the other. Usually, V (z) is the sum of a repulsive and an
attractive potentials. A typical example is provided by the following potential
[22]
V (z) = Vh (z) +
VvdW (z) , (2.0)
where
Vh (z) =
Ahe-z/Ah (2.0)
represents
the repulsive hydration potential due to the water molecules inserted between
hydrophilic lipid heads [22]. The amplitude Ah and the potential-range
ëh are of the order of : Ah ^, 0.2
J/m2 and ëh ^, 0.2-0.3 nm. In fact,
the amplitude Ah is Ah = Ph xëh, with
the hydration pressure Ph ^, 108-109 Pa. There,
VvdW (z) accounts for the van der Waals potential
between one wall and biomembrane, which are a distance z apart. Its
form is as follows
[ ]
H 1 1
VvdW (z) = - ,
z2 - 2
(z + ä)2 + (2.0)
12ð (z + 2ä)2
with the Hamaker constant H ^, 10-22 -
10-21 J, and ä ^, 4 nm denotes the membrane thickness.
For large distance z, this implies
Wä2
VvdW (z) ? z4 .
(2.0)
Generally, in addition to the distance z, the interaction
potential V (z) depends on certain length-scales,
(î1, ...,în), which are the
interactions ranges. The fluid membrane then experiences the following total
potential
I D ) I D ) , -D
U (z) = V 2 - z + V
2 + z 2 < z < D 2 .
(2.0)
In the Monge representation, a point on the membrane can be
described by the three-dimensional position vector r = (x,
y, z = h (x, y)), where h (x, y) E
[-D/2, D/2] is the height-field. The latter then fluctuates
around the mid-plane located at z = 0.
The Statistical Mechanics for the description of such a
(tensionless) fluid membrane is based on the standard Canham-Helfrich
Hamiltonian [9, 23]
? [ê ]
1-l [h] = dxdy 2
(?h)2 + W (h) , (2.0)
with the
membrane bending rigidity constant ê. The latter is comparable
to the thermal energy kBT, where T is the absolute
temperature and kB is the Boltzmann's constant. There, W
(h) is the interaction potential per unit area, that is
U (h)
W (h) = L2 , (2.0)
where
the potential U (h) is defined in Eq. (2), and L is
the lateral linear size of the biomembrane. Let us discuss the pair-potential
W (h).
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
Firstly, Eq. (2) suggests that this total potential is an
even function of the perpendicular distance h, that is
W (-h) = W (h) .
(2.0)
In particular, we have W (-D/2) = W
(D/2).
Secondly, when they exist, the zeros h0's of the
potential function U (h) are such that
(D ) (D )
V 2 - h0 = -V 2 +
h0 . (2.0)
This equality indicates that, if h0 is a zero of the
potential function, then, -h0 is a zero too. The number of zeros is
then an even number. In addition, the zero h0's are different
from 0, in all cases. Indeed, the quantity V (D/2) does not
vanish, since it represents the potential created by one wall at the middle of
the film. We emphasize that, when the potential processes no zero, it is either
repulsive or attractive. When this same potential vanishes at some points,
then, it is either repulsive of attractive between two consecutive zeros.
Thirdly, we first note that, from relation (2), we deduce that
the first derivative of the potential function, with respect to distance
h, is an odd function, that is W'
(-h) = -W' (h). Applying this relation to
the midpoint h = 0 yields : W' (0) = 0. Therefore,
the potential W exhibits an extremum at h = 0, whatever the
form of the function V (h). We find that this extremum is a
maximum, if V ?(D/2) < 0, and a
minimum, if V ?(D/2) > 0. The
potential U presents an horizontal tangent at h = 0, if only
if V ?(D/2) = 0. On the other hand, the general
condition giving the extrema {hm} is
|
dV dh
|
????h= D 2 -hm
|
dV =
dh
|
????h= D 2 +hm
|
. (2.0)
|
Since the first derivative W' (h)
is an odd function of distance h, it must have an odd number
of extremum points. The point h = hm is a maximum,
if
|
and a minimum, if
|
d2V dh2
|
????h= D 2 -hm
|
<
|
d2V dh2
|
????h= D 2 +hm
|
,
|
(2.0)
|
|
d2V dh2
|
????h= D 2 -hm
|
>
|
d2V dh2
|
????h= D 2 +hm
|
. (2.0)
|
At point h = hm, we have an
horizontal tangent, if
d2V
dh2
????h= D 2 +hm
. (2.0)
d2V dh2
????h= D 2 -hm
104
The above deductions depends, of course, on the form of the
interaction potential V (h).
Fourthly, a simple dimensional analysis shows that the total
interaction potential can be rewritten on the following scaling form
|
W (h) kBT
|
D2Ö( = 1 h1n 1
(2.0)
D, D,..., D J ,
|
where (î1, ...,în)
are the ranges of various interactions experienced by the membrane, and
Ö(x1, ..., xn+1) is a (n + 1)-factor
scaling-function.
Finally, we note that the pair-potential W
(h) cannot be singular at h = 0. It is rather an
analytic function in the h variable. Therefore, at fixed ratios
îi/D, an expansion of the scaling-function Ö,
around the value h = 0, yields
W (h) kBT
h2
2 D4
= ã + (h4) .
(2.0)
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
105
We restrict ourselves to the class of potentials that exhibit
a minimum at the mid-plane h = 0. This assumption implies that the
coefficient ã is positive definite, i.e. ã >
0. Of course, such a coefficient depends on the ratios of the
scale-lengths îi to the separation D.
In confinement regime where the distance h is small
enough, we can approximate the total interaction potential by its quadratic
part. In these conditions, the Canham-Helfrich Hamiltonian becomes
W0 [h] = 2 J dxdy
[1ê (?h)2 + uhl
, (2.0)
with the elastic constant
u = ã kBT
D4 .(2.0)
The prefactor ã will be computed below. The
above expression for the elastic constant u gives an idea on its
dependance on the film thickness D. In addition, we state that this
coefficient may be regarded as a Lagrange multiplier that fixes the
value of the membrane roughness.
Thanks to the above Hamiltonian, we calculate the
mean-expectation value of the physical quantities, like the height-correlation
function (propagator or Green function), defined by
G (x - x', y -
y') = (h (x, y) h
(x',y')) - (h (x,
y)) (h (x',y')) .
(2.0)
The latter solves the linear differential equation
(îc?2 + u)G(x -
x',y - y') = ä (x -
x')ä (y - y') , (2.0)
where ä (x) denotes the one-dimensional
Dirac function, and ? = ?2/?x2 +
?2/?y2 represents the two-dimensional
Laplacian operator. We have used the notations : = ê/kBT and u =
u/kBT, to mean the reduced membrane elastic constants.
From the propagator, we deduce the expression of the membrane
roughness
L2? = (h2)
- (h)2 = G(0,0) . (2.0)
Such a quantity measures the fluctuations of the
height-function (fluctuations amplitude) around the equilibrium plane located
at z = 0. We show in Appendix that the membrane roughness is exactly
given by
2
L2 = 12, (2.0)
provided that one is in the confinement-regime, i.e. D
<< L0?. Notice that the above equality
indicates that the roughness is independent on the geometrical properties of
the membrane (through ê). We emphasize that this relation can be
recovered using the argument that each point of the membrane has equal
probability to be found anywhere between the walls [24].
The elastic constant u may be calculated using the known
relation
L2 1 kBT = (2.0)
?8 ,urs .
This gives
u =
9 (kBT)2
êD4 . (2.0)
4
This formula clearly shows that this elastic constant decays
with separation D as D-4. The term
uh2/2 then describes a confinement potential that
ensures the localization of the membrane around the mid-plane. Integral over
the hole plane R2 of this term represents the loss
entropy due to the confinement of the membrane. The value (19) of the elastic
constant is compatible with the constraint (17).
Therefore, the elaborated model is based on the Hamiltonian
(13), with a quadratic confinement potential. We can say that the presence of
the walls simply leads to a confinement of the membrane in a region
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
of the infinite space of perpendicular size L?.
We define now another length-scale that is the in-plane
correlation length, L?. The latter measures the correlations extent
along the parallel directions to the walls. More precisely, the propagator
G (x - x', y -
y') fails exponentially beyond L?, that is for
distances d such that d =
v(x - x')2
+ (y - y')2
> L?. From the standard relation
L2 ? = kBT
16ê L2 ? , (2.0)
we deduce
L
(2.0)
( ê )1/2
2
? = v3 D .
kBT
In contrary to L?, the length-scale L?
depends on the geometrical characteristics of the membrane (through
ê).
The next steps consist in the computation of the Casimir force at
and out equilibrium.
III. STATIC CASIMIR FORCE
When viewed under the microscope, the membranes of vesicles
present thermally excited shape fluctuations. Generally, objects such as
interfaces, membranes or polymers undergo such fluctuations, in order to
increase their configurational entropy. For bilayer biomembranes and
surfactants, the consequence of these undulations is that, they give rise to an
induced force called Casimir force.
To compute the desired force, we start from the partition
function constructed with the Hamiltonian defined in Eq. (13). This partition
function is the following functional integral
f { }
-H0 [h]
Z = Dh exp , (3.0)
kBT
where integration is performed over all height-field
configurations. The associated free energy is such that : F = -kBT
lnZ, which is, of course, a function of the separation D. If we
denote by Ó = L2 the common area of plates, the
Casimir force (per unit area) is minus the first derivative of the
free energy (per unit area) with respect to the film-thickness D, that
is
This force per unit area is called disjoining pressure. In
fact, II is the required pressure to maintain the two plates at some distance
D apart. In term of the partition function, the disjoining pressure
rewrites
|
II
kBT =
|
1 Ó
|
? lnZ 1 ?u ? lnZ
?D = ?u . (3.0)
Ó ?D
|
Using definition (19) together with Eqs. (23) and (24) yields
1 ?u
II = -(3.0)
2 ?D L2 ? .
Explicitly, we obtain the desired formula
êD3 . (3.0)
3
II = 8
(kBT)2
106
From this relation, we extract the expression of the disjoining
potential (per unit area) [25]
f D II (D') dD'
= 3 (kBT )2
Vd (D) = - êD2 . (3.0)
16
8
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
107
The above expression of the Casimir force (per unit area)
calls the following remarks.
Firstly, this force decays with distance more slowly in
comparison to the Coulombian one that decreases rather as
D-2.
Secondly, this same force depends on the nature of lipids
forming the bilayer (through ê). In this sense, contrarily to
the Casimir effect in Quantum Field Theory [16] and in Critical Phenomena [20],
the present force is not universal. Incidentally, if this force is
multiplied by ê, then, it will become a universal quantity.
Thirdly, at fixed temperature and distance, the force amplitude has significant
values only for those bilayer membrane of small bending rigidity constant.
Fourthly, as it should be, such a force increases with
increasing temperature. Indeed, at high temperature, the membrane undulations
are strong enough.
Finally, the numerical prefactor 3/8 (Helfrich's
cH-amplitude [9]) is close to the value obtained using Monte Carlo
simulation [26].
In Fig. 1, we superpose the variations of the reduced static
Casimir force Ð/kBT upon separation D, for two
lipid systems, namely SOPC and DAPC [27], at temperature T =
18?C. The respective membrane bending rigidity constants are :
ê = 0.96 x 10-19 J and ê =
0.49 x 10-19 J. These values correspond to the renormalized
bending rigidity constants : ?ê = 23.9 and ?ê
= 12.2. The used methods for the measurement of these rigidity
constants were entropic tension and micropipet [27]. These
curves reflect the discussion made above.
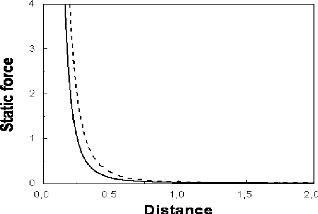
FIG. 1. Reduced static Casimir force,
ll/kBT, versus separation D, for two lipid
systems that are SOPC (solid line) and DAPC (dashed line), of respective
membrane bending rigidity constants : k = 0.96 ×
10-19 J and k = 0.49 ×
10-19 J, at temperature T =
18?C. The reduced force and separation are expressed in
arbitrary units.
IV. DYNAMIC CASIMIR FORCE
To study the dynamic phenomena, the main physical quantity to
consider is the time height-field, h (r, t), where r
= (x, y) E R2 denotes the position
vector and t the time. The latter represents the time observation of
the system before it reaches its final equilibrium state. We recall that the
time height function h (r, t) solves a non-dissipative
Langevin equation (with noise) [28]
|
?h(r,t) ?t
|
= - äH0 [h]
äh (r, t) + í (r,
t) , (4.0)
|
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
where > 0 is a kinetic coefficient. The latter has
the dimension : [] = L4 0T -1
0 , where L0 is some length
and T0 the time unit. Here, í (r,
t) is a Gaussian random force with mean zero and variance
?í (r,t)í
(r',t')? = 2ä2
(r - r')ä (t -
t') , (4.0)
and H0 is the static Hamiltonian (divided by
kBT), defined in Eq. (13).
The bare time correlation function, whose Fourier transform is
the dynamic structure factor, is defined by the expectation mean-value over
noise í
G(r - r',t -
t') =
?h(r,t)h(r',t')??
- ?h(r,t)??
?h(r',t')?? , t
> t' . (4.0)
The dynamic equation (28) shows that the time height function
h is a functional of noise í, and we write : h
= h [í]. Instead of solving the Langevin equation
for h [í] and then averaging over the noise
distribution P [í], the correlation and response functions can
be directly computed by means of a suitable field-theory, of action [28 -
31]
A [h, h] = J dt J
d2r { h?th +
?häâh°
h?h } , (4.0)
so that, for an arbitrary observable, O [æ], one
has 111 JJJ
|
?
?O?? = [dí] O [ö
[í]] P [í] =
|
f DhD?hOe-A[h,?h]
(4.0)
f DhD?he-A[h,h]
|
where h (r, t) is an auxiliary field,
coupled to an external field h (r, t). The correlation and
response functions can be computed replacing the static Hamiltonian H0
appearing in Eq. (13), by a new one : H0 [h, J] = H0 [h] -
f d2rJh. Consequently, for a given observable O,
we have
|
ä ?O?J äJ
(r,t)
|
J=0
|
? )
= ?h (r, t) O . (4.0)
|
108
[ ]
The notation ? . ?J means the average taken
with respect to the action A h, ?h, J associated with
the
Hamiltonian H0 [h, J]. In view of the structure of
equality (33), h is called response field. Now, if O =
h, we get the response of the order parameter field to the external
perturbation J
|
R (r - r',t -
t') =
|
?
ä ?h(r',t')?J =
(ti
(r,t)h(r',t')).
(4.0)
äJ (r, t) J=0
|
The causality implies that the response function vanishes for
t < t'. In fact, this function can be related to the
time-dependent (connected) correlation function using the
fluctuation-dissipation theorem, according to which
? )
?h (r, t) h
(r', t') = -è
(t - t') ?t ?h (r,
t) h (r',
t')?c . (4.0)
The above important formula shows that the time correlation
function C (r - r', t -
t') = ?ö (r, t) ö
(r', t')?c may be
determined by the knowledge of the response function. In particular, we show
that
(4.0)
t
L2? (t) =
(h2 (r, t))c = -2
f dt' Ch (r, t')
h (r, t')) .
8
The limit t ? -8 gives the natural value
L2? (-8) = 0, since, as assumed, the initial
state corresponds to a completely flat interface.
Consider now a membrane at temperature T that is
initially in a flat state away from thermal equilibrium. At a later time
t, the membrane possesses a certain roughness, L?
(t). Of course, the latter is time-dependent, and we are interested in
how it increases in time.
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
109
We point out that the thermal fluctuations give rise to some
roughness that is characterized by the appearance of anisotropic humps.
Therefore, a segment of linear size L effectuates excursions of size
[32]
L? = BL? . (4.0)
Such a relation defines the roughness exponent
æ. Notice that L is of the order of the in-plane
correlation length, L?. From relation (20), we deduce the exponent
æ and the amplitude B. Their respective values
are : æ = 1 and B es.,
(kBT/ê)1/2.
In order to determine the growth of roughness L? in
time, the key is to consider the excess free energy (per unit area) due to the
confinement, ?F. Such an excess is related to the fact that the
confining membrane suffers a loss of entropy. Formula (27) tells us how ?F
must decay with separation. The result reads [32]
?F es., kBT/L2max es.,
kBT (B/L?)2/? , (4.0)
where Lmax represents the wavelength above
which all shape fluctuations are not accessible by the confined membrane. The
repulsive fluctuation-induced interaction leads to the disjoining pressure
|
??F
_
Ð DL?
|
es., L-(1+2/?). (4.0)
?
|
In addition, a care analysis of the Langevin equation (28) shows
that
|
?L???F ?tes., -
?L?
|
= × Ð es., L-(1+2/?) .
(4.0)
?
|
(4.0)
2 + 2æ 4
We emphasize that this scaling form agrees with Monte Carlo
predictions [32, 33]. Solving this first-order differential equation
yields [34]
1
= .
L? (t) es.,
?lt?l , è? = æ
This implies the following scaling form for the linear size
|
L (t) es.,
?iit?ii , è? =
|
1= 1
2 + 2æ 4 . (4.0)
|
Let us comment about the obtained result (39).
Firstly, as it should be, the roughness increases with time (the
exponent è? is positive definite). In addition, the exponent
è? is universal, independently on the membrane bending
rigidity constant ê. Secondly, we note that, in Eq. (39), we
have ignored some non-universal amplitude that scales as ê-1/4.
This means that the time roughness is significant only for those biomembranes
of small bending rigidity constant.
Fourthly, this time roughness can be interpreted as the
perpendicular size of holes and valleys at time t. Fifthly, the
roughness increases until a fine time, ô. The latter can be
interpreted as the time over which the system reaches its final equilibrium
state. This characteristic time then scales as
ô es., -1L1/?l
? , (4.0)
where we have ignored some non-universal amplitude that scales
as ê. Here, L? es., D is the final
roughness. Explicitly, we have
ô es., -1D4 .
(4.0)
As it should be, the final time increases with increasing film
thickness D. On the other hand, we can rewrite the behavior (39) as
|
L? (t) L?
(ô)
|
= I T I?l. (4.0)
|
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
This equality means that the roughness ratio, as a function of
the reduced time, is universal.
Now, to compute the dynamic Casimir force, we start from a
formula analog to that defined in Eq. (24), that is
11(t) 1
=
kBT Ó
? ln Z? 1 ?u ? ln
Z?
?D = ?u , (4.0)
Ó ?D
with the new partition function
fZ? =
DhD?he-A[h,?h] .
(4.0)
11(t) 1
kBT 2
?u
A simple algebra taking into account the basic relation
(35a) gives
?D L2 ? (t) , (4.0)
which is very similar to the static relation defined in Eq. (25),
but with a time-dependent membrane roughness, L? (t).
Combining formulae (43) and (46) leads to the desired expression
for the time Casimir force (per unit area)
|
11(t) 11(ô)
|
( t \?'
= ,
ô
|
(4.0)
|
where 11 (ô) is the final static Casimir force,
relation (25). The force exponent, èf, is such that
æ 1
èf = 2è? =
(4.0)
1 + æ 2
= .
110
The induced force then grows with time as
t1/2 until it reaches its final value 11
(ô). At fixed time and separation D, the force
amplitude depends, of course, on ê, and decreases in this
parameter according to ê-3/2. Also, we note that the
above equality means that the force ratio as a function of the reduced time is
universal.
In Fig. 2, we draw the reduced dynamic Casimir force, 11
(t) /11 (ô), upon the renormalized time
t/ô.

K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
FIG. 2. Reduced dynamic Casimir force, 11 (t) /11 (r), upon the
renormalized time t/r.
Finally, consider again a membrane which is initially flat but
is now coupled to overdamped surface waves. This real situation corresponds to
a confined membrane subject to hydrodynamic interactions. The roughness now
grows as [35]
|
?L? (t) t???
|
,
|
?è? = æ
1 + 2æ
|
1
= 3 . (4.0)
|
111
Therefore, the roughness increases with time more rapidly
than that relative to biomembranes free from hydrodynamic interactions.
In this case, the dynamic Casimir force is such that
|
11h (t) 11(ôh)
|
( t )
= ôh
|
??f
|
,
|
(4.0)
|
where 11 (ôh) is the final static Casimir force,
relation (25). The new force exponent is
|
- èf = 2-è? =
2æ
1 + 2æ
|
2
= 3 . (4.0)
|
There, ôh D3 accounts for
the new time-scale over which the confined membrane reaches its final
equilibrium state. Therefore, the dynamic Casimir force decays
with time as t2/3, that is more rapidly than
that where the hydrodynamic interactions are ignored, which scales rather as
t1/2. As we said before, this drastic change can
be attributed to the overdamped surface waves that develop larger and larger
humps.
We depict, in Fig. 3, the variation of the reduced dynamic
force (with hydrodynamic interactions), 11h (t) /11
(ôh), upon the renormalized time t/ôh.

K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
112
FIG. 3. Reduced dynamic Casimir force (with hydrodynamic
interactions), 11h (t)
/11 (r), upon the renormalized time
t/rh.
V. CONCLUSIONS
In this work, we have reexamined the computation of the
Casimir force between two parallel walls delimitating a fluctuating fluid
membrane that is immersed in some liquid. This force is caused by the thermal
fluctuations of the membrane. We have studied the problem from both static and
dynamic point of view.
We were first interested in the time variation of the
roughening, L1 (t), starting with a membrane that is inially
in a flat state, at a certain temperature. Of course, this length grows with
time, and we found that : L1 (t) t°?
(91 = 1/4), provided that the hydrodynamic
interactions are ignored. For real systems, however, these interactions are
important, and we have shown that the roughness increases more rapidly
as : ?L1 (t)
t?°? (91 = 1/3). The
dynamic process is then stopped at a final r (or rh) that
represents the required time over which the biomembrane reaches its final
equilibrium state. The final time behaves as : r D4 (or
rh ? D3), with D the film thickness.
Now, assume that the system is explored at scales of the order
of the wavelength q-1, where q =
(4ð/À) sin (9/2) is the wave vector modulus, with
À the wavelength of the incident radiation and 9
the
scattering-angle. In these conditions, the relaxation rate,
r (q), scales with q as : r-1
(q) q1/°? = q4
( h (q) q1/?°? = q3)
or r-1 . Physically speaking, the relaxation
rate characterizes the local growth of the
height fluctuations.
Afterwards, the question was addressed to the computation of
the Casimir force, II. At equilibrium, using an appropriate field theory, we
found that this force decays with separation D as : II
D-3, with a known amplitude scaling as
#c-1, where #c is the membrane bending rigidity
constant. Such a force is then very small in comparison with the Coulombian
one. In addition, this force disappears when the
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
temperature of the medium is sufficiently lowered.
The dynamic Casimir force, II (t), was computed using
a non-dissipative Langevin equation (with noise), solved by the time
height-field. We have shown that : II (t)
t°f
(èf = 2è1 =
1/2). When the hydrodynamic interactions effects are important, we
found that the dynamic force increases more rapidly as :
( )
IIh (t) '--
t?°f
?èf =
2?è1 = 2/3 .
Notice that we have ignored some details such as the role of
inclusions (proteins, cholesterol, glycolipids, other macromolecules) and
chemical mismatch on the force expression. It is well-established that these
details simply lead to an additive renormalization of the bending rigidity
constant. Indeed, we write êeffective =
ê + äê, where ê is the
bending rigidity constant of the membrane free from inclusions, and
äê is the contribution of the incorporated entities.
Generally, the shift äê is a function of the inclusion
concentration and compositions of species of different chemical nature (various
phospholipids forming the bilayer). Hence, to take into account the presence of
inclusions and chemical mismatch, it would be sufficient to replace ê
by êeffective, in the above
established relations.
As last word, we emphasize that the results derived in this
paper may be extended to bilayer surfactants, although the two systems are not
of the same structure and composition. One of the differences is the magnitude
order of the bending rigidity constant.
APPENDIX
To show formula (17), we start from the partition function that
we rewrite on the following form
|
J I j
-H [h]
Z = Dh exp =
kBT
|
D/2
f
-D/2
|
dz (z) . (5.0)
|
113
Also, it is easy to see that the membrane mean-roughness is given
by
L2 1 =
D/2
f dzz2 (z)
. (5.0)
-D/2
D/2
f
-D/2
dz (z)
The restricted partition function is
? { j
-H [h]
(z) = Dhä [z - h
(x0, y0)] exp .
(5.0)
kBT
Here, H [h] is the original Hamiltonian defined in
Eq. (3). Of course, this definition is independent on the chosen point
(x0, y0), because of the
translation symmetry along the parallel directions to plates. Notice that the
above function is not singular, whatever the value of the perpendicular
distance.
Since we are interested in the confinement-regime, that is
when the separation D is much smaller than (z h <<
L0
the membrane mean-roughness L0
), we can replace the function par its value at z =
0,
1 1
denoted 0. In this limit, Eq. (A.2)
gives the desired result.
This ends the proof of the expected formula.
ACKNOWLEDGMENTS
We are much indebted to Professors T. Bickel, J.-F. Joanny and
C. Marques for helpful discussions, during the »First International
Workshop On Soft-Condensed Matter Physics and Biological Systems», 14-17
November 2006, Marrakech, Morocco. One of us (M.B.) would like to thank the
Professor C. Misbah for fruitful correspondences, and the Laboratoire de
Spectroscopie Physique (Joseph Fourier University of Grenoble) for their
kinds of hospitalities during his regular visits.
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
114
REFERENCES
1 M.S. Bretscher and S. Munro, Science
261, 12801281 (1993).
2 J. Dai and M.P. Sheetz, Meth. Cell Biol.
55, 157171 (1998).
3 M. Edidin, Curr. Opin. Struc. Biol.
7, 528532 (1997).
4 C.R. Hackenbrock, Trends Biochem. Sci.
6, 151154 (1981).
5 C. Tanford, The Hydrophobic Effect, 2d
ed., Wiley, 1980.
6 D.E. Vance and J. Vance, eds., Biochemistry
of Lipids, Lipoproteins, and Membranes, Elsevier, 1996.
7 F. Zhang, G.M. Lee, and K. Jacobson, BioEssays
15, 579588 (1993).
8 S. Safran, Statistical Thermodynamics of
Surfaces, Interfaces and Membranes, Addison-Wesley, Reading, MA, 1994.
9 W. Helfrich, Z. Naturforsch.
28c, 693 (1973).
10 For a recent review, see U. Seifert, Advances in
Physics 46, 13 (1997).
11 H. Ringsdorf and B. Schmidt, How to Bridge
the Gap Between Membrane, Biology and Polymers Science, P.M. Bungay et
al., eds, Synthetic Membranes: Science, Engineering and
Applications, p. 701, D. Reiidel Pulishing Compagny, 1986.
12 D.D. Lasic, American Scientist
80, 250 (1992).
13 V.P. Torchilin, Effect of Polymers Attached
to the Lipid Head Groups on Properties of Liposomes, D.D. Lasic and Y.
Barenholz, eds, Handbook of Nonmedical Applications of Liposomes,
Volume 1, p. 263, RCC Press, Boca Raton, 1996.
14 R. Joannic, L. Auvray, and D.D. Lasic, Phys.
Rev. Lett. 78, 3402 (1997).
15 P.-G. de Gennes, Scaling Concept in Polymer
Physics, Cornell University Press, 1979.
16 H.B.G. Casimir, Proc. Kon. Ned. Akad. Wetenschap
B 51, 793 (1948).
17 S.K. Lamoreaux, Phys. Rev. Lett.
78, 5 (1997).
18 U. Mohideen and A. Roy, Phys. Rev. Lett.
81, 4549 (1998).
19 M.E. Fisher and P.-G. de Gennes, C. R. Acad.
Sci. (Paris) Sér. B 287, 207 (1978); P.-G. de Gennes,
C. R. Acad. Sci. (Paris) II 292, 701 (1981).
20 M. Krech, The Casimir Effect in Critical
Systems, World Scientific, Singapore, 1994.
21 More recent references can be found in : F.
Schlesener, A. Hanke, and S. Dietrich, J. Stat. Phys. 110, 981
(2003); M. Benhamou, M. El Yaznasni, H. Ridouane, and E.-K. Hachem, Braz. J.
Phys. 36, 1 (2006).
22 R. Lipowsky, Handbook of Biological
Physics, R. Lipowsky and E. Sackmann, eds, Volume 1, p. 521, Elsevier,
1995.
23 P.B. Canham, J. Theoret. Biol.
26, 61 (1970).
24 O. Farago, Phys. Rev. E 78,
051919 (2008).
25 We recover the power law II -
D-3 that is known in literature (see, for
instance, Ref. [8]), but the corresponding amplitude depends on the used
model.
26 G. Gompper and D.M. Kroll, Europhys. Lett.
9, 59 (1989).
27 U. Seifert and R. Lipowsky, in Structure and
Dynamics of Membranes, Handbook of Biological Physics, R.
Lipowsky and E. Sackmann, eds, Elsevier, North-Holland, 1995.
28 J. Zinn-Justin, Quantum Field Theory and
Critical Phenomena, Clarendon Press, Oxford, 1989.
29 H.K. Jansen, Z. Phys. B 23, 377
(1976).
30 R. Bausch, H.K. Jansen, and H. Wagner, Z. Phys.
B 24, 113 (1976).
31 F. Langouche, D. Roekaerts, and E. Tirapegui,
Physica A 95, 252 (1979).
32 R. Lipowsky, in Random Fluctuations and
Growth, H.E. Stanley and N. Ostrowsky, eds, p. 227-245, Kluwer Academic
Publishers, Dordrecht 1988.
33 R. Lipowsky, J. Phys. A 18,
L-585 (1985).
34 R. Lipowsky, Physica Scripta T
29, 259 (1989).
35 F. Brochard and J.F. Lennon, J. Phys.
(Paris) 36, 1035 (1975).

Dans cette deuxième contribution
originale, nous considérons une solution colloïdale
au contact d'une biomembrane, qui est confinée dans une fente. L'on
suppose que l'épaisseur de cette fente est beaucoup plus petite que la
rugosité en volume, afin d'assurer le confinement de la membrane. Le but
étant l'étude de la dynamique Brownienne de ces particules, sous
la variation d'un paramètre adéquat, tel que la
température, par exemple. L'objet de base est la densité locale
des particules.
Nous déterminons exactement cette densité, qui est
fonctionde la distance et du temps. L'outil pour cela est l'équation de
Smolokowski
Article N°2
Dynamique Brownienne de colloïdes
au contact d'une biomembrane confinée.
101

|
African Journal Of Mathematical Physics Volume
8(2010)101-114
|
Casimir force in confined biomembranes
K. El Hasnaoui, Y. Madmoune, H. Kaidi,
M. Chahid, and M.
Benhamou
Laboratoire de Physique des Polymères et
Phénomènes Critiques
Facultédes Sciences Ben M'sik, P.O. 7955,
Casablanca, Morocco
m.benhamou@univh2m.ac.ma
abstract
We reexamine the computation of the Casimir force between two
parallel interacting plates delimitating a liquid with an immersed biomembrane.
We denote by D their separation, which is assumed to be much smaller
than the bulk roughness, in order to ensure the membrane confinement. This
repulsive force originates from the thermal undulations of the membrane. To
this end, we first introduce a field theory, where the field is noting else but
the height-function. The field model depends on two parameters, namely the
membrane bending rigidity constant, k, and some elastic constant,
u - D-4. We first compute the static Casimir force
(per unit area), 11, and find that the latter decays with separation D
as : 11 - D-3, with a known amplitude scaling as
k-1. Therefore, the force has significant values only for
those biomembranes of small enough k. Second, we consider a
biomembrane (at temperature T) that is initially in a flat state away
from thermal equilibrium, and we are interested in how the dynamic force, 11
(t), grows in time. To do calculations, use is made of a
non-dissipative Langevin equation (with noise) that is solved by the time
height-field. We first show that the membrane roughness, L?
(t), increases with time as : L? (t) -
t1/4 (t < r), with the final time
r - D4 (required time over which the final
equilibrium state is reached). Also, we find that the force increases in time
according to : 11 (t) - t1/2 (t
< r). The discussion is extended to the real situation where the
biomembrane is subject to hydrodynamic interactions caused by the surrounding
liquid. In this case, we show that : L? (t) -
t1/3 (t < rh) and 11h
(t) - t2/3 (t < rh),
with the new final time rh - D3. Consequently, the
hydrodynamic interactions lead to substantial changes of the dynamic properties
of the confined membrane, because both roughness and induced force grow more
rapidly. Finally, the study may be extended, in a straightforward way, to
bilayer surfactants confined to the same geometry.
Key words: Biomembranes - Confinement - Casimir force -
Dynamics.
I. INTRODUCTION
The cell membranes are of great importance to life, because
they separate the cell from the surrounding environment and act as a selective
barrier for the import and export of materials. More details concerning the
structural organization and basic functions of biomembranes can be found in
Refs. [1 - 7]. It is well-recognized by the scientific community that the cell
membranes essentially present as a phospho-lipid bilayer combined with a
variety of proteins and cholesterol (mosaic fluid model). In
particular, the function of the cholesterol molecules is to ensure the bilayer
fluidity. A phospholipid is an amphiphile
0 ?c a GNPHE publication 2010,
ajmp@fsr.ac.ma
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
102
molecule possessing a hydrophilic polar head attached to two
hydrophobic (fatty acyl) chains. The phos-pholipids move freely on the membrane
surface. On the other hand, the thickness of a bilayer membrane is of the order
of 50 Angstroms. These two properties allow to consider it as a two-dimensional
fluid membrane. The fluid membranes, self-assembled from surfactant solutions,
may have a variety of shapes and topologies [8], which have been explained in
terms of bending energy [9, 10].
In real situations, the biomembranes are not trapped in
liquids of infinite extent, but they rather confined to geometrical boundaries,
such as white and red globules or liposomes (as drugs transport agents [11 -
14]) in blood vessels. For simplicity, we consider the situation where the
biomembrane is confined in a liquid domain that is finite in one spatial
direction. We denote by D its size in this direction. For a tube,
D being the diameter, and for a liquid domain delimitated by two
parallel plates, this size is simply the separation between walls. Naturally,
the length D must be compared to the bulk roughness, L0
1, which is the typical size of humps caused by the thermal
fluctuations of the membrane. The latter depends on the nature of lipid
molecules forming the bilayer. The biomembrane is confined only when D
is much smaller than the bulk roughness L0
1. This condition is similar to that usually
encountered in confined polymers context [15].
The membrane undulations give rise to repulsive effective
interactions between the confining geometrical boundaries. The induced force we
term Casimir force is naturally a function of the size D, and
must decays as this scale is increased. In this paper, we are interested in how
this force decays with distance. To simplify calculations, we assume that the
membrane is confined to two parallel plates that are a finite distance D
< L01 apart.
The word »Casimir» is inspired from the traditional
Casimir effect. Such an effect, predicted, for the first time, by Hendrick
Casimir in 1948 [16], is one of the fundamental discoveries in the last
century. According to Casimir, the vacuum quantum fluctuations of a confined
electromagnetic field generate an attractive force between two parallel
uncharged conducting plates. The Casimir effect has been confirmed in more
recent experiments by Lamoreaux [17] and by Mohideen and Roy [18]. Thereafter,
Fisher and de Gennes [19], in a short note, remarked that the Casimir effect
also appears in the context of critical systems, such as fluids, simple liquid
mixtures, polymer blends, liquid 4He, or liquid-crystals, confined
to restricted geometries or in the presence of immersed colloidal particles.
For these systems, the critical fluctuations of the order parameter play the
role of the vacuum quantum fluctuations, and then, they lead to long-ranged
forces between the confining walls or between immersed colloids [20,
21].
To compute the Casimir force between the confining walls, we
first elaborate a more general field theory that takes into account the
primitive interactions experienced by the confined membrane. As we shall see
below, in confinement regime, the field model depends only on two parameters
that are the membrane bending rigidity constant and a coupling constant
containing all infirmation concerning the interaction potential exerting by the
walls. In addition, the last parameter is a known function of the separation
D. With the help of the constructed free energy, we first computed the
static Casimir force (per unit area), II. The exact calculations show that the
latter decays with separation D according to a power law, that is II
#c-1 (kBT)2
D-3, with a known amplitude. Here, kBT
denotes the thermal energy, and #c the membrane bending rigidity
constant. Of course, this force increases with temperature, and has significant
values only for those biomembranes of small enough #c. The second
problem we examined is the computation of the dynamic Casimir force, II
(t). More precisely, we considered a biomembrane at temperature T
that is initially in a flat state away from the thermal equilibrium, and
we were interested in how the expected force grows in time, before the final
state is reached. Using a scaling argument, we first showed that the membrane
roughness, L1 (t), grows with time as : L1
(t) t1/4 (t < r), with
the final time r D4. The latter can be interpreted as the
required time over which the final equilibrium state is reached. Second, using
a non-dissipative Langevin equation, we found that the force increases in time
according to the power law : II (t) t1/2
(t < r). Third, the discussion is extended to the real
situation where the biomembrane is subject to hydrodynamic interactions caused
by the flow of the surrounding
liquid. In this case, we show that : L1 (t)
t1/3 (t < rh) and II (t)
t2/3 (t < rh), with the new
final
time rh D3. Consequently, the
hydrodynamic interactions give rise to drastic changes of the dynamic
properties of the confined membrane, since both roughness and induced force
grow more rapidly.
This paper is organized as follows. In Sec. II, we present the
field model allowing the determination of the Casimir force from a static and
dynamic point of view. The Sec. III and Sec. IV are devoted to the computation
of the static and dynamic induced forces, respectively. We draw our conclusions
in the last section. Some technical details are presented in Appendix.
K. El Hasnaoui et al. African Journal Of Mathematical
Physics Volume 8(2010)101-114
103
II. THEORETICAL FORMULATION
Consider a fluctuating fluid membrane that is confined to two
interacting parallel walls 1 and 2. We denote by D their finite
separation. Naturally, the separation D must be compared to the bulk
membrane roughness, L01, when the system is
unconfined (free membrane). The membrane is confined only when the condition
L << L01 is fulfilled. For the opposite
condition, that is L >> L01, we expect
finite size corrections.
We assume that these walls are located at z =
-D/2 and z = D/2, respectively. Here, z
means the perpendicular distance. For simplicity, we suppose that the two
surfaces are physically equivalent. We design by V (z) the
interaction potential exerted by one wall on the fluid membrane, in the absence
of the other. Usually, V (z) is the sum of a repulsive and an
attractive potentials. A typical example is provided by the following potential
[22]
V (z) = Vh (z) +
VvdW (z) , (2.0)
where
Vh (z) =
Ahe-z/Ah (2.0)
represents
the repulsive hydration potential due to the water molecules inserted between
hydrophilic lipid heads [22]. The amplitude Ah and the potential-range
ëh are of the order of : Ah ^, 0.2
J/m2 and ëh ^, 0.2-0.3 nm. In fact,
the amplitude Ah is Ah = Ph xëh, with
the hydration pressure Ph ^, 108-109 Pa. There,
VvdW (z) accounts for the van der Waals potential
between one wall and biomembrane, which are a distance z apart. Its
form is as follows
[ ]
H 1 1
VvdW (z) = - ,
z2 - 2
(z + ä)2 + (2.0)
12ð (z + 2ä)2
with the Hamaker constant H ^, 10-22 -
10-21 J, and ä ^, 4 nm denotes the membrane thickness.
For large distance z, this implies
Wä2
VvdW (z) ? z4 .
(2.0)
Generally, in addition to the distance z, the interaction
potential V (z) depends on certain length-scales,
(î1, ...,în), which are the
interactions ranges. The fluid membrane then experiences the following total
potential
I D ) I D ) , -D
U (z) = V 2 - z + V
2 + z 2 < z < D 2 .
(2.0)
In the Monge representation, a point on the membrane can be
described by the three-dimensional position vector r = (x,
y, z = h (x, y)), where h (x, y) E
[-D/2, D/2] is the height-field. The latter then fluctuates
around the mid-plane located at z = 0.
The Statistical Mechanics for the description of such a
(tensionless) fluid membrane is based on the standard Canham-Helfrich
Hamiltonian [9, 23]
? [ê ]
1-l [h] = dxdy 2
(?h)2 + W (h) , (2.0)
with the
membrane bending rigidity constant ê. The latter is comparable
to the thermal energy kBT, where T is the absolute
temperature and kB is the Boltzmann's constant. There, W
(h) is the interaction potential per unit area, that is
U (h)
W (h) = L2 , (2.0)
where
the potential U (h) is defined in Eq. (2), and L is
the lateral linear size of the biomembrane. Let us discuss the pair-potential
W (h).
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
Firstly, Eq. (2) suggests that this total potential is an
even function of the perpendicular distance h, that is
W (-h) = W (h) .
(2.0)
In particular, we have W (-D/2) = W
(D/2).
Secondly, when they exist, the zeros h0's of the
potential function U (h) are such that
(D ) (D )
V 2 - h0 = -V 2 +
h0 . (2.0)
This equality indicates that, if h0 is a zero of the
potential function, then, -h0 is a zero too. The number of zeros is
then an even number. In addition, the zero h0's are different
from 0, in all cases. Indeed, the quantity V (D/2) does not
vanish, since it represents the potential created by one wall at the middle of
the film. We emphasize that, when the potential processes no zero, it is either
repulsive or attractive. When this same potential vanishes at some points,
then, it is either repulsive of attractive between two consecutive zeros.
Thirdly, we first note that, from relation (2), we deduce that
the first derivative of the potential function, with respect to distance
h, is an odd function, that is W'
(-h) = -W' (h). Applying this relation to
the midpoint h = 0 yields : W' (0) = 0. Therefore,
the potential W exhibits an extremum at h = 0, whatever the
form of the function V (h). We find that this extremum is a
maximum, if V ?(D/2) < 0, and a
minimum, if V ?(D/2) > 0. The
potential U presents an horizontal tangent at h = 0, if only
if V ?(D/2) = 0. On the other hand, the general
condition giving the extrema {hm} is
|
dV dh
|
????h= D 2 -hm
|
dV =
dh
|
????h= D 2 +hm
|
. (2.0)
|
Since the first derivative W' (h)
is an odd function of distance h, it must have an odd number
of extremum points. The point h = hm is a maximum,
if
|
and a minimum, if
|
d2V dh2
|
????h= D 2 -hm
|
<
|
d2V dh2
|
????h= D 2 +hm
|
,
|
(2.0)
|
|
d2V dh2
|
????h= D 2 -hm
|
>
|
d2V dh2
|
????h= D 2 +hm
|
. (2.0)
|
At point h = hm, we have an
horizontal tangent, if
d2V
dh2
????h= D 2 +hm
. (2.0)
d2V dh2
????h= D 2 -hm
104
The above deductions depends, of course, on the form of the
interaction potential V (h).
Fourthly, a simple dimensional analysis shows that the total
interaction potential can be rewritten on the following scaling form
|
W (h) kBT
|
D2Ö( = 1 h1n 1
(2.0)
D, D,..., D J ,
|
where (î1, ...,în)
are the ranges of various interactions experienced by the membrane, and
Ö(x1, ..., xn+1) is a (n + 1)-factor
scaling-function.
Finally, we note that the pair-potential W
(h) cannot be singular at h = 0. It is rather an
analytic function in the h variable. Therefore, at fixed ratios
îi/D, an expansion of the scaling-function Ö,
around the value h = 0, yields
W (h) kBT
h2
2 D4
= ã + (h4) .
(2.0)
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
105
We restrict ourselves to the class of potentials that exhibit
a minimum at the mid-plane h = 0. This assumption implies that the
coefficient ã is positive definite, i.e. ã >
0. Of course, such a coefficient depends on the ratios of the
scale-lengths îi to the separation D.
In confinement regime where the distance h is small
enough, we can approximate the total interaction potential by its quadratic
part. In these conditions, the Canham-Helfrich Hamiltonian becomes
W0 [h] = 2 J dxdy
[1ê (?h)2 + uhl
, (2.0)
with the elastic constant
u = ã kBT
D4 .(2.0)
The prefactor ã will be computed below. The
above expression for the elastic constant u gives an idea on its
dependance on the film thickness D. In addition, we state that this
coefficient may be regarded as a Lagrange multiplier that fixes the
value of the membrane roughness.
Thanks to the above Hamiltonian, we calculate the
mean-expectation value of the physical quantities, like the height-correlation
function (propagator or Green function), defined by
G (x - x', y -
y') = (h (x, y) h
(x',y')) - (h (x,
y)) (h (x',y')) .
(2.0)
The latter solves the linear differential equation
(îc?2 + u)G(x -
x',y - y') = ä (x -
x')ä (y - y') , (2.0)
where ä (x) denotes the one-dimensional
Dirac function, and ? = ?2/?x2 +
?2/?y2 represents the two-dimensional
Laplacian operator. We have used the notations : = ê/kBT and u =
u/kBT, to mean the reduced membrane elastic constants.
From the propagator, we deduce the expression of the membrane
roughness
L2? = (h2)
- (h)2 = G(0,0) . (2.0)
Such a quantity measures the fluctuations of the
height-function (fluctuations amplitude) around the equilibrium plane located
at z = 0. We show in Appendix that the membrane roughness is exactly
given by
2
L2 = 12, (2.0)
provided that one is in the confinement-regime, i.e. D
<< L0?. Notice that the above equality
indicates that the roughness is independent on the geometrical properties of
the membrane (through ê). We emphasize that this relation can be
recovered using the argument that each point of the membrane has equal
probability to be found anywhere between the walls [24].
The elastic constant u may be calculated using the known
relation
L2 1 kBT = (2.0)
?8 ,urs .
This gives
u =
9 (kBT)2
êD4 . (2.0)
4
This formula clearly shows that this elastic constant decays
with separation D as D-4. The term
uh2/2 then describes a confinement potential that
ensures the localization of the membrane around the mid-plane. Integral over
the hole plane R2 of this term represents the loss
entropy due to the confinement of the membrane. The value (19) of the elastic
constant is compatible with the constraint (17).
Therefore, the elaborated model is based on the Hamiltonian
(13), with a quadratic confinement potential. We can say that the presence of
the walls simply leads to a confinement of the membrane in a region
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
of the infinite space of perpendicular size L?.
We define now another length-scale that is the in-plane
correlation length, L?. The latter measures the correlations extent
along the parallel directions to the walls. More precisely, the propagator
G (x - x', y -
y') fails exponentially beyond L?, that is for
distances d such that d =
v(x - x')2
+ (y - y')2
> L?. From the standard relation
L2 ? = kBT
16ê L2 ? , (2.0)
we deduce
L
(2.0)
( ê )1/2
2
? = v3 D .
kBT
In contrary to L?, the length-scale L?
depends on the geometrical characteristics of the membrane (through
ê).
The next steps consist in the computation of the Casimir force at
and out equilibrium.
III. STATIC CASIMIR FORCE
When viewed under the microscope, the membranes of vesicles
present thermally excited shape fluctuations. Generally, objects such as
interfaces, membranes or polymers undergo such fluctuations, in order to
increase their configurational entropy. For bilayer biomembranes and
surfactants, the consequence of these undulations is that, they give rise to an
induced force called Casimir force.
To compute the desired force, we start from the partition
function constructed with the Hamiltonian defined in Eq. (13). This partition
function is the following functional integral
f { }
-H0 [h]
Z = Dh exp , (3.0)
kBT
where integration is performed over all height-field
configurations. The associated free energy is such that : F = -kBT
lnZ, which is, of course, a function of the separation D. If we
denote by Ó = L2 the common area of plates, the
Casimir force (per unit area) is minus the first derivative of the
free energy (per unit area) with respect to the film-thickness D, that
is
This force per unit area is called disjoining pressure. In
fact, II is the required pressure to maintain the two plates at some distance
D apart. In term of the partition function, the disjoining pressure
rewrites
|
II
kBT =
|
1 Ó
|
? lnZ 1 ?u ? lnZ
?D = ?u . (3.0)
Ó ?D
|
Using definition (19) together with Eqs. (23) and (24) yields
1 ?u
II = -(3.0)
2 ?D L2 ? .
Explicitly, we obtain the desired formula
êD3 . (3.0)
3
II = 8
(kBT)2
106
From this relation, we extract the expression of the disjoining
potential (per unit area) [25]
f D II (D') dD'
= 3 (kBT )2
Vd (D) = - êD2 . (3.0)
16
8
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
107
The above expression of the Casimir force (per unit area)
calls the following remarks.
Firstly, this force decays with distance more slowly in
comparison to the Coulombian one that decreases rather as
D-2.
Secondly, this same force depends on the nature of lipids
forming the bilayer (through ê). In this sense, contrarily to
the Casimir effect in Quantum Field Theory [16] and in Critical Phenomena [20],
the present force is not universal. Incidentally, if this force is
multiplied by ê, then, it will become a universal quantity.
Thirdly, at fixed temperature and distance, the force amplitude has significant
values only for those bilayer membrane of small bending rigidity constant.
Fourthly, as it should be, such a force increases with
increasing temperature. Indeed, at high temperature, the membrane undulations
are strong enough.
Finally, the numerical prefactor 3/8 (Helfrich's
cH-amplitude [9]) is close to the value obtained using Monte Carlo
simulation [26].
In Fig. 1, we superpose the variations of the reduced static
Casimir force Ð/kBT upon separation D, for two
lipid systems, namely SOPC and DAPC [27], at temperature T =
18?C. The respective membrane bending rigidity constants are :
ê = 0.96 x 10-19 J and ê =
0.49 x 10-19 J. These values correspond to the renormalized
bending rigidity constants : ?ê = 23.9 and ?ê
= 12.2. The used methods for the measurement of these rigidity
constants were entropic tension and micropipet [27]. These
curves reflect the discussion made above.
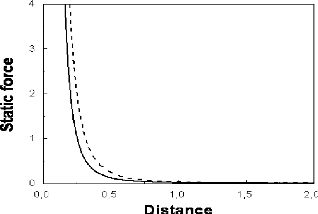
FIG. 1. Reduced static Casimir force,
ll/kBT, versus separation D, for two lipid
systems that are SOPC (solid line) and DAPC (dashed line), of respective
membrane bending rigidity constants : k = 0.96 ×
10-19 J and k = 0.49 ×
10-19 J, at temperature T =
18?C. The reduced force and separation are expressed in
arbitrary units.
IV. DYNAMIC CASIMIR FORCE
To study the dynamic phenomena, the main physical quantity to
consider is the time height-field, h (r, t), where r
= (x, y) E R2 denotes the position
vector and t the time. The latter represents the time observation of
the system before it reaches its final equilibrium state. We recall that the
time height function h (r, t) solves a non-dissipative
Langevin equation (with noise) [28]
|
?h(r,t) ?t
|
= - äH0 [h]
äh (r, t) + í (r,
t) , (4.0)
|
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
where > 0 is a kinetic coefficient. The latter has
the dimension : [] = L4 0T -1
0 , where L0 is some length
and T0 the time unit. Here, í (r,
t) is a Gaussian random force with mean zero and variance
?í (r,t)í
(r',t')? = 2ä2
(r - r')ä (t -
t') , (4.0)
and H0 is the static Hamiltonian (divided by
kBT), defined in Eq. (13).
The bare time correlation function, whose Fourier transform is
the dynamic structure factor, is defined by the expectation mean-value over
noise í
G(r - r',t -
t') =
?h(r,t)h(r',t')??
- ?h(r,t)??
?h(r',t')?? , t
> t' . (4.0)
The dynamic equation (28) shows that the time height function
h is a functional of noise í, and we write : h
= h [í]. Instead of solving the Langevin equation
for h [í] and then averaging over the noise
distribution P [í], the correlation and response functions can
be directly computed by means of a suitable field-theory, of action [28 -
31]
A [h, h] = J dt J
d2r { h?th +
?häâh°
h?h } , (4.0)
so that, for an arbitrary observable, O [æ], one
has 111 JJJ
|
?
?O?? = [dí] O [ö
[í]] P [í] =
|
f DhD?hOe-A[h,?h]
(4.0)
f DhD?he-A[h,h]
|
where h (r, t) is an auxiliary field,
coupled to an external field h (r, t). The correlation and
response functions can be computed replacing the static Hamiltonian H0
appearing in Eq. (13), by a new one : H0 [h, J] = H0 [h] -
f d2rJh. Consequently, for a given observable O,
we have
|
ä ?O?J äJ
(r,t)
|
J=0
|
? )
= ?h (r, t) O . (4.0)
|
108
[ ]
The notation ? . ?J means the average taken
with respect to the action A h, ?h, J associated with
the
Hamiltonian H0 [h, J]. In view of the structure of
equality (33), h is called response field. Now, if O =
h, we get the response of the order parameter field to the external
perturbation J
|
R (r - r',t -
t') =
|
?
ä ?h(r',t')?J =
(ti
(r,t)h(r',t')).
(4.0)
äJ (r, t) J=0
|
The causality implies that the response function vanishes for
t < t'. In fact, this function can be related to the
time-dependent (connected) correlation function using the
fluctuation-dissipation theorem, according to which
? )
?h (r, t) h
(r', t') = -è
(t - t') ?t ?h (r,
t) h (r',
t')?c . (4.0)
The above important formula shows that the time correlation
function C (r - r', t -
t') = ?ö (r, t) ö
(r', t')?c may be
determined by the knowledge of the response function. In particular, we show
that
(4.0)
t
L2? (t) =
(h2 (r, t))c = -2
f dt' Ch (r, t')
h (r, t')) .
8
The limit t ? -8 gives the natural value
L2? (-8) = 0, since, as assumed, the initial
state corresponds to a completely flat interface.
Consider now a membrane at temperature T that is
initially in a flat state away from thermal equilibrium. At a later time
t, the membrane possesses a certain roughness, L?
(t). Of course, the latter is time-dependent, and we are interested in
how it increases in time.
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
109
We point out that the thermal fluctuations give rise to some
roughness that is characterized by the appearance of anisotropic humps.
Therefore, a segment of linear size L effectuates excursions of size
[32]
L? = BL? . (4.0)
Such a relation defines the roughness exponent
æ. Notice that L is of the order of the in-plane
correlation length, L?. From relation (20), we deduce the exponent
æ and the amplitude B. Their respective values
are : æ = 1 and B es.,
(kBT/ê)1/2.
In order to determine the growth of roughness L? in
time, the key is to consider the excess free energy (per unit area) due to the
confinement, ?F. Such an excess is related to the fact that the
confining membrane suffers a loss of entropy. Formula (27) tells us how ?F
must decay with separation. The result reads [32]
?F es., kBT/L2max es.,
kBT (B/L?)2/? , (4.0)
where Lmax represents the wavelength above
which all shape fluctuations are not accessible by the confined membrane. The
repulsive fluctuation-induced interaction leads to the disjoining pressure
|
??F
_
Ð DL?
|
es., L-(1+2/?). (4.0)
?
|
In addition, a care analysis of the Langevin equation (28) shows
that
|
?L???F ?tes., -
?L?
|
= × Ð es., L-(1+2/?) .
(4.0)
?
|
(4.0)
2 + 2æ 4
We emphasize that this scaling form agrees with Monte Carlo
predictions [32, 33]. Solving this first-order differential equation
yields [34]
1
= .
L? (t) es.,
?lt?l , è? = æ
This implies the following scaling form for the linear size
|
L (t) es.,
?iit?ii , è? =
|
1= 1
2 + 2æ 4 . (4.0)
|
Let us comment about the obtained result (39).
Firstly, as it should be, the roughness increases with time (the
exponent è? is positive definite). In addition, the exponent
è? is universal, independently on the membrane bending
rigidity constant ê. Secondly, we note that, in Eq. (39), we
have ignored some non-universal amplitude that scales as ê-1/4.
This means that the time roughness is significant only for those biomembranes
of small bending rigidity constant.
Fourthly, this time roughness can be interpreted as the
perpendicular size of holes and valleys at time t. Fifthly, the
roughness increases until a fine time, ô. The latter can be
interpreted as the time over which the system reaches its final equilibrium
state. This characteristic time then scales as
ô es., -1L1/?l
? , (4.0)
where we have ignored some non-universal amplitude that scales
as ê. Here, L? es., D is the final
roughness. Explicitly, we have
ô es., -1D4 .
(4.0)
As it should be, the final time increases with increasing film
thickness D. On the other hand, we can rewrite the behavior (39) as
|
L? (t) L?
(ô)
|
= I T I?l. (4.0)
|
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
This equality means that the roughness ratio, as a function of
the reduced time, is universal.
Now, to compute the dynamic Casimir force, we start from a
formula analog to that defined in Eq. (24), that is
11(t) 1
=
kBT Ó
? ln Z? 1 ?u ? ln
Z?
?D = ?u , (4.0)
Ó ?D
with the new partition function
fZ? =
DhD?he-A[h,?h] .
(4.0)
11(t) 1
kBT 2
?u
A simple algebra taking into account the basic relation
(35a) gives
?D L2 ? (t) , (4.0)
which is very similar to the static relation defined in Eq. (25),
but with a time-dependent membrane roughness, L? (t).
Combining formulae (43) and (46) leads to the desired expression
for the time Casimir force (per unit area)
|
11(t) 11(ô)
|
( t \?'
= ,
ô
|
(4.0)
|
where 11 (ô) is the final static Casimir force,
relation (25). The force exponent, èf, is such that
æ 1
èf = 2è? =
(4.0)
1 + æ 2
= .
110
The induced force then grows with time as
t1/2 until it reaches its final value 11
(ô). At fixed time and separation D, the force
amplitude depends, of course, on ê, and decreases in this
parameter according to ê-3/2. Also, we note that the
above equality means that the force ratio as a function of the reduced time is
universal.
In Fig. 2, we draw the reduced dynamic Casimir force, 11
(t) /11 (ô), upon the renormalized time
t/ô.

K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
FIG. 2. Reduced dynamic Casimir force, 11 (t) /11 (r), upon the
renormalized time t/r.
Finally, consider again a membrane which is initially flat but
is now coupled to overdamped surface waves. This real situation corresponds to
a confined membrane subject to hydrodynamic interactions. The roughness now
grows as [35]
|
?L? (t) t???
|
,
|
?è? = æ
1 + 2æ
|
1
= 3 . (4.0)
|
111
Therefore, the roughness increases with time more rapidly
than that relative to biomembranes free from hydrodynamic interactions.
In this case, the dynamic Casimir force is such that
|
11h (t) 11(ôh)
|
( t )
= ôh
|
??f
|
,
|
(4.0)
|
where 11 (ôh) is the final static Casimir force,
relation (25). The new force exponent is
|
- èf = 2-è? =
2æ
1 + 2æ
|
2
= 3 . (4.0)
|
There, ôh D3 accounts for
the new time-scale over which the confined membrane reaches its final
equilibrium state. Therefore, the dynamic Casimir force decays
with time as t2/3, that is more rapidly than
that where the hydrodynamic interactions are ignored, which scales rather as
t1/2. As we said before, this drastic change can
be attributed to the overdamped surface waves that develop larger and larger
humps.
We depict, in Fig. 3, the variation of the reduced dynamic
force (with hydrodynamic interactions), 11h (t) /11
(ôh), upon the renormalized time t/ôh.
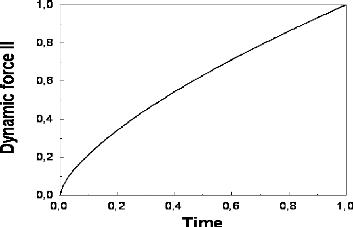
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
112
FIG. 3. Reduced dynamic Casimir force (with hydrodynamic
interactions), 11h (t)
/11 (r), upon the renormalized time
t/rh.
V. CONCLUSIONS
In this work, we have reexamined the computation of the
Casimir force between two parallel walls delimitating a fluctuating fluid
membrane that is immersed in some liquid. This force is caused by the thermal
fluctuations of the membrane. We have studied the problem from both static and
dynamic point of view.
We were first interested in the time variation of the
roughening, L1 (t), starting with a membrane that is inially
in a flat state, at a certain temperature. Of course, this length grows with
time, and we found that : L1 (t) t°?
(91 = 1/4), provided that the hydrodynamic
interactions are ignored. For real systems, however, these interactions are
important, and we have shown that the roughness increases more rapidly
as : ?L1 (t)
t?°? (91 = 1/3). The
dynamic process is then stopped at a final r (or rh) that
represents the required time over which the biomembrane reaches its final
equilibrium state. The final time behaves as : r D4 (or
rh ? D3), with D the film thickness.
Now, assume that the system is explored at scales of the order
of the wavelength q-1, where q =
(4ð/À) sin (9/2) is the wave vector modulus, with
À the wavelength of the incident radiation and 9
the
scattering-angle. In these conditions, the relaxation rate,
r (q), scales with q as : r-1
(q) q1/°? = q4
( h (q) q1/?°? = q3)
or r-1 . Physically speaking, the relaxation
rate characterizes the local growth of the
height fluctuations.
Afterwards, the question was addressed to the computation of
the Casimir force, II. At equilibrium, using an appropriate field theory, we
found that this force decays with separation D as : II
D-3, with a known amplitude scaling as
#c-1, where #c is the membrane bending rigidity
constant. Such a force is then very small in comparison with the Coulombian
one. In addition, this force disappears when the
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
temperature of the medium is sufficiently lowered.
The dynamic Casimir force, II (t), was computed using
a non-dissipative Langevin equation (with noise), solved by the time
height-field. We have shown that : II (t)
t°f
(èf = 2è1 =
1/2). When the hydrodynamic interactions effects are important, we
found that the dynamic force increases more rapidly as :
( )
IIh (t) '--
t?°f
?èf =
2?è1 = 2/3 .
Notice that we have ignored some details such as the role of
inclusions (proteins, cholesterol, glycolipids, other macromolecules) and
chemical mismatch on the force expression. It is well-established that these
details simply lead to an additive renormalization of the bending rigidity
constant. Indeed, we write êeffective =
ê + äê, where ê is the
bending rigidity constant of the membrane free from inclusions, and
äê is the contribution of the incorporated entities.
Generally, the shift äê is a function of the inclusion
concentration and compositions of species of different chemical nature (various
phospholipids forming the bilayer). Hence, to take into account the presence of
inclusions and chemical mismatch, it would be sufficient to replace ê
by êeffective, in the above
established relations.
As last word, we emphasize that the results derived in this
paper may be extended to bilayer surfactants, although the two systems are not
of the same structure and composition. One of the differences is the magnitude
order of the bending rigidity constant.
APPENDIX
To show formula (17), we start from the partition function that
we rewrite on the following form
|
J I j
-H [h]
Z = Dh exp =
kBT
|
D/2
f
-D/2
|
dz (z) . (5.0)
|
113
Also, it is easy to see that the membrane mean-roughness is given
by
L2 1 =
D/2
f dzz2 (z)
. (5.0)
-D/2
D/2
f
-D/2
dz (z)
The restricted partition function is
? { j
-H [h]
(z) = Dhä [z - h
(x0, y0)] exp .
(5.0)
kBT
Here, H [h] is the original Hamiltonian defined in
Eq. (3). Of course, this definition is independent on the chosen point
(x0, y0), because of the
translation symmetry along the parallel directions to plates. Notice that the
above function is not singular, whatever the value of the perpendicular
distance.
Since we are interested in the confinement-regime, that is
when the separation D is much smaller than (z h <<
L0
the membrane mean-roughness L0
), we can replace the function par its value at z =
0,
1 1
denoted 0. In this limit, Eq. (A.2)
gives the desired result.
This ends the proof of the expected formula.
ACKNOWLEDGMENTS
We are much indebted to Professors T. Bickel, J.-F. Joanny and
C. Marques for helpful discussions, during the »First International
Workshop On Soft-Condensed Matter Physics and Biological Systems», 14-17
November 2006, Marrakech, Morocco. One of us (M.B.) would like to thank the
Professor C. Misbah for fruitful correspondences, and the Laboratoire de
Spectroscopie Physique (Joseph Fourier University of Grenoble) for their
kinds of hospitalities during his regular visits.
K. El Hasnaoui et al. African Journal Of Mathematical Physics
Volume 8(2010)101-114
114
REFERENCES
1 M.S. Bretscher and S. Munro, Science
261, 12801281 (1993).
2 J. Dai and M.P. Sheetz, Meth. Cell Biol.
55, 157171 (1998).
3 M. Edidin, Curr. Opin. Struc. Biol.
7, 528532 (1997).
4 C.R. Hackenbrock, Trends Biochem. Sci.
6, 151154 (1981).
5 C. Tanford, The Hydrophobic Effect, 2d
ed., Wiley, 1980.
6 D.E. Vance and J. Vance, eds., Biochemistry
of Lipids, Lipoproteins, and Membranes, Elsevier, 1996.
7 F. Zhang, G.M. Lee, and K. Jacobson, BioEssays
15, 579588 (1993).
8 S. Safran, Statistical Thermodynamics of
Surfaces, Interfaces and Membranes, Addison-Wesley, Reading, MA, 1994.
9 W. Helfrich, Z. Naturforsch.
28c, 693 (1973).
10 For a recent review, see U. Seifert, Advances in
Physics 46, 13 (1997).
11 H. Ringsdorf and B. Schmidt, How to Bridge
the Gap Between Membrane, Biology and Polymers Science, P.M. Bungay et
al., eds, Synthetic Membranes: Science, Engineering and
Applications, p. 701, D. Reiidel Pulishing Compagny, 1986.
12 D.D. Lasic, American Scientist
80, 250 (1992).
13 V.P. Torchilin, Effect of Polymers Attached
to the Lipid Head Groups on Properties of Liposomes, D.D. Lasic and Y.
Barenholz, eds, Handbook of Nonmedical Applications of Liposomes,
Volume 1, p. 263, RCC Press, Boca Raton, 1996.
14 R. Joannic, L. Auvray, and D.D. Lasic, Phys.
Rev. Lett. 78, 3402 (1997).
15 P.-G. de Gennes, Scaling Concept in Polymer
Physics, Cornell University Press, 1979.
16 H.B.G. Casimir, Proc. Kon. Ned. Akad. Wetenschap
B 51, 793 (1948).
17 S.K. Lamoreaux, Phys. Rev. Lett.
78, 5 (1997).
18 U. Mohideen and A. Roy, Phys. Rev. Lett.
81, 4549 (1998).
19 M.E. Fisher and P.-G. de Gennes, C. R. Acad.
Sci. (Paris) Sér. B 287, 207 (1978); P.-G. de Gennes,
C. R. Acad. Sci. (Paris) II 292, 701 (1981).
20 M. Krech, The Casimir Effect in Critical
Systems, World Scientific, Singapore, 1994.
21 More recent references can be found in : F.
Schlesener, A. Hanke, and S. Dietrich, J. Stat. Phys. 110, 981
(2003); M. Benhamou, M. El Yaznasni, H. Ridouane, and E.-K. Hachem, Braz. J.
Phys. 36, 1 (2006).
22 R. Lipowsky, Handbook of Biological
Physics, R. Lipowsky and E. Sackmann, eds, Volume 1, p. 521, Elsevier,
1995.
23 P.B. Canham, J. Theoret. Biol.
26, 61 (1970).
24 O. Farago, Phys. Rev. E 78,
051919 (2008).
25 We recover the power law II -
D-3 that is known in literature (see, for
instance, Ref. [8]), but the corresponding amplitude depends on the used
model.
26 G. Gompper and D.M. Kroll, Europhys. Lett.
9, 59 (1989).
27 U. Seifert and R. Lipowsky, in Structure and
Dynamics of Membranes, Handbook of Biological Physics, R.
Lipowsky and E. Sackmann, eds, Elsevier, North-Holland, 1995.
28 J. Zinn-Justin, Quantum Field Theory and
Critical Phenomena, Clarendon Press, Oxford, 1989.
29 H.K. Jansen, Z. Phys. B 23, 377
(1976).
30 R. Bausch, H.K. Jansen, and H. Wagner, Z. Phys.
B 24, 113 (1976).
31 F. Langouche, D. Roekaerts, and E. Tirapegui,
Physica A 95, 252 (1979).
32 R. Lipowsky, in Random Fluctuations and
Growth, H.E. Stanley and N. Ostrowsky, eds, p. 227-245, Kluwer Academic
Publishers, Dordrecht 1988.
33 R. Lipowsky, J. Phys. A 18,
L-585 (1985).
34 R. Lipowsky, Physica Scripta T
29, 259 (1989).
35 F. Brochard and J.F. Lennon, J. Phys.
(Paris) 36, 1035 (1975).

Article N°3
Mécanique Statistique des membranes
confinées dans un liquide trouble

Dans cette troisième contribution originale, nous
étudions les effets d'impuretés sur les propriétés
statistiques des membranes fluides. Celles peuvent être attractives ou
répulsives. En premier lieu, nous déterminons la rugosité
moyenne de la membrane, en combinant la technique des répliques avec la
méthode variationnelle. Le résultat s'exprime en fonction de la
concentration des impuretés et l'amplitude de leur interaction avec la
membrane. En second lieu, nous déterminons la taille d'une
vésicule isolée, en fonction de ces mêmes
paramètres. Enfin, l'étude est étendue à
l'adhésion membranaire.


This article appeared in a journal published by
Elsevier. The attached copy is furnished to the author for internal
non-commercial research and education use, including for instruction at the
authors institution and sharing with colleagues.
Other uses, including reproduction and distribution, or
selling or licensing copies, or posting to personal, institutional or third
party websites are prohibited.
In most cases authors are permitted to post their
version of the
article (e.g. in Word or Tex form) to their personal website
or
institutional repository. Authors requiring further
information
regarding Elsevier's archiving and manuscript policies
are
encouraged to visit:
http://www.elsevier.com/copyright
Author's personal copy
Physica A 389 (2010) 3465-3475
Statistical mechanics of bilayer membranes in troubled aqueous
media
M. Benhamou*, K. Elhasnaoui, H. Kaidi, M. Chahid
Laboratoire de Physique des Polymères et
Phénomènes Critiques, Faculté des Sciences Ben M'sik, P.O.
7955, Casablanca, Morocco
Article history:
Received 30 March 2010 Available online 14 April 2010
Keywords:
Bilayer membranes Vesicles
Impurities Equilibrium
Statistical mechanics
1. Introduction
We consider a bilayer membrane surrounded by small impurities,
assumed to be attractive or repulsive. The purpose is a quantitative study of
the effects of these impurities on the statistical properties of the supported
membrane. Using the replica trick combined with a variational method, we
compute the membrane mean-roughness and the height correlation function for
almost-flat membranes, as functions of the primitive elastic constants of the
membrane and some parameter that is proportional to the volume fraction of
impurities and their interaction strength. As results, the attractive
impurities increase the shape fluctuations due to the membrane undulations,
while repulsive ones suppress these fluctuations. Second, we compute the
equilibrium diameter of (spherical) vesicles surrounded by small random
particles starting from the curvature equation. Third, the study is extended to
a lamellar phase composed of two parallel fluid membranes, which are separated
by a finite distance. This lamellar phase undergoes an unbinding transition. We
demonstrate that the attractive impurities increase the unbinding critical
temperature, while repulsive ones decrease this temperature. Finally, we say
that the presence of small impurities in an aqueous medium may be a mechanism
to suppress or to produce an unbinding transition, even the temperature and
polarizability of the aqueous medium are fixed, in lamellar phases formed by
parallel lipid bilayers.
(c) 2010 Elsevier B.V. All rights reserved.
Usually, the aqueous media supporting biological membranes are
assumed to be homogeneous. Actually, any real system inevitably contains
impurities. Under well-controlled conditions, the particles can be removed from
the surrounding medium. But, if these entities are present, it is also
interesting to study their effect on the statistical properties of the
biomembranes, such as fluctuations' spectrum and dynamical behavior. In
general, random inhomogeneities tend to disorder the system. It is important to
make a distinction between annealed and quenched disorders.
The former is used when impurities and host constituents
(phospholipids) are in equilibrium [1]. This means that their respective
mobilities are comparable. If it is not the case, that is host constituents and
impurities are out of equilibrium, the disorder is rather quenched [1]. When
the Statistical Mechanics is used, the latter consists to trace over all
membrane undulations, before performing the summation over the impurities'
disorder. Although the quenched disorder is harder to analyze, it remains more
realistic than its annealed counterpart. Indeed, the thermal and the noise
averaging have very different roles.
In this paper, the physical system we consider is a fluid
membrane (flat or closed) trapped in a troubled aqueous medium. The latter is
impregnated by a weak amount of impurities that may be attractive or repulsive
regarding the membrane. The aim is to show how these entities can modify the
statistical properties of the fluid membrane. These properties will be studied
through the fluctuations' amplitude. To model the system, we suppose that the
impurities act as a random external potential with a Gaussian distribution
(uncorrelated disorder). In addition, we suppose that the disorder is quenched.
To
* Corresponding author.
E-mail address:
benhamou.mabrouk@gmail.com
(M. Benhamou).
0378-4371/$ - see front matter (c) 2010 Elsevier B.V. All rights
reserved. doi:10.1016/j.physa.2010.03.049
Author's personal copy
3466 M. Benhamou et al. / Physica A 389 (2010)
3465-3475
do calculations, the replica theory [2,3] that is based on a
mathematical analytical continuation, usually encountered in Quantum Mechanics
[4] and Critical Phenomena will be made use of [5,6].
Our finding are as follows. First, using the above evoked
theory, we compute the mean-roughness of an almost-flat membrane, as a function
of the primitive parameters of the pure membrane (free from impurities) and a
certain parameter depending on the volume fraction of impurities and their
interaction strength. The main conclusion is that, attractive impurities
increase the shape fluctuations due to the thermal undulations, while repulsive
ones tend to suppress these fluctuations and then lead to a strong membrane
confinement. Second, we analyze the impurities effects on the equilibrium shape
of closed vesicles solving the curvature equation (for spherical vesicles). We
show that the vesicle is more stable in the presence of repulsive impurities,
in comparison with attractive ones. Thereafter, the study is extended to
lamellar phases formed by two parallel fluid membranes. We demonstrate that the
presence of random impurities drastically affects the physical properties of
the lamellar phase, in particular, the unbinding transition driving the system
from a bind state to a state where the two membranes are completely
separated.
This paper is organized as follows. In Section 2, we describe
the fundamentals of the used model. Section 3 deals with the computation of the
fluctuations amplitude of a single almost-flat fluid membrane, surrounded by
attractive or repulsive impurities. We compute, in Section 4, the equilibrium
diameter of a closed vesicle in the presence of impurities. Extension of study
to lamellar phases is the aim of Section 5. Finally, some concluding remarks
are drawn in the last section.
2. Effective field theory
Consider a fluctuating fluid membrane embedded in a
three-dimensional liquid surrounded by very small impurities. For the sake of
simplicity, we suppose that the impurities are point like. Within the framework
of the Monge representation, a point on the membrane can be described by the
position-vector (r, z = h (r)), where r
= (x, y) ? R2 is the
transverse vector and h (r) is the height function.
The Statistical Mechanics of fluid membranes free from impurities
is based on the Canham-Helfrich Hamiltonian [7]
f [ê 2
h2]
R0 [h] = d2r 2
(Äh)2 + u , (1)
with ê the membrane bending modulus. The confinement
energy (per unit area) uh2/2 (u > 0) is responsible for
the localization of the membrane in some region of the Euclidean space, where
it fluctuates around an equilibrium plane located at h = 0. Therefore,
the height h takes either positive and negative values. For
simplicity, the membrane is assumed to be tensionless. In fact, this assumption
does not change conclusions made below.
To model the impurities effects on the statistical properties
of the system, we suppose that these tend to reinforce the membrane
confinement, if they are repulsive, or to render this membrane more free, if
the particles are rather attractive. These tendencies can be explained assuming
that the confinement parameter is local in space and making the substitution
u ? u + V (r) , (2)
in the above Hamiltonian, where the variation V
(r) can be regarded as a random external potential. To simplify,
the corresponding probability distribution is supposed to be Gaussian
(uncorrelated disorder), that is
V (r) = 0, V (r) V
(r0) = -vä2 (r
- r0) . (3)
Here, -v is a positive constant proportional to both
concentration of impurities and strength of their interaction potential, and
ä2 (r) denotes the two-dimensional Dirac distribution.
Therefore, the new effective Canham-Helfrich Hamiltonian reads
f Lê
]
R [h] = d2r 2
(Äh)2 + 2 1 (u + V (r))
h2 , (4)
for attractive impurities. For repulsive ones, V
(r) must be replaced by iV (r), with
i2 = -1. Since the disorder distribution is Gaussian, all
its odd moments vanish, but the even ones do not. This implies that all
physical quantities, calculated with the pure imaginary potential iV,
are entire numbers.
Since the impurities and membranes are not in equilibrium, the
disorder is rather quenched, that is we have to average not the
partition function, Z, but its logarithm, ln Z. The latter
defines the free energy.
For a given (quenched) configuration of impurities, the partition
function is
fZ =
Dhe-A[h], (5)
with the action
|
R [h]
A [h] =
kBT
|
f [bê
]
= d2r (bu +
bV (r))
h2
2 (Äh)2 + 1 . (6)
2
|
Author's personal copy
M. Benhamou et al. / Physica A 389 (2010) 3465-3475
3467
We have used the notations
ê
u
bê =
bV =
bu =
kBT ,
kBT ,
V
. (7)
kBT
In term of the reduced impurities potential
bV, the second disorder law in Eq. (3) becomes: bV
(r)bV (r') = -bvä (r -
r'), with
bv = v/ (kBT)2. A simple dimensional analysis
shows that: [bê] = L0, [bu] = L-4
and [bv] = L-6, where L is some length that may be
the membrane thickness.
The main quantity to consider is the average of the logarithm of
the partition function, ln Z, over disorder. To compute such a
quantity, we use the replica trick [2]. This method consists to formally
write
Zn - 1
. (8)
n
ln Z = lim
n?0
After performing the average over disorder, we get
ZZn = Dh1 ...
Dhne-A[h1, ,hn], (9)
with the
n-replicated effective action
Z " ! nX !#
Xn Xn
bê
A [h1, ... , hn] =
d2r
(Ähá)2 + bu á + bv
Xn
h2 h2 h2 ,
(10)
á â
2 2 8
á=1 á=1 á=1 â=1
where Greek indices denote replicas. The last term introduces
an additional coupling constant bv < 0, which is directly responsible for
the effective interaction between replicas due to the presence of impurities.
The above action describes attractive impurities. For repulsive ones, the
coupling bv must be replaced by -bv. The additive quartic term in the above
action means that the presence of impurities is accompanied by an increase of
entropy, when these are attractive, and by an entropy loss, if they are rather
repulsive.
The following paragraph is devoted to a quantitative
determination of the fluctuations spectrum in the presence of impurities.
3. Single almost-flat membrane
We start by considering the attractive impurities problem. Of
course, the functional integral (9) cannot be exactly computed. One way is the
use of a variational method. To this end, we consider a bilayer membrane in the
presence of the following bare action
Z " #
Xn (Ähá)2 +
bç Xn
bê
Aç [h1, ... ,
hn] = d2r h2 , (11)
á
2 2
á=1 á=1
with the new confinement couplingbç > 0. With this
action, the partition function, Zç, is
exact. We have
Zç =
(Z0)n , (12)
with
Z ~ Z ~bê ~~
Z0 = Dh exp - d2r
2 (Äh)2 + bç 2 h2 .
(13)
The latter accounts for the usual partition function of a bilayer
membrane free from impurities.
Introduce the mean-value of a functional X [h1,
... , hn], calculated with the bare action
Aç [h1, ... , hn],
(X)0 = Z Dh1 ... DhnX
[h1, ... , hn] exp {-A,~
[h1, ... , hn]} .
Zç (14)
1
In term of this mean-value, the averaged partition function may
write
~~~
Zn = Zç ~exp ~-~A -
Aç 0 . (15)
Using the standard inequality
(eX)0 > e(X)0, (16)
we get
Zn > Zç exp~-~A -
Aç ~ ~. (17)
0
Author's personal copy
3468 M. Benhamou et al. / Physica A 389 (2010)
3465-3475
This implies that
- ln Z = lim
n?0
|
1 - Zn
|
= lim
n?0
|
1 - Zç exp{-(A -
Aç10}
|
|
(18)
|
|
n
|
n
|
.
|
On the other hand, we have
Z " #
A - Aç~ Xn ~ Xn
Xn
h2
bu -bç h2
0 = d2r 0 + bv ~
áh2 . (19)
á â
2 8 0
á=1 á=1 â=1
It is easy to see that
|
Xn á=1
|
h2 ~
á 0 = nó2,
|
Xn
á=1
|
Xn â=1
|
h2 ~
áh2 0 = n (n + 2) ~ó2~2
, (19a)
â
|
with the squared membrane roughness
|
1
ó2 (ç) =
8
|
1
(20)
pêbç.
|
With these considerations,
bu -bç
2 ó2 + bv ~ó2~2~
- ln Z = -ln Z0 + Ó , (21)
4
where Ó is the area of the reference plane.
Notice that the right-hand side of this inequality
isbç-dependent function. Therefore, a good approximate value of -ln
Z
is
- [ln Z JMF = min [-ln Z0 +
Ó(bu2çó2
+4(ó2)2)] (22)
(The subscript MF is for mean-field theory).
The variational parameterbç is such that
~ bu -bç ~ó2~2~~
? 2 ó2 + bv
- ln Z0 + Ó = 0. (23)
?bç 4
Combining the relationship
|
2 2
ó = -
Ó
|
? ?bç
|
ln Z0 (24)
|
and Eq. (20) yields the minimum value ofbç, which
satisfies the following implicit relation
bç = bu +bvó2. (25)
?
?
?
1 ó2 =
The squared membrane roughness, ó2, is then
given by the parametric equations 1
(26)
p ,
bç =
8 bê bç
bu +bvó2.
Eliminatingbç between these equations gives the implicit
relation
q8 bê Cbu +bvó2).
1
(28)
1 ó2 =
p
Introduce the usual squared roughness of a membrane free from
impurities, ó2 0 = 1/8 bê bu. Then, we have 1
ó2 = ó2 .
0 (28)
p1 +bvó2/bu
3 > 0, as
The latter may be rewritten, in terms of dimensionless variables
ó2/ó0 2 ,bê, and w = -64bê bv
~óÔ
ó2
=
ó2
0
1
q1 - wó2/óÔ
, (attractive impurities) . (29)
Author's personal copy
M. Benhamou et al. / Physica A 389 (2010) 3465-3475
3469
Table 1
Some values of the coupling w and their corresponding ratios
ó2/óô , for attractive impurities.
|
w ó2/ó02
|
|
0.1 1.0575
0.15 1.0937
0.2 1.1378
0.25 1.1939
0.3 1.2715
w* v3
|
Notice that the coupling constant w > 0 is directly
proportional to the volume fraction of impurities and their interaction
strength.
Let us comment about the obtained result.
Firstly, this makes sense only when ó2/ó0 2 <
1/w. This condition is fulfilled for very weak disorders (w is small enough).
Secondly, since w is positive definite, we have: ó2 >
ó02. A comparison between this inequality and that
just evoked above implies that 0 < w < 1.
Thirdly, if we set x =
ó2/ó02, the above relation can
be rewritten as
x2 - 1
w = .
(30)
x3
Therefore, w is a direct function of x (Fig. 1). This
formula may be experimentally used to estimate the impurities coupling w,
knowing the experimental value of the ratio
ó2/ó20 . If w is fixed to some
value, the x-variable then solves the following third-degree algebraic
equation
wx3 - x2 + 1 = 0. (31)
The existence of its roots then depends on the value of the
renormalized coupling w. We show that there exists a typical v
value w* = 2/3 3 of the coupling w, such that:
(1) For w > w* (strong disorder), we have
only one root that is negative ; v
(2) For w = w* (medium disorder), we have
one negative root and a positive unique root, which is x =
ó2/ó0 2 = 3. Then, the maximal value of the membrane roughness is
ó* = 31/4ó0. This constraint
means that the lipid bilayer cannot support undulations of perpendicular size
(hunt size) greater than ó*. This is realized if only if the
impurities volume fraction ö is below some value ö*,
directly proportional to the threshold w*;
(3) For w < w* (weak disorder), we
have one negative root and two positive ones. Only one positive root is
acceptable (the smallest one). At this particular root, the free energy
-kBT [ln Z ]MF is minimal. We show that the absolute minimum
satisfies the inequality
- 4wx6 + 3x4 - 1 > 0.
(32)
In this case, the ratio
ó2/ó02 can be obtained by
numerically solving Eq. (31). We report in Table 1 some values of the
impurities coupling w and the corresponding dimensionless squared membrane
roughness ó2/ó02. It is easy to
see that, the ratio ó2/ó02
increases with increasing coupling w, provided that w is in the interval
w < w*.
ó2
=
ó2
0
1
, (repulsive impurities) , (33)
Now, for repulsive impurities, the fundamental relationship (29)
is replaced by
q1- wó2/ó02
or equivalently
- wx3 - x2 + 1 = 0,
(34)
with the stability condition
4wx6 + 3x4 - 1 > 0.
(35)
The equality (34) can be transformed into the following direct function
(Fig. 2)
x2 - 1
w =3 (36)
x
with x < 1 and w < 0.
As it should be, the membrane roughness is reduced by the
presence of repulsive impurities, that is ó2 <
óô, and in addition, ó2 decreases with
increasing impurities coupling -w. As a matter of fact, the effect of these
particles is to reinforce
Author's personal copy

3470 M. Benhamou et al. / Physica A 389 (2010)
3465-3475
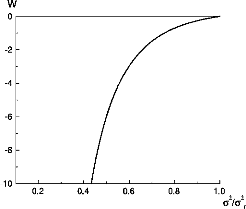
Fig. 1. Impurities' coupling w versus
the ratio ó2/ó0 2 , for attractive
impurities.
Fig. 2. Impurities' coupling w versus
the ratio ó2/ó2 0 , for repulsive
impurities.
Table 2
Some values of the coupling w and their corresponding
ratios ó2/ó0 2 , for attractive
impurities.
|
w
|
ó2/ó2 0
|
|
-0.1
|
0.9554
|
|
-0.15
|
0.9364
|
|
-0.2
|
0.9190
|
|
-0.25
|
0.9032
|
|
-0.3
|
0.8885
|
|
-0.4
|
0.8622
|
the confinement of the considered fluid membrane. Therefore, a
bilayer membrane collapses, when it is trapped in a troubled aqueous media with
repulsive impurities. In this case, it is easy to see that the algebraic
equation has only one positive root. In Table 2, we give some values of the
coupling w and the corresponding ratio
ó2/ó2 0 .
Another interesting physical quantity is the (connected) height
correlation function: G (r - r') = (h (r) h
(r')) -
(h (r)) (h (r')). The latter measures
the fluctuations of the height function h around its mean-value
(h). Here, (.) denotes the thermal expectation mean-value,
which must not be confused with average over disorder.
Author's personal copy
M. Benhamou et al. / Physica A 389 (2010) 3465-3475
3471
To compute the correlation functions, we start from the
generating functional
Z ~ Z ~
Z [J] = Loh exp -A
[h] + d2r J (r) h
(r) , (37)
with the action A [h] = X'
[h] /kBT, where X' [h] is the effective
Canham-Helfrich Hamiltonian defined in Eq. (4). Here, J is an
auxiliary source coupled to the field h. Functional derivatives of
Z [J] with respect to source J give all height
correlation functions, in particular, the propagator
~~
ä2ln Z [J]
(38)
) J=0.
G~r - r0) =
ä
ä
0
J (r)
J (r
This definition indicates that the main object to compute
is the averaged connected generating functional ln Z [J]. To
compute the functional ln Z [J], as before, we use the
replica method based on the limit
|
|
|
Zn [J] - 1
|
|
|
|
lnZ [J] = lim
n?0
|
|
(39)
|
|
with
|
|
n
|
,
|
Zn [J] = Z Loh1 ... Lohn
exp -A [h1, ... , hn] +
XZd2r J (r) hi (r) ,
(40)
i=1
where A [h1, ... , hn] is
the action, relation (10).
Using the standard cumulant method [5,6] based on the approximate
formula
hexp {X}i0 = exp {hXi0 + (1/2!)
((X2)0 - hXi2 ~ + · · ·~ , (41)
0
we find that
Z
Zn [J] ' Zç
exp~-~A - Aç ~ 0 + ···~exp~n
Z d2r0J
(r)G0~r - r0~J
~r0~~
d2r , (42)
2
with the usual bare propagator
eiq.(r-r0)
G0(r - r0)= Z
d2q (43)
(2ð)2 bêq4 +bç
.
In Eq. (42), we have ignored high-order terms in J
that do not contribute to the propagator. After performing the limit n
= 0, we find that the averaged connected generating functional reads
bu -bç Z Z
2 ó2 + bv ~ó2~2~ + 1 ~r -
r0 J ~r0~ .
ln Z [J] ' - ln Z0 + Ó
d2r d2r0J
(r) G0 (44)
4 2
By simple functional derivation, we obtain the expected
propagator
eiq.(r-r0)
d2q
G{r - r0) =
G0{r - r0) =Z (45)
(2ð)2bêq4 +bç
.
Then, the expected propagator identifies with the bare one.
Here, the variational parameterbç satisfies the implicit equation
(25).
We then recover the relationship: ó2 = G
(0), where ó2 is the squared membrane roughness computed
above.
The next step consists to extend the study to a closed vesicle
surrounded by attractive or repulsive impurities.
4. Single vesicle
We start by recalling some basic backgrounds dealt with the
equilibrium shape of (spherical) vesicles, which may studied using Differential
Geometry techniques.
The vesicle is essentially formed by two adjacent monolayers
(inner and outer) that are formed by amphiphile lipid molecules. These
permanently diffuse with the molecules of the surrounded aqueous medium. Such a
diffusion then provokes thermal fluctuations (undulations) of the membrane.
This means that the latter experiences fluctuations around an equilibrium
plane.
Consider a biomembrane of arbitrary topology. A point of this
membrane (surface) can be described by two local coordinates (u1,
u2). At each point of the surface, there exists two particular
curvatures (minimal and maximal), called
Author's personal copy
3472 M. Benhamou et al. / Physica A 389 (2010)
3465-3475
principal curvatures, denoted C1 =
1/R1 and C2 = 1/R2. The quantities
R1 and R2 are the principal curvature radii. With the help of
the principal curvatures, one constructs two invariants that are the
mean-curvature
1
C =
2 (C1 + C2) , (46)
and the Gauss curvature
R
R0 = 1 #177; 8ky2 ö
+ O (ö2) , (56)
K = C1C2. (47)
The principal curvatures C1 and C2 are
nothing else but the eigenvalues of the curvature tensor [8].
To comprehend the geometrical and physical properties of the
biomembranes, one needs a good model. The widely accepted one is the fluid
mosaic model proposed by Singer and Nicolson in 1972 [9]. This model consists
to regard the cell membrane as a lipid bilayer, where the lipid molecules can
move freely in the membrane surface like a fluid, while the proteins and other
amphiphile molecules (cholesterol, sugar molecules, ...) are simply embedded in
the lipid bilayer. We note that the elasticity of cell membranes crucially
depends on the bilayers in this model. The elastic properties of bilayer
biomembranes were first studied, in 1973, by Helfrich [7]. The author
recognized that the lipid bilayer could be regarded as smectic-A liquid
crystals at room temperature, and proposed the following curvature free energy
(without impurities)
F = 2 f (2C)2 dA +
êG f KdA + f ãdA + p f
dV. (48)
where dA denotes the area element, and V is
the volume enclosed within the lipid bilayer. In the above definition, ê
accounts for the bending rigidity constant, êG for the Gaussian
curvature, ã for the surface tension, and p for the pressure
difference between the outer and inner sides of the vesicle. The spontaneous
curvature is ignored. The first-order variation gives the shape equation of
lipid vesicles [10]
p - 2ãC + 4êC (C2
- K) + ê?2 (2C) = 0,
(49)
with the surface Laplace-Bertolami operator
|
1
?2 =
vg
|
? ~vggij ?~, (50)
?ui ?uj
|
where gij is the metric tensor on the surface
and g = det (gij). For open or tension-line vesicles, local
differential equation
(49) must be supplemented by additional boundary conditions we
do not write [11]. The above equation have known three v
analytic solutions corresponding to sphere [10], 2-torus [12-15]
and biconcave disk [16].
For spherical vesicles, the solution to the above curvature
equation is exact, and we find that the equilibrium radius is
2ã
R0 = . (51)
p
Now, assume that the vesicle is trapped in a troubled aqueous
medium. Usually, to take into account the presence of impurities, a low-order
coupling between their volume fraction, ö, and the mean-curvature C
is added to the above free energy F, that is
fF ? F #177; kBT öCdA. (52)
The positive sign is for attractive impurities and the negative
sign for repulsive ones. The new free energy is then
F = 2 f(2C #177; 2C0)2
dA + êGfKdA +fãIdA +
pfdV (53)
|
with the notation
ö
C0 = kBT 4ê,
|
ÿ = ã -
2êC20. (54)
|
Then, the impurities generate an extra spontaneous curvature.
This means that these give arise to an asymmetry of the vesicle when its
membrane is crossed. In addition, these impurities additively renormalize the
interfacial tension coefficient. Minimizing this new curvature free energy
yields
p - 2ÿC + ê (2C #177; C0)
(2C2 F C0C - 2K) +
ê?2 (2C) = 0. (55)
For a spherical vesicle, the mean curvature is a constant, and
we have K = C2. In this case, the mean-curvature C
is a root of a polynomial of degree 2. This means that we have an
exact solution we do not write. In particular, for very small volume
fractions (ö « 1), we find that the vesicle equilibrium
radius writes
Author's personal copy
M. Benhamou et al. / Physica A 389 (2010) 3465-3475
3473
or
~~
~~ R - R0 ~
~ ~
R0
pkBT
^-' 8ã 2 ö. (57)
The signs (+) and (-) describe attractive and repulsive
impurities, respectively. Here, R0 = 2ã/p denotes the
equilibrium radius for a spherical vesicle free from impurities.
The above results call the following remarks.
Firstly, as it should be, the equilibrium radius of the
vesicle increases with increasing volume fraction of impurities, when these are
attractive. This means that the vesicle is swollen, but it radius remains close
to the unperturbed one R0, as long as the volume fraction of
impurities is very small. For repulsive impurities, however, the vesicle is
collapsed.
Secondly, formula (57) makes sense only when the volume
fraction ö is below some threshold ö* =
8ã2/kBTp. Since the latter must be small in
comparison with unity, the vesicle bears interfacial tensions of coefficients
that do not exceed some typical value ã* =
.ABTp/8.
Finally, at fixed volume fraction ö <
ö*, this formula may be used to estimate the experimental value
of the ratio p/ã2, by a simple measurement of the
equilibrium radii R (with impurities) and R0 (without
impurities).
The following paragraph will be devoted to the study of lamellar
phases made of two parallel lipid bilayers.
5. Lamellar phases
The natural question is the extension of the study to the case
when we have more than one membrane immersed in a aqueous media, which is
impregnated by small random impurities.
In our analysis, we start from a lamellar phase composed of
two parallel (neutral) fluid membranes free from impurities. The effects of
these entities on physics will be discussed below. The cohesion between these
bilayer membranes is ensured by long-ranged attractive van der Waals forces
[17], which are balanced, at short membrane separation, by strong repulsion
coming from hydration forces [18] and by steric shape fluctuations ones
resulting from the membrane undulations [7].
For two parallel bilayer membranes separated by a finite distance
l, the total interaction energy per unit area is
V (l) = VH (l) + VW
(l) + VS (l) . (58)
The first part
VH (l) =
AHe-l/ëH
(59)
represents the hydration potential (per unit area) that acts at small
separations of the order of 1 nm. The corresponding amplitude AH and
potential-range ëH are about AH ^-' 0.2 J/m2
and ëH ^-' 0.3 nm. The second part
~ 1 ~
W VW (l) = - (60)
l2 - 2
(l + ä)2 + 1
12ð (l + 2ä)2
is the attractive van der Waals potential (per unit area) that
originates from polarizabilities of lipid molecules and water molecules. Here,
W accounts for the Hamaker constant that is in the range W
^-' 10-22 - 10-21 J, and ä for the bilayer
thickness. The latter is of the order of ä ^-' 4 mm. The last part is the
steric shape fluctuations potential (per unit area) [7]
Vs (l) = cH
(kBT)2
, (61)
with kB the Boltzmann's constant, T
the absolute temperature, and ê the common bending rigidity constant
of the two membranes. But in the case of two bilayers of different bending
rigidity constants ê1 and ê2, we have ê = ê1ê2/
(ê1 + ê2). There, the coefficient cH is a known
numerical coefficient [7].
We note that the lamellar phase remains stable at the minimum
of the potential, provided that the potential depth is comparable to the
thermal energy kBT. This depends, in particular, on the value of
amplitude W of the direct van der Waals energy. The Hamaker constant
W may be varied changing the polarizability of the aqueous medium.
In a pioneered theoretical paper, Lipowsky and Leibler [19]
have shown that there exists a certain threshold Wc beyond
which the van der Waals attractive interactions are sufficient to bind the
membranes together, while below this characteristic amplitude, the membrane
undulations dominate the attractive forces, and then, the membranes separate
completely. According to the authors, Wc is in the interval
Wc ^-' (6.3 - 0.61) x 10-21 J when the bending
rigidity constant is in the range ê ^-' (1 - 20) x 10-19 J. We
note that the typical value Wc corresponds to some
temperature, Tc, called unbinding critical
temperature [19,20]. In particular, it was found [19] that, when the
critical amplitude is approached from above, the mean-separation between the
two membranes, (l)0, diverges according to
(l)0=î0?~
(Tc -T)-ø,
T?Tc-, (62)
with ø a
critical exponent whose value is [19]: ø ^-' 1.00 #177; 0.03.
The latter was computed using field-theoretical Renormalization-Group.
Author's personal copy
3474 M. Benhamou et al. / Physica A 389 (2010)
3465-3475
Now, assume that the lamellar phase is trapped in a troubled
aqueous medium. As first implication, the impurities drastically modify the
unbinding transition phenomenon, in particular, the critical temperature. For
simplicity, suppose that the two adjacent fluid membranes are physically
identical. Then, we have to consider two distinct physical situations: The
impurities attract or push the two membranes. As we have shown above, for
attractive impurities, the membrane roughness î? is important, and then,
the steric shape fluctuation energy dominates. Therefore, we expect that the
unbinding transition occurs at a low critical temperature
Tc* we will determine below. For repulsive
impurities, however, we have an opposite tendency, that is the unbinding
transition takes place at a high temperature greater than
Tc (absence of impurities). This can be explained by the fact
that the membrane roughness is less important, and then, the direct
van der Waals energy dominates. In any case, the mean-separation hli
scales as
hli = î? -- (Tc* -
T)-ø , T ?
Tc- . (63)
The new unbinding critical temperature
Tc* can be estimated as follows. Using formulae
(29) and (33), we show that, at first order in the impurities coupling w,
|
î? ' 1
+
|
w
+ (9
4
w + (9 4
|
(w2) , (w2)
,
|
(attractive impurities) , (repulsive
impurities) .
|
(64)
(65)
|
|
î0?
î?' 1
-
|
|
î0?
|
Combing Eqs. (62) to (65), we find that the difference between
the two critical temperatures Tc and
Tc* (without and with impurities) is as
follows
Tc - Tc* -- w
+ (9 (w2) , (attractive impurities) ,
(66)
Tc - Tc* -- -w
+ (9 (w2) , (repulsive impurities) .
(67)
The prefactors in the above behaviors remain unknown. The
temperature shift is then proportional to the volume fraction of impurities and
their interaction strength through the coupling w. Then, we are in a situation
similar to finite size scaling. For charged membranes forming the lamellar
phase, it was found [19] that the mean-separation between two adjacent bilayers
scales as [19]
hli0 = î0? -- (÷ -
÷c)-ø , (68)
in the vicinity of ÷c, with ÷
the ionic concentration of the aqueous medium and ÷c
its critical value. For instance, for DPPC in CaCl2 solutions,
÷c is in the interval [21]:
÷c ' 84-10 mM. In the presence of impurities, we state
that the mean-separation behaves as
hli = î? -- (÷ - ÷*
)-ø , (69)
c
with the same exponent ø. In this case, we have
÷*c -
÷c -- w + (9 (w2) ,
(attractive impurities) , (70)
÷*c -
÷c -- -w + (9 (w2) ,
(repulsive impurities) . (71)
We note that the same comments may by done in this case.
6. Conclusions
In this paper, we presented a large scope about the effects of
impurities on the statistical properties of fluid membranes. In fact, these
drastically affect the living systems behavior. As an example, we can quote a
very recent experimental study [22], where the authors have undertaken a series
of comparative experiments, in order to explore the effect of impurities in the
form of proteins and lipids on the crystallization of membrane proteins in
vapor diffusion.
For the present study, the impurities were assumed to be
attractive or repulsive. Using the replica trick combined with a variational
method, we have computed the membrane mean-roughness, as a function of the
parameters associated with the pure membrane and some parameter that is
proportional to the volume fraction of impurities and their interaction
strength. The main conclusion is that, attractive impurities increase the shape
fluctuations due to the membrane undulations, but repulsive ones tend to
suppress these fluctuations.
Also, we have computed the equilibrium diameter of (spherical)
vesicles surrounded by small random particles solving the curvature
equation.
Thereafter, we extended discussion to lamellar phase formed by
two parallel fluid membranes that are a finite distance apart. This lamellar
phase may undergo an unbinding transition. We have shown that, attractive
impurities increase the unbinding critical temperature, while repulsive ones
tend to decrease this temperature.
Author's personal copy
M. Benhamou et al. / Physica A 389 (2010) 3465-3475
3475
We point out that, the incorporation of a small amount of
impurities in an aqueous medium may be a mechanism to suppress or to produce an
unbinding transition (even the temperature and polarizability of the aqueous
medium are fixed) within lamellar phases composed of fluid membranes.
Finally, the present study may be extended to bilayer
membranes of arbitrary topology. The essential conclusion is that, attractive
impurities tend to swell the membrane, while in the presence of repulsive ones,
this membrane is collapsed. Also, the used method can be applied to multilayers
constituted by several parallel lamellar phases.
Acknowledgements
We are much indebted to Professors T. Bickel, J.-F. Joanny and
C. Marques for helpful discussions, during the «First International
Workshop On Soft-Condensed Matter Physics and Biological Systems», 14-17
November 2006, Marrakech, Morocco. One of us (M.B.) would like to thank
Professor C. Misbah for fruitful correspondences, and the Laboratoire de
Spectroscopie Physique (Joseph Fourier University of Grenoble) for their
kind hospitality during his regular visits.
References
111 J. Cardy, Scaling and Renormalization in Statistical Physics,
Cambridge University Press, 1996.
121 V.J. Emery, Phys. Rev. B 11 (1975) 239.
131 S.F. Edvards, P.W. Anderson, J. Phys. (France) 5 (1975)
965.
141 L.D. Landau, E.M. Lifshitz, Quantum Mechanics, 3rd edition,
Pergamin Press, 1991.
151 J. Zinn-Justin, Quantum Field Theory and Critical Phenomena,
Clarendon Press, Oxford, 1989.
161 C. Itzykson, J.-M. Drouffe, Statistical Field Theory: 1 and
2, Cambridge University Press, 1989.
171 W. Helfrich, Z. Natureforsch 28c (1973) 693.
181 K. Wolfgang, Differential Geometry: Curves - Surfaces -
Manifolds, American Mathematical Society, 2005.
191 S.J. Singer, G.L. Nicolson, Science 175 (1972) 720.
1101 O.-Y. Zhong-Can, W. Helfrich, Phys. Rev. Lett. 59 (1987)
2486.
1111 Z.C. Tu, Z.C. Ou-Yang, Phys. Rev. E 68 (2003) 061915.
1121 O.-Y. Zhong-Can, Phys. Rev. A 41 (1990) 4517.
1131 Z. Lin, R.M. Hill, H.T. Davis, L.E. Scriven, Y. Talmon,
Langmuir 10 (1994) 1008.
1141 M. Mutz, D. Bensimon, Phys. Rev. A 43 (1991) 4525.
1151 A.S. Rudolph, B.R. Ratna, B. Kahn, Nature 352 (1991) 52.
1161 H. Naito, M. Okuda, O.Y. Zhong-Can, Phys. Rev. E 48 (1993)
2304.
1171 J.N. Israelachvili, Intermolecular and Surface Forces, 2nd
edition, Academic Press, London, 1991.
1181 R.P. Rand, V.A. Parsegian, Biochim. Biophys. Acta 988 (1989)
351.
1191 R. Lipowsky, S. Leibler, Phys. Rev. Lett. 56 (1986) 2541.
1201 R. Lipowsky, E. Sackmann (Eds.), An Extensive List of
References on the Subject can be Found in: Structure and Dynamics of Membranes:
Generic and
Specific Interactions, vol. 1B, Elsevier, 1995.
1211 L.J. Lis, W.T. Lis, V.A. Parsegian, R.P. Rand, Biochemistry
20 (1981) 1771.
1221 A. Christopher, et al., Acta Cryst. D 65 (2009)
1062-1073.
Article N°4
Conformation d'un polymère
confiné
dans des domaines délimités par
des


biomembranes
Dans cette quatrième contribution originale, nous
étudions la conformation d'un polymère isolé, qui est
confiné entre deux membranes lipidiques parallèles ou dans une
vésicule tubulaire.
Pour rester plus général, nous supposons que le
polymère est de topologie arbitraire, qu'on appelle
D-manifold, où D est la dimension spectrale
(par exemple,
D =1, pour les polymères linéaires, et
D =4?3, pour les polymères branchés). En fait,
D est le nombre de coordonnées locales permettant de
caractériser géométriquement le polymère
55

|
African Journal Of Mathematical Physics Volume
10(2011)55-64
|
Statistics of a single D-manifold restricted to two
parallel
biomembranes or a tubular vesicle
M. Benhamou* , K. Elhasnaoui, H. Kaidi, M.
Chahid
Laboratoire de Physique des Polymères et
Phénomènes Critiques
Facultédes Sciences Ben M'sik,
P.O. Box 7955, Casablanca, Morocco
*
benhamou.mabrouk@gmail.com
abstract
The purpose is an extensive conformational study of a single
polymer immersed in an aqueous medium (good solvent) delimitated by bilayer
membranes. To be more general, we assume that the polymer is of arbitrary
topology we term D-polymeric fractal or D-manifold, where
D is the spectral dimension (for instance, D = 1, for linear
polymers, and 4/3, for branched ones). The main quantity to consider
is the parallel extension of the confined polymer. To make explicit
calculations, we suppose that the polymer is restricted to a tubular vesicle or
two parallel biomembranes. We first show that, for the first geometry, the
polymer is confined only when the tubular vesicle is in equilibrium state. For
the second geometry, the confinement is possible if only if the two parallel
membranes are in their binding state, that is below the unbinding or adhesion
temperature. In any case, the parallel gyration radius of the confined polymer
is computed using an extended Flory-de Gennes theory. As result, this radius
strongly depends on the polymer topology (through the spectral dimension
D) and on the membranes sizes, which are the equilibrium diameter
(function of bending modulus, pressure difference between inner and outer sides
of the membrane, and interfacial tension coefficient), for the first geometry,
and the mean-separation (function of temperature and interaction strength
between the adjacent membranes), for the second one. Finally, we give the
expression of the confinement free energy, as a function of the polymer size,
and discuss the effects of external pressure or lateral tension on the radius
expression for two confining parallel membranes.
Key words: D-Polymeric fractals, Biomembranes, Vesicles,
Confinement.
I. INTRODUCTION
The polymer confinement finds many applications in various
domains, such as biological functions, filtration, gel permeation
chromatography, heterogeneous catalysis, and oil recuperation.
The physics of polymer confinement is a rich and exciting
problem. Recently, much attention has been paid to the structure and dynamics
of polymer chains confined to two surfaces, or inside cylindrical pores [1
- 7]. Thereafter, the study has been extended to more complex
polymers, called D-polymeric fractals or D-manifolds [8] that
are restricted to the same geometries. Here, D is the spectral
dimension that measures the degree of the connectivity of monomers inside the
polymer [9]. For instance, this intrinsic dimension is 1 for linear polymers
and 4/3 for branched ones. The D-manifolds may be polymerized
(or
M. Benhamou et al. African Journal Of Mathematical Physics
Volume 10(2011)55-64
56
crumpled) vesicles [10]. The polymer confinement between two
surfaces and in cylinders with sinusoidal undulations was also investigated
[11, 12].
The confining geometries may be soft-bodies, as bilayer
biomembranes and surfactants, and spherical and tubular vesicles. A particular
question has been addressed to polymer confinement in surfactant bilayers of a
lyotropic lamellar phase [13], where the authors reported on small-angle X-ray
scattering and free-fracture electron microscopy studies of a nonionic
surfactant/water/polyelectrolyte system in the lamellar phase region. The
fundamental remark is that, the polymer molecules cause both local deformation
and softening of the bilayer.
In the same context, it was experimentally demonstrated [14]
that the polymer confinement may induce a nematic transition of microemulsion
droplets. More precisely, the authors showed that upon confinement, spherical
droplets deform to prolate ellipsoid droplets. The origin of such a structural
transition may be attributed to a loss of the conformational entropy of polymer
chains due to the confinement.
In other experiments [15 - 17], a new phase has been
observed adding an neutral hydrosoluble polymer (PVP) in the lyotropic lamellar
phase (CPCI/hexanol/water). Also, one has studied the effect of a neutral
water-soluble polymer on the lamellar phase of a zwitterionic surfactant system
[18].
The polymer confinement is also relevant for living systems
and governs many biological processes. As example, we can quote membrane
nanotubes that play a major role in intercellular traffic, in particular for
lipid and proteins exchange between various compartments in eukaryotic cells
[19 - 22]. The traffic of macromolecules and vesicles in nanotubes is
ensured by molecular motors [23]. Also, these are responsible for the
extraction of nanotubes [24]. The formation of tubular membrane tethers or
spicules [25 - 33] results from the action of localized forces that
are perpendicular to the membrane. These forces may originate from the
polymerization of fibers [34], as actin [35], tubulin [36], or sickle
hemoglobin [37]. Inspired by biological processes, as macromolecules and
vesicles transport, we aim at a conformational study of confined polymers in
aqueous media delimitated by biomembranes. More precisely, the purpose is to
see how these biomembranes can modify the conformational properties of the
constrained polymer. To this end, we choose two geometries : a tubular vesicle
(Geometry I), and two parallel biomembranes (Geometry II). To
be more general, we consider polymers or arbitrary connectivity called
D-polymeric fractals or D-manifolds [38]. Linear and branched
polymers, and polymerized vesicles constitute typical examples. We note that
this conformational study in necessary for the description of dynamic
properties of polymers restricted to these geometries.
As we shall below, the polymer confinement is entirely
controlled by the confining biomembranes state. Indeed, for Geometry I, the
polymer may be confined only when the confining tubular vesicle is at
equilibrium. For Geometry II, the confinement is possible if only if the two
parallel membranes are in the binding state.
This paper is organized as follows. In Sec. II, we briefly
recall the conformational study of unconfined D-polymeric fractals in
good solvent. Sec. III deals with the conformational study of polymers confined
inside a tubular vesicle. In Sec. IV, we extend the study to
D-polymeric fractals confined to two parallel biomembranes. Some
concluding remarks are drawn in the last section.
II. UNCONFINED POLYMERIC FRACTAL
Consider a single polymeric fractal of arbitrary topology
(linear polymers, branched polymers, polymer networks, ...). We assume that the
considered polymer is trapped in a good solvent. We denote by
RF aM1/dF (1)
its gyration (or Flory) radius, where dF is the
Hausdorff fractal dimension, M is the molecular-weight (total mass) of
the considered polymer, and a denotes the monomer size. The mass M
is related to the linear dimension N by : M =
ND, where D is the spectral dimension [9]. The
latter is defined as the Hausdorff dimension corresponding to the maximal
extension of the fractal.
Naturally, the Hausdorff dimension depends on the Euclidean
dimensionality d, the spectral dimension D and the solvent
quality. When the polymer is ideal (without excluded volume forces), its
Hausdorff dimension, d0F, is a known simpler
function of D [9]
M. Benhamou et al. African Journal Of Mathematical Physics
Volume 10(2011)55-64
For linear polymers (D = 1),
d0F = 2 [2], for ideal branched ones
(D = 4/3), d0F = 4
[9], and for crumpled membranes (D = 2),
d0F = 8.
Because of the positivity of the Hausdorff dimension, the
above expression makes sense only for D < 2. Indeed, this condition
is fulfilled for any complex polymer with spectral dimension in the interval 1
= D < 2 [9].
A polymeric fractal in good solvent is swollen, because of the
presence of the excluded volume forces. The polymer size increases with
increasing total mass M according to the power law (1). The first
implication of the polymer swelling is that, the actual Hausdorff dimension
dF is quite different from the Gaussian one, defined in Eq. (2).
However, there exists a special value of the Euclidean dimensionality
called upper critical dimension duc [39,40],
beyond which the polymeric fractal becomes ideal. This upper dimension is
naturally a D-dependent function, which can be determined [39] using a
criterion of Ginzburg type, usually encountered in critical phenomena
[41,42]. According to Ref. [39], duc is given
by
4D
duc =
2 - D . (3)
For instance, the upper critical dimension is 4 for linear
polymers [2], and 8 for branched ones [39]. We emphasize that, in general, the
Hausdorff fractal dimension dF cannot be exactly computed. Many
techniques have been used to determine its approximate value, in particular,
the Flory-de Gennes (FD) theory [2]. Using a generalized FD approach, it was
found that the fractal dimension is given by [39]
dF = D d + 2
D + 2 , (4)
below the critical dimension, and it equals the Gaussian
fractal dimension d0F described above.
For dimension 3, we have
5D
dF (3) =
D + 2 . (5)
57
For instance, for linear polymers, dF (3) =
5/3, and dF (3) = 2, for branched ones (animals).
In the following paragraph, we shall focus our attention on
the conformational study of a single polymeric fractal confined to a long
tubular vesicle.
III. CONFINED POLYMERIC FRACTAL IN GEOMETRY I
A.
Useful backgrounds
Before studying the conformation of a single polymeric
fractal, we recall some basic backgrounds concerning the equilibrium shape of
tubular vesicles. This can be done using Differential Geometry machineries.
The tubular vesicle is essentially formed by two adjacent
leaflets (inner and outer) that are composed of amphiphile lipid molecules.
These permanently diffuse with the molecules of the surrounded aqueous medium.
Such a diffusion then provokes thermal fluctuations (undulations) of the
membrane. This means that the latter experiences fluctuations around an
equilibrium plane we are interested in.
Consider a biomembrane of arbitrary topology. A point of this
membrane can be described by two local coordinates (u1, u2).
From surfaces theory point of view, at each point, there exists two particular
curvatures (minimal and maximal), called principal curvatures, denoted
C1 = 1/R1 and C2 = 1/R2. The quantities
R1 and R2 are the principal curvature radii. With the help of
the principal curvatures, one constructs two invariants that are the
mean-curvature
and the Gauss curvature
K = C1C2 . (7)
M. Benhamou et al. African Journal Of Mathematical Physics
Volume 10(2011)55-64
58
We recall that C1 and C2 are nothing else
but the eigenvalues of the curvature tensor [43].
To comprehend the geometrical and physical properties of the
biomembranes, one needs a good model. The widely accepted one is the fluid
mosaic model proposed by Singer and Nicholson in 1972 [44]. This model consists
to regard the cell membrane as a lipid bilayer, where the lipid molecules can
move freely in the membrane surface like a fluid, while the proteins and other
amphiphile molecules (cholesterol, sugar molecules, ...) are simply embedded in
the lipid bilayer. We note that the elasticity of cell membranes crucially
depends on the bilayers in this model. The elastic properties of bilayer
biomembranes were first studied, in 1973, by Helfrich [45]. The author
recognized that the lipid bilayer could be regarded as smectic-A liquid
crystals at room temperature, and proposed the following curvature free
energy
? ? ? ?
?
F = (2C +
2C0)2 dA + ?G KdA +
?dA + p dV . (8)
2
where dA denotes the area element, and V is
the volume enclosed within the lipid bilayer. In the above definition, ?
accounts for the bending rigidity constant, C0 for the
spontaneous curvature, ?G for the Gaussian curvature, ? for
the surface tension, and p for the pressure difference between the
outer and inner sides of the vesicles. The first order variation gives the
shape equation of lipid vesicles [46]
p - 2?C + ? (2C +
C0) (2C2 - C0C - 2K) +
??2 (2C) = 0 , (9)
|
with the surface Laplace-Bertlami operator
?2 = 1
vg
|
? (vggij ? ) ,
(10)
?ui ?uj
|
where gij is the metric tensor on the
surface and g = det (gij). For open or
tension-line vesicles, local differential equation (9) must be supplemented by
additional boundary conditions we do not write [47]. The above equation have
known three analytic solutions corresponding to sphere [46], v2-torus
[48 - 51] and biconcave disk [52].
For cylindrical (or tubular) vesicles, one of the principal
curvature is zero, and we have
1
C = - R , K = 0 , (11)
where R is the radius of the cylinder. If we ignore
the boundary conditions (assumption valid for very long tubes), the uniform
solution to equation (9) is
(4?)1/3
H = 2 , (12)
p
where H is the equilibrium diameter. We have
neglected the surface tension and spontaneous curvature contributions, in order
to have a simplified expression for the equilibrium diameter.
The above relation makes sense as long as the pressure
difference is smaller than a critical value pc that scales
as [53] : pc ? ?/R3. The latter is in
the range 1 to 2 Pa. The meaning of the critical pressure is that, beyond
pc, the vesicle is unstable. This implies that the
equilibrium diameter must be greater than the critical one
Hc = 2
(4?/pc)1/3.
In what follows, we shall use the idea that consists to regard
the tubular vesicle as a rigid cylinder of effective diameter H that
depends on the characteristics of the bilayer through the parameters ?
and p.
B. Parallel extension to the cylinder-axis
Consider now a polymeric fractal of arbitrary topology
confined inside a tubular vesicle of equilibrium diameter H. The host
solvent is assumed to be a good solvent. The polymer is confined if only if its
three-dimensional Flory radius RF3 is much larger
than the diameter H, that is H << RF3. At
fixed parameters ? and p, this condition implies that the
polymer mass M must be greater than some typical value
M* that scales as M*
(?/p)5D/3(D+2). Now, if the
parameter M and p are fixed, the polymer is
M. Benhamou et al. African Journal Of Mathematical Physics
Volume 10(2011)55-64
(14)
59
confined is only if ? << ?* ^,
pM3(D+2)/5D. This behavior
clearly indicates that the confinement is more favorable when the tubular
vesicle is of small bending rigidity constant. We note that the confinement
condition depends on the nature of the polymeric fractal through its spectral
dimension D. Also, the solvent quality is another factor that
influences this confinement.
The confinement of polymers of arbitrary topology inside a
rigid tube is largely investigated in Ref. [8]. In this paper, to achieve the
conformational study of a confined polymer, we use a generalized FD theory
based on the following free energy [8]
|
F
kBT =
|
R2
?
+ v R20
|
M2
(13)
R?H2
|
where R? denotes the polymer parallel extension to the
tube-axis, and v is the excluded volume parameter.
There, R0 ^,
aM1/d°, is the ideal radius and
R?H2 represents the volume occupied by the fractal.
Minimizing the above free energies with respect to R? yields the
desired result
l 2/9

R? ^,
aM(D+2)/3D (a-3?
.
p
We have used relationship (12).
Let us comment about the obtained result.
Firstly, notice that, in any case, the parallel radius naturally
depends on polymer and tubular vesicle
characteristics, through M and parameters (?,
p), respectively.
Secondly, at fixed polymer mass M, the parallel
extension is important for those tubular vesicles of small
bending modulus.
Finally, the above behavior is valid as long as the parallel
extension R? remains below the maximal
extension of the polymer, that is we must have R? <
aM1/D (maximal extension). This gives a
minimal tube diameter
Hmin ^,
aM(D-1)/2D . (15)
Therefore, the confinement of the polymeric fractal implies
that the tube diameter is in the interval Hmin < H <
RF3. For instance, for linear polymers, Hmin ^,
a, and Hmin ^,
aM1/8, for branched ones. The minimum
pore size for linear polymers is then independent on the molecular-weight. This
means that the linear polymers find their way even through a very small pore.
It is not the case for branched polymers, for which the minimum pore size
increases with the total mass. As pointed out in Ref. [8], it should be
possible to construct a porous medium that may separate a mixture of branched
and linear molecules on a basis of their connectivity. Indeed, one can choose
an appropriate minimum pore size through which linear polymers can pass,
whereas branched polymers cannot. Now, combining relations (12) and (15) yields
a minimal value for the bending rigidity constant (at fixed pressure
difference)
?min ^,
a3pM3(D-1)/2D .
(16)
Thus, a tubular membrane confines a polymeric fractal only if
its bending modulus is in the interval ?min < ? < ?*,
where the typical value ?* is that given above.
The following paragraph is devoted to the confinement of a
polymer of arbitrary topology to two parallel fluctuating fluid membranes.
IV. CONFINED POLYMERIC FRACTAL IN GEOMETRY II
A.
Basic backgrounds
Consider a lamellar phase formed by two parallel bilayer
membranes. The cohesion between these lipid bilayers is provided by long-ranged
van der Waals forces [54]. But these attractive interactions are balanced, at
short membrane separation, by strong repulsion coming from hydration forces for
uncharged bilayers [55]. In addition, for bilayers carrying electric charges,
the attractive interaction is reduced by
M. Benhamou et al. African Journal Of Mathematical Physics
Volume 10(2011)55-64
60
the presence of electrostatic forces [54, 56,
57].
For two parallel bilayer membranes that are a finite distance
l apart, the total interaction energy (per unit area) is the following
sum
V (l) = VH (l) + VE
(l) + VW (l) . (17)
The first part represents the hydration energy. The hydration
forces that act at small separation of the order of 1 nm, have been discovered
for multilayers under external stress [55]. The adopted form for the hydration
energy is an empirical exponential decay
VH (l) =
AHe-l/?H .
(18)
The typical values of amplitude AH and
potential-range ?H are AH ? 0.2
J/m2 and ?H ? 0.3 nm. The electrostatic
energy between two charged membranes also decays exponentially, that is
VE (l) =
AEe-l/?E ,
(19)
provided that the separation l is greater than the
Debye-H·uckel length. The potential amplitude and its range depend on
ionic concentration in the aqueous solution, ?, and the surface charge
density at membranes, ?0. More precisely, ?E and AE
scale as : ?E ?-1/2 and AE
?2 0?-1/2. The
last part is the attractive van der Waals energy that results from
polarizabilities of lipid molecules and water molecules. This interaction
energy has the standard form
VW (l) =
12? Ll2 (l + ?)2 + (l
+ 2?)2] (20)
The Hamaker constant is in the range W ?
10-22 -10-21 J. In the
above expression, the bilayer thickness ? is of the order of ? ?
4 mm.
In principle, one must add a steric interaction energy that
originates from membranes undulations. According to Helfrich [45], this energy
(per unit area) is
2
Vs (l) = cH
(k?l2) , (21)
with kB the Boltzmann's constant, T the
absolute temperature, and ? the common bending rigidity constant of
the two membranes. But, for two bilayers of different bending rigidity
constants ?1 and ?2, we have ? =
?1?2/ (?1 + ?2). The precise value
of coefficient cH remains an open debate. Indeed, Helfrich gave for
this coefficient the value cH ? 0.23 [45], but
computer simulations predict smaller prefactors, namely, cH ?
0.16 [58], cH ? 0.1 [59], cH
? 0.07 [60] and cH ? 0.08 [61].
Therefore, the steric interaction energy is significant only for those
membranes of small bending modulus. Of course, this energy vanishes for rigid
interfaces (? ? 8).
We note that the lamellar phase remains stable at the minimum
of the potential, provided that the potential-depth is comparable to the
thermal energy kBT. This depends, in particular, on the value
of W-amplitude.
From a theoretical point of view, Lipowsky and Leibler [62]
had predicted a phase transition that drives the system from a state where the
membranes are bound to a state where they completely separated. Such a phase
transition is first-order if the steric repulsive energy is taken into
account. But, if this energy is ignored (for relatively rigid membranes), the
transition is rather second-order. We restrict ourselves to
second-order phase transitions, only. The authors have shown that there exists
a certain threshold Wc beyond which the van der attractive
interactions are sufficient to bind the membranes together, while below this
characteristic amplitude, the membrane undulations dominate the attractive
forces, and then, the membranes separate completely. In fact, the critical
value Wc depends on the parameter of the problem, which are
temperature T, and parameters AH, ?H, ? and
?. For room temperatures and AH ? 0.2
J/m2, ?H ? 0.3 nm, and ? ? 4 nm,
one has Wc ? (6.3 -
0.61) × 10-21 J, when the
bending rigidity constant is in the range ? ? (1 - 20)
× 10-19 J. For instance, for egg lecithin,
one has [63] ? ? (1 - 2) ×
10-19 J, and the corresponding threshold
Wc is in the interval Wc ?
(6.3 - 4.1) ×
10-21 J. We note that the typical value
Wc corresponds to some temperature, Tc,
called unbinding critical temperature [62, 64].
M. Benhamou et al. African Journal Of Mathematical Physics
Volume 10(2011)55-64
61
Let us first consider uncharged membranes, and notice that the
Hamaker constant may be varied changing the polarizability of the aqueous
medium. It was found [62] that, when the critical amplitude is approached from
above, the mean-separation between the two membranes diverges according to
H ,,, (Tc -
T)-? ,,, (W -
Wc)-? , (W ?
Wc+ or T ? T- ) . (22)
c
Here, 0 is a critical exponent whose value is
[62]
0 ,, 1.00 #177; 0.03 .
(23)
Such an exponent was computed using field-theoretical
Renormalization-Group.
From an experimental point of view, critical fluctuations in
membranes were considered in some experiment [65], and in particular, the
mean-separation was measured.
We have now all ingredients to study the conformation of a
single polymeric fractal of arbitrary topology, which is confined to two
parallel fluid membranes forming a lamellar phase.
B. Polymer parallel extension
First, we note that the polymer is confined only when its
three-dimensional gyration radius RF3 ,,,
aM(D+2)/5D is much greater than the mean-separation
H (Tc - T)-?, that is
H << RF3. This condition implies that the polymer
confinement is possible only when temperature T is below some value
T* = Tc - aM-(D+2)/5D?.
This temperature is then smaller than the critical unbinding one
Tc, and the shift Tc -
T* essentially depends on the polymer mass M and its
spectral dimension D.
The first implication of the polymer confinement is that, its
behavior becomes two-dimensional. This means that the polymer can be regarded
as a two-dimensional polymeric fractal formed by blobs (pancakes) of
size H. To determine the parallel extension of the polymer,
R?, as before, we start from a FD free energy
|
F= kBT
|
R2
? + v R2 0
|
M2
R2H , (24)
?
|
where v denotes the excluded volume parameter. There,
R0 aM1/d0F is the ideal radius and
R2?H
represents the volume occupied by the fractal. Minimization of
the above free energy with respect to R? gives
R? aM(D+2)/4D
(W - Wc)?/4
aM(D+2)/4D
(Tc - T)?/4 , (T <<
T*) . (25)
We have used Eq. (22).
The above result calls the following remarks.
First, the expression of the polymer parallel extension
combines two critical phenomena, one is related to the long-mass limit of the
polymeric fractal and the other to the vicinity of the unbinding transition of
the membranes.
Second, in this formula, naturally appears the fractal
dimension (D + 2) /4D of a two-dimensional polymeric
fractal.
Third, the parallel radius becomes more and more smaller as the
unbinding transition is reached. In other word, this radius is important only
when the two adjacent membranes are strongly bound. Finally, the parallel
radius expression may be used to determine the unbinding critical exponent
0, in X-ray experiment, for instance.
V. CONCLUDING REMARKS
In this paper, we have two objectives, namely the
conformational study of a polymeric fractal inside a tubular vesicle or between
two parallel membranes forming an equilibrium lamellar phase. For the former,
the length scale is the equilibrium diameter that depends on the
characteristics of the membrane, which are the bending modulus and the pressure
difference between inner and outer aqueous media. For
M. Benhamou et al. African Journal Of Mathematical Physics
Volume 10(2011)55-64
62
the second geometry, the length scale is the mean-separation
between the adjacent membranes.
The main quantity to consider was the parallel extension of
the confined polymeric fractal. Such a quantity was computed within the
framework of an extended Flory-de Gennes theory. Notice that the same result
may be recovered using scaling argument or blob model [8].
Another physical quantity to consider is the confinement free
energy, denoted ?F. It is the reduced free energy of the polymer,
measured from the state with H = oo. Here, H is the
tube diameter or the mean-separation. The confinement free energy must have the
scaling form : ?F = kBT f (RF3/H),
where the unknown scaling function f (x) has the following
features : f (x) 0, for x << 1 and f
(x) xm, for x >> 1. The
exponent m can be obtained using the fact that ?F must be
extensive as a function of the total mass M. This gives m =
dF (3) = 5D/ (D + 2). Therefore, ?F =
kBTM (H/a)-5D/(D+2),
with H (?/p)1/3, for tubular
vesicles, and H (W - Wc)-?,
for lamellar phases. Notice that ?F
may be measured by comparison of the two concentrations in the
pore (tube or slab) and in the bulk solution. We have
Cpore/Cbulk = ? exp
(-?F/kBT), where ? is a certain coefficient
depending on the ratio RF3/H.
We emphasize that for charged membranes forming the lamellar
phase, it was demonstrated [62] that the mean-separation between two adjacent
bilayers scales as : H (? -
?c)-?, as ? ?
?+c , where ? is the ionic concentration of
the aqueous medium and ?c is its critical value. Of course,
the latter depends on the nature of the lipid system. For instance, for DPPC in
CaCl2 solutions, experimental measurements [66] showed that
?c is in the range ?c ' 84
- 10 mM. In this case, the parallel radius of the polymer
aM(D+2)/4D (x --
xo)~G/4.
scales as : R11
We said above that, for T > Tc, the
shape fluctuations drive the membranes forming lamellar phase apart even in the
presence of the direct attractive forces. In this case, the system recovers its
bound state by a simple application of an external pressure or a lateral
tension.
In the presence of an external pressure P, it was
found [64] that the mean-separation H scales as : H ?L
P-1/3 (?L being the membrane
mean-roughness). Such a behavior agrees with MC data [67]. In this case, the
parallel extension of the polymer obeys the scaling law : R11
aM(D+2)/4DP1/12. As it should be, this extension increases with
increasing external pressure.
The role of a lateral tension is to suppress the bending
undulations and the fluctuation-induced repulsion. In fact, the latter becomes
short-ranged, and the long-ranged van der Waals attraction then dominates
[64]. For this case, it was found [64] that the
mean-separation behaves as : H ?L Ó-1/2,
where
Ó represents the lateral tension. Then, the resulting
parallel extension is : R11 aM(D+2)/4DÓ1/8. As
expected, the parallel radius of the polymer increases as the
lateral tension is augmented.
For tubular vesicles, we have assumed that they are
tensionless. If it is not the case, and if the pressure difference between
inner and outer aqueous media can be neglected, the equilibrium diameter is :
H = 2 (2?/?)1/2, which is solution to Eq. (9).
Here, ? is the interfacial tension coefficient. In this case, the
parallel extension of the polymer is : R11 ^'
aM(D+2)/3D (a2?/?)1/3.
Naturally, this extension increases with increasing interfacial tension
coefficient. The minimal diameter corresponds to a typical value ?min
^' a-2?M(1-D)/D of ? (? is fixed).
Therefore, the polymer is confined if only if ? < ?min.
Finally, further questions in relation with the subject are under
consideration.
ACKNOWLEDGMENTS
We are much indebted to Professors T. Bickel, J.-F. Joanny and
C. Marques for helpful discussions, during the »First International
Workshop On Soft-Condensed Matter Physics and Biological Systems», 14-17
November 2006, Marrakech, Morocco. One of us (M.B.) would like to thank the
Professor C. Misbah for fruitful correspondences, and the Laboratoire de
Spectroscopie Physique (Joseph Fourier University of Grenoble) for their
kinds of hospitalities during his regular visits.
M. Benhamou et al. African Journal Of Mathematical Physics
Volume 10(2011)55-64
63
REFERENCES
1 E.F. Cassasa, J. Polym. Sci. B 5,
773 (1967).
2 P.-G. de Gennes, Scaling Concepts in Polymer
Physics, Cornell University Press, Ithaca, 1979.
3 M. Daoud and P.-G. de Gennes, J. Phys. (France)
38, 85 (1977).
4 F. Brochard and P.-G. de Gennes, J. Phys. (France)
40, L-399 (1979).
5 E. Raphael and P. Pincus, J. Phys. II (France)
2, 1341 (1992).
6 J.T. Brooks and M.E. Cates, J. Chem. Phys.
99, 5467 (1993).
7 J. Lal, S.K. Sinha, and L. Auvray, J. Phys. II
(France) 7, 1597 (1997).
8 T.A. Vilgis, P. Haronska, and M. Benhamou, J. Phys.
II (France) 4, 2139 (1994).
9 S. Orbach and R. Orbach, J. Phys. (France)
43, 1341 (1992).
10 B. Duplantier, Phys. Rev. Lett.
62, 23372341 (1989), and references therein.
11 T. Dotera and Y.Y. Suzuki, Phys. Rev. E
62, 53185323 (2000).
12 Y.Y. Suzuki, T. Dotera, and M. Hirabayashi,
Simulation of Gaussian and Excluded-Volume Chains in Curved Slits,
3rd International Symposium on Slow Dynamics in Complex Systems, AIP
Conference Proceedings, Volume 708, pp. 257-258, 2004.
13 E.Z. Radlinska et al., Phys. Rev. Lett.
74, 42374240 (1994).
14 K. Nakaya et al., Europhys. Lett.
71, 494 (2005).
15 G. Bouglet, Thesis, Montpellier II
University, France, 1997.
16 C. Ligoure, G. Bouglet, and G. Porte, Phys. Rev.
Lett. 71, 3600 (1993).
17 C. Ligoure, G. Bouglet, G. Porte, and O. Diat, J.
Phys. II (France) 7, 473 (1997).
18 A. Maldonado et al., Journal of Colloid
and Interface Science 296, 365 (2006).
19 P.A. Halban and J.C. Irminger, Biochem. J.
299, 1 (1994).
20 M.G. Farquhar and H.P. Hauri, Protein Sorting
and Vesicular Traffic in the Golgi Apparatus, in The Golgi
Apparatus, E.G. Berger and J. Roth, Eds., pp. 63-129, 1997.
21 B. Alberts, Transport des Protéines dans
la Cellule : Essentiel de la Biologie Cellulaire, Garland Eds., 1999.
22 C. Leduc et al., PNAS
101, 17095 (2004).
23 J.C. Howard, Mechanics of Motors Proteins and
the Cytoskeleton, Sinauer, Sunderland, MA, 2001.
24 A. Roux et al., Proc. Nath. Acad. Sci. USA
99, 5394 (2002).
25 I. Derenyi, F. Julicher, and J. Prost, Phys. Rev.
Lett. 88, 238101 (2002).
26 B. Bozic, V. Heinrich, S. Svetina, and B. Zeks,
Eur. Phys. J. E. 6, 91 (2001).
27 D.J. Bukman, J.H. Yao, and M. Wortis, Phys. Rev. E.
54, 5463 (1996).
28 V. Heinrich, B. Bozic, S. Svetina, and B. Zeks,
Biophys. J. 76, 2056 (1999).
29 S. Zhang, J. Phys. Soc. Japan. 68,
3603 (1999).
30 A. Smith, E. Sackmann, and U. Seifert, Phys. Rev.
Lett. 92, 208101 (2004).
31 T.R. Powers, G. Huber, and R.E. Goldstein, Phys.
Rev. E. 65, 041901 (2002).
32 D. Raucher and M.P. Sheetz, Biophys. J.
77, 1992 (1999).
33 D.K. Fygenson et al., Phys. Rev. Lett.
79, 4497 (1997).
34 More details can be found in : D.R. Daniels and
M.S. Turner, Phys. Rev. Lett. 95, 238101 (2005).
35 D. Boal, Mechanics of the Cell, Cambridge
University Press, 2001.
36 B. Alberts et al., Molecular Biology
of the Cell, Garland, New York, 2002.
37 R.W. Briehl et. al., J. Mol. Biol.
245, 710 (1995).
38 See Ref. [8], and references therein.
39 D. Lhuillier, J. Phys. (France)
49, 705 (1988).
40 T.A. Vilgis, J. Phys. (France) 49,
1481 (1988).
41 J. Zinn-Justin, Quantum Field Theory and
Critical Phenomena, Clarendon Press, Oxford, 1989.
42 C. Itzykson and J.-M. Drouffe, Statistical
Field Theory: 1 and 2, Cambridge University Press, 1989.
43 K. Wolfgang, Differential Geometry:
Curves - Surfaces - Manifolds, American Mathematical Society, 2005.
44 S.J. Singer and G.L. Nicolson, Science
175, 720 (1972).
45 W. Helfrich, Z. Natureforsch 28c,
693 (1973).
46 O.-Y. Zhong-Can and W. Helfrich, Phys. Rev. Lett.
59, 2486 (1987).
47 Z.C. Tu and Z.C. Ou-Yang, Phys. Rev. E
68, 061915 (2003).
48 O.-Y. Zhong-Can, Phys. Rev. A 41,
4517 (1990).
49 Z. Lin, R.M. Hill and H.T. Davis, L.E. Scriven, and
Y. Talmon, Langmuir 10, 1008 (1994).
50 M. Mutz and D. Bensimon, Phys. Rev. A
43, 4525 (1991).
M. Benhamou et al. African Journal Of Mathematical Physics
Volume 10(2011)55-64
64
51 A.S. Rudolph, B.R. Ratna, and B. Kahn, Nature
352, 52 (1991).
52 H. Naito, M. Okuda, and O.Y. Zhong-Can, Phys. Rev.
E 48, 2304 (1993).
53 Z.C. Tu, L.Q. Ge, J.B. Li, and Z.C. Ou-Yang, Phys.
Rev. E 72, 021806 (2005).
54 J.N. Israelachvili, Intermolecular and Surface
Forces, 2nd edition, Academic Press, London, 1991.
55 R.P. Rand and V.A. Parsegian, Biochim. Biophys.
Acta 988, 351 (1989).
56 E.J.W. Verwey and J.Th.G. Overbeek, Theory of
the Stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948.
57 B.V. Derjaguin, N.V. Churaev and V.M. Muller,
Surface Forces, Consultants Bureau, New York, 1987.
58 R. Lipowsky and B. Zielinska, Phys. Rev. Lett.
62, 1572 (1989).
59 N. Gouliaev and K.J.F. Nagle, Phys. Rev. Lett.
81, 2610 (1998).
60 W. Janke and H. Kleinert, Phys. Rev. Lett.
58, 144 (1987); Phys. Lett. A 117, 353
(1986).
61 G. Gompper and D.M. Kroll, Europhys. Lett.
9, 59 (1989).
62 R. Lipowsky and S. Leibler, Phys. Rev. Lett.
56, 2541 (1986).
63 W. Harbich and W. Helfrich, Chem. Phys. Lipids
36, 39 (1984).
64 An extensive list of references can be found in :
Structure and Dynamics of Membranes : Generic and Specific
Interactions, R. Lipowsky and E. Sackmann, Eds, Volume 1B, Elsevier,
1995.
65 R. Zhang et al., Phys. Rev. Lett.
74, 2832 (1995).
66 L.J. Lis, W.T. Lis, V.A. Parsegian, and R.P. Rand,
Biochemistry 20, 1771 (1981).
67 R. Lipowsky and B. Zielinska, Phys. Rev. Lett.
62, 1572 (1989).

Dans cette cinquième contribution originale, nous
présentons une vue large sur le phénomène de
ségrégation entre les phospholipides et des chaînes de
polymère greffées sur une membrane en bicouche.
En particulier, nous discutons l'influence de la qualité
du solvant et la polydispersité des chaînes de polymère
greffées sur le comportement de phase critique du mélange.
Nous rappelons que la qualité du solvant apparaît
à travers l'expression générale de l'énergie libre
du mélange, qui nous permettra la détermination du diagramme de
phase relatif à l'agrégation des chaînes de polymère
ancrées
Article N°5
Condensation des polymères greffés
sur
une biomembrane

Home Search Collections Journals About Contact us My
IOPscience
An extended study of the phase separation between phospholipids
and grafted polymers on a bilayer biomembrane
This article has been downloaded from IOPscience. Please scroll
down to see the full text article. 2011 Phys. Scr. 83 065801
(
http://iopscience.iop.org/1402-4896/83/6/065801)
View the table of contents for this issue, or go to the
journal homepage for more
Download details:
IP Address: 41.137.25.75
The article was downloaded on 20/06/2011 at 23:39
Please note that terms and conditions apply.
IOP PUBLISHING PHYSICA SCRIPTA
Phys. Scr. 83 (2011) 065801 (6pp)
doi:10.1088/0031-8949/83/06/065801
An extended study of the phase separation
between phospholipids and grafted
polymers on a bilayer biomembrane
M Benhamou, I Joudar, H Kaidi, K Elhasnaoui, H Ridouane
and H Qamar
Laboratoire de Physique des Polymères et
Phénomènes Critiques, Faculté des Sciences, Ben M'sik, PO
Box 7955, Casablanca, Morocco
E-mail:
benhamou.mabrouk@gmail.com
Received 4 April 2010
Accepted for publication 9 May 2011
Published 26 May 2011
Online at
stacks.iop.org/PhysScr/83/065801
Abstract
We re-examine here the phase separation between phospholipids and
adsorbed polymer chains on a fluid membrane with a change in some suitable
parameter (temperature). Our purpose is to quantify the significant effects of
the solvent quality and of the polydispersity of adsorbed loops formed by
grafted polymer chains on the segregation phenomenon. To this end, we elaborate
on a theoretical model that allows us to derive the expression for the mixing
free energy. From this, we extract the phase diagram shape in the
composition-temperature plane. Our main conclusion is that the polymer chain
condensation is very sensitive to the solvent quality and to the polydispersity
of loops of adsorbed chains.
PACS numbers: 87.16.Dg, 47.57.Ng, 64.60.F
1. Introduction
Biological membranes are of great importance to life, because
they separate the cell from the outside environment and separate the
compartments inside the cell in order to protect important processes and
specific events.
Nowadays, it is largely recognized that biological membranes
are present as a lipid bilayer composed of two adjacent leaflets [1, 2], which
are formed by amphiphile molecules possessing hydrophilic polar-heads pointing
outward and hydrophobic fatty acyl chains that form the core. The majority of
lipid molecules are phospholipids. These have a polar-head group and two
non-polar hydrocarbon tails, whose length is of the order of 5 nm.
0031-8949/11/065801+06$33.00 Printed in the UK & the USA 1
(c) 2011 The Royal Swedish Academy of Sciences
Also, the cell membranes incorporate another type of lipid,
cholesterol [1, 2]. The cholesterol molecules have several functions in the
membrane. For example, they give rigidity or stability to the cell membrane and
prevent crystallization of hydrocarbons. The biomembranes also contain
glycolipids (sugars), which are lipid molecules that microaggregate in the
membrane, and may be protective and act as insulators. Certain kinds of
molecules are bounded by sphingolipids such as cholera and tetanus toxins.
Sphingolipids and cholesterol favor the aggregation of proteins in microdomains
called rafts. In fact, these play the role of a platform for the
attachment of proteins while the membranes are moved around the cell and also
during signal transduction.
Proteins (long macromolecules) are another principal component
of cell membranes. Transmembrane proteins are amphipathic and are formed by
hydrophobic and hydrophilic regions having the same orientation as other lipid
molecules. These proteins are also called integral proteins. Their function is
to transport substances, such as ions and macromolecules, across the membrane.
There exist other types of proteins that may be attached to the cytoplasm
surface by fatty acyl chains or to the external cell surface by
oligosaccharides. These are termed peripheral membrane proteins. They have many
functions; in particular, they protect the membrane surface, regulate cell
signaling and participate in many other important cellular events. In addition,
some peripheral membrane proteins (those having basic residues) tend to bind
electrostatically to negatively charged membranes, such as the inner leaflet of
the plasma membrane.
Phys. Scr. 83 (2011) 065801 M Benhamou
etal
We note that the majority of macromolecules forming the
bilayer are simply anchored on the membrane and form a soft branched
polymer brush [3, 4].
The study of grafted polymers on soft interfaces was motivated
by the fact that they have potential applications in biological materials, such
as liposomes [5-8]. These soft materials were discovered by A Bangham.
Currently, they are major tools in biology, biochemistry and medicine (as drugs
transport agents). Liposomes are artificial vesicles of spherical shape that
can be produced from natural nontoxic phospholipids and cholesterol. But the
lipid bilayers have a short lifetime, because of the weak stability of the
vesicles and their extermination by white blood cells. To have stable vesicles
in time, one useful method consists of protecting them with a coat of flexible
polymer chains (coat size of the order of 50 nm [1]), which prevents the
adhesion of marker proteins [6, 7]. In fact, these polymer chains stabilize the
liposomes, due to the excluded volume forces between monomers [8]. Liposomes
can also be synthesized from A-B diblock-copolymers immersed
in a selective solvent that prefers to be contacted by the polymer A.
The hydrophobic B-polymer chains then aggregate and form a thin
bilayer, while the hydrophilic polymer chains A float in the solvent.
These copolymer-based liposomes have properties that are slightly different
from those of the lipid ones [9] (high resistance, high rigidity and weak
permeability to water). Depending on the choice of copolymers, these liposomes
are resistant to detergents [10].
The grafting of polymers onto lipid membranes was considered
in a very recent paper [11]. More precisely, the purpose was to investigate of
the phase separation between phospholipids and anchored polymers. As
assumptions, the aqueous medium was assumed to be a good solvent, and in
addition, the polymer chains were anchored to the interface only by one
extremity, a big amphiphile molecule. The latter is chemically different from
the phospholipid molecules. In this paper, however, we assume that the polymer
chains may be adsorbed on the membrane by many monomers that are directly
attached to some polar-heads of the host lipid molecules (mobile anchors), and
then organize in polydisperse loops. The surrounding liquid may be a good
solvent or a theta solvent. As we shall see below, the loops' polydispersity
and solvent quality drastically affect the phase behavior of the system. Under
a change in a suitable parameter, such as temperature, the phospholipids and
adsorbed polymer chains phase separate into macroscopic domains alternately
rich in the two components. For the determination of the phase diagram shape,
we elaborate on a theoretical model that takes into account both the loops'
polydispersity and the solvent quality.
This paper is organized as follows. In section 2, we derive
the expression for the mixing free energy of the phospholipid-anchor mixture.
To investigate the phase diagram shape is the aim of section 3. Finally, some
concluding remarks are given in section 4.
2. Mixing free energy
Polymers can adhere to biomembranes in several ways: (i) by
lipid anchors; that is, the polymer is covalently
2
bound to the polar-head of a lipid molecule (for many
proteins, the lipid anchors are glycosylphosphatidylinositol units) [12, 13];
(ii) by hydrophobic side-groups of the polymers which are integrated into the
bilayer [14, 15]; (iii) by membrane spanning hydrophobic domains of the polymer
(membrane-bound proteins, for example); and (iv) by a strong adsorption that
drives the polymer from a desorbed state to an adsorbed one [16]. For a single
polymer chain, the adsorption (on solid substrates) can be theoretically
studied using a scaling argument [17], for instance. In addition to the
polymerization degree of the polymer chain, N, and the excluded volume
parameter, v, the study was based on an additional parameter,
8, which is the energy (per kBT unit) required to
adsorb one monomer on the surface. For a strong adsorption, 8-1
defines the adsorbed-layer thickness. An adsorption transition takes
place at some typical value 8* of 8 scaling as [17]:
8* ~ R-1 F ~ aN-VF
(VF = 3/5), where RF is the Flory
radius of the polymer chain. For dilute and semi-dilute polymer solutions, the
adsorption phenomenon depends, in addition to the parameter 8, on the
polymer concentration.
In this paper, we consider situation (iv), where each monomer
has the same probability of being adsorbed on the membrane surface
[18]1. More precisely, a given monomer is susceptible to becoming
linked to a polar-head of a phospholipid molecule (anchor). As a result, the
polymer chains form polydisperse loops (with eventually one or two tails
floating in the aqueous medium). In fact, this assumption conforms to what was
considered in [19]. The case where no loops are present (adsorption only by one
extremity) was considered in [11]. Contrary to the adsorption on the solid
surface, the anchored polymer chains are mobile on the host membrane and may
undergo the aggregation transition that we are interested in. To be more
general, the fluid membrane is assumed to be in contact with a good solvent or
a theta solvent.
The purpose is to write a general expression for the mixing
free energy. The latter will allow the determination of the phase diagram
related to the aggregation of anchored polymer chains.
First, we start with the free energy (per unit area) of the
polymer layer (for solid substrates), which is given by [20]
|
F0 ' kBT
|
Z N (
1 [b2S (n)]â
+ [-b2S0 (n)] ln
b2 1
|
~ l\
- S0 (n) dn.
S1
(1)
|
For the configuration study, Guiselin [21] considered that
each loop can be viewed as two linear strands (two half-loop). Here, S(n)
is the number of strands having more than n monomers per unit
area, and b represents the monomer size. The number N denotes
the length of the longest strand. Hereafter, we shall use the notation
S1 = /a, which denotes the total number of grafted chains per
unit area, with 8 being the volume fraction of anchors and a
their area. If the mixture is assumed to be incompressible, then 1 - 8
is the volume fraction of the phospholipid molecules.
Let us come back to the free energy expression (1); note that
the first term of the right-hand side represents the
1 The adsorption of an adequate polymer on a fluid membrane
made of two phospholipids of different chemical nature may be a mechanism of
phase separation between these two unlike components as was pointed out.
Phys. Scr. 83 (2011) 065801 M Benhamou et
al
contribution of the (two- or three-body) repulsive
interactions between monomers belonging to the polymer layer. The second term
is simply the entropy contribution describing all possible rearrangements of
the grafted chains in the polymer layer. There, the exponent â depends on
the solvent quality [20]. When the grafting is accomplished in a dilute
solution with a good solvent or a theta solvent, the values of â are
â = 11/6 (blob model) or â = 2, respectively.
For polydisperse polymer layers, the distribution
S(n) is known in the literature [20]. This can be obtained by
minimizing the above free energy with respect to this distribution.
Without presenting details, we simply sketch the general
result that [20]
8
S(n) ~ an1/(â-1) . (2)
For usual solvents, we have
8
8
S(n) ~
(good solvents), (3)
(theta solvents). (4)
an
We shall rewrite the distribution S(n) as
8
S(n) = f (n), (5)
a
with f (n) ~
1/n1/(â-1), for polydisperse
polymer layers, and f (n) = 1 (for all n), for
polymer brushes. Therefore, F0 can be approximated by
F0
= a
kBT
-1u8â
+ç(N)8, (6)
where the linear term in 8 describes the contribution of
entropy to the free energy, where the coefficient ç(N) is as
follows (see the appendix):
lç(N) = a-1 [â
+ln(â - 1)] (1 - N1/(1-â)~
Explicitly, we have
æ(N) = 1 (polymer brushes), (11)
æ(N) ~ Nâ/(1-â) (polydisperse
systems). (12)
Note that æ(N) < 1, since, in all cases,
â > 1. Therefore, the polydispersity of loops decreases the repulsive
interaction energy.
Now, we have all the ingredients for the determination of the
expression for the mixing free energy. To this end, we imagine that the
interface is present as a two-dimensional (2D) Flory-Huggins lattice [17, 22],
where each site is occupied by an anchor or by a phospholipid molecule. Hence,
we can regard the volume fraction of anchors 8 as the probability that a given
site is occupied by an anchor. Therefore, 1 - 8 is the occupation probability
of phospholipids.
Before the determination of the desired mixing free energy
(per site), we note that the latter is the sum of three contributions, which
are the mixing entropy (per site), the volume free energy (per site) and the
interaction energy (per site) coming from the membrane undulations. Actually,
the induced attractive forces due to the membrane undulations are responsible
for the condensation of anchors. These forces balance the repulsive ones
between monomers along the connected polymer chains. We then write
F
kBT = 8ln8+(1-8)ln(1-8)+÷8(1-8)
+u8â +ç(N) 8. (13)
We note that, for polymer chains anchored by one extremity, a
big amphiphile molecule (the polymer brush case), the first contribution of
entropy, 8 ln 8, should be divided by some factor q, which represents
the ratio of the anchor area to the area of polar-heads of the host
phospholipids. In the present case, we have q = 1. In equality (11),
÷ accounts for the Flory interaction parameter
|
+ N1/(1-â) ln N }. (7)
â -1 JJJ
|
÷ = ÷0
|
(14)
1 D
A2 C -kBT
,
|
In the asymptotic limit N ? 8, this coefficient goes
to
ç(N) ? a-1 [â
+ln(â - 1)], (8)
provided that â > 1 (note that â =
11/6, for good solvents, and â = 2, for theta ones). This asymptotic
limit is always positive definite and inversely proportional to the polar-head
area a. In fact, the positive sign of the coefficient
ç(N) agrees with the entropy loss due to the polymer chains
grafting. As we shall see below, this linear contribution does not change the
phase diagram in the composition-critical parameter plane. Here, the coupling
constant u is as follows:
u
(9)
with
æ(N) =
=(b2 1f-1 a) Næ(N),
1N
N J1[ f
(n)]â dn. (10)
3
where the positive coefficients C and D are
such that (in dimension 2) [23]
D = -ð f°°
rU(r) dr, C = ð2
ó2 (covolume). (15)
Here, U(r) is the pair potential induced by
the membrane undulations ([11]; [24] and references therein)
cr
i
U(r) =
8, r < ó,
-AH(
ól4 (16)
/ , r >
ó, r
where ó is the hard disc diameter, which is
proportional to the square root of the anchor area a. There, the
potential amplitude AH plays the role of the Hamaker constant. It was
found that the latter decays with the bending rigidity constant according to
([11]; [24] and reference therein)
AH ~ ê-2. (17)
Phys. Scr. 83 (2011) 065801 M Benhamou et
al
But this amplitude is also sensitive to temperature. We remark
that the above mixing free energy is not symmetric under the change 8 ? 1-8.
Some straightforward algebra gives the following expression for
the attraction parameter D:
ð
2ó2 ~
D = AH
ê-2
ó2 . (18)
Therefore, those membranes with a small bending modulus induce
significant attraction between anchors.
In formula (12), ÷0 > 0 is the Flory interaction
parameter describing the chemical segregation between amphiphile molecules that
are phospholipids and anchors. This segregation parameter is usually written
as
ã0
÷0 = á0 + T , (19)
where the coefficients á0 and ã0 depend on the
chemical nature of the various species. Also, the total interaction parameter
÷ can be written as
ã
÷ = á + T , (20)
with the new coefficients
C D
á = á0 A2, ã =ã0+
kB A2 . (21)
These coefficients then depend on the chemical nature of the
unlike components and on the membrane's characteristics through its bending
modulus ê.
If we admit that the coupling constant u has a slight
dependence on temperature, we will draw the phase diagram in the plane of
variables (8, ÷). Indeed, all of the temperature dependence is contained
in the Flory interaction parameter ÷. interactions widen the compatibility
domain, and then, the separation transition appears at low temperature.
Now, to see the influence of the solvent quality, we rewrite
the interaction parameter u as u =
u0æ(N) ~ u0Nâ/(1-â) <
u0, where u0 is the interaction parameter relative to a
monodisperse system. Thus, the polydispersity of loops has a tendency to reduce
the compatibility domain in comparison with the monodisperse case.
The critical volume fraction, 8c, can be obtained
by minimizing the critical parameter ÷(8) with respect to the 8-variable.
We then obtain
1 1
(1 - 8c)2 82 c
+â(â - 1) (â - 2)
u8â-3
c = 0. (23)
For good solvents (â = 11/6), we have
1
(1 - 8c)2
1
216u8-7/6
55 c = 0. (24)
82 c
Therefore, the critical volume fraction is the abscissa of the
intersection point of the curve of the equation (2x - 1)/
x5/6(1 - x)2 and the
horizontal straight line of the equation y = (55/216)u. Note
that this critical volume fraction is unique, and in addition, it must be
greater than the value 1/2 (for mathematical compatibility). The coordinates of
the critical point are (8c, ÷c), where 8c
solves the above equation and ÷c = ÷(8c).
The latter can be determined by combining equations (19) and (21). For theta
solvents (â = 2), the coordinates of the critical point are exact,
8c = 12, ÷c =
2+u, (25)
where the interaction parameter u scales as
u =
b2 N-1. (26)
a
3. Phase diagram
With the help of the above mixing free energy, we can
determine the shape of the phase diagram in the (8, ÷)-plane that is
associated with the aggregation process that drives the anchors from a
dispersed phase (gas) to a dense one (liquid). We focus only on the spinodal
curve along which the thermal compressibility diverges. The spinodal curve
equation can be obtained by equating to zero the second derivative of the
mixing free energy with respect to the anchor volume fraction 8; that is,
?2F/?82 = 0. Then, we obtain the following
expression for the critical Flory interaction parameter:
÷(8) = 2 (8(11 8)
+â(â - 1) u8â-2 I. (22)
Above this critical interaction parameter appear two phases:
one is homogeneous and the other is separated. Of course, the linear term in 8
appearing in equality (11) does not contribute to the critical parameter
expression.
We remark that, in usual solvents, this critical interaction
parameter is increased due to the presence of (two-or three-body) repulsive
interactions between monomers belonging to the polymer layer. This means that
these
The above relation clearly shows that the polymer chains'
condensation rapidly takes place only when the characteristic mass N
is high enough. The same tendency is also seen in the case of good
solvents.
4
It is straightforward to show that the critical fraction and
the critical parameter are shifted to lower values in the case of polydisperse
systems, whatever be the quality of the surrounding solvent.
In figure 1, we present the spinodal curve for monodisperse
(with no loops) and polydisperse (with loops) systems, with a fixed parameter
N. We have chosen the good solvents situation. For theta solvents, the
same tendency is seen.
We present in figure 2 the spinodal curve for a polydisperse
system (with loops), at various values of the parameter N. As expected
the critical parameter is shifted to higher values when we augmented the
typical polymerization degree.
Finally, we compare, in figure 3, the spinodal curves for a
polydisperse system (with loops) for the case of theta solvents and those for
the case of good solvents, at fixed parameters b and N. All
the curves in the figure reflect our discussions above.
Phys. Scr. 83 (2011) 065801 M Benhamou
etal
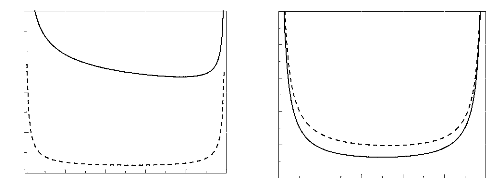
÷
80
60
40
20
0
0,0 0,2 0,4 0,6 0,8 1,0
÷
20
16
12
8
4
0
0,0 0,2 0,4 0,6 0,8 1,0
Ö
Figure 1. Spinodal curves (in a good solvent)
for monodisperse (dashed line) and polydisperse (solid line) systems, when
N = 100, with the parameter b2 = 0.5a.
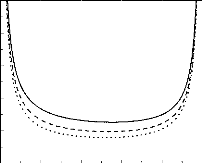
÷
20
16
12
8
4
0
0,0 0,2 0,4 0,6 0,8 1,0
Ö
Figure 2. Spinodal curves for a polydisperse
system, when N = 50 (solid line), 100 (dashed line) and 150 (dotted
line), with the parameter b2 = 0.5a . We assumed
that the surrounding liquid is a good solvent. For theta solvents, the tendency
is the same.
4. Discussion and conclusions
This paper is devoted to the thermodynamic study of the
aggregation of the polymer chains adsorbed on a soft surface. Such an
aggregation is caused by competition between the chemical segregation between
phospholipids and grafted polymer chains, their volumic interactions and the
membrane undulations. More precisely, we addressed the question of how these
polymer chains can be driven from a dispersed phase (gas) to a dense one
(liquid), under a change in a suitable parameter, e.g. the absolute
temperature.
To be more general, we achieved the study in a unified way;
that is, we have considered more realistic physical situations: the solvent
quality (good or theta solvents) and the polydispersity of the adsorbed loops
formed by the grafted
Ö
5
Figure 3. Superposition of spinodal curves for a
polydisperse system for the case of theta solvents (solid line) on those for
the case of good solvents (dashed line). For these curves, we chose N
= 100 and b2 = 0.5a.
polymer chains. The latter were taken into account through the
well-known form of the chains' length distribution.
In doing so, we first computed the expression for the mixing
free energy by adopting the Flory-Huggins lattice image usually encountered in
polymer physics [17, 22]. Such an expression shows that there is competition
between four contributions: entropy, chemical mismatch between unlike species,
interaction energy induced by the membrane undulations and the interaction
energy between monomers belonging to the grafted layer. Such a competition
governs the phases succession.
We emphasize that the present work and a previous work [11]
differ from another previous work that was concerned with the same problem, but
in which the substrate was assumed to be a rigid surface [3]. Therefore, the
membrane undulations were neglected. As we have seen, these undulations
increase the segregation parameter ÷ by an additive term,
÷m, scaling as ê-2. This means that
the phase separation is accentuated due to the presence of thermal
fluctuations. Compared with the previous work [11], which was concerned with
soft brushes with monodisperse end-grafted polymers, the present work is more
general, since it takes into account both the polydispersity of loops forming
the adsorbed polymer chains and the solvent quality. Thus, the present study
was achieved in a unified way. As we have seen, these details drastically
affect the phase diagram architecture.
Now, let us discuss further the influence of solvent quality
on the critical phase behavior. We recall that the solvent quality appears in
the free energy (11) through the repulsion parameter u, defined in
equation (7). We find, in the N ? 8 limit, that ug
~ N1/5uè, where the
subscripts g and è stand for good and theta solvents,
respectively. This implies that the good solvent plays the role of a stabilizer
regarding the phase separation.
Finally, this work must be considered as a natural extension
of a study reported previously [11], which was concerned with monodisperse
end-grafted polymer chains
Phys. Scr. 83 (2011) 065801 M Benhamou
etal
trapped in a good solvent. Therefore, the present work
presents a wide perspective on the phenomenon of segregation between the host
phospholipids and grafted polymer chains on bilayer membranes.
Acknowledgments
We are indebted to Professors T Bickel, J-F Joanny and C
Marques for helpful discussions during the First International Workshop on
Soft-Condensed Matter Physics and Biological Systems (14-17 November 2006,
Marrakech, Morocco). MB thanks Professor C Misbah for fruitful correspondence
and the Laboratoire de Spectroscopie Physique (Joseph Fourier University of
Grenoble) for their kind hospitality during his visit. We are grateful to the
referee for critical remarks and useful suggestions that helped us to improve
the scientific content of this paper.
Appendix
The aim is to determine the coefficient ç(N)
appearing in formula (6). We start with the entropy contribution to the free
energy
|
Fentropic
kBT
|
Z N
1
(~-b2S0(n)~ ln
'
b2 1
|
~ ~~
- S0(n)
S1
|
dn, (A.1)
|
where the loop-size distribution is defined in equation (2).
Then, the above expression can be rewritten as
= ç(N) 8, (A.2)
Fentropic kBT
with
Z N ( 1 ])
ç(N) = a-1 1
nâ/(1-â) ln â - 1nâ/(1-â)
dn.
â - 1 1
(A.3)
Straightforward algebra gives
{ç(N) = a-1 [â
+ln(â - 1)] (1 - N1/(1-â)~
~
â
+ â - 1 N1/(1-â) ln N. (A.4)
This concludes the determination of the coefficient
ç(N).
References
[1]
6
Lipowsky R and Sasckmann S (ed) 1995 Structure and
Dynamics of Membranes: From Cells to Vesicles vol 1A (New York:
Elsevier)
[2] Benhamou M 2008 Lipids Insights 1
2
[3] Nicolas A and Fourcade B 2003 Eur. Phys. J.
E 10 355
[4] Aubouy M et al 2000 Phys. Rev.
Lett. 84 4858 Aubouy M et al 1996 Macromolecules 29
7261
[5] Ringsdorf H and Schmidt B 1986 How to bridge the gap
between membrane, biology and polymers science Synthetic Membranes:
Science, Engineering and Applications ed P M Bungay et al
(Dordrecht: D Reidel) p 701
[6] Lasic D D 1992 Am. Sci. 80 250
[7] Torchilin V P 1996 Effect of polymers attached to
the lipid head groups on properties of liposomes Handbook of Nonmedical
Applications of Liposomes vol 1, ed D D Lasic and Y Barenholz (Boca Raton,
FL: RCC Press) p 263
[8] Joannic R, Auvray L and Lasic D D 1997 Phys.
Rev. Lett. 78 3402
[9] Discher B M et al 1999 Science 284
1143
[10] Elferink M G L et al 1992 Biochim.
Biophys. Acta 1106 23
[11] Benhamou M, Joudar J and Kaidi H 2007 Eur.
Phys. J. E 24 343
[12] Blume G and Cev G 1990 Biochim. Biophys. Acta
1029 91
[13] Lasic D D, Martin F J, Gabizon A, Huang S K and
Papahadjopoulos D 1991 Biochim. Biophys. Acta 1070 187
[14] Decher G et al 1989 Angew. Makromol.
Chem. 166 71
[15] Simon J, Kuhner M, Ringsdorf H and Sackmann E
1995 Chem. Phys. Lipids 76 241
[16] Garel1 T, Kardar M and Orland H 1995 Europhys.
Lett. 29 303
Chatellier X and Andelman D 1995 Europhys.
Lett. 32 567 Lipowsky R 1995 Europhys. Lett. 30 197
Xie A F and Granick S 2002 Nature Mater. 1
129
[17] de Gennes P-G 1979 Scaling Concept in Polymer
Physics (Ithaca, NY: Cornell University Press)
[18] Binder W H, Barragan V and Menger F M 2003
Angew. Chem. Int. Edn Engl. 42 5802
[19] Manghi M and Aubouy M 2001 Adv. Coll. Interf.
Sci. 94 21
[20] Manghi M and Aubouy M 2003 Phys. Rev. E 68
041802
[21] Guiselin O 1992 Euro. Phys. Lett. 17 225
Guiselin O 1992 PhD Thesis Paris VI University
[22] Flory P J 1953 Principles of Polymer Chemistry
(Ithaca, NY: Cornell University Press)
[23] Balian R 2006 From Microphysics to
Macrophysics--Methods and Applications of Statistical Physics (Berlin:
Springer)
[24] Marchenko V I and Misbah C 2002 Eur. Phys.
J. E 8 477
elhasnaouikhalid@gmail.com
elhasnaouikhalid@hotmail.fr
| 


