Parcs à karité (Vitellaria paradoxa) (Gaertn. c. f. ) (Sapotaceae) au Bénin: importance socio-culturelle, caractérisations morphologique, structurale et régénération naturelle

5.4.2.6 Relation hauteur totale-diamètre à 1,30 m au-dessus du sol

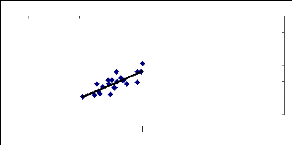
Cette relation s'ajuste au mieux à la fonction linéaire de la forme Ln(1/H) = 0,6658Ln(1/D) + 0,1667 au seuil de 5% avec R² =67% Ln = logarithme népérien, H = hauteur totale de l'arbre et

D= diamètre à 1,30 m au-dessus du sol (figure 37).

0

-5 -4 -3 -2 -1 0

-0.5

-3

Ln(1/D)

-1

-1.5

-2

-2.5

Ln (1/Y) = 0.6658Ln(1/x)+ 0.1667
R2 = 0.6702

Ln(l/H)

Figure 36 : Diagramme hauteur totale-diamètre à 1,30m au-dessus du sol des arbres du parc à karité

de la région de Savè

5.4.2.7 Relation diamètre cime-diamètre à 1,30 m au-dessus du sol

La relation s'ajuste à l'équation de type Y= 0,6658Lndbh - 0,1667 avec R² =67%. Y= Ln(diamètre cime) ; X = Ln (diamètre à 1,30 m au-dessus du sol) (figure 38).

3

2.5

2

LnDcime

1.5

1

0.5

0

y = 0.6658x - 0.1667
R2 = 0.6702

0 1 2 3 4 5

Lndbh

Figure 37 : Diagramme diamètre cime-diamètre à 1,30 m au-dessus du sol des arbres du parc à karité de la

région de Savè

5.4.2.8 Relation hauteur totale-diamètre cime

Le nuage de points représenté par la figure 39 illustre la relation existant entre la hauteur totale et le diamètre cime des arbres du parc à karité de la région de Savè s'ajuste au mieux à l'équation puissance de type Y= 1,5218x 0,4691 avec R² =37%. Y= hauteur totale et X = diamètre cime.

	3 2.5				y = 1.5218x^0.4691 R2 = 0.369
2					LnH
1.5

1

0.5

0

0 1 2 3

LnDcime

Figure 38 : Diagramme hauteur totale-diamètre cime des arbres du parc à karité de la région de Savè