
 |
Identification et commande des systèmes non linéaires( Télécharger le fichier original )par LEMMOU Amira- BELLAKHDAR Khaoukha- LEDJEDEL Adila université de M'Sila Algérie - Ingénieur en électronique 2011 |
CHAPITRE II : LES RESEAUX DE NEURONESINTRODUCTION .13 II.1.LES NEURONES ARTIFICIELS .13 II.2.FONCTION D'ACTIVATION ..14 II.2.1.Fonction binaire a seuil~ «« ««« «««« «..14 II.2.2.Fonction linéaire««««««««««««««««««««««~.15 II.2.3.Fonction linéaire à seuil ou multiseuil ««« ««««««.15 II.2.4.Fonction sigmoúde«««««««««««««««««««««~..15 II.3.ARCHITECTURE DES RESEAUX DE NEURONES 16 II.3.1.Les reseaux non bouclés««««««««««««««««««« 16 II.3.2.Reseaux bouclés««««««««««««««««««««««~.17 II.4.L'APPRENTISSAGE 17 II.4.1.Types d'apprentissage«««««««««««««««««««« 17 II.4.1.1.Apprentissage supervisé«««««««««««««««« 17 II.4.1.2.Apprentissage non supervisé««««««««««««««~ 18 II.4.1.3.Apprentissage autosupervisé««««««««««««««~ 18 II.4.2.Les methodes d'apprentissage««««««««««««««««~ 18 II.4.2.1.Regle de hebb««««««««««««««««««««~ 18 II.4.2.2.Retropropagation du gradient de l'erreur~ « ~ 18 II.4.2.2.1.Avantages et inconvénients««««««««~..19 >
Aventage«««««««««««««««
..19 II.4.3.Le perceptron«««««««««««««««««««««««~..20 II.4.3.1.Description««««««««««««««««««««« ...20 II.5.STRUCTURE A PERCEPTRON MULTICOUCHE(PMC) ..21
II.7.2.La capacité d'adaptation~~~~~~~~~~~~~~~~~~..23 II.7.3 .La mémoire distribuée~~~~~~~~~~~~~~~~~~~.23 II.7.4.La capacité de généralisation.~~~~~~~~~~~~~~~...24 II.8.MODELISATION NEURONALE DES SYSTEMES NONLINEAIRES.....24II.9.IDENTIFICATION DES PROCESSUS PAR RESEAUXDE NEURONES .25 II.9.1.Identification
directe~~~~~~~~~~~~~~~~~~~~.25 II.9.2.Identification inverse
.27 DE NEURONES ..27 II.10.1.Avantages des reseaux de neurones~~~~~~~~~~~~~~..27 II.10.2.Inconvénient des reseaux de neurones~~~~~~~~~~~~~..28 CONCLUSION ..28 CHAPITRE III : LES TYPES DE LA COMMANDEINTRODUCTION ..30 III.1.COMMANDE DE PROCESSUS .30 III.2.LES RESEAUX DE NEURONES DANS LA COMMANDEDES SYSTEMES 31 III.2.1.La commande inverse~~~~~~~~~~~~~~~~~~~~ 32 III.2.2.Commande basée sur l'erreur de sortie~~~~~~~~~~~~~ 33 III.2.3.Commande adaptative neuronale~~~~~~~~~~~~~~~ 34 III.2.3.1. Commande adaptative neuronale indirecte~~~~~~~~ 35 III.2.3.2.Commande adaptative neuronale directe~~~~~~~~~ 36 III.3.STRUCTURE BASE DE LA COMMANDE ADAPTATIVENEURONALE A RETOUR D'ETAT .36 III.3.1.Les reseaux de neurones~~~~~~~~~~~~~~~~~~~.36 III.4.STRUCTURE DE LA COMMANDE ADAPTATIVE NEURONALE A RETOUR DE SORTIE 37 III.4.1.La structure de base~~~~~~~~~~~~~~~~~~~........37 III.4.2.Les observateurs non linéaire~~~~~~~~~~~~~~~ 38 III.5.APPRENTISSAGE D'UN CONTROLEUR CONVENTIONNEL ..39 CONCLUSION 40 CHAPITRE IV : LES RESULTATS DE SIMULATIONINTRODUCTION 42 IV.1.PRESENTATION DES SYSTEMES A IDENTIFIER ET RESULTAT 42 IV.2. LA SIMULATION 47 IV.3 .INTERPRETATION DE RESULTAT 57 CONCLUSION 58 Introduction générale :La commande de processus au moyen des réseaux de neurones, a connu un très grand essor cette dernière décennie. La vision de la biologie a pris, dans le domaine de la théorie des Systèmes dynamiques, une tournure particulièrement intéressante. Elle a ouvert des perspectives de compréhension à la fois plus larges et plus méfiantes. Dans le dut d'élargir son champ d'application, la théorie de contrôle ressent actuellement un besoin d'intégrer de nouveaux concepts regroupés sous le terme de commande intelligente. L'objectif est d'introduire de nouveaux mécanismes permettant une commande plus simple, capable de s'adapter à des variations de l'environnement et démontrant des capacités d'apprentissage, telles les efforts et les interventions de l'home, tant dans les phases de conception que de conduite proprement dite, en soient significativement réduits. La plupart des commandes utilisant un réseau de neurones en tant que contrôleur se distinguent par une étape d'identification et une étape de contrôle. L'identification consiste à élaborer un modèle neuronal qui est une estimation du processus à commander et cela au moyen d'une phase d'apprentissage. Celle-ci peut être soit préalable (hors ligne), ou bien elle peut se faire intégralement en ligne. La commande utilise les connaissances acquises pendant la phase d'identification et/ou de l'apprentissage en ligne pour élaborer des signaux de commande. Un apprentissage en ligne, pendant la commande du système, est intéressant si des perturbations viennent affecter le processus ou son environnement. L'ensemble des travaux est regroupé dans quatre chapitres
Dans ce chapitre, tous les résultats de simulation vont être présentés .enfin, nous terminons par une conclusion générale et la liste des références. Chapitre IMODELISATION ET IDENTIFICATIONDES SYSTEMES NON LINEAIRESIntroduction : La modélisation des systèmes non linéaires par réseaux de neurones a fait l'objet de nombreux travaux de recherche depuis une dizaine d'années à cause de la capacité d'apprentissage, d'approximation et de généralisation que possèdent ces réseaux. En Effet systèmes non linéaires peuvent être modélisés sans une description mathématique précise. L'identification, c'est l'opération de détermination du modèle dynamique d'un système à partir des mesures entrées/sorties. Souvent la sortie mesurée des systèmes est entachée du bruit. Cela est dû soit à l'effet des perturbations agissant à différents endroits du procédé, soi à des bruits de mesure. Ces perturbations introduisent des erreurs dans l'identification des paramètres du modèle. Dans ce chapitre, nous présentons la modélisation et l'identification des systèmes non-linéaires. I.1.Modélisation:On dit qu'on a modélisé un processus physique, si on est capable de prédire quel était son comportement (sortie) lorsqu'on le soumet a une sollicitation (entrée) connus. Le problème de modélisation se pose lorsque l'ingénieur doit prendre une décision au sujet du phénomène dont il ne connaît le comportement qu'a partir des données expérimentales. Dans certains cas, la connaissance fondamentale des phénomènes en question nous permet de proposer un modèle mathématique précis, déterministe que l'on nomme modèle de connaissance. Pour des raisons de commodité pratique, le modèle sera mathématique afin d'être simulé sur calculateur numérique .On cherche donc une relation mathématique É qui lie les variables mesurées d'entrée u et de sortie y. É (u, ?)= 0 (I-1) Cette relation mathématique prend une certaine forme qui définit la structure du modèle. Elle fait intervenir des paramètres ? dont on ignore généralement a priori les valeurs numériques [4]. I.1.1.Modélisation de données statiques :Il existe une immense variété de phénomènes statiques qui peuvent être caractérisés par une relation déterministe entre des causes et des effets ; les réseaux de neurones sont de bons candidats pour modéliser de telles relations à partir d'RENi1YalIRnN expérimentales, sous réserve que celles-ci soient suffisamment nombreuses et présentatives [1]. I.1.2.La modélisation de processus dynamiques non linéaires :Modéliser un processus, c'est trouver un ensemble d'équations mathématiques qui décrivent le comportement dynamique du processus, c'est-à-dire l'évolution de ses sorties en fonction de celle de ses entrées ; c'est donc typiquement un problème qui peut être avantageusement résolu par un réseau de neurones si le phénomène que l'on désire modéliser est non-linéaire. La prédiction de séries chronologiques (prédictions financières, prédiction de consommation, etc.) entre dans ce cadre [1]. I.1.2.1.Les modèles dynamiques "boîtes noires":Qui sont établis uniquement à partir des mesures effectuées sur le processus, sans intervention d'autre connaissance. Les réseaux de neurones sont souvent utilisés comme des modèles "boîtes noires". Néanmoins, nous verrons plus loin qu'ils peuvent aussi mettre en 0 FiEinl FRP S1RP iN inl1i liN P RCèliNITERtvliN noires" et les modèles de connaissances. Pour réaliser un modèle dynamique, il convient alors d'utiliser des réseaux bouclés, qui comme indiqué plus haut, sont eux-mêmes des systèmes dynamiques. Comme précédemment, l'apprentissage est l'estimation des paramètres du modèle neuronal utilisé, l'objectif de l'apprentissage n'est pas ici d'annuler l'erreur de prédiction, puisque, si tel était le cas, le réseau serait capable de reproduire l'effet des perturbations non mesurables il s'agit plutôt d'obtenir une erreur de prédiction dont la variance est minimale, c'est-à- dire égale à celle du bruit. Si l'on peut obtenir un tel résultat, le réseau reproduit complètement le comportement déterministe du processus, bien que l'apprentissage ait été effectué en présence de perturbations. Des résultats théoriques prouvent que cet objectif est accessible, et de nombreux exemples montrent qu'il est effectivement atteint [1] I.1.2.2.Modèle de connaissance :Basé sur les lois de la physique, chimie, etc.... Ces modèle permettent une description assez complète des systèmes et sont utilisés pour la simulation et la conception de procédé. Les paramètres ?i du modèle de connaissance ont alors un sens physique : longueur, résistance électrique, inertie, etc. ... c'est-à-dire que l'on est susceptible de les retrouver avec la même signification dans les modèles d'autres processus. C'est en fait la voie classique de la mise en équation ou analyse phtisique conventionnelle qui tend à utiliser au mieux toutes les connaissances scientifiques et techniques disponibles : y= É (u,?i) (I-2) Ces modèles sont beaucoup plus riches en signification que les modèles de représentation et contiennent toutes les informations utiles sur les processus. Ils sont par contre beaucoup plus onéreux et difficiles à obtenir [4]. I.1.2.3. Modèle de représentation:Ces modèles n'ont aucun pouvoir explicatif de la structure physique du système. Leur structure n'est qu'une relation mathématique qui va relier localement les mesures des différentes variables du processus. Les modèles de représentation sont de type « Boite noir » et ne sont informatif [4]. Un modèle est quantitatif lorsque les fonctions qui définissent les équations sont spécifiées analytiquement. Dans un modèle quantitatif, une suite d'opération permet le calcul de la valeur numérique des fonctions du modèle à partir de leurs arguments (et des entrées du système) [6]. I.2.Étape de modélisation :I.2.1. Caractérisation :La première étape du processus de modélisation consiste à faire une hypothèse sur la structure du système, c'est-à-dire à choisir un type de relation mathématique f liant les entrées et les sorties. Les paramètres structuraux, au départ inconnus, seront déterminés numériquement dans l'étape suivante dite l'identification dans ce choix de structure, on peut être guidé par :
I.3.Principe de la modélisation et l'estimation [6]:
I.4.Intérêt de la modélisation:
I.5. L'identification :
I.6.Identification des systèmes statiques et dynamiques :
I.7.Procédure d'identification:
Figure I.1.Schéma de Procédure d'identification I.8.Architecture des schémas d'identification : Nous focalisons l'attention ici sur la nature paramétrique ou non des schémas proposés. En effet, cet aspect revêt une importance plus grande en identification des systèmes non linéaires en blocs dans la mesure où ces derniers sont constitués de plusieurs sous- systèmes, le choix entre une représentation paramétrique ou non se pose pour chacun de ces sous-systèmes [10]. > Système entièrement paramétrique : les deux sous-systèmes (linéaire et non Linéaire) sont caractérisés par une représentation paramétrique. > Système partiellement paramétrique : un des deux sous-systèmes est non paramétrique. > Système entièrement non paramétrique : les deux sous-systèmes sont non paramétriques I.9.Nature des perturbations et des erreurs de modélisation dans les Schémas d'identification :Les perturbations sont un fait réel que l'on peut difficilement ignorer dans le processus de modélisation ou d'identification des systèmes physiques. Elles représentent en fait l'influence non contrôlée de l'environnement du système sur celui-ci. Quand on essaie d'en tenir compte, on est confronté a deux types d'incertitudes : la nature (stochastique ou déterministe) de la source génératrice de ces perturbations et la manière dont celles-ci affectent le système (leurs points d'action). En identification des systèmes non linéaires, l'effet des perturbations est très souvent pris en compte dans le modèle à travers une erreur de sortie de type bruit blanc (avec des distributions plus ou moins clairement spécifiées) éventuellement filtré par un filtre stable. Toutefois certains travaux ont suggéré une prise en compte des perturbations à travers une erreur d'équation ou d'entrée assimilée a un bruit blanc filtré ou non. Les cas extrêmes sont ceux où aucune hypothèse n'est émise sur le processus générateur des erreurs et le cas opposé où ces erreurs sont supposées nulles. Il va sans dire que les hypothèses considérées dans tel ou tel travail sont avant tout motivées par le souci d'analyse de consistance des estimateurs considérés. Il convient de remarquer aussi que les erreurs en question (de sortie, d'équation et d'entrée) sont aussi le résultat d'erreurs de modélisation inhérente a l'approche « boite noire » [10]. I.10.Importance et utilité de l'identification :Les systèmes abondent dans l'environnement de l'homme. Toute les choses qui nous entourent (la machine, l'économie, la plante, la société, etc....) Ó compris nous même les êtres humains, peuvent être étudiées et considérés comme des systèmes, à savoir modélisées, c'est-à-dire réduits à des formes de représentations plus abstraits et moins physiques que le système réel. L'analyse du modèle de représentation permet d'obtenir de meilleures connaissances sur le système et de le corrige par la suite dans le sens désiré. L'importance de la modélisation des systèmes et de l'analyse s'est fait sentir récemment, dans de nombreux domaines tels que l'économie, la biologie, la médecine et naturellement dans la commande automatique. Les modèles mathématiques développés a travers les techniques d'identification doivent être adéquats et robustes car ils peuvent être utilisée pour : > L'obtention d'une meilleure connaissance du procédé. > L'obtention des propriétés du modèle par étude des simulations temporelles et des propriétés structurelles (ordre, commandabilité, observabilité, stabilité) :C'est l'analyse du modèle. La conception et la mise en oeuvre d'un système performant de régulation. Le choix entre un ou plusieurs algorithmes de commande suivant les performances requises et test du schéma adopté par simulation de la boucle fermée, constituée du modèle initial et du régulateur : c'est la synthèse du système de commande [4]. La prédiction des signaux. > L'optimisation du comportement du procédé. > Le calcul des variables expérimentalement inaccessibles. Conclusion :Dans ce chapitre nous considérons le problème de l'identification et modélisation des systèmes non linéaires .L'objectif est de construire un modèle pour le système à identifier e nous avons présentées la relation entre la modélisation et l'identification. Chapitre IILes Réseaux de neuronesIntroduction :L'un des défis de l'homme aujourd'hui est de copier la nature et de reproduire des modes de raisonnement et de comportement qui lui sont propre. Les réseaux de neurones, sont nés de cette envie ils constituent une famille de fonctions non linéaires paramétrées, utilisées dans de nombreux domaines (physique, chimie, biologie, finance, etc.), notamment pour la modélisation de processus et la synthèse de lois de commandes, leur application dans le domaine de l'électronique est assez récente. Ce chapitre décrit une technique intelligente nouvellement introduite dans le monde de l'électronique. Il s'agit principalement des réseaux de neurones artificiels et les différentes structures qui leurs sont associées ainsi que nous abordons par la suite l'identification et le contrôle de processus par les réseaux de neurones pour la synthèse de lois de commandes. II.1.Les neurones artificiels :Les réseaux de neurones biologiques réalisent facilement un certain nombre d'applications telles que la reconnaissance des formes, le traitement de signal, l'apprentissage par l'exemple la mémorisation et la généralisation. Ces applications sont pourtant, malgré tout les efforts déployés en algorithmique et en intelligence artificielle, à la limite des possibilités actuelles .C'est à partir de l'hypothèse que le comportement intelligent émerge de la structure et du comportement des éléments de base du cerveau que les réseaux de neurones artificiels se sont développes. Les réseaux de neurones artificiels sont des modèles, à ce titre ils peuvent être décrits par leurs composants, leurs variables descriptives et les interactions des composants.
Figure II.1. Le modèle d'un neurone artificiel.
Chaque neurone artificiel est un processeur élémentaire, il reçoit un nombre de variable d'entrées en provenance de neurones amont. A chacune de ces entrées est associé un poids (W) abréviation de poids représentatif de la force de connexion. Chaque processeur élémentaire est dote d'une sortie unique, qui se ramifie ensuite pour alimenter un nombre variable de neurones avals. A chaque connexion est associé un poids synaptique. Cette structure élémentaire est appelée perceptron [2]. II.2. Fonctions d'activation :Cette fonction permet de définir l'état interne du neurone en fonction de son entré totale, Citons à titre d'exemple quelques fonctions souvent utilisées [11]. II.2.1. Fonction binaire a seuil :Fonction Heaviside (figure II.2) définie par : f1, x> 0 h(x) =10, sinon (II.1) Fonction Signe (figure II.3) définie par : (+1, x > 0 sgr(x) = t-1, sinon (II.2)
Le seuil introduit une non-linéarité dans le comportement du neurone, cependant il limite la gamme des réponses possibles à deux valeurs [11]. II.2.2 Fonction linéaire :C'est l'une des fonctions d'activations les plus simples, sa fonction est définie par [11] : F(x)=x
Figure. II.4. Fonction linéaire. II.2.3 Fonction linéaire à seuil ou multi-seuils : On peut la définir comme suit :IX , X E [U, v] F(X) = v ,Si X v (II.3) U , Si X < U II.2.4 Fonction sigmoïde :Elle est l'équivalent continu de la fonction linéaire. Etant continu elle est dérivable, d'autant plus que sa dérivée est simple à calculer, (figure. II.5) elle est définie par [11] : ??1 ??) = 1 ??2 ??~ = 1-??-?? 1+??-?? 1+??-??
Figure. II.5. Fonction sigmoïde. II.3.Architecture des réseaux de neurones :II.3.1.Les réseaux non bouclés :Ce sont des réseaux unidirectionnels sans retour arrière (feedforward). Le signal de sortie est directement obtenu après l'application du signal d'entrée. Si tous les neurones ne sont pas des organes de sortie, on parle de neurones cachés [2]
II.3.2.Réseaux bouclés :Il s'agit de réseaux de neurones avec retour en arrière (feedback network ou récurrent Network) [2].
Figure II.7.Réseau bouclé. II.4.L'apprentissage :II.4.1.Types d'apprentissages :L'apprentissage et l'adaptation constituent deux caractéristiques essentielles des réseaux de neurones. Le rôle de l'apprentissage est de définir le poids de chaque connexion. De nombreuses règles existent pour modifier le poids des connexions et donc pour arriver à un apprentissage correct lorsque la phase d'apprentissage est achevée, le réseau doit etre capable de faire les bonnes associations pour les vecteurs d'entrées qu'il n'aura pas appris. C'est l'une des propriétés importante dans les réseaux de neurones, car elle permet de donner la capacité de reconnaître des formes ressemblantes et meme dégradées des prototypes, c'est la phase de reconnaissance. Les techniques d'apprentissage peuvent etre classées en trois catégories [2]: Un superviseur ou professeur, fournit au réseau des couples d'entrées-sorties. Il fait apprendre au réseau l'ensemble de ces couples, par une méthode d'apprentissage comme la rétro-propagation du gradient de l'erreur, en comparant pour chacun d'entre eux la sortie effective du réseau et la sortie désirée. L'apprentissage est terminé lorsque tous les couples entrées-sorties sont reconnus par le réseau. Ce type d'apprentissage se retrouve, entres autres dans le perceptron [2]. II.4.1.2. Apprentissage non supervisé :Cet apprentissage consiste à détecter automatiquement des régularités qui figurent dans les exemples présentés et à modifier les poids des connexions pour que les exemples ayant les mêmes caractéristiques de régularité provoquent la même sortie. Les réseaux autoorganisateurs de Kohonen sont les réseaux à apprentissage non supervisé les plus connus [2]. II.4.1.3. Apprentissage auto-supervisé :Le réseau de neurone évalue lui-mrme ses performances, sans l'aide d'un «professeur ». Un objet est présenté à l'entrée du réseau de neurones, à qui on a indiqué la classe à laquelle appartient cet objet. Si le réseau ne le classe pas correctement, il mesure lui-mrme l'erreur qui le faîte, et propage cette erreur vers l'entrée. Le réseau procède à autant d'itérations qu'il est nécessaire jusqu'à obtenir la réponse correcte [2]. II.4.2Les méthodes d'apprentissage :Dans les systèmes experts, les connaissances de l'expert ont une forme énumérée : elles sont exprimées sous forme de règles. Dans le cas des réseaux de neurones, les connaissances ont une forme distribuée : elles sont codées dans les poids des connexions, la topologie du réseau, les fonctions de transfert de chaque neurone, le seuil de ces fonctions, la méthode d'apprentissage utilisée. Il existe un certain nombre de méthodes d'apprentissage [2]: II.4.2.1. Règle de Hebb :C'est la méthode d'apprentissage la plus ancienne (1949), elle est inspirée de la biologie. Elle traduit le renforcement des connexions liant deux neurones activés. Si un des deux neurones au moins n'est pas activé, le poids de la connexion n'est pas modifié. II.4.2.2. Rétro-propagation du gradient de l'erreur :Cet algorithme est utilisé dans les réseaux de type feedforward, ce sont des réseaux de neurones à couche, ayant une couche d'entrée, une couche de sortie, et au moins une couche cachée. Il n'y a pas de récursivité dans les connexions, et pas de connexions entre neurones de la même couche. Le principe de la rétro-propagation consiste à présenter au réseau un vecteur d'entrées, de procéder au calcul de la sortie par propagation à travers les couches, de la couche d'entrées vers la couche de sortie n passant par les couches. Cette sortie obtenue est comparée à la sortie désirée, une erreur est alors obtenue. A partir de cette erreur, est calculé le gradient de l'erreur qui est à son tour propagé de la couche de sortie vers la couche d'entrée, d'où le terme de rétro-propagation. Cela permet la modification des poids du réseau et donc l'apprentissage. L'opération est réitérée pour chaque vecteur d'entrée et cela jusqu'à ce que le critère d'arr~t soit vérifié [2]. II.4.2.2.1Avantages et inconvénients de retro propagation du gradient de l'erreur : > Les Avantages : Ce f~t un des premiers algorithmes développés pour l'apprentissage des réseaux de neurones multicouches de types feedforward. Il permet de pallier une carence de l'algorithme du perceptron qui est incapable de modifier les poids des couches cachées , l'implémentation informatique ne présente pas de difficultés [2]. > Les Inconvénients : En ce qui concerne l'algorithme : L'algorithme de rétro-propagation du gradient de l'erreur suit la descente du gradient de L'erreur [2] : un minimum local peut rapidement bloquer la recherche des optima globaux : > L'algorithme de rétro-propagation est gourmand en temps de calcul. > Importance du choix du coefficient d'apprentissage, si le coefficient est trop grand la dynamique du réseau va osciller autour de l'optimum, s'il est trop petit la convergence est lente. II.4.3.Le perceptron :Depuis les résultats des travaux de Mac Culloch et Pitts (1943), qui ont abouti à La définition du neurone formel, ainsi ceux de Hebb, expliquant les effets d'apprentissage de mémoire et de conditionnement à partir de groupes de cellules. Pour expliquer ces effets d'apprentissage, Hebb propose que les cellules apprennent à modifier l'intensité des connexions qui les relient, en fonction de leur activité simultanée. L'idée de certains chercheurs fut d'utiliser les modélisations des neurones et de l'évolution des synapses pour simuler des réseaux de neurones. Le premier modèle solide fut présenté en 1959 par F. Rosenblatt il s'agit du perceptron, autrement dit un réseau réduit à un seul neurone formel [2]. II .4.3.1. Description :Les perceptrons sont des réseaux de type feedforward, possédant la structure suivante : Une couche de connexions fixes, située entre les unités d'entrée, la rétine, et les unités d'association. La seconde couche relie les unités d'association et les unités de réponse : c'est sur ces poids que l'adaptation agit. Dans le perceptron, il n'y a qu'une seule couche qui varie en fonction de l'adaptation. Dans le neurone du perceptron on utilise la fonction d'activation à seuil. Le modèle du neurone linéaire à seuil du perceptron à une cellule de décision et relié à N cellules d'entrée est présenté sur la (figure II.8)
Le neurone linéaire à seuil réalise donc, une partition des vecteurs d'entrée qui lui sont soumis en entrée en deux domaines. La frontière entre ces deux dom S = E ?????? * Xj (II-4)
En effet, pour ?? E???? * Xj > S , le neurone répond 1 ; Pour ??E???? * Xj < S , il répond -1 La frontière séparant ces deux domaines sera donc un hyperplan. : II.5.Structure à perceptron multicouche(PMC)Les perceptrons sont les réseaux de neurones artificiels les plus courants, ils correspondent de trois couches, la première correspond a la couche d'entrée, la deuxième est nommée couche cachée et la dernière est la couche de sortie. La première couche est constituée neurones formels ,les neurones d'une couche à une autre sont relies par les poids synaptiques .Chaque neurone formel constitue une cellule effectuant une somme pondérée des entrées Xij du neurone (j) par les poids synaptiques Wij correspondant a ces entrées .Sa sortie est ensuite obtenue par l'intermédiaire de la fonction fj dite fonction d'activation .Cette fonction est en générale croissante ,monotone et bornée ,les plus utilisées sont les fonction signes de saturations ainsi que les fonction sigmoïde ,nous avons ajoute des termes d'entrées X0ij correspondant au biais .Il n'existe pas de regèle pour fixer l'architecture du réseaux ,les neurones des couches d'entrée et de sortie sont lies respectivement au nombre d'entrées et de sorties .Ainsi il a été prouver récemment que les réseaux a une seule couche cachée constitue un outil d'approximation .Pour notre cas ,l'information se propage de la couche d'entrée vers la couche de sortie ,qui fourni une réponse réelle (Y^ ) correspondant à la sortie désirée Y) .En résume pour enseigner une tache a ce réseau (adaptation des poids ) nous devons lui présente un couple d'exemple(entrées /sorties) ou(Ucom,Y).l'apprentissage des poids se fait par retro ~ propagation de l'erreur( å) entre la grandeur de sortie du réseau (Y^ )et la grandeur désirée (Y) (critère de minimisation).l'algorithme permettant un telle apprentissage est dit « algorithme de retro-propagation »de Windrow --Hoff il est base sur la méthode du gradient toutes ces méthodes consistent a réduire une fonction se rapportant a l'erreur quadratique moyenne. Cet algorithme d'apprentissage permet de déterminer les variations des poids synaptiques ?W1(k) et les biais ?b1(k) .il peut etre exprime par les relations suivantes [14] : ??????,?? ??) = ?? ???? ??) ?????? ???????(??) ????? ??~ (???? ??~)? (II-5) ??????,?? ??) = ?????? ??) ?????? ???????(??) ????? ??~ (II-6) Xi(n) : représente le vecteur d'entrée du neurone (i) de la couche m ; l'équation de mise à jour de ces poids synaptiques et biais s'effectue sur la base relation suivante :
?????? ?? + ??) = ?????? ??) + ? ?????? (??) (II-8) Le calcul des grandeurs d'activation des unités d'entrées s'exprime symboliquement par : ?? ???????? ?? ??~ = ????,?? ?? ??~??????,?? ?? ??~ + ???? ??(??) (II-9) ??=??
11 ??) = ?? ??[?????????? ??)] (II-10)
| ||||||||||||||||||||||||||||||
|
|
||
Z (k+1)=z(k)-???? ??l??) (II-13)
L'intér~t porté aujourd'hui aux réseaux de neurones tient sa justification dans les quelques propriétés intéressantes qu'ils possèdent et qui devraient permettre de dépasser les limitations de l'informatique traditionnelle, tant au niveau programmation qu'au niveau machine [11].
Cette notion se situe à la base de l'architecture des réseaux de neurones considérés comme ensemble d'entités élémentaires travaillant simultanément. Par l'étude du fonctionnement des réseaux de neurones, on pourrait aboutir à des nouvelles techniques de formalisation de problème qui permettraient de les traiter en parallèle [11].
caractérisent aussi par leur capacité d'auto organisation qui assure leur stabilité en tant que systèmes dynamiques capables de tenir compte de situations non encore connues [11].
Dans les réseaux de neurones, la mémoire correspond à une carte d'activation de neurones. Cette carte est en quelque sorte un codage du fait mémorisé ce qui attribue à ces réseaux l'avantage de résister aux bruits (pannes) car la perte d'un élément ne correspond pas jà la perte d'un fait mémorisé.
Cette capacité est important surtout dans le cas oil la constitution de recueils d'expertise pour un système expert devient difficile (reconnaissance intuitive ou implicite). Les réseaux
neuronaux peuvent apprendre à retrouver des règles à partir d'exemple [11].
L'utilisation des réseaux de neurones pour la modélisation des systèmes non linéaires découle naturellement des aptitudes de ces derniers à l'approximation et la généralisation. La détermination du modèle dynamique d'un système comporte en général les étapes suivantes
[3] :
> Acquisition des données d'apprentissage et de test.
> Choix de la structure du modèle.
> Estimation des paramètres du modèle.
> Validation du modèle identifié.
La première étape fournit les données entrées/sorties susceptibles de permettre l'extraction d'un modèle de procédé significatif. La deuxième étape consiste à choisir la structure du modèle susceptible de représenter la dynamique du système, l'architecture du réseau de neurones et ses entrées. Les réseaux multicouches statiques sont les plus utilisés à cause de la simplicité de leurs algorithmes d'apprentissage et leurs aptitudes à l'approximation et à la généralisation. Il n'existe pas de méthodes générales pour le choix du nombre de neurones sur chaque couche cachée ainsi que le nombre de ces dernières. Cependant un réseau à une seule couche cachée est dans la majorité des cas suffisant. En référence à la théorie des systèmes linéaires, plusieurs modèles non linéaires ont été proposés
- Le modèle NFIR : la régression est composée uniquement des entrées passées. yà(k) = f (u (k -1),..., u (k - n)) (II-14)
- Le modèle NARX : dans ce cas la régression est composée de sorties et entrées passées.
yà(k) = f (u (k -1),..., u (k - n), y (k -1),..., y (k -m)) (II-15)- Le modèle NOE : la régression est composée d'entrées et sorties estimées passées. yà(k) = f (u (k -1),..., u (k - n), yà (k -1),..., yà (k -m)) (II-16)
-Le modèle NARMAX : la régression est composée de sorties et entrées passées Ainsi que d'erreurs d'estimation.
yà(k) = f (u(k -1),...,u(k - n), y(k -1),..., y(k -m),e(k-1),...,e(k-l)) (II-17)
Le principe de l'identification par réseau neuronaux consiste à substituer aux modèles paramétriques classiques des modèles neuronaux, c'est-à-dire proposer un modèle établissant une relation entre son entrée et sa sortie et à déterminer, à partir du couple des signaux d'entrée-sortie, le comportement du modèle. Deux raisons importantes nous motivent [2] :
> Prédire le comportement d'un système pour différentes conditions de fonctionnement.
> Élaborer une loi de commande à appliquer au processus pour qu'il réalise l'objectif
assigné.
Nous citerons deux techniques d'identification à base de réseaux de neurones multicouches : la méthode d'identification directe et la méthode d'identification inverse.
La figure (II .9) montre le schéma général d'identification directe d'un processus. Sur cette figure, le réseau de neurones identificateur RNI est utilisé en parallèle avec un processus de type boite noire. La sortie du processus, y, est comparée avec la sortie du réseau de
neurones, y, puis l'erreur e=y-y est utilisée afin d'affiner les paramètres du système neuronal
[2].
Figure. II.9 .Schéma d'identification directe d'un processus par réseau de neurones.
Pour considérer l'aspect dynamique du système, on a le choix d'utiliser les réseaux de neurones récurrents, ou bien d'accroître les entrées du réseau de neurones avec les signaux
En considérant l'aspect dynamique du système, l'équation différentielle de la sortie y l'instant t + 1peut être écrite de la façon suivante :
y(t+1)=f (y(t),..., y(t-1+n),..., u(t),...,u(t-1+m)) (II-18)
Ou y (t+1) est la sortie du processus à l'instant t+1 et f est la fonction non linéaire régissant le
fonctionnement du processus. Cette fonction dépend des sorties antérieures jusqu'à l'ordre n et des entrées antérieures jusqu'à l'ordre m du processus la sortie y(t+1) du réseau de neurones à l'instant t +1est décrite comme suit :
y(t+1)= ?? ^(y(t),...,y(t-1+n),...,u(t),...,u(t-1+m)) (II-19)
Ou ?? ^ représente la fonction d'approximation non-linéaire de la fonction f du processus. La sortie du réseau neurones y(t+1) dépend des sorties et entrées antérieures du processus respectivement jusqu'aux ordres n et m. Elle ne dépend pas des sorties antérieures du réseau neurones. Si la sortie de l'identificateur neuronal se rapproche de celle du processus après quelques itérations d'apprentissage, alors nous pouvons l'utiliser comme entrée. On aura ceci :
y (t+1)=?? ^ (y(t),..., y(t-1+n),..., u(t),..., u(t-1+m)) (II-20)
Dans cette méthode, l'entrée du processus est comparée avec la sortie de l'identificateur
neuronal RNI est la sortie du processus est injectée comme entrée du réseau de neurones après
un apprentissage hors ligne du modèle inverse, le RNI peut être configuré afin d'assurer un
Figure. II.10. Schéma d'identification inverse d'un processus avec un réseau de neurones.
> Capacité de représenter n'importe quelle fonction, linéaire ou pas, simple ou complexe.
> Faculté d'apprentissage à partir d'exemples représentatifs, par « rétro propagation des Erreurs ». L'apprentissage (ou construction du modèle) est automatique
> Résistance au bruit ou au manque de fiabilité des données.
> Simple à manier, beaucoup moins de travail personnel à fournir que dans l'analyse
statistique classique. Aucune compétence en matis, informatique statistique requise.> Comportement moins mauvais en cas de faible quantité de données.
> Pour l'utilisateur novice, l'idée d'apprentissage est plus simple à comprendre que les
complexités des statistiques multi variables [2].
> L'absence de méthode systématique permettant de définir la meilleure topologie du réseau et le nombre de neurones à placer dans la (ou les) couche(s) cachée(s).
> L e choix des valeurs initiales des poids du réseau et le réglage du pas d'apprentissage,
qui jouent un rôle important dans la vitesse de convergence.
· Le problème du sur apprentissage (apprentissage au détriment de la généralisation).
> L a connaissance acquise par un réseau de neurone est codée par les valeurs des poids
sont inintelligibles pour l'utilisateur [2].
Nous avons présenté dans ce chapitre les principes de base des réseaux de neurones
inspiré de l'étude du cerveau humain, dont il s'est développé depuis des modèles plus complexes grâce à l'évolution de la neurobiologie et à l'utilisation d'outils théoriques plus puissants comme l'algorithme de rétro-propagation. Il est à noter que l'emplacement idéal pour l'intégration des réseaux de neurones artificielle, pourrait etre d'un intéret particulier pour l'identification du processus.
Les réseaux de neurones artificiels ont trouvé une large utilisation dans le domaine de la commande des systèmes non linéaires. Ceci est d à leur propriété d'approximation universelle qui les rend capables d'approximer, avec un degré de précision arbitraire fixé, n'importe quelle fonction non linéaire. Les réseaux à base de perceptrons multicouches, (Multi Layer Perceptrons), MLP, et les fonctions radiales de base RBF, sont les plus utilisés. Les premières applications des réseaux de neurones en commande n'étaient pas basées sur des analyses de stabilité rigoureuses. En général, la loi de commande est exprimée en fonction des non linéarités du modèle du système suivant la méthode de linéarisation entrée-sortie. Les réseaux de neurones sont ensuite utilisés soit pour approcher directement la loi de commande soit pour approcher les non Linéarités formant ainsi une loi de commande neuronale adaptative. Le modèle non Linéaire utilisé dans ces études satisfait les conditions de linéarisation entrée sortie. Dans tous ces travaux, le signal erreur utilisé pour l'apprentissage dans les lois d'adaptations est basé sur l'erreur de poursuite. Dans ce mémoire, une structure de commande neuronale avec des lois d'adaptation basée sur le signal erreur de commande est étudiée. Dans ce cas la fonction à optimiser dépend alors directement des poids.
L'utilisation des réseaux de neurones pour la commande (adaptative ou non) de processus non linéaires découle naturellement des aptitudes de ces derniers à la modélisation. Il s'agit essentiellement d'une extension non linéaire de la commande optimale avec coût quadratique sur un horizon infini. Considérons en effet une structure de commande typique (la commande avec modèle interne) représentée Sur la Figure III.1.
Figure .III.1.Exemple d'architecture pour la commande neuronale robuste.
Elle comprend :
> Un modèle neuronal, obtenu comme indiqué au paragraphe précédent
> Un correcteur neuronal dont les coefficients sont mis à jour périodiquement si la commande est adaptative ; dans le cas contraire, ses coefficients sont fixes une fois l'apprentissage terminé.
Pour l'apprentissage de systèmes de poursuite, il est nécessaire de surcroît d'utiliser un modèle de référence qui traduit le cahier des charges en termes de dynamique de poursuite désirée. La commande de processus non linéaires semble être l'un des domaines les plus prometteurs pour es réseaux de neurones à l'heure actuelle. Les comparaisons entre commandes "neuronales" (faisant intervenir des connaissances a priori sur le processus) et commandes non linéaires redditionnelles ont montré que les réseaux de neurones permettent d'obtenir des résultats au moins aussi bons, et souvent meilleurs, mais surtout qu'ils sont de mise en oeuvre beaucoup plus simple en raison du caractère générique des algorithmes mis en oeuvre : quelle que soit l'architecture du réseau bouclé utilisé, c'est toujours le mrme algorithme qui est mis en oeuvre.
Par leur capacité d'approximation universelle, les réseaux de neurones sont bien adaptés pour la commande des systèmes non linéaires. En effet dans ce cas la fonction commande est une fonction non linéaire, l'objectif est alors d'approximer cette fonction par les RNA (réseaux de neurones artificiels). Cette approximation est réalisée par apprentissage des poids du réseau, l'apprentissage peut se faire hors ligne ou en ligne :
ü Dans le cas de hors ligne, l'apprentissage est basé sur un ensemble de données définissant la fonction commande.
ü Dans le cas de en ligne, la mise à jour des poids est essentiellement adaptative. Il existe alors plusieurs algorithmes de commande par RNA basés sur ces deux structures, principalement on peut distinguer :
> La commande inverse (basée sur l'erreur de commande).
> Commande basée sur l'erreur de sortie (d'état).
> Commande adaptative.
> Commande basée sur le critique adaptatif (Adaptif Critique).
> Commande apprentissage d'un contrôleur conventionnel.
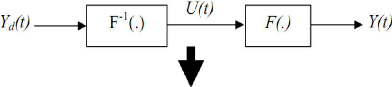
Considérons un système non linéaire avec une entrée u(t) et une sortie y(t) peut dépendre de u(t) seulement ou de u(t) et les états précédents de y et/ou u
y(t)= F (u(t)) (III-1)
Ou
y(t)=F (u(t), u(t-1), u(t-2),..., y(t-1), y(t-2),...) (III-2)
L'objectif est de faire suivre y(t) une trajectoire de référenceyd(t). Le contrôleur idéal réalise l'égalité : y(t)=yd (t), mathématiquement il doit réaliser l'inverse F-1 de la fonction F.
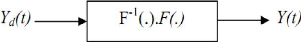
Figure III.2.principe de la commande neuronale inverse.
Le principe de la commande inverse par réseau de neurones consiste à construire le réseau (en générale MLP) qui approxime la fonction F-1, cette approximation se fait par apprentissage hors ligne. Etant donné la fonction F, il faut construire un RNA pour réaliser l'approximation, on génère une base de données à partir de F. L'objectif de l'apprentissage est de déterminer la fonction inverse à partir de ces données. A l'instant t on donne au RNA : y(t), y(t-1), y(t-2) et on obtient à la sortie ur(t). La mise à jour des poids du réseau est basée sur la minimisation de l'erreur entre ur(t) et u(t)
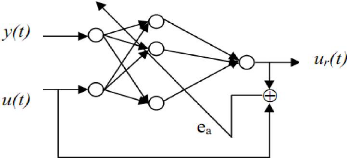
Figure III.3.Apprentissage de la commande inverse.
/ RIAINMESSIFQtiAAMAeAMIPiAPIDLOéAeIu SIIt ~IIIIMIliAPIFRP P 11FRQtrôleur
iQverAe. Cette
méthode peut être appliquée aux systèmes invariants dans le temps.
DIQAADIFIA UAFeMMISSERFK, IIEA'pBfiiliéIMP 1Qe10 1FRQt> TS 61 $ MEP IQiP iAe I
MilECTeQtrIRI ARLIHNEMPIpIeQTH IIl A'PBarlRrAuIRQaiP eQtueP eQt dIPQ aSSIFQtiAAMITQT boucle fermée, alors faut il le réaliser en ligne ou hors ligne. La AtIuFIMI KI111SSIeQtiAAaIe est donnée par la Figure .III.4
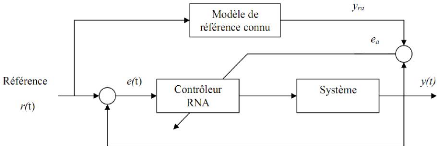
Figure .III.4.commande à modèle de référence.
/ IRENFtiIITAt O'eQtIaîQILID14hAeIXESROUIRMllileA SRIdA qX3P IQiP 1A1Qt
J=1/2[37ra(0 -- 37(??)] 2=1/2[ea(??)]2 (III-4)
La commande u(t) dépend des poids du réseau, la mise à jour est alors de la forme :
???? ???? ????
??(t+1)=??(t)-?? (III-5)
???? ???? ????
Mais on ne connaît pas le Jacobien ????

????
Plusieurs propositions ont été faites pour résoudre le problème du Jacobien, une des premières a été de créer un émulateur qui modélise le système.
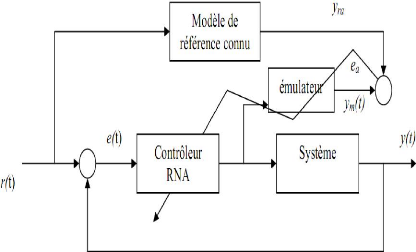
Figure III.5.structure de commande neuronale avec émulateur Cette méthode fonctionne si ???? ??) = ??(t) les étapes pour le développement de Cette approche :
> Construire le RNA émulateur (à partir des données).
> Initialiser hors ligne le contrôleur RNA.
Dans cette stratégie de contrôle, les réseaux de neurones sont introduits pour construire des systèmes de commande adaptative stable basés sur la théorie de la stabilité de Lyapunov. Deux
classes de méthodes ont été développées: directe et indirecte.
Dans la première approche appelée commande adaptative neuronale indirecte, les réseaux de neurones sont utilisés pour approximer les non linéarités du système non linéaire. Une des méthodes qui a connu le plus de développement est basée sur la méthode de linéarisation par retour (feedback linearization) avec un système non linéaire sous forme affine :
x (t) = É (x) + 9(x)u(t) (III-6)
Y(t) = h(x)
La loi de commande linéaire est de la forme :
U(t)=v-É(x)
(III-7)
9(x)
Lorsque les fonctions non linéaires f(x) et g(x) sont inconnues, deux réseaux de neurones sont utilisés pour obtenir leur approximations É à(x) et g(x) et construire la commande C(t) approximée dans cette approche se pose cependant un problème de singularité de la commande lorsque g(x) = 0. Plusieurs techniques ont été proposées pour éviter cette singularité, la plus intéressante étant la commande indirecte ci-dessous.
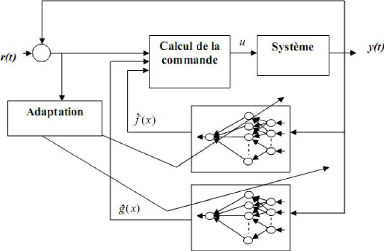
La deuxième approche appelée commande adaptative directe le seul réseau de neurones est introduit pour approximer directement la loi de commande idéale non constructible u(t) cidessus. Dans ces méthodes le signal d'adaptation est l'erreur de poursuite. Il faut noter cependant que les développements mathématiques sont plus élaborés pour cette méthode. Par exemple la méthode proposée dans consiste à approximer la loi :
U (??)= ??
??(??)(É (??) +??) +2????)2 ???? (III-8)
Où
????= ????
?? ??=?? ???? (III-9)
Avec e =[????, ????, . . ????]??=????-??????-?? i=1,...n
Et
??-??
??=-???? ??~+ ????
??=?? ???? (III-10)
???? est un signal de référence borné et supposé n fois dérivable. Les coefficients ???? Sont choisit tel que le polynôme ????+????-??????+...+???? a tous ses racines strictement dans le demi plan complexe gauche et ????=1 donc e(t)?0 tan que ???? ?0.
Dans ce paragraphe nous introduisons un contrôleur adaptatif u(t) à retour d'état pour un système non linéaire mono variable sous la forme générale :
?? = É(??,??)
(III-11)
?? = ??(??)
??=[?? ??, ????, ... , ??]?? ? ???? est le vecteur d'état supposé complètement disponible U, y ? ?? sont
l'entrée et la sortie du système respectivement. III.3 .1.Les réseaux de neurones :
La sortie du réseau de neurones est donnée par :
u(??)=????. ?? (???? .Z) (III-12)
Où V= [??1, ??2, ..., ????]? R(??+1)×?? et W=[??1,??2, ... , ????]?? ? R??
Sont les poids du réseau de neurones, z est le vecteur d'entrée, ?? = [??1, ??2, ... , ????]??est le vecteur d'état du système. La fonction lisse u* peut être approximée comme suit:
??*(??)=W??* .S (??*?. ??)+E (??) ? ?? ? ??? (III-13)
Où å (z) est l'erreur d'approximation du réseau de neurones. La sortie du contrôleur neuronal avec les poids W à et V à peut ~tre écrite sous la forme :
û (??)=W??.S(??à??. Z) (III-14)
On définit l'erreur de commande :
??*??= û(??) -??*(??) (III-15)
Si on veut trouver les poids qui minimisent cette erreur, l'objectif sera :
??
J=?? (??*??)2 (III-16)
Les lois de la mise à jour des poids sont obtenues par la dérivation de cette équation par rapport aux ces poids et en utilisant l'algorithme du gradient avec un pas prédéterminé :
W =-??
(??*?? . S (??à??. Z) + ???? . ??*?? .W) (III-17)
??à = -??
(??*?? .Z.W??.OE( ??à?? . Z) + ???? . ??*?? .Và) (III-18)
Où OE( ??à??. Z) = diag {oe1,
oe2, ... , oe??} et oe?? =
d[S(Z)] /dz ?? =???? , ??à??.Z=[??1, ??2, ... ,
????]??
Et ?? = ????.I > 0, ?? =
????.I > 0 sont les taux de mise à jour de ??*?? L'erreur
de commande. III.4. Structure de la commande adaptative neuronale
à retour de sortie:
Dans la section précédente, nous avons introduit la structure de commande neuronale en supposant que les états du système sont disponibles. Ceci n'est généralement pas le cas, pour cela nous introduisons maintenant une structure à retour de sortie basée sur un observateur non linéaire. Dans ce qui suit nous rappelons brièvement la théorie des observateurs non linéaires à gain élevé.
Dans les systèmes de commande à retour d'état la présence des variables d'états inconnues et non mesurables devient une difficulté qui peut être maîtrisée avec l'introduction d'un estimateur d'état approprié. Le développement d'algorithme pour permettre l'estimation a attiré l'attention de plusieurs chercheurs. Plusieurs techniques ont été introduites pour estimer les variables d'état en connaissant juste les valeurs mesurables du système. Il existe plusieurs formes d'estimateur qui peuvent être utilisées dépendant à la structure mathématique du modèle du processus et l'information du système. La forme non linéaire de certains processus a nécessité le développement d'observateurs non linéaire. Ces observateurs sont conçus de sorte qu'ils peuvent prendre en compte la non linéarité intrinsèque du processus dynamique. Nous considérons ici un modèle d'observateur appelé l'observateur à gain élevé (High-gain observer), pour un système non linéaire de la forme générale
?? = É(??) ??=h (??) ??? R??
Supposons que la fonction y(t) et ses n dérivées sont bornées. Considérons le système linéaire suivant :
???? ??=?? ??+?? (III-19)
E????=- ????
?? ??=?? .????-??+??+ y(t) (III-20)
Oil
Les paramètres ??1, ???? sont choisis tel que le polynôme ????+??1????-1 + ~ ????-1S +1 a tous ses racines strictement dans le demi-plan complexe gauche et avec ????=1 Alors il existe des constantes positives????, k2,3, ,n, et t* telles que pour tout t>t* on a:
????+?? v (??) =- ????(??+??) ,k = 1i ,n-1 (III-21)
???? -' --
????+?? (??) '-- _
Y -??????+?? , k = 1I Q-1 (III-22)
???? -
Avec å un petit nombre positif, ??= ????
?? ??=1 . ????-??+1 Et ???? = ????
, ???? la dérivée d'ordre k de ??
Alors l'estimé xà du vecteur x est donné par :
?? ???? ???? )T ??à=[?? ??, ?? ??, ... ??à??lT = [????, ?? , ???? , ... ????-??]?? (III-23)
Un réseau de neurones peut reproduire le comportement d'un contrôleur conventionnel déjà existant (PI, PID, RST, ...) grkce à ses facultés d'apprentissage et d'approximation. Il suffit de le soumettre à un apprentissage hors ligne pendant une phase d'identification directe en considérant que le contrôleur est lui-même un processus. La figure III.8 montre le principe de l'identification directe d'un contrôleur conventionnel.
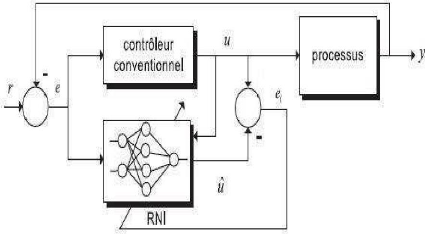
Figure III.8. Schéma d'identification directe d'un contrôleur conventionnel avec un RNI
Le but de cette architecture n'est pas de perfectionner les performances du contrôleur conventionnel déjà existant, mais de s'affranchir des contraintes d'implémentations matérielles que peuvent nécessiter certains régulateurs. La méthode de régulation de type RST par exemple est reconnue pour ses bonnes performances en commande mais elle pose de sérieux problèmes en intégration numérique.
Dans ce chapitre nous avons présentées des notions fondamentales sur la commande, un algorithme de commande adaptative neuronale permettant une adaptation directe des poids du réseau de neurones. L'algorithme est basé sur la minimisation du signal erreur sur la commande. La fonction à optimiser dépend alors directement des poids. Le signal de commande idéale ne pouvant ~tre calculé, il est remplacé par une estimée. L'estimée ayant un signe correct, elle n'influe que sur le pas d'apprentissage.
Plusieurs méthodes d'identification ont été établies pour les systèmes non linéaires
l'avènement de la méthode des réseaux de neurones (MNN), présente des approches d'identification très efficace au non linéarité des systèmes
Dans ce chapitre on va appliquer la technique d'identification sur quatre systèmes non
linéaires selon leur complexité, et pour cela on va utiliser l'algorithme du rétro-propagation
Système 1 :
Le système 1 à identifier sera donné par l'équation récurrente suivante :
y (k+1) =0.3y(k)+0 .6y(k -- 1)+f [u(k)] (IV-1)
Où la fonction inconnue f a la forme :
f (u)=0.6sin (ðu) +0.3sin (3ðu) +0.1sin (5ðu)
(k + 1)=0.3y(k) + 0.6y(k -- 1) + f [u (k)] Pour le modèle neuronal, l'identification de F
· L'entrée du système et du modèle doit etre u(k) = sin (2ðk / 250)
· Pour l'identification nous avons trouvé 10000 itérations pour minimiser l'erreur avec
une entrée aléatoire entre [ 1,1], le résultat est obtenu après 405s.
· 02 couches cachées
· 20 neurones dans la pr
· 10 neurones dans la de
· U
· La fonction d'activation utilisée dans les deux couches cachées est la fonction sigmoïde.
·
y (k)y (k -- 1)[y (k) + 2.5]
Gain d'ajustement 0.1.
v Calcul La commande de poursuite :
Le modèle de référence est décrit par l'équation de différence de premier ordre
m ù r(k)=sin (2*pi*k/250)
La comm
u(k)= -f^ [u(k)] +0,6y(k) +r(k)
v Système 2 : e système 2 à identifier sera donné par l'équation récurrente suivante :
y(k + 1) = f [y(k), yp (k -- 1)] + u(k) (IV-2)
ù la fonction inconnue f a la forme :
f [y(k), y (k -- 1)] =
1 + y2 (k) + y2(k -- 1)
Le modèle d'identification sera décrit par l'équation suivante :
y^ (k + 1) = f [y(k), y(k -- 1)] + u(k)
our le modèle neuronal, l'identification de on a choisis les paramètres suivants :
· L'entrée du système et du modèle doit etre u(k) = sin (2ðk / 25)
· Pour l'identification nous avons trouvé 10000 itérations pour minimiser l'erreur avec une entrée aléatoire entre [ 2,2], le résultat est obtenu après 129s.
· 02 couches cachées.
· 20 neurones dans la première couche cachée.
· La fonction d'activation utilisée dans les deux couches cachées est la fonction sigmoïde.
· Gain d'ajustement 0.1.
v Calcul La commande de poursuite :
Le modèle de référence est décrit par l'équation de différence de premier ordre yrn (k + 1) = 0,6yrn (k) + 0,2yrn (k -- 1) + (k)
m ù r(k)=sin (2*pi*k/25)
La commande de poursuite est calculée on utilisant :
u(k)= -f^ [y(k), y (k-1)] +0,6y(k) + 0 ,2y (k-1) +r(k)
v Système 3 :
Le système 3 à identifier sera donné par l'équation récurrente suivante : y(k + 1) = f [y(k)] + g[u (k)] (IV-3)
y(k)
f [y(k)] =
ù la fonction inconnue f est définie par :
1 + y2(k)
t la fonction g est définie par :
g[u (k)] = u3(k)
e modèle d'identification est décrit par l'équation suivante :
y7 (k + 1) = f [y(k)] + g [u (k)]
our le modèle neuronal, l'identification de on a choisis les paramètres suivants :
· L'entrée du système et du modèle doit etre
· Pour l'identification nous avons trouvé 2000 itérations pour minimiser l'erreur avec
· 02 couches cachées.
?
· 10 neurones dans la deuxième couche cachée.· Un seul neurone dans la couche de la sortie.
· La fonction d'activation utilisée dans les deux couches cachées est la fonction sigmoïde.
· Gain d'ajustement 0.1.
Pour le modèle neuronal l'identification de on a choisis les paramètres suivants :
· L'entrée du système et du modèle doit ~tre
· Pour l'identification nous avons trouvé 50000 itérations pour minimiser l'erreur avec une entrée aléatoire entre [-2,2], le résultat est obtenu après 1.5111 e+003s.
· 02 couches cachées.
· 20 neurones dans la première couche cachée.
· 10 neurones dans la deuxième couche cachée.
· Un seul neurone dans la couche de la sortie.
· La fonction d'activation utilisée dans les deux couches cachées est la fonction sigmoïde.
· Gain d'ajustement 0.1
v Calcul La commande de poursuite :
Le modèle de référence est décrit par l'équation de différence de premier ordre :
Où
La commande de poursuite est calculée on utilisant
v Système 4 :
Le système 4 à identifier sera donné par l'équation récurrente suivante :
y(k + 1) = f [y(k), y(k -- 1), y(k -- 2), u (k), u (k -- 1)] (IV-4)
Où la fonction f a la forme :
??1??2??3??5 ??3 - 1 + ??4
?? ??1, ??2, ??3, ??4, ??5~ =
1 + ??32 + ??22
Le modèle d'identification est décrit par l'équation suivante :
??^ ?? + 1) = ?? [?? ??), ?? ?? - 1), ?? ?? - 2), u ??), u(?? - 1)]
Pour le modèle neuronal, l'identification de on a choisis les paramètres suivants :
L'entrée du système et du modèle doit ~tre :
u ??) = sin 2ðk/250), ?? = 500
0.8sin 2ð??/250) + 0.2sin 2ð??/25) ,?? = 500
Pour l'identification nous avons trouvé 50000 itérations pour minimiser l'erreur avec une entrée aléatoire entre [-1,1], le résultat est obtenu après 1.465 e+3s.
· 02 couches cachées.
· 20 neurones dans la première couche cachée.
· 10 neurones dans la deuxième couche cachée.
· Un seul neurone dans la couche de la sortie.
· La fonction d'activation utilisée dans les deux couches cachées est la fonction sigmoïde.
· Gain d'ajustement 0.1.
Calcul La commande de poursuite :
Le modèle de référence est décrit par l'équation de différence de premier ordre :
???? ?? + 1) = 0,5???? ??) + ??(??)
Où r(k)=cos (2*pi*k/250)
La commande de poursuite est calculée on utilisant :
u(k)= -f^ [y(k), y (k-1), y (k-2), u(k), u (k-1)] +0,5y(k) + r(k)
+ Système 1 :
? Identification neuronale :
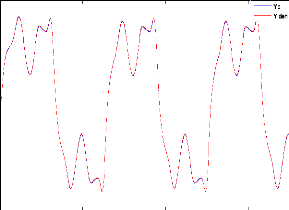
Figure .IV.1. Le modèle(Yiden) et le système 1(Yp).
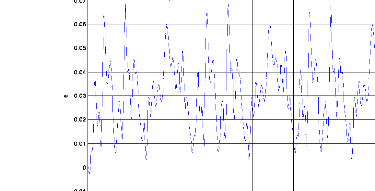
? La commande neuronale :
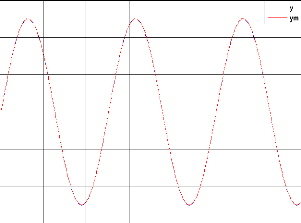
Figure IV.3.le système1 et le modèle de référence.
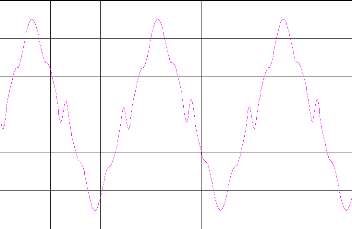
Figure. IV.4. la commande de poursuite.
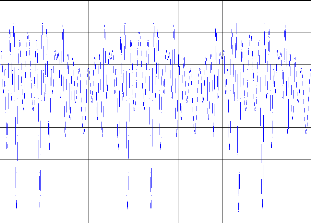
Figure. IV.5. MSE entre le système1 et la sortie désirée. + Système 2 :
? Identification neuronale :
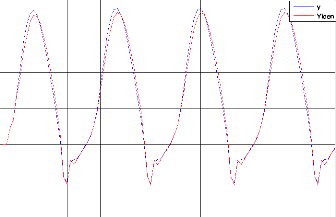
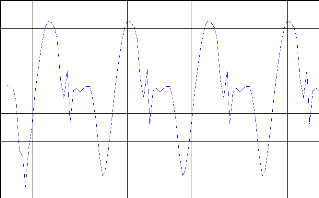
Figure. IV .7.MSE entre le modèle et le procédé.
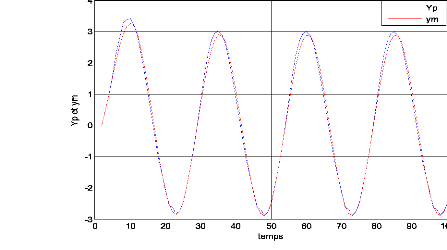
? La commande neuronale :
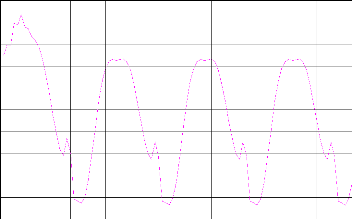
Figure. IV.9. la commande de poursuite.
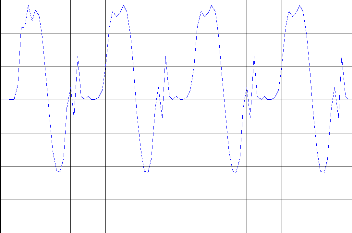
Figure. IV .10. MSE entre le système2 et la sortie désirée.
·:
· Système
3:
. Identification neuronale :
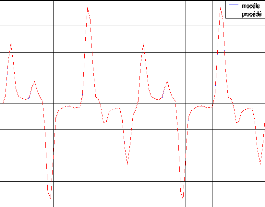
Figure. IV .11. Le modèle et le système 3.
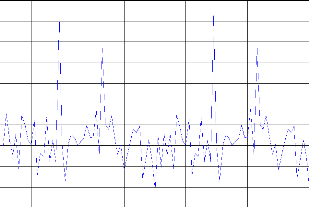
? La commande neuronale :
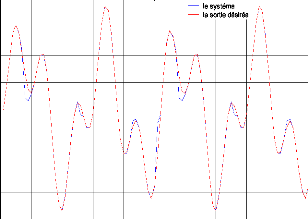
Figure. IV .13. Le système3 et le modèle de référence.
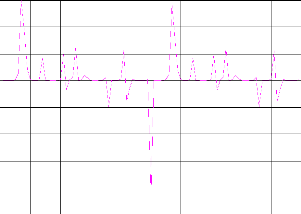
Figure. IV .14. La commande de poursuite.
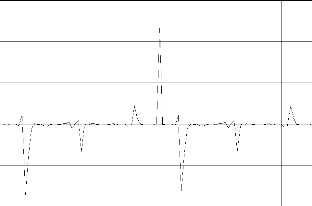
Figure. IV .15. MSE entre le système3et la sortie désirée. + Système 4 :
? Identification neuronale :
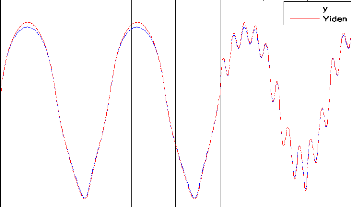
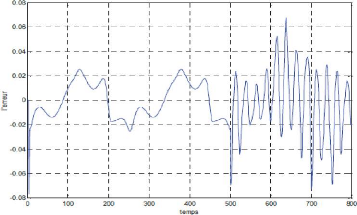
Figure. IV .17. MSE entre le modèle et le procédé. ? La commande neuronale :
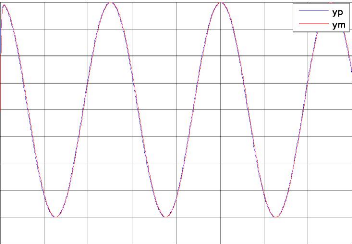
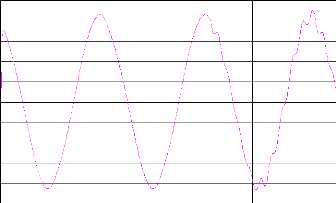
Figure. IV.19.La commande de poursuite.
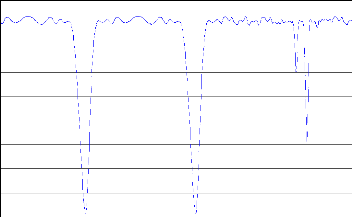
Nous avons étudié l'identification des systèmes non linéaires selon leur complexité. Le système 1 est un système SISO (Single Input Single Output) d'entrée u(k) et de sortie fà Le système 2 est un système TISO (Two Input Single Output), est un système TISO d'entrée [y(k), y (k i-1)] et de sortie f^ .Le système 3 est un système SISO complexe contient deux parties à identifier F et G, F d'entrée [y(k)] et de sortie f^ G d'entrée [u(k)] et de sortie gà. Le système 4 est le plus complexe, est un système MISO d'entrées
[ y(k) , y(k i-1) , y(k i- 2) ,u(k) ,u(k i-1) ] et de sortie y(k +1) .
Le résultat Ede la simulation du système 1 ampliatif dans la figure (IV.1) pour la méthode neuronale dans la phase d'apprentissage, nous remarquons que le modèle convergent vers la sortie du système 1. Comme excitation nous avons pris pour entrée aléatoire. Nous avons opté comme critère la moyenne de la somme des erreurs au carré MSE (Mean Square Error).Égal à 1,2 e-3 qui est montre dans la figure (IV.2)
Pour la commande nous avons trouvé la somme des erreurs moyennes entre la sortie désiré et la sortie du système est de 4,2454e-005.Et le temps de calcul qui nous allons trouver que pour l'identification est 405s pour 10000 itérations.
La figure (IV-6) montre le résultat d'identification du système 2. Nous remarquons aussi une convergence de modèle vers la sortie du système 2. Comme excitation nous avons pris pour l'entrée aléatoire.
Nous avons trouvé MSE égal à 2,47 e-2 ampliatif dans la figure (IV.7). Nous allons trouver que le temps de calcul pour l'identification est 129 s avec 10000 itérations. Pour la commande nous avons trouvé la somme des erreurs moyennes entre la sortie désiré et la sortie du système est de 2 ,5 e-2 montre dans la figure (IV.10).
Pour le système 3 le résultat d'identification montre dans la figure (IV-11). La convergence des modèles vers le système est toujours assurée. Comme excitation nous avons pris pour l'entrée aléatoire pour F et G. nous avons trouvé MSE égal à 1.2289e-005.et le MSE égal à 0.0339 pour la commande montre dans figure. (IV-15)
La figure (IV-16) montre le résultat d'identification du système 4. La convergence de modèle vers le système est toujours assurée. Comme excitation nous avons pris pour entrée aléatoire toujours. Pour l'identification nous avons trouvé MSE égal à 1,5 e-3 avec nombre d'itération 50000 et temps de calcul égale 1,465 e+3 s et MSE pour la commande égal à 2 e-3 montre dans figure. (IV-20).
Dans ce chapitre nous avons illustré l'identification et la commande et les réseaux de neurone par la simulation, nous avons pris quelques systèmes particuliers de niveaux de complexité différente, ainsi dans ce chapitre nous avons Interprété les résultats.
L'identification et la commande des systèmes non linéaires ne sont pas des taches triviales à cause de non linéarité qui les caractérise. La commande et l'identification doivent être appliqué par un système capable de parier à ce problème, La simulation étendue a montré qu'avec quelque information antérieure à propos d'un système non linéaire inconnu peut être contrôlé, tels identificateurs et contrôleurs résultent en performance satisfaisante. Pour une classe spécifique de système non linéaire, il a été montré que les lois adaptatives donnent la stabilité globale du système total. Et l'identification pour la commande consiste à trouver dans un ensemble des modèles un modèle qui a une distance minimale avec le vrai système et à quantifier L'incertitude du modèle dans une norme compatible avec celle de la commande. On peut considérer deux approches générales pour l'identification des systèmes. Dans l'approche probabiliste le modèle est considéré comme un élément aléatoire qui appartient à une classe paramétrique de distributions probabilistes et l'objectif est d'identifier asymptotiquement le vrai système considéré comme un élément de cette classe. Dans cette approche l'erreur du modèle est souvent quantifiée par des bornes probabilistes et déterministes. Au contraire l'approche ensembliste pour l'identification souvent suppose que
le vrai système appartient à un ensemble connu de modèles et que les données expérimentales
sont contaminées par une perturbation inconnue mais avec une borne connue. Contrairement
au cas probabiliste, on présume très peu sur la perturbation et par conséquent on n'établit pas la convergence exacte du modèle vers le vrai système. On peut donc seulement parler de la convergence asymptotique du modèle vers un voisinage du vrai système.
Les réseaux neuronaux artificiels ont été utilisés avec succès comme blocs structurels dans l'architecture de l'identification et la commande des systèmes dynamiques non linéaires. Cette architecture est basée sur l'entraînement du réseau utilisant les données d'entrée-sortie du système. En général, les paramètres du réseau sont ajustés en utilisant la méthode du gradient. Pour une classe spécifique de systèmes non linéaires.
[1] :G.DREYFUS « les réseaux de neurones »Ecole supérieure de physique et de chimie industrielle de la ville de Paris (ESPCI) laboratoire d'électronique 1998
[2] : CHEKROUNE .Soufyane «commande neuro-floue sans capteur de vitesse d'une machine asynchrone triphasée », thèse magister Ecole Normale supérieure d'enseignement 2009
[3] :k.kara « Application des réseaux de neurones à l'identification des systèmes non linéaire », thèse de magister Université de Constantine 1995.
[4] : « modélisation et identification du signal ECG par logique floue »mémoire d'ingénieure université de M'sila, juin 2008.
[5] :A.AOUICHE « rejection des perturbations dans les systèmes non linéaire : étude comparative », thèse de magister université de M'sila ,2006.
[6] : « cours Identification » (PDF).
[7] : « identification et contrôle par réseaux de neurones » mémoire d'ingénieure université de M'sila, juin 2006
[8] : AHMIDA ZAHIR « contribution à la commande prédictive : stabilisation prédictive non linéaire d'une commande en poursuite basée sure une classe de réseaux neuroniques », thèse doctorat université Mentouri de Constantine .2006
[9] : MEHRZAD .NAMVAR « Interaction entre Identification et commande », thèse doctorat, institut national polytechnique de Grenoble.2001
[10] :YOUSSEF.ROCHDI « identification des systèmes non linéaire blocs », thèse doctorat .université de CEAN /basse #177;Normandie .2006
[11] : « Application des réseaux de neurones artificiels dans le domaine de surveillance des eaux potables », thèse d'ingénieure universite M'sila 2006
[12] : GUITANI .ISSAM « commande adaptation neuronale par retour de sortie des systèmes non linéaire », thèse magister .université Mentouri de Constantine 2007
[13]: k .NARENDRA « identification and control of dynamical systems using neural networks », IEEE transactions on neural networks vol1NO1, March 1990
[14]:AHRICHE.Aimad «réalisation d'une commande numérique avec différentes stratégies de commande et identification par réseaux de neurones artificiels .application au réglage de température », thèse de magister université Boumerdes, 2008.
MEMOIRE DE FIN D'ETUDES D'INGINIORAT EN GENIE
ELECTRONIQUE
Proposé et dirigé par : Monsieur
AOUICHE ABDELAZIZ
Présenté par : Amira Lemmou, Khaoukha Bellakhdar, ledjdel Adila
THEME :
IDENTIFICATION ET COMMANDE DES SYSTEMES NON LINEAIRE RESUME :
Les réseaux neuronaux avec ces architectures différentes ont été utilisés avec succès ces dernières années pour l'identification et la commande de systèmes non linéaires d'une classe large. Dans ce mémoire, Des systèmes dans une forme de simulation sont étudié utilisant cette méthode. Plusieurs étapes de complexité croissante sont discutées en détail, la justification théorique été fournie pour l'existence de solutions au problème de l'TdentTfTFItTon et la commande.
MOTS CLES :
Modélisation , Identification, Réseau de neurone, Commande ,Système non linéaire

