|
ROYAUME DU MAROC
*-*-*-*-*
HAUT COMMISSARIAT AU
PLAN
*-*-*-*-*-*-*-*
INSTITUT NATIONAL
DE STATISTIQUE ET D'ECONOMIE
APPLIQUEE

Stage d'application
*-*-*-*-*
L'APPLICATION DE LA THEORIE DES REPONSES AUX
ITEMS
DANS LA COMPARAISON DES RESULTATS AUX
TESTS D'ACQUISITION : CAS DU
CAMEROUN
Préparé par : Mlle. BELHAJ
Karima
Sous la direction de : M. VARLY Pierre
(VARLYPROJECT)
Option : Actuariat-Finance
Année universitaire
2011/2012
Résumé
Résumé
La qualité de l'éducation et de la formation est
une question qui revêt la plus haute priorité politique. On estime
que des niveaux élevés de connaissances, de compétences et
de qualifications sont des conditions fondamentales de la citoyenneté
active, de l'emploi et de la cohésion sociale. La qualité de
l'éducation a ainsi constitué une question prioritaire à
analyser.
Le présent rapport présente une nouvelle
approche permettant d'évaluer la qualité de l'éducation :
la théorie des réponses aux items (TRI ou IRT de son acronyme
anglais). Pour illustrer l'utilisation de cette théorie, cette
étude se fera sur le cas du Cameroun à travers deux tests
administrés aux élèves de 5ème
année du primaire en 2005 et 2011.
Mots dles: Théorie de Réponses aux
Items, Fiabilité, Unidimensionnalité, Test equating.

Dédicaces
Dédicaces
Ce travail est dédié à mes chers parents
sans qui ces lignes
n'auraient guerre étaient écrites.
Je tiens également à le dédier à
Ismail mon grand frère ainsi que mes amies : Salma El Hamri, Imane
Motia, Imane Benajiba et Chaimae Belhadj en leurs souhaitant beaucoup de
succes...
Je vous aime tous du plus profond de mon coeur.
K.B
Remerciements
Remerciements
Avant d'entamer mon rapport, je tiens tout d'abord
à adresser mes sincères remerciements à M. Varly P. pour
m'avoir accordé toute sa confiance, pour le temps qu'il m'a
consacré tout au long de cette période sachant répondre
à toutes mes interrogations, sans oublier son soutien technique et ses
précieuses remarques qui ont grandement contribué à
améliorer la qualité de ce rapport
Je tiens également à exprimer ma plus
profonde gratitude à l'équipe d'Education et Territoire Magreb
pour leur accueil, leur sympathie, ainsi que leurs idées constructives.
C'est avec un réel plaisir que j'ai effectué mon stage au sein de
ses locaux
Je remercie tout particulièrement Justine,
étudiante en économétrie à l'université
lumiqre Lyon 2, stagiaire avec qui j'ai travaillé au sein des locaux
Varlyproject.
D'une façon plus générale je remercie
tous ceux qui ont participé de prés ou de loin au cheminement de
ce modeste travail. Qu'ils trouvent ici l'expression de mes sentiments les plus
sincères.
Table des matières
RESUME 3
DEDICACES 4
REMERCIEMENTS 5
TABLE DES MATIERES 6
LISTE DES FIGURES 9
LISTE DES TABLEAUX 10
LISTE DES GRAPHIQUES 11
LISTE DES ENCADRES 12
LISTE DES ABREVIATIONS 13
INTRODUCTION ET PROBLEMATIQUE 14
CHAPITRE PRELIMINAIRE : 17
I. Présentation de l'organisme d'accueil : VARLYPROJECT
18
CHAPITRE 1 : 20
I. Bref aperçus sur la théorie classique 21
II. Analyse des items 22
II.1. Principe 22
II.2. Analyse qualitative 22
II.3. Analyse statistique 23
II.3.1. I '1XpK1l1tIl&roJ?1IK 23
II.3.2. Le point bi-sérial 25
III. Théorie des réponses aux items 26
III.1. Limites de la théorie classique et principes
fondamentales de la
théorie des réponses aux items 26
III.2. Hypothèse de la théorie des réponses
aux items 27
III.2.1. L'unidimensionnalité 27
III.2.2. L'indépendance locale 28
III.2.3. La monotonocité 28
III.3. Formulation mathématique du modèle 29
III.3.1. Courbe caractéristique d'items 30
III.3.2. Interprétation des paramètres du
modèle 32
a) Paramètre de difficulté 32
b) Paramètre de discrimination 33
c) Paramètre de pseudo chance 35
III.4. Les différents modèles IRT 36
III.4.1. Le modèle de Rasch 36
a) Propriétés du modèle 36
III.4.2. Le modèle à deux et trois
paramètres 38
a) Le modèle à deux paramètres ou le
modèle de BIRNBHAUM 38
b) Le modèle à trois paramètres
39
III.5. Estimation des paramètres avec les modèles
IRT et test d'ajustement 39
III.5.1. Estimation des paramètres 39
a) L'estimation des paramqtres pour le modle de Rasch
39
Estimation des paramètres de difficulté des items
: spécification du modèle
43
Estimation de la variable latente et spécification du
modèle. 43
b) Estimation des paramètres de difficulté et
de trait latent pour le modèle de BIRNBAUM. 44
III.6. L'ajustement du modèle aux données 44
III.6.1. Choix du modèle 45
III.6.2. Test d'ajustement 46
CHAPITRE 2 : 48
I. Principe de base 49
II. Hypothèses 50
III. Méthodologie 50
III.1. Selon le modèle de Rasch 50
III.2. Selon le modèle à deux paramètres
51
CHAPITRE 3 : 54
I. Analyse des items 55
I.1. Fiabilité et validité du test 55
I.2. Items discriminants 57
II. Validation des postulats de base de TRI 58
II.1. Unidimensionnalité 58
II.2. La monotonocité 60
III. Estimation des paramètres et tests d'ajustement 61
III.1. Choix du modèle 62
III.2. Ajustement du modèle 64
III.2.1. Ajustement graphique 64
III.2.2. Ajustement statistique 66
IV. Mise à l'échelle des tests 2005 et 2011 71
IV.1. Vérification des hypothèses de la mise
à l'échelle 71
IV.2. Choix de la méthode de la mise à
l'échelle 73
CONCLUSION 77
BIBLIOGRAPHIE 78
WEBOGRAPHIE 78
ANNEXES 80
ANNEXE I 81
ANNEXE II 82
ANNEXE III 86
Liste des figures
Liste des figures
Figure 1: courbe caractéristique d'item 31
Figure 2 : courbe caractéristique d'item d'un test de
langue (courbe théorique vs courbe empirique) 32
Figure 3 : courbe caractéristique d'item ayant même
pouvoire discriminant mais des niveaux de difficulté différents
33
Figure 4 : courbe caractéristique d'item ayant un
même niveau de difficultémais des pouvoir discriminants
différents 34
Figure 5 : courbes caractéristique d'items ayant des
paramètres de pseudo-
chance différents 35
Figure 6: analyse en composante principale (avec STATA) 60
Liste des tableaux
Liste des tableaux
Tableau 1 : Modèles et hypothèses
spécifiques 45
Tableau 2: L'alpha de Cronbach des 39 items du test de langue
francophone
(modifié sur Excel 56
Tableau 3: Estimations des
paramètres de difficulté et de discrimination selon le
modèle à deux paramètres 63
Tableau 4 :
Les moyennes et variances des paramètres de difficulté et de
discrimination des cinq sous-échantillons sont
affichées comme suit : 68
Tableau 5: L'indice de discrimination des
39 items du test de langue
francophone (modifié sur Excel) 82
Tableau 6: L'indice de discrimination des 26 items du test de
mathématique 83
Liste des graphiques
Liste des graphiques
Graphique 1 : indice de discrimination des items du test de
langue francophone
58
Graphique 2 : analyse en composante principale (avec R) 59
Graphique 3: courbe caractéristique des items du test
langue francophone
(estimé selon le modèle de Rasch) 61
Graphique 4: courbes caractéristiques d'un item bien
ajusté au modèle 65
Graphique 5: exemple d'un item qui ne s'ajuste pas bien aux
données 65
Graphique 6 : CCI d'items anglophone et francophone ayants un
même pourvoir discriminant et un même niveau de difficulté
70
Graphique 7 : CCI d'items anglophone et francophone ayants des niveaux
de
difficulté différent mais un même pourvoir
discriminant 70
Graphique 8: le score vrai estimé de 2005 vs le score vrai
estimé de 2011 75
Graphique 9 : package Irtoys vs Résultats produit avec
notre programme R 76
Liste des Encadrés
Liste des Encadrés
Encadré 1 : Notations et notions préliminaires
à l'estimation 41
Encadré 2 : Choix du modèle avec R (Output) 62
Encadré 3 : Comparaison des modèles avec R 62
Encadré 4: Test d'ajustement avec R 66
Liste des abréviations
Liste des abréviations
|
AFD
|
Agence Française
de Développement
|
|
AIC
|
Akaike Criterium
Information
|
|
CCI
|
Courbe Caractéristique
de l'Item
|
|
ID
|
Indice de Discrimination
|
|
IRT
|
Items Responses
Theorie
|
|
MRI
|
Modèle de
Réponses aux Items
|
|
OMD
|
Objectifs du Millénaire
pour le Développement
|
|
ONU
|
Organisation des Nations
Unies
|
|
PASEC
|
Programme l'Analyse du
Système Educatif de la
CONFEMEN
|
|
QCM
|
Question à Choix
Multiple
|
|
TRI
|
Théorie de
Réponses aux Items
|
Introduction et problématique
« Il nous reste encore un long chemin à
parcourir pour intégrer les jeunes filles et donner du pouvoir aux
femmes, pour promouvoir le développement durable et protéger les
plus vulnérables» a déclaré le Secrétaire
général de l'ONU, M. Ban Ki-moon. En effet, des études ont
montré que parmi tous les ODM, c'est l'éducation des enfants, en
particulier des filles, qui a le plus d'impact sur la lutte contre la
pauvreté. C'est dans cette perspective que l'appui à
l'éducation primaire a été une priorité pour
différente institutions et associations internationales de
développement, la Banque mondiale par exemple a mis l'éducation
au premier plan de sa mission de lutte contre la pauvreté depuis 1962,
elle constitue dans ce secteur la première source de financement
extérieur pour le monde en développement.
Par conséquent, plusieurs recherches se sont
penchées sur l'évaluation de l'éducation en
général, et des acquis scolaires en particulier.
La recherche sur ces objets remplit plusieurs fonctions
d'accompagnement de cette évolution : celle de prendre en compte et
d'étayer la diversification des problématiques
d'évaluation; celle de contribuer à l'approfondissement des
méthodologies de l'évaluation, celle d'éclairer la
production de connaissances. Ainsi, elle vise à insuffler au sein du
système éducatif tout entier une nouvelle culture de
l'évaluation fondée sur la recherche de la performance.
La mesure, c'est à dire l'assignation de grandeurs
à des objets en respectant certaines propriétés de
ceux-ci, a posé en psychologie des problèmes particuliers qui ont
abouti au développement de solutions originales au sein de cette
discipline. Ces méthodes se sont trouvées rassemblées dans
la psychométrie qui définit les méthodes à mettre
en oeuvre, depuis les dispositifs de collecte des données jusqu'à
la définition de normes de fiabilité ; pour une
présentation des théories et méthodes
psychométriques.
Des modèles statistiques de mesure ont pris une place
importante dans les recherches concernant l'évaluation quantitative de
l'éducation. Ces modèles de mesure sont
généralement regroupes en deux grandes familles : la
théorie classique et la théorie « moderne » dites aussi
théorie de réponse aux items TRI ou IRT (Item Response
Theory).
Les modèles classiques sont basés sur la
décomposition du score observé (qui est égal à la
somme pondérée des réponses) en un vrai score et une
erreur. Les modèles IRT sont des modèles linéaires
généralisés qui décrivent la probabilité
d'une réponse comme une fonction du trait psychologique :
L'aptitude mentale. Cette dernière est devenue, pour
les psychométriciens contemporains, un moyen très en vogue, et
assez prisé en vue d'une évaluation objective.
Dans cet esprit, notre stage d'application s'est
articulé d'une part sur l'analyse par les différents
modèles cités ci-dessus, des données provenant des tests
administrés aux élèves et d'autre part sur son
application, encore très récente, dans le cadre de la comparaison
du niveau des élève issu de deux groupes différent. Le but
étant ainsi de donner une idée du niveau individuel des
élèves sur la base de leurs résultats.
Pour ce faire, et dans un premier chapitre, nous aurons
à traiter deux sections. La première décrit, dans le cadre
de la théorie classique, la manière de s'assurer de la
validité et de la fiabilité des instruments de mesure des
acquisitions scolaires des élèves. La deuxième expose,
cette fois dans le cadre de la TRI, les différents modèles de
mesure de l'éducation.
Dans le deuxième Chapitre, nous tenterons d'expliciter
quelques méthodes de standardisation des tests afin de comparer deux
groupes d'individu n'ayant pas passé le même test.
Pour illustrer l'importance de ces questions, cette
étude se fera sur le cas du Cameroun à travers deux tests
administrés aux élèves de 5ème
année du primaire en 2005 et 2011 Ainsi, le troisième chapitre
portera sur les différents résultats et constats en se basant sur
ce qu'on a vu dans les chapitres précédent.
Le Cameroun ayant bénéficié d'une subvention
de l'AFD de 50 millions d'euros à travers le programme Contrat de
Désendettement et développement, la question est de savoir si ces
investissements ont eu les effets escomptés sur la qualité des
apprentissages : le niveau des élèves s'est-il maintenu entre
2005 et 2011. Les tests utilisés en 2005 et 2011 sont différents
mais comportent quelques items communs. L'objectif du stage est donc de
mettre sur une même échelle les deux tests afin de mesurer
l'évolution du niveau des niveaux des élèves.
Chapitre préliminaire :
Contexte et justification du stage
Chapitre préliminaire
Contexte et justification du stage
I. Présentation de l'organisme d'accueil :
VARLYPROJECT
Varlyproject est une SARL individuelle basée à
Rabat, Maroc, spécialisée dans l'évaluation des acquis
scolaires et l'analyse des données sur l'éducation. Varlyproject
s'engage dans la recherche et le développement à travers un blog
et la production d'articles pour le compte d'organisations non
gouvernementales, comme le projet One Laptop Per Child. La
principale activité de Varlyproject reste l'analyse de données
sur l'éducation pour le compte de gouvernements ou d'organismes
privées, où la société agit comme sous-contractant
ou en contrat direct.
La société est dirigée par Pierre VARLY,
statisticien, titulaire d'un Master en Econométrie et ayant plus de 10
ans d'expérience dans l'analyse de données sur
l'éducation. En tant que coordonnateur du PASEC, à Dakar de 2005
à 2009, Monsieur VARLY a encadré une équipe de six jeunes
statisticiens appuyée ponctuellement par des contractuels et des
stagiaires. Le PASEC a pris régulièrement en stage deux
stagiaires de l'école de statistique de Dakar, mais également
accueilli des élèves de l'Ecole Polytechnique par le
passé. Un des stagiaires, Makan Doumbouya, a reçu un prix
international de Statistiques grâce à un article tiré de
son stage. Les thèmes de ces stages de recherche tournent autour de
l'amélioration des méthodes économétriques
utilisées en éducation (pondérations, imputations,
méthodes de pseudo panels, analyses multi niveaux, théorie de
réponse à l'item). La théorie de réponse aux items
et ses applications Le calcul des scores aux épreuves
d'évaluation des acquis scolaires mobilise de plus en plus des
techniques sophistiquées, regroupées au sein des modèles
de réponse aux items. Il s'agit non plus de calculer un simple score ou
une note mais de modéliser la relation entre la probabilité de
réussir un item (un exercice) et l'aptitude des élèves.
De tels modèles permettent de tester la validité
des tests utilisés mais permettent également de vérifier
l'équivalence de versions de tests rédigés dans des
langues différentes ou de produire une mesure comparable dans le temps,
à partir d'items d'ancrage. Ces modèles sont largement
utilisés dans le domaine de la psychométrie ou du marketing afin
de mettre au point des profils de comportement.
Chapitre 1 :
Modèles de mesure
I. Bref aperçus sur la théorie
classique
Le modèle de mesure dit classique permet
d'évaluer jusqu'à quel point un score obtenu à un test
reflète bien la compétence ou l'aptitude de l'individu en
question.
L'équation de base du modèle classique est
donnée par :
X = V + E
Où X est le score observé d'un individu, V est
le score vrai de cet individu et E est l'erreur de mesure.
L'équation de base signifie que, selon le modèle
classique, le score observé à un test est constitué de
deux composantes additives : V et E. le score observé à un test
est obtenu lors d'une administration particulière de ce test. Chaque
individu qui a passé ce test, à ce moment particulier, a donc un
score observé. Ce score observé varie d'une
répétition à l'autre du même test. Typiquement le
score observé peut être une fonction de la somme des items
réussis d'un test lorsque ces items sont corrigés de façon
dichotomique : 1 pour une bonne réponse 0 pour une mauvaise
réponse (Bertrand R., BLAIS J. (2004), p.39).
Il est bon de souligner que :
- le score observé est variable d'une
répétition à l'autre du test
- Le score vrai est intuitivement lié à un
individu particulier et à un test particulier : ainsi le score vrai
changera non seulement d'un individu à un autre mais aussi d'un test
à l'autre.
- l'erreur de mesure est une entité non observable,
inconnue, variable d'une
répétition à l'autre du test.
II. Analyse des items
II.1. Principe
Il est important dans toute évaluation d'examiner les
items du test en question, afin de s'assurer que ce dernier appréhende
bien la variable qu'on cherche à mesurer répondant ainsi aux deux
critères de fiabilité et validité. Avant de
développer cette analyse, nous allons expliquer brièvement ce que
signifient ces deux concepts dans le cadre des évaluations
psychométriques.
La fiabilité indique si un test est susceptible de
produire les mêmes résultats s'il est administré à
un même groupe de personnes testées plusieurs fois, de même
s'il est administré à différentes population. On parle
d'homogénéité ou de consistance interne des items
(appréciée à partir de leurs
inter-corrélations).
La validité indique si le test mesure bien ce qu'il
prétend mesurer .Par exemple un test d'algèbre est censé
mesurer uniquement les compétences des élèves en
algèbre. Mais s'il comprend des problèmes de texte, un tel test
peut être un défi pour les étudiants avec de faibles
compétences en langue. Il mesurerait ainsi non seulement leurs
compétences en algèbre mais aussi leurs compétences de
langue, s'écartant ainsi de son objectif principal.
L'analyse des items se fait en deux étapes : une
analyse qualitative et une analyse statistique.
II.2. Analyse qualitative
Nous appelons analyse qualitative la procédure à
suivre pour évaluer le test à priori. Cet examen est essentiel
dans l'élaboration du test. Il s'agit de tester les items sur un
échantillon d'élève.
« En pratique, il n'est pas toujours possible de mettre
le test à l'essai avec un groupe cobaye.par exemple si les individus du
groupe cobaye savent que le test ne compte pas leur comportement risque de
différer, situation susceptible d'affecter
les réponses aux items [...] biaisant de la sorte les
résultats de l'analyse » (R. Bertrand, JG BLAIS, 2004 p.56).
II.3. Analyse statistique
Dans le cadre de la théorie classique on peut mesurer,
à posteriori, la confiance à accorder aux données afin de
s'assurer que le score qui représente l'acquisition, est calculé
avec précision, avec un minimum d'erreur et de biais. En effet, les
conditions de passation du test, le contexte particulier de l'évaluation
(culture) et les caractéristiques du sujet peuvent être des
sources potentielles de biais et d'erreur. Cette remarque est
particulièrement valable dans le contexte camerounais où la
variété sociolinguistique est très importante avec plus de
280 langues parlées.
Il s'agit ainsi d'identifier voire de rejeter les items
aberrants, à savoir ceux qui n'apportent aucune valeur ajoutée au
test ; autrement dit les items faiblement liés à notre variable
latente, pire ceux qui y sont négativement liés.
Pour ce faire on a recourt à différents indices
statistiques qui permettent de juger de la fiabilité du test dans son
ensemble ainsi que la cohérence interne des items. Les indices les plus
couramment utilisés sont l'indice bi-sérial et l'alpha de
Cronbach. Rappelons que ces deux indices se rapportent à la
théorie du score vrai.
II.3.1. I Ial1Ka Ie &ronbaIK
L'alpha de Cronbach est utilisé pour mesurer la
cohérence interne des concepts tels qu'ils sont mis en oeuvre par les
questions posées (les réponses aux questions portant sur le
même sujet devant être corrélées). Il permet donc
l'estimation de la fiabilité du test au niveau globale.
L'alpha de Cronbach se calcule en appliquant la formule
suivante:
où k est le nombre d'items, est la variance du score
total et est la
variance de l'item i.
Cronbach, l'inventeur de cet indice, a
également développé un alpha standardisé qui
s'exprime comme suit :
avec la moyenne des corrélations entre les k
items.
Il s'agit d'une mesure de corrélation au carré
entre les scores observés et les scores vrai. Autrement dit, la
fiabilité est mesurée en termes de ratio de variance. Un test
fiable doit minimiser l'erreur de mesure de telle sorte que l'erreur n'est pas
fortement corrélée avec le score vrai. D'autre part, la relation
entre le score vrai et le score observé doit être forte l'alpha de
Cronbach examine cette relation.
Il varie entre 0 et 1 et plus le test est fiable, plus l'alpha
est proche de 1. En pratique on valide les données si l'alpha de
Cronbach est supérieur ou égale à 0,8. Cependant et bien
que la littérature ne fasse pas état de consensus sur le sujet,
beaucoup d'auteurs considèrent qu'une valeur alpha supérieure
à 0,7 est satisfaisante, un coefficient supérieur à 0,9
tendant à montrer une redondance entre items.
L'alpha de Cronbach n'est pas un test statistique c'est un
coefficient de fiabilité (ou consistance). Cependant, un alpha
élevé ne signifie pas que la mesure est
unidimensionnelle1. Si, en plus de mesurer la cohérence
interne, on souhaite apporter la preuve que l'échelle en question est
unidimensionnelle des analyses supplémentaires peuvent être
effectuées. Cette approche permet de repérer les poires au milieu
d'un
1 Voir III.2.1.
panier de pommes, c'est-à dire les items qui ne
s'inscrivent pas dans la meme dimension que les autres ou qui ne mesure pas la
même compétence.
II.3.2. Le point bi-sérial
Le point-bi-sérial (rpbis) décrit la
cohérence d'un item par rapport à l'objectif global du test dans
lequel il s'inscrit. Il est un indice de discrimination2, de
précision (fidélité) d'un item. Il varie entre -1 et +1,
cependant le seuil de validité est généralement
fixé à 0,2.

oil :
Al1 représente la moyenne
des scores totaux pour les seuls sujets qui ont réussi l'item j,
Al2 représente la moyenne
des scores totaux pour les seuls sujets qui ont échoué à
l'item j,
n1 le nombre de sujets dans le
groupe 1,
n2 le nombre de sujets dans le
groupe 2,
Sn est la
déviation standard utilisée lorsque vous avez des données
pour chaque membre de la population:

Il existe une certaine relation entre ces deux indicateurs.
Plus un test est composé d'items aux valeurs de point bi-sérial
faibles, plus l'alpha est faible et moins le test est fiable. Cette relation va
nous servir dans la validation des données.
2 Voir b)
III. Théorie des réponses aux items
III.1. Limites de la théorie classique et principes
fondamentales de la
théorie des réponses aux items
Dans de nombreux domaines en sciences humaines et sociales,
les chercheurs et les praticiens sont amenés à mettre au point
divers dispositifs ou instruments d'évaluation destinés à
recueillir des données quantitatives : tests, épreuves,
échelles, questionnaires. Ce faisant, ils doivent s'assurer de la
fiabilité des mesures qu'ils obtiennent.
La théorie de la réponse à l'item (TRI),
développée au début des années 1960, est apparue
comme une réponse aux limites de la théorie classique des tests
et notamment à la dépendance existant entre les
différentes mesures (estimations) et l'échantillon.
La TRI offre des techniques pour construire une échelle
de mesure invariante, rendant possible une mesure objective de traits
psychologiques. Le principe fondamental de cette théorie est que
personnes et items peuvent être localisés sur un même
continuum latent qui décrit simultanément la compétence de
la personne et la difficulté de l'item. La non-dépendance
à l'échantillon tient au caractère linéaire et
invariant de l'échelle qui autorise l'addition ultérieure d'items
mesurant le même trait latent.
Ainsi la TRI s'efforce de produire une estimation des
propriétés de l'item qui soit indépendante d'un groupe
particulier d'individus. En d'autres termes, elle cherche à
élaborer des instruments de mesure dont les caractéristiques ne
soient pas excessivement influencées par tel ou tel autre groupe de
référence.
Cette propriété d'invariance est le coeur
même de la justification de l'utilisation des modèles de la
théorie des réponses. Une de ses applications, thème de
stage, est la mise à l'échelle de deux tests différents
passés à deux époques distinctes.
Par ailleurs, la TRI permet d'obtenir des erreurs d'estimation
séparées pour chaque item et pour chaque personne, il sera
possible alors de quantifier les sources d'erreurs et d'identifier les plus
importantes afin de les corriger. Rappelons que dans la théorie du score
vrai l'erreur de mesure est estimée globalement dans le test elle n'est
pas différentiable mais estimée globalement sur les items du
test.
Enfin, la TRI permet de calibrer la difficulté des items
indépendamment des répondants cibles.
Une des reproches que les praticiens adressent à la
TRI, notamment dans les pas du Sud, est sa relative complexité de mise
en oeuvre. Ce rapport s'inscrit dans la suite des travaux initiés par le
PASEC pour vulgariser ces techniques dans l'espace francophone.
III.2. Hypothèse de la théorie des
réponses aux items
L'IRT repose sur trois hypothèses fondamentales :
l'unidimensionnalité, la monotonicité et l'indépendance
globale.
III.2.1. I VKidiPHKliRKK3lit'
La TRI postule l'unidimensionnalité de l'instrument de
mesure (le test) auquel elle est appliquée. Concrètement cela
suppose que tous les items contribuent à appréhender chez les
élèves un unique attribut: leur niveau de compétence.
Il existe différente approches qui permettent
d'évaluer la validité de cette hypothèse, parmi lesquelles
on peut citer le coefficient alpha de Cronbach ou l'analyse factorielle et
notamment l'analyse en composantes principales.
III.2.2. / 'iXCaliCDXFl lRFDll
En TRI, la validité des estimations relatives aux
caractéristiques des individus suppose que la condition dite
d'indépendance locale soit satisfaite ; condition selon laquelle, pour
un niveau d'aptitude donné, les réponses d'un sujet sont
statistiquement indépendantes, c'est-à-dire que la performance
(échec ou réussite) à chaque item n'est pas
influencée par la performance relative aux restes items.
Ainsi pour un niveau de compétence donné, la
corrélation entre les résultats des individus à deux items
quelconques doit être nulle ou, tout au moins, proche de zéro.
En termes de probabilité elle se traduit par la relation
suivante :
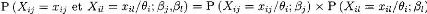
III.2.3. La monotonocité
La monotonocité concerne la fonction de réponse
aux items, elle doit être non décroissantes et monotone du trait
latent thêta, en d'autres termes, on doit avoir :
????(?????? = ??????/?? ??,????) >
0
?? ????
oil íj est un vecteur de param~tres
caractérisant l'item j.
Aussi, il est important de signaler que La taille de
l'échantillon est un facteur à prendre en compte car plus le
modèle est complexe, plus il nécessitera de sujets. Avec des
échantillons de 100 à 200 personnes, le modèle de Rasch
est le
seul choix possible. Le modèle à deux
paramètres demandera au moins trois fois plus de sujets, et le
modèle à trois paramètres dix fois plus (Jones, 1992).
Dans notre cas, nous avons des échantillons de 2361
élèves en 2005 et 2553 élèves en 2011.
III.3. Formulation mathématique du modèle
En psychométrie les modèles IRT décrivent
la relation entre la probabilité de répondre correctement
à un item et l'aptitude de l'élève. Il s'agit d'une
relation non linéaire dont la formulation dépend d'un certain
nombre de facteurs et notamment du nombre de paramètres que le
modèle comporte.
La formulation mathématique générale
s'exprime comme suit :
?? ?????? = ?? = ???? + ?? - ???? .?? ???? ??? - ???? )
Où
· F représente la fonction de répartition
d'une loi de probabilité.
· Xij la réponse de l'individu i à la
question j (i = 1,...,n et j = 1,...,k)
· ?? ??????= ?? est la probabilité que
l'individu i réponde correctement à l'item j
· ??? est (?? ?° ??) un scalaire
qui représente le niveau d'acquisition scolaire de l'individu i,
étant supposé normalement distribué au sein de la
population, il est exprimé sur une échelle de scores, dont les
valeurs sont pratiquement comprises entre -3 et +3 (distribution centrée
et réduite).
· ???? est un scalaire (????° ??) qui
représente le niveau de difficulté de l'item j ;
· ???? est un scalaire positif (???? ° ??) qui
représente le pouvoir discriminant de la question j
· ?? ??°[0;1[ , appelé paramètre de
pseudo-chance est introduit dans le modèle
quand on suppose que les répondants ont la
possibilité de trouver par hasard la réponse correcte à la
question. Cela est particulièrement valable dans les tests
composés de Questions à Choix Multiples (QCM).
Les pionniers de la théorie ont approximé les
modèles IRT par une fonction logistique du type :
?? ?????? = ?? = ???? + ?? - ????
?????? ?? ?? ??? - ???? )
?? + ?????? ???? ??? - ???? )
Les modèles Logit sont autant utilisés pour des
items à réponses dichotomiques que pour des items à
réponses polytomiques. On entend par items à réponses
dichotomiques une question qui n'a que deux possibilité de
réponse: une réponse correcte qui est codée 1 et une
réponse fausse qui est codée 0. Cependant, il ne s'agit pas d'une
attribution de valeurs comme dans les bases de données où l'on
recode, par exemple, le sexe 0=féminin et 1=masculin. Un score
dichotomique est un score basé sur les valeurs 0 et 1, où 1 a une
valeur réelle plus élevée que 0. Puisque les
données que nous utilisons portent sur des items à
réponses dichotomique on ne travaillera que dans ce sens.
Notons que dans la littérature on retrouve d'autres
formulations mathématiques, cependant les modèles Logit sont les
plus souvent utilisés dans la mesure où ils sont simples à
manipuler aussi les choisira t-on dans le cadre de ce présent
travail.
En se basant sur cette formule il est facile de voir que plus le
sujet se situe à un niveau élevé sur le trait, plus sa
probabilité de réussir l'item augmente.
III.3.1. Courbe caractéristique d'items
La TRI postule que la performance (réussite ou
échec) à un item peut être expliquée par un facteur
appelé trait latent noté è, il s'agit dans notre cas de
l'aptitude cognitive en langue. Graphiquement, cette relation est
représentée par une courbe appelé courbe
caractéristique d'un item, la courbe prend souvent la forme
suivante :
Figure 1: courbe caractéristique
d'item

Source : Richard Bertrand(2004), p.111
L'axe des abscisses représente le trait latent qui est,
dans le cadre de la mesure des acquis scolaires, la compétence de
l'élève. En ordonné est représentée la
probabilité de réussir à l'item. Le trait latent
étant supposé normalement distribué au sein de la
population, il est exprimé sur une échelle de scores z, dont les
valeurs sont pratiquement comprises entre -3 et +3 (distribution centrée
réduite). On remarque que pour un trait latent qui est de l'ordre de -3
la probabilité de réussite est presque nulle tandis qu'elle est
proche de 1 pour des très latents prochent de 3.
On remarque aussi l'existence d'un point d'inflexion aux
milieux de la courbe, ce point indique que 50% des élèves
d'habilité moyenne (è=0) ont réussi cet item. Toutefois
gardons à l'esprit que ce graphique représente la
modélisation théorique et non des données empiriques,
c'est un cas quasi-idéal d'un MRI.
Notons également, que l'allure de la CCI dépend
des caractéristiques métriques de l'item ainsi au simple regard
à la courbe on peut évaluer les qualités
psychométrique de ce dernier (voir figure 2).
Figure 2 : courbe caractéristique d'item d'un
test de langue (courbe
théorique vs courbe empirique)

III.3.2. Interprétation des paramètres du
modèle
Dans les modèle IRT chaque item est
caractérisé pas trois indices à savoir l'indice de
difficulté, l'indice de discrimination et l'indice de pseudo-chance.
Chacun de ces indices décrit une propriété
particulière de l'item auquel ils sont associés.
a) Paramètre de
difficultéComme son nom l'indique ce
paramètre exprime le degré de difficulté de
l'item. Il est défini par convention comme la valeur de
thêta qui correspond à une probabilité de réussite
exactement égale à 0.5. C'est précisément cette
valeur de thêta qu'on appelle paramètre de difficulté de
l'item.
Figure 3 : courbe caractéristique d'item ayant
même pouvoire
discriminant mais des niveaux de difficulté
différents

Source : Richard Bertrand et jean-gays Blais (2004) p.
128
Cette figure montre que plus la CCI se trouve à droite
plus l'item est difficile, ainsi l'item 3 est plus difficile que l'item 2,
lui-même plus difficile que l'item 1. Aussi, on peut voir que ces courbes
ne se coupent pas, elles sont translatées les unes par rapport aux
autres. Cela signifie qu'un seul paramètre influence la réponse
des individus à la question.
b) Paramètre de
discrimination
La discrimination de l'item renseigne sur la qualité et
la quantité d'information apportées par l'item pour
déterminer la compétence du sujet. Un item au pouvoir
discriminant élevé apporte beaucoup d'information sur la
compétence du sujet, un item peu discriminant renseigne peu sur la
compétence du sujet.
La valeur de ce paramètre est proportionnelle à la
pente de la CCI au point d'inflexion I. Ainsi plus la pente est abrupte plus
l'item discrimine mieux.
Figure 4 : courbe caractéristique d'item ayant
un même niveau de
difficulté mais des pouvoir discriminants
différents

Source :
http://luna.cas.usf.edu/~mbrannic/files/pmet/irt.htm,
accédé le 9 septembre 2011.
Le pouvoir discriminant est un des principaux critères de
sélection des items pour la construction définitive d'une
épreuve.
On notera que la théorie du score vrai propose aussi
une définition de l'indice de discrimination (comme étant le
score des 27% des élèves les plus forts - le score des 27% les
plus faibles. Dans cet optique, Ebel (1954) propose les valeurs repère
suivantes pour interpréter ce coefficient :
0,40 et plus => item discrimine très bien ;
0,30 à 0,39 => item discrimine bien ;
0,20 et 0,29 => item discrimine peu ;
0,10 et 0,19 => item-limite. A améliorer ;
Inf. à 0,10 => item n'a aucune utilité.
c) Paramètre de pseudo chance
Comme on est dans un modèle portant sur des items
dichotomiques il est essentiel d'introduire le paramètre de
réponse au hasard. En terme mathématique, ce paramètre est
égal à la probabilité de réussir un item avec un
niveau d'habilitétrès faible. La figure ci-dessous illustre un
exemple de trois courbes produites à partir d'un modèle à
trois paramètres :
Figure 5 : courbes caractéristique d'items
ayant des paramètres de pseudo-chance différents
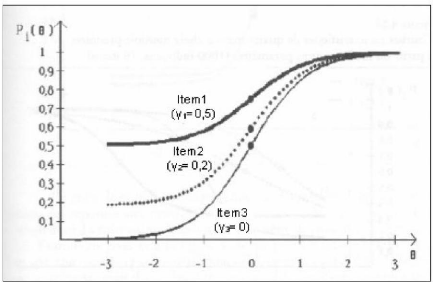
Source : Richard Bertrand et jean-gays Blais (2004) p.
135
On remarque que la probabilité de réussir un item
varie surtout pour les élèves les plus faibles.
De par leur nature, les tests à QCM ont des
paramètres de pseudo chances supérieurs à des items
à questions ouvertes (portant sur le même stimulus).
III.4. Les différents modèles IRT
On distingue habituellement trois grands types de
modèle : le modèle logistique à un paramètre plus
connu sous le nom du modèle de Rasch et les modèles à deux
(Birnbaum) et trois paramètres. Ces modèles regroupés sous
l'appellation générique de modèles de riSRnsHLIj
LIl'LJHm (MRI) - Item Response Modeling (IRM) en anglais -- ont
été créés il y a une trentaine d'années. Il
faut signaler qu'ils ont été « inventés »
à peu près simultanément et de manière
indépendante au Danemark par le mathématicien Georg Rasch (1960)
qui cherchait un modèle permettant de comparer des compétences
d'élèves en lecture à plusieurs années d'intervalle
et, aux États-Unis, par le statisticien Allan Birnbaum (1959,
cité dans Birnbaum, 1968) qui cherchait à améliorer les
modèles de mesure en psychométrie.
Des modèles comportant un nombre de paramètres
supérieur à trois sont cités par certains auteurs. Nous
n'en parlerons pas ici, car ils sont très peu utilisés en
sciences de l'éducation.
III.4.1. Le modèle de Rasch
Le modèle de Rasch est un des modèles les plus
simplifiés de l'IRT puisque chaque item est modélisé par
un paramètre unique appelé le paramètre de
difficulté de l'item. Il s'écrit comme suit :
|
?? ?????? = ?? =
|
?????? ??? - ???? )
??+ ?????? ??? - ???? )
|
a) Propriétés du
modèle
Les défenseurs du modèle à un
paramètre ou modèle de Rasch revendiquent que seul ce
modèle permet d'obtenir une mesure objective et exhaustive. De plus, il
est plus facile à manipuler mais les données doivent
répondre à de nombreuses contraintes.
Une mesure objective
G. Rasch argumentait que l'estimation de la difficulté
des items et de la compétence des sujets étaient
indépendantes, ce qui fondait, selon lui, le concept
d'objectivité3 spécifique. Quels que soient les items
passés par un sujet, on obtiendra une même estimation de sa
compétence. Quels que soient les groupes de sujets auxquels l'item a
été administré, on obtiendra une même estimation de
sa difficulté.
Le modèle de Rasch n'est pas un `modèle de
données', mais une `définition de la mesure'. En d'autres termes,
avec le modèle de Rasch, si les items du test ne correspondent pas au
modèle, ce sont les items qui posent problème et non le
modèle. Par opposition, les modèles plus complexes sont
perçus comme imposant des contraintes arbitraires sur les valeurs que
les paramètres peuvent prendre dans le processus d'estimation (Jones,
1992). Selon Bond et Fox (2001), « c'est précisément
l'addition de paramètres supplémentaires qui dépouille les
données de leurs propriétés fondamentales de mesure »
(p. 191, trad.).
En termes mathématiques cette propriété
s'exprime comme suit : étant donné deux individu i1et i2, la
probabilité que le premier donne une réponse correcte à
l'item j et que le deuxième y donne une réponse correcte sachant
que l'un des deux y a répondu positivement est indépendante du
paramètre de difficulté de l'item en question :
??(?????? = ??,?????? = ??/???? = ??) =
???????(??????)
?????? ??????~+???????(??????)
Une mesure exhaustive
Cette propriété4 est très
importante dans la mesure où elle justifie l'utilisation du score
observé comme résumé de l'information portée par
3 La démonstration de cette
propriété est présentée en Annexe (annexe I)
4 La démonstration de la
propriété d'exhaustivité est présentée en
annexe (annexe I)
l'instrument de mesure ; c'est-à-dire que toute
l'information disponible sur le trait latent d'un élève est
contenue dans le score simple .
En bref, choisir le modèle de Rasch, c'est accorder la
primauté au modèle de mesure et non aux données. De plus
l'exigence plus réduite en termes de nombre de sujets fait du
modèle de Rasch le plus économique du point de vue du temps comme
du point de vue du coût.
III.4.2. Le modèle à deux et trois
paramètres
a) Le modèle à deux paramètres
ou le modèle de BIRNBHAUM Sa formulation
mathématique se présente comme suit :
|
?? ?????? = ?? =
|
?????? ???? ??? - ???? )
??+ ?????? ???? ??? - ???? )
|
Le modèle logistique à deux paramètres
généralise le modèle de Rasch. Il nécessite en plus
du paramètre de difficulté, un paramètre pour le
caractère discriminant de l'item.
Dans ce cas ces deux paramètres sont libres de varier
permettant ainsi aux CCI de se croiser.

Cependant ce modèle ne possède pas de
statistique exhaustive contrairement au modèle de Rasch. Toutefois, si
l'on suppose les valeurs des pouvoirs discriminant áj
connues alors le score pondéré est exhaustif pour le
trait latent è.
Cependant les paramètres ne sont pas connus a priori ce
qui empêche l'utilisation de cette propriété.
b) Le modèle à trois
paramètres
Ce modèle prend en compte le paramètre de chance,
il s'écrit comme suit :
|
?? ?????? = ?? = ???? + ??- ????
|
?????? ???? ??? - ???? )
??+
?????? ???? ??? - ???? )
|
Il est le plus approprié dans le cas où tous les
paramètres sont nécessaires pour expliquer les données,
c'est-à-dire dans le cas où les items varient beaucoup du point
de vue de la discrimination, et où la conjecture est un facteur incident
dans les scores. Cependant il perd la propriété
d'exhaustivité et d'objectivité de la mesure.
III.5. Estimation des paramètres avec les
modèles IRT et test
d'ajustement
III.5.1. Estimation des paramètres
a) L'estimation des param~tres pour le modle de
Rasch
On considère deux types de modèle de RASCH : le
modèle de RASCH à effets aléatoires selon lequel le trait
latent è est aléatoire et le modèle de RASCH à
effets fixes où la variable è est considérée fixe.
Dans l'encadré ci-dessous on voit que la log-vraisemblance des
observations est la somme de la log-vraisemblance marginale des scores (LM) et
de la log-vraisemblance conditionnellement au score qui ne dépend que
des paramètres de difficultés. Ainsi on fait une estimation en
deux étapes. La première consiste à une estimation par
maximum de vraisemblance conditionnelle et la seconde à une estimation
par maximum de vraisemblance marginale.
L'estimation par maximum de vraisemblance conditionnelle
permet d'estimer les paramètres de difficulté. En effet, la
log-vraisemblance conditionnelle au score ne dépend que des
paramètres de difficultés. Les paramètres de
difficultés estimés sont ensuite utilisés dans
l'estimation des niveaux d'acquisition par la méthode du maximum de
vraisemblance marginale.
Encadré 1 : Notations et notions
préliminaires à l'estimation
Notations
La variable aléatoire de bernouilli
le vecteur de réponse de l'individu i qui est la
1 ~~
......
) ( ) 1 )
x x
X x P T P dG T )
j
réalisation de la variable aléatoire
la matrice des réponses de N individus aux J items, qui
est
la réalisation de la variable
aléatoire
Notions préliminaires
P X x S s
Soit la fonction de répartition de la variable latente
pour un individu i, la
(( ) ( ))
i
, i
X x S s
? / )
? ?
i 1 J i i
probabilité d'observer le vecteur de réponse
s'écrit :
[2]
La probabilité d'observer un vecteur de réponse
donné sachant que l'individu à eu un score donné est
définie ci-dessous : [2]
.
Pour N individus ayant répondu individuellement à J
questions, La probabilité jointe de réponse des N individus aux J
questions s'écrit : [2]
N
= L x ? s
( , / ) ? =L s G s
( )
C M
? ? ?
De cette écritur, on obtient la log Vraisemblance qui suit
: [2]
? ? ?
( )
s exp( )
? j ?
Log vraisemblance du modèle de
RASCH
Où
Enfin
avec
la log vraisemblance conditionnelle au
score
et
log vraisemblance marginale des scores
On en déduit que la log-vraisemblance des observations
est la somme de la log-vraisemblance marginale des scores (LM) et de la
log-vraisemblance conditionnellement au score qui ne dépend que des
paramètres de difficultés.
Estimation des paramètres de difficulté des
items : spécification du modèle
? 1 si k
?
Le modèle transformé donne pour un individu
répondant à un item j :
Avec
Log ? p ? ? ?
I ?
i et
? ? 1)
? une variable aléatoire égale à
l'erreur
k j
de spécification
Dans la pratique, la variable à
expliquer est la réponse aux items et les
variables explicatives sont des indicatrices
Ikj . A chaque item j correspond un paramètre de
difficulté .
On crée donc J variables indicatrices Ikj
telles que pour k=1 ;2 ;...... ;J.
On obtient le modèle suivant :
.
On fait ensuite une estimation logistique conditionnelle sur le
modèle cidessus. Cette estimation permet d'obtenir uniquement les
paramètres de difficultépour chaque item à un signe
près. Les estimateurs obtenus sont convergents.
Estimation de la variable latente et spécification
du modèle.
On a N individus mais on a J-i-1 score (S= 0 ; 1 ; 2 ;... ; J).
Puisque le score S est une statistique exhaustive pour la variable latent, on
aura à estimer J-i-1 traits latents
(dans le cas où N>J). On crée J+1 variables
indicatrices associées au score obtenu par chaque éleve.
La variable expliquée est la
réponse aux items et les variables
explicatives sont les indicatricesSsi
. Les parametres de difficulté déjà estimés sont
introduits dans la
modélisation comme variables offset. Une variable offset
est une variable à laquelle on associe le coefficient 1 dans une
modélisation :
Le modele estimé est sans constante. Les estimations des
modeles présentés ci-dessus requierent la transformation des
données.
b) Estimation des paramètres de
difficulté et de trait latent pour
le modèle de BIRNBAUM.
Pour l'estimation du modèle à deux
paramètres, on se réfère aux modeles linéaires
généralisés. En effet, Les modeles IRT entrent dans le
cadre des modeles linéaires généralisés. De plus le
modele de BIRNBAUM perd la propriété d'exhaustivité du
score simple. Dans ce cas, on ne peut plus utiliser la méthode
d'estimation par maximum de vraisemblance conditionnelle.
Le modele à estimer ici est :
La variable expliquée est la
réponse aux items et les variables
explicatives sont les indicatrices Ikj définies
plus hauts. A chaque item j correspond un parametre de difficulté .
Cette estimation requiert des travaux préliminaires
liés à la transformation des données. En
annexe, est présentée la démarche à suivre et la
mise en oeuvre sous stata.
III.6. L'ajustement du mod~le aux données
Les trois modeles cités précédemment
à savoir le modele de rasch le modele de BIRNAUM et le modele à
trois parametres sont utilisés dans les évaluations à
grande échelle. Cependant, il n'existe pas de consensus quant au
modèle qui
conviendrait le mieux à toutes les situations. En effet
le choix d'un modèle ne constitue qu'une hypothèse parmi d'autres
pour formaliser la relation entre la probabilité de réussir un
item et l'habilité de l'élève. Toutefois, comme nous
l'avons déjà exprimé, chaque modèle possède
des propriétés qui le rendent plus désirable que d'autres
pour une situation donnée. Dans le cadre de cette étude, nous
allons mettre les trois modèles sur un même pied
d'égalité.
Ainsi, pour évaluer la qualité d'ajustement des
données au modèle, nous proposerons une procédure qui se
fait en deux étapes : la première, générale, qui
consiste à comparer les modèles, et l'autre, plus
particulière, qui nous livrera des informations précises
concernant chaque item du test une fois le modèle choisi.
III.6.1. Choix du modèle
Ce choix tient compte des hypothèses spécifiques de
chaque modèle, les hypothèses générales ayant
été vérifiées par les procédures de
sélection des items.
Ces hypothèses spécifiques, relatives aux
paramètres des items, sont regroupées dans les tableaux
ci-dessous.
Tableau 1 : Modèles et hypothèses
spécifiques
|
Les
paramètres
|
Modè
le de Rasch
|
Modèle à
deux
paramètres
|
Modèle
à
trois
paramètres
|
|
Discri
mination de
l'item j :
|
= 1
|
1
|
|
1
|
|
Param ètre de pseudo - chance de
l'item j :
|
=
0
|
|
= 0
|
0
|
Dans cette section on se limitera uniquement aux deux
modèles, le modèle à deux paramètres et le
modèle de Rasch.
On a donc à choisir entre le modèle de BIRNBAUM et
le modèle de RASCH en testant les hypothèses suivantes :
Ce test consiste donc à comparer le modèle de Rasch
( = 1
) au modèle de Birnbaum ( 1). Pour ce faire, nous
disposons du critère
? j J 1
d'information d'Akaike (AIC) et du LR test (test du rapport de
vraisemblance). Le AIC est calculé de la manière suivante :
Avec la log- vraisemblance du modèle et K le nombre de
paramètres à estimer. La règle de décision consiste
à choisir le modèle dont le AIC est le plus faible.
III.6.2. Test d'ajustement
A partir du moment où nous avons choisi le modèle,
il importe d'évaluer la qualité de l'ajustement des
données au modèle (goodness-of-fit).
Il existe plusieurs approches pour apprécier
l'ajustement du modèle, dans le cadre de cette étude nous allons
nous limiter à deux d'entre elle, la première graphique et la
deuxième analytique.
a) Ajustement graphique
Cette première forme d'analyse repose sur l'examen de
la différence entre la CCI prédite par le modèle et la CCI
empirique construite à partir des données observées. On
cherche à savoir si la courbe observé adopte l'allure
générale de la courbe théorique et ceci en évaluant
l'aire comprise entre ces deux courbes. Des outils informatiques ont
été mis au point pour cette fin (CONQUEST).
L'analyse graphique ne suffit pas, il faut souvent s'aider de
statistiques d'ajustement qui permettent une analyse beaucoup plus fine.
b) Ajustement statistique
Si nous désirons aller au -- delà d'une analyse
visuelle, des tests ont été développé pour mieux
appréhender la qualité d'ajustement.
« Ainsi , Bock(1972) accompagnait sa présentation
du modèle nominale d'une statistique, BCHI, donc la distribution est
celle de khi-carré pour tester l'ajustement du modèle :
|
BCHI =
|
I
j=1
|
Nj (Oij --Eij )2
Eij ( 1 -- Eij )
|
Ou Oij et Eij correspondent respectivement à la
proportion observée de réponses endossée et à la
proportion attendue selon le modèle pour l'item i et la catégorie
j. la statistique BCHI possède une distribution du khi-carré avec
J-m degrés de liberté où J le nombre de catégorie
et m le nombre de paramètre estimés » (BERTRAND R. p
197).
Chapitre 2 :
Calibrage des tests d'évaluatio
Chapitre 2
Calibrage des tests d'évaluation
I. Principe de base
L'objectif de ce présent chapitre est de fournir une
méthode simple pour comparer, d'une manière objective, deux
groupes d'élèves ayant passé deux tests différents.
En effet, dans le cadre de notre études, l'estimation du score vrai a
pour but l'évaluation des capacités des élèves de
la manière la plus juste et équitable possible.
Ainsi, après estimation du modèle, on obtient
les valeurs de la variable latente ainsi que celles des paramètres de
difficulté et de discrimination des items pour des modèles
IRT.
Pour deux groupes d'élèves ayant
été évalués avec des tests d'acquisition
différents, il convient de mettre ces estimations sur une même
échelle afin de pouvoir les comparer. On utilise, dans ce cas, des items
communs aux deux tests. Ceci grâce à la particularité des
IRT qui mette sur une même échelle le niveau de difficulté
des items et la variable latente.
Soient deux groupes A et B évalués
respectivement par les tests d'acquisition X et Y. Ceux-ci ont en commun des
items qui forment un sous test W (confère le schéma ci-dessous).
L'un des groupes, en occurrence le groupe A, sera considéré comme
le groupe de référence. Les paramètres de
difficulté du sous-test W estimés dans les deux groupes seront
utilisés pour mettre les traits latents des individus du groupe B sur
l'échelle de groupe A. Selon le modèle utilisé dans
l'estimation, les transformations sont différentes. Pour celles-ci nous
utilisons des méthodes de calcul qui sont reprises par LINDA L. Cook et
Daniel R. Eignor dans leur document « IRT Equating Methods
».
II. Hypothèses
Pour pouvoir les mettre à l'échelle, il faut
vérifier quelques conditions (Angoff et Kolen):
1. le nombre d'items d'ancrage doivent correspondre à 20%
du nombre total d'items du test
2. les tests doivent mesurer les mêmes aptitudes
3. les tests doivent vérifier l'indépendance des
réponses aux items
4. les tests doivent être unidimensionnels
5. l'échantillon doit etre de taille suffisante (au moins
1800 élèves)
6. les items d'ancrage doivent etre placés dans le meme
ordre dans les deux tests
7. les items d'ancrage doivent etre représentatifs en
contenu et en valeurs statistiques des deux tests
8. les deux tests contiennent le meme nombre d'items
III. Méthodologie
III.1. Selon le modèle de Rasch
Dans ce modèle, les deux tests sont sur une même
échelle si la moyenne des paramètres de difficulté
estimés du test W est la même dans les deux groupes. Soit k le
nombre d'items communs on a:
On postule que les paramètres estimés du test Y
sont mis sur l'échelle du test X par les transformations suivantes :
P1* - P w(y) = P1 - Pw(x)
D'où
P1* = P1 - Pw(x) + Pw(y)
??
?? ?? ??~ = ?? ?? ?????? ??~ ?? ?????? ??~
|
???? *
|
=
|
?? ????
|
??~
|
+ ??
|
(1)
|
|
|
??
|
|
|
|
|
*
????
|
=
|
?? ????
|
??0
|
|
(2)
|
De même pour le trait latent è :
???? * = ?? ?? ?? (??) + ?? (3)
Ainsi, par un simple calcule on peut vérifier que :
???? ????*~ = ????(???? ??~) ;
avec ???? ????) la fonction de réponse à l'item j
de l'individu i qui s'exprime,
rappelons le, comme suit :
|
???? ????) =
|
?????? (???? ??? - ????))
?? + ?????? (???? ??? - ????))
|
Les coefficients A et B se déterminent à partir
de l'équation suivante :
|
?????? ??o - ????(??)
|
?????? ??) - ????(??)
=
????(??)
|
|
????(??)
|
Avec ????(??) et ???? (??)les variances du paramètre de
difficulté du sous test W estimés respectivement dans le groupe A
et B.
Sachant que ces paramètres de difficulté
vérifient l'équation (1) on tire les coefficients a et b:
|
??=
|
????(??)
|
et ?? = ?? ??(??) - ?? ??(??) ????(??)
????(??)
|
|
????(??)
|
On notera que pour le modèle à trois
paramètres on applique la même procédure pour l'indice de
difficulté ainsi que l'indice de discrimination. Vous devinerez que,
puisque le paramètre de pseudo-chance est déterminer à
partir de l'axe des ordonnés de la courbe caractéristique
c'est-à-dire indépendamment du trait latent, aucune mise à
l'échelle n'est requise ; il reste inchangé.
A partir du moment où les paramètres
estimés sont mis sur une même échelle, on peut calculer le
score vrai (true score) des deux groupes pour comparer ainsi leur niveau de
compétence. On obtient ainsi le score vrai estimé par la relation
suivante :
?? ?? = ?? ??
????
??=1 ??),
?? ?? = ?? ??
Chapitre 3 :
Applications et Résultats
Chapitre 3
Application et Résultats
I. Analyse des items
I.1. Fiabilité et validité du test
Le but de la première phase de l'étude est de
vérifier la fiabilité et la validité de notre instrument
de mesure (test). L'analyse et l'interprétation porte sur les indices
statistiques évoqués plus haut, à savoir l'alpha de
cronbach et le point bi-sérial.
La commande qui permet, sous STATA, de calculer ces
statistiques de fiabilité est la commande « alpha
liste_item , std item »
Cette procédure a permit de sélectionner presque
tout les items.
Prenons l'exemple du test francophone de langue. Le
résultat de l'estimation se trouve exposé dans le tableau
ci-dessous (modifié avec Excel). La première et la
deuxième colonne comportent respectivement le nom des items et le nombre
d'observations utilisé pour chaque item. Les colonnes 3 à 4 sont
relatives au rpbis : signe, valeur et valeur ajustée. La dernière
colonne donne la valeur de l'alpha de Cronbach.
Ce test se compose de 39 items. Nous constatons que l'item
lang_f génère un rpbis inférieur au seuil de
validité (0,0687<0,2), par conséquent le supprimer de la base
a pour effet d'améliorer la qualité de mesure. Les autres items
par contre présentent des résultats satisfaisants.
Tableau 2: L'alpha de Cronbach des 39 items du test de
langue
francophone (modifié sur Excel
|
langue average
item-test item-rest interitem
Item Obs Sign correlation correlation correlation
alpha
|
|
lang_a
|
2557
|
+
|
0,5118
|
0,4754
|
0,2882
|
0,9374
|
|
lang_b
|
2557
|
+
|
0,4056
|
0,3647
|
0,2916
|
0,9384
|
|
lang_c
|
2557
|
+
|
0,5724
|
0,5391
|
0,2863
|
0,9369
|
|
lang_d
|
2557
|
+
|
0,5098
|
0,4733
|
0,2883
|
0,9374
|
|
lang_e
|
2557
|
+
|
0,3247
|
0,2811
|
0,2941
|
0,9391
|
|
lang_f
|
2557
|
+
|
0,0687
|
0,0211
|
0,3022
|
0,9413
|
|
lang_g
|
2557
|
+
|
0,6346
|
0,6049
|
0,2843
|
0,9363
|
|
lang_h
|
2557
|
+
|
0,5843
|
0,5516
|
0,2859
|
0,9368
|
|
lang_i
|
2557
|
+
|
0,6673
|
0,6396
|
0,2833
|
0,936
|
|
langj
|
2557
|
+
|
0,6468
|
0,6178
|
0,284
|
0,9362
|
|
lang_k
|
2557
|
+
|
0,6505
|
0,6217
|
0,2838
|
0,9362
|
|
lang_l
|
2557
|
+
|
0,518
|
0,4819
|
0,288
|
0,9374
|
|
lang_m
|
2557
|
+
|
0,4544
|
0,4154
|
0,29
|
0,9379
|
|
lang_n
|
2557
|
+
|
0,5243
|
0,4885
|
0,2878
|
0,9373
|
|
lang_o
|
2557
|
+
|
0,4943
|
0,4571
|
0,2888
|
0,9376
|
|
lang_p
|
2557
|
+
|
0,4446
|
0,4052
|
0,2903
|
0,938
|
|
lang_q
|
2557
|
+
|
0,3906
|
0,3492
|
0,292
|
0,9385
|
|
lang_r
|
2557
|
+
|
0,4852
|
0,4475
|
0,2891
|
0,9377
|
|
lang_s
|
2557
|
+
|
0,7058
|
0,6807
|
0,2821
|
0,9356
|
|
lang_t
|
2557
|
+
|
0,6959
|
0,6701
|
0,2824
|
0,9357
|
|
lang_u
|
2557
|
+
|
0,6704
|
0,6429
|
0,2832
|
0,936
|
|
lang_v
|
2557
|
+
|
0,7012
|
0,6757
|
0,2822
|
0,9357
|
|
lang_w
|
2557
|
+
|
0,6963
|
0,6705
|
0,2824
|
0,9357
|
|
lang_x
|
2557
|
+
|
0,5989
|
0,5671
|
0,2855
|
0,9366
|
|
lang_y
|
2557
|
+
|
0,5443
|
0,5094
|
0,2872
|
0,9371
|
|
lang_z
|
2557
|
+
|
0,4852
|
0,4475
|
0,2891
|
0,9377
|
|
lang_aa
|
2557
|
+
|
0,2869
|
0,2424
|
0,2953
|
0,9394
|
|
lang_ab
|
2557
|
+
|
0,6166
|
0,5858
|
0,2849
|
0,9365
|
|
lang_ac
|
2557
|
+
|
0,6268
|
0,5966
|
0,2846
|
0,9364
|
|
lang_ad
|
2557
|
+
|
0,6129
|
0,5818
|
0,285
|
0,9365
|
|
lang_ae
|
2557
|
+
|
0,7089
|
0,684
|
0,282
|
0,9356
|
|
lang_af
|
2557
|
+
|
0,6995
|
0,6739
|
0,2823
|
0,9357
|
|
lang_ag
|
2557
|
+
|
0,5834
|
0,5507
|
0,286
|
0,9368
|
|
lang_ah
|
2557
|
+
|
0,6014
|
0,5697
|
0,2854
|
0,9366
|
|
lang_ai
|
2557
|
+
|
0,6077
|
0,5764
|
0,2852
|
0,9366
|
|
lang_aj
|
2557
|
+
|
0,485
|
0,4474
|
0,2891
|
0,9377
|
|
lang_ak
|
2557
|
+
|
0,5996
|
0,5678
|
0,2854
|
0,9366
|
|
lang_al
|
2557
|
+
|
0,595
|
0,5629
|
0,2856
|
0,9367
|
|
Test
scale
|
|
|
|
|
0,2869
|
0,9386
|
I.2. Items discriminants
Pour renforcer notre analyse, nous avons calculé, dans
le cadre de la théorie du score vrai, l'indice de discrimination, qui
rappelons-le est la différence entre le score des 27% des
élèves les plus forts « UPPER » et le
score des 27% les plus faibles « LOWER ».
On reprend le même exemple précédent
(Graphique ci-dessous).On remarque que ce résultat rejoint ce qui
précède : l'item f affiche un indice de discrimination
très faible (inférieur à 0,1). Les résultats
chiffrés sont présentés en annexe.
Graphique 1 : indice de discrimination des items du
test de langue francophone
Indices de discrimination langues
|
1,00 0,80 0,60 0,40 0,20 0,00
|
|
|
|
a b c d e f g h i j k l m flop q r s t u v w x y z aa ab ac ad
ae af ag ah ai aj ak al am
|
Suite aux analyses effectuées dans cette
première phase, nous avons pu identifier les items déviant (voir
les résultats pour le test mathématique en annexe II).
II. Validation des postulats de base de TRI
Comme signaler précédemment, la TRI repose sur
trois hypothèses fondamentales à savoir l'indépendance
locale, l'unidimensionnalité et la monotonocité. Dans notre cas,
les items sont indépendant par construction, par conséquent il ne
s'agira, dans cette rubrique, que de vérifier la validité des
deux autres hypothèses.
II.1. Unidimensionnalité
Cette analyse portera sur deux graphiques représentants
les résultats d'une analyse en composante principale le premier
réalisé avec R et le deuxième avec
STATA ; tout deux convergent vers le même résultat
l'unidimensionnalité des items.
Reprenons le même exemple du test langue francophone
2011, Au regard des deux graphiques ci-dessous, on peut affirmer que les items
mesurent bien un seul trait latent.
Graphique 2 : analyse en composante principale (avec
R)

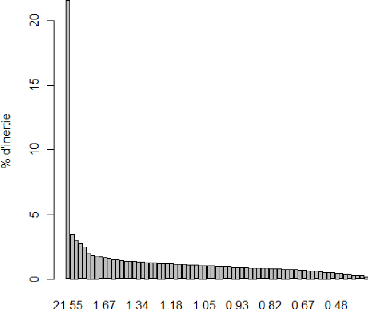
Pour réaliser cette procédure on utilise la
fonction « dudi.pca() » du package « ade4 ».Comme l'indique
le graphique ci-dessus, l'axe 1 explique 22,55% de l'inertie et l'axe 2 1,67%.
Il y a donc a priori une seule composante principale, donc le test est
unidimensionnel.
Figure 6: analyse en composante principale (avec
STATA)
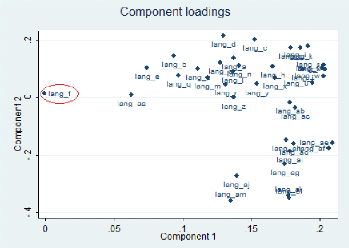
On voit bien que l'item « lang_f » » est proche du
point d'intersection des deux axes (0,0) donc ne contribue pas beaucoup
à l'inertie.
II.2. La monotonocité
Un modèle économétrique simple (le
modèle de Rach par exemple) permet d'avoir une représentation
graphique de la relation fonctionnelle entre le trait latent (l'habilité
de l'élève) et la probabilité de réussite à
l'item. Comme nous pouvons le voir dans le graphique ci-dessous les CCI du test
de langue suivent une fonction monotone non décroissante.
Graphique 3: courbe caractéristique des items
du test langue francophone
(estimé selon le modèle de Rasch)
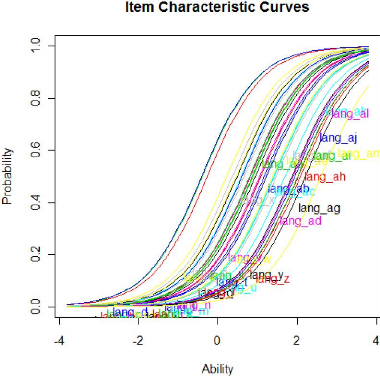
III. Estimation des paramètres et tests
d'ajustement
Dans cette partie on prendra comme exemple le test de langue
francophone dont on a éliminé les items déviants suite
à l'analyse effectuée plus haut.
Le test est constitué de 33 items. , contre 39 au
départ. Six items ont été éliminés car
porteurs de comportements déviant ou différentiés selon la
langue du test. Il s'agit d'abord de choisir le modèle le plus
adéquat aux données.
III.1. Choix du modèle
Pour cela nous disposons du critère d'information
d'Akaike (AIC). Cette statistique rappelons le, permet de comparer les
modèles et de déterminer celui qui s'ajuste le mieux aux
données. On choisi le modèle dont le (AIC) est le plus petit.
La fonction « anova () » du package « ltm
»permet de calculer cette statistique.
Comparons tout d'abord le modèle de Rasch au modèle
de BIRNBHAUM, les résultats des estimations sont présenté
en annexe.
Le test ANOVA donne :
Encadré 2 : Choix du modèle avec R
(Output)
|
>anova(RSh,BIR)
Likelihood Ratio Table
AIC BIC log.Lik LRT df p.value
RSh 70746.21 70944.94 -35339.11
BIR 68484.15 68869.92 -34176.07 2326.07 32 <0.001
|
On constate que AIC(BIR)<AIC(RSh) et la p-value est
inférieur à 0 ,01, par conséquent le modèle
à deux paramètres est plus approprié aux données
que le modèle à un paramètre.
Comparons maintenant le modèle de deux paramètres
au modèle de trois paramètres :
Encadré 3 : Comparaison des modèles avec
R
|
Likelihood Ratio Table
AIC BIC log.Lik LRT df p.value BIR 68484.15 68869.92 -34176.07
TP 69154.89 69546.51 -34510.45 -668.75 1 1
|
On remarque que la AIC(BIR)<AIC(TP) et la p-value est
supérieur à 1, le modèle à deux paramètres
reste le plus approprié aux données.
Les estimations des paramètres de difficulté et de
discrimination sont données dans le tableau ci-dessous :
Tableau 3: Estimations des paramètres de
difficulté et de discrimination selon le modèle à deux
paramètres
|
coefficients
(2011)
|
|
|
items(2011)
|
Dffclt
|
Dscrmn
|
|
FIN5F__E
|
0,9773348
|
1,376736
|
|
FIN5F__A
|
0,45209506
|
1,2223902
|
|
FIN5F__Q
|
0,63504961
|
1,075596
|
|
FIN5F__B
|
1,43787687
|
0,9001128
|
|
FIN5F__S
|
1,29374018
|
1,2656595
|
|
lang_a
|
0,69128905
|
1,2758679
|
|
lang_b
|
-
0,06218079
|
0,9501138
|
|
lang_c
|
-
0,14287979
|
2,0462499
|
|
lang_d
|
-
0,17249183
|
1,542806
|
|
lang_e
|
1,27306386
|
0,6364286
|
|
lang_g
|
0,54200864
|
2,008758
|
|
lang_h
|
1,1671953
|
1,8903242
|
|
lang_i
|
0,83860182
|
2,3858874
|
|
langj
|
0,82042118
|
2,0285716
|
|
lang_k
|
0,84027917
|
2,2530731
|
|
lang_l
|
0,80506933
|
1,3109121
|
|
lang_m
|
1,24769438
|
1,1064497
|
|
lang_s
|
0,81026022
|
2,8482186
|
|
lang_t
|
1,00876845
|
2,9108182
|
|
lang_u
|
1,19978817
|
2,8347749
|
|
lang_v
|
0,92215826
|
2,9226913
|
|
lang_w
|
1,04348279
|
3,0076832
|
|
lang_x
|
0,75172019
|
1,7392454
|
|
lang_y
|
1,64206232
|
2,0389886
|
|
lang_z
|
1,87819997
|
1,8473199
|
|
lang_aa
|
1,90539814
|
0,5322742
|
|
lang_ab
|
1,15619583
|
2,0674709
|
|
lang_ac
|
1,25411229
|
2,2851117
|
|
lang_ad
|
1,53950906
|
2,5921828
|
|
lang_ae
|
1,16336052
|
2,9071115
|
|
lang_af
|
1,22585772
|
2,9066453
|
|
lang_ah
|
1,5973621
|
2,788262
|
|
lang_ai
|
1,59615799
|
2,7598394
|
III.2. Ajustement du modèle
III.2.1. Ajustement graphique
Il est souvent plus facile avec les modèles IRT d'utiliser
les courbes caractéristiques pour analyser les items. CONCQOUEST offre
la possibilitéd'avoir ces courbes. Le code est donné
en annexe.
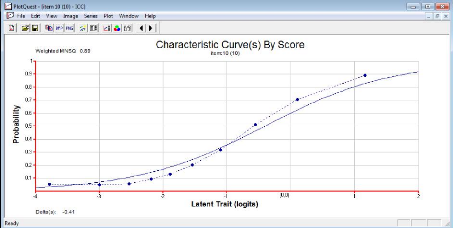
Nous avons ci-dessous deux exemples de CCI du test de langue
francophone. En trait continu, nous avons la courbe la courbe
quasi-idéal produite par le modèle et en pointillés la
courbe empirique. La CCI de l'item langj donne l'exemple d'un item qui s'ajuste
bien au modèle. L'ajustement parfait est difficile voire impossible
à obtenir.
La courbe observée, malgré l'oscillation,
épouse l'allure de la courbe théorique.
Graphique 4: courbes
caractéristiques d'un item bien ajusté au
modèle
Nous avons, à l'opposé ici, un item déviant
toujours le même item lang_f (l'item 6 pour CONQUEST)
Graphique 5: exemple d'un item qui ne s'ajuste
pas bien aux données

La courbe empirique s'écarte complètement de la
courbe théorique. Pire elle décroit pour des traits latents
compris entre -1 et 1 violant l'hypothèse de monotonicité.
III.2.2. Ajustement statistique
a) Application sur R
Comme nous l'avons déjà exprimé, cette
ajustement a pour but de déterminer les items qui s'ajustent
significativement au modèle.
>item.fit(BIR)
Encadré 4: Test d'ajustement avec
R
Item-Fit Statistics and P-value Call:
ltm(formula = data ~ z1)
Alternative: Items do not fit the model Ability Categories: 10
X'2 Pr(>X'2)
FIN5F__E 24.1134 0.0022 FIN5F__A 57.8623 <0.0001 FIN5F__Q
63.7090 <0.0001 FIN5F__B 17.6695 0.0238 FIN5F__S 20.6680 0.0081
|
lang_a
|
24.6577
|
0.0018
|
|
lang_b
|
18.5878
|
0.0172
|
|
lang_c
|
36.6025
|
<0.0001
|
|
lang_d
|
33.7865
|
<0.0001
|
|
lang_e
|
30.2248
|
0.0002
|
|
lang_g
|
16.0449
|
0.0417
|
|
lang_h
|
27.9201
|
0.0005
|
|
lang_i
|
18.7033
|
0.0165
|
|
langj
|
25.2253
|
0.0014
|
|
lang_k
|
22.5732
|
0.004
|
|
lang_l
|
38.8514
|
<0.0001
|
|
lang_m 43.8923
|
<0.0001
|
|
lang_s
|
19.2971
|
0.0133
|
|
lang_t
|
20.4608
|
0.0087
|
|
lang_u
|
26.9626
|
0.0007
|
|
lang_v
|
13.5028
|
0.0957
|
|
lang_w
|
16.7123
|
0.0332
|
|
lang_x
|
26.0067
|
0.001
|
|
lang_y
|
14.7331
|
0.0645
|
|
lang_z
|
10.4916
|
0.2322
|
lang_aa 45.9957 <0.0001 lang_ab 13.2897 0.1023 lang_ac
17.0671 0.0294 lang_ad 12.5607 0.1279 lang_ae 15.4527 0.0509 lang_af 12.9743
0.1127 lang_ah 13.3439 0.1006 lang_ai 16.2935 0.0384
On conclue que 7 items seulement ne s'ajustent pas
significativement au modèle.
Notons aussi que pour évaluer la robustesse de nos
estimations nous avons testé le modèle sur un cinq sous
échantillon de l'échantillon principal (50%) tirés
aléatoirement. Les moyennes des estimations des paramètres du
modèle convergent vers le même résultat trouvé
précédemment. Nous avons développé cette
procédure sur R (voir code en annexe III).
Tableau 4 : Les moyennes et variances des
paramètres de difficulté et de discrimination des cinq
sous-échantillons sont affichées comme suit :
|
Moy. Dif
|
Var. Dif.
|
Moy. Dis.
|
Var. Dis.
|
|
FIN5F__E
|
0,9617
|
0,0013
|
1,3706
|
0,0031
|
|
FIN5F__A
|
0,4208
|
0,0009
|
1,2625
|
0,0070
|
|
FIN5F__Q
|
0,5753
|
0,0011
|
1,1143
|
0,0032
|
|
FIN5F__B
|
1,5011
|
0,0130
|
0,8576
|
0,0055
|
|
FIN5F__S
|
1,2687
|
0,0043
|
1,2627
|
0,0079
|
|
lang_a
|
0,6680
|
0,0013
|
1,3304
|
0,0098
|
|
lang_b
|
-0,0800
|
0,0023
|
0,9513
|
0,0005
|
|
lang_c
|
-0,1608
|
0,0007
|
1,9604
|
0,0029
|
|
lang_d
|
-0,1980
|
0,0011
|
1,5349
|
0,0079
|
|
lang_e
|
1,2020
|
0,0078
|
0,6503
|
0,0020
|
|
lang_g
|
0,5125
|
0,0009
|
1,9389
|
0,0017
|
|
lang_h
|
1,1426
|
0,0017
|
1,8865
|
0,0037
|
|
lang_i
|
0,8068
|
0,0016
|
2,3657
|
0,0119
|
|
lang_j
|
0,7892
|
0,0013
|
2,0160
|
0,0134
|
|
lang_k
|
0,8024
|
0,0015
|
2,2156
|
0,0240
|
|
lang_l
|
0,7655
|
0,0106
|
1,3366
|
0,0069
|
|
lang_m
|
1,2267
|
0,0023
|
1,1381
|
0,0015
|
|
lang_s
|
0,7895
|
0,0018
|
2,8302
|
0,0397
|
|
lang_t
|
0,9907
|
0,0013
|
2,8860
|
0,0210
|
|
lang_u
|
1,1847
|
0,0011
|
2,8698
|
0,0231
|
|
lang_v
|
0,9243
|
0,0004
|
2,8993
|
0,0186
|
|
lang_w
|
1,0338
|
0,0008
|
3,0018
|
0,0211
|
|
lang_x
|
0,7468
|
0,0019
|
1,6812
|
0,0061
|
|
lang_y
|
1,6409
|
0,0021
|
1,9735
|
0,0144
|
|
lang_z
|
1,9007
|
0,0078
|
1,8264
|
0,0106
|
|
lang_aa
|
1,8879
|
0,0673
|
0,5489
|
0,0075
|
|
lang_ab
|
1,1594
|
0,0010
|
2,0034
|
0,0047
|
|
lang_ac
|
1,2356
|
0,0020
|
2,2813
|
0,0081
|
|
lang_ad
|
1,5244
|
0,0035
|
2,5665
|
0,0116
|
|
lang_ae
|
1,1327
|
0,0016
|
3,0144
|
0,0105
|
|
lang_af
|
1,1924
|
0,0019
|
2,9807
|
0,0194
|
|
lang_ah
|
1,5701
|
0,0012
|
2,8218
|
0,0152
|
|
lang_ai
|
1,5667
|
0,0041
|
2,8253
|
0,0517
|
Ces résultats témoignent de la robustesse de nos
estimations. b) IIs F'a's dP'JIP
Une des contraintes majeures du cahier de charge des tests
était de s'assurer de l'équivalence des versions francophones et
anglophones des items. Le contenu des tests a été
réalisé de manière à établir un
dénominateur commun entre les programmes et méthodes
d'enseignement des deux sous-systèmes francophone et anglophone du
Cameroun. Les traductions des tests ont été
vérifiées par un cabinet spécialisé et les items
ayant des comportements similaires dans les deux versions ont été
sélectionnés après la mise à l'essai.
Les tests finaux devraient donc être équivalents
dans leur fonctionnement entre élèves francophones et
anglophones.
En première instance, une analyse comparée des
taux de réussite, indices de difficulté et de discrimination des
versions francophones et anglophones a été réalisé
et montre une grande similarité des différents valeurs des
indices calculés sur la base de la théorie du score vrai dans les
deux sous-systèmes.
Ceci étant, la théorie du score vrai ne nous
permet pas d'affirmer que les tests sont équivalents ni de
déterminer si les élèves francophones et anglophones
performent identiquement.
Il nous faut donc mobiliser une fois de plus la théorie
de réponse aux items qui proposent plusieurs méthodes
d'étude des biais ou fonctionnement différentié des items
(diferential item functionning, DIF). Ces méthodes reposent sur
deux grands principes : soit sur une fonction de l'aire entre les deux courbes
caractéristiques des items, soit un test de signification en rapport
avec les paramètres des items.
Pour simplifier, nous avons opté pour une
méthode graphique, en visualisant l'écart entre les courbes
francophones et anglophones des items. Les courbes ont été
tracées avec le logiciel Conquest.
Nous avons ci-dessous deux exemples de CCI du test anglophone et
francophone.
Le premier exemple montre une grande similarité entre
les deux items des deux tests. Quant au deuxième graphique, on remarque,
en terme de difficulté, un écart entre les deux courbes mais le
pouvoir discriminant des deux items est pratiquement le même.
Graphique 6 : CCI d'items anglophone et francophone
ayants un même pourvoir discriminant et un même niveau de
difficulté
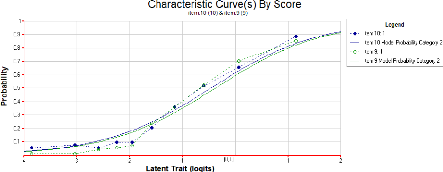

Graphique 7 : CCI d'items anglophone et francophone
ayants des niveaux de difficulté différent mais un même
pourvoir discriminant
Les graphiques n'ont pas fait ressortir d'écart
important entre courbes francophones et anglophones des items. On notera que
les items d'ancrage ont été sélectionnés
également sur la base de l'équivalence des versions francophones
et anglophones. Par la suite, nous avons donc considéré comme
équivalents (et donc sur une même échelle) les tests
francophones et anglophones.
IV. Mise à l'échelle des tests 2005 et
2011
IV.1. Vérification des hypothqses de la mise
à l'échelle
Pour pouvoir comparer le niveau d'acquisition des
élève du Cameroun de 2005 (TEST PASEC 2005) à celui des
élèves de 2011 il a fallu mettre les deux test sur une même
échelle, par convention on prend la première année (2005)
comme référence.
Pour ce faire on a repris la procédure
développée dans le chapitre III.
Pour faciliter les calculs on a développé sur R
un programme qui permet, en un seul clic de donner les résultats,
partant ainsi de l'estimation des paramètres, jusqu'au calcul des scores
calibrés passant par la mise à l'échelle. Le programme est
donné en annexe III.
Nous avons comparé les résultats de notre
programme avec le package R Irtoys mis au point très récemment et
qui permet la mise en oeuvre d'un test equating.
Toutefois, il faut au préalable s'assurer de la
validité des hypothèses postulées auparavant.
1. le nombre d'items d'ancrage doivent correspondre à 20%
du nombre total d'items du test
2. les tests doivent mesurer les mêmes aptitudes
3. les tests doivent vérifier l'indépendance des
réponses aux items
4. les tests doivent être unidimensionnels
5. l'échantillon doit être de taille suffisante (au
moins 1800 élèves)
6. les items d'ancrage doivent être placés dans le
même ordre dans les deux tests
7. les items d'ancrage doivent être représentatifs
en contenu et en valeurs statistiques des deux tests
8. les deux tests contiennent le même nombre d'items
Voyons donc si nos tests vérifient bien les
différentes hypothèses.
Le test PASEC contient 42 items et le test 2011 contient 39
items. Ils ne sont pas tout à fait égaux en contenus car le test
2011 contient des items de production d'écrits mobilisant des
compétences supérieures et faisant appel à des questions
ouvertes à réponse longue.
De même, le test 2011 contient beaucoup de questions
ouvertes à réponse courte, alors que le test PASEC contient
principalement des QCM.
Pour pallier à cette situation, 6 items de production
d'écrits du test 2011 ont été supprimés, ainsi que
9 items du test PASEC sur la base des corrélations item-test et indices
de difficulté, ou fonctionnement différentié
anglophone-francophone.
On obtient ainsi deux sous test de 33 items chacun, qui
mesurent les mêmes habiletés (compréhension en lecture et
outils de la langue) et qui serviront à faire la mise à
l'échelle, sur la base de cinq items communs (soit 15% du test
total).
Les cinq items PASEC ont été choisis sur la base
de l'indice de difficulté (proche de 0.5), et surtout de
l'équivalence des versions francophones et anglophones des items tant
sur le plan linguistique que sur le plan psychométrique (pas de biais
d'items).
Les hypothèses 2, 7 et 8 sont donc
vérifiées.
L'hypothèse 3 d'indépendance des items est
également respectée par la construction des tests.
L'hypothèse 4 d'unidimensionnalité est
également vérifiée sur la base de la cohérence
interne des tests et des corrélations item-test mais également
par l'analyse factorielle (voir Monseur pour l'analyse des réponses aux
items des tests PASEC).
Ces deux hypothèses étant vérifiées,
la mise en oeuvre des modèles de réponse à l'item est
possible.
S'agissant de l'hypothèse 5, les échantillons
sont respectivement de 2361 élèves en 2005 et de 2553
élèves en 2011. Par contre, l'hypothèse 6 n'est pas
vérifiée, les items communs se situent au milieu du test 2011 et
dans diverses parties du test PASEC 2005.
Globalement, les sous-tests qui vont servir à la mise
à l'échelle respectent bien les différentes conditions,
bien que le nombre d'items d'ancrage soit assez faible.
Après comparaison des différents critères
tels que AIK, etc.., un modèle à deux paramètres s'ajuste
bien aux deux échantillons.
Les statistiques d'ajustement des items aux modèles
montrent que 7 items du test 2011 et 7 items du test 2005 ne suivent pas bien
le modèle.
Néanmoins, ces items seront conservés pour la mise
à l'échelle. IV.2. &KRiI
-GT-la-PptKRGT-GT-la-PIIT-E-l'pFKTllT
Il existe quatre méthodes permettant de mettre sur une
même échelle des tests comportant des items communs Davier (2011)
:
1. La méthode mean/mean se base sur les moyennes des
paramètres des items communs ;
2. La méthode mean/sigma se base sur les moyennes et les
écarts types des paramètres des items communs ;
3. La méthode Stocking-Lord ;
4. La méthode Haebara .
Les deux premières méthodes reposent sur
l'utilisation d'une transformation linéaire des paramètres des
items d'ancrage, tandis que les deux autres méthodes se basent sur une
minimisation de différences de carrés.
Nous allons utiliser la méthode N°2 qui peut
être facilement mise en oeuvre et qui fournit des estimations
raisonnables des différences d'habiletés des élèves
entre deux vagues d'évaluation.
Cette méthode sera mise en oeuvre sur Excel, puis sur R en
mettant au point un programme puis avec le package Irtoys5 mis au
point récemment.
Les courbes ci-dessous présentent les scores vrais
estimés en fonction du niveau d'habilité des
élèves. La courbe en vert est pour 2005, la courbe en rouge est
pour 2011.
5 On notera que le package Plink permet aussi la mise
à l'échelle mais s'avère compliqué à
paramétrer.
Graphique 8: le score vrai estimé de 2005 vs le
score vrai estimé de 2011
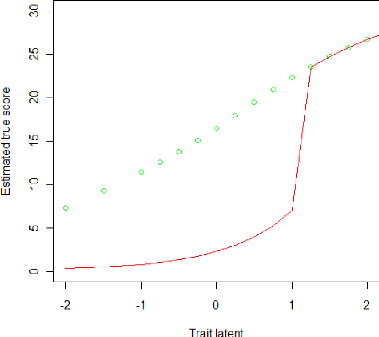
Comme la courbe rouge est globalement en dessous de la courbe
verte, cela signifie que le score vrai estimé a baissé
entre 2005 et 2011. Ainsi, on en conclut que le niveau d'acquisition
des élèves a globalement baissé; aussi, on remarque que
pour les élèves de niveau moyen, c'est-à-dire pour des
thêtas compris entre -1 et 1, la baisse est beaucoup plus importante
pendant que les forts se maintiennent à leur niveau.
La méthode mean/ sigma peut être mis en oeuvre en
plusieurs étapes grâce aux package ltm et irtoys sur le logiciel R
(Voir code en annexe III). On a mis sur
une même graphique les 3 courbes, en vert le <<
true score >> 2005, en bleu le << true score >> avec le
package irtoys, et en rouge le true score avec la méthode décrite
cidessous.
Graphique 9 : package Irtoys vs Résultats
produit avec notre programme R


Les résultats obtenus avec le package Irtoys convergent
avec les résultats produits avec notre programme sur R, à savoir
que le niveau des élèves a baissé entre 2005 et 2011.
Conclusion
CONCLUSION
L'objectif tracé pour ce travail était de
présenter une nouvelle approche de mesure en psychométrie.
Ainsi, le premier chapitre a présenté les
différentes méthodes de mesure de l'éducation et ainsi il
nous a permis d'avoir une vision approfondie sur les points forts de chacune
d'entre elles.
Quant au deuxième chapitre, il a été
consacré à la présentation des différentes
techniques de mise à l'échelle des tests. Aussi, avons-nous
essayé de détailler la méthode du « test equating
».
Dans le cadre de la dernière partie, nous avons
exposé les différents modèles de mesure à savoir la
méthode classique que nous nous somme contentés uniquement de
présenter, et la théorie de réponse aux items, but de
notre analyse. En effet, au cours de cette deuxième partie, nous avons
présenté le cadre théorique de cette méthode de
mesure, ses différents modèles à savoir le modèle
de Rasch, le modèle à deux et trois paramètres. Nous avons
pu, ainsi, détecter les points forts de chacun d'entre eux.
Dans le dernier chapitre, nous avons tenté d'appliquer
la théorie vue précédemment sur des données
empiriques issues d'une enquête auprès des élèves de
5ème année du Cameroun.
On en conclut que le niveau des élèves a
baissé entre 2005 et 2011 et ces analyses ont pu être
utilisées dans le rapport fait par Varlyproject aux autorités du
Cameroun.
Notre étude a été finalisée par la
conception et la réalisation d'une application informatique qui servira
d'outil de calibrage des paramètres des items.
Pour clore ce travail, nous pouvons dire que les
modèles IRT sont des sujets qui ne cessent de susciter
l'intérêt des chercheurs et spécialistes et ce, en raison
de la grande valeur ajoutée qu'ils peuvent apporter s'ils sont bien
maitrisés mais surtout bien appliqués en interne.
BIBLIOGRAPHIE
- Monseur (2007), Guide méthodologique sur les
tests, PASEC.
- Bertrand R., Blais J. (2004), 0 RGICIIIIIPIIAL
H A ESSRLIFEHl EIlicoRLiIBILV réponses aux items, Press
de l'Université du Québec.
- Baker F. (2002), The Basics of Item Response Theory,
ERIC.
- Rizopoulos D. (2006), ltm: An R Package for Latent
Variable Modeling and Item, Journal of Statistical Software, Volume 17,
Issue 5Response Theory Analyses
- Kolen M., Brennan R. (2010), Test equating, Scaling and
Linking, Method and practices, Springer.
- Alina A., Davier V. (2011), Statistical Models for Test
Equating, Scaling, and Linking, Springer.
- Cook L., Eignor D. (), IRT equating methods, ETS.
- Angoff W.H (1984), Scales, norms and equivalent scores,
Princeton, NJ: Educational testing service.
- Kpodar K. (2007), Manuel d'initi EtiRn à1751 Et
EMILsiRTI). Centre d'Etudes et de Recherches sur le Développement
International.
- Emmanuel P. (2005), R pour les débutants,
Institut des Science de l'Evolution Université de Monpellier II.
WEBOGRAPHIE
-
http://luna.cas.usf.edu/~mbrannic/files/pmet/irt.htm
-
http://anaqol.org/index.php?file=raschtest.php?fr=1
-
http://statmath.wu.ac.at/research/talks/resources/PresIRT.pdf
- http://cran.cict.fr/
-
http://www.psycho-psysoc.site.ulb.ac.be/ressources-en-statistiques/154-lalphade-cronbach
-
http://www.umoncton.ca/crde/files/crde/wf/wf/pdf/AtelierRasch_UMoncton200
9 JGrondin.pdf
Annexes
Annexes

Annexe I : Démonstrations
Annexe I
Démonstration de la propriété
d'objectivité
Considérons deux individus et ayant répondu
à l'itemet notons et
J
? j
leurs aptitudes respectives. La statistique étant
exhaustive pour le
j ? 1
paramètre :
Démonstration de la propriété
d'exhaustivité du score
L'exhaustivité du score sur le trait latent signifie que,
sous le modèle de Rasch, toute l'information disponible sur la valeur du
trait latent d'un individu est
? 0 / 1)
2 contenue dans la statistique exhaustive
R ? ?
J j P R
( 1)
?
( X , X
(score). L'exhaustivité du score
i j i j
)
découle du fait que le modèle de RASCH appartient
à la famille exponentielle [2].
1
=
Soit la densité conjointe de la loi logistique suivant
:
( ? ? ( ? ? ) (
( ? )
2 j
)(+ e )
nf
ex( ?
Annexe II
Résultats des
estimations
Tableau 5: L'indice de discrimination des 39
items du test de langue francophone (modifié sur Excel)
|
langue
|
|
|
|
|
|
item
|
UPPER
|
tx de reussite U
|
LOWER
|
tx de réussite L
|
ID
|
|
a
|
480
|
0,690647482
|
44
|
0,06918239
|
0,62
|
|
b
|
548
|
0,788489209
|
105
|
0,16509434
|
0,62
|
|
c
|
657
|
0,945323741
|
64
|
0,100628931
|
0,84
|
|
d
|
631
|
0,907913669
|
83
|
0,130503145
|
0,78
|
|
e
|
387
|
0,556834532
|
78
|
0,122641509
|
0,43
|
|
f
|
170
|
0,244604317
|
129
|
0,202830189
|
0,04
|
|
g
|
568
|
0,817266187
|
21
|
0,033018868
|
0,78
|
|
h
|
384
|
0,552517986
|
3
|
0,004716981
|
0,55
|
|
i
|
490
|
0,705035971
|
5
|
0,007861635
|
0,70
|
|
j
|
493
|
0,709352518
|
24
|
0,037735849
|
0,67
|
|
k
|
482
|
0,69352518
|
6
|
0,009433962
|
0,68
|
|
l
|
456
|
0,656115108
|
17
|
0,02672956
|
0,63
|
|
m
|
358
|
0,515107914
|
12
|
0,018867925
|
0,50
|
|
n
|
423
|
0,608633094
|
17
|
0,02672956
|
0,58
|
|
o
|
502
|
0,722302158
|
33
|
0,051886792
|
0,67
|
|
p
|
448
|
0,644604317
|
33
|
0,051886792
|
0,59
|
|
q
|
334
|
0,48057554
|
21
|
0,033018868
|
0,45
|
|
r
|
359
|
0,516546763
|
12
|
0,018867925
|
0,50
|
|
s
|
501
|
0,720863309
|
2
|
0,003144654
|
0,72
|
|
t
|
452
|
0,650359712
|
0
|
0
|
0,65
|
|
u
|
383
|
0,551079137
|
0
|
0
|
0,55
|
|
v
|
473
|
0,68057554
|
1
|
0,001572327
|
0,68
|
|
w
|
426
|
0,61294964
|
1
|
0,001572327
|
0,61
|
|
x
|
484
|
0,696402878
|
22
|
0,034591195
|
0,66
|
|
y
|
244
|
0,351079137
|
2
|
0,003144654
|
0,35
|
|
z
|
196
|
0,282014388
|
2
|
0,003144654
|
0,28
|
|
aa
|
305
|
0,438848921
|
66
|
0,103773585
|
0,34
|
|
ab
|
389
|
0,55971223
|
2
|
0,003144654
|
0,56
|
|
ac
|
360
|
0,517985612
|
1
|
0,001572327
|
0,52
|
|
ad
|
256
|
0,368345324
|
0
|
0
|
0,37
|
|
ae
|
392
|
0,564028777
|
0
|
0
|
0,56
|
|
af
|
197
|
0,283453237
|
0
|
0
|
0,28
|
|
ag
|
368
|
0,529496403
|
0
|
0
|
0,53
|
|
ah
|
226
|
0,325179856
|
1
|
0,001572327
|
0,32
|
|
ai
|
229
|
0,329496403
|
3
|
0,004716981
|
0,32
|
|
aj
|
219
|
0,315107914
|
1
|
0,001572327
|
0,31
|
|
ak
|
281
|
0,404316547
|
2
|
0,003144654
|
0,40
|
|
al
|
247
|
0,355395683
|
0
|
0
|
0,36
|
|
am
|
117
|
0,168345324
|
0
|
0
|
0,17
|
Tableau 6: L'indice de discrimination des 26
items du test de mathématique
|
math
|
|
|
|
|
|
UPPER
|
tx de reussite U
|
Lower
|
tx de réussite L
|
ID
|
|
a
|
654
|
0,712418301
|
73
|
0,118506494
|
0,59
|
|
b
|
654
|
0,712418301
|
60
|
0,097402597
|
0,62
|
|
c
|
441
|
0,480392157
|
14
|
0,022727273
|
0,46
|
|
d
|
668
|
0,727668845
|
65
|
0,105519481
|
0,62
|
|
e
|
167
|
0,181917211
|
3
|
0,00487013
|
0,18
|
|
f
|
376
|
0,409586057
|
42
|
0,068181818
|
0,34
|
|
g
|
298
|
0,324618736
|
39
|
0,063311688
|
0,26
|
|
h
|
552
|
0,60130719
|
12
|
0,019480519
|
0,58
|
|
i
|
338
|
0,368191721
|
8
|
0,012987013
|
0,36
|
|
j
|
104
|
0,11328976
|
1
|
0,001623377
|
0,11
|
|
k
|
146
|
0,159041394
|
3
|
0,00487013
|
0,15
|
|
l
|
436
|
0,474945534
|
30
|
0,048701299
|
0,43
|
|
m
|
642
|
0,699346405
|
49
|
0,079545455
|
0,62
|
|
n
|
290
|
0,315904139
|
5
|
0,008116883
|
0,31
|
|
o
|
663
|
0,722222222
|
75
|
0,121753247
|
0,60
|
|
p
|
397
|
0,432461874
|
103
|
0,167207792
|
0,27
|
|
q
|
440
|
0,479302832
|
15
|
0,024350649
|
0,45
|
|
r
|
257
|
0,279956427
|
25
|
0,040584416
|
0,24
|
|
s
|
221
|
0,240740741
|
30
|
0,048701299
|
0,19
|
|
t
|
401
|
0,436819172
|
14
|
0,022727273
|
0,41
|
|
u
|
232
|
0,252723312
|
32
|
0,051948052
|
0,20
|
|
v
|
192
|
0,209150327
|
114
|
0,185064935
|
0,02
|
|
w
|
98
|
0,106753813
|
0
|
0
|
0,11
|
|
x
|
524
|
0,5708061
|
16
|
0,025974026
|
0,54
|
|
y
|
469
|
0,510893246
|
11
|
0,017857143
|
0,49
|
|
z
|
179
|
0,194989107
|
1
|
0,001623377
|
0,19
|
Tableau4 : L'alpha de cronbach des 26 items du test de
Mathématique
|
Math average
item-rest Inter-item
Item Obs Sign correlation correlation correlation
alpha
|
|
math_a
|
2557
|
+
|
0,4683
|
0,3915
|
0,1383
|
0,8005
|
|
math_b
|
2557
|
+
|
0,457
|
0,3793
|
0,1387
|
0,801
|
|
math_c
|
2557
|
+
|
0,5204
|
0,448
|
0,1364
|
0,798
|
|
math_d
|
2557
|
+
|
0,4964
|
0,4219
|
0,1373
|
0,7991
|
|
math_e
|
2557
|
+
|
0,5118
|
0,4387
|
0,1367
|
0,7984
|
|
math_f
|
2557
|
+
|
0,3625
|
0,2784
|
0,1421
|
0,8055
|
|
math_g
|
2557
|
+
|
0,3501
|
0,2652
|
0,1426
|
0,8061
|
|
math_h
|
2557
|
+
|
0,5838
|
0,5177
|
0,1341
|
0,794
|
|
math_i
|
2557
|
+
|
0,5605
|
0,4921
|
0,135
|
0,796
|
|
mathj
|
2557
|
+
|
0,4126
|
0,3316
|
0,1403
|
0,8032
|
|
math_k
|
2557
|
+
|
0,4677
|
0,3909
|
0,1383
|
0,8005
|
|
math_l
|
2557
|
+
|
0,4392
|
0,3601
|
0,1394
|
0,8019
|
|
math_m
|
2557
|
+
|
0,5224
|
0,4502
|
0,1364
|
0,7979
|
|
math_n
|
2557
|
+
|
0,3845
|
0,3017
|
0,1413
|
0,8045
|
|
math_o
|
2557
|
+
|
0,4316
|
0,352
|
0,1396
|
0,8023
|
|
math_p
|
2557
|
+
|
0,2119
|
0,1214
|
0,1475
|
0,8123
|
|
math_q
|
2557
|
+
|
0,4557
|
0,3778
|
0,1388
|
0,8011
|
|
math_r
|
2557
|
+
|
0,2685
|
0,1798
|
0,1455
|
0,8098
|
|
math_s
|
2557
|
+
|
0,3422
|
0,2569
|
0,1429
|
0,8064
|
|
math_t
|
2557
|
+
|
0,506
|
0,4324
|
0,1369
|
0,7987
|
|
math_u
|
2557
|
+
|
0,3041
|
0,217
|
0,1442
|
0,8082
|
|
math_v
|
2557
|
+
|
0,1303
|
0,0382
|
0,1505
|
0,8158
|
|
math_w
|
2557
|
+
|
0,3678
|
0,284
|
0,1419
|
0,8053
|
|
math_x
|
2557
|
+
|
0,456
|
0,3782
|
0,1387
|
0,8011
|
|
math_y
|
2557
|
+
|
0,4151
|
0,3343
|
0,1402
|
0,803
|
|
math_z
|
2557
|
+
|
0,3956
|
0,3135
|
0,1409
|
0,804
|
|
Test scale
|
|
|
|
|
0,1402
|
0,8091
|
Annexe III
I. Code R pour le test de robustesse
#création d'une fonction qui estime les paramètre
du modèle# #sur 50% de l'échantillon tirer
aléatoirement#
estimation<- function (data11) {
echantillon <- sample(1:nrow(data11),
ceiling(nrow(data11)*0.5)) y<-ltm(data11[echantillon, ] ~ z1)
coef<-coef(y)}
estimation(data11)
#appeler la fonction 5 fois avec la fonction replicate()#
resultat <- replicate(5, estimation(data11))
resultat[1,1,1]
resultat[1,1,]
#calculer la moyenne de l'indice de difficulté de l'item #
#FIN5F__E dans les cinq itération#
mean(resultat[1,1,])
#toutes les moyennes et variances de tout les items#
#et des deux indices#
apply(resultat, MARGIN = c(1,2),FUN=mean)
apply(resultat, MARGIN = c(1,2),FUN=var)
II. &RGFB SRXLII IPB11111190101e
#Importation des données au format csv #
data11<-read.csv("
C:/Users/acer/Desktop/stage/data11.csv",
header =
TRUE,sep = ",") #
data05<-read.csv("
C:/Users/acer/Desktop/stage/data05.csv",
header =
TRUE,sep = ",") #
summary(data05) ############### #library#
###############
library(ltm)
#
#
#############################################################
#le modèle à deux paramètres non contraint
(BIR)#
#############################################################
#Données PASEC# P<- ltm(data11 ~ z1)
Y<-coef(P)
#indice de difficulté (2011)#
y<-Y[1:33,1]
y<- as.matrix(y)
#indice de difficulté des items communs (2011)#
p<-Y[1:5,1]
p<- as.matrix(p)
#indice de discrimination des items communs (2011)#
d<-Y[1:33,2]
d<- as.matrix(d)
#moyenne et ecart-type des indices de difficulté des items
communs (2005)# mean(p)
var(p)
SP<-sqrt(var(p))
#Données Cameroun 2005#
V<- ltm(data05 ~ z1)
X<-coef(V)
#indice de difficulté des items communs#
v<-X[1:5,1]
v<- as.matrix(v)
#moyenne et ecart-type des indices de difficulté des items
communs (2005)# mean(v)
SV<-sqrt(var(v))
#les paramètre de transformation linéaire
(slope/intercept)#
slope<-SV/SP
intercept<-(mean(p)*slope)+mean(v)
#paramètre de difficulté de 2011 mis à
l'echelle de 2005#
Diff11<- y*rep(slope)+rep(intercept) Diff11[1:5,1]<-
y[1:5,1]
#paramètre de discrimination de 2005 mis à
l'echelle de 2005# Dis11<-d/rep(slope)
Dis11[1:5,1]<- d[1:5,1]
#proba de réussite à l'item i#
theta<-c(-1,0,1)
proba11<- function(Dis11, Diff11, theta)
{inv.logit(Dis11*(theta-Diff11))} score11<- function (theta)
{sum(proba11(Dis11,Diff11,theta))}
prcscore11<-function(theta){score11(theta)/33}
#2005#
#indice de difficulté (PASEC)#
Diff5<-X[1:33,1]
Diff5<- as.matrix(Diff5)
#indice de dicrimination#
Dis5<-X[1:33,2]
Dis5<- as.matrix(Dis5)
proba5<- function(Dis5, Diff5, theta)
{inv.logit(Dis5*(theta-Diff5))} score5<- function (theta)
{sum(proba5(Dis5,Diff5,theta))}
prcscore5<-function(theta){score5(theta)/33}
#courbe#
score11_bis<-c(score11(-1), score11(0), score11(1))
score5_bis<-c(score5(-1), score5(0), score5(1))
plot ( theta,score5_bis,col="green",ylab="Estimated true
score",xlab="Trait
latent",ylim=c(0,30),xlim=c(-2,2))
lines ( theta,score11_bis, col="red")
proba11_P<- function(Dis11, Diff11, theta1)
{inv.logit(Dis11*(theta1-
Diff11))}
score11_P<- function (theta1)
{sum(proba11(Dis11,Diff11,theta1))} proba5_P<- function(Dis5, Diff5, theta1)
{inv.logit(Dis5*(theta1-Diff5))} score5_P<- function (theta1)
{sum(proba11(Dis5,Diff5,theta1))}
theta1<-c(-2,-1.5,-1,-0.75,-0.5,-
0.25,0,0.25,0.5,0.75,1,1.25,1.5,1.75,2,2.25,2.5,2.75,3)
length(theta1) length(score5_bis_P)
score5_bis_P<-c(score5_P(-2),score5_P(-1.5),score5_P(-1),score5_P(-
0.75),score5_P(-0.5),score5_P(-
0.25),score5_P(0),score5_P(0.25),score5_P(0.5),score5_P(0.75),score5_P(1),
score5_P(1.25), score5_P(1.5), score5_P(1.75),score5_P(2), score5_P(2.25),
score5_P(2.5), score5_P(2.75),score5_P(3))
score11_bis_P<-c(score11_P(-2),score11_P(-1.5),score11_P(-
1),score11_P(-0.75),score11_P(-0.5),score11_P(-
0.25),score11_P(0),score11_P(0.25),score11_P(0.5),score11_P(0.75),score11_P(1),
score5_P(1.25), score5_P(1.5), score5_P(1.75),score5_P(2), score5_P(2.25),
score5_P(2.5), score5_P(2.75),score5_P(3))
plot ( theta1,score5_bis_P,col="green",ylab="Estimated true
score",xlab="Trait latent",ylim=c(0,30),xlim=c(-2,2))
lines ( theta1,score11_bis_P, col="red")
III. &RdI-I5 SRXLID IPisI-AIIIéERI-RI-
DAI-E lI- SDEkDge Irtoys
# La méthode MS est mean/sigma est appliquée #
scaling_11on5_bis<-sca(old.ip=coef5,
new.ip=coef11,old.items=1:5,new.items=1:5,old.qu = NULL, new.qu
=
NULL,method="MS",bec=FALSE)
#On récupère les coef mis à l'échelle
# coef11_scaled5_bis<-scaling_11on5_bis$scaled.ip
coef11scaled5bis
# estimated true score #
true_score <- function (coef, theta) {
sum(inv.logit(coef[34:66]*(rep(theta,33)-coef[1:33]))) }
# comparaison des true score #
true_score2005<-c(true_score(coef5,-2),true_score(coef5,-
1.5),true_score(coef5,-1),true_score(coef5,-0.75),+
true_score(coef5,-0.5),true_score(coef5,-0.25),true_score(coef5,0),+
true_score(coef5,0.25),true_score(coef5,0.5),true_score(coef5,0.75),true_score(c
oef5,1),true_score(coef5,1.5),true_score(coef5,2))
true_score_scaled5_bis <- c(true_score(coef11_scaled5_bis,-
2),true_score(coef11_scaled5_bis,-1.5),+
true_score(coef11_scaled5_bis,-1),true_score(coef11_scaled5_bis,-
0.75),true_score(coef11_scaled5_bis,-0.5),true_score(coef11_scaled5_bis,-0.25),+
true_score(coef11_scaled5_bis,0),true_score(coef11_scaled5_bis,0.25),true_scor
e(coef11_scaled5_bis,0.5),+
true_score(coef11_scaled5_bis,0.75),true_score(coef11_scaled5_bis,1),true_scor
e(coef11_scaled5_bis,1.5),true_score(coef11_scaled5_bis,2))
theta1<-c(-2,-1.5,-1,-0.75,-0.5,-0.25,0,0.25,0.5,0.75,1,1.5,2)
plot ( theta1,true_score2005,col="green",main="Test
characteristisc curves 2005-scaled2011",type="l",ylab="Estimated true
score",xlab="Ability scale",ylim=c(0,30),xlim=c(-2,2))
lines ( theta1,true_score_scaled5_bis, col="red")
|
|



