Annexe C : Resultats stochastiques des
series du modèle
C1. Caractéristiques stochastiques de la série
LPIB RH
Evolution de la série LPIBRH et
corrélogramme de la série D(LPIBRH)

1980 1985 1990 1995 2000 2005
LPIB_RH
13.4
13.3
13.2
13.1
13.0
12.9
12.8
Source : Sortie Eviews
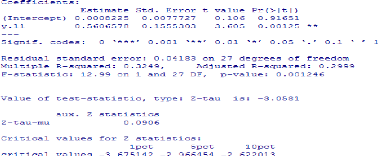
Test ADF réalisé sur logiciel R de la
série LPIBRH

Test PP réalisé sur logiciel R de la
série LPIBRH
. Caractéristiques stochastiques de la série LINV
P
Evolution de la série LINVP et
corrélogramme de la série D(LINVP)

28.6
28.4
28.2
28.0
27.8
27.6
27.4
27.2
LINV_P
1980 1985 1990 1995 2000 2005
Source : sortie Eviews
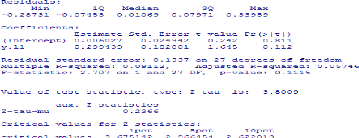
Test ADF sur le logiciel R de la série
LINVP

Test PP sur le logiciel R de la série
LINVP
C3. Caractéristiques stochastiques de la série
LPREST TOT
Evolution de LPRESTTOT et corrélogramme de
D(LPRESTTOT)
|
25.0 24.5 24.0 23.5 23.0 22.5 22.0
|
|
|
|
1980 1985 1990 1995 2000 2005
|
|
|
LPREST_TOT
|
|
Source : sortie Eviews
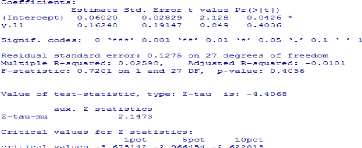
Test ADF réalisé sur logiciel R de la
série LPRESTTOT

Test PP réalisé sur logiciel R de la
série LPRESTTOT
C4. Caractéristiques stochastiques de la série LREC
TOT

25.6
25.2
24.8
24.4
24.0
23.6
23.2
Evolution de LRECTOT et corrélogramme de
D(LRECTOT)
1980 1985 1990 1995 2000 2005
LREC_TOT
Source : Sortie Eviews
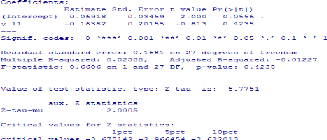
Test ADF
réalisé sur logiciel R de la série LRECTOT

Test PP sur le logiciel R de la série
LRECTOT
IX
Annexe D : Cointégration et Modèle a`
correction d'erreur par la méthode de
Johansen
|
EncadréD1 : La notion de cointégration
Cette notion a étéintroduite dès 1974 par
Engle et Newbold, sous le nom de »spurious regressions», ou
regression fallacieuse, puis formalisée par Engle et Granger en 1987, et
enfin par Johansen en 1991 et 1995.
1. Définition de la cointégration
Deux séries Xt et Yt sont cointégrées si
:
- Xt et Yt sont intégrés d'ordre d ;
- il existe une combinaison linéaire de ces séries
qui soit intégrée d'ordre strictement inférieur a` d,
notéd-b;
2. Modèles a` correction d'erreur (ECM)
On considère deux variables (Xt) et (Yt)
cointégrées d'ordre 1 et soit [â, -1] le vecteur de
cointégration. L'idée des modèles a` correction d'erreur
est de considérer des relations de la forme :
ÄYt = ëÄXt + u[Yt_1 -
âXt_1] + St (1)
Ce qui revient a` décomposer un processus stationnaire
(ÄYt) en une somme de deux processus stationnaires (ÄXt et
(Yt_1 - âXt_1)). De facon plus
générale que (1), ces modèles s'écrivent :
ÄYt = u + Pp i=1 aiÄYt_i + Pq j=0 biÄXt_i +
c[Yt_1 - âXt_1] + çt
o`u les variables interviennent soit a` travers leurs
différences premièressuposées stationnaires, soit a`
travers un terme d'écart a` la cible a` long terme, a` la période
précédentequi doit être stationnaire si la théorie
économique sous-jacente est pertinente.
Source : Charpentier A., Séries temporelles et
applications.
|
EncadréD2 : Cointégration entre plusieurs
variables: L'approche de Johansen
La cointégration selon l'approche de Johansen vient
généraliser celle de Engle et Granger formalisée en 1987.
La procédure de test de cointégration et d'estimation du VECM par
Johansen, se résume en cing étapes.
Etape 1 : Test de stationnaritésur les séries pour
déterminer s'il y a possibilitéde cointégration ou non.
Etape 2 : Si le test de stationnaritémontre que les
séries sont intégrées d'un même ordre, il y a alors
risque de cointégration. On peut envisager l'estimation d'un
modèle VECM. Pour ce faire, on commence par déterminer le nombre
de retards p du modèle VAR(p) a` l'aide des critères
d'information.
Etape 3 : Mise en place du test de Johansen permettant de
connaàýtre le nombre de relations de cointégration.
Etape 4 : Identification des relations de cointégration,
c'est a` dire des relations de long terme entre les variables.
Etape 5 : Estimation du modèle VECM et validation des
tests usuels : Significativitédes coefficients, vérification que
les résidus sont bruits blancs, etc.
Source : Hamisultane H., Modèle a` correction
d'erreur et application.
La détermination du retard optimal p* se
fait au moyen des critères d'information. Elle est préalable a`
l'estimation des paramètres du modèle. La littérature en
propose au moins cinq.
- Le sequential modified likelihood ratio LR = (T-m) {ln
|11p-1| - ln|11p|} ~ ÷2(k2) o`u m est le
nombre de paramètres a` estimer et T la longueur des séries. On
teste l'hypothèse nulle de nullitéconjointe des coefficients.
[ ]
+ 2k2p
- L'Akaike Information Criterion AIC(p) = ln det 11à T
[ ] + 2k2p ln(T )
- Le Schwarz Information Criterion SC(p) = ln det 11à T
[ ] + 2k2p ln(ln(T ))
- L'Hannan-Quinn Information criterion HQ(p) = ln det 11à
T
|
Le Final Prediction Error FPE(p) = det
|
ip
11à hT +kp+1
T +kp-1
|
Pour les quatre derniers critères, le retard optimal est
celui qui minimise le critère d'information.
Source : KEMOE L. (2010), p119
| 


