2.1.7.2. Correlation: Research Questions (c) & (d)
· To which extent can we say that the relationship
between subsequent
scores in translation and prior scores in language is
systematic?
In the previous analysis procedure, the second independent
variable i.e. cultural knowledge was found to have no significant relation to
the students' translation scores. As a result, only one independent variable,
i.e. language scores, remained to be investigated in the second research
question.
This question is concerned with the magnitude of the
relationship existing between one dependent variable and one independent
variable. These variables were both measured at an interval scale. Therefore,
the appropriate statistics procedure was Pearson product-moment. It is
one of the best known techniques used to measure correlation or
association between two variables (Cohen & Manion, 1980). In other
words, it measures the two variables' "tendency to vary consistently"
(Cohen & Manion, 1980, p.126). Consequently, this type of analysis
fits the mentioned research question.
Pearson product-moment correlation coefficient (r) is
a statistical value that indicates the strength and the direction of the
relationship between variables. It can be as high as (+1) when the relationship
is positive. This implies that if one variable increases, so does the other
and
vice versa. When the relationship is negative r can
have a value as high as (-1). This means that when one variable increases, the
other decreases and vice versa. When there is a weak or no relationship between
the variables, the coefficient can be as low as (0). To sum up, the nearer is
r to (1) or to (-1) the stronger is the relationship and vice versa.
If it is preceded by (-), the relationship is negative. Otherwise, it is
positive. (Brown, 1988; Cohen & Manion, 1980).
The research hypotheses this analysis intended to test were the
following:
H 1: There is a systematic positive relationship
between language scores and subsequent translation scores. In other words,
H 1: the higher the prior language scores the
higher the subsequent translation scores.
The null hypothesis was also stated so that it could be tested as
well.
Ho: There is no systematic positive relationship
between prior language scores and subsequent translation scores.
Statistically speaking:
Hi: r > 0
Ho: r = 0
Alpha Decision Level
a < 0.01 directional.
This decision implied that there was only 1% probability (p)
that rejecting the null hypothesis be an error. In other words, it meant that
99% of the correlation represented by r was due to factors other than
chance. "Directional" meant that this study assumed that any relationship
proved to exist between the two variables would be positive.
Calculating the Pearson Coefficient
The formula is as follows:
(IXY) - (j()
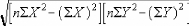
r=
|
r=
|
|
274307,99 - 264094,43
|
|
|
|
1"[298864,57-287049,49 [257294,4825 - 242975,06]
|
r = 10213,56
13007.12
r= 0.79
In order to know if this observed value of Pearson
product-moment correlation coefficient was statistically significant, we
consulted a table of r critical values. With a sample size of 44,
which made a degree of freedom of 42 (df= n-2), r crit = 0.3578. It
was obvious that: r obs > r crit
(0.79 > 0.3578). At p < 0.01 directional, there was only
1% probability that this observed correlation coefficient was due to chance.
This result permitted the rejection of the null hypothesis (Ho: r =
0). And as the relationship was expected to be positive, only one
alternative hypothesis was there (Hi : r > 0). This is, hence,
automatically accepted with only 1% probability that the observed correlation
(r obs =0.79) was due to chance alone.
Once the significance of the observed Pearson correlation
coefficient had been established remained to investigate its
meaningfulness. One way to do so is to examine its magnitude. It is
clear that it reflects a strong relationship since it is much doser to (1),
which indicates perfect correlation, than it is to zero, which indicates no
correlation. Another way to check the outcome's meaningfulness is to calculate
the coefficient of determination (r2). This coefficient
provides us with the percentage of variation of each variable that is due to
the variation of the other i.e. the covariance. It is calculated
simply by squaring the value of the observed r.
r = 0.79
This coefficient implied that 62% of the two variables
correlated with each other, which is quite meaningful. Only 38%, the remaining
of the relationship, could then be explained by other variables.
The following table summarises the process of hypothesis
testing.
Table 3: Summary of the Correlational
Analysis
111:r> 0 Ho: r = 0 n = 44
a < 0.01. Directional
df = 42
r obs= 0.79
r crit = 0.3578
r obs > r crit ( 0.79 > 0.3578)
At p < 0.01 Ho is rejected and Hi accepted.
r2 = 0.62
62% of covariance are accounted for.
The following scatter diagram represents correlation between each
student's translation score and his Baccalaureate language mean.
Figure 2 : Correlation Between Language
Scores and Translation Scores
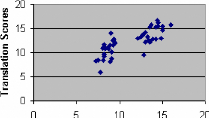
Language Bac Scores
This pattern indicates a strong correlation. The gap in the
middle of the two groups of points represents the absent marks of average
students, who were not included in the sample. It is clear that the points of
the whole population would form a linear shape that goes up toward the right.
This is a typical shape for a strong positive correlation. This is supported by
the assumption that correlations ranging from 0.65 to over 0.85 "make
possible group predictions" ( Cohen & Manion, 1980, pp. 138-9). This
means that, with this strong correlation, it is possible to predict a student's
translation score from his language score, which suggests that the relationship
is systematic.
Figure 5: Overall Students' Performance
on the English General Culture Test
|
|
q Correct
1=1 Partially Correct
q No Answer
q Wrong
|
|
1 2 3 4 5 6
Question Numbers
|
|
Qualitative description
Question one is correctly answered by 56% of the students. What
is worth mentioning is that most of them don't write the correct spelling of
film titles. They simply transcribe the words as they heard them. The least we
can deduce from this is the lack of interest in accurate information about the
movie. Partially correct answers reflected, for example, confusion between
titles or between British and American actors or movies.
Second World War is one of the main subjects of the History
program of third year of secondary school. Winston Churchill is, therefore,
frequently mentioned in the course. This is not reflected in the high
percentage of wrong answers: 38% and "no answer": 27%. To
illustrate this better, here are some answer examples: Churchill
is "a German soldier"," an ancient president of the USA" ,"the commandant
of the Americans during the Cold War".
The correct answers of the third question (38%) were all a
literal translation of the Arabic equivalent of "World Trade Centre", which is
quite comprehensible. The partially correct answers (11%) included the
"Pentagon". The wrong answers (11%) and the "no answer" cases (38%) seemed to
reflect a considerable disinterest in what's happening in the world.
As to question four, only two students (6%) wrote "Times".
We considered it as a partially correct answer because we assumed that it
was just a failure to write "Thames" correctly. The rest either did not answer
(66%), or answered wrongly (26%). "The Amazon" ,"the Danube" and the
"Rayne" are examples of wrong answers.
Question five concerned the British currency. Not more than 23%
answered correctly --some in Arabic. The rest either did not answer at all
(38%), or answered incorrectly (38%). These are some wrong answers:
"Lira"," Oro" ,"Dollar" , and "American Dollar".
The last question was about American political parties. "No
answer" cases represented 66% of the sample, partially correct answers, 11% and
correct, 6%. This was unexpected because, as stated earlier, the presidential
campaign was the first headline in every news edition of the
day. The two most important American Political Parties were
mentioned each time. In addition, what characterised an important number of
wrong answers, which represented 16% of the sample, is that students did not
understand the question at all. Some answers were: "war and race toward
weapons","Dollar and petroP' ,"Washington and New York".
| 


