|
ENSEIGNEMENT SUPERIEUR ET UNIVERSITAIRE
INSTITUT SUPERIEUR
PEDAGOGIQUE DE KAZIBA
I.S.P/KAZIBA

SECTION DES SCIENCES EXACTES
DÉPARTEMENT DE
MATHÉMATIQUE-PHYSIQUE
Prédiction de Durée De Séjour
hospitalier
en Gynécologie basée sur le Machine
Learning : Cas de quelques hôpitaux au
Sud-Kivu
Présenté par : CUBAKA ZAHINDA
René
Mémoire présenté et défendu pour
l'obtention du diplôme de Licence en Pédagogie Appliquée
Option : Mathématique-Physique
Directeur : Prof. Dr. ZIHINDULA MUSHENGEZI
Elie
Encadreur : CT. AMBO AMANDURE
Jean-Médard
ANNéE ACADéMIQUE : 2022-2023
Epigraphe
Change is the end result of all true learning
-- Leo Buscaglia Écrivain, professeur
d'éducation
Research is to see what everybody else has seen, and to think
what nobody else has thought -- Albert szent-Györgyi
Prix Nobel de physiologie ou médecine
I
René CUBAKA ZAHINDA
Dédicace
A toute personne vouée du bon sens dans ce monde
cassé A tous les amoureux de l'Intelligence Artificielle
Je dédie ce travail !!!
II
René CUBAKA ZAHINDA
III
Remerciements
Le présent travail n'est pas seulement le fruit d'un
labeur individuel, mais aussi celui
de plusieurs personnes que je tiens à remercier. Parmi
les personnes qui ont collaboré à la
réalisation de ce travail en offrant soit un support
moral, soit un support technique je
pense particulièrement à ma famille, à
mes amis et à mes collègues.
Sans doute, des personnes auront été,
involontairement oubliées dans l'énumération
suivante, je tiens en premier lieu à remercier mon Dieu
tout puissant, le créateur de
l'univers.
J'exprime toute ma reconnaissance à l'équipe de
direction de ce travail notamment le
Prof. Dr. ELIE ZIHINDULA et Msc. AMBO
AMANDURE.
Je tiens à remercier ma famille, en particulier mes
parents ZAHINDA KASHOSHO Faustin
et sa dulcinée NSIMIRE M'MUSOBO Adolphine
qui m'ont soutenu à réaliser mes études et
qui m'ont toujours encouragé dans mon destin. Je leurs
exprime toute ma reconnaissance.
Mes remerciements sont adressés au CT. BASHIGE
NTUGA Innocent et le Professeur
Balagizi Karhagomba Innocent pour leur appuie
matériel, moral durant notre cursus
de 5 ans à l'ISP Kaziba.
A toutes les autorités académiques et
administratives de l'Institut Supérieur Pédagogique
de Kaziba, plus particulièrement celles de la section
des sciences exactes.
A toutes les autorités scolaires de l'Institut Saint
Jean-Paul II Bugoye et de l'EP
Karhala, trouvez ici la plus profonde considération
à votre endroit.
Mes sincères et profondes gratitudes nous
assujettissent à remercier le Doctorant
ZIRHUMANANA BALIKE Dieudonné, NGANIZA
LUGERERO Bernadette et Msc. AGISHA Albert
pour les multiples conseils à mon égard dans
tout le cursus de ma formation.
Aux Réverendes Soeurs de la Paroisse de Burhinyi et aux
Réverends Prêtres de la
Congrégation des Franciscains de la paroisse de
Burhinyi, plus précisement le Père Jean
Claude.
A tous mes formateurs depuis l'école primaire
jusqu'à ce niveau, dans le cadre scientifique, spirituel, ... trouvez
ici, l'expression de ma profonde gratitude. Vous avez fait de moi ce que je
suis.
A mes frères, soeurs, cousins, cousines, neveux et
nièces : BISIMWA ZAHINDA, BULONZA ZAHINDA, KULONDWA ZAHINDA, MUSAFIRI
ZAHINDA, RHUGWASANYE ZAHINDA, FADHILI ZAHINDA, ZIRUKA ZAHINDA, CHRISTIAN
LUSHUHA, MUTABESHA MIHIGO, ...
A tous mes beaux-frères et belles-soeurs : NZIGIRE
M'MUSHOSHERE, OLINAMUNGU M'MUTABESHA, NEEMA KAGAYO, IZUBA MASHEGEYE, BAHATI
ONESPH0RE trouvez ici l'expression de ma profonde gratitude.
A mes amis, mes camarades étudiants du département
de maths et ceux de l'ISP KAZIBA en général : BIJIRAMUNGU BEKA,
MUSHAGALUSA BAHOYA, BWIRHONDE ZIHINDULA, CHOMBO NAMIKERE, ALEXANDRE BASHUSHANA,
BAHATI BASHIMBE, VOLONTE MINEKE, MUNGU WAMPAGA Innocent, ... trouvez ici
l'expression de ma gratitude.
A cette personne, laquelle la destinée nous unira et que
j'aimerai de tout mon coeur, j'espère qu'elle existe, elle trouvera,
dans la copie de ce travail mes sincères remerciements.
IV
René CUBAKA ZAHINDA
1
Introduction générale
Au cours de ces dernières années, la nouvelle
technologie est en train de prendre le devant dans la prise de décision
dans plusieurs domaines. Dans le domaine hospitalier, selon [18] et [19] une
rigoureuse collaboration entre les chercheurs universitaires et les agents de
santé dans plusieurs contextes est importante. Cette collaboration
cherche à rassembler les efforts de chaque partie pour améliorer
les performances d'efficacité des services des établissements de
soins. Avec l'apparition de la pandémie à Covid19 en 2019,
où le monde a fait face à un cas plus particulier du galopage du
taux d'hospitalisation dans plusieurs hopitaux du monde, les gestionnaires de
santé seraient peut-être confrontés à un
dilèmme : d'une part, du nombre de personnel soignant qui doit
assumer la permanance, et du nombre de patients pouvant être
réadmit dans une unité de soins de santé, ou alors, d'une
éventuelle sortie d'un patient x à l'hopital d'autre part.
Le cas concret est celui de la France car selon [18], elle a atteint le
nombre d'hospitalisation de 7,1 millions durant l'an 2019.
La Durée de Séjour Hospitalier (DDS) constitue
un des indicateurs de base d'évaluation de la pertinence d'un
hôpital. Cette durée représente l'intervalle de temps entre
l'admission du patient dans un service (ou hôpital) et sa sortie du
service (ou hôpital). Elle est donc le parcours suivi lors du
séjour [18]. Pendant que plusieurs services sanitaires au monde
s'approprient les nouvelles technologies de l'information et de la
communication pour rendre meilleures et fiables leurs structures sanitaires. Il
s'oberve jusque là, dans notre pays la non considération de la
nouvelle technologie de l'Information et de la Communication expliquée
par le fait que les institutions sanitaires ne sont pas
numérisées.
2
Les établissements de soin sont des systèmes
à plusieurs dimensions car, ils doivent gérer concomitamment la
pertinance des personnels soignants, de la gestion des malades, etc. En RDC
plus particulièrement au Sud-Kivu, le service de gynécologie
réçoit un nombre important de patientes car, des mamans en
processus de procréation, des cas de règles douloureuses, des
violences sexuelles, ... C'est ainsi que, dans ce travail, nous allons plus
nous intérésset à la Durée de Séjour du
service de Gynécologie dans certains hopitaux de la province du
Sud-Kivu.
Face aux besoins sanitaires croissants de la population,
à la surcharge du travail des
professionnels de santé et à l'allongement des
délais d'attente des patients, l'estimation de
la DDS doit être établie au moment de l'admission du
patient, suivie et la mise à jour
tout au long du séjour hospitalier. La prédiction
de la DDS contribue à :
- La planification des activités de soins des services
médicaux.
- L'amélioration des conditions organisationnelles de
l'hôpital.
- L'analyse du taux journalier d'admission des patients et le
suivi de leur séjour.
- La gestion des lits hospitaliers.
- L'optimisation des ressources matérielles et humaines de
l'hôpital.
Un des avantages les plus importants de la prédiction de
la DDS est la maîtrise des
contraintes budgétaires à la quelle les
hôpitaux sont tenus [19].
La prédiction de la durée de séjour
hospitalier, est une discipline complexe dont nous ne sommes pas les
précursseurs. C'est comme par exemple, MEKHALDI RASHDA NAILA
dans sa thèse de doctorant présentée et soutenue
le 27 janvier 2022, il fait des algorithmes pour la prédiction de la DDS
dans plusieurs unités de soins, notamment dans les services suivants :
le service de cardiologie, le service de médecine polyvalente, le
service de pédiatrie et le service de néonatologie. A chaque
fois, il faisait deux algorithmes l'un en apprentissage supervisé et
l'autre en apprentissage non supervisé et faire une comparaison et faire
une étude de savoir quel algorithme prédit mieux que l'autre. Il
génère deux modèles, l'un statique, le modèle qui
sera formulé au moment de l'admission du patient; et l'autre
séquentiel, qui intègre les données disponibles pendant le
séjour du patient.
3
Etant donné que la durée de séjour
hospitalier (DDS) joue un grand rôle dans la
définition d'un hopital fiable, la rédaction de ce papier est
axée sur le problème de la modélisation de la durée
de séjour hospitalier basée sur quelques techniques de Machine
Learning. Nous tâcherons de répondre à la question suivante
: Comment pouvons-nous faire un algorthme de préduction de durée
de séjour hospitalier (DDS) dans l'unité médicale de la
gynécologie et qu'il puisse prédire à quelques erreurs
près cette DDS ?
La prédiction de la durée de séjour
hospitalier sérait possible grâce aux données des hopitaux
se rapportant sur les informations des patients et voir même depuis
l'admission de ce dernier. Cet algorithme approximerait la population, au cas
où elle serait associée d'une technique et des algorithmes de
l'apprentissage automatique de l'intelligence artificielle.
Pour répondre d'une manière claire et
précise à notre problématique de
recherche, il nous sera impératif de définir deux algorithmes en
machine learning. L'un en apprentissage supérvisé et l'autre en
apprentissage non supérvisé; et à chaque
instant, étudier la pertinance de l'un ou l'autre. Ces algorithmes
seront possibles, après avoir étudié les
différentes causes d'un séjour quelconque dans une unité
de gynécologie, spécialement dans certainss hôpitaux du
Sud-Kivu. Mais aussi, une recolte de données qui nous conduira
à la méthode documentaire nous sera utile dans
la construction de l'algorithme de l'apprentissage supervisé.
Ce travail est constitué de quatres chapitres
bornés par l'introduction générale et la conclusion
générale. Le premier chapitre porte sur les
systèmes d'informations hospitaliers où nous essayons de
faire un apperçu sur les données d'hospitalisation et leur
origines ainsi que de la propriété de ces dernières. Dans
ce dernier, nous parlons aussi de la durée de séjour hospitalier
et des facteurs infuençant cette dernière. Le deuxième
chapitre parle des modèles de prédiction de Machine Learning.
Dans ce dernier, nous différencions les différentes formes
d'apprendissange avant de parler de quelques modèles de Machine Learning
(oui, quelques modèles car notre liste n'est pas exaustive) avant de
chutter par la pertinence d'un modèle de Machine Learning car, bien
évidement différentes modèles prédisent
différemment. Ce qui veut dire qu'il y a des erreurs qui peuvent surgir.
Ainsi donc, le meilleur modèle de prédiction sera celui qui
prédit à moins d'erreurs. Le troisième
4
chapitre est celui consacré à la
présentation des données que nous allons utiliser. Ces
données proviennent de plusieurs structures sanitaires de la province
car, bien évidemment, nous n'avons pas trouvé des données
pour toute la province stockées en un seul endroit. Et finalement, le
quatrième et dernier chapitre est celui où nous allons construire
nos différents modèles de machine Learning pour prédire le
séjour hospitalier dans l'unité médicale de la
gynécologie en province du Sud-Kivu. Pour ce faire, nous allons
constituer des modèles tantôt en apprentissage supervisé,
tantôt en apprentissage non supervisé et à chaque
étape nous allons nous rassurer de la pertinence de chaque modèle
pour en fin finir par une meilleure selection du modèle à
considérer.
5
Chapitre 1
Les systèmes d'informations
hospitaliers et la gestion hospitalière
1.1 Introduction
Actuellement, les établissements de soins font face
à une forte croissante du nombre de cas d'hospitalisation, et ceci,
c'est depuis l'apparution de la pandémie à COVID-19 où le
nombre d'hospitalisation a accru dans plusieurs pays du monde [7]. Pour ce
faire, il est donc question pour les services de santé,
d'améliorer leurs conditions de fonctionnement par une bonne gestion des
structures sanitaires et ainsi, parvenir à consolider la qualité
de soin pour permettre les entrées et sorties au sein de n'importe
quelle unité médicale. Ceci sera alors effectif, par le fait de
bien conserver les informations médicales, pour savoir administrer un
médicament à un quelconque patient et ne pas le faire
fortuitement.
D'une manière plus générale, les
Systèmes d'Informations Hospitaliers (SIH) s'occupent de la gestion de
l'ensemble des informations, de leurs règles d'utilisation et de leur
circulation. De plus, ils font face au stockage et au traitement des
données pour répondre aux besoins quotidiens des
établissements de soins ([11] et[19]).
Les performances et la qualité des services de soins
reposent sur la qualité et la quantité des informations
collectées dans les SIH. La DDS constitue un des indicateurs
d'évaluation le plus utilisé et sa prédiction basée
sur les données disponibles dans les SIH a été au centre
d'un grand nombre de travaux de recherche. Le problème de la
prédiction des durées
6
de séjours hospitaliers a été
abordé sous différents angles dans des recherches
précédentes. [19].
Le but de ce chapitre est de vouloir mettre à la
lumière du soleil certaines informations sur le Système
d'Information Hospitalier en partant de la sorte : tout d'abord nous allons
décrire les systèmes d'Information Hospitalier d'une
manière générale en parlant de la sources de ces
informations ainsi que des propriétés y afferantes. En suite,
nous allons parler de la durée de séjour hospitalier et les
facteurs influençant cette dernière pour enfin chutter avec le
rôle des machines learning dans tout ceci.
1.2 Les systèmes d'informations hospitaliers 1.2.1
Terminologie
Définition 1.1 Un Système
d'Information Hospitalier (SIH) est un Système
informatique destiné à faciliter la gestion de l'ensemble des
informations médicales et administratives d'un hôpital. Selon
[19], on appelle système d'information l'ensemble des
outils matériels, des logiciels et des réseaux de
télécommunications utilisés pour recueillir, créer
et distribuer des données utiles dans des organisations.
En particulier, un Système d'Informations Hospitalier
(SIH) désigne un système conçu pour gérer
l'ensemble des données médicales et administratives d'un
hôpital. Il se constitue d'un groupe d'éléments en
communication qui rassemblent, traitent et fournissent les informations
nécessaires à son activité.
Définition 1.2 Un Système
d'information de l'hôpital est un ensemble des
éléments en interaction ayant pour objectif de rassembler,
traiter et fournir les informations nécessaires à son
activité.
Définition 1.3 Un Système
d'Information de Santé (SIS) est un Système
d'information global, regroupant tous les types d'acteurs et ressources de
santé.
1.2.2 Type d'informations
Dans un milieu hospitalier, plusieurs informations sont
récueillies, tantôt lors de l'admission du patient et au fur et
à mesure que le patient augmente son séjour à l'hopital.
On a donc besoin souvent des informations antérieures du patient et
quelques informations administratives. Selon [19], ces informations comprennent
les données démographiques sur les patients, les
étapes de son suivi, les complications, les médicaments, les
signes vitaux, les antécédents médicaux, les
immunisations, les données de laboratoire et les rapports de radiologie
[HIM]. Les informations administratives concernent la gestion
opérationnelle d'un hôpital en matière de soins de
santé. Elles englobent les informations de la gestion des patients
(parcours, facturation, actes médicaux), la gestion de la finance et de
la comptabilité (budget, ressources matérielles, achats) et la
gestion des ressources humaines (affectations, planning, payement).
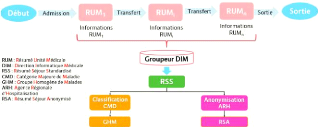
Le SIH est scindé en trois sous-systèmes comme
illustre la figure 1.1 ([11], [18] et[19] )
:

7
FIGURE 1.1 - Composantes des Systèmes d'Informations
Hospitaliers [11]
8
Le sous-système de production des
soins
Ce volet s'occupe de l'administration des données
patients, les unités de soins, la communication entre ces unités
et la gestion de la recherche et de l'enseignement médicaux. Il contient
toutes les données liées au patient comme par exemple : le
diagnostic médical, les prescriptions et la réalisation des actes
médicaux, l'édition des comptes rendus et les
résumés de dossier sont présentes au sein de ce
sous-système.
Le sous-système d'information
logistique
L'objectif est donc de mieux organiser les activités et
les structurer afin d'assurer une meilleure qualité de soins des
patients. Le sous-système d'information logistique permet de
gérer les différents ressources matérielles, humaines,
physiques et financières de l'hôpital. Il englobe la gestion de
stocks et des approvisionnements, la gestion des locaux, la gestion des
facturations et des commandes, la gestion des lits d'hospitalisation et de
soins ainsi que les archives et la documentation des établissements de
soins.
Le sous-système de pilotage
Il veille à la prise en charge de la gestion
médicoéconomique de l'hôpital. Il concerne la
qualité des soins et la gestion des risques. De plus, il
s'intéresse à l'allocation budgétaire des
différentes unités de soins .
Ces sous-systèmes sont souvent en interaction afin
d'assurer la continuité des services de soins, améliorer leur
qualité et gérer les ressources et les contraintes
budgétaires. Compte tenu du grand volume des données des SIH,
divers formats de stockage sont apparus. Ces données proviennent de
multiples sources et font l'objet de plusieurs études dans le domaine
médical. Quoi que ces données existent, elles proviennent de
quelque part effectivement. Dans la partie suivante, nous allons parler des
différentes sources des données hospitalières.
9
1.3 Sources des données des SIH
Les progrès technologiques et les progrès des
processus de traitement des données ont permis une augmentation
exponentielle de la quantité des données collectées dans
le domaine de la santé. Le volume des données contenues dans les
SIH ne cessent de croître. En fonction de leur type, les données
sont recueillies à partir de différentes sources. Ces sources de
données sont nombreuses et diffèrent selon le type de collecte,
le format de représentation et la nature des informations. Les
principales sources des données médicales sont : les dossiers
médicaux, les enquêtes auprès des patients et les
données administratives utilisées pour payer les factures ou
gérer les soins ([20],[19]). Dans ce qui suit, nous détaillons
les sources de données .
1.3.1 Dossier médical du patient
Il comporte les données démographiques du
patient acquises au moment de son admission : sa date de naissance, son
adresse, son statut marital et son sexe. Il contient également les
données liées à son état de santé comme les
résultats des analyses biologiques et les transcriptions
médicales, les résultats d'examens radiologiques, le diagnostic
médical, les antécédents médicaux et les rapports
textuels cliniques.
1.3.2 Les données administratives
Elles peuvent inclure les données des facturations et
des remboursements des séjours hospitaliers des patients. Les
données de facturation sont souvent liées aux motifs
d'hospitalisation représentés à l'aide de la Codification
Internationale des Maladies (CIM) et aux procédures que le patient a
subi au cours de son séjour. Les données administratives
comportent aussi des informations sur le type de l'unité
médicale, l'admission du patient, le nombre d'unités dans
lesquelles le patient est passé (ou le nombre de jours passés
dans chaque unité).
10
1.3.3 Les données issues des enquêtes et de
la recherche clinique
Une source importante des données médicales est
apparue avec l'explosion de l'utilisation d'internet comme moyen de
communication. Les données de santé peuvent provenir des
échanges des patients sur les réseaux sociaux et des recherches
effectuées sur le web. Elles proviennent également des
études cliniques réalisées par les professionnels de
santé, les scientifiques et les industriels.
1.4 Propriétés des données
médicales
"S'agissant des données de santé,
informations éminemment sensibles, la tentation est exacerbée de
se prévaloir d'un droit de propriété pour se garantir une
meilleure protection contre tout usage préjudiciable" N.
MALLET-POUJOL cité dans [9].
Vu que les données médicales doivent être
protégées comme vu dans la section 1.3, il existe des
données à caractère privé. Des lois pour palier
à un quelconque dérapage des données médicales sont
aussi de structe application.
Les données médicales sont à conserver
jalousement non seulement du fait qu'elles sont sensibles, mais aussi car elles
sont utilisées par des chercheurs, les hopitaux eux-mêmes, ... ces
dernières nous aident même à l'organisation des
établissements de soins, l'identification de profils homogènes de
patients, le suivi des parcours des patients et la recherche de leur diagnostic
médical. Cependant, avant d'utiliser ces données, il est
primordial de procéder à leur annotation, de les intégrer
et de les pré-renseigner de manière appropriée afin de
faciliter leur compréhension. La compréhension et la manipulation
des données médicales se heurtent à des défis
liés à leur complexité, la richesse des informations aussi
qu'à des contraintes de confidentialité [19]. Il existe donc des
garentis juridiques pour n'importe quel dérapage de la part des
données médicales [20].
La figure 1.2 nous illustre les différentes
propriétés des données médicales ainsi que leurs
sources. Particulièrement, les données que nous avons
utilisées dans l'analyse de ce présent travail ne sont pas loin
de respecter ces critères ici.
Les sous-sections suiventes nous servirons de détail
pour les propriétés du SIH en paraphrasant [19].

11
FIGURE 1.2 - Données médicales : sources et
propriétés [19]
1.4.1 Confidentialité
Selon l'article 4 du Règlement Général
sur la Protection des Données (RGPD) de l'Union Européenne :
« les données relatives à la santé physique ou
mentale d'une personne physique, y compris la prestation de services de soins
de santé, qui révèlent des informations sur l'état
de santé de cette personne » sont définies comme
données à caractère personnel. Ces donnes doivent donc
être protégées et une politique et une démarche de
sécurité de ces données doivent être définies
pour les protéger. Si la protection des données est un enjeu
majeur, d'autres risques liés au matériel et à
l'infrastructure informatique sont également des points d'attention
récurrents. Les données médicales sont exploitées
dans plusieurs recherches et études académiques et industrielles.
Elles peuvent être utilisées dans la conception des
systèmes d'aide à la décision du domaine médical,
l'amélioration des prestations de soins de santé, l'optimisation
des ressources matérielles et humaines des hôpitaux. Un processus
d'anonymisation ou de pseudo-anonymisation des données est donc utile
avant toute manipulation. L'anonymisation des données médicales
est définie comme la suppression de tout caractère identifiant un
ensemble de données d'une
12
manière irréversible. Toutes les informations
directement ou indirectement identifiables sont supprimées ou
modifiées afin d'empêcher toute ré-identification des
personnes. Quant à la pseudo-anonymisation, elle permet le retour
à l'information originale en cas de besoin particulier. Elle consiste
à remplacer les données à caractère personnel par
des pseudonymes. Cette technique est réversible et permet donc la
ré-identification ou l'étude de corrélations entre les
informations codifiées en cas de besoin particulier. De cette
manière, la réutilisation des données médicales est
possible ce qui suscite un intérêt et une demande croissante.
1.4.2 Données incrémentales
A l'aire du Big data, les données médicales ne
sont plus à ignorer. L'analyse des données massives est un
domaine en pleine croissance qui peut fournir des informations utiles dans le
domaine des soins de santé. Dans les systèmes d'aide à la
décision ou de prédiction, les éléments
collectés sont insérés dès leur
disponibilité dans le modèle comme des évènements
successifs. Un exemple qui caractérise cette particularité est de
modéliser le séjour hospitalier par un processus de trois
étapes : moment d'admission du patient, le séjour
hospitalier et la sortie du patient.
Lors de l'admission du (de la) patient(e), des informations
démographiques comme l'âge, l'adresse, le genre et l'état
civil sont acquises ainsi que des informations administratives comme le type
d'admission au service concerné, le motif d'hospitalisation et
l'unité médicale dans laquelle le patient est admis.
Au cours du séjour hospitalier, d'autres informations
médicales et administratives s'ajoutent. Par exemple les actes
médicaux réalisés pour le patient, les complications
médicales et les transferts entre unités médicales.
Et au finish, à la sortie du (de la) patient(e), les
rapports médicaux effectués par les médecins ou les
infirmiers sont élaborés. La régularisation de la facture,
la durée de séjour du patient et son mode de sortie sont
prélevés.
13
1.4.3
Hétérogénéité
De nos jours, il est nécessaire d'utiliser conjointement
des données provenant de systèmes d'information qui utilisent
différentes sources de connaissances comme par exemple, les rapports
médicaux textuels et les résultats d'imagerie médicale
pour l'enregistrement des données et les utiliser dans la
résolution de nombreux problèmes dans le domaine médical.
L'exploration de ces données dites hétérogènes pour
extraire des connaissances est un processus fastidieux imposant des contraintes
opérationnelles importantes. Les données
hétérogènes sont des données dont les types et les
formats présentent une grande variabilité. Il existe
principalement 4 types d'hétérogénéité :
- L'hétérogénéité
syntaxique : Elle se produit lorsque deux sources de données ne sont pas
exprimées dans le même langage.
- L'hétérogénéité
sémantique ou conceptuelle : Elle désigne les différences
de modélisation d'un même domaine d'intérêt.
- L'hétérogénéité
terminologique : Elle désigne les variations de noms lorsqu'on se
réfère aux mêmes entités à partir de
différentes sources de données.
- L'hétérogénéité
pragmatique : Elle correspond à des interprétations
différentes des entités.
De plus, nous rajoutons
l'hétérogénéité par type de données.
Elle réside dans ce cas dans la présence de données
quantitatives ou dites numériques et qualitatives ou dites
catégorielles. Les données quantitatives sont celles qui peuvent
être comptées ou comparées sur une échelle
numérique. On distingue alors les données quantitatives continues
et discrètes. Pour le type qualitatif, on sépare le qualitatif
nominal et le qualitatif ordinal. Par exemple l'âge d'un patient est une
donnée numérique discrète, sa taille est une donnée
numérique continue, son genre est une donnée catégorielle
nominale et son niveau d'étude est une donnée catégorielle
ordinale. Nous définissons aussi le type de donnée
catégorielle multivaluée comme par exemple les diagnostics
médicaux si le patient possède plusieurs diagnostics. Le format
des données médicales peut être structuré ou non
structuré. Le format des données structurées est
organisé et formaté. Par conséquent, il est facile de
saisir, rechercher et manipuler les données structurées. A
l'inverse, les données non structurées comme par exemple les
rapports médicaux en format textuel ou les images de
14
radiologie médicale, souvent classées comme des
données qualitatives, sont plus difficiles à traiter et à
analyser. Un processus d'intégration des données
hétérogènes est crucial pour permettre aux utilisateurs de
définir leurs requêtes sans connaître leurs sources et
donner une vue uniforme de l'ensemble de ces sources.
1.4.4 Complexité
La grande quantité d'informations
générées par les systèmes d'informations de
santé, la variété des sources des données
médicales et l'hétérogénéité des
données rendent leur traitement et leur analyse plus difficile et plus
complexe soulevant ainsi plusieurs défis. Parmi ces défis, nous
retrouvons la présence de plusieurs variables ce qui engendre une grande
dimension. De plus, ces données sont souvent incomplètes et
contiennent des variables fortement corrélées entre elles
résultant de la redondance de l'information. Les données
médicales présentent également d'autres problèmes
comme la présence des données aberrantes ou des erreurs dans les
informations enregistrées. Ces problèmes imposent des
méthodes de pré-traitement des données avant de les
utiliser afin de rendre leur exploitation plus facile et fiable. La
complexité des données médicales rend primordiale
l'implication de l'expertise médicale dans leur exploitation par les
utilisateurs afin de valider, interpréter et mieux valoriser leur
contenu.
1.5 Durée De Séjour hospitalier
Définition 1.4 La Durée de
Séjour Hospitalier peut être définie
comme un séjour pendant lequel le patient peut être
hospitalisé dans plusieurs services, que l'on appelle actuellement des "
unités médicales "[4].
La figure 1.3 explique en quelques sortes la durée de
séjour hospitalier dans un hopital en passant par une ou plusieurs
unités médicales.
Face à un accroissement sans précédent du
nombre de cas d'hospitalisation, l'apparution des nouvelles maladies et ou
épidémies, la famine en RDC, les institutions sanitaires font
face à un nombre accru des patients pouvant même dépasser
la capacité d'accueil de ces derniers.
15
FIGURE 1.3 - Évaluation des systèmes de
santé : DDS [19]
Pour faire face à tout ceci, la prédiction de la
durée de séjour hospitalier est un facteur clé dans un
service de santé, car contribue à la planification et à
l'organisation des activités de soins, ainsi qu'au management des lits
réduisant leur occupation inutile [19], mais aussi savoir gérer
le personnel soignant et ouvrier pour l'assurance des malades. Chaque structure
sanitaire est donc confrontée à faire face à un
système de santé sans pareil pour permettre une bonne
compétitivité au marché des hopitaux.
Selon [19], il existe trois facteurs importants pour
définir la pertinance d'un système de santé, on peut citer
: le taux de mortalité, le nombre de réadmissions et
la durée de séjour hospitalier (DDS) .
Quant à l'unité de mesure de la DDS, elle est
mesurée en journée. Cette définition peut changer
constamment dans d'autres contextes. Dans les services d'urgence et
ambulatoire, l'admission et la sortie du patient sont réalisées
dans la même journée. De ce fait, la DDS est égale à
0 jour. La valeur de la DDS est alors calculée en nombre d'heures et
peut s'étaler sur 24 heures au maximum. Plusieurs travaux ont
étudié les flux des patients en service d'urgence en se basant
sur l'estimation du nombre d'heures du séjour du patient dans ce
service. Nous distinguons donc deux définitions majeures de la DDS : la
DDS dans des unités médicales dites « programmées
» calculée en nombre de jours passés dans ces unités
et la DDS dans des services dits « non programmés »
calculée en nombre d'heures. Dans ces deux cas, la DDS est
quantifiée par une valeur numérique discrète.
Ce qui nous permet d'affirmer qu'une Durée de
Séjour Hospitalier au délà de la moyenne provoquerait des
coûts matériels que financiers suplémentaires à
l'hopital. C'est ainsi alors
16
que la prédiction de DDS dans un service sanitaire est
d'une importance capitale pour palier à ce problème.
1.6 Facteurs influençant la DDS
La durée de séjour hospitalieur est souvent
dû à plusieurs facteurs qui sont tantôt d'origine du patient
lui-même ( c'est à dire de son âge, de sa maladie, de son
état psychique, ...) ou d'un autre facteurs exterieur. D'où alors
la durée de séjour hospitalier dépend aussi de
l'Unité médicale dans laquelle le patient est admis ([19]).
Parmi les facteurs influançant la DDS, on peut citer
([18]) :
1. Les facteurs démographiques :
l'âge, le genre et la situation familiale du patient;
2. L'historique médicale du patient
3. Les mesures des signes vitaux et des résultats
du laboratoire,
4. Etc.
Ce travail étant borné dans le service de
Gynécologie, à part les facteurs vus ci-haut, les hopitaux aussi
jouent un rôle dans la prédiction de la DDS. C'est comme le cas
par exemple de la Gynécologie obstétrique où, pour un
accouchement eutocique la DDS va de 2 à 5 jours selon les hopitaux
consultés et pour un accouchement distocique, elle va de 4 à 9
jours.
1.7 Que vient faire l'intelligence artificielle dans tous
ça ?
L'intelligence artificielle (Artificial intelligence en
anglais) englobe plusieurs techniques comme par exemple l'apprentissage
automatique (Machine Learning), la vision par ordinateur, le raisonnement, la
représentation des connaissances et la fouille de données. Ces
techniques font partie des techniques les plus utilisées de nos jours
dans les différents domaines de recherche. Les applications de l'IA
s'étendent à des domaines que l'on pensait auparavant
réservés aux experts humains des données
numérisées, d'infrastructure informatique, d'amélioration
de la puissance et de la capacité de stockage des ordinateurs,
17
le domaine médical est identifié comme l'un des
domaines les plus promoteurs de l'IA. L'apprentissage automatique ou le Machine
Learning (ML) en anglais, est une technique de l'IA largement employée
dans les recherches cliniques. Elle est apparue dans les années
1950 avec Alan Turing quand il a écrit
un article sur « Computing machinery and intelligence » dans
lequel il explique que pour démontrer l'intelligence d'une machine, elle
doit être capable d'exécuter des tâches humaines de telle
sorte que personne ne peut la différencier de celle d'un être
humain.
La figure 1.4 illustre les principales techniques de
l'Intelligence Artificielle et leurs applications [19].

FIGURE 1.4 - Techniques de l'Intelligence Artificielle et leurs
applications [19]
L'apprentissage automatique consiste à doter les machines
de capacités d'analyse, d'apprentissage et de
généralisation à partir des données. L'objectif est
de résoudre des problèmes pour lesquels il aurait
été difficile de trouver une solution avec des approches
informatiques traditionnelles. Il existe quatre types d'apprentissage
automatique : l'apprentissage supervisé, l'apprentissage
non-supervisé, l'apprentissage semi-supervisé et l'apprentissage
par renforcement. En médecine, selon les nouvelles techniques de l'IA,
plusieurs solutions sont en train de voir le jour comme c'est le cas par
exemple de la prédiction du cancer, dans la prédiction d'une
quelconque réadmission à l'hopital [13], ...
Comme nous pouvons le constanter, la Nouvelle Technologie de
l'Information et de la Communication (NTIC) est au service de toute la
communauté et ceci par l'apparution de l'Intelligence Artificielle
où les machines prennent certaines décisions que prennaient
18
les humains dans l'ancien temps. Faudra-t-il que ceci soit
possible sans nous interroger comment ça marche ? La mise en place d'un
Algorithme de Machine Learning se fait le plus souvent par le canal de certains
algorithmes (Modèles de prédiction). La partie suivante sera
concencrée à certains modèles de machine learning qui nous
servirons dans les deux derniers chapitres.
19
Chapitre 2
Modèles de prédiction en Machine
Learning
2.1 Introduction
La durée de séjour hospitalier est sans doute un
facteur qui indique en quelques sortes la force et la viabilité d'un
système hospitalier. Cette prédiction a vu son essort depuis que
l'Intelligence Artificielle, spéciallement les Machines Learning sont
entrain de s'imposer dans la prise de décision dans presque tous les
domaines de la vie. Parfois, on ne sait pas distinguer ce qui est
intélligence artificielle, apprentissage automatique et
apprentissage profond.
Le but de ce chapitre est tout d'abord de présenter le
machine learning, son historique et ses champs d'application, en suite nous
mettrons au courant les differents modèles de prédiction de
machine learning, ainsi que la définition d'un modèle pertinant
et en fin, comprendre le rôle de ces modèles dans la
prédiction de DDS.
2.2 Intelligence Artificielle, Machine Learning et Apprentissage
Profond
Premièrement, nous devons définir clairement ce
dont nous parlons lorsqu'il est question d'IA. Que sont l'intelligence
artificielle, l'apprentissage automatique et l'apprentissage
20
profond ? Quels liens existent entre eux (figure 2.1) ?
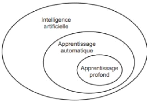
FIGURE 2.1 - Les relations entre l'intelligence artificielle,
l'apprentissage automatique et l'apprentissage profond [10]
2.2.1 Intelligence Artificielle : Artificial
Intelligent (AI)
L'intelligence artificielle est née dans les
années 50, quand une poignée de pionniers de l'informatique
naissante ont commencé à se demander si les ordinateurs
pouvaient
être conçus pour « penser » une
question dont nous continuons aujourd'hui d'explorer
les ramifications. Une
définition précise de ce domaine serait la suivante : c'est
l'effort d'automatisation des tâches intellectuelles normalement
effectuées par des humains [10].
L'intelligence artificielle est donc un domaine
général qui englobe l'apprentissage automatique et
l'apprentissage profond, mais qui comprend également de nombreuses
autres approches qui n'impliquent aucun apprentissage. Pendant très
longtemps, de nombreux experts ont cru qu'une intelligence artificielle
équivalente à celle de l'homme pouvait être atteinte en
faisant en sorte que les programmeurs fabriquent un ensemble suffisamment large
de règles explicites pour manipuler les connaissances. Cette approche
est connue sous le nom d'intelligence artificielle symbolique (symbolic AI), et
ce fut le paradigme dominant de l'IA des années 1950 à la fin des
années 1980. Elle a atteint son apogée pendant le boom des
systèmes experts (expert systems) dans les années 1980 [10].
Bien que l'IA symbolique se soit révélée
apte à résoudre des problèmes logiques bien
définis, tels que jouer aux échecs, elle s'est
avérée incapable de définir des règles explicites
pour résoudre des problèmes plus complexes et flous, tels que la
classification d'images, la reconnaissance de la parole et la traduction
linguistique. Une nouvelle approche est apparue, et elle a pris la place de
l'intelligence artificielle symbolique : c'est
l'apprentissage
21
automatique (machine learning) [10].
2.2.2 Apprentissage automatique : Machine
Learning
Dans l'Angleterre victorienne, Lady Ada Lovelace était
une amie et une collaboratrice de Charles Babbage, l'inventeur de la machine
analytique (Analytical Engine) : le premier ordinateur mécanique
polyvalent connu. Bien que visionnaire et très en avance sur son temps,
la machine analytique n'était pas conçue comme un ordinateur
polyvalent (general purpose computer) lorsqu'elle a été
pensée dans les années 1830 et 1840, car le concept de calcul
polyvalent n'avait pas encore été inventé. C'était
simplement un moyen d'utiliser des opérations mécaniques pour
automatiser certains calculs du domaine de l'analyse
mathématique d'où le nom de machine analytique.
En 1843, Ada Lovelace a ainsi
commenté l'invention : « le moteur
analytique n'a aucune prétention à être à l'origine
de quoi que ce soit. Il peut faire toutes les tâches dont nous savons
comment lui ordonner de les effectuer [...]. Son domaine de compétence
est de nous aider à rendre disponible ce que nous connaissons
déjà. » Le pionnier de l'IA, Alan Turing, a cité
cette remarque plus tard comme « l'objection de Lady Lovelace » dans
son article phare de 1950 appelé « Computing Machinery and
Intelligence » qui présentait le test de Turing ainsi que les
concepts clés qui façonneront plus tard l'IA. Turing citait Ada
Lovelace en se demandant si les ordinateurs polyvalents pourraient être
un jour capables d'apprendre et de faire preuve de créativité, et
il en vint à la conclusion qu'ils en seraient capables. L'apprentissage
automatique découle de cette question : un ordinateur pourrait-il aller
au-delà des « tâches dont nous savons comment lui ordonner de
les effectuer », et apprendre par lui-même comment effectuer une
tâche spécifique ? Un ordinateur pourrait-il nous surprendre ?
À la place de programmeurs élaborant à la main des
règles de traitement de données, un ordinateur pourrait-il
apprendre automatiquement ces règles par l'exposition aux données
?
Cette question ouvre la porte à un nouveau paradigme de
programmation. En programmation classique, le paradigme de l'IA symbolique,
l'homme saisit des règles (un programme) et des données à
traiter conformément à ces règles, et il en découle
des réponses en sortie. Avec l'apprentissage automatique, les humains
entrent des données,
22
ainsi que les réponses attendues à partir de ces
données, et ils obtiennent des règles en sortie. Ces
règles peuvent ensuite être appliquées à de
nouvelles données pour produire des réponses originales.
Un système d'apprentissage automatique est
entraîné plutôt qu'explicitement programmé. De
nombreux exemples pertinents pour une tâche lui sont
présentés. Puis il trouve dans ces exemples une structure
statistique qui lui permet à terme d'élaborer des règles
pour l'automatisation de la tâche. Par exemple, si vous souhaitez
automatiser l'étiquetage de vos photos de vacances, vous pouvez
présenter à un système d'apprentissage automatique de
nombreux exemples d'images déjà étiquetées par des
humains, et le système apprendra des règles statistiques pour
associer, à des images spécifiques, des étiquettes
spécifiques. Bien que l'apprentissage automatique n'ait commencé
à prospérer que dans les années 1990, il est rapidement
devenu le sous-domaine de l'IA le plus populaire et le plus performant. Cette
tendance est alimentée par la disponibilité de matériels
informatiques plus rapides et de plus grands ensembles de données.
L'apprentissage automatique est étroitement lié aux statistiques
mathématiques, mais il diffère des statistiques sur plusieurs
points importants. À la différence des statistiques,
l'apprentissage automatique traite généralement de vastes et
complexes ensembles de données (par exemple un ensemble de
données de millions d'images, chacune comprenant des dizaines de
milliers de pixels) pour lesquels une analyse statistique classique telle
qu'une analyse bayésienne serait impossible à mettre en oeuvre.
En conséquence, l'apprentissage automatique, et en particulier
l'apprentissage profond : Deep Learning,
présente relativement peu de théorie mathématique
peut-être trop
peu et est axé sur l'ingénierie. C'est une
discipline pratique dans laquelle les idées sont
plus souvent
prouvées empiriquement que théoriquement.
2.2.3 Apprentissage des représentations à
partir de données
Pour définir l'apprentissage profond (deep learning en
anglais) et comprendre la différence entre l'apprentissage profond et
les autres approches d'apprentissage automatique, nous devons d'abord avoir une
idée du fonctionnement des algorithmes d'apprentissage automatique. Nous
venons juste d'énoncer que l'apprentissage automatique découvre
des règles permettant d'exécuter une tâche de traitement de
données, lorsque lui sont fournis
23
des exemples de résultats attendus. Pour faire de
l'apprentissage automatique, nous avons donc besoin de trois choses :
- des points de données d'entrée (input data
points) par exemple, si la tâche est
la reconnaissance vocale, ces
points de données peuvent être des fichiers audio de personnes qui
parlent ; si la tâche est l'étiquetage d'images, ces points de
données peuvent être des images ; si c'est dans le cas de ce
papier, on aura donc besoin de données d'entrées de la
patiente.
- des exemples de sortie attendue (expected output) dans une
tâche de reconnaissance vocale, il peut s'agir de transcriptions de
fichiers sonores générés par l'homme ; dans une
tâche d'étiquetage d'images, les sorties attendues peuvent
être des étiquettes telles que « chien », « chat
», etc. ; dans une tâche de séjour hospitalier les output
sont donc des séjours moyens de chacune des patientes.
- un moyen de mesurer la performance de l'algorithme c'est un
élément nécessaire pour déterminer la distance, au
sens mathématique, entre la sortie effective de l'algorithme et la
sortie attendue ; la mesure est utilisée comme un signal de retour
(feedback) pour ajuster le fonctionnement de l'algorithme ; cette étape
d'ajustement est ce que nous appelons l'apprentissage.
Un modèle d'apprentissage automatique transforme ses
données d'entrée en sorties qui ont un sens, c'est un processus
qui est « appris » à partir de l'exposition à des
exemples connus d'entrées et de sorties. Par conséquent, le
problème central de l'apprentissage automatique et de l'apprentissage
profond est de transformer de manière utile les données : en
d'autres termes, d'apprendre des représentations utiles des
données d'entrée disponibles
des représentations qui nous rapprochent du
résultat attendu. Avant d'aller plus loin : qu'est-ce qu'une
représentation ? Fondamentalement, c'est une façon
différente
de considérer les données de représenter
ou d'encoder les données. Les modèles
d'apprentissage
automatique ont pour but de trouver des représentations
appropriées pour
leurs données d'entrée des transformations de
données qui les rendent plus adaptées à
la tâche
à accomplir, telle que par exemple une tâche de classification.
Techniquement, voici ce qu'est l'apprentissage automatique :
c'est la recherche de représentations utiles de certaines données
d'entrée, dans un espace des possibilités
prédéfini, en s'appuyant sur un signal de retour. Cette
idée simple permet de résoudre un
24
très large éventail de tâches
intellectuelles, de la reconnaissance automatique de la parole à la
conduite automobile autonome.
Disons, ce qui est profond de
l'apprentissage profond est donc une nouvelle approche de
l'apprentissage des représentations à partir des données
qui met l'accent sur l'apprentissage de couches (layers) successives de
représentations qui sont de plus en plus significatives.
L'adjectif « profond » de l'apprentissage profond ne
fait pas référence à une forme de compréhension
plus approfondie réalisée par l'approche mise en oeuvre ; il
représente plutôt l'idée de couches successives de
représentations.
2.3 Les apprentissages en Machine Learning 2.3.1
Introduction
Dans cette section, nous allons voir quelques algorithmes de
prédictions de Machine Learning tantôt en apprentissange
supervisé, en apprentissage non supervisé ou en apprentissage par
renforcement.
Au delà de ces différents apprentissages, il
existe des algorithmes utiliés dans l'un ou l'autre apprentissage. Ces
modèles au finish nous serviront en grande partie dans la conception du
modèle de prédiction en Gynécologie qui fera l'objet de ce
mémoire.
Parlons d'abord de ce qui est de l'apprentissage
supervisé, l'apprentissage non supervisé et l'apprentissage par
renforcement ([19] et[25]).
2.3.2 Apprentissage supervisé
L'apprentissage supervisé est fait en utilisant une
vérité, c'est-à-dire qu'on a une connaissance
préalable de ce que les valeurs de sortie pour nos échantillons
devraient être. Par conséquent, le but de ce type d'apprentissage
est d'apprendre une fonction qui, compte tenu d'un échantillon de
données et de résultats souhaités, se rapproche le mieux
de la relation entre les entrées et les sorties observables dans les
données. La figure 2.2 est un exemple d'un modèle de traitement
de données en apprentissage supervisé.
Dans l'apprentissage supervisé, on a deux types
d'algorithmes :
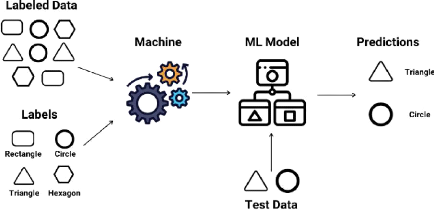
25
FIGURE 2.2 - Modèle de traitement de données en
apprentissage supervisé [1]
- Les algorithmes de régression, qui cherchent à
prédire une valeur continue, une quantité.
- Les algorithmes de classification, qui cherchent à
prédire une classe/catégorie.
2.3.3 Apprentissage non supervisé
Dans l'apprentissage non supervisé (clustering en
anglais), l'ensemble de données est divisé en sous-groupes
homogènes pour obtenir une représentation simplifiée de
l'ensemble de départ [19]. Les algorithmes d'apprentissage automatique
non supervisés sont utilisés lorsque l'information
utilisée pour entraîner le modèle n'est ni
classifiée ni étiquetée. Le modèle en question
étudie ses données d'entrainement dans le but de déduire
une fonction pour décrire une structure cachée à partir
des données (figure 2.3). À aucun moment le système ne
connaît la sortie correcte avec certitude. Au lieu de cela, il tire des
inférences des ensembles de données quant à ce que la
sortie devrait être. [1].
Les algorithmes de ce type d'apprentissage peuvent être
utilisés pour trois types en problèmes.
- Association : un problème où
on désire découvrir des règles qui décrivent de
grandes portions de ses données. Par exemple, dans un contexte d'une
étude de
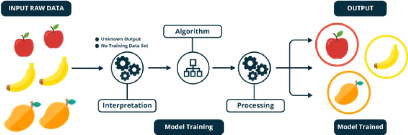
26
27
FIGURE 2.3 - Modèle de traitement de données en
apprentissage non supervisé [1]
comportement d'achat d'un groupe de clients, les personnes qui
achètent tel produit ont également tendance à acheter un
autre produit spécifique.
- Regroupement : un problème où
on veut découvrir les groupements inhérents
aux données, comme le regroupement des clients par le
comportement d'achat. - La réduction de dimension : on
vise à réduire le nombre de variables à prendre
en compte dans l'analyse.
2.3.4 Apprentissage semi-supervisé
Ce type d'algorithme est la combinaison entre l'apprentissage
supervisé et l'apprentissage non supervisé. Ces algorithmes sont
capables d'apprendre à partir d'ensembles de données
partiellement étiquetées [19].
2.3.5 Apprentissage par renforcement
L'apprentissage par renforcement est une méthode qui
consiste à optimiser de manière itérative un algorithme
uniquement à partir des actions qu'il entreprend et de la réponse
associée de l'environnement dans lequel il évolue (figure
2.4).
Cette méthode permet aux machines et aux agents de
déterminer automatiquement le comportement idéal dans un contexte
spécifique pour maximiser ses performances. Une simple
rétroaction de récompense, connue sous le nom de signal de
renforcement, est
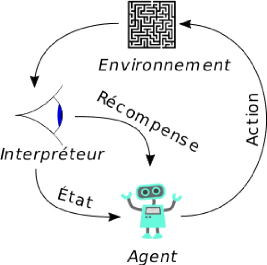
FIGURE 2.4 - Modèle de traitement de données en
apprentissage par renforcement
nécessaire pour que l'agent apprenne quelle action est la
meilleure.
La plus part des problèmes de la DDS utilisent les
algorithmes de l'apprentissage supervisé car, avant d'étudier la
DDS d'un patient, il faut donc savoir pour les précédents, leurs
DDS et ainsi, les faire appliquer au nouveau modèle.
2.4 Algorithmes de l'apprentissage automatique
Dans la partie suivante nous allons parcourir quelques
algorithmes en apprentissage supervisé car, sont eux qui nous serviront
dans la suite de ce travail.
Pour résoudre un problème en apprentissage
supervisé, on fait recours à plusieurs méthodes qui sont
applicables dans plusieurs domaines [1]. Dans la suite, nous allons essayer de
voir certains algorithmes en apprentissage automatique. Précisons que la
liste n'est pas exhaustive mais nous allons juste essayer de présenter
ici quelques modèles mais pas les tous.
28
2.4.1 Régression linéaire
La régression linéaire est l'une des
méthodes de prédiction en ML. Elle utilise des variables
quantitatives et l'idée plus générale ici est juste
d'exprimer les variables par une fonction f(x).
L'un de ses principaux mérites est de fournir une
illustration pédagogique élémentaire des différents
concepts du ML. Il suppose que la fonction de prédiction f qui
lie les variables prédictives x1, ..., xp
à la variable cible a la forme :
f(x) = a0x0 +
a1x1 + a2x2... +
apxp = a x x + b (2.1)
La régression linéaire est utilisée pour
l'estimation de certaines tendances en économétrie et dans le
marketing lorsqu'on a des raisons de penser qu'il existe une relation
linéaire entre la variable explicative et la cible. Établir la
relation entre l'augmentation du prix d'un produit et sa demande,
évaluer l'impact d'une campagne publicitaire en fonction des frais
engagés sont des exemples d'utilisation [15].
L' apprentissage du modèle consiste en l'occurrence
à calculer les coefficients ai qui minimisent les erreurs de
prédiction sur un jeu de données d'apprentissage. Le plus souvent
l'erreur est définie comme la somme des carrés des écarts
entre les valeurs prédites f(x(i))
et les valeurs observées yi. On parle à ce
titre de méthode des moindres carrés. Le
carré ici des erreurs nous permet de ne pas avoir des valeurs
négatives qui pourraient probablement se simplifier et ainsi faire
penser au concepteur du modèle que nous est correct or il y a des
valeurs érronées.
Erreur et la fonction coût
Un modèle de ML le plus souhaité, est celui qui
minimise l'erreur. C'est ainsi que dans la conception d'un algorithme de
Machine Learning, on cherche toujours à prendre le modèle qui a
moins d'erreurs.
En effet, pour chaque point xi, l'erreur unitaire
pour ce point xi est donné par la différence entre la
valeur prédite et la vraie valeur. Pour se rassurer que cette valeur
sera positive pour que l'équation 2.3 ne soit pas nulle, on
élève cette difference au carré :
(f(xi) - yi)2.
L'erreur unitaire étant déjà
définie, faisons une sommation de ces erreurs pour plusieurs points.
L'équation 2.2 donne [12] :
Xm (f(xi) -
yi)2. (2.2)
i=1
La fonction coût (équation 2.3) est
définie en normant cette somme de l'équation 2.2 par le nombre
m de points dans la base [12] :
m
1
J(è0, è1) = 2
X (f(xi) - yi)2 (2.3)
m i=1
29
Il existe aussi des modèles linéaires
généralisés qui se basent sur des lois de
probabilité. Les modèles linéaires
généralisés (GLM) étendent les modèles
linéaires de deux manières [2]. Premièrement, les valeurs
prédites y sont liés à une combinaison
linéaire des variables d'entrée x via une fonction de
lien inverse. Deuxièmement, la fonction de perte au carré est
remplacée par la déviance unitaire d'une distribution dans la
famille exponentielle (ou plus précisément, un modèle de
dispersion exponentielle reproductive (EDM).On fait alors le choix d'une
distribution statistique à faire. Ceci est guidé par la
caractéristique de données qu'on a [2] :
- Si les valeurs cibles y sont des nombres (valeur
entière non négative) ou des fréquences relatives (non
négatives), vous pouvez utiliser une distribution de Poisson avec un
lien logarithmique.
- Si les valeurs cibles y sont positives et
asymétriques, vous pouvez essayer une distribution Gamma avec un lien de
journal.
- Si les valeurs cibles y semblent avoir une queue
plus lourde qu'une distribution Gamma, vous pouvez essayer une distribution
gaussienne inverse (ou des puissances de variance encore plus
élevées de la famille Tweedie).
- Si les valeurs cibles y sont des
probabilités, vous pouvez utiliser la distribution de Bernoulli. La
distribution de Bernoulli avec un lien logit peut être utilisée
pour la classification binaire. La distribution catégorielle avec un
lien softmax peut être utilisée pour la classification
multiclasse.
30
D'après l'équation 2.1, nous pouvons encore
définir par 'q la DDS prédite à un moment
t [22]. Cette équation devient donc :
'17 = a0 + Xp
aixi (2.4)
i=1
2.4.2 Les k plus proches voisins
Le modèle des k plus proches voisins (KNN pour
k Nearest Neighbors) est un des modèles
prédictifs les plus simples. Il ne fait aucune hypthèse
mathématique et ne demande pas non plus toute une litanie des choses. Il
nécessite très peu de choses [15] :
- une notion de distance;
- et l'hypothèse que des points proches les uns des
autres sont similaires.
L'opérateur de distance le plus souvent utilisé
est la distance Euclidienne, cependant, en fonction du problème, on peut
encore utiliser d'autres distances [26], etc
Principe de l'algorithme
On suppose que l'ensemble E contient n
données labellisées et u , une autre donnée
n'appartenant pas à E qui ne possède pas de label. Soit
d une fonction qui renvoie la distance (qui reste à choisir)
entre la donnée u et une donnée quelconque appartenant
à E. Soit un entier k inférieur ou égal
à n [8]. Le principe de l'algorithme de k-plus proches voisins
est le suivant [3] et [8] :
- On calcule les distances entre la donnée u
et chaque donnée appartenant à E à l'aide de
la fonction d.
- On retient les k données du jeu de
données E les plus proches de u, c'est-à-dire,
les données déjà classifiées qui ont une distance
d la plus proche avec la nouvelle donnée entrée.
- On attribue à u la classe qui est la plus
fréquente parmi les k données les plus proches.
Les distances utilisées [3]
Les distances les plus souvent utilisées ici sont les
distances euclidienne et Manhattan.
1. Distance euclidienne
La distance Euclidienne est la distance utilisée pour
calculer la distance entre deux points. La distance Euclidienne d
entre les points A et B est donnée par la
relation suivante :
|
d(A, B) =
|
v u u Xn
tk=1
|
(yk -
xk)2. (2.5)
|
31
2. Distance Manhattan d
La distance de Manhattan est nommée ainsi car elle
permet de mesurer la distance parcourue entre deux points par une voiture dans
une ville où les rues sont agencées selon un quadrillage.
La distance de Manhattan d entre deux données
A et B est donnée par la relation suivante :
d(A,B) = Xn |
yk - xk |.
(2.6)
k=1
2.4.3 Les arbres de décision
Les arbres de décision sont des
modèles de ML supervisés et non paramétriques
extrêmement flexibles. Ils sont utilisables aussi bien pour la
classification que pour la régression. Nous décrirons ici
brièvement les principes utilisés pour la classification. Les
arbres de décision utilisent des méthodes purement algorithmiques
qui ne reposent sur aucun modèle probabiliste. L' idée de base
consiste à classer une observation au moyen d'une succession de
questions (ou critères de segmentation) concernant les valeurs des
variables prédictives Xi de cette observation.
Chaque question est représentée par un noeud d'un arbre de
décision. Chaque branche sortante du noeud correspond à une
réponse possible à la question posée. La classe de la
variable cible est alors déterminée par la feuille (ou noeud
terminal) dans laquelle parvient l'observation à l'issue de la suite de
questions [23].
Un modèle de Machine Learning comprend trois sortes de
noeuds [16] : les racines, les noeuds intermédiaires et les
branches. Deux noeuds sont reliés par des branches. La
figure 2.5 illustre ces diffentes parties d'un arbre de décision. Selon
la figure 2.5, on constate que la racine de cet arbre est
x0, les noeuds intermédiaires sont
x2, x3 et
x4. Par

32
FIGURE 2.5 - Exemple d'un arbre avec ses differentes parties
[16]
contre, les branches sont x1, x5;
x6, x7 et x8. On comprend dans ce sens que l'arbre
de décision n'est rien autre qu'une suite de questions où les
réponses constituent des branches et des feuilles.
La question de la profondeur de l'arbre qu'il faut retenir est
délicate et est directement liée au problème du
surapprentissage. Exiger que toutes les observations soient parfaitement
rangées peut rapidement mener au surapprentissage. Pour cette raison on
décide généralement de ne plus rajouter de noeuds lorsque
la profondeur de l'arbre excède un certain seuil, qui caractérise
la complexité maximale de l'arbre de décision, ou lorsque le
nombre d'observations par feuille est trop faible pour être
représentatif des différentes classes (on parle de
pré-élagage). On pratique aussi des opérations
d'élagage a posteriori (prunning) sur des arbres dont les feuilles sont
homogènes en utilisant un jeu de données distinct (prunning set)
de celui qui a permis la construction de l'arbre original [23].
Une fois l'arbre construit à partir des données
d'apprentissage, on peut prédire un nouveau cas en le
faisant descendre le long de l'arbre, jusqu'à une feuille.
Comme la feuille correspond à une classe, l'exemple sera
prédit comme faisant partie de cette classe [26].
Les arbres de décisions interviennent par ailleurs
comme brique de base de l'algorithme plus sophistiqué des forêts
aléatoires que nous présenterons au paragraphe suivant.
33
Quoi que l'arbre de décision soit un algorithme
important en prédiction, elle présente
aussi quelques faiblesses comme nous pouvons le lire selon [26]
:
- C'est un algorithme Glouton, sans backtrack (sans retracer ou
trace arrière).
- Transposables en règles avec des règles ayant des
attributs communs, en particulier
l'attribut utilisé à la racine.
- Présentent des difficultés avec les concepts
disjonctifs.
- Etc.
Aspect mathématiques
Dans cette partie, nous allons voir quelques fonctions
mathématiques utiles pour un arbre de décision. L'algorithme
utilise l'entropie (c'est une théorie tirant ses origines dans la
théorie de l'information. L'entropie en statistique designe le
désordre qui règne dans une population. La constuction de l'arbre
visera à minimiser ce bruit [12]) et le gain d'information comme
fonctions [6].
Etant donné un ensemble C de données
labélisées +, - et p la population totale,
l'entropie sur C de l'ensemble de données S est
donnée par l'équation 2.7
Entropie(C) = X
(-Pcilog2Pci)
(2.7)
ciEC
où Pci =
|Ci|
|S| représente une
probabilité de l'eventualité ci.
L'entropie étant déjà minimisée,
l'étape critialle est de savoir quel attribut testé en premier
(on choisira l'attribut qui maximisera le gain d'information ou, son
équivalent : qui minimisera l'entropie [6] [12] ). Il faut
connaître la notion de gain d'information. Le gain est défini par
un ensemble d'exemples et par un attribut. L'équation 2.8
formulée va donc servir à calculer ce que cet attribut apporte au
désordre de l'ensemble. Plus un attribut contribue au désordre,
plus il est important de le tester pour séparer l'ensemble en plus
petits sous-ensembles ayant une entropie moins élevée [6].
|
Gain(S, A) = Entropie(S) - X
cEvaleur(A)
|
| Sv |
| S | x Entropie(Sv)
(2.8)
|
Les arbres de décisions interviennent par ailleurs comme
éléments de base de l'algorithme
34
plus sophistiqué des forêts aléatoires que
nous présenterons au paragraphe suivant.
2.4.4 Les forêts aléatoires
Il est connu qu'une forêt est un ensemble de plusieurs
arbres (figure 2.6). Les forêts aléatoires sont donc un ensemble
de plusieurs arbres de décisions.
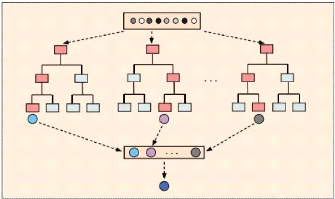
FIGURE 2.6 - Généralisation du modèle
prédictif Forêt aléatoire [16]
Prenons l'exemple suivant : imaginez-vous, vous vous
rendez à l'hôpital pour le CPN et d'un coût, un
médecin vous annonce que vous allez subir une opération (la
prémière après sept naissances d'avant.) Parfois vous
n'allez pas vous imaginer que cela soit possible. Il vous faut donc un
récours vers un autre médecin car vous supposez que
celui-là n'est pas soit à la hauteur de sa tâche.
[12]
Comme pour l'algorithme de l'arbre de décision, quoi
qu'il y a un seul arbre, mais à l'intérieur de ce dernier sont
groupés plusieurs autres questionnement qui permettent de bien
répondre à une certaine question. L'ensemble de ces portions
d'arbre à l'intérieur d'un arbre constituent pour ce faire un
algorithme appelé forêt aléatoire (Random Forest en
anglais) [12].
Origine des forêts aléatoires
[12]
On doit les random forests au fantastique Leo Breiman,
éminent statisticien américain connu pour ses travaux sur les
arbres décisionnels et sur la méthode CART, introduite
35
précédemment. Lui-même avait parfaitement
conscience du défaut majeur d'un arbre de décision : sa
performance est trop fortement dépendante de l'échantillon de
départ. De plus, on peut s'attendre à ce que l'ajout de quelques
nouvelles données dans la base d'apprentissage (ce qui est une bonne
nouvelle en soit !) ne modifie pas drastiquement le modèle, qu'il le
modifie de façon marginale pour l'améliorer. Ce n'est pas le cas
avec un arbre de décision, dont la topologie peut totalement changer
avec l'ajout de quelques observations supplémentaires. Plutôt que
de lutter contre ces défauts des arbres de décisions, Breiman a
eu l'idée géniale d'utiliser plusieurs arbres pour faire des...
forêts d'arbres ! Vous avez compris le forest dans random forest. Et
random alors ? Pour éviter de se retrouver avec des arbres égaux,
il donne à chaque arbre une vision parcellaire du problème, tant
sur les observations en entrée que sur les variables à utiliser.
Ce double échantillonnage est tout simplement tiré
aléatoirement. Notons que l'assemblage d'arbres de décision
construits sur la base d'un tirage aléatoire parmi les observations
constitue déjà un algorithme à part entière connu
sous le nom de tree bagging. Les random forests ajoutent au tree bagging un
échantillonnage sur les variables du problème, qu'on appelle
feature sampling. On retiendra que :
Random forest = tree
bagging + feature sampling
Avant d'entrer dans le détail de son fonctionnement,
notons enfin que l'on retrouve dans le random forest la polyvalence des arbres
de décision. En effet, on peut les utiliser :
- en classification, le résultat final étant obtenu
en faisant « voter » chaque arbre ;
- en régression, en moyennant le résultat des
arbres.
Le but de l'algorithme des forêts aléatoires est
de conserver la plupart des atouts des arbres de décision tout en
éliminant leurs inconvénients, en particulier leur
vulnérabilité au surapprentissage et la complexité des
opérations d'élagage. C'est un algorithme de classification ou de
régression non paramétrique qui s'avère à la fois
très fléxible et très robuste.
L' algorithme des forêts aléatoires repose sur trois
idées principales :
1. À partir d'un échantillon initial de N
observations (x(1), . . .
x(n)), dont chacune est décrite au moyen de
p variables prédictives, on crée « artificiellement
» B nouveaux échantillons de même taille N
par tirage avec remise. On appelle cette technique
36
le bootstrap. Grâce à ces B
échantillons, on entraîne alors B arbres de
décisions différents.
2. Parmi les p variables prédictives
disponibles pour effectuer la segmentation associée au noeud d'un arbre,
on n'en utilise qu'un nombre in < p choisies « au hasard
». Celles-ci sont alors utilisées pour effectuer la meilleure
segmentation possible.
3. L' algorithme combine plusieurs algorithmes « faibles
», en l'occurrence les B arbres de décisions, pour en
constituer un plus puissant en procédant par vote. Concrètement,
lors qu'il s'agit de classer une nouvelle observation x, on la fait
passer par les B arbres et l'on sélectionne la classe
majoritaire parmi les B prédictions. C'est un exemple d'une
méthode d'ensemble.
Le nombre B d'arbres s'échelonne
généralement entre quelques centaines et quelques milliers selon
la taille des données d'apprentissage. Le choix du nombre in de
variables à retenir à chaque noeud est le résultat d'un
compromis. Il a été démontré que les
prédictions d'une forêt aléatoire sont d'autant plus
précises que les arbres individuels qui la composent sont
prédictifs et que les corrélations entre prédictions de
deux arbres différents sont faibles. Augmenter le nombre in de
variables augmente la qualité de prédiction des arbres
individuels mais accroît aussi les corrélations entre arbres. Une
valeur in de l'ordre de /p constitue un bon compromis
[23].
2.4.5 Les réseaux de neurones
artificiels
Les réseaux de neurones artificiels sont
utilisés tantôt dans plusieurs disciplines mais ne constituent pas
en quelques sortes eux mêmes une discipline [27]. Un réseau de
neurone artificiel (parfois simplement réseau de neurones) est un
modèle de prédiction qui met en exergue le fonctionnement du
cerveau. Le cerveau ici considéré est une collection de neurones
connectés les uns aux autres. Chaque neurone examine les sorties des
autres neurones, qui deviennent ses entrées, effectue un calcul, puis se
déclenche ou pas [15]. La figure 2.7 est un exemple illustratif d'un
réseau de neurones.
Les réseaux de neurones résolvent nombreux
problèmes tels que la réconnaissance de l'écriture, la
réconnaissance faciale [25],[15], voire même la fonction du
système nerveu central [24].
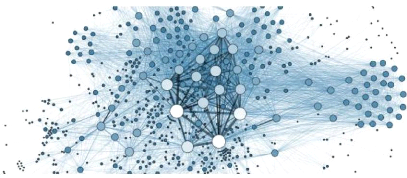
37
FIGURE 2.7 - Réseau de neurones [25]
Définition 2.1 Les réseaux
de neurones artificiels sont des réseaux fortement connectés de
processeurs élémentaires fonctionnant en parallèle. Chaque
processeur élémentaire calcule une sortie unique sur la base des
informations qu'il reçoit. Toute structure hiérarchique de
réseaux est évidemment un réseau.
Cependant, développer un réseau de neurones
à moindre coût est l'appanage de [25] : - Un Dataset beaucoup plus
grand (des millions de données)
- Un temps d'apprentissage plus long (parfois plusieurs
jours)
- Une plus grande puissance de calcul.
Pour dépasser ces challenges, les chercheurs dans le
domaine ont développés des variantes du Gradient Descent ainsi
que d'autres techniques pour calculer plus rapidement les
dérivées sur des millions de données. Parmi ces solutions
on trouve [25] :
- Mini-Batch Gradient Descent : Technique
pour laquelle le Dataset est fragmenté en petits lots pour simplifier le
calcul du gradient à chaque itération.
- Batch Normalization : Mettre à la
même échelle toutes les variables d'entrée et de sortie
internes au Réseau de Neurone pour éviter d'avoir des calculs de
gradients extrêmes.
- Distributed Deep Learning : Utilisation du
Cloud pour diviser le travail et le confier à plusieurs
machines.
Historique [27]
- 1890 : W. James, célèbre psychologue
américain introduit le concept de mémoire associative, et propose
ce qui deviendra une loi de fonctionnement pour l'apprentissage sur les
réseaux de neurones connue plus tard sous le nom de loi de Hebb.
- 1943 : J. Mc Culloch et W. Pitts laissent leurs noms
à une modélisation du neurone biologique (un neurone au
comportement binaire). Ce sont les premiers à montrer que des
réseaux de neurones formels simples peuvent réaliser des
fonctions logiques, arithmétiques et symboliques complexes (tout au
moins au niveau théorique).
- 1949 : D. Hebb, physiologiste américain explique le
conditionnement chez l'animal par les propriétés des neurones
eux-mêmes. Ainsi, un conditionnement de type pavlovien tel que, nourrir
tous les jours à la même heure un chien, entraîne chez cet
animal la sécrétion de salive à cette heure précise
même en l'absence de nourriture. La loi de modification des
propriétés des connexions entre neurones qu'il propose explique
en partie ce type de résultats expérimentaux.
Comment comprendre un réseau de neurones
?
La réponse à cette question viendra à l'aide
de l'exemple sur la figure 2.8. Sur cette
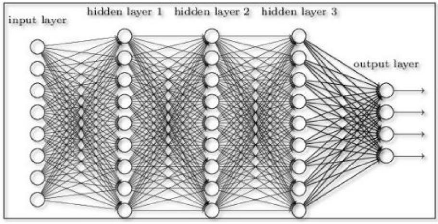
FIGURE 2.8 - Réseau de neurones à plusieurs
neurones [25]
38
39
figure, on remarque à gauche des entrées
appelées input layers et à gauche des sorties
appelées Output layers. Les petits ronds sont
appelés les neurones et représentent des fonctions d'activation
[25].
Ils sont classés suivant le nombre de neurones de chaque
réseau.
Réseau de Neurone à 1 Neurone : Le
perceptron
Le réseau de Neurones le plus simple qui existe porte
le nom de perceptron. Il est identique à la
Régression Logistique de la section précedente.
Les entrées du neurone sont les x
multipliées par des paramètres c à
apprendre. Il existe deux étapes pour le calcul d'un réseau de
neurone d'abord, un calcul linéaire par la somme de toutes les
entrées et le calcul de la fonction d'activation ou la fonction
logistique [25].
On utilise souvent d'autres fonctions d'activation que la
fonction sigmoïde pour simplifier le calcul du gradient et ainsi obtenir
des cycles d'apprentissage plus rapides [25] :
- La fonction tangente hyperbolique tanh(z)
- La fonction Relu(z)
Réseaux à plusieurs neurones : le Deep
Learning
Cette méthode se fait en étapes en liant plusieurs
perceptrons [25] :
- On réunit les neurones en colonne (on dit qu'on les
réunit en couche, en layer). Au sein de leur colonne, les neurones ne
sont pas connectés entre eux.
- On connecte toutes les sorties des neurones d'une colonne
à gauche aux entrées de tous les neurones de la colonne de droite
qui suit.
On peut ainsi construire un réseau avec autant de
couches et de neurones que l'on veut. Plus il y a de couches,
plus on dit que le réseau est profond (deep)
et plus le modèle devient riche, mais aussi
difficile à entraîner. C'est ça, le
Deep Learning [25].
Les réseaux de neurones entrent dans la
catégorie des modèles non linéaires en
leurs paramètres. La forme la plus courante de réseau de neurones
statique est une extension
simple de l'équation [14] :
g(x,w) = Xp w f (x,w')
(2.9)
=1
où les fonctions f (x, w') ,
appelées "neurones", sont des fonctions paramètrées qui
seront définies dans la suite.
La fonction f peut être
paramétrée de manière quelconque. Deux types de
paramétrage sont fréquemment utilisés [14] :
- les paramètres sont attachés aux variables du
neurone : la sortie du neurone est une fonction non linéaire d'une
combinaison des variables {x } pondérées par les
paramètres {w }, qui sont alors souvent désignés
sous le nom de « poids » ou, en raison de l'inspiration biologique
des réseaux de neurones, « poids synaptiques ».
Conformément à l'usage (également inspiré par la
biologie), cette combinaison linéaire sera appelée «
potentiel » dans tout cet ouvrage. Le potentiel v le plus
fréquemment utilisé est la somme pondérée, à
laquelle s'ajoute un terme constant ou « biais » :
v = wo + Xn w x (2.10)
=1
La fonction f est appelée fonction
d'activation.
- les paramètres sont attachés à la
non-linéarité du neurone : ils interviennent directement dans la
fonction f ; cette dernière peut être une fonction
radiale ou RBF (en anglais Radial Basis Function), ou encore une ondelette ; la
première tire son origine de la théorie de l'approximation, la
seconde de la théorie du signal . Par exemple, la sortie d'un neurone
RBF à non-linéarité gaussienne a pour équation :
2w2 n+1
Pn =1(x - w )2
y = exp(-
) (2.11)
40
2.5 Pertinence d'un modèle de
prédiction
Comme vu dans les chapitres précedents, il existre
plusieurs algorithme de prédiction en apprentissage automatique. Mais la
question qui reste toujours en jachère est celle de savoir si
réellement toutes ces méthodes ont les mêmes chances de
prédiction. C'est dans cette
perpective que dans cette section, nous allons essayer de voir
comment on peut parvenir à faire un choix des algorithmes à
maintenir pour la prédiction en Machine Learning. Nous allons parler de
quelques mesures d'estimation des algorithmes de regression [2].
2.5.1 Score R2,
coefficient de détermination
l représente la proportion de variance (de y)
qui a été expliquée par le variables indépendantes
dans le modèle. Il fournit une indication de la bonté de et donc
une mesure de la probabilité que les échantillons non vus soient
prédit par le modèle, à travers la proportion de variance
expliquée.
Étant donné que cette variance dépend de
l'ensemble de données, peut ne pas être significativement
comparable dans différents ensembles de données. Le meilleur
score possible est de 1,0 et il peut être négatif (parce que le
modèle peut être arbitrairement pire). Ceci veut dire que lorsque
le modèle coefficient de détermination est nul, inférieur
à zéro ceci s'explique en disant que quand la variable x
croit d'une valeur quelconque, la variable y décroit.
La formule 2.12 nous permet de calculer ce
coéfficient.
P(y -
ypred)2
R2 = 1
(2.12)
P(y -
moyenne(y))2
|
1
MAE =
n
|
n-1X
i=0
|
| yi - yi pred
(2.13)
|
41
2.5.2 Erreur absolue moyenne
La fonction calcule la moyenne absolue erreur, un risque
métrique correspondant à la valeur attendue de la perte d'erreur
absolue ou de la perte -norm.
Si est la valeur prédite du -ième
échantillon, et est la valeur vraie correspondante, alors l'erreur
absolue moyenne (MAE) estimé sur est défini comme suit :
2.5.3 Erreur quadratique moyenne
La fonction calcule le carré moyen erreur, un risque
métrique correspondant à la valeur attendue de l'erreur au
carré (quadratique) ou perte.
Si est la valeur prédite du -ième
échantillon, et est la valeur vraie correspondante, alors l'erreur
quadratique moyenne (MSE) estimé sur est défini comme suit :
|
1
MSE = n
|
n-1X
i=0
|
(yi - yi
pred)2 (2.14)
|
42
Il existe plusieurs autres mesures de performences d'un
modèle de regression, mais dans le cadre de ce travail, nous allons nous
limiter à ces trois mesures linéaires.
Ce deuxième chapitre étant celui consacré
à la description des modèles de machine Learning car au
début nous avons signifié que c'est un domaine qui n'est pas cher
à nous. Dans le chapitre suivant, nous allons essayer de classer et
grouper les données qui nous servirons dans la construction du nouveau
modèle de prédiction de séjour hospitalier, le principal
objectif de ce travail.
43
Chapitre 3
Cadre méthodologique
3.1 Introduction
En Apprentissage automatique et dans toute science
expériementale, une connaissance de certaines données anciennes
permettant de prendre des décisions sur des données nouvelles est
necéssaire. Ainsi, dans ce chapitre, nous allons nous
intérésser à la présentation de la base de
données récueillies dans plusieurs hopitaux de la, aussi, par le
trichement de ces données, nous allons montrer comment nous
procédérons à l'analyse de ces dernières d'abord
par le traitement des données.
Nous avons recolté des données dans certains
hopitaux de la Province du Sud-Kivu notamment à l'Hopital
Général de Référence de Kaziba à Kaziba, aux
Centres Hospitaliers BIOPHARM à Bukavu, KAKWENDE à Burhinyi, et
ORANGE à Twangiza dans l'unité médicale de
Gynécologie (image 3.1 ). Ces données sont à
caractère confidentiel et pour y avoir accès, nous avons
été d'abord formé et informé de la
confidentialité des données médicales. Le cas
écheant entraine des peines.
3.2 Type d'informations récuillies
Les enregistrements de cette base de données concerne
des informations des patientes admises dans le service de Gynécologie
dans des hopitaux que nous avons visité. Les données incluent les
variables suivantes :
- Adresse
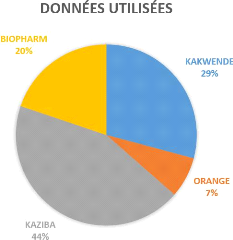
44
FIGURE 3.1 - Diagramme circulaire des données
utilisées
-- Age
- Diagnostic
- Traitement
-- DDS
Le tableau 3.1 montre un exemple d'un extrait de la base des
données. Par exemple, la premiere ligne présente une patiente
habitant à Kakwende âgée de 24 ans où les
premières informations diagnostiquées lors de son admission sont
: Anémie, Paludisme grave. Les traitements qu'elle a suivi sont
une transfusion 450m de sang; ampi3; arthemeter, Gentamiciline 160mg, pendant
19 jours. Sa durée de séjour hospitalier est de 5 jours.
Comme nous pouvons observer dans ce tableau, il ya certaines
informations manquantes. Ce qui est normal car le plus souvent la base de
données souffre de ceci. Nous allons présenter dans la partie
à suivre comment nous nous sommes mis pour faire face à ceci.
3.3 Récolte et Pré-traitement des données
Il a été observé dans plusieurs
structures sanitaires que les informations sont parfois stockuées d'une
manière traditionnelle (c'est-à-dire dans un cahier qui peut soit
se perdre
45
Tableau 3.1 - Exemple de la base de données
|
N°
|
Adresse
|
Age
|
Diagnostic
|
Traitement
|
DDS
|
|
1
|
KAKWENDE
|
24
|
- Anémie
- Paludisme grave
|
Transfusion
450ml de
sang Ampi
3, Arthemeter,
Genta 160mg/l 9 jours
|
5
|
|
2
|
MULI
|
35
|
Avortement incomplet
|
10u d'ocytocine
dans SG 5%
500ml, ampi
3Xsg
|
5
|
|
3
|
CIDAHO
|
-
|
- Paludisme grave - IU
- MAV
|
vinine 1000mg,
puis 500mg,
Aceftriaxène
sg/5jrs Genta
160mg/5jrs
|
7
|
|
4
|
BUDAHA
|
-
|
Paludisme grave
|
Arthemeter 160mg , Ampi genta mebenda,
letro, vit A
100.000U DU IU
|
4
|
|
5
|
CIBINDYE
|
21
|
- Paludisme grave insufisament trété
- UI
-- MAV
|
Quinine 100mg,
puis 800mg,
ceftriaxène sg/
sjs Genta 160mg / 5js
|
6
|
avec toutes les données de l'hopital). C'est ce qui va
faire l'objet de cette section.
3.3.1 Récolte de données
Nous sommes partie des structures sanitaires. De ces registres
manuscrites nous on été données et de ces registres, nous
y avons tirés des informations que nous avons jugées bonnes pour
ce travail.
3.3.2 Pré-traitement des
données
Comme indiqué dans le tableau 3.1, certaines informations
ne sont pas disponibles. Ceci nous a permis de passer à leur
préparation (appelé en anglais data pre-processing).
46
Certaines variables sont quantitatives et d'autres
qualitatives. Nous avons d'abord transformer la variable adresse
par la distance entre le domicile et la structure sanitaire que nous
avons calculé en utilisant le logiciel Google Earth Pro
et ceci en utilisant un milieu connu dans la contrée comme
l'église, l'école, etc., les identifiants tels que les noms sont
remplacés par les numéros pour nous permettre de garder les
données discrètes.
D'après l'hystogramme 3.1, nous constatons que les
données proviennent de 4 hopitaux, c'est ainsi que, l'étiquette
Hopital de Kaziba a été modifiée par 1,
Hopital de Kaziba remplacé par 2, CH Biopharm
par 3 et CH Orange par 4. Ceci pour nous permettre
d'avoir des données numériques pour cette variable aussi
catégorielle Hopital.
Quant à la catégorie Diagnostic
qui est catégorielle, pour avoir des données plus
manipulables, nous sommes passés à la subdivision des diagnostics
en fonction des maladies fréquemment trouvées dans notre base de
données (Grossesse, Infection Urinaire, malformation
artério-veineuse ou mesure de l'acuité visuelle,
Hémoragie, Paludisme Avortement, Infections, Autres
1). Ce qu'il faudra rétenir ici est que, les
avortements qu'ils soient provoqués, volontaires ou des ménaces
d'avortement, nous les avons ainsi classés dans cette variable.
Quant à la catégorie Traitement
réçu qui est aussi catégorielle, nous avons fait
la même chose comme pour le cas précédent, subdiviser les
médicaments par classes thérapeutiques. Nous les avons donc
regroupé de la sorte. On a donc scindé cette colonne en 12
colonnes [17], [21] : Anti-Bactériens,
Anti-palidéens, Ocytociques, Anthelmintiques Intestinaux,
Antispasmodique musculotrope, Analgesiques Non Opioides et Ains,
Antiallergiques / Antianaphylactiques, Vitamines, Cephalosporines, Antiamibiens
et Antigiardiens, Transfusion, Autres.
Malgré cette fusion, nous avons toujours des variables
qui n'ont pas assez d'importance dans la prédiction. Nous avons
utilisé la la fonction python display_feat_imp_rforest (figure 3.2 ).
Quant à la Durée de Séjour Hospitalier,
nous avons pris la Durée de séjour moyenne par hopital. On a
l'histogramme (figure 3.3) suivant pour la variable DDS.
En subdivisant nos différentes catégories, nous
sommes passé de 6 colonnes à 25 colonnes. Et plusieurs variables
sont catégorielles Nous sommes passés pour ce faire de 6
1. Cette colonne conserne uniquement des diagnostiques qui ne
sont pas pris en silo
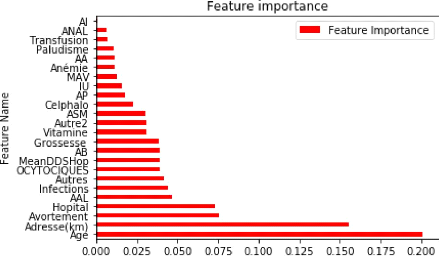
47
FIGURE 3.2 - Importance de chaque variable colonnes à 25
colonnes.
Quant à la gestion des données
manquantes, nous avons utilisé la médiane pour les
données quantitatives (adresse, âge, ) et la
durée de séjour hospitalier nous avons supprimé toutes les
lignes qui n'ont pas de DDS. Ceci pour nous permettre de faire une
préduction plus ou moins bonne où notre basse de données
est passée de 538 lignes à 344 lignes.
Nous avons en suite utilisé la fonction .dropna() de
Python pour supprimer des lignes comptenant des données manquantes
où notre base de données est passée à 333 lignes.
Une base de données parfois contient des enregistrements qui semblent
être les mêmes. Nous avons dans ce sens utilisé la fonction
.drop_duplicates pour nous permettre de supprimer les lignes qui peuvent
être dupliquées.
Nous passons dans ce cas, d'une base de données de 333
à 332 observations.
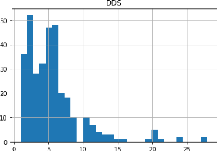
48
FIGURE 3.3 - Histogramme de la Durée de
Séjour Hospitalier
3.3.3 Normalisation et Standardisation des
données
La standardisation des données, également
appelée normalisation, fait référence au processus de
transformation des données brutes en une forme standardisée. La
plupart du temps, cela implique de procéder à la modification des
données afin que ces dernières obtiennent une moyenne de
zéro et un écart-type de un. En d'autres termes, la
standardisation consiste à trier, organiser et
homogénéiser des données suivant certains standards
préalablement définis. [5]
Dans ce travail, nous avons utilisé la fonction
StandardScaler(). Mathématiquement, la normalisation StandardScaler est
:
avec :
- x la valeur qu'on veut standardiser (input
variable)
- u la moyenne (mean) des observations pour cette
feature
- ó est l'ecart-type (Standard Deviation) des
observations pour cette variable (feature)
Cette transformation a été faite juste dans le
cadre de vouloir expirmer nos unités dans la même unité.
Comme c'est le cas par exemple de l'âge en année et de la distance
en kilomètre.
49
3.3.4 Descripition des données
Dans cette partie nous allons présenter dans le tableau
3.2 les différentes corrélations entre les données en
étudiant la moyenne de chaque variable, le maximum, le minimun,
l'écart-type (tableau 3.2), ...
Tableau 3.2 - Description des variables quantitatives non
continues
|
Variable
|
Nombre
|
moyenne
|
std
|
min
|
25%
|
50%
|
75%
|
max
|
|
Adresse(km)
|
332.0
|
3.563193
|
3.995763
|
0.34
|
1.41
|
2.43
|
4.925
|
54.0
|
|
Age
|
332.0
|
26.313253
|
6.725840
|
14.00
|
21.00
|
25.00
|
30.000
|
50.0
|
|
Durée de
Séjour
|
332.0
|
5.539157
|
4.351786
|
1.00
|
2.00
|
5.00
|
7.000
|
28.0
|
|
Mean DDSHop
|
332.0
|
5.54
|
0.49
|
5.0
|
5.0
|
6.0
|
6.0
|
6.0
|
3.3.5 Corrélation entre les données
quantitatives
Pour éviter d'autres problèmes de
surapprentissage, nous avons catégorisé certaines colones en
variables catégorielles comme le diagnostique, l'hopital où les
données ont été tirées ainsi que le traitement
réçu. La corrération de SPEARMAN trouvée pour nos
variables est (figure 3.4) :
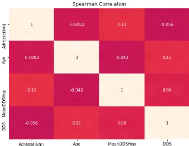
FIGURE 3.4 - Corrélation de spearman entre variables
quantitatives
Selon la figure 3.4, nous constatons que la distance du
ménage et la Durée de Séjour Hospitalier ne
corrélent pas. Par contre, la Durée de Séjour
corrèle avec les autres variables.
50
Ce chapitre étant consacré à la
présentation de la méthode utilisée pour parvenir à
avoir les données utilisables dans l'apprentissage de notre base de
données. Nous avons fait des descentes au sein des hôpitaux
ci-haut énumérés. Les différentes transformations
ont été faites dans le cadre d'avoir une base de données
plus ou moins manipulable. Le chapitre qui suivra sera consacré à
l'apprentissage de la nouvelle base de données avec 332
entrées.
51
Chapitre 4
Modélisation de la prédiction de la
Durée de Séjour Hospitalier en
Gynécologie
4.1 Introduction
Les institutions de santé et toute entreprise qui se
veulent émerger cherchent sans doute à produire un travail de
qualité tout en minimisant le temps et les coûts. Pour les
établissements de soins, ils cherchent aussi à optimiser les
fonctionnements de leurs services tout en assurant un travail de soin de
qualité (on peut lire la pertinance d'une structure sanitaire à
la section 1.5, page 15 ). Le système hospitalier est très
complexe car il fait intervenir plusieurs catégories d'agents : les
médecins, les infirmiers, les personnels administratifs et les patients.
Et toutes ces catégories pourraient avoir un impact solide dans le
changement de la structure hospitalière. Prédire la durée
de séjour hospitalier est dans ce sens un pas d'avance pour les
tructures sanitaires rêvant un épanouissement de grande envergure.
La DDS est identifiée comme une variable complexe dépendant de
plusieurs facteurs liés au contexte médical du patient, aux
conditions de son admission et à l'organisation de l'hôpital ou du
service hospitalier [19].
Dans ce chapitre, nous proposons un modèle de
prédiction de la durée de séjour hospitalier en nous
servant des données de certains hôpitaux de la Province du
Sud-Kivu.
52
Ce modèle se servira des données disponibles
lors de l'admission de la patiente à l'hôpital. Nous
commençons d'abord par expliquer les méthodes de
prédiction de la DDS, le rôle du Machine Learning dans un
système hospitalier, surtout dans la prédiction de la
durée de séjour, nous expliquons aussi les differents algorithmes
qui ont entrainé le modèle avec un score raisonnable pour enfin
finir par une conclusion et le choix d'un meilleur algorithme selon nos
données.
4.2 Méthode de prédiction de Durée de
Séjour Hospitalier
Le milieu hospitalier est complexe, car regroupant plusieurs
acteurs : d'une part, de spécialité médicale tels que les
médecins, les infirmiers et les biologistes, d'autre part nous
retrouvons les administratifs, les financiers et les logisticiens. Dans ce
contexte institutionnel et organisationnel la définition du
séjour hospitalier ainsi que la Durée De Séjour
hospitalier (DDS) doit prendre en compte cette dynamique et interaction entre
plusieurs acteurs [19].
4.2.1 Périmètre d'étude
Le périmètre d'étude représente
dans ce sens, le secteur où la DDS sera considérée. La
définition du périmètre d'étude permet d'identifier
l'ensemble des facteurs qui impactent la DDS [19].
Dans le cadre de ce mémoire, le périmètre
d'étude concerne l'unité médicale de Gynécologie
dans quatre hôpitaux du Sud-Kivu. Dans ce sens, la Durée de
Séjour Hospitalier ne sera pas calculée en fonction du nombre
d'heures comme c'est le cas dans le service d'urgence ou les soins ambulatoires
mais plutôt en jours. Pour nous permettre de faire une
généralisation, dans le cadre de ce mémoire nous avons
pris quatre structures sanitaires.
D'après la définition 1.4, la durée de
séjour hospitalier étant définie comme le séjour
pendant lequel un patient peut-être admis dans un ou plusieurs
unités médicales. Dans le
53
cadre de ce travail, nous ne nous focalisons qu'à la
seule unité médicale de Gynécologie. Alors, la DDS sera le
temps entre l'admission de la patiente et sa sortie dans l'unité
médicale de Gynécologie.
Dans la partie suivante, nous montrons les différents
paramètres que nous allons utiliser dans la modélisation de la
DDS.
4.2.2 Modélisation et processus de prédiction de
la Durée de Séjour
Lors de l'admission dans une unité médicale, les
données disponibles englobent les données démographiques
de la patiente : son nom, son prénom, son identifiant, sa date de
naissance, sa situation familiale et son adresse. Puis doivent suivre des
plaintes qui l'amène à l'hopital et ainsi, de ces plaintes
sortent des diagnostiques de la part des médecins. Et on chute avec une
administration des médicaments.
Comme nous l'avons vu dans le chapitre 3, section 3.3.2, les
informations à caratère personnel sont labélisées
pour rester avec des données distrètes. Nous n'avons pas tenu
conte des antécédents médicaux car nous ne les avons pas
trouvées dans les tructures sanitaires concernées. La
disponibilité de ces données est alors le point de départ
dans le processus de prédiction.
A partir des bases de données médicales,
l'historique des données est trouvée. Cette étape est
suivie par une analyse des données. Ensuite, une phase de
pré-traitement de données est réalisée. Elle inclut
le nettoyage des données, la sélection de variables, la
transformation et l'encodage des données (tout ceci dans le chapitre 3).
L'ensemble de données est séparé en 2 sous-ensembles :
ensemble d'apprentissage qui compte 80% des données et
l'ensemble de test avec 20% de données. L'ensemble
d'apprentissage sert à l'apprentissage du modèle et à la
validation des résultats et l'ensemble de test pour l'évaluation
des résultats obtenus.
54
4.3 Évaluation des modèles de prédiction de
DDS
Cette section concerne les résultats obtenus suite
à l'implémentation des différents processus pour
l'apprentissage automatique décrits dans le chapitre 2 et le chapitre 3.
Les résultats ici présentés sont issus des données
des algorithmes de regression.
4.3.1 Le réseau de neurone dans la prédiction de
Durée de Séjour Hospitalier
En prédisant par l'algorithme des réseaux de
neurones (Neural Network), nous avons trouvé par rapport à nos
données que la prédiction a un score négatif, soit de 78%
pris négativement pour les données de test et 97,6% pour
les données d'apprentissage. La figure suivante (figure 4.1) est une
représentation des valeurs prédites contre les valeurs
réelles.

FIGURE 4.1 - Valeurs actuelles contre les valeurs prédites
en utilisant le réseau de neurone
4.3.2 Les arbres de décision dans la prédiction
de Durée de Séjour Hospitalier
Dans la prédiction de la DDS par la méthode des
arbres de decision (decision Tree), le score pour ce modèle est positif
et il est évalué à 0.13.
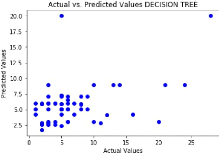
55
FIGURE 4.2 - Valeurs actuelles contre les
valeurs prédites en utilisant les arbres de décision
4.3.3 Le modèle linéaire
généralisé
Nous avons une DDS des données de comptage, ce qui nous
permet d'affirmer que nous pouvons utiliser deux distributions : soit
la distribution Binomiale ou la distribution de poisson. Dans cette
partie, nous allons examiner les deux distributions et tirer une meilleure
conclusion.
1. Distribution de poisson
Ce modèle a été utilisé avec la
distribution de poisson et vous avons été satisfait de son score
qui est de 97%. Nous nous sommes rendu compte que c'est le vrai dans la
prédiction telle que celle ci.
Le resumé du modèle linéaire
généralisé est présenté dans le tableau
4.1.
La deuxième colonne du tableau indique les
coéfficients du MLG. Etant donné que la confiance du
modèle est d'à peu près 97%, le p - value
est donc de 0.03. Certains coéfficients sont
statistiquement significatifs car, ayant un p - value
inférieur à 0.03. Comme c'est le cas par exemple de
Adresse, l'âge, la grossesse, lers Inféctions Urinaires, les
avortements, les Anti Inféctieux, les Analgésiques, les
Vitamines, les céphalo, autres et la moyenne de DDS par hopital.
D'après l'équation 2.4, page 30 la DDS prédite est
supposée être ij, et la fonction de lien dans ce
modèle est la fonction logarithme néperien
56
Tableau 4.1 - Résumé du modèle
linéaire généralisé avec la distribution de
poisson
Generalized Linear Model Regression Results (Poisson
Distribution)
Dep. Variable : DDS No. Observations : 256
Model : GLM Df Residuals : 232
Model Family : Poisson Df Model : 23
Link Function : log Scale : 1.0000
Method : IRLS Log-Likelihood : -720.25
Date : Thu, 12 Oct 2023 Deviance : 587.32
Time : 21 :06 :40 Pearson chi2 : 766.
No. Iterations : 5
|
Covariance Type
|
:
coef
|
nonrobust std err
|
z
|
P>|z|
|
[0.025
|
0.975]
|
|
Adresse(km)
|
-0.0899
|
0.029
|
-3.106
|
0.002
|
-0.147
|
-0.033
|
|
Age
|
0.1283
|
0.028
|
4.644
|
0.000
|
0.074
|
0.182
|
|
Hopital
|
-0.0342
|
0.034
|
-1.008
|
0.314
|
-0.101
|
0.032
|
|
Grossesse
|
0.3048
|
0.083
|
3.686
|
0.000
|
0.143
|
0.467
|
|
IU
|
-0.2051
|
0.089
|
-2.299
|
0.022
|
-0.380
|
-0.030
|
|
MAV
|
-0.1270
|
0.085
|
-1.496
|
0.135
|
-0.293
|
0.039
|
|
Anémie
|
-0.0498
|
0.082
|
-0.608
|
0.543
|
-0.210
|
0.111
|
|
Paludisme
|
0.1256
|
0.093
|
1.353
|
0.176
|
-0.056
|
0.308
|
|
Avortement
|
-0.4229
|
0.077
|
-5.518
|
0.000
|
-0.573
|
-0.273
|
|
Infections
|
0.0844
|
0.079
|
1.063
|
0.288
|
-0.071
|
0.240
|
|
Autres
|
0.0872
|
0.065
|
1.333
|
0.183
|
-0.041
|
0.215
|
|
AB
|
-0.0349
|
0.068
|
-0.514
|
0.607
|
-0.168
|
0.098
|
|
AP
|
-0.0680
|
0.103
|
-0.661
|
0.509
|
-0.270
|
0.134
|
|
OCYTOCIQUES
|
-0.0971
|
0.079
|
-1.234
|
0.217
|
-0.251
|
0.057
|
|
AI
|
-0.5020
|
0.235
|
-2.136
|
0.033
|
-0.963
|
-0.041
|
|
ASM
|
0.0689
|
0.067
|
1.024
|
0.306
|
-0.063
|
0.201
|
|
ANAL
|
-0.2039
|
0.110
|
-1.856
|
0.064
|
-0.419
|
0.011
|
|
AAL
|
0.3220
|
0.090
|
3.598
|
0.000
|
0.147
|
0.497
|
|
Vitamine
|
0.5866
|
0.133
|
4.403
|
0.000
|
0.326
|
0.848
|
|
Cephalo
|
0.3184
|
0.096
|
3.318
|
0.001
|
0.130
|
0.506
|
|
AA
|
-0.0572
|
0.130
|
-0.438
|
0.661
|
-0.313
|
0.199
|
|
Transfusion
|
0.2113
|
0.169
|
1.248
|
0.212
|
-0.121
|
0.543
|
|
Autre2
|
0.1285
|
0.059
|
2.190
|
0.028
|
0.014
|
0.244
|
|
MeanDDSHop
|
0.2852
|
0.025
|
11.414
|
0.000
|
0.236
|
0.334
|
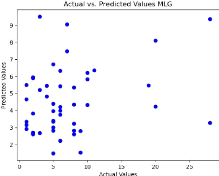
57
FIGURE 4.3 - Valeurs actuelles contre les
valeurs prédites en utilisant le modèle linéaire
généralisé avec la distribution de poisson
('q = log(i)). Avec ,u la moyenne de
la durée de séjour. L'équation 2.4 devient donc :
log(1a) = a0 + Xp aixi
(4.1)
i=1
En guide de l'équation 4.1, en utilisant les variables
significatives telles que trouvées dans le tableau 4.1, la DDS 'q
sera :
- 'q est multipliée par
e-0.0899 lorsque la variable Adresse est
augmentée d'une unité. La valeur
e-0.0899 E]0, 1[, la DDS va donc
diminuer
- 'q est multipliée par e0.1283
lorsque la variable Age est augmentée d'une
unité. La quantité e-0.1283 est
supérieure à 1, ce qui signifie que plus l'âge augmente, la
DDS aussi augmente.
- 'q est multipliée par e0.2852
lorsque la variable Durée Moyenne de DDS est
augmentée d'une unité. La quantité e0.2852
est supérieure à 1, ce qui signifie que plus
l'âge augmente, la DDS aussi augmente.
- pour les variables dichotomiques, on ne fait pas trop de
commentaires car on constate qu'elles ne prendrons pas des valeurs au
délà de 0 et 1.
On peut donc voir qu'il y a des variables significatives
à coéfficients positifs ont tendences à augmenter la DDS
d'un patient à l'Hopital.
Par rapport aux données prédites par ce
modèle, la variance est de 6.549 et la moyenne est de
5.867. Ceci nous montre que, la différence sur ces deux est
d'environs 1.364, où il
58
n'y a pas un écart considérable entre les deux.
2. Distribution Binomiale Négative
Pour cette distribution, nous avons un degré de
confiance de 95%. Le tableau 4.2 nous présente le résumé
de ce modèle. L'interprétation des coéfficients de ce
tableau utilise la même procédure que pour le tableau 4.1. Par
contre, nous n'avons qu'une seule variable significative qui est la
durée moyenne de DDS par Hopital. Cette variable lorsqu'elle
augmente d'une unité, la DDS est multipliée par un facteur de
e0.3064.
D'après les analyses des tableaux 4.1 et 4.2 et comme
nous avons deux modèles différents, nous allons comparer leurs
prédictions par la méthode AIC (Akaike Information Criterion ) de
python où le AIC des modèles linéaires
généralisés en utilisant respectivement les distributions
de poisson et binomiale négative sont : 1569 et 1578.
Il s'en suit donc que la distribution de poisson est celle qui
est plus adaptée (car ayant le plus petit AIC) à ces
données que l'autre. Ceci était déjà visible par le
biais de la signification des variables.
4.3.4 Le k Plus proches voisins
Dans le cadre de cette étude, le modèle des
k plus proches voisins a prédit avec un score approximatif qui
est de 0.09 soit moins de 10%. La figure 4.4 est une
représentation des valeurs prédites contres les séjours
réels des malades.

FIGURE 4.4 - Valeurs actuelles contre les valeurs
prédites en utilisant le k Plus proches voisins
59
Tableau 4.2 - Résumé du modèle
linéaire généralisé avec la distribution binomiale
négative
Generalized Linear Model Regression Results
Dep. Variable : DDS No. Observations : 281
Model : GLM Df Residuals : 257
Model Family : NegativeBinomial Df Model : 23
Link Function : log Scale : 1.0000
Method : IRLS Log-Likelihood : -765.21
Date : Mon, 16 Oct 2023 Deviance : 97.379
Time : 00 :01 :23 Pearson chi2 : 123.
No. Iterations : 9
|
Covariance Type
|
:
coef
|
nonrobust std err
|
z
|
P>|z|
|
[0.025
|
0.975]
|
|
Adresse(km)
|
0.0155
|
0.074
|
0.210
|
0.834
|
-0.129
|
0.160
|
|
Age
|
0.0509
|
0.070
|
0.722
|
0.470
|
-0.087
|
0.189
|
|
Hopital
|
-0.0045
|
0.079
|
-0.056
|
0.955
|
-0.160
|
0.151
|
|
Grossesse
|
0.0667
|
0.191
|
0.349
|
0.727
|
-0.308
|
0.441
|
|
IU
|
-0.0739
|
0.208
|
-0.355
|
0.723
|
-0.482
|
0.334
|
|
MAV
|
-0.1880
|
0.212
|
-0.887
|
0.375
|
-0.604
|
0.228
|
|
Anémie
|
-0.1224
|
0.194
|
-0.632
|
0.527
|
-0.502
|
0.257
|
|
Paludisme
|
-0.0099
|
0.229
|
-0.043
|
0.965
|
-0.458
|
0.438
|
|
Avortement
|
-0.3523
|
0.183
|
-1.930
|
0.054
|
-0.710
|
0.005
|
|
Infections
|
-0.1126
|
0.204
|
-0.551
|
0.581
|
-0.513
|
0.288
|
|
Autres
|
0.0388
|
0.168
|
0.230
|
0.818
|
-0.291
|
0.369
|
|
AB
|
-0.0008
|
0.171
|
-0.005
|
0.996
|
-0.335
|
0.334
|
|
AP
|
0.0533
|
0.227
|
0.235
|
0.814
|
-0.391
|
0.498
|
|
OCYTOCIQUES
|
-0.0898
|
0.191
|
-0.470
|
0.639
|
-0.464
|
0.285
|
|
AI
|
-0.5137
|
0.540
|
-0.951
|
0.341
|
-1.572
|
0.545
|
|
ASM
|
0.2355
|
0.178
|
1.321
|
0.186
|
-0.114
|
0.585
|
|
ANAL
|
-0.0299
|
0.232
|
-0.129
|
0.898
|
-0.485
|
0.425
|
|
AAL
|
0.0568
|
0.252
|
0.226
|
0.821
|
-0.436
|
0.550
|
|
Vitamine
|
0.4917
|
0.385
|
1.276
|
0.202
|
-0.263
|
1.247
|
|
Cephalo
|
0.1706
|
0.279
|
0.612
|
0.541
|
-0.376
|
0.717
|
|
AA
|
0.0415
|
0.313
|
0.133
|
0.894
|
-0.572
|
0.655
|
|
Transfusion
|
0.0846
|
0.316
|
0.268
|
0.789
|
-0.534
|
0.704
|
|
Autre2
|
0.0038
|
0.141
|
0.027
|
0.978
|
-0.272
|
0.280
|
|
MeanDDSHop
|
0.3064
|
0.061
|
5.026
|
0.000
|
0.187
|
0.426
|
60
4.3.5 Tableau synthètique
Nous avons déjà vu d'après les trois
sous-sections précédentes les deux algorithmes de l'apprentissage
supervisé en regression que nous avons utilisé sur nos
données. Le tableau suivant reprend pour chacun des modèles le
score, le F1-score, etc.
Tableau 4.3 - Évaluation du modèle statique de
prédiction de DDS : régression
|
Algorithme
|
Réseau de
neurone
|
Arbre de décision
|
K plus
proches voisins
|
Forêt aléatoire
|
MLG
|
|
Erreur Quadratique
moyenne
|
29.49
|
19.91
|
26.99
|
27.99
|
14.24
|
|
Erreur absolue
moyenne
|
4.11
|
3.02
|
3.15
|
3.55
|
2.77
|
|
Score R2
|
-0.78
|
0.13
|
0.09
|
0.11
|
0.97
|
D'après le tableau 4.3, le modèle
linéiare généralisé est celui qui approxime la
durée de séjour hospitalier en minimisant les erreurs.
Ce chapitre étant concentré sur la
modélisation de la prédiction de la durée de séjour
hospitalier, nous sommes parti des bases de données décrites dans
le chapitre 3, pour faire une prédiction de la DDS. Les méthodes
de prédiction de la DDS au moment de l'admission de la patiente sont
basées sur des fouilles des données. Nous avons trouvé que
le modèle linéaire généralisé est le
modèle très fidele dans la prédiction d'un quelconque
séjour hospitalier.
61
Conclusion
Résumé conclusif
Les établissements de soins sont toujours à la
quête de l'excellence par le canal d'une amélioration de la
qualité des soins et de l'efficacité des services notamment en
terme de gestion hospitalière et humaine. La Durée De
Séjour hospitalier (DDS) savère un indicateur d'évaluation
des performances des hôpitaux. Dans ce mémoire, nous avons
passé en revu des différents modèles de prédiction
des Durées de Séjour Hospitalier qui se basent sur des
données issues de certains hopitaux du Sud-Kivu dans l'unité
médicale de gynécologie. Ces données sont
exploitées pour prédire la DDS au moment de l'admission de la
patiente.
Le grand travail présenté dans ce mémoire
est sans doute celui de la proposition d'un modèle de prédiction
de DDS. Cette dernière était de prédire la DDS depuis lors
que la patiente arrive à l'hopital en se basant à certains
diagnostiques des agents de santé et le traitement administré
à la patiente. Nous nous sommes basé sur des techniques et
méthodes de l'apprentissage automatique et la fouille de
données.
Contributions
La Durée de Sejour hospitalier est un facteur tout
à fait complexe du fait qu'elle est facteur de plusieurs acteurs qui
doivent conjuguer plusieurs efforts pour rendre meilleure la structure
sanitaire. D'abord, nous avons étudié les facteurs pouvant
influencer la durée de séjour hospitalier en
général, en suite nous avons recolté des données
pour les exploiter et en fin faire un algorithme de prédiction de DDS
dans une unité médicale de gynécologie.
62
De ceci, nous avons fait une approche méthodologique de
la sorte :
Définition d'un paramètre d'étude
: dans ce mémoire, nous sommes parti d'une seule unité
médicale qui est celle de gynécologie.
Modélisation générique de la DDS
: une étude minitieuse a été ménée
pour savoir les facteurs qui impactent la DDS dans une unité
médicale. L'ensemble des facteurs démographiques (l'âge, le
sexe, l'adresse) et des facteurs médicaux (motif d'hospitalisation,
diagnostics et traitement réçus). Cette modélisation de la
DDS est la porte d'entrée aux processus de prédiction. Les
processus de prédiction se sont appuyés sur les méthodes
d'apprentissage automatique et de fouille de données (où nous
avons l'encodage, le traitement de données, ...).
Modèle statique de prédiction de DDS
: nous avons présenté un modèle de
prédiction de la DDS dans l'unité de gynécologie en nous
appuyant aux données disponibles lors de l'admission de la patiente
à l'hôpital. Nous avons utilisé des techniques
d'apprentissage supervisé (Neural Network, Decision Tree, ... ). Les
résultats obtenus ont montré que les algorithmes d'apprentissage
automatique sont performants en terme de précision et de taux d'erreurs
dans la prédiction des DDS en milieu hospitalier. L'algorithme qui a
très bien entrainé nos données est le modèle
linéaire généralisé étant donné que
son score est positif et minimise les erreurs (avec un score de 97%).
Perspectives
Le domaine de Machine Learning est encore en plein essort
surtout dans les pays en voie de développement comme notre pays la RDC
où plusieurs entreprises ont encore une gestion manuelle de
données. La prédiction de la DDS s'avère un facteur
clé d'indication de la fiabilité et de la viabilité d'une
structure sanitaire, parvenir à prédire avec moins d'erreur
possible est une réponse à une panoplie de questions que les
gestionnaires de santé se posent du jour au lendemain. La porte de
sortie étant prometeuse par rapport aux différents algorithmes
utilisés dans la construction du modèle, mais quelques
perspectives peuvent être sorties pour des prochaines recherches :
- quant au périmètre d'étude, il serait
plus intéressant de faire part d'autres unités médicales
et ainsi, faire une prédiction de DDS dans plusieurs unités
médicales et
63
pas dans une seule unité médicale ;
- par rapport à la modélisation, associer les
experts médicaux dans le choix des facteurs influançant la DDS
est un atout ;
- Regardant la complexité des données
médicales, l'expert médical doit aussi être impliqué
dans l'analyse des profils atypiques pour les détecter et les distinguer
des données aberrantes.
- Afin d'améliorer les performances des algorithmes
d'apprentissage automatique, une piste serait d'enrichir l'ensemble de
données utilisé dans l'apprentissage et celui utilisé dans
la validation des processus de prédiction [19]. L'ajout des nouvelles
données et qui présentent une richesse dans les informations
permet aux algorithmes d'apprentissage automatique d'apprendre sur plus de cas
et de ce fait, ils aboutissent à des résultats plus précis
[19].
La prédiction de DDS s'avère un axe de recherche
important dans le domaine médical. Les méthodes que nous avons
proposées peuvent avoir des imperfections inhérentes à
notre volonté, c'est ainsi que nous resterons receptifs aux suggestions
et recommendations de la part de nos lecteurs.
64
Bibliographie
[1]
https://blent.ai/blog/a/apprentissage-supervise-definition.
[2]
https://scikit-learn.org/stable/index.html.
[3]
https://www.maxicours.com/se/cours/comprendre-et-utiliser-l-algorithme-des-k-plu
[4]
https://www.vocabulaire-medical.fr/encyclopedie/264-seance-sejour#:~:
text=Lorsqu'un%20patient%20est%20hospitalis%C3%A9,actuellement%20des%
20%%AB%20unit%C3%A9s%20m%C3%A9dicales%20%%BB.
[5]
https://www.yzr.ai/articles/comment-standardiser-des-donnees/.
[6]
https://zestedesavoir.com/tutoriels/962/les-arbres-de-decisions/.
[7] A. K. Alahmari. actors Associated with Length of
Hospital Stay among COVID-19 Patients in Saudi Arabia : A Retrospective Study
during the First Pandemic Wave. Healthcare, 2022.
[8] J. A.LOUGHANI. Algorithme des k-plus proches
voisins.
Acadéie Lille, Paris, Disponible sur
https://www.google.
com/url?q=
http://www.planeteisn.fr/k-voisins.pdf&sa=
U&ved=2ahUKEwiAlPjh4Y2AAxUBjZUCHdS6DB4QFnoECAAQAg&usg=
AOvVaw0PvUZRG8qzODxZGwin7T8W.
[9] M. Cavalier. La propriété des
données de santé. Thèse de doctorat,
Université Jean Moulin (Lyon 3), Lyon, 2016.
[10] F. CHOLLET. L'apprentissage profond avec Python.
Collection Les Essentiels de
l'IA, 37540 Saint-Cyr sur Loire France, 2020.
[11] P. Degoulet. Systèmes d'Information
Hospitaliers. HEGP,Faculté de Médecine
Broussais-Hôtel-Dieu, Ecole d'été Corte, juillet 2001.
[12]
65
M. L. Erick Biernat. Data Science fondamentaux et
étude des cas Machine Learning avec Python et R. Edition EYROLLES,
Paris, 2015.
[13] S. B. et All. Design d'un algorithme d'IA en grande
dimension pour prédire la réadmission à l'hôpital.
IA & Santé, 2018.
[14] M. S.-M. B. G. F. B. S. T. G. Dreyfus, J.-M. Martinez.
Apprentissage statistique. Edition EYROLLES, Paris, 2008.
[15] J. Grus. Data Science par la pratique. Edition
EYROLLES, Paris, 2017.
[16] S. Hull. Machine Learning for Economics and Finance
in TensorFlow 2 Deep Learning Models for Research and Industry. Apress
Media LLC : Welmoed Spahr, California, 2021.
[17] F. J.-J. Joseph. Liste nationale des
médicaments essentiels. Direction de la Pharmacie, du
Médicament et de la Médecine Traditionnelle, République
d'HAITI, 1e édition, Mai 2012.
[18] M. R. Naila. Apprentissage automatique dans la
prédiction des durées de séjour hospitalier.
ResearchGate, 2020.
[19] M. R. Naila. Conception et développement des
méthodes de prédiction de la durée de séjour
hospitalier centrées sur des techniques de machine learning.
Thèse de Doctorat, Polytechnique Hauts-de-France, Valencienne, 27
janvier 2022.
[20] F. nationale des observatoires régionaux de la
santé. Les données de santé. Conférence
nationale de santé, Paris, Octobre 2009.
[21] OMS. Liste des médicaments essentiels par
classe thérapeutique. Direction de la Pharmacie, du
Médicament, Programme de Médicaments Essentiels, 2021.
[22] G. S. Peter Kunt Dunn. Generalized Linear Models
With Examples in R. Springer, New-York, 2018.
[23] M. M. J.-L. R. Pirmin Lemberger, Marc Batty. Big
Data et Machine Learning Manuel du Data scientist. Dunod, Paris, 2015.
[24] F. Rossi. Réseaux de neurones le perceptron
multi-couches. Universit'e Paris-IX Dauphine, sur
http://apiacoa.org/contact.html.
[25] G. Saint-Cirgue. Apprendre les Machines Learning en
une semaine. 2019.
[26]
66
M. TAFFAR. Initiation à l'apprentissage automatique.
Université de Jijel.
[27] C. Touzet. Les réseaux de neurones
artificiels, introduction au connexionnisme : cours, exercices et travaux
pratiques. E, Collection de l'EERIE, N. Giambiasi, 1992.
67
Liste des tableaux
3.1 Exemple de la base de données 45
3.2 Description des variables quantitatives non continues
49
4.1 Résumé du modèle linéaire
généralisé avec la distribution de poisson . . . 56
4.2 Résumé du modèle linéaire
généralisé avec la distribution binomiale négative
59
4.3 Évaluation du modèle statique de
prédiction de DDS : régression . . . . 60
68
Table des figures
1.1 Composantes des Systèmes d'Informations Hospitaliers
[11] 7
1.2 Données médicales : sources et
propriétés [19] 11
1.3 Évaluation des systèmes de santé : DDS
[19] 15
1.4 Techniques de l'Intelligence Artificielle et leurs
applications [19] 17
2.1 Les relations entre l'intelligence artificielle,
l'apprentissage automatique et
l'apprentissage profond [10] 20
2.2 Modèle de traitement de données en
apprentissage supervisé [1] 25
2.3 Modèle de traitement de données en
apprentissage non supervisé [1] . . 26
2.4 Modèle de traitement de données en
apprentissage par renforcement . 27
2.5 Exemple d'un arbre avec ses differentes parties [16] 32
2.6 Généralisation du modèle
prédictif Forêt aléatoire [16] 34
2.7 Réseau de neurones [25] 37
2.8 Réseau de neurones à plusieurs neurones [25]
38
3.1 Diagramme circulaire des données utilisées
44
3.2 Importance de chaque variable 47
3.3 Histogramme de la Durée de Séjour Hospitalier
48
3.4 Corrélation de spearman entre variables quantitatives
49
4.1 Valeurs actuelles contre les valeurs prédites en
utilisant le réseau de neurone 54 4.2 Valeurs actuelles contre les
valeurs prédites en utilisant les arbres de décision 55 4.3
Valeurs actuelles contre les valeurs prédites en utilisant le
modèle linéaire
généralisé avec la distribution de poisson
57
69
4.4 Valeurs actuelles contre les valeurs prédites en
utilisant le k Plus proches
voisins 58
70
Table des matières
Epigraphe I
Dédicace II
Remerciements III
Introduction générale 1
1 Les systèmes d'informations hospitaliers et la
gestion hospitalière 5
1.1 Introduction 5
1.2 Les systèmes d'informations hospitaliers 6
1.2.1 Terminologie 6
1.2.2 Type d'informations 7
1.3 Sources des données des SIH 9
1.3.1 Dossier médical du patient 9
1.3.2 Les données administratives 9
1.3.3 Les données issues des enquêtes et de la
recherche clinique . . . 10
1.4 Propriétés des données médicales
10
1.4.1 Confidentialité 11
1.4.2 Données incrémentales 12
1.4.3 Hétérogénéité 13
1.4.4 Complexité 14
1.5 Durée De Séjour hospitalier 14
1.6 Facteurs influençant la DDS 16
1.7 Que vient faire l'intelligence artificielle dans tous
ça ? 16
71
2
|
Modèles de prédiction en Machine
Learning
|
19
|
|
2.1
|
Introduction
|
19
|
|
2.2
|
Intelligence Artificielle, Machine Learning et
|
|
|
|
Apprentissage Profond
|
19
|
|
|
2.2.1 Intelligence Artificielle : Artificial Intelligent
(AI)
|
20
|
|
|
2.2.2 Apprentissage automatique : Machine Learning
|
21
|
|
|
2.2.3 Apprentissage des représentations à partir de
données
|
22
|
|
2.3
|
Les apprentissages en Machine Learning
|
24
|
|
|
2.3.1 Introduction
|
24
|
|
|
2.3.2 Apprentissage supervisé
|
24
|
|
|
2.3.3 Apprentissage non supervisé
|
25
|
|
|
2.3.4 Apprentissage semi-supervisé
|
26
|
|
|
2.3.5 Apprentissage par renforcement
|
26
|
|
2.4
|
Algorithmes de l'apprentissage automatique
|
27
|
|
|
2.4.1 Régression linéaire
|
28
|
|
|
2.4.2 Les k plus proches voisins
|
30
|
|
|
2.4.3 Les arbres de décision
|
31
|
|
|
2.4.4 Les forêts aléatoires
|
34
|
|
|
2.4.5 Les réseaux de neurones artificiels
|
36
|
|
2.5
|
Pertinence d'un modèle de prédiction
|
40
|
|
|
2.5.1 Score R2, coefficient de
détermination
|
41
|
|
|
2.5.2 Erreur absolue moyenne
|
41
|
|
|
2.5.3 Erreur quadratique moyenne
|
42
|
|
3
|
Cadre méthodologique
|
43
|
|
3.1
|
Introduction
|
43
|
|
3.2
|
Type d'informations récuillies
|
43
|
|
3.3
|
Récolte et Pré-traitement des données
|
44
|
|
|
3.3.1 Récolte de données
|
45
|
|
|
3.3.2 Pré-traitement des données
|
45
|
|
|
3.3.3 Normalisation et Standardisation des données
|
48
|
72
|
|
3.3.4 Descripition des données
3.3.5 Corrélation entre les données quantitatives
|
49
49
|
|
4
|
Modélisation de la prédiction de la
Durée de Séjour Hospitalier en
|
|
|
Gynécologie
|
51
|
|
4.1
|
Introduction
|
51
|
|
4.2
|
Méthode de prédiction de Durée de
Séjour
|
|
|
|
Hospitalier
|
52
|
|
|
4.2.1 Périmètre d'étude
|
52
|
|
|
4.2.2 Modélisation et processus de prédiction de la
Durée de Séjour . .
|
53
|
|
4.3
|
Évaluation des modèles de prédiction de DDS
|
54
|
4.3.1 Le réseau de neurone dans la prédiction de
Durée de Séjour Hospitalier 54 4.3.2 Les arbres de
décision dans la prédiction de Durée de Séjour
Hospitalier 54
4.3.3 Le modèle linéaire
généralisé 55
4.3.4 Le k Plus proches voisins 58
4.3.5 Tableau synthètique 60
Conclusion 61
Résumé conclusif 61
Contributions 61
Perspectives 62
Bibliographie 64
Liste des tableaux 67
Table des figures 68
Table des matières 70
Annexe I
Annexe I : Base de données I
Annexe II : Subdivision de la base de données II
Annexe III : Entrainement des modèles III
I
Annexe
Annexe I : Information de notre base de
données
1 DATABASE. info ()
<class 'pandas core frame DataFrame'> Int64Index : 332
entries, 0 to 331 Data columns (total 25 columns) :
|
#
|
Column
|
Non-Null Count
|
Dtype
|
|
0
|
Adresse(km)
|
332 non-null
|
float64
|
|
1
|
Age
|
332 non-null
|
float64
|
|
2
|
Hopital
|
332 non-null
|
category
|
|
3
|
Grossesse
|
332 non-null
|
category
|
|
4
|
IU
|
332 non-null
|
category
|
|
5
|
MAV
|
332 non-null
|
category
|
|
6
|
Anémie
|
332 non-null
|
category
|
|
7
|
Paludisme
|
332 non-null
|
category
|
|
8
|
Avortement
|
332 non-null
|
category
|
|
9
|
Infections
|
332 non-null
|
category
|
|
10
|
Autres
|
332 non-null
|
category
|
|
11
|
AB
|
332 non-null
|
category
|
|
12
|
AP
|
332 non-null
|
category
|
II
13
|
OCYTOCIQUES
|
332 non-null
|
category
|
|
14
|
AI
|
332 non-null
|
category
|
|
15
|
ASM
|
332 non-null
|
category
|
|
16
|
ANAL
|
332 non-null
|
category
|
|
17
|
AAL
|
332 non-null
|
category
|
|
18
|
Vitamine
|
332 non-null
|
category
|
|
19
|
Celphalo
|
332 non-null
|
category
|
|
20
|
AA
|
332 non-null
|
category
|
|
21
|
Transfusion
|
332 non-null
|
category
|
|
22
|
Autre2
|
332 non-null
|
category
|
|
23
|
MeanDDSHop
|
332 non-null
|
float64
|
|
24
|
DDS
|
332 non-null
|
int32
|
dtypes : category(21), float64(3), int32(1) memory usage : 19.6
KB memory usage : 70.4 KB
Annexe II : Subdivision de la base de
données
1 #Subdivision de la base de données en
target et data
2 data=BASE[ [ ' Adresse (km) ', 'Age ' , '
Hopital ' , ' Grossesse ', 'IU ' , 'MAV' , 'Ané mie' ,
3 ' Paludisme' , ' Avortement' , ' Infections '
, ' Autres' , 'AB' , 'AP' ,
4 'OCYTOCIQUES' , 'AI ' , 'ASM' , 'ANAL' , 'AAL'
, ' Vitamine ' , ' Celphalo ' , 'AA' ,
5 ' Transfusion ', ' Autre2 ' , 'MeanDDSHop ' ]
]
6 target=BASE[ [ 'DDS' ] ]
7
8 #Données de test et données d '
entrainement
9 x , y=data , target
10 x_train , x_test , y_train , y_test=
train_test_split (x , y , test_size =0.20)
III
Annexe III :Entrainement de nos données aux
modèles de machine learning
Arbes de décision
1
2
3 # Split the data into training and testing
sets
4 x_train , x_test , y_train , y_test =
train_test_split (x , y , test_size =0.20 , random_state=0) # Adjust test_size
and random_state as needed
5
6 # Model initialization and training
7 model1 =t ree . DecisionTreeRegressor
(max_depth=300, min_samples_split =25)
8 model1 . fit ( x_train , y_train )
9
10 # Model evaluation
11 y_pred = model1 . predict ( x_test )
12 # Compute various scores
13 mae = mean_absolute_error ( y_test ,
y_pred)
14 mse = mean_squared_error ( y_test ,
y_pred)
15 r_squared = r2_score ( y_test , y_pred)
16
17 # Print the scores in a formatted manner
18 print ("Mean Absolute Error : { :.2 f }".
format (mae) )
19 print ("Mean Squared Error : { :.2 f }".
format (mse) )
20 print ("R-squared : { :.2 f }". format (
r_squared ) )
21
22 # Print the R-squared score in a formatted
manner
23 print ("R-squared : { :.2 f }". format (
r_squared ) )
k plus proches voisins
1 import numpy as np
2 import matplotlib . pyplot as plt
3 from sklearn . datasets import load_digits
4 from sklearn . neighbors import
KNeighborsRegressor
IV
5 from sklearn . model_selection import
train_test_split
6 from sklearn . metrics import
mean_absolute_error , mean_squared_error , r2_score
7
8 # Assuming x and y are your data and target
9 x , y = data, target
10
11 # Split the data into training and testing
sets
12 x_train , x_test , y_train , y_test =
train_test_split (x , y , test_size =0.20 , random_state=42)
13 # Adjust random_state as needed
14
15 # Model initialization and training
16 MODEL = KNeighborsRegressor ( leaf_size
=30000000, metric='minkowski ' , n_neighbors=10, p=4000, weights ='uniform '
)
17 MODEL. fit ( x_train , y_train )
18
19 # Model evaluation
20 y_pred = MODEL. predict ( x_test )
21
22 # Compute various scores
23 mae = mean_absolute_error ( y_test ,
y_pred)
24 mse = mean_squared_error ( y_test ,
y_pred)
25 r_squared = r2_score ( y_test , y_pred)
26
27 # Print the scores
28 print ("Mean Absolute Error :" , mae)
29 print ("Mean Squared Error :" , mse)
30 print ("R-squared :" , r_squared )
31
32 # Visualize the results
33 plt . scatter ( y_test , y_pred , color
='blue ' )
34 plt . xlabel ("Actual Values")
35 plt . ylabel (" Predicted Values")
36 plt . title ("Actual vs . Predicted
Values")
37 plt . show ()
V
Réseau de neurone
1 import numpy as np
2 from sklearn . datasets import load_digits
3 from sklearn . neural_network import MLPRegressor
4 from sklearn . model_selection import train_test_split
5 from sklearn . preprocessing import StandardScaler
6 from sklearn . metrics import mean_squared_error , r2_score
7
8 # Assuming x and y are your data and target
9 x , y = data, target
10
11 # Split the data into training and testing sets
12 x_train , x_test , y_train , y_test = train_test_split (x , y
, test_size =0.20 , random_state=42)
13
14 # Feature scaling
15 scaler = StandardScaler ()
16 x_train_scaled = scaler . fit_transform ( x_train )
17 x_test_scaled = scaler. transform ( x_test )
18
19 # Model initialization and training
20 model = MLPRegressor( hidden_layer_sizes =(300, 700 , 1) ,
max_iter=1000)
21 model. fit ( x_train_scaled , y_train )
22
23 # Model evaluation
24 y_pred = model. predict ( x_test_scaled )
25 # Compute various scores
26 mae = mean_absolute_error ( y_test , y_pred)
27 mse = mean_squared_error ( y_test , y_pred)
28 r_squared = r2_score ( y_test , y_pred)
29
30 # Print the scores in a formatted manner
31 print ("Mean Absolute Error : { :.2 f }". format (mae) )
32 print ("Mean Squared Error : { :.2 f }". format (mse) )
VI
33 print ("R-squared : { :.2 f } " . format (
r_squared ) )
34
35 # Visualize the results
36 plt . scatter ( y_test , y_pred , color
='blue ' )
37 plt . xlabel ( " Actual Values " )
38 plt . ylabel ( " Predicted Values " )
39 plt . title ( " Actual vs . Predicted
Values " )
40 plt . show ()
Modèle linéaire
généralisé avec la distribution de poisson
|
1 import pandas as pd
2 from patsy import dmatrices
3 import numpy as np
4 import statsmodels . api as sm
5 import matplotlib . pyplot as plt
6 poisson_training_results = sm.GLM( y_train ,
x_train , family=sm. families . Poisson()). fit ()
7 print ( poisson_training_results . summary())
#affichage du résumé
|
Modèle linéaire
généralisé avec la distribution de Binomiale
négative
|
1 import pandas as pd
2 from patsy import dmatrices
3 import numpy as np
4 import statsmodels . api as sm
5 import matplotlib . pyplot as plt
6 nb_training_results = sm.GLM( y_train ,
X_train , family=sm. families. NegativeBinomial () ) . fit ()
7 print ( nb_training_results . summary ( ) )
#affichage du résumé
|
| 


