Dans un premier temps, nous avons réalisé un
graphique qui nous permet de ressortir la variance qui est expliquée par
chaque dimension.
Graphique 14 : Variance expliquée par chaque
dimension
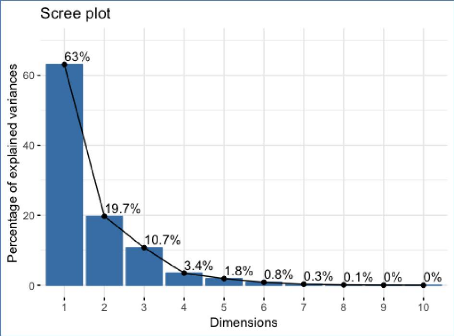
Le graphique 14 montre que l'inertie ressort principalement
des trois premières composantes. En effet, la première dimension
est dominante car elle ressort 63% de l'inertie de l'analyse en composante
principale tandis que la seconde dimension en ressort seulement 19,7%. Enfin,
la troisième dimension ressort 10,7% de l'inertie de l'ACP. En observant
le graphique, les autres dimensions ressortes très peu d'inertie voir
pas du tout.
A présent, nous allons observer la qualité de
la représentation de nos variables sur le graphique. Nous allons donc
regarder les cosinus carrés associés à nos variables.
39
Graphique 15 : Cosinus des dimensions
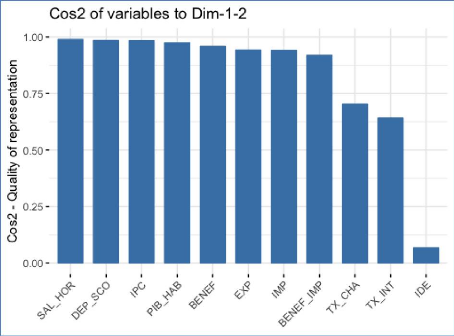
Tout d'abord, il est important de souligner que si la valeur
du cosinus est élevée alors la variable aura une meilleure
représentation sur les axes considérés. De plus, une
variable dont le cosinus carré est élevé sera proche de
l'origine du cercle de corrélation. D'après le graphique 15, les
variables SAL_HOR, DEP_SCO, IPC et PIB_HAB sont très bien
représentées. En effet, la valeur de leurs cosinus carrés
est proche de un. Le TX_CHA présente un cosinus carré d'environ
0,70 tandis que celui du TX_INT est d'environ 0,65. En revanche, la variable
à expliquer (IDE) ne semble pas bien représentée car la
valeur de son cosinus est très faible (environ 0,10).
Dans l'étape suivante, nous allons procéder
à la représentation de nos variables sur le cercle de
corrélation. Pour cela, nous allons observer la contribution des
variables dans la définition des composantes.
40
Graphique 16 : Contribution de chaque variable à la
définition des composantes
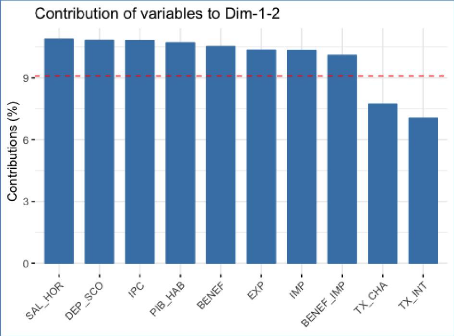
Le graphique 16 nous montre les contributions de chaque
variable à la définition des composantes dans le cadre des deux
premières dimensions. Les résultats obtenus à partir de ce
graphique sont très similaires à ceux des corrélations
variables composantes. En effet, les variables fortement
corrélées avec la première dimension participent davantage
à expliquer la variabilité de l'échantillon. De
manière identique, les variables qui ne sont pas ou très peu
corrélées avec une composante ne participent pas ou très
peu à expliquer la variabilité de l'échantillon. Le trait
en pointillé rouge représente la contribution moyenne. Les
variables les mieux représentées dans le cadre des deux
premières dimensions sont le SAL_HOR, DEP_SCO et l'IPC. Il est beaucoup
plus simple d'observer ces indicateurs sur un graphique qui favorise
l'interprétation des données.
41
Graphique 17 : Cercle de corrélation
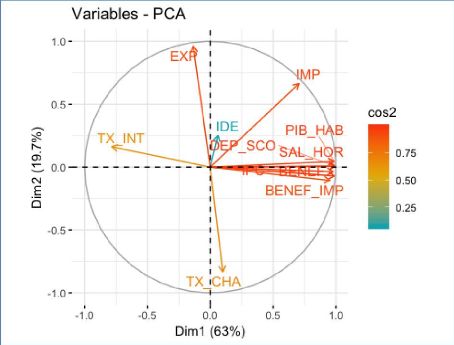
A partir du graphique 17 représentant le cercle de
corrélation, les variables IDE, IMP, PIB_HAB, DEP_SCO, SAL_HOR, BENEF,
BENEF_IMP, IPC et TX_CHA ont une corrélation positive avec la dimension
1. En revanche, les variables TX_INT et EXP sont corrélés
négativement car elles se situent sur la partie gauche du cercle. Par
exemple, les variables EXP, IMP et BENEF_IMP font parties des variables qui
sont très bien représentées car leurs flèches sont
très proches du cercle. Dans le cas de la seconde dimension, les
variables IPC, BENEF, BENEF_IMP et TX_CHA sont corrélées
négativement tandis que les variables SAL_HOR, DEP_SCO, PIB_HAB, IMP,
IDE, EXP et TX_INT sont corrélés positivement. La somme des
dimensions dépasse les 80%, ce qui permet d'affirmer que le
modèle est bien représenté. Cependant, la variable
à expliquer est très mal représentée car sa
flèche est proche de l'origine du cercle. Pour conclure sur l'analyse en
composante principale, il est possible de dire que le modèle semble
plutôt satisfaisant et le choix des variables explicatives semble
pertinent.
42
Graphique 18 : Représentation des observations
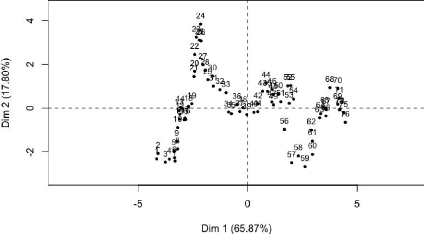
D'après le graphique 18, nous observons que les
observations 75 et 76 contribuent très fortement à l'axe 1. En
effet, ces deux observations correspondent au troisième et
quatrième trimestre 2013. Par conséquent, on peut dire que les
investissements directs étrangers ont été satisfaisants
sur ces deux trimestres.
En revanche, pour l'axe 2, l'observation 24 semble la plus
contributive. Elle représente le quatrième trimestre 2010. Ce
point est le plus contributif car il s'agit du point le plus haut sur l'axe 2.
Globalement, les observations les moins bien représentées sont
celles qui correspondent à la période de crise
économique.



