étude des atténuations dans une transmission par fibre optique.

ATHÉNÉE SAINT JOSEPH ANTSIRABE (A.S.J.A)

MÉMOIRE DE FIN D'ÉTUDE EN VUE DE L'OBTENTION DU DIPLÔME DE MASTER II

Mention : Informatique

Parcours : Télécommunications

ÉTUDE DES ATTÉNUATIONS

DANS UNE TRANSMISSION PAR

FIBRE OPTIQUE

Présenté par : RABESALAMA Iabaina Isidor Soutenu publiquement le : 07 Novembre 2016

Devant les membres du jury composés de :

Président : Examinateurs :

Monsieur RASAMIMANANA François de Salle Monsieur RAKOTOMALALA

Monsieur RATIANARIVO Paul Ezekel

Encadreur pédagogique : Monsieur RANDRIAMIHAJARISON Mparany Jimmy

Année académique : 2015 - 2016

REMERCIEMENTS

I

Ce présent mémoire n'aurait jamais pu être réalisé sans la grâce Divine et la collaboration des quelques personnes.

Nous tenons donc à remercier avant tout, notre Seigneur Dieu Tout Puissant de nous avoir donné la santé, la force et le courage afin que nous puissions mener à bien ce mémoire.

L'existence de l'université Athénée Saint Joseph Antsirabe (ASJA) nous offre la possibilité d'acquérir des connaissances durant 5 ans et de réaliser ce présent travail.

Nous exprimons donc nos vifs remerciements :

> Au Révérend Père CUOMO Mario Giuseppe pour la création de l'ASJA et sa contribution à assurer l'avenir des jeunes étudiants ;

> À son Excellence, Monseigneur Rosario SARO VELLA qui nous a aidé financièrement durant notre étude universitaire ;

> À Monsieur Le Recteur TSIRINIRINDRAVO Herisetra Lalaina pour ses efforts afin d'assurer une bonne administration de l'ASJA ;

> À Monsieur RASAMIMANANA François de Salle qui a accepté d'être le Président de jury ;

> À Monsieur RATIANARIVO Paul Ezekel et Monsieur RAKOTOMALALA de bien vouloir examiner ce mémoire ;

> À mon encadreur pédagogique, Monsieur RANDRIAMIHAJARISON Mparany Jimmy de nous avoir bénéficié d'une aide précieuse par ses conseils et son encadrement durant la réalisation de ce travail.

Notre profonde gratitude s'adresse également à ma famille pour leurs soutiens moraux et financiers tout au long de notre étude.

Ainsi, nous présentons aussi nos plus humbles remerciements à tous les professeurs de l'ASJA ainsi que mes ami(e)s, pour toutes les bienveillances et les aides qu'ils nous ont octroyées.

II

RÉSUMÉ

La fibre optique est actuellement l'un des moyens de communication le plus efficace et le plus attirant dans le monde du fait de sa performance. De ce fait, nombreuses sont les études qui sont en cours afin de la rendre plus puissante mais aussi de l'améliorer car celle-ci ne semble être un support de transmission parfait.

Le présent mémoire s'est basé sur les problèmes dans une liaison par fibre optique selon son intitulé « Étude des atténuations dans une transmission par fibre optique ».

Les atténuations dans ce support de transmission sont tributaires du type de la fibre utilisée. Les principaux éléments qui entrent en jeu dans une liaison par fibres tels que les interfaces optoélectroniques d'émission et de réception ainsi que les amplificateurs optiques, qui sont tous relatés dans la seconde partie, peuvent contribuer à l'affaiblissement du signal.

On trouve également dans cette même partie la base de notre étude qui expose les deux types d'atténuations dont l'une est intrinsèque c'est-à-dire lié à la structure et impureté d'une fibre et l'autre l'atténuation extrinsèque dépendante du positionnement ou du milieu d'installation. Au terme de cet ouvrage, quelques solutions sont proposées afin de minimiser les problèmes dans une fibre. Celles-ci sont suivies d'une étude plus pratique du thème proposé, en concevant un logiciel qui permet de simuler ces atténuations.

Mots clés: fibre optique, atténuation, lumière, liaison, signal, transmission, problème.

ABSTRACT

Nowadays, the optical fiber is an attractive and adequate physical transmission support. To this end, several studies are underway to improve and find a new type of fiber more efficient. Basically, this memory presents the problems on the links by optical fibers and the title is « Attenuations study in the transmission by optical fiber ».

To differ a kind of fiber allows specifying efficiently the attenuation.

The basics component including in the links of optical fiber such as transmitter, receiver and amplifier describing in this thesis can to contribute to weaken the signal.

We can see also the basis of our study whose we show two kinds of attenuations. The first is an intrinsic attenuation of which concerns the fiber structure and its defect. The second attenuation is extrinsic of which depend on the installation and place.

In order to minimize the problem by attenuation, some solutions are giving in the last chapter. At last, we are developed software to simulate these losses.

Keywords: optical fiber, attenuation, light, link, signal, transmission, problem.

III

TABLE DES MATIÈRES

REMERCIEMENTS I

RÉSUMÉ II

ABSTRACT II

TABLE DES MATIÈRES III

LISTE DES ABRÉVIATIONS VI

LISTE DES TABLEAUX VIII

LISTE DES FIGURES VIII

INTRODUCTION GÉNÉRALE 1

PARTIE I : GÉNÉRALITÉS SUR LA FIBRE OPTIQUE

Chapitre 1 : DESCRIPTION D'UNE FIBRE OPTIQUE 2

1.1 Historique 2

1.2 Structures d'une fibre optique 3

1.3 Les avantages et inconvénients d'une fibre optique 5

1.3.1 Les avantages 5

1.3.2 Les inconvénients 6

1.4 Les domaines d'utilisation de la fibre optique 6

1.5 Propagation de la lumière 8

1.5.1 Spectre de la lumière 8

1.5.2 La réflexion et la réfraction 9

1.5.3 Les lois de Snell-Descartes 10

1.5.4 Angle limite et condition de guidage 12

1.6 Principe de propagation de la lumière dans une fibre optique 13

1.7 L'ouverture numérique et la fréquence normalisée 14

Chapitre 2 : LES DIFFÉRENTS TYPES DE FIBRE OPTIQUE 17

2.1 Notion de mode de propagation 17

2.2 La fibre multimode 17

2.2.1 La fibre multimode à saut d'indice 18

2.2.2 La fibre multimode à gradient d'indice 20

2.3 La fibre monomode 23

2.3.1 Conditions de monomodalité d'une fibre optique 24

2.3.2 Diamètre de mode d'une fibre monomode 25

2.3.3 Facteur de confinement 27

IV

2.4 Les Recommandations G.652 à G.657 de l'UIT 28

PARTIE II : LES PARAMÈTRES DE TRANSMISSION ET ATTÉNUATIONS DANS UNE LIAISON OPTIQUE

Chapitre 3 : LES PARAMÈTRES DE TRANSMISSION PAR FIBRE 32

3.1 Les éléments d'un système de transmission par fibre optique 32

3.2 L'interface optoélectronique d'émission 33

3.2.1 La diode électroluminescente 33

3.2.2 Diode LASER 34

3.3 Techniques de modulation 37

3.3.1 La modulation directe 37

3.3.2 La modulation externe 38

3.4 Répéteur ou amplificateur optique 38

3.4.1 Définition et principe d'un amplificateur 38

3.4.2 Bruit d'un amplificateur optique 39

3.5 Interface optoélectronique de réception 39

3.5.1 Photodiodes PIN 41

3.5.2 Photodiodes à avalanche (PDA) 41

3.5.3 Bruits des photodiodes 42

3.6 Multiplexage 43

3.6.1 Multiplexage temporelle (TDM) 44

3.6.2 Multiplexage en longueur d'onde (WDM) 44

3.6.3 Multiplexage fréquentielle (FDM) 45

Chapitre 4 : LES ATTÉNUATIONS DANS UNE LIAISON PAR FIBRE OPTIQUE 46

4.1 Description de l'atténuation 46

4.1.1 Définition 46

4.1.2 Les différents types d'atténuations 46

4.2 Les atténuations extrinsèques 47

4.2.1 Pertes par courbure 47

4.2.2 Pertes par microcourbure 48

4.2.3 Pertes de jonction 48

4.2.4 Pertes par injection de la lumière dans la fibre 51

4.3 Les atténuations intrinsèques 52

4.3.1 L'atténuation linéique 52

V

4.3.2 Pertes par diffusion 54

4.3.3 Pertes par absorption 55

4.3.4 Dispersion modale 58

4.3.5 Dispersion chromatique 60

4.3.6 Dispersion de polarisation 65

PARTIE III : LES SOLUTIONS ET SIMULATION DES ATTÉNUATIONS DANS UNE FIBRE OPTIQUE

Chapitre 5 : LES SOLUTIONS ET SIMULATION DES ATTÉNUATIONS 68

5.1 Les solutions des atténuations 68

5.1.1 Solutions pour l'atténuation due à la dispersion chromatique 68

5.1.2 Diverses solutions possibles pour minimiser les problèmes d'atténuations 71

5.2 Bilan énergétique d'une liaison par fibre optique 73

5.2.1 Puissance de réception 73

5.2.2 Puissance maximale et minimale de réception 74

5.2.3 Exemple du bilan de liaison 74

5.3 Étude quantitative des atténuations 76

5.3.1 Description du logiciel de simulation MATLAB 76

5.3.2 Présentation du programme de simulation 77

CONCLUSION GÉNÉRALE 85

ANNEXES X

BIBLIOGRAPHIE XIV

WEBOGRAPHIE XV

PAGE DE RENSEIGNEMENT XVI

VI

LISTE DES ABRÉVIATIONS

AlGa : Arséniure de Galium

AlGaAs : Arséniure de Galium Aluminium

ASN : Amplified Spontaneous Noise

ATM : Asynchronous Transfer Mode

dB : déciBel

dBm : déciBel milliwatt

DCF : Dispersion Compensating Fiber

DEL : Diode ELectroluminescente

DGD : Differential Group Delay

DSF : Dispersion Shifted Fiber

FDM : Frequency Division Multiplexing

GaAs : Arséniure de Gallium

GHz : GigaHertz

GVD : Group Velocity Dispersion

IOE : Interface Optique d'Émission

IOR : Interface Optique de Réception

IR : InfraRouge

InP : Phosphure d'Indium

InGaAsP : Phosphure d'Arséniure de Galium-Aluminium et Indium

IT : Intervalle de temps

km : kilomètre

LASER : Light Amplification by Stimulated Emission of Radiation

LED : Light Emitting Diode

mA : miliAmpère

MATLAB : MATrix LABoratory

MMF : Multi Mode Fiber

MRT : Multiplexage à répartition dans le temps

mW : milliWatt

nm : nanomètre

NZDSF : Non Zero Dispersion Shifted Fiber

OH : Hydroxyde

ON : Ouverture Numérique

VII

ONU : Organisation des Nations Unies

PDA : PhotoDiode à Avalanche

PIN : Positive Intrinsec Negative

PMD : Polarisation Mode Dispersion

RIN : Relative Intensity Noise

SiO2 : Dioxyde de Silicium

SMF : Single Mode Fiber

TDM : Time Division Multiplexing

THz : Terahertz

TDM : Time Division Multiplexing

TDMA : Time Division Multiple Access

THz : Terahertz

UIT-T : Union International de Télécommunication et de la Télégraphe

UV : UltraViolet

w : watt

WDM : Wave Division Multiplexing

ìm : Micromètre

ZCE : Zone de Charge d'Espace

VIII

LISTE DES TABLEAUX

Tableau 2.01 : Les Recommandations G652 à G657 de l'UIT 28

Tableau 4.01 : Comparaison entre les trois fenêtres de transmission 57

Tableau 5.01 : Tableau montrant les effets de la variation du rayon du coeur et d'indice 72

Tableau 5.02 : Comparaison des atténuations dues au raccordement des fibres 84

LISTE DES FIGURES

Figure 1.01 : Structure générale d'une fibre optique 4

Figure 1.02 : Principales structures d'interconnexion d'une fibre 4

Figure1.03 : Spectre de la lumière 8

Figure 1.04 : Domaine du spectre électromagnétique 9

Figure 1.05 : Phénomène de la réflexion et réfraction............................................................................................10 Figure 1.06 : a) Le faisceau réfracté n'existe plus......................................................................................................12

b) Le faisceau incident est entièrement réfléchi ............................................................................12 Figure 1.07 : Propagation de la lumière dans la fibre par réflexion totale ..............................................13 Figure 1.08 : Cône d'acceptance ...............................................................................................................................................14

Figure 2.01 : Profil d'indice d'une fibre multimode à saut d'indice 18
Figure 2.02 : Chemins optiques empruntés par les rayons lumineux et l'impulsion d'entrée

etsortie 19

Figure 2.03 : Exemples du profil d'indice d'une fibre à gradient d'indice 21

Figure 2.04 : Impulsion d'entrée et sortie des rayons lumineux et leurs trajets 22

Figure 2.05 : Signal d'entrée et sortie dans une propagation par fibre monomode 23

Figure 2.06 : Profil d'indice d'une fibre monomode 25

Figure 2.07 : Distribution d'intensité de mode fondamental (ligne continue) et son

approximation par une forme gaussienne (ligne discontinue 26

Figure 2.08 : Facteur de confinement 27

Figure 3.01 : Les éléments d'une transmission point à point par fibre optique 32

Figure 3.02 : Symbole d'une diode électroluminescente 33

Figure 3.03 : Spectre d'émission d'une DEL 34

Figure 3.04 : Symbole d'une diode laser 35

Figure 3.05 : Puissance émise par diode laser 36

Figure 3.06 : Synoptique de la modulation directe 37

Figure 3.07 : Synoptique de la modulation externe 38

IX

Figure 3.08 : Symbole normalisé d'une photodiode 40

Figure 3.09 : Structure d'une photodiode 40

Figure 3.10 : Symbole d'une photodiode PIN 41

Figure3.11 : Principe du multiplexage 43

Figure 3.12 : Principe du multiplexage à répartition dans le temps 44

Figure 3.13 : Multiplexage en longueur d'onde 44

Figure 4.01 : Différentes pertes dans une fibre optique 47

Figure 4.02 : Séparation longitudinale des deux fibres 49

Figure4.03 : Désalignement axial 50

Figure4.04 : Écartement angulaire 50

Figure 4.05 : Deux fibres de diamètres différents 51

Figure4.06 : Portion d'une fibre 52

Figure 4.07 : Diffusion de Rayleigh dans une fibre optique 54

Figure 4.08 : Courbe d'atténuation par diffusion en fonction de la longueur d'onde 55

Figure 4.09 : Allure d'atténuation par absorption 56

Figure 4.10 : Courbe d'atténuation par absorption et fenêtres de transmission 57

Figure 4.11 : Parcours du rayon lumineux axial et réfléchi dans une fibre à saut d'indice 59

Figure 4.12 : Influence de la dispersion due aux matériaux sur une impulsion optique 62

Figure 4.13 : Dispersion d'une partie de la puissance optique dans la gaine 63

Figure 4.14 : Influence de la dispersion modale de polarisation sur une impulsion optique......66

Figure 5.01 : Exemple de compensation de dispersion de 100% 69

Figure 5.02 : Courbes de dispersion chromatique des fibres G652, G653, G655 70

Figure 5.03 : Effet d'une fibre à réseau de Bragg à pas variable sur un signal 71

Figure 5.04 : Fenêtre d'accueil 78

Figure 5.05 : Fenêtre d'évaluation des atténuations intrinsèques 79

Figure 5.06 : Exemple d'application sur le calcul des atténuations intrinsèques 80

Figure 5.07 : Fenêtre des atténuations extrinsèques 82

Figure 5.08 : Exemple de calcul des atténuations extrinsèques 83

1

INTRODUCTION GÉNÉRALE

De nos jours, les supports de transmission ont une très grande importance dans l'utilisation quotidienne du réseau informatique et de la télécommunication. Ils sont utilisés pour transporter un signal depuis une entité émetteur jusqu'au récepteur. Que ce soit dans le domaine du travail professionnel ou divertissement, ces supports de transmission permettent un échange des informations vitales dans notre société de communication.

Autrefois, la transmission des informations via des câbles électriques et des ondes hertziennes semblait être satisfaisante pour la télécommunication. Face à la croissance considérable des nouvelles technologies, de l'avènement de l'Internet et de l'apparition des nouveaux services liés au développement du multimédia, ces types de supports de transmission n'arrivent plus à échanger correctement des grandes quantités d'informations surtout sur une longue distance.

Ce qui nécessite un système de communication plus performant et fiable qui répond aux besoins des utilisateurs notamment en termes de qualité de service.

Avec une bande passante plus large et une possibilité de conduire plusieurs signaux sur un même support, la fibre optique apparait comme une solution idéale pour les transmissions à haut débit. Dès l'apparition de la source laser à très faible divergence, on note un regain d'intérêt pour la transmission d'information par voie optique. Ainsi, la fibre optique, par rapport aux autres supports de transmission, semble avoir toutes les qualifications techniques nécessaires pour satisfaire les besoins croissants des actuels réseaux de télécommunication et des réseaux informatiques.

Néanmoins, étant le meilleur support de transmission recensé jusqu'ici, la fibre optique n'en est pas moins un support parfait. Des nombreux problèmes tels que les différentes atténuations dues à la structure de la fibre, des atténuations au niveau de la ligne de transmission, ainsi que celles au niveau des installations doivent être minimisées, et des recherches sont encore en cours dans ce sens. D'où l'intitulé de notre mémoire « Étude des atténuations dans une transmission par fibre optique ». Ce travail consiste à bien identifier tous les paramètres relatifs à l'affaiblissement du signal provoquant des pertes d'information afin de faciliter la recherche des solutions correspondantes.

Dans ce présent mémoire, nous présenterons des divers aspects liés à la transmission par fibre optique et les atténuations. Pour en faire, nous adopterons trois grandes parties entamées par généralités sur la fibre optique suivi des paramètres de transmission et atténuations dans une liaison optique, enfin les solutions et la simulation de ces atténuations sous un logiciel approprié sont présentées au terme de cet ouvrage.

2

PARTIE I : GÉNÉRALITÉS SUR LA FIBRE OPTIQUE

Chapitre 1 : DESCRIPTION D'UNE FIBRE OPTIQUE

L'initiation d'une étude sur un objet particulier doit être entamée par son apprentissage généralisé en parlant de son origine, sa définition, ses structures, ses avantages et inconvénients ainsi que le domaine de son utilisation. On parle évidemment ici de la fibre optique qui est un support de transmission si récent. Dans le système de communication optique, c'est la lumière qui porte l'information à travers la fibre. Dans ce cas, la connaissance du principe de la propagation de la lumière s'avère aussi très importante. Tous ceux-ci font l'objet de ce chapitre.

1.1 Historique

À l'époque des Grecs anciens, le phénomène du transport de la lumière dans des cylindres de verre était déjà connu.

La première démonstration scientifique du principe de la réflexion totale interne fut faite par les physiciens suisses et français Jean-Daniel Colladon à Genève et Jacques Babinet à Paris au début des années 1840. L'Irlandais John Tyndall répéta l'expérience devant la Société Royale Britannique en 1853. À l'époque, l'idée de courber la trajectoire de la lumière, de quelque façon que ce soit, était révolutionnaire puisque les scientifiques considéraient que la lumière voyageait uniquement en ligne droite. Leur démonstration consistait à guider la lumière dans un jet d'eau déversé d'un trou à la base d'un réservoir. En injectant de la lumière dans ce jet, celle-ci suivait bien la courbure du jet d'eau, démontrant ainsi qu'elle pouvait être déviée de sa trajectoire rectiligne. Cette expérience a permis d'envisager l'application du même principe sur une trajectoire à base de la fibre optique.

La possibilité de transporter de la lumière le long de fine fibre de verre fut exploitée vers 1900. Quelques années plus tard, en 1930, Heinrich Lamm réussit à transmettre l'image d'un filament de lampe électrique grâce à un assemblage rudimentaire de fibres de quartz. Cependant, il était encore difficile à cette époque de concevoir que ces fibres de verre puissent trouver une application.

La première application fructueuse de la fibre optique eut lieu au début des années 1950, lorsque le fibroscope flexible fut inventé par Abraham Van Heel et Harold Hopkins. Malheureusement, la transmission ne pouvait pas être faite sur une grande distance étant donnée la piètre qualité des fibres utilisées.

Les télécommunications par fibre optique restèrent impossibles jusqu'à l'invention du laser en 1960. Le laser offrit en effet la possibilité de transmettre un signal de faible perte sur une longue distance.

3

En 1966, Charles Kao démontra expérimentalement, avec la collaboration de Georges Hockman, qu'il était possible de transporter de l'information sur une grande distance sous forme de lumière grâce à la fibre optique. Cette expérience est souvent considérée comme la première transmission de données par fibre optique. Cependant, les pertes dans cette fibre optique étaient telles que le signal disparaissait au bout de quelques mètres. Cela la rendait encore peu avantageuse par rapport au fil de cuivre traditionnel. L'atténuation linéaire entrainée par l'usage d'une fibre de verre homogène constituait le principal obstacle à l'utilisation courante de la fibre optique.

En 1970, trois scientifiques de la compagnie Corning Glass Works de New York : Robert Maurer, Peter Schultz et Donald Keck produisirent la première fibre optique avec une atténuation linéaire suffisamment faible pour être utilisée dans les réseaux de télécommunications (20 décibels par kilomètre) ; mais aujourd'hui la fibre conventionnelle affiche des pertes de moins de 0,25 décibel par kilomètre pour la longueur d'onde 1 550 nm, utilisée dans les télécommunications.

Le premier système de communication téléphonique optique fut installé au centre-ville de Chicago en 1977. La première liaison optique fut réalisée en France Paris en 1980 reliant les centraux téléphoniques des Tuileries et Philippe-Auguste.

La fibre optique s'est, dans une première phase, de l'année 1984 à 2000, limitée à l'interconnexion des centraux téléphoniques, eux seuls nécessitant de forts débits. Cependant, avec la baisse des coûts du fait de sa fabrication en masse et les besoins croissants des particuliers en très haut débit, on envisage depuis 1994 et 2005 son arrivée même chez les particuliers. [3] [18]

1.2 Structures d'une fibre optique

Dans la télécommunication optique, les signaux sont transmis sous forme d'onde lumineuse. Une fibre optique est un fil en verre ou en plastique très fin qui a la propriété d'être un conducteur de la lumière. Elle est constituée de deux couches diélectriques de même axe, entourés d'un élément protecteur. Ces deux couches diélectriques possèdent des indices de réfraction différents.

La fibre optique est composée généralement de :

o La couche centrale ou le coeur dans lequel se propage la lumière. Il peut être fabriqué à base de silice, de quartz ou de plastique et son diamètre est variable suivant le type de fibre à concevoir ;

o La couche périphérique ou la gaine optique : en général, fait de mêmes matériaux que le coeur mais avec des additifs qui la permet d'avoir un indice de réfraction inférieur à celui

4

du coeur ; ce qui assure le confinement du rayon lumineux dans ce dernier ; o La couche protectrice ou revêtement de protection : généralement en plastique, qui

assure la protection mécanique de la fibre et à piéger la lumière qui se propage dans la gaine.

Cette structure est illustrée par la figure ci-dessous :



Figure 1.01 : Structure générale d'une fibre optique

En réalité, le diamètre de la fibre optique mesure un peu plus de quelques centaines de micromètre (ìm) par rapport au diamètre du cheveu du corps humain. [13]

Il existe deux principales structures d'une fibre qui sont mises en oeuvre lors de son conditionnement [6] :

? Fibre à structure libre :

Deux ou plusieurs fibres sont placées « libres » à l'intérieur d'un tube. Ce type de fibre est à usage extérieur, elle sera donc particulièrement mise en oeuvre dans les liaisons entre plusieurs destinataires. L'inconvénient de cette structure est son encombrement, son poids, la rigidité et mise oeuvre des connexions assez complexes.

? Fibre à structure serrée :

Une seule gaine optique est placée à l'intérieur de la gaine protectrice. Elle a comme avantages sa légèreté, flexibilité et faible encombrement.

La figure ci-dessous illustre cette structure serrée (figure de droite) et celle décrit précédemment (figure de gauche).



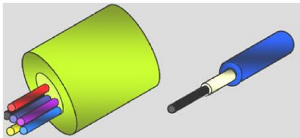
Figure 1.02 : Principales structures d'interconnexion d'une fibre

5

1.3 Les avantages et inconvénients d'une fibre optique

1.3.1 Les avantages

En tant que support de transmission de communication relativement récent, la fibre optique présente des nombreux avantages. L'avantage décisif n'est pas toujours le même suivant l'utilisation envisagée.

Ces avantages sont observés au niveau de :

? La performance de transmission :

La fibre optique a une très large bande passante de l'ordre de quelques gigahertz (GHz) permettant d'atteindre des débits de l'ordre de quelques Gigabits par seconde. [22]

En général, la capacité de communication dépend du type de la fibre en fonction du profil d'indice.

? L'insensibilité aux interférences électromagnétiques et perturbation extérieur :

Les signaux optiques dans les fibres optiques sont généralement rayonnés à l'intérieur du coeur, de sorte que les informations à transmettre en elles sont hautement sécurisées vis à vis des interférences et perturbations diverses du milieu extérieur.

Les fibres optiques, réalisées en verre, ou parfois en polymère plastique, sont des isolants électriques et sont immunes vis-à-vis des interférences électromagnétiques. Elles peuvent être utilisées dans des environnements électromagnétiques. L'interférence croisée parmi plusieurs signaux optiques distincts (diaphonie) ne se produit pas lorsque l'on transmet simultanément des différentes lumières situées dans le même câble. [3]

? L'insensibilité thermique :

A haute fréquence, il n y a pas d'échauffement de la fibre optique tandis que le câble à base de cuivre nécessite un refroidissement pour des hautes fréquences et hautes puissances. [22]

? Petite taille et poids faible :

Les fibres optiques présentent un diamètre très petit, souvent comparé au diamètre d'un cheveu humain. Même si elles sont recouvertes de revêtements protecteurs, elles sont plus petites et plus légères que les câbles en cuivre. Les fibres optiques n'ont pas besoin beaucoup d'espace pour l'installation et s'avèrent très pratiques à transporter.

? Riches en ressources et une longue durée de vie :

La matière première utilisée pour fabriquer la fibre optique est le dioxyde de silicium SiO2, il est abondant dans la nature, contrairement à celle du cuivre.

6

Enfin, un autre point fort de la fibre optique est sa durée de vie plus longue par rapport aux autres supports de transmission. En effet, la fibre optique est estimée utilisable pendant une durée d'environ 25 ans, or une station relais ou terminale d'une liaison par faisceau hertzien dure environ 10 ans et la durée de vie maximale d'un satellite géostationnaire est autour de 10 à 15 ans. Elle nécessite peu d'interventions en maintenance. [20]

1.3.2 Les inconvénients

Cependant, la fibre optique possède également des inconvénients : parmi lesquels, des difficultés au niveau de l'installation du fait de la taille en miniature des composants utilisés dans une liaison par fibre optique et des exigences micromécaniques importantes (connexions, alignement). À cause de cette complexité d'installation, le coût de la mise en place d'une liaison est souvent cher par rapport celui d'une liaison radio terrestre. En plus, suite à l'exigence de précision lors de la fabrication des divers composants optoélectroniques, ces derniers sont aussi onéreux.

Malgré les performances avérées des fibres optiques, les signaux qui les traversent subissent des atténuations lors de la propagation. Les différents types de pertes sont liés à la diffusion de Rayleigh, l'absorption, la dispersion modale et chromatique, l'imperfection des connexions, la présence des courbures et micro-courbures dans la fibre. L'atténuation du signal dépend essentiellement de la nature de la fibre (monomode ou multimode).

Les fibres monomodes SMF (Single Mode Fiber) exploitées à la longueur d'onde de 1550 nm présentent des atténuations minimales de l'ordre de 0,2 dB/km. Par contre les fibres multimodes MMF (Multi Mode Fiber) utilisées à cette même longueur d'onde présentent des atténuations plus importantes de l'ordre de 1dB/km pour les fibres multimodes à gradient d'indice et 4 dB/km pour les fibres multimodes à saut d'indice. [6]

1.4 Les domaines d'utilisation de la fibre optique

Le principal est bien entendu celui des télécommunications, mais les fibres optiques débordent largement ce secteur et connaissent un grand nombre d'applications industrielles.

Ces domaines d'applications sont les suivant [18] [20]:

? Télécommunications :

Les deux premiers grands domaines d'utilisation, liés aux besoins des réseaux, ont été les liaisons urbaines, de capacités considérables et les liaisons sous-marines telles que les liaisons transocéaniques ou les liaisons côtières sans répéteurs.

7

Les liaisons terrestres régionales, nationales et internationales connaissent un très fort développement. Grâce au multiplexage qui consiste à envoyer en même temps plusieurs signaux portés par des longueurs d'onde différentes sur la même fibre, un seul câble de 144 fibres peut transmettre simultanément 40 000 conversations téléphoniques. Le débit est 250 fois plus fort que celui des fils de cuivre.

Aux Etats Unis, quasiment tous les appels téléphoniques interurbains et 90% des appels transcontinentaux passent par les installations à fibres optiques.

? Éclairage :

Les fibres optiques plastiques, transparentes à la lumière visible, conduisent facilement la lumière d'un endroit à un autre. Une source illumine l'extrémité d'un faisceau de fibres optiques. Son énergie transite à travers l'ensemble des fibres jusqu'à leurs extrémités. Outre l'aspect décoratif de ces pointes lumineuses, cette lumière visible éclaire les oeuvres d'art, les vitrines, etc. Grâce à la faible sensibilité des fibres plastiques à l'humidité, elles participent aussi à l'éclairage des fontaines lumineuses, des piscines et du balisage routier.

? Médecine :

La fibre optique est utilisée dans le domaine de la médecine pour filmer des endroits sensibles ou inaccessibles du corps humain, du fait de la réalisation de caméra et du câble de très petite taille. La fibre de verre a été mise au service de la médecine pour l'examen des infections de l'organisme humain. Leur bande passante se situe dans le visible et le proche infrarouge. On introduit dans le corps du patient un câble souple appelé endoscope muni d'une mèche (ou un lot) d'une centaine de fibres par un conduit ou une cavité de l'organisme. La lumière est insérée à une des extrémités et éclaire le tissu à examiner. Un autre faisceau de fibres optiques contenu dans l'endoscope renvoie l'image à travers un système optique vers l'observateur. Dans certains dispositifs, une mini-caméra transmet les images à un écran vidéo. Parfois, l'endoscope se termine par un outil chirurgical pour un prélèvement sur la zone observée.

? Scalpel optique :

Au système précédent de visualisation peut être associée une fibre polycristalline d'halogénure métallique qui transporte les impulsions d'un laser. L'extrémité de l'endoscope devient un outil chirurgical optique. Le médecin peut alors pulvériser les calculs rénaux, découper une tumeur, réparer une rétine, sans « ouvrir » le patient. Celui-ci voit sa convalescence considérablement réduite, comparée à une opération classique.

? Applications diverses :

- Dans l'armé, la fibre a son utilité dans le Polyphème qui est un missile à fibre optique venant d'être inventée. Ce missile possède derrière lui une bobine de fibre optique qui le relie au poste de tir et qui permet de le guider jusqu'à sa cible via un opérateur agissant grâce à une caméra embarquée.

- Des capteurs comme le gyromètre à fibre optique est un instrument utilisé par les navires, les sous-marins, les avions ou les satellites pour donner la vitesse angulaire. Il contient des fibres à maintien de polarisation.

- Ses propriétés sont également exploitées dans le domaine des capteurs que ce soit température, pression ou autre. Grâce à ces capteurs, on peut calculer la distance d'un objet par rapport à un autre, la vitesse de rotation, les vibrations. [22]

1.5 Propagation de la lumière

Dans une liaison optique les signaux sont transmis sous forme d'onde lumineuse. Par suite, une connaissance de certaines caractéristiques de la lumière sera nécessaire.

1.5.1 Spectre de la lumière

Le spectre de la lumière n'est qu'une infime frange d'une énergie plus générale qu'on nomme rayonnement électromagnétique. Ce dernier peut être décomposé en différentes catégories selon leur longueur d'onde ou selon leur fréquence, c'est le spectre des ondes électromagnétiques. La lumière fait partie de ces ondes électromagnétiques. Elle est constituée d'un ensemble des rayons lumineux formant une palette allant de l'ultraviolet à l'infrarouge.

En fonction de la longueur d'onde, la lumière change soit de couleur, soit du type.

La décomposition de la lumière en plusieurs franges colorées s'appelle le spectre de la lumière. L'homme ne peut voir qu'une partie des ondes. Le rayonnement électromagnétique probablement le plus connu est la lumière visible. Il ne constitue cependant qu'une très faible partie du spectre électromagnétique.

La partie qui correspond à la lumière visible s'étend sur une gamme de longueurs d'ondes approximativement comprises entre 400 nm et 750 nm.

Voici la figure qui montre le spectre de la lumière :



Figure 1.03 : Spectre de la lumière

8

9

Dans une lumière visible, les rayonnements de haute fréquence (faible longueur d'onde) sont de couleur plus près du violet, tandis que les ondes de basses fréquences (grandes longueurs d'ondes) sont rouges. Entre les deux sont réparties toutes les couleurs de l'arc-en-ciel. Il y a 5 couleurs principales distinctes dans le spectre (rouge, jaune, vert, bleu, violet) mais il existe des mélanges intermédiaires qui donnent des nombreuses couleurs.

Si l'on superpose des rayons de toutes les couleurs d'intensité identique, on obtient une lumière blanche, tandis que l'absence totale de lumière donne bien entendu le noir.

Les longueurs d'ondes inférieures à 400 nm correspondent au rayonnement ultraviolet ; celles encore plus basses caractérisent les rayons X et Gamma. Au dessus de 750 nm, il y a les rayons infrarouges. C'est à partir de 750 nm, aux alentours des rayons infrarouges, que se situent les longueurs d'ondes utilisées pour la fibre optique. Juste en dessous de la fréquence de l'infrarouge, nous trouvons les micro-ondes et aux fréquences les plus basses se situent les ondes radio.

La figure ci-dessous présente les domaines du spectre électromagnétique.



Figure 1.04 : Domaine du spectre électromagnétique

Il convient de signaler que la frontière entre ces bandes de fréquences n'est pas définie de manière nette : il n'existe ainsi aucune fréquence caractéristique en dessous de laquelle le rayonnement est de type ultraviolet et au-delà de laquelle il est un rayon X ; ces définitions recouvrent plutôt des bandes de fréquences, et l'appellation dépend parfois de l'application que l'on en fait. [2] [7] [20]

1.5.2 La réflexion et la réfraction

La propagation de la lumière à travers une fibre optique est basée sur le principe de la réflexion successive du faisceau lumineux. Il est alors nécessaire de prendre en compte les notions fondamentales sur le déplacement de la lumière au niveau d'une surface réfléchissante appelée « dioptre » séparant deux milieux plus ou moins transparents d'indices de réfraction différents. Lorsqu'un rayon lumineux monochromatique heurte obliquement un dioptre qui sépare deux milieux d'indice différents n1 et n2, il se divise généralement en deux : une partie est réfléchie

10

tandis que l'autre est réfractée c'est-à-dire transmise dans le second milieu en changeant de direction. On obtient donc le rayon réfléchi et rayon réfracté.

Le rayon lumineux est dit incident avant d'avoir rencontré la surface réfléchissante. Le point de rencontre du rayon incident et de la surface réfléchissante ou dioptre est appelé point d'incidence. La droite orthogonale au dioptre au point d'incidence est dite normale au dioptre.

L'angle d'incidence, de réflexion et de réfraction sont mesurés par rapport à la normale au dioptre.

Ce phénomène de réflexion et de réfraction est illustré dans la figure ci-dessous.



Figure 1.05 : Phénomène de la réflexion et réfraction

L'indice de réfraction est une grandeur caractéristique des propriétés optiques d'un matériau. La vitesse de la lumière dans un matériau d'indice n est donnée par la formule :

[ rn/si

Où c : vitesse de lumière dans le vide, c = 299 792 458 m/s (cette valeur est exacte) ; n : indice du milieu auquel la lumière traverse.

La lumière voyage donc plus rapidement dans un matériau avec un indice de réfraction plus petit. Il est à noter que l'indice de réfraction du vide est de 1. On dit aussi que l'indice de l'air est égal à 1 puisque la vitesse de la lumière dans l'air est à peu près égale à celle dans le vide.

Pour guider la lumière, la fibre utilise le phénomène de réflexion totale qui se produit à l'interface de deux milieux d'indices différents. Ces deux milieux sont définis par le coeur et la gaine. L'indice de réfraction de la gaine doit être inférieur à celui du coeur.

1.5.3 Les lois de Snell-Descartes

Il y a des lois qui correspondent à ces phénomènes de réflexion et de réfraction. On appelle cette loi : Lois de Snell-Descartes. Elles s'énoncent comme suit [7] [16] :

11

? Première loi :

Le plan d'incidence est le plan qui contient le rayon incident et la droite normale au dioptre au point d'incidence.

La première loi de Snell-Descartes stipule que les rayons réfléchi et réfracté sont dans le plan d'incidence. Donc le rayon incident, le rayon réfléchi, le rayon réfracté, et la normale au dioptre appartiennent au même plan. On en déduit que le plan de réfraction et le plan de réflexion sont dans le plan d'incidence.

? Deuxième loi :

Cette loi évoque les relations entre les différents angles.

Lorsqu'un rayon est réfléchi, il est symétrique du rayon incident par rapport à la normale au dioptre et l'angle de réflexion r1 est de même valeur que l'angle d'incidence i1, c'est la loi de réflexion. En prenant comme l'angle nul la normale au dioptre et en tournant vers le sens trigonométrique, on obtient la relation en valeur absolue :

r1 = i1 (1.02)

Avec

r1 : angle de réflexion dans le milieu d'indice n1 i1 : angle d'incidence dans le milieu d'indice n1

Lorsqu'un rayon est réfracté, on a la loi de réfraction :

n1.sin i1= n2.sin r2 (1.03)

Où r2 : angle de réfraction dans le milieu d'indice n2

On remarque que :

Pour n1 < n2

Puisque sin i1/sin r2= n2/n1 < 1, l'équation (1.03) devient :

sin i1 > sin r2 (1.04)
Comme la fonction sinus est croissante, donc on a :

i1 > r2 (1.05)

Le rayon réfracté se rapproche donc de la normale en traversant le dioptre.

Pour n1 > n2

On a :

i1 < r2 (1.06)
Cela signifie que le rayon réfracté s'écarte de la normale lorsque l'angle d'incidence augmente.

1.5.4 Angle limite et condition de guidage

L'angle limite est la valeur de l'angle incident i1 à partir duquel il y a réflexion totale.

On remarque que pour n1 > n2, le rayon réfracté s'écarte de la normale lorsqu'on augmente

progressivement la valeur de l'angle d'incidence. Quand l'angle de réfraction arrive à 90°, l'angle d'incidence atteint sa limite c'est-à-dire la valeur minimum sur laquelle il n'y a pas de

rayon réfracté. Au-delà de cet angle limite, noté t le faisceau réfracté disparait car le faisceau incident est alors entièrement réfléchie (Figure 1.06b). On parle alors de « réflexion totale ». [7]



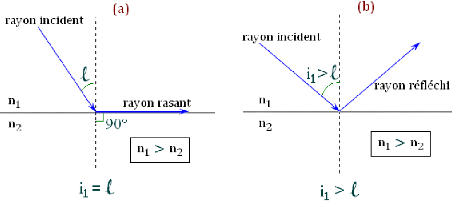
12

Figure 1.06 : a) Le faisceau réfracté n'existe plus ; b) Le faisceau incident est entièrement réfléchi.

Pour i1 = t on a i2 = 90°

La relation (1. 03) permet d'écrire :

n1.sin t = n2.sin 90° (1.07)

Ce qui entraine :

sin t = (1.08)

Finalement, l'angle limite s'écrit :

t = arcsin

(1.09)

( )

Par exemple, si la lumière passe d'un verre quelconque d'indice n1=1,5 dans l'air d'indice n2=1,

alors l'angle limite est tel que sin t = . Il est alors proche de 42°.

Ainsi,

o Si l'angle d'incidence est inférieur à 42°, le faisceau est réfracté dans l'air ;

o S'il vaut 42°, il est alors rasant ;

o S'il est plus grand que 42°, il est entièrement réfléchi par l'air et reste dans le verre.

13

La condition de guidage est la condition pour que tous les rayons circulant dans la fibre optique soient réfléchis par la gaine. Elle est obtenue par la relation :

i1 > arcsin (ⁿ_n ²_', (1.10)

1.6 Principe de propagation de la lumière dans une fibre optique

Les propriétés de guidage de la lumière reposent sur le principe physique de la réflexion totale décrit précédemment. Dans la fibre optique, le coeur et la gaine ont des indices de réfraction différents. Pour qu'il y ait propagation de la lumière, l'indice de réfraction du coeur doit être plus grand que celui de la gaine de sorte qu'on retrouve un effet miroir à l'intérieur de la gaine. La lumière est donc confinée à l'intérieur du coeur. [1][6][24]

Pour avoir la propagation de la lumière avec une moindre perte dans la fibre optique, tous les rayons lumineux heurtant l'interface entre le coeur et la gaine devront respecter la condition de réflexion totale interne. L'angle d'entrée de la lumière, calculé en fonction des indices, devra donc scrupuleusement respecté.

Lorsqu'un rayon lumineux entre dans une fibre optique à l'une de ses extrémités avec un angle adéquat, il subit de multiples réflexions totales. Ce rayon se propage alors jusqu'à l'autre extrémité de la fibre optique, en empruntant un parcours en zigzag comme la figure ci-dessous nous montre.



Figure 1.07 : Propagation de la lumière dans la fibre par réflexion totale

Dans cette figure précédente, n0 représente l'indice du milieu entre émetteur et fibre (souvent de l'air). La condition de guidage dans le coeur de la fibre pour que la lumière subisse une réflexion

totale est : i1 > l

Si cette condition n'est pas vérifiée alors le rayon est réfracté dans la gaine de la fibre optique. Mais partant de l'émetteur, le rayon lumineux doit subir une réfraction pour qu'il puisse entrer dans le coeur de la fibre. Il doit suivre la relation (1.03).

14

1.7 L'ouverture numérique et la fréquence normalisée

En plus des conditions de guidage, pour qu'un rayon lumineux soit effectivement guidé dans la fibre optique, il faut que le faisceau incident i0 appartienne à un cône dit d'acceptance.

L'angle d'acceptance de la fibre est l'angle d'incidence limite maximal i0lim qui permet à la lumière, issue de l'émetteur, une propagation par réflexion successive dans la fibre.

Pour un angle d'incidence en dehors de l'angle d'acceptance, la lumière est transmise soit du coeur vers la gaine, soit réfléchi et retourné à l'extérieur de la fibre. L'information alors transportée par la lumière est perdue car non propagée jusqu'à la sortie de la fibre. [1][24] Observons la figure suivante afin d'énoncer la formule de l'ouverture numérique:



Figure 1.08 : Cône d'acceptance

Un faisceau de lumière rentre dans la fibre avec un angle i0 par rapport à la normale à la surface (axe central de la fibre).

Puisqu'il y a un changement du milieu, appliquons le principe de Descartes pour calculer l'angle d'incidence limite i0lim .

En appliquant la loi de Descartes, formule (1.03), l'angle de réfraction á1 dans le matériau d'indice n1 vérifie :

n0.sin i0lim = n1.sin ?? (1.11)

Avec :

?? ? i? (1.12)

Pour l'angle limite, on a :

?1lim = i1lim (1.13)

On a alors :

sin ?1lim= sin( ) =

sin i0lim = cos i1lim (1.14)

Ce qui donne :

sin i0lim = v (1.15)

15

D'après la condition de guidage : i1lim arcsin

( )

Alors :

= v

sin i0lim (1.16)

v ( )

Or, en général, n0 représente l'indice de réfraction de l'air qui est égal à 1. Donc :

sin i0lim v (1.17)

Dans ce cas, l'angle d'acceptance est :

i0lim arcsin (v ) (1.18)

L'ouverture numérique (O.N) ou en anglais « numerical aperture » (N.A.) d'une fibre caractérise l'angle d'incidence que doit faire le faisceau à l'entrée pour assurer sa propagation. Elle est ainsi définie par :

ON= sin i0lim v (1.19)

Sur la figure précédente (Figure 1.08), lorsque l'angle d'incidence est inférieur à l'angle d'acceptance _i0lim , la propagation du faisceau lumineux dans la fibre est assurée tandis que pour un faisceau lumineux qui n'appartient pas dans le cône d'acceptance c'est-à-dire d'angle d'incidence supérieur à celui d'acceptance, le rayon lumineux est perdu. [7]

Afin de faciliter l'injection de la lumière dans la fibre, on a intérêt à avoir l'angle limite le plus grand possible. Ceci s'obtient pratiquement en choisissant l'indice de la gaine et du coeur le plus proche.

En effet, une fibre optique est souvent décrite selon deux paramètres :

o La différence d'indice normalisé, qui donne une mesure du saut d'indice entre le coeur et la gaine. Elle est donnée par la formule :

(1.20)

o L'ouverture numérique de la fibre, qui est concrètement le sinus de l'angle d'entrée maximal de la lumière dans la fibre pour que la lumière puisse être guidée sans perte et mesuré par rapport à l'axe de la fibre.

A partir de cette ouverture numérique, et sachant le rayon du coeur de la fibre, on peut déduire la fréquence normalisée. Elle permet de prédire le nombre de modes (chemins possibles) qu'une fibre peut contenir.

La fréquence normalisée est exprimée par :

V = v =

(1.21)

16

Avec :

a : rayon du coeur de la fibre

: longueur d'onde dans le vide

À mesure que V augmente, le nombre de modes supportés par la fibre va augmenter. Ce paramètre V est important pour définir les conditions de propagation monomode.

Conclusion

Dans ce chapitre, nous avons parlé de la fibre optique depuis son apparition suivi de ses structures. Ce support de transmission offre des avantages en particulier au niveau du débit et de son faible poids par rapport aux autres supports câblés. Aussi récente et performante qu'elle est, la fibre optique présente quand même des inconvénients conduisant à l'atténuation des signaux. La fibre et la lumière sont deux choses inhérentes et l'analyse des comportements de la lumière dans une liaison par fibre optique est aussi apportée dans ce chapitre.

17

Chapitre 2 : LES DIFFÉRENTS TYPES DE FIBRE OPTIQUE

Introduction

Nous avons vu dans le chapitre précédent que la fibre optique présente des problèmes entrainant l'atténuation des signaux transmis. Ces inconvénients ne sont pas tous les mêmes selon la structure dont une fibre a été conçue. En fonction de cette structure, il existe différents types de fibre optique et nous allons voir dans ce présent chapitre ces types de la fibre et leurs spécificités.

2.1 Notion de mode de propagation

Les faisceaux lumineux, sortant de leur source pour être transmis vers la fibre, peuvent subir de la réflexion ou réfraction. Selon le phénomène auxquelles ils sont soumis, ces rayons lumineux peuvent être, soient restés confiner dans le coeur de la fibre, soient dirigés vers l'extérieur et perdus.

Le rayon incident, s'il fait partie du cône d'acceptance, doit pouvoir se propager dans la fibre. Chaque direction du rayon incident qui satisfait les conditions de propagation est associée à un mode. Dans ce cas, toutes les directions permettant aux rayons lumineux de rester dans le coeur constituent les modes de propagation.

Les fibres optiques peuvent être classées en deux grandes catégories selon le nombre des modes des ondes lumineuses.

Le rayon du coeur entre en jeu pour définir le nombre de mode qui peut s'introduire dans la fibre. En d'autre terme, plus le rayon du coeur de la fibre est grand, plus l'ouverture numérique s'élargit et le nombre de rayon lumineux entrant dans la fibre augmente ; ce qui donne plusieurs modes. [14]

Suivant le nombre de modes N des ondes lumineuses, on distingue :

o la fibre multimode (N>1) et

o la fibre monomode (N=1).

2.2 La fibre multimode

Dans ce type de fibre, le signal lumineux se propage par des multitudes des rayons le long de la fibre. Le terme « multimode » signifie que la lumière repartit dans plusieurs modes (trajets lumineux interne) simultanément. Donc plusieurs chemins de propagation y sont possibles. Elles sont caractérisées par un diamètre de coeur de plusieurs dizaines à quelques centaines de micromètres.

Les fibres multimodes (dites MMF, pour Multi Mode Fiber), ont été les premières sur le marché. Elles sont maniables grâce à ses dimensions relativement grandes ou encore une ouverture numérique élevée.

18

Le problème de la fibre multimode est que les modes n'arrivent au même moment en bout de fibre. Ce qui entraine la « dispersion modale ». Il y a donc élargissement des impulsions lumineuses émises. Du fait de la dispersion modale, on constate un étalement temporel du signal proportionnel à la longueur de la fibre. Par conséquent, l'utilisation la plus fréquente pour ce type de fibre est la transmission à bas débit ou à courte distance.

La dispersion modale peut cependant être minimisée en réalisant un gradient d'indice dans le coeur de la fibre.

Il existe deux types de fibre multimode :

o la fibre à saut d'indice et

o la fibre à gradient d'indice.

Leur différence réside principalement au niveau de l'homogénéité ou non de l'indice du coeur.

2.2.1 La fibre multimode à saut d'indice

2.2.1.1 Profil d'indice

La fibre est caractérisée par son profil d'indice. Il s'agit de la représentation de l'indice de la fibre en fonction de la distance r à l'axe centrale de la fibre : n(r).

Soit 2a le diamètre du coeur, le profil d'indice est représenté comme suit :



Figure 2.01 : Profil d'indice d'une fibre multimode à saut d'indice

2.2.1.2 Caractéristiques

Dans ce type de fibre, le coeur et la gaine présentent des indices de réfraction différents et constants. Le passage d'un milieu vers l'autre est caractérisé par un saut d'indice.

Le « saut d'indice » signifie que la différence entre l'indice de réfraction du coeur et celui de la gaine est assez importante et constitue de ce fait un palier.

19

Dans cette structure, lorsque la lumière rencontre la gaine, il est brusquement réfléchi.

Cette fibre est caractérisée par son indice de réfraction du coeur n1 homogène de valeur normalisée entre 1,40 à 1,55. Ce coeur est entouré d'une gaine optique d'indice n2 inférieure à n1 de valeur se trouvant dans un même intervalle que celle du coeur. Ces valeurs d'indice sont aussi valables aux autres types de fibres.

En moyenne, le diamètre du coeur est de 50 à 200 ìm et celui de la gaine est de 125 à 400 ìm. Le faisceau lumineux injecté à l'entrée de la fibre va atteindre la sortie en empruntant des chemins optiques différents. Le rayon est guidé par la réflexion totale au niveau de l'interface coeur-gaine.

La figure ci-dessous montre les différents trajets de chaque rayon lumineux et la différence entre l'impulsion d'entrée et celle de la sortie.



Figure 2.02 : Chemins optiques empruntés par les rayons lumineux et

l'impulsion d'entrée et sortie

Dans cette figure, chaque faisceau lumineux possède son angle de départ et angle de réflexion différent l'un de l'autre.

En analysant la propagation dans une fibre à saut d'indice, on voit une propagation par chemins multiples. Les rayons lumineux qui s'y propagent suivent des trajets différents les uns des autres et se déplacent à différentes vitesses en fonction de leurs longueurs d'onde. Ce qui entraine des temps de propagation différents des signaux transmis. Ce retard provoque une dispersion du signal dans le temps qui se traduit par un accroissement de la durée de l'impulsion. Il y a donc à l'arrivée un étalement du spectre conséquent. Ce phénomène est appelé dispersion intermodale. La capacité de transmission de ce type de fibre est d'environ 100 à 200Mbits/s.

Cette valeur correspond également à la bande passante. On peut exprimer la bande passante en Mhz*km. Ici pour la fibre à saut d'indice elle est de 20 à 100Mhz*km. Cette capacité est assez faible car chaque rayon a parcouru une distance plus ou moins différente. Par conséquent il faut à l'extrémité attendre que tous les faisceaux soient arrivés. [19] [22]

20

2.2.1.3 Modes

Les modes sont l'expression des différents chemins optiques que peut suivre le signal dans la fibre. Le nombre de modes se calcule en fonction de la fréquence normalisée V décrit auparavant par la formule (1.21). Pour les fibres multimodes à saut d'indice, le nombre de modes est donné expérimentalement par [19] :

N = (2.01)

2.2.2 La fibre multimode à gradient d'indice

La fibre à gradient d'indice est la plus courante. Elle connaît plusieurs améliorations par rapport à la fibre à saut d'indice.

Le but, pour ce profil d'indice est de rendre la vitesse de propagation des différents rayons plus proche, c'est-a-dire de minimiser l'étalement du signal en rendant plus lents les rayons qui sont proches de l'axe de la fibre et rapides ceux qui s'en éloignent.

Dans cette catégorie le coeur n'est plus homogène : la valeur de l'indice décroît légèrement depuis l'axe du coeur jusqu'à l'interface coeur-gaine. Alors, les chemins optiques empruntés par les rayons lumineux prennent une allure sinusoïdale.

L'avantage essentiel de ce type de fibre est la minimisation de la dispersion du temps de propagation entre les rayons. [7]

2.2.2.1 Profil d'indice

Le profil d'indice est représenté mathématiquement comme suit. Dans le coeur : 0 < r < a

J i-2L(r/a)" (2.02)

Dans la gaine : r > a

(2.03)

Avec :

r : distance à l'axe ;

a : rayon du coeur ;

a : exposant du profil d'indice (souvent 1 à 2)

L : différence relative d'indice (diminution relative de l'indice entre l'axe et la gaine)

Exemple du profil d'indice :

o Pour a = 2, le profil est parabolique.

o Pour a = 1, le profil devient triangulaire.

o Pour a -00, on est ramené au cas d'une fibre à saut d'indice.



21

Figure 2.03 : Exemples du profil d'indice d'une fibre à gradient d'indice

2.2.2.2 Ouverture numérique

Pour une fibre à saut d'indice l'ouverture numérique est égale à . n_i² -- n₂² (formule 1.19). Pour une fibre à gradient d'indice, en raison de la variation de l'indice du coeur, on définit une ouverture numérique locale :

ON = . n(r)²--n₂² (2.04)

oca

Où n(r) : indice à la distance r de l'axe du coeur. On remarque que :

o L'ouverture numérique est maximale pour r = 0. On a alors n(r) = nl

o Elle est minimale (et même nulle) pour r = a .On a alors n(r) = n2

Plus l'ouverture numérique est grande, plus l'angle d'acceptance est grand, et plus la puissance véhiculée est importante. Ainsi, une fibre à saut d'indice transporte plus de puissance lumineuse que celle à gradient d'indice. [3]

2.2.2.3 Caractéristiques

Contrairement aux fibres à saut d'indice, le coeur, n'est pas homogène.

Il est constitué de plusieurs couches de verre ayant chacune un indice de réfraction légèrement différent de la couche contigüe.

Alors le rayon lumineux n'est pas brusquement réfléchi lorsqu'il rencontre la gaine, mais sa trajectoire est déviée progressivement à chaque fois qu'il traverse une nouvelle couche.

Le guidage est cette fois dû à l'effet du gradient d'indice. La gaine optique n'intervient pas directement mais elle élimine les rayons trop inclinés.

Pour ce type de fibre, le diamètre du coeur mesure entre 50 et 100 um et celui de la gaine se situe entre 125 et 140 um. La fibre multimode à gradient d'indice est caractérisée par la variation linéaire de l'indice n1 du coeur de la fibre optique en fonction de la distance r à l'axe suivant la formule (2.02).



22

La trajectoire du rayon lumineux dans une fibre à gradient d'indice est incurvée et la vitesse des rayonnements étant de plus en plus faible quand il se rapproche du centre du coeur. Ceci est dû à la non homogénéité de l'indice de réfraction du coeur. Cet indice est très élevé au centre du coeur et diminue jusqu'à la gaine optique grâce aux différentes couches de verre.

L'avantage avec ce type de fibre est la minimisation de la dispersion du temps de propagation entre les rayons, sans utiliser pour cela l'ouverture numérique trop faible ainsi qu'un étalement du spectre moins important étant donné que les faisceaux lumineux arrivent presque à un même moment lorsqu'ils passent par l'axe du coeur.

La bande passante est de l'ordre de 500Mbits/s. Cette capacité est plus élevée que celle pour une fibre à saut d'indice car le temps d'arrivée de chaque rayon se rapproche.

Pour une fibre à gradient d'indice fabriquée en silice dopée qui possède un coeur de diamètre 50 à 62,5 ìm, la bande passante est entre 100 et 1000MHz*km et l'affaiblissement à une longueur d'onde de 1550 nm est inférieur à 2dB/km. [2] [23]

Elle peut être utilisée pour une liaison à grande distance.

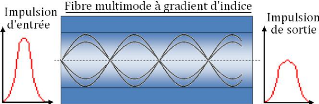
Ces améliorations apportées à cette fibre ont permet de réduire l'atténuation de l'information par rapport à la fibre à saut d'indice, ce qui fonctionne parfaitement car l'impulsion du signal de sortie représente plus de la moitié du signal d'entrée comme le montre la figure suivante.

Figure 2.04 : Impulsion d'entrée et sortie des rayons lumineux et leurs trajets

Nous pouvons remarquer que les résultats sont nettement améliorés par rapport à ceux procurés par la fibre à saut d'indice.

2.2.2.4 Modes

Le nombre de modes N dans ce type de fibre est donné par la relation :

N = (2.05)

-. -.

23

On a donc :

_y2

o Pour une fibre à profil d'indice parabolique (a ? 2), N vaut

_y2

o Pour une fibre à profil triangulaire (a ? 1), le nombre de mode est

6

o Pour un paramètre de profil d'indice très grand (a - 00), N revient à ^y22 (fibre à saut

d'indice)

2.3 La fibre monomode

Vu le problème de la fibre multimode (dispersion modale), une des solutions est de rétrécir le diamètre de la fibre pour avoir un seul mode, d'où la naissance de la fibre monomode.

Le but recherché dans cette fibre est que le chemin parcouru par le faisceau soit le plus direct possible. Pour cela, on réduit fortement le diamètre du coeur qui est dans la plupart des cas

environ 10ìm. Les rayons lumineux ont un parcours rectiligne et dans la figure ci-dessous, le signal de sortie ressemble presque au signal d'entrée.



Figure 2.05 : Signal d'entrée et sortie dans une propagation par fibre monomode

Le fait que le coeur soit si fin va obliger le signal lumineux à se propager en ligne droite.

Comme la trajectoire ne change pas, le temps de parcours du rayon lumineux diminue et la vitesse de transmission augmente.

Dans ce cas :

o Le faisceau de lumière ne rencontre pas la gaine ;

o La déformation du signal dans ce type de fibre est quasi inexistante ;

o La dispersion modale est quasi nulle.

Étant donné que les faisceaux lumineux ne se dispersent pas, la bande passante est donc augmentée, plus de10 GHz*km. [21]

Du fait de ces précieux avantages, la fibre monomode a pris une ampleur considérable dans les transmissions sur des grandes distances.

Le problème de la fibre monomode est le raccord entre fibres, ou entre fibre et connecteur qui nécessite un alignement parfait. De plus, le petit diamètre du coeur requiert une grande puissance d'émission, donc des diodes laser qui sont relativement onéreuses.

24

2.3.1 Conditions de monomodalité d'une fibre optique

2.3.1.1 Longueur d'onde critique ou de coupure

Il s'agit de la valeur de la longueur d'onde à partir de laquelle la fibre n'est plus monomode.

La fibre reste toujours monomode si V< 2,404, où V est la fréquence normalisée définie par la

formule (1.21).

On a donc :

< 2,404 (2.06)

Ce qui entraine :

(2.07)

>

La longueur d'onde critique est la limite de cette équation et qui est définie par :

=

(2.08)

D'après cette condition sur la valeur de la fréquence normalisée, pour vérifier la monomodalité

d'une fibre, la longueur d'onde utilisée doit être supérieure à longueur d'onde de coupure (en

dessous de cette valeur un deuxième mode apparaît dans la fibre). C'est-à-dire pour > , la

fibre est dite monomode. [11]

Par exemple, soit une fibre dont a = 3 um, ON = 0,151 et = 1,3um.

La fibre a donc un rayon de coeur de 3 um, une ouverture numérique de 0,151 et elle est prévue pour transmettre la longueur d'onde 1,3 um. A partir de la formule (1.21), on obtient comme fréquence normalisée V = 2,19.

Comme V est ici inférieur à 2,404 ; on conclut donc que la fibre est monomode.

De plus, si on calcul la longueur d'onde critique on trouve = 1,184um qui est réellement inférieure à la longueur d'onde = 1,3 um.

2.3.1.2 Profil d'indice d'une fibre monomode

Le profil d'indice est représenté par la courbe n(r) dans la figure 2.06 sur la page suivante.

Les fibres monomodes ont un profil à saut d'indice, avec un coeur beaucoup plus étroit que pour

les fibres multimodes.

Comme pour la fibre multimode à saut d'indice, l'indice du coeur est homogène.



25

Figure 2.06 : Profil d'indice d'une fibre monomode 2.3.2 Diamètre de mode d'une fibre monomode

2.3.2.1 Définition du diamètre de mode

Il se peut que la largeur du rayon lumineux touche la gaine lorsque le diamètre du coeur est très étroit ou lorsque la fibre n'est plus en position rectiligne.

En raison de la diffraction de l'onde dans une fibre monomode, une partie transverse du champ modal optique s'élargi jusqu'à l'intérieur de la gaine. C'est pourquoi, on définit un nouveau diamètre de mode, plus large que le diamètre du coeur, qui caractérise la largeur réelle du faisceau lumineux.

En monomode, la lumière est généralement guidée par le coeur, mais, une certaine partie de la puissance est transmise dans la gaine. La répartition de cette puissance lumineuse est à peu près « gaussienne », c'est-à-dire en forme de cloche.

L'intensité du mode fondamental varie en fonction du rayon transverse de la fibre dont le point culminant correspond à l'origine au centre du coeur.

Le diamètre du mode est défini par 2w0 sur lequel w0 représente la demi-largeur du mode. [12][23]

2.3.2.2 Valeur du diamètre de mode

En général, le diamètre de mode fondamental d'une fibre optique monomode peut être assimilé à une distribution gaussienne. La figure suivante présente la distribution réelle (mesurée expérimentalement) du mode fondamental et son approximation gaussienne.



26

Figure 2.07 : Distribution d'intensité de mode fondamental (ligne continue) et son approximation par une forme gaussienne (ligne discontinue).

Où r est la distance par rapport à l'axe central de la fibre.

Il est à noter que l'intensité lumineuse aux alentours de cet axe est très importante vis-à-vis de celui plus près de la gaine. C'est pour cette raison que les faisceaux lumineux sont supposés toujours placés au centre du coeur.

Il existe une expression analytique empirique qui permet de déterminer en fonction de la
fréquence normalisée V et rayon du coeur a pour une fibre standard à saut d'indice qui est aussi valable pour une fibre monomode. Il s'agit de la formule de Marcuse définit par [9]:

(2.09)

Avec a : rayon du coeur de la fibre V : Fréquence normalisée Par exemple :

o Pour V = 2,404 (à la limite du monomode) on obtient. w0 = 1,11a ;

o Pour V = 2, on obtient w0 = 1,26a ;

o Pour V = 1,5, on a : w0 = 1,78a ;

o Pour V = 1, on obtient : w0 = 5,15a. On remarque qu'ici, le rayon du mode pour cette valeur de V=1 s'étend de plus en plus dans la gaine.

27

Pour la fibre monomode, le diamètre de la gaine mesure souvent entre 100 et 150um.

Le diamètre de mode est une caractéristique des fibres monomodes. Il augmente très rapidement avec la longueur d'onde, ce qui rend la transmission de plus en plus sensible aux déformations.

2.3.3 Facteur de confinement

Le facteur de confinement décrit la fraction de puissance du mode contenue dans le coeur par rapport à la puissance totale du mode.

Il est donné par la formule suivante :

P_c

F = = 1 - exp (_2 a 2) (2.10)

Pc+Pg

Avec P_c : puissance du mode dans le coeur

Pg : puissance du rayon dans la gaine et avoisinant l'interface coeur-gaine.

Plus la fréquence normalisée augmente, plus la quantité de lumière transportée par la gaine diminue (donc plus le facteur de confinement F augmente).



Figure 2.08 : Facteur de confinement

La figure ci-dessus présente la dépendance en V du facteur de confinement. On remarque que F n'est pas égal à 1 si V = 2,404, ce qui veut dire qu'une certaine partie de la puissance se propage dans la gaine.

28

2.4 Les Recommandations G.652 à G.657 de l'UIT

L'UIT (Union Internationale des Télécommunications) est un organe de l'Organisation des Nations Unies (ONU) chargé de la réglementation et la normalisation des télécommunications dans le monde. Les Recommandations G.652 à G.657 de l'UIT sont spécialement dédiées à la fibre optique monomode.

Les points essentiels de cette série sont représentés par le tableau suivant. [25]

G.652				G.652.A
Attribut
Détail		Valeur	Coefficient de dispersion chromatique
2Omin		1300 nm
		1324 nm
		0,092 ps/nm^2 km	Coefficient d'atténuation
Maximum à 1310 nm		0,5 dB/km
		0,4 dB/km	G.652.B
Attribut
Détail		Valeur	Coefficient de dispersion chromatique
2Omin		1300 nm
		1324 nm
		0,092 ps/nm^2 km	Coefficient d'atténuation
Maximum à 1310 nm		0,4 dB/km
		0,35 dB/km
		0,4 dB/km	G.652.C / G.652.D
Coefficient de dispersion chromatique
2Omin		1300 nm
		1324 nm
		0,092 ps/nm^2 km	Coefficient d'atténuation
Maximum de 1310 nm à 1625 nm		0,4 dB/km
		= 0,4 dB/km
		0,3 dB/km

29

G.653

G.653.A
Attribut
Détail	Valeur	Coefficient de dispersion chromatique
??min	1500 nm
	1600 nm
	3,5 ps/ nm.km
	0,085 ps/nm^2 km	Coefficient d'atténuation
Maximum à 1550 nm	0,35 dB/km	G.653.B
Coefficient de dispersion chromatique
Dmin (?) : 1460 - 1525 nm	0,085(? ? ????) ? ???
	3,5(? ? ????)/75
	3,5(? ? ????)/75
	0,085(? ? ????) + 3,5	Coefficient d'atténuation
Maximum à 1550 nm	0,35 dB/km	G.654
G.654.A / G.654.B / G.654.C
Attribut
Détail	Valeur	Coefficient de dispersion chromatique
D1550max	20 ps/ nm.km
	0,070 ps/nm^2 km	Coefficient d'atténuation
Maximum à 1550 nm	0,22 dB/km	G.655
G.655.C
Attribut
Détail	Valeur	Coefficient de dispersion chromatique
?0min	1530 nm
	1565 nm
	1,0 ps/ nm.km
	10,0 ps/ nm.km	Coefficient d'atténuation
Maximum à 1550 nm	0,35 dB/km
	0,4 dB/km	G.655.D
Coefficient de dispersion
Dmin (?) : 1460 - 1550 nm	7,00(? ? ????)/90 ? ????
	2,97(? ? ????)/75 + ????

30

chromatique

Dmax (X) : 1460 - 1550 nm	2,91(X -- 1460)/90 + 3,29
	5,06(X -- 1550)/75 + 6,20
	Coefficient d'atténuation
Maximum à 1550 nm	0,35 dB/km
	0,4 dB/km	G.655.E
Coefficient de dispersion chromatique
Dmin (X) : 1460 - 1550 nm	5,42(X -- 1460)/90 + 0,64
	3,30(X -- 1550)/75 + 6,06
	4,65(X -- 1460)/90 + 4,66
	4,12(X -- 1550)/75 + 9,31	Coefficient d'atténuation
Maximum à 1550 nm	0,35 dB/km
	0,4 dB/km	G.656
Coefficient de dispersion chromatique
Dmin (X) : 1460 - 1550 nm	2,60(X -- 1460)/90+ 1,00
	0,98(X -- 1550)/75+ 3,60
	4,68(X -- 1460)/90 + 4,60
	4,72(X -- 1550)/75 + 9,28	Coefficient d'atténuation
Maximum à 1460 nm	0,4 dB/km
	0,35 dB/km
	0,4 dB/km	G.657
G.657.A
Coefficient de dispersion chromatique
X0min	1300 nm
	1324 nm
	0,092 ps/nm^2 km	Coefficient d'atténuation
Maximum de 1310 nm à 1625 nm	0,4 dB/km
	= 0,4 dB/km
	0,3 dB/km	G.657.B
Coefficient de dispersion chromatique
X0min	1300 nm
	1424 nm
	0,10 ps/nm^2 km

31

Coefficient d'atténuation

Maximum à 1310 nm	0,5 dB/km
	0,3 dB/km
	0,4 dB/km

Tableau 2.01 : Les Recommandations G652 à G657 de l'UIT

Le coefficient de dispersion chromatique D est spécifié en imposant des limites aux paramètres d'une courbe de dispersion chromatique qui est une fonction de la longueur d'onde.

La limite du coefficient de dispersion chromatique pour n'importe quelle longueur d'onde X est calculée à l'aide de la longueur d'onde minimale de dispersion nulle X0min , de la longueur d'onde maximale de dispersion nulle X0max et du coefficient maximal de pente à la dispersion nulle S0max

Conclusion

Ainsi, nous pouvons dire que ce chapitre permet de distinguer les trois types de fibre optique et leurs particularités au niveau de la performance. Ce sont la dimension et l'indice du coeur qui les différencient principalement et le nombre de mode ou faisceaux lumineux pouvant se propager dans la fibre dépend de cette dimension du coeur. Ce qui donne le nom du multimode comme étant une fibre capable de transmettre plusieurs modes et le monomode pour un seul mode.

PARTIE II : LES PARAMÈTRES DE TRANSMISSION ET
ATTÉNUATIONS DANS UNE LIAISON OPTIQUE

Chapitre 3 : LES PARAMÈTRES DE TRANSMISSION PAR FIBRE

Introduction

Lors d'une transmission par fibre optique, il existe plusieurs paramètres qui coopèrent à l'acheminement des signaux lumineux. Nous allons décrire quelques éléments nécessaires dans une liaison par fibre optique contribuant à l'affaiblissement du signal. Il s'agit des composants qui émettent et captent de la lumière ainsi que des régénérateurs. Les techniques de modulation et de multiplexage sont aussi abordées dans ce présent chapitre.

3.1 Les éléments d'un système de transmission par fibre optique

Dans les fils métalliques, on transmet les informations par l'intermédiaire d'un courant électrique modulé. Avec la fibre optique, on utilise un faisceau lumineux pour faire transiter l'information. La transmission d'un signal par fibre optique nécessite une double transformation : à l'émission, le signal électrique est transformé en signal optique et à la réception la transformation est inverse.

Une liaison point à point par fibres optiques comprend : [2] [13] [24]

o les fibres optiques elles-mêmes, contenues dans un câble qui la protège et qui peut comporter un grand nombre de fibres ;

o l'interface optique d'émission, constituée du composant optoélectronique d'émission qui est le plus souvent une diode électroluminescente (DEL) ou une diode laser (DL) ayant pour rôle de transformer le signal électrique en signal optique. L'interface contient également des circuits permettant le fonctionnement correct de l'émission et l'adaptation du signal ;

o l'interface optique de réception constituée d'une interface optoélectronique de réception généralement la photodiode qui effectue la conversion inverse de la précédente, des circuits d'adaptation et d'un amplificateur compensant l'atténuation de la fibre optique.

o Les répéteurs ou amplificateur, lorsque la longueur de la liaison le nécessite, on y insère un ou plusieurs entre plusieurs fibres pour amplifier le signal affaibli le long d'une fibre.



Figure 3.01 : Les éléments d'une transmission point à point par fibre optique

32

33

3.2 L'interface optoélectronique d'émission

Les sources en transmission par fibre optique servent à convertir le signal électrique en signal lumineux qui est plus adapté au support de transmission. Pour cela, on a besoin des composants à semi-conducteurs tels que les diodes électroluminescentes DEL et les diodes LASER dont leurs dimensions sont bien adaptées au diamètre du coeur de la fibre. Ces composants peuvent en effet être modulés à des fréquences élevées sous des tensions faibles. [16]

Les semi-conducteurs sont des matériaux présentant une conductivité électrique intermédiaire entre les métaux et les isolants.

3.2.1 La diode électroluminescente

3.2.1.1 Principe d'émission de lumière dans une DEL

Dans un semi-conducteur, un courant électrique est favorisé par deux types de porteurs : les électrons et les trous. Les propriétés d'un semi-conducteur (c'est-à dire le nombre de porteurs, électrons ou trous) peuvent être contrôlées en le dopant avec des impuretés (autres matériaux). Un semi-conducteur présentant plus d'électrons que de trous est alors dit de type N, tandis qu'un semi-conducteur présentant plus de trous que d'électrons est dit de type P.

Les transitions dans la diode à semi-conducteur correspondent à une recombinaison des niveaux tendant à combler les trous de la bande de valence par la transition des électrons en provenance de la bande de conduction. Cette recombinaison d'une paire électron-trou est radiative : il y a alors émission de rayonnement et c'est le cas des diodes électroluminescentes

Une diode électroluminescente, couramment abrégée sous le sigle DEL et le plus souvent sous l'anglicisme LED (Light Emitting Diode) est un composant électronique capable d'émettre de la lumière lorsqu'il est parcouru par un courant électrique. C'est le composant le plus simple, qui réalise directement l'émission de photons par recombinaison de paires électron-trou. [14][19]

3.2.1.2 Caractéristiques des diodes DEL

Une diode électroluminescente ne laisse passer le courant électrique que dans un seul sens et produit un rayonnement non cohérent à partir de la conversion d'énergie électrique lorsqu'un courant la traverse. Une diode électroluminescente se symbolise comme suit :



Figure 3.02 : Symbole d'une diode électroluminescente

Ces diodes sont polarisées : on raccorde le pôle « - » à la cathode et donc le pôle « + » à l'anode. Les DEL sont généralement constituées par des matériaux semi-conducteurs d'Arséniure de

34

Gallium (GaAs) à la longueur d'onde 850 nm qui fonctionnent dans le rouge visible et Arséniure de Galium-Aluminium (AlGaAs) pour diode infrarouge qui émette un rayon invisible à 1300 nm. Elles peuvent travailler dans la gamme de courant de quelques milliampères jusqu'à des centaines de milliampères.

La puissance lumineuse émise est alors pratiquement proportionnelle au courant injecté, avec un rendement externe médiocre ; en particulier, seule une faible partie peut être couplée dans une fibre optique à cause de la forte divergence. En effet, une diode électroluminescente convertit environ 40 à 60% de l'énergie électrique en lumière, le reste étant dégagé sous forme de chaleur. Le spectre typique de l'émission spontanée, est continu et assez large, d'où forte sensibilité à la dispersion chromatique. La largeur de spectre d'une DEL est environ 50 nm et représenté dans la figure ci-dessous.



Figure 3.03 : Spectre d'émission d'une DEL

Quant au rendement, la technologie actuelle permet d'avoir un rendement d'émission de l'ordre de 20 à 200 mW/A. [7]

Dans les liaisons longues distances, les DEL ne sont pas très convaincantes vue leur largeur de bande un peu large et leur sensibilité à la dispersion chromatique.

En contre partie une DEL présente une faible quantité de bruit ainsi qu'un coût relativement faible. Elles sont employées dans les réseaux locaux.

3.2.2 Diode LASER

3.2.2.1 Caractéristiques d'une diode Laser

Le mot LASER vient de l'acronyme anglais « Light Amplification by Stimulated Emission of Radiation » ce qui peut être traduit en français comme amplification de la lumière par émission stimulée de radiation.

35

Ce dispositif d'émission de lumière se symbolise comme suit :



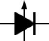
Figure 3.04 : Symbole d'une diode laser

C'est un dispositif qui amplifie la lumière et la rassemble en un étroit faisceau. Ce dernier est cohérent, tous les rayons ont la même longueur d'onde et se propagent en phase dans la même direction. Le laser émet donc de la lumière à très haute intensité.

Une diode laser est un composant optoélectronique à base de matériaux semi-conducteurs destiné à produire un faisceau laser à l'aide des matériaux semi-conducteurs comme par exemple AlGaAs à la longueur d'onde 1300 nm et InGaAsP à 1550 nm.

Une diode laser est caractérisée par son courant de seuil, en dessous duquel, il effectue une émission spontanée, c'est-à-dire qu'il se comporte comme une simple diode électroluminescente. L'avantage de l'utilisation des diodes lasers est qu'on peut avoir de puissance relativement élevée par rapport à une DEL. De plus, un rayon laser a une largeur spectrale faible moins de 5nm et une directivité parfaite. [20]

Son aspect très fin le rend très compatible avec l'ouverture numérique d'une fibre monomode. Les diodes lasers sont donc utilisées comme sources dans les liaisons longues distances.

3.2.2.2 Principe d'émission

Le concept d'émission consiste à exciter un milieu actif qui est un réservoir d'électron, par un apport d'énergie ; ceci dans le but d'élever le niveau d'énergie de ces électrons à un niveau supérieur. Cette excitation du milieu actif est appelée « pompage ». Le pompage se fait à l'aide d'un courant électrique.

Le mouvement aléatoire de ces électrons dans le niveau d'énergie plus faible s'accompagne de l'émission de particule lumineuse appelée Photon. Lorsque ces photons rencontrent d'autres atomes excités, des particules identiques (photons) se forment et se propagent à la même longueur d'onde.

La lumière est produite au niveau de la jonction par la recombinaison des trous et des électrons. Elle est amplifiée lorsqu'il y a beaucoup de photons qui se déplacent dans le dispositif.

Le résonateur est une cavité optique dans laquelle l'onde lumineuse se réfléchit et s'amplifie.

Les diodes laser sont des semi-conducteurs dans lesquels on a recréé un milieu amplificateur avec sa cavité résonnante et dont l'inversion de la population est réalisée par un courant.

36

Tant que l'on reste en dessous d'une valeur seuil de ce courant, la diode laser se comporte comme une diode électroluminescente classique ; dès que le seuil est atteint, l'inversion de population est réalisée et l'effet laser est déclenché. [2] [23]



Figure 3.05 : Puissance émise par une diode laser

3.2.2.3 Bruit des diodes lasers

Néanmoins, les diodes lasers présentent quelques imperfections.

En effet, on constate que le rayon laser fourni est affecté par des bruits d'amplitude et de phase qui peuvent dégrader la performance des systèmes de communications. Ce bruit est provoqué par l'émission spontanée dans la diode laser. Chaque photon émis spontanément ajoute une petite composante aléatoire en phase au champ optique cohérent (généré par émission stimulée) et perturbe ainsi à la fois l'amplitude et la phase du signal de sortie du laser de manière aléatoire.

Le bruit d'amplitude ou la fluctuation de l'amplitude est caractérisé par le bruit d'intensité rin (Relative Intensity Noise) défini par le rapport entre la densité spectrale des fluctuations de la puissance optique <?P> et le carré de cette puissance.

On utilise habituellement la quantité RIN(f), expression en décibels de rin(f), exprimant la puissance relative dans une bande de 1 Hz en dB/Hz.

( LP(f))²

rin(f) = (3.01)

( P(f)) 2

RIN(f) = 10 log[rin(f)] (3.02)

37

Les photons émis spontanément qui changent aléatoirement la phase du champ optique constituent un mécanisme contribuant aux fluctuations de phase. [11]

Le bruit de phase induit un élargissement du spectre de la lumière émise à la sortie du laser.

3.3 Techniques de modulation

Afin de transmettre des informations dans les systèmes numériques optiques, il faut les imprimer sur le signal et les adapter au support de transmission qui est la fibre optique ; c'est ce que l'on entend par modulation.

Il existe principalement deux techniques de modulation optique : la modulation directe et la modulation externe.

3.3.1 La modulation directe

Un des principaux avantages de l'utilisation des lasers à semi-conducteur pour les systèmes de télécommunications par fibres optiques réside sur le fait qu'il est possible de les moduler facilement : la modulation du courant qui les traverse entraîne directement la modulation en intensité de la lumière émise. Cette technique est appelée modulation directe.

Ainsi, il suffit d'inscrire les données sur l'alimentation du laser.

Cette solution de modulation directe requiert assez peu de composants. En dehors de la source optique, le laser, seuls un générateur de courant et un driver sont nécessaires.

Le premier va émettre à un débit donné une séquence de données, expression de l'information à transmettre. Le second a pour rôle de commander la source optique au niveau des puissances émises (en fixant les valeurs du courant d'alimentation).

Pour cela, il modifie et transforme les niveaux du courant issu du générateur.



Figure 3.06 : Synoptique de la modulation directe

La modulation directe connaît beaucoup d'avantages, en particulier le faible coût de mise en oeuvre. Mais elle comporte aussi des limites. Les lasers en sont souvent la cause. Leur temps de réaction, le bruit créé font que la modulation directe engendre, pour les hauts et très hauts débits, certaines dégradations sur le signal optique modulé. A cela, la modulation externe constitue un remède. [20]

3.3.2 La modulation externe

La modulation externe consiste à écrire les données électriques sur un signal optique continu. Elle est obtenue en modulant directement le faisceau lumineux en sortie du laser et non plus le courant d'alimentation à l'entrée du laser.

Ainsi les défauts de la modulation directe favorisés par le laser ne seront plus présents sur le signal optique. La modulation est effectuée par un composant indispensable : le modulateur externe. Celui-ci est commandé par une tension externe v(t), modulée et représentative de l'information à transmettre. Cette tension appliquée au modulateur a pour propriété de modifier le facteur de transmission en intensité à la sortie. Le signal optique continu émis par le laser alimenté par un courant constant est donc peu dégradé.

En traversant le modulateur, il subit les modifications du facteur de transmission et le signal de sortie se trouve modulé selon v(t).

Un driver est souvent présent entre les données et le modulateur afin de fixer les niveaux de v(t) et de choisir les modifications du facteur de transmission.



38

Figure 3.07 : Synoptique de la modulation externe

La modulation directe, plus simple et moins coûteuse est encore très utilisée si les données sont transmises à un débit de quelques gigabits/s, selon la qualité du laser. Mais au-delà de 5 Gbits/s, la modulation externe est indispensable pour maintenir une qualité de transmission correcte. Cependant, les modulateurs ne sont pas totalement parfaits et peuvent quand même engendrer des défauts mais leurs impacts sont moins importants. [12] [14] [19]

3.4 Répéteur ou amplificateur optique

3.4.1 Définition et principe d'un amplificateur

L'évolution des systèmes de transmission par fibre optique a connu une véritable révolution avec la mise au point et le développement industriel des amplificateurs optiques, qui ont permis au

39

multiplexage un meilleur contrôle des pertes, mais surtout a fourni un avantage économique décisif par sa capacité d'amplifier le signal. Ce sont des dispositifs qui amplifient la lumière transmise dans les fibres optiques et augmentent sa puissance pour étendre la distance de transmission des systèmes à fibre optique vu que le signal est atténué au cours de son parcours dans la fibre optique.

Les répéteurs optiques servent à régénérer le signal entre deux segments de fibres. Ils captent l'information affaiblie en sortie de la première fibre, la remettent en forme, l'amplifient et la réinsèrent dans la seconde fibre par modulation.

Dans la plupart des cas, un amplificateur intensifie un signal lumineux sans avoir besoin de le convertir en signal électrique avant de l'amplifier avec les techniques classiques de l'électronique. Dans ce cas l'apport d'énergie extérieur augmente la quantité de photon constituant le signal lumineux, on effectue un système de pompage. [21]

3.4.2 Bruit d'un amplificateur optique

Les amplificateurs optiques génèrent des bruits que l'on appelle bruit de l'émission spontanée

amplifiée (Amplified Spontaneous Noise ou ASN).

Ce bruit est le résultat d'une émission parasite de photons par certains ions dans la fibre.

La densité spectrale du bruit est donnée par [7] :

(v) = nsp (G - 1) hv (3.03)

Avec G : gain en puissance

nsp : paramètre d'émission spontanée de l'amplificateur

h : constante de Planck (h= 6,626.10^-34 J.s)

v : fréquence optique

Un amplificateur optique est aussi caractérisé par son facteur de bruit Fa exprimé par :

+

F_a= nsp (3.04)

3.5 Interface optoélectronique de réception

L'interface optoélectronique de réception, dans une liaison par fibre optique, est chargée de convertir le signal lumineux en signal électrique, en lui apportant le minimum de dégradation. Ce rôle est tenu par le photodétecteur. Deux variantes de photodétecteur sont fréquemment utilisées dans une liaison par fibre optique :

o la photodiode PIN et

o la photodiode à avalanche (PDA).

40

Mais avant de décrire ces deux types de photodiodes, il est nécessaire de reprendre quelque notion sur la photodiode en générale.

Une photodiode est un composant semi-conducteur ayant la capacité de détecter un rayonnement du domaine optique et de le transformer en signal électrique.

C'est une diode qui entre en conduction seulement lorsqu'elle est frappée par une source lumineuse. Elle peut être reconnue par son symbole normalisée suivant.



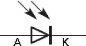
Figure 3.08 : Symbole normalisé d'une photodiode

Une photodiode est un semi-conducteur formé par une simple jonction P-N photoréceptrice généralement non amplificatrice. Sa structure générale est illustré dans la figure ci-dessous.



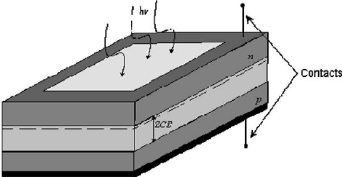
Figure 3.09 : Structure d'une photodiode

Dans cette configuration il y a apparition de trois zones (ou régions), une zone de charge d'espace (ZCE) appelée couramment zone de déplétion de diffusion ainsi que deux régions neutre de type N et P.

Quand un semi-conducteur est exposé à un flux lumineux, les photons sont absorbés.

Lorsque les photons d'énergie _Eph pénètrent dans le semi-conducteur, pourvu qu'ils aient une énergie suffisante, ils peuvent créer des photoporteurs en excès dans les matériaux.

Ces photoporteurs sont des paires d'électrons-trous et ils sont minoritaires dans la zone de déplétion. Dans la couche de déplétion, le champ électrique accélère les électrons vers la couche N et les trous vers la couche P où ils sont majoritaires.

41

Il en résulte une charge positive dans la couche P et une charge négative dans la couche N, proportionnelle au nombre de photons absorbés, et donc à l'intensité du faisceau lumineux incident. [20]

3.5.1 Photodiodes PIN

La photodiode PIN est un composant semi-conducteur de l'optoélectronique. Elle est utilisée comme photodétecteur dans de nombreuses applications industrielles. Sa particularité vient de sa jonction composée d'une région à forte résistivité (zone intrinsèque I) intercalée entre deux zones porteurs : une région fortement dopée P et une autre fortement dopée N. Elle est symbolisée comme suit :



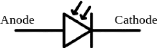
Figure 3.10 : Symbole d'une photodiode PIN

Elle utilise la photodétection (conversion d'un photon en une paire d'électron-trou) dans un semi-conducteur.

Comme a déjà parlé, seuls les photons d'énergie suffisante hí pourront être détectés.

Afin d'obtenir un bon rendement, on utilise une structure de diode PIN polarisée en inverse ; les photons sont absorbés dans la zone intrinsèque qui, du fait de la polarisation, est vide de porteurs mobiles ; les électrons et les trous ainsi crées ont une faible probabilité d'être recombinés.

Ils sont séparés par un champ électrique E qui règne dans la zone intrinsèque et qui les dirige vers la zone n et p où ils sont majoritaires. Le déplacement de ces porteurs est à l'origine du photocourant.

Le seuil typique de détection pour un taux d'erreur binaire de 10^-9 pour ce photodétecteur est environ -10 à -45dBm pour un débit de 1 à 10Gbits/s. [15] [24]

3.5.2 Photodiodes à avalanche (PDA)

Le signal reçu peut être très faible, il est nécessaire d'amplifier le photocourant.

La photodiode est suivie d'un amplificateur, mais le bruit de celle-ci est souvent prépondérant. On peut avoir l'intérêt à utiliser un composant à gain interne, la photodiode à avalanche (PDA). L'effet d'avalanche se produit à l'intérieur de semi-conducteur lorsque le champ électrique à l'intérieur du matériau est suffisamment important pour accélérer les électrons jusqu'au point où, lorsqu'ils percutent des atomes, ils libèrent d'autres électrons : le nombre d'électrons libres augmente alors rapidement car les nouveaux électrons libres en entraînent à nouveau d'autres, dans un phénomène comparable à celui d'une avalanche neigeuse.

42

Ce principe est l'ionisation en chaîne, par impact, des porteurs, sous l'effet d'un champ électrique très intense. C'est l'effet d'avalanche qui, s'il n'est pas contrôlé, aboutit au claquage de la jonction. Pour un taux d'erreur binaire de 10^-9, la photodiode à avalanche a un taux d'erreur binaire de -12 à -42dBm. [14]

3.5.3 Bruits des photodiodes

3.5.3.1 Bruit de grenaille ou bruit quantique

Comme dans toute jonction pn polarisée en sens inverse, un bruit de grenaille apparaît dans la photodiode. Ce bruit résulte de la nature corpusculaire du photocourant.

Le caractère aléatoire de l'arrivée des photons est responsable de ce bruit dont les effets prédominent largement sur ceux du bruit thermique. Il se manifeste par la fluctuation du courant détecté autour de sa valeur moyenne. C'est un bruit blanc dont la densité spectral est donnée par la formule de Schottky [16] :

g ( f ) = e.I (3.05)
Avec, e : charge d'électron (e = -1,6.10^-19C) ;

I : courant dans la photodiode

Ce bruit quantique constitue la limite théorique à la capacité des systèmes de transmission. Dans une bande B, la puissance de bruit recueillie est alors 2.e.I.B .

Si l'on admet que les photons arrivent de manière purement aléatoire (phénomène de type poissonnien), la probabilité de recevoir x photons pendant un intervalle de temps T est donnée par la loi de poisson.

Prob(x, T) = exp( ) (3.06)

Où représente le nombre moyen de photons reçus pendant le temps T . [14]

3.5.3.2 Bruit des diodes à avalanche

Dans les photodiodes à avalanche, un excès de bruit apparaît du fait de la multiplication. La densité spectrale du courant de bruit de la PDA est donnée par :

g ( f ) = e.iD . M ².F(M) (3.07)
Avec M : gain d'avalanche ;

F(M) : fonction croissante du gain M, dit facteur d'accès de bruit ; iD : courant d'obscurité

Le courant d'obscurité iD qui circule dans la jonction en absence d'éclairement, a des origines multiples : génération thermique dans la zone intrinsèque I, courant de surface, courant de fuite.

43

Il dépend beaucoup du matériau et augmente avec la température suivant une loi :

iD = exp?? E kT? (3.08)

Où, E : désigne le champ électrique ;

k : constante de Boltzman (1,38.10^-23 Ws/K) ; T : température absolue (K).

3.5.3.3 Bruit thermique

Ce bruit, lié à l'agitation thermique apparaît souvent dans tout conducteur quelque soit sa nature. Sa densité spectrale n'est pas considérée comme uniforme. La puissance de bruit thermique est donnée par la relation [16] :

dNth= dv (3.09)

hv

Avec k : constante de Boltzman ; T : température absolue.

3.6 Multiplexage

Le multiplexage est une technique qui permet de faire passer sur un seul canal les signaux issus de plusieurs canaux.

Les signaux entrant dans le multiplexeur (MUX) et sortant du démultiplexeur (DEMUX) sont dits voies basse vitesse. Entre ces deux équipements se trouve une voie haute vitesse.



Figure 3.11 : Principe du multiplexage Il existe 3 techniques de multiplexage optique :

o Le multiplexage temporel : on partage dans le temps l'utilisation de la voie haute vitesse en l'attribuant successivement aux différentes voies basses vitesses ;

o Le multiplexage fréquentiel : on attribue à chaque signal une bande passante particulière en s'assurant qu'aucune bande passante de voie basse vitesse ne se chevauche ;

o Le multiplexage en longueur d'onde : plusieurs signaux de longueur d'onde différente sont transmis dans un seul canal.

44

3.6.1 Multiplexage temporelle (TDM)

Le multiplexage TDM (Time Division Multiplexing) ou MRT (Multiplexage à répartition dans le temps) consiste à affecter à un utilisateur unique la totalité de la bande passante pendant un court instant appelé IT (intervalle de temps) et à tour de rôle pour chaque utilisateur.



Figure 3.12 : Principe du multiplexage à répartition dans le temps

Le multiplexage TDM permet alors de regrouper plusieurs canaux de communications à bas débits sur un seul canal à débit plus élevé (par exemple, conception d'un débit 40 Gbits/s, à partir de 4 séquences à 10 Gbits/s).

Pour émettre la suite de son message chaque utilisateur doit attendre une période afin que l'intervalle de temps qui lui a été attribué soit à nouveau disponible.

L'émetteur n'émet donc pas en continu, mais les messages sont compressés et insérés dans l'IT alloué. [21]

3.6.2 Multiplexage en longueur d'onde (WDM)

Le multiplexage en longueur d'onde (WDM ou Wavelength Division Multiplexing) consiste à juxtaposer plusieurs ondes de longueur d'ondes différentes sur une même fibre. Cette technique de multiplexage est illustrée comme suit :



Figure 3.13 : Multiplexage en longueur d'onde

Il repose sur la propriété physique de la lumière. Chaque signal lumineux possède sa propre longueur d'onde. Ainsi, plutôt que de transmettre de l'information sur une seule longueur d'onde, on va utiliser plusieurs longueurs d'onde et multiplier d'autant le débit de la liaison.

45

De cette façon, on peut aisément augmenter le débit de transmission d'une fibre sans avoir à la remplacer par une autre. Il suffit tout simplement de disposer d'un émetteur et d'un récepteur capables de distinguer les différentes longueurs d'onde utilisées.

Ainsi à l'émission, on doit multiplexer plusieurs canaux en attribuant à chacun une longueur d'onde. Le signal lumineux composé de toutes ces longueurs d'onde va transiter sur la fibre, et le récepteur n'aura qu'à démultiplexer le signal pour obtenir les différents canaux de départ.

Le défaut de ce type de multiplexage réside sur le fait que le nombre de longueur d'onde qu'une fibre peut transporter est limité. La norme internationale UIT-T G692 autorise l'utilisation de longueurs d'onde comprises entre 1530 et 1565 nm. Une des caractéristiques du WDM est l'intervalle minimum entre deux longueurs d'onde utilisable.

3.6.3 Multiplexage fréquentielle (FDM)

Le multiplexage fréquentiel consiste à partager la bande de fréquence disponible en un certain nombre de canaux ou sous-bandes plus étroits et à affecter en permanence chacun de ces canaux à un utilisateur ou à un usage particulier.

Ainsi plusieurs transmissions peuvent être faites simultanément, chacune sur une bande de fréquences particulières.

Ce procédé est encore appelé multiplexage en longueur d'onde WDM. Ces deux termes recouvrent la même notion, mais par habitude, on parle de multiplexage en longueur d'onde lorsque la séparation entre deux canaux est relativement grande (typiquement plus de 1 nm), tandis que l'on parle de multiplexage en fréquence lorsque cet écart est relativement petit.

Conclusion

Une description des éléments optoélectroniques d'émission et de réception a été apportée précédemment. A l'émission, deux composants tels que les diodes DEL et les diodes LASER peuvent être utilisés pour convertir le signal électrique en signal optique. Ce sont la photodiode à avalanche et la photodiode PIN qui sont les plus utilisées pour la reconversion du signal optique à son état initial. Ces composants présentent tout de même quelques imperfections plus précisément des bruits. Nous avons également décrit dans ce chapitre deux types de modulations ainsi que les techniques de multiplexage temporel, fréquentiel et en longueur d'onde.

46

Chapitre 4 : LES ATTÉNUATIONS DANS UNE LIAISON PAR FIBRE OPTIQUE

Introduction

Après avoir acquis des diverses notions sur la fibre optique et ses paramètres de transmission, nous allons aborder, d'une manière plus attentive, les problèmes dans une transmission par fibre optique notamment les atténuations du signal. Il est à noter que nous ne nous lancerons pas dans une étude approfondie de ces phénomènes ; ce qui semble être une tâche très complexe et persistante compte tenue des multitudes des données à manipuler, mais nous nous contenterons d'en exposer tous les faits essentiels afin de les comprendre et de les caractériser.

Pour cela, nous allons élucider les deux types d'atténuations dans une fibre optique qui sont les atténuations extrinsèques et les atténuations intrinsèques.

4.1 Description de l'atténuation

4.1.1 Définition

Une information codée en signal lumineux transite vers le récepteur par l'intermédiaire d'une fibre optique. A la réception, l'information doit être restituée sans défaut. Mais lors de la transmission, les pertes et la dispersion de la lumière dans la fibre risquent de déformer le signal. L'atténuation est la perte de puissance que subit la lumière au cours de sa propagation dans la fibre optique. Cette perte est soit locale soit régulièrement repartie sur toute la longueur de la fibre. Dans le premier cas, la perte ou l'atténuation s'exprime en décibels (dB) alors que dans le deuxième cas, elle se mesure en décibel par kilomètre (dB/km) pour une longueur de fibre traversée. [3]

4.1.2 Les différents types d'atténuations

D'une manière générale, les liaisons optiques présentent des caractéristiques d'atténuation de la puissance optique transmise, qui peuvent être divisées en deux grandes catégories [8]:

o Les atténuations intrinsèques : Ces types d'atténuations sont liés à la structure et les matériaux constituant une fibre elle-même. Elles dépendent des caractéristiques typiques du processus technologique de fabrication ou de vieillissement de la fibre qui se manifestent généralement par des pertes par diffusion, l'atténuation linéique, la dispersion de la lumière et pertes par absorption engendrées par les impuretés présentes dans la fibre. Ces défauts se repartissent souvent le long d'une fibre optique.

o Les atténuations extrinsèques : Ce sont des pertes dues à l'installation et le milieu d'installation d'une fibre optique par les défauts de positionnement et d'interconnexion

47

des plusieurs fibres entre eux (épissures, connecteurs, courbures,...). Elles apparaissent lors de la réalisation de la liaison. Ces pertes sont locales et uniquement présentent dans une partie ou une portion de la fibre où le défaut a lieu.

Les différents types de pertes sont illustrés dans la figure suivante :



Figure 4.01 : Différentes pertes dans une fibre optique 4.2 Les atténuations extrinsèques

4.2.1 Pertes par courbure

Les obstacles sur le lieu d'installation peuvent nécessairement nous obligent à courber la fibre optique afin de les franchir. Dans ce cas, la fibre suit donc un trajet curviligne et cette courbure peut provoquer une atténuation plus ou moins importante car le rayon est transmis dans la gaine ; ce qui se traduit par une perte d'énergie transmise.

Lorsque le coeur de la fibre décrit un arc de cercle de rayon très petit, les rayons lumineux pénètrent majoritairement dans la gaine qu'à l'intérieur du coeur et pourrait être complètement dégradés au-delà d'une certaine flexion.

En pratique, l'effet de cette perte de courbure est négligeable lorsque le rayon de courbure R est grand par rapport au rayon critique Rc. On calcule ce dernier à l'aide de la relation suivante et à préciser que son unité est en centimètre :

o pour les fibres multimodes :

Rc = [cm] (4.01)

48

o pour les fibres monomodes :

[cm] (4.02)

Rc = 20 x ( )

Avec :

a : rayon du coeur [um] ; ON : ouverture numérique ;

n1 : indice du coeur ;

n2 : indice de la gaine ;

? ? longueur d'onde utilisée [um] ; ?c ? longueur d'onde critique [um] ;

Dans les deux cas précédents, on peut remarquer que plus la différence d'indice entre le coeur et la gaine optique est grande, moins la fibre est sensible à la perte par courbure.

Mais pour une fibre possédant un diamètre de coeur grand, elle est plus vulnérable à la courbure. En pratique, l'ordre de grandeur de Rc est environ de quelque centimètre. [9] [22]

4.2.2 Pertes par microcourbure

Elles sont dues à une déformation locale de la dimension d'une fibre lors de sa fabrication ou par une forte pression qu'elle subisse sur son lieu d'installation et elle provoque le même effet que celui causé par la courbure et souvent la cause de la dispersion de polarisation.

Elle ne dépend pas de la longueur d'onde utilisée mais de la fibre proprement dite, surtout avec une fibre optique de diamètre très petit.

Les microcourbures sont des variations aléatoires du diamètre du coeur ou de la gaine (de l'ordre de quelques micromètres). Il y a donc un risque, pour un rayon lumineux, de ne pas remplir la condition de réflexion totale, d'où la perte dans la gaine par réfraction. [22]

4.2.3 Pertes de jonction

Les pertes de jonction ou de raccordement sont provoquées par le défaut d'alignement et la réflexion dans les épissures et au niveau des connecteurs optiques. Inévitablement, une partie de la lumière quittant la fibre est perdue par la divergence du faisceau et par réflexion : le faisceau repart en sens inverse, c'est le « return loss ».

L'épissurage est le mode de raccordement de deux fibres et il en existe deux sortes : celle qui se fait avec une soudure, et celle qui utilise des connecteurs. Mais dans ces deux cas, une perte de raccordement est toujours présente.

L'épissurage par soudure est moins sensible au défaut par rapport à celui utilisant des connecteurs. Ce type de jonction est relativement fragile et le raccordement est définitif. [5][20]

L'alignement des fibres n'est jamais totalement parfait, il existe donc une perte de lumière lors du passage de celle-ci d'un côté à l'autre. Cette perte est plus ou moins importante suivant les défauts résiduels d'alignement.

Il existe plusieurs causes des pertes de jonction telles que : la séparation longitudinale, le désalignement axial, l'écartement angulaire et les dimensions différentes des fibres.

4.2.3.1 La séparation longitudinale

La séparation longitudinale se traduit par un petit écartement entre deux fibres qui devraient être parfaitement connectées. Il existe une variation d'indice dans la partie vide qui sépare les deux fibres, donc le rayon lumineux peut être réfracté ou réfléchi selon le cas. La perte due à cette séparation est critique mais non rédhibitoire.

Dans ce défaut, les faces des fibres sont écartées l'une de l'autre d'une distance l comme la figure ci-dessous nous montre.



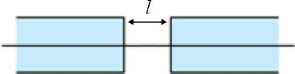
Figure 4.02 : Séparation longitudinale des deux fibres

L'atténuation est exprimée par [6] :

^rr

A[dB] = -- 10 log L1+

(4.03)

l2. )2]

(

21cn1D

Avec A : longueur d'onde utilisée [um] ;

l : distance de séparation entre deux fibres [um] ; n1 : indice du coeur de la fibre ;

D : diamètre de la fibre optique [um].

49

Soient deux fibres de même dimension de coeur jointes par un connecteur supposé parfait. Lorsqu'une mince épaisseur d'air les sépare, recherchons les facteurs de réflexion théorique liée à cet écartement.

Au niveau de chaque dioptre séparant l'air de la fibre, une partie de la lumière peut subir une réflexion dans cette interface air-verre. Alors, le facteur de réflexion en intensité s'exprime par :

Re = (ni_1)2 (4.04)

n₁+1

Avec n1 : indice du coeur.

50

Et le coefficient de transmission en intensité est :

T = 1 - Re (4.05)

Pour un indice de 1,5 du coeur de la fibre, Re = 4 % à chaque dioptre et T vaut 1 - Re = 96 %.

4.2.3.2 Le désalignement axial

Le défaut se présente par le non alignement des axes des deux fibres. Elles sont écartées d'une distance e l'un de l'autre.

L'atténuation est donnée par [6] :

A[dB] = 10 log * ( )+ (4.06)

Ce désalignement radial est illustré dans la figure 4.04 suivante. Les coeurs et les gaines optique des fibres raccordées présentent une pente et l'effet de celle-ci se déduit en fonction du rapport de l'excentrement par le diamètre des fibres.



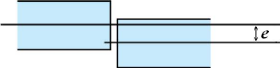
Figure 4.03 : Désalignement axial

4.2.3.3 L'écartement angulaire

Dans le désalignement angulaire (figure 4.04), il y a une présence d'un angle d'écartement entre l'axe des deux fibres.



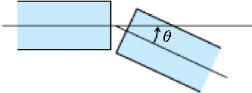
Figure 4.04 : Écartement angulaire

Les rayons lumineux arrivant à la deuxième fibre subissent une déviation qui peut se traduire par une perte. Cette dernière dépend de l'angle que font les deux fibres à raccorder.

L'axe de la deuxième fibre fait un angle ? par rapport à celui du premier. L'atténuation est calculée par [6] :

A[dB] = 10 log [ ( ( ) )] (4.07)

51

4.2.3.4 Les dimensions différentes des fibres raccordées

Pour une répartition uniforme de l'énergie lumineuse, le rapport est égal au rapport où S1 est la surface de la section transverse du coeur de la première fibre et S2 celle de la seconde fibre.



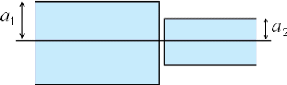
Figure 4.05 : Deux fibres de diamètres différents

La perte locale vaut :

A[dB] = 10 log = 10 log = 10 log ( ) (4.08)

Finalement :

A[dB]= 20 log( ) (4.09)
Où a1 et a2 désignent respectivement le rayon du coeur (plus grand) et celui (plus petit) des deux

fibres.

4.2.4 Pertes par injection de la lumière dans la fibre

Lors d'une insertion des rayons lumineux dans le coeur de la fibre, il se peut qu'il ait une perte importante des signaux. Cette perte du rayonnement lumineux se manifeste lorsque l'angle d'incidence dépasse une valeur minimale dite angle d'acceptance _i0lim qui dépend de l'indice de réfraction du coeur et de la gaine.

La condition permettant de récupérer la lumière issue d'un émetteur se présente comme suit :

i1 < i0lim (4.10)

Avec i1 : angle d'incidence ;

i0lim : angle d'acceptance définie par la relation 1.18 du premier chapitre

Outre la valeur de l'angle d'incidence, la divergence de la lumière provenant de la source lumineuse contribue aussi à cette perte d'insertion. En effet les diodes DEL, présentant une grande largeur spectrale, dispersent une partie de la lumière considérable.

Par contre, la diode laser constitue une source la plus intéressante pour faire injecter la lumière dans la fibre, mais celui-ci présente quand même des bruits parfois non négligeables.

52

4.3 Les atténuations intrinsèques

4.3.1 L'atténuation linéique

L'atténuation linéique est une perte régulièrement repartie le long d'une fibre. Cette atténuation est toujours présente dans toutes les fibres. Elle est due aux matériaux constituants la fibre optique et les constructeurs en donnent souvent sa valeur. On pourra tout de même calculer cette atténuation en connaissant la puissance du signal à une distance donnée.

Soit une fibre optique de diamètre constant. Calculons la perte de puissance lumineuse, pour une certaine longueur de fibre en choisissant deux sections de droites (perpendiculaires à la direction de propagation) distantes d'une petite distance dL appelée distance élémentaire. La puissance lumineuse (ou flux) est le rapport de la qualité d'énergie lumineuse traversant une section sur l'unité de temps.



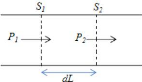
Figure 4.06 : Portion d'une fibre

Soit P1, la puissance lumineuse traversant S1, et P2 la puissance lumineuse traversant S2.

En raison de l'atténuation dans une fibre, on a P2 < P1.

La variation élémentaire de puissance dP = P2 - P1 est négative et :

o Proportionnelle à dL : une longueur x fois dL donne des pertes x fois plus grandes ;

o Proportionnelle à un coefficient d'atténuation linéique á caractérisant la fibre.

La quantification des pertes est calculée suivant la loi de décroissance de la puissance optique de Beer-Lambert, pour une distance dL faible tel que :

= a .P (4.11)

Équivalent à :

= a .dL (4.12)

Par intégration sur une longueur L2 et L1 mesurée respectivement au niveau de la section S2 et S1 de la fibre correspondant à la puissance P2 et P1, on obtient :

?

= a. ? (4.13)

On en déduit que :

Ln = a (L2 L1) (4.14)

53

Alors :

=??xp [ ? ?L2 L1)] (4.15)

Donc, pour Pe et Ps la puissance à l'entrée et à la sortie de la fibre, le bilan de puissance d'entrée et sortie du signal de l'atténuation linéaire se traduit par la décroissance exponentielle de puissance injectée en fonction de la longueur de la fibre. C'est la loi de Beer-Lambert se définissant comme suit :

Ps = Pe .?? (4.16)
Avec Ps : Puissance à la sortie de la fibre [en Watt]

Pe : Puissance à l'entrée de la fibre [en Watt]

: coefficient d'atténuation linéique [en ]

L : Longueur de la fibre [en km]

L'atténuation en dB/km de la lumière dans une fibre de longueur L se caractérise par un terme d'atténuation linéique ?. Elle est exprimée par la relation suivante :

??

? ?

[dB/km] (4.17)

L'accroissement de cet affaiblissement reste constant pour toute distance traversée dans une fibre optique ou plusieurs fibres raccordées de même structure.

On en déduit le bilan de puissance d'entrée et sortie du signal de l'atténuation linéique qui se traduit par :

= (4.18)

On peut utiliser la relation de mesure suivante pour une conversion : ? [dB.km^-1] = ? [km^-1]

L'atténuation linéique totale pour une fibre de longueur L est donnée par :

? linéique ? ? x L [dB] (4.19)

Exemple de calcul d'atténuation linéique :

A l'entrée d'une fibre, on injecte une puissance P1 = 36 dBm. Au bout d'1 km, on récupère une puissance P2 = 35,8 dBm. Cherchons le coefficient d'atténuation de la fibre puis la puissance P3 à la sortie de la fibre de longueur totale 100 km et l'atténuation linéique totale.

D'abord, il est impératif de savoir que la puissance en Watt est obtenue par :

P[W] = 1W. [ ]

Alors P1 = 36dBm = 3,981W et P2 = 35,8 dBm = 3,802W

54

L'atténuation linéique exprimée en [dB/km] vaut : a [ dB.km^-1] = 10. =10.log10 = 0,2
On en déduit sa conversion en [km^-1] par :

a[ dB.km^-1] x

a [ km^-1] = = 0,046
Pour trouver P3, on peut utiliser :

o Soit la relation 4.06 : P3 = P1 . = 3,981

o Ou bien la formule 4.08 : P3 = P1 . = 3,981 .
Ce qui donne le même résultat :

P3 = 0,03981 W = 16 dBm

Donc, l'atténuation linéique totale pour une fibre de 100 km est :

Alinéique = a[dB.km^-1] . L = 0,2 .100 = 20 dB

4.3.2 Pertes par diffusion

Les pertes par diffusion sont créées par les irrégularités des compositions et d'indice de réfraction de la fibre.

Cette perte appelée perte de RAYLEIGH proviennent de la diffusion de la lumière. Quand la lumière rencontre une irrégularité, le phénomène de diffusion disperse l'énergie lumineuse dans toutes les directions.



Figure 4.07 : Diffusion de Rayleigh dans une fibre optique

Quelques rayons ne satisfont plus les conditions de réflexion totale et ne coopèrent plus à la transmission du signal. [7]

55

La diffusion de Rayleigh dépend de la longueur d'onde de la lumière incidente. Elle est d'autant plus grande que la longueur d'onde est petite mais plus la longueur d'onde du photon est grande, moins il y aura d'interaction et de perte par diffusion.

L'atténuation varie comme l'inverse de la puissance quatrième de la longueur d'onde :

A{dB] = (4.20)

L'allure de l'atténuation est donc représentée comme suit :



Figure 4.08 : Courbe d'atténuation par diffusion en fonction de la longueur d'onde

4.3.3 Pertes par absorption

Les matériaux qui constituent le coeur de la fibre ne sont pas parfaitement transparents, plus précisément ils n'ont pas un indice de réfraction pur.

Ces matériaux sont plus ou moins absorbants et par conséquent, une partie de l'énergie électromagnétique est convertie en chaleur par effet joule.

Les impuretés de la fibre se présentent sous forme de molécules qui absorbent la lumière à des fréquences spécifiques, ce qui entraine alors une atténuation de la lumière transmise.

Cette perte présente un pic lorsque la longueur d'onde utilisée est au milieu de 1300 et 1550 nm notamment au voisinage de 1380 nm comme la montre la figure 4.09 suivante. Celle-ci est due à

la présence des petites quantités des ions hydroxydes dans la silice.

La liaison entre l'oxygène et l'hydrogène (dans ) donne de la résonnance et absorbe
fortement la longueur d'onde aux alentours de 1230 nm et 1380 nm.

Les molécules de dioxyde de Silice (SiO2) qui est le principal constituant de la fibre se lient aux

ions et vibrent à une fréquence équivalente à ? = 2730 nm. Les harmoniques suscitent une
accrue d'atténuation à partir de cette valeur de longueur d'onde.

Une onde qui se propage dans ce milieu est donc de la forme donnée par la relation (4.21) qui comporte un terme réel d'amplitude exponentiel associé au terme imaginaire de phase ; il lui correspond un affaiblissement linéique exprimé en dB/km.

?? ?? (4.21)



56

Figure 4.09 : Allure d'atténuation par absorption

En outre, une infime présence de métal (chrome, fer, cobalt, cuivre, nickel...) dans la fibre optique produit aussi une très forte absorption. [4][11]

Comme toute trace de métal absorbe une grande partie de l'énergie lumineuse transportée, la fabrication des fibres optiques exige des produits extrêmement purs.

4.3.3.1 Fenêtre de transmission

Historiquement, les premières fibres optiques furent utilisées dans une fenêtre optique comprise entre 800 nm et 900 nm car ces longueurs d'ondes correspondaient à l'époque au minimum d'absorption de ces fibres, mais aussi à cause du moindre coût des sources et des détecteurs fonctionnant dans cette fenêtre.

A partir des années 80, de nouveaux composants réalisés sur substrat de Phosphure d'Indium (InP) ont permis de travailler dans une nouvelle fenêtre optique autour de 1300 nm. Cette longueur d'onde correspond à une moyenne relative d'atténuation (0,4 dB/km) de la fibre optique moderne. Elle a une dispersion chromatique minimale et est utilisée couramment en transmission à moyenne distance ainsi qu'à haut débit en réseau d'accès et réseau métropolitain.

Pour les télécommunications sur longue distance (plus de 100 km), les longueurs d'onde les plus intéressantes se trouvent dans une troisième fenêtre qui est situé aux voisinages de 1550 nm. En effet, celle-ci correspond au minimum d'atténuation de la silice (0,2 dB/km) et de plus, coïncide parfaitement aux longueurs d'onde de fonctionnement des amplificateurs optiques disponibles aujourd'hui. Cependant, elle demande des composants plus coûteux parce que la dispersion chromatique apparait facilement dans cette fenêtre.

57

La figure ci-dessous présente l'allure typique de l'atténuation par absorption d'une fibre optique en fonction de la longueur d'onde, ainsi que les trois fenêtres optiques d'utilisation.



Figure 4.10 : Courbe d'atténuation par absorption et fenêtres de transmission

On constate d'après la figure précédente que les longueurs d'onde 1300 nm et 1550 nm sont favorables à la transmission car c'est dans ces valeurs que l'atténuation est minimale. C'est pour cela que l'on prend ces valeurs dans la plupart des expériences effectuées récemment.[6] [8] [14] Voici le tableau montrant la différence entre les trois principales fenêtres de transmission optimale :

Première fenêtre (800 - 900 um)	Deuxième fenêtre (1280 -1330nm)		Troisième fenêtre (1525-1625nm)	- Atténuation élevée
- Atténuation moyenne	- Atténuation minimale ( -0,2dB/km) ;		( -3,5dB/km);
(-0,4dB/km) ;	- Lasers et amplificateurs performants		- Composants très bon marché
- Lasers disponibles depuis	(assez onéreux) ;		(Diodes LED) ;
longtemps et peu couteux ;
	- Composé de deux sous-bandes :		- Ne peut être utilisée qu'en
- Utilisation en multimode et	C (1525-1565nm) et L (1565-1625 nm)		multimode ;
monomode ;
	- Fenêtre de choix pour les applications		- Assez commode pour le réseau
- Largement utilisée pour les	modernes de hauts débits et à longue		LAN ; - Utilisation en cours de décroissance.
réseaux MAN et WAN mais aussi pour LAN.	distance ; - Utilisation en phase d'accroissement.

Tableau 4.01 : Comparaison entre les trois fenêtres de transmission

58

4.3.4 Dispersion modale

L'information se propage dans la fibre sous forme d'impulsion lumineuse. Cette dernière subit un phénomène de dispersion qui se traduit par un étalement temporel plus ou moins important selon la structure d'une fibre.

Les rayons lumineux s'écartent et une impulsion de courte durée à l'entrée de la fibre s'élargit et s'atténue lors de la propagation dans la fibre optique : c'est la dispersion de la lumière.

Cette dispersion se manifeste sous diverses manières en fonction du type de la fibre optique dont on parle de dispersion modale ou intermodale pour les fibres multimodes. [9]

Les fibres multimodes permettent à la lumière de se propager selon plusieurs modes. Chaque mode parcourt un chemin différent dans la fibre optique. Les ordres faibles se propagent près du centre du coeur alors que les ordres élevés s'approchent de la gaine. Les trajets extrêmes constituent les chemins les plus longs à la propagation que les trajets situés sur l'axe optique. Ainsi des impulsions initiales transmises dans la fibre, transitant par plusieurs modes, ressort à des instants différents de la fibre selon les modes qui l'ont transportée. L'impulsion est élargie en sortie de fibre : il s'agit de la « dispersion modale ».

La longueur de la liaison et l'ouverture numérique influent sur la distorsion de l'impulsion lumineuse. En effet, plus grande est la distance que parcourent les rayons lumineux, plus grands sont les retards engendrés ; donc plus grande est la distorsion. De même, pour l'ouverture numérique, plus elle est grande, nombreux sont les rayons dans la fibre, engendrant ainsi une dispersion modale plus importante.

La dispersion intermodale n'est présente que dans les fibres multimodes car il s'agit d'une dispersion liée à la multitude des chemins parcourus par les rayons lumineux.

4.3.4.1 Cas d'une fibre à saut d'indice

Les rayons lumineux traversant la fibre optique multimode est décomposé en plusieurs rayons qui présentent des angles d'incidences différents, ce qui procure pour chaque rayon une distance de parcours différent.

Pour la fibre à saut d'indice, le mode arrivant en premier à la sortie de la fibre est celui qui traverse longitudinalement le coeur (angle d'incidence 0°). Le mode qui arrive en dernier est celui dont l'angle d'incidence est l'angle d'injection critique.

Le délai modal est caractérisé par la différence de durée maximale et minimale ?? de la transmission de la puissance lumineuse. Il est mesuré à la mi-hauteur de l'impulsion de sortie de la fibre. [23]

59

Pour une fibre à saut d'indice, l'expression de la dispersion modale en ps/km est donnée par :

Dmod = (4.22)

Avec ON : ouverture numérique ;

n1 : indice du coeur ;

c : vitesse de la lumière dans le vide [m/s].

Le calcul du délai modal dépend de l'indice du coeur et de la gaine ainsi que du diamètre du coeur. Soit deux rayons lumineux qui se propagent dans la fibre à saut d'indice dont l'un parcourt le chemin le plus long et l'autre celui le plus court illustré par la figure ci-dessous.



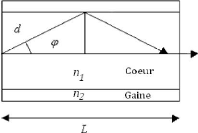
Figure 4.11 : Parcours du rayon lumineux axial et réfléchi dans une
fibre à saut d'indice

D'après la figure précédente, on a :
d =					(4.23)
=	d =				(4.24)
	=				(4.25)
	=				(4.26)
							Alors l'écart du temps est :
							=
		=			(4.27)
			(	)

En fonction de la différence relative d'indice , la différence temporelle pour une fibre à saut

d'indice, après un trajet d'une distance L est décrit par [8] :

=

(4.28)

60

4.3.4.2 Cas d'une fibre à gradient d'indice

La lumière transite dans la fibre sous plusieurs modes mais le délai modal de la fibre à gradient d'indice est plus faible que celui d'une fibre à saut d'indice.

En effet, quand un mode s'écarte de l'axe de la fibre, il traverse du milieu dont l'indice diminue légèrement. Il en résulte une augmentation de la vitesse de transmission de la lumière. Le parcours du rayon lumineux décrit un trajet sinusoïdal dans le coeur d'indice variable. Les modes d'ordre élevé, possédant la plus grande longueur de chemin à cause de leur excursion supplémentaire par rapport à l'axe, ont une vitesse moyenne qui s'élève résultant d'une diminution relative d'indice en fonction de la distance partant l'axe du coeur.

Ce qui donne, un temps de parcours qui se rapproche entre les modes de faibles vitesses et les modes de hautes vitesses, donnant ainsi un croisement proche de l'axe central.

Pour une fibre à gradient d'indice, l'expression de la dispersion modale s'écrit [8] :

Dmod = (4.29)

[ ]

Avec n(r) : l'indice du coeur à une distance r par rapport à l'axe D'où le décalage temporel de propagation des modes est donné par :

?? = L x Dmod (4.30)

4.3.5 Dispersion chromatique

4.3.5.1 Définition de la dispersion chromatique

Cette dispersion vient du fait que l'indice de réfraction de la fibre dépend de la longueur d'onde et que les sources utilisées pour transmettre le signal ne sont pas purement monochromatiques. La dispersion chromatique (ou GVD pour Group Velocity Dispersion) est un phénomène qui se traduit par un élargissement d'une impulsion lumineuse du fait de la différence de vitesse de groupe en fonction des différentes longueurs d'onde.

La dispersion chromatique introduit différents retards de propagation pour différentes composantes spectrales du signal et elle concerne généralement la fibre monomode. [5]

61

4.3.5.2 La vitesse de groupe et vitesse de phase

Une onde sinusoïdale est caractérisée par sa fréquence ou pulsation w (en rad/s), et par son vecteur d'onde de norme :

k = [rad/m] (4.31)

Où X est la longueur d'onde.

Il existe deux vitesses caractéristiques différentes [7] :

o La vitesse de phase : qui est la vitesse à laquelle la phase de l'onde se propage dans l'espace et définit par :

v_? = (4.32)

o La vitesse de groupe : qui correspond à la dérivée de la pulsation par rapport au nombre

d'onde associée à cette pulsation. Elle peut être définie comme étant la vitesse à laquelle le sommet d'une impulsion se déplace :

vG = (4.33)

Si :

? = 0 (4.34)

Alors :

v_g = v_? (4.35)

On peut dire ainsi qu'il n'y a pas de dispersion.

Mais si,

? ? 0 (4.36)

Alors, il existe une dispersion.

4.3.5.3 Les principales causes de la dispersion chromatique

La dispersion chromatique provient de deux causes principales : la dispersion due aux matériaux et celle provoquée par le guide. [15]

a) La dispersion due aux matériaux :

Elle est liée à la dépendance de l'indice de réfraction du milieu dit « dispersif » à la longueur d'onde. En optique, un matériau est qualifié « dispersif » si son indice varie en fonction des longueurs d'onde que l'on transmet.

Par exemple, la silice (composant de base des fibres) est un matériau très dispersif dont l'indice obéit à la relation de Cauchy :

n(?) = A + (4.37)

Où A et B sont des constantes

En conséquence, chaque « couleur » se déplace à une vitesse qui lui est propre :

(4.38)

On a : c est la vitesse de la lumière dans le vide et l'indice de groupe relatif à la longueur

d'onde de la « couleur ».

Pour mieux comprendre le phénomène de la dispersion due aux matériaux, on peut se référer à l'expérience de NEWTON : un faisceau de lumière blanche, après avoir traversé un prisme de verre se décompose en une série de couleurs diverses, l'ensemble représente le spectre de la lumière visible.

Il en de même dans la fibre optique, si une impulsion de lumière blanche est injectée à l'entrée d'une fibre de silice, les longueurs d'onde rouges émergent de la fibre premièrement suivies de l'orange, du jaune, du vert et du bleu et la durée de l'impulsion en sortie est plus longue qu'en entrée (figure 4.12). Aux longueurs d'ondes visibles, le rouge va plus vite que le bleu. C'est ce que l'on appelle la dispersion de vitesse de groupe normale ou positive. Alors, les grandes longueurs d'onde se propagent plus rapidement que les longueurs d'onde plus courtes.



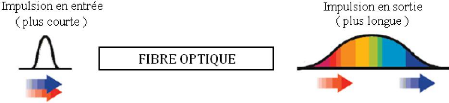
62

Figure 4.12 : Influence de la dispersion due aux matériaux sur une impulsion optique

La dispersion du matériau D_m est donnée par :

D_m = (4.39)

Pour la silice, D_m varie d'environ -100 ps/nm/km à 0,85um et +25 ps/nm/km à 1,55 um ; elle s'annule à 1,27 um.

La différence dans le temps de propagation est donnée comme étant :

(= ) (4.40)

Où est la largeur du spectre de la source, L est la longueur d'onde nominale de la source et

la dérivée seconde de l'indice du coeur avec réfraction. [5][9]

63

b) La dispersion dans le guide

Ce phénomène est essentiellement dû à la structure géométrique de la fibre, et en particulier aux dimensions réduites du diamètre du coeur (10 à 50 ìm). Cette dispersion est particulièrement spécifique aux fibres monomodes.

En effet, une partie de la puissance optique transportée par le mode fondamental se propage aussi dans la gaine (figure 4.13). Les indices de réfraction de la gaine et du coeur étant différents; la lumière se propage donc à des vitesses différentes (v = c/n).

Cette dispersion est liée à la structure géométrique du guide d'onde et résulte de la variation de la constante de propagation â avec la fréquence normalisée V; la dispersion du guide dépend des paramètres de la fibre. [5] [9]



Figure 4.13 : Dispersion d'une partie de la puissance optique dans la gaine

On peut définir la constante de propagation normalisée qui est très utile dans le calcul de la dispersion du guide, elle est donnée par :

( ) ( )

b = (4.41)

Une expression de ? peut être écrite comme :

? (4.42)
Dans ce cas, la dispersion du guide est donnée par :

*Dg + (4.43)

Où

0,08 + 0,5439 (2,834 - (4.44)

En particulier, le délai causé par la dispersion du guide est :

?guide = (4.45)

64

La différence dans le temps de propagation est :

??guide = ?? (4.46)

4.3.5.4 Les paramètres de la dispersion chromatique

La dispersion chromatique résulte de la somme de la dispersion propre au matériau et la dispersion du guide liée à la forme du profil d'indice. À cause de la dispersion chromatique, la vitesse de groupe v_g à l'intérieur d'un mode de propagation varie en fonction de la longueur d'onde ?. Le retard de groupe du signal après une longueur de propagation L sera alors :

t_g (?) = (4.47)
= L

La dispersion chromatique en fonction de la longueur d'onde D(?) est alors définie par :

D(?) = (4.48)

Dans la silice, dans la région du proche infrarouge pour les longueurs d'ondes croissantes la dispersion est d'abord négative, c'est la dispersion normale, passe par un zéro à ?=1310 nm, appelé zéro de dispersion, et puis devient positive. Le zéro de dispersion est important puisque pour cette longueur d'onde les signaux ne subissent pas, en théorie, de distorsion. Les fibres optiques monomodes standards présentent une dispersion chromatique de 17 ps/nm/km autour de 1500 nm.

Pour déterminer la valeur de la dispersion, la constante de propagation ? est développée en série de Taylor autour de la pulsation centrale ?0 de l'onde :

(4.49)

?_n = , n = 1,2,3,... (4.50)

Le paramètre ?1 est lié à la vitesse de groupe des ondes (?1 = ). Le terme ?2 est lié au

coefficient de dispersion D(?) par la relation suivante :

D(?) = = ?2 [ps/nm/km] (4.51)

Où D(?) est la dispersion chromatique tributaire de la longueur d'onde et mesurée dans une distance d'1 kilomètre. L'unité de la dispersion (ps/nm/km) signifie que pour chaque kilomètre de propagation, deux longueurs d'onde écartées de 1 nm ont un écart temporel en picoseconde égal à D(?) à la sortie. Cette dispersion doit être fournie par le constructeur et la recommandation de l'UIT précise la valeur maximale et minimale selon la longueur d'onde utilisée.

65

La dispersion chromatique induit un élargissement temporel des impulsions se propageant dans la fibre. Elle limite aussi la distance sur laquelle un signal peut être transmis sans régénération électronique du signal numérique d'origine. [5] [9] [15]

Pour qu'un signal puisse traverser la distance totale de la liaison, il y a une limite maximale de dispersion appelée dispersion maximale admissible _Dmax. Elle est en générale donnée par le constructeur de la fibre elle-même. La limite de dispersion estimée permet de calculer la largeur spectrale d'un signal AX en tenant compte de l'atténuation linéique et le débit :

[nm] (4.52)

?? =

Avec :

Alinéique : Atténuation linéique par km

? : Débit binaire de transmission (en bit/s).

Ainsi la dispersion chromatique totale _Dtotale pour un signal optique possédant un spectre de largeur ?? s'écrit :

Dtotale = D(?).??.L [ps] (4.53)

Où L est la longueur totale de la fibre

Une variation de temps de propagation de groupe en fonction de la longueur d'onde est définie par la relation :

?? = D(?).?? ?ps/km? (4.54)
D'une manière générale, un rapport de 0,25 entre la dispersion chromatique totale et la durée de l'impulsion ? constitue une limite acceptable pour une transmission le mieux convenable. On en déduit le taux d'élargissement :

TE = ??

< 0,25 (4.55)

Avec ? = 1/?

On peut alors calculer l'atténuation due à la dispersion chromatique à l'aide de la formule empirique:

ADispersion = 10.log [?? ( ) ]

(4.56)

4.3.6 Dispersion de polarisation

Il existe aussi une autre forme de dispersion qui perturbe la propagation des signaux dans une fibre optique : la dispersion de polarisation (ou PMD : Polarisation Mode Dispersion).

Ce phénomène de PMD représente une autre cause de l'élargissement temporel d'une impulsion à la traversée de la fibre par le changement de l'état de polarisation du mode.

Les fibres optiques monomodes permettent en fait la transmission de deux modes de propagation partant ensemble dont leur polarisation est orthogonale. Lorsque la fibre présente une symétrie circulaire, ces deux modes de polarisation se propagent avec la même vitesse de groupe. En revanche, lorsque la symétrie circulaire est brisée, les vitesses de groupe sont différentes : la PMD représente alors la différence entre les temps de groupes associés aux deux modes de polarisation orthogonaux et elle a la propriété de provoquer la déformation temporelle du signal transmis.

Lors de la fabrication de la fibre, celle-ci peut présenter certains défauts tels qu'une ellipticité du coeur ou alors des contraintes résiduelles. De plus, les fibres déjà installées peuvent aussi subir des contraintes mécaniques (courbures, microcourbures,...). Tous ces phénomènes se manifestent pour induire ce qu'on appelle la biréfringence dans la fibre optique.

Lorsque la fibre présente une biréfringence, on observe une levée de dégénérescence des constantes de propagation (3x ? (3y (on suppose ici une biréfringence linéaire d'axe propre Ox et Oy). Les 2 modes se propagent alors à des vitesses de groupe différentes ce qui entraîne l'élargissement de l'impulsion.

Dans une fibre de longueur L avec une biréfringence constante, l'élargissement de l'impulsion peut être estimé à partir du retard temporel 4T entre les deux composantes de polarisation pendant la propagation de l'impulsion, appelé le retard différentiel de groupe (DGD : Differential Group Delay) définit par la relation suivante.

4T = |L L | = L | | L4(3 (4.57)

où les indices x et y identifient les deux modes de polarisation orthogonaux et 4(3 est liée à la

différence des vitesses de groupe _(vg,x ^et _vg,y) le long des deux axes principaux de polarisation. Cet effet de dispersion de polarisation sur une impulsion du signal de sortie est représenté graphiquement comme suit :



66

Figure 4.14 : Influence de la dispersion modale de polarisation sur une impulsion optique

67

Pour les fibres longues, le DGD est proportionnel à la racine carrée de la distance de propagation L :

?T = D_p VL (4.58)

On introduit alors le paramètre de dispersion de polarisation D_p caractéristique de la fibre qui s'exprime en (ps/Vkm) :

D_p = V (4.60)

Les valeurs typiques pour Dp sont de 0,01 à 10 (ps/Vkm). En raison de la dépendance en VL, l'élargissement de l'impulsion induite par la PMD est relativement faible par rapport aux effets de la GVD. Toutefois, la PMD devient un facteur limitant pour les systèmes conçus pour fonctionner sur de très longues distances à des débits élevés. [5] [9]

Conclusion

La transmission de la lumière à travers une fibre optique est souvent soumise à des nombreux écueils. D'abord, la structure et les matériaux constituants une fibre elle-même peut se présenter comme causes de l'atténuation du signal. Cette atténuation dite intrinsèque se manifeste par la diffusion, absorption et dispersion de la lumière accompagnée d'une atténuation linéique. Le positionnement d'une fibre lors de son installation et le mode de raccordement de plusieurs fibres entre eux font parti des facteurs qui accentuent l'atténuation des signaux. Pourtant il existe des solutions qui peuvent être efficace pour minimiser ces problèmes. Ces remèdes sont trouvés dans le chapitre suivant.

PARTIE III : LES SOLUTIONS ET SIMULATION DES
ATTÉNUATIONS DANS UNE FIBRE OPTIQUE

68

Chapitre 5 : LES SOLUTIONS ET SIMULATION DES ATTÉNUATIONS

Introduction

Il est rarissime d'avoir une liaison par fibre optique exempte d'atténuation étant donné qu'il existe plusieurs causes qui peuvent contribuer à l'apparition de celle-ci. Face à cette circonstance, il y a d'autant de solutions que l'on peut choisir afin de minimiser ce problème. Le fait de quantifier ces atténuations permet de faciliter la recherche des solutions relatives à chaque type d'atténuation. Pour cela nous allons apporter les diverses solutions possibles pour réduire ces problèmes et nous établissons ensuite un bilan de liaison. Une étude quantitative de ces atténuations utilisant un programme de simulation développé sous un logiciel Matlab sera présentée en dernier.

5.1 Les solutions des atténuations

Nombreuses sont les solutions proposées pour réduire, voire annuler ces atténuations dans une fibre optique donnée. Ceci afin d'exploiter aux maximum l'énorme potentiel de ce type de support de transmission. Voici quelques-unes de ces solutions aussi efficaces les unes aux autres. Les solutions présentées ici ne paraissent pas être exhaustives mais elles font parties de celles les plus utilisées.

5.1.1 Solutions pour l'atténuation due à la dispersion chromatique

5.1.1.1 Fibres compensatrices de dispersion

La compensation permet de remettre en forme les impulsions optiques étalées par la dispersion chromatique. Pour cela on utilise des fibres compensatrices de dispersion ou « Dispersion Compensating Fiber » (DCF).

Les fibres à compensation de dispersion ont une dispersion négative et une valeur absolue très élevée du coefficient de dispersion chromatique (de l'ordre de 100 ps/nm/km).

Comme la dispersion chromatique est stable et prévisible, il est possible de la compenser afin de rétablir la forme initiale de l'impulsion lumineuse émise.

A partir des caractéristiques de la fibre, fournit par le fabricant, dont principalement, le zéro de dispersion et la pente de dispersion il est possible de prévoir la valeur de la dispersion à un endroit donné et concevoir par la suite des modules de compensation. La dispersion totale est la somme de la dispersion de la ligne et de celle de la compensatrice.

Dtotale = Dligne + Dcompensatrice (5.01)

69

La figure ci-dessous illustre cette technique de compensation de la dispersion :



Figure 5.01 : Exemple de compensation de dispersion de 100%

Dans l'exemple illustré par cette figure, la liaison est constituée de 100 km de fibre standard G652 de coefficient de dispersion D = 17 ps/nm/km, donc Dligne = 1700 ps/nm. Le module de compensation est formé par une DCF de coefficient de dispersion égal à -100 ps/nm/km sur 17 km. C'est ainsi qu'on réalise la compensation de dispersion de 100%.

Certes, la technique est efficace mais le problème est que les fibres compensatrices présentent une atténuation linéique plus élevée que les fibres standards (0.6 au lieu 0.2 dB/km). [5] [15]

5.1.1.2 Les fibres à dispersion décalées

Dans une fibre donnée, il est possible de décaler la courbe de dispersion en optimisant son profil d'indice. Cela permet de sélectionner des valeurs de la longueur d'onde pour lesquelles D = 0 (zéro de dispersion).

On distingue principalement deux types de fibres à dispersion décalée ou DSF (Dispersion Shifted Fiber) :

o La fibre à dispersion décalée dont le zéro de dispersion se situe dans la bande C (autour de 1550 nm). Ces types de fibres sont définit par la recommandation G653 de l'UIT. Cette fibre élimine le problème de dispersion mais elle crée des complexités sur le multiplexage.

o La fibre à dispersion décalée non-nulle dont le zéro de dispersion se situe près de la bande C (à 1525 nm) ou NZDSF (Non Zero Dispersion Shifted Fiber). Elles font l'objet de la recommandation G655 de l'UIT.

C'est au niveau de la fabrication que l'on peut concevoir des fibres à dispersion décalée.

La fibre G653 de l'UIT élimine le problème de dispersion mais elle crée des difficultés au niveau du multiplexage WDM. Comme remède à cela fut créée la fibre NZDSF.

NZDSF désigne un type de fibre monomode qui présente un zéro de dispersion juste à coté de la bande C (utilisée pour les télécommunications). Cela signifie que la dispersion reste très faible dans cette bande, et permet toutefois d'éliminer les problèmes sur la fibre précédente. [5]

70

La figure 5.02 suivante nous montre les différentes courbes de dispersion des fibres G652, G653 (DSF) et de la G655 (NZDSF).



Figure 5.02 : Courbes de dispersion chromatique des fibres G652, G653, G655

On constate que par rapport à la G652, les fibres DSF et NZDSF sont très performantes du point de vue de la dispersion chromatique.

5.1.1.3 Réseau de Bragg

On entend par réseau de Bragg dans une fibre optique une modification permanente et partielle de l'indice de réfraction du coeur. Pour corriger la dispersion chromatique, on fait parfois appel à un réseau de Bragg à pas variable. Un réseau de Bragg à pas constant se comporte comme un filtre pour une longueur d'onde donnée. Avec un réseau à pas variable, on travaille sur toute une bande spectrale, on ralentit les longueurs d'onde les plus rapides. Si on propage de la lumière dans un tel système, on aura un effet positif si la longueur d'onde coïncide avec la longueur d'onde de Bragg selon la Loi de Bragg :

ABragg = ².neff. p (5.02)

Dans cette relation, p désigne la période de modulation ou modification d'indice et _neff l'indice de réfraction effective.

Dans un réseau à pas variable deux longueurs d'onde différentes ne sont pas décélérées dans un même tronçon de fibre. Ainsi la dispersion est compensée et le signal d'origine est rétabli et retrouve sa forme initiale.



71

Figure 5.03 : Effet d'une fibre à réseau de Bragg à pas variable sur un signal

Un réseau de Bragg est inscrit dans la fibre par holographie ou bien par chauffage, tension ou pression, sur un segment de quelques centimètres. [14]

5.1.2 Diverses solutions possibles pour minimiser les problèmes d'atténuations

Le choix d'une interface optique d'émission adéquate à l'usage conçu devrait être la première chose qu'il faut prendre en considération pour éviter la perte significative des signaux depuis la source. Il en est de même à la réception, sinon toutes les améliorations apportées durant le long du trajet de transmission sont annihilées.

Quant aux pertes par raccordement des fibres, il faut réunir donc des nombreuses conditions afin de réaliser une connexion qui minimisera les pertes, parmi lesquelles :

o Aplanir la face de contact, ou la rendre parfaitement sphérique par polissage, en veillant à ce qu'elle soit perpendiculaire à l'axe optique ;

o Bien aligner les deux fibres à raccorder en utilisant les outils spécialisés tels qu'une bague d'alignement, connecteur, épissureuse, etc ;

o Vérifier la soudure s'il y en a et l'entourer d'une gaine de protection.

Réaliser toutes ces conditions sur un câble de l'ordre de micromètre en laboratoire et plus encore sur le terrain n'est pas une chose aisée. Cela requiert du matériel de pointe. Si on n'utilise pas les connecteurs pour la jonction des fibres, il faut alors travailler avec les nanotechnologies. [20]

Autres moyens permettant d'éviter les pertes reposent sur l'amélioration de la fabrication de la fibre optique qui est souvent la source des pertes par absorption et diffusion ainsi que les dispersions. Par suite de cela, les utilisateurs sont incités à opter la fibre optique le mieux adapter

72

à leur usage étant donné que le diamètre du coeur et la différence d'indice ont des influences défavorables sur les différentes sortes d'atténuations. Le tableau suivant récapitule ces effets dont la flèche dirigée vers le haut et celle vers le bas signifie respectivement un accroissement et une diminution, le symbole égal « = » montre qu'il n'y a aucune variation.



Tableau 5.01: Tableau montrant les effets de la variation du rayon du coeur et d'indice

Un compromis dépendant des conditions d'utilisation telles que courbures, contraintes, distance entre les raccordements et qualité de ceux-ci est donc à trouver.

Il se traduit par un choix de la fibre optique parmi les standards existants et il suffit de déterminer la valeur optimale du diamètre et de la différence d'indice en fonction de l'utilisation de la fibre.

Eu égard à des nombreuses contraintes qui se rapportent à l'utilisation de la fibre, l'optimum correspond ainsi à un petit diamètre de coeur et une différence d'indice relativement faible.

Afin de faciliter le choix d'une fibre à utilisée, l'UIT a instauré des normes internationales pour les fibres optiques déployées dans les réseaux de télécommunications.

Voici quelques standards [5] :

o G.651: fibre multimode

Souvent utilisée pour une transmission à courte distance.

o G.652 : NDSF (Non-Dispersion Shifted Fiber)

Elle admet une dispersion nulle à la longueur d'onde de 1310 nm. Son atténuation est moins importante lorsque la longueur d'onde arrive à 1550 nm. En général, ce sont les fibres les plus couramment installées dans le monde.

o G.653 : DSF (Dispersion Shifted Fiber)

La dispersion nulle et l'atténuation minimale se coïncident autour d'une valeur de longueur d'onde de 1550 nm. On utilise cette fibre pour une transmission très longue distance.

73

o G.654 : Cut off shifted fiber

Elle a un coeur très large en silice pure et une faible atténuation, mais une forte dispersion chromatique. Elle est utilisée pour une transmission très longue distance, par exemple une liaison sous-marine.

En plus de ces standards donnés, les caractéristiques des fibres optiques monomodes correspondant à la recommandation de l'UIT qui montre les valeurs d'atténuation et de dispersion (tableau 2.01 du second chapitre) constituent une sorte d'indication afin de prévenir les éventuelles pertes avant que la fibre ne soit pas installée.

5.2 Bilan énergétique d'une liaison par fibre optique

Le bilan de liaison consiste à identifier le maximum de perte permise entre l'émetteur et le récepteur. Cela a pour but d'obtenir une puissance du signal à la réception le plus convenable. L'atténuation totale durant la transmission est évaluée dans ce bilan.

L'utilisation d'un système de transmission jusqu'à la limite de leur capacité n'est pas conseillée. Il faut toujours tenir compte des différentes perturbations dans leur fonctionnement (dérive en température, incident entrainant l'épissure, remplacement des composants...) afin d'assurer un fonctionnement stable. C'est la raison pour laquelle, lors de la conception d'une liaison par fibre optique, il est nécessaire d'inclure dans le bilan de liaison une certaine marge de sécurité MS (entre 3 et 10 dB).

La marge de sécurité choisie doit être plus importante pour les systèmes utilisant des diodes électroluminescentes (DEL ou LED) que ceux utilisant des diodes LASER. Ceci s'explique par le fait que les caractéristiques des diodes LED sont beaucoup moins stables en température. La marge de fonctionnement est la marge dans laquelle une transmission peut s'effectuer. Elle est égale à la différence entre la puissance minimale reçue et le seuil de réception.

L'atténuation totale en ligne occasionnées par la fibre et ses connexions doivent être inférieure à la puissance minimale émise compte tenu de la marge de sécurité.

5.2.1 Puissance de réception

La puissance du signal qui doit être envoyée dans la fibre optique dépend des caractéristiques de bruit du récepteur, de la bande passante de la fibre, des pertes des connecteurs et des atténuations intrinsèques de la fibre.

74

La puissance reçue PR est donnée par la relation suivante en décibel :

PR = PE -- AAbsorption -- ADispersion -- Alinéique -- PEpissures -- PConnecteurs (5.03)

Avec PR : puissance reçue

PE : puissance émise

A : atténuation

P : perte

Cette puissance reçue doit être supérieure au seuil de réception _S(TEB) pour un taux d'erreur

binaire TEB donné, avec une certaine marge de fonctionnement MF , et inférieure à la puissance maximale admissible _PRmax , sous peine de dégradation, avec une marge de sécurité MS .

S(TEB) + MF < PR < PRmax - MS (5.04)

5.2.2 Puissance maximale et minimale de réception

Le fabricant indique en général deux caractéristiques de puissance d'émission : l'une est la

puissance minimale _PEmin, qui correspond à la valeur garantie en fin de vie, et l'autre à la puissance maximale PEmax.

En conséquence, en appelant _ATotale l'atténuation totale, la puissance de réception est comprise entre les valeurs :

PEmin -- ATotale < PR < PEmax - ATotale (5.05)

Avec ATotal = AAbsorption + _ADispersion + _AEpissures + _Alinéique + _{PConnecteurs+Psupplémentaires} (5.06) On admet donc comme puissance minimale et maximale de réception comme suit:

PRmin = PEmin -- ATotale (5.07)

PRmax = PEmax -- ATotale (5.08)

5.2.3 Exemple du bilan de liaison

Considérons une liaison par fibre optique réalisée avec un débit nominal de 2,5 Gbits/s dont la longueur d'onde de transmission est de 1,55 um. Les fibres utilisées ont une longueur totale de 100 km composé de 20 fibres monomodes de type G652 de longueur 5 km chacune dont les caractéristiques sont les suivantes :

Atténuation linéique : ? ? 0,2 dB. km^-1

Dispersion chromatique : D(?) = 17 ps. nm^-1. km^-1

Perte par épissure : PEpissure = 0,05Db

Atténuation par diffusion : 0,17 dB

75

Les caractéristiques des équipements sont :

Dispersion maximale admissible : Dmax = 3000 ps/nm

Débit nominal : a = 2510 Mbit/s
Puissance maximale d'émission : PEmax = 40 dBm Puissance minimale d'émission : PEmin = 36 dBm

Seuil de réception : S(TEB) = -- 15 dBm

Pertes des connecteurs : PConnecteur = 1,25 dB

On en déduit le bilan de transmission suivant :

: T =

Durée du bit 0- i / = 398,40 ps

T

Largeur spectrale du laser : AX = ? = 0,026 nm

a. L = 20 dB

Dmax

Atténuation linéique totale : Alinéique =

Atténuation par les épissures : AEpissures = PEpissures . L = 1 dB

Dispersion chromatique totale : Dtotal = D(X).AX.L = 45,15 ps

Taux d'élargissement : TE= Dt_T al = 0,11

RO 0 614 l Atténuation chromatique : ADispersion = 10.log (expL ( )²]

) = 0,

, .0- 11 dB
Dtota

L'atténuation totale de la transmission est donc :

ATotale = Alinéique + _ADiffusion + AEpissure+ ADispersion + Pconnecteur = 22,53 dB En tenant compte la marge de sécurité de 4 dB :

ATotale = 26,53 dB

La puissance de réception se situe dans l'intervalle fermée des deux puissances suivantes:

Puissance maximale reçue : PRmax = PEmax - ATotale = 13,47 dBm

Puissance minimale reçue : PRmin = PEmin - ATotale = 9,47 dBm La marge de fonctionnement est : MF = PRmin - S(TEB) = 24,47 dBm

Parmi les atténuations montrées dans ce bilan, l'atténuation linéique semble être la plus dominante. La puissance maximale et minimale reçue dépend majoritairement de cette atténuation. On peut remarquer que la puissance minimale reçue est supérieure au seuil de réception avec la marge de fonctionnement, et inférieure à la puissance maximale admissible sous l'influence de la marge de sécurité, donc la puissance à l'émission parviendra à émettre les rayons lumineux.

76

5.3 Étude quantitative des atténuations

5.3.1 Description du logiciel de simulation MATLAB

5.3.1.1 Généralité sur le logiciel Matlab

Matlab est un environnement puissant destiné aux calcules scientifiques. Il intègre le calcul matriciel et l'analyse numérique dans les fonctions de base. De plus, son architecture graphique orientée objets permet la génération graphiques de qualité.

Matlab tire son nom de l'anglais et constitue une contraction de MATrix LABoratory. C'est donc un logiciel qui a été développé pour traiter spécifiquement les problèmes nécessitant un formalisme matriciel important.

L'ensemble Matlab est formé d'un noyau et de nombreuses bibliothèques de fonctions spécialisées. Le noyau est le logiciel Matlab en lui-même : c'était à l'origine le logiciel à part entier. Il intègre de nombreuses fonctions mathématiques codées en langage Matlab sous forme d'extension « .m » (les m-files). Les bibliothèques de fonctions Matlab spécialisées permettent de personnaliser l'environnement de travail. Elles ont été ajoutées au noyau sous forme de « boites à outils » (ou Toolbox). Ces toolbox sont donc des bibliothèques de fonctions écrites en langage Matlab : elles regroupent des m-files par thème. Par exemple Image Processing (pour le traitement d'image), Signal Processing (pour le traitement du signal), Control system (pour l'automatique), etc. [10]

5.3.1.2 Caractéristiques du Matlab

La particularité de Matlab est qu'il permet le travail interactif soit en mode commande, soit en mode programmation; tout en ayant toujours la possibilité de faire des visualisations graphiques. Considéré comme un des meilleurs langages de programmations, MATLAB possède les caractéristiques suivantes :

o La programmation facile ;

o La continuité parmi les valeurs entières, réelles et complexe ;

o La gamme étendue des nombres et leurs précisions ;

o La bibliothèque mathématique compréhensible ;

o L'outil graphique qui inclut les fonctions d'interface graphique et les utilisateurs ;

o La possibilité de liaison avec les autres langages classiques de programmations.

Dans MATLAB, aucune déclaration n'est à effectuer sur les nombres. En effet, il n'existe pas de distinction entre les nombres entiers, les nombres réels, les nombres complexes. Cette caractéristique rend le mode de programmation très facile et très rapide.

77

La bibliothèque des fonctions mathématiques dans MATLAB donne des analyses mathématiques très simples. En effet, l'utilisateur peut exécuter dans le mode commande n'importe quelle fonction mathématique se trouvant dans la bibliothèque sans avoir à recourir à la programmation. Pour l'interface graphique, des représentations scientifiques et même artistiques des objets peuvent être créées sur l'écran en utilisant les expressions mathématiques. [10]

5.3.1.3 Motif de choix de ce logiciel

Nous avons choisi le logiciel de programmation Matlab puisqu'il est un système interactif et convivial de calcul numérique et de visualisations graphiques destiné aux ingénieurs, chercheurs et tous scientifiques. C'est un environnement performant, ouvert et programmable qui permet de remarquable gain de productivité et de créativité.

Matlab dispose de plusieurs centaines voire des milliers de fonctions mathématiques, scientifiques et techniques, selon les versions. Il est un outil performant capable d'afficher des données en trois dimensions (3D).

Par ailleurs, les possibilités de représentations graphiques offertes par Matlab et ses fonctionnalités nous permettent d'établir aisément notre logiciel de simulation et de créer ainsi une interface graphique que nous allons décrire par la suite.

La version 7.10.0 (R2010a) de Matlab que nous avons utilisée est tout à fait satisfaisante sachant qu'elle inclut déjà toutes les fonctions de base précédentes et qu'elle prend également en charge les autres fonctions indispensables pour réaliser notre simulation.

5.3.2 Présentation du programme de simulation

Le logiciel élaboré permet d'une part, de faire l'étude quantitative des atténuations, et d'autre part, d'établir le bilan énergétique d'une liaison à fibre optique.

Il ne s'agit pas en aucun cas d'un logiciel parfaitement conçu pour être utilisé dans le domaine professionnel rattaché au secteur de télécommunications et réseau par fibre optique, mais il s'agit uniquement d'un programme que nous avons développé pour montrer d'une manière plus pragmatique la présence des atténuations dans une liaison par fibre optique.

Ce programme est composé de trois fenêtres distinctes qui sont :

o La fenêtre principale (accueil),

o L'interface représentant les atténuations intrinsèques,

o La fenêtre d'évaluation des atténuations extrinsèques.

78

5.3.2.1 La fenêtre principale (accueil)

C'est l'interface principale du programme de simulation. Elle met en exergue le thème étudié ainsi que d'autres informations. Le bouton « Suivant » placé au dessous constitue un lien vers l'interface d' « Atténuations intrinsèques ».

La figure ci-dessous nous montre cette fenêtre d'accueil.



Figure 5.04 : Fenêtre d'accueil

5.3.2.2 L'interface représentant les atténuations intrinsèques

Plusieurs paramètres sont présentés dans cette fenêtre. Il est à noter que les éléments colorés en bleu sont les données résultats et ceux qui sont en noir les données d'entrées. Il en est de même pour les autres fenêtres. Cette interface d'atténuation intrinsèque est montrée par la figure suivante.



79

Figure 5.05 : Fenêtre d'évaluation des atténuations intrinsèques

Comme il est déjà expliqué dans le chapitre précédent, cette atténuation intrinsèque concerne la structure d'une fibre elle-même (valeur d'indice, dimension, impureté des matériaux constitutifs, longueur, etc). Dans ce cas, pour étudier ce type d'atténuation, il est indispensable de séparer le type de la fibre utilisée et c'est le cas qui est illustré par cette figure 5.05. Pour les fibres multimodes (à saut d'indice et à gradient d'indice), la dispersion modale qui se traduit par le retard des modes est majoritaire. Par contre pour les fibres monomodes, c'est la dispersion chromatique qui modifie l'impulsion du signal.

L'atténuation linéique et celle par diffusion dans la zone placées en haut de cette fenêtre sont communes à ces trois types de fibres.

On peut visualiser graphiquement l'allure de l'atténuation linéique et de l'atténuation par diffusion dans la zone de représentation graphique placée dans la partie supérieure à droite. Une fonctionnalité zoom permet de voir de plus près la courbe depuis le centre de l'axe. Cet agrandissement prenne uniquement effet en appuyant sur le bouton « Actualiser ».

80

Tous les résultats et les courbes hormis celles de dispersion et atténuation chromatique, sont affichés après avoir introduit dans les champs de saisi toutes les données en entrées suivi d'un appui sur le bouton « Afficher les résultats ».

Pour la représentation graphique de la dispersion et atténuation chromatique, on est amené à choisir d'abord la courbe à afficher.

Les autres boutons existants nous donnent la possibilité d'accéder à d'autre fenêtre.

a) Exemple d'application

Considérons un exemple montré dans la figure ci-dessous dont les valeurs introduites sont celles correspondant aux données du bilan de liaison énoncé dans la seconde section du présent chapitre.



Figure 5.06 : Exemple d'application sur le calcul des atténuations intrinsèques

Dans une fibre de longueur totale de 100 km, l'atténuation linéique, résultant de la différence entre une puissance d'entrée (36dBm) et celle de sortie (16dBm), est de 0,2dB pour chaque distance d'1 km.

81

En choisissant une fenêtre de transmission de 1,55um de longueur d'onde, l'atténuation par diffusion est de 0,17 dB.

Dans le cas où la fibre utilisée est multimode, la valeur de la dispersion et celle du retard modal sont obtenues une fois que l'indice du coeur et de la gaine sont connus et nous optons comme valeur d'indice du coeur 1,48 et celle de la gaine 1,47. L'indice du coeur de la fibre à gradient d'indice varie évidemment dans cet intervalle.

Les données fournies par le fabricant de la fibre monomode tels que la dispersion maximale admissible, débit nominale de transmission et la dispersion chromatique par kilomètre nous permettent de calculer la largeur spectrale de la lumière émise, le retard par kilomètre, la dispersion chromatique totale ainsi que l'atténuation chromatique.

b) Interprétation des résultats

Si on veut étudier l'influence d'une seule donnée d'entrée, il faut varier sa valeur.

En diminuant la valeur de la puissance de sortie de la fibre, on constate que l'atténuation linéique devient de plus en plus importante. De plus, d'après la courbe représentative de ladite atténuation, elle croit progressivement en fonction de la distance parcourue dans une fibre. Cela signifie que plus la fibre est longue plus la puissance du signal s'atténue.

Quant à l'atténuation par diffusion, elle décroit fortement lorsque la longueur d'onde est inférieure à 1 et elle s'annule petit à petit au-delà de cette valeur. La représentation graphique de cette atténuation nous montre qu'elle décroit légèrement à partir d'une certaine valeur de la longueur d'onde environ 1.5 um. Donc le choix de la troisième fenêtre de transmission à une longueur d'onde aux alentours de 1,55 um est plus avantageux.

La différence entre la fibre multimode à saut d'indice et celle à gradient d'indice est apparente d'après ces résultats de dispersion modale et du retard des modes. Ces derniers diminuent lorsque la valeur d'indice du coeur et de la gaine se rapproche.

Pour la fibre monomode, le retard est presque négligeable par rapport à celui des fibres multimodes. Sa dispersion chromatique croit linéairement de l'ordre de 20 ps pour tous les 1/100 de largeur spectrale. Mais l'atténuation chromatique varie légèrement d'une manière croissante en fonction de la largeur spectrale et on peut dire qu'elle est assez faible par rapport à l'atténuation linéique et celle par diffusion pour une distance de 100 km.

82

5.3.2.3 La fenêtre d'évaluation des atténuations extrinsèques

On utilise cette fenêtre pour calculer la valeur numérique de quelques atténuations extrinsèques et représenter graphiquement chaque courbe d'atténuation en comparant les unes aux autres. La figure suivante nous montre cette interface.



Figure 5.07 : Fenêtre des atténuations extrinsèques

L'étude effectuée ici se focalise sur les atténuations liées à l'installation d'une fibre optique notamment le raccordement des fibres.

Pour en faire, on introduit d'abord les valeurs des 7 paramètres suivants :

o la distance de séparation longitudinale entre 2 fibres raccordées,

o la distance de désalignement de leur axe,

o l'angle d'écartement de l'axe de la deuxième fibre,

o l'indice du coeur en supposant qu'il soit le même pour chaque fibre,

o le rayon du coeur de la 1^ere et 2^e fibre et

o la longueur d'onde utilisée.

83

Puis en appuyant sur le bouton « Calculer les atténuations », on pourra alors caractériser les influences de ces paramètres d'entrés en observant les valeurs affichées dans la zone des résultats au dessous de ce bouton et la courbe représentative de chaque atténuation.

Il est aussi possible d'ouvrir soit la fenêtre des atténuations intrinsèques soit retourner à la fenêtre d'accueil à l'aide des boutons correspondants placés au dessous à gauche.

a) Exemple de calcul

L'étude des atténuations que nous allons effectuée dans cette fenêtre s'est basée sur la comparaison de chaque atténuation afin d'identifier celle la plus prépondérante dans une liaison par fibre. Pour cela nous allons commencer par introduire des valeurs identiques dans le champ de saisi pour la séparation longitudinale, le désalignement axial, l'angle d'écartement et le rayon du coeur de la deuxième fibre. La figure ci-dessous nous montre cet exemple.



Figure 5.08 : Exemple de calcul des atténuations extrinsèques

Les fibres utilisées dans cet exemple sont des fibres multimodes à saut d'indice dont le rayon de la première fibre est de 60 um et celui de la seconde est 50 um. Il y a donc une différence de la dimension du coeur de 10 um.

84

Considérons un deuxième et troisième exemple sur lesquels nous prenons respectivement les valeurs 20 et 30 à la place de 10 montré dans la figure 5.08 précédente.

b) Résultats et discussion

D'après les résultats d'atténuations présentés dans la figure précédente, toutes les atténuations sauf celle par séparation longitudinale sont à peu près égales à 3,6 dB.

En tenant compte le deuxième et troisième exemple, les résultats sont illustrés dans le tableau suivant.

Atténuation par :		Résultats en décibel (dB)
		2^e exemple	3^e exemple	- séparation longitudinale
0,00083		0,0033	0,0075	- désalignement axial
3,61		14,47	32,57	- écartement angulaire
3,69		7,38	11,07	- dimension (rayon) différente des fibres
3,64		8,10	13,86

Tableau 5.02 : Comparaison des atténuations dues au raccordement des fibres

Les résultats dans le tableau ci-dessous nous montrent qu'une liaison par fibre optique est beaucoup plus sensible au désalignement axial tandis que l'effet de la séparation longitudinale est moins apparent. Cette affirmation reste vraie quelle que soit la valeur de l'indice et de la longueur d'onde utilisée.

En observant la courbe représentative du désalignement axial et d'écartement angulaire, l'atténuation est maximale lorsque la distance de désalignement axial de la seconde fibre est égale au rayon de la première fibre et le maximum est atteint pour l'atténuation par écartement angulaire lorsque l'angle d'écartement est supérieur à 90°.

Conclusion

Dans ce dernier chapitre, nous avons apporté quelques solutions sur la dispersion chromatique, la dispersion modale et sur les atténuations extrinsèques. On a pu remarquer que le choix d'une fibre à utiliser semble aussi très indispensable avant la mise en place d'une liaison. Le bilan de liaison établi nous a permis de quantifier l'ensemble des atténuations ainsi que la puissance du signal restante à la réception. La quantité d'une atténuation et sa variation en fonction d'un ou plusieurs paramètres sont bien visibles grâce à l'utilisation d'un programme spécialement conçu à cet effet.

85

CONCLUSION GÉNÉRALE

L'esquisse d'étude décrit dans ce présent mémoire se porte sur les notions fondamentales de la transmission par fibre optique en parlant de la description de ce support de transmission et le principe d'émission de l'information dans celle-ci. La transmission d'information dans une fibre optique se fait à l'aide d'un rayon lumineux qui possède aussi ses propres caractéristiques.

La fibre optique apporte des nombreux intérêts dans divers domaines étant donné sa performance notamment au niveau du débit et de la bande passante vis-à-vis des autres supports.

Malgré des nombreux avantages auxquels la fibre procure, elle présente quand même des inconvénients qui peuvent être très désavantageux à son utilisation. La lumière portant les informations qui traverse le long d'une fibre optique est soumise à des nombreuses phénomènes tels que la réflexion, réfraction et elle peut s'atténuer en fonction du milieu ou la structure de la fibre qu'elle traverse. Ce phénomène d'atténuation constitue l'objet de notre étude présenté dans ce mémoire selon son intitulé « Étude des atténuations dans une transmission par fibre optique ». Ces problèmes dans la fibre optique se manifestent différemment selon le type de la fibre utilisée et nous avons constaté que les pertes sont plus faibles pour la fibre monomode par rapport aux fibres multimodes. En comparant ces derniers, on peut dire que la fibre multimode à gradient d'indice est plus avantageuse que celle à saut d'indice. Les équipements d'émission, de réception et de régénération du signal font parti des facteurs qui contribuent à ce phénomène d'atténuation. A l'aide d'un programme de simulation développé sous un logiciel Matlab, la quantification de ces atténuations a été donnée et on a vu qu'elles ne sont pas tous les mêmes mais il y a celles qui sont plus prépondérantes que les autres.

Face à ces problèmes qui dégénèrent le signal transmis dans une fibre, il existe toutefois des solutions que l'on peut prendre afin de les contourner. Ainsi, la mise en place d'une liaison par fibre optique requiert des études préalables au niveau du milieu d'installation, de la fibre utilisée et ses équipements ainsi que l'usage auquel elle est conçue.

X

ANNEXES

ANNEXE 1 : Fabrication d'une fibre optique

La fabrication d'une fibre optique ayant les qualités requises pour les télécommunications a nécessité la mise au point des procédés techniques très complexes.

La technique générale de fabrication comporte d'abord la fabrication d'une préforme, que l'on tire ensuite en fibre. La préforme est un barreau cylindrique qui représente la géométrie de la fibre. Ce barreau peut être imaginé comme une grosse fibre de courte longueur. Une fois étirée, la fibre préserve le même profil d'indice et le même rapport entre le diamètre du coeur et celui de la gaine que ceux présents dans la préforme du départ. En l'étirant, on obtient un cylindre beaucoup plus long mais beaucoup plus mince. Alors, une préforme de dix centimètres de diamètre et d'un mètre de long peut former par étirement une fibre de 150 kilomètres et de quelques micromètres de diamètre.

A1.1 Étapes de fabrication

La préforme est fabriquée par dépôt des composants chimiques sous forme vapeur à l'intérieur d'un tube de verre ou en périphérie d'une tige de substrat. Les couches successives de coeur et de gaine ainsi superposées subissent ensuite une compression (opération de restreint), pour l'obtention de la préforme.

La dernière étape (le fibrage) étire la préforme pour lui donner la dimension finale de la fibre. En fin d'opération, la fibre est recouverte de diverses gaines protectrices.

A1.2 Préparations des composants

Le verre et les dopants sont préparés en phase vapeur à partir des chlorures ou des bromures. Ces produits créent des préformes pour fibres monomodes et multimodes avec l'atténuation linéique de l'ordre de 0,2 dB/km à 0,5 dB/km.

La variation de l'indice du verre est obtenue par des additifs, les dopants : l'oxyde de bore (B2O3) diminue l'indice alors que l'oxyde de phosphore (P2O5) et l'oxyde de germanium (GeO2) l'augmentent. [12]

A1.3 Obtention de la préforme

Pour fabriquer des préformes, on utilise la méthode du dépôt chimique en phase vapeur, plus communément appelée méthode CVD (Chemical Vapour Deposition). Cette technique permet de fabriquer des verres de très haute qualité à partir d'une réaction chimique de produits en phase vapeur. Les chlorures utilisés (SiCl4, GeCl4, POCl3, BCl3) sont transformées en oxydes (SiO2,

XI

GeO2, P2O5, B2O3). La silice (SiO2) constitue la matière de base de la préforme. L'addition de GeO2 et de P2O5 augmente l'indice de la silice mais l'ajout de B2O3 le réduit. Il existe plusieurs variantes de cette technique pour la fabrication de préformes.

o La technique par dépôt interne est appelée MCVD (Modified Chemical Vapour Deposition ou dépôt de vapeurs chimiques modifiées).

o Il y a aussi les techniques de dépôts externes des oxydes. Ce sont la méthode OVPO (Outside Vapour Phase Oxydation) et la méthode VAD (Vapor Axial Deposition).

A2.4 Fibrage

La préforme est placée verticalement et est étirée pour donner à la fibre la dimension finale.





XII

Figure A2.02 : Étirage du préforme

On réalise le tirage de la fibre en plaçant la préforme dans un four à induction qui fond la silice. On fixe sur un tambour en rotation le filament de verre qui s'est étiré par gravitation. On rajoute un revêtement en silicone qui assure une protection mécanique de la fibre. La vitesse de rotation du tambour définit le diamètre de la fibre.

ANNEXE 2 : Interface principal du logiciel MATLAB



XIII

XIV

BIBLIOGRAPHIE

[1] Berinon GRISTO, Tann F. ZENO, 2001, « Cours de DESS et de DEA d'optique et optoélectrique », In Université de Nante (ed), 210pp, DUNOD, Paris.

[2] Cassan ELOÏQUE, 2005, « Étude des propriétés physiques des fibres optiques à partir d'un modèle simple », 142pp, Institut d'Électroniques Fondamentale, Eyrolles, Paris.

[3] Claude Georges CYRILLAN, s.d, « La fibre optique », 89pp, Cordat, ENST, s.l

[4] Claire JULANNE ERNONE, 1997, « Télécommunications optiques : Introduction à l'optique intégrée », 117pp, Mass'On, Nante.

[5] Colomer LOBREU, 2005, « Les mesures de dispersion chromatique », PhotonLine, s.l.

[6] Cozannet ARDON, Fleuret JUMERR, 2001, « Optique et Télécommunications», 413pp, Eyrolles, Paris.

[7] François WILLIAM, s.d, « Optique moderne »,80p, Ellipses, Paris.

[8] Ismael J., Thomas MOULINET, 1996, « Les télécommunications par fibre optique, Collection Technique et Scientifique des Télécommunications », Dunod, Paris.

[9] Jacques MERSIER, 2000, « Fibres optiques pour télécommunications», 164, pE7, s.l.

[10] Mulaff MOKHTARI, 2009, « MATLAB 7.10 and GRAPHICAL PLOT », 297pp, ISBN, s.l

[11] Morvan De Salle SAM, s.d, « Transmission par Fibres optiques : Base d'ingénierie », In Dép Optique-ENST (ed), CNAM, Bruxelle.

[12] Réné BOUILLIT, Vessam OUBON MOA,1990, « Sytèmes de transmission numérique sur fibres optiques », In Traité Électronique (ed) ,175pp, ESSET, 1990

XV

WEBOGRAPHIE

[13] Christian F. CALECA, « La fibre optique », [Réf du 25 Mai 2016], Format PDF, Disponible sur http://www.christian.caleca.free.fr

[14] Cordat GRASSINO, 2003, « Transmission par Fibre optique », [Réf du 25 Mai 2016], Format World Wide Web, Disponible sur http://www.mptranss.free.fr/

[15] Hugues Philipe, Irenn Patrick RENAUD, « Mesure de dispersion chromatique (DC) », [Réf du 11 Juillet 2016], Format PDF, Disponible sur http://www.telecomparistech-fr/

[16] Ismael JULIENO, Marinnet GASPAR, 1999, « Fibres optique pour télécommunications, techniques et principes de l'Ingénieur », [Réf du Juin 2016], Format PDF, Disponible sur http://www.technique-ingénieur.fr

[17] Jean Rodin DINO, 2003, « La fibre NZDSF (Non Zero Dispersion Shifted Fiber) », [Réf du 11 Juillet 2016], Format Word, Disponible sur http:// http://www.enstbretagne.fr/

[18] Jerôme Jeff STEFFE, s.d, « Fibre optique», [Réf du Mai 2016], Format World Wide Web, Disponible sur http://www.fr.wikipedia.org/wiki/

[19] Léon GERARD, 2005, « Aspect sur la transmission physique de la lumière par fibre », [Réf du 30 Mai 2016], Format PDF, Disponible sur http://www.opt-fibre.phys.polymtl.ca/

[20] Lionel P. CORPECHAUT, « Cours fibre optique », [Réf du 25 Mai 2016], Format World Wide Web, Disponible sur http://www.httr.ups_tlse.fr/pedagogie/cours/fibre/

[21] Lionel CASSARD, « Télécommunication optique », [Réf du 25 Mai 2016], Format PDF, Disponible sur http://www.cem2.univ-mont p 2.fr/-moreau/cours/

[22] Libson DONDAU, Jules MERRAIN « Tout sur fibre optique », [Réf du 18 Juin 2016], Format World Wide Web, Disponible sur http://www.fibre-optique.org/

[23] Monique BORIES, Rénaud JOULIER, « Liaison par fibre optique », [Réf du 18 Juin 2016], Format World Wide Web, Disponible sur http://www.fibre_optique.org/

[24] Olivier J. HUGUE, Pierre COLEY, SUZANNA, « Transmission des ondes lumineuses dans un verre », [Réf du 18 Juin 2016], Format PDF, Disponible sur http://www.profil-onde.com/

[25] Théophile LEFÈVRE, Torry FAYNAM, Grivann JOY, « Recommandations sur les télécommunications », [Réf du Mai 2016], Format World Wide Web, Disponible sur http://www.itu.int/

XVI

PAGE DE RENSEIGNEMENT

Nom : RABESALAMA Prénoms : Iabaina Isidor Adresse : Lot 300PA Est-Météo Tombontsoa Tsaravavaka Antsirabe II ANTSIRABE 110 E-mail : [e-mail] Contact : 033 74 923 00

Titre de mémoire :

« ÉTUDE DES ATTÉNUATIONS DANS UNE TRANSMISSION PAR FIBRE OPTIQUE »

Nombre de pages : 85 Nombre de tableaux : 04 Nombre de figures : 51

Mots clés : fibre optique, atténuation, transmission, perte, lumière, réflexion, dispersion, signal, longueur d'onde.

Encadreur pédagogique :

Monsieur RANDRIAMIHAJARISON Mparany Jimmy