L'atténuation linéique est une perte
régulièrement repartie le long d'une fibre. Cette
atténuation est toujours présente dans toutes les fibres. Elle
est due aux matériaux constituants la fibre optique et les constructeurs
en donnent souvent sa valeur. On pourra tout de même calculer cette
atténuation en connaissant la puissance du signal à une distance
donnée.
Soit une fibre optique de diamètre constant. Calculons
la perte de puissance lumineuse, pour une certaine longueur de fibre en
choisissant deux sections de droites (perpendiculaires à la direction de
propagation) distantes d'une petite distance dL appelée
distance élémentaire. La puissance lumineuse (ou flux) est le
rapport de la qualité d'énergie lumineuse traversant une section
sur l'unité de temps.
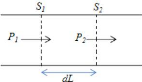
Figure 4.06 : Portion d'une fibre
Soit P1, la puissance lumineuse traversant S1, et P2 la
puissance lumineuse traversant S2.
En raison de l'atténuation dans une fibre, on a P2 <
P1.
La variation élémentaire de puissance dP = P2 - P1
est négative et :
o Proportionnelle à dL : une longueur x fois dL donne des
pertes x fois plus grandes ;
o Proportionnelle à un coefficient d'atténuation
linéique á caractérisant la fibre.
La quantification des pertes est calculée suivant la loi
de décroissance de la puissance optique de Beer-Lambert, pour une
distance dL faible tel que :
= a .P (4.11)
Équivalent à :
= a .dL (4.12)
Par intégration sur une longueur L2 et L1 mesurée
respectivement au niveau de la section S2 et S1 de la fibre correspondant
à la puissance P2 et P1, on obtient :
?
= a. ? (4.13)
On en déduit que :
Ln = a (L2 L1) (4.14)
53
Alors :
=??xp [ ? ?L2 L1)] (4.15)
Donc, pour Pe et Ps la puissance à l'entrée et
à la sortie de la fibre, le bilan de puissance d'entrée et sortie
du signal de l'atténuation linéaire se traduit par la
décroissance exponentielle de puissance injectée en fonction de
la longueur de la fibre. C'est la loi de Beer-Lambert se définissant
comme suit :
Ps = Pe .?? (4.16)
Avec Ps : Puissance à la
sortie de la fibre [en Watt]
Pe : Puissance à l'entrée de la fibre [en Watt]
: coefficient d'atténuation linéique [en ]
L : Longueur de la fibre [en km]
L'atténuation en dB/km de la lumière dans une
fibre de longueur L se caractérise par un terme d'atténuation
linéique ?. Elle est exprimée par la relation suivante :
??
? ?
[dB/km] (4.17)
L'accroissement de cet affaiblissement reste constant pour
toute distance traversée dans une fibre optique ou plusieurs fibres
raccordées de même structure.
On en déduit le bilan de puissance d'entrée et
sortie du signal de l'atténuation linéique qui se traduit par
:
= (4.18)
On peut utiliser la relation de mesure suivante pour une
conversion : ? [dB.km-1] = ? [km-1]
L'atténuation linéique totale pour une fibre de
longueur L est donnée par :
? linéique ? ? x L [dB]
(4.19)
Exemple de calcul d'atténuation linéique
:
A l'entrée d'une fibre, on injecte une puissance P1 =
36 dBm. Au bout d'1 km, on récupère une puissance P2 = 35,8 dBm.
Cherchons le coefficient d'atténuation de la fibre puis la puissance P3
à la sortie de la fibre de longueur totale 100 km et
l'atténuation linéique totale.
D'abord, il est impératif de savoir que la puissance en
Watt est obtenue par :
P[W] = 1W. [ ]
Alors P1 = 36dBm = 3,981W et P2 = 35,8 dBm = 3,802W
54
L'atténuation linéique exprimée en [dB/km]
vaut : a [ dB.km-1] = 10. =10.log10 = 0,2
On en déduit sa
conversion en [km-1] par :
a[ dB.km-1] x
a [ km-1] = = 0,046
Pour trouver P3, on peut
utiliser :
o Soit la relation 4.06 : P3 = P1 . = 3,981
o Ou bien la formule 4.08 : P3 = P1 . = 3,981
.
Ce qui donne le même résultat :
P3 = 0,03981 W = 16 dBm
Donc, l'atténuation linéique totale pour une fibre
de 100 km est :
Alinéique = a[dB.km-1] . L =
0,2 .100 = 20 dB



