4.2.1 Pertes par courbure
Les obstacles sur le lieu d'installation peuvent
nécessairement nous obligent à courber la fibre optique afin de
les franchir. Dans ce cas, la fibre suit donc un trajet curviligne et cette
courbure peut provoquer une atténuation plus ou moins importante car le
rayon est transmis dans la gaine ; ce qui se traduit par une perte
d'énergie transmise.
Lorsque le coeur de la fibre décrit un arc de cercle
de rayon très petit, les rayons lumineux pénètrent
majoritairement dans la gaine qu'à l'intérieur du coeur et
pourrait être complètement dégradés au-delà
d'une certaine flexion.
En pratique, l'effet de cette perte de courbure est
négligeable lorsque le rayon de courbure R est grand par
rapport au rayon critique Rc. On calcule ce dernier à l'aide de
la relation suivante et à préciser que son unité est en
centimètre :
o pour les fibres multimodes :
Rc = [cm] (4.01)
48
o pour les fibres monomodes :
[cm] (4.02)
Rc = 20 x ( )
Avec :
a : rayon du coeur [um] ; ON : ouverture
numérique ;
n1 : indice du coeur ;
n2 : indice de la gaine ;
? ? longueur d'onde utilisée [um] ; ?c
? longueur d'onde critique [um] ;
Dans les deux cas précédents, on peut remarquer
que plus la différence d'indice entre le coeur et la gaine optique est
grande, moins la fibre est sensible à la perte par courbure.
Mais pour une fibre possédant un diamètre de
coeur grand, elle est plus vulnérable à la courbure. En pratique,
l'ordre de grandeur de Rc est environ de quelque centimètre.
[9] [22]
4.2.2 Pertes par microcourbure
Elles sont dues à une déformation locale de la
dimension d'une fibre lors de sa fabrication ou par une forte pression qu'elle
subisse sur son lieu d'installation et elle provoque le même effet que
celui causé par la courbure et souvent la cause de la dispersion de
polarisation.
Elle ne dépend pas de la longueur d'onde
utilisée mais de la fibre proprement dite, surtout avec une fibre
optique de diamètre très petit.
Les microcourbures sont des variations aléatoires du
diamètre du coeur ou de la gaine (de l'ordre de quelques
micromètres). Il y a donc un risque, pour un rayon lumineux, de ne pas
remplir la condition de réflexion totale, d'où la perte dans la
gaine par réfraction. [22]
4.2.3 Pertes de jonction
Les pertes de jonction ou de raccordement sont
provoquées par le défaut d'alignement et la réflexion dans
les épissures et au niveau des connecteurs optiques.
Inévitablement, une partie de la lumière quittant la fibre est
perdue par la divergence du faisceau et par réflexion : le faisceau
repart en sens inverse, c'est le « return loss ».
L'épissurage est le mode de raccordement de deux
fibres et il en existe deux sortes : celle qui se fait avec une soudure, et
celle qui utilise des connecteurs. Mais dans ces deux cas, une perte de
raccordement est toujours présente.
L'épissurage par soudure est moins sensible au
défaut par rapport à celui utilisant des connecteurs. Ce type de
jonction est relativement fragile et le raccordement est définitif.
[5][20]
L'alignement des fibres n'est jamais totalement parfait, il
existe donc une perte de lumière lors du passage de celle-ci d'un
côté à l'autre. Cette perte est plus ou moins importante
suivant les défauts résiduels d'alignement.
Il existe plusieurs causes des pertes de jonction telles que
: la séparation longitudinale, le désalignement axial,
l'écartement angulaire et les dimensions différentes des
fibres.
4.2.3.1 La séparation longitudinale
La séparation longitudinale se traduit par un petit
écartement entre deux fibres qui devraient être parfaitement
connectées. Il existe une variation d'indice dans la partie vide qui
sépare les deux fibres, donc le rayon lumineux peut être
réfracté ou réfléchi selon le cas. La perte due
à cette séparation est critique mais non rédhibitoire.
Dans ce défaut, les faces des fibres sont
écartées l'une de l'autre d'une distance l
comme la figure ci-dessous nous montre.
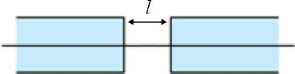
Figure 4.02 : Séparation longitudinale des
deux fibres
L'atténuation est exprimée par [6] :
rr
A[dB] = -- 10 log L1+
(4.03)
l2. )2]
(
21cn1D
Avec A : longueur d'onde utilisée [um] ;
l : distance de séparation entre deux fibres
[um] ; n1 : indice du coeur de la fibre ;
D : diamètre de la fibre optique [um].
49
Soient deux fibres de même dimension de coeur jointes par
un connecteur supposé parfait. Lorsqu'une mince épaisseur d'air
les sépare, recherchons les facteurs de réflexion
théorique liée à cet écartement.
Au niveau de chaque dioptre séparant l'air de la
fibre, une partie de la lumière peut subir une réflexion dans
cette interface air-verre. Alors, le facteur de réflexion en
intensité s'exprime par :
Re = (ni_1)2 (4.04)
n1+1
Avec n1 : indice du coeur.
50
Et le coefficient de transmission en intensité est :
T = 1 - Re (4.05)
Pour un indice de 1,5 du coeur de la fibre, Re = 4 % à
chaque dioptre et T vaut 1 - Re = 96 %.
| 


