Conception et calcul d'un pont suspendu.

1

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

1

TRAVAIL DE FIN D'ETUDE

EPIGRAPHE

Tout homme donc qui entend mes paroles que voici et les met en pratique sera comparé à un homme avisé, qui a bâti sa maison sur le roc. Et la pluie est tombée à verse, et les inondations sont venues, et les vents ont soufflé et ont battu cette maison, mais elle ne s'est pas effondrée, car elle avait été fondée sur le roc.

Matthieu 7 : 24 - 25

2

TRAVAIL DE FIN D'ETUDE

DEDICACE

Je dédie ce travail à :

- Mon père Okundji Lotengo Médard

- Victorine Nlandu Zakuadia

- Aselo Otemakumi Mervi

- Tous ceux qui m'ont aidé à grandir sur le plan scientifique.

2

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

3

TRAVAIL DE FIN D'ETUDE

SYMBOLES ET ABREVIATIONS

C.T : chef des travaux

f : flèche

L : portée du pont

H : Hauteur totale du pylône

e : Épaisseur de la dalle

l : largeur de la dalle

L : Longueur de la poutre

t : Épaisseur de la semelle

t : Épaisseur de l'âme

b : base de poutre

: Base de l'entretoise

e : Épaisseur de la semelle de l'entretoise

N : Nombre d'entretoise

N : Nombre d'entre axe des entretoises

l : Entre axe des entretoises

l : Distance à nu des entretoises

H : Hauteur des suspentes

N : Nombre des suspentes

H : Hauteur totale du pylône

H : Hauteur supérieure du pylône

l : Largeur du pont

H : Hauteur inferieure du pylône

r : rayon d'inclinaison du profilé de la poutre

A : section de la poutre

3

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

4

TRAVAIL DE FIN D'ETUDE

h : Hauteur à nu de la poutre

d : hauteur de l'âme

P : Poids de la dalle

: Poids spécifique de béton bitumineux

N : Nombre des poutres

N : Nombre d'entre axe des poutres

l : Largeur entre axe des poutres

l : Distance à nu des poutres

H Hauteur de l'entretoise intermédiaire

H Hauteur de l'entretoise extrême

P poids du couche de roulement

P Poids de la couche d'isolation

P : Poids de la couche de forme en béton

: Poids spécifique de béton armé

: Poids spécifique du béton

: Poids spécifique de l'acier

P : Poids de la chaussée

LCPC : laboratoire central des ponts et chaussées

P : Poids d'une roue

4

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

5

TRAVAIL DE FIN D'ETUDE

LISTE DES FIGURES

Figure 1 : Pont suspendu ancré au sol, année 1832-1834 de 246,26 mètres de portée Figure 2 : le pont suspendu à chaines, le pont de menai année 1819-1826 de 176 mètres

de portée.

Figure 3 : Eléments d'un Pont suspendu

Figure 4 : Tablier du pont suspendu

Figure 5 : Les différents câbles

Figure 6 : Les suspentes

Figure 7 : Les suspentes

Figure 8 : Collier de suspension et suspentes

Figure 9 : Les formes des pylônes

Figure 10 : Les massifs d'ancrage

Figure 11 : Les massifs d'ancrage

Figure 12 : Les massifs d'ancrage

Figure 13 : Pont suspendu à travée unique

Figure 14 : Pont suspendu à 3 travées suspendues

Figure 15 : Pont suspendu à 3 travées

Figure 16 : Pont suspendu à 3 travées

Figure 17 : Pont suspendu à multi travées

Figure 18 : Description du site

Figure 19 : Description du site

Figure 20 : Carte topographique de la ville de Kinshasa

Figure 21 : Les grès d'Inkisi

Figure 22 : Les grès d'Inkisi

Figure 23 : Représentation de la coupe longitudinale du pont

Figure 24 : Les différents profilés

Figure 25 : Les profilés IPE

5

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

6

TRAVAIL DE FIN D'ETUDE

Figure 26 : Les profilés HE

Figure 27 : Tableau des différentes classes des aciers

Figure 28 : La coupe transversale du pont

Figure 29 : Coupe transversale du tablier

Figure 30 : coupe longitudinale du tablier

Figure 31 : Vue de dessus du tablier

Figure 32 : vue en plan du tablier

Figure 33 : Corps de la chaussée

Figure 34 : La superstructure du pont

Figure 35 : Schéma du pré-dimensionnement de la superstructure

Figure 36 : Tablier métallique du pont

Figure 37 : Les poutres transversales

Figure 38 : Le convoi

Figure 39 : La répartition des charges du convoi

Figure 40 : La transmission de charge de la roue sur le tablier

Figure 41 : Les panneaux de la dalle

Figure 42 : Plan d'armature du ta lier

Figure 43 : Calcul des contraintes

Figure 44 : Répartition transversale des charges

Figure 45 : Calcul des surfaces des lignes d'influence de moment

Figure 46 : La répartition des charges du convoi

Figure 47 : Ligne d'influence de l'entretoise (charge unitaire au milieu)

Figure 48 : ligne d'influence de l'entretoise (charge unitaire au point 5)

Figure 49 : diagramme de moment de l'entretoise

Figure 51 : La poutre du treillis la plus chargé

Figure 52 : premier chargement de la poutre principale

6

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

7

TRAVAIL DE FIN D'ETUDE

Figure 53 : les réactions d'appuis de la poutre principale

Figure 54 : deuxième chargement de la poutre principale

Figure 55 : les réactions d'appuis de la poutre principale

Figure 56 : Chargement du treillis transversal

Figure 57 : Réaction d'appui du treillis transversal

Figure 58 : Chargement du treillis longitudinal

Figure 59 : Les réactions des suspentes et d'appui du treillis longitudinal

Figure 60 : deux suspentes en un point du câble principal

Figure 61 : effort dans le câble principal et pylône

Figure 62 : chargement du câble principal

Figure 63 : chargement du demi-câble principal

Figure 64 : effort de compression du pylône

Figure 65 : la section du pylône

Figure 66 : la longueur du câble principal

Figure 67 : diagramme des contraintes

Figure 68 : massif d'ancrage

Figure 69 : vue en plan de la fondation

Figure 70 : coupe transversale de la fondation

Figure 71 : chargement de la semelle

Figure 72 : les réactions d'appui de la semelle

Figure 73 : diagramme de moment de la semelle

Figure 74 : diagramme des efforts tranchants de la semelle

Figure 75 : diagramme des efforts normals de la semelle

Figure 76 : diagramme de la déformée de la semelle

Figure 77 : la représentation des noeuds et arres

7

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

8

TRAVAIL DE FIN D'ETUDE

AVANT PROPOS

La logique académique de l'enseignement supérieur et universitaire veut qu'à la fin du cursus académique, les finalistes défendent leurs mémoires ou travail de fin d'études (T.F.E) dans un domaine scientifique de leur choix en rapport avec leur formation.

L'Institut national du bâtiment et travaux publics (INBTP) ne fait pas exception à cette logique. Voilà pourquoi nous y conformons, en optant pour domaine des ponts (pont spécial à grande portée) pour la défense de notre mémoire enfin d'être qualifié en tant qu'ingénieur en bâtiment et travaux publics.

Nous remercions d'une manière particulière notre directeur de travail en la personne du Professeur Docteur Ingénieur Mutondo wa Mutondo et notre encadreur en la personne de l'assistant Ingénieur Zenga Mbala Fils, pour toutes leurs disponibilités, sacrifices qu'ils ont pu mettre à notre service afin de nous encadrer malgré leurs multiples occupations.

Nous remercions également tous les professeurs, Chef des travaux et assistants des cours que sont le C.T Dédé Bovulu, Assistant Kiaka, Assistant Zenga Mbala Fils, Assistant Mukinayi Mukendi Joel, Assistant Mutonkole Patrick...

Nous remercions aussi toutes les couches sociales de l'INBTP.

8

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

9

TRAVAIL DE FIN D'ETUDE

CHAPITRE I. INTRODUCTION

I.1 SUJET

Conception et calcul d'un pont suspendu de 1.210 mètres de portée devrant relier le Congo Kinshasa au Congo Brazzaville via le quartier mbudi dans la commune de mont-ngafula

I.2 PROBLEMATIQUE

Le monde actuel se développe très rapidement. Les pays développés sont interconnectés par diverses voies de circulation dont notamment la voie routière, maritime, aérienne, souterraine, ferroviaire, etc

En ce qui concerne le transport routier qui est le plus exploité et qui nous intéresse, ce dernier et souvent sujet à des o stacles tant naturels qu'artificiels dont la route doit franchir et cela grâce notamment aux ouvrages d'art du type pont.

Depuis plusieurs années, on cherche à relier les deux capitales le plus proche du monde : Brazzaville et Kinshasa qui sont séparée par un obstacle naturel qui est le fleuve Congo.

On note notamment le projet du groupe économique français BOLLORE qui est actuellement occupé à préparer les travaux de construction d'un pont entre les deux Congo au niveau de Maluku. C'est dans ce cadre qu'il construit déjà un port sec à Brazzaville pour contraindre Kinshasa à l'acceptation de cette option¹.

Ainsi dans le but de nous pencher sur cette idée nous avions jugé bon de travailler sur un projet similaire à Mbudi pour rendre plus fiable et facile cette interconnexion entre les ceux capitales via un pont suspendu de 1.210 mètres de portée.

Notre travail porte donc sur « la conception et calcul d'un pont suspendu de 1.210 mètres de portée devrant relier le Congo Kinshasa au Congo Brazzaville via le quartier Mbudi dans la commune de Mont - Ngafula »

Les quelques questions suivantes méritent d'être posées :

- Comment se justifie le choix de ce site?

- En quoi se justifie le choix d'un pont suspendu pour ce site?
- Quels avantages sociaux économiques de ce projet

I.3 HYPOTHESE DE TRAVAIL

L'hypothèse est une proposition de réponse à la question posée. Elle est une affirmation provisoire concernant la relation entre deux ou plusieurs variables. Concernant la question dont nous nous sommes posées, il nous revient de donner des réponses provisoires ci-après :

¹ JOURNAL INTERPRETE N° 1608 DU 23 à 25 FEVRIER 2016

9

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

10

TRAVAIL DE FIN D'ETUDE

? Cette analyse permettrait à l'ingénieur de pont de mieux connaitre les structures ou les ponts à câbles.

? Des conceptions du genre, renforce la connaissance architecturale, l'analyse structurelle et une bonne connaissance de la géotechnique du sol.

? Ce pont une fois construit, va encore accroitre le trafic et les échanges commerciaux entre les deux villes.

I.4 LES CHOIX ET INTERET DU SUJET

De par sa conception et son étude, notre pont va résoudre deux grands problèmes primordiaux :

1. Relier deux capitales les plus proches du monde via un pont suspendu qui fait partis ponts spéciaux connus.

2. Offrir au pays un tel ouvrage d'art, deuxième du genre après le pont MARECHAL lorsque l'autorité compétente le matérialisera.

Ce projet de pont suspendu nous aidera à combler deux grands besoins essentielles dont se pose un ingénieur constructeur et concepteur de pont :

1. Comment faut-il réaliser un pont à une travée adapté à la portée, et aux réalités du site ?

2. Quels sont les calculs, les méthodes et les matériaux appropriés à ce genre d'ouvrage ?

Sur ce nous demandons et espérons que ces genres des projets verront le jour pour mettre en relation deux coins, deux cultures donc deux modes de vie différentes séparés par un obstacle naturel qu'est le fleuve Congo.

I.5 DELIMITATION DU TRAVAIL

Notre travail comprend huit (8) chapitres qui suivent :

CHAPITRE 1 : INTRODUCTION

CHAPITRE 2 : GENERALITES SUR LES PONTS

CHAPITRE 3 : DONNEES DU PROJET

CHAPITRE 4 : CONCEPTION ET PRE-DIMENSIONNEMNT DES ELEMENTS DU PONT

CHAPITRE 5 : CALCUL DE LA SUPERSTRUCTURE

CHAPITRE 6 : CALCUL DE L'INFRASTRUCTURE

CHAPITRE 7 : ETUDES DES IMPACTS ENVIRONEMENTAUX ET EVALUATION DU PROJET

CHAPITRE 8 : CONCLUSION

10

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

11

TRAVAIL DE FIN D'ETUDE

CHAPITRE 2. GENERALITES

2.1 DEFINITION D'UN PONT

Un pont est un ouvrage permettant de franchir un obstacle naturel ou une voie de circulation terrestre, fluviale ou maritime².

Le pont, c'est un ouvrage d'art par excellence, occupe une place très particulière parmi les constructions ; il est un symbole, lui-même paradoxal : franchissant un fleuve, il est un moyen de communication entre les hommes, d'expansion de la civilisation, mais aussi un instrument de conquête et d'invasion³.

2.2 HISTORIQUE DES PONTS4

L'histoire de pont peut se résumer en des étapes suivantes :

· Avant 1500 (après jésus christ): période empirique ; la construction de pont sans calculé

· De 1500 à 1800 : c'est la période des grands savants, le début des études théorique du pont et la naissance de l'acier; il s'agit de Newton, Galilée, Hooke.

· De 1800 à 1900 : Naissance de l'industrialisation, d'où dé ut des chemins de fer et construction des 1er ponts métalliques pour des chemins de fer. A la fin de cette période, il y a apparition du béton armé.

· De 1900 à 1950 : apparition des voitures, d'où des ouvrages en éton armé. Apparition du béton précontraint.

· De 1950 à 1975 : la période du développement de l'autoroute.

· De 1975 jusqu'à nos jours : à cause de la crise pétrolière due à la guerre de KIPPUR (guerre entre les israéliens et les arabes en 1973). Ce qui entraina la crise économique mondiale, est à cause de l'apparition des écologistes, nous assistons à un frein dans la construction des routes.

Les grandes lignes de l'évolution de la construction des ponts ces dernières années sont les suivantes :

· Evolution du trafic en flèche : le trafic a évolué quantitativement et qualitativement et le confort aussi.

· Evolution des techniques des constructions : les techniques à mettre à la disposition des ingénieurs, des moyens de plus en plus sûrs du point de vue matériaux, calculs et exécutions.

² Rufin MUTONDO, cours de pont 3 BTP, INBTP, 2013 2014, inedit

3 Jean-Armand CALGARO et Roger LACROIX, PATHOLOGIE ET EVALUATION DES PONTS

⁴ Rufin MUTONDO, Op.cit.

11

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

12

TRAVAIL DE FIN D'ETUDE

2.3 CLASSIFICATION DES PONTS5

Les ponts sont classés de diverses manières :

- Suivant les matériaux

- Suivant la longueur

- Du point de vue genre de charge (nature de la voie portée)

- Du point de vue niveau de circulation

- Du point de vue mobilité

- Du point de vue orientation des voies

- Du point de vue résistance des matériaux

- Du point de la structure en général

- Du point de vue de la durée de vie

2.3.1. SELON LES MATERIAUX CONSTITUTIFS

2.3.1.1. PONTS EN BOIS.

Sa durée de vie est limitée, il est employé pour les ponts provisoires. Les formes les plus usitées sont les poutres à treillis et les arcs.

2.3.1.2. PONTS EN PIERRE.

Etant donné que la construction en maçonnerie résiste très bien aux efforts de compression, et très mal à la traction, la réalisation des voûtes en pierre pour lesquelles chaque section reste constamment comprimée est employée. Par contre, celui-ci est en nette régression parce que les conditions actuelles, principalement de main-d'oeuvre et de temps, ne permettent plus la taille de la pierre.

2.3.1.3. PONTS EN BETON.

Le béton non armé a été utilisé comme la pierre de taille pour la réalisation de voûtes, car il n'est pas suscepti le de s'opposer aux grands efforts de traction.

2.3.1.4. PONTS EN BETON ARME.

Le mode de mise en oeuvre du éton armé permet d'envisager la réalisation de toutes les formes d'ouvrages que l'on peut imaginer.

Cependant, dans un ut d'économie, le projeteur recherche les formes simples qui permettent de réduire au minimum le prix des coffrages.

⁵ Rufin MUTONDO, cours de pont 3 BTP, INBTP, 2013 2014, inedit

12

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

13

TRAVAIL DE FIN D'ETUDE

2.3.1.5. PONTS EN BETON PRECONTRAINT.

Il permet en particulier de réaliser de travées indépendantes par poutres préfabriquées de plus grande portée et à un prix moindre lorsqu' il y a un grand nom re de poutres identiques. Grâce à celui-ci, des méthodes nouvelles de construction sont apparues, telle la construction par encorbellement, qui permet de supprimer les cintres et les échafaudages.

2.3.1.6. PONTS METALLIQUES

2.3.1.6.1. PONTS EN FONTE ET EN FER

Pour la réalisation des ponts, ces matériaux sont maintenant abandonnés par ce que :

- La fonte est trop fragile, résiste mal à l'application de surcharges dynamiques et se fissure ;

- Le fer est plus cher et moindre résistant que l'acier.

2.3.1.6.2. PONTS EN ACIER

Diverses nuances d'acier, de qualités différentes, permettent la réalisation de ponts métallique modernes. Les pièces métalliques élémentaires (fers plats, corniches...) sont assemblées soit par rivetage, soit par soudure, soit par boulonnage. Un ouvrage métallique réclame une surveillance et un entretient permanents, après son achèvement.

2.3.1.7. PONTS MIXTES

Ce sont des ouvrages métalliques pour lesquels la dalle de couverture en Béton Armé intervient dans la résistance générale de l'ensem le à la flexion longitudinale.

2.3.2. SELON LA CONCEPTION MECANIQUE.

On distingue deux catégories :

- Les ouvrages isostatiques :

? Arcs à trois articulations ;

? Pont à travées indépendantes ;

? Ponts cantilever ou ponts Gerber ;

? Les consoles.

13

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

14

TRAVAIL DE FIN D'ETUDE

- Les ouvrages hyperstatiques : ? Les ponts cadres ; ? Ponts à travées continues ; ? Les ponts à béquilles.

2.3.2.1. PONTS EN TRAVEE INDEPENDANTE.

Ce sont des ouvrages isostatiques : Poutres sur appuis simple. On réalise ainsi des ouvrages ayant jusque 30m en béton armé, 50m en béton précontraint et jusque 80m en métal.

C'est la solution quasi idéale que l'on rencontre par exemple dans les viaducs d'accès aux grands ouvrages ou dans les ponts particulièrement longs.

2.3.2.2. PONTS A POUTRE CONTINUE.

Ce sont des ouvrages hyperstatiques, qui répondent bien au franchissement de larges brèches avec implantation d'appuis intermédiaires.

La continuité permet de réduire les moments en travée et fait apparaître des moments négatifs sur appuis. Ceci permet une variation de la hauteur des poutres, donc de respecter, dans certains cas, les gabarits imposés par la voie franchie.

2.3.2.3. PONTS CANTILEVERS.

Ce sont des ouvrages isostatiques que les projeteurs n'envisagent plus guère actuellement à cause des pro lèmes qui se posent au droit de l'articulation pour le joint de chaussée et qui n'ont pas trouvé de solution jugée accepta le.

2.3.2.4. PONTS VOUTES ET ARCS.

Ces sont des ouvrages hyperstatiques, qui engendrent des poussées horizontales sur le sol de fondation, d'où la nécessité pour celui-ci d'être particulièrement résistant.

2.3.2.5. PONTS EN PORTIQUES.

Ils engendrent des poussées horizontales à leur ase comme les arcs. L'évolution de la précontrainte permet la réalisation de formes nouvelles dans les portiques.

14

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

15

TRAVAIL DE FIN D'ETUDE

2.3.2. SELON L'UTILISATION

2.3.3.1. PONTS RAILS.

Il est destiné à supporter une ou plusieurs voies ferrées. 2.3.3.2. PONTS ROUTES.

Il supporte des voies de circulation routière. 2.3.3.3. PASSERELLE.

C'est un ponceau réservé aux piétons. Il est de fai le largeur, avec des rampes ou des escaliers d'accès.

2.3.3.4. PONTS CANAUX.

Le pro lème de l'étanchéité y est particulièrement important. 2.3.3.5. AQUEDUCS ET BACHES.

C'est un petit ouvrage généralement voûte et inférieur à 2m utilisé pour le transport de l'eau pota le.

On appelle bâche, un petit aqueduc.

2.3.3.6. PONTS ALEODUC.

C'est un pont, qui livre passage à une canalisation conçue pour le transport des huiles.

2.3.3.7. PONTS MOBILES. Ils peuvent être :

V' Levant : Le tablier est équilibré par des contre poids auxquels il est relié par des câbles, passant au sommet de deux pilonnes placées sur les rives.

V' Tournant : Le ta lier pivote autour d'un axe vertical.

V' Basculants : Le tablier est muni d'un contre poids qui ascule soit en pivotant autour d'un axe horizontal, soit en roulant sur une plate-forme.

V' Transbordeurs : Les véhicules sont placés sur une plate-forme suspendue à une traverse pour passer d'un ord à l'autre de la rèche.

V' Flottants : Le tablier est appuyé sur des bateaux.

15

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

16

TRAVAIL DE FIN D'ETUDE

2.3.4. SELON LA FORME DES POUTRES.

La forme des poutres peut être différente suivant que l'on est en présence d'un pont à poutres latérales, à poutres sous chaussée ou s'il n'y a pas de poutre du tout.

2.3.4.1. POUTRES EN CAISSON.

Elles sont constituées par deux âmes ou plus reliées entre elles par des membrures supérieure et inférieure. Ces mem rures s'appellent également hourdis dans les ouvrages en béton précontraint

2.3.4.2. POUTRE A AME PLEINE.

C'est le cas des ponts à poutres latérales de hauteur relativement fai le ou des poutres multiples sous chaussée.

2.3.4.3. POUTRE A TREILLIS.

Lorsque la hauteur des poutres devient trop importante (cas des ouvrages à poutres latérales de grande portée), et afin de réduire le poids du matériau utilisé, on réalise des poutres treillis. Ceci est une forme des poutres très répandue dans les ouvrages métalliques.

2.3.4.4. POUTRES DE HAUTEUR CONSTANTE OU VARIABLE.

La hauteur, plus grande sur appui qu'à la clé, peut varier suivant une loi para olique sur toute la longueur de la travée.

Mais, la hauteur peut également varier paraboliquement ou linéairement sur une partie de la portée : Ce sont les poutres à goussets.

2.3.4.5. PONTS DALLE.

Il n'y a plus des poutres, la dalle est à la fois élément de couverture et élément porteur. Ils sont souvent réalisés pour les ouvrages de faible portée et pour lesquels le gabarit de la voie franchie et le profil en long de la voie portée ne permettent qu'une fai le hauteur du tablier.

16

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

17

TRAVAIL DE FIN D'ETUDE

2.3.5. SELON LA FORME EN PLAN.

2.3.5.1. PONTS DROIT.

Ce sont ceux pour lesquels l'axe de la voie portée est perpendiculaire à l'axe de la voie franchie (ou à la direction principale du courant de la rivière).

2.3.5.2. PONT BIAIS.

Dont l'angle des deux axes c'est -à-dire l'axe de la voie de circulation et celle de la rivière sont différent de 90°.

2.3.5.3. PONTS COURBES.

Le pont cour e c'est un pont avec des charges excentrées. 2.3.6. SELON LA DUREE DU SERVICE ENVISAGE

2.3.6.1. PONTS PROVISOIRES.

Ils doivent être construits rapidement et pour une durée relativement brève permettant la construction d'un ouvrage définitif.

Ils sont en bois ou métal (poutres de récupération). On utilise également les ponts militaires Bellay.

2.3.6.2. PONTS DEFINITIFS.

Ils sont théoriquement pour une durée de l'ordre d'un siècle et sont évidemment beaucoup plus soignés que les ponts provisoires.

2.4.1 DEFINITION6

Un pont suspendu est un ouvrage métallique dont le tablier est attaché par l'intermédiaire de tiges de suspension verticales a un certain nom re de câbles flexibles ou de chaines dont les extrémités sont reliées aux culées, sur les berges

2.4.2 HISTORIQUE

Les premiers ponts, dont on peut dater l'apparition à cause de leurs anciennetés, permettaient aux hommes de traverser des obstacles naturels comme rivières. On peut alors parler de l'apparition de l'ancêtre du pont suspendu, car ces ponts n'étaient fixés que sur deux bords de la rivière et donc pas supportés par des piliers.

⁶ WW.GOOGLE.WIKIPEDIA

17

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

18

TRAVAIL DE FIN D'ETUDE

Lors de leur apparitions, traverser un pont signifiait rejoindre Dieu, car il traversait un obstacle que Dieu avait placé enfin de se cacher des hommes. Aujourd'hui encore, le pont a une signification religieuse importante et il est à l'origine du surnom du pape, « le souverain pontife ». En effet, le pape est par cette métaphore considéré comme celui qui doit montrer la voie de Dieu.

Dans les civilisations chinoises, incas, ou Africaines, le pont suspendu fut très tôt un moyen de franchissement traditionnel, principalement dans les régions montagneuses ou se présentait la difficulté de gorges à franchir. Ainsi on estime que l'on trouvait plus

de 200 ponts suspendus chez les incas au XVI siècles à l'arrivée des espagnols,
pièces maitresses du vaste réseau de chemins de l'empire amérindien. Ils atteignaient couramment les 50 mètres de longueur, pro a lement plus, soit plus long qu'aucune arche de maçonnerie européenne de l'époque.

Seule l'apparition du pont à structure métallique permettra de dépasser cette distance franchissement sans pilier intermédiaire. Si les Incas furent la seule civilisation amérindienne à développer de tels ponts suspendus, ils existaient dans d'autres civilisations de régions montagneuses du monde, dans l'Himalaya et en Chine ancienne.

On trouvait déjà en Chine des ponts suspendus avec chaines d'acier au III siècle
avant Jésus Christ. Mais ces ponts antiques étaient le plus souvent composés de lianes, et d'un ta lier en ois, permettant le passage d'une charge modeste avec une structure de pont légère. Comme à l'instar de cette passerelle suspendue, au Népal.

C'est en Amérique que nait le pont suspendu moderne. Un juge, James Finley, a l'idée d'un pont suspendu avec des chaines en fer forgé. Le pont Jaco 's Creek est achevé en 1802, à l'ouest de la Pennsylvanie. Jammes Finley, devant le succès de cette formule qui maximum. Mais l'utilisation des ponts fait apparaitre un problème d'oscillation : le pont entre facilement en résonance, et la pression qui s'exerce sur les chaines les faits céder. En réalité, le savoir-faire américain en ingénierie et dans la qualité du fer forgé est bien trop faible. Le développement des ponts est limité en taille, et en charge. De nombreux accidents interrompent le succès naissant du pont suspendu.

La technique va alors franchir l'atlantique pour trouver de nouveaux adeptes chez les Britanniques, qui possèdent une énorme avance dans la métallurgie. Les chaines sont considérablement améliorées. En conséquence, les ponts suspendus deviennent très ambitieux. Les premiers ponts britanniques sont construits vers 1815 et les dimensions ne cessent de croitre. En 1826, le célèbre ingénieur Thomas Telford construit le pont suspendu de menai (menai bridge), de 125 mètres de portée, qui permet le passage des

ateaux à voiles. C'est alors le plus grand pont du monde, la plus part des ponts de l'époque se situant entre 70 et 100 mètres de portées. Le pont suspendu est le seul moyen pour atteindre de telles longueurs, et devient monument à la gloire du progrès, en pleine révolution industrielle européenne.

18

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

19

TRAVAIL DE FIN D'ETUDE

C'est justement l'essor européen de celle-ci qui exporte le pont suspendu sur le continent. En France, la technologie est connue au travers des exploits britanniques relatés dans les journaux. Une mission d'étude des ponts et chaussés et menée en 1821, sans aboutir. Le territoire contient un des fleuves les plus difficilement franchissables à l'époque : le Rhône. Les ponts sont très peu nombreux : 3, dont un rompu (le pont d'Avignon) entre Lyon et l'estuaire. En effet, le fleuve est large, très puissant, et ne connait pas de baisse notable de son flux puisque subissant la fonte des neiges. Sans saison « sèche », il est donc impossi le d'édifier des piles selon la méthode éprouvée. La compagnie Seguin Frère (Annonay, Ardèche), dirigée par Marc Seguin, propose donc un projet innovant en 1822 : le pont suspendu de Tournon.

L'entreprise comprend très vite qu'un pont suspendu classique est impossi le en France du fait de la qualité médiocre des chaines. On tente alors de les remplacer par des faisceaux de fil de fer. C'est la naissance du câble. Apres plusieurs essais et un refus des ponts et chaussées, le projet est finalement accepté. A l'innovation des câbles est ajoutée l'utilisation de béton hydraulique pour la fondation, du béton armé (25 ans avant les premiers brevets) pour les superstructures, et des structures de renforcement rigidifient le tablier en bois. Le pont suspendu a pris sa forme moderne.

En 1823 est construit à Genève la passerelle de Saint-Antoine, puis des 1832 à Fribourg le grand pont suspendu dont le câble en fils tréfilés à 87 kilos de rupture, et utilisés à 27 kilos (fils parallèle) permet d'atteindre 273 mètres de portée. De nombreux pont léger sont ainsi construits : Bercy et Constantine à Paris (101 mètres), Gray, Chateaulin, La Roche-Bernard... mais ces ouvrages étaient très mobiles et les charges de circulation devaient y être limitées. Ils subirent une éclipse en France jusqu'au moment où la création de la poutre de rigidité permit de réaliser des ouvrages d'une tenue compara le à celle des ponts en charpente.

D'après un premier décompte, environ 400 ponts furent construits pendant XIX siècle, une grande majorité entre 1825 et 1850. Nombre sont encore les réalisations toujours en place.

Figure 1 : Pont suspendu ancré au sol, année 1832-1834 de 246,26 mètres de portée

19

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

20

TRAVAIL DE FIN D'ETUDE

Figure 2 : le pont suspendu à chaines, le pont de menai année 1819-1826 de 176 mètres de portée

2.4.3 LES ELEMENTS D'UN PONT SUSPENDU

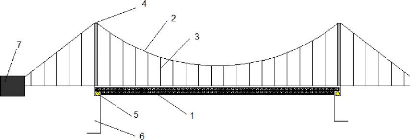
Figure 3 : Eléments d'un Pont suspendu

1. Tablier

2. Câble

3. Suspentes

4. Pylône

5. Appareil d'appuis

6. Culée

7. Massif d'ancrage

A. LA SUPERSTRUCTURE

A.1 LE TABLIER

? Le tablier est une plate-forme horizontale qui supporte la chaussée ou la voie de circulation.

? Le ta lier d'un pont est une structure porteuse qui supporte les charges du trafic routier et les transmet aux appuis ou aux éléments de suspension (suspentes ou arcs)

20

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

21

TRAVAIL DE FIN D'ETUDE

? Le présent chapitre traite d'un élément que l'on retrouve dans tous les ponts, mais on relèvera une différence fondamentale entre un tablier d'ouvrage classique, à poutres sous chaussée ou latérales par exemple, et un tablier d'ouvrage suspendu.

Dans le premier cas, en effet, le tablier assure à la fois une fonction de continuité de la voie portée et une fonction porteuse : il doit supporter son poids propre, les charges permanentes diverses et les charges roulantes.

Dans le second cas, la fonction porteuse est assurée par la suspension et le tablier remplit alors seulement les fonctions de continuité de la voie, de répartition et de transmission des charges.

Dans le cadre de notre travail nous avons un tablier métallique⁷.

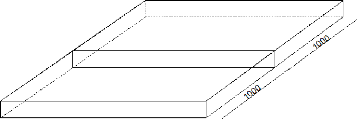
Figure 4 : Tablier du pont suspendu

L = 1210 m (121 travées de 10 mètres) ; l = 24 m et e = 2 m A.2 LES CABLES

Un pont suspendu est un pont dont le tablier est maintenu en suspension par des câbles verticaux qui à leur tour, transmettent les efforts à des câ les porteuses flexi les d'allure parabolique, passant par les sommets des pylônes et dont les extrémités, appelés câbles d'ancrages, sont solidement ancrés aux massifs d'ancrages des deux rives.⁸

On distingue :

- Les câ les d'ancrages

- Les câ les d'équili re

- Les câbles porteurs ou câbles de retenues.

Ici nous considérons les câbles porteurs ou câbles de retenues qui sont des câbles

principaux, d'allure para olique, qui reprennent les efforts transmis par les suspentes

en rejoignant deux pylônes.

Le câble porteur est étendu sur tout le long du pont, et passe par les sommets de deux

piliers. Il maintient le pont et en particulier les multiples suspentes.

Les câbles sont utilisés notamment pour les ponts suspendus ou haubanés, les

⁷ LCPC, les ponts suspendus en France

⁸ www.google.com

21

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

22

TRAVAIL DE FIN D'ETUDE

Pylônes haubanés, les couvertures suspendues ou les contreventements.

Les torons sont des assemblages de fils métalliques enroulés hélicoïdalement autour d'un fil central et constitués d'acier à très haute limite d'élasticité atteignant plusieurs fois celle de l'acier traditionnel de charpente. Ils peuvent contenir des centaines de fils et atteindre des limites de rupture de plusieurs centaines de tonnes. Leur module d'élasticité intrinsèque Ec est plus petit que celui du matériau acier à cause de l'enroulement des fils en hélice : une valeur de 170.000 [MPa] n'est pas rare.

Les câbles sont constitués d'un ensemble de torons alignés (on parle de câbles à torons parallèles) ou enroulés autour d'une âme centrale métallique ou textile (on parle alors de cordages).

Les cordages possèdent un module d'élasticité intrinsèque encore plus faible, qui peut être inférieur à 140.000 [MPa].

Le calcul exact d'une structure composée de câbles est souvent laborieux pour une raison évidente : contrairement aux structures à éléments rigides, la géométrie déformée d'un câble après chargement est très différente de sa géométrie initiale. Cette particularité a une double conséquence : d'une part, le principe de superposition n'est plus applicable et, d'autre part, le calculateur ne peut plus se baser sur la géométrie de la structure non chargée pour écrire les équations d'équilibre.⁹

Les ponts à câbles regroupent essentiellement les ponts suspendus et les ponts à haubans.

Les principaux types de câbles porteurs des ponts suspendus sont :

-- les câ les à fils parallèles, qui se présenter sous forme d'un faisceau de fils maintenus jointifs par des frettes (fils métalliques enroulés sous tension) disposées à intervalles réguliers ; chaque fil est protégé individuellement à l'aide de rai de houille ;

-- les câbles torsadés, dont les fils constitutifs sont assemblés entre eux en torons de 7 à 19 fils, puis ces torons sont câ lés en hélice autour d'un toron central métallique ou textile;

-- les câbles toronnés, clos ou non : ce sont les plus fréquemment rencontrés sur les ponts suspendus ; ils sont constitués de fils enroulés en hélice autour d'un fil d'âme, en couches successives à pas inversés. Les câbles clos sont dotés de fils profilés en Z dans leurs couches périphériques.¹⁰

⁹ Cours de pont à câble

¹⁰ Jean-Armand CALGARO et Roger LACROIX ; Pathologie et évaluation des ponts existants

22

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

23

TRAVAIL DE FIN D'ETUDE

Figure 5 : Les différents câbles

On a les câbles a fils parallèles, les câbles torsadé et Câble toronné non clos A.3 LES SUSPENTES

Dans un pont suspendu, les suspentes désignent les tiges verticales qui relient le tablier du pont aux câbles porteur.¹¹

Les suspentes, organes de liaison entre les câbles et le tablier, peuvent être constituées soit de torons, soit de barres en acier ou en fer forgé.

? Les suspentes en fer forgé¹²

Les suspentes en fer forgé sont les plus anciennes. Elles sont en une seule pièce et comportent, d'une façon générale, des boucles à chaque extrémité dans lesquelles viennent s'accrocher des étriers. Du fait même de la nature du matériau et des systèmes d'attache, elles sont peu sensibles à la corrosion

? Les suspentes toronnées¹³

Les suspentes toronnées sont, comme les câbles, composées de fils tréfilés, mais le diamètre de ces derniers est plus faible. De même que les câbles, elles peuvent être

¹¹ www.google.com Wikipédia

¹² , 13 et 14 LCPC, les ponts suspendus en France

23

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

24

TRAVAIL DE FIN D'ETUDE

soumises aux effets de la corrosion due à la circulation d'eau à l'intérieur des torons. Les suspentes peuvent se présenter sous deux formes :

? suspentes à brin unique, munies d'un culot à chaque extrémité ; l'eau peut s'infiltrer, soit par le culot supérieur, soit le long de la suspente et stagner au niveau du culot inférieur qui constitue alors un foyer préférentiel de corrosion ;

? suspentes à deux brins, il s'agit en général d'un toron unique passant au-dessus d'un collier fixé sur les câbles de suspension ; l'ancrage est assuré en partie basse, à l'aide de deux culots. Dans ce cas, le faible rayon de courbure, au passage au-dessus des câbles, donne lieu à un écrasement de la suspente et à un écartement des fils des couches périphériques, favorisant les entrées d'eau. Comme précédemment, l'eau circule à l'intérieur de la suspente et stagne en partie basse, au niveau des culots, entraînant des risques de corrosion.

? Les suspentes en barre d'acier¹⁴

Les suspentes en barre d'acier sont réalisées le plus généralement en acier mi-dur du type XC-38, par exemple. Elles sont utilisées à l'état brut de laminage ou, de préférence, après un traitement de normalisation ; elles comportent, à chaque extrémité, un filetage permettant l'accrochage sur les organes d'attache, disposition préférable à une liaison par soudage qui ne permet pas de réglage et requiert des techniques d'exécution particulières. A la différence des suspentes toronnées, ce sont des suspentes rigides qui ne peuvent encaisser, principalement pour les suspentes courtes, les moments de flexion dus aux mouvements relatifs du tablier et de la suspension. Il convient donc que les organes d'attache, en parties haute et basse, soient convenablement articulés, faute de quoi on assiste à des concentrations de contraintes en fond de filetage, dues aux efforts parasites et pouvant entraîner des fissurations, voire même des ruptures. Des applications ont, par ailleurs, été effectuées avec des barres en acier E 36 .3 comportant des extrémités refoulées et filetées. Cette solution présente deux avantages :

- D'une part, la partie filetée ayant un diamètre plus important que la partie courante de la barre, le poids d'acier mis en oeuvre est inférieur

- d'autre part, l'acier E 36 .3 présente des caractéristiques de résilience meilleures que l'acier XC-38, ce qui réduit les risques de fissuration à fond de filet.

Sous réserve que les conditions d'articulation des attaches citées plus haut soient respectées, il apparait que ce type de suspente présente les meilleures garanties.

24

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

25

TRAVAIL DE FIN D'ETUDE

? ANCRAGES ET ORGANES D'ATTACHE DES CÂBLES ET SUSPENTES¹⁵ ? Les culots

Les câbles élémentaires sont fixés à leurs points d'attache par des pièces appelées "culots". Ceux-ci sont des pièces massives en fonte pour les anciens culots ou en acier moulé pour les culots plus récents. Ils comportent deux, trois ou quatre trous (selon le diamètre du câble élémentaire) pour le passage des tirants de fixation, et un trou central pour le passage du câble.

a) Culottage des câbles

Le culottage des câbles se fait en plusieurs opérations :

- pose des ligatures dont une se trouvera en un point situé sous le bas du culot ;

- préparation du câble en "chignon" (ou perruque). Cette opération consiste à détrôner la partie du câble située au-dessus de la dernière ligature, à mettre les fils en gerbe régulière et à retourner l'extrémité de chaque fil vers l'intérieur du chignon;

- enfoncement du chignon dans son logement par traction au vérin ;

- chauffage du culot pour éviter le refroidissement trop rapide du métal fusible, et remplissage de la cavité par le métal fusible.

Ce métal fusible était :

- soit un alliage binaire composé de 90 % de zinc de haute teneur, et de 10 % d'antimoine, coulé à une température de 500-550 °C (point de fusion 450 °C) ; - soit un alliage ternaire composé de 84 % de plomb, 7 % d'étain et 9 %

d'antimoine. Cet alliage se coule à une température de 340-350 °C (point de fusion 240 °C). Actuellement, on utilise Cu zinc pur à haute teneur (> 99,5 %) porté à une température de 500 °C recommandé pour son efficacité contre la corrosion (point de fusion 420 °C). Cette température doit être respectée : plus élevée, le zinc recuirait les fils élémentaires, particulièrement ceux des petits câbles ; plus basse, le zinc se solidifierait avant d'avoir atteint la base du culot.

Dans le cas où le remplissage du culot s'effectue avec du zinc pur, on peut vérifier la température de celui-ci avec une baguette de sapin. Celle-ci, plongée dans le zinc et retirée vivement, ne devra comporter aucune trace de zinc et n'être que légèrement décolorée par la chaleur. Si le zinc adhère à la baguette, c'est qu'il est trop froid, si la baguette carbonise, c'est qu'il est trop chaud.

Toutes ces opérations se déroulent avec le câble en position verticale pour permettre au métal fusible de descendre à l'extrémité inférieure du culot. Il est nécessaire, pour garantir un bon remplissage, que le métal fusible ressorte à l'extrémité inférieure du culot.

b) Forme des culots

Le logement dans lequel s'engage le "chignon" peut avoir plusieurs formes. Dans les premiers culots en fonte. La trop grande longueur de la partie cylindrique ne permettait

¹⁵ LCPC, les ponts suspendus en France

25

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

26

TRAVAIL DE FIN D'ETUDE

pas au métal fusible d'arriver jusqu'à l'extrémité, ce qui permettait l'entrée de l'eau dans le vide subsistant entre câble et culot.

Dans les derniers culots en fonte, puis les culots en acier moulé, cette longueur de la partie cylindrique a été réduite. La solution adoptée maintenant pour les nouveaux culots en acier moulé est la forme dite "en tulipe", de façon à avoir un gradient de pression uniforme de l'extrémité du culot à l'orifice de sortie du câble, et un meilleur remplissage du culot par l'alliage fusible.

c) Défauts au niveau des culots

Avant culottage, un câble coupé droit. Pour recevoir l'alliage fusible, le culot doit se présenter verticalement, avec son ouverture en haut et lors de la mise en position, il risque d'y avoir un glissement relatif des couches de fils entre elles (de 30 à 60 mm). Après culottage lors de la mise en position "câbles en service" le phénomène inverse se produit et les fils extérieurs sont plus tendus. C'est la raison pour laquelle, dans la plupart des cas, les ruptures de fils se produisent souvent sur les couches périphériques qui subissent des contraintes plus élevées. Ces fils des couches périphériques représentent une part importante de la section des câbles d'où diminution

Importante du coefficient de sécurité (pour un câble courant de 169 fils, la dernière couche, 42 fils, représente le quart de la section). Le problème le plus important est la corrosion des fils due au séjour de l'eau au voisinage des culots. Dans le cas d'un mauvais remplissage, l'eau s'arrête à l'intérieur du culot au contact du métal fusible et entraîne la rupture des fils par corrosion fissurant. Cette rupture d'un certain nombre de fils entraîne un report de contrainte sur les autres fils élémentaires et une rupture du câble à brève échéance.

Figure 6 : Les suspentes

26

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

27

TRAVAIL DE FIN D'ETUDE

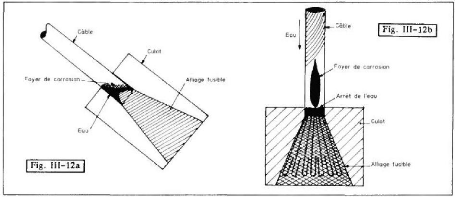
Figure 7 : Les suspentes

La suspension classique à dou le nappe continue à s'imposer, même si des tentatives sont faites pour introduire le monocâble porteur.

Pour améliorer la sta ilité d'ensem le des ponts de très grandes portées, les suspentes verticales sont remplacées par des suspentes inclinées formant un réseau triangulé procurant une bonne rigidité longitudinale.

Les suspentes sont faites d'une paire de câ les et relient le ta lier aux câ les porteurs tous les 10 à 20 m. Côté câble porteur, les suspentes sont soit attachées à un collier par une articulation de type axe sur chape, soit formées en boucle pour ceinturer le collier dans des gorges rainurées.

Les colliers, constitués de deux demi-coquilles cylindriques, sont serrés par des boulons à haute résistance pour produire la résistance de friction nécessaire et s'opposer à tout glissement sur le câble. Côté ta lier, la liaison est réalisée par un étrier s'articulant sur une pièce spéciale fixée au tablier, ou par ancrage sur un appendice extérieur à la poutre et prolongeant la pièce de pont.¹⁶

Figure 8 : Collier de suspension et suspentes

¹⁶ Jean-Pierre DUCOUT ; Ponts métalliques Applications spécifiques

27

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

28

TRAVAIL DE FIN D'ETUDE

A.4 LES APPAREILS D'APPUI

Un appareil d'appui est un élément d'un pont placé entre le ta lier et les appuis, dont le rôle est de transmettre les actions verticales dues à la charge permanente et aux charges d'exploitation et de permettre des mouvements de rotation ou de translation.

Il existe de nombreux types d'appareils d'appui, qui ont été classés ci-après suivant leur fonction, leur conception, qui a évolué au cours du temps, dépend souvent de l'importance de l'ouvrage

? Appareils d'appui métalliques fixes¹⁷

Ils sont conçus pour permettre les rotations et empêcher les déplacements. Il en existe quatre familles (tableau 1).

17 Jean-Armand CALGARO et Roger LACROIX ; Pathologie et évaluation des ponts existants

28

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

29

TRAVAIL DE FIN D'ETUDE

? Appareils d'appui métalliques mo iles

Ils permettent les rotations et les déplacements suivant l'axe longitudinal de l'ouvrage. On distingue quatre types principaux (Tableau 2).

29

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

30

TRAVAIL DE FIN D'ETUDE

? Appareils d'appui en éton Ils sont étudiés dans le tableau 3.

L'appareil d'appuis est un équipement que l'on retrouve dans tous les ouvrages, les appareils d'appui méritent, dans le cas des ponts suspendus, un développement particulier dans la mesure où ils peuvent jouer le double rôle d'initiateur ou de révélateur de désordres liés au comportement général de l'ouvrage.

? ROLE DES APPAREILS D'APPUI

Les appareils d'appui doivent interdire les déplacements d'ensemble du tablier, mais permettre leur libre déformation, de manière à éviter des réactions excessives.

A.5 PYLONE

Les pylônes sont un élément spécifique dont la fonction principale est de transmettre aux appuis la réaction verticale des câbles.

Les pylônes sont les organes d'appui des câbles.

Une pile peut porter de lx pylônes isolés portant chacun une nappe ou un faisceau de câbles. Souvent, pour mieux supporter les efforts transversaux ou pour des raisons

30

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

31

TRAVAIL DE FIN D'ETUDE

relevant de l'architecture, ils sont reliés par une ou plusieurs traverses et forment un portique. Ce portique est couramment appelé "pylône".

Le pylône transmet à la pile la réaction verticale des câbles et les sollicitations secondaires correspondant aux déplacements longitudinaux de ces derniers, ainsi qu'une part des efforts transversaux dus au vent.

La constitution des pylônes a évolué avec les matériaux de construction, maçonnerie à l'origine, puis fonte et fer, et maintenant acier ou béton armé. Suivant la conception générale de l'ouvrage, les pylônes peuvent être :

- encastrés rigides, c'est-à-dire peu déformables ;

- encastrés flexible, volontairement déformables pour suivre le déplacement des câbles à leur sommet

- articulés à la base, pour suivre sans contrainte ces déplacements.

? Pylônes encastrés rigides

Tous les pylônes en maçonnerie ont été conçus et considérés comme encastrés rigides. La majorité des pylônes en béton armé ou en acier sont conçus de la même manière.

? Pylônes encastrés flexibles

Ces pylônes sont toujours soit en acier, soit en béton armé. La différence avec les pylônes "encastrés rigides", est que leurs sections ont été dimensionnées et calculées pour que le mouvement maximal des câbles fixés au sommet sous les charges de calcul et les écarts de température, n'entraîne pas de contraintes excessives. Cela est d'autant plus facile que la hauteur fléchie est plus grande et peut être comptée jusqu'à la fondation (mais en tenant compte aussi des réactions au niveau du tablier).

? Pylônes articulés

Dans ce cas, l'appui à la base du pylône est articulé; le pylône ne subit qu'un effort simple de compression et peut être réalisé avec une section minimale économique. Mais il faut aussi considérer le coût supplémentaire des articulations et de la sujétion d'un encastrement provisoire pendant la construction.

Les premiers pylônes de ce genre, qui étaient appelés colonnes ou fléaux, étaient constitués en bois, puis en fonte, et ensuite en acier et en béton armé.¹⁸

Ils sont ancrés sur de puissantes fondations. Leur construction fait plus souvent appel au

éton qu'à l'acier. Les montants, réalisés en caissons, sont entretoisés sur leur hauteur pour rigidifier la structure sous les effets de compression et de flexion transversale. La solution en acier est intéressante lorsque le montage par grande section est facilité par l'utilisation de puissantes igues flottantes, ce qui implique que le chantier soit maritime.

¹⁸ LCPC, les ponts suspendus en France

31

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

32

TRAVAIL DE FIN D'ETUDE

? LES FORMES DES PYLONES

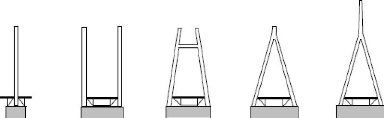
Figure 9 : Les formes des pylônes

Ils supportent toutes les charges affectant le tablier (poids mort, surcharges de chaussée et climatiques) et les conduisent aux fondations.

Ils constituent donc le dispositif essentiel de sta ilité et de résistance de l'ensem le. Plusieurs formes se combinent avec le schéma de haubanage et le type de tablier : mât central unique (figure a), double mât latéral

Indépendant (figure b) ou entretoisé (figure c), pylône en V renversé (figure d) ou en Y renversé (figure e).¹⁹

B. INFRASTRUCTURE

B.1 CULEE ET/OU PILE, FONDATION

? La culée est la partie située sur la rive destinée à supporter le poids d'un ta lier à poutre ou la poussée de la voute d'un pont en arc.²⁰

La culée est un appui extrême du pont.

? La pile d'un pont est un appui intermédiaire supportant le ta lier de l'ouvrage. Il s'agit d'un appui massif et permanent, par opposition aux palées qui sont des appuis plus légers et temporaire.²¹

Les piles et les culées dépendent des deux éléments qu'elles unissent :

- Le sol et

- Le tablier.

Elles sont donc conçues au mieux, en tenant compte de ces facteurs, ce qui se traduit par la résistance mécanique, la sta ilité et l'aspect.

En plus de leur rôle de support des extrémités des ouvrages d'art, les culées doivent souvent soutenir les terres des ouvrages d'accès et sont étudiées en conséquence.

¹⁹ Jean - pierre DU COUT, cours de ponts suspendus métalliques

²⁰ www.google.com, Wikipédia

²¹ www.google.com, Wikipédia

32

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

33

TRAVAIL DE FIN D'ETUDE

? La fondation est l'élément qui permet de transmettre au sol les charges d'une structure. Son étude nécessite :

- d'une part, l'examen de la capacité portante des terrains servant d'assise - d'autre part, la détermination de la fondation proprement dite.

On distingue :

- les fondations superficielles (semelles, radiers) qui transmettent directement aux couches superficielles du sol les efforts apportés par la superstructure ;

- les semelles sur pieux, le rôle de ces derniers étant de descendre les charges de la structure jusqu'à la couche profonde du sol de fondation.

B.2 PIEUX22

On distingue les fondations profondes des fondations superficielles par la définition suivante : toute fondation dont la largeur est inférieure au dixième de la hauteur, elle-même supérieure à 3 mètres, est une fondation profonde.

Les fondations profondes peuvent être réalisées au moyen de pieux ou barrettes, parois, puits.

Dans cette nous parlerons que de la fondation profonde (pieux).

Tableau N° 1 : Les dimensions des pieux

Dimensions	Valeurs extrêmes	Valeurs courantes
Pieux
Diamètres	0,25 m à 2,70 m	0,40 m à 1,50 m
profondeur	5 m à 50 m	10 m à 20 m

Les pieux peuvent être soumis à :

- des forces verticales descendantes, voire ascendantes

- des forces horizontales dues au vent, à des poussées latérales.

? LA FORCE PORTANTE DES PIEUX La force de pieux est limitée par :

- La capacité du sol par sa résistance de pointe et son frottement latéral - La résistance du matériau constitutif du fut du pieu.

Nous distinguons des pieux en béton, acier, bois ou mixte.

²² Henry Thonier ; Conception et calcul des structures de bâtiment, tome 2

33

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

34

TRAVAIL DE FIN D'ETUDE

B.3 MASSIF D'ANCRAGE

Le massif d'ancrage désigne une fondation en éton destiné à l'accrochage d'un tirant ou d'un hau an.

Le massif d'ancrage de la rive est constitué d'une structure creuse en éton armé ( éton dans lequel sont mises des tiges en acier) qui s'appuie sur quatre massifs de fondations. Les tiges d'ancrages, support de suspension sont encastrée dans les murs latéraux du massif dont les dimensions sont approximativement 40 m de longueur et 50 m de hauteur. La traction des tiges est reprise par les câbles de précontraintes.

Hormis pour les ponts dits à "auto-ancrage " où les câbles sont ancrés directement sur le tablier qui supporte en compression la composante horizontale de leur tension, les autres types de ponts suspendus comportent des points d'ancrage situés soit sur les pylônes eux-mêmes, soit sur des massifs ou dans des chambres d'ancrage indépendants.

La solution la plus couramment retenue est celle des massifs ou chambres d'ancrage, dont la conception est fonction de la disposition de l'ouvrage lui-même, de la nature et de la résistance du terrain, des risques d'érosion par affouillement, notamment en cas de crues et de courants violents, voire de la disposition des constructions voisines.

Le massif d'ancrage, disposé à l'arrière des pylônes de rive, enterré ou en partie en élévation, s'impose de lui-même quand on ne dispose pas de terrain rocheux suffisamment dur pour y constituer un ancrage par tirants.

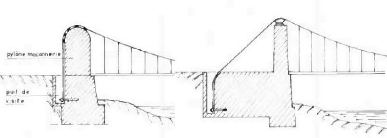
Figure 10 : Les massifs d'ancrage figure 11 : Les massifs d'ancrage

Figure 12 : Les massifs d'ancrage

34

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

35

TRAVAIL DE FIN D'ETUDE

2.4.4 TYPE DES PONTS SUSPENDUS23 ? Selon la forme

Les ponts suspendus se présentent sous trois formes selon que la travée de rive est suspendue ou non :

? Les ponts à travée suspendue unique avec câble d'ancrage direct sur rive (travée de rive, si elle existe, franchie par des tabliers en charpente), donnant des travées de rives réduites ;

Figure 13 : Pont suspendu à travée unique

Pont suspendu à travée unique, avec ancrage sur les rives par des câbles d'ancrage.

? Les ponts à trois travées suspendues (travées centrale et de rives), forme normale du pont suspendu qui doit être un ouvrage de grande portée, donc à travée de rive importante et qu'il faut également suspendre.

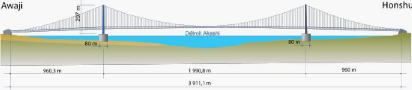
Figure 14 : Pont suspendu à 3 travées suspendues Pont à trois travées suspendues

.

Figure 15 : Pont suspendu à 3 travées Figure 16 : Pont suspendu à 3 travées

²³ www.google.com; pont suspendu Wikipédia

35

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

36

TRAVAIL DE FIN D'ETUDE

? Les formes avec l'une ou l'autre disposition de rive, mais à travées

multiples correspondant aux très longs ponts, ou à ceux permettant des appuis intermédiaires faciles,

Figure 17 : Pont suspendu à multi travées

Pont à trois travées, travée latérale gauche suspendue, travée latérale droite en poutre

? Selon la rigidité On distingue :

? Les ponts suspendus flexibles, soutenus par des câbles ou chaînes parfaitement flexibles;

? Les ponts suspendus rigides où le câble flexible est remplacé par deux poutres rigides articulées chacune avec une culée, et réunies aussi l'une à l'autre par une articulation placée au milieu de la portée.

2.4.5 AVANTAGES ET INCONVENIENTS D'UN PONT SUSPENDU ? AVATANGES

Les avantages sont les suivants :

- Sa structure permet de franchir des plus grandes distances.

- Le tablier étant plus flexible que le tablier des autres ponts, il est plus de donner à la structure une trajectoire courbée.

- L'a sence de nom reux piliers facilite la circulation maritime et terrestre sous le pont.

? INCONVENIENTS

Les ponts suspendus possèdent de nombreux inconvénients mais nous énumérons quelques un :

- Le vent, en effet si sa prise au vent est mal étudiée lors de la conception, cela peut provoquer sa rupture. Lors de ce phénomène on dit que le pont entre en résonnance.

- Il nécessite la présence d'un massif d'ancrage important, volumineux, imposant et surtout très lourd. Ce genre de massif d'ancrage ne peut pas ou très difficilement

36

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

37

TRAVAIL DE FIN D'ETUDE

être implanté sur n'importe quel sol, du fait de son impressionnant volume et de son poids.

- L'entretient des câ les, un travail difficile et dangereux car ce sont ces câ les qui portent l'entière masse du pont. C'est un travail long est couteux car dans la majorité des cas le pont doit être fermé afin de garantir la sécurité des automobilistes.

2.4.6 QUELQUES PONTS SUSPENDUS DANS LE MONDE

Nous dressons un tableau récapitulatif de quelques 10 ponts suspendus dans le monde. Tableau N°2 : les ponts suspendu dans le monde

N°	NOM	Portée (m)	Longueur (m)	Date	Pays
1	Pont du détroit d'Akashi	1991	3911	1998	Japon
2	Pont de Xihoumen	1650	5452	2009	Chine
3	Pont est du Grand Belt	1624	6790	1998	Danemark
4	Pont Osman Gazy	1550	4000	2016	Turquie
5	Pont Yi sun-sin	1545	2260	2012	Corée de sud
6	Pont Runyang	1490	7210	2005	Chine
7	Quatrième pont de Nankin	1418	5437	2012	Chine
8	Pont Humber	1410	2220	1981	Angleterre
9	Pont de Jiangyn	1385	3071	1999	Chine
10	Pont Tsing Ma	1377	3523	1997	Hong-Kong

En général nous avons 104 ponts suspendus dans le monde, en commençant par le Pont du détroit d'Akashi 1991 mètres de portée au pont de Namhae 404 mètres de portée, le

nôtre pont Matadi (République Démocratique du Congo) occupe la 78 position avec
520 mètres de portée, 722 mètres de longueur et construite en 1983.

37

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

38

TRAVAIL DE FIN D'ETUDE

2.5 TERMINOLOGIE SUR LES PONTS

- Tablier : partie supérieur du pont qui reçoit directement les véhicules, la dalle sur

le pont soit platelage.

- Poutres principales : ce sont les poutres de pont dans le sens de la circulation

- Entretoises : ce sont des poutres transversales d'un pont, c'est-à-dire

perpendiculaire aux poutres principales et ont pour rôle d'éviter le asculement.

- Culée : appuis extrêmes (massif d'encrage)

- Appareil d'appuis : pièce en élastomère qui autorise des rotations tout en

transmettant les charges des poutres aux culées

- Dalle flottante : sert de transition entre voie et pont en pour empêcher le

tassement

- Travée : la distance successive entre deux appuis (pile ou culée)

- Portée : la distance comprise entre deux appuis

- Lits majeurs ou mineurs : espaces minimums ou maximums que l'eau occupe

pendant une période.

- Affouillement : érosion sous-eaux provoquée par le courant

38

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

39

TRAVAIL DE FIN D'ETUDE

CHAPITRE 3. DONNEES DU PROJET

3.1 DONNEES NATURELLES DU SITE

3.1.1 DESCRIPTION DU SITE

Grace au logiciel de traitement d'images satellitaires dénommé GOOGLE EARTH, nous avons pu situer notre site, qui quant à lui, est situé au-delà de la concession Kimbanguiste de Lutendele, entre la commune de Ngaliema et Mont Ngafula dans la ville province de Kinshasa.

La commune de Ngaliema est une commune de l'ouest de la ville de Kinshasa en R.D.Congo, elle a une superficie de 224,3 Km ; une densité de 3041 hab/Km et une population d'environ 682.135 ha itant.

La commune de Mont Ngafula est une commune du sud de la ville de Kinshasa en R.D.Congo, elle a une superficie de 358,92 Km ; une densité de 727 hab/Km et une population d'environ 261004 ha itants.

L'avenue principale c'est la route Lutendele via le terminus de M udi passant par la concession Kimbanguiste.

Figure 18 : Description du site

39

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

40

TRAVAIL DE FIN D'ETUDE

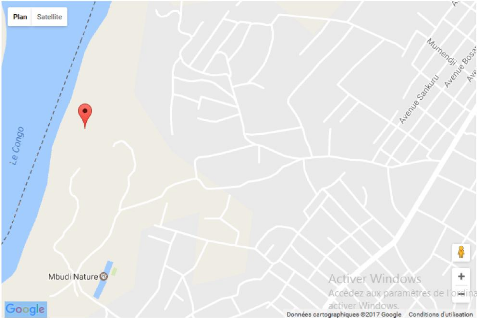
Figure 19 : Description du site

3.1.2 DONNEES TOPOGRAPHIQUE DU SITE

La géomorphologie de Kinshasa est subdivisée en deux parties :

- La zone de plaine (18 communes : Gombe, Barumbu, Kinshasa, Lingwala, Limete, Bandalungwa, Kintambo, Kasa-Vubu, Ngiri-ngiri, Ngaba, Lemba, Matete, Kalamu, Bum u, Masina, Ndjili, Kim anseke et N'sele) constituée généralement des sa les fins argileux et des sables limoneux.

- La zone des collines (6 collines : Maluku, Kinsenso, Makala, Selembao, Mont Ngafula et Ngaliema) constituée de sable de faible cohésion.

40

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

41

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

41

TRAVAIL DE FIN D'ETUDE

- La carte topographique de la ville de Kinshasa

Figure 20 : Carte topographique de la ville de Kinshasa

3.1.3 DONNEES GEOLOGIQUE DU SITE

Dans le site nous avons une carrière des roches ou le long du site nous avons des roches. La roche qui s'y trouve c'est le Grès d'INKISI

Figure 21 : Les grès d'Inkisi figure 22 : Les grès d'Inkisi

42

TRAVAIL DE FIN D'ETUDE

? Le grès est une roche sédimentaire détritique, issue de l'agrégation et la cimentation (ou diagenèse) des grains de sa le. Il peut s'agir d'une roche cohérente et dure

? Les caractéristiques du grès

Tableau N°3 : les caractéristiques de la roche d'Inkisi

Catégorie	Roche sédimentaire
Sous-catégorie	Roche détritique
Principaux éléments chimique	Variable
Minéraux principaux	Variable
Texture	Sable consolidé
Couleur	Variable (rouge, rose, vert, gris, blanc, jaune, marron, violet, doré et argenté)
Utilisation	Pierre de construction, pierre à meule, pavage et sculpture

? L'Inkisi est une rivière qui a sa source en Angola et qui se jette dans le fleuve Congo

3.1.4 DONNEES HYDROLOGIQUES DU SITE

Le fleuve Congo avec un débit moyen de 41.654 , est le plus important fleuve en

Afrique et le second au monde.

La profondeur variant de 200 mètres à 550 mètres

La longueur est de 4.700 km

Le bassin du fleuve est de 3.680.000 Km

L'altitude est de 1.760 mètres

Notre site ne pas naviga le mais néanmoins cela n'empêche que des grands travaux hydraulique soient effectué à la long pour rendre cette passe navigable.

Selon la norme Européenne les bateaux au gabarit Freycinet ne doivent pas dépasser 38,5 mètres avec un tirant d'air de 3 mètres.

42

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

43

TRAVAIL DE FIN D'ETUDE

Figure 23 : Représentation de la coupe longitudinale du pont

N.F.E = + 0.00

N.P.B.E = 86,5 mètres

N.P.H.E = 110 mètres

Gabarit = 38,5 mètres

Tirant d'air = 3 mètres

La somme nous donne 151,5 mètres.

Vue la hauteur inferieur de notre pylône ceci n'empêchera a rien même cette partie du fleuve devienne navigable.

3.1.5 DONNEES GEOTECHNIQUES DU SITE

La géotechnique a pour but de déterminer les caractéristiques mécaniques du sol. Ces derniers ont une grande importance sur la profondeur et le type de fondation à réaliser. La nature et la capacité portante du sol en place guident le choix du type de structure et des méthodes de construction de l'ouvrage.

Dans notre étude nous nous sommes retrouvés dans un site de Plaine où le sol concerné est purement cohérents (sols rocheux) avec influence de la nappe phréatique. Les valeurs des contraintes admissibles en fonction des matériaux sont reprises dans le tableau ci-après :

Tableau N°4 : Les contraintes admissibles

Matériaux	Contrainte admissible de compression en kg/cm^2
Maçonnerie à sec	1 -	1,5
Maçonnerie + mortier de chaux	2,5	- 3,5
Maçonnerie + mortier de ciment	4	- 7
Maçonnerie de briques pleines	10	- 12
Maçonnerie de béton	20	- 25

43

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

44

TRAVAIL DE FIN D'ETUDE

D'autres données relevées sont :

o La teneur en eau uniforme en fonction des profondeurs ci-haut est 20,3% ;

o La cohésion C = 0,25 bars x 100 C = 25,0 KN/m²

o Type de sol : rocheux

o Contrainte admissible : = 3 daN cm

o L'angle de frottement interne = 30°

o ' de jaugé = 0,62 d or d = 16,2 KN/m³ D'où 'jaugé = 10,0 KN/m³ (Valeur uniforme)

o Le convoi est de 56 tonnes

3.2 LES MATERIAUX

Un matériau désigne toute matière utilisée pour réaliser un objet au sens large. Des matériaux de construction sont des matériaux utilisés dans les secteurs de la construction : bâtiment, pont, barrage, route, travaux hydraulique en bref les travaux publics.

Les matériaux utilisés pour la calcul et réalisation de pont sont :

- Le béton

- L'armature (acier)

- L'acier

- Le éton et l'armature forme le éton armé (B.A)

3.2.1 LE BETON

Le béton est un matériau de construction usuel, qui s'apparente à une pierre artificielle. Ses constituants essentiels sont :

- un mélange granulaire de sable et graviers formant le squelette du matériau

- un liant hydraulique, le ciment, assurant la cohésion entre les différents grains du squelette

- l'eau est le réactif chimique provocant la prise du ciment (hydratation)

- éventuellement, et en faible quantité, des produits d'addition, les adjuvants, influençant certaines propriétés ou comportements du matériau béton.

44

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

45

TRAVAIL DE FIN D'ETUDE

L'intérêt du matériau béton réside dans sa facilité de mise en oeuvre puisqu'il se présente à l'état pâteux et qu'il suffit de remplir des moules (coffrages) de la forme de

l'élément à réaliser²⁴.

Son poids volumique est de l'ordre 23 à 24 KN m³, s'il est armé la norme P06 - 004 du B.A.E.L le considère à 25 KN/m^3.

Dans les calculs de béton, on caractérise le béton par sa « résistance caractéristique » en compression à j jours d'âge. Elle est notéef .

Sa valeur est issue d'essais réalisés sur des éprouvettes de éton cylindrique dont la hauteur fait le double de diamètre. La résistance caractéristique est inférieure à la résistance moyenne des essais d'environ 40%.

Les valeurs courantes de f (à 28 jours) sont de 16 à 35 MPa, mais on peut obtenir de valeurs très supérieures avec des bétons à haute performances. Le champ d'application de règle général du BAEL 91 est limité à 60 MPa.

Avant 28 jours, le béton a une résistance f inférieure à f .

f=		pour f = 40 MPa

, ,

Après 28 jours, le béton à une résistance égale à fc28 (nous allons prendre f = 30 MPa) la résistance du béton à la traction est très inférieur à f :

f = 0,6 + 0,06 f

La contrainte limite ultime du béton en compression est :

f = , , X f =

,

X 30 = 17 MPa = 1, 7 KN/cm^2

Avec : =1,5 en général ; c'est un coefficient de béton

: Est fonction de la durée d'application de charge qui vaut 1 lorsque la durée probable d'application des charges considérées est supérieure à 24 heures.

Le éton est un matériau qui, sous l'application de charges de longue durée, va opérer une modification de sa structure interne afin de mieux accepter les sollicitations. C'est le phénomène de fluage.

Le BEAL définit donc deux module d'élasticité :

? Module de déformation longitudinale instantanée (durée d'application des

Charges < 24 heures)

E = 11000 X f (MPa) = 34,17955757 MPa

²⁴ Pascal legrand et J.M.tchouani nana, cours de béton arme-suivant les Règles BAEL 91 Et modifications 99

45

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

46

TRAVAIL DE FIN D'ETUDE

? Module de déformation différée (longue durée d'application)

E = 3700 X f (MPa) = 11,49676027 MPa

3.2.2 ACIERS

3.2.2.1 ACIERS (armatures)

Les armatures pour le béton armé sont sollicitées par des aciers qui distinguent par leur nuance et leur état de surface : on trouve les ronds lisses et les barres à haute adhérence. Pour les ronds lisses, il existe deux nuances : F E215 et F E235, correspondant à des limites d'élasticité garantie de 215 et 235 MPA (les diamètres disponibles sont 6-8-10 et 12 mm) ; pour les barres à haute adhérence, les nuances sont F E400 et F E500 (les diamètres disponibles sont 6-8-10-12-14-16-20-25-32 et 40 mm). Les aciers sont également disponibles sous forme de treillis soudés²⁵.

3.2.2.2 ACIERS26

L'acier est un materiau constitué essentiellement de fer et d'un peu de car one, qui sont extrait de matieres premieres naturelles tirées du sous sol (mine de fer et de charbon). Le car one n'intervient, dans la composition, que pour une tres faible part (generalement à 1%).

? ESSAIS DE CONTROLE DES ACIERS

Les essais de contrôle des aciers sont de deux types :

? Les essais destructifs, qui renseignent sur les qualités mecaniques des aciers. Ce

sont :

- L'essai de traction

- L'essai de dureté

- L'essai de resilience

- L'essai de pliage

- L'essai de fatigue

? Les essais non destructifs, qui renseignent sur la composition et la structure des

aciers. Ce sont :

- La macrographie

- La micrographie

- La radiographie

- Les ultrasons

²⁵ BAEL 91 modifier 99 et DTU associés ; Jean Pierre Mougin

²⁶ Calcul des structures métalliques selon l'Euro code 3 ; Jean Morel

46

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

47

TRAVAIL DE FIN D'ETUDE

? Les caracteristiques mecaniques des aciers

Les valeurs des principales caracteristiques mecaniques des aciers de construction sont :

- Module d'elasticité longitunale : E = 210 000 MPA - Coefficient de poisson : v = 0, 3

- Module d'elasticité transversale : G = 81 000 MPA - Coefficient de dilatation lineaire : A = 11 * 10

- Masse volumique de l'acier : = 78,50

- Contrainte limite elastique de cisaillement pur : = v = 0,58 f

? QUELQUES PROFILES DES ACIERS

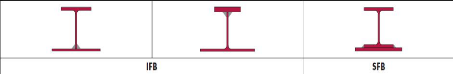
Figure 24 : Les différents profilés

47

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

48

TRAVAIL DE FIN D'ETUDE

Dans le cadre de notre travail nous utiliserons le profilé IPE et HE

? LE PROFILE IPE

Figure 25 : Les profilés IPE

? LE PROFILE HE

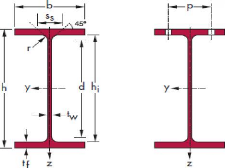
Figure 26 : Les profilés HE

? CLASSIFICATION DES SECTIONS TRANSVERSALES

Quatre classes de sections ont été définies, allant de la section 1 (la plus performante) à la section 4 (la plus fragile), soit :

- classe 1 : sections transversales pouvant atteindre leur résistance plastique, sans risque de voilement local, et possédant une capacité de rotation importante pour former une rotule plastique

- classe 2 : sections transversales pouvant atteindre leur résistance plastique, sans risque de voilement local, mais avec une capacité de rotation limitée

- classe 3 : sections transversales pouvant atteindre leur résistance élastique en fibre extrême, mais non leur résistance plastique, du fait des risques de voilement local.

48

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

49

TRAVAIL DE FIN D'ETUDE

- Classe 4 : sections transversales ne pouvant atteindre leur résistance élastique, du fait des risques voilement local.

Nous considérons seulement les profilés IPE et HE

Tableau N°5 : les contraintes admissibles des aciers

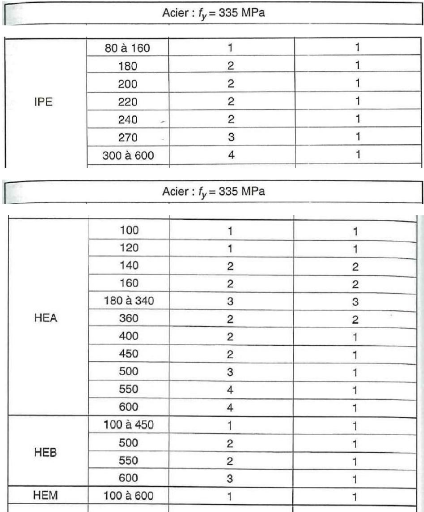
49

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

50

TRAVAIL DE FIN D'ETUDE

3.3 NORME ET METHODE DE CALCUL

3.3.1 NORMES

Une norme est une règle, une loi auxquelles on doit se conformer. La norme est l'ensem le des règles de conduite qu'il convient de suivre au sein d'une évaluation.

Dans le cadre de ce travail nous avons utilisés 3 normes (B.A.E.L, Belge et EUROCODE 1 et 3)

? B.A.E.L

Béton armé aux états limites.

On appel « Etat limite », tout état d'une structure (ou d'une partie de celle-ci) au-delà du quelle elle cesserait de remplir les fonctions ou ne satisferait plus aux conditions pour lesquelles elle a été conçu.

Les états limites peuvent être classés en deux catégories :

? Etas limite ultime, correspond à la ruine de l'ouvrage de l'un de ses

composants par perte d'équili re, rupture ou flam ement (E.L.U)

? Etat limite de service, au-delà desquels ne sont plus satisfaites aux
conditions normales d'exploitation ou de dura ilité (déformation successives, ouvertures des fissures) (E.L.S)

Dans le cas de calcul aux états limites, on considère des coefficients de sécurité partiels :

- Des coefficients minorants appliqués aux matériaux et - Des coefficients de majorations appliqués aux actions.

Ces coefficients sont fixés par le BAEL 91 selon la nature de l'action, les différents types d'actions en présence, l'état limite considéré.

La vérification de la sécurité consiste à s'assurer que l'on a ien, pour chaque état limite : =

Les sollicitations sont les valeurs de N, T, M calculées à partir des actions, où : N : effort normal ; T : effort tranchant et M : moment fléchissant

La règle demande d'envisager plusieurs com inaisons d'actions, les plus courants sont : E.L.U : 1,35 G 1,5 Q

E.L.S : G Q

50

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

51

TRAVAIL DE FIN D'ETUDE

? EUROCODE

L'Euro code 1 : nous a fixés sur les actions du pont

L'Euro code 2 : nous a permis de pré-dimensionner et de dimensionner les structures métalliques (Profilés)

3.3.2 METHODE DES CALCULS

La méthode désigne le chemin celui, tracé à l'avance, qui conduit à un résultat. La méthode se rapporte à la meilleure façon de conduire un raisonnement.

Dans le souci de conférer le caractère scientifique au présent travail et

d'opérationnaliser nos hypothèses, il nous faut utiliser les méthodes comme définit par DESCARTES :

Un procédé destiné à atteindre des règles pour bien conduire sa pensée.

C'est ainsi nous avons recouru aux méthodes historique, fonctionnaliste, analytique et comparative.

- La méthode historique : nous a permis de retracer la genèse des ponts ;

- La méthode fonctionnaliste : nous a permis de comprendre et d'expliquer les faits

mécaniques de la structure à tous les niveaux de son développement en se référant à la fonction que remplit notre ouvrage.

- La méthode analytique : Par cette méthode, nous avons analysé les différentes parties qui nous déterminent les différents éléments nécessaires à la réalisation de notre projet.

- La méthode comparative : nous a permis d'analyser les données de notre structure par rapport aux principes des bases de résistance des matériaux en vue d'en dégager une confirmation de nos hypothèses du départ, pour nous

permettre de déclarer notre structure stable aux sollicitations auxquelles elle est soumise.

3.4 ACTIONS PRISE EN COMPTE ? DEFINITION

On appelle action toute cause sollicitant une structure ou une section c'est-à-dire produisant un jeu des forces dans une structure.

? TYPE DES ACTIONS

On peut citer :

- le poids propre

- Les Charges (exploitation et concentrée) - Les Actions indirectes

- Les Actions dynamiques etc.

51

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

52

TRAVAIL DE FIN D'ETUDE

Les actions sont a priori connus, elles sont chiffrer avec une certaine précision. Les actions sont provoquées par des phénomènes naturels ou artificiels.

NB : Le grand travail consiste à déterminer les actions, leur intensité et leur combinaison.

? LES CHARGES

Les charges regroupent l'ensem le des actions qui peuvent envahir la construction en fonction de sa destination, dites aussi charges utiles, vives, mo iles ou d'exploitation et toutes les actions d'origine extérieure qu'on peut visualiser sous forme des forces.

Les actions dues au trafic routier à considérer sont définies dans l'Euro code 1991-3 section 4 « Actions du trafic routier et autres actions spécifiques sur les ponts routes ».

? LE POID PROPRE

Notons qu'une structure est aussi sollicitée par son propre poids.

P = m g (1) ; = (2) et = (3)

(1) Dans (2) : = = g or =

= g (4)

P = V

P = V g

On a le poids :

- Linéaire : P = * S * g - Surfacique : P = * e * g - Volumique : P = * g - Concentré : P = * V * g

Avec P : poids ; m : masse ; g : 9.81 m/s accélération de la pesanteur

: poids volumique ; : masse volumique ; e : épaisseur ou largeur ou hauteur ou longueur et s : surface

52

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

53

TRAVAIL DE FIN D'ETUDE

? LES ACTIONS INDIRECTES

Ici on peut comprendre que ce sont des actions qui ne peuvent se concrétiser d'em lée sous forme des forces, mais font néanmoins naitre un jeu des forces internes dans une structure :

- Variation de la température

- Tassement du sol

- Fluage

- Retrait des matériaux

- Etc

Tassement : action de diminuer le volume de quelque chose en serrant, en pressant ; son résultat.

Retrait : action de se retirer, de s'éloigner (retrait des matériaux cad ils sèchent ou se refroidit).

Fluage : déformation progressive d'un matériau soumis à un effort prolongée.

53

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

54

TRAVAIL DE FIN D'ETUDE

CHAPITRE 4. CONCEPTION ET PRE-DIMENSIONNEMNT DES ELEMENTS DU PONT

4.1 PRESENTATION DE L'OUVRAGE

- 2 voies

- 3 bandes par voie : 2 * 3 = 6 bandes de circulation

- 3,00 mètres par bande de circulation

- 2 caniveaux de 0,5O mètre par caniveau

- 2 trottoirs de 2 mètres par trottoirs

- 2 bordures le deux cotés (L = 0,50 mètre et h = 0,50 mètre)

- 2 gardes corps le deux cotés (h = 1,00 mètre)

Figure 28 : La coupe transversale du pont

1. Garde-corps

2. Trottoir

3. Caniveaux

4. Bordure

5. Chaussée

4.1.1 COUPE TRANSVERSALE, COUPE LONGITUDINALE, VUE DE DESSUS ET VUE EN PLAN DU TABLIER

Figure 29 : Coupe transversale du tablier

Figure 30 : Coupe longitudinale du tablier

54

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

55

TRAVAIL DE FIN D'ETUDE

Figure 31 : Vue de dessus du tablier

Figure 32 : vue en plan du tablier

55

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

56

TRAVAIL DE FIN D'ETUDE

Nous avons 49 barres dans le treillis transversal Maillage carré : (2 * 2) mètres

4.1.2 CORPS DE LA CHAUSSE

Figure 33 : Corps de la chaussée

1. Couche de roulement en béton bitumineux (5 cm)

2. Couche d'isolation (3 cm)

3. Couche de forme en béton (4 cm)

4. Bac en acier ou tôle en acier (1 cm)

4.2 CONCEPTION ET PRE-DIMENSIONNEMENT DE LA SUPERSTRUCTURE

Figure 34 : La superstructure du pont

La portée : L = 1210 mètres

Les travées extrême : = 201,67 mètres 200 mètres La travée centrale : 810 mètres

56

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

57

TRAVAIL DE FIN D'ETUDE

4.2.1. PREDIMENSIONNEMENT

4.2.1.1 FLECHE

f = = = 134,44 mètres ? f = 135 mètres

4.2.1.2 HAUTEUR TOTALE DE LA PYLONE

=0,2 { 0,22 ? 0,2= =0,22? 0,2 L =H =0,22 L

0,2 * 1210 = H = 0,22 1210 ? 242 m = H = 266,2 m Nous adoptons : H = 250 mètres

· HAUTEUR SUPERIEURE DU PYLONE H = f 2 m = 135 2 = 137 mètres

· HAUTEUR INFERIEURE DU PYLONE

H = H H = 250 137 = 113 mètres

· SCHEMA

Figure 35 : représentation du pré-dimensionnement de la superstructure

57

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

58

TRAVAIL DE FIN D'ETUDE

4.2.1.3 LES POUTRES

Figure 36 : Tablier métallique du pont Nous avons au total 121 travées de la sorte.

4.2.1.3.1 HAUTEUR DE LA POUTRE

H Avec L : la distance entre poutre principale (L = 10 m)

H = = 0,4 m = 40 cm = 400 mm

Nous adoptons : H = 500 mm

4.2.1.3.2 PROFILE

Nous avons le profilé IPE 500

h = 500 mm; b = 200 mm; t = 10,2 mm; t = 16 mm; r = 21 mm; A = 116 * 10 mm ; h =468 mm et d = 426 mm

4.2.1.3.3 NOMBRE DES POUTRES

Nous considérons une poutre sur chaque noeud de 2 mètres, on à 11 noeuds. N = 11 poutres

58

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

59

TRAVAIL DE FIN D'ETUDE

Figure 37 : Les poutres transversales

4.2.1.3.4 NOMBRE D'ENTRE AXES DES POUTRES

N = N 1 = 11 1 = 10 Entre axe des poutres 4.2.1.3.5 ENTRE AXES DES POUTRES

l = 2m = 2000 m

4.2.1.3.6 DISTANCE A NU DES POUTRES

l = l t = 2000 10,2 = 1989,8 mm 2000 mm

4.2.1.4 DALLE

4.2.1.4.1 EPAISSEUR DE LA DALLE

L'épaisseur de la dalle est fonction de l'entre axe des poutres. Voir le tableau ci-dessous.

Tableau N°6 : pré-dimensionnement de la dalle

ENTRE DISTANCE DES POUTRES		EPAISSEUR DE LA DALLE (cm)
	2	16
2	- 3	18
3	- 4	20

Comme l = 2m ; voir 2 m à 3 m ? e = 18 cm 4.2.1.5 ENTRETOISE

Ici nous distinguons deux types d'entretoises : - Entretoise extrême

- Entretoise intermédiaire

4.2.1.5.1 ENTRETOISE EXTREME

H = H = 500 mm

Profilé IPE 500

4.2.1.5.2 ENTRETOISE INTEMEDIARE

H = 500 = 333,3 mm

H =

Nous adoptons : H = 360 mm

59

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

60

TRAVAIL DE FIN D'ETUDE

4.2.1.5.2.1 PROFILE

Nous utilisons le profilé IPE 360

h = 360 mm; b = 170 mm; t = 8 mm; t = 12,7 mm; r = 18 mm; A = 72,7 * 10 mm ; h = 334,6 mm et d = 298,6 mm

4.2.1.5.3 NOMBRE DES ENTRETOISES

La distance entre poutre principale est de 5 m.

L = 5 m = 2 * 5 = 10 m

- Nous considérons une entretoise sur chaque noeud après 2m on aura 4 entretoise

après 2 poutre principales

- N = 4 entretoises/2 treillis

- Nous avons 121 travées de 10 m

- Le nombre des entretoises total : N = 484 entretoises

4.2.1.5.4 NOMBRE D'ENTRE AXES DES ENTRETOISES N = N - 1 = 4 - 1 = 3 entre axe / 2 treillis

4.2.1.5.5 ENTRE AXES DES ENTRETOISES

l = 2 m

4.2.1.5. DISTANCE A NUS DES ENTRETOISES l = 1,9898 m = 1989,8 mm 2000 mm

4.2.1.5 LES SUSPENTES

4.2.1.5.1 NOMBRE DES SUSPENTES

Nous aurons une suspente par noeud du ta lier (après 5 m) L = 810 m (travée centrale)

=

Nom re des noeuds = = 162 noeuds
4.2.1.5.2 HAUTEUR DES SUSPENTES

L'équation qui définit la hauteur de chaque suspente :

H = X (L X)

Avec X : Espace entre suspente (5 m)

L : la portée centrale du pont (810 m) f : flèche (135 m)

60

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

61

TRAVAIL DE FIN D'ETUDE

H =

X (810 X) = 0,66X - 0,000823X 4.2.2. EVALUATION DES CHARGES

4.2.2.1 CHARGE PERMANENTE

4.2.2.1.1 DALLE

P = = 0,18 2500 = 450
4.2.2.1.2 CHAUSSE

- Couche de roulement : P = e = 0,05 2200 = 110

- Couche d'isolation : P = e * = 0,03 * 2300 = 69 Kg/m

- Couche de forme en béton : P = e = 0,04 2200 = 88

- Bac en acier : P = e = 0,01 7850 = 78,5

P = 345,5

G = P P = 450 345,5 = 795,5

4.2.2.2 CHARGE ROULANTE

Nous avons 6 bandes de 3 mètres chacune, donc nous considérons 6 convois de 560 KN :

Q = 6 * 560 = 3360 KN = 336000 Kg

Nous considérons : P = 190 KN = 19000 Kg

S = 24 * 10 = 240 m

= = 1400

Figure 40 : La transmission de charge de la roue sur le tablier

61

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

62

TRAVAIL DE FIN D'ETUDE

h = 0,18 m h = 0,13 m U = 0,35 m V = 0,35 m Arc tg = 36,9 Tg 36,9° = =

? 0,75 =

?X = 0,2325 m

, ,

X' = X - 0,18 = 0,2325 - 0,18 = 0,0525 m = 5,25 cm

a 1,5h = 0,0525 1,5 0,13 = 0,2475 m

V = V 1,5 h 2 h = 0,35 + 1,5 * 0,13 + 2 * 0,18 = 0,905 m

U = U 1,5 h 2 h = 0,35 1,5 0,13 2 0,18 = 1,575 m

S = U * V = 1,575 * 0,905 = 1,43 m

Nous aurons : P = =

,

= 132,86 = 13286

COEFFICIENT DYNAMIQUE DE LA DALLE

,

S= 1 ,

,

,

, = 1,18

= 1 ,

,

4.2.2.3 LA SURCHARGE ROULANTE FIXE

La surcharge roulante fixe due à la foule, d'après la norme Européenne (Euro code 1) nous considérons : 5 KN/m Q = 500

4.2.2.4 LE POIDS TOTAL PONDERE

P = 1,35G + 1,5Q 1,5 S P P = 1,35 795,5 + 1,5 * 500 + 1,5 * 1,18 * 13286 = 25340,145

62

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

63

TRAVAIL DE FIN D'ETUDE

4.2.3. CALCUL DE LA DALLE

? PLAN DE POUTRAISON

Nous avons 3 panneaux à calculer vue qu'ils sont identiques

Figure 41 : Les panneaux de la dalle
Panneau 1

á = = = 1 0,4 la dalle porte dans les deux sens

= = = 1

K = K = 0,027 et K = K = 0,070

M = M = K P L = 0,027 253401,45 2 = 27367,3 Nm M = M = K P L = 0,070 253401,45 2 = 70952,4 Nm

63

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

64

TRAVAIL DE FIN D'ETUDE

Panneau 2

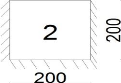
á = = = 1 0,4 la dalle porte dans les deux sens

= K M	=	= 1 ; K = P L		0,025; K = 0,021
	= 0,021 = K
M	= K	P	L	= 0,025
M	= K	P	L	= 0,055
M	= K	P	L	= 0,062

= 0,055 et K = 0,062 253401,45 2 = 21285,7 Nm 253401,45 2 = 25340,1 Nm 253401,45 2 = 55748,3 Nm 253401,45 2 = 62843,5 Nm

Panneau 3

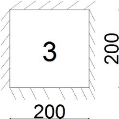
á = ; = = 1 0,4 la dalle porte dans les deux sens

= = = 1

K = K = 0,020 et K = K = 0,052

M = M = K P L = 0,020 253401,45 2 = 20272,1 Nm

M = M = K P L = - 0,052 253401,45 2 = - 52707,5 Nm

64

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

65

TRAVAIL DE FIN D'ETUDE

Tableau N°7 : le résumé des moments dans les panneaux

N°	M	M			M	M
1	27367,3	27367,3			70952,4	70952,4
2	21285,7	25340,1			55748,3	62843,5
3	20272,1	20272,1			- 52707,5	- 52707,5
max	27367,3	27367,3			70952,4	70952,4
? CALCUL DES ARMATURES f = 20 MPA ? f = , = ,				= 11,33 MPA
			,

f = 400 MPA ? f = = = 348 MPA

,

b = 1 m = 100 cm

d = e a = 18 5 = 13 cm

n Calcul des moments réduit : =

.

n Comparaison des moments réduit :

Armature simple Armature double

n Calcul du paramètre de déformation : á = 1,25(1 ?1 2 )

n Calcul du ras de levier : Z = d(1 0,4á)

n Calcul de la section d'acier : A Mu
_st=

.

Dans le cas ou Le calcul de la section en armature simple conduit à utiliser les

aciers à une contrainte faible. Dans ce cas deux possibilités existent :

n Calcul du moment résistant du éton : M = . . d . f

Si alors M M Donc la section nécessite des aciers comprimés.

n Calcul du moment résiduel : M = M M La section d'acier fictive A

Pour équilibre le momentM , il faut une section d'acier A . Le bras de levier du couple interne est : Z = d(1 0,4á )

65

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

66

TRAVAIL DE FIN D'ETUDE

D'où la section d'acier tendue nécessaire est : A =

.

La section fictive : Pour équilibre le moment résiduel, il faut : A = ( )

n La section d'acier comprimée est: A = ( )

La section d'acier tendue total est: A A A

> SUIVANT M = 27367,3 Nm

	,	= 0,14
,

á = 1,25 (1 - v1 2 0,14 ) = 0,189 Z = (1 - 0,4 * 0,189) * 13 = 12 cm

A = , = 6,55 cm ? A = 7,7 cm (5HA 14 m)

> SUIVANT M = 70952,4 Nm

	,	= 0,37
,

á = 1,25 (1 - v1 2 0,37 ) = 0,61 Z = (1 - 0,4 * 0,61) * 13 = 9,828 cm

A = , = 20,7 cm ? A = 21,98 cm (7HA 20 m)

,

66

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

67

TRAVAIL DE FIN D'ETUDE

? PLA N D'ARMATURE

Figure 42 : Plan d'armature du ta lier

4.2.4. CALCUL DES MOMENTS

4.2.4.1 POIDS PROPRES

4.2.4.1.1 POUTRE

Profilé IPE 500 : A = 11600 mm ; e = 18 cm et h = 500 mm

P = h e A = 25000 0,18 0,5 78500 0,0116
= 3160,5 N/m

4.2.4.1.2 ENTRETOISE

H = 500 mm et = 200 mm

H = 360 mm et = 170 mm

L = 10 m ; l = 24 m et l = 2 m

P = = , , = 960,84

P = p p = 0,31605 0,096 = 0,412

4.2.4.2 SURCHARGE FIXE (p') POUR 1/2 PONT

? Garde-corps : 1 KN/m = 0,01 t/m ? Tablette : 0,3 0,15 2,5 = 0,1125

? Trottoir :

- pierre de taille : 0,15 * 0,15 * 2,3 = 0,0518 t/m - sable : 0,1 * 2 * 1,8 = 0,36 t/m

67

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

68

TRAVAIL DE FIN D'ETUDE

- Dallette : 0,05 * 2 * 2,2 = 0,22 t/m

- couche de roulement : 0,05 * 1 * 2,3 = 0,115 t/m

- couche de forme en béton : 0,04 * 1 * 2,3 = 0,092 t/m

- couche d'isolation : 0,03 * 1 * 2,2 = 0,066 t/m

- bac en acier : 0,01 * 1 * 7,8 = 0,078 t/m

La somme donne : 1,1053 t/m

Pour 1/2 pont, nous avons 5,5 poutres, on a :

P` = , , = 0,2 t m

P P' = 0,412 0,2 = 0,612 t m ? CALCUL DES CONTRAINTES

= avec M = P * d

P : charge unitaire

d : Distance entre P et l'axe du pont Ù : aire totale

I : moment d'inertie

Figure 43 : Calcul des contraintes

Avec : d = 10 m ; d = 8 m; d = 6 m; d = 4 m; d = 2 m et d = 0

Nous avons une section unitaire pour chaque poutre : W = 1

Avec 11 poutres : W = à = W = 1 m

L'aire totale : Ù = ? W = 1 11 =

11 m

68

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

I = I =	I = W I = W		d d			= 1 = 1	10 8	69 TRAVAIL DE FIN D'ETUDE = 100 m = 64 m
I = I = I =	I = W I = W I = W		d d d			= 1 = 1 = 1	6 4 2	= 36 m = 16 m = 4 m
I = W d		=		1	0 = 0
I = 2 (I I M = P * d =		I 1 *		10	I I ) = = 10 tm				440 m

- Si P = 1t ; au milieu du pont, donc le coefficient de répartition des charges est

:C = = 0,09 t car chaque poutre sera chargée identiquement

- Si P = 1 t est placé à l'appui 1 du pont, on a une rotation de la section autour de 0, l'axe de la coupe transversale

Ainsi on a à

Tableau N°8 : calcul des contraintes

					_
	=		0,317 =		1		=	0,044
						2
			/	6$	1	1		0
	=		0,2/ 1 =		=	--	=
	=				=
			0,226 =			44	=	0,046
						6
	=				=
			0,18 = --				=	0,0918
	=				=
			0,135 =				=	0,137
6	=	0
		440	0,09 =

P = W

69

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

70

TRAVAIL DE FIN D'ETUDE

Tableau N°9 : calcul des forces

P = 1 * 0,317 = 0,317 t	P =		1 * 0,044 = 0,044 t
P = 1 * 0,271 = 0,271 t	P =	1 * 0	= 0 t
P = 1 * 0,226 = 0,226 t	P = 1	* (-	0,046) = - 0,046 t
P = 1 * 0,18 = 0,18 t	P =	1 *	(-	0,0918) = - 0,0918 t
P = 1 * 0,135 = 0,135 t	P =	1 *	(-	0,137) = - 0,137 t
P = 1 * 0,09 = 0,09 t
? P = 0,9882 t 1 t

? REPARTITION TRANSVERSALE DES CHARGES

Figure 44 : Répartition transversale des charges
Tableau N°10 : calcul des surfaces

Ligne d'influence	Valeur des surfaces des diagrammes (m )
	S = (0,43 * 15)/2	S = (0,19 * 8)/2
1 et 11	= 3,225	= 0,76	S = 2,465
2 et 10	S = (16 ,7 * 0,31)/2	S = (7 * 0,14)/2	S = 2,1
	= 2,59	= 0,49

70

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

71

TRAVAIL DE FIN D'ETUDE

3 et 9	S = (18 * 0,26)/2	S = (5,5 * 0,08)/2	S = 2,12
	= 2,34	= 0,22
4 et 8	S = (20 ,8 * 0,2)/2	S = 0	S = 2,08
	= 2,08
5 et 7	S =	S = 0	S = 2,04
	(0,02 + 0,15)*24 /2
	= 2,04
6	S =	S = 0	S = 2,16
	(0,09 + 0,09)*24 /2
	= 2,16

? LA SURCHARGE DE LA FOULE

Q = 5 KN/m 1,5 = 7,5 = 0,75 t m

4.2.4.2 FOULE

-

-

q (charge positive) :	0,75 *	S =	0,75 *	3,225	= 2,4 t/m
q (charge negative) :	0,75 *	S =	0,75 *	0,76	= 0,57 t/m

? CHARGE DE LA POUTRE LONGITUDINALE LA PLUS CHARGEE

? CALCUL DES SURFACES DES LIGNES D'INFLUENCE DE MOMENT Soit la poutre principale divisée en 10 parties

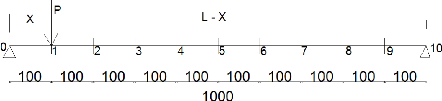
Figure 45 : Calcul des surfaces des lignes d'influence de moment

M =

avec X' = L - X ? M = (L X)X

71

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

72

TRAVAIL DE FIN D'ETUDE

Tableau N°11 : calcul des moments

M = M =	0		M = M = (1	* 3 * 7)/10	= 2,1 tm
= =		0,9 tm =	= =	=
M M			M M	2,4 tm
= =		1,6 tm =	1 5 5	= 2,5
M M
			M = 10

4.2.4.3 CONVOI

Le convoi est de 56t constitué de 4 essieux de 9t, 19t , 14t et 14t, chacun placé dans la position les plus défavorables pour produire des valeurs maximales.

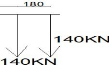
Figure 46 : La répartition des charges du convoi

? ETUDE DE LA POUTRE LA PLUS CHARGEE

? VALEUR DES ORDONNEES DUES AU CONVOI (CAS DES MOMENTS)

? SOIT LE CONVOI AU MILIEU DE LA POUTRE PRINCIPALE L'UN DES ESSIEUX A LA

SECTION 5

Echelle :

X : 10 m 15 cm

Y : 1 tm 2 cm

? SECTION 1

,

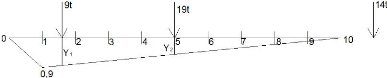
= ?Y =0,5 et = ,

?Y = 0,84

,

72

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

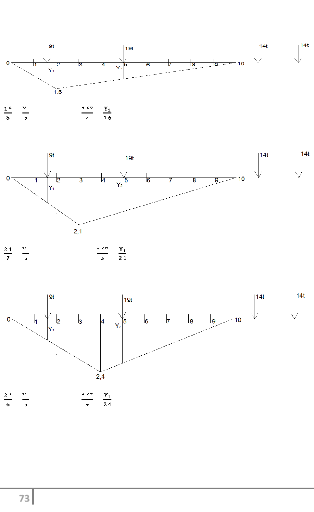
, = ? Y = 1 et ,

=

,

? SECTION 3

? Y = 1,336

= ? Y = 1,785 et ,

=

? Y = 1,169

,

? Y = 1

, = ? Y = 2 et ,

=

73

TRAVAIL DE FIN D'ETUDE

? SECTION 2

,

? SECTION 4

,

73

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

74

TRAVAIL DE FIN D'ETUDE

? SECTION 5

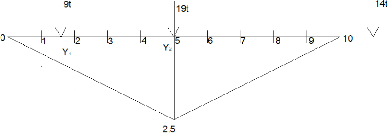
Y = 2,5 et , = ? Y = 0,84

,

Tableau N°12 : calcul des lignes d'influence des poutres

SECTION	Y	Y	9 Y	19 Y	? 9Y 19Y	0,566? 9Y 19Y
1	0,84	0,5	7,56	9,5	17,06	9,65
2	1,336	1	12,024	19	31,024	17,55
3	1,169	1,785	10,521	33,915	44,436	25,15
4	1	2	9	38	47	26,6
5	0,84	2,5	7,56	47,5	55,06	31,16

? EVALUATION DES SURFACES

Surface =

Avec Base = 10 m et Hauteur = le moment à chaque section

Tableau N°13 : calcul des surfaces

S =	S =	0	S =	S =		, 10,5 = m
S =	S =	, 4,5 = m	S =	S =		, 12 = m
S =	S =	, 8 = m	S =	,	=	12,5 m

74

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

75

TRAVAIL DE FIN D'ETUDE

Tableau N°14 : calcul des moments fléchissant

SECTION	S	S (P P )	S q	CONVOI	MOME NTS
		(1)	(2)	(3)	(1)+(2)+(3)
1	4,5	2,754	10,8	9,65	23,2
2	8	4,896	19,2	17,55	41,646
3	10,5	6,426	25,2	25,15	56,776
4	12	7,344	28,8	26,6	62,744
5	12,5	7,65	30	31,16	68,81

M = M = 68,81 MNm = 688100 N; c'est le moment maximal de la poutre ? ETUDE DE LA POUTRE TRANSVERSALE LA PLUS CHARGEE

Nous calculons les entretoises comme des poutres

1. DETERMINONS LES LIGNES D'INFLUENCE DE L'ENTRETOISE POUR 1/2 PONT 1.a SOIT LA CHARGE UNITAIRE (1t) AU MILIEU DE L'ENTRETOISE

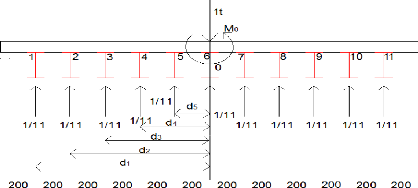
Figure 47 : Ligne d'influence de l'entretoise (charge unitaire au milieu)

M = d d d d d = (10 8 6 4 2) = 2,7 tm

75

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

76

TRAVAIL DE FIN D'ETUDE

1. SOIT LA CHARGE UNITAIRE (1t) A L'APPUI 5

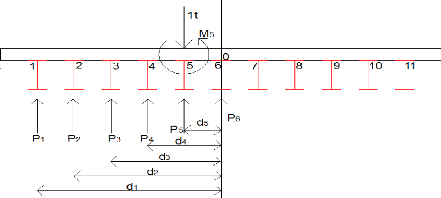
Figure 48 : Ligne d'influence de l'entretoise (charge unitaire est au point 5)

P =

Tableau N°15 : calcul des forces

=	=		=
P	0,14 t	P =	0,11 t
=	=	=	=
P	0,123 t	P	0,1 t
P =	= t	P =	= t
	0,12		0,09

M = P d P d P d P d P d P d 1d

M = 0,14 10 0,123 8 0,12 6 0,11 4 0,1 2 0,09 0 2 M = 1,7 tm

? DIAGRAMME DES MOMENTS DE L'ENTRETOISE

ECHELLE

X : 1m 0,5 cm

Y : 1tm 2 cm

76

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

77

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

77

TRAVAIL DE FIN D'ETUDE

Figure 49 : diagramme de moment de l'entretoise
Tableau N°16 : calcul des moments de l'entretoise

M	= 4,4 cm = 2,2 tm	M	= 0,7 cm = 0,35 tm	M	= 1,744 tm
M	= 2,6 cm = 1,3 tm	M	= 1,3 cm = 0,65 tm	M	= 2,73 tm

? EVALUATION DES SURFACES

- Surface positive : S = , ,

= 6,8 m

- Surface négative : S = , , = 5 m

? DETERMINATION DES CHARGES APPLIQUEES

a) LE POIDS PROPRES

Ces charges ne provoquant aucune flexion de l'entretoise car tout est repris par les poutres principales

b) LA FOULE

La ligne d'influence de la réaction de la dalle sur l'entretoise considérée liée isostatique

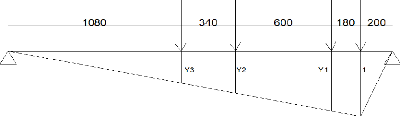
Figure 50

78

TRAVAIL DE FIN D'ETUDE

= ; ? Y = 0,727

,

, , ? Y = 0,511

,

, , ? Y = 0,39

Foule : 0,5 t/m 1,5 = 0,75 tm

M = 0,75 S = 0,75 6,825 = 5 tm

M = 0,75 S = 0,75 5,06 = 3,7 tm

c) CONVOI

Le convoi étant 56 t disposés de 9t, 19t, 14t et 14t par essieu, on a :

(9 * 0,39) + (19 * 0,511) + (14 * 0,727) + (14 * 1) = 37,3 t

Soit : , = 18,6 t

> COEFFICIENT DYNAMIQUE POUR LES POUTRES ET LES ENTRETOISES

,

ä= 1 ,

,

A. CALCUL DE P

> Chaussée : 34,5 Kg/m (déjà calculé)

> Entretoise : P = H N = 0,5 * 2 * 7850 = 7850 Kg/m P = H N = 0,36 * 2 * 7850 = 5652 Kg/m

> Poutre : P = H = 0,5 7850 = 3925

> Dalle : 450 Kg/m (déjà calculé)

> Trottoirs :

- Dallette : 0,05 * 2500 = 125 Kg/m

- Tablette (15*30) cm : 0,30 * 2500 = 750 Kg/m

- Garde-corps : 1 KN/m = 1 KN/m

- Sable : 0,10 * 1800 = 180 Kg/m

P = 1155 Kg/m

D'où : P = 345,5 + 7850 + 5652 + 3925 + 450 + 1155 = 19377,5 Kg/m

78

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

79

TRAVAIL DE FIN D'ETUDE

B. CALCUL DE Q

Q = 1400 Kg/m (déjà calculé)

ä= Les ?	,	: 0,09	0,044)	=	2,526
	1 , 1,012 , = ,
	lignes d'influences des moments donnent 2(0,317 0,271 0,226 0,18 0,135
?	2(0,046 0,0918 0,137) = 0,54
M	= 18,699 2,526 1,012 = 47,3 tm
M	= 18,699 2,526 1,012 = 0,2748 tm
M	= 5 47,3 = 52,3 tm
M	= 3,795 0,2748 = 4,06 tm
M	= M = 52,3 tm = 523000 Nm

? CALCUL DES EFFORTS TRANCHANTS

? CALCUL DES SURFACES DES LIGNES D'INFLUENCE DES EFFORTS TRANCHANTS

T = R =

= P(1 )

Tableau N°17 : calcul des efforts tranchants

T	=	1 t =	T	=	0,6 t =	T	=	, 0,2 t =
T	=	= t	T	=	= t	T	=	, = t
		0,9			0,5			0,1
T	=	= t	T	=	, = t	T	=	0 =
		0,8			0,4
T	=	0,7 t =	T	=	, = t
					0,3

79

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

80

TRAVAIL DE FIN D'ETUDE

· EVALUATION DES SURFACES

Tableau N°18 : calcul des surfaces positives et négatives

SURFACES POSITIVES			SURFACES NEGATIVES			1 S =
10 5 tm		0 S =	0	0 tm
2 =			2 =
9 4,05 tm =		0,1 S	1 =	0,05 tm	2
		= 2
8 3,2 tm =		0,2 S	2 =	0,2 tm	=2
		= 2
7 = tm		S =0,32	^3=	0,45 tm
2,45
6 1,8 tm =		0,4 S	4 =	0,8 tm	=2
		= 2
5 1,25 tm =		0,5 S	5 =	1,25 tm	2
		= 2
4 0,8 tm =		0,6 S	6 =	1,8 tm	=2
		= 2
3 = tm		0,7 S	7 =	2,45 tm	2
0,45		= 2
2 =		0,8 S	8 =	3,2 tm	=2
0,2 tm		= 2
1= 0,05 tm		S =0,92	9 =	4,05 tm
0 0 tm		1 S =	10	5 tm
2 =			2 =

? VALEUR DES ORDONNEES DUES AU CONVOI (CAS DES EFFORTS)

· SOIT LE CONVOI EST PLACE AU DROIT DES DIFFERENTES SECTIONS

Echelles :

X : 10 m 15 cm

Y : 1 tm 4 cm SECTION 0

80

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

81

TRAVAIL DE FIN D'ETUDE

Y = 1

1 Y

10 = 6,6 ? Y = 0,66

1 Y

10

= ? Y = 0,06 0,6

Y = 0 SECTION 1

			Y = 0,9 0,9 = Y 9 5,6
? Y = 0,56

Y = Y = 0 SECTION 2

			Y = 0,8 0,8 = Y 8 4,6
? Y = 0,46

Y = Y = 0

81

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

82

TRAVAIL DE FIN D'ETUDE

SECTION 3

			Y = 0,7 0,7 = Y 7 3,6
? Y = 0,36

Y = Y = 0 SECTION 4

			Y = 0,6 0,6 = Y 6 2,6
? Y = 0,26

Y = Y = 0

82

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

83

TRAVAIL DE FIN D'ETUDE

SECTION 5

			Y = 0,5 0,5 = Y 5 1,6
? Y = 0,16

Y = Y = 0

SECTION 6

			Y = 0,4 0,4 = Y 4 0,6
? Y = 0,06

Y = Y = 0

83

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

84

TRAVAIL DE FIN D'ETUDE

SECTION 7

Y = 0,3

Y = Y = Y = 0

SECTION 8

Y = 0,2 et Y = Y = Y = 0

SECTION 9

Y = 0,1 et Y = Y = Y = 0

SECTION 10

Y = Y = Y = Y = 0

TABLEAU DES VALEURS DES ORDONNEES DUES AU CONVOI

Tableau N°19 : calcul des lignes d'influence des entretoises

section	Y	Y	Y	Y	9Y	19Y	14Y	14Y	?9 Y 19Y 14Y 14Y )		0,566 ? 9Y 19Y 14Y 14Y	0
1	0,66	0,06	0	9	12,54	0,84	0	22,38	12,66		1
0,9	0,56	0	0	8,1	10,64	0	0	18,74	10,6		2
0,8	0,46	0	0	7,2	8,74	0	0	15,94	9,02		3
0,7	0,36	0	0	6,3	6,84	0	0	13,14	7,43		4
0,6	0,26	0	0	5,4	4,94	0	0	10,34	5,85		5
0,5	0,16	0	0	4,5	3,04	0	0	7,54	4,26		6
0,4	0	0	0	3,6	0	0	0	3,6	2,03		7
0,3	0	0	0	2,7	0	0	0	2,7	1,52		8
0,2	0	0	0	1,8	0	0	0	1,8	1,01		9
0,1	0	0	0	0,9	0	0	0	0,9	0,509		10
0	0	0	0	0	0	0	0	0	0

84

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

85

TRAVAIL DE FIN D'ETUDE

VALEURS DES EFFORTS TRANCHANTS
Tableau N°20 : calcul des efforts tranchants

Section	S	S	S	S (P P ) (1)	S q (2)	S q (3)	Convoi (4)		Effort (5)	0
5	0	5	3,06	12	0	12,66	27,72		1
4,05	0,05	4	2,448	9,72	0,0285	10,6	22,79		2
3,2	0,2	3	1,836	7,68	0,114	9,02	18,65		3
2,45	0,45	2	1,224	5,88	0,256	7,43	14,79		4
1,8	0,8	1	0,612	4,32	0,456	5,85	11,238		5
1,25	1,25	0	0	3	0,712	4,26	7,972		6
0,8	1,8	- 1	-0,612	1,92	1,026	2,03	4,364		7
0,45	2,45	-2	-1,224	1,08	1,396	1,52	2,772		8
0,2	3,2	-3	-1,836	0,48	1,824	1,01	1,478		9
0,05	4,05	-4	-2,448	0,12	2,308	0,509	0,489		10
0	5	-5	-3,06	0	2,85	0	-0,21

T = 27,72 t = 27720 Kg = 277200 N

? DIMENSIONNEMENT DES POUTRES ET ENTRETOISES A. LES POUTRES

Le dimensionnement se fait à la flexion :

Notre section est de classe 4 (IPE 300 à 600). IPE 500 et f = 335 MPA

Condition : le moment fléchissant M dans chaque section transversale doit être inférieur au moment résistant, soit : M = M

Avec : M = ; = 1,1 et M = 68,81 tm = 6881 * 10 Nmm

,

On aura : M = M = ? W =

W 2259432,836 mm

Nous adoptons : W = 2441 10 mm Nous avons le profilé IPE 550

85

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

86

TRAVAIL DE FIN D'ETUDE

B. LES ENTRETOISES

W

Avec : M = 52,3 tm = 523 10 Nmm

W = = 1717313 mm

,

Nous adoptons : W = 1728 10 mm Nous avons le profilé IPEA 500

? CALCUL DU TREILLIS

Le treillis principal

Figure 51 : La poutre du treillis la plus chargé

Le cas le plus défavorable, la poutre transversale au milieu qui sera la plus chargée et la poutre longitudinale de 1O mètres de portée

l = 2 m

? EVALUATION DES CHARGES

- Le poids propre de la dalle et chaussée : G = 795,5 Kg/m

- La surcharge roulante : (9000, 19000, 14000 et 14000) Kg

- La surcharge de la foule : Q = 500

86

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

87

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

87

TRAVAIL DE FIN D'ETUDE

? CHARGE SURFACIQUE

P = 1,35 G 1,5 Q = 1,35 795,5 1,5 500 = 1823,925

P = 1823,925 l = 1823,925 2 = 3647,85 Par rapport aux charges linéaires nous aurons

R = R = = , = 18239,25 Kg

Nous avons deux poutres identiques qui concourent vers ce noeud, on aura : 2 R = 2 18239,25 = 36478,5 Kg

? LES CHARGES CONCENTREES

On aura : ? 1,5						P	1,5 *
1,18	* 9	=	15,93 t = 15930 Kg	1,5 *
1,18	*1	9	=	33,63 t = 33630 Kg		1,5 *
1,18	* 14	=		24,78 t = 24780 Kg

Nous aurons :

? Le 1 cas

Figure 52 : premier chargement de la poutre principale du tablier Apres résolution nous avons les réactions d'appuis suivant

Figure 53 : Les réactions d'appuis de la poutre principale du ta lier

88

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

88

TRAVAIL DE FIN D'ETUDE

? Le 2 cas

Figure 54 : deuxième chargement de la poutre principale du tablier Apres résolution nous avons les réactions d'appuis suivant

Figure 55 : Les réactions d'appuis de la poutre principale du ta lier La somme donne :

R = R R = 70304,4 Kg et R = R R = 87225 Kg
Nous considérons : R = 87225 Kg

? CHARGEMENT DU TREILLIS TRANSVERASAL

Noeuds extrêmes : R R = 18239,25 87225,6 = 105464,85 Kg

Noeuds intermédiaire : 2R R = 36478,5 87225,6 = 123704,1 Kg

Figure 56 : chargement du treillis transversal

Apres résolution nous avons les résultats suivants :

Figure 57 : les réactions d'appui du treillis transversal

89

TRAVAIL DE FIN D'ETUDE

Les extrêmes globaux

N = 2171,50 t = 21715000 N ? DIMENSIONNEMENT

= ,

N = N = = ? A = 71302,98 mm

Nous adoptons : A = 743,7 10 mm (le profilé HE100*584 )

? CHARGEMENT DU TREILLIS LONGITUDINAL

Le treillis est sollicité par les réactions aux appuis venant de la poutre

R = R = 785,85 t

L = 810 mètres

l = 10 mètres

Nombre des travées = 81

Nombre des suspentes = 80

? LE TREILLI CHARGE

Figure 58 : chargement du treillis longitudinal

? LES REACTIONS

Figure 59 : les réactions d'appui

R = 27343 t et R = 100 t (réaction des suspentes) Effort dans les barres maximales : 783,06 t

89

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

90

TRAVAIL DE FIN D'ETUDE

> LE PROFILE TUBULAIRE POUR LES SUSPENTES

> DIMENSIONNEMENT

· LES BARRES

N = = ? avec N = 7830600 N

A = ,

= 25712,4 mm

Nous adoptons : A = 270 10 mm (HE600 B)

· LES SUSPENTES

A avec N = 100 t = 1.000.000 t

A , = 3283,58 mm 3284 mm

Nous aurons deux suspentes en un point de câble principal

Figure 60: deux suspentes sur câble principal

A = 1642 mm

Nous adoptons : A = 1680 mm (D = 82,5 mm et t = 7,1 mm)

90

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

91

TRAVAIL DE FIN D'ETUDE

Tableau N° 21 : les caractéristiques des profilés tubulaire

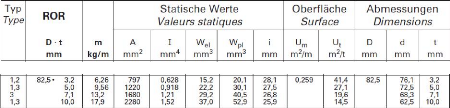
A. CALCUL DE H ET

Figure 61 : les efforts dans le câble principal et pylône

Figure 62 : chargement du câble principal Vue la symétrie nous considérons une partie de la structure

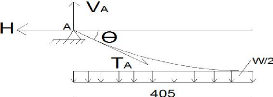
Figure 63 : chargement du demi-câble principal

91

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

92

TRAVAIL DE FIN D'ETUDE

W = ? = , = 77,61 t m

W = = , = 38,8 t m

?M = H Y =0

En remplaçant X par L/2, on a : H =

= ,

= 47148,075 t

,

V = V =

= = 31432,05 t

,

tg = = , =0,66 =33,69

En A, la pente de la tangent au câble est égale à 33,69° La traction en A dans le câble sera égale à

T = vV H = v31432,05 47148,075 = 56664,93 t

, Ou T = -- = ,

= 56664,889 t

tg â = = 1,25 ? â = 51,34

,

T = = ,

= 75473,429 t

B. CALCUL DE LA FORCE DE COMPRESSION DANS LE POTEAU La compression dans le poteau AE sera égale à

Figure 64 : effort de compression du pylône

92

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

93

TRAVAIL DE FIN D'ETUDE

P = T sin T sin â = 56664,889 sin 33,69 75473,429 sin 51,34

P = 90366,658 t = 903666580 N

A = ,

= 2967263,397 mm

Nous adoptons une section carrée : a = b = 2000 mm = 2 m

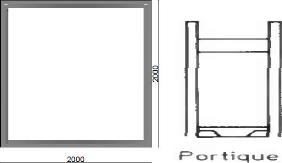
Figure 65 : la section du portique

Nous avons deux pylônes en portique

C. CALCUL DE LA LONGUEUR DU CABLE ENTRE A ET B

On sait que le câ le prend la forme para olique sous l'action des charges verticales W uniformément distribuées.

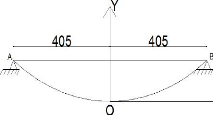
Figure 66 : la longueur du câble principal

L'équation de la parabole est donnée par : Y = a X

Pour : X = 0 ; Y = 0

X = = 405 m ; Y = flèche maximale du câble à mi portée

Y = = ,		= 135 m

,

93

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

94

TRAVAIL DE FIN D'ETUDE

Y = a X si X = et Y =

= a ( ) ? a = ? Y = X ? Y' = ? Y =
On sait que : ds = vdx dy = v1 Y dx

La longueur du câble est donnée par : S = 2 ? ds = 2 ? v1 Y dx

[

S = 2 ? 1 dx= v X ln (X v X )

S = 4759,94 m 4760 m

D. CABLE PRINCIPAL

T = 56664,93 t = 566649300 N

A = , = 1860639,493 mm

Nous adoptons : A = 1.860.700 mm

D = v = v4 , = 1539,58 mm

Nous considérons : D = 1540 mm et A = 1.861.706 mm

E. CABLE TENDU

T = 75473,429 t = 754734290 N

A = ,

= 2478231,997 mm

Nous adoptons : A = 2.478.232 mm

D = v = v4 . .

, = 1776,79 mm

Nous considérons : D = 1778 mm et A = 2.481.607,94 mm

? VERIFICATION DES STABILITES

1. EVALUATION DES CHARGES VERTICALES 1.1. POIDS PROPRE DE LA SEMELLE

P = 60 15 2,5 = 2250 t m

X = = 30 m

94

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

95

TRAVAIL DE FIN D'ETUDE

1.2. POIDS DE LA SUPERSTRUCTURE

P = P P P P P é

- P = 450 24 810 = 8748000 kg = 8748 t

- P = 7,8 0,0116 810 = 73,288 t

- P = 7,8 0,0116 24 = 2,17152 t

- P = 1,155 2 810 = 1871,1 t

- P é = 345,5 24 810 = 6716,520 t

P = 17411 t ? P = = 21,5 t/m

X = = 30 m

1.3. REACTION DES CHARGES

P = T S (P P ) = 14,6 3,06 = 11,54 t

P = , = 0,4808

X = = 30 m

? TABLEAU RECAPITULATIF DES CHARGES VERTICALES

Tableau N° 22 : les charges verticales

CHARGES	EFFORTS	BRAS DE LEVIER	MOMENTS
P	2250	30	67500
P	21,5	30	645
P	0,4808	30	14,424
	E V = 2271,98 t		E M =68159,424 tm

2. EVALUATION DES CHARGES HORIZONTALES

2.1. POUSSEE DUE A LA SURCHARGE DU REMBLAI

H = Q h K or K = tg ( ) avec = 30

K = tg ( ) = 0,33

Q = 1 t m h = 15 m

H = 1 60 0,33 = 19,8 t m X = = 7,5 m

95

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

96

TRAVAIL DE FIN D'ETUDE

2.2. POUSSEE DES TERRES

H = h K= 1,8 15 = 202,5
X = = 5 m

2.3. EFFORT DE FREINAGE

=

H

Avec k = 0,33 ; C = 56 t ; n = 6 et l = 24 m

H = , = 4,62
X = 15 m

> TABLEAU RECAPITULATIF DES CHARGES HORIZONTALES Tableau N° 23 : les charges horizontales

CHARGES	EFFORTS	BRAS DE LEVIER		MOMENTS	H
19,8	7,5	148,5		H
202,5	5	1012,5		H
4,62	15	69,3
? H = 226,92 t		? M =1230,3 tm

> STABILITE AU GLISSEMENT Condition à vérifier : 0,75 ?

? 1,5 ? 0,75 , , = 7,5 1,5

Donc pas de glissement

> STABILITE AU RENVERSEMENT

Condition à vérifier : ? 1,5 ? , = 55,4 1,5

? ,

Donc pas de renversement

> STABILITE A LA CAPACITE PORTANTE

Pour que la résistance passe par le tiers central, il faut que la condition suivante soit vérifiée : e

- e = = ?	, ,	= 9,8 m
	,

- = = 10 m

96

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

97

TRAVAIL DE FIN D'ETUDE

Comparaison : e = 9,8 m 10 m ; donc la résultante passe par le tiers central

	?	CALCUL DES CONTRAINTES
=	?	(1	)	=	, (1 ,	)	=	74,89
=	?	(1	)	=	, (1	)	=
								0,75

DIAGRAMME DES CONTRAINTES :

Figure 67 : le diagramme des contraintes

? LES ASSEMBLAGES

Nous allons utiliser les boulons à haute adhérence (HR)

Nous allons faire le dimensionnement des boulons par rapport aux plus grands efforts dans les barres.

Nous avons :

- un gousset de 8 mm d'épaisseur : t = 8 mm

- effort dans les barres : N

- Classe de boulon : acier S335

- La limite d'élasticité d'un acier : f = 335

- Coefficient de frottement des pièces : = O, 3O

- = = 1,25

- Boulon HR10.9

- La section brute de profilé : A

- La section nette minimale : A =

- La section de perçage : Ù = A A

- La résistance au glissement des boulons

F = or F = 0,7 f A

- Nombre des boulons : n =

- La pression diamétrale : F = ,

97

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

98

TRAVAIL DE FIN D'ETUDE

- La vérification : F F

A. TREILLIS DU TABLIER TRANSVERSAL

Nous les caractéristiques suivantes des boulons :

Les boulons de 30 mm de diamètre (d = 30 mm)

Le diamètre de perçage des trous de boulonnage de 32 mm (d = 32 mm)

K = 1; m = 1 ; = 0,30; f = 1000 MPA ; A = 561 mm et = 1,25
N = 2171,50 t = 21715000 N

, ,

F = ,

,

F =

,

= 94248 N

= 480000 N

n = = 231 oulons

Vérification : F = 94248 N F = 480000 N ; la condition a vérifiée B. LE TREILLIS DU TABLIER LONGITUDINAL

N = 783,06 t = 7830600 N

, F = ,				= 94248 N
	,
F = ,			= 480000 N
	,

n = = 83 oulons

Vérification : F = 94248 N F = 480000 N ; la condition a vérifiée

4.3 CONCEPTION ET PRE-DIMENSIONNEMENT DE L'INFRASTRUCTURE A. MASSIF D'ANCRAGE

Condition : P T

Or : P = V = a c

Le massif d'ancrage a une forme cu ique rectangulaire (a = = c)

C T ? C v

= v

= 31,13 m

,

,

Nous adoptons : C = 35 m

98

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

99

TRAVAIL DE FIN D'ETUDE

Si nous considérons a = b = c = 35 m, il y aura chevauchement entre les deux massifs d'ancrage.

Nous changeons les dimensions : a = 10 m et b = c = 65,25 m

Figure 68 : le massif d'ancrage

B. FONDATION

Nous avons deux pylônes sous semelle, donc une semelle filante

Figure 69 : vue en plan de la fondation

Condition :

· Aux dimensions : = ? B

or = = 2 m

(2)

B B (1)

· Aux contraintes : = B

Avec P = 903666580 N et = 3

= 30

v v

(1) = (2) : B = ?B = = = 54,88 cm

99

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

100

TRAVAIL DE FIN D'ETUDE

Nous adoptons : B = B = 60 m

h = 5 cm = 5 = 1455 cm = 14,55 m

Nous adoptons : h = 15 m

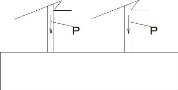
Figure 70 : coupe transversale de la fondation

,

=

G = B B h = 60 60 15 25000 = 135 10 N

=	,		= 100,8

P = B = 1008000 60 = 6,049 10 N m On aura :

Figure 71 : chargement de la semelle

Les réactions d'appui

Figure 72 : les réactions d'appui de la semelle

100

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

101

TRAVAIL DE FIN D'ETUDE

Moment

Figure 73 : diagramme de moment de la semelle
Effort tranchant

Figure 74 : diagramme des efforts tranchants de la semelle

Effort normal

Figure 75 : diagramme des efforts normals de la semelle
Déformée

Figure 76 : diagramme de la déformée de la semelle

101

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

102

TRAVAIL DE FIN D'ETUDE

Efforts

Tableau N° 24 : les valeurs des efforts intérieurs

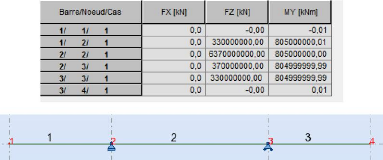
Figure 77 : les noeuds et arres de la poutre

Nous uniformisons les armatures inférieures à ceux des supérieurs (appuis et travée) par rapport au plus grand moment

M = 805000000 Nm

? CALCUL DES ARMATURES

f = 25 MPA ? f = 14,2 MPA f = 400 MPA ? f = 348 MPA a = a' = 5 cm

d = 1500 - 5 = 1495 cm

d' = d - a' = 1495 - 5 = 1490 cm M = 805000000 Nm

=			= 0,00422

,

= 0,00422 = 0,39 ; Simplement armé

= 1,25(1 V1 2 0,00422) = 0,005286 Z = 0,9 1495 = 1345,5 cm

A =

= 1719,2 cm

,

102

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

103

TRAVAIL DE FIN D'ETUDE

Section d'une arre de 40 : S = , = 12,56 cm

N = , = 136,87 137 HA 40

,

A = A = 1720,72 cm (137 HA 40)

- Armature transversal

= = 13,33 mm ? = 14 mm (HA14)

- Espacement des barres

t = 15 = 15 40 = 600 mm = 60 cm ? t = 20 cm ? PLAN D'ARMATURE

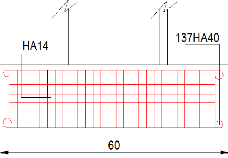
Figure 78 : plan d'armature de la semelle ? LES RESULTATS FINALS

Figure 79 : la description du pont suspendu coté

103

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

104

TRAVAIL DE FIN D'ETUDE

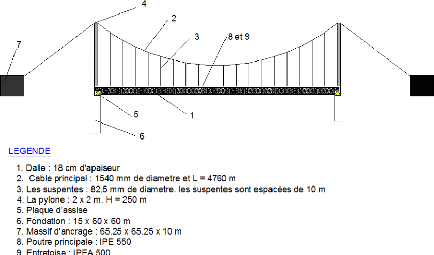
Figure 80 : les nomenclatures et dimensions des éléments du pont

Figure 81 : la représentation du pylône coté

104

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

105

TRAVAIL DE FIN D'ETUDE

CHAPITRE 7. ETUDES DES IMPACTS ENVIRONEMENTAUX ET EVALUATION DU PROJET

7.1 LES IMPACTS ENVIRONNEMENTAUX

7.1.1 DEFINITION :

L'impact environnemental désigne l'ensem le des modifications qualitatives, quantitatives et fonctionnelles de l'environnement engendrées par un projet, un processus, un procédé, un ou des organismes et un ou des produits, de sa conception à sa fin de vie²⁷.

L'o jectif principal de l'étude d'impact est de s'assurer de la faisa ilité technique, socioéconomique et environnementale du projet à la lumière des informations issues des études techniques et de celles recueillies lors des inventaires du milieu récepteur ou dans la littérature existante.

7.1.2 LES ENJEUX DU PROJET

L'étude des impacts environnementaux de la construction du pont a fait ressortir des enjeux qui porteront des dommages sur la iodiversité, l'aménagement du territoire et les diversités culturelles.

? Les différents enjeux sont :

- Pendant les travaux et l'entretien du pont, la poussière et les fumées (COx, NOx, SOx et HAP) générées par les travaux routiers et aux sites de préparation du itume affecteront localement la qualité de l'air. Dans les zones ur aines, villageoises ou du site les vibrations des engins de terrassement pourraient entamer la stabilité du patrimoine bâti.

- Dans les zones de travaux, le bruit des engins de terrassement et des motopompes bouleversera le calme habituel du milieu naturel.

- Pendant les travaux, le passage des engins et véhicules de chantier provoquera un tassement des sols. Ce tassement sera marginal.

- Les sols pourront être souillés par le rejet direct de déchets liquides, notamment les huiles de vidanges usagées, huiles de suintements et de déversements accidentels, les eaux usées de la base vie, et de déchets solides dont les gravats et les déchets divers provenant du chantier.

- Au total, l'impact sur les sols est direct, négatif et de moyenne importance.

- Les eaux de surface polluées pourraient également souiller les eaux souterraines

par infiltration. Cet impact est négligeable au regard de la quantité probable

d'eaux de surface qui seront polluées.

- Au total, l'impact est négatif et d'importance fai le et négligeable.

- Pendant les travaux les bruits des machines des engins de terrassement

perturberont la quiétude de la faune sauvage en général et des oiseaux en particulier.

- Les déversements d'hydrocar ures pourront éventuellement détruire la microfaune aquatique dans le site de prélèvement.

²⁷ WWW.GOOGLE.COM Wikipédia

105

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

106

TRAVAIL DE FIN D'ETUDE

- Les ouvriers prélèveront la faune pour leur alimentation.

- De même, on pourrait assister à des risques de contamination du SIDA et autres IST au niveau des ouvriers et de la population des agglomérations.

- Le projet renforcera davantage la cohésion internationale et rapprochera les deux capitales de cultures différentes.

- Il contribuera à améliorer le mode vie des nomades.

- Le pont sera un facteur de cohésion sociale au niveau local, régional, national et internationale.

4.3.1 Bilan des Impacts et des mesures d'atténuation du projet de construction

Composante affectée	Période	Source d'impact	Description de l'impact		Mesures préconisées	Air et
Travaux et	Activités du	Poussière et	· Arroser les sites et		Ambiance
Exploitation	chantier et	fumée	régler correctement les
	travaux	générée par les	moteurs des engins
	d'entretien	travaux	· Installer les sites de
	et trafic	sur les chantiers, les zones d'emprunt et les sites de préparation du bitume. Fumées provenant du trafic après les travaux.	préparation du bitume loin des agglomérations · Port de masques anti- poussière pour les travailleurs obligatoire · Application stricte de la disposition de limitation des vitesses en agglomération		Sols
Travaux et	Activités de	Terrassement	· Incorporation de
Exploitation	chantier, travaux en	du sol par les engins et	clauses techniques environnementales
	zones d'emprunt et érosion	camions, déchets, érosion des	dans le cahier de charges des entreprises
	hydrique au	sols accrue à	· O liger les
	droit du	cause des	entreprises à restaurer
	pont et des	ouvrages	les zones
	ouvrages	réalisés.	d'emprunt des travaux
	de drainage	Destruction du sol dans les zones d'emprunt et les carrières. Risques de pollution des sols par les déchets	· Protection contre l'érosion des accotements des ouvrages. Mettre en place des dispositifs biologiques de traitement des déchets · Mettre en place des dispositifs biologiques de

106

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

107

TRAVAIL DE FIN D'ETUDE

			liquides et solides des		lutte contre l'ensa lement
		chantiers.	· Exécuter des descentes d'eau sur les remblais

107

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

108

TRAVAIL DE FIN D'ETUDE

ANNEXES

108

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

109

TRAVAIL DE FIN D'ETUDE

Annexe 1 : La représentation d'une partie de la structure

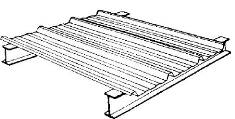
Annexe 2 : Bac en acier

Annexe 3 : Espace vert avant d'atteindre le site

109

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

110

TRAVAIL DE FIN D'ETUDE

Annexe 4 : Vue de loin du site

Annexe 5 : A la recherche du site avec l'aide de GPS et la carte

110

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

111

TRAVAIL DE FIN D'ETUDE

Annexe 6 : Les appuis des suspentes sur le tablier du pont Marechal

Annexe 7 : Les suspentes torsadées du pont Marechal

111

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

112

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

112

TRAVAIL DE FIN D'ETUDE

Annexe 8 : Vue du pont Marechal

Les annexes 9 : Les assemblages

113

TRAVAIL DE FIN D'ETUDE

CHAPITRE 8 : CONCLUSION

Nous voici au terme de notre travail de fin d'études en Bâtiment et travaux publics, dont le sujet a été : CONCEPTION ET CALCUL D'UN PONT SUSPENDU DE 1.210 METRES DE PORTEE DEVRANT RELIER LE CONGO KINSHASA AU CONGO BRAZAVILLE VIA LE QUARTIER MBUDI DANS LA COMMUNE DE MONT-NGAFULA.

C'est avec eaucoup de gratitude que cette modeste étude nous a permis d'avoir un aperçu sur la réalisation d'un ouvrage d'art de très grandes envergures.

Ce pont suspendu va relier les deux capitales le plus proche du monde (Kinshasa et Brazzaville). Nous avons volontiers apporté notre contribution sur la future probable réalisation de ce projet pour le développement intégral de deux pays.

Ce travail est un outil important que nous mettions à la disposition des étudiants, chercheurs, autorités gouvernementales etc.

Il est vrai que l'ouvrage étant principalement métallique, il nécessitera un entretien suffisant pour lutter contre toutes dégradations, corrosions ou tout autre agent destructeur, surtout celles des parties exposées à l'eau et aux intempéries. Pour cela, nous encourageons les autorités à adopter une politique adéquate dans la gestion des ouvrages d'arts car ceci peut être un atout majeur pour l'office national de tourisme (ONT).

En somme, nous osons croire que tous ceux qui auront parcouru ce travail de fin d'étude

énéficieront du fruit de notre formation à l'Institut National du Bâtiment et des Travaux Publics(INBTP).

Nous pouvons enfin conclure que l'ouvrage projeté : pont suspendu de 1210 mètre est un ouvrage qui répond aux normes modernes ou la matière et nous y avons tenu compte des aspects esthétiques, sécuritaires et économiques.

Toutefois, nous n'avions pas de la prétention d'avoir réaliser un travail parfait. C'est ainsi que nous sollicitons l'indulgence de tous les lecteurs pour certaines imperfections qui se seraient glisser indépendamment de notre volonté et nous nous disposons volontiers à toutes les suggestions pouvant contri uer à l'amélioration du dit travail.

113

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

114

TRAVAIL DE FIN D'ETUDE

BIBLIOGRAPHIE

A. Ouvrages

1. J.P. Mougin, Béton armé BAEL 91 modifié 99 et DTU associés, Eyrolls,2000.

2. Euro code 1

3. Norme NBN B03-101

4. Jean-Armand CALGARO, Projet et construction des ponts.

5. Etude d'impact environnemental est social « pose des pipelines traversant le canal de virdi (Cote d'Ivoire)

6. Louis FRUITET et Guy MURRY, construction métallique

7. SETRA Guide technique : Appareils d'appuis en élastomère fretté

8. MOREL J, Calcul des structures métalliques selon l'Euro code 3, Paris Eyrolles (6e tirage), 2005

9. Otemakumi Lotengo M. Guide de la statique appliquée et de la R.D.M édition 2017

10. B. gely et J. A. CALGARO : Conception des Ponts. Presses de l'école nationale des Ponts et Chaussées

B. Notes de cours

1. Kitoko di sola, Cours de béton armé, INBTP, 2011 et Cours de stabilité des constructions, INBTP, 2011.

2. Kuka di mabula, Cours d'analyse des travaux, INBTP, 2011.

3. mbuyamba mukundi, Cours de résistance des matériaux, INBTP, 2014.

4. Mutondo wa mutondo, Cours de ponts et ponts spéciaux INBTP, 2011.

5. Xavier mbutabuba, cours d'étude d'impacts environnemental, BTP5 (INBTP)

114

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

115

TRAVAIL DE FIN D'ETUDE

REMERCIEMENT

Mes remerciements s'adressent à :

- Jéhovah Dieu et Jésus christ

- Ma famille biologique (la famille Lotengo) : Papa Médard, maman Louise, Augustin Welo, Noëlla Aselo, Armel Edungu, Didi Dimandja, Divine Pala, Osongo Exaucé, Abigaël Ndjakambolo.

- La famille Zakuadia : papa Modeste, maman Grace, Espoir Luzolo, VICTORINE NLANDU, Christelle Lukombo, Modeste Nsukulu et Kidima dieu le veut

- Aux ingénieurs BTP : Tsabika Kahungu Sosthène, Bola Bonyange Souvenir, Nsimba Lukeba Fils, Ohanga Ndjeka Evariste, Powa Lokasha, Onzeama Mondanga Celia, Guhwima Gwanzambi Guy, Nkulu Azevedo, Roland Wala, Malongo Joel, Odia Etumbil, Tibasima Wamara Remis, Beauniche Lukombo, Osako Osenge, Omalosombe Raphael, Ntumba Mudiande Jonathan, Etayaka Mondanga Nash, Ngoy Mwiyande Saint, Lukoki Gosi Peter

- Mes encadreurs : Ir MOKE MBENGA EMMANUEL, Ir Assistant MUKINAYI MUKENDJI JOEL, Ir Zina, Ir Gustave Cyani

- Ir Assistant Mutonkole Patrick

- Ebwa Naomie

- Mariana Kafumba et Mervedie Kabala

- Tous les anciens élèves du complexe scolaire les bambins : Muboyayi Corneil, Hénoch Luyeye, Mani, Gaza Monuc, Chimelle Mandudi, Adeseni Patricia, Bofenda Nathan, Samy Ngunde, Grace Mukeveri, Edith Mbaya, Louise Mpialu, Yasser Kele, Jérôme Malilo, Kabedi Kabwe Claudia, Luvefua Armel, Tshukamenga Josiane

- Mes connaissances : Agnes Mbuyi, Pauline Mukongo, Naomie Meki, Elysee Tundanga, Laura Tshikudi, Leaticia Kavungu, Rachel Tshibangu, Mamitsho, Nadege, Marie Kafumba, Divine Kanza, Omambo Charle, Judith Mbokoso, Kisimba Benedicte

- Mes joueurs : Mputu Trésor, Mbayo Kibemba, Gladis Bokese, Mbala Biscotte, tous les champions des Chans 2009 et 2016

- Tous les joueurs du Fc Barcelone : Lionel Messi, André Iniesta, Xavi, Carles Puyol, Ronaldinho, Samuel Eto'o...

- Tous ceux qui m'ont quitté (mort) : ALINE YENGA IPOMA, Fr Bokungu Roger, Papa Wemba, King Kester, Prefet Eustache Ndarabu, Etienne Tshisekedi wa Mulumba

- Toutes les congrégations des Témoins de Jéhovah

- ASELO OTEMAKUMI MERVI

- MAMAN CHRISTINE TOYITOYI

- D.C.M.P (Daring Club Motema Pembe)

- TP. Mazembe (Moise Katumbi)

- Tous les étudiants et étudiantes de l'INBTP KINSHASA (Institut National du Bâtiment et des Travaux Publics)

115

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

116

TRAVAIL DE FIN D'ETUDE

TABLE DES MATIERES

116

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN