Conception et dimensionnement d'un pont en béton armé de 17,00m de portée à ériger sur la rivière Tshuenge dans la ville province de Kinshasa.

[1]

CONCEPTION ET DIMMENSIONNEMENT D'UN PONT EN BETON ARME DE 17m DE PORTEE A ERIGER SUR LA RIVIERE TSHUENGE DANS LA VILLE PROVINCE DE KINSHASA.

Présentés par :

? Ir Dimbi Makoso Jérémie ? Ir Mboy Kupa Vladimir

Pour plus d'infos contactez : [phone], [phone] Facebook : Jérémie Dimbi et Mboy Kupa

[2]

Avant-propos

Le présent travail vient mettre un terme à notre formation au cycle de graduat pour l'obtention du titre d'ingénieur technicien en bâtiment et travaux publics. En effet, ce travail demeure le résultat de beaucoup d'années de travail. Il est à noter que sa réalisation a été rendu possible grâce à l'apport tant instructif, moral, matériel, que financier d'innombrables personnes dont nous proposons ici-bas une liste exhaustive et a qui nous exprimons nos sincères remerciements :

- En premier lieu, nous tenons à remercier le DIEU TOUT PUISSANT créateur du ciel et de la terre pour son immense bonté, lui qui nous a gardés, et a permis que ce jour arrive.

- Le corps enseignant de l'institut national du bâtiment et travaux publics, pour la formation dont nous avons bénéficié et nous saluons leur dévouement. Ces remerciements s'adressent particulièrement à :

? Professeur, docteur, ingénieur, MUTONDO WA MUTONDO pour avoir accepté de diriger le présent travail ainsi qu'à l'assistant ingénieur BTP JEAN PIERRE KIAKA LWATA pour avoir accepté de codiriger le présent travail.

? A toutes les autorités académiques.

? A nos parents pour leur inlassable soutient dans bien des choses. ? A tous nos amis et frères pour leur conseil et assistance.

[3]

PARTIE 1 : GENERALITES

CHAPITRE 1 : Introduction

La fin de tout étude d'ingénieur est sanctionnée par un travail de fin de cycle et c'est dans cette perceptive que s'inscrit le présent travail.

1.1.Problématique

Les habitants des quartiers BIKUKU et BADARA éprouvent des difficultés pour le franchissement de la rivière TSHUENGE qui constitue un obstacle. La route qu'empruntent les usagers est en terre. Cette route qui autrefois permettait de partir de l'aéroport de N'DJILI jusqu'à l'UNIKIN ne permet plus à ses usagés d'effectuer ce trajet et les obligeant ainsi à emprunter le grand boulevard Lumumba et cela suite à la destruction du pont qui reliait les deux rives de la rivière TSHUENGE. Il s'agissait d'un tuyau de la SEP ZAIRE qui parcourrait la route en passant par un autre pont oléoduc sur la rivière. Tous ces ouvrages ont été détruites faute d'entretient témoignent la population trouvée sur place. Malgré le projet de construction de cette route par l'OVD, le constat aujourd'hui est qu'il n'y a pas de chaussé proprement dite. Cette route se trouve aujourd'hui comme oubliée ; seulement quelques motards qui peuvent traverser la rivière pendant la période de décrue (d'étiage) ou au moins s'approcher de la rivière pendant la période de crue. Ce problème se pose à cause de la discontinuité de la route due à l'obstacle qui est la rivière TSHUENGE. Cela empêche non seulement le Trafic routier et des piétons mais aussi des marchandises d'un côté à l'autre de la rivière ce qui ne facilite pas les petits commerces. Les lignes qui suivent en disent long.

1.2.Choix et intérêt du sujet

Ce travail de fin de cycle consiste à résoudre les problèmes auxquels fait face la population qui habite ou fréquente cette route. Pour ce faire, nous avons choisi de faire la conception et le dimensionnement d'un pont à poutre en béton armé de 34m de long à deux travées de 17m de portée qui va relier la commune de la N'SELE et celle de KIMBANSEKE par leurs quartiers respectives BADARA et BIKUKU. Notre plus grande préoccupation sera de construire un ouvrage qui assure parfaitement son service avec un cout optimal. Ce pont contribuera à faciliter le franchissement de la rivière. Cela va influencer le trafic routier de la ville province de Kinshasa et aussi faciliter les petits commerces. Il est exigé de cette étude de produire finalement des détails qui devront permettre de construire un pont possédant une bonne aptitude technico-fonctionnelle pour une durée utile.

[4]

1.3.Méthodologie

La méthode consiste à déterminer la marche que nous avons suivi pour la réalisation de ce travail. Nous avons divisé notre travail en 5 parties :

- Partie 1. Généralités : dans cette partie nous avons énuméré les difficultés que rencontrent la population assortit d'une solution. De situer et de décrire l'ouvrage projetée qui est le pont.

- Partie 2. Collecte des données : cela nous a permis d'obtenir les renseignements sur l'ouvrage porté et le site ;

- Partie 3. Calcul de l'ouvrage : cette partie nous a permis de dimensionner le pont en déterminant les sollicitations et de de trouver les armatures pouvant résister à ces efforts.

- Partie 4. Construction de l'ouvrage : cette partie nous a permis d'évaluer le cout de l'ouvrage.

- Partie 5. Conclusion : nous avons donné un aperçu global du travail, ses avantages sur la société.

Pour la réussite de ce travail, nous avons utilisé la méthode analytique qui est une méthode qui aide à un chercheur de pouvoir faire une analyse de la situation d'un problème étudié par le sujet. C'est ainsi que cette méthode a été très utile dans la conception de l'ouvrage(pont) de notre sujet. Nous allons donner les différentes étapes qui ont conduits à la réussite de ce travail.

? Collecte des données :

Concernant la collecte des données ; nous nous sommes servis de : ? Collecte des données sur le site :

Nous sommes allés sur terrain pour mieux évaluer la situation. C'est ainsi que nous nous sommes servi des techniques suivantes :

? Technique d'interview : pour recueillir certaines informations sur l'obstacle à franchir en interviewant les habitants du quartier.

[5]

Pendant l'interview d'une femme du quartier

? Technique d'observation libre : qui nous a permis à juger en tant qu'observateurs avertis, les informations fournies par les habitants avec la réalité. Par exemple ; nos yeux nous ont permis de voir et de déterminer le niveau de plus haute eaux rien qu'en observant les traces sur les murs des maisons abandonnées dans le lit majeur.

Ruine d'une ancienne habitation dans le lit majeur près du lit mineur en compagnie du plongeur

[6]

? Collecte des données auprès des structures spécialisées :

Nous avons consulté le laboratoire national des travaux publics pour obtenir des informations relatives au sol en place. Nous avons aussi consulté d'autres structures tels que UBA pour nous permettre de bien faire l'évaluation du cout de l'ouvrage.

? Traitement des données :

La zone du projet est très reculée (pas d'électricité, pas d'accès à l'eau potable), on n'a pas pu observer des constructions importantes(R+N). Cela nous a rendu la tâche très difficile pour ce qui est de comparer les données différentes en vue d'en tirer des conclusions. C'est ainsi que faute d'informations, nous nous sommes servi des seules données que disposaient le LNTP sur ladite région. Il s'agit des travaux effectués à LUEBO dans la commune de KIMBANSEKE non loin de la zone du projet. Nous avons donc fait une similitude entre LUEBO et notre zone du projet.

? Consolidation des données :

Nous avons consulté des ouvrages sur le pont en béton armé, les mémoires et TFC de nos prédécesseurs, les notes de calculs des ponts notamment celui du professeur MUTONDO ; en vue d'enrichir notre travail des données à la source.

? Calcul de l'ouvrage :

Nous nous sommes servi de ces données pour le calcul de l'ouvrage c'est-à-dire la conception et le dimensionnement. Dans le respect des étapes et des règles fournies par l'encadreur.

[7]

CHAPITRE 2 : Présentation de l'ouvrage

2.1. Localisation du site

Du point de vue géographique, la zone de projet se situe dans la région KIN-OUEST plus précisément entre la commune de la N'SELE et la commune de KIMBANSEKE. La rivière TSHUENGE sépare les deux communes respectivement par le quartier BADARA et le quartier BIKUKU et cela suivant la direction du tuyau.

PLAN DE SITUATION

2.2. Parties et fonctionnalités

Notre pont est constitué de deux parties : ? La superstructure

? L'infrastructure

2.2.1. Superstructure

C'est la partie supérieure du pont soumis aux charges dues au trafic sur le pont et d'autres actions extérieures. Elle comprend le tablier qui est formé par :

? Poutres principales : ce sont les éléments porteurs qui sont parallèles à l'axe

longitudinal de l'ouvrage porté(route).

Elles ont pour rôle :

- de supporter les charges et surcharges(Trafic) des éléments porteurs se trouvant au-

dessus,

- de permettre la transmission des charges et surcharges du tablier aux appuis par

l'intermédiaire des appareils d'appuis.

? Entretoises ou poutres secondaires : ce sont les éléments porteurs transversalement

aux poutres principales.

Elles ont pour rôles :

- De rigidifier le tablier,

- D'éviter le déversement de poutres principales

[8]

+ Dalle : la partie supérieure du tablier.

Elle a pour rôle :

- De reprendre les efforts dus à la circulation sur le pont,

- De repartir les charges et les surcharges sur les poutres et les entretoises.

+ Couche de roulement : C'est la partie de la route destinée à la circulation des

véhicules.

+ Trottoirs : Ce sont les parties du pont destinées à la circulation des piétons. Ils sont

surélevés à un niveau par rapport à la chaussé pour protéger les piétons.

+ Et d'autres équipements : tels que le garde-corps et les appareils d'appuis.

2.2.2. Infrastructure

C'est la partie inférieure du pont comprenant les appuis et les fondations. Elle constitue le support du tablier. Elle est composée de :

+ Culées : ce sont les appuis extrêmes du pont. Elles ont pour rôles :

> De supporter les efforts horizontaux et verticaux provenant de la superstructure et des

remblais pour les transmettre au bon sol par leurs semelles fondations. Elles sont constituées de :

o Mur garde grève : qui sert à éviter le contact du tablier avec le remblai ; il sert de support pour la dalle de transition (par le corbeau) ; à maintenir le tablier en place.

o Corps de la culée : qui est un voile en béton armé qui permet de transmettre les charges reçues de la superstructure aux semelles.

o Semelles : qui sont les parties supérieures de la fondation qui reçoivent et repartissent les charges de la structure au bon sol

+ Dalle de transition : c'est une dalle placée sous la chaussé aux extrémités du pont. Elle est appuyée d'un côté par la culée(corbeau) et de l'autre coté sur le sol. Elle a pour rôle de limiter les déformations dus au tassement des remblais et aussi d'éviter les chocs dus à la circulation au contact sur la culée.

+ Appareils d'appuis : servent de liaisons entre le tablier et les appuis. Ils ont pour rôles de permettre la transmission des charges du tablier aux appuis, de faciliter les

[9]

rotations libres et la translation du tablier Pa rapport aux appuis. Ils contribuent aux fonctionnements d'ensemble d'ouvrage.

? Mur en aile : sert à maintenir le remblai (sol) qui contribue à la stabilité de la

semelle ; à bloquer le sol situé en amont et à équilibrer la culée qui aura tendance à se renverser.

? Piles :

Ce sont les appuis intermédiaires elles ont pour rôle de transmettre les charges du tablier au bon sol par leurs semelles de fondation.

o Pile de type colonne (poteaux) : les colonnes peuvent être libre en tête ou liées par une poutre chevêtre

NB : Poutre chevêtre : C'est la membrane supérieure horizontale qui relie les colonnes d'une pile. Elle a pour rôles de :

? De réduire la longueur du flambement ;

? Joue le rôle de raidisseur et de solidification des appuis ;

? Sert d'appuis aux vérins lors de changement des appareils d'appuis

2.3. Matériaux utilisés et leurs caractéristiques

Il s'agit d'énumérer les différents matériaux utilisés et de donner leurs caractéristiques : 2.3.1. Béton

Le béton est un matériau composé de ciment, sable, gravillon, eau ainsi que d'autres

adjuvants. Le béton est défini par sa résistance à la compression à l'âge de 28 jours notée fc28 et par sa classe de résistance (30 MPA). Il s'agit de :

o Résistance caractéristique à la compression (fcj) dépend de la classe de ciment, du dosage et des conditions de la fabrication.

fcj = a Rc (C/E-0,5) ( Bollomey)

Avec a : -coefficient dépendant du matériau égal à 0,55 pour les concassés de bonne qualité,

-Rc : résistance du ciment - C/E : rapport ciment-eau - 0,5 : équivalence

Avec - fe : limite d'élasticité de l'acier

[10]

o Résistance caractéristique à la traction (ftj) qui est liée à la résistance à la compression du béton(fcj)

ftj = 0,6+0,06fcj

o La contrainte à la compression à l'état limite ultime(fbu)

Avec - O : coefficient de durée de charge égale à 1 puis que la durée d'application de la charge est supérieure à 24heure ;

o ?b : coefficient de sécurité du béton. Il vaut 1,5 dans le cas général

o La contrainte de compression à l'état limite de service (fbu)

Fbu =0,6fcj

On notera :

? Le coefficient de poisson (y) : représente la variation relative des dimensions transversale d'une pièce soumise à la variation relative de dimensions longitudinale y=0,2 pour le calcul des déformations (ELS) y=0 pour le calcul des sollicitations (ELU) 2.3.2. Acier :

Matériaux obtenue par alliage de fer, de carbone en faible pourcentage (0,15% à 0,25%) pour la nuance semi dure et dure. Module d'élasticité de l'acier est de 2. 1O⁵MPA. Contrairement au béton, l'acier possède une bonne résistance en compression et en traction.

o Résistance caractéristique de l'acier en ELU :

[11]

> ?s : coefficient de sécurité de l'acier valant 1,15 dans le cas générale et 1,00 dans le cas accidentel

o Résistance caractéristique de l'acier en ELS,

fs = min{ v }

NB : - l'infrastructure est en contact avec l'eau. La fissuration n'est pas souhaitable pour la culée et la pile (fissuration préjudiciable).

> Nous ne tenons pas compte de l'effet du vent et des intempéries puisque notre pont est en béton armé (lourd) et s'élève à moins de 4m au-dessus de l'eau.

Le béton armé est caractérisé par sa grande résistance à la compression et à la traction. Cette propriété très particulière est due à l'association de deux matériaux complémentaires :

> Le béton pour sa résistance à la compression > L'acier pour sa résistance à la traction

2.4. Normes utilisées

> Norme belge NBN B 03-101 : pour le train de charge et autres chargements > B.A.E.L. 91 R 99 Février 2000 : pour le calcul du béton armé

[12]

PARTIE 2 : COLLECTE DES DONNEES

CHAPITRE 3 : Données du site

3.1. Données topographiques et bathymétriques

3.1.1. Données topographiques Le site de Kinshasa comprend deux zones géomorphologiques :

? La plaine du pool bordant le fleuve Congo au nord et constituée par deux terrasses emboitées dont l'altitude varie de 275 à 340 m

? La zone des collines, dont le sommet culmine à 550 m d'altitude, présentant dans

l'ensemble des pentes de l'ordre de 12 à 30 % pour les altitudes variant de 345 à 550m ; elle est située au sud, et sud-ouest de la ville.

Le terrain étudié est situé dans la zone de la plaine.

3.1.2. Données bathymétriques

Pour obtenir la bathymétrie de la rivière, nous nous sommes servi d'un plongeur équipé d'une tige. La tâche de ce dernier était de plonger le bâton aux endroits indiqués, de maintenir son doigt à la profondeur à laquelle s'est plongé le bâton pour que nous la prélevons à l'aide du ruban. Voici comment se présente la coupe bathymétrique de la rivière :

Fig.4

3.2. Données hydrauliques et géologiques
3.2.1. Données hydrauliques

L'ouvrage prévu est un pont qui surplombe une rivière et celle-ci à un débit qui varie au fil de saison et des années. Afin de pouvoir implanter adéquatement le pont et d'installer les fondations aux meilleurs endroits, Il est nécessaire d'analyser le comportement de la rivière.

[13]

Pour obtenir la vitesse d'écoulement des eaux, nous nous sommes servi de la technique de flottage. Nous avons laissé un objet léger en plastique flotter sur l'eau suivant le courant en déterminant nous-même la distance que cela devrait parcourir. Nous avons noté le temps mis par l'objet pour parcourir cette distance. Nous avons divisé la distance parcourue par le temps pour obtenir la vitesse que nous considérons dans notre travail.

> Vitesse d'écoulement (V_e) : 0,9177 m/s

> La profondeur de basses eaux (PBE) : 0,50m

> La profondeur de hautes eaux (PHE) : 1,20m

3.2.2. Données géologiques

D'après l'esquisse géologique du sous-sol de Léopoldville au 1/40.000^eme dressée par A. EGOROFF (1955), la zone reconnue est couverte principalement de sables de la Lemba. Ce sont des sables généralement fins, très mal classés, avec de gros grains épars et de rares débris de gros polymorphe. Ils sont parfois argileux en profondeur et humifères en surface ; au contact avec le sable kaolineux, ils se chargent de débris de plantes et deviennent noirs ou bruns. Il est à noter qu'en absence d'un levé topographique, toutes les profondeurs sont mesurées à partir de la surface du terrain naturel. Il a été effectué un sondage par puits manuel, suivi d'un sondage à la tarière pour identifier la nature et évaluer l'épaisseur des sols traversés dont voici les résultats :

> Résultats de sondage par puits manuel

> De 0,00 à 0,60 m : sable fin noirâtre + racine ;

> De 0,60 à 1,00 m : sable fin brunâtre ;

> De 1,00 à 2,00 m : sable limoneux jaunâtre.

> Résultats de sondage à la tarière

> De 0,00 à 0,60 m : sable fin noirâtre + racine ;

> De 0,60 à 1,00 m : sable fin brunâtre ;

> De 1,00 à 5,00 m : sable limoneux jaunâtre.

Généralement le tirant d'air varie de 1,0m à 2,0m. Nous adoptons un tirant d'air est de 1,50m.

[14]

3.2.3. Données hydrologique

La nappe aquifère n'a été repérée dans tous les sondages lors de la campagne géotechnique réalisée à la fin du mois de juillet 2019.

3.3. Données géotechniques

Dans cette partie se trouve consignés tous les renseignements relatifs aux sondages et essais réalisés, à leur interprétation, au calcul de la contrainte admissible, ainsi qu'au type de niveau d'assise de fondation de l'ouvrage projeté. L'étude géotechnique est l'une des informations les plus importantes en début de projet, car elle constitue le pilier des décisions à prendre lors de l'activité de conception structurale de l'ouvrage. Les résultats de cette étude influencent la conception de l'ouvrages, les dimensions des éléments de soutiens de la superstructure. Il a été effectué un essai de pénétration dynamique et des essais en laboratoire dont voici les résultats :

? La résistance dynamique de pointe du sol d'assise :

- à 4m, RA = 2,4 MPa

- à 3m RA = 2,2 MPa

? [a contrainte admissible :

- à 4m, óadm = 0,24 MPa

- à 3m, óadm = 0,22 MPa

? L'angle de frottement interne : õ = 25°

? [a cohésion du sol : C_u = 0,10 bars = 1 t/m²

? Profondeur d'encrage : 5m

NB : elles constituent l'un des éléments du choix de la solution pour le franchissement projeté.

3.4. Tirant d'air

[15]

CHAPITRE 4 : Données relatives à l'ouvrage porté 4.1. Profils en long de la voie porté

C'est une coupe longitudinale de la voie qui permet d'en obtenir l'allure de la route. Etant donné que la route est en terre nous nous sommes servis de celui du terrain naturel.

PROFIL EN LONG DU TERRAIN NATUREL

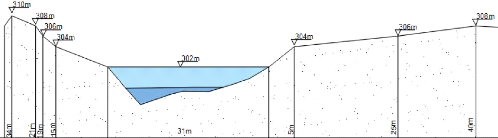
Après avoir prise en compte les différents paramètres liés à l'obstacle naturel(rivière), notre ouvrage présente une longueur de 34m.

4.2. Profil en travers

C'est la coupe transversale de l'ouvrage porté qui donne les détails de la géométrie et des équipements de l'ouvrage. Etant donné que la route n'est pas en terre

proprement dite, le profil en travers n'existe pas. C'est ainsi que nous nous sommes proposés ce profil en travers :

PROFIL E N TRAVERS PROJECTE

. Ceci nous permet d'obtenir la largeur du pont dont voici les composantes : ? Largeur de la bande : 3,50m ? Largeur du trottoir : 1,50m ? Bordure : 0,30m

[16]

? Séparateur en béton : 0,40m

? Nombre des voies de circulation : 2

? Fossé : 0,50m

4.3. Gabarit sur le pont

Le gabarit sur le pont est donné en fonction de la hauteur sous d'autres ouvrages dans la ville de Kinshasa. Nous adoptons le gabarit est de 4,50m comme c'est le cas de saut de moutons de rond pont Mandela.

[17]

PARTIE 3 : CALCUL DE L'OUVRAGE

Le chapitre vise à calculer la stabilité et de s'assurer que l'ouvrage va travailler dans les conditions requises. Le pont aura deux travées indépendantes de 17m de portée. Le calcul consistera à stabiliser l'une de travée ainsi l'autre le sera puisqu'elles sont identiques.

3.1. Conception du pont

Largeur utile du pont = (2×3,50m) + (2×0,50m) + (2×0,30m) + (2×1,50m) + (0,40m) = 12m CHAPITRE 5 : Pré dimensionnement

5.1. Superstructure

5.1.1. Poutre principale

V' Hauteur économique (hp) :

Généralement la hauteur de la poutre est déterminée par la relation :

L/15= h_p =L/10

Pour le pont à poutre en béton armé, la hauteur économique de la poutre est donnée par :

L

li p = on a : lip = 1127= 1,416m

1 2

Nous optons pour h_p= 1500cm ? h_p= 1,50m

V' La base de la poutre(B_p) :

Généralement, la base de la poutre est déterminée par la relation :

0,3hp =B_p= 0,5hp

0,3(1,50) = B_p =0,5(1,50)
0,45= B_p= 0,75

Nous prenons : B_p = 0,50m

V' Entraxe entre poutres principales (l1) :

De manière générale, l'entraxe entre les poutres principales varie de 2m à 4m. Nous optons pour 3m. Le nombre d'entraxes : Np-1= 3 entraxes

[18]

ü Encorbellement(l3) :

L'encorbellement est obtenu par : l3 = = 1,5m l3= 1,5m

ü Ecartement entre nu des poutres principales (l2) : l2= l1-2(Bp/2) = 3-2(0,50/2) = 2,5m alors ; l2= 2,5m

ü Nombre des poutres (N_p) :

Le nombre de poutres principales s'obtiendra par la relation :

= 4

5.1.2. Dalle

L'épaisseur de la dalle varie généralement de 16 à 20cm en fonction des entraxes entre poutres principales. C'est ainsi que nous optons une épaisseur de 18cm pour 3m d'entraxe.

Soit ; hd = 18cm
5.1.3. Entretoise

ü Hauteur :

> Aux appuis :

Pour faciliter l'accès aux appareils d'appuis lors des travaux d'entretien du pont, la hauteur de l'entretoise sera réduite. Généralement, cette hauteur est donné par : h_a= h_p = (1,5)= 1,00m

> En travée :

Généralement la hauteur de l'entretoise en travée ne dépasse pas celui de la poutre principale. Nous prenons : ht= hp-hd = 1,5m-0,18m= 1,32m

ü Base de l'entretoise :

> Aux appuis : 0,3h_a < be1 < 0,5h_a ? 0,3(1m) < be1 < 0,5(1m) ? 0,3m< _be1 <0,5m ? Nous prenons : be1=0,40m

[19]

? En travée : 0,3ht= _be2 =0,5ht ? 0,3(1,32m) = be2 =0,5 (1,32m) ? 0,396m _=be2 =0,66m

?Nous prenons : b_e2=0,40m

? Entraxe (l4) :

Généralement l'entraxe entre les entretoises varie de 5 à 8m. Nous adoptons 5,65m

? Ecartement (l5) :

L5 = l4 - 2(b_e/2) = 8m - 0,40m = 7,60m

? Nombre d'entretoise(N_e) :

En considérant les distances axe par axe, le nombre d'entretoises sera donné par la relation :

(N_e - 1) l4 = L_p ? N_e = = 4,008 4 entretoises

? La partie en encorbellement :

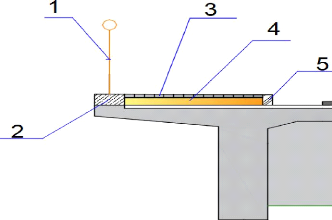
Avec :

1. Garde-corps (en acier) : h = 1,0m

2. Bordure externe : b = 0,30m ; h = 0,15m

3. Carrelage en dallètte : h = 0,04m

4. Sable : h = 0,10m ; b = 1,40m

5. Bordure interne : b = 0,10 ; h = 0,15m

[20]

? Séparateur en béton :

B = 0,40m ; b = 0,15m ; h = 0,70m

5.2. Infrastructure

5.2.1. Culée

Pour ce travail, nous avons choisi la culée du type 1 qui est plus courant :

Fig.5

? Détermination de la hauteur _(Hculée) de la culée : Hculée = ht + Tirant d'air + PHE + PBS

Avec :

? Hauteur du tablier (ht) = 1,50m ? Tirant d'air = 1,50m

[21]

> Profondeur de hautes eaux (P"E) = 1,20m

> Profondeur du bon sol (PBS) = 3m ; prit rapport au niveau du sol naturel

Alors :

"culée = 1,50m + 1,50m + 1,20m + (3,00m - 1,20m) = 6,00m

> Base de la culée(Bculée) :

-- 0,6m<m<1,2m

0,5"culée <Bculée < 0,7"culée -- 0,5(6,0m) <Bculée<0,7(6,0m) -- 3,0m _<Bculée< 4,2m. Généralement la largeur de la base de la culée varie de 4 à 6m, ainsi, nous prenons : --Bculée= 6m

> Corps de la culée ou mur (m ; n ; d) :

Le corps de la culée est obtenu par les relations : < m <

Etant donné que la largeur du corps de la culée varie de 0,8m à 1m, nous prenons :

-- m = 1,0m

n : n= -- n= -- n=0,6m

Étant donné que la largeur n varie de 1 à 2 m, nous adoptons : n = 2m d : d = Bculée - (m + n) -- d = 6m - (1+2,0) -- d = 3m

> Mur garde grève

Nous savons que b varie de 20cm à 30cm nous adoptons : b = 30cm et a varie de 25cm à

30cm et que le minimum à ne pas dépasser et de 20cm d'où nous prenons : a = 25cm

> Epaisseur de la semelle

Epaisseur de la semelle est de 1m. Avec : f = 0,6m ; r = 0,4m ; k=0,5m ; j=0,5m

> Béton de propreté :

Généralement, l'épaisseur du béton de propreté varie de 10 à 15cm. Nous adoptons une

épaisseur de 15cm

> Corbeau

L'épaisseur du corbeau h, est de 25cm

[22]

Longueur du corbeau : Lcor = 1m

Fig.

5.2.2. Mur en aile

Il a les dimensions suivantes :

Avec : une pente de 2/3 et une épaisseur de 80cm

[23]

5.2.3. Dalle de transition

L'épaisseur varie de 20cm à 30cm aussi, c'est ainsi que nous adoptons b = 25cm, la longueur de 4m à 6m, nous adoptons Ldt = 5m avec une pente variant de 5 à 10% nous adoptons une pente de 8%.

Fig. 7

5.2.2. Pile

Nous avons choisi la pile type colonne avec poutre chevêtre

Fig. 8

? Epaisseur de la semelle

Avec : r= 0,50m ; f=0,50m soit i = 1,00m ; B = 5,80m

? Colonnes :

La colonne aura une section circulaire de diamètre 100cm et une hauteur de 4,38m

[24]

? Poutre chevêtre :

La poutre chevêtre aura une section carré (100cm x 100cm) et une longueur de 10m.

Fig.

(dimension en cm)

[25]

5.3. Vues et coupes

PROFIL EN LONG DU PONT

(dimension en cm)

PROFIL EN TRAVERS DU PONT

[26]

CHAPITRE 6 : Dimensionnement des éléments de la superstructure

Dans ce chapitre, nous allons évaluer les charges, étudier les sollicitations dans chaque élément du tablier et pour finir, nous allons faire le calcul du béton armé.

6.1. Poutres principales

Nous allons ici faire l'étude de la répartition transversale en vue de déterminer le coefficient de répartition transversale pour trouver la poutre la plus chargé afin la stabiliser et puisque les éléments de notre pont sont symétriques toutes les poutres seront stabilisées.

6.1.1. Répartition transversale

Le but de l'étude de répartition transversale de charge est de pouvoir permettre au concepteur de projet de pont de pouvoir arriver à déterminer la part de charges que chacune des poutres reçoive suite aux charges qui leurs seront appliquées.

Cette part de charge, sera prise en compte dans le calcul sous forme d'un coefficient de majoration qu'ont appelé coefficient de répartition transversale des charges. En effet, le coefficient de répartition transversale est une valeur qui nous permet de trouver la poutre la plus chargée et de déterminer la charge qui s'applique sur cette poutre.

Le Trafic étant une série des charges ponctuelles mobiles, les efforts intérieurs dépendent de la position des véhicules ce qui fait que l'effet de chaque véhicule se calcul à l'aide des lignes d'influences. Nous prenons les hypothèses suivantes :

? La dalle reçoit les efforts dus au convoi, à la foule, et aux surcharges fixes et les transmet aux entretoises et ces derniers les transmettent aux poutres principales. En considérant que les éléments que comporte le tablier fonctionnent ou travaillent ensemble comme un corps unique.

? Le tablier reste un élément monolithique qui ne peut subir qu'une rotation et non une flexion.

NB : pour les ponts routes ; le rapport entre l'inertie des entretoises et celles des poutres doit tendre vers l'infinie cela traduit l'idée selon laquelle plus la poutre est chargée, moins l'entretoise l'est.

[27]

Fig. 9

^{P1 P2 P3 P4}

^{15 30 30 30 15}

(Dimensions en dm)

Nous prenons une charge unitaire pour trouver les équations des lignes d'influences qui nous permettrons de déterminer en lisant en abscisse la valeur de l'effet à la position de la charge.

Considérons les cas extrêmes de chargements suivantes : 1er cas : la charge unitaire P(1t) se trouve au milieu du pont.

Fig. 10

^P=1t

^{P1 P2 P3 P4}

^{15 30 30 30 15}

(Dimensions en dm)

On constatera que chaque poutre est chargée de la même façon. Tel que :

? P = charge unitaire

? n= nombres des poutres principales ? Qi= charges reprise par la poutre ? i= variant de 1 à n

ici nous avons p=1t, n= 4 et i varie de 1 à 4 ; c'est ainsi que Q1 = Q2 = Q3 = Q4

[28]

Pour trouver la contrainte, nous savons que la contrainte c'est l'action d'une charge sur l'unité de la surface. Ainsi, nous prenons les surfaces des poutres en réduisant chaque surface à l'unité. C'est de cette façon que nous avons : S1=S2=S3=S4= 1cm². Pour avoir la contrainte sur chaque poutre on prend la charge unitaire sur la somme des surfaces de chaque poutre.

D'où :

Avec : S= S1+S2+S3+S4 = 4cm²

= 0,25 t/m²

2eme cas : la charge unitaire P=1t se trouve au droit de la poutre principale 1.

Fig. 11

(Dimensions en dm)

On constatera que la charge P provoque un basculement du tablier et donc un moment en plus de sa charge unitaire. On sait qu'une force peut subir une déviation suivant son support qui tend à l'amener vers le centre de ce dernier. Ainsi, nous voulons connaitre l'effet de cette charge sur les poutres. C'est de cette façon que nous la plaçons au milieu du pont en l'associant de son moment qui est un moment de transfert.

[29]
Fig. 12

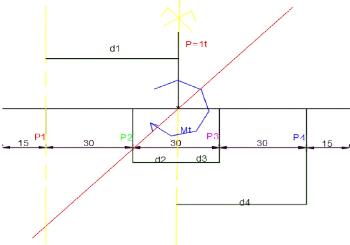
Où :

> d1 : distance de la poutre principale numéro 1 à l'axe du pont = 4,5m

> d2 : distance de la poutre principale numéro 2 à l'axe du pont = 1,5m

> d3 : distance de la poutre principale numéro 3 à l'axe du pont = 1,5m

> d4 : distance de la poutre principale numéro 4 à l'axe du pont = 4,5m

> Mt : moment de transfert = P. di

Etant donné que les poutres sont identiques nous évaluons les surfaces comme dans le premier cas où S'était égale à 4cm2.

La contrainte que recevra chaque poutre sera obtenue par la formule suivante :

Où : - Mt : le moment de transfert

- di= distance de la poutre numéro i à l'axe de la poutre

- I= moment d'inertie de la section transversale en ne considérant que les surface des poutres principales. C'est le moment de la section transversale par rapport à la charge unitaire P qui est centrée au milieu de la poutre. Elle sera obtenue par :

I= S.di

[30]

Où S est la somme des toutes les sections des poutres

Alors : I= _S1d12 + _S2d22 + _S3d32 + S4d4² = 1x (4,5)² + 1x (1,5)² + 1x(1,5)² + 1x(4,5)² I = 20,25m⁴ + 2,25 m⁴+ 2,25 m⁴ + 20,25 m⁴ = 45 m4

> Considérons que la poutre assimilée ci-dessus est d'abord soumise à l'action du moment de transfert de la charge ; alors la contrainte engendrée au droit de chaque poutre sera obtenue par :

Ainsi :

=

= 0,45t/m²

= 0 15t/m²

, =

= 0 15t/m²

, =

= 0 45t/m²

,

On sait que , alors l'effort normale sera : Ni = i x Si ; avec Si = s1+s2+s3+s4 = 1m² ;
alors : Ni = i

> Considérons cette fois que la poutre assimilée ci-dessus est soumise à la charge unitaire P, la charge Qi que reprendra chaque poutres principale (Pi) dû à l'action de Pi ; sera :

Qi = = = 0,25t

> Ainsi, en combinant les actions dues au moment de transfert et à la charge unitaire Pi , sur la poutre assimilée, l'effort total dans chaque poutres principales Pi sera donné par :

#177; Ni

Bi = #177; ou Bi =

Il est à noter que l'on additionne : Compression +compression et traction + traction On soustrait : Compression - traction et Traction - compression

[31]

Fig. 13

B1 =	#177; N1 =	+ 0,45t = 0,70 t/m^2 x 1m^2 -- P1= 0,70t
B2 =	#177; N2 =	+ 0,15t = 0,40 t/m^2 x 1m^2 -- P2= 0,40t
B3 =	#177; N3 =	- 0,15t = 0,10 t/m^2 x 1m^2 -- P3= 0,10t
B4 =	#177; N4 =	- 0,45t = - 0,20 t/m^2 x 1m^2 -- P4= -0,20t

Fig. 14

Lignes d'influences

[32]

6.1.2. Evaluation des charges

> Poids de la dalle : Pdalle= ép. x l_p x L_p x ?b = 0,18m x 17m x 12m x 25KN/m³ = 918 KN

> Poids de la chaussé :

- Revêtement : 0,08m x (2x3,50m) x 17m x 24KN/m³ = 228,48 KN

- Chape d'étanchéité : 0,04 x (2x3,50m) x 17m x 21KN/m³ = 99,96 KN

- Couche de forme : 0,04 x (2x3,50m) x 17m x 22KN/m³ = 104,72 KN

Poids de la chaussé : Pchaussée = 433,16 KN

> Poids du trottoir :

- Carrelage en dallette : 2 x 0,04m x 1,40m x 17m x 25KN/m³ = 47,6 KN

- Mortier de pose :2 x 0,01m x 1,40m x 17m x 22KN/m³ = 10,472 KN

- Sable : 2 x 0,10m x 1,40m x 17m x 18KN/m³ = 85,68 KN

- Bordure externe : 2 x 0,15m x 0,30m x 17m x 25KN/m³ = 38,25 KN

- Bordure interne : 2 x 0,15m x 0,10m x 17m x 25KN/m³ = 12,75 KN

Poids du trottoir : PTrottoir = 194,752 KN

> Garde-corps : PGarde-corps = 1KN/m x 17m x 2 = 34KN > Séparateur en béton :

- Trapèze : P1 = x 0,60m x 17m x 25KN/m³ = 70,125 KN

- Rectangle : P2 = 0,40m x 0,10m x 17m x 25KN/m³ = 17 KN

Poids du séparateur : Pseparateur = 87,125 KN

> Gousset : les 2 triangles : 2 x (0,30m x 0,10m) x 17m x 25KN/m³ = 25,5 KN

Il y a 4 poutres et les goussets sont placés dans chaque poutres on a : PGousset = 25,5KN x4 =

102KN

> Poids de la poutre : Ppoutre = 4 x (1,50m - 0,18m) x 0,50m x 17m x 25KN/m³ = 1122KN

> Poids de l'entretoise :

- Aux appuis : 2 x (1m - 0,18m) x 0,40m x (12m - 3m) x 25KN/m³ = 147,6 KN - En travée : 2 x (1,32m - 0,18m) x 0,40m x (12m - 3m) x 25KN/m³ = 205,2 KN

Poids de l'entretoise : PEntretoise= 352,8 KN

[33]

6.1.3. Calcul des coefficients d'impact dynamique

õ = 1+ +

6.1.3.1. Coefficient dynamique de la dalle

[a dalle doit supporter son poids propre est toute les surcharges fixes, alors :

P1 = Pdalle + _Pchaussée + _PTrottoir + _PGarde-corps + Pseparateur = 918 KN + 433,16 KN+ 194,752KN + 34 KN + 87,125 KN = 1667,037 KN

õdalle = 1+ + ? õdalle = 1,1824128 1,2

6.1.3.2. Coefficient dynamique de la poutre

[a poutre doit supporter son poids propre, le poids de la dalle, le poids des entretoises et les surcharges fixes ; ainsi :

P2 = P1 + _Ppoutre + _PGousset + PEntretoise = 1667,037 KN + 1122 KN + 102 KN + 352,8 KN P2 = 3243,837 KN

õpoutre = 1+ + ? õpoutre = 1,14170149 1,14

6.1.4. Coefficient de répartition transversale

Nous utiliserons les lignes d'influences transversales pour déterminer les valeurs de réactions par essieux. Pour le calcul des surface d'influences, les valeurs lues en ordonnée sont considérées adimensionnelles. Nous considérons que deux convois de 60t passent au même moment sur le pont ce qui manifeste le cas le plus défavorable.

[34]

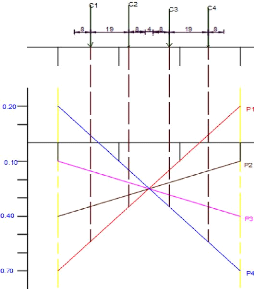
Le coefficient de répartition transversale est obtenue par la relation k = , où :

- m : le maximum des sommes de réactions par poutre due au convois

- n : le nombre d'essieux

Ces valeurs sont obtenues dans le tableau suivant :

CONVOIS	M1	M2	M3	M4	SOMME
POUTRE
P1	0,55	0,355	0,1451	-0,05	1,0001
P2	0,35	0,285	0,2149	0,15	0,9999
P3	0,15	0,2149	0,285	0,35	0,9999
P4	-0,05	0,1451	0,355	0,55	1,0001
SOMME	1	1	1	1	4

Alors : k = = 0,50005 0,5

On y affecte le coefficient dynamique de la poutre, alors on obtient un coefficient

K = k x õpoutre = 0,57

[35]

6.1.5. Calcul de la poutre la plus chargée
6.1.5.1. Calcul des efforts internes (M, N, T)

Pour déterminer, nous allons subdiviser la poutre en 10 sections égales et trouver les efforts au droit de chaque section.

Pour ce faire, nous allons faire l'étude des lignes d'influences longitudinales en plaçant une charge unitaire.

6.1.5.2. Calcul des moments fléchissant

Nous prenons pour hypothèse : La charge unitaire se déplace le long de la poutre ainsi défini en parcourant les deux sens de circulation.

^1t

^S

^{A B}

^Xs

^X

^{RA L RB}

RA = (1- ) et RB =

La somme de moment en un point est égale à zéro, nous considérons le moment à gauche de la section. Même en considérant le moment à droite, les deux auront la même valeur juste la différence de signe. Nous prenons le moment positif car nos poutres sont isostatiques non continues.

Moment à gauche de la section S : MS = RA . XS = (1- ) . XS - Si X=L ; MS = 0 m

Xs

- Si X = XS ; MS = (1- ) . XS

[36]

TABLEAU DES MOMENTS ET DES EFFORTS TRANCHANTS

TABLEAU DES MOMENTS
SECTION	XS (m)	L(m)	Ms= (1-Xs/L)Xs
0	0	17	0
1	1,7		1,53
2	3,4		2,72
3	5,1		3,57
4	6,8		4,08
5	8,5		4,25
6	10,2		4,08
7	11,9		3,57
8	13,6		2,72
9	15,3		1,53
10	17		0

Lignes d'influences longitudinales des moments fléchissant :

^1t

^S

^{A B}

^Xs

^X

^{RA L} RB

6.1.5.3. Calcul des efforts tranchants Nous considérons la même hypothèse :

[37]

Les efforts tranchants équivalent aux réactions d'appuis. Avec RA = 1- et RB =

TABLEAU DES EFFORTS TRANCHANTS
SECTION	Xs	L	RA	RB
0	0	17	1	0
1	1,7		0,9	0,1
2	3,4		0,8	0,2
3	5,1		0,7	0,3
4	6,8		0,6	0,4
5	8,5		0,5	0,5
6	10,2		0,4	0,6
7	11,9		0,3	0,7
8	13,6		0,2	0,8
9	15,3		0,1	0,9
10	17		0	1

Lignes d'influences longitudinales des efforts tranchants :

Pour déterminer l'effort tranchant max, nous considérons 3 cas :

[38]

6.1.6. Application des lignes d'influences 6.1.6.1. Lignes d'influences des moments fléchissant Pour déterminer le moment max ; nous considérons 3 cas :

1er CAS : le train de charge se trouve au milieu du pont, on considère qu'un essieu se trouve au milieu du pont et un autre à 1,5m de celui-ci.

? Section 0 : le moment est nul au niveau des appuis.

? Section 1 :

^{30t 30t}

^Y1

^Y2

^1,50

Avec : y1 = 0,85m et y2 = 0,7m ; ? Section 2 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 1,7m et y2 = 1,4m ? Section 3 :

[39]

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 2,55m et y2 = 2,1m ? Section 4 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 3,4m et y2 = 2,8m ? Section 5 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 4,25m et y2 = 3,5m ? Section 6 :

^Y1

^1,50

Y2

^{30t 30t}

[40]

Avec : y1 = 3,4m et y2 = 3,9m

> Section 7 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 2,55m et y2 = 3,00m

> Section 8 :

^{30t 30t}

> Section 9 :

^{30t 30t}

^1,50

^Y1

^1,50

^Y2

^{Y1 Y2}

Avec : y1 = 0,85m et y2 = 1,00m

> Section 10 : le moment est nul

[41]

2ème CAS : L'un de train de charge se trouve au droit de la première section et l'autre à 1,50m de celui-ci :

? Section 1 :

^{30t 30t}

^Y1

^Y2

^1,50

Avec : y1 = 1,53m et y2 = 1,38m ? Section 2 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 1,36m et y2 = 2,56m ? Section 3 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 1,19m et y2 = 2,24m ? Section 4 :

^{30t 30t}

^1,50

^Y1

^Y2

[42]

Avec : y1 = 1,08m et y2 = 1,92m ? Section 5 :

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1 = 0,85m et y2 = 1,6m ? Section 6 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 0,68m et y2 = 1,28m ? Section 7 :

[43]

^{30t 30t}

^Y1

^1,50

^Y2

Y1 Y2

Avec : y1 = 0,17m et y2 = 0,32m

Avec : y1 = 0,51m et y2 = 0,96m ? Section 8 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 0,34m et y2 = 0,68m ? Section 9 :

^{30t 30t}

^1,50

[44]

^V1

^1,50

^V2

Avec : y1 = 2,77m et y2 = 2,32m

3ème CAS : le train de charge se trouve à égale distance de l'axe du pont :

? Section 1 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 0,99m et y2 = 0,77m ? Section 2 :

^{30t 30t}

^1,50

^Y2

^Y1

Avec : y1 = 1,85m et y2 = 1,55m ? Section 3 :

^{30t 30t}

[45]

? Section 4 :

^{30t 30t}

^1,50

^{Y1 Y2}

Avec : y1 = 3,7m et y2 = 3,1m ? Section 5 :

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1 = 3,87m et y2 = 3,87m ? Section 6 :

^30t

^30t

^1,50

^Y1

^Y2

Avec : y1 = 3,1m et y2 = 3,7m ? Section 7 :

[46]

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1 = 2,32m et y2 = 2,77m ? Section 8 :

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1 = 1,55m et y2 = 1,85m ? Section 9 :

^30t

^30t

^1,50

^Y2

^Y1

Avec : y1 = 0,75m et y2 = 0,92m

Les surfaces d'influences des moments donnent : S0 = S10 = 0 tm²

S1 = S9 = = 13,005 m²

S2 = S8 = = 23,12 m2

[47]

S3 = S7 = = 30,345 m²

S4 = S6 = = 34,68 m²

S5 = = 36,125 m²

6.1.6.1.1. Moments dus au convoi

^MOMENT FLECHISSANT (CONVOIS)

^SECTION

^CAS 1

^CAS 2

^CAS 3

^à retenir

^MxK

^Y2

^M=(Y1+Y2)30

^Y1

^Y2

^M=(Y1+Y2)30

^Y1

^Y2

^M=(Y1+Y2)30

^0

^0

^0

^0

^0

^0

^0

^0

^0

^0

^0

^1

^0,85

^0,7

^46,5

^1,53

^1,38

^87,3

^0,92

^0,77

^50,7

^87,3

^49,761

^2

^1,7

^1,4

^93

^1,36

^2,56

^117,6

^1,85

^1,55

^102

^117,6

^67,032

^3

^2,55

^2,1

^139,5

^1,19

^2,24

^102,9

^2,77

^2,32

^152,7

^152,7

^87,039

^4

^3,4

^2,8

^186

^1,08

^1,92

^90

^3,7

^3,1

^204

^204

^116,28

^5

^4,25

^3,5

^232,5

^0,85

^1,6

^73,5

^3,87

^3,87

^232,2

^232,2

^132,354

^6

^3,4

^3,9

^219

^0,68

^1,28

^58,8

^3,1

^3,7

^204

^219

^124,83

^7

^2,55

^3

^166,5

^0,51

^0,96

^44,1

^2,32

^2,77

^152,7

^166,5

^94,905

^8

^1,7

^2

^111

^0,34

^0,68

^30,6

^1,55

^1,85

^102

^111

^63,27

^9

^0,85

^1

^55,5

^0,17

^0,32

^14,7

^0,75

^0,92

^50,1

^50,1

^28,557

^10

^0

^0

^0

^0

^0

^0

^0

^0

^0

^0

0

[48]

6.1.6.1.2. Moments dus au poids propre

Evaluation des charges linéaires :

> Poids de la dalle : 0,18m x 12m x 25KN/m³ = 54 KN/m

> Poids de la chaussée :

- Revêtement : 0,08m x (2 x 3,50m) x 24 KN/m³ = 13,44 KN/m

- Chape d'étanchéité : 0,04m x (2 x 3,50m) x 21 KN/m³ = 5,88 KN/m

- Couche de forme : 0,04m x (2 x 3,50m) x 22 KN/m³ = 6,16 KN/m

Poids de la chaussée par mètre linéaire : P_c = 25,48 KN/m

> Poids du trottoir :

- Carrelage en dallettes : 2 x 0,04m x 1,40m x 25 KN/m³ = 2,8 KN/m

- Mortier de pose : 2 x 0,01m x 1,40m x 22 KN/m³ = 0,616 KN/m

- Sable : 2 x 0,10m x 1,40m x 18 KN/m³ = 5,04 KN/m

- Bordure externe : 2 x 0,15m x 0,30m x 25 KN/m³ = 2,25 KN/m

- Bordure interne : 2 x 0,10m x 0,15m x 25 KN/m³ = 0,75 KN/m

Poids propre du trottoir : PT = 11,456 KN/m

> Garde-corps : 2x1 KN/m = 2 KN/m

> Poids propre du séparateur : 0,205m² x 25 KN/m³ = 5,125 KN/m

> Poids propre des poutres : 4 x 1,32m x 0,50m x 25 KN/m³ = 66 KN/m

> Poids propre des goussets : 4 x 2 x 0,30m x 0,10m x 25 KN/m³ = 6 KN/m

> Poids propre des entretoises :

- Au appuis : 2 x (1,0m - 0,18m) x 0,40m x 25 KN/m³ = 16,4 KN/m

- En travée : 2 x (1,32m - 0,18m) x 0,40m x 25 KN/m³ = 22,8 KN/m

Poids propre des entretoises : PE = 39,2 KN/m

Ptotale = 54 KN/m + 25,48 KN/m + 11,456 KN/m + 2 KN/m + 5,125 KN/m + 66 KN/m+ 6 KN/m + 39,2 KN/m = 209,261 KN/m

? Ptotale = 209,261 KN/m.

La charge reprise par poutre sera : Ppoutre = = = 52,31525 KN/m

Soit Ppoutre = 5,231525 t/m

[49]

TABLEAU ES MOMENTS DUS AUX POIDS PROPRES

		^MOMENT DU AU POIDS PROPRE ^Poids propre par ^poutre(t/m)
				^SECTION
^SURFACE (m2)
				^0
^0				^1
^13,005				^2
^23,12				^3
^30,705

^5,231525

^68,03598263

^160,6339751

⁴

^34,68

⁵

^36,125

^188,9888406

⁶

^34,68

⁷

^30,705

^160,6339751

^68,03598263

6.1.6.1.3. Moment dus à la foule

La norme belge prévoit une charge de 0,4 t/m² pour la foule.

Les surfaces d'influence dans la répartition transversale ont donné :

^8 ^9 ^10 N° POUTRE	^23,12 13,005 0S+	S-		Somme	P1
2,45	0,20	2,25		P2
2,25	0	2,25		P3
2,25	0	2,25		P4
2,45	0,20	2,25

^(tm)

^{0 120,952858 181,429287 181,429287 120,952858}

⁰

Nous multiplions la charge de la foule par les surfaces d'influences ci-haut :

? PFoule : S⁺ = 2,45m x 0,4 t/m² = 0,98 t/m

[50]

? PFoule : S^- = 0,20m x 0,4 t/m² = 0,08 t/m

On retient : PFoule = 0,98 t/m

TABLEAU DES MOMENTS DU A LA FOULE

		^MOMENT DU A LA FOULE ^FOULE
				^SECTION
^SURFACE
				^0
^0				^1
^13,005				^2
^23,12				^3
^30,705

^{Mfoule=SxFoule}

^0,98

⁰

^12,7449

^22,6576

^30,0909

⁴

^34,68

^33,9864

⁵

^36,125

^35,4025

⁶

^34,68

^33,9864

⁷

^30,705

^30,0909

⁸

^23,12

^22,6576

⁹

^13,005

^12,7449

¹⁰

⁰

⁰

NB : De tous ces tableaux, c'est-à-dire celui des moments dus à la foule, des moments dus au convoi et des moments dus au poids propre seront repris dans un tableau récapitulatif duquel on tirera la valeur du moment ultime maximum (le plus contraignant). C'est cette valeur de moment ultime max qui fera l'objet des calculs d'armatures. On fait de même pour les efforts tranchants.

[51]

VOICI LE TABLEAU RECAPITULATIF

			^TABLEAU RECAPUTILATIF
						^SECTION
^MOMENT DU ^AU POIDS		^MOMENT DU ^A LA FOULE	^MOMENT DU ^AU CONVOIS	^MOMENT ULTIME ^Mu=1,35Mp+1,5(	^MOMENT DE
^PROPRE						^0
^0		^0	^0	^0		^1
^68,03598263		^12,7449	^49,761	^185,6074265		^2
^120,952858		^22,6576	^67,032	^297,8207583		^3
^160,6339751		^30,0909	^87,039	^392,5507164

^Mf+Mq)

^33,9864

^116,28

^470,3291375

^35,4025

^132,354

^506,7696848

^33,9864

^124,83

^483,1541375

^30,0909

^94,905

^404,3497164

^22,6576

^63,27

^292,1777583

^12,7449

^28,557

^153,8014265

⁰

⁰

⁰

COURBE ENVELOPPE DES MOMENTS

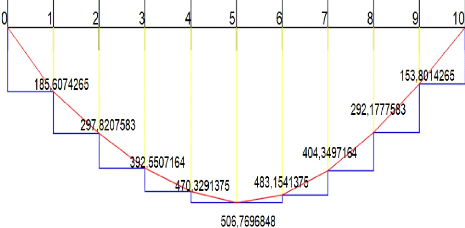
[52]

6.1.6.2. Lignes d'influences des efforts tranchants

1er CAS : : le train de charge se trouve au milieu du pont, on considère qu'un essieu se trouve au milieu du pont et un autre à 1,5m de celui-ci.

? Section 0 :

^V1

^{30t 30t}

^1,50

^V2

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m ? Section 1 :

^0.9t

^Y1

^{30t 30t}

^1,50

^Y2

^0.1t

^{30t 30t}

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m ? Section 2 :

^1,50

Y2

^Y1

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m ? Section 3 :

^{30t 30t}

^V1

^1,50

^V2

[53]

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m ? Section 4 :

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m

? Section 5 :

^1,50

^V2

^{30t 30t}

^V1

Avec : y1 = y1⁺ + y1^- = 0,5m - 0,5m = 0m et y2 = 0,41m

? Section 6 :

[54]

^{30t 30t}

^1,50

^Y2

^Y1

Avec : y1^- = 0,5m et y2^- = 0,58m ? Section 10 :

Avec : y1^- = 0,5m et y2^- = 0,58m ? Section 7 :

^{30t 30t}

^1,50

^V1

^V2

Avec : y1^- = 0,5m et y2^- = 0,58m ? Section 8 :

^{30t 30t}

^1,50

^Y1

^Y2

^{30t 30t}

^1,50

^0.1t

^V1

^V2

0.9t

Avec : y1^- = 0,5m et y2^- = 0,58m ? Section 9 :

[55]

^{30t 30t}

^1,50

^Y1

^Y2

^1t

Avec : y1^- = 0,5m et y2^- = 0,58m

2ème CAS : L'un de train de charge se trouve au droit de la première section et l'autre à 1,50m de celui-ci :

> Section 0 : ^1t

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1⁺ = 0,9m et y2⁺ = 0,81m

> Section 1 :

^0.9t

^{30t 30t}

^Y1

^1,50

^Y2

^0.1t

Avec : y1 = 0,8m et y2⁺ = 0,81m

> Section 2 :

[56]

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 6 :

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 3 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 4 :

^{30t 30t}

^1,50

^Y1

^Y2

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 5 :

^{30t 30t}

^1,50

^Y1

^Y2

[57]

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 7 :

^{30t 30t}

^V1

^1,50

^V2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 8 :

^{30t 30t}

^Y1

^1,50

^Y2

^{30t 30t}

^1,50

^0.1t

^Y1

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 10 :

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 9 :

[58]

^Y1

^1,50

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m

3ème CAS : le train de charge se trouve à égale distance de l'axe du pont :

> Section 0 :

^1t

^{30t 30t}

^1,50

^Y2

Avec : y1 = 0,54m et y2 = 0,45m

> Section 1 :

^0.9t

^Y1

^30t

^1,50

^30t

Y2

^0.1t

Avec : y1 = 0,54m et y2 = 0,45m

> Section 2 :

^Y1

[59]

^{30t 30t}

^1,50

^Y2

Avec : y1 = 0,54m et y2 = 0,45m ? Section 3 :

^30t

^1,50

^30t

^Y2

^Y1

^Y1

^{30t 30t}

^1,50

Y2

Avec : y1 = 0,54m et y2 = 0,45m ? Section 4 :

^{30t 30t}

^Y1

^Y2

^1,50

Avec : y1 = 0,54m et y2 = 0,45m ? Section 5 :

[60]

Avec : y1^- = 0,50m et y2⁺ = 0,45m ? Section 6 :

^30t

^1,50

^V2

^V1

Avec : y1^- = 0,45m et y2^- = 0,54m ? Section 7 :

^30t

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1^- = 0,45m et y2^- = 0,54m ? Section 8 :

^{30t 30t}

^1,50

^'f1

^'f2

Avec : y1^- = 0,45m et y2^- = 0,54m ? Section 9 :

[61]

^{30t 30t}

^1,50

^0.1t

^Y1

^Y2

Avec : y1^- = 0,45m et y2^- = 0,54m ? Section 10 :

^30t

^30t

^Y1

^1,50

^Y2

Avec : y1^- = 0,45m et y2^- = 0,54m

Les surfaces d'influences des efforts tranchants donnent :

S0^+ =	m	S10 - =	m
	= 8,5		= 8,5t
S1^+ =	= 6,885 m	S9^- =	= 6,885 m
S2^+ =	m	S8^- =	m
	= 5,44		= 5,44
S3^+ =	m	S7^- =	m
	= 4,165		= 4,165
S4^+ =	m	S6^- =	m
	= 3,06		= 3,06
S5^+ =	m	S5^- =	m
	= 2,125		= 2,125
S6^+ =	m	S4^- =	m
	= 1,36		= 1,36
S7^+ =	= 0,765 m	S3^- =	= 0,765 m

[62]

S8^+ =	=	0,34 m	S2^-	=	=	0,34 m
S9^+ =	=	0,085 m	S1^-	=	=	0,085 m
S10^+ = 0 m			S0^-	= 0 m

6.1.6.2.1. Efforts tranchants dus au convois

^EFFORTS TRANCHANT (CONVOIS)
^SECTION	^CAS 1			^CAS 2			^CAS 3			^à retenir	^TxK
	^Y1	^Y2	^T=(Y1+Y2)30	^Y1	^Y2	^T=(Y1+Y2)30	^Y1	^Y2	^T=(Y1+Y2)30
^0	^0,5	^0,41	^27,3	^0,9	^0,81	^51,3	^0,54	^0,45	^29,7	^51,3	^29,241
^1	^0,5	^0,41	^27,3	^0,9	^0,81	^51,3	^0,54	^0,45	^29,7	^51,3	^29,241
^2	^0,5	^0,41	^27,3	^-0,1	^-0,18	^-8,4	^0,54	^0,45	^29,7	^29,7	^16,929
^3	^0,5	^0,41	^27,3	^-0,1	^-0,18	^-8,4	^0,54	^0,45	^29,7	^29,7	^16,929
^4	^0,5	^0,41	^27,3	^-0,1	^-0,18	^-8,4	^0,54	^0,45	^29,7	^29,7	^16,929
^5	^0	^0,41	^12,3	^-0,1	^-0,18	^-8,4	^-0,5	^0,45	^-1,5	^12,3	^7,011
^6	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	^-18,468
^7	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	^-18,468
^8	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	^-18,468
^9	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	^-18,468
^10	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	-18,468

[63]

6.1.5.2.2. Efforts tranchants dus au poids propre

			^P propre
^SECTION	^S+	^S-		T+= ^S+ Ppropre
^0	^8,5	^0		^44,4679625
^1	^6,885	^0,085		^36,01904963

^{EFFORTS TRANCHANTS DUS AU POIDS PROPRE}

^0,34

^28,459496

^0,765

^21,78930163

6.1.5.2.3. Efforts tranchants dus à la foule

^4 ^3,06 ^1,36 ^16,0084665
^5	^2,125	^2,125	^5,231525	^11,11699063
^6	^1,36	^3,06	^EFFORTS TRANCHANTS DUS AU POIDS PROPRE ^P Foule ^0,98	^7,114874
^7	^0,765	^4,165		^4,002116625
^8 ^SECTION	^0,34 ^S+	^5,44 ^S-		^1,7787185 T+= ^S+ Ppropre	^T- = ^S- Ppropre
^9 ^0	^0,085 ^8,5	^6,885 ^0		^0,444679625 ^8,33	^0
^10 ^1	^0 ^6,885	^8,5 ^0,085		^0 ^6,7473	^0,0833
^2	^5,44	^0,34		^5,3312	^0,3332
^3	^4,165	^0,765		^4,0817	^0,7497
^4	^3,06	^1,36		^2,9988	^1,3328
^5	^2,125	^2,125		^2,0825
^6	^1,36	^3,06		^1,3328
^7	^0,765	^4,165		^0,7497

[64]

TABLEAUX RECAPITULATIF DES EFFORTS TRANCHANTS Efforts tranchants positifs

^SECTION	^T propre	^T foule	^T convois	^T= 1,35Tp + ^1,5(Tf + ^Tc)
^0	^44,4679625	^8,33	^29,241	^116,3882494
^1	^36,01904963	^6,7473	^29,241	^102,608167
^2	^28,459496	^5,3312	^16,929	^71,8106196

^{TABLEAU RECAPITULATIF DES EFFORTS TRANCHANTS POSITIFS}

^4,0817

^16,929

^4,0817

^16,929

^2,0825

^7,011

Efforts tranchants négatifs

^6 ^7,114874 ^1,3328 ^-18,468 ^-16,0977201
^7	^4,002116625	^0,7497	^-18,468	^-21,17459256
^8	^1,7787185	^0,3332	^-18,468 ^TABLEAU RECAPITULATIF DES EFFORTS TRANCHANTS NEGATIFS	^-24,80093003
^9 ^SECTION	^0,444679625 ^T propre	^0,0833 ^T foule	^-18,468 ^T convois	^-26,97673251 ^T= 1,35Tp + ^1,5(Tf + ^Tc)	^Tserv
^10 ^0	^0 ^0	^0 ^0	^-18,468 ^-18,468	^-27,702 ^-27,702	^-18,468
^1	^0,444679625	^0,0833	^-18,468	^-26,97673251	^-17,94002038
^2	^1,7787185	^0,3332	^-18,468	^-24,80093003	^-16,3560815
^3	^4,002116625	^0,7497	^-18,468	^-21,17459256	^-13,71618338
^4	^7,114874	^1,3328	^-18,468	^-16,0977201	^-10,020326
^5	^11,11699063	^2,0825	^7,011	^28,64818734	^20,21049063
^6	^16,0084665	^2,9988	^16,929	^51,50312978	^35,9362665
^7	^21,78930163	^4,0817	^16,929	^60,93160719	^42,80000163
^8	^28,459496	^5,3312	^16,929	^71,8106196

[65]

COURBE ENVELOPPE DES EFFORTS TRANCHANTS

6.2. Calcul de l'entretoise

L'entretoise se calcul comme une poutre reposant sur une(des) poutre(s)s principale(s) :

^Entretoises

^{3m 3m 3m}

^Poutre

1er Cas : On applique une charge unitaire au milieu du pont ; on constate que toutes les poutres sont chargées de la même façon, d'une charge de 0,25t

[66]

^{d1 1t}

^{0,25t 0,25t 0,25t 0,25t}

MO = 0,25t (3m + 1,5m) + 0,25t (1,5m) = 1,125tm + 0,375tm = 1,5 tm

2eme Cas : On applique une charge unitaire au droit de la poutre P1 ; on constate que les poutres ne sont plus chargées de la même façon :

^1t

^{0,70t 0,40t 0,10t 0,20t}

MO = 0,70t (3,0m + 1,5m) + 0,40t (1,5m) - 1t (3,0m + 1,5m) = - 0,75tm

Lignes d'influences des moments au centre du pont :

^{0,75tm 0,75tm}

- -

^{1,5m 6,0m 1,5m}

+

1,5tm

[67]

Pour le calcul de surfaces d'influences nous considérons les valeurs en ordonnées adimensionnelles alors les surfaces d'influences de l'entretoise donnent :

? S⁺ = = 4,5 m²

? S^- = 2( = - 1,125 m²

6.2.1. Calcul des moments

6.2.1.1. Moments dus aux charges permanentes

Ce sont les charges fixes et le poids propre. Ces éléments ne causent pas de flexion de l'entretoise. Ces charges sont reprises par les poutre principales. Tout le pont fléchi et les entretoise restent parallèles à elles-mêmes.

6.2.1.2. Moments dus à la charge de la foule La charge de la foule prévue par la norme est de 0,4 t/m.

Le coefficient dynamique : õ = 1,14

On trouve les lignes d'influences de la réaction de l'entretoise suite à l'action de la dalle considérée isostatiquement liée à l'entretoise.

^{Sens de circulation}

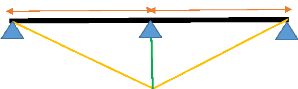
^{5,65 5,65}

^1t

la charge repartie de la foule sera : 0,4t/m² x 1,14 x 2( ) = 2,5764 t/m

Pour usage des lignes d'influences de moments en O. M+ = 2,5764 t/m x 4,5 m² = 11,5938 tm

M- = 2,5764 t/m x 1,125 m² = 2,89845 tm

[68]

6.2.1.3. Moments dus à la charge du convoi

Nous considérons que deux convois passent en même temps sur le pont et leurs essieux passent sur l'entretoise au même moment (cas le plus défavorable). Nous avons un convoi de 60t soit 30t par essieux. Nous avons une charge de 15t par roues espacé de 1,90m.

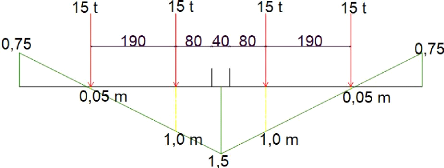
Les lignes d'influences des moments donnent : y1 = y4 = 0,05m et y2 = y3 = 1,0m ; alors le moment du au convois sera :

M ⁺convois = 15t x 1,14 x 2(0,05 + 1,0) = 35,91 tm M ^-convois = 15t x 1,14 x 2(0) = 0 tm

M⁺max = 1,5(11,5938 tm + 35,91 tm) = 71,2557 tm M^-max = 1,5(2,89845 tm + 0 tm) = 4,347675 tm

6.3. Etude de la dalle

Fig.

[69]

=

Elancement : á = = 0,530 ? 0,4

La dalle porte dans deux sens.

6.3.1. Evaluation des charges

6.3.1.1. Dalle sous la chaussée

? Poids propre : 0,18m x 25 KN/m³ = 4,5 KN/m²

? Poids de la chaussé :

? Revetement : 0,08m x 24KN/m³ = 1,92 KN/m²

? Chape d'étanchéité : 0,04m x 21KN/m³ = 0,84 KN/m²

? Couche de forme : 0,04m x 22KN/m³ = 0,88 KN/m²

Pchaussé = 3,64 KN/m2

[70]

? Séparateur : 0,70m x 25KN/m³ = 17,5 KN/m²

v G = 25,64 KN/m² = 2,5464 t/m²

v La foule : Pfoule = 4 KN/m² ou 0,4 t/m² x 1,2 = 0,48 t/m²

v Convoi : 60t où 600 KN

Les surfaces d'influences de la dalle seront données par : > Sens de x :

S1 = L1 x L2

L1 = a1 + 1,5 h_r + 2 hd + = 0,30m + 1,5 (0,16m) + 2 (0,18m) + = 1,9 m

L2 = a2 + 1,5 h_r + 2 hd = 0,30m + 1,5 (0,16m) + 2 (0,18m) = 0,9 m D'où S1 = 1,9m x 0,9m = 1,71 m²

Alors la densité sera : x õdalle = x 1,2 = 5,263 t/m²

> Sens de y :

S2 = L1 x L2

L2 = a2 + 1,5 h_r + 2 hd = 0,30m + 1,5 (0,16m) + 2 (0,18m) = 0,9 m

L1 = a1 + 1,5 h_r + 2 hd + = 0,30m + 1,5 (0,16m) + 2 (0,18m) + = 2,783 m

D'où S1 = 0,9m x 2,783m = 2,505 m²

Alors la densité sera : x õdalle = x 1,2 = 3,593 t/m²

La charge du convoi est donc : Pconvois = 8,856 t/m²

Charge ultime de la dalle sera :

PUd = 1,35(G) + 1,5(Pconvoi + Foule) = 1,35(2,564 t/m²) + 1,5(8,856 t/m² + 0,48 t/m²

PUd = 17,4654 t/m²

PS = 2,564 + 8,856 + 0,48 = 11,9 t/m²

6.3.1.1.1. Calculs des moments

[71]

Nous optons pour la méthode forfaitaire de dalle continue. Les panneaux de rives sont identiques. Nous calculons un panneau de rive et nous affectons ce moment à tous les panneaux.

> Moments isostatiques :

Mox = ìx. PUd. l_x² et Moy = ì_y . Mox avec : ì_x =0,0922 ; ì_y = 0,2500

Alors : Mox = 0,0922 x 17,4654 x (3) ² = 14,492788 tm et Moy = 0,2500 x 14,492788 = 3,623197 tm

> Moments en travée et aux appuis :

Nous ne considérerons que les valeurs des moments obtenues par le calcul du panneau de rive puisqu'elles sont supérieures aux valeurs obtenues au panneau courant.

Dans le sens de x : Mtx = 0,85.Mox = 0,85 x 14,492788 tm = 12,3188698 tm

Max = - 0,5.Mox = - 0,5 x 14,492788 tm = - 7,246394 tm Dans le sens de y : Mty = 0,85. Moy = 0,85 x 3,623197 tm = 3,07971745 tm

May = - 0,5.Mox = - 0,5 x 14,492788 tm = - 7,246394 tm

6.4. Etude de l'encorbellement

L'encorbellement sera calculé comme une poutre encastrée d'un seul côté. Cela par bande d'un 1,00m.

6.4.1. Evaluation des charges

> Poids de la dalle : 0,18m x 25KN/m³ x 1m = 4,5 KN/m

> Poids du trottoir :

? Carrelage en dallèttes : 0,04m x 25 KN/m³ x 1m = 1 KN/m

? Mortier de pose : 0,01m x 22 KN/m³ x 1m = 0,22 KN/m

? Sable : 0,10m x 18KN/m³ x 1m = 1,8 KN/m

? Bordure externe : 0,15 m x 0,30m x 25 KN/m³ x 1m = 1,125 KN

> Garde-corps : 1 KN/m x 1m = 1 KN

> Force horizontale : 100 kg/m = 1 KN/m x 1m = 1 KN

+ Charges réparties : 4,5 KN/m + 1 KN/m + 0,22 KN/m + 1,8 KN/m = 7,52KN/m

= 0,752 t/m

[72]

? Charges concentrées : 1,125 KN + 1 KN = 2,125 KN = 0,2125 t Combinaison des charges :

? Charges réparties : 1,35(0,752t/m) + 1,5(0,4t/m) = 1,6152 t/m

? Charges concentrées : 1,35(0,2125 t) + 1,5(0,1t) = 0,436875 t

Schéma statique

^0,436875t

^1,6152t/m

^1,50m

Nous utiliserons la méthode de superposition pour calculer les sollicitations :

6.4.1.1. Calcul de moment

^0,436875t

^1,50m

^1,6152t/m

^1,50m

M1 = - PL + M2 = -

M1 = 0,436875t x 1,50m = - 0,6553 tm

²

M2 = - 1 , 6 1 52 ( 1 , 5 0 )= - 1,8171 tm

2

Mtotale = - 0,6553 tm - 1,8171 tm = - 2,4724 tm

[73]

6.4.1.1. Calcul de l'effort tranchant

^0,436875t

	^1,50m

T1 = P + T2 = PL

T1 = 0,436875 t

T2 = 1,6152t/m x 1,50m = 2,4228 t

Ttotale = 0,436875t + 2,4228 t = 2,859675 t

[74]

6.5. Calculs d'armatures des éléments de la superstructure

Nous calculons les armatures des éléments de la superstructure aux états limites ultime et nous vérifions les contraintes aux états limites de services cas de la fissuration préjudiciable.

? Poutres principales :

MU = 506,7696848 tm et TU = 116,3882494 t ; M_s = 356,7453406 tm et Ts = 82,0389625 t

· Largeur de la table de compression :

Nous utilisons la formule suivante : B = 12hd + bO = 12(0,18) + 0,50 = 2,66 m

Nous avons : B = 2,66 m ; d = h_p - e = 1,50 - 0,05 = 1,45 m ; f8 = 30 MPa alors

fbu = _ = 17 MPa or 1 MPa = 100 t/m2 -- fbu = 1700 t/m2 ; f_e = 500 MPa alors

f_s = = 434,78 MPa 435 MPa = 43500 t/m2

· Moment résistant de la table de compression :

Mt = B x hO x _fbu (d - ² ) = 2,66m x 0,18m x 1700 t/m2 x (1,45m - ² ) = 1106,9856 tm

M_u < Mt ; d'où la poutre est simplement armée.

· Moment réduit ultime :

ìbu = ~~v = 0,053 < 0,186 (pivot A)

=

· Paramètre de déformation :

á = 1,25 (1 - v ) = 0,068

· Position de l'axe neutre :

y = á x d = 0,068 x 1,45 = 0,0986 m -- la position est donnée tel que : 0,8.y < hd ; nous aurons : 0,8 x 0,0986m < 0,18 -- 0,0788 < 0,18 (Poutre rectangulaire)

St < 22,0 cm ? St = 20 cm

[75]

· Bras de levier :

Z = d (1 - 0,4 á) = 1,45 (1 - 0,4(0,068)) = 1,41 m

· Armatures principales :

AS = = 0,008262 m2 = 82,62 cm² soit 12HA30 ? 84,78 cm²

· Armatures transversales : T_u = 116,3882494 t

La contrainte tangentielle ultime moyenne : ôuo = = = 160,5355 t/m²

Etant donné qu'on est en fissuration peu préjudiciable

ôlim < min (

; 5 MPa)

ôlim < min ( ; 5 MPa)

ôlim < min (4MPa ; 5 MPa) ôlim = 4 MPa = 400 t/m²

ôuo ? ôlim ; d'où l'utilisation des armature transversale droite.

Section d'armature doit être tel que: dit < min ( ; ; )

dit < min ( ; ; 30mm )

dit < 30mm ; nous adoptons : dit = 12 mm

= =

At = 113,04 mm² = 1,1304 cm²
At = 1,1304 cm2 x 4 brins = 4,5216 cm2

· Ecartement d'armatures :

S < t-= -

= 0,220 m = 22,0 cm

verifié.

[76]

· Armatures de peau :

A_p ? x parement( 2R+bo) ? A_p ? x ( 2(1,32)+0,50)

A_p ? 9,42 cm² soit 4HA18 ? 10,18 cm²

Vérification des contraintes

MS = 356,7453406 tm ; d = 1,45m ; b = 2,66m ; AS = 84,78 cm² ; f8 = 30 MPa ; f_e = 500MPa

· Position de l'axe neutre :

b - nAS (d - y) = 0 ; avec n = = = 16,6

	- 0,1407348(1,45 - y) = 0				(2,66) - 16,6 (0,008478)(1,45 - y) = 0 ? 2,66
	+ 0,1407348 y - 0,20406546		= 0	? 2,66 y^2 + 0,2814696 y - 0,40813092 = 0
				? = b^2 - 4ac = (0,2814696) ^2 - 4(2,66) (-0,40813092)
=	4,349

v = #177;2,085

= 0,339 m

y =

· Moment d'inertie : I = Ib + nISt

avec Ib = y³ = (0,339)³ = 0,0345 m⁴ et ISt = AS (d - y)² = 0,008478(1,45 - 0,339)² =

0,01046 m4

I = Ib + nISt = 0,0345m⁴ + 16,6(0,01046 m⁴⁾ = 0,208136 m4

Les contraintes sont : c = Ms

xy = 581,046 t/m² et fst= n.Ms(d--y)

f = 31610,637 t/m²

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m² ; nous savons que : fbc ? la condition est

[77]

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : f _st = min{ ³ f e ; max (0,5 f e ;110.nf t28}
avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m² f = min{ (50000) ;m (0,5 50

st 000 ;110.1,6(240)}
f = min{ 33333,3 ;m (25000 ;2

st 155,55)} ; nous adoptons f st = 25000 t/m² ; nous
savons que : fSt ? f ^st la condition n'est pas vérifiée dans ce cas nous recalculons la section d'aciers tendus aux états limites de service.

Calcul d'armature :

·		, =
	0,544
Axe neutre : y = á x d = 0,544 x 1,45m = 0,79m				·
, levier	1,187m
Moment résistant de la table : MRS = (b x y)	x Z = (2,66 x 0,79 )	1800 x 1,187

MRS = 2244,925 tm ? MS (poutre simplement armée)

· Sections d'armature :

AS = = 0,012021 m² = 120,21 cm² soit 16HA32 ? 128,61 cm²

= ,

? Entretoises :

· En travée :

Mû = 71,2557 tm et Mu- = 4,347675 tm

· Largeur de la table de compression : B = 12ho + bo = 12(0,18) + 0,40 = 2,56m

MS = 47,5038 tm ; d = 1,27m ; b = 2,56m ; AS = 14,73 cm2 ; f8 = 30 MPa ; f_e = 500 MPa

[78]

Donnés : B = 2,56 m ; d = hP - e = 1,32 - 0,05 = 1,27m ; fbu = 1700 t/m² ; fsu = 43500 t/m²

· Moment de la table :

Mt = b x ho x _fbu x (d - ) = 2,56m x 0,18m x 1700 x (1,27 - ) = 924,3648 tm

· Pour le moment positif : Mû = 71,2557 tm M_u < Mt : section rectangulaire (B x h)

= 0,010151 < 0,186 (pivot A)

ìbu = =

á = 1,25 (1 - v ) = 0,01275

Z = d (1 - 0,4 á) = 1,27 (1 - 0,4(0,01275)) = 1,2635

_ _

AS 1 - 0,00129644 m2 = 12,9644 cm² soit 3HA25 ? 14,73 cm²

· Pour le moment négatif : Mu- = 4,347675 tm

= .( = 0,00061938 < 0,186 (pivot A)

ìbu = (1

b 1700.,27)x.2

á = 1,25 (1 - v ) = 0,00077446

Z = d (1 - 0,4 á) = 1,27 (1 - 0,4(0,00077446)) = 1,2696m

AS = _ = 0,00007872 m2 = 0,7872 cm² soit 4HA8 ? 2,01 cm²

· Armatures de peau :

A_p > x parement( 2R+bo) ? A_p > x ( 2(1,14)+0,40)

A_p > 8,04 cm² soit 4HA16 ? 8,04 cm²

Vérification des contraintes

Pour le moment positif :

[79]

· Position de l'axe neutre :

b - nAS (d - y) = 0 ; avec n = = = 16,6

(2,56) - 16,6 (0,001473)(1,45 - y) = 0 ? (2,56) - 0,02445(1,45 - y) = 0

? (2,56) - 0,03545 + 0,02445 y = 0 ? 2,56 + 0,02445 y - 0,03545 = 0

? 2,56 y² + 0,0489 y - 0,0709 = 0

? = b² - 4ac = (0,0489) ² - 4(2,56) (-0,0709) = 0,7284 v = 0,85

y = = 0,156 m

· Moment d'inertie :

I = Ib + nISt

avec Ib = y³ = (0,156)³ = 0,003239 m⁴ et ISt = AS (d - y)² = 0,001473(1,27 - 0,156)² =

0,00183 m4

I = Ib + nISt = 0,03239m⁴ + 16,6(0,00183 m⁴⁾ = 0,033617 m4

Les contraintes sont : fbc = = 220,44 t/m² et fSt = = 26131,39t/m²

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m² ; nous savons que : fbc ? la condition est

verifié.

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : = min{ v }

Avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m²

= min{

v }

[80]

= min{ } ; nous adoptons = 25000 t/m² ; nous

savons que : fSt ? la condition n'est pas vérifiée dans ce cas nous recalculons la section

d'aciers tendus aux états limites de service. Calcul d'armature : · Paramètre de déformation : á =		=		= 0,544

· Axe neutre : y = á x d = 0,544 x 1,27m = 0,69 m

· Bras de levier : Z = d (1 - ) = 1,27(1 - ) = 1,039m

· Moment résistant de la table : MRS = (b x y) x Z = (2,56 x 0,69 ) 1800 x 1,039

MRS = 1651,760 tm ? MS (poutre simplement armée)

· Sections d'armature :

AS = = = 0,001829 m² = 18,29 cm² soit 6HA20 ? 18,84 cm²

· Aux appuis :

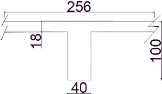
B = 2,56 m ; d = h_p - e = 1 - 0,05 = 0,95 m ; fbu = 1700 t/m² ; fsu = 43500 t/m²

· Moment de la table de compression :

Mt = 2,56 x 0,18 x 1700 x ( 0,95 - ) = 673,6896 tm

M_u ? Mt : section rectangulaire (B x h)

· Moment réduit ultime :

ìbu == 0,018141 ? 0,186 (pivot A)

=

· Paramètre de déformation :

[81]

á = 1,25 (1 - v ) = 0,02288

· Bras de levier :

Z = d (1 - 0,4 á) = 0,95 (1 - 0,4(0,02288)) = 0,939m

· Section d'armature :

AS = = 0,0017444 m2 = 17,444 cm² soit 6HA20 ? 18,84 cm²

· Pour le moment négatif : Mu^- = 4,347675 tm

ìb

=
· = 0 001106 < 0 186(pivot
u = , ₇ A)

á = 1,25 (1 - v ) = 0,001383

Z = d (1 - 0,4 á) = 0,95 (1 - 0,4(0,001383)) = 0,949m

AS = = 0,0001053 m² = 1,053 cm² soit 4HA8 ? 2,01 cm²

Pour les armatures transversales, nous adoptons les même que celles des poutres.

· Armatures de peau :

A_p ? x parement( 2R+bo) ? A_p ? x ( 2(0,82)+0,40)

A_p ? 6,12 cm2 soit 4HA14 ? 6,16 cm²

Vérification des contraintes

Pour le moment positif :

MS = 47,5038 tm ; d = 0,95m ; b = 2,56m ; AS = 18,84 cm² ; f8 = 30 MPa ; f_e = 500 MPa

· Position de l'axe neutre :

b - nAS (d - y) = 0 ; avec n = = = 16,6

(2,56) - 16,6 (0,001884)(0,95 - y) = 0 ? (2,56) - 0,03127(0,95 - y) = 0

? (2,56) - 0,0297 + 0,03127 y = 0 ? 2,56 + 0,03127 y - 0,0297= 0

? 2,56 y² + 0,06254 y - 0,0594 = 0

[82]

? = b² - 4ac = (0,06254) ² - 4(2,56) (-0,0594) = 0,61217 v = 0,78

y = = 0,14 m

· Moment d'inertie :

I = Ib + nISt

avec Ib = y³ = (0,14)³ = 0,0023 m⁴ et ISt = AS (d - y)² = 0,001884(0,95 - 0,14)² =

0,001236 m4

I = Ib + nISt = 0,0023 m⁴ + 16,6(0,001236 m⁴⁾ = 0,0228 m4

Les contraintes sont : fbc = = 291,68 t/m² et fSt = = 28014,74t/m²

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m² ; nous savons que : fbc ? la condition est

verifié.

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : = min{ v }
avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m²

= min{ v }

= min{ } ; nous adoptons = 25000 t/m² ; nous

savons que : fSt ? la condition n'est pas vérifiée dans ce cas nous recalculons la section

=

d'aciers tendus aux états limites de service.

· Calcul d'armature :

·

= 0,544

Paramètre de déformation : á =

· Axe neutre : y = á x d = 0,544 x 0,95m = 0,5168 m

· Bras de levier : Z = d (1 - ) = 0,95(1 - ) = 0,778m

verifié.

[83]

· Moment résistant de la table : MRS = (b x y) x Z = (2,56 x 0,5168 ) 1800 x 0,778

MRS = 926,37 tm ? MS (poutre simplement armée)

· Sections d'armature :

AS = = 0,002442 m² = 24,42 cm² soit 8HA20 ? 25,14 cm²

Pour le moment négatif :

MS = 2,89845 tm ; d = 0,95m ; b = 2,56m ; AS = 2,01 cm2 ; f8 = 30 MPa ; f_e = 500 MPa

· Position de l'axe neutre :
b - nAS (d - y) = 0 ; avec n =	=		=	16,6
(2,56) - 16,6 (0,000201)(0,95	- y) =	0	?	(2,56)	- 0,0033366(0,95 - y) = 0

? (2,56) - 0,003169 + 0,0033366 y = 0 ? 2,56 + 0,0033366 y - 0,003169 = 0

? 2,56 y² + 0,0066732 y - 0,006338 = 0

? = b² - 4ac = (0,0066732) ² - 4(2,56) (-0,006338) = 0,06494 v = 0,2548

y

= = 0,048 m

· Moment d'inertie : I = Ib + nISt

avec Ib = y³ = (0,048)³ = 0,000094 m⁴ et ISt = AS (d - y)² = 0,000201(0,95 - 0,048)² =

0,00016 m4

I = Ib + nISt = 0,000094 m⁴ + 16,6(0,00016 m⁴⁾ = 0,00275 m4

Les contraintes sont : fbc = = 50,59 t/m² et fSt = = 15781,48 t/m²

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m2 ; nous savons que : fbc ? la condition est

[84]

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : = min{ v }
avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m²

= min{ v }

= min{ } ; nous adoptons = 25000 t/m² ; nous

savons que : fSt ? ? Dalle : · En travée :

la condition est vérifiée

Suivant le sens transversale(x) :

Mû = 12,3188698 tm ; d = 0,18m - 0,05m = 0,13m ; b =1m

· Moment réduit ultime :

' = 0,4287 0,430 ? 0,186 (doublement armé)

ìbu = =

· Sections d'armatures :

As = fl_u x b x d x et As^' = fl_u^' x b x d x avec : fl_u = 0,5591 et fl_u^' = 0,0656

· Armatures inférieures :

As = 0,5591 x 1,00 x 0,13 x = 0,00284 mm² = 28,4 cm² soit 12HA18/m ?30,52 cm²

· Armatures supérieures :

As^' = 0,0656 x 1,00 x 0,13 x = 0,00033327 = 3,3327 cm² soit 3HA14/m ? 4,62 cm²

Suivant le sens de la circulation(y) :

Mû = 3,07971745 tm ; d = 0,18m - 0,05m = 0,13m ; b =1m

· Moment réduit ultime :

--

M

=

= 0107 < O 186

ìbu-- , 7

[85]

· Paramètre de déformation :

á = 1,25 (1 - v ) = 0,141

· Bras de levier :

Z = d (1 - 0,4 á) = 0,13 (1 - 0,4(0,141)) = 0,122m

· Section d'armature :

AS = = 0,0005803 m² = 5,803 cm² soit 8HA10/m ? 6,28 cm²

· Aux appuis : M_u^- = 7,246394 tm

· Moment réduit ultime :

ìbu = =

= 0,252 ? 0,186

0,186 ? 0,2522 ? 0,371 (dalle simplement armée)

As = â_u x b x d x avec : â_u = 0,2957

· Section d'armatures :

As = 0,2957 x 1,00 x 0,13 x = 0,0015022 m² = 15,022 cm² soit 10HA14/m ? As =

15,39 cm²

· Espacement :

Stx = min { = min { ? Stx = 33cm l'espacement entre les barres principales d'une

dalle ne dépasse pas 30 cm.

Sty = min { = min { ? Sty = 44cm.

? Encorbellement : Mu^- = 2,4724 tm

· Moment réduit ultime :

[86]

= 0,086 ? 0,186 (pivot A)

ìbu = =

· Paramètre de déformation :

á = 1,25 (1 - v ) = 0,112

· Bras de levier :

Z = d (1 - 0,4 á) = 0,13 (1 - 0,4(0,112)) = 0,124 m

· Section d'armatures :

AS =

_ = 0,0004583 m2 = 4,583 cm² soit 3HA14 /m? 4,62 cm² Armatures de répartition : Ar = ; ( 4,62) = 1,155 cm² soit 2HA10 ? 1,57 cm² ? Vérification de l'effort tranchant :

? 21,9975 < 182,60869 : condition vérifiée

< <

?

· Espacements :

Stx < min { < min { ? Stx < 33cm l'espacement entre les barres principales d'une

dalle ne dépasse pas 30 cm. D'où nous adoptons Stx = 20 cm

Sty < min { < min { ? Sty < 44cm. D'où nous adoptons Sty = 30 cm

Vérification des contraintes

MS = 1,76475 tm ; d = 0,13m ; b = 1,0 m ; AS = 4,62 cm2 ; f8 = 30 MPa ; f_e = 500 MPa

· Position de l'axe neutre : b - nAS (d - y) = 0 ; avec n = = = 16,6

(1) - 16,6 (0,000462)(0,13 - y) = 0 ? - 0,00767(0,13 - y) = 0

? - 0,00099 + 0,00767 y = 0 ? + 0,00767 y - 0,00099 = 0

? y² + 0,01534 y - 0,00198 = 0

[87]

? = b² - 4ac = (0,01534) ² - 4(1) (-0,00198) = 0,0081 v = 0,09

= 0,037 m

y =

· Moment d'inertie :

I = Ib + nISt

avec Ib = y³ = (0,037)³ = 0,0000168 m⁴ et ISt = AS (d - y)² = 0,000462(0,13 - 0,037)² =

0,00000399 m4

I = Ib + nISt = 0,0000168 m⁴ + 16,6(0,00000399 m⁴⁾ = 0,0000830 m4

fb_c = M =fst= n. = 32824,35 t/m²

Les contraintes sont : 786 69 t/m² et

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m2 ; nous savons que : fbc ? la condition est

verifié.

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : = min{ v }
avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m²

= min{ v }

= min{ } ; nous adoptons = 25000 t/m² ; nous

savons que : fSt ? la condition n'est pas vérifiée dans ce cas nous recalculons la section

d'aciers tendus aux états limites de service. Calcul d'armature : · Paramètre de déformation : á =		=		= 0,544

· Bras de levier : Z = d (1 - ) = 0,13(1 - ) = 0,106 m

· Moment résistant de la table : MRS = (b x y) x Z = (1 x 0,07 ) 1800 x 0,106

[88]

MRS = 6,678 tm ? MS (poutre simplement armée) ? Sections d'armature :

AS = = = 0,000665 m² = 6,65 cm² soit 5HA14 ? 7,70 cm²

Armatures de répartition : Ar = ( 7,70) = 1,92 cm² soit 3HA10 ? 2,36 cm2

[89]

CHAPITRE.7. Calcul des éléments de l'infrastructure

Dans ce chapitre, nous allons évaluer les charges, étudier la stabilité des éléments de l'infrastructure (en considérant les charges en ELU pour l'appareil d'appuis). Enfin, nous allons faire le calcul du béton armé aux états limite de services.

7.1. Appareils d'appuis

Nous utiliserons des appareils d'appuis fixes qui assurent l'immobilité de la section reposant sur eux et les rotations. Nous avons opté pour les appareils d'appuis en élastomères frettés ou néoprène qui a pour avantage :

· Une bonne résistance au cisaillement et à la traction ;

· Présente un pouvoir remarquable d'élasticité et d'allongement ;

· Très disponible sur le marché ;

Une plaque en néoprène est composée d'une tôle en acier et d'une couche d'élastomère(caoutchouc).

Fig.

Le calcul se fait en fonction des conditions suivantes :

· Vérification des contraintes à vide et sous charge ;

· La distorsion due à la variation de la température ;

· La distorsion due à l'effort de freinage ; ? Quelques spécifications techniques :

· Limite de contraintes à la compression :

- A vide : 95 bars (poids propre du tablier et la charge de la foule) - Sous charge : 135 bars (le trafic y compris)

[90]

· Variation de la température : ÄT = 10°C

· Coefficient thermique : X = 1,2 x 10^-5

· Module d'élasticité : E = 10 bars

v Pré-dimensionnement :

Nous optons pour une plaque de 10 mm c'est-à-dire 1mm pour la tôle en acier et 9mm pour l'élastomère (en caoutchouc) soit 1cm en tout.

v Vérification

ü A la compression :

On sait que :

· Tconvois = 29,241 t x 1,5 = 43,8615 t

· Tfoule = 8,33 t x 1,5 = 12,495 t

· Tpoids propre = 44,4679625 t x 1,35 = 60,03174 t

A vide : R1 = Tfoule + Tpoids propre = 72,52674 t = 72526,74 kg

< 95 bars ? < 95 kg/cm² ? < 95 kg/cm² ? S1 = 763,43cm²

Sous charge : R2 = Tconvois + _Tfoule + Tpoids propre = 116,38824 t = 116388,24 kg

,2

< 135 bars ? < 135 kg/cm2 ? < 135 kg/cm2 ? S2 = 862,1351cm²

Pour trouver la section d'appareil d'appuis nous prenons : Sappareil d'appuis ? Smax et

Smax = max (S1 ; S2) ? Smax = max (763,43cm² ; 862,1351cm²) ? Smax = 862,1351 cm², nous adoptons : Sappareils d'appuis = 900 cm²

Nous cherchons à déterminer la section (a x b) qui va résister à l'effort de freinage et l'épaisseur (e) qui va résister à la variation de la température.

ü A la distorsion :

Distorsion due à la variation de Température (d1) :

Ici : d1 < 0,5. e avec : d1 = X. ÄT. où L est la portée

d1 = 1,2 x 10^-5 x 10 x = 0,102cm ? 0,102cm < 0,5.e d'où e ? ? e ? 0,204 cm

nous adoptons : e = 12 cm

[91]

Distorsion due à l'effort de freinage (d2) :

Ici : d2 = avec F =

Alors : ? Effort de freinage =

=

x 1m = 4 t = 4000 kg

? Nombre de poutre : 4 ? Nombre d'appuis : 2

Avec E = 10 bar = 10 kg/cm² d'où F = = 500 kg

Ainsi : d2 = = 0,666 cm

? Condition : d1 + d2 ? 0,7 e

? 0,102 cm + 0,666 cm ? 0,7 x 12 cm ? 0,768 cm ? 8,4 cm d'où la condition est vérifiée.

7.2. Dalle de transition

Fig.

La dalle de transition est appuyée d'un côté par le mur garde grève (corbeau) et de l'autre côté sur le remblai (appuis élastique). Elle s'étant sur une longueur de 5m et a une largeur correspondant à celle du pont soit 12m.

CL = = = 0,4166 0,42 ? 0,40 ; la dalle porte dans deux sens.

? Evaluation des charges :

? Poids propre de la dalle : 0,25m x 2,5 t/m³ = 0,625 t/m2

[92]

· Poids de la chaussée :

· Revetement : 0,08m x 2,4 t/m³ = 0,192 t/m²

· Chape d'étanchéité : 0,04m x 2,1 t/m² = 0,084 t/m²

· Couche de forme : 0,04m x 2,2 t/m² = 0,088 t/m² Poids de la chaussée : PChaussée = 0,364 t/m²

· Surcharge sur remblais : 1 t/m2

· Convoi :

Les surfaces d'influences de la dalle seront données par :

> Sens de x :

S1 = L1 x L2

L1 = a1 + 1,5 h_r + 2 hd + = 0,30m + 1,5 (0,16m) + 2 (0,25m) + = 2,706 m

L2 = a2 + 1,5 h_r + 2 hd = 0,30m + 1,5 (0,16m) + 2 (0,25m) = 1,04 m D'où S1 = 2,706 m x 1,04 m = 2,814 m2

Alors la densité sera : x õdalle = x 1,2 = 3,198 t/m²

> Sens de y :

S2 = L1 x L2

L2 = a2 + 1,5 h_r + 2 hd = 0,30m + 1,5 (0,16m) + 2 (0,25m) = 1,04 m

L1 = a1 + 1,5 h_r + 2 hd + = 0,30m + 1,5 (0,16m) + 2 (0,25m) + = 5,04 m

D'où S1 = 1,04 m x 5,04 m = 5,2416 m2

Alors la densité sera : x õdalle = x 1,2 = 1,717 t/m²

La charge du convoi est donc : Pconvois = 4,915 t/m²

Combinaisons des charges : PS = 0,625 t/m2 + 0,364 t/m2 + 1 t/m2 + 4,915 t/m2 = 7,268 t/m2

? Calcul des moments :

Par la méthode forfaitaire on a : pour á = 0,42 ; u_x = 0,1098 et u_y = 0,3000 ; l_x = 5m

[93]

Mox = ì_x. Ps. l_x² = 0,1098 x 7,268 t/m² x (5m)² = 19,951 tm Moy = ì_y. Mox = 0,3000 x 19,951 tm = 5,9853 tm

Suivant le petit côté X :

? Moment en travée :

Mtx = 0,85. Mox = 0,85 x 19,951 tm = 16,958 tm

? Moment aux appuis :

Max = - 0,5. Mox = - 0,5 x 19,951 tm = - 9,9755 tm

Suivant le grand côté Y :

? Moment en travée :

Mty = 0,85. Moy = 0,85 x 5,9853 tm = 5,0875 tm

? Moment aux appuis :

May = - 0,5. Mox = - 0,5 x 19,951 tm = - 9,9755 tm

7.3. Culée

Fig.

[94]

Les sollicitations sur la culée sont calculées par une tranche d'un mètre. Le bras de levier est pris par rapport au point O.

7.3.1. Evaluation des charges.

Fig.

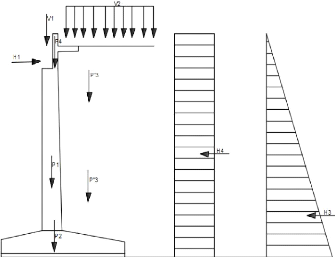
? Charges verticales :

? Poids des terres derrière le mur (P3) :

P'3 = (1m+3,0m) x 3,0m x 1,8t/m³ x 1m = 21,6 t

P»3 = (2m - 0,50m) x 3,0m x 2,60 t/m³ x 1m = 11,7 t P3 = P'3 + P»3 = 21,6 t + 11,7t = 33,3 t

Excentricité : x = ¹(3,0m) + 1m + 2,0m = 4,0m ? Poids de la semelle (P2) :

[95]

S1 = = 0,4 m² ; S2 = 0,60m x 2,0 = 1,2 m²

S3 = 1,00m x 1,00m = 1 m² ; S4 = = 0,75 m²

S5 = 0,50 x 3,0m = 1,50 m²

St = 0,4 m² + 1 m² + 1,50 m² + 1,2 m² + 0,75 m² = 4,85 m² P2 = 4,85 m² x 2,5 t/m³ x 1m = 12,125 t

Excentricité: X1 = (2,0m) = 1,33m ; X2 = (2,0m) = 1 m ; X3 = (1m) + 2,0m = 2,50 m ; X4 = (3,0m) + 1m + 2,0m = 4 m ; X5 = (3,0m)+ 1m + 2,0m = 4,5m

?

?

X

= 2,985 m

? Poids du corps de la culée(P1) :

S1 = 0,80m x 3,38 m = 2,704 m² ; S2 = = 0,338 m²

St = 2,704 m² + 0,338 m² = 3,042 m²

P1 = 3,042 m² x 2,5 t/m³ x 1m = 7,605 t

Excentricité : X1 = (0,80) + 2,0m = 2,40m ; X2 = (0,20) + 0,80m + 2,0m = 2,86m

?

?

X

= 2,451 m

? Poids du mur garde grève (P4) :

S1 = 0,30 m x 1,62m = 0,486 m² ; S2 = 1m x 0,25m = 0,25 m² St = 0,25 m² + 0,486 m² = 0,736 m²

P4 = 0,736 m² x 2,5 t/m³ x 1m = 1,84 t

Excentricité : X1 = (0,30m) + 0,50m+ 2,0m = 2,65 m ; X2 = (1m) + 0,30m + 0,50m + 2,0m = 3,30m

= 2,870 m

?

?

X

[96]

? La réaction verticale due à l'action des charges verticales (V1) : L'effort tranchant max(ELS) : Tmax = 82,0389625 t

Comme il y a 4 appuis sur la culée, on obtient :

V1 = x 1m = 27,346320 t

Excentricité : X= (0,50m) + 2,0m = 2,25m ? Poids de la surcharge(V2) : 1t/m²

V2 = x 1m = 1,95 t

Excentricité : x = (3,0m) + 1m + 2,0m = 4,0m

? Poids de la dalle de transition (V3) : P_s = 0,625t/m² + 0,364t/m² = 0,989 t/m² V3= 0,989 t/m² x 5m x 1m = 4,945 t

Excentricité : x = (3,0m) + 1m + 2,0m = 4,0m

? Charges horizontales :

Le coefficient des poussées des terres k est donné par :

Pour le sable : Nõ = tg²(45+ ) = tg²(45+ ) = 3 ; k = = = 0,33

Pour le sable limoneux : Nõ = tg²(45+ ) = tg²(45+ ) = 2,46 ; k = = = 0,40

Pour le calcul de l'effort de freinage et de la poussé due à la surcharge, nous utiliserons le

coefficient des poussées des terres le plus élevé soit k = 0,40 ? Effort de freinage (H1) :

H1 =

Avec : - k : coefficient des poussées des terres = 0,40

- N : nombre de bandes = 2

[97]

- C : convois : 60t

- lp : largeur du pont = 12 m

t

H1 = o,4ox2x6o x 1m = 4 t
12m

162m

Excentricité : X = 6,0 - , = 5,19 m

· Poussées des terres due au poids du sol (H3^' et H3^») :

ü Pour le sable :

H'3 = ₂¹(?sable x h² x k) = ₂¹(1,8t/m³ x (4,0)² x 0,33) x 1m = 4,752 t

Excentricité : X= ¹(6,0 - 2,0) = 1,33 m

ü Pour le sable limoneux :

cu

Contrainte horizontale : 6h = - 2 avec 6_v = (2,6 t/m³ x 2m ) = 5,20 t/m²
tpf tp

5,2 2(1)

6h _2,46 - 1/2,46 = 0,838 ^t/m2

H»3 = 1 (0,838 t/m² x 2m ) x 1m = 0,838 t

²

Excentricité : X= ¹(2m) = 0,67m

· Poussée de terres due à la surcharge (H4) : H4 = k x V2 x Hculée = 0,40 x 1t/m² x 6,0 m x 1m = 2,4 t Excentricité : X= ₂¹(6,0m) = 3,0m

[98]

^TABLEAU DES FORCES VERTICALES
^Charges verticales	^CHARGES (t)		^(m)		^Moment stabilisant ( ^tm)
^P1	^7,605		^2,451		^18,639855
^P2	^12,125		^2,985		^36,193125
^P3	^33,3		^4		^133,2
^P4	^1,84		^2,87		^5,2808
^V1	^27,34632		^2,25		^61,52922
^V2	^1,95		^4		^7,8
^V3	^6,675		^4		^26,7
^SOMMES	^90,84132				^289,343
^Excentricité ^TABLEAU DES FORCES HORIZONTALES
^Charge horizontale		CHARGE(t)		^(m)	^Moment renversant ^(tm)
^H1		^4		^5,19	^20,76
^H'3		^4,752		^1,33	^6,32016
^H"3		^0,838		^0,67	^0,56146
^H4		^2,4		^3	^7,2
^SOMMES		^11,99		^Excentricité	^34,84162

7.3.2. Etude de la stabilité

E Ms 289,343 Stabilité au renversement : > 1 5 ? >	1,5 ?	? 8,3 7,57 >	> 1,5 · la ' 1,5 ; la condition
E Mr - ' 34,84162 condition est vérifiée. Fi; 90,84132
v > > 1,5 Stabilité au glissement : Fh 1,5 ? 11,99

est vérifiée.

v Stabilité face aux contraintes transmise par le sol :

Condition : Emax ? Esol et Emin ? 0

Pour le choix du type de fondation, nous avons choisi les fondations directes (avec semelles) ; la profondeur du bon sol étant de 5m. La condition est que la contrainte admissible du sol support doit être d'au moins : Esol = R_p / 10 > 0,1 MPa

[99]

Notre sol présente une contrainte de rupture à la pointe minimum de 1,4 MPa ; alors la

contrainte admissible du sol sera : ósol = _ = 0,22 MPa > 0,1 MPa

La culée travaille en flexion composée. D'où :

? ?

ómax = X (1 + ) et ómin = x (1 - )

· Calcul de l'excentricité (e) : e = - x

=

or x=

? ?

?

= 2,80 m

e = - 2,80m = 0,20 m

condition : 0 ? e = ? 0 ? 0,20 = ? 0 ? 0,20 = 1. Condition vérifiée l'excentricité

se trouve dans le noyau central.

· Vérification des contraintes :

ómax = T x (1 + ) = 18,168 t/m²

ómin = x (1 - ) = 12,112 t/m²

ómax ? ósol et ómin > 0 ? 18,168 t/m² ? 22 t/m² et 12,112 t/m² > 0. Condition vérifiée

· Diagramme de contrainte :

^ómin = ^{12,112 t/m2}

^ómax = ^18,168 t/m2

[100]

7.3.3. Calcul proprement dit de la culée

Fig.

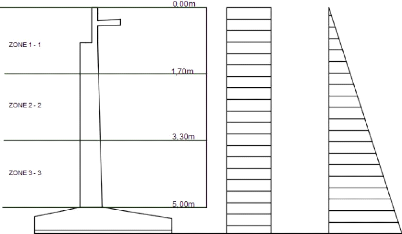
7.3.3.1. Calcul du corps de la culée et mur garde grève
7.3.3.1.1. Calcul des moments

? Effort de freinage

=

H1 = x 1m = 4 t ; alors H1' = H1» = H1''' ; c'est-à-dire que l'effort
de freinage reste ainsi dans chaque zones.

On trouve l'excentricité dans chaque zones : x = Hi-i

x1 = 0,89m ; x2 = 2,49m ; x3 = 4,19m

? Poussée due à la surcharge

H2 = k x V2 x H2-2

1 - 1 : H2^' = (0,40 x 1t/m² x 1,70m) x 1m = 0,68 t ; x1 = = 0,85 m

2 - 2 : H2» = (0,40 x 1t/m² x 3,3m) x 1m = 1,32 t ; x2 = = 1,65 m

3 - 3 : H2^''' = (0,40 x 1t/m² x 5,0m) x 1m = 2,0 t ; x3 = = 2,5 m

[101]

? Poussée des terres :

H3 = k x ySol ^x (H3-3)2 , nous évaluons la poussée par zone en tenant compte du sol le plus dominant ;
1 - 1	: H3^' =	0,33 x 1,8 x (1,70m)^2 x 1m = 0,858 t ; x = (1,70m) =						1,13m
2 - 2	: H3^» =	0,33 x 1,8 t/m^3 x (3,3m)^2 x 1m = 3,234 t ; x = (3,3m)						= 2,2m
3 - 3	: H3^''' =	0,40 x 2,6 t/m^3 x (5,0m)^2 x 1m = 13 t ; x = (5,0m) =						3,33m
					^TABLEAU ZONE 1 - ^1
^Zone 1 - ^1				^CHARGE	^Excentricité
^H1				^4	^0,89
^H2 ^0,68 ^0,85
^H3			^0,858		^1,13
^Somme			^5,538		^TABLEAU ZONE 2 - ^2
^Zone 2 - ^2			^CHARGE		^Excentricité		^MOMENT
^H1			^4		^2,49		^9,96
^H2			^1,32		^1,65

[102]

^{TABLEAU ZONE 3} - ³

^{Zone 3} - ³

^CHARGE

^{Excentricité}

7.3.3.2. Calcul de la semelle

^MOMENT

^H1

⁴

^4,19

^16,76

^H2

²

^2,5

⁵

^H3

¹³

^3,33

^43,29

^Somme

¹⁹

^65,05

La semelle est sollicitée par toutes les charges situées au-dessus c'est-à-dire : la réaction

verticale due à l'action des charges provenant de la superstructure, le poids du corps de la

culée, le poids du mur garde grève, le poids du remblai, la surcharge sur remblais et son poids

propre ; en dessous par la réaction du sol. On sait que l'action est égale à la réaction. Nous

considérons l'effet de la réaction du sol sous semelle puisqu'il tend à soulever la semelle.

Nous calculons la semelle comme un élément encastré avec une charge correspondant à la

réaction du sol.

Calcul des moments

Tronçons A - B :

^{18,168 t/m2}

^{0,018 t/m}

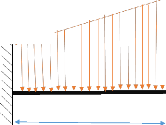
^15,644

^{17,122 t/m2}

^{2,5 m}

FAB1 = x 1m = x 1m = 3,155 t ; x= (2,5) = 1,6m

^2,

FAB2 = 15,644 t/m² x 2,50m x 1m = 39,11 t ; x = (2,50) = 1,25m FAB = 3,155 t + 39,11 t = 42,265 t

[103]

Excentricité : X = = 1,27 m

MAB = - FAB x X = - 42,265 t x 1,27 m = 53,676 tm

Tronçons B - C :

^{12,112 t/m2}

^{3,5 m}

^{15,644 t/m2}

FBC1 = x 1m = x 1m = 6,181 t ; x= (3,5) = 1,16m

FB = 12,112 t/m² x 3,50m x 1m = 42,392 t ; x = (3,50) = 1,75m FBC = 6,181 t + 42,392 t = 48,573 t

Excentricité : X = = 1,67 m

MBC = - _FBC x X = - 48,573 t x 1,67 m = - 81,11691 tm

7.3.3.3. Corbeau

Le corbeau se calcul comme une poutre encastrée d'un seul côté (mur garde grève) par bande d'un mètre.

? Evaluation des charges

Le corbeau sert d'appuis pour la dalle de transition. Nous allons considérer la charge de la dalle de transition par bande d'un mètre et le poids propre du corbeau soit :

[104]

PS = (7,268 t/m² x 1 m) +(0,25m x 1m x 2,5 t/m³) = 7,893 t/m

? Calcul de moment

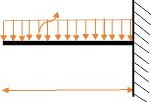
^7,893t/m

^1,0m

M = - = - = - 3,9465 tm

? Calcul de l'effort tranchant

T = PL = 7,893 t/m x 1,0m = 7,893 t

7.4. Mur en aile

Les murs en ailes sont des voiles de part et d'autre de la culée pour retenir les remblais derrière cette dernière. Il est soumis aux sollicitation suivantes :

? Horizontalement il est soumis à la poussée des terres et à la poussée due aux surcharges sur le remblai ;

? Verticalement il est soumis à son poids propre ;

7.4.1. Evaluation des charges

[105]

? Charges verticales :

? Poids des terres derrière le mur (P3) : P'3 = (1m+3,0m) x 2,0m x 1,8t/m³ x 1m = 14,4 t P»3 = (2m - 0,50m) x 2,0m x 2,60 t/m³ x 1m = 7,8 t P3 = P'3 + P»3 = 14,4 t + 7,8t = 22,2 t

Excentricité : x = (2,0m) + 0,80m + 1,20m = 2,67m ? Poids de la semelle (P2) :

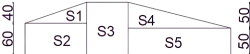
S1 = = 0,24 m² ; S2 = 0,60m x 1,20 = 0,72 m²

S3 = 0,80m x 1,00m = 0,80 m² ; S4 = = 0,50 m²

S5 = 0,50 x 2,0m = 1,0 m²

St = 0,24 m² + 0,72 m² + 0,80 m² + 0,50 m² + 1 m² = 3,26 m²

=

P2 = 3,26 m² x 2,5 t/m³ x 1m = 8,15 t

Excentricité: X1 = (1,20m) = 0,80m ;	X2 = (1,20m) =	0,60 m ; X3 =	(0,80m)	+ 1,20m
1,60 m ; X4 = (2,0m) + 0,80m + 1,20m	= 2,67 m ; X5 =	(2m)+ 0,80m	+ 1,20m	= 3,0m

?

X ?

= 1,913 m

? Poids du corps du Mur (P1) :

S = 0,80m x 5 m = 4 m² ; P1 = 4 m² x 2,5 t/m³ x 1m = 10 t

Excentricité : X = (0,80) + 1,20m = 1,60m ;

[106]

? Charges horizontales :

· Poussées des terres dues au poids du sol (H3^' et H3^») :

ü Pour le sable :

H'3 = ₂¹(?sable x h² x k) = ₂¹(1,8t/m³ x (4,0)² x 0,33) x 1m = 4,752 t

Excentricité : X= ¹(6,0 - 2,0) = 1,33m

ü Pour le sable limoneux :

Contrainte horizontale : óh = - v2 avec ó_v = (2,6 t/m³ x 2m ) = 5,20 t/m²

5,20 2(1)

óh _=2,46 - V2,46 = 0,838 ^t/m2H»3 = 1 (0,838 t/m² x 2m ) x 1m = 0,838 t 2

Excentricité : X= ¹(2m) = 0,67m

· Poussée de terres due à la surcharge (H4) : H4 = k x V2 x Hculée = 0,40 x 1t/m² x 6,0 m x 1m = 2,4 t Excentricité : X= ₂¹(6,0m) = 3,0m

^TABLEAU DES FORCES VERTICALES
^Charges verticales	^(t)	^Excentricit ^é (m)	^Moment ^stabilisant
^P1	^10	^1,6	^16
^P2	^CHARGES ^8,15	^1,913	^15,59095
^P3	^22,2	^2,67	^59,274
^SOMMES	^40,35		90,86495

[107]

^TABLEAU DES FORCES HORIZONTALES
^Charge horizontale	CHARGE(t)	^Excentricit ^é (m)	^Moment ^renversant
^H'3	^4,752	^1,33	^6,32016
^H"3	^0,838	^0,67	^0,56146
^H4	^2,4	^3	^7,2
^SOMMES	^7,99		^14,08162

7.4.2. Etude de la stabilité

v Stabilité au renversement : ? >1,5 ? > 1,5 ? 6,45 > 1, ; 5 la condition
? --

--

est vérifiée.

v Stabilité au glissement : E Fh > 1,5 ? 9 > 1,5 ? 5,050 > 1,5 ; la condition est vérifiée.

v Stabilité face aux contraintes transmise par le sol : Le calcul des contraintes se fera comme dans le cas de la culée. La culée travaille en flexion composée. D'où :

? ómax =

x (1 + ) et ómin = ? x (1 -

)

· Calcul de l'excentricité (e) : e = ' - x

? ?

or

= = 1,90 m

?

e = - 1,90m = 0,10 m

condition : 0 ? e = ? 0 ? 0,10 = ? 0 ? 0,10 = 0,67 condition vérifiée l'excentricité se trouve dans le noyau central.

· Vérification des contraintes :

ómax = x (1 + ) = 13,265 t/m²

ómin = x (1 - ) = 6,909 t/m2

[108]

ómax < ósol ^et ómin > 0 ? 13,265 t/m² < 22 t/m² et 6,909 t/m² > 0. Condition vérifiée ? Diagramme de contrainte :

^ómin = ^{6,909 t/m2}

^ómax = ^{13,265 t/m2}

7.5. Calcul proprement dit du mur en aile

Nous allons calculer le moment et l'effort normal par zone et nous considèrerons la zone qui aura les valeurs les plus élevées.

7.5.1. Calcul du corps du mur

Fig.

[109]

7.5.1.1. Calcul des moments

· Poussées des terres due au poids du sol (H3^' et H3^») :

ü Pour le sable :

H'3 = (?sable x h² x k) = (1,8t/m³ x (4,0)² x 0,33) x 1m = 4,752 t

Excentricité : X= (6,0 - 2,0) = 1,33 m

ü Pour le sable limoneux :

Contrainte horizontale : óh =
· -
· v avec ó_v = (2,6 t/m³ x 2m ) = 5,20 t/m²

óh = - v = 0,838 ^t/m2

H»3 = (0,838 t/m² x 2m ) x 1m = 0,838 t

Excentricité : X= (2m) = 0,67m

· Poussée de terres due à la surcharge (H4) : H4 = k x V2 x Hculée = 0,40 x 1t/m² x 6,0 m x 1m = 2,4 t Excentricité : X= (6,0m) = 3,0m

TABLEAU DES MOMENTS

^TABLEAU ZONE 1- ^1					^Zone 1- ^1
^CHARGE		^Excentricité	^MOMENT	^H2
^0,68		^0,85	^0,578	^H3
^0,858		^1,13	^0,96954	^Somme
^1,538			1,54754

[110]

^TABLEAU ZONE 2 - ^2					^Zone 2 - ^2
^CHARGE		^Excentricité		^H2
^1,32		^1,65		^H3
^3,234		^2,2		^Somme
^4,554

^MOMENT

^{2,178 7,1148 9,2928 TABLEAU ZONE 3} - ³

^{Zone 3} - ³

^CHARGE

^{Excentricité}

^MOMENT

^H2

²

^2,5

^H3

¹³

^3,33

^43,29

^Somme

¹⁵

^48,29

7.5.1.2. Calcul de l'effort normal

L'effort tranchant correspond au poids propre soit NS = 10 t

7.5.2. Calcul de la semelle

⁵

La semelle est sollicitée par toutes les charges situées au-dessus c'est-à-dire : le poids du

corps du mur en aile, le poids du remblai et son poids propre ; en dessous par la réaction du

sol. Le principe de calcul reste le même que celui de la semelle de la culée.

Calcul des moments :

Tronçon A - B :

^{13,265 t/m2}

^10,7

^{17,122 t/m2}

^{1,60 m}

,

^{0,018 t/m}

[111]

FAB1 = x 1m = x 1m = 2,034 t ; x= (1,60) = 1,06m

FAB2 = 10,722 t/m² x 1,60m x 1m = 17,155 t ; x = (1,60) = 0,80m FAB = 2,034 t + 17,155 t = 19,189 t

Excentricité : X = = 0,827 m

MAB = - FAB x X = - 19,189 t x 0,827 m = - 15,869 tm Tronçon B - C :

^{6,909 t/m2}

^{2,4 m}

^{10,722 t/m2}

FBC1 = x 1m = " " x 1m = 4,575 t ; x= (2,4) = 0,8mFB = 6,909 t/m² x 2,40m x 1m = 16,581 t ; x = (2,40) = 1,20m

FBC = 4,575 t + 16,581 t = 21,156 t

Excentricité : X = = 1,11 m

MBC = - _FBC x X = - 21,156 t x 1,11 m = - 23,483 tm

[112]

7.6. Piles
Fig.

Les sollicitations sur la pile se calculera par bande d'un mètre.

7.5.1. Evaluation des charges

? Charges verticales : ? Poids des terre (P3)

P3(gauche) = b x h x ?sable = 2,40m x (2,80m - 0,50m) x 2,60 t/m³ x 1m = 14,35 t P3(droite) = b x h x ?sable = 2,40m x (2,80m - 0,50m) x 2,60 t/m³ x 1m = 14,35 t

Excentricité : Xdrroite = (2,40m) = 1,6 m et Xgauche = (2,40m) + 1m + 2,40 m = 4,2m ? Poids de la semelle (P2)

[113]

S1 = S4 = x 2 = 1,2 m² ; S2 = S5 = (0,50m x 2,40m) x 2 = 2,4 m² et S3 = 1,00m

x 1,00m = 1,00m²

? = 1,2 m² + 2,4 m² x 1,00 m² = 4,6 m² P2 = 4,6 m² x 2,5 t/m³ x 1 m = 11,5 t

Excentricité : X1 = (2,40m) + 1m + 2,40m = 4,2m ; X2 = (2,40m) + 1m + 2,40 m = 4,6 m ; X3 = (1,00 m) + 2,40 m = 2,9 m ; X4 = (2,40m) = 1,6 m ; X5 = (2,40m) = 1,2 m

?

X = ? = 4,96 m

? Poids de la colonne(P1) :

P1 = x 4,38 x 2,5 t/m³ = 8,595 t ; on a 4 colonnes alors P1 = 8,595 t x 4 = 34,38 t

P1 = x 1m = 2,865 t

Excentricité : X = (1m) + 2,40 m = 2,9 m

? Poids de la poutre chevêtre(P4) : P4 = 1m x 1m x 2,5t/m³ x 6m = 15 t

Excentricité : X = (1m) + 2,40 m = 2,9 m

? Réaction verticale due à l'action des charges (V1) : L'effort tranchant max en ELS : Tmax = 82,0389625 t Comme il y a 4 appuis sur la pile, on obtient :

V1 = x 1m = 27,34632 t

La pile recevra le double de cette réaction. Soit V1 = 27,34632 x 2 = 54,6926 t Excentricité : X = (1m) + 2,40 m = 2,9 m

? Charges horizontales

Le coefficient des poussées des terres k est donné par :

[114]

Pour le sable limoneux : Nõ = tg²(45+ ) = tg²(45+ ) = 2,46 ; k = = = 0,40

? Effort de freinage (H1) :

H1 =

Avec : - k : coefficient des poussées des terres = 0,40

- N : nombre de bandes = 2 - C : convois : 60t

- lp : largeur du pont = 12 m

H1 = x 1m = 4 t

Nous considérons le cas où deux convois freinent simultanément sur une voie de circulation.

Alors : H1 = 2 x 4 t = 8 t Excentricité : X = 5,38 m

? Poussée des terres due au poids du sol (H2) :

? Pour le sable limoneux :

Contrainte horizontale : óh = - v avec ó_v = (2,6 t/m³ x 2,80m ) = 7,28 t/m²

óh = - v = 1,684 t/m²

H2 = (1,684 t/m² x 2,80m ) x 1m = 2,357 t Excentricité : X= (2,80m) = 0,93m

Etant donné qu'il y a des terres de mêmes natures de part et d'autre de la pile ; les poussées dues à ces premiers s'annulent et maintient la pile en équilibre.

? Poussée hydrodynamique(H2) :

La poussée hydrodynamique sera évaluée en fonction du PHE (profondeur des hautes eaux ; soit 1,20 m).

H2 = h x b x W x ?eau x V2

[115]

Avec :

· h : la hauteur de l'eau (1,20m)

· b : la largeur de l'obstacle (1m)

· W : le coefficient de forme dépendant du type de pile (W=0,32 ; section circulaire)

· ?eau : le poids spécifique de l'eau (1 t/m³)

· V : la vitesse d'écoulement de l'eau (V = 0,9177m/s)

H2 = 1 (1,20) x (1) x (0,32) x (1 t/m³) x (0,9177)² = 0,1616 t

Excentricité : X = (1,20m) = 0,4 m

^CHARGES VERTICALES
^Type de charge	^Charges		^Excentricité ^(m)		^Moment ^tm
^P1	^2,865		^2,9		^8,3085
^P2	^11,5		^4,96		^57,04
^P3(gauche)	^14,35		^1,6		^22,96
^P3(droite)	^14,35		^4,2		^60,27
^P4	( ^t ) ^15		^2,9		^stabilisant en ^43,5
^V1	^54,6926		^2,9		^158,60854
^somme	^112,7576				^350,68704
^CHARGES HORIZONTALES
^Type de charge		^Charges		Excentricité ^(m)	Moment ^tm
^H1		^8		^5,38	^43,04
^H2		( ^t ) ^0,1616		^0,4	^renversant en ^0,06464
^somme		^8,1616			^43,10464

7.5.2. Etude de la stabilité

E Ms 350,68704

? Stabilité au renversement : , Mr = 2 ?

43,10464 = 2 ? 8,13 = 2 ; la condition

est vérifiée.

[116]

?

v Stabilité au glissement : > 2 = 2 ? 13,81 = 2 ; la condition est

vérifiée.

v Stabilité face aux contraintes transmise par le sol :

La pile travaille en flexion composée. D'où :

? ?

ómax X (1 + ) et ómin = x (1 - )

· Calcul de l'excentricité (e) : e = - x

? ?

=

or x=

?

= 2,7278 m

e = - 2,7278 m = 0,1722 m

condition : 0 ? e = ? 0 ? 0,1722 = 6 ? 0 ? 0,1722 = 0,966 condition ^vérifiéel'excentricité se trouve dans le noyau central.

· Vérification des contraintes :

ómax = x (1 + ) = 22,904 t/m²

ómin = x (1 - ) = 15,977 t/m²

· Diagramme de contrainte :

^ómin = ^{15,977 t/m2}

^ómax = ^22,904 t/m2

[117]

7.5.3. Calcul proprement dit de la pile
7.5.3.1. Calcul de la poutre chevêtre

La poutre chevêtre se calculera comme une poutre reposant sur 4 colonnes (appuis). Elle ne va supporter que son poids propre parce que les colonnes qui composent la pile sont placées au droit des appareils d'appuis. Les charges du tablier seront transmises directement sur les colonnes, ce qui manifeste le cas le plus défavorable.

Le poids propre de la poutre est donné par : P4 = 1m x 1m x 2,5 t/m³ = 2,5 t/m
D'où le schéma statique suivant :

^{2,5 t/m}

^{3m 3m 3m}

? Calcul des moments aux appuis :
? Tronçons A-B-C :

^{2,5 t/m}

^{3m 3m}

3MA + 2( 3+3) MB + 3MC = - ( 2,5 x 3³ + 2,5 x 3³ )
? 3 MA + 12 MB + 3 MC = - ( 67,5 + 67,5 )
? 3 MA + 12 MB + 3 MC = - ( 135)

? 3 MA + 12 MB + 3 MC = - 33,75 ? 12 MB + 3 MC = - 33,75 (1) ? Tronçons B-C-D :

[118]

^{2,5 t/m}

^{3m 3m}

3MB + 2( 3+3) MC + 3MD = - ( 2,5 x 3³ + 2,5 x 3³ )
-- 3 MB + 12 MC + 3 MD = - ( 67 + 67 )
-- 3 MB + 12 MC + 3 MD = - ( 135)

-- 3 MB + 12 MC + 3 MD = - 33,75

3 MB + 12 MC = - 33,75 (2)
On obtient le système suivant :

12 MB + 3 MC = - 33,75 (1)

3 MB + 12 MC = - 33,75 (2)

Après résolution du système, on a les valeurs des moments aux appuis :

MA = 0 tm ; MB = - 2,25 tm ; MC = - 2,25 tm ; MD = 0 tm

? Calcul des moments en travées :

? Travée A-B :

^{2,5 t/m}

^{MC MD}

^3m

MAB = - MA = - 0 = 1,8 tm

TAB = + = + = 3 t

TBA = + = + = 4,5 t

MDC = - MD = - 0 = 1,8 tm

[119]

MBA = - MB = - 2,25 = 1,8 tm

Position Mmax : XAB = = 1,2 m et XBA = = 1,8 m

> Travée B-C

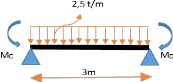
TBC = + = + = 3,75 t

TBC = + = + = 3,75 t

MBC = - MB =

- 2,25 = 0,5625 tm

MBC = - MB =

- 2,25 = 0,5625 tm

Position Mmax : XBC = = 1,5 m et XCB = = 1,5 m

> Travée C-D

TCD = + = + = 4,5 t

TDC = + = + = 3 t

MCD = - MC =

- 2,25 = 1,8 tm

[120]

Position Mmax : XCD = = 1,8 m et XDC = = 1,2 m

Diagrammes : ? Moments :

+ + +

^{2,25 tm 2,25 tm}

- -

^{0,5625 tm}

^{1,8 tm 1,8 tm}

? Efforts tranchants :

^{3 t 3,75 t 4,5 t}

+

^{4,5 t 3,75 t}

^{3 t}

+

+

-

TABLEAUX RECAPITULATIFS

- -
^Travée ^travée en tm	^AB	^BC	^TABLEAU RECAPITULATIF DES MOMENTS ^CD	^A retenir Mtmax
^Moments en	^1,8	^0,5625	^1,8		^1,8
^Appuis ^appuis en tm	^A	^B	^C	^D

[121]

				^A retenir

^{TABLEAU RECAPITULATIF DES EFFORTS TRANCHANTS}

^4,5

³

7.5.3.2. Calcul de la colonne

^Travée

^AB

^BC

^CD

^Tmax

^{A GAUCHE}

^(t)

³

^3,75

^4,5

Les colonnes reçoivent la charge de la superstructure par l'intermédiaire

des appareils d'appuis. Pour calculer une colonne, on considèrera la part de charge qui lui est

transmise par la poutre avec laquelle elle est reliée et cela se fait en flexion composée (E.L.S)

en considérant le moment à la base de la colonne. Elle devra supporter :

^{A DROITE}

^(t)

^4,5

^3,75

? Son poids propre (P1) ;

? La réaction due à l'action des charges (V1), pour une poutre ;

? Le poids propre de la poutre chevêtre (P4) ;

? Evaluation des sollicitations sur la colonne

- Poids propre de la colonne : P1 = 8,595 t ;

- La réaction due à l'action des charges :

L'effort tranchant max(ELS) : Tmax = 82,0389625 t

Comme il y a 2 appuis sur la colonne de la pile, on obtient :

V1 = 82,0389625 t x 2 = 164,0779 t

- Réaction due au poids de la poutre chevêtre :

V3 = Efforts tranchants = 3,75 + 4,5 t = 8,25 t ; Pour la colonne la plus chargée

? L'effort normal (NS) :

- Charges permanentes (G) ;

G = 8,595 t + 8,25 t = 16,845 t

- La charge d'exploitation (Q) :

Q = 164,0779 t

[122]

D'où : - NS = 16,845 t +164,0779 t = 180,9229 t ? Moment

Le moment à la base de la colonne est donné par :

MH1 = H1 x hcolonne = 8 t x 4,38m = 35,04 tm

MH2 = H2 x (heau) = 0,1616 t x 0,4m = 0,06464 tm

MS = MH2 + MH1 = 35,04 tm + 0,06464 tm = 35,10464 tm

7.5.3.3. Calcul de la semelle

Calcul des moments :

Tronçon A - B :

^{22,904 t/m2}

^{0,018 t/m}

^{19,4405 t/m2}

^{17122 t/m2}

^2,5

^{2,90 m}

FAB1 = x 1m = x 1m = 5,022 t ; x= (2,9) = 1,93m

FAB2 = 19,4405 t/m2 x 2,9m x 1m = 56,377 t ; x = (2,9) = 1,45m FAB = 5,022 t + 56,377 t = 61,399 t

Excentricité : X = = 1,489 m
MAB = - _FAB x X = - 61,399 t x 1,489 m = - 91,423 tm

[123]

Tronçon B - C :

^{15,977 t/m2}

^{2,9 m}

^{19,4405 t/m2}

FBC1 = x 1m = x 1m = 5,022 t ; x= (2,9) = 0,96m

FB = 15,977 t/m² x 2,9m x 1m = 46,333 t ; x = (2,9) = 1,45m FBC = 5,022 t + 46,333 t = 51,355 t

Excentricité : X = = 1,402 m
MBC = - _FBC x X = - 51,355 t x 1,402 m = - 71,999 tm

[124]

7.6. Calcul d'armatures des éléments de l'infrastructure Nous considérons la fissuration préjudiciable.

? Dalle de transition

ü Moment en travée (sens de X) :

MS = 16,958 tm ; d = h - e = 25cm - 5cm = 20 cm ; b = 1m ; fbs = 1800 t/m2 ; f_s = 25000t/m² ;

· Paramètre de déformation : á =	·	=		= 0,544

· Bras de levier : Z = d (1 - ) = 0,20(1 - ) = 0,1637m

· Sections d'armature : AS =

= = 0,004143 m² = 41,43 cm² soit 14HA20/m -- 43,96 cm²

ü Moment en travée (sens de Y) :

MS = 5,0875 tm ; d = 20 cm ; b = 1m ; fbs = 1800 t/m² ; f_s = 25000 t/m² ;

· Paramètre de déformation : á =	·	·		= 0,544

· Bras de levier : Z = d (1 - ) = 0,20(1 - ) = 0,1637m

· Sections d'armature : AS =

= = 0,001243 m² = 12,43 cm² soit 5HA18/m -- 12,72 cm²

ü Moments aux appuis :

MS = - 9,9755 tm ; d = 20 cm ; b = 1m ; fbs = 1800 t/m² ; f_s = 25000 t/m² ;

· Paramètre de déformation : á =	·	=		= 0,544

· Bras de levier : Z = d (1 - ) = 0,20(1 - ) = 0,1637m

· Sections d'armature : AS =

= = 0,002437 m² = 24,37 cm² soit 8HA20 -- 25,14 cm²

· Espacements :

[125]

Stx < min {3 < min { ? Stx < 33cm l'espacement entre les barres principales d'une

dalle ne dépasse pas 30 cm.

Sty < min { < min { ? Sty < 44cm.

? Culée

Les armatures se calculerons par bande d'un mètre en flexion composé. ? Corps de la culée et mur garde grève

Le moment le plus défavorable a été obtenu dans la zone 3-3 d'où : MS = 65,05 tm ;

Tmax(ELS) = 82,0389625 t

R = x 1m = x 1m = 27,346320 t

NS = R + P4 + P1 = 27,346320 t + 1,84 + 7,605 = 36,79132 t b = 1m ; a = 1m ; h = 5,0 m ; fbs = 1800 t/m² ; f_s = 25000 t/m²

· Calcul du flambement : Lf = 2 x h = 2 x 5,0m = 10 m

ë = v = v = 34,64 ? 35 ; il n'y a pas risque de flambement.

· Calcul de l'excentricité :

e1 = = = 1,768 m

e_a = max { } =

{ } = { } = 2 cm = 0,02 m

e2 = ~~ x (2+(á x õ)) = ~~~ x (2+(0,5 x 2)) = 0,018 m

et = e1 + e2 + e3 = 1,768 m + 0,02 m + 0,018 m = 1,806 m

· Coefficient de remplissage :

Ø1 = ; avec: Nmax = b x h x fbs = 1m x 5,0m x 1800 t/m2 = 9000 t

[126]

Ø1 = = 0,00408 ? 0,81

· Excentricité critique :	·	·		·

on a = 1+v9 _ 1+.~1+,/9 ,00408),00408)

Puisque Ø1 = 0,00408 ? =

3 ' 4(3 v v 0,166553

· Excentricité du noyau centrale :

enc = î x h = 0,166553 x 5,0 m = 0,832765 m ? et ; d'où la section est partiellement comprimée ou tendue.

· Moment fictif :

Mf = N_s (e + d - ^ ) = 36,79132 t (1,806 m + 4,95m - ) = 156,583857 tm

· Paramètre de déformation : á =	·	=		= 0,544

· Bras de levier : Z = d (1 - ) = 4,95(1 - ) = 4,0524 m

· Section fictive :

Afictif = = = 0,001545 m²

· Section réelle d'armature :

Aréelle = Afictive - = 0,001545 m² - = 0,00007334 m² = 0,7334 cm² soit 4HA12/m

? 4,52 cm²

· Armatures transversales :

Öt = Öl = (12 mm) = 4 mm soit un cadre de HA10

· Espacement : St = min{ } = min{ }
Alors St = 40 cm ; soit St = 20 cm

Afin de faciliter la mise en oeuvre des armatures(ferraillage) nous prolongeons les armatures du corps de la culée jusqu'au mur garde-grève.

· Armature de frettage :

[127]

Nous savons que ces armatures servent à bloquer la déformation transversale du béton qui se produit par l'effet de poisson sous l'action d'une compression, à augmenter la résistance à la rupture du béton. C'est ainsi que nous adoptons les mêmes armatures transversales tout en réduisant l'écartement soit HA10 espacées de 5cm.

? Corbeau :

MS = - 3,9465 tm ; d = h - e = 25cm - 5cm = 20 cm ; b = 1m ; fbs = 1800 t/m² ; f_s = 25000t/m2 ;

·	Paramètre de déformation = : á	=		= 0,544
Axe neutre : y = á x d = 0,544 x 0,20m	= 0,108 m			·
Bras de levier : Z = d (1 - ) = 0,20(1 -	= 0,1637m )
Moment résistant : MRS = (b x y)	x Z = (1 x 0,108 )	1800 x 0,1637

MRS = 15,911 tm ? MS (simplement armée)

· Sections d'armature : AS =

= = 0,0009643 m² = 9,643 cm² soit 4HA18/m ? 10,18 cm²
Armatures de répartition : Ar = ( 10,18) = 2,545 cm² soit 4HA10/m ? 3,14 cm² ? Vérification de l'effort tranchant :

<

,0

< ? 39,465 < 182,60869 : condition vérifiée

· Espacements :

Stx < min { < min { ? Stx < 33cm l'espacement entre les barres principales d'une
dalle ne dépasse pas 30 cm

Sty < min { . {

< min ? Sty < 44cm.

[128]

? Semelle

Nous ne considérons que le tronçon B-C parce que c'est là que la sollicitation est le plus à craindre.

MS = - 81,11691 tm ; d = 95 cm ; b = 1m ; fbs = 1800 t/m² ; fsu = 25000 t/m² ;

· Paramètre de déformation : á =	·	=		= 0,544

· Bras de levier : Z = d (1 - ) = 0,95(1 - ) = 0,777m

· Section d'armature :

AS = = = 0,004175 m2 = 41,75 cm² soit 10HA25/m ? 49,09 cm²

· Armatures de répartitions :

ASt = ASl = (49,09) = 12,27 cm² soit 4HA20/m -- 12,57 cm²

· Espacements :

Stx < min { < min { -- Stx < 33cm.

Sty < min { < min { -- Sty < 44cm.

? Mur en aile :

Les armatures se calculerons par bande d'un mètre en flexion composée.

? Corps du mur

Le moment le plus défavorable a été obtenu dans la zone 3-3 d'où :

MS = 48,29 tm ; NS = 10 t

b = 1m ; a = 1m ; h = 5,0 m ; fbs = 1800 t/m² ; f_s = 25000 t/m2

· Calcul du flambement : Lf = 2 x h = 2 x 5,0m = 10 m

ë = v = v = 34,64 ? 35 ; il n'y a pas risque de flambement.

[129]

· Calcul de l'excentricité :

e1 = = = 4,829 m

e_a = max { } =

{ } = { } = 2 cm = 0,02 m

e2 = ~ x (2+(á x õ)) = ~~ x (2+(0,5 x 2)) = 0,018 m

et = e1 + e2 + e3 = 4,829 m + 0,02 m + 0,018 m = 4,867 m

· Coefficient de remplissage :

T1 = ; avec: Nmax = b x h x fbs = 1m x 5,0m x 1800 t/m² = 9000 t

T1 = = 0,0011 < 0,81

90

· Excentricité critique :

Puisque T1 = 0,0011 <
· on a î = v = v = 0,166636

' v v '

· Excentricité du noyau centrale :

enc = î x h = 0,166636 x 5,0 m = 0,83318 m < et ; d'où la section est partiellement comprimée ou tendue.

· Moment fictif :

Mf = N_s (e + d - ) = 10 t (4,867 m + 4,95m - ) = 73,17 tm

· Paramètre de déformation : á =	·	=		= 0,544

·

Aréelle = Afictive - = 0,0007222 m² - = 0,000322 m² = 3,22 cm² soit 5HA10/m ?

3,39 cm2

Bras de levier : Z = d (1 - ) = 4,95(1 - ) = 4,0524m

· Section fictive :

Afictif = = = 0,0007222 m²

· Section réelle d'armature :

[130]

· Armatures transversales :

Öt = Öl = (10 mm) = 3,33 mm soit un cadre de HA8

· Espacement : St < min{ } = min{ }
Alors St < 40 cm ; soit St = 20 cm

Afin de faciliter la mise en oeuvre des armatures(ferraillage) nous prolongeons les armatures du corps du mur.

? Semelle

Nous ne considérons que le tronçon B-C parce que c'est là que la sollicitation est le plus à craindre.

MS = - 23,483 tm ; d = 95 cm ; b = 1m ; fbs = 1800 t/m² ; fsu = 25000 t/m² ;

· Paramètre de déformation : á =	·	=		= 0,544

· Bras de levier : Z = d (1 - ) = 0,95(1 - ) = 0,777m

· Section d'armature : AS =

= = 0,001208 m² = 12,08 cm² soit 8HA14 /m ? 12,32 cm²

· Armatures de répartitions :

ASt = ASl = (17,81) = 4,45 cm² soit 4HA12/m ? 4,52 cm²

· Espacements :

Stx < min { <~ { 3 3 ? Stx < 33cm.

--

Sty < min { < min { ? Sty < 44cm.

[131]

? Pile

? Poutre chevêtre :

ü En travée :

MS = 1,8 tm ; d = 95 cm ; b = 1m ; fbs = 1800 t/m² ; fsu = 25000 t/m² ;

·	Paramètre de déformation = : á	=	= 0,544
·	Axe neutre : y = á x d = 0,544 x 0,95m	= 0,5168 m
·	Bras de levier : Z = d (1 - ) = 0,95(1 -	= 0,777m )
·	Moment résistant : MRS = (b x y)	x Z = (1 x 0,5168	) 1800 x 0,777

MRS = 361,723 tm > MS (simplement armée)

· Section d'armature : AS =

= = 0,0000926 m² = 0,926 cm² nous adoptons 4HA12 ? 4,52 cm²

ü Aux appuis :

MS = 2,25 tm ; d = 95 cm ; b = 1m ; fbs = 1800 t/m² ; fsu = 25000 t/m² ;

·	Paramètre de déformation = : á	=	= 0,544
·	Axe neutre : y = á x d = 0,544 x 0,95m	= 0,5168 m
·	Bras de levier : Z = d (1 - ) = 0,95(1 -	= 0,777m )
·	Moment résistant : MRS = (b x y)	x Z = (1 x 0,5168	) 1800 x 0,777

MRS = 361,723 tm > MS (simplement armée)

· Section d'armature : AS =

= = 0,0001158 m² = 1,158 cm² nous adoptons 3HA12 ? 3,39 cm²

· Armatures transversales : TS = 4,5 t

[132]

La contrainte tangentielle : Tso = = = 4,7368 t/m2

Etant donné qu'on est en fissuration préjudiciable

Tlim < min ( ; 4 MPa)

Tlim < min ( ; 4 MPa)

Tlim < min (3 MPa ; 4 MPa) Tlim = 3 MPa = 300 t/m²

Tso ? Tlim ; d'où les armature transversale droite.

.

Section d'armature : Ö rrv

_t < n ( h 3 ; b '

10 ÖL )

Öt < min ( ; ; 8mm )

Öt < 8mm ; nous adoptons : Öt = 8 mm

=

At= 50,24 mm² = 0,5024 cm² At = 0,5024 cm² x 2 brins = 1,0048 cm² soit HA8

· Ecartement d'armatures :

St < = = 0,83 m = 83cm

St < 83 cm ? St = 20 cm

· Armatures de peau :

A_p > x parement( 2R+bo) ? A_p > x ( 2(1)+1)

A_p > 9 cm² soit 8HA12 ? 9,05 cm² ? Colonne :

MS = 35,10464 tm ;

NS = 180,9229 t

D = 1,0 m ; h = 4,38 m ; fbs = 1800 t/m² ; f_s = 25000 t/m2

[133]

· Calcul du flambement : Lf = 2 x h = 2 x 4,38 m = 8,76 m

ë = = = 35,04 = 35 ; il y a risque de flambement.

· Calcul de l'excentricité : e1 = = = 01940 m

,

e_a = max { } = { } = { } = 1,75 cm = 0,0175 m

e2 = x (2+(á x õ)) = x (2+(0,5 x 2)) = 0,02365 m
et = e1 + e2 + e3 = 0,1940 m + 0,0175 m + 0,02365 m = 0,23515 m

· Coefficient de remplissage :

Ø1 = ; avec: Nmax = D x h x fbs = 1m x 4,38m x 1800 t/m² = 7884 t
Ø1 = = 0,02294 < 0,81

v v

Puisque Ø1 = 0,02294 < ; on a î =

^v

v

· Excentricité critique :

3 4(3+

9 4(3+

9 = 0,166019

· Excentricité du noyau centrale :

enc = î x h = 0,166019 x 4,38 m = 0,727 m ? et ; d'où la section est entièrement comprimée.

AS = max { avec : B = ï.D = 3,14 m

AS = max {

AS = 15,7cm2 soit 8HA16 ? 16,08 cm²

· Armatures transversales :

Öt = Öl = ; (16 mm) = 5,33 mm soit un cadre de HA10

[134]

· Espacement : St < min{ } = min{ }
Alors St < 40 cm ; soit St = 20 cm

? Semelle

Nous ne considérons que le tronçon A-B parce que c'est là que la sollicitation est le plus à craindre.

MS = - 91,423 tm ; d = 95 cm ; b = 1m ; fbs = 1800 t/m² ; fsu = 25000 t/m² ;

· Paramètre de déformation : á =	·	=	= 0,544

· Bras de levier : Z = d (1 - ) = 0,95(1 - ) = 0,777m

· Section d'armature :

AS =

= = 0,004706 m² = 47,06 cm² soit 10HA25/m ? 49,09 cm²

· Armatures de répartitions :

ASt = ASl = (49,09) = 12,2725 cm² soit 4HA20/m ? 12,57 cm²

· Espacements :

Stx < min { min { 33cm ? Stx < 33cm.
--

Sty < min { < min { ? Sty < 44cm.

[135]

CHAPITRE 8. Plans d'armatures

8.1. Armatures de chaque élément

? Poutres principales

? Entretoises ? En travée :

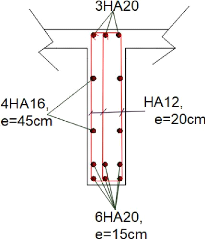
[136]

? Aux appuis :

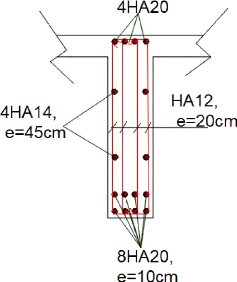
? Dalle de platelage

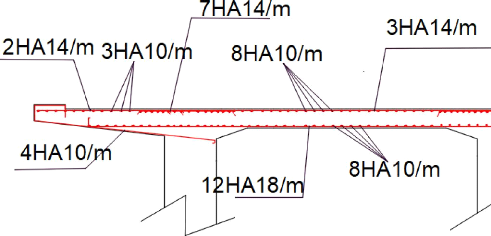
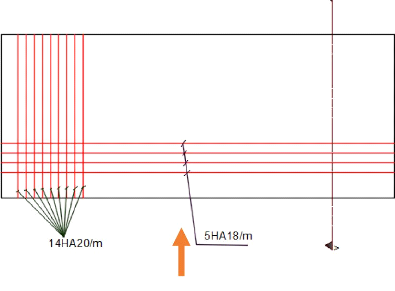
SENS DE CIRCULATION

[137]

? Dalle de transition

[138]

? Culée

[139]

? Mur en aile

? Pile

[140]

[141]

8.2. Armatures d'ensemble(superstructure)

COUPE TRANSVERSALE

COUPE LONGITUDINALE

[142]

PARTIE 4 : CONSTRUCTION DE L'OUVRAGE

CHAPITRE 9 : Evaluation du coût de l'ouvrage

AVANT METRE

é é ence	Désignation des parties	Nombre des parties semblables	DIMENSIONS			SURFACES OU CUBE			OBSERVATION
			Longueur (m)	Largeur (m)	H (m)	Auxiliaires	Partiels	Définitifs
0	1	2	3	4	5	6	7	8	9
A. Terrassement
1	Déblais
	Culée	2	15	9	3	135	405	810	3+L ou l
	Pile	1	15	7	2,8	105	294	294
	Mur en aile	4	13,5	7	3	94,5	283,5	1134
Volume Total déblais								2238
2	Remblais
	culée AB	2	15	9	3	135	405	810
	Culée B'	2	12	5	3	60	180	360
	Pile	1	15	7	2,8	105	294	294
	Mur en aile AB	4	13,5	7	3	94,5	283,5	1134
	Mur en aile B'	4	10,5	5	3	52,5	157,5	630
Volume Total Remblais								3228
Volume total de terrassement								5466
B. Béton de propreté dosé à 250 kg/m3
	Culée	2	15	9	0,15	135	20,25	40,5
	Pile	1	15	7	0,15	105	15,75	15,75
	Mur en aile	4	13,5	7	0,15	94,5	14,175	56,7
Volume total du béton de propreté								112,95
C. Béton dosé à 450 kg/m3
1	Infrastructure
1.1.	Culée
	semelle	2	12			4,85	58,2	116,4

[143]

	Corps de la culée	2	12			3,042	36,504	73,008
	Mur garde- grève et corbeau	2	12			0,736	8,832	17,664
	Volume total culée							207,072
	Coffrage	2	12	20,7				496,8
1.2.	Dalle de transition	2	12	5	0,25	60	15	30
	volume total dalle de transition							30
	Coffrage	2	0,25	34				17
1.3.	Pile
	semelle	1	12			3,4	40,8	40,8
	colonnes	4			4,38	0,785	3,4383	13,7532
	poutre chevêtre	1	6	1	1	6	6	6
	Volume total de la pile							60,5532
	Coffrage	1	12					152,93
1.4.	Mur en aile
	semelle	4	7,8			3,26	25,428	101,712
	Corps du mur	4		0,8		39	31,2	124,8
	Volume total du mur							226,512
	Coffrage	4	10,5	18,499				776,958
2	Superstructure
	Poutre principale	8	17,4	0,5	1,32	8,7	11,484	91,872	Lp + 2(0,20)
	Gousset	16	16			0,00015	0,0024	0,0384
	Entretoise aux appuis	4	7	0,4	0,82	2,8	2,296	9,184
	Entretoise en travée	4	7	0,4	1,14	2,8	3,192	12,768
	Dalle platelage	2	17,4	12	0,18	208,8	37,584	75,168
Volume total du béton dosé à 450kg/m3								713,1676
Coffrage 2								579,676	1159,352

[144]

D. Béton dosé à 350 kg/m3
1	Bordures
	Bordure interne	4	17,4	0,1	0,15	1,74	0,261	1,044
	Bordure externe	4	17,4	0,3	0,15	5,22	0,783	3,132
2	Séparateur en béton	2	17,4			0,205	3,567	7,134
3	Carrelage en dallette	4	17,4	1,4	0,04	24,36	0,9744	3,8976
Coffrage 4								5,31	21,24
Volume total du béton dosé à 350 kg/m3								15,2076
E. Mortier
1	Couche de forme	2	17,4	7,4	0,04	128,76	5,1504	10,3008
2	Chape d'étanchéité	2	17,4	7,4	0,04	128,76	5,1504	10,3008
3	Mortier de pose pour dallette	4	17,4	1,4	0,01	24,36	0,2436	0,9744
Volume total de mortier								21,576
F. Revêtement (enrobé)
1	Sur la dalle platelage	2	17,4	7,4	0,08	128,76	10,3008	20,6016
2	Sur la dalle de transition	2	5	7,4	0,08	37	2,96	5,92
3	Imprégnation	2	22,4	7,4	0,01	165,76	1,6576	3,3152
Volume total de Revêtement								26,5216
G. Autres équipements
1	Garde-corps	4	17,4					69,6
2	Appareils d'appuis	16
3	Cornière IPN pour joints	6	12	1	0,008	12	0,096	0,576

[145]

^BORDEREAU D'ARMATURES

POIDS

^LONG

POIDS

^LOCALISATION

SCHEMAS

^ö(nn)

^(kg/m)

UNITAIRE

NOMBRES

^TOTALE (kg)

^A. Infrastructure

^a. Culée

^1. Semelle

Armatures

^longitudinales

^5,9m

^25

^3,851

^6,38

^119

^2924

^Armaturesde

^répartitions

12,9m

^20

^2,466

^13,14

^24

^778

^Armaturesde ^transversales

60,18m

^10

^0,617

^60,18

^119

^4419

^Armatures de retrait

^8,06m

^14

^1,208

^8,06

^119

^1159

^Armatures de ^repartition (retrait)

13,02m

^10

^0,617

^13,02

^59

^474

^Poids total semelles

^2

^19508

^2. Corps

^de la culée

Armatures ^longitudinales

7,95m

^12

^0,888

^8,95

^47,6

^379

^Armature ^transversales

^10

^0,617

^3,8

^476

^1117

^Armatures de frettage

^10

^0,617

^0,45

^47,6

^14

^Poids total corps des culées

^2

^3020

^3. ^Corbeau

Armatures

^longitudinales

^1,2m

^18

^1,998

^1,308

^47,6

^125

^Armatures

^transversales

^10

^0,617

^2,22

^71,4

^98

^Poids totale corbeaux

^2

^446

^4. Dalle

^de transition

^Armatures suivantle ^sens de circulation

4,90m

^20

^2,466

^5,2

^187,6

^2406

^Armatures suivant le

^11,9m

^transversale à la ^18 ^1,998 ^12 ^sens ^circulation

^24,5

^588

^Poids total dalles de transitions

^2

[146]

^b. Pile
Armatures				1. ^Semelle
3,9m	^25			^3,851	^4,38	^144,54	^2439
12,9m	^20			^2,456	^13,14	^29,5	^953
0,90m	^10			^0,617	^1,02	^126,4	^80
^2,95m	^14			^1,208	^5,932	^95,2	^683
^24							^193	^Poids total semelle ^1 ^4348
^Armatures
	2. ^Colonnes
	6,28m		^16	^1,578	^7,28	^8	^92
	^10			^0,617	^3,26	^31	^63	^Armatures de frettage ^10 ^0,617 ^0,9
^8							^5	^Poids total colonnes ^4 ^640
^Armatures
	3. ^Poutre chevètre
^longitudinales ^Armatures		8,90m		^12	^0,888	^9,04	^4	^33
^transversales				^8	^0,395	^3,648	^30	^44
	^0,5m
^Armatures Chapeaux				^12	^0,888	^0,57	^6	^4
^Armatures de peau ^8,90m ^12 ^0,888 ^9,04							^8	^65
^Poids total d'armature poutre chevètre							^1 ^146

[147]

^c. Mur en aile
						^1. Semelle
Armatures
^longitudinales	3,9m					^14	^1,208	^4,28	^72,8	^377
^Armatures de
^repartition	7,7m					^12	^0,888	^7,84	^11,7	^82
Armatures
^transversales	^0,90m					^10	^0,617	^1,02	^499,2	^315
^Armatures de retrait	5,10m					^12	^0,888	^5,24	^41,6	^194
^Armatures de	10,4m
^repartition (retrait)						^10	^0,617	^10,52	^12,8	^84
	^Poids total d'armatures semelles								^4	^4208
						^2. Corps ^du mur
Armatures	7,0m
^longitudinales						^10	^0,617	^7,06	^72,8	^318
^Armatures
						^8	^0,395	^2,12	^410,8	^345
^transversales	^Poids total armatures corps
	^Poids total d'armatures du mur					^du mur			^4	^2652
	^Poids					^en aile				^6860
	^total d'armatures pour l'infrastructure									^40956
						^B. Superstructure
	^a. Poutre					^principales
^Armatures	18,30m
^longitudinales ^Armatures						^32	^6,313	^18,68	^20	^2359
^transversales						^12	^0,888	^3,744	^84,5	^281
^Armatures	1,40m
^transversales ^Armatures de						^12	^0,888	^1,54	^84,5	^116
	^18,3m
^peau						^18	^1,998	^18,52	^8	^297
	^0,90m
^Armatures de retrait ^10 ^0,617 ^1,02									^84,5	^54

[148]

				b.1. ^Entretoises en travée
	8,90m		^20	^2,466	^9,14	^9	^203	^Armatures ^transversales
	^12			^0,888	^3,18	^44,5	^126
1,22m	^12			^0,888	^1,36	^44,5	^54
^4							^65	^Poids total d'armatures pour entretoises en travée ^4 ^1792
	b.2. ^Entretoise aux appuis
^Armatures ^longitudinales		8,90m		^20	^2,466	^9,14	^12	^271
^Armatures ^transversales				^12	^0,888	^2,54	^44,5	^101
^Armatures ^transversales	0,90m			^12	^0,888	^1,04	^44,5	^42
^Armatures de peau ^8,90m ^14 ^1,208 ^9,08							^4	^44
^Poids total d'armatures pour entretoises aux appuis ^4 ^1832
				^c. Dalle sous la chaussée
^Armatures suivant le ^sens de circulation	17,30			^10	^0,617	^17,42	^152	^1634
^Armatures ^transversales	11,90m			^25	^3,851	^12,2	^103,8	^4877
^Armatures ^transversales	11,90m			^14	^1,208	^12,06	^51,9	^757
^Armatures aux appuis ^14 ^1,208 ^5,25							^121,1

[149]

		^d. Encorbellement
^Armatures ^longitudinales 17,30m ^14 ^1,208 ^17,46					^7,25	^153
^Armatures de ^repartition 1,45m ^10 ^0,617 ^1,57 ^51,9 ^51
^Armatures de retrait		^10	^0,17	^2,6	^84,5	^38
	^2,48m
					^4	^968
	^Poids total d'armatures pour encorbellement
e.1. ^Bordures externes
^Armatures ^longitudinales 17,30m ^10 ^0,617 ^17,42 ^2 ^22
^Armatures ^transversales		^8	^0,395	^0,3	^86,5	^11
	0,20m
					^4
	^Poids total d'armatures bordures externes
^Armatures 17,30m ^10 ^0,617 ^17,42					^2
^Armatures 0,10m ^8 ^0,395 ^0,2					^86,5

[150]

BODEREAU QUANTITATIF
N°	DESIGNATION	Unité	Quantité
0	IMPLANTATION	m^2	408
1 ère PHASE : GROS OEUVRES
1	TERRASSEMENT	m3
	Déblai	m3	2238,00
	Remblai	m3	3228,00
2	BETON DE SEMELLE(Propreté) DOSE A 250 kg/m3	m3	112,95
	Sable	T	45,18
	Caillasse 8/15	T	90,36
	Ciment	Sac	565,00
3	BETON DOSE A 450 kg/m3	m3	713,17
	Sable	T	285,27
	Caillasse 8/15	T	570,53
	Ciment	Sac	6418,51
4	BETON DOSE A 350 kg/m3	m3	15,21
	Sable	T	6,08
	Caillasse 8/15	T	12,168
	Ciment	Sac	106,47
5	COFFRAGE	m^2	2603,04
6	MORTIER DOSE 350 kg/m3	m3	21,58
	Sable	T	8,63
	Ciment	Sac	152,00
7	COUCHE DE REVETEMENT	m^2	331,52
8	IMPREGNATION	m^2	331,52
9	ARMATURES	kg	86726,00
10	APPAREILS D'APPUIS	pce	16,00
	2ème PHASE : FINITION
11	GARDE CORPS	m	69,6
12	CORNIERE	m	72,00

[151]

DEVIS

DEVIS QUANTITATIF ET ESTIMATIF
N°	DESIGNATION	Unité	Quantité	PU	PT
0	IMPLANTATION	m^2	408	21	8568
1 ère PHASE : GROS OEUVRES
1	TERRASSEMENT
	Déblai	m^3	2238,00	15	33570
	Remblai	m^3	3228,00	15	48420
2	BETON DE SEMELLE(Propreté) DOSE A 250 kg/m3	m3	112,95
	Sable	T	45,18	20	903,6
	Caillasse 8/15	T	90,36	24	2168,64
	Ciment	Sac	565,00	8,9	5028,5
3	BETON DOSE A 450 kg/m3	m^3	713,17
	Sable	T	285,27	20	5705,3408
	Caillasse 8/15	T	570,53	24	13692,818
	Ciment	Sac	6418,51	8,9	57124,725
4	BETON DOSE A 350 kg/m3	m3	15,21		15,2076
	Sable	T	6,08	20	121,68
	Caillasse 8/15	T	12,168	24	292,032
	Ciment	Sac	106,47	8,9	947,583
5	COFFRAGE	m^2	2603,04	8	20824,32
6	MORTIER DOSE 350 kg/m3	m3	21,58		21,576
	Sable	T	8,63	20	172,64
	Ciment	Sac	152,00	8,9	1352,8
7	COUCHE DE REVETEMENT	m^2	331,52	60	19891,2
8	IMPREGNATION	m^2	331,52	10	3315,2
9	ARMATURES	kg	86726,00	2,57	222885,82
10	APPAREILS D'APPUIS	pce	16,00	120	1920
	2ème PHASE : FINITION
11	GARDE CORPS	m	69,6	90	6 264,00 $
12	CORNIERE	m	72,00	2,2	158,40 $
PRIX TOTAL HT				453 364,08 $
TVA 16,18%				73 354,31 $
MAIN D'0EUVRE OUVRIERS 30%				158 015,52 $
PRIX TOTAL TTC				684 734,00 $

[152]

PARTIE 5 : CONCLUSION

Ce projet de fin de cycle a fait l'objet de la conception et dimensionnement d'un pont en béton armé. La construction de cet ouvrage d'art sur la rivière Tshuenge contribuera au développement de cette contrée de la Ville Province de Kinshasa. Notre projet s'est déroulé en deux grandes étapes ; dans la première étape, nous avons fait la conception de l'ouvrage ; dans la deuxième étape nous avons fait le calcul de l'ouvrage dans les conditions de stabilité et de résistance. Ce travail nous a permis de découvrir certaines spécialités liées aux différentes étapes de l'étude d'un projet de pont. Cela nous a approché tout près du domaine pratique ainsi que de nous initier avec les calculs d'un ouvrage d'art, d'approfondir et de compléter les connaissances acquises tout au long de notre cursus. Nous avons bénéficié de l'expérience et conseils de nos prédécesseurs dans le domaine.

[153]

BIBLIOGRAPHIE

1. MUTONDO WA MUTONDO R. ; Notes de cours de pont 3^eme BTP, INBTP, Kinshasa, 2021.

2. POINEAU MM et EDON ; SETRA : Guide d'emploi du règlement français de béton armé aux états limites BAEL 83, exemple d'application aux ponts ; Paris ;1987

3. J.A. Calgaro ; Conception des ponts

4. MOUGIN JP. ; BAEL modifié 99 ; béton armé aux états limites ;

5. MANGIZI, Notes de cours de calcul des structures en béton armé, INBTP, Kinshasa 2021,

6. Technologie des ponts

7. Notes de calcul d'un pont en béton armé, prof. MUTONDO