Tableau 6 : Breusch-Goffrey
|
Breusch-Godfrey Serial Correlation LM Test:
|
|
|
|
|
F-statistic
|
1.317576
|
Prob. F(2,18)
|
0.2924
|
|
Obs*R-squared
|
3.192552
|
Prob. Chi-Square(2)
|
0.2026
|
Source : Estimation de l'auteur à partir du logiciel
Eviews6
Le test de Breusch-Godfrey obtenu à partir des MCO (lags =
2) donne deux probabilités (Prob = 0,292 etProb=0,203).
Nous constatons que ces deux probabilités sont
supérieures à 5%.
Alors on ne rejette pas H0. Les erreurs du modèle ne sont
pas corrélées. Les estimations obtenues par les MCO sont donc
optimales.
· Test de Ramsey
Ce test nous renseigne sur la spécification d'un
modèle.
Les hypothèses du modèle sont :
H0 : le modèle est bien
spécifié
H1 : le modèle est mal
spécifié
Les résultats du test de Ramsey sont consignés dans
le tableau suivant :
Tableau 7 : Test de Ramsey
|
Ramsey RESET Test :
|
|
|
|
|
F-statistic
|
0.538000
|
Prob F(1,19)
|
0.4722
|
|
Log likelihood ratio
|
0.698058
|
Prob Chi-Square(1)
|
0.4034
|
Source : Estimation de l'auteur à partir du logiciel
Eviews6
Le test de Ramsey obtenu à partir des MCO (lags = 1) donne
les deux probabilités (Prob =0,472 et 0,403).Nous constatons que les
probabilités sont supérieures à 5%.Alors on ne rejette pas
H0. Ce qui nous amène à dire que le modèle est bien
spécifié.
e-Test CUSUM de stabilité (Brown, Durbin,
Ewans)
· Test de CUSUM
Ce test permet de détecter d'éventuels mouvements
dans des coefficients reflétant une position d'instabilités
structurelles du modèle.
Les hypothèses du test sont :
H0 : le modèle est structurellement
stable
H1 : le modèle est structurellement
instable
La règle de décision est la suivante :
v Si la courbe ne coupe pas les bornes du corridor, alors le
modèle est stable
v Si la courbe coupe les bornes du corridor, alors le
modèle est instable
Les résultats du test sont présentés dans le
graphique suivant :
Figure 6 : Test de
CUSUM
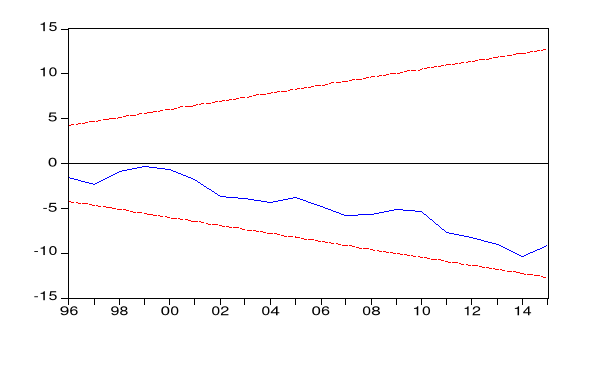
Source : réalisé par l'auteur sur l'Eviews6
Conclusion : la courbe ne coupe pas le corridor, donc le
modèle est structurellement stable.
· Test de CUSUM Carré
Ce test permet de détecter les instabilités
ponctuelles du modèle.
Les hypothèses du test sont :
H0 : le modèle est ponctuellement
stable
H1 : le modèle est ponctuellement
instable
La règle de décision est la suivante :
v Si la courbe ne coupe pas les bornes du corridor alors le
modèle est stable
v Si la courbe coupe les bornes du corridor alors le
modèle est instable. Dans ce cas, la courbe indique la période
d'instabilité.
| 


