II.1.2. Méthode
d'estimation
Dans ce deuxième volet, nous
présenterons d'abord le principe de l'estimation et par la suite, nous
passerons en revue les principaux tests de robustesse.
a) Principe de l'estimation
La modélisation sous forme de panel dynamique
entraîne le problème d'endogenéité. En
général, ce problème peut résulter de l'omission de
variables explicatives pertinentes dans la spécification du
modèle ; de la simultanéité qui apparaît
lorsque la variable dépendante et certaines variables explicatives sont
déterminées en « même temps », ou
encore des erreurs de mesures sur les variables indépendantes et/ou de
la variable dépendante. Dans le cas particulier de notre étude,
la méthodologie relative au calcul des indicateurs de la dette
extérieure peut être sujette à des limites et de ce fait
conduire à des erreurs de mesure. Dès lors, l'hypothèse
d'exogénéité des indicateurs de la dette extérieure
peut ne plus être vérifiée.
De plus, la spécification en panel dynamique
nécessite que soit introduite, parmi les variables explicatives, la
variable dépendante retardée d'au moins une période. La
présence de celle-ci dans le membre de droite de nos équations
entraîne automatiquement le biais d'endogenéité. Dès
lors, l'utilisation des méthodes traditionnelles notamment celle des MCO
n'est plus adéquate puisqu'elle donne des estimateurs biaisés et
non convergents à cause de la corrélation entre la variable
endogène retardée et le terme d'erreur, lorsque les
résidus sont autorégressifs. Il nous faut donc recourir à
des méthodes d'estimation plus performantes en l'occurrence la
méthode des moments généralisés (GMM)
développée par Holtz-Eakin et al. (1988) et Arellano et
Bond (1991). A cet effet, Arellano et Bond (1991) proposent de passer
l'équation de référence (1) en différences
premières permettant ainsi d'éliminer l'effet spécifique
aux pays.
 (3) (3)
Cependant, ce passage soulève un nouveau
problème puisque la variable dépendante retardée est par
construction corrélée avec le terme d'erreur. Pour apporter une
solution à ce problème, les auteurs postulent deux
hypothèses à savoir l'absence d'autocorrélation des termes
d'erreurs ainsi que la faible exogénéité des variables
explicatives (les variables explicatives sont non corrélées avec
les réalisations futures des termes d'erreurs). Dès lors,
Arellano et Bond (1991) proposent les conditions des moments suivantes :
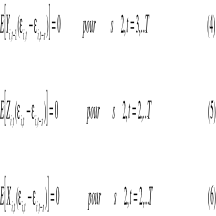
Les conditions (4) (5) et (6) soulignent l'absence de
corrélation entre les variables explicatives retardées ainsi que
les variables endogènes retardées avec les variations du terme
d'erreur. De ce fait, les conditions (4) (5) et (6) permettent l'utilisation
des variables retardées en niveau comme instruments pour estimer
l'équation (3).
Cette méthode bien que procurant des résultats
plus précis que les techniques usuelles, présente
néanmoins quelques limites, car l'utilisation des variables
retardées en niveau comme instruments n'est pas toujours
adéquate. En effet, Blundell et Bond (1998) ont montré que, sur
de petits échantillons, les coefficients pouvaient être
sérieusement biaisés si les variables explicatives en niveau
présentent une forte corrélation. Aussi, l'approche qui sera
privilégiée dans le cadre de cette étude, est l'estimateur
GMM en systèmes d'Arellano-Bover (1995)/Blundell-Bond (1998). Elle
consiste à combiner pour chaque période l'équation en
différence première avec celle en niveau. Dans l'équation
en différence première, les variables sont alors
instrumentées par leurs valeurs en niveau retardées d'au moins
une période. En revanche, dans l'équation en niveau, les
variables sont instrumentées par leurs différences
premières (Jeanneney, Guillaumont et Kangni, 2006).
| 


