Tracker solaire à deux axes

	Université Sidi Mohamed Ben Abdellah Faculté des Sciences et Techniques Fès Département Génie Electrique

Mémoire de Projet de fin
d'étude

Préparé par

Samira BOUJENANE

Pour l'obtention du diplôme

Tracker Solaire Page 1

Master Sciences et Techniques
Electronique, Signaux et Systèmes Automatisés
(E.S.S.A)
Intitulé

Tracker solaire

Encadré par :

Pr Hassan EL MOUSSAOUI

Mr Abdellatif GHENNIOUI (Green Energie Park)

Soutenu le 14 Juin 2017, devant le jury composé de :

Pr Hassan EL MOUSSAOUI : Encadrant

Mr Abdellatif GHENNIOUI : Encadrant

Pr Hassane EL MARKHI .: Examinateur

Pr Ali AHAITOUF : Examinateur

Pr Najia ES-SBAI : Examinatrice

Dédicace

Tracker Solaire Page 2

Je dédie ce modeste travail à :

À mes très chers parents, Mohamed et Tifa que dieu les garde et les protège pour leurs soutien moral et financier, pour leurs encouragements et les sacrifices qu'ils ont endures.

À mes chers Frères Rachid et Azzeddine. À mes chères Soeurs Fatima et Oumaima.

À tous mes chères Amis.

À tous les Amis (es) d'études surtout ceux de master ESSA promotion 2017. À tous les Gens que je connais.

Remerciement

Tracker Solaire Page 3

Remerciement

Le projet de fin d'études auquel j'ai été initié a été une expérience intellectuellement utile et humainement motivante. Rien de cela n'aurait été possible sans ceux qui ont partagé avec moi leur savoir, leurs efforts et qui m'ont permis d'éviter les difficultés par leurs bons conseils.

Ce stage a été effectué au centre de recherche IRESEN (Green Enegy Park). Au cours de ces travaux, j'ai été encadré par Monsieur GHENNIOUI Abdellatif, directeur de la division modélisation, je tiens à le remercier pour bien voulu m'accueillir comme stagiaire dans sa division, pour la qualité du sujet de recherche qu'il m'a proposé, pour m'avoir fait bénéficier de ses connaissances scientifiques, ses conseils et son énorme aide.

J'adresse mes vifs remerciements à Hassan EL MOUSSAOUI Professeur à la Faculté des Sciences et Techniques de Fès, pour son encadrement, ses clairs conseils, j'ai beaucoup appris en travaillant avec lui, sa disponibilité aussi pour la confiance et la compréhension qu'il m'a manifestée, je le remercie également de m'avoir supporté pendant la durée du stage.

C'est également avec plaisir que je remercie les membres du jury le professeur H. EL MARKHI, A. AHAITOUF et Madame N. ES-SBAI, je mesure à leur juste valeur le temps qu'ils m'ont accordé.

Mes vifs remerciements à tous les enseignants qui ont contribué à ma formation du primaire à l'université, à ceux qui ont marqué ma formation électrique.

Un immense merci aux membres de l'équipe de Green Energie Park qui j'ai eu l'opportunité d'embêter, en particulier Monsieur Abdellah El Hassani El Alaoui pour sa rigueur scientifique et les conseils judicieux qu'il m'a prodigués pour l'élaboration de ce travail, je lui remercie également pour sa disponibilité et sa gentillesse toute la durée de mon stage.

Je souhaite remercier tous mes amis de master ESSA avec qui j'ai partagé d'agréables moments au cours de ces dernières années.

Merci également à tous les collègues avec lesquelles j'ai effectué mon stage (Zemmouri Med Noor, DAHR Fatima Ezzahra et Oumaima EL ALANI) de leurs encouragements et les bons moments qu'on a passés ensemble, une chance énorme de vous avoir connu à vous tous.

Je ne peux pas finir mes remerciements sans rendre un grand hommage à AZEROUAL Mohamed et EL KARKRI Yassir pour leurs conseils et leur énorme aide.

Enfin, je remercie tous ceux qui ont contribué de près ou de loin à la concrétisation de ce travail.

Merci aux lecteurs de ce rapport.

Tracker Solaire Page 4

Remerciement

Résumé

Dans l'optique de maximisation de la production des panneaux solaires d'une part, et de réduction des coûts d'installation en facilitant la maintenance et l'entretien des trackers d'autre part, ce travail se focalise sur l'amélioration de la précision et la réduction du coût de la stratégie de génération de la trajectoire du tracker. Un modèle du tracker à deux axes a été développé en trois parties: une modélisation mécanique sous SolidWorks, un modèle dynamique sous Matlab/Simulink et un modèle de commande. Ainsi, l'analyse d'une nouvelle approche sans capteur s'appuyant sur un calcul astronomique de la position de soleil a été effectuée, en effet, la position du soleil varie d'une manière continue durant la journée de l'Est vers l'Ouest selon l'axe azimutal (Est-Ouest), et aussi pendant les saisons selon un axe zénithal (Nord-Sud).

Mots clés : Tracker à deux axes, Modèle du tracker, SolidWorks, Matlab/Simulink, calcul astronomique, l'axe azimutal, l'axe azimutal.

Abstract

In order to maximize the production of solar panels on the one hand and reduce installation costs by facilitating the maintenance of trackers on the other hand, this work focuses on improving Accuracy and reduction of the cost of the tracker's tracking strategy. A two-axis tracker model has been developed in three parts: a mechanical modeling under SolidWorks, a dynamic model under Matlab / Simulink and a control model. Thus, the analysis of a new approach without sensor based on an astronomical calculation of the position of sun was carried out, in fact, the position of the sun varies in a continuous way during the day from the East to the 'West along the azimuthal axis (East-West), and also during the seasons along a zenithal axis (North-South).

Key words: Two-axis tracker, Tracker model, SolidWorks, Matlab / Simulink, astronomical calculation, azimuth axis, azimuth axis.

Tracker Solaire Page 5

Résumé

Sommaire

Dédicace 2

Remerciement 3

Résumé/Abstract 4

Sommaire 5

Liste des figures 8

Liste des tableaux 10

Abréviations 10

Introduction générale 11

Chapitre I : Présentation de l'organisme d'accueil 13

1. Présentation de l'institution 13

2. La Structure D'IRESEN 14

3. Les grands projets pilotes de la plateforme : 15

Chapitre II : Gisement solaire et le générateur photovoltaïque 16

1. Introduction 16

2. Aspects géométriques 16

2.1. Mouvement de la Terre autour du soleil 16

2.2. Trajectoire apparente du soleil 17

2.3. Coordonnées du soleil 17

2.4. Les coordonnées terrestres (géographiques) 19

2.5. Durée d'insolation 19

2.6. Le taux d'insolation 19

3. Aspects énergétiques 20

4. Énergie solaire : 23

4.1.1. Modélisation de la cellule photovoltaïque 25

4.1.2. Le générateur photovoltaïque et ses performances 25

4.1.3. Type et rendement des cellules photovoltaïques 26

5. Conclusion 27

Chapitre III : Position du soleil & les trackers solaires 29

1. Introduction 29

2. L'intérêt des panneaux mobiles par rapport aux panneaux fixes 29

3. Orientation et inclinaison d'une surface 30

4. Les points positifs et négatifs des suiveurs 31

Tracker Solaire Page 6

Sommaire

5. Les types des suiveurs 31

5.1. Mécanisme d'orientation (système de positionnement) 31

5.2. Type de commande 32

5.2.1. Commande en boucle ouverte 32

5.2.2. Commande en boucle fermée 32

5.2.3. Commande hybride 32

5.2.4. Commande tenant compte de la consommation 32

5.3.1. Traqueurs Mono axiaux : 33

5.3.2. Traqueurs Bi axiaux : 33

6. Description du suiveur solaire : 34

7. Angle d'incidence sur un plan incliné(i) 35

8. Conclusion 35

Chapitre IV: Modélisation des trackers 36

1. Introduction 36

2. Modèle mécanique 36

2.1. Représentation du logiciel utilisé 37

2.1.1. Définition de la CAO 37

2.1.2. Outil CAO utilisé dans notre projet 37

2.2. Conception et Modélisation géométrique du système 38

2.2.1. Description générale des systèmes 38

2.2.2. Système de poursuite 38

3. Modèle dynamique 39

3.1. Modèle du soleil 40

3.2. Modèle dynamique des actionneurs 42

3.2.1. Analyse des éléments 42

3.2.2. Vitesse de rotation du panneau 43

3.2.3. Le vent 44

3.2.4. Modèle de Capteur 45

3.3. Modélisation du moteur asynchrone 46

3.3.1. Modèle dynamique de la machine asynchrone 46

3.3.2. Modèle mécanique du tracker 48

3.3.3. Calcul de l'inertie du tracker azimut et élévation 48

3.3.4. Relation entre la position angulaire et la course du vérin 49

3.3.5. Estimation du couple résistant 50

Sommaire

3.3.6. Modélisation et simulation du modèle dynamique 50

3.4. Commande scalaire 53

3.4.1. Contrôle en V/f de la machine asynchrone 54

3.4.2. Modélisation de l'onduleur triphasé 54

3.4.3. Les Techniques de commande de l'onduleur triphasé 56

3.4.4. La modulation de largeur d'impulsions 56

3.4.5. Modélisation de la commande scalaire 57

4. Commande et stratégie de génération de trajectoire d'un tracker 59

5. Conclusion 59

Chapitre V : Test et simulation de la Commande du tracker 60

1. Introduction 60

2. Contexte logiciel 60

3. Écriture du programme 61

4. Description du HARDWARE 61

4.1. Réalisation de la commande de l'onduleur 61

4.1.1. Schéma de principe 61

4.1.2. Circuit de l'onduleur 62

4.1.3. Gâte drives circuit 62

4.2. Réalisation de la carte de commande du moteur asynchrone 64

5.1.1. Étage de la puissance 64

5.1.2. Relai électromagnétique 64

4.3. Teste de la carte 65

5. Conclusion 65

Conclusion générale et Perspectives 66

Références 68

Annexes 70

Tracker Solaire Page 7

Tracker Solaire Page 8

Sommaire

Liste des figures

Chapitre 1 :

Fig. I. 1 Dessin schématique des principaux contributeurs d'IRESEN. 13

Fig. I. 2 Modèle 3D de Green Energy Park. 14

Fig. I. 3 Structure D'IRESEN. 14

Chapitre 2 :

Fig. II. 1 Le mouvement de la Terre autour du soleil [4]. 17

Fig. II. 2 Trajectoire du soleil [5]. 17

Fig. II. 3 Le plan équatorial de la terre avec l'angle de Déclinaison solaire (ô) et Angle horaire .

18

Fig. II. 4 Le plan horizontal de la terre avec l'azimut du soleil a et son élévation h. 19

Fig. II. 5 Coordonnées terrestre. 19

Fig. II. 6 Analyse spectrale du rayonnement solaire. 20

Fig. II. 7 Le rayonnement solaire et le nombre d'air masse. 20

Fig. II. 8 Types de rayonnement solaire reçus au sol [6]. 21

Fig. II. 9 - a- Rayonnement solaire capté par un plan horizontal et incliné [2]]. 23

Fig. II. 10 L'énergie émise par le soleil. 24

Fig. II. 11 Conversion de l'énergie solaire en énergie électrique. 24

Fig. II. 12 Capacité mondiale d'énergie solaire photovoltaïque [7]. 25

Fig. II. 13 Schéma équivalent électrique d'une cellule PV [5] 25

Fig. II. 14 Courbes I(V) et P(V) d'un panneau photovoltaïque [5]. 26

Fig. II. 15 Caractéristiques d'un générateur photovoltaïque pour différents éclairements [5]. 26

Chapitre 3 :

Fig. III. 1 Un panneau photovoltaïque fixe (a) et avec système suiveur (b) [11]. 29

Fig. III. 2 Diagramme de comparaison entre la production avec suiveur et la production avec

système fixe [5]. 30

Fig. III. 3 Les angles de l'inclinaison, de projection et de l'incidence [5]. 30

Fig. III. 4 Exemple et fonctionnement du suiveur passif [13]. 31

Fig. III. 5 Commande en boucle ouverte d'un tracker PV [14]. 32

Fig. III. 6 Commande en boucle fermée d'un tracker [14]. 32

Fig. III. 7 Génération de trajectoire discontinue [14]. 33

Fig. III. 8 Traqueur à un seul axe avec angle d'inclinaison de Latitude [5]. 33

Fig. III. 9 Traqueur à deux axes avec angle d'inclinaison de Latitude [5]. 34

Fig. III. 10 Traqueur à deux axes Azimut/Élévation [5]. 34

Fig. III. 11 Description de suiveur solaire [12]. 35

Chapitre 4 :

Fig. IV. 1 Modélisation d'un tracker PV et de son command. 36

Fig. IV. 2 Le diagramme représentant les cinq générations de systèmes de CAO [15]. 37

Fig. IV. 3 Le modèle mécanique réalisé sous SolidWorks. 38

Fig. IV. 4 Description des différents éléments du tracker. 39

Fig. IV. 5 Schéma synoptique du modèle de tracker proposé. 40

Fig. IV. 6Angle d'Azimute et l'altitude en fonction du temps. 40

Tracker Solaire Page 9

Liste des figures

Fig. IV. 7 Le rayonnement reçu sur la surface d'un panneau incline. 41

Fig. IV. 8 Comparaison entre l'Altitude/Azimut calculé et mesuré. 42

Fig. IV. 9 Réducteur de roue et vis [18]. 44

Fig. IV. 10 La rose de vent de Ben Guerir 44

Fig. IV. 11 Élévation mesurée avec notre inclinomètre [19]. 45

Fig. IV. 12 Moteur asynchrone [20]. 46

Fig. IV. 13 Modèle électromécanique asservi du tracker. 47

Fig. IV. 14 Inertie du panneau (Elévation). 49

Fig. IV.15 Inertie du panneau (azimut). 49

Fig. IV.16 Schéma des paramètres de calcul. 49

Fig. IV.17 Modéle Interne du MAS. 51

Fig. IV. 18 Modèle en bloc Simulink de la MAS alimentée en tension. 51

Fig. IV. 19 Le schéma interne de MAS modèle dq. 52

Fig. IV. 20 Les Résultats de la simulation du démarrage à vide du moteur asynchrone. 53

Fig. IV. 21 Commande scalaire du moteur asynchrone [22] 54

Fig. IV. 22 Le schéma d'un onduleur triphasé alimentant le MAS. 54

Fig. IV. 23 Schéma équivalent de l'onduleur. 55

Fig. IV. 24 Modèle de l'onduleur triphasé. 55

Fig. IV. 25 La sortie d'onduleur triphasé. 56

Fig. IV. 26 Modèle Simulink de la commande MLI. 57

Fig. IV.27 Le signal de sortie de la commande MLI. 57

Fig. IV.28 Modèle dynamique du MAS asservie en position. 58

Fig. IV. 29 Les résultats de simulation. 58

Fig. IV. 30 Réponses indicielles d'un axe du tracker asservi en position. 59

Chapitre 5 :

Fig. V. 1 Carte de commande d'un tracker solaire. 60

Fig. V. 2 Cheminement de la programmation et de la simulation [1]. 61

Fig. V. 3 Circuit de commande d'un onduleur triphasé. 62

Fig. V. 4 L'onduleur triphasé avec trois bras. 62

Fig. V. 5 La structure du circuit tampon (BC547 et 2N3019). 63

Fig. V. 6 La structure de l'opto-isolateur. 63

Fig. V. 7 La structure de Darlington pair amplifiée (TIP122). 64

Fig. V. 8 Connexion d'IR2112. 64

Fig. V. 9 Description d'un relais électromagnétique. 64

Fig. V. 10 Les signaux PWM. 65

Les tableaux et Abréviations

Tracker Solaire Page 10

Liste des tableaux

Tableau 1 : Performance des différentes technologies des cellules PV [8]. 27

Tableau 2 : les indicateurs statistiques 42

Tableau 3: Matrice de choix du moteur nature de la motorisation. 43

Tableau 4 : La comparaison entre les différents capteurs de position [19] 45

Tableau 5 : Récapitulation de l'influence d'un PID série sur le système. 47

Abréviations

MAS Moteur Asynchrone.

MLI Modulation de largeur d'impulsion.

AM Masse d'air.

PV Photovoltaïque.

TSV Temps solaire vrai.

MPPT Maximum power point tracking : recherche du maximum de puissance.

PPM Point de puissance maximale

DNI Direct normal Irradiance : Ensoleillement direct.

GHI Global Horizontal Irradiance : Ensoleillement global.

DHI Diffus Horizontale Irradiance.

MSE Mean square error : Erreur quadratique moyenne.

PPM Point de puissance maximale.

RMSE Racine carrée de l'erreur quadratique moyenne.

TU Temps universels.

ET Équation du temps.

TL Temps légal.

TS-2 Tracker solaire à 2 axes.

CAO Conception Assistée par Ordinateur.

MCAO Mécanique Conception Assistée par Ordinateur.

Tracker Solaire Page 11

Les tableaux et Abréviations

Introduction générale

Dans un contexte énergétique et économique difficile, les attentes en termes d'énergies renouvelables en général et d'énergie solaire en particulier, sont de plus en plus importantes. Les enjeux majeurs des chercheurs et des industriels dans ce domaine sont l'amélioration du rendement et diminution des coûts des cellules, des modules et des systèmes photovoltaïques afin de les rendre les plus compétitifs possible.

Il y a deux manières pour maximiser le taux d'énergie utile en optimisant la conversion et le degré d'absorption, et en augmentant le taux de rayonnement d'incidence en employant les systèmes d'orientation mécanique. Ces systèmes appelés suiveurs solaires aussi « trackers » permettent d'orienter les modules tout au long de la journée. Les systèmes de suiveurs solaires sont utilisés pour plusieurs applications incluant : les cellules solaires photovoltaïques, les concentrateurs solaires et les télescopes.

Ce travail présente la conception et l'exécution d'un algorithme de commande pour une structure mécanique à prix réduit qui peut soutenir les modules photovoltaïques et qui agit en tant que traqueur du soleil.

Plusieurs classes de structure peuvent être distinguées selon les critères de classification. Concernant des possibilités de mouvement, trois principaux types de traqueurs du soleil existent: surfaces fixes, traqueurs un axe et traqueurs deux axes. La différence principale parmi eux est la capacité de réduire l'erreur d'orientation, en augmentant l'irradiation quotidienne que les cellules solaires reçoivent et, ainsi, l'énergie électrique qu'elles produisent. Notre projet a pour but d'étudier un tracker solaire à deux axes.

Ce rapport est composé de cinq chapitres :

? Le premier chapitre est dédié à la présentation de l'organisme d'accueil Green Energy Parck de Ben Guérir, branche du centre de recherche IRESEN.

? Dans le chapitre 2, nous rappelons les généralités sur l'énergie solaire photovoltaïque ainsi que les principales caractéristiques de fonctionnement d'un générateur PV à sa puissance maximale.

? Dans le chapitre 3, nous présentons les coordonnées astronomiques et les angles correspondants à la trajectoire du soleil dans la sphère céleste pour repérer sa position dans le ciel. Nous présentons aussi une méthode algorithmique pour calculer cette position.

? Le chapitre 4, porte sur la conception du suiveur solaire et son principe de fonctionnement. Une première partie, est dédiée à la modélisation mécanique de la structure du tracker générée sous le logiciel SOLIDWORKS®. Une deuxième partie, est consacrée à la modélisation dynamique sous Matlab/Simulink : le premier élément de ce simulateur est un modèle de génération des données atmosphériques et des données théoriques de la position du tracker correspondant à la trajectoire du soleil, le deuxième élément est un modèle électromécanique du tracker asservi permettant de calculer la position réelle du tracker en tenant compte du comportement dynamique électrique de l'actionneur et du comportement dynamique mécanique du tracker. Une troisième partie de ce chapitre aborde la commande du tracker solaire à l'aide d'un microcontrôleur.

Introduction générale

? Le chapitre 5 est consacré â la commande d'un système du suiveur de soleil â deux axes et la

programmation du PIC sous mikroC et ISIS.

Tracker Solaire Page 12

Chapitre I : Présentation de l'organisme d'accueil

Chapitre I : Présentation de

l'organisme d'accueil

Tracker Solaire Page 13

Présentation de l'institution

IRESEN est un institut de recherche créé en 2011 par le Ministère de l'Énergie, des Mines, de l'Eau et de l'Environnement et plusieurs acteurs clés du secteur de l'énergie au Maroc (Figure I. 1) pour accompagner la stratégie énergétique nationale en soutenant appliquée la recherche et développement dans le domaine de l'énergie solaire et de nouvelles énergies. C'est aussi la mission de l'organisme d'orienter les grands axes de recherche et de financer les projets, qui sont pertinents. L'un des succès les plus étonnants d'IRESEN a été le développement du Green Energy Park.

Fig. I. 1 Dessin schématique des principaux contributeurs d'IRESEN.

Green Energy Park est une plate-forme d'essai, de recherche et de formation solaire couvrant une superficie totale de huit hectares situés dans la ville verte de BenGuerir Il a été développé par IRESEN (Institut de Recherche en Energie Solaire et Energies Nouvelles) avec le soutien du Ministère de l'Énergie, des Mines, de l'Eau et de l'Environnement le long du Groupe OCP (Figure I. 2).

Chapitre I : Présentation de l'organisme d'accueil

Fig. I. 2 Modèle 3D de Green Energy Park.

Cette plate-forme de recherche (le premier de son genre en Afrique) permet de réaliser deux objectifs principaux :

? Création de synergies et mise en commun des infrastructures de recherche afin d'atteindre l'excellence ;

? Fournir aux différentes universités partenaires ainsi qu'aux industriels les informations nécessaires sur les panneaux solaires photovoltaïques ou thermiques.

La Structure D'IRESEN

La structure d'IRESEN est sur la figure I.3 suivante:

Fig. I. 3 Structure D'IRESEN.

Tracker Solaire Page 14

Chapitre I : Présentation de l'organisme d'accueil

Les grands projets pilotes de la plateforme :

Centrale CSP (CHAMS1) : L'objectif du projet CHAMS 1 est le développement d'un champ solaire thermodynamique nouvelle génération, basse concentration et utilisant un champ solaire de type Fresnel innovant [1].

Centrale PV : Installation d'une centrale pilote photovoltaïque 120 - 200 kWc, utilisant 5 technologies différentes pour la caractérisation des performances et l'identification de la complémentarité des technologies existantes sous les conditions climatiques marocaines [1].

Centrale SUNPOWER C7 : Installation d'une nouvelle génération de CPV à basse concentration, pour mettre en évidence les preuves de ce nouveau concept et pour comparer sa performance à celle des technologies PV conventionnelle [1].

Centrale HCPV : Mise en place d'un système CPV à haute concentration combiné à un système d'accumulateurs, pour l'étude et la caractérisation de ses performances [1].

Tracker Solaire Page 15

Chapitre II : Gisement solaire et le générateur photovoltaïque

Tracker Solaire Page 16

Chapitre II : Gisement solaire

et le générateur photovoltaïque

1. Introduction

Le gisement solaire est un ensemble de données décrivant l'évolution du rayonnement solaire disponible au cours d'une période donnée.

Le soleil est une source énergétique quasiment illimitée, il pourrait couvrir plusieurs milliers de fois notre consommation globale d'énergie [2]. C'est pourquoi, l'homme cherche depuis longtemps à mettre à profit cette énergie importante et diffusée sur l'ensemble de la planète, il est arrivé à réaliser ce but par le moyen dit cellule photovoltaïque.

Le nom photovoltaïque vient du grec, il est composé de deux parties :

? Photos : Lumière.

? Volt : Unité de tension électrique, du nom Alessandro Volta.

Aujourd'hui, grâce à sa fiabilité et à son concept respectueux de l'environnement, le photovoltaïque prend une place prépondérante.

Dans ce chapitre, nous allons rappeler quelques notions de base sur la géométrie solaire, le rayonnement et l'énergie solaire, ensuite une description du système photovoltaïque sera donnée.

Aspects géométriques

Mouvement de la Terre autour du soleil

Le mouvement de la Terre autour du soleil s'effectue dans un plan nommé le plan de l'écliptique. L'axe des pôles, autour duquel s'effectue le mouvement de rotation de la Terre, n'est pas perpendiculaire sur le plan de l'écliptique. Le centre de gravité de la Terre décrit une ellipse dont le soleil occupe l'un des foyers [3] (voir Figure II.1).

Les deux déplacements distincts de la terre (Figure II.1).

? Le premier est une rotation de celle-ci autour de son axe en 24 heures.

? Le second est une rotation de la Terre autour du soleil en 365 jours 5h 48 min 40s 365,25 jours. Ce mouvement s'effectue dans le sens trigonométrique et provoque le cycle des saisons

Tracker Solaire Page 17

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. II. 1 Le mouvement de la Terre autour du soleil [4]. Trajectoire apparente du soleil

Sur la figure II.2, les trajectoires et en même temps les hauteurs du Soleil sont tracées pour tous les pays qui sont à la même latitude. Plus on monte vers le Nord, plus le Soleil à son lever, s'écarte de l'Est à l'époque des solstices. L'angle que fait un point de l'horizon avec la direction du Sud s'appelle l'azimut [5].

L'équateur céleste est pratiquement la ligne que trace pour nous le Soleil dans le ciel, aux premiers jours du printemps et de l'automne (appelés jours d'équinoxes).

L'observateur est ici face au Soleil couchant. Le parcours du Soleil est le plus long au solstice d'été. Au solstice d'hiver, en revanche, le parcours du Soleil est le plus court.

Fig. II. 2 Trajectoire du soleil [5]. Coordonnées du soleil

Pour un lieu donné, la position du soleil est repérée à chaque instant de la journée et de l'année par deux systèmes de coordonnées différents [6].

Par rapport au plan équatorial de la terre (repère équatorial).

Par rapport au plan horizontal du lieu (repère horizontal).

- Coordonnées équatoriales

Le mouvement du soleil est repéré par rapport au plan équatorial de la terre à l'aide de deux angles.

Déclinaison solaire (ô)

C'est l'angle que fait la direction du soleil avec sa projection sur le plan équatorial (voir figure II.3). La déclinaison du soleil varie quotidiennement selon la relation :

Chapitre II : Gisement solaire et le générateur photovoltaïque

* * ( ) ( )++ E. 1

Avec :

J : le numéro du jour de l'année compté à partir du 1^er janvier, c.-à-d. varie de 1 à 365 ou 366 selon l'année

On dit que la déclinaison du Soleil est égale à zéro lorsque la trajectoire du Soleil suit l'équateur céleste. Cette déclinaison atteint +23.45° au début de l'été, et -23.45° au début de l'hiver. C'est l'écart que fait le Soleil avec l'équateur céleste à l'époque des solstices.

Angle horaire du soleil C'est l'angle que fait la projection de la direction du soleil avec la direction du méridien

du lieu, l'angle horaire du soleil varie à chaque instant de la journée selon la relation (Figure. II.3):

( ) E. 2

( ) ( ) E. 3

(

( )) ( ( )) ( ( )) E. 4

( ) ( ) ( ) ( ) E. 5

Avec

TSV : temps solaire vrai,

TU: Temps universel c'est le décalage horaire

par rapport au méridien de Greenwich.

Pour le Maroc : TU= 0.

TL: Temps légal : temps donné par une montre.

At : correction de l'équation du temps.

: Longitude du lieu.

>0 : après midi.

<0 : le matin.

=0 : midi TSV.

x:

( ) - Coordonnées horizontales du soleil

Fig. II. 3 Le plan équatorial de la terre avec l'angle de Déclinaison solaire (ä) et Angle horaire??.

La position du soleil à un instant considéré est donnée par l'azimut du soleil a et son élévation h (voir figure II.5).

Azimut ( )

C'est l'angle que fait la projection du soleil sur le plan horizontal avec la direction du Sud, l'azimut du soleil varie à chaque instant de la journée selon la relation :

E. 6

Hauteur, Elévation ou l'altitude (h)

C'est l'angle vertical entre le plan horizontal et la direction du soleil (Figure II. 4). La hauteur du soleil varie à chaque instant de la journée et de l'année selon la relation suivante :

E. 7

La hauteur du soleil varie entre -90° et +90°.

h= 0 pour le plan horizontal (aux lever et coucher),

Tracker Solaire Page 18

Chapitre II : Gisement solaire et le générateur photovoltaïque
h> 0 le jour, h< 0 la nuit, h = 90° pour le zénith. L'azimut a: varie entre -180° et 180°. On prend : > 0 : vers l'ouest, < 0 : vers l'est, = 0 : direction du sud, = 180° pour le Nord.

Fig. II. 4 Le plan horizontal de la terre avec l'azimut

du soleil a et son élévation h.

Les coordonnées terrestres (ggpq)

Les coordonnées polaires terrestres portent les noms de latitude (notée ö) et longitudes (notée L) terrestres (Figure II. 5).

La latitude ö est une valeur angulaire, expression du positionnement nord ou sud d'un point sur Terre, 4)varie de -90° à 90° tel que: 4) > 0 vers le nord et 4) < 0 vers le sud.

La longitude L est une valeur angulaire, expression du positionnement est ou ouest d'un point

sur Terre, L varie de -180° à 180° tel que : L >0 à l'est du méridien de Greenwich & L<0 à l'ouest du méridien de Greenwich.

Duré

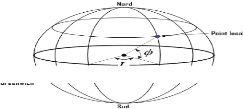
Fig. II. 5 Coordonnées terrestre.

.

La durée d'insolation représente la durée maximale de la journée, entre le lever et coucher du soleil

Le temps du lever (sunset) du soleil est :

( --t9( 5) t9( p)) / 15 E. 8

Le temps du coucher (sunrise) du soleil est :

t = 12 + arcco ( --t9( ) t9( )) / 1 E. 9

vcoucner

Durée du jour :

( --t9( s) t9( 0)) E. 10

Le taux d'insolation

Le sol reçoit le rayonnement solaire maximal pendant la durée de jours d'ensoleillement T (du lever au coucher du soleil) et par ciel clair, mais la durée effective d'ensoleillement s d'une journée ordinaire est inférieure à cette durée maximale [3].

Le taux d'insolation est donné par l'expression ci-après :

E. 11

Tracker Solaire Page 19

Tracker Solaire Page 20

Chapitre II : Gisement solaire et le générateur photovoltaïque

Aspects énergétiques

3.1. Potentiel solaire

L'ensoleillement, qui représente le flux d'énergie émit par unité de temps et par unité de surface du soleil, exprimé en W/m est donné par la loi de Stefan-Boltzmann :

E. 12

Où a = 5.67 * 10^-$ W/m². K⁴est la constante de Stefan-Boltzmann ;

T est la température absolue du corps noir.

L'ensoleillement reçu en dehors de l'atmosphère terrestreE0, nommée la constante solaire et les mesures, par satellite, indiquent que la valeur moyenne de l'année est de E₀ =1367W/m.

L'ensoleillement extraterrestre sur une surface perpendiculaire au faisceau du soleil dans le jour n de l'année est donné (n variant de 1 à 365 et ce du 01/01 au 31/12 de l'année) par l'équation suivante [2]:

(n) = (1 + 0.033 ₂₃₆₅₎ E₀ E. 13

3.2. Rayonnement solaire

Le rayonnement solaire est constitué de photons dont la longueur d'onde s'étend de l'ultraviolet (0,2 um) à l'infrarouge lointain (2,5 um).

3.3. Répartition spectrale du rayonnement

L'énergie associée à ce rayonnement solaire comme l'indique la figure II. 6 se décompose approximativement de :

- 9% dans la bande des ultraviolets (<0,4 um),

- 47% dans la bande visible (0,4 à 0,8 um),

- 44% dans la bande des infrarouges (>0,8 um).

Fig. II. 6 Analyse spectrale du rayonnement solaire. 3.4. Masse d'air

La masse d'air est définit comme une zone stable au sens des paramètres physiques mesurés en son sein, et c'est le rapport entre l'épaisseur d'atmosphérique traversée par le rayonnement direct pour atteindre le sol et l'épaisseur traversée à la verticale du lieu [6].

Chapitre II : Gisement solaire et le générateur photovoltaïque

Donc, l'Air Mass

3.5. Composition du rayonnement solaire

Le rayonnement solaire sur une surface au sol est composé comme suit (Figure II. 8) [2]:

Fig. II. 8 Types de rayonnement solaire reçus au sol [6]. - Rayonnement direct DHI

C'est la fraction du rayonnement solaire qui arrive directement au sol.

E. 14

Avec

h: hauteur du soleil.

J: Rayonnement direct d'une surface normale

n

J = J E. 15

n [ +0.0 *c s( *')+

0 = 1367

- Rayonnement diffus DNI

Le rayonnement diffus est le rayonnement provenant de toute la voûte céleste.

- Rayonnement réfléchi (L'albédo)

Le rayonnement solaire réfléchi est le rayonnement qui est réfléchi par le sol ou par des objets se trouvant à sa surface. Ce rayonnement dépend de l'albédo du sol [6].

E. 16

- Rayonnement global GHI Une surface horizontale

C'est l'ensemble du rayonnement d'origine solaire qui parvient sur une surface horizontale. Il comprend deux types de rayonnements directs et diffus.

Une surface inclinée

Rayonnement global sur une surface inclinée est la somme des rayonnements :Direct, diffus et réfléchi.

Tracker Solaire Page 21

Tracker Solaire Page 22

Chapitre II : Gisement solaire et le générateur photovoltaïque

3.6. Calcul du rayonnement solaire

Rayonnement solaire direct sur un plan horizontal [3]

DHI,h = F*sin(h) [ ] E. 17

Avec

h : est la hauteur angulaire du soleil,

F : est le flux incident reçu sur une surface face aux rayons solaires et peut être évalué.

Par :

F = Esol × exp(TL /(0.9 + 9.4sin(h))) [ ] E. 18

Avec

Esol= 1370

TL le facteur de trouble de Linke défini comme suit :

TL = 2.4 + 14.6B + 0.4(1+2B)ln(Pv) E. 19

Où B est le coefficient de trouble atmosphérique qui prend une des valeurs :

B = 0.02 pour un lieu situé en montagne

B = 0.05 pour un lieu rural

B = 0.10 pour un lieu urbain

B = 0.20 pour un lieu industriel (atmosphère polluée)

Pv est la pression partielle de vapeur d'eau, qui se calcule par :

Pv = Pvs×HR E. 20

Avec Pvs la pression de vapeur saturante, HR le taux moyen d'humidité relative et :

Pvs = 2.165 (1.098 + T/100)^8.02 E. 21

Où T est la température de l'air en °C.

Rayonnement diffus sur un plan horizontal

Le rayonnement solaire diffus sur un plan horizontal peut être déterminé par [3] :

DNI,h= 54.8 vsin(h) × (T - 0.5 - vsin(h) ) E. 22

Où TL est le facteur de trouble de Linke calculé par la formule.

Rayonnement solaire direct sur un plan incliné

Le rayonnement direct est celui qui traverse l'atmosphère sans subir de modifications, il est possible de l'estimer par la formule suivante [3] :

DHI,i= F × CI E. 23

CI étant le coefficient d'orientation, c'est l'angle formé par le rayonnement solaire avec la perpendiculaire d'une surface. Ce coefficient est défini d'une part par la hauteur du soleil (h) et son azimut (a) et d'autre part par l'orientation (o) et l'inclinaison (??) du plan récepteur. L'orientation (o) est négative vers l'Est, positive vers l'Ouest et nulle vers le sud.

Le calcul du coefficient d'incidence CI est obtenu par la formule suivante :

CI= (sin(??)cos(h) cos(o - a) cos(??)sin(h)) E. 24

Rayonnement diffus sur un plan incliné

Le rayonnement solaire diffus D arrive sur le plan récepteur incliné après avoir été diffusé par les particules solides ou liquides en suspension dans l'atmosphère, il n'a pas de

Tracker Solaire Page 23

Chapitre II : Gisement solaire et le générateur photovoltaïque

direction privilégiée, de ce fait, l'orientation du plan (l'azimut) n'a pas d'importance, seule son inclinaison en a.

Ainsi sur un plan récepteur d'inclinaison (f.?), DNI se calcule [3] :

DNI,i =125 X sin(h)^0.4((1+ cos(f.?)) / 2) + 211.86 X sin(h)^1.22 ((1-cos(f.?)) / 2) E. 25

Le rayonnement diffus pour un plan incliné fixe est un cas particulier du rayonnement diffus pour un plan incliné mobile, l'inclinaison (f.?) doit être prédéfinie.

Rayonnement réfléchi sur un plan incliné

La composante réfléchie, Gr est donnée par la relation suivante [3]:

Gr = ñX GHI (1 - cos(â)/2) E. 26

Où ñ représente l'albédo et â l'inclinaison du champ PV.

3.7. L'intensité du rayonnement solaire

L'intensité du rayonnement solaire reçu sur un plan quelconque à un moment donné est appelée irradiation ou éclairement (noté généralement par la lettre G), il s'exprime en watts paramètre carré ( w/m²).

La valeur du rayonnement reçu par la surface du module photovoltaïque varie selon la position de ce dernier. Le rayonnement solaire atteint son intensité maximale lorsque le plan du module photovoltaïque est perpendiculaire aux rayons [2].

Dans la figure. II.9 ci-après est illustré l'effet de l'inclinaison des modules photovoltaïques sur l'intensité de l'éclairement reçu sur leurs surfaces du lever au coucher du soleil.

Fig. II. 9 - a- Rayonnement solaire capté Fig. II. 9 - b- Intensité de l'ensoleillement reçu

par un plan horizontal et incliné [2]. sur un plan horizontal et incliné [2].

Énergie solaire :

L'énergie solaire est la fraction de l'énergie électromagnétique provenant du soleil et parvenant à la surface de la Terre, après filtrage par l'atmosphère terrestre (Figure II. 10).

Tracker Solaire Page 24

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. II. 10 L'énergie émise par le soleil.

Les techniques pour capter une partie de cette énergie (énergie absorbée par la terre) sont disponibles et sont constamment améliorées. On peut distinguer le solaire passif, le solaire photovoltaïque et le solaire thermique.

? Le type qui nous intéresse c'est l'énergie solaire photovoltaïque. L'énergie solaire photovoltaïque

L'énergie solaire photovoltaïque provient de la conversion de la lumière du soleil en électricité au sein de matériaux semi-conducteurs comme le silicium ou recouverts d'une mince couche métallique.

Ces matériaux photosensibles ont la propriété de libérer leurs électrons sous l'influence d'une énergie extérieure. C'est l'effet photovoltaïque. L'énergie est apportée par les photons (composants de la lumière) qui heurtent les électrons et les libèrent, induisant un courant électrique. Ce courant continu de micro-puissance calculé en watt crête (Wc) peut être transformé en courant alternatif grâce à un onduleur (Figure II.11).

Fig. II. 11 Conversion de l'énergie solaire en énergie électrique. Évolution de l'utilisation de l'énergie solaire

Au cours de la dernière décennie, l'énergie solaire PV a monté son énorme potentiel. La quantité de puissance PV installée a rapidement augmenté. Actuellement, la puissance PV installée à l'échelle mondiale est d'environ 227 GW. La figure II.12 montre la puissance PV

installée cumulée.

Tracker Solaire Page 25

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. II. 12 Capacité mondiale d'énergie solaire photovoltaïque [7]. Les panneaux solaires

Modélisation de la cellule photovoltaïque

Une cellule PV peut se modéliser à partir de l'équation définissant le comportement statique de la jonction PN d'une diode classique. Ainsi, la figure.1.2 illustre le schéma équivalent électrique d'une cellule PV réelle. Dans cette équation, on prend en compte le courant de court-circuit et les différentes résistances modélisant les pertes dues à la connectique. Ainsi, en statique, le comportement d'une cellule PV constituée d'une jonction PN à base de silicium peut être décrit par l'équation suivante [5]:

f exp(VCELL+ICELLRS)l VCELL+ICELLRS E. 27

_L

MIT J Rp

Avec :

Où IsAT est le courant de saturation, VT le potentiel thermo dynamique, K la constante de Boltzmann, T la température effective de la cellule en Kelvin, e la charge de l'électron, n le facteur de non idéalité de la jonction, ICELL est le courant fourni par la cellule, VCELL la tension à ses bornes, Iccle courant de court-circuit de la cellule dépendant de l'éclairement et la température, Rp la résistance shunt caractérisant les courants de fuite de la jonction et Rs la résistance série représentant les diverses résistances des contacts et de connexions.

La figure II. 13 montre la schématique adoptée pour une cellule PV élémentaire.

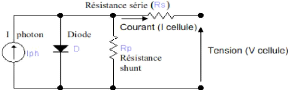
Fig. II. 13 Schéma équivalent électrique d'une cellule PV *5].

Le générateur photovoltaïque et ses performances

Un générateur photovoltaïque ou module est constitué d'un ensemble des cellules photovoltaïques élémentaires montés en série et/ou parallèle afin d'obtenir des caractéristiques électriques désirés tels que la puissance, le courant de court-circuit (Icc) ou la tension en circuit ouvert (V. O.

Tracker Solaire Page 26

Chapitre II : Gisement solaire et le générateur photovoltaïque

? Caractéristiques courant tension

La figure II. 14 ci-dessous montre la caractéristique courante tension d'un panneau photovoltaïque typique dans des conditions constantes d'irradiation et température.

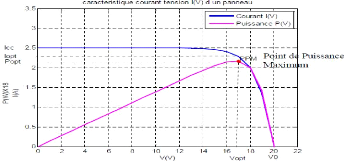
Fig. II. 14 Courbes I(V) et P(V) d'un panneau photovoltaïque [5]. ? L'influence de l'éclairement :

La figure II.15 présente un exemple des courbes pour différents niveaux de rayonnements :

Fig. II. 15 Caractéristiques d'un générateur photovoltaïque pour différents éclairements [5].

On remarque que la valeur du courant de court-circuit est proportionnelle à l'intensité du rayonnement. Par contre, la tension en circuit ouvert ne varie pas dans les mêmes proportions, elle reste quasiment identique même à faible éclairement. L'irradiation standard, internationalement acceptée, pour mesurer la réponse des panneaux photovoltaïques est l'intensité rayonnante de 1000 w/m² et une température de 25°C.

Type et rendement des cellules photovoltaïques

Il existe différents types de cellules solaires, et chaque type de cellules à un rendement qui lui est propre. Cependant, quel que soit leur type, leur rendement reste assez faible : de 8 à 23% de l'énergie qu'elles reçoivent [2].

Dans le tableau 1, ci-dessous on résume les différentes performances des technologies des cellules photovoltaïques :

Tracker Solaire Page 27

Chapitre II : Gisement solaire et le générateur photovoltaïque

Tableau 1 : Performance des différentes technologies des cellules PV [8].

Les avantages et les inconvénients de l'énergie PV

- Avantages

? L'énergie photovoltaïque peut être installée partout, même en ville.

? L'énergie photovoltaïque est renouvelable et gratuite.

? Sur les sites isolés, l'énergie photovoltaïque offre une solution pratique pour obtenir de

l'électricité à moindre coût.

? Les systèmes photovoltaïques sont fiables : aucune pièce employée n'est en mouvement.

Les matériaux utilisés (silicium, verre, aluminium) résistent aux conditions

météorologiques extrêmes.

? L'énergie photovoltaïque est totalement modulable et peut donc répondre à un large

éventail de besoins. La taille des installations peut aussi être augmentée par la suite pour

suivre les besoins de son propriétaire.

- Inconvénients

? Le coût d'investissement des panneaux photovoltaïques est élevé.

? Le rendement électrique diminue avec le temps (20% de moins au bout de 20 ans).

? Les panneaux contiennent des produits toxiques et la filière de recyclage n'est pas encore

existante.

? Lorsque le stockage de l'énergie électrique par des batteries est nécessaire, le coût du

système photovoltaïque augmente.

? Le rendement réel de conversion d'un module est faible.

Conclusion

Dans ce chapitre nous avons présenté des généralités sur la technologie photovoltaïque. Les technologies PV actuelles permet de transformer directement le rayonnement solaire en

Chapitre II : Gisement solaire et le générateur photovoltaïque

électricité avec un taux de conversion d'environ 15%. L'amélioration du rendement des systèmes photovoltaïques PV dépend du rayonnement absorbé par les panneaux solaire.

Afin que le rayonnement solaire soit perpendiculaire au panneau solaire, il est nécessaire de recourir à la technique de poursuite du soleil. Ainsi on se propose dans le chapitre suivant d'étudier la position du soleil et les systèmes de poursuite `'solar traker» pour maximiser l'énergie produite par les cellules PV.

Tracker Solaire Page 28

Tracker Solaire Page 29

Chapitre II : Gisement solaire et le générateur photovoltaïque

Chapitre III : Position du soleil &

les trackers solaires

1. Introduction

La puissance électrique produite par un panneau photovoltaïque dépend fortement de l'ensoleillement et à un degré moins important de la température des cellules. Ces deux variables influençant sur le comportement du système et présentent des fluctuations quotidiennes et saisonnières. Pour ces raisons, un dispositif de contrôle devra être intégré dans le circuit de commande. Ce dernier doit être capable de faire fonctionner le panneau photovoltaïque à sa puissance maximale. On peut distinguer 2 techniques de suivi ou "Tracking"[9]:

1- La méthode de MPPT (Maximum Power Point Tracking) est basée sur l'utilisation d'un algorithme de recherche du maximum de la courbe de puissance du panneau photovoltaïque.

2- Systèmes de poursuite solaire (sun tracking systems) qui permettent d'orienter les panneaux solaires tout au long de la journée pour mieux exploiter les cellules photovoltaïques. En effet, beaucoup de travaux centrent leur intérêt sur la poursuite du soleil afin de maximiser l'ensoleillement en gardant la surface active du module solaire perpendiculaire aux radiations solaires [10].

L'intérêt des panneaux mobiles par rapport aux panneaux fixes

Au cours de la journée, le soleil se déplace continuellement, alors qu'un générateur photovoltaïque est fixe dans sa position, perdant ainsi une considérable quantité d'énergie, qui pourrait être disponible.

Lorsqu'un panneau photovoltaïque est fixe par rapport au sol et orienté vers le sud (implantation en hémisphère nord), son rendement énergétique n'est pas constant au cours de la journée : en début et en fin de journée, le mauvais angle d'éclairement du panneau diminue le rendement de la production électrique.

Lorsqu'un système suiveur oriente le panneau solaire en le faisant pivoter en direction du soleil et en maintenant en permanence un angle d'incidence des rayons idéal, voisin de 9Ø°, la production électrique par m² de panneau atteint alors son maximum [11] (Figure III. 1).

Fig. III. 1 Un panneau photovoltaïque fixe (a) et avec système suiveur (b) [11].

Le diagramme comparatif de production électrique (Figure III. 2) montre pour une journée ensoleillée d'été, le gain de production électrique obtenu en passant d'une installation fixe à une installation équipée.

Tracker Solaire Page 30

Chapitre II : Gisement solaire et le générateur photovoltaïque

Au cours d'une journée complètement ensoleillée, un système fixe de 1 kW bien orienté, produit 5,5 kWh d'énergie, alors que le même système avec suiveur, dans les mêmes conditions d'ensoleillement, produit 11 kWh d'énergie.

Fig. III. 2 Diagramme de comparaison entre la production avec suiveur et la production avec système fixe [5].

Orientation et inclinaison d'une surface

3.1. Angle d'inclinaison du panneau

L'angle d'inclinaison (Figure III. 3) est l'angle entre le panneau et le plan horizontal, il vérifié

la condition suivant [5]: ??

3.2. L'angle d'incidence

L'angle d'incidence (Figure III. 3) est l'angle qui se trouve entre le rayon du soleil et

la normale de la surface du plan, il est donné par l'équation suivante [3]:

( ) (??) ( ) ( ) (??) ( ) E. 28

Avec :

i: L'angle d'incidence.

â: L'inclinaison du plan récepteur

h: La hauteur du soleil

á: l'azimut du plan récepteur

a: l'azimut solaire

: Angle de la projection horizontale d la normale au palan considéré avec N-S.

??: Angle de la normal au plan considéré avec le plan horizontal.

Fig. III. 3 Les angles de l'inclinaison, de projection et de l'incidence *5].

Le rendement en puissance solaire exploitée peut être calculé à l'aide de l'équation suivante :

Tracker Solaire Page 31

Chapitre II : Gisement solaire et le générateur photovoltaïque

( 9) *100 E. 29

La valeur de B qui donne le meilleur rendement c'est B =90 .

Les points positifs et négatifs des suiveurs

- Avantages

? + 40 % de production à surface de panneaux solaires égale

? Augmente le nombre de cas d'implantation quand les solutions classiques ne sont pas possibles

? Peut valoriser les espaces de terrains perdus

- Inconvénients

? Le principal inconvénient des traqueurs solaires est leur faible résistance aux vents. En effet, ceux-ci se replient lorsque le vent atteint des vitesses supérieures à 11.11-13.88 m/s.

? Nécessité d'un permis communal

? Encombrant. Demande un grand terrain

? Risque de panne du suiveur

Les types des suiveurs

La stratégie de commande d'un tracker consiste essentiellement à générer la trajectoire du tracker afin de poursuivre parfaitement le soleil dans le but de maximiser la production. En effet, l'asservissement des actionneurs des trackers est généralement considéré comme maitrisé et n'est par conséquent pas abordé.

Cette stratégie de commande peut avoir d'autres objectifs et d'autres contraintes comme la minimisation de l'énergie consommée, l'adaptation aux variations des conditions météorologiques.

Les traqueurs solaires peuvent être divisés en deux types principaux selon le type de la commande et de la sensibilisation ou du système de positionnement qu'ils incorporent [5] [12].

Mécanisme d'orientation (système de positionnement)

1- Les traqueurs passifs: en cas de mises en mouvement par des phénomènes physiques autonomes, emploient le rayonnement des soleils pour chauffer gaz qui déplace le traqueur à travers le ciel utilisé, ne nécessitant pas d'énergie électrique (Figure III.4).

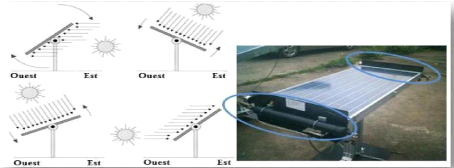
Fig. III. 4 Exemple et fonctionnement du suiveur passif [13].

Tracker Solaire Page 32

Chapitre II : Gisement solaire et le générateur photovoltaïque

2- Les traqueurs actifs: en cas de mise en mouvement par des éléments électromécaniques, emploient les commandes électriques ou hydrauliques pour déplacer le traqueur.

Type de commande

Beaucoup de travaux ont été menés sur les stratégies de commande des trackers solaires dans le cas des modules PV ou CPV. Trois grandes catégories de stratégies se dégagent, la troisième, hybride étant une combinaison des deux premières, dites stratégie en boucle ouverte et en boucle fermée [14].

Commande en boucle ouverte

La commande dite en boucle ouverte (Figure III.5) est une commande active de poursuite basée uniquement sur des calculs astronomiques de la position du soleil (calcul d'éphémérides), sans mesure de la position du soleil. En fait, elle permet de générer les consignes de la trajectoire de poursuite du tracker (dans notre cas l'angle d'azimut et l'élévation) à partir de l'heure et des coordonnées GPS d'une centrale. Comme toute commande en boucle ouverte, elle est très sensible aux perturbations (absence de feedback) et aux erreurs de modélisation.

Fig. III. 5 Commande en boucle ouverte d'un tracker PV *141.

Commande en boucle fermée

La commande en boucle fermée est une commande active qui se base sur une mesure de l'erreur de poursuite réelle pour contrôler les actionneurs du tracker. Cette mesure de l'erreur (Figure III.6) est fournie généralement par un capteur solaire, aussi appelé viseur solaire. Dans certains cas, le retour n'est pas une erreur de poursuite mais une puissance produite par le module.

En effet, cette stratégie consiste à orienter les trackers suivant la position du tracker le mieux orienté, en partant de n'importe quelle position (position aléatoire).

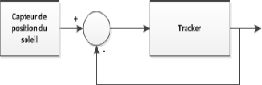
Fig. III. 6 Commande en boucle fermée d'un tracker *141.

Commande hybride

La commande hybride est une commande de poursuite qui combine le calcul de la position de référence proposée par la « boucle ouverte », et la donnée de retour proposée par la commande à boucle fermée.

Commande tenant compte de la consommation

Tracker Solaire Page 33

Chapitre II : Gisement solaire et le générateur photovoltaïque

Les stratégies de commandes présentées précédemment ont un seul objectif qui est la maximisation de l'ensoleillement, et donc de la production, sans tenir compte de l'état de fonctionnement des actionneurs ni de leur consommation d'énergie.

Le principe de la commande, comme illustré par la figure III. 7, est le suivant : le tracker reste en arrêt jusqu'à ce que l'écart entre la position (théorique) du soleil et la position du tracker atteigne un certain seuil de tolérance ("Initial tolérance"). A ce moment, le tracker rattrape la position du soleil et prend de l'avance ("Final tolérance").

Fig. III. 7 Génération de trajectoire discontinue [14].

Degrés de liberté de mouvement 5.3.1. Traqueurs Mono axiaux :

Suiveur Mono-axiaux disposent d'un seul degré de liberté et tournent autour d'un seul axe.Le plan de ce type de traqueur est incliné à un angle de latitude de lieu dirigé en plein sud et l'angle de suivi égal à l'angle horaire [5](Figure III. 8).

Fig. III. 8 Traqueur à un seul axe avec angle d'inclinaison de Latitude *5].

5.3.2. Traqueurs Bi axiaux :

Ils disposent de deux degrés de liberté grâce auxquels l'axe perpendiculaire aux panneaux photovoltaïques est aligné parfaitement et en temps réel avec les rayons du soleil, au détriment en revanche d'une plus grande complexité de construction [5].

1- Traqueur équatorial

Dans ce type de traqueur, le panneau est incliné par l'angle local (latitude), et l'angle de

suivi de cet axe tourne avec un angle égal à l'angle horaire (Figure III. 9).

L'angle de suivi du deuxième axe tourne avec un angle égal à l'angle de

. La variation horaire de l'angle de déclinaison est considérée très lente ; par conséquent l'orientation de ce dernier peut être ajustée une ou plusieurs fois par saison [5].

Tracker Solaire Page 34

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. III. 9 Traqueur à deux axes avec angle d'inclinaison de Latitude *5].

2- Traqueur azimut/élévation

L'idée consiste à la rotation de l'axe autour de zénith avec un angle de rotation égal à l'angle d'azimut, tandis que l'autre axe est parallèle à la surface de la Terre et tourne avec un angle de rotation égale à l'angle d'altitude (Figure III.10).

Les traqueurs d'altitude/azimut emploient des données ou des algorithmes astronomiques de position du soleil pour déterminer la position du soleil pendant n'importe quelles heures et endroits donnés. Le lieu, la date et le temps de traqueur sont saisis par un contrôleur pour fixer la position du soleil.

Fig. III. 10 Traqueur à deux axes Azimut/Élévation [5].

L'avantage principal de ce système est que la position du soleil peut être déterminée indépendamment de la couverture de nuage.

En outre, des variations saisonnières de la position du soleil sont prises en considération.

Description du suiveur solaire :

Le système de poursuite se compose essentiellement de deux parties (Figure III. 11) :

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. III. 11 Description de suiveur solaire [12].

La partie commande ou programmation

Cette partie apte à traiter les informations de position du soleil et les transmettent aux actionneurs pour effectuer la poursuite du soleil, détecter les anomalies de fonctionnement et effectuer les opérations de mise en sécurité de l'équipement [12].

Il assure, aussi, d'autres fonctions, dont :

? Le contrôle des mouvements mécaniques du système en limitant les angles de rotation à

partir des fins de courses (0° à 200° sur l'horizontal et 0° à 90° sur la verticale) ;

? L'orientation du panneau en fin de journée vers la position de départ ou de démarrage du système.

La partie opérative ou électronique

Cette partie repose sur des systèmes qui permettent la réception des ordres envoyés par le calculateur, leur conversion en signaux électriques et leur transmission au système mécanique articulé, ainsi que l'activation du monteur (vérin). Cette opération assure que le rayonnement solaire soit toujours perpendiculaire au panneau.

Angle d'incidence sur un plan incliné(i)

L'expression de l'angle incidence est [14] : cos = ?

On trouve :

cos = sin sin cos ?? sin cos .sin ?? cos + cos cos cos ?? cos + cos sin

cos ?? cos + cos sin sin E. 30

Cas particuliers :

? Capteur orienté plein sud ( = 0) :

cos = sin sin( ??) + cos cos cos( ??)
? Pour un captage annuel de type (?? = )

cos = cos .cos

? Pour une incidence parfaite (cas d'un système de poursuite du soleil) = 0.

Conclusion

Le système de poursuite solaire consiste à contrôler le mouvement de rotation du panneau et le commander par un programme informatique pour mettre la normale du collecteur face au soleil pendant toute la journée.

L'importance de ce système est de capter le rayonnement solaire parallèle venant directement du disque solaire (rayonnement direct). Donc nous obtenons une nette amélioration du niveau de l'éclairement solaire et un meilleur rendement du système tout au long de l'année en utilisant ce système.

Tracker Solaire Page 35

Tracker Solaire Page 36

Chapitre II : Gisement solaire et le générateur photovoltaïque

Chapitre IV: Modélisation des

trackers

1. Introduction

La modélisation d'un tracker diffère selon l'objectif d'utilisation. Il existe des modèles de prédiction de la production d'un tracker et d'une centrale PV sur trackers. Ces modèles utilisent une régression linéaire et une estimation de l'ensoleillement ainsi que l'historique des données météorologiques (ensoleillement direct, ensoleillement global...).

On obtient aussi un modèle basé sur la réponse spectrale de la cellule multi-jonctions III-V. Ces modèles, destinés plutôt à des centrales CPV, permettent de prédire la production sur un mois ou sur une année en fonction des modules utilisés et du lieu de la centrale [13]. Par contre ces modèles ne sont pas dédiés à tester, ni à simuler et valider les commandes ou les stratégies de commande des trackers, car ils se basent sur un suivi parfait du soleil. Ce manque de travaux concernant la modélisation physique comportementale des trackers a redirigé nos recherches vers des modèles de trackers PV classiques. Malgré les différences de comportement et de caractéristiques, ces modèles de trackers PV peuvent présenter une base pour le développement d'un modèle de tracker.

Dans l'optique de caractérisation du comportement dynamique des trackers en prenant en considération la performance du suivi (de la commande), en effet ce modeste travail propose un modèle géométrique et dynamique 3D de la structure mécanique et la motorisation d'un tracker PV en tenant compte de sa commande de trajectoire. Le modèle de conception du tracker contenant la structure mécanique rigide et l'actionneur (moteur) a été rédigé sous le logiciel «SolidWorks». Le modèle dynamique du tracker est développé sous Matlab/Simulink. La commande adoptée dans ce travail est une commande en boucle ouverte, basée sur un calcul astronomique pour déterminer la position de référence pour l'asservissement de position du moteur (Figure IV. 1).

Fig. IV. 1 Modélisation d'un tracker PV et de son command.

2. Modèle mécanique

Le système mécanique comporte également deux organes, le premier organe est une partie fixe et le deuxième qui est mobile, les deux parties sont reliées par un mécanisme de rotation (roulements).

Nous avons mis deux roulements l'un pour faire orienter la partie mobile dont elle supporte le panneau horizontalement (azimutal), est le deuxième est dédié au déplacement

Tracker Solaire Page 37

Chapitre II : Gisement solaire et le générateur photovoltaïque

vertical (élévation). Nous avons ainsi associé à chaque déplacement (horizontal/vertical) un moteur asynchrone muni d'un vérin à déplacement linéaire pour l'axe d'élévation.

2.1. Représentation du logiciel utilisé

La conception assistée par ordinateur CAO est devenue un outil technologique puissant dans l'ingénierie moderne complexe et multidisciplinaire.

Le travail présenté a pour objectif de la conception et la modélisation géométrique détaillée à l'échelle réelle (l'esquisse de tous les composants, l'assemblage, la vérification et la simulation d'animation) de structure du TS-2. Cette conception a été réalisée par le logiciel de C.A.O SOLIDWORKS.

2.1.1. Définition de la CAO

Nous pouvons définir la CAO par l'ensemble des outils logiciels et des techniques informatiques qui permettent d'assister les concepteurs dans la conception et la mise au point d'un produit. Un logiciel de CAO se compose généralement de quatre parties majeures qui peuvent être organisées comme suit [15] (Figure IV. 2) :

? Le modeleur géométrique: il représente "la planche à dessin". Nous trouvons dans cette partie les composants géométriques essentiels : points, droites, cercles, ellipses, plans, sphères, cylindres, cônes, courbes de Bézier ou B-Splines, surfaces NURBS, surfaces de révolution, surfaces de balayage, etc. Il intègre également les composants topologiques : sommets, faces, arêtes, orientations, coïncidences, adjacences, intersections, soustractions, unions, etc.

? L'outil de visualisation.

? Un certain nombre d'applications: nous retrouvons le calcul des grandeurs géométriques (distances, inerties, volumes, masses, etc.), les fonctions métiers, assemblage de pièces, production de plans, simulation d'usinage, moulage, fraisage, etc.

? Un contrôleur: il gère et manipule les intersections entre les trois outils cités précédemment.

Fig. IV. 2 Le diagramme représentant les cinq générations de systèmes de CAO [15]. 2.1.2. Outil CAO utilisé dans notre projet

Dans ce travail nous avons choisi le logiciel CAO-SOLIDWORKS pour développer la conception et la modélisation géométrique du tracker.

Tracker Solaire Page 38

Chapitre II : Gisement solaire et le générateur photovoltaïque

SOLIDWORKS est un logiciel 3D Mécanique Conception Assistée par Ordinateur (MCAO) développé par SOLIDWORKS Corporation des États-Unis. SOLIDWORKS Corporation a été fondé en décembre 1993 par Jon Hirschtick. En juillet 1997, DASSAULT SYSTEM rachète la société qui est détentrice de la licence du produit et l'intègre dans l'univers DASSAULT. SOLIDWORKS est un logiciel commercial largement utilisé dans la modélisation et dans la conception des systèmes mécaniques assistée par ordinateur [15].

2.2. Conception et Modélisation géométrique du système 2.2.1. Description générale des systèmes

La structure représentée sur la figure IV.3 possède deux degrés de liberté, la rotation horizontale permet de suivre le mouvement du soleil tout au long de la journée. Le déplacement vertical permet d'orienter la structure selon la déclinaison saisonnière du soleil, pour permettre une exposition maximale des modules PV au rayonnement solaire.

Fig. IV. 3 Le modèle mécanique réalisé sous SolidWorks.

2.2.2. Système de poursuite

Les deux mouvements pour les deux systèmes de suiveur sont assurés par deux dispositifs mécaniques de réduction découplés.

Le premier mécanisme est un motoréducteur pour l'entraînement en azimut (vertical), comportant, pour le mouvement d'élévation est assuré par un vérin mécanique d'actionnement électrique. Comme illustré sur la figure IV. 4.

Tracker Solaire Page 39

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. IV. 4 Description des différents éléments du tracker.

3. Modèle dynamique

Cette partie a pour objectif de tester le modèle dynamique adaptée au tracker, essentiellement en termes de performance de suivi qui résulte de la stratégie de commande adoptée.

Une étude de l'évolution de la puissance électrique consommée par les actionneurs du tracker doit être menée en parallèle. La figure IV. 5 présente un schéma descriptif de l'objectif du simulateur. Il s'articule autour du modèle du tracker à deux axes (azimut et élévation) contenant les sous modèles suivants :

? Un modèle du soleil, basé sur un calcul astronomique, capable de calculer les positions

d'azimut et d'élévation (hauteur) (A, h) théoriques, que le tracker doit viser, en fonction de l'heure et de la date. Dans le contexte de cette étude, le résultat de ce calcul est également utilisé comme position réelle du soleil pour servir d'entrée au modèle des modules PV ((A, h) soleil = (A, h) théorique).

? Un bloc de stratégie de commande du tracker qui sert à calculer la position de référence du tracker servant de consigne aux deux actionneurs.

? Un modèle dynamique de moto-variateur (les actionneurs) asservi en position pour les axes d'élévation et d'azimut.

? Un modèle mécanique du tracker est implémenté afin de calculer la position réelle du tracker en tenant compte des réducteurs de vitesses utilisés, des inerties du tracker et des frottements estimés.

? Un modèle du capteur.

Tracker Solaire Page 40

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. IV. 5 Schéma synoptique du modèle de tracker proposé.

Grâce à ses différents sous-modèles, ce simulateur permet l'étude de l'influence de la performance du suivi du soleil sur la production des modules PV.

3.1. Modèle du soleil

Le modèle du soleil proposé est un modèle de génération de données. En effet, il est capable d'estimer l'ensoleillement global et direct. Il permet aussi de calculer les données de position théorique du soleil à viser par le tracker. Les positions théoriques en élévation et azimut ((As, hs) théoriques), à viser par le tracker, sont générées à partir d'un calcul astronomique en fonction de l'heure, de la date et des coordonnées géographiques du tracker (coordonnées GPS : (longitude et latitude). Les algorithmes de calcul astronomique sont issus de la référence [16].

a) Calcul des vecteurs de position solaire (altitude/azimut)

Le schéma de la figure IV.6 illustre les variations horaires du vecteur de la position solaire (Altitude/azimute) pendant une journée d'été pour la ville de Ben Guerir (Figure IV. 6). Nous voyons que la hauteur (altitude) du soleil à midi atteint 77°.

Fig. IV. 6Angle d'Azimute et l'altitude en fonction du temps.

Les variations de la trajectoire

du soleil en vue du sens horizontal

(azimutale) sont considérées presque identiques pendant les différentes périodes de l'année. Elles sont d'une forme ligne droite.

b) Le rayonnement reçu sur la surface d'un panneau incline

La figure IV.7 montre que le rayonnement reçu sur un panneau est important cela veut dire que les rayons de la lumière sont perpendiculaires à sa surface.

Tracker Solaire Page 41

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. IV. 7 Le rayonnement reçu sur la surface d'un panneau incline. c) Méthode d'évaluation du modèle

Les résultats de l'algorithme de calcul de la position théorique du soleil ont été validés par comparaison avec les données mesurées par la station de Green Energy Park (Annexe 1).

Calcul statistique

Plusieurs indicateurs statistiques utilisés dans la littérature vont nous permettre de

confronter les données obtenues par le modèle développé et les données mesurées.

Les indicateurs utilisés sont :

RMSE, Racine carrée de l'erreur quadratique moyenne.

v? ( ) E. 31

Avec n Nombre d'heures, c'est l'élévation calculé et l'élévation mesuré.

La RMSE est une mesure de la variation des valeurs calculées autour des valeurs mesurées, plus sa valeur est petite et plus le modèle est meilleur.

MBE : Erreur de biais moyen.

La MBE donne une indication sur la déviation moyenne des valeurs calculées par rapport aux valeurs mesurées. Une valeur positive indique une sur estimation par contre une valeur négative indique une sous-estimation.

( )

? E. 32

R² : Coefficient de détermination.

? ( ) ( )

E. 33

v? ( ) ? ( )

Avec hcmean: élévation moyenne journalière calculée et hmmean est élévation moyenne journalière mesurée.

L'indicateur R² varie entre 0 et 1. Une valeur de 1 ou proche de 1 indique un parfait accord entre la valeur mesurée et calculée. Par contre, une valeur proche de 0 indique un total désaccord.

Les indicateurs statistiques RMSE, MBE, R2 sont résumés dans le tableau suivant.

Chapitre II : Gisement solaire et le générateur photovoltaïque

	Tableau 2 : les indicateurs statistiques
RMSE	17.3940
MBE	27.9243
ind_R2	0.33407

D'après ces calcules le RMSE calculée donne un écart minimum donc les deux modèles sont proche. Le MBE donne une valeur positive c.-à-d on a une sur estimation des valeurs mesurées enfin la valeur du coefficient de détermination indique un accord entre les valeurs mesurées et calculées.

Résultats de simulation

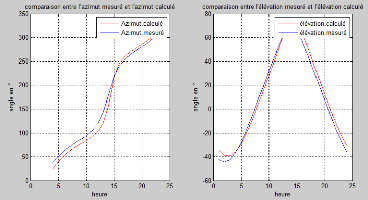
Fig. IV. 8 Comparaison entre l'Altitude/Azimut calculé et mesuré.

Nous constatons d'après la figure IV.8 que les angles de l'Altitude/Azimut du soleil calculés avec notre programme sont très rapprochés de ceux donnés par la base des données ce qui signifie la validité du programme élaboré.

3.2. Modèle dynamique des actionneurs

Le système intégré complet inclut généralement les éléments et composants suivants :

? Moteurs électriques : moteurs électriques à courant continu ou à courant alternatif pour conduire les entraînements mécaniques, par le biais du courant, de la fréquence ou du contrôle de la vitesse.

? Sous-système d'entraînement mécanique transmission / actionneur : les actionneurs linéaires, les engrenages à vis sans fin, les entraînements linéaires, les entraînements dynamiques et les entraînements à engrenages planétaires font partie du système de positionnement pour déplacer le réflecteur face au soleil.

3.2.1. Analyse des éléments

Comme tous les systèmes automatisés, le tracker nécessite des systèmes de motorisation offrant couple et vitesse pilotable pour suivre le soleil. Afin de trouver un système de motorisation adapté au tracker, une analyse des éléments relatifs impactant ce système a été réalisé.

Tracker Solaire Page 42

Chapitre II : Gisement solaire et le générateur photovoltaïque

Le tableau 2 permet de visualiser très rapidement l'ensemble des moteurs électriques disponibles, leurs principales caractéristiques et leurs domaines d'emploi. Il faut souligner la place tenue par les moteurs asynchrones à cage triphasée dont le qualificatif de « standard » est de nos jours renforcé par une parfaite adaptation à l'emploi consécutive au développement des dispositifs électroniques qui autorisent la variation de vitesse.

Tableau 3: Matrice de choix du moteur nature de la motorisation.

	Asynchrone à cage Triphasé Monophasé			Asynchrone à bague	Synchrone À rotor bobiné	Rotor terres rares	Pas à pas	A courant continu
TYPE DE MOTEUR
Cout du moteur	Faible		Faible	Elevé	Elevé	Elevé	Faible	Elevé
Moteur étanche	Standard		Possible	Sur demande, coûteux	Sur demande, coûteux	Standard	Standard	Possible Très couteux
Démarrage direct de sur le réseau	Aisé		Aisé	Dispositif de démarrage particulier	Impossible à partir de quelques KW.	Non prévu	Non prévu	Non prévu
Variation de vitesse	Facile		Très rare	Possible	Fréquent	Toujours	Toujours	Toujours
Coût de la	De plus	en	Très	Economique	Très	Assez	Très	Très
solution variation de vitesse	plus économique		économique		économique	économique	économique	économique
Performance en variation de vitesse	De plus plus élevée	en	Très faible	Moyenne	Elevée	Très élevée	Moyenne à élevée	Elevée à très élevée
Emploi	Vitesse constante variable	ou	En majorité, vitesse constante	Vitesse constante ou variable	Vitesse constante ou variable	Vitesse variable	Vitesse variable	Vitesse variable
Utilisation	Universelle		Pour les	En	Dans les	Machine	Positionnem	En
industrielle			petites puissances	diminution	grandes puissances en moyenne tension	outils, forte dynamique	ent en boucle ouvert, pour les petites	diminution

puissances

Tout d'abord, tous ces moteurs peuvent offrir une puissance assez importante, supérieure à 1,2 kW. Comme nous voulons diminuer le coût de maintenance sur 20 ans, les machines à courant continu ne conviennent pas vraiment à l'utilisation de dans un désert. Il faut également que l'entreprise achète plusieurs moteurs il y a beaucoup d'argent à investir. Le coût est donc un facteur déterminant dans le choix du moteur. D'après ces caractéristiques, les machines asynchrones conviendront le mieux à l'application.

3.2.2. Vitesse de rotation du panneau La vitesse de rotation du panneau se calcule par la relation [1] :

L'angle d~azimut maximal (°)

ladureé dujour (h)

Nous avons besoin du nombre d'heures à partir du lever du soleil jusqu'à son coucher. Ce

nombre est égal à 14 heures en été et à 9 heures en hiver. Ainsi, nous avons pris la moyenne qui est égale à 12h.

oJ (°/ ) = °= oJ( /s) = * =7.27* - oJ(tr/min) = 60*360 = 0.000694 E. 34

(tr/min)

(tr/min) E. 35

Rapport de réducti on = 2161383.2853

On obtient un rapport d'engrenage anormalement élevé, parce qu'en règle générale, un

système de transmission de vitesse plus pratique et réaliste pour le suivi solaire utilise un système de transmission avec un rapport de réduction compris entre [18] 10 000 : 1 et 30 000 : 1.

Tracker Solaire Page 43

Chapitre II : Gisement solaire et le générateur photovoltaïque

Le mouvement de rotation du pisteur solaire est normalement plus rapide que la vitesse de rotation du soleil (0,000694 tr / min). C'est la raison pour laquelle on utilise des systèmes de contrôle de suivi solaire de type on / off pour synchroniser le mouvement de rotation angulaire des actionneurs avec le mouvement du soleil (contrôle de suivi solaire décrit dans le paragraphe 3.4).

D'après une étude faite par (Gerro Prinsloo, Robert Dobson) [18] un réducteur roue vis sans fin a été choisi avec une couronne pour assurer le bon rapport de réduction (Figure IV. 9).

Fig. IV. 9 Réducteur de roue et vis [18].

L'absence de freins s'explique parce que la vis peut entrainer la roue mais le roue ne peut pas entrainer la vis, ce qui est le plus grand avantage d'un réducteur de roue et vis sans fin [19].

3.2.3. Le vent

De toutes les charges auxquelles les trackers solaires sont exposés, le changement du vent est le plus important. Il provoque les plus grandes forces de charge qui varient dans toutes les directions et peuvent causer des dommages mécaniques ainsi qu'ils déstabilisent le panneau solaire, ce qui réduit sa capacité à capter la lumière du soleil efficacement.

Grâce à l'équipement de la station météorologique de Green Energy Park (comme l'indicateur de pluie, le capteur de pression / humidité et l'anémomètre - voir Annexe 1), un énorme ensemble de données a été collecté et transformé en une rose de vent dans la figure IV. 10 à l'aide d'un code Matlab.

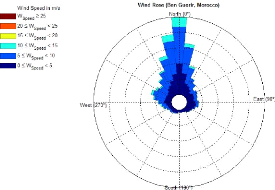
Tracker Solaire Page 44

Fig. IV. 10 La rose de vent de Ben Guerir.

Il semble que le vent le plus décontracté provient du nord avec beaucoup moins d'intensité dans la partie nord-ouest de la région. Cependant, il a également été prouvé que la

Tracker Solaire Page 45

Chapitre II : Gisement solaire et le générateur photovoltaïque

plus haute vitesse du vent, même si elle est extrêmement rare, provient du Sud et atteint en Mars 2015 à Mars2016 un maximum de 23.6 m/s.

3.2.4. Modèle de Capteur

? Dispositifs de sous-système de détection de mouvement : encodeurs d'arbres linéaires ou rotatifs, capteurs d'inclinaison, inclinomètres, photodiodes, résistances photosensibles pour surveiller la position actuelle du plat pendant qu'il se déplace jusqu'à la position désirée [18].

? Interrupteurs de fin de course : Dispositifs pour empêcher un mouvement mécanique au-delà des limites prédéfinies afin d'éviter les dommages au tracker ou au câble [18].

? Dispositifs de détection ambiante environnementaux ou atmosphériques : détection de l'intensité lumineuse, solormètre, pyranomètre, capteur d'anémomètre / vent, capteur de température ambiante, capteur d'humidité et capteurs de pression atmosphérique pour détecter tout risque environnemental ou menaçant pour l'environnement.

a) Connaître la position des modules

? La matrice (tableau 3) de choix pour la position des modules (suivant l'élévation):

Tableau 4 : La comparaison entre les différents capteurs de position [19].

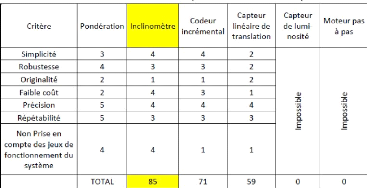
Les critères de répétabilité et de précision sont très importants. En effet, on veut que notre capteur soit précis et que la mesure soit repérable (c'est-à-dire que l'on obtient toujours la même valeur).

La solution retenue pour l'élévation est un inclinomètre. Ce capteur est très avantageux, car il permet de mesurer directement l'élévation du panneau ce qui permet d'atteindre de hautes précisions et de s'affranchir des défauts de montage contrairement à une mesure indirecte qui doit prendre en compte les jeux de fonctionnements (Figure IV. 11).

Fig. IV. 11 Élévation mesurée avec notre inclinomètre [19]. ? Matrice de choix pour l'azimut

Chapitre II : Gisement solaire et le générateur photovoltaïque

Inutile de faire une matrice de choix pour la solution. Pour connaître l'angle de l'azimut de notre tracker, nous utiliserons un codeur incrémental. C'est le seul capteur qui répond aux critères [19].

3.3. Modélisation du moteur asynchrone

La machine asynchrone est composée de deux parties séparées par un entrefer. Le stator ou l'inducteur : c'est la partie fixe de la machine asynchrone comportant un enroulement triphasé couplé en étoile ou en triangle. Le rotor ou l'induit : c'est la partie tournante de la machine asynchrone. Ils sont (les rotors) constitués d'un bobinage similaire à celui du stator fermé sur un rhéostat extérieur via des bagues et des balais ; ou ils sont de type à cage constitué de barres conductrices en court-circuit. Ces derniers sont plus robustes et moins onéreux [20] (Figure IV. 12).

Fig. IV. 12 Moteur asynchrone [20].

3.3.1. Modèle dynamique de la machine asynchrone

Un modèle dynamique basé sur des hypothèses simplificatrices a été adopté, afin de modéliser la machine asynchrone contrôlée en boucle ouverte par un variateur de vitesse. Ce modèle prend en compte la conversion électromécanique et les pertes de la machine. Cette modélisation dynamique est adoptée afin de modéliser correctement les régimes transitoires du système. Concernant la commande, un contrôle scalaire est choisi pour se rapprocher au plus du système.

Il existe plusieurs modèles de la machine asynchrone triphasée dans la littérature. Ils sont basés sur les équations générales décrivant le fonctionnement de la machine, supposée en régime linéaire (machine non saturée), dans un référentiel de Park d-q qui est obtenu par la transformation du Park pour passer d'un modèle sur 3 axes fixes à 2 axes tournants notés d et q.

Le modèle proposé par (Caron.J-P, 1995) [13] a été choisi pour le développement du simulateur, car il est facile à manipuler et possède un nombre raisonnable de paramètres à identifier. En effet, ce modèle est caractérisé par 4 paramètres électriques :

? La constante de temps rotorique Tr.

? Le coefficient de dispersion a.

? La résistance propre d'une phase statorique Rs.

? L'inductance cyclique statorique Ls.

Le modèle électrique de la machine est donné par l'équation suivante :

E. 36

Tracker Solaire Page 46

? Remarque : L'opérateur ( ) est employé comme notation de la dérivation appliquée aux

courants statoriques et rotoriques. Cette notation est reprise de (Caron.J-P, 1995).Diverses formes du calcul du couple électromagnétique sont proposées dans (Caron.J-P, 1995). L'expression du couple de ce modèle est représentée comme suit [13]:

P I D

Chapitre II : Gisement solaire et le générateur photovoltaïque

( )( ) E. 37

Les coefficients p, Lr, M, isq et isd sont respectivement le nombre de paires de pôles, l'inductance cyclique rotorique, l'inductance mutuelle cyclique entre rotor et stator et les courants statoriques dans le repère de Park. Les flux rotoriques dans le repère de Park sont calculés à partir des équations [13]:

( ) E. 38

( ) E. 39

La figure IV.13 présente les entrées et les sorties du modèle dynamique de la machine asynchrone triphasée. En effet, le modèle permet de calculer le couple électromagnétique en fonction des tensions statoriques dans le repère de Park, Vsd et Vsq, et des pulsations statorique et rotorique ws et wr.

Fig. IV. 13 Modèle électromécanique asservi du tracker.

La modélisation de la machine asynchrone triphasée présentée ci-dessus est précédée d'une modélisation du variateur de vitesse et des transformations du repère triphasé au repère diphasé puis au repère de Park. Ce modèle du variateur de vitesse assure une commande scalaire pour la machine asynchrone. Pour le système étudié (tracker de référence), la vitesse de la machine asynchrone n'est pas asservie, mais simplement contrôlée "en boucle ouverte".

La fréquence de consigne en entrée du modèle provient d'un régulateur à actions proportionnelles, intégrale et dérivée (PID). Les tensions Vsd et Vsq ainsi que la pulsation statorique d'alimentation sont obtenues après application de la transformation de Park. La fonction de transfert, dans le domaine de Laplace, du régulateur PID, assurant l'asservissement de position, est représentée par l'équation [13]:

( ) ( ) E. 40

Le réglage de ces paramètres a été effectué par la méthode empirique de Ziegler et Nichols ne nécessitant pas une connaissance parfaite du modèle du procédé à commander. En effet, cette technique de réglage du régulateur a été retenue de manière à obtenir des performances équivalentes à celles du système pris pour référence.

Les paramètres du PID (tableau 4) influencent le comportement du système de la manière suivante si l'on augmente séparément l'action proportionnelle (P), intégrale (I) ou dérivée (D)

[21].

Tableau 5 : Récapitulation de l'influence d'un PID série sur le système.

Précision Stabilité Rapidité

Tracker Solaire Page 47

Tracker Solaire Page 48

Chapitre II : Gisement solaire et le générateur photovoltaïque

3.3.2. Modèle mécanique du tracker

L'objectif de la modélisation de la partie mécanique est de calculer les positions angulaires en azimut et en élévation (A, h) du tracker en fonction du couple des moteurs, des différents étages de réduction de vitesse ainsi que des inerties et des frottements du tracker. Pour cette première modélisation, nous considérons que l'ensemble de la chaine de transformation de mouvement est indéformable [13].

Le principe fondamental de la dynamique donne [13] :

[ ] ( ) E. 41

En appliquant le principe fondamental de la dynamique :

? ?? ( ) E. 42

On obtient la relation suivante :

( )

E. 43

Les coefficients feq, Jeq et C_r sont respectivement le coefficient de frottement équivalent du système mécanique, l'inertie équivalente de l'axe considéré ramenée à l'arbre du moteur et le couple résistant. L'expression de la vitesse mécanique du tracker est la solution de l'équation fondamentale de la dynamique après passage au domaine de Laplace :

( ) ( )

( ) E. 44

Avec

Le coefficient _mecest la constante de temps mécanique.

La position est calculée en intégrant la vitesse mécanique et en prenant en considération les étages de réduction.

Le calcul de la vitesse mécanique du moteur basé sur l'équation est précédé par une estimation de l'inertie équivalente ramenée au moteur, des coefficients de frottement et d'un calcul du couple résistant.

L'expression de l'inertie équivalente ramenée au moteur est déterminée à partir de l'expression de l'énergie cinétique :

E. 45

Le coefficient de frottement équivalent ramené au moteur est déterminé à partir de l'équation :

E. 46

3.3.3. Calcul de l'inertie du tracker azimut et élévation

a) L'axe d'élévation

Chapitre II : Gisement solaire et le générateur photovoltaïque

Pour l'axe d'élévation, les paramètres concernés pour calculer l'inertie sont montré par la figure IV.14.

Dimensions du plateau Longueur= 4 m Hauteur= 2 m Epaisseur= 0.25 m Poids total = 480 kg

Tracker Solaire Page 49

Fig. IV. 14 Inertie du panneau (Elévation).

b) Calcul d'inertie

On calcule l'inertie de l'axe d'élévation par la relation suivante [19] :

? ? ( )

E. 47

c) L'axe d'azimut

La figure IV. 15montre les parties concernées pour calculer l'inertie.

Fig. IV.15 Inertie du panneau (azimut).

d) Calcul d'inertie

? ? ( )

E. 48

3.3.4. Relation entre la position angulaire et la course du vérin

Fig. IV.16 Schéma des paramètres de calcul.

Chapitre II : Gisement solaire et le générateur photovoltaïque

Calcul de la course du vérin [19] :

X = XO -- ( h * cos (elévation) + C² -- ( e + h * sin(elévation)²)) E. 49

X0 : Position du vérin par rapport à l'état initial.

X = + ²+e²

0

X : sortie du vérin par rapport à sa position initiale.

3.3.5. Estimation du couple résistant

Le couple résistant est supposé nul pour le mouvement en azimut (Cr Azimut =0), car ce mouvement n'est pas influencé par la gravité et en adoptant l'hypothèse qu'il n'y a pas d'efforts externes (perturbation). Pour le mouvement en élévation, le couple résistant évolue avec l'angle d'élévation du tracker. L'expression du couple résistant est donc écrite sous la forme suivante [13]:

(elévation) * d E. 50

Avec mplateau+modules, g et d sont respectivement la masse du plateau et des modules, l'intensité de la pesanteur (9,81 m/s²) et la distance entre le centre de gravité et le centre de la rotation.

3.3.6. Modélisation et simulation du modèle dynamique

Il s'agit dans ce volet de faire la simulation du modèle dynamique d'un moteur asynchrone, ainsi on est amené à élaborer l'ensemble des équations qui caractérisent ce modèle et l'implanter sur MATLAB et plus précisément sous son module de simulation SIMULINK (Figure. IV. 17).

L'interface principale du simulateur ainsi que les différents blocs principaux développés sont présentés ci-après.

a) Diagramme fonctionnel du MAS

Tracker Solaire Page 50

Tracker Solaire Page 51

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. IV.17 Modéle Interne du MAS.

La machine asynchrone présente des entrées :

? w_s (1), _Vds ^(2), _Vqs (3) : composantes de PARK et pulsation de la tension d'alimentation.

? Le couple résistant Cr (4), caractéristique de la charge.

Les sorties suivantes sont accessibles : Ids ^(3), _Iqs (4) composantes de PARK du courant moteur, C_e (6) : couple moteur (C_e) et w (7) vitesse de rotation.

b) Démarrage direct du moteur

Il faut encore réaliser la transformée de PARK du réseau d'alimentation pour l'appliquer au schéma fonctionnel du moteur et calculer l'angle 8_ypar intégration deco_y.

La transformation de PARK inverse permet de revenir aux grandeurs réelles de la machine (courant I dans notre cas). C'est ce qui est présenté dans le schéma suivant (figure IV. 18) :

Fig. IV. 18 Modèle en bloc Simulink de la MAS alimentée en tension.

Chapitre II : Gisement solaire et le générateur photovoltaïque

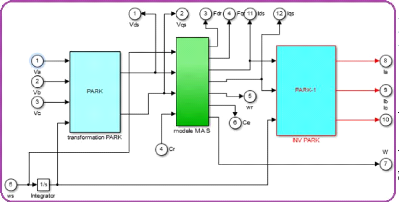
Fig. IV. 19 Le schéma interne de MAS modèle dq.

Le bloc MAS correspond à la modélisation faite plus haut. Sources sinusoïdales triphasées est une source triphasée équilibrée de tension de valeur efficace 230 V et de fréquence 50 Hz. PARK permet de calculer les composantes de PARK du réseau de tension et PARK-1 permet de reconstituer les courants absorbés par le moteur à partir de ses composantes de PARK. L'intégrateur permet d'obtenir sà partir de l'intégration de wS.

c) Résultats de la modélisation

La simulation du modèle présenté dans la figure IV. 18 donne des réponses en boucle ouverte de la machine asynchrone à vide comme la figure IV. 20 suivante:

Tracker Solaire Page 52

Tracker Solaire Page 53

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. IV. 20 Les Résultats de la simulation du démarrage à vide du moteur asynchrone.

L'oscillogramme de la figure IV. 20 représente l'évolution du courant, de la vitesse et du couple au démarrage d'un moteur asynchrone à vide. On note un appel d'un fort courant à la mise sous tension ; la valeur instantanée de ce courant peut atteindre trois fois le courant nominal pour le cas étudié. Des oscillations de couple apparaissent et peuvent atteindre trois fois le couple nominal, après disparition du régime transitoire, le couple tend vers zéro puisque le couple résistant et nul.

? Remarque : Le démarrage à vide et sous tension nominale permet un

établissement rapide de la vitesse et un couple électromagnétique instantané. L'application d'une charge introduit une chute de vitesse.

Lorsque la charge est appliquée, le couple électromagnétique répond instantanément et la vitesse est légèrement perturbée. La commande en courant donne une réponse à fort dépassement pour le couple électromagnétique par conséquent il est déconseillé de l'utiliser dans un système à boucle ouverte pour des raisons de stabilité.

3.4. Commande scalaire

Cette technique est facile d'implantation, moins coûteuse donnant aussi des performances statiques acceptables plusieurs commandes scalaires existent selon que l'on agit sur le courant ou sur la tension. Elles dépendent surtout de la topologie de l'actionneur utilisé (onduleur de tension ou de courant) et pour notre cas on a utilisé l'onduleur de tension alimentant la machine asynchrone commandée par une commande scalaire (V/f)=cst (Figure IV. 21).

Chapitre II : Gisement solaire et le générateur photovoltaïque

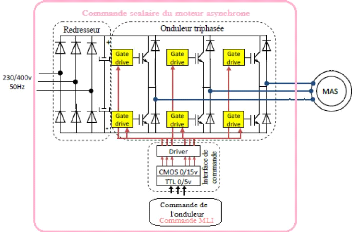
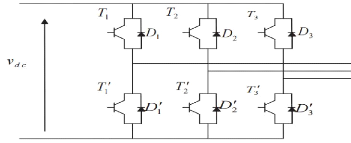
Tracker Solaire Page 54

Fig. IV. 21 Commande scalaire du moteur asynchrone [22]. 3.4.1. Contrôle en V/f de la machine asynchrone

Son principe est de maintenir V/f = Constant ce qui signifie garder le flux constant. Le contrôle du couple se fait par l'action sur le glissement. En effet, d'après le modèle établi en régime permanent, le couple maximum s'écrit :

( ) E. 51

On voit bien que le couple est directement proportionnel au carré du rapport de la tension sur la fréquence statorique [23].

3.4.2. Modélisation de l'onduleur triphasé

La figure IV. 22 présente le schéma d'un onduleur triphasé alimentant le MAS [24].

Fig. IV. 22 Le schéma d'un onduleur triphasé alimentant le MAS.

L'onduleur de tension triphasé se compose de trois bras identiques. Chaque bras composé de deux cellules comportant chacune une diode et un transistor. Tous ces éléments sont considérés comme des interrupteurs parfaits [24]. Alors l'onduleur de tension peut être représenté dans le cas idéal sous la forme suivante dans la figure IV.24.

Chapitre II : Gisement solaire et le générateur photovoltaïque

Tracker Solaire Page 55

Fig. IV. 23 Schéma équivalent de l'onduleur.

L'onduleur est modélisé en associant à chaque bras une fonction logique F qui détermine son état de conduction [24] :

{

1 si Icifermé et Ici^' ouvert Avec i=1, 2, 3.
0 si Ici^'fermé et Ici ouvert L'expression sous forme matricielle des tensions simples de l'onduleur au

moyen des fonctions logiques de connexions est obtenue à partir des équations :

(Vas(2 --1 --1 F1

Vbs = ^v3^c--1 2 --1 F2 E. 52

Vcs --1 --1 2 F3

Vdc: C'est la tension d'alimentation continue de l'onduleur.

Le modèle (E.52) peut être représenté sous Simulink par le schéma suivant figure IV. 24 :

Fig. IV. 24 Modèle de l'onduleur triphasé.

La figure VI. 25 suivante illustre la forme des tensions obtenus à la sortie de l'onduleur.

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. IV. 25 La sortie d'onduleur triphasé.

3.4.3. Les Techniques de commande de l'onduleur triphasé On distingue les trois types de commandes :

? Commande 180° chaque transistor est commandé pendant 180°. Les commandes de deux transistors d'un même bras sont décalées de 120° par rapport aux transistors du bras voisin.

? Commande 120° elle est identique à celle d'un pont triphasé à thyristors. Chaque transistor conduit pendant le 120°, ce qui correspond à une zone vide de 60° entre la commande de deux transistors d'un même bras.

? Commande MLI, la modulation de largeur d'impulsions (MLI), est une technique couramment utilisée pour synthétiser des signaux continus à l'aide de circuits à fonctionnement tout ou rien, ou plus généralement à états discrets.

Dans notre projet on a choisi l'utilisation de la commande MLI.

3.4.4. La modulation de largeur d'impulsions

Commande de l'onduleur par modulation de largeur d'impulsion (MLI) (Figure IV. 26) permet de convertir une tension de référence appelée modulante en une tension sous forme de créneaux, le principe de la MLI consiste à comparer le signal de référence (modulante), à un signal porteur (triangulaire) de fréquence supérieure. Cette commande utilisée afin d'atténuer certaines harmoniques de la tension, on module les largeurs des impulsions. Cette technique permet d'éviter l'emploi d'un filtre encombrant et onéreux en sortie de l'onduleur [24].

Tracker Solaire Page 56

Tracker Solaire Page 57

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. IV. 26 Modèle Simulink de la commande MLI.

Le signal de sortie de notre système qui va servir à commander les instants de

commutation des interrupteurs de l'onduleur triphasé est présenté par la troisième courbe de la figure IV. 27.

Fig. IV.27 Le signal de sortie de la commande MLI.

Le signal de sortie (modulée) vaut 1 si la modulante est plus grande que la porteuse et 0

sinon, le signal de sortie change donc d'état à chaque intersection de la modulante et de la porteuse.

3.4.5. Modélisation de la commande scalaire

La figure IV. 28 montres l'implémentation de la commande V/f constante de la machine asynchrone avec générateur de tension de commande.

Tracker Solaire Page 58

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. IV.28 Modèle dynamique du MAS asservie en position.

a) Résultats de simulation

La figure IV. 29 présente la simulation du modèle électromécanique du tracker :

Fig. IV. 29 Les résultats de simulation.

D'après la figure IV. 29la vitesse suit correctement la référence et le rejet de perturbation est rapide sans oscillations.

Chapitre II : Gisement solaire et le générateur photovoltaïque

Tracker Solaire Page 59

Le couple présente des fluctuations à chaque variation de régime. Les performances sont acceptables. La variation de la vitesse en charge est lente et le couple est très fluctué. La réponse indicielle ainsi obtenue est donnée à la figure IV. 30 qui montre que le tracker atteint sa position de référence (1°) et le temps de réponse est moins de 2s.

Fig. IV. 30 Réponses indicielles d'un axe du tracker asservi en position.

4. Commande et stratégie de génération de trajectoire d'un tracker

L'unité de commande est un dispositif programmable pour coordonner les modes de fonctionnement, ainsi que la stratégie de contrôle pour positionner le système selon l'algorithme de position solaire. Dons notre cas nous avons procédé par une programmation en langage mikroC et par une simulation sous ISIS.

L'élément de base du montage est le microcontrôleur 18F458 de la famille des PIC Midrange et architecture RISC (35 instructions de durée 1ou 2 cycles) avec une consommation moins de 2mA sous 5V et 4MHZ [25]. Cette partie est développée dans le chapitre suivant.

5. Conclusion

Ce chapitre décrit les différentes parties de conception du suiveur solaire et son principe de fonctionnement. Une simulation a été menée pour mettre en évidence la partie dynamique du suiveur, dans cette partie nous avons simulé la commande scalaire du MAS avec un contrôleur PID sous MATLAB, puis une simulation virtuelle du suiveur en boucle ouverte basée sur les équations astronomiques a été effectuée. Sur la partie mécanique, nous avons généré un modèle sous SolidWorks. Enfin, nous avons élaboré la commande du suiveur basé sur le microcontrôleur PIC 18F458.

Tracker Solaire Page 60

Chapitre II : Gisement solaire et le générateur photovoltaïque

Chapitre V : Test et simulation de

la Commande du tracker

1. Introduction

Cette dernière étape est consacrée à l'implémentation matérielle, tests et simulations de la technique adoptée dans cette étude, c'est la partie électronique qui va assurer la commande de tout le système. Pour ce faire, il est indispensable d'identifier la technologie choisie ainsi que les blocs qui seront utilisés (Figure V. 1). Notre choix s'est porté sur l'utilisation du microcontrôleur PIC comme un circuit intégré pour l'exécution du programme qui seront traduits en langage C, bien que d'autres cartes puissent être utilisées aussi. Une présentation de l'environnement logiciel est éventuellement décrite dans ce chapitre, expliquant la procédure adoptée pour une simulation en temps réel de ce projet et la description de la réalisation d'une carte de commande du tracker solaire.

Fig. V. 1 Carte de commande d'un tracker solaire.

2. Contexte logiciel

Les microcontrôleurs sont aujourd'hui implantés dans la plupart des grandes applications publiques ou professionnelles, il en existe plusieurs familles. La société Américaine Micro chip Technologie a mis au point dans les années 90 un microcontrôleur : le PIC (Peripheral Interface Contrôler). Ce composant encore très utilisé à l'heure actuelle est un compromis entre simplicité d'emploi, rapidité et prix de revient.

Dans notre cas on a utilisé le microcontrôleur PIC 18F458 programmé avec le langage mikroC, Le mikroC est un compilateur C complet pour PIC de Microchip. Le code source est simulé via PROTEUS.

La figure V. 2 représente la méthodologie suivie pour la simulation de la carte de

commande.

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. V. 2 Cheminement de la programmation et de la simulation [1].

3. Écriture du programme

On peut distinguer deux parties dans le programme rédigé avec mikroC le premier consiste à la commande scalaire du moteur le deuxième programme permet de calculer la position solaire et orienter le moteur a cette position.

? Description de l'algorithme

Dans cette stratégie et à partir des données enregistrées au préalables le microcontrôleur lit les variables suivantes : les données du lieu géographique, la latitude et la longitude, la date actuelle, l'horloge en temps réel (RTC : Real Time Clock) et les positions des angles (élévation et azimutale du panneau : détectés via les capteurs de position p1, p2), comme il est montré dans (chapitre 4, la partie 3.1 ) (Méthode pour calculer la position du soleil) .puis, le microcontrôleur calcule les paramètres et les angles suivants :l'angle horaire, et l'angle altitude, azimut, plus Heure de lever et de coucher.

Après avoir terminé le calcul, le système se déplace vers l'Est si la condition (abs (p1-az) >1 et p1> azimut) est vérifiée sinon (p1< azimut) vers l'Ouest sinon il s'arrête (la position azimutale est détectée) et la même chose la méthode est identique pour le deuxième moteur d'élévation avec la condition (abs (p2-altitude) > 1et p2> altitude). Si l'horloge atteint l'heure du coucher, le système se déplace automatiquement vers la position prévue pour l'heure du lever le jour prochain et s'arrête pour recommencer de nouveau.

4. Description du HARDWARE

Après avoir réalisé les études précédentes, on a pu construire un schéma de principe sur lequel on va se baser pour réaliser la carte de contrôle.

4.1. Réalisation de la commande de l'onduleur 4.1.1. Schéma de principe

La figure V. 3 montre le circuit de commande d'un onduleur triphasé. Il se compose

d'une mémoire tampon (BC547 et 2N3019), d'un opto-isolateur, d'un amplificateur Darlington et d'un driver MOSFET.

Tracker Solaire Page 61

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. V. 3 Circuit de commande d'un onduleur triphasé. L'élément de base du montage est le microcontrôleur PIC 18F458.

4.1.2. Circuit de l'onduleur

La figure V. 4 présente l'onduleur triphasé, il se compose de six MOSFET connectés en trois membres. Il convertit la liaison continue d'entrée en une tension alternative triphasée correspondante. Le circuit de microcontrôleur et de commande de grille sert à contrôler le temps de marche / arrêt (signal PWM) des MOSFET dans une séquence particulière. La séquence de conduite des MOSFET est de 1-5, 2-6, 3-4 et répétée. Dans cette séquence de MOSFET conducteurs, chaque paire de MOSFET conduit après chaque 120° [26] [27].

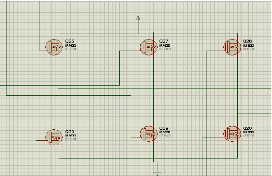
Fig. V. 4 L'onduleur triphasé avec trois bras.

4.1.3. Gâte drives circuit

Les signaux PWM sont utilisés pour contrôler la vitesse du moteur. Ils sont générés par le

microcontrôleur. Ces impulsions sont données au circuit de commande. Ce dernier fournit les signaux de grille pour déclencher les MOSFET qui entraînent le moteur à induction triphasé.

Tracker Solaire Page 62

Tracker Solaire Page 63

Chapitre II : Gisement solaire et le générateur photovoltaïque

a) Circuit tampon (BC547 et 2N3019)

L'impulsion PWM générée par le microcontrôleur PIC n'est pas capable de commander

l'opto-isolateur. Pour sur monter ce problème, le circuit tampon est utilisé comme le montre la figure V. 5 [27].

Fig. V. 5 La structure du circuit tampon (BC547 et 2N3019).

b) Opto-isolateurs (MCT2E)

La figure V. 6 présente la structure de l'opto-isolateur. C'est la combinaison de la diode

électroluminescente IR LED et NPN phototransistor. La fonction principale de l'opto-isolateur est d'isoler les circuits de puissance des circuits de commande [26] [27].

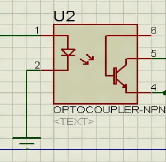
Fig. V. 6 La structure de l'opto-isolateur.

Le circuit tampon alimente le signal d'entrée de la diode électroluminescente. La LED conduit et émet la lumière qui attaque le phototransistor conduit.

c) Darlington pair Amplifier (TIP122)

Le TIP122 est un transistor de puissance NPN de pair Darlington évalué comme 100V, 5A ayant un gain de plus de 1000 avec une dissipation de puissance de 50W. Il est destiné à être utilisé dans des applications électriques, linéaires et de commutation [26][27].

Le TIP122 est un transistor de puissance NPN de pair de Darlington, classé comme 100V, 5A ayant un gain de 1000 avec une dissipation de puissance de 50W. Le circuit amplificateur Darlington est illustré sur la figure V. 7 suivante.

Tracker Solaire Page 64

Chapitre II : Gisement solaire et le générateur photovoltaïque

Fig. V. 7 La structure de Darlington pair amplifiée (TIP122).

d) IR 2112

IR2110 est un MOSFET haute tension et haute vitesse conductrice avec sortie côté gauche et côté gauche indépendant canaux de tension (FigureV.8). Il est capable de contrôler deux entrées en même temps et produit des impulsions de sortie latérales élevées et secondaires. Les entrées logiques sont compatibles avec une logique de 3,3 V. la fonction de pilote de sortie dispose d'un stade de tampon de courant à impulsions élevées conçu pour une section minimale du conducteur[26] [27].

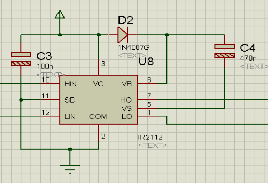
Fig. V. 8 Connexion d'IR2112.

4.2. Réalisation de la carte de commande du moteur asynchrone

5.1.1. Étage de la puissance

Ce montage est constitué d'un relais électromagnétique de commande et d'un contacteur pour chacun des moteurs (horizontal/vertical).

Fig. V. 9 Description d'un relais électromagnétique. 5.1.2. Relai électromagnétique

Chapitre II : Gisement solaire et le générateur photovoltaïque

Tracker Solaire Page 65

Comme son nom l'indique, il sert à faire une transition entre un courant faible et un courant fort. Il est constitué d'une bobine ou solénoïde qui lorsqu'elle est sous-tension attire par un phénomène électromagnétique une armature ferromagnétique qui déplace des contacts, voir figure ci-dessus.

4.3. Teste de la carte

Pour tester la carte de notre projet et pour visualiser les signaux de commande de l'onduleur nous avons branché un oscilloscope. La figure suivante représente les signaux PWM.

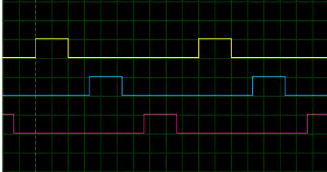
Fig. V. 10 Les signaux PWM.

5. Conclusion

Ce chapitre présente les résultats finaux de l'implémentation matérielle de la technique de poursuite étudiée lors de ce projet ainsi que les différentes étapes et la méthodologie de la programmation et l'implémentation. Ensuite, nous avons décrit les différents composants utilisés dans la carte de contrôle soit pour la commande de l'onduleur ou bien la commande des moteurs d'élévation et d'azimut.

Chapitre II : Gisement solaire et le générateur photovoltaïque

Conclusion générale et Perspectives

Dans ce rapport une étude de modélisation, simulation et commande d'un tracker a été présentée. L'objectif était de proposer et de développer un modèle permettant d'améliorer le rendement d'un module photovoltaïque, et de réduire les coûts de conception et développement de la commande. Afin de valider et de tester les performances de ce modèle, un simulateur de tracker a été développé.

? Synthèse des travaux réalisés

Dans un premier temps, nous avons présenté le gisement solaire, puis un bref historique sur l'énergie solaire et l'énergie photovoltaïque ainsi que l'évolution de son utilisation est décrites. Ensuite, nous avons présenté l'algorithme qui permet de calculer la position solaire, en citant par la suite les différents types du tracker avec leurs avantages et leurs inconvénients.

La conclusion tirée de cette étude bibliographique concerne l'utilisation du capteur solaire très répandue dans le cas de commandes hybrides ou en boucle fermée. L'élimination du coût supplémentaire de ce capteur constitue donc un des objectifs de notre travail.

La deuxième partie du présent rapport a été consacrée au développement d'un simulateur de tracker. Puis, une description de chaque bloc ou sous modèle constituant ce simulateur a été présentée. Un modèle de soleil a ensuite été proposé permettant de générer, par calcul astronomique, la trajectoire théorique du soleil à viser par le tracker. Le modèle permet aussi de générer les données d'ensoleillement en fonction de la date, de l'heure et les coordonnées GPS du tracker. Les résultats obtenus avec notre modèle sont comparés avec les données issues de la base de données de green énergies Park.

Nous avons ensuite développé un modèle électromécanique asservi en position du tracker basé sur la modélisation d'une machine asynchrone contrôlée en boucle ouverte par un variateur de vitesse et sur un modèle rigide de la structure mécanique du tracker. Classiquement, cette modélisation dynamique est proposée dans le repère diphasé de Park associée à un modèle de variateur de vitesse basé sur la commande scalaire.

? Perspectives

Les activités de modélisation et de commande du tracker doivent être prolongées et validées sur une installation réelle en exploitation. Parmi les perspectives de ces travaux, la première concerne l'amélioration de la modélisation et le développement du simulateur du tracker.

Notamment, une deuxième version du modèle du soleil pourrait inclure avantageusement un bloc d'estimation et de calcul de l'ensoleillement global et direct, ou d'un modèle à paramètres réduits basé sur les réseaux de neurones artificiels. Par ailleurs, le contrôle des actionneurs doit être amélioré en remplaçant la commande scalaire par une commande vectorielle ou une commande DTC avec un asservissement de la position et de la vitesse de la machine asynchrone. De même, un modèle mécanique plus complet et précis permettait de mettre en évidence les déformations mécaniques des trackers de grandes dimensions et leurs influences sur la production des modules.

Tracker Solaire Page 66

Chapitre II : Gisement solaire et le générateur photovoltaïque

Tracker Solaire Page 67

Références

[1]. BOUNOUA ZINEB, « Etude de l'impact des aérosols sur le rayonnement solaire au sol par ciel clair en utilisant le modèlen McClear de la méthode Heliosat-4 » Mémoire de Projet de fin d'étude Master ESSA, FST Fes 2015- 2016

[2]. M. SLAMA Fateh « Modélisation d'un système multi générateurs
photovoltaïques interconnectés au réseau électrique », Mémoire de Magister 2011-2012.

[3]. Rahmani djelloul « Analyse d'un système de concentration solaire pour la production d'hydrogène (cas de l'Algérie)». Mémoire d'ingénieur d'état en électronique 2011-2012.

[4]. Jacques Teller « confort thermique », chap.II : géométrie solaire, mémoire à Université de Liège.

[5]. Mr : Boughoufala Mohamed « Conception et réalisation d'un système de Suiveur Solaire pour des systèmes photovoltaïques » Mémoire de Magister en électronique 2010/2011

[6]. Mohamed djelloul « Contribution de l'énergie photovoltaïque dans la performance énergétique de l'habitat à haute qualité énergétique en Algérie » Mémoire de Magister 20102011.

[7]. http://www.lemonde.fr/energies/article/2016/06/01/2015-annee-record-pour-les-energies-renouvelables-dans-le-monde_4929916_1653054.html , 2015.

[8]. AOUFI Saliha « Modélisation et commande d'un système de pompage photovoltaïque » Mémoire De Magister, Option : Commande Electrique, Université Ferhat Abbas Setif-1ufas (Algérie)

2014/2015.

[9]. Benzahia Ayoub « Réalisation d'un prototype d'un système de poursuite solaire », Université Mohamed Khider Biskra Faculté des Sciences et de la Technologie, Mémoire de Magister 2013 / 2014.

[10]. R. Rezoug et A. Zaatri1 « Optimisation du rendement d'un système photovoltaïque par poursuite du soleil », 2015.

[11]. Baccalauréat général session 2008 série s sciences de l'ingénieur ; étude d'un système pluri technique « suiveur de trajectoire pour panneau solaire ».

[12]. Lucas Hadjeres « LE TRACKER SOLAIRE », Lycée Colbert, Tourcoing, article 2015.

[13]. Mohamed Aymen Sahnoun « Contribution à la modélisation et au contrôle de trajectoire de Trackers photovoltaïques à haute concentration (HCPV) ». Automatique / Robotique. Ecole nationale supérieure d'arts et métiers - ENSAM, 2015. Français. <NNT : 2015ENAM0043>. <tel-01269847>

[14]. Aghilas BRAHIMI « Etude de performances d'un capteur solaire plan à eau », Mémoire de Master en Mécanique et Energétique 2015-2016.

[15]. FERROUDJI Fateh « Conception et optimisation en dynamique forcée d'un nouveau prototype de système de suiveur solaire à deux axes »,thèse du doctorat sciences en mécanique 2015-2016.

[16]. REDA, Ibrahim et ANDREAS, Afshin. « Solar position algorithm for solar radiation applications. Solar energy », 2004, vol. 76, no 5, p. 577-589

[17]. KERKOUCHE, K., CHERFA, F., ARAB, A. Hadj, et al. « Evaluation de l'irradiation solaire globale sur une surface inclinée selon différents modèles pour le site de Bouzaréah». Revue des Energies Renouvelables, 2013, vol. 16, no 2, p. 269-284.

[18]. Prinsloo, G.J., Dobson, R.T. (2015). « Solar Tracking ». Stellenbosch : SolarBooks. ISBN 978-0-620-61576-1, p 1-542.

[19]. Salem AKKARI, Flavien LUCAS, Etienne GRENIER, Nicolas LUCAS, Yinchao LI, Yihuan SUN, Anthony CARRATALA, « Projet mécatronique intégrée 5A : Réalisation d'un tracker » .

ANNEE UNIVERSITAIRE 2016- 2017

[20].

http://electrotechnique1.blogspot.com/p/la-machine-asynchrone.html.2017.

[21]. https://fr.wikipedia.org/wiki/R%C3%A9gulateur_PID. 2017.

[22]. Soufien Gdaim. « Commande directe de couple d'un moteur asynchrone à base de techniques intelligentes. Intelligence artificielle» [cs.AI]. Ecole Nationale d'Ingénieurs de Monastir. Tunisia, 2013. Français. <tel-01456394v2> , Submitted on 8 Feb 2017.

[23]. L. BAGHLI « Modélisation et Commande de la Machine Asynchrone», 2015.

[24]. DIAF YOUSSOUF, BEN ANTER DJAMAL « Modélisation et commande d'un onduleur triphasé pilote par mli a structure multiniveaux », PROJET DE FIN D'ETUDES de Master en Génie électrique Filière : Génie électrique Spécialité : Electrotechnique Industriel, 2011/2012.

[25]. PIC18FXX8 Data Sheet, 2004 Microchip Technology Inc.

[26]. Jamadar JAMADAR, B. N., KUMBHAR, S. R., GAVANE, P. M., et al. « Design and Development of Control System for Three Phase Induction Motor using PIC Microcontroller». IFAC Proceedings Volumes, 2014, vol. 47, no 1, p. 807-811.

[27]. JAMADAR, B. N., KUMBHAR, Dr SR, et SUTRAVE, D. S « PICMicrocontroller Based Speed Control of Three Phase Induction Motor Using Single Phase Supply». IJRCSIT I ISSN, 2013, no 2319-5010 PIC.

ANNEE UNIVERSITAIRE 2016- 2017

Annexes

Annexe 1. Description de la station météorologie

Le paramètre mesuré	Equipment de mesure	Photos
Global Irradiation Horizontal (GHI).	Pyranomètre I.
Irritation normale directe (DNI).	Pyrhéliomètre.
L'irradiation Diffuse horizontale (DNI).	Pyranomètre I.
Les précipitations.	Pluviométrie de Kipp & Zonen.
La température, d'humidité et de pression.	Capteur de Kipp & Zonen.
Mesure la vitesse du vent.	Anémomètre de Kipp & Zonen.

Annexe 2. Detaille de calcule astronomique

L'annexe suivant décrit le calcul astronomique utilisé pour calculer la position théorique du soleil en fonction de la date, de l'heure et des coordonnées géographique du site.

Suivi du soleil :

ANNEE UNIVERSITAIRE 2016- 2017

Le suivi du soleil est réalisé sur la base d'un calcul astronomique théorique de la position du soleil à partir des

coordonnées GPS du Tracker et de l'heure UTC. Les formules du calcul astronomique sont issues de (Meeus.J, 1998).

Calcul du jour julien

- Les calculs astronomiques sont réalisés à partir de dates converties en jour Julien comme décrit au chapitre 7 de

l'ouvrage.

Si = 1 ou = 2 alors {

?? = ?? - 1

= + 12

?? = ??+( +(( +( /60))/60))/24

On pose = floor (D/100) et = 2 - + floor ( /4)

Y, M, D, h, m, s sont respectivement l'année, le mois, le jour du calendrier Grégorien, l'heure UTC, la minute et la seconde.

- Le jour julien est donc calculé comme suit :

?? = floor (365.25 (?? + 4716)) + floor (30.6001 ( + 1)) + ?? + - 1524.5

Calcul de la position apparente du soleil

La position apparente du soleil est obtenue en coordonnées équatoriales á (Ascension Droite) et ä (Déclinaison) à partir des équations suivantes :

· Siècle Julien J2000 = ( ?? - 2451545.0) / 36525

· Longitude moyenne du Soleil

0 = 280.46645° + 36000.76983° + 0.0003032° 2

· Anomalie moyenne du Soleil

= 357.52910° + 35999.05030° - 0.0001559° 2 - 0.00000048° 3

· Equation du Centre du Soleil

= (1.914600° - 0.004817° - 0.000014° 2) sin + (0.019993° - 0.000101° ) sin 2M + 0.000290° sin
3

· Longitude vraie du soleil ?? = 0 + + ????

????? permet une amélioration du calcul de la longitude vraie du soleil en introduisant les corrections suivantes :

- Corrections dues à l'action de Venus

A = 153.23° + 22518.7541°

B = 216.57° + 45037.5082°

- Correction due à l'action de Jupiter

C = 312.69° + 32964.3577°

- Correction due à l'action de la Lune

D = 350.74° + 445267.1142° - 0.00144° 2

· Inégalité de longue période

E = 231.19 + 20.20 Ä?? = 0.00134° cos ( ) + 0.00154° cos ( ) + 0.00200° cos ( ) + 0.00179° sin (??) + 0.00178° sin ( )

· Paramètre de nutation de la terre = 125.04452° - 1934.136261°

· Longitude apparente du soleil

= Revolution (?? - 0.00569° - 0.00478° sin )

· Ascension droite et Déclinaison du Soleil tan = cos ?? sin cos sin = sin ?? sin

= 2(cos ; cos ?? sin )

= asin(sin ?? sin )

Transformation de coordonnées

ANNEE UNIVERSITAIRE 2016- 2017

La position apparente du soleil est donnée en coordonnées équatoriales, les coordonnées dans le repère horizontal sont obtenues grâce aux transformations décrites dans (Meeus.J,1998). Les coordonnées du soleil dans le repère horizontal (Azimut A et Elévation h) sont obtenues à partir des coordonnées équatoriales (Ascension Droite á et Déclinaison ä), des coordonnées GPS de l'observateur (Latitude ö et Longitude L) et du temps sidéral à Greenwich è.

· Angle Horaire Local H = 00 - L - a

· Azimut

tanA = sin H cos H*sin cp-tan 6*cos cp

A = atan2(cos H* sin cp - tan 6* cos cp , sin H)

· Elévation

sin h = sin cp* sin 6 + cos cp* cos 6* cos H , h = asin(sin cp* sin 6 + cos cp* cos 6* cos H)

Annexe 3. Informatique sur PIC

· Les caractéristiques du PIC :

· Brochage du 16f877 :

· Structure interne d'un microcontrôleur :

· Schéma bloc de PIC :

ANNEE UNIVERSITAIRE 2016- 2017

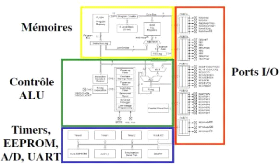
ANNEE UNIVERSITAIRE 2016- 2017