Une approche IDM du transformation du modèle ecore vers event-b.

Résumé

Le travail présenté dans cette mémoire est une contribution dans le domaine de l'Ingénierie Dirigée par les Modèles (IDM). Son principal objectif est l'application des techniques de la transformation de modèles, et plus précisément les approches hybrides, pour pouvoir appliquer des outils d'analyse et de vérification durant le processus de développement des systèmes complexes.

Le travail présenté dans ce cadre consiste en une approche et un outil pour la modélisation et la transformation des modèles ECore en modèles Event-B. L'outil est conçu en langage ATL sous l'environnement de développement Eclipse. Nous présenterons d'abord les deux méta-modèles de notre approche, ensuite nous présenterons un outil pour la transformation de ces modèles ECore en leurs équivalents dans le formalisme Event-B. Nous utiliserons l'outil RODIN pour prouver les propriétés des modèles Event-B.

Mots clés : Ingénierie Dirigée par les Modèles, Méta-modélisation, ECore, Méthode

Formelle Event-B.

Remerciements

Je remercie Dieu de m'avoir accorde des connaissances de la science et de m'avoir aidé à
réaliser ce travail.
Je souhaiterais manifester ma reconnaissance particulièrement à Mr "Mohamed Graiet"
pour son soutien et sa disponibilité. Son aide, son encouragement continu et ses conseils
m'ont été précieux afin de mener mon travail à bon port. J'espère être à la hauteur de sa
confiance. Qu'ils trouvent dans ce travail l'expression de ma profonde gratitude.
Par la même occasion, je tiens à remercier vivement tous les membres de jury pour leur
présence et leur coopération.
Encore, je remercie sincèrement tous les membres de ma famille, et plus particulièrement
mes parents, pour leur incessant soutien.
Un grand merci à tous et à toutes qui ont contribué de prés ou de loin au bon déroulement
de ce travail en particulier "Marwa Hamdi".
Enfin,merci à tout le corps enseignant qui a contribué à ma formation.

Dédicaces

À mon cher père "Boujemaa" (Dieu a son âme)
Qui a fait de moi ce que je suis aujourd'hui, qui m'a donné l'aide, le courage et l'amour
avec patience illimitée pour lequel je resterai redevable,mais il m'a quitté,je lui dédie ce
travail et j'espère qu'il soit content de moi.

À ma très chère mère " Fayza"

La personne qui m'a donné toute sa vie, qui a été très stressée pour ce projet, je lui dédie

ce travail.

À ma soeur « Henda », à son mari « Lacheheb » et à leur petit « Mohamed Yassine » À mes frères, à mes soeurs,

Que Dieu vous garde tous unis et vous procure tout le bonheur.

À mon amie « Marwa »,

Qui m'aide et m'encourage toujours avec toute façon.

À mes amies « Radhya », « Khouloud », et à tous mes amis,
Que je leur souhaite un grand succès dans leurs études et du bonheur.

À tous ceux que j'aime, à tous ceux qui m'aiment.

Qu'ils trouvent dans ce travail le témoignage de ma profonde gratitude.

BOUAZIZI Hana

i

Table des matières

Introduction générale 2

I Etat de l'art 5

1 Ingénierie dirigée par les modèles 6

1.1 Introduction 7

1.2 L'Ingénierie dirigée par les modèles(IDM) 7

1.2.1 Principe et concepts généraux de l'IDM 7

1.2.2 L 'Approche MDA (Model Driven Architecture) 8

1.3 Transformation de modèles 10

1.3.1 Principe géneral d'une transformation 10

1.3.2 Types de transformation 11

1.3.3 Taxonomies des transformations 12

1.3.4 Paradigmes de transformation 12

1.3.4.1 Transformation Modèle vers Modèle 13

1.3.4.2 Transformation Modèle vers Code 14

1.4 Langage de transformation de modèles ATL 14

1.4.1 Vue d'ensemble sur la transformation ATL 15

1.4.2 Présentation d'ATL 16

1.5 La plateforme de modélisation sous Eclipse 18

1.5.1 Eclipse Modeling Framework (EMF) 18

1.5.2 XML Metadata Interchange (XMI) 19

1.6 Le langage de génération de code Xpand 20

1.6.1 Structure générale d'un template Xpand 20

1.7 Le langage Check pour la vérification de contraintes 21

page ii

TABLE DES MATIÈRES

2	1.8 MWE (Modeling Workflow Engine) 1.9 Conclusion Méta-modélisation :Le méta-modèle ECore		22 23 24
	2.1	Introduction	25
	2.2	La méta-modélisation	25
	2.3	Les langages de méta-modélisation	26
		2.3.1 MOF (Meta Object Facility)	26
		2.3.2 ECore	26
	2.4	Le Méta-modèle ECore	27
		2.4.1 Noyau d'ECore	27
		2.4.2 Caractéristiques structurelles	28
		2.4.2.1 EAttribute	30
		2.4.2.2 ERéférence	30
		2.4.3 Caractéristiques comportementales	31
		2.4.4 Classificateurs	33
		2.4.4.1 Les classes	33
		2.4.4.2 Types de données	34
		2.4.4.3 Types énumérés	35
		2.4.4.4 Package	36
	2.5	Etude de cas	36
		2.5.1 Présentation informelle	37
		2.5.2 Spécification du système bancaire en ECore	37
	2.6	Conclusion	38
3	La méthode formelle Event-B		39
	3.1	Introduction	40
	3.2	Quelques langages formels	40
		3.2.1 Le langage Z	40
		3.2.2 La méthode B	41
		3.2.3 La méthode Event-B	41
	3.3	Modèle Event-B	42
		3.3.1 Structure d'une Machine	42

page iii

TABLE DES MATIÈRES

3.3.2 Structure d'un Contexte 43

3.3.3 Structure d'un Evénement 43

3.3.3.1 Les différentes formes des événements 44

3.3.3.2 Obligations de preuves 46

3.4 Exemple de machine en Event-B 47

3.5 RODIN : l'outil support d'Event-B 48

3.6 Conclusion 49

II Contribution 50

4 Une approche IDM pour la génération de modèle Event-B à partir de

modèle ECore 51

4.1 Introduction 52

4.2 Les méta-modèles de notre approche 52

4.2.1 Méta-modèle Event-B 52

4.2.1.1 Méta-Classe de Context 52

4.2.1.2 Méta-Classe Machine 53

4.2.1.3 Méta-Classe Event 55

4.2.1.4 Vue d'ensemble sur le méta-modèle Event-B 55

4.2.1.5 Les règles de cohérences sous forme d'OCL (.chk) 57

4.2.2 Méta-modèle ECore 59

4.2.2.1 Les règles de cohérence du méta-modèle ECore sous forme

d'OCL (OCLinECore) 62

4.3 Formalisation en Event-B 63

4.3.1 Formalisation du concept EPackage en Event-B 63

4.3.2 Formalisation du concept EClass en Event-B 64

4.3.3 Formalisation du concept EEnum en Event-B 64

4.3.4 Formalisation du concept EAttribute en Event-B 65

4.3.5 Formalisation du concept EReference en Event-B 67

4.3.6 Formalisation du concept EOperation en Event-B 69

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche

IDM (Ingénierie Dirigée par les Modèles). 70

4.4.1 Transformation de modèles M2M 71

page iv

TABLE DES MATIÈRES

4.4.1.1 Exemple des règles en ATL 73

Règle générant Context et Machine 74

Règle générant les ensembles abstraits(Sets) 75

Règle générant les événements (Event) 76

Règle générant les Constants (Constants) 77

Règle générant les ensembles (Sets) 78

4.4.1.2 Exécution du programme ECore2Event-B.atl 79

4.4.2 Transformation de modèle M2T 81

4.4.2.1 Présentation de la transformation M2T 81

4.4.2.2 Modèle Event-B en texte: Extraction via Xpand 82

4.4.2.3 Le moteur de validation et de génération de code Ada . . 84

4.4.2.4 Exemple d'utilisation : Système bancaire(Bank) 85

4.5 Vérification formelle par l'outil Rodin 88

4.5.1 Preuves d'une machine 88

4.6 Conclusion 91

Conclusion et perspectives 92

Appendices 94

Annexes 95

A Les règles de cohérence du métamodèle Event-B sous forme d'OCL (.chk) 95

B Les règles de cohérence du métamodèle ECore sous forme d'OCLinECore 98

C Les règles de transformation M2M (Ecore2EventB.atl) 101

D Le template de génération de code EventB en Xpand 110

v

Table des figures

1.1 les relations de bases dans IDM 8

1.2 Exemple montrant les relations de bases dans IDM 8

1.3 Pyramide de modélisation de l'OMG 10

1.4 Transformation de modèles 11

1.5 Approches de transformations de modèles 13

1.6 Vue d'ensemble sur la transformation ATL 15

1.7 Les règles de transformation ATL 17

1.8 Aperçu d'un fichier ECore ouvert avec son éditeur 19

1.9 Exemple d'un fichier XMI 20

2.1 Notions de base de la méta-modélisation 25

2.2 Les concepts du méta-modèle ECore 27

2.3 Noyau d'ECore 28

2.4 Concept EStructuralFeature 29

2.5 Concept EAttribute 30

2.6 Concept EReference 31

2.7 Concept EOperation et EParameter 32

2.8 Concept EClassifier 33

2.9 Concept EClass 34

2.10 Concept EDataType, EEnum et EEnumLiteral 35

2.11 Concept EPackage 36

2.12 Modèle ECore d'un Bank 37

2.13 Modèle ECore d'un Bank validé 38

3.1 L'unité de spécification de Z 41

3.2 Relation entre un contexte et une machine 43

page vi

TABLE DES FIGURES

3.3 La plateforme RODIN 49

4.1 Structure d'un contexte 53

4.2 Méta-Classe Context 53

4.3 Structure d'une machine 54

4.4 Méta-Classe Machine 54

4.5 Méta-Classe Event 55

4.6 Méta-modèle Event-B 56

4.7 Méta-modèle Event-B ouvert avec son éditeur 57

4.8 Cas d'erreur 58

4.9 Cas de warning 59

4.10 Méta-modèle ECore ouvert avec son éditeur 60

4.11 Méta-modèle ECore partiel 61

4.12 Règle sous forme d'OCLinECore. 62

4.13 Cas d'erreur 63

4.14 Formalisation du concept EPackage 63

4.15 Formalisation du concept Eclass 64

4.16 Formalisation du concept EEnum 65

4.17 Formalisation du concept EAttribute 66

4.18 Formalisation du concept EAttribute 68

4.19 Formalisation du concept EOperation 69

4.20 Schéma de notre approche 70

4.21 Vue d'ensemble sur le programme ECore2Event-B 72

4.22 Exemple règle ATL 73

4.23 Règle générant Context et Machine 75

4.24 Règle générant Sets 76

4.25 Règle générant Event 77

4.26 Règle générant Constants 78

4.27 Règle générant Sets 79

4.28 Modèle ECore d'un Bank (modèle source) 80

4.29 Modèle Event-B d'un Bank (modèle cible) 80

4.30 Schéma de transformation de modèle Event-B vers texte Event-B 81

4.31 Schéma de transformation de modèle Event-B vers texte Event-B 86

page vii

TABLE DES FIGURES

4.32 Les OPs sous Rodin de la machine 89

4.33 Preuve automatique 90

4.34 Preuves interactif 91

1

Liste des tableaux

3.1 prédicats avant-après 46

4.1 prédicats avant-après 66

4.2 diverses relations fonctionnelles en Event-B 67

2

Introduction générale

L

es logiciels et systèmes informatiques sont présents aujourd'hui dans tous les domaines

de l'activité humaine (industrie, construction, communication...). Avec le temps ces
logiciels deviennent de plus en plus complexes, et par conséquent, leur analyse et leur vérification représentent un enjeu capital. Ceci les rend très sensibles aux erreurs produites durant le cycle de vie d'un système. En effet, ces erreurs logicielles peuvent être introduites durant la phase de conception.

Pour la conception du logiciel, Les méthodes les plus utilisées en conception de systèmes d'information (ECore, UML) dites semi-formelles, sont basées principalement sur l'utilisation de divers diagrammes. Ces méthodes présentent des avantages indéniables. Elles représentent le système d'une manière à la fois intuitive et synthétique. De ce fait, elles sont bien adaptées à la plupart des utilisateurs. Ces avantages ont contribué à répandre largement leur utilisation dans l'industrie. Mais leur principal défaut est l'absence d'une sémantique précise des diverses notations utilisées, ce qui entraîne souvent des ambiguïtés. En outre, il est impossible de prouver la cohérence du système, ce qui limite la fiabilité des logiciels produits.

Pour réagir face à ces problèmes, il est nécessaire d'offrir des méthodes permettant d'éviter les erreurs inhérentes au développement des logiciels et systèmes complexes. Le génie logiciel offre des méthodes, techniques et outils permettant de vérifier et d'éviter les erreurs. En effet, les méthodes formelles du génie logiciel fournissent des notations issues des mathématiques, en particulier de la logique, permettant de décrire très précisément les propriétés des systèmes à construire. De ce fait, ces méthodes disposent de techniques de preuve permettant de vérifier complètement le raffinement des spécifications en code exécutable. Ces avantages apportent des réponses pertinentes à la problématique de construction des logiciels et systèmes complexes.

page 3

Introduction générale

L'objectif de ce mémoire est de proposer une approche IDM de la transformation Du méta-modèle ECore vers la méthode formelle Event-B basée sur le principe « tout est modèle » [6]. Pour y parvenir, nous avons élaboré deux méta-modèles : le méta-modèle ECore jouant le rôle de méta-modèle source et le méta-modèle Event-B jouant le rôle de méta-modèle cible pour l'opération de transformation d'ECore vers Event-B. De plus, nous avons réalisé un programme ECore2Event-B écrit en ATL [8] permettant de transformer un modèle source conforme au méta-modèle ECore vers un modèle cible conforme au méta-modèle Event-B. En outre nous avons utilisé avec profit l'outil de Xpand pour la transformation du modèle Event-B à un code Event-B. Enfin, nous avons testé notre travail sur une étude de cas d'un Système Bancaire « BANK » décrite en [3].

Ce mémoire contient deux grandes parties qui sont organisées de la manière suivante :

~ Partie I : Etat de l'art

-- Le chapitre 1

premier chapitre donne une vue d'ensemble sur l'approche IDM. En outre, il présente ATL comme un langage de transformation M2M, aussi Xpand comme un langage de transformation M2T et enfin la plateforme Eclipse utilisé dans ce mémoire.

-- Le chapitre 2

Le second présente la méta-modélisation semi-formelle ECore et les concepts du méta-modèle ECore qui joue le rôle de méta-modèle source de notre approche de transformation.

-- Le chapitre 3

Le troisième chapitre présente d'une façon rigoureuse les principes du langage Event-B (machine abstraite, contexte, langage de substitutions, obligations de preuves) permettant de développer des modèles corrects par construction. Il présente aussi un aperçu sur la plateforme RODIN [27] [28] supportant la méthode Event-B.

page 4

Introduction générale

~ Partie II : Contribution

-- Le chapitre 4

Le dernier chapitre est consacré au passage du modèle ECore vers Event-B. Ce chapitre comporte quatre sections, la première section présente les méta-modèles, Event-B et ECore que nous les utilisons dans notre contexte de transformation. Dans la deuxième section nous présentons notre contribution consiste à la formalisation en Event-B des concepts ECore. Dans la troisième section nous présentons la transformation des modèles M2M (ECore2Event-B) et la transformation M2T (Event-B2TexteEvent-B).Et enfin nous présentons la validation du modèle cible Event-B sur la plateforme RODIN.

Enfin, nous achèverons notre mémoire par une conclusion et des perspectives.

Première partie

5

Etat de l'art

6

1 Ingénierie dirigée par les modèles

Sommaire

1.1 Introduction 7

1.2 L'Ingénierie dirigée par les modèles(IDM) 7

1.2.1 Principe et concepts généraux de l'IDM 7

1.2.2 L 'Approche MDA (Model Driven Architecture) 8

1.3 Transformation de modèles 10

1.3.1 Principe géneral d'une transformation 10

1.3.2 Types de transformation 11

1.3.3 Taxonomies des transformations 12

1.3.4 Paradigmes de transformation 12

1.4 Langage de transformation de modèles ATL 14

1.4.1 Vue d'ensemble sur la transformation ATL 15

1.4.2 Présentation d'ATL 16

1.5 La plateforme de modélisation sous Eclipse 18

1.5.1 Eclipse Modeling Framework (EMF) 18

1.5.2 XML Metadata Interchange (XMI) 19

1.6 Le langage de génération de code Xpand 20

1.6.1 Structure générale d'un template Xpand 20

1.7 Le langage Check pour la vérification de contraintes 21

1.8 MWE (Modeling Workflow Engine) 22

1.9 Conclusion 23

page 7

1.1 Introduction

1.1 Introduction

L

a complexité, la variété des technologies existantes et l'accroissement des besoins font

aujourd'hui le domaine dans du développement logiciel un véritable défi. Pour réagir
face, il est nécessaire d'offrir une approche permettant d'abstraire toutes les complexités technologique. Dans ce contexte, l'approche Ingénierie Dirigée par les Modèles(IDM) a émergé comme une discipline récente du génie logiciel en ouvrant des nouvelles voies d'investigation pour répondre aux nouveaux besoins et présenter des nouvelles solutions conceptuelles qui permettent de suivre l'évolution croissante des applications.

Dans ce chapitre, nous consacrerons aux concepts de base de l'Ingénierie Dirigée par les Modèles (IDM) qui couvrent les disciplines dans lesquelles les modèles jouent un rôle principal. Nous nous intéresserons également à la transformation des modèles. Et enfin nous présenterons la plateforme Eclipse utilisée dans ce mémoire.

1.2 L'Ingénierie dirigée par les modèles(IDM)

L'Ingénierie Dirigée par les Modèles (IDM), ou Model Driven Engineering (MDE) en anglais, évoque plusieurs améliorations significatives dans le développement de systèmes complexes en permettant de se concentrer sur une préoccupation plus abstraite que la programmation classique.

1.2.1 Principe et concepts généraux de l'IDM

Le principe de l'IDM consiste à utiliser intensivement les modèles tout au long du processus de développement logiciel. Les modèles devront des entités interprétables par les machines non seulement au coeur du processus. Donc le principe de base de cette approche consiste à dire que « tout est modèle »[10].

page 8

1.2 L'Ingénierie dirigée par les modèles(IDM)

La figure 1.1 présente les relations de bases dans IDM.

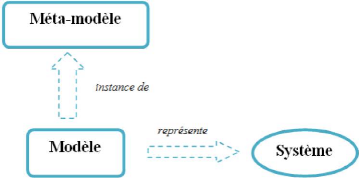
FIGURE 1.1 - les relations de bases dans IDM

La Figure 1.1 représente les concepts généraux de l'IDM ainsi que la relation entre ces concepts. En effet, le modèle écrit dans un méta-modèle donné sera dit « instance de ». On rencontre également cette relation sous la forme « conforme à » c'est-à-dire un modèle est conforme à son méta-modèle.

La Figure 1.2 monte un exemple qui présente les relations de bases dans IDM.

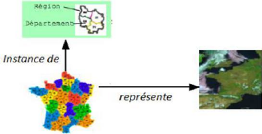
FIGURE 1.2 - Exemple montrant les relations de bases dans IDM.

1.2.2 L 'Approche MDA (Model Driven Architecture)

L'approche Model Driven Architecture (MDA) est une initiative de l'OMG rendue publique en 2000. C'est une proposition à la fois d'une architecture et d'une démarche de

page 9

1.2 L'Ingénierie dirigée par les modèles(IDM)

développement [9]. L'idée de base du MDA est la séparation des spécifications fonctionnelles d'un système des détails de son implémentation sur une plate-forme donnée. Pour cela, le MDA classe les modèles en modèles indépendants des plates-formes appelés PIM (Platform-Independent Models) et en modèles spécifiques appelés PSM (Platform-SpecificModels).

L'initiative MDA a donné lieu à une standardisation des approches pour la modélisation sous la forme d'une structure en 4 niveaux de modélisation (appelée communément Pile de modélisation).

La proposition initiale était d'utiliser le langage UML et ses différentes vues comme unique langage de modélisation. Cependant, il a fallu rapidement ajouter la possibilité d'étendre le langage UML, par exemple en créant des profils, afin d'exprimer de nouveaux concepts relatifs à des domaines d'application spécifiques. Ces extensions devenant de plus en plus importantes, la communauté MDA a élargi son point de vue en considérant les langages de modélisation spécifiques à un domaine.

L'OMG se dégage une hiérarchie de quatre niveaux d'abstraction pour la modélisation des systèmes : méta-méta-modèle, méta-modèle, modèle et information.

~ Niveau M0 : Le niveau M0 (ou information) correspond au monde réel. Il ne s'agit pas d'un niveau de modélisation proprement dit. Ce niveau contient les informations réelles de l'utilisateur, c'est une instance du modèle de niveau M1.

~ Niveau M1 (M) : Le niveau M1 (ou modèle) est composé de modèles d'informations. Il décrit les informations de M0. Ce niveau contient les modèles UML, les PIM et les PSM. Les éléments d'un modèle (M1) sont des instances des concepts décrits dans un méta-modèle(M2).

~ Niveau M2 (MM) : Le niveau M2 (ou méta-modèle) définit le langage de modélisation et la grammaire de représentation des modèles M1. Ce niveau contient le méta-modèle UML qui définit la structure interne des modèles UML ainsi que les profils UML qui étendent le méta-modèle. Les concepts définis par un méta-modèle sont des instances des concepts du MOF.

~ Niveau M3 (MMM) : Dans l'approche MDA, le niveau M3 (ou méta-méta-modèle) est composé d'une seule entité réflexive appelée le MOF (Meta Object Facility) [13], permettant de décrire la structure des méta-modèles, d'étendre ou de modifier les méta-modèles existants.

page 10

1.3 Transformation de modèles

La Figure 1.3 illustre ce que nous venons de dire :

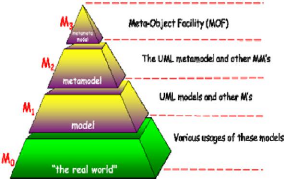
FIGURE 1.3 - Pyramide de modélisation de l'OMG

Et pour mieux illustrer la hiérarchie de modélisation à 4 niveaux existe en dehors du MOF et d'UML, dans d'autres espaces technologiques que celui de l'OMG, on prend le cas de langage de programmation.

On peut dire que le niveau M0 représente l'exécution d'un programme, le niveau M1 est le programme, le niveau M2 méta-méta-modèle définissant le méta-modèle et enfin le dernier niveau est le concept de grammaire EBNF [6].

1.3 Transformation de modèles

La transformation de modèle est une opération fondamentale dans toute approche orientée modèle. La définition et l'automatisation des transformations a pour objectif de rendre les modèles plus opérationnels et d'augmenter la productivité du développement dans une approche IDM.

1.3.1 Principe géneral d'une transformation

La définition la plus générale et qui fait l'unanimité au sein de la communauté IDM consiste à dire qu'une transformation de modèles est la génération d'un ou de plusieurs modèles cibles à partir d'un ou de plusieurs modèles sources [8] [7].

Dans l'approche par modélisation, cette transformation se fait par l'intermédiaire de

page 11

1.3 Transformation de modèles

règles de transformations qui décrivent la correspondance entre les entités du modèle source et celles du modèle cible.

En réalité, la transformation se situe entre les méta-modèles source et cible qui décrivent la structure des modèles cible et source. Le moteur de transformation de modèles prend en entrée un ou plusieurs modèles sources et crée en sortie un ou plusieurs modèles cibles.

Une transformation des entités du modèle source met en jeu deux étapes :

~ Première étape : permet d'identifier les correspondances entre les concepts des modèles source et cible au niveau de leurs méta-modèles, ce qui induit l'existence d'une fonction de transformation applicable à toutes les instances du méta-modèle source..

~ Deuxième étape : consiste à appliquer la transformation du modèle source afin de générer automatiquement le modèle cible par un programme appelé moteur de transformation ou d'exécution.

La Figure 1.4 illustre ces deux étapes de transformation de modèles [5].

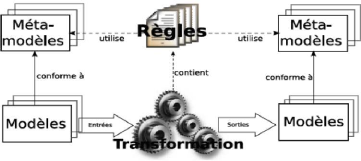
FIGURE 1.4 - Transformation de modèles

1.3.2 Types de transformation

Une transformation de modèles met en correspondances des éléments des modèles cibles et sources. On distingue les types de transformation suivant :

~ Les transformations simples (1 vers 1) : qui associent à tout élément du modèle source au plus un élément du modèle cible.

page 12

1.3 Transformation de modèles

~ Les transformations multiples (M vers N) : qui prennent en entrée un ensemble d'éléments du modèle source et produisent en sortie un ensemble d'éléments (généralement différent) du modèle cible (par exemple, la fusion de modèles est une transformation M vers 1).

~ Les transformations de mise à jour : appelées aussi modifications sur place (ajout, suppression, changement de propriétés, etc.). Ces transformations sont caractérisées par l'absence de modèle cible, et agissent donc directement sur le modèle source. Les transformations de restructuration sont des exemples typiques de ce type de transformation.

1.3.3 Taxonomies des transformations

En fonction du changement de niveau d'abstraction engendré par la transformation et de la nature des méta-modèles source et cible impliqués, plusieurs types de transformation sont à considérer.

Il existe 2 types de transformation :

~ Exogène :

1. Les modèles source et cible sont conformes à des méta-modèles différents.

2. Transformation d'un modèle UML en programme Java.

3. Transformation d'un fichier XML en schéma de BDD. ~ Endogène :

1. Les modèles source et cible sont conformes au même méta-modèle.

2. Transformation d'un modèle UML en un autre modèle UML [5].

1.3.4 Paradigmes de transformation

Les transformations de modèles se partagent également en deux grandes classes [11] : les transformations « Modèle vers Code », et les transformations « Modèle vers Modèle » largement étudiées dans l'approche MDA.

Dans chacune de ces deux grandes classes, on distingue plusieurs sous classes comme le montre la Figure 1.5.

page 13

1.3 Transformation de modèles

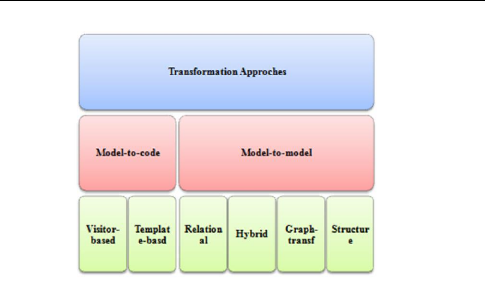
FIGURE 1.5 - Approches de transformations de modèles

1.3.4.1 Transformation Modèle vers Modèle

Ces transformations ont beaucoup évolué depuis l'apparition de MDA. Ce type de transformation permet la génération de plusieurs modèles intermédiaires avant d'atteindre le modèle de code, afin d'étudier les différentes vues du système, son optimisation, la vérification de ses propriétés et sa validation.

Nous distinguons cinq techniques de transformation « Modèle vers Modèle » [12] : ~ Approche par manipulation directe : Cette approche est basée sur une représentation interne des modèles source et cible, en plus des API (Application Programming Interface) pour les manipuler.

~ Approche relationnelle : Cette approche utilise les contraintes pour spécifier les relations entre les éléments du modèle source et celles du modèle cible en utilisant une logique déclarative basée sur des relations mathématiques.

~ Approche basée sur les transformations de graphes : Cette approche convient lorsque les modèles sont représentés par des graphes. Elle exprime les transformations sous une forme déclarative. Les règles de transformation sont définies sur des parties du modèle et non pas sur des éléments basiques. Une opération de filtrage de motifs (Pattern Matching) est ensuite lancée. Le moteur de transformation compare à chaque

page 14

1.4 Langage de transformation de modèles ATL

fois des fragments du modèle source pour trouver des règles applicables. Ce fragment est ensuite remplacé par son équivalent dans la règle appliquée.

~ Approche basée sur la structure : Divisée en deux étapes, la première se charge de la création d'une structure hiérarchique du modèle cible, la seconde ajuste ses attributs et ses références.

~ Approche hybride : Comme ATL, les approches hybrides sont la combinaison des différentes techniques ou alors celle d'approches utilisant à la fois des règles à logique déclarative et impérative.

1.3.4.2 Transformation Modèle vers Code

La génération de code peut être considérée comme un cas particulier de transformation de type modèle vers texte. Pour cela, il faut définir un méta-modèle correspondant au langage de programmation cible.

Pour des raisons pratiques liées à la réutilisation des compilateurs existants, le code produit est souvent donné sous format texte. Ceci conduit à considérer deux types d'approche. ~ Sous le premier type, on range les approches basées sur un mécanisme de « visiteur » dont le principe repose sur le balayage de la représentation interne du modèle et l'écriture du code dans un fichier de sortie sous format texte.

~ Le deuxième type rassemble les approches qui sont basées sur des Template de transformation des modèles vers du code. Dans cette catégorie on trouve plusieurs outils MDA open source et commerciaux tels que Xpand, Acceleo, qui est intégré à la plate-forme Eclipse et au framework EMF.

1.4 Langage de transformation de modèles ATL

Plusieurs langages de transformation ont été proposés pour réaliser des transformations de modèle selon l'approche par méta-modélisation, parmi lesquels le standard MOF2.0 QVT et le langage ATL (ATLAS Transformation Langage) [7].

Dans ce mémoire, notre choix s'est porté sur ce dernier langage. En effet, ATL est largement utilisé maintenant par la communauté et il est aussi considéré comme un standard de transformation dans Eclipse.

ATL [8], acronyme de «ATLAS Transformation Langage» est un langage de transfor-

page 15

1.4 Langage de transformation de modèles ATL

mation de modèles dans le domaine de l'IDM (Ingénierie Dirigée par les Modèles) ou MDE (Model-Driven Engineering). Il fournit aux développeurs un moyen de spécifier la manière de produire un certain nombre de modèles cibles à partir de modèles sources.

1.4.1 Vue d'ensemble sur la transformation ATL

Une transformation de modèles définit la façon de générer un modèle Mb, conforme au méta-modèle MMb, à partir du modèle Ma conforme au méta-modèle MMa. Un élément majeur dans l'ingénierie des modèles est de considérer, dans la mesure du possible, tous les objets traités comme des modèles. La transformation de modèles doit être elle-même définie comme un modèle (MMa2MMb.atl). Ce modèle de transformation doit être conforme au méta-modèle qui définit la sémantique de transformation de modèles (ATL). Tous les méta-modèles doivent être conformes au méta-méta-modèle considéré (ECore). La Figure 1.6 donne une vue d'ensemble sur la transformation ATL [5].

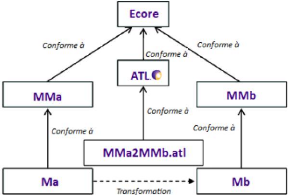
FIGURE 1.6 - Vue d'ensemble sur la transformation ATL

Le langage ATL offre différents types d'unités, qui sont définis dans des fichiers d'extension «.atl» distincts. Ces unités sont le module permettant de définir les opérations des transformations des modèles, des requêtes ATL et des bibliothèques qui peuvent être importées par les différents types d'unités ATL, y compris les autres bibliothèques. Un aperçu de ces différents types d'unités est fourni dans la suite.

page 16

1.4 Langage de transformation de modèles ATL

1.4.2 Présentation d'ATL

Un programme ATL qui définit la transformation d'un modèle en un autre modèle est appelé module et est stocké dans un fichier (.atl). Le module est composé d'une section entête, d'une section d'importation de bibliothèques, d'une section de déclaration des fonctions auxiliaires (helpers) et d'une section de spécification des règles de transformation.

Les règles de transformation en ATL peuvent être spécifiées dans un style déclaratif (mat-ched/lazy rules) ou impératif (called rules).

Dans ce qui suit, nous décrivons en détails les différentes sections ATL utilisées dans le cadre de notre programme de transformation.

~ La section d'en-tête (header)

La section d'en-tête définit le nom du module de transformation ainsi que le nom des variables correspondantes aux modèles sources et cibles. Elle encode également le mode d'exécution. La syntaxe de la section d'en-tête est définie comme suit :

module MMa2MMb;

create Mb : MMb [from|refining] Ma : MMa ;

~ La section d'importation

La section d'en-tête définit le nom du module de transformation ainsi que le nom des variables correspondantes aux modèles sources et cibles. Elle encode également le mode d'exécution. La syntaxe de la section d'en-tête est définie comme suit :

uses nom bibliothèque;

~ Les helpers

Les fonctions ATL sont appelées des helpers d'après le standard OCL (Object Constraint Language (OCL)) sur le quel ATL se base. OCL définit deux sortes de helpers : opération et attribut.

1. La syntaxe d'un helper opération est définie comme suit :

helper [context type_du_contexte]? def : nom_du_helper ( nom_paramètre1 : type_paramètre1 , nom_paramètre2 : type_paramètre2) :

type_de_retour = expression;

page 17

1.4 Langage de transformation de modèles ATL

2. La syntaxe d'un helper attribut est définie comme suit :

helper [context type_du_contexte]? def : nom_du_helper : type_de_retour = expression;

Il existe une différence dans la sémantique d'exécution du helper opération et du helper attribut. Le premier est calculé à chaque appel tandis que le deuxième est calculé une seule fois selon l'ordre de sa déclaration dans le fichier ATL.

~ Les règles

Le langage ATL est un langage hybride, il contient aussi bien les constructions déclaratives que les constructions impératives. Le style recommandé est le style déclaratif, cependant, pour faciliter les constructions plus ou moins compliqués il est possible d'avoir recourt au style impératif. Le langage comprend trois types de règles déclaratives et un type de règles impératives. La Figure 1.7 présente la syntaxe abstraite des règles de transformation ATL.

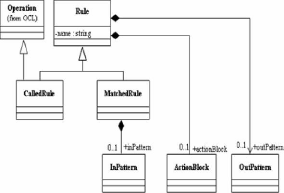
FIGURE 1.7 - Les règles de transformation ATL.

Les règles standards (Matchedrules) :

Ils constituent le noyau de la transformation déclarative. Elles sont appelées une seule fois pour chaque tuple correspondant à leurs motifs d'entrée trouvée dans les modèles source. Elles permettent de spécifier pour quels éléments sources les éléments cibles sont générés ainsi que la façon dont ces éléments cibles sont initialisés.

Les règles paresseuses (lazyrule) :

Elles ressemblent aux règles standards, à la différence qu'elles ne sont déclenchées que par d'autres règles. Elles sont appliquées sur chaque tuple autant de fois qu'elles sont référencées.

page 18

1.5 La plateforme de modélisation sous Eclipse

Les règles paresseuses uniques (unique lazyrule) :

Identiques aux règles paresseuses non uniques, à la différence qu'elles sont appliquées une

unique fois pour chaque tuple.

Les règles appelées (calledrules) :

Elles fournissent le style de programmation impératif. Elles peuvent être vues comme des

helper particuliers. Elles doivent être déclenchées.

~ Les bibliothèques ATL

Une bibliothèque ATL permet de définir un ensemble de helpers qui peuvent être appelés à

partir des différentes unités ATL. Ce fichier est défini par l'en-tête :

library nom_bib;

1.5 La plateforme de modélisation sous Eclipse

Nous présentons brièvement les outils de modélisation de la plateforme Eclipse utilisés au cours de notre travail. Cette présentation concerne EMF, XMI.

1.5.1 Eclipse Modeling Framework (EMF)

L'outil principal utilisé durant ce mémoire est Eclipse Modeling Framework, EMF est une plate-forme de modélisation et de génération de code qui facilite la construction d'outils. Il s'agit d'un ensemble d'outils de développement intégré à l'environnement Eclipse sous forme de plugins.EMF a été conçu pour simplifier le chargement, la manipulation et la sauvegarde de modèles au sein de l'environnement Eclipse.

Il repose sur un formalisme de description de méta-modèles nommé ECore. Ce formalisme est un sous-ensemble de la norme EMOF (Essential MOF), elle-même étant un sous-ensemble de MOF [13].

Parmi les fonctionnalités d'EMF, on peut citer :

~ La génération automatique d'un simple éditeur graphique permettant l'édition des modèles sous forme arborescente, c'est-dire générer automatiquement, à partir d'un méta-modèle,

~ La génération des interfaces de manipulation des modèles consiste à fournir des interfaces graphiques génériques pour manipuler des modèles.

page 19

1.5 La plateforme de modélisation sous Eclipse

~ Un éditeur graphique offrant une vue arborescente d'un modèle. Chacun des noeuds de l'éditeur représentera une instance d'une méta-classe,

~ Enfin, la génération de code, c'est bien là son objectif premier, améliore la productivité de développement d'application par l'automatisation de la génération de code à partir du modèle. Effectivement, une fois le modèle créé « quelques clics » suffisent à cette génération.

Un aperçu d'un fichier ECore ouvert avec son éditeur est illustré par la Figure 1.8.

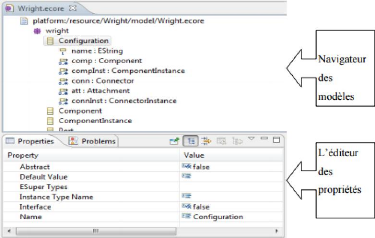
FIGURE 1.8 - Aperçu d'un fichier ECore ouvert avec son éditeur

L'arbre de navigation est utilisé pour naviguer et créer des éléments ECore avec un clic sur l'emplacement souhaité, on a aussi l'éditeur des propriétés est utilisé pour modifier des éléments ECore.

1.5.2 XML Metadata Interchange (XMI)

Le format XMI permet la sérialisation des modèles sous un format physique. Comme son nom l'indique, XMI reprend la syntaxe XML (Extensible Markup Langage), conçue autour du principe de balises [13].

page 20

1.6 Le langage de génération de code Xpand

Un aperçu d'un fichier XMI ouvert avec son éditeur est donné par la Figure 1.9.

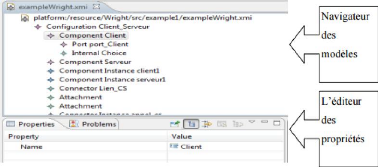
FIGURE 1.9 - Exemple d'un fichier XMI

L'arbre de navigation est utilisé pour naviguer et créer de nouvelles instances XMI avec un clic sur l'emplacement souhaité. La deuxième ligne définit l'instance racine. L'éditeur de propriétés est utilisé pour modifier les instances et établir les liens entre les instances.

1.6 Le langage de génération de code Xpand

Le langage Xpand est utilisé pour contrôler la génération de code. Le template Xpand assure ce contrôle, il est stocké dans un fichier ayant l'extension «.xpt »[14].

1.6.1 Structure générale d'un template Xpand

1. IMPORT

Cette instruction permet d'importer le méta-modèle. Ceci est similaire à une déclaration d'importation JAVA, elle permet de faciliter l'accès aux métaclasses et leurs attributs à partir de l'espace méta-modèle(s) importé(s).

«IMPORT metamodel»

2. le bloc DEFINE

Le concept central de Xpand est le bloc DEFFINE. Ceci l'unité la plus petite identifiable dans le template. L'étiquette se compose d'un nom (templateName), une liste de paramètres ainsi que le nom de la classe du méta-modèle (MetaClasseName) pour

page 21

1.7 Le langage Check pour la vérification de contraintes

laquelle le modèle est défini. Le format de l'instruction DEFFINE se présente comme

suit :

«DEFINE templateName(formalParameterList) FOR MetaClass» a sequence of statements

«ENDDEFINE».

3. L'instruction FILE

Cette instruction, et à partir de ces directives, redirige la sortie produite à une cible spécifique. Le format de l'instruction FILE se présente comme suit :

«FILE expression »

a sequence of statements«ENDFILE»

4. L'Instruction EXPAND

L'instruction EXPAND appelle un bloc DEFINE et insère sa production "output" à son emplacement. Il s'agit d'un concept similaire à un appel de méthode. Le format de l'instruction EXPAND se présente comme suit :

«EXPAND definitionName [(parameterList)] [FOR expression | FOREACH expression [SEPARATOR expression]]»

1.7 Le langage Check pour la vérification de contraintes

La plate forme (OAW) Open Architecture Ware fournit aussi un langage formel appelé Chek (Xpand) pour la spécification des contraintes que le modèle doit respecter pour être correct est basé sur OCL.

Les contraintes spécifiées avec ce langage doivent être stockées dans des fichiers avec l'extension « .Chk ». Ce fichier doit commencer par une importation du méta-modèle selon le format « import metamodel; ».

Chaque contrainte est spécifiée dans un contexte, soit une méta-classe du méta-modèle importé, pour lequel la contrainte s'applique.

Les contraintes peuvent être de deux types :

~ Warning : dans ce cas, si la contrainte n'est pas vérifiée un message sera affiché sans que l'exécution s'arrête.

~ Error : dans ce cas, si la contrainte n'est pas vérifiée un message sera affiché et l'exécution sera arrêtée.

page 22

1.8 MWE (Modeling Workflow Engine)

Example:

context Entity WARNING

"Names have to be more than one character long" : name.length > 1;

Cette contrainte avertit que l'attribut name des instances de la méta-classe Entity doit normalement être plus long qu'un caractère. Le langage Check est basé sur OCL (OCL).

1.8 MWE (Modeling Workflow Engine)

MWE, est une composante d'EMFT (EMF Technology), est un moteur de génération déclaratif configurable qui s'exécute sous Eclipse. Il fournit un langage de configuration simple, basé sur les balises XML. Un générateur workflow est composé d'un ensemble de composants qui sont exécutées séquentiellement dans une JVM (Java Virtual Machine) unique.

~ Les propriétés

Ce sont des variables qui contiennent des valeurs utilisables par d'autres éléments. Les propriétés peuvent être déclarées n'importe où dans un fichier workflow. Ils seront disponibles après leurs déclarations.

Il y a deux types de propriétés : les propriétés fichiers et les propriétés simples. L'utilisa-tion d'une propriété se fait selon le format.

La balise <property> possède plusieurs attributs :

1. name : cet attribut définit le nom de la propriété.

2. value : cet attribut définit la valeur de la propriété .

3. file : cet attribut permet de préciser le nom d'un fichier qui contient la définition d'un ensemble de propriétés. Ce fichier sera lu et les propriétés qu'il contient seront définies.

Example 1

<component

class="org.eclipse.emf.mwe.utils.DirectoryCleaner"> <directory="${runtimeProject}/src-gen"> </component>

page 23

1.9 Conclusion

~ Les composants

Les composants workflow représentent une partie du processus générateur. Ils représentent généralement les analyseurs modèles, validateurs de modèles, les transformateurs de modèles et les générateurs de codes.

Example 1

<component

class="org.eclipse.emf.mwe.utils.DirectoryCleaner"> <directory="${runtimeProject}/src-gen"> </component>

Le composant DirectoryCleaner contient, entre autre, la propriété directory. Il permet de nettoyer le répertoire, ici runtimeProject/src-gen, qui contient des artefacts générés avant de (re-) produire ces artefacts.

Example 2

<bean class="org.eclipse.emf.mwe.utils.StandaloneSetup"> <platformUri="${runtimeProject}/..">

</bean>

La classe StandaloneSetup n'est pas un composant du workflow au sens étroit. Toutefois, cette classe a besoin d'être référencée dans le workflow afin de mettre en place le méta-modèle EMF défini en mode autonome. Elle contient, entre autre, la propriété platformUri.

1.9 Conclusion

D

ans ce chapitre, nous avons présenté une étude sur l'Ingénierie Dirigé par les modèles (IDM) et les outils que nous allons l'utiliser dans la suite de cet mémoire: EMF, XMI, ATL, Xpand, check et MWE, autour de la plate forme Eclipse. Dans le prochain chapitre nous présenterons un aperçu sur la méta-modélisation semi-formelle avec ECore.

24

2 Méta-modélisation :Le méta-modèle

ECore

Sommaire
2.1 2.2 2.3 2.4	Introduction La méta-modélisation Les langages de méta-modélisation 2.3.1 MOF (Meta Object Facility) 2.3.2 ECore Le Méta-modèle ECore		25 25 26 26 26 27
	2.4.1	Noyau d'ECore	27
	2.4.2	Caractéristiques structurelles	28
	2.4.3	Caractéristiques comportementales	31
	2.4.4	Classificateurs	33
2.5	Etude de cas		36
	2.5.1	Présentation informelle	37
	2.5.2	Spécification du système bancaire en ECore	37
2.6	Conclusion		38

page 25

2.1 Introduction

2.1 Introduction

L

a méta-modélisation est l'activité de construire des méta-modèles, elle représente un

concept fondamental sur lequel se base l'ingénierie, et son utilisation s'est accentuée
avec l'arrivée de l'IDM. Elle vise à fournir des langages de méta-modélisation plus abstraites et facilement maîtrisables que des langages de programmation.

Ce chapitre intitulé la méta-modélisation semi-formelle avec ECore est composé de quatre sections, la première section présente la méta-modélisation dans le domaine de l'informatique, la deuxième section présente un aperçu sur certain langages de méta-modélisation dans le contexte de l'ingénierie des modèles, la troisième présente les concepts du méta-modèle ECore, et dans la dernière section nous éditons un exemple de modèle ECore conforme à son méta-modèle ECore.

2.2 La méta-modélisation

Dans le domaine de l'informatique, la méta-modélisation se définit comme la mise en évidence d'un ensemble des concepts pour un domaine particulier. Un langage de modélisation conceptuel peut servir dans la plupart des cas comme un langage de méta-modélisation. La Figure 2.1 illustre les notions de base de la méta-modélisation.

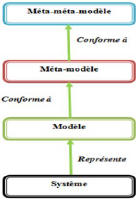
FIGURE 2.1 - Notions de base de la méta-modélisation

page 26

2.3 Les langages de méta-modélisation

Plusieurs technologies sont disponibles pour l'expression de ces langages, telles que le standard MOF 2.0 de l'OMG [25][26], le Framework EMF dans la sphère Eclipse. Ces technologies de méta-modélisation offrent aux utilisateurs un cadre pour la définition de la syntaxe abstraite des langages de modélisation en utilisant une notation semi-formelle souvent orientée objet. Ainsi, plusieurs environnements et langages de méta-modélisation sont apparus comme EMF/ECore [24].

2.3 Les langages de méta-modélisation

Les premiers travaux de la communauté IDM se sont portés sur la définition du bon niveau d'abstraction des concepts pour définir des langages de méta-modélisation. Parmi ces travaux on cite à titre d'exemple MOF, et aussi ECore implémenté dans le projet EMF d'Eclipse.

Dans cette section, nous allons présenter les langages de méta-modélisation les plus connus en détaillant ECore.

2.3.1 MOF (Meta Object Facility)

Le MOF est un standard de l'OMG (Object Management Group) depuis novembre 1997. C'est un formalisme, pour établir des langages de modélisation (méta-modèles) permettant eux-mêmes de définir des modèles. Le but du MOF est de définir un langage de méta-modélisation (méta-métamodèle) pour représenter des méta-modèles et des modèles. Le MOF peut être étendu par héritage ou par composition de manière à représenter des modèles plus

2.3.2 ECore

ECore est un méta-modèle très proche du MOF. Il est important de savoir que les méta-modèles conformes à ce méta-modèle sont composés d'EClass contenant des EAttributes et des EReferences. Le méta-modèle ECore a été conçu proprement à des implémentations Java [23].

page 27

2.4 Le Méta-modèle ECore

La Figure 2.2 illustre les 17 éléments qui composent le méta-modèle ECore.

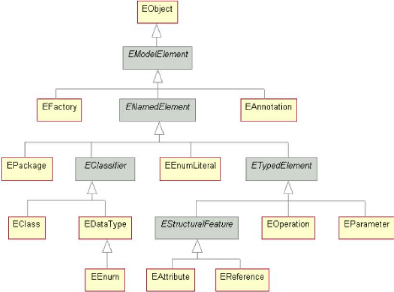
FIGURE 2.2 - Les concepts du méta-modèle ECore

2.4 Le Méta-modèle ECore

Dans cette partie, nous allons examiner ECore en détail, dans le but de l'utiliser dans notre contexte de transformation comme méta-modèle source.

2.4.1 Noyau d'ECore

Nous commençons par une illustration d'un sous-ensemble simplifié du méta-modèle ECore. Nous le décrivons comme le noyau d'ECore avec des ajouts d'autres concepts. Ce modèle est illustré sur la Figure 2.3, et définit quatre types d'objets qui sont quatre classes :

1. EClass : modélise les classes elles-mêmes. Les classes sont identifiées par leur nom et peuvent contenir un certain nombre d'EAttributes et d'EReferences. Pour soutenir l'héritage, une classe peut se référer à un certain nombre d'autres classes que ses supertypes.

page 28

2.4 Le Méta-modèle ECore

2. EAttribute : modélise les attributs, les composantes des données d'un objet. Ils sont identifiés par leur nom, et ils ont un type.

3. EDataType : modélise les types d'attributs, représentant des types de données primitifs et objets qui sont définis dans Java, mais pas dans EMF. Les types de données sont également identifiés par leur nom.

4. EReference : est utilisé dans les associations de modélisation entre les classes; il modélise une extrémité d'une telle association. Tout comme les attributs, les références sont identifiés par leur nom et ont un type. Cependant, ce type doit être EClass à l'autre extrémité de l'association. Si l'association est navigable dans la direction opposée, il y aura une autre référence correspondante. Une référence précise bornes inférieures et supérieures sur sa multiplicité.

Maintenant, avec ce sous-ensemble d'ECore, nous pouvons aborder le reste du modèle.

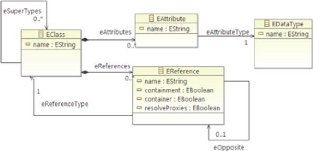
FIGURE 2.3 - Noyau d'ECore

2.4.2 Caractéristiques structurelles

En regardant le noyau ECore, nous remarquons un certain nombre de similitudes entre «EAttribute» et «EReference», ils ont tous deux noms et types. Pour capturer ces similitudes, ECore comprend une base commune pour ces deux classes, appelé EStructuralFeature.

page 29

2.4 Le Méta-modèle ECore

La situation est illustrée dans la Figure 2.4.

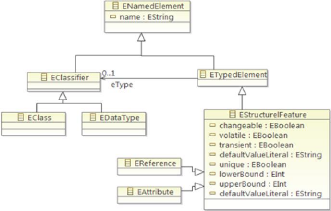
FIGURE 2.4 - Concept EStructuralFeature

Comme le montre la Figure, EStructuralFeature est, elle-même, provenant d'autres super-types. «ENamedElement» définit un seul attribut, le nom que nous avons vu dans chaque classe discuté jusqu'à présent. La plupart des classes en ECore étendent cette classe afin d'hériter de cet attribut.

Un autre aspect commun d'EAttribute et EReference que nous avons observé est la notion d'un type. Parce que cela est également partagé avec d'autres classes d'ECore, comme nous le verrons bientôt, l'attribut eType est pris en dehors dans «ETypedElement», le supertype immédiat de «EStructuralFeature».

Le type de «eType» est EClassifier, une classe de base commune de «EDataType» et «Eclass» qui étaient les types requis pour «eAttrbituteType» et «eFeatureType».

EStructuralFeature comprend un certain nombre d'attributs utilisés pour caractériser les deux, «EAttribute» et «EReference». Cinq attributs booléens définissent les caractéristiques structurelles :

~ Changeable : détermine si la valeur de la fonction peut être réglée de l'extérieur. ~ Transient : détermine si la fonction est omise de la sérialisation de l'objet auquel il appartient.

~ Unique : qui n'a de sens que pour les fonctions de multiplicité, spécifie si une seule valeur est empêché de se produire plus d'une fois dans la fonction.

page 30

2.4 Le Méta-modèle ECore

~ Unsettable : précise si la fonction a une valeur supplémentaire possible, appelé unset, qui est unique à partir de l'une des valeurs juridiques de son type.

~ Volatile : précise si la fonction n'a pas de stockage directement; ce qui est généralement le cas lorsque la valeur de la fonction est dérivée uniquement à partir des valeurs d'autres caractéristiques.

2.4.2.1 EAttribute

Après avoir ce que les EAttributes ont en commun avec des EReferences, nous allons maintenant examiner ce qui les distingue.

Figure 2.5 illustre les aspects uniques de «EAttribute».

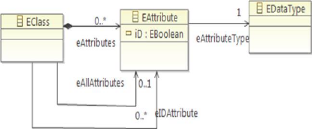
FIGURE 2.5 - Concept EAttribute

EAttribute définit également une référence «eAttributeType», qui fait référence à la même «EClassifier» que «eType», que nous avons décrit dans le paragraphe précédent. Cependant, le type d'un attribut doit être un type de données et non pas une classe, donc cette référence jette cet objet à un «EDataType».

Comme nous l'avons vu dans la Figure 2.3, «EAttribute» sont contenus par un «Eclass» via sa référence de «eAttributes».

2.4.2.2 ERéférence

Les aspects uniques de «EReference» sont illustrés à la Figure 2.6

page 31

2.4 Le Méta-modèle ECore

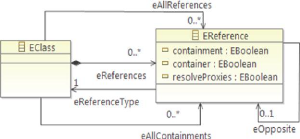
FIGURE 2.6 - Concept EReference

EReference ajoute deux références et trois attributs à ceux définis par « EStructuralFea-ture ». La première référence « eReferenceType », est analogue au « eAttributeType » de EAttribute. Il se réfère à la même EClassifier que « eType » de EStructuralFeature, mais castée à « Eclass ». La référence « eOpposite », se réfère à la référence représentant la direction opposée d'une association bidirectionnelle. Ainsi, une telle association est représentée par les deux EReferences, chacun définissant l'autre comme eOpposite.

EReference est également analogue à EAttribute dans sa relation de confinement avec « Eclass ». Un EClass contient EReference via sa référence « eReferences ».

2.4.3 Caractéristiques comportementales

En plus de leurs caractéristiques structurelles, ECore peut modéliser les caractéristiques comportementales d'un EClass comme « EOperation ». Un modèle de base ne donne aucune indication sur le comportement réel des opérations. Les corps des opérations doivent être codés à la main dans les classes Java générées.

page 32

2.4 Le Méta-modèle ECore

EOperation et EParameter illustré dans la Figure 2.7.

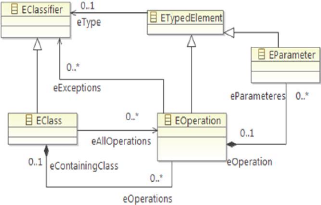
FIGURE 2.7 - Concept EOperation et EParameter

La relation « eOperations » avec EClass est tout à fait semblable à ceux de « eAttributes » et « eReferences ».

EOperations sont contenus par un EClass via la référence de « eOperations », et une référence de « eAllOperations » est définie pour inclure les opérations d'une classe et ses supertypes. Aussi EOperation fait partie d'une association bidirectionnelle, ce qui permet une EOperation d'obtenir facilement Eclass qui contient via la référence en face « eContai-ningClass ».

Un EOperation contient zéro ou plusieurs EParameter, accessibles via « eParameters », qui modélisent les paramètres d'entrée de l'opération, cette référence constitue la moitié d'une association bidirectionnelle; les EParameters peuvent accéder au « EOperation » auquel ils appartiennent via « eOperation ».

Les deux EOperation et EParameter héritent de l'attribut « name » et la référence « eType » de « ETypedElement ». Ces références de « eType » modélisent le type de retour de l'opération et le type de paramètre, et peuvent se référer à tout EClassifier (si EClass ou EDataType).

Enfin, EOperation définit une référence supplémentaire « eExceptions » à zéro ou plusieurs EClassifiers.

page 33

2.4 Le Méta-modèle ECore

2.4.4 Classificateurs

Après avoir présenté les caractéristiques structurelles et comportementales d'ECore, nous allons maintenant revenir et prendre un regard détaillé sur les classes. Comme nous l'avons déjà vu, EClass partage une classe de base avec EDataType, donc nous allons devoir discuter les deux ensembles.

Cette classe de base « EClassifier » agit comme un objectif commun pour la référence « eType » de ETypedElement, permettant de spécifier les types de caractéristiques structurelles, des opérations et des paramètres, soit des classes ou des types de donnés. Comme la montre la Figure 2.8

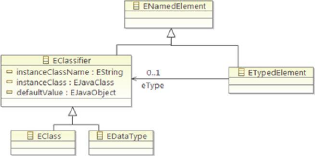
FIGURE 2.8 - Concept EClassifier

EClassifier contribue un certain nombre d'attributs et des opérations. Aussi, il hérite d'un

attribut name d'ENamedElement. 2.4.4.1 Les classes

Les aspects uniques de « Eclass » sont illustrés à la Figure 2.9.

page 34

2.4 Le Méta-modèle ECore

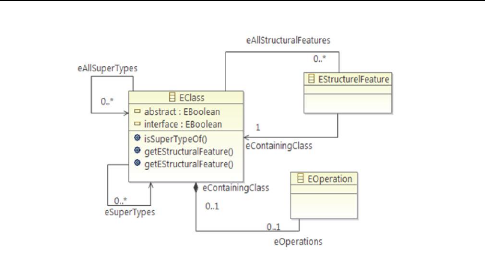
FIGURE 2.9 - Concept EClass

Nous avons déjà discuté les relations entre EClass et les classes qui représentent les caractéristiques structurelles et comportementales.

Nous avons vu la référence « eOperations » de confinement et son contraire « eCon-tainingClass », qui relient un EClass avec ses EOperations. Nous avons également vu « eAttributes » et « eReferences », qui ne sont pas bidirectionnel, mais de même connecter un EClass à ses EAttributes et EReferences.

EClass définit également une référence appelée « eAllStructuralFeatures » qui regroupe les objets accessibles via « eAllAttributes » et « eAllReferences », il comprend toutes les caractéristiques structurelles définies et héritées par une classe.

Les deux attributs définis par EClass lui-même peut être utilisé pour spécifier le type particulier de la classe en cours de modélisation. Si l'interface est vraie, EClass représente une interface, qui ne peut pas être instanciée. Si abstraite est vrai, le EClass représente une classe abstraite, à partir de laquelle d'autres classes peuvent hériter des caractéristiques.

ECore comprend un certain nombre de classes abstraites, dont la plupart nous l'avons déjà vu : ENamedElement, EClassifier, ETypedElement et EStructuralFeature.

2.4.4.2 Types de données

Alors que les classes définissent plusieurs caractéristiques structurelles et comportementales, les types de données représentent un seul élément de données «simples». Cette dis-

page 35

2.4 Le Méta-modèle ECore

tinction est assez similaire, mais pas identique, qu'entre les classes et les types primitifs en Java.

En général, il est considéré comme une mauvaise idée de représenter une classe Java très complexe en tant que type de données. Au lieu de cela, il est préférable de modéliser directement la classe EMF avec un EClass et, par conséquent, de bénéficier de l'assistance du cadre en matière de sérialisation, la notification et la réflexion. En règle générale, si ses valeurs ne peuvent pas être simplement représentées comme une chaîne sans l'utilisation d'une notation d'imposer la structure, il ne devrait probablement pas être modélisée comme un type de données [4].

2.4.4.3 Types énumérés

Un type énuméré est un type de données spécial qui est défini par une liste explicite des valeurs qu'il peut éventuellement prendre, appelés littéraux.

La Figure 2.10 illustre EDataType, EEnum et EEnumLiteral, les types de données du modèle, les types énumérés, et littéraux, respectivement.

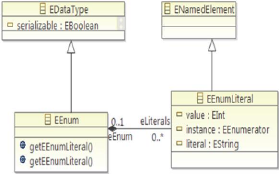
FIGURE 2.10 - Concept EDataType, EEnum et EEnumLiteral

Un EEnum spécifie zéro ou plus EEnumLiteral via la référence de confinement «eLiterals» qui est bidirectionnelle avec un «eEnum» opposé. EEnumLiteral hérite d'un attribut name de «ENamedElement ». EEnum définit une opération «getEEnumLiteral» pour retourner le «EEnumLiteral» de «eLiterals» avec un nom.

page 36

2.5 Etude de cas

2.4.4.4 Package

En ECore, les classes et les types de données sont groupées en paquets, EPackage apporte des facilités pour accéder aux métadonnées du modèle. Elle contient des accesseurs aux EClasses, EAttributes et EReferences implémentées dans le modèle.

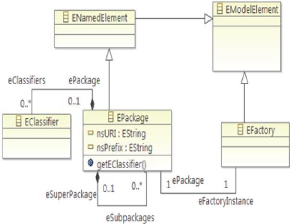
FIGURE 2.11 - Concept EPackage

EPackage hérite d'un attribut name de « ENamedElement ». Le nom d'un paquet doit être unique. Au lieu de cela, un URI est utilisé pour identifier de manière unique le paquet, est également utilisé dans la sérialisation des documents d'instance pour identifier un espace de noms, Cette URI est donnée à l'attribut « nsURI » du EPackage. Et l'attribut « nsPrefix » est utilisé pour spécifier le préfixe d'espace de noms correspondant.

Les EClassifiers regroupés par un EPackage sont contenus via la référence de « eClassifiers », qui a une référence en face appelé « ePackage ». Une opération de « getEClassifier » est également définie, pour obtenir commodément un de ces EClassifiers par nom.

2.5 Etude de cas

Dans cette section, nous présentons un exemple pour bien illustrer nos propos, il s'agit d'une application de `Système Bancaire (BANK) » décrit par J-R Abrial [4].

page 37

2.5 Etude de cas

2.5.1 Présentation informelle

La fonction de ce système « Système Bancaire » est de modéliser le comportement d'un Bank. Un Bank gère des comptes pour des personnes. On va développer le modèle simple d'un Bank où les gens (clients de la banque) peuvent ouvrir ou fermer un compte et faire un dépôt ou retirer de l'argent sur leur compte, aussi peuvent transférer et économiser d'argent entre les comptes.

On pourrait définir deux classes CLIENTS et ACCOUNTS. Chacun de ces comptes doit être connecté à un seul client. Les personnes peuvent devenir des clients des Bank, puis ouvrir successivement un ou plusieurs comptes. On pourrait définir aussi un type énuméré « KIND » qui contient deux littéraux définissant les type d'un compte bancaire qui peut être un compte normal ou bien compte Savings « normal et Savings ».

2.5.2 Spécification du système bancaire en ECore

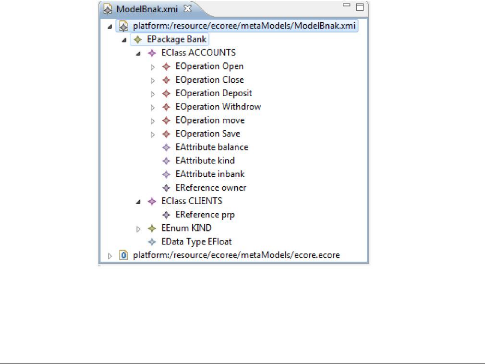
FIGURE 2.12 - Modèle ECore d'un Bank

Les deux figures Figure 2.12 et Figure 2.13 representent le modèle Ecore d'un Système bancaire"Bank".

page 38

2.6 Conclusion

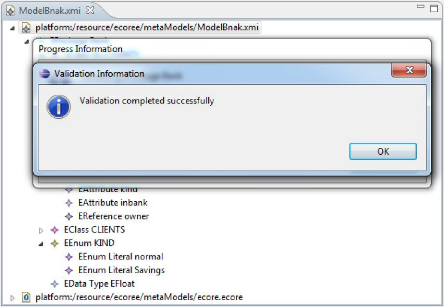
FIGURE 2.13 - Modèle ECore d'un Bank validé

2.6 Conclusion

D

ans ce chapitre, nous avons présenté la méta-modélisation ECore en détaillant les concepts de ce méta-modèle pour l'utiliser dans notre approche de transformation .Aussi nous avons édité un modèle ECore d'un Système Bancaire « Bank » conforme au méta-modèle ECore.

Dans le chapitre suivant, nous allons présenter un aperçu sur le langage formel Event-B que nous avons choisi dans notre contexte de transformation.

39

3 La méthode formelle Event-B

Sommaire

3.1 Introduction 40

3.2 Quelques langages formels 40

3.2.1 Le langage Z 40

3.2.2 La méthode B 41

3.2.3 La méthode Event-B 41

3.3 Modèle Event-B 42

3.3.1 Structure d'une Machine 42

3.3.2 Structure d'un Contexte 43

3.3.3 Structure d'un Evénement 43

3.4 Exemple de machine en Event-B 47

3.5 RODIN : l'outil support d'Event-B 48

3.6 Conclusion 49

page 40

3.1 Introduction

3.1 Introduction

B

ien que les méthodes formelles demandent des efforts importants dans leur mise en oeuvre et qu'elles soient consommatrices de temps, les études ont montré l'intérêt de leur utilisation lors de chacune des phases du cycle de développement logiciel pour aider à structurer le raisonnement et apporter des garanties sur le développement.

Ce chapitre est composé de quatre sections. La première section présente un aperçu sur quelques langages formels. La deuxième section présente la structure d'une machine, d'un contexte et d'un Evénement. La troisième section présente un exemple de machine en Event-B. Enfin, la quatrième section présente la plateforme de développement RODIN.

3.2 Quelques langages formels

Les méthodes formelles sont des techniques qui peuvent être utilisées lors de chacune des phases du cycle de développement logiciel pour aider à structurer le raisonnement et apporter des garanties sur le développement. Pour cela, ces méthodes reposent sur un raisonnement mathématique rigoureux fondé sur un langage formel.

Les langages formels servent à spécifier de manière mathématique, via la théorie des ensembles et la logique de prédicat du premier ordre, un système complexe.

3.2.1 Le langage Z

Le langage Z est un langage pour exprimer les spécifications formelles de systèmes informatiques [22]. La notation de langage Z s'inspire de la formalisation de la théorie de ensembles et de la théorie du premier ordre. Il est basé sur la notation d'un schéma qui se compose d'une collection d'objets nommés variables et spécifiés par certains axiomes. Le schéma est une unité de spécification de Z, encapsule une partie déclaration et une partie contrainte, comme le montre la Figure 3.1.

page 41

3.2 Quelques langages formels

FIGURE 3.1 - L'unité de spécification de Z

Le schéma illustré par la Figure 3.1 représente une boite contenant des descriptions utilisant les notations Z. Les schémas sont utilisés pour décrire les états d'un système, les états initiaux ou bien les opérations.

3.2.2 La méthode B

La méthode B est une méthode de spécification formelle permettant de décrire un système de son analyse à son implémentation [1] [2]. Son formalisme s'appuie sur des notations mathématiques utilisant la théorie des ensembles et la logique du premier ordre pour spécifier à la fois le système et ses propriétés. La méthode B se base sur le concept de machine abstraite représentant le système. Cette machine abstraite décrivant le comportement général est détaillée au fur et à mesure de la modélisation pour devenir plus concrète et plus proche de 1'implémentation finale du système. Ce processus est appelé raffinement. Il joue un rôle central dans la méthode B. Les étapes de raffinement sont prouvées afin de garantir que les modèles successifs modélisent le même système et qu'aucune erreur n'est introduite lors de la modélisation. De nombreux outils comme l'atelier B, les éprouveurs B ou ProB [30] appuient le développement de systèmes avec la méthode B.

3.2.3 La méthode Event-B

Event-B [4] est une méthode basée sur la méthode B avec un aspect événementiel. Elle permet de spécifier le comportement d'un système appelé « système d'événements » de manière à inclure ses propriétés critiques dans la conception. Dans la méthode Event-B, le modèle initial est successivement raffiné plusieurs fois pour atteindre une modélisation correcte par construction [3]. Les propriétés introduites sont également prouvées et l'utilisation d'une notation mathématique permet une modélisation indépendante de toute considération

page 42

3.3 Modèle Event-B

informatique. La communauté Event-B étant très active, et du fait de l'utilisation industrielle de la méthode, des outils performants sont proposés. Des outils de preuve et des vérificateurs de modèles (model checkers).

3.3 Modèle Event-B

Le modèle est le premier concept d'Event-B. Il est composé d'un ensemble des machines et des contextes. Un modèle Event-B peut contenir des contextes seulement, des machines seulement ou les deux. Dans le premier cas, le modèle représente une structure mathématique pure. Le deuxième cas représente un modèle non paramétré.

3.3.1 Structure d'une Machine

La machine Event-B contient des éléments dynamiques qui décrivent l'état du système. Une machine est constituée de trois sections principales : les variables sont données dans la clause VARIABLES et initialisées dans la clause Initialisation, aussi les invariants définit l'espace d'état des variables, et les évènements. La machine est constituée de plusieurs clauses, ces clauses sont décrites comme suit :

~ MACHINE : La clause MACHINE représente le nom du composant qui devrait être unique dans un modèle.

~ SEES : la clause SEES spécifie la liste des contextes « vus » par la machine. Dans ce cas la machine peut utiliser les constantes les ensembles et les axiomes figurant dans le contexte.

~ VARIABLES : définit la liste des variables introduites dans la machine qui constituent l'état du système. Les valeurs de ces variables sont initialisées dans Initialisation et peuvent changer par les évènements.

~ INVARIANTS : sert au typage des variables et à décrire les contraintes qu'elles doivent respecter sous forme des prédicats.

~ EVENTS : contient la liste des événements qui opèrent une ou plusieurs substitutions sur la valeur des variables. L'événement INTIALISATION donne une valeur initiale aux variables.

page 43

3.3 Modèle Event-B

3.3.2 Structure d'un Contexte

Un contexte représente la partie statique du modèle, il est composé de constantes et d'axiomes décrivant les propriétés de ces constantes. Un contexte peut être visible pour une machine en utilisant la clause « SEES ».

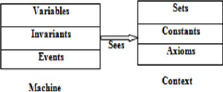
FIGURE 3.2 - Relation entre un contexte et une machine

La structure du contexte est constituée d'un ensemble de clauses introduites par des mots clés, ces clauses sont décrites comme suit :

~ CONTEXT : représente le nom du composant qui devrait être unique dans un modèle.

~ SETS : définit les ensembles porteurs du modèle. Ces ensembles non vides servent à typer le reste des entités du modèle.

~ CONSTANTS : cette clause contient la liste des constantes utilisées par le modèle. Dans la suite nous présentons les constituants d'un évènement Event-B.

3.3.3 Structure d'un Evénement

En Event-B, les événements remplacent les opérations. Un événement d'initialisation permet de définir les valeurs initiales des variables. Ces valeurs doivent établir les invariants. Les autres événements ont des gardes qui garantissent des propriétés. Les gardes sont définies dans la clause WHEN et sont mises en conjonction. Si l'une des gardes d'un événement est fausse, l'événement ne peut pas être déclenché. Les actions d'un événement sont exécutées de manière concurrente, et il n'est pas possible de modifier la même variable dans deux actions d'un même événement.

page 44

3.3 Modèle Event-B

La structure d'un évènement est constituée d'un ensemble de clauses introduites par des mots clés. Ces clauses sont décrites comme suit :

~ ANY : énumèe la liste des paramètres de l'évènement.

~ WHERE : contient les différentes gardes de l'évènement. Ces gardes sont des conditions nécessaires pour déclencher l'évènement. Il faut noter que si la clause « any » est omise le mot clé « where » est remplacé par « when ».

~ WITH : lorsqu'un paramètre abstrait disparait dans la version concrète de cet évènement, il est indispensable de définir un témoin sur l'existence de ce paramètre. ~ THEN : décrit la liste des actions de l'évènement.

3.3.3.1 Les différentes formes des événements

Les évènements, dans Event-B, peuvent avoir l'une des trois formes : indéterminée, gardée ou simple. La sémantique formelle d'un évènement s'exprime à partir de la sémantique de la substitution autrement dit la relation qui existe entre la valeur des variables avant et après le déclenchement de l'évènement.

La première est la forme dite indéterministe où x est une variable d'état du système et t une variable locale. L'évènement ne se déclenche que s'il existe une valeur de la variable t qui satisfait le prédicat G(x, t).x : P (x', x, t) est l'action de l'évènement. La présence de la variable locale t fait que cet évènement est non déterministe.

EVENT nom
ANY
t
WHERE
G(x, t)
THEN
x : P(x, x0, t)
END

page 45

3.3 Modèle Event-B

La seconde forme est celle dite gardée dans laquelle il n'y a pas de variable locale et où la garde et l'action ne dépendent que des variables d'états du modèle.

EVENT nom
WHEN
G(x)
THEN
x : P(x, x0)
END

La forme simple inclut seulement une action. Cela équivaut donc à une garde qui est toujours vraie.

EVENT nom
BEGIN
x : P(x, x0)
END

Il existe aussi un évènement avec une action et une garde vide : l'évènement skip. Rappelons qu'il existe un évènement obligatoire, nommé INITIALISATION, qui est toujours de la forme simple. A la différence d'un véritable évènement, cet évènement permet d'initialiser le système en spécifiant les valeurs initiales possibles (qui doivent bien sûr respecter les invariants).

Avant de passer aux obligations de preuve d'un modèle B, il faut présenter les prédicats avant-après des événements traditionnellement notés BA (pour before after en anglais). Ces prédicats définissent la relation entre la valeur des variables d'état avant et après le déclenchement des événements. La valeur d'une variable x après le déclenchement d'un événement est notée x'. Par exemple le prédicat avant-après de l'événement TICK de la machine HORLOGE est heure' = heure+1.Le tableau 3.1 résume les prédicats avant-après selon la forme des événements.

page 46

3.3 Modèle Event-B

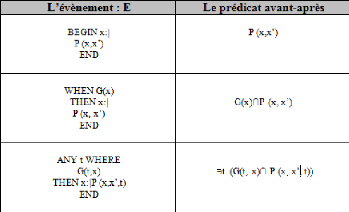
TABLE 3.1 - prédicats avant-après 3.3.3.2 Obligations de preuves

Les obligations de preuve définissent ce que doit être prouvée pour un modèle Event-B. Ils sont générés automatiquement par un générateur d'obligations de preuve. Ce générateur vérifie les machines et les contextes et il décide ce que doit être prouvé dans ces machines et contextes.

Nous décrivons dans ce qui suit les obligations de preuve associées à une machine abstraite d'un modèle Event-B.

L'obligation de preuve de préservation de l'invariant : INV

Cette obligation de preuve assure que chaque invariant d'une machine soit préservé par chaque évènement. Pour un évènement evt et un invariant inv (x), l'obligation de preuve associée est "evt / inv / INV". Si I(x) est l'invariant du système, alors pour tout évènement E du système qui a comme prédicat avant-après BA l'obligation de preuve est comme suit:

I(x)?BA(x, x^') = I(x^')

Par rapport à notre exemple l'obligation de preuve est la suivante :

Heure E 0..23 heure < 23

F-

heure := heure + 1

page 47

3.4 Exemple de machine en Event-B

L'obligation de preuve de Faisabilité : FIS

Le but de cette obligation de preuve est de s'assurer que l'action non-déterministe est réalisable. Pour un évènement evt et une action act l'obligation de preuve associée est "evt/act/-FIS". I étant l'invariant du système, alors l'obligation de preuve qui correspondant à un évènement E est comme suit :

I (x)?grd(E) = x^'.P(x, x^')

Heure E 0..23 heure < 23

F-

?i.i E 0..23 ?i := heure + 1

Par rapport à notre exemple l'obligation de preuve est la suivante :

3.4 Exemple de machine en Event-B

Dans cette section nous présentons un petit exemple pour illustrer nos propos. Il s'agit d'une machine Event-B modélisant le comportement d'une horloge. Le modèle contient une variable heure qui contient l'heure courante, cette variable est un entier naturel compris entre 0 et 23.Un événement TICK fait évoluer l'heure courante et un autre événement RAZ remet l'heure à zéro quant celle-ci dépasse 23.L'initialisation met la valeur de l'horloge à 0.

page 48

3.5 RODIN : l'outil support d'Event-B

MACHINE horloge VARIABLES heure

INVARIANT Heure E 0..23 INITIALISATION heure := 0 EVENTS

EVENT TICK WHERE

Heure < 23 THEN

Heure := heure + 1 END

EVENT RAZ WHERE

heure = 23 THEN

heure := 0 END

3.5 RODIN : l'outil support d'Event-B

Event-B fournit actuellement un logiciel libre sous la forme d'une plateforme (dérivée de « Eclipse ») de spécification et de preuve, appelé RODIN [27] [28]. Cette dernière a été initialement développée dans le cadre d'un projet européen.

page 49

3.6 Conclusion

La plate-forme Rodin, illustrée dans la Figure 3.3

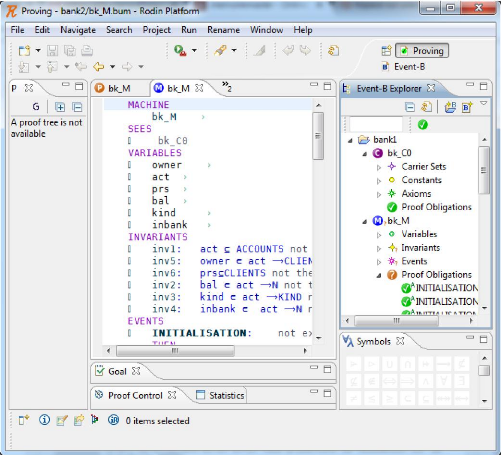
FIGURE 3.3 - La plateforme RODIN

3.6 Conclusion

D

ans ce chapitre, nous avons présenté d'une façon rigoureuse les concepts de base de la méthode formelle Event-B. Une telle méthode permet le développement pas-à-pas des logiciels corrects par construction.

Deuxième partie

50

Contribution

51

4 Une approche IDM pour la généra-

tion de modèle Event-B à partir de

modèle ECore

Sommaire

4.1 Introduction 52

4.2 Les méta-modèles de notre approche 52

4.2.1 Méta-modèle Event-B 52

4.2.2 Méta-modèle ECore 59

4.3 Formalisation en Event-B 63

4.3.1 Formalisation du concept EPackage en Event-B 63

4.3.2 Formalisation du concept EClass en Event-B 64

4.3.3 Formalisation du concept EEnum en Event-B 64

4.3.4 Formalisation du concept EAttribute en Event-B 65

4.3.5 Formalisation du concept EReference en Event-B 67

4.3.6 Formalisation du concept EOperation en Event-B 69

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles). . . . 70

4.4.1 Transformation de modèles M2M 71

4.4.2 Transformation de modèle M2T 81

4.5 Vérification formelle par l'outil Rodin 88

4.5.1 Preuves d'une machine 88

4.6 Conclusion 91

page 52

4.1 Introduction

4.1 Introduction

C

e chapitre comporte quatre sections, la première section présente les méta-modèles Event-B et ECore que nous utilisons dans notre contexte de transformation. Dans la deuxième section nous présentons notre contribution qui consiste à la formalisation en Event-B des concepts ECore. Dans la troisième section nous présentons la transformation des modèles M2M (ECore2Event-B) en utilisant ATL comme langage de transformation, ensuite nous présentons la transformation M2T (Event-B2TexteEvent-B).Et enfin nous présentons la validation sur la plateforme RODIN.

4.2 Les méta-modèles de notre approche

Pour définir un langage de modélisation, il est nécessaire de définir sa syntaxe abstraite et sa syntaxe concrète. Les méta-modèles représentent pour notre approche la base de la transformation. Pour chacune de ces transformations, chaque modèle est défini dans son propre méta-modèle.

4.2.1 Méta-modèle Event-B

Le méta-modèle que nous proposons pour Event-B donne une vue structurelle de haut niveau reprenant les notions définies au niveau de la syntaxe Event-B. Nous nous en servons ici pour donner une vision globale des dépendances entre les différentes constructions du langage Event-B. Dans un premier temps, nous procéderons à la spécification du fragment du méta-modèle correspondant à une machine Event-B, ensuite nous proposerons un fragment du méta-modèle exprimant le contexte Event-B ainsi qu'un fragment du méta-modèle exprimant l'événement. Et Enfin nous terminerons par une vue d'ensemble de notre méta-modèle Event-B utilisé comme méta-modèle cible pour notre approche de transformation ECore vers Event-B.

4.2.1.1 Méta-Classe de Context

Un Context représenté est constitué de plusieurs clauses permettant de spécifier les parties statiques du système. La partie statique correspond aux déclarations d'ensembles, de constantes et d'axiomes décrivant les propriétés de ces constantes.

page 53

4.2 Les méta-modèles de notre approche

La description du contexte est constituée d'un ensemble de clauses et est montrée par la Figure 4.1 suivant :

CONTEXT Context_ identifier_list SETS set_identifier 1

CONSTANTS constant_identifier1 AXIOMS * label_1 : <predicate_1> END

FIGURE 4.1 - Structure d'un contexte

De cette description nous pouvons dériver le méta-modèle d'un contexte montré dans la Figure 4.2 au dessous :

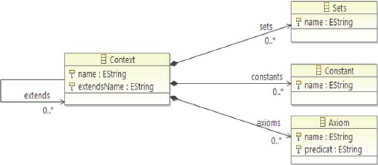
FIGURE 4.2 - Méta-Classe Context

La Méta-Classe « Context » définit la partie statique du modèle Event-B. Elle est composée de trois sous Méta-Classe `Sets','Constants' et `Axioms'. Chacune d'entre elles contient un Méta-Attribut `name' (de type chaine de caractères).

4.2.1.2 Méta-Classe Machine

Comme indiqué dans le chapitre 3, une machine est constituée de plusieurs clauses permettant de spécifier les parties statiques et dynamiques du système. La partie statique

4.2 Les méta-modèles de notre approche

correspond aux déclarations de variables et une caractérisation de ces données en termes d'invariants. Quant à la partie dynamique, elle est spécifiée par EVENT et INTIALISA-TION qui permettent de représenter respectivement les événements et l'initialisation d'une spécification Event-B. La description de la machine est constituée d'un ensemble de clauses et est montré par la Figure 4.3 suivante :

MACHINE Machine_identifier SEES * context_identifier_list VARIABLES Variable_identifier_list INVARIANTS label: <predicate> EVENTS <event_list> INTIALISATION

END

FIGURE 4.3 - Structure d'une machine

De cette description nous pouvons dériver le méta-modèle d'une machine comme il est montré par la Figure 4.4 :

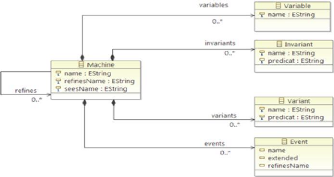
page 54

FIGURE 4.4 - Méta-Classe Machine

Les méta-classes `Event','Variable, `Variant','Invariant' sont incluses dans la méta-classe `Machine' qui définit la partie dynamique du modèle Event-B.

page 55

4.2 Les méta-modèles de notre approche

4.2.1.3 Méta-Classe Event

La méta-classe `Event' est une sous classe de 'Machine'. Celle-ci est composée de quatre sous méta-classes `Parameter' , `Guard' , `Action' , `Witness' présentées par la Figure 4.5.

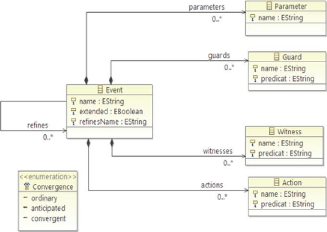
FIGURE 4.5 - Méta-Classe Event

4.2.1.4 Vue d'ensemble sur le méta-modèle Event-B

Le méta-modèle Event-B utilisé comme méta-modèle cible pour notre approche de transformation de ECore vers Event-B est l'assemblage de toutes les méta-classes (Context, Machine, Event) déjà présentées dans cette section. Les Figures 4.6 et 4.7 illustrent ce méta-modèle.

variables

4.2 Les méta-modèles de notre approche

Vatiable

C...

name : EString

irr ariantt

p Invariant

	4 name : EStrittg § refinesName : ratting § seesNarne : EShing
refines

0..¹ mine ; EStnog

preckat:ESbi

o,.

			Variant
	variants		T maw:^. E5trrng § pretCcat : E51rin9	§	§
			Event

refines

0.' $ name : EStriurg

$ extended : Boolean

§ retinesNwme ; ES#r.rg

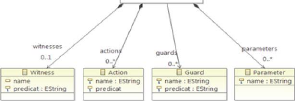
senumeralionJ coriverse_

- Y

- .tamergent

- anticipated

SeS

sees

o,.

extends

o,.

A Sets

_Q-.

name : E51nng

Context

§ 4Sar1é; ESteinsj

? extendedName ; EStr.'ig

- Constant

$

€ons[ants name : Mring

o..

fl Axiam $ name : EString predieat _ EStrin9

ao iorns

o.,

FIGURE 4.6 -- Méta-modèle Event-B

page 56

page 57

4.2 Les méta-modèles de notre approche

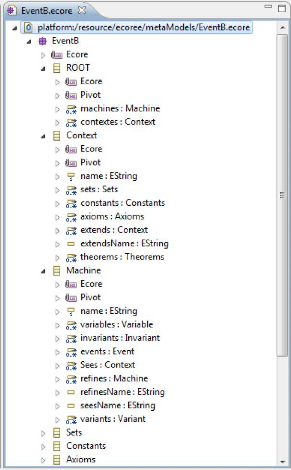
FIGURE 4.7 - Méta-modèle Event-B ouvert avec son éditeur

4.2.1.5 Les règles de cohérences sous forme d'OCL (.chk)

Nous avons établi des propriétés décrivant des contraintes d'utilisation d'Event-B. De telles propriétés sont décrites d'une façon informelle et formelle en se servant d'OCL. ~ Le cas d'ERROR

Tous les contextes attachés à un ROOT doivent avoir des noms deux à deux différents. Une formalisation partielle de cette propriété en OCL est :

page 58

4.2 Les méta-modèles de notre approche

context Machine ERROR

"Le nom de variable doit etre unique":

variables.forAll(var1| variables.notExists(var2|var1!=var2 var1.name==var2.name));

En cas d'erreur un message sera affiché et l'exécution sera arrêtée. Ceci est illustré par la Figure 4.8 suivante :

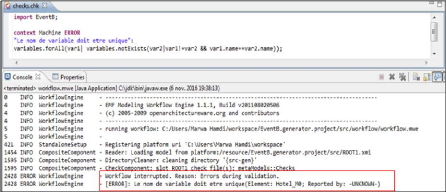
FIGURE 4.8 - Cas d'erreur

~ Le cas de WARNING

Le nom de la machine doit commencer avec une majuscule. Ceci est formalisé en OCL comme suit :

context Machine WARNING

"le nom doit etre commencer par majuscule" : Machine.name.startsWith("M");

Le type de contrainte « WARNING » n'arrête pas le workflow, il affiche seulement un message. Ceci est illustré par la Figure 4.9 suivante :

page 59

4.2 Les méta-modèles de notre approche

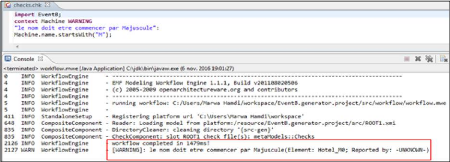
FIGURE 4.9 - Cas de warning

L'annexe A présente le reste des contraintes « OCL ».

4.2.2 Méta-modèle ECore

Le méta-modèle ECore utilisé comme méta-modèle source pour notre approche de transformation de ECore vers Event-B est donné par la Figure 4.10 (sous forme du diagramme) et par la Figure 4.11 (Méta-modèle ECore ouvert avec son éditeur).

page 60

4.2 Les méta-modèles de notre approche

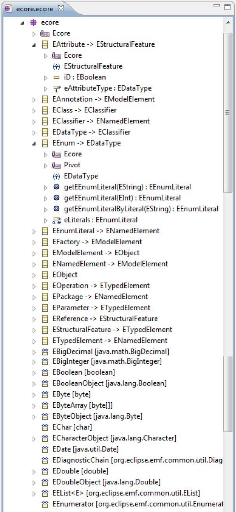
FIGURE 4.10 - Méta-modèle ECore ouvert avec son éditeur

page 61

4.2 Les méta-modèles de notre approche

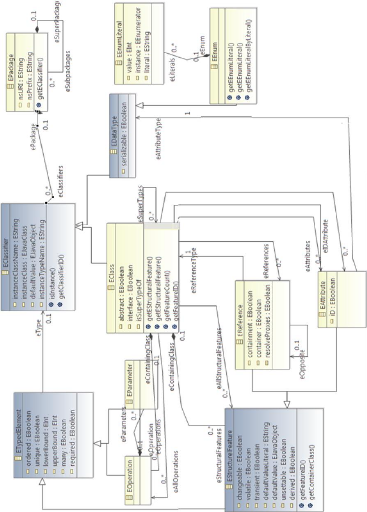
FIGURE 4.11 - Méta-modèle ECore partiel

page 62

4.2 Les méta-modèles de notre approche

4.2.2.1 Les règles de cohérence du méta-modèle ECore sous forme d'OCL (OCLi-nECore)

Nous avons établi des propriétés décrivant des contraintes d'utilisation d'ECore. De telles propriétés sont décrites d'une façon informelle et formelle en se servant d'OCL.

~ Propriété 1 :

Dans une même EClass une EOperation, un EAttribute et une EReference doivent avoir des noms deux à deux différents. Ceci, est formalisé en OCL comme suit et montré par la Figure 4.12 :

Invariant CheckNamesEClass:

eStructuralFeatures->collect(self eStructuralFeatures->collect(name)) ->excludesAll(self eOperations->collect(self eOperations->collect(name )));

FIGURE 4.12 - Règle sous forme d'OCLinECore.

En cas d'erreur un message sera affiché et l'exécution sera arrêtée. Ceci est illustré par la Figure 13 suivante :

page 63

4.3 Formalisation en Event-B

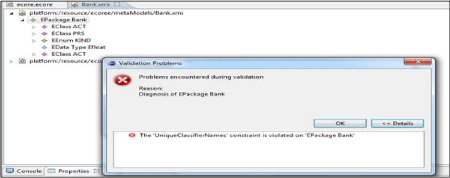
FIGURE 4.13 - Cas d'erreur

L'annexe B présente le reste des contraintes « OCL ».

4.3 Formalisation en Event-B

Formaliser en Event-B consiste essentiellement à la génération des deux composants Event- B : CONTEXT et MACHINE. Le CONTEXT Event-B contient éventuellement la description statique du modèle (déclaration des types, des constantes, etc) alors que la MACHINE Event- B se focalise sur les aspects dynamiques du modèle (déclaration des variables, des invariants, des évènements, etc). Le processus de formalisation est abordé en se basant sur le méta-modèle ECore contenant les concepts structurels et comportementaux.

4.3.1 Formalisation du concept EPackage en Event-B

Dans le méta-modèle ECore, un package est représenté par le méta-classe racine <EPa-ckage>. En Event-B, un package sera représenté par CONTEXT, et aussi par MACHINE (voir Figure 4.14).

FIGURE 4.14 - Formalisation du concept EPackage

page 64

4.3 Formalisation en Event-B

4.3.2 Formalisation du concept EClass en Event-B

En ECore, un class est représenté par la méta-classe <EClass>. En Event-B, un class sera représenté, dans le CONTEXT par l'ensemble EClassSet, et dans la MACHINE par la variable EClassVariable. Pour chaque variable nous avons associé un invariant de typage. Tel est l'invariant inv1 dans la Figure 4.15, et cette variable doit être initialisée dans Event INITIALISATION.

FIGURE 4.15 - Formalisation du concept Eclass

4.3.3 Formalisation du concept EEnum en Event-B

Dans le méta-modèle ECore, les types énumérés sont représentés par le concept <EE-num>. En Event-B, Les types énumérés seront traduits par des ensembles énumérés EEnum-Set dans la clause SETS et tous ces EEnumLiteral sont formalisés en des constantes(EEnumLiteral) dans CONTEXT Event-B. Pour chaque constant nous avons associé un Axioms de typage. Tel est l'axioms axm1 dans la Figure 4.16.

4.3 Formalisation en Event-B

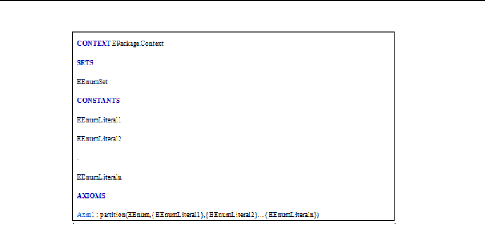
FIGURE 4.16 - Formalisation du concept EEnum

4.3.4 Formalisation du concept EAttribute en Event-B

Dans le méta-modèle ECore, un attribut d'EClass est représenté par le concept <EAt-tribute>. En Event-B, EAttribute sera représenté directement dans la MACHINE par la variable « EAttributeVariable ». La fonction associée à cette variable est donnée par l'invariant (inv2, inv3, inv4, inv5) qui est une relation entre un EClass et le type de l'attribut « EDataType ». Pour chaque variable nous avons associé un invariant de typage, et cette variable doit être initialisée dans Event INITIALISATION.

La formalisation des attributs se fait naturellement à l'aide des relations' entre les classes `EClass' et les types des attributs'EDataType'. Cette approche est similaire à celle de [21] [22].

Les spécialisations de la relation dépendent de la nature de l'attribut : Selon que l'attribut est volatile ou non volatile, unique ou non unique, la relation peut devenir une fonction partielle ou totale. Le Tableau 4.1 donne les différentes valeurs de relation.

page 65

page 66

4.3 Formalisation en Event-B

TABLE 4.1 - prédicats avant-après

FIGURE 4.17 - Formalisation du concept EAttribute

La formalisation du concept "EAttribute" est donné par la Figure 4.17.

page 67

4.3 Formalisation en Event-B

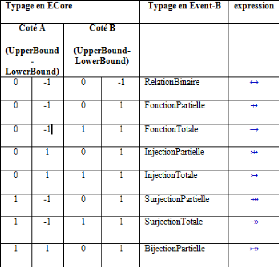
TABLE 4.2 - diverses relations fonctionnelles en Event-B

4.3.5 Formalisation du concept EReference en Event-B

Une reference liant deux classes EClassA et EClassB (seront représenté dans le CONTEXT par l'ensemble EClassASewt et EClassBSet), est représentée dans le méta-modèle ECore par la méta-classe <EReference>. En Event-B, une reference sera traduite par une variable « EReferenceVariable » dans la clause VARIABLES, typée ainsi au niveau de l'invariant de typage et initialisé dans l'Event INITIALISATION. La variable EReferenceVariable est une fonction entre EClassASet et EClassBSet.

Les spécialisations de la fonction dépendent des multiplicités de « EReference » et leur EReference opposé (UpperBound et LowerBound). Par exemple, des multiplicités 0 et 1 respectivement du coté de EClasssA et de EClassB, donnent lieu à une fonction injection partielle de `EClassASet `vers `EClassBSet'. La Figure 4.18 liste les diverses relations fonctionnelles en Event-B en leur associant des multiplicités ECore.

4.3 Formalisation en Event-B

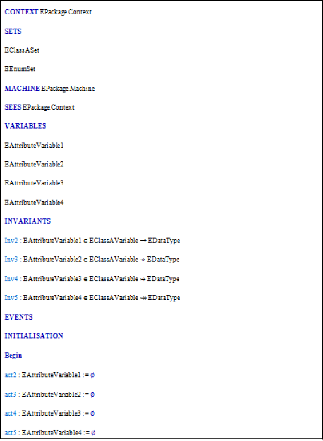
FIGURE 4.18 - Formalisation du concept EAttribute

page 68

page 69

4.3 Formalisation en Event-B

4.3.6 Formalisation du concept EOperation en Event-B

En ECore, une opération est définit par le méta-classe « EOperation » qui désigne les opérations d'une classe, identifiée par un nom et des paramètres « EParameter ». En Event-B, une opération se traduit par un événement « EVENT », et ces paramètres « EParameter » se traduit par PARAMETER.

Pour chaque paramètre<PARAMETER> d'un événement<EVENT> nous avons associé un grade de typage.

Example :

EOperation_name(parameter1 : type, , .. . , parametern : type).

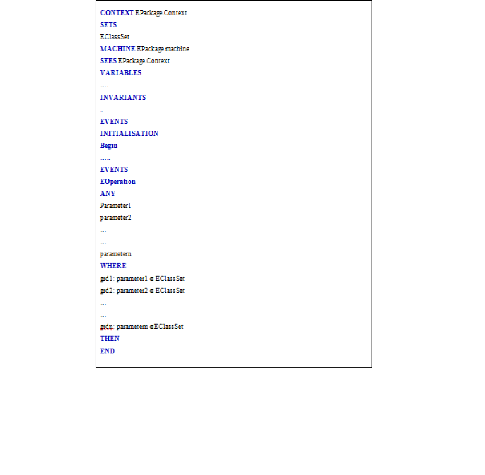
FIGURE 4.19 - Formalisation du concept EOperation

La formalisation de concept EOperation « est donné par la Figure 4.19.

page 70

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

Dans cette section, nous proposons une approche et un outil pour la transformation de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles). Notre approche est basée sur la transformation de modèles. Le résultat de la transformation (code Event-B) sera ensuite l'entrée de l'outil RODIN pour vérifier la cohérence et la fiabilité du modèle Event-B obtenu.

Notre approche suit le schéma suivant :

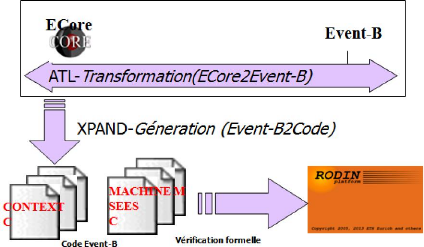
FIGURE 4.20 - Schéma de notre approche

Le passage des modèles ECore vers leurs équivalents en Event-B a été réalisé par une transformation de modèle en utilisant une approche IDM. Cette transformation est réalisée sous l'environnement de programmation Java Eclipse en utilisant ATL comme langage de transformation M2M et Xpand pour la transformation M2T. Les modèles ECore et Event-B sont réalisés en conformité avec leurs méta-modèles respectifs.

page 71

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

4.4.1 Transformation de modèles M2M

Nous allons présenter les règles de transformation permettant le passage d'un modèle ECore vers un modèle Event-B. Ces règles sont établies entre le méta-modèle source et le méta-modèle cible, autrement dit entre tous les concepts des méta-modèles source et cible. Ces règles sont expliquées brièvement suivant en langage naturel.

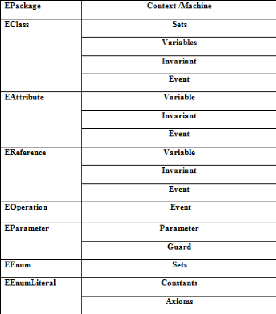
Après la présentation des règles de transformation, maintenant nous allons définir quelques règles en utilisant ATL comme langage de transformation d'un modèle ECore en un modèle Event-B.

La Figure 4.22 donne le contexte de notre programme ECore2Event-B permettant de transformer une modélisation ECore vers une spécification Event-B.

page 72

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

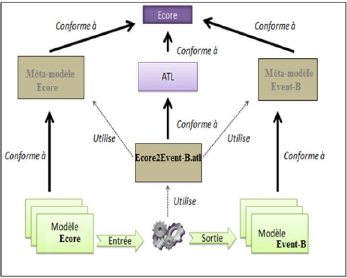
FIGURE 4.21 - Vue d'ensemble sur le programme ECore2Event-B

Les modèles source et cible (modélisation en ECore et spécification en Event-B) ainsi que le programme ECore2Event-B sont conformes à leurs méta-modèles ECore, Event-B et ATL. Dans un premier temps, nous avons développé deux modèles correspondant aux méta-modèles source ECore et cible Event-B. Ces méta-modèles sont conformes au méta-méta-modèle ECore.

L'entête du programme ECore2Event-B stockée dans le fichier ECore2Event-B.atl se présente comme suit :

module ECore2Event-B;

create modeleEvent-B: Event-B modeleECore : ECore

Dans notre programme le modèle cible est représenté par la variable modèle Event-B à partir du modèle source représenté par modeleECore.

Les modèles source et cible sont respectivement conformes aux méta-modèles ECore et Event-B. Notre programme ECore2Event-B opère sur le modèle source modeleECore en lecture seule et produit le modèle cible modèle Event-B en écriture seule.

page 73

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

4.4.1.1 Exemple des règles en ATL

Avant de commencer à définir des règles de transformation, nous allons donner la forme générale de celles-ci dans la Figure 4.23 :

ruleForExample {

from

i :inputMetamodel !InputElement

to

a :OutputMetaModel !OutputElement (

attributeA<-i.attributeA,

attributeB<-i.attributeC

)}

FIGURE 4.22 - Exemple règle ATL

~ Forexample : est le nom de la règle de transformation.

~ I (resp. O) : est le nom de la variable représentant la source d'élément identifié que, dans le corps de la règle (resp. élément cible créé).

~ InputMetaModel (resp. OutputMetaModel) : est le méta-modèle dans lequel le modèle de source (resp. le modèle de cible) de la transformation est constante.

~ InputElement : signifie la méta-classe d'éléments de modèle de source à laquelle cette règle sera appliquée.

~ OutputElement : signifie la méta-classe à partir de laquelle la règle instancie les éléments cibles.

~ Le point d'exclamation! : est utilisé pour spécifier à quel méta-modèle appartient une classe méta.

~ AttributeA et attributeB : sont des attributs de la méta-classe OutputElement, leurs valeurs sont initialisées à l'aide des valeurs des attributs i.attributeA, i.attributeCde l'InputElement.

Après la présentation des règles de transformation, maintenant nous allons définir quelques règles en utilisant ATL comme langage de transformation d'un modèle ECore en un modèle Event-B.

page 74

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

Règle générant Context et Machine

Reprenons l'exemple de la Règle qui transforme un EPackage ECore en CONTEXT Event-B et aussi en MACHINE Event-B. Le résultat de cette transformation est montré dans la Figure 4.24.

2

4

6

8

10

12

14

16

18

20

22

24

rule EPackage2RootContextMachine

{ from z :MM! EPackage

to

a :MM1!ROOT (

contextes<-Sequence {ctx } ,

contextes <-Sequence {mch}) , ctx : MM1! Context

(

name<- z . name+' ctx ',

sets <-z . eC la s si f ie rs ->select ( el | el . oclIsTypeOf (MM! EClass ) ) , sets <-z . eC la s si f ie rs ->select ( el | el . oclIsTypeOf (MM!EEnum) ) ,

constants <- Sequence {thisModule . GetEEnumLiteral1->c o l l e c t ( e | thisModule . resolveTemp (e , ' const1 ' ) ) } ,

constants <- Sequence

axioms <- Sequence {thisModule . GetEReference1->c o l l e c t

( e | thisModule . resolveTemp (e , ' f f ' ) )} ) ,

mch : MM1! Machine ( name <- z . name+'M' ,

variables <-Sequence{thisModule . GetEClass1 ->collect ( e | thisModule . resolveTemp

(e , ' const4 ' ) )}

. . . .

)}

Voici la règle écrite en ATL.

page 75

3

5

7

9

11

13

3

5

7

3

5

7

9

11

13

23

25

27

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

FIGURE 4.23 - Règle générant Context et Machine

Règle générant les ensembles abstraits(Sets)

2

4

6

8

10

12

14

16

Reprenons l'exemple de la Règle qui transforme le concept EClass en « EVENT » dans MACHINE Event-B. Le résultat de cette transformation est montré dans la Figure 4.25. Voici la règle écrite en ATL.

rule EClass2Sets {

from cc : MM! EClass

to const3 : MM1! Sets (

name <- cc . name . firstToLower ()

) ,

const4 : MM1! Variable (

name <- cc . instanceClassName ) ,

inv : MM1! Invariant (

name <-' inv0 ' ,

predicat <-cc . instanceClassName+'IN '+cc . name ) ,

i n it :MM1! Event (

name <- 'INITIALISATION' ,

actions <-Sequence{ action2 }

) ,

action2 : MM1! Action (

name <-' act ',

predicat <-cc . instanceClassName+' := '+'empty' ) }

page 76

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

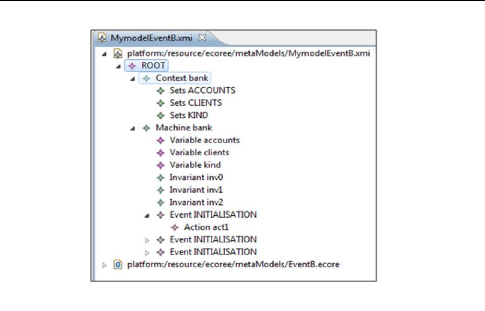
FIGURE 4.24 - Règle générant Sets

Règle générant les événements (Event)

Reprenons l'exemple de la Règle qui transforme le concept EOperation en « EVENT » dans MACHINE Event-B. Le résultat de cette transformation est montré dans la Figure 4.26.

1

Ci-dessous la règle écrite en ATL.

rule Eoperation2Event {

from

H: MM! EOperation

Toevt : MM1! Event (

name <- H. name,

parameters <-H. eParameters ,

guards <- Sequence {thisModule . allMethodDefsprm->

collect ( e | thisModule . resolveTemp (e , ' grd ' ) ) }) }

rule EParameter2ParameterAndGuard {

from

Z: MM! EParameter

to

ZZ: MM1! Parameter (

name <- Z. name

15

17

page 77

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

) ,

grd : MM1! Guard (

name <- ' gdr1 ',

predicat<-Z. name+' '+'IN '+' '+Z. eType . name)}

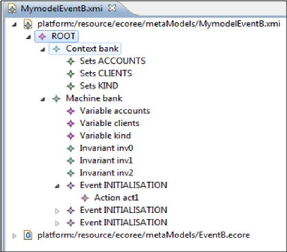
FIGURE 4.25 - Règle générant Event

Règle générant les Constants (Constants)

1

Reprenons l'exemple de la Règle qui transforme le concept EEnumLiteral en « Constants » dans Context Event-B. Le résultat de cette transformation est montré dans la Figure 4.27. Ci-après la règle écrite en ATL.

rule EEnumLiteral2ConstantsAndAxioms {

from

EnumLiteral : MM! EEnumLiteral

to

const1 : MM1! Constants (

name <- EnumLiteral . name

) ,

const2 :MM1! Axioms (

9

11

page 78

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

name <- 'axm1-1 ',

predicat <-'PARTITION '+' '+' ( '+EnumLiteral . eEnum. name +','+'{ '+EnumLiteral . name+'} '+' ) ' ) }

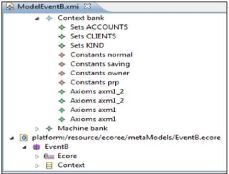
FIGURE 4.26 - Règle générant Constants

Règle générant les ensembles (Sets)

1

Reprenons l'exemple de la Règle qui transforme le concept EEnum en « SETS » dans CONTEXT Event-B. Le résultat de cette transformation est montré dans la Figure 4.28. Ci-dessous la règle écrite en ATL.

rule EEnum2Sets {

from

Enum: MM!EEnum

to

sets: MM1! Sets (

name <- Enum. name

) ,

enum : MM1! Variable (

name <- Enum. instanceClassName

) ,

inv1 : MM1! Invariant (

name <-' inv0 ' ,

predicat <-Enum. instanceClassName+'IN '+Enum. name

) ,

15

17

19

21

page 79

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

init1 :MM1! Event (

name <- 'INITIALISATION' ,

actions <-Sequence{ action1 }

) ,

action1 : MM1! Action (

name <-' act ',

predicat <-Enum. instanceClassName+':= '+' isEmpty () '

)

actions <-Sequence{ action3 } ) ,

action3 : MM1! Action (

name <-' act ',

predicat <-a . name+':= '+' isEmpty () '

)}

FIGURE 4.27 - Règle générant Sets

L'annexe C présente le reste des règles de transformation « .atl ». 4.4.1.2 Exécution du programme ECore2Event-B.atl

Le moteur de transformation permet de générer le modèle Event-B, ce qui est conforme au méta-modèle Event-B, à partir du modèle ECore qui est conforme au méta-modèle ECore en utilisant le programme ECore2Event-B.atl, qui doit être également conforme au méta-modèle qui définit la sémantique de la transformation ATL. Tous les méta-modèles doivent être conformes à la méta-méta-modèle ECore.

Pour valider nos règles de transformation, nous avons réalisé un test. A titre d'illustration,

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

nous considérons l'exemple d'un compte bancaire présenté dans le chapitre 2. (Voir Figure 4.29).

FIGURE 4.28 - Modèle ECore d'un Bank (modèle source)

Lorsque le modèle est validé et il n'y a pas d'erreurs, et après l'ajout des contraintes OCL attachées au modèle, l'utilisateur peut exécuter le programme de transformation de modèle ATL pour transformer le modèle ECore en Event-B. Le résultat de cette transformation est représenté sur la Figure 4.30 ci-dessous.

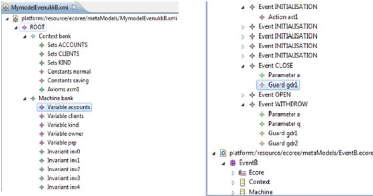
page 80

FIGURE 4.29 - Modèle Event-B d'un Bank (modèle cible)

page 81

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

4.4.2 Transformation de modèle M2T

Cette section présente la validation du modèle Event-B conforme au méta-modèle Event-B et la transformation de ce modèle vers un texte Event-B. Le principe d'extraction est montré par la Figure 4.31. Pour y parvenir, nous avons utilisé avec profit les outils Check pour la validation et Xpand pour la transformation.

4.4.2.1 Présentation de la transformation M2T

La Figure 4.31 suivante donne le contexte de notre programme permettant la transformation de modèle Event-B vers texte Event-B.

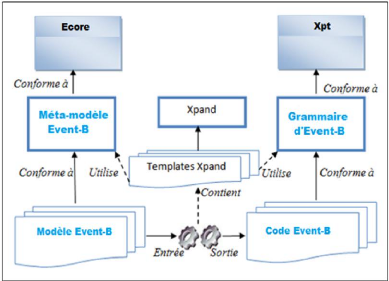
FIGURE 4.30 - Schéma de transformation de modèle Event-B vers texte Event-B

La transformation proposée comporte quatre étapes. La première étape a pour objectif de créer le méta-modèle Event-B. Puis, la deuxième étape consiste à créer un template. Xpt pour générer le code Event-B. Ensuite, la troisième a pour objectif de créer un modèle XMI conforme au méta-modèle Event-B puis valider ce modèle xmi conforme via OclInECore. Finalement, la quatrième partie consiste à exécuter le générateur de code (generateur.mwe).

page 82

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

La première et troisième partie sont déjà faite dans la section précédente(le méta-modèle Event-B est le méta-modèle cible de la transformation M2M et le modèle XMI conforme au méta-modèle Event-B qui est le résultat de la transformation ECore vers Event-B).

4.4.2.2 Modèle Event-B en texte : Extraction via Xpand

L'outil Xpand est intégré dans l'environnement EMF. Il permet la génération de code en partant d'un modèle. Ce dernier doit être conforme à un méta-modèle comme nous l'avons déjà mentionné. Un fichier templateXpand (d'extension .xpt) comporte des instructions d'import qui servent à importer le méta-modèle, de zéro ou plusieurs EXTENSION avec le langage Xtend et d'un ou plusieurs blocks DEFINE.

~ IMPORT

L'instruction IMPORT nous permet d'importer notre méta-modèle contenant les méta-classes et leurs attributs pour les utiliser dans notre approche template. Dans notre cas c'est le méta-modèle nommé «Event-B » qui va être utilisé.

« IMPORT Event-B»

~ Bloc DEFINE Les lignes suivantes dans le fichier de modèle servent à définir le modèle pour le fichier « Invariant ».Nous commençons par le modèle en spécifiant son nom (INVARIANTS).

La déclaration de `Invariant' se traduit par le code suivant :

«DEFINE INVARIANTS FOR Invariant»

«IFname.trim().length !=0 predicat.trim().length !=0» «this.name» : «this.predicat»

«ENDIF»

«ENDDEFINE»

~ Instruction FILE Nous utilisons « FILE » pour spécifier le type et l'extension de fichier de sortie qui va être générée. Le nom du fichier est obtenu par la concaténation de l'attribut « name » de « context » actuelle et la chaine littérale `.buc'.

page 83

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

«DEFINEContenuContextFORContext"

'FILEname + ".buc""

...

...

'ENDFILE"

'ENDDEFINE"

o Instruction EXPAND EXPAND invoque un autre sous modèle avec le nom « Contenu_context"(respectivement'Contenu_machine").

Ce sous modèle sera appelé pour chaque élément dans les champs attribut (de référence) de méta-classe « Context » actuelle (respectivement méta-classe « Machine »).

«DEFINEContenuContextFORContext"

'FILEname + ".buc""

Context

'name"

'EXPANDEXTENDSFOREACHextends"

'IF!sets.isEmpty"

SETS

'EXPANDSET SFOREACHsets"

'ENDIF"

'IF!constants.isEmpty"

CONSTANTS

'EXPANDCONSTANT SFOREACHconstants"

'ENDIF"

'IF!axioms.isEmpty"

'ENDIF"

END

'ENDFILE"

'ENDDEFINE"

page 84

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

On trouve la version complète des règles de transformation « model to text via Xpand » dans l'annexe C.

4.4.2.3 Le moteur de validation et de génération de code Ada

Après avoir fait notre projet Xpand et les règles de cohérences sous forme d'OCL. Nous avons testé notre programme en utilisant un générateur.

Ce générateur, dans notre cas utile deux variables, l'une nommée « model » avec comme valeur « k », précise le modèle XMI à entrer.

Et l'autre « src-gen » de valeur « src-gen », précisant la place ou les fichiers générés vont être enregistrés.

De plus notre générateur contient quatre composants :

~ Reader : Il permet de lire le modèle XMI à utiliser pour la transformation.

~ DirectoryCleaner : Il permet de nettoyer le répertoire, ici « src-gen », qui contient les artefacts générés.

~ CheckComponent : Ce composant contient le fichier de contraintes OCL « Check » pour valider notre modèle XMI à entrer.

~ Generator : Ce composant permet de préciser le générateur de code à utiliser dans notre workflow pour générer notre code.

Le workflow donné ci-dessous permet de générer le code Event-B relatif au modèle XMI conforme au méta-modèle Event-Ben utilisant les templates Xpand fournis précédemment.

3

1

<?xml version=" 1.0 "?>

<workflow>

<propertyname="SCEH" value=" Event-B. generator . project / src /SCEH. xmi"

5

/>

<propertyname=" src-gen " value=" src-gen "/>

7 <!-- set up EMF for standalone execution -->

<beanclass=" org . eclipse . emf .mwe. u t i l s . StandaloneSetup ">

9 <platformUrivalue=" .. "/>

</bean>

11 <!-- instantiate metamodel -->

<beanid="mm_emf"

13 class=" org . eclipse . xtend . typesystem . emf . EmfRegistryMetaModel "/>

<!-- load model and store i t in slot ' model' -->

15 <componentclass=" org . eclipse. emf .mwe. u t ils . Reader">

page 85

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

31

33

35

37

39

<urivalue= platform : / resource /\${SCEH} />

<modelSlotvalue= SCEH /> </component>

19 <componentclass= org . eclipse . emf .mwe. u t ils . DirectoryCleaner > <directoryvalue= {src -gen} />

21 </component>

<!-- check model -->

23 <componentclass= org . eclipse . xtend . check. CheckComponent > <metaModelidRef= mm_emf />

25 <checkFilevalue= src :: Checks /> <emfAllChildrenSlotvalue= SCEH />

27 </component>

<!--generate code -->

29 <componentclass= org . eclipse . xpand2 . Generator > <metaModelidRef= mm_emf />

<expand

value= template :: Template:: main FOR SCEH />

<outletpath= {src-gen} >

<postprocessorclass= org . eclipse . xpand2 . output. JavaBeautifier />

</outlet>

<resourceManagerclass= org . eclipse . xtend . expression . ResourceManagerDefaultImpl >

<fileEncodingvalue= ISO-8859-1 /> </resourceManager>

</component> </workflow>

17

4.4.2.4 Exemple d'utilisation: Système bancaire(Bank)

En exécutant le workflow sur le modèle Event-B « Bank » présenté dans la partie précédente (modèle cible de la transformation de modèle ECore vers Event-B), nous obtenons les deux fichiers générés « Bank.buc » et« Bank.bum ».

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

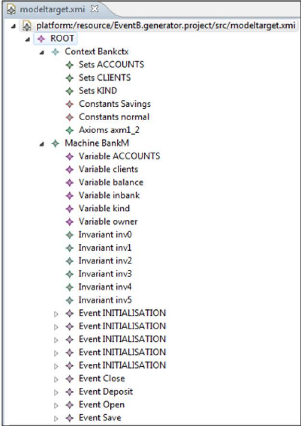
FIGURE 4.31 - Schéma de transformation de modèle Event-B vers texte Event-B

Le fichier avec l'extension .buc représente le fichier contexte dans un projet RODIN, Le contenu du ce fichier « Bank.buc »est le suivant :(après une intervention manuelle).

page 86

page 87

4.4 Transformations de modèle ECore vers Event-B en utilisant une approche IDM (Ingénierie Dirigée par les Modèles).

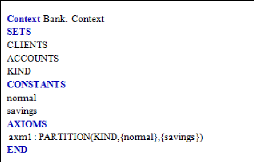
Le fichier avec l'extension .bum représente une machine dans un projet RODIN, Le contenu du ce fichier « Bank.bum » est le suivant :(après une intervention manuelle)

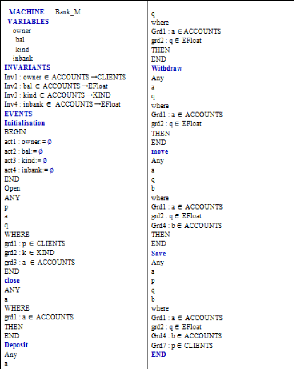
page 88

4.5 Vérification formelle par l'outil Rodin

4.5 Vérification formelle par l'outil Rodin

Dans cette section, nous présentons comment nous procédons pour vérifier la cohérence et la fiabilité du modèle Event-B obtenu. Pour chaque concept et règle que nous avons formalisé, nous allons montrer comment nous l'avons prouvés à l'aide des outils de vérifications fournis par la plateforme RODIN.

~ RODIN : un atelier qui a été développé dans le cadre d'un projet européen. Il est basé sur Eclipse. RODIN stocke les modèles dans une base de données et fournit des nouveaux prouveurs puissants, qui peuvent être manipulés à l'aide d'une interface graphique.

4.5.1 Preuves d'une machine

Dans une machine Event-B, il est nécessaire de vérifier que l'état initial (initialisation) satisfait les invariants. Ainsi, pour un tel évènement il faut s'assurer que l'action non-déterministe est réalisable. Cela se fait à l'aide de l'obligation de preuve de faisabilité.

Dans le modèle abstrait les propriétés souhaitées du système sont exprimées dans les invariants, il est nécessaire de prouver la cohérence de ces invariants par rapport aux évènements du système par des preuves.

Une Obligation de Preuve (OP) : est une formule mathématique à démontrer afin d'assurer qu'un composant B (CONTEXT ou MACHINE) est correct. Les outils, support la spécification en Event-B comme Rodin, peuvent générer les OPs et les prouver.

Corrections guidées par la preuve : Une OP non prouvée indique une erreur dans le modèle.

Vérification par la preuve : Rodin génère l'ensemble des OPs nécessaires à la validation de la cohérence de modèle, et de la préservation de l'invariant par ce modèle.

Dans notre modèle, nous trouvons des obligations de preuve Figure 4.32. Chacun d'eux a un nom composé, par exemple, evt / inv / INV. Un logo vert situé à gauche du nom de l'obligation de preuve mentionne qu'elle a été prouvée, un A signifie qu'elle a été prouvée automatiquement.

page 89

4.5 Vérification formelle par l'outil Rodin

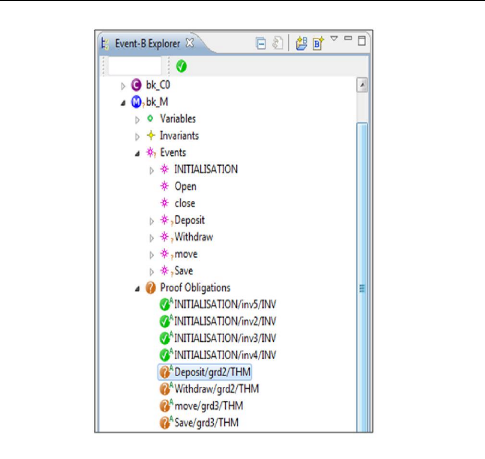
FIGURE 4.32 - Les OPs sous Rodin de la machine

Dans la Figure 4.33, les obligations de preuve associées à chaque invariant ont été générer automatiquement. Soit l'exemple suivant : INITIALISATION / inv2 / INV. Cette règle d'obligation de preuve assure que l'invariant inv2, dans la machine, soit préservé par l'évène-ment INITIALISATION. Cette obligation de preuve a été déchargée automatiquement par le RODIN prover.

page 90

4.5 Vérification formelle par l'outil Rodin

FIGURE 4.33 - Preuve automatique

Toutefois, les obligations de preuve produites par les générateurs de preuve, pourraient exiger une preuve interactive au lieu de preuves automatiques. Tel est l'exemple, dans la Figure 4.34, de l'obligation de preuve Deposit / grd1 / THM qui a été prouvée interactive-ment.

page 91

4.6 Conclusion

FIGURE 4.34 - Preuves interactif

Dans le développement de notre modèle des obligations de preuve n'ont pas été déchargées par les outils de preuves automatiques et interactifs, mais les spécifications sont correctes.

4.6 Conclusion

D

ans ce chapitre, nous avons proposé un méta-modèle Event-B ainsi qu'une transformation de modèle ECore en modèle Event-B en respectant des contraintes exprimées en OCLinECore et en utilisant ATL comme langage de transformation M2M. Nous avons, par ailleurs, proposé une transformation de modèle Event-B en texte en respectant des contraintes exprimées en Check et en utilisant l'outil Xpand qui nous a permis de transformer un modèle Event-B vers code moyennant l'écriture des templates Xpand. Nous avons vérifié le modèle Event-B obtenu avec l'outil RODIN.

92

Conclusion et perspectives

D

ans ce mémoire, nous avons abordé la problématique de développement des logiciels et systèmes complexes sensibles aux erreurs. Pour éviter les erreurs inhérentes au développement de ces logiciels et systèmes, nous avons proposé une approche IDM permettant de transformer une modélisation semi-formelle ECore vers une spécification formelle Event-B, qui permet d'obtenir une spécification cohérente et digne de confiance du futur système en utilisant les outils associés à Event-B : générateur d'obligations de preuves, prouveur automatique et interactif, animateur et model-checker.

Pour y parvenir, nous avons élaboré deux méta-modèles : le méta-modèle ECore qui joue le rôle de méta-modèle source dans notre approche IDM de transformation d'une modélisation décrite en ECore vers une spécification en Event-B. Et le méta-modèle Event-B qui joue le rôle de méta-modèle cible. De plus, nous avons conçu et réalisé un programme ECore2Event-B.atl permettant de transformer un modèle source ECore conforme au méta-modèle ECore vers un modèle cible Event-B conforme au méta-modèle Event-B en respectant des contraintes exprimées en OCLinECore et en utilisant un langage déclaratif ATL comme langage de transformation M2M. Notre programme ECore2Event-B.atl est purement déclaratif et utilise avec profit les constructions déclaratives fournis par ATL : telles que helpers (attribut, opération), règles standard, règles paresseuses. En outre, nous avons proposé une transformation du modèle Event-B vers texte Event-B en respectant des contraintes exprimées en Check et en utilisant l'outil Xpand qui nous a permis de transformer un modèle Event-B vers code moyennant l'écriture des templates Xpand.

Quant aux perspectives de ce travail, nous pourrions envisager les prolongements suivants:

1. Enrichir notre méta-modèle Event-B on ajoutant d'autres concepts et d'autres propriétés décrivant des contraintes d'utilisation des constructions Event-B.

Conclusion et perspectives

2. Améliorer notre programme ECore2Event-B.atl par de helpers (opération).

3. Proposer l'opération de transformation inverse d'Event-B vers ECore.

page 93

94

Appendices

95

A Les règles de cohérence du méta-

modèle Event-B sous forme d'OCL

(.chk)

1 import ecore ;

3 /* Contrainte attach EPackage */

context EPackage ERROR

5 " UniqueClassifierNames " :

e C l a s s i f i e r s . forAll ( a1| e C l a s s i f i e r s . notExists ( a2 | a1!=a2 && a1 . name==a2 . name)) ;

7 context EPackage ERROR

" UniqueSubpackageNames " :

9 eSubpackages . forAll ( a1 | eSubpackages . notExists ( a2 | a1!=a2 && a1 . name==a2 . name) ) ;

context EPackage ERROR

11 " WellFormedNsURI " :

nsURI!= null;

13

context EPackage ERROR

15 " WellFormedNsPrefixI " :

this . nsURI> 0;

17 /*Contrainte attach EClass */

context EClass ERROR

19 " UniqueOperationSignatures " :

eOperations . forAll ( a1 | eOperations . notExists ( a2 | a1!=a2 && a1 . name==a2 . name));

21 /* context EClass ERROR

" noAttributesInInterface " :

23 i f ( this . interface==true ) then

eAttributes==0 ; :

25 context EClass ERROR

27

29

31

33

35 37 39 41 43 45 47 49

page 96

" CheckNamesEClass " :

eStructuralFeatures ->c o l l e c t ( self. eStructuralFeatures ->c o l l e c t (name))->

excludesAll ( self. eOperations->c o l l e c t ( self. eOperations->c o l l e c t (name))) ;

context EClass ERROR

" UniqueFeatureNames " :

eStructuralFeatures . forAll ( a1 | eStructuralFeatures . notExists ( a2 | a1!=a2 && a1 .

name==a2 . name));

/* Contrainte attach abstract class EClassifier */

context EClassifier ERROR

" UniqueTypeParameterNames " :

eTypeParameters . forAll ( a1 | eTypeParameters . notExists ( a2 | a1!=a2 && a1 . name==a2 .

name));

context EClassifier ERROR

" WellFormedInstanceTypeName " :

this . name > 0;

/* Contrainte attach abstract class ENamedElement */

context ENamedElement ERROR

" WellFormedName " :

this . name>0;

/* Contrainte attach EAnnotation

context EAnnotation ERROR

" WellFormedName " :

this . name!= null; */

/* Contrainte attach abstract class ETypedElement */

context ETypedElement ERROR

" ValidLowerBound " :

lowerBound!=0 implies lowerBound >0 ;

51 context ETypedElement ERROR

" ValidUpperBound " :

55

57

53 upperBound!=0 implies ( lowerBound == 1 && upperBound == -1) ;

/* Contrainte attach EEnum */

context EEnum ERROR

" UniqueEnumeratorNames " :

eLiterals . forAll ( a1 | eLiterals . notExists ( a2 | a1!=a2 && a1 . name==a2 . name) ) ;

59

61

/* Contrainte attach EOperation */ context EOperation ERROR

			uniqueTypeNames :
63		eTypeParameters . forAll ( a1 | eTypeParameters . notExists ( a2 | a1!=a2 && a1 . name==a2 . name));
65 context EOperation ERROR UniqueParameterNames : 67 eParameters . forAll ( a1| eParameters . notExists ( a2 | a1!=a2 && a1 . name==a2 . name)) ;
			Checks.chk

page 97

98

B Les règles de cohérence du méta-

modèle ECore sous forme d'OCLi-

2

4

6

8

10

12

14

16

nECore

P r o p r i t 1 :

Les m ta-attributs nsURI et nsPrefix de la m ta-classe EPackage doit stocker

un identificateur valide qui doit tre non vide. Ceci peut tre
f o r m a l i s en OCL comme suit :

invariant WellFormedNsURI :

nsURI . size () > 0;

invariant WellFormedNsPrefix : nsURI . size () > 0;

P r o p r i t 2 :

Tous les EClassifier ( EClass , EDataType ,EEnum) attach s un EPackage doivent

avoir des noms deux deux d i f f rents . Ceci peut tre f o r m a l i s en
OCL comme suit :

invariant UniqueClassifierNames :

eClassifier s ->forAll (a : EClassifier , b : EClassifier a . name = b . name

implies a = b) ;

P r o p r i t 3 :

Un EPackage doit avoir un nom unique. Ceci peut tre f o r m a l i s en OCL comme suit :

invariant UniqueSubpackageNames :

eSubpackages->forAll ( r1 : EPackage , r2 : EPackage r1 <> r2 implies r1 . name

<> r2 . name) ;

P r o p r i t 4 :

Une interface est une classe sans attribut. Ceci peut tre f o r m a l i s en OCL

comme suit :

invariant noAttributesInInterface :

18

20

22 24 26 28

30 32 34 36 38

40

42

page 99

eAttributes->isEmpty () ;

P r o p r i t 5 :

Tous les EOperation attach s un EClass doivent avoir des signatures deux

deux d i f f rents . Ceci peut tre f o r m a l i s en OCL comme suit :
invariant UniqueOperationSignatures :

eOperations->forAll (a : EOperation , b : EOperation a . name = b . name implies a

= b) ;

P r o p r i t 6 :

Toutes les Features ( EAttribute , EReference ) attach e s un EClass doivent

avoir des noms deux deux d i f f rents .

Une formalisation partielle de cette p r o p r i t en OCL est:

invariant UniqueFeatureNames :

eStructuralFeatures ->forAll (a : EStructuralFeature , b : EStructuralFeature a
. name = b . name implies a = b) ;

P r o p r i t 7 :

Dans un m me EClass une EOperation , un EAttribute et une EReference doivent

avoir des noms deux deux d i f f rents . Ceci, est f o r m a l i s en OCL comme
suit :

invariant CheckNamesEClass :

eStructuralFeatures ->c o l l e c t ( self. eStructuralFeatures ->c o l l e c t (name))-> excludesAll ( self. eOperations->c o l l e c t ( self. eOperations->c o l l e c t (name))) ;

P r o p r i t 8 :

Un param tre attach un EOperation doit avoir un nom et type unique. Ceci
, est f o r m a l i s en OCL comme suit :

invariant UniqueParameterNames :

eParameters->forAll ( a1 : EParameter , a2 : EParameter a1 <> a2 implies a1 .
name <> a2 . name) ;

invariant UniqueTypeParameterNames :

eTypeParameters->forAll ( t1 : ETypeParameter , t2 : ETypeParameter t1 <> t2
implies t1 . name <> t2 . name) ;

P r o p r i t 9 :

Le m ta-attribut name de la m ta-classe abstrait ENamedElement doit

stocker un identificateur valide qui doit tre non vide. Ceci peut tre
f o r m a l i s en OCL comme suit :

invariant WellFormedName : this . name . size () <> 0;

P r o p r i t 10 :

Un EEnum doit avoir un nom unique. Ceci peut tre f o r m a l i s en OCL comme suit :

44

46

48

50

52

54

56

58

invariant UniqueEnumeratorNames :

eClassifier s ->forAll (a : EEnum, b : EEnum a . name = b . name implies a = b) ;

P r o p r i t 11 :

Tous les EEnumLiteral attach s un composant doivent avoir des noms deux

deux d i f f rents . Ceci peut tre f o r m a l i s en OCL comme suit :

invariant UniqueEnumeratorLiterals ;

eLiterals ->forAll (a : EEnumLiteral , b : EEnumLiteral a . name = b . name implies
a = b) ;

P r o p r i t 12 :

Le m ta-attribut source de la m ta-classe abstrait EAnnotation doit

stocker un identificateur valide qui doit tre non vide. Ceci peut tre
f o r m a l i s en OCL comme suit :

invariant WellFormedSourceURI : name. size () > 0;

P r o p r i t 13 :

Le m ta-attribut LowerBound de la m ta-classe abstrait ETypedElement

doit stocker un identificateur valide qui doit tre e 0 ou 1 .

Et Le m ta-attribut UpperBound doit tre -1 ou 1 . Ceci
peut tre f o r m a l i s en OCL comme suit :

invariant ValidlowerBoundd :

this . lowerBound = 0 or lowerBound = 1; invariant ValidUpperBoundd :

this . upperBound = - 1 or lowerBound = 1;

page 100

101

C Les règles de transformation M2M

(Ecore2EventB.atl)

-- @path MM=/ecoree /metaModels/ ecore . ecore

2 -- @path MM1=/ecoree /metaModels/EventB . ecore

4 module aaa ;

create OUT : MM1 from IN : MM;

6 helper context MM! EReference def : getExtendedName () : String =

i f s e l f . changeable=f a l s e then

8 ' '

else

10 s e l f . name

endif ;

12 helper context MM! EReference def : getERefernceName () : String =

i f ( s e l f . changeable=f a l s e ) and ( s e l f . v o l a t i l e=true ) then

14 s e l f . name

else

16 OclUndefined

endif ;

18 helper context String def : firsttoUpper () : String =

s e l f . substring (1 , s e l f . size ( ) ) . toLower () ;

20 helper context String def : firstToLower () : String =

self. substring (1 , self. size () ) . toUpper () ;

22 helper def : GetEEnumLiteral1 : Sequence (MM! EEnumLiteral ) =

MM! EEnumLiteral . allInstances ( ) ->

24 sortedBy ( e e . name) ;

helper def : GetEEnumLiteral2 : Sequence (MM! EEnumLiteral ) = 26 MM! EEnumLiteral . allInstances ( ) ->

sortedBy ( e e . name) ;

28 helper def : GetEClass1 : Sequence (MM! EClass ) =

page 102

30

32

34

36

38

40

42

44

46

48

50

52

54

56

58

60

62

64

66

MM! EClass allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEClass2 : Sequence (MM! EClass ) =

MM! EClass allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEEnum : Sequence (MM!EEnum) =

MM!EEnum allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEClass3 : Sequence (MM! EClass ) =

MM! EClass allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEEnum1 : Sequence (MM!EEnum) =

MM!EEnum allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEEnum2 : Sequence (MM!EEnum) =

MM!EEnum allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEAttribute : Sequence (MM! EAttribute ) =

MM! EAttribute allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEAttribute1 : Sequence (MM! EAttribute ) =

MM! EAttribute allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEattribute : Sequence (MM! EAttribute ) =

MM! EAttribute allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEReference2 : Sequence (MM! EReference ) =

MM! EReference allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEReference3 : Sequence (MM! EReference ) =

MM! EReference allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetERef : Sequence (MM! EReference ) =

MM! EReference allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEvent : Sequence (MM! EOperation ) =

MM! EOperation allInstances ( ) ->

sortedBy ( e e name) ;

helper def : GetEParameter : Sequence (MM! EParameter ) =

68

MM! EParameter . allInstances ( ) -> sortedBy ( e | e . name) ;

70

72

74

82

(

rule EPackage2RootContextMachine

{

76

from z :MM! EPackage

to

78

a :MM1!ROOT (

80

contextes <-Sequence {ctx } , contextes <-Sequence {mch}

) ,

ctx : MM1! Context

84

name <- z . name+' ctx ' ,

86

sets <-z . eClassifiers ->s e l e c t ( el | el . oclIsTypeOf (MM! EClass ) ) ,

sets <-z . eClassifiers ->s e l e c t ( el | el . oclIsTypeOf (MM!EEnum) ) ,

constants <- Sequence {thisModule . GetEEnumLiteral1->c o l l e c t ( e | thisModule .

resolveTemp (e , ' const1 ')) } ,

axioms <- Sequence {thisModule. GetEEnumLiteral2->c o l l e c t ( e | thisModule .

resolveTemp (e , ' const2 ')) }

88

90

92

page 103

) ,

94

mch : MM1! Machine

(

name <- z.name+'M',

variables <-Sequence {thisModule . GetEClass1->c o l l e c t ( e | thisModule .

96

resolveTemp (e , ' const4 ')) } ,

variables <-Sequence {thisModule .GetEEnum->c o l l e c t ( e | thisModule . resolveTemp (

e,'enum'))},

98

variables <-Sequence {thisModule . GetEAttribute->c o l l e c t ( e | thisModule.

resolveTemp (e , 'A')) } ,

variables <-Sequence {thisModule . GetEReference3->c o l l e c t ( e | thisModule.

resolveTemp (e , ' s ')) } ,

invariants <-Sequence {thisModule . GetEClass2->c o l l e c t ( e | thisModule .

resolveTemp (e , ' inv ')) } ,

100 102 104 106

invariants <-Sequence {thisModule .GetEEnum1->c o l l e c t ( e | thisModule . resolveTemp (e , ' inv1 ')) } ,

invariants <-Sequence {thisModule . GetEAttribute1->c o l l e c t ( e | thisModule. resolveTemp (e , 'B')) } ,

invariants <-Sequence {thisModule . GetEReference2->c o l l e c t ( e | thisModule. resolveTemp (e , ' ss ') ) } ,

events <-Sequence {thisModule. GetEClass3->c o l l e c t ( e | thisModule . resolveTemp (e ,'init'))},

events <-Sequence {thisModule . GetEEnum2->c o l l e c t ( e | thisModule . resolveTemp (e , ' init1 ' ) ) } ,

events <-Sequence {thisModule. GetEattribute->c o l l e c t ( e | thisModule . resolveTemp (e , ' init2 ')) } ,

events <-Sequence {thisModule . GetERef->c o l l e c t ( e | thisModule . resolveTemp (e,' sss'))},

events <-Sequence {thisModule . GetEvent->c o l l e c t ( e | thisModule . resolveTemp (e , ' evt'))}

108 ) }

110 116	rule EClass2Sets { from ) ,

112

cc : MM! EClass

to

114

const3 : MM1! Sets (

name <- cc . name. firstToLower ()

118

const4 : MM1! Variable (

name <- cc . instanceClassName

120

) ,

inv : MM1! Invariant ( name <- ' inv0 ' ,

122

predicat <-cc . instanceClassName+' '+' Subset '+' '+cc . name ) ,

124

126

i n i t :MM1! Event ( name <- 'INITIALISATION ' , actions <-Sequence{ action2 }

128

page 104

) ,

130

action2: MM1! Action (

132

136 138 140 142 144 146 148 150 152 154

156 158 160 162 164 166

name <-' act ',

predicat <-cc . instanceClassName+' := '+' isEmpty () '

)

134 }

rule EEnum2Sets { from

Enum: MM!EEnum

to

sets: MM1! Sets ( name <- Enum. name

)

}

rule EEnumLiteral2ConstantsAndAxioms {

from

to

EnumLiteral : MM! EEnumLiteral

const1 : MM1! Constants (

name <- EnumLiteral . name

) ,

const2 :MM1! Axioms (

name <- 'axm1_2 ',

predicat <-'PARTITION'+' '+' ( '+EnumLiteral .eEnum. name+', '+'{ '+

EnumLiteral . name+' } '+' ) '

)

}

rule EAttribute2Variable {

from

a : MM! EAttribute (a . changeable=true )

to

A: MM1! Variable (

page 105

name <-a . name

) ,

B: MM1! Invariant (

name <-' inv ' ,

predicat <-i f a . v o l a t i l e=true and a . unique=true then

a . name+' '+'IN '+' '+' PartialInjective '+' ( '+ a . eContainingClass .

instanceClassName+' , '+a . eAttributeType . name+' ) '

168

else i f a . v o l a t i l e=true and a . unique=f a l s e then

a . name+' '+'IN '+' '+' PartialFunction '+' ( '+ a . eContainingClass .

instanceClassName+' , '+a . eAttributeType . name+' ) '

170

else i f a . v o l a t i l e=f a l s e and a . unique=true then

a . name+' '+'IN '+' '+' TotalBijective '+' ( '+ a . eContainingClass .

instanceClassName+' , '+a . eAttributeType . name+' ) '

172

else

a . name+' '+'IN '+' '+' TotalFunction '+' ( '+ a . eContainingClass .

instanceClassName+' , '+a . eAttributeType . name+' ) '

174

endif endif

176

endif

) ,

178

init2 :MM1! Event (

180

name <- 'INITIALISATION' , actions <-Sequence{ action3 }

182

) ,

action3 : MM1! Action (

184

name <-' act ',

predicat <-a . name+':= '+' isEmpty () '

186

)

}

188

190

page 106

rule EReference2Variable {

from

192

u : MM! EReference (u . changeable=true )

to

194

s : MM1! Variable (

name <- u . getExtendedName ()

196

) ,

ss : MM1! Invariant (

198

name <-' inv1_1 ',

predicat <-i f ( u . changeable=true and u . lowerBound=0 and u . upperBound

=-1)and(u . eOpposite . lowerBound=0 and u . eOpposite . upperBound=-1) then

200

u . getExtendedName ()+' '+'IN '+' '+' BinaryRelation '+' ( '+ u .

eContainingClass . name+' , '+u . eReferenceType . name+' ) '

else i f

202

(u . lowerBound=0 and u . upperBound=-1)and(u . eOpposite . lowerBound=0 and u .

eOpposite . upperBound=1) then

u . getExtendedName ( )+' '+'IN '+' '+' PartialFunction '+' ( '+ u .

eContainingClass . name+' , '+u . eReferenceType . name+' ) '

204

else i f

(u . lowerBound=0 and u . upperBound=-1)and(u . eOpposite . lowerBound=1 and u .

eOpposite . upperBound=1) then

206

u . getExtendedName ( )+' '+'IN '+' '+' TotalFunction '+' ( '+ u .

eContainingClass . name+' , '+u . eReferenceType . name+' ) '

else i f

208

(u . lowerBound=0 and u . upperBound=1)and(u . eOpposite . lowerBound=0 and u .

eOpposite . upperBound=1) then

u . getExtendedName ( )+' '+'IN '+' '+' PartialInjective '+' ( '+ u .

eContainingClass . name+' , '+u . eReferenceType . name+' ) '

210

else i f

(u . lowerBound=0 and u . upperBound=1)and(u . eOpposite . lowerBound=1 and u .

eOpposite . upperBound=1) then

212

u . getExtendedName ( )+' '+'IN '+' '+' TotalInjective '+' ( '+ u .

eContainingClass . name+' , '+u . eReferenceType . name+' ) '

else i f

214

(u . lowerBound=1 and u . upperBound=-1)and(u . eOpposite . lowerBound=0 and u .

eOpposite . upperBound=1) then

u . getExtendedName ( )+' '+'IN '+' '+' PartialSurjective '+' ( '+ u .

eContainingClass . name+' , '+u . eReferenceType . name+' ) '

216

page 107

else i f

218

(u . lowerBound=1 and u . upperBound=-1)and(u . eOpposite . lowerBound=1 and u .

eOpposite . upperBound=1) then

u . getExtendedName ( )+' '+'IN '+' '+' TotalSurjective '+' ( '+ u .

eContainingClass . name+' , '+u . eReferenceType . name+' ) '

220

else i f

(u . lowerBound=1 and u . upperBound=1)and (u . eOpposite . lowerBound=1 and u .

eOpposite . upperBound=1) then

222

u . getExtendedName ( )+' '+'IN '+' '+' TotalBijective '+' ( '+ u .

eContainingClass . name+' , '+u . eReferenceType . name+' ) '

else i f

224

(u . lowerBound=1 and u . upperBound=1)and(u . eOpposite . lowerBound=0 and u .

eOpposite . upperBound=1) then

226

u . getExtendedName ( )+' '+'IN '+' '+' PartialBijective '+' ( '+ u . eContainingClass . name+' , '+u . eReferenceType . name+' ) '

else

228

230

u . getExtendedName ( )+' '+'IN '+' '+' TotalBijective '+' ( '+ u . eContainingClass . name+' , '+u . eReferenceType . name+' ) '

232

234

236

endif endif endif endif endif endif endif endif

238

240

endif

242

) ,

244

sss :MM1! Event (

name <- 'INITIALISATION' , actions <-Sequence{actionA} ) ,

246

248

actionA : MM1! Action (

name <-' act ',

predicat <-u . getExtendedName ( )+' := '+' isEmpty () ' )

250

}

252

254

page 108

rule Eoperation2Event {

256

from

H: MM! EOperation

258

to

evt : MM1! Event (

260

name <- H. name ,

parameters <-H. eParameters ,

guards <- Sequence {thisModule . GetEParameter->c o l l e c t ( e | thisModule .

resolveTemp (e , ' grd ' ) )}

		)
262
		}
264		rule EParameter2ParameterAndGuard { from
266				Z: MM! EParameter
				to
268 270 272 274 276				ZZ: MM1! Parameter ( name <- Z. name ) , grd : MM1! Guard ( name <- ' gdr1 ', predicat <-Z. name+' '+'IN '+' '+Z. eType . name )
278 }
			ECore2Event-B.atl

page 109

110

D Le template de génération de code

6

8

10

12

14

16

18

20

22

24

26

28

2 IMPORT EventB

DEFINE main FOR ROOT

4 EXPAND Contenu_Context FOREACH contextes EXPAND Contenu_machine FOREACH machines

ENDDEFINE

REM ******* ICI ON PRESENTE LE CONTENU DU contexte ******ENDREM

DEFINE Contenu_Context FOR C ont ext

FILE name+" .buc"

Context

name

EXPAND EXTENDS FOREACH ex t ends

I F sets . isEmpty

SETS

EXPAND SETS FOREACH s e t s

ENDIF

I F constants. isEmpty

CONSTANTS

EXPAND CONSTANTS FOREACH cons t a n t s

ENDIF

I F axioms. isEmpty

AXIOMS

EXPAND AXIOMS FOREACH axioms

ENDIF

I F theorems. isEmpty

THEOREMS

EXPAND THEOREMS FOREACH theorems

ENDIF

EventB en Xpand

END

ENDFILE

ENDDEFINE

DEFINE EXTENDS FOR Context

I F ! extends. isEmpty

EXTENDS

this . extends . toString ()

ENDIF

ENDDEFINE

DEFINE SETS FOR Sets

this . name

ENDDEFINE

DEFINE CONSTANTS FOR Constants

this . name

ENDDEFINE

DEFINE AXIOMS FOR Axioms

t h i s . name : t h i s . p r e d i c a t

30 32 34 36 38 40 42 44 46 48 50

ENDDEFINE

DEFINE THEOREMS FOR Theorems t h i s . name : t h i s . p r e d i c a t ENDDEFINE

REM ******* ICI ON PRESENTE LE CONTENU DU MACHINE******ENDREM 52 DEFINE Contenu_machine FOR Machine

FILE name+" .bum"

54 56 58 60 62 64 66

MACHINE

page 111

name

I F ! refines . isEmpty

REFINES

FOREACH r e fin e s . name AS e ITERATOR i t e r SEPARATOR''

e

ENDFOREACH

ENDIF

I F ! Sees . isEmpty

SEES

FOREACH Sees . name AS e ITERATOR i t e r SEPARATOR'' e

ENDFOREACH

ENDIF

I F ! variables. isEmpty

VARIABLES

EXPAND VARIABLES FOREACH variables

ENDIF

I F ! invariants . isEmpty

INVARIANTS

EXPAND INVARIANTS FOREACH invariants

ENDIF

I F ! variants . isEmpty

VARIANT

EXPAND INVARIANTS FOREACH invariants

ENDIF

I F ! events. isEmpty

EVENTS

EXPAND EVENTS FOREACH events

ENDIF

END

ENDFILE

ENDDEFINE

DEFINE VARIABLES FOR Variable

I F name. trim () . length !=0

this . name

ENDIF

ENDDEFINE

DEFINE INVARIANTS FOR Invariant

I F name. trim () . length !=0 && predicat . trim () . length !=0

this . name : this. p r e d i c a t

ENDIF

ENDDEFINE

DEFINE EVENTS FOR Event

n a m e

I F extended

extended

ENDIF

STATUS

68 70 72 74 76 78 80 82 84 86 88 90 92 94 96 98 100 102

104

106

REFINES

I F ! refines . isEmpty

page 112

EXPAND REFINES FOREACH r e f i n e s

108

110

112

114

116

118

120

122 124 126 128

130

132

134

136

138

140

ENDIF

I F ! parameters . isEmpty && guards . isEmpty && Witnesses . isEmpty && actions . isEmpty

ANY

EXPAND PARAMETER FOREACH parameters

BEGIN

ELSEIF ! parameters . isEmpty && ! guards . isEmpty && Witnesses.

isEmpty && actions . isEmpty

ANY

EXPAND PARAMETER FOREACH parameters

WHERE

EXPAND GUARDS FOREACH guards

THEN

skip

ELSEIF ! parameters . isEmpty && ! Witnesses . isEmpty && guards.

isEmpty && actions . isEmpty

ANY

EXPAND PARAMETER FOREACH parameters WITH

EXPAND WITNESSES FOREACH Witnesses BEGINREM Then <ENDREM

skip

ELSEIF ! parameters . isEmpty && ! actions . isEmpty && guards. isEmpty && witnesses . isEmpty

ANY

EXPAND PARAMETER FOREACH

paramet ers

BEGINREMThenENDREM

EXPAND ACTION FOREACH actions

ELSEIF ! parameters . isEmpty && ! actions . isEmpty && ! guards. isEmpty && ! Witnesses . isEmpty && actions. i s E m p t y

ANY

EXPAND PARAMETER FOREACH

paramet ers

WHERE

page 113

EXPAND GUARDS FOREACH guards

142

144

146

148 150 152 154 156

158

160

162

164

166

168

170

172

174

WITH EXPAND WITNESSES FOREACH Witnesses THEN skip

ELSEIF parameters . isEmpty && actions . isEmpty && guards. isEmpty && Witnesses . isEmpty && actions . isEmpty

ANY

EXPAND PARAMETER FOREACH parameters

WHERE

EXPAND GUARDS FOREACH guards

WITH

EXPAND WITNESSES FOREACH Witnesses

THEN

EXPAND ACTION FOREACH actions

ELSEIF actions . isEmpty && parameters . isEmpty && guards.

isEmpty && Witnesses. isEmpty

ANY

EXPAND PARAMETER FOREACH parameters

WHERE

EXPAND GUARDS FOREACH guards

THEN

EXPAND ACTION FOREACH actions

ELSEIF guards . isEmpty && Witnesses . isEmpty && parameters.

isEmpty && actions . isEmpty

WHERE EXPAND GUARDS FOREACH guards THEN skip

skip

ELSEIF guards . isEmpty && Witnesses . isEmpty && parameters.

isEmpty && actions . isEmpty

WHERE

EXPAND GUARDS FOREACH guards

WITH

EXPAND WITNESSES FOREACH Witnesses

THEN

page 114

ELSEIF guards . isEmpty && actions . isEmpty && Witnesses . isEmpty && parameters . isEmpty

176

178

WHERE

EXPAND GUARDS FOREACH guards

THEN

180

EXPAND ACTION FOREACH actions

ELSEIF guards . isEmpty && Witnesses . isEmpty && actions.

isEmpty && parameters. isEmpty

182

WHERE

EXPAND GUARDS FOREACH guards

184

WITH

EXPAND WITNESSES FOREACH Witnesses

186

THEN

EXPAND ACTION FOREACH actions

188

ELSEIF Witnesses . isEmpty && parameters . isEmpty && guards.

isEmpty && actions . isEmpty

WITH

190

EXPAND WITNESSES FOREACH Witnesses

BEGINREMThenENDREM

192

skip

ELSEIF Witnesses . isEmpty && actions . isEmpty && parameters.

isEmpty && guards. isEmpty

194

196

WITH EXPAND WITNESSES FOREACH Witnesses BEGIN EXPAND ACTION FOREACH actions

198

i . name

208

ELSEIF actions . isEmpty && parameters . isEmpty && guards.

isEmpty && Witnesses. isEmpty

BEGIN

200

EXPAND ACTION FOREACH actions

ELSE

202

skip

ENDIF

204

END

ENDDEFINE

206

DEFINE REFINES FOR Event

FOREACH refines AS i SEPARATOR ' '

page 115

210

212

214

216

218

220

222

ENDFOREACH

ENDDEFINE

DEFINE PARAMETER FOR Parameter

this . name

ENDDEFINE

DEFINE GUARDS FOR Guard

this . name : this. p r e d i c a t

ENDDEFINE

DEFINE WITNESSES FOR Witness

this . name : this. p r e d i c a t

ENDDEFINE

DEFINE ACTION FOR Action

this . name : this . p r e d i c a t

ENDDEFINE

Template.xpt

page 116