|
1

|
République Tunisienne
Ministère de
l'Enseignement Supérieur et
de la Recherche
Scientifique
Université de Sousse
|
|
****
Institut Supérieur du Transport et de la
Logistique de Sousse
****
MEMOIRE
Réalisé par :
NAJEH CHAOUCH
POUR OBTENIR LE DIPLÔME DE MASTERE DE
RECHERCHE
|
Planification des ressources humaines au sein de la compagnie
d'assistance aérienne à l'aide des données du panel et
l'algorithme multi-objectif
|
Soutenu le ../../2014 devant le Jury composé de
Mr ... Président
Mr Examinateur
Mme. Mounira Tlili Encadreur
Mr. Aymen Ghedira Invité (Co-encadreur)
Le mémoire a été préparé au
sein (de la société de TAV Handling)
Résumé :
Lorsqu'un avion atterrit, les compagnies d'assistance
aéroportuaire fournis aux aéronefs et aux passagers un nombre
important de tâches effectuées par les différents groupes
de personnel au sol. De ce fait, les sociétés d'assistance sont
soumises à des nombreux problèmes de décision et de
planification qui doit continuellement être résolu afin d'offrir
un service rapide et fiable dans un environnement concurrentiel. Dans ce
mémoire, nous nous intéressons à analyser la
problématique de la planification et de modéliser l'algorithme
d'optimisation des ressources humaines au sein d'une compagnie d'assistance
aérienne. Les objectifs pratiques du mémoire sont la
résolution des différents problèmes de planification en
tenant compte des objectifs et de défis opérationnels
soulevés par l'établissement de plannings à savoir les
problèmes d'ordonnancement dans un environnement dynamique à
l'aide la programmation linéaire en nombre entière et les
données du panel.
Mots clés : Planification, assistance
aéroportuaire, programmation linéaire en nombre entière,
données du panel.
Abstract :
When an airline lands, ground handling societies provided a
huge number of services to aircraft and passengers performed by different
ground staff. Therefore, ground handling companies are subject to many planning
and decisions problems that must continually be solved to provide a fast and
reliable service in a competitive environment. In this work, we analyze the
planning problems and modeling an optimization human resources algorithm. Main
objectives of this work are solving different planning problems taking into
account operational challenges in a dynamic environment raised by the
establishment of schedules using integer linear programming and the panel
data.
2
Key Words : planning, ground handling, integer linear
programming, panel data.
3
Dédicace
Cette mémoire représente l'aboutissement du
soutien que mes parents m'ont
prodigués tout au long ma vie.
La
patience et l'encouragement de mon mari m'ont aidé à surmonter
toutes les
difficultés rencontrées au cours de cette
mémoire.
L'amour de mes soeur, mon frère et mes deux enfants
ont était la cause de ma
réussite.
Je vous remercie d'être dans ma vie.
4
Remerciement
Au terme de ce travail, je souhaite adresser mes
sincères remerciements à toutes les personnes qui ont
contribué à sa réalisation et ont permis par leur soutien
et leurs conseils, de le mener à bien. Qu'elles trouvent dans ce travail
l'expression de mes plus sincères remerciements.
Je remercie particulièrement Mme Mounira Tlili pour
avoir acceptée et encadrée cette mémoire. Ses conseils et
remarques, toujours pertinents, m'ont permis de confronter et ajuster mes
travaux à des problématiques pratiques et réelles.
Nonobstant, sa relecture finale du mémoire m'a sans aucun doute permis
de préciser mon propos.
Mes profondes reconnaissances s'adressent à mon
Co-encadreur Mr Aymen Ghedira qui ma aider tout au long de la
réalisation de ce mémoire.
Je remercie beaucoup Mlle Imen Gam, pour ses efforts dans la
réalisation de la partie expérimentale de cette
mémoire.
J'aimerai aussi remercier Mr Sukru Kaya, directeur de
planification auprès TAV Handling, pour la confiance qu'il m'a
témoignée du début à la fin du travail, pour sa
disponibilité à comprendre et à communiquer et sans
oublier ses précieuses intuitions.
Je remercie les membres du jury pour avoir accepté de
participer à mon jury de mémoire.
5
Table de matières
Introduction Générale 1
Chapitre 1 Le Processus de planification 3
Introduction 3
1 Notion de la planification 3
1.1 La planification du personnel de l'entreprise 3
1.2 L'apport de la planification du personnel à la
performance de l'entreprise 5
1.3 Le planning 7
2 La planification du personnel dans la compagnie d'assistance
9
2.1 Le problèmes de planification 9
2.2 Le modèle de la planification au sol 13
2.3 Les étapes de la planification 13
3 L'horizon de planification 14
3.1 Les scenarios de planification 14
3.2 Les planifications tactique, opérationnelle et en
temps réel 16
3.3 Les limite de processus planification 17
4 Les méthodes de résolution dans la
littérature 17
4.1 Le positionnement des jours de repos Day-Off Scheduling 19
4.2 La planification des vacations 19
4.3 Le tournement de l'horaire 20
4.4 Modèles PLNE et PPC 20
Conclusion 21
Chapitre 2 La modélisation de la demande
22
Introduction 22
1 Représentation de la demande 22
6
1.1 La courbe de la demande 22
1.2 Les sources de la demande 25
1.3 La flexibilité de la demande 26
2 Estimation de la demande 26
2.1 Estimation de la demande à l'aide du PLNE 27
2.2 Estimation de la demande incertaine 28
2.3 Estimation de la demande incertaine à l'aide du PANEL
31
3 Les contraintes et L'écart entre l'offre et la demande
36
3.1 Les contraintes 36
3.2 L'écart entre l'offre et la demande 38
3.3 Le valeur de l'écart entre l'offre et la demande
39
4 La demande hétérogène 40
4.1 L'hétérogénéité de la
demande aérienne 40
4.2 Les exigences du service et les qualifications
nécessaires 41
4.3 La couverture de la charge de travail 42
Conclusion 43
Chapitre 3 Le dimensionnement et la création des
vacations 44
1 Le dimensionnement 44
1.1 La notion de dimensionnement 44
1.2 Les contraintes de dimensionnement 45
1.3 Le processus de dimensionnement 46
2 Le dimensionnement de l'effectif et les vacations 47
2.1 le dimensionnent de l'effectif 47
2.2 Le problème de dimensionnent de vacation 50
2.3 La formulation du probleme de construction de vacation 51
3 Les modèles de création des vacations 53
3.1 La recherche opérationnelle 53
3.2 Les approche par couverture 53
3.3 Les approches implicites 55
4 Enumérations des vacations 55
7
4.1 Algorithme d'énumération des vacations 56
4.2 Optimisation de l'algorithme d'énumération des
vacations 59
4.3 L'algorithme d'énumération proposé 61
Conclusion 66
Chapitre 4 Le tournée du personnel 67
1 Le concept de la tournée 67
1.1 Enonce du problème 67
1.2 Grille de besoins 68
1.3 Le tableau de tournées 69
2 La formulation mathématique a l'aide de PLNE 71
2.1 Choix des variables du modèle 71
2.2 Formulation de l'objectif 72
2.3 Formulation des contraintes 73
3 La solution algorithmique 76
3.1 Solution avec deux jours de repos consécutifs 76
3.2 Solution avec deux jours de repos non-consécutifs
78
3.3 Solution avec un jour de repos 79
4 Les résultats obtenus et les axes pour la future
recherche 80
4.1 Les résultats obtenus 80
4.2 Les axes pour la future recherche : compétence et
répartition des taches 83
Conclusion 83
Chapitre 5 Proposition d'un prototype de planification
des personnels 84
Introduction 84
1 Choix des programmes et du langage de programmation 84
1.1 Environnement de développement : Microsoft Visual
Studio 2010 85
1.2 Base de donnes SQL server et utilisation interactive avec
Vb.Net 86
1.3 Présentation de MATLAB 87
2 Spécifications des besoins 88
2.1 Utilisateurs du système 88
2.2 Les besoins fonctionnels 89
2.3 Les modules principaux de l'application 89
3 Implémentations de l'algorithme de tournée sous
MATLAB 90
4 Présentations du progiciel 92
4.1 Les interface 92
Conclusion 94
8
Conclusion générale 95
9
Liste des tableaux
Table 1. Exemple de planning non-cyclique sur 2 semaines pour 4
employés (M : vacation du
|
Matin, E : vacation du soir, N : vacation de nuit)
|
.18
|
|
Table 2. Estimation du modèle homogène sous Eviews
|
33
|
|
Table 3. Estimation du modèle à Effet Fixe sous
Eviews
|
34
|
|
Table 4. Estimation du modèle à effets
aléatoires sous Eviews
|
35
|
|
Table 5. Test d'Hausman
|
36
|
|
Table 6. Tableau de dominance des vacations matinée
|
62
|
|
Table 7. Les nombres requis et nécessaires des agents
|
68
|
|
Table 8. Grille de besoins pour le service de piste pendant la
vacation Matinée M
|
69
|
|
Table 9. Le tableau de tournée
|
70
|
|
Table 10. Le tableau de tournée cyclique
|
70
|
|
Table 11. Schéma de 5 jours de travail par semaine
|
72
|
Table 12. Schéma de 5 jours de travail par semaine et
deux jours de repos consécutifs...........78 Table 13. Schéma de
5 jours de travail par semaine et deux jours de repos
non-consécutifs......78
Table 14. Les nombres requis et nécessaires des agents
79
Table 15. Schéma de 5 jours de travail par semaine et deux jours
de repos non-consécutifs......80
10
Liste des figures
|
Figure 1. Schéma illustrant le problème de la
planification - Dr. Chan Peter
|
5
|
|
Figure 2. L'apport de la planification du personnel à la
performance de l'entreprise
|
.7
|
|
Figure 3. Processus d'élaboration du planning
|
9
|
Figure 4. Les tâches se produisant autour de l'avion
selon l'association internationale du
transport aérien IATA 11
Figure 5. Charges de travail typique de l'aéroport
Enfidha-Hammamet au cours de la journée
pour l'année 2014 .13
Figure 6.La chronologie des problèmes dans le
modèle de planification du personnel de
manutention au sol 14
Figure 7 . Les scénarios de planification en fonction
du temps 16
Figure 8. Charges de travail au cours de la journée
dans l'aéroport Enfidha-Hammamet 24
Figure 9. Regroupement des vols au cours de la journée
dans l'aéroport Enfidha-Hammamet 25
Figure 10. La détermination des tâches 26
Figure 11. Évolution du retard en fonction du trafic :
aéroport Enfidha-Hammamet année 2010-
2012 30
Figure 12. Détail des causes de retards selon l'Air
Trafic Flow Management (ATFM) en 2001....30
Figure 13. La modélisation de la demande incertaine au
cours de la journée de dimanche année
2011 31
Figure 14. Exemple d'une partie de matrice des facteurs de
retards par jour : saison d'été 2010.32
Figure 15. Regroupement des tâches et les
déplacements au cours de la journée 37
Figure 16. Processus de décisionnel ....45
11
|
Figure 17. Besoins par semaine type
|
48
|
|
Figure 18. Plages horaires par semaine type
|
....49
|
|
Figure 19. Définition d'une vacation
|
....51
|
|
Figure 20. Construction d'une vacation
|
....52
|
Figure 21.Exemple de matrice de couverture journalière par
les vacations (vacation matin (M) présenté en vert, vacation soir
(E) présenté en orangé et vacation de nuit (N)
présenté en bleu) ...57
|
Figure 22. Exemple de chevauchement des vacations de matin M et
soir E
|
.....59
|
|
Figure 23. Matrice de couverture journalière
|
...60
|
|
Figure 24. Chevauchement des vacations
|
61
|
|
Figure 25. Exemple de dominance des vacations matinée
|
62
|
|
Figure 26. Des courbes de demande distinctes selon les services
|
63
|
|
Figure 27. Le principe de l'algorithme d'optimisation
|
64
|
|
Figure 28. Interface général du Microsoft Visual
Studio 2010
|
85
|
|
Figure 29. Utilisation interactive de
VB.Net SQL Server
|
86
|
|
Figure 30. L'espace de travail MATLAB
|
87
|
|
Figure 31.Nombre max des agents par un jour type
|
91
|
|
Figure 32. Interface « Empoyee »
|
92
|
|
Figure 33. Interface « Empoyee Teams »
|
92
|
|
Figure 34. Interface « Empoyee Teams Membership »
|
93
|
|
Figure 35.Interface « Flight »
|
93
|
|
Figure 36. Interface « Rules»
|
93
|
|
Figure 37. Interface « Roster»
|
94
|
12
Introduction générale
Déterminer les horaires de travail des employés
est un enjeu important pour les organisations de grande taille. Donc, la
planification des horaires conditionne la satisfaction des besoins des clients,
le respect des contraintes juridiques et techniques, tout en assurant une
gestion optimale de la masse salariale. Dans ce mémoire, nous nous
intéressons à la modélisation et à la
résolution de différents problèmes d'optimisation
soulevés par la construction de planning pour le personnel de la
compagnie d'assistance aérienne au sol.
La planification des besoins en ressources humaines de la
compagnie d'assistance au sol est l'un des plus grands défis auxquels
sont confrontés les gestionnaires et les dirigeants. Donc, elle
représente, en général, la plus grande partie des
coûts de fonctionnement. Pour relever ce défi, un processus qui
assure l'adaptation des ressources humaines aux besoins prévus de
l'organisation est un outil fondamental et essentiel à la performance de
la qualité.
Le présent travail est organisé comme suit :
Le premier chapitre décrit les enjeux et l'apport de la
planification à la performance de l'entreprise dans un cadre
général puis dans un contexte aéronautique, nous
détaillons le processus de planification et nous synthétisons la
multitude d'approches présentées dans la littérature. Nous
étudions par la suite les différentes étapes du
problème de la planification en fonction du temps commençant par
la modélisation de la demande à long terme (stratégie
tactique) jusqu'au l'affectation du personnel dans le court terme
(stratégie opérationnelle). Cependant, l'intervention du jour de
l'opération (stratégie en temps réel) ne sera pas
traitée dans ce mémoire.
Dans ce cadre, nous notons que le processus de planification
passe en premier lieu par le recensement des activités futures afin de
déterminer les capacités et les besoins en personnel et aboutir
à la création du planning efficace. En effet, le deuxième
chapitre est consacré à la présentation de la demande
à l'aide des courbes de charges. Ainsi que la modélisation de la
demande globale y compris la demande incertaine à l'aide de la
programmation linéaire et à
13
l'aide d'une analyse économétrique des
données de Panel. Nous finissons par la détermination des
contraintes et l'écart entre l'offre et la demande.
La résolution de cet écart s'effectue à
travers la prévision des effectifs nécessaires par vacation afin
de concevoir l'adéquation de l'effectif à la demande. En effet,
dans le troisième chapitre, nous examinons en détail le
dimensionnement de l'effectif et les vacations et nous nous intéressons,
en particulier, au problème de construction de vacations couvrant une
courbe de charge à coût minimal. Après avoir comparé
différentes modélisations et approches de résolution, nous
proposons un algorithme de création de vacation qui permet de couvrir
les charges à moindre coût. Ce modèle
d'énumération serra adopter dans la planification des ressources
dans les chapitres suivants.
Le quatrième chapitre décrit, en premier lieu,
l'énoncé du problème de tournée du personnel et les
modèles mathématiques seront. Nous présentons la fonction
objective et les contraints du problème de tournée du personnel
tout en réduisant le nombre total de travailleurs, mais, en respectant
le nombre minimum requis d'employés pour chaque jour de la semaine. En
deuxième lieu, nous présentons la solution algorithmique
où chaque employé fonctionne six jours par semaine et prend un
jour de congé, ou il travaille cinq jours par semaine et prend deux
jours de congé (consécutive, ou pas nécessairement
consécutives). Les résultats obtenus seront analysés dans
la dernière partie qui décrit aussi les axes pour les futures
recherches.
Toutes ces approches de modélisation et algorithmes
seront motivés, dans le cinquième chapitre, par la proposition
d'un progiciel crée à l'aide du langage de programmation VB dot
net et le logiciel MATLAB. Ce progiciel a comme objectif principal
l'affectation des personnes disponibles de façon pertinente au bon
endroit et au bon moment et en conformité avec la loi et les exigences
du marché.
14
Chapitre 1
Le Processus de planification
Introduction
Dans un environnement purement concurrentiel, les compagnies
d'assistance aérienne ont intérêt à planifier le
travail de personnel et la gestion du temps de manière efficace et
exacte afin d'améliorer la productivité et la
compétitivité en termes de compétence, coût et
qualité.
Ce chapitre est consacré à la
présentation de la problématique de la « planification
» dans un cadre général puis dans un contexte
aéronautique. Nous commençons par définir la planification
tout en déterminant son apport à la performance de l'entreprise
et ses enjeux dans la première section. Ensuite dans la deuxième
section, nous traitons la complexité du processus de la planification au
quotidien de la compagnie d'assistance ce qui permet de présenter par la
suite l'horizon de la planification dans la troisième section. En
finissant par quelques méthodes de résolution proposées
dans la littérature dans la quatrième section.
1 Notion de la planification
Les coûts d'exploitation, le capital
élevés et la faible marge bénéficiaire rendent
l'industrie du transport aérien international extrêmement
concurrentiel ce qui pousse les compagnies d'assistance aériennes
à chercher continuellement la réduction des coûts en
augmentant la productivité et l'efficacité. Dans ce cadre, la
planification du personnel est primordiale pour les entreprises de grande
taille.
1.1 La planification du personnel de l'entreprise
L'objectif principal des compagnies est d'atteindre un
rendement financier raisonnable, tout en veillant à ce que les normes de
service ne sont pas érodées. Parmi les coûts que les
entreprises essayent de réduire sont les coûts relatifs à
la gestion du personnel à savoir les coûts
15
de recrutement, de formation, de gestion et de
rémunération du personnel. Ces coûts constituent une
composante importante des coûts de fonctionnement des compagnies.
Dans ce cadre, la planification du personnel est une
nécessité pour chaque entreprise dont l'objectif est d'aboutir
à des programmes permettant d'organiser et planifier le travail des
salariés afin de rester pérenne dans l'économie globale.
Ceci passe par l'affectation de la bonne personne à la bonne place au
bon moment tout en satisfaisant les objectifs de la compagnie et les exigences
des employés.
En effet, la planification est considérée comme
un processus très complexe qui « vise à affecter les
ressources humaines pour chaque intervalle de temps sur un horizon
donné, de telle sorte que les besoins par intervalle soient couverts et
que les différentes contraintes soient satisfaites » [Chan Peter].
Bien qui ils sont parfois contradictoires à savoir l'environnement du
travail (satisfaction du personnel, sécurité...), les contraintes
juridiques (durées de travail et de repos...), les contraintes sociales
(répartition équitable du temps de travail et du repos), les
contraintes techniques (caractéristiques des tâches) et les
contraintes économiques.

Figure 1. Schéma illustrant le problème de la
planification - Dr. Chan Peter
16
En d'autres termes, la planification du personnel correspond
à la construction d'emplois du temps spécifiant pour chaque
employé ses jours et horaires de travail, ainsi que ses jours de repos,
tout en respectant un ensemble de contraintes. Dont le but est de trouver le
meilleur arbitrage possible entre trois critères le coût, la
qualité de service et la satisfaction sociale :
- Le coût : apparais sous la forme du
coût de la main d'oeuvre directe nécessaire pour réaliser
la charge de travail.
- La qualité de service : correspond à
la mesure de l'efficacité pour répondre à la demande des
clients internes et / ou externes. Ainsi que la réalisation des
tâches dans les meilleurs délais et en conformité avec les
exigences du client.
- Les critères de satisfaction sociale :
concernes la satisfaction des employés vis-à-vis de leurs
horaires et de leurs conditions de travail. La satisfaction des exigences de
sécurité et d'environnement est devenue un enjeu de
compétitivité.
Dans ce cadre, nous notons l'importance de la planification du
personnel dans l'amélioration de la performance de l'entreprise.
1.2 L'apport de la planification du personnel à la
performance de l'entreprise
La véritable richesse d'une organisation est sa
ressource humaine dont la différence entre une entreprise performante et
une entreprise non-performante, ce sont avant tout les employés, leur
enthousiasme, leurs compétences et leur créativité. En
effet, la planification des ressources humaines prend une importance
grandissante de nos jours. Dû à la nécessité d'une
adaptation permanente de plus en plus rapide et réactive de l'entreprise
et ses employés aux environnements technique, économique,
politique et social afin d'atteindre les objectifs de performances.
En effet, le concept de performance peut faire l'objet d'un
vaste débat. Son contenu est variable et entraine des estimations
différentes, notamment en ce qui concerne sa mesure. Mesurer l'apport de
la planification des ressources humaines à la performance de
l'entreprise
permet de mieux gérer les ressources humaines et donc
d'optimiser la contribution à la performance des organisations à
savoir la performance financière, la performance économique, la
performance organisationnelle et la performance sociale.
- D'un point de vue financière, la
planification assure une coordination optimale des salariés permettant
de réduire le risque d'affaires (en termes d'absentéisme,
accident...) d'une entreprise et atteindre le rendement visé de ses
actifs.
- D'un point de vue économique, la
planification des ressources humaines peut s'appuyer sur des arguments de la
théorie du capital humain, les connaissances, les habiletés et
les compétences détenues par les individus représentent
une source de valeur économique pour la compagnie (Jackson et Schuler,
1995 ; Ducharme, 1998).
- De point de vue sociale, la motivation et la
satisfaction des travailleurs sont les piliers de la planification et ils
présentent les facteurs principaux qui influent le comportement des
employés.
- De point de vue organisationnelle, la motivation et
la satisfaction des travailleurs permettent d'avoir un impact sur la
qualité de production et la rentabilité des entreprises.

17
Figure 2. L'apport de la planification du
personnel à la performance de l'entreprise
18
Nous pouvons conclure que la planification du personnel
conduit à avoir un planning où pour un horizon donné, nous
optimisons la gestion des ressources humaines de façon à couvrir
un besoin exprimé par une charge de travail prévisionnelle tout
en respectant un ensemble de contraintes précises. De ce fait, la
construction du planning suit un processus bien défini.
1.3 Le planning
La construction du planning débute par le recensement
des activités futures afin de déterminer les capacités et
les besoins en personnel. L'entreprise doit satisfaire ces derniers en
affectant la bonne personne, à la bonne place au bon moment et en
respectant les contraintes sociales, juridiques, économiques et
techniques.
L'analyse des déséquilibres entre les besoins
futurs et les ressources humaines déjà en place permet de mettre
en lumière les dysfonctionnements qui perturberaient l'évolution
de l'organisation. Ce dysfonctionnement exige le ré-recensement des
besoins en termes de personnel.
En cas d'adéquation des activités futures avec
les capacités en personnel, nous précédons à
l'élaboration du calendrier qui doit satisfaire les exigences des
différents acteurs. Nous déduisons que le processus de planning
se compose de :
- La détermination des activités future de
l'entreprise,
- Le recensement de besoins en tenant compte les ressources
nécessaires et les ressources
disponibles,
- La vérification du respect des contraintes social,
économique, juridique et technique,
- La détermination des tâches à
exécuter et l'horizon de la planification (une semaine),
- Élaboration du calendrier de travail,
- La vérification de réalisation des objectifs des
différents acteurs,
- La publication du planning,

19
Figure 3. Processus d'élaboration du planning
De ce qui précède nous déduisons que les
plannings sont des calendriers de travail, où figurent à la fois
le temps, l'affectation du personnel, les jours et horaires de travail, et les
congés et repos.
20
Certains plannings spécifient les pauses et les
périodes de travail de la journée de chaque employé et
selon l'horizon de la planification, le planning peut être journalier,
hebdomadaire, mensuel ou annuel.
D'autres affectent le personnel en fonction des tâches
et compétences ce qui exige la décomposition, le repérage
des tâches en gammes opératoires que chaque personne est capable
d'accomplir, nous parlons de plannings des tâches.
Certains autres plannings sont cycliques, c'est-à-dire
qu'ils reflètent une certaine périodicité des horaires
individuels tant que les contraintes restent inchangées sur une
période définie. Ces plannings présentent une
facilité de construction, mais une difficulté réside dans
la prise en compte des souhaits du personnel. Cependant, dans un processus de
planification non-cyclique, dit acycliques, un nouveau planning est
généré pour chaque période de planification et peut
tenir compte les souhaits du personnel.
Dans le cadre aérien aussi le planning peut être
l'un des types déjà cité, mais la planification du
personnel dans la compagnie d'assistance se caractérise par la
diversité des contraintes à prendre en considération.
2 La planification du personnel dans la compagnie
d'assistance 2.1 Les problèmes de planification
Les compagnies d'assistance aériennes d'aujourd'hui
sont confrontées à une pression des coûts énormes.
Compte tenu de nouveaux concurrents et de la croissance du marché du
transport aérien, les compagnies d'assistance tentent d'accroître
leur compétitivité et réduire leur coût y compris
les coûts du personnel au sol.
Ces prestataires du service de manutention au sol sont
rarement de petites entreprises indépendantes qui fournissent un seul
service. Généralement, ces compagnies vont gérer plusieurs
services interalliés simultanément pour une seule compagnie
aérienne ou pour plusieurs compagnies selon un programme des vols.
21
Ainsi, il important de noter que le programme des vols d'une
compagnie aérienne impose un ensemble de tâches qui peuvent
être distinguées par les opérations de piste et les
opérations de services passagers :
- Les tâches de piste : regroupent les
tâches effectuées au niveau ou à proximité de
l'avion dans la piste y est inclue la manutention des bagages, nettoyage des
appareils, les services d'eau potable, le transport par autobus, le fret, la
planification et le contrôle du chargement.
- Les services passagers : effectués à
l'arrivée ou au départ de l'avion dans le terminal de
l'aéroport se réfèrent principalement à l'accueil,
l'enregistrement, l'embarquement, services d'assistance.
En d'autre terme, les opérations au sol regroupent les
tâches de piste et les tâches du terminal. La « figure 4
» illustre un aperçu général des tâches selon
l'association internationale du transport aérien IATA.

Figure 4. Les tâches se produisant autour de l'avion
selon l'association internationale du
transport aérien IATA
22
Nous notons que la demande, manifester dans les tâches
à exécuter, peut être très irrégulière
et spécifiée sur des intervalles de temps aussi court que cinq
minutes ce qui nécessite un haut degré de coopération et
de spécialisation et ce qui exigent la planification des
différentes qualifications. Ainsi, en raison de la taille de ces
opérations même des petites améliorations se traduisent par
d'importants gains économiques.
De ce fait, nous considérons le problème de
planification du personnel dans la compagnie d'assistance comme un
problème de planification de main d'oeuvre
hétérogène avec des compétences multiples pour
couvrir une demande donnée tout en minimisant les coûts.
Notons que la planification efficace, nonobstant que c'est une
tâche très complexe, est cruciale dans la maîtrise des
coûts. Du fait, qu'elle implique souvent plusieurs centaines
d'employés, plusieurs tâches par semaine et une multitude de
contraintes. À savoir contraint social, technique, économique ou
encore juridique. Dans ce cadre, nous notons que la réglementation du
travail et les organisations de réglementation aérienne nationale
et internationale définies des nombreuses règles et restrictions
aux différentes opérations d'assistance au sol. Ainsi, les
aéroports, souvent, travaillent sur une base continue 24 heures, sur
sept jours par semaine.
De plus, la complexité de planification du personnel
dans la compagnie d'assistance se manifeste dans l'enivrement de travail
incertain. Dû fait que, dans la plupart des cas, les ressources humaines
sont planifiées selon le calendrier des vols et les tâches
à effectuer, mais cette planification peut subir une modification due
aux changements connexes à savoir les limitations dans les
capacités actuelles (absences, retards...) et les perturbations des
vols. Et comme la compagnie fonctionne à pleine capacité, la
planification efficace de ces ressources est, de plus, en plus importante dont
elle doit couvrir toutes les opérations. Cependant, il est important de
noter que la demande de main d'oeuvre est soumise à de fortes variations
à différents moments de la journée ce qui se traduit par
trois ou quatre périodes de pointe de charge de travail
élevée au sein de chaque jour.
La planification prévoit donc l'estimation de la charge
de travail, à l'aide des courbes de charge (voir figure 5), afin de
planifier les personnels avant plusieurs jours ou semaines des
23
opérations à partir d'un horaire fixe des vols,
le nombre prévu des passagers et des bagages et les exigences des
compagnies aériennes.

Figure 5. Charges de travail typique de l'aéroport
Enfidha-Hammamet au cours de la journée
pour l'année 2014.
Cependant, il est important de noter que la planification du
personnel au sol n'est pas directement formulée à partir des
tâches à effectuer. Il y a une étape intermédiaire
dont les tâches doivent être groupées en vacations
affectées par la suite au personnel en tenant compte certaines
contraintes.
Dans ce cadre, nous notons que nous n'allons pas traiter
l'aspect de temps réel, c'est-à-dire les questions relatives aux
changements d'horaire à court terme ou de maladie ne seront pas prises
en considération. Les modèles d'optimisation et les algorithmes
développés seront génériques et s'appliquent
à un large éventail d'activités d'assistance en escale.
Toutefois, certains services peuvent ne pas être couverts dus à la
diversité considérable des tâches exécutables.
De ce fait, nous visons à concevoir un modèle de
planification du personnel dans une compagnie d'assistance,
spécifiquement la compagnie d'assistance TAV Handling, robuste sur un
large éventail d'informations pertinentes et des scénarios de
planification différente.
24
2.2 Le modèle de la planification au sol
En référence à la chronologie de la
planification de la section précédente, nous pouvons
présenter un modèle de planification qui conçoit les
étapes et les flux de planification du personnel au sol.
Les étapes de ce modèle de planning
reflètent également comment et quand les différents
niveaux de décisions sont introduits dans le processus de planification.
Le modèle de planification présenté dans la « Figure
6 » illustre les étapes spécifiques observées dans la
compagnie d'assistance. Ces étapes ne doivent pas être
considérées comme des problèmes isolés dont le
résultat d'un problème contribue aux problèmes
ultérieurs

Figure 6.La chronologie des problèmes dans le
modèle de planification du personnel de
manutention au sol.
2.3 Les étapes de la planification
Une boucle de rétroaction peut être
imaginée entre chaque étape de la planification, de sorte qu'une
étape puisse modifier les conditions des étapes
ultérieures. Les principales étapes du modèle de
planification sont présentées brièvement ci-dessous, mais
elles seront présentées en détail dans les chapitres
suivants :
- La modélisation de la demande : la
modélisation de la demande porte sur la détermination de la
charge de travail qui doit être effectuée en fonction de
prévision des vols dans laquelle des exigences temporelles sont
analysées dans leur évolution dans le temps et en
25
tenant compte des périodes de pointe. La
modélisation de la demande est décrite en détail dans le
chapitre 2.
- La Conception des vacations : la conception des
vacations consiste à déterminer des prévisions d'horaire
qui couvrent la demande. Cette étape est considérée comme
stratégie tactique lorsqu'elle est utilisée pour
déterminer la taille minimale de la main d'oeuvre pour une
opération donnée compte tenu des caractéristiques des
personnels. Elle tient en considération la demande globale (obtenue
à travers le programme des vols) dans l'élaboration de la liste
des vacations.
- La planification de la main d'oeuvre : consiste
à planifier les personnels en tenant compte la réglementation du
travail, les contraintes techniques et sociales. Il utilise les sorties du
deuxième module pour répartir les vacations sur un jour
particulier au personnel qui sont inscrites au tableau de service ce
jour-là.
- L'affectation du personnel : est le processus
d'affectation des tâches du travail à chaque employé.
L'affectation du personnel ne fait pas objet d'étude dans ce
mémoire.
- Modification journalière : c'est la
planification des personnels aux tâches selon les changements du jour de
l'opération.
Nous pouvons déduire que la planification du personnel
est évolutive dans le temps. De ce fait, nous allons élaborer,
dans la section qui suit, un modèle général de
problème de planification selon le temps de prise de décision
puis nous introduisons un modèle de planification pour les
opérations de manutention au sol.
3 L'horizon de planification
3.1 Les scénarios de planification
Comme nous avons déjà dit, les problèmes
de planification existent dans une grande variété, certains
problèmes peuvent nécessiter la solution d'un autre
problème de planification. À titre d'exemple, prenons deux
décisions qui doivent être compatibles
1. Quels sont les objectifs pour les dix prochains jours ?
2. Que faire demain ?
Ce sont deux questions très différentes qui auront
des exigences complexes :
- La première question .
· demande au
décideur de générer une stratégie aux dix prochains
jours pour l'entreprise.
- La deuxième question .
· demande un
plan détaillé pour le lendemain en tenant compte les ressources
nécessaires.
Néanmoins, le problème à moyen terme
devrait être résolu avant le problème de court terme
dû fait que les plans quotidiens doivent être compatibles aux
stratégies formulées. Il est typique de classer les
problèmes de planification en fonction de la dépendance
temporelle entre eux (voir figure 7) :
- Les solutions des problèmes à mi-parcours sont
désignées stratégies tactiques,
- Les solutions des problèmes du jour sont notées
stratégies opérationnelles,
- Et la modification de la planification selon les changements
journaliers est les stratégies en temps réel.

26
Figure 7 . Les scénarios de planification en fonction du
temps
27
3.2 Les planifications tactique, opérationnelle et en
temps réel
Comme nous avons déjà annoncé, la
planification tactique se produit à la date prévue de production
du calendrier, elle inclut l'analyse de scénarios, et la
détermination de la main d'oeuvre pour les opérations. Un
scénario typique de la planification tactique est de créer des
calendriers qui couvrent les opérations pour une période future,
comme la semaine prochaine ou le mois prochain, et qui peuvent inclure des
changements dans la gestion du personnel.
La planification opérationnelle consiste à
générer des plans d'exécution détaillés pour
la journée d'opération. À ce stade, la demande et la
disponibilité des ressources sont considérés comme fixe.
Le problème est alors d'attribuer les travaux aux différentes
ressources en tenant compte de la planification antérieure et en
satisfaisant les contraintes d'exploitation.
La planification opérationnelle couvre les
décisions spécifiques à un jour de l'opération dont
elle consiste à couvrir principalement les problèmes de
planification quotidienne des tâches considérant le changement de
vacation, les maladies et les heures supplémentaires.
Planification en temps réel dans la phase finale est
préoccupée par l'adaptation d'un plan de services afin de traiter
les perturbations qui peuvent survenir au cours de la journée
d'opération. De ce fait, la planification en temps réel (ou
dynamique) réagit aux événements survenus au cours du jour
de l'opération.
Nous pouvons conclure que certaines décisions sont
naturellement faites avant d'autres. De même dans le contexte
aérien, la détermination du taille de la main d'oeuvre dans la
période prévue (planification tactique) est
réalisée avant l'affectation des ressources humaines
(planification opérationnelle) ainsi la planification journalière
(planification en temps réel) est générée en
fonction des informations fiables et disponibles aux différents moments
de l'horizon de planification, où les événements
réels sont différents aux événements attendus.
Comme la journée d'opération se rapproche, ces informations ou
ces facteurs de perturbation deviennent, de plus en plus, connus. Ces facteurs
résultent à la fois des décisions extérieures
(comme les voeux des employés, les retards des vols...) et aussi les
besoins de planification (conception des
28
horaires de repos...). Nous pouvons conclure que le processus
de planification est délimité par certaines contraintes et
facteurs qui seront détaillés par la suite.
3.3 Les limites de processus planification
Les limites de processus planification sont de plusieurs natures
à savoir :
- Limite de décomposition .
· les
méthodes courantes décomposent la planification en
sous-étapes séquentielles et irrévocables la
modélisation de la demande, la conception des vacations, la
planification de la main d'oeuvre, l'affectation du personnel et la
modification journalière. La somme des sous-solutions optimales n'est
pas toujours optimale globalement.
- Limites des modèles .
· il est
absolument nécessaire de proposer des plannings qui prennent compte les
individus, les qualifications, les préférences, et l'historique
pour générer des plannings équitables.
- Limites de prise compte du contexte dynamique
.
· les plannings sont sujets à aléas en ressources
et en charge et qu'il faut les réviser en conséquence.
Ces limites ont été débordées dans
plusieurs revues et plusieurs solutions ont été proposées.
Cependant, le problème de la planification des emplois du temps de
salariés est un problème qui se pose dans de nombreux domaines,
et qui a été étudié de façon
spécifique, il n'existe pas de modèle générique
pour un tel problème. Dont chaque domaine a ses contraintes et la taille
du problème elle-même est liée au nombre de contraintes.
4 Les méthodes de résolution dans la
littérature
Les méthodes de résolution utilisées se
situent dans un large éventail de recherche datent des années 50
suite à la création d'horaires de travail pour les agents d'un
poste de péage par Dantzig. Ce modèle est considéré
le modèle de base de la planification.
Par la suite de nombreux secteurs ont été
visés à savoir le secteur bancaire (Jacques 93), les services
hospitaliers (Brusco, M. J., Futch, J., & Showalter, M. J. 1993), les
compagnies de transport ferroviaire (A.Caprara 1998), etc. Dans l'article de
A.T.Ernst date 2004 nous trouvons
29
une revue de littérature sur la planification de
personnel en général. Des outils, des modèles et des
méthodes utilisées dans différents secteurs sont
détaillés. Ces méthodes permettent la classification du
problème de planification à savoir cyclique et non-cyclique
(Table 1), journalier, hebdomadaire ou mensuelle.
Les méthodes de résolution ont dû
être adaptées aux modèles proposés pour
résoudre les programmes linéaires obtenus, des méthodes de
génération de colonnes ont été utilisées (en
Allemagne [Fahle Junker Karisch Kohl Sellmann Vaaben 99], et au Royaume-Uni
[Fores 96]), ainsi que des méthodes heuristiques basées sur une
relaxation lagrangienne du problème [Sanders Takkula Wedelin 99], pour
des tailles importantes. Nous noterons aussi l'utilisation de la méthode
de recherche tabou [Chiarandini Schaerf Tiozzo 99].
|
LUN
|
MAR
|
MER
|
JEU
|
VEN
|
SAM
|
DIM
|
LUN
|
MAR
|
MER
|
JEU
|
VEN
|
SAM
|
DIM
|
|
AGENT 1
|
M
|
E
|
N
|
|
M
|
E
|
N
|
|
M
|
E
|
N
|
|
M
|
E
|
|
AGENT 2
|
E
|
E
|
E
|
E
|
E
|
|
M
|
N
|
N
|
|
|
M
|
M
|
M
|
|
AGENT 3
|
M
|
N
|
N
|
|
|
M
|
M
|
M
|
E
|
E
|
|
E
|
E
|
E
|
Table 1. Exemple de planning non-cyclique sur 2 semaines pour 4
employés (M : vacation du
Matin, E : vacation du soir, N : vacation
de nuit)
Cependant, Baker (1976) classifie les méthodes de
résolution du problème de planification en trois types :
- Le positionnement des jours de repos : consiste
à déterminer le nombre de personnes à affecter à
des jours de repos.
- La planification des vacations : qui consiste
à définir le nombre de personnes à affecter à
chaque vacation afin de respecter une charge et de minimiser le coût des
vacations.
- La planification des tours : qui combine les deux
autres types de problèmes et qui consiste à déterminer le
nombre de personnes à affecter à chaque tour en respectant la
charge et la politique de repos.
30
4.1 Le positionnement des jours de repos Day-Off
Scheduling
Dans la littérature, l'approche d'optimisation de jour
de repos est l'approche de planification la plus popularités. Cela peut
être dû au fait qu'il est plus facile à gérer le
problème de planification avec la fixation du jour de repos. Tibrewala
(1972) a trouvé un algorithme simple qui fournit une solution optimale
pour la planification cyclique de deux jours de repos successifs. Baker et
Magazine ont étudié ce problème sous une
variété de propositions de jours de repos : deux jours de repos,
deux jours de repos consécutifs et quatre jours de repos toutes les deux
semaines. Ils ont tiré des formules explicites pour déterminer la
taille de l'effectif et ont développé des algorithmes pour
construire un calendrier réalisable dans chaque cas. Rosenbloom et
Goertzen (1978) ont examiné le problème de planification des
infirmières sous une variété de règles de travail,
les jours d'opération (de travail) et les jours de repos. Dans une
étude récente, Emmons et Fuh (1997) ont examiné le
problème de jours de repos pour sept jours de travail où la
demande est considérée constante. Leur contribution est qu'ils
ont considéré deux types d'employés à temps partiel
pour compléter les travailleurs à plein temps.
4.2 La planification des vacations
La programmation des vacations de travail tente à
planifier l'horaire d'un seul jour et si la demande pendant les périodes
différentes est constante pendant toute la semaine la planification
cyclique peut être appliquée. Les études de planification
de vacation ne mention pas explicitement la variabilité de la demande
toute la semaine, mais ils supposent implicitement que le calendrier sera
cyclique. Dans le cas contraire, le problème de planification des
vacations peut être résolu pour chaque jour
séparément. Dans la littérature, beaucoup de
méthodes de résolution du problème de création des
vacations reposent sur des approches par recouvrement d'ensemble. Dans une
première étape, tout ou une partie de l'ensemble des vacations
candidates sont générées (Easton et Rossin91). Ensuite,
les vacations faisant partie de la solution finale sont
sélectionnées selon différentes méthodes à
partir d'une première solution générée par la
résolution d'un problème de recouvrement d'ensemble
relâché de Dantzig (1954) (présente en détails dans
le chapitre 3).
31
4.3 La tournée d'horaire
Le problème de tournée d'horaire a eu plus de
popularités dans les études ultérieures, car il
présente un cadre plus réaliste et fourni une solution plus
flexible. Burns et Koop (1988) ont introduit un algorithme modulaire pour
résoudre la planification des vacations cyclique en tenant compte les
contraintes jour de repos et la minimisation de nombre de travailleurs.
Brusco(1998) a étudié le problème tourné du
calendrier du personnel en fixant des limites à temps partiel et
à plein temps. En effet, dans la littérature, tous ces
modèles sont regroupés dans deux approches de modélisation
et de résolution l'une basée sur les techniques de Programmation
Linéaire en Nombres Entier (PLNE), l'autre sur les Principes de la
Programmation Par Contraintes (PPC). Chacune des approches vise à
obtenir le planning le plus équitable possible.
4.4 Modèles PLNE et PPC
Les modèles en Programmation Linéaire en Nombre
Entière (PLNE) peuvent exprimer les contraintes sur les durées de
travail journalier et en traitant des variables en nombres entiers, nous
obtenons le nombre de salariés homogènes qui effectuent un
travail. Le premier modèle de couverture de charge est dû à
Dantzig (1954) repose sur la construction des vacations qui assure la
couverture des charges. Le second modèle est le modèle implicite
de Moondra (1976) où chaque vacation n'est plus
représentée qu'implicitement par le nombre d'agents qui
travaillent au cours d'un intervalle p. Cependant, le problème
des pauses a étaient résolu par Bechtold et Jacobs (1990). Un
modèle doublement implicite est proposé par Thompson (1995)
permettant de tenir compte à la fois des heures de début de
vacations et les pauses. Le modèle de Jarrah(1994) a
intégré la modélisation implicite des pauses avec les
algorithmes exacts de positionnement de repos développés et de
plus traité les travailleurs à temps partiel.
En effet, les modèles conçus pour la PLNE ne
peuvent pas être traités avec la même efficacité en
PPC, Programmation Par Contraintes, qui traite des contraintes de nature
globale (contraintes cumulatives) et non-locale à un nombre de
variables.
32
Les modèles PPC sont multiples à savoir le
modèle explicite de Partouche (1998) présente une liste de
vacations comme un objet contenant 3 vecteurs de même longueur le vecteur
des heures de début, le vecteur des heures de fin et le vecteur des
durées, cependant ce modèle est très peu performant.
Partouche présente un deuxième modèle implicite de
planning individuel avec des variables de début et de fin de vacation,
proche de celui de Moondra, ce qui évite d'énumérer toutes
les vacations possibles.
Conclusion
La planification d'horaires de personnel est indispensable
pour la performance de l'entreprise. Cependant, elle donne naissance à
des problèmes difficiles à résoudre provenant autant des
différentes règles de travail que de la variété des
employés. Du fait, qu'il était nécessaire de suivre un
processus qui permet de trouver des solutions respectant toutes les contraintes
de ces problèmes. Ce processus se compose de plusieurs étapes qui
diffèrent selon la stratégie de planification adopte (tactique,
stratégique ou opérationnel). Dans le chapitre suivant, nous
allons présenter en détail la première étape du
processus de planification tactique à savoir la modélisation de
la demande.
33
Chapitre 2
Modélisation de la demande
Introduction
Ce chapitre est consacré à la
présentation détaillée de la première étape
de processus de planification à savoir la phase de modélisation
de la demande. Elle consiste à déterminer le nombre des
employés nécessaires pour assurer l'assistance des vols en tenant
compte les différentes contraintes.
Pour se faire, une représentation graphique de la
demande serra étudiée dans la première section. Cette
présentation serra modélisé, dans la deuxième
section, à l'aide de la programmation linéaire et à l'aide
des données de Panel. Cependant, les contraintes et l'écart entre
l'offre et la demande seront discutés dans la troisième section.
La quatrième section présentera les aspects de la demande
hétérogène.
1 Représentation de la demande
La planification de la main d'oeuvre utilise une description
agrégée de travail. Dont nous nous n'intéressons pas lors
de la planification tactique aux demandes particulière. Les courbes de
demande ont pour but de modéliser la demande globale. Ainsi, dans les
compagnies d'assistance aérienne, il est fréquent de
modéliser les charges de travail à l'aide des courbes de la
demande sous forme d'un histogramme des tâches parallèles dans
l'horizon de planification (voir figure 8).
34
1.1 La courbe de la demande
Les courbes de la demande sont communément
désignées charge de travail ou prévisions de la demande
dont il permet de spécifier le nombre de travailleurs requis au cours de
chaque intervalle de temps pour la période de planification.
Ainsi, dû fait que chaque tâche de travail exige un
employé, cette représentation permet une analyse simple des
besoins de main d'oeuvre, par exemple pour une seule journée nous
pouvons déterminer pour chaque intervalle de temps la
valeur entière du nombre des agents requis .
La courbe de la demande est aussi une abstraction commune de la
charge de travail dont il permet d'analyser facilement les pics de charges de
travail et par conséquent permet aux planificateurs de fixer des
vacations appropriées couvrant la demande.

Figure 8. Charges de travail au cours de la journée dans
l'aéroport Enfidha-Hammamet. Cependant, il important de noter que dans
le domaine aérien, la demande est liée à l'arrivée
ou au départ des vols dont l'attribution et la durée des
tâches doivent être exécutées en se
référant soit à l'arrivée, le départ ou le
temps d'escale, à titre d'exemple à l'arrivée, il faut
décharger le bagage cinq minutes après l'atterrissage et dont la
durée dépendent de nombres de bagages. En revanche, les
tâches de nettoyage de la cabine se réfèrent aux temps
d'escale de l'avion.
35
Toutefois, les tâches peuvent être
générées pour plusieurs vols en commun à savoir
l'enregistrement des passagers qui sert souvent des groupes de vols ou le
déchargement de bagages si les postes de stationnement sont adjacents.
La charge de travail résulte dans ces cas selon les nombres de passagers
et des bagages à être desservis par un groupe de vols.
De ce fait, les compagnies d'assistance aériennes ont
tendance à regrouper les vols dans des «banques» dans un court
laps de temps (voir figure 9) puis décomposer ces vols en
arrivées et départs tout au long de la journée afin de
minimiser les retards des avions.
Dans le reste de ce chapitre, nous adoptons la courbe de la
demande qui représente la charge de travail total et qui correspond
à la figure 8.
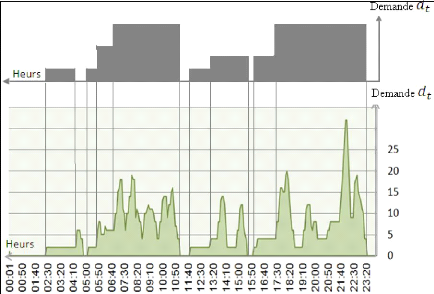
Figure 9. Regroupement des vols au cours de la journée
dans l'aéroport Enfidha-Hammamet.
Afin de présenter les courbes de la demande, nous
devons tout d'abord estimer la demande. Cette estimation peut être
déterminée par une variété de manières
suivant les sources de la demande.
36
1.2 Les sources de la demande
La plupart des travaux d'assistance au sol proviennent des
tâches dans une période de
temps limitée dont leurs regroupements peuvent
être convertis en demande globale . Pour les tâches
individuelles qui sont gérées de façon identique comme
l'enregistrement des passagers et des bagages, il est fréquent
d'utiliser les prévisions afin de déterminer le volume de
tâches à chaque unité du temps. Cette prévision
serra effectuer sur la base des programmes des vols, les
caractéristiques de chaque vol et les engagements des compagnies.

Figure 10. La détermination des tâches
En effet, la figure au dessus représente le schéma
de base de la détermination des tâches à l'aide de trois
piliers :
- Une première entrée .
· le
programme des vols qui souvent contient des informations relatives au
positionnement du vol à savoir le stationnement des avions, les portes
d'arrivée et les comptoirs d'enregistrement.
- La deuxième entrée .
· les
caractéristiques de chaque vol à savoir le nombre de passagers et
le nombre de bagages.
- La troisième entrée .
· les
engagements de la compagnie d'assistance envers les compagnies aériennes
sous forme de contrat d'assistance. Ces engagements représentent les
règles de détermination des tâches selon les
spécificités de vol à savoir le type d'aéronef,
itinéraires, des intervalles de charges de bagages, etc., dont une norme
d'engagement peut fixer le nombre des agents nécessaires à
effectuer une tâche, à titre d'exemple, quatre agents de nettoyage
pendant 25 minutes pour un Boeing 738.
37
Cependant, la détermination des tâches n'est pas
totalement déterministe dû à l'enivrement aérien
incertain (retards des vols, absence des employés...). Ce qui exige de
déterminer une flexibilité minimale de la demande.
1.3 La flexibilité de la demande
La flexibilité du travail est l'un des moyens
permettant à une entreprise de s'adapter aux évolutions de sa
demande et de son environnement. Cette flexibilité est l'une des
composantes de sa réactivité industrielle dont elle implique
toutes les ressources de l'entreprise et en particulier son personnel.
En effet, l'utilisation de techniques de prévisions
à savoir la transformation des charges de travail par la courbe de la
demande permet de déterminer pour chaque intervalle du temps la demande
exigée. Cette demande peut être regroupée pour former une
plus grande masse de charge de travail prévisionnel.
Ce regroupement est efficace quand il n'y a pas de
flexibilité minimale de la demande particulièrement pour les
tâches fixes. Cependant lorsque la demande est plus complexe certaines
décisions doivent être prises pour créer la charge de
travail conduisant à la transformation de la demande à des
problèmes de modélisation. Dû fait que le problème
de la mise en place des tâches pour générer une charge de
travail aussi lisse que possible est connu comme le problème de
nivellement des ressources.
Ce problème d'égalisation de la demande à
l'offre (ressources disponibles pour la réalisation de service)
nécessite une estimation approximative de la demande globale.
2 Estimation de la demande
Plusieurs représentations de la demande peuvent
être faisables pour la même quantité de travail et dans ce
cas, il est désiré d'obtenir la représentation la plus
efficace.
38
2.1 Estimation de la demande à l'aide du PLNE
La détermination des besoins en personnel pour chaque
période de l'horizon peut être faite sous forme linaire tenant
compte la réduction des coûts.
Nous supposons que le coût de prévision de la
demande du service pour l'intervalle du
temps t est noté . Et nous supposons que
l'estimation du coût du service est notée
, le coût de manque du service est noté et le
coût d'une heure de rémunération du
personnel est noté . La fonction linéaire serra
donc la suivante :
Cependant, cette fonction ne présente pas explicitement
le coût et l'estimation du personnel.
Pour ce faire, nous devons se baser sur les modèles qui
utilisent la représentation de la courbe de la demande du travail et qui
peuvent dans leur forme de base se présenter comme une variante du
modèle d'origine de programmation linéaire de George Dantzig
1947.
À fin d'adopter ce modèle au problème de
planification des employés dans une
compagnie d'assistance aérienne nous supposons que est
le nombre des employés affectes à
la vacation v tel
que v = 1,..,3 (avec 1= Vacation du Matin, 2=Vacation du soir, 3=
Vacation de nuit). ). Le modèle réduit au minimum le coût
en agissant sur la demande (nombre des agents
requis) pendant l'intervalle de temps t =1,...,24.
Sous la contrainte que dans l'intervalle
39
de temps t soit égale au nombre des agents
Xt réellement affectés dans l'intervalle de temps
t
pour couvrir le travail at = (0, 1).
at est une variable binaire qui égale à 1
s'il y a de travail à couvrir et 0 s'il n'y a pas de
travail à couvrir.
(1)
(2)
(3)
Selon la fonction (1) et (3) il est facile de formuler le
problème d'estimation de la demande. Il suffit de déterminer
quelle valeur dt avec t = 1, ... , 24 décrivent le mieux
la
charge de travail réel afin de générer
des horaires de travail qui couvrent la totalité de la demande et non
pas seulement les pics. Dû fait que le couvrement d'un seul pic peut
nécessite beaucoup de travailleurs, qui peuvent être en repos
avant et après le pic. Par conséquent, il appartient au
planificateur de trouver un équilibre entre la couverture de la
totalité de la demande et la minimisation des dépenses.
Cependant, lorsque la demande est irrégulière,
il est peu probable de couvrir parfaitement la demande, ou même s'en
approcher. Cela souligne la nécessité de considérer
à la fois le manque et le surplus de personnel dans la prévision
de la « demande incertaine ». Cette demande née suit aux
irrégularités du programme de vols.
2.2 Estimation de la « demande incertaine »
La demande fixe a été modélisée
dans la section précédente sans tenir compte la demande «
incertaine ». Cette demande, comme nous avons déjà
énoncé, est née due aux changements du programme des vols
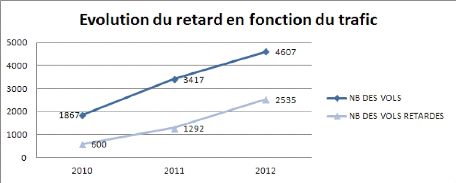
(avance, retards ou encore même l'annulation des vols) qui s'accru avec
l'augmentation du trafic (voir figure 11) à cause de plusieurs facteurs
regroupés et numérisés par IATA sous forme des codes (voir
Annexe 1).
40
Figure 11. Évolution du retard en fonction du trafic :
aéroport Enfidha-Hammamet année 2010-2012
Parmi ces facteurs de retard, nous notons le manque du
personnel des compagnies d'assistance aérienne aux services du passager,
piste (toutes tâches autour de l'avion) et marchandises dont notre
objectif est de les minimiser à travers l'estimation et la
prévision des retards. Le détail des causes relatives à la
compagnie d'assistance ont été présenté par
l'organisme de gestion des flux de trafic aérien (l'Air Trafic Flow
Management ATFM). Les retards dus à l'assistance au sol étaient
d'ordre 28 % (voir figure 12).

Figure 12. Détail des causes de retards selon l'Air Trafic
Flow Management (ATFM) en 2001
Ainsi, la détermination des retards d'arrivé
s'effectue à travers la comparaison de l'heure d'arrivée
prévue avec l'heure d'arrivée effective. La détermination
des retards de départ
41
s'effectue à travers la comparaison de l'heure de
départ prévue avec l'heure départ effective. Nous
supposons que TRD est l'heure réelle de départ et TPD est l'heure
programmée de départ nous pouvons formule le RMD qui
représente le retard moyen par mouvement de départ comme suit
:
De même pour le retard moyen par mouvement
d'arrivée RMA avec TRA est l'heure réelle d'arrivée et TPA
est l'heure programme d'arrivée :
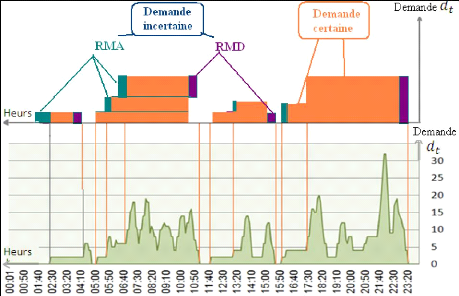
Figure 13. La modélisation de la demande incertaine au
cours de la journée de dimanche année
2011
Par conséquent, la modélisation de la demande
incertaine par l'extension de l'intervalle du temps des tâches avec un
temps moyen de retard (pour l'aéroport Enfidha-Hammamet la demande
incertaine est supposée égale à 20 min) permet de
gérer les imprévues et éviter le manque du personnel.
Cependant, la problématique est comment attribuer cette
demande aux tâches au cours du temps, car certain vols peuvent ne pas
faire de retards, (voir figure 13). De ce fait, il nécessaire de faire
recours à la base de données afin de déterminer la liste
des vols (par compagnie) qui ont tendance d'effectuer des retards. Cette
analyse de base de données doit être effectuée par saison
(été ou hiver), par jour, par compagnie et par facteur de
retards. D'où la nécessité d'utiliser les données
de panel qui sont des coupes transversales répétées
à travers le temps.
2.3 Estimation de la « demande incertaine »
à l'aide du PANEL : cas de la compagnie d'assistance TAV Handling
2010-2013
Afin de déterminer la demande incertaine du trafic
aérien à l'aide d'un modèle de données de panel,
nous faisons appel à des méthodes économétriques
permettant d'aboutir à des conclusions présentant une certaine
robustesse. Ainsi, il est important de noter que les données de panel
consistent à regrouper les données en coupes transversales (un
échantillon aléatoire d'unités (les Vols) observées
à un moment donné (par jour) à travers le temps (Ex :
pendant chaque jour des années 2010-2013, voir Annexe 2 qui contient une
partie de la matrice). Ces données ont donc une double dimension: la
dimension en coupe transversale et la dimension chronologique.

Figure 14. Exemple d'une partie de matrice des facteurs de
retards par jour : 2010-2013
42
43
Dans cette partie empirique, nous choisissons d'utiliser le
logiciel Eviews. En effet, Eviews est un logiciel de système
d'exploitation Windows qui donne une prévision de l'analyse des
données scientifique, l'analyse financière, les prévisions
des ventes et les prévisions économiques.
Nous vérifiions, tout d'abord, la stationnarité
de nos variables. L'étude de la stationnarité des séries
temporelles est incontournable, dû au fait que la plupart des analyses se
faisant sur des séries longues subissent des perturbations d'origine
diverses qui tendent à modifier la variance des données.
Ainsi, selon les résultats obtenus à l'aide du
logiciel Eviews (voir Annexe 3) nous conclurons que toutes les variables sont
globalement stationnaires en niveau du fait que valeur-p < 5 %. Toutefois,
afin de formaliser ces estimations sous forme d'équation avec des
grandeurs économétrique, il faut procéder par quatre
étapes.
Étape 1 : Estimer un Modèle Pooled
(modèle homogène)
Cette étape consiste à vérifier la
capacité du modèle à interpréter les données
disponibles. Le but est de voir si le modèle théorique est
homogène pour tous les individus étudiés ou au contraire,
il existe des spécificités. La fonction générale du
modèle homogène se présente sous la forme suivante :
Ainsi, à l'aide des résultats abstenus à
l'aide du logiciel Eviews nous comparons la valeur-p à un seuil
préalablement défini (traditionnellement 5 %) :
44
- Si la valeur-p est inférieure à ce seuil, on
rejette l'hypothèse nulle en faveur de l'hypothèse alternative,
et le résultat du test est déclaré « statistiquement
significatif » et par conséquent le modèle est
homogène.
- Dans le cas contraire, si la valeur-p est supérieure
au seuil, on ne rejette pas l'hypothèse nulle.

Table 2. Estimation du modèle homogène sous
Eviews
Nous remarquons que valeur-p (F-statistic) < 5% confirme
l'homogénéité du modèle. Nous passons par la suite
à estimer le modèle à effet fixe.
45
Étape 2 : modèle à Effets
Fixes
La fonction générale du modèle à
effets fixes se présente sous la forme suivante :

Table 3. Estimation du modèle à Effet Fixe sous
Eviews
Nous remarquons que valeur-p (F-statistic) < 5% confirme
l'hétérogénéité des individus sous la forme
d'un effet fixe. Nous pouvons donc retenir ce modèle.
Étape 3 : modèle à Effets
Aléatoires
La fonction générale se présente sous la
forme suivante :
dont les résidus sont décomposés en une
partie spécifique à l'individu et une partie variant
au cours du temps. Avec et sont distribuées selon une
loi normale d'espérance nulle.

Table 4. Estimation du modèle à effets
aléatoires sous Eviews
46
47
Les résultats de l'estimation du modèle à
effets aléatoires consignés dans le tableau 4 démontrent
que le modèle à effets aléatoires ne peut pas être
rejeté.
Ainsi, afin de choisir entre les modèles à effets
aléatoires et ceux à effets fixes, qui fournissent des
résultats extrêmement proches, nous appliquons le test de Hausman
:
Étape 4 : test
d'Hausman
Le test de spécification d'Hausman (1978) est un test
général qui peut être appliqué à des nombreux
problèmes de spécification en économétrie. Le test
de spécification de Hausman repose sur le corps d'hypothèses
suivant :
H0 : E ( effets aléatoires )
H1 : E ( (effets fixes)
À l'aide du logiciel Eviews nous obtenons les
résultats suivants :

Table 5. Test d'Hausman
Nous remarquons que Prob < 5% : donc nous rejetons H0. Par
conséquent, nous devons retenir seulement le modèle à
Effets fixes.
3 Les contraintes et L'écart entre l'offre et la
demande
Les estimations et la prévision de demande sont
limitées par certaines contraintes qui peuvent génère des
écarts entre l'offre et la demande :
3.1 Les contraintes
Le problème de la planification et l'ordonnancement du
personnel dans le domaine du transport aérien se manifestent dans le
commencement d'une tâche dans un emplacement défini
48
et son accomplissement dans un autre après une
période de temps. Notons que l'assistance au sol se compose de nombreux
types d'opérations centrées, soit dans la piste, soit dans le
terminal à savoir les comptoirs d'enregistrement des passagers, les
portes d'embarquement, les stands d'avions, etc. Les personnels s'obligent de
se déplacer entre les emplacements pour effectuer leurs tâches. De
ce fait, nous conclusions que le temps de déplacement et le lieu
d'affectation du tâche sont les limitent principales qui affectent la
capacité du personnel à effectuer d'autres tâches.

Figure 15. Regroupement des tâches et les
déplacements au cours de la journée.
Ainsi, une estimation du temps de déplacement peut
être modélisée par l'extension de l'intervalle du temps des
tâches avec un temps moyen de déplacement, (voir figure 15
où les tâches de travail sont affichées en orangé,
les temps de déplacement sont affichés en violet). Dont chaque
circuit peut être interprété comme une séquence de
tâches qui doit être effectuée par un ou plusieurs
travailleurs. Cela peut suffire quand les temps de déplacement ne sont
pas significatifs.
49
Cependant, l'estimation du temps de déplacement ne
serra pas faisable si l'intervalle de temps ou d'autres caractéristiques
des tâches sont significatifs. Dans ce dernier cas, il sera
efficace d'appliquer une approche simple qui regroupe la demande
globale par heure et qui
par simple calcul peut fournir une charge de travail approximatif
à chaque heure.
De toute évidence, la minimisation du nombre de
déplacement correspond à la résolution du problème
d'investissement en ressources humaines notamment dans la planification du
personnel dans les pics.
En général, la courbe de la demande fournie une
meilleure base pour la détermination du décalage entre la demande
et planification, comme il est décrit dans la section suivante.
3.2 L'écart entre l'offre et la demande
Dans le modèle d'origine de la programmation
linéaire de Dantzig spécifiquement les fonctions (1) et (3) la
demande par unité de temps a été considérée
comme des contraintes qui doivent être respectées dont le
défaut de répondre à la demande entraîneraient une
solution irréalisable. Le coût total par vacation (en tenant
compte le coût de personnel) a été réduit minimisant
ainsi implicitement le surplus des travailleurs par unité de temps, mais
sans prise en considération le sur ou le manque d'effectif en cas
d'existence.
(1)
(2)
(3)
Cependant, il est important de traiter l'écart par
rapport à la demande en tenant compte la disponibilité, la
satisfaction des employés en termes d'équité et la
possibilité d'absorber les changements.
Dans certains cas, il est peut-être souhaitable ou
inévitable de considérer le manque de personnel notamment lorsque
la taille de la main d'oeuvre est fixée comme dans le modèle
Bailey
50
(1985) où le manque de personnel est
considéré comme un « inconvénient à la
clientèle » et
reçoit une pénalité linéaire par
unité de temps :
(4)
S/c (5)
(6)
Les fonctions (4) et (6) introduisent un modèle
généralisé qui s'étendent le recouvrement des
fonctions (1) et (3) du modèle de Dantzig. La fonction objective (4) est
une somme pondérée
de trois termes : le coût , le manque de personnel
et sureffectifs . Les fonctions du
manque de personnel et de sureffectifs est une
représentation généralisée du coût de
l'écart de l'offre par rapport à la demande.
Pour simplifier le modèle, nous utilisons le vecteur
variable et
pour le manque de personnel et le sureffectif. La contrainte (5
) équilibre les
vacations, le manque de personnel et le sureffectif à la
demande à chaque unité de
temps
Cependant, dans la littérature il existe plusieurs
modèles qui estiment la valeur de l'écart entre l'offre et la
demande.
3.3 La valeur de l'écart entre l'offre et la
demande
Les fonctions du coût relatif au manque de personnel et au
sureffectif varient
considérablement dans la littérature.
Brusco et Johns (1998) utilisent une approche en deux
étapes dont la deuxième étape minimise au maximum le ratio
de la demande et de sureffectifs. Dowling (1997) mettre en carré la
valeur du sureffectif à chaque unité de temps. Chu (1993)
minimise le sureffectif maximum.
51
Lusby (2010) ajoute une demande d'urgence
supplémentaire de valeur maximum de 15 % de la demande d'origine par
unité de temps.
Cependant, la méthode la plus simple est de
pénaliser le manque de personnel linéairement en imposant un
coût identique pour chaque unité de manque de personnel et les
sureffectifs. Cette approche, a été utilisée par Thompson
(1993) pour satisfaire la demande, mais elle ne tient pas compte la
répartition des sous-effectifs ou sureffectifs dans le temps. Dû
fait que Thompson décrit un modèle où les personnels sont
polyvalents et peuvent effectuer les différents services.
L'approche de Thompson permet de satisfaire les exigences de
la demande aérienne qui se caractérise par
l'hétérogénéité.
4 La demande hétérogène
4.1 L'hétérogénéité de
la demande aérienne
La demande de services d'assistance est considère
hétérogène, dû fait que les services diffères
ou bien ces services sont identiques, mais exprimés à des moments
différents ou dans des lieux différents.
Cette hétérogénéité
nécessite la mise en place de structures de réponses
adéquates afin que la demande soit satisfaite dans un délai
convenable. En effet, l'hétérogénéité de la
demande exige un personnel hétérogène divisé en
différents groupes assez dissemblables considérés comme
des sous-problèmes.
La planification d'un personnel
hétérogène peut s'avérer un travail long, sujet
à erreurs et parfois tout simplement frustrant, dont les employés
subissent le même ensemble de contraintes, mais avec des valeurs
différentes. En effet, tous les employés sont productifs, mais
avec des capacités différentes. Dû fait que le personnel
expérimenté peut être capable d'effectuer des tâches
plus avancées, en plus de leur travail de base.
52
Plus généralement, la main d'oeuvre peut
être multi-compétences divisé en plusieurs types de
capacités regroupées et programmées
séparément. Par exemple, un groupe de nettoyage ou de chargement
ou encore d'enregistrement selon les exigences du service et les qualifications
nécessaires.
4.2 Les exigences du service et les qualifications
nécessaires
Le problème planification d'un personnel
hétérogène se résume dans la conception d'un
ensemble de détails de travail qui précisent les exigences
techniques relatives à la demande à travers la transformation de
la demande, à partir d'une courbe de la demande, aux exigences de base
plus simples.
Ceci fournit un outil fatal pour les organisations à
évaluer les capacités de la main-d'oeuvre existante ou la
nécessité d'adapter la main-d'oeuvre pour répondre
adéquatement à la demande.
En effet, pour décrire le niveau de cohésion
entre les exigences du service et la
qualification du personnel (capacités) , nous pouvons
utiliser la fonction suivante :
(7)
Les niveaux d'interaction calculent le nombre moyen d'exigences
couvertes par
qualification où représente la qualification afin
de couvrir exigence .
Une des principales difficultés dans la
modélisation de personnel technique est la non-similarité des
tâches ce qui peut nécessite de nombreuses combinaisons
différentes de travailleurs ou de ressources.
En effet, différents vols appartenant à
différentes compagnies peuvent nécessiter différents
équipements, ou peuvent nécessiter différentes formes de
service, et différentes exigences particulières. Par exemple,
lors de l'enregistrement et de l'embarquement, certaines
53
compagnies aériennes exigent l'ouverture de certains
nombres de comptoirs d'enregistrement, des compétences linguistiques
spécifiques peuvent également être une exigence pour
certains vols.
Dans la piste, tous les types d'appareils peuvent être
compatibles avec tout type d'équipement néanmoins certain
équipement, des chargeurs ou des véhicules repoussage peuvent
seulement servir certains appareils. Pour le nettoyage, les différentes
compagnies aériennes auront contracté différents niveaux
de service pour leur flotte, ou pour des vols spécifiques.
En effet, la charge de travail qui nécessite des
différentes compétences doit être représentée
à l'aide des courbes de demande distinctes afin de créer des
vacations qui peuvent la couvrir
4.3 La couverture de la charge de travail
Le calcul de la couverture de la charge de travail peut
être considéré comme l'affectation des vacations à
unités de charge par période de temps. Donc toutes les vacations
doivent être associées à une unité appropriée
de charge de travail afin d'éviter le sureffectif et le manque de
personnel.
Cependant, dans un effectif homogène l'affectation
à la vacation, le manque du personnel et les sureffectifs à la
demande est futile due à l'évaluation de la fonction objective du
modèle (4) et le modèle (6) toutefois, dans un effectif
hétérogène l'affectation à la vacation, le manque
du personnel et les sureffectifs à la demande peuvent être
détectés aux différentes parties de la charge de
travail.
Cela signifie que pour un ensemble de vacations de travail le
problème d'affectation doit être résolu afin de trouver un
compromis entre les sureffectifs et le manque de personnel. De ce fait, le
problème de planification de la main-d'oeuvre
hétérogène peut être modélisé comme
suit :
54
En comparaison avec le modèle homogène les
variables , et ont a été remplacés
par des matrices et . Les exigences représentent un
ensemble minimal de
compétences requis pour couvrir un type de demande
donnée.
La demande et le manque de personnel existent pour chaque
exigence. Les qualifications représentent les compétences
combinées de l'agent dans une vacation. La matrice
de sureffectifs contient une valeur distincte pour chaque
qualification.
La fonction objective (8) est une somme pondérée
des coûts et les fonctions du manque
de personnel et sureffectif . Elle est identique à la
fonction objective (4) dans le modèle
homogène sauf que les vecteurs manque de personnel et les
sureffectifs ont été remplacés par des matrices à
deux dimensions. La contrainte (9) impose le nombre des agents pour chaque
exigence et la contrainte (10) relie les agents avec les exigences et les
qualifications.
Conclusion
Dans ce chapitre, nous avons modélisé la demande
pour chaque intervalle de temps pendant la journée. Nous avons fait
recours à la programmation linaire et l'analyse des données de
panel. Ainsi compte tenu du période de planification, nous pouvons
dresser une liste des tâches ainsi que le nombre et le besoin en
compétences du personnel requit pour effectuer chacun d'eux. Dans le
chapitre suivant, nous allons présenter en détail le
dimensionnement du personnel et vacations.
55
Chapitre 3
Le Dimensionnement et la création
des
vacations
Introduction
Selon Tien et Kamiyama (1982) le problème de
planification est précédé par la traite de deux
problèmes la prévision de la demande (effectuer dans le chapitre
précédent) et la prévision des effectifs
nécessaires par vacation capables d'accomplir efficacement le travail
spécifié par les contrats de service.
Pour ce faire, nous donnons un aperçu
général du problème de dimensionnement dans la
première section puis nous détaillons le concept de
dimensionnement de l'effectif et les vacations dans la deuxième section.
Les modèles de créations des vacations seront analysés
dans la troisième section. Finalement, nous représenterons les
problèmes d'énumération des vacations de travail. Les
décisions de planification (positionnement des congés et jours de
repos et affectation des emplois du temps) ne seront pas prises en compte dans
ce mémoire.
1 Le dimensionnement
1.1 La notion de dimensionnement
L'objectif principal de la planification de la main d'oeuvre
est la détermination des horaires qui répond aux exigences de la
demande. Cependant, la prise de décision de la planification en fonction
du temps illustré par le planning permet de subdiviser la planification
en un certain nombre de problèmes d'optimisations successives. Dû
fait que la planification peut être considérée comme un
processus décisionnel où le dimensionnement est une étape
fondamentale.
56
Le dimensionnement de la main d'oeuvre peut être
défini comme le processus qui assure l'adéquation optimale des
ressources humaines disponible avec les besoins d'une organisation en tenant
compte la qualité de service. Ainsi comme illustré dans la figure
16, le dimensionnement est la première décision à prendre
en matière de gestion des ressources humaines. Les décisions de
planification (positionnement des congés et jours de repos et
affectation des emplois du temps) sont prises ultérieurement.

Figure 16. Processus de décisionnel
1.2 Les contraintes de dimensionnement
Comme nous l'avons mentionné l'objectif du
dimensionnement est de déterminer le nombre de personnel
nécessaire en tenant compte la qualité de service que
l'entreprise souhaite garantir. Le dimensionnement devrait donc être
conçu de telles sortes qu'il permet à l'organisation de
satisfaire les différentes contraintes y compris les contraintes
techniques. Tenant compte que beaucoup aéroports sont extrêmement
occupés et fonctionnent déjà à plaine ou
quasi-complète capacité, tout en s'attendant à la
croissance du nombre de passagers à l'avenir.
En outre, l'émergence des compagnies aériennes
low-cost a créé des exigences supplémentaires pour les
courts temps d'escale des avions, tandis que les structures de réseau
hub-and-spoke de grands transporteurs créent aussi une demande pour les
temps de connexion réduits entre aéroports. Ainsi, nous notons
que l'arrivée de vol ou les heures de départ sont souvent
placées dans des périodes de pics. Ceci signifie que
l'activité de l'aéroport peut être
57
extrêmement élevée pendant les
fréquentes périodes des arrivées et les départs,
tandis que d'autres périodes de la journée sont relativement
calmes.
De ce fait, il est important de noter que selon les conditions
particulières et les politiques de l'organisation, il y a plusieurs
contraintes qui doivent être prises en compte dans le processus de
dimensionnement à savoir les contraintes citées par Dowsland
(1998) ;
- Nature de la demande en personnel constante ou variable au
cours des jours, cyclique ou non-cyclique.
- Type d'horaire de travail utilisé les plus communs
six jours standards, 48 heures par semaine.
- Nombre et la tendance des vacations quotidiennes admissibles
(il y a peut être des équipes de jour, de soir et de nuit).
- Les règles de travail concernant les jours de travail et
du repos pour les agents.
- Le maximum de jours de travail consécutifs
autorisé.
- Les attributs de la main d'oeuvre, il peut y avoir des
compétences différentes des travailleurs.
1.3 Le processus de dimensionnement
Pour ce faire, le dimensionnement peut être
subdivisé en des sous-problèmes. En effet, Baker cite trois
sous-problèmes :
- Le premier sous problème est la programmation de jour de
repos, il consiste à déterminer les jours sans travail (ou de
manière analogue les jours ouvrables) pour chaque employé. - Le
deuxième sous-problème détermine les horaires de travail
pour chaque journée.
- Le troisième sous-problème représente la
combinaison des deux premiers problèmes.
Cependant, Tien (1982) présente une procédure
plus détaillée en cinq étapes plus pour élaborer
l'ordonnancement :
- Prévision de la demande : détermine
le nombre de travailleurs requis pour garantir une meilleure la qualité
de service. L'usage habituel consiste à imposer une contrainte de
58
qualité de service identique pour chaque période de
la journée. Cette contrainte est, par la suite, convertie en nombre
d'effectifs nécessaire
- Détermination de l'effectif minimal :
détermine la taille totale de la main d'oeuvres nécessaires
pour satisfaire la demande tout en minimisant le coût salarial et en
respectant les contraintes de qualité de service.
- Détermination du nombre optimal de salariés
à affecter à chaque vacation.
- Positionnement des jours de repos de chaque
salarié.
- Détermination du planning de chaque
employé.
Cette subdivision illustre l'introduction progressive des
détails dans le processus décisionnel et la complexité de
chaque étape.
2 Le dimensionnement de l'effectif et les vacations 2.1
Le dimensionnent de l'effectif
Avant de pouvoir planifier l'emploi du temps d'une
équipe, il est nécessaire de connaître sa taille. Dans la
littérature scientifique, de nombreux auteurs proposent des
méthodes de calcul de la borne inférieure avec des règles
de travail contraignantes. Burns et Carter ont été les premiers
à proposer une méthodologie basée sur le calcul de
plusieurs bornes inférieures (charge de week-end, charge totale de la
semaine et charge maximale journalière), la taille étant le
maximum de ces bornes.
Ils ont considéré le cas d'une seule vacation
par jour et le besoin est d(j), J=1 pour le dimanche,..., 7 pour le samedi.
D = nombre total de salariés, D=Max(d(1),...,d(7)).Hun94 propose
une méthode de calcul de la taille minimale d'une équipe. Chaque
jour il y a V vacations (ex. J=3 pour le matin, 2=soir et 3=nuit).
Pendant la semaine, il faut au moins D(v) personnes sur la
vacation v pour v=1,..., V.
Nous nous s'intéressant à la tournée de
type 3*8 dont chaque jour dispose d'au moins
3 vacations et puisque les compagnies d'assistance travaillent
tous les jours le nombre des
plages requis = 3 (nombre des vacations / jour)* 365
(nombre de jours par ans) = 1095. Ces plages doivent être couvrir
par un certain nombre d'agents.
Cependant l'agent travaille 365 moins quatre jours de
repos par mois de travail, si l'agent a droit à un jour de repos par
semaine, et moins le congé annuel 30jrs. Donc l'agent travaille
365-4*11(jours de repos pars ans) - 30(jours de congé annuel) = 291
jours (ou vacation).
De ce fait, afin d'assurer un service 24/24 toute
l'année nous sommes besoin de 1095/291=3.76 donc au minimum
4 agents par jour. Cependant, le nombre des agents
nécessaires doivent satisfaire les besoins en termes de
plages à couvrir. Pour ce faire, nous referons à une semaine type
et à travers laquelle nous déterminons les plages
nécessaires (voir figure 17). Si nous avons N lignes de plages
d'horaire nous aurons en tout 7*N besoins par
semaine, soit 365*N par ans.
Exemple
Soit N lignes de plages d'horaire par semaine
=5
Le nombre des agents nécessaires par semaine égale
à :
agents.
=
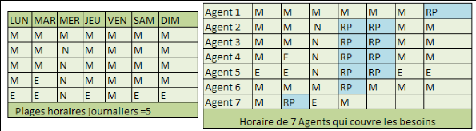
59
Figure 17. Besoins par semaine type
60
Cependant dans le cadre aérien le nombre des agents
nécessaires diffèrent d'un jour à un autre dont les
besoins se diffèrent d'un jour à un autre dans une semaine.
Afin de satisfaire les besoins, nous referons à une
semaine type et nous calculons les plages horaires totales à satisfaire
(voir figure 18).
Si nous avons N plages d'horaire par semaine nous aurons
en tout 52 (nombres des semaines par ans)* N par ans.
Exemple
Soit N plages d'horaire par semaine =62
Le nombre des agents nécessaires par semaine égale
à :
=
agents.

Figure 18. Plages horaires par semaine type
Cependant, la planification d'un personnel
hétérogène dans le cas des compagnies d'assistance tient
compte que tous les employés sont productifs mais avec des
capacités
61
différentes dont le personnel expérimenté
peut être capable d'effectuer des tâches plus avancées, en
plus de le travail de base. Pour décrire le niveau de cohésion
entre les exigences du service
et la qualification du personnelles (capacités) , nous
pouvons utiliser la fonction
suivante déjà citée :
2.2 Le problème de dimensionnent de vacation
Dans la planification de la main-d'oeuvre, les horaires sont
créés pour les travailleurs, de telle sorte que chaque
travailleur a une séquence de vacations et des jours de repos qui, en
combinaison satisfait une demande définie.
De ce fait, le problème de la planification du
personnel considère durant ses différents niveaux de
planification la disposition des données pertinentes et
détaillées concernant la demande, l'effectif et les vacations. Il
est donc courant de subdiviser le problème en plusieurs
sous-problèmes que peuvent être résolus à des
moments différents. Une telle division en cinq sous-problèmes (ou
étapes) est proposée par Tien et Kamiyama (1982) dans le premier
et la deuxième étape concerne le problème de
dimensionnement de vacations.
En effet, le problème de dimensionnement de vacations
est un problème de planification de personnel. Dont il consiste, pour
une journée donnée, à affecter des employés
à un ensemble de vacations autorisées afin, d'une part de couvrir
une courbe de charge traduisant une demande et d'autre part, de minimiser le
coût de travail. La résolution du problème de
dimensionnement de vacations suppose que la demande dans les aéroports
est habituellement représentée par une courbe de demande, dans
lequel la période de planification est divisée en un certain
nombre de périodes de taille égale (une heure) ayant chacun un
nombre de travailleurs requis.
Les vacations représentent des périodes de
travail pour un seul travailleur commençant par son arrive au travail et
finissant par son départ. Et pendant lequel un travailleur peut

62
accomplir des missions, se déplacer entre les
tâches, prendre des pauses ou être inactif. (Voir Figure 19).
Figure 19. Définition d'une vacation
Cependant, le déplacement entre les tâches ne
peut pas être évité dont il s'inscrit dans le cadre de la
journée de l'ouvrier, mais peut être minimisé par la
répartition des tâches entre les travailleurs d'une manière
efficace. C'est la principale préoccupation de problèmes
d'ordonnancement de tâches. Le temps consacré aux pauses est
obligatoire et prévu par la réglementation du travail ou les
conventions collectives.
2.3 La formulation du problème de construction de
vacation
La conception et l'attribution des quarts de travail peuvent
faire l'objet d'ensemble diversifié de contraintes. Les règles de
base couvrent les longueurs de déplacement minimal et maximal, le nombre
des pauses et leur placement pendant un quart, les temps de repos minimum entre
les quarts et un nombre minimum et maximum de jours de travail
consécutifs autorisés
63
avant que le travailleur a droit à un ou plusieurs
jours de repos. Le problème de la création de vacation pour le
personnel est un problème complexe qui vise à couvrir
efficacement la demande tout en respectant les spécificités de la
main d'oeuvre.
Ainsi, la première formulation du problème de
construction de vacation sous forme de programme linéaire entier a
été proposée par Dantzig. Ce modèle cherche en
premier lieu les besoins en personnel puis en deuxième lieu
optimisé la couverture de la charge en minimisant le temps de
présence du personnel nécessaire (voir figure 20).

Figure 20. Construction d'une vacation
En effet comme entrée, nous disposons des besoins en
personnel pour chaque intervalle de temps, la courbe de charge indique le
nombre de personnes nécessaires. En support du processus, nous disposons
d'un ensemble de règles légales qui définissent la
journée de travail, ainsi qu'un ensemble de règles d'usage. En
sortie, nous voulons savoir comment faire travailler
64
les salariés, soit la définition des horaires de
début et fin et des horaires de pause, de telle sorte que la somme de
leurs disponibilités couvre au mieux la courbe de charges avec un
minimum de surplus.
3 Les modèles de création des
vacations
Le problème de construction des vacations a
été le premier problème de planification d'horaires de
personnel traité dans la littérature relative à la
recherche opérationnelle. Et qui peuvent être soit des approches
par couverture, soit des approches implicites, soit des approches
explicites.
3.1 La recherche opérationnelle
Des différentes méthodes ont été
proposées, parmi lesquels nous pouvons citer la programmation
linéaire, la programmation par contrainte ou encore la recherche locale
(méthode Tabou).
D'une manière générale, ces
modèles prennent comme entrée les besoins en personnel et
l'ensemble de règles juridiques. Et comme sortie, ces modèles
repartirent les agents de telle sorte que la somme de leurs
disponibilités couvre au mieux la courbe de charges avec un minimum de
surplus.
Cependant, nous notons que ces approches proposées sont
soit des approches par couverture, soit des approches implicites, soit des
approches explicites.
3.2 Les approches par couverture
Le problème de création de vacations peut
être modélisé comme un problème de recouvrement
d'ensemble. Le premier modèle de couverture de charge dû à
Edie (1954), Dantzig (1954) traitent le cas où l'on aurait un seul type
d'activité, donc une seule courbe de demande à couvrir.
65
La construction des vacations se repose sur des modèles
simplifiés et non-linéaires de couverture ensemblistes qui
cherchent à couvrir une charge en minimisant le nombre de vacations.
Cependant, le modèle Dantzig permet de prendre en compte tout type de
vacation avec un nombre quelconque de pauses. En effet, dans le contexte
aérien, nous préférons de ne pas spécifier de
débuts et fins de pause due aux caractéristiques du travail.
Ainsi afin d'améliorer la solution de Dantzig(1954),
Henderson et Berry ont proposé deux méthodes de résolution
journalière du problème à partir d'un sous-ensemble de
vacations faisables défini à l'aide de plusieurs
paramètres, soit par l'itération de la vacation qui couvre le
plus de tâches non encore couvertes soit par choisir aléatoirement
les vacations du sous-ensemble.
Par la suite afin de choisir les vacations parmi le
sous-ensemble trois méthodes ont été proposés :
- La première méthode est celle utilisée par
Dantzig avec un arrondissement à l'entier supérieur, tout en
essayant de supprimer un agent pour chaque vacation.
- La seconde utilise le résultat de la première et
tente de remplacer deux vacations par une troisième qui fait partie du
sous-ensemble de départ.
- La troisième méthode est identique à la
seconde sauf qu'elle part d'une solution obtenue au hasard.
Les performances de ces méthodes sont, a priori, bonnes
sur des intervalles de temps réduit, mais deviennent plus discutables
lorsque le nombre de quarts augmente.
Segal (1974) inspiré aussi du modèle de Dantzig,
a proposé un algorithme baser sur les modèles de flots. Ce
modèle consiste à modifier dynamiquement la demande en
employés en fonction du temps, sans tenir compte des pauses. Puis, il
fait intervenir une procédure heuristique pour réintégrer
les pauses. Malheureusement, cette méthode de résolution peut
difficilement être étendue au cas multi-activités en
considérant les durées minimales et maximales ainsi que des
coûts de transitions entre les activités distinctes.
66
3.3 Les approches implicites
Les approches implicites permettent de réduire le
nombre d'effectif requis par chaque type de vacation candidate
caractérisé par une fenêtre d'heure de début, une
fenêtre de durée et des fenêtres de pause. Dans ce cadre,
Moondra (1976) a proposé un modèle implicite dans lequel les
variables correspondent au nombre d'agents commençant et terminant
à chaque période, au cours d'un intervalle p qui doit
couvrir les besoins, ainsi que des équations pour limiter la
durée maximale et minimale des vacations.
Cependant, l'approche implicite de Moondra ne prend pas en
compte le cas où l'on a une flexibilité sur le positionnement de
la pause dont le modèle ne tient compte que d'une pause de durée
fixe et d'une heure de début fixe par vacation. Bechtold et Jacobs
(1990) ont apporté une solution qui suppose que les pauses peuvent
démarrer à des intervalles différents. Ils ont
proposé un modèle implicite avec affectation flexible des pauses
d'un seul type aux quarts de travail, c'est-à-dire la fenêtre de
pause d'un type de vacation v n'est pas strictement incluse dans celle
d'un autre type v1.
Thompson a proposé un modèle doublement
implicite en exploitant la modélisation implicite des débuts des
vacations de Moondret la modélisation implicite des pauses de Bechtold
et Jacobs (1990) pour traiter des problèmes d'un très haut niveau
de flexibilité dans l'étendue des vacations concernées
tout en garantissant l'obtention d'un solution optimale. Un autre modèle
proposé par Aykin (2000) traite l'intégration d'une pause
supplémentaire, située avant et/ou après la pause
repas.
Dans ce mémoire, nous proposons un algorithme pour la
création des vacations basées sur les variables de Moondra et les
paramètres de couverture de charge de Dantizig tout en tenant compte de
la dynamique la demande en employés en fonction du temps proposé
par Segal.
4 Énumération des vacations
Comme nous l'avons vu dans la partie précédente,
l'approche de Dantzig nécessite d'énumérer toutes les
vacations possibles dans le modèle afin de réduire les
coûts. Le modèle que nous proposons tente de conserver autant que
possible le caractère générique du modèle de
67
Dantzig dans la traduction des contraintes de temps de
travail, tout en gardant les avantages d'une formulation implicite
4.1 Algorithme d'énumération des
vacations
Les vacations envisageables doivent être
énumérées avant de lancer le modèle d'optimisation,
qui sélectionnera un ensemble de ces vacations et déterminera le
nombre d'employés nécessaires par vacations. En effet,
l'énumération des vacations revient à construire une
matrice de couverture dont les lignes sont les périodes de la
journée en périodes ayant une durée d'une heure, les
colonnes sont vacation découpé en périodes ayant une
durée d'une heure et les intersections correspondent à la
couverture de la période par la vacation.
Nous notons que les compagnies d'assistance aérienne
offre un service 24/7 d'où la nécessité des vacations qui
couvre toute la journée. Nous se limitons ici à l'étude de
l'organisation des journées et des semaines normales de travail des
actifs occupés à plein temps, en laissant de côté
l'analyse des situations à temps partiel et celle des périodes de
congé.
Nous supposons que la durée max de la vacation est de
huit heurs et que les journées sont découpées en trois
tranches horaires (Voir figure 21) :
- Le matin (M) qui commence soit à 6 h ou 8 h et se
termine successivement soit à 14h ou 16h, - (E) le soir qui commence
soit à 14 h ou 16 h et se termine successivement soit à 20 h ou
22 h, -(N) la nuit qui commence soit à 20 h ou 22 h et se termine
successivement soit à 6 ou 8 h,

68
Figure 21.Exemple de matrice de couverture journalière par
les vacations (vacation matin (M) présenté en vert, vacation soir
(E) présenté en orangé et vacation de nuit (N)
présenté en bleu)
69
En effet, afin d'assurer l'énumération des
vacations v et la couverture de la période t
et , il est nécessaire de respecter les contraintes de
début et de fin de vacation et
la durée de la vacation. Un algorithme de
génération sera appliqué en tenant compte que la
journée est découpée en périodes ayant une
durée d'une heure. Dans l'algorithme que nous nous proposons nous ne
tenons pas en compte de la durée, de l'heure de début et de fin
des pauses due à la complexité des tâches à
effectuer aux cours de l'assistance d'un vol. Ainsi les variables et les
paramètres à utiliser sont :
= L'ensemble des indices représentant les
périodes journalière ; {0,..,24}.
= L'ensemble des indices représentant les jours
par semaine = L'ensemble des vacations (1=matin, ...3= nuit).
= Variable binaire détermine la charge de travail
La couverture de la période t par la vacation .
DebutTotv = Heure de début au plus tôt du type
de vacation v. DebutTardv = Heure de début au plus
tard du type de vacation v. Dureemax = Durée max de vacation
est 8 heure
Debutv = L'heure de début de vacation
v
Finv = L'heure de fin de vacation
v
t= 0 ; /initialiser l'heure t=0.....24 /
T = 1 ; /initialiser le jour j=1.....7 dont 1 est lundi, ...,
7 est dimanche /
f = 0; / f=0 pas de demande à couvrir /
Pour j=
1...7 faire
Pour i = 1,.....24 faire
Si f=0 alors /si f=0 pas de vol /
/ =0 pas de couverture /
Sinon
1
i++
Fin pour j++
Fin pour
Dureemax=8 / durée max de vacation est 8 heure
/
Pour v=1....3 faire
Pour = ..... faire
Si
Fin pour
+Dureemax
Fin pour
70
4.2 Optimisation de l'algorithme
d'énumération des vacations
Les vacations envisageables doivent être
énumérées en tenant compte du volume de la couverture afin
de réduire le nombre des agents et par conséquent, réduire
le coût de vacation. Comme nous avons déjà vu les vacations
peut se chevaucher ce qui permet d'utiliser les employés de deux
vacations dans un travail commun.
Par exemple si la vacation de matin (M) débute à
8h et termine à 16h et la vacation de soir (E) débute à
14h et termine à 22h, il aura un chevauchement de deux heures entre 14h
et 16h et pendant lesquels nous pouvons utiliser les employés des deux
vacations (voir figure 22).

Figure 22. Exemple de chevauchement des vacations de matin M et
soir E
Ainsi, nous rappelons que la version la plus commune du
modèle de Dantzig qui tient compte les aspects de coûts
liés aux vacations est la suivante :
En effet, afin d'optimiser l'énumération des
vacations V tenant compte de la couverture
de la période t et la vacation , il
est nécessaire de déterminer la valeur de
la demande pendant
la période t et la vacation
Pour se faire nous supposons que le nombre des vols
reflète le volume de la demande, par exemple, si nous avons à 5h
quatre vols nous supposons que nous avons une demande égale à
quatre agents, voir la matrice de couverture (figure 23).
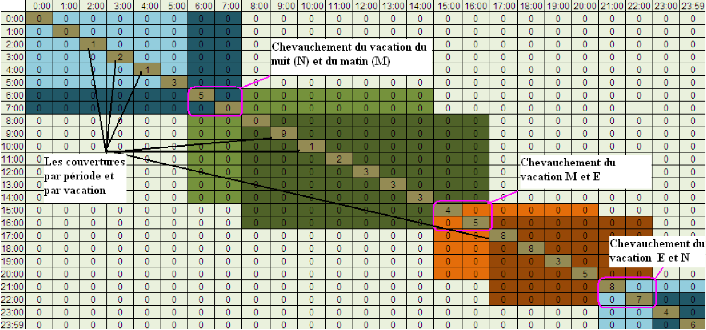
71
Figure 23. Matrice de couverture journalière

72
4.3 L'algorithme d'énumération
proposée
Afin d'assurer la couverture, nous proposons trois vacations
le matin (M) qui commence soit à 6 h ou 8 h et se termine successivement
soit à 14h ou 16h, (E) soir qui commence soit à 14 h ou 16 h et
se termine successivement soit à 20 h ou 22 h, (N) nuit qui commence
soit à 20 h ou 22 h et se termine successivement soit à 6 ou 8
h.
Nous remarquons que ces vacations peuvent se chevaucher
(figure 24) et dans la période de chevauchement, nous pouvons utiliser
les agents des deux vacations.
Figure 24. Chevauchement des vacations
Ainsi à l'aide des algorithmes génétiques
multi-objectifs plus précisément à l'aide de la notion
Rang de dominance, nous pouvons choisir de chevaucher ou non deux vacations. En
effet, la stratégie Rang de dominance consiste à associer
à chaque vacation un rang proportionnel au nombre de vacations qui la
dominent. De ce fait, une vacation sera meilleure qu'une autre si elle a un
rang plus petit. Nous proposons une méthode dans laquelle chaque
vacation est rangée en fonction du nombre des vacations qui le
dominent.
En effet, une vacation Va E V1 , en domine une
autre si elle est meilleure vis-à-vis de l'ensemble des critères
indépendamment les uns des autres, avec i = {1..3} (1 matin,2
soir et 3
nuit) et avec a les possibilités
qu'une vacation peut avoir (vacation matinée peut être Vml:
débute a 6h et se termine à 14h, Vm2 :
débute a 7h et se termine à 15h, ou Vm3 : débute a 8h et
se termine à 16h) . Le concept de dominance peut être
illustré par la figure 25.
En s'appuyant sur ce concept de dominance, nous utilisons une
fonction de notation permettant de prendre en compte le rang de la vacation et
le nombre des vacations ayant même rang.
Soit une vacation à la génération ,
dominée par vacations. Le rang de cette
vacation est Rang = 1+ . Toutes les vacations non dominées
sont de rang 1 (les
meilleurs).
Exemple :
Soient les vacations , et trois types de vacation matinée
dont :
- débute a 6h et se termine à 14h,
- débute a 7h et se termine à 15h,
- débute a 8h et se termine à 16h,
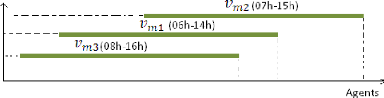
Figure 25. Exemple de dominance des vacations matinée Le
tableau de dominance est le suivant :
|
Vacations
|
Dominé par
|
Rang
|
|
|
2
|
|
et
|
3
|
|
Aucun
|
1
|
Table 6. Tableau de dominance des vacations matinée
73
La meilleure vacation à choisir qui réduit le
coût est de Rang 1.
En effet, le modèle proposé compte le nombre des
salariés à chaque vacation, de telle sorte que les besoins par
intervalle P sont satisfaits, tout en minimisant le
coût total des affectations.
Pour se faire nous supposons que S ( , p)
est le nombre des agents sur une vacation du
type qui se termine à la fin de l'intervalle
p. En effet S ( , p)
reflète le nombre max des
agents sur une vacation dont
S ( , p) égal au Max B ( ,
p). Et nous supposons que B(T)
est le nombre des agents sur la période de chevauchement
T entre deux vacations successive
et (comme indiqué dans la figure 27) et dont B(T) =
-[S ( , p) + S ( , p)] .
Ainsi, fin d'éviter les sureffectifs nous faisons appel
au modèle de Brusco et Johns qui
minimise au maximum le ratio de la demande et de sureffectifs
dont est le nombre
de postes actifs au temps est la demande au temps . Mais afin
d'éviter le manque
.
d'effectif nous proposons un modèle qui au minimum
égalise le nombre d'effectifs à la demande dans une
période de temps p :
Cependant, la charge de travail dans les compagnies
d'assistance aérienne nécessite des différentes
compétences qui doivent être représentées à
l'aide des courbes de demande distinctes, en tenant compte des qualifications
exigées, afin de créer des vacations qui peuvent la couvrir.

Figure 26. Des courbes de demande distinctes selon les
services
74
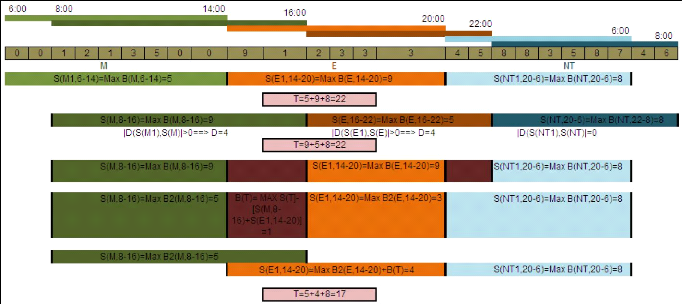
75
Figure 27. Le principe de l'algorithme d'optimisation
76
Et comme nous avons déjà annoncé dans le
cas d'un effectif hétérogène pour un ensemble de vacations
de travail le problème d'affectation doit être résolu afin
de trouver un compromis entre les sureffectifs et le manque de personnel. Nous
notons, que le problème de planification de la main-d'oeuvre
hétérogène peut être modélisé comme
suit :
En effet nous ne tenons compte du nombre des agents dans la
période du chevauchement que si la différence D entre le
nombre des agents de la vacation vti (par exemple vacation du matin M)
noté S(vti) et le nombre des agents de la vacation
v ( r e e le c tion du tin v noté S(v )est
supérieure à zéro :
)
Dans ce cadre nous proposons la fonction linaire suivante :
|
B (T) = Max B(p)- [S
(v1, p) + S (v1+1, p)]
|
|
Avec
S ( , p) Nombre d'agents à la fin de la vacation du
type durant l'intervalle de temps p ; Nombre des employés
affectés à la vacation ;
Nombre des employés nécessaires pendant la
période du chevauchement T; Nombre des employés
nécessaires pendant l'intervalle de temps p; p Un période de
temps dans un jour donnée;
i Types des vacations;
T La période du chevauchement entre deux vacations
successive et Le nombre de postes actifs au temps
La demande au temps
|
77
Conclusion
Le dimensionnement de l'effectif permet de déterminer
le nombre des agents nécessaires pour fournir un service en respectant
certaines contraintes y compris la contrainte de couverture des vacations. Dans
ce cadre, le dimensionnement et l'énumération des vacations
à l'aide de la recherche opérationnelle, par couverture ou par
approche implicite doivent offrir une solution optimale.
Cette solution était le résultat d'un algorithme
multi-objectif basé sur la notion des dominances des vacations qui
réduit le maximum les coûts tous en adoptant la tournée des
agents. Dans le chapitre suivant nous allons détailler le concept de la
tournée du personnel.
78
Chapitre 4
La tournée du personnel
Introduction
Un problème important se pose dans la planification de
la main-d'oeuvre est la détermination et la minimisation du nombre des
employés en respectant certaines contraintes et réduisant les
coûts. En effet, ce chapitre se compose de quatre parties.
La première section décrit
l'énoncé du problème de tournée. La deuxième
section présente le modèle mathématique en traitant la
fonction objective et les contraints. La troisième partie
présente la solution algorithmique et la quatrième section
présente les résultats obtenus et les points pour la future
recherche.
1 Le concept de la tournée 1.1 Enoncé du
problème
Comme nous avons déjà cité dans le
chapitre 3, les compagnies d'assistance aérienne offrent des services
sans interruption au cours d'une journée (24h) et au cours de
l'année d'où la nécessité du personnel suffisant en
nombre et en compétence pour effectuer des tâches toute la
journée.
Dans la partie « dimensionnement de l'effectif »
afin de satisfaire les besoins nous avions eu utilisé une semaine type
et nous avions eu calculé les plages horaires totales à
satisfaire «N» afin d'avoir en tout 52 (nombres des
semaines par ans)* N (nombre de plages) agents requis par ans.
79
Cependant, cette méthode ne tient pas compte des
qualifications des agents et ne tient pas compte de la minimisation des
coûts. Pour ce faire, nous supposons que le nombre
d'employés requis pour chaque jour j de la
semaine S diffère selon la charge de travail à
chaque
jour. La charge de travail est déterminée selon le type des
tâches à exécuter et la qualification nécessaire. Il
est nécessaire donc de déterminer les capacités humaines
assignées pour chaque jour j tous en réduisant les
coûts.
|
SEMAINE 1
|
|
Jours j
|
1 (Lun)
|
2 (Mar)
|
3 (Mer)
|
4 (Jeu)
|
5 (Ven)
|
6 (Sam)
|
7 (Dim)
|
|
Nombre requis
|
|
|
|
|
|
|
|
|
Nombre assigné
|
|
|
|
|
|
|
|
Table 7. Les nombres requis et nécessaires des agents
1.2 Grille de besoins
Notons que le travail effectué dans les
aéroports est hautement spécialisé. La capacité
d'effectuer une tâche spécifique peut nécessite certaines
autorisations de sécurité, de formation ou équipements
spécialisés. Ainsi, les exigences peuvent varier
considérablement entre les tâches ou même d'un type
d'aéronef à un autre dont certaines peuvent nécessitent
différents types d'équipement, différents endroits dans
l'aéroport (parking éloigné ou passerelle) ou des
différents systèmes informatiques.
Cependant, beaucoup de travailleurs peuvent avoir une
formation dans plusieurs tâches ou des certificats différents, qui
leur fournissent des capacités de travailler des différentes
tâches dans des différentes zones. Par conséquent, la
conception de la tournée du personnel de compagnie d'assistance au sol
doit gérer une demande hétérogène et main-d'oeuvre
divisée en groupes dont la spécialisation est
modélisée à l'aide plusieurs courbes de demande et une
grille de besoin.
On suppose qu'il existe un certain nombre de postes
prédéfinis et chacun d'eux nécessite des
compétences particulières. Avant d'élaborer donc les
grilles de tournée du
80
personnel, nous déterminons les grilles de besoin pour
chaque poste, nous déterminons le nombre d'agents dont nous aurons
besoin pour chaque vacation (Matinée M 6h-14h, Soiré S 14h-22h et
Nuit N 22h-6h). Par exemple, pour les services de piste, à savoir le
nettoyage, le bagage ou chargement, et pour chaque jour et pour chaque
vacation, nous déterminons le nombre des agents nécessaires dans
une grille de besoins.

Table 8. Grille de besoins pour le service de piste pendant la
vacation Matinée M
1.3 Le tableau de tournées
L'élaboration des tournées consiste donc
à couvrir la grille des besoins en tenant en compte qu'un agent (X) est
affecté à une vacation (V) et à une tâche et qu'il a
droit à un jour de repos (RP) par semaine (S) et après un minimum
de travaille (MT) situe entre 4 et 6 jours.
Une fois le nombre des agents est déterminé,
à travers la grille de besoin, nous les repartions sur les vacations
dans le tableau de tournée équitablement. Nous supposons que le
tableau de tournée se compose de 7*S colonnes et de X lignes (voir
tableau 9). Le tableau de tournée est donc composé de 7*S*X
cases, dans chaque case, nous notons le service que doit tenir l'agent pour
cette journée.
81
7*S Colonnes =7*3 =21
|
|
SEMAINE 1
|
|
SEMAINE N
|
|
Lun
|
Mar
|
Mer
|
Jeu
|
Ven
|
Sam
|
|
Dim
|
Lun
|
Mar
|
Mer
|
Jeu
|
Ven
|
Sam
|
Dim
|
|
X
|
AGENT 1
|
M
|
M
|
M
|
E
|
E
|
RP
|
RP
|
.......
|
N
|
N
|
N
|
N
|
N
|
RP
|
RP
|
|
AGENT 2
|
E
|
E
|
E
|
E
|
RP
|
E
|
E
|
.......
|
M
|
M
|
RP
|
RP
|
M
|
E
|
E
|
|
LIGNES
|
|
|
|
|
|
|
|
.......
|
|
|
|
|
|
|
|
|
AGENT 3
|
N
|
N
|
N
|
N
|
RP
|
RP
|
M
|
.......
|
M
|
M
|
M
|
E
|
E
|
RP
|
RP
|
Table 9. Le tableau de tournée
Il convient de remarquer que les tournées cycliques de
personnel sont organisées en un certain nombre de cycles (C)
répétitif. Dont nous supposons que les agents effectuent tous les
mêmes services, mais avec un décalage par rapport aux autres
agents quand l'agent 1 effectue le
cycle l'agent 2 effectue le cycle .
Nous supposons que le cycle est légal au niveau du
nombre d'heures travaillées, et nous ne faisons que dérouler les
cycles. En conséquence, nous pouvons ignorer les horaires précis
de chaque vacation, mais nous faisons l'hypothèse que le repos
hebdomadaire est compris dans le cycle comme indique dans le tableau 10.
|
SEMAINE 1
|
SEMAINE N
|
|
Lun
|
Mar
|
Mer
|
Jeu
|
Ven
|
Sam
|
Dim
|
Lun
|
Mar
|
Mer
|
Jeu
|
Ven
|
Sam
|
Dim
|
|
Cycle 1
|
M
|
M
|
M
|
M
|
M
|
RP
|
RP
|
E
|
E
|
E
|
E
|
E
|
RP
|
RP
|
|
Cycle 2
|
RP
|
M
|
M
|
M
|
M
|
M
|
RP
|
RP
|
E
|
E
|
E
|
E
|
E
|
RP
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cycle C
|
E
|
E
|
E
|
E
|
E
|
RP
|
RP
|
M
|
M
|
M
|
M
|
M
|
RP
|
RP
|
Table 10. Le tableau de tournée cyclique
Cependant pour élaborer un tableau de tournée
non-cyclique, nous indiquerons pour
chaque vacation de chaque journée si l'agent travaille
(1) ou non (0). De ce fait,
l'outil le plus performant pour la formulation
de ce problème est incontestablement les variables binaires 0-1 dont
elles permettent de représenter le fait qu'un événement se
réalise ou non au sein d'une solution qu'on recherche.
82
La formulation conduit à un Programme Linéaire en
Nombre Entiers à variables binaires 0-1 (PLNE0-1) dont voici la
structure algébrique générale :
(1)
(2)
(3)
Dans ce cadre afin de formuler le problème de
planification la formulation sous forme d'un programme linéaire à
variables mixtes, nous supposons que les principales variables de
décision sont les variables binaires qui correspondent
à l'affectation de
l'agent (avec m la matricule de l'agent), au jour ,
à la vacation v et
prennent la valeur 0 ou 1 :
Par la suite, nous présentons en détail la
formulation mathématique à l'aide de Programme Linéaire en
Nombre Entiers à variables binaires 0-1 (PLNE0-1)
2 La formulation mathématique à l'aide de
PLNE
La formulation d'un problème d'optimisation comporte
toujours les trois étapes
- choix des variables du modèle; - formulation de
l'objectif;
- formulation des contraintes.
2.1 Choix des variables du modèle
La première étape consiste à choisir les
variables du problème qui représentent « toute
quantité utile à la résolution du problème dont le
modèle doit déterminer la valeur. Cette
83
définition permet de différencier les variables qui
sont des données qui peuvent varier d'une période à
l'autre ou d'un scénario à l'autre. Dans notre cas, les
quantités que le modèle doit déterminer est le nombre des
agents nécessaires par vacation, par jour et par semaine.
Pour se faire nous supposons que le nombre des employés
qui commencent le travail le
lundi est présenté par et ceux qui commencent le
mardi présenté par , ..., et ceux de
dimanche
présenté par comme indiquer dans le tableau 11.

Table 11. Schéma de 5 jours de travail successif par
semaine
2.2 Formulation de l'objectif
La deuxième étape consiste à formuler
mathématiquement l'objectif. Cependant nous déduisons que la
détermination du nombre des employés nécessite
l'utilisation de variables entières à l'aide du Programme
Linéaire en Nombre Entiers (PLNE) sous sa forme
général:
Soit un ensemble de solutions admissibles pour chaque jour
à partir le lundi (présenté par ) jusqu'au dimanche
(présenté par ). Il s'agit de déterminer une solution ,
appartenant
84
à . L'ensemble des solutions admissibles est
supposé fini et est en général défini par un
ensemble C de contraintes. En effet nous pouvons présenter
la fonction objective comme suit :
La résolution de ce problème consiste à
minimiser au mieux ces fonctions
objectives :
La solution optimale obtenue indiquera le nombre optimal
d'employés prévus pour chaque jour de la semaine. Le nombre
minimum requis d'employés de l'organisation est alors
2.3 Formulation des contraintes
La troisième étape est la formulation des
contraintes du problème. Nous appelons contraintes du problème
toutes les relations limitant le choix des valeurs possibles des variables.
De ce fait, nous considérons que le nombre des
employés qui travaillent le lundi peuvent être formulé
comme suit :
Ainsi, pour l'élaboration d'un planning, certaines
règles sont à respecter. Elles sont issues de la
réglementation, mais également des accords convenus entre
responsables et employés ;
On défini des contraintes similaires pour les autres jours
afin d'obtenir un programme complet :
Supposons que la charge minimale ne doit pas être
inférieure à un certain
nombre . Dans un tel cas, les contraintes de charge de travail
auront la forme suivante :
Ainsi, afin de générer un planning
équilibré nous devons tenir compte d'autres variables
à savoir la pénibilité de l'agent le plus
chargé pour chaque jour j et chaque vacation v et
celle de l'agent le moins chargé . Ainsi, la contrainte
d'équité peut être formulée de la
manière suivante :
|
Avec C est la contrainte d'équité
|
V' C1 : La non-négativité et
l'intégralité des variables :
V' : Un MT est entre 3 et 6 jours ;
V' C3 : 2 MT consécutifs doivent être
séparés par une période de repos d'au moins un jour,
et de 2 jours lorsque la première MT dure 6 jours ;
V' C4 : Une période de repos ne peut pas être
composée de plus de 3 jours consécutifs ;
V' C5 : A chaque vacation de chaque journée, le personnel
doit être en nombre suffisant
pour satisfaire la grille des besoins. La contrainte de
couverture est exprimée par
l'équation suivante où représente le
nombre des agents requis pour la vacation v et le
jour j.
? C6 : Les contraintes de disponibilité : cette contrainte
spécifie les différentes vacations
admises pour cet agent ce jour (les préférences des
employés).
? C7 : Les contraintes de transitions qui permettent de
spécifier des suites obligatoires ou
interdites :
- Jours de repos après une vacation de nuit,
- Vacation de matin interdite après vacation de nuit, -
Vacation de matin interdite après vacation de soir.
? C8 : Le temps de travail par jour ne doit pas excéder 12
heures par jour.
? C9 : Le temps de travail par semaine travaillée doit
s'approcher de 38h. Il peut le
dépasser dans la limite de 48h par semaine.
? C10 : Un repos journalier minimum de 11 heures entre les
vacations doit être respecté
? C11 : Si un agent est affecté à deux nuit
successives, alors le lendemain est un repos.
3 La solution algorithmique
La résolution de ce problème est
effectuée en deux étapes. La première étape
consiste à résoudre le problème avec deux jours repos
consécutifs en utilisant un modèle de programmation
linéaire en nombres entiers. La deuxième étape consiste
à résoudre le problème avec deux jours repos
non-consécutifs en utilisant un modèle de programmation
linéaire en nombre binaire.
Considérons que chaque employé travaille cinq
jours consécutifs et prend deux jours de repos successifs. Le
modèle mathématique est formulé en prenant en compte le
nombre des
3.1 Solution avec deux jours de repos
consécutifs
employés qui commencent à travailler le lundi ,
ceux qui commencent à travailler le
mardi ,..., et ceux qui commencent à travailler le
dimanche . Ainsi, selon la section
précédente, nous déduisons le modèle
mathématique complet voir tableau 12 :
La solution optimale obtenue indiquera le nombre optimal
d'employés prévus pour chaque jour de la semaine.

Table 12. Schéma de 5 jours de travail par semaine et
deux jours de repos consécutifs
Le nombre minimum requis d'employés de l'organisation est
alors :
3.2 Solution avec deux jours de repos
non-consécutifs
Dans cette étape, nous allons considérer que
chaque employé travaille cinq jours pas nécessairement
consécutifs et prend deux jours de repos par semaine. Pour ce faire,
nous considérons que la solution optimale obtenue dans la
première étape est une solution utilisable dans la
deuxième étape.
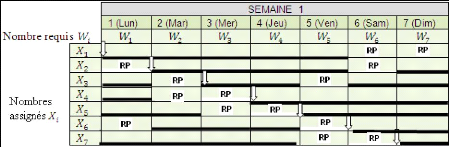
Table 13. Schéma de 5 jours de travail par semaine et
deux jours de repos non-consécutifs
Ainsi, nous supposons en premier lieu que le nombre des
employés requis le premier jour est fixe et puis nous allons supprimer
ces employés qui seront en repos dans la solution finale.
Nous supposons les variables de décision des variables de
décision binaires, où j
représente le nombre de jours (de telle sorte que 1 =
lundi, 2 = mardi, ..., et 7 = dimanche) et m
représente le nombre assigné des employés
(m = 1, 2, ..., est le nombre minimum des
employés obtenus
dans l'étape 1.
3.3 Solution avec un jour de repos
Supposons que chaque employé travaille six jours par
semaine, et prend un jour de repos RP. Afin de résoudre ce
problème, nous supposons que le nombre d'employés
nécessaires pour chaque jour de la semaine se diffère selon la
charge de travail. Donc il est nécessaire de déterminer les
capacités humaines à assigner pour chaque jour j tous en
réduisant les coûts.
|
SEMAINE 1
|
|
Jours j
|
1 (Lun)
|
2 (Mar)
|
3 (Mer)
|
4 (Jeu)
|
5 (Ven)
|
6 (Sam)
|
7 (Dim)
|
|
Nombre requis
|
|
|
|
|
|
|
|
|
Nombre assigné
|
|
|
|
|
|
|
|
Table 14. Les nombres requis et nécessaires des
agents
Le modèle mathématique est formulé en
prenant en compte le nombre des employés qui commencent à
travailler le lundi , ceux qui commencent à travailler le mardi ,..., et
ceux qui commencent à travailler le dimanche
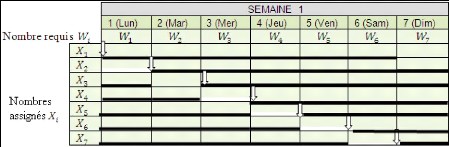
Table 15. Schéma de 5 jours de travail par semaine et
deux jours de repos non-consécutifs
La solution optimale obtenue indiquera le nombre optimal
d'employés prévus pour chaque jour de la semaine.
4 Les résultats obtenus et les axes pour la future
recherche : 4.1 Les résultats obtenus
Dans le chapitre précédant, nous avons
proposé une fonction linéaire qui permet de planifier les
employés, mais sans tenir compte les jours de repos :
|
B (T) = - [S ( , p) + S ( , p)]
|
|
Avec :
S ( , p) Nombre d'agents à la fin de la vacation du
type Nombre des employés affectés à la vacation ; Nombre
des employés nécessaires pendant la période du
chevauchement T; Nombre des employés nécessaires pendant
l'intervalle de temps p;
p Un période de temps dans un jour
donnée;
i Types des vacations;
T La période du chevauchement entre deux vacations
successive et
Le nombre de postes actifs au temps
La demande au temps
|
En effet, suite à la grande charge des compagnies
d'assistance aérienne, nous allons suppose que les employés aient
droit qu'à un seul jour de repos :
Dans ce cas notre la résolution mathématique
proposée est la suivante :
B (T) = - [S ( , p) + S ( , p)]
Avec :
S ( , p) Nombre d'agents à la fin de la vacation du
type
Nombre des employés affectés à la
vacation ;
Nombre des employés nécessaires pendant la
période du chevauchement T;
Nombre des employés nécessaires pendant
l'intervalle de temps p;
p Un période de temps dans un jour
donnée;
i Types des vacations;
T La période du chevauchement entre deux vacations
successive et Le nombre de postes actifs au temps
La demande au temps
4.2 Les axes pour la future recherche: compétence
et répartition des tâches
Suivant une étude menée par (Letouzey, 2001) sur
19 entreprises afin d'obtenir leur avis sur le problème d'affectation
des opérateurs. Cette étude a montré que la gestion du
personnel, en fonction de leurs compétences, est importante pour les
leaders de l'industrie. 79% des entreprises pensent que la gestion du personnel
est utile ou essentielle en ordonnancement.
Pour ce faire, la gestion des compétences
représente un enjeu stratégique pour beaucoup d'entreprises. Il
ne suffit plus d'avoir des compétences disponibles au sein de
l'entreprise, il faut être en mesure de déterminer les besoins
(recrutement, formations,...) (Harzallah et al., 2001). Afin de gérer de
manière plus flexible et équitable la répartition des
tâches entre les employés. Dans ce cadre, nous notons que les
compétences peuvent être soient :
- Des compétences génériques :
utilisées dans différentes situations professionnelles,
- Des compétences spécifiques : celles-ci sont
liées au domaine et au secteur d'activité.
De plus, les compétences peuvent être
identifiées à la fois sur la tâche (compétences
requises : compétences nécessaires pour la réalisation de
la tâche, de missions ou d'actions stratégiques) et sur l'agent
(compétences acquises : compétences que possède l'agent).
De ce fait, dans les futures recherches, nous pouvons tenir compte les
compétences d'employés lors de la planification d'horaire ainsi
que la répartition des tâches. L'intervention le jour de
l'opération (stratégie en temps réel) ne sera pas
traitée dans ce mémoire.
Conclusion
La détermination et la minimisation du nombre des
employés en respectant la grille de besoin est un plié important
dans la planification des employés dont il permet de réduire les
couts salariaux. Cependant, la tournée du personnel exige la
satisfaction des contraintes différentes à savoir l'affectation
du jour de repos qui peut être un jour ou deux jours successifs ou
non-successifs. De ce fait, la tournée du personnel était
résolue à l'aide PLNE. Dans le chapitre suivant nous
présentons un prototype de progiciel de planification des personnels.
La résolution de la programmation linéaire du
problème de planification serra effectuer à l'aide du Matlab.
Chapitre 5
Proposition d'un prototype de
planification des personnels
Introduction
Nous présentons dans ce chapitre les perspectives afin
d'optimiser de la résolution du problème de planification. En
effet, à ce niveau, il est question de réaliser la base de
données et d'élaborer des programmes qui concrétisent
toute la conception. Dans ce chapitre, nous présentons brièvement
les besoins de conception du logiciel. Nous procédons à
l'établissement du modèle physique et la conception de
l'interface.
1 Choix des programmes et du Langage de
Programmation
Nous avons choisi le langage de programmation
VB.Net et le logiciel Visual Basic 2010 pour
créer le progiciel. Dû fait que le Visual Basic 2010 permet de
créer des grandes applications et a beaucoup d'avantages à savoir
:
? La possibilité de communiquer avec n'importe quel
SGBD.
? La création des applications qui peuvent être
exécutées sur le net.
? La création des applications qui peuvent se communiquer
à distance. ? L'exportation d'autres applications à savoir le
Matlab.
1.1 Environnement de développement : Microsoft
Visual Studio 2010
Visual Basic (VB) est un langage de programmation
événementielle de la troisième génération
ainsi qu'un environnement de développement intégré,
créé par Microsoft pour son modèle de programmation (COM).
Visual Basic est directement dérivé du BASIC et permet le
développement rapide d'applications, la création d'interfaces
utilisateur graphiques, l'accès aux bases de données en utilisant
les technologies (DAO), (ADO) et (RDO), ainsi que la création de
contrôles ou objets ActiveX.

Figure 28. Interface générale du Microsoft Visual
Studio 2010
Les modifications apportées à
VB.Net sont telles qu'on peut parler d'un
nouveau langage, plutôt que d'une simple mise à niveau. Mais ces
changements étaient nécessaires pour offrir aux
développeurs les fonctions qu'ils réclamaient depuis longtemps
sous Visual
Basic. VB.NET est maintenant un
véritable langage orienté objet, avec un déploiement
simplifié autour
d'un environnement de développement cohérent qui
peut permettre le développement d'applications traditionnelles, client
serveur et web.
Visual Studio .NET fournit un environnement de
développement intégré (IDE) qui permet aux
développeurs de créer des solutions plus rapidement en utilisant
des fonctionnalités de productivité clé accessibles avec
n'importe quel langage .NET. L'IDE est un environnement personnalisable qui
permet aux développeurs les meilleures performances. Il fournit un
accès unifié aux concepteurs, éditeurs et outils de Visual
Studio à partir de n'importe quel langage .NET.
1.2 Base de données SQL Server et utilisation
interactive avec
VB.Net
Le SQL Server persiste avec le seul problème, est que
l'on ne peut pas lui parler directement, c'est à ce moment-là
qu'intervient le
VB.NET par l'intermédiaire d'ADO.NET
et de la chaine de connexion de SQL Client. Le langage Visual
basic. NET sert comme un
intermédiaire entre l'utilisateur et SQL Server.

Figure 29. Utilisation interactive de
VB.Net SQL Server
Selon la figure :
1. Le serveur utilise
VB.NET
2. Le code
VB.NET demande à SQL Server
d'enregistrer une information dans la base de données.
3. SQL Server va "répondre" à
VB.NET en lui disant "OK, c'est bon, je
stocke l'information".
4.
VB.NET va alors renvoyer au serveur que tout
c'est bien déroulé (donc SQL Server a bien fait son travail).
1.3 Présentation de MATLAB :
MATLAB est un logiciel interactif essentiellement basé
sur le calcul matriciel d'où son nom MATrix LABoratory. Il est
utilisé dans les calculs scientifiques et les problèmes
d'ingénierie étant donner qu'il permet la résolution des
problèmes numériques complexes en moins de temps requis par les
langages de programmation, et ce grâce à une multitude de
fonctions intégrées et à plusieurs programmes outils
testés et regroupés selon usage (boites à outils ou
Toolbox).

Figure 30. L'espace de travail MATLAB
MATLAB possède les particularités suivantes:
- La programmation facile,
- La continuité parmi les valeurs entières,
réelles et complexes,
- La gamme étendue des nombres et leurs
précisions,
- La bibliothèque mathématique très
compréhensive,
- L'outil graphique qui inclut les fonctions d'interface
graphique et les utilitaires,
- La possibilité de liaison avec les autres langages de
programmation,
Ainsi, grâce aux fonctions graphiques de MATLAB, il
devient très facile de modifier interactivement les différents
paramètres des graphiques pour les adapter selon nos souhaits.
2 Spécification des besoins
Pour atteindre nos objectifs dans les meilleures conditions,
nous devons spécifier les besoins de notre application. Dans cette
section, nous procéderons à déterminer les utilisateurs du
système puis analyser les besoins auxquels doit répondre
l'application.
2.1 Utilisateurs du système
Nous distinguerons deux grands types d'utilisateurs du
système :
- Les administrateurs ayant le droit de créer d'autres
utilisateurs et de spécifier leurs droits d'accès. C'est un
utilisateur unique ayant les privilèges administrateurs, mais qui est
créé automatiquement par le système lors de son
installation. C'est cet utilisateur initial qui permettra de créer tous
les autres utilisateurs directement ou indirectement.
- Les utilisateurs ayant tout juste le droit d'utiliser le
système sans avoir de privilège administrateur.
Ainsi, le système devra pouvoir spécifier pour
chaque utilisateur s'il a le droit ou non d'utiliser un écran quelconque
de l'application. Le système devra aussi donner la possibilité de
spécifier si à travers tel écran l'utilisateur a le droit
de consulter, modifier ou supprimer les informations de la base de
données.
2.2 Les besoins fonctionnels
L'application doit permettre :
- Un accès rapide aux menus et aux données.
- Un accès sécurisé et les utilisateurs
doivent avoir un accès individualisé et limité aux
données.
- Édition des données : le système devra
permettre d'éditer les informations des employés,
les caractéristiques et tout type d'informations.
- Modifier les données enregistrées.
- Établir des statistiques relatives aux informations
enregistrées.
- Imprimer des documents administratifs.
- Gérer l'emploi du temps.
- Gérer les absences : le système devra consigner
toutes les absences des employés avec le
détail fourni par l'emploi du temps.
2.3 Les modules principaux de l'application
L'application comprendra principalement six modules
accessibles à l'aide de menu :
- Un module d'édition employée : ce
module permet d'ajouter des employés en remplissant certains champs (Nom
et prénom, Code national de l'employée, Date et lieu de
naissance, L'adresse principale...). Ensuite, toutes les informations seront
enregistrées dans la base de données.
- Un module de gestion des absences : ce module
permet de marquer l'absence des employés avec les détails fournis
par l'emploi du temps (Date et heure d'absence, Durée d'absence,
l'information si absence a été justifiée ou pas). Ensuite,
toutes ses informations seront enregistrées dans la base.
- Un module d'édition des documents administratifs
: ce module permet d'éditer certain documents (Liste des vols,
listes des équipes, emploi du temps, fiches employés...)
- Un module d'emploi du temps : L'application devra
gérer l'emploi du temps et la gestion des employés
- Un module des statistiques : les informations
statistiques pertinentes sont la répartition
des vols, la répartition des employés par sexe et
par qualification.
- Un module de gestion des ressources humaines :
l'application devra pouvoir gérer les ressources humaines et leurs
qualifications. Toutes ces informations doivent être gérables par
le système.
3 Implémentation de l'algorithme de tournée
sous MATLAB
Afin de réussir l'implémentation de l'algorithme,
il faut déterminer et initialiser les variables. Pour ce faire, nous
rappelons tout d'abord l'algorithme à implémenter :
B (T) = - [S ( , p) + S ( , p)]
S ( , p) Nombre d'agents à la fin de la vacation du
type
Nombre des employés affectés à la
vacation ;
Nombre des employés nécessaires pendant la
période du chevauchement T;
Nombre des employés nécessaires pendant
l'intervalle de temps p;
p Un période de temps dans un jour
donnée;
i Types des vacations;
T La période du chevauchement entre deux vacations
successive et
|
Le nombre de postes actifs au temps La demande au
temps
|
Les variables de la solution Matlab sont donc :
|
Demande = Nombre d'employés nécessaires à
déterminer pendant l'intervalle de temps p et
qui reflète la variable ;
Heurparjour = 8 (données fixes qui reflètent la
contrainte juridique)
|
Ainsi, comme nous avons déjà annoncé, afin
d'implémenter l'application sous Matlab il
faut déterminer la demande par intervalle de temps
à l'aide de la courbe des charges comme
designer dans la figure
31.
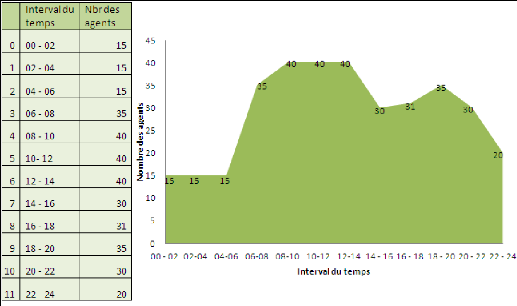
Figure 31.Nombre max des agents par un jour type Dans ce cas, les
variables auront les valeurs suivantes:
Demande = [15 15 15 35 40 40 40 30 31 35 30 20]';
Heurparjour = 8;
4 Présentation du progiciel
Nous présentation dans cette section, les interfaces
qui permettent de satisfaire les besoins des utilisateurs.
4.1 Les interfaces
Interface « Empoyee » permet à l'utilisateur
d'identifier les données de tous les employés (figure 32).
Figure 32. Interface « Empoyee »
Interface « Empoyee Teams » permet à
l'utilisateur d'identifier les groupes de travail (figure 33).
Figure 33. Interface « Empoyee Teams »
Interface « Empoyee Teams Membership » permet
à l'utilisateur d'identifier les groupes de travail de tous les
employés (figure 34).
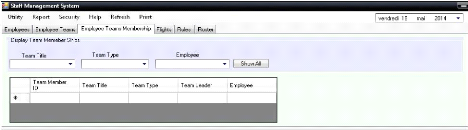
Figure 34. Interface « Empoyee Teams Membership »
Interface « Flight » permet à l'utilisateur
d'identifier la liste des vols journaliers ou hebdomadaires ou mensuels (figure
35).
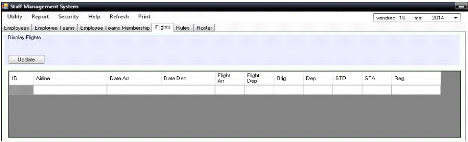
Figure 35.Interface « Flight »
Interface « Rules» permet à l'utilisateur
d'identifier la demande journalière ou hebdomadaire ou mensuelle (figure
36).

Figure 36. Interface « Rules»
Interface « Roster» permet à l'utilisateur
d'afficher la planification hebdomadaire ou mensuelle (figure 37).
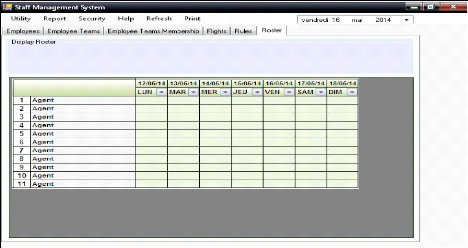
Figure 37. Interface « Roster»
Conclusion
L'automatisation de la planification du personnel est une
tâche compliquer, mais primordial pour le gain du temps et l'optimisation
de la planification. En effet, l'automatisation permet aux responsables de
créer des plannings alignant les effectifs sur la demande
anticipée tout en respectant les conventions collectives et la
réglementation du travail en matière de temps de travail. Du
fait, qu'en fonction des besoins en capacité, le système
génère spontanément un planning que l'on peut adapter
aisément.
Conclusion générale
Dans ce travail, nous avons présenté la
problématique de planification du personnel. Il s'agit d'un
problème original, issu de la réalité industrielle et
comportant un certain nombre de contraintes spécifiques comme par
exemple les contraintes sociales, techniques, juridiques...etc. Ce
problème est central et se situe à la base de
problématique gestion du personnel comme le problème des
tournées ou encore le problème de création des
vacations.
Dans un premier temps, nous avons présenté la
demande dans le contexte aérienne tous en spécifiant les
différentes étapes et scénarios de planification. Dans ce
cadre, nous avons étudié les trois stratégies de
planifications à savoir les stratégies tactiques,
opérationnelles et en temps réel tous en se
référant à la littérature et présentant les
différentes méthodes de résolution.
En deuxième lieu, nous avons détaillé la
première étape de planification à savoir la
modélisation de la demande. Nous avons formalisé et
modélisé la demande à l'aide de la programmation linaire
en nombre entière et les données de Panel.
Dimensionnement des effectifs, étais bien
détaillé dans ce travail. Du fait que le dimensionnement peut
être exploité pour détecter des insuffisances au cours de
planification en termes de manque de personnel. Ainsi, la création de
vacations étant un problème qui repose sur la satisfaction de
nombreuses contraintes temporelles, nous avons proposé une approche de
modélisation basée sur le concept d'énumération.
Ces différentes approches et modèles ont
était pris en compte lors de l'élaboration l'algorithme et la
solution proposée pour la planification du personnel.
Bibliographie
[1] - Arthur, J.B. (1994): Effects of Human
Resource Systems on manufacturing
Performance and Turnover.
[2] - Azah Mohamed (2010):Modelling,
Simulation and Identification
[3] - Aykin. A (2000): comparative
evaluation of modeling approaches to the labor shift
scheduling problem.
[4] - Badr D, Youness C (2012):
Modélisation d'un problème d'allocation des agents
de
maintenance.
[5] - Brusco, M. J., Futch, J., &
Showalter, M. J. (1993). Nurse staff planning under
conditions of a nursing
shortage. Journal of Nursing Administration, 23 (7/8), 58-64.
[6] - Carmen DRAGHICI(2006) :
Modélisation et conception d'algorithmes pour la
planification
automatique du personnel de compagnies
[7] - Chan, P. (2002): La planification du
personnel: acteurs, actions et termes multiples pour
une planification
opérationnelle des personnes.
[8] - Claude McMillan (1986): the general
employee scheduling problem: an integration of
MS and AI.
[9] - Dowsland.K (1998): Nurse scheduling
with Tabu Search and Strategic Oscillation.
[10] - Evrim Didem Gunes (2003):
Planification de la main-d'oeuvre.
[11] - Evrim Didem Gunes (1999): Workforce
Scheduling.
[12] - Ernst, A. T., Jiang, H., (2004):
Staff scheduling and rostering: A review of applications, methods and
models.
[13] - Frédéric Albert(2007):
Réalisation d'un outil de prototypage des plateaux chirurgicaux
[14] - Fantassin Kakule katsuva (2010) :
Problématique de gestion des ressources humaines dans une ONG
internationale, cas de AVSI.
[15] - Jorg Herbers (2005) : Models and
Algorithms for Ground Staff Scheduling on Airports
[16] - J.Agard (1970): Automatisation du
planning mensuel du personnel Navigant commercial.
[17] - Jonathan F. et Hadi W (2004):
Preference scheduling for nurses using column generation
[18] - Lorraine T et Alain G (2005):
Planification de ressources mutualisées : le cas des infirmiers
anesthésistes.
[19] - Lise C, Guy A, (2005): Impacts des
pratiques de gestion des ressources humaines sur la performance
organisationnelle des entreprises de gestion de projets.
[20] - Lorraine T et Alain G (2007) :
Planification des infirmiers anesthésistes : analyse comparative des
performances de différents solveurs.
[21] - P. Brucker (1998): Scheduling
algorithms, 2nd edition, Springer, Heidelberg.
[22] - Rodolphe Donald (2010) : Pratiques de
GRH et performance sociale de Benin Telecoms SA
[23] - Rehbein AOS (2007): Review of Passenger
Functions.
[24] - Rémy-Robert, Alexandre (2003) :
Systèmes Interactifs d'Aide à l'Élaboration de Plannings
de Travail de Personnel.
[25] - Stolletz, Raik (2009): Operational
workforce planning for check-in counters at airports
[26] - Trilling,L Guinet,A (2006): Nurse
scheduling using integer linear programming and constraint programming.
Webographie:
[1] -
http://acustaf.com
[2] -
http://www.daskoo.org/325-lasticite-de-la-demande-par-rapport-au-prix.cours
[3] -
http://www.hindawi.com/journals/mpe/2012/214607/
[4] -
http://www.kappix.com/download.htm
[5] -
http://www.lindo.com/index.php?option=com_content&view=article&id=38&Itemid=24
[6]
Annexes
-
http://www.mathworks.com/help/optim/examples/office-assignments-by-binary-integer-programming.html
[7] -
http://plasserre.developpez.com/cours/chart/
Les causes de retards selon IATA Ref:AHM730
|
|
[8] -
http://personnel.isae.fr
[9] -
http://personnel.isae.fr/emmanuel-zenou/supaero/1ere-annee-l3/article/initiation-matlab.html
[10] -
http://shift-work.com/articlesnewsletters/shiftwork-articles/
[11] - http://trainingzone.eurocontrol.int/
[12] -
http://www.metaheuristics.org/index.php?main=3&sub=32
|
Les causes de retards
|
Les codes
|
|
Passagers et bagage
|
1
|
|
Fret
|
2
|
|
Avion et services de piste
|
3
|
|
Equipement appareil
|
4
|
|
Dommage appareil
|
5
|
|
Equipage
|
6
|
|
Météo
|
7
|
|
Aéroport et autorité
|
8
|
|
Divers
|
9
|
Annexe : 1 : Les causes de retards selon
IATA
Annexe : 2 : Les causes de retards de 2010-2013
Annexe : 3 : Etude de la stationnarité
Pool unit root test: Summary
Series: RET1_BER, RET1_BHP, RET1_BLX, RET1_CND, RET1_I,
RET1_OXL, RET1_JAF, RET1_LBT, RET1_LOL, RET1_PRI,
RET1_SAS, RET1_TAR, RET1_TCVV, RET1_TCX
Date: 05117114 Time: 12:26
Sample: 2010M01 2013M12
Exogenous variables: Individual effects, individual linear
trends
Automatic selection of maximum lags
Automatic selection of lags based on SIC: 0 to 1
Newey-West bandwidth selection using Bartlett kernel
|
Method Statistic Prob.**
|
Cross-
sections
|
Ohs
|
|
Null: Unit root (assumes common unit root process)
|
|
|
|
Levin, Lin & Chu t*
|
-19.0822 0.0000
|
10
|
469
|
|
Breitung t-stat
|
-11.2600 0.0000
|
10
|
459
|
|
Null: Unit root (assumes individual unit root process)
|
|
|
|
Im, Pesaran and Shin W-stat
|
-16.4701 0.0000
|
10
|
469
|
|
ADF - Fisher Chi-square
|
226.765 0.0000
|
10
|
469
|
|
PP - Fisher Chi-square
|
456.791 0.0000
|
10
|
470
|
Probabilities for Fisher tests are computed using an asymptotic
Chi -square distribution. All other tests assume asymptotic normality.
Pool unit root test: Summary
Series: RET3_BER, RET3_9HP, RET3_BLX, RET3_CND, RET3_OVVI,
RET3_CXL, RET3_JAF, RET3_LBT, RET3_LCL, RET3_PRI,
RET3_SAS, RET3_TAR, RET3_TCW, RET3_TCX
Date: 05117114 Time: 12:31
Sample: 2010M01 2013M12
Exogenous variables: Individual effects, individual linear
trends
Automatic selection of maximum lags
Automatic selection of lags based on SIC: 0 to 8
Newey-West bandwidth selection using Bartlett kernel
|
Method Statistic Prob.**
|
Cross-
sections
|
Obs
|
|
Null: Unit root (assumes common unit root process)
|
|
|
|
Levin, Lin & Chu t*
|
-14.8763 0.0000
|
14
|
632
|
|
Breitung t-stat
|
-10.8405 0.0000
|
14
|
618
|
|
Null: Unit root (assumes individual unit root process)
|
|
|
|
Im, Pesaran and Shin W-stat
|
-19.5790 0.0000
|
14
|
632
|
|
ADF - Fisher Chi-square
|
325.790 0.0000
|
14
|
632
|
|
PP - Fisher Chi-square
|
614.688 0.0000
|
14
|
644
|
**Probabilities for Fisher tests are computed using an asymptotic
Chi -square distribution. All other tests assume asymptotic normality.
Pool unitroottest: Summary
Series: RET4_BER, RET4_BHP, RET4_BLX, RET4_CND, RET4_GWI,
RET4_GXL, RET4_JAF, RET4_LBT, RET4_L0L, RET4_PRI,
RET4_SAS, RET4_TAR, RET4_TCW, RET4_TCX
Date: 05117114 Time: 12:31
Sample: 2010M01 2013M12
Exogenous variables: Individual effects, individual linear
trends
Automatic selection of maximum lags
Automatic selection of lags based on SIC: 0 to 9
Newey-West bandwidth selection using Bartlett kernel
|
Method Statistic Prob.**
|
Cross-
sections
|
Obs
|
|
Null: Unit root (assumes common unit root process)
|
|
|
|
Levin, Lin & Chu t*
|
-9.70038 0.0000
|
9
|
390
|
|
Breitung t-stat
|
-12.0045 0.0000
|
9
|
381
|
|
Null: Unit root (assumes individual unit root process)
|
|
|
|
Im, Pesaran and Shin VV-stat
|
-12.6786 0.0000
|
9
|
390
|
|
ADF - Fisher Chi-square
|
168.105 0.0000
|
9
|
390
|
|
PP - Fisher Chi-square
|
1381.94 0.0000
|
9
|
414
|
**Probabilities for Fisher tests are computed using an asymptotic
Chi -square distribution. All other tests assume asymptotic normality.
|
Pool unit root test: Summary
|
|
|
Series: RETS_BER, RET5_BHP, RET5_BLX, RETS_CND, RETS_OWI,
|
|
|
RETS_GXL, RETS_JAF, RETS_LBT, RETS_LOL, RETS_PRI,
|
|
|
RETS_SAS, RETS_TAR, RETS_TCW, RETS_TC
|
|
|
Date: 05117114 Time: 12:32
|
|
|
Sample: 2010M01 2013M12
|
|
|
Exogenous variables: Individual effects, individual linear
trends
|
|
|
Automatic selection of maximum lags
|
|
|
Automatic selection of lags based on SIC: 0
|
|
|
Newey-West bandwidth selection using Bartlett kernel
|
|
|
Balanced observations for each test
|
|
|
Cross-
|
|
|
Method Statistic Prob.** sections Obs
|
|
|
Null: Unit root (assumes common unit root process)
|
|
|
Levin, Lin & Chu t* -7.57497 0.0000 1
|
46
|
|
Breitung t-stat -6.86507 0.0000 1
|
45
|
|
Null: Unit root (assumes individual unit root process)
|
|
|
Im, Pesaran and Shin W-stat -7.49944 0.0000 1
|
46
|
|
ADF - Fisher Chi-square 35.1928 0.0000 1
|
46
|
|
PP - Fisher Chi-square 58.9634 0.0000 1
|
46
|
|
**Probabilities for Fisher tests are computed using an asymptotic
Chi -square distribution. All other tests assume asymptotic normality.
|
|
Pool unit root test: Summary
Series: RET6_BER, RET6_9HP, RET6_BLX, RET6_CND, RET6_OWI,
RET6_OXL, RET6_JAF, RET6_LBT, RET6_LOL, RET6_PRI,
RET6_SAS, RET6_TAR, RET6_TCW, RET6_TCX
Date: 05I17114 Time: 12:32
Sample: 2010M01 2013M12
Exogenous variables: Individual effects, individual linear
trends
Automatic selection of maximum lags
Automatic selection of lags based on SIC: 0 to 9
Newey-West bandwidth selection using Bartlett kernel
|
Method Statistic Prob.**
|
Cross-
sections
|
Obs
|
|
Null: Unit root (assumes common unit root process)
|
|
|
|
Levin, Lin & Chu t*
|
-17.3297 0.0000
|
4
|
174
|
|
Breitung t-stat
|
-11.0757 0.0000
|
4
|
170
|
|
Null: Unit root (assumes individual unit root process)
|
|
|
|
Im, Pesaran and Shin W-stat
|
-19.4327 0.0000
|
4
|
174
|
|
ADF - Fisher Chi-square
|
384.441 0.0000
|
4
|
174
|
|
PP - Fisher Chi-square
|
665.452 0.0000
|
4
|
184
|
**Probabilities for Fisher tests are computed using an asymptotic
Chi -square distribution. All other tests assume asymptotic normality.
|
Pool unit root test: Summary
Series: RET7_BER, RET7_BHP, RET7_BLX, RET7_CND, RET7_GWI,
RET7_OXL, RET7_JAF, RET7_LBT, RET7_LOL, RET7_PRI, RET7_SAS, RET7_TAR, RET7_TCW,
RET7_TCX
Date: 05117114 Time: 12:33
Sample: 2010M01 2013M12
Exogenous variables: Individual effects, individual linear
trends
Automatic selection of maximum lags
Automatic selection of lags based on SIC: 0
Newey-West bandwidth selection using Bartlett kernel
Balanced observations for each test
|
|
Cross-
Method Statistic Prob.** sections Obs
|
|
Null: Unit root (assumes common unit root process)
|
|
Levin, Lin & Chu t* -23.0790 0.0000 3 138
Breitung t-stat -20.0781 0.0000 3 135
Null: Unit root (assumes individual unit root process)
|
|
Im, Pesaran and Shin W-stat -22.2602 0.0000 3 138
ADF - Fisher Chi-square 325.369 0.0000 3 138
PP - Fisher Chi-square 605.741 0.0000 3 138
|
|
**Probabilities for Fisher tests are computed using an asymptotic
Chi -square distribution. All other tests assume asymptotic normality.
|
|
Pool unit root test: Summary
Series: RET8_BER, RET8_BHP, RET8_BLX, RET8_CND, RET8_OWI, RET8_O
L, RET8_JAF, RET8_LBT, RET8_LOL, RET8_PRI, RET8_SAS, RET8_TAR, RET8_TCW,
RET8_TC>C
Date: 05117114 Time: 12:33
Sample: 2010M01 2013M12
Exogenous variables: Individual effects, individual linear
trends
Automatic selection of maximum lags
Automatic selection of lags based on SIC: 0 to 9
Newey-West bandwidth selection using Bartlett kernel
|
|
Cross-
Method Statistic Prob.** sections Obs
|
|
Null: Unit root (assumes common unit root process)
|
|
Levin, Lin & Chu t* -23.5248 0.0000 11 492
Breitung t-stat -17.8301 0.0000 11 481
Null: Unit root (assumes individual unit root process)
|
|
Im, Pesaran and Shin W-stat -25.2998 0.0000 11 492
ADF - Fisher Chi-square 567.080 0.0000 11 492
PP - Fisher Chi-square 1378.94 0.0000 11 506
|
|
**Probabilities for Fisher tests are computed using an asymptotic
Chi -square distribution. All other tests assume asymptotic normality.
|
|
Pool unit roottest: Summary
Series: RET9_BER, RET9_BHP, RET9_BL, RET9_CND, RET9_OWI, RET9_0L,
RET9_JAF, RET9_LBT, RET9_LOL, RET9_PRI, RET9_SAS, RET9_TAR, RET9_TCW,
RET9_TC}{
Date: 05117114 Time: 12:34
Sample: 2010M01 2013M12
Exogenous variables: Individual effects, individual linear
trends
Automatic selection of maximum lags
Automatic selection of lags based on SIC: 0 to 7
Newey-West bandwidth selection using Bartlett kernel
|
|
Cross-
Method Statistic Prob.** sections Obs
|
|
Null: Unit root (assumes common unit root process)
|
|
Levin, Lin & Chu r -24.5597 0.0000 14 635
Breitung t-stat -15.5729 0.0000 14 621
Null: Unit root (assumes individual unit root process)
|
|
Im, Pesaran and Shin W-stat -24.6658 0.0000 14 635
ADF - Fisher Chi-square 598.827 0.0000 14 635
PP - Fisher Chi-square 664.434 0.0000 14 644
|
|
**Probabilities for Fisher tests are computed using an asymptotic
Chi -square distribution. All other tests assume asymptotic normality.
|
|
Pool unit root test: Summary
Series: Y_BER, Y_BHP, Y_BLX, Y_CND, Y_OWI, Y_CL, Y_JAF, Y_LBT,
Y_LOL, Y_PRI, Y_SAS, Y_TAR, Y_TOW, Y_TC7<
Date: 05/17114 Time: 12:35
Sample: 2010M01 2013M12
Exogenous variables: Individual effects, individual linear
trends
Automatic selection of maximum lags
Automatic selection of lags based on SIC: 0 to 9
Newey-West bandwidth selection using Bartlett kernel
|
|
Cross-
Method Statistic Prob.** sections Ohs
|
|
Null: Unit root (assumes common unit root process)
|
|
Levin, Lin & Chu r -11.9364 0.0000 14 613
Breitung t-stat -10.7704 0.0000 14 599
Null: Unit root (assumes individual unit root process)
|
|
Im, Pesaran and Shin W-stat -19.5125 0.0000 14 613
ADF - Fisher Chi-square 383.974 0.0000 14 613
PP - Fisher Chi-square 333.316 0.0000 14 644
|
|
**Probabilities for Fisher tests are computed using an asymptotic
Chi -square distribution. All other tests assume asymptotic normality.
|
Liste des abréviations
ATFM :La gestion des flux de trafic
aérien (en anglais Air Traffic Flow Management).
IATA :L'Association internationale du
transport aérien (en anglais International Air Transport
Association, ou IATA).
MCO : La méthode des moindres
carrés ordinaire (MCO).
PLNE: Programmes Linéaires en
Nombres Entiers.
PPC : Programmation Par Contraintes.
RMA : Retard moyen par mouvement
d'arrivée.
RMD : Retard moyen par mouvement de
depart.
TPA : L'heur programme d'arrivée .
TPD : L'heur programmé de
départ.
TRA : L'heur réel d'arrivée.
TRD : L'heur réel de départ.
Glossaires
A
Acycliques : planification non cyclique.
Affectation: l'affectation des personnes
disponibles dans le tableau de service.
B
Besoins futurs : besoins prévus de
l'organisation.
C
Charge de travail: un besoin à couvrir
par l'ensemble des salariés.
Contrainte : une relation portant sur des
variables de décision.
Courbe de charges : les tâches peuvent
dépasser 24H en durée
Courbes de demande distinctes : les tâches
ne dépassent pas 24H en durée
Cycle de travail : le planning des
salariés qui suit un cycle est répétitif.
Cycle de travail hebdomadaire : est
défini par une séquence de vacations hebdomadaires.
Cycle de travail journalier : est défini
par une séquence de vacations journalières
D
Demande incertaine : demande est née due aux changements
du programme des vols. Demande globale : demande global obtenue à
travers le programme des vols.
Dimensionnement : le processus qui assure l'adéquation
optimale des ressources humaines disponible avec les besoins d'une
organisation.
E
Equipe : groupe de salariés effectuant le
même planning au même moment.
Élasticité : mesure la variation
d'une grandeur provoquée par la variation d'une autre grandeur.
Énumération des vacations : création d'un
ensemble de vacation.
F
Fenêtre d'heure de début :
intervalle durant lequel les vacations peuvent commencer.
G
Grille de travail: planning nominatif ou non,
avec des étiquettes, défini sur un horizon.
Grille de besoins : pour chaque jour et pour
chaque vacation, elle détermine le nombre des agents
nécessaires.
H
Heure de pointe: ou heures de pic dont on note
le nombre max des vols.
I
J
K
L
M
N
O
P
Pause : l'ensemble de périodes non
travaillées au cours de la journée.
Planification d'horaires : sur un horizon d'un
jour à quelques mois, donner l'utilisation des ressources de
façon à couvrir un besoin exprimé par une charge de
travaille prévisionnelle, tout en respectant des contraintes
précises.
Planning : un emploi du temps pour les
salariés.
Planning journalier : un emploi du temps pour
les salariés pour un horizon d'un jour.
Planning mensuel : un emploi du temps pour les
salariés pour un horizon d'un mois.
Planning annuel : un emploi du temps pour les
salariés pour un horizon d'un an.
Programmation par contraintes PPC :
méthode de résolution des problèmes de satisfaction des
contraintes.
Programmation Linéaire en Nombres
Entiers: méthodes de résolution d'un système
d'équations linéaires.
Q
Qualification : la capacité d'un salarié à
travailler sur une tâche qui exige des connaissances défini.
R
S
T
U
V
Vacation : une journée de travail,
défini par des horaires de début et de fin, précisant les
pauses. Variable de décision : pouvant prendre une
valeur prise dans le domaine de la variable.
Index
A
Absences 11
Activités 12, 52
Acycliques 9
Affectation des ressources humaines 17
Affectation du personnel 1, 8,15,59,75
Algorithme 2, 12,20, 21, 22, 52, 53, 55,
57, 58, 59,75
Analyse de scénarios 16
Approches explicites 51
Approches implicites 51, 53
Approches par couverture 51
Assistance 3, 4, 9, 11, 12, 24, 26, 27, 31,
35, 46, 48, 54, 55, 60, 63
Augmentation du trafic 31
B
Besoins de main d'oeuvre 25
Besoins en personnel 2, 7, 29, 50, 51 Besoins futurs 8
Borne inférieure 46
Construction de vacation 23, 49, 51, 52
Contexte aérien 17, 52
Contexte dynamique 18
Contraintes cumulatives 23
Contraintes de début 55
Contraintes de nature globale 23
Contraintes social 8
Contraintes techniques 4, 14, 43
Courbe de charges 51
Courbe de demande 24, 27, 28, 36,39, 49, 52,60
Courbes de demande distinctes 60
Court terme 12, 16
Coût de vacation 30, 56
Coût relatif 37, 38
Coûts d'exploitation 4 Coût de recrutement, 4 Contraintes 35
Coûts d'exploitation 4
Couverture de la charge 23,40, 50
Couverture de la période 54
Création d'horaires 19
Cyclique 9,19, 20, 21, 22, 44, 65, 66
D
Day-Off Scheduling 20
Décideur 16
Décisions extérieures 18
|
Demande
|
|
1,
|
2, 5, 10, 11, 14, 15, 17, 18,
|
|
21,
|
24,
|
25,
|
26,
|
27,
|
28,
|
29,
|
30,
|
31,
|
33,
|
34,
|
|
35,
|
36,
|
37,
|
38,
|
39,
|
40,
|
41,
|
42,
|
44,
|
45,
|
48,
|
|
50,
|
52,
|
53,
|
56,
|
57,
|
59,
|
60,
|
62,
|
64,
|
71,
|
75
|
Demande incertaine 31, 33
Demande globale 14
Dépendance temporelle 16
Description
agrégée 24
Détermination des tâches 28
Détermination
du nombre optimal 45
C
Calendrier 8,11, 16, 21, 22
Capacités actuelles 11
Capital humain 6
Changements d'horaire 12
Charge de travail 5, 7, 11, 12, 25, 26,
27, 29, 30, 36, 40, 60, 63, 69
Chevauchement 56, 57, 58,59, 61
Chronologie 13
Compétences 6, 8, 11, 38, 39, 40, 41, 44, 60, 64
Compétitivité 3, 5, 9
Concept de dominance 58
Concept de la tournée 62
Conception des vacations 14
Congés 8, 42, 43, 54
Dimensionnement 41, 42, 43, 44, 45, 48,
62, 63
Dimensionnent de l'effectif 46 Disponibilité 17, 36, 71
Durée max de la vacation 4, 22, 23,
52,54
E
Effectif minimal 45
Écart 2, 24, 35, 36, 37
Économie globale 4
Élasticité 31, 32
Énumération des vacations 53,54, 56
Équitables 18
Escale 12, 26, 44
Estimation de la charge 12
Estimation de la demande 27
Estimation du temps 35
Estimation du coût 29
Étape 12, 14, 21, 24, 37, 43, 45, 48, 67, 68,
69, 72, 73, 74
Événements 17, 18
Evolution du retard en fonction du trafic
32
Exigences complexes 15
Exigences du service 38, 39, 48
Exigences techniques 39
F
Facteurs de perturbation 18
Facteurs de retard 31
Flexibilité 28, 53
Flux de planification 13
Fonction objectif 2, 40, 41, 62, 68
Forme linaire 29
Formulation de l'objectif 67,68
Formulation des contraintes
67, 69 Formulation mathématique 67
G
Génération de colonnes 19
Gestion des ressources humaines 7, 43
Gestion du personnel
17
Grille de besoins 63, 64, 65, 71
H
Hebdomadaire 8, 19, 65
Hétérogène 11, 24, 38, 39, 40, 48, 60,64
Heures de début 23
Heures de fin 23
Heure de pointe 34
Heures supplémentaires 17
Homogène 40, 41
Horaire fixe 12
Horaires de travail 1, 5, 8, 30, 45
Horaires individuels 9
Horizon 3, 4, 7, 8, 15, 18, 25, 29
I
Implicite 23, 53, 54
Intervalles de temps 10, 25, 52
J
Jour de l'opération 1, 15, 17
Journalier 8, 19, 22, 71
Journée d'opération 17,
18,21 Jours de repos 20, 21, 46, 50
K
L
Limite de décomposition 18
Limite de processus planification 18, 22,
38
Limites de prise compte 18
Limites des modèles 18
Littérature 1, 4, 19, 20, 21, 22, 37, 46,
51, 75
M
Manque de personnel 36, 37, 40, 41, 60 Matrice de couverture 54,
55, 57 Main d'oeuvre 5, 14, 17, 18, 36
Mensuel 8
Méthodes de résolution 4, 19, 20, 21,
52
Méthodes heuristiques 19
Minimisation de nombre de travailleurs 22
Minimiser le coût 20, 48
|
13,
|
14,
|
15
|
14,
|
24
|
|
|
15,
|
|
18
|
|
|
|
|
29
|
|
|
|
|
30,
|
41,
|
46,
|
47,
|
Modèle implicite 23
Modèle de base 19
Modèle de la planification
Modèle explicite 23
Modèle générique 19
Modélisation de la demande Modification journalière
Moyen terme 16
N
Nature de la demande 44 Niveaux de décisions 13 Niveaux
d'interaction 39 Nivellement des ressources. Nombre des agents 25, 28,
56, 59, 61, 64, 65, 67, 71
Nombres requis 63
Non cyclique 9, 19, 44, 66 Non
négativité 70
O
Opérations 9, 11, 12, 15, 16, 35
Optimisation 1, 12, 20, 54, 58, 59, 67, 75 Optimisation de
l'algorithme 56
Ordonnancement 35, 45, 49
Pics de charges 25
Plages horaires 47, 63
Planification des tours 20
Planification journalière 17
Planification
opérationnelle 17
Planification quotidienne 17
Planification tactique 16, 17
Planning 1, 2, 7, 8, 13, 20, 22, 23, 42,
45, 70,
Positionnement des jours 20
Positionnement des jours de repos
45
Positionnement du vol 28
Productivité 4
Préférences 18, 71, 75
Prévision 2, 14, 29, 31, 42
Prévision de la demande 25,45
Prévisions
d'horaire 14
Problème de dimensionnent 48
Problème tournée 22
Processus d'affectation 15, 75
Processus de décisionnel 43
Processus de dimensionnement 44
Processus de planification 1, 9, 13, 18
Processus
décisionnel 43, 45
Programmation linéaire 2, 24, 30, 36,
51, 72
Programme Linéaire en Nombres Entier 19, 22, 66, 67, 68
Programmation Par Contraintes 22, 23
Programme des vols 9,
14, 28, 31, 34
P
Pauses 8, 23, 49, 50, 52, 53, 55
Q
Qualification du personnel 39, 48 Qualifications 10, 18, 38, 41,
60, 63
Pénalité linéaire 36
Performance économique 6
Performance financière 6
Performance organisationnel 7
Période de planification 9,
Période future 17
Périodes de pic 44
Périodes de pointe 11, 14
Périodes de travail 8, 49
Périodicité 9
Perspective financière 6 Perturbations 11, 17
Qualité de service 5, 43,45
Quantité de travail 14, 29
|
25, 49 R
|
|
|
|
|
|
Recensement des activités
|
1, 7
|
|
|
|
|
Recherche opérationnelle
|
51
|
|
|
|
|
Recherche tabou 20
|
|
|
|
|
|
Recouvrement d'ensemble
|
21,
|
51
|
|
|
|
Réglementation du travail
|
11,
|
14,
|
21,
|
23,
|
|
44,49
|
|
|
|
|
|
Regroupement des vols
|
27,
|
29
|
|
|
Rémunération 4
Ressources nécessaires 16
Retards 11, 18, 26, 31, 32, 33, 34, 75
Rétroaction
14
Revue de littérature 19
S
Salariés homogènes 22
Satisfaction des employés 5, 36
Satisfaction sociale
5
Scenarios de planification 13,15, 16, 67
Solution optimale 21, 53, 69, 73
Solutions admissibles 68
Solutions candidates. 58
Sources de la demande 27
Spécificités de vol 28
Stationnement 26, 28
Stratégie 1, 14, 16
Stratégie tactique 1, 14
Stratégies opérationnelles 16
Stratégies
tactiques 16
Sureffectifs 37, 40, 41, 59, 60
T
Tableau de service 15
Tableau de tournement 65, 66
Tâches 4, 5, 8, 9, 10, 11, 12, 15, 17, 25, 26,
27, 28, 29, 33, 35, 38, 39, 41, 48, 49, 52, 63, 64, 75
Tâches de piste 9, 10
Tâches individuelles 27
Taille minimum 14
Temps moyen 33, 35 Temps partiel 21, 22, 23,
54 Temps plein 21, 22, 54
Temps réel 1, 12, 16, 17, 75
Tournée d'horaire 22
Tournée du personnel 62,
64
Tournement de l'horaire 65,22
Transformation de la demande 29, 39
Travaille commun 57
Type d'horaire 44
V
|
Vacations
|
|
2,
|
12,
|
14,
|
15,
|
18,
|
20,
|
21,
|
22,
|
|
23,
|
25,
|
30,
|
37,
|
40,
|
41,
|
42,
|
44,
|
45,
|
46,
|
48,
|
|
49,
61,
|
51,
62,
|
52,
64,
|
53,
65,
|
54,
71,
|
55,
75
|
56,
|
57,
|
58,
|
59,
|
60,
|
Vacations candidates 21 Vacations possibles 23 Valeur
économique 6
Variables binaires 66, 67
Variables de début 23
Variables de décision 66, 74 Variables en nombres entiers 22
Variables mixtes 66
Volume de la couverture 56
| 


