5 Coûts d'insertion
Cette section, illustre plus de détailles pour le
calcul des coûts d'insertions. Le calcul du coût d'insertion du
noeud k entre i et j est une pondération des trois fonctions des
coûts: un coût lié à la capacité, un
coût lié à la distance (ou bien le temps), et un coût
lié à l'ordre :
|
1 1 2 2 3 3
c ijk = W c ijk + W c ijk + W c ijk
|
(9)
(10)
3
Où W t : coefficient de pondération du coût
cijk Avec E W t = 1
t =1
1
Le premier coût cijk = F1 (t ik + t
kj - tij ) correspond à la variation du temps suite à
l'insertion du
2
k entre i et j cijk = F2 (qk) coût de la variation de la
charge du véhicule à l'arrivée au client j suite
à
3
)l'insertion du client k. Le troisième cijk =F3(t. - t J y
J .c est la variation du temps d'arrivée
J
au point j après avoir inséré k, où
tj = Sup (tk + tkj, aj) est le nouveau temps d'arrivée au
point j, telle
que tk = Sup (ti + tik, ak) et yj est une variable binaire
qui vaut 1 si le véhicule arrive en retard en j 0 sinon et c
une
pénalité de retard ( si le retard n'est pas pris en
considération il suffit donner à yi ou bien c une
valeur
nulle)
cvk Le coût d'insertion du client k dans une position
précise de la route v. cvk = 1nf {cijk }
(i,j)E v
cv*k Le coût optimal d'insertion du client k dans la
meilleure route donc la route est à repérer cv*k = 1nf {cvk}
v E V
6 Amélioration
Les solutions réalisables obtenues à la fin de
l'étape de construction ne sont bien évidemment optimales.
L'application d'une méthode de recherche du voisinage permet souvent de
les améliorer. Cette méthode démarre à partir d'une
solution réalisable qui est successivement remplacée par une
meilleure solution appartenant à son voisinage. Un voisinage V associe
à chaque solution un sous-ensemble V(S) de solutions. La solution S est
un optimum local par rapport au voisinage V(S) s'il n'existe pas de solution
strictement meilleure que S dans V(S). L'itération s'arrête
lorsqu'un optimum local est atteint, c'est à dire, lorsque toutes les
solutions voisines de la solution courante lui sont de qualité
inférieure.
La clef du succès pour un algorithme de recherche
locale consiste dans le choix convenable de la structure du voisinage, et aussi
la solution du démarrage. En outre des méthodes classiques
d'amélioration à savoir le recuit simulé, la recherche
taboue, la méthode de descente, la méthode VNS...
Méthode d'éjection des chaînes
Ce processus permet de réduire le nombre des routes
pour le VRPTW. 1l suffit d'utiliser un nouveau type de la structure du
voisinage : échanger quelques clients (arcs successifs) d'une route
donnée par d'autres clients d'une autre route distincte sans violer les
contraintes du capacité ou bien d'intervalles du temps.
Méthode du transfert des chaînes.
Cette méthode consiste à choisir une succession
des arcs pour les échanger d'une route à une autre tout en
respectant les contraintes de précédences entre les clients ; une
telle procédure est appliquée sauf si elle réduit la
distance totale. Le choix de la chaîne à déplacer est
guidé par des critères prédéfinis pour
éviter les déplacements indésirables. Cependant on peut ne
pas changer la route mais juste modifier l'ordre des chaînes.
Méthode du choix par villes
Durant cette méthode, on sélectionne une ville
pour la permuter avec une autre afin de réduire la distance parcourue ou
bien permettre l'insertion d'autres clients sans construire des sous tours.. 1l
est à noter que la permutation des clients peut se faire dans une
même route comme entre les routes on parle donc d'échange interne
et d'échange externe. Cette dernière méthode est celle
adoptée pour notre étude, vu son efficacité et son
exécution simple
Soit Z*ipv coût total optimal de la réalisation si
le client i est dans la position p dans une route v; aucune permutation n'est
acceptée sauf si elle va améliorer le coût optimal de la
solution finale
Si Ziqu < Z* ipv alors introduire le client j dans la
position q de la route v. Lorsque u = v alors on parle d'un changement intra
route alors que pour le cas où i = j et u # v il s'agit d'un changement
du même client dans d'une route vers une autre. Si i # j et u # v alors
il s'agit d'un échange de deux clients de routes différentes.

Algorithme 3 ~
Début
Une fois tous les clients sont affectés
Pour i = 1...n ; j= 1...n ; V p et V q
Soit Dij = Z* ipv Z*jqu
Tant que Dij > 0 introduire j dans la position q. Mettre
à jours cijk .
Si Dij très faible arrêter le processus. Fin tant
que
Fin
Pendant la permutation la formulation du coût
d'insertion prend en considération les changements possibles quant
à la charge et aussi les distances parcourues ce qui permet de
vérifier la proximité entre les routes puisqu'un échange
entre deux routes éloignées va engendrer un coût
élevé qui bloquer la permutation.
i
i
u
u
0
Dépôt
0
Dépôt
v
v
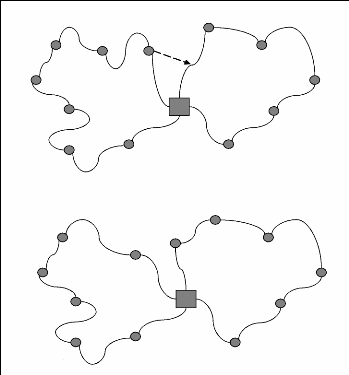
Figure 1 : Procédure d'Amélioration
La discrimination des principes des méthodes de
construction ainsi que ceux d'amélioration laisse les horizons ouverts
pour plusieurs possibilités d'hybridation vu que la problématique
commence à avoir autres extensions par l'introduction des nouvelles
exigences.
Pour notre cas et afin de tester ses performances ; la
méthode GRASP a été appliquée à quelques
exemples de tailles différentes. L'objectif été la
minimisation de la distance totale parcourue par l'ensemble des
véhicules. Les résultats sont résumés
ci-dessous.
|
Problèmes
|
Données
|
Solutions
|
|
I
|
V
|
D*
|
V*
|
Z*
|
|
Exemple 1
|
10
|
5
|
67.9
|
3
|
136.25
|
|
Exemple 2
|
12
|
3
|
83.2
|
3
|
419.65
|
|
Problème 1
|
22
|
9
|
314.65
|
6
|
734.45
|
|
Problème2
|
145
|
15
|
2193.56
|
16
|
50 31.75
|
T1 Tableau récapitulatif des
résultats
En plus de la minimisation du temps de la tournée
totale D* la méthode permet aussi, et à travers son processus
d'amélioration, de réduire le nombre V* de véhicules
utilisés ce qui revient à réduire le coût total Z* ;
parfois il s'agit de chercher un compromis entre la réduction du nombre
de véhicules utilisés et la distance totale parcourue.
| 


