2.2.2. Analyse des données structurales.
a. rosace de fréquence
La rosace est une représentation graphique des
fréquences des valeurs de données structurales dans les classes
de 10 degrés d'amplitude, dans notre cas.
Comme la montre la figure 3.4 la rosace des fréquences
est un outil d'évaluation qui permet d'apprécier les valeurs des
données structurales en fonction des classes respectives. Elle nous
permet de déterminer les directions que doivent prendre les galeries
principales, les refentes, etc....
. 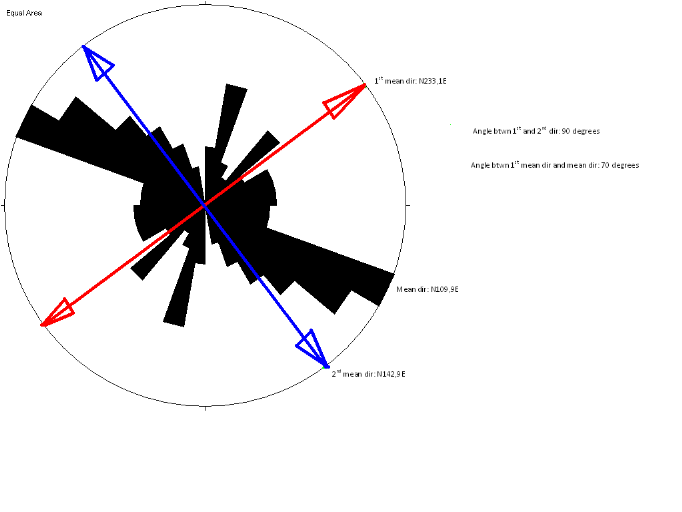
Figure 3.4. Rosace des fréquences et directions
principales des ouvrages

Figure 3.5. Rosace des fréquences des plans de
stratification
B pôles et cyclogrammes.
La représentation des données structurales
collectées sur le terrain est faite à partir d'une technique de
projection sphérique suivant laquelle le plan D est
représenté par un grand cercle, en 2D. L'intersection du plan
avec la sphère de référence définit un grand
cercle (cyclogrammes) lorsqu'on fait sa projection en 2D.
Le Pole est défini par le point où le segment de
droite, tracé du c entre de la sphère perpendiculairement au plan
touche la sphère.
Pour arriver à nos fins, nous avons utilisé le
logiciel de projection stéréographique STEREOWIN 1.2. qui est un
programme de projection dans l'hémisphère inférieure de la
sphère.
Pour enter les données correspondant à
l'orientation des plans, nous avons utilisé les commandes
suivantes :
File/new/planes/ok/plot data to stereo net/enter.
Comme l'illustre les figure 3.6, 3.7, 3.8 et 3.9 un click sur
l'onglet «Scatter» du meme plot donnent les pôles de tous les
plans.
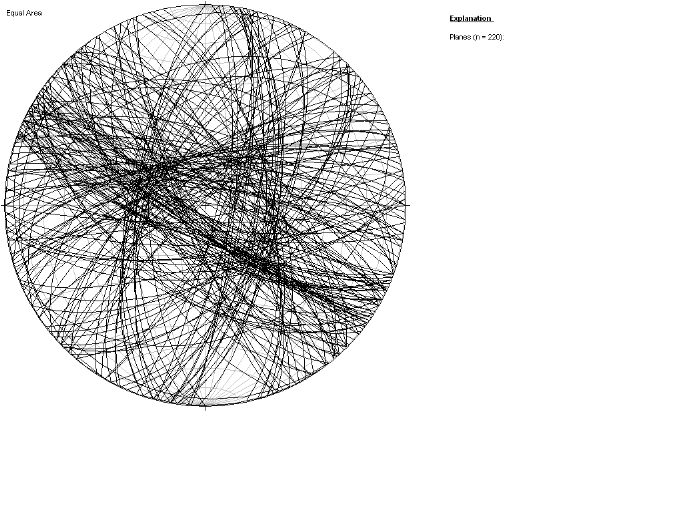
Figure 3.6. Cyclogrammes des plans des fractures
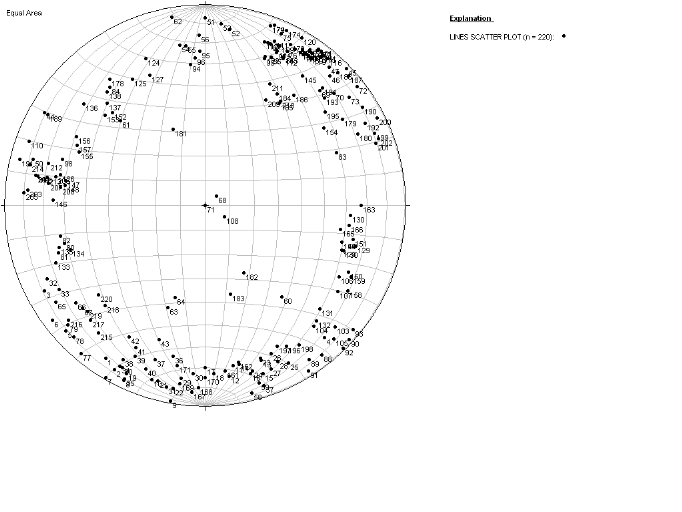
Figure 3.7. Pôles des plans des fractures
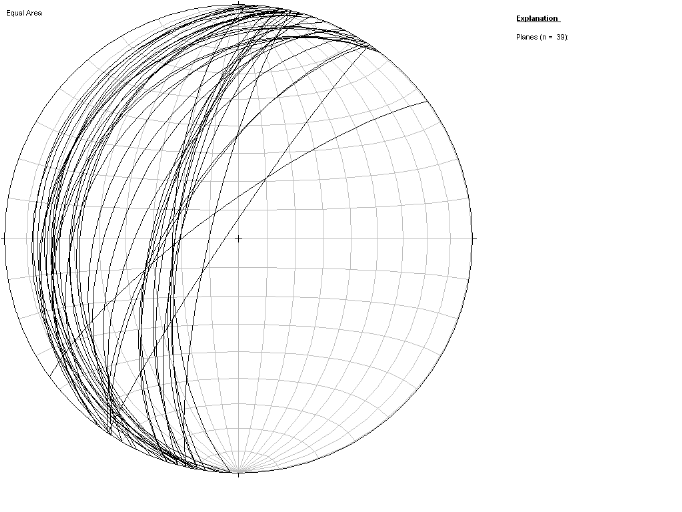
Figure 3.8. Cyclogrammes des plans de stratification
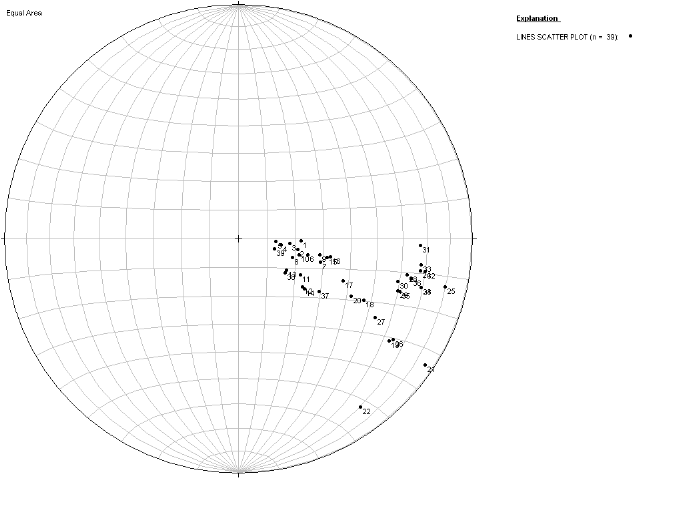
Figure 3.9. Pôles des plans de stratification
c. pole de densité
Stereowin 1.2, use de la méthode de Kamb (1959) pour
déterminer les pôles de densité. Pour y parvenir nous avons
utilisé les commandes ci-après
Plot/Kamb contour/oui.
Cela est illustré par les figures 3.10 et 3.11.
Les pôles de densité nous permettent de
déterminer le paramètre Jn de la classification de Barton et al(
annexe...).
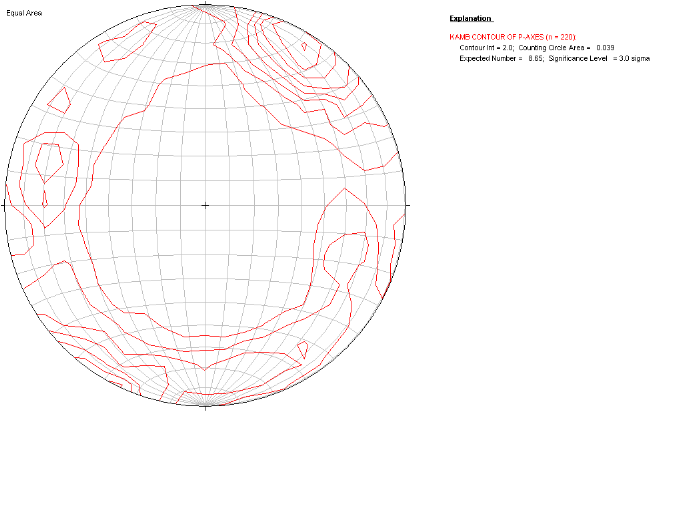
Figure 3.10. Pôles de densité des fractures
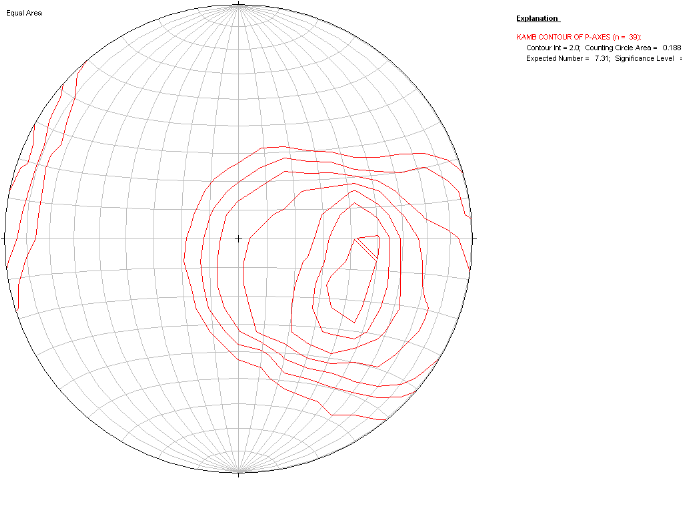
Figure 3.11. Pôles de densité des plans de
stratification
d. contrainte, champs de stabilité, de
glissement et champs métastable.
La projection des pôles des plans de cassures en 2D
aboutit à la détermination du plan deviatorique  des réseaux de fractures des réseaux de fractures  et et , des champs de stabilités de glissements, etc. , des champs de stabilités de glissements, etc.
Par deux grands réseaux de fracture, on fait passer des
cyclogrammes partageant les nuages des pôles respectifs en deux.
L'intersection de ces deux cyclogrammes (réseaux de fractures).est le
point d'application de la contrainte  qui, elle est le pole du plan deviatorique qui, elle est le pole du plan deviatorique . .
A partir de l'angle  qui est l'égale à 2 qui est l'égale à 2 , on déduit l'angle de frottement interne , on déduit l'angle de frottement interne  correspondant à 90° - 2 correspondant à 90° - 2 . Le milieu de l'arc P1P2 est le point
d'application de la contrainte T1 et le cyclogramme
passant par T1 et T2 est
le plan bissecteur . Le milieu de l'arc P1P2 est le point
d'application de la contrainte T1 et le cyclogramme
passant par T1 et T2 est
le plan bissecteur  . .
Le point d'application de T1 est le
pole du cyclogramme dont l'intersection avec le plan déviatoire est
le point d'application de la contrainte T3. T1
est le centre d'un cercle de rayon  qui détermine le champ de stabilité.(Hoek E. et
al,1980) qui détermine le champ de stabilité.(Hoek E. et
al,1980)
P1 et P2 sont les pôles des plans
 et et  dont l'intersection avec le cyclogramme tangent, en
P3, au cercle de stabilité permet de définir
P4 et P5 l'intersection du plan dont l'intersection avec le cyclogramme tangent, en
P3, au cercle de stabilité permet de définir
P4 et P5 l'intersection du plan  avec les plans avec les plans  et et  donne respectivement les points P6 et
P7. Ces derniers, enfin permettent de définir
respectivement deux cercles de centres P6 et P7
et des rayon P6P7 et
P7P5 qui sont les champs de glissement. donne respectivement les points P6 et
P7. Ces derniers, enfin permettent de définir
respectivement deux cercles de centres P6 et P7
et des rayon P6P7 et
P7P5 qui sont les champs de glissement.
Les zones se trouvant entre le champ de stabilité et le
champ métastable.(Barton N. et al,1974)
Vu la multitude des valeurs à ploter, nous utilisons
Stereowin 1.2, lequel logiciel qui nous permet d'arriver à nos fins en
nous basant sur l'algorithme présenté dans l'annexe....
Cela est illustré par la figure 3.12.
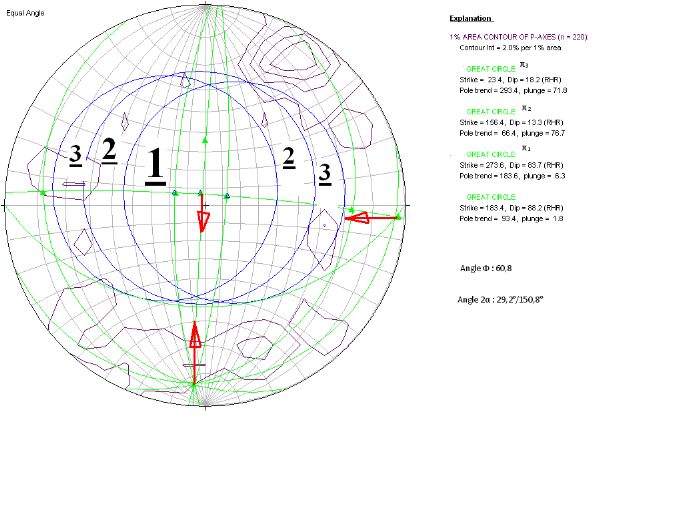
Figure 3.12. Champs de stabilité, champs de glissement,
champs métastable et les contraintes
| 


