Estimation non-paramétrique par noyaux associés et données de panel en marketing

?e_?????_q?? ????s?????
????ster? ?? ????s??_??????t ??_?éri??r, ???l????e??e?S???n??fiq?e?et??e ?a??????_???c
U????rs?té ?? ? \u9670·?????r? a ??rt??_??

Ecole Superieure de la Statisti_que et de l'Anal_yse de l'Information

Projet de Fin d'Etude

EsTIMATION NON-PARAMETRI_QUE PAR NOYAUX AssOCIIs
ET DONNEEs DE PANEL EN MARKETING

Pres??te _??r?:
I??? BEN KHALIFA

??s ?? ??r??t?? ???

Celestin C. KOKONENDJI, HDR
U????rs?te ?? P?? ?t ??s P?_\u9313‡As ?? ????r
???r?t?r? ?? ??t?e??t?_q??s ?_????_q?e?s ?- U?? ???? ?\u9670·??
E-mail: [e-mail]

Dhafer MALOUCHE, MA
???? ?_?er???r? ?? ?? ?t?t?st?_q?? ?t ?? ??????_\u9313‡As? ?? ??_?r??t??
E-mail: [e-mail]

Résumé

Dans ce rapport, nous nous interessons a la notion destimation non-parametri_que d'une densite (fonction de masse) inconnue sur ? ? R par la methode des no_yaux associes. Pour ce faire,nous presentons dabord une definition(unifiee)dun no_yau associeà une loi de probabilite _quelcon_que (continue ou discrete) Nous etudions de maniere detaillee _quel_ques exemples des no_yaux continus s_ymetri_ques(??_??_? normal, Epanechnikov, etc.), continus as_ymetri_ques (????? beta, _gamma, _gaussien-inverse et _gaussien-inverserecipro_que), discret cate_goriel (Aitchison & Aitken 1976) et discret de denombrement (????? trian_gulaires s_ymetri_ques, standards as_ymetri_ques dordre 1 tels _que Poisson, binomial et binomial ne_gatif). Ensuite,nous donnonsla definition delestimateur no_yau associe. Nous montrons la conver_gence ponctuelle de cet estimateur Nous verifions si cet estimateur est bien de masse totale e_gale lunite Dautres proprietes (_globales) sont etudiees, telles _que biais, variance et erreur _quadrati_que mo_yenne inte_gree. Nous proposons une extension dans le cas multivarie (? ? R^d) pour des fonctions de densite (fonction de masse) et de re_gression. Enfin nous illustrons une partie de la methode sur des donnees de panel en marketin_g, les_quelles donnees sont de compta_ge et parsemees.

?ts ??es? ?\u9313‡A?? ?ss??e_????etr? ????ss?_??_?????i_???a?????_??er??u ???d?a?_i???_\u9313‡A??????te_?re?_? ???é?s _??rs??e?s

Abstract

In this report, we are interested in the notion of nonparametric estimation of an unknown densit_y (mass function) in ? ? R b_y usin_g associated-kernel method First we present an unified definition of a kernelassociated to a probabilit_ylawthatmi_ght be eithercontinuousordiscrete.Then,weprovideathorou_ghtreatmentofsomes_ymmetric andcontinuouskernels(??_??_?Gaussian,Epanechnikov,etc.) as_ymmetricandcontinuous (????? beta, _gamma, inverse _gaussian, reciprocal inverse _gaussian) ; discrete cate_gorical (Aitchison & Aitken,1976) and discrete count data (????? s_ymmetric trian_gular,or some knownas_ymmetricdistributionssuchasPoisson,binomialandne_gativebinomial)Furthermore, we define the associated kernel estimators and investi_gate some of their finite andas_ymptoticproperties.Moreprecisel_yweverif_yiftheproposedestimatorsarebona fidedensitiesormassfunctions(i.efunctionswhicharesimultaneousl_ynonne_gativeand inte_grate/sum up to one). Their pointwise consistenc_y bias, variance and mean inte_grated s_quared error are tackled as well Moreover we extend these estimators to the multivariate settin_g ? ? R^d for both densit_y/mass and re_gression functionsFinall_ythe practical usefulness of this approach is illustrated b_y a case stud_y based on some sparse count data obtained from a marketin_g panel research surve_y

?\u9313‡A ?r?s? ?ss???t?? ??r???_? s?t???_? ???????t?_? ???a_? ??a?????_? ???? ?n?_?g?a?? s_q??r?? ?rrr_? s_??rs? ??t??

Remerciements

J???r? ???t??? a ???_?re?????

?? s??s ?\u9312‡@trê?????t ???r??s? ????r ??????? ?? ????i _ç?ça, ?? _???t ?? ?? ?a?i?_???r? ?????t?_??? ?? r????r??? ?? _????s?r ???_???_q???t????? _??s ? ?é??es?it ??e ????nt ??_?????s _??r _q?? ?? _???ss? s???r ?? _q?? ?? ???r???? ?? _q?? ??es ??? ?u?? ?? _????i?i ??? ???st ?? r????r???_? ?? ??et??s _??s ?????? ?? ?é??t ???t ?? ?v?? ?d_? e??i ???u???i?e??e ????ts ?e_????s??ts ???? ??s ???s??s_??r ?tt???r??_???s??i??? (?a??_????

P?r ??s ????ts ???????????s?

?? t???s t?t ????r? d r???r???r Ce??st?? C? K?????_?? ?????r ?????re ?? tr????? ??????????? ?? ??_?et????_? ????t??s??s?? ?tet ?? ??s_???????it_? ; M?r?? C???st?? _??r t???????? ??????r??\u9312‡@_{? ?}?r t?s ??s ?_\u9313‡A??s _q?? t? ?s ??s a ?? ??i_?s?i??_{? ?}?u ?????i _???t ???????? ?????r t?_??rs s? r???t?r ?? r?????_? ?? ????i_?r??_??é ??e ??n???l ???ses_? ????? ?? t? r???r??? _??r ?stes ??_?s ????r?_?????tt ?e ?e ?ot ??_??u?

?? s??s _??rt?????ar????t r??????ss??t? a D??_??r M?????? _??r t?t? ?????? _q???? ????_??rte ??tt? ???e?_? M?r?? D??_??r _??r t?t? ?? ??????? _??s ??ss? ?? r???r???r ???????r??s????t t?t ??s ??s??_????ts?

???\u9312‡@_?r??? ??s r???r??????ts ??s _???s ??_?s C B??????? A???s _??r s? s_\u9313‡A?_??t???_? s? t????t ?? _?e??_???? ?t s? t???? ?\u9312‡@??_?t???????_?; M?r?? B??????? _??r t? ??????? ?t t?s ????r?_?????ts ?? r???r??? ? ??r??rt ??stér??_{? ?}r_??es??u ?? ??a??e??_? a ???????_?er???r? ?? ????r?? ?? P??_? ?? ??s ???r _??r?? ?tet ?\u9312‡@_???_q?é ?? ?de???l ?e ???é?s?

??s r???r??????ts ??t e_???????t a

Tr?st?? S??_?? K??sse_{? ?}?r s? ???e_???t???? s?t???? M?r?? Tr?st?? _??r ??s ????ts ?? ?e_?????r_? ??s ??_???s ??s??ss??s_? ??sles ????r?_?????tt ?e ? ??_?????it?

M?r??? Z???_? ??? _??rs??? _q?? ???? ?? ?? ?????? ?? ??s??ér?r ???? ???? ??????????? M?r?? M?r??? _??r t?s ??s???s_? t? s???????t? ???s??? ?tet ?e ??????e _??oo?

L??? Gr?_??rs??t?_? L?_\u9313‡A?? L?\u9314‡B???_? A?? S?????_? D????? G?s_??r ?t a t?s ???\u9312‡@ _q?? ??? ???? _????s?r ?? ?ot_\u9313‡A?r ??r??t _q??tr?s ??l

M?r?? P?_?? & M???? _??r ??????s ?? r??s?s_? ??s ?? ????\u9314‡B _??r ?_?rs _??r ??? t??t ?????r ?t ?? ???????

M?r?? ?? ???r _?rar? A???? _??r t?t ??????r _q?? t? ?_?r?s_{? ?}?r ??s r?_?????s_? ?e _??t?t?s s?r_?r?s?s ?t _??r t?s ?????s?

?? ?? s??s _??s ?????t ?\u9312‡@_?r???r s??_??????t ??cc _q?? _??je ??ff d ??e _???u ??,a?e ??n?e_???t? H?s??_? ??t? AT?_??t ?t a ?? ??r???? R????. M???? M?r?? _??r ????? ?t ??? r??s?s?

U? M?r?? tras ???r _??r ??s s?_??rs ???s Rima, M_yriam & Omar.
U? _?r??? M?r?? ??ss? _??r t?s ???\u9312‡@ ?t ?????s _q?? ??????t?

Table des matières

Présentation _générale du sta_ge 13

1 Introduction a l'estimation non-paramétri_que 15

2 No_yau continu s_ymétri_que 17

2.1 Cas univarié .................. . . .. . . . . . . . . . . 17

2.1.1 Propriétés élémentaires. . . . . . . . . . . . . . . . . 18

2.1.2 Biais ponctuel . ... . . . . . . . . . . . . . . . . . . . . . . . . . 19

2.1.3 Variance ponctuelle .... . ... . .. . . .. . . . . . . . . . . 21

2.1.4 Erreur _quadrati_que mo_yenne (MSE) 22

2.1.5 Erreur _quadrati_que mo_yenne inté_grée (MISE) 22

2.1.6 Choix du no_yau .......... . .. . . .. . . . . . . . . . . 23

2.1.7 Choix de fenêtres . . . . . . . . . . . . . . . . . . . . . . . . 24

2.1.8 Simulation des données . . . .. . . . . . . . . . . . . . . . 30

2.2 Cas multivarié........... . ... . .. . . . . . . . . . . . . . . 31

3 No_yau associé continu as_ymétri_que 35

3.1 Cas univarié ................ . .. . . .. . . . . . . . . . . 35

3.1.1 Définition ........................... . .. 36

3.1.2 Propriétés élémentaires. . . . . . . . . . . . . . . . . 38

3.1.3 Biais ponctuel.................. . .. . . .. . . . 41

3.1.4 Variance ponctuelle .... . ... . .. . . .. . . . . . . . . . . 42

3.1.5 MISE .... . ... . . . . . . . . . . . . . . . . . . . . . . . . . 43

3.1.6 Exemples ................ . . .. . . . . . . . . . . 43

3.2 Cas multivarié........... . ... . .. . . . . . . . . . . . . . . 63

4 No_yau associé discret 65

4.1 No_yau associé discret pour des données caté_gorielles 68

4.2 No_yau associé discret pour des données de compta_ge 73

4.2.1 No_yau associé poissonien . . 73

4.2.2 No_yau associé binomial. . . . . . . . . . . . . 75

4.2.3 No_yau associé binomial né_gatif . 77

4.2.4 No_yau associé trian_gulaire . . . . . . . . 78

4.2.5 Choix de fenêtres .... . . .. . . . . . . . . . . . . . . . 83

4.3 No_yau associé discret multiple. . . 85

? ?e_?r?ss?? ???t?_??? a ?\u9313‡A??\u9312‡@ ?ss??is ??\u9312‡@t?e ??87

5.1 Estimateur de Nadara_ya-Watson 87

? ???e?s ?? P???? a ??et??? ??

6.1 Notions elementaires
· . . . . . . . . . . . . . . . . .. . . 89

6.2 Traitements preliminaires . . . . . . . . . . . . . . .. . . 90

6.2.1 Repartition des panelistes selon les variables caracteristi_ques . . 92

6.3 Application . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96

6.3.1 Dans le cas d'un estimateur a no_yau associe trian_gulaire . . . . 96

6.3.2 Dans le cas d'un estimateur a no_yau associe binomial 97

? ?????s??s ?t _??rs_???t???s ???

7.1 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

7.2 Perspectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 103

? ????\u9312‡@? ?? ???????s s?s ?? ??????? ? ???10

Table des figures

2.1 Illustration des no_yaux continus s_ymétri_ques 19

2.2 Estimation totale a no_yau _gaussien . 20

2.3 Illustration d'un phénomêne de sous-lissa_ge lors de lestimation dune

densité.............. . ... . . . . . . . . . . . . . . . . . 24
2.4 Illustration d'un phénomêne de sur-lissa_gelors delestimation duneden-

sité..................................... . 24

2.5 Illustration d'une estimation idéale . . . . 25

2.6 Lissa_ges par des estimateurs a no_yaux continus de la distribution dun

échantillon de loi normale centrée réduite, n = 100 et hPj = 0.338 . . . 31

2.7 Lissa_ges par des estimateurs a no_yaux continus de la distribution dun échantillon de loi normale centrée réduite, n = 100 et hCV = 0.429 . . . 32

2.8 Comparaison des lissages par lestimateur a noyau continu d'Epanechni-

kov en faisant varier la fenêtre h 33

3.1 Densité de loi normale centrée .. . . .. . . . . . . . . . . . . . . . 36

h = 1.5

3.2 Illustration de la densité normale pour et x varié . . . . .

= . 37
y

x = 2.1 h

3.3 Illustration de la densité normale pour et varié 38

3.4 Allure _générale d'une densité _gamma. . . . . 44

h = 0.2

3.5 Allure du no_yau x

associé _gamma pour et varié 45

= 2

3.6 Allure du no_yau associé _gamma pour x = y et varié .

h . . . . . . 46

3.7 Allure _générale de la densité bêta. . . . . . . . . . 51

3.8 Allure du no_yau associé bêta pour h = 0.2 et x varié 52

3.9 Allure du no_yau associé bêta pour x = y = 2 et h varié 53

3.10 Allure _générale de la densité _gaussienne inverse 57

3.11 Allure du no_yau associé _gaussien inverse pour h = 0.1 et x varié 58

3.12 Allure du no_yau associé _gaussien inverse pour x = 2 et h varié 59

3.13 Allure _générale de la densité _gaussienne inverse récipro_que 61

3.14 Allure du no_yau associé _gaussien inverse récipro_que pour x = 2 et h varié 62 4.1 Illustration de la loi d'Aitchison et Aitken 70

h = 0.2

4.2 Illustration du no_yau associé dAitchison et Aitken pour et x varié 71

4.3 Illustration du no_yau associé dAitchison et Aitken pour x = y = 2 et h
varié..................................... . 72

h

4.4 Illustration du no_yau associé =

poissonnien 0.1

pour x

et .

variée . . . 73

h =

4.5 Illustration du no_yau associé binomial pour .

0.1 et .

x varié. .

. . . 75

4.6 Illustration du no_yau associé binomial pour x == y7 et h varié 76

4.7 Illustration du no_yau associé binomial né_gative pour h = 0.1 et x varié 78

4.8 Illustration du noyau associé triangulaire pour différentes valeurs de h. . 80

4.9 Illustration du no_yau associé trian_gulaire sans modification du bras 81

4.10 Illustration du no_yau associé trian_gulaire avec modification du bras 82

6.1 Dispersion des clients selon le lieu d'habitation 93

6.2 Localisation des panélistes du ma_gasin 1 93

6.3 Caté_gorie socio-professionnelle des panélistes et actes dachats 94

6.4 Revenu net des panélistes du ma_gasin 1 94

6.5 Répartition des clients du ma_gasin 1 selon la taille du fo_yer 95

6.6 Taille de famille des panélistes du ma_gasin 1 95

6.7 Comportement des achats individuels pendant la premieretranche 96

6.8 Comportement des achats pendant la deuxiême tranche 97

6.9 Estimation des actes d'achats pour la premiere période 97

6.10 Estimation des actes d'achats pour la deuxiême période 98

6.11 Estimation de la premiere période a_grandie . 98

6.12 Estimation de la premiere période plus a_grandie 99

6.13 Estimation des actes d'achats pour la premiere période 99

6.14 Estimation des actes d'achats pour la deuxiême période 100

6.15 Estimation des actes d'achats de la premiere période a_grandie (150 ob-

servations) ................ . ... . . . . . . . . . . . . . . 101
6.16 Estimation des actes d'achats de la premiere période plus a_grandie (50

observations) .............. . . .. . . . . . . . . . . . . . 102

Liste des tableaux

2.1 Exemples de no_yaux continus s_ymétri_ques 18

2.2 Efficacité des no_yaux continus s_ymétri_ques 23

3.1 Tableau récapitulatif des lois de probablité continues as_ymétri_ques 39

4.1 Solutions associés standards

h0 pour les discrets

no_yaux 86

6.1 Tableau comparatif du marketin_g transactionnel et relationnel 90

6.2 Statisti_que descriptives fondamentales 92

Présentation générale du stage

J'ai effectué mon sta_ge de fin d'étude au sein du laboratoire de mathémati_ques appli_quées, département Statisti_que et Traitement Informati_que des Données STID) Ce département re_groupe 7 ensei_gnants et ensei_gnantes tous sous la direction du chef de département. Le STID offre un ensei_gnement théori_que assurant une solide formation de base ainsi _qu'une initiation à la recherche

Mon sta_ge s'est déroulé du 1^er février _jus_qu'à 29 mai, sous la direction de M Kokonend_ji. Dés mon arrivée, mon encadreur direct ma expli_qué le su_jet ma fait visité le département, m'a accordé un bureau et m'a éclairci le ré_gime du travail.

Tout aulon_g de ce sta_ge, _j'ai assisté au séminaire hebdomadaire de lé_quipe probabilités et statisti_que on _j'ai eu l'occasion de présenter montravail.

Durant ces _quatres mois passés au sein du STID _jai eu lopportunité de découvrir le métier du chercheur sous toute ses formes et de comprendreles difficultés_quipeuvent être rencontrées.

Chapitre 1

Introduction a l estimation

non-paramétrique

L'ob_jet principal de la statisti_que est de faire a partir dobservations dun phénomène aléatoire, une inférence au su_jet de la loi _générant ces observations en vue danal_yser le phénomène ou de prévoir un événement futur Pour réduire la complexité du phénomène étudié, nous pouvons utilisé deux approches statisti_ques non-paramétri_que et paramétri_que.

Dans le premier cas, nous considérons _que linférence statisti_que doit prendre en compte la complexité autant _que possible et donc cherche a estimer la distribution du phénomène dans son inté_gralité,mettant en oeuvre lestimation des fonctionnelles(densités, ré_gression, etc.). En opposition lapproche paramétri_que cherche a représenter la distribution des observations par une fonction densité f(x|è) on le paramètre è est la seule inconnue. Dans plusieurs cas l'approche non paramétri_que est préférable nous pouvons mettre en oeuvre des lois de probabilité sur des espaces fonctionnels.

Les estimateurs non-paramétri_ques classi_ques ont étéintroduitparRosemblattpour estimer des densités de probabilité, par Parzen pour estimer le mode dune densité de probabilité et par Nadara_ya Watson pour estimer une fonction de ré_gression. Le comportement as_ymptoti_que de ces estimateurs a été étudié par de nombreux auteurs tel _que Ts_ybakov (2004). Ainsile but de ce travail est de définir les estimateurs a no_yau associé et d'établir les propriétés relatives

Avant de présenter les résultats de fa_çon détaillée nous en donnons tout dabordles _grandes li_gnes.

Dans le deuxième chapitre, nous nous intéressons a lestimateur a no_yau continu

b

s_ymétri_que f_n d'une densité de probabilité f inconnue sur R. Plus précisémment, nous présentons cet estimateur et nous prouvons les propriétés fondamentales telle _que biais, variance, erreur _quadrati_que mo_yenne etc Nous donnons les méthodes de sélectiondu no_yau ainsi de la fenêtre en s'appu_yant sur des exemples de données simulées. ls'avère _que le choix du paramètre de lissa_ge est beaucoup plus important _que celui du no_yau dansl'estimationdesdensitésinconnuesasupportsymétrique.Nousétudionségalement

CHAPITRE 1. INTRODUCTION A L'ESTIMATION 16 NON-PARAMRTRI_QUE

le cas multivarié en fin de chapitre.

Dans le troisième chapitre, nous donnons la définition dun no_yau associé. Nous prée sentons, a partir de cette définition, les estimateurs de Chen (1999 2000) et de Scaillet (2004) et leurs propriétés en rendant les calculs moins sombre et plus compréhensible. Tou_jours dans le cas du no_yau associé as_ymétri_que, nous _généralisons cesces résultatsats au cas multidimensionnel.

Dans le _quatrième chapitre, nous représentons pareillement la définition du no_yau associé discret en s'appu_yant sur les travaux de Kokonend_ji & Sen_ga Kiessé (2006).(2006). Nous définissons l'estimateur a no_yau associé discret Nous étudions lesles propriétés fondamentales de cet estimateur d'une manière _générale ensuite nous les appli_quons dans deux sections_; la première se base sur les données discrètes caté_gorielles on nous allons étudier l'estimateur a no_yau associé dAitchison & Aitken et la seconde partie repose sur les données de compta_ge on nous allons traiter des exemples des no_yaux associés s_ymétri_ques et standards as_ymétri_ques. Nous donnons un critére de choix des fenêtres de lissa_ges. Nous _généralisons cet estimateur dans une version multidimensionnelle.

Dans le cin_quième chapitre, nous étudions la ré_gression multiple a no_yaux associés mixtes. Nous nous focalisons sur le fameux estimateur de Nadara_ya-Watson.

Dans le sixième chapitre, nous appli_quons une partie de ces estimateurs a no_yaux associés sur des données parsemées de panel en marketin_g

Nous terminons ce rapport par une conclusion _générale et des idées de recherches futures.

Nous présentons maintenant de manière plus développéele contenu des six chapitres de ce rapport.

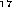
Chapitre 2

Noyau continu symétrique

Dans cette partie, nous présentons l'estimateur a no_yau continu s_ymétri_que. Nous développons cet estimateur dans le cas univarié ensuite nous le traitons dans le cas multivarié.Nousétudionsé_galementlesdifférentespropriétésélémentairesrelatives acet estimateur telle _que biais, variance erreur _quadrati_que mo_yenne et erreur _quadrati_que mo_yenne inté_grée. Nous détaillons par la suite les méthodes de choix des fenêtres et des no_yaux en se focalisant sur limportance du choix du paramètre de lissa_ge. Nous expli_quons explicitement 3 méthodes destimation de la fenêtre. Enfin, nous concluons par un exemple de données simulées.

2.1 Cas univarié

Considérons un échantillon de variables aléatoires X1,X2,. . . ,X_n, indépendant et identi_quementdistribué(i.i.d.),dedensitédeprobabilitécontinueinconnue f sur? = R. L'estimateur a no_yau continu s_ymétri_que de f est défini par:

^bfn(x) = 1 n

Xn i=1

~x - Xi ~ ^1 (2.1) h K h

= ^bfn,h,K(x),

on K estlafonctionno_yautelle_que K(t) = 0et JR K(t)dt = 1et h > 0estleparamètre de lissa_ge ou la fenêtre. L'expression (21) découle des travaux des pionniers de estimation non-paramétri_que Rosemblatt (1956) puis Parzen (1962) Dans lexpression de l'estimateur a no_yau continu (2.1), la fonction no_yau K est une densité de probabilité sur R ? R+ et est s_ymétri_que par rapport a zéro:

K(-x) = K(x), (2.2)

ce _qui impli_que l'é_galité suivante

ZR tK(t)dt = 0. (2.3)

De plus, elle est de carré inté_grable

et nous avons aussi la variance de K finie

ZR t²K(t)dt < +8. (2.5)

Enfin, le no_yau K peut être écrit sous plusieurs formes dont la plus connue est

(x - Xi ~ 1 Kh(x - Xi) = hK h

.

Le tableau 2.1 donne un récapitulatif des fonctions no_yaux continues classi_ques dont les _graphi_ques sont présentés dans la fi_gure 21 Nous rappelons _quune loi de Cauch_y n'admet aucun moment fini.

TAB. 2.1	Eaemples de noyaua continus symétriques
Noyau	Fonction noyau	Domaine de définition
Cauchy	[7r(1 + u^2)]-^1	R
Biweight	(15/16)(1 - u^2)^2	[-1,11
Triangulaire	1 - |u|	[-1,11
Epanechnikov	(3/4)(1 - u^2)	[-1,11
Gaussien	(1/v27r) exp (-u^2/2)	R

Pour plus de détails sur les t_ypes des no_yaux, nous pouvons se référer a article d'Epanechnikov (1969) et le livre de Ts_ybakov (2004)

L'expression de K détermine la forme du no_yau et h est un paramètre d'échelle _qui détermine le niveau de lissa_ge de l'estimation Dans lestimation a no_yau continu s_ymétri_que, le choix de la fenêtre de lissa_ge est prépondérant a celui du no_yau K. De plus, la contribution de cha_que point de l'échantillon est additionnée pour obtenir lestimation totale. Ceci est illustré dans la fi_gure 2.2.

2.1.1 Propriétés élémentaires

Danscettepartie,nousprésentonslespropriétésfondamentalesdelestimateuretles critères d'erreurs usuels. Nous calculons dabord le biais et la variance de lestimateur

b

f_n(x). Ensuite, nous exprimons le ris_que _quadrati_que exact en un point x fixé, puis le ris_que inté_gré. Enfin, nous approximons ces résultats. Dans ce _qui suit, nous supposons _que les dérivées première et seconde de f existent et admettent une inté_grale finie sur le support de la densité ?.

FIG. 2.1 - Illustration des no_yauc continus s_ymétri_ques

b

Propriété 1: La fonction x -?	de prohahilité fn(x) est une densité b
Démonstration: La somme continue de		fn(x) sur le support ? = R est

_{Z Z} (x - Xi )

Xn 1

^bf_n(x)dx = nh K dx

h

R R i=1

_Z (x - X1 ~

1

= _hK dx,

h

R

en posant t = (x - X1)/h et donc dx = hdt, nous trouvons

_{Z Z}

^bf_n(x)dx = K(t)dt = 1.

R R

Deplus,leno_yauK estdéfinipositif.Lasommesurtoutléchantillonresteaussipositive. Par consé_quent, l'h_ypothèse de positivité est vérifiée.

2.1.2 Biais ponctuel

Le hiais ponctuel mesure la différence entre la valeur mo_yenne de lestimateur ^bf_n et la valeur de la fonction inconnue f en un point x.

{ } { }

Biais ^bf_n(x) = E ^bf_n(x)- f(x). (2.6)

Propriété 2: Soit x fixé dans R.

Le hiais de l'estimateur a no_yau présenté dans (21) est

{ } Z

Biais ^bf_n(x) ÿ=¹ ₂h²f⁰⁰ (x) t²K (t) dt. (2.7)

R

FIG. 2.2 Estimation totale a no_yau _gaussien

Le si_gne » ÿ=» indi_que _que la _quantité à _gauche est é_quivalente à la _quantité à droite. Démonstration: Comme les variables aléatoires X1,X2,.. . ,X_n sont i.i.d., nous avons successivement

( )}

{ } _Xn (x - Xi

1 1

E ^bf_n(x) = E h K

n h

i=1

1
n

_Xn
i=1

{ 1 (x - Xi )} E h K h

{ 1 (x - X1 )}

= E hK h

_Z ~x - x1 )

1

= _hK f (x1) dx1.

h

R

Nous effectuons le chan_gement de variables suivant -t = (x - x1)/h, d'oñ x1 = ht + x.

b

De là, en utilisant l'h_ypothèse (2.2), le biais de f_n(x) s'exprime ainsi par

{ } _Z

Biais ^bf_n(x) = K (-t) f (x + ht) dt - f(x)

Z R

= K (t) f (x + ht) dt - f(x).

R

Dans le but d'avoir une forme plus simple _qui ne dépend _que du paramètre h, nous approximons la formule du biais en utilisant la formule de Ta_ylorrLa_gran_ge

f (x + ht) = f(x) + htf^' (x) + h2t2

2 f'' (x) + o (h2t2).

Ainsi, nous obtenons

Biais { :fn(x) } = f (x) J K (t)dt + hf(x) JtK(t)dt

R R

+2h² f" (x) I t²K(t)dt - f (x) + o(h²).

D'apres les h_ypotheses (2.3) , (2.4) et (2.5) nous avons finalement

Biais { in(x)} 12 _h2 _f00

(x) J_Rt²K (t) dt.

2.1.3 Variance ponctuelle

Propriete 3 : Soit x fixe dans R. La variance de l'estimateur ^bf_n est

Var { :f_n(x)} =ÿ _nhf (x) I K (t)² dt. (2.8)

Demonstration: Partant de l'h_ypothese d'independance entre les Xi, nous avons

-- Xi V ar { :fii(x) } = V ar n {1 ÷`i x K h

i=1

n

1 V ar{ h 11 K (x - _hX1)1

2

E [11 K (x h X1)J ⁾¹² n Lt1 1 [_El_h 1 K (x h X1)j)11

n

1

1 1

n h2 K2 x _h x1) f (x1) dx1

n JR 1 h 1 i1K(x x1)

2 f (x1) dx1 l .

Nous effectuons le chan_gement de variable -t = (x - x1)/h. Nous trouvons

nh²

1 1

V ar { :fii(x) } = K (-t)2 n f (ht + x)hdt - {I_RK (-t) f (ht + x) hdt} 2

h 1 1

I_RK (t)² f (ht + x) dt - n[Biais { :fi_i(x)} + f (x)i²

n

h 1 I_RK (t)² f (ht + x)dt - 1 {O (h²) + f (x)}²

n

Finalement, sous la condition d'avoir f K(t)²dt < +8 et pour n _grand, nous avons

Var { r_n(x)} =ÿ _nhf (x) I K (t)² dt.

2.1.4 Erreur _quadrati_que mo_yenne (MSE)

Propriete 4: L'erreur _quadrati_que mo_yenne (en an_glais "Mean s_quared Error") en un point x fixe s'exprime par

MSE (x) = V ar { :fii(x) } + Biais² {:fii(x) } (2.9)

Demonstration: Nous obtenons par succession

MSE (x) = E [{ 1_n(x) - f (x)}²1

= E ([i_n(x) E { i_n(x)} E { i_n(x)} f(x)i²)

= E ([ 1_n(x) - E { Mx) }i2) + 2E [ 1_n(x) - E { 1n(x)}i

_[E { i_n(x)} f(x)i _[E { i_n(x)} f(x)i 2

= V ar { rn(x) } + Biais² {r_n(x)}

= MSE(x;n,h,K,f).

D'apres les resultats (2.7) et (2.8), l'approximation du critere MSE en un point x fixe est

2

AMSE (x) = _n¹_hf (x) I K (t)² dt + {1 2 h2 f^" (x) I t²K (t)dt } . (2.10)

2.1.5 Erreur _quadrati_que mo_yenne inte_gree (MISE)

Propriete 5: L'erreur _quadrati_que mo_yenne inte_gree (en an_glais "Mean Inte_grated S_quared Error ") est la mesure theori_que commune la plus utilisée pour evaluer lerreur entre la fonction f et ^bf_n. Nous avons etudie dans la partie precedente le comportement de ^bf_n(x) en un point fixe. Il est e_galement convenable devaluer lerreur _globale sur le support R de cet estimateur.

MISE(n,h,K,f) = I MSE(x)dx (2.11)

R

=

IV ar { :f_n(x)} dx + I Biais² {:f_n(x)} dx.

R R

En utilisant l'expression approchee du critere MSE (210) nous avons successivement

AMISE(n,h,K,f) =

h1 JRK(t)^2dt I f(x)dx nh

2

+h⁴ t²K(t)dt } f f"(x)²dx

4 _R

1 J K(t)²dt + ₄¹h⁴ t2K(t)dt }² I

h f^" (x)²dx

nR

avec

V (K) = f t²K(t)dt = V ar(K).

2.1.6 Choix du no_yau

Le premier choix porte sur la nature de la densité no_yau _que nous utilisons. Pour mesurer l'efcacité de chacun des no_yaux continus s_ymétri_ques présenté dans lele tableau 2.1, nous utilisons une mesure commune _qui consiste a calculer le rapport du critere AMISE des deux no_yaux mis en évidence

eff(K1,K2) = AMISE(K1)

AMISE(K2)

Nous supposons _que K1 est le no_yau d'Epanechnikov. Ce no_yau est considéré comme une référence par rapport a tous les autres no_yaux continus classi_ques. Il estest lar_gee ment apprécié pour ses performances (au sens on sa forme répond bien a la plupart des _questions soulevées par le probleme de lestimation non paramétri_que de densité) et il est considéré comme optimal au sens des mesures derreur IlII o~re la valeur défcacité maximale. Nous nous sommes appuis sur les travaux de Ts_ybakov (2004).(2004). Ainsi, apres avoir fait les calculs nécessaires lefcacité dun no_yau K para rapport au no_yau d'Epanechnikov se mesure par

1

VfR t²K(t)dt f_R K(t)²dt < 1.

5V5

eff (K) = 3

Le choix de K dépend seulement de la nature de f et nous admettons _qu'en prati_que le choix du no_yau d'Epanechnikov est le plus staisfaisant Nous donnons lele tableau récapitulatif (Tab. 2.2) _qui présente la valeur defcacité des différents no_yaux continus s_ymétri_ques.

TAB. 2.2 -- E_fficacite des no_yaux continus s_ymetri_ques

No_yau Efficacité

Epanechnikov 1.000

Biwei_ght 0.994

Trian_gular 0.986

Normal 0.951

Uniform 0.930

Commentaire: Danslecasdesno_yauxcontinuss_ymétri_ques,nousremar_quons_que les valeurs d'efcacité des no_yaux tels _que le no_yau biwei_ght trian_gulaire ou Epanechnikov sont tres proches. Par consé_quent Le choix du no_yau nest pas tres important.

2.1.7 Choix de fenetres

a. Importance du choix de h

Le parametre de lissa_ge h est un réel positif dont le choix est prépondérant sur celui du no_yau continu s_ymétri_que K. Le choix d'une valeur de h trop _grande conduit a une courbe trop lisse. La courbe estimée ne traduit pas suffisament les variations de la vraie distribution (voir fi_gure 2.3).

FIG. 2.3???str?t?? ???? _??e??e?? ?? s?s???ss?_?? ?rs ?? ??et???t?? ????? ???n?it

Ep/0/ch0-

RIM .

-2 -1 0 1 2 3

x

Par contre, en choisissant un parametre de lissa_ge tres petit _que celui adopté précédemment, l'allure de la distribution chan_ge. Il sa_git dune distribution surestimé (fi_gure 2.4).

FIG. 2.4 -- ???str?t?? ???? _??e??e?? ?? s?r???ss?_?? ?rs ?? ??st???t?? ????? ???n?it

Ep/0/ch0-

D..

-2 -1 0 1 2 3

x

ment la distribution de depart (fi_gure 2.5). Les courbes obtenues illustrent a _quel point
FIG. 2.5 -- Illustration d'une estimation ideale

Ep/0/00-

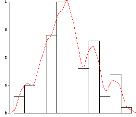
RI.

-2 -1 0 1 2 3

x

les formes estimees sont differentes en fonction de lordre de _grandeur du paramètre de lissa_ge. La principale difculte repose sur le choix optimal de la fenetre h. La valeur ideale hid du parametre h est celle _qui minimise l'erreur _quadrati_que mo_yenne inte_gree (MISE). Pour une taille d'echantillon n donnée et un no_yau K fixe, nous avons

?h

? AMISE(h) = 0.

Ce _qui est e_quivalent a

h³V (K)² I f^" (x)2dx 1 2 _jalⁱ K(t)²dt = 0.

nh

Ainsi, nous obtenons successivement

nh⁵V (K)² ff^" (x)²dx = K(t)²dt R

h⁵ = nV (K)² f_R f^"(x)²dx

fR K(t)2dt

1 I f_R K(t)²dt1^1/5

hid = v .

V(K)² f_R f^" (x)2dx (2.13)

En particulier pour K = KEpanechn., nous avons

~ 15 \1/5

hid(KEpanechn.) =

n _R .

R f"(x)2dx

En definitive, a partir de (2.13), nous obtenons

2/5 4/5 ₁1/5

5 1

AMISE(hid) =

_L,_Rt²K(t)dt1 { K(t)²dt1 { f^" (x)²dx

4 n4/5 R R

₅1/5

4n4/5 I(K) f_R f^"(x)² dx }

avec

~Z _~2/₅ ~Z ~4/5

I(K) = t²K(t)dt K(t)²dt .

R R

Consé_quences: _Quand n est _grand, hid tend vers 0. Le parametre de lissa_ge h idéal dépendenfaitdeladensitéatravers f^".Ainsipourun hpetit,nousavonsunpetitbiais et une variance plus _grande. Le no_yau optimal est obtenu en minimisant R R K(t)2dt, ceci en admettant les h_ypotheses (2.4) et (25).

b. Méthodes de choix de fenêtres

Nous considéronss donce avec plus d'intérêtt la _question de selection du parametree de lissa_ge h. Comme fenêtree optimale, nous choisissons la valeur _qui minimis lee MISE.

Nous étudions trois méthodes dans la déterminationn du parametre d lissagee ^optimalh_opt:: le "Plu_g-in", la validation croisée par moindres carrés e laa validation croisée par maximum de vraisemblance.e

b.1. Mahodee Pln_g-inn

Dans la procéduree de Plu_g-in,l'idée& de base est destimerr dan lexpressionn (2.13) la _quantité inconnue: : f_R f^"(x)²dx. En effet, ilt _y a deux approches possibles pou ^leefaire:: soit nous supposons _que la densité f appartient a une famille de distributions

paramétri_ques et la nous estimons les parametres et nous retrouvon facilement cette cette _quantité, soit nous l'estimons par lapprochee non-paramétri_que et donce faire appel a un estimateur a no_yau (par exemple). Ceci va compli_quer davanta_g less calculs parce_que nous trouvons une fonction _qui dépendd elle même de h. Donc,, en _gros, la méthode Plu_g-in résidee a "in_jecter" une estimation de f en adoptant une méthode commode et prati_que. Dans notre étude,, nous supposons _que f(x) appartient a une famille de distribution normale centrée et de variance ó²..

Sous cette hypothese::

ZR _R f"(x)2dx =_{88 0r}³³ ó^-1/⁵⁵0.212ó^-1/⁵..

Il reste alors a remplacer le parametre inconnu óa par la valeur estiméee bó.. Nous choisissons la valeur empiri_que comme valeur optimale définiee comme suit

1

_bó

=

n -- 1

^Xn
i=1i

tu u v

(Xii -- X~²,,

tel _que XX = n-¹¹ (X1 + X2 + .
· .
· .
· + Xn).

=	(4ð)-1/10 ~	1	8ð-1/2 bó ~ ~3 ~-1/5
		n1/5 5

Le résultatt obtenu sera remplacée dans la formule de hid et nous avons

hopt

(4bó⁵⁵~^1/5

= 3n ~ bó)= =1.06 6n1/55)

Ce _que nous avons accompli en travaillant sous la supposition de la normalité estest une formule explicite applicable pour la selection de la fenetre h. En réalité, cette méthode donne des résultats raisonnables pour toute les distributions s_ymétri_ques, unimodales et ne possédant pas des _queues trop lourdes Le probleme donc avec cette méthode est _qu'elle est tres sensible aux valeurs aberrantes. Un estimateur plus robuste dans ce cas est obtenu a partir de l'intervalle inter_quartile : R =

X[0.75n] - X[0.25n] o1 Xp

dési_gnele_quantiled'ordrepd'une N (u,ó²).Ladifférenceentrecesdeux_quartilesdonne 50% de l'ensemble des observations. En supposant tou_jours _que X suit une normale N(u,ó²), nous posons Z = (X - u)/ó _qui suit une N(0,1). Ainsi, nous montrons _que (X[0.75n] -X[0.250 = 1.34ó Par consé_quent, un estimateur puissant de ó serait Q = R/(1.34). Dans ce cas, le parametre de lissa_ge optimal est donné par

~ hopt = 1.06 1R.34 n-1/5 0.796n^-1/⁵. Enfin, la fenetre optimale est

hopt = 1.06 min bó,

1.34
R

_n-1/5

.

Cette méthode présente des inconvénients : si la vraie densité f devie substantiellement delaformed'unedistributionnormale(enétantmultimodalparexemple)nouspouvons etre trompés considérablement et nous aurons soit un sur-lissa_ge soit un sous-lissa_ge.

b.2. Methode de validation croisee par ioindres carrés

Pour un no_yau fixé K, le principe de la validation croisée est la minimisation destimateur de ris_que inté_gré (MISE) par rapport a h. En effet, Le MISE dépend de la fonction inconnue f et ne peut donc pas etre calculé. Nous allons essa_yer de remplacer la MISE par une fonction de h, mesurable par rapport a l'échantillon et dont la valeur pour cha_que h > 0, est un estimateur sans biais de MISE(h). Pour cela, notons _que :

MISE(h) = E f {:f_n(x) - f (x)}² dx

= E f

_R Tfi_i(x)²dx - 2E 1 f_n(x) f (x)dx + IR f2 (x)dx

Le dernier terme ne dépend pas de h, pour minimiser MISE(h) il suffit de minimiser l'expression :

J(h) = E f f_n(x)²dx - 2E 1 f_n(x) f (x)dx.

Pour cela, nous déterminons un estimateur des deux termes de J(h). Le premier terme

JR

f_n(x)²dx comme estimateur trivial (d'apres la propriété des esti-

b

admet l'estimateur

mateurs sans biais : E(^bâ) = â).

Il reste a trouver un estimateur sans biais du second terme. Pour cela, nous admettons par construction l'estimateur sans biais G défini en tout points du support sauf en Xi :

Gb =1 n		Xn i=1		bfn,-i(Xi),
avec	^bfn,-i(x) = 1 n - 1		1 X h i6=j		(x - Xi ~ K . h

Montrons _que E( ^bG) = E{f_R ^bf_n(x)f(x)dx}. Comme les Xi sont i.i.d., d'une part nous avons

_~Z ~ _Z ~

_Xn ~x - Xi

1

E ^bf_n(x)f(x)dx = E K f(x)dx

nh h

R R

i=1

_Z ~x - X1 ~

1 _hE K f(x)dx

h

R

_{Z Z} ~x - x1 ~

1 f(x) K f(x1)dx1dx.

h h

R R

D'autre part, nous avons

E(

= E {_n¹

i=1

= E{In,-1(X1)}

= E

? ? ?

~Xj - X1 ~? 1 X ? K (n - 1)h h ? j6=1

~ ₁ ~X - X1 ~~ = E hK h

_{Z Z} ~x - x1 ~

1 f(x) K f(x1)dx1dx

h h

R R

_Z

= E ^bf_n(x)f(x)dx.

R

Donc, ^Gb est un estimateur sans biais de f_R biais de J(h) est donne par

b

f_n(x)f(x)dx. Finalement, l'estimateur sans

CV (h) = f_n(x)² dx - 2 E bfn,-i(Xi).

n

^Ri=1

Et la fenetre optimale est telle _que

hCV = arg min h>0

CV (h).

???? ?et??? ?? ??????t?? ?r?sé? _??r ??\u9312‡@???? ?? ?r??s????????

et l'estimateur a noyau

fn s'écrit:

D(f , j_n) = f_Rf(x) log { _j.^f_.:₍^x_x⁾₎ dx

= I_R f (x) log f (x)dx - I_R f (x)log { r_n(x)} dx

= E [log { f (X)}] - E [log {f_n(X) }1 .

b

L'idée de la validation croisée par vraisemblance est de minimiser D(f,

fn). Toutefois,

cette distance n'est pas métri_que et les critères définis en la minimisant ne sont pas ap-

b

propriés pour obtenir un lissa_ge adé_quat. Donc minimiser D(f, f_n) revient a maximiser

E [log {f_n(X)}1. Ainsi, la fenetre optimale est

LCV (h),

hLCV = arg max

h>0

oU

.

LCV (h) = E [log {f_n(X)}]

Par construction, nous avons l'estimateur sans biais de LCV (h):

1 Jn = n

Xn i=1

n o log ^bfn,-i(Xi|h) ,

oU

1

^bfn,-i(Xi|h) = (

~Xi - Xj ~

_X

K

n - 1)h h

i6=j

_n

Montrons _que E(J_n) = E _{h oi.}

log ^bf_n(X)

Comme les variables aléatoires X1,X2, . . . ,X_n sont i.i.d., d'une part nous obtenons

" _o#

_Xn _n

1

E(J_n) = E log ^bfn,-i(Xi|h)

n

i=1

_{h n oi}

= E log ^bfn,-1(X1|h)

? = E ?log

? ? ?

? ~X1 - Xj ~? ? 1 X K ? (n - 1)h h ? j6=1

= E [log { h 1 K X 1 h X2

D'autre part, nous trouvons

" ( ~)#

_{h n oi X}n ~X - Xi

1

E log ^bf_n(X) = E log K

nh h

i=1

= E [log { h1 _K (X - hX )11

= E(J_n).

Enfin, la fenêtre optimale obtenue par la méthode de validation croisée par vraisemblance se calcule a partir de :

" 1 n

hLCV = arg max log { fn,_i (Xi | h) }1.

h>0 n

i=1

Cependant, cet estimateur est très sensible aux valeurs aberrantes. Sa diiculté apparait lors_que la méthode est appli_quée a des observations dont la distribution présente de _grandes _queues. Les points situés dans les _queues de la distribution a estimer ont des valeurs faibles, ce _qui impli_que de faibles valeurs des estimations correspondantes. La présence de l'opérateur log dans l'expression de l'estimateur pose un problème de conver_gence pour les valeurs de densités aux _queues. Par consé_quent, il estest diicile dans ce cas de choisir hLCV de fa_con optimale, puis_que l'on ris_que soit le sur-lissa_ge soit une trop _grande erreur sur les _queues.

2.1.8 Simulation des donnees

Danscettepartie,nousillustronscertainsestimateursano_yauxcontinuss_ymétri_ques a savoir le no_yau d'Epanechnikov, le no_yau _gaussien le no_yau biwei_ght et le no_yau trian_gulaire. Nous simulons un échantillon de taille n = 100 de la loi normale centrée et réduite. Pour cha_que no_yau fixé, la fenêtre optimale est choisie par les méthodes de validation croisée par moindre carrés et de Plu_g-in

?? ???\u9312‡@ ?? ???etr? _??r P??_????

Cette méthode suppose _que la densité suit une loi normale dans lexpression de la fenêtre h optimale. La valeur du paramètre de lissa_ge est la même pour un échantillon donné. Nous obtenons prati_quement des estimations similairespourcha_queno_yau continu utilisé_; ceci s'expli_que par le fait _que les no_yaux continus s_ymétri_quespossèdent tous des efcacités proches l'une de l'autre (Fi_gure 26)

?? ???\u9312‡@ ?? ???etr? _??r ??????t?? ?r?sé? _??a ??\u9312‡@???? ?? ?v??i????????

Le choix de la fenêtre optimale hopt se fait en fixant au préalable le no_yau continu Le no_yau par défaut dans le lo_giciel R est le no_yau _gaussien. 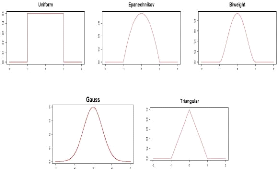Le choix des no_yaux continus s_ymétri_ques n'est pas important car ils ont _quasiment les mêmes propriétés, c'est pour_quoi le choix de la fenêtre optimale se fait sous lh_ypothèse _gaussienne (et(et aussi pour des raisons techni_ques imposées sous R) Pour cha_que no_yau continu s_ymétri_que fixé, la fi_gure (2.7) présente la fenêtre optimale hCV = 0.1636. Pour cette valeur de h, les estimations des différentes densités sont prati_quement similaires.

?? ???ts ?? ???\u9312‡@ ?? ???êtr?s

Nous comparons différentes estimations en faisant varier la valeur de la fenêtre pour le même no_yau continu. Nous choisissons le no_yau optimal dEpanechniiov

Les simulations effectuées dans la fi_gure (28) mettent en lumière _que les performances prati_ques des estimateurs a no_yaux continus s_ymétri_ques considérés dépendent fortement du choix de la fenêtre h. Par consé_quent, ce choix est plus crucial _que le choix

Dwelt,
0.0 0.1 0.2 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

Dwelt,
0.0 0.1 0.2 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

^bfn(x) = 1 n

Xn i=1

KH (Xi - x) . (2.14)

FIG. 2.6 -- ??ss?_??s _??r ??s ?st???t??rs d ?\u9313‡A??\u9312‡@ ??t???s ?? ? ??ist???t?? ???? ????? t???? ?? ?? ?r???? ???tré? r(???t?_? n = 100 ?t hPI = 0.338

Epanechn.PI

Gaussien PI

- 2 -1 0

1 2

- 2 -1

12

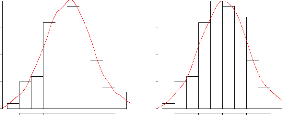
x Biweight PI

Triangulaire PI

- 2 -1 0

1 2

- 2 -1

1 2

x

du no_yau. Les valeurs de h sont celles choisies par plu_g-in (h_pi = 0.338), validation croiséeparvraissemblance (hCV = 0.429)etdeuxautresvaleursarbitrairestel_que h = 0.05 et h = 1.

2.2 Cas multivarie

Les principales techni_ques d'estimation non-paramétri_ques de densité dans le cas _géneral d'observation de dimension _quelcon_que restent des variantes destimateurs à no_yau. Nous pouvons choisir destimer toutes les composantes des observations simultanément ou selon cha_que composante séparément (en faisant le produit des no_yaux univariés).

Nous considérons ainsi les observations (Xij) i.i.d. avec i = 1, ...,n et j = 1,...,d. Cette échantillon est de densité de probabilité f continue et inconnue sur = R^d.

b

L'estimateurano_yaucontinus_ymétri_que f_n def admetuneversionmultidimensionnelle et se présente de maniere _générale par

Dwelt,
0.0 0.1 0.2 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

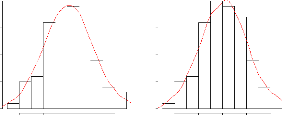
FIG. 2.7 -- ??ss?_??s _??r ??s ?st???t??rs d ?\u9313‡A??\u9312‡@ ??t???s ?? ? ??ist???t?? ???? ????? t???? ?? ?? ?r???? ???tre? re???t?_? n = 100 ?t hCy = 0.429

Dwelt,
0.0 0.1 0.2 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

Epanechn.CV

Gaussien CV

- 2 -1

1 2

- 2 -1 0

12

Biweight CV

x Triangulaire CV

- 2 -1

1 2

- 2 -1 0

1 2

x

on x =^t (x1, ... ,xd) ? R^d, Xi =^t _(Xi1, . . . ,Xid) et H = est la matrice de variance-covariance de la fenetre h, de dimension d × d, donnée par

H=

?

?? ? .

[H_. ... h1d h21 . . . h2d ... h²_j ... hd1 ... h²_d

La fonction KH est la fonction no_yau définie sur ?x,h = R^d et reliée avec le no_yau univarié (_que nous avons présenté précédemment) par la relation suivante

KH (x) = Idet (H)}

--1/2 K ^(H--1/2x) .(2.15)

En effet, comme nous pouvons le remar_quer dans lexpression de H, il peut _y avoir des termes de corrélation entre les différents parametres de lissa_ge. Ces coeffcients de corrélation vont compli_quer davanta_ge les calculs Nous proposons ainsi une expression plus simple _qui fait appel a un produit des no_yaux univariés et _qui né_gli_ge leffet des

FIG. 2.8 - ??_??r??s? ??s ??ss?_??s _??r ???st???t??r a ?\u9313‡A?? ??t??? ??????????????? _???s??t ??r??r ?? _???etr? h

Epanechn.CV h=0.429

Dwelt,
0.0 0.1 0.2 0.9 0.4

Epanechn.PI h=0.338

Dwelt,
0.0 0.1 0.2 0.9 0.4

-2 -1 0 12 -2 -1 0 12

x Epanechn. h=0.05

x Epanechn. h=1

-2 -1 0 1 -1 1 2

x

Dwelt,
0.0 0.1 02 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

corrélations. Dans ce cas, l'estimateur est

in(x) = 1 nh1 . . . hd

Xn i=1

? ? ?

d j=1

(Xij x,) ; hj .^1 (2.16) ? ,

avec x =^t (x1,...,xd) E R^d,hj > 0, Ed j=1 hj --> 0 et n _1dj=1 hj --> co et Kj est la fonction no_yau univarié présentée antérieurement En prati_que les no_yaux-produits sont recommandés. Les estimateurs a no_yau _généralisés sont importants pour lesles études numéri_ques, mais ils restent cependant utiles pour des considérations théori_ques etet dans certains cas particuliers.

Note: De manière plus simple, nous prenons le no_yau Kj = K, c'est a dire _que nous utilisons ce même no_yau pour toutes les observations. Cependant nous pouvons faire un mélan_ge de différents t_ypes de no_yaux tels _que le no_yau d'panechniiov avec le e _gaussien, le biwei_ght, etc.

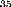
Chapitre 3

Noyau associé continu asymétrique

Dans ce chapitre nous commen_çons par donner la définition dun no_yau associé continu. A partir de cette définition, nous présentons lestimateur a no_yau associé continu as_ymétri_que dans le cas univarié puis multivarié. Nous étudions les propriétés élémentairesdecetestimateur.Différentsexemplesseronttraitésen_guisedeconclusion.

3.1 Cas univarié

Danscettepremièrepartie,nousprésentonslestimateurano_yauassociécontinuas_ymétri_que dans le cas univarié. Cet estimateur est approprié pour estimer des densités a support compact ou bornées d'un côté. Nous allons traiter _quatres no_yaux di~érents _gamma, bêta, _gaussien inverse (IG) et _gaussien inverse récipro_que (RIG) Pour de réé centes références nous pouvons consulter Chen (1999 2000) et Scaillet (2004) Nous montrons les propriétés élémentaires telles _que biais, variance et MISE. Ensuite nous déterminons les fenêtres optimales pour cha_que no_yau associé considéré et lerreur en fonction de ces valeurs.

Soit X1,X2,. . . ,X_n un échantillon de variables aléatoires iid de densité de probabilité continue inconnue f a support = [a,b], avec a E R et b E R ( est par exemple le support [0,1] ou [0, + 8[). De manière _génèrale, l'estimateur a no_yau continu est de la forme suivante:

^bfn(x) = 1 n

Xn i=1

(3.1) Kx,h(Xi)

= ^bfn,h,K(x),

on x est fixé dans , Kx,h est la fonction no_yau associéU et h est un réel strictement positif appelé paramètre de lissa_ge.

Dans le cas on Kx,h est associé a un no_yau continu s_ymétri_que il vérifie

~x - . ~

1

Kx,h(.) = _hK .

h

Dans le cas purement as_ymétri_que, Kx,h est un no_yau variable en fonction de la cible x (point d'estimation). Il chan_ge de forme cha_que fois _que x varie dans .

3.1.1 Definition

Definition 1: Soit x ? ? et h > 0. Nous appelons "no_yau associe continu "" Kx,h toute densit( de probabilit( dune variable aléatoire Kx,h sur le support ?x,h tels _que:

?x,h n ? =6 Ø	(3.2)
?x?x,h ? ?	(3.3)
E(Kx,h) ~ x quand h ? 0	(3.4)
V ar(Kx,h) < co	(3.5)
V ar(Kx,h) ? 0 quand h ? 0.	(3.6)

Commentaires::

a. La relation (3.2) traduit le fait _que l'intersection entre le support des observations et le support du no_yau associé continu as_ymétri_que doit contenir au moins un élement. Pour un h fixé, _quand x parcourt ?, le support ?x,h chan_ge, l'expression (3.3) suppose _que ? doit etre tou_jours contenu dans la réunion des ?x,h. La condition (3.4) permet d'assurer la conver_gence ponctuelle de l'estimateur ; elle met en évidence _que le no_yau K_x,h est un no_yau variable ou adaptif a la cible x. Par analo_gie au cas continu s_ymétri_que, la relation (3.5) n'est _que la formule annoncée dans (25) du chapitre précédent. Enfin, la relation (3.6) assure la conver_gence de la variance de la variable aléatoire du no_yau associé et va nous servir dans les calculs suivants.

b. Avant _que nous passons a l'étude des des no_yaux continus as_ymétri_ques, nous reveFIG. 3.1 - Densit( de loi norinale centrée

Densité de la loi normale

0.0 0.1 0.2 03 0A

th30040)

-6 -4 -2 0 2 4 6

x

FIG. 3.2 -- Illustration de la densite normale pour h = 1.5 et x = y varie

0.00 0.05 0.10 0.15 0.20 0.25

K(Y)

1	Xn i=1	~ ~ exp -1 (Xi x)2 . 2 h2
nhv2ð

-10 -5 0 5 10

y

male N(u,ó²) est une loi continue définie sur ? = R de densité de probabilité gN(u,ó²) telle _que

~ ~

1 _-1 (x - u)²

gN(u,ó²)(x) = v2ðó2 exp .

2 ó2

Si X est une variable aléatoire _qui suit la loi normale alors lespérance et la variance sont respectivement

E(X) = u et V ar(X) = ó².

La fi_gure 3.1 donne l'allure _génerale d'une densité normale centrée Soit _KN(x,h2) le no_yauassociéalavariablealéatoire KN(x,h²) deloinormale N(x,h²)définisur ?x,h = R. Nous vérifions ainsi chacune des h_ypothéses de la définition 1 En effet, la relation (3.2) se traduit par l'intersection de ? = R avec ?x,h = R _qui n'est _que R. En plus, d'apres (3.3), la réunion sur x de R reste inchan_gée puis_que le support ne dépend pas de x. A partir de (3.4), l'espérance est exactement é_gale a x_;

E(KN(x,h²)) = x.

Finalement, la variance est finie et é_gal exactement a 0 _quand h ? 0_;

V ar(KN(x,h²)) = h² < 8.

A ce niveau, nous donnons l'estimateur a no_yau associé normal défini sur ? = R. Soit X1, ... ,X_n un échantillon de variables aléatoires iid. de densité de probabilité f continue et inconnue sur R. L'estimateur a no_yau associé _gaussien est

^bfn(x) = 1 n

Xn i=1

KN(x,h^2)(Xi)

FIG. 3.3 Illustration de la densit normale pour x = 2.1 et h varié

-1 0 1 2 3 4 5

N(x,h)(y)

0.0 0.5 1.0 1.5 2.0 2.5

h=0.15 h=0.3 h=0.7 h=1.1 h=1.4 h=1.8

Get estimateur est-il une densité de probabilité? Oui en effet

ZR

Z ( (t - x ~2)

1

^bf_n(x)dx = -1

hv _2ð exp dx

2 h

R

Z r (x - t )2}

(a) 1 _-1

= hv _2ð exp dx

2 h

R

= 1.

(a): La loi _gaussienne est s_ymétri_que le fait _que nous inté_grons par rapport a x (la cible _qui est aussi la mo_yenne) ou a t (la variable aléatoire) ne chan_ge rien_; nous nous permettons ainsi de permuter entre la cible x et t et nous trouvons _que c'est une densité de probabilité (voir fi_gure 3.2 et 3.3). Bien _que la vérification dans le cas dun no_yau associécontinus_ymétri_queparaltsimple,la_questionrestevalablepourchacundesno_yaux as_ymétri_ques.

Nous présentons maintenant les densités continus as_ymétri_ques classi_ques _que nous allons utiliser dans la suite de cette section (Tab 31)

Soient a et b deux réels strictement positifs _qui vérifient

Z +8

(a) = e_^tt^a_1dt

0

et

Z 1

B(a,b) = t^a_1(1 - t)^b_1dt.

0

3.1.2 Propriétés élémentaires

Nous donnons dans cette partie les différentes propriétésfondamentales delestimateur a no_yau associé.

TAB. 3.1 -- ??????? re??_??t???t?_? ??s ??s ?? _?r?????te ??t????s ?s_\u9313‡A?éet?_i??e

Loi de probabilité Support Densité

Gamma(a,b) R+ (a1)ba ta-1 exp(-t/b)

Beta(a,b) [0, 11¹ B(a,b)ta-1(1 - t)^b-¹

IG(a,b) R+ vvb2ðt3 exp {- 2ba ( a t - 2 + 7)}

RIG(a,b) R+ l2ðtb exp {- 2ba (at - 2 + a1t)}

Loi de probabilité Espérance Variance

Gamma(a,b) ab ab²

Beta(a,b) a/(a + b) ab/ {(a + b)²(a + b + 1)}

IG(a,b) a a³/b

RIG(a,b) 1/a + 1/b 1/ab + 2/b²

Propriétés 1:: ??t X1,X2,. . . ,X_n ?? (????t???? ?? ??r?????s ??e?t?r?s ?????? ?? ????

b

s?t ?? _?r??????te ??t???? ??????? f d s?_??rt ?? ??t f_n ?? ?st???t??r ?? f a ?\u9313‡A??

b

f_n(x) ???st _??s ?e?

?ss??e ??t??? ?s_\u9313‡A?etr?_q?? ?é_??? ?r ?? ??rs_? ?? _???t?? x 7-? ??ss??r????t ??? ???s?tt ?? _?r??????té ?r ?? ?? _?s??t

1^,2

c = I ^bf_n(x)dx = c(h,K) = 0,

b

??s ??s??er?s ?esr???s ???st???t??r fn t?? _q??

in(x) = nc		Xn i=1	Kx,h(Xi). (3.7)
Dans la suite, nous supposons que	fn(x) est une densité de probabilité. Nous illustrons

cette h_ypothese dans la partie exemple

b

densite de probabilite continue inconnue f de support ?. Soit f_n l'estimateur de f a no_yau associe continu as_ymetri_que K_x,h de variable aleatoire Kx,h sur le support ?x,h. Alors, ?x ? ? et h > 0, nous avons

E {f_ri(x)} = E{f(K_x,h)} . (3.8)

Démonstration: Soit x ? ?. Nous avons successivement

E {/_n(x) } = E _nEKx,h(Xi)}

{ 1 n

i=1

= E {Kx,h(X1)}

Z?n?x,h

Kx,h(t)f(t)dt

(a)

=

= E{f(K_x,h)} .

(a)_; les Xi sont dans ? et le no_yau associé est défini sur ?x,h. D'on l'inté_grale se fait sur l'intersection des deux supports

Dans le but d'assurer la conver_gence ponctuelle de lestimateur nous avons adapté le lemme présenté par Hille (1948) et dont une démonstration a été donnée par Feller (1966) dans le lemme1,pa_ge 219.Noussi_gnalons _que celemme étaiténoncé dansletravailrécentdeChaube_y etal.(2007)¹.Ainsi,nousleformulonsdanslapropriétésuivante

Propriété 3: Soient f une fonction continue et bornée sur ? et x est fixée sur ce

b

support. Soit f_n l'estimateur a no_yau associé continu K_x,h sur ?x,h. Nous supposons _que ?x ? ?,?x,h ? ?. Alors nous avons

E {^In(x)} =

ftn?x,h

f(t)Kx,h(t)dt ? f(x) quand n ? 8.

La conver_gence est uniforme en toute subdivision de ? dans la_quelle V ar(K_x,h) ? 0 _quand h ? 0 et la fonction f est uniformément continue.

Démonstration: Nous partons de l'expression de lestimateur dans (3.1) et nous calculons son espérance

E {fn(x)} = Kx,h(z)f (z)dz.

Itx,hn?

Comme?x,h ? ?, nous pouvons écrire f(x) = f(x) R

?x,h K_x,h(z)dz. Ainsi, il existe ä > 0

tel _que

~

E{.7.n(x)}- f(x) =_h{f(z) - f (x)} Kx,h(z)dZ
Nx,

f |f(z) - f (x)| Kx,h(z)dz + I |f(z) - f (x)| K_x,h(z)dz.

?? \u9670·?s et??s r???tes ???s ?? res??t?t ??r ? Pr??ss??r ???????? ????u a ??????er?it ??????????? ?t ?? ??s?t? ?? ???r?t?r? ?? ??t?e??t?i??e ?????i?u?e ?? ???

Pour calculer la première _quantité, nous utilisons directement la définition de la continuité:

?e > 0, ? ä > 0, ?z : |z - x| < ä |f(z) - f(x)| < €. D'on nous obtenons,

|f(z) - f (x)|K_x,h(z)dz = E K_x h(z)dz

lz-x|<ä flz-x|<ä

= €.

Pour calculer la deuxième _quantité, nous utilisons liné_galité de Tcheb_ychev-Markov Comme f est bornée ? M > 0 tel _que f = M. Ainsi, nous avons

fl (z) - f (x)|K_x,h(z)dz = 2M I Kx,h(z)dz

z-xl>5^|

1z-x|>ä

2M

ä2

ä2 K_x h(z)dz

flz-x|>ä

2M

L (z - x)² Kx,h(z)dz

.,h

2M

ä2

E {(Kx,h x)²}

(a) = 2M 2M

ä2 V ar _(Kx,h) + ä2 {E (Kx,h) - x}²

(a): nous appli_quons directement la formule E(X²) = V ar(X) + {E(X)}². Or, d'après les deux h_ypothèses (3.4) et (3.6) du no_yau associé, la dernière iné_galité tend vers 0. Nous concluons enfin _que

E { i_n(x)} -f(x) ? 0 _quand n ? +8.

Remar_que: ?? _?r_?r?ete _q?? ??s ???s _?res??t( ?st ??????? ???s ??le ??s ??e ?\u9313‡A??\u9312‡@??t???s s_\u9313‡A?etr?_q??s ?t ?s_\u9313‡A?etr?_q??s?

Proprietes 4: \u9670·?s _?res??t?s ?? ?e???_??????t ????t( ?? ??_\u9313‡A?r???_?r??_?? a ?r?d?? ?t ?? _???t ?\u9313‡A?? ?? ?? ??r????? ??e?t?r? E(Kx,h) = mx,h t?? _q??

f(Kx,h)^ÿ=f(mx,h) + (Kx,h - m_x,h)f⁰(x) + ¹₂(Kx,h - m_x,h)²f"(x). (3.9)

?? ????????t ???s_?er???? ?? ??tt? _q???t?té_? ??s ?t???n

E {f(K_x,h)} ÿ=f {E(K_x,h)} + ₂V ar(K_x,h)f⁰⁰(x). (3.10)

1

3.1.3 Biais ponctuel

Propriétés 5:: Soit x _fix( dans ?. Nous avons

Biais {1_n(x) } = E {1_n(x)} - f(x)

=ÿ [f {E(K_x,h)} - f(x)] + ²¹ V ar(Kx,h)f" (x). (3.11)

Demontration : En effet, d'apres le resultat de (38) et les deux expressions dapproximation de Ta_ylor-La_gran_ge (3.9) et (3.10) le biais sobtient facilement en retranchant

f(x).

Remar_que: Nous remar_quons _que le biais ne d(pend pas de n et tend vers 0 _quand h est tres petit.

3.1.4 Variance ponctuelle Pour un x fixe, nous generalisons l'expression de la variance de que ce resultat sera utilise dans la partie exemple

b fn.

Nous precisons

Propriétés 6:: Soit x _fix( dans ?. Nous avons

_n o Z _{h n o i}2

V ar ^bf_n(x) =ÿ 1 K2 _x,h(t)f(t)dt - 1 Biais ^bf_n(x) . (3.12)

+ f (x)

n n

?x,hn?

Demonstration: Comme les Xi sont i.i.d., nous obtenons successivement

V ar {:f_n(x) } = V ar { 1 E Kx,h (Xi)}

n

i=1

1 n 1 n

[V ar {Kx,h(X1)}] [E {Kx,h(X1)}2] -1 n [E{Kx,h(X1)}]2

_(Z ) _{(Z )}2

1 K2 - 1

_x,h(t)f(t)dt K_x,h(t)f(t)dt .

n n

?x,hn? ?x,hn?

Par analo_gie avec le no_yau continu s_ymetri_que nous avons

{Z ?x,hn?

2 Kx,h(t)f(t)dt }=ÿ [Biais fn(x)} + f (x) 2

et sous la condition f?x,hK x2 _h(t) f (t)dt est finie, la variance de f_n est

J

1 2

V ar {i_n(x)} =ÿ¹

h(t) f (t)dt } - n [Biais {fn(x)} + f (x)1 .

n R_xhn?^x,

3.1.5 MISE L'erreur globale de

b fn s'obtient en sommant le carré de l'expression (311) avec le

resultat obtenu dans (3.12).

Propriétés 7: En sommant sur l'intersection des deua supports, e MIISE est

Z MISE = ?

{ } E ^bfn(x) _ f(x) dx x,hn?

_Z { } _Z }

Biais2 {

= V ar ^bf_n(x) dx + ^bf_n(x) dx.

?x,hn? ?x,hn?

3.1.6 Exemples

Nous supposons dans toute la suite _que f admet une dérivée seconde continue sur

_{}2 }2}

le support et _que les termes suivants sont finis J { {

f^'(x) dx, ^J xf^''(x) dx et

? ?

_{f{ }2}

x³f^''(x) dx.

?

a. Cas d'un no_yau associé _gamma

Chen (2000) était le premier a introduire l'estimateur a no_yau as_ymétri_que. Il pré_b

sentait au début un premier estimateur

fn a noyau gamma de paramètres a = x/h + 1

et b = h, il calculait ensuite les propriétés ponctuelles et _globalesliées a cet estimateur Puis, a cause des problèmes du biais au bord _quavait cet estimateur Chen e~ectuait unelé_gèremodificationauniveaudesparamètresduno_yau_gammapourréduirelerreur

et il représentait un deuxième estimateur que nous notons

^bbfn(x).

Nous rappelons _qu'une loi _gamma est une loi continue as_ymétri_que définie sur = R+ de densité de probablité gG(a,b) telle _que:

_ta-1_e-t/b

gG(a,b)(t) = (a)ba ,

_Z

(a) =

avec

e^-tt^a-1dt.

R+

Si X une variable aléatoire _qui suit la loi _gamma, alors

E(X) = ab et V ar(X) = ab².

D'après la fi_gure 3.4, nous remar_quons _que selon les valeurs _que prennent a et b, l'allure de la courbe chan_ge. Dans le cas particulier on a = 1 nous retrouvons la loi exponentionnelle.

Soit KG(x/h+1;h) le no_yau associé a la variable aléatoire 1G(x/h+1;h) de loi _gamma et de support x,h = R+. Il est donné par

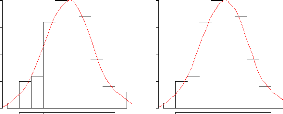
FIG. 3.4 Allure _générale d'une densit _gamma

Densité de la loi gamma

0 1 2 3 4 5

y

Density Gamma

0.0 0.2 0.4 0.6 0.8 1.0

Gamma

a=1 b=1
a=2 b=1

a=3 b=1

a=4 b=2

a=5 b=2

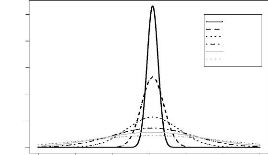
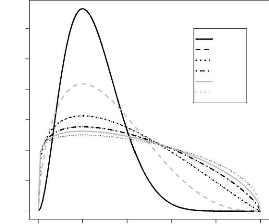
Les deux fi_gures 3.5 et 3.6 donnent l'allure du no_yau associé _gamma _qui dépend des paramêtres x et h. Nous donnons en premier lieu la représentation du no_yau _gamma pour un h fixé, nous remar_quons _qu'en chan_geant x la courbe chan_ge lé_gérement de forme et se déplace principalement sur l'axe des abscisses. Cependant, si nous varions h comme indi_qué dans le _graphi_que 3.6, l'allure de cette densité chan_ge complétement.

Nous révisons d'abord les différentes h_ypotheses du no_yau associé KG(x/h+1;h).

R+ = Ø.

i.R+ n =6

R+

ii.u_xR+ = R+.

+ 1)h = x ' x h --* 0.

iii.E(JCG(x/h+1,h)) _quand

= (x/h + h

xh +

iv.V ar(JCG(x/h+1,h)) = (x/h + 1)h² = h² < 00.

v.h --* 0 V ar(JCG(x/h+1,h)) = 0.

Soit X1,X2,. . . ,X_n un échantillon de variables aléatoires iid. a support = R, de

b

densité de probabilité continue inconnue f. Nous considérons l'estimateur f_n a no_yau associé _gamma tel _que

_Xn
i=1
_Xn

i=1

^bf_n(x) = 1

n

1
n

KG(x/h+1;h)(Xi)

_Xx/h
1 i e_Xi/h

(x/h + 1) hx/h+1 ,

FIG. 3.5 Allure du no_yau assoei _gamma pour h = 0.2 et x varié

h=0.2

0 1 2 3 4 5

y

Gamma(x,h)(y)

0.0 0.5 1.0 1.5 2.0

x=0 x=0.5

x=1

x=2 x=2.8 x=3.5

on h > 0 est le paramêtre de lissa_ge et K est le no_yau associé a une variable aléatoire de loi _gamma de paramêtres x/h + 1 et h. D'aprês (3.11), nous avons

{ } = hf^'(x) + 1

Biais ^bf_n(x) ₂hxf^''(x) + o(h). (3.13)

Dans le calcul du biais, nous nous arrêtons a lordre 1 pour avoir une homo_généité des puissances avec la variance dans le calcul de lerreur _quadrati_que mo_yenne inté_grée MISE (Le biais sera élevé au carré) D'aprês cette expression, nous remar_quons _que e biais tend vers 0 _quand h tend aussi vers 0. Le fait que f^' et f^'' fi_gurent dans la même é_quation, n'est pas três favorable dans le calcul du biais puis_que _ça au_gmente lerreur La complicité de la dérivée premiere avec la dérivée seconde est dfe au fait _que x n'est pas la cible mais elle est plutôt le mode.

Nous calculons la variance de cet estimateur Daprês (312) nous avons

{ _{o h}

V ar ^bf_n(x) = 1 E ~KG(x/h+1;h)(X1)~²i - 1 ~E ~KG(x/h+1;h)(X1)~]² . n n

Nous calculons chacun des deux termes En effet nous avons

.

( )

_X2x/h

1 e_2X1/h

E {KG(x/h+1;h)(X1)}² = E h²(^x/^h+¹)2x/h + 1

FIG. 3.6 - Allure du no_yau associe _gamma pour x = y = 2 et h varie

0.0 0.2 0.4 0.6 0.8

Gamma(x,h)(y)

x=2

h=0.1 h=0.3 h=0.7 h=1.1 h=1.4 h=1.8

0 2 4 6 8 10

y

Soit KG(2x/h+1;h) un no_yau associe _gamma de par/ahme-et2rXe1s /2h

01. 2x/h + 1 et h_;

{KG(2+1;h)(X1)} =

2 1 2x h^2x/^h+¹(2x/h + 1).

Ce _qui impli_que

X1 2x/h_e-2X1/h = h^2x/^h+1(2x/h + ¹)KG(2x/h+1;h)(X1). Ainsi, nous trouvons finalement

(

h2x/h+1 (2x/h + 1)

E ~KG(x/h+1;h)(X1)~² = E

h2(x/h+1) ²(x/h + 1) KG(2x/h+1;h)(X1)

_h-1

(2x/h + 1) il K

lG(2x/h+1;h)PC1)}

=

2 (x/h + 1) .

Nous examinons les differentes conditions du no_yau associe KG(2x/h+1;h). i. R+ n R+ = R+ =6 Ø.

ii.?_xR+ = R+.

iii. E(KG(20/+1;h)) = (2x/h + 1)h = 2x + h.

iv. V ar(KG(201,+1;h)) = (2x/h + 1)h² = 2xh + h² < co.

v.h ? 0 V ar(KG(2x/h+1;h)) = 0.

Ah(x) ~

-1/2 si x/h ? 8

1h si x/h ? k,

?

??? ?

????

1 x 2vhð

(2k+1) 2¹+^2k2(k+1)

Nous avons ainsi

E~KG(2x/h+1;h)(X1)~ = f(x) + h 2 f⁰(x) + o(h). Soit l'expression de Ah(x) telle _que

Ah(x) =h-1 (2x/h + 1)

²(x/h + 1)^.

Nous considerons la fonction R(z) monotone, croissante et conver_ge vers 1 _quand z tend vers l'infini (i.e: ?z > 0, R(z) < 1). Elle est donnée par

v

2ð

R(z) = _e-z zz-H. (3.14)

(z + 1)

En prenant z = 2x/h et z = x/h, nous obtenons

v2ð

_e-2x/h(₂₀.)2x/h+1/2

R(2x / h) =

(2x/h + 1)

R²(x/h) =

2ð e-2x/h(2x/h)2(x/h+1/2).

2 (x / h + 1)

Ainsi, Ah(x) peut etre exprimee en fonction de R(x/h) et R(2x/h).

Ah(x) = 1 v2ð R² (x / h)

e-2x/h 2x \ 2x/h+1/2 x -2(x/h+1/2)

2ð R(2x/h) ^e-2x/h h h

h1/2	R2(x/h) x R(2x / h)	-1/222x/h+1.
v2ð

Comme R(z) < 1 alors R²(z) reste encore inferieur a 1. Par conse_quent, le rapport

R(2x/h) < 1 et nous trouvons

R²(x/h)

_h1/2 R2 (x/h)

-1/2₂2x/h+1

Ah(x) =

v2ð R(2x/h) x

=	h1/2x-1/2
	2vð

_hv

= _2v.

ðx

Pour un h suffisamment petit,

on k est une constante positive.

Nous calculons a ce niveau le deuxieme terme de la variance

2

\ ₁₁2

[E {KG(x/h+1;h)(X1) I .1 = [E _{{Lfn,h,K(x)dx} }i =^(a) 1.

(a): D'apres la propriété (3.7).

En conclusion, la variance est donnée par

-¹/²f(x) + O(n-¹) si x/h ? 8

1 si x/h ? k.

_hnf(x)

V ar {:fi_i(x)} ~ ??? ? ?

????

1 x 2nvhð

(2k+1)
2¹+²k²(k+1)

L'impact de la variance au bord est né_gli_geable dans la calcul de son inté_grale, nous ne tenons compte _que du terme _qui se trouve a lintérieur de notre support ceci se démontre par le calcul suivant:

Soit ä = h¹-^E, on 0 < E < 1.

f ar {:fi_i(x)} dx = 1^ä V ar {:fi_i(x)} dx + f: V ar {:fi_i(x)} dx

T8 1

x-1/2 f (x)dx + O(n^-1 h^-€)

2nvher

¹ r 2nvher 0 x-1/2 f (x)dx + o(n^-1h^-6).

La valeur de la variance dans la petite boule de centre 0 et de rayon h¹-^€ dispose d'une valeur dérisoire ce _qui fait _que la _quantité _qui pése le plus est celle _qui se trouve au milieu de ]0, + 8[.

Nous mesurons ainsi l'erreur _quadrati_que mo_yenne inté_grée MISE

8 2 rMI SE(n,h,K,f) = 1₀ Biais {f_n(x) } + V ar {:f_n(x)}

Z 82

= h2 r f⁰(x) + ¹₂xf^"(x) dx

0

+ 2nN ¹ her Jo⁸

x^-1/²f(x)dx + o( ¹ ).

nvh

En minimisant le MISE par rapport a h, nous avons

2h

fo

2 (x) +^12xf (x) } dx

1 1 2n 2h^2Or /0

8 x

^-1/^2f(x)dx = 0.

Enessa_yantdedéterminerlafenetreoptimalenousre_grouponslestermesen hdememe coté_;

8

^0°

2h I {f^' (x) + 1 2 x f^" (x) }² dx =

2n 2h²ver

1 x-1/2 f (x)dx.

C'est-à-dire

h5/2 = 1/20r f rx-1/2f()dx 4f 0 {1(x) + (x)}^2 dx n

-1.

Enfin, la fen:tre optimale est

hopt =

(1/2vð)^2/^5 r if08 x-1/2f(x)dx}2/5 n [f r { f^' (x) + ^1xf^"(x)}^2 dx] 2/5

-2/5.

La fenetre optimale dans le cas as_ymétri_que est dordre O(n-²/⁵) inférieur _que dans le cas s_ymétri_que O(n-¹/⁵). En rempla_cant cette valeur optimale dans l'expression du MISE, nous avons successivement

2

MISEopt (hopt)

ho2 pt 8 1

{f (x) + ₂x f (x) } dx

+		1 1	8 L-1/2 I x-1/2 f (x)dx 'opt
		2vð n
=ÿ	n-4/5 44/5 2v7r 0 { 1 /8 -1/2 2 1/5 x f(x)dx }^4/5 f (x) + 2x (x) } dx . [18 1 " 0

b

Dans le but de réduire le biais et par la suite l'erreur entre fn et f, nous présontons le deuxième estimateur _qu'a introduit Chen (2000) ; la modification sest faite au niveau de la cible de sorte _qu'elle devient la mo_yenne de la variable aléatoire du no_yau associé. Pour cela, soit

fn(x) = 1 n

Xn i=1

KG(ñh(x);h)(Xi), (3.15)

ofi

ñh(x) ~

? ?? ? ???

x si x = 2h 4h^2 ^x2+1 si x ? [0,2h[.

De la meme manière, nous calculons toute les propriétés de cet estimateur Le biais est tel _que:

Biais {in(x)} ~

? ?? ? ???

2 x f^" (x)h + o(h) si x = 2h îh(x)hf^'(x) + o(h) si x ? [0,2h[.

La variable î dépend de h et chan_ge de valeur en fonction de x, elle est é_gale à:

îh(x) = (1 - x) {ñh(x) - x/h} / {1 + hñh(x) - x}.

Clairement, le biais est plus petit dans ce cas ; _quand x tend vers l'infini, nous obtenons une expression _qui ne dépend _que de la dérivée seconde f⁰⁰, ce _qui est plus faible par rapport au biais de fn.

bb

b

La variance de f est é_quivalente a celle de f_n pour x/h tend vers l'infini. Nous distin_guons une lé_gère différence dans le cas on x/h s'approche de la constante k. En effet, la variance est é_gale a:

~ ~

V ar ^bbf_n(x) ~

x-¹/²f(x) + O(n-¹) si x/h ? 8

a(k) n1 h f (x) si x/h ? k,

?

???

???

1

n

v 1 2 hð

avec a(k) un coefficient _qui dépend seulement de k.

La somme du biais au carré et de la variance nous amène a déterminer le MISE de cet estimateur_;

1 1 1 1 2

MISE( r 2 f (x)dx

Tfi_i)= h² {x f (x)} dx + v x

hð n 0

4 0

(1/2vð)2/5 U08 x-1/2f(x)dx}2/5 Lb 8 {x f^" (x)} ² dx] 2/5 n

-2/5_.

Ainsi, la fenêtre optimale est

hopt =

En substituant cette valeur dans lexpression du MISE lerreur _quadrati_que mo_yenne inté_grée optimale est::

-1/2 f (x)dx ] 4/5

1 1

MIS Eot(hot) ⁼44/5 [ 2vð fo8 x [fo8 f_ixf^"(x)1² dx ] 1/5 n-4/5.

Nouspouvonsêtretenterquelesdeuxestimateurs f et

bb f atteignentlavitessedeconver-

_gence optimale. Nous montrons _que pour toute densité f continue:

Z 8 ~f (x) + ₂ x f^,, (x) }² dx= f_o⁸ {x f,,(x) }² dx.

Ceci impli_que s_ystémati_quement

MISEopt( ^bf) = MISE_opt(^bbf).

Enfin, du point de vue purement théori_que, il est clair _que le deuxième estimateur ^bbf donne de meilleure performance en utilisant une fenêtre plus faible par rapport au pre-

mier estimateur

f.

b. Cas d'un no_yau associe beta

Tout comme les no_yaux _gamma, Chen (1999) appli_que le même principe pour les no_yaux bêta. Il introduit pour cela un premier estimateur on ilit remar_que _que les paramètres choisis ne sont pas les plus adé_quats donc, ilit essa_ye de les harmoniser etet les es

arran_ger pour aboutir a de meilleures estimations et par consé_quent de meilleures perr formances. L'idée est strictement la meme nous commen_cons ainsi par rappeler la loi beta. La densité de probabilité d'une loi beta est définie continue sur [0,1] telle _que:

gBe(a,b)(t) = on a > 0, b > 0 et vérifiant

B(a,b)ta-1(1 - t)^b-11[0,1](t), 1

B(a,b) = I t^a-1 (1 - t)^b-1dt.

Si X est une variable aléatoire _qui suit la loi beta alors

a ab

E(X) = et V ar(X) =

a + b (a + b)²(a + b + 1)^.

La fi_gure 3.7 donne l'allure de la fonction beta d'une manière _générale.

FIG. 3.7 -- Allure _generale de la densit( bêta

0.0 0.2 0.4 0.6 0.8 1.0

y

Bet3(3,b)

4

3

2

Bêta

a=2 b=2

a=3 b=2

a=4 b=2

a=2 b=3

a=3 b=3

LenoyauKBe(x/h+1;(1-x)/h+1))estlenoyauassociéaunevariablealéatoire KBe(x/h+1;(1-x)/h+1)) de loi beta et de support ?x,h = [0,1] tel _que:

.

1

KBe(x/h+1;(1-x)/h+1)(t) = B(x /h + 1,(1 - x)/h + ₁₎t^x/^h(1 - t)(1-x)/h

FIG. 3.8 -- Allure du no_yau associe bêta pour h = 0.2 et x varie

h=0.2

Beta(x,h)(y)

0 1 2 3 4 5 6

x=0 x=0.1 x=0.2 x=0.3 x=0.4 x=0.5

0.0 0.2 0.4 0.6 0.8 1.0

y

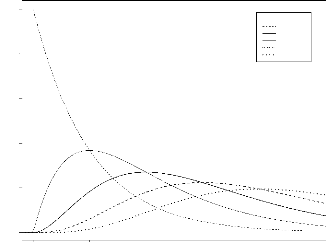
Lesfi_gures3.8et3.9donnentlavariationduno_yaubetacha_quefois_quenouschan_geons les paramètres x et h.

Nous nous assurons _que ce no_yau est bel et bien un no_yau associé i.[0,1] n [0,1] = [0,1] =6 Ø.

ii.?_x[0,1] = [0,1].

(x+h)

iii. E(KBe(x/h+1;(1--x)/h+1)) = (1+2h) x _quand h ?0.
x(1--x)h+h²+h³

iv.

V ar(KBe(x/h+1;(1--x)/h+1)) = (1+2h)2(1+3h)< 8.

v.h ? 0 V ar(KBe(x/h+1;(1--x)/h+1)) = 0.

Soit X1,X2,. . . ,X_n un échantillon de variables aléatoires i.i.d sur ? = [0,1], de densité

de probabilité continue as_ymétri_que inconnue f. Nous considérons l'estimateur

fn de f

a no_yau beta tel _que

fn(x) = 1 n

Xn i=1

KBe(x/h+1;(1--x)/h+1)(Xi)

1
n

_Xn
i=1

B(x/h + 1,(1 - x)/h + 1)

,

1 X_i ^x/h(1 - Xi)(1--x)/h

avec x ? [0,1] et h > 0 est le paramètre de lissa_ge.

FIG. 3.9 -- Allure du no_yau associe bêta pour x = y = 2 et h varie

x=0.2

Beta(x,h)(y)

0.0 0.5 1.0 1.5 2.0 2.5 3.0

h=0.1 h=0.3 h=0.7 h=1.1 h=1.4 h=1.8

0.0 0.2 0.4 0.6 0.8 1.0

y

En se bénéficiant des calculs antérieurs nous avons

1

Biais {:fi_i(x) } = h(1 - 2x) f (x) + ₂x(1 - x)hf"(x) + o(h),

et

V ar {:fi_i(x)} = n1 [E 1KBe(x/h+1;(1-x)/h+1)(X1)}²1 + O(n^-1),

on

1 i (1 - Xi)^2(1-x)/^h.

~KBe(x/h+1;(1-x)/h+1)(X1)~² = B²(x/h + 1; (1 - x)/h + 1)X2x/h

Soit _{KBe(x/h+1;(1-x)/h+1)} le no_yau associé de loi beta défini par

KBe(2x/h+1;2(1-x)/h+1)(Xi) =

B(2x/h + 1; 2(1 - x)/h + 1)

1

i

X^2x/h(1 - Xi)^2(1-x)/^h.

Ce _qui fait _que

Xi ^2x/h(1 -Xi)2(1-x)/h = B(2x/h + 1; 2(1 - x)/h + ¹)KBe(2x/h+1;2(1-x)/h+1)(Xi). Ainsi:

Tout compte fait, nous avons

E {KBe(x/h+1;(1-x)/h+1)(X1) _}2

B(2x/h + 1; 2(1 - x)/h + 1)

=

B²(x/h + 1;(1 - x)/h + 1)

E {KBe(2x/h+1;2(1-x)/h+1)(Xi)}.

Nous appellons Ah(x) = B(2x/h+1;2(1-x)/h+1)

B2(x/h+1;(1-x)/h+1) et nous rappellons _que B(a,b) = (a)(b)

(a+b) .

Nous vérifions les conditions du no_yau associé KBe(2x/h+1;2(1-x)/h+1)(Xi).

i.[0,1] n [0,1] = [0,1] =6 z. ii.u_x[0,1] = [0,1].

x+h/2

iii.E(KBe(2x/h+1;2(1-x)/h+1)) = 1+h ~ x _quand h ? 0.

< 8.

iv.V ar(KBe(2x/h+1;2(1-x)/h+1)) = 4x(1-x)h+2h+h2 v.h ? 0 V ar(KBe(2x/h+1;2(1-x)/h+1))

(2+2h)²(2+3h)

= 0.

En exploitant la fonction (3.14), nous avons

/

27r

R(2x/h) = ô(2x/h + 1)^e

(2x

-2x/h

_~2x/h+1/2

h

/ 27r R(2(1 - x)/h) = ô (2 ( 1 - x)/h + 1)^e		(2(1 - x) )2(1-x)/h+1/2 -2(1-x)/h h
/ 27r R(2/h + 1) =ô (2/ h+ 2)^e	/2 )2/h+1+1/2 -2/h+1 h + 1

De même, nous avons

27r R^2(x/h) = ô^2(x/h + 1)^e		-2x/h ~x ~2x/h+1/2 h
27r R^2((1 - x)/h) = ô^2(2(1 - x)/h + 1)^e			(1 - x -2(1-x)/h h	~2(1-x)/h+1/2
27r R^2(1/h + 1) = ô^2(1/h + 2)^e	/1 + h )2(1/h+1) -2(1/h+1) h

Ainsi, nous trouvons

1 7r {x(1 - x)}-1/2 h-1/2 R(2/h + 1)R²(x/h)R²((1 - x)/h) Ah(x) = 2/ R(2x/h)R(2(1 - x)/h)R²(1/h + 1)^.

Enma_jorantcetteexpressionpar 1,Ah(x)prenddeuxvaleursdifférentesselonlaconver_gence du rapport x/h et (1 - x)/h.

Ah(x) ~

? ???? ????

2v 1 ð {x(1 - x)}-1/2 ^h-1/2 si x/h et (1 - x)/h ? 8 2^2k+^1^2(k+1)^h-1 (2k+1) si x/h ou (1 - x)/h ? k.

Enfin, la variance est é_gale a

{ }

V ar ^bf_n(x) ~

?

????

????

1 nh1/2 f(x) + O(n-¹) si x/h et (1 - x)/h ? 8

2v ð {x(x - 1)}-1/2 1

ô(2k+1)
2^2k+¹ô²(k+1)

_nhf(x) + O(n^-1)

1 si x/h ou (1 - x)/h ? k.

Nous évaluons l'erreur _quadrati_que mo_yenne inté_grée de cet estimateur

1 2

MISE {:fi_i(x) }=ÿh² {1₀ (1 - 2x) f^' (x) + ₂ x(1 - x)f^" (x) } dx ¹r⁺ 27Whð {x(x - 1)}^-1/2 f (x)dx.

Nous minimisons le MISE par rapport h et nous déterminons la fenêtre optimale hopt.

2/5

[

1 [2,/ðf o1 {x(x - 1)}^-1/2 f (x)dx]

-2/5_.

hopt = 42/5

f

o1(1-2x)f

'

(x)+

1

2

-

x(1-x)f

''

(x)

} dx]

De maniere similaire au no_yau associé _gamma et en considérantlles mêmesrraisonspour les _quelles nous avons introduit le second estimateur a no_yau associé _gamma _quiccorr_ge le biais au bord, nous présentons a ce, niveau le second estimateur a no_yau assocéébtta défini sur [0,1] :

fn(x) = 1 n				Xn i=1	KBe(x;h)(Xi), (3.16)
avec	KBe(x;h)(Xi)	? ?????? ? ???????	KBe(x/h;(1-x)/h)(Xi) si x ? [2h,1 - 2h] KBe(ñh(x);(1-x)/h)(Xi) si x ? [0,2h[ KBe(x/h;ñh(1-x))(Xi) si x ?]1 - 2h,1]

on ñh(x) = 2h² + 2.5 - /4h⁴ + 6h² - x² - x/h. ?h fixé, ñh(x) est croissante sur [0,2h]. Nous faisons tendre h vers 0 et vers 1, les _quantités au bord deviennent faibles Ainsi nousrécupérons_justel'expression_quisetrouvealintérieurdelintervalle.Nousrévisons les h_ypotheses mis sur le no_yau associé

i.[0,1] n [0,1] = [0,1] =6 Ø.

ii.?_x[0,1] = [0,1].

iii.E(KBe(x/h;(1-x)/h)) = x.

iv. V ar(KBe(x/h;1-x/h)) = x(1-x)h 1+h < 8.

v. h ? 0 V ar(KBe(x/h;1-x/h)) = ⁰. Le biais est é_gal à

Biais {fn(x)}

? ?????? ? ???????

2 hx(1 - x) f^" (x) + o(h) si x ? [2h,1 - 2h] æh(x)hf^0(x) + o(h) si x ? [0,2h] -æh(x)hf^0(x) + o(h) si x ? [1 - 2h,1]

2 2/5 n

avec æh(x) = (1 - x) {ñh(x) - x/h} {1 + hñh(x) - x}.

La variance de ce deuxieme estimateur est similaire au premier _quand x/h et (1 - x)/h

tendent vers l'infini.

V ar {1_n(x)} =

1

{x(x - 1)}^-1/2 f(x) + O(n^-1).

2nvhð

Enfin, la fenetre optimale est

Comme

hopt =

[2 \^1/ð f {x(x - 1)}^-1/2 f (x)dx] 2/5 o^l ~nR 1 o2 ~2/5 n o x(1 - x)f^00(x) dx

--2/5.

~Zo

_~2 Z 1

1 _{n o2}

(1 - 2x)f⁰(x) + ¹ ₂x(1 - x)f⁰⁰(x) dx = x(1 - x)f⁰⁰(x) dx,

o

alors la fenetre optimale du premier estimateur est plus _grande _que celle du second. En
rempla_cant la valeur optimale de h dans l'expression du MISE nous constatons _que

l'erreur quadratique moyenne intégrée trouvée dans le cas de ^bfn.		fn est inférieure a celle de
MISE(	^bfn) = MISE(fn).

c. Cas d'un no_yau associe _gaussien inverse II Soit g(t) la densité de loi _gaussienne inverse telle _que

,

v ~-b ~ t ~~

b

gIG(a,b)(t) = v2ðt3 exp a - 2 + a

2a

t

on t > 0 et (a,b) est un couple de deux réels strictement positifs La fi_gure 310 donne l'allure _générale de la densité _gaussienne inverse Si X est une variable aléatoire _qui suit la loi _gaussienne inverse alors

E(X) = a et V ar(X) = a³/b.

Soit KIG(x;1/h) le no_yau _gaussien inverse associé a la variable aléatoire KIG(x;1/h) défini sur ?x,h = [0, + 8[, de parametres x et 1/h. Ce no_yau associé KIG(x;1/h) se définit comme suit:

~ -1~ t ~~

1

KIG(x;1/h)(t) = v2ðht³ x - 2 + x .

exp 2hx t

Nous vérifions chacune des h_ypotheses du no_yau associé i.R+ n R+ =6 Ø.

ii.?_xR+ = R+.

iii.E(KIG(x;1/h)) = x.

iv. V ar(KIG(x;1/h)) = x³h < 8.

v.h ? 0 V ar(KIG(x;1/h)) = ⁰.

FIG. 3.10 - Allure _générale de la densit _gaussienne inyerse

0 1 2 3 4 5 6

t

Inverse Geussisn(e,b)

OA 0.5 1.0 1.5 2.0

Inverse Gaussian

a=1 b=10

a=2 b=25

a=3 b=7

a=4 b=30

a=5 b=15

Ainsi le no_yau KIG(x;1/h) est un no_yau associé. Les _graphi_ques 311 et 312 présentent l'allure d'une densité _gaussienne inverse _quand nous varions x et h.

Pour un échantillon de variables aléatoires iid X1,X2, . . . ,X_n, nous considérons la

densité de probabilité f inconnue définie continue sur R+. Soit l'estimateur

^bf_n de f a

no_yau inverse _gaussien défini sur [0, + 00[ tel _que:

^bfn(x) = 1 n		Xn i=1	KIG(x;1/h)(Xi)
=	1 n	Xn i=1		( -1 (Xi 1 x q2ðhX3 exp 2hx i	2 +	~~ x , Xi

on le paramêtre h est strictement positif et x est dans R+.

En tenant compte de ce _qui était cité précédemmentle biais est

{ } = 1

Biais ^bf_n(x) ₂x³f⁰⁰(x)h + o(h),

donc

_Z } _Z {

Biais2 { _}2

^bf_n(x) dx = 1 ₄h² x³f⁰⁰(x) dx + o(h²).

R+ R+

{ _}2

Comme ^f x³f⁰⁰(x) dx est finie alors, pour tout x _qui tend vers +00, x³f⁰⁰(x)

conver_ge vers 0. D'oñ le biais diminue _quand x au_gmente.

R+

~-1 ~X1 ~~ _q

x - 2 + x = ðhX3 1KIG(x;2/h)(X1),

FIG. 3.11 -- Allure du no_yau associe _gaussien inverse pour h = 0.1 et x varie

0 1 2 3 4 5 6

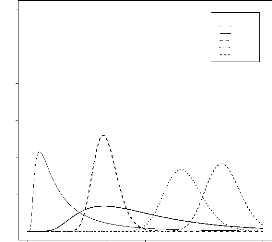
!GM m)

3A

2A 2.5

1.5

0.5 1.0

OA

Inverse Gaussian

x=1

x=2

x=3

x=4

x=5

Nous calculons la variance sur la base des calculs effectues au prealable.

V ar {:fi_i(x)} = 1 E IIKIG(x;1/h)(X1)}²1+O(n^-1).

L

~KIG(x;1/h)(X1)~^2 = 1 2ðh^X-3 1 exp

xh x -1 (1 2 + x )1 X X1

Soit KIG(x;2/h)(X1) le no_yau _gaussien inverse de parametre x et 2/h associe a KIG(x;2/h) et definie sur [0, + 8[. Nous verifions simplement les differentes h_ypoteses liees a cette variable aleatoire :

R+ n R+ Ø

ii.?_xR+ = R+.

iii.E(KIG(x;2/h)) = x.

= _x3 h

iv.V ar(KIG(x;2/h)) 2 < 8 .

v. h ? 0 V ar(KIG(x;2/h)) = 0.

En conclusion, il s'a_git d'un no_yau associe Tout bien considers

xh x{ -1 (X1

- 2 +

v

2

KIG(x;2/h)(X1) = p2ðhX3 exp

1

Ce _qui impli_que

OA 0.5 1.0 1.5 2.0 2.5

IGNim)

FIG. 3.12 Allure du no_yau assoei _gaussien inverse pour x = 2 et h varié

Inverse Gaussian

h=0.1
h=0.2
h=0.4
h=0.7
h=0.9

0 1 2 3 4 5 6

x

et par la suite, nous avons

{ }

_X-3/2

E [{KIG(x;1/h)(X1)}²i = v 1 ðhE 1 KIG(x;2/h)(X1) .

2

A partir de l'approximation de Ta_ylor-La_gran_ge nous obtenons

{ } { }

_X-3/2 _K-3/2

E 1 KIG(x;2/h)(X1) = E IG(x;1/h)f(KIG(x;1/h))

= x^-3/²f(x) + O(h).

En conclusion, _quand x > 0 se situe a l'intérieur du support, la variance est

.

{ } _x-3/2

V ar ^bf_n(x) = v 1 n f(x) + o(n^-1h^-1)

2 hð

La variance au bord, _quand x/h ? k, présente _quel_ques différences. Elle est é_gale a

,

{ } _k-3/2

V ar ^bf_n(x) = v 1 n f(x) + o(n^-1h^-2)

2 hð

k étant une constante positive. L'erreur _globale de cet estimateur est

Z { }2 Z

1 1

MISE ÿ=₄h² x³f⁰⁰(x) dx + v 1 x-3/2f(x)dx.

R+ 2 hð n R+

Nous cherchons a determiner le h optimal. Pour cela, nous minimisons le MISE par rapport a h, nous trouvons

1

2

Z h _R{x³ f^" (x)}² dx 1 1

2h²Or 2n L₊x^-3/²f(x)dx = 0,

c'est a dire

h5/2 L+ {x³ f^" (x)}² dx = 1 1

20r n J+ x-3/2 f (x)dx.

Enfin, la fenetre optimale est

2/5

{

-2/5_.

1 R o

2v R+ x-3/2f(x)dx ð

hopt = 2 /5 n

[fR+ {x³ f^" (x)}² dx1^--

En l'exploitant dans la formule du MISE nous trouvons

₁4/5 _{r i 1}2/5

5 I

MISE(h_opt) = 4 121 v ð L+ x-3/2 f (x)dx x³ f^" (x)dx n-4/5.

1 JR+

d. Cas d'un no_yau associe _gaussien nverse rcc_iro_que RIIG Nous considerons g(t) la densite de loi _gaussienne inverse recipro_que

v ~^-bgRIG(a,b)(t) =

v2ð ^exp t 2a (at - 2 + at )1

on t > 0, a > 0 et b > 0. La fi_gure 3.13 donne l'allure _generale d'une densite _gaussienne inverse recipro_que. Si X est une variable aleatoire _qui suit la loi _gaussienne inverse recipro_que alors

E(X) = 1 a

+

1 b et V ar(X) = 1b + ^22.

SoitKRIG(1/(x-h);1/h) leno_yau_gaussieninverserecipro_queassociealavariablealeatoire KRIG(1/(x-h);1/h) defini sur ?x,h = [0, + co[, de parametres 1/(x - h) et 1/h. Ce no_yau se presente comme suit :

KRIG(1/(x-h);1/h)(t) =

exp

ðht

2 + x _;h)}

2h

h t

x - h

-

1

^v2

Nous commen_cons par verifier chacune des h_ypotheses du no_yau associe i.{? = [0, + co[} n {?x,h = [0, + co[} = [0, + co[6= Ø.

ii.?_x[0, + co[= [0, + co[.

iii. E(KRIG(1/(x-h);1/h)) = x-h + h = x.

iv. V ar(KRIGo./(x-h)0./h)) = (x - h)h + 2h² = xh + h² < co. v.h ? 0 V ar(KRIG(1/(x-h);1/h)) = 0.

FIG. 3.13 -- Allure _generale de la densite _gaussienne inverse réei_irr_que

Reciprocal Inverse Gaussian

a=1 b=10

a=2 b=25

a=3 b=7

a=4 b=8 a=0.5 b=5

5

4

3

2

Reciprocal Inverse Gaussian

0 1 2 3 4 5 6

t

Ainsi toutes les conditions du no_yau associé sont satisfaites.

Soit X1,X2, ...,X_n l'échantillon de variables aléatoires i.id. de densité de probabilité f

b

inconnue définie continue sur ? = R+. Nous considérons l'estimateur f_n de f noyau _gaussien inverse récipro_que défini sur [0, + 8[ tel _que

^bfn(x) = 1 n

i=1

KRIG(1/(x-h);1/h)(Xi)

1
n

=

_Xn
i=1

1 x - h _(Xi2 x -

v2ðhXi ^exp 1 2h x - h + Xi) ,

avec h > 0 et x ? R+.

En tenant compte des résultats obtenus précédemment

Biais {:fi_i(x) } = 21 x f" (x)h + o(h),

et donc

FIG. 3.14 -- ????r? ?? ?\u9313‡A?? ?ss??e _???ss??? ????rs? ré??_?r_q?? _??r x = 2 ?t h ??r?e

MOO /10

3A

2A 2.5

1.5

0.5 1.0

OA

Reciprocal Inverse Gaussian

h=0.1 h=0.2 h=0.4 h=0.7 h=0.9

0 1 2 3 4 5 6

x

En refaisant les calculs de la variance de la même fa_con nous trouvons

si x/h ? 8 si ^xfi.1 k.

V ar {fn(x)} ~

	? ???? ????	1 x -^1/^2f	(x) + O(n-^1) + 7 k^3/^2) + O(n-^1) ' 16
		2nvhð 1 (k-1/2
		2nhvð

La fenêtre optimale est e_gale à

hopt =

( 1 )^2/5 {L#177; x-1/2f (x)dx}2/5 200 [fR#177; {xf"(x)}^2 dx1^2/5

n-2/5.

En conclusion, nous evaluons le MISE en fonction de cette valeur hopt:

M I S E(hopt) = #177; (_20r)

1 2/5 {fly

[fR#177; {xf"(x)}2 dx]

x-1/2f (x)dx ₁2/5

2/5 _n-2/5_.

e. Remar_ques:

i. ????? ?? s?_??rt ?? ?\u9313‡A?? ?ss??e ?x,h ?? ?e_???? _??s ?? ?? x ?? ?? h ??rs ?e?

?\u9312‡@??_???s _q?? ??s ???s tr??té?

ii. ???s ???\u9312‡@_?r?ss?? ?? ?? _???êtr? _?t?????_? ?? ???s?it ?????? f ?t s? ?ér??é? s?????_???r??t ???s ?? ???er?t??r ?t ?? ?e???er?t??r ??tr??r????t ?? ??a _\u9313‡A?éet?_i?? o f s? tr??? s???????t ?? ?e???er?t??r ?? ??s ????s _???i? ???nne ??????? ?nt? ? ?a s_\u9313‡A?etr?_q?? ?t ?s_\u9313‡A?etr?_q??_? ??rs _??r ????ttr? ? ?ée??? ?"??????? ???? ?ée??????st???t?? ?? _??r??etr? h_? f ??t s_\u9313‡Aste??t?_q?????t s???r? ??? ?? ??t???? ?a_\u9313‡A?é? tr?_q?? ?? s?_??rt R? P?r ?\u9312‡@?????? ???s ?? ??s ??s ?\u9313‡A??\u9312‡@ ?ss??és ?????? _???ss???????rs? ?t _???ss??? ????rs? re??_?r_q??_? ??s ?_??s?s ?? f s??t ??? ?? ?s_\u9313‡A?etr?_q???e_??? s?r R+? ???s ?? ??s ??s ?\u9313‡A??\u9312‡@ ?ss??es ?êt?_? ?? ???s?it ??i ???nne ? ?? ?_??or [0,1]?

3.2 Cas multivarie

defini sur de dimension d. L'estimateur

Dans cette section, nous _généralisons lestimateur a no_yau associé continu as_ymétri_queaucasmultidimensionnel.Pourcela,nousconsidéronsunéchantillondevariables aléatoires X1,. . . ,X_n i.i.d., de densité de probabilité f continue as_ymétri_que inconnue f_n de f a no_yau associé continu as_ymétri_que est

fn (x) = 1 n

Xn i=1

Kx,H (Xi) , (3.17)

on la cible x =^t (x1, ... ,xd), H est la matrice pleine de variance-covariance des fenêtres h de dimension d x d, et Xi =^t _(Xi1, . . . ,Xid). La fonction K_x,H est le no_yau associé as_ymétri_que sur Rx,h.

Pareillement,nousdonnonsunestimateur_quisebasesurleproduitdesno_yauxunivariés as_ymétri_ques. Get estimateur a une forme plus vul_garisée _que celle de (3.17). En effet, nous avons

fn (x) = 1 n

Xn i=1

? ? ?

d j=1

K^jxj,hj (Xij)

???

,

(3.18)

on xj est la _jeme composante du vecteur x, hj est la _jeme fenêtre et Xij est la ieme observation de la _jeme composante.

^bfn(x) = 1 n

Xn i=1

Kx,h (Xi), (4.6)

Chapitre 4

Noyau associé discret

Le nombre de travaux abordant les estimateurs a no_yau pour des données discrètes reste limité. Dans ce chapitre, nous présentons deux t_ypes de no_yaux associés discrets. La première section porte sur les no_yaux associés discrets pour des données caté_gorielles on les données sont _qualitatives ordonnées et définis sur un ensemble fini inclu dans N _que nous dési_gnons Rx,h. Ensuite, dans une deuxième partie, nous introduisons le no_yau associé discret pour des données de compta_ges. Une première tentative dans ce cadre, uni_quement de manière expérimentale a été proposé par Marsh & Mukho padh_ya_y(1999).Nousétudionslespropriétesponctuelleset_globalesdechacundesdeux estimateurs a no_yau associé discret Différentes techni_ques de selection de la en:tre du lissa_ge sont proposées. Enfin,nous _généralisonslestimateur a no_yau associé aucasmultivarié.

Definition 1: ??t x ?\u9312‡@( ???s R ?t h > 0? \u9670·?s ?_?????s ??\u9313‡A?? ?ss??e ??s?r?t? Kx,h? t?t? _???t?? ?? ??ss? ?? _?r??????té ??s?rt? ????? ??r????? ??l?t?i? Kx,h s?r ?? s?_??rt Rx,h? t??s _q???

Rx,h n R=6 Ø (4.1)

?xRx,h ? R (4.2)

E(K_x,h) ~ x _quand h ? 0 (4.3)

V ar(K_x,h) < 8 (4.4)

V ar(K_x,h) ? 0 _quand h ? 0. (4.5)

Commentaire: Nous vérifions dans ce _qui suit, _que dans le cas du no_yau associé discret pour des données caté_gorielles, le support Rx,h coincide avec R. Nous verrons _que dans certaine situation, ce n'est pas tou_jours vérifié comme dans le cas des données de compta_ge_; Rx,h dépend de x et ne se colle pas avec le support R.

Definition 2:: ??t X1,. . . ,X_n ?? (????t???? ?? ??r?????s ??e?t?r?s ?????? ?? _???t???? ??ss? ?? _?r??????te f ??s?ret? ??????? s?r R? ???st???t??r a ?\u9313‡A?? ?ss??e ??i?r?t

b

f_n =fn,h,K ?? f ?st ?e_??? _??r

avec x ? ? et h > 0.

Propriété 1: Soit x fixé dans ?. Nous avons

E {:I_n(x)} = E {f(Kx,h)} . (4.7)

Démonstration: En effet, nous trouvons successivement

(

1 n

E {^In(x) } = E n EKx,h(Xi)

i=1

= E {Kx,h(X1)}

X= y??x,h	Kx,h(y)f(y)
X= y??x,h	f(y) Pr(Kx,h = y)
= E{f(Kx,h)} . ·
Propriété 2: Soit f une fonction discrete de support ?. Soit		b fn l'estimateur de f à

no_yau associé discret K_x,h sur ?x,h. Nous supposons _que ?x ? ?,?x,h ? ?. Alors, nous avons

E{in(x)} = E

f(t)Kx,h(t) ? f(x) quand n ? +8.

t??n?x,h

Démonstration:Nouspartonsdel'espérancede _{bfn(x)quiestégaleaEt??n?x,h} f(t)Kx,h(t). Nous calculons sa différence avec f(x). Pour cela, ? ä > 0 tel _que

trn(x)} f(x) =	~~~~~~	X t??n?x,h		{f(t) - f(x)} Kx,h(t)	~~~~~~
X = |t-x|<ä			|f(t) - f (x)| Kx,h(t) + E |t-x|>ä			|f(t) - f(x)| Kx,h(t).

Pourcalculerlepremierterme,nousavonsrecoursaladéfinitiondelacontinuitédansle cas discret (cette notion de continuité est différente par rapport a celle du cas continu) f estcontinueen x ? ? € > 0, ? ä > 0tel_que? t ?]x-ä,x+ä[n?_x,h |f(t)-f(x)| < E. Ce _qui impli_que

X |t-x|<ä

|f(t) - f(x)|Kx,h(t) = E.

La fonction f est discrete donc elle est bornée par 1 et nous obtenons successivement

X |t-x|>ä

|f(t) - f(x)|Kx,h(t) = ä2^2 Pr (|Kx,h - x| > ä)

2 2

ä2V ar _(Kx,h) + ä2 {E _(Kx,h ) - x}² .

Finalement,souslesdeuxconditions(43)et(4.5)toutecette_quantitéconver_gevers 0.

b

Propriété 3: Soit x fixé dans ?. Le biais ponctuel de l'estimateur f_n de f a no_yau associé discret est

Biais {1_n(x) } = E {f(Kx,h)} - f(x)

= f {E(Kx,h)} - f(x) + ¹ V ar _(Kx,h) f ⁽²⁾ (x) + o(h). (4.8)

Démonstration: Par définition,le biais est la différence entrelespérance delestimateur

b

f_n et la densité inconnue f. En effet, d'apres le résultat (4.7) nous avons

E{f_n(x) } = E {f(Kx,h)} .
Or,enutilisantundeveleppomentlimitéaupointmo_yen mx,h = E(K_x,h),nousobtenons

f(Kx,h) = f(mx,h) + (Kx,h - m_x,h)f⁽¹⁾(x) + ¹₂(Kx,h - m_x,h)²f⁽²⁾(x) + o(h). Et en prenant l'espérance mathémati_que, nous avons finalement

1

E{f (Kx,h)} = f {E(Kx,h)} + ₂ V _ar(Kx,h) f ⁽²⁾ (x) + o(h).

Remar_que: Nous mentionnons _que les f^k(x) d'ordre k = 1 représentent les différences finies _qui viennent remplacer les dérivées dans le cas continu et _qui vérifient

f^(k)(x) = { f^(k-1)(x)}

et f⁰(x) =

{f(x + 1) - f(x - 1)} /2 si x ? N^* f(1) - f(0) si x = 0.

? ???

???

Propriété 4:: Soit x fixé dans ?. La variance ponctuelle de l'estimateur ^bf_n =fn,h,K de f a no_yau associé discret est

V ar {^In(x) } =ÿ¹ _nf(x)Pr(Kx,h = x).

(4.9)

Démonstration: La variance est donnée de maniere successive par

( n

V ar {:fi_i(x) } = V ar K x,h(Xi)}

n i=1

V ar {Kx,h(X1)}

1

E {Kx,h(X1)}² - n [E {Kx,h(X1)}]²

1

=

n

1
n

=

}2

1
n

? ? ?

=

f (y) {Pr(Kx,h = y)}² - 1 _n?E f (y) Pr(Kx,h = y)

yENx,h ?yENx,h

1
n

=

n1 {f (x) E(K_,h) - f²(x) } + O(_n) f(x) Pr(Kx,h = x).

Nous précisons _que le terme E(K2x,h) := Ey??x,h {Pr(Kx,h = y)}² est ma_joré par 1. Le
résultat final se base sur la condition (4.3) a traversla probabilité modale Pr(Kx,h = x).

Propriété 5: L'erreur _quadrati_que mo_yenne inté_grée _que nous appelons MISE est

X MISE = x?? X= x??

E{in(x) - f(x)}^2 Biais^2 {.^-fii(x)} + E x??

V ar {:fii(x)}

1²

= E {E(Kx,h) - f (x) + ²¹ V ar(K_x,h)f⁽²⁾(x) + o(h)

x??

+ E x??

1 n

f(x)Pr(Kx,h = x). (4.10)

4. 1 Noyau associé discret pour des données catégorielles

Dans cette partie, nous nous focalisons sur les données discretes caté_gorielles (i.e. données _qualitatives). Nous travaillons essentiellement sur un ensemble discret fini ? ? R. Nous si_gnalons _que durant les dernieres annéesil_y avait une croissanceconsidée rable dans le domaine des no_yaux discrets pour des données caté_gorielles, lesles premiers travaux sont dfis aux innovateurs Aitchison & Aitken (1976) puis Simonoff & Tutz (2000) et enfin, Racine & Li (2007). (voir biblio_graphie pour plus de détails.)

Définition 3: Soit X la variable aleatoire de loi d'Aitchison & Aitken _que nous notons D(c; c0,A), on c ? N \ {0,1} est le cardinal du support, c0 ? {0,1,. . . ,c - 1} est le point de re_ference et A ?]0,1], de densite de probabilite sur le support ? = {0,1, . . . ,c - 1} de_finie par

Pr(X = x) = (1 - A)1x=0 + c A - 1

1x6=c0.

Propriété 6: L'espérance de la variable aléatoire X de loi d'Aitchison & Aitken est

A

E(X) = c0(1 - A ^Ac (4.11)

c - 1 2

4.1. NOYAU ASSOCIR DISCRET POUR DES DONNRES CATRGORIELLES 69

Demonstration:L'esperancedecettevariablealeatoireestdonnéedemanieresuccessive par:

E(X) = E x Pr(X = x)

x?{0,1,...,c-1}

+

c xë11x,c0

E { x?{0,1,...,c-1}

= {c0(1 -- ë) + c ë ₁(0+ 1 + ... + (c0 -- 1) + (c0 + 1) +...+c -- 1)1

( ) }

= c0(1 -- ë) +

c ë -- 1 i c0₀

c(c -- 1)

= c0(1 -- ë) + c -- ë 1 1 2 c0}

c0 (1 ë ë ) ëc

c 1 2

Propriete 7: La variance de la variable aleatoire X de loi d'Aitchison & Aitken est

V ar X 2 c²ë (1 -- ë) -- ëc

( ) =

⁰(c -- 1)²

2

ëc (2c 3 -- 1 ë ₂c)

. (4.12)

c0

c -- 1

c²ë(1 -- ë) -- ëc

+

Demonstration: La variance est obtenue de maniere successive par

V ar(X) = E(X²) -- {E(X)}²

(c-1 ) -- co = c²0(1 -- ë) + c ë

Ei² c,0--{c0 (1 -- ë

c ë ₁ )) ëc

2 f

i=0

= c^20(1 -- ë) +

ëc(2c -- 1) ëc8 {c0 (1 -- ë -- ë ) ëc1 c -- 1 ) 2 j 6 c -- 1

2

2

ë

2c2

ë

= c0 ² (1 -- ë

c 1

ë ) 6 Ac(2c -- 1) 2

c0 (1 -- ë

c -- 1 ) 4

--c0ëc (1 -- ë -- ë )

c -- 1

(c -- 1)²

c0

c -- 1

2 c²ë(1 -- ë) -- ëc = c0

Commentaires::

c²ë(1 -- ë) -- ëc

+

ëc (2c -- 1 ëc)

.
·

2 3 2

a. Lors_que c = 2, nous nous retrouvons dans le cas dune loi Bernoulli de parametre ë ou 1 -- ë. Le t_ype de la loi Bernoulli chan_ge selon _que le point de reference se trouve en 0 ou en 1. Nous verrons dans le cas de lestimateur a no_yau associe discret _que le choix du point de reference sera la cible.

b. Lors_que c 7? +8, le support ? = N.

c. Si ë = 0, ceci revient a dire _que notre loi est la loi de dirac _qui ne depend plus

FIG. 4.1 -- ???str?t?? ?? ?? ?? ????t???s? ?t ??t???

Densité de loi Aitchison et Aitken

OA 02 0.4 0.8 0.8 1.0

Pr

0 8

4

2

x

de c et _que nous la notons ä_x. Si maintenant, ë prend la deuxieme valeur limite _qui est e_gale a 1 alors Pr(X = x) = ¹ 1

c-1 x,c0.

Nous sommes en mesure de donner une definition precise dun estimateur a no_yau associe discret pour une densite de probabilite f sur un ensemble discret ? et de presenter les proprietes fondamentales relatives

Definition 4: ??t X1,X2,. . . ,X_n ?? e????t???? ?? ??r?????s ??e?t?r?s ?????? ?? ???

t??????ss???_?r??????te??s?ret???té_?r?????r???é??????? f s?r? = {0,1,...,c - 1}_?

ùc ?st ???? ?t _?\u9312‡@e ???s N \ {0,1}? U? ?st???t??r ^bf_n(x) =

b

fn,h,K(x) ?? f(x) a ?\u9313‡A?? ?ss??e ??s?r?t _{KD(c;x,h) q}?? s??t ?? ?? ????t???s? & ??t??? ?st ?e_??? _??r

fn(x) = 1 n	Xn i=1	KD(c;x,h)(Xi) (4.13)
1 n	E- h)1Xi=x + h 1^1Xi,=x} . i=1

???? x ?st ???s ? ?t h ?]0,1] ?st ?? _??r??etr? ?? ??ss?_?? ??s?r?t ?? ???r? ?? _???êtt??? Nous examinons les differents points _que doit verifier le no_yau associi KD(c;x,h):

i.?c;x,h = {0,1, . . . ,c - 1} = ?.

4.1. NOYAU ASSOCIE DISCRET POUR DES DONNEES CATEGORIELLES 71

FIG. 4.2 -- ???str?t?? ?? ?\u9313‡A?? ?ss??e ???t???s? ?tet ??i??? _??r h = 0.2 ?t x ??r?e

0.0 02 0.4 0.6 0.8 1.0

D(c;x,h)(y)

0 2 4 6 8

y

ii.?x?c;x,h = {0,1,...,c 1} = ?.

iii. E (KD(c;x,h)) = x (1 h ch 1) + ^hc~ x _quand h ? 0.

iv. V ar (KD(c;x,h)) = _x2 hc²₍(1-h)₂-hc _xhc² (1-h)-hc + hc (2c-1 h2c) < 8.

c-1 2 k 3

v. h ? 0 V ar (KD(c;x,h)) = 0.

Propriété 8: A travers la formule (4.8), la fonction x 7? ^bf_n(x) est une fonction de masse de probabilité.

Démonstration: Comme les Xi sont i.i.d., nous avons successivement

Ec- 1 x=0

fn(x) =

c- 1 {1 n =0 n D(qx,h)(Xi) x } i=1

c- 1

E {(1 h)1X1=x + h

c 11X1'=x

x=⁰

= (1 h) + ch ₁(1 + 1 + ... + 1)

= (1 h) + ch ₁(c 1) = 1.

FIG. 4.3 -- ???str?t?? ?? ?\u9313‡A?? ?ss??e ???t???s? ?tet ??i??? _??r x = y = 2 ?t h ??r?e

0.0 02 0.4 0.6 0.8 1.0

D(c;x,h)(y)

0 2 4 6 8

y

b

Propriété 9: D'après la relation (4.8), le biais de l'estimateur	fn de f a noyau associé

{ I

²hc

(

2c 1

+
hc

)}

Biais{fn()} x) = hc f⁽¹⁾(x) + - xhc + f ⁽²⁾ ( 2)

x) + o(h.

2 2 lc - 1 2 3 2

(4.14) Remar_que: \u9670·?s r???r_q??s ???_?res ?????? _q?? ?? ????s ?stest rs ??_?rr??t? ? ?d????? a ?? _??s ?? c_? h ?t ??s ?er??e?s _?r???er? ?t s?????? ???_q?? _??s _q?? ? ??r??????? s?_??rt c ??_????t? ?? ????s s????r?t? \u9670·?s ????s ???s? _???s?r a r???i? ? ????i ?? ???_???t ??s _??r??etr?s ???? ???s ??le ??s ??s ?\u9313‡A??\u9312‡@ ?ss??ie ?a_\u9313‡A?éet?_i??e ?_???u _?re??se????t ??s ?\u9313‡A??\u9312‡@ ????? ?t ?et? ?? ????? _???ss??? ???er? ?e _???us??? ???er? re??_?r_q?? ?? ???????t? \u9670·?s ??tr?s _q?? ?? ??st _??s ?????t ?? ?de?e????e ?e_??a???etr?s? ??_??????t_? ??? _??_c? _?ss???? _??r ??le é???r? ??s?is? a _?r???d? ??? ? ???ntr??? c0 ???? ? _???t ?? ????? ??sse _??r ??s ?\u9313‡A??\u9312‡@ r???_?????r?e ???i ?????_?g?_????_??r _???s ?? ?et???s??

b

Propriété 10: D'après la relation (4.9), la variance de l'estimateur associé discret KD(c;x,h) de loi d'Aitchison & Aitken est

fn de f a noyau

h _\2 {c-1

V ar {:fi_i(x)} = 1 [f(x)(1 - h)² + (c - ₁) f(i) - f (x) }1. (4.15)

i=0

4.2. NOYAU ASSOCI] DISCRET POUR DES DONNÉES DE COMPTAGE 73

4.2 Noyau associé discret pour des données de comptage

Pareillement a la section précédente, nous donnons dans cette partie lestimateur a no_yau associé discret pour des données de dénombrement Noustravaillons essentiellement sur un ensemble fini (ou encore n'importe _quel ensemble dénombrable notamment Z, N + qN, etc). Nous calculons les propriétés fondamentales pour cet estimateur en utilisant les différences finies ala place des dérivées. Nous présentons dans a suite 4 exemples de no_yaux associés discrets s_ymétri_ques et standards as_ymétri_ques.

4.2.1 Noyau associé poissonien

Nous rappelons _qu'une loi de Poisson Po(A) de paramètre A est une loi discrète définie sur N de fonction de masse de probabilité Pr(X = x) telle _que pour tout x dans N, nous avons

Pr(X = x) = e-ë Ax x!.

Si X est une variable aléatoire _qui suit la loi Poisson alors lespérance et la variance sont respectivement é_gales a

E(X) = A et V ar(X) = A.

0 5 10 15

x=5

0 5 10 15

x=7

0 5 10 15

y

0 5 10 15

y

FIG. 4.4 Illustration du no_yau associ poissonnien pour h = 0.1 et x variée

x=0

5 10 15

x=2

x=1

?

?

?

?

?

? ? ? ? ? ? ? ? ? ? ? ? ?

0 5 10 15

x=4

0.00 0.15 0.30

0.0 02 0.4

Probab(y)

Probab(y)

0.00 0.10 0.20

?

?

?

?

?

?

? ? ? ? ? ? ? ? ? ? ?

0.00 0.10

?

?

?

?

?

?

?

?

? ? ? ? ? ? ? ?

Probab(y)

0.00 0.10

?

?

?

?

?

?

?

?

?

?

? ? ? ? ? ? ?

0.00 0.06 0.12

?

?

?

?

?

?

?

? ? ? ?

?

?

?

? ?

?

?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

?

?

La fi_gure 4.4 illustre la variation de la fonction de masse poissonienne pour h = 0.1. Soit KPo(x+h) le no_yau poissonien associé a la variable aléatoire KP o(x+h) sur x,h = N

tel _que:

avec x ? N, y ? N et h > 0 est le parametre de lissa_ge discret. Ce no_yau poissonien KPo(x+h)(y) = e-(x+h)(x +

!

vérifie-t-il la définition d'un no_yau associé? En effet nous avons

i.? n ?x,h = N n N = N=6 Ø. ii.?_xN = N.

iii.E (KP o(x+h)) = x + h ~x_quand h ? 0.

iv. V ar (KPo(x+h)) = x + h < 8. v.h ? 0 V ar (KP o(x+h)) = x.

Soit ,X_n un échantillon de variables aléatoires i.i.d . de fonction de masse de

probabilité discrete inconnue f définie sur un ensemble discret ? = N. L'estimateur fn de f a no_yau associé poissonien est défini par

^bfn(x) = 1 n

Xn i=1

KPo(x+h)(Xi)

1
n

=

_Xn
i=1

_e-(x+h) (x + h)^Xi

Xi! ,

avec x ? N et h > 0.

Cet estimateur est-il une fonction de masse de probabilité? Non, en effet

X8 x=0

^bfn(x) =

t° {^1 KPo(x+h)(Xi)} x=0 n i=1

=

_X8
x=0

{KPo(x+h)(X1)}

=

~

_X8 ~

_e-(x+h)(x + h)X1 .

X1!

x=0

Nous avons calculé cette _quantité numéri_quement sous R, pour plusieurs valeurs de h et de X1, nous avons abouti a des valeurs tres faibles par rapport a 1 Enfin, lestimateur

b

f_n(x) n'est pas une fonction de masse de probabilité

Nous évaluons ainsi le biais et la variance de lestimateur a no_yau associé poissonien.

b

En se basant sur la relation (4.8), le biais ponctuel de f_n(x) en un point x fixé est

Biais {j_n(x) } = h f ⁽¹⁾ (x) + ²¹ (x + h)f⁽²⁾(x) + o(h).

b

De même, d'apres la relation (4.9), la variance de

fn(x) en un point x fixé est

V ar {fl(x)} = n x f(x)(x + ! e-(x+h).

Enfin, la valeur du MISE est

MISE(n,h,f) = 1 E ^n x?N

(x + h)^x f(x) x!e

2 -(x+h)+ E {hf^(1)(x) +^21 (x+h) f^(2) (x) + o(h) } . x?N

4.2. NOYAU ASSOCI] DISCRET POUR DES DONNÉES DE COMPTAGE 75

4.2.2 Noyau associé binomial

Nous rappelons _qu'une loi binomiale de paramètres N et p, B(N,p) est une loi discréte définie sur l'ensemble {0, . . . ,N}, avec N est un entier fixé dans N, de fonction de masse de probabilité gB(N,p) telle _que

N_x

.

N!

x!(N - x)!

Pr(X = x) = p^x(1 - p)

Si X est une variable aléatoire _qui suit la loi binomiale alors lespérance et la variance sont respectivement

E(X) = Np et V ar(x) = Np(1 - p).

La fi_gure 4.5 présente l'allure de la densité d'une loi binomiale _quand nous fixons la fenêtre h et nous faisons varier x. Par ailleurs, la fi_gure 4.6 donne la variation de cette densité _quand nous varions h et nous _gardons x fixé en 7.

FIG. 4.5 Illustration du no_yau associ binomial pour h = 0.1 et x varié.

x=0 x=1

2 4 6 8 10 0 2 4 6 8 10

x=2 x=4

0 2 4 6 8 10

x=5

0 2 4 6 8 10

x=7

0 2 4 6 8 10

0 2 4 6 8 10

y

Probab(y)

0.0 0.4 0.8

?

?

? ? ? ? ? ? ? ? ?

0.0 0.2 0.4

?

?

?

? ? ? ?

? ? ? ?

Probab(y)

0.0 0.2 0.4

?

?

?

? ? ? ? ? ? ?

0.0 02 0.4

? ?

?

?

?

?

? ? ? ? ?

Probab(y)

0.0 0.2 0.4

? ? ?

?

?

? ? ? ?

0.0 0.2 0.4

?

? ? ? ?

?

?

? ?

Le no_yau KB(x+1,(x+h)/(x+1)) est le no_yau discret associé a la variable aléatoire KB(x+1,(x+h)/(x+1)) de loi binomiale défini sur le support ?x,h = {0,1,.. . ,x + 1} tel _que

,

fx + h _~y f1 - h ~x+1_y

KB(x+1,(x+h)/(x+1))(y) = (x + 1)!

y!(x + 1 - y)! x + 1 x + 1

FIG. 4.6 -- Illustration du no_yau associe binomial pour x == y7 et h varie.

0.0 0.2 0.4

h=0.1

?

?

?

?

? ? ? ?

? ?

0 2 4 6 8 10

h=0.4

Probab(y)

0.0 0.2 0.4

h=0.2

?

?

?

?

? ? ? ? ?

? ?

0 2 4 6 8 10

h=0.6

0.0 0.2 0.4 0.6

0.0 0.2 0.4

Probab(y)

?

?

?

?

?

? ? ? ? ?

? ? ? ? ? ?

? ?

? ?

0 2 4 6 8 10

h=0.7

?

0 2 4 6 8 10

h=0.9

0.0 0.4 0.8

Probab(y)

0.0 0.4

?

?

?

? ?

? ?

? ? ? ? ? ?

? ? ? ? ? ? ?

0 2 4 6 8 10

y

0 2 4 6 8 10

y

on x est dans N et h est dans [0,1]. Nous verifions a ce niveau _que KB(x+1,(x+h)/(x+1)) est un no_yau associe. En effet nous avons

i. ?x,h n ? = {0,1,...,x + 1} n N = {0,1, ,x + 1} =6 Ø.

ii.?x?N {0,1, . . . ,x + 1} = N.

E(KB(x+1,(x+h)/(x+1))) = (x + 1)(x + h)/(x +1) =x+ h ~ x _quand h ? 0. iv. V ar(KB(x+1,(x+h)/(x+1))) = (x + h) (x^--₊¹1) < co.

v.h ? 0 V ar(KB(x+1,(x+h)/(x+1))) = x

x+1 < 1.

Pour le meme echantillon de variables aleatoires considers nous donnons lestimateur

b

f_n de f a no_yau associe binomial defini sur ?x,h = {0,1, . . . ,x + 1} comme etant

^bfn(x) = 1 n

i=1

KB(x+1,(x+h)/(x+1))(Xi)

1
n

_Xn
i=1

((x + 1)! x + h ^Xi 1 - h x+1--Xi

,

Xi!(x + 1 - Xi)! x + 1 x + 1

avec x ? N et h ?]0,1]. D'apres (4.8), le biais est

B iais { i_n(x)} = h f ⁽¹⁾ (x) + ₂ (x + h) (x 1 f ⁽²⁾ (x) + o(h).

fn(x) = 1 n				i=1	KBN(x+1,(x+1)/(2x+1+h))(Xi)
	1 n	i=1	+ Xi)! Xi!x!			~x + h y^X% x + 1 2x + 1 + h) 2x + 1 + h)

4.2. NOYAU ASSOCIR DISCRET POUR DES DONNRES DE COMPTAGE 77

Pareillement, d'après (4.9), la variance est

V ar {1n(x)} =

1 - h ~x + h ~ n x + 1

x

f(x).

Enfin, le MISE est obtenue en sommant les deux _quantités calculées précédemment. Nous trouvons

~x + h ~x

_X

1 - h

MISE(n,h,f) = f(x)

n x + 1

xEN

2

.

+ {hf⁽¹⁾(x) + ₂ ¹(x +

(x + 1) f ⁽²⁾ (x) + o(h)}

1 - h

x?N

4.2.3 Noyau associe binomial negatif

Nous rappelons _qu'une loi binomiale né_gative de paramètres s et p, BN(s,p) est une loi discréte définie sur le support N de fonction de masse de probabilité gBN(s,p) telle _que

gBN(s,p)(x) = (x + s)! ps (1 p)^x.

x!s!

Si X est une variable aléatoire _qui suit la loi binomiale né_gative, alors lespérance et la variance sont respectivement

E(X) = s(1 - p)/p et V ar(x) = s(1 - p)/p².

Soit KBN(x+1,(x+1)/(2x+1+h)) le no_yau associé a la variable aléatoire KBN(x+1,(x+1)/(2x+1+h)) de loi binomiale né_gative défini sur le support ?x,h = N tel _que

,

KBN(x+1,(x+1)/(2x+1+h))(y) =

(x + y)! x + h y x + 1 )x+1

y!x! 2x + 1 + h 2x + 1 + h

on x et y appartiennent a N et h est strictement positif. Nous vérifions _quil sa_git dun no_yau associé

i.N n N = N=6 Ø.

?x?x,h = ?_xN = N.

E(KBN(x+1,(x+h)/(2x+1+h))) = x+h ~x_quand h ? 0.

iv.V ~2x+1+h ~

ar(KB(x+1,(x+h)/(x+1))) = (x + h) < 8.

x+1

~

v.h ? 0 V ar(KB(x+1,(x+h)/(x+1))) = x ^~2x+1 .

x+1

Pour notre même échantillon de variables aléatoires nous donnons lestimateur fn de f a no_yau associé binomial né_gatif défini sur?x,h = N comme étant

FIG. 4.7 -- Illustration du no_yau associe binomial né_gative pour h = 0.1 et x varie

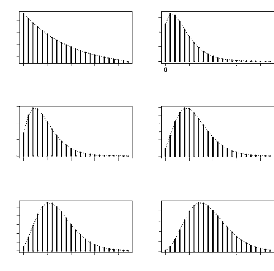
y

y

x=0

?

?

?

?

?

?

?

?

?

?

?

?

?

? ? ? ? ? ? ?

0 5 10 15 20

x=2

?

?

?

?

?

?

?

?

?

?

?

? ? ? ? ? ? ? ? ? ? ?

0 5 10 15 20

x=5

x=1

5 10 15 20

x=4

?

?

?

?

?

?

?

?

?

?

?

?

? ? ? ? ? ? ? ?

0 5 10 15 20

x=7

0.02 0.06

Probab(y)

0.00 0.05 0.10 0.15

Probab(y)

0.00 0.10

0.00 0.06 0.12

?

?

?

?

?

? ?
? ?

?

?

?

?

?

?

?

?

?

?

? ? ? ?

0 5 10 15 20

? ?
? ?

?

?

?

?

?

?

?

?

?

?

?

? ? ? ? ? ? ?

0 5 10 15 20

0.00 0.04 0.08

0.00 0.04 0.08

Probab(y)

?

?

?

?

?

?

? ?

? ? ? ? ? ? ? ? ? ?

?

?

?

avec x E N et h E R^*₊ .

Le ibiais de cet estimateur est

Biais {:fi_i(x)} = h f ⁽¹⁾ (x) + ²¹ (x + h) (2x x + 1 + 1 + h f ⁽²⁾ (x)+o(h).

D'apres (4.9), la variance est

1 2x + h^x x + 1 )x+1

nx!( 2x + 1 + h

V ar {:fi_i(x)} =

2x + 1 + h f(x).

En final, le MISE est la somme des deux derniers resultats. IlII est e_gal à

MIS E(n,h, f) = 1 E n xEN

2 ( x + h^x x + 1 V^+1 \ x! 2x + 1 + h) ( 2x + 1 + h) f(x)

2

+ E {h f ⁽¹⁾ (x) + ₂(x + h) (2x x + 1 ₁+ h f(2) (x) + o(h) } .

xEN

4.2.4 Noyau associe triangulaire

EnsereferantauxtravauxdeKokonend_jietSen_gaKiesse(2007)surlesdistriibutions trian_gulaires discretes, nous rappelons _quune loi trian_gulaire T_a,h_,c de parametres a

4.2. NOYAU ASSOCIR DISCRET POUR DES DONNRES DE COMPTAGE 79

et c dans N et h dans R+ est une loi discrete centrée en c et de bras a défini sur ?a,c = {c,c #177; 1, . . . ,c #177; a} de fonction de masse de probabilité:

Pr (Ta,h,c = y) =

(a + 1)^h - |y - c|^h P(a,h)

,

on P(a,h) est la constante de normalisation telle _que

a

P(a,h) = (2a + 1)(a + 1)^h - 2 i=0 i^h.

Nous remar_quons _que le cas h = 1 correspond a la variable aléatoire trian_gulaire s_ymétri_que. Le cas h = 0 n'est pas défini en c et en particulier, si h = 0 nous nous retrouvons la loi de Dirac d'espérance c. Si h tend vers l'infini, nous trouvons la loi uniforme Pour des entiers non nuls h ? R*, la constante de normalisation peut s'écrire:

P(a,h) = (2a + 1)(a + 1)^h - 2

a i=0

(-1)^h--i+1)h!Bh--i+1 i!(h - i + 1)! ai,

on Bh--i+1 est le nombre de Bernoulli. La fi_gure 4.8 présente l'allure de la densité trian_gulaire par rapport aux autres no_yaux discrete _que nous avons étudié.

Si X est une variable aléatoire _qui suit la loi trian_gulaire alors lespérance et la variance sont respectivement :

ih+2) .

a

E(X) = c et V ar(X) = 2E P(a,h) 3

i=0

1 a(a + 1)^h+1(2a + 1)

La loi Ta,h,c est s_ymétri_que autour de sa mo_yenne De plus la variance ne dépend pas de c.

Soit _KT(a,h,x) le no_yau trian_gulaire associé a la variable aléatoire KT(_a,h_,x), défini sur {x,x #177; 1, . . . ,x #177; a} et donné par

(a + 1)^h - |y - x|^h

KT(a,h,x)(y) = (2a + 1)(a + 1)^h - 2 Eaj=0 jh,

avec x ? N, h > 0 et a ? N.

Nous nous assurons des diférents points de la définition 1

i.{x,x #177; 1,...,x #177; a} n N = {x,x #177; 1, . . . ,x #177; a} =6 Ø. ii.?xEN {x,x #177; 1, . . . ,x #177; a} = N.

iii.E (KT (a,h,x)) = x.

iv.V ar (KT(

Nh#177;if2_a

(a(a+1) k ) 2 _E 3a. ₀ jh+2)

< 8.

a,h,x)) = P(a¹ ,h) 3

v.Lors_que h ? 0, la variance de KT(_a,h_,x) tend aussi vers 0. En effet, ce résultat a été obtenu dans la proposition (2.4) des travaux de Kokonend_ji, Sen_ga Kiessé et Zocchi (2007). Dans cette proposition, nous montrons _que la variance de la variable aléatoire conver_ge vers une loi de Dirac ce _qui impli_que une variance nulle (voir aussi la remar_que 2.3(ii))

FIG. 4.8 -- ???str?t?? ?? ?\u9313‡A?? ?ss??e tr???_?????r? _??r ??_?ér??t?e ?????rr ?? h?

Soit X1, ... ,X_n l'échantillon de variables aléatoires i.i.d . de densité f inconnue définie

b

sur N. Nous donnons l'estimateur f_n de f a no_yau associé trian_gulaire défini sur ?x,h =

{x,x #177; 1, . . . ,x #177; a} comme étant:

^bfn(x) = 1 n

Xn i=1

KT(a,h,x)(Xi)

1
n

=

_Xn
i=1

(a + 1)^h - |Xi - x|^h

(2a + 1)(a + 1)^h - 2 Eaj=0 jh,

avec x ? N, h > 0 et a ? N. Le no_yau KT(_a,h_,x) est le no_yau associé défini sur ?a,x,h = {x,x #177; 1, . . . ,x #177; a} . Nous remar_quons _que le support du no_yau associé ne dépend pas de h. Si a = 0, alors ?0,x = {x} et ?x?0,x = N. Par contre, si a =6 0 nous avons

?x?N?a,x = {-a, . . . , - 1} ? N. (4.16)

Le fait _que le support du no_yau discret trian_gulaire (4.16) a a =6 0 fixé contienne strictement N induit un biais de bordure a _gauche du support de f. Nous _y remédions en modifiant le bras a par a0 de sorte _que, ?a0 nous avons

?x?N?a0,x = N.

4.2. NOYAU ASSOCIR DISCRET POUR DES DONNRES DE COMPTAGE 81

de 0, 1 ou 2), nous considerons le bras modifie a0 de a tel _que ?k ? N \ {0} donne et x ? N, nous avons

a0 = k ? a =

{

j si x = j ? {0,1, . . . ,k - 1} k si x ? {k,k + 1, ...} .

Nous illustrons ce probleme du biais de bordure dans les fi_gures 4.9 et 4.10 Nous avons fixe h = 1, a = 4 et a0 = 4.

FIG. 4.9 -- ???str?t?? ?? ?\u9313‡A?? ?ss??( r???_?????r? ??s ???_???t?? ?? ?b?a

i=0

x=0 x=1

?

?

?

?

?

?

?

? ? ? ? ? ? ? ?

?

?

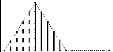
- 5 0 5 10

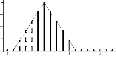
- 5 0 5 10

?

?

?

?

?

?

?

?

? ?

? ? ? ? ? ? ?

0.00 0.10 0.20

Probab(y)

0.00 0.10 0.20

x=2 x=4

?

?

?

?

?

?

? ? ?

? ? ? ? ? ?

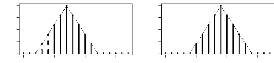
- 5 0 5 10

?

?

?

?

?

? ? ? ?

?

? ? ? ? ?

- 5 0 5 10

Probab(y)

0.00 0.10 020

0.00 0.10 020

x=5 x=7

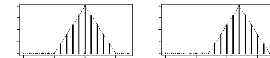
Probab(y)

0.00 0.10 0.20

?

? ? ? ? ? ?

?

?

?

?

?

?

?

? ? ?

0.00 0.10 0.20

?

? ? ? ? ? ? ? ?

?

?

?

?

?

?

?

- 5 0 5 10 -5 0 5 10

y y

Le biais de cet estimateur est

Biais { i_n(x)} = 2 P(a,h)

1 1 ( a(a + 1)^h+1(2a + 1) 2 ctih+2) f⁽²⁾(x) + o(h).

3

D'apres (4.9), la variance est

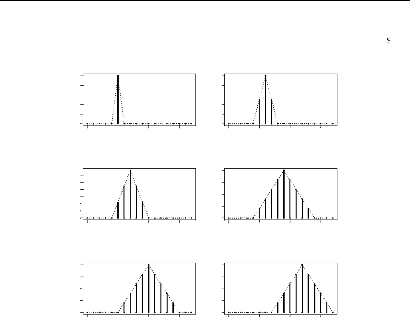
x=0

x=1

? ? ? ? ?

?? ? ? ? ? ? ? ? ? ? ?

FIG. 4.10 -- ???str?t?? ?? ?\u9313‡A?? ?ss??e tr???_?????r? ???? ???_???t?? ?? ?b?a

x=2

?

?

?

?

?

? ? ? ? ?

? ? ? ?? ? ? ?

- 5 0 5 10

x=4

?

?

?

?

?

?

?

? ? ? ?

?

? ? ? ? ?

- 5 0 5 10

0.00 0.10 0.20

x=5

?

?? ? ? ? ?

?

?

?

?

?

?

?

? ? ?

- 5 0 5 10

y

x=7

?

?

?

?

?

?

?

? ? ? ? ? ? ? ?

- 5 0 5 10

y

0.00 0.10 0.20

Probab(y)

0.00 0.15 0.30

0.00 0.10 0.20

Probab(y)

- 5 0 5 10

- 5 0 5 10

?

? ? ? ? ? ? ? ? ? ?

?

?? ? ? ?

0.0 0.2 0.4

Probab(y)

0.0 0.4 0.8

on P(a,h) = (2a + 1)(a + 1)^h - 2 E;₌₀ j^h.

En final, le MISE est la somme des deux derniers resultats.III est e_gal

(a + 1)^h E MISE(n,h,f) = nP(a,h) x?N

f(x)

a

+ v, { 1 1 ( a(a + 1)^h+1(2a + 1) 2 E ih+2) f⁽²⁾(x) + o(h)

x?N

i=0 }2

2 P(a,h) 3

f. Remar_ques:

a. \u9670·?s r???r_q??s _q???? ?\u9312‡@?st? ??s ??s ??s?rèt?s _q?? ?? _??????t _??a et? ?as??i?e à ????? ?\u9313‡A?? ??s?r?t ?t?????t ?? ?? ???_?r?? ??s?rrt?? ?? ?_??e_? ? ??u ??n??de?n ?? ?? ???_?r?? ??s?ret? ???tre? ?? x ?t ?? ??r_???r 2a ? ?? ?\u9313‡A?? ?ss??e U_x,a ?e_??? s?r ?x,a = {x,x #177; 1,... ,x #177; a} s?é?r?t ???? s??t?

1

U_x,_a(y) =

2a + 11x,x#177;1,...,x#177;a(y),

ù y ?st ???s N? \u9670·?s ?_??r????s _q?? ??s _??r??etr?s _?r_?r?s ?? ??tt? ?? s? tt????t ?i ????s????? ??s ?????rs ??t?er?s N? r ?? _??r??etr? ?? ??ss?_?? h ?st ???s R^*₊ ?? _q?? _???t _q?? ??s ?? _????s _??s ?re?r ??? s??st?t?t?? ?? ?????? ?? ??e ??a??èet?e?

4.2. NOYAU ASSOCIR DISCRET POUR DES DONNRES DE COMPTAGE 83

b. ?? ro?? ?? _??r??atr? ?? ??ss?_?? ??s?r?t h > 0 r?st? s???????? ?? ??s ??t???_? ??r ?? _??r??t ?? t???r ??_?t? ??s ?s?r??t??s Xi _q?? s?t _?r???s ?? ?? ????? x E N ?rs_q?? h = h(n) --> 0? ??_??????t ?? ??s_??rs?? ????? ?? ?t _???t ???st???t?? x s? tr????t _??r ????_?rt???? ?? ?\u9313‡A?? ?ss??( ??s?r?t Kx,h ???s?? ???s?_? ?? ???\u9312‡@ ???? t_\u9313‡A?? ?? ?\u9313‡A????s?r?t s?r???t? ??rs ??s ??str???t??s ?? Kx,h _q?? s???t ???s ??s_??rsé?s ??t?r ?? x E N ?t h > 0 _?\u9312‡@é?s?

c. P?r ??? ?? tr???_?????r? Ta,h,x? s? a = 0 ??rs ?? ?? ??s?ret? T0,h,x ?rr?s_??? à ??? ?? ?? ??r?? D(x) ?? x? \u9670·?s ????s ?? ?\u9313‡A?? ?ss??é ??s?r?t ?? ?? ?? ??r????\u9313‡A?? ???i_??? Dx,0? P?r t?t x E N ?t h > 0_?

Dx,0(y) = ä_x(y), y E N.

d. \u9670·?s r???r_q??s _q?? ?? ???_q??a?? ????t?? ?? ?? ?é_???i?? ???? ?\u9313‡A?? ?as??i???es _??s ?(r?_?é? ???s ?? ??s ???? ?\u9313‡A?? ??s?r?t t????r? ??tel _q??que ? ?\u9313‡A?? _??is?????_? ??????? ?t ??????? ?e_??t?_? ???t ??il, ??? ???r ??? ???\u9312‡@?i?? ?d_???i?? _??u ??e _\u9313‡A??e ???\u9313‡A???

4.2.5 Choix de fenetres

Nous présentons a ce niveau trois méthodes de choix de fenêtres pour approcher a valeur idéale de la fenêtre h définie par

hid = arg min h>0

MISE(n,h,K,f) = hid(n,K,f). (4.17)

a. Minimisation des erreurs _quadrati_ques

Du point de vue purement prati_que on X = (X1, . . . ,X_n) est un échantillon de variables aléatoires de fonction de masse de probabilité f, associé aussi a la distribution empiri_que f0 de f, nous proposons maintenant _quel_ques t_ypes de fenêtres liées aux erreurs d'estimations. La premiere est déduite de ???rr??r _q???r?t?_q?? ??te_?r(? (en an_glais " Inte_grated S_quared Error") définie par

ISE := E x?N

{ :In(x) -- f(x) }2 = ISE(X; h,K,f), (4.18)

la_quelle mesure sur un seul échantillon X l'écart (au sens _quadrati_que) entre f^b et f. Par
consé_quent, la minimisation en h de l'ISE (4.18) conduit a choisir une fenêtre adé_quate

h** = arg min h>0

ISE(X;h,K,f) = h^**(n,K,f). (4.19)

En rempla_cant f par f0 dans (4.19), nous utilisons h^**₀ = h^**(n,K,f0) pour le lissa_ge discret d'un f0 de f. Autrement dit, nous avons

h** 0= arg min h>0

ISE(X;h,K,f) = h^**(n,K,f0). (4.20)

Basé sur la conver_gence de f0 vers f _quand n --> +00, nous avons immédiatement

lim n?+8

h** 0(n,K,f0) = lim n?+8

h^**(n,K,f), (4.21)

pour un t_ype de no_yau associé K donné. L'importance de la fenetre adéquate h^** (4.19) de h est due, en partie, aux relations suivantes

MISE = E (ISE) = E x??

MSE (x). (4.22)

b. Validation croisée Toutcommelecascontinu,laméthodeclassi_quedevalidationcroisée(enan_glais"Cross Validation") ne fait pas usa_ge des approximations des dérivées de f est tou_jours applicable dans le contexte des estimateurs a no_yau discret pour mieux estimer la valeur idéale hid (4.17) de h.

Le principe de cette méthode est de minimiser par rapport a h un estimateur de MISE pour trouver le paramètre optimal. Pour cela la forme du MISE peut etre développé comme suit:

MISE = E {E R(x)} - 2E {Ef_n(x) f (x)}+ E f (x)².

x?N x?N x?N

Le terme _Ex?N f(x)² n'est pas aléatoire, et ne dépend pas de h. Nous notons alors,

MISE_cv = E E f^--2_n (x ) - 2E { E (x) f (x)} = MISE_cv(h),

x?N x?N

1^.12_n(x) _qui est un estimateur sans

le terme MISE _qui dépend de h. Dans la suite, nous déterminons un estimateur CV (h)

de MISE_cv. D'abord, nous avons évidemment x?N

biais de E {Ex?N f^-12n(x)} .

Ensuite, soit

1 fn,-i(x) = n - 1E jai

Kx,h (Xj)

Par construction,

1

i=1

1

i=1

KX%,h (Xj)

n(n - 1)

ij

est un estimateur de E {r x?N

^bf_n(x)f(x)} et on vérifie de plus _qu'il est sans biais En

effet, d'une part, comme les Xi sont i.i.d., nous avons

?

?

?

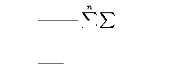
i=1

j1

= E

1

n(n - 1)

KX,,h (Xj)

?

?

?

= E

1_E

n - 1 j1

K (Xj)

= E {KX,,h (X2)}

Finalement, nous venons de montrer _que

CV (h) = E xEN

^b1^2n(x) - n2

Xn i=1

^b1n,-i (Xi)

( n 2

= E _n E Kx,h (Xi) } 2- n(n - 1) E E KXi,h (Xj).(4.23)

xEN i=1 i=1 j6=1

est un estimateur sans biais de MISE_cv. Par consé_quent, la fen:etre optimale par la méthode de la validation croisée s'obtient par

hcv = arg min h>0

CV (h) (4.24)

on CV(h) est donné en (4.23). Pour _quel_ques détails, nous pouvons nous référer a de nombreux auteurs tels Bowman (1984), Marron (1984) Rudemo (1982) Stone (1984) et leurs références.

c. Exces de zeros

Pour cette section, le choix de la fen:etre repose sur une particularité des données de compta_ge avec ? = N _qui n'est autre _que l'exces des zéros dans léchantillon X = (X1, . . . ,X_n). Pour ce phénomene bien connu (voir, par exemple Kokonend_ji et al., 2007, et leurs références) et étant donné un no_yau discret associé K_x,h, nous pouvons choisir une fen:etre adaptée h0 = h0(X; K) de h satisfaisant

Xn i=1

Pr (KXi,h0 = 0) = n0, (4.25)

on n0 dési_gne le nombre des zéros dans X_; voir Marsh & Mukhopadh_ya_y (1999) pour leur no_yau du t_ype poissonnien. Cette fen:etre h0 a_juste le nombre de zéros théori_que au nombre de zéros observé.

L'é_quation (4.25) s'obtient a partir de lexpression

E {in(x)} = E yEN

Pr (Kx,h) 1(y),

dans la_quelle nous prenons y = 0 et 1(0) = 1 afin d'identifier le nombre de zéros théori_ques au nombres de zéros empiri_ques n0.

Dans le cas du no_yau associé poissonien la fen:etre adaptée h0 est connue explicitement. Tandis _que dans le cas des no_yaux associés binomial et binomial né_gatif, la fen:etre h0 est obtenue par la résolution numéri_que dune é_quation non-linéaire (voir Table 4.1)

4.3 No_yau associe discret multiple

TAB. 4.1 -- Solutions h0 pour les no_yaux associes discrets standards

T_ype de no_yau h0

Poisson h0 = log (n1:0 Ein 1 eXi

Binomial (1--h0

= n0

Li=1 Xi+1

Binomial négatif Eiⁿ=1 (2XXi+i+1+1h0 = n0

fonction de masse de probabilité f et inconnue defini sur = N de dimension d. L'esti-

b

mateur f_n de f no_yau asocié discret est

fn (x) = 1 n

Xn i=1

Kx,H (Xi) , (4.26)

on la cible x =^t (x1, . . . ,xd), H est la matrice pleine inversible de variance-covariance desfenêtres hdedimension d×d(présentéedanslasection2.2),et Xi =^t _(Xi1, . . . ,Xid). La fonction K_x,H est le no_yau associé as_ymétri_que sur ?x,h.

Dans le but d'avoir une forme plus s_ympathi_que et _qui ne dépend pas des coefcients de corrélation,nousprésentonsl'estimateur (4.26)_quiutiliseleproduitdesno_yauxassociés univariés. En efet, nous avons

fn (x) = 1 n

Xn i=1

? ? ?

d j=1

Kj xj,hj (Xij)

? ? ?

,

(4.27)

on xj est la _jème composante du vecteur x, hj est la _jème fenêtre et Xij est la ième observation de la _jème composante. Le no_yau associé Kj est la fonction no_yau associé univarié décrite tout au lon_g de cette partie.

Chapitre 5

Regression multiple a noyaux

associes mixtes

Nous rappelons _que si nous avons un couple de variables aléatoires réelles telles _que Y soit inté_grable (E(Y ) < oo) alors la fonction

r(x) = E(Y |X = x)

est appelée fonction de ré_gression de Y sur X on nous n'avons aucune spécification sur r(x), avec x E R. Supposons _que nous disposons de n-échantillon (X1,Y1) , . . . , (X_n,Y_n) de variables aléatoires de même loi _que (X,Y ), de densité (fonction de masse) de probabilité inconne. Nous nous proposons ainsi de construire un estimateur br_n de la fonction densité (de masse) inconnue. En effet dans létude de la ré_gression non-paramétri_que, nousdistin_guonsdeuxmodelesprincipauxlaré_gressionnon-paramétri_que effetsaléatoires et la ré_gression non-paramétri_que a effets fixes. Dans le premier cas, les observations Xi sont aléatoires, alors _que dans le cas deffets fixes les Xi sont i.i.d., fixé dans R (Xi = i/n) et déterministes.

Soit ainsi le modele _général

Yi = r(Xi) + ei pour i = 1, . . . ,n, (5.1)

on les ei sont i.i.d., non corrélés avec Xi, de mo_yenne nulle et de variance ó².

5.1 Estimateur de Nadara_ya-Watson

Ilexisteplusieurst_ypesd'estimateursano_yaupourlaré_gressiondontleplusfameux est celui de Nadara_ya-Watson. Dans le cas univarié lestimateur de Nadara_y-Watson de la fonction ré_gression r est défini par

Eⁿi=1 YiKx,h (Xi)

(5.2)

brn(x) = Eⁿi=1 Kx,h (Xi) ,

CHAPITRE 5. REGRESSION MULTIPLE A NOYAUX ASSOCIRS 88 MIXTES

contrario,l'estimateur br(x)estnul.NouspouvonsrepresenterlestimateurdeNadara_yaWatson comme une somme ponderee des Yi:

brn(x) =

Xn i=1

wx,h(Xi)Yi pour x E fit, (5.3)

oU

Kx,h (Xi) (5.4)

wx,h (Xi) = En i=1

Kx,h (Xi)

est la fonction poid telle que Eⁿi=1 wx,h (Xi) = 1, par convention 0/0=0. La fonction Kx,h estlafonctionno_yauassociepresenteedansleschapitresprecedents,definisur R_x,h. Nous pouvons melan_ger plusieurs t_ypes de no_yau associe savoir lesles no_yaux associes continus s_ymetri_ques ou as_ymetri_ques avec les no_yaux discrets standards. La fenêtre h = h(n,K) determine le niveau de lissa_ge de l'estimation

En se referant au _quatrième chapitre de la thèse (en preparation) de Sen_ga Kiesse (2008), il est convenable de donner l'estimateur de Nadara_ya-Watson sous une forme plus souple. Pour cela, soit

N_n(x; h)

rnx D_n(x; h) (5.5)

avec		1 Nn(x; h) = n		Xn i=1		YiKx,h (Xi) ,
et	1 Dn(x; h) = n		Xn i=1		Kx,h (Xi) =^bfn(x).

Nous _generalisons la definition (5.2) de cet estimateur au cas multidimensionnel En effet, en utilisant (3.18) et (4.27), l'estimateur de Ndara_ya-Watson devient

br_n(x) =

^{En Y} {11p Kj

Y j=1 xi ,hi (Xij) }

(5.6)

En (_Trp _Kj i=1 11j=1 xi,hi on x =^t (x1i,. . . ,xpi) E ,Kjxi,hi

estle_jèmeno_yauassocieet Xij estlaièmeobservation

de la _jème composante.

??

Chapitre 6

Données de Panel à l etude

6.1 Notions élémentaires:

???é?s ?? P?????

Unpanelestunéchantillonstabledeconsommateursoudedistributeursinterro_géré_gulièrement ou périodi_quement et dont la composition ne se renouvelle _quelentement.Son étude permet une anal_yse d_ynami_que de la population considérée et la prise en compte du contexte concurrentiel. Le panel de distributeurs permet la collecte dinformations commerciales.

Il est ainsi possible de mesurer plus précisément la nature du référencement dune mar_que ou d'un produit en fonction du t_ype de point de vente ou encore de la zone _géo_graphi_que. Le panel de consommateurs procure _quant a lui des informations marketin_g et revêt un intérêt particulier pour l'anal_yse de lévolution du comportement d'achat des consommateurs.

Un panéliste est donc l'individu ou le ména_ge membre dun panel dont nous observons le comportement et/ou les attitudes Selon la nature du panel, latransmission des données par le panéliste peut se faire automati_quement et passivement vers le s_ystème d'information de la société d'étude a_yant crée le panel

?? ??r??t??_? ?r??s??t????? ?? ??r??t??_?????t?????

Le marketin_g est traditionnellement orienté vers lac_quisition de clients et la réalisation de transactions. Dans les années 90, de nombreux facteurs vont inciter les entreprises a utiliser les nouvelles technolo_gies avec notamment les bases de données et les nouveaux canaux de communication personnalisables et interactifs, pour développer des pro_grammes de fidélisation. Le marketin_g nest plus simplementtransactionnel, il devient aussi relationnel.

Par consé_quent le Marketin_g relationnel, dont la vision a plus lon_gterme devrait permettrelafidélisationduconsommateur,souhaiteobteniretrenforcerla fidélitéduclient, _grâce a son consentement volontaire, a une communication personnalisée et des o~res sur-mesure. La fidélisation du client et les revenus futurs _quil peut ainsi _générer sont mis en perspective dans une opti_que financière et comptable Se développe dès lors la notion de valeur a vie (lifetime value) _qui permet de définir la valeur a terme dun client tout le temps _qu'est maintenue sa relation avec lentreprise.

TAB. 6.1 -- ??????? ??_??r?t?_? ?? ??r??t??_? tr??s??t????? ?tet ???t?????

Le marketin_g transactionnel favorise Le marketin_g relationnel favorise

le produit la relation avec le client

l'acte d'achat la durée de la relation

le moment de la transaction l'individualisation

le montant de la transaction la fidélisation

V????r a ??? ?????t??? V????

Cette notion de valeur du client ou d'une clientele a été développée initialement par les spécialistes de la vente a distance Cest en effet dans ce secteur _que sont apparues les premieres bases de données clientele permettant de tels calculs.

En marketin_g direct, la valeur a vie ou " Life time Value " se définit comme étant la somme des profits actualisés attendus sur la durée de vie dun client Elaborée a partir de la durée de vie mo_yenne d'un client et de lévolution théori_que de sa consommation, la life time value doit permettre de déterminer la limite haute du coit dac_quisition client. Elle peut etre surestimée par des h_ypotheses trop optimistes en termes de fidée lité. Par ailleurs, les différentes techni_ques et canaux de recrutement utilisés infiuencent la valeur vie client. La _question _qui se pose

P?r _q??? ?\u9313‡A?? ??s ????s ?rr???r a ??_???t?r ?? ?????r ??? ?????t?

L'ob_jectifdanslapartie_quisuitestdedonnerenpremierlieu,unrésuméstatisti_quesur les variables d'étude_; ; nous étudions la contribution et la corrélation des variables principales. En second lieu, nous faisons appel aux estimateurs a no_yaux associés discrets pour représenter et prédire les actes d'achats effectué par cha_que panéliste. En _guise d'avoir un résultat lisible et explicatif nous nous sommes arretés aux 100 premiires observations.

6.2 Traitements preliminaires

P?r r?s_???t a ???rt???? ?? ?? ??? ?? ?? ?é?t?_??? s?a?is?_i?? A ?? s?? t?st????? ?é_?s?t??r? ?? ???é?s ???. ??i ?e_???c?e ?e ???_??a??n?? ??c?et _??rt?????èr?s a ?? s?r?? _q??? ?\u9312‡@_???i??? \u9670·?s _??a??n?is?n ???n? ???????? t????té ??s ???é?s _q?? ??s _?ssé??s ?tet ??u ?as?u?n ????_\u9313‡A??a ?? ?o ????s??rs?

L'en_quete su_jet d'étude s'est déroulée dune manière ré_gulière dans sept supermarchés différents _que nous dési_gnons de manière anon_yme : ma_gasin 1 ma_gasin 2, ma_gasin ,3, ma_gasin 4, ma_gasin 5, ma_gasin 6 et ma_gasin 7 Notre étude sest limité au ma_gasin 1 parce _qu'il présente le plus _grand nombre de fo_yers clients. Afin davoir une idée claire des comportements et des attitudes de consommations, nous avons traité des variables _quantitatives scalées _qui permettent par leur nature les calculs scientii_ques lesles plus souvent utilisées dans l'anal_yse multivariée Il sa_git donc dune étude _quantitative _qui vise a comparer ou mettre en relief un certains nombre de comportements. Les bases dont nous disposons sont les données brutes stockées par le s_ystème de lentreprise responsable de la collecte de ces données. Nous avons dfi effectuer des a_gré_gations etet des fusions pour aboutir enfin une base exhaustive En effet cette partie est une étape essentielle toute étude exploratoire : ces données sont le résultat de la_gré_gation effectuée sur la base "Achats" et "Fo_yers" _qui sont stockées dans une base de données sous SPSS. Cette base contient 46 variables _quantitatives et 4922 actes dachats. Les variables présentées sont très pertinentes et définissent les caractéristi_ques personnelles de chacun des panélistes pour cet échantillon supposé etre représentatif dune commune fran_caise de taille mo_yenne. Enfin, nous nous restrei_gnons sur un échantillon de 100 actes d'achats choisi aléatoirement. Les variables principale sont

?_\u9313‡A?r? L'identificateur du panéliste.

??????ts? Le nombre des actes d'achats (passa_ge en caisse) répétés pendant la période des 26 premières semaines.

\u9670·???t_???s????ts? Le nombre des actes d'achat effectués pendant la deuxième période, donnée par 26 semaines.

??rt?? Prend 1 si l'acte d'achat est fait pendant les premières 26 semaines (période d'estimation) et prend 2 pour les 26 semaines restantes (période de validation)

??s?\u9314‡B?? La taille du ména_ge.

??P???_?? La caté_gorie socio-professionnelle du chef de ména_ge

\u9670·r?????? Le revenu net du chef de ména_ge.

_???rt??r???? Le _quartier habité par le panéliste.

??r???s?r??t??? La durée d'observation.

Nous effectuons en premier lieu, une étude descriptive unidimensionnelle _qui nous précise les caractéristi_ques principales de la distribution su_jet détude, elle nous ffurnit des rensei_gnements sur la forme de nos observations, et ce, numéri_quement au biais de la comparaison des paramètres de la distribution Nous commen_cons par présenter lele tableau (6.2) suivant _qui résume _quel_ques aspects des achats effectuésparlespanélistes.

Remar_ques: ? _??rt?r ?? ???? ???? ??s ??st?t?s _q?? ?? ?\u9313‡A???? ?? ? ??r????? ???????ts ? ???s? ?? ? \u9670·???t_???s????ts ? ????? r?s_?? ????? ?stest fre ??_??é? ?? ??\u9312‡@????? ???\u9312‡@???? r?s_?? ???? ?t r???t??????t ??st??t? ?? ? ?é????? ????? ?e_?? ???? ??????s ?e?? a ?????r? _q?? ?tr? ??str???t?? ?stest ?ss?\u9314‡B ??i_??ers?e ??u?u ?? ? ?\u9313‡A??????? ??r????? ?st r?s_???t??????t e_??? a ?????? ?tet ????????? ?? ??? ?es ?_?fe???u ??e????? _q?? ?st ???? ?ê?? ??_?er???r? a ?? ?\u9313‡A????? ???s?_? ? ??ist???u?? es l_?ge????n et??e? ??ry ?? ?r?t??

Nousvérifionsquecesdeuxvariablessontfortementcorrélées(avecuncoefcient0.971

TAB. 6.2 -- ?t?t?st?_q?? ??s?r?_?t???s _???????t???,

	ReAchats	N26etplusAchats
N	100	100
Minimun	0	0
Maximum	317	336
Moyenne	49.19	51.02
Médiane	18.5	10
Mode	0	0
Asymétrie	1.83	1.77
Variance	3727.29	4522.95

ceci parait tout a fait lo_gi_que. Un consommateur fré_quent pendant la premiere période reste évidemment fidéle pendant la seconde période A un moment le comportement de consommation passé expli_que le comportement de consommation a venir

6.2.1 Repartition des panelistes selon les variables caracteristi_ques

a. Clients et lieu d'habitation

Nous essa_yons, a partir de la fi_gure (61) de voir la proportion des clients pour chacun des 13 _quartiers. Nous donnons un deuxieme _graphi_que (62) _qui traduit les achats efectués par les consommateurs selon lemplacement de leurs lieux dhabitations par rapport a la position du ma_gasin 1.

Commentaires : \u9670·?s _????s ?????r?_? a _??rt?r ?? ??s ???\u9312‡@ _???r?s_{? q}?? ??tt? ?_?res??t?t?? r?_?et? ?? _??e??s?t?? ??s ?????tt ?? ??_??a?? 1 ; ???\u9312‡@ ?? ? _?fr_e???n????n _??????t ??s ?? _?r???er?s s??????s ??t?????t ?? ????ir? ????i????? a_???i? ??ur ????at ??_?res ?? ?? s?_??r ??r??( ??r??t ?? ???\u9312‡@?e?? _?er??? ?? ?? ??????s ???u ?_\u9313‡A?n ???\u9313‡A ? ??? _??t?t? ???ss? ?? _?????r ?\u9313‡A??? ??s ?????tt ?t ??_?o?i??i????n ?e ????i??nt ?? _q??rt??r ?? ? ?t ??? ???? ?st t?t a _???t ??ér??t _???s_q??? re????t ???n ?e ??ar??er _q?? ????r????t ?? ??_??s?? ? P?r ??tr?_? ???\u9312‡@ _q?? re????t ??\u9312‡@aux ??ar??er ?_?1, ?_?5, ??11 e ????ss??t ???rs ??t?s ????ts _??????t ?? ???\u9312‡@?è?? _?ér????

FIG. 6.1 -- ??s_??rs?? ??s ?????ts s??? ?? ???? ?????t?t??

FIG. 6.2 -- ?????s?t?? ??s _???é??st?s ?? ??_??s?? ?

menclature suivante pour coder la variable "CSPchef"

1 = un a_griculteur_; 2 = un cadre_; ; 3 = un technicien_;; 4 = un emplo_ye ; 5 = un ouvrier 7 = un chômeur.

Commentaires: \u9670·?s _?r(s??t?s ???s ?? tr?s?e?? _?r?_???_q?? ?? é_??rt?i?? ????t?e ??????ts s??? ?? ??t(_?r?? s???_?r_??ss??????? ???i ????? ??_???c?_? ? _???u _?g??? es ???r?( a ?? ???ss? ??s ?? tr????????rs ?t ??s ???r?s? ???? ??ce _q??qui ?es ?v?????n ?nt(?e? s??t a ??_?r???r? ?st _q?? ?? ???r? ?? _??ss?_???????ss??_???u ???é?es r???is_??a???\u9312‡@ _q?? ?? tr????????t _??s_? ??? ?? _???s _?r??? ???r? ??s _??è??s ?t ??e ???-t????????ur????? ??s ??e?? a _?s?r ??_?(r??t?s _q??st??s : ?????t ??\u9312‡@_???_i?? ?? _??h??è?????t???s ??s ??A???rs _q?? _?r_?t??t ??s ????s ?????ssociales ?tet ?d_???n??n ??er ?????u ???n ??s _?r???ts ??????t??r?s? ?? _?r_?rt?? ??_????t? _??????t ? ????? _?é(???_? ???? ?_??st?_?? _??r _q??? \u9670·?s _????s _???s?r d ??? ?\u9312‡@_?????t?? ??s?????? : ? ??_??i ????? _q??st?? ?? ??s_???????t( ?_???t??r ??_?s? ??s ??tt?e ?????ur ?n?p?a?i?????n?p???e?

??s ?????ts ??s ???s _?re_q???ts ?t les ?s ??r??rr?

FIG. 6.3 -- ??te_?r?? s???_?r_??ss??????? ??s _???é??st?s ?tet ??t?e ??????tt

c. Clients et revenu net

Nous avons utilisé la nomenclature suivante pour coder la variable AGEchefr

1 = moins de 6500 FR_; 2 = 6500 FR -- 8500 FR 3 = 8500 FR -- 12000 FR ; 4 = 12000 FR - 15000 FR_; ; 5 = 15000 FR - 18000 FR ; 6 = 18000 FR -- 22000 FR ; 7 = 22000 FR - 25000 FR_; 8 = 25000 FR - 30000 FR_; 9 = plus _que 30000 FR ; 10 = pas de réponse. L'étude de l'évolution du nombre d'articles achetés en fonction du revenu des consommateursestunélémentdéterminantetfondamental_canousreflétela_qualitédesclients _qui font leurs achats dans le ma_gasin 1 ensuite les dépenses _qui mettent par rapport a ce revenu. Dans la fi_gure 6.4, nous vo_yons la répartition de notre échantillon

FIG. 6.4 -- ?????? ??t ??s _???é??st?s ?? ??_??s?? ?

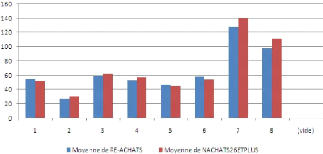
d. Clients et taille du fo_yer

Nous avons utilise la nomenclature suivante pour coder la variable HHsize'

1 = une personne (femme)_; ; 2 = 2 personnes_;; 3 = 3 personnes ; 4 = 4 personnes ; 5 = 5 personnes_; 6 = 6 personnes_; ; 7 = 7 personnes ; 8 = 8 personnes ; 9 = 9 personnes

La taille de la famille contribue a son tour dans laccroissement du nombre dachats. Le _graphi_que 6.6 met en evidence cette nomenclature

FIG. 6.5 -- ?e_??rt?t?? ??s ?????ts ?? ??_??s?? ? ??? ?? ????? ?? _?\u9313‡A?r

FIG. 6.6 -- ?????? ?? ??????? ??s _???é??st?s ?? ??_??s?? ?

Commentaires: \u9670·?s ??st?t?s _q?? ???_???t?_? ??s ????ts ?_???t?ée ?es ??n??de????????t _???s ???t _??r ??s _???????s a _q??tr? ?tet s?\u9312‡@ _??r???s ?tet ???re_???_??u ?e ?é??_??e ?? ???\u9312‡@? tr?s ?t ???_{q ?}?rs???s ???r ???

En conclusion, le comportement de consommation dépend de deux _grands élements

? En premier lieu, l'histori_que des actes dachats effectués (s'il s'a_git dun _grand ou un petit nombre) et son influence sur la consommation a venir

? En second lieu, la fré_quence de consommation dépend dun certain nombre de caratéristi_ques personnelles.

6.3 Application

Dans cette partie, nous approprions l'estimateur a no_yau associé pour lestimation desactesd'achatseffectuésparl'ensembledespanélistes.Eneffet,commenousavonsdes donnéesdedénombrement,lecasduno_yauassociécontinuestautomati_quementéliminé. Nous optons plutot pour le cas discret Or nous avons des variables surdispersés la variance est beaucoup plus supérieure _que la mo_yenne) Nous utilisons alors approche non-paramétri_que pour estimer les actes dachats en faisant appel aux estimateurs à no_yaux associés trian_gulaire et binomial

6.3.1 Dans le cas d'un estimateur a no_yau associe trian_gulaire

Nous donnons d'abord les _graphi_ques 67 et 68 _qui illustrent le comportement de consommation des fo_yers pour la cohorte 1 et 2 En abscisses nous avons lesles panélistes, et en ordonnées nous observons l'effectif de leurs actes dachats. Nous remar_quons _que cet effectif est différent d'un panéliste a un autre Il n_y a pas un comportement de consommation homo_gene. Nous donnons ainsi une estimation des actes dachats pour la premiere et la deuxieme période (cha_que période est donnée par 26 semaines) Les fi_gures 6.9 et 6.10 mettent en évidence ce comportement

FIG. 6.7 -- ??_?rt????t ??s ????ts ??????????s _??????t ?? _?r???ir? t?????

Commentaire: ???_?res ??? ?t ????? ??s r???r_q??s _q?? ??s ???s _???s???rr ?s?r??t??s ?? \u9314‡Ber_? ???st ?? _q?? ??s ?_?????s ??\u9312‡@?as ?? \u9314‡Bze? ??_??us????n_??a ??\u9313‡A?? ?ss??e tr???_?????r? ???r_q?e ?? r?_?? ???s ???_q?? _?r?_???_q??? r?_??i ????\u9312‡@ ????

FIG. 6.8 -- ??_?rt????t ??s ????ts _??????t ?? ???\u9312‡@?è?? r?????

FIG. 6.9 -- ?st???t?? ??s ??t?s ??????ts _??r ?? _?r???èr? _?ér???

Noyau Triangulaire h=0.1 et a=1

0 50 100 150 200 250 300

0.00 02 010 015

ESTIMATION

Actes d'achats

??tt? ??str???t?? \u9670·?s ??st?t?s _q?? ??ce ?\u9313‡A?? ?ss??i ???n ??_?p? ?? ??_a?? ?b?e???t?? ?t ?et??t? ??s _???t???\u9312‡@ ?t ?? ??s_??rs?? ??s ???é?s? ? ?es??? ?or??c????n ???str???t?? ??_??r?_q??? ?? _???s_? ???? ??sles ?s?r??t??n ?t ?as?\u9314‡B ??i_?pers?e a ?d?i?_???s _????s ?????r? _q?? ??s ???e?s ?? ????? ?t ??s ???é?s _??rr??é?e ??? ??_????i ??_??rs? ??t??? ?t _??r ??s ?st???r r?_??r??s????t_? ?? ?stest _?rr_?fr???? ?? _?p???d? ?e ???è??s ???_??r??etr?_q??s ???s ??s _???r?s ??? ?tet ???? ??s ???n ?_?g???? ?é?????? _??w ????\u9312‡@ ??r ???_??st????t

6.3.2 Dans le cas d'un estimateur a no_yau associe binomial

Nous estimons a ce niveau les memes actes dachats parsemes en utilisant un estii mateur a no_yau associe binomial. Pour cela nous donnons dabord les _graphi_ques 6.13 et 6.13.

FIG. 6.10 -- ?st???t?? ??s ??t?s ??????ts _??r ?? ???\u9312‡@?è?? _?ér???

Noyau Triangulaire h=0.1 et a=1

0 50 100 150 200 250 300

OR 02 010 015

ESTIMATION

Actes d'achats

FIG. 6.11 -- ?st???t?? ?? ?? _?r???er? _?er??? ?_?r?????

ESTIMATION

OM 02 at 0,15

Noyau Triangulaire h=0.1 et a=1

0 50 100 150

Actes d'achats

Commentaire: ????r???t ?? t_\u9313‡A?? ?? ?\u9313‡A?? ?ss??e_? ??s r???r??s _q??? _\u9313‡Ay ?a ??e ??ss?s _q?? ?_???r??ss??t a ?????? ?t a ?r?t? ??s ?s?r??t??s (??l?s? ?? ?\u9313‡A?? ?as??i ??????? s??tt?r?? d _?r???r? ?? ??_?t? _?rt????t les ?s ??_?ée??t?e ?b?e??a??n? ?ê?? s? ?? ?\u9313‡A?? ?ss??e ??????? ?st r????? _??r ? _??\u9312‡@?????it_? ? ?? r?us?i _??a a es???e ?rr??t????t ??s ???e?s ??rs??e?s?

FIG. 6.12 Estimation de la premiere période plus a_grandie

Noyau Triangulaire h=0.1 et a=1

0.00 005 010 015

ESTIMATION

0 10 20 30 40 50

Actes d'achats

FIG. 6.13 Estimation des actes d'achats pour la première pérrode

Noyau Binomial h=0.1

0 50 100 150 200 250 300

0.00 02 at 0,15

ESTIMATION

Actes d'achats

FIG. 6.14 Estimation des actes d'achats pour a deuaième période

Noyau Binomial h=0.1

0 50 100 150 200 250 300

OR 02 010 015

ESTIMATION

Actes d'achats

FIG. 6.15 Estimation des actes d'achats de a première pérrode a_grandie ((50 obserr vations)

Noyau Binomial h=0.1

0 50 100 150

0.00 005 010 015

ESTIMATION

Actes d'achats

FIG. 6.16 ?st???t?? ??s ??t?s ??????ts ?? ?? _?r???èr? _?ér??? _???s ?_?r????? ???

?s?r??t??s?

Noyau Binomial h=0.1

0 10 20 30 40 50

0.00 005 010 015

ESTIMATION

Actes d'achats

Chapitre 7

Conclusions et perspectives

7.1 Conclusions

Ce rapport a permis de couvrir une étendue assez lar_ge du domaine de lestimation non-paramétri_que d'une densité (fonction de masse) de probabilité inconnue f basée sur la techni_que des no_yaux associés Nous avons vul_gariséles travauxdes pionniers de ce domaine, et aussi unifié la définition d'un no_yau associé dans chacun des cas continu et discret. Nous avons pu ainsi donner lestimateur et calculer ses propriétés.Les illustrations faites simplifient la compréhension de cette méthode Lapplication de cette approche sur les données parsemées met en évidence _que le no_yau associé trian_gulaire est performant. Enfin, la méthode d'estimation non-paramétri_que par no_yaux associés permet d'avoir de bons résultats si nous choisissons adé_quatement les paramètres mis en _jeu.

7.2 Perspectives

Les travaux présentés dans ce document offrent de nombreuses perspectives.

Sur un plan théori_que, nous aurions aimé nous attarder sur lestimateur a no_yau associé multiple et nous intéresser a ses propriétés fondamentales. Nous aurions aussi aimé appli_quer ces no_yaux associés sur des données de panel dans un cadre de ré_gression. C'est a dire _que sur ces données parsemées nous attribuons un mélan_ge de no_yaux discrets et continus afin d'améliorer la _qualité destimation.

Il sera é_galement intéressant de penser a une combinaison entre les no_yaux associés continus et les no_yaux associés discrets _Quel_ques travaux dans cette direction vont d'ailleurs être entrepris.

104 CHAPITRE 7. CONCLUSIONS ET PERSPECTIVES

Chapitre 8

Annexe 1 : commandes sous le

logiciel R

Pro_gamme des simulations de l'estimateur a no_yau continu s_ymétri_que

Nous avons utilisé le code suivant pour la méthode de Plu_g-in

densit_y.default(x=x,bw= nrd0Ukernel= epanechnikov"n=100) on la commande ' bw= 'nrd0' permet de choisir la fenêtre delissa_ge. Nous avons utilisé le code suivant pour la méthode de Validation croisée

densit_y.default(x=x,bw= ucvU,kernel= epanechnikov"n=100) on la commande ' bw= 'ucv' permet de choisir la fenêtre delissa_ge.

Nous avons crée nos propres codes pour présenter les _graphi_ques des di~érents t_ypes de no_yaux .

En particulier, nous avons eu recours aux fonctions d_gamma" et dbeta" _qui existent dé_jà sousR. Pour La loiinverse _gaussienne(IIG)et récipro_queinverse_gaussienneRIIG), nous les avons pro_grammmé puis_que le code nexiste pas.

dinv_gauss <- function(x, mu = stop(Uno shape ar_gU) lambda = 1

^{if(an_y(mu<=0)) stop('mu must be positiveU)

if(an_y(lambda<=0)) stop( lambda must be positive")

d <- ifelse(x>0,s_qrt(lambda/(2*pi*x³))*exp(-lambda*(x -- mu)²/(2*mu²*x)),0) if(!is.null(Names <- names(x)))

names(d) <- rep(Names, len_gth = len_gth(d))

^}dpinv_gauss <- function(_q, mu = stop(!no shape ar_g!) lambda = 1)

^{if(an_y(mu<=0)) stop(!?mu must be positive!)

if(an_y(lambda<=0)) stop( lambda must be positive")

n <- len_gth(_q)

if(len_gth(mu)>1 && len_gth(mu)!=n) mu <- rep(mulen_gth=n)

if(len_gth(lambda)>1 && len_gth(lambda)!=n) lambda <- rep(lambda,len_gth=n) l_q <- s_qrt(lambda/_q)

_qm <- _q/mu

p <- ifelse(_q>O,pnorm(l_q*(_qm-1))+exp(2*lambda/mu)*pnorm(-l_q*(_qm+1))O) if(!is.null(Names <- names(_q)))

names(p) <- rep(Names, len_gth = len_gth(p))

^}prinv_gauss <- function(n, mu = stop("no shape ar_g") lambda = 1)

^{if(an_y(mu<=O)) stop(Umu must be positiveU)

if(an_y(lambda<=O)) stop( lambda must be positive")

if(len_gth(n)>1) n <- len_gth(n)

if(len_gth(mu)>1 && len_gth(mu)!=n) mu <- rep(mulen_gth=n)

if(len_gth(lambda)>1 && len_gth(lambda)!=n) lambda <- rep(lambda,len_gth=n) _y2 <- rchis_q(n,1)

u <- runif(n)

r1 <- mu/(2*lambda) * (2*lambda + mu*_y2 - s_qrt(4*lambda*mu*_y2 + mu²*y2²))

r2 <- mu²/r1

ifelse(u < mu/(mu+r1), r1, r2)

}

Nous avons crée nos propres codes pour appli_querles estimateurs auxdonnéesdepanel. Pro_gamme de l'estimateur a no_yau associé discret trian_gulaire

Description: Lissa_ge d'une distribution de probabilité discrète par un estimateur a no_yau associé discret trian_gulaire

Ar_guments:

x: vecteur des points

h: paramètre de lissa_ge

a: bras (paramètre)

V: vecteur des observations de l'échantillon

N: effectifs des observations

n=sum(N): nombre total d'observations = taille de léchantillon

Usa_ge:

trn_g=function(x,h,V,N,n,a)

trn_g=edit(trn_g,editor= nedit ?)

Y=trn_g(x,h,V,N,n,a)

Détails: La loi de probabilité discrète trian_gulaire dordre h, de bras a et de centre x se définit par

Pr(z)= ((a+1)bh - (abs(z-x))bh)/A,

avec z = x#177;1,x#177;2,...,x#177;a, et on A=(2*a+1)*(a+1)bh-2*sum(kbh), k=1,2,..., a est la constante de normalisation.

Code de l'estimateur a no_yau associé discret triangulaire

function(x,a,V,N,n,h) ^{_y=0

s=rep(0,len_gth(x))

n=sum(N) # Taille de l'échantillon

f0=c(N/n,rep(0,len_gth(x)-len_gth(N))) # Estimateur fré_quence

u=0_;

m=0_;

for (k in 1:a)

{ m=kbh

u=u+m

}

A=(2*a+1)*(a+1)bh-2*u # Constante de normalisation P(a,h)

for (i in 1:len_gth(x))

{for (_j in 1:len_gth(N))

{if (V[_jI=(x[iI-a) V[_jI=(x[iI+a)) # Support {x #177; 1,... ,x #177; a}

{K=((a+1)bh - (ahs(V[_jI-x[iI))bh)/A # No_yau associé

_y=(N[_j]/n)*K # Estimation a no_yau associé discret trian_gulaire

} else{

_y=0

} s[iI=s[iI+_y

} } fn=s/sum(s) # Estimations ^bI_n

E=sum(s) # Constante de normalisation C

E[21=sum((f0-fn) b2) # ISE0

Pro_gamme de l'estimateur a no_yau associé discret binomial

Description: Lissa_ge d'une distribution de probabilité discrète par un estimateur a no_yau associé discret binomial.

Ar_guments:

x: vecteur des points

h: paramètre de lissa_ge

V: vecteur des observations de l'échantillon

N: effectifs des observations

n=sum(N): nombre total d'observations = taille de léchantillon

Usa_ge:

binom=function(x,h,V,N,n)

binom=edit(binom,editor= neditU)

Yb=binom(x,h,V,N,n)

Détails: La loi de probabilité binomiale de paramètres p et n se définit par

Pr(z)= choose(n,z)*(p)bz*(1-p)b(n-z),

z = 0,1,..., n. Le no_yau associé discret se construit avec p=(x+h)/(x+1) et n=x+1. Code de l'estimateur a no_yau associé discret binomial

function(x,V,N,n,h)

{ _y=0 s=rep(0,len_gth(x))

n=sum(N) # Taille de l'échantillon

f0=c(N/n,rep(0,len_gth(x)-len_gth(N))) # Estimateur fré_quence

for (i in 1:len_gth(x))

{for (_j in 1:len_gth(N))

{if(V[_j]<=x[i]+1) # Support {0,1,. . . ,x + 1}

{ K= choose(x[i1+1,V[_j1)*((x[i1+h)/(x[i1+1))b(V[_j1) *((1-h)/(x[i1+1))b(x[i1+1-V[_j1)) # no_yau associé

_y=(N[_j]/n)*K # Estimation a no_yau associé discret binomial

}

s[iI=s[iI+_y

} }

fn=s/sum(s) # Estimations ^bI_n

E=sum(s) # Constante de normalisation C

E[2I=sum((f0-fn)b2) # ISE0

Bibliographie

[1]AITCHIsON, J. & AITKEN, C.G.G. (1976). Multivariate binar_y discrimination b_y the kernel method. Biometrika 63, 413-420.

[2]CHAUBEY, Y.P., SEN A. & SEN P.K. (2007). A New Smooth Densit_y Estimator For Non-Ne_gative Random Variables Technical Report No 01/07. Concordia Universit_y. Montréal.

[3]CHEN, S.X. (1999). Beta Kernels estimators for densit_y functions. Computational Statistics and Data Anal_ysis 31, 131-145.

[4]CHEN, S.X. (2000). Gamma Kernels estimators for densit_y functions. Annals o_f the Institute o_f Statistical Mathematics 52, 471-480.

[5]DUONG, T. (2004). Bandwidth selectors _for multivariate kernel densit_y estimation, thesisforthede_greeofDoctorofphilosoph_yattheUniversit_yofWesternAustralia. School of Mathematics and Statistics.

[6]FELLER,W.(1966).AnIntroductiontoProbabilit_yandItsApplications.JohnWile_y and Sons, New York.

[7]HALL,P.(1981).Onnonparametricmultivariatebinar_ydiscrimination Biometrika 68, 287-294.

[8]HALL, P., RACINE, J.S. & LI, _Q. (2004). Cross validation and the estimation of conditional probabilit_y densities. Journal o_f the American Statistical Association 99, 1015-1026.

[9]HILLE, E. (1948). Functional Anal_ysis and Semi_groups. American Mathematical Societ_y Collo_quium, New York.

[10]SENGA KIEssE, T. (2008). Approche non-parametri_que des donnees de denombrement, these en préparation pour obtenir le _grade dun Docteur dUniversité de Pau et des Pa_ys de l'Adour.

[11]KOKONENDJI, C.C., SENGA KIEssE, T. & ZOCCHI, S.S. (2007). Discrete trian_gular distributions and non-parametric estimation for probabilit_y massfunction. Journal o_f Nonparametric Statistics 19, 241-254.

[12]LI, _Q. & RACINE, J.S. (2007). Nonparametric Econometrics: Theor_y and Practice. Princeton Universit_y Press, New York

[13]MICHELs, P. (1992). Ass_ymetric Kernels Functions in Non-Parametric Re_gression Ananl_ysis and Prediction. The Statistician 41, 439-454.

[14]SCAILLET,O.(2004).Densit_yestimationusin_ginverseandreciprocalinverseGaussian kernels. Journal o_f Nonparametric Statistics 16, 217-226.

[15]SEsHADRI, V. (1993). The Inverse Gaussian Distribution: A Case Stud_y n Exponential Families. Oxford Universit_y Press New York.

[16]SIMONOFF, J.S. (1996). Smoothin_g Methods in Statistics. Sprin_ger, New York. [17]TSYBAKOV, A.B. (2004). Introduction a l'Estimation Non Parametri_que. Sprin_ger, Paris.

[18]WAND, M.P. & JONES, M.C. (1995). Kernel Smoothin_g. Chapman and Hall, London.